

Preview text:
40 Đề TSA | Phạm Tú Khanh
Ngày:___/___/_____. Điểm: ___/40.
Đề Thi Thử Đánh Giá Tư Duy Toán Học.
Câu 1. [Mức 1] Bạn Hiếu bắt đầu đếm từ số theo cấp số cộng . Đồng thời, với cùng
tốc độ, bạn Sang cũng bắt đầu đếm từ số theo cấp số cộng . Tại một
thời điểm nào đó, hai bạn sẽ cùng nói một số . Giá trị của bằng? ➢ Điền đáp án: .
Câu 2. [Mức 1] Cho đường tròn có phương trình trong hệ trục toạ độ . Biết rằng
có tâm và bán kính , xét tính đúng/sai của các mệnh đề sau: Mệnh đề Đúng Sai
a. Bán kính của đường tròn là . ○ ○
b. Tâm của đường tròn có toạ độ . ○ ○ c. Cho hai điểm thuộc thuộc sao cho góc ○ ○ . Khi đó độ dài cung bằng .
Câu 3. [Mức 1] Một khối lập phương có độ dài các cạnh bằng bị lấy mất
đi nhiều khối vuông đơn vị nhỏ có kích thước bằng nhau (như hình vẽ bên).
Khi đó, cần gắn lại bao nhiêu khối vuông đơn vị để sửa khối lập phương đã cho về như ban đầu? A. . C. . B. . D. .
Câu 4. [Mức 2] Tập hợp những nghiệm dương của bất phương trình là . Khi đó, bằng? ➢ Điền đáp án: .
Câu 5. [Mức 2] Cho hai số thực thoả mãn . Khi đó, giá trị của biểu thức bằng? A. . B. . C. . D. .
Câu 6. [Mức 2] Trong một buổi lái xe, tỉ lệ người lái xe thắt dây an toàn là . Biết rằng khi người
lái xe có thắt dây an toàn thì xác suất để người đó bị tai nạn là
và khi người lái xe không thắt dây
an toàn thì xác suất người đó bị tai nạn là
. Khi đó, xác suất để người lái xe bị tan nạn trong một buổi lái xe bằng? A. . B. . C. . D. .
Câu 7. [Mức 2] Bạn Hải có ba túi đựng bi. Trong đó, số bi ở túi thứ nhất bằng một nửa số bi ở túi
hai, số bi trong túi ba gấp ba lần số bi ở túi thứ nhất. Mặt khác, một nửa số bi ở túi một, một phần ba
số bi ở túi hai và một phần tư số bi ở túi ba có màu xanh. Hải đổ hết bi từ cả ba túi vào một chiếc hộp
40 Đề TSA | Phạm Tú Khanh
rồi chọn ngẫu nhiên một viên bi trong hộp đó, xác suất để chọn được viên bi màu xanh là . Khi đó, tổng bằng? ➢ Điền đáp án: .
Câu 8. [Mức 1] Biết rằng trung bình cộng của ba số thực
bằng 22, khi đó trung bình cộng của ba số và bằng? ➢ Điền đáp án: .
Câu 9. [Mức 1] Cho hình chóp có , vuông tại , độ dài các cạnh và
. Khoảng cách từ điểm đến mặt phẳng bằng , giá trị của bằng? ➢ Điền đáp án: .
Câu 10. [Mức 1] Cho hàm số có đạo hàm . Xét tính
đúng/sai của các mệnh đề sau: Mệnh đề Đúng Sai a. Hàm số có điểm cực trị. ○ ○ b. Với mọi và thoả ○ ○ mãn thì hiệu .
Câu 11. [Mức 1] Diện tích phần được giới hạn bởi đồ thị hàm số
và phần trên của đường tròn
là? (làm tròn kết quả đến hàng phần chục) ➢ Điền đáp án: .
Câu 12. [Mức 2] Cho tam giác có các góc
, mệnh đề nào sau đây đúng? A. . C. . B. . D. .
Câu 13. [Mức 1] Bạn An đang uống một lon nước ngọt hình trụ thì đọc thấy trên nhãn dán có ghi “Dung tích:
”. Thấy vậy, An liền lấy thước kẻ ra và đo được chiều cao của lon nước bằng
. Khi đó, bán kính đáy của lon nước đó bằng bao nhiêu ? ➢ Điền đáp án: .
Câu 14. [Mức 1] Diện tích bề mặt của một khối cầu được đo bằng , khi
đó đường kính của của khối cầu đó bằng? A. . C. . B. . D. .
Câu 15. [Mức 1] Cho hình chóp có
lần lượt là trung điểm của , và . Tỉ lệ thể tích bằng? A. . B. . C. . D. .
Câu 16. [Mức 1] Cho cấp số cộng có số hạng đầu
và công sai , cấp số nhân có số hạng đầu và công bội
. Xét tính đúng/sai của các mệnh đề sau: Mệnh đề Đúng Sai a. Nếu thì . ○ ○
40 Đề TSA | Phạm Tú Khanh b. Nếu thì . ○ ○
Câu 17. [Mức 2] Tập hợp những nghiệm dương của bất phương trình là . Khi đó, bằng? ➢ Điền đáp án: .
Câu 18. [Mức 1] Ta định nghĩa hai hàm số lượng giác và . Khi đó, tích phân bằng? ➢ Điền đáp án: .
Câu 19. [Mức 1] Kéo và thả các phương án thích hợp vào chỗ trống. 1 2 3 4 5 6 15625 3125 Cho cấp số nhân có . Biết rằng . a. Giá trị của . b. Số hạng .
Câu 20. [Mức 1] Nếu hai số chia cho
có cùng số dư thì ta nói đồng dư với theo module , kí hiệu
. Những khẳng định nào sau đây đúng? (Chọn nhiều đáp án) A. . C. . B. . D. .
Câu 21. [Mức 2] Cho hai hàm số bậc nhất và thoả mãn . Biết và và ta coi
, xét tính đúng/sai của các mệnh đề sau: Mệnh đề Đúng Sai a. Giá trị của . ○ ○ b. Hàm số . ○ ○
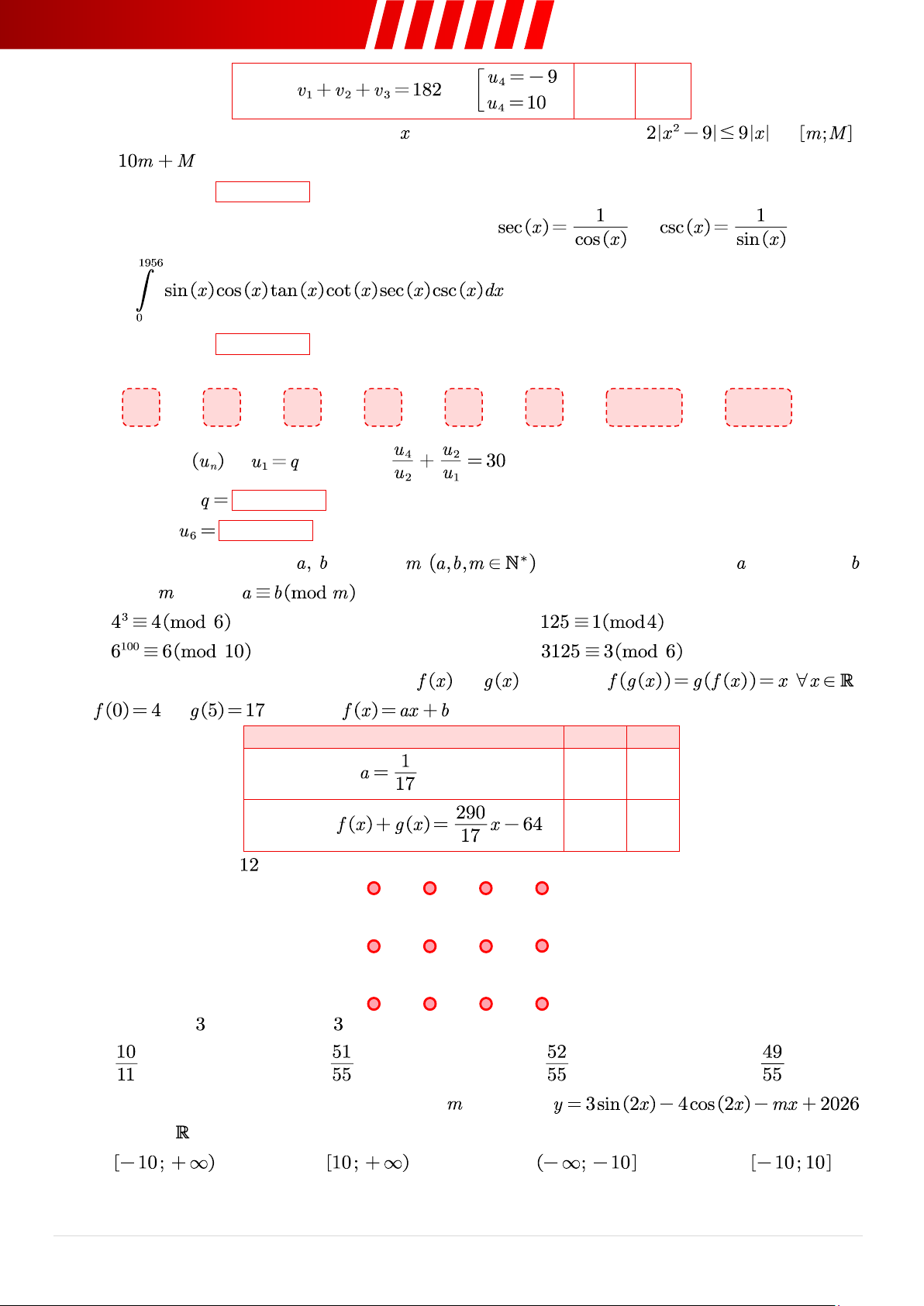
Câu 22. [Mức 2] Cho chấm tròn được sắp xếp như hình vẽ sau:
Chọn ngẫu nhiên chấm, xác suất chấm chọn được tạo thành một tam giác là? A. . B. . C. . D. .
Câu 23. [Mức 2] Tập hợp tất cả các giá trị của để hàm số đồng biến trên là? A. . B. . C. . D. .
40 Đề TSA | Phạm Tú Khanh
Câu 24. [Mức 2] Cho hai hàm số và . Biết đồ thị hàm số
đi qua hai điểm cực trị của đồ thị hàm số
và tiếp xúc với đường thẳng . Khi đó, giá trị của bằng? ➢ Điền đáp án: .
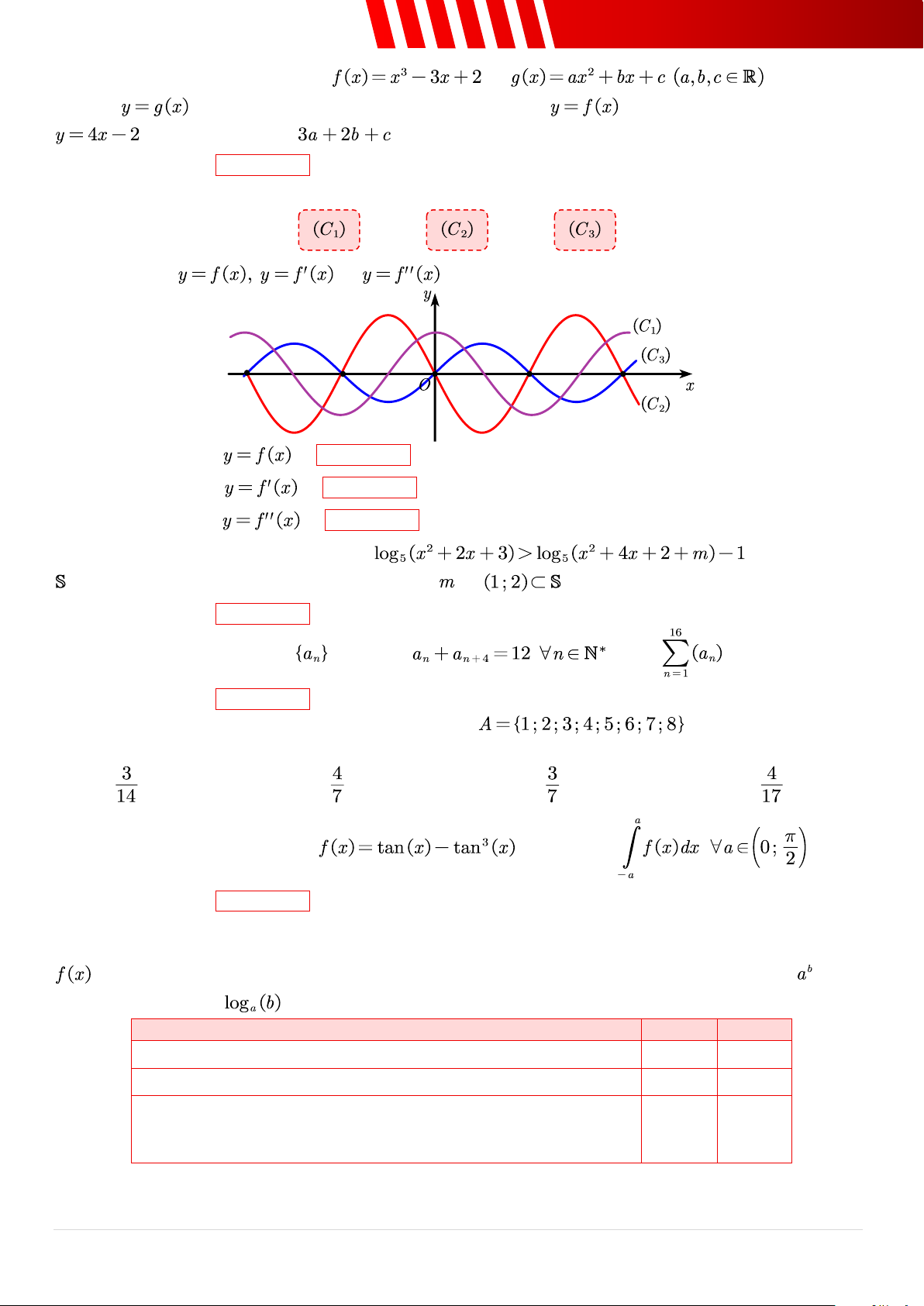
Câu 25. [Mức 3] Kéo và thả các phương án thích hợp vào chỗ trống. Cho ba hàm số và
có đồ thị như hình vẽ sau đây:
a. Đồ thị hàm số là .
b. Đồ thị hàm số là .
c. Đồ thị hàm số là .
Câu 26. [Mức 3] Cho bất phương trình có tập nghiệm
. Tồn tại bao nhiêu giá trị nguyên của tham số để ? ➢ Điền đáp án: .
Câu 27. [Mức 2] Cho dãy số thoả mãn . Tổng bằng? ➢ Điền đáp án: .
Câu 28. [Mức 1] Chọn ngẫu nhiên hai số trong tập
. Xác suất để tổng hai
số được chọn là một số chẵn là? A. . B. . C. . D. .
Câu 29. [Mức 1] Cho hàm số lẻ . Giá trị của bằng? ➢ Điền đáp án: .
Câu 30. [Mức 3] Trong ngôn ngữ lập trình của phần mềm soạn thảo LaTeX, ta có một vài mã lệnh
thường gặp như sau: Lệnh “\int_{a}^{b}{\f(x)}dx” biểu thị tích phân cận từ a đến b của một hàm
, lệnh “\floor{x}” nhằm chỉ số nguyên lớn nhất bé hơn x, lệnh “\a^{b}” nhằm chỉ , lệnh “\log_a(b)” biểu thị
,… Xét tính đúng/sai của các mệnh đề sau: Mệnh đề Sai Đúng
a. Kết quả của phép “\floor{12,3}=” là 3. ○ ○
b. Kết quả của phép “\floor{\log_10(2^{2026})}+1” là 610. ○ ○
c. Kết quả của phép toán:
“\int_{-e^2}^{e^2}{\tan(x)-tan^3(x)}dx” ○ ○ là một số nguyên.
40 Đề TSA | Phạm Tú Khanh
Câu 31. [Mức 3] Cho dãy số thoả mãn
. Giá trị nhỏ nhất của để là ? ➢ Điền đáp án: .
Câu 32. [Mức 3] Trong một dự án trang trí, cô giáo chủ nghiệm của lớp 12A
muốn thiết kế một món đồ chơi hình trụ được bọc trong lớp vỏ hình cầu, có
đường kính bằng , sao cho lớp vỏ luôn ngoại tiếp món đồ chơi. Biết rằng độ
dày của lớp vỏ không đáng kể và cô giáo muốn thiết kế món đồ chơi sao cho
diện tích xung quanh là lớn nhất nhằm cho học sinh tô màu tráng trí lên món
đồ đó. Xét tính đúng/sai của các mệnh đề sau: Mệnh đề Đúng Sai
a. Gọi và lần lượt là bán kính đáy và chiều ○ ○
cao của món đồ chơi, khi đó .
b. Bán kính của món đồ chơi bằng . ○ ○
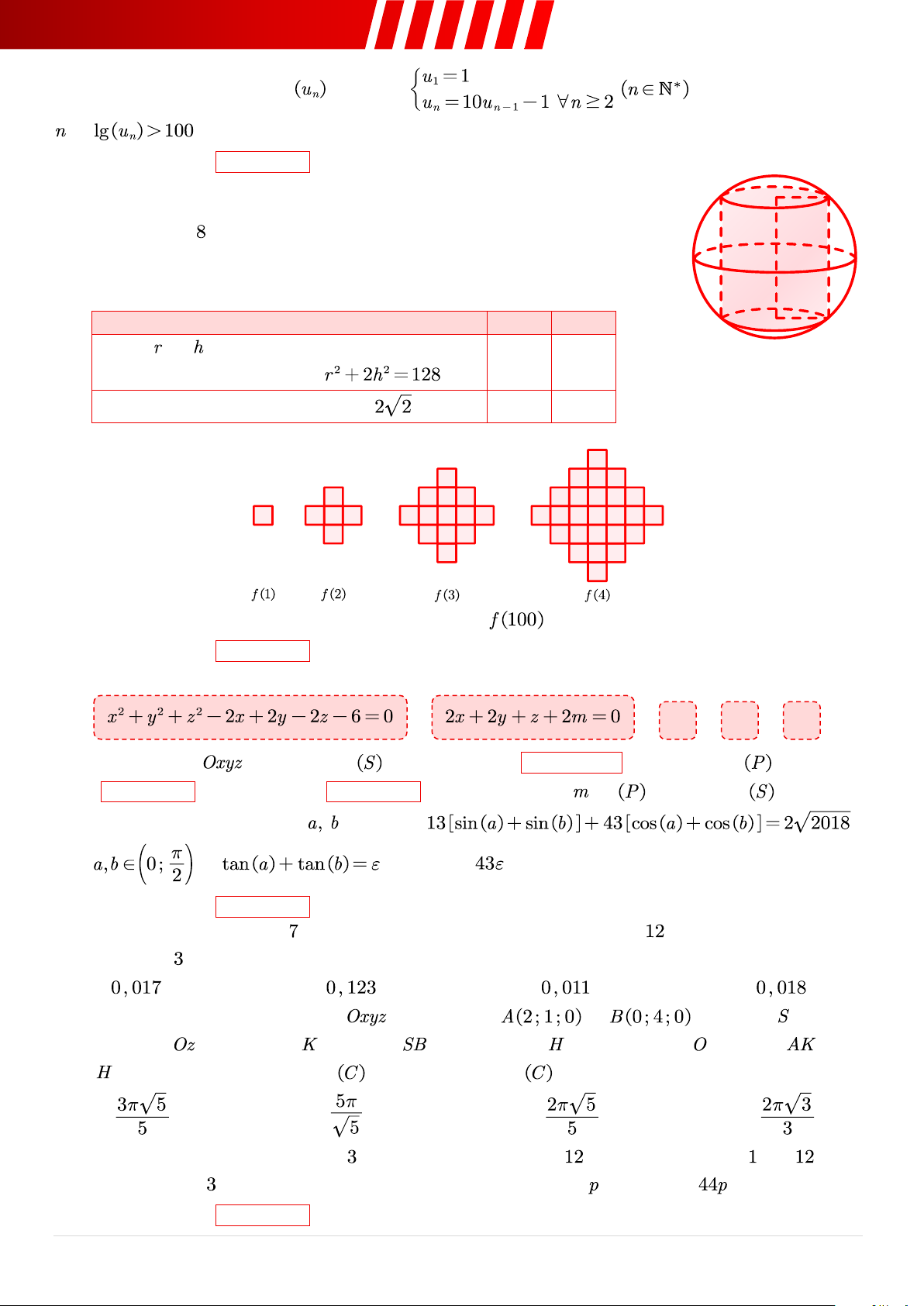
Câu 33. [Mức 3] Cho một dãy các hình như sau:
Cứ vẽ thêm các hình vuông như quy luật trên thì hình có bao nhiêu hình vuông? ➢ Điền đáp án: .
Câu 34. [Mức 2] Kéo và thả các phương án thích hợp vào chỗ trống. 1 2 3 Trong không gian , cho mặt cầu
có phương trình và mặt phẳng có phương
trình . Khi đó, tồn tại giá trị nguyên của để tiếp xúc với .
Câu 35. [Mức 3] Cho số thực thoả mãn . Biết và , giá trị của bằng? ➢ Điền đáp án: .
Câu 36. [Mức 3] Một đoàn hành khách chuẩn bị lên một toa tàu gồm toa trở khách. Xác suất
để chỉ có đúng toa có người bằng? A. . B. . C. . D. .
Câu 37. [Mức 3] Trong không gian , cho hai điểm và . Xét điểm thay đổi nằm trên trục , trung điểm của đoạn và hình chiếu
của gốc toạ độ lên cạnh . Biết
rằng luôn thuộc một đường tròn cố định, chu vi của bằng? A. . B. . C. . D. .
Câu 38. [Mức 3] Chọn ngẫu nhiên lá bài từ một bộ bài gồm lá (được đánh số từ đến ), xác
suất để các số trên lá bài được chọn lập thành một cấp số cộng là . Giá trị của bằng? ➢ Điền đáp án: .
40 Đề TSA | Phạm Tú Khanh
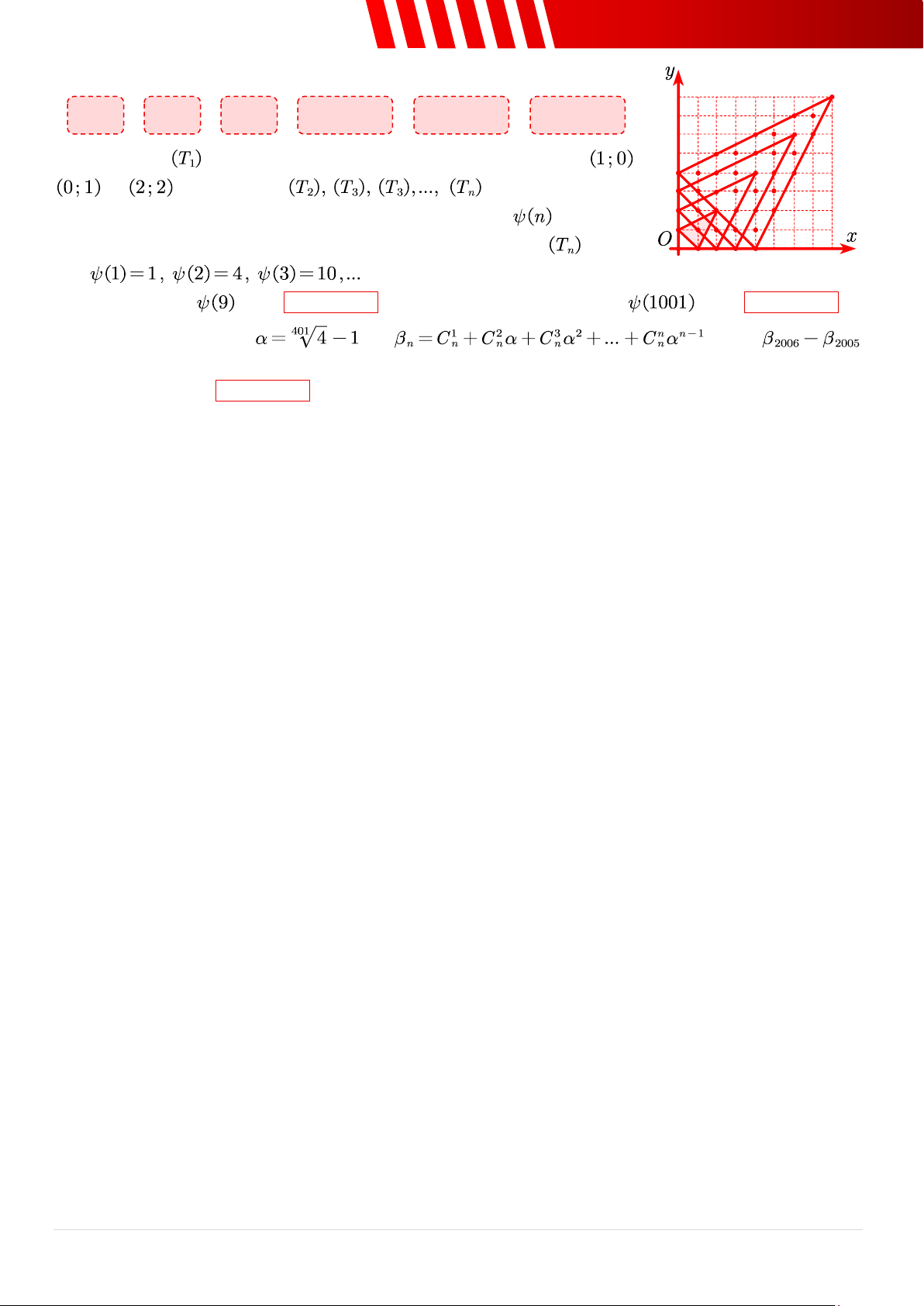
Câu 39. [Mức 3] Kéo và thả các phương án thích hợp vào chỗ trống. 202 108 109 1501501 1501500 1501503 Cho tam giác
(vùng tô đậm) được tạo bởi ba đỉnh có toạ độ , và . Các tam giác đồng dạng với nhau
và có các toạ độ đỉnh nguyên (như hình vẽ bên). Ta đặt là số điểm
có toạ độ nguyên nằm trong miền được giới hạn bởi tam giác , chẳng hạn . a. Giá trị của bằng . b. Giá trị của bằng .
Câu 40. [Mức 3] Đặt và . Hiệu bằng? ➢ Điền đáp án: .
-=-=-=-=-=-=-=-HẾT-=-=-=-=-=-=-=-
40 Đề TSA | Phạm Tú Khanh Đáp Án. Câu Đáp Án Câu Đáp Án 1 757 21
a. Đúng b. Đúng 2
a. Đúng b. Sai c. Sai 22 B 3 D 23 C 4 21 24 4 5 A 25 a. b. c. 6 B 26 22 7 95 27 96 8 726 28 C 9 3 29 0 10 a. Sai b. Sai 30
a. Sai b. Đúng c. Đúng 11 31 102 12 C 32
a. Sai b. Đúng 13 2 33 20201 a. 14 B 34 b. c. 2 15 C 35 26 16
a. Sai b. Đúng 36 A 17 21 37 A 18 1956 38 6 19 a. 5 b. 15625 39
a. 109 b. 1501501 20 A, B, C 40 1024
40 Đề TSA | Phạm Tú Khanh
Ngày:___/___/_____. Điểm: ___/40.
Đề Thi Thử Đánh Giá Tư Duy Toán Học.
Câu 1. [Mức 1] Theo một công thức nấu ăn, để làm một chiếc bánh ngọt cần cốc bột mì. Bạn
Giang mua một hộp làm bánh có chứa
cốc bột mì, vậy Giang cần dùng bao nhiêu lượng bột mì trong hộp để làm
chiếc bánh ngọt theo công thức trên? ➢ Điền đáp án: .
Câu 2. [Mức 1] Cho khối chóp
có đáy là tam giác đều cạnh , cạnh bên vuông góc với đáy và
. Thể tích của khối chóp bằng? A. . B. . C. . D. .
Câu 3. [Mức 2] Vào một buổi chiều rảnh rỗi, bạn Hoàng đã ngồi viết hết tất cả các số tự nhiên có 3
chữ số vào vở. Sau khi viết xong, Hoàng đã viết chữ số 5 tổng cộng bao nhiêu lần? ➢ Điền đáp án: .
Câu 4. [Mức 2] Cho hai vector thoả mãn và . Độ dài vector bằng? A. . B. . C. . D. .
Câu 5. [Mức 3] Có bao nhiêu cách để chia bạn học sinh thành nhóm học nhỏ, với ba nhóm có
thành viên và hai nhóm có thành viên? ➢ Điền đáp án: .
Câu 6. [Mức 3] Tồn tại bao nhiêu cặp số nguyên thoả mãn ? ➢ Điền đáp án: .
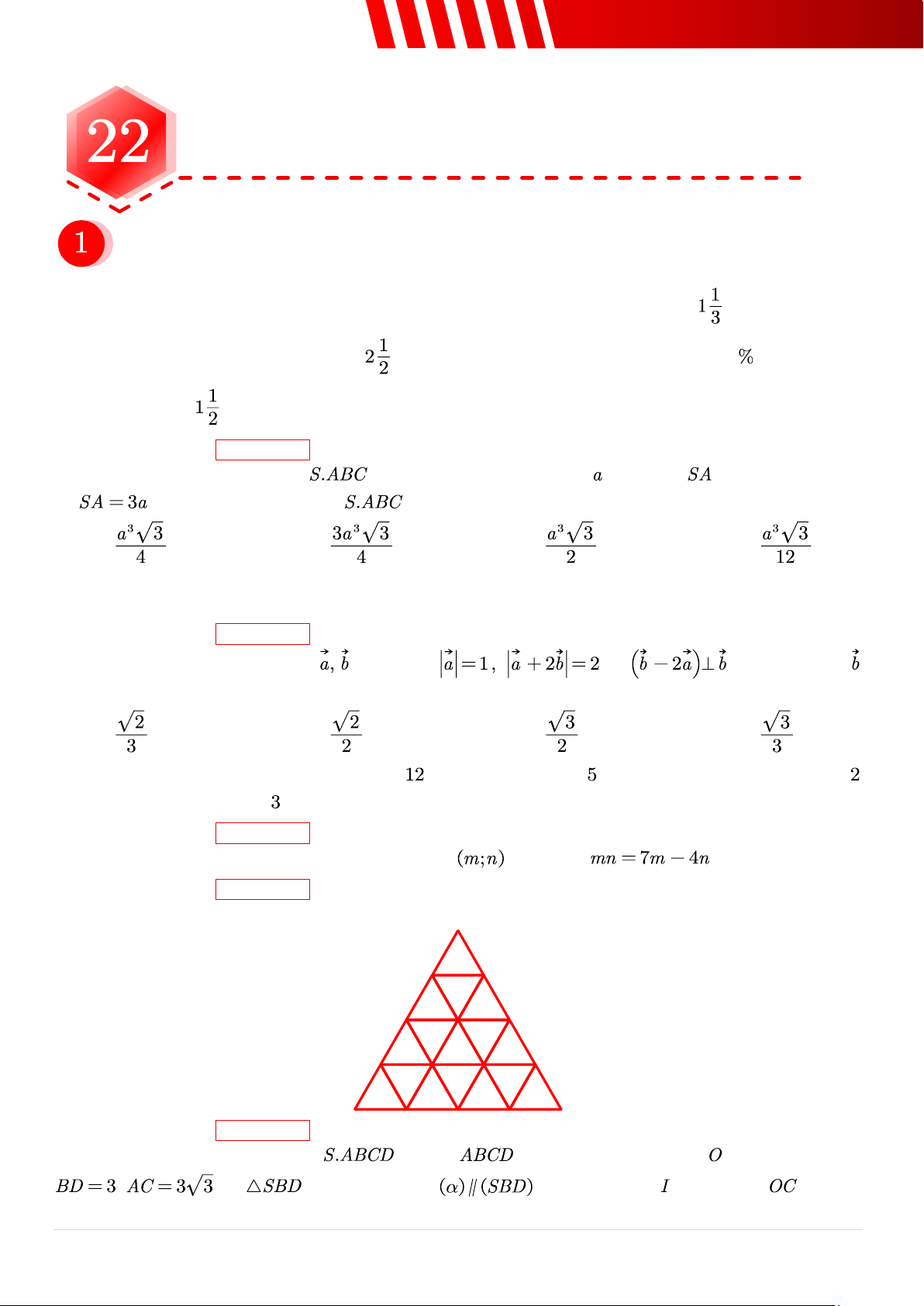
Câu 7. [Mức 2] Có bao nhiêu tam giác trong hình dưới đây? ➢ Điền đáp án: .
Câu 8. [Mức 3] Cho hình chóp có đáy
là hình bình hành tâm , độ dài các cạnh , và đều. Mặt phẳng
và đi qua điểm thuộc đoạn sao cho
40 Đề TSA | Phạm Tú Khanh . Biết cắt các cạnh , , lần lượt tại
, xét tính đúng/sai của các mệnh đề sau: Mệnh đề Đúng Sai a. cân tại . ○ ○ b. Diện tích gấp lần diện tích . ○ ○ c. Diện tích bằng . ○ ○
Câu 9. [Mức 2] Điền số nguyên thích hợp vào chỗ trống. Cho bảng ô vuông
với các giá trị của mỗi ô tương ứng như sau: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
Chọn 4 ô sao cho mỗi hàng và mỗi cột đều có đúng 1 ô được chọn.
a. Có cách chọn như trên.
b. Tổng lớn nhất các số trong 4 ô được chọn là .
Câu 10. [Mức 2] Cho là tổng của số hạng đầu tiên của cấp số cộng . Nếu và thì giá trị của bằng? ➢ Điền đáp án: .
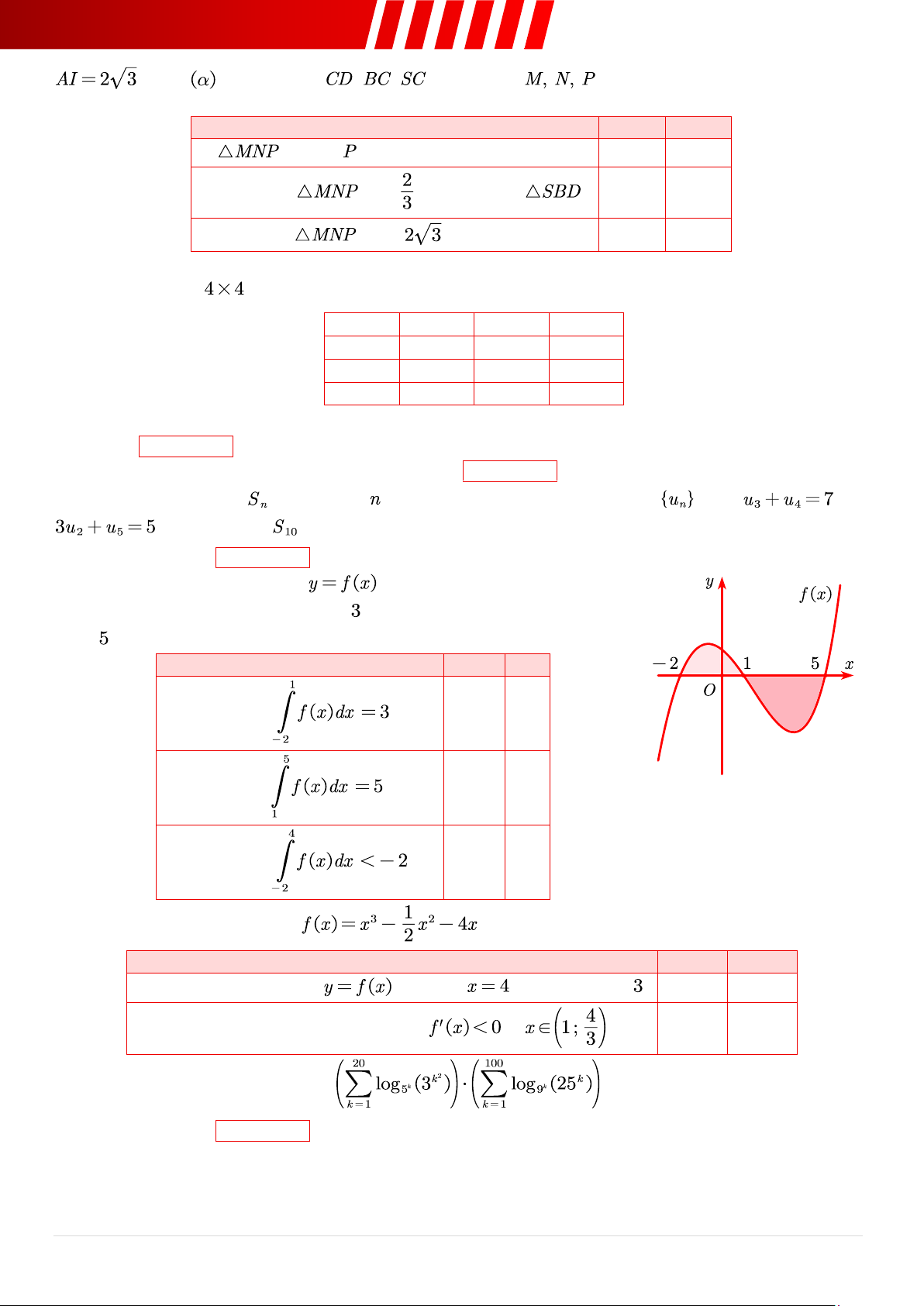
Câu 11. [Mức 1] Cho hàm số
có đồ thị như hình vẽ bên. Biết
diện tích phần tô màu nhạt hơn bằng và diện tích phần tô màu đậm hơn
bằng , xét tính đúng/sai của các mệnh đề sau: Mệnh đề Đúng Sai a. Tích phân . ○ ○ b. Tích phân . ○ ○ c. Tích phân . ○ ○
Câu 12. [Mức 1] Cho hàm số
. Xét tính đúng/sai của các mệnh đề sau: Mệnh đề Đúng Sai
a. Đạo hàm của hàm số tại điểm có giá trị bằng . ○ ○
b. Tập nghiệm của bất phương trình là . ○ ○
Câu 13. [Mức 1] Giá trị của tổng bằng? ➢ Điền đáp án: .
40 Đề TSA | Phạm Tú Khanh
Câu 14. [Mức 1] Cho hai biến cố thoả mãn . Khi đó, bằng? A. . B. . C. . D. .
Câu 15. [Mức 1] Tập nghiệm của bất phương là ? A. . B. . C. . D. .
Câu 16. [Mức 1] Trong không gian , cho các điểm , , .
Đường thẳng đi qua gốc toạ độ và trọng tâm của có phương trình là? A. . C. . B. . D. .
Câu 17. [Mức 1] Với số thực dương , ta có . Tổng bằng? ➢ Điền đáp án: .
Câu 18. [Mức 1] Kéo và thả các phương án thích hợp vào chỗ trống. ellipse hyperbol tròn parabol
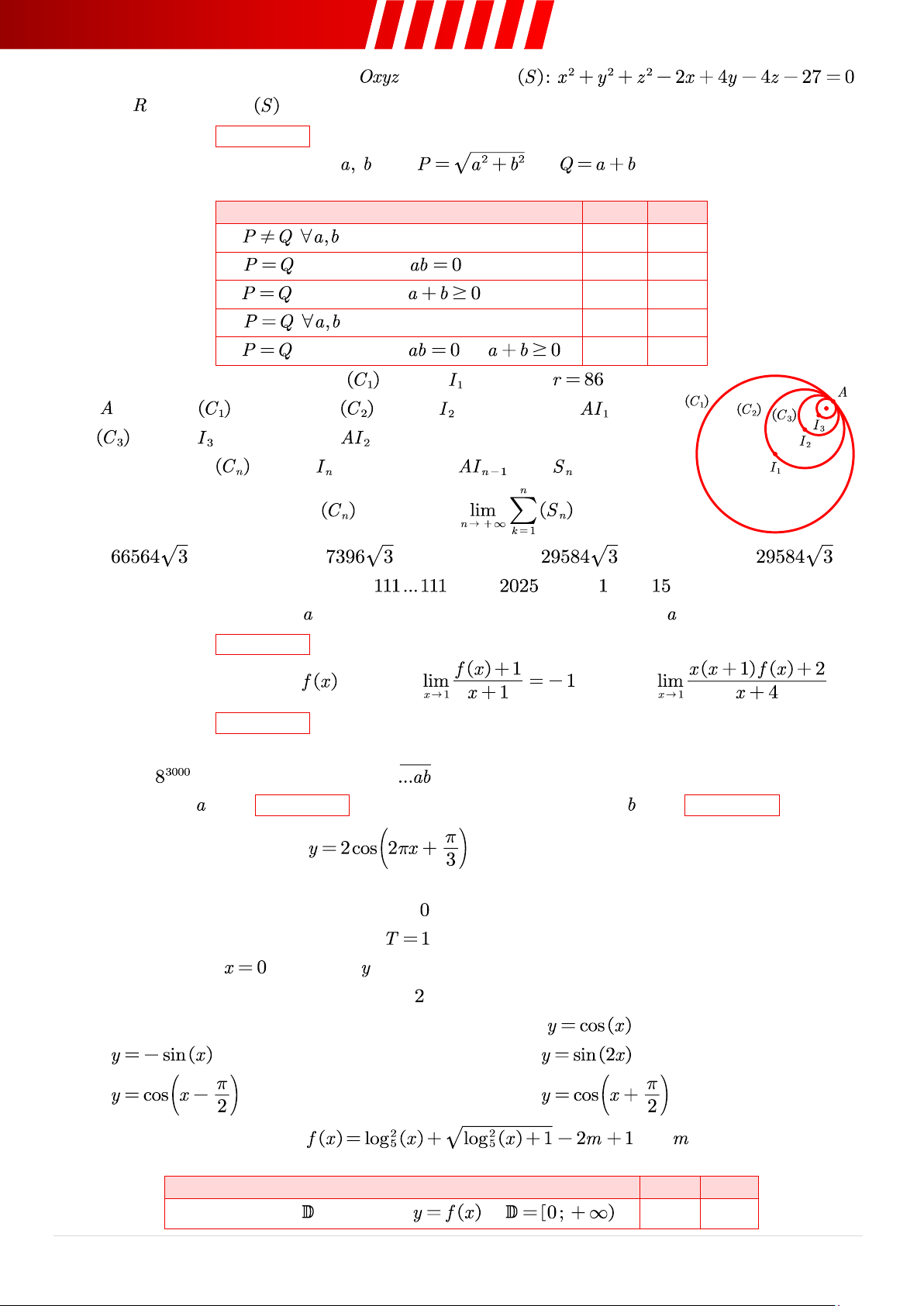
Cho hai hình nón tiếp xúc với nhau tại hai đỉnh, tạo thành một hình “đồng hồ cát”. Một mặt phẳng
cắt hình nón tại các vị trí khác nhau như hình vẽ sau đây. Ta xét các đường cong thuộc và
nằm trên bề mặt ngoài của hình nón. a. Đường cong ở là đường . c. Đường cong ở là đường . b. Đường cong ở là đường . d. Đường cong ở là đường .
Câu 19. [Mức 1] Bạn Nam đang cầm quả bóng đá hình cầu của mình để ra sân chơi thì đã vô tình
làm rơi vào một xô chứa đầy nước. Quan sát, Nam nhận thấy rằng có đúng một nửa quả bóng chìm
xuống nước và thể tích nước tràn ra bằng
. Đường kính của quả bóng đó bằng bao nhiêu ? A. . B. . C. . D. .
Câu 20. [Mức 1] Cho dãy số
có công thức tổng quát
. Xét tính đúng/sai của các mệnh đề sau: Mệnh đề Đúng Sai
a. Dãy số trên không bị chặn dưới. ○ ○ b. Giới hạn . ○ ○
c. Dãy số trên là dãy số bị chặn. ○ ○
40 Đề TSA | Phạm Tú Khanh
Câu 21. [Mức 1] Trong không gian , cho mặt cầu . Bán kính của mặt cầu bằng? ➢ Điền đáp án: .
Câu 22. [Mức 1] Với hai số thực , đặt và
. Xét tính đúng/sai của các mệnh đề sau: Mệnh đề Đúng Sai a. . ○ ○ b. khi và chỉ khi . ○ ○ c. khi và chỉ khi . ○ ○ d. . ○ ○ e. khi và chỉ khi và . ○ ○
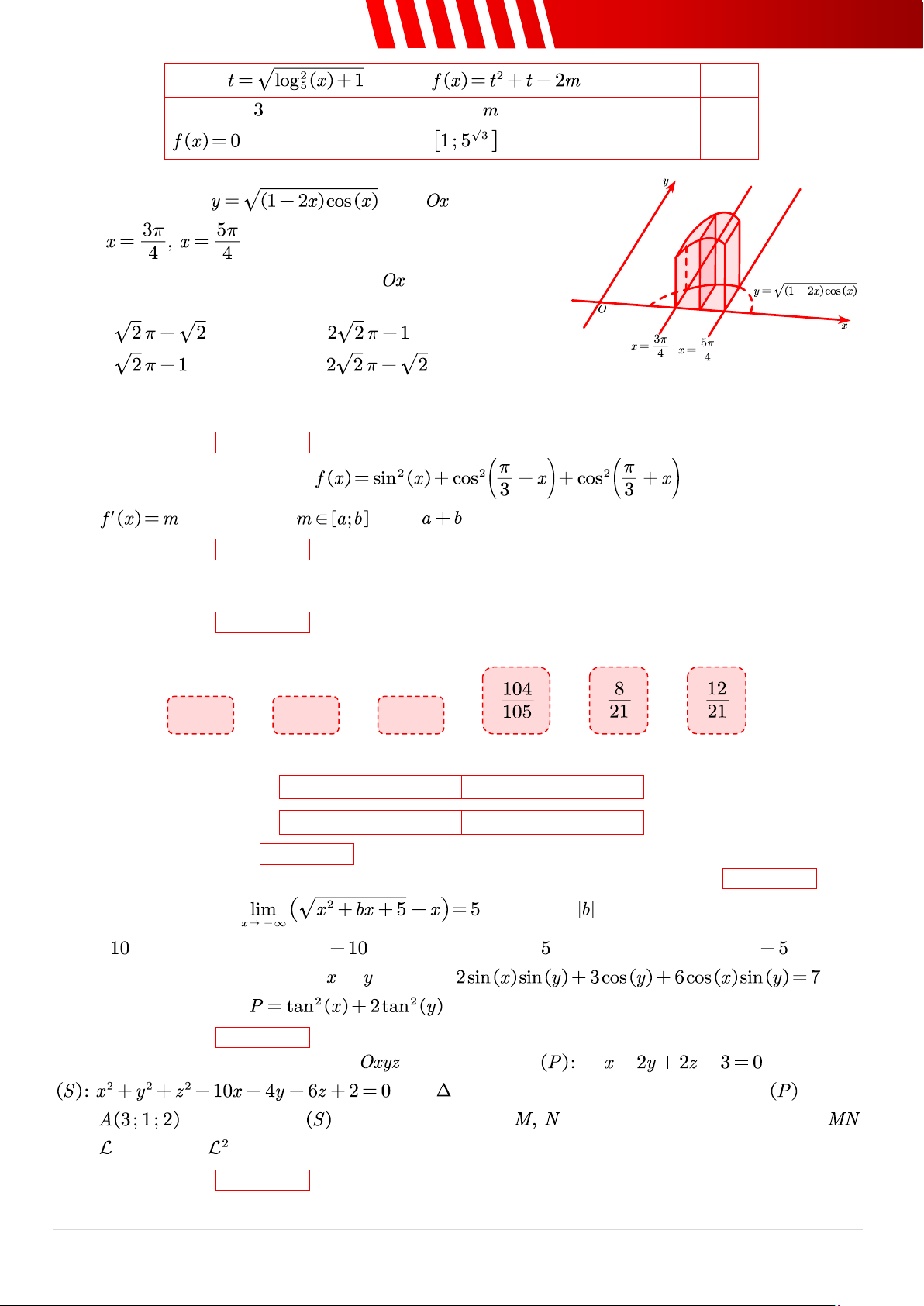
Câu 23. [Mức 3] Cho đường tròn có tâm , bán kính và một điểm nằm trên . Đường tròn có tâm và đường kính , đường tròn có tâm và đường kính
,… quá trình này được lặp lại vô tận sao cho đường tròn có tâm và đường kính . Đặt là diện tích
tam giác đều nội tiếp đường tròn , khi đó tổng bằng? A. . B. . C. . D. .
Câu 24. [Mức 3] Biết rằng khi chia số (gồm chữ số ) cho
thì thu được kết quả là
một số có duy nhất một chữ số ở hàng phần chục sau dấu phẩy. Giá trị của bằng? ➢ Điền đáp án: .
Câu 25. [Mức 3] Cho hàm số thoả mãn . Giới hạn là? ➢ Điền đáp án: .
Câu 26. [Mức 3] Điền số nguyên thích hợp vào chỗ trống. Biết rằng số
có hai chữ số tận cùng là .
a. Giá trị của bằng .
b. Giá trị của bằng .
Câu 27. [Mức 1] Cho hàm số
. Trong các mệnh đề sau đây, có những mệnh đề
nào là đúng? (Chọn nhiều đáp án)
A. Giá trị nhỏ nhất của hàm số trên bằng .
B. Hàm số trên tuần hoàn với chu kỳ .
C. Tại thời điểm
, giá trị của là một số lẻ.
D. Giá trị lớn nhất của hàm số trên bằng .
Câu 28. [Mức 1] Hàm số nào sau đây có một nguyên hàm là ? A. . C. . B. . D. .
Câu 29. [Mức 2] Cho hàm số
, với là tham số thực. Xét
tính đúng/sai của các mệnh đề sau: Mệnh đề Đúng Sai
a. Tập xác định của hàm số là . ○ ○
40 Đề TSA | Phạm Tú Khanh b. Đặt , khi đó . ○ ○
c. Tồn tại giá trị nguyên của tham số để phương trình ○ ○ có nghiệm trên khoảng .
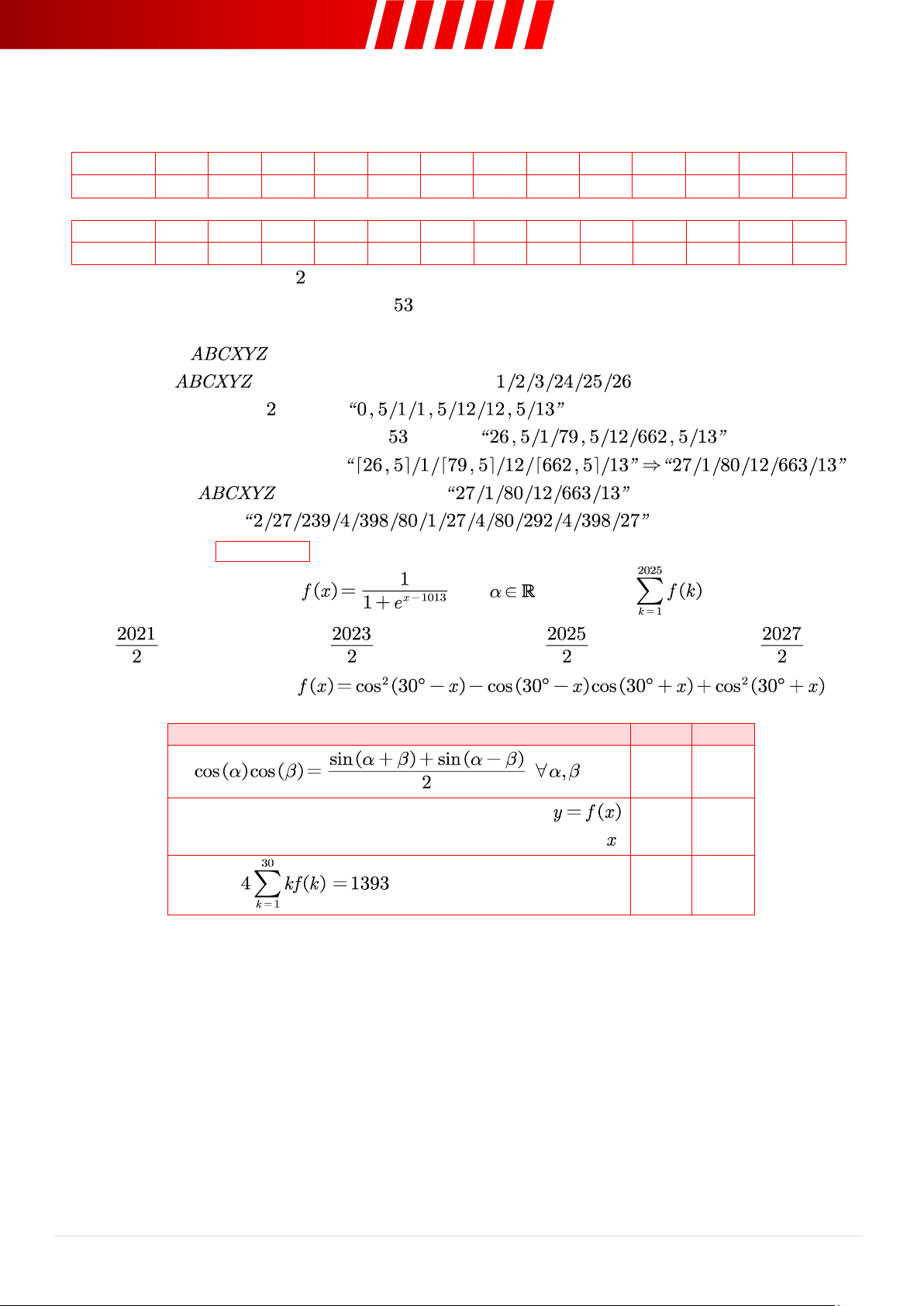
Câu 30. [Mức 2] Một khối rắn có mặt đáy là hình phẳng giới hạn bởi đường cong , trục và hai đường thẳng
. Biết tất cả các mặt cắt ngang của khối
rắn này với mặt phẳng vuông góc với trục đều là hình vuông,
thể tích của khối rắn này bằng? A. . C. . B. . D. .
Câu 31. [Mức 2] Cho một dãy gồm 20 số tự nhiên khác nhau và khác 0. Biết rằng tổng của chúng
bằng 211, số lớn nhất trong dãy trên là? ➢ Điền đáp án: .
Câu 32. [Mức 2] Cho hàm số
. Biết rằng để phương trình có nghiệm thì , tổng bằng? ➢ Điền đáp án: .
Câu 33. [Mức 2] Sắp xếp ngẫu nhiên một chuỗi gồm các ký tự BACHKHOA, xác suất để hai chữ H đứng cạnh nhau là? ➢ Điền đáp án: .
Câu 34. [Mức 2] Kéo và thả các phương án thích hợp vào chỗ trống. 2525 2515 2520
Xếp 8 chữ số thuộc dãy “3; 3; 5; 5; 7; 7; 9; 9” vào tám ô trống sau:
a. Số cách sắp xếp là .
b. Xác suất để hai số giống nhau không đứng cạnh nhau (trong cùng 1 hàng) là .
Câu 35. [Mức 2] Biết , giá trị của bằng? A. . B. . C. . D. .
Câu 36. [Mức 3] Cho hai số thực và thoả mãn . Khi
đó, giá trị của biểu thức bằng? ➢ Điền đáp án: .
Câu 37. [Mức 3] Trong không gian , cho mặt phẳng và mặt cầu . Gọi
là đường thẳng nằm trong mặt phẳng , đi qua điểm và cắt mặt cầu
tại hai điểm phân biệt
. Độ dài nhỏ nhất của đoạn thẳng bằng , giá trị của bằng? ➢ Điền đáp án: .
40 Đề TSA | Phạm Tú Khanh
Câu 38. [Mức 3] Mật mã bảo mật Icarus được sử dụng để mã hoá các thông điệp bí mật bằng cách
thay đổi thông điệp ban đầu thành các ký tự khác. Quy trình mã hoá Icarus được thực hiện như sau:
Với các thông điệp ban đầu là các chữ cái, ta quy đổi chúng thành số thứ tự tương ứng trong bảng
chữ cái tiếng Anh như sau: Chữ cái A B C D E F G H I J K L M Số 1 2 3 4 5 6 7 8 9 10 11 12 13 Chữ cái N O P Q R S T U V W X Y Z Số 14 15 16 17 18 19 20 21 22 23 24 25 26
Sau đó, ta chia các giá trị cho và lấy kết quả làm thông điệp mã hoá (thông điệp đầu ra). Nếu phép
chia cho ra kết quả không nguyên, ta nhân
vào kết quả rồi lấy phần nguyên trên làm thông điệp mã
hoá. Mỗi chữ cái trong thông điệp đầu ra được ngăn cách nhau bởi dấu “/”. Ví dụ, bắt đầu với thông điệp đầu vào là “
”, ta mã hoá theo mật mã Icarus như sau: 1. Quy đổi “
” sang số thứ tự tương ứng là “ ”.
2. Chia từng giá trị cho , ta được .
3. Nhân các phần tử không nguyên với , ta được .
4. Lấy phần nguyên trên, ta được . Vậy, thông điệp “ ” được mã hoá thành
theo mật mã Icarus. Khi đó,
với thông điệp đầu ra là
thì thông điệp đầu vào là? ➢ Điền đáp án: .
Câu 39. [Mức 3] Cho hàm số , với . Giá trị của bằng? A. . B. . C. . D. .
Câu 40. [Mức 3] Cho hàm số , xét
tính đúng/sai của các mệnh đề sau: Mệnh đề Sai Đúng a. . ○ ○
b. Đường thẳng tiếp tuyến của đồ thị hàm số ○ ○
luôn song song với trục hoành với mọi giá trị thực của . c. Tổng . ○ ○
-=-=-=-=-=-=-=-HẾT-=-=-=-=-=-=-=-
40 Đề TSA | Phạm Tú Khanh Đáp Án. Câu Đáp Án Câu Đáp Án 1 80 21 6 2 A 22 Chỉ có e. đúng 3 280 23 B 4 B 24 4 5 138600 25 6 12 26 a. 7 b. 6 7 27 27 B, C, D 8
a. Đúng b. Sai c. Sai 28 D 9 a. 24 b. 34 29
a. Sai b. Đúng c. Sai 10 95 30 D 11
a. Đúng b. Sai c. Sai 31 21 12 a. Sai b. Sai 32 0 13 21000 33 14 A 34 a. 2520 b. 15 D 35 A 16 B 36 9 17 49 37 120
a. parabol b. tròn 18 38 DAIHOCBAHCKHOA
c. ellipse d. hyperbol 19 C 39 C 20
a. Sai b. Đúng c. Đúng 40
a. Sai b. Đúng c. Sai
40 Đề TSA | Phạm Tú Khanh
Ngày:___/___/_____. Điểm: ___/40.
Đề Thi Thử Đánh Giá Tư Duy Toán Học.
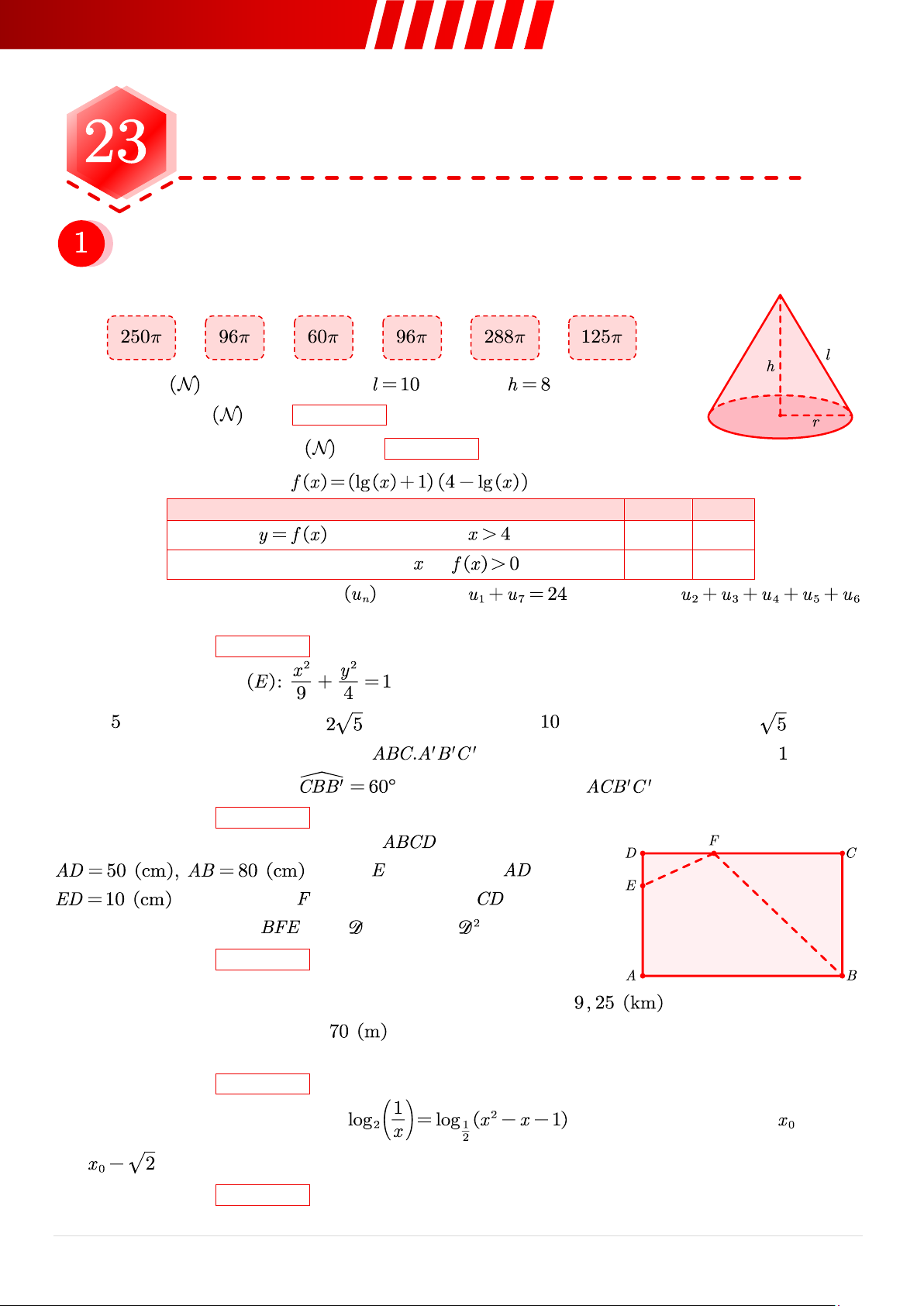
Câu 1. [Mức 1] Kéo và thả các phương án thích hợp vào chỗ trống. Một hình nón
có độ dài đường sinh , chiều cao . a. Thể tích của bằng .
b. Diện tích toàn phần của bằng .
Câu 2. [Mức 1] Cho hàm số
. Xét tính đúng/sai của các mệnh đề sau: Mệnh đề Sai Đúng a. Hàm số xác định với mọi . ○ ○
b. Có 9999 giá trị nguyên của để . ○ ○
Câu 3. [Mức 1] Cho cấp số cộng thoả mãn , khi đó tổng bằng? ➢ Điền đáp án: .
Câu 4. [Mức 1] Elipse có tiêu cự bằng? A. . B. . C. . D. .
Câu 5. [Mức 3] Cho lăng trụ tam giác
có đáy là tam giác đều với cạnh bằng , các mặt
bên là các hình thoi. Biết rằng
, thể tích của khối chóp bằng? ➢ Điền đáp án: .
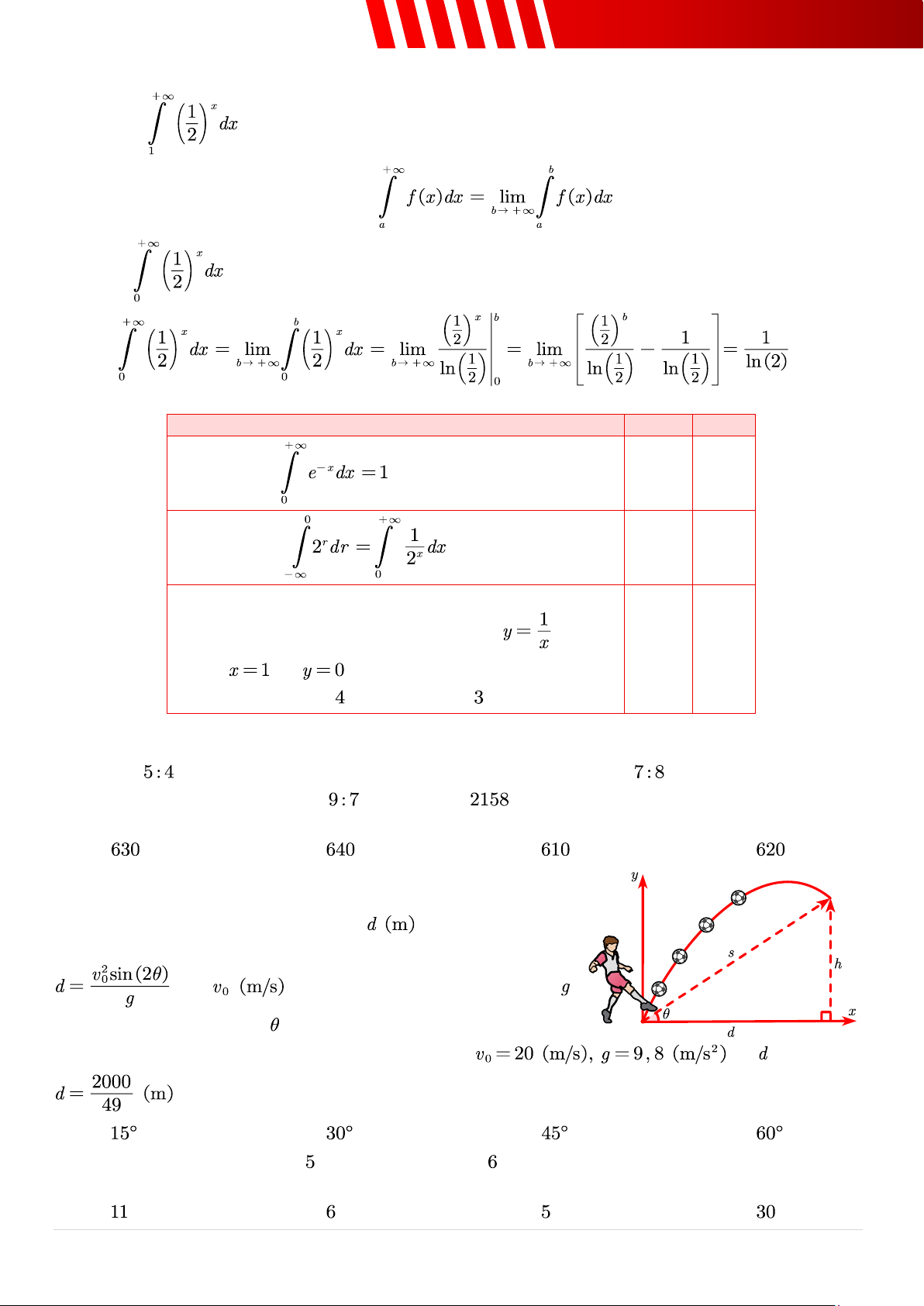
Câu 6. [Mức 3] Cho hình chữ nhật có độ dài các cạnh , điểm thuộc cạnh sao cho
. Với một điểm linh động trên cạnh , độ dài ngắn
nhất của đường gấp khúc bằng , giá trị của bằng? ➢ Điền đáp án: .
Câu 7. [Mức 1] Sau một cơn bão, trên một đoạn đường đại lộ dài
đã có rất nhiều cây xanh
bị đổ. Người ta nhận thấy rằng cứ
thì có một cây bị đổ, vậy trên đường đại lộ đó có bao nhiêu
cây bị đổ? (biết rằng cây đầu tiên bị đổ ở ngay đầu đoạn đường) ➢ Điền đáp án: .
Câu 8. [Mức 1] Biết phương trình
có một nghiệm duy nhất . Giá trị của bằng? ➢ Điền đáp án: .
40 Đề TSA | Phạm Tú Khanh
Câu 9. [Mức 3] Tích phân suy rộng là một dạng tích phân có một (hay cả hai) cận tiến đến vô cùng, chẳng hạn:
. Để tính toán, ta coi cận vô cùng là một ẩn số rồi đi xác định giới hạn của tích
phân khi ẩn đó tiến đến vô cùng, cụ thể: . Ví dụ với , ta có: .
Xét tính đúng/sai của các mệnh đề sau: Mệnh đề Đúng Sai a. Tích phân . ○ ○ b. Tích phân . ○ ○
c. “Kèn của Gabriel” là vật thể được tạo thành khi xoay
phần diện tích giới hạn bởi đường cong , đường ○ ○ thẳng và
quanh trục hoành. Thể tích của
chiếc kèn đó bé hơn , nhưng lớn hơn .
Câu 10. [Mức 1] Trong một buổi khảo sát số lượng sinh viên theo ngành Kỹ Thuật Địa Vật Lý,
trường Đại Học Mỏ Địa Chất thống kê được rằng tỉ lệ giữa số lượng sinh viên năm nhất với số sinh viên năm hai là
, tỉ lệ giữa số sinh viên năm hai với số sinh viên năm ba là
và tỉ lệ giữa số sinh viên
năm ba với số sinh viên năm tư là . Nếu có tổng
sinh viên theo ngành Kỹ Thuật Địa Vật Lý
thì có bao nhiêu sinh viên trong đó là năm nhất? A. . B. . C. . D. .
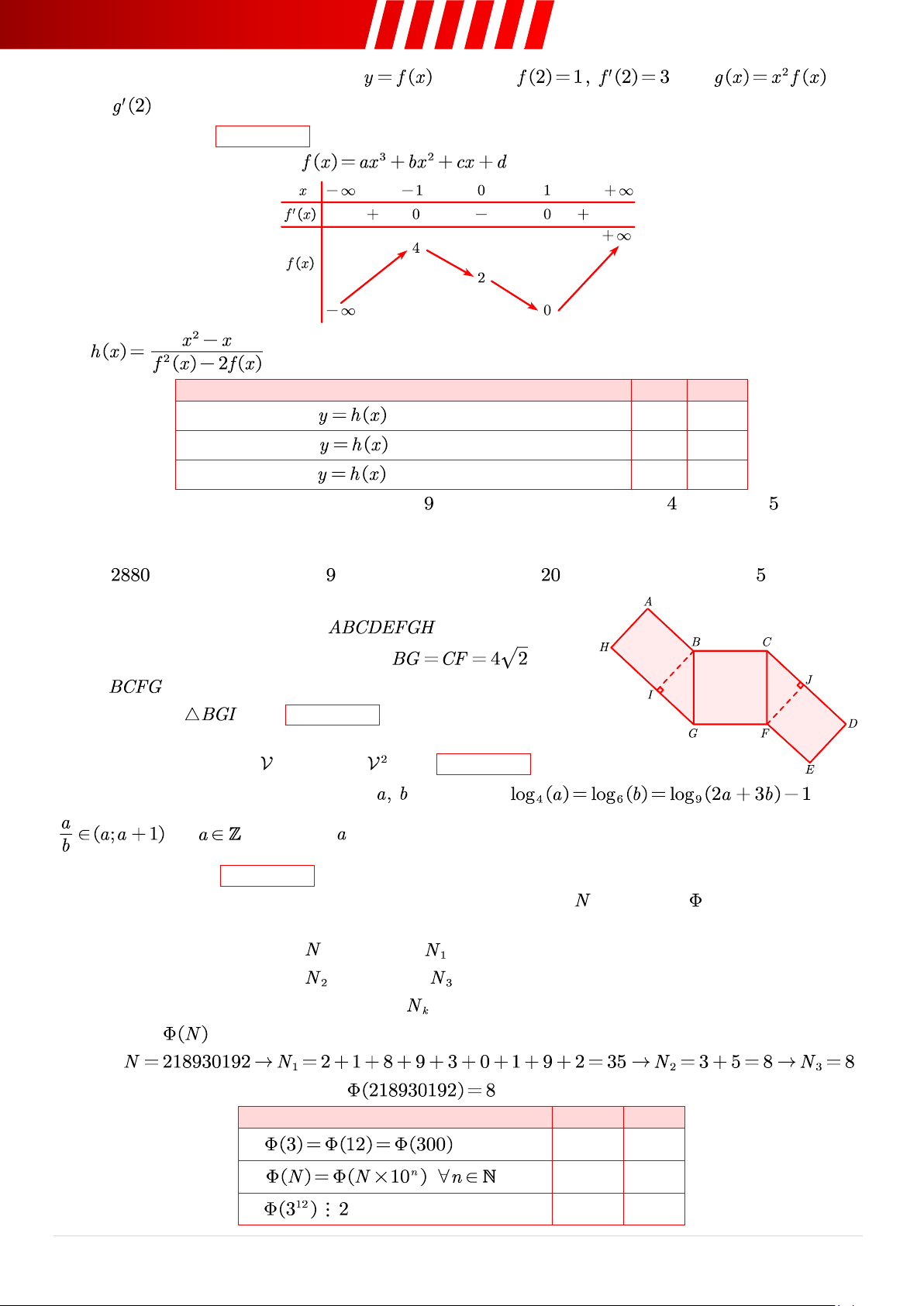
Câu 11. [Mức 1] Một cầu thủ sút quả bóng lên không trung theo
quỹ đạo như hình vẽ bên. Từ lúc quả bóng được sút đến khi chạm
đất, nó di chuyển được một khoảng theo phương nằm
ngang. Khoảng cách này được xác định theo công thức , với
là vận tốc ban đầu của quả bóng,
là gia tốc trọng trường và là góc quả bóng được sút lên so với
phương nằm ngang. Khi quả bóng được sút lên với và được đo là
thì góc sút ban đầu của quá bóng bằng? A. . B. . C. . D. .
Câu 12. [Mức 1] Bạn Lan có quyển sách Toán và quyển sách Văn học, các quyển sách là khác
nhau. Có bao nhiêu cách để Lan chọn một quyển để đọc? A. . B. . C. . D. .
40 Đề TSA | Phạm Tú Khanh
Câu 13. [Mức 1] Cho hàm số đa thức thoả mãn . Đặt , giá trị của bằng? ➢ Điền đáp án: .
Câu 14. [Mức 3] Cho hàm số
có đồ thị như hình vẽ sau: Đặt
, xét tính đúng/sai của các mệnh đề sau: Mệnh đề Sai Đúng
a. Đồ thị hàm số
có 4 đường tiệm cận đứng. ○ ○
b. Đồ thị hàm số
có 1 đường tiệm cận ngang. ○ ○
c. Đồ thị hàm số
có 5 đường tiệm cận. ○ ○
Câu 15. [Mức 1] Trong một giờ chào cờ, có bạn lớp 12TA1, trong đó có bạn nữ và bạn nam,
được lên sân khấu nhận giải. Có bao nhiêu cách để sắp xếp các bạn trên thành một hàng ngang sao cho
các bạn nam và nữ đứng xen kẽ nhau? A. . B. . C. . D. .
Câu 16. [Mức 2] Điền số nguyên thích hợp vào chỗ trống.
Hình vẽ bên miêu tả một đa giác , được kết hợp bởi
hai tam giác vuông cân có kích thước , hình vuông và hai hình chữ nhật. a. Diện tích bằng .
b. Gập hình theo đường nét đứt, ta được một hình lăng trụ
đứng có thể tích bằng , giá trị của bằng .
Câu 17. [Mức 2] Cho hai số thực thoả mãn . Biết với , giá trị của bằng? ➢ Điền đáp án: .
Câu 18. [Mức 1] Xuất phát với giá trị đầu vào là một số nguyên , thuật toán được tiến hành như sau:
1. Tính tổng các chữ số của để thu được .
2. Tính tổng các chữ số của để thu được .
3. Cứ như vậy cho đến lúc giá trị của các
không thay đổi nữa thì dừng lại và ghi kết quả làm giá trị đầu ra . Ví dụ: .
Do vậy, giá trị đầu ra của phép toán
. Xét tính đúng/sai của các mệnh đề sau: Mệnh đề Đúng Sai a. . ○ ○ b. . ○ ○ c. . ○ ○
40 Đề TSA | Phạm Tú Khanh
Câu 19. [Mức 1] Trong không gian , cho và là hai
đường thẳng vuông góc với nhau. Giá trị của bằng? ➢ Điền đáp án: .
Câu 20. [Mức 1] Bạn Bình mua quyển sổ, chiếc bút chì và chiếc bút mực với giá . Bạn Phương mua quyển sổ, chiếc bút chì và
chiếc bút mực với giá
. Nếu bạn Thắng muốn mua quyển sổ, chiếc bút chì và
chiếc bút mực thì sẽ mất bao nhiêu tiền ? A. 49. B. 50. C. 51. D. 52.
Câu 21. [Mức 2] Cho tam giác
vuông cận tại . Biết rằng khi ta quay quanh cạnh
thì thu được hình nón có diện tích là và khi ta quay quanh ( là trung điểm của
) thì thu được hình nón có diện tích là
. Khi đó, tỉ lệ diện tích bằng? ➢ Điền đáp án: .
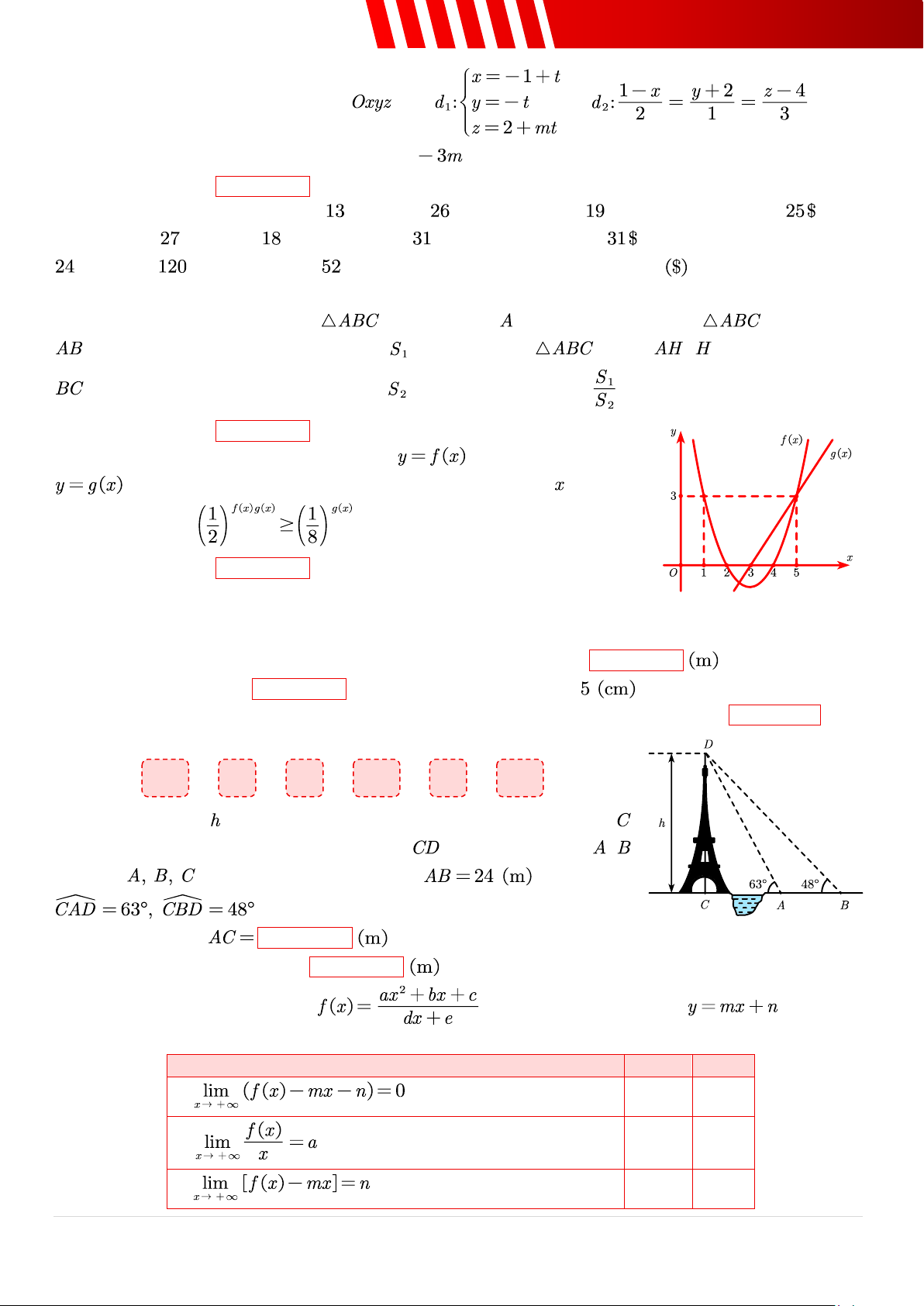
Câu 22. [Mức 2] Cho hàm số bậc hai và hàm số bậc nhất
có đồ thị như hình vẽ bên. Tổng các giá trị nguyên của thoả mãn bất phương trình bằng? ➢ Điền đáp án: .
Câu 23. [Mức 2] Điền số nguyên thích hợp vào chỗ trống.
Cho Một quả bóng được thả từ độ cao 5 (m) so với mặt đất. Sau mỗi lần tiếp đất, quả bóng sẽ nảy lên
với độ cai tối đa bằng 75% độ cao tối đa của lần nảy trước đó. Kết quả được làm tròn đến hàng đơn vị.
a. Độ cao tối đa của quả bóng sau khi chạm đất lần thứ 6 bằng .
b. Cần nảy tối thiểu lần để độ cao tối đa đạt dưới .
c. Từ lúc nảy đến lúc quả bóng nằm yên, tổng quãng đường đã di chuyển được là (m).
Câu 24. [Mức 2] Kéo và thả các phương án thích hợp vào chỗ trống. 17 8 9 16 7 15
Muốn đo chiều cao của một toà tháp mà ta không thể đến được tâm
của chân tháp. Trong mặt phẳng chứa trục , ta chọn hai điểm , sao cho
thẳng hàng. Giả sử đoạn và các góc
. (Các kết quả được làm tròn đến hàng đơn vị) a. Độ dài đoạn .
b. Chiều cao của tháp bằng .
Câu 25. [Mức 2] Cho hàm số
có đường tiệm cận xiên . Xét tính
đúng/sai của các mệnh đề sau: Mệnh đề Đúng Sai a. . ○ ○ b. . ○ ○ c. . ○ ○
40 Đề TSA | Phạm Tú Khanh
Câu 26. [Mức 3] Cho hàm số
có đạo hàm liên tục trên khoảng thoả mãn và
. Xét tính đúng/sai của các mệnh đề sau: Mệnh đề Sai Đúng a. . ○ ○ b. Giá trị của . ○ ○
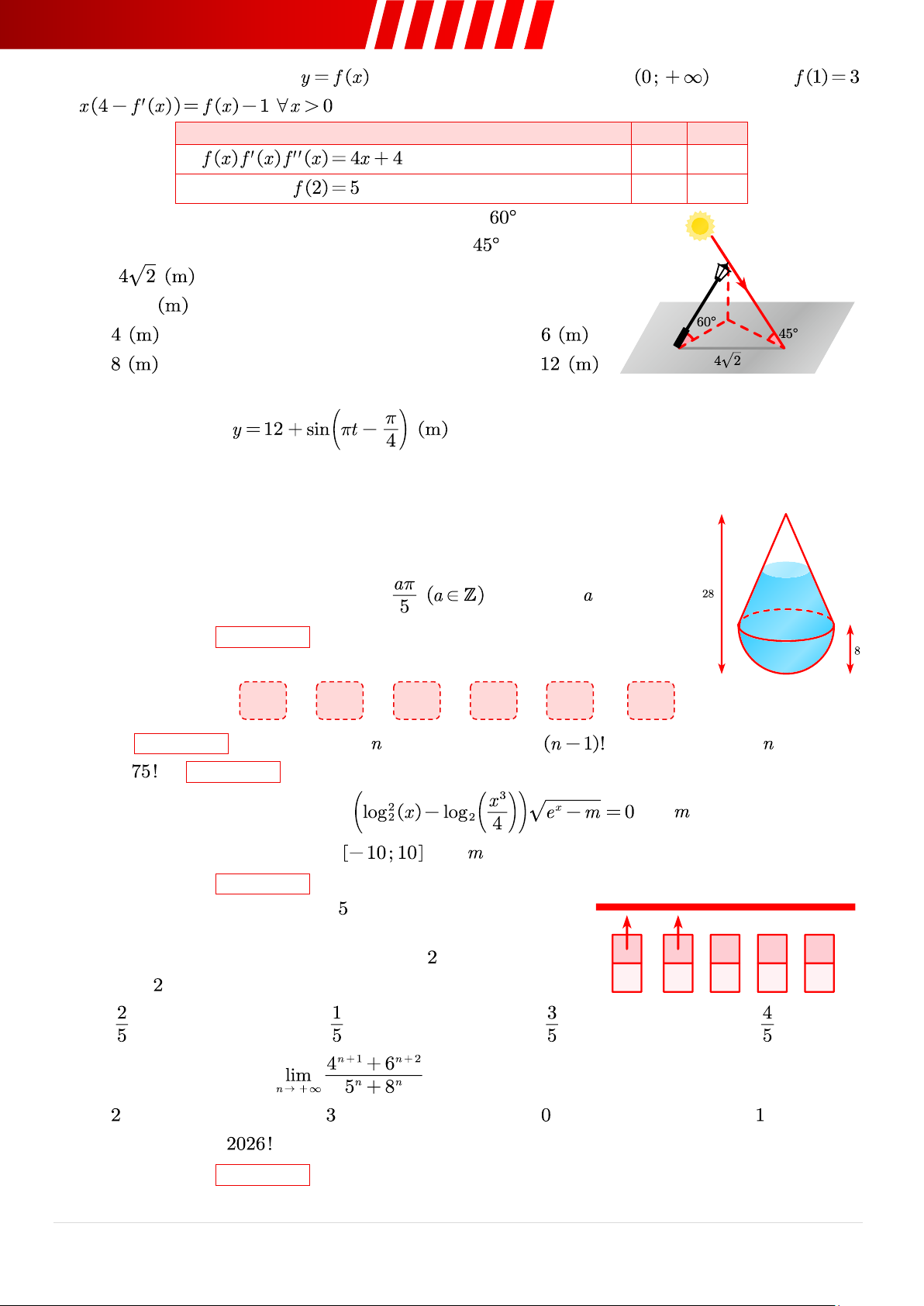
Câu 27. [Mức 2] Một cột đèn bị đổ nghiêng một góc so với mặt
đất. Khi ánh sáng mặt trời tạo với mặt đất một góc thì bóng của đèn dài
và vuông góc với cột đèn. Chiều cao của cột đèn đó là bao nhiêu ? A. . C. . B. . D. .
Câu 28. [Mức 2] Chuyển động của một xô nước nằm trên guồng quay hình tròn theo thời gian được xác định bằng hàm số
(t tính bằng phút). Trong 10 phút, xô nước này đạt
độ cao 12 (m) bao nhiêu lần? A. 8. B. 10. C. 9. D. 12.
Câu 29. [Mức 2] Cho bình chứa nước được tạo bởi một hình nón không đáy và
hình bán cầu và đặt thẳng đứng trên mặt bàn như hình vẽ. Bình được đổ một
lượng nước bằng 70% dung tích của bình. Coi kích thước vỏ bình không đáng kể,
chiều cao của mực nước so với mặt bàn là . Giá trị của bằng? ➢ Điền đáp án: .
Câu 30. [Mức 3] Kéo và thả các phương án thích hợp vào chỗ trống. 13 14 15 16 17 18
a. Có số nguyên dương nhỏ hơn 50 sao cho không chia hết cho . b. Số
có chữ 0 tận cùng bên phải.
Câu 31. [Mức 2] Cho phương trình
, với là tham số. Tổng tất
cả các giá trị nguyên, trong khoảng
, của để phương trình trên có đúng 2 nghiệm bằng? ➢ Điền đáp án: .
Câu 32. [Mức 2] Cho thanh sắt và thanh nam châm với cực Bắc
và cực Nam nằm ngẫu nhiên (như hình vẽ bên). Biết rằng khi đưa
thanh sắt gần vào các nam châm thì sẽ chỉ có thanh bị hút lên.
Xác suất để thanh nam châm cạnh nhau bị hút lên bằng? A. . B. . C. . D. .
Câu 33. [Mức 1] Giới hạn bằng? A. . B. . C. . D. .
Câu 34. [Mức 3] Số có bao nhiêu chữ số? ➢ Điền đáp án: .
40 Đề TSA | Phạm Tú Khanh
Câu 35. [Mức 3] Cho hình lăng trụ
, gọi và lần lượt là trung điểm của và , điểm thuộc sao cho . Biết rằng . Khi đó, giá trị của bằng? ➢ Điền đáp án: .
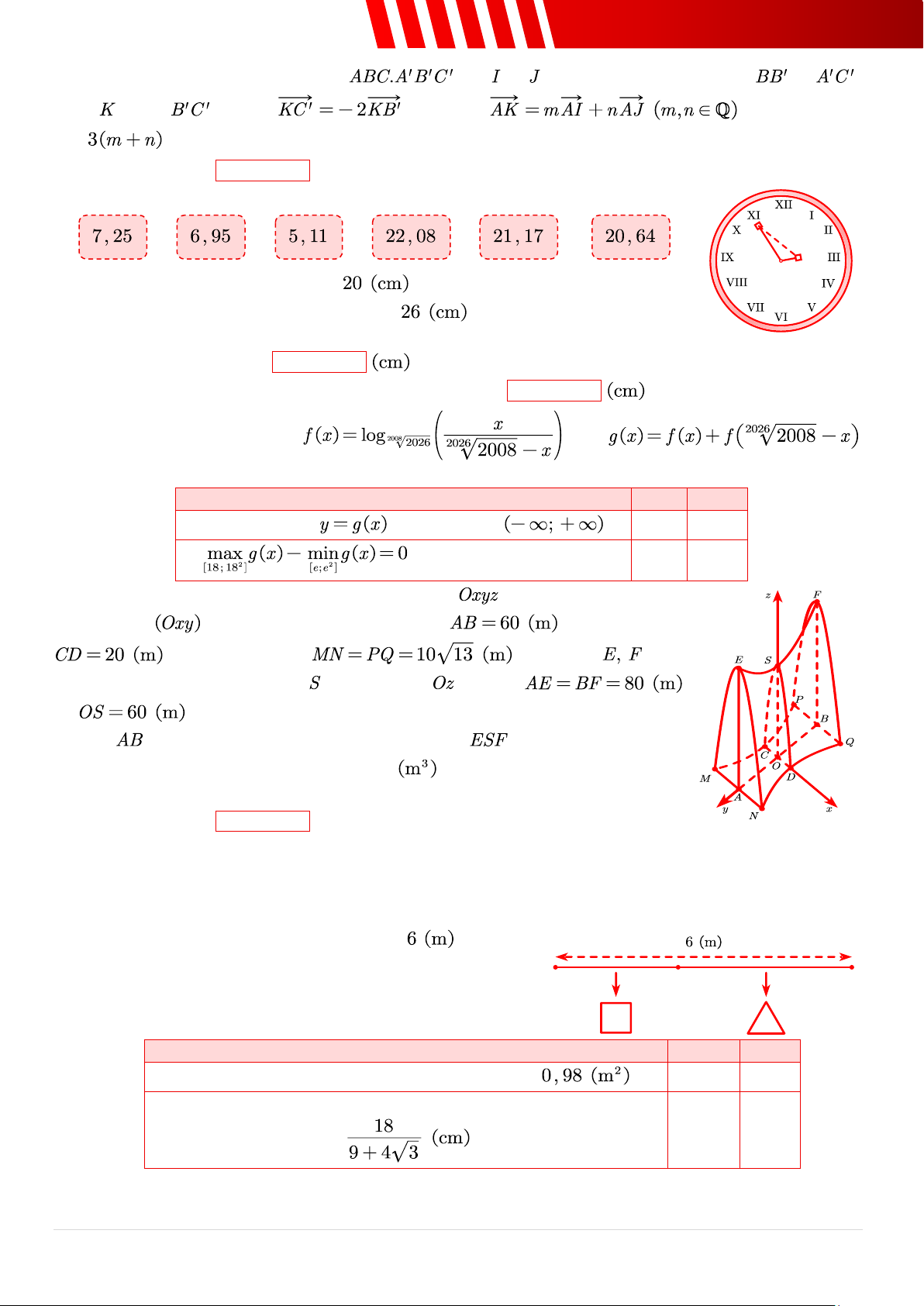
Câu 36. [Mức 1] Kéo và thả các phương án thích hợp vào chỗ trống.
Một chiếc đồng hồ có kim phút dài
. Vào lúc 3 giờ kém 10, hai đầu của
hai kim đang cách nhau một khoảng bằng
. (Làm tròn các kết quả đến hàng phần trăm)
a. Độ dài kim giờ bằng .
b. Vào lúc 3 giờ, khoảng cách giữa hai đầu kim bằng .
Câu 37. [Mức 3] Cho hàm số . Đặt
, xét tính đúng/sai của các mệnh đề sau: Mệnh đề Sai Đúng
b. Đồ thị hàm số đơn điệu trên . ○ ○ c. . ○ ○
Câu 38. [Mức 3] Một toà nhà trong không gian có mặt sàn nằm trong mặt phẳng
là hình hyperbol với độ dài , chỗ hẹp nhất và chỗ rộng nhất . Hai điểm nằm
trên đỉnh toà nhà và một điểm nằm trên tia sao cho và
. Biết rằng thiết diện của toà nhà khi cắt bởi mặt phẳng vuông góc với
luôn là một hình parabol và đường cong cũng là một phần của
parabol, thể tích toà nhà bằng bao nhiêu
? (Kết quả được làm tròn đến hàng đơn vị) ➢ Điền đáp án: .
Câu 39. [Mức 3] Thực hiện 30 nhát cắt lên một tờ giấy A4. Biết rằng mỗi nhát cắt theo hướng đường
thẳng, trong đó không có hai nhát cắt nào song song và không có ba nhát cắt nào đi qua cùng một vị
trí. Sau khi cắt, ta thu được tối đa bao nhiêu mảnh giấy? A. 479. B. 529. C. 497. D. 466.
Câu 40. [Mức 3] Một sợi dây có chiều dài được chia
thành hai phần. Phần thứ nhất được uốn thành hình tam
giác, phần thứ hai được uống thành hình vuông. Làm tròn
các kết quả (nếu cần) đến hàng phần trăm. Xét tính đúng/sai của các mệnh đề sau: Mệnh đề Đúng Sai
a. Tổng diện tích nhỏ nhất của hai hình là xấp sỉ . ○ ○
b. Khi tổng diện tích hai hình đạt nhỏ nhất th độ dài mỗi cạnh ○ ○ của hình tam giác bằng .
-=-=-=-=-=-=-=-HẾT-=-=-=-=-=-=-=-




