Áp dụng thuật giải heuristic cho bài toán tô màu tối ưu trên đồ thị | Trường đại học Điện Lực

TRƯỜNG ĐẠI HỌC ĐIỆN LỰC
KHOA CÔNG NGHỆ THÔNG TIN
BÁO CÁO CHUYÊN ĐỀ HỌC PHẦN
NHẬP MÔN TRÍ TUỆ NHÂN TẠO ĐỀ TI:
Áp dụng thuật giải heuristic cho bài toán tô màu tối ưu trên đồ thị
Sinh viên thực hiện : PHẠM VĂN TUẤN NGUYỄN HONG HIỆU NGUYỄN DỨC THUẬN
Giảng viên hướng dẫn : VŨ VĂN ĐỊNH Ngành
: CÔNG NGHỆ THÔNG TIN Chuyên ngành
: HỆ THỐNG THƯƠNG MẠI ĐIỆN TỬ Lớp : D14HTTMDT1 Khóa : 2019
Hà Nội, tháng 10 năm 2021
Phiếu chấm điểm STT Họ tên sinh viên
Nội dung thực hiện Điểm Chữ ký 1 Phạm Văn Tuấn Làm báo cáo Làm chương trình 2 Nguyễn Hoàng Hiệu Làm báo cáo Làm chương trình 3 Nguyễn Đức Thuận Làm báo cáo Làm chương trình
Họ tên giảng viên Chữ ký Ghi chú M C L Ụ Ụ C I.
GIỚI THIỆU BI TOÁN..................................................................................................................4 1.
Tổng quan về heuristic..................................................................................................................4
1.1. Heuristic và các cách biểu diễn đồ thị.......................................................................................4
1.2. Các bài toán điển hình................................................................................................................6 2.
Bài toán tô mầu đồ thị...................................................................................................................6
2.1. Bài toán tô mầu cạnh..................................................................................................................6
2.2. Bài toán tô mầu đỉnh..................................................................................................................6
2.3. Các khái niệm liên quan.............................................................................................................7
2.4. Ứng dụng......................................................................................................................................8 II.
GIẢI THUẬT.................................................................................................................................9 1.
Bài toán tô mầu đỉnh.....................................................................................................................9 1.1.
Các định nghĩa sử dụng:........................................................................................................9 1.2.
Thuật toán............................................................................................................................10 1.3.
Ví dụ......................................................................................................................................12 2.
Bài toán tô mầu cạnh...................................................................................................................17 2.1.
Giải thuật..............................................................................................................................17 2.3.
Độ phức tạp:.........................................................................................................................23 III.
CI ĐẶT THUẬT TOÁN...........................................................................................................24
1. Bài toán tô mầu đỉnh.......................................................................................................................24
2. Bài toán tô mầu cạnh.......................................................................................................................30 2.1. Đọ c dữ li ệ u t ừ fle
..................................................................................................................30 2.2. Dữ li ệ u vào t
ừ bàn phím........................................................................................................40 3.
Mã nguồn......................................................................................................................................51 IV.
TI LIỆU THAM KHẢO...........................................................................................................52
PHỤ LỤC 1: DANH MỤC CÁC HÌNH ẢNH TRONG TI LIỆU...................................................53
PHỤ LỤC 2: PHÂN CHIA CÔNG VIỆC..............................................................................................53
I. GIỚI THIỆU BI TOÁN
1. Thuật giải heuristic
1.1.khái niệm heuristic
Là mở rộng khái niệm thuật toán.
o Thuờng tìm lời giải tốt nhưng không tốt nhất.
o Nhanh chóng tìm ra kết quả hơn so với giải thuật tối ưu, vì vậy chi phí thấp hơn.
o Thuờng thể hiện khá tự nhiên, gần gũi với cách suy nghĩ và hành động của con nguời.
Các nguyên lý của thuật giải heuristic Vét cạ n thông minh Nguyên lý thứ tự Nguyên lý tham lam Hàm heuristic Kyỹ thuậ t heuristic: Theo T đi ừ n tiêếng ể
Anh Oxford: “Heuristics là nghệ thuật tm kiêếm chân lý. Nói riêng,
heuristics là đặ c trư ng củ a quá trình họ c nhờ đó các họ c sinh họ c đ ượ c cách t ự tm ra cách gi i
ả thích các hiệ n tượ ng tự nhiên”. T “Heuristics” có cùng m ừ t gôếc tiêếng Hy L ộ
ạ p như từ Eureka. Feigenbaum Feldman đã đư a ra đị nh nghĩa :
“Heuristics (Các quy tắếc heuristics, các ph
ng pháp heuristics) là các quy t ươ ắếc, phươ ng pháp, chiêến l c, m ượ o gi ẹ i hay ả ph
ng cách nào đó nhắằm làm gi ươ m khôếi l ả ượ ng tm kiêếm l ờ i gi i
ả trong không gian bài tóan c c l ự ớ n”.
2. Bài toán tô mầu đồ thị
Tô màu đồ thị và sự tổng quát của nó là công cụ hữu dụng trong việc mô hình hóa rất nhiều bài
toán khác nhau trong vấn đề xếp lịch, xây dựng chương trình và vấn đề phân công công việc. Bài
toán tô màu đồ thị bao gồm nhiều loại: tô màu đỉnh đồ thị (vertex graph coloring) , tô màu cạnh
đồ thị (edge graph coloring) ...
2.1. Bài toán tô mầu cạnh Bài toán
Cho G=(V,E) là đơn đồ thị vô hướng ( G không là đồ thị khuyên) , hãy tìm cách gán (tô màu) cho
mỗi cạnh của đồ thị một màu sao cho hai cạnh có cùng chung 1 đỉnh không bị tô bởi cùng một
màu. Một phép gán màu cho các cạnh như vậy gọi là một phép tô màu cạnh đồ thị. Nói cách
khác, phép tô cạnh đồ thị bởi k màu nói trên có thể được hiểu là một phân hoạch của tập cạnh E
của G thành k tập con (tương ứng với k màu) sao cho mỗi tập con ứng với một màu i nhất định.
Bài toán đặt ra là tìm cách tô màu nào sử dụng số màu ít nhất có thể. Ví dụ
Đồ thị trong hình trên có thể tô bởi 4 màu. Đồ thị G gọi là tô được bởi k màu-cạnh nếu G có một
phép tô k màu-cạnh phù hợp.Thông thường hầu hết các đồ thị không là đồ thị khuyên đều tô
được.Và nếu G có tính chất như vậy thì G cũng có thể tô bởi l màu với l>k.
2.2. Bài toán tô mầu đỉnh
Một phép tô mầu sử dụng nhiều nhất k mầu gọi là một phép tô k mầu. Số lượng mầu nhỏ nhất
cần để tô các đỉnh của đồ thị G gọi là sắc số đỉnh của đồ thị G, sao cho không có hai đỉnh kề
nhau nào được tô cùng mầu.
Một đồ thị có thể tô được bằng k mầu, trong đó mỗi một tập các đỉnh cùng mầu gọi là một lớp mầu.
Một đồ thị có thể được tô bằng k mầu nghĩa là có có k tập độc lập trong đồ thị
2.3. Các nguyên lý của thuật giải heuristic 1.Vét cạ n thông minh
H n chêế vùng không gian tm kiêếm và ạ
có sự đị nh hướ ng để nhanh chóng tm đêến mụ c tiêu. T o miêằn D’ ạ râết nh so v ỏ ớ i D Vét c n trên D’ ạ
2.Nguyên lý tham lam (Greedy): Lâếy tiêu chu n
ẩ tôếi ư u (trên phạ m vi toàn cụ c) c
ủ a bài toán để làm tiêu chu n
ẩ chọn lự a hành động cho phạm vi cụ c bộ củ a từ ng bướ c. a)Thu t gi ậ i GTS1: ả (Greedy-Traveling Saleman) Xây d ng m ự t l ộ ch trình du l ị ch có chi phí Cost t ị
ôếi thiể u cho bài toán trong tr ng h ườ p ph ợ i qua n thành phôế v ả i ma tr ớ
nậ chi phí C và bắết đâằu tạ i mộ t đỉ nh U nào đó. Thu t gi ậ ả i : B ước 1 : {Kh i đâằu} ở Đ t ặTour := {}; Cost := 0; V := U; {V là đ nh hi ỉ n t ệ i đang làm vi ạ ệ c} B
ước 2 : {Thắm tâết c cá ả c thành phôế} For k := 1 To n Do qua bước 3; B ước 3 : {Ch n cung k ọ êế tiêếp} Đ t (V
ặ , W) là cung có chi phí nh nhâết tnh t ỏ V
ừ đêến các đỉ nh W chư a dùng: Tour := Tour + {(V,W)}; Cost := Cost + Cost(V,W); Nhãn W được sử dụ ng Đ t V := ặ W; {Gán đ xét b ể c kêế tiêếp} ướ B
ước 4 : {Chuyêến đi hoàn thành} Đ t T ặ our := Tour + {(V,U)}; Cost := Cost + Cost(V,U); Dừng. U = A Tour = {} Cost = 0 V = A W
∈ {B, C, D, E}{Các đ nh có th ỉ đêến ể từ A}
→ W = B{Vì qua B có giá thành bé nhâết} Tour = {(A, B)} Cost = 1 V = B W ∈ {C, D, E}→ W = EA Tour = {(A, B),(B, E)} Cost = 1 + 3 = 4 V = E W ∈ {C, D} → W = C b.Thu t gi ậ ải GTS2: T o r ạ a l ch trình t ị
p thành phôế xuâết phát riêng b ừ
iệt. Tìm chu trình của ngườ i bán
hàng qua n thành phôế (1

c t ượ o ra và ạ
ch chu trình tôết nhâết tr ỉ ong p chu trình đ c gi ượ l
ữ ạ i mà thôi (thuậ t giả i này đòi hỏ i phả i nhậ p n, p và C) Thu t gi ậ ả i : B ước 1 : {Kh i đâằu} ở
k := 0; {Đêếm sôế thành phôế đi qua}
Tour = {(A, B), (B, E), (E, C)}
Bước 2: {Bắết đâằu chu trình 2.4. Ứng dụng m i} ớ Chuy n
ể qua bướ c 3 khi k

ng c l ượ ạ i dừ ng. B ước 3 : {T o chu trình m ạ ớ i} k := k + 1; Call (GTS1(Vk)) : Tr v ả êằ mộ t chu trình T(k) ng v ứ i chi phí C(k). ớ B ước 4 : {C p nh ậ ật chu trình tôết nhâết} Nêếu C(k)< Cost thì Best := T(k); Cost := C(k); B
ước 2 : {Bắết đâằu chu trình m i} ớ Chuy n
ể qua bướ c 3 khi k

ng c l ượ ạ i dừ ng. B ước 3 : {T o chu trình m ạ ớ i} k := k + 1; Call (GTS1(Vk)) : Tr v ả êằ mộ t chu trình T(k) ng v ứ i chi phí C(k). ớ B ước 4 : {C p nh ậ ật chu trình tôết nhâết} Nêếu C(k)< Cost thì Best := T(k); Cost := C(k); 2.Bài toán dồ thị
- Bài toán lập lịch:
Ở đây nhóm xin đưa ra một ví dụ cụ thể là bài toán lập lịch thi: hãy lập lịch thi trong một trường
đại học sao cho không có sinh viên nào thi hai môn cùng một lúc Giải pháp:
Biểu diễn bằng đồ thị với:
Mỗi môn học là một đỉnh
Nếu hai môn học nào được dự thi bởi cùng 1 sinh viên thì sẽ nối bằng 1 cạnh
Các lập lịch sẽ tương ứng với bài toán tô mầu của đồ thị này: số các mầu được tô là số các
đợt thi, các đỉnh có cùng mầu sẽ thi cùng 1 đợt. Ví dụ:
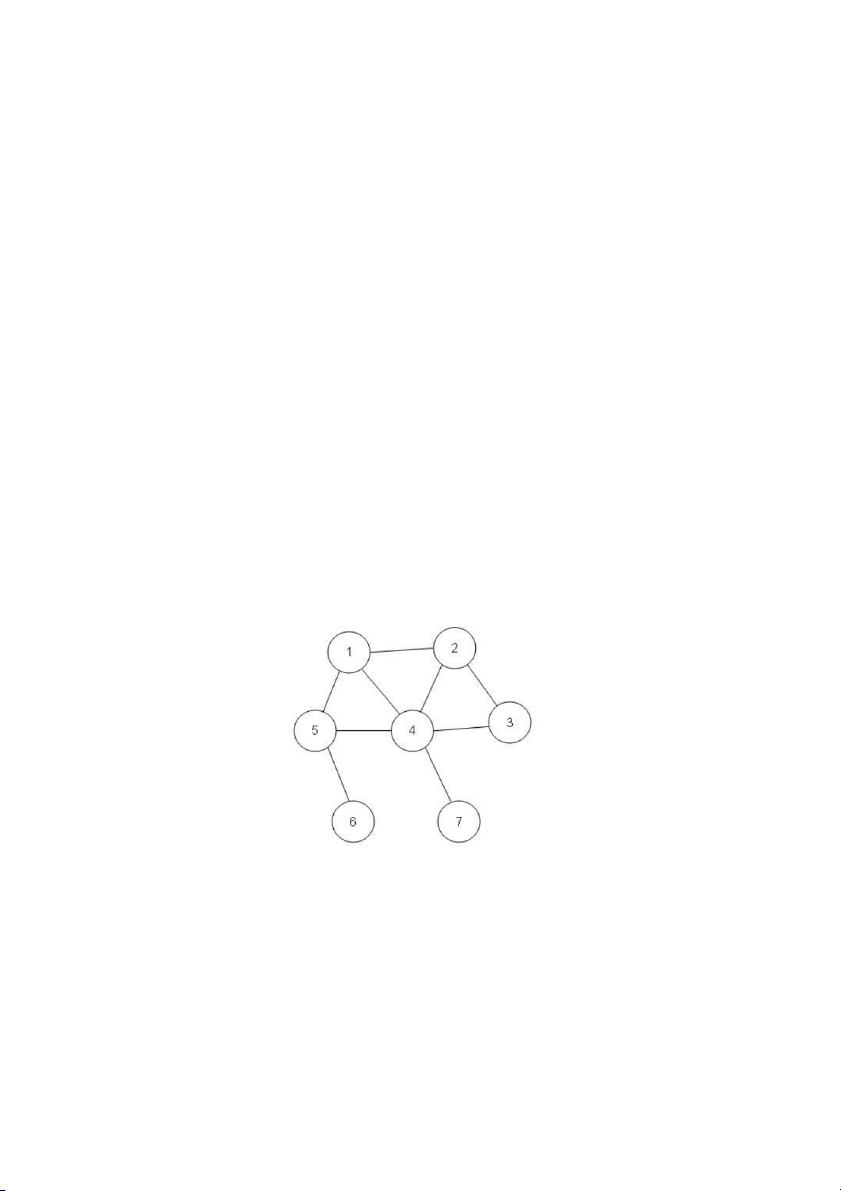
Có 7 môn thi với thông tin như sau:
Môn 1: có các sinh viên A, B, C và D thi
Môn 2: có các sinh viên A, E, F, G và H thi
Môn 3: có các sinh viên B, E, I, J và K thi
Môn 4: có các sinh viên B, F, L và M thi
Môn 5: có các sinh viên G, L, N và O thi
Môn 6: có các sinh viên J, M, N và P thi
Môn 7: có các sinh viên D, H, K, O và P thi
Hãy xếp lịch thi thành các đợt sao cho các sinh viên đều có thể dự thi tuần tự các môn mình đăng ký
Hình 02: Đồ thị G của bài toán lập lịch trên -
Bài toán phân phối các thanh ghi chỉ số (register allocation)
Trong lập trình các thanh ghi thường được dung để lưu trữ giá trị các biến tạm thời. Bài toán yêu
cầu tìm số thanh ghi ít nhất cần sử dụng trong một chương trình Giải pháp:
Biểu diễn bằng đồ thị với:
Mỗi biến tương ứng là 1 đỉnh
Hai đỉnh được nối với nhau nếu hai biến cùng được ghi xuống tại một thời điểm
Số thanh ghi ít nhất cần sử dụng sẽ là số mầu của đồ thị trên II. GIẢI THUẬT
1. Bài toán tô mầu đỉnh 1.1.
Các định nghĩa sử dụng:
Để mô tả giải thuật nhóm bắt đầu với việc diễn giải các thuật ngữ, định nghĩa mà giải thuật đề cập tới. - ⌊x ⌋
: biểu thị các chức năng sàn tức là số nguyên lớn nhất không lớn hơn x - ⌈ ⌉
x : biểu thị chức năng trần nghĩa là số nguyên bé nhất là không bé hơn x -
Một đồ thị đơn giản G với đỉnh n
bao gồm một tập các đỉnh V,với | V |= n, và một bộ các
cạnh E, sao cho mỗi cạnh là một cặp không có thứ tự của các đỉnh khác nhau. Lưu ý rằng
định nghĩa của G rõ ràng cấm các vòng lặp(cạnh nối một đỉnh với chính nó) và các cạnh
đa (nhiều cạnh tham gia một cặp đỉnh), khi thiết lập E cũng phải được giới hạn. Chúng tôi có
thể gán nhãn các đỉnh của G với 1 số nguyên, 2, ..., n. -
Nếu các cặp không có thứ tự của các đỉnh {u, v} là một cạnh trong G, chúng ta nói đó u là
một lân cận của (hoặc v u kề với v) và viết
uv ∈ E. Lân cận đối xứng rõ ràng là một mối quan hệ: uv
∈ E nếu và chỉ nếu vu ∈ E . -
Bậc của một đỉnh v, ký hiệu là d (v), là số lân cận của v. Số bậc tối đa của tất cả các đỉnh
của G được ký hiệu là Δ. -
Các ma trận kề của G là một ma trận n ×
n với các mục trong hàng u và cột v bằng 1 nếu
uv ∈ E và bằng 0 nếu ngược lại. -
Cho đồ thị G và H, tích đề các G × H được định nghĩa là các đồ thị mà tập các đỉnh là V
(G) × V (H)với một cạnh đang kết nối đỉnh (u v 1, 1) với đỉnh (u v 2,
2) nếu và chỉ nếu hoặc u = 1 u và 2 {v v 1,
2} là một cạnh trong H hoặc v = 1 v 2 và {u 1, u 2} là một cạnh trong G. -
Đồ thị đầy đủ với m đỉnh được ký hiệu là K m. -
Tập độc lập S của đồ thị G là một tập các đỉnh như vậy mà không chứa cặp không có thứ tự
của các đỉnh trong S là một cạnh. Với một bộ độc lập S củaG và một đỉnh bên v
ngoài S, chúng ta nói v là có thể thêm vào nếu đặt S∪
{v} vẫn là một tập độc lập của G. Ký
hiệu ρ (S) là số đỉnh có thể thêm vào của một tập độc lập S của G. Một tập độc lập tối đa
không có đỉnh có thể thêm vào. Một tập độc lập tối đa là một tập độc lập với số lượng các
đỉnh lớn nhất. Lưu ý rằng một tập độc lập tối đa luôn luôn là tối đa, nhưng không nhất thiết phải ngược lại. -
Cho một tập m màu {1, 2, ..., một tập m},
m-màu của các đỉnh của đồ thị G là sự phân một
màu duy nhất cho mỗi đỉnh của G sao cho không có hai đỉnh kề nhau có cùng màu. Số màu
χ(G) của đồ thị G là giá trị nhỏ nhất của m mà tồn tại tương ứng một một m-màu của các đỉnh củaG. -
Thuật toán là một phương pháp giải quyết vấn đề thích hợp để thực hiện như một chương
trình máy tính. Trong khi thiết kế thuật toán chúng ta thường phải đối mặt với một số phương
pháp tiếp cận khác nhau. -
Thuật toán thời gian
- đa thức A có số lượng các bước tính toán luôn luôn bị chặn bởi một
hàm đa thức của các kích thước của đầu vào. Do đó, một thuật toán thời gian đa thức là một
vấn đề thực sự hữu ích trong thực tế. Các lớp của tất cả các vấn đề như vậy có thuật toán thời
gian đa thức được ký hiệu là P. Đối với một số vấn đề, không có thuật toán thời gian đa thức
được biết đến, nhưng những vấn đề này có thuật toán thời gian đa thức bất định: hãy thử tất
cả các ứng viên cho các giải pháp cùng một lúc và cho mỗi ứng viên nhất định, xác minh
xem đó là một giải pháp chính xác trong thời gian đa thức. 1.2. Thuật toán
Nhóm bắt đầu với tích Đề Các cho phép chúng ta chuyển đổi các vấn đề của việc tìm kiếm một tập m-màu của các đỉnh của n
một đồ thị tương đương như việc tìm kiếm một bộ độc lập kích
thước n trong tích đề các G × Km . - Tích Đề Các
Một đơn đồ thị G với đỉnh là n
tô được bằng m mầu khi và chỉ khi tích đề các G × K m có một tập độc lập kích thước n. Chứng minh.
Giả sử có một tập m-màu của các đỉnh của G. Xác định một tập con S của các đỉnh của tích đề
các G × K m như sau. Một đỉnh (u, v) của G × Km thuộc S nếu và chỉ nếu đỉnh u của G được giao
màu v đối với tập m màu thích hợp. Vì mỗi đỉnh của G được giao một màu duy nhất, | S | = n.
Bây giờ chúng ta sẽ chỉ ra rằng S là một tập độc lập. Cho (u 1, v 1) và (u
2, v 2) thuộc S, giả sử có
một cạnh {(u 1, v 1), (u 2, v 2)}
trong G × K m. Do đó, theo định nghĩa của tích đề các, có hai khả năng: u = 1 u và 2 {v 1, v
2} là một cạnh trong K m. Nhưng u = 1 u với 2 v = 1 v2, từ mỗi đỉnh
trong G đượcgiao một màu duy nhất. Nhưng sau đó {v
1, v1} không thể là một cạnh
trong K m khi K m là một đơn đồ thị (mâu thuẫn). {U u 1,
2} là một cạnh trong G, và v = 1 v Nhưng 2.
điều này vi phạm các định nghĩa của
một tập m màu của G từ đỉnh kề phải được giao các màu khác nhau (mâu thuẫn).
Vì vậy không thể có một cạnh giữa hai đỉnh trong S và S phải là một tập độc lập.
Ngược lại, giả sử có một tập độc lập S kích thước n trong tích đề các G × K m. Chúng ta sẽ chỉ ra
rằng G có m màu riêng biệt. Nếu m lớn hơn hoặc bằng thì n
G có thể được m màu một cách tầm
thường , do đó giả sử m nhỏ hơn n. Sự phân chia các đỉnh của S vào nhiều nhất là m lớp tương đương C 1, C C ,..., 2
m, nơi một đỉnh (u, v) trong S thuộc về lớp tương đương C i khi và chỉ khi =
v v i. Rõ ràng , điều này đưa ra một định nghĩa phân chia tốt của các đỉnh trong S. Bây giờ
các đỉnh của G vào nhiều nhất là m lớp tương đương C '1, C' 2, ..., 'm, C nơi một đỉnh u của G thuộc
lớp tương đương C 'i nếu và chỉ nếu (u, v i) thuộc về lớp tương đương C i. Để chứng tỏ điều đó ta
đưa ra một định nghĩa phân chia tốt của các đỉnh các đỉnh của G tuân theo:
Cho một đỉnh u của G, nếu thuộc u
về cả hai C 'i và C' j thì (u, v i) thuộcC i và (u, v j) C thuộc j. Khi K mđầy {v đủ,
i, v k} là một cạnh trong K m, do đó, {(u, v i), (u, v j)} là một
cạnh trong tích đề các G ×K m. Điều này mâu thuẫn với thực tế là S là một tập độc lập .Vì
vậy, các bộ C '1, C' 2 ,..., C 'm là cặp phân chia.
Danh sách các phần tử của S sắp xếp như sau: o (U 1, 1 1 1 v 1), (u 2, v 1), ..., (u i (1), 1) v o (U 2 2, 2 1, v 2), (u 2 v 2), ..., (u i (2), v 2) o ... o (U m v m 1, m), (u 2, v m), (u ..., m i (m), m v)
Nếu một số u i j = l trong u k
danh sách, thì, khi K m đầy đủ, {v i, v l} là một cạnh trong K i k
m, do đó, {(u j, v i), (u l , v l)} là một cạnh trong tích đề các G × K m. Điều này mâu
thuẫn với thực tế S là một tập độc lập. Vì vậy, tất cả các u i j xuất hiện trong danh sách là
riêng biệt và từ | S | = ,
n có n u i j i phân biệt mọi đỉnh của G được chứa trong một số
lớp tương đương 'C Do đó,..
Chỉ định màu i đến đỉnh của u G nếu thuộc u
về các lớp tương đương C i' . Điều này tạo ra một
tập m-màu của các đỉnh của G.
Bây giờ chúng ta định nghĩa hai thủ tục để thực hiện với tập độc lập trong tích đề các G × K m. - Thủ tục 1
Với một tập độc lập S của tích đề các G×Km nếu S không có đỉnh có thể thêm, đầu ra S. Ngược
lại, cho mỗi đỉnh có thể thêm (u, v) của S, tìm số ρ (S∪ {(u, v)}) của đỉnh có thể thêm của tập độc
lập S ∪ {(u, v)}. Cho (u,v ) max biểu thị một đỉnh có thể thêm sao cho ρ (S ∪ {(u, v) max}) là lớn
nhất và chứa tập độc lập S ∪ {(u,
v) max}. Lặp lại cho đến khi tập độc lập không có đỉnh có thể thêm vào. - Thủ tục 2
Cho một tập độc lập tối đa S của tích đề các G × K m, nếu không có đỉnh (u 1, v 1) bên ngoài S sao cho (u
1, v 1) có đúng một lân cận (u
2, v 2 ) trong S, đầu ra S.Ngược lại, tìm thấy một đỉnh (u u , v ), (u , v 1, v 1) ngoài S sao cho (u 1,
v 1) có đúng một lân cận (u 2, v 2) trong S Xác 1. định S( ) 1 1 2 2 bằng cách thêm (u , (u v (u v 1 v1) vào S và bỏ (u
2, v 2) từ S. Thực hiện thủ tục 3.1 trên S 1, 1), 2, 2) và đầu
ra các tập độc lập kết quả. Giải thuật
Với đầu vào là một đơn đồ thị G với đỉnh, n
tìm kiếm một tập m-màu của các đỉnh của G. Để {u u 1, ..., 2,
u n} biểu thị các đỉnh của G và để {v1, v 2, ..., v biểu m}
thị các đỉnh của K m.. Chúng ta
tạo các tập độc lập tối đa trong tích đề các G×Km. Ở mỗi giai đoạn, nếu tập độc lập thu được có
kích thước n nhỏ nhất, thì đi đến phần III.
Phần I. Đối với i = 1, 2, ..., n và j = 1, 2, ..., n lần lượt o
Khởi tạo tập độc lập S i, j = {(u i, v j)}. o
Thực hiện thủ tục 3.1 trên S i, j. o
Đối với r = 1, 2, ..., n thực hiện thủ tục 3.2 lặp lại r lần. o
Kết quả là một tập độc lập tối đa S i, j.
Phần II. Với mỗi cặp tập độc lập tối đa S i, j, S k, l tìm thấy trong phần I o
Khởi tạo S đặt độc lập i, j, k, l = S i, j ∩ S k, l. o
Thực hiện thủ tục 3,1 trên S i, j, k, l. o
Đối với r = 1, 2, ..., n thực hiện thủ tục 3,2 lần r lặp đi lặp lại. o
Kết quả là một tập độc lập tối đa S i, j, k, l.
Phần III. Nếu một tập độc lập S với kích thước n đã được tìm thấy tại bất kỳ giai
đoạn của phần I hoặc phần II, đầu ra S như là một tập m-màu của các đỉnh
của G theo Bổ đề Đề các. Ngược lại, kết luận thuật toán không thể tìm thấy bất kỳ
tương ứng m-màu của các đỉnh của G. 1.3. Ví dụ
Chúng ta thể hiện các bước của thuật toán bằng một ví dụ nhỏ. Đồ thị đầu vào được thể hiện
dưới đây trong hình 3.1 với =
n 4 đỉnh có nhãn V = {1, 2, 3, 4}. Các thuật toán tìm kiếm cho một
tương ứng 3- màu của các đỉnh bằng cách sử dụng các thiết lập của các màu {1, 2, 3} đại diện
bởi màu xanh lá cây, đỏ và màu xanh tương ứng.
Hình 03.Các đồ thị đầu vào G với 3- màu tương ứng của các đỉnh của nó được tìm thấy bởi thuật toán
Thuật toán đầu tiên xây dựng tích đề các G × K 3 hiển thị dưới đây trong các con số 3,2 với 12
đỉnh {(1,1), (1,2), (1,3), (2,1), (2,2), (2,3), (3,1), (3,2), (3,3), (4,1), (4,2), (4,3)}. Chúng ta tách
các đỉnh {1, 2, 3} của thành phần thứ hai K 3 như các màu sắc xanh, đỏ và màu xanh tương ứng.
Hình 04: tích đề các G×K với một tập độc lập với kích thước 4 được tìm thấy bằng thuật toán 3
Thuật toán bây giờ tìm kiếm một tập độc lập với kích thước 4 trong tích đề các G × K .3 Phần I
cho i = 1 và j = 1 khởi tạo tập độc lập như S = {(1, 1)}. 1,1
Bây giờ chúng ta thực hiện các thủ tục 1. Sau đây là các kết quả dưới dạng bảng:
Tập độc lập S = {(1, 1)}. Kích thước: 1. 1,1
Đỉnh có thể thêm (u, Đỉnh có thể thêm ρ S ∪ {(u, v)}) v) S của (1,1 1,1 của S 1,1 ∪{(u, v)} (2, 2) (3, 3), (4, 2), (4, 3) 3 (3, 2), (4, (2, 3) 3 2), (4, 3) (3, 2) (2, 3), (4, 3) 2 (3, 3) (2, 2), (4, 2) 2
Trong đó thuật toán tô màu theo dãy lại được ứng dụng theo nhiều cách khác nhau.
Ý tưởng của thuật toán này xoay quanh việc sắp xếp thứ tự các cạnh của đồ thị theo một thứ
tự nhất định. Đánh trọng số cho các màu được dung để tô. Sau đó duyệt các cạnh theo thứ tự nêu
trên. Trong quá trình duyệt sẽ tô màu cho cạnh bằng màu có trọng số nhỏ nhất mà chưa được sử
dụng để tô cho các cạnh kề. Đây là một vận dụng của sử dụng thuật toán tham lam. Kết quả của
bài toán khác nhau nếu chúng ta chọn được thứ tự của các cạnh khác nhau. Do đó các cải tiến
hay các thuật toán khác nhau dựa trên thuật toán này hầu hết đều là cải tiến việc lựa chọn thứ tự cho các cạnh ban đầu.
Trong chương trình ứng dụng của nhóm, giải thuật đưa ra ở mức minh hoạ một cách tô màu
cạnh của đồ thị vô hướng. Trong đó, việc xếp thứ tự của đỉnh được đồng nghĩa với thứ tự các
đỉnh được sắp xếp của đầu vào. Do đó thuật toán được thu gọn như sau :
Thứ tự các cạnh được sắp xếp trong quá trình nhập dữ liệu về đồ thị. Các cạnh được đánh số theo thứ tự E , E 1 , ...,E 2 n.
Tìm bậc lớn nhất của đồ thị (Δ)
Chuẩn bị (Δ+1) màu để tô
Bước i: Tô màu cạnh Ei bởi màu có chỉ số nhỏ nhất trong số các màu chưa được sử dụng
để tô màu cạnh kề của nó. Trong đó ở bước i tùy theo cách cài đặt sẽ có những cách đánh màu khác nhau.
Với thuật toán trên chúng ta có thể tìm được 1 cách tô màu cho các cạnh của đồ thị với số
màu không quá Δ+1 màu ( vấn đề này sẽ thấy rõ hơn khi đi sâu vào phần cài dặt). Vậy đó đã là
số màu nhỏ nhất hay chưa. Theo định lý Vizing chúng ta phát biểu ở trên, ta có Δ(G)≤ χ′(G) ≤
Δ(G) + 1. Vậy sắc số cạnh chỉ có thể nằm ở 1 trong hai giá trị là Δ(G) và Δ(G) + 1. Với việc
chọn số màu lớn nhất có thể tô là Δ(G)+1, thuật toán đã kẹp được cận trên của sắc số cạnh. Với
việc lựa chọn màu có chỉ số nhỏ nhất chưa được sử dụng để tô các cạnh kề cho một cạnh, số màu
được sử dụng là số màu nhỏ nhất. 2.2. Ví dụ Ta có đồ thị sau:
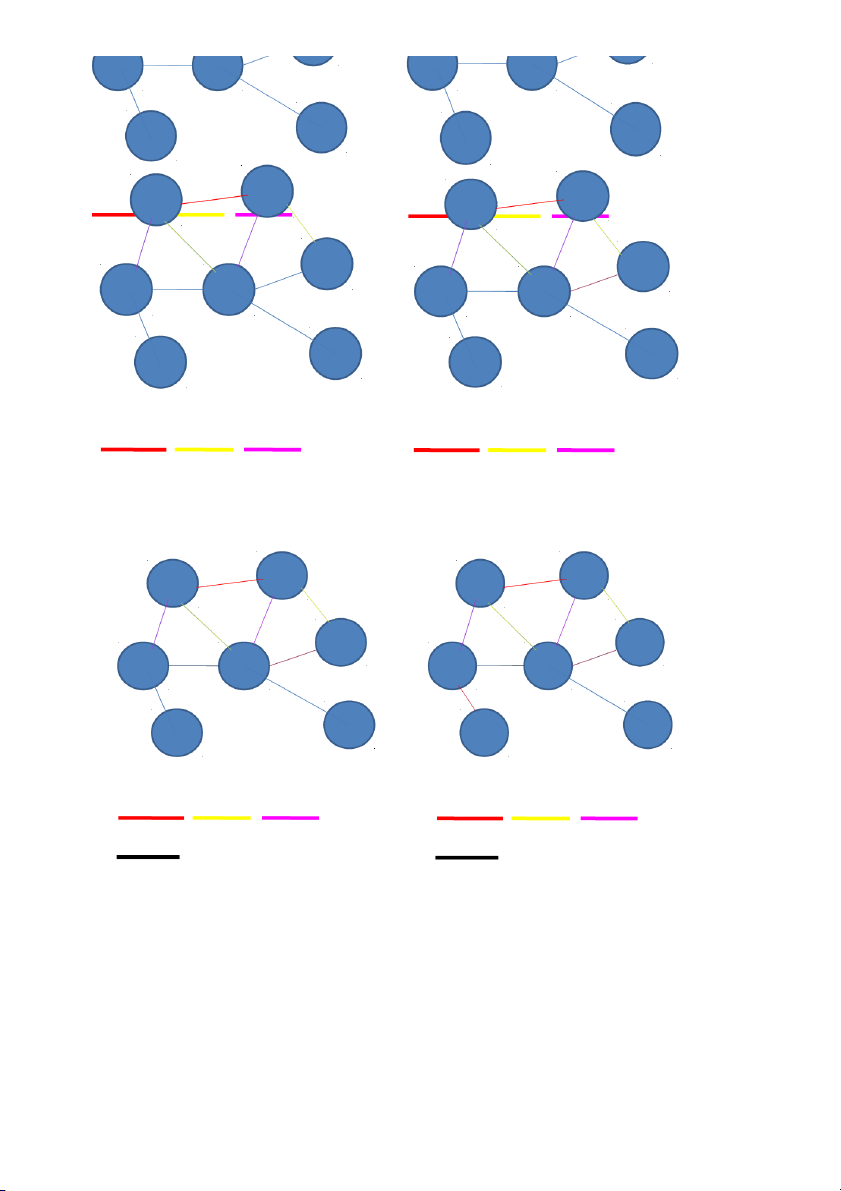
Ta sắp xếp các cạnh theo thứ tự như sau: Bước 1
: tô màu cạnh thứ 1
Cạnh này tô màu đỏ trước tiên Bước 2 : tô màu cạnh 2.
Cạnh 2 kề với cạnh 1 (tô màu đỏ) do đó cạnh 2 sẽ tô màu xanh lá cây Bước 3: tô màu cạnh 3
Cạnh 3 kề với cạnh 1 (tô màu đỏ), cạnh 2 (tô màu xanh lá cây) do đó cạnh 3 phải tô màu xanh da trời Bước 4: tô màu cạnh 4
Cạnh 4 kề với cạnh 1 (tô màu đỏ) nên sẽ tô màu xanh lá cây Bước 5: tô màu cạnh 5
Cạnh 5 kề với cạnh 3 (tô màu xanh da trời), cạnh 4 (tô màu xanh lá cây) nên cạnh 5 tô màu đỏ Bước 6: tô màu cạnh 6
Cạnh 6 kề với cạnh 1,5 (tô màu đỏ), cạnh 3 (tô màu xanh da trời), cạnh 4 (tô màu xanh lá cây)
nên cạnh 6 phải tô màu tím Bước 7: tô màu cạnh 7
Cạnh 7 kề với cạnh 2 (tô màu xanh lá cây), cạnh 3 (tô màu xanh da trời), cạnh 5 (tô màu đỏ),
cạnh 6 (tô màu tím) do đó cạnh này tô màu vàng
Bước 8: tô màu cho cạnh thứ 8
Cạnh 8 kề với cạnh 5 (tô màu đỏ), cạnh 7 (tô màu vàng) nên sẽ tô màu xanh lá cây Bước 9: tô màu cạnh 9
Cạnh 9 kề với cạnh 4 (tô màu xanh lá cây), cạnh 5 (tô màu đỏ) nên sẽ tô màu xanh da trời
Kết luận: Đồ thị này có thể tô được với 5 màu. Mặt khác Δ = 5 nên đây chính là số màu nhỏ nhất
có thể dùng để tô cạnh của đồ thị trong trường hợp này. 2.3. Độ phức tạp:
Độ phức tạp của giải thuật là: O (E+V ) 2
III.CI ĐẶT THUẬT TOÁN
Trong phần cài đặt này bài toán tô mầu cạnh có 2 cách nhập dữ liệu (bằng file và nhập từ bàn
phím), bài toán tô mầu đỉnh cho phép nhập dữ liệu từ file.
Menu chương trình hiển thị các lựa chọn nhập dữ liệu:
1. Bài toán tô mầu đỉnh - Cài đặt:
Đọc dữ liệu từ file: graph.txt
Kết quả sẽ trả ra ở file: coloring.txt - Mã nguồn chương trình #include #include #include using namespace std; int n, a[7][7],sm=0,m[7];
void docfile(){ //Dung de doc file, sau do gan vao mang a[][] int q,p;
ifstream dothi ("C:/data/dothi.txt"); if (dothi.is_open()) { dothi >> n;
while (!dothi.eof()) //Doc file cho den cuoi file { dothi >> q; dothi >> p; a[q][p]=9; a[p][q]=9; } dothi.close(); }
else cout << "Khong mo duoc file"; }
void xuly(){ //Xu ly de cho ra ket qua vao mang m[] int kt; for(int i=1;i<=n;i++) if(!m[i]) { sm++; //Dem so mau m[i]=sm;
for(int j=i+1;j<=n;j++) //Kiem tra xem nhung dinh nao co the gan bang mau sm nua khong
if((a[i][j]==0)&&(m[j]==0)){ kt=1;
for(int k=i+1;k if((a[k][j]==1)&&(m[i]==m[k])){ kt=0; break; } if(kt==1) m[j]=sm; } } }
void xuatkq(){ //In ket qua ra man hinh for(int i=1;i<=sm;i++){
cout << "Mau " << i << ": ";
for(int j=1;j<=n;j++) if(m[j]==i) cout << j << " "; cout << endl; } } int main(){ docfile();
cout << n << endl;
for(int i=1;i<=n;i++){ //In mang ra man hinh de theo doi
for(int j=1;j<=n;j++) cout << a[i][j] << " "; cout << endl; }cout << endl; xuly(); xuatkq(); return 0; } a.
Đồ thị 2 phía K (3,3):
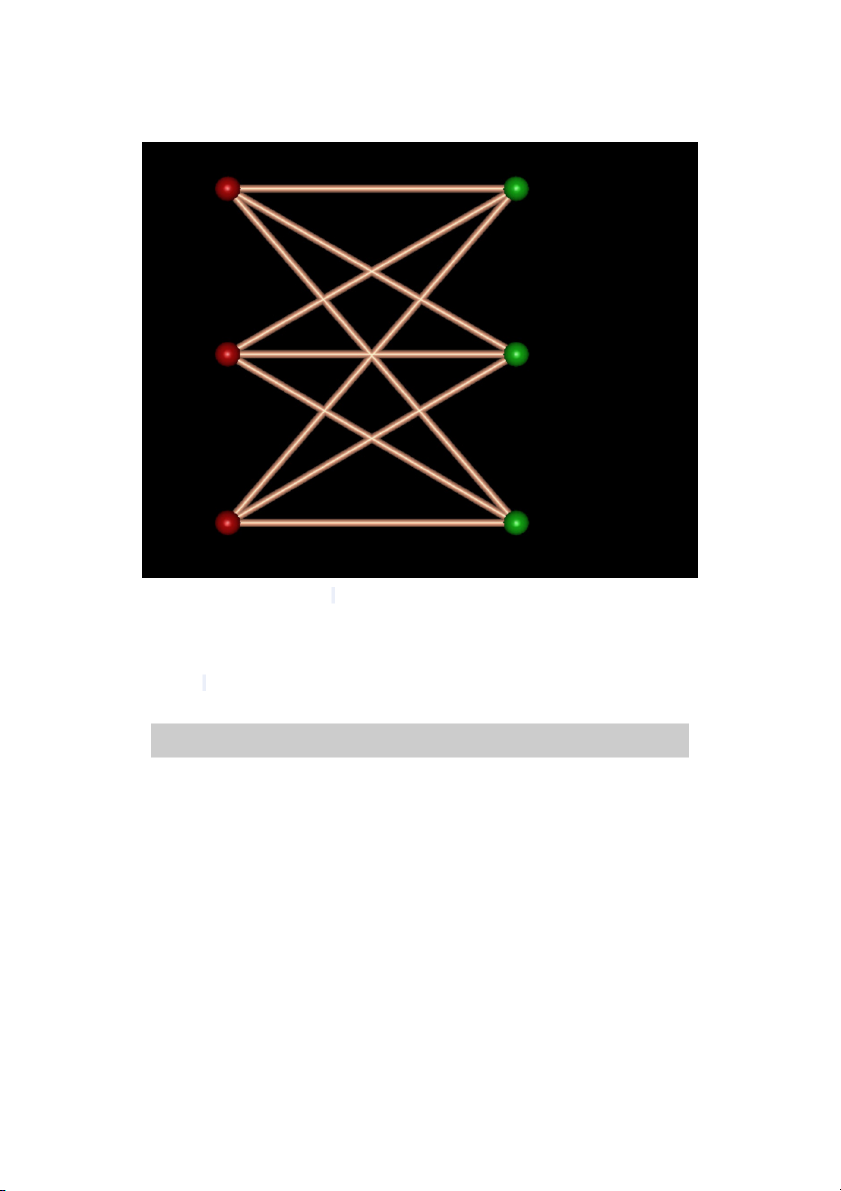
Chúng ta chạy chương trình trên đồ thị hai phía Kuratowski K3, 3 với n = 6 đỉnh. Thuật toán
tìm được đúng m-màu của các đỉnh graph.txt 6 0 0 0 1 1 1 0 0 0 1 1 1 0 0 0 1 1 1 1 1 1 0 0 0 1 1 1 0 0 0 1 1 1 0 0 0 coloring.txt
Vertex Coloring ( 6 ): ( 1 , 1 ) ( 2 , 1 ) ( 3 , 1 ) ( 4 , 2 ) ( 5 , 2 ) ( 6 , 2 )
Hình 05: Đồ thị hai phía Kuratowski K3, 3 với tập đúng m-màu b. Đồ thị Octahedron
Chúng ta chạy chương trình trên đồ thị Octahedron với n = 6 đỉnh. graph.txt 6 0 1 1 0 1 1 1 0 1 1 0 1 1 1 0 1 1 0 0 1 1 0 1 1 1 0 1 1 0 1 1 1 0 1 1 0 coloring.txt
Vertex Coloring ( 6 ): ( 1 , 1 ) ( 2 , 2 ) ( 3 , 3 ) ( 4 , 1 ) ( 5 , 2 ) ( 6 , 3 )
Hình 05: Đồ thị Octahedron với tập đúng m-màu (n= 6,m= χ(G) = 3 )
c. Đồ thị Bondy-Murty G1
Chúng ta chạy chương trình trên đồ thị Bondy-Murty G 1 với n = 7 đỉnh. graph.txt 7 0 1 1 0 1 1 0 1 0 1 1 0 1 0 1 1 0 1 1 0 0 0 1 1 0 0 0 1 1 0 1 0 0 0 1 1 1 0 0 0 0 1 0 0 0 1 1 1 0 coloring.txt
Vertex Coloring ( 7 ): ( 1 , 1 ) ( 2 , 2 ) ( 3 , 3 ) ( 4 , 1
) ( 5 , 2 ) ( 6 , 3 ) ( 7 , 4 )
Hình 06: Đồ thị Bondy-Murty G1 với tập đúng m-màu (n= 7,m= χ(G) = 4 )
2. Bài toán tô mầu cạnh
2.1. Đọc dữ liệu từ file - Cài đặt
Đọc dữ liệu từ File văn bản .txt ,file .txt có cấu trúc dạng
Dòng đầu là số đỉnh, các dòng tiếp theo dòng thứ i là các đỉnh kể với đỉnh i.
Với ví dụ minh họa ở phần trước Ta sẽ có file .txt dạng 7 0 1 0 1 1 0 0 1 0 1 1 0 0 0 0 1 0 1 0 0 0 1 1 1 0 1 0 1 1 0 0 1 0 1 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0
Dữ liệu được đọc từ file được lưu vào mảng 2 chiều a.
Khởi tạo các giá trị ban đầu cho màu với giá trị mã nhỏ nhất là 2
Tìm bậc lớn nhất của đồ thị (Δ)
Chuẩn bị (Δ+1) màu để tô Tô màu các cạnh: Tại bước thứ i:
+) Với các đỉnh j kề với i trong danh sách đã được xây dựng ở trên
+)A[i][j] = t (t>1) tức là cạnh [I,j] được tô bởi màu có mã là t
+)A[i][j] = 1 tức là có cạnh [i,j] và cạnh [I,j] chưa được tô
Khi tô cạnh i,j ta xét đỉnh i và đỉnh j
Ta tất cả các cạnh có 1 đầu cạnh là I hoặc j và đánh dấu các màu đã được tô
Sau đó ta tìm mã màu gần nhất chưa được tô bởi các cạnh có 1 đầu cạnh là i hoặc j và gắn mã màu cho a[i][j] Gán a[j][i] = a[i][j]
Lấy lại ví dụ trên ta được kết quả như sau: Bước 1 Bước 2: 2 2 1 1 3 3 5 4 5 4 Bư 3 Bước 4 7 7 6 6 Màu 2 Màu 3 âếy l i ạ ví d ụ trên ta được kêết quả như sau: 2 . 2 1 1 .. .......... .......... 3 3 ..... 5 4 5 4 bày 2 cách cài đặt k 7 6 7 6 u c 5 Bước 6 Màu 2 Màu 3 M 2 Màu 2 Màu 3 M 1 2 1 3 3 5 4 5 4 B 7 Bước 8 7 7 6 6 Màu 2 Màu 3 Màu 4 Màu 2 Màu 3 Màu 4 1 2 1 2 3 3 5 4 5 4 6 7 6 7 Màu 2 Màu 3 Màu 4 Màu 2 Màu 4 Màu 3 Màu Màu 5 5 Bước 9: 2 1 3 5 4 7
Vậy trong ví dụ trên đồ thị đư 6
ng 5 màu đánh số từ 2 cho .
- Mô tả chương trình và đánh giá độ phức tạp cài đặt Màu 2 Màu 3 Màu 4
Đọc dữ liệu từ file lưu các giá trị vào mảng 2 chiều a
int input(filename) // lay so lieu dau vao tu file du lieu Màu Màu 6 { int i,j; 5
f = fopen(filename,"r"); //mở file
if (f== NULL) //nếu không có file như vậy {
printf("\n Khong ton tai file \n"); return(1); } else //nếu có file {
printf("File mane: %s \n",filename); printf("Content :\n");
fscanf(f,"%d",&n); //lấy số đỉnh printf("Co % d dinh\n",n); for(i=1;i<=n;i++) {
for(j=1;j<=n;j++) //đưa vào ma trận a { fscanf(f,"%d",&a[i][j]); printf("%d ",a[i][j]); } printf("\n"); } return(0); } }
Hàm có 2 câu lệnh for lồng nhau nên độ phức tạp là O(n ) 2
Hàm khởi tạo các mã màu ,mã màu nhỏ nhất là 2 void initcolor()
// khoi tao mau ban dau co toi da somau_max
// voi somau_max bang bac lon nhat cua dinh do thi { int i; for(i=2;i<=somau_max;i++) mau[i]= i; }
Hàm trên có độ phức tạp O(n)
Hàm tìm bậc lớn nhất có độ phức tạp O(n) int maxbac() // ham tinh gia tri maxbac { int max; int i; int j; int dem=0; for(i=1;i<=n;i++) { dem = 0; for(j=1;j<=n;j++) if (a[i][j] == 1) dem++ ; if (max < dem) max = dem; } return max+1; }
Hàm duyệt đồ thị void duyet(int x,int y) có độ phức tạp O(n) void duyet(int x,int y)
// kiem tra cac canh mau xung quanh no { int i; initcolor();
// moi dinh lai su dung mang mau 1 lan for(i=1;i<=n;i++) {
if (a[x][i] != 0) // neu canh [x,ke[i]] duoc to mau t
mau[a[x][i]] = 0; // thi mau[t] = 0 } for(i=1;i<=n;i++) { if (a[y][i] != 0) mau[a[y][i]] = 0; } }
Ví dụ với cạnh [3,4] lúc này trạng thái các cạnh như hình sau 2 1 3 5 4 7 6 Đỉnh 3 Vàng Đỉnh 4 tím Vàng
Từ đó suy ra màu vàng và tím bị loại
Hàm Tô màu các cạnh.Dùng hàm duyệt để kiểm tra xem những màu nào Ko được phép tô
sau đó tìm màu gần nhất có thể tô được. Hàm này có độ phức tạp O(n ) 3 void tomau() { int i,j; int t; for(i=1;i<=n;i++) for(j=1;j<=n;j++) if (a[i][j] == 1) { duyet(i,j) ; for(t=2;t<=somau_max;t++) if (mau[t] == t) { a[i][j] = t; a[j][i] = t; break; } } }
Qua bước trên ta đã loại màu vàng và tím, màu gần nhất được phép tô là màu đỏ nên ta tô [3,4] màu đỏ
Hàm void main() : hàm sử dụng các hàm con có độ phức tạp O(n ) 3 (như hàm tô màu), độ phức tạp O(n )
2 ( như hàm input()), độ phức tạp O(n) ( như hàm tìm bậc lớn nhất maxbac())
nên chương trình có độ phức tạp là O(n ) 3 initcolor(); somau_max = maxbac() ; tomau(); printf("\n Result:\n"); for(i=1;i<=n;i++) { for(j=1;j<=n;j++) if (a[i][j] >0) {
printf(" Canh [%d,%d] duoc to mau %d ",i,j,a[i][j]) ; a[i][j] = 0; a[j][i] = 0; } printf("\n") ; } 2 1 3 5 4 - Hướng dẫnsử dụng c ng trình
Với cách cài đặt đầu tiên này, việc nhập dữ liệu đượ
ra thành một khâu riêng bằng cách
chúng ta phải tạo một file o chuẩn đã trình bày 7
( Trong bộ báo cáo có một bộ các 6
file txt chính là ví dụ đi k
i cách cài đặt này). Với ách nhập dữ liệu như thế này sẽ đơn
giản hơn khi thực hiện chương trình. Lúc này việc nhập dữ liệu chỉ còn là nhập filename của file
chứa ví dụ cần thực hiện và xem kết quả Nhập filename
Sau đó ấn enter để xem nội dung file và kết quả - Kết quả thực nghiệm
Trong phần kết quả sẽ in ra
Nội dung của ma trận biểu diễn đồ thị
Các cạnh cụ thể được tô màu theo thứ tự
Kết quả của ví dụ trên
Kết quả này hòan tòan phù hợp với ví dụ chúng ta đã trình bày ở phần mô tả giải thuật. Sau đây ta sẽ so sánh lại : Màu 2 Màu 3 Màu 4 Màu Màu 6 5
2.2. Dữ liệu vào từ bàn m 1 2 - ặt
Sắp xếp các cạnh theo thứ , E2, ...,En
Tìm bậc lớn hất của đồ 3 5 Chuẩn bị 4 màu để tô
Bước i: tô c h Ei bởi màu có chỉ số nhỏ nhất trong số các màu chưa được sử dụng để tô cạnh kề của nó
Trong đó ệc sắp xếp các cạnh th
tự được người sử dụng nhập vào. 6 7
- Mô tả c ơng trình và đánh giá độ phức tạp
Trước tiên ta tổ chức các cạnh là một danh sách gồm 3 thông tin: - Đỉnh đầu của cạnh - Đỉnh cuối của cạnh - Màu của cạnh typedef struct { int dau; int cuoi; int mau; } Danhsachcanh;
Để lưu những màu đã tô của cạnh giao tại một đỉnh ta tổ chức n mảng (n là số đỉnh) với độ lớn là (Δ+1) phần tử.
Trước hết ta đưa tất cả các phần tử này về 0 (chưa có màu nào được tô)
Ta sử dụng con trỏ để trỏ tới vị trí mảng màu của một đỉnh:
int *p[20]; //mảng con trỏ đến các mảng màu của đồ thị
Để xác định vị trí của con trỏ của một đỉnh ta dùng đoạn code sau:
int temp[20]; //mảng lưu vị trí con trỏ của các đỉnh int j=0; for (i=0;i {
if (temp[G[i].dau]<0) {temp[G[i].dau]=j;j++;}
if (temp[G[i].cuoi]<0) {temp[G[i].cuoi]=j;j++;} }
Để xác định bậc lớn nhất của đồ thị ta dùng hàm maxdegree:
Độ phức tạp của hàm là O(E) với E là số cạnh của đồ thị
int maxdegree(Danhsachcanh a[],int edge) //hàm tìm bậc lớn nhất của đỉnh { int temp[20];
for (int i=0;i<20;i++) temp[i]=0; for (i=0;i { temp[a[i].dau-1]++; temp[a[i].cuoi-1]++; } int max=temp[0];
for (i=1;i<21;i++) if (max return max; } Hàm findcolor:
Trong trường hợp tồi nhất độ phức tạp của hàm là O(V) với V là số đỉnh
int findcolor(int *a,int *b,int maxdegree) //Hàm tìm màu tô cho cạnh { int i=0;
while (((a[i]>0)||(b[i]>0))&&(i return i; }
Hàm này sẽ duyệt 2 mảng màu của 2 đỉnh và đưa ra vị trí thứ i đầu tiên là vị
trí mà chưa có màu nào được tô, tại vị trí đó các phần tử của 2 mảng đều bằng 0.
Ví dụ: với 2 mảng màu của 2 đỉnh 1 và 2
Thì hàm findcolor sẽ trả về giá trị là 2.
Thì hàm findcolor sẽ trả về giá trị là 3.
Theo cách này thì cạnh đầu tiên sẽ luôn được tô là màu đỏ (màu đỏ là màu có chỉ số thấp nhất)
Đoạn chương trình thực hiện tô màu từng cạnh, khi duyệt qua lần lượt mỗi cạnh sẽ thực hiện những công việc sau:
- Tìm vị trí thứ j là vị trí đầu tiên trong 2 mảng màu của 2 đỉnh chưa có màu tô
- Sử dụng biến maxcolor để ghi nhận số màu lớn nhất khi đã tô cạnh này - Gán màu cho cạnh
- Lưu lại vị trí j trong mảng màu của 2 đỉnh thuộc cạnh for (i=0;i {
j=findcolor(p[temp[G[i].dau]],p[temp[G[i].cuoi]],maxdeg); if(maxcolor G[i].mau=j; *(p[temp[G[i].dau]]+j)=j+1; *(p[temp[G[i].cuoi]]+j)=j+1; }
Dựa vào những đánh giá trên và dựa vào chương trình nguồn ta có thể đánh giá được độ phức tạp
của chương trình Cai_dat_2 này là : O(E+V2) - Một ví dụ
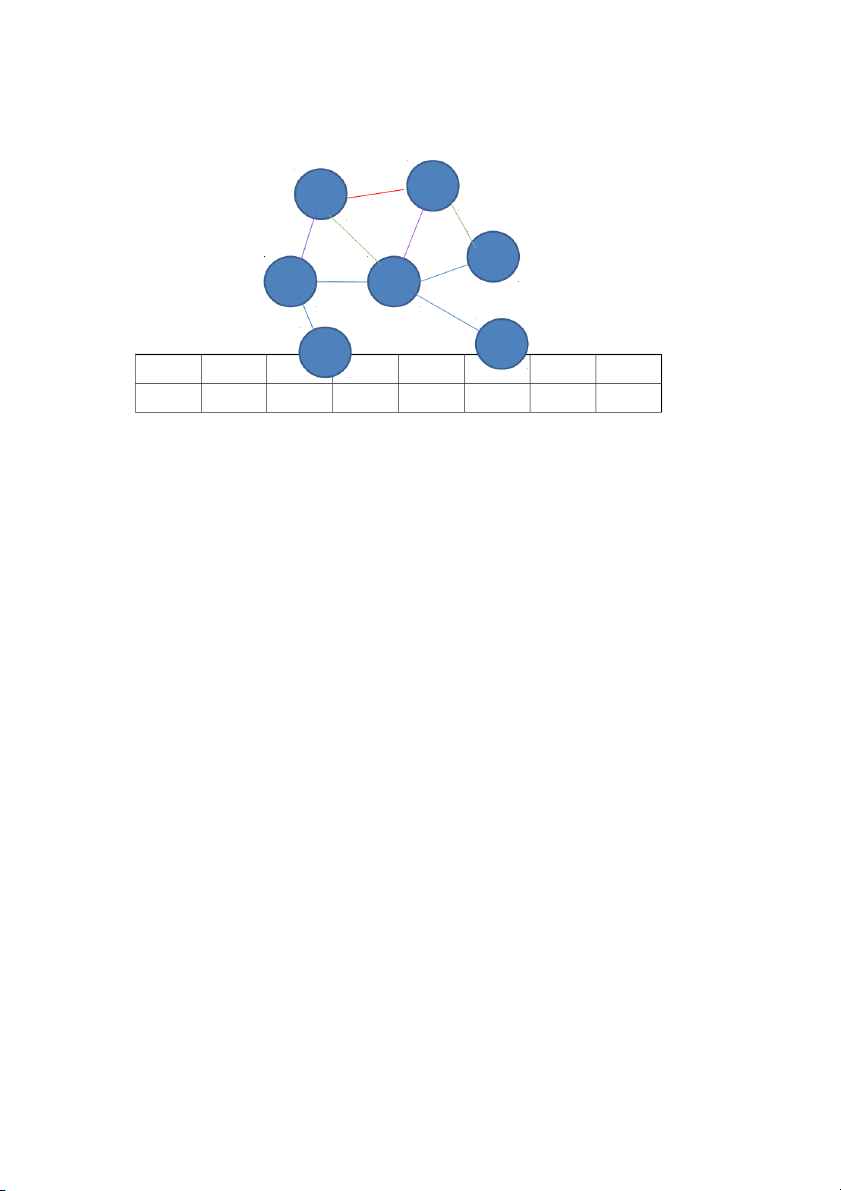
Ta có đồ thị với 8 đỉnh và 10 cạnh như sau:
Ta có bậc lớn nhất: maxdeg=5.
Mảng màu các đỉnh được tạo như sau: Các bước tô màu: Bước 1: Bước 2: Bước 3: Bước 4: Bước 5: Bước 6: Bước 7: Bước 8: Bước 9: Bước 10: Kết quả:
- Đồ thị tô được bởi 5 màu: red, blue, yellow, green, pink Cạnh 1(5,1): red Cạnh 2(2,1): blue Cạnh 3(4,5): blue Cạnh 4(7,8): red Cạnh 5(6,5): yellow Cạnh 6(5,7): green Cạnh 7(4,8): yellow Cạnh 8(3,1): yellow Cạnh 9(4,3): red Cạnh 10(5,2): pink
- Hướng dẫn sử dụng chương trình
Bước 1:Với cách cài đặt này người sử dụng phải tự nhập các đỉnh và các cạnh của đồ thị với quy tắc cho trước như sau:
Yêu cầu người dùng nhập số đỉnh và số cạnh của đồ thị
Với mỗi cạnh yêu cầu người dùng nhập vào 2 đỉnh là đỉnh đầu và đỉnh cuối
Ví dụ như trong đồ thị trình bày ở trên ta có thể nhập như sau :
Với thứ tự nhập các cạnh: Cạnh Đỉnh đầu Đỉnh cuối 1 5 1 2 2 1 3 4 5 4 7 8 5 6 5 6 5 7 7 4 8 8 3 1 9 4 3 10 5 2
Bước 2: Xem từng bước các kết quả. Với cách cài đặt này, người sử dụng được xem từng bước
của quá trình tính tóan, tô màu thực hiện trong chương trình. Ấn enter trong mỗi lần chuyển đến
bước kế tiếp. Kết quả cuối cùng sẽ được hiện lên màn hình - Kết quả thực nghiệm
Kết quả sẽ hiện ra theo từng cạnh và màu tương ứng
Sau đây là kết quả của ví dụ trên theo từng bước
Kết quả này phù hợp với ví dụ ta trình bày trước đó 3. Mã nguồn
- File mã nguồn: Algo2010N15.cpp
- File biên dịch: Algo2010N15
- File dữ liệu đầu vào của cài đặt tô mầu cạnh: dothi.txt
- File dữ liệu đầu vào của cài đặt tô mầu đỉnh: dothi.txt
- File dữ liệu đầu ra của cài đặt tô mầu đỉnh: dothi.txt
IV. TI LIỆU THAM KHẢO
1. Bài giảng của thầy Vũ Văn Định.
2. Coloring random graphs : organization of solutión and computational hardness - Lenka
Zdeborova’ và Florent Krzakala
3. Graph coloring problems and their applications in scheduling - Da’niel Mark
4. Graph coloring algorithms - Walter Klotz
5. Reducibility among combinatorial problems, Complexity of Computer Computations, Plenum Press, 1972- R.M. Karp
6. The Vertex Coloring Algorithm - Ashay Dharwadker
7. Các bài viết trên wikipedia và các trang web:
http://en.wikipedia.org/wiki/Register_alloc ation
http://en.wikipedia.org/wiki/Edge_coloring http://www
.cs.sunysb.edu/~algorith/files/edge-coloring.shtml
PHỤ LỤC 1: DANH MỤC CÁC HÌNH ẢNH TRONG TI LIỆU
Hình 01: Đồ thị vô hướng
Hình 02: Đồ thị G của bài toán lập lịch trên
Hình 03: Các đồ thị đầu vào G với 3- màu tương ứng của các đỉnh của nó được tìm thấy bởi thuật toán
Hình 04: tích đề các G×K với một tập độc lập với kích thước 4 được tìm thấy bằng thuật toán 3
Hình 05: Đồ thị Octahedron với tập đúng m-màu (n = 6, m = χ( G ) = 3 ).
Hình 06: Đồ thị Bondy-Murty G1 với tập đúng m-màu
PHỤ LỤC 2: PHÂN CHIA CÔNG VIỆC Họ tên SV Nội dung công việc Đóng góp Phạm Văn Tuấn -
Cài đặt bài toán tô mầu đỉnh 35% - Lập báo cáo Nguyễn Hoàng Hiệu -
Cài đặt bài toán tô mầu cạnh với dữ liệu từ file 35% -
Tìm hiểu thuật toán giải quyết bài toán tô mầu cạnh Nguyễn Đức Thuận -
Cài đặt bài toán tô mầu cạnh với dữ liệu nhập từ 30% bàn phím -
Tìm hiểu thuật toán giải quyết bài toán tô mầu đỉnh