Bài 2: Thông lượng điện trường môn Vật lý đại cương | Đại học Kinh tế Thành phố Hồ Chí Minh

Bài 2: THÔNG LƯỢNG ĐIỆN TRƯỜNG
Đường sức iện trường ( ường thông lượng – ường dòng)
Đường sức là hệ thống các ường cong có hướng thể hiện hình ảnh của một trường vectơ.
Liên hệ giữa ường sức và vectơ của trường
Tiếp tuyến tại mỗi iểm của ường sức trùng với phương của vectơ cường ộ iện trường.
Chiều của ường sức là chiều của vectơ cường ộ iện trường.
Số ường sức qua một ơn vị diện tích vuông góc các ường sức tỷ lệ với ộ lớn của trường tại nơi ó.
Tính chất ường sức iện trường:
Trường tĩnh iện là một trường thế hay còn ược gọi là trường có nguồn. -
Đường sức có iểm xuất phát (nơi iện tích dương – nguồn phát sinh) và có iểm kết thúc ường
sức (iện tích âm – nguồn hấp thu) -
Đường sức là các ường cong không khép kín (các ường cong hở)
Các loại trường lực
Trường thế: trường có nguồn. Đường sức là các ường cong hở, xuất phát và kết thúc tại các iểm
nguồn. Trường tĩnh iện, trường hấp dẫn, trường lực àn hồi, trường gió do áp suất khí quyển.
Trường xoáy: trường không có nguồn. Đường sức là các ường cong khép kín (không có iểm xuất
phát và kết thúc các ường sức).
Thông lượng iện trường gởi qua một mặt hở
Thông lượng iện trường là ại lượng ặc trưng cho lưu lượng iện
trường gởi qua một mặt nào ó.
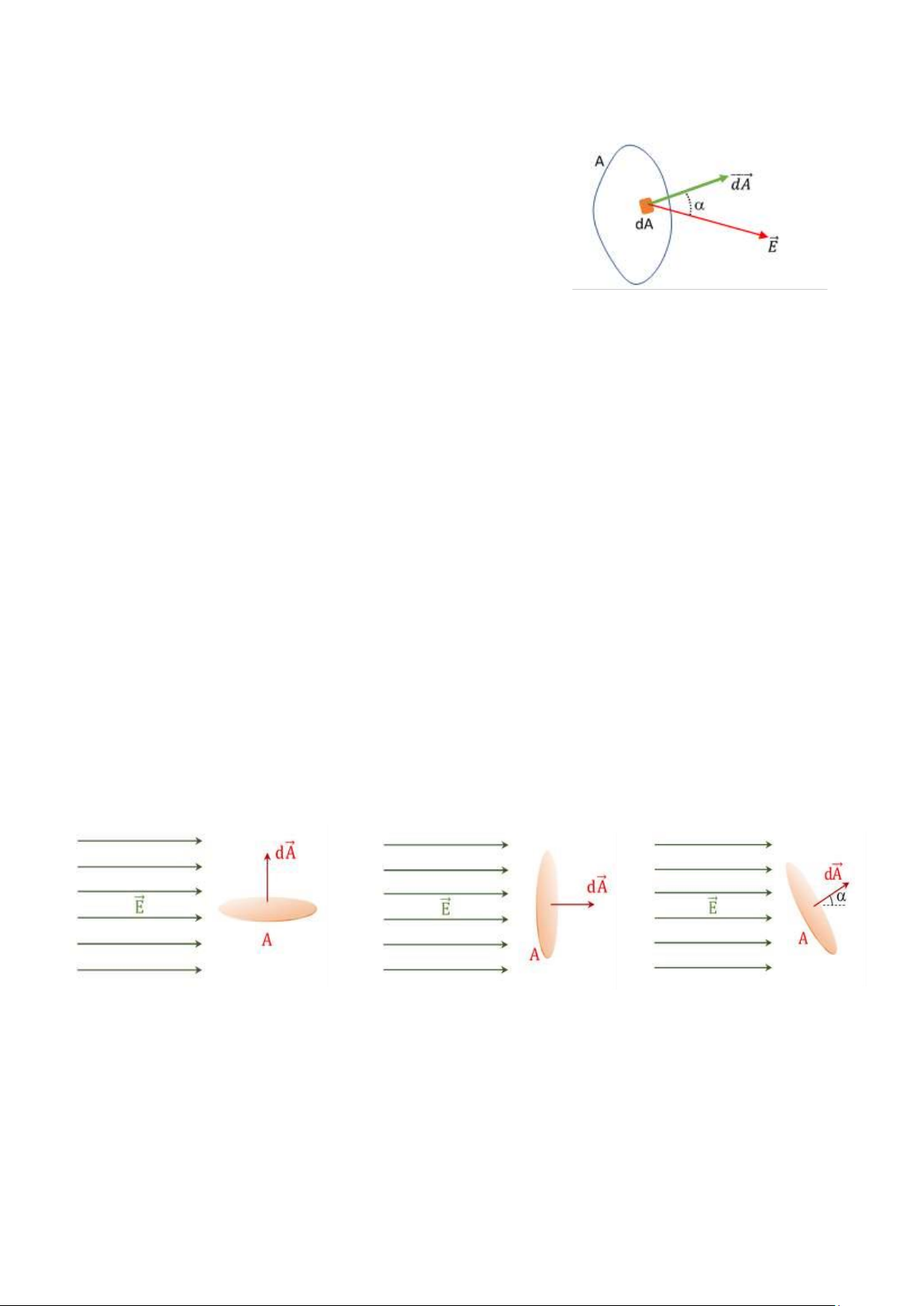
Chia nhỏ mặt A thành các phần diện tích vô cùng bé dA.
Thông lượng iện trường gởi qua một mặt vô cùng bé dA bất kỳ là ại lượng:
dΦ = E⃗. dA⃗ = 끫롰.dA.cosα
Với α là góc hợp bởi E⃗ và dA⃗: α = (E⃗, dA⃗)
Trong ó d 끫룐⃗ là vectơ vô cùng bé, có ộ lớn bằng diện tích dA và vuông góc với mặt dA.
Thông lượng iện trường gởi qua toàn bộ mặt A bất kỳ bằng tổng (trong một phân bố liên tục của mặt
thì tổng có nghĩa là tích phân ∫ ) tất cả các thông lượng vô cùng bé dΦ.
끫뵺 = 끫레⃗. 끫렺끫렀⃗ = 끫레. 끫뤊끫룐. 끫렸끫렸끫렸끫렸
Đơn vị của thông lượng iện trường trong hệ thống SI là V.m Cách
tính thông lượng iện trường:
Mặt phẳng ặt trong iện trường ều:
Mặt A song song với E⃗ (끫롰⃗ ⊥ d 끫롨⃗): Φ = 0
Mặt A vuông góc với E⃗ (끫롰⃗ ∥ d 끫롨⃗): Φ = E.A
Phương vuông góc với mặt A hợp với vectơ cường ộ iện trường E⃗ một góc α: Φ = E.A.cosα.Trong ó α = (E⃗, dA⃗)
Thông lượng gởi qua một mặt bất kỳ:
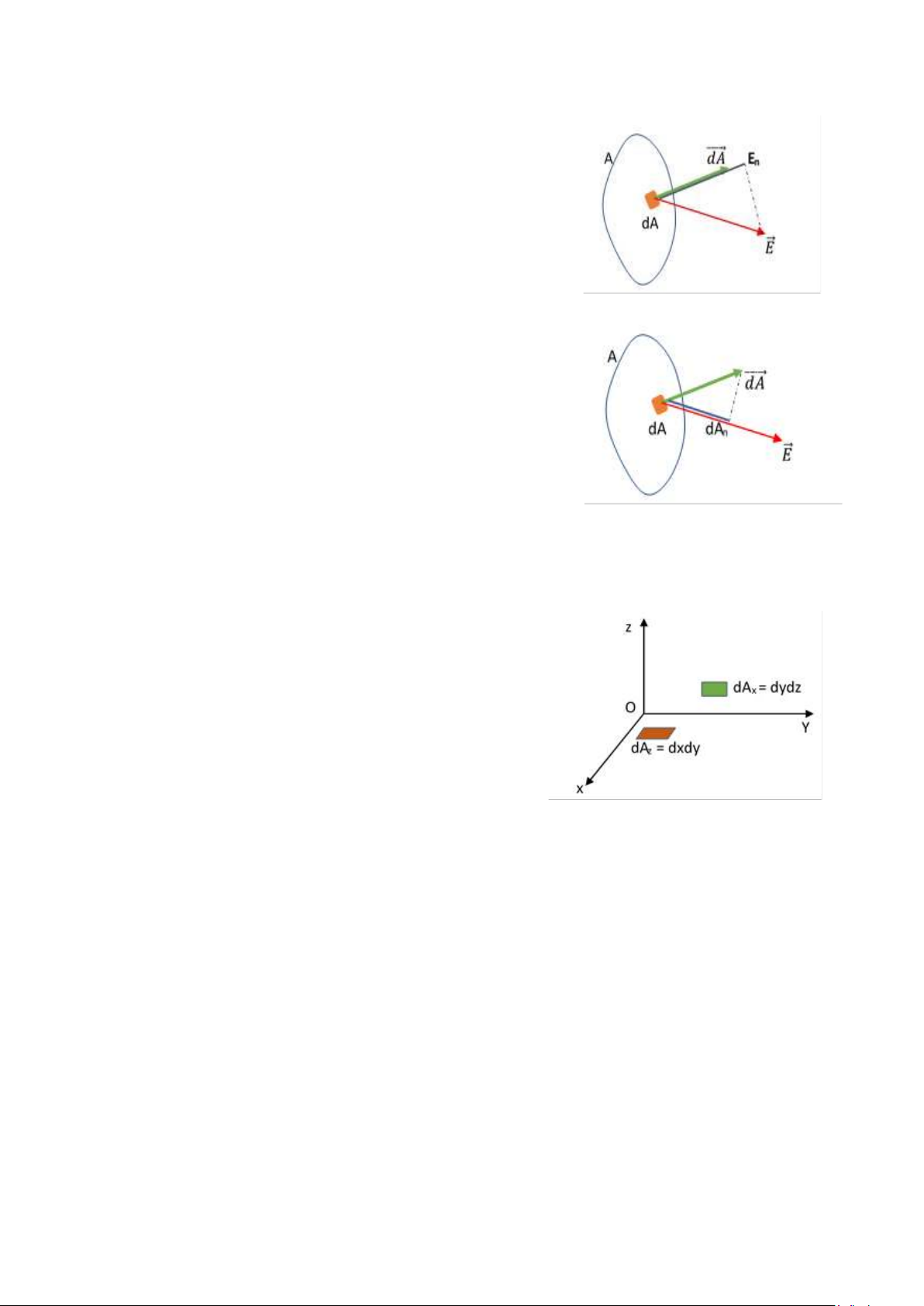
Trước hết, tính dΦ thông lượng gởi qua diện tích vô cùng bé dA. Rồi sau ó tính toàn bộ thông lượng
gởi qua cả mặt A: Φ = ∫끫뢢끫뢢 = ∫ E⃗. 끫뢢 A⃗
Vì E⃗. dA⃗ = E.dA.cosα nên có thể viết: E⃗. dA⃗ = En.dA thành
phần En của E⃗ vuông góc với dA (thành phần En cùng phương 끫뢢 A⃗)
Hoặc tính theo E⃗. dA⃗ = E. dAn
thành phần diện tích dAn vuông góc với E⃗ (thành phần dAn cùng phương E⃗)
Cả hai cách tính ều có kết quả như nhau và nghĩa là chỉ cần tính
tích số của các thành phần cùng phương của 끫롰⃗ và 끫뢢끫롨⃗.
Dạng giải tích của thông lượng iện trường:
Trong hệ trục tọa ộ Oxy cho trước iện trường có dạng:
끫롰⃗ = 끫롰끫룊끫뵈⃗ + 끫롰끫료끫뵊⃗ + 끫롰끫룎끫뢰⃗ và
끫뢢끫롨⃗ = 끫뢢끫롨끫룊끫뵈⃗ + 끫뢢끫롨끫료끫뵊⃗ +
끫뢢끫롨끫룎끫뢰⃗ thì dΦ = 끫레⃗. 끫렺끫렀⃗ =
끫룘끫뤲.끫뤊끫룐끫뤲 + 끫룘끫뤴.끫뤊끫룐끫뤴 + 끫룘끫뤶.끫뤊끫룐끫뤶 dAx = dy.dz dAy = dz.dx dAz = dx.dy
1. Một iện trường không ều có cường ộ iện trường 끫롰⃗ = 끫뢜끫뢜끫뵈⃗ + 끫뢞끫뢞끫뵊⃗ +
끫뢠끫뢠끫뢰⃗ , trong ó a, b, và c là các hằng số.
Xác ịnh thông lượng iện trường qua một mặt hình chữ nhật trong mặt phẳng Oxy ược giới hạn bởi
phạm vi từ 끫뢠 = 0 ến 끫뢠 = 끫룈 và từ 끫뢜 = 0 ến 끫뢜 = ℎ.
Ý nghĩa của thông lượng iện trường:
Bất kỳ một trường vectơ (끫롰⃗, trường hấp dẫn, từ trường 끫롪⃗, trường vận tốc nước trong sông,
trường vận tốc gió trong khí quyển,…) ều có một ại lượng ặc trưng là thông lượng gởi qua một mặt nào ó.
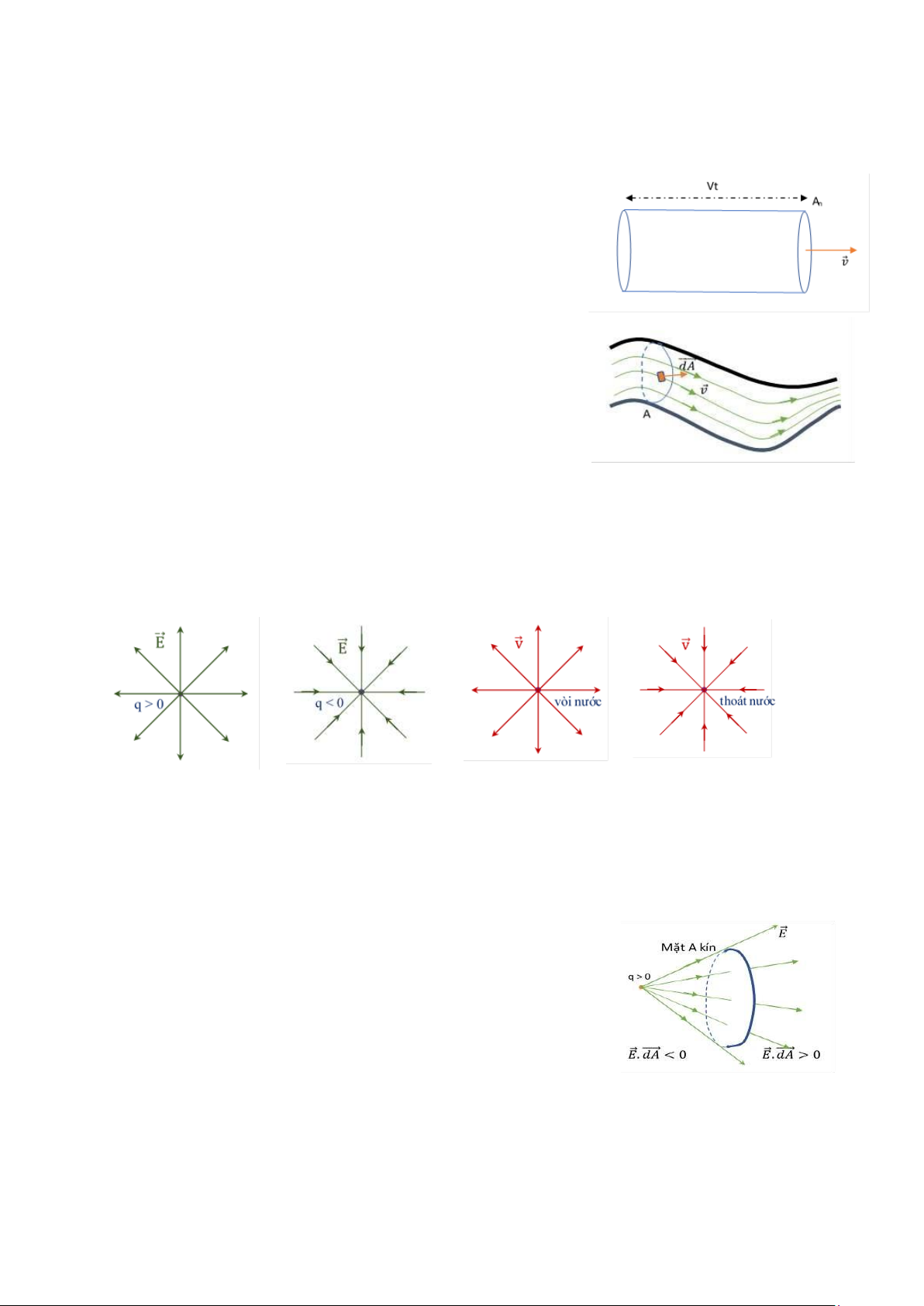
Tính lưu lượng nước của con sông (thể tích nước chuyển qua một
mặt nào ó trong ơn vị thời gian (m3/s)).
Mô hình ơn giản: oạn sông thẳng và vận tốc nước chảy 끫룆⃗ không ổi: Q = v.An (m3/s)
Mô hình thực: Lưu lượng nước gởi qua diện tích vô cùng bé dA⃗:
dQ = v⃗.dA⃗ = v.dAn
Lưu lượng nước gởi qua toàn bộ mặt A bao quanh dòng sông: Q = ∫v⃗.dA⃗
So sánh thông lượng iện trường và lưu lượng nước chuyển qua con sông:
Φ = ∫ E⃗. dA⃗ (V.m) và Q = ∫ v⃗. dA⃗ (m3/s) cường ộ iện trường E⃗ ⇔ vận tốc nước v⃗
q > 0 ⇔ nguồn phát sinh (vòi nước)
q < 0 ⇔ nguồn hấp thu (lỗ thoát nước)
Thông lượng iện trường gởi qua một mặt kín – Đĩnh lý Gauss ối với iện trường
Đối với một mặt kín (không hở tức là nó chứa thể tích trong nó): quy ước chiều của vectơ 끫뢢 A⃗
hướng về phía lồi của mặt A. 끫뵺 = ∮끫레⃗. 끫뤊끫렀⃗
Thông lượng gởi ra khỏi mặt A là dương (Φ > 0) và ngược lại, thông
lượng gởi vào mặt A là âm (Φ < 0)
Trường hợp vật mang iện (hay iện tích) hoặc các nguồn mang iện nằm
bên ngoài mặt A kín thì thông lượng iện trường gởi qua toàn bộ mặt kín ó bằng 0:
끫뵺 = ∮끫레⃗. 끫뤊끫렀⃗ = 0 khi iện tích q nằm bên ngoài
mặt kín Định lý Gauss ối với iện trường:
Thông lượng iện trường gởi qua mặt kín bất kỳ bằng tổng các iện tích chứa bên trong nó và chia cho
hằng số iện εo. ∑끫롔끫롄
끫뵺 = 끫레⃗. 끫렺끫렀⃗ = 끫붌끫렸
Trong ó qi là các iện tích nằm bên trong mặt A kín.
Chú ý: Φ có thể dương hay âm phụ thuộc vào giá trị các iện tích.
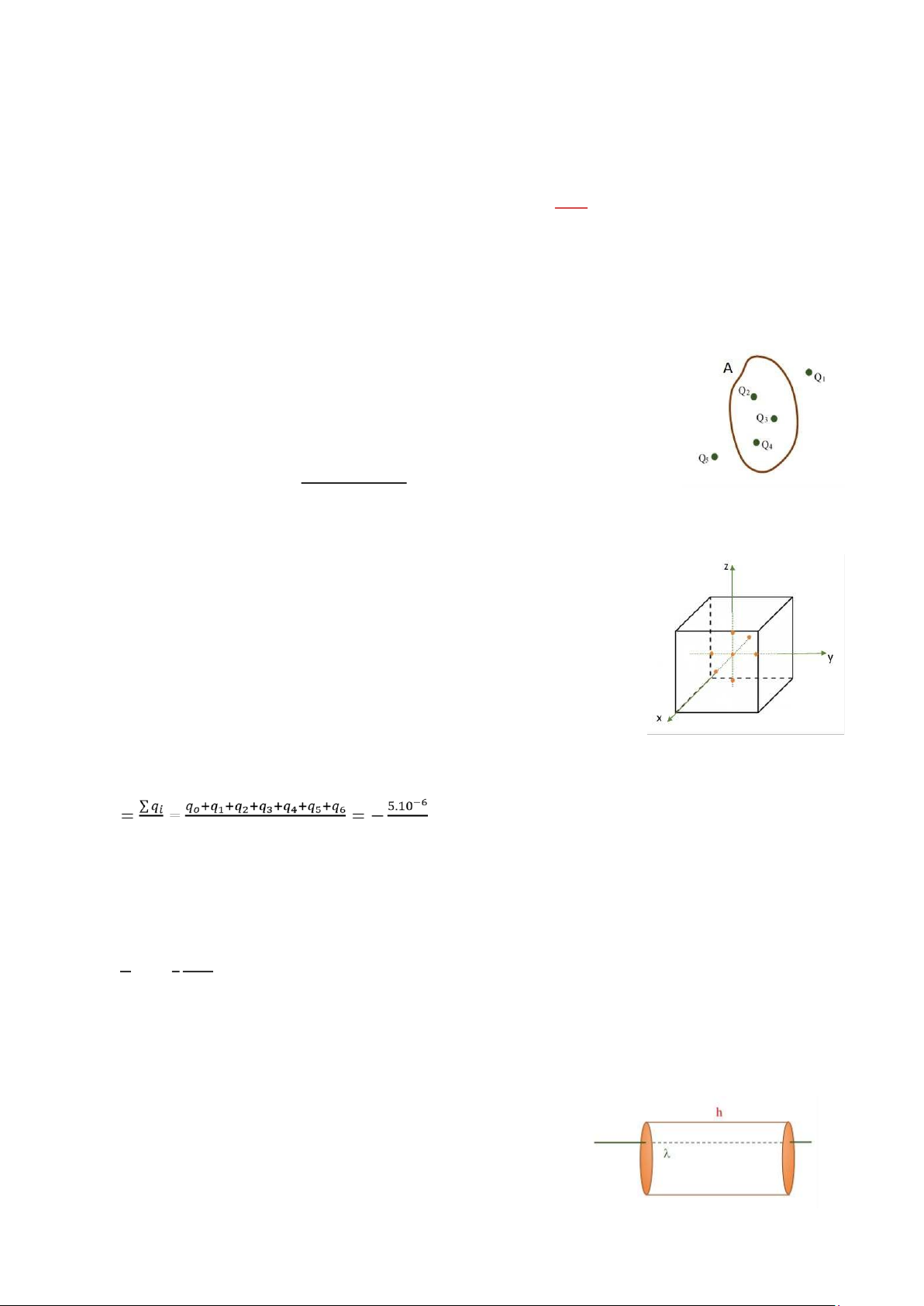
2. Tính thông lượng iện trường gởi qua mặt A kín như hình vẽ
Các iện tích q1 và q5 nằm bên ngoài mặt A nên không gây ảnh hưởng ến thông
lượng iện trường gởi qua mặt A.
끫뢈 2 + 끫뢈 3 + 끫뢈 4 끫뢢 = 끫븀끫뢸
3. Cho iện tích qo = 10−6C ặt tại gốc tọa ộ. Các iện tích q1 = q2 = q3 = q4
= q5 = q6 = −10−6C lần lượt ặt tại các vị trí A(1,0,0); B(−1,0,0);
C(0,1,0); D(0,−1,0); E(0,0,1) và F(0,0,−1).
Tính thông lượng iện trường gởi qua mỗi mặt của khối lập phương, có
cạnh a = 4 ơn vị và tâm tại gốc tọa ộ.
Tất cả các iện tích ều nằm trong khối lập phương nên: 끫뢢 끫븀끫뢸 끫븀끫뢸 끫븀끫뢸
(Dấu trừ là quy ước thông lượng hướng vào khối lập phương).
Điện tích và vị trí các iện tích ều ối xứng qua O. Khối lập phương cũng ối xứng qua O nên
thông lượng iện trường gởi quả mỗi mặt của khối lập phương là: 끫뢢 o = 끫뷮 = −5 10−6 = − 9,4.104 V.m 6 6 끫븀끫뢸
4. Cho một mặt trụ, có ường sinh là h và một sợi dây iện thẳng,
ược xem dài vô hạn, có mật ộ iện dài λ và song song với ường
sinh mà có một phần nằm bên trong mặt trụ.
Tính thông lượng iện trường gởi qua mặt trụ do dây iện tạo ra. 끫뢢 = 끫브 ℎ 끫븀끫뢸
5. Cho một mặt cầu tâm O, bán kính R và hai mặt phẳng mang iện song song (xem như rộng vô hạn) cắt mặt cầu.
Mặt mang mật ộ iện mặt σ cắt mặt cầu ở tâm.Mặt mang iện − σ cắt mặt
cầu ở khoảng cách R/2 tính từ tâm O. Tính thông lượng iện trường do hai
mặt phẳng mang iện gởi qua mặt cầu. Diện tích mặt σ là A1 = πR2. Diện
tích mặt − σ là A2 = 3 πR2. Thông 4
lượng iện trường gởi qua mặt cầu: 끫뢢 = 끫븜끫븜 1−끫븜끫븜 2 = 끫븜끫븜끫뢊 2 끫븀끫뢸 4 끫븀끫뢸
6. Một iện tích q > 0 ặt tại ỉnh một hình lập phương cạnh a. Hãy tính thông lượng iện trường gởi qua
mỗi mặt của khối lập phương ó.