










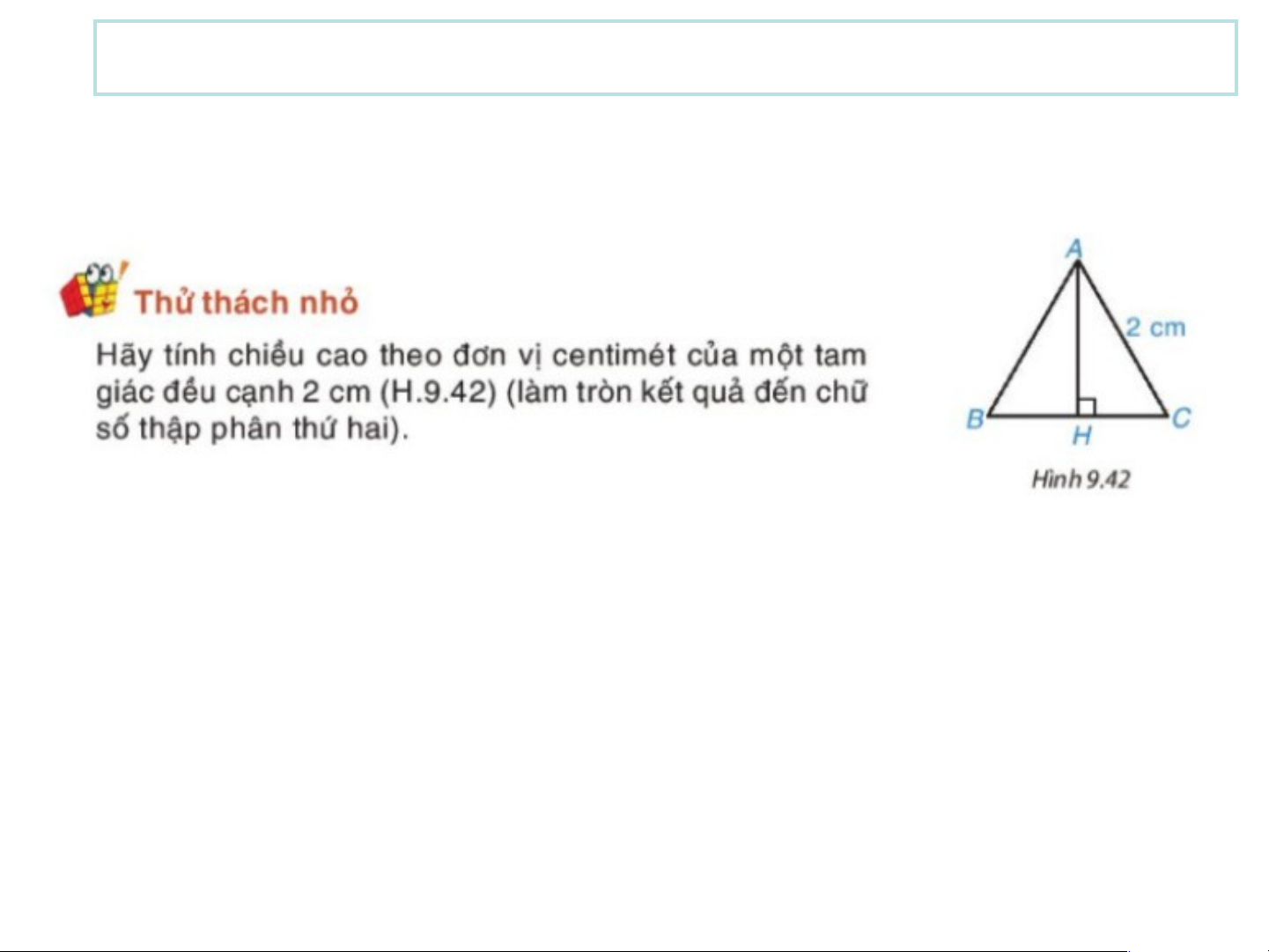



Preview text:
TOÁN 8 BÀI 35:
ĐỊNH LÝ PYTHAGORE VÀ ỨNG DỤNG
BÀI 35: ĐỊNH LÝ PYTHAGORE VÀ ỨNG DỤNG
1. ĐỊNH LÍ PYTHAGORE: BC 5 cm 2 2 2 2 AB AC 3 4 2 5 2 2 BC 5 2 5 2 2 2
AB AC BC
BÀI 35: ĐỊNH LÝ PYTHAGORE VÀ ỨNG DỤNG
1. ĐỊNH LÍ PYTHAGORE: a+b
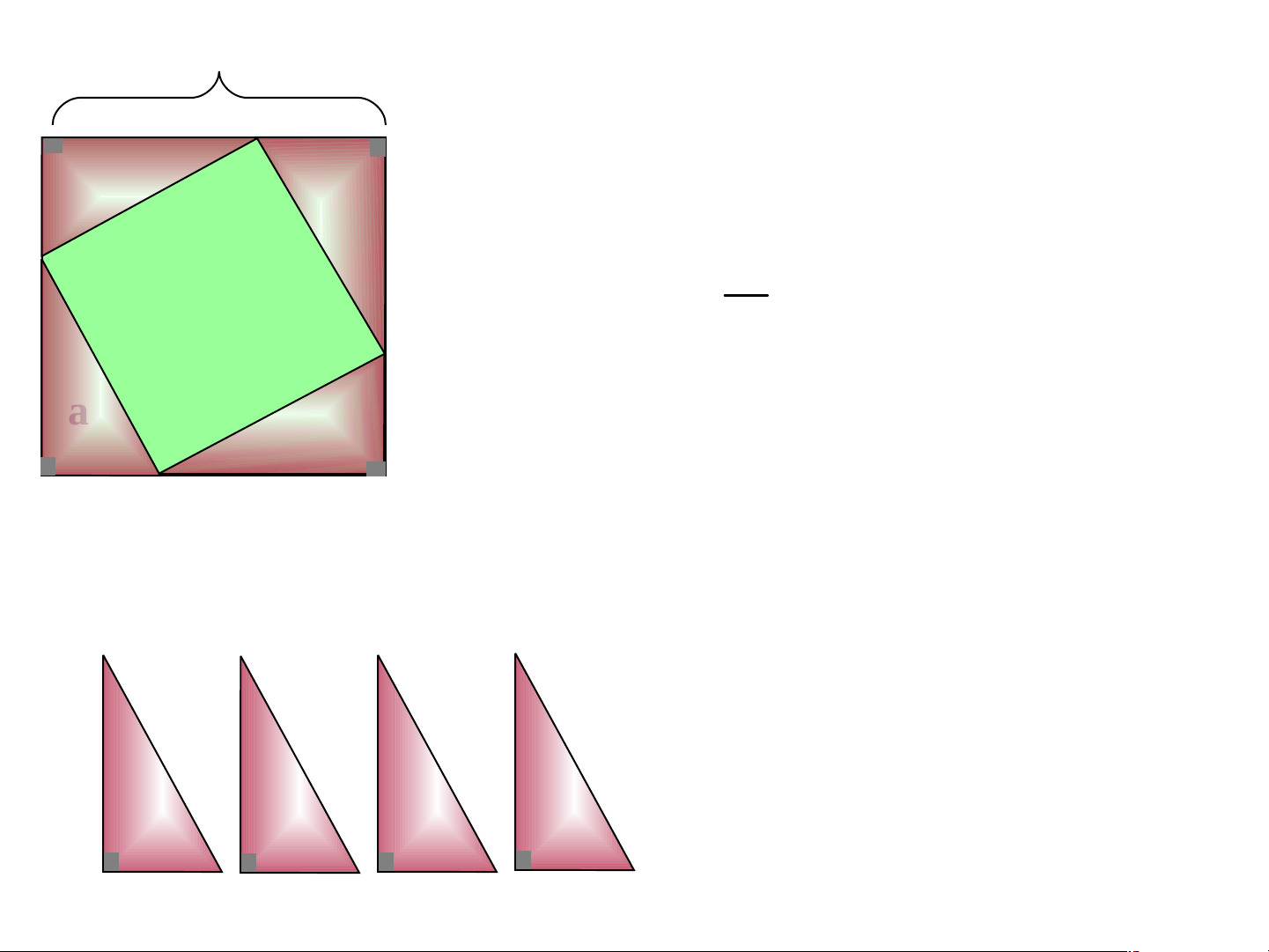
Diện tích phần bìa hình vuông màu xanh cạnh là c là: a 2 b c b c c
Tổng diện tích bốn tam giác vuông là: a c2 ab .4 2 ab 2 a
Diện tích cả tấm bìa hình vuông cạnh a +b ac c b là: 2 (a b) b a Kết luận: Hình 121 2 2 2 c a b a c a c a c a c b b b b H·y ph¸t biÓu hÖ thøc c2= a2 + b2 b»ng lêi ? c2 = a2 + b2 Trong một tam giác vuông,
bình phương của cạnh huyền
bằng tổng các bình phương của hai cạnh góc vuông
BÀI 35: ĐỊNH LÝ PYTHAGORE VÀ ỨNG DỤNG
1. ĐỊNH LÍ PYTHAGORE: • Định lí Pythagore:
Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng các
bình phương của hai cạnh góc vuông.
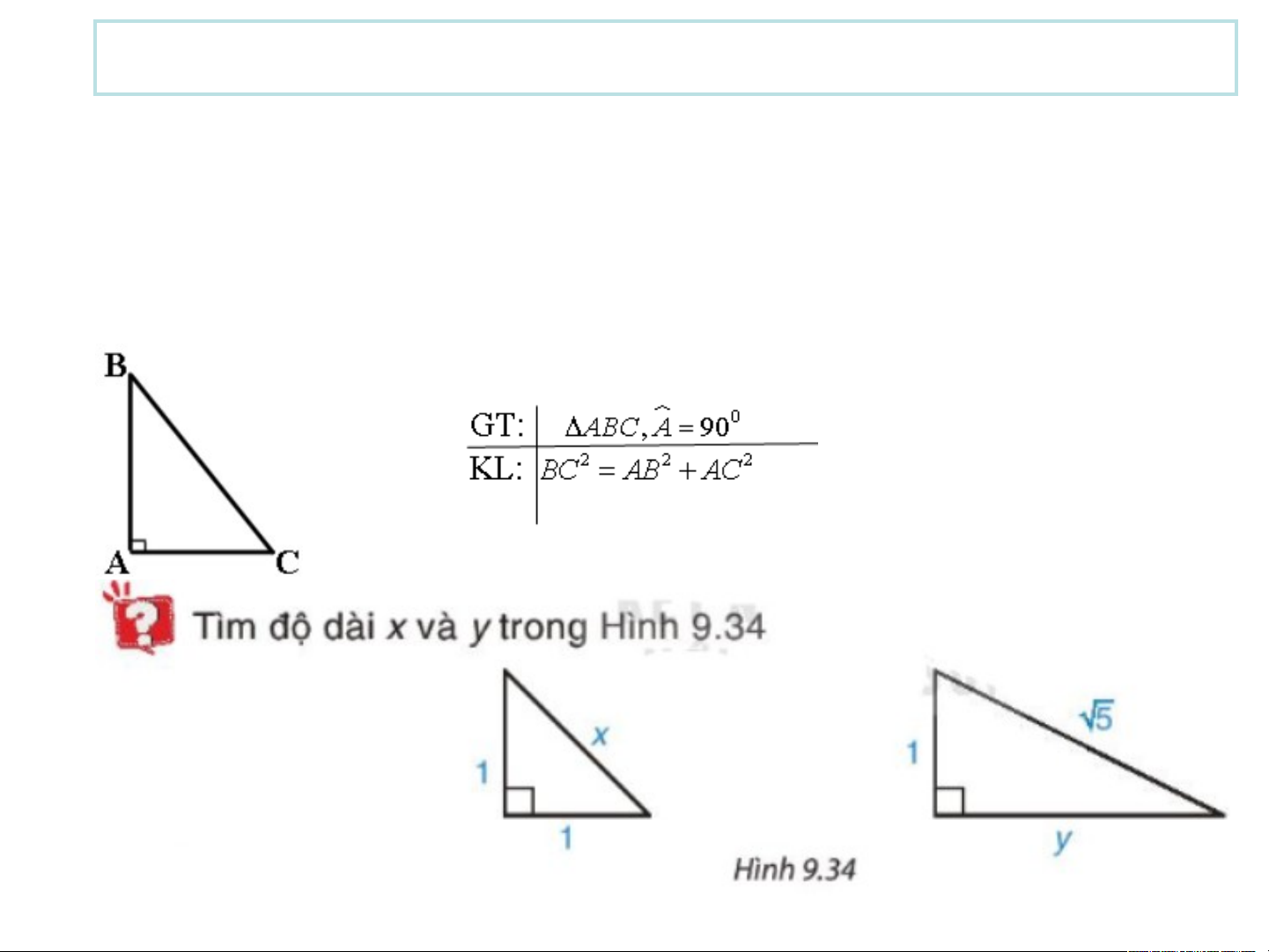
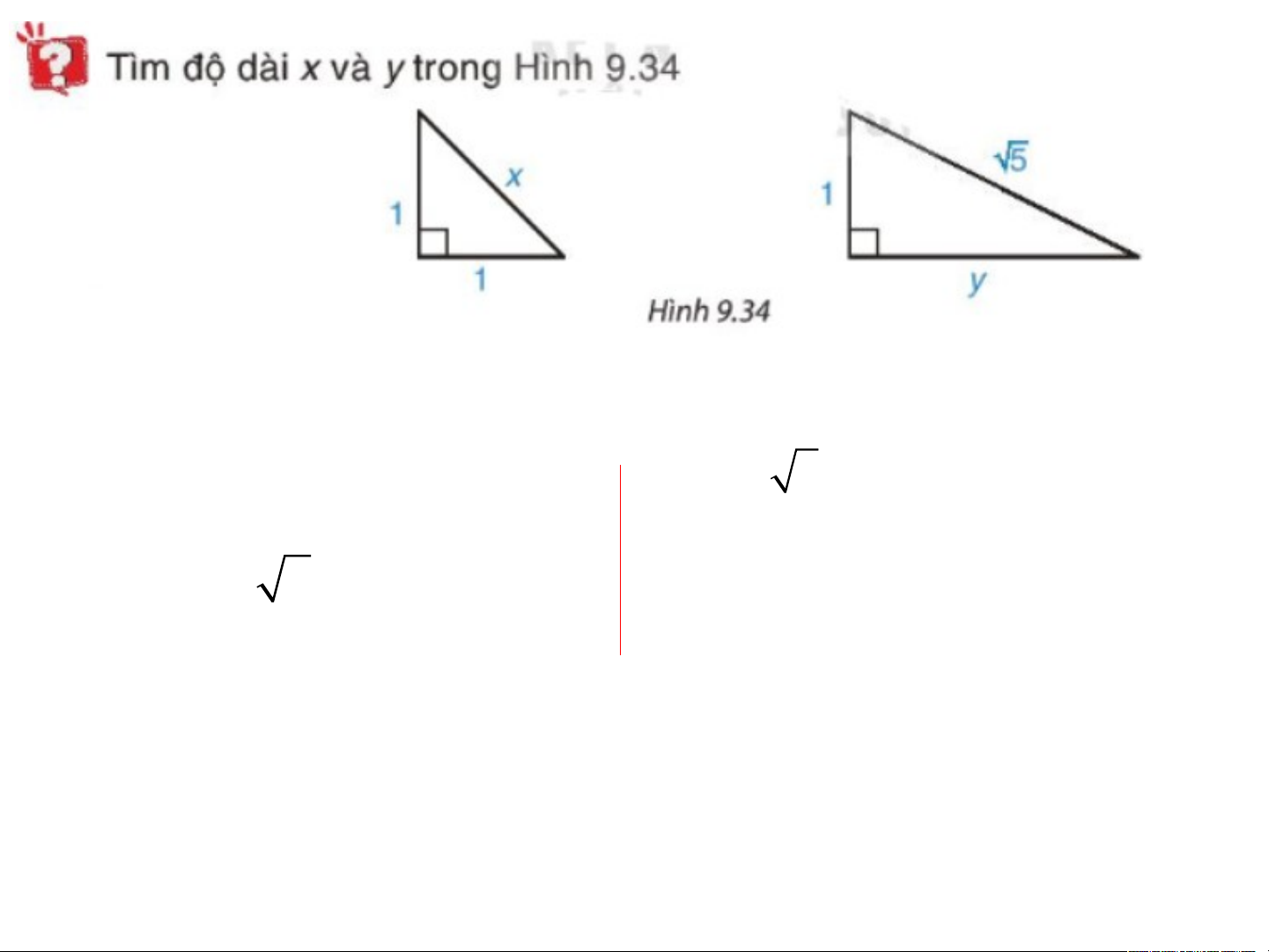
Theo định lí Pythagore trong tam giác vuông, ta có: 2 2 2 5 1 y 2 2 2 x 1 1 2 2 y 4 x 2 y 2
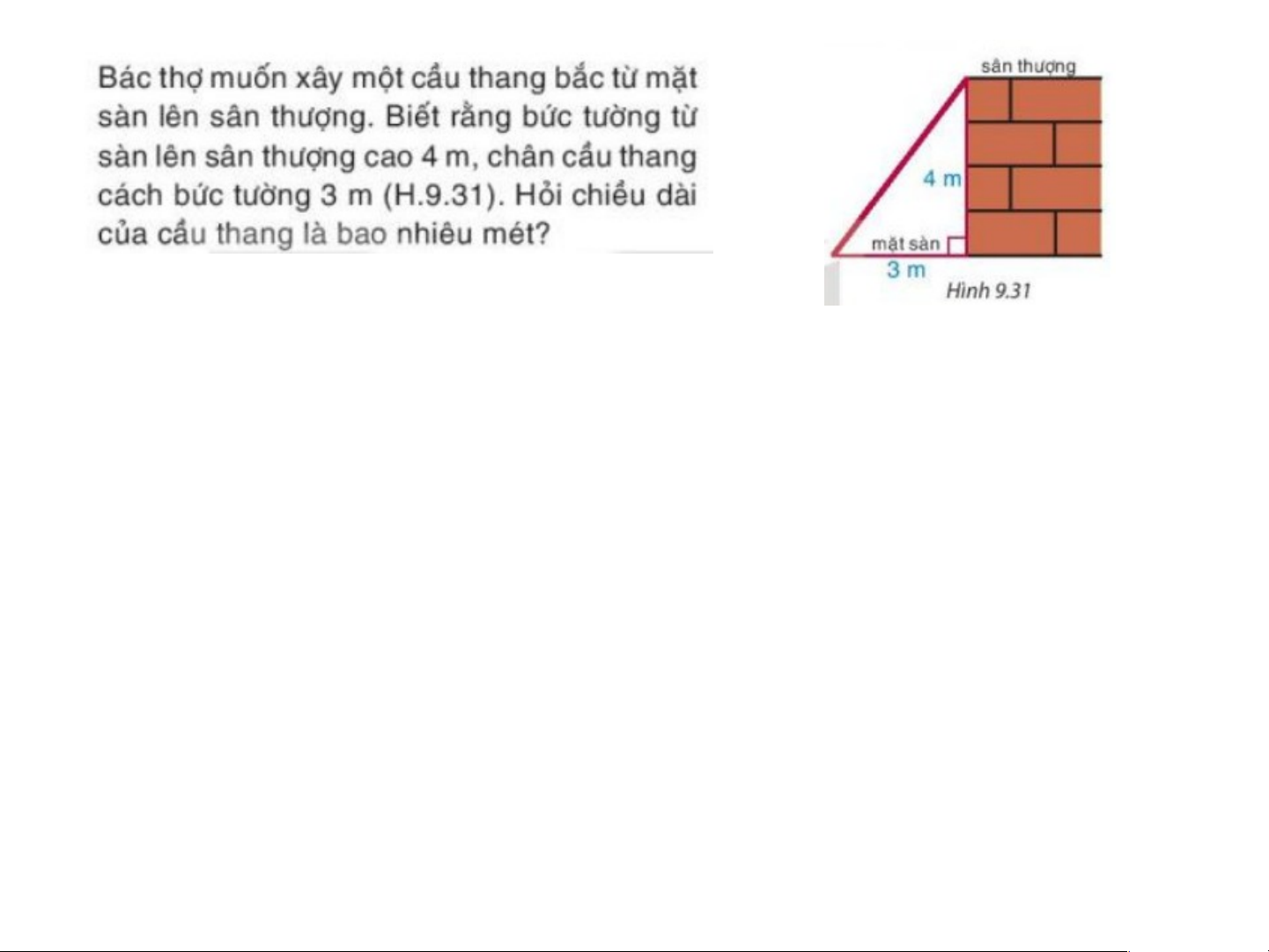
Giải: Gọi chiều dài của cầu thang là x. Theo định lí Pythagore
trong tam giác vuông, ta có: 2 2 2 x 3 4 2 x 9 16 2 x 25 x 5 (m)
Vậy chiều dài của cầu thang là 5m.
BÀI 35: ĐỊNH LÝ PYTHAGORE VÀ ỨNG DỤNG
1. ĐỊNH LÍ PYTHAGORE: • Định lí Pythagore:
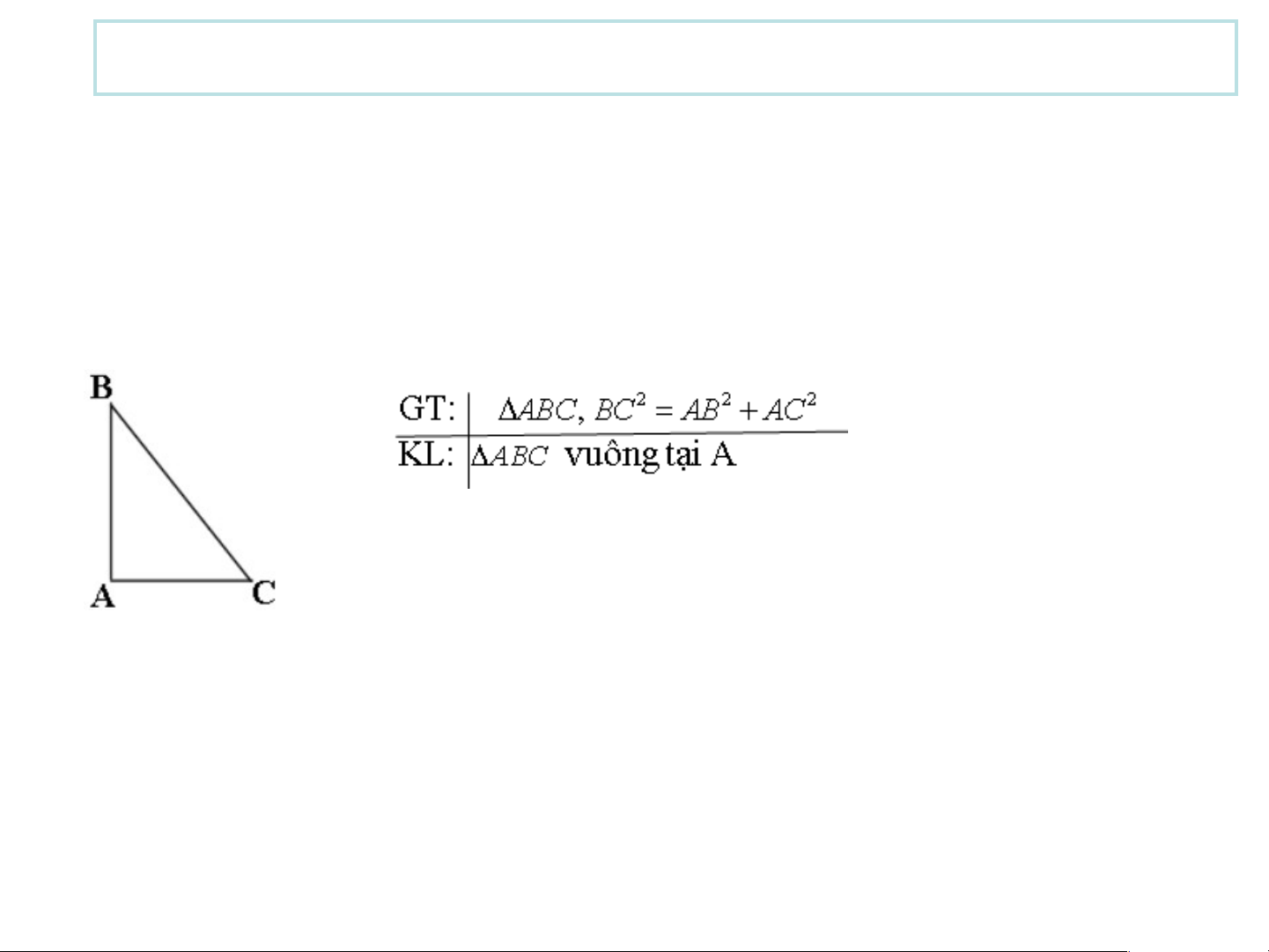
• Định lí Pythagore đảo:
Nếu tam giác có bình phương của một cạnh bằng tổng các bình phương
của hai cạnh kia thì tam giác đó là tam giác vuông.
BÀI 35: ĐỊNH LÝ PYTHAGORE VÀ ỨNG DỤNG
1. ĐỊNH LÍ PYTHAGORE:
BÀI 35: ĐỊNH LÝ PYTHAGORE VÀ ỨNG DỤNG
1. ĐỊNH LÍ PYTHAGORE:
BÀI 35: ĐỊNH LÝ PYTHAGORE VÀ ỨNG DỤNG
1. ĐỊNH LÍ PYTHAGORE:
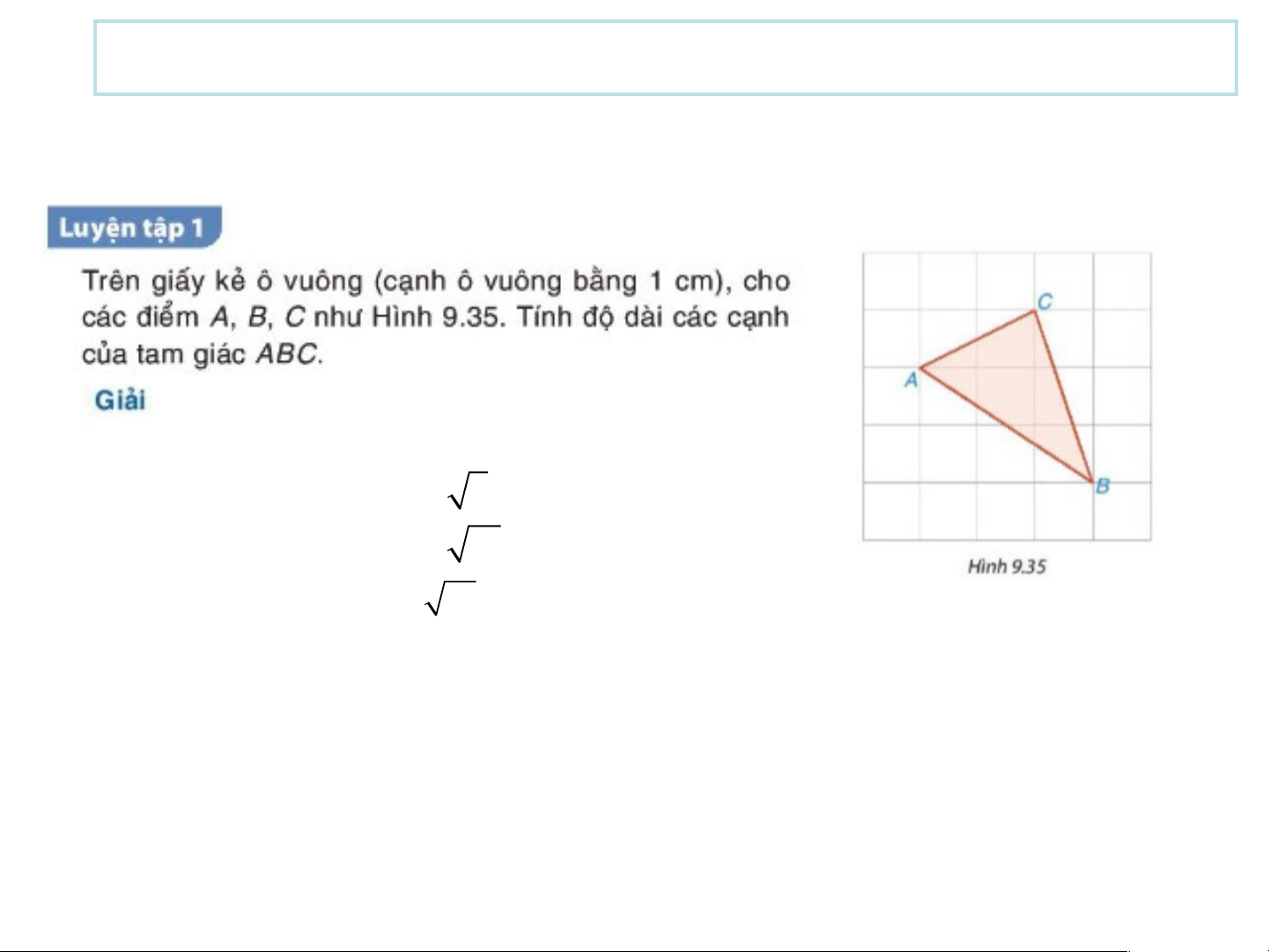
Theo định lí Pythagore trong tam giác vuông, ta có: 2 2 2 AC 1 2 5
AC 5cm 2 2 2 AB 3 2 13 AB 13cm 2 2 2 BC 1 3 1
0 BC 10cm
BÀI 35: ĐỊNH LÝ PYTHAGORE VÀ ỨNG DỤNG 1. ĐỊNH LÍ PYTHAGORE:
2. ỨNG DỤNG CỦA ĐỊNH LÍ PYTHAGORE:
Tính độ dài đoạn thẳng:
Bài toán 1:Cho tam giác ABC vuông tại A có AB = 6 cm, AC = 8 cm.
Hãy tính độ dài cạnh BC, đường cao AH và các đoạn thẳng BH, CH.
Nhận xét: Nếu tam giác ABC vuông tại A có đường cao có AH = h, các cạnh
BC = a, AC = b, AB = c thì h . a = b . c
BÀI 35: ĐỊNH LÝ PYTHAGORE VÀ ỨNG DỤNG 1. ĐỊNH LÍ PYTHAGORE:
2. ỨNG DỤNG CỦA ĐỊNH LÍ PYTHAGORE:
BÀI 35: ĐỊNH LÝ PYTHAGORE VÀ ỨNG DỤNG 1. ĐỊNH LÍ PYTHAGORE:
2. ỨNG DỤNG CỦA ĐỊNH LÍ PYTHAGORE:
BÀI 35: ĐỊNH LÝ PYTHAGORE VÀ ỨNG DỤNG 1. ĐỊNH LÍ PYTHAGORE:
2. ỨNG DỤNG CỦA ĐỊNH LÍ PYTHAGORE:
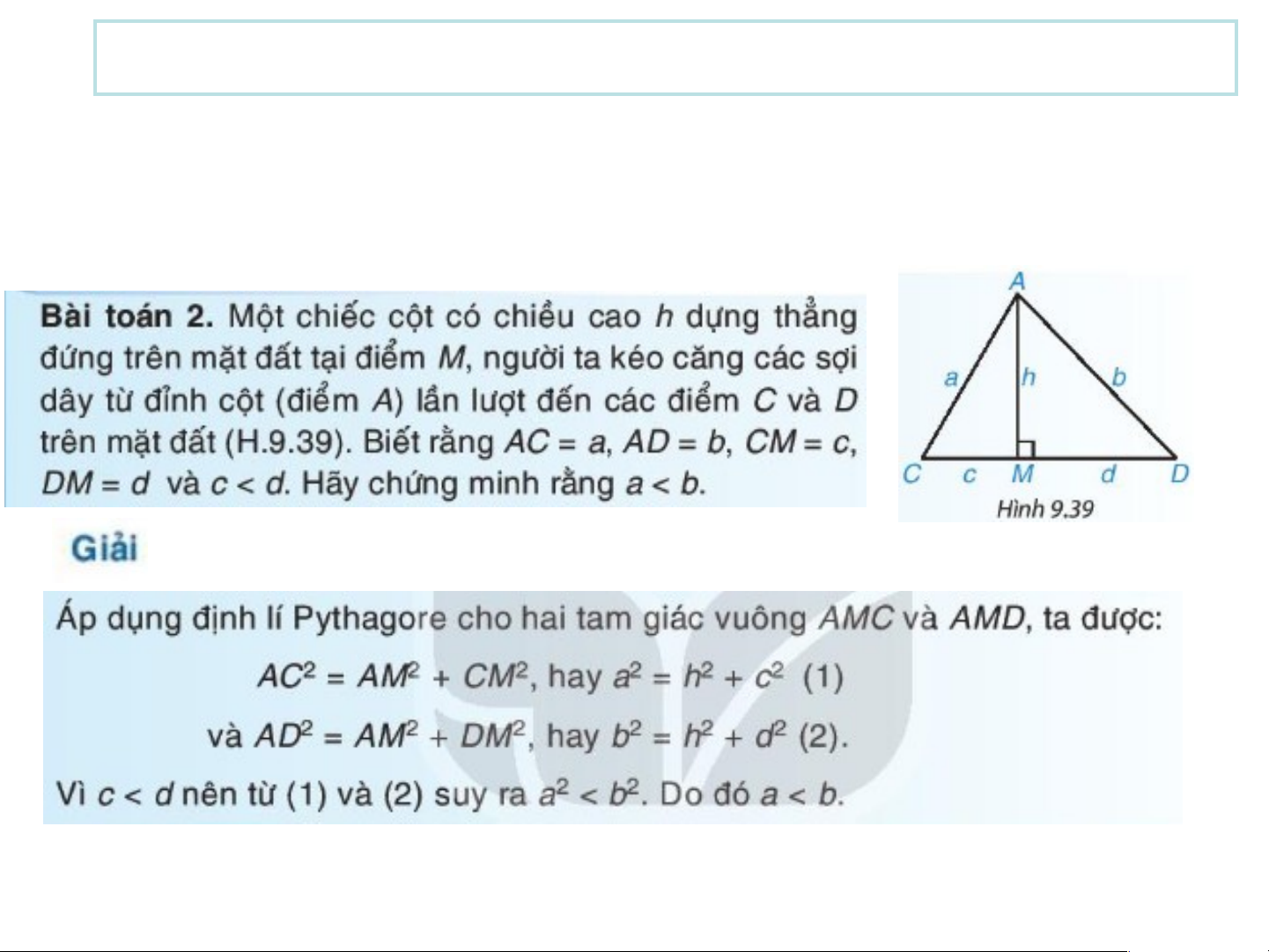
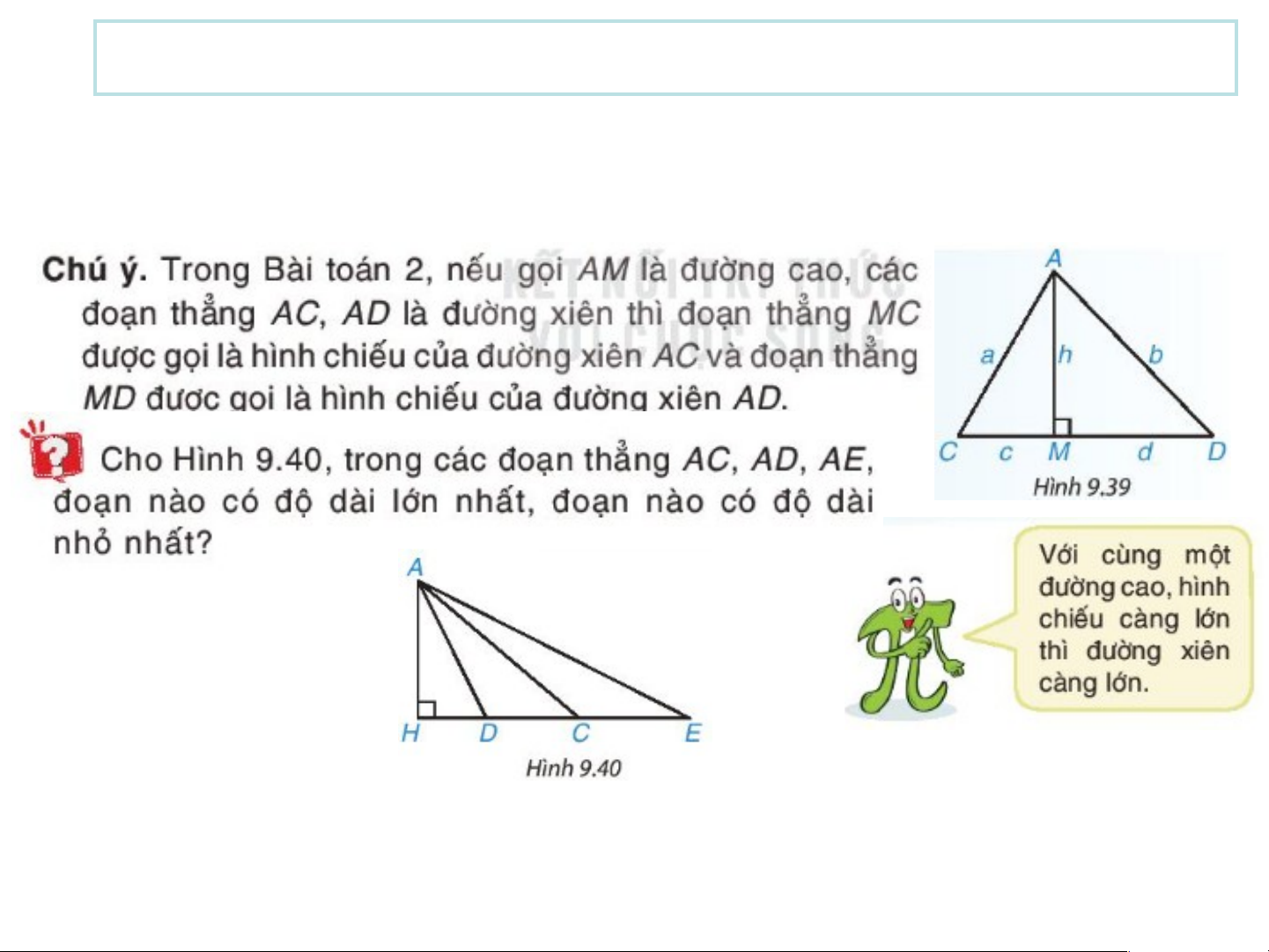
Chứng minh tính chất hình học:
BÀI 35: ĐỊNH LÝ PYTHAGORE VÀ ỨNG DỤNG 1. ĐỊNH LÍ PYTHAGORE:
2. ỨNG DỤNG CỦA ĐỊNH LÍ PYTHAGORE:
BÀI 35: ĐỊNH LÝ PYTHAGORE VÀ ỨNG DỤNG 1. ĐỊNH LÍ PYTHAGORE:
2. ỨNG DỤNG CỦA ĐỊNH LÍ PYTHAGORE:
BÀI 35: ĐỊNH LÝ PYTHAGORE VÀ ỨNG DỤNG 1. ĐỊNH LÍ PYTHAGORE:
2. ỨNG DỤNG CỦA ĐỊNH LÍ PYTHAGORE:
LUYỆN TẬP VÀ CỦNG CỐ
Bài tập 1: Cho tam giác MNP, MN = 6cm, NQ= 8cm. Tìm giá trị của x.
Một bạn học sinh làm như sau: M Xét tam giác MNP 6 cm x
có: MQ2 = MN2 + NQ2 (định lí Pythagore)
x2 = 62 + 82 = 36 + 64 = 100 Q N 8 x = 10 ( cm ) cm
Bạn đó làm đúng hay sai? A. Đúng B. Sai
Bài tập 2: Tìm x trên hình E 5 x D F 3
DEF vuông tại D => EF2 = DE2 + DF2 ( định lí Pythagore ) Hay 52 = x2 + 32 25 = x2 + 9 x2 = 25 – 9 =16 x 16 4
Bài tập 3: Cho tam giác nào ABC có AB = 13cm , AC = 12cm và
BC = 5cm. Hỏi tam giác ABC có là tam giác vuông không ? Ta có : C AB2 = 132 =169 AC2 = 122 = 144 BC2 = 52 = 25 A Do 169 = 144 + 25 B Nên AB2 = AC2 + BC2
Vậy tam giác ABC vuông tại C (theo
định lí Pythagore đảo)
Như vậy : Để nhận biết tam giác giác vuông hay không khi biết độ dài ba cạnh
Ta lấy bình phương cạnh có độ dài lớn nhất so sánh với tổng
bình phương độ dài hai cạnh còn lại TIỂU SỬ PYtHagoRE
• Pythagore sinh tr ưởng trong mét gia ®ình
quý téc ë đảo Xa-m«t, mét ®ảo giµu cã
ë ven biÓn £-giª thuéc ĐÞa Trung Hải
• Míi 16 tuæi, cËu bÐ Pythagore ®· næi tiÕng
vÒ trÝ th«ng minh kh¸c th ưêng. ĐÓ tìm
hiÓu nÒn khoa häc cña c¸c d©n téc,
Pythagore ®· dµnh nhiÒu năm ®Õn Ên
Đé, Ba-bi-lon, Ai CËp vµ ®· trë thµnh uyªn b¸c trong
hÇu hÕt c¸c lÜnh vùc quan träng: sè häc, hình häc,
thiªn văn, ®Þa lý, ©m nh¹c, y häc, triÕt häc.
• Mét trong những c«ng trình næi tiÕng cña «ng lµ hÖ
thøc giữa ®é dµi c¸c c¹nh cña mét tam gi¸c vu«ng,
®ã chÝnh lµ ®Þnh lý Pythagore mµ h«m nay chóng ta häc. TIỂU SỬ PYtHagoRE
* Pythagore sinh khoảng năm 580 đến 572 TCN -
mất khoảng năm 500 đến 490 TCN) là một nhà triết học người Hy Lạp .
* Pythagore đã chứng minh được rằng tổng 3 góc
của một tam giác bằng 180° và nổi tiếng nhất
nhờ định lý toán học mang tên ông. Ông cũng được
biết đến là "cha đẻ của số".
* Mới 16 tuổi, cậu bé Pythagore đã nổi tiếng về trí
thông minh khác thường. Cậu bé theo học nhà toán
học nổi tiếng Talét, và chính talét cũng phải kinh ngạc
về tài năng của cậu. Để tìm hiểu nền khoa học của
các dân tộc, Pythagore đã dành nhiều năm đến ấn
Độ, Babilon, Ai Cập và đã trở nên uyên bác trong hầu
hết các lĩnh vực quan trọng: số học, hình học, thiên
văn, địa lí, y học, triết học.
Cã thÓ em ch ưa biÕt Khi lµm nhµ tre, A nhµ gç, ng êi thî . méc ®ôc c¸c lç A,B,C cña trô chèng AB, phÇn . . . qu¸ giang AC, về B C kÌo BC sao cho AB, AC, BC tØ lÖ víi 3; 4; 5 thì khi dùng lªn, bao giê trô chèng còng vu«ng gãc víi qu¸ giang
Cã thÓ em ch ưa biÕt Khi x©y mãng nhµ, ®Ó kiÓm tra xem A C 4 hai phÇn mãng AB vµ AC cã vu«ng gãc víi nhau hay kh«ng, 3
ng êi thî cả thường lÊy AB=3dm, AC= B 4dm, råi ®o BC, nÕu BC = 5dm thì hai phÇn mãng AB
vµ AC vu«ng gãc víi nhau
TỔNG KẾT VÀ HƯỚNG DẪN TỰ HỌC
1) Lí thuyết: Định lí Pythagore, Định lí Pythagore đảo
2) BTVN: 9.17 đến 9.20 SGK/97
Document Outline
- BÀI 35: ĐỊNH LÝ PYTHAGORE VÀ ỨNG DỤNG
- PowerPoint Presentation
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- TIỂU SỬ PYtHagoRE
- Slide 25
- Cã thÓ em chưa biÕt
- Slide 27
- Slide 28





