30 trang
93 lượt tải
Bài 4. Hai mặt phẳng vuông góc | Toán 11
186
1. Định nghĩa Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó. Nếu hai mặt phẳng song song hoặc trùng nhau thì ta nói góc giữa hai mặt phẳng đó bằng 0 . 2. Diện tích hình chiếu của một đa giác Cho đa giác H nằm trong mặt phẳng có diện tích S và đa giác H là hình chiếu vuông góc của H trên mặt phẳng . Khi đó diện tích S của H được tính theo công thức: S S cos Với là góc giữa. Tài liệu được sưu tầm giúp bạn tham khảo, ôn tập và đạt kết quả cao trong kì thi sắp tới. Mời bạn đọc đón xem!
Chủ đề: Chương 7: Quan hệ vuông góc trong không gian (KNTT) 74 tài liệu
Môn: Toán 11 3.5 K tài liệu
Tác giả:
Danh sách Quiz
TÀI LIỆU TỰ HỌC TOÁN
11
I. LÝ THUYẾT TRỌNG TÂM
I. GÓC GIỮA HAI MẶT PHẲNG
1. Định nghĩa
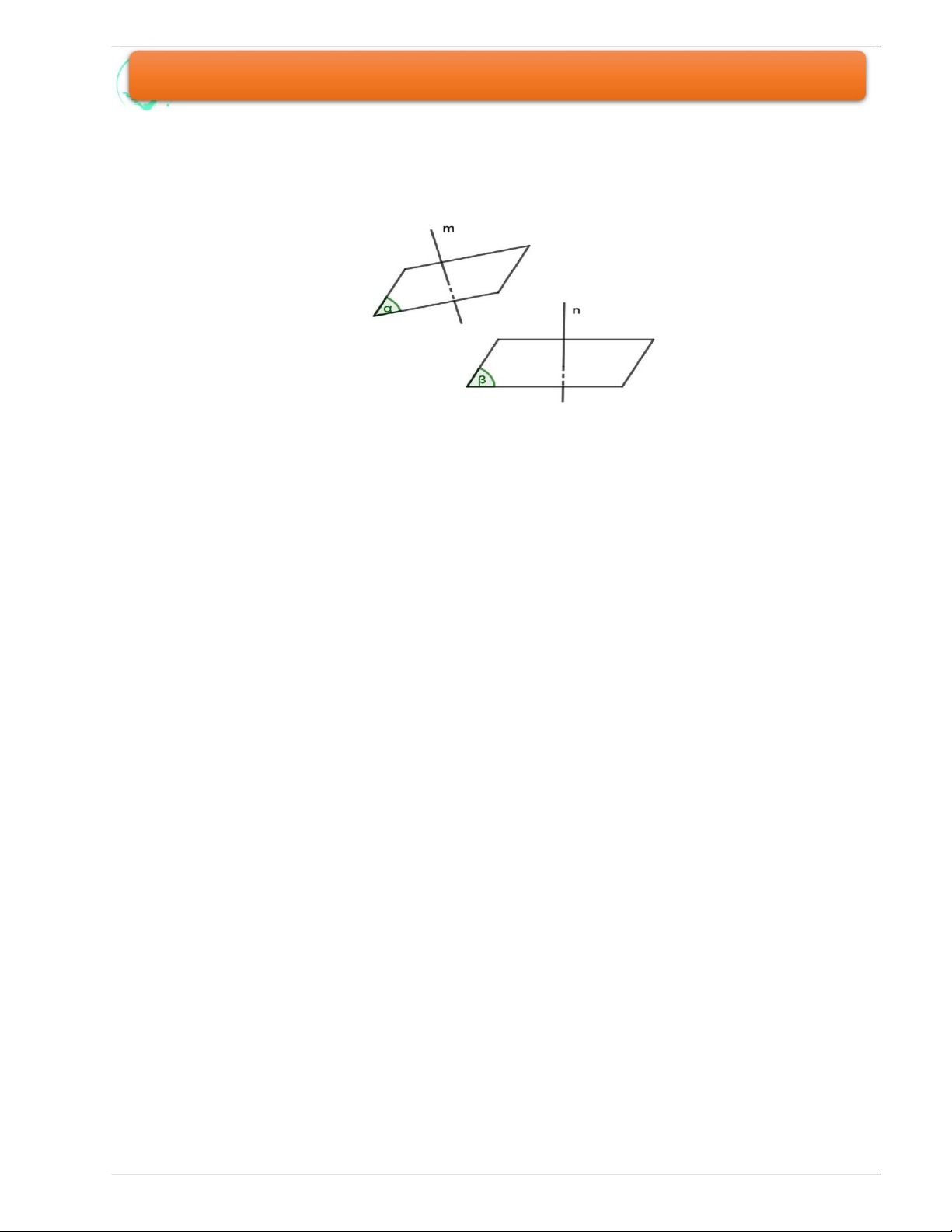
Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó.
Nếu hai mặt phẳng song song hoặc trùng nhau thì ta nói góc giữa hai mặt phẳng đó bằng 0 .
2. Diện tích hình chiếu của một đa giác
Cho đa giác H nằm trong mặt phẳng
có diện tích
S
và đa giác H
là hình chiếu vuông góc
của H trên mặt phẳng
. Khi đó diện tích
S
của H
được tính theo công thức:
S
S cos
Với
là góc giữa
và
.
II. HAI MẶT PHẲNG VUÔNG GÓC
1. Định nghĩa
Hai mặt phẳng gọi là vuông góc với nhau nếu góc giữa hai mặt phẳng đó bằng
90 .
Kí hiệu
.
2. Các định lí
Định lí 1 (điều kiện để hai mặt phẳng vuông góc)
Điều kiện cần và đủ để hai mặt phẳng vuông góc với nhau là mặt phẳng này chứa một đường
thẳng vuông góc với mặt phẳng kia.
Định lí 2 (tính chất của hai mặt phẳng vuông góc)
Nếu hai mặt phẳng vuông góc với nhau thì bất cứ đường thẳng nào nằm trong mặt phẳng này và
vuông góc với giao tuyến thì vuông góc với mặt phẳng kia.
Hệ quả 1
Cho hai mặt phẳng
và
vuông góc với nhau. Nếu từ một điểm thuộc mặt phẳng
ta
dựng
một đường thẳng vuông góc với mặt phẳng
thì đường thẳng này nằm trong mặt phẳng
.
Hệ quả 2
Nếu hai mặt phẳng cắt nhau và cùng vuông góc với mặt phẳng thứ ba thì giao tuyến của chúng
vuông góc với mặt phẳng thứ ba đó.
Hệ quả 3
Bài 4. HAI M T PH NG VUÔNG GÓCẶ Ẳ
Chương 3. QUAN HỆ VUÔNG GÓC
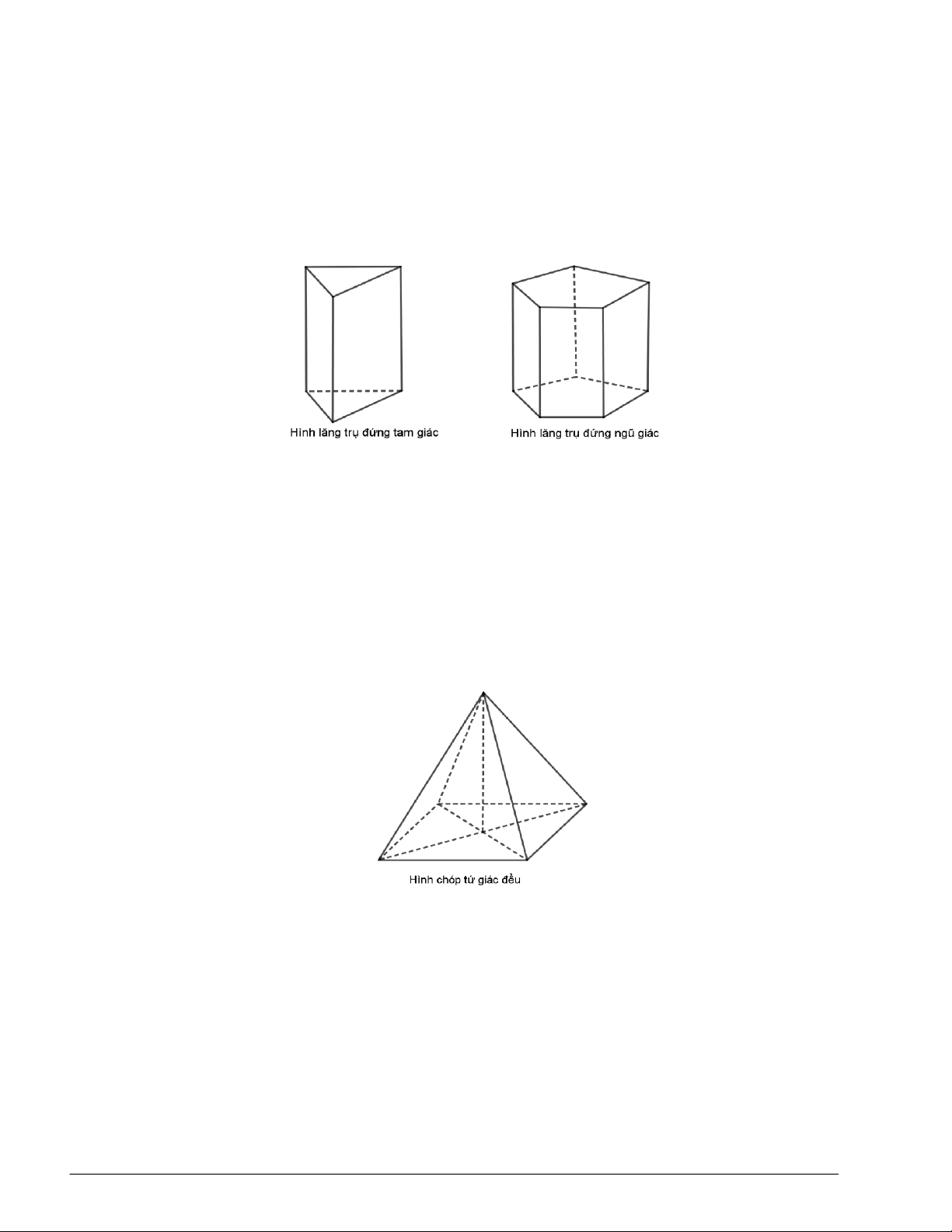
III. HÌNH LĂNG TRỤ ĐỨNG, HÌNH HỘP CHỮ NHẬT, HÌNH LẬP PHƯƠNG
1. Định nghĩa
Hình lăng trụ đứng là hình lăng trụ có các cạnh bên vuông góc với các mặt đáy. Độ dài cạnh bên
được gọi là chiều cao của hình lăng trụ đứng.
Các mặt bên của hình lăng trụ đứng luôn luôn vuông góc với mặt phẳng đáy và là những hình chữ
nhật.
Hình lăng trụ đứng có đáy là tam giác, tứ giác,... được gọi là hình lăng trụ đứng tam giác, hình
lăng trụ đứng tứ giác,...
2. Một số lăng trụ đặc biệt
● Hình lăng trụ đứng có đáy là đa giác đều được gọi là hình lăng trụ đều.
● Hình lăng trụ đứng có đáy là hình bình hành được gọi là hình hộp đứng.
● Hình lăng trụ đứng có đáy là hình chữ nhật được gọi là hình hộp chữ nhật.
● Hình lăng trụ đứng có đáy là hình vuông và các mặt bên đều là hình vuông được gọi là hình lập
phương.
III. HÌNH CHÓP ĐỀU VÀ HÌNH CHÓP CỤT ĐỀU
1. Hình chóp đều
Định nghĩa. Một hình chóp được gọi là hình chóp đều nếu đáy của nó là đa giác đều và các cạnh
bên bằng nhau.
Tính chất.
Một hình chóp là hình chóp đều khi và chỉ khi đáy của nó là đa giác đều
và chân đường cao của hình chóp đi qua tâm đường tròn ngoại tiếp của đa giác đáy.
Hình chóp đều có các mặt bên là những tam giác cân bằng nhau. Các mặt
bên tạo với mặt đáy các góc bằng nhau. Các cạnh bên tạo với mặt đáy các góc bằng nhau.
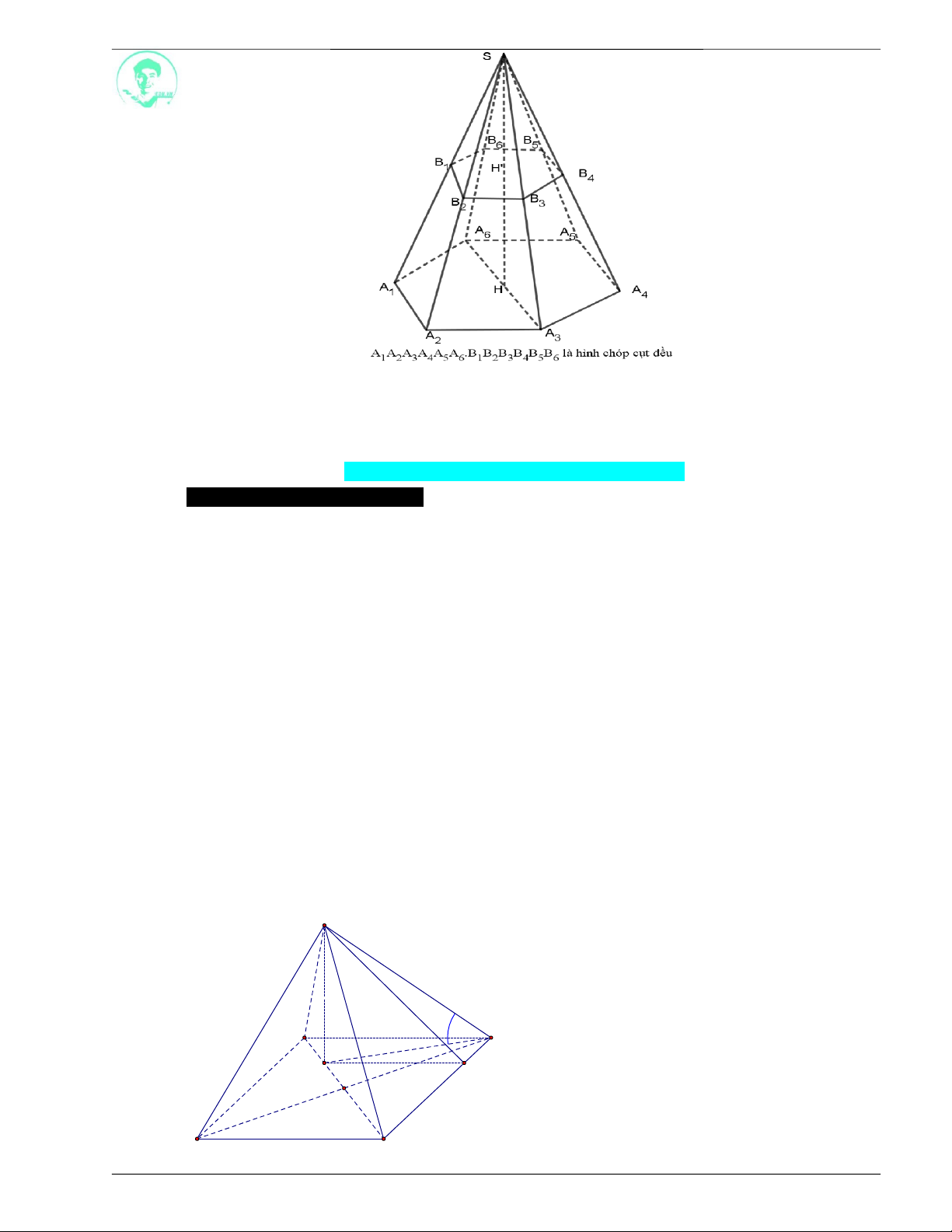
2. Hình chóp cụt đều
Phần của hình chóp đều nằm giữa đáy và một thiết diện song song với đáy cắt các cạnh bên của
hình chóp đều được gọi là hình chóp cụt đều.
TÀI LIỆU TỰ HỌC TOÁN
11
Các mặt bên của hình chóp cụt đều là những hình thang cân và các cạnh bên của hình chóp cụt
đều có độ dài bằng nhau.
Hai đáy của hình chóp cụt đều là hai đa giác đều và đồng dạng với nhau.
Đoạn nối tâm của hai đáy được gọi là đường cao của hình chóp cụt đều.
PHẦN 1. CÁC DẠNG TOÁN THƯỜNG GẶP
Dạng 1. Góc giữa hai mặt phẳng
Phương pháp giải
Để xác định góc giữa hai mặt phẳng
P
và
Q
+ Xác định giao tuyến
P
Q
ta thực hiện như sau:
+ Tìm mặt phẳng trung gian
R
mà
R
, (Đây là bước quan trọng nhất)
+ Xác định các đoạn giao tuyến thành phần:
a
R
P
P
;
Q
a;b
b
R
Q
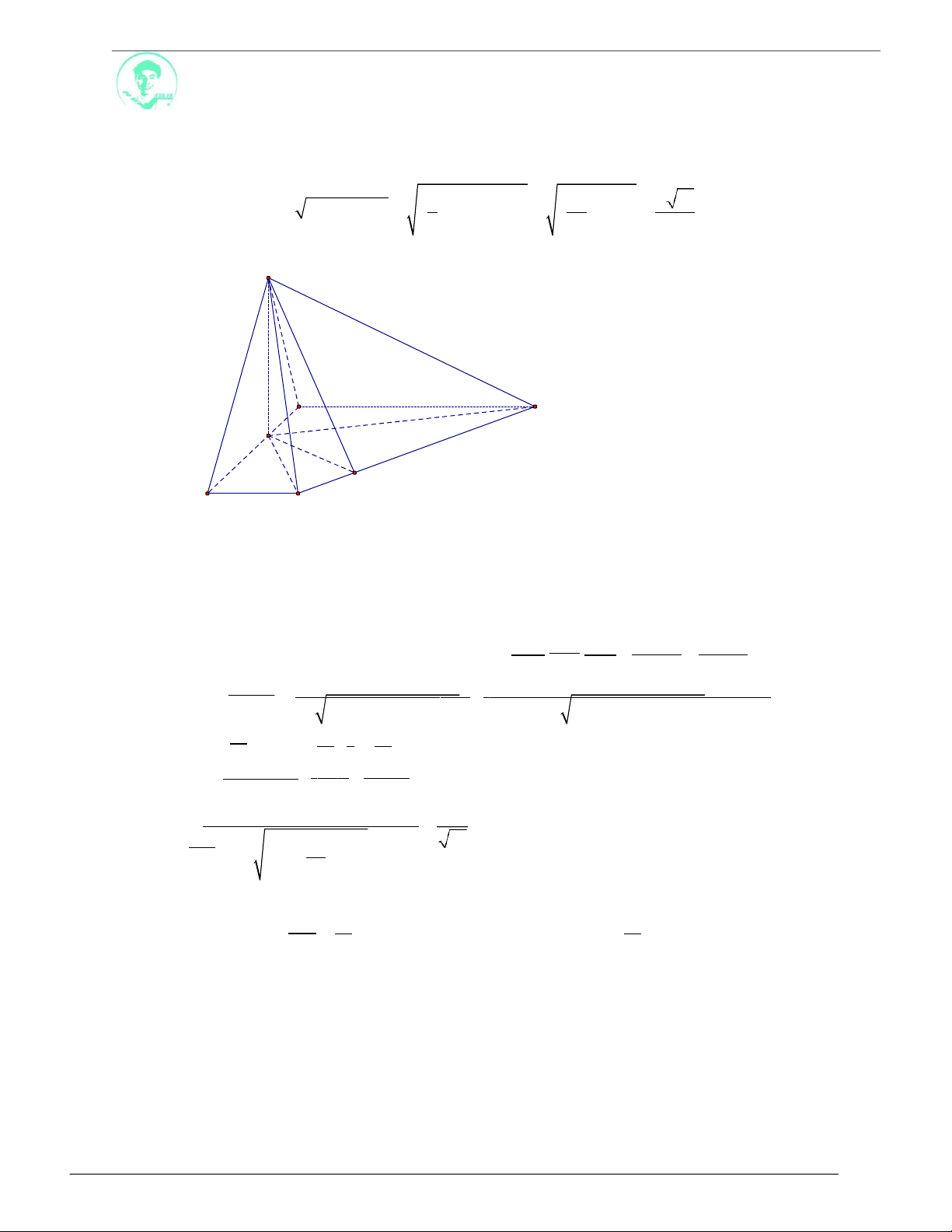
Câu 1. Cho hình chóp S.ABCD
có đáy
ABCD là hình vuông cạnh 2a , O là tâm đáy. Hình chiếu vuông
góc của S xuống
ABCD
a)
SCD
và
ABCD
.
là trung điểm
H
của OA , biết
SD; ABCD
60 . Tính góc giữa
b)
MBC
và
ABCD
, với M là trung điểm SA .
Lời giải
a)
S
D
B C
A
60°
H
I
O
3
SHD : SH HD. tan 60
a
10
.
a
30
2 2
a) Ta có:
SCD
ABCD
CD
HI
CD
Trong mặt phẳng
ABCD
, kẻ HI
AD, HI CD I
HI
3
.2a
3a
4 2
Lại có: SH CD CD
SHI
SCD
,
ABCD
SI , HI
S
IH
(do
S
IH 90 )
Xét SHI : tan
S
IH
SH
30
SCD, ABCD
S
IH
arctan
30
.
HI 3 3
b)
S
B
D C
Ta có:
MBC
ABCD
BC
Gọi E là trung điểm
AH
EM
ABCD
EM
1
SH
a 60
.
2 4
EK
BC
Trong mặt phẳng
ABCD
, kẻ EK
AB, EK BC K
7 7 7a
EK
AB .2a
8 8 4
Lại có:
EM BC BC
MEK
MBC
,
ABCD
MK , EK
M
KE
Xét MEK : tan
M
KE
EM
60
MBC
, ABCD
M
KE
arctan
60
.
EK 7 7
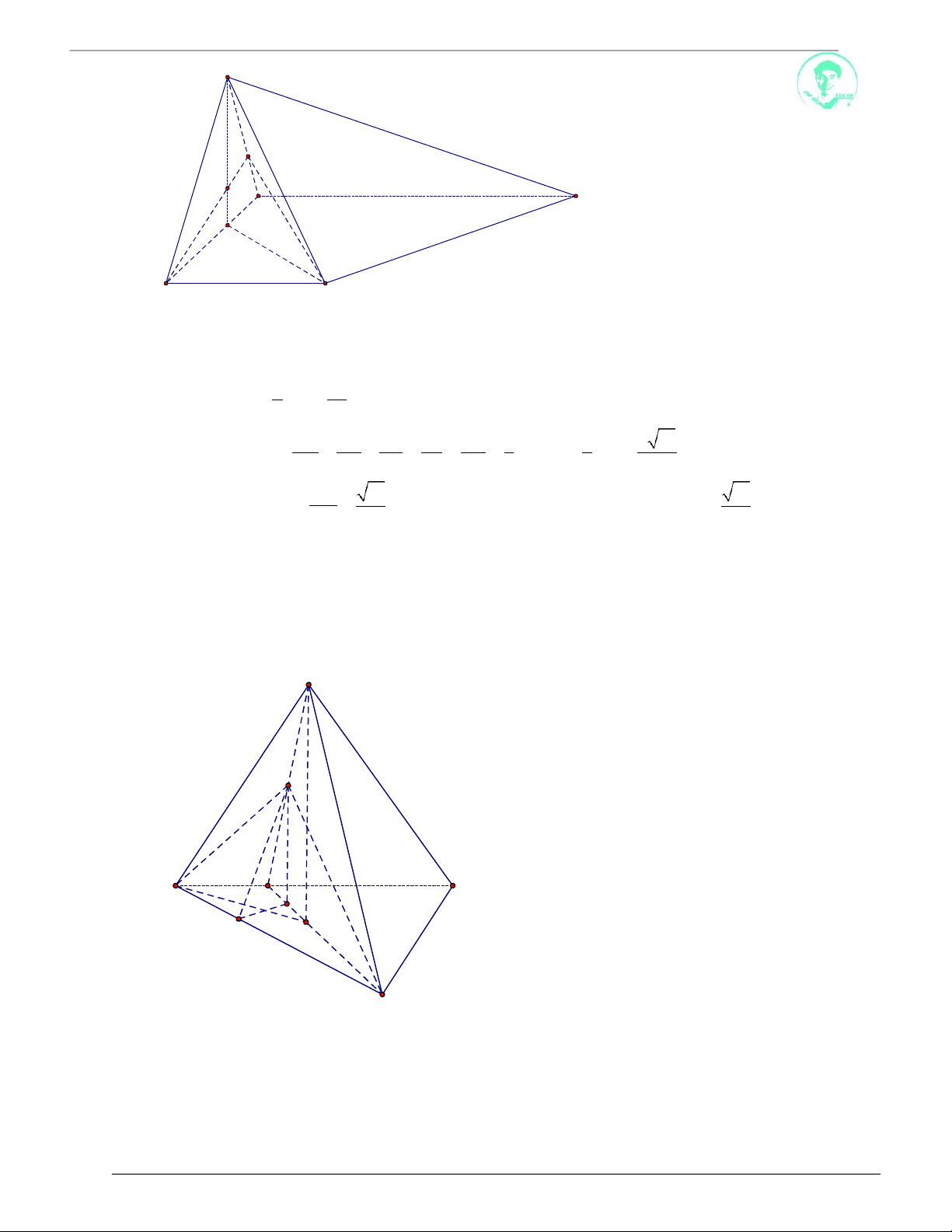
Câu 2. Cho hình chóp
M
A
E
K
H
O
Ta có: SH
ABCD
SD,
ABCD
SD, HD
S
DH
60
OHD
:
HO
1
AC
a
2 ,
OD
a
2
HD
HO
2
OD
2
a
2
2
4 2
2
a
2 2
a
10
2
TÀI LIỆU TỰ HỌC TOÁN
11
S.ABCD có đáy
ABCD là hình thang
vuông tại
A, B với AB BC a ;
AD
5a
.
2
Hình chiếu vuông góc của S xuống
ABCD
SC; ABCD
45 . Tính góc giữa
là điểm H thuộc đoạn AB với
BH 2AH . Biết
2
a
2
3
a
2
AB
2
AD
BC
2 AB
2
AD
BC
2
a
2
a
5
a
2
2
13
Lời giải
Ta có: SH ABCD
SC, ABCD
SC, HC S
CH 45
SH HC
a)
S
3
A
D
H
K
B C
Ta có:
SCD
ABCD
CD
Trong mặt phẳng
ABCD
, kẻ HK
CD
Lại có: SH CD CD SHK
SCD, ABCD
SK , HK S
KH
Xét SHK :
2
AD
BC
AB
AD . AH
BH . BC
2S
2
S
S
S
2 2 2
HK
SHK
CD
ABCD AHD BHC
5a
a
a
5a
.
a 2a
.a
2
2
2
3
3
2 2 2
4a
tan S
KH
SH
HK
13
SCD
,
ABCD
S
KH
arctan
13
12 12
b)
2
3
AB
BC
2
2
BH
2
BC
2
a 13
SCD
và
ABCD
.
IBC
và
ABCD
, v i ớ
I
thu c o n ộ đ ạ
SA
sao cho
SI
2
IA
.
N
I
J
E
H
TÀI LIỆU TỰ HỌC TOÁN
11
B C
Ta có:
IBC
ABCD
BC
Lại có:
BC
SBA
IBC
,
ABCD
BI , BA
I
BA
Xét SAB : BH
2
AB
2a
3 3
Gọi P IB SH
HP
IP
HI
IA
HA
1
HP
1
SH
a 13
SP BP SB SA BA 3 4 12
Xét BHP : tan
H
BP
HP
13
tan
ABI
IBC , ABCD
A
BI
arctan
13
.
BH 8 8
Câu 3. Cho hình chóp S.ABC có đáy là tam giác đều cạnh 2a , I là điểm trên cạnh BC
s
a
o cho
C
I
2BI .
Hình chiếu vuông góc của S lên mặt phẳng
ABC
là điểm H thuộc AI với HA
2HI
0 , biết
SB;
ABC
60 . Tính góc giữa hai mặt phẳng NAB và ABC với N
là trung điểm SI .
Lời giải
S
B
C
A
+ Gọi
J
là trung điểm
IH NJ / / SH
, mà
SH
ABC
NJ
ABC
NJ AB
Trong mặt phẳng
ABC
, kẻ
JE AB
E AB
AB
NEJ
Lại có: AB
NAB
ABC
,
NAB
NEJ
NE,
ABC
NEJ
EJ
NAB
,
ABC
NE,
EJ
N
EJ
S
I
P
A
D
H
+ SH
ABC
SB,
ABC
SB, HB
S
BH 60
+ Ta có:
AB
BC
CA
2
a
,
BI
BC
2
a
,
NJ
SH
3 3
2
2a 19
3
Q
H
P
A
E
TÀI LIỆU TỰ HỌC TOÁN
11
2
HA 2HI 0 3BH BA 2BI 9BH
2
BA
2
4BI
2
4BA.BI
2 2 2
2
4a
2
2a
76a
2
9BH BA
4BI 4BA.BI.cos ABI 4a
4. 4.2a. .cos 60
9 3 9
BH
76a
2
BH SH BH. tan
60
.
81 9 9 9
NJ
Lại có:
S
ABJ
AJ
5
;
S
ABI
BI
1
S
ABJ
5
S
ABI AI 6
S
ABC
BC
3
S
ABC
18
5 5 4a
2
3 5a
2
3 JE.AB 2.5a
2
3 2.5a
2
3 5a
3
S
ABJ
18
.S
ABC
18
.
4
18
2
JE
18. AB
18.2
a 18
+ Xét tam giác NJE vuông tại J
tan
N
EJ
NJ
2a 57
9
4 19
JE
NAB
,
ABC
N
EJ arctan
4 19
.
5
5a
3
5
18
Câu 4. Cho hình chóp S.ABCD có SA
ABCD
và SA
a 2 , đáy ABCD là hình thang vuông tại
A
và
D với AB 2a, AD DC a . Tính góc giữa các cặp mặt phẳng sau:
a)
SBC
và
ABC
.
b)
SAB
và
SBC
.
c)
*
SBC
và
SCD
.
S
Lời giải
B
D C
a)
Ta có:
SBC
ABC
BC
2a 19 2a 57
2a 57
9
Gọi E là trung điểm AB AECD là hình vuông và BCDE là hình bình hành
AC BC , mà
SA BC BC
SAC
SBC
,
ABC
S
CA
a 2.a
a
2 2 2
a
2
a 2.a
SA
2
AB
2
3
CD. AD
2
SA
2
CD
2
SD
2
a. a
2
a a
2
a
2
a
2 2
2 2
2
3
7
TÀI LIỆU TỰ HỌC TOÁN
11
Xét tam giác SAC vuông tại A , có
b)
Ta có:
SAB
SBC
SB
AC a
2
SA nên
SBC , ABC
S
CA 45 .
Ta có:
CE
AB
CE
SB , kẻ EH
SB
H
SB
SB
CHE
CE SA
Do đó:
SAB
,
SBC
HE, HC
E
HC
Tam giác EHC vuông tại E , có
CE a, HE
SA.BE
a
3
SB 3
tan E
HC
CE
EH
SAB, SBC
E
HC 60.
c)
Ta có:
SBC
SCD
SC
Kẻ
DP SC
P SC
, PQ SC
Q SB
SC
DPQ
SBC
,
SCD
DP, PQ
Ta chứng minh được:
PQ / / BC
PQ / /OD
PQ
1
BC
PQ OD
a
2
DP,
PQ
DP,
DO
2
2
DP
CD.SD
a
3
SC 2
Lại có:
OD
SA
OD AC
OD
SAC
OD
OP
Tam giác DOP vuông tại O
cos O
DP
OD
6
DP 3
Vậy
SBC
,
SCD
arccos
6
.
3
Câu 5. Cho tứ diện ABCD có ABC là tam giác đều, DBC
Tính góc giữa
ABC
và
DBC
.
vuông cân tại D . Biết
AB 2a ,
AD a .
Lời giải
2
a
3 .
a
DE BC
A
Ta có:
ABC
BCD
BC
Gọi E là trung điểm BC
AE
BC
ADE
BC
ABC
,
BCD
AE, DE
Tam giác
ADE
có AE
2a
3
a
3, DE
BC
2a
a, AD a
2 2 2
2 2 2
a 3
2
a
2
a 7
2
Do đó: cos
AED
AE
DE
AD
3
AED 150
2 AE.DE 2
Vậy
ABC
,
BCD
AE, DE
180 150 30.
Câu 6. Cho hình chóp
S.ABC , có đáy
ABC
là tam giác vuông cân với
BA
BC
a; SA
ABC
và
SA a . Gọi E, F lần lượt là trung điểm của các cạnh AB và AC .
a)
Tính góc giữa hai mặt phẳng
SAC
và
SBC
.
b)
Tính góc giữa hai mặt phẳng
SEF
và
SBC
.
Lời giải
x
C
B
a)
Ta có:
SAC
ABC
AC
7
S
H
A
F
E
I
K
D
a 7
B
E
C
2a
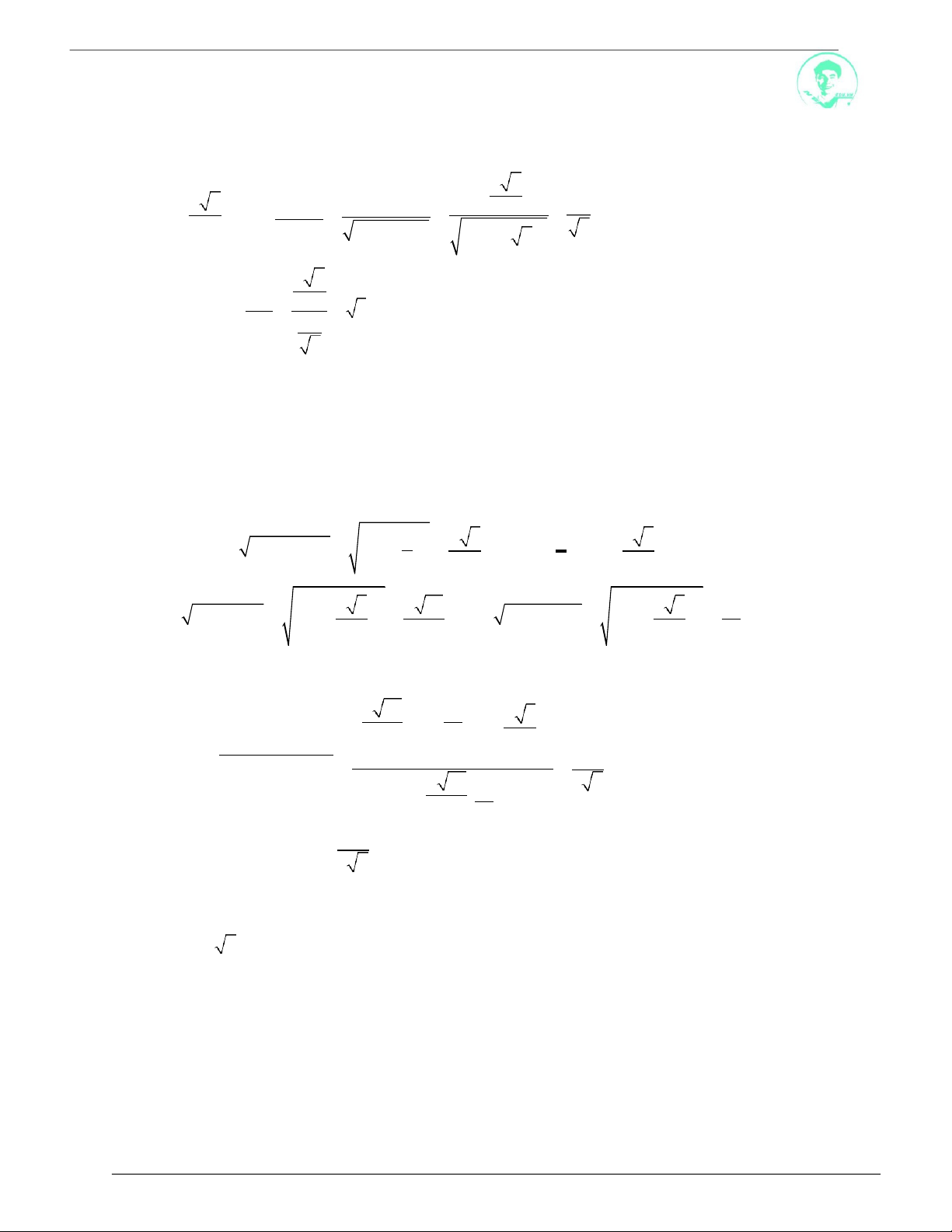
SA
2
FC
2
a
2
a
2 2
a
2
a
2
5
2
2
3 7
TÀI LIỆU TỰ HỌC TOÁN
11
Kẻ
FH SC
H SC
SC
BHF
SAC
, ABC
HF
,
HB Tam giác BHF vuông tại F có:
BF
a
2
, FH
SA.FC
2 SC
SA
.FC
a.
a 2
2
a
a
2
tan F
HB
BF
2
HF a
Vậy
SAC
,
ABC
HF , HB
F
HB
60 .
b) Vì
EF / / BC
SEF
SBC
Sx / / BC / / EF
Gọi I , K lần lượt là trung điểm EF, BC
Sx
SIK
,
SIK
SEF
SI ,
SIK
SBC
SK
SEF
,
SBC
SI
,
SK
1
Ta có:
AK , AI IK
AK
2 2 4
3a
SI
4
, SK
2
Xét tam giác SIK có:
a
21
2
3a
2
a
5
2
2 2 2
4
2
4
cos I
SK
SI
SK
IK
13
.
2SI.SK
Vậy
cos
SEF
,
SBC
13
.
2.
a
21
.
3a
4 2
Câu 7. Cho hình chóp
S.ABCD
có
SA
ABCD
có đáy
ABCD là hình vuông cạnh 2a ;
SA
ABCD
và SA a . Tính góc giữa
a)
SCD
và
ABCD
.
b)
SBD
và
ABCD
.
c)
SDI
và
ABCD
, với I là trung điểm BC .
Lời giải
Gọi F là trung điểm AC
BF
AC
BF
SAC
BF
SC
BF
SA
6
3
a
2
a
2
2
AB
2
BK
2
a 5a 5
a
2
a
2
5
4
SA
2
AI
2
SA
2
AK
2
a 21
3 7
6
2
2
2 2
3
AD
2
DJ
2
3
BD SA
DI SA
a) Ta có:
CD
SA
CD AD
CD
SAD
ABCD
,
SCD
SD, SA
S
DA
tan S
DA
SA
SD
1
ABCD, SCD
S
DA
arctan
1
.
b) Ta có:
BD
AC
BD
SAC
ABCD
,
SBD
SO,
AC
S
OA
(do
S
OA
90
)
tan
S
OA
SA
ABCD, SBD
S
OA arctan .
SD
c) Gọi J là trung điểm CD .
Ta có:
DI
JA
BD
SJA
ABCD
,
SDJ
SJ , JA
S
JA
(do
S
OA 90 )
tan
S
JA
SA
JA
SA
1
ABCD, SDJ
S
JA
arctan
1
.
Câu 8. Cho hình chóp S.ABC
có đáy là tam giác đều cạnh
a 2 , I là trung
đ
iểm
c
ủ
a B
C . Hình
chiếu
vuông góc của S lên mặt phẳng
ABC
Tính góc giữa
a) BC và SA .
b)
SBC
và
ABC
.
c)
SAB
và
ABC
.
là điểm H thuộc AI với IH 2 AH 0 và SH 2a .
Lời giải
TÀI LIỆU TỰ HỌC TOÁN
11
a) Dựng hình thoi ABCD
BC
/ /
AD
SAD
BC, SA
S
AD
1a
Do 2
AH
AI
AHIH0
6
SA
SH
2
AH
2
a
6
SH
2
HD
2
7
SH
2
HK
2
73
3 6 6
Xét AHD : HD
a SD a
Nhận
xét: SA
2
AD
2
SD
2
tam giác SAD vuông tại A S
AD 90
Vậy
BC;
SA
90
.
b)
Ta có:
SBC
ABC
BC
Nhận xét: tam giác SBC cân tại A SI BC
Mà AI
BC
BC
SAI
Suy
ra:
SBC , ABC
SI , AI S
IA
Tính được:
AI
a 6
; HI
a
6
SI
a
42
2 3 3
SI
2
IA
2
SA
2
1
Xét SAI : cos SIA SIA 67,8
2SI.IA
Suy ra:
SBC
,
ABC
67,8 .
c)
Ta có:
SAB
ABC
AB
Từ H dựng HK
AB
AB
SHK
SAB
;
ABC
S
KH
Ta dễ dàng chứng minh được: HK
1
BI
a
2
; SK
a 146
3 6 6
SK
2
KH
2
SH
2
1
Xét SHK : cos SKH SKH 83, 3
2SK.KH
Suy
ra:
SAB,
ABC
S
KH
83, 3 .
Vậy MN
SAM
SMN
SAM
.
Câu 9. Cho lăng trụ ABC.A
B
C
có đáy là tam giác đều cạnh a , AA
vuông góc với đáy và AA
a . Tính
góc giữa
ABC
và
BCA
.
Lời giải
AD
2
AH
2
13
6
37
6
3
7
TÀI LIỆU TỰ HỌC TOÁN
11
BT KT
a
B
Ta có giao tuyến hai mặt phẳng là đoạn BK , với K là tâm hình vuông A
C
CA .
Gọi T là trung điểm của AC thì
BT
AC
KTB
ABC
.
Từ T kẻ TM
vuông góc với KB thì
AC
BK
BK
AMC
ABC
,
A
BC
A
MC
TM BK
.
180
0
A
MC
Ta có KT
a
; BT
a
2 2
3
BK a TM
KT .BT
a
BK
3
MC
a 7
.
4 4
a
3
Dẫn đến cosT
MC
MT
4
cos A
MC 2 cos
2
T
MC 1
1
.
MC
a
7
7
4
A
MC 98
0
ABC
, A
BC
82
0
.
Dạng 2. Chứng minh vuông góc
Phương pháp:
Để chứng minh hai mặt phẳng
và
vuông góc với nhau ta có thể dùng một trong các cách
sau:
Cách 1. Xác định góc giữa hai mặt phẳng , rồi tính trực tiếp góc đó bằng 90
0
.
,
900
.
Cách 2. Chứng minh trong mặt phẳng này có một đường thẳng vuông góc với mặt phẳng kia.
a
.
Cách 3. Tìm hai vec tơ
n
1
.n
2
0
.
n
1
,
n
2
lần lượt vuông góc với các mặt phẳng
,
rồi chứng minh
Câu 1. Cho hình chóp S.ABC có đáy
ABC
là tam giác vuông tại C , SAC là tam giác đều và nằm trong
mặt phẳng vuông góc với
ABC
. Gọi I
là trung điểm SC .
a) Chứng minh
SBC
SAC
.
A'
C'
B'K
M
A
T
C
a 6
3
a)
Gọi
H
là trung điểm của
AC
SH
AC
SH
ABC
SH
BC .
Kết hợp với
BC AC BC
SAC
SBC
SAC
.
b)
Theo câu a, BC
SAC
, AI
SAC
BC
AI .
Tam giác SAC đều, AI là trung tuyến nên AI
SC
AI
SBC
ABI
SBC
.
Câu 2. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Biết SA
ABC
. Gọi M , N
lần
lượt là hai điểm trên BC và DC sao cho
SAM
SMN
.
MB
a
,
2
DN
3a
. Chứng minh rằng
4
Lời giải
Ta có
2
2 2 2
a
2
5a
2
AM AB
BM
a
4 4
3a
2
25a
2
AN
2
AD
2
DN
2
a
2
a
2
MN
2
MC
2
NC
2
4
a
2
16
5a
2
2
4
16
Khi đó AM
2
MN
2
AN
2
AM MN .
Mà SA
ABCD
SA
MN .
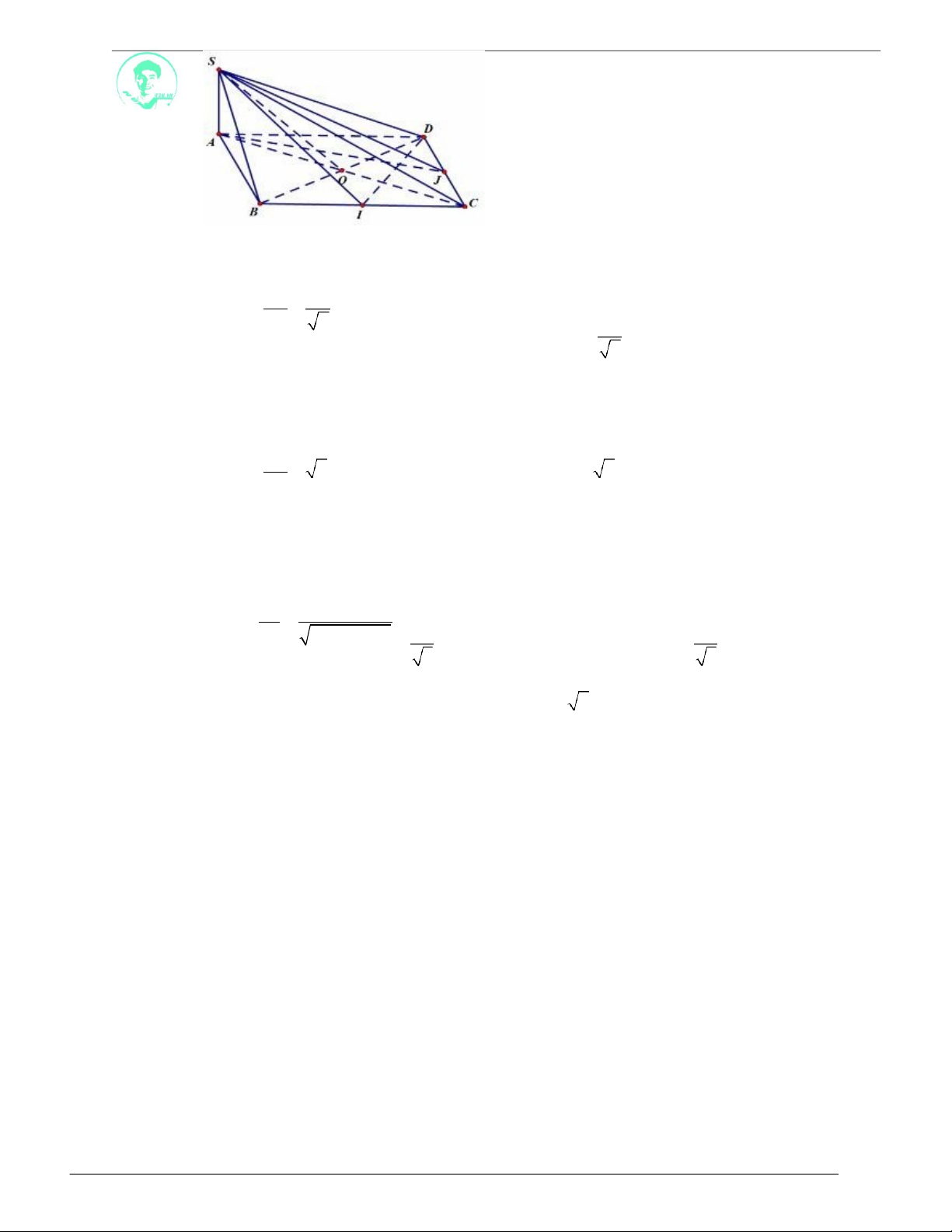
Câu 3. Cho hình thoi ABCD cạnh a có tâm O và OB
a 3
,
3
minh rằng:
a)
A
SC
90o .
b)
SAB
SAD
.
dựng SO
ABCD
và SO
. Chứng
Lời giải
b) Chứng minh
ABI
SBC
.
Lời giải
a
3
2
a 6
TÀI LIỆU TỰ HỌC TOÁN
11
a) Xét tam giác OAB vuông tại O , OA
2
AB
2
OB
2
a
2
a
3
3
SAO vuông cân tại O SCO cũng vuông cân tại O
SAC vuông cân tại
S
ASC 90
o
.
2 2 2 2 2 2 2
4a
2
b) Ta có: SB
SO
OB
a SB a, SA SO
OA
SA
3 3
Gọi I là trung điểm SA BI SA .
Xét tam giác BAI vuông tại I , có BI AB
2
IA
2
a
2
a
3
DI
12a
2
2a
3
2
3
3 3
IB2
ID2
BD2
BID vuông cân tại I
IB
ID
IB
SAD
9
3
SAB
SAD
.
Câu 4. Cho hình chóp SABCD
có đáy
ABCD
là hình thoi tâm I cạnh a và có góc
A bằng 60
0
, cạnh
SC
a 6
2
và SC
ABCD
.
a)
Chứng minh
SBD
SAC
.
b) Trong tam giác SCK kẻ IK SA tại K . Tính độ dài IK
c)
Chứng minh
B
KD
900
và từ đó suy ra
SAB
SAD
.
Lời giải
S
C
A
a)
Chứng minh
SBD
SAC
.
Ta có:
6
2a 3
a 6
K
D
I
B
S
I
D
C
A
O
B
2
AC
2
SC
2
AB
2
BM
2
b) Tính độ dài IK .
BD AD AB a
AC 2 AI a
Ta có:
IK AI.sin
S
AI
AI.
SC
SA
AI
.SC
a
3
.
a
6
2 2
a
.
2
c)
Chứng minh
B
KD
90
và từ đó suy ra
SAB
SAD
Trong DKB có:
KI ID IB
a
2
BKD
vuông tại K
B
KD 90 ,
Chứng minh:
SAB
SAD
học sinh tự làm
Câu 5. Cho hình chóp SABCD , có đáy ABCD là hình vuông cạnh a , SA
ABCD
. Gọi M , N lần lượt
là hai điểm nằm trên hai cạnh BC, DC sao cho
BM
a
,
2
DN
3a
. Chứng minh hai mặt phẳng
4
SAM
và
SMN
vuông góc với nhau.
S
Lời giải
D
B
M C
Hạ AO SM
Ta có
AM
a
2
5
3
a
3
2
a
6
2
2
a 5
4
O
A
N
M t khác: ặ
BD
SBD
SBD
SAC
SC
BD
AC
BD
BD
SAC
.
Bấm Tải xuống để xem toàn bộ.