Bài 5: Hệ phương trình tuyến tính | Bài giảng môn Đại số các nhóm ngành chuẩn | Đại học Bách khoa hà nội

Hệ phương trình tuyến tính n pt, n ẩn số mà ma trận hệ số không suy biến được gọi là hệ Cramer. Tài liệu trắc nghiệm môn Đại số các nhóm ngành chuẩn giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời bạn đọc đón xem!

17 9 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Môn: Đại số các nhóm ngành chuẩn (THH)

Trường: Đại học Bách Khoa Hà Nội

Thông tin:

52 trang 1 tháng trước

Tác giả:

Profile Lê Na
1
BÀI 5
2
§5: Hệ phương trình tuyến tính
5.1 Dạng tổng quát và dạng ma trận của hệ
phương trình tuyến tính.
5.1.1. Định nghĩa: Hệ phương trình tuyến tính m phương trình, n
ẩn số có dạng:
n n
n n
m m mn n m
a x a x a x b
a x a x a x b
a x a x a x b
11 1 12 2 1 1
21 1 22 2 2 2
1 1 2 2
...
...
(*)
...
...
trong đó a
ij
là hệ số của pt thứ i của ẩn x
j ,
b
i
là hệ số tự do của
phương trình thứ i
,
x
j
là các ẩn số (i=1,..,m, j=1,..,n).
3
§5: Hệ phương trình tuyến
tính
- Nếu b
= 0 với mọi i=1,2,…,m thì hệ được gọi là hệ
tuyến tính thuần nhất.
1 2 3 4
1 2 3 4
1 2 3 4
2 3 4
2 3 5 2
2 3 4 0
3 8 5 3 2
4 2 7 9
x x x x
x x x x
x x x x
x x x
Ví dụ
Hệ 4 phương trình 4 ẩn
Là hệ không thuần nhất
4
§5: Hệ phương trình tuyến
tính
ij m n
A a
[ ]
+ Ma trận gọi là ma trận hệ số của hệ phương trình
(*).
+ Ma trận gọi là ma trận hệ số tự do của hệ phương trình
(*).
m
b
b
b
...
b
1
2
+ Ma trận gọi là ma trận ẩn số của hệ phương trình (*).
n
x
x
x
...
x
1
2
5
§5: Hệ phương trình tuyến tính
Ví dụ: Cho hệ phương trình
1 2 3 4
1 2 3 4
1 2 3 4
2 3 4
1
2
3
4
2 3 5 2
2 3 4 0
3 8 5 3 2
4 2 7 9
2 3 5 1 2
1 2 3 4 0
, ,
3 8 5 3 2
0 4 2 7 9
x x x x
x x x x
x x x x
x x x
x
x
A b x
x
x
6
§5: Hệ phương trình tuyến tính
b s
A A A | b
Ma trận bổ sung của hệ (*):
Ví dụ: Cho hệ phương trình
1 2 3 4
1 2 3 4
1 2 3 4
2 3 4
2 3 5 2
2 3 5 1 2
2 3 4 0
1 2 3 4 0
[A|b]
3 8 5 3 2 3 8 5 3 2
0 4 2 7 9
4 2 7 9
bs
x x x x
x x x x
A A
x x x x
x x x
Nhận xét: Các hệ số của phương trình thứ i là các phần tử ở hàng thứ
i của A
bs
và ngược lại.
7
§5: Hệ phương trình tuyến tính
Với các kí hiệu đó, hệ (*) được đưa về dạng
Ax b (**)
gọi là dạng ma trận của hệ (*).
Ví dụ:
2 7 1 9
3 1 4 0
5 9 2 5
x
y
z
2 7 9
3 4 0
5 9 2 5
x y z
x y z
x y z
8
§5: Hệ phương trình tuyến tính
5.2. Hệ Cramer
Định nghĩa: Hệ phương trình tuyến tính n pt, n
ẩn số mà ma trận hệ số không suy biến được
gọi là hệ Cramer
Ví dụ: Giải hệ phương trình tuyến tính sau:
9
5.2 Hệ Crame
Định lý: Mọi hệ Cramer n pt đều có nghiệm duy
nhất (x
1
, x
2
, …,x
n
) được xác định bởi công
thức
j
j
D
x
D
10
5.2 Hệ Crame
11
5.2 Hệ Crame
Ví dụ: Giải hệ phương trình tuyến tính sau:
12
5.2 Hệ Crame
13
5.2 Hệ Crame
14
5.2 Hệ Crame
15
5.2 Hệ Crame
B
ài tập
: Giải hệ phương trình sau:
1 2 3
1 2 3
1 2 3
2 1
2 3 5
3 2 1
x x x
x x x
x x x
1 1 2
2 1 3
3 2 1
D
1
1 1 2
5 1 3
1 2 1
D
2
1 1 2
2 5 3
3 1 1
D
3
1 1 1
2 1 5
3 2 1
D
= = --1919
= = --2929
= = --99
= = --88
16
5.2 Hệ Crame
1
1
2
2
3
3
19
8
29
8
9
8
D
x
D
D
x
D
D
x
D
17
§5: Hệ phương trình tuyến tính
5.3.1. Các phép biến đổi tương đương hệ phương trình5.3.1. Các phép biến đổi tương đương hệ phương trình
Nhân một số ( ) vào 2 vế của 1 PT của hệ.Nhân một số ( ) vào 2 vế của 1 PT của hệ.
Đổi chỗ hai PT của hệ.Đổi chỗ hai PT của hệ.
Nhân một số ( ) vào một PT rồi cộng vào Nhân một số ( ) vào một PT rồi cộng vào
PT khác của hệ.PT khác của hệ.
0
0
1
2 3 2
2 5
x y z
x y z
x y z
3 2
2 4 2 1
1
2 3 2
0
pt
x y z
x y z
x y z
2 3
1
2 3 2
2 4 2 10
pt pt
x y z
x y z
x y z
5.3. Giải hệ phương trình bằng PP Gauss
18
5. Giải hệ PT bằng PP Gauss
Như vậy các phép biến đổi tương đương hệ
PT chính là các phép BĐSC trên dòng của
ma trận bổ sung tương ứng..
1 1 1 1
2 1 3 2
1 2 1 5
A
1
2 3 2
2 5
x y z
x y z
x y z
2 ( 2) 1
3 ( 1) 1
1
3 5 0
3 4
pt pt
pt pt
x y z
y z
y
3 2
1
3 4
3 5 0
pt pt
x y z
y
y z
2 1
3 1
( 2)
( 1)
1 1 1 1
0 3 5 0
0 3 0 4
h h
h h
3 2
1 1 1 1
0 3 0 4
0 3 50
h h
VD
19
5.3. Giải hệ PT bằng PP Gauss
5.3.2. Định lí Kronecker-Capelli
a. ĐL: Cho hệ phương trình Ax=b
Hệ có nghiệm
r( A) r( A)
Cụ thể hơn, ta có kết quả sau: Nếu Ax=b là hệ n ẩn số, ta có
+ hệ vô nghiệm
r( A) r( A)
+ hệ có nghiệm duy nhất
r( A) r( A) n
+ hệ có vô số nghiệm phụ thuộc (n-r)
tham số
r( A) r( A) r n
20
5.3. Giải hệ PT bằng PP Gauss
Xét hệ phương trình tổng quát sau:
Chứng minh.
Giả sử A có hạng là r
| 1/52
| | Tải xuống

Có thể bạn quan tâm:

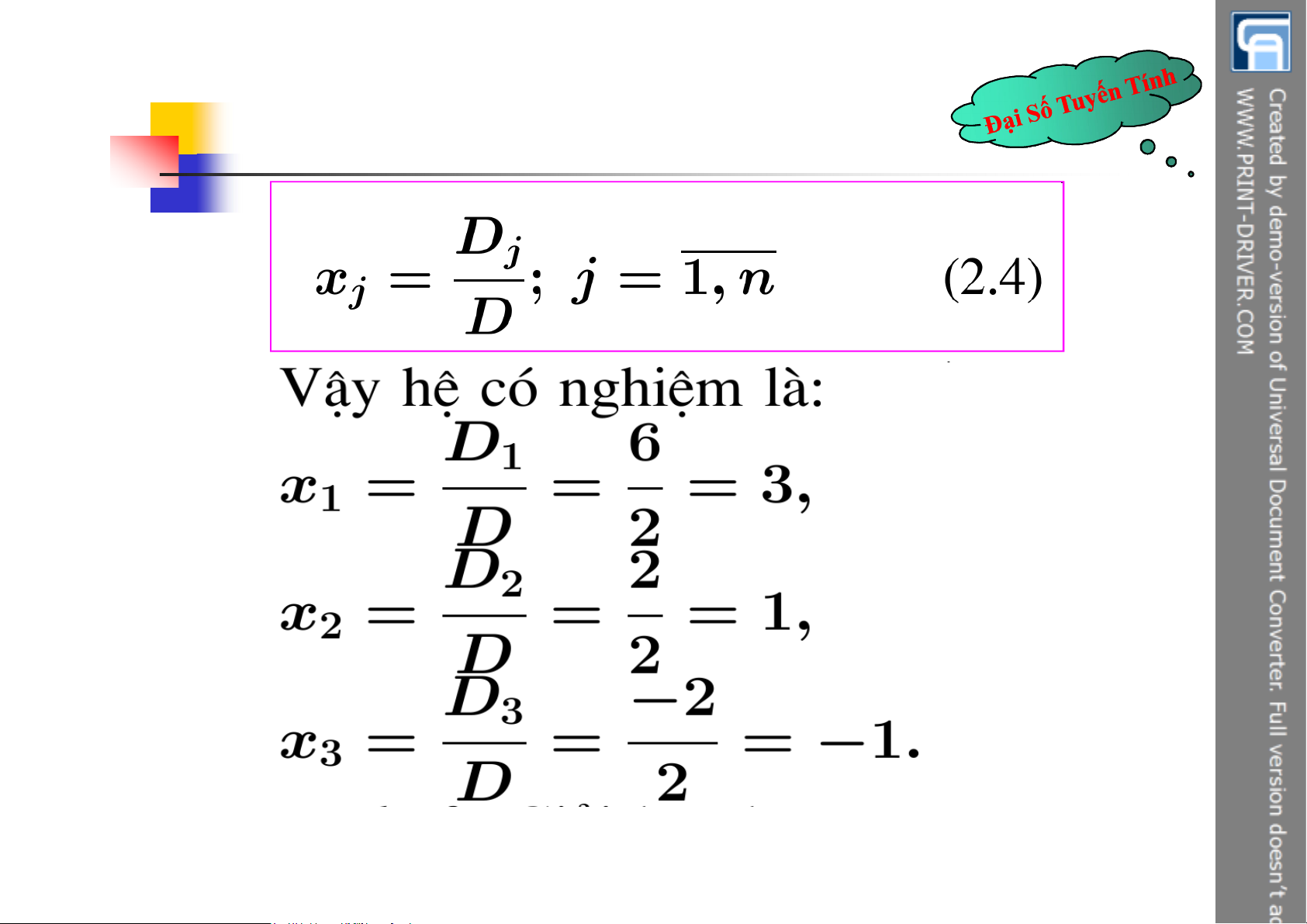
Preview text:

BÀI 5 1
§5: Hệ phương trình tuyến tính
5.1 Dạng tổng quát và dạng ma trận của hệ
phương trình tuyến tính.
5.1.1. Định nghĩa: Hệ phương trình tuyến tính m phương trình, n ẩn số có dạng:
a x a x  ...  a x b 11 1 12 2 1n n 1 
a x a x  ...  a x b 21 1 22 2 2 n n 2  (*) ...
a x a x  ...  a x bm1 1 m2 2 mn n m
trong đó a là hệ số của pt thứ i của ẩn x b là hệ số tự do của ij j , i
phương trình thứ i, x là các ẩn số (i=1,..,m, j=1,..,n). j 2
§5: Hệ phương trình tuyến tính
- Nếu b = 0 với mọi i=1,2,…,m thì hệ được gọi là hệ i tuyến tính thuần nhất.
2x  3x  5x x  2 Ví dụ 1 2 3 4
x  2x  3x  4x  0 
Hệ 4 phương trình 4 ẩn 1 2 3 4
3x 8x 5x  3x  2
Là hệ không thuần nhất 1 2 3 4  
 4x  2x  7x  9  2 3 4 3
§5: Hệ phương trình tuyến tính + Ma trận Aa
[ ] gọi là ma trận hệ số của hệ phương trình
ij mn (*).  b  1   + Ma trận
b 2 gọi là ma trận hệ số tự do của hệ phương trình b    (*).  ...    bm   x  1   x + Ma trận x  2  
gọi là ma trận ẩn số của hệ phương trình (*).  ...    xn  4
§5: Hệ phương trình tuyến tính
Ví dụ: Cho hệ phương trình
2 x  3x  5 x x  2 1 2 3 4
x  2x  3x  4x  0  1 2 3 4
3x  8x  5x  3x  2 1 2 3 4  
 4 x  2 x  7 x  9  2 3 4  2 3 5 1  2   x  1       1 2 3 4 0 x2   A ,     b  ,   x   3 8 5 3  2  x  3       0 4 2 7 9      x4  5
§5: Hệ phương trình tuyến tính
Ma trận bổ sung của hệ (*): b s A  A  A | b 
Ví dụ: Cho hệ phương trình 2
x 3x 5x x  2  2 3  5 1  2  1 2 3 4   
x 2x 3x 4x  0  1  2  3 4 0 1 2 3 4 bsA A [A|b]      
3x 8x 5x 3x  2   3 8 5  3 2 1 2 3 4    
4x 2x 7x  9   0 4  2 7  9 2 3 4  
Nhận xét: Các hệ số của phương trình thứ i là các phần tử ở hàng thứ
i của Abs và ngược lại. 6
§5: Hệ phương trình tuyến tính
Với các kí hiệu đó, hệ (*) được đưa về dạng
Ax b (**)
gọi là dạng ma trận của hệ (*).  Ví dụ:
2 x  7 y z  9  2 7 1   x  9        
3x y  4 z  0  3  1 4 y  0      
5x  9 y  2z  5  5 9 2   z   5         7
§5: Hệ phương trình tuyến tính 5.2. Hệ Cramer
Định nghĩa: Hệ phương trình tuyến tính n pt, n
ẩn số mà ma trận hệ số không suy biến được gọi là hệ Cramer
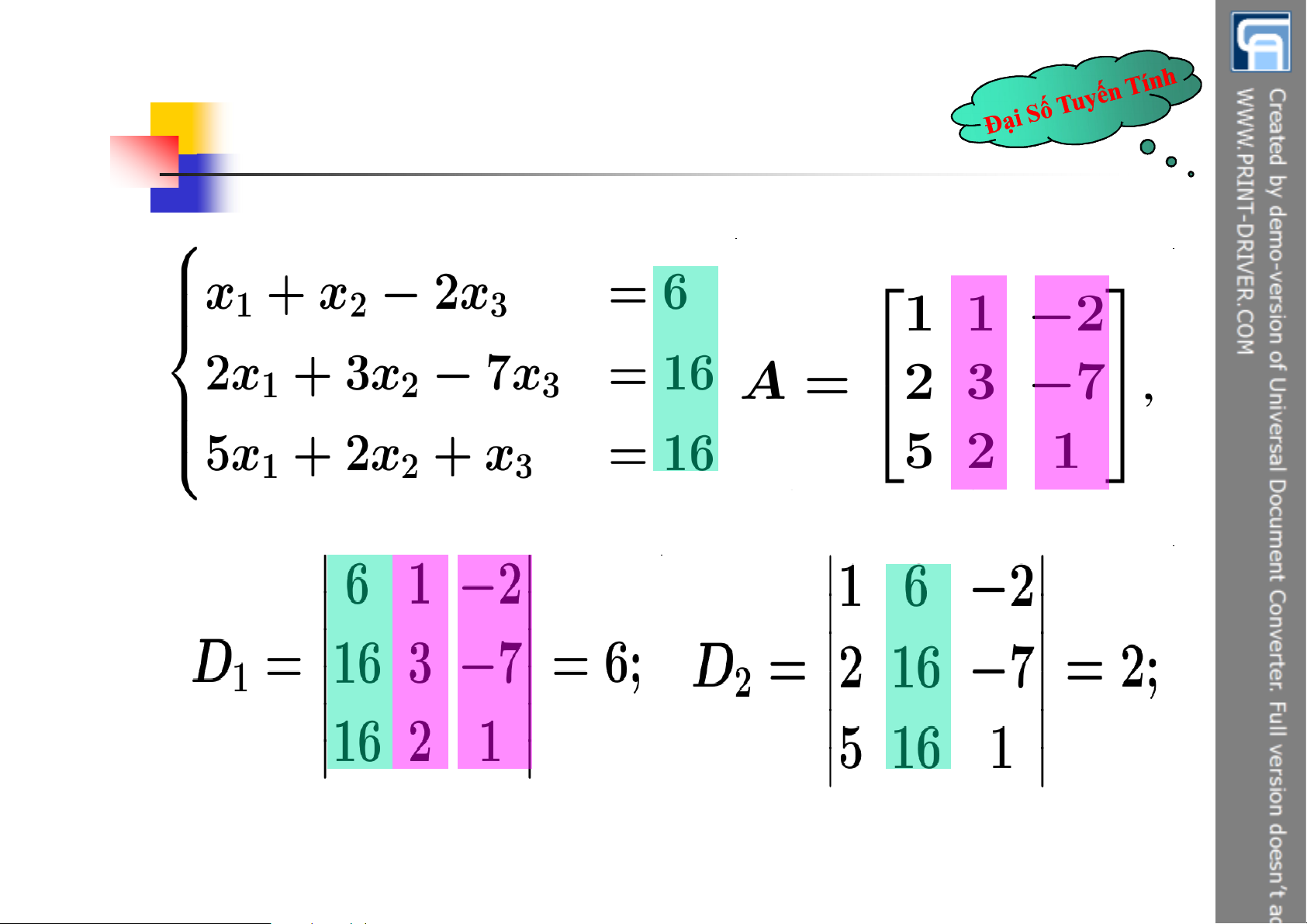
Ví dụ: Giải hệ phương trình tuyến tính sau: 8  5.2 Hệ Crame
Định lý: Mọi hệ Cramer n pt đều có nghiệm duy
nhất (x , x , …,x ) được xác định bởi công 1 2 n thức D j xj D 9  5.2 Hệ Crame 10  5.2 Hệ Crame
Ví dụ: Giải hệ phương trình tuyến tính sau: 11  5.2 Hệ Crame 12  5.2 Hệ Crame 13  5.2 Hệ Crame 14  5.2 Hệ Crame
Bài tập: Giải hệ phương trình sau:
x x  2x  1 1 1 2 1 2 3  D  5 1 3  = = -19 1 1
2x x  3x  5 1 2 3 1 2 1 3
x  2x x 1  1 2 3 1 1 2 D  2 5 3  2 = = -29 2 1 1 2 3 1 1 D  2 1 3  = = -8 1 1  1 3 2  1 D  2 1 5 = = -9 3 3 2  1 15  5.2 Hệ Crame D1 1  9 x   1 D 8  D2 2  9 x   2 D 8  D3 9 x    3 D 8  16
§5: Hệ phương trình tuyến tính
5.3. Giải hệ phương trình bằng PP Gauss 5.3 . . 3 1 . . 1 . C á C c á p h p ép é bi b ến ế đổi ổ i tươ ư n ơ g đư đ ơn ơ g g hệ h p h p ươ ư n ơ g g tr t ìn ì h Nh N â h n â m ộ m t ộ số s ố (   0) v à v o à 2 v ế v ế củ c a a 1 1 P T T c ủ c a a hệ. ệ Đổ Đ i ổ c h c ỗ ỗ h a h i a P T T c ủ c a ủ a hệ h . ệ Nh N â h n â m ộ m t ộ số s ố ( ) v à v o à m ộ m t P T T rồ r i c ộ c n ộ g v à v o à   0 PT T k h k ác á c c ủ c a a h ệ. ệ
x y z  1
x yxz 1 y z  1 
pt 32 pt2 pt3 
2x y  3z  2  2x   y2 3 x z  4 2 y  2z  10
x  2y z  5    2x  4 y  2x 2 z y 1  0  3z  2  17
5. Giải hệ PT bằng PP Gauss
 Như vậy các phép biến đổi tương đương hệ
PT chính là các phép BĐSC trên dòng của
ma trận bổ sung tương ứng.
VDxyz 1 
xy z 1 
x y z 1  pt pt  2 2 (  2  ) 1 pt pt
xy 3z 2  y z 3 2 pt pt  3 5 0 3 (  1  ) 1    3y  4
x2yz 5   3 y 4 
 3y 5z 0  1  1  1 1 1 1  1 1 1  1  1 1   h h   A 2 1 3  2 h ( 2  ) h   3 2   0 3 0 4   2 1   0 3 5 0 h ( 1  ) h   3 1   1  2 1 5      0 3 0 4 0 3 5 0     18 
5.3. Giải hệ PT bằng PP Gauss
5.3.2. Định lí Kronecker-Capelli
a. ĐL: Cho hệ phương trình Ax=b
Hệ có nghiệm r( A) r( A)
Cụ thể hơn, ta có kết quả sau: Nếu Ax=b là hệ n ẩn số, ta có +
r ( A )
r (
A )  hệ vô nghiệm
+ r( A) r( A) n  hệ có nghiệm duy nhất
+ r( A) r( A) r n  hệ có vô số nghiệm phụ thuộc (n-r) tham số 19
5.3. Giải hệ PT bằng PP Gauss Chứng minh.
Xét hệ phương trình tổng quát sau: Giả sử A có hạng là r 20