Bài 6 Công thức xác suất có điều kiện (Phần 1) môn Toán 12

Khoá học SSLive Toán học 2k8 | S1 Toán học MÔN TOÁN
21:00 Học tương tác S-REAL trên Classin
Xem lại bài giảng và làm bài tập trên ssstudy.vn
CÔNG THỨC XÁC SUẤT BÀI 6
CÓ ĐIỀU KIỆN (PHẦN 1)
1. Công thức xác suất có điều kiện
Cho hai biến cố A và B . Xác suất của biến cố A với điều kiện biến cố B đã xảy ra được gọi
là xác suất của A với điều kiện B , kí hiệu là P  A∣B . P  AB n  AB
Công thức xác suất có điều kiện: P  A∣B   . P  B n  B
2. Công thức nhân xác suất
P  AB  P  A.P  B A  P  B.P  A B Chú ý:
 P  A  P  A  1
 P  A B  P  A B  1
 P  A | B  P A B 1
 P  AB  P  AB  P  A
 P  AB  P  AB  P B
 Cho hai biến cố độc lập A và B . Khi đó
- P  A  P  A B  P  A B
- P  B  P  B A  P B A
Trên bước đường thành công, không có bước chân của những con người lười biếng.
Khoá học SSLive Toán học 2k8 | S1 Toán học MÔN TOÁN
21:00 Học tương tác S-REAL trên Classin
Xem lại bài giảng và làm bài tập trên ssstudy.vn
DẠNG 1: BÀI TOÁN DÙNG CÔNG THỨC TRỰC TIẾP
Ví dụ 1: Cho hai biến cố ,
A B có P  A  0,5; P  B  0,8; P  AB  0, 4 . Tính P  A | B và P  B | A .
Ví dụ 2: Cho hai biến cố ,
A B với P  A  0, 6; P  B  0,8; P  A  B  0, 4. Tính các xác suất sau: a) P  B A b) P B A c) P  AB.
Ví dụ 3: Cho hai biến cố ,
A B có P  A  0, 4; P  B  0,8; P  A  B  0,9. Tính:
a) P  A | B
b) P  A | B
c) P  A | B
Ví dụ 4: Cho P  A  0,5; P  B  0,6; P  B | A  0,9. Tính P  A | B.
Ví dụ 5: Cho hai biến cố A và B có P  A  0,3 ; P  B  0,5 và P  A B  0, 4 . Tính P  AB và P  A B.
DẠNG 2: BÀI TOÁN XÁC SUẤT CÓ ĐIỀU KIỆN CƠ BẢN
Ví dụ 6: Cho hai xúc xắc cân đối và đồng chất. Gieo lần lượt từng xúc xắc trong hai xúc xắc đó.
Tính xác suất để tổng số chấm xuất hiện trên hai xúc xắc bằng 6, biết rằng xúc xắc thứ
nhất xuất hiện mặt 4 chấm.
Ví dụ 7: Một hộp có 12 quả bóng bàn bàn màu trắng và 10 quả bóng bàn màu vàng; các quả bóng
có kích thước và khối lượng như nhau. Có 10 quả bóng bàn trong hộp được đánh số, trong
đó có 4 quả bóng bàn màu trắng và 6 quả bóng bàn màu vàng. Lấy ngẫu nhiên một quả
bóng bàn trong hộp. Tính xác suất để bóng bàn được lấy ra có màu trắng, biết rằng quả
bóng bàn đó được đánh số.
Ví dụ 8: Trong kì kiểm tra môn Toán của một trường trung học phổ thông 200 học sinh tham gia,
trong đó có 95 học sinh nam và 105 học sinh nữ. Khi công bố kết quả của kì kiểm tra dó,
có 50 học sinh đạt điểm giỏi, trong đó có 24 học sinh nam và 26 học sinh nữ. Chọn ra
ngẫu nhiên một học sinh trong số 200 học sinh đó. Tính xác suất để học sinh được chọn
ra đạt điểm giỏi, biết rằng học sinh đó là nữ (làm tròn kết quả đến hàng phần trăm).
Trên bước đường thành công, không có bước chân của những con người lười biếng.
Khoá học SSLive Toán học 2k8 | S1 Toán học MÔN TOÁN
21:00 Học tương tác S-REAL trên Classin
Xem lại bài giảng và làm bài tập trên ssstudy.vn
Ví dụ 9: Câu lạc bộ cờ vua của nhà trường gồm 35 thành viên, mỗi thành viên biết chơi ít nhất một
trong hai môn cờ vua hoặc cờ tướng. Biết rằng có 25 thành viên biết chơi cờ vua và 20
thành viên biết chơi cờ tướng. Chọn ngẫu nhiên 1 thành viên của câu lạc bộ. Tính xác suất
thành viên được chọn biết chơi cờ vua, biết rằng thành viên đó biết chơi cờ tường.
Ví dụ 10: Mỗi bạn học sinh trong lớp của Minh lựa chọn học một trong hai ngoại ngữ là tiếng Anh
hoặc tiếng Nhật. Xác suất chọn tiếng Anh của mỗi bạn học sinh nữ là 0, 6 và của mỗi bạn
học sinh nam là 0, 7 . Lớp của Minh có 25 bạn nữ và 20 bạn nam. Chọn ra ngẫu nhiên
một bạn trong lớp. Tính xác suất của các biến cố:
M : “Bạn được chọn là nam, biết học sinh đó học tiếng Nhật”.
N : “Bạn được chọn là nữ, biết học sinh đó học tiếng Anh”.
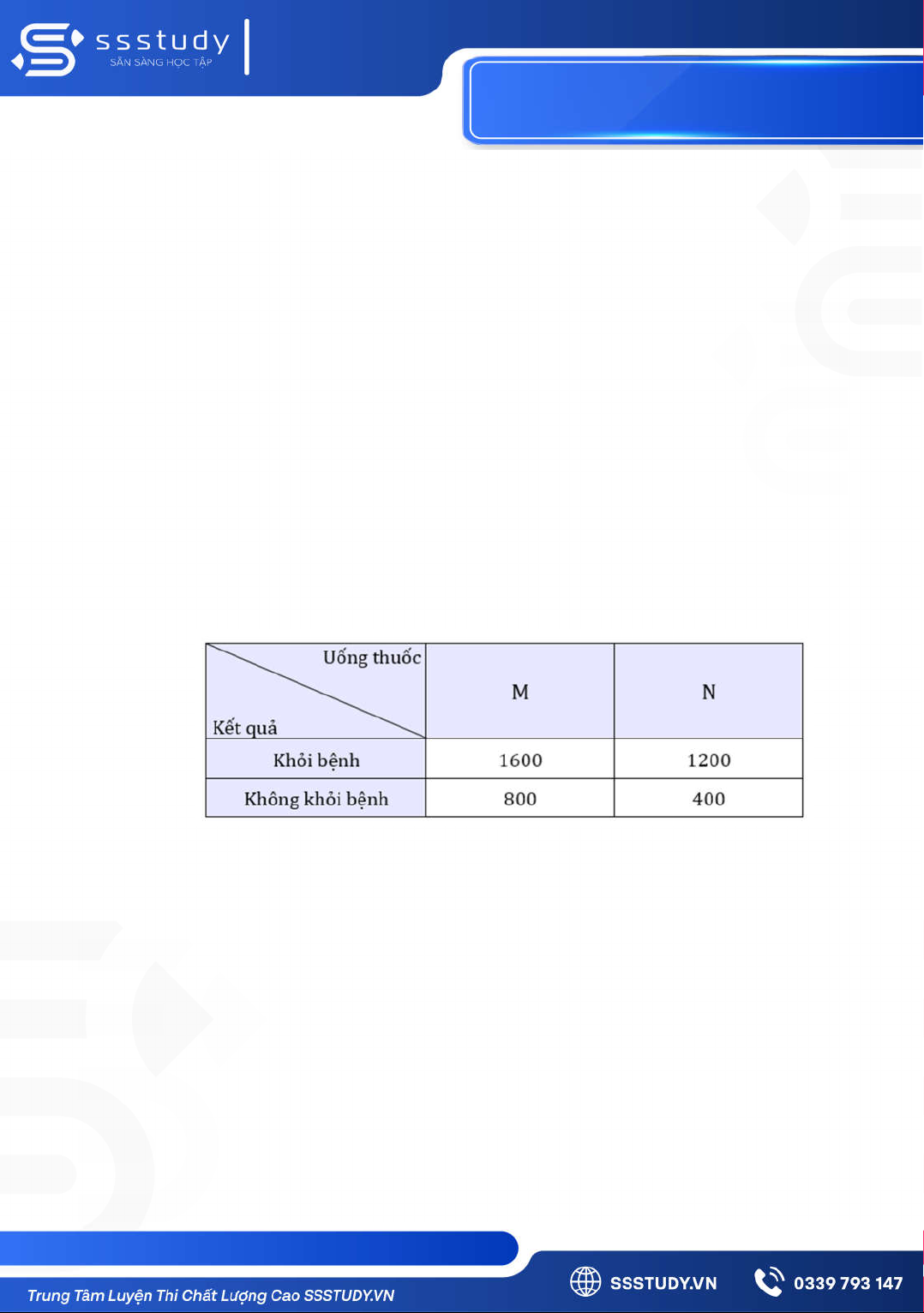
Ví dụ 11: Một công ty dược phẩm muốn so sánh tác dụng điều trị bệnh X của hai loại thuốc M và N.
Công ty đã tiến hành thử nghiệm với 4000 bệnh nhân mắc bệnh X trong đó 2400 bệnh nhân
dùng thuốc M, 1600 bệnh nhân còn lại dung thuốc N. Kết quả được cho trong bảng dữ liệu thống kê 2x2 như sau:
Chọn ngẫu nhiên một bệnh nhân trong 4000 bệnh nhân thử nghiệm sau khi uống thuốc.
Tính xác suất để bệnh nhân đó:
a) Uống thuốc M, biết rằng bệnh nhân đó khỏi bệnh.
b) Uống thuốc N, biết rằng bệnh nhân đó không khỏi bệnh.
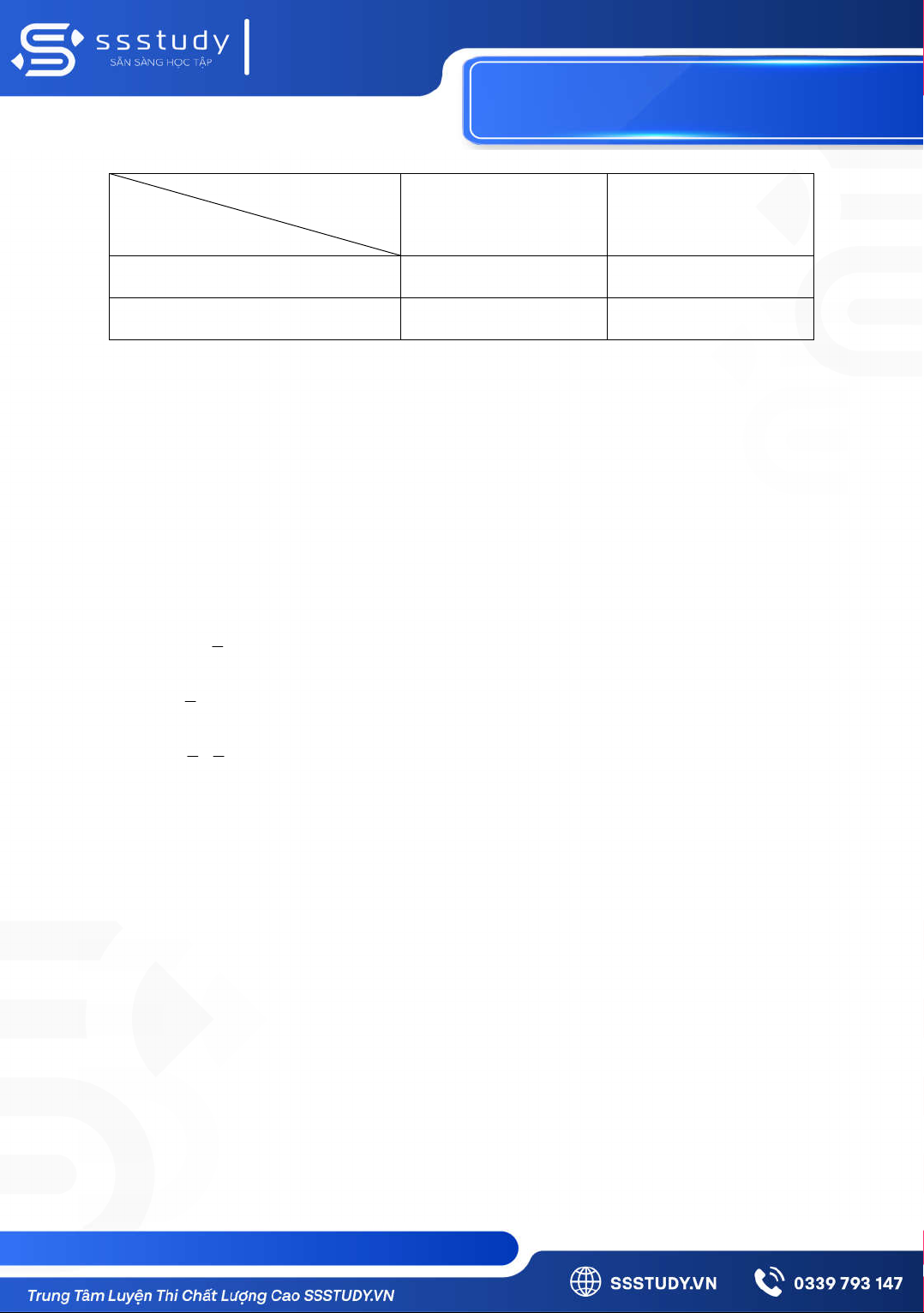
Ví dụ 12: Một công ty dược phẩm giới thiệu một dụng cụ kiểm tra sớm bệnh sốt xuất huyết. Về kiểm
định chất lượng của sản phẩm, họ cho biết như sau: Số người được thử là 9000 , trong đó
có 1500 người đã bị nhiễm bệnh sốt xuất huyết và có 7500 người không bị nhiễm bệnh
sốt xuất huyết. Khi thử bằng dụng cụ của công ty, trong 1500 người đã bị nhiễm bệnh sốt
xuất huyết, có 76% số người đó cho kết quả dương tính, còn lại cho kết quả âm tính. Mặt
khác, 7500 người không bị nhiễm bệnh sốt xuất huyết, có 7% số người đó cho kết quả
dương tính, còn lại cho kết quả âm tính khi kiểm tra.
Trên bước đường thành công, không có bước chân của những con người lười biếng.
Khoá học SSLive Toán học 2k8 | S1 Toán học MÔN TOÁN
21:00 Học tương tác S-REAL trên Classin
Xem lại bài giảng và làm bài tập trên ssstudy.vn Kết quả thử nghiệm Dương tính Âm tính Tình trạng bệnh Nhiễm bệnh Không nhiễm bệnh
Chọn ngẫu nhiên một người trong số những người thử nghiệm. Tính xác suất để người
được chọn ra bị nhiễm bệnh sốt xuất huyết, biết rằng người đó có kết quả thử nghiệm dương
tính (làm tròn kết quả đến hàng phần mười).
Ví dụ 13: Một lớp học có 17 học sinh nam và 24 học sinh nữ. Cô giáo gọi ngẫu nhiên lần lượt 2 học
sinh (có thứ tự) lên trả lời câu hỏi. Xét các biến cố:
A: "Lần thứ nhất cô giáo gọi 1 học sinh nam";
B : "Lần thứ hai cô giáo gọi 1 học sinh nữ".
a) P  B∣A  0,575 .
b) P  B∣A  0,6 .
c) P  B∣A  0, 425.
d) P B∣A  0, 4 .
Trên bước đường thành công, không có bước chân của những con người lười biếng.