119 trang 7 lượt tải

Bài giảng các kỹ thuật giải phương trình lượng giác | Toán 11

14

Bài giảng các kỹ thuật giải phương trình lượng giác | Toán học 11. Tài liệu gồm 119 trang, giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời bạn đọc đón xem!

Chủ đề: Chương 1: Hàm số lượng giác và phương trình lượng giác (KNTT) 134 tài liệu

Môn: Toán 11 3.6 K tài liệu

Tác giả:

Profile

Sang

1 năm trước
Tải xuống Chia sẻ Báo cáo
Danh sách Quiz
Tải xuống
/119
CÁC KĨ THUẬT GIẢI PHƯƠNG TRÌNH
LƯỢNG GIÁC
Giáo viên giảng dạy: NGUYỄN THÀNH LONG
Email: Changngoc203@gmail.com
Bỉm sơn: 10 – 02 – 2014
Giáo viên: Nguyễn Thành Long Email: Changngoc203@gmail.com
https://www.facebook.com/trithuc.viet.37
1
Phương trình lượng giác và ứng dụng của nó là một phần rất quan trọng trong đề thi đại học và ứng dụng
của nó trong đại số cũng như hình học. Và đặc biệt là giải phương trình lượng giác là một câu không thể
thiếu trong đề thi đại học các năm. Vậy muốn làm tốt lượng giác trước tiên ta phải nắm được công thức
lượng giác
TÓM TẮT CÁC CÔNG THỨC LƯỢNG GIÁC CẦN NHỚ
I. Các công thức lượng giác cần nhớ
1. Các công thức cơ bản
sin
tan
cos
a
a
a
với
2
a k
cot
sin
a
a
a
với
a k
tan .cot 1
a a
2 2
2 2
2 2
sin 1 cos (1 cos )(1 cos )
sin cos 1
cos 1 sin (1 sin )(1 sin )
a a a a
a a
a a a a
2
2
1
1 tan
cos
a
a
2
2
1
1 cot
sin
a
a
2. Công thức cộng và trừ
a. Với sin và cos
sin sin .cos cos .sin
a b a b a b
cos cos .cos sin .sin
a b a b a b
sin sin .cos cos .sin
a b a b a b
cos cos .cos sin .sin
a b a b a b
b. Với tan
tan tan
tan
1 tan .tan
a b
a b
a b
tan tan
tan
1 tan .tan
a b
a b
a b
3. Công thức tính tích thành tổng
1
cos .cos cos( ) cos( )
2
a b a b a b
1
sin .cos sin( ) sin( )
2
a b a b a b
1
sin .sin cos( ) cos( )
2
a b a b a b
1
cos .sin sin( ) sin( )
2
a b b a a b
4. Công thức biến đổi tổng thành tích
a. Công thức sin và cos
cos cos 2cos cos
2 2
a b a b
a b
cos cos 2sin sin
2 2
a b a b
a b
sin sin 2sin cos
2 2
a b a b
a b
sin sin 2cos sin
2 2
a b a b
a b
b.Công thức tan và cot
sin( )
tan tan
cos .cos
a b
a b
a b
sin( )
tan tan
cos .cos
a b
a b
a b
sin( )
cot cot
sin .sin
a b
a b
a b
sin( )
cot cot
sin .sin
b a
a b
a b
5. Công thức nhân đôi và nhân ba, nhân bốn
2 2
sin 2 2sin .cos
(sin cos ) 1 1 (sin cos )
a a a
a a a a
2 2 2 2
4 4
cos2 2cos 1 1 2sin cos sin
cos sin
a a a a a
a a
2
2tan
tan2
1 tan
a
a
a
;
3
2
3tan tan
tan3 =
1 3tan
a a
a
a
3 2
2
sin3 3sin 4sin sin 3 4sin
sin 4cos 1 sin 2cos 1 2cos 1
a a a a a
a a a a a
3 2
2
cos3 4cos 3cos cos 4cos 3
cos 1 4sin cos 1 2sin 1 2sin
a a a a a
a a a a a
Giáo viên: Nguyễn Thành Long Email: Changngoc203@gmail.com
https://www.facebook.com/trithuc.viet.37
2
4 2
sin 4 4sin 2sin
a a a
4 2
cos4 8cos 8cos 1
a a a
6. Công thức hạ bậc
2
1 cos2
cos
2
a
a
2
1 cos2
sin
2
a
a
2
2
2
sin 1 cos2
tan
1 cos2
cos
a a
a
a
a
2
2
2
cos 1 cos2
cot
1 cos2
sin
a a
a
a
a
3
cos3 3cos
cos
4
a a
a
3
3sin sin3
sin
4
a a
a
II. Giá tri lượng giác của các góc liên quan đặc biệt
1. Bỏ chẵn lần pi thì không thay đổi
sin 2 sin
cos 2 cos
x k x
x k x
tan 2 tan
cot 2 cot
x k x
x k x
2. Bỏ pi hay lẻ lần pi thì thành cộng biến thành trừ
sin sin
cos cos
tan tan
cot cot
x x
x x
x x
x x
TQ:
sin( 2 ) sin
k x x
cos( 2 ) cos
k x x
sin sin
cos cos
tan tan
cot cot
x x
x x
x x
x x
TQ:
sin( 2 ) sin
k x x
cos( 2 ) cos
k x x
3. Bỏ pi trên hai
sin cos
2
cos sin
2
tan cot
2
cot tan
2
x x
x x
x x
x x
sin cos
2
cos sin
2
tan cot
2
cot tan
2
x x
x x
x x
x x
d. Đổi dấu
sin sin
cos cos
x x
x x
tan tan
cot cot
x x
x x
III. Công thức tính sina, cosa theo
2
a
t
Ta có
2
2 2
2
2
2
sin
1
1 1
cos cot
2
1
2
tan
1
t
a
t
t t
a a
t
t
t
a
t
Một số công thức khác
Giáo viên: Nguyễn Thành Long Email: Changngoc203@gmail.com
https://www.facebook.com/trithuc.viet.37
3
2
cos sin cos cos 2cos .cos 2. cos
2 4 4 2 4
3 3
2.sin 2.sin 2.sin 2.sin
2 4 4 4 4
a a a a a a
a a a a
Vậy
cos sin 2 cos 2 sin 2 cos
4 4 4
a a a a x
Tương tự:
cos sin 2 cos 2 cos 2 sin 2sin
4 4 4 4
a a a a a a
3 3 2 2
sin cos sin cos sin sin .cos cos sin cos 1 sin .cos
x x x x x x x x x x x x
3 3 2 2
sin cos sin cos sin sin .cos cos sin cos 1 sin .cos
x x x x x x x x x x x x
4 4 2 2 2 2
1 1 1 3 1
sin cos 1 2sin .cos 1 sin 2 cos 2 cos4
2 2 2 4 4
x x x x x x x
4 4 2 2 2 2
cos sin cos sin cos sin cos2
x x x x x
6 6 4 4 2 2 2 2
3 1 3 3 5
sin cos sin cos sin cos 1 sin 2 cos 2 cos4
4 4 4 8 8
x x x x x x x x x
6 6 4 4 2 2
cos sin cos2 (sin cos sin cos )
x x x x x x x
sin cos 2 sin 2 cos
4 4
x x x x
2
2 2
1 sin 2 sin cos 2sin cos sin cos
x x x x x x x
2 2 2
1 sin 2 sin cos 2sin cos (sin cos )
x x x x x x x
2 2
sin 2
sin cos ,1 cos2 2cos ,1 cos2 2sin
2
x
x x x x x x
ĐƯỜNG TRÒN LƯỢNG GIÁC
Giá trị các hàm số lượng giác của các cung (góc) đặc biệt (ta nên sử dụng đường tròn lượng giác để
ghi nhớ các giá trị đặc biệt)
Giáo viên: Nguyễn Thành Long Email: Changngoc203@gmail.com
https://www.facebook.com/trithuc.viet.37
4
- 3
-1
- 3
/3
(Ñieåm goác)
t
t'
y
y'
x
x'
u
u'
- 3
-1
- 3
/3
1
1
-1
-1
-
/2
5/6
3/4
2
/3
-/6
-
/4
-/3
-1/2
- 2
/2
- 3
/2
-1/2- 2
/2- 3 /2
3
/2
2 /2
1/2
3
/2
2
/2
1/2
A
/3
/4
/6
3
/3
3
B
/2
3
/3
1
3
O
Bảng lượng giác của một số góc đặc biệt
Hoặc: Đường tròn lượng giác
Một điểm M thuộc đường tròn lượng giác sẽ có tọa độ
cos ;sin
M
ứng với mỗi góc
ta sẽ được
một điểm M cụ thể trên đường tròn
0
0
30
0
45
0
60
0
90
0
120
0
135
0
150
0
180
0
360
0
Góc
Hslg
0
6
4
3
2
2
3
3
4
5
6
2
sin
0
1
2
2
2
3
2
1
3
2
2
2
1
2
0 0
cos
1
3
2
2
2
1
2
0
1
2
2
2
3
2
-1 1
tan
0
3
3
1
3
kxđ
3
-1
3
3
0 0
cot
kxđ
3
1
3
3
0
3
3
-1
3
kxđ kxđ
Giáo viên: Nguyễn Thành Long Email: Changngoc203@gmail.com
https://www.facebook.com/trithuc.viet.37
5
Để giải được phương trình lượng giác chúng ta nắm được các bước giải sau
Bước 1: Đặt điều kiện cho phương trình có nghĩa (nếu có). Điều kiện gồm, phương trình chứa
mẫu, chứa cot hoặc tan, chứa căn bậc chẵn…
Cụ thể:
- Phương trình chứa
tan
x
, điều kiện: cos 0 ,
2
x x k k
.
- Phương trình chứa
cot
x
, điều kiện: sin 0 ,x x k k
.
- Phương trình chứa cả
tan
x
và
cot
x
, điều kiện:
,
2
x k k
.
Bước 2: Sử dụng công thức lượng giác, các phép biến đổi lượng giác. Các phương pháp giải
phương trình nói chung, tìm ra nghiệm của phương trình
Bước 3: Đối chiếu với điều kiện ban đầu để tìm ra nghiệm thỏa mãn và kết luận (xem mục kĩ
năng 5 loại nghiệm và kết hợp nghiệm)
Chú ý:
Đối với phương trình
2
2
1 1
cos cos
2 2
1 1
sin sin
2 2
x x
x x
ta không nên giải trực tiếp vì khi đó có tới 4 nghiệm,
khi kết hợp và so sánh với điều kiện rất phức tạp, ta nên hạ bậc là tối ưu nhất. Nghĩa là:
2
2
2
2
1
cos
2cos 1 0 cos2 0
2
1 cos2 0
2sin 1 0
sin
2
x
x x
x
x
x
.
Tương tự đối với phương trình
2
2
sin 1 sin 1
cos 1
cos 1
x x
x
x
ta không nên hạ bậc, mà nên biến đổi dựa vào
công thức
2 2
sin cos 1
x x
. Lúc đó:
2 2
2 2
sin 1 cos 0 cos 0
sin 0
cos 1 sin 0
x x x
x
x x
Giáo viên: Nguyễn Thành Long Email: Changngoc203@gmail.com
https://www.facebook.com/trithuc.viet.37
6
Đối với phương trình
cos cos2 0
x x
. Chúng ta có thể chuyển về dạng
cos cos 2x x
nhưng đơn giản hơn là thay
2
cos2 2cos 1
x x
để phương trình trở thành phương trình bậc hai với cosx
Tương tự với phương trình
sin cos2 0
x x
Khi đặt ẩn phụ
sin , cos
t x t x
thì điều kiện của t là
1
t
. Khi đặt ẩn phụ
2 2
sin , cos
t x t x
thì điều kiện của t là
0 1
t
. Khi đặt ẩn phụ
sin cos
t x x
thì điều kiện của t là
2
t .
Một số phương trình lượng giác cơ bản cần nhớ
Dạng 1:
2
sin sin ,
2
u v k
u v k
u v k
Đặc biệt:
sin 0
sin 1 2 ,
2
sin 1 2
2
x x k
x x k k
x x k
Dạng 2:
2
cos cos ,
2
u v k
u v k
u v k
Đặc biệt:
cos 0 2
2 2
cos 1 2 ,
cos 1 2
x x k k
x x k k
x x k
Dạng 3:
tan tan
,
,
2
u v u v k
k
u v k
Đặc biệt:
tan 0
,
tan 1
4
x x k
k
x x k
Dạng 4:
cot cot
,
,
u v u v k
k
u v k
Đặc biệt:
cot 0
2
,
cot 1
4
x x k
k
x x k
Giáo viên: Nguyễn Thành Long Email: Changngoc203@gmail.com
https://www.facebook.com/trithuc.viet.37
7
§ 1: CÁC DẠNG PHƯƠNG TRÌNH THƯỜNG GẶP
1. Phương trình bậc nhất đối với
sin ,cos
x x
a. Định nghĩa: Phương trình
sin cos (1)
a x b x c
trong đó a, b, c
và
2 2
0
a b
được gọi là
phương trình bậc nhất đối với
sin ,cos
x x
b. Cách giải.
Ta có thể lựa chọn 1 trong 2 cách sau:
Cách 1: Thực hiện theo các bước
Bước 1: Kiểm tra
- Nếu
2 2 2
a b c
phương trình vô nghiệm
- Nếu
2 2 2
a b c
khi đó để tìm nghiệm của phương trình ta thực hiện tiếp bước 2
Bước 2: Chia cả 2 vế phương trình (1) cho
2 2
a b
, ta được
2 2 2 2 2 2
sin cos
a b c
x x
a b a b a b
Vì
2 2
2 2 2 2
1
a b
a b a b
nên tồn tại góc
sao cho
2 2 2 2
cos , sin
a b
a b a b
Khi đó phương trình (1) có dạng
2 2 2 2
sin .cos sin .cos sin( )
c c
x x x
a b a b
Đây là phương trình cơ bản của sin mà ta đã biết cách giải
Cách 2: Thực hiện theo các bước
Bước 1: Với
cos 0 2 ,
2
x
x k k
thử vào phương trình (1) xem có là nghiệm hay không?
Bước 2: Với
cos 0 2 ,
2
x
x k k
Đặt
tan
2
x
t suy ra
2
2 2
2 1
sin , cos
1 1
t t
x x
t t
Khi đó phương trình (1) có dạng
2
2
2 2
2 1
( ) 2 0 (2)
1 1
t t
a b c c b t at c b
t t
Bước 3: Giải phương trình (2) theo t, sau đó giải tìm x.
Dạng đặc biệt:
sin cos 0 tan 1 ,
4
x x x x k k
sin cos 0 tan 1 ,
4
x x x x k k
.
sin cos 0
x x k k
sử dụng công thức sin cos 2 sin 2 cos
4 4
x x x x
Chú ý: Từ cách 1 ta có kết quả sau
2 2 2 2
sin cos
a b a x b x a b
từ kết quả đó ta có thể áp dụng tìm GTLN và GTNN của các
hàm số có dạng
sin cos
y a x b x
,
sin cos
sin cos
a x b x
y
c x d x
và phương pháp đánh giá cho một số phương
trình lượng giác .
THÍ DỤ MINH HỌA
Thí dụ 1: Giải phương trình:
sin 2 3cos2 3
x x
Giải:
Giáo viên: Nguyễn Thành Long Email: Changngoc203@gmail.com
https://www.facebook.com/trithuc.viet.37
8
Cách 1:
Chia cả hai vế phương trình cho
2 2
1 3 10
ta được
1 3 3
sin 2 cos2
10 10 10
x x
Đặt
3 1
sin , cos
10 10
. Lúc đó phương trình viết được dưới dạng
cos sin 2 sin cos2 sin sin(2 ) sin
2 2
,
2 2
2
x x x x
x k
x k
k
x k
x k
Vậy phương trình có 2 nghiệm
Cách 2:
Ta nhận thấy
cos 0
x
là nghiệm của phương trình
Với
cos 0 ,
2
x x k k
.
Đặt
tan
t x
, lúc đó
2
2 2
2 1
sin 2 , cos2
1 1
t t
x x
t t
Phương trình sẽ có dạng
2
2 2
2 2
2 1
3 3 2 3(1 ) 3(1 ) 3
1 1
t t
t t t t
t t
Hay tan 3 tan ,x x k k
Vậy phương trình có 2 họ nghiệm
Cách 3: Biến đổi phương trình về dạng
2
sin 2 3(1 cos2 ) 2sin .cos 6cos
cos 0 cos 0
(sin 3cos )cos 0
sin 3cos 0 tan 3 tan
x x x x x
x x
x x x
x x x
,
2
x k
k
x k
Vậy phương trình có hai họ nghiệm
Chú ý:
Khi làm bài toán dạng này chúng ta nên kiểm tra điều kiện trước khi bắt tay vào giải phương trình bởi có
một số bài toán đã cố tình tạo ra những phương trình không thoả mãn điều kiện. Ta xét ví dụ sau:
Thí dụ 2: (Đại học Giao thông Vận tải Hà Nội 2000) Giải phương trình sau:
2 2 sin cos cos 3 cos2
x x x x
Giải:
Phương trình
2 2 sin cos cos 3 cos2
x x x x
2sin 2 1 cos2 3 2
x x
Ta có
2 2
2 2
2
2
2 2 1 5 2 2
3 2 11 6 2
a b
c
Ta sẽ chứng minh:
2 2 2
a b c
5 2 2 11 6 2
2
2
4 2 6 4 2 6
32 36
(đúng)
Vậy phương trình vô nghiệm.
Ngoài ra chúng ta cần lưu ý rằng việc biến đổi lượng giác cho phù hợp với từng bài toán sẽ biểu diễn
chẵn các họ nghiệm . Ta xét ví dụ sau
Thí dụ 3: Giải phương trình
(1 3)sin (1 3)cos 2
x x
Giáo viên: Nguyễn Thành Long Email: Changngoc203@gmail.com
https://www.facebook.com/trithuc.viet.37
9
Giải:
Cách 1:
Thực hiện phép biến đổi
PT
1 3 1 3 2 1
sin cos
2 2 2 2 2 2 2
x x
Đặt
1 3 1 3
cos ; sin
2 2 2 2
x x
Phương trình được viết thành
1
sin .cos sin .cos sin( ) sin
4
2
x x x
2 2
4 4
,
3
2 2
4 4
x k x k
k
x k x k
Vậy phương trình có hai họ nghiệm
Cách 2:
Biến đổi phương trình về dạng
(sin cos ) 3(sin cos ) 2 2 sin 6 cos 2
4 4
1 3 1 1
sin cos sin cos cos sin
2 4 2 4 4 3 4 3
2 2
2
2
312 4
sin sin
4 3 4
2
12 4
x x x x x x
x x x x
x k
x k
x
x k x
,
5
2
6
k
k
Vậy phương trình có hai họ nghiệm
Qua hai cách giải ở bài trên ta nhận thấy bằng cách 2 ta thu được nghiệm phương trình chẵn.
Bài trên cũng có thể sử dụng cách đặt
2
x
t
và ta cũng thu được nghiệm chẵn
Thí dụ 4: (ĐH – D 2007) Giải phương trình:
2
sin cos 3cos 2
2 2
x x
x
Giải:
Phương trình
2 2
sin 2sin cos cos 3 cos 2
2 2 2 2
x x x x
x
sin 3cos 1
x x
1 3 1
sin cos
2 2 2
x x
1
sin .cos cos .sin
3 3 2
x x
1
sin
3 2
x
2 2
3 6
6
,
5
2 2
3 6 2
x k x k
k
x k x k
Vậy phương trình có các nghiệm là
2 , 2 ,
2 6
x k x k k
Chú ý:
Giáo viên: Nguyễn Thành Long Email: Changngoc203@gmail.com
https://www.facebook.com/trithuc.viet.37
10
Đối với phương trình dạng
sin ( ) cos ( ) sin ( ) cos ( ) (*)
a P x b Q x c Q x d P x
trong đó a, b, c, d
thoả mãn
2 2 2 2
0
a b c d
và
,
P x Q x
không đồng thời là các hàm hằng số. Bằng phép chia cho
2 2
a b
ta có (*)
sin ( ) sin ( )P x Q x
hoặc
(*)
cos ( ) cos ( )P x Q x
trong đó
,
là các góc phụ thích hợp. Ta xét ví dụ sau:
Thí dụ 5: (ĐH – D 2009) Giải phương trình:
3 cos5 2sin3 cos2 sin 0
x x x x
Giải:
PT
3 1
3cos5 sin5 2sin cos5 sin5 sin sin 5 sin
2 2 3
x x x x x x x x
5 2
3 18 3
,
5 2
3 6 2
k
x x k x
k
k
x x k x
Vậy phương trình có nghiệm là
, ,
18 3 6 2
k k
x x k
Thí dụ 6: Giải phương trình:
cos7 sin5 3(cos5 sin7 )
x x x x
Giải:
PT
cos7 3 sin7 3 cos5 sin5
x x x x
1 3 3 1
cos7 sin7 cos5 sin5
2 2 2 2
x x x x
cos cos7 sin sin7 cos cos5 sin sin5
3 3 6 6
x x x x
7 5 2
3 6
cos 7 cos 5
3 6
7 5 2
3 6
x x k
x x
x x k
2 2
6 12
,
3
12 2
8 62
x k x k
k
k
x
x k
Vậy phương trình có hai nghiệm
Thí dụ 7: (ĐH – B 2012) Giải phương trình
2(cos 3sin )cos cos 3sin 1.
x x x x x
Giải:
Nhận xét 1: Sau khi nhân phá ra ta nhóm cụm
2
2cos 1 cos2
x x
và
2 3sin cos 3sin 2
x x x
, không
còn hệ số tự do và chuyển cung 2x sang một bên, cung 1x sang một bên thì bài toán trở thành bài toán cơ
bản nhưng mở rộng của bài phương trình bậc nhất đổi với sin và cos nên ta có lời giải sau
Cách 1:
2 cos 3sin cos cos 3sin 1 cos2 3sin 2 cos 3sin
x x x x x x x x x
(*)
Chia hai vế cho 2 và biến đổi thành
2
2
3
cos 2 cos 2 2 ,
2
3 3 3 3
3
x k
x x x x k k
x k
Chú ý:
- Ta có thể biến đổi về sin như sau
Giáo viên: Nguyễn Thành Long Email: Changngoc203@gmail.com
https://www.facebook.com/trithuc.viet.37
11
M
2
M
3
M
1
cos2 3sin 2 cos 3sin
2
2 2
2
6 6
3
sin 2 sin ,
2
6 6
2 2
6 6
3
x x x x
x x k
x k
x x k
x x k
x k
- Có thể giải phương trình (*) như sau
cos2 cos 3 sin 2 sin 0
3 3
2sin sin 2 3sin cos 0
2 2 2 2
2
3
sin 0
3
2
,
2
tan 3 2
2 3
x x x x
x x x x
x
x k
k
x
x k
Nhận xét 2: Sau khi nhân phá ra chuyển về một vế và nhóm thành hai cặp
2
2cos cos 1
x x
và
3sin 2cos 1
x x
ta thấy chúng có nhân tử chung là
2cos 1
x
và ta có lời giải sau
Cách 2:
2
2(cos 3sin )cos cos 3sin 1 2cos cos 1 3sin 2cos 1 0
x x x x x x x x x
2cos 1 cos 1 3sin 2cos 1 0 2cos 1 3sin cos 1 0
x x x x x x x
2
2
1
cos
3
2cos 1 0
2
2 ,
1
3sin cos 1 0
cos
2
3 2 2
3
x k
x
x
x k k
x x
x
x k
Sử dụng đường tròn lượng giác tổng hợp nghiệm ta thấy
Với nghiệm
2
x k
tương ứng trên đường tròn là điểm
M
1
Với nghiệm
2
2
3
x k
tương ứng trên đường tròn là điểm M
2
Với nghiệm
2
2
3
x k
tương ứng trên đường tròn là điểm
M
3
Nhận thấy 3 điểm nghiệm không trùng với hai điểm điều kiện mà
3 điểm nghiệm này cách đều nhau một góc
2
3
nên ta có gộp 3 điểm
nghiệm thành
2
,
3
x k k
.
Vậy phương trình có nghiệm là
2 2
2 , ,
3 3
x k x k k
Chú ý:
- Ta cũng có thể biến đổi về sin như sau
1
3sin cos 1 0 sin sin
6 2 6
x x x
- Ta có bài toán tổng quát như sau khi xuất hiện
cos2
x
(hoặc
2
sin
x
hoặc
2
cos
x
),
sin 2 ,sin ,cos
x x x
và
hệ số tự do ta có bài toán tổng quát sau
sin 2 cos2 sin cos 0
a x b x c x d x e
ta biến đổi về một
trong hai dạng
Giáo viên: Nguyễn Thành Long Email: Changngoc203@gmail.com
https://www.facebook.com/trithuc.viet.37
12
2
2
2
2
2 sin cos 2cos 1 sin cos 0
2 sin cos 1 2sin sin cos 0
2 cos cos sin 2 cos 0
2 sin sin cos 2 sin 0
a x x b x c x d x e
a x x b x c x d x e
b x d x b e x a x c
b x c x b e a x d
Từ đó sẽ xuất hiện nhân tử chung (với các hệ số
, , , ,
a b c d e
theo một tỉ lệ nào đó), với dạng bài này đề
thi khối D năm 2010 (xem ở mục kĩ năng đưa về phương trình tích)
Tương tự: Giải phương trình
6 6
8 sin cos 3 3sin 4 3 3 cos2 9sin 2 11
x x x x x
Phương trình
2
3
8 1 sin 2 6 3sin 2 cos2 3 3 cos2 9sin 2 11 0
4
x x x x x
2
3cos2 2sin 2 1 2sin 2 3sin 2 1 0
3cos2 2sin 2 1 sin 2 1 2sin 2 1 0
2sin 2 1 3 cos2 sin 2 1 0
1
sin 2
2sin2 1 0
2
3cos2 sin 2 1 0
sin 2 sin
3 6
12
5
12
4
5
12
x x x x
x x x x
x x x
x
x
x x
x
x k
x k
x k
x k
,k
Thí dụ 8: (ĐH – B 2009) Giải phương trình:
3
sin cos sin2 3cos3 2 cos4 sin
x x x x x x
Giải:
Phương trình
2
sin 1 2sin cos .sin2 3cos3 2cos4
x x x x x x
1 3
sin3 3 cos3 2cos4 sin3 cos3 cos4
2 2
x x x x x x
cos4 cos 3
6
x x
4 3 2
6
x x k
2
6
,
2
42 7
x k
k
x k
Hoặc: Phương trình
1 3 1
sin sin3 sin 3cos3 2 cos4 sin sin3
2 4 4
x x x x x x x
1 3 3 1
sin3 sin 3cos3 2cos4 sin sin3
2 2 2 2
x x x x x x
Giáo viên: Nguyễn Thành Long Email: Changngoc203@gmail.com
https://www.facebook.com/trithuc.viet.37
13
1 3
sin3 3 cos3 2cos4 sin3 cos3 cos4
2 2
x x x x x x
Vậy phương trình có nghiệm là
2
, 2 ,
42 7 6
k
x x k k
Thí dụ 9: Giải phương trình
8sin tan cot 4cot 2
6
x x x x
Giải:
Điều kiện:
sin 0
sin 2 0
cos 0
x
x
x
(*)
Phương trình
2
8sin 4cot2
6 sin2
x x
x
2 2
4sin sin 2 1 2cos2 2 3sin cos .sin 2 3sin – cos 0
6
x x x x x x x x
( 3sin cos )(2sin 2 3sin cos ) 0
3sin cos 0
2sin2 3sin cos 0
x x x x x
x x
x x x
TH1: 3sin cos 0 cot 3 ,
6
x x x x k k
3 1
TH2: 2sin 2 3sin cos 0 sin cos sin2
2 2
5
2
6
sin sin 2 ,
2
6
18 3
x x x x x x
x k
x x k
k
x
Các nghiệm trên đều thỏa mãn (*). Vậy phương trình có 3 nghiệm trên
Thí dụ 10: Giải phương trình
tan 3cot 4 sin 3 cos
x x x x
Giải:
Phương trình
2 2
sin 3cos 1 3
8 sin cos
sin cos 2 2
x x
x x
x x
1 2cos2 4sin 2 .sin
3
x x x
2
cos cos2 cos cos 3
3 3 3
2
cos2 cos cos 3 cos 0
3 3 3
x x x
x x x
3 3
2cos cos cos 0
2 6 2 6 2 2
3
4cos sin sin 0
2 6 3 2 6
x x x
x x
x
Giáo viên: Nguyễn Thành Long Email: Changngoc203@gmail.com
https://www.facebook.com/trithuc.viet.37
14
sin 0
2 6
3
sin 0 ,
4 2
3
9 3
3
4cos 0
2 6
x
x k
x k
k
x
x
Vậy nghiệm của phương trình là
4 2
; ,
3 9 3
k
x k x k
Vậy phương trình có ba nghiệm trên
Chú ý: Cách khác xem ở Ví dụ 3 trang 23
Dạng 2: Phương trình thuần nhất bậc hai đối với
sin
x
và
cos
x
.
a. Định nghĩa: Phương trình thuần nhất bậc hai đối với
sin
x
,
cos
x
là phương trình.
2 2
sin sin .cos cos
a x b x x c x d
(1) trong đó a, b, c, d
b. Cách giải :
Cách 1:
Chia từng vế của phương trình (1) cho một trong ba hạng tử
2
sin
x
hoặc
2
cos
x
hoặc
sin .cos
x x
.
Chẳng hạn nếu chia cho
2
cos
x
ta làm theo các bước sau:
Bước 1: Kiểm tra:
cos 0 ,
2
x x k k
xem nó có phải là nghiệm của phương trình (1) hay
không?
Bước 2: Với
cos 0
x
chia cả hai vế cho
2
cos
x
lúc đó phương trình (1) trở thành
2 2 2
tan tan (1 tan ) ( )tan tan 0
a x b x c d x a d x b x c d
Đây là phương trình bậc hai theo tan ta đã biết cách giải bằng cách đặt
tan
t x
.
Cách 2:
Dùng công thức hạ bậc
2 2
1 cos2 1 cos2 sin 2
sin ;cos ;sin .cos
2 2 2
x x x
x x x x
đưa phương trình đã
cho về phương trình sin 2 ( )cos2
b x c a x d c a
Đây là phương trình bậc nhất đối với sin và cos ta đã biết cách giải (dạng 1)
Chú ý:
- Khi
0
d
thì
2 2
sin sin .cos cos 0
a x b x x c x
gọi là phương trình đẳng cấp bậc 2
- Đối với phương trình đẳng cấp bậc n (n
3) với dạng tổng quát
(sin ,cos ,sin cos ) 0
n n k h
A x x x x
trong đó ; , ,k h n k h n
Khi đó ta cũng làm theo 2 bước:
Bước 1: Kiểm tra xem
cos 0
x
có phải là nghiệm của phương trình hay không?
Bước 2: Nếu
cos 0
x
. Chia cả hai vế của phương trình trên cho
cos
n
x
ta sẽ được phương trình bậc n
theo tan. Giải phương trình này ta được nghiệm của phương trình ban đầu.
THÍ DỤ MINH HỌA
Thí dụ 1:
(ĐH – B 2008) Giải phương trình: xxxxxx cossin3cossincos3sin
2233
Giải:
Nhận xét 1: Đây là phương trình đẳng cấp bậc 3 nên ta giải như sau
Cách 1:
Thay
cos 0 ,
2
x x k k
vào phương trình ta được
3
sin 0 sin 0
x x
nên ,x k k
không phải là nghiệm của phương trình
Khi
cos 0
x
chia cả hai vế của phương trình cho
3
cos
x
ta được
Giáo viên: Nguyễn Thành Long Email: Changngoc203@gmail.com
https://www.facebook.com/trithuc.viet.37
15
3 2 2 2
tan 3 tan 3.tan tan tan 1 3 tan 1 0
x x x x x x
2
tan 1
tan 1 tan 3 0
tan 3
x
x x
x
4
,
3
x k
k
x k
Nhận xét 2: Ta nhận thấy có các nhân tử chung và các hệ số tương ứng tỉ lệ nên ta có lời giải sau
Cách 2:
Phương trình
3 2 3 2
sin sin cos 3cos 3sin cos 0
x x x x x x
2 2 2 2
sin sin cos 3 cos cos sin 0
sin sin cos sin cos 3cos cos sin cos sin 0
sin cos sin cos sin 3 cos 0
sin cos 0
tan 1
4
sin cos 0 ;
tan 3
sin 3 cos
3
x x x x x x
x x x x x x x x x x
x x x x x x
x x
x k
x
x x k
x
x k
x x
Vậy phương trình có các nghiệm là
; ,
4 2 3
x k x k k
Chú ý:
- Kết hợp hai nghiệm
4
x k
thành một nghiệm
4 2
x k
vì chúng hợp với nhau một góc
2
- Cũng có thể biến đổi
Phương trình
3 2 3 2
sin sin cos 3cos 3sin cos 0
x x x x x x
2 2 2 2
sin sin cos 3 cos cos sin 0
sin cos2 3 cos cos2 0
cos2 sin 3 cos 0
cos2 0
2 2
;
sin 3 cos
3
x x x x x x
x x x x
x x x
x k
x
k
x x
x k
Thí dụ 2: (ĐHCĐ – 2000) Giải phương trình
1 3tan 2sin2
x x
Giải:
Cách 1: Điều kiện:
cos 0
x
(*)
Phương trình
2
sin
1 3 4sin cos cos 3sin 4sin cos
cos
x
x x x x x x
x
Nhận xét: Đây là phương trình đẳng cấp bậc ba nên ta chia hai vế của phương trình cho
3
cos
x
Ta được
2 2
2 2
3 2 2
1 tan
3 4tan 1 tan 3tan 1 tan 4tan
cos cos
3tan tan tan 1 0 tan 1 3tan 2 tan 1 0
x
x x x x
x x
x x x x x x
tan 1 ,
4
x x k k
(thỏa mãn (*)) vì
2
3tan 2tan 1 0
x x
vô nghiệm
Chú ý:
- Ta có thể chia từ đầu hai vế của phương trình cho
2
cos
x
- Nhìn vào phương trình ta thấy xuất hiện
tan
x
và
sin 2
x
ta nghĩ tới mối quan hệ như giữa chúng
Giáo viên: Nguyễn Thành Long Email: Changngoc203@gmail.com
https://www.facebook.com/trithuc.viet.37
16
2 2 2
2sin cos 2tan
sin 2
sin cos 1 tan
x x x
x
x x x
hoặc
2
2
2
2sin cos
2tan
cos
sin 2 2sin cos
1
1 tan
cos
x x
x
x
x x x
x
x
từ đó ta đặt
tan
t x
Cách 2:
Đặt
2
2
tan sin 2
1
t
t x x
t
Khi đó ta được
3 2 2
2
4
1 3 3 1 0 ( 1)(3 2 1) 0
1
t
t t t t t t t
t
1 tan 1 ,
4
t x x k k
(thỏa mãn (*))
Vậy phương trình có duy nhất 1 họ nghiệm
,
4
x k k
Cách 3: Phân tích hệ số
3 1 2
Ta có phương trình
1 tan 2tan 4sin cos
x x x x
2
sin cos 2cos 1
2sin 0
cos cos
x x x
x
x x
sin cos 1 2sin cos sin 0
x x x x x
sin cos 0
tan 1
1 2sin cos sin
sin 2 cos2 2
x x
x
x x x x x
,
4
x k k
(Vì phương trình
sin 2 cos2 2
x x
vô nghiệm)
Cách 4: Phân tích hệ số
1 3 2
Ta có phương trình
3 1 tan 2 1 sin
x x
2
2
2
sin cos
3 2 sin cos sin cos 3 sin 2 2cos 0
cos
sin cos 0
tan 1
sin 2 cos2 2
3 sin 2 2cos 0
x x
x x x x x x
x
x x
x
x x
x x
,
4
x k k
(Vì phương trình
sin 2 cos2 2
x x
vô nghiệm)
Thí dụ 3: (ĐHQG HCM – 1998) Giải phương trình:
3
sin 2 sin
4
x x
Giải:
Cách 1:
Ta nhận thấy
sin
4
x
có thể biểu diễn được qua
sin cos
x x
. Luỹ thừa bậc ba biểu thức
sin cos
x x
ta sẽ đưa phương trình về dạng thuần nhất đã biết cách giải
Phương trình
3
3
2 2 sin 4sin 2 sin 4sin
4 4
x x x x
3
(sin cos ) 4sin
x x x
(*)
Xét với
cos 0 2 ,
2
x x k k
. Khi đó phương trình có dạng
3
sin 4sin
2 2
k k
mâu thuẫn
Giáo viên: Nguyễn Thành Long Email: Changngoc203@gmail.com
https://www.facebook.com/trithuc.viet.37
17
Vậy phương trình không nhận
2
2
x k
làm nghiệm
Với
cos 0
x
. Chia cả hai vế của phương trình (2) cho
3
cos
x
ta được:
3 2 3 2
(tan 1) 4(1 tan )tan 3tan 3tan tan 1 0
x x x x x x
.
Đặt
tan
t x
phương trình có được đưa về dạng:
3 2 2
3 3 1 0 ( 1)(3 1) 0 1 ,
4
t t t t t t x k k
Họ nghiệm trên thoả mãn điều kiện của phương trình .
Cách 2:
Từ phương trình (*)
3 2
(*) (sin cos ) 4sin (sin cos )(sin cos ) 4sin
x x x x x x x x
2 2
(sin cos )(1 2sin cos ) 4sin cos 3sin 2sin cos 2sin
cos 0
x x x x x x x x x x x
2 2
cos ( 2sin 1) sin (2cos 3) 0 cos (cos2 2) sin (cos2 2
) 0
x x x x x x x x
(cos2 2)(cos sin ) 0 cos2 2
x x x x
(loại) hoặc tan 1 ,
4
x x k k
Vậy phương trình có duy nhất 1 họ nghiệm
,
4
x k k
Cách 3.1: Đặt
4 4
t x x t
khi đó ta được phương trình
3
sin 2sin sin cos
4
t t t t
(**)
2 2
sin sin 1 cos sin cos cos
cos sin 2 2 0 cos 0 ,
2
t t t t t t
t t t t k k
Với
3
,
2 4
t k x k k
Cách 3.1: Từ phương trình (**) ta thấy nếu
sin 0 cos 1
x x
thì phương trình (**) vô nghiệm nên
sin 0
x
. Chia cả hai vế của (**) cho
3
sin
x
ta được phương trình
2 2
1 1 cot cot 1 cot cot 0
t t t t
3
,
2 4
t k x k k
Chú ý:
Ngoài phương pháp giải phương trình thuần nhất đã nêu ở trên có những phương trình có thể giải bằng
phương pháp khác tuỳ thuộc vào từng bài toán để giải sao cho cách giải nhanh nhất, khoa học nhất.
Thí dụ 4: Giải phương trình:
1 tan
1 sin 2
1 tan
x
x
x
Giải:
Điều kiện
cos 0
2
,
tan 1
4
x k
x
k
x
x k
Cách 1:
Biến đổi phương trình về dạng:
2 3
cos sin
cos sin cos sin cos sin
cos sin
x x
x x x x x x
x x
Chia cả hai vế của phương trình (3) cho
3
cos 0
x
ta được:
Giáo viên: Nguyễn Thành Long Email: Changngoc203@gmail.com
https://www.facebook.com/trithuc.viet.37
18
3
2 2
3 2 2
1 tan 1 tan tan 1 tan
tan tan 2tan 0 tan tan 2 tan 0 (*)
x x x x
x x x x x x
(do
2
tan tan 2 0
x x
vô nghiệm) nên:
Phương trình (*) tan 0 ,x x k k
Cách 2:
Biến đổi phương trình về dạng
2
2
2
cos
cos sin 2
4
cos sin 2sin cot
cos sin 4 4
sin 1 cot
4 4
x
x x
x x x x
x x
x x
Đặt cot
4
t x
ta được:
3 2
2
2
2 0 1 2 0 1
1
t t t t t t t
t
Hay
cot 1 ,
4 4 4
x x k x k k
Vậy phương trình có một họ nghiệm là ,x k k
Cách 3:
Phương trình
2
cos sin sin cos sin cos
x x x x x x
3 3
2 3
2 3
cos sin sin cos 3sin cos sin cos
cos 1 cos sin sin 3sin cos sin cos 0
cos sin sin sin 3sin cos sin cos 0
sin sin 2 cos2 3 0
x x x x x x x x
x x x x x x x x
x x x x x x x x
x x x
sin 0 ,x x k k
(Vì phương trình
sin 2 cos2 3 0
x x
vô nghiệm)
Cách 4: Đặt
2
2
tan sin 2
1
t
t x x
t
ta được phương trình
3 2
2
1 2
1 2 0
1
1
t t
t t t
t
t
2
2 0 0
t t t t
(vì phương trình
2
2 0
t t
vô nghiệm)
Với tan 0 ,x x k k
Thí dụ 5: (Đại học Y Dược Thành phố Hồ Chí Minh 1997)
Giải phương trình:
3
sin .sin 2 sin3 6cos
x x x x
Giải:
PT
3 3
sin 2sin cos 3sin 4sin 6cos
x x x x x x
3 2 3
4sin 3sin 2sin cos 6cos 0
x x x x x
(*)
Nếu
cos 0
x
là nghiệm (*) của thì:
3
3
sin 1
cos 0
sin 1
4sin 3sin 0
4sin 3sin 0
x
x
x
x x
x x
vô lý
Chia 2 vế của (*) cho
3
cos 0
x
ta được phương trình tương đương:
3 2 2
* tan 2tan 3tan 6 0 tan 2 tan 3 0
x x x x x
tan 2 tan
,
tan 3 tan
3 3
x x k
k
x x k
Giáo viên: Nguyễn Thành Long Email: Changngoc203@gmail.com
https://www.facebook.com/trithuc.viet.37
19
Vậy phương trình có các nghiệm là
; ,
3
x k x k k
với
tan 2
Thí dụ 6: Giải phương trình
cos2
tan 2 sin 2 0
1 cot 4
x
x x
x
Giải:
Điều kiện:
1 cot 0
sin 0
cos 0
x
x
x
Phương trình
cos2 .sin sin
sin 2 cos2 0
sin cos cos
x x x
x x
x x x
sin 1
cos2 1 sin 2cos 0
sin cos cos
cos2 .cos sin .cos2
0
sin cos cos
x
x x x
x x x
x x x x
x x x
2 2
2 2
sin cos
cos2 0
cos sin cos
cos2 (sin sin .cos cos ) 0
cos2 0 (1)
sin sin .cos cos 0 (2)
x x
x
x x x
x x x x x
x
x x x x
2
(1) ,
4 2
1 5 1 5
(2) tan tan 1 0 tan arctan ,
2 2
x k k
x x x x l l
Đối chiếu điều kiện ta có nghiệm phương trình là:
4
1 5
arctan
2
x k
x l
Dạng 3: Phương trình đối xứng đối với
sin
x
và
cos
x
.
a. Định nghĩa: Phương trình đối xứng đối với
sin
x
và
cos
x
là phương trình dạng
(sin cos ) sin cos 0
a x x b x x c
trong đó , ,a b c
b. Cách giải:
Cách 1:
Do
2
(sin cos ) 1 sin cos
a x x x x
nên ta đặt
sin cos 2sin 2 cos
4 4
t x x x x
. Điều kiện
| | 2
t
Suy ra
2
1
sin cos
2
t
x x
và phương trình được viết lại:
2
2 ( 2 ) 0
bt at b c
Đó là phương trình bậc hai đã biết cách giải
Cách 2:
Đặt
4
t x
thì
sin cos 2 cos 2 cos
4
x x x t
2
1 1 1 1
sin cos sin2 cos 2 cos2 cos
2 2 2 2 2
x x x x t t
nên phương trình trở thành

Tài liệu khác của Toán 11

Preview text:


CÁC KĨ THUẬT GIẢI PHƯƠNG TRÌNH LƯỢNG GIÁC
Giáo viên giảng dạy: NGUYỄN THÀNH LONG
Email: Changngoc203@gmail.com
Bỉm sơn: 10 – 02 – 2014
Giáo viên: Nguyễn Thành Long Email: Changngoc203@gmail.com
Phương trình lượng giác và ứng dụng của nó là một phần rất quan trọng trong đề thi đại học và ứng dụng
của nó trong đại số cũng như hình học. Và đặc biệt là giải phương trình lượng giác là một câu không thể
thiếu trong đề thi đại học các năm. Vậy muốn làm tốt lượng giác trước tiên ta phải nắm được công thức lượng giác
TÓM TẮT CÁC CÔNG THỨC LƯỢNG GIÁC CẦN NHỚ
I. Các công thức lượng giác cần nhớ
1. Các công thức cơ bản sin a cos a tan a  với a   k cot a
với a k cos a 2 sin a tan .
a cot a  1 2 2 s  in a
 1 cos a  (1 cosa)(1 cosa) 2 2
sin a  cos a  1   2 2 cos a
 1 sin a  (1 sin a)(1 sin a) 1 1 2 1  tan a  2 1  cot a  2 cos a 2 sin a
2. Công thức cộng và trừ a. Với sin và cos
sin a b  sin .
a cos b  cos . a sin b
cos a b  cos .
a cos b  sin . a sin b
sin a b  sin .
a cos b  cos . a sin b
cos a b  cos .
a cos b  sin . a sin b b. Với tan   a b a b tan a tan b tan  a b  1    tan tan tan tan . a tan b 1  tan . a tan b
3. Công thức tính tích thành tổng 1 1 cos .
a cos b  cos(a b)  cos(a b) sin .
a cos b  sin(a b)  sin(a b) 2 2 1 1 sin .
a sin b  cos(a b)  cos(a b) cos .
a sin b  sin(b a)  sin(a b) 2 2
4. Công thức biến đổi tổng thành tích
a. Công thức sin và cos a b a b a b a b
cos a  cos b  2cos cos
cos a  cosb  2  sin sin 2 2 2 2 a b a b a b a b
sin a  sin b  2sin cos
sin a  sin b  2 cos sin 2 2 2 2
b.Công thức tan và cot sin(a b) sin(a b)
tan a  tan b
tan a  tan b  cos . a cos b cos . a cos b sin(a b) sin(b a)
cot a  cot b
cot a  cot b  sin . a sin b sin . a sin b
5. Công thức nhân đôi và nhân ba, nhân bốn sin 2a  2sin . a cos a 2 2 2 2
cos 2a  2cos a 1  1  2sin a  cos a  sin a 2 2
 (sin a  cosa ) 1  1 (sin a  cosa ) 4 4
 cos a  sin a 2 tan a 3
3 tan a  tan a 3
sin 3a  3sin a  4sin a  sin a  2 3  4sin a tan 2a  ; tan 3a = 2 1  tan a 2 1  3 tan a  sin a 2 4 cos a  
1  sin a 2cos a   1 2cos a   1 3
cos 3a  4cos a  3cos a  cos a  2 4 cos a  3  cosa 2
1  4sin a  cosa1 2sin a1 2sin a
https://www.facebook.com/trithuc.viet.37 1
Giáo viên: Nguyễn Thành Long Email: Changngoc203@gmail.com 4 2
sin 4a  4sin a  2sin a 4 2
cos 4a  8cos a  8cos a 1
6. Công thức hạ bậc 1  cos 2a 1  cos 2a 2 cos a 2 sin a 2 2 2 sin a 1  cos 2a 2 cos a 1  cos 2a 2 tan a   2 cot a   2 cos a 1  cos 2a 2 sin a 1  cos 2a
cos 3a  3cos a
3sin a  sin 3a 3 cos a 3 sin a 4 4
II. Giá tri lượng giác của các góc liên quan đặc biệt
1. Bỏ chẵn lần pi thì không thay đổi
sin  x k2  sin x
tan x k2  tan x
cos  x k2  cos x
cot  x k2  cot x
2. Bỏ pi hay lẻ lần pi thì thành cộng biến thành trừ
sin x  sin x
sin x  sin x
cos x  cos x
cos x   cos x
tan x   tan x
tan x  tan x
cot x   cot x
cot x  cot x
TQ: sin(k2x)  sin x
TQ: sin(k2x)  sin x
cos(k2x)   cos x
cos(k2x)  cos x 3. Bỏ pi trên hai  
sin   x  cos x
sin   x  cos x 2   2     
cos   x  sin x
cos   x  sin x 2   2     
tan   x  cot x
tan   x  cot x 2   2     
cot   x  tan x
cot   x   tan x 2   2   d. Đổi dấu
sin x  sin x
tan x   tan x
cos x  cos x
cot x   cot x a
III. Công thức tính sina, cosa theo t  tan 2  2t sin a  2  1  t  2 2  1  t 1  t Ta có cos a    cot a  2 1  t 2t   2t tan a   2 1   t
Một số công thức khác
https://www.facebook.com/trithuc.viet.37 2
Giáo viên: Nguyễn Thành Long Email: Changngoc203@gmail.com  2 
cos a  sin a  cos a  cos   a   2cos .cos a     2. cos a    2 4 4 2 4         3    3     2.sin  a     2.sin
a  2.sin   a  2.sin a    2 4 4 4 4               
Vậy cos a  sin a  2 cos a     2 sin a
    2 cos  x 4 4 4       Tươ       
ng tự: cos a  sin a  2 cos a    2 cos a
    2 sina     2 sin a     4   4   4   4  3 3 x x   x x 2 2 sin cos sin cos sin x  sin .
x cos x  cos x  sin x  cos x1 sin .xcos x 3 3 x x   x x 2 2 sin cos sin cos sin x  sin .
x cos x  cos x  sin x  cos x1 sin .xcos x 1 1 1 3 1 4 4 2 2 2 2
sin x  cos x  1  2sin .
x cos x  1 sin 2x
 cos 2x   cos4x 2 2 2 4 4 4 4 x x   2 2  x 2 2 cos sin cos sin
cos  sin x  cos2x 3 1 3 3 5 6 6 4 4 2 2 2 2
sin x  cos x  sin x  cos x  sin x cos x  1 sin 2x
 cos 2x  cos4x  4 4 4 8 8 6 6 4 4 2 2
cos x  sin x  cos 2x(sin x  cos x  sin x cos x)   
sin x  cos x  2 sin x     2 cos x     4   4   x x x x x   x x2 2 2 1 sin 2 sin cos 2 sin cos sin cos 2 2 2
1  sin 2x  sin x  cos x  2sin x cos x  (sin x  cos x) sin 2x 2 2 sin x cos x
,1  cos 2x  2 cos x,1  cos 2x  2sin x 2
ĐƯỜNG TRÒN LƯỢNG GIÁC
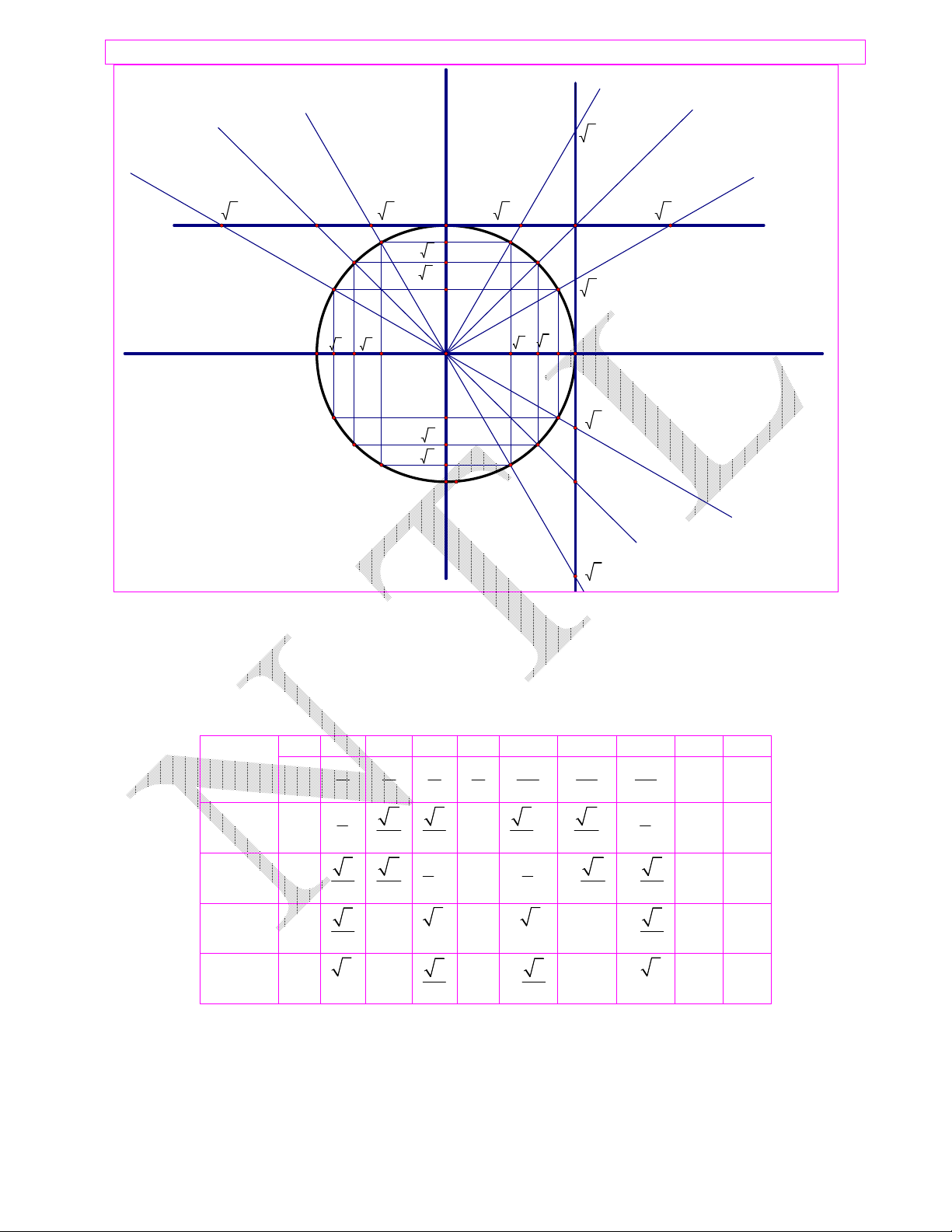
Giá trị các hàm số lượng giác của các cung (góc) đặc biệt (ta nên sử dụng đường tròn lượng giác để
ghi nhớ các giá trị đặc biệt)
https://www.facebook.com/trithuc.viet.37 3
Giáo viên: Nguyễn Thành Long Email: Changngoc203@gmail.com y t 3 - 3 -1 - 3 /3 B /2 3 /3 1 3 u' 1 /3 u 2/3 3 /2 /4 3/4 2 /2 /6 5/6 3 /3 1/2 x' - 3 /2 - 2 /2 -1/2 1/2 3 /2 2 /2
1 A (Ñieåm goác) x -1 O -1/2 - 3 /3 -/6 - 2 /2 - 3 /2 -/4 -1 -/3 -1 -/2 - 3 y' t'
Bảng lượng giác của một số góc đặc biệt 00 300 450 600 900 1200 1350 1500 1800 3600 Góc 0 2 3 5 2 Hslg 6 4 3 2 3 4 6 sin 0 1 1 1 0 0 2 3 3 2 2 2 2 2 2 2 cos 1 3 2 1 0 1 -1 1  2 3   2 2 2 2 2 2 tan 0 1  0 0 3 3 kxđ 3 -1 3  3 3 cot kxđ 3 1 3 0 3 -1  3 kxđ kxđ  3 3
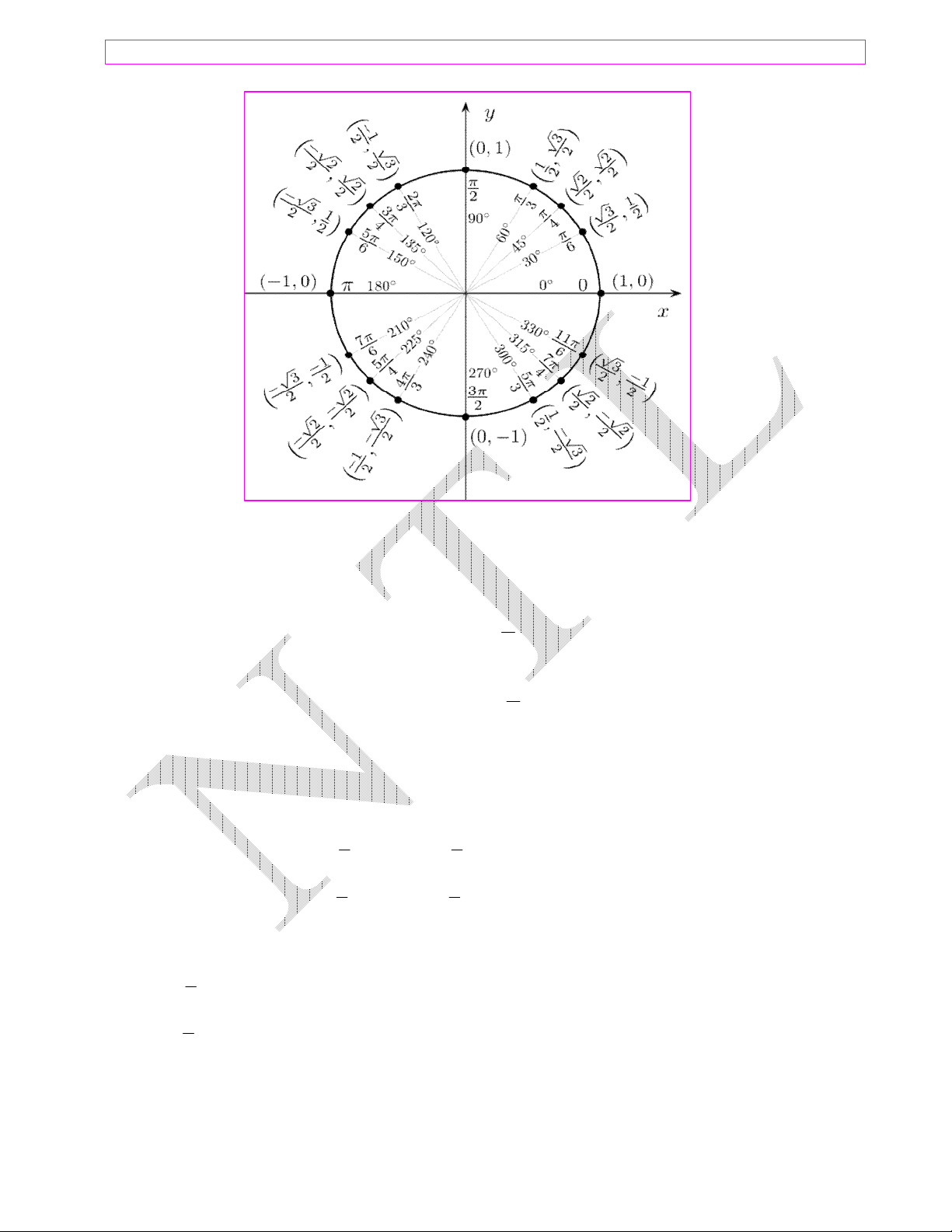
Hoặc: Đường tròn lượng giác
Một điểm M thuộc đường tròn lượng giác sẽ có tọa độ M cos;sin ứng với mỗi góc ta sẽ được
một điểm M cụ thể trên đường tròn
https://www.facebook.com/trithuc.viet.37 4
Giáo viên: Nguyễn Thành Long Email: Changngoc203@gmail.com
Để giải được phương trình lượng giác chúng ta nắm được các bước giải sau
Bước 1: Đặt điều kiện cho phương trình có nghĩa (nếu có). Điều kiện gồm, phương trình chứa
mẫu, chứa cot hoặc tan, chứa căn bậc chẵn… Cụ thể:
- Phương trình chứa tan x , điều kiện: cos x  0  x
k ,k  . 2
- Phương trình chứa cot x , điều kiện: sin x  0  x k , k   .
- Phương trình chứa cả tan x và cot x , điều kiện: x k , k   . 2
Bước 2: Sử dụng công thức lượng giác, các phép biến đổi lượng giác. Các phương pháp giải
phương trình nói chung, tìm ra nghiệm của phương trình
Bước 3: Đối chiếu với điều kiện ban đầu để tìm ra nghiệm thỏa mãn và kết luận (xem mục kĩ
năng 5 loại nghiệm và kết hợp nghiệm) Chú ý:  1  1 2 cos x  cos x     Đố 2 2 i với phương trình   
ta không nên giải trực tiếp vì khi đó có tới 4 nghiệm, 1 1 2   sin x  sin x    2  2
khi kết hợp và so sánh với điều kiện rất phức tạp, ta nên hạ bậc là tối ưu nhất. Nghĩa là:  1 2 cos x  2  2cos x 1  0 cos2x  0 2      . 2 1  2sin x   1  0 cos 2x   0 2 sin x  2 2      Tương tự đố sin x 1 sin x 1 i với phương trình   
ta không nên hạ bậc, mà nên biến đổi dựa vào 2 cos x   1 cos x   1  2 2 s  in x  1 cos x  0 cos x  0 công thức 2 2
sin x  cos x  1. Lúc đó:      2 2 cos x   1 sin x   0 sin x   0
https://www.facebook.com/trithuc.viet.37 5
Giáo viên: Nguyễn Thành Long Email: Changngoc203@gmail.com
Đối với phương trình cos x  cos 2x  0. Chúng ta có thể chuyển về dạng cos x  cos2x
nhưng đơn giản hơn là thay 2
cos 2x  2 cos x 1 để phương trình trở thành phương trình bậc hai với cosx
Tương tự với phương trình sin x  cos2x  0
Khi đặt ẩn phụ t  sin x,t  cos x thì điều kiện của t là t  1. Khi đặt ẩn phụ 2 2
t  sin x,t  cos x
thì điều kiện của t là 0  t  1. Khi đặt ẩn phụ t  sin x  cos x thì điều kiện của t là t  2 .
Một số phương trình lượng giác cơ bản cần nhớ
sinx  0 x k    Dạ u v k 2 
ng 1: sin u  sin v  , k  
Đặc biệt: sin x
 1  x   k2 , k u
  v k2 2  
sin x  1  x    k2  2    Dạ u v k2
ng 2: cos u  cos v  , k   Đặc biệt: u
  v k2
cos x  0  x   k
  k2 2 2   cosx
 1  x k2 , k
cos x  1 x k2  
tanu  tan v u v k
tan x  0  x k Dạ   ng 3: , k Đặc biệt: , k u, v   k
       tan x 1 x k  2  4      
cot x  0  x   k Dạ cot u cot v u v k  2 ng 4: , k   Đặc biệt: , k   u, v   k
 cot x  1  x    k  4
https://www.facebook.com/trithuc.viet.37 6
Giáo viên: Nguyễn Thành Long Email: Changngoc203@gmail.com
§ 1: CÁC DẠNG PHƯƠNG TRÌNH THƯỜNG GẶP
1. Phương trình bậc nhất đối với sin x,cos x
a. Định nghĩa: Phương trình a sin x b cos x c (1) trong đó a, b, c  và 2 2
a b  0 được gọi là
phương trình bậc nhất đối với sin x,cos x b. Cách giải.
Ta có thể lựa chọn 1 trong 2 cách sau:
Cách 1: Thực hiện theo các bước Bước 1: Kiểm tra - Nếu 2 2 2
a b c phương trình vô nghiệm - Nếu 2 2 2
a b c khi đó để tìm nghiệm của phương trình ta thực hiện tiếp bước 2
Bước 2: Chia cả 2 vế phương trình (1) cho 2 2
a b , ta được a b c sin x  cos x  2 2 2 2 2 2 a b a b a b 2 2  a   ba b Vì       1 
nên tồn tại góc sao cho  cos,  sin 2 2   2 2 
a b   a b  2 2 2 2 a b a b Khi đó phương tr c c ình (1) có dạng sin .
x cos sin.cos x
 sin(x )  2 2 2 2 a b a b
Đây là phương trình cơ bản của sin mà ta đã biết cách giải
Cách 2: Thực hiện theo các bước Bước 1: x Với cos
 0  x k2,k  thử vào phương trình (1) xem có là nghiệm hay không? 2 Bước 2: x Với cos
 0  x k2,k 2 2 Đặt x 2t 1  t
t  tan suy ra sin x  , cos x  2 2 2 1  t 1  t
Khi đó phương trình (1) có dạng 2 2t 1  t 2 ab
c  (c b)t  2at c b  0 (2) 2 2 1  t 1  t
Bước 3: Giải phương trình (2) theo t, sau đó giải tìm x. Dạng đặc biệt:
sin x  cos x  0  tan x  1  x  
k,k  4
sin x  cos x  0  tan x  1  x
k,k   . 4   
sin x  cos x k k  0 sử dụng công thức sin x  cos x  2 sin x     2 cos x    4 4    
Chú ý: Từ cách 1 ta có kết quả sau 2 2 2 2
a b asin x bcos x a b từ kết quả đó ta có thể áp dụng tìm GTLN và GTNN của các
a sin x b cos x
hàm số có dạng y a sin x b cos x , y
và phương pháp đánh giá cho một số phương
c sin x d cos x trình lượng giác . THÍ DỤ MINH HỌA
Thí dụ 1: Giải phương trình: sin 2x  3cos 2x  3 Giải:
https://www.facebook.com/trithuc.viet.37 7
Giáo viên: Nguyễn Thành Long Email: Changngoc203@gmail.com Cách 1:
Chia cả hai vế phương trình cho 2 2 1  3  10 ta được 1 3 3 sin 2x  cos 2x  10 10 10 Đặt 3 1  sin,
 cos. Lúc đó phương trình viết được dưới dạng 10 10
cossin 2x  sincos 2x  sin sin(2x )  sin x
x k
2x k2     , k 2x
 k2
x   k  2
Vậy phương trình có 2 nghiệm Cách 2:
Ta nhận thấy cos x  0 là nghiệm của phương trình
Với cos x  0  x
k ,k . 2 2 Đặt 2t 1  t
t  tan x , lúc đó sin 2x  , cos 2x  2 2 1  t 1  t 2 Phương tr 2t 1  t ình sẽ có dạng 2 2  3
 3  2t  3(1 t )  3(1 t )  t  3 2 2 1  t 1  t
Hay tan x  3  tanx k , k  
Vậy phương trình có 2 họ nghiệm
Cách 3: Biến đổi phương trình về dạng 2
sin 2x  3(1  cos 2x)  2sin .
x cos x  6 cos x cos x  0 cos x  0
 (sin x  3cos x)cos x  0     sin x   3cos x  0 tan x   3  tan x   k   2 , k   x
  k
Vậy phương trình có hai họ nghiệm Chú ý:
Khi làm bài toán dạng này chúng ta nên kiểm tra điều kiện trước khi bắt tay vào giải phương trình bởi có
một số bài toán đã cố tình tạo ra những phương trình không thoả mãn điều kiện. Ta xét ví dụ sau:
Thí dụ 2: (Đại học Giao thông Vận tải Hà Nội 2000) Giải phương trình sau:
2 2 sin x  cos xcos x  3  cos 2x Giải:
Phương trình 2 2 sin x  cos xcos x  3cos2x
 2 sin x   2  1cos2x  3 2 a b    22  2 2 2 2 1  5  2 2 Ta có  c   3 22 2 11 6 2 Ta sẽ chứng minh: 2 2 2
a b c  5  2 2  11  6 2     2 2 4 2 6 4 2  6  32  36(đúng)
Vậy phương trình vô nghiệm.
Ngoài ra chúng ta cần lưu ý rằng việc biến đổi lượng giác cho phù hợp với từng bài toán sẽ biểu diễn
chẵn các họ nghiệm . Ta xét ví dụ sau
Thí dụ 3: Giải phương trình (1  3) sin x  (1  3) cos x  2
https://www.facebook.com/trithuc.viet.37 8
Giáo viên: Nguyễn Thành Long Email: Changngoc203@gmail.com Giải: Cách 1:
Thực hiện phép biến đổi 1 3  1 3  2 1 PT  sin x    cos x         2 2 2 2 2 2 2     Đặt 1 3 1  3  cos x;  sin x 2 2 2 2 Phương tr 1
ình được viết thành sin .
x cos sin.cos x
 sin(x )  sin 2 4  x   k2 x
k2   4 4     , k    3 
x   k2 x
k2  4  4
Vậy phương trình có hai họ nghiệm Cách 2:
Biến đổi phương trình về dạng   
(sin x  cos x)  3(sin x  cos x)  2  2 sin x     6 cos x     2 4 4     1   3   1  1  sin x     cos x      sin x   cos   cos x   sin   2  4  2  4  2  4  3  4  3 2    x    k2 x   k2       12 4 3  sin x
     sin     , k    4 3  4  5  x
  k2 x    k 2 12 4  6
Vậy phương trình có hai họ nghiệm
Qua hai cách giải ở bài trên ta nhận thấy bằng cách 2 ta thu được nghiệm phương trình chẵn. x
Bài trên cũng có thể sử dụng cách đặt t  tan và ta cũng thu được nghiệm chẵn 2 2  x x
Thí dụ 4: (ĐH – D 2007) Giải phương trình: sin 
 cos   3cos x  2  2 2  Giải: Phương tr x x x x ình 2 2  sin  2sin cos  cos  3 cos x  2 2 2 2 2
 sin x  3 cos x  1 3 1 1  sin x  cos x  2 2 2 1    sin . x cos  cos .xsin  1  sin x     3 3 2  3  2    x    k2 x    k2   3 6 6     , k 5 x    k2 x   k2  3 6  2
Vậy phương trình có các nghiệm là x
k2, x    k2,k 2 6 Chú ý:
https://www.facebook.com/trithuc.viet.37 9
Giáo viên: Nguyễn Thành Long Email: Changngoc203@gmail.com
Đối với phương trình dạng asin P(x)  bcosQ(x)  csinQ(x)  d cos P(x) (*) trong đó a, b, c, d  thoả mãn 2 2 2 2
a b c d  0 và P x,Q x không đồng thời là các hàm hằng số. Bằng phép chia cho 2 2
a b ta có (*)  sinP(x)    sinQ(x)   hoặc
(*)  cosP(x)    cosQ(x)   trong đó , là các góc phụ thích hợp. Ta xét ví dụ sau:
Thí dụ 5: (ĐH – D 2009) Giải phương trình: 3 cos5x  2sin 3x cos 2x  sin x  0 Giải: 3 1 
PT  3 cos 5x  sin 5x  2sin x
cos 5x  sin 5x  sin x  sin   5x  sin x 2 2 3    k
 5x x  2k x     3 18 3     , k  k
 5x x  2k x     3  6 2  k  k
Vậy phương trình có nghiệm là x   , x    , k 18 3 6 2
Thí dụ 6: Giải phương trình: cos 7x  sin 5x  3(cos 5x  sin 7x) Giải:
PT  cos 7x  3 sin 7x  3 cos5x  sin 5x 1 3 3 1  cos7x  sin 7x
cos 5x  sin 5x 2 2 2 2
 cos cos7x  sin sin 7x  cos cos5x  sin sin5x 3 3 6 6  7x
 5x   k2      3 6  cos 7x     cos 5x      3 6       7x    5x
    k2 3   6   2x   k2 x   k   6 12     , k 3   k 12x   k2 x    2  8 6
Vậy phương trình có hai nghiệm
Thí dụ 7: (ĐH – B 2012) Giải phương trình 2(cos x  3 sin x) cos x  cos x  3 sin x 1. Giải:
Nhận xét 1: Sau khi nhân phá ra ta nhóm cụm 2
2 cos x 1  cos 2x và 2 3 sin x cos x  3 sin 2x , không
còn hệ số tự do và chuyển cung 2x sang một bên, cung 1x sang một bên thì bài toán trở thành bài toán cơ
bản nhưng mở rộng của bài phương trình bậc nhất đổi với sin và cos nên ta có lời giải sau Cách 1:
2 cos x  3sin xcos x  cos x  3sin x 1  cos2x  3sin 2x  cos x  3 sin x (*)
Chia hai vế cho 2 và biến đổi thành  2 x   k2        3 cos 2x     cos x
    2x    x
    k2  , k 3 3 3 3 2        x k  3 Chú ý:
- Ta có thể biến đổi về sin như sau
https://www.facebook.com/trithuc.viet.37 10
Giáo viên: Nguyễn Thành Long Email: Changngoc203@gmail.com
 cos2x  3 sin 2x  cos x  3sin x   2 2x
  x k2 x    k2 6 6      3  sin 2x
    sin  x     , k  6   6    2  2x    
  x  k2 x k 6   6   3
- Có thể giải phương trình (*) như sau
 cos2x  cos x  3 sin 2x  sin x  0 3x x 3x x  2
 sin sin  2 3sin cos  0 2 2 2 2  3x  2 sin  0 x k   2 3     , k x 2   tan  3 x   k2  2  3
Nhận xét 2: Sau khi nhân phá ra chuyển về một vế và nhóm thành hai cặp  2
2 cos x  cos x   1 và
3 sin x 2cos x  
1 ta thấy chúng có nhân tử chung là 2cos x   1 và ta có lời giải sau Cách 2: 2
2(cos x  3 sin x) cos x  cos x  3 sin x  1  2cos x  cos x  1 3 sin x 2cos x   1  0
 2cos x  1cos x  1  3sin x2cos x  1  0  2cos x  1 3sin x cosx  1  0  2  1 x    k2 cos x    3 2cos x 1  0  2       x   k2 , k 3 sin x   cos x 1  0    1 cos x       2   3  2 x   k2  3
Sử dụng đường tròn lượng giác tổng hợp nghiệm ta thấy M2
Với nghiệm x k 2 tương ứng trên đường tròn là điểm M1 Với nghiệm 2 x
k2 tương ứng trên đường tròn là điểm M2 3 Với nghiệm 2 x  
k2 tương ứng trên đường tròn là điểm M1 3 M3
Nhận thấy 3 điểm nghiệm không trùng với hai điểm điều kiện mà
3 điểm nghiệm này cách đều nhau một góc 2 nên ta có gộp 3 điểm 3 M3 2
nghiệm thành x k , k . 3 2 2
Vậy phương trình có nghiệm là x
k2, x k , k 3 3 Chú ý:
- Ta cũng có thể biến đổi về sin như sau   1
3 sin x  cos x 1  0  sin x      sin  6  2 6
- Ta có bài toán tổng quát như sau khi xuất hiện cos 2x (hoặc 2 sin x hoặc 2
cos x ), sin 2x,sin x, cos x và
hệ số tự do ta có bài toán tổng quát sau a sin 2x b cos 2x c sin x d cos x e  0 ta biến đổi về một trong hai dạng
https://www.facebook.com/trithuc.viet.37 11
Giáo viên: Nguyễn Thành Long Email: Changngoc203@gmail.com
2asin xcos x b 2 2 cos x  
1  c sin x d cos x e  0 
2asin xcos x b   2
1  2sin x  csin x d cos x e  0 2
2bcos x d cos x b e  sin x2acos x c  0   2
2bsin x csin x b e  cos 
2asin x d  0
Từ đó sẽ xuất hiện nhân tử chung (với các hệ số a, ,
b c, d , e theo một tỉ lệ nào đó), với dạng bài này đề
thi khối D năm 2010 (xem ở mục kĩ năng đưa về phương trình tích)
Tương tự: Giải phương trình  6 6
8 sin x  cos x  3 3sin 4x  3 3 cos2x  9sin 2x 11 Phương tr  3  ình 2  8 1
  sin 2x  6 3sin 2x cos2x  3 3 cos2x  9sin 2x 11  0  4   x x   2 3 cos 2 2 sin 2
1  2sin 2x  3sin 2x 1  0
 3 cos2x2sin2x  1  sin2x  12sin2x  1  0
 2sin 2x  1 3cos2x sin2x  1  0  1 sin 2x  2sin 2x 1  0  2     3 cos 2x   sin 2x 1  0      sin
   2x  sin   3 6       x   k  12  5  x   k  12    , k
x   k  4  5x    k  12
Thí dụ 8: (ĐH – B 2009) Giải phương trình: x x x x   3 sin cos sin 2 3 cos 3
2 cos 4x  sin xGiải: Phương trình  x 2 sin
1 2sin xcos .xsin2x 3cos3x  2cos4x 1 3
 sin3x  3 cos3x  2cos4x  sin3x
cos 3x  cos 4x 2 2    
cos 4x  cos 3x
    4x   3x
    k2  6   6   x    k2  6   , k 2 x   k  42 7
Hoặc: Phương trình 1    x   x x 3 1 sin sin 3 sin
 3 cos3x  2 cos4x
 sin x  sin3x 2  4 4  1 3 3 1
 sin3x  sin x  3 cos3x  2cos4x  sin x  sin3x 2 2 2 2
https://www.facebook.com/trithuc.viet.37 12
Giáo viên: Nguyễn Thành Long Email: Changngoc203@gmail.com 1 3
 sin3x  3 cos3x  2cos4x  sin3x
cos 3x  cos 4x 2 2 2k
Vậy phương trình có nghiệm là x   , x  
 2k,k 42 7 6 
Thí dụ 9: Giải phương trình 8sin x
    tan x  cot x  4cot 2x  6  Giải:   Điều kiện: sin x 0   sin 2x  0 (*) cos x   0  Phương tr  2 ình  8sin x      4cot 2x 6 sin 2x      x   x    x   x x  2 2 4 sin sin 2 1 2 cos 2 2 3 sin cos
.sin 2x  3sin x – cos x  0  6 
 ( 3sin x  cos x)(2sin 2x  3sin x  cos x)  0
 3sin x  cos x  0   2sin 2x
 3sin x  cos x  0 TH1:
3 sin x  cos x  0  cot x   3  x  
k,k 6 3 1 TH2:
2 sin 2x  3 sin x  cos x  0 
sin x  cos x   sin 2x 2 2  5 x   k2     x      x 6 sin sin 2   , k  6    k2 x     18 3
Các nghiệm trên đều thỏa mãn (*). Vậy phương trình có 3 nghiệm trên
Thí dụ 10: Giải phương trình tan x  3cot x  4sin x  3 cos xGiải: 2 2    Phương tr sin x 3cos x 1 3 ình   8 sin x   cos x  sin x cos x  2 2       1
  2cos2x  4sin 2 .xsin x     3  2    cos
 cos2x  cos x     cos 3x    3  3   3        2
 cos2x  cos x      cos 3x       cos  0    3    3  3   3x     x    3x    2cos  cos
      cos    0  2 6 2 6 2 2         3x   
  x    4cos  sin x    sin      0 2 6 3 2 6      
https://www.facebook.com/trithuc.viet.37 13
Giáo viên: Nguyễn Thành Long Email: Changngoc203@gmail.com   x   sin      0  2 6    x    k     3  sin x      0   , k    3 4     k2 x     3x    9 3 4 cos      0 2 6    4 k 2
Vậy nghiệm của phương trình là x    k; x   , k   3 9 3
Vậy phương trình có ba nghiệm trên
Chú ý: Cách khác xem ở Ví dụ 3 trang 23
Dạng 2: Phương trình thuần nhất bậc hai đối với sin x và cos x .
a. Định nghĩa: Phương trình thuần nhất bậc hai đối với sin x , cos x là phương trình. 2 2
a sin x bsin .
x cos x c cos x d (1) trong đó a, b, c, d   b. Cách giải : Cách 1:
Chia từng vế của phương trình (1) cho một trong ba hạng tử 2 sin x hoặc 2 cos x hoặc sin . x cos x . Chẳng hạn nếu chia cho 2
cos x ta làm theo các bước sau: Bước 1:
Kiểm tra: cos x  0  x
k ,k  xem nó có phải là nghiệm của phương trình (1) hay 2 không?
Bước 2: Với cos x  0 chia cả hai vế cho 2
cos x lúc đó phương trình (1) trở thành 2 2 2
a tan x b tan x c d(1  tan x)  (a d ) tan x b tan x c d  0
Đây là phương trình bậc hai theo tan ta đã biết cách giải bằng cách đặt t  tan x . Cách 2: 1  cos 2x 1  cos 2x sin 2x Dùng công thức hạ bậc 2 2 sin x  ;cos x  ;sin . x cos x  đưa phương trình đã 2 2 2
cho về phương trình bsin 2x  (c a) cos 2x d c a
Đây là phương trình bậc nhất đối với sin và cos ta đã biết cách giải (dạng 1) Chú ý: - Khi d  0 thì 2 2
a sin x bsin .
x cos x c cos x  0 gọi là phương trình đẳng cấp bậc 2
- Đối với phương trình đẳng cấp bậc n (n  3) với dạng tổng quát
(sinn , cosn ,sink cosh A x x x
x)  0 trong đó k h  ;
n k, h, n  
Khi đó ta cũng làm theo 2 bước:
Bước 1: Kiểm tra xem cos x  0 có phải là nghiệm của phương trình hay không?
Bước 2: Nếu cos x  0. Chia cả hai vế của phương trình trên cho cosn x ta sẽ được phương trình bậc n
theo tan. Giải phương trình này ta được nghiệm của phương trình ban đầu. THÍ DỤ MINH HỌA
Thí dụ 1: (ĐH – B 2008) Giải phương trình: sin 3 x  3 cos3 x  sin x cos2 x  3 sin 2 x cos x Giải:
Nhận xét 1: Đây là phương trình đẳng cấp bậc 3 nên ta giải như sau Cách 1:
Thay cos x  0  x
k,k vào phương trình ta được 3
sin x  0  sin x  0 nên x k , k 2
không phải là nghiệm của phương trình
Khi cos x  0 chia cả hai vế của phương trình cho 3 cos x ta được
https://www.facebook.com/trithuc.viet.37 14
Giáo viên: Nguyễn Thành Long Email: Changngoc203@gmail.com 3 2 x   x x
x  2 x     2 tan 3 tan 3. tan tan tan 1 3 tan x   1  0  x    k    tan x  1 2 tan x  
1 tan x  3  0   4   , k tan x    3  x    k  3
Nhận xét 2: Ta nhận thấy có các nhân tử chung và các hệ số tương ứng tỉ lệ nên ta có lời giải sau Cách 2: Phương trình   3 2 x x x   3 2 sin sin cos
3 cos x  3 sin x cos x  0  x  2 2 x x   x  2 2 sin sin cos 3 cos
cos x  sin x  0
 sin xsin x  cos xsin x  cos x  3cos xcos x sin xcos x  sin x  0
 sin x  cos xsin x  cos xsin x  3cosx  0  
sin x  cos x  0     tan  1 x k x  4
 sin x  cos x  0      ; k tan x     3  sin   3 cos x    k x x  3
Vậy phương trình có các nghiệm là x
k ; x    k , k 4 2 3 Chú ý:
- Kết hợp hai nghiệm x  
k thành một nghiệm x   k vì chúng hợp với nhau một góc 4 4 2 2
- Cũng có thể biến đổi Phương trình   3 2 x x x   3 2 sin sin cos
3 cos x  3 sin x cos x  0  x  2 2 x x  x  2 2 sin sin cos 3 cos
cos x  sin x  0
 sin xcos2x  3 cos xcos2x  0
 cos2xsin x  3cosx  0    cos2  0 x k x  2 2     ; k sin x   3 cos x x    k  3
Thí dụ 2: (ĐHCĐ – 2000) Giải phương trình 1  3 tan x  2sin 2x Giải:
Cách 1: Điều kiện: cos x  0 (*) Phương tr sin x ình 2 1  3
 4sin x cos x  cos x  3sin x  4sin x cos x cos x
Nhận xét: Đây là phương trình đẳng cấp bậc ba nên ta chia hai vế của phương trình cho 3 cos x Ta được 1 tan x 2  3
 4tan x  1 tan x  3tan 2
1  tan x  4 tan x 2 2  cos x cos x 3 2
 3tan x  tan x  tan x 1  0  tan x  1 2
3 tan x  2 tan x   1  0  tan x  1
  x    k ,k (thỏa mãn (*)) vì 2
3 tan x  2 tan x 1  0 vô nghiệm 4 Chú ý:
- Ta có thể chia từ đầu hai vế của phương trình cho 2 cos x
- Nhìn vào phương trình ta thấy xuất hiện tan x và sin 2x ta nghĩ tới mối quan hệ như giữa chúng
https://www.facebook.com/trithuc.viet.37 15
Giáo viên: Nguyễn Thành Long Email: Changngoc203@gmail.com 2 sin x cos x 2 sin x cos x 2 tan x 2 2 tan x sin 2x   cos sin 2  2sin cos x x x x   2 2 2 sin x  cos x 1  hoặc tan x 2 1 1  từ đó ta đặt tan x 2 cos x t  tan x Cách 2: Đặt 2t
t  tan x  sin 2x  2 1  t Khi đó ta được 4t 3 2 2 1  3t
 3t t t 1  0  (t 1)(3t  2t 1)  0 2 1  t
t  1  tan x  1  x    k ,k (thỏa mãn (*)) 4
Vậy phương trình có duy nhất 1 họ nghiệm x  
k ,k  4
Cách 3: Phân tích hệ số 3  1  2
Ta có phương trình  1 tan x  2tan x  4sin xcos x 2 sin x  cos x 2 cos x 1   2sin x  0 cos x cos x
 sin x  cos x 1 2sin x
cosx sin x  0 
sin x  cos x  0 tan x  1      1  2sin x
cosx sin x sin 2x   cos2x  2
x    k,k   (Vì phương trình sin 2x  cos2x  2 vô nghiệm) 4
Cách 4: Phân tích hệ số 1  3  2
Ta có phương trình  31 tan x  21 sin x sin x  cos x  3
 2sin x  cos x2  sin x  cos x 2
3  sin 2x  2cos x  0 cos x
sin x  cos x  0 tan x  1     2 3
  sin 2x  2cos x  0 sin 2x   cos2x  2
x    k,k   (Vì phương trình sin 2x  cos2x  2 vô nghiệm) 4 
Thí dụ 3: (ĐHQG HCM – 1998) Giải phương trình: 3 sin x
    2 sin x  4  Giải: Cách 1:  Ta nhận thấy sin x
   có thể biểu diễn được qua sin x  cos x . Luỹ thừa bậc ba biểu thức  4 
sin x  cos x
ta sẽ đưa phương trình về dạng thuần nhất đã biết cách giải 3 Phương tr      ình 3  2 2 sin x
    4sin x  2 sin x      4sin x  4 4      3
 (sin x  cos x)  4sin x (*)
Xét với cos x  0  x
k2,k . Khi đó phương trình có dạng 2     3
sin   k   4sin   k   mâu thuẫn 2 2    
https://www.facebook.com/trithuc.viet.37 16
Giáo viên: Nguyễn Thành Long Email: Changngoc203@gmail.com
Vậy phương trình không nhận x
k2 làm nghiệm 2
Với cos x  0 . Chia cả hai vế của phương trình (2) cho 3 cos x ta được: 3 2 3 2
(tan x 1)  4(1  tan x) tan x  3tan x  3 tan x  tan x 1  0 .
Đặt t  tan x phương trình có được đưa về dạng: 3 2 2
3t  3t t 1  0  (t  1)(3t  1)  0  t  1  x  
k,k   4
Họ nghiệm trên thoả mãn điều kiện của phương trình . Cách 2: Từ phương trình (*) 3 2
(*)  (sin x  cos x)  4sin x  (sin x  cos x)(sin x  cos x)  4sin x 2 2
 (sin x  cos x)(1 2sin xcos x)  4sin x  cos x  3sin x  2sin xcos x  2sin xcos x  0 2 2
 cos x(2sin x 1)  sin x(2cos x  3)  0  cos x(cos2x  2)  sin x(cos2x  2)  0
(cos 2x  2)(cos x  sin x)  0  cos 2x  2 (loại) hoặc tan x  1  x  
k,k 4
Vậy phương trình có duy nhất 1 họ nghiệm x  
k ,k  4
Cách 3.1: Đặt t x
x t  khi đó ta được phương trình 4 4   3
sin t  2 sin t
    sin t  cost (**)  4  
t  2 t   2 sin sin
1  cost  sin t cos t  cos t
 cost sin2t  2  0  cost  0  t   k,k 2 3 Với t
k x
k,k 2 4
Cách 3.1: Từ phương trình (**) ta thấy nếu sin x  0  cos x  1
 thì phương trình (**) vô nghiệm nên sin x  0. Chia cả hai vế của (**) cho 3 sin x ta được phương trình 2   t t  2 1 1 cot
cot 1 cot t  cott  0 3
t   k x
k ,k 2 4 Chú ý:
Ngoài phương pháp giải phương trình thuần nhất đã nêu ở trên có những phương trình có thể giải bằng
phương pháp khác tuỳ thuộc vào từng bài toán để giải sao cho cách giải nhanh nhất, khoa học nhất. 1  tan x
Thí dụ 4: Giải phương trình:  1 sin 2x 1  tan x Giải: x   k    Điều kiện cos x 0  2   , k    tan x   1
x    k  4 Cách 1:
Biến đổi phương trình về dạng:
cos x  sin x  cos x  sin x2  cos x sin x  cosx sin x3 cos x  sin x
Chia cả hai vế của phương trình (3) cho 3
cos x  0 ta được:
https://www.facebook.com/trithuc.viet.37 17
Giáo viên: Nguyễn Thành Long Email: Changngoc203@gmail.com
1  tan x  1 tan xtan x  1 tan x3 2 2 3 2
 tan x  tan x  2tan x  0   2
tan x  tan x  2tan x  0 (*) (do 2
tan x  tan x  2  0 vô nghiệm) nên:
Phương trình (*)  tan x  0  x k,k Cách 2:
Biến đổi phương trình về dạng   cos x   
cos x  sin x       
cos x  sin x2 4 2 2   2sin x     cot x     cos x  sin x 4 4       2 sin x   1   cot x    4 4     Đặt   2 t  cot x    ta được: 3 t
t t  2  0  t  1 2t t  2  0  t 1 2   4  1  t  Hay cot x
    1 x    k x k,k   4 4 4  
Vậy phương trình có một họ nghiệm là x k , k   Cách 3: Phương trình  x x   x x  x x 2 cos sin sin cos sin cos 3 3
 cos x  sin x  sin x  cos x  3sin xcos xsin x  cos x  cos x 2 1  cos x 3
 sin x  sin x  3sin xcos xsin x  cos x  0 2 3
 cos xsin x  sin x  sin x  3sin xcos xsin x  cos x  0
 sin xsin 2x  cos2x  3  0
 sin x  0  x k ,k  (Vì phương trình sin 2x  cos2x  3  0 vô nghiệm) 2t
Cách 4: Đặt t  tan x  sin 2x  ta được phương trình 2 1  t 1  t 2t 3 2  1
t t  2t  0 2 1  t 1  t
t  2t t  2  0  t  0 (vì phương trình 2t t  2  0 vô nghiệm)
Với tan x  0  x k ,k
Thí dụ 5: (Đại học Y Dược Thành phố Hồ Chí Minh 1997) Giải phương trình: 3 sin .
x sin 2x  sin 3x  6cos x Giải: PT  x x x  3 3 sin 2 sin cos
 3sin x  4sin x  6cos x 3 2 3
 4sin x 3sin x  2sin x cos x  6cos x  0 (*)
Nếu cos x  0 là nghiệm (*) của thì: sin x 1 cos x  0    sin x   1  vô lý 3 4 sin x  3sin x  0  3 4 sin x  3sin x  0 Chia 2 vế của (*) cho 3
cos x  0 ta được phương trình tương đương:   3 2  x x x     x   2 * tan 2 tan 3 tan 6 0 tan 2 tan x  3  0
tan x  2  tan
x k     , k  
tan x   3   tan
x    k  3  3
https://www.facebook.com/trithuc.viet.37 18
Giáo viên: Nguyễn Thành Long Email: Changngoc203@gmail.com
Vậy phương trình có các nghiệm là x k; x  
k,k với tan 2 3 cos 2x
Thí dụ 6: Giải phương trình
 tan x  2 sin 2x     0 1  cot x  4  Giải: 1   cot x  0
Điều kiện: sin x   0 cos x   0 Phương tr cos 2 . x sin x sin x ình  
 sin 2x  cos2x  0 sin x  cos x cos x  sin x   1   cos2x
1  sin x 2cos x     0
 sin x  cos x   cos x
cos2 .xcos x sin .xcos2x    0 sin x  cos x cos x  sin x cos x   cos2x    0 cos x sin x   cos x  2 2
 cos2x(sin x  sin .xcos x  cos x)  0 cos2x  0 (1)   2 2 sin x
 sin .xcos x  cos x  0 (2) (1)  x
k ,k 4 2 1 5 1 5 2
(2)  tan x  tan x 1  0  tan x   x  arctan
l,l 2 2  x   k
Đối chiếu điều kiện ta có nghiệm phương tr 4 ình là:   1 5 x  arctan  l  2
Dạng 3: Phương trình đối xứng đối với sin x và cos x .
a. Định nghĩa: Phương trình đối xứng đối với sin x và cos x là phương trình dạng
a(sin x  cos x)  b sin x cos x c  0 trong đó a, , b c   b. Cách giải: Cách 1: Do 2
a(sin x  cos x)  1 sin x cos x nên ta đặt   
t  sin x  cos x  2 sin x
    2 cos  x . Điều kiện | t |  2  4   4  2 t 1
Suy ra sin x cos x
và phương trình được viết lại: 2
bt  2at  (b  2c)  0 2
Đó là phương trình bậc hai đã biết cách giải Cách 2: Đặt t
x thì sin x  cos x  2 cos  x  2 cost 4  4  1 1   1 1 2
sin x cos x  sin 2x  cos  2x  cos 2t  cos t  nên phương trình trở thành 2 2 2 2 2  
https://www.facebook.com/trithuc.viet.37 19

Tài liệu liên quan: