






















































































































Preview text:
lOMoARcPSD| 36067889
HỌC VIỆN CÔNG NGHỆ BƯU CHÍNH VIỄN THÔNG
-------------------- NGÔ ĐỨC THIỆN BÀI GIẢNG
LÝ THUYẾT TRƯỜNG ĐIỆN TỪ VÀ SIÊU CAO TẦN LỜI MỞ ĐẦU lOMoARcPSD| 36067889
Học phần Lý thuyết trường iện từ và Siêu cao tần thuộc phần kiến thức cơ sở cho các
chuyên ngành iện – iện tử và viễn thông. Học phần này có mục ích nêu những khái niệm cơ
bản chung liên quan ến trường iện từ, xây dựng những phương pháp khảo sát tương tác trường
– chất. Trình bày các ịnh luật, các nguyên lý cơ bản của trường iện từ, cùng các quy luật và
tính chất lan truyền của sóng iện từ trong chân không, trong không gian vô hạn và các quá
trình lan truyền sóng siêu cao tần trong các loại ường truyền dẫn phổ biến. Mô tả các quá
trình dao ộng iện từ ở dải siêu cao tần trong các mạch dao ộng cộng hưởng khác nhau. Nghiên
cứu nguyên lý các mạng nhiều cực siêu cao tần và các linh kiện iện tử và bán dẫn siêu cao tần.
Cuốn bài giảng “Lý thuyết trường iện từ và Siêu cao tần” bao gồm 6 chương, trong ó
3 chương ầu là các nội dung về Lý thuyết trường iện từ:
Chương 1: Các ịnh luật và nguyên lý cơ bản của trường iện từ. Chương này ưa ra các
thông số cơ bản ặc trưng cho trường iện từ và môi trường chất, các ịnh luật, hệ phương trình
Maxwell, các ặc iểm và phương trình của trường iện từ tĩnh và trường iện từ dừng.
Chương 2: Bức xạ sóng iện từ. Chương này trình bày nghiệm của hệ phương trình
Maxwell, nghiệm của phương trình thế, và bức xạ sóng iện từ của dipol iện.
Chương 3: Sóng iện từ phẳng. Chương này khảo sát quá trình lan truyền của sóng iện
từ phẳng trong các môi trường ồng nhất ẳng hướng và môi trường không ẳng hướng, sự phân
cực của sóng iện từ, hiện tượng phản xạ và khúc xạ sóng iện từ…
Ba chương tiếp theo là các nội dung về kỹ thuật siêu cao tần, bao gồm:
Chương 4: Sóng iện từ trong các hệ ịnh hướng. Chương này trình bày các hệ ịnh hướng
sóng iện từ như dây song hành, cáp ồng trục, ống dẫn sóng…
Chương 5: Hộp cộng hưởng. Trình bày khái niệm về hộp cộng hưởng, các loại hệ số
phẩm chất, các hộp cộng hưởng ơn giản và phức tạp, kích thích năng lượng và iều chỉnh tần số cộng hưởng.
Chương 6: Mạng nhiều cực siêu cao tần. Chương này tập trung vào các vấn ền về
mạng 2n cực siêu cao tần, các mạng 2 cực, 4 cực, 6 cực. Vấn ề phối hợp trở kháng ở mạch siêu cao tần.
Trong quá trình biên soạn bài giảng này không thể tránh ược những sai sót, tác giả rất
mong nhận ược các ý kiến góp ý của bạn ọc.
Hà nội, tháng 10 năm 2013 MỤC LỤC
LỜI MỞ ĐẦU ........................................................................................................................... 1
MỤC LỤC ............................................................................................................................... 2
CHƯƠNG 1. CÁC THAM SỐ VÀ ĐỊNH LUẬT CƠ BẢN CỦA TRƯỜNG ĐIỆN TỪ .............. 6
1.1. Các ại lượng ặc trưng cơ bản cho trường iện từ và môi trường chất ......................... 6 lOMoARcPSD| 36067889 6
1.1.1. Vec tơ cường ộ iện trường E .......................................................................................... 6
1.1.2. Vec tơ iện cảm D ............................................................................................................ 7
1.1.3. Vectơ cường ộ từ cảm B ................................................................................................. 8
1.1.4. Vec tơ cường ộ từ trường H ........................................................................................... 8
1.1.5. Các tham số ặc trưng cơ bản của môi trường .............................................................. 10
1.2. Các phương trình Maxwell ...................................................................................... 10
1.2.1. Một số khái niệm và ịnh luật cơ bản ............................................................................ 10
1.2.2. Các dạng của hệ phương trình Maxwell ....................................................................... 15
1.2.3. Ý nghĩa của hệ phương trình Maxwell ......................................................................... 18
1.3. Điều kiện bờ ối với các vec tơ của trường iện từ..................................................... 19
1.4. Năng lượng của trường iện từ - Định lý Poynting ................................................... 21
1.5. Trường tĩnh iện ........................................................................................................ 25
1.5.1. Các phương trình ặc trưng cơ bản ............................................................................... 25
1.5.2. Một số bài toán về trường tĩnh iện ............................................................................... 28
1.6. Từ trường của dòng iện không ổi ............................................................................. 31
1.6.1. Điện trường dừng ......................................................................................................... 31
1.6.2. Từ trường dừng ............................................................................................................ 32
1.7. Trường iện từ biến thiên .......................................................................................... 33
1.7.1. Các phương trình cơ bản.............................................................................................. 33
1.7.2. Hiện tượng sóng của trường iện từ biến thiên .............................................................. 38
BÀI TẬP CHƯƠNG 1 ...................................................................................................... 40
CHƯƠNG 2. BỨC XẠ SÓNG ĐIỆN TỪ ................................................................................ 42
2.1. Bức xạ của lưỡng cực iện ......................................................................................... 42
2.1.1. Tìm nghiệm tổng quát ................................................................................................... 42
2.1.2. Trường bức xạ ở khu gần ............................................................................................. 44
2.1.3. Trường bức xạ ở khu xa ............................................................................................... 46
2.2. Trường iện từ của vòng dây ..................................................................................... 49
2.3. Trường bức xạ của hệ thống anten .......................................................................... 53
2.3.1. Trường bức xạ của anten nửa sóng .............................................................................. 53
2.3.2. Trường bức xạ của hai anten nửa sóng ặt song song cách nhau một khoảng d .......... 54 lOMoARcPSD| 36067889
BÀI TẬP CHƯƠNG 2 ...................................................................................................... 58
CHƯƠNG 3. SÓNG ĐIỆN TỪ PHẲNG ................................................................................. 59
3.1. Khái niệm về sóng iện từ phẳng ............................................................................... 59
3.2. Sự phân cực của sóng iện từ .................................................................................... 60
3.2.1. Phân cực Ellip .............................................................................................................. 60
3.2.2. Phân cực tròn ............................................................................................................... 61
3.2.3. Phân cực thẳng ............................................................................................................. 62
3.3. Nghiệm phương trình sóng ối với sóng phẳng ......................................................... 63
3.4. Sóng phẳng trong các môi trường ồng nhất, ẳng hướng .......................................... 66
3.4.1. Sóng phẳng trong môi trường iện môi lý tưởng ........................................................... 66
3.4.2. Sóng iện từ phẳng trong vật dẫn tốt ............................................................................. 68
3.4.3. Sóng iện từ phẳng trong môi trường bán dẫn .............................................................. 71
3.5. Hiệu ứng bề mặt ....................................................................................................... 72
3.5.1. Khái niệm chung ........................................................................................................... 72
3.5.2. Hiệu ứng bề mặt về iện trong một phiến dẫn phẳng ..................................................... 72
3.6. Sự phản xạ và khúc xạ sóng iện từ ........................................................................... 76
3.6.1. Sóng tới phân cực ngang ............................................................................................. 76
3.6.2. Sóng tới phân cực ứng ................................................................................................. 79
3.7. Sóng phẳng trong môi trường không ẳng hướng ..................................................... 80
BÀI TẬP CHƯƠNG 3 ...................................................................................................... 82
CHƯƠNG 4. SÓNG ĐIỆN TỪ TRONG CÁC HỆ ĐỊNH HƯỚNG ......................................... 83
4.1. Phân loại dải sóng siêu cao tần và ặc iểm của sóng siêu cao tần ............................ 83
4.2. Khái niệm về hệ ịnh hướng sóng iện từ .................................................................... 84
4.3. Ống dẫn sóng chữ nhật ............................................................................................ 85
4.3.1. Trường iện ngang ......................................................................................................... 88
4.3.2. Trường từ ngang .......................................................................................................... 93
4.4. Ống dẫn sóng trụ tròn .............................................................................................. 95
4.4.1. Trường iện ngang ......................................................................................................... 96
4.4.2. Trường từ ngang ......................................................................................................... 99
4.5. Cáp ồng trục .......................................................................................................... 102
4.6. Đường dây song hành............................................................................................ 105
4.7. Mạch dải ................................................................................................................ 107
4.8. Ống dẫn sóng iện môi ............................................................................................ 107
CÂU HỎI VÀ BÀI TẬP CHƯƠNG 4 ............................................................................... 107
CHƯƠNG 5. HỘP CỘNG HƯỞNG ......................................................................................108
5.1. Khái niệm về hộp cộng hưởng................................................................................ 108 lOMoARcPSD| 36067889
5.2. Hệ số phẩm chất của hộp công hưởng ................................................................... 110
5.2.1. Khái niệm chung ......................................................................................................... 110
5.2.2. Các loại hệ số phẩm chất của hộp cộng hưởng .......................................................... 110
5.3. Hộp cộng hưởng chữ nhật ...................................................................................... 111
5.3.1. Trường từ ngang TM .................................................................................................. 112
5.3.2. Trường iện ngang TE ................................................................................................. 114
5.3.3. Điều chỉnh tần số cộng hưởng ................................................................................... 115
5.3.4. Kích thích và ghép năng lượng trong ống dẫn sóng và hộp cộng hưởng .................. 116
BÀI TẬP CHƯƠNG 5 .................................................................................................... 117
CHƯƠNG 6. MẠNG NHIỀU CỰC SIÊU CAO TẦN ................................................................118
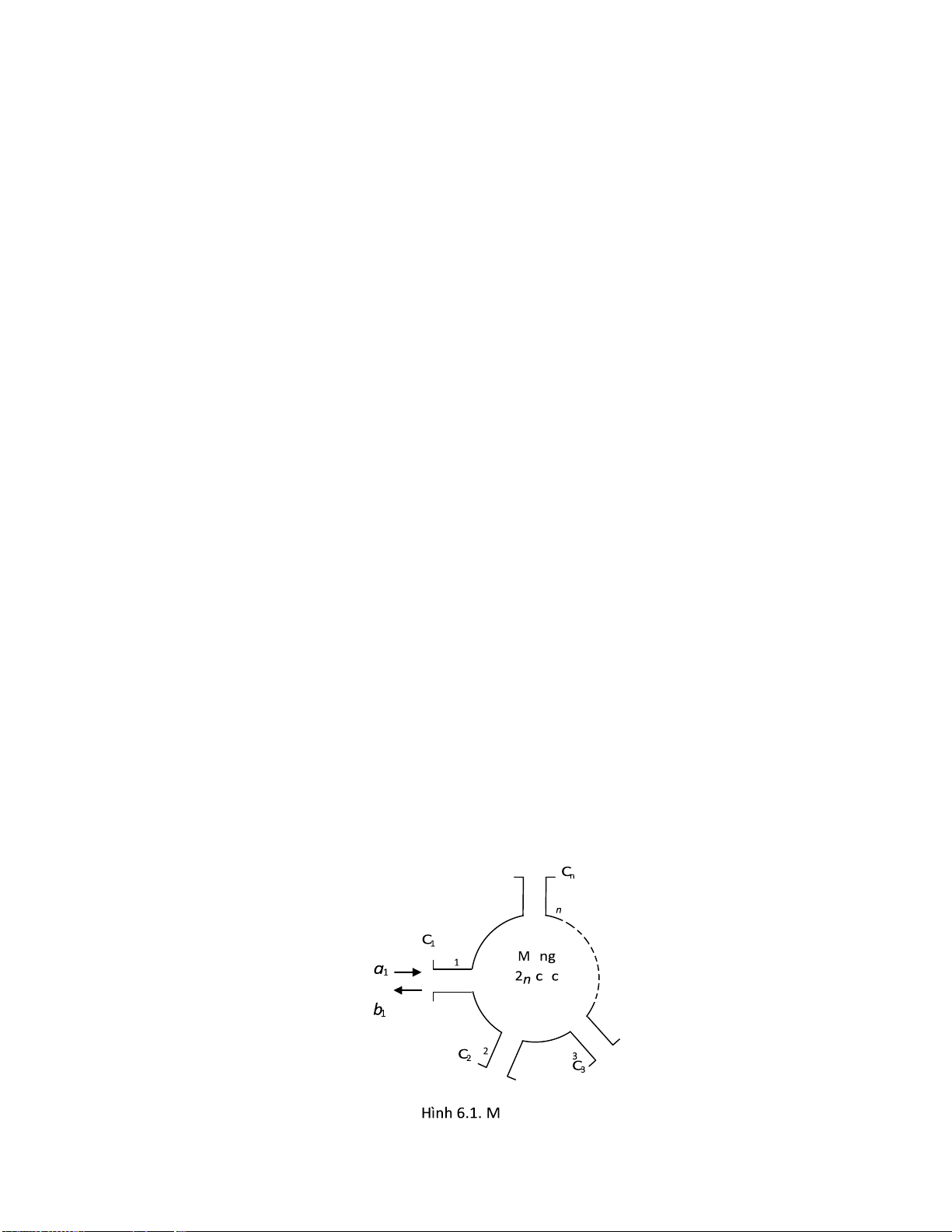
6.1. Mạng nhiều cực siêu cao tần ................................................................................. 118
6.1.1. Khái niệm .................................................................................................................... 118
6.1.2. Công suất phức ........................................................................................................... 119
6.1.3. Sóng chuẩn hóa .......................................................................................................... 120
6.2. Ma trận sóng của mạng nhiều cực siêu cao .......................................................... 123
6.2.1. Ma trận tán xạ ............................................................................................................ 123
6.2.2. Ma trận truyền ........................................................................................................... 126
6.2.3. Ma trận trở kháng và ma trận dẫn nạp ...................................................................... 128
6.2.4. Mối quan hệ giữa các ma trận sóng........................................................................... 130
6.3. Mạng 2 cực ............................................................................................................ 131
6.3.1. Hệ số phản xạ và trở kháng chuẩn hóa ...................................................................... 131
6.3.2. Một ví dụ về mạng 2 cực ............................................................................................ 133
6.4. Mạng 4 cực ............................................................................................................ 133
6.4.1. Ma trận sóng .............................................................................................................. 133
6.4.2. Mạng 4 cực không tổn hao ........................................................................................ 136
6.4.3. Biến thế lý tưởng ......................................................................................................... 139
6.4.4. Trở kháng mắc song song ........................................................................................... 141
6.4.5. Dẫn nạp mắc nối tiếp ................................................................................................. 142
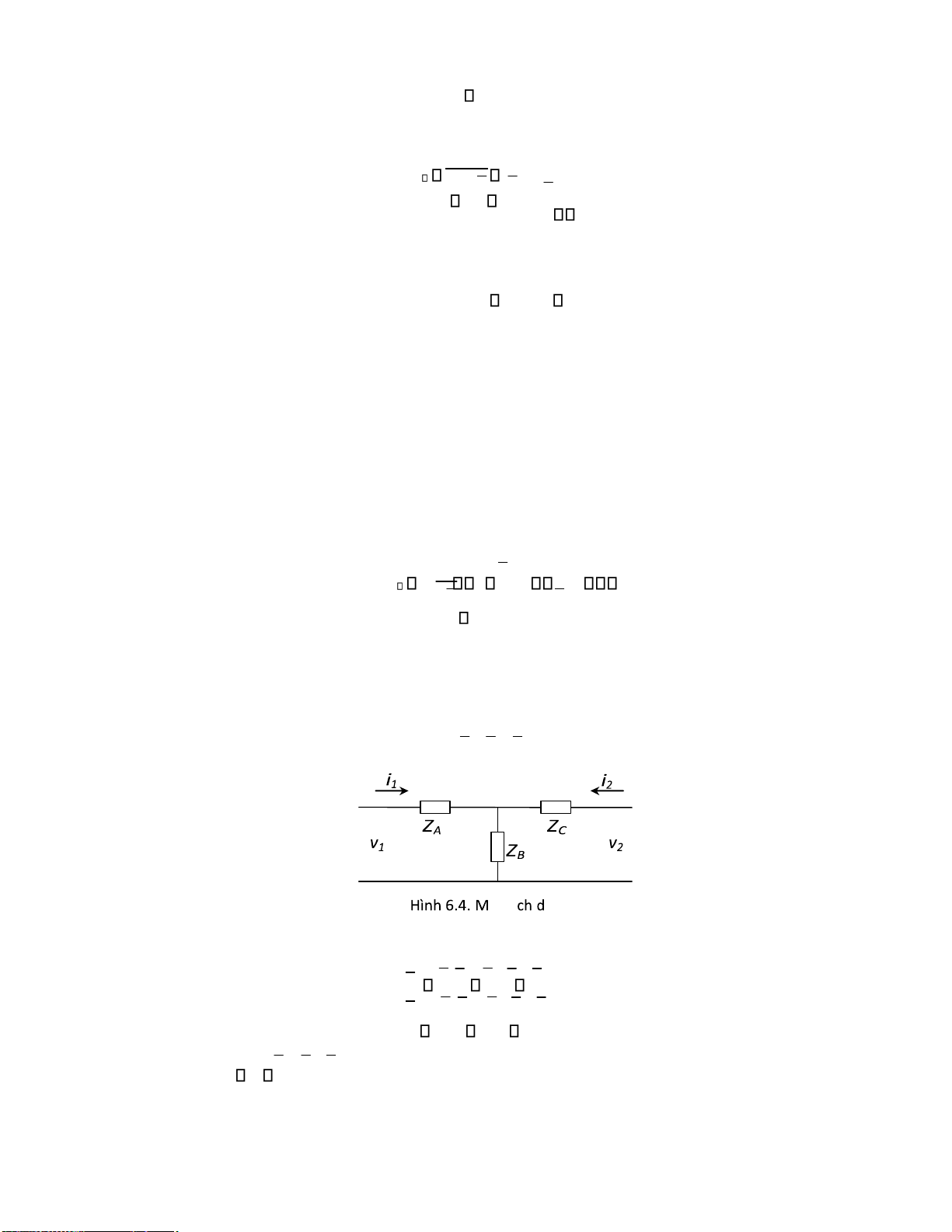
6.4.6. Mắt xích dạng T các trở kháng chuẩn hóa................................................................. 143
6.4.7. Mắt xích dạng ......................................................................................................... 144
6.4.8. Ứng dụng của mạng 4 cực ......................................................................................... 146
6.5. Các bộ ghép ịnh hướng .......................................................................................... 150
6.6. Các bộ cầu siêu cao ............................................................................................... 152
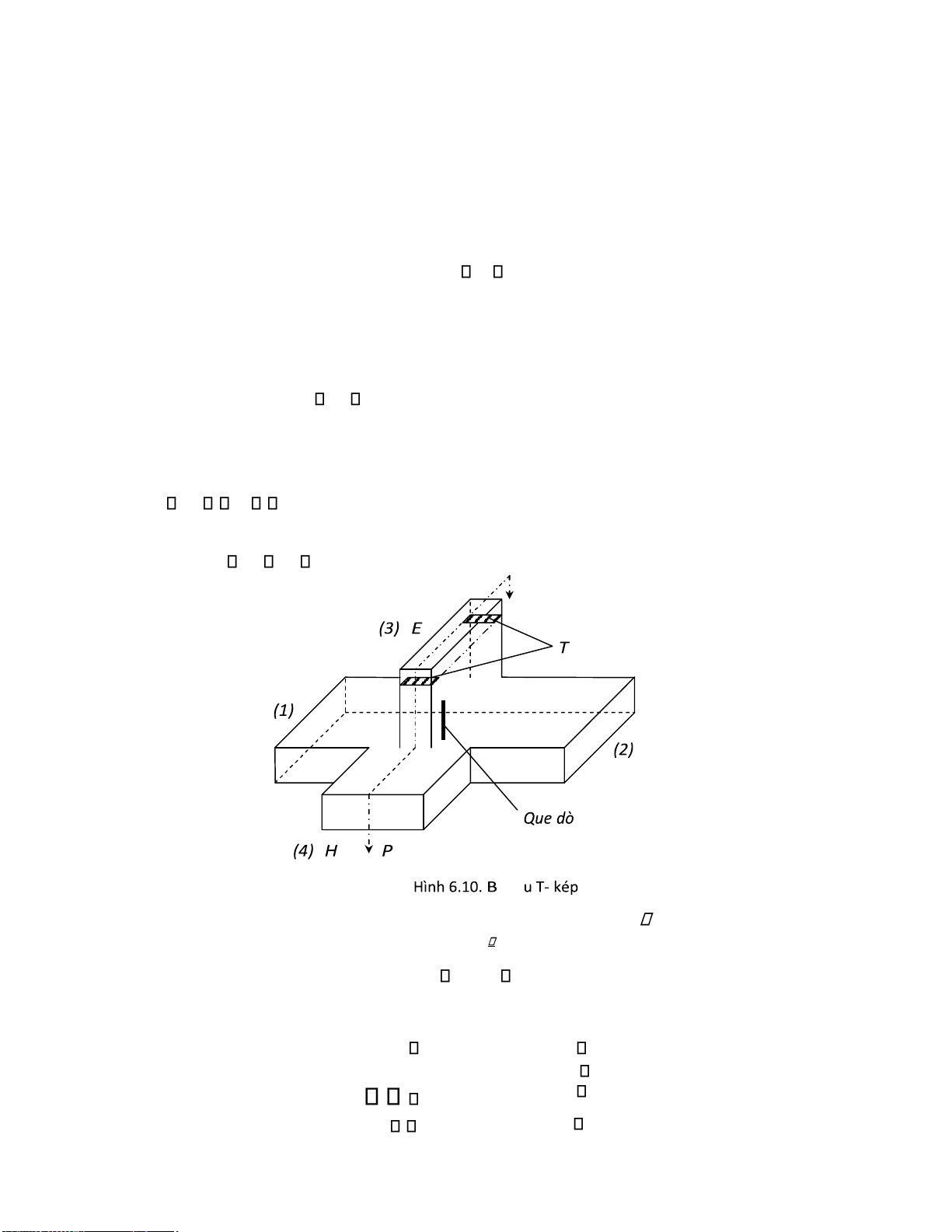
6.6.1. Cầu T - kép ................................................................................................................. 152
6.6.2. Cầu vòng..................................................................................................................... 154
6.7. Các phần tử siêu cao tần có ferít ........................................................................... 156
6.7.1. Tính chất của ferít bị từ hóa ....................................................................................... 156 lOMoARcPSD| 36067889
6.7.2. Các phần tử có ferít trong ống dẫn sóng chữ nhật ..................................................... 158
6.7.3. Các phần tử có ferít trong ống dẫn sóng tròn ............................................................ 162
6.7.4. Một số ứng dụng của các phần tử siêu cao có ferít ................................................... 164
6.8. Phối hợp trở kháng ở siêu cao tần ......................................................................... 166
6.8.1. Ý nghĩa của việc phối hợp trở kháng .......................................................................... 166
6.8.2. Các phương pháp phối hợp trở kháng ....................................................................... 167
6.9. Giới thiệu một số cấu kiện siêu cao tần ................................................................. 172
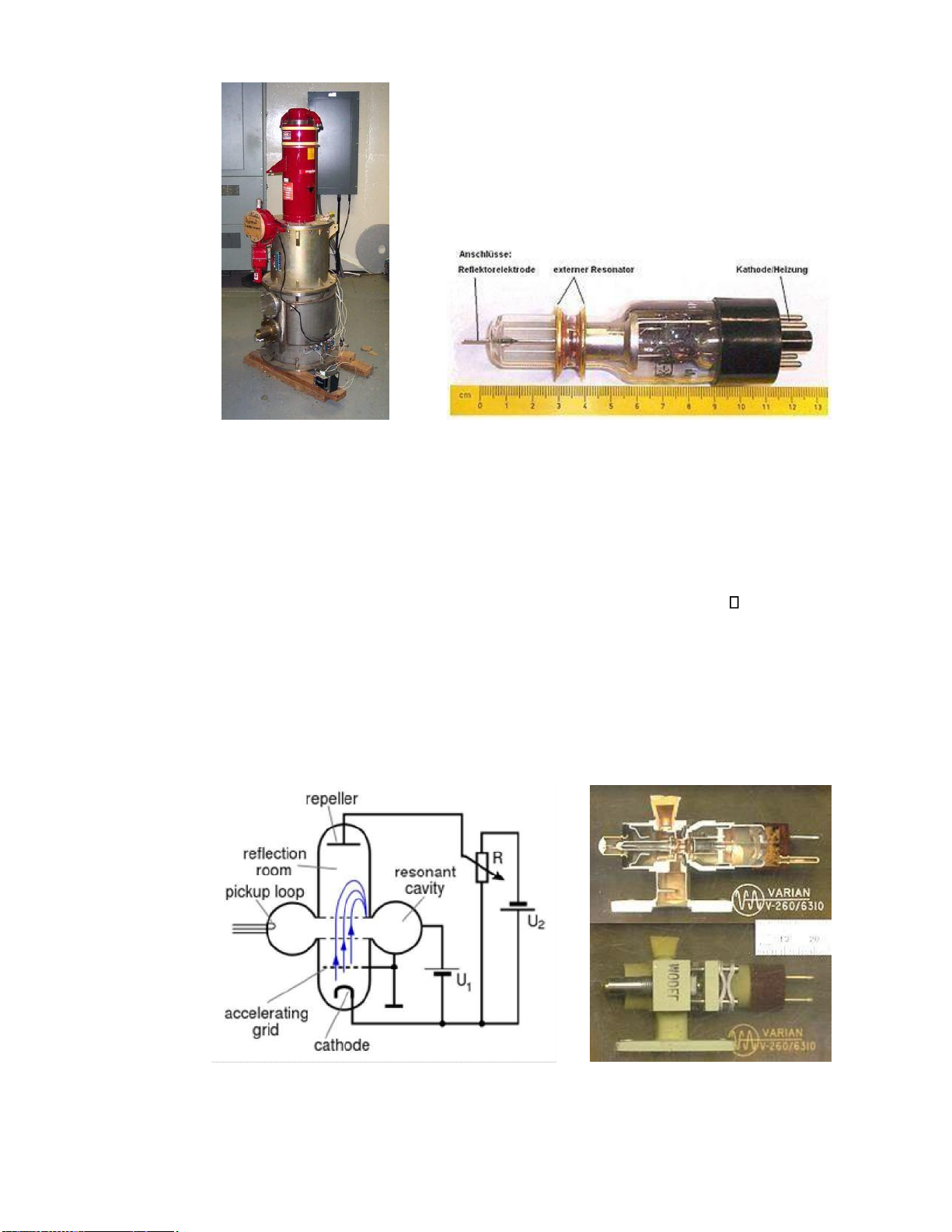
6.9.1. Đèn Klystron trực xạ .................................................................................................. 172
6.9.2. Đèn Klystron phản xạ ................................................................................................ 174
6.9.3. Đèn sóng chạy ............................................................................................................ 175
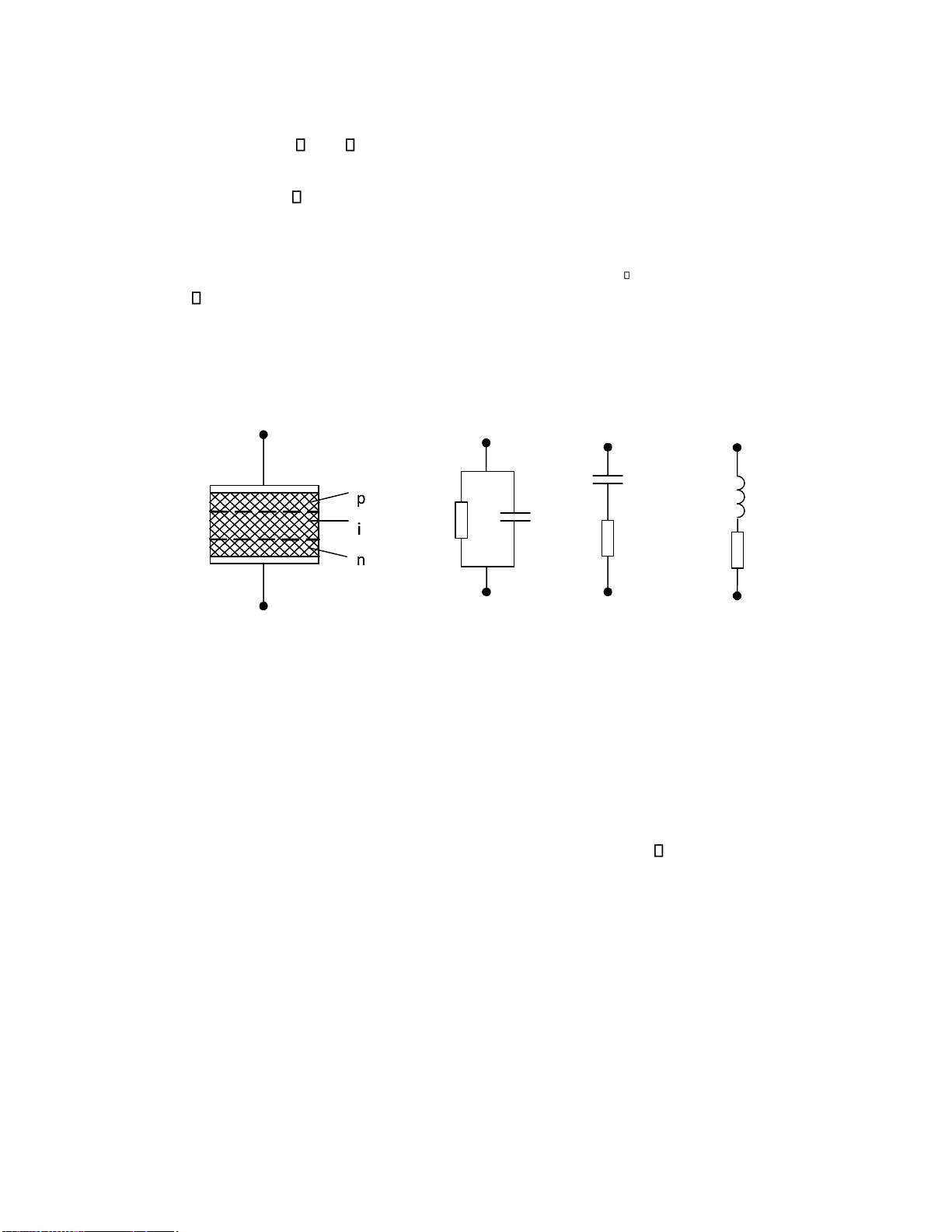
6.9.4. Diode PIN .................................................................................................................... 175
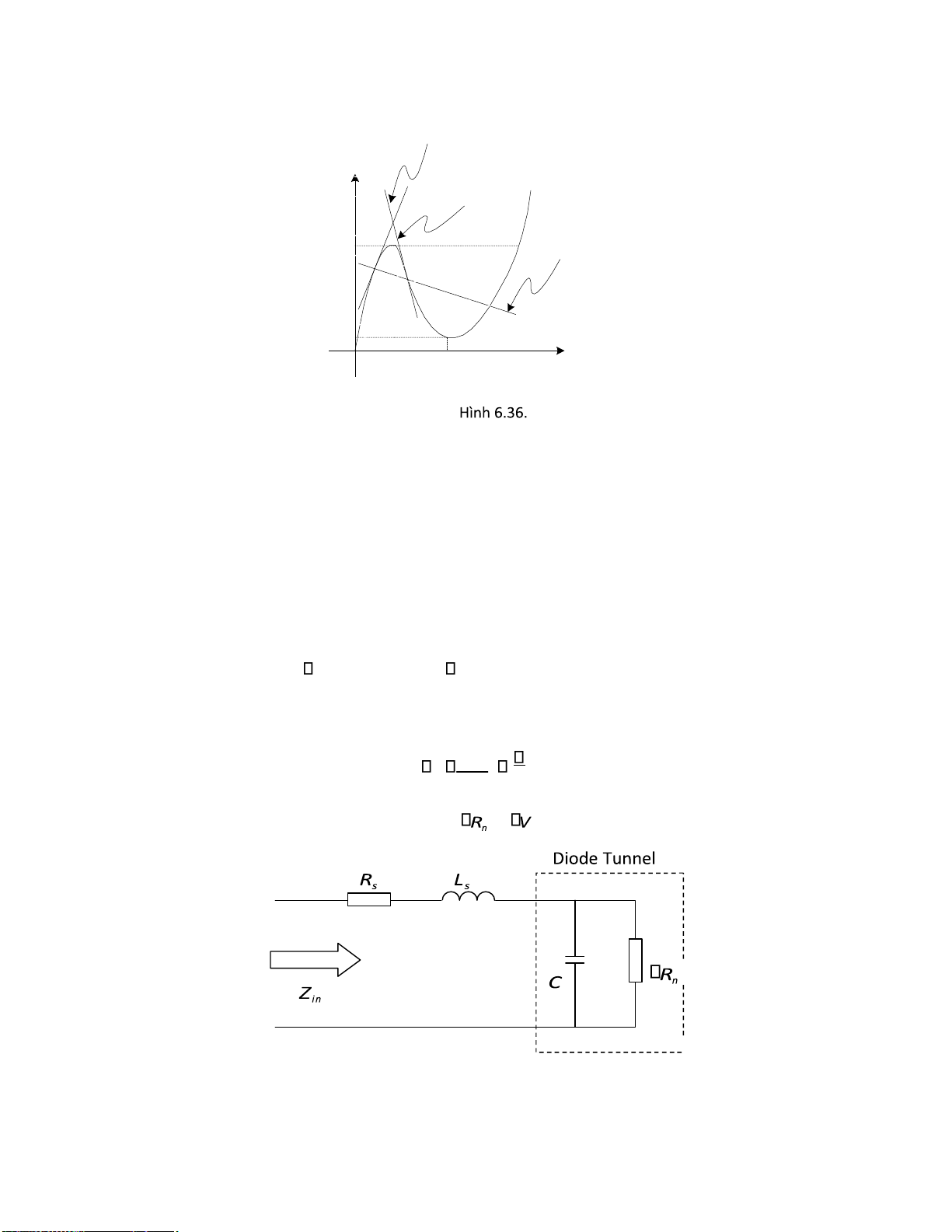
6.9.5. Diode Tunnel .............................................................................................................. 176
PHỤ LỤC 1: MỘT SỐ KÝ HIỆU ...........................................................................................180
PHỤ LỤC 2: CÁC CÔNG THỨC VÀ ĐỊNH LÝ GIẢI TÍCH VECTƠ ..................................182
TÀI LIỆU THAM KHẢO ........................................................................................................182
CHƯƠNG 1. CÁC THAM SỐ VÀ ĐỊNH LUẬT CƠ BẢN CỦA TRƯỜNG ĐIỆN TỪ
1.1. Các ại lượng ặc trưng cơ bản cho trường iện từ và môi trường chất
1.1.1. Vec tơ cường ộ iện trường E
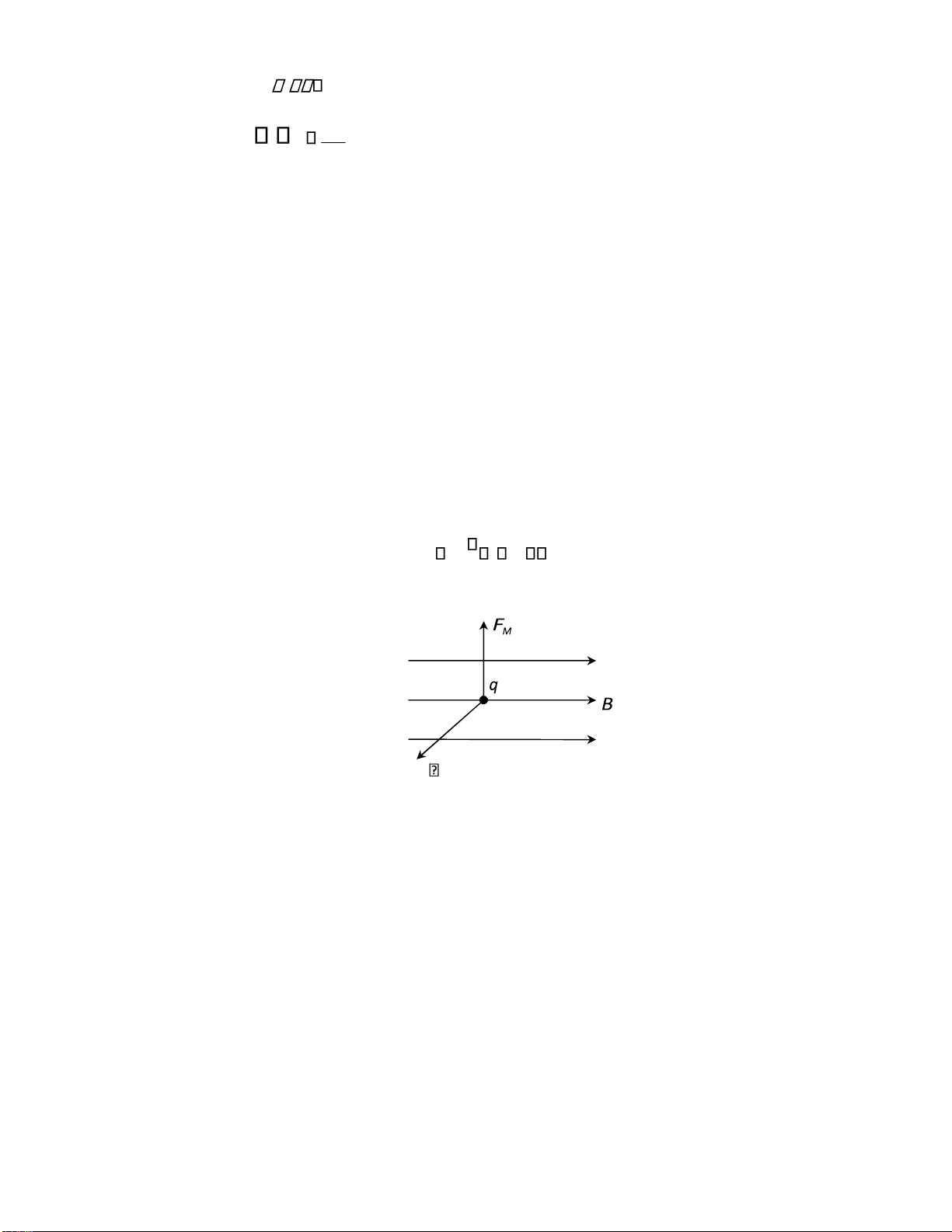
Khi một iện tích thử q ặt cố ịnh tại iểm M trong một hệ quy chiếu quán tính, chịu
một tác dụng F , người ta nói rằng tại lân cận iểm M có một iện trường. Để o lực tác E
ộng về iện tại M người ta dùng véc tơ trạng thái gọi là cường ộ iện trường, ký hiệu E FE E (1.1) q E
Fq CN CmNm Vm M F q E lOMoARcPSD| 36067889
Hình 1.1. Lực iện trường tác ộng lên iện tích q
1.1.2. Vec tơ iện cảm D
Chất iện môi ược hiểu là những môi trường chỉ tồn tại các hạt mang iện ràng buộc,
khi ặt iện môi vào iện trường E , các iện tích rằng buộc tiếp nhận năng lượng iện trường dịch
chuyển khỏi vị trí cân bằng. Tâm quỹ ạo iện tử bị kéo ra xa những nút có iện
tích dương một oạn l nào ó và hình thành các lưỡng cực iện. Đây là hiện tương phân cực iện của iện môi.
Trạng thái phân cực iện của iện môi phụ thuộc vào q và l , và có thể o trạng thái ó bằng
mômen iện của lưỡng cực: p q.l (1.2)
Nếu số lưỡng cực trung bình cho một ơn vị thể tích là N , thì mômen iện tổng của
chúng, gọi là vec tơ phân cực iện, ký hiệu là P :
P Np Nql (1.3)
Trong môi trường iện môi tuyến tính l tỷ lệ với E , nên P tỷ lệ với E . P kp 0E (1.4)
Trong ó: kp là hệ số phân cực iện. 0
361 10 9 F m là hằng số iện môi.
Điện trường trong iện môi ược ặc trưng bởi vectơ D có dạng sau: D 0E P 1 kp 0E r 0E r E (1.5) Trong ó: r
1 kp là hệ số iện môi tương ối. lOMoARcPSD| 36067889
r 0 là hệ số iện môi tuyệt ối. Đơn vị của D C2 . m
1.1.3. Vectơ cường ộ từ cảm B
Một iện tích thử q chuyển ộng với vận tốc v trong một hệ quy chiếu quán tính nếu
chịu một lực tác ộng FM (phân biệt với lực iện FE ), thì người ta nói tại lân cận qtồn tại một từ trường.
Vectơ cường ộ từ cảm B ặc trưng cho lực tác dụng của từ trường lên iện tích chuyển ộng
hay dòng iện theo inh luật Lorentz sau: FM q v B (1.6) v
Hình 1.2. Lực từ trường tác ộng lên iện tích chuyển ộng
1.1.4. Vec tơ cường ộ từ trường H
Trong nhiều chất, từ môi ược hiểu là những môi trường có các dòng phân tử ràng buộc,
dưới tác dụng của từ trường với từ cảm B , các spin và dòng phân tử giống như những nam
châm nhỏ thường bị xoay trục ít nhiều theo chiều của B và hình thành các cực từ nhỏ. Đó là
hiện tương phân cực từ.
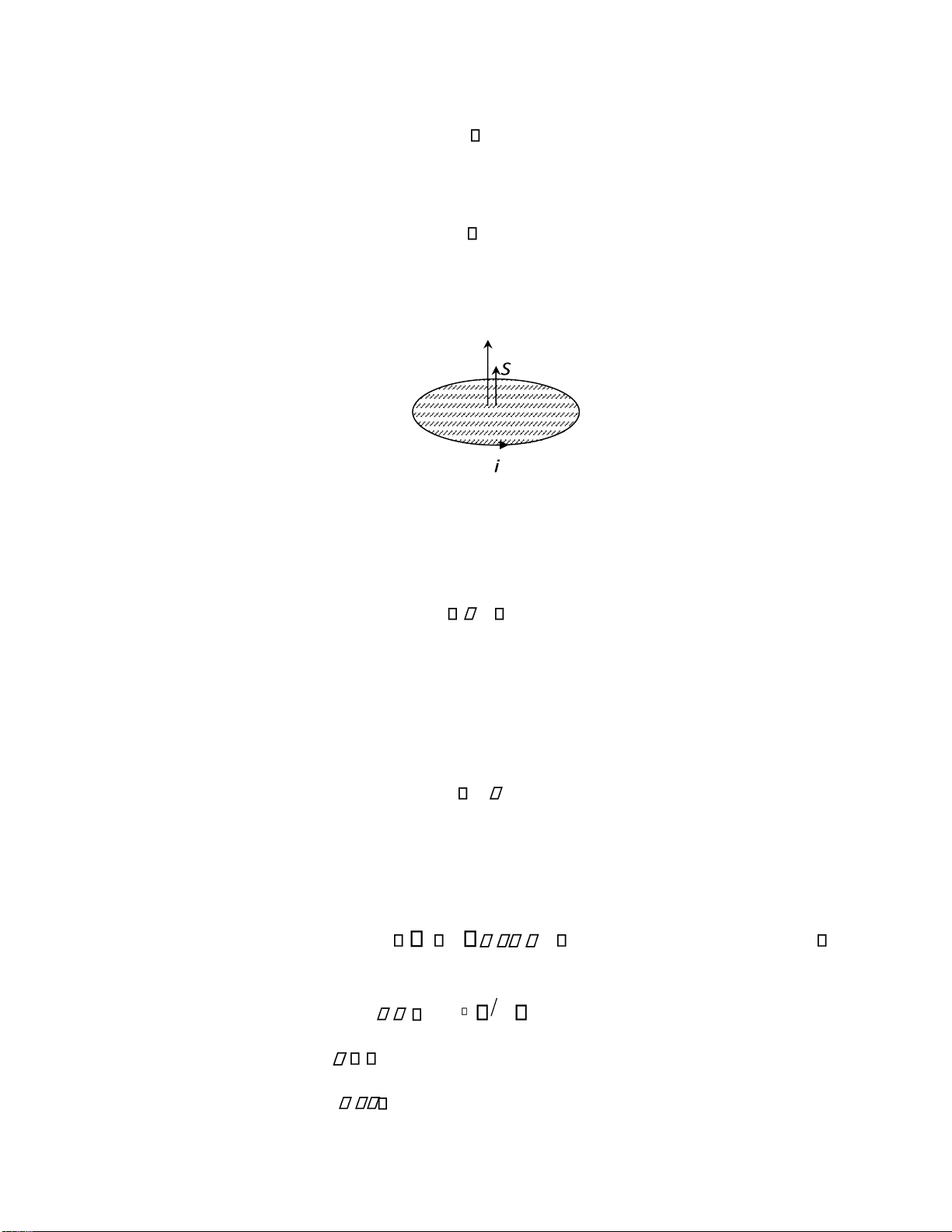
Mômen của một cực từ ược tính như sau: lOMoARcPSD| 36067889 m i S.
Mômen tổng hay mômen phân cực từ của từ môi: M Nm
Với N là số cực từ. m
Hình 1.3. Mô men phân cực từ Vect
ơ cường ộ từ trường H . B 0H M (1.7)
Trong a số chất từ môi khi cường ộ từ trường không quá mạnh, thì M tỷ kệ với
cường ộ từ trường H : M km 0H
với km là hệ số phân cực từ. Ta có: B 1 k m 0H r 0H H (1.8) Trong ó: 0
4 .10 7 H m là ộ từ thẩm trong chân không. r
1 km là ộ từ thẩm tương ối. r
0 là ộ từ thẩm tuyệt ối lOMoARcPSD| 36067889 Đơn vị của H A . m
Đối với một số chất như sắt, vật liệu sắt từ thì r 103 104
1.1.5. Các tham số ặc trưng cơ bản của môi trường
Đặc tính của môi trường vật chất ược thể hiện qua các tham số iện và từ của nó bao gồm:
Hệ số iện môi tuyệt ối (F/m).
Hệ số iện môi tương ối r (không thứ nguyên)
Độ từ thẩm tuyệt ối (H/m)
Độ từ thẩm tương ối r (không thứ nguyên) Độ dẫn iện (S/m)
Dựa trên các tham số iện và từ, người ta chia vật chất (môi trường iện từ) ra thành các loại sau:
Môi trường tuyến tính: các tham số , , và không phụ thuộc cường ộ trường.
Khi ó, các phương trình liên hệ là tuyến tính.
Môi trường ồng nhất và ẳng hướng: các tham số iện và từ là hằng số. Trong môi
trường này, các vectơ của cùng một phương trình liên hệ song song với nhau.
Nếu các tham số iện từ theo các hướng khác nhau có các giá trị không ổi khác nhau
thì ược gọi là không ẳng hướng.
Môi trường có các ại lượng iện từ là các hàm của tọa ộ ược gọi là môi trường không ồng nhất.
Trong tự nhiên, hầu hết các chất có hệ số iện môi tương ối r 1 và là môi trường tuyến tính.
Môi trường có ộ từ thẩm tương ối r
1 gọi là chất thuận từ, còn r 1 gọi là chất nghịch từ.
Chất dẫn iện là chất có
104 S / m . Chất bán dẫn là chất có 104 10 10 S m/
Chất cách iện là chất có 10 10 S m/ Điện môi lý tưởng có
0 , còn vật dẫn lý tưởng là môi trường có . lOMoARcPSD| 36067889
1.2. Các phương trình Maxwell
1.2.1. Một số khái niệm và ịnh luật cơ bản
1.2.1.1. Định nghĩa dòng iện
Xét một thể tích V ược giới hạn bởi một mặt kín S . Giả sử lượng iện tích q nằm trong
thể tính này giảm theo thời gian, nếu thừa nhận iện tích không tự biến mất thì iện tích ã chảy
ra khỏi thể tích ó (qua mặt S ). Ngược lại, sự tăng iện tích trong thể tích ang xét theo thời gian
chỉ có thể xảy ra do iện tích chảy từ ngoài vào, qua mặt S . Sự chuyển dịch của iện tích qua S
ã tạo ra dòng iện ược xác dòng iện ược xác ịnh bằng tốc ộ biến thiên của iện tích q trong thể
tích giới hạn bởi mặt S , lấy với dấu âm. dq I (1.9) dt
Như vậy dòng iện sẽ dương trong trường hợp iện tích q trong thể tích V giảm theo thời
gian, do các iện tích chảy ra ngoài và ngược lại. Căn cứ (1.9) có thể ịnh nghĩa dòng iện theo
cách ơn giản: Dòng iện có giá trị bằng lượng iện tích chảy qua mặt S trong một ơn vị thời gian.
Để mô tả ầy ủ hơn sự chuyển ộng có hướng của các hạt mang iện, người ta ưa ra
khái niệm mật ộ dòng iện J với ịnh nghĩa: Mật ộ dòng iện dẫn là một ại lượng vectơ, có hướng
trùng với hướng chuyển ộng của iện tích tại iểm ang xét, còn ộ lớn bằng lượng iện tích chảy
qua một ơn vị bề mặt ặt vuông góc với hướng chuyển ộng, trong một ơn vị thời gian. Quan hệ
giữa I và J như sau: I JdS (1.10) S
1.2.1.2. Định luật bảo toàn iện tích
Về thực chất, biểu thức (1.9) là ịnh luật bảo toàn iện tích dạng vi phân, nó liên hệ giữa
thông lượng của vectơ mật ộ dòng iện qua mặt kín với sự biến ổi của iện tích trong thể tích
giới hạn bởi mặt ấy.
Thay I từ biểu thức (1.10) vào (1.9) và thay Q trong (1.9) bởi: q tddV V
trong ó td là mật ộ iện tích trong thể tích V. Ta nhận ược: lOMoARcPSD| 36067889 (1.11 S JdS dt d V tddV V ddttd dV )
Áp dụng phép biến ổi Gauss cho vế trái của (1.11) ta có: td divJdV dV V V t Từ ây suy ra: td divJ (1.12 ) t
Biểu thức (1.12) là biểu thức vi phân của ịnh luật bảo toàn iện tích.
1.2.1.3. Định luật Ohm
Là ịnh luật liên hệ giữa mật ộ dòng iện trong môi trường dẫn iện với cường ộ iện trường.
Biểu thức toán học của ịnh luật có dạng: J E (1.13)
là hệ số phụ thuộc vào tính dẫn iện của môi trường, ược gọi là iện dẫn suất (hay ộ dẫn iện).
Biểu thức (1.13) là công thức của ịnh luật Ohm dạng vi phân. Bây giờ xét ịnh luậ Ohm
dạng tích phân cho oạn dây có dòng iện. E lOMoARcPSD| 36067889 l J Từ (1.13) suy ra: E (1.14) Nhân
hai vế của (1.14) với dl ta có: Jdl dl Edl J
Nhân S với tử số và mẫu số vế phải của biểu thức trên, sau ó lấy tích phân theo chiều dài cả hai vế ta ược: l l Sdl Edl J 0 0 S
Giả sử J phân bố ều trên theo tiết diện, ta có: JS I , do ó: l l dl Edl I (1.15) 0 0 S
Vế trái của (1.15) chính là hiệu iện thế tại hai ầu oạn l . l
Edl U 1 U 2 0
Còn tích phân vế phải chính bằng iện trở của oạn dây: l R dl 0 S
Cuối cùng ta viết ược ịnh luật Ohm cho oạn dây: lOMoARcPSD| 36067889 U 1 U 2 IR
1.2.1.4. Đinh luật dòng iện toàn phần
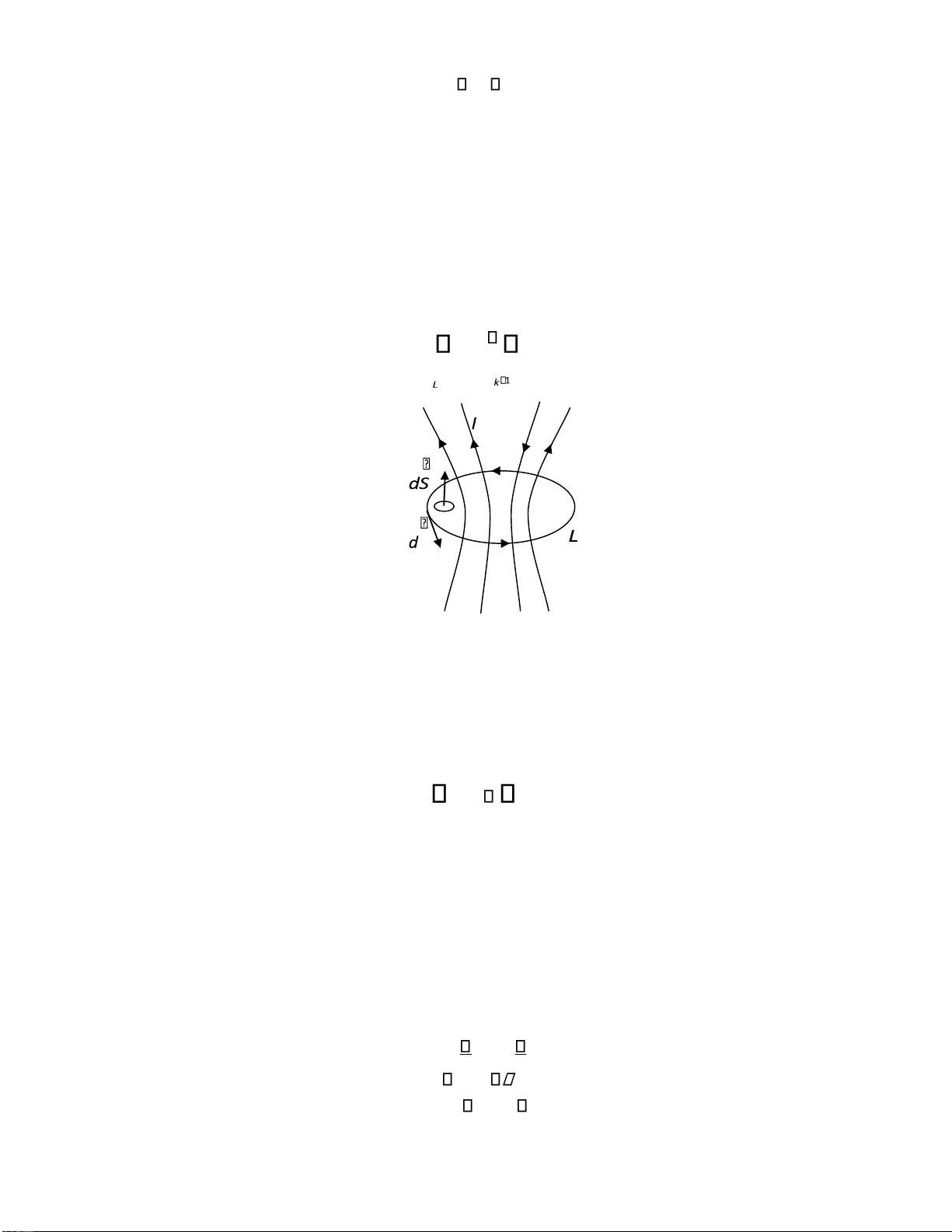
Định luật dòng iện toàn phần của nhà bác học Ampe người Pháp ược phát biểu như
sau: Lưu thông của vectơ cường ộ từ trường H dọc theo một ường cong kín bất kỳ bằng tổng
ại số các dòng iện chảy qua diện tích bao bởi ường cong này. Biểu thức toán học của ịnh luật
dòng iện toàn phần có dạng: n Hdl I k (1.16) l
Hình 1.5. Lưu thông của cường ộ từ trường qua ường cong kín L
Nếu dòng iện chảy qua mặt S phân bố ều liên tục với mật ộ J thì ịnh luật dòng iện toàn
phần ược viết dưới dạng sau: Hdl JdS (1.17) L S
1.2.1.5. Khái niệm về dòng iện dịch
Khi nghiên cứu ịnh luật cảm ứng iện từ của Fara ây và ịnh luật dòng iện toàn phần của
Ampe nhà vật lý người Anh Maxwell bằng lý thuyết ã chỉ ra sự tác dụng tương hỗ giữa iện
trường và từ trường với việc dẫn ra khái niệm mới về dòng iện là dòng iện dịch. Theo Maxwell
dòng iện dịch có mật ộ ược xác ịnh bằng biểu thức: D E J dc (1.18) t t lOMoARcPSD| 36067889
Theo Maxwell mật ộ dòng iện toàn phần gồm hai số hạng: mật ộ dòng iện iện dẫn
J (tỷ lệ với cường ộ iện trường) và mật ộ dòng chuyển dịch (J cd ) tỷ lệ với biến thiên của
cường ộ iện trường theo thời gian. J J J cd (1.19)
1.2.2. Các dạng của hệ phương trình Maxwell
1.2.2.1. Phương trình Maxwell thứ nhất
Bằng cách bổ sung dòng iện dịch vào vế phải của biểu thức ịnh luật dòng iện toàn phần
cùng với dòng iện dẫn Maxwell xây dựng ược phương trình thứ nhất dạng tích phân như sau: L
Hdl S JdS S Dt dS (1.20)
Phương trình (1.20) mô tả quan hệ giữa các vectơ của trường (H và D ) trong một
vòng bất kỳ và các dòng iện (dòng dẫn và dòng dịch) chảy qua nó.
Phương trình Maxwell dạng vi phân có dạng như sau: D rotH J J J cd (1.21) t
Với iện môi lý tưởng và chân không thì J
E 0 nên (1.21) có dạng: E rotH J cd (1.22) t
Phương trình (1.21) cho thấy vai trò của dòng iện dịch và dòng iện dẫn là như nhau
trong quá trình tạo ra từ trường xoáy.
1.2.2.2. Phương trình Maxwell thứ hai
Maxwell cho rằng biểu thức của ịnh luật cảm ứng iện từ áp dụng không chỉ cho một
vòng dây dẫn iện kín mà còn úng cho một vòng kín nào ó (không nhất thiết là dẫn iện) trong
không gian. Trong trường hợp tổng quát vòng kín này có thể một phần nằm trong chân không,
phần khác nằm trong iện môi hay trong kim loại.
Phương trình Maxwell thứ hai dạng tích phân như sau: lOMoARcPSD| 36067889 B L Edl S t dS (1.23)
Áp dụng phép biến ổi Green-Stoke cho vế trái của (1.23) ta nhận ược phương trình
Maxwell thứ hai dạng vi phân: B rotE (1.24) t
Phương trình (1.24) cho thấy từ trường biến thiên sẽ sinh ra iện trường xoáy.
Từ hai phương trình (1.22) và (1.24) cho thấy iện trường và từ trường có tác dụng tương
hỗ lẫn nhau. Điện trường biến thiên tạo ra dòng iện dịch và từ trường biến thiên, ồng thời từ
trường biến thiên lại tạo ra iện trường biến thiên.
1.2.2.3. Phương trình Maxwell thứ ba và thứ tư
Phương trình Maxwell thứ ba và thứ tư ược dẫn ra từ ịnh luật Gauss ối với iện trường
và từ trường. Dạng tích phân của hai phương trình này như sau: DdS tddV q (1.25) S V BdS 0 (1.26) S
Áp dụng phép biến ổi Gauss cho vế trái của hai phương trình trên ta ược: divDdV tddV V V divBdV 0 V
Vì thể tích V là tùy ý nên nhận ược các phương trình Maxwell dạng vi phân: lOMoAR cPSD| 36067889 divD td (1.27) (1.28) divB 0
1.2.2.4. Hệ thống các phương trình Maxwell Dạng vi phân: (1.29)
D rotH J t B rotE t divD td divB Dạng tích phân: 0 L
Hdl S JdS S Dt dS B L Edl S t dS (1.30)
DdS tddV q S V S BdS 0
Hệ phương trình Maxwell dạng phức:
Nếu các ại lượng iện trường và từ trường biến thiên tuần hoàn theo thời gian với tần số
, tức là có thể mô tả chúng như sau: E Ee j t , H
He j t thì phương trình Maxwell 1
và 2 dạng phức có dạng như sau: lOMoARcPSD| 36067889 rotH ( j)E rotE j H (1.31)
1.2.3. Ý nghĩa của hệ phương trình Maxwell
1.2.3.1. Mô tả mối quan hệ giữa hai mặt iện trường và từ trường của trường iện từ biến thiên
Theo phương trình Maxwell 1: ở những vùng có iện trường biến thiên, tức là mật ộ
dòng iện J D t 0 biến thiên thì ở ó có từ trường biến thiên và từ trường ó có tính
chất xoáy (vì rotH 0). Ngược lại theo phương trình Maxwell 2 nêu rõ ở những vùng có từ
trường biến thiên B t
0 thì ở ó có iện trường biến thien và iện trường ó cũng có tính
chất xoáy (rotE 0 ). Vậy hai phương trình Maxwell 1 và 2 cho thấy từ trường và iện trường
biến thiên luôn gắn bó với nhau và luôn có tính chất xoáy.
1.2.3.2. Mô tả hình học của hai mặt thể hiện iện trường và từ trường
Theo phương trình Maxwell 4: divB 0 hoặc BdS 0 ta nhận thấy B luôn chảy S
liên tục. Với mọi mặt kín S thông lượng củaB chảy vào và ra luôn bằng nhau, không có vùng
nào là vùng xuất phát hoặc tận cùng của B , ó là hình học của véctơ từ cảm B .
Theo phương trình Maxwell 3: divD td hoặc DdS q nêu lên một hình học khác. S
Thông lượng của véctơ D chảy ra khỏi một mặt kín S bằng lượng iện tích tự do bao quanh
mặt ấy. Vậy ối với véctơ D có thể có những vùng xuất phát là vùng có td 0 và những
vùng tận cùng là những nơi có phân bố td
0 . Nó có thể chảy không liên tục, khép kín khắp
nơi như B . Đó là hình học của véctơ D . lOMoARcPSD| 36067889
1.2.3.3. Các phương trình Maxwell mô tả quan hệ khăng khít giữa trường và môi trường chất
Thật vậy phương trình Maxwell 1 nêu rõ ộ xoáy của từ trường gắn liền với dòng iện,
có nghĩa là ường sức từ H xoáy quanh những dòng iện (dòng dẫn hoặc dòng dịch) là một dạng
chuyển ộng của vật chất.
Phương trình Maxwell 3 nêu rõ sự gắn bó giữa iện trường và sự phân bố các hạt mang
iện. Đường sức của D tỏa ra từ những hạt mang iện td , trong tự nhiên tồn tại các iện tích tựa
như những hạt này là các "nguồn" của iện trường. (Chú ý phương trình Maxwell 4 cho
thấy từ trường B không có "nguồn" iểm thuộc loại như vậy, thực tế cho thấy rằng không tồn tại những từ tích).
Nhìn chung sự gắn bó trường-chất thể hiện ở những hệ số của phương trình
td là những biến và thông số hành vi của môi trường. Với những hệ số khác nhau
ta có những dạng phương trình khác nhau và do ó quy luật tương tác của hệ sẽ khác nhau.
1.3. Điều kiện bờ ối với các vec tơ của trường iện từ
Điều kiện bờ ối với các vectơ của trường iện từ là hệ thức giữa các thành phần của các
vectơ trường iện từ ở hai bên, sát mặt giới hạn phân cách hai môi trường khác nhau. Điều
kiện bờ có tầm quan trọng trong cả nghiên cứu lý thuyết lẫn tìm nghiệm các bài toán iện từ
trong thực tiễn. Trong mục này, chúng ta sẽ i tìm quan hệ của cùng các vectơ
E D B H, ,
, ở hai bên của mặt phân cách hai môi trường khác nhau.
Giả sử có hai môi trường ược phân cách nhau bằng mặt giới hạn S nào ó. Các tham số
iện và từ của hai môi trường tương ứng là: 1 , 1 , 1, 2 , 2 ,
2 và E1,D1,B1,H 1
E 2 ,D2 ,B 2 ,H 2 .
Điều kiện bờ với thành phần tiếp tuyến.
Phát biểu 1: Nếu trên bờ tiếp giáp hai môi trường, một vectơ F thỏa mãn phương trình
rotF = hữu hạn, thì các thành phần tiếp tuyến phải chuyển tiếp liên tục [3].
F1t S F2t S (1.32) lOMoARcPSD| 36067889
Hệ luận. Từ (1.31) suy ra trường hợp ặc biệt, khi trên bờ S thành phần tiếp tuyến rot F
t có dạng phân bố Đi-rắc theo chiều pháp tuyến A. n
thì F1t S và F2t S sẽ
chuyển tiếp gián oạn loại 1: F 1t F2t A (1.33)
Ta có iều kiện bờ ối với thành phần tiếp tuyến của iện trường và từ trường như sau: a)
Với vectơ từ trường:
H 1t H 2t J S với J S là mật ộ dòng iện mặt.
* Khi cả hai môi trường là iện môi thì J S 0 , ta có:
H 1t H 2t
* Khi môi trường 1 là iện môi, môi trường 2 là vật dẫn lý tưởng thì:
H 1t J S , H 2t 0 .
b) Với vectơ iện trường:
E1t E 2t
Đúng cho mọi trường hợp tổng quát với hai môi trường có tham số tùy ý.
* Khi môi trường 2 là dẫn iện lý tưởng thì: E 12
0 , do ó: E1t E 2t 0
Điều kiện bờ với thành phần pháp tuyến.
Phát biểu 2: Nếu trên bờ tiếp giáp hai môi trường, một vectơ F thỏa mãn phương trình
divF = hữu hạn, thì các thành phần pháp tuyến phải chuyển tiếp liên tục [3].
F1n S F2n S (1.34)
Hệ luận. Từ (1.34) suy ra trường hợp ặc biệt, khi trên bờ S divF có dạng phân bố Đirắc
theo bề dầy thì Fn sẽ có gián oạn loại 1: F 2n F1n S n .dn S (1.35)
Từ phát biểu 2 và hệ luận ta có thể có iều kiện bờ với thành phần pháp tuyến của vectơ iện trường như sau: lOMoARcPSD| 36067889 D 2n D1n s (1.36)
Trong ó S là mật ộ iện tích mặt.
Biểu thức (1.36) úng cho trường hợp tổng quát với 2 môi trường có tham số tùy ý. Khi
môi trường 1 là vật dẫn lý tưởng thì ta có:
D1n 0,D 2n s
1.4. Năng lượng của trường iện từ - Định lý Poynting
Định lý Poynting thiết lập mối liên hệ giữa sự thay ổi năng lượng iện từ trong một thể
tích V với dòng năng lượng iện từ chảy qua mặt kín S bao quanh thể tích này.
Trong một thể tích V tùy ý, trường iện từ sẽ có năng lượng tích tụ bằng: W V E2 2 H2 2 dV V wE wH dV (1.37) E 2
Trong ó: wE là mật ộ năng lượng iện trường. 2 H 2
wH là mật ộ năng lượng từ trường. 2
Từ các phương trình Maxwell 1 và 2 ta có thể viết lại: E t rotH J ( )a (1.38) Ht rotE ( )b
Nhân vô hướng ẳng thức (1.38)(a) với E và ẳng thức (1.38)(b) với H rồi cộng vế với vế
hai ẳng thức lại ta có: E H ErotH HrotE JE (1.39) t t Biến ổi (1.39) ta ược: lOMoAR cPSD| 36067889 (1.40) t E2 2 H2 2
div E H JE
Lấy tích phân theo thể tích hai vế phương trình (1.40) ta có: (1.41) t V E2 2 H2 2 dV V div E H dV V JEdV
Dùng phép biến ổi Gauss cho tích phân thứ nhất của vế phải (1.41) ta có: div E
H dV E H dS dS V S S Trong ó: E H (1.42) E H
gọi là vectơ Poynting (vectơ mật ộ công suất của trường iện từ). Cuối cùng ta có: t lOMoARcPSD| 36067889 V E2 2 H2 2
dV S dS V JEdV (1.43) Hay: W
S dS Q (1.44) t
Các biểu thức (1.43) và (1.44) là dạng toán học của ịnh lý Poynting và cũng là ịnh lý về
sự bảo toàn năng lượng trong trường iện từ. Trong ó: Q
JEdV là công suất tổn hao dưới dạng nhiệt của dòng iện trong thể V tích V.
Theo (1.42) thì năng lượng của trường iện từ ở mỗi iểm sẽ dịch chuyển theo phương
pháp tuyến với mặt phẳng tạo bởi E và H .
Phương trình (1.44) là biểu thức của ịnh lý Poynting. Định lý này do hai nhà bác học
Poynting (người Anh) và Umôv (người Nga) ưa ra, nên còn gọi là ịnh lý Umôv-Poynting.
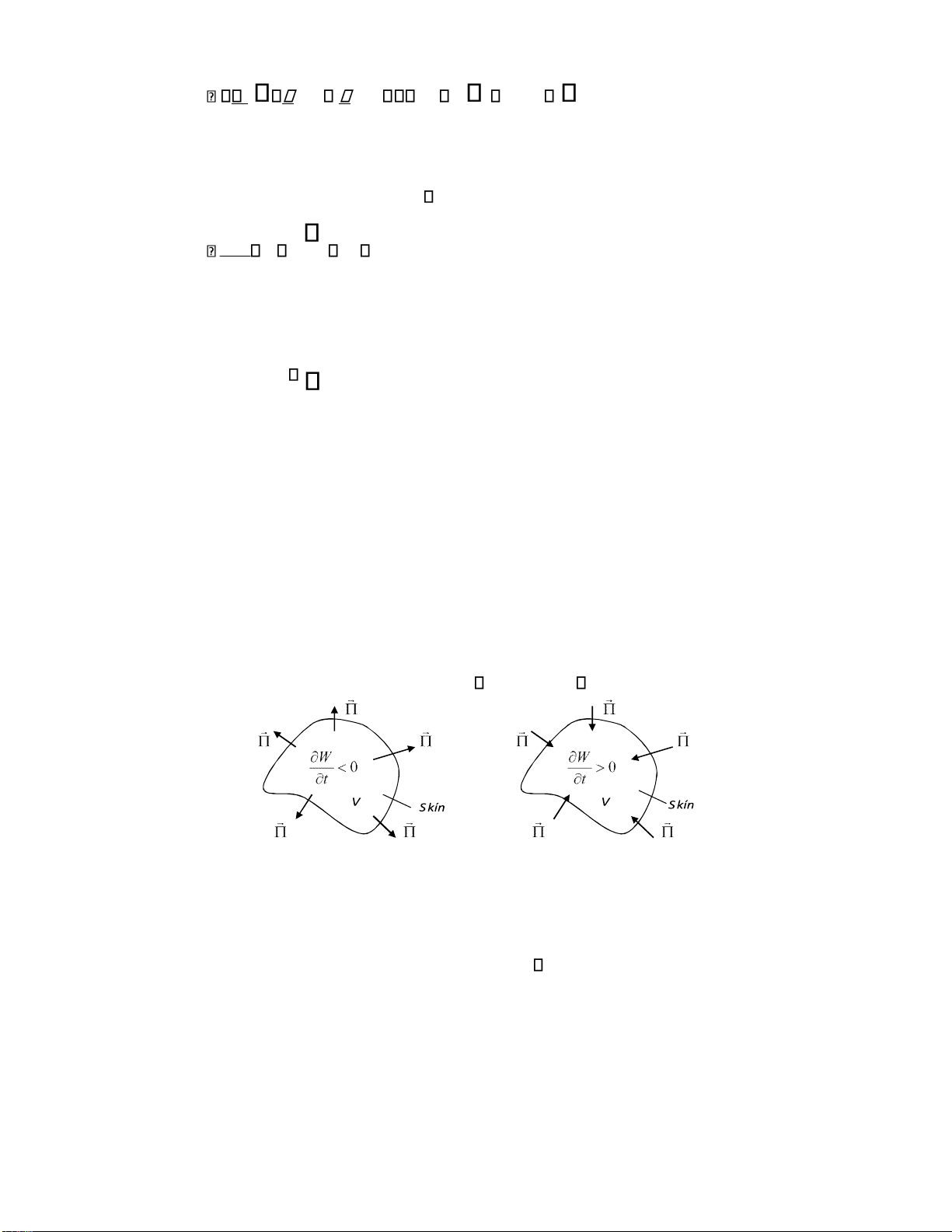
Dấu (-) ở vế trái của phương trình (1.44) thể hiện sự bảo toàn năng lượng. Khảo sát
trường hợp môi trường iện môi lý tưởng (J 0 và do ó Q 0 ). Xét hai trường hợp sau: a) b)
Hình 1.6. Thông lượng của qua mặt kín S lOMoARcPSD| 36067889 W
Trường hợp Hình 1.6.a vectơ tỏa ra ngoài S nên S dS 0 và do ó t 0 tức
là năng lượng trong V giảm dần theo thời gian. W
Ngược lại: Trường hợp Hình 1.6.b vectơ i vào S nên S dS 0 và do ó t
0 tức là năng lượng trong V tăng dần theo thời gian.
* Vec tơ Poynting trung bình dạng phức:
Đối với trường iện từ iều hòa, các ại lượng cơ bản tính trung bình trong một chu kỳ dao
ộng T của trường có ý nghĩa thiết thực vì thế người ta thường biểu diễn một số ại lượng theo
dạng phức. Ta có thể viết các ại lượng thực của trường thông qua các ại lượng phức và liên
hợp phức của nó như sau:
E reE 1
E E* 21
H H* H reH 2
Ở ây dấu (*) là ại lượng lấy liên hợp phức. Vectơ Poynting có thể biểu diễn qua ại lượng phức như sau:
reE reH 14
E E*
H H* lOMoARcPSD| 36067889
Biến ổi phương trình này và lấy tích phân trong 1 chu kỳ T ta có vectơ Poyting trung bình tính như sau: tb 1 re E H* 2
Với vectơ Poynting dạng phức: 12 E H * từ ó ta có: tb re
Bằng cách tương tự người ta biểu diễn các ại lượng trung bình khác như sau: WEtb 1 | E |2 dV 4 V WMtb 1 |H |2 dV 4 V
Công suất tiêu tán trung bình 1 re JE dV
* 1 | E|2 dV P ttb 2 V 2 V
1.5. Trường tĩnh iện
1.5.1. Các phương trình ặc trưng cơ bản
1.5.1.1. Hệ phương trình Maxwell cho trường tĩnh iện
Trường ịên từ tĩnh là trường iện từ thỏa mãn hai iều kiện sau:
Các ại lượng iện và từ không thay ổi theo thời gian, tức là ạo hàm riêng các ại
luợng của trường theo thời gian ều bằng không t 0 . lOMoAR cPSD| 36067889
Không có sự chuyển ộng của các hạt mang iện, nghĩa là mật ộ dòng iện dẫn luôn bằng không J 0 .
Từ hai iều kiện này ta sẽ có hệ phương trình Maxwell cho trường iện từ tĩnh như sau: rotH 0 rotE 0 (1.45) divD td divB 0
Từ (1.45) ta có vài nhận xét: iện trường và từ trường ều có tính chất thế, và chúng không
có quan hệ trực tiếp với nhau, tức là iện trường và từ trường ộc lập. Ta có thể khảo sát riêng
rẽ iện trường và từ trường. Trong tài liệu này chỉ khảo sát iện trường tĩnh, ó là iện trường
không thay ổi theo thời gian của các iện tích ứng yên.
1.5.1.2. Thế vô hướng của trường tĩnh iện
Ở trường tĩnh công dịch chuyển một iện tích từ iểm nọ ến iểm kia hoàn toàn xác ịnh bởi
vị trí 2 iểm mà không phụ thuộc vào ường i. Điều ó nghĩa là công dịch chuyển một iện tích
theo một vòng kín luôn triệt tiêu, iều này thể hiện tính chất thế của trường iện từ tĩnh.
Công của lực iện tĩnh khi di chuyển một iện tích q theo một ường cong kín C như sau:
A qE d. l q rotE dS . 0 C S
Từ ặc iểm này suy ra, nếu chọn một iểm M 0 nào ó làm gốc, thì công dịch chuyển một
ơn vị iện tích (q 1C ) từ M 0 ến mọi iểm M sẽ có giá trị xác ịnh tùy thuộc vị trí của M . Ta
ịnh nghĩa công dịch chuyển iện tích 1C từ M 0 ến M là thế năng ( iện thế) ứng với iểm M x y z, , . lOMoAR cPSD| 36067889 (1.46) , , E x y z E M Edl M 0
Đại lượng ặc trưng cho vị trí ó ược gọi là iện thế , ơn vị l E à Volt (V).
Từ (1.46) ta có thể biểu diễn E qua E như sau: E E dl l Hay: E grad E E (1.47) M
Biểu thức (1.47) thỏa mãn phương trình Maxwell 1: rotE rotgrad E 0
Dấu trừ ở (1.47) chỉ là quy ước: chiều của vec tơ cường ộ iện trường là chiều giảm của E .
1.5.1.3. Phương trình Laplace – Poisson
Thay phương trình (1.47) vào phương trình Maxwell 4 ta ược: divD divE divgrad E
Nếu miền khảo sát là ồng nhất, hệ số iện môi là hằng số thì ta có: divgrad E E (1.48) lOMoARcPSD| 36067889
Với là toán tử Laplace. Phương trình (1.48) là phương trình Laplace - Poisson. Phương
trình này thể hiện quan hệ giữa iện thế của trường tĩnh iện với phân bố iện tích tạo nên trường tĩnh iện ó.
Nếu trong miền khảo sát không có iện tích, phương trình (1.48) trở thành: E 0 (1.49)
Phương trình (1.49) ược gọi là phương trình Laplace.
1.5.1.4. Từ trường tĩnh và khái niệm từ thế vô hướng M
Từ trường tĩnh không gắn với iện trường nên tách ra ược cặp phương trình Maxwell cho từ trường tĩnh:
rotH 0, divB div H 0
Tương tự như iện trường tĩnh ta thấy H cũng có tính chất thế và ta cũng có: H grad M (1.50)
Trong ó M là từ thế vô hướng biểu diễn trạng thái từ trường tĩnh. Kết hợp với phương
trình Maxwell 4 ta cũng có phương trình Laplace cho từ thế vô hướng như sau: M 0
1.5.2. Một số bài toán về trường tĩnh iện
Dưới ây là một số ví dụ vận dụng trực tiếp luật Gauss tĩnh iện ể giải phương trình Laplace.
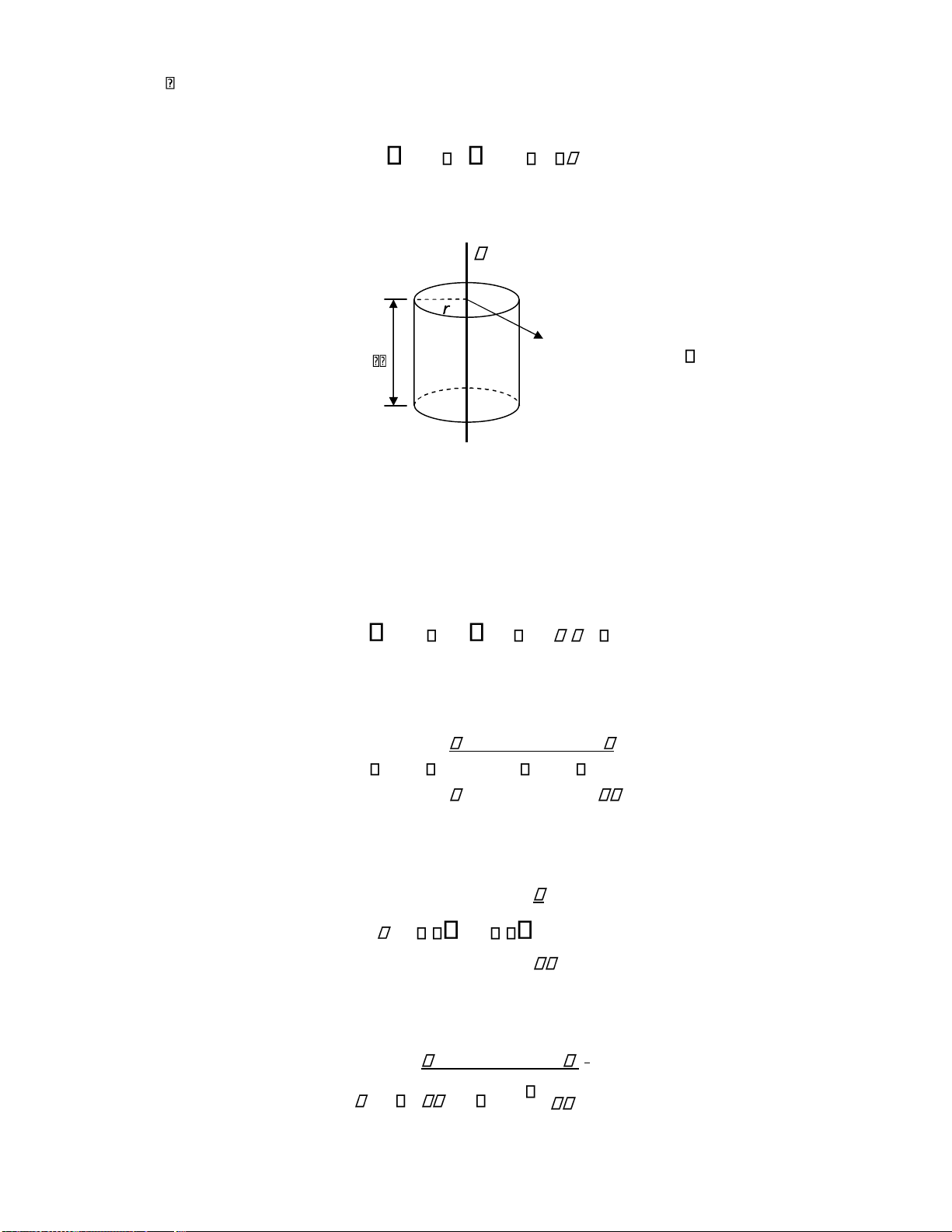
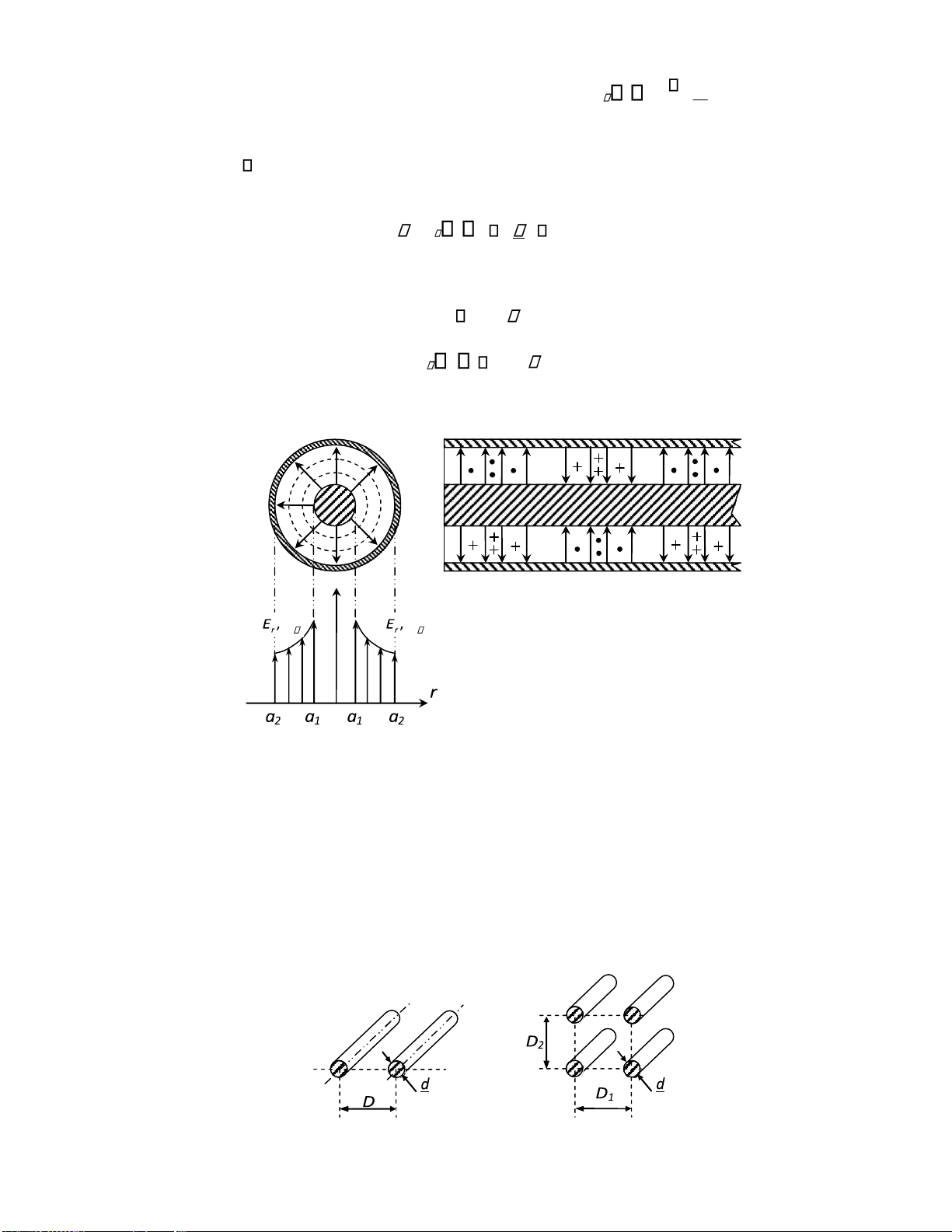
1.5.2.1. Điện trường ối xứng xuyên tâm hình cầu
Xét một iện tích iểm hoặc một vật dẫn hình cầu mang iện ặt trong môi trường iện môi lúc này
iện trường có tính ối xứng xuyên tâm rõ rệt. Các ại lượng E D,
, E sẽ chỉ phụ thuộc
khoảng cách r ến tâm cầu (như Hình 1.7).
Hình 1.7. Điện trường ối xứng xuyên tâm hình cầu lOMoARcPSD| 36067889
Các iểm trên mặt cầu có cùng iện thế và cùng cường ộ iện trường, hay mặt cầu chính là mặt ẳng thế.
Ở ây E và D chỉ có thành phần xuyên tâm: E Er , D Dr . Vì vậy khi ta lấy mặt cầu
S có bán kính r và áp dụng luật Gauss cho mặt S ta có:
DdS D dS r DdS q S S S
Trong ó q là iện tích nằm trong S. Do D phân bố ều trên mặt cầu nên ta có:
DdS D dS 4 r D2 q (1.51) S S Hay:D r( ) D q r ( )r
4 qr 2 và E r( ) 4 r 2
Từ kết quả này ta tính ược iện thế của một iểm trên mặt cầu với mốc lấy ở xa vô cùng E ( ) 0 như sau: r r q r dr E ( )r E drr E drr 2 4 r
Ở ây ta coi môi trường là ồng nhất và tuyến tính tức là
const tại mọi vị trí, và ta có
biểu thức quen thuộc tính iện thế như sau: q E (1.52) 4 r
1.5.2.2. Điện trường ối xứng xuyên trục
Xét một trục mang iện hoặc một vật dẫn hình trụ tròn, thẳng và dài vô hạn ặt trong môi
trường iện môi, lúc này iện trường sẽ ối xứng qua trục và chỉ phụ thuộc vào khoảng cách r ến
trục. Xét một dây dẫn iện thẳng và dài vô hạn, tích iện ều với mật ộ tính chiều theo chiều dài là như Hình 1.8.
Với trường hợp này các thành phần E ,E D,
chỉ phụ thuộc vào khoảng cách ến dây, tức là: E E . Để r ,D Dr
tính D r( ) và E r( ) ta lấy một mặt trụ có bán kính r và chiều dài là lOMoAR cPSD| 36067889
, ồng trục với dây dẫn. Áp dụng luật Gauss ta có:
DdS D dS r q l S S
Trong ó: q chính là lượng iện tích nằm trong S. D Dr
Hình 1.8. Điện trường ối xứng xuyên trục
Ta nhận thấy Dr phân bố ều trên diện tích xung quanh của hình trụ S, và Dr không i qua
diện tích 2 áy của hình trụ, do ó ta có: D dS r Dr
dS Dr 2 r l l S S Hay:
D r( ) Dr ( )r
; E r( ) Er ( )r (1.53) 2 r 2 r
Chọn một mặt trụ bán kính r0 làm mốc ta tính ược iện thế của một iểm cách dây một
khoảng cách r như sau: r r E ( )r E drr dr r0 r0 2 r
Với môi trường tuyến tính ẳng hướng ta tính ược: r0 E (1.54) ( )r 2 (lnr 0 lnr ) 2 ln r lOMoARcPSD| 36067889
1.6. Từ trường của dòng iện không ổi
Trạng thái riêng thứ hai của trường iện từ là trường do dòng iện không ổi tạo ra, ây
là trạng thái dừng của trường iện từ. Từ trường dừng là trường gắn với phân bố dòng dẫn J
không ổi theo thời gian (J const 0). Do ó các ại lượng của trường cũng không ổi theo
0 . Hệ phương trình Maxwell của trường iện từ dừng là: thời gian t rotH J E rotE 0 (1.55) divD 0 divB 0 Với B H J; E .
Nhận xét: theo phương trình Maxwell 1 và 2 trong hệ (1.55) ta thấy: H có tính xoáy và
phụ thuộc và E , còn E có tính chất thế và ộc lập so với H .
1.6.1. Điện trường dừng
Trong vật dẫn không tồn tại iện trường tĩnh, nếu bỏ qua hiện tượng phân cực, coi
0 ta có D 0 và nếu bỏ qua hiện tượng dẫn trong iện môi 0, tức là coi 0 , có
thể tách ra hai vùng: Vật dẫn có phân bố dòng iện dẫn J và vùng iện môi quanh ó có
phân bố D và E . Do ó ta có các phương trình sau: Vật dẫn: rotE 0 ; divJ 0 ; J E Điện môi: rotE 0 ; divD 0; D E lOMoARcPSD| 36067889
Khái niệm về iện thế và phương trình quan hệ giữa iện thế với E tương tự như trường iện từ tĩnh, ta có: E grad E
Thay phương trình này vào các phương trình divJ 0 và divD 0 ối với cả hai vùng ều
có chung một phương trình Laplace cho iện thế vô hướng , nó mô tả ủ iện trường dừng: divgrad E E 0 (1.56)
1.6.2. Từ trường dừng
Hệ phương trình Maxwell ối với từ trường dừng:
rotH J , divB 0; B H
Từ phương trình rotH J
0 ta thấy từ trường dừng có tính chất xoáy, do ó không
thể xây dựng hàm thế vô hướng ược. Chú ý rằng ở mọi vùng J có triệt tiêu hay không thì
cường ộ từ cảm B luôn chảy liên tục: divB 0
So sánh biểu thức này với hằng ẳng thức div rotA M
0, nên có thể o từ trường bằng
một hàm thế AM , gọi là từ thế vectơ. B rotA (1.57)
Thay (1.57) vào phương trình thứ nhất của hệ (1.55), ta nhận ược: A J (1.58)
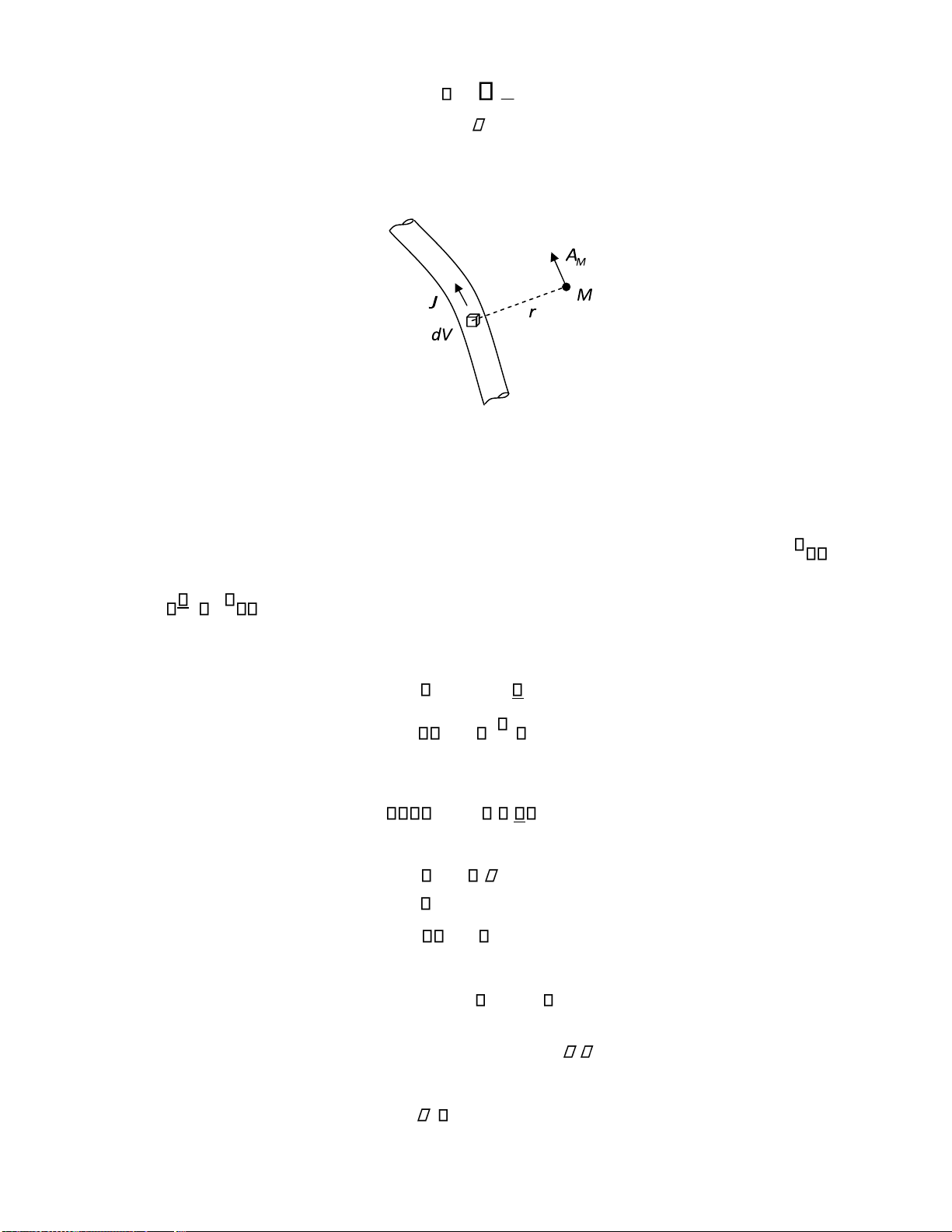
Đây là phương trình Poisson cho thế véctơ AM , và nghiệm của phương trình (1.58) có dạng sau: J lOMoARcPSD| 36067889 A dV 4 V r
Trong ó: r là khoảng cách từ iểm ang xét M ến nguyên tố nguồn JdV trong thể tích V của dây dẫn.
Hình 1.9. Từ thế véctơ A của dây dẫn iện
1.7. Trường iện từ biến thiên
1.7.1. Các phương trình cơ bản
Trong trường iện từ biến thiên các trạng thái của trường biến thiên theo thời gian t 0
và do ó hệ phương trình Maxwell như sau: D rotH J t rotE Bt divD td divB 0
Từ hệ phương trình này ta thấy rotH 0, rotE 0 nên cả E và H ều có tính chất xoáy,
ngoài ra chúng luôn gắn bó khăng khít với nhau. Do ó ta không thể biểu diễn trạng thái của
trường biến thiên bằng riêng những hàm thế vô hướng E , M ược, mà phải biểu diễn
thêm bằng hàm thế véctơ A (ở nơi td
0) hoặc ồng thời cả hai. Ở ây ta sử dụng từ thế lOMoAR cPSD| 36067889
véctơ A như trình bày ở trên cho trường iện từ biến thiên trong môi trường ồng nhất,
ẳng hướng, tuyến tính.
Từ phương trình Maxwell 2 và phương trình (1.57) ta có: B A rotE rotA rot t t t A Hay: rot E 0 t
Chú ý hằng ẳng thức rotgrad E 0 , ta có thể ặt: A rot E grad E 0 t Suy ra: A E grad E F t( ) t
Trong ó F t( ) là một hàm véctơ tùy ý chỉ phụ thuộc riêng vào thời gian và thỏa mãn
iều kiện rotF 0. Để xác ịnh F ta lập luận rằng khi trường chưa thành lập trong không gian E 0,B 0, E
0,A 0, do ó suy raF 0. Vậy ta ược: A E grad E 0 t lOMoARcPSD| 36067889 A E grad E t
Về ý nghĩa vật lý số hạng
grad E chính là thành phần iện trường ứng với một phân
bố iện tích như biểu thức (1.47). Trường hợp ơn giản nhất ó là thành phần trường tĩnh hoặc
dừng xếp chồng lên trường biến thiên. Nếu khắp nơi trong không gian không có phân bố iện
tích tự do, như khi xét trường iện từ biến thiên trong vật dẫn, trong bức xạ vô tuyến iện bằng
những anten ở tầng khí quyển thấp, sẽ không có thành phần grad E và ta có: A E (1.59) t
Để xác ịnh A như một trường véctơ, về toán học cần ịnh nghĩa hai phép toán không
gian rotA divA, và phép toán thời gian A t . Tất nhiên việc ịnh nghĩa các phép toán ấy nhằm
mục ích mô tả những hiện tường iện từ. Ở trên ta ã ịnh nghĩa một phép toán thời gian và một phép toán không gian. rotA B
ồng nhất với divB 0 (1.60) A t E grad E
ồng nhất với rotE B t (1.61)
Chú ý muốn mô tả trường B ta ngoài phép toán không gian rotA ở (1.60) ta còn cần
thêm phép divA mới hoàn toàn xác ịnh.
Ta có hệ phương trình Maxwell biểu diễn theo dạng sau: D rotH J t (1') lOMoARcPSD| 36067889 (1.62) rotE t ®ång nhÊt víi E t grad E (2') divD divE td (3')
divB 0 ®ång nhÊt víi B rotA (4')
Thay (2') và (3') vào (1') ta có: 1 J E J 2tA2 grad tE rotH rotrotA t Hoặc: 2A E rotrotA J t 2 grad t (1.63) B A
Vận dụng công thức giải tích véctơ: rotrotA graddivA divgradA vào vế trái công thức (1.63) ta có: grad divA tE divgradA 2tA2 J Để ược
phương trình ơn giản ta có thể chọn divA như sau: lOMoARcPSD| 36067889 E E divA 0 divA (1.64) t t
Điều kiện (1.64) ược gọi là iều kiện liên tục của Lorentz. Về vật lý nó phản ảnh dưới
dạng khác một hiện tượng quan trọng của trường iện từ là tính liên tục của dòng iện toàn phần.
Cuối cùng ta ược phương trình cho A của trường iện từ biến thiên: 2A 2A J trong vËt dÉn divgradA t 2 A t 2 0, trong ®iÖn m«i (1.65)
Trong trường hợp toàn không gian không có iện tích tự do, ta không có khái niệm iện thế E , lúc ó: A J E t Ta có thêm dạng: A A 2A2 t , trong vËt dÉn (1.66) t 0, trong ®iÖn m«i
Cần nhấn mạnh riêng trong môi trường iện môi với 0,J 0, ặt: 12 (1.67) v Ta có: 2A 2A A t 2 A (vt)2 0 (1.68) lOMoARcPSD| 36067889
Các biểu thức (1.65)b, (1.66)b và (1.68) là những phương trình 'Alamber (d'Alamber) về
truyền sóng của trường iện từ bién thiên trong iện môi.
1.7.2. Hiện tượng sóng của trường iện từ biến thiên
1.7.2.1. Định nghĩa sóng
Sóng là hình thái dao ộng hoặc chuyển ộng, di chuyển, của một dạng vật chất phân bố
một cách liên tục trong không gian.
Các không gian có thể là không khí, nước, một môi trường chất rắn. Trong khi dao ộng,
chuyển ộng, lan truyền thì năng lượng của sóng cũng lan truyền theo, do ó chúng có thể tiếp
cận ể trao ổi năng lượng với những vật chất có khả năng tiếp nhận hoặc ưa trả năng lượng ấy
(khả năng i xuyên của sóng qua nhiều môi trường).
Dòng năng lượng sóng phải lan truyền cùng chiều với dòng lan truyền của dạng vật
chất hay của trường, tức là cùng chiều truyền sóng. Từ ó ta có thể ịnh nghĩa chiều truyền
sóng ở mỗi iểm là chiều truyền vật chất (hoặc trường), cũng là chiều truyền năng lượng. Ví
dụ nếu không khí ở một miền nào ó ột nhiên dãn nở mạnh, sẽ hình thành những sóng khí
truyền ra xung quanh. Đồng thời năng lượng cũng lan ra theo bán kính, vậy ở ây chiều
truyền sóng là chiều bán kính, tỏa ra từ miền dãn nở.
Kèm theo sóng trường hoặc sóng chất, những trạng thái như khối lượng, mật ộ năng
lượng, áp suất, cường ộ trường...cũng dao ộng lan truyền và biến thiên theo không gian và
thời gian. Ta cũng gọi hình thái lan truyền, dao ộng của những trạng thái ó là sóng (sóng
trạng thái): sóng khối lượng, sóng năng lượng, sóng áp suất, sóng E , sóng H v.v...
1.7.2.2. Phương trình truyền của trường iện từ biến thiên
Như ã nêu các hàm thế A, của trường iện từ với: A B rotA E, grad E t
Cũng ã nêu quy luật vận ộng, lan truyền của chúng miêu tả bởi những phương trình truyền: 2A A t 2 J (1.69) E 2 t td lOMoARcPSD| 36067889
Phương trình (1.69) hàm những ý nghĩa quan trọng, chúng mô tả một cách ầy ủ và
gọn sự vận ộng của trường và quan hệ giữa trường và chất (giữa A với J , , ; giữa E với td , , ).
Đặc biệt với các hệ số
khác nhau chúng mô tả một cách tổng quát và ầy ủ tính
chất lan truyền của trường trong các môi trường khác nhau.
Ví dụ trong môi trường iện môi thuần túy và không trễ ta có
0 và là số thực, phương
trình trong môi trường không tiêu tán có dạng phương trình truyền sóng 'Alamber. 2A 2 A 2 0, E t 2 0 (1.70) t
Trong môi trường vật dẫn không trễ, ta có là số thực nếu coi 0 và toàn không
gian không có phân bố iện tích tự do ta có E
0 và phương trình A có dạng: 2A A A t 2 t 0 (1.71)
Đây là phương trình truyền có tiêu tán.
Nếu bỏ qua số hạng ạo hàm bậc 2 theo t, tức là về hình thức coi 0 , phương trình
sóng trong vật dẫn sẽ có dạng: A A 0 (1.72) t
Đây là một phương trình truyền nhiệt, hoặc phương trình khuếch tán có tiêu tán.
Để dẫn ra các phương trình truyền ối với E H, trong môi trường tuyến tính, không có
phân bố iện tích tự do, ta thực hiện tính rot với hai vế phương trình Maxwell 1 sau ó giải với
phương trình Maxwell 2 và phương trình Maxwell 4. Tương tự như vậy tác ộng rot vào hai vế
phương trình Maxwell 2, ồng thời kết hợp phương trình Maxwell 1 và phương trình Maxwell 3 với td
0 ta có phương trình sóng ối với thành phần từ trường và iện trường như sau: lOMoARcPSD| 36067889 2H H H 2t2 t 0 (1.73) E tE2 Et 0
Vậy tóm lại trường iện từ biến thiên trong một môi trường tuyến tính ược mô tả bởi
những phương trình (1.69) hoặc (1.73). Tùy vào từng trường hợp ta sẽ chọn phương trình nào. BÀI TẬP CHƯƠNG 1
Bài 1-1: Giữa hai bản cực của một tụ iện phẳng ặt cách nhau theo chiều x , có phân bố hàm
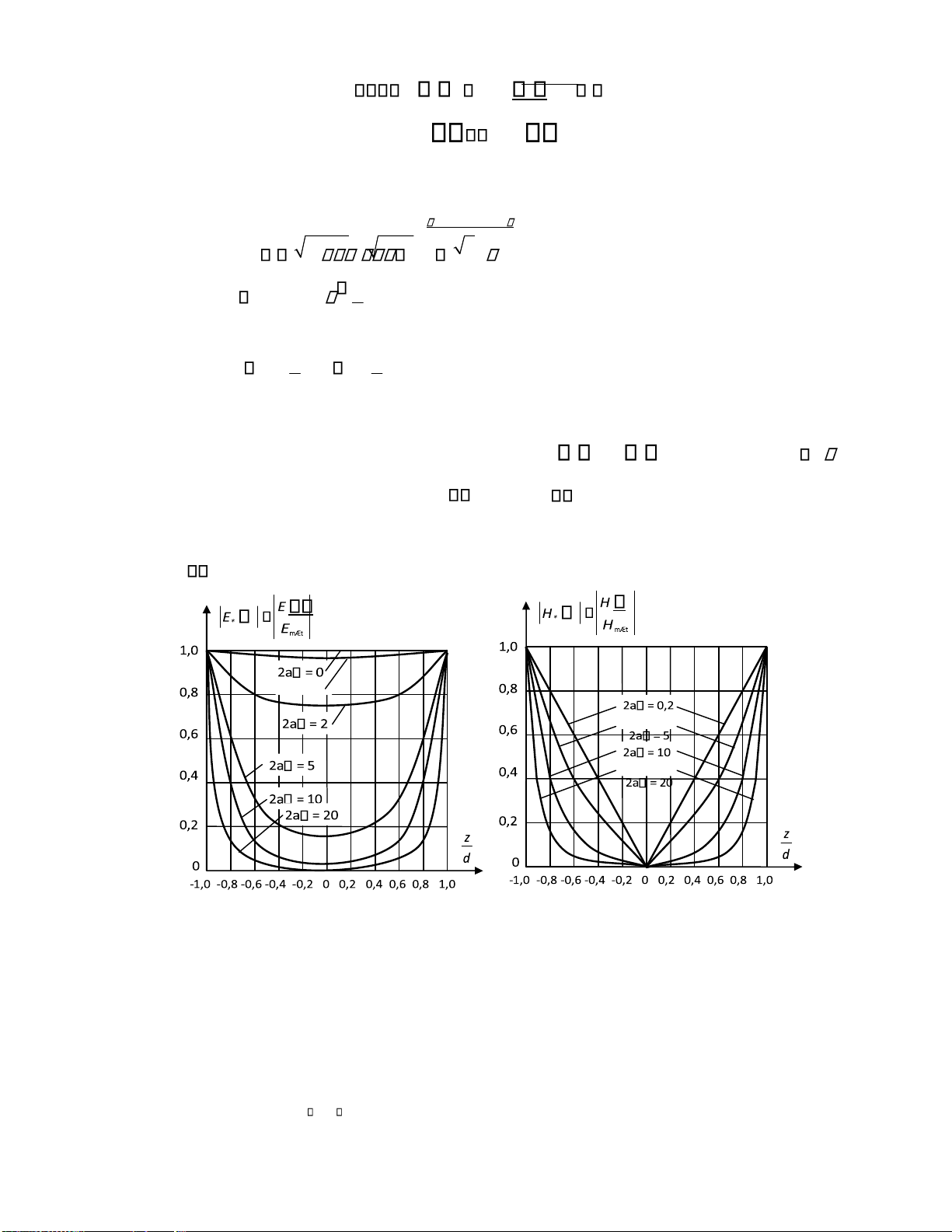
thế E ax 2 bx . Hãy tìm sự phân bố cường ộ trường E , D , phân bố iện tích E1 E1; E 2 E
2 và xem trường có tính chất gì?
Bài 1-2: Một quả cầu vật chất bán kính a có hằng số iện môi tuyệt ối ặt trong không k
hí. Có phân bố ều iện tích trong thể tích quả cầu. Hãy tìm cường ộ iện trường E ở trong và ngoài mặt cầu.
Bài 1-3: Tìm cường ộ iện trường E và iện thế E tại một iểm cách một sợi chỉ mảnh một khoảng
cách r , sợi chỉ dài vô hạn ặt trong không khí và tích iện ều với mật ộ iện tích dài là l .
Bài 1-4: Tính cường ộ iện trường E và thế E của hai sợi chỉ mảnh dài vô hạn ặt song song
cách nhau một khoảng cách d trong không khí. Mỗi sợi chỉ tích iện với mật ộ iện tích dài là l và l .
Bài 1-5: Đặt một hệ ba iện tích iểm q, q / 2, q / 2 trên 3 ỉnh của một tam giác ều ABC
như hình 1.10 Hãy tìm iện thế vô hướng E và cường ộ iện trường E ở trọng tâm tam giác. Cho
biết cạnh tam giác là a. lOMoARcPSD| 36067889 Hình 1.10.
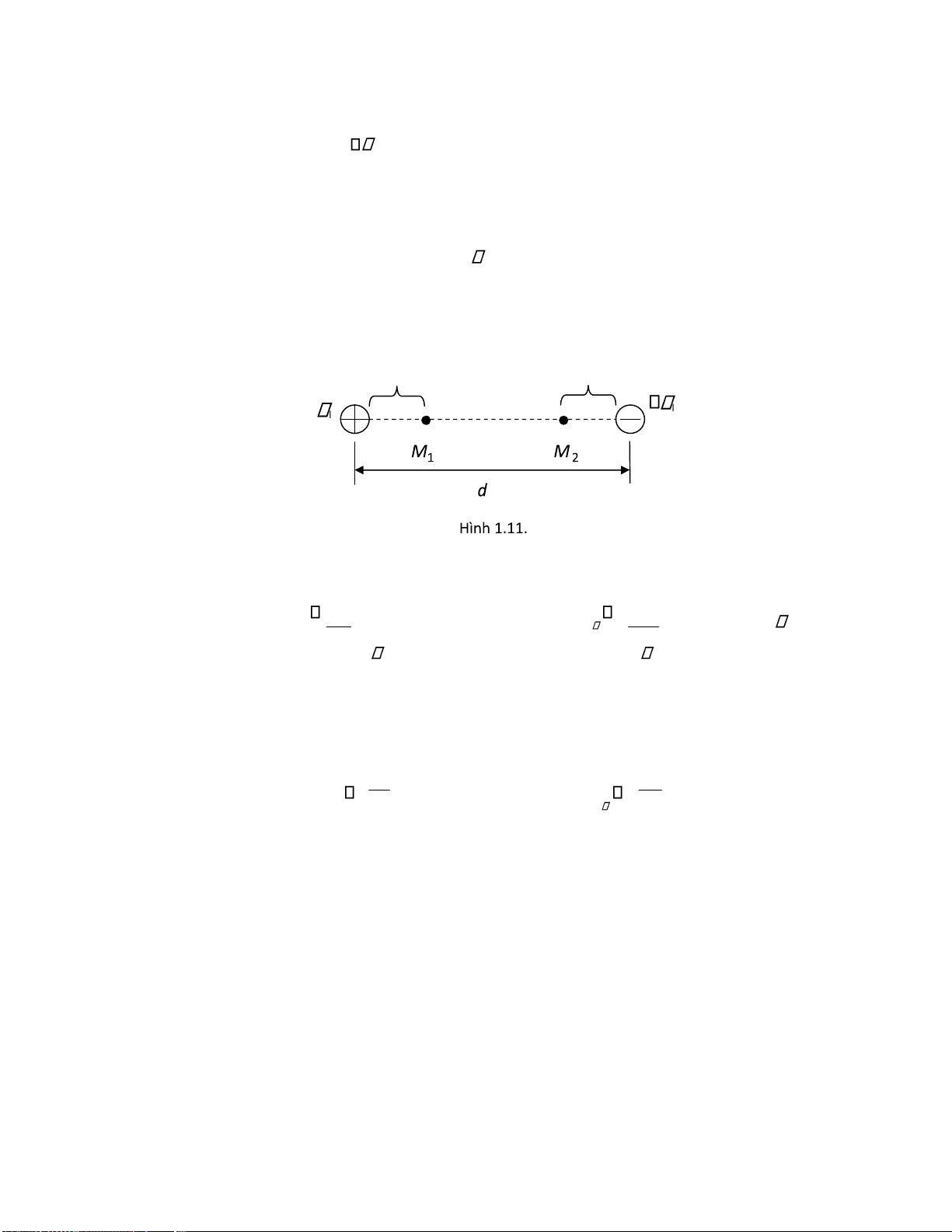
Bài 1-6: Cho hai dây dẫn iện mảnh ặt song song và tích iện trái dấu với cùng một mật ộ iện
tích tính theo chiều dài là
l (Hình 1.11). Khoảng cách giữa hai dây là d . Hãy tính:
a) Điện thế giữa hai iểm M 1,M 2 : U M M ? 1 2
b) Tìm cường ộ iện trường E và iện thế E tại một iểm nằm trên mặt phẳng
trung trực? E cực ại tại vị trí nào trên mặt phẳng trung trực? a a l l
Bài 1-7: Trên mặt một dây iện hình trụ tròn có chiều dài l , thành phần dọc trục của cường
ộ iện trường bằng E i
, cường ộ từ trường bằng i z H
, trong ó i S, , ,a, l là S 2 a
dòng iện, tiết diện, iện dẫn suất, bán kính của dây và chiều dài của dây. Hãy tìm vectơ Poynting
chảy vào dây, công suất iện ưa vào dây (tổn hao) và iện trở của oạn dây ó. Bài 1-8: Một cáp
ồng trục có các bán kính lõi và vỏ tương ứng a a1, 2 ; trong ó phân bố một
iện trường xuyên trục E E 0 H 0 r
và một từ trường phương vị H
. Tính công suất truyền r r dọc cáp? lOMoARcPSD| 36067889
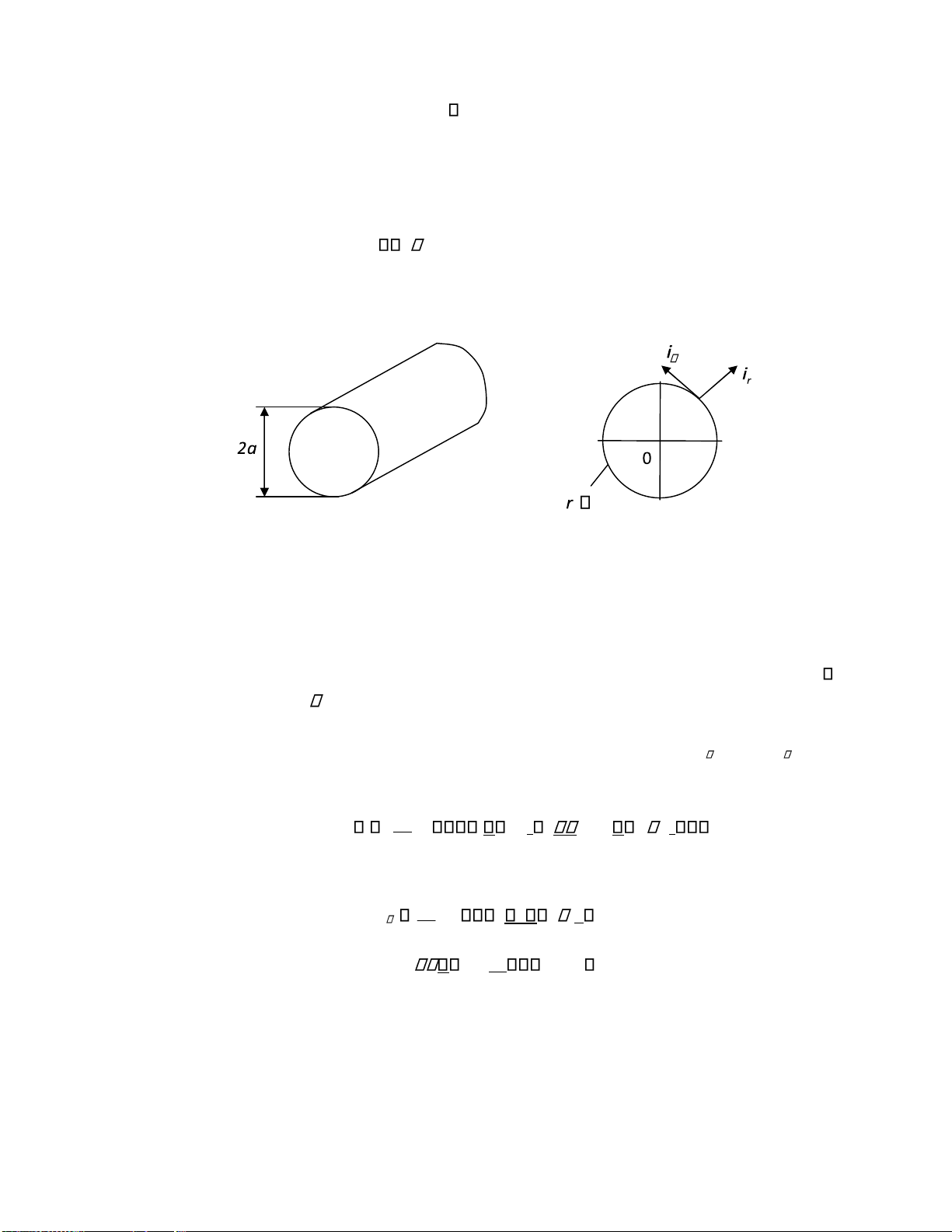
CHƯƠNG 2. BỨC XẠ SÓNG ĐIỆN TỪ
2.1. Bức xạ của lưỡng cực iện
2.1.1. Tìm nghiệm tổng quát
Khảo sát sự bức xạ của một phần tử bức xạ ơn giản nhất là dipol iện hoặc còn gọi là
lưỡng cực iện. Đó là một oạn dây dẫn có chiều dài l rất nhỏ hơn bước sóng, trên ó có dòng
iện biến ổi I phân bố ều theo chiều dài. Theo ịnh luật bảo toàn iện tích, có thể tồn tại dòng
iện như vậy nếu ở hai ầu dây dẫn có các iện tích q và q biến ổi theo thời gian. Các iện tích
này có liên hệ với dòng iện theo biểu thức: I dq y l
Hình 2.1. Lưỡng cực iện
Vì phương của A trùng với phương của I nên nếu xét trong hệ tọa ộ vuông góc thì A
chỉ có 1 thành phần là Az :
A I t r /v .l (2.1) z 4 r
Trong hệ tọa ộ cầu, A có các thành phần như sau: A r Az cos I l cos 4 r A Az sin I l sin lOMoARcPSD| 36067889 H (2.2) r 0 H 0 H 1 1r r rA Ar l vr1 I t r /v
r 12 I t r /v sin 4
Tương tự ta tìm ược các thành phần của E :
l I t r /v q Er 2 vr 2 r 3 cos E l I
t 2r /v I t r2 /v sin (2.3) 4 r A 0
Sử dụng biểu thức tính rotA trong hệ tọa ộ cầu, ta có: 4 v r vr E 0 Trong ó: I dq dt
Các công thức (2.2) và (2.3) là các công thức tổng quát cho phép ta xác ịnh các thành lOMoARcPSD| 36067889
phần trường bức xạ của dipol iện.
Trường hợp dòng iện biến ổi iều hòa theo thời gian.
Với trường hợp này các biểu thức liên quan ến dòng iện như sau:
I t r /v I emj t r v/ I me jkrej t I
t r /v j I me jkrej t
q t r /v 1 I em jkrej t j
Thay các giá trị này vào (2.2) và (2.3) ta nhận ược: H I m l j kr r12 sin .e jkr (2.4) 4 Er kI m l r12 j kr13 cos .e jkr (2.5) 2 E kI m l j k 12 j13 sin . e jkr (2.6) 4 r r kr Trong ó: k
2 và ể ơn giản ta tạm bỏ thừa số ej t . v
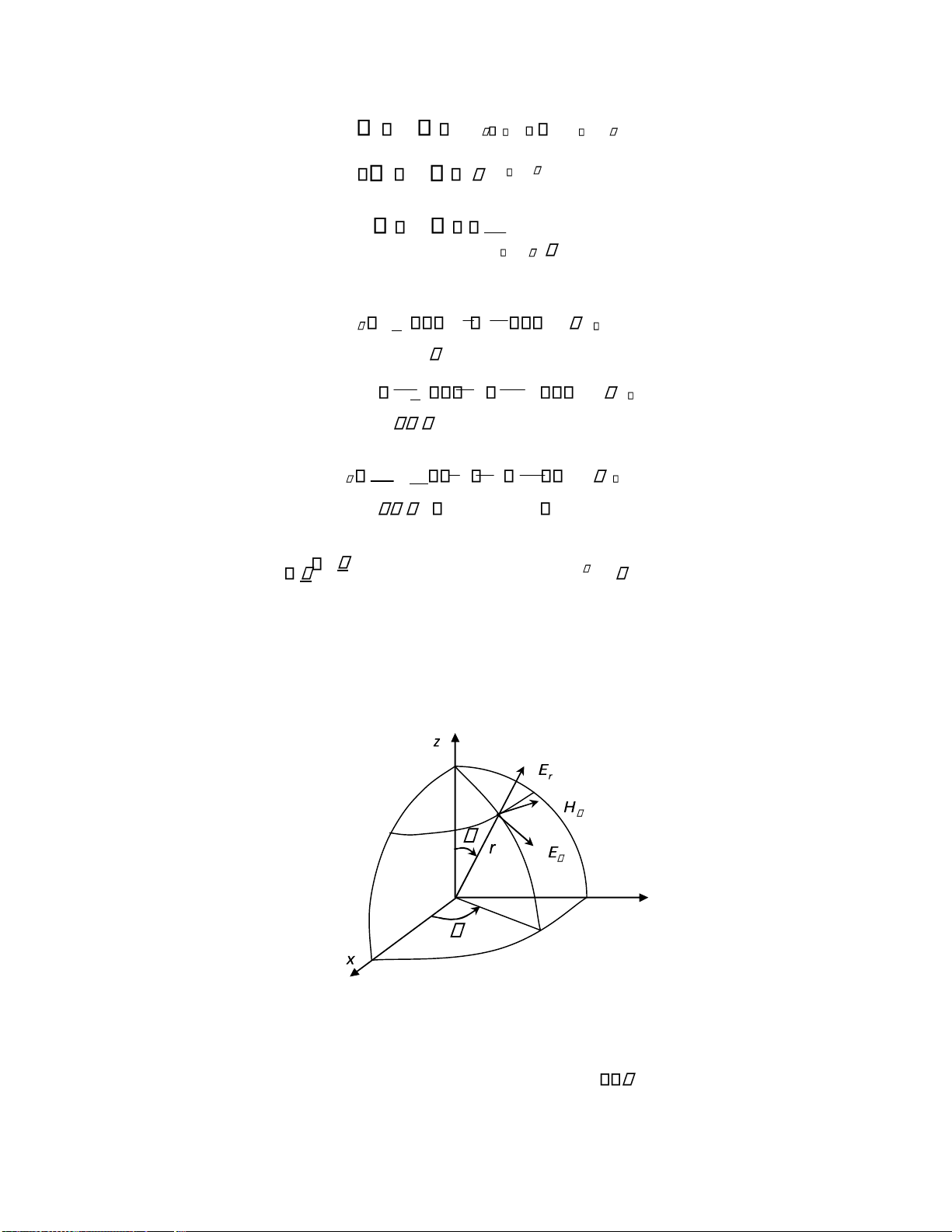
Quan hệ về hướng của các vectơ E và H trong trường bức xạ của dipol iện như trong Hình 2.2.
Từ các biểu thức nhận ược ở trên ối với các thành phần trường bức xạ, ta thấy có thể
phân biệt các trường hợp bức xạ ở khu gần và ở khu xa. y
Hình 2.2. Bức xạ của lưỡng cực iện
2.1.2. Trường bức xạ ở khu gần
Khu gần ược coi là khu vực có các khoảng cách r
. Khi ấy trong biểu thức của lOMoARcPSD| 36067889
H thì số hạng chủ yếu là số hạng tỷ lệ với 1/ r 2 , còn trong các biểu thức của Er ,E thì số hạng
chủ yếu là số hạng tỷ lệ với 1/ r 3 .
Thừa số e jkr coi gần úng bằng 1.
e jkr e j 2 r 1
Điều này có nghĩa khi r
, sự chậm pha của trường so với nguồn có thể bỏ qua, tương
tự như trường hợp chuẩn tĩnh. Áp dụng các nhận xét ó vào các biểu thức (2.4) ến (2.6) ta có
các thành phần trường khu gần: 1 H I (2.7) m l sin r Er j
Z2 s 3 I m l cos (2.8) 4 r E j
Z2 s 3 I m l sin (2.9) 8 r Trong ó: Z s
/ (trở kháng sóng, sẽ ề cập trong chương 3)
Phân tích các công thức trên ta nhận thấy ở trường khu gần, các thành phần iện
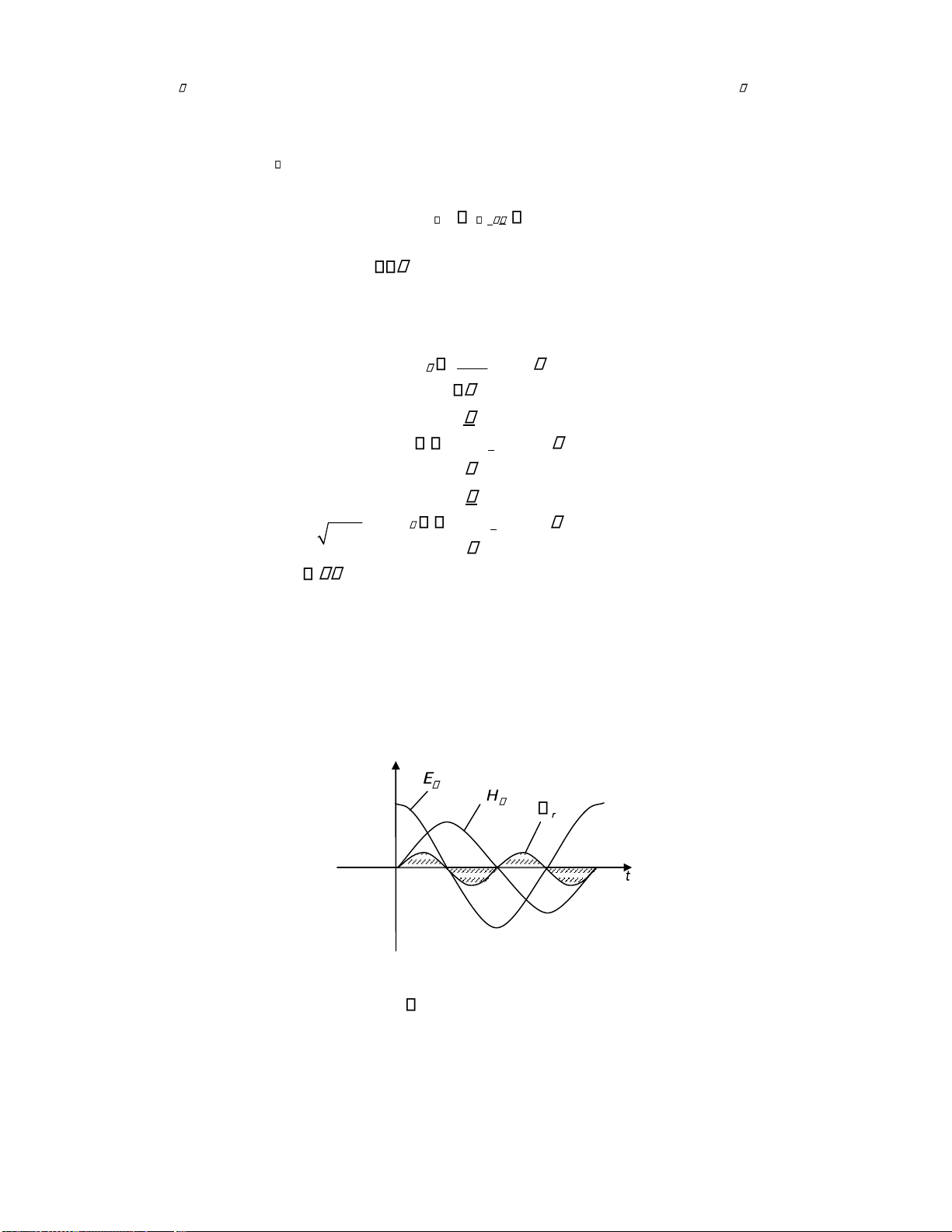
trường và từ trường lệch pha nhau 900 theo thời gian. Do ó vectơ Poynting trung bình sẽ có
giá trị bằng 0. Điều này chứng tỏ năng lượng của trường khu gần có tính dao ộng. Năng
lượng này trong một phần tư chu kỳ ầu thì dịch chuyển từ nguồn trường ra không gian xung
quanh và trong phần tư chu kỳ tiếp theo lại dịch chuyển ngược lại. Vì vậy ở trường khu gần
còn gọi là trường cảm ứng và khu gần còn gọi là khu cảm ứng.
Hình 2.3. Quan hệ giữa với E và H ở trường khu gần của lưỡng cực iện
Hình 2.3 cho thấy sự biến ổi của các thành phần iện trường và từ trường theo thời gian,
với góc lệch pha 900. Vectơ Poynting bằng tích E và H sẽ biến ổi với tần số gấp ôi tần số của
nguồn trường, có giá trị khi âm, khi dương. Giá trị trung bình của nó trong một chu kỳ sẽ bằng không. lOMoARcPSD| 36067889
2.1.3. Trường bức xạ ở khu xa
Khu vực xa là khu vực có các khoảng cách r , ồng thời r 1. Sự chậm pha của
trường không thể bỏ qua. Giá trị gần úng của E và H trong miền này có thể ược tính theo các
công thức tổng quát (2.4) ến (2.6) khi chỉ giữ lại các số hạng chủ yếu là các số hạng tỷ lệ với 1/ r . Ta có: H I l sin .e jkr (2.10) 2 r
E I l sin . e jkr Z Hs (2.11) 2 r Er 0 y
Hình 2.4. Trường bức xạ khu xa của lưỡng cực iện.
Phân tích các biểu thức (2.10) và (2.11) ta nhận thấy iện trường và từ trường ở khu xa
luôn ồng pha. Do ó giá trị trung bình của vectơ Poynting luôn khác không và năng lượng bức
xạ ược dịch chuyển từ nguồn vào không gian xung quanh.
Trường bức xạ ở khu xa có dạng sóng cầu, trong ó các vectơ iện và từ vuông góc với
hướng truyền lan. Sóng như vậy ược gọi là sóng iện từ ngang.
Nhận xét về trường bức xạ
Phân tích các công thức (2.10) và (2.11) ta có thể rút ra một vài nhận xét ối với trường
bức xạ ở khu xa của dipol iện như sau:
+ Vectơ iện trường hướng theo tiếp tuyến với ường tọa ộ , còn vectơ từ trường
hướng theo tiếp tuyến với ường tọa ộ . lOMoARcPSD| 36067889
+ Giá trị của cả hai vectơ E và H ều giảm tỷ lệ nghịch với khoảng cách. + Giữa
E và H có quan hệ với nhau bởi các hệ thức: E Zs H
+ Giá trị cường ộ trường bức xạ phụ thuộc vào góc . Theo hướng trục của dipol khi
0 trường bức xạ bằng 0. Giá trị cực ại của trường tại mặt phẳng vuông góc với dipol, khi / 2.
Nếu ký hiệu giá trị cực ại của các biên ộ trường ứng với góc / 2 là Emax và H
max , ta có thể viết các biểu thức biên ộ của E và H ứng với khoảng
cách r cho trước, phụ thuộc vào góc như sau: E m Emax sin H m H max sin Hoặc có thể viết: E m sin Emax (2.12) HH mmax sin
* Hàm phương hướng và ồ thị phương hướng
Các biểu thức (2.12) biểu thị sự phụ thuộc tương ối của biên ộ trường bức xạ theo các
hướng không gian khác nhau, ược gọi là hàm phương hướng biên ộ của dipol iện, ký hiệu bởi: f Em sin (2.13) Emax
Đồ thị phương hướng của dipol iện trong hệ tọa ộ cực như trong Hình 2.5. lOMoARcPSD| 36067889 y y
Hình 2.5. Đồ thị phương hướng của lưỡng cực iện
* Công suất bức xạ của dipol iện:
Để xác ịnh công suất bức xạ của dipol iện, ta bao bọc dipol bằng mặt cầu kín có bán
kính tùy ý và lấy tích phân của véctơ Poynting trung bình trên toàn mặt cầu ó: (2.14) P tbdS S
Ở ây dS là phần tử diện tích mặt cầu, bằng dS r 2 sin d d . Ta có: I l 2 (2.15) tb Zs m2 2 sin2 8r
Thay (2.15) vào (2.14) và tính toán ta có:
Z l 2 2 l 2 Pbx s
I m2 Zs I hd2 (2.16) 3 3 lOMoARcPSD| 36067889
Từ biểu thức (2.16) ta thấy công suất bức xạ tỷ lệ với bình phương của biên ộ dòng iện
trên dipol và tỷ lệ với bình phương của ộ dài tương ối so với bước sóng, nghĩa là tỷ lệ l 2 với .
* Điện trở bức xa của dipol iện:
Ta có công suất bức xạ theo công thức thông thường: Pbx hd (2.17) 2
Gọi R là iện trở bức xạ thì: P 2 l 2 R bx 2 Zs (2.18) I 2 R I hd 3
Đối với chân không Z s Z 0 120
, ta có iện trở bức xạ của dipol iện bằng: R 80 2 l 2
2.2. Trường iện từ của vòng dây
Trong thực tế, người ta tạo ra nguyên tố bức xạ ra trường iện từ tương ương như trường
của lưỡng cực từ bằng cách cho dòng iện biến ổi I chạy qua một vòng dây dẫn nhỏ mảnh.
Sau ây ta sẽ áp dụng phương pháp thế chậm ể tìm trường bức xạ của nguyên tố anten khung này.
Giả sử rằng mặt phẳng của vòng dây nằm trùng với mặt phẳng vĩ tuyến của tọa ộ cầu.
Vòng dây có bán kính a ủ nhỏ so với bước sóng, ể có thể coi dòng iện là như nhau trên tròn
vòng dây i I m sin t .
Lấy một oạn ngắn dl của vòng dây (hình 2.6). Có thể coi nó là một nguyên tố anten
thẳng, có thế vectơ như sau:
dA Idl e jkr (2.19) lOMoARcPSD| 36067889 4 r y ố anten v
Do tính ối xứng ối với trục Oz, thế vectơ A của dòng iện vòng ở một iểm M có góc
phương vị xác ịnh, sẽ chỉ có thành phần phương vị A , nên: (2.20) A dAi. Iea.cos d I a.cos d e 0 4 r0 4 0 r0
Xét riêng vùng xa so với bán kính vòng a r ta có: r 0 r a.cos sin (2.21) 2 jkr 0 2 jkr0
Ở ây, cần chú ý ta có thể thay gần úng r0 ở mẫu số (2.20) bằng r , nhưng ở tử số, trong
e jkr0 phải thay r0 theo (2.37) vì sự lệch pha có ảnh hưởng lớn ến thế vectơ trong (2.20). Từ ó: A aIe jkr0 2 ejkasin cos cos d 4 r 0 Do: ka 2 a
1 nên ejkasin cos 1jka sin cos Và A
aIe r jkr0 2 0 cos +jka sin cos2 d 4
Sau khi lấy tích phân, ta ược: lOMoARcPSD| 36067889 A j
a kIe2 jkr0 sin (2.22) 4 r
Ta xét cường ộ iện trường và cường ộ từ trường ở vùng xa r . Các cường ộ trường
tính theo phương trình sau: H 1 rotA E 1 rotH j Với iều kiện r
, cường ộ iện trường chí có thành phần phương vị E và cường ộ từ
trường chỉ có thành phần tà H . H r (2.23) s 2a I2 2 jkr Z Hs
E Z sin . e r
Chuyển từ ảnh phức sang giá trị tức thời ta ược: 2a I2 H 2 sin .sin t R r v (2.24)
2a I2 2 sin . e jkr 2a I2 R lOMoARcPSD| 36067889 E Zs 2 sin .sin t r v
Biểu thức (2.40) chứng tỏ sóng iện từ ở vùng xa cũng là sóng cầu, nhưng so với trường
của anten thẳng thì các sóng E và H ã ổi chỗ cho nhau (như hình 2.7). y
Hình 2.7. Các thành phần sóng bức xạ của vòng dây
Tuy bây giờ E và H ngược pha nhau nhưng vectơ Poynting vẫn luôn luôn hướng theo
bán kính rời khỏi gốc tọa ộ.
Công suất bức xạ của anten vòng tìm ược như sau:
Pbx Zs a I h2d (2.25) 6 Tổng trở bức xạ: 2 (2.26)
Rbx Zs a 4 6
Trong chân không Zs 120 ta có: Pbx 20 2 2 a 4 I hd2 (2.27) 2 4 lOMoARcPSD| 36067889 4 Rbx 20 2 2 a (2.28)
So sánh công suất bức xạ của anten vòng và anten thẳng nếu chúng có chiều dài như nhau, tức là 2 l a
1 và dòng iện như nhau, ta thấy công suất của anten thẳng lớn hơn
công suất của anten vòng nhiều lần. Đó là vì anten thẳng có kết cấu hở, dòng iện dẫn trong
oạn dây ược khép kín mạch bởi dòng iện chuyển dịch chảy trong iện môi xung quanh, do ó
từ trường và iện trường cùng phân bố trong không gian xa rộng xung quanh dây. Còn ối với
anten vòng dòng chảy khép kín, từ trường tập trung nhiều hơn ở gần vòng dây, do ó hiện
tượng bức xạ yếu hơn.
2.3. Trường bức xạ của hệ thống anten
Ta thấy trường bức xạ của anten thẳng có ộ dài rất nhỏ với bước sóng l . Trên thực
tế, ể tăng công suất bức xạ, người ta phải tăng chiều dài anten, do ó anten thường có chiều dài
so ược với bước sóng. Thường dùng nhất là anten nửa sóng l
/ 2. Hơn nữa ể tăng tính ịnh
hướng người ta không dùng 1 anten mà dùng hệ thống anten sắp ặt một cách thích hợp.
2.3.1. Trường bức xạ của anten nửa sóng Hình 2.8. Anten nửa sóng
Ta xét một anten thẳng, có dòng iện hình sin, có ộ dài l
/ 2 . Dòng iện phân bố trên
chiều dài bây giờ không ều nữa.
Để tính trường của anten có dòng iện phân bố không ều, ta chia anten thành những
nguyên tố anten thẳng là những oạn vô cùng nhỏ dz , trên ó dòng iện coi là phân bố ều với trị
hiệu dụng I z . Ở một iểm tại vùng xa, cường ộ từ trường ứng với oạn dây I dz z ược tính như sau: lOMoARcPSD| 36067889 (2.29)
dH 1 j I dzz sin e jkrz 2 .rz
Trong ó rz là khoảng cách từ vi phân dây dz ến iểm xét. Từ hình 2.8 ta có: (2.30) r z r0 z.cos ,
z Isin 2 z I
Mẫu số của biểu thức (2.29) coi r z
r0 , có tử số theo (2.30) ta có:
H 1 j Isin e jkR0
/4 ejk cos sin 2 zdz. 2 .r0 /4
Sau khi tích phân ta ược: (2.31) H j Icos 2 cos e jkR0 2 . r0 sin
Còn cường ộ iện trường ta cũng có: E Z Hs (2.32)
Theo (2.31) ta có thể vẽ ồ thị ịnh hướng của anten nửa sóng trong mặt phẳng kinh tuyến
(Hình 2.9). Trường của anten nửa sóng cũng ối xứng qua z. y
Hình 2.9. Đồ thị ịnh hướng của anten nửa sóng.
2.3.2. Trường bức xạ của hai anten nửa sóng ặt song song cách nhau một khoảng d.
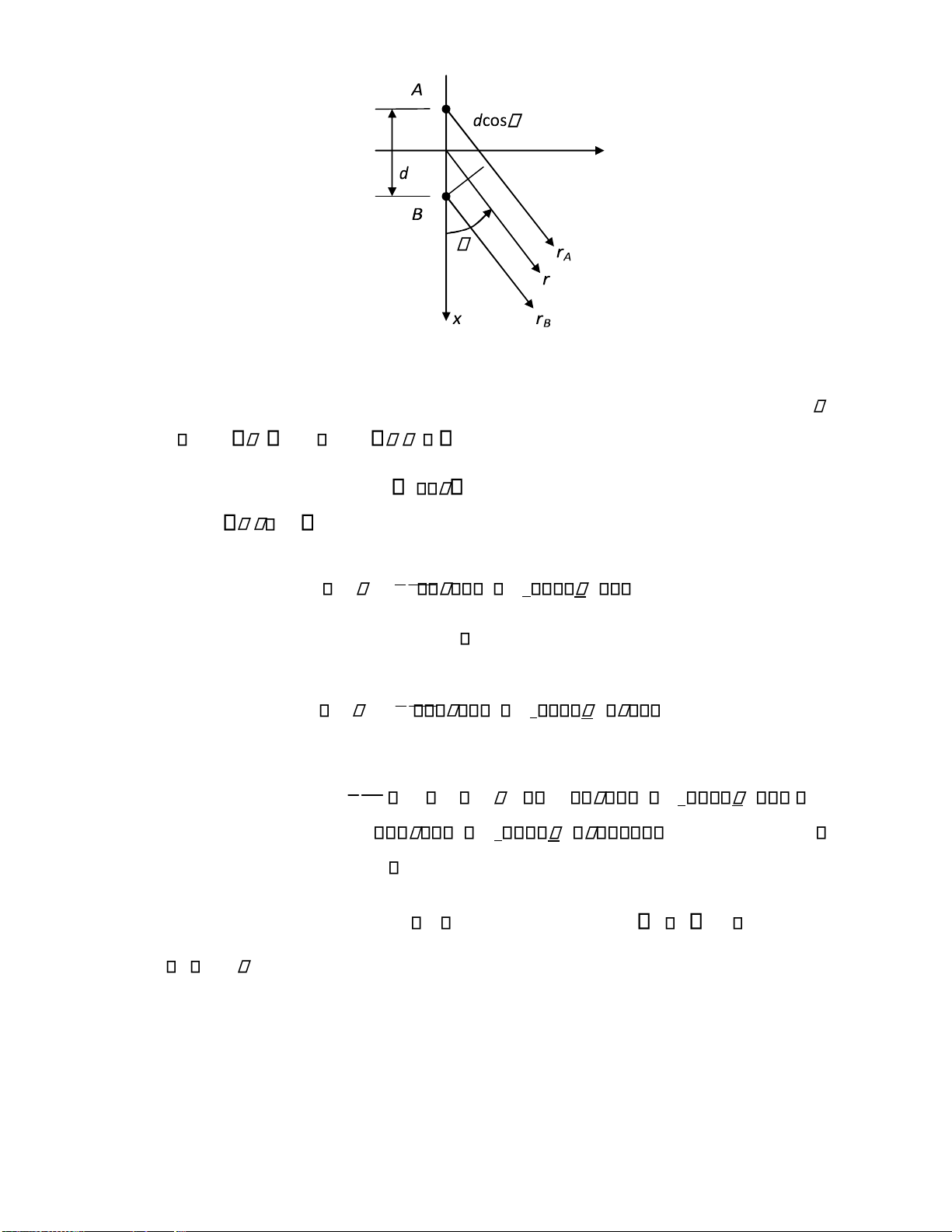
Để ịnh hướng bức xạ theo chiều phương vị trong mặt phẳng ngang, người ta dùng hệ
thống nhiều anten ặt thẳng ứng, song song cách nhau những quãng d . Xét trường hợp hai
anten nửa sóng ặt song song cách nhau d trên trục Ox (Hình 2.10). lOMoARcPSD| 36067889 y
Hình 2.10. Hai anten nửa sóng ặt song song
Giả thiết dòng iện trong hai anten có biên ộ bằng nhau những lệch pha nhau một góc , sin sin i A I m t và iB I m t .
Tại một iểm M ở vùng xa r
cường ộ từ trường của mỗi anten trong mặt phẳng xích ạo / 2 như sau: A 12 IrmA sin t rvA 2 ; H (2.33)
H B 12 IrmB sin t rvB 2
Cường ộ từ trường tổng bằng:
H H A H B 12 I m sin t rvA 2 sin t rvB 2 (2.34) r Ở mẫu số của ấy (2.34), ã coi r A
rB r . Còn trong góc pha l rA rB
/ 2 r , nhưng rA rB d cos , ta ược: lOMoARcPSD| 36067889 H j e (2.35) jkr cos cos 2 r Trong ó: I Iej 2
Nếu hai dòng iện cùng pha nhau 0 ta có: H j Ie jkr cos d cos (2.36) I d r
Tương tự cường ộ iện trường tình ược như sau: E Z Hs
Từ (2.36) có thể vẽ ược ồ thị ịnh hướng các cường ộ trường trong mặt phẳng ngang. Với
các giá trị d khác nhau, ồ thị ịnh hướng có dạng rất khác nhau. Trong hình 2.11
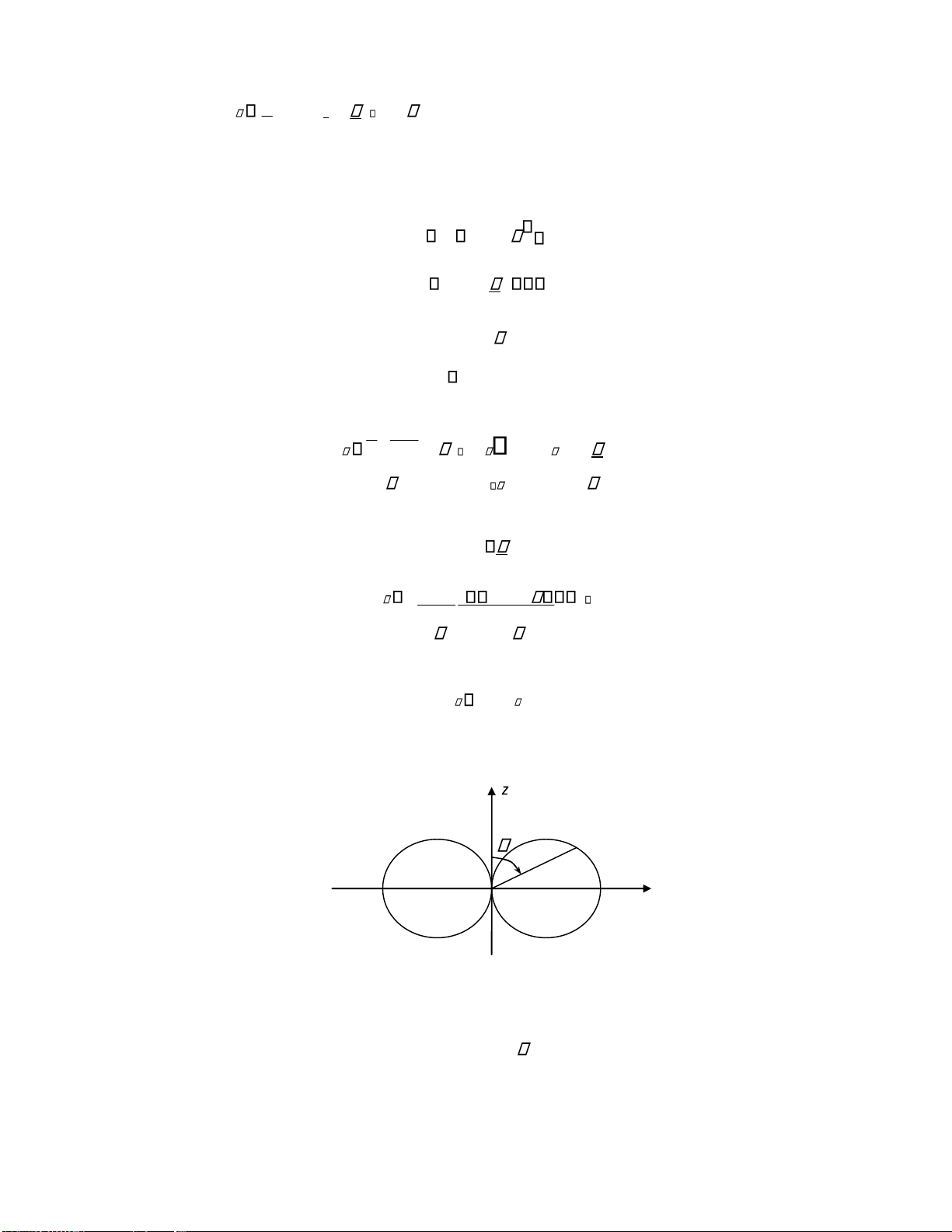
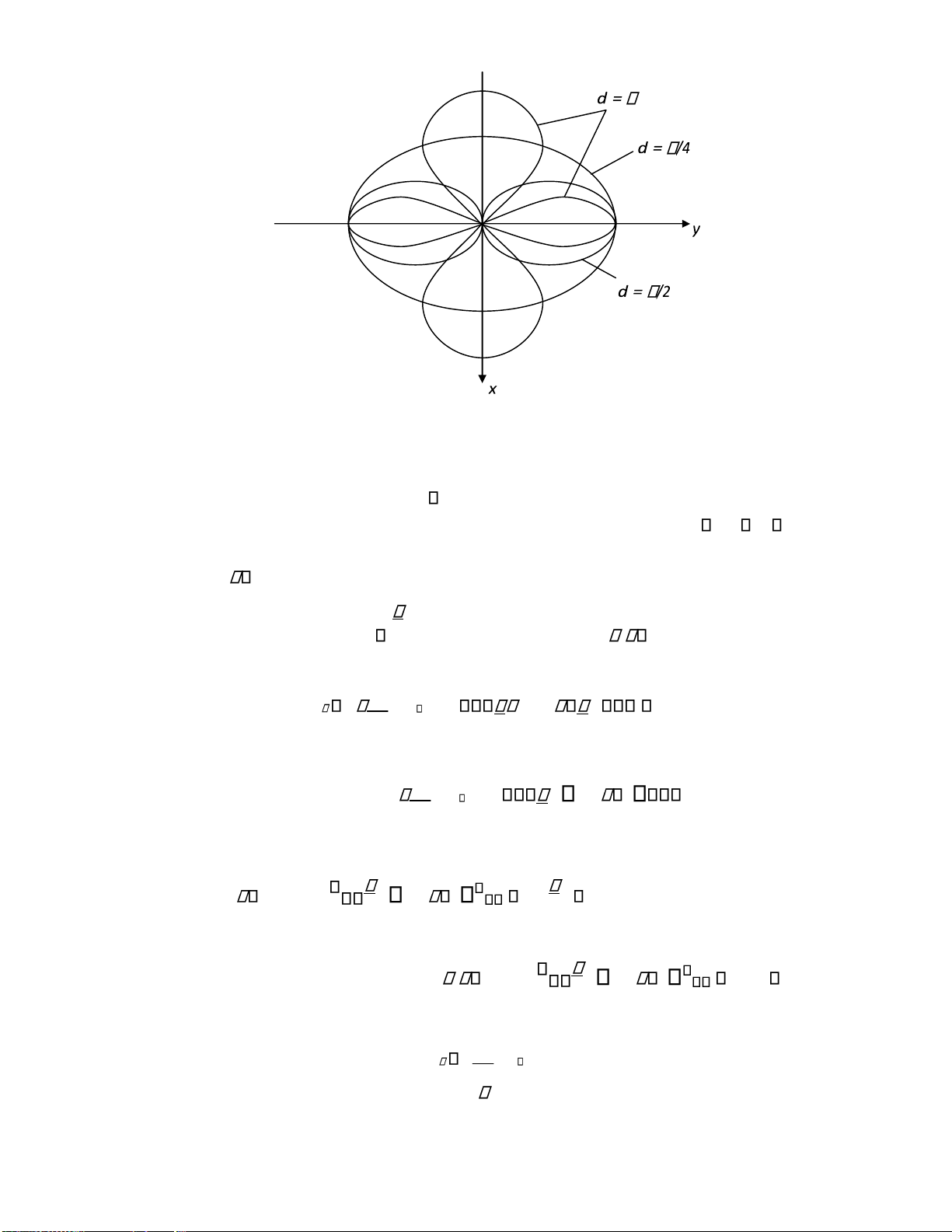
vẽ ồ thị ịnh hướng của 2 anten có dòng iện ồng pha ứng với các trường hợp d và 4
d . Có thể giải thích tính ịnh hướng theo chiều phương vị của 2 anten có dòng iện 2 cùng
pha ặt cách nhau 1 khoảng d , bằng sự giao thoa của 2 anten. Do ó khoảng cách từ mỗi anten
ến iểm xét khác nha, pha của cường ộ trường của mỗi anten ở iểm ó sẽ khác nhau. Do ó khi
xếp chồng trường 2 anten, có những iểm cường ộ trường tổng yếu i hoặc triệt tiêu. lOMoARcPSD| 36067889
Hình 2.11. Đồ thị ịnh hướng của hai anten nửa sóng ặt song song
Từ Hình 2.11 ta thấy trường của 2 anten có dòng iện cùng pha, ặt cách nhau d , tuy
không giống nhau theo mọi phương nhưng vẫn còn ối xứng qua gốc tọa ộ O (búp sóng ối
xứng qua trục Ox và Oy) tức là cường ộ trường theo 2 phương ối nhau ( và + ) bằng
nhau. Muốn có ồ thị ịnh hướng không ối xứng ta cho dòng iện trên 2 anten lệch pha nhau một góc 0.
Ví dụ, xét trường hợp d và hai dòng iện lệch pha nhau / 2, ta có: 4 H j Ir e jkr cos d cos 2 (2.37) = j Ir e jkr cos 4 cos 1 Với 0 thì cos 4 cos 1
cos 2 0 , nên về phía dương của trục x ,
cường ộ trường bằng 0. Ngược lại với thì cos 4 cos 1 cos0 1 và H j Ie jkr r
tức gấp ôi cường ộ trường của một anten ơn. Đồ thị ịnh hướng như Hình 2.12. lOMoARcPSD| 36067889
Hình 2.12. Đồ thị ịnh hướng của 2 anten nửa sóng có
dòng iện lệch pha nhau 900. BÀI TẬP CHƯƠNG 2
Bài 2-1: Cho một nguyên tố anten thẳng, dài l 5m , có dòng iện I hd 10A , tần số f 106Hz
ặt trong không khí. Tính công suất bức xạ và tổng trở bức xạ. Tính trị hiệu dụng của cường ộ
iện trường, cường ộ từ trường và vectơ Poynting tại các iểm cách anten r 100km ứng với các
góc tà bằng 00 ,30 ,45 ,60 ,0 0 0 900 . Vẽ ồ thị ịnh hướng.
Bài 2-2: Cho một vòng dây có chu vi l 5m , dòng iện I hd 10A , tần số f 106 Hz ặt trong
không khí. Tính công suất bức xạ và tổng trở bức xạ. Tính trị hiệu dụng của cường ộ iện
trường, cường ộ từ trường và vectơ Poynting tại các iểm cách anten r 100km ứng với các
góc tà bằng 00 ,30 ,45 ,60 ,0 0 0 900 . Vẽ ồ thị ịnh hướng. So sánh với kết quả ở bài 2-1.
Bài 2-3: Một vòng dây có diện tích S 3m2 , dòng iện I hd
10A , tần số f 50Hz . Hỏi công
suất tiêu tán do bức xạ bằng bao nhiêu?
Bài 2-4: Cho một anten nửa sóng có dòng iện I hd
10A , tần số f 3.108 Hz ặt thẳng ứng. Tính
trị hiệu dụng cường ộ từ trường và iện trường tại những iểm cách anten 1km, trong mặt phẳng ngang xOy?
Bài 2-5: Cho hai anten nửa sóng có dòng iện I hd
10A , tần số f 3.108Hz ặt thẳng ứng, song song, cách nhau d
/ 4 trên trục Ox. Tính trị hiệu dụng cường ộ từ trường và iện trường tai
những iểm cách anten r 10km trong mặt phẳng ngang xOy ứng với các góc phương vị
00 ,30 ,45 ,60 ,0 0 0 900 nếu các dòng iện trong hai anten cùng pha? Vẽ ồ thị ịnh hướng?
Bài 2-6: Giải bài 2-5 trong trường hợp các dòng iện lệch pha nhau / 2. lOMoARcPSD| 36067889
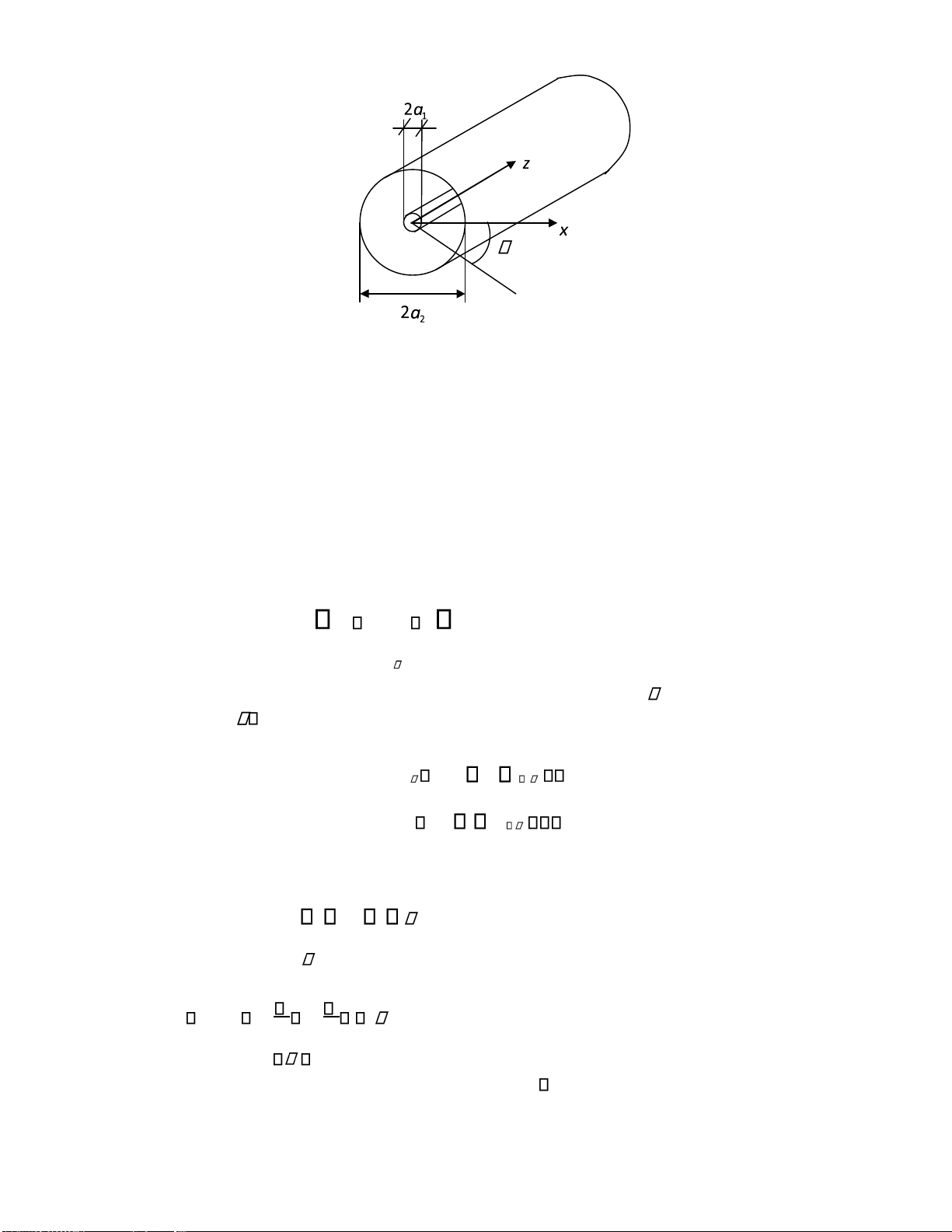
CHƯƠNG 3. SÓNG ĐIỆN TỪ PHẲNG
3.1. Khái niệm về sóng iện từ phẳng
Giả sử có nguồn bức xạ nào ó tạo ra sóng iện từ truyền tới không gian khảo sát. Nếu
không ể ý ến các nguồn tạo ra trường ở khu xa mà chỉ ơn thuần coi sự tồn tại của trường ở
miền khảo sát, ta có thể áp dụng các phương trình Maxwell cho không gian không có nguồn ể
nghiên cứu các tính chất của trường ấy.
Trong không gian ồng nhất, ẳng hướng và rộng vô hạn, sóng iện từ sẽ tạo ra tại mỗi iểm
và ở mỗi thời iểm các vectơ iện và từ có biên ộ và pha xác ịnh. Những iểm của trường có biên
ộ giống nhau hợp thành những mặt ồng biên, còn những iểm của trường có
pha giống hợp thành mặt ồng pha. Các vectơ E và H luôn biến ổi theo thời gian, sự biến ổi pha
khiến cho các mặt ồng pha sẽ dịch chuyển. Vận tốc dịch chuyển của mặt ồng pha gọi là vận
tốc pha vph của sóng.
Nếu tại tất cả các iểm trên mặt ồng pha, biên ộ của vectơ E và H cùng bằng nhau thì mặt
ồng pha chính là là mặt ồng biên, sóng ược gọi là sóng ồng nhất. các mặt ồng nhất này ược
gọi là mặt sóng. Nếu mặt ồng pha và ồng biên là những mặt phẳng (mặt trụ, mặt cầu), ta có
sóng iện từ phẳng (sóng trụ, sóng cầu).
Mặc dù trong thực tế sóng iện từ bức xạ từ anten không phải là sóng phẳng thuần túy
mà thường là sóng trụ hoặc sóng cầu. Tuy nhiên, tại những iểm khảo sát cách xa nguồn, và
trong một phạm vi không gian hẹp ta có thể coi gần úng mặt sóng là những mặt phẳng.
Phân loại kiểu sóng:
Trong chương này ta sẽ xét sóng phẳng trong hệ tọa ộ Descartes xyz và chọn trục z làm
phương truyền sóng, trên cơ sở ó ta có các kiểu sóng như sau:
+ Sóng iện từ ngang (TEM): Sóng iện từ ngang là sóng có véctơ E và H luôn vuông
góc với phương truyền sóng (phương z). Tức là các thành phần E z
0 và H z 0 . Đây là loại
sóng phổ biến trong thực tế.
+ Sóng iện ngang (TE): Sóng iện từ ngang là sóng có véctơ E luôn vuông góc với
phương truyền sóng. Tức là các thành phần E z
0, loại sóng này còn ược gọi là sóng từ dọc (són
g H) vì có thành phần từ trường dọc theo phương truyền sóngH z 0. lOMoARcPSD| 36067889
+ Sóng từ ngang (TM): Sóng iện từ ngang là sóng có véctơ H luôn vuông góc với
phương truyền sóng, tức là các thành phần H z
0 , loại sóng này còn gọi là sóng iện dọc (són
g E) vì có thành phần từ trường dọc theo phương truyền sóngE z 0 .
Hai loại sóng TE và TM ược sử dụng trong ống dẫn sóng (sẽ ược trình bày trong chương 4).
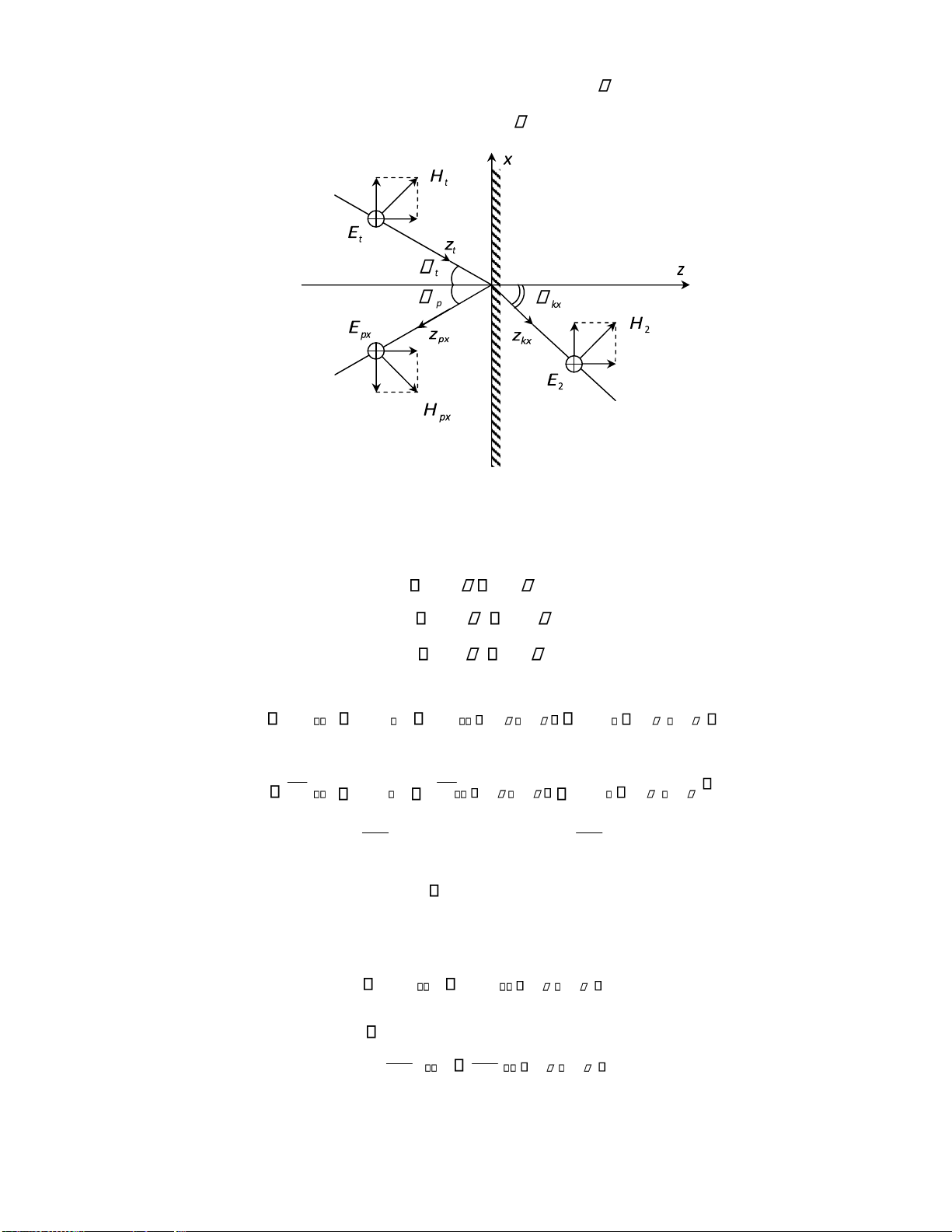
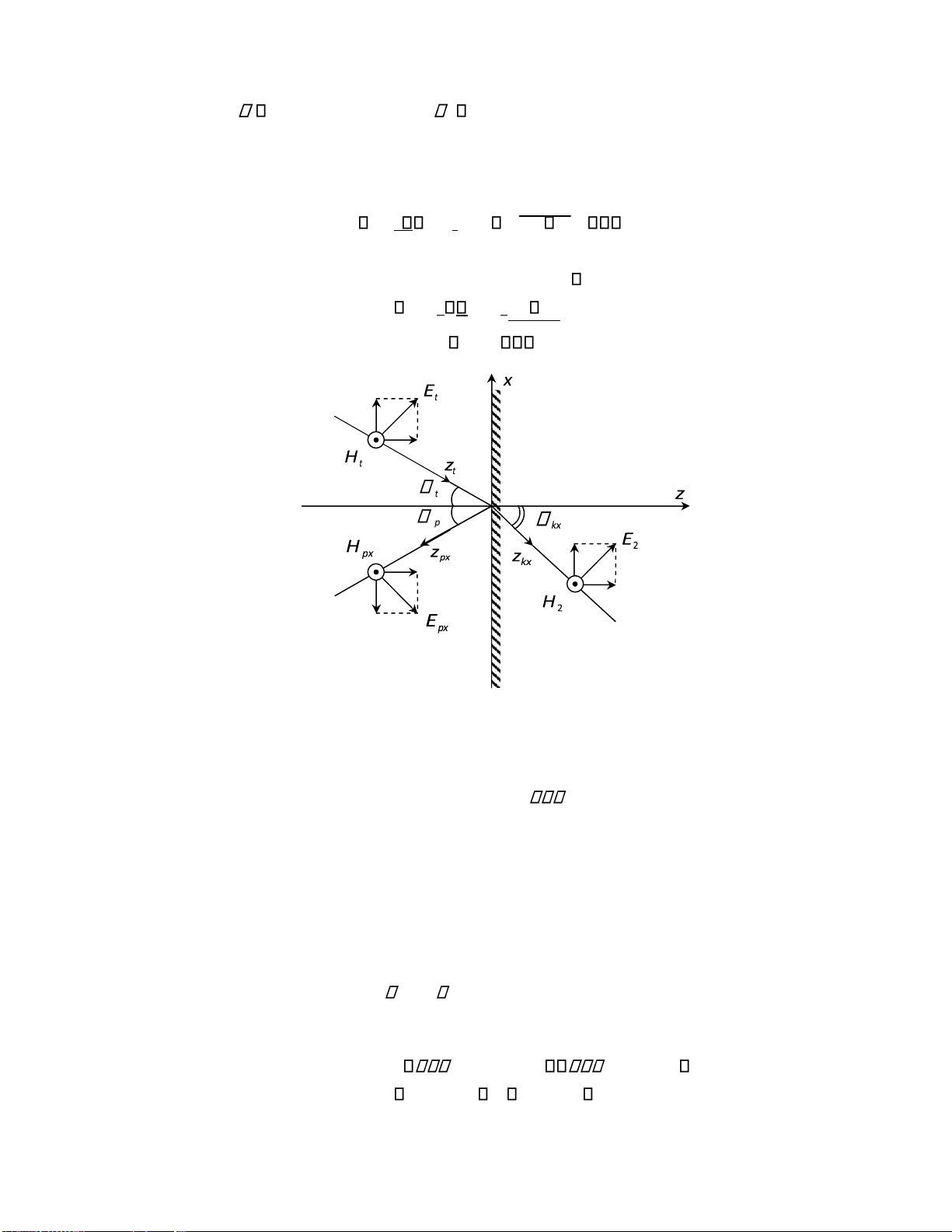
3.2. Sự phân cực của sóng iện từ
Sóng iện từ khi truyền lan trong một môi trường, vectơ cường ộ iện trường và cường ộ
từ trường có thể thay ổi cả trị số và hướng. Trong quá trình truyền lan của sóng nếu quan
sát iểm cuối của vectơ E thì nó vạch ra một quỹ ạo nào ó, dạng quỹ ạo này biểu thị dạng phân cực của sóng.
Mặt phẳng phân cực là mặt phẳng chứa phương truyền sóng và vectơ cường ộ iện
trường E . Sóng iện từ phẳng có nhiều dạng phân cực như: phân cực ellip, phân cực tròn và
phân cực thẳng. Các dạng phân cực trên có nhiều ứng dụng trong kỹ thuật.
3.2.1. Phân cực Ellip
Giả sử ta nhìn từ nguồn phát sóng theo hướng truyền sóng (quy ịnh là phương z ), nếu
ầu cuối của vectơ cường ộ iện trường của sóng vạch nên hình ellip trong không gian thì gọi là sóng phân cực ellip.
Chúng ta có thể phân tích sóng phân cực ellip thành hai thành phần sóng có cùng tần
số, cùng phương truyền và các vectơ cường ộ trường vuông góc với nhau trong không gian.
Giả sử ta có hai sóng phẳng như sau:
E1 Emx cos( t z i). x E 2
Emy cos( t z ).iy
Ở ây Emx ,Emy là các biên ộ của các sóng thành phần, là góc lệch pha ban ầu của hai sóng.
Vectơ cường ộ iện trường của sóng tổng hợp sẽ thực hiện theo quy tắc tổng hợp 2 vectơ,
chúng ta hãy tìm phương trình cho ầu cuối của vectơ cường ộ trường của sóng tổng hợp. Ta
lần lượt bình phương hai vế của các biểu thức trên và biến ổi ôi chút sẽ nhận ược biểu thức sau: 2 2 E1 E 2 lOMoARcPSD| 36067889 Emx Emy
2cos EE Emx1E2my sin 2 (3.1)
Từ hình học giải tích, ta nhận thấy biểu thức (3.1) là phương trình mô tả ường cong ellip
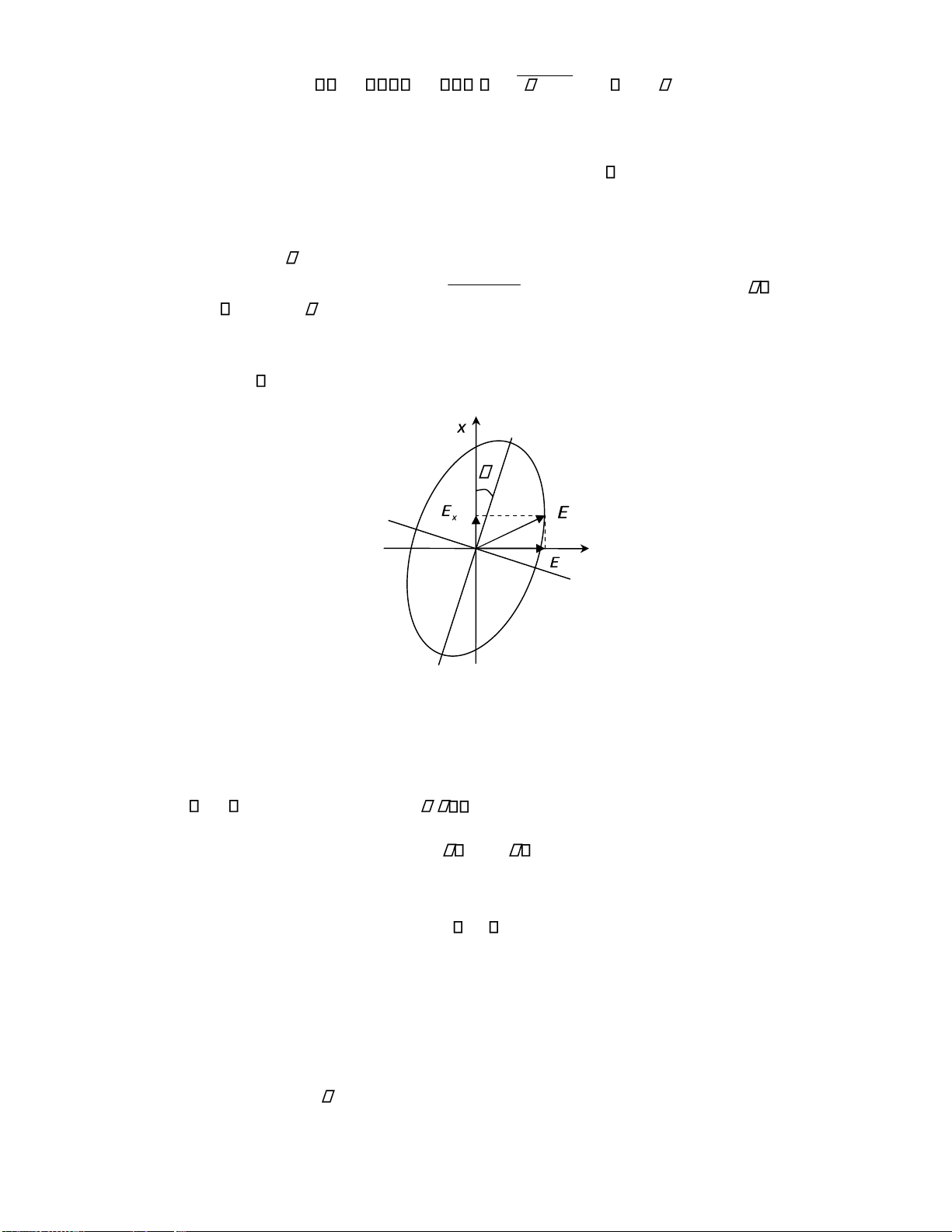
trong mặt phẳng tọa ộ E1,E 2 . Ellip này có trục lớn tạo một góc với trục tọa ộ x . Do vậy trong
quá trình truyền sóng theo trục z ầu cuối của vectơ iện trường của sóng tổng hợp sẽ vạch ra
một ường xoắn trong không gian.
Giá trị của có thể tính theo biểu thức sau: 2 2mxE2 mx
EEmymy2 cos (3.2) tg E với E mx Emy y y Hình 3.1. Phân cực Ellip
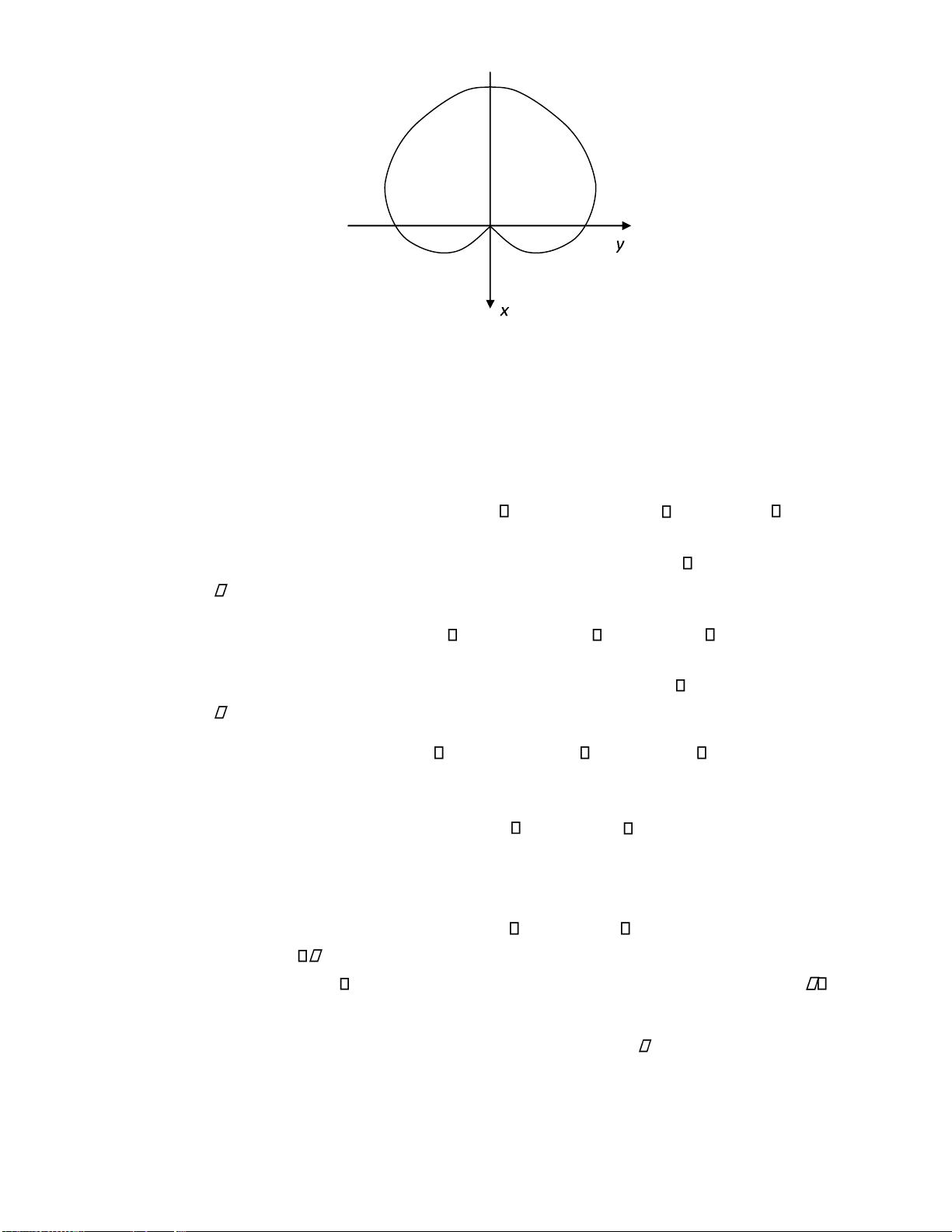
3.2.2. Phân cực tròn
Trong trường hợp thành phần iện trường của hai sóng thành phần có biên ộ bằng nhau: E mx
Emy Em và lệnh pha nhau góc / 2 thì ta có: sin2 1,cos 0
Nên phương trình (3.1) trở thành: E 2 2 2 1 E 2 Em (3.3)
Đây là phương trình ường tròn trong mặt phẳng tọa ộ E1,E 2 . Trong trường hợp này, ầu
cuối của vectơ iện trường vẽ nên ường xoắn tròn trong không gian. Sóng ược gọi là phân cực
tròn. Nếu nhìn theo chiều truyền sóng, vectơ iện trường quay theo chiều kim ồng hồ thì ta có
sóng phân cực tròn quay phải, trường hợp vectơ iện trường quay ngược chiều kim ồng hồ ta
gọi là sóng phân cực tròn quay trái. Chiều quay của vectơ cường ộ iện trường phụ thuộc vào dấu của góc lệch pha . lOMoARcPSD| 36067889 y ực tr
3.2.3. Phân cực thẳng
Sóng có vectơ cường ộ trường E luôn hướng song song theo một ường thẳng trong
quá trình truyền sóng gọi là sóng phân cực thẳng hay phân cực tuyến tính.
Trong trường hợp này góc lệch pha của 2 sóng thành phần Ex và Ey có giá trị: 0, , 2 ,...
Nên sin = 0, cos = 1 và phương trình (3.24) trở về dạng: E1 E 2 2 0 Emx Emy Emy Suy ra: E 2 E1 (3.4) Emx
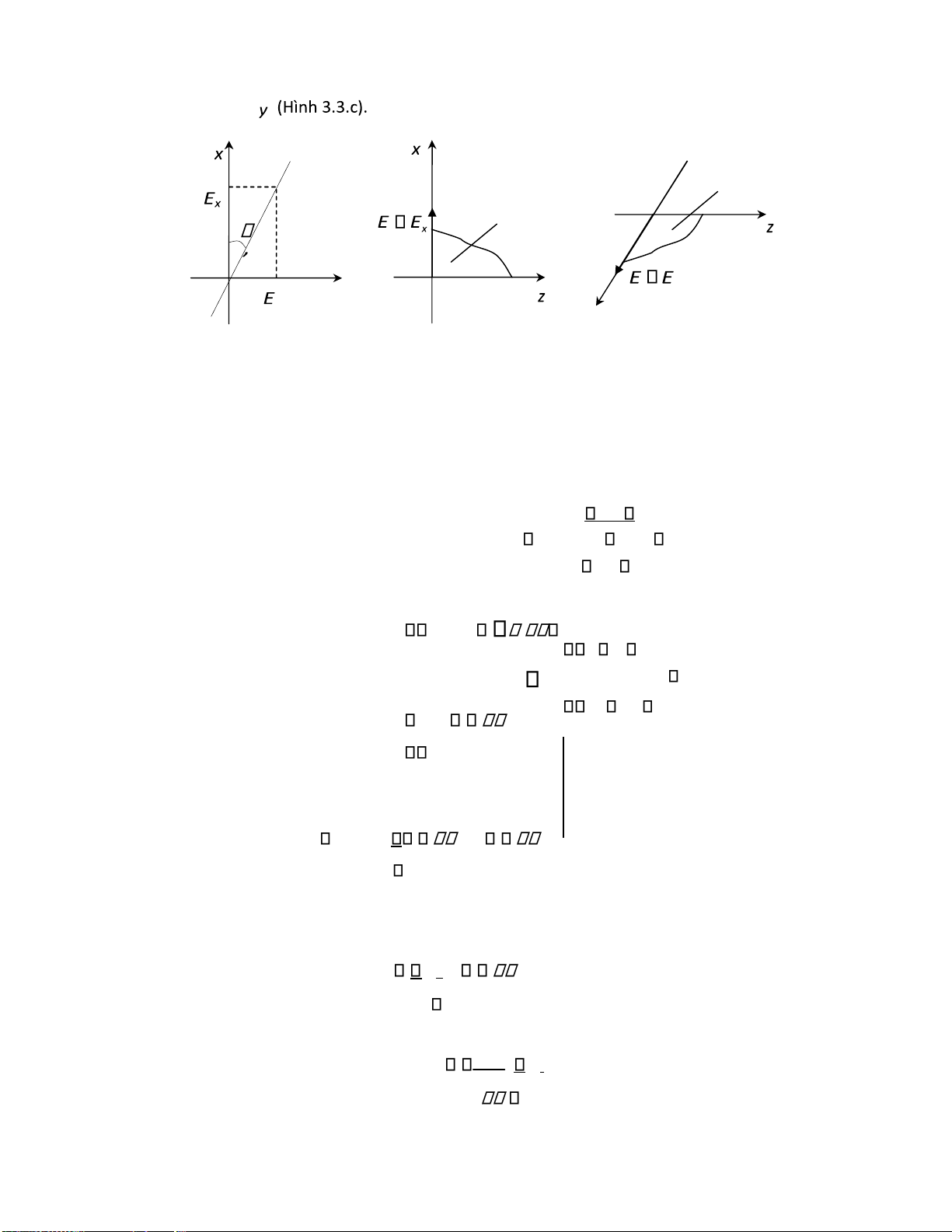
Đây là phương trình ường thẳng i qua gốc tọa ộ, nghiêng một góc so với trục x là ' ược
xác ịnh bởi biểu thức, như mô ta trong hình 3.3.a: Emy tg ' (3.5) Emx
Đối với phân cực thẳng tùy theo hướng của vectơ cường ộ iện trường, người ta còn phân
làm hai trường hợp là phân cực ngang và phân cực ứng.
+ Sóng phân cực ứng (phân cực V): Trường hợp này vectơ E chỉ có một thành phần theo
phương x (Hình 3.3.b). lOMoARcPSD| 36067889
+ Sóng phân cực ngang (phân cực H): Trường hợp này vectơ E chỉ có một thành phần theo phương Mặt phẳng phân cực Mặt phẳng phân cực y y y y a) b) c)
Hình 3.3. Phân cực thẳng (a), ứng (b), ngang (c)
3.3. Nghiệm phương trình sóng ối với sóng phẳng
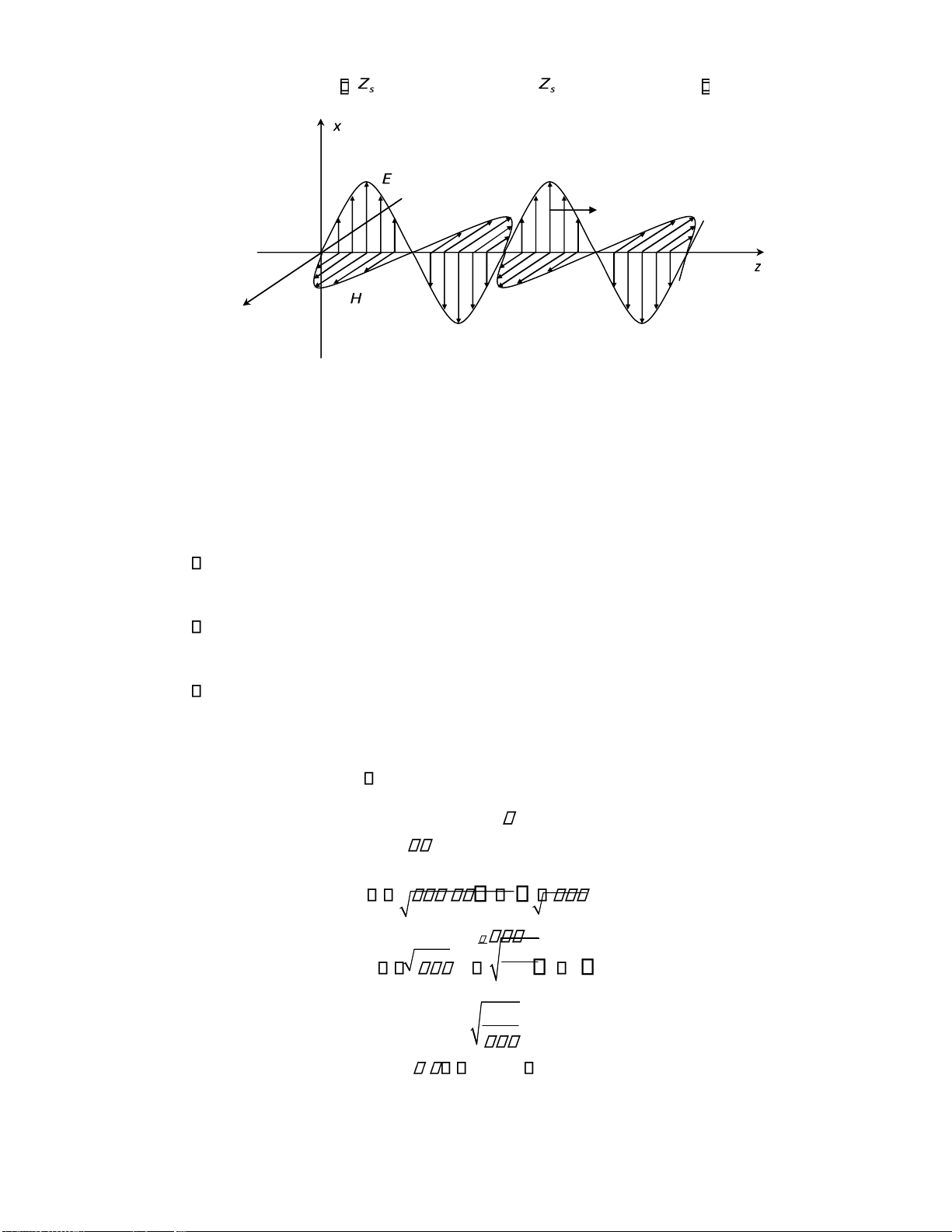
Để ơn giản ta chọn hệ tọa ộ Descartes, sóng iện từ phẳng là ơn sắc và chỉ truyền
theo phương z. Mặt sóng vuông góc với phương z 0. Áp dụng hệ phương x y trình Maxwell phức:
Xét sóng TEM và phân cực ứng: rotH E E 0 y z j E H x H z 0 j H rotE
ix iy iz
Ta có: rotE 0 0 j H j H iy y z Ex 0 0
Ex iy j H iy y z hay Hy 1 Ex (3.6) j z Tương tự: lOMoAR cPSD| 36067889 ix iy i rotH 0 0 j E j E ix x 0 H y j Ex (3.7)
Thay (3.6) vào (3.7) ta ược: 1 2zE2x j Ex j 2E Hay: x (3.8) 2 j j Ex 0 z Đặt: j (3.9) j j
Gọi là hệ số truyền sóng, trong ó:
+ Phần thực : là hệ số suy hao, có ơn vị là 1/ m .
+ Phần ảo : là hệ số pha ( ặc trưng cho sự lan truyền), ơn vị rad /m
Ta có phương trình sóng phẳng như sau: (3.10) 2E 2x 2Ex 0 z
Giải phương trình (3.10) ta có nghiệm:
Ex E et z E epx z (3.11)
Trong biểu thức (3.11) cường ộ iện trường bao gồm hai thành phần, thành phần thứ nhất: E E e z z t
là thành phần sóng thuận (sóng tới) và E E e px là thành phần sóng
ngược (phản xạ) (Chú ý: z ở ây là trục tọa ộ chứ không phải trở kháng sóng Z s ). Trong ó; E j j t
E et 1;E px E epx 2 là các biên ộ phức của sóng tới và sóng phản xạ, 1, 2
là các góc pha ầu của sóng. lOMoARcPSD| 36067889
Thay (3.11) vào (3.6) ta ược: Hy 1
E et z E pxe z j H y
E et z Epxe z (3.12) j Đặt: Zs j Z es j (3.13)
Z s gọi là trở kháng sóng.
Trong ó: phần modul ặc trưng cho ộ lệch biên ộ giữa iện trường và từ trường, còn
arguymen ặc trưng cho sự lệch pha giữa E và H . Ta ược: Hy
EZst e z EZpsx ej z (3.14)
Theo biểu thức (3.14) ta thấy H y cũng có hai thành phần:
Sóng thuận: H Et Zs
Sóng ngược: H EZ p xs
Ta cũng có quan hệ: Zs HE HE lOMoARcPSD| 36067889
3.4. Sóng phẳng trong các môi trường ồng nhất, ẳng hướng
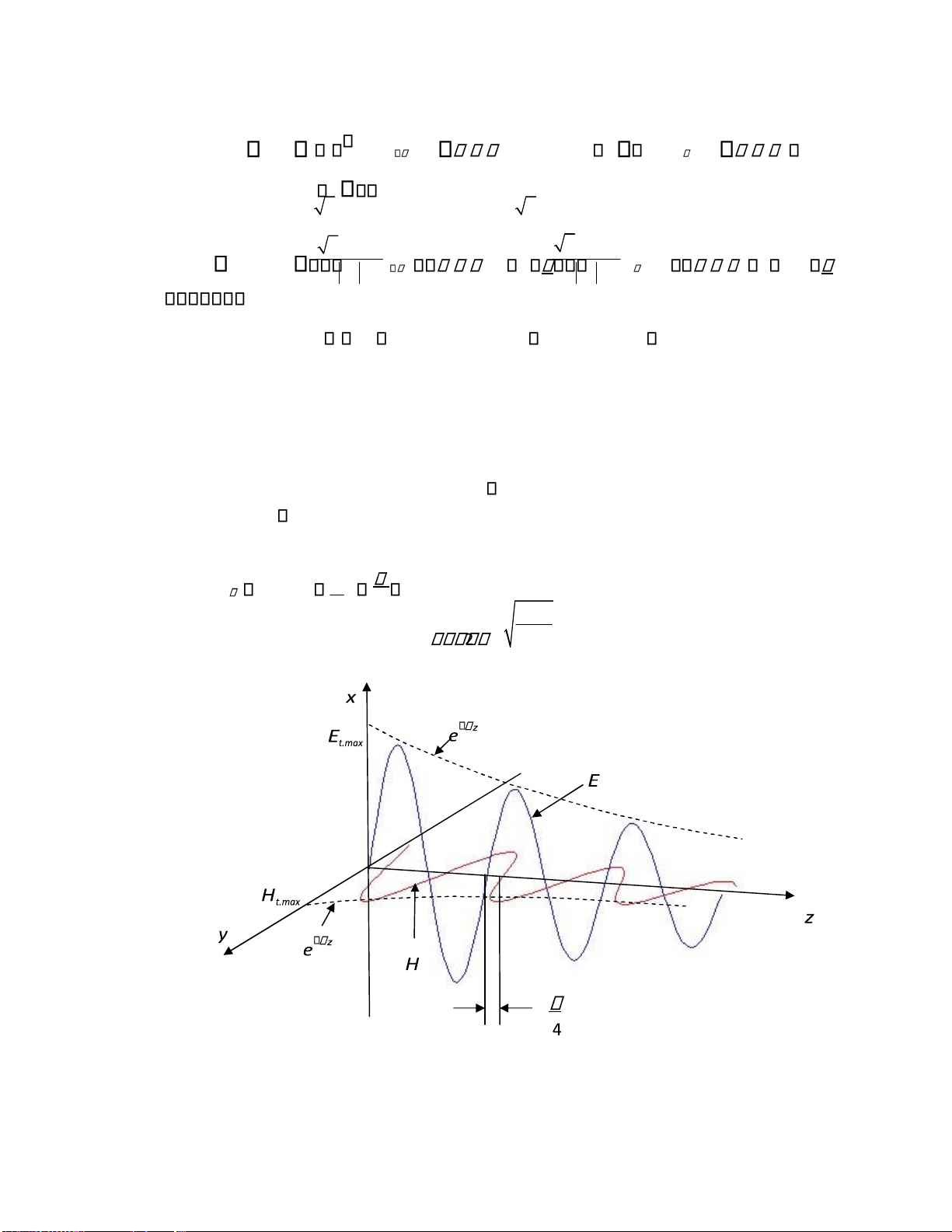
3.4.1. Sóng phẳng trong môi trường iện môi lý tưởng
Nghiên cứu các tính chất của sóng iện từ phẳng ồng nhất truyền dọc theo trục z 0 trong
môi trường iện môi lý tưởng ồng nhất và ẳng hướng rộng vô hạn. Vì iện môi lý tưởng có ộ dẫn iện
0 nên các tham số iện của nó là các số thực.
3.4.1.1. Hệ số truyền sóng j j j 2 2 j j Ta thấy: +
0 nên sóng truyền trong iện môi lý tưởng không bị suy hao. + .
3.4.1.2. Vận tốc pha
Vận tốc truyền sóng v là vận tốc truyền tín hiệu hay vận tốc truyền năng lượng, ây là một
ại lượng vật lý nên v c . 1 v (3.15)
Vận tốc pha vph là vận tốc dịch chuyển của các trạng thái pha, hay vận tốc dịch chuyển của
mặt ồng pha. Mặt ồng pha của sóng thuận có dạng: t z const (3.16) Do ó: d
dt dz 0 , nên vận tốc pha ược xác ịnh như sau: dz v ph (3.17) dt
Chú ý vận tốc pha là một ại lượng quy ước.
Với môi trường iện môi lý tưởng ta có: 1 v v ph
Ta thấy vận tốc pha bằng với vận tốc sóng, và nó không phụ thuộc vào tần số, môi trường
như vậy người ta nói là môi trường không tán sắc.
3.4.1.3. Trở kháng sóng lOMoARcPSD| 36067889
Theo công thức (3.13) ta có: Zs j j j (3.18)
Ta thấy rằng trở kháng sóng là một số thực, arguymen
0 hay E và H khi truyền i luôn ồng pha nhau.
3.4.1.4. Biểu thức sóng
Thay j và Z s
Zs vào nghiệm của phương trình sóng phẳng các biểu thức (3.11) và (3.14) ta có:
Ex E et z Epxe z E etj z 1 Epxej z 2
y EZst
z Epxs ej z EZst ej z 1 EZpxs ej z 2 H e Z
Dạng tức thời của cường ộ trường như sau: E x y z t , , , 2Et cos t - z 1 2E px cos t z 2 ix
H x y z t, , , 2E t t - z 1 2Epx cos t z 2 iy (3.19) cos lOMoARcPSD| 36067889 v y
Hình 3.4. Dạng sóng iện từ phẳng trong iện môi lý tưởng
Hình 3.4 là dạng sóng thuận của iện trường và từ trường trong iện môi lý tưởng, biên ộ
của sóng giữ cố ịnh theo phương truyền sóng, pha của cường ộ iện trường và cường ộ từ trường trùng nhau.
Ta nhận xét tính chất của sóng phẳng trong iện môi lý tưởng như sau:
Các vectơE vàH luôn vuông góc với nhau và vuông góc với phương truyền sóng. Từ
trường và iện trường luôn ồng pha và có biên ộ không ổi dọc theo phương truyền sóng.
Vận tốc pha của sóng phẳng bằng vận tốc truyền sóng trong cùng môi trường. Và iện
môi lý tưởng là môi trường không tán sắc.
Năng lượng sóng không tổn hao và trở kháng sóng là một số thực.
3.4.2. Sóng iện từ phẳng trong vật dẫn tốt
3.4.2.1. Hệ số truyền sóng
Môi trường dẫn iện tốt là môi trường có rất lớn, nên trong biểu thức của hệ số truyền
sóng ta có thể bỏ qua thành phần . j j j Hay ej 4 1 j (3.20) 2 Do ó: 0 (3.21) 2 lOMoAR cPSD| 36067889
Vậy sóng truyền trong vật dẫn sẽ bị suy hao, với hệ số suy hao ~ tức là khi tần số của
sóng càng tăng thì hệ số suy hao càng lớn và sóng sẽ khó có thể i sâu vào vật dẫn.
3.4.2.2. Vận tốc pha
Theo biểu thức (3.17) ta có: v 2 ph (3.22) 2
Với vật dẫn tốt ta thấy vph phụ thuộc vào tần số, môi trường như vậy người ta nói là môi trường tán sắc.
3.4.2.3. Trở kháng sóng
Theo công thức tính trở kháng sóng ta có: Zs j j ej 4 (3.23) j Z s ; 4 và H truyền i
Ta thấy rằng trở kháng sóng là một số phức có arguymen hay E 4
lệch pha nhau một góc / 4 .
3.4.2.4. Biểu thức sóng Thay j và Z j 4 s
Z e s vào nghiệm của phương trình sóng phẳng các biểu thức (3.11) và (3.14) ta có:
Ex E et zej z 1
E pxe e zj z 2 y E etZs zj z 1 4 Epxes z ej z 2 4 H e Z lOMoARcPSD| 36067889
Dạng tức thời của cường ộ trường như sau: E x y z t , , ,
2E et z cos t - z 1 2E pxe z cos t z 2 ix
H x y z t, , , 2E eZ ts z t -z 1 2E pxs e z cos t z 2 4 iy cos 4 Z
3.4.2.5. Độ sâu thâm nhập d
Để o mức ộ tắt của sóng khi lan truyền trong vật dẫn người ta ưa ra ại lượng ộ sâu thâm
nhập, ký hiệu là d . Đó là khoảng cách tính theo phương truyền sóng sao cho sóng truyền qua
khoảng cách d ấy thì biên ộ sóng sẽ giảm i e 2,718 lần, và do ó vectơ Poynting, dòng năng
lượng giảm i e2 7, 45 lần.
Theo ịnh nghĩa trên, ta có:
e d e hay d 1 2 (3.24)
Hình 3.5. Dạng sóng iện từ phẳng trong vật dẫn tốt lOMoARcPSD| 36067889
3.4.3. Sóng iện từ phẳng trong môi trường bán dẫn
3.4.3.1. Hệ số truyền sóng
Môi trường bán dẫn là môi trường có ầy ủ các tham số
, , ộ dẫn iện không là một
số rất lớn. Theo (3.9) ta có: j j 12 2 2 2 11
v12tg2 e 1 12 (3.25) 12 2 2 2 11 v 21 tg2 e 1 12 Trong ó: tg e
gọi là tang của góc tiêu hao iện.
3.4.3.2. Vận tốc pha v 1 (3.26) ph 12 2 2 2 11
3.4.3.3. Trở kháng sóng
Zs Z es j Z s 4 2 22 2 2 (3.27) arctg
Trường hợp môi trường gần với môi trường iện môi lý tưởng, nghĩa là ta có: 1
Các công thức (3.25) ến (3.27) ược giản ước gần úng như sau: lOMoARcPSD| 36067889 2 ; ; 4 2
3.5. Hiệu ứng bề mặt
3.5.1. Khái niệm chung
Khi dòng iện chạy trên một dây dẫn iện thì mật ộ dòng iện sẽ phân bố ều trên toàn bộ tiết diện ngang của dây.
Tuy nhiên nếu trên dây dẫn có dòng iện xoay chiều chạy qua thì mật ộ dòng iện sẽ không
còn phân bố ều trên tiết diện ngang nữa. Lúc này mật ộ dòng iện sẽ tập trung ra sát bề mặt
bên ngoài của dây dẫn. Khi tần số của dòng iện càng tăng thì hiện tượng này xảy ra càng
mạnh, hiệu ứng này gọi là hiệu ứng bề mặt (skin effect).
Các ảnh hưởng của hiệu ứng bề mặt:
+ Diện tích tham gia dẫn iện của vật dẫn giảm và làm cho iện trở của vật dẫn tăng lên,
tức là tổn hao sẽ tăng lên.
+ Điện cảm của vật dẫn cũng thay ổi.
Điều này làm ảnh hưởng nhiều ến việc truyền dẫn năng lượng ở tần số cao và siêu cao.
Trong thực tế ở tần số siêu cao người ta không dùng dây dẫn iện mà thường dùng các
hệ ịnh hướng sóng iện từ ể truyền năng lượng (sẽ ề cập trong chương 4), với các ưu iểm:
+ Hạn chế tiêu hao năng lượng do bức xạ sóng iện từ.
+ Hạn chế tiêu hao năng lượng do hiệu ứng bề mặt.
3.5.2. Hiệu ứng bề mặt về iện trong một phiến dẫn phẳng
Phiến dẫn phẳng là một tấm kim loại mỏng với các kích thước bề dầy 2a (rất mỏng), bề
ngang là b và chiều dài là l ủ nhỏ (so với bước sóng trong không khí), với iều kiện 2a b. Do
bề ngang b ủ rộng, không kể ến hiệu ứng ở biên và các góc cạnh của phiến dẫn, có thể thấy
trên các bề mặt z a và các mặt a z a cường ộ trường cũng như mật ộ dòng iện phân
bố ều ặn, chúng chỉ phụ thuộc vào tọa ộ z . Do ó chọn hệ trục tọa ộ như Hình 3.6. y lOMoARcPSD| 36067889
Hình 3.6. Hiệu ứng bề mặt về iện trên phiến dẫn phẳng
Trên phiến dẫn có dòng iện xoay chiều I
I hd .ej t chạy theo chiều x như Hình 3.6, giả sử
hiệu ứng bề mặt chỉ xảy ra trên bề dày (trục z) của phiến dẫn. Ta nhận thấy: E z a E z a (Đối xứng chẵn) H z a H z a (Đối xứng lẻ)
Khi hiệu ứng bề mặt xảy ra trên phiến dẫn thì biên ộ của E H, sẽ lớn nhất tại 2 bề mặt (z
a z; a ), còn giá trị của chúng bên trong ược tính như sau:
Z HsmÆt ch z E sh a (3.28)
H HmÆt sh a H mÆt I 2b
Thay z a vào (3.28) ta có: E mÆt Z H smÆtcth a E * zE z mÆt chch ..az E (3.29) z sh lOMoARcPSD| 36067889
z HH mÆtz shsh ..az H * Ta thấy j ej 4 2. . ej 4 Hay tỷ lệ với
1 (d là ộ sâu thâm nhập). d Vậy: a ~ a ; z ~ z . d d
Hình 3.7 là sự phân bố tương ối về modul của E * z ,H * z theo thông số a d/ a. .
Dễ thấy khi phiến ủ mỏng với 2a
d tức a d/ 1 sự phân bố của E*,H * theo bề dày
coi là ều ặn, ó là vì các sóng chạy trong phiến mỏng chưa ủ ể tắt. Ta gọi phiến có bề dầy 2a ủ
nhỏ (so với d) như vậy là một phiến “trong suốt” ối với sóng iện từ. Ngược lại ở phiến ủ dầy 2a
d hiệu ứng bề mặt thể hiện rất rõ, ta bảo phiến này “ ục”. * *
Hình 3.7. Phân bố tương ối về modul của E và H trong phiến dẫn
Với cùng một phiến, nhưng ối với những tần số khác nhau, sẽ có những ộ sâu thâm nhập
d khác nhau và phiến có thể là “trong” hoặc “ ục”. Nó là “trong suốt” ối với tần số thấp,
nhưng lại “ ục” ối với tần số cao ứng với ộ sâu thâm nhập d bé hơn. Vậy ở tấn số cao hiệu
ứng bề mặt càng mạnh, vật dẫn càng “ ục”.
Ta có khái niệm trở kháng sóng Zs là tỷ số giữa trị hiệu dụng phức của các sóng thuận
hoặc sóng ngược E ,H . Với quan niệm sóng iện từ truyền từ bên ngoài khúc xạ vào phiến lOMoARcPSD| 36067889
dẫn ến một phân bố nào ó, ta dẫn ra thêm khái niệm tổng trở vào của sóng Zvµo. Nó bằng tỷ số
EmÆt với H mÆt ở trên bề mặt phiến z a . Ta có: Z vµo Z cths a (3.30)
Tổng trở iện của một phiến dẫn
Từ kết quả phân tích về một phiến dẫn phẳng khi có dòng iện xoay chiểu I chảy dọc phiến,
ta có một cơ sở ể xét tổng trở về iện của phiến.
Chú ý rằng một mặt tổng trở iện bằng tỷ số của công suất phức trung bình và bình phương của dòng iện. S Z 2 (3.31) I
Mặt khác công suất phức ưa vào phiến phải bằng thông lượng vectơ Poynting phức chảy
vào phiến ó, khi trong phiến có dòng iện I . Vectơ Poynting trên mặt z a ều có chiều chảy
vào phiến với trị số bằng: E mÆtHmÆt ZvµoH mÆt2 (3.32)
Đối với phiến phẳng thông lượng vectơ Poynting ưa vào phiến bằng: 2
S 2lb ZvaoH mat2 2lb Zvao l I (3.33) 2b
Và tổng trở về iện của phiến:
Z S2 Zvao2b.l (3.34) I
Đặc biệt ở tần số ủ cao, hiệu ứng bề mặt xảy ra rất mạnh, phiến rất “ ục”, có thể coi các
sóng lan truyền từ phía mặt này sang mặt kia ã tắt hết trên dọc ường i trong khoảng 2a d
nên trên bề mặt phiến chỉ có các sóng thuận i vào. Trên bề mặt phiến, sóng sẽ chỉ gặp tổng trở
vào vừa bằng tổng trở sóng Z vµo
Z s . Cũng có thể từ (3.30) suy ra iều ấy, với a 1, cth a 1 và:
Zvµo Zs (3.35) lOMoARcPSD| 36067889
Vậy ối với một phiến “ ục”, thay (3.35) vào các biểu thức (3.32), (3.33), (3.34) có các biểu
thức của vectơ Poynting và tổng trở dây: s mat (3.36)
Z Zs. / 2lb R jX
Nếu tính Zs theo các thông số d và , ta có thể viết:
Z R jX l 1 j (3.37) Z H 2 2bd
Biểu thức này cho ta tìm ược iện trở R và iện kháng X (ứng với phần bên trong của phiến)
của phiến theo tần số. Ta thấy trong trường hợp này hai giá trị R và X vừa bằng nhau, argumen của Z bằng / 4 .
3.6. Sự phản xạ và khúc xạ sóng iện từ
Khi sóng iện từ bức xạ ra từ một nguồn thì các thông số của sóng phụ thuộc vào nguồn,
sau ó nó phụ thuộc vào môi trường. Nếu trên ường i của sóng nó gặp phải một môi trường có
thông số khác thì tại bề mặt phân chia giữa hai môi trường sẽ xảy ra hiện tượng phản xạ và khúc xạ sóng iện từ.
Hiện tượng phản xạ và khúc xạ sóng iện từ làm thay ổi phương truyền sóng tại bề mặt
phân cách hai môi trường có tham số khác nhau. Sự phản xạ và khúc xạ sóng ược ứng dụng nhiều trong kỹ thuật.
Để cho ơn giản, ta chỉ xét ối với trường hợp sóng phẳng tới phân cực ngang và ứng, các
trường hợp phân cực khác của sóng phẳng là tổ hợp của hai dạng sóng phân cực thẳng ngang và ứng.
3.6.1. Sóng tới phân cực ngang
Sóng phân cực thẳng ược gọi là phân cực ngang nếu vectơ cường ộ iện trường của sóng
tới vuông góc với mặt phẳng tới. Mặt phẳng tới là mặt phẳng chứa phương truyền sóng và
pháp tuyến của mặt phân cách hai môi trường.Trong trường hợp này, vectơ cường ộ iện
trường của sóng tới sẽ song song với mặt phân cách hai môi trường. Để tìm quy luật của sóng
phản xạ và khúc xạ, ta chọn hệ tọa ộ Descartes có mặt xOy trùng với mặt phẳng giới hạn phân
cách hai môi trường, trụcz trùng với pháp tuyến của mặt giới hạn, hai môi trường iện môi có các tham số iện 1, 1, , 2 tương ứng.
Giả sử sóng tới truyền theo phương zt lập với pháp tuyến của mặt phân chia 2 môi tường một góc t . lOMoARcPSD| 36067889
Sóng phản xạ truyền theo phương zpx với góc phản xạ px , còn sóng khúc xạ truyền theo
phương zkx i vào môi trường thứ hai ứng với góc kx . px Môi trường 1 Môi trường 2
Hình 3.8. Phản xạ và khúc xạ của sóng phân cực ngang
Sử dụng công thức chuyển ổi tọa ộ, chuyển các phương z zt , px ,zkx về tọa ộ x và z. z t
z cos t x sin t z px
z cos px x sin px z kx
zcos kx x sin kx
Biểu thức sóng trong môi trường 1 là:
E1 E et 1zt
E epx 1zpx E et 1 z cos t x sin t
Epxe 1 z cos px x sin px
H Et e 1zt
Epx e 1zpx Et e 1 zcos t x sin t
Epx e 1 z cos px x sin px (3.38) 1 Z1 Z1 Z1 Z1
Giả sử môi trường 2 từ vị trí z 0 trở i theo trục z là môi trường ồng nhất và rộng vô
hạn, tức là sẽ không có sóng phản xạ trong môi trường 2. Biểu thức sóng trong môi trường
lúc này chỉ có thành phần sóng thuận, chính là sóng khúc xạ.
E2 E ekx 2zkx
E ekx 2 zcos kx x sin kx (3.39) H 2 Ekx e 2zkx
Ekx e 2 zcos kx x sin kx Z 2 Z 2 lOMoARcPSD| 36067889
Vì hai môi trường là iện môi ta có thể áp dụng iều kiện bờ.
E1 E 2 z 0 Ta nhận thấy: E (3.40) 1
E1; E 2 E 2 vậy: E1 E 2 z 0
H 1 H 2 z 0 Hay H (3.41) 1 cos t H 2 cos kx z 0
Từ các biểu thức từ (3.38) ến (3.41) ta có: E et 1x sin t
Epxe 1xsin px E ekx 2xsin kx (3.42)
Biểu thức (3.42) phải úng với mọi giá trị của x , tức là phải úng với x 0 , hay:
Et Epx Ekx (3.43)
Tương tự như thế ta có: (3.44)
EZ1t EZpx1
cos t EZkx2 cos kx
Giải 2 phương trình (3.43) và (3.44) ta có:
Epx Z2 coscos tt ZZ11 coscos kxkx Et Z 2 (3.45) 2Z2 cos t
Ekx Zcos t Z1 cos kx Et 2
Để mô tả mối quan hệ giữa các biên ộ phức của sóng tới, sóng phản xạ, sóng khúc xạ,
người ta ưa ra khái niệm hệ số phản xạ và hệ số khúc xạ.
Với sóng phân cực ngang ta có: t 2 t 1 kx (3.46) T ng
Ekxt Z2 cos2 Zt2 cosZ 1 cost kx E
Kết hợp (3.42) và (3.43) ta ược một iều kiện: 1 sin t 1 sin px 2 sin kx (3.47) lOMoARcPSD| 36067889
Rng Epx ZZ2 coscos t ZZ1 coscos kx E sin t sin px hay t px sin t 2 (3.48) Ngoài ra ta cũng có: sin kx 1
Xét trường hợp 2 môi trường ều là iện môi có thông số khác nhau, khi ó: 1 j 1 1 ; 2 j
2 2 , thông thường với iện môi ộ từ thẩm tương ối bằng 1, tức là 1 2 0 , ta ược: 2 2 n2 1 1 n1 sin t 2 n2 (3.49) Hay sin kx 1 n1
Trong ó: n gọi là chiết suất của môi trường.
3.6.2. Sóng tới phân cực ứng
Ta lập lại các bước tiến hành tương tự như với sóng phân cực ngang, áp dụng iều kiện
bờ cho các thành phần tiếp tuyến của iện trường và từ trường tại mặt giới hạn phân cách hai
môi trường x0y, sẽ nhận ược các biểu thức của song phản xạ và khúc xạ như sau:
Rd HHpxt ZZ11 coscos tt ZZ22 coscos kxkx (3.50)
Td HHkxt Z1 cos2 Zt1 cosZ 2 cost kx lOMoARcPSD| 36067889
Trong trường hợp ặc biệt, khi sóng tới vuông góc với mặt phân chia hai môi trường, tức là góc tới t
0 và do ó góc khúc xạ kx 0 .
Lúc này các hệ số phản xạ và khúc xạ có dạng ơn giản là: Rng Z2
ZZ11 ;Tng Z22Z 2Z1 Z 2 (3.51) Rd ZZ11 ZZ22 ;Td
Z12 ZZ12 px Môi trường 1 Môi trường 2
Hình 3.9. Phản xạ và khúc xạ của sóng phân cực ứng
3.7. Sóng phẳng trong môi trường không ẳng hướng
Ở các phần trước, chúng ta ã tìm hiểu sóng iện từ phẳng trong các môi trường ẳng hướng.
Trong các môi trường này, các tham số iện từ như
, , là các hằng số và các vectơ
của trường iện từ E song song với D , B song song với H qua các phương trình chất.
Trong tự nhiên, ngoài các môi trường ẳng hướng còn tồn tại những môi trường mà theo
các hướng khác nhau các tham số iện từ của chúng có các giá trị khác nhau. Những môi trường
như vậy ược gọi là môi trường không ẳng hướng. Độ từ thẩm và iện thẩm của môi trường
không ẳng hướng gồm một số các giá trị khác nhau tạo thành một bảng gọi là tenxơ
ộ từ thẩm và . Chúng có dạng sau: xx xy xz xx xy xz lOMoARcPSD| 36067889 yx yy yz , yx yy yz (3.52) zx zy zz zx zy zz
Các phương trình chất trong môi trường không ẳng hướng sẽ là: D E; B H (3.53)
Triển khai (3.53) cho các thành phần theo các trục tọa ộ Descartes ược: Dx xxEx xyEy xzEz Dy yxEx yyEy yzEz D z zxEx zyEy zzEz (3.54) Bx xxH x xyH y xzH z By yxH x yyH y yzH z Bz zxH x zyH y zzH z
Từ (3.54), ta thấy trong môi trường không ẳng hướng các vectơ của trường E không
song song vớiD ,B không song song vớiH .
Trong thực tế chỉ tồn tại các môi trường mà ộ từ thẩm và iện thẩm ều là các tenxơ, chỉ có
các môi trường không ẳng hướng loại như sau:
Môi trường có và là các hằng số mà ộ từ thẩm là tenxơ
ược gọi là môi trường
không ẳng hướng từ quay. Ferit bị từ hóa bởi từ trường không ổi là môi trường từ quay
ối với sóng iện từ. Nó ược ứng dụng trong kỹ thuật siêu cao tần làm các thiết bị iều khiển sự truyền sóng.
Môi trường có và là các hằng số, còn ộ iện thẩm là tenxơ
ược gọi là môi trường
không ẳng hướng iện quay. Chất khí bị ion hóa (còn gọi là plazma) dưới tác dụng của
từ trường không ổi cũng biểu hiện tính không ẳng hướng của môi trường iện quay ối
với sóng iện từ. Tầng ion hóa của khí quyển trái ất cũng là plazma dưới tác dụng của
từ trường trái ất cũng là môi trường iện quay. Khi truyền sóng vô tuyến trong tầng ion
hóa cần xét ến tính chất không ẳng hướng của nó. Điều này ược nghiên cứu kỹ trong
các tài liệu về truyền sóng vô tuyến. lOMoARcPSD| 36067889 BÀI TẬP CHƯƠNG 3
Bài 3-1: Một sóng phẳng iều hòa là truyền trong môi trường ồng nhất, vô hạn với các thông số 0 , 0 và
0. Biết Em 500 mV/m, tần số 108rad /s . Hãy xác ịnh các thông số
của sóng: hệ sồ truyền sóng , trở kháng sóng Z s , vận tốc sóng v, bước sóng , cường ộ từ
trường H , vectơ Poynting và mật ộ dòng dịch J dc .
Bài 3-2: Hãy tìm các thông số của một sóng phẳng iều hòa: hệ số pha , trở kháng sóng Z s , vận
tốc sóng v trong không khí và nước. Cho biết thông số của nước là 1 81 0 ; 1 0 .
Xét trường hợp tần số f 1Mhz và f 10Mhz.
Bài 3-3: Một sóng phẳng iều hòa lan truyền trong môi trường bán dẫn ( iện môi có tiêu tán),
biết các thông số môi trường
10 0 ; 0 ; 10 2 S m/ và tần số
108rad /s . Đã biết
cường ộ trường tại x y z 0 là E m
600mV /m . Hãy viết biểu thức sóng chạy?
Bài 3-4: Một sóng phẳng iều hòa lan truyền theo phương z vuông góc với mặt chia cắt hai iện
môi. Thông số hai môi trường tại z 0 là: r 1 1; r 1 1; 1 0 và tại 0 z : r 2
4; r 2 1; 1 0 . Biết tần số sóng
3.108rad /s , biên
ộ sóng tại z 0 bằng
Em 1V /m , cho biết sóng phân cực ngang E Ey
. Hãy tìm biểu thức sóng trong hai môi
trường ó: E1 t ,H 1 t , E 2 t ,H 2 t ?
Bài 3-5: Một sóng phẳng iều hòa phân cực theo chiều x lan truyền theo phương z, tại vị trí z
0 sóng chuyển từ không khí có r 1
1; r 1 1 sang một môi trường dẫn iện r 2
1; 2 5.102S m/ . Biết biên ộ cường
ộ trường của sóng tới Et 1V / m , tần số
106rad /s. Hãy tìm giá trị tức thời của các vectơ trường E và H trong hai miền sau khi ã khúc
xạ, phản xạ. Tìm vectơ Poynting thấm vào mặt vật dẫn và tím ộ sâu thâm nhập d ?
Bài 3-6 : Một sóng phẳng phân cực ngang H t lOMoARcPSD| 36067889
lan truyền theo phươngzt tạo với pháp tuyến của x mặt phẳng phân chia giữa 2 ới
môi trường (mặt E t phẳng xoy) một góc t 300 , biết: Môi trường 1 có Môi trường 1 Môi trường 2 Môi trường 2 có r 2 1; r 2 1; 2 0 ; Tần số sóng
3.108rad/s ; Biên ộ sóng tới: E t max 500mV / m . a)
Hãy tìm các góc phản xạ px , góc khúc xạ kx và biểu thức sóng trong hai môi
trường E1 t ;E 2 t ;H 1 t ;H 2 t ? b)
Vẽ các véc tơ thành phần sóng theo các phương sóng tới zt , phương sóng phản xạ zpx
và phương sóng khúc xạ zkx ?
CHƯƠNG 4. SÓNG ĐIỆN TỪ TRONG CÁC HỆ ĐỊNH HƯỚNG
4.1. Phân loại dải sóng siêu cao tần và ặc iểm của sóng siêu cao tần
Ở các chương 1, 2 và 3 ta ã khảo sát các vấn ề thuộc phần lý thuyết trường iện từ. Bắt ầu
từ chương 4 là các vấn ề về kỹ thuật siêu cao tần.
Dải sóng siêu cao tần là một phần của dải sóng iện từ có bước sóng nằm trong khoảng
từ 10m ến 1mm, tương ứng với dải tần số f từ 3.107Hz ến 3.1011Hz. Nó ược phân ra bốn dải nhỏ là: Dải sóng m hay VHF
10m 1m f; 30MHz 300Mhz
Dải sóng dm hay UHF
10dm 1dm f; 300MHz 3GHz
Dải sóng cm hay SHF
10cm 1cm f; 3GHz 30GHz
Dải sóng mm hay EHF
10mm 1mm f; 30GHz 300GHz
Các dải sóng siêu cao tần trên ược sử dụng ngày càn rộng rãi trong các thiết bị vô tuyến
iện tử ở các lĩnh vực khác nhau như: truyền hình, phát thanh FM, thông tin vệ tinh, thông tin
di ộng, radar, ạo hàng…
Sở dĩ như vậy vì sóng siêu cao tần có các tính chất ặc biệt sau:
1. Sóng siêu cao tần truyền thẳng trong phạm vi nhìn thấy trực tiếp. Hầu hết các dải sóng
này ều có khả năng xuyên qua bầu khí quyển của trái ất và thay ổi ít về công suất và phương truyền sóng. lOMoARcPSD| 36067889
2. Sóng siêu cao tần có tính ịnh hướng cao khi bức xạ từ những vật có kích thước lớn
hơn nhiều so với bước sóng.
3. Sóng siêu cao tần cho phép khoảng tần số sử dụng lớn, tức là chúng ta có thể sử dụng
số kênh rất lớn trong dải sóng siêu cao tần, áp ứng ược nhu cầu truyền thông tin ngày càng tăng.
Ví dụ: trong tất cả các dải sóng ngắn
100m 10m f; 3MHz 30MHz chỉ có thể
phân bố ược khoảng 4000 kênh thoại hay 4 kênh video của truyền hình không nhiễu ến nhau.
Song với lượng kênh cần sử dụng như trên khi dùng dải sóng cm, chỉ cần một khoảng khá nhỏ từ bước sóng 2,992 ến 3cm.
4. Ở dải sóng siêu cao tần nhất là hai dải nhỏ là cm và mm thì kích thước của các phần
tử và thiết bị so sánh ược với chiều dài bước sóng, thậm chí có trường hợp chúng còn lớn hơn
nhiều so với bước sóng. Do ó trong các trường hợp như vậy phải chú ý ến hiệu ứng giữ chậm
của sóng iện từ. Trong các èn iện tử chân không thông thường thời gian bay của iện tử giữa
các cực của èn có thể so sánh hoặc lớn hơn chu kỳ dao ộng siêu cao tần (nhất là ở dải cm và
mm). Nên ta phải chú ý ến hiệu ứng quán tính bay của iện tử. Trong các dụng cụ bán dẫn
thông thường ở dải sóng siêu cao tần cũng có hiệu ứng quán tính dịch chuyển của iện tử và lỗ trống.
Do các ặc iểm riêng của dải sóng siêu cao tần, nên các khái niệm về các phần tử tập
trung ở ây không còn áp dụng ược, mà ta phải thay bằng khái niệm về các phần tử phân bố.
Đồng thời chúng cũng ặt ra nhiều vấn ề lớn cần giải quyết như: các hệ thống truyền dẫn năng
lượng, các mạch dao ộng, các hệ bức xạ và các dụng cụ iện tử và bán dẫn ể tạo ra các dao ộng siêu cao tần.
4.2. Khái niệm về hệ ịnh hướng sóng iện từ
Chúng ta gọi ường truyền là các thiết bị hay hệ ể giới hạn ường truyền lan các dao ộng
iện từ hay các dòng năng lượng iện từ theo hướng ã cho. Đường truyền dùng ể truyền dẫn
năng lượng siêu cao tần hay sóng siêu cao gọi là ường truyền năng lượng siêu cao tần ( ường truyền siêu cao).
Đường truyền siêu cao ược gọi là ường truyền ồng nhất nếu như dọc theo hướng truyền
sóng tiết diện ngang không thay ổi và môi trường chứa trong nó là ồng nhất. Trong kỹ thuật
siêu cao tần, ường truyền ồng nhất ược sử dụng là chủ yếu. Người ta có thể phân loại ường
truyền ồng nhất ra các loại sau: ường truyền hở và ường truyền kín.
Trong ường truyền hở, tại tiết diện ngang không có vòng kim loại bao bọc vùng truyền
năng lượng siêu cao tần. Đường truyền hở có nhiều dạng khác nhau như: ường dây ôi, mạch
dải, ường truyền sóng mặt …
Đối với ường truyền kín, trong nó phải có ít nhất một mặt vật dẫn kim loại bao bọc
hoàn toàn vùng truyền năng lượng siêu cao tần. Đường truyền kín là các ống kim loại rỗng
có tiết diện khác nhau, bên trong có thể nhét ầy các chất iện môi ồng nhất khác nhau hoặc
không khí hay chân không. Chúng ược gọi là ống dẫn sóng. lOMoARcPSD| 36067889
Có nhiều loại ống dẫn sóng ược dùng trong kỹ thuật siêu cao tần như: ống dẫn sóng ồng
trục, ống dẫn sóng chữ nhật, ống dẫn sóng trụ tròn …
Ở dải sóng mét, người ta ứng dụng ường dây ôi (song hành) và cáp ồng trục hay ống
dẫn sóng ồng trục ể truyền dẫn năng lượng siêu cao. Đường dây ôi có cấu trúc ơn giản và cho
kích thước ngang khá gọn, dễ iều chỉnh phối hợp. Nhưng ở dải sóng decimet, ống dẫn sóng
ồng trục hay cáp ồng trục ược dung phổ biến ể truyền dẫn năng lượng siêu cao. Đường dây
ôi không ược sử dụng rộng rãi trong dải sóng này vì tổn hao do bức xạ và hiệu ứng bề mặt.
Trong dải sóng centimet, ường truyền siêu cao phổ biến là các ống dẫn sóng chữ nhật
và trụ tròn vì nó cho tiêu hao nhỏ, kích thước phù hợp, ống dẫn sóng ồng trục hay cáp ồng
trục ít ược dung vì tổn hao do hiệu ứng bề mặt ở lõi trong và tổn hao trong iện môi rất lớn.
Nó chỉ dùng ở khoảng cách ngắn và công suất nhỏ.
Trong dải milimet, các ống dẫn sóng chữ nhật và tròn không ược dùng phổ biến do kích
thước nhỏ, khó chế tạo và tiêu hao lớn. Ở dải sóng này, ường truyền siêu cao phổ biến là
mạch dải, ường truyền sóng mặt như: ống dẫn sóng iện môi, dây dẫn ơn có phủ chất iện môi.
Trong chương này, chúng ta sẽ tìm hiểu trường iện từ tồn tại và lan truyền trong các
dạng ường truyền siêu cao phổ biến như: ống dẫn sóng chữ nhật, ống dẫn sóng trụ tròn, ống
dẫn sóng hoặc cáp ồng trục, ống dẫn sóng iện môi, ường dây ôi, mạch dải… Chúng ta cũng
tiến hành xét iều kiện truyền lan các dạng trường TEM, TE, TM trong chúng và nghiên cứu
các ại lượng ặc trưng cho trường và cho ường truyền ể từ ó áp dụng chúng có hiệu quả nhất
khi truyền dẫn năng lượng siêu cao.
4.3. Ống dẫn sóng chữ nhật
Ống dẫn sóng chữ nhật là một cấu trúc ược tạo bởi 4 vách kim loại như hình 4.1. Khoảng
không gian bên trong ống là iện môi. Phần lớn các trường hợp, iện môi là không khí, có
trường hợp là khí trơ. Các vách kim loại làm bằng vật liệu có ộ dẫn cao, ví dụ ồng hoặc hợp
kim của ồng. Đồng thời ể chống rỉ và tăng thêm ộ dẫn, người ta có thể mạ bên trong ống bằng 1 lớp bạc mỏng. y
Hình 4.1. Ống dẫn sóng chữ nhật
Để tìm trường có thể tồn tại trong ống dẫn sóng chữ nhật không tổn hao, cần giải hệ
phương trình Maxwell ối với miền giới hạn bởi các vách kim loại dẫn iện lý tưởng, với iều kiện bờ E t 0 .
Để ơn giản ta xét ống dẫn sóng với các iều kiện sau ây: lOMoAR cPSD| 36067889 Thành ống có
Điện môi bên trong lý tưởng: dm 0 .
Ta coi ống dẫn sóng dài vô hạn và trong miền khảo sát không tồn tại nguồn trường 0 .
Sử dụng hệ toạ ộ vuông góc (Hình 4.1) ta có iều kiện bờ trên các thành ống có dạng: E t
0 tại x 0,x a y, 0,y b (4.1)
Ta sẽ quan tâm ến iều kiện ể lời giải của các phương trình sẽ có dạng sóng chạy truyền
lan dọc theo trục ống dẫn sóng (trục z). Vì vậy, sự phụ thuộc của các thành phần vectơ E H,
với toạ ộ z trong chế ộ xác lập có thể biểu diễn bởi hàm số: ej t z (4.2)
Với là hệ số truyền sóng chưa biết.
Theo (4.2) thì vi phân của một thành phần bất kỳ của vectơ E hoặc H theo biến số z sẽ
tương ương với tích của hàm số ấy với . Ví dụ: Ex
Ex0 x y e, z Ex z z
Do ó, khai triển các phương trình Maxwell theo hệ toạ ộ vuông góc, ối với miền trong của
ống dẫn sóng, khi J 0 và 0 ta sẽ có:
ix iy iz rotH j E (4.3) x y z H x H y H z rotE j H (4.4)
Cho các thành phần tương ứng theo 3 trục x y z, , của hai vế phương trình (4.3) và (4.4) bằng nhau ta ược: lOMoARcPSD| 36067889 Hz
Hy j E (1)
Eyz Ey j Hx y x Hz x j E (4) Ez Ex j H H (2) (4.5) x y x y (5)
Hy Hx
Ey Ex j H j E (3) (6) x y z x y z Trong ó:
là các hằng số của môi trường bên trong ống dẫn sóng.
Nếu thay H x và H y từ phương trình (4) và (5) vào phương trình (1), (2) của hệ phương
trình (4.5), sau ó thay E x và E y từ phương trình (1), (2) vào phương trình (4), (5) thì các ại
lượng chưa biết Ex ,Ey ,Hx ,Hy sẽ ược biểu thị qua E z ,H z : Ex 1c2 Exz j Hyz k Ey k 1c2 Eyz j Hz x (4.6) x 1c2 j Eyz Hxz H k
Hy k 1c2 j Exz Hyz 2 c k 2 2 , với k Trong ó k v lOMoARcPSD| 36067889
Đối với sóng truyền lan theo hướng ngược, cần thay trong các biểu thức (4.5) và (4.6) bởi .
Như vậy nếu ta tìm ược E z ,H z thì sẽ tìm ược các thành phần sóng còn lại trong ống dẫn
sóng. Thay E x ,E y từ (4.6) vào (6) của (4.5) và thay H x ,H y vào (3) của (4.5) ta sẽ nhận ược
phương trình của các thành phần E z và H z : (4.7) 2z
y 2z k Hc2 z 0 x 2E 2E 2z
y 2z k Ec2 z 0 x (4.8) E (4.9) x j kc2
Hyz ;Ey j kc2
Hxz ;Ez 0
x c2 xz y k c2
Hyz z 0
H ;H ;H H k
Ex k c2
Exz ;Ey k c2
Eyz ;Ez 0 (4.10) 2H 2H
Từ các biểu thức (4.6) ta thấy trường iện từ trong ống dẫn sóng, trong trường hợp tổng
quát là tổng của hai trường ộc lập nhau:
Hx j c2
Eyz ;Hy jk c2
Exz ;Hz 0 k
Dễ dàng nhận thấy biểu thức (4.9) là trường iện ngang TE (E z
0) , (4.10) là trường từ ngang TM (H z 0).
4.3.1. Trường iện ngang
Theo (4.9) trường iện ngang trong ống dẫn sóng ược xác ịnh bởi thành phần dọc H z .
Thành phần này thoả mãn (4.7). Điều kiện bờ có thể tìm ược từ iều kiện bờ tổng quát. lOMoAR cPSD| 36067889
Điều kiện này ược áp dụng cho trường TE như sau: E (4.11) z 0y 0;y b x 0;x a Áp dụng (4.9) sẽ có: (4.12) Hz
0 t¹i x 0;x a x
H z 0 t¹i y 0;y b y
Lời giải của (4.7) có thể biểu thị dưới dạng:
Hz X x Y y e z (4.13)
Trong ó X x và Y y là các hàm chỉ phụ thuộc vào x và y . Thay các biểu thức trên
vào (4.7) và thực hiện các phép biến ổi ơn giải ta sẽ nhận ược: X Y kc2 0 X Y Từ ây ta có: X p X2 0; Y
q Y2 0 víi p2 q2 k 2 c
ở ây p và q là các hằng số phân ly tuỳ ý (giải bằng phương pháp phân ly biến số).
Ta viết lời giải tổng quát của các phương trình vi phân trên dưới dạng sau:
X A1 cospx B1 sin px ,
Y A2 cosqy B2 sinqy
Theo (4.13), thành phần H z sẽ bằng: H z
A1 cospx B1 sin px
A2 cosqy B 2 sinqy e z (4.14)
ở ây hệ số truyền sóng 2 p2 q2 k 2
Để tìm các ại lượng chưa biết, ta áp dụng iều kiện bờ (4.12). Từ iều kiện thứ hai ta có: lOMoAR cPSD| 36067889 B 2 0;sinqb 0
hay q n ;n 0,1,2,... b
Từ iều kiện thứ nhất ta nhận ược: B 1
0;sin pa 0 hay p m ;m 0,1,2,... a Do ó: kc2 m 2 n 2 a b
mn kc2 k 2 m 2 n 2 k 2 a b
Hz Amn cos m x cos n y e z a b ở ây ký hiệu A mn A A1 2
Bây giờ thay giá trị của H z vào (4.9) ta sẽ tìm ược các biểu thức cuối cùng ối với
hình chiếu của các vectơ trường iện ngang trong ống dẫn sóng chữ nhật. Ex j kc2nb Amn cos ma x sin nb y e z Ey j 2 m Amn sin m x cos n y e z kc a a b Ez 0
x mn2m Amn sin m x cos n y e z (4.15) H kc a a b lOMoAR cPSD| 36067889
Hy mn2 n Amn cos m x sin n y e z k c b a b z mn m n z H A cos x cos y e a b
Từ các ẳng thức trong (4.15) ta thấy khi m n 0 thì tất cả các thành phần của trường
ều bằng 0, trừ H . Do ó số z
m và n có thể nhận bất kỳ giá trị nào bằng 0,1,2,3,... nhưng không
ồng thời ược lấy bằng 0.
Như vậy trong ống dẫn sóng chữ nhật tồn tại vô số kiểu trường iện ngang khác nhau, ặc
trưng bởi các giá trị m n, khác nhau (ta ký hiệu trường TEmn hoặc H mn ). Theo (4.15) phân bố
trường theo các cạnh a b, có sóng ứng, ồng thời số m xác ịnh số nửa sóng trong khoảng 0
x a , còn n là số nửa sóng trong khoảng 0 y b.
Rõ ràng là trường (4.15) sẽ có dạng sóng chạy, truyền theo trục z nếu hệ số truyền sóng là một số thuần ảo. 2 2 mn j mn jk2 m n (4.16) a b
mn là hệ số pha. Muốn vậy, cần thực hiện bất ẳng thức sau: k 2 2 m 2 n 2 a b Nếu k 2 m 2 n
2 thì trường sẽ là trường suy giảm. a b
Do ó, trong ống dẫn sóng cũng như trong khoảng không gian giữa các mặt phẳng dẫn
iện, trường TEmn sẽ tồn tại nếu tần số dao ộng f lớn hơn tần số tới hạn fth xác ịnh từ iều kiện mn 0 .
Áp dụng (4.16), sau một vài biến ổi ơn giản sẽ nhận ược fth : lOMoARcPSD| 36067889
fth 1 k vc v m 2 n 2 m n, 0,1,2,3,... (4.17) 2 2 a b
Bước sóng tới hạn (ứng với tần số tới hạn ã tìm ược) sẽ xác ịnh theo công thức: th c 2 c 2 (4.18) fth kc v m 2 n 2 0 0 a b
Điều kiện truyền sóng trong ống dẫn sóng: f fth hoặc th (4.19)
Tiếp theo, có thể dễ dàng tính ược vận tốc pha và bước sóng trong ống dẫn sóng. Vận tốc pha vph bằng: v v ph (4.20) fth 2 1 f
Còn bước sóng trong ống dẫn sóng sẽ là: vph s (4.21)
Do ó s có giá trị khác với bước sóng trong không gian tự do tính theo các thông số 0 và 0 .
Vận tốc nhóm vnh có dạng: vnh d mn v 1 ffth 2 (4.22) d
Từ các công thức ối với vận tốc pha và vận tốc nhóm (4.20) và (4.22) ta thấy ống dẫn sóng
chữ nhật là môi trường tán sắc.
Trở kháng của ống dẫn sóng trong trường hợp sóng iện ngang có giá trị bằng:
Zs TE Exy HEyx mn Z 0fth 2 (4.23) H lOMoARcPSD| 36067889 1 f
Từ biểu thức (4.17) có thể thấy rằng với các kích thước ngang của ống dẫn sóng cho
trước, khi tăng m và n , tần số tới hạn sẽ tăng, nghĩa là sóng với m n, lớn sẽ có tần số tới hạn
cao hơn là sóng với m n, nhỏ. Do ó, ể truyền năng lượng iện từ có tần số dao ộng cho trước
trong ống dẫn sóng có kich thước ngang nho nhất cần sử dụng sóng với các giá trị m n, nhỏ.
4.3.2. Trường từ ngang
Trường từ ngang trong ống dẫn sóng ược xác ịnh bởi thành phần E z ,thành phần này
thoả mãn phương trình (4.8) và các iều kiện bờ: E z
A1 cospx B1 sin px
A2 cosqy B 2 sinqy e z (4.25) Với
p2 q2 k 2 và 2 p2 q2 k 2 (4.26)
Khi thoả mãn các iều kiện bờ (4.24) ta sẽ nhận ược: A 1
0; sin pa 0; p m ;m 0,1,2,... a (4.27)
E z 0 t¹i x 0,x a z 0 t¹i y 0,y b (4.24) E
Vì phương trình (4.7) và (4.8) tương tự nhau nên lời giải của (4.8) cũng sẽ có dạng giống (4.14) nghĩa là: A 2
0; sinqb 0; q nb ;n 0,1,2,...
Áp dụng kết quả này vào (4.25) ta sẽ có:
Ez Bmn sin m x sin n y e z a b ở ây B mn B B1 2
Thay giá trị Ez vào công thức (4.10) ta sẽ nhận ược các biểu thức cuối cùng của các thành
phần vectơ trường từ ngang trong ống dẫn sóng chữ nhật. lOMoAR cPSD| 36067889
Ex kmnc2ma Bmn cos ma x sin nb y e mnz
Ey mn2 n Bmn sin m x cos n y e mnz
kc b a b
Ez Bmn sin m x sin n y e mnz a b (4.28)
Hx j 2 n Bmn sin m x cos n y e mnz
kc b a b
Hy jk c2ma Bmn cos ma x sin nb y e mnz Hz 0
Đồng thời theo (4.26) và (4.27) ta nhận ược: 2 2 kc2 m n a b mn m 2 n 2 k 2 a b
Như vậy, trong ống dẫn sóng chữ nhật có thể tồn tại vô số kiểu sóng từ ngang, ặc trưng
bởi các chỉ số m n,
khác nhau (sóng TM mn hay Emn )
Các số m n, ở ây cũng có ý nghĩa giống như trong trường hợp TE .
Dễ dàng nhận thấy khi m hoặc n bằng 0 thì tất cả các vectơ trường sẽ bằng 0. Do ó trong
ống dẫn sóng chữ nhật sẽ không tồn tại các trường TM 00 ,TM m 0 hoặc TM 0n , và m n, sẽ nhận
các giá trị: m 1, 2,3,...,n 1,2,3,...
Cũng lập luận tương tự như ối với “trường iện ngang” ta sẽ nhận ược công thức của tần
số tới hạn, bước sóng tới hạn và các ặc trưng khác ối với sóng từ ngang khác nhau. Các công
thức này có dạng gần giống với các công thức của sóng iện ngang. Công thức ối với trở kháng
ặc tính của ống dẫn sóng trong trường hợp sóng từ ngang có dạng: Zs TM mn Z 0 1 ffth 2 (4.29) lOMoARcPSD| 36067889
Như vậy tất cả các lời giải có thể có trong ống dẫn sóng chữ nhật ã ược thể hiện ầy ủ
bởi các trường (4.15) và (4.28) với m n, 0,1,2,... Các trường hợp này ược gọi là trường riêng
hay sóng riêng của ống dẫn sóng chữ nhật. Hiển nhiên là nếu có một trường bất kỳ, với cấu
trúc phức tạp thì tại các iểm không có nguồn ta cũng có thể biểu thị nó dưới dạng tổ hợp của
các trường riêng nói trên.
Chú ý, trong các công thức trên ây, khi tính toán với trường hợp iện môi bên trong ống
dẫn sóng lý tưởng ta thay thế j .
4.4. Ống dẫn sóng trụ tròn a) b)
Hình 4.2. Ống dẫn sóng trụ tròn
Ống dẫn sóng trụ tròn là 1 ống hình trụ bằng kim loại rỗng bên trong chứa chất iện môi
(thường là không khí), bán kính của ống là a .
Ta sẽ khảo sát ống dẫn sóng trụ tròn mà bề mặt của nó ược xác ịnh bởi phương trình r a
trong hệ toạ ộ trụ r , ,z (Hình 4.2.b).
Áp dụng các phương trình Maxwell ta sẽ biểu thị các thành phần Er ,E và Hr ,H qua Ez
,Hz như sau: Er k 1c2 Erz j r H z E 1c2 E z j Hrz k r (4.30) lOMoARcPSD| 36067889 Hr 1c2 j E z Hrz k r H k 1c2 j
Erz r H z
4.4.1. Trường iện ngang
Biểu thức tổng quát của các thành phần vectơ E H, của trường iện ngang trong ống dẫn sóng trụ tròn có dạng: Er k 1c2 j r
H z ;E j kc2
Hrz ;Ez 0 r kc z
c 1 Hz z 0 (4.31) H 2
H ;H k 2 r ;H
Các iều kiện bờ mà H z phải thỏa mãn sẽ dễ dàng nhận ược từ iều kiện thành phần
tiếp tuyến của vectơ E trên mặt ống dẫn sóng bằng 0.
Theo (4.31) hình chiếu E t
E sẽ bằng 0 tại r a nếu: Hz 0 t¹i r a (4.32) r
Trong hệ tọa ộ này, hướng bán kính sẽ trùng với hướng pháp tuyến ngoài của mặt r a
nên biểu thức (4.32) có thể viết như sau: Hz 0 t¹i r a (4.33) n
Áp dụng các tính toán như ống dẫn sóng chữ nhật và chú ý các tính toán trong hệ tọa ộ trụ ta có: lOMoAR cPSD| 36067889 Hz A Jmm k rc B Nmm k rc Cm cosm Dm sinm e z
Trong ó: J m k rc và N m k rc là các hàm Bessel loại 1 và loại 2.
Gốc ể tính có thể chọn tùy ý. Ta sẽ lấy nửa mặt phẳng
const mà trong ó thành phần
H z có giá trị cực ại ể làm gốc. Do ó H z sẽ bằng: cos H z A Jmm k rc B Nmm k rc m .e z (4.34)
Hàm số Bessel loại 2 sẽ bằng khi r 0. Thế nhưng theo quan iểm vật lý thì trường ở
tâm ống r 0 phải có giá trị hữu hạn. Vì vậy, trong (4.34) cần ặt B m 0 . Lời giải của
phương trình này bây giờ sẽ có dạng:
Hz A Jmm k rc cos m .e z (4.35)
Vì hàm số H z không ược biến ổi khi bằng
2 nên m chỉ có thể là số nguyên: m 0,1,2,3,...
Tiếp theo, iều kiện bờ (4.32) sẽ ược thỏa mãn nếu: dJ m k rc 0 tại r a dr Hoặc: J m k ac 0;m 0,1,2,... (4.36)
ở ây dấu “ ' “ là ký hiệu ạo hàm theo argumen.
Lý thuyết hàm số Bessel cho biết với mỗi giá trị m sẽ có vô số nghiệm của phương trình J m
0. Ta ký hiệu các nghiệm này là mn ở ây n là số thứ tự nghiệm. Giá trị của một
vài nghiệm ầu, với m 0,1,2,... cho trong bảng 4.1.
Bảng 4.1. Nghiệm của ạo hàm hàm số Bessel Số thứ tự nghiệm (n) m 0 m 1 m 2 1 3,832 1,840 3,054 2 7,016 5,335 6,705 3 10,174 8,536 9,965 lOMoARcPSD| 36067889
Từ biểu thức (4.36) ta có: k ac mn Từ ó suy ra: k mn (4.37) c
;m 0,1,2,...;n 1,2,3,... a Thay giá trị của k 2
c vào biểu thức: kc k 2 2 ta có: mn mn 2 k2 a Và tương ứng ta có: mn k2 mn 2 a
Từ các biểu thức (4.31), (4.35) và (4.36) ta nhận ược các thành phần của các vectơ trường
iện ngang trong ống dẫn sóng trụ tròn: Er j kc2m r AmnJ m amn r sin m .e mnz E j 2 AmnJ m mn r cos m .e mnz kc a E z 0
r mn2 AmnJ m mn r cos m .e mnz (4.38) H k c a H mn2 AmnJ m mn r sin m .e mnz kc a lOMoARcPSD| 36067889
Hz AmnJ m amn r cos m .e mnz
Như vậy trong ống dẫn sóng trụ tròn tồn tại vô số trường iện ngang TEmn (hoặc H mn ) với
các số m n, khác nhau. Các số này có quan hệ ến cấu trúc trường trong mặt cắt ngang của ống
dẫn sóng: n ặc trưng cho sự biến ổi trường theo bán kính, m ặc trưng cho sự biến ổi trường
theo chu vi. Cũng giống như ống dẫn sóng chữ nhật, mỗi kiểu trường sẽ có tần số tới hạn và
bước sóng tới hạn riêng.
Tần số tới hạn của trường TEmn ược xác ịnh bởi: f (4.39) th TE kc mn 2 2 a
Còn bước sóng tới hạn: 1 th TE 2 a (4.40) mn 0 0
Các công thức ối với vận tốc pha và vận tốc nhóm của sóng TEmn trong ống dẫn sóng có dạng sau: 2 v 2 ph vfth ; vnh v 1 ffth (4.41) 1 f
Trở kháng của ống dẫn sóng trụ tròn trong trường hợp này bằng: Zc TE Z0 2 1 ffth
4.4.2. Trường từ ngang
Biểu thức gốc ối với các thành phần của vectơ trường từ ngang trong ống dẫn sóng tròn có dạng: lOMoARcPSD| 36067889 c c c (4.42) r 1c2 j
E z ;H k1c2 j
E z ;Hz 0 H k r
Phương trình cho thành phần E z trong hệ tọa ộ trụ là; (4.43) 2E 2 r 2z r1 Erz r12
E2z k Ec2 z 0
Hàm E z phải thỏa mãn iều kiện bờ trên mặt ống dẫn sóng. E z 0 tại r a (4.44) Er 2
Ez ;E 2 12
Erz ;Ez 0 k r k k
Khi thực hiện iều kiện này, tất cả các thành phần tiếp tuyến của vectơ Ez trên mặt ống dẫn sóng sẽ bằng 0.
Để ảm bảo trường có giá trị hữu hạn trên trục, nghiệm của phương trình (4.43)sẽ có dạng:
Ez B Jmm k rc cos m
e z ;m 0,1,2,...
Nghiệm này sẽ thỏa mãn iều kiện (4.44) nếu: mn k c (4.45) lOMoARcPSD| 36067889 a ở ây
mn là nghiệm của phương trình J m
0;m 0,1,2,...;n 1,2,3,...
Giá trị của một số nghiệm ầu của phương trình J m
0; khi m 0,1,2,... như trong bảng 4.2.
Bảng 4.2. Nghiệm của hàm Bessel Số thứ tự nghiệm (n) m 0 m 1 m 2 1 2,405 3,832 5,135 2 5,520 7,016 8,417 3 8,654 10,173 11,620
Thay giá trị E z ã tìm ược vào (4.42) ta ược:
Er kmnc2 BmnJ m amn r cos m .e mnz E mn2 m BmnJ m mn r sin m .e mnz kc r a z mn m mn m .e mnz
E B J r cos a (4.46)
Hr j 2 m BmnJ m mn r sin m .e mnz kc r a H jk c2 BmnJ m amn r cos m .e mnz H z
0;m 0,1,2,... n 1,2,3,... mn mn 2 k 2 a lOMoARcPSD| 36067889
Ta cũng nhận ược vô số kiểu trường TM mn (hay Emn ) ặc trưng bởi các số m và n khác nhau.
Các số này cũng có ý nghĩa giống như trường hợp TEmn .
Tần số tới hạn của trường từ ngang trong ống dẫn sóng trụ tròn: f (4.47) th TM k vc mn 2 2 a Bước sóng tới hạn: 1 th TM 2 a (4.48) mn 0 0
Nếu f fth TM hoặc
th TM thì trường sẽ truyền lan trong ống dẫn sóng dưới dạng sóng chạy.
Cuối cùng cần lưu ý rằng trong ống dẫn sóng chỉ có các sóng iện ngang (TE) hoặc từ
ngang (TM) là có thể tồn tại. Sóng iện từ ngang (TEM) không thể tồn tại trong bất cứ hệ
thống ống dẫn sóng nào. Điều này có thể suy luận một cách ơn giản như sau: Giả sử ường
sức vectơ H nằm hoàn toàn trong mặt cắt ngang của ống dẫn sóng (nghĩa là H chỉ có thành
phần ngang). Theo lý thuyết các ường sức từ khép kín phải bao quanh ường sức dòng iện
tổng, không phân biệt dòng dẫn hay dòng dịch. Nhưng trong ống dẫn sóng không có dây dẫn
nên dòng iện này chỉ có thể là dòng iện dịch. Do ó vectơ E trong trường hợp này phải có
thành phần theo trục z. Điều ó có nghĩa trường trong ống dẫn sóng không phải là trường iện từ ngang nữa. 4.5. Cáp ồng trục
Khi sử dụng ống dẫn sóng ể truyền sóng thì kích thước ngang của ống dẫn sóng phải có
cùng cỡ với bước sóng. Vì vậy ể khả thi thường người ta chỉ dùng ống dẫn sóng có bước sóng
cực ngắn cỡ vài cm, tức tần số siêu cao cỡ 1010Hz . Để truyền năng lượng và tín hiệu iện từ ở
tần số không cao lắm (bước sóng từ vài trăm mét ến vài mét) người ta dùng cáp ồng trục.
Cáp ồng trục là một hệ thống gồm lõi và vỏ trụ tròn bằng vật dẫn, có trục trùng nhau (Hình 4.3). lOMoARcPSD| 36067889
Hình 4.3. Cấu tạo nguyên lý của cáp ồng trục
Cáp ồng trục là loại ường truyền kín và cũng có ưu iểm của ống dẫn sóng là tránh ược
bức xạ năng lượng iện từ ra xung quanh. Nhưng khác với ống dẫn sóng, do cáp có lõi nên
ngoài sóng TE, TM nó còn có thể cho qua sóng iện từ ngang TEM với mọi bước sóng, về
nguyên tắc không bị hạn chế bởi kích thước tiết diện.
Ta cũng ưa ra giải thiết cáp dài vô hạn với ộ dẫn của vỏ là vô cùng lớn, và ộ dẫn iện của
lớp iện môi coi như bằng 0. Ta chọn hệ tọa ộ trụ tròn với trục z hướng theo trục cáp (như trong hình 4.3).
Để ơn giản ta chỉ xét sóng iện từ ngang TEM tức là các cường ộ trường ều không có thành phần dọc trục E z
0,Hz 0 . Do tính ối xứng của lõi và vỏ nên cường ộ từ trường
chỉ có thành phần phương vị H và cường ộ iện trường chỉ có thành phần xuyên trục E r với
trị hiệu dụng chỉ phụ thuộc một tọa ộ r , không phụ thuộc các tọa ộ ,z . Gọi
kz là hệ số pha dọc trục, ta có thể ặt:
H H0 r e j z r E0 r e j z (4.49) E
Trong ó: H 0 r ,E 0 r , là những hàm và thông số chưa biết.
Để tìm ta xuất phát từ các phương trình Maxwell 1,2 trong hệ tọa ộ trụ tròn với E z 0,H z 0; 0; j ta có: z lOMoARcPSD| 36067889 j H j E r , r j H (4.50) j E drdrH 0
Nhân hai vế phương trình (4.49a), (4.49b) với nhau rồi chia hai vế cho H ,E r ta ược: 2 2 hay (4.51)
Vì là một số thực, nên hệ số truyền sóng j là một số ảo không phụ thuộc tần số sóng
và kích thước tiết diện cáp. Tần số tới hạn ứng với
0 trong trường hợp này bằng th 0 .
Điều này có nghĩa là sóng TEM ở mọi tần số, mọi bước sóng ều truyền qua ược dây cáp ồng trục.
Từ (4.49a) và (4.49b) suy ra quan hệ giữa Er ,H : H
Er H H Z H. v
Tức là Er ,H biến thiên cùng pha.
Biểu thức tức thời của chúng có dạng:
H t r , Hm r cos t z , m r cos t z
(4.52) E t r, H
Như vậy sóng iện từ ngang trong cáp hoàn toàn giống sóng phẳng trong không gian tự
do. Bây giờ ta xét sự phân bố của H và E r theo tọa ộ r . Từ công thức (4.50c) ta có: rH
r C const lOMoARcPSD| 36067889 Hay C H r r
Trong ó có thể xác ịnh ược hằng số C theo luật dòng iện toàn phần ối với một ường tròn
bán kính r a1 , ôm sát lõi cáp. 2 aH
a 2 C Im a Từ ó có: C I / 2 Và: H r I/ 2 r (4.53)
Tức trị hiệu dụng của cường ộ từ trường và cường ộ iện trường tỷ lệ nghịch với bán kính
r . Hình 4.4 vẽ phân bố iện trường và từ trường trong cáp ồng trục.
Hình 4.4. Phân bố iện trường và từ trường TEM trong dây cáp ồng trục.
4.6. Đường dây song hành
Ở dải sóng mét, ường truyền năng lượng siêu cao tần dạng phổ biến có cấu tạo ơn giản,
kích thước ngang nhỏ là ường dây song hành. Đường dây song hành ơn giản nhất, gồm có hai
dây dẫn kim loại trụ tròn như nhau ường kính d ặt song song với nhau, cách nhau một khoảng
D giữa hai trục của chúng trong môi trường ồng nhất và ẳng hướng. Môi trường ồng nhất và
ẳng hướng có thể là không khí hay iện môi. Ngoài loại ơn giản nhất hai dây, ường dây song
hành có thể gồm 4 dây hoặc 2 dây có màn chắn kim loại. lOMoARcPSD| 36067889 a) b)
Hình 4.5. Dây song hành loại 2 dây (a) và 4 dây (b)
Sau ây ta chỉ xét trường hợp ường dây song hành ơn giản gồm hai dây dẫn hở. Trường
iện từ truyền dọc ường dây song hành này là trường TEM.
Khi nghiên cứu trường tĩnh iện ở vùng không gian bao quanh hai dây dẫn mảnh ặt song
song cách nhau một khoảng ược tích iện (có cùng iện lượng song trái dấu). Đường sức iện
trường tĩnh của hệ luôn vuông góc với các ường ẳng thế (là họ vòng tròn nằm trong mặt
phẳng vuông góc với trục của hai dây dẫn), nên iện trường nằm trong mặt phẳng ngang với
trục hai dây dẫn. Từ trường sinh ra ở vùng không gian bao quanh hai dây dẫn có dòng iện
không ổi chảy (dòng trong mỗi dây có cùng giá trị song ngược chiều). Nên ường sức từ trường
của hệ trùng với các ường ẳng thế của chúng (cũng là các họ vòng tròn dạng như các ường
ẳng thế của iện trường tĩnh). Do ó từ trường cũng nằm trong mặt phẳng ngang với trục của hai dây dẫn.
Điện áp và dòng iện trên ường dây của sóng thuận (truyền theo chiều dương trục z của hệ) có dạng:
U z( ) U m .e jkz I m .e jkz (4.54) I z( )
Trở sóng ặc tính của ường dây song hành không tiêu hao có dạng: Z CT U U m L0 1 ln
2D (4.55) I I m C 0 d
Ở ây U m ,I m là biên ộ của iện áp và dòng trên dây. L0 ln 2dD ; C 0 ln 2D (4.56) d
là iện cảm và iện dung tính trên một ơn vị ộ dài của ường dây song hành.
Nếu ường dây song hành ược ặt trong không khí ( 0 và
0 ) thì trở sóng ặc tính
của ường dây này có dạng ơn giản là: ZCT 0 120ln 2D 2 276lg D ( ) d d lOMoARcPSD| 36067889 4.7. Mạch dải
Trong kỹ thuật o lường và các thiết bị thu ở các dải sóng từ dm ến mm, người ta thường
sử dụng một loại ường truyền năng lượng siêu cao tần có kích thước gọn nhẹ, ó là các mạch
dải siêu cao tần. Vì các mạch dải siêu cao tần ược chế tạo dưới dạng mạch in nên chúng ược
dùng rất phổ biến trong vi mạch siêu cao. Mạch dải siêu cao thường cấu tạo theo các dạng:
dạng ối xứng, dạng không ối xứng, dạng ường khe và dạng cáp phẳng.
Các tấm iện môi dùng làm ế của mạch dải có hệ số iện môi tương ối lớn cỡ từ 7 ến 13, có
tiêu hao rất nhỏ, có ộ dầy h = 1,5 ến 5mm.
Để tạo ra các dải kim loại dẫn sóng, người ta dùng các kim loại phun, tạo ra trên mặt
tấm iện môi các dải dẫn sóng có ộ dày lớn hơn nhiều lần ộ thấm sâu của trường, cỡ 15 m ến
100 m . Dải kim loại rộng gọi là bản áy hay ất, còn dải hẹp có ộ rộng 0,05mm ến
10mm ược gọi là dải trung tâm dẫn sóng. Độ rộng của mạch dải thường lớn gấp nhiều lần chiều cao tổng cộng của nó.
4.8. Ống dẫn sóng iện môi
Ở dải sóng mm hoặc ngắn hơn (dưới mm hoặc hồng ngoại hay quang học), người ta
dùng ống dẫn sóng iện môi ể truyền dẫn năng lượng iện từ rất thuận tiện vì có năng lượng
tiêu hao nhỏ, kích thước bé và dễ chế tạo. Ống dẫn sóng iện môi có cấu tạo từ một thanh iện
môi ồng nhất dạng phẳng hay trụ tròn gồm một hay nhiều lớp. Nếu các lớp iện môi có chiết
suất ồng nhất và khác nhau thì ược gọi là có dạng nhảy bậc. Còn nếu trong một lớp chính
(thường là lớp giữa) mà chiết suất biến ổi theo theo một hàm số của tốc ộ thì ược gọi là ống
dẫn sóng dạng Gradient. Sóng truyền dọc ống dẫn sóng iện môi là sóng mặt chậm.
Ống dẫn sóng iện môi phẳng ược dùng trong các kỹ thuật quang tích phân, trong các thiết bị laze bán dẫn.
Ống dẫn sóng iện môi trụ tròn dùng chủ yếu ể dẫn năng lượng ở dải sóng mm hay dải
sóng quang học dưới dạng sợi quang.
CÂU HỎI VÀ BÀI TẬP CHƯƠNG 4
Bài 4-1: Tại sao ở tần số cao ể dẫn năng lượng iện từ phải dùng ống dẫn sóng hoặc cáp ồng trục
mà không dùng ược ường dây thông thường như ở tần số thấp?
Bài 4-2: Tại sao sóng TEM không truyền ược trong ống dẫn sóng? Tại sao cáp ồng trục có thể
cho tất cả các loại sóng TEM, TE, TM i qua?
Bài 4-3: Bước sóng tới hạn của ống dẫn sóng là gì? Nó phụ thuộc những yếu tố nào? Chứng minh rằng nếu
th thì sóng sẽ tắt mà không chạy trong ống dẫn sóng. lOMoARcPSD| 36067889
Bài 4-4: Cho một ống dẫn sóng chữ nhật có kích thước a 2,5cm và b 5cm . Độ dẫn iện của
thành ống vô cùng lớn. Điện môi bên trong ống là không khí. Hỏi ở tần số f 7,5Ghz những
mode sóng nào có thể truyền ược trong ống? Tính th và s của các mode sóng ó?
Bài 4-5: Cho một ống dẫn sóng hình trụ tròn bán kính a 2cm , ộ dẫn iện của thành ống lớn
vô cùng, iện môi trong ống là không khí. Hỏi ở tần số f 1010 Hz những mode sóng nào có thể
truyền qua ống ược? Tính bước sóng tới hạn và bước sóng trong ống dẫn sóng của những mode sóng ó?
Bài 4-6: Tính và biểu diễn lên trục số các bước sóng tới hạn và bước sóng của các dạng sóng
trong ống dẫn sóng chữ nhật bên trong chứa không khí có kích thước tiết diện ngang
a 7, 2cm b; 3,4cm , bước sóng = 3,9cm.
CHƯƠNG 5. HỘP CỘNG HƯỞNG
5.1. Khái niệm về hộp cộng hưởng
Thông thường mỗi hệ thống dao ộng là một mạch iện gồm iện cảm L và C . Hai thông số
quan trọng của mạch là tần số cộng hưởng và hệ số phẩm chất. Ở môn học Lý thuyết mạch,
chúng ta ã biết mạch LC cho tần số cộng hưởng riêng là: 1 f0 (5.1) 2 LC 1
Còn hệ số phẩm chất: Q L R C
Nhưng ở dải tần số siêu cao (trừ sóng dài của dải sóng m), ta không thể dùng mạch LC
cho hiện tượng cộng hưởng, do các nguyên nhân sau:
1. Để nhận ược tần số cộng hưởng f0 lớn, ta phải giảm nhỏ các giá trị L và C của cuộn
cảm hay tụ iện. Do kích thước chế tạo, ta không thể có các giá trị L và C nhỏ như yêu cầu ược.
2. Ở dải sóng siêu cao, kích thước của các cuộn cảm hay tụ iện so sánh ược với bước
sóng nên tại các tần số này, bản thân mạch dao ộng cũng óng vai trò như các phần
tử bức xạ năng lượng iện từ làm tăng tiêu hao năng lượng áng kể trong mạch dao ộng
và mạch không duy trì ược dao ộng ở dải này. lOMoAR cPSD| 36067889
3. Khi tần số tăng, tiêu hao do hiệu ứng bề mặt và tiêu hao trong iện môi của cuộn cảm
và tụ iện tăng áng kể làm giảm phẩm chất của mạch dao ộng LC, làm cho nó mất
tính chọn lọc cộng hưởng.
Vì vậy, ở dải sóng siêu cao, người ta sử dụng các mạch dao ộng có tham số phân bố,
thường gọi là hộp cộng hưởng.
Định nghĩa: Hộp cộng hưởng là một vùng không gian hữu hạn mà ở trong nó sau
khoảng thời gian lớn hơn nhiều chu kỳ dao ộng siêu cao tần có sự tích lũy năng lượng iện từ.
Hộp cộng hưởng thường có dạng kín, tức là ược bao bọc bởi thành kim loại. Tuy nhiên
cũng có hộp cộng hưởng dạng không kín như hộp cộng hưởng iện môi, hộp cộng hưởng hở ở
dải mm hay dải quang học, bao gồm hai bản phản xạ ặt song song cách nhau một khoảng nhất
ịnh. Các hộp cộng hưởng kín lại chia làm hai loại:
1. Các hộp cộng hưởng có cấu trúc tương ối ơn giản ược tạo nên từ các oạn ống dẫn
sóng ồng nhất rỗng như: hộp cộng hưởng chữ nhật, hộp cộng hưởng trụ tròn, hộp
cộng hưởng ồng trục, hộp cộng hưởng xuyên tâm…
2. Các hộp cộng hưởng có cấu trúc phức tạp hơn như: hộp cộng hưởng hình xuyến, hộp
cộng hưởng dạng một khâu của èn Manhetron, hộp cộng hưởng ồng trục có khe hở…
Đối với các hộp cộng hưởng từ oạn ống dẫn sóng rỗng, do cấu trúc ơn giản nên ta có
thể tìm ược trường iện từ các dạng tồn tại bên trong chúng bằng cách tìm nghiệm của các
phương trình Maxwell với các iều kiện bờ ã cho rồi từ ó tìm ược các ại lượng ặc trưng cơ bản
là bước sóng cộng hưởng riêng hay tần số cộng hưởng riêng và hệ số phẩm chất của hộp cộng
hưởng ứng với các dạng dao ộng khác nhau trong hộp.
Đối với các hộp cộng hưởng phức tạp thì do cấu trúc iều kiện bờ phức tạp, ta chỉ xét cấu
trúc của trường iện từ của các dao ộng hay sóng trong chúng, kết hợp với tìm biểu thức cho
bước sóng hay tần số cộng hưởng riêng của dạng dao ộng ược sử dụng và nêu ứng dụng của chúng.
Khác với các mạch cộng hưởng LC chỉ có một tần số cộng hưởng riêng f0 khi ã cho các
giá trị của L và C, trong hộp cộng hưởng với kích thước ã cho có thể tồn tại vô số các dao
ộng riêng có cấu trúc trường khác nhau và tương ứng cho các bước sóng cộng hưởng hay tần
số cộng hưởng và hệ số phẩm chất khác nhau.
Các hộp cộng hưởng ược ứng dụng trong kỹ thuật siêu cao làm mạch dao ộng trong các
lĩnh vực như: trong chế ộ dao ộng tự do nó ược dùng làm hộp tiếng vọng ể kiểm tra các trạm
phát xung. Trong chế ộ dao ộng cưỡng bức, hộp cộng hưởng óng vai trò của hệ cộng hưởng
chọn lọc cho các thiết bị thu, phát, o lường. Trong các dụng cụ iện tử và bán dẫn siêu cao,
hộp cộng hưởng tạo ra không gian tương tác và trao ổi năng lượng giữa trường iện từ và các
iện tử hoặc lỗ trống ể tạo hoặc khuếch ại các dao ộng siêu cao tần. lOMoARcPSD| 36067889
5.2. Hệ số phẩm chất của hộp công hưởng
5.2.1. Khái niệm chung
Hệ số phẩm chất của hộp cộng hưởng là một tham số cơ bản, nó ặc trưng cho khả năng
duy trì các dao ộng tự do trong hộp và dải thông của hộp. Nếu hộp cộng hưởng ược sử dụng
làm mạch dao ộng cộng hưởng trong máy thu thì hệ số phẩm chất của nó ánh giá khả năng
chọn lọc tần số của máy thu.
Hệ số phẩm chất của mạch cộng hưởng ối với một dạng mạch dao ộng riêng ược xác ịnh bởi biểu thức sau: Q W 0 (5.1) Pth Hoặc: Q 2 W (5.2) Wth 0 Ở ây:
W là năng lượng của trường iện từ tích lũy trong hộp.
Wth = Pth.T là năng lượng iện từ tiêu hao trong hộp sau một chu kỳ của trường,
Pth là công suất tiêu hao của trường trong hộp, 0 là tần số cộng hưởng của dạng dao ộng.
Vì trong hộp cộng hưởng tồn tại vô số các dao ộng riêng, mỗi dạng có cấu trúc trường
riêng nên có năng lượng tích lũy, năng lượng tiêu hao hay công suất tiêu hao riêng, do ó hộp
cộng hưởng cũng có vô số ộ phẩm chất. Từ nay về sau, khi xét hệ số phẩm chất của hộp cộng
hưởng, ta hiểu ngầm là chỉ cho một dạng dao ộng riêng không suy biến tồn tại trong hộp.
5.2.2. Các loại hệ số phẩm chất của hộp cộng hưởng
Tiêu hao năng lượng của trường iện từ trong hộp cộng hưởng do các nguyên nhân sau:
tiêu hao trên bề mặt bên trong của hộp do hiệu ứng bề mặt, tiêu hao trong chất iện môi chứa
trong hộp, tiêu hao do ghép với tải bên ngoài của hộp. Nên ta có thể viết:
Pth Pthkl Pthdm Ptht (5.3)
Và ta viết (5.3) dưới dạng sau: 1 Pth 1 1 1 1 1 (5.4) Qt 0W Qkl Qdm Qng Q0 Qng
Ta ưa vào các loại hệ số phẩm chất sau của hộp: lOMoARcPSD| 36067889
Hệ số phẩm chất của hộp khi chỉ tính tiêu hao do hiệu ứng bề mặt trong hộp: Q W kl 0 (5.5) Pthkl
Hệ số phẩm chất của hộp khi chỉ tính ến tiêu hao trong chất iện môi chứa trong hộp: Q W dm 0 (5.6) Pthdm
Hệ số phẩm chất ngoài khi chỉ tính ến tiêu hao do ghép tải ở ngoài hộp: Q W (5.7) ng 0 Ptht
Trong trường hợp chung thì hệ số phẩm chất của hộp cộng hưởng là hệ số phẩm chất
tải Qt. Q0 ược gọi là hệ số phẩm chất không tải hay hệ số phẩm chất riêng của hộp. Nó chỉ
liên quan ến tiêu hao xảy ra trong bản thân hộp mà không tính ến ảnh hưởng của tải. Ta có: 1 1 1 (5.8) Q0 Qkl Qdm
Để chỉ mức ộ liên kết giữa hộp cộng hưởng và tải bên ngoài, người ta còn ưa vào khái
niệm hiệu suất của hộp cộng hưởng và ký hiệu bởi chữ h ược xác ịnh bởi biểu thức sau: Ptht h (5.9) Pth Từ
(5.4), (5.7) và (5.9) ta tính ược: th Qt Q0 1 Qt (5.10) Qng Q0 Qng Q0
Khi Q0 Qng ta có sự ghép giữa hộp cộng hưởng và tải ở chế ộ tới hạn.
- Khi Qng Q0 ta có chế ộ ghép chặt,
- Ngược lại chế ộ ghép lỏng ứng với trường hợp Qng Q0 .
5.3. Hộp cộng hưởng chữ nhật lOMoARcPSD| 36067889 y
Hình 5.1. Hộp cộng hưởng chữ nhật
Trường ở trong hộp cộng hưởng có thể xác ịnh theo phương pháp tương tự như với ống
dẫn sóng, nhưng ở ây cần lưu ý là theo hướng z trường cũng có dạng sóng ứng do kích thước
của ống dẫn sóng theo chiều z không phải là vô hạn mà bị giới hạn bởi các vách kim loại.
Sóng phản xạ từ hai vách kim loại này sẽ tạo ra sóng ứng, giống như sóng ứng theo các trục
x và y của ống dẫn sóng.
Tương tự như ối với ống dẫn sóng, ta sẽ nhận ược kết quả là trong hộp cộng hưởng có
thể tồn tại vô số kiểu trường iện ngang và trường từ ngang khác nhau ặc trưng bởi 3 chỉ số m
n, và p ó là TEmnp và TM mnp . Ở ây hai chỉ số ầu m và n cũng có ý nghĩa như trường hợp ống dẫn
sóng, nghĩa là ặc trưng cho số nửa sóng của sóng ứng theo hai cạnh x và y , còn chỉ số p ặc
trưng cho số nửa sóng của sóng ứng theo cạnh z . Mỗi kiểu trường iện ngang và từ ngang này
là một dao ộng riêng của hộp cộng hưởng.
5.3.1. Trường từ ngang TM
Áp dụng kết quả của phân bố trường theo tọa ộ ngang trong ống dẫn sóng chữ nhật, ta
nhận ược biểu thức biên ộ của trường TM trong hộp cộng hưởng chữ nhật như sau: Ez Em sin m x sin n y cos p z a b L
Ex Em2 p m cos m x sin n y sin p z
kc L a a b L
Ey Em2 p n sin m x cos n y sin p z (5.11) kc L b a b L H x jEm2 n sin m x cos n y cos p z kc b a b L H y jEm2 m cos m x sin n y cos p z kc a a b L lOMoARcPSD| 36067889 E m
2A là một hằng số tùy ý, nó ược xác ịnh từ kết quả của việc kích thích trường. kc2 2 k 2 m n, 1,2,3,... p 1,2,...
Bước sóng cộng hưởng riêng trong hộp cộng hưởng chữ nhật ược tính theo biểu thức sau ây:
kc2 k 2 2 k 2 / 0 , j j p , L kc2 m 2 n 2 a b Suy ra: 2 (5.12) 0 2 2 2 m n p a b L
Từ biểu thức của các thành phần trường TMmnp, ta thấy các thành phần ngang của iện
trường và từ trường lệch pha nhau 900. Do ó vectơ mật ộ công suất trung bình theo phương
trục z bằng 0. Ngoài ra, thành phần dọc Ez ồng pha với các thành phần ngang Ex ,Ey song iểm
cực ại của chúng lại lệch nhau theo trục z i một khoảng t / 4 . Trong ống dẫn sóng chữ nhật,
ta ã biết hệ số pha biểu thị qua bước sóng trong ống dẫn sóng t có dạng:
= 2 mà = p nên ta suy ra: t L
L p t , p = 1, 2, 3,… (5.13)
Biểu thức (5.13) gọi là iều kiện cộng hưởng của hộp cộng hưởng chữ nhật. Điều kiện
(5.13) mô tả hiện tượng là từ một tiết diện z bất kỳ, sóng truyền dọc theo trụczvà và sóng phản
xạ liên tiếp hai lần tại hai áy z 0,z L có pha cách nhau 2p tức là chúng ồng pha. Dạng lOMoARcPSD| 36067889
dao ộng ơn vị nào thỏa mãn iều kiện cộng hưởng sẽ có biên ộ rất lớn trong hộp, còn các dạng
dao ộng khác sẽ bị tiêu hao nên tắt rất nhanh.
5.3.2. Trường iện ngang TE
Các thành phần trường TE trong hộp cộng hưởng chữ nhật sau: H z H m cos m x cos n y sin p z a b L
H x H 2m p m sin m x cos n y cos p z
kc L a a b L
H y H 2m p n cos
m x sin n y cos p z (5.14) kc L b a b L Ex H m j2 n cos m x sin n y sin p z kc b a b L Ey H m j2 m sin m x cos n y sin p z kc a a b L ở ây ta chọn: H m
2A với m n, 0,1,2,...; p 1,2,3,...
Bước sóng cộng hưởng riêng của dạng trường TEmnp trong hộp này cũng ược biểu thị
bởi (5.12). Điều kiện cộng hưởng cho dạng trường TE trong hộp cộng hưởng chữ nhật cũng
tuân theo biểu thức (5.13). Từ các biểu thức (5.11) và (5.14) ta thấy ứng với một cặp ba số
nguyên m n p, , trong hộp cộng hưởng chữ nhật tồn tại các dạng trường ơn vị dạng TMmnp(Emnp) và TEmnp(Hmnp).
Chúng ược gọi là các dạng dao ộng riêng trong hộp cộng hưởng. Mỗi dạng dao ộng
riêng có bước sóng cộng hưởng riêng theo công thức (5.12) khi ã cho kích thước của hộp,
dao ộng riêng có bước sóng cộng hưởng lớn nhất gọi là dạng dao ộng cơ bản, các dạng dao
ộng khác gọi là dạng dao ộng bậc cao. Chẳng hạn nếu ta có kích thước của hộp: L a b 0 thì:
0(H101) a22aL L2 max
Nên dạng dao ộng H101 là cơ bản trong hộp cộng hưởng chữ nhật. lOMoARcPSD| 36067889
Các dạng dao ộng riêng trong hộp cộng hưởng chữ nhật có cấu trúc trường khác nhau,
nhưng có cùng tần số hay bước sóng cộng hưởng riêng gọi là dạng dao ộng suy biến. Chẳng
hạn các dạng dao ộng TMmnp và TEmnp khi có cùng chỉ số là các dạng suy biến. Dạng dao ộng
cơ bản trong hộp cộng hưởng không óng vai trò quan trọng như trường cơ bản trong ống dẫn sóng.
5.3.3. Điều chỉnh tần số cộng hưởng
Từ các mục trước, chúng ta ã biết rằng tần số cộng hưởng có liên quan ến kích thước
của hộp cộng hưởng qua biểu thức của iều kiện cộng hưởng. Do vậy, khi thay ổi kích thước
của hộp ta nhận ược các giá trị khác nhau của tần số cộng hưởng hay bước sóng cộng hưởng.
Điều này thường hay thực hiện bởi pittông dịch chuyển ược. Tuy nhiên trong một số trường
hợp chỉ cần iều chỉnh tần số cộng hưởng của một dạng dao ộng ã cho trong hộp ở phạm vi
nhỏ, mà cấu trúc của hộp ỡ phức tạp và giảm tiêu hao do có dòng mặt ở chỗ tiếp xúc của
pittông với thành hộp, người ta không dùng pit-tông dịch chuyển mà dùng phương pháp nhiễu loạn nhỏ.
Việc iều chỉnh tần số cộng hưởng của hộp theo phương pháp này ược thực hiện bằng
cách ưa vào bên trong hộp một vật thể có kích thước nhỏ hơn nhiều so với kích thước hộp.
Vật thể ưa vào trong hộp có thể là iện môi, ferit hay kim loại dẫn iện lý tưởng. Phương pháp
iều chỉnh cộng hưởng này cho phép ta khắc phục ược các nhược iểm khi chế tạo hộp không
chính xác và bù ược một số sai sót do bất ồng nhất gây ra làm ảnh hưởng ến iều kiện cộng
hưởng và cách thực hiện khá ơn giản. Vì thể tích của vật thể ưa vào rất nhỏ so với thể tích
của hộp nên nó không gây ra méo áng kể ến cấu trúc trường của dạng dao ộng trong hộp, từ
ó ta coi vật thể ưa vào như một nhiễu loạn nhỏ.
Giả sử ta có hộp cộng hưởng dạng tùy ý có thể tích V, bên trong chứa không khí với
hằng số 0, 0 ang làm việc với một dạng dao ộng nào ó ở tần số . Bây giờ ta ưa vào trong
hộp một vật thể rất nhỏ có thể tích là V0 với hằng số , , .
Theo kết quả của phương pháp nhiễu loạn nhỏ thì sự thay ổi tần số tương ối trong hộp ược
xác ịnh bởi biểu thức sau: WH WE (5.15) 2W V( ) 1 1 Ở ây: W V() 0 E dV2 0 H dV2 2 V 2 V
Là năng lượng tích lũy cực ại của iện trường hoặc từ trường trong hộp cộng hưởng không
nhiễu loạn (chưa ưa vật thể vào).
Trường hợp vật thể ưa vào là kim loại thì: WE WE V0 (5.16) lOMoARcPSD| 36067889 WH WH V0
WE(V0), WH(V0) là iện năng và từ năng cực ại trong thể tích V0 ã có trước ây của hộp khi chưa ưa vật thể vào.
Nếu vật ưa vào là iện môi hay ferit thì: E 0 0 WE (V0 ) W (5.17) W H 00 WH (V0 )
5.3.4. Kích thích và ghép năng lượng trong ống dẫn sóng và hộp cộng hưởng
Ta ã xét các dạng trường iện từ tồn tại trong ống dẫn sóng và trong hộp cộng hưởng
cùng các tính chất quan trọng của chúng. Tuy nhiên lại xuất hiện một vấn ề là các dạng trường
trong ống dẫn sóng và trong hộp cộng hưởng ược tạo ra như thế nào và cần dẫn năng lượng
từ chúng ra mạch ngoài ra sao.
Các phần tử dùng ể tạo ra dạng trường mong muốn trong ống dẫn sóng hay hộp cộng
hưởng ược gọi là phần tử kích thích. Ngược lại các phần tử dùng ể ghép năng lượng của dạng
trường ã cho ra mạch ngoài gọi là phần tử liên kết hay phần tử ghép.
Theo nguyên lý tương hỗ trong lý thuyết trường iện từ, chúng ta nhận thấy nguyên tắc
làm hoạt ộng của các phần tử kích thích và các phần tử ghép là tương tự nhau. Tức là cùng
một phần tử có thể làm chức năng của phần tử kích thích và ngược lại cũng có thể làm chức
năng của phần tử ghép tùy theo từng ứng dụng. Vì vậy, ở ây ta chỉ xét trường hợp phần tử kích thích.
Bài toán kích thích trường trong ống dẫn sóng và trong hộp cộng hưởng là bài toán tìm
trường iện từ trong ống dẫn sóng và trong hộp cộng hưởng của nguồn ã cho với phân bố dòng
ã biết trong phần tử kích thích. Để tìm nghiệm của nó, người ta tiến hành như sau: biểu diễn
trường cần tìm trong ống dẫn sóng và trong hộp cộng hưởng dưới dạng tổ hợp của các dạng
trường ơn vị trong ống dẫn sóng và tổ hợp các dao ộng riêng trong hộp cộng hưởng với các
hệ số khai triển cần tìm. Yêu cầu ặt ra là trường phải tìm tại vị trí ặt phần tử kích thích trùng
với trường của nó có phân bố dòng ã cho. Khi ồng nhất các hệ số triển khai của chúng, ta tìm
ược kết quả của bài toán. Việc tính toán ịnh lượng bài toán này sẽ dẫn ến việc xây dựng các
sơ ồ tương ương thay thế của các phần tử kích thích.
Sau ây ta chỉ trình bày nguyên tắc hoạt ộng theo quan iểm ịnh tính của các phần tử kích
thích trường trong ống dẫn sóng và trong hộp cộng hưởng.
Theo lý thuyết trường iện từ, các phần tử kích thích trường chính là các bức xạ nguyên
tố. Chúng có dạng là các lưỡng cực iện, lưỡng cực từ hoặc tổ hợp của cả hai dạng trên. Do
vậy, các phần tử kích thích trường trong ống dẫn sóng và trong hộp cộng hưởng cũng gồm ba
loại: loại iện, loại từ và loại nhiễu xạ. Nguyên tắc tạo trường của chúng tuân theo nguyên tắc
của các bức xạ nguyên tố. lOMoARcPSD| 36067889
5.3.4.1. Phần tử kích thích dạng iện
Phần tử kích thích dạng iện ược thực hiện bằng các que dò hay thăm kim loại mảnh ưa
vào bên trong ống dẫn sóng hoặc hộp cộng hưởng. Muốn tạo ra dạng trường ơn vị hoặc dạng
dao ộng riêng mong ợi, ta phải ặt que dò hay que thăm ở vị trí mà iện trường của trường ơn
vị hay dạng dao ộng riêng là cực ại và phương của dò hay thăm phải song song với ường sức
của iện trường. Phần tử kích thích loại iện này thường là phần kéo dài của lõi giữa ống dẫn
sóng ồng trục hay cáp ồng trục ưa vào bên trong ống dẫn sóng có chiều dài xác ịnh, còn lõi
ngoài của ống ồng trục nối với thành ống dẫn sóng hay hộp cộng hưởng.
5.3.4.2. Phần tử kích thích dạng từ
Phần tử kích thích dạng từ ược thực hiện dưới dạng vòng dây dẫn mảnh có diện tích
nhỏ (lưỡng cực từ) ược ưa vào trong ống dẫn sóng hay hộp cộng hưởng. Muốn tạo ra dạng
trường ơn vị hoặc dạng dao ộng riêng mong muốn, ta ặt vòng dây kích thích dẫn năng lượng
siêu cao tần từ nguồn ngoài vào trong ống dẫn sóng hay hộp cộng hưởng tại vị trí từ trường
của dạng trường ơn vị hay dạng dao ộng riêng là cực ại và mặt phẳng vòng dây vuông góc với
ường sức từ trường của chúng.
5.3.4.3. Phần tử kích thích dạng nhiễu xạ
Phần tử kích thích dạng nhiễu xạ ược thực hiện bằng cách xẻ các khe hẹp hay lỗ nhỏ
trên thành ống dẫn sóng hay hộp cộng hưởng. Vì trên thành hay bên trong của ống dẫn sóng
hay hộp cộng hưởng ứng với một dạng trường ơn vị hay dạng dao ộng riêng ã cho có phân
bố dòng iện mặt xác ịnh. Việc xẻ các khe hay lỗ trên thành ống dẫn sóng hay hộp cộng hưởng
sẽ làm biến dạng phân bố của dòng iện mặt và thành phần tiếp tuyến của từ trường tại ây và
khe hoặc lỗ trở thành nguồn bức xạ thứ cấp tương ương như một lưỡng cực từ hoặc tổ hợp
của cả lưỡng cực iện và từ tùy theo vị trí và hình dạng của lỗ hay khe. Kích thích dạng nhiễu
xạ rất thích hợp khi ghép nối giữa các ống dẫn sóng với nhau hoặc giữa ống dẫn sóng và hộp
cộng hưởng. Để tạo ra dạng trường ơn vị hay dạng dao ộng riêng mong muốn trong ống dẫn
sóng và trong hộp cộng hưởng, ta cần xẻ khe hẹp hay lỗ nhỏ ở chỗ trên thành có dòng iện
mặt của trường ã cho cực ại và cắt ngang dòng mặt này hoặc ở chỗ có thành phần tiếp tuyến
của từ trường cực ại và khe hay lỗ song song với tiếp tuyến từ trường. BÀI TẬP CHƯƠNG 5
Bài 5-1: Một hộp cộng hưởng chữ nhật có các kích thước a 10cm b; 20cm L; 30cm . Độ
dẫn iện của thành hộp là vô cùng lớn, iện môi bên trong là không khí. Tính tần số sóng trong
hộp cộng hưởng với m 1,n 0, p 1.
Bài 5-2: Tính và lập bảng các bước sóng cộng hưởng riêng trong hộp cộng hưởng chữ nhật
rỗng có kích thước a 7, 2cm b; 3,4cm L; 10cm với các dạng dao ộng hoạt ộng có trong dải sóng có t 5,3cm . lOMoARcPSD| 36067889
CHƯƠNG 6. MẠNG NHIỀU CỰC SIÊU CAO TẦN
Ngoài ường truyền và hộp cộng hưởng, trong kỹ thuật siêu cao tần còn sử dụng các
phần tử thụ ộng tuyến tính và không tuyến tính khác nhau. Những phần tử này có cấu trúc rất
a dạng và có những tính chất ặc thù ể ảm nhiệm các chức năng cần thiết. Khi nghiên cứu và
ứng dụng các phần tử này, nếu dựa trên sự tính toán cấu trúc trường iện từ và tính các tham
số ặc trưng bên trong của thiết bị thường gặp nhiều khó khăn do cấu trúc và iều kiện biên của
chúng phức tạp. Hơn nữa với các phần tử này, người ta quan tâm chủ yếu ến công suất truyền,
hệ số phản xạ và sự phối hợp trở kháng trên ường truyền. Các ặc tính iện bên ngoài của các
phần tử (tức là các tham số phản ánh tính chất iện của các phần tử tại các mặt cuối của chúng)
ủ cho phép ta giải quyết các nhu cầu trên. Khi nghiên cứu các tham số iện bên ngoài, ta sử
dụng công cụ toán là ại số tuyến tính và các phép tính ma trận. Các phần tử siêu cao tần ược
xem là các “mạng nhiều cực siêu cao”
6.1. Mạng nhiều cực siêu cao tần
6.1.1. Khái niệm
Một cách tổng quát, ta hiểu mạng nhiều cực siêu cao tần là một vùng không gian ược
giới hạn bởi các mặt dẫn kim loại dẫn iện tốt (còn gọi là bọc kim loại) chỉ thông ra ngoài qua
những nhánh là các oạn ường truyền dẫn năng lượng siêu cao.
Nếu mạng có n nhánh ( l1, l 2 ,..., ln ) thì gọi ó là mạng 2n cực siêu cao. Các nhánh có thể
có tiết diện khác nhau hoặc cấu trúc khác nhau. Tiết diện cuối cùng của các nhánh (C1,C2, …
Cn) ược gọi là các mặt cuối của mạng 2n cực. Khi nghiên cứu các mạng 2n cực siêu cao, ta
giả thiết rằng trong mỗi nhánh của nó chỉ tồn tại một dạng trường, ồng thời các mặt cuối C
phải chọn cách ủ xa chỗ nối vào bọc kim loại ể tại các mặt cuối không tồn tại các trường bậc cao. Ta quy ước rằng:
- Sóng i từ ngoài qua mặt cuối C vào mạng nhiều cực ược gọi là sóng tới a , -
Còn sóng i từ trong mạng ra ngoài qua C ược gọi là sóng phản xạ b . l l l l ạng 2n cực lOMoARcPSD| 36067889
6.1.2. Công suất phức
Có một oạn ường truyền L nối giữa máy phát và một nhánh l của mạng nhiều cực như hình 6.2. l ạng cực
Hình 6.2. Ghép nối một cổng với máy phát
Như vậy tại mặt cuối C sẽ có sóng tới từ máy phát truyền vào mạng nhiều cực và cũng có
sóng phản xạ từ mạng nhiều cực qua C.
Trên oạn ường truyền L có sóng ứng. Nếu ta gọi E và H là cường ộ trường của sóng ứng
tại C thì theo lý thuyết trường, công suất của sóng qua C phải là:
P 1 [E H*]dS (6.1) 2 S Ở ây:
Dấu (*) chỉ ại lượng liên hiệp phức
S là tiết diện của ường truyền tại C.
dS là vi phân diện tích tiết diện
Công thức (6.1) cho ta công suất phức của sóng qua mặt cuối C. Công suất trung bình của
nó là phần thực của biểu thức (6.1).
Ta có thể chuyển công thức (6.1) về dạng sau:
P 1 [Eq Hq*]dS (6.2) 2 S
Ở ây, Eq và H q là các thành phần ngang của iện và từ trường của sóng. Do vậy về sau ta
sẽ ề cập chủ yếu ến các thành phần ngang của trường.
Với một sóng chạy bất kỳ theo hướng truyền sóng gọi là sóng tới, thành phần ngang của
iện từ trường ược biểu diễn như sau: lOMoARcPSD| 36067889
qt q E10qt (q q1, 2 ).e z E qt
q H20qt (q q1, 2 ).e z (6.3) H
q 10 ,q 20 Là các vector ơn vị hướng theo 2 trục tọa ộ ngang q q1, 2
E t (q q1, 2 ) và H t (q q1, 2 )là biên ộ phức,
là hệ số truyền sóng.
Còn z là tọa ộ dọc theo phương truyền sóng.
Từ (6.2) và (6.3) ta nhận ược:
P 1 E Hqtqt *dS (6.4) 2 S
6.1.3. Sóng chuẩn hóa
Để tiện lợi cho việc nghiên cứu sự truyền sóng trong tuyến siêu cao, người ta ưa vào
khái niệm “sóng chuẩn hóa”. Sóng chuẩn hóa là sóng chạy trên ường truyền của một dạng
sóng nhất ịnh ở tần số công tác có công suất truyền trung bình qua tiết diện S của ường truyền
bằng ½ (công suất cực ại bằng 1).
Nếu ta gọi ech là biên ộ phức iện trường của sóng chuẩn hóa và hch là biên ộ phức từ trường
của nó thì iều kiện chuẩn hóa trên có dạng: e * ch .h dSch 1 (6.5) S
ech ,hch là các hàm của tọa ộ ngang tại tiết diện S của ường truyền. Khi ó một sóng chạy
tới theo chiều dương z trên ường truyền tại tiết diện S bất kỳ có biên ộ iện và từ trường ngang
ược biểu diễn qua biên ộ sóng chuẩn hóa như sau: Eqt e ach t (6.6) H q h ach a
là biên ộ sóng tới (hoặc gọi tắt là sóng tới). Nó là một ại lượng phức không
phụ thuộc vào các tọa ộ ngang của tiết diện S trên ường truyền, nó tỉ lệ với biên ộ iện trường ngang của sóng tới.
Đối với sóng chạy phản xạ (theo chiều z âm), ta cũng có biểu thức tương tự sau: lOMoARcPSD| 36067889 Eqpx e bch px (6.7) H q h bch b
là biên ộ sóng phản xạ, nó cũng là một ại lượng phức và tỉ lệ với biên ộ iện
trường ngang của sóng phản xạ.
Từ (6.4), (6.5), (6.6) và (6.7) ta biểu diễn ược công suất của sóng tới và sóng phản xạ như sau: Pt 1 E H dSqt qt * 1 aa*e h dSch ch* 1 |a |2 (6.8) 2 S 2 S 2
Ppx 1 EqpxHqpxdS 1 bb e h dS* ch ch* 1 |b |2 (6.9) 2 S 2 S 2
Ta ưa vào khái niệm iện áp chuẩn hóa và dòng chuẩn hóa tại một tiết diện S bất kỳ trên
ường truyền sẽ giúp ích cho việc tính và phân tích các mạch iện siêu cao tần về sau. Chúng ược ịnh nghĩa như sau: u a b (6.10) i a b
u là iện áp chuẩn hóa, i là dòng iện chuẩn hóa.
Tương tự như ở mạch iện với tham số tập trung, ta gọi tỉ số iện áp chuẩn hóa và dòng iện
chuẩn hóa là trở kháng chuẩn hóa, ký hiệu là zch , ta có: z u (6.11) i ch i
Từ (6.10) ta có thể viết: a
(6.12) b ( u i ) lOMoAR cPSD| 36067889
Hệ số phản xạ tại tiết diện S tùy ý trên ường truyền là tỉ số giữa biên ộ iện trường ngang
của sóng phản xạ trên biên ộ iện trường ngang của sóng tới. Ký hiệu là Rpx, ta có biểu thức:
Rpx Eqpxt b (6.13) Eq a
Từ (6.10), (6.11) và (6.13) ta suy ra mối quan hệ giữa trở kháng chuẩn hóa và hệ số phản xạ sau: a b 1 Rch (6.14) Z ch a b 1 Rch Và ngược lại:
R Zch 1 (6.15) px Zch 1
Trên ường truyền, khi có cả sóng tới và sóng chạy phản xạ ồng thời thì sóng tổng hợp sẽ
là sóng ứng. Điện trường ngang của sóng ứng có biên ộ là:
Eq Eqt Eqpx Eqt (1 Rpx )
Giá trị lớn nhất của E ược gọi là iểm bụng của sóng ứng:
Eqb Eqmax Eqt (1 |Rpx |)
Còn giá trị nhỏ nhất của E ược gọi là iểm nút của sóng ứng:
Eqn Eqmin Eqt (1 |Rpx |)
Tỉ số giữa iện trường cực ại và iện trường cực tiểu ược gọi là hệ số sóng ứng iện áp, ký
hiệu là Kd và có biểu thức: d
Eq max 1 | Rpx | (6.16) K
Eq min 1 | Rpx |
Nghịch ảo của hệ số sóng ứng ược gọi là hệ số sóng chạy: 1 1 |Rpx | (6.17) K d K d 1 |Rpx |
Vì module của hệ số phản xạ R biến thiên từ 0 ến 1 nên K d có giá trị từ 1còn Kch có giá trị từ 0 ến 1. lOMoARcPSD| 36067889
Với các khái niệm và ịnh nghĩa trên ây, ta nghiên cứu mạng nhiều cực siêu cao với phương pháp ma trận sóng ứng.
6.2. Ma trận sóng của mạng nhiều cực siêu cao
6.2.1. Ma trận tán xạ
Giả sử ta có một mạng 2n cực, nhánh p của nó ược nối với máy phát siêu cao có sóng
tới qua mặt cuối Cp là ap, các nhánh còn lại của mạng 2n cực ược lắp tải không phản xạ (gọi
là tải phối hợp). Trong một nhánh q bất kỳ khác sẽ có sóng i ra khỏi mạng 2n cực qua mặt
cuối Cq vào tải là bq. Đồng thời tại mặt Cp cũng có một sóng phản xạ lại máy phát là bp. Ta có
mối quan hệ giữa các sóng bp, bq, và ap như sau:
bp S app p với p khácq; p q, 1, 2,...,n bq S aqpp
Ở ây, Spp ,Sqp là các hệ số tỉ lệ, mô tả tính chất của mạng 2n cực không phụ thuộc và ap ,b
bp , q chúng là các ại lượng phức. Rõ ràng trong trường hợp tổng quát nhất khi các nhánh của
2n cực có sóng tới thì bất kỳ một sóng phản xạ nào tại mỗi nhánh phải phụ thuộc vào sóng
tới ở tất cả các nhánh của nó. Vì mạng 2n cực là tuyến tính nên ta có biểu thức sau: n (6.18) bp S apq q q 1
Biểu thức (6.18) viết cho tất cả n nhánh là:
b1 S a111 S a122 ... S a1nn
2 S a21 1 S a22 2 ... S a2n n b
............................................ (6.19)
bn S an1 1 S an 2 2 ... S ann
n Ta ưa vào các ma trận sau: b 1 a1 [ ]b b2 ; [ ]a a2 b n an S11 S12 ... S1
[ ]S S21 S22 ... S2nn (6.20) ... ... ... ... lOMoAR cPSD| 36067889
Sn1 Sn 2 ... Snn
Thì (6.19) ược viết dưới dạng gọn hơn là: b S a (6.21)
[a] ược gọi là ma trận sóng tới,
[b] ược gọi là ma trận sóng phản xạ,
[S] là ma trận tán xạ của mạng 2n cực, nó là ma trận vuông cấp n.
Các hệ thức (6.19) và (6.21) mô tả quan hệ giữa các sóng phản xạ và sóng tới tại các
mặt cuối của các nhánh mạng 2n cực qua các yếu tố ma trận tán xạ của mạng 2n cực ó. Ma
trận tán xạ của một mạng 2n cực ã cho là hoàn toàn xác ịnh, nó không phụ thuộc vào các
sóng tới cũng như các tải mắc tại các nhánh. Từ (6.19) ta thấy: bp Spq l p q p, ; q aq a l 0 (6.22) bp
Spp l p;l 1,2,...,n a p al 0
Như vậy ta suy ra rằng: các yếu tố ngoài ường chéo chính Spq của ma trận [S] mang ý
nghĩa của hệ số truyền của sóng từ nhánhq sang nhánhp . Yếu tố nằm trên ường chéo chính
của [S] chính là hệ số phản xạ riêng tại mắt cuối Cp của nhánh p của mạng 2n cực.
Ta cũng nhận thấy rằng ma trận tán xạ [S] của mạng 2n cực ược xác ịnh với các mặt
cuối ã cho. Khi thay ổi vị trí của các mặt cuối Cp ở các nhánh thì các yếu tố liên quan ến nó sẽ
biến ổi, nhưng chỉ có pha là thay ổi còn module của chúng thì vẫn giữ nguyên (nếu trong các
nhánh và trong 2n cực không tiêu hao năng lượng)
Ta hãy xem các yếu tố này thay ổi ra sao. Nếu mặt cuối Cp của nhánh p dịch chuyển về
phía mạng 2n cực một oạn là d ' '
p ến vị trí mới là C p sóng tới tại mặt cuối C p sẽ có pha giảm i 2 góc p
dp so với sóng tới ở vị trí Cp. Ta có: a j p a ep p (6.23)
Còn sóng phản xạ tại C p
so với sóng ở Cp sẽ có pha tăng lên một góc p , tức là: lOMoAR cPSD| 36067889 b j p b ep p (6.24)
Nếu ở nhánh q ta cũng dịch chuyển mặt cuối Cq i một khoảng dq về phía mạng 2n cực ến vị trí mới C q
một góc pha là q 2 dq thì cũng nhận ược: aq a eq j q q beq j q b
Như vậy các yếu tố mới của ma trận tán xạ [S’] so với yếu tố của ma trận [S] là:
Spp bp' bp ej 2 p S epp2j p ' ap ap
Sqq' bq'' bq ej 2 q
S eqq 2 j q (6.25) aq aq
Spq' bp'' bp ej ( q p ) S epq j ( p q ) aq aq
Một cách tổng quát, nếu ở nhánh 1 dịch chuyển mặt cuối C1 i một góc pha 1, ở nhánh
C2 dịch chuyển i góc pha 2 …,Cn i góc n. Thì theo (6.23) và (6.24) ta có mối quan hệ:
[ ]b ' [G] [ ]* b
[ ]a ' [G].[ ]a (6.26)
Ở ây ma trận chuyển ổi [G] có dạng: e j 0 0 1 j 0 2 (6.27) [G] 0 e . . j n 0 e
Còn [G]* là ma trận lấy liên hiệp phức tất cả các phần tử của ma trận [G], từ ó rút ra ược
ma trận tán xạ mới của mạng 2n cực so với ma trận khi chưa thay ổi các mặt cuối: [S]’ = [G]*[S] [G]* (6.28) Hay: lOMoARcPSD| 36067889 [S] = [G] [S]’[G] (6.29)
Ma trận tán xạ [S] của mạng 2n cực siêu cao có các tính chất quan trọng sau:
Nếu môi trường trong mạng 2n cực là ẳng hướng thì ma trận tán xạ [S] của nó ối xứng, tức là: Spq Sqp Hay: [S] [S]T (6.30)
[S]T là ma trận chuyển vị của ma trận [S] qua ường chéo chính. Mạng 2n cực
như thế gọi là phần tử thuận nghịch.
Nếu mạng 2n cực không tiêu hao năng lượng thì ma trận tán xạ [S] của nó sẽ ơn nguyên (Unita), nghĩa là:
[S] [H S] [ ]I (6.31)
[I] là ma trận ơn vị cùng cấp với [S], các yếu tố ường chéo chính là ơn vị còn các yếu tố khác là 0.
[S]H = ([S]*)T là ma trận liên hợp Hecmitic của ma trận [S].
Từ tính chất trên của ma trận, ta dễ dàng kiểm tra mạng 2n cực trên phương diện năng
lượng. Vì nếu mạng 2n cực là không tiêu hao năng lượng thì tổng công suất của sóng tới tất
cả các nhánh phải bằng tổng công suất sóng phản xạ ở tất cả các nhánh. Tính chất trên ược
biểu thị bởi hệ thức sau: n (6.32)
|Spq |2 1;p 1,2,...,n q 1
Về pha, ta cũng có hệ thức sau: (6.33) n S Splql* 0 l 1 p 1,2,...,n q 1,2,...,n p khácq
6.2.2. Ma trận truyền
Ngoài ma trận tán xạ [S], khi phân tích và tổng hợp các mạng nhiều cực, người ta còn
dùng một số ma trận khác thuận tiện cho việc nghiên cứu. Đó là các ma trận truyền [T ], ma
trận trở kháng [Z ] và ma trận dẫn nạp [Y ]. lOMoAR cPSD| 36067889
Ma trận truyền T của mạng 2n cực mô tả mối quan hệ giữa biên ộ phức của sóng tới
và sóng phản xạ ở nhóm nhánh vào với nhóm nhánh ra. Với mạng 4 cực, nếu ta gọi nhánh 1
là nhánh vào, nhành 2 là nhánh ra thì ma trận truyền T 4 sẽ cho ta các hệ thức sau: ba11 TT1121 TT1222 ba22 (6.34) . (6.35) T . . . Tm 1,n Tba Tbb Tm 1,1 Tm 1,m 1 Tnn T n1 Tn m, 1 bII T Trong ó: [T ] ... 12 4 TT1121 T 22 là ma trận truyền an của mạng 4 cực
Với mạng 2n cực, nếu n = 2m,
ta gọi các nhánh từ 1 ến m là nhóm T11
nhánh vào I, các nhánh còn lại từ m
+ 1 ến n là nhóm nhánh ra II và ưa
vào các ma trận dạng sau: T1m a I ... T Tmm bm aII b m 1 Tm 1,1 T T a 1 ... Tnm ... bI b am n b1 am 1 . T1,m 1 T1n lOMoARcPSD| 36067889 . aa ab m1 . Tm m, 1 Tmn
Thì hệ thức mô tả giữa các sóng tới và phản xạ giữa nhóm nhánh ra và nhóm nhánh vào
qua ma trận truyền của mạng 2n cực có dạng sau: aII TTaabaTTbbab baIIII (6.36) b
Khác với ma trận tán xạ [S], các yếu tố của ma trận truyền [T] nói chung cũng là ại lượng
phức, nhưng không nhất thiết có một ý nghĩa vật lý nào. Ma trận truyền ược sử dụng rất thuận
tiện khi có nối tầng các mạng nhiều cực, tức là việc ghép nối các nhóm nhánh vào của một
mạng nhiều cực với nhóm nhánh ra của mạng nhiều cực khác.
Chẳng hạn với mạng 4 cực ta có tính chất sau: nếu thực hiện việc ghép nối tầng liên tiếp
các mạng 4 cực khác nhau, thì ma trận truyền [T] của mạng 4 cực hợp thành bằng tích theo
thứ tự truyền sóng các ma trận truyền của các mạng 4 cực thành phần.
Gọi [T1], [T2], [T3] là ma trận truyền của các mạng 4 cực thành phần, 1, 2, 3 mắc liên
tiếp nhau, [T] là ma trận truyền của mạng 4 cực hợp thành sau khi ghép nối, ta có: [T] = [T1].[T2].[T3] (6.37)
6.2.3. Ma trận trở kháng và ma trận dẫn nạp
Ma trận trở kháng của mạng 2n siêu cao mô tả quan hệ giữa iện áp chuẩn hóa với dòng
iện chuẩn hóa tại các mặt cuối của nó. Nếu gọi v v1, 2 ,...,vn là iện áp chuẩn hóa và
i1,i2 ,...,in là dòng iện chuẩn hóa tại các mặt cuối Cp của các nhánh thì ta có các hệ thức sau:
u1 z i11 1 z i12 2 .... z i1n n
u2 z i21 1 z i22 2 .... z2n ni (6.38) ............
un z in1 1 zn 2 2i .... znn ni Hay ưa vào các ma trận: u 1 i i [ ]u u2 ; [ ]i 2 ... ... lOMoAR cPSD| 36067889 n in u z11 z12 z1n [Z ] 22 21 (6.39) 2n z n 2 zn1 znn z z z
Thì (6.38) có dạng gọn hơn là:
[u ] [Z ].[ ]i (6.40)
[u]gọi là ma trận iện áp chuẩn hóa,
[i ]gọi là ma trận dòng iện chuẩn hóa,
còn [Z ] là ma trận trở kháng, nó là ma trận vuông cấp n.
Bây giờ ta biểu diễn ngược lại iện áp qua dòng iện với các hệ thức (6.38) thì ược dạng sau:
i1 y u11 1 y u12 2 ... y u1n
n i y u y u ... y u 2 21 1 22 2 2n n (6.41) ......................
in y un1 1 yn 2u2 ... ynnun Hay
viết dưới dạng ma trận: (6.42) i ... y1n Y
...21...22......y...2n (6.43)
yn1 yn 2 . ... ynn lOMoARcPSD| 36067889
Gọi là ma trận dẫn nạp của mạng 2n cực, nó cũng là ma trận vuông cấp n , các yếu tố
nói chung là các ại lượng phức.
Từ (6.40) và (6.42) ta thấy 2 ma trận [Z ] và [Y ] là nghịch ảo của nhau. Tức là:
[Y ][Z ] [ ]I
Ma trận trở kháng [Z ] và ma trận dẫn nạp [Y ]của mạng2n cực thuận nghịch (chứa môi
trường ẳng hướng) thì ối xứng: zpq zqp (6.44) ypq yqp
Nếu mạng2n cực không tổn hao năng lượng thì các yếu tố của ma trận trở kháng [Z ]
của 2n cực là các số thuần ảo.
6.2.4. Mối quan hệ giữa các ma trận sóng
Việc dẫn ra các ma trận tán xạ [S] có thuận lợi lớn vì có thể o ạc các yếu tố của nó dựa
trên việc o công suất và hệ số sóng ứng iện áp. Ngoài ra khi dịch chuyển các mặt cuối của
mạng 2n cực chỉ có pha của các yếu tố Spq thay ổi, trong khi ó các yếu tố của ma trận [Z ] và
ẽ thay ổi cả pha lẫn module. Sử dụng ma trận tán xạ [Y ]s
S thuận tiện khi phân
tích các mạng nhiều cực có số cực lớn hờn. Còn khi với mạng 2 cực thì dùng ma trận [Y ]hoặc
[Z ] sẽ dễ dàng hơn. Khi phân tích các mạng 4 cực nối tầng, sử dụng ma trận truyền [T] sẽ nhanh gọn hơn.
Các ma trận [T], [Z ] và [Y ]không xác ịnh ược bằng thực nghiệm, nhưng ta có thể nhận
ược chúng khi biết ma trận tán xạ [S] qua các mối quan hệ giữa [S] với [T], [Z ] và [Y ] Từ các
biểu thức (6.10), (6.12), (6.14), (6.40) và (6.42) ta có mối quan hệ giữa S với [Z ] và
[Y ]cho mạng 2n cực như sau:
[ ]S ([Z ] [ ])([ ]IZ [ ])I 1 ([ ]I [Y ])([ ]I [Y ]) 1
[Z ] ([ ]I [ ])([ ]S I [ ])S 1 (6.45)
[Y ] ([ ]I [ ])([ ]SI [ ])S 1
Với mạng 4 cực, từ các biểu thức (6.21) và (6.34) có quan hệ giữa S và T : S S S S (6.46) [ ]S 11211222
T121/T/T1111
det[ ]/ TT12 /TT1111 Ở ây: lOMoARcPSD| 36067889 det [T] = T11T22 – T12T21 det [S] = S11S22 – S12S21
Dấu (-1) trong biểu thức (6.45) chỉ ma trận nghịch ảo.
Các mạng nhiều cực siêu cao ược ứng dụng rộng rãi trong kỹ thuật nhất là các mạng 2,
4, 6, và 8 cực. Sau ây ta lần lượt nghiên cứu các mạng trên. 6.3. Mạng 2 cực
6.3.1. Hệ số phản xạ và trở kháng chuẩn hóa
Mạng 2 cực siêu cao tần là phần tử siêu cao ơn giản nhất trong tuyến siêu cao. Chúng
ược dùng khá rộng rãi trong kỹ thuật siêu cao. Đó là: tải không phản xạ, ầu nồi tắt có pittông
dịch chuyển, ầu tách sóng, một hộp cộng hưởng nối với oạn ường truyền, tải tiêu thụ v.v… ạng ực l ạng 2 cực si ần
Ta hãy xét quy luật biến ổi của hệ số phản xạ và trở kháng chuẩn hóa ở ầu vào C của
mạng 2 cực nói chung. Giả sử có một mạng 2 cực mắc trên ường truyền L với máy phát năng
lượng siêu cao như hình 6.3, tại mặt phẳng cuối C1 ta có sóng tới là a và sóng phản xạ là b.
Hệ số phản xạ tại C1 là: Rpx1 b a/
Và trở kháng chuẩn hóa tại C1 theo (6.14) là: 1 Rpx1 Zch1 1 Rpx1
Bây giờ ta dịch chuyển mặt cuối của mạng 2 cực từ C1 về C2 một khoảng l thì tại C2 ta
có sóng tới và sóng phản xạ theo (6.23) và (6.24) là: b be l a ae l
j : hệ số truyền
là hệ số tiêu hao, là hệ số pha lOMoARcPSD| 36067889 2
Như vậy hệ số phản xạ và trở kháng chuẩn hóa tại mặt cuối C2 là:
Rpx2 b' R epx1 2 l a ' 1 Rpx ch2 1 l 2 1 Zch1 Rpx 2 Zch1th Hay là:
Rpx1 Rpx 2e2 l Zch1 Z chZ2 ch 2thth ll 1 (6.50) th l (6.49) Z
Nếu ường truyền L không tổn hao năng lượng = 0 thì:
Rpx1 Rpx 2e 2 l Rpx 2.e j 4 l Zch1 jZch2tg 2 l (6.51) 1
Nếu oạn ường truyền l
/ 4 thì (6.51) có dạng: Rpx1 Rpx 2 Zch1 1 (6.52) Zch2 jtg 2 l lOMoARcPSD| 36067889 Zch 2
Từ (6.52) ta thấy rằng một tiết diện nối tắt có thể trở thành một trở kháng vô cùng (
ường truyền hở mạch ở cuối) khi qua một oạn ường truyền có chiều dài l / 4 hoặc ngược lại.
Nếu gọi trở kháng ặc tính của ường truyền Zco thì trở kháng của mạng 2 cực tại tiết diện cuối C sẽ là:
Z1 Zch1Zco ,Z 2 Zch 2Zco (6.53)
Các biểu thức (6.51) và (6.52) có thể viết như sau cho các trở kháng:
Z1 Zco Z 2 jZ tgco22 l (6.54) Z co jZ tg2 l Z Z (6.55) 2 1 Zco2
6.3.2. Một ví dụ về mạng 2 cực
Có rất nhiều phần tử trong mạng siêu cao tần thuộc loại mạng 2 cực. Trong phần này,
ta chỉ xét một ví dụ ó là tải không phản xạ.
Tải không phản xạ dùng trong tuyến siêu cao tần với mục ích tạo ra trong tuyến sóng
chạy hoàn toàn, dùng trong khi o ạc ở siêu cao và làm anten tương ương khi iều chỉnh máy
phát siêu cao. Tải không phản xạ có cấu tạo a dạng tùy theo cấu trúc của ường truyền và mức
công suất cần hấp thụ. Đặc trưng iện cơ bản của tải không phản xạ là module của hệ số phản
xạ (hay hệ số sóng ứng) trong một dải tần công tác. Trong thực tế kỹ thuật có khả năng tạo ra
những tải với module của hệ số phản xạ R px
0,01 trong dải tần tương ối f f 0
20 30% hoặc lớn hơn. Còn pha của hệ số phản xạ có thể có giá trị bất kỳ trong
khoảng từ 0 ến 2 . Một ặc trưng quan trong của tải không phản xạ là giá trị công suất hấp thụ
cho phép. Tải với mức công suất nhỏ thì công suất hấp thụ Pt 1W còn lớn hơn 1W là tải ở mức công suất lớn. 6.4. Mạng 4 cực
6.4.1. Ma trận sóng
Mạng 4 cực siêu cao là phần tử ược sử dụng rộng rãi nhất trong tuyến siêu cao tần, nó
rất a dạng và ảm nhiệm các chức năng khác nhau. Từ các phần tử ơn giản như: tấm chắn, que
dò, cửa sổ cộng hưởng, 1 oạn ường truyền ến phần tử phức tạp như các bộ suy giảm, quay
pha, bộ lọc ều là những mạng 4 cực siêu cao và chúng không thể thiếu trong tuyến siêu cao.
Trước hết chúng ta nghiên cứu các ma trận sóng của chúng.
Giả sử ta có một mạng 4 cực siêu cao tần có nhánh vào 1 và nhánh ra 2. Với các sóng
tới a1, a2, sóng phản xạ b1, b2, iện áp và dòng chuẩn hóa: v1, ,i v1 2 ,i2 . lOMoAR cPSD| 36067889
Quan hệ giữa các sóng tới và sóng phản xạ ở các nhánh của mạng 4 cực này ược biểu
diễn bởi ma trận tán xạ [S] và ma trận truyền [T] có dạng: b1 S aS a1121 11 S aS a1222 22 (6.56) b2
a1 T b11 2 T a12 2 (6.57) b 1 S b21 2 S b22 2
Mối quan hệ giữa iện áp chuẩn hóa và dòng iện chuẩn hóa của mạng 4 cực ược mô tả
qua ma trận trở kháng và ma trận dẫn nạp như sau:
v1 z i11 1 z i12 2 (6.58)
v2 z i21 1 z i22 2
i1 y v111 y v12 2 (6.59)
i2 y v211 y v222
Các yếu tố của các ma trận của mạng 4 cực quan hệ với nhau như sau: (z [ ]S SS1121 SS1222 A A
(1 y11 )(1 y22 ) y y1221 2y12 B B (6.60) 2y21
(1 y11 )(1 y22 ) y y1221 B B lOMoARcPSD| 36067889 ở ây:
A (z11 1)(z22 1) z z12 21
B (1 y11)(1 y22 ) y y12 21
(1 S11)(1 S22 ) S S12 21 2S12 z
2CS21(1 S11)(1 CS22 ) S S12 21 (6.61) 21 C C
(1 S11)(1 S22 ) S S12 21 2S12 21 y22
2DS21(1 S11)(1 DS22 ) S S12 21 (6.62) D D ở ây:
C = (1 – S11)(1 - S22) – S12S21
D = (1 + S11)(1 + S22) – S12S21 z 22 z12 (6.63) E E Y z
E z z11 22 z z12 21 z11 21 E E y22 F y 12 [Z] (6.64) y F 21
F y y11 22 y y12 21 y11 F F
Trong trường hợp mạng 4 cực chứa môi trường ẳng hướng, tức là nó thuận nghịch thì
các ma trận [S], [Z ]và [Y ] sẽ ối xứng, tức là có: S 12
S21 z12 z21 y12 y21
Thì các biểu thức (6.60), (6.61) và (6.62) sẽ có dạng ơn giản hơn: (6.65) lOMoARcPSD| 36067889 B B
(1 S11 )(1 S22 ) S122 2S12 [Z] C (6.66) C 2S12
(1 S11 )(1 S22 ) S122 C C (1 S 2S12
11 )(1 S22 ) S122 Y D D 2 (6.67) 2S12
(1 S11 )(1 S22 ) S12 D D
6.4.2. Mạng 4 cực không tổn hao
Nếu mạng 4 cực không tổn hao năng lượng và thuận nghịch từ tính Unita của ma trận
tán xạ [S] ta thấy có thể ặt:
S11 j cos e j 1 S 22 j cos e j 2 (6.68)
S12 S21 sin e j ( 1 2 )/2
, 1, 2 là các số thực có giá trị từ 0 ến 2 . Với ký hiệu mới, ma trận tán xạ của một
mạng 4 cực thuận nghịch không tổn hao có thể viết:
[ ]S e j ( (6.69) 1 2 )/2
j cos e j 2 sin
Còn ma trận truyền [T] của mạng 4 cực này theo (6.46) có dạng: 1ej 1 2 2 j cotg ej 1 2 2 (6.70) lOMoARcPSD| 36067889
sin 1 2 j 1 2 2 [ ]T j cotg ej 1 2 e sin
j cos e j sin 1 e j ( 1 2 )/2
Từ (6.68) ta thấy rằng |S11| = |S22| nó ược gọi là hệ số phản xạ riêng của mạng 4 cực
không tổn hao. Nếu mắc một ường truyền với mạng 4 cực này, trên ường truyền sẽ có sóng ứng với hệ số: K d 11 ||SS1111 || 11 coscos cotg2 2 (6.71)
Và góc ược gọi là góc mở.
Hoàn toàn tương tự từ (6.65), (6.66) và (6.67) ta có thể dẫn ra ược các ma trận [Z ] và
[Y ]cho 4 cực không tổn hao thuận nghịch.
Nếu mạng 4 cực không tổn hao mà có: S11 = S22 tức là 1 = 2 =
Thì ược gọi là ối xứng.
Với một mạng 4 cực không tổn hao ối xứng thì các ma trận tán xạ [S] và truyền [T] sẽ có dạng ơn giản hơn:
[ ]S e i jsincos jsincos lOMoARcPSD| 36067889 j e i j cos cos [ ]T i (6.72) e
Như vậy với một mạng 4 cực không tổn hao ối xứng, các ma trận sóng ược xác ịnh bởi
2 tham số ộc lập là và .
Một ví dụ rất ơn giản về một mạng 4 cực không tổn hao ối xứng là một oạn ường truyền
ồng nhất không tổn hao có chiều dài l với góc pha 2 l / .
Ở ây vì không có phản xạ nên góc = /2 và do ó = 0 nào ó, và lúc này ma trận tán
xạ và ma trận truyền của nó sẽ là: 0 e j 0 [ ]S j 0 (6.73) e 0 [ ]T ej 0 0j 0 (6.74) 0 e
Nếu bây giờ ta ặt một ường truyền không tổn hao có ma trận [T] như (6.74) trước một
mạng 4 cực ối xứng không tổn hao có ma trận truyền [T] như ở (6.72) thì theo (6.75) ma
trận truyền của mạng 4 cực mới tạo thành có dạng: e j 0 0 ej j cos 1 [ ]T 0 e j 0
j cos e j sin (6.75) sin1 j cos .ej (
e0 )i 0 jecos . j ( e0 )i 0
So sánh (6.75) và (6.70) ta thấy mạng 4 cực mới này cũng không tổn hao có dạng tùy ý.
Nó ược xác ịnh bởi ba tham số thực ộc lập , , và 0. Nó có dạng giống như ma trận (6.70)
nếu ta giữ nguyên và ặt = 0 và: 1 2 (6.76) 0 2
Như vậy khi không có tổn hao, ở mỗi tần số, một mạng 4 cực không ối xứng có thể ược
thay thế bởi một mạng 4 cực ối xứng ặt sau một oạn ường truyền ồng nhất.
Ở ây, góc 0 của oạn ường truyền mô tả tính không ối xứng của mạng 4 cực nên nó ược
gọi là góc bất ối xứng của mạng 4 cực, ma trận tán xạ của mạng 4 cực này có dạng: lOMoARcPSD| 36067889 [ ]T j sin .cos . ee jj( (
20 )0 ) sin .j cos . e je( j 0 ) (6.77)
Theo (6.66) và (6.73) ta dễ dàng viết ược ma trận trở kháng va dẫn nạp của một mạng 4 cực ối xứng như sau: 1 cos sin (6.78) [Z ] sin cos cos sin 1 cos sin [Y ] cos sin sin cos (6.79)
6.4.3. Biến thế lý tưởng
Ta nhận thấy rằng vì các yếu tố của ma trận tán xạ [S] của mạng 4 cực ược xác ịnh bằng
thực nghiệm nên nó luôn tồn tại. Còn các ma trận trở kháng và ma trận dẫn nạp của mạng 4
cực chỉ tồn tại khi thỏa mãn iều kiện sau:
C = (1 – S11)(1 – S22) – S12S21 0
D = (1 + S11)(1 + S22) – S12S21 0 (6.80)
Ta xem xét trường hợp khi cả hai iều kiện trên ều không thỏa mãn tức là ối với một
mạng 4 cực thuận nghịch xảy ra ồng thời hai ẳng thức: (1 – S 2 11)(1 – S22) – S12 = 0 (1 + S 2 11)(1 + S22) – S12 = 0 (6.81)
Điều kiện (6.81) cho ta hệ thức sau: lOMoAR cPSD| 36067889 - S22 = S11 = S 2 2
11 + S12 = 1 S12 = t = (1 - 2)1/2 (6.82)
Lúc này ma trận truyền [T] của mạng 4 cực có dạng: 1 1 [ ]T (6.83) 1 2 1
Hay có mối quan hệ giữa các sóng ở lối vào và lối ra của mạng 4 cực: a1 1 2 b2 1 2 a2 1 b1 1 1 2 b2 1 2 a2
Ta cộng và trừ hai vế của hai ẳng thức trên và chú ý ến biểu thức (6.10) sẽ nhận ược kết quả: u1 11 2 ; u2 11 i1 11 2 ; i2 11 Nếu ta ặt: n 1 (6.84) 1
Thì biểu thức trên viết dưới dạng mới là: u2 1 u1 n (6.85) i 2 ni1
Một mạng 4 cực như trên ược gọi là một biến thế lý tưởng. Còn n ược gọi là hệ số của biến thế.
Từ (6.82) và (6.84) ta biểu diễn ngược lại các hệ số ma trận [S] qua hệ số biến thế n : lOMoARcPSD| 36067889 n 2 1 S11 1 n 2 (6.86) S12 t 1 2nn 2 Do ó: [ ]S 1 1n 2 (12 nn 2 ) (1 2nn 2 ) (6.87)
Ta nhận thấy rằng vì n thực cho nên tất cả các yếu tố của ma trận [S] ều là thực, ồng
thời từ (6.82) ma trận [S] Unita. Như vậy một mạng 4 cực chỉ có thể biểu diễn dưới dạng
một biến thế lý tưởng chỉ khi nó không tổn hao năng lượng và các mặt cuối phải ặt ở vị trí
một là bụng sóng, một là nút sóng ứng.
Khi n 0 thì mặt cuối C1 (có S11 > 0) ặt ở bụng sóng ứng, C2 ở nút sóng ứng và ngược
lại n 0 thì C1 sẽ ở nút sóng và C2 ở iểm bụng sóng.
Với cách chọn các vị trí thích hợp của các mặt cuối C1, C2, một mạng 4 cực không tổn
hao tuỳ ý có thể biểu diễn dưới dạng là một biến thế lý tưởng ghép nối ở hai ầu oạn ường
truyền ồng nhất không tiêu hao. Ở ây các oạn l l1, 2 chọn sao cho các góc pha: 1 2l1 / , 2 2 l 2 /
Thực hiện ược iều kiện: S ' 2j 11
S e11 1 là thực và dương (hoặc âm) S ' 2j 22 S e22
2 là thực và dương (hoặc âm) Lúc ó: S ' j ( 12 S e12 1
2 ) sẽ tự ộng thỏa mãn là thực. ở ây
dấu phẩy chỉ các yếu tố của biến thế lý tưởng.
6.4.4. Trở kháng mắc song song
Một trở kháng [Z ] mắc song song vào ường truyền ược xem như là một mạng 4 cực
với lối vào và ra cùng nằm tại chỗ mắc trở kháng.
Hệ thức giữa iện áp và dòng iện chuẩn hóa: u1 zi 1 zi2 lOMoARcPSD| 36067889 u 2 zi1 zi2 Ma trận trở kháng là: z z [Z ] z z
Từ ó theo (6.65) tính ược ma trận tán xạ và ma trận truyền: [ ]S / / (6.88) 2z 2z 1 Từ (6.26) có dạng: 1 1 1 2z 1 2z 2z 1 2z 1 Như vậy ta có: S11 – S12 = -1 (6.90) 1 1 (6.89) [ ]T //
Người ta ã chứng minh ược rằng nếu một mạng 4 cực thực hiện ược iều kiện (6.90) thì
sơ ồ tương ương của nó có dạng như một trở kháng mắc song song vào ường truyền siêu cao.
6.4.5. Dẫn nạp mắc nối tiếp
Một dẫn nạp [Y ] mắc nối tiếp trên ường truyền chính là một mạng 4 cực ơn giản.
Hệ thức giữa các dòng và áp chuẩn hóa của nó có dạng:
i1 y u. 1 y u. 2 i 2 y u. 1 y u. 2
Ma trận dẫn nạp [y ] là: y y [Y ] y y lOMoARcPSD| 36067889
Ma trận tán xạ ược tính từ (6.65): [ ]S 2y (6.91) 1 2y 1
Từ (6.91) suy ra iều kiện: S11 + S12 = 1 (6.92) 1 1 2 y
Người ta cũng chứng minh ược rằng khi một mạng 4 cực nào thỏa mãn iều kiện (6.92)
thì sơ ồ tương ương của nó ược biểu diễn bằng một dẫn nạp mắc nối tiếp vào ường truyền siêu cao tần.
Ma trận truyền của nó có dạng: [ ]T 21y 1 12y1 21y (6.93)
6.4.6. Mắt xích dạng T các trở kháng chuẩn hóa
Sau ây ta có thể biểu diễn sơ ồ tương của một mạng 4 cực thuận nghịch dưới dạng một
mắc xích dạng T với 3 trở kháng chuẩn hóa.
Giả sử ta có 3 trở kháng chuẩn hóa ZA ,ZB ,ZC mắc dạng chữ T như hình 6.4. ắt xí ạng T
Ta có mối quan hệ giữa các dòng iện và iện áp chuẩn hóa của chúng là:
u1 Z iA 1 ZB (i1 i2 )
u2 Z iC 2 ZB (i1 i2 ) Vì ở
ây i i1 i2 hay viết dạng ma trận ta có: lOMoARcPSD| 36067889 u 1 (ZA BZB ) B BZC ) u2 Z (Z
Như vậy ma trận trở kháng của mạch này là: ZB (ZB ZC ) Z 21 Z 22 Từ ó suy ra quan hệ sau: Z11 Z12 (ZA ZB ) B (6.94) [ ]Z
ZA Z11 Z12 Z B Z12 Z 21 (6.95)
ZC Z 22 Z12
Từ biểu thức (6.66) ta có:
ZA (1 (1S11 )(1S11 )(1S22 S) 22S) 12 2 S 1222S12
ZB (1 S11 2S 2
(6.96) )(1 S22 ) S12
ZC (1 (1S 22 S)(111 )(1S 11S) 22S) 12 2 S 1222S12
Chú ý rằng việc biểu diễn theo sơ ồ dạng chữ T chỉ thực hiện ược trong iều kiện: C = (1- S 2
11)(1 – S22) – S12 khác 0 (6.97)
6.4.7. Mắt xích dạng
Ta có thể biểu diễn một mạng 4 cực thuận nghịch bất kỳ bằng sơ ồ tương ương dạng
với 3 dẫn nạp Y ' ' '
A ,YB ,YC như hình 6.5. lOMoAR cPSD| 36067889 Hình 6.5. Mắt xích dạng
Mối quan hệ giữa các dòng iện và iện áp chuẩn hóa của mạng trên là:
i1 y uA' 1 yB' (u1 u2 )
i2 y uC' 2 yB' (u1 u2 ) Và
ma trận dẫn nạp có dạng: y11 y12 y21 y22 YB' ) (YA' YB' ) YB' (YB' YC' Ta suy ra ược: (6.98) [Y ]
YA' y11 y12 Y ' B y12 y21 (6.99)
YC y22 y12
Hay các yếu tố ma trận tán xạ ược các biểu thức cho các dẫn nạp là:
YA' (1 S11)(1 S22 ) S122 22S12
(1 S11)(1 S22 ) S12 YB 2S 2 (6.100) '
(1 S11)(1 S22 ) S12
YC' (1 (1S11 )(1S11 )(1S22 S) 22S) 12 2 S 1222S12
Rõ ràng biểu diễn theo sơ ồ tương ương dạng chỉ thực hiện ược trong iều kiện: D = (1 + S 2 11)(1 + S22) – S12 khác 0 (6.101) lOMoARcPSD| 36067889
6.4.8. Ứng dụng của mạng 4 cực
6.4.8.1. Các loại chuyển tiếp
Để ghép nối các loại ường truyền khác nhau với các dạng sóng làm việc thích hợp trong
tuyến siêu cao tần, người ta dùng các phần tử chuyển tiếp. Một số loại chuyển tiếp phổ biến
trong kỹ thuật như: chuyển tiếp từ ường dây ồng trục sang ống dẫn sóng tròn và chữ nhật,
chuyển tiếp từ dây ồng trục sang mạch dải, chuyển tiếp từ ống dẫn sóng chữ nhật sang ống
dẫn sóng tròn. Tất cả các chuyển tiếp ều là các mạng 4 cực siêu cao.
a) Chuyển tiếp dạng ồng trục - ống dẫn sóng Gồm hai loại chính:
Chuyển tiếp từ ống ồng trục hay cáp ồng trục sang ống dẫn sóng chữ nhật.
Được dùng ể truyền năng lượng trong ống ồng trục với sóng TEM sang ống dẫn sóng
chữ nhật với sóng cơ bản H10 hay ngược lại. Tuỳ theo yêu cầu về công suất và dải tần mà
dạng chuyển tiếp này có cấu tạo khác nhau như dạng que dò (hình 6.6a), dạng Slaypher (hình
6.6.b), dạng có thanh ngang hay dạng cúc áo.
Hình 6.6. Chuyển tiếp ồng trục – ống dẫn sóng chữ nhật.
Đối với chuyển tiếp dạng que dò, việc phối hợp giữa hai loại ống dẫn sóng ược bảo ảm
bởi chọn thích hợp chiều dài của que dò ld và khoảng cách từ que dò ến thành ngắn mạch của
ống dẫn sóng l . Để mở rộng dải tần, việc phối hợp ược thực hiện bằng cách tăng ường kính
d của que dò và việc chọn cả ộ lệch a của que dò. Khi chọn khoảng cách và các kích thước
trên một cách tỉ mỉ, loại chuyển tiếp dạng que dò này phải ảm bảo phối hợp ược trong dải tần
cỡ ến 15 ến 20 % với hệ số sóng chạy Kch lớn hơn hoặc bằng 0,95. Nhược iểm của loại chuyển
tiếp que dò là làm giảm ộ bền iện do tập trung ường sức iện trường ở ầu của que dò.
Khắc phục nhược iểm trên, người ta làm chuyển tiếp dạng Slaypher. Khi chọn các kích
thước l và chiều dài oạn Slaypher ld thì dải tần công tác tương ối cũng chỉ ạt ến khoảng 7%.
Để ạt ược sự phối hợp tốt ồng thời tăng ộ bền iện người ta còn có chuyển tiếp dạng có
thanh ngang ược bổ sung bằng một tấm chắn iện cảm. Dạng chuyển tiếp này có thể ạt ến 20%
khi hệ số sóng chạy Kch lớn hơn 0,95. Khi truyền công suất lớn và ể có ộ bền iện cao ta dùng
chuyển tiếp dạng cúc. Trong dạng chuyển tiếp ồng trục ống dẫn sóng này cần phải chọn tỉ mỉ
dạng của dây dẫn chỗ chuyển tiếp và bổ sung bằng tấm chắn iện cảm. Dạng chuyển tiếp này
ược dùng ể dẫn năng lượng từ èn dao ộng Magnetron ra tuyến siêu cao. lOMoARcPSD| 36067889
Chuyển tiếp từ ống ồng trục sang ống dẫn sóng tròn
Để kích thích sóng trong ống dẫn sóng tròn dạng sóng cơ bản H11 từ ường dây ồng
trục, ta dùng bộ chuyển tiếp ồng trục - ống dẫn sóng tròn (hình 6.7).
Hình 6.7. Chuyển tiếp ồng trục – ống dẫn sóng trụ tròn
Ở ây lõi của dây ồng trục kéo dài ra thành một que dò ặt song song với ường sức iện
trường của sóng H11 trong ống dẫn sóng tròn.
Để kích thích sóng E01 trong ống dẫn sóng tròn từ dây ồng trục, ta dùng chuyển tiếp có
lõi của dây ồng trục kéo dài ra tạo thành que dò ặt song song với trục của ống dẫn sóng tròn
và song song với ường sức iện trường của sóng E01.
Loại chuyển tiếp này ược sử dụng trong các khớp quay anten ài rada.
b) Chuyển tiếp dạng ống dẫn sóng chữ nhật - ống dẫn sóng tròn
Để kích thích sóng cơ bản H11 trong ống dẫn sóng tròn từ sóng cơ bản H10 trong ống
dẫn sóng chữ nhật, người ta dùng chuyển tiếp từ từ. Ở loại chuyển tiếp này, tiết diện ngang
của nó biến dạng dần ều ều từ tiết diện chữ nhật sang tròn.
Để tránh phản xạ trong một dải tần thì chiều dài của chuyển tiếp phải lớn hơn bước sóng trong ống dẫn sóng.
Một dạng chuyển tiếp khác từ ống dẫn sóng chữ nhật sang ống dẫn sóng tròn với sóng
cơ bản H11 và H10 chắc chắn hơn về mặt cơ khí có tiết diện chữ nhật chuyển sang tiết diện
tròn ược thực hiện qua một oạn biến áp /4 có tiết diện hình oval. Hình 6.8. Hình 6.9.
Để kích thích sóng E01 trong ống dẫn sóng tròn từ sóng H10 ở trong ống dẫn sóng chữ
nhật, ta dùng chuyển tiếp dạng khác. Trong loại chuyển tiếp này, ống dẫn sóng chữ nhật nối
với ống dẫn sóng tròn qua tiết diện của ống chữ nhật. Một ầu của ống sóng tròn ược ngắn
mạch có ộ dài /2 so với bước sóng của sóng E01 trong ống dẫn sóng trên tính từ tâm chỗ nối
với ống dẫn sóng chữ nhật.
Để lọc sóng không mong muốn là H11 trong ống dẫn sóng tròn, trong oạn nối tắt của
ống dẫn sóng tròn người ta ặt một vòng xuyến kim loại mỏng, chu vi của xuyến gắn với bước lOMoAR cPSD| 36067889
sóng 0 trong không gian tự do. Vị trí của xuyến ặt cách tâm lỗ ghép một khoảng /4 bước
sóng của sóng H11. Xuyến cộng hưởng này tác dụng lên sóng H11 như một oạn ngắn mạch.
Đối với sóng E01 ường sức iện trường E vuông góc với xuyến nên nó không bị ảnh hưởng.
Việc kích thích sóng H01 trong ống dẫn sóng tròn từ sóng H10 trong ống dẫn sóng chữ
nhật ược thực hiện bởi chuyển tiếp từ từ. Trong dạng chuyển tiếp này, tiết diện ngang của nó
ược biến dạng từ dạng chữ nhật sang tròn nhưng ảm bảo cho ường sức iện trường biến chuyển
dần từ thẳng sang dạng ồng tâm với trục.
Vì sóng dạng H01 là bậc cao nên muốn có nó ta phải dùng một bộ lọc bỏ các dạng sóng
bậc thấp hơn chẳng hạn như lọc sóng E01. Bộ lọc như vậy gọi là bộ lọc dạng sóng. Nó chính
là một oạn ống dẫn sóng tròn, bên trong có ặt các phiến mỏng kim loại theo phương bán kính.
Một dạng bộ lọc khác có xẻ các khe tròn hẹp song song chạy vòng quanh ống tròn. Khe
này sẽ làm cho các sóng bậc thấp như H11 và E01 bức xạ qua khe ra ngoài, cò sóng H01 truyền bên trong ống dẫn sóng.
Ngoài các loại chuyển tiếp trên, còn có chuyển tiếp ồng trục - mạch dải và chuyển tiếp
ống dẫn sóng - mạch dải. Do thời lượng của môn học nên tài liệu không bàn ến hai loại chuyển tiếp này.
6.4.8.2. Các bộ suy giảm
Chúng ta tìm hiểu một loại mạng 4 cực siêu cao tần khác là các bộ suy giảm. Đó là các
phần tử 4 cực siêu cao mà khi sóng iện từ i qua nó sẽ bị giảm i một phần năng lượng ở ầu ra
so với ầu vào. Các bộ suy giảm ược lắp ở ầu ra của máy phát và tuyến siêu cao hoặc ể o ạc
trong các thiết bị o lường. Người ta chia làm ba loại suy giảm: suy giảm kiểu hấp thụ, suy
giảm tới hạn và suy giảm có iều khiển iện.
a) Suy giảm kiểu hấp thụ
Bộ suy giảm kiểu hấp thụ gồm một một oạn ống dẫn sóng chữ nhật, bên trong nó ược ưa
vào một bản hấp thụ năng lượng iện từ trường. Bản hấp thụ này có thể là iện môi ược kim loại
hóa. Tùy theo vị trí ặt tấm hấp thụ mà ta ạt ược mức ộ khác nhau về suy giảm năng lượng siêu cao tần.
Các bộ suy giảm kiểu hấp thụ có ưu iểm là cấu trúc ơn giản, phản xạ ít. Tuy nhiên chúng
có nhược iểm là ộ suy giảm không lớn quá 50dB và rất nhạy ối với tần số. Do ó với các tần
số khác nhau phải lấy chuẩn cho từng tần số.
b) Suy giảm tới hạn
Nguyên tắc làm việc của bộ suy giảm tới hạn là sự suy giảm cường ộ trường theo hàm
mũ trong ống dẫn sóng có kích thước sao cho bước sóng tới hạn của dạng sóng ã chọn nhỏ
hơn bước sóng công tác. Ta có biểu thức: 1th2 12 1t2 lOMoAR cPSD| 36067889
nếu > th thì t là số ảo, sóng trong ống dẫn sóng không lan truyền ược mà bị suy
giảm theo hàm mũ với hệ số suy giảm ược tính: 2 th 2 1 khi > > th thì ta có: 2 th
Nghĩa là ộ suy giảm không phụ thuộc vào tần số.
Các bộ suy giảm tới hạn có ưu iểm là ộ suy giả thay ổi trong phạm vi lớn và chịu ược
công suất lớn khi chọn ộ suy giảm thay ổi tuyến tính theo chiều dài L tốt. Do ó chúng ược
dùng làm các bộ suy giảm chuẩn. Nhược iểm của chúng là gây ra phản xạ lớn do bất ồng nhất.
Để giảm phản xạ, người ta dùng các phần tử phối hợp ở hai ầu như là các iện trở hay ĩa iện môi.
Ngoài hai loại trên, trong kỹ thuật còn sử dụng các bộ suy giảm có iều khiển iện. Người
ta lợi dụng tính chất ặc biệt của ferit bị từ hoá trong từ trường không ổi ể tạo ra các bộ suy
giảm không thuận nghịch gọi là các bộ van. Ngoài ra còn dùng các diode loại PIN tạo ra các
bộ suy giảm có thể iều khiển iện khi thay ổi thiên áp cho các diode trên.
6.4.8.3. Các bộ quay pha
Một loại mạng 4 cực khác là các bộ quay pha. Các bộ quay pha ược sử dụng nhiều trong
tuyến siêu cao và trong các thiết bị o lường.
Bộ quay pha ơn giản cố ịnh chính là một oạn ường truyền ồng nhất có chiều dài l sẽ cho
một bộ quay pha cố ịnh với góc pha: 2 l
Một bộ quay pha biến ổi ơn giản ược thực hiện bởi ống ồng trục khi thay ổi chiều dài l của bộ quay pha.
Người ta còn tạo ra bộ quay pha biến ổi bằng cách làm thay ổi bước sóng tới hạn của
ống dẫn sóng H10 trong ống dẫn sóng chữ nhật.
Tất cả các bộ quay pha trên ều có mức ộ quay pha như nhau không phụ thuộc vào chiều
truyền sóng. Các bộ quay pha như vậy gọi là các bộ quay pha thuận nghịch.
Người ta sử dụng tính chất ặc biệt của ferit bị từ hoá trong từ trường không ổi ể tạo ra
các bộ quay pha theo chiều truyền sóng gọi là các bộ quay pha không thuận nghịch. lOMoARcPSD| 36067889
6.5. Các bộ ghép ịnh hướng
Bộ ghép ịnh hướng là một mạng 8 cực ược sử dụng phổ biến trong kỹ thuật siêu cao
tần. Ta giả thiết rằng ây là một mạng 8 cực không tổn hao năng lượng. 1 3 Mạng ực 2 4
Cho một mạng 8 cực với các nhánh1, 2, 3 và 4. Ta nhóm các nhánh trên thành 2
nhóm: nhóm 1 gồm các nhánh 1 và 2, nhóm 2 gồm các nhánh 3 và 4.
Ta nói rằng mạng 8 cực này là một bộ ghép ịnh hướng nếu các nhánh của một nhóm
hoàn toàn cách ly khi các nhánh của nhóm kia ược phối hợp.
Ví dụ ta nối vào hai nhánh 3 và 4 các tải không phản xạ, cho sóng vào nhánh 1 thì không có sóng ra nhánh 2.
Các iều kiện ược thể hiện bởi hệ thức: S12 = S21 = S34 = S43 = 0
Ma trận tán xạ của bộ ghép ịnh hướng có dạng: S11 0 S13 S14 (6.102)
0 S22 S23 S24 [ ]S S13 S23 S33 0 S14 S24 0 S44
Các bộ ghép ịnh hướng có ba tính chất sau:
Các hệ số phản xạ của bộ ghép ịnh hướng có cùng module.
Từ tính chất Unita của ma trận tán xạ [S] của bộ ghép ịnh hướng ta có:
S S1311* S S3314* 0
S S22 24* S S2444* 0 S S11 14* S S14 44*
0 Ta suy ra ược kết quả: |S11| = |S22| = |S33| = |S44| (6.103)
Nếu bộ ghép ịnh hướng ối xứng ể cho: lOMoAR cPSD| 36067889 S14 = S23 và S13 = S24 (6.104)
Thì nó hoàn toàn phối hợp, tức: S11 = S22 = S33 = S44 (6.105)
Thật vậy, từ (6.102) và iều kiện (6.103), (6.104) ta có dạng ma trận tán xạ của bộ ghép ịnh hướng là: S11 0 S13 S 14 0 0 S 22 S14 [ ]S S S 13 0 14 S33 0 (6.106) S13 S13 0 0 S14 44 0 S
Ta có thể chọn mạng 8 cực ối xứng với các mặt cuối ể ạt ược các hệ số phản xạ tại các
nhánh là thực và dương là .
Từ tính Unita và ối xứng của ma trận [S] (6.106), ta suy ra các ịnh thức con ứng với
các số hạng 0 của ma trận [S] (6.106) sẽ bằng không. Cụ thể ta có; 0 0 2 0 0
Suy ra: hoặc = 0 hoặc = 0 hoặc = 0. Nếu = S11 = S22 = S33 = S44 = 0 thì trùng với (6.105)
Còn trường hợp = = 0 ứng với hai trường hợp mạng 8 cực suy biến thành hai mạng
4 cực. Rõ ràng là bộ ghép ịnh hướng ối xứng là hoàn toàn phối hợp.
Ngược lại nếu một mạng 8 cực thuận nghịch hoàn toàn phối hợp là một bộ ghép ịnh hướng.
Ta viết ma trận tán xạ của mạng 8 cực hoàn toàn phối hợp này dạng:
0 S12 S13 S14 0 S S23 0 12 [ ]S
S23 S34 S24 S13 S24 S34 S14 0
Vì ma trận Unita, nên các ịnh thức con ứng với các số hạng 0 sẽ bằng 0. Do ó ta nhận ược các hệ thức:
S23 S24 S34 0;
S13 S14 S34 0 (6.107)
S12 S14 S24 0;
S12 S13 S23 0 lOMoARcPSD| 36067889
Hệ (6.107) có 3 nghiệm cặp: (A): S12 = 0; S34 = 0 (B): S13 = 0; S24 = 0 (C): S14 = 0; S23 = 0
3 nghiệm (A), (B), (C) sẽ cho ta 3 cách tạo ra bộ ghép ịnh hướng khác nhau.
Như vậy ma trận tán xạ của một bộ ghép ịnh hướng hoàn toàn phối hợp dạng: 0 0 S13 S14 [ ]S 0 0 S14 S13 (6.108) S13 S14 0 0 S14 S13 0 0 với iều kiện: |S13|2 + |S14|2 = 1 S13S14* + S14S13* = 0
Các tính chất trên là nói với các bộ ghép hoàn toàn lý tưởng. Tuy nhiên các bộ ghép
ịnh hướng thực tế bao giờ cũng có sóng ra nhánh cách ly. Để ặc trưng cho chất lượng của bộ
ghép ịnh hướng, ta dùng 2 khái niệm là hệ số ghép C và hệ cố ịnh hướng D. Chúng ược ịnh nghĩa như sau:
Hệ số ghép là tỉ số của biên ộ sóng ở nhánh ghép tính theo Decibel:
C = 20 lg |a1/b4| (dB) (6.109)
Hệ số ịnh hướng là tỉ số biên ộ sóng ở nhánh ghép và biên ộ sóng ở nhánh cách ly tính theo Decibel: D = 20 lg |b4/b2| (6.110)
Ở ây, sóng vào các nhánh 1 và ra ở nhánh 3, còn một phần năng lượng sẽ sang nhánh
ghép ịnh hướng 4 và phản xạ sang nhánh cách ly 2.
6.6. Các bộ cầu siêu cao
Mạch cầu siêu cao là những mạng 8 cực chia ôi công suất hay là những bộ phân mạch
ịnh hướng với ộ ghép C = 3 dB. Các bộ cầu siêu cao tần có thể thực hiện trên ống dẫn sóng
chữ nhật, ống ồng trục hoặc mạch dải. Các bộ cầu siêu cao iển hình là: cầu T kép, cầu khe và cầu vòng.
6.6.1. Cầu T - kép
Cầu T – kép ược cấu tạo từ việc ghép 2 chạc 3 vuông góc (chữ T) loại E và H có chung
mặt phẳng ối xứng P với nhau (hình 6.10). Do kết hợp 2 loại chạc 3 vuông góc loại E và H
nên cầu T – kép mang tính chất của 2 loại chạc 3 này. lOMoARcPSD| 36067889
Tức là nếu truyền sóng H10 vào nhánh 3 (E) thì tại nhánh (1) và (2) có 2 sóng ra ồng biên
và ngược pha, còn trong nhánh (4) không có sóng ra.
Nếu ta lại truyền sóng H 10 vào nhánh (4) thị tại nhánh (1) và (2) có 2 sóng ồng biên và
ồng pha mà không có sóng ra nhánh (3).
Như vậy, giữa hai nhánh (3) và (4) cách ly iện với nhau, tức là: S34 S43 0
Việc phối hợp trở kháng ở nhánh (3) ược thực hiện bởi tấm chắn iện cảm ặt ở nhánh E,
còn que dò ặt vuông góc với thành phần rộng của nhánh H sẽ làm cho nhánh này ược phối hợp. Ta có: S 33 S44 0
Vì bộ cầu T kép là ối xứng qua P va thuận nghịch, không tiêu hao năng lượng nên ma
trận tán xạ [S] sẽ ối xứng và Unita. Với tính chất của các chạc 3 vuông góc E và H ta có: S13
S31 S23 S32
S14 S41 S24 S42
ấm chắn iện cảm ộ cầ
Ngoài ra các hệ số truyền giữa 1-E và 1-H còn lệch pha nhau / 2 nên:
S14 S e13 j 2 jS13
Như vậy ma trận [S] của cầu T- kép có dạng:
S11 S12 S13 jS13 S 22 - -S13 S jS13 12 S13 jS13 0 S 0 0 lOMoARcPSD| 36067889 S13 0 jS13
Từ tính Unita của [S] ta có: 22 S12 2 S13 1 22 2 2 S13 2 1 1 Từ ó suy ra: 22 S 12 0
Như vậy cầu T- kép ược phối hợp hoàn toàn ở các nhánh và giữa nhánh 1 và nhánh 2
cũng cách ly iện. Do tính chất kỳ lạ này nên cầu T-kép còn ược gọi là cầu T magic.
Nếu chọn các mặt cuối của cầu T-kép một cách thích hợp thì ta có thể nhận ược ma trận
tán xạ [S] của nó có dạng gọn như sau: 0 0 1 j S 1 01 01 010j (6.111) 2 j j 0 0
6.6.2. Cầu vòng
Cầu vòng ược tạo thành trên ống dẫn sóng ồng trục hay trên mạch dải. Nó có cấu tạo như hình 6.11. ộ cầu v lOMoAR cPSD| 36067889
Thân cầu là một oạn ường truyền uốn vòng tròn cố chiều dài 6 / 4 và dẫn nạp ặc tính Y T
C . Các nhánh (1), (4) và (3) ghép song song với cầu cũng là các oạn ường truyền có dẫn sóng ặc tính Y T nh .
Chúng ặt cách nhau một khoảng cách /4. Còn nhánh (2) cũng có dẫn nạp ặc tính là Y T nh
ặt cách nhánh (3) một khoảng /4 và cách nhánh (4) một khoảng 3 /4.
Nguyên tắc làm việc của cầu vòng như sau: nếu sóng TEM vào nhánh (1) thì sóng sẽ
truyền vào cầu theo 2 phía của chỗ ghép i về các nhánh (3) và (4) hai sóng i theo hai phía của
cầu có cùng biên ộ và cùng pha (giả thiết không có tiêu hao trên cầu vòng) còn tại chỗ ghép
với nhánh (2) thì hai sóng này ồng biên và ngược pha. Tại tiết diện nối với nhánh (2) ta có nút
iện áp. Nên dẫn nạp vào tiết diện này bằng . Do ó tại các tiết diện ghép với các nhánh (3) và
(4) dẫn nạp vào bằng dẫn nạp ặc tính của các nhánh (3) và (4). Khi ó dẫn nạp vào tại tiết diện
ghép với nhánh (1) tiết diện AA trên hình 6.11 sẽ là tổng dẫn nạp của hai nhánh (3) và (4) mắc
song song tính chuyển qua một oạn /4 và bằng: YCT 2 YCT 2 YCT 2 YVAA T T 2 T Ynh Ynh Ynh
Muốn ể cầu vòng ược phối hợp thì yêu cầu dẫn nạp vào ở tiết diện ghép với nhánh (1)
phải bằng dẫn nạp ặc tính của nhánh, tức là ta có iều kiện phối hợp sau:
YnhT YVAA 2YCTT2 Ynh Từ ó rút ra hệ thức: Y T T nh 2YC (6.112)
Với trở kháng ặc tính thì iều kiện phối hợp của cầu vòng là: Z T T c 2Znh (6.113)
Nếu chọn các mặt cuối ở các nhánh một cách thích hợp, thì ta nhận ược ma trận tán xạ
[S] của cầu vòng thuận nghịch không tiêu hao dạng ơn giản như sau: 0 0 1 1 S 1 0101 10 01 (6.114) 2 1 1 0 0 lOMoARcPSD| 36067889
6.7. Các phần tử siêu cao tần có ferít
Các phần tử siêu cao tần sử dụng tính chất ặc biệt của ferít từ hóa bởi từ trường không
ổi ảm nhiệm nhiều chức năng quan trọng khác nhau trong tuyến siêu cao. Chúng thường ược
gọi là các phần tử không thuận nghịch. Các phần tử này thường là các mạng 4 cực, 6 cực và 8 cực.
6.7.1. Tính chất của ferít bị từ hóa
Ferít là một chất vừa có tính như môi trường iện môi vừa là chất sắt từ. Về hóa học ferít
là hỗn hợp của oxyt sắt (Fe2O3) với một số oxyt kim loại khác như Mg, Mn, Ni,… nó thường
ược chế tạo bằng cách nén bột ferít trong áp suất và nhiệt ộ thích hợp ể tạo nên dạng cần thiết.
Ferít có hằng số iện môi tương ối r
5 16 . Độ từ thẩm tương ối của ferít ở âm tần khá lớn,
còn khi tần số siêu cao thì nó giảm xuống bằng ơn vị.
Ferít khi không có từ trường không ổi từ hóa, ối với sóng iện từ biểu hiện như một môi
trường ẳng hướng bình thường. Nhưng nó mang những tính chất ặc biệt của môi trường không
ẳng hướng khi bị từ hóa bởi từ trường không ổi, khi truyền sóng iện từ siêu cao tần. Với môi
trường không ẳng hướng ộ từ thẩm ược o bằng tenxơ có dạng sau: x ja 0 ja x 0 0 0 z
Trong ó x,a, z là các hằng số, chúng phụ thuộc vào tính chất của ferít, cường ộ từ
trường không ổi từ hóa H0, vào tần số của trường siêu cao tần. Nói chung chúng là các ại lượng phức.
Một số tính chất ặc biệt của ferít từ hóa bởi từ trường không ổi khi truyền sóng siêu cao:
Khi truyền sóng iện từ vectơ cường ộ từ trường H phân cực tròn quay phải, mặt
phẳng vectơ H vuông góc với từ trường không ổi H0, vào ferít bị từ hóa. Vectơ từ cảm B cũng
phân cực tròn quay phải. Và như vậy môi trường ferít bị từ hóa có thể coi như môi trường ẳng
hướng với sóng phân cực tròn quay phải với hằng số từ môi mới là x a và sóng quay
phải truyền với vận tốc pha: Vph 1 x a
Nếu ta lại truyền sóng siêu cao tần có vectơ cường ộ từ trường H phân cực tròn quay lOMoARcPSD| 36067889
trái mà vectơ H vuông góc với vectơ từ trường không ổi H0, khi i vào ferít bị từ hóa, thì vectơ
từ cảm của sóng siêu cao tần cũng phân cực tròn quay trái. Tức là ferít bị từ hóa bởi từ trường
không ổi có tác dụng như một môi trường ẳng hướng ối với việc truyền sóng phân cực tròn
quay trái, nhưng có ộ từ thẩm là: x a
Và vận tốc pha: V 1 ph x a
Như vậy ferít bị từ hóa bởi từ trường không ổi có tác dụng khác nhau lên phân cực tròn
quay trái và quay phải. Độ từ thẩm của ferít ối với 2 sóng này khi kể ến suy hao là một số phức:
x a 1 j 2 x a 1 j 2 Phần thực
1 , 1 biểu thị sự biến ổi của vận tốc pha của các sóng khi truyền qua ferít,
còn phần ảo 2 ; 2 biểu thị mức ộ tiêu hao của 2 sóng trong ferít. Khi nghiên cứu tỉ mỉ,
người ta vẽ ược các ường cong ộ từ thẩm phụ thuộc vào cường ộ từ trường từ hóa H0 như trên hình 6.12.
Hình 6.12. Sự phụ thuộc của từ thẩm vào cường ộ từ trường từ hóa của ferít
Từ ồ thị ta thấy có một giá trị của H H 0
och , tại ây vận tốc pha của sóng phân cực tròn
quay phải biến ổi lớn và nó bị tiêu hao năng lượng nhiều. Đường cong 2 có dạng ường cong lOMoARcPSD| 36067889
cộng hưởng. Hiện tượng sóng phân cực tròn quay phải bị tiêu hao năng lượng gọi là sự cộng
hưởng sắt từ trong ferít từ hóa.
Bây giờ ta lại truyền sóng siêu cao tần dọc theo phương của vectơ từ trường không ổi
H0 từ hóa ferít có phân cực thẳng tùy ý. Khi i ra khỏi ferít từ hóa, mặt phẳng phân cực của sóng
siêu cao bị quay i một góc so với hướng ban ầu. Hiện tượng trên gọi là hiệu ứng Faraday trong
ferít từ hóa. Độ lớn của góc quay và chiều quay mặt phẳng phân cực phụ thuộc
vào chiều và ộ lớn của vectơ từ trường H0 và kích thước của ferít.
Hiệu ứng Faraday có thể giải thích gọn như sau: một phân cực thẳng bất kỳ của vectơ
cường ộ từ trường H của sóng siêu cao có thể coi như tổng của 2 sóng phân cực tròn quay
trái và quay phải có modul vectơ H như nhau. Khi truyền dọc theo thanh ferít bị từ hóa bởi
từ trường không ổi H0 hướng theo trục thanh ferít thì các sóng quay trái và quay phải bị lệch pha các góc khác nhau
l; l ở ây l là chiều dài thanh ferít, còn , là các
hệ số pha của hai sóng quay phải và quay trái. 2 x a 2 x a
Do ó tổng hợp 2 sóng phân cực trò quay trái và quay phải khi ra khỏi ferít bị tè hóa cũng
là sóng phân cực thẳng, nhưng mặt phân cực của nó bị lệch so với vị trí ban ầu một góc . l = 2 l x a x a
Dựa trên các tính chất ã nêu của ferít bị từ hóa ta xét một số các phần tử siêu cao tần có
ứng dụng ferít bị từ hóa.
6.7.2. Các phần tử có ferít trong ống dẫn sóng chữ nhật
6.7.2.1. Van cộng hưởng lOMoARcPSD| 36067889
Van cộng hưởng ược cấu tạo từ một oạn ống dẫn sóng chữ nhật, bên trong nó tại tiết
diện x1 ; chỗ sóng H10 có từ trường phân cực tròn ta ặt một bản ferít mỏng song song với thành
hẹp dọc theo tiết diện này (hình 6.13) từ trường từ hóa không ổi H 0 hướng vuông góc với
thành rộng ống dẫn sóng.
Giả sử khi sóng H10 ược truyền theo phương z 0 vào ống dẫn sóng chữ nhật có thanh
ferít; thì tại tiết diện x1 này từ trường của sóng H 10 là phân cực tròn quay phải. Còn nếu sóng
truyền theo chiều ngược lại z 0 thì tại x1 từ trường sẽ phân cực tròn quay trái.
Nếu ta chọn cường ộ từ trường không ổi có giá trị H 0
H 0ch , thì thanh ferít sẽ hấp thụ áng kể
năng lượng của sóng phân cực tròn quay phải, do vậy khi sóng H 10 truyền theo phương z 0
bị suy giảm nhiều. Khi truyền ngược lại z 0 thanh ferít không hấp thụ năng lượng sóng phân
cực tròn quay trái, nên sóng H10 không bị suy giảm. Như vậy phần tử trên làm việc như một
chiếc van, cho sóng i theo một chiều, nó ược gọi là van cộng hưởng. ộng hưởng
Để tăng cường hiệu quả của van, tại tiết diện x 2 trường H 10 cũng phân cực tròn ta ặt
thêm một tấm ferít mỏng nữa dọc theo thành hẹp, còn từ trường không ổi từ hóa ặt hướng
vuông góc với thành rộng nhưng có chiều ngược lại.
6.7.2.2. Bộ quay pha không thuận nghịch
Về cấu tạo, bộ quay pha này ược tạo thành từ một oạn ống dẫn sóng chữ nhật, tại tiết
diện x ta ặt một bản ferít mỏng song song với thành hẹp, từ trường từ hóa không ổi H 0 cũng
hướng vuông góc với thành rộng ống sóng (hình 6.14) nhưng về ộ lớn thì ta chọn nhỏ hơn
nhiều so với H 0ch . lOMoARcPSD| 36067889 Hình 6.14.
Bộ quay pha không thuận nghịch làm việc theo nguyên tắc: thanh ferít bị từ hóa bởi từ
trường không ổi sẽ tác dụng lên 2 sóng quay trái và quay phải với các ộ từ thẩm , khác nhau. Khi H 0
H 0ch thi tiêu hao của cả 2 sóng là không áng kể và từ ồ thị hình 6.14 ta thấy
nên sóng quay trái khi truyền qua thanh ferít sẽ bị lệch pha nhiều hơn sóng phân cực
tròn quay phải. Do ó khi sóng H10 truyền vào bộ quay pha theo 2 hướng khác nhau z 0 và z
0 sẽ có góc lệch pha khác nhau. Hiệu góc lệch pha giữa chúng sẽ có một giá trị nào ó. Và
như vậy phần tử trên có tác dụng như một bộ quay pha không thuận nghịch. Góc quay pha
phụ thuộc vào cường ộ từ trường H 0 , chiều dài thanh ferít và vị trí ặt thanh ferít. Trên hình
6.14 vẽ sự thay ổi góc pha phụ thuộc vào vị trí x ặt tấm ferít.
6.7.2.3. Phân mạch vòng tuần hoàn (Circulator) kiểu chữ Y
Bộ phân mạch vòng tuần hoàn ược thực hiện trên một chạc 3 ối xứng Y kiểu H trên ống
dẫn sóng chữ nhật. Tại tâm của chạc 3 có một thanh ferít hình trụ ược gắn với một vỏ iện môi
hình trụ ặt vuông góc với thành rộng của ống dẫn sóng. Tại 3 ầu vào có gắn thêm 3 thanh nhỏ
iện môi hình trụ vuông góc với thành rộng và ở giữa chúng (hình 6.15). Từ trường không ổi H
0 ặt vuông góc với thành rộng của ống dẫn sóng. lOMoARcPSD| 36067889
Hình 6.15. Circulator kiểu chữ Y
Nguyên tắc làm việc của circulator chữ Y như sau: sóng H 10 truyền vào nhánh (1) i
ến vùng có ferít rẽ làm 2 sóng i vòng theo 2 chiều ngược nhau quanh thanh ferít. Vùng
quay của từ trường 2 sóng này nằm trong mẫu ferít bị từ hóa và hướng quay H của chúng
theo phương của vectơ từ hóa H10 là ngược chiều nhau, và ferít sẽ biểu hiện ộ từ thẩm có giá
trị và khác nhau và góc lệch pha khác nhau. Ta chịn kích thước của thanh ferít và cường
ộ từ trường từ hóa H 0 sao cho 2 sóng này i vào nhánh (2) sẽ ồng pha, còn vào nhánh 3 chúng
ngược pha. Kết quả sóng i nhánh (1) sẽ ra nhánh (2) mà không vào nhánh (3). Do tính ối xứng
của circulator mà ta thấy ngay rằng nếu truyền sóng vào nhánh (2) thì có sóng rẽ sang nhánh
(3) không vào nhánh (1), hoặc nếu sóng truyền vào nhánh (3) thì sẽ chỉ rẽ sang nhánh (1).
Tóm lại ta có chu trình làm việc của circulator như sau: 1 2 3 1
Nếu ta ổi chiều H 0 thì circulator sẽ làm việc theo chu trình sau: 1 3 2 1
Thanh iện môi bao thanh ferít có tác dụng nâng cao tính ổn ịnh nhiệt và sự bền chắc của
circulator. Còn 3 thanh nhỏ iện môi ở 3 nhánh có tác dụng phối hợp giữa các nhánh. Do cấu
trúc ơn giản, kích thước gọn nhẹ nên circulator chữ Y ược dùng khá rộng rãi trong kỹ thuật
siêu cao tần, nó có dải làm việc ến 30% tần số trung tâm.
6.7.2.4. Bộ phân mạch vòng tuần hoàn 4 nhánh (circulator kiểu pha)
Bộ phân mạch vòng tuần hoàn kiểu pha là một mạng 8 cực. Nó ược cấu tạo từ 2 bộ cầu
khe ống dẫn sóng và một bộ quay pha không thuận nghịch ghép với nhau như hình 6.16. ểu pha
Bộ quay pha không thuận nghịch làm quay một góc pha theo chiều mũi tên. Bộ
circulator này làm việc theo chu trình sau: 1 2 3 4 1 lOMoARcPSD| 36067889
Thật vậy, nếu truyền sóng H 10 vào nhánh (1) thì sóng sẽ sang nhánh bên của cầu khe thứ
nhất một nửa năng lượng với góc lệch pha / 2 so với sóng i trong nhánh chính của cầu khe
này. Sóng i trong nhánh chính qua bộ quay pha không thuận nghịch lệch pha thêm một góc
và tiếp tục i sang nhánh (2) của cầu khe thứ 2. Trong khi ó sóng i ở nhánh phụ sẽ qua lỗ cầu
khe thứ hai một phần rẽ sang nhánh (2) và lệch pha thêm một góc / 2. Do ó 2 sóng i vào
nhánh (2) sẽ ồng pha và chúng ược cộng lại. Còn 2 sóng i vào nhánh (4) sẽ lệch pha nhau các góc
/ 2 và / 2 nên kết quả chúng triệt tiêu nhau. Còn do tính chất của cầu khe mà sóng
ở nhánh (1) không rẽ sang nhánh (3).
Ta cũng có thể nhận ược bộ circulator 4 nhánh trên ống dẫn sóng tương tự như trên, nếu
thay một trong hai cầu khe bằng một T-kép.
6.7.3. Các phần tử có ferít trong ống dẫn sóng tròn.
6.7.3.1. Circulator 4 nhánh (kiểu phân cực)
Nguyên tắc hoạt ộng của bộ circulator trên ống dẫn sóng trụ tròn là ứng dụng hiệu ứng
Faraday trong ferít từ hóa.
Bộ circulator này có cấu tạo như hình 6.17. Nó gồm một oạn ống dẫn sóng tròn ấu ghép
với hai oạn chuyển tiếp dẫn thành ống dẫn sóng chữ nhật nhưng có thành rộng quay với nhau
một góc 450. Ở giữa trục của ống dẫn sóng tròn ta ặt một thanh ferít hình trụ mảnh vát nhọn
2 ầu ể tránh phản xạ, từ trường từ hóa H 0 hướng dọc theo trục ống dẫn sóng.
Cũng tại 2 ầu oạn ống dẫn sóng tròn còn gắn hai oạn ống dẫn sóng chữ nhật có thành rộng
vuông góc với trục ống dẫn sóng tròn, và lập với nhau cũng một góc 450. Để tăng sự phối hợp
và tránh sự phản xạ tại 2 ầu các nhánh (1) và (2) ta ặt 2 tấm iện môi mảnh song song với thành
rộng của ống dẫn sóng chữ nhật. Chiều dài thanh ferít và cường ộ từ trường từ hóa H 0 chọn
sao cho khi sóng cơ bản H11 truyền dọc theo thanh ferít bị từ hóa sẽ quay mặt phẳng phân cực
i một góc 450 theo chiều kim ồng hồ. Circulator này làm việc theo chu trình sau: 1 2 3 4 1 lOMoARcPSD| 36067889
Hình 6.17. Circulator 4 nhánh kiểu phân cực
Nguyên tắc hoạt ộng của circulator trên này có thể giải thích qua giản ồ vectơ của ường
sức iện trường của sóng H 10 và H 11 thì sẽ ược chu trình làm việc của circulator như sau: 1 4 3 2 1
Do ứng dụng sự qua mặt phẳng phân cực của sóng, nên nó còn ược gọi là circulator phân cực. 6.7.3.2. Van Faraday
Van Faraday có cấu tạo giống circulator phân cực, nhưng không có hai nhánh (3) và (4).
Từ trường H 0 từ hóa và chiều dài thanh ferít l vẫn chọn sao cho sóng H11 truyền dọc theo thanh
ferít mặt phẳng phân cực của sóng bị quay i một góc 450 theo chiều kim ồng hồ, ở ầu nhánh
(1) ta chỉ ặt một tấm iện môi song song với thành rộng của ống dẫn sóng.
Rõ ràng từ giản ồ vectơ hình 6.18, ta thấy khi sóng i từ nhánh (1) rẽ sang nhánh (2), còn
nếu truyền sóng từ nhánh (2) sẽ không có sóng vào nhánh (1). Sóng sẽ bị tấm iện môi ở phía
nhánh (1) ặt song song với ường sức iện trường lúc này hấp thụ rất mạnh. Phần tử làm việc
cho sóng i theo một chiều từ (1) sang (2) nên ược gọi là van Faraday.
Ngoài các phần tử có ferít trong ống dẫn sóng chữ nhật và tròn, còn có một số phần tử
có ferít trên ống dẫn sóng ồng trục và mạch dải. Các thiết bị này cũng có tính chất tương tự
như ống dẫn sóng chữ nhật và tròn. lOMoARcPSD| 36067889 (4)
6.7.4. Một số ứng dụng của các phần tử siêu cao có ferít.
6.7.4.1. Bộ chuyển mạch nhanh
Bộ chuyển mạch nhanh ược sử dụng trên circulator ối xứng chữ Y. Nhánh (1) lắp với
mạy phát năng lượng siêu cao tần, còn nhánh (2) và (3) nối với 2 tuyến cần dẫn sóng (hình 6.19)
Hình 6.19. Bộ chuyển mạch nhanh trên circulator ối xứng chữ Y
Việc thay ổi chiều từ trường không ổi H 0 ược thực hiện bằng nam châm iện khi thay ổi
chiều dòng iện. Khi thay ổi chiều dòng iện chảy trong nam châm ta thực hiện việc dẫn năng
lượng siêu cao lần lượt từ máy phát vào các tuyến (1) và tuyến (2). Tốc ộ của chuyển mạch này khá lớn. lOMoARcPSD| 36067889
Bộ chuyển mạch nhanh cũng có thể thực hiện trên circulator 4 nhánh loại phân cực (hình
6.20). Ở ây máy phát ược lắp vào nhánh (1), hai tuyến dẫn năng lượng lắp vào nhánh (2) và
(4). Ta không dùng nhánh (3).
Hình 6.20. Bộ chuyển mạch nhanh trên circulator 4 nhánh
6.7.4.2. Bộ ảo mạch anten rada
Trong các rada một anten dùng chung cho cả máy phát và máy thu, người ta sử dụng bộ
circulator làm bộ phân ường cho tín hiệu thu và phát. Nhánh (1) của circulator 4 nhánh lắp
với máy phát, nhánh (2) lắp với anten chung, nhánh (3) lắp với ầu vào máy thu qua bộ phóng
iện bảo vệ, còn nhánh (4) lắp với tải hấp thụ (hình 6.21).
Khi máy phát làm việc công suất lớn từ máy phát i ra anten có thể một phần năng lượng
phản xạ từ anten sang máy thu nhưng lúc này bộ phóng iện làm việc, làm ngắn mạch máy thu
và tín hiệu sẽ i ến tải hấp thụ mà không về máy phát làm máy phát hoạt ộng ổn ịnh. Khi máy
phát nghỉ các tín hiệu phản xạ từ mục tiêu qua anten i vào máy thu, lúc này bộ phóng iện không làm việc. Máy Máy
Hình 6.21. Bộ ảo mạch anten rada
6.7.4.3. Bộ tách các kênh tần số
Trong thông tin tiếp sức có nhiều kênh tần số cao tần, ở nơi thu ta cần tách các kênh
riêng rẽ bằng cách sử dụng bộ tách kênh tần số. Bộ tách kênh tần số này ược hình thành từ
các circulator và các bộ lọc thông dải. Trên hình 6.22 mô tả một bộ tách kênh 4 tần số cao
dùng 2 circulator và 4 bộ lọc thông dải F F1, 2 ,F3,F4 . lOMoARcPSD| 36067889 ả hiệu
Hình 6.22. Bộ tách các kênh tần số
6.8. Phối hợp trở kháng ở siêu cao tần
Nhiệm vụ cơ bản của vấn ề phối hợp trở kháng ở siêu cao tần là làm sao bảo ảm trong
tuyến siêu cao tần, sóng phản xạ là ít nhất hoặc ảm bảo trong tuyến siêu cao tần hệ số sóng
ứng K d hay hệ số sóng chạy K ch ạt yêu cầu ề ra trong một dải tần nhất ịnh.
6.8.1. Ý nghĩa của việc phối hợp trở kháng a)
Do mất phối hợp nên trong tuyến siêu cao có sóng ứng. Thực hiện việc phối
hợp trở kháng ở siêu cao có nghĩa là dùng những phần tử phối hợp ưa vào ường truyền ể
giảm ến mức tối a sự phản xạ sóng trong một dải tần xác ịnh. Khi trong tuyến siêu cao ã
ược phối hợp trở kháng lý tưởng thì chỉ có sóng chạy thuần tuý, tức là có K ch 1 Việc phối
hợp trở kháng óng vai trò rất quan trọng trong thực tiễn và là vấn ề hay gặp trong kỹ thuật
siêu cao tần. Thật vậy, nếu trong tuyến siêu cao tần khi mất phối hợp trở kháng sẽ gây ra
các tác hại xấu như sau:
Ta biết rằng công suất truyền lan từ máy phát ến tải trên ường truyền ược xác ịnh theo công thức:
Ptải = Ptới – Ppx = Ptới(1 - |Rpx|2)
Khi tải ược phối hợp với ường truyền thì:
|Rpx| = 0, Ptải = Ptới và ạt giá trị cực ại
Khi mất phối hợp với ường truyền, do |Rpx| > 0 nên Ptải < Ptải max
Như vậy công suất truyền từ máy phát ến tải giảm. b)
từ lý thuyết ường truyền, ta có biểu thức xác ịnh công suất truyền lan tới hạn dọc ường truyền là:
Pth = Pthmax(1 - |Rpx|)/(1 + |Rpx|) = Pth.max/Kd lOMoARcPSD| 36067889
Ở ây, Pth.max là công suất truyền lan tới hạn khi ường truyền ược phối hợp hoàn toàn
|Rpx| = 0. Rõ ràng nó là công suất truyền lan lớn nhất ường truyền có thể chịu ựng ược mà
không xảy ra hiện tượng ánh lửa. Khi mất phối hợp trở kháng, tức |Rpx| khác 0 thì Pth < Pthmax
tức là công suất truyền lan tới hạn trên ường truyền giảm i, trên ường truyền có sóng ứng và
tại các iểm bụng của nó dễ xảy ra hiện tượng ánh lửa nếu truyền công suất lớn hơn giá trị tới hạn. c)
Nếu trong ường truyền mất phối hợp thì sự suy giảm sóng trong nó lớn, tiêu hao
năng lượng lớn làm giảm hiệu suất của ường truyền.
Hàm suy giảm công tác L của một oạn ường truyền dài l với sóng truyền trên nó ược xác ịnh theo công thức: pvao 1 |Rpx |2 e 4 l L 10lg ra 10lg (1 |Rpx | )2 e 2 l P với là hệ số suy hao.
Khi ường truyền ược phối hợp hoàn toàn, tức là |Rpx| = 0 thì:
L L min 10lge2 1 20 1 lge 8,68 1 dB
Nếu ường truyền bị mất phối hợp, tức là |R| khác 0 thì L > Lmin tức là tiêu hao trong
ường truyền tăng lên làm giảm hiệu suất của nó. d)
Ngoài ra khi ường truyền bị mất phối hợp trở kháng, sóng phản xạ sẽ trở về
máy phát làm ảnh hưởng ến chế ộ làm việc ổn ịnh của máy phát cả về phương diện công suất lẫn tần số.
Do ó trong tuyến siêu cao tần, máy phát thường ược lắp qua thiết bị phối hợp với ường
truyền. Các thiết bị này có thể là các phần tử cách ly như; các bộ suy giảm biến ổi hoặc các bộ van.
Vấn ề phối hợp trở kháng thường ược chia làm hai loại: phối hợp trở kháng dải rộng và
phối hợp trở kháng dải hẹp.
6.8.2. Các phương pháp phối hợp trở kháng
6.8.2.1. Phối hợp trở kháng dải hẹp
Phối hợp trở kháng ở một tần số cố ịnh hay xung quanh nó với dải hẹp về mặt lý thuyết
có thể ảm bảo dùng các phần tử phối hợp ạt ược chế ộ gần lý tưởng. Các phần tử phối hợp
ược ưa vào trong ường truyền chỉ cần dùng các phần tử thuần kháng nên không gây ra tiêu
hao năng lượng. Đó là các biến áp /4 và các phần tử thuần kháng như que dò, tấm chắn hay
Sleypher. Sau ây ta xét một trường hợp là nguyên tắc dùng biến áp /4. lOMoARcPSD| 36067889
Biến áp /4 chính là một oạn ường truyền ồng nhất không tiêu hao năng lượng có ộ dài
bằng 1/4 bước sóng công tác và có trở sóng ặc tính ZCT. Dùng biến áp /4 mắc vào giữa
ường truyền và tải có thể ảm bảo phối hợp sao cho trên oạn ường truyền từ chỗ nối biến áp
trở về máy phát không có sóng phản xạ. Về mặt vật lý, iều ó ược giải thích là do sóng phản
xạ tại hai ầu nối của biến áp /4 sẽ ngược pha nhau, nếu biên ộ của các sóng phản xạ này
chọn ược bằng nhau, chúng sẽ triệt tiêu nhau ở lối vào của biến áp.
Ta có thể tính toán ịnh lượng bài toán phối hợp trở kháng dùng biến áp /4 qua ồ thị vòng Smith.
6.8.2.2. Phối hợp trở kháng dải rộng
Vấn ề phối hợp trở kháng dải rộng là vấn ề khá phức tạp, óng vai trò thiết thực trong các
bài toán thực tiễn. Phối hợp trở kháng dải rộng hay phối hợp trở kháng trong một dải tần ã
cho yêu cầu phải ảm bảo ạt ược chỉ tiêu ã cho như hệ số sóng chạy không ược nhỏ hơn giá trị
Kchmin nào ó trong dải hoặc ảm bảo thực hiện ược theo một hàm ặc trưng nào ó chẳng hạn theo
ặc trưng của hàm suy giảm công tác L.
Các phần tử phối hợp trở kháng trong một dải tần ã cho có cấu tạo rất a dạng và có thể
theo hai hướng khác nhau: dùng các phần tử tiêu hao năng lượng và các phần tử không tiêu hao năng lượng.
Một số phương pháp phổ biến là: phối hợp dùng tải hấp thụ hay bộ van, phối hợp dùng
oạn ường truyền không ồng nhất, phối hợp dùng mạch cộng hưởng.
6.8.2.3. Giản ồ Smith
Khi giải các bài toán về phối hợp trở kháng, người ta sử dụng một công cụ rất có hiệu
quả cả trong lý thuyết lẫn thực tế là ồ thị vòng Smith. Trong tài liệu này chỉ giới thiệu tóm tắt
cấu tạo ồ thị vòng và một số ứng dụng cơ bản.
Đồ thị vòng Smith ược xây dựng trên tọa ộ cực của mặt phẳng phức, nó biểu diễn các
tham số cơ bản trong ường truyền như: hệ số phản xạ, hệ số sóng ứng Kd hoặc hệ số sóng
chạy Kch, trở kháng chuẩn hóa Z ch ( )z và dẫn nạp chuẩn hóa Y ch ( )z tại một tiết diện bất kỳ. Nó có cấu trúc như sau:
- Họ vòng tròn ồng tâm O với bán kính R từ 0 ến 1 mô tả module của hệ số phản xạ
hoặc giá trị của hệ số sóng ứng hoặc sóng chạy. Tại vòng tròn tâm O bán kính lớn nhất R 1,
ta khắc ộ các pha của hệ số phản xạ theo giá trị tương ối l/ có giá trị từ 0 ến 0,5 theo hai
chiều ngược nhau với gốc ở iểm A. Hình 6.23. 1
- Họ vòng tròn có tâm nằm trên trục thực AB trong oạn OB có bán kính bằng ối 1 r
1 với trở kháng hay bằng ối với dẫn nạp, nó biến ổi từ 0 ến 1.
Họ vòng tròn này chỉ 1 g
các giá trị dẫn thuần g const hay trở thuần r const Các vòng tròn ều tiếp xúc nhau tại iểm B. lOMoARcPSD| 36067889
- Họ vòng tròn có tâm nằm trên ường thẳng song song với trục ảo i qua iểm B với 1
1 bán kính bằng ối với trở kháng và bằng ối với dẫn nạp, có bán
kính thay ổi từ 0 ến x z
vô cực. Họ vòng tròn này mô tả các giá trị kháng thuần x const và iện nạp b const . Chúng
cũng tiếp xúc với nhau tại iểm B. Một phần của họ vòng tròn trên trong vòng tròn bán kính
ơn vị ược vẽ ở hình 6.24. Phía phải trục thực các vòng tròn chỉ x 0 hoặc b 0 , phía trái
trục thực các vòng tròn cho ta giá trị x 0 hoặc b 0.
Giao iểm của hai họ vòng tròn trên mô tả iểm có trở kháng chuẩn hóa Z ch r jx hoặc
dẫn nạp chuẩn hóa Y ch
g jb trên ường truyền. Hình 6.24.
Tại iểm A, trở kháng và dẫn nạp bằng 0 (r x 0;g b 0) còn ở iểm B thì trở kháng
và dẫn nạp bằng (r x ;g b )
Trục thực AB mô tả các giá trị trở thuần và dẫn thuần. Bán kính OA là quỹ tích các iểm
nút iện áp ( ối với ồ thị trở kháng) và là quỹ tích các iểm bụng áp ( ối với ồ thị dẫn nạp), bán
kính OB là quỹ tích các iểm bụng áp (với trở kháng) hay nút áp (với dẫn nạp).
Vòng tròn lớn nhất (bán kính ơn vị) chỉ các giá trị của kháng thuần x hoặc iện nạp b (vì r 0;g 0 ).
Tâm O của ồ thị biểu diễn chế ộ phối hợp trở kháng lý tưởng trong ường truyền (r 1,g 1;x b 0) . lOMoARcPSD| 36067889
Từ gốc A theo ường tròn tâm O quay theo chiều kim ồng hồ cho chiều chuyển ộng trên
ường truyền từ tải về máy phát, còn ngược chiều kim ồng hồ ứng với dịch chuyển trên ường
truyền từ máy phát về tải.
Hình 6.25. Đồ thị vòng Smith
6.8.2.4. Các ứng dụng của giản ồ Smith
a) Biểu diễn trở kháng chuẩn hóa của tải và hệ số sóng ứng
Giả sử có ường truyền siêu cao có trở sóng ặc tính là Zco, ở cuối ường mắc tải với giá trị
Zt. Hãy tìm iểm biểu diễn Zt trên ồ thị vòng và hệ số sóng ứng trên ường truyền.
Vì ồ thị vòng trở kháng dùng cho các ơn vị tương ối tức là với các trở kháng chuẩn hóa,
nên hãy tính với tải chuẩn hóa:
zt zt rt jxt zco lOMoARcPSD| 36067889
Ta tìm trên giản ồ giao iểm của hai vòng tròn r rt ;x xt Giao iểm này chính là iểm biểu
diễn tải cần tìm. Trên hình 6.26 là iểm C. Từ iểm C ta vẽ vòng tròn tâm O bán kính OC sẽ ược
vòng tròn chỉ Kd cần tìm. Vòng tròn này cắt trục thực AB tại iểm có khắc ộ sẽ cho giá trị Kd.
b) Xác ịnh trở kháng vào của ường truyền cách tải một khoảng l khi biết trở tải
Giả sử ta có ường truyền không tổn hao với trở sóng ặc tính là Zco ở cuối có mắc tải Zt,
hãy xác ịnh trở kháng lối vào của ường truyền cách tải một khoảng l , bước sóng công tác trên ường truyền là .
Trước hết ta tìm iểm biểu diễn tải chuẩn hóa trên ồ thị vòng. Đó là iểm C trên hình
6.26 giống như ở mục a).
zt zt rt jxt zco
Vẽ vòng tròn tâm O bán kính OC sẽ là vòng tròn K d
const trên ường truyền. từ O kẻ
bán kính qua C cắt vòng tròn ơn vị theo chiều kim ồng hồ (tức là theo chiều về máy phát)
một oạn tương ối là l/ sẽ ược iểm D’. Nối bán kính OD’ cắt vòng tròn, K d const tại D. Từ
ây ta nhận ược 2 giá trị ứng với giao iểm của 2 vòng tròn r v
r const x, v x const
Trở vào tại tiết diện cách Zt một khoảng l là: z v zco (rv jxv )
c) Xác ịnh trở tải
Bây giờ ta xác ịnh trở kháng tải mắc ở cuối ường truyền khi ã xác ịnh ược hệ số sóng ứng
Kd và khoảng cách từ tải tới iểm nút áp ầu tiên là dmin. Đường truyền có trở sóng ặc tính Zco
và công tác ở bước sóng .
Ta biết rằng quỹ tích các iểm nút áp của sóng ứng biểu diễn trên oạn OA của ồ thị vòng
với trở kháng. Do ó ta dựng vòng tròn Kd = const cắt trục AB tại E. Điểm này chính là iểm
biểu diễn nút ầu tiên trên ường truyền cách tải một khoảng dmin. Ta lấy A làm gốc dịch chuyển
trên vòng tròn lớn (bán kính ơn vị) theo chiều về tải (ngược chiều kim ồng hồ) một oạn là lOMoARcPSD| 36067889
dmin/ sẽ nhận ược iểm C. Nối OC cắt vòng tròn Kd = const tại F. Qua F ta nhận ược 2 vòng
tròn có giá trị r const x, const Cuối cùng nhận ược trở kháng tải là: z t zco rt jxt
d) Xác ịnh dẫn nạp khi biết trở kháng
Ta ã biết dẫn nạp tại một iểm tiết diện Z bất kỳ trên ường truyền có thể tính dựa trên
phép lấy nghịch ảo của trở kháng dựa vào ồ thị vòng một cách dễ dàng hơn. Từ các biểu thức
(6.54) và (6.55) ta nhận ược mối quan hệ giữa trở kháng ở hai tiết diện Z1 và Z2 cách nhau một oạn bằng /4 là: z1 zco zco z2 1 hay z 1 y2 z2
Như vậy ta nhận ược quan hệ: trở kháng tại tiết diện bất kỳ bằng dẫn nạp tại tiết diện
cách tiết diện trên một khoảng bằng /4. Việc tìm trở kháng chuẩn hóa ở tiết diện cách một
khoảng /4 ược thực hiện trên ồ thị vòng tròn bằng cách dịch chuyển theo vòng tròn Kd =
const i một khoảng l/ = 0,25. Hay là thực hiện phép lấy ối xứng trên vòng tròn Kd = const qua
tâm O. Vậy ta có thể nhận ược dẫn nạp từ trở kháng qua phép lấy ối xứng qua vòng tròn Kd =
const. Điểm C biểu diễn trở kháng còn iểm D biểu diễn dẫn nạp trên ồ thị vòng tròn ở hình 6.27.
6.9. Giới thiệu một số cấu kiện siêu cao tần
6.9.1. Đèn Klystron trực xạ
Đèn Klystron là một loại linh kiện èn iện tử hiện vẫn còn ang ược sử dụng rộng rãi trong
kỹ thuật siêu cao tần do khả năng công suất lớn, hiệu suất cao với một dải tần số tương ối
rộng. Đèn Klystron bao gồm hai loại: èn Klystron trực xạ và èn Klystron phản xạ. nguyên lý
hoạt ộng của chúng có những iểm tương ồng nhau. lOMoARcPSD| 36067889
Nguyên lý hoạt ộng của èn Klystron trực xạ:
Đèn Klystron trực xạ ược sử dụng trong mạch khuếch ại siêu cao tần công suất lớn, dựa
trên nguyên lý iều chế vận tốc và iều chế cường ộ dòng iện của chùm tia electron. Đèn có hai
hốc cộng hưởng 1 và 2, ặt thẳng hàng lần lượt trên ường i của chùm tia electron.
Hình 6.28. Đèn Klystron trực xạ
Khi cathode ược sưởi nóng và có iện thế ban ầu – B0, các electron bức xạ bởi cathode ã
có một vận tốc ban ầu. Chúng ược một iện cực anode, mang iện thế - U0, dương hơn so với –
B0, gia tốc và do ó chúng di chuyển thành một chùm tia với vận tốc ều nhau v0. hốc cộng
hưởng 1, ặt trên ường i của chùm tia electron (có tiết diện dạng lưới, cho phép chùm tia
electron xuyên qua), nhận một tín hiệu RF ở siêu cao tần từ bên ngoài và tạo ra một hiệu iện
thế siêu cao tần giữa hai chùm vách của hốc cộng hưởng (cách nhau khoảng d). Khi chùm
electron i xuyên qua hốc cộng hưởng 1, hiệu iện thế này có tác dụng gia tốc thêm cho các
electron ở bán kỳ dương hoặc làm giảm vận tốc của electron ở bán kỳ âm. Kết quả là các
electron ược gia tốc sẽ di chuyển nhanh và bắt kịp các electron phía trước, các electron bị
giảm vận tốc sẽ di chuyển chậm lại và gặp các electron phía sau. Khi hiện tượng trên xảy ra
tuần tự liên tiếp, chùm electron ban ầu sẽ lần lượt bị kết nhóm electron sau khi ra khỏi hốc
cộng hưởng 1 và các nhóm electron này sẽ di chuyển trong vùng không gian giữa hộc cộng
hưởng 1 và hốc cộng hưởng 2.
Khi các nhóm electron này i xuyên qua hốc cộng hưởng 2, sự dịch chuyển thành nhóm
của hạt mang iện sẽ tương ương dòng iện bị iều chế cường ộ và do ó cảm ứng hiệu iện thế RF
ở tần số cao trong hốc. Hiệu thế này ồng dạng với tín hiệu RF vào, sẽ ược lấy ra từ hốc cộng
hưởng 2 (tín hiệu RF ra), nhờ vậy ta tạo ược mạch khuếch ại siêu cao tần.
Các electron sau khi ra khỏi hốc cộng hưởng 2 sẽ ược thu nhận bởi iện cực collector.
Đèn Klystron trực xạ có một số ặc tính kỹ thuật chính như sau:
- Hiệu suất công suất: trong lý thuyết hiệu suất công suất = Pout/Pin có thể ạt cực ại ến
58%, nhưng trong thực tế thường ạt từ 15% ến 30%
- Công suất phát lớn, có thể ạt ến 500 kW với tín hiệu liên tục và hàng chục MW cho
tín hiệu xung, tại các tần số từ 10 GHz ến 20 GHz.
- Hệ số khuếch ại công suất lớn, có thể ạt ến 40 dB. lOMoARcPSD| 36067889
Hình 6.29. Một số hình ảnh èn Klystron
6.9.2. Đèn Klystron phản xạ
Với èn Klystron trực xạ, năng lượng của chùm tia electron khi ra khỏi hộc cộng hưởng
1 sẽ ược trao cho hốc cộng hưởng 2. Nếu cấu trúc chỉ có một hốc cộng hưởng và tia electron
sau khi ra khỏi hốc cộng hưởng này sẽ bị ẩy ngược trở lại vào hốc cộng hưởng ó một lần nữa
sẽ có khả năng xảy ra hồi tiếp dương của tín hiệu iều chế vận tốc của các nhóm electron trong
quá trình trên (nếu tổng quãng ường i tương ứng với ộ trễ pha là bội số của 2 ). Lúc này èn
Klystron sẽ tạo ra dao ộng siêu cao tần. Đây là loại èn Klystron phản xạ.
Đèn Klystron phản xạ ược dùng ể làm các bộ nguồn tín hiệu siêu cao tần công suất thấp
(từ 10mW ến 500mW) với dải tần số từ 1GHz ến 25GHz. Hiệu suất của èn ạt từ 20% ến 30%.
Đèn Klystron phản xạ có thể ược sử dụng trong phòng thí nghiệm ể thực tập, o lường siêu cao
tần hoặc có thể làm bộ dao ộng nội của máy thu trong các thiết bị radar, tên lửa quân sự, dân dụng hoặc hàng không.
Hình 6.30. Đèn Klystron phản xạ lOMoARcPSD| 36067889
6.9.3. Đèn sóng chạy
Đèn sóng chạy (TWT: Traveling-Wave Tube) cũng là một loại linh kiện siêu cao tần, ược
sử dụng trong mạch khuếch ại RF công suất cao hoặc mạch tạo sóng có công suất trung bình
và dải tần số rộng. Dải tần số hoạt ộng từ 300MHz ến 50GHz, hệ số khuếch ại khoảng 70dB.
Có hai loại èn sóng chạy: èn sóng chạy dùng phần tử làm chậm sóng hình xoắn và èn sóng
chạy dùng các hốc cộng hưởng ghép. Chúng ta chỉ khảo sát èn sóng chạy dùng phần tử làm chậm hình xoắn.
Hình 6.31. Đèn sóng chạy hình xoắn
(1) Súng iện tử; (2) Đầu vào RF; (3) Nam châm; (4) Bộ suy giảm; (5)
Lõi xoắn; (6) Đầu ra RF; (7) Ống chân không; (8) Collector.
Đèn gồm một cathode nung nóng bức xạ chùm tia electron, ược gia tốc bởi cực anode
và hấp thụ bởi cực thu. Khối hội tụ dùng từ trường có tác dụng làm hội tụ thành chùm tia
electron khi chúng i qua vùng cấu trúc làm chậm sóng. Cấu trúc này thường có dạng xoắn,
thực chất là một ống dẫn sóng, là nơi ta ặt tín hiệu siêu cao tần vào. Khi tín hiệu siêu cao tần
này lan truyền dọc theo ường ống xoắn, vô hình chung sẽ tạo một iện trường hướng dọc theo
trục của ống xoắn. Điện trường này cũng lan truyền dọc trục với vận tốc ược tính gần úng
bằng vận tốc lan truyền của sóng dọc theo chu vi mỗi vòng xoắn.
Khi chùm tia electron di chuyển dọc theo trục ống xoắn, sẽ xảy ra sự tương tác giữa iện
trường vì: các electron i vào tại thời iểm bán kỳ dương của iện trường sẽ ược gia tốc trong khi
các electron i vào tại thời iểm bán kỳ âm sẽ bị giảm tốc. Kết quả là sẽ xảy ra sự kết nhóm của
chùm tia electron. Người ta tính toán sao cho các nhóm electron này ra khỏi ống xoắn tại thời
iểm vuông pha với iện trường, do ó ộng năng của chúng ược chuyển thành năng lượng của tín
hiệu trong ống xoắn. Quá trình này ược ứng dụng ể khuếch ại tín hiệu siêu cao tần hoặc tạo
dao ộng, tương tự như ối với èn Klystron. Tuy nhiên, sự khác biệt chính giữa hai loại èn này là
trong èn sóng chạy, sự tương tác giữa chùm tia electron và iện trường xảy ra liên tiếp dọc suốt
chiều dài di chuyển của chùm tia trong khi trong èn Klystron sự tương tác chỉ xảy ra tại úng
thời iểm khi tia electron i ngang qua khe của hốc cộng hưởng.
6.9.4. Diode PIN
Diode bán dẫn PIN gồm có một bản silic cao ôm phẳng có ộ dày khoảng 75 m (trong
giới hạn từ 10 ến 200 m), ở hai mặt phẳng ầu có trộn tạp chất là Bo (ể tạo ra vùng dẫn loại p)
và phốt pho (ể tạo ra vùng bán dẫn loại n ), với kỹ thuật khuếch tán tạo ra các lớp chuyển tiếp
p i và i n ở sát hai mặt phẳng hai ầu. Vùng cao ôm ở giữa ược gọi là vùng i rất nghèo iện
tích tự do. Tại hai mặt phẳng của hai vùngpvà n gắn hai tiếp xúc kim loại ể làm anode và lOMoARcPSD| 36067889
cathode cho diode (như Hình 6.32). Diode PIN có ặc tính như sau: nếu ặt vào diode một thiên
áp âm một chiều ( iện áp âm ặt vào vùng p) hoặc thiên áp không thì hiệu thế tiếp xúc của các
lớp chuyển tiếp p i và i n sẽ ngăn cản các iện tích tự do từ vùng p(các lỗ trống) và vùng n
(các iện tử) phun vào vùng i (còn gọi là vùng Base) nên diode có trở kháng rất lớn (R cỡ từ ơn
vị ến hàng chục k ). Diode trong trường hợp này không cho qua tín hiệu siêu cao tần, nó ở
chế ộ ngắt mạch. Khi ặt thiên áp thuận lên diode thì hàng rào thế của các lớp chuyển tiếp hạ
thấp làm cho các iện tử và lỗ trống phun từ vùng n và vùng p vào vùng i làm cho diode thông.
Trạng thái này diode ược biểu diễn bởi sơ ồ ở Hình 6.32d. Ở ây r là iện trở thuần khá nhỏ (cỡ
vài ), Ls chỉ iện cảm ký sinh ầu ra của diode (cỡ 0,2-2nH).
Trong trạng thái thông diode PIN cho qua tín hiệu siêu cao có dòng khá lớn. Ta dùng hai
trạng thái thông và tắt của diode PIN cùng các tham số của nó khi mắc vào ường truyền siêu
cao sẽ tạo ra các thiết bị iều khiển sự truyền sóng mong muốn như các bộ chuyển mạch và quay pha. C_ LS R Ci r_ r+ a) b) c) d) Hình 6.32. Diode PIN
6.9.5. Diode Tunnel
Hiệu ứng Tunnel xảy ra trên các hạt mang iện tại tiếp xúc p n mật ộ rất cao, không
giống như hiệu ứng iện trường thông thường trong lớp bán dẫn (các hạt mang iện dịch chuyển
dưới tác dụng của một iện trường bên ngoài và thời gian dịch chuyển qua vùng tiếp xúc bằng
bề rộng vùng tiếp xúc chia cho vận tốc của hạt), mà do sự dịch chuyển lượng tử của các hạt
nhân trên cùng một mức năng lượng.
Diode Tunnel ược sử dụng nhiều trong mạch khuếc ại, mạch dao ộng siêu cao tần, mạch
flip-flop dùng trong bộ nhớ. Lý do chính là kích thước nhỏ, giá thành hạ, tốc ộ cao, công suất
tiêu thụ thấp, nhiễu thấp và tỉ số dòng iện ỉnh – thung lũng rất cao.
6.9.5.1. Nguyên lý hoạt ộng
Diode tunnel là diode tiếp xúc p-n có iện trở âm. Mật ộ tạp chất ở cả hai vùng bán dẫn
p và n rất cao (khoảng từ 1025 ến 1026 nguyên tử/m3) và bề dày miền rào thế tiếp xúc rất lOMoARcPSD| 36067889
nhỏ (khoảng từ 100 A ến 10-6 cm). Theo quy luật thông thường, một hạt
mang iện không thể vượt qua rào thế tiếp xúc trừ phi nó tích lũy ủ mức năng lượng lớn hơn
hàng rào thế năng này. Tuy nhiên, khi bề dày của miền rào thế tiếp xúc quá nhỏ, có thể xảy ra
trường hợp các hạt mang iện chui xuyên qua miền rào thế (hiệu ứng ường hầm tunnel) dù
rằng ộng năng của hạt chưa ủ lớn. Hình 6.33.
Chúng ta hãy quan sát Hình 6.33, diode tunnel ở trạng thái hở mạch (trạng thái tĩnh).
Do mật ộ tạp chất ở hai vùng pvà n rất cao nên khi chúng tạo thành vùng tiếp xúc chung mức
Fermi EF ở cả hai bên lấn sâu vào vùng hóa trị p và vùng dẫn n và phải bằng nhau), vùnng hóa
trị của bán dẫn p lại có mức năng lượng cao hơn vùng dẫn của bán dẫn n . Kết quả là các hạt
iện tử ở vùng hoá trị p chui hầm sang lấp ầy vùng dẫn n có mức năng lượng thấp hơn. Ở trạng
thái hở mạch (không có nguồn bên ngoài ặt vào), sẽ xuất hiện vùng không chứa electron ở
vùng hóa trị p và vùng chứa ầy electron ở vùng dẫn n , trạng thái cân bằng ược duy trì và
không có dòng dịch chuyển của các hạt mang iện, do ó không có dòng iện. (a) (b) (c) (d) Hình 6.34. lOMoARcPSD| 36067889
Khi diode tunnel ược phân cực thuận bởi nguồn iện bên ngoài V, sẽ có sự dịch chuyển
mức năng lượng ở vùng p và n , tạo ra dòng iện qua diode I có ặc tuyến I(V) như trên Hình
6.35. Đặc tuyến này có 4 vùng (1), (2), (3), và (4), ta lần lượt xét từng vùng, tương ứng với
hình Hình 6.34 a, b, c, và d. Đặc tuyến V ủa diode tunnel
Khi nguồn V bắt ầu tăng dương, mức Fermi EFn cao hơn so vói EFp, xảy ra hiệu ứng chui
hầm của electron từ vùng dẫn n chứa ầy electron sang vùng hóa trị p không chứa electron
(Hình 6.34a). Nguồn V cáng tăng, hiệu ứng chui hầm càng tăng, do ó dòng iện I qua diode
càng tăng, tương ứng với oạn ặc tuyến (1) ở Hình 6.35.
Khi nguồn V ạt ến giá trị Vp, toàn bộ vùng dẫn n chứa ầy electron nằm ngang mức năng
lượng với vùng hóa trị p không chứa electron (Hình 6.34b), do ó, hiệu ứng chui hầm xảy ra
với mật ộ hạt rất lớn, dòng I ạt mức cực ại ỉnh Ip, tương ứng với iểm ỉnh (2) trên ặc tuyến Hình 6.35.
Khi nguồn V tăng lớn hơn Vp, khoảng cân bằng mức năng lượng giữa vùng dẫn n chứa
ầy electron với vùng hóa trị p không chứa electron bị giảm i, (Hình 6.34c), do ó, dòng iện do
hiện tượng chui hầm giảm, tương ứng oạn ặc tuyến (3) trên Hình 6.35. Đây là oạn có iện trở âm của ặc tuyến I(V).
Khi nguồn V lớn hơn giá trị Vv, không còn hiệu ứng chui hầm nữa (Hình 6.34d), dòng
iện I qua diode lúc này hoàn toàn giống như dòng iện khuếch tán của các hạt mang iện khi
vượt qua rào thế tiếp xúc trong một diode thông thường. Do ó, ặc tuyến I(V) ở vùng (4) của
Hình 6.35 có dạng hàm mũ.
Tỉ số giữa mức dòng iện ỉnh Ip với mức dòng iện thung lũng Iv thường ạt từ mười ến vài chục lần.
6.9.5.2. Đặc tính iện trở âm
Ta có thể phân cực diode tunnel ở 3 loại ường tải khác nhau, tương ứng với 3 chế ộ hoạt ộng (Hình 6.36).
Với ường tải lưỡng ổn cắt ặc tuyến I(V) ở ba iểm a, b, c, ta nhận thấy chỉ có iểm a và c
là tương ứng với trạng thái ổn ịnh của mạch iện, nghĩa là khi mạch iện ã tồn tại ở trạng thái
này thì nó sẽ tồn tại mãi mãi ở trạng thái ó nếu không có tác nhân kích thích từ bên ngoài.
Điểm b tương ứng với trạng thái không ổn ịnh, nghĩa là mạch iện sẽ tự ộng chuyển sang trạng lOMoARcPSD| 36067889
thái khác nếu ang tồn tại ở trạng thái không ổn ịnh. Vì lúc này diode tunnel có 2 trạng thái ổn
ịnh nên ược gọi là lưỡng ổn và có thể ựơc dùng trong các mạch flip-flop, giao hoán, v.v…
Với ường tải ơn ổn cắt ặc tuyến I(V) chỉ ở iểm a (trạng thái ổn ịnh), dù ban ầu diode
tunnel ang ở iểm hoạt ộng khác nhau nhưng sau ó sẽ nhanh chóng chuyển sang trạng thái về
iểm a và giữ nguyên mãi mãi ở trạng thái ó nếu không có tác nhân kích thích từ bên ngoài. Ta
nói rằng trạng thái này là ơn ổn, ựơc dùng trong các mạch tạo xung theo nhịp iều khiển.
Với ường tải bất ổn cắt ặc tuyến I(V) chỉ ở iểm b (vùng iện trở âm của ặc tuyến), mạch
iện sẽ không thể tồn tại lâu ở trạng thái này mà liên tục thay ổi iểm hoạt ộng chung quanh b,
tạo ra các dao ộng iện tần số cao. Ta nói rằng trạng thái này là bất ổn, ược dùng trong các
mạch khuếch ại hoặc dao ộng siêu cao tần.
Điện dẫn âm g hoặc iện trở âm Rn của diode tunnel ươc ịnh nghĩa trên ặc tuyến I(V) như sau: 1 g I (6.115) Hình 6.37. lOMoARcPSD| 36067889
Mạch iện tương ương của một diode tunnel ược vẽ ở Hình 6.37. Điện trở RS và iện cảm
LS tượng trưng cho các thông số của dây nối chân linh kiện từ bên ngoài. Tụ C là iện dung
vùng tiếp xúc của diode thường ược o tại iểm thung lũng Vv trên ặc tuyến. Các giá trị tiêu biểu: Rn 30 C 20pF R s 1 Ls 5nH
Từ Hình 6.37, ta suy ra tổng trở tương ương Zin của diode là:
Zin Rs j Ls ( Rn ) jC Rn jC (6.116) Rs Rnn2 j Ls 1 ( R CR Cn2n )2 1 ( R C )
Tần số cắt, tại ó trở kháng Zn của diode tunnel là thuần kháng ược suy ra từ (6.116): f 1 Rn c 1 (6.117) 2 R Cn Rs
Tần số cắt, tại ó trở kháng Zin là thuần trở (âm hoặc dương) là: fr 1 R Cn2 1 (6.118) 2 R Cn Ls
PHỤ LỤC 1: MỘT SỐ KÝ HIỆU Hệ số tiêu hao Hệ số pha Hệ số truyền sóng ,
Các loại bước sóng trong môi trường truyền dẫn 0 , t , th
Độ dẫn iện ( iện dẫn suất) của môi trường ,
Các loại hằng số iện môi của môi trường 0 , r lOMoARcPSD| 36067889 ,
Các loại ộ từ thẩm của môi trường 0 , r ,
Đơn vị iện trở (ôm), tần số vòng. Hiệu suất của mạch 2 , Toán tử Laplace lOMoARcPSD| 36067889
PHỤ LỤC 2: CÁC CÔNG THỨC VÀ ĐỊNH LÝ GIẢI TÍCH VECTƠ 1) grad 1 2 1grad 2 2grad 1 2) div .A .divA A grad. 3) rot A .rotA grad A 4) div A B B rotA. A rotB. 5) rot grad 0 6) div rotA 0 7) rot rotA grad divA A Định lý Green-Stokes
A d. l rotAdS. L S
Định lý Oxtrogradski-Gauss A dS. divAdv. S V
TÀI LIỆU THAM KHẢO
[1] Kiều Khắc Lâu, Lý thuyết trường Điện từ, NXB Giáo dục, 1999. lOMoAR cPSD| 36067889
[2] Kiều Khắc Lâu, Cơ sở kỹ thuật siêu cao tần, NXB Giáo dục, 1998.
[3] Nguyễn Bình Thành, Nguyễn Trần Quân, Lê Văn Bảng, Cơ sở lý thuyết trường iện
từ, NXB Đại học và Trung học chuyên nghiệp, 1970.
[4] Phan Anh, Trường iện từ và truyền sóng, NXB ĐHQG Hà Nội, 2000.
[5] Ngô Nhật Ảnh, Trương Trọng Tuấn Mỹ, Trường iện từ, NXB Đại học Quốc gia Tp.HCM, 2000.
[6] Vũ Đình Thành, Lý thuyết cơ sở kỹ thuật siêu cao tần, NXB Khoa học và Kỹ thuật, 1997.
[7] Nguyễn Văn Hùng, Điện ộng lực học, Nhà xuất bản Đại học Quốc gia Hà nội, 2005.
[8] David M.Pozar, Microwave Engineering – 2nd edition, John Wiley & Sons, Inc., 1998.
[9] J.Van Bladet, Electromagnetic fields, Mc.Graw Hill book company Inc. New York and London 1964.




