lOMoARcPSD|36067889
H
Ọ
C VI
Ệ
N CÔNG NGH
Ệ
BƯU CHÍNH VIỄ
N THÔNG
KHOA VI
Ễ
N THÔNG 1
BÀI GI
Ả
NG
LÝ THUY
Ế
T TRUY
Ề
N TIN
Mã môn h
ọ
c: TEL1344
Chuyên ngành Điệ
n t
ử
Vi
ễ
n thông
ộ

lOMoARcPSD|36067889
- MỤC LỤC -
LỜI NÓI ĐẦU ............................................................................................................. iv
THUẬT NGỮ VIẾT TẮT ......................................................................................... vii
CHƯƠNG 1- GIỚI THIỆU VỀ LÝ THUYẾT TRUYỀN TIN ................................
1
1.1. SƠ LƯỢC LỊCH SỬ PHÁT TRIỂN CỦA LÝ THUYẾT TRUYỀN TIN ............. 1
1.2. MỘT SỐ KHÁI NIỆM CƠ BẢN ............................................................................
2
1.2.1. Tin tức ....................................................................................................... 2
1.2.2. Thông tin ...................................................................................................
2
1.2.3. Tín hiệu ......................................................................................................
3
1.3. MÔ HÌNH TỔNG QUÁT HỆ THỐNG TRUYỀN TIN .........................................
4
1.3.1. Phân loại hệ thống truyền tin .....................................................................
4
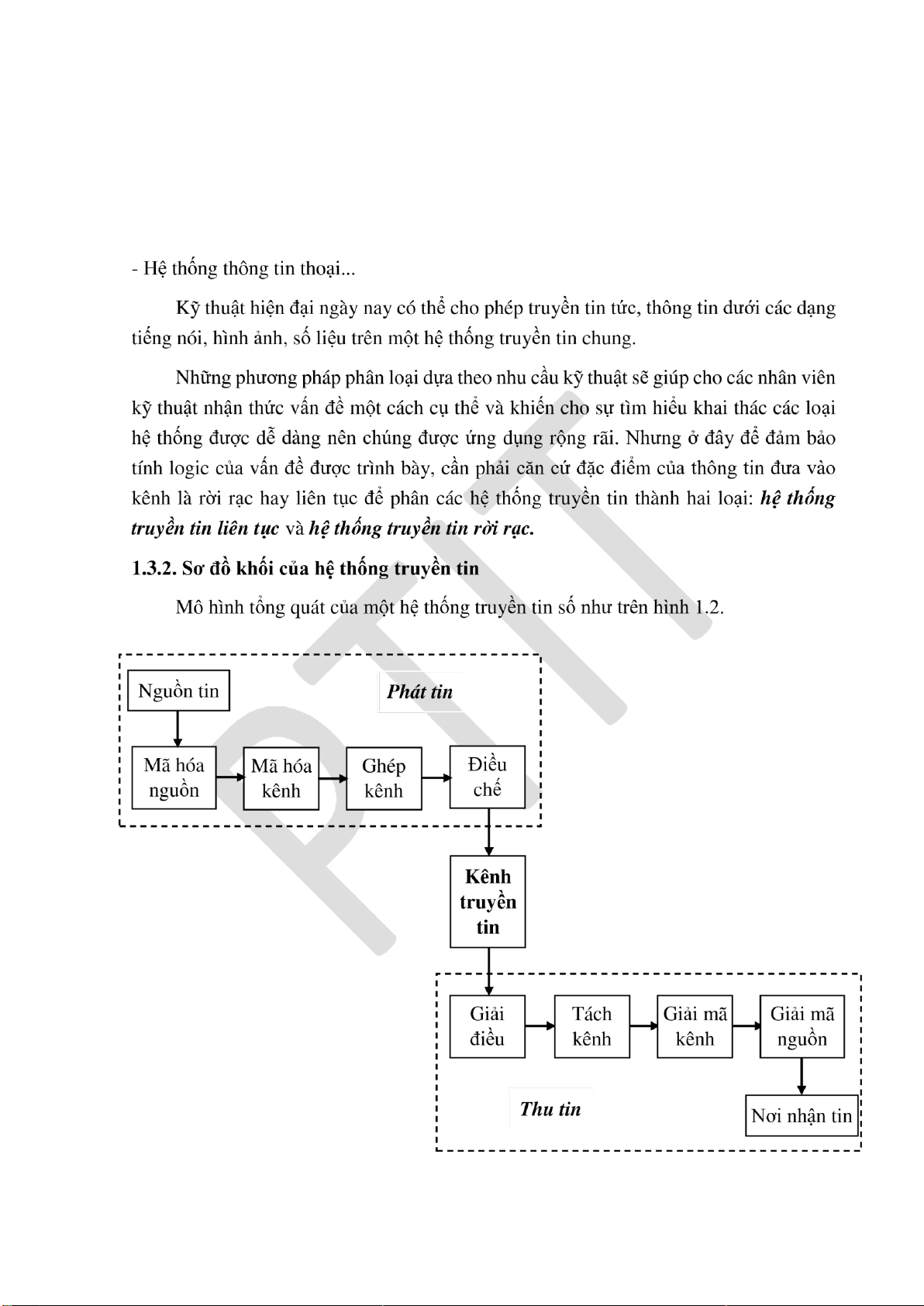
1.3.2. Sơ ồ khối của hệ thống truyền tin ............................................................ 5
1.3.3. Những chỉ tiêu chất lượng cơ bản của một hệ truyền tin ........................ 10
1.4. TỔNG KẾT CHƯƠNG .........................................................................................
11
CÂU HỎI/BÀI TẬP CHƯƠNG 1 ................................................................................
11
CHƯƠNG 2- CƠ SỞ LÝ THUYẾT TRUYỀN TIN ................................................
12
2.1. XÁC SUẤT VÀ QUÁ TRÌNH NGẪU NHIÊN ................................................... 12
2.1.1. Xác suất ...................................................................................................
12
2.1.2. Quá trình ngẫu nhiên ............................................................................... 23
2.2. LƯỢNG TIN VÀ PHẾP ĐO CỦA NGUỒN ........................................................ 32

lOMoARcPSD| 36067889
2.2.1. Nguồn rời rạc ...........................................................................................
32
2.2.2. Nguồn liên tục ......................................................................................... 38
2.3. LƯỢNG TIN VÀ PHẾP ĐO CỦA KÊNH ........................................................... 39
2.3.1. Kênh rời rạc .............................................................................................
39
2.3.2. Kênh liên tục ........................................................................................... 44
2.3.3. Kênh Gaussian .........................................................................................
45 2.4. TỔNG KẾT CHƯƠNG
......................................................................................... 48
CÂU HỎI/BÀI TẬP CHƯƠNG 2 ................................................................................
48
CHƯƠNG 3 – MÃ HÓA ............................................................................................
50
3.1. TỔNG QUAN VỀ MÃ HÓA ................................................................................ 50
3.2. MỘT SỐ VẤN ĐỀ CƠ BẢN TRONG MÃ HÓA ................................................ 50
3.2.1. Mã hiệu và thông số cơ bản của mã hiệu ................................................ 50
3.2.2. Phương pháp biểu diễn mã ...................................................................... 53
3.2.3. Điều kiện phân tách của mã hiệu............................................................. 56
3.2.4. Mã hệ thống .............................................................................................
60
3.2.5. Phát hiện và sửa lỗi.................................................................................. 63
3.3. MÃ HÓA NGUỒN ................................................................................................
64
3.3.1. Một số khái niệm chung .......................................................................... 64
3.3.2. Mã hóa cho các nguồn tin rời rạc ............................................................ 65
3.3.3. Mã hóa cho các nguồn tin liên tục ........................................................... 75
3.4. MÃ HÓA KÊNH ...................................................................................................
88
3.4.1. Mã kiểm tra chẵn lẻ ................................................................................. 89
3.4.2. Các mã a thức ........................................................................................ 94
3.4.3. Mã khối tuyến tính .................................................................................. 98
3.4.4. Các mã chập .......................................................................................... 104

lOMoARcPSD| 36067889
3.5. TỔNG KẾT CHƯƠNG .......................................................................................
112
CÂU HỎI/ BÀI TẬP CHƯƠNG 3 ............................................................................. 112
CHƯƠNG 4 - GHP KÊNH ................................................................................... 115
4.1. TỔNG QUAN VỀ KỸ THUẬT GHÉP KÊNH .................................................. 115
4.2. KỸ THUẬT GHÉP KÊNH ................................................................................. 116
4.2.1. Kỹ thuật ghép kênh phân chia theo tần số (FDM) ................................ 116
4.2.2. Kỹ thuật ghép kênh phân chia theo thời gian (TDM) ........................... 118
4.2.3. Các kỹ thuật ghép kênh khác ................................................................. 123
4.3. ỨNG DỤNG KỸ THUẬT GHÉP KÊNH TRONG HỆ THỐNG TRUYỀN THÔNG
SỐ ...............................................................................................................................
125
4.3.1. Kỹ thuật ghép kênh TDM-PCM ............................................................ 125
4.3.2. Kỹ thuật ghép kênh SDH .......................................................................
128 4.4. TỔNG KẾT CHƯƠNG
....................................................................................... 131
CÂU HỎI/ BÀI TẬP CHƯƠNG 4 ............................................................................. 131
CHƯƠNG 5 – ĐIỀU CHẾ TÍN HIỆU ....................................................................
133
5.1. KHÁI NIỆM VỂ ĐIỀU CHẾ .............................................................................. 133
5.2. BIỂU DIỄN TÍN HIỆU ....................................................................................... 135
5.2.1. Biểu diễn thông thấp tín hiệu và hệ thống truyền tin ............................ 135
5.2.2. Không gian tín hiệu ............................................................................... 138
5.2.3. Biểu diễn các tín hiệu iều chế số ......................................................... 139
5.3. ĐIÊU CHẾ TÍN HIỆU TƯƠNG TỰ................................................................... 152
5.3.1. Điều chế tín hiệu liên tục ....................................................................... 152
5.3.2. Điều chế xung ........................................................................................
156
5.4. ĐIỀU CHẾ TÍN HIỆU SỐ .................................................................................. 162
5.4.1. Điều chế khóa dịch biên ộ (ASK) ....................................................... 163
5.4.2. Điều chế khoá dịch tần số (FSK)........................................................... 165
5.4.3. Điều chế khóa dịch pha (PSK) .............................................................. 167

lOMoARcPSD|36067889
5.4.4. Điều chế biên ộ cầu phương (QAM) ................................................... 170
5.5. TỔNG KẾT CHƯƠNG .......................................................................................
172
CÂU HỎI/ BÀI TẬP CHƯƠNG 5 ............................................................................. 173
CHƯƠNG 6 – NHIỄU VÀ BỘ THU TỐI ƯU .......................................................
174
6.1. NHIỄU .................................................................................................................
174
6.1.1. Định nghĩa và phân loại nhiễu ............................................................... 174
6.1.2. Các tham số ặc trưng mô tả nhiễu ....................................................... 174
6.1.3. Một số loại nhiễu cơ bản ....................................................................... 180
6.2. BỘ THU TỐI ƯU ................................................................................................
187
6.2.1. Khái niệm về bộ thu tối ưu .................................................................... 187
6.2.2. Các vấn ề thu tối ưu ............................................................................. 188
6.2.3. Bộ thu tối ưu cho kênh có nhiễu cọng Gaussian ................................... 190
6.2.4. Hiệu quả của bộ thu tối ưu .................................................................... 203
6.3. TỔNG KẾT CHƯƠNG .......................................................................................
221
CÂU HỎI/ BÀI TẬP CHƯƠNG 6 .............................................................................
221 TÀI LIỆU THAM KHẢO
........................................................................................ 222
LỜI NÓI ĐẦU
Bài giảng “Lý thuyết truyền tin” ược biên soạn theo ề cương của Học viện công
nghệ bưu chính viễn thông phê duyệt năm 2021 dành cho sinh viên hệ ào tạo Đại học
chính qui, ngành iện tử- Viễn thông.
Cuốn bài giảng này ược viết ể cung cấp cho sinh viên những kiến thức bổ ích nhằm
chuẩn bị tốt kiến thức cơ sở ể học tập và nắm vững các môn kỹ thuật chuyên ngành, ảm

lOMoARcPSD| 36067889
bảo cho sinh viên có thể ánh giá ược các chỉ tiêu chất lượng cơ bản của một hệ thống
truyền tin một cách có căn cứ khoa học.
Cụ thể, cấu trúc của bài giảng bao gồm 6 chương với các nội dung cơ bản như sau:
Chương 1: Giới thiệu về lý thuyết truyền tin. Nội dung chương này trình bày sơ lược
về lịch sử phát triển của lý thuyết truyền tin, ưa ra một số khái niệm cơ bản trong truyền
tin và giới thiệu mô hình tổng quát của một hệ thống truyền tin.
Chương 2: Cơ sở lý thuyết truyền tin. Chương này trình bày cụ thể các vấn ề cơ bản
về xác suất thống kê, lượng tin và phép o của nguồn cũng như lượng tin và phép o của
kênh thông tin. Trong ó giới thiệu về phương pháp ịnh lượng thông tin trong nguồn,
kênh tin. Đưa ra các khái niệm lượng tin trung bình, entropi, tốc ộ lập tin của nguồn,
thông lượng của kênh và giải thích rõ ý nghĩa các ịnh lý Shannon.
Chương 3: Mã hóa. Nội dung của chương này trình bày về những vấn ề cơ bản trong
mã hóa như: khái niệm mã hóa, mã hiệu, ưa ra các thông số cơ bản của mã hiệu, iều kiện
thiết lập mã và các phương pháp biểu diễn mã. Ngoài ra còn trình bày về khái niệm mã
hóa thống kê tối ưu và mã hóa chống nhiễu, các bước mã hóa/giải mã của các phương
pháp mã hóa thống kê tối ưu và các phương pháp mã hóa chống nhiễu.
Chương 4: Ghép kênh. Nội dung chủ yếu của chương này ề cập những vấn ề cơ bản
về ghép kênh. Trong ó giải thích rõ các kỹ thuật ghép kênh ược sử dụng ể chia sẻ các
tài nguyên truyền dẫn, ặc biệt là ghép kênh phân chia tần số (FDM) và ghép kênh phân
chia thời gian (TDM). Chương 4 còn trình bày cụ thể về ứng dụng kỹ thuật ghép kênh
trong hệ thống truyền thông số.
Chương 5: Điều chế tín hiệu. Chương này trình bày cụ thể về khái niệm iều chế, cách
biểu diễn tín hiệu. Ngoài ra trong chương 5 còn trình bày về iều chế cho tín hiệu tương
tự, và iều chế cho tín hiệu số.
Chương 6: Nhiễu và bộ thu tối ưu. Nội dung của chương này trình bày về những vấn
ề cơ bản của nhiễu như: ịnh nghĩa và phân loại nhiễu, ưa ra các tham số ặc trưng mô tả
nhiễu và giới thiệu một số loại nhiễu cơ bản. Vấn ề về bộ thu tối ưu cho kênh có nhiễu
cọng Gaussian cũng ược phân tích kỹ trong chương này.
Sau mỗi chương có các bài tập hoặc câu hỏi ể sinh viên tự kiểm tra và ánh giá kiến
thức của mình.
Chúng tôi hy vọng rằng cuốn bài giảng không chỉ là tài liệu hữu ích cho sinh viên
chuyên ngành viễn thông của Học viện Công nghệ Bưu chính Viễn thông mà còn là một

lOMoARcPSD|36067889
tài liệu tham khảo hữu ích cho các sinh viên chuyên ngành Điện - Điện tử và Công nghệ
thông tin, cũng như những người quan tâm khác. Đây cũng là phiên bản ầu tiên ược viết
trong thời gian ngắn do vậy sẽ không tránh khỏi những sai sót. Chúng tôi rất mong nhận
ược ý kiến óng góp của các quí thầy cô, các bạn sinh viên và những người quan tâm ể
hoàn thiện hơn bài giảng này.
Những ý kiến óng góp xin gửi về:
Bộ môn Tín hiệu và Hệ thống
-
Khoa Viễn thông 1
Học Viện Công nghệ Bưu chính Viễn thông
Địa chỉ: Km 10, ường Hà Nội
-
Hà Đông, Hà Đông, Hà Nội
Tel: 0243-8549352
Xin trân trọng cám ơn!
Hà Nội, tháng 12 năm 2021
Tác giả

lOMoARcPSD|36067889
THUẬT NGỮ VIẾT TẮT
lOMoARcPSD|36067889
lOMoARcPSD|36067889

lOMoARcPSD|36067889

lOMoARcPSD|36067889
MPE-LPC Multipulse Excited LPC

lOMoARcPSD|36067889
- CHƯƠNG I -
GIỚI THIỆU VỀ LÝ THUYẾT TRUYỀN TIN
Trong cuộc sống, con người luôn có nhu cầu trao ổi thông tin với nhau. Những thông
tin khi truyền ược mang dưới những dạng năng lượng khác nhau như sóng âm, sóng iện
TDM
Time Division Multiplexing
Ghép kênh theo thời gian
TIFF
Tagged Image File Format
ịnh dạng tệp hình ảnh ược gắn thẻ
V
VC
Virtual Container
Contenơ ảo
VCG
Virtual Concatenation Group
Nhóm kết chuỗi ảo
VCO
Voltage Controlled Oscillator
Bộ tạo dao ộng iều khiển bằng iệ
n áp
VLC
Variable Length Code
Mã hóa chiều dài thay ổi
W
WDM
Wavelength Division Multiplexing
Ghép kênh theo bước sóng

lOMoARcPSD| 36067889
từ, sóng ánh sáng… Để hiểu rõ hơn về quá trình truyền tin, trong chương I sẽ giới thiệu
về lý thuyết truyền tin.
1.1. SƠ LƯỢC LỊCH SỬ PHÁT TRIỂN CỦA LÝ THUYẾT TRUYỀN TIN
Cơ sở lý thuyết truyền tin chỉ là một bộ phận của lý thuyết thông tin chung – Nó là
phần áp dụng của “Lý thuyết thông tin” vào kỹ thuật thông tin liên lạc.
Do sự phát triển mạnh mẽ của kỹ thuật tính toán và các hệ tự ộng, một ngành khoa
học mới ra ời và phát triển nhanh chóng, ó là: “Lý thuyết thông tin”. Là một ngành khoa
học nhưng nó không ngừng phát triển và thâm nhập vào nhiều ngành khoa học khác như:
Toán học; Triết học; Hoá học; Xibecnetic; Lý thuyết hệ thống; Lý thuyết và Kỹ thuật
thông tin liên lạc… và ã ạt ược nhiều kết quả. Tuy vậy vẫn còn nhiều vấn ề cần ược giải
quyết hoặc giải quyết hoàn chỉnh hơn.
Người ặt viên gạch ầu tiên ể xây dựng lý thuyết thông tin là Hartley R.V.L. Năm
1928, ông ã ưa ra số o lượng tin là một khái niệm cơ bản rất quan trọng của lý thuyết
thông tin. Dựa vào khái niệm này, ể có thể so sánh ịnh lượng các hệ thống truyền tin.
Năm 1933, V.A Kachenhicov chứng minh một loạt những luận iểm quan trọng của
lý thuyết thông tin trong bài báo “Về khả năng thông qua của không trung và dây dẫn
trong hệ thống liên lạc iện”.
Năm 1935, D.V Ageev ưa ra công trình “Lý thuyết tách tuyến tính”, trong ó ông
phát biểu những nguyên tắc cơ bản về lý thuyết tách các tín hiệu.
Năm 1946, V.A Kachenhicov công bố công trình “Lý thuyết thế chống nhiễu ánh
dấu một bước phát triển rất quan trọng của lý thuyết thông tin.
Trong hai năm 1948 – 1949, Shanon C.E công bố một loạt các công trình vĩ ại, ưa
sự phát triển của lý thuyết thông tin lên một bước tiến mới chưa từng có. Trong các công
trình này, nhờ việc ưa ra khái niệm lượng thông tin và tính ến cấu trúc thống kê của tin,
ông ã chứng minh một loạt ịnh lý về khả năng thông qua của kênh truyền tin khi có nhiễu
và các ịnh lý mã hoá. Những công trình này là nền tảng vững chắc của lý thuyết thông
tin.
Ngày nay, lý thuyết thông tin phát triển theo hai hướng chủ yếu sau:
Lý thuyết thông tin toán học: Xây dựng những luận iểm thuần tuý toán học và
những cơ sở toán học chặt chẽ của lý thuyết thông tin. Cống hiến chủ yếu trong lĩnh vực
này thuộc về các nhà bác học lỗi lạc như: N.Wiener, A. Feinstain, C.E Shanon, A.N.
Kanmôgorov, A.JA Khintrin.
Lý thuyết thông tin ứng dụng: còn ược gọi là lý thuyết truyền tin.

lOMoARcPSD|36067889
Chuyên nghiên cứu các bài toán thực tế quan trọng do kỹ thuật liên lạc ặt ra có liên
quan ến vấn ề chống nhiễu và nâng cao ộ tin cậy của việc truyền tin. Các bác học C.E
Shanon, S.O RiCe, D. Midleton, W. Peterson, A.A Khakevich, V. Kachenhicov ã có
những công trình quý báu trong lĩnh vực này.
1.2. MỘT SỐ KHÁI NIỆM CƠ BẢN
1.2.1. Tin tức
Vật liệu ban ầu ược gia công trong một hệ thống truyền tin (hệ thống thông tin liên
lạc) là tin tức. Tin tức (news) là sự phản ảnh của sự vật khách quan ối với sự nhận biết
của con người. Tin tức có tính chất là sự “mới mẻ”.
1.2.2. Thông tin
Thông tin (information) là sự phản ánh mang tính ịnh hướng (sự quan tâm của
người nhận) của sự vật khách quan ối với sự nhận biết của con người. Hay nói cách
khác, thông tin là sự cảm hiểu của con người về thế giới xung quanh thông qua sự tiếp
xúc với nó. Ví dụ: Hai người nói chuyện với nhau, cái ược trao ổi giữa họ chính là thông
tin. Một người ang xem tivi hoặc nghe ài hoặc ọc báo, người ó ang nhận thông tin. Đàm
thoại, tham dự diễn àn, gửi/nhận thư iện tử... chỉ là những ví dụ trong hàng nghìn ví dụ
khác nhau về thông tin liên lạc. Thông tin xuất hiện dưới nhiều dạng: âm thanh, hình
ảnh, ký hiệu,... Những dạng này chỉ là “vỏ bọc” vật chất chứa thông tin, “vỏ bọc” là
phần “xác”, thông tin là phần “hồn”. Ngữ nghĩa của thông tin chỉ có thể hiểu ược khi
bên thu hiểu ược cách biểu diễn ngữ nghĩa của bên phát.
Một tin nếu ược một ai ó quan tâm thì ó chính là thông tin ối với người ó. Như vậy,
càng tiếp xúc với thế giới xung quanh, lượng thông tin mà con người thu nhận ược càng
nhiều, vì thế họ càng tăng thêm sự hiểu biết và nhận thức tốt hơn về những ối tượng
trong ời sống xã hội, trong thiên nhiên,… giúp cho họ thực hiện hợp lý công việc cần
làm ể ạt tới mục ích một cách tốt nhất. Khi tiếp nhận ược thông tin, con người có thể
truyền, lưu trữ, nhân bản hoặc phải xử lý nó ể tạo ra những thông tin mới có ích hơn, từ
ó có những phản ứng nhất ịnh.
Ví dụ 1-1:
- Những ám mây en xuất hiện ở chân trời phía Đông chứa ựng thông tin báo hiệu về
trận mưa lớn sắp xảy ra.
- Những nốt nhạc trong bản xô-nát Ánh trăng của Beethoven làm cho người nghe
cảm thấy ược sự tươi mát, êm dịu của êm trăng.

lOMoARcPSD|36067889
- Người tài xế chăm chú quan sát người tham gia giao thông, xe cộ i lại trên ường, ộ
tốt xấu của mặt ường, tính năng kỹ thuật cũng như vị trí chiếc xe ể quyết ịnh cần tăng
tốc ộ hay hãm phanh, cần lái sang trái hay sang phải,.... ể ảm bảo an toàn tối a cho chuyến
i.
1.2.3. Tín hiệu
Thông tin là một hiện tượng vật lý, nó thường tồn tại và ược truyền i dưới một dạng
vật chất nào ó. Về nguyên tắc, bất kỳ cấu trúc vật chất hoặc bất kỳ dòng năng lượng nào
cũng có thể mang thông tin. Chúng ược gọi là những sóng mang hay còn gọi là vật mang
tin. Sóng mang ã chứa thông tin trong nó và là một ại diện của thông tin, sẽ ược gọi là
tín hiệu (signal).
Như vậy, tín hiệu là các ại lượng vật lý biến thiên, phản ánh tin cần truyền. Chú ý
là không phải bản thân quá trình vật lý là tín hiệu, mà sự biến ổi các tham số riêng của
quá trình vật lý mới là tín hiệu. Các ặc trưng vật lý có thể là dòng iện, iện áp, ánh sáng,
âm thanh, trường iện từ.
Thông tin là một quá trình ngẫu nhiên. Tín hiệu mang tin tức cũng là tín hiệu ngẫu
nhiên và mô hình toán học của nó cũng là các quá trình ngẫu nhiên. Vì vậy, lý thuyết
truyền tin là lý thuyết ngẫu nhiên của tin tức, có nghĩa là nó xét ến tính bất ngờ của tin
tức ối với nơi nhận tin.
Trước ây, người ta nghiên cứu ịnh lượng hệ thống truyền tin bằng cách tính toán
và thực nghiệm sự biến ổi năng lượng mang tin trong các hệ thống ó. Trên quan iểm
năng lượng, lý thuyết mạch và tín hiệu ã giải quyết những vấn ề tổng quát về phân tích,
tổng hợp mạch và tín hiệu, nhờ ó mà kỹ thuật truyền tin ã có những bước tiến bộ khá
dài. Nhưng ồng thời với sự phát triển mạnh mẽ của mình, trong ngành kỹ thuật truyền
tin ã nảy sinh những vấn ề mà lý thuyết xây dựng trên quan iểm năng lượng không giải
thích ược trọn vẹn như: mối liên hệ cơ bản giữa các hệ thống truyền tin sử dụng những
năng lượng khác nhau; vấn ề lưu giữ tin tức trong các hệ thống truyền tin vũ trụ mà ở ó
năng lượng tải tin rất nhỏ... Do ó, các lý thuyết xây dựng trên quan iểm năng lượng cần
phải ược bổ sung bằng những lý thuyết xây dựng trên quan iểm thông tin.
1.3. MÔ HÌNH TỔNG QUÁT HỆ THỐNG TRUYỀN TIN
1.3.1. Phân loại hệ thống truyền tin
Trong cuộc sống, con người luôn có nhu cầu trao ổi thông tin với nhau, có nghĩa
là có nhu cầu truyền tin. Các dạng trao ổi thông tin có thể như: àm thoại giữa người với
người, ọc sách báo, nghe radio, gửi và nhận thư, nói chuyện qua iện thoại, xem truyền
hình, tham dự diễn àn, truy cập thông tin trên internet,... Nếu không có giao lưu trao ổi
thì sẽ không thành tin tức hoặc thông tin.

lOMoARcPSD| 36067889
Ví dụ 1-2: Anh A muốn thông báo cho chị B một thông tin là tại một ịa iểm nào ó
dưới dạng dữ liệu (còn gọi là số liệu). Mạng truyền và xử lý thông tin dưới dạng dữ liệu
ược gọi là mạng truyền số liệu.
Những hệ thống truyền tin mà con người sử dụng và khai thác có rất nhiều dạng
và khi phân loại chúng có thể dựa trên nhiều cơ sở khác nhau. Chặng hạn, dựa trên cơ
sở năng lượng mang tin, có thể phân hệ thống truyền tin thành các loại:
- Hệ thống iện tín: dùng năng lượng iện một chiều.
- Hệ thống thông tin vô tuyến iện: dùng năng lượng sóng iện từ.
- Hệ thống thông tin quang (hệ thống báo hiệu, thông tin hồng ngoại, laser, cáp quang):
dùng năng lượng quang học.
- Hệ thống thông tin dùng sóng âm, siêu âm...: dùng năng lượng cơ học.
ang có mưa thì sự
truy
ề
n tin có th
ể
x
ảy ra như
minh h
ọ
a trên hình 1.1.
Hình 1.1: Ví d
ụ
vê h
ệ
th
ố
ng truy
ề
n tin
M
ộ
t h
ệ
th
ống mà thông tin ượ
c truy
ề
n t
ả
i t
ừ
nơi phát ến nơi
thu
ượ
c g
ọ
i là h
ệ
th
ố
ng truy
ề
n tin (ho
ặ
c h
ệ
th
ố
ng vi
ễ
n thông).
Trong các h
ệ
th
ố
ng truy
ề
n tin có s
ự
tham gia c
ủ
a máy tính, thông t
in ượ
c bi
ể
u th
ị
lOMoARcPSD|36067889
Có thể phân loại hệ thống truyền tin dựa trên cơ sở biểu hiện bên ngoài của thông tin
như:
- Hệ thống phát thanh, truyền hình.
- Hệ thống truyền số liệu.
Hình 1.2: Mô hình tổng quát của hệ thống truyền tin số

lOMoARcPSD|36067889
1.3.2.1. Nguồn tin
Là nơi sinh ra thông tin. Các nguồn tin thường thấy trong tự nhiên ược gọi là các
nguồn tin nguyên thủy. Đây là các nguồn tin chưa qua bất kỳ một phép biến ổi nào.
Trong quá trình truyền tin, nguồn tin có thể truyền i một chuỗi các tin (còn gọi là
bản tin). Có thể coi nguồn là một tập các tin và khả năng xuất hiện tại mỗi thời iểm của
mỗi tin.
Nếu tập tin là hữu hạn thì nguồn sinh ra nó ược gọi là nguồn rời rạc. Nếu tập tin là vô
hạn thì nguồn sinh ra nó ược gọi là nguồn liên tục.
Nguồn tin có hai tính chất: Tính thống kê và tính hàm ý. Với nguồn rời rạc, tính
thống kê biểu hiện ở xác suất xuất hiện các tin là khác nhau. Tính hàm ý biểu hiện ở xác
suất xuất hiện của một tin nào ó sau một dãy tin khác nhau nào ó là khác nhau.
Sự phân biệt về bản chất của nguồn rời rạc với nguồn liên tục là số lượng các tin trong
nguồn rời rạc là hữu hạn, số lượng các tin trong nguồn liên tục là không ếm ược.
Thông tin có thể thuộc nhiều loại như:
Đối với nguồn nguyên thủy rời rạc:
- Một dãy ký tự (các tin) như trong iện tín của hệ thống gửi iện tín.
- Bảng chữ cái của một ngôn ngữ.
- Các lệnh iều khiển trong hệ thống iều khiển.
Đối với nguồn nguyên thuỷ liên tục:
- Một hàm chỉ theo một biến thời gian () như trong phát thanh và iện thoại.
- Một vài hàm của một vài biến như trong trường hợp truyền hình màu - ở ây, thông tin bao
gồm ba hàm (, , ), (, , , , ) biểu diễn cường ộ sáng của ba thành phần cơ
bản (xanh lá cây, ỏ, xanh dương).
Những tin nguyên thuỷ có thể trực tiếp ưa vào kênh ể truyền, i nhưng chỉ ở trong
phạm vi rất nhỏ. Muốn truyền tin trong phạm vi xa hơn thì phải qua các phép biến ổi
nhân tạo (xử lý tín hiệu).
Mô hình hóa toán học nguồn tin:
Để phân tích, nghiên cứu các hệ thống truyền tin, người ta thường sử dụng các mô
hình toán học hoặc thống kê nguồn, kênh và người sử dụng. Nếu các mô hình của nguồn,
kênh và người sử dụng ược xây dựng sơ sài thì các bộ thu, bộ phát dù ược thiết kế cẩn
thận ến âu cũng không phục vụ hiệu quả quá trình truyền tin. Nhưng nếu các mô hình

lOMoARcPSD|36067889
này ược xây dựng quá phức tạp về mặt thống kê hoặc toán học thì cũng không thể thiết
kế ược các bộ thu, bộ phát thích hợp. Vì vậy, phải có sự phù hợp ở các mặt này.
Có thể xây dựng mô hình toán học cho nguồn tin như sau: Một bản tin xuất phát
từ một nguồn tin nào ó ều phản ánh tính chất thống kê của nguồn, bản tin càng dài sự
phản ánh càng trung thực. Có thể xem một bản tin cụ thể là thể hiện một quá trình ngẫu
nhiên và ứng trên quan iểm toán học, xem nguồn tin là cấu trúc thống kê của quá trình
ó. Như vậy, ể xác ịnh một nguồn tin, hay nói cách khác ể xác ịnh cấu trúc thống kê của
một quá trình ngẫu nhiên, chúng ta cần phải biết ược các quy luật thống kê của quá trình.
Để nghiên cứu ịnh lượng nguồn tin cũng như hệ thống truyền tin, có thể mô hình hoá
toán học nguồn tin bằng bốn quá trình sau:
Quá trình ngẫu nhiên liên tục: Nguồn tiếng nói, âm nhạc, hình ảnh là tiêu biểu cho quá
trình này. Trong các hệ thống thông tin thoại, truyền thanh, truyền hình với các tín hiệu
iều biên, iều tần thông thường chúng ta gặp các nguồn như vậy.
Quá trình ngẫu nhiên rời rạc: Một quá trình ngẫu nhiên liên tục sau khi lượng tử hoá
theo mức sẽ trở thành quá trình này. Một ngôn ngữ, tín hiệu iện tín, các lệnh iêu khiển
là những nguồn rời rạc thuộc loại này
Dãy ngẫu nhiên liên tục: Đây là trường hợp nguồn liên tục ã ược gián oạn hoá theo thời
gian, như thường gặp trong các hộ thống thông tin iều biên xung (PAM), iều pha xung
(PPM), iều tần xung (PFM),... không bị lượng tử hoá.
Dãy ngẫu nhiên rời rạc: Dãy ngẫu nhiên liên tục ược tiếp tục lượng tử hoá theo mức. ví dụ
các hệ thống iều biên (pha, tần), xung lượng tử hóa, iều chế xung mã PCM.
1.3.2.2. Khối mã hóa/ Giải mã
Khối mã hoá: Làm ứng mỗi tin với một tổ hợp các ký hiệu ã chọn nhằm tăng mật
ộ, tăng khả năng chống nhiễu, tăng tốc ộ truyền tin. Cụ thể:
- Biến ổi các cấu trúc thống kê của nguồn, làm cho các thông số thống kê của nguồn
thích ứng với các thông số của kênh như: tốc ộ hình thành tin gần với khả năng cho
thông qua của kênh, tính chỗng nhiễu của tin khi truyền qua kênh tăng lên.
- Đối với việc mã hóa thống kê tối ưu: những tin có xác suất xuất hiện nhiều sẽ ược
thay thế bởi những từ mã ngắn và ngược lại, ể ảm bảo ộ dài trung bình của mã hiệu tối
thiểu.
- Đối với mã hóa chống nhiễu: sử dụng thêm một số bit bổ sung phục vụ cho việc
chống nhiễu (phát hiện, sửa lỗi) nhằm tăng ộ tin cậy truyền tin.

lOMoARcPSD|36067889
Tóm lại, hai nhiệm vụ lớn mà mã hóa cần phải ạt ược là: tăng hiệu suất truyền tin
và tăng ộ tin cậy.
Khối giải mã: Biến ổi các tin ã mã hoá thành các tin tương ứng ban ầu (các tin của
nguồn phát i).
1.3.2.3. Khối ghép kênh/ Tách kênh Khối
ghép kênh:
- Thuật ngữ “ghép kênh”: chỉ quá trình kết hợp hay tổ hợp nhiều tín hiệu ầu vào (có
tốc ộ bit thấp) tạo nên một tín hiệu ầu ra (có tốc ộ bit cao hơn).
- Điều kiện ơn kênh: Tại một thời iểm, môi trường truyền dẫn chỉ cho phép duy nhất
một kênh truyền/tín hiệu truyền qua.
- Trong trường hợp nhiều kênh truyền cùng chia sẻ một môi trường truyền dẫn: khi
ó tài nguyên của môi trường truyền sẽ phải chia nhỏ, mỗi kênh truyền sẽ ược chia một
phần tài nguyên ó. Tài nguyên của môi trường truyền dẫn là thời gian, tần số (bước
sóng), mã, không gian.
Khối tách kênh: Tách tín hiệu thu ược thành nhiều tín hiệu ầu ra.
1.3.2.4. Khối iều chế/ Giải iều chế
Điều chế có nghĩa là chuyển tin tức trong một dạng năng lượng thích hợp với môi
trường truyền lan. Dạng năng lượng ược dùng, phải ít bị suy hao và bị biến dạng do tác
ộng của nhiễu. Thực chất của quá trình iều chế là biến ổi một hoặc nhiều thông số của
dạng năng lượng ã chọn theo quy luật ại diện cho tin tức. Trong các hệ thống truyền tin
hiện nay, các phương pháp iều chế thường ược dùng ối với tin tức liên tục là iều chế
biên ộ (AM), iều chế tần số (FM) và iều chế pha (PM). Để tăng tính chống nhiễu dùng
các phương pháp iều chế xung như: iều chế pha xung (PPM), iều chế ộ rộng xung
(PWM), iều chế tần số xung (PFM) và iều chế biên ộ xung (PAM). Một phương pháp
iều chế thường dùng là iều chế mã xung (PCM) và iều chế delta. Đối với các tin tức rời
rạc, các phương pháp iều chế cũng giống như dối với các trường hợp tin tức liên tục
nhưng làm việc gián oạn theo thời gian, ược gọi là khóa dịch. Cụ thể là có các phương
pháp khóa dịch biên ộ (ASK), khóa dịch pha (PSK) và khóa dịch tần số (FSK), iều chế
biên ộ cầu phương (QAM).
Giải iều chế là phép biến ổi ngược lại của quá trình iều chế. Điểm khác là ầu vào
của thiết bị giải iều chế không phải là tín hiệu ầu ra của thiết bị iều chế mà nó là hỗn hợp
của tín hiệu iều chế và nhiễu. Nhiệm vụ của thiết bị giải iều chế là từ trong hỗn hợp ó
lọc ra ược những tin tức dưới dạng một hàm iện áp liên tục hoặc là một dãy xung rời rạc
giống như tin tức ở ầu vào của thiết bị iều chế với một sai số trong phạm vị cho phép.

lOMoARcPSD|36067889
Phương pháp giải iều chế, nói cách khác là phép lọc tin, ược thực hiện tuỳ theo hỗn hợp
tín hiệu và nhiễu với các chỉ tiêu tối ưu về sai số ( ộ chính xác) ề ra cho nó. Chúng ta có
các phương pháp lọc tin thông thường như tách sóng biên ộ, tách sóng tần số, tách sóng
pha, tách sóng ồng bộ, lọc tin liên kết, lọc tin bằng phương pháp tương quan, lọc tối ưu.
Như vậy, có thể tóm lược các chức năng của các khối iều chế và giải iều chế như
sau:
Khối iều chế: Là thiết bị biến tập tin ( ã hoặc không mã hoá) thành các tín hiệu ể phát
xạ/phát vào không gian/ống dẫn sóng quang dưới dạng sóng iện từ cao tần/ánh sáng. Về
nguyên tắc, bất kỳ một máy phát nào cũng có khối này. Cụ thể:
- Sử dụng sóng mang có tần số phù hợp với môi trường truyển tin, thay ổi các tính
chất dữ liệu (tín hiệu iều chế) theo dữ liệu ầu vào (tín hiệu mang tin). Ví dụ: iều chế theo
biên ộ, theo tần số, theo góc pha... - Sử dụng tối ưu môi trường truyền tin.
- Tuỳ thuộc vào nhiễu trong kênh mà xây dựng những hệ thống tín hiệu có hệ số phân
biệt với nhau rõ ràng ể quá trình giải iều chế dễ dàng phân biệt dù có bị nhiễu làm biến
dạng.
Khối giải iều chế: Biến ổi tín hiệu thu ược thành tin ã mã hoá.
1.3.2.5. Kênh truyền tin
Là môi trường vật lý, trong ó tín hiệu truyền i từ nguồn tin ến nơi nhận tin. Môi
trường truyền tin gồm: môi trường ịnh hướng (cáp kim loại, cáp quang,..) hoặc môi
trường không ịnh hướng (không khí, tầng iện ly, sóng âm...).
Trên ường truyền có những tác ộng làm mất năng lượng, làm mất thông tin của tín
hiệu, ó chính là nhiễu. Nhiễu là các yếu tố ngẫu nhiên có ảnh hưởng xấu ến việc nhận
tin. Do ó có thể lấy nhiễu làm ặc tính chung của môi trường truyền tin và ể phân tích,
phân loại môi trường này có thể dựa trên sự phân tích, phân loại nhiễu. Tuy môi trường
truyền tin trong thực tế rất khác nhau, song vẫn có thể xem xét chúng theo các dạng cơ
bản sau: Môi trường có tác ộng nhiễu cộng là chủ yếu, Môi trường có tác ộng của nhiễu
nhân là chủ yếu; Môi trường gồm cả nhiễu cộng và nhiễu nhân. Nhiễu cộng do các nguồn
nhiễu công nghiệp và vũ trụ tạo ra, luôn luôn tồn tại trong các môi trường truyền lan của
tín hiệu. Nhiễu nhân là do phương thức truyền lan của tín hiệu hay là sự thay ổi thông
số vật lý của bộ phận môi trường truyền lan khi tín hiệu i qua.
Nhiệm vụ của kênh truyền tin là chuyển tín hiệu mang tin từ nguồn tin ến nơi nhận
tin và ảm bảo tính toàn vẹn của tin tức với thời gian quy ịnh.
Trong lý thuyết truyền tin: kênh truyền tin ặc trưng bởi hỗn hợp tín hiệu và nhiễu.

lOMoARcPSD|36067889
1.3.2.6. Nơi nhận tin
Nơi nhận tin: Hiện thị thông tin chuyển ến và có ba chức năng:
- Ghi lưu giữ tin (ví dụ bộ nhớ của máy tính, băng ghi âm, ghi hình,…)
- Biểu thị tin: Làm cho các giác quan của con người hoặc các bộ cảm biến của máy thụ
cảm ược ể xử lý tin (ví dụ băng âm thanh, chữ số, hình ảnh,…)
- Xử lý tin: Biến ổi tin ể ưa nó về dạng dễ sử dụng. Chức năng này có thể thực hiện bằng
con người hoặc bằng máy.
Nhận tin thường gồm có bộ nhận biết thông tin ược phát và xử lý thông tin. Bộ xử
lý thông tin có thể là người, cũng có thể là thiết bị. Nếu bộ phận xử lý thông tin là thiết
bị tự ộng chúng ta có một hệ thống truyền tin tự ộng.
1.3.3. Những chỉ tiêu chất lượng cơ bản của một hệ truyền tin
1.3.3.1. Tính hiệu quả Thể
hiện trên các mặt sau:
- Tốc ộ truyền tin cao.
- Truyền ược ồng thời nhiều tin khác nhau.
- Chi phí cho một bit thông tin thấp.
1.2.3.2. Độ tin cậy
Đảm bảo ộ chính xác của việc thu nhận tin cao, xác suất lỗi (hoặc tỉ số lỗi bít
(BER)) thấp.
Hai chỉ tiêu trên mâu thuẫn nhau. Giải quyết mâu thuẫn trên là nhiệm vụ của lý
thuyết thông tin.
1.3.3.3. An toàn
Thể hiện trên các mặt sau:
- Bí mật:
+ Không thể khai thác thông tin trái phép.
+ Chỉ có người thu hợp lệ mới hiểu ược thông tin.
- Xác thực: Gắn trách nhiệm của bên gửi – bên thu với bản tin (chữ ký số).
- Toàn vẹn:
+ Thông tin không bị bóp méo (cắt xén, xuyên tạc, sửa ổi).
+ Thông tin ược thu phải nguyên vẹn cả về nội dung và hình thức.

lOMoARcPSD|36067889
- Khả dụng: Mọi tài nguyên và dịch vụ của hệ thống phải ược cung cấp ầy ủ cho người
dùng hợp pháp.
1.3.3.4. Đảm bảo chất lượng dịch vụ (QoS)
Đây là một chỉ tiêu rất quan trọng ặc biệt là ối với các dịch vụ thời gian thực, nhạy
cảm với ộ trễ (truyền tiếng nói, hình ảnh,…).
1.4. TỔNG KẾT CHƯƠNG
Chương 1 ã trình bày sơ lược về lịch sử phát triển của lý thuyết truyền tin, một số
khái niệm cơ bản trong truyền tin và giới thiệu mô hình tổng quát của một hệ thống
truyền tin.
Trong ó ã ề cập các chức năng của
các thành phần chính trong hệ thống
truyền tin và ưa
ra n
hững chỉ tiêu chất lượng cơ bản của một hệ
thống
truyền tin
.
Câu hỏi/bài tập chương 1
1-
Nêu khái niệm hệ thống truyền tin và phân loại chúng
?
2-
Trình bày quá trình phát triển của hệ thống truyền tin?
3-
Vẽ
mô hình
tổng quát của một hệ thống truyền tin và giải thích chức năng của từng
thành phần chính trong mô hình ó.
4-
Trình bày các chỉ tiêu chất lượng cơ bản của một hệ thống truyền tin?

lOMoARcPSD|36067889
- CHƯƠNG 2 -
CƠ SỞ LÝ THUYẾT TRUYỀN TIN
Trong chương I, ã trình bày một cách tổng quát hệ thống truyền tin và các vấn ề cơ
bản của hệ thống. Chương này sẽ khảo sát kỹ hơn các cơ sở lý thuyết và các phép xử lý
tin tức ở khối nguồn tin. Do thông tin là một quá trình ngẫu nhiên, tín hiệu mang tin tức
cũng là tín hiệu ngẫu nhiên, cho nên lý thuyết xác suất và quá trình ngẫu nhiên chính là
công cụ toán học ể nghiên cứu các hệ thống truyền tin. Trên cơ sở trình bày một số kiến
thức cơ bản về xác suất thống kê sẽ rút ra ược những kết quả cần thiết ứng dụng vào việc
nghiên cứu hệ thống truyền tin.
2.1. XÁC SUẤT VÀ QUÁ TRÌNH NGẪU NHIÊN
2.1.1. Xác suất
2.1.1.1. Khái niệm về xác suất
a) Không gian mẫu
Là tập hay không gian tất cả các kết quả có thể có của một thí nghiệm và thường
ược ký hiệu là hoặc . Nếu không gian mẫu là rời rạc thì có thể biểu diễn bằng =
{
1
,
2
}.
b) Sự kiện, sự kiện cơ bản
Mỗi phần tử của (không gian mẫu) ược gọi là một sự kiện cơ bản, mỗi tập con của
ược gọi là một sự kiện.
Ví dụ 2-1: Trong phép thử gieo một con xúc xắc thì tập các giá trị có thể xuất hiện là
= {1, 2, 3, 4, 5, 6}. Ở ây, mỗi giá trị xuất hiện chính là số lượng iểm chấm có trên mặt
ngửa của con xúc xắc và chúng ược gọi là sự kiện cơ bản. Khi gieo một số con xúc xắc
thì một tập con các giá trị của sẽ xuất hiện và sự xuất hiện này là một sự kiện. Chẳng
hạn sự kiện là việc xuất hiện hai giá trị 2 và 4 thì = {2, 4}.
Sự kiện bù của sự kiện ược ký hiệu là , là một tập con gồm các phần tử của
nhưng không thuộc . Ví dụ, = {1, 3, 5, 6}.
Hai sự kiện ược gọi là loại trừ nhau nếu chúng không chứa một giá trị chung nào.
Chẳng hạn, nếu = {1, 3} thì và là loại trừ nhau.
Hợp của hai sự kiện là sự kiện chứa tất cả các giá trị có trong hai sự kiện. Phép hợp
ược ký hiệu là ‘ ’. Ví dụ: nếu = {1, 2, 6} thì = = {1, 2, 4, 6}.

lOMoARcPSD|36067889
Giao của hai sự kiện là sự kiện chứa các giá trị chung trong hai sự kiện. Giao ược
ký hiệu là ‘ ’. Ví dụ: = {3, 4, 6} thì = = {4, 6}. c)
Định nghĩa xác suất
Thực hiện phép thử lần. Giả sử sự kiện xuất hiện lần. Khi ó ược gọi là
tần số của sự kiện và tỷ số ( ược gọi là tần suất xuất hiện sự kiện trong loạt
phép thử. Cho số phép thử tăng lên vô hạn, tần suất xuất hiện sự kiện dần về một số
xác ịnh gọi là xác suất xuất hiện sự kiện , ký hiệu là () và ược xác ịnh như sau:
() = lim
(2.1)
Ví dụ 2-2: Một xạ thủ bắn 100 viên ạn vào bia, có 70 viên trúng bia. Khi ó, xác suất mà
xạ thủ bắn trúng bia là = 70%.
Ví dụ 2-3: Nếu gieo xúc xắc (xúc xắc ồng nhất) thì xác suất:
(1) = , , (1, 3, Rõ
ràng với ịnh nghĩa trên thì luôn có (1.
Nếu có một tập các sự kiện loại trừ nhau
, thuộc tập , thì xác suất
xuất hiện của sự kiện hợp của chúng bằng tổng các xác suất xuất hiện của các sự kiện
thành phần:
(
=1
(
) (2.2)
d) Sự kiện ồng thời và xác suất ồng thời
Sự kiện ồng thời là sự kiện mà hai sự kiện riêng ồng thời xuất hiện.
Cụ thể: nếu thực hiện một phép thử làm xuất hiện sự kiện
, = và phép
thử thứ hai làm xuất hiện sự kiện
, thì phép thử ồng thời sẽ làm xuất
hiện sự kiện ồng thời (
,
), = 1, 2, . . . , , = 1, 2, . . . , .
Ứng với mỗi sự kiện ổng thời này là một khả năng xuất hiện của nó và ược gọi là xác
suất xuất hiện ồng thời (
,
).
Nếu các sự kiện
loại trừ nhau thì:
=1
(
,
) = (
)
Tương tự, nếu các sự kiện
loại trừ nhau thì:
=1
(
,
) = (
)
Nếu tất cả các sự kiện
và
loại trừ nhau thì:
=1
=1
(
,
) = 1.

lOMoARcPSD|36067889
e) Xác suất có iều kiện
Giả thiết một thực nghiệm ồng thời ã ược xác ịnh và sự kiện ồng thời với xác suất
(, ). Khi ang thực nghiệm, giả thiết sự kiện ã xuất hiện và cần xác ịnh xác suất
xuất hiện sự kiện . Xác suất này gọi là xác suất có iều kiện của sự kiện với iều kiện
sự kiện ã xuất hiện và ược ịnh nghĩa:
(|) = (, ) ( ) (2.3)
Tương tự, xác suất có iều kiện của sự kiện với iều kiện sự kiện ã xuất hiện là:
(|) = (, ) ( ) (2.4)
Với iều kiện () > 0 hoặc () > 0 kết hợp cả hai biểu thức (2-3) và (2-4) ta có:
(, ) = (). (|) = (). (|) (2.5)
Một quan hệ thường dùng của xác suất có iều kiện là công thức Bayes. Công thức
này nói rằng: nếu các sự kiện
, là loại trừ nhau và là một sự kiện xuất
hiện dồng thời với các sự kiện
và () > 0 thì:
(|
).(
) (
|) = (
,
)/() =
=1
(|
).(
)
(2.6)
Trong hệ thống truyền tín hiệu số, các sự kiện
sẽ ược coi là các tin có thể ược
phát, ược coi là tin thu ược khi phía nguồn phát tin
và có nhiễu tác ộng, xác suất
(
|) ược coi là xác suất ể nguồn tin phát tin
khi phía thu ã thu ược tin . Trong
công thức Bayes, (
|) ược gọi là xác suất hậu nghiệm, còn (
) ược gọi là xác suất
tiền nghiệm.
f) Tính ộc lập thống kê của các sự kiện
Tính ộc lập thống kê của các sự kiện là một khái niệm quan trọng trong lý thuyết
xác suất. Để giải thích khái niệm này, xem xét hai sự kiện và và xác suất có iều kiện
của chúng là (|) hoặc (|). Giả thiết việc xuất hiện của sự kiện không phụ
thuộc vào sự xuất hiện của sự kiện hoặc ngược lại thì:
(|) = ()
(|) = ()
(2.7)
Suy ra: (, ) = (). () (2.8)
Lúc này xác suất ồng thời là tích trực tiếp của hai xác suất thành phần. Trong lý
thuyết xác suất, người ta nói hai sự kiện là ộc lập thống kê khi chúng thỏa mãn quan hệ
(2.8).

lOMoARcPSD|36067889
2.1.1.2. Đại lượng ngẫu nhiên và phân bố xác suất
a) Đại lượng ngẫu nhiên
Đại lượng ngẫu nhiên là ại lượng biến ổi biểu thị giá trị kết quả của một phép
thử ngẫu nhiên. Để ký hiệu ại lượng ngẫu nhiên, thường dùng các chữ cái hoa như , ,
.
b) Đại lượng ngẫu nhiên rời rạc
Đại lượng ngẫu nhiên ược gọi là rời rạc nếu nó chỉ nhận một số hữu hạn hoặc một
số vô hạn ếm ược các giá trị. Có thể liệt kê các giá trị của ại lượng ngẫu nhiên rời rạc
1
,
2
. Ký hiệu ại lượng ngẫu nhiên nhận giá trị
là =
và xác suất ể nhận
giá trị
là ( =
).
Ví dụ 2-4: Gọi là số chấm xuất hiện trên mặt con xúc sắc thì là một ại lượng ngẫu
Hàm phân bố xác suất của ại lượng ngẫu nhiên , ký hiệu () là hàm ược ịnh nghĩa
như sau:
() = ( < ) (2.10) Nếu
là ại lượng ngẫu nhiên rời rạc nhận các giá trị có thể
1
,
2
thì:
nhiên r
ờ
i r
ạ
c. S
ố
h
ọ
c sinh v
ắ
ng m
ặ
t trong m
ộ
t bu
ổ
i h
ọc cũng là một ại lượ
ng ng
ẫ
u
nhiên r
ờ
i r
ạ
c.
c) Đại lượ
ng ng
ẫ
u nhiên liên t
ụ
c
Đại lượ
ng ng
ẫu nhiên ượ
c g
ọ
i là liên t
ụ
c n
ế
u các giá tr
ị
có th
ể
c
ủ
a nó l
ấp ầ
y m
ộ
t
kho
ả
ng trên tr
ụ
c s
ố
. Ví d
ụ
:
nhi
ệt ộ
không khí
ở
m
ỗ
i th
ời iểm nào ó, sai số
khi o
lườ
ng m
ột ại lượ
ng v
ậ
t lý.
Hàm m
ật ộ
xác su
ấ
t:
Hàm m
ật ộ
xác su
ấ
t c
ủa ại lượ
ng ng
ẫ
u nhiên liên t
ụ
c
là hàm không âm
()
,
xác ị
nh v
ớ
i m
ọ
i
và tho
ả
mãn:
(
)
=
()
(2.9)
v
ớ
i m
ọ
i t
ậ
p s
ố
th
ự
c
.
Tính ch
ấ
t c
ủ
a hàm m
ật ộ
xác su
ấ
t:
+
(
)
+
()
+
=1
Hàm phân b
ố
xác su
ấ
t:

lOMoARcPSD|36067889
1
,
2
2
)=
2
1
(
<
( =
<
(
= ( =
)) (2.11) Nếu
là ại lượng ngẫu nhiên liên tục có hàm mật ộ xác suất () thì:
(
() (2.12)
Ý nghĩa: Hàm phân bố xác suất () phản ánh mức ộ tập trung xác suất về bên trái của iểm
.
Tính chất của hàm phân bố xác suất:
+ 0 < (
+ F(x) là hàm không giảm (
1
2
(
1
(
2
)
+
() = (.
d) Đại lượng ngẫu nhiên nhiều chiều, hàm phân bố, hàm mật ộ xác suất của biến ngẫu
nhiên nhiều chiều
Khi thực hiện ồng thời nhiều phép thử hoặc thực hiện một phép thử phức tạp, chúng
ta sẽ gặp một ại lượng ngẫu nhiên nhiều chiều. Đại lượng này nhận một bộ giá trị ngẫu
nhiên mà mỗi giá trị có thể là một giá trị ại lượng ngẫu nhiên thành phần. Hàm phân bố
xác suất và hàm mật ộ phân bố xác suất của ại lượng này ược gọi là hàm phân bố xác
suất và mật ộ phân bố xác suất nhiều chiều.
Giả sử biến ngẫu nhiên gồm hai ại lượng ngẫu nhiên thành phần
1
,
2
. Hàm phân
bố xác suất hai chiều sẽ là:
(
1
,
2
) = (
1
(
1
,
2
)
1
2
(2.13)
Hàm mật ộ phân bố xác suất hai chiều là:
2
(
1
,
2
) =
1
2 (
1
,
2
) (2.14)
Khi lấy tích phân hàm mật ộ phân bố xác suất hai chiều theo một ại lượng, sẽ ược hàm
mật ộ phân bố xác suất của ại lượng kia, có nghĩa là:
(
1,
2
)
1
= (
2
) (2.15)
(
1,
2
)
2
= (
1
) (2.16)
Các hàm mật ộ phân bố xác suất p(x
1
) và p(x
2
) thu ược từ hàm mật ộ phân bố ồng
thời gọi là các hàm mật ộ phân bố xác suất biên. Hơn nữa, ta có:
(
1,
2
)
1
2
= 1 (2.17)

lOMoARcPSD|36067889
1
1
|
2
2
<
2
2
)=
1
2
2
2
2
1
2
2
2
=
(
1
,
2
(
1
,
2
2
)
Có thể tổng quát hóa các khái niệm và ịnh nghĩa trên cho các biến ngẫu nhiên nhiều
chiều một cách tương tự. Các biến ngẫu nhiên
, = 1, 2. . . , có hàm phân bố xác suất
ược ịnh nghĩa như sau:
(
1
,
2
) = (
1
,
2
2
)
(
1
,
2
, . . . ,
)
1
2
(2.18)
với (
1
,
2
. . . ,
) là hàm mật ộ phân bố xác suất ồng thời, ta cũng có:
(
1
,
2
. . . ,
)
=
1
2
...
(
1
,
2
. . . ,
) (2.19)
e) Hàm phân bố xác suất có iều kiện
Xét hai biến ngẫu nhiên
1
,
2
có hàm mật ộ phân bố xác suất ồng thời (
1,
2
).
Giả sử muốn xác ịnh xác suất ể biến ngẫu nhiên
1
1
với iều kiện:
2
2
<
2
2
trong ó:
2
dương.
Điều ó có nghĩa là muốn xác ịnh xác suất của sự kiện (
1
1
|
2
2
<
2
2
). Sử dụng những quan hệ ã thiết lập ở trên cho xác suất có iều kiện của một sự kiện,
xác suất của sự kiện (
1
1
|
2
2
<
2
2
) sẽ bằng xác suất của sự kiện ồng thời
(
1
1
|
2
2
<
2
2
) chia cho xác suất của sự kiện (
2
2
<
2
2
):
(1,2)
(
(2)2 (2(22)
(2.20)
Giả sử các hàm mật ộ phân bố xác suất p(x
1
, x
2
)và p(x
2
) là các hàm liên tục trong
khoảng (
2
2
,
2
), có thể chia cả tử số và mẫu số của biểu thức (2.20) cho
2
và
lấy giới hạn khi
2
0 và nhận ược:
1 (1,2)12]/2
(1 1|2 = 2) = (1|2) = ((1,2)2/)/2 2 = (2)2]/2
1
(
1
,
2
)1
=
(2.21)
(2)

lOMoARcPSD|36067889
ó chính là hàm phân bố xác suất của biến ngẫu nhiên
1
, trong iều kiện biến
2
ã xác
ịnh. Rõ ràng là:
2
) = 0 và
2
) = 1. Lấy ạo hàm (2.21) theo
1
nhận ược
hàm mật ộ phân bố xác suất tương ứng (
1
|
2
) như sau:
(
1
|
2
) =
(
(
1,
2
)
2)
(2.22)
Có thể biểu diễn hàm mật ộ phân bố xác suất p(x
1
, x
2
) theo các hàm mật ộ phân bố
xác suất có iều kiện:
(
1
,
2
) = (
1
|
2
)(
2
) = (
2
|
1
)(
1
) (2.23)
Tương tự sẽ mở rộng các quan hệ trên cho các biến ngẫu nhiên nhiều chiều. Hàm mật
ộ phân bố xác suất ồng thời của các biến ngẫu nhiên
, = 1, 2, . . . , như sau: (
1
,
2
,
. . . ,
) = (
1
,
2
, . . . ,
|
+1
, . . . ,
)(
+1
, . . . ,
) (2.24)
Hàm phân bố xác suất có iều kiện ồng thời tương ứng với hàm mật ộ phân bố xác suất
(
1
,
2
, . . . ,
|
+1
, . . . ,
) là:
1
(1,2...,,+1,...,)1 (2.25)
(
1
,
2
, . . . ,
|
+1
, . . . ,
) =
(+1,...,)
2.1.1.3. Một số phân bố xác suất thường gặp
Trong phần này sẽ xem xét các biến ngẫu nhiên hay gặp trong thực tế và các hàm
phân bố xác suất, hàm mật ộ phân bố xác suất. Đầu tiên là phân bố nhị thức, phân bố

lOMoARcPSD|36067889
Hình 2.1: Hàm phân bố xác suất biến ngẫu nhiên X Hàm mật ộ phân bố xác suất của
ược xác ịnh như sau:
(
=0
( = )(
=0
(
)
)
( ) (2.27) Hàm
phân bố xác suất của là:
=0
(2.28)
ở ây: [] là số nguyên lớn nhất mà . Hàm phân bố xác suất trong (2.28) ặc trưng
cho một biến ngẫu nhiên có phân bố nhị thức.
b) Phân bố ều
Hàm mật ộ phân bố xác suất và phân bố xác suất của biến ngẫu nhiên phân bố ều
ược trình bày trên hình 2.2.
này là phân b
ố
c
ủ
a m
ộ
t bi
ế
n ng
ẫ
u nhiên r
ờ
i r
ạc, và sau
ó s
ẽ
xét phân b
ố
xác su
ấ
t c
ủ
a
m
ộ
t s
ố
bi
ế
n ng
ẫ
u nhiên liên t
ụ
c.
a) Phân b
ố
nh
ị
th
ứ
c
Cho
là m
ộ
t bi
ế
n ng
ẫ
u nhiên r
ờ
i r
ạ
c, ch
ỉ
nh
ậ
n hai giá tr
ị
=0
ho
ặ
c
=1
v
ớ
i
xác su
ất tương ứ
ng là
và
. Hàm m
ật ộ
phân b
ố
xác su
ấ
t c
ủ
a
ượ
c bi
ể
u di
ễ
n
trên hình 2.1. Bây gi
ờ
gi
ả
thi
ế
t r
ằ
ng:
=
=1
(2.26)
ở
ây:
,
=1,2,...,
là các bi
ế
n ng
ẫu nhiên ộ
c l
ậ
p th
ố
ng kê và phân b
ố
ồ
ng nh
ấ
t
v
ớ
i hàm m
ật ộ
xác su
ấ
t bi
ể
u th
ị
trong hình 2.1.
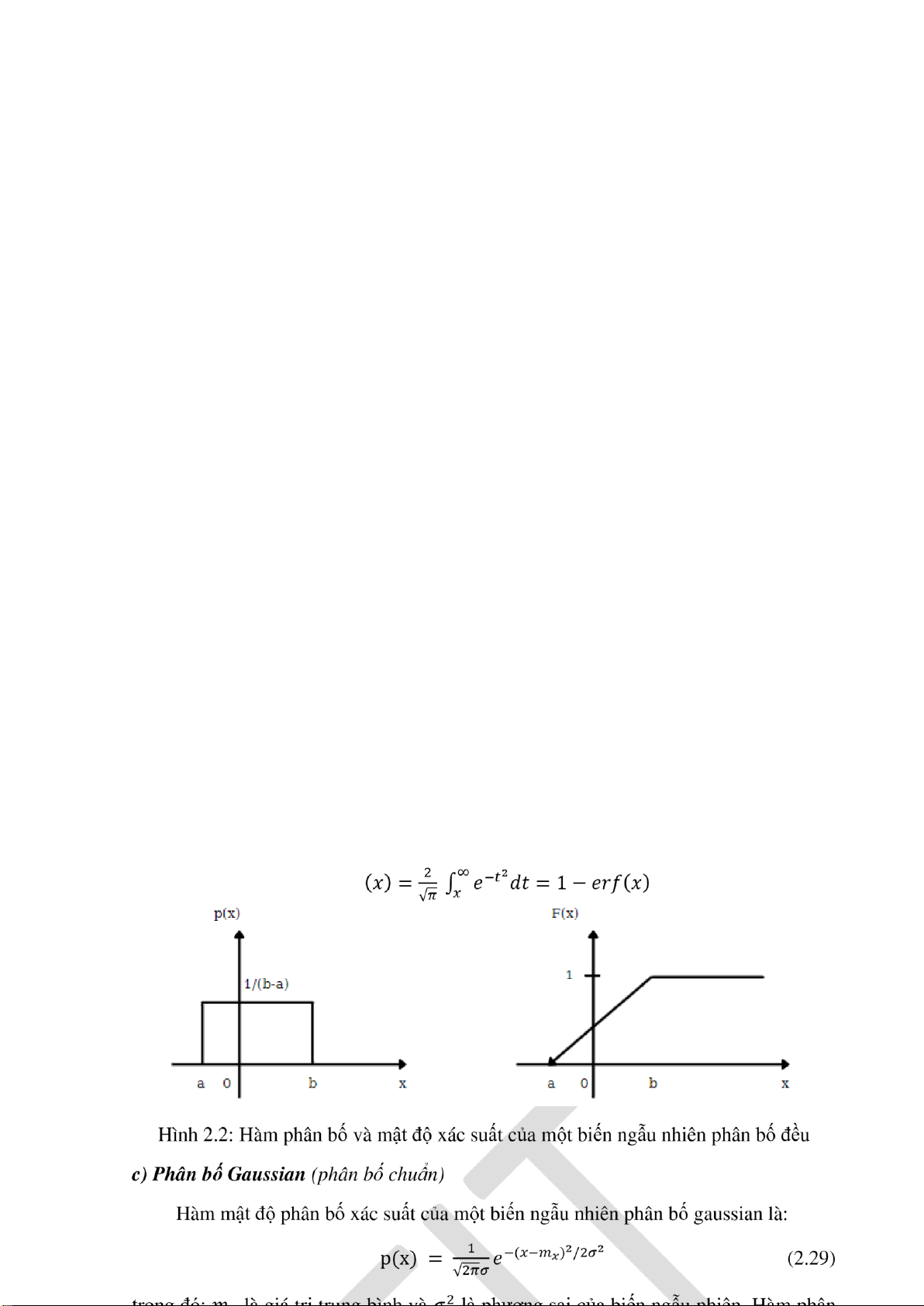
lOMoARcPSD|36067889
lOMoARcPSD|36067889
Lưu ý là: (), (), (0) =
và (0) = 1. Với >
thì hàm bù lỗi và vùng bên dưới ngưỡng của
hàm mật ộ phân bố xác suất gaussian. Với lớn, hàm bù lỗi () có thể ược biểu
diễn gần úng bằng chuỗi như sau:
2
(2.34)
trong ó: sai số của phép xấp xỉ nhỏ hơn số hạng cuối cùng.
Hàm thường ược dùng cho vùng dưới ngưỡng của hàm mật ộ phân bố xác suất
gaussian ược ký hiệu là () và ược ịnh nghĩa như sau:
=
2/2
, x0
(2.35)
So sánh (2.33) và (2.35) ta có:
() =
(2.36)
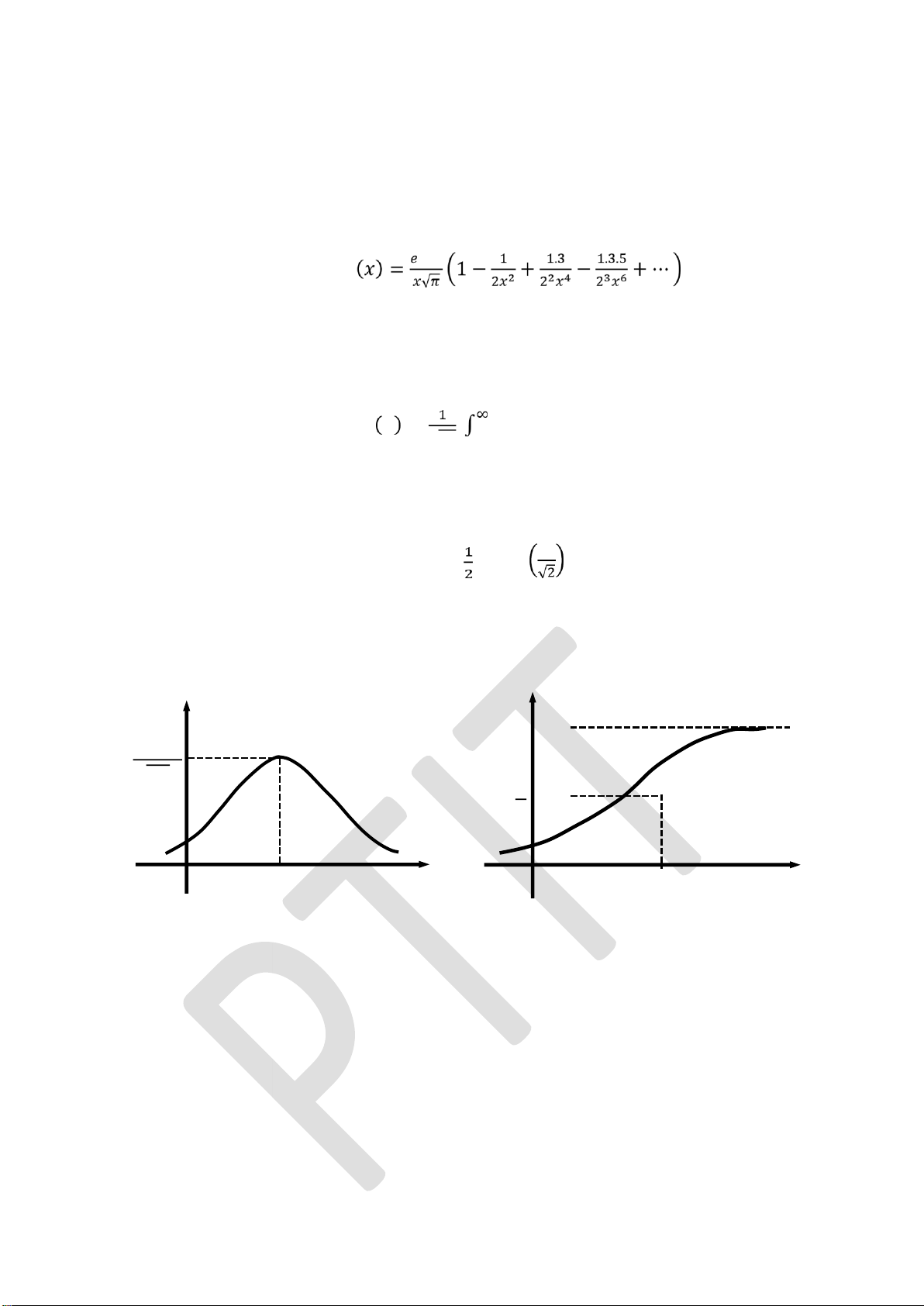
Hàm phân bố và mật ộ xác suất của một biến ngẫu nhiên phân bố Gaussian như
bi
ể
u th
ị
trên hình 2.3.
Hình 2.3: Hàm phân b
ố
và m
ật ộ
xác su
ấ
t c
ủ
a m
ộ
t bi
ế
n ng
ẫ
u nhiên phân b
ố
Gaussian
d) Phân b
ố
Khi-
bình phương
(Khi-Square Distribution)
N
ế
u
=
2
trong ó
là m
ộ
t bi
ế
n ng
ẫ
u nhiên gaussian thì
s
ẽ
có phân b
ố
Khi-
bình phương. Phân biệ
t hai lo
ạ
i phân b
ố
Khi-
bình phương. Loạ
i th
ứ
nh
ất ượ
c g
ọ
i là
phân b
ố
Khi-bì
nh phương trung tâm
khi
có tr
ị
trung bình b
ằ
ng không. Lo
ạ
i th
ứ
hai
g
ọ
i là
phân b
ố
Khi-
bình phươn
g không trung tâm
khi
có tr
ị
trung bình khác không.
Trướ
c h
ế
t xét phân b
ố
Khi-
bình phương tru
ng tâm
v
ớ
i
có phân b
ố
gaussian v
ớ
i
tr
ị
trung bình b
ằng 0 và ộ
l
ệch trung bình bình phương là
2
. Hàm m
ật ộ
phân b
ố
xác
su
ấ
t c
ủ
a
như sau:
()
1
1
2
()
1
1
2
0
0
)
(
(
)
lOMoARcPSD|36067889
() = [
2
/22
] , 0 (2.37)
và hàm phân bố xác suất của là:
/22
(2.38)
Hàm này không biểu diễn ược dưới dạng ẩn, tuy nhiên hàm ặc tính có thể ược biểu
diễn dưới dạng ẩn:
(jv) =
1
2 1/2
(2.39)
2 )
Tổng quát hóa, giả thiết biến ngẫu nhiên ược ịnh nghĩa như sau:
=1
2
(2.40)
trong ó:
, = 1, 2, . . . , là các biến ngẫu nhiên có phân bố gaussian, ộc lập thống kê và
có phân bố ồng nhất với trị trung bình bằng 0 và phương sai
2
.
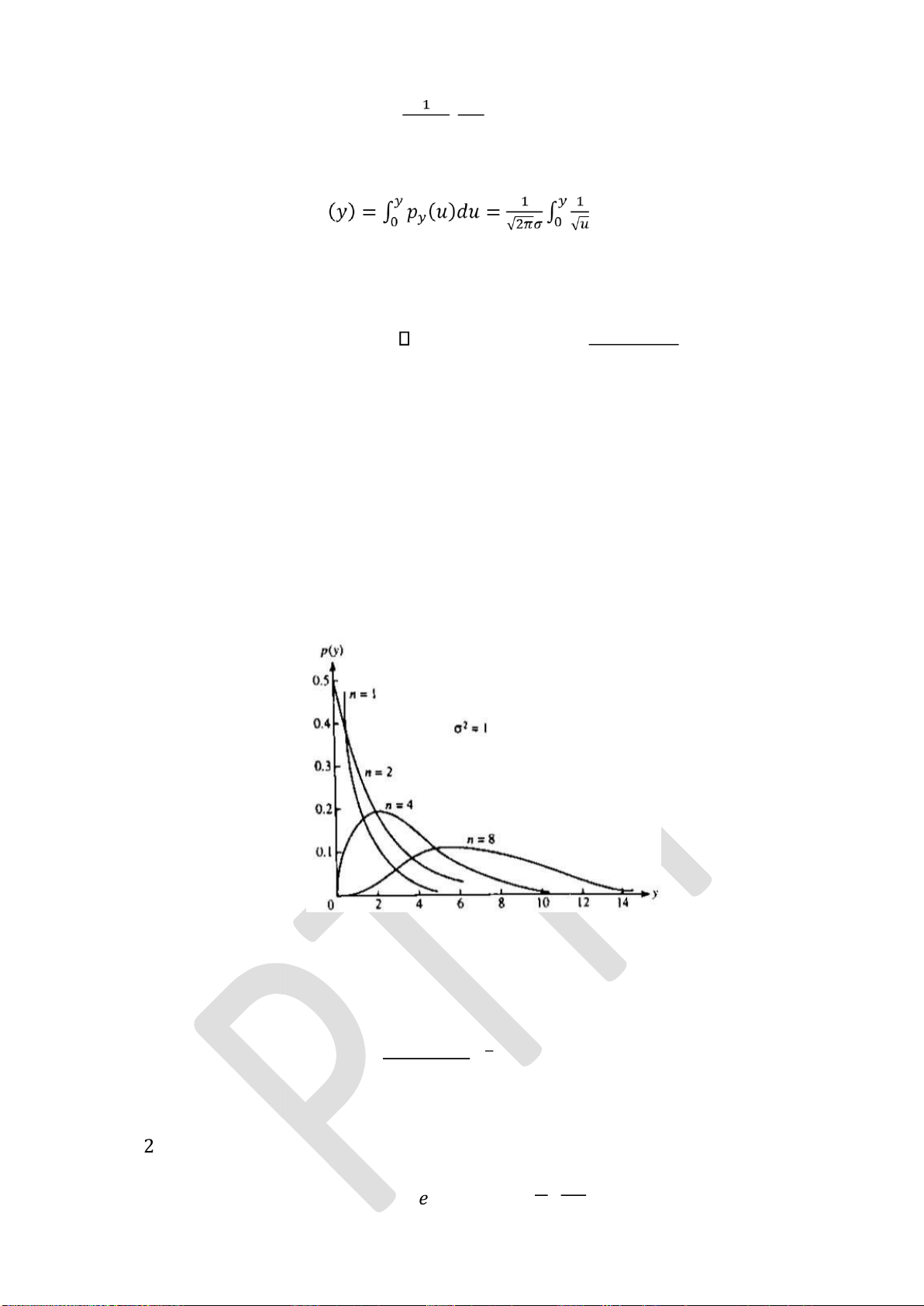
Hàm mật ộ phân bố xác suất của biến ngẫu nhiên khi phân bố Khi-bình phương như
trên hình 2.4.
Hình 2.4: Hàm m
ật ộ
phân b
ố
xác su
ấ
t c
ủ
a bi
ế
n ng
ẫ
u nhiên khi phân b
ố
Khi-bình
phương
Hàm phân b
ố
xác su
ấ
t c
ủ
a
là:
(
)
=
1
2
/2
(
1
2
)
2
1
/2
2
,0
0
(2.41)
Khi
ch
ẵ
n phép tích phân (2.41) có th
ể
bi
ể
u di
ễn dướ
i d
ạ
ng
ẩ
n. C
ụ
th
ể, ặ
t
=
2
trong ó
là s
ố
nguyên, b
ằ
ng phép tích phân t
ừ
ng ph
ần thu ượ
c bi
ể
u th
ứ
c:
(
)
/2
2
1
!
(
2
2
)
,0
1
=0
(2.42)

lOMoARcPSD|36067889
(
)
=
2
2
(
2
)
2
1
(
2
)
0
(
)
(
)
=0
(
)
(
,
)
Tiếp theo sẽ xem xét phân bố Khi-bình phương không trung tâm, thu ược từ việc
bình phương của một biến ngẫu nhiên gaussian có trị trung bình khác không. Nếu là
biến ngẫu nhiên gaussian với trị trung bình
, và phương sai là
2
, thì biến ngẫu nhiên
=
2
có hàm mật ộ phân bố xác suất thu ược bằng:
() =
2
(+2)/22
(2.43) Hàm
ặc tính tương ứng với hàm mật ộ phân bố xác suất này là:
(jv) =
1
2 1/2
2/22)
(2.44)
2 )
Để tổng quát hóa kết quả này, ặt là tổng bình phương của các biến ngẫu nhiên
gaussian ược ịnh nghĩa ở (2.40). Với
, = 1, 2, . . . , là các biến ngẫu nhiên ộc lập
thống kê với trị trung bình
, và phương sai ồng nhất bằng
2
, khi ó hàm ặc tính của
thu ược là:
1
2
(jv) =
2 /2
(2.45) 2 ) 2
Hàm phân bố xác suất của phân bố Khi-bình phương không trung tâm với bậc tự do
là:
1 (2)/4 (2+)/22 (2.46)
Không có biểu thức dạng ẩn cho tích phân này. Tuy nhiên khi = là một số
nguyên, hàm phân bố xác suất có thể biểu diễn ở dạng hàm (gọi là hàm Marcum tổng
quát) ược ịnh nghĩa như sau:
1 (2+2)
(, ( ) 2 1()
(2+2)/2 1=1 ()
() (2.47)
= 1(, ) +
trong ó:
1
(, ) = (2+2)/2
, > > 0 (2.48)
Nếu ổi biến tích phân trong (2.46) từ thành với
2
=
2
và ặt
2
=
2
2
a
2
=s
2
/
2
thì sẽ thu ược:
(
2
)
,0

lOMoARcPSD|36067889
(2.49) e) Phân bố
Rayleigh
Phân bố Rayleigh thường ược dùng làm mô hình thống kê của những tín hiệu
truyền qua các kênh vô tuyến. Phân bố này có liên hệ với phân bố Khi-bình phương
trung tâm. Để minh hoạ iều này, xét biến ngẫu nhiên =
1
2
+
2
2
, trong ó
1
và
2
là
những biến ngẫu nhiên gaussian ộc lập thống kê có trị trung bình bằng 0, phương sai
2
.
Từ ó ta thấy có phân bố Khi bình phương với hai bậc tự do. Hàm mật ộ phân bố xác
suất của ược xác ịnh như sau:
() =
2
1
2
/22
, (2.50) Bây giờ ịnh
nghĩa một biến ngẫu nhiên mới:
=
(2.51)
Hàm mật ộ phân bố xác suất của là:
() =
2
1
/
2
2
, 0 (2.52)
1
(2/22 1=0 !1 2 , 0 (2.56)
2
.1.2. Quá trình ngẫu nhiên
Có rất nhiều hiện tượng ngẫu nhiên xảy ra trong tự nhiên là các hàm của thời gian.
Ví dụ các hiện tượng trong khí tượng học như các hiện tượng tăng giảm ngẫu nhiên của
nhiệt ộ và áp suất không khí là những hàm theo thời gian. Sự dao ộng của iện áp do
nhiễu nhiệt sinh ra trong những iện trở của một thiết bị iện tử cũng là một hàm của thời
gian. Tương tự, tín hiệu ở ầu ra của một nguồn phát thông tin ược ặc trưng như một tín
hiệu ngẫu nhiên biến ổi theo thời gian. Tín hiệu truyền trên kênh thoại là một ví dụ của
loại tín hiệu như vậy. Tất cả những ví dụ này ều là những quá trình ngẫu nhiên. Trong
nghiên cứu về truyền thông tin số, chúng ta sẽ gặp các quá trình ngẫu nhiên khi ặc tính
hóa và mô hình hóa các tín hiệu ược tạo ra bởi các nguồn thông tin, trong việc mô hình
hóa các kênh truyền thông dùng ể truyền thông tin, trong việc biểu diễn nhiễu trong máy
thu và trong việc thiết kế các máy thu tối ưu cho các quá trình xử lý và thu các tín hiệu
ngẫu nhiên.

lOMoARcPSD|36067889
(
2
)
Đây là hàm mật ộ phân bố xác suất của biến ngẫu nhiên có phân bố Rayleigh và hàm
phân bố xác suất tương ứng là:
2
/22
(2.53)
Để tổng quát hóa những kết quả trên, xét biến ngẫu nhiên:
=1
2
(2.54)
trong ó:
, = 1, 2, . . . , là các biến ngẫu nhiên gaussian ộc lập thống kê, phân bố ồng
nhất và có trị trung bình bằng không. Biến ngẫu nhiên gọi là biến ngẫu nhiên có phân
bố Rayleigh tổng quát. Như vậy =
2
là phân bố Khi-bình phương với bậc tự do.
Hàm mật ộ phân bố xác suất của nó ược xác ịnh bởi (2.41). Dễ dàng tìm ra hàm mật ộ
phân bố xác suất của R bằng cách ổi biến trong (2.41):
() = (2)/21 1 2/22, 0 (2.55)
2 (
) 2
Từ sự liên hệ giữa phân bố Khi-bình phương trung tâm và phân bố Rayleigh, có
thể suy ra sự liên hệ giữa các hàm phân bố xác suất tương ứng. Do vậy, với mọi hàm
phân bố xác suất của có thể biểu diễn qua hàm gamma. Đặc biệt khi = 2 thì hàm
phân bố xác suất của có thể biểu diễn ở dạng ẩn như sau:
Tại một thời iểm nào ó, giá trị của một quá trình ngẫu nhiên là một biến ngẫu nhiên,
ví dụ như giá trị iện áp nhiễu phát sinh bởi một iện trở hay biên ộ của tín hiệu phát ra
bởi một nguồn âm thanh. Tiếp theo sẽ xem một quá trình ngẫu nhiên như là một biến
ngẫu nhiên theo tham số thời gian. Ký hiệu các quá trình như thế là (). Một cách tổng
quát, tham số là liên tục, trong khi có thể là liên tục hoặc rời rạc phụ thuộc vào ặc
iểm của nguồn phát tạo ra quá trình ngẫu nhiên.
Điện áp nhiễu sinh ra từ một iện trở hoặc một nguồn thông tin cho ta thấy việc tạo
ra một thể hiện của quá trình ngẫu nhiên, ược gọi là một mẫu của quá trình ngẫu nhiên.
Tập hợp tất cả các mẫu, nghĩa là tập hợp tất cả iện áp nhiễu phát ra từ các iện trở, tạo
nên một quá trình ngẫu nhiên (). Một cách tổng quát, số các mẫu trong tập hợp các
mẫu có thể là vô hạn, nhưng thường thì hữu hạn.
Ta ã ịnh nghĩa một quá trình ngẫu nhiên như tất cả các mẫu có thể xuất hiện, chúng
ta lại có thể quan tâm tới các giá trị của quá trình tại các thời iểm
1
>
2
>…>
, với
là số nguyên dương. Tổng quát, các biến ngẫu nhiên
(
), = 1, 2, . . . , ược ặc
trưng thống kê bởi hàm mật ộ xác suất ồng thời (
1
,
2
). Nói rộng ra, tất cả
(
)
=
2
2
0

lOMoARcPSD|36067889
(
1
2
)
=
1
2
các quan hệ xác suất ã ược ịnh nghĩa trong phần xác suất cho các biến ngẫu nhiên nhiều
chiều cũng ược sử dụng cho các biến ngẫu nhiên
, = 1, 2, . . . , .
Quá trình ngẫu nhiên dừng: Như ã nói ở trên, các biến ngẫu nhiên
, = 1, 2, . . . ,
thu ược từ quá trình ngẫu nhiên () tại các thời iểm
1
>
2
>…>
và với bất kỳ,
ược ặc trưng thống kê bằng hàm mật ộ xác suất ồng thời (
1
,
2
). Cần chú ý
tới một tập hợp gồm biến ngẫu nhiên khác
+
= (
+ ), = 1, 2, . . . , ở ây là ộ
dịch thời gian tùy ý. Các biến ngẫu nhiên này ược ặc trưng bằng hàm mật ộ xác suất ồng
thời (
1
,
2
). Các hàm mật ộ xác suất ồng thời của các biến ngẫu nhiên
và
+
, = 1, 2, . . . , có thể là giống nhau hoặc không giống nhau. Trong trường hợp
chúng giống nhau, nếu:
(
1
,
2
) = (
1
+
,
2+
+
) (2.57)
với mọi và thì quá trình ngẫu nhiên ược gọi là dừng chặt. Điều ó có nghĩa là tính chất
thống kê của quá trình ngẫu nhiên dừng là không ổi với bất kỳ sự dịch chuyển nào của
trục thời gian. Mặt khác, khi các hàm mật ộ xác suất ồng thời không giống nhau, quá
trình ngẫu nhiên là không dừng.
2.1.2.1. Các trị trung bình thống kê
Như ã ịnh nghĩa các trị trung bình thống kê cho các biến ngẫu nhiên, tương tự
chúng ta cũng có thể ịnh nghĩa các trị trung bình thống kê cho một quá trình ngẫu nhiên.
Các trị trung bình này ược gọi là các trị trung bình theo tập hợp. Với () biểu thị một
quá trình ngẫu nhiên và
(
), mô men cấp của biến ngẫu nhiên
ược ịnh nghĩa
là:
(
) =
(
)
(2.58)
Nói chung giá trị của mô men cấp phụ thuộc vào thời iểm
nếu hàm mật ộ phân
bố xác suất của (
) phụ thuộc vào
, khi quá trình là dừng (
) = (
+
) với mọi .
Vì vậy hàm mật ộ phổ xác suất và mô men cấp không phụ thuộc vào gốc thời gian.
Tiếp theo chúng ta quan tâm tới hai biến ngẫu nhiên
(
), = 1, 2. Tương quan
giữa
1
và
2
ược o bằng mô men ồng thời:
(
1
,
2
)
1
2
(2.59)
Do mô men ồng thời này phụ thuộc vào các thời iểm
1
,
2
nó ược ký hiệu bằng
hàm (
1
,
2
). Hàm này ược gọi là hàm tự tương quan của quá trình ngẫu nhiên. Khi quá
trình () là dừng, hàm mật ộ xác suất ồng thời của cặp (
1
,
2
) giống với hàm mật ộ
xác suất ồng thời của cặp (
1
+
,
2+
) với mọi . Điều này nói lên rằng hàm tự tương

lOMoARcPSD| 36067889
quan của () không phụ thuộc vào các thời iểm riêng biệt
1
và
2
, mà chỉ phụ thuộc
vào hiệu
1
2
. Do ó ối với một quá trình ngẫu nhiên dừng mô men ồng thời ược viết
như sau:
(
1
2
) = (
1
,
2
) = (
1
2
) = () (2.60)
với: =
1
2
hay
2
=
1
. Nếu ặt
2
=
1
+ ta sẽ có:
) = (
1
1
+
) = (
) = ()
Như vậy, hàm () là hàm chẵn và (0) = (
2
) biểu thị công suất trung bình của
quá trình ngẫu nhiên ().
Có thể nhận thấy tồn tại các quá trình ngẫu nhiên không dừng với tính chất là trị
trung bình của quá trình không phụ thuộc thời gian (là hằng số) và hàm tự tương quan
thỏa mãn iều kiện (
1
,
2
) = (
1
2
). Những quá trình ngẫu nhiên như thế ược gọi
là dừng theo nghĩa rộng. Do ó dừng theo nghĩa rộng là một iều kiện kém chặt chẽ hơn
dừng chặt. Về sau, khi nói tới quá trình ngẫu nhiên dừng là ta quy ước là quá trình ngẫu
nhiên dừng theo nghĩa rộng.
Tương ứng với hàm tự tương quan là hàm tự hiệp biến của một quá trình ngẫu nhiên
và ược ịnh nghĩa như sau:
(
1
,
2
) = {[
1
(
1
)][
2
(
2
)]} = (
1
,
2
(
1
)(
2
) (2.61) ở
ây (
1
) và (
2
) theo thứ tự là các trị trung bình của
1
và
2
. Khi quá trình ngẫu
nhiên là dừng, hàm tự hợp biến ược viết ơn giản thành:
(
1
,
2
) = (
1
2
) = () = (
2
(2.62)
ở ây =
1
2
.
Những mômen ồng thời cấp cao hơn của hai hoặc nhiều biến ngẫu nhiên thu ược
từ một quá trình ngẫu nhiên () ược ịnh nghĩa tương tự như trên. Ngoại trừ quá trình
ngẫu nhiên gaussian, những mô men cấp cao có thể ược biểu diễn qua các mô men bậc
một và bậc hai, các mômen bậc cao thường rất ít gặp trong thực nghiệm.
Trị trung bình của một quá trình gaussian. Giả thiết rằng () là một quá trình ngẫu
nhiên gaussian. Do ó tại các thời iểm =
, = 1, 2, . . , , các biến ngẫu nhiên
, =
1, 2, . . , là gaussian với các trị trung bình (
) và các hàm tự hợp biến là:
(
,
) = {[
(
)] [
(
)]}, , , (2.63)

lOMoARcPSD|36067889
(
)
Nếu biểu thị là ma trận hiệp biến cỡ × với các phần tử là (
,
) và các trị
trung bình là véc tơ
, thì hàm mật ộ phân bố xác suất ồng thời của các biến
ã ược
xét tới trong công thức trước.
Nếu quá trình gaussian là dừng thì (
) = mọi
và (
,
) = (
). Có
thể nhận xét rằng quá trình ngẫu nhiên gaussian ược xác ịnh hoàn toàn bởi trị trung bình
và các hàm tự hiệp biến. Từ ó nếu quá trình gaussian là dừng theo nghĩa rộng thì nó cũng
dừng theo nghĩa hẹp. Tất nhiên iều ngược lại luôn úng cho mọi quá trình ngẫu nhiên.
Trị trung bình ồng thời của quá trình ngẫu nhiên. Cho () và () biểu thị hai quá
trình ngẫu nhiên
(
) và
, , = 1, 2, . . , là các biến ngẫu nhiên
tại các thời iểm
1
>
2
và
1
>
2
. Đặc trưng thống kê của hai qua
trình ược biểu thị bằng hàm mật ộ xác suất ồng thời:
(
1
,
2
,
,
) với mọi
1
,
2
,
1
,
2
và với mọi số nguyên
dương , .
Hàm tương quan chéo giữa () và () biểu thị bằng
(
1
,
2
), ược ịnh nghĩa
như là mô men ồng thời:
,
2
)
1
2
(2.64)
và hàm hiệp biến chéo là:
(
1
,
2
) =
(
1
,
2
(
1
)
(
2
) (2.65)
Khi các quá trình là dừng ồng thời và dừng riêng biệt, chúng ta có
(
1
,
2
) =
(
1
,
2
) và
(
1
,
2
) =
(
1
2
). Trong trường hợp này ta chú ý rằng:
)
= (
1
1
+
) = (
1
1
) (2.66)
Các quá trình ngẫu nhiên () và () ược gọi là ộc lập thống kê nếu và chỉ
nếu: (
1
,
2
,
,
,
) = (
1
,
2
)(
) với mọi
và
và mọi số nguyên dương , . Các quá trình ược gọi là không tương quan nếu:
(
1
,
2
) = (
1
)(
2
) vì vậy:
(
1
,
2
) = 0.
Quá trình ngẫu nhiên phức () ược ịnh nghĩa như sau:
() = () + () (2.67)

lOMoARcPSD|36067889
(
1
,
2
)
=
1
2
(
1
2
)
=
1
2
(
1
+
1
)(
2
2
)
=
1
2
{
(
1
,
2
)
+
(
1
,
2
)
+
[
(
1
,
2
)
(
1
,
2
)
]}
(
)
=
1
2
(
1
1
)
=
1
2
(
1
với: () và () là các quá trình ngẫu nhiên. Hàm mật ộ phân bố xác suất ồng thời của
các biến ngẫu nhiên
= (
), ược xác ịnh bởi hàm mật ộ phân bố xác
suất ồng thời của các thành phần (
,
), . Như vậy hàm mật ộ
xác suất ặc trưng cho
là: (
1
,
2
,
,
1
,
2
).
Quá trình ngẫu nhiên phức () thường gặp trong khi biểu diễn nhiễu băng hẹp
bằng tín hiệu tần số thấp tương ương. Một ặc tính quan trọng của quá trình như vậy là
hàm tự tương quan, ược ịnh nghĩa như sau:
(2.68)
với:
(
1
,
2
) và
(
1
,
2
) là các hàm tự tương quan của () và (), và
(
1
,
2
),
(
1
,
2
) là các hàm tương quan chéo, hệ số ½ trong ịnh nghĩa của hàm tự tương quan
một quá trình ngẫu nhiên phức có ý nghĩa về mặt chuẩn hóa toán học.
Khi các quá trình () và () là dừng ộc lập và dừng ồng thời, hàm tự tương quan
của () trở thành:
(
1
,
2
) =
(
1
2
) =
() với:
2
=
1
. Như vậy, hàm
liên hợp phức sẽ là:
+
1
) =
) (2.69)
vì vậy:
() =
)
Bây giờ giả thiết rằng () = () + () và () = () + () là hai quá
trình ngẫu nhiên phức, hàm tương quan chéo của () và () ược ịnh nghĩa như sau:
(2.70)
Khi (), (), (), và
2
dừng ồng thời từng cặp, hàm tương quan chéo trên trở
thành các hàm của thời gian chênh lệch =
1
2
. Tức là:
+
1
) =
) (2.71)
2.1.2.2. Phổ mật ộ công suất
Đặc tính tần số của một tín hiệu là ặc tính cơ bản, nó cho phép phân biệt các tín
hiệu với nhau. Nói chung một tín hiệu có thể ược phân loại là có công suất trung bình
hữu hạn hay vô hạn, có năng lượng vô hạn hay hữu hạn. Đặc tính tần số của tín hiệu có
lOMoARcPSD|36067889
năng lượng hữu hạn thu ược qua phép biến ổi Fourier của biểu diễn tín hiệu theo thời
gian. Nếu tín hiệu là tuần hoàn, năng lượng tín hiệu là vô hạn nên không tồn tại biến ổi
Fourier. Thay vào ó dùng chuỗi Fourier cho biết sự phân bố công suất tín hiệu tại các
tần số rời rạc.
Một quá trình ngẫu nhiên dừng có năng lượng vô hạn và ặc tính phổ của quá trình
ngẫu nhiên dừng ược cho bởi phép biến ổi Fourier của hàm tự tương quan. Sự phân bố
công suất tín hiệu theo tần số ược cho bởi hàm:
()
2
(2.72) Biến ổi Fourier ngược là:
()
2
(2.73) Có nhận xét:
() = (|
|
2
0 (2.74)
Do hàm (0) biểu diễn công suất trung bình của tín hiệu ngẫu nhiên nên () là
phân bố công suất của tín hiệu ngẫu nhiên theo tần số. Bởi vậy () ược gọi là phổ mật
ộ công suất của quá trình ngẫu nhiên.
Nếu quá trình ngẫu nhiên là thực, là hàm thực và chẵn, hàm () cũng thực và
chẵn. Mặt khác nếu quá trình là phức,
, vì vậy ta có:
2 2
2
= () (2.75)
do ó: () là thực.
Định nghĩa của mật ộ phổ công suất có thể suy rộng ra cho hai quá trình ngẫu nhiên
dừng ồng thời () và (), hai quá trình này có hàm tương quan chéo
(). Biến ổi
Fourier của
() ược gọi là phổ mật ộ công suất chéo:
()
2
(2.76) Nếu kết hợp 2 vế của (2.76) ta có:
2 2
2
=
() (2.77) Nếu
() và () là các quá trình ngẫu nhiên thực ta có:
2
=
) (2.78)

lOMoARcPSD|36067889
(
)
=
(
)
=
[
()
]
(
)
=
(
)
Kết hợp (2.77) và (2.78) ta thấy mật ộ phổ công suất chéo của hai quá trình thực hiện
thoả mãn iều kiện:
() =
) (2.79)
2.1.2.3. Đáp ứng của một hệ thống tuyến tính bất biến theo thời gian với một tín hiệu
vào ngẫu nhiên
Xét một hệ thống tuyến tính bất biến theo thời gian ược mô tả bởi áp ứng xung
(), áp ứng tần số (), () và () là một cặp của biến ổi Fourier, với () là tín
hiệu vào của hệ thống và () là tín hiệu ầu ra. Tín hiệu ra của hệ thống có thể biểu diễn
dưới dạng tích chập:
( ) (2.80)
Giả thiết rằng () là một thể hiện của quá trình ngẫu nhiên dừng () thì tín hiệu
ầu ra () là một thể hiện của một quá trình ngẫu nhiên (). Chúng ta hãy xác ịnh trị
trung bình và hàm tự tương quan của tín hiệu ra.
Do phép toán chập là một phép biến ổi tuyến tính tác ộng lên tín hiệu vào (), giá
trị trung bình của tích phân bằng tích phân của giá trị trung bình. Do ó trị trung bình của
() là:
[( )] =
(0) (2.81)
trong ó: (0) là áp ứng tần số của một hệ thống tuyến tính tại tần số = 0. Vì vậy giá trị
trung bình của tín hiệu là một hằng số.
Hàm tự tương quan của tín hiệu ầu ra là:
()
(
1
2
+ )
Như vậy tích phân kép là một hàm của tín hiệu thời gian
1
2
. Nói cách khác, nếu
quá trình ầu vào là dừng thì quá trình ở ầu ra cũng là dừng, vì vậy ta có:
( + ) (2.82)
Bằng tính toán biến ồi Fourier hai vế ta thu ược mật ộ phổ công suất của quá trình ầu
ra:
()
2
( + )
2
=
()|()|
2
(2.83)

lOMoARcPSD|36067889
(
)
=
=
(
)
=
Từ công thức trên sẽ có một kết quả quan trọng là phổ mật ộ công suất của tín hiệu
ầu ra là tích của phổ mật ộ công suất của tín hiệu vào với bình phương biên dộ áp ứng
tần số của hệ thống tuyến tính.
Khi muốn tính hàm tự tương quan
(), thông thường có thể tính phổ mật ộ công
suất
() và sau ó tính biến ổi Fourier ngược. Ta có:
()2 ()|()|22 (2.84) Công suất trung
bình của tín hiệu ầu ra là:
()|()|
2
(2.85)
Do
(0) =
2
), suy ra
()|()|
2
0
Ví dụ 2.5:
Giả thiết rằng mạch lọc thông thấp ược minh hoạ trong hình 2.5 ược kích bởi một tín
hiệu ngẫu nhiên () có mật ộ phổ công suất:
() =
1
2
0
với mọi
Một quá trình ngẫu nhiên có mật ộ phổ công suất ồng ều (phẳng) gọi là nhiều trắng.
Chúng ta xác ịnh phổ mật ộ công suất của trình ngẫu nhiên ở ầu ra, Hàm truyền ạt của
mạch lọc thông thấp là:
1
() = =
+ 2 1 + 2/ Vì vậy: |H(f)|
2
=
1
2 2 (2.86)
1+( ) f
R
Hình 2.5: Ví dụ một mạch lọc thông thấp Phổ
mật ộ công suất của quá trình ra là:
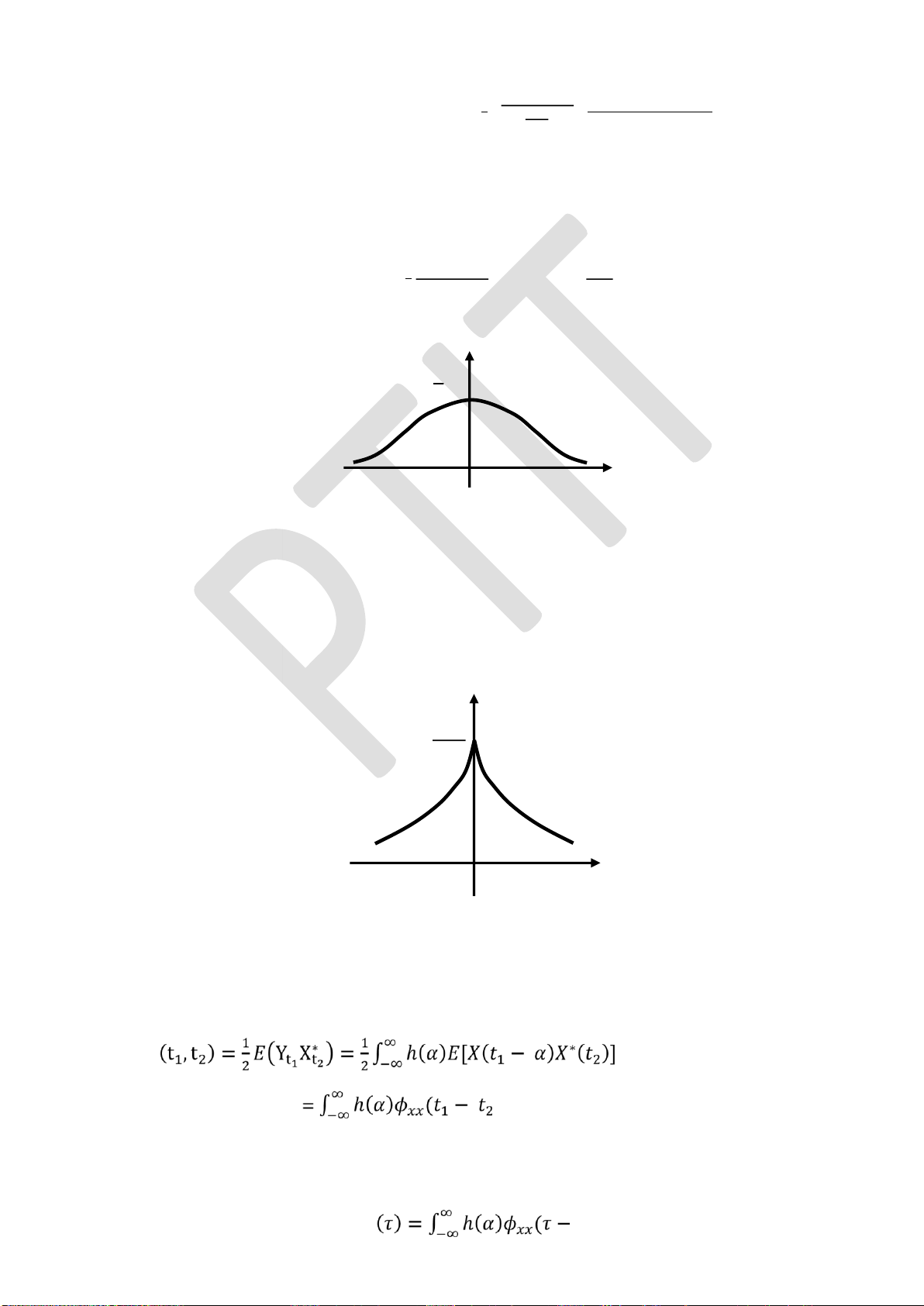
lOMoARcPSD|36067889
() =
2
0 1
)
(2.87)
R
Phổ mật ộ công suất ược minh hoạ trong hình 2.6. Biến ổi Fourier ngược thu
Hình 2.7: Hàm tự tương quan của tín hiệu ra của mạch lọc thông thấp khi tín hiệu vào
là nhiễu trắng.
Bây giờ sẽ xác ịnh hàm tương quan chéo giữa () và (), ở ây () và () lần lượt
là tín hiệu ầu ra và ầu vào của hệ thống tuyến tính. Ta có:
) =
(
1
2
)
Như vậy quá trình ngẫu nhiên () và () là các quá trình dừng ồng thời. Với
1
2
= ta có:
) (2.89)
ượ
c hàm t
ự
tương quan:
(
)
=
0
2
1
1+(
2
R
)
2
f
2
e
=
0
4
(
)
||
(2.88)
Hình 2.6: Ph
ổ
m
ật ộ
công su
ấ
t tín hi
ệ
u ra m
ạ
ch l
ọ
c thông th
ấ
p khi tín hi
ệ
u vào là
nhi
ễ
u tr
ắ
ng
Hàm t
ự
tương quan
(
)
ượ
c bi
ể
u di
ễ
n trong hình 2.7. Chúng ta nh
ậ
n xét r
ằ
ng
momen b
ậ
c 2 c
ủ
a quá trình
()
là
(
)
=
R
0
/4
.
(
)
1
2
0
0
(
)
0
4
0
1+(
2
2
f
2

lOMoARcPSD|36067889
Chú ý rằng tích phân trong (2.89) là một tích chập, do ó công thức (2.89) biểu diễn ở
miền tần số sẽ trở thành:
() =
()() (2.90)
2.2. LƯỢNG TIN VÀ PHẾP ĐO CỦA NGUỒN
2.2.1. Nguồn rời rạc
2.2.1.1. Khái niệm nguồn rời rạc
Định nghĩa: Nguồn tin rời rạc là nguồn tin tạo ra các tin (biến ngẫu nhiên) dưới dạng rời
rạc:
1
,
2
.
- Ký hiệu (
) là phần tử nhỏ nhất có chứa thông tin.
- Bộ ký hiệu, = {
1
,
2
} là tập hợp tất cả các ký hiệu có thể, còn ược gọi là bảng
chữ cái.
- Từ là tập hợp hữu hạn các ký hiệu (trong trường hợp ặc biệt, mỗi từ có thể chỉ chứa một
ký hiệu).
- Bộ từ là tập hợp tất cả các từ mà một bộ ký hiệu có thể tạo ra.
Nguồn rời rạc ặc trưng bởi xác suất {, ()}, = {
1
,
2
}
Nguồn rời rạc không nhớ là nguồn rời rạc mà xác suất xuất hiện một ký hiệu không
phụ thuộc vào các ký hiệu xuất hiện trước ó.
(
|
1
,
2
1
) = (
) (2.91)
trong ó:
là một ký hiệu nào ó của bộ ký hiệu do nguồn tạo ra tại thời iểm
.
Nguồn rời rạc có nhớ là nguồn rời rạc mà xác suất xuất hiện một ký hiệu phụ thuộc
vào một hay nhiều ký hiệu ã xuất hiện trước ó nếu khả năng nhớ của nguồn ủ lớn.
(
|
1
,
2
1
) < (
) (2.92)
Nguồn dừng là nguồn rời rạc mà xác suất xuất hiện các ký hiệu không phụ thuộc
vào gốc thời gian mà chỉ phụ thuộc vào vị trí tương quan giữa các ký hiệu, có nghĩa là:
(
,
) = (
+
) (2.93)
Nguồn có tốc ộ thông tin iều khiển ược là nguồn có thể tạo ra các tin với tốc ộ phụ
thuộc vào các yếu tố bên ngoài nguồn và không có các ràng buộc nội tại về mặt thời gian
trong việc tạo ra các tin. Ví dụ về loại nguồn này là nguồn iện báo. Rõ ràng ối với hệ
thống iện báo thì không có các ràng buộc về mặt thời gian ối với các ký hiệu tạo ra ược
truyền i.

lOMoARcPSD|36067889
Nguồn có tốc ộ thông tin không iều khiển ược là nguồn tạo ra các bản tin với tốc ộ
cố ịnh, không iều khiển ược từ bên ngoài nguồn, tốc ộ này là một tính chất nội tại của
nguồn. Ví dụ trong trường hợp này là nguồn rời rạc tạo ra khi lấy mẫu một tín hiệu liên
tục theo thời gian. Các mẫu ược tạo ra liên tiếp nhau, cách nhau một khoảng thời gian
cố ịnh phụ thuộc vào các tín hiệu liên tục.
Nguồn Markov giữ vai trò trong trọng trong lĩnh vực truyền thông. Đây là nguồn rời
rạc mà xác suất của một ký hiệu chỉ phụ thuộc vào ký hiệu trước ó:
(
|
1
,
2
(
|
1
) (2.94)
2.2.1.2. Lượng tin riêng, lượng tin tương hỗ, lượng tin có iều kiện
Lượng tin của mỗi tin
là (
(
), ược gọi là lượng tin riêng của tin
.
Nếu nguồn thông qua một phép biến ổi trở thành nguồn , ví dụ như thông qua
sự truyền lan trong kênh thì phép biến ổi ó có thể không phải là một - một. Trong quá
trình truyền lan trong kênh, nhiễu phá hoại làm cho một tin
có thể chuyển thành
một tin
bất kỳ trong nguồn ở ầu ra của kênh với những xác suất chuyển ổi khác
nhau tuỳ theo tính chất của nhiễu trong kênh.
Bài toán thu tin:
Các tin của nguồn truyền qua hệ thống biến ổi trở thành ầu ra . Cho biết:
- Cấu trúc thống kê của nguồn.
- Cấu trúc thống kê của nhiễu và phép biến ổi (cho bảng xác suất chuyển ổi).
- Với mỗi ầu ra
, xác ịnh ầu vào
ã sinh ra
.
Lời giải:
- Chính xác: Không có
- Xác suất: Xác ịnh ầu vào có khả năng nhất.
- Thông tin: Tách thông tin ầu vào chứa trong ầu ra.
+ Xác ịnh lượng thông tin của mỗi tin
chứa trong
. Lượng tin này chính là lượng
tin tương hỗ = lượng tin ban ầu - lượng tin bị mất i do nhiễu.
+ Chọn ầu vào là lượng tin tương hỗ lớn nhất.
Xác suất của
khi biết
là (
|
)
Lượng tin bị nhiễu phá huỷ không ến ược ầu thu chính là lượng tin còn lại của tin
, sau khi ã nhận ược
là:

lOMoARcPSD|36067889
(
|
(
|
) (2.95)
còn ược gọi là lượng tin có iều kiện.
Lượng tin tương hỗ của
trong
là:
(
|
) (
|
)
(
,
) = (
(
|
) =
(
)
=
(
)(
|
)
(2.96)
2.2.1.3. Tính chất của lượng tin
Tính chất 1: Lượng tin riêng của một tin
bao giờ cũng lớn hơn lượng tin tương hỗ
trong một tin khác
.
Khi
và
ộc lập thống kê với nhau thì lượng tin tương hỗ bằng không.
Nếu từ
xác ịnh ược
thì lượng tin tương hỗ cực ại, lượng tin riêng chính là
lượng tin tương hỗ cực ại.
(
|
) (
|
)
(
(
(
,
) = (
) = (
)
Do ó có thể giải thích ý nghĩa lượng tin riêng như là lượng tin tương hỗ cực ại giữa
và
.
Tính chất 2: Lượng tin riêng là một ại lượng không âm vì (
, nhưng lượng tin
tương hỗ có thể dương hoặc âm.
Khi xác suất xuất hiện
với iều kiện ã xảy ra
lớn hơn xác suất của
khi nó xảy
ra ộc lập với
thì lượng tin tương hỗ dương, ngược lại lượng tin tương hỗ sẽ là một ại
lượng âm.
Tính chất 3: Lượng tin của một cặp (
) bằng tổng lượng tin riêng của từng tin trừ i
lượng tin tương hỗ giữa chúng.
(
) = (
) + (
(
,
) (2.97)
Khi chúng ộc lập thống kê với nhau thì lượng tin tương hỗ với nhau bằng không,
khi ó:
(
) = (
) + (
) (2.98)
2.2.1.4. Lượng tin trung bình
Nguồn tin là một tập hợp các tin. Lượng tin riêng chỉ có ý nghĩa với một tin nào ó
nhưng không thể phản ánh ược tin tức của nguồn tin. Nói cách khác, (
) mới ánh giá

lOMoARcPSD|36067889
ược về mặt tin tức của một tin
khi nó ứng riêng rẽ, nhưng không thể dùng ể ánh giá
về mặt tin tức của một tập hợp trong ó
tham gia. Trong thực tế, iều cần quan tâm là
giá trị tin tức của một tập hợp chứ không phải là của một phần tử nào ó trong tập hợp.
Ví dụ 2-6: một nguồn tin chỉ gồm có hai tin = {
1
,
2
} với xác suất xuất hiện là (
1
)
= 99 %, (
2
) = 1 %. Khi thu ược một ký hiệu của nguồn, có thể cầm chắc ến 99% là
tin
1
và có thể xem như là một tin ã biết trước. Đứng về quan iểm tin tức mà xét, lượng
tin thu ược của nguồn tin này ít có giá trị mặc dù lượng tin riêng của tin
2
(= bit/ký hiệu) khá lớn. Do ó, trong thực tế ể ánh giá một tin thu ược
của một nguồn ã cho, người ta dùng khái niệm lượng tin trung bình (trị trung bình theo
tập hợp):
(
() log () (2.99)
Lượng tin trung bình là lượng tin tức trung bình chứa trong một ký hiệu bất kỳ của
nguồn ã cho.
Đối với ví dụ trên lượng tin trung bình của nguồn là:
(
2
2
0,01 = 0,081 (bit/ký hiệu)
Tương tự lượng tin riêng, lượng tin tương hỗ không mang ầy ủ ý nghĩa thực tế cần
thiết, nó chỉ cho biết lượng tìn về một ký hiệu ã cho chứa trong một ký hiệu xác ịnh,
nghĩa là mới cho biết sự ràng buộc thống kê giữa một cặp (
,
) nào ó. Nhưng iều quan
trọng hơn là cần phải xác ịnh trong thực tế mối liên hệ thống kê giữa hai tập , , nghĩa
là lượng tin trung bình về một tin bất kỳ của nguồn chứa trong một tin bất kỳ thuộc
nguồn hay còn ược gọi là lượng tin tương hỗ trung bình:
(,
(, )
(|)
()
(2.100)
Tương tự, lượng tin riêng trung bình có iều kiện (|) là lượng tin trung bình của
một tin bất kỳ của khi ã biết một tin bất kỳ của và ược xác ịnh như sau:
(|
(, ) log (|) (2.101)
Quan hệ giữa các lượng tin trung bình:
(, ) = ((|) (2.102)
(, ) = (, 0 (2.103)
2.2.1.5. Entropi của nguồn rời rạc
a) Khái niệm Entropi

lOMoARcPSD|36067889
Khi thu ược một tin, ộ bất ngờ về tin ó ược giải thoát (tin ã biết, ộ bất ngờ = 0) ổng
thời thu ược một lượng tin. Vì vậy, ộ bất ngờ bằng lượng tin về số o nhưng trái ngược
nhau về ý nghĩa vật lý.
Độ bất ngờ của tin
, sẽ là:
(
(
) = (
) (2.104) Độ
bất ngờ trung bình của một nguồn tin sẽ là:
(
() log () = () (2.105)
Độ bất ngờ () gọi là entropi của nguồn, ược o bằng lượng tin trung bình của các
tin do nguồn phát ra và ây là thông số phản ánh khả năng phát tin (trung bình) của nguồn
và là một thông số thống kê cơ bản của nguồn.
b) Tính chất của entropi
Tính chất 1: Entropi là một ại lượng luôn luôn không âm (0.
Tính chất 2: Entropi sẽ bằng không khi nguồn có một ký hiệu có xác suất xuất hiện bằng
1 và tất cả các ký hiệu còn lại có xác suất bằng 0.
Tính chất 3: Entropi có giá trị cực ại khi tất cả các ký hiệu có cùng xác suất.
Lấy một ví dụ ơn giản về nguồn có hai tin = {
0
,
1
} với xác suất tương ứng là
0
và
1
ể minh hoạ iều trên, ta có quy luật phân bố xác suất:
0
+
1
1
0
Entropi của nguồn sẽ là:
(
0
log
0
1
log
1
0
log
0
0
) log(1
0
)
Biểu diễn () theo
0
như ưa ra trên hình 2.8.
Đường biểu diễn cho ta thấy ()
khi
0
= 1/2 (khi ó
1
0
= 1/2 =
0
và
()
= 2. Nếu dùng cơ số 2 thì () = 1 (bit/ký hiệu).
Từ ó, có thể giải thích ý nghĩa của ơn vị bit là entropi của một nguồn gồm hai ký
hiệu ồng xác suất.
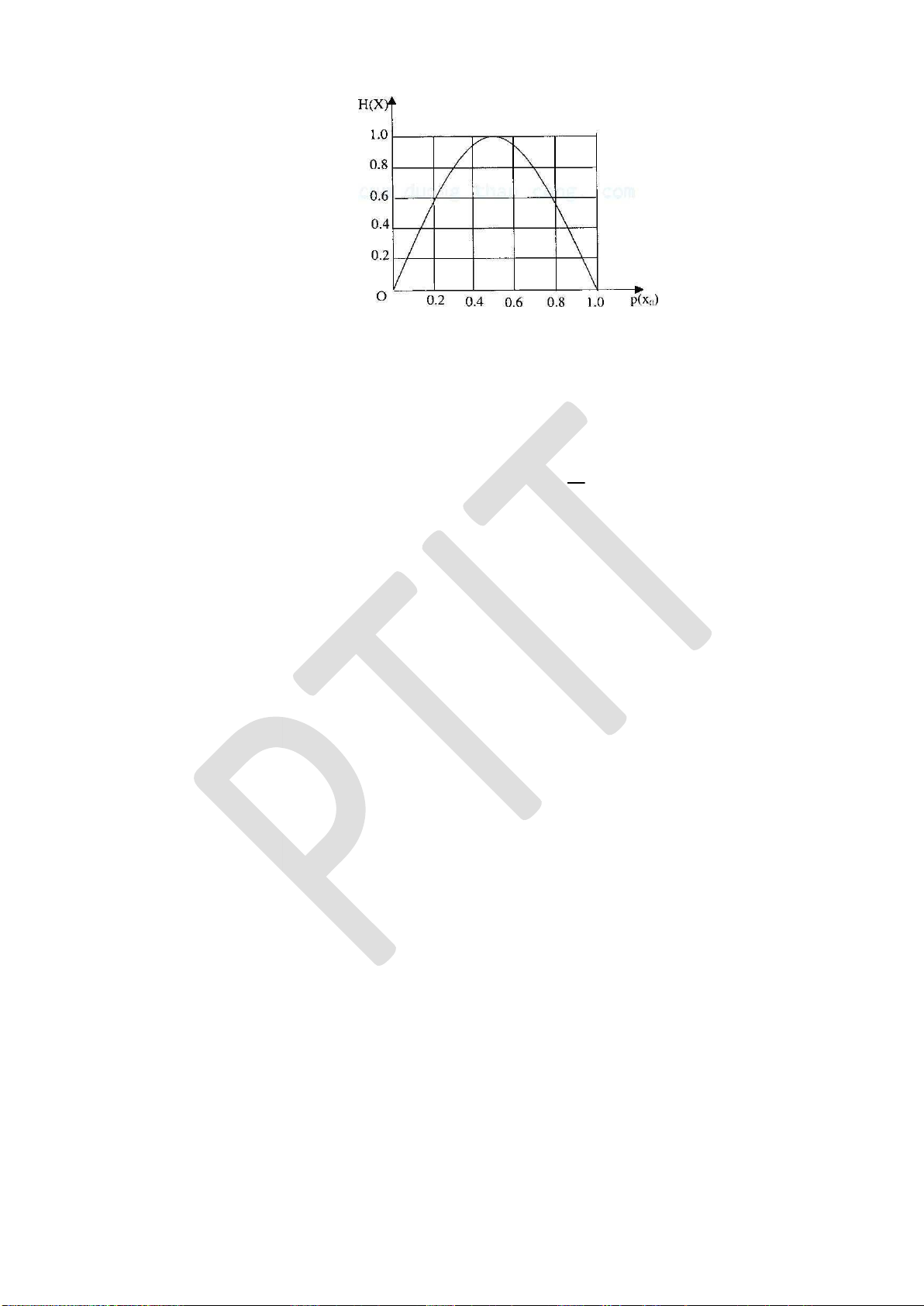
lOMoARcPSD|36067889
1
=
2
=
=
=
1
Hình 2.8: Biểu diễn H(X) theo p
0
Tổng quát, nếu nguồn gồm ký hiệu, entropi sẽ có giá trị lớn nhất khi các ký hiệu
ồng xác suất:
Khi ó sẽ có:
()
=1
log
= (2.106) Nếu dùng
loga cơ số 2, sẽ có ()
=
2
(bit/ký hiệu).
2.2.1.6. Tốc ộ lập tin của nguồn
Thông số thống kê cơ bản thứ nhất của nguồn là entropi, nó tuỳ thuộc vào cấu trúc
thống kê của nguồn. Nhưng tốc ộ tạo ra các tin (các ký hiệu) của nguồn nhanh hay chậm
còn phụ thuộc vào các tính chất vật lý của nguồn như quán tính, ộ phân biệt,... Ví dụ: cơ
cấu cơ quan phát âm của con người bị hạn chế, mỗi giây chỉ có thể phát ược từ 5 ến 7
ký hiệu (âm tiết) trong lời nói thông thường, trong khi ó máy iện báo có thể phát từ 50
ến 70 ký hiệu trong một giây.
Như vậy, thông số thống kê cơ bản thứ hai của nguồn là tốc ộ thiết lập tin , bằng
tích của entropi, () với số ký hiệu
0
ược lập trong một ơn vị thời gian. Đơn vị của
là lượng tin trên ơn vị thời gian, trong trường hợp dùng loga cơ số hai ơn vị của sẽ
là bit/s.
=
0
() (bit/s) (2.107) Để
có tốc ộ lập tin lớn nhất với
0
(nguồn vật lý) cố ịnh, cần ()
.
Để ()
thì phải thay ổi cấu trúc thống kê của nguồn bằng các phương pháp
mã hóa thống kê.
Để chỉ ra sự chênh lệch giữa entropi của nguồn và giá trị cực ại có thể có của nó,
người ta ịnh nghĩa ộ dư của nguồn như sau:

lOMoARcPSD|36067889
(
)
(
)
= ()
() (2.108)
Độ dư tương ối của nguồn ược ịnh nghĩa như sau:
= [ ()
()]/()
()/()
(2.109)
2.2.2. Nguồn liên tục
2.2.2.1. Khái niệm nguồn liên tục
Nguồn liên tục là một quá trình ngẫu nhiên liên tục. Để có thế nghiên cứu, xem xét
nguồn liên tục cần rời rạc hóa nguồn liên tục.
Với iều kiện nguồn có phổ hữu hạn, có thời gian tồn tại hữu hạn, nguồn liên tục có
thể ược lấy mẫu với tần số tại các thời iểm {
}, .
Mỗi thể hiện () của nguồn liên tục là một hàm theo thời gian tồn tại trong quãng
thời gian
, ược ặc trưng bởi giá trị tức thời {
}, .
Tính chất thống kê của nguồn ược ặc trưng bởi phân bố xác suất ồng thời (nhiều
chiều): (
1
,
2
).
Trong thực tế truyền tin, thường gặp các quá trình ngẫu nhiên dừng, tính chất thống
kê của các quá trình này không phụ thuộc vào gốc thời gian.
(
,) = (
+
)
2.2.2.2. Entropi nguồn liên tục
Entropi là ại lượng o ộ bất ịnh trung bình của một giá trị bất kỳ mà mẫu (
) có
thể lấy ược, về số o, entropi cũng là lượng tin trung bình của một giá trị bất kỳ thuộc
(
).
Entropi của nguồn liên tục dừng (các mẫu (
) ộc lập thống kê với nhau và cùng một
quy luật phân bố xác suất ()).
log () (2.110) Entropi của nguồn
liên tục không dừng:
,
2
) log (
1
,
2
)
1
2
(2.111) Tốc ộ lập tin của nguồn liên tục sẽ là :
=
0
() = (/
)( () (bit/s) (2.112)
Khi sự truyền tin xảy ra trong kênh có nhiễu, ứng với một thể hiện () ở ầu vào
kênh có một thể hiện () ở ầu ra ã bị sai lệch ít nhiều. Tại một thời iểm bất kỳ một trị

lOMoARcPSD|36067889
(
,
)
(
,
)
(
,
)
=
(
,
)
log
(
,
)
log
nào ó (
) qua kênh sẽ chuyển ổi thành một trị nào ó (
) theo quy luật phân bố có iều
kiện (|).
Quy luật phân bố (|) cho phép xác ịnh ộ bất ịnh trung bình về một giá trị nào
ó khi nhận ược một giá trị , nghĩa là xác ịnh ược entropi có iều kiện của nguồn liên tục.
log (|) (2.113)
log (|) (2.114)
với: (, ) là quy luật phân bố ồng thời của và . Quy luật này dùng ể tính entropi ồng
thời:
log (, ) (2.115)
Lượng tin tương hỗ trung bình giữa một tin bất kỳ của tập nhận và một tin bất kỳ
của tập gửi ược xác ịnh theo biểu thức:
(|) (|) =
() ()
(2.116)
Quan hệ giữa các entropi với lượng tin tương hỗ như sau:
(, ) = () + (|) = () + (|) (2.117) (,
) = ((|) = ((|) (2.118)
2.3. LƯỢNG TIN VÀ PHÉP ĐO CỦA KÊNH
2.3.1. Kênh rời rạc
2.3.1.1. Khái niệm kênh rời rạc
Nguồn tin và nơi nhận tin liên hệ với nhau qua kênh truyền tin. Kênh truyền tin
thực hiện một phép biến ổi từ không gian các ký hiệu vào ến không gian ký hiệu ở ầu ra
của kênh.
Kênh ược gọi là rời rạc nếu không gian tín hiệu vào và không gian tín hiệu ra là rời
rạc.
Nếu sự truyền tin chỉ thực hiện ở những thời iểm rời rạc theo thời gian thì kênh ược
gọi là rời rạc theo thời gian.
Nếu sự chuyển ổi ký hiệu vào là thành ký hiệu ra là không phụ thuộc vào các
chuyển ổi trưóc ó thì kênh ược gọi là không nhớ. Nếu sự chuyển ổi ó phụ thuộc vào việc
chọn gốc thời gian thì kênh ược gọi là dừng.
Trong phần này, chỉ quan tâm chủ yếu ến kênh rời rạc dừng, không nhớ.

lOMoARcPSD|36067889
2.3.1.2. Entropi ở ầu vào và ở ầu ra của kênh
Kí hiệu [] là tập hợp tất cả các kí hiệu ở ầu vào kênh, tạo nên một trường các sự
kiện. Ví dụ trong một kênh telex sử dụng mã Morse, [] gồm 4 kí hiệu
1
,
2
,
3
,
4
.
Nếu có kí hiệu thì không gian kí hiệu ở ầu vào của kênh là:
[] = [
1
2
] Giả sử
mỗi kí hiệu
ược sử dụng với xác suất (
):
[
] = [(
1
)(
2
(
)]
Các xác suất [
] không phải là tính chất của kênh, chúng là một tính chất của nguồn
tin.
Tập hợp tất cả các kí hiệu ở ầu ra của kênh là:
[] = [
1
2
] Và
xác suất của các kí hiệu:
[
] = [(
1
)(
2
(
)]
Do tính chất của nhiễu trên kênh, không gian [] có thể khác với không gian [],
cũng như các xác suất [
] cũng có thể khác các xác suất ở ầu vào [
]. Với không gian
kí hiệu ở ầu vào kênh và ở ầu ra kênh, ta có thể ịnh nghĩa một trường tích:
1
1
1
2
1
[, ] = [21 22 2 ] (2.119)
1
2
trong ó: tích
là sự xuất hiện ồng thời hai sự kiện
và
. Tương ứng với ma trận xác
suất:
(
1
1
) (
1
2
(
1
)
[(, )] = [(
2
1
) (
2
2
(
2
)] (2.120)
(
1
)
(
2
(
)
Từ ma trận xác suất (2.120) ta có:
=1
(
,
) (2.121)
Và
=1
(
,
) (2.122)
Như vậy, ta có thể ịnh nghĩa ba sự kiện:
- Trường ầu vào của kênh với entropy H(X):

lOMoARcPSD|36067889
và
Để
xác ịnh các entropy có iề
u ki
ệ
n, c
ầ
n ph
ả
i bi
ế
t các xác su
ất có iề
u ki
ệ
n:
[
(|
)]=
[
(
|
)
=
=1
(
|
)
=
=1
=1
(
). log (
) (2.123) -
Trường ầu ra của kênh với entropy H(Y):
(
=1
(
). log (
) (2.124)
- Trường hợp giữa ầu vào và ầu ra với entropy H(X,Y):
1
(
,
). log (
,
) (2.125)
2.3.1.3. Entropi có iều kiện
Khi trường các sự kiện ở ầu ra của kênh, do có nhiễu tác ộng, vẫn còn sự bất ịnh về
trường vào kênh. Giá trị trung bình của sự bất ịnh này gọi là entropy của trường khi
biết trường , kí hiệu (|). Xuất phát từ các xác suất có iều kiện (|) và (|)
cũng như theo ịnh nghĩa về entropy, ta ược biểu thức entropy có iều kiện
(|):
=1
(
,
). log (
|
) (2.126) Tương tự xác ịnh
ược entropy của trường ra khi biết trường vào kênh:
1
(
,
). log (
|
) (2.127)
Nếu trên kênh không có nhiễu thì (
|
) = 1 và log (
|
) = 1 do ó:
(|) = (|) = 0 (2.128)
Nếu nhiễu trên kênh ủ lớn ể trường vào kênh và trường ra kênh ộc lập thống kê với
nhau, tức là (
|
) = (
) và (
|
) = (
) thì:
(|) = () (2.129)
(|) = () (2.130)
(
1
|
1
) (
1
|
2
) (
1
|
)
(
2
|
1
) (
2
|
2
(
2
|
)] (2.131) (
|
1
)
(
|
2(
|
)
(
1
|
1
)
[(|)] = [(
1
|
2
)
(
1
|
)
(
2
|
1
)
(
2
|
2
(
2
|
)
(
|
1
)
(
|
2
)] (2.132)
(
|
)
Các xác suất này có thể xác ịnh từ ma trận [(, )]. Ma trận [(|)] ược gọi là ma trận
nhiễu trên kênh.

lOMoARcPSD|36067889
Sự liên hệ giữa các entropi:
Từ các công thức (2.123), (2.125), (2.126) ta ược:
(, ) = () + (|) = () + (|) (2.133)
Nếu trên kênh không có nhiễu, giữa ầu vào và ầu ra có một quan hệ một - một, sai số
trung bình cũng như ộ mập mờ bằng không, khi ó:
(, ) = () = () (2.134)
Khi nhiễu trên kênh ủ lớn làm cho trường vào và trường ra của kênh ộc lập với
nhau thì:
(, ) = () + () (2.135)
và chứng minh ược bất ẳng thức: ((|); ((|). Nghĩa là ộ bất ịnh
trung bình của một tin bất kỳ bao giờ cũng lớn hơn ộ bất ịnh trung bình của tin ó khi ã
biết một tin bất kỳ khác có liên hệ thống kê với nó. Các bất ẳng thức trên sẽ trở thành
ẳng thức trong trường hợp hai tập X và Y ộc lập.
Sự liên hệ giữa lượng tin tương hỗ trung bình và entropy ược biểu diễn:
(, ) = ((|) = ((|) (2.136) (,
) = () + ( (, ) (2.137)
Các biểu thức này có một ý nghĩa cụ thể khi dùng chúng ể mô tả sự truyền tin trong
một kênh có nhiễu. Lượng tin trung bình nhận ược về tin phát bằng tổng các ộ bất ịnh
trung bình về tin phát i và tin thu ược xét một cách ộc lập với nhau trừ cho ộ bất ịnh
trung bình về sự xuất hiện ồng thời của chúng. Nếu giữa tin thu và tin phát không có liên
quan gì với nhau nghĩa là tập phát X và tập thu Y ộc lập thống kê với nhau, thì lượng tin
trung bình nhận ược về tin phát sẽ bằng không vì:
(, ) = () + () và (, ) = 0
Từ ó có thể giải thích lượng tin tương hỗ như một số o mỗi liên hệ thống kê giữa X
và Y.
2.3.1.4. Thông lượng kênh rời rạc
a) Khái niệm thông lượng của kênh
Thông lượng của kênh là lượng tin tối a mà kênh cho i qua trong một ơn vị thời
gian mà không gây lỗi. Ký hiệu là . Đơn vị bit/s.
Là tốc ộ lập tin tối a ở ầu ra của kênh.
Tốc ộ lập tin của nguồn thường nhỏ hơn nhiều so với thông lượng của kênh.

lOMoARcPSD|36067889
<< (2.138)
Tận dụng thông lượng của kênh như sau:
+ Tối a tốc ộ lập tin của nguồn cho phù hợp với kênh: mã hóa thống kê ể có tốc ộ lập
tin cực ại, gần với thông lượng của kênh ( ồng bộ kênh - nguồn) - cơ sở lý thuyết là ịnh luật
Shannon cho kênh không nhiễu.
+ Sử dụng phần còn lại của thông lượng kênh ể chống nhiễu (mã chống nhiễu) - cơ
sở lý thuyết là ịnh luật Shannon cho kênh có nhiễu.
b) Thông lượng của kênh rời rạc không nhiễu
Khi kênh không có nhiễu thì thông tin do nguồn thiết lập truyền sẽ không có lỗi, do ó
thông lượng kênh khi ó bằng tốc ộ lập tin cực ại của nguồn:
=
=
0
()
(2.139)
Để tối ưu hệ thống cần cực ại entropi của nguồn. Hai câu hỏi ặt ra là: Thứ nhất,
liệu có tồn tại một phương pháp mã hóa làm tăng entropi của nguồn ạt ến mức cực ại
hay không; Thứ hai, giới hạn của tốc ộ truyền tin khi ó là bao nhiêu?
Điều này ược Shannon phát biểu trong một ịnh lý cơ bản của lý thuyết tin tức với nội
dung như sau:
Giả sử nguồn có entropi (bit/ký hiệu) và kênh có thông lượng (bit/s), có thể mã
hoá tin tức ở ầu ra của nguồn làm cho sự truyền tin trong kênh không nhiễu theo một
tốc ộ trung hình
(ký hiệu/s) với là lượng bé tùy ý và không thể truyền nhanh
hơn
(ký hiệu/s).
Tốc ộ lập tin tối a tiệm cận và có thể bằng thông lượng của kênh. Phép mã hóa
tương ứng gọi là phép mã hóa thống kê tối ưu. Có thể nói, ịnh luật trên chính là cơ sở lý
thuyết của phương pháp mã hóa thống kê tối ưu. Phép mã hóa thống kê tối ưu không sử
dụng hết thông lượng của kênh.
Khi tốc ộ lập tin của nguồn chưa ạt cực ại, còn khả năng ể tối ưu nguồn thì khả
năng này ược o bằng ộ dư của nguồn.
Độ dư của nguồn ược ịnh nghĩa như sau:
= ()
() (2.140)
Độ dư tương ối của nguồn ược ịnh nghĩa như sau:

lOMoARcPSD|36067889
()
() ()
=
()
()
(2.141) Để có thể xây dựng mã chống nhiễu,
iều kiện ầu tiên là phải có ộ dư.
c) Thông lượng của kênh rời rạc có nhiễu
Xét kênh không nhớ, nghĩa là những tin thu ược sau không phụ thuộc vào những
tin thu ược trước, nói cách khác chúng ộc lập thống kê với nhau. Độ chính xác của tin
truyền i trong kênh chỉ còn bị ảnh hưởng của nhiễu làm giảm i mà thôi, ở ây có thể xảy
ra hai trường hợp:
- Nếu các tin thu ược sai lệch với các tin gửi i nhưng vẫn phân biệt ược các tin ầu vào
thì sự truyền tin như vậy vẫn ảm bảo chính xác.
- Nếu các tin ầu vào bị lẫn nhau ở ầu ra (nhiều tin ầu vào cho một tin ầu ra), trường
hợp này làm giảm ộ chính xác truyền tin và xuất hiện sai số truyền tin. Chúng ta sẽ khảo
sát trường hợp này.
Xét hệ thống gồm ầu vào = {
}, = 1, 2, . . . , và ầu ra của kênh thu ược các
tin tương ứng hợp lại thành tập = {
}, = . Do kênh có nhiễu, nên phép biến
ổi giữa X và Y ược biểu diễn bằng ma trận xác suất chuyển ổi = (
|
).
Trong trường hợp này lượng tin tương hỗ trung bình giữa và ược xác ịnh bằng:
(, ) = () (|)
(, ) = ((|)
Tốc ộ lập tin ở ầu ra của kênh trong trường hợp kênh có nhiễu bằng:
=
0
(, ) =
0
(((|)) (bit/s) (2.142)
trong ó:
0
(, ) là lượng tin bị nhiễu phá hủy trong một ơn vị thời gian.
Khi các thông số của kênh ã ược xác ịnh, muốn nâng cao tốc ộ lập tin ở ầu ra của
kênh nhất thiết phải tăng entropi bằng phương pháp mã hóa. Thông lượng kênh lúc này
chính là tốc ộ lập tin tối a ở ầu ra của kênh.
=
=
0
(, ) =
0
(((|)) (2.143) Nếu
xem băng thông của kênh =
0
, thì thông lượng của kênh có nhiễu là:
(((|))
(2.144)
Vấn ề ặt ra cho sự truyền tin trong kênh có nhiễu là bằng cách nào có thể truyền tin
chính xác và mức ộ chính xác là bao nhiêu. Trả lời cho vấn ề này, Shannon ã phát biểu
trong một ịnh lý cơ bản thứ hai của lý thuyết truyền tin. Nội dung ịnh lý như sau:

lOMoARcPSD|36067889
Kênh rời rạc có thông lượng (bit/s), tốc ộ lập tin của nguồn .
- Nếu R < C: Phần dư của nguồn ược dùng ể bổ sung các thông tin chống nhiễu. Cần
truyền lượng tin lớn hơn so với thông tin cần truyền.
- Nếu R > C: Phần thông tin không ược truyền i sẽ trở thành sai số (tối thiểu). Tồn
tại cách mã hóa ể có sai số bé hơn + ( là lượng bé tùy ý). Không tồn tại mã
hiệu ảm bảo ộ sai lỗi của quá trình truyền tin bé hơn .
2.3.2. Kênh liên tục
2.3.2.1. Khái niệm kênh liên tục
Kênh ược gọi là liên tục nếu cả hai không gian ký hiệu vào và ra là liên tục.
Nếu sự truyền tin trong kênh liên tục theo thời gian thì kênh ược gọi là liên tục theo
thời gian.
2.3.2.2. Thông lượng của kênh liên tục
Giả thiết tín hiệu ầu vào của kênh là (), tín hiệu ở ầu ra của kênh là () tương ứng
là kết hợp của () và nhiễu cộng ():
() = () + ()
Giả thiết (, ( và ( với là tập nguồn, là tập thu, là tập
nhiễu và (), (), () là entropi các tập tương ứng. Giữa nguồn tin và nguồn
nhiễu không có liên hệ thống kê nào, có thể viết entropi ồng thời của và như sau:
(, ) = (, + ) = (, ) = () + () (2.145) Mặt
khác entropi ổng thời có thể viết lại như sau:
(, ) = () + (|) So
sánh hai công thức cho thấy:
(|) = () (2.146) Vậy
(|) là entropi của nguồn nhiễu.
Tốc ộ lập tin ở ầu ra của kênh ược xác ịnh theo:
=
0
(((|((()) (2.147)
Thông lượng của kênh bằng tốc ộ lập tin cực ại ở ầu ra:
=
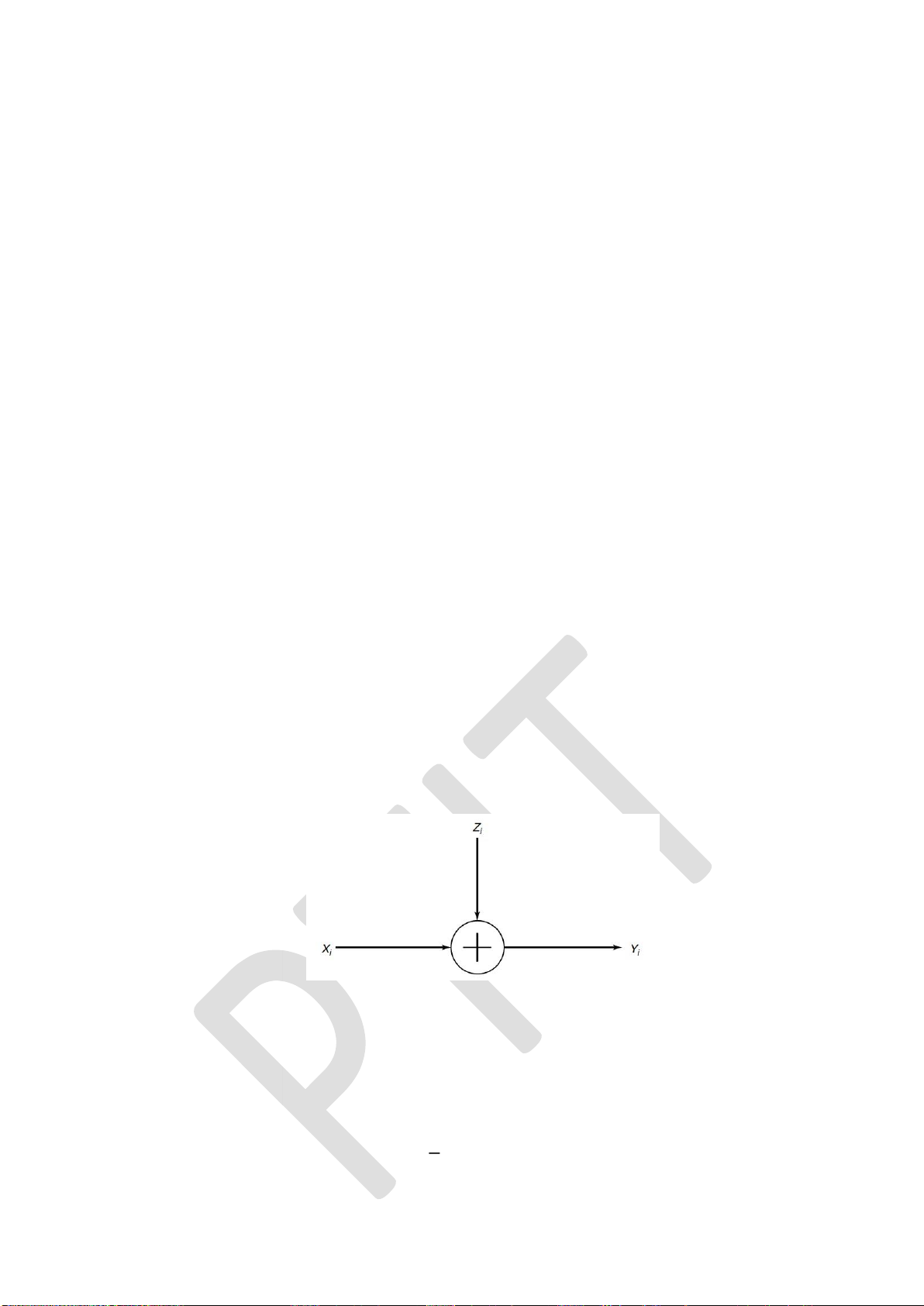
lOMoARcPSD|36067889
1
Tốc ộ lập tin cực ại khi () cực ại. Các tin của gồm hai thành phần từ và .
Phụ thuộc vào các hạn chế của , có thể xác ịnh qui luật phân bố của ể thông lượng
kênh ạt cực ại.
2.3.3. Kênh Gaussian
2.3.3.1. Khái niệm kênh Gaussian
Kênh bảng chữ cái liên tục quan trọng nhất là kênh Gaussian ược mô tả trong hình
2.9. Đây là một kênh rời rạc theo thời gian với ầu ra
ở thời gian i, trong ó
là tổng của
ầu vào
và nhiễu
. Nhiễu
~(0, ) là biến ngẫu nhiên Gaussian với giá trị trung bình
0 và phương sai . Do ó:
=
+
(2.148)
Nhiễu
ược giả thiết là ộc lập với tín hiệu
. Kênh này là một mô hình cho một
số kênh truyền thông phổ biến, chẳng hạn như các kênh thoại có dây và không dây và
các liên kết vệ tinh. Nếu không có thêm iều kiện, dung lượng của kênh này có thể là vô
hạn. Nếu phương sai nhiễu bằng 0, máy thu sẽ nhận ược ký hiệu phát một cách hoàn
hảo. Vì có thể lấy bất kỳ giá trị thực nào, nên kênh có thể truyền một số thực tùy ý mà
không có lỗi.
Nếu phương sai nhiễu khác không và không có ràng buộc nào ối với ầu vào, có thể
chọn một tập con vô hạn các ầu vào cách xa nhau một cách tùy ý, ể chúng có thể phân
biệt ược ở ầu ra với xác suất lỗi nhỏ tùy ý. Một sơ ồ như vậy có dung lượng vô hạn là
rất tốt. Do ó, nếu phương sai nhiễu bằng 0 hoặc ầu vào không bị giới hạn, thì dung lượng
của kênh là vô hạn.
Hình 2.9: Kênh Gaussian
Hạn chế phổ biến nhất ối với ầu vào là hạn chế về năng lượng hoặc công suất.
Giả thiết hạn chế công suất trung bình. Đối với bất kỳ từ mã nào (
1
,
2
, . . . ,
) ược truyền
qua kênh, yêu cầu là:
=1
2
(2.149)
Kênh truyền thông này ược mô hình hóa cho nhiều kênh thực tế, bao gồm các liên
kết vô tuyến và vệ tinh. Nhiễu cộng thêm vào trong các kênh như vậy có thể do nhiều
nguyên nhân. Tuy nhiên, theo ịnh lý giới hạn trung tâm, hiệu ứng tích lũy của một số

lOMoARcPSD|36067889
1
2
lượng lớn các hiệu ứng ngẫu nhiên nhỏ sẽ là xấp xỉ bình thường, vì vậy giả thiết Gaussian
có giá trị hợp lệ trong hầu hết các tình huống.
Trước tiên, sẽ phân tích một cách ơn giản dưới mức tối ưu ể sử dụng kênh này. Giả
thiết gửi 1 bit qua kênh trong một lần sử dụng kênh. Do hạn chế về công suất, cách tốt
nhất có thể làm là gửi một trong mức, hoặc . Máy thu dựa vào ã nhận
tương ứng và ể quyết ịnh mức nào trong hai mức ã ược gửi. Giả ịnh rằng cả hai mức ều
bằng nhau ( ây sẽ là trường hợp nếu muốn gửi chính xác 1 bit thông tin), quy tắc giải mã
tối ưu là quyết ịnh + ược gửi nếu > 0 và quyết ịnh ược gửi nếu < 0. Xác
suất lỗi với một sơ ồ giải mã như vậy là:
= Pr( < 0| = + ( > 0|
| = Pr( | = +
= Pr( > (2.150)
trong ó: () là hàm chuẩn tích lũy
1 2
(
2
2 (2.151)
Sử dụng sơ ồ như vậy, ã chuyển ổi kênh Gaussian thành một kênh ối xứng nhị phân
rời rạc với xác suất chéo
. Tương tự, bằng cách sử dụng tín hiệu ầu vào bốn mức, có
thể chuyển ổi kênh Gaussian thành một kênh bốn ầu vào rời rạc. Trong một số sơ ồ iều
chế thực tế, những ý tưởng tương tự ược sử dụng ể chuyển ổi kênh liên tục thành một
kênh rời rạc. Ưu iểm chính của kênh rời rạc là dễ xử lý tín hiệu ầu ra ể sửa lỗi, nhưng
một số thông tin bị mất trong quá trình lượng tử hóa.
2.3.3.2. Dung lượng kênh Gaussian
a) Định nghĩa dung lượng kênh Gaussian
Dung lượng (thông tin) của kênh là mức tối a của thông tin tương hỗ giữa ầu vào và
ầu ra trên tất cả các phân bố ầu vào thỏa mãn giới hạn công suất.
Định nghĩa: Dung lượng thông tin của kênh Gaussian với phương sai nhiễu và giới hạn
công suất là:
= max (, ) = (1 +
) (2.152)
():
2
Dung lượng kênh Gaussian ạt cực ại khi ~(0, ).
Dung lượng này cũng là cận trên của tốc ộ ạt ược ối với kênh. Nghĩa là:
)
+
1
2
Pr
(
>

lOMoARcPSD|36067889
1
2
(1 +
)
(2.153)
b) Dung lượng kênh Gaussian băng tần giới hạn
Một mô hình chung ể truyền thông qua mạng vô tuyến hoặc ường dây iện thoại là một
kênh giới hạn băng tần với nhiễu trắng cộng. Đây là một kênh thời gian liên tục.
Đầu ra của kênh ược mô tả là tích chập:
() = (() + () (2.154)
trong ó: () là dạng sóng tín hiệu, () là dạng sóng của nhiễu Gaussian trắng cọng
() là áp ứng xung của một bộ lọc thông dải lý tưởng, loại bỏ tất cả các tần số lớn hơn
.
Để kênh ược sử dụng trong khoảng thời gian [0, T]. Trong trường hợp này, năng lượng
trên mỗi mẫu là 2 = 2 , phương sai nhiễu trên mỗi mẫu là
0
2 2 2 =
0
2, do ó dung lượng trên mỗi mẫu là:
= (1 +
2
0
) =
1
(1 +
) (bit/mẫu) (2.155)
2
2 0
Vì mỗi giây có 2 mẫu nên dung lượng kênh ược viết thành:
= (1 +
) (bit/s) (2.156) 0
Phương trình (2.153) là một trong những công thức nổi tiếng nhất của lý thuyết
thông tin. Nó ưa ra dung lượng của một kênh Gauss băng tần giới hạn với mật ộ phổ
nhiễu
0
[W/Hz] và công suất [W]. 2
2.4. TỔNG KẾT CHƯƠNG
Chương 2 ã trình bày cụ thể các vấn ề cơ bản về xác suất thống kê, lượng tin và
phép o của nguồn cũng như lượng tin và phép o của kênh thông tin. Trong ó ã nghiên
cứu phương pháp ịnh lượng thông tin trong nguồn, kênh tin. Đưa ra các khái niệm lượng
tin trung bình, entropi, tốc ộ lập tin của nguồn, thông lượng của kênh và ã giải thích rõ
ý nghĩa các ịnh lý Shannon.
Câu hỏi/bài tập chương 2
1- Hãy viết các công thức mô tả mối quan hệ giữa các ại lượng (), (), (/),

lOMoARcPSD| 36067889
(/), (, ) và (, )?
2- Một nguồn tin rời rạc trong một hệ thống thông tin số phát ra 6 ký hiệu {
1
,
2
6
} với tốc ộ 5000 ký hiệu/giây. Các ký hiệu có xác suất (
, ) xuất hiện
tương ứng là: 0,1; 0,01; 0,13; 0,33; 0,15 và 0,08. Xác ịnh Entropy () và tốc ộ thông
tin của nguồn ã cho?
3- Xác ịnh entropi của biến ngẫu nhiên có phân bố ều:
1
() = { 0 á á á
trong các trường hợp: a)
a=1
b) a=4
c) a=1/4
4- Hai biến ngẫu nhiên và nhị phân có phân bố ồng thời:
( = = 0) = ( = 0, = 1) = ( = = 1) = 1/3
Tính (), (), (|), (|) và ().
5- Cho nguồn tin có 4 ký hiệu là
1
,
2
,
3
,
4
có xác suất xuất hiện tương ứng là 0,5;
0,25; 0,12; 0,13. Hãy tính lượng tin riêng tương ứng với từng kí hiệu và entropi của
nguồn.
6- Nguồn tin là một èn LED 7 thanh. Hãy xác ịnh ().
7- Một thử nghiệm có bốn kết quả loại trừ nhau
, i=1,2,3,4 và thử nghiệm thứ hai có ba
kết quả loại trừ nhau
, j=1,2,3. Các xác suất chung ( ồng thời) (
,
) là:
(
1
,
1
) = 0,1; (
1
,
2
) = 0,08; (
1
,
3
) = 0,13;
(
2
,
1
) = 0,05; (
2
,
2
) = 0,03; (
2
,
3
) = 0,09;
(
3
,
1
) = 0,05; (
3
,
2
) = 0,12; (
3
,
3
) = 0,14;
(
4
,
1
) = 0,11; (
4
,
2
) = 0,04; (
4
,
3
) = 0,06;
Hãy xác ịnh xác suất (
) i=1,2,3,4 và (
) j=1,2,3.
8- Xác ịnh entropi của các biến ngẫu nhiên liên tục sau ây:
a) là biến ngẫu nhiên hàm mũ với tham số > 0:
() = {1/ > 0 0
0
b) là biến ngẫu nhiên Laplace với tham số > 0:
() =
1
||/
2

lOMoARcPSD|36067889
- CHƯƠNG III -
MÃ HÓA
Khi thực hiện truyền tin tức qua hệ thống truyền tin, cần phải ảm bảo tốc ộ hình
thành tin gần hơn với khả năng cho thông qua của kênh và phải tăng tính chống nhiễu
của tin tức khi truyền qua kênh. Để áp ứng ược các yêu cầu này phải thực hiện một phép
biến ổi cấu trúc thống kê của nguồn thông qua chức năng mã hóa. Do ó, nội dung của
chương này sẽ ề cập ến một số vấn ề cơ bản trong mã hóa. Trên cơ sở ó sẽ nghiên cứu
cụ thể các phương pháp mã hóa nguồn và mã hóa kênh.
3.1. TỔNG QUAN VỀ MÃ HÓA
Trong các hệ thống truyền tin rời rạc hoặc truyền các tín hiệu liên tục nhưng ã ược
rời rạc hóa, bản tin thường phải qua một một số phép chuyển ổi: ở phía phát bản tin ược
chuyển ổi thành số (thường là số nhị phân) dưới dạng các từ mã nhờ quá trình mã hóa,
ở phía thu thực hiện chuyển ổi ngược lại từ các từ mã thành bản tin thông qua quá trình
giải mã.
Mã hóa thông tin cho phép ký hiệu hóa thông tin hay sử dụng các ký hiệu quy ước
ể biểu diễn bản tin ở dạng phù hợp với các ứng dụng. Nhờ mã hóa, có thể nhìn thấy hay
hiển thị ược thông tin có bản chất là các khái niệm (thông tin là hiểu biết của con người).
Đối với một hệ thống truyền tin, việc mã hóa sẽ cho phép tăng tính hiệu quả và ộ tin cậy
của hệ thống truyền tin, nghĩa là tăng tốc ộ truyền tin và khả năng chống nhiễu của hệ
thống.
Như ã ề cập trong chương II, khi tốc ộ lập tin của nguồn còn cách xa thông lượng
của kênh, nhiệm vụ của mã hóa là biến ổi tính thống kê của nguồn làm cho tốc ộ lập tin
tiệm cận với khả năng truyền của kênh. Trong trường hợp truyền tin trong kênh có nhiễu,
iều cần quan tâm nhất là ộ chính xác của quá trình truyền tin, hay các tin truyền i ít bị
sai lỗi. Đây chính là nhiệm vụ thứ hai của mã hóa.
3.2. MỘT SỐ VẤN ĐỀ CƠ BẢN TRONG MÃ HÓA
3.2.1. Mã hiệu và thông số cơ bản của mã hiệu
3.2.1.1. Khái niệm mã hiệu
Trong các hệ thống truyền tin, các nguồn tin nguyên thủy thường phải qua các phép
chuyển ổi ể trở thành các nguồn tin trung gian phù hợp với các quá trình xử lý, với môi

lOMoARcPSD| 36067889
trường truyền... nhằm nâng cao hiệu suất truyền tin hoặc nâng cao tính chống nhiễu của
hệ thống. Tại phía thu, chuyển ổi nguồn tin trung gian trở thành nguồn tin có dạng ban
ầu. Quá trình mã hóa chuyển ổi nguồn tin thành các nguồn tin trung gian và mã hiệu
dùng ể biểu diễn các nguồn tin trung gian này.
Mã hiệu ược ịnh nghĩa là một tập hữu hạn các ký hiệu (thường là các chữ số) và
phép ánh xạ các tin/bản tin của nguồn tin thành các dãy ký hiệu tương ứng. Tập các ký
hiệu và phép ánh xạ này phải áp ứng các yêu cầu của từng hệ thống truyền tin ặt ra.
Mã hóa (encoding) là phép biến ổi từ nguồn tin thành mã hiệu hay mã hóa là phép
biến ổi nguồn tin này thành nguồn tin khác có tính thống kê (entropi, chiều dài các tin,
ộ chính xác) theo yêu cầu.
Các khái niệm liên quan ến mã hiệu:
- Mã hiệu gồm một tập hữu hạn các ký hiệu có phân bố xác suất nào ó, gọi là dấu mã hay
ký hiệu mã.
- Tập hợp một số dấu mã gọi là tổ hợp mã.
- Trong tập hợp tất cả các tổ hợp mã, một tập hợp các tổ hợp mã ược xây dựng theo một
quy luật nào ó, gọi là tổ hợp mã hợp lệ.
- Trong quá trình mã hóa, một tin nguyên thủy ược ánh xạ vào một tổ hợp mã. Một tổ hợp
mã như vậy gọi là từ mã. Những tổ hợp mã khác gọi là tổ hợp cấm.
- Nguồn tin rời rạc gồm nhiều tin tạo thành các bản tin. Các nguồn tin trong thực tế có số
lượng các tin rất lớn. Ngược lại các mã hiệu thường có số lượng các ký hiệu tương ối nhỏ.
Do ó một tin của nguồn ban ầu thường ược mã hóa thành một chuỗi các ký hiệu mã (từ
mã).
- Một dãy từ mã bất kỳ tạo thành một từ thông tin.
- Quá trình ngược lại của quá trình mã hóa ược gọi là giải mã. 3.2.1.2. Các thông số cơ
bản của mã hiệu
a) Cơ số mã
Tập các ký hiệu mã dùng ể biểu diễn các tin ược gọi là bảng ký hiệu mã, còn số
các ký hiệu mã khác nhau trong bảng mã ó ược gọi là cơ số mã. Cơ số mã thường ược
ký hiệu là .
Đối với iện báo khóa dịch tần số (FSK) hoặc khóa dịch pha (PSK) chỉ dùng hai tần
số hoặc hai góc pha ngược nhau 180°, cơ số của mã bằng hai ( = 2). Điện báo Morse
dùng ba loại ký hiệu: gạch, chấm, nghỉ có ộ dài khác nhau thì cơ số của mã bằng ba (
= 3). Khi mã có cơ số hai gọi là mã nhị phân, ây là loại mã ược dùng rộng rãi nhất. Mã

lOMoARcPSD| 36067889
có cơ số bằng ba, bốn ược gọi là mã tam phân, tứ phân,...Trong thực tế máy tính và các
thiết bị iện tử thường dùng mã nhị phân, nhưng mã nhị phân thường rất dài nên trong
máy tính còn dùng hệ mã Hecxa (mã có cơ số bằng 16).
b) Độ dài từ mã
Tổ hợp các ký hiệu mã dùng ể mã hoá một tin ược gọi là ộ dài từ mã. Độ dài từ mã
thường ược ký hiệu là . Có thể nói mã hoá là một phép biến ổi một - một giữa một tin
của nguồn với một từ mã của bộ mã. Trong một số trường hợp nhất ịnh, không thay thế
mỗi tin của nguồn bằng một từ mã mà một khối tin của nguồn mới ược mã hóa bằng một
từ mã thì từ mã sẽ là một tổ hợp dùng ể mã hóa một khối tin của nguồn. Lúc này có khái
niệm là mã khối.
c) Độ dài trung bình từ mã
Nếu một bộ mã mà các từ mã có ộ dài như nhau gọi là mã ều, ngược lại gọi là mã
không ều. Đối với mã không ều, còn có thêm một tham số cơ bản nữa ó là ộ dài trung
bình của từ mã.
=1
(
) (3.1)
trong ó: (
) là xác suất xuất hiện tin
của nguồn sẽ ược mã hóa;
là ộ dài từ mã
tương ứng với tin ; là tổng số từ mă ứng với tổng số tin của .
d) Tổng số từ mã
Tất cả các từ mã ể mã hóa các tin của nguồn làm thành bộ mã hóa nguồn. Tổng số
từ mã bằng số tin ược mã hóa. Trong trường hợp mã khối thì tổng số từ mã bằng tổng
số khối tin sẽ ược mã hóa. Trong trường hợp mã ều, nếu tất cả các tổ hợp mã gồm ký
hiệu với trị khác nhau ều ược dùng làm từ mã, chúng ta sẽ có:
=
(3.2) Khi này bộ mã
ược gọi là mã ầy. Nếu L < m", bộ mã ược gọi là mã vơi.
Căn cứ sự phát triển của lý thuyết và kỹ thuật mã hiện nay, có thể có hai xu hướng
nghiên cứu về mã. Thứ nhất, nghiên cứu cấu trúc các loại mã ều, chủ yếu là loại mã vơi
có tính chất phát hiện và sửa sai. Thứ hai là, nghiên cứu các loại mã không ều ể xây
dựng những loại mã có ộ dài trung bình ngắn nhất, gọi là mã thống kê tối ưu hoặc là mã
kinh tế (về quan iểm thời gian truyền tin). Hiện nay cũng có những công trình nghiên
cứu phương pháp xây dựng các loại mã không ều có tính chất chống nhiễu. e) Trọng số
từ mã
lOMoARcPSD|36067889
Để thuận tiện cho việc sử dụng mã hiệu, mỗi từ mã ược gán cho một giá trị còn gọi
là trọng số từ mã. Trọng số của từ mã là tổng các giá trị của các ký hiệu mã có trong từ
mã.
1
=0
(3.3)
trong ó: Chỉ số là số thứ tự của mỗi ký hiệu mã trong từ mã, ược ánh số 0 từ phải qua
trái; Trọng số vị trí
là hệ số nhân của từng vị trí ký hiệu (
=
). Mỗi ký hiệu mã
ược gán cho một giá trị gọi là giá trị riêng
. Đối với mã nhị phân ( = 2) có 2 ký hiệu
mã ‘0’ và ‘1’ ược gán giá trị riêng 0 và 1.
Ví dụ 3-1: Trọng số của từ mã 1011 là:
= 1 × 2
0
+ 0 × 2
1
+ 1 × 2
2
+ 1 × 2
3
= 13
3.2.2. Phương pháp biểu diễn mã
Phương pháp biểu diễn mã là cách trình bày toàn bộ mã hiệu với các tin ược mã
hóa. Các dạng biểu diễn mã thường ược dùng là các bảng mã, ồ hình mã và các hàm cấu
trúc mã.
3.2.2.1. Các bảng mã
Các bảng mã thường ược dùng rộng rãi ể mô tả một mã hiệu (bộ mã) là bảng ối chiếu
và mặt tọa ộ mã.
a) Bảng ối chiếu mã:
Là cách trình bày ơn giản nhất: liệt kê trong một bảng các tin của nguồn và chỉ rõ
những từ mã tương ứng với nó. Bảng ối chiếu mã có ưu iểm là cho thấy cụ thể và tức
thời bản tin và từ mã của nó.
Ví dụ 3-2: Nguồn tin = {
1
,
2
,
3
,
4
,
5
} các tin của nó ược mã hoá như sau:
Tin
1
2
3
4
5
Từ mã 00 01 100 1010 1011
Trong bảng ối chiếu mã, số thứ tự của từ mã trong bộ mã là số thứ tự ã liệt kê từ mã.
Cách biểu diễn này tuy rõ ràng nhưng không thích hợp với các bộ mã lớn và cồng
kềnh.
b) Mặt tọa ộ mã:
Mặt tọa ộ mã là một cách biểu diễn mã dựa vào hai thông số: ộ dài từ mã và trọng
số của từ mã ể lập một mặt phẳng toạ ộ, trên ó mỗi từ mã ược biểu diễn bằng một iểm.
Bộ mã trình bày trong bảng ối chiếu mã ở trên ược biểu diễn trong mặt tọa ộ mã ở
hình 3.1 như sau:

lOMoARcPSD|36067889
b
13
x
5
5 x4
2 x2 x3
x1
0 1 2
3 4 n
Hình 3.1: Biểu diễn mã bằng mặt toạ ộ mã
Mỗi từ mã sẽ hoàn toàn xác ịnh khi xác ịnh ược cặp (, ) của nó. Như vậy mỗi từ
mã ược biểu diền bởi một cặp tọa ộ (, ) duy nhất.
3.2.2.2. Đồ hình mã
Các phương pháp ồ hình cho phép trình bày bộ mã một cách gọn hơn các bảng mã,
ồng thời cho thấy rõ hơn các tính chất của mã hiệu như tính phân tách ược hay tính
prefix.... Các phương pháp ồ hình thường dùng gồm có: cây mã và ồ hình kết cấu.
a) Cây mã:
Cây mã là một ồ hình gồm các nút và các nhánh. Gốc của cây gọi là nút gốc (mức
0). Từ nút gốc phân i nhánh hoặc ít hơn, mỗi nhánh ại diện cho một trị của ký hiệu.
Mỗi nhánh kết thúc tại một nút ở cấp cao hơn nút xuất phát. Tiếp tục từ mỗi nút ở cấp
sẽ phân ra m nhánh hoặc ít hơn. Mỗi nhánh ại diện cho một trị của ký hiệu có tại vị trí
+ 1 (tính từ bên trái) của những từ mã mà ký hiệu bên trái nó ược biểu diễn bằng một
ường liên tục các nhánh tính từ nút gốc ến nút cấp thứ ược phân nhánh này. Mỗi nhánh
phân ra từ nút cấp này sẽ kết thúc ở một nút cấp + 1.
Mỗi nút cuối (còn gọi là nút lá) là nút kết thúc của nhánh sẽ ại diện cho một từ mã,
thứ tự các trị ký hiệu mã là thứ tự các trị trên các nhánh i từ nút gốc ến nút cuối qua các
nút trung gian.
Rõ ràng có thể có những nút cuối mà không có nhánh nào i ra từ nó, và cũng có thể
có những nút cuối của từ mã này là nút trung gian của từ mã khác.

lOMoARcPSD| 36067889
Mã hiệu có nút cuối trùng với nút trung gian của từ mã khác sẽ có ặc iểm là từ mã
ngắn hơn là phần ầu từ mã dài hơn và nó không cho phép phân tách một chuỗi mã bất kỳ
thành một dãy duy nhất các từ mã.
Ví dụ 3-3: Cây mã cho bộ mã 00, 01, 100, 1010, 1011 như ược biểu diễn trên hình 3.2.
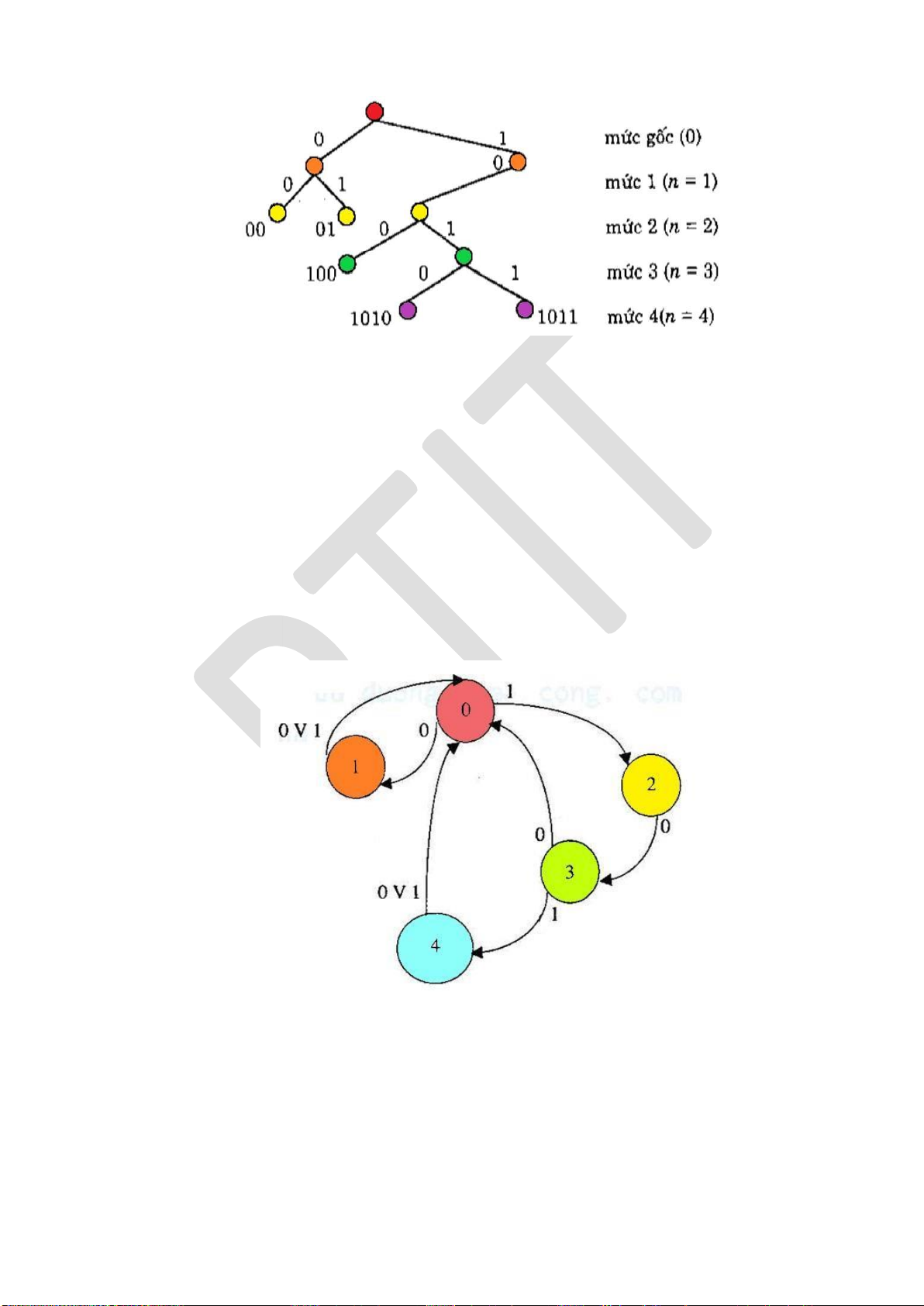
lOMoARcPSD| 36067889
ều.
1011.
Hình 3.2: Ví d
ụ
v
ề
cây mã
T
ừ
ví d
ụ
trên có th
ể
nh
ậ
n th
ấ
y: khi nhìn vào cây mã có th
ể
bi
ết mã ã cho thuộ
c
lo
ại mã ề
u (khi các nút lá cùng b
ậc) hay không ều, mã ầ
y (t
ấ
t c
ả
các nút trung gian
b
ậc trướ
c
các nút lá ề
u có
nhánh) hay mã vơi.
Cây mã hình 3.2 thu
ộ
c lo
ạ
i mã không
b)
Đồ
hình k
ế
t c
ấ
u:
Đồ
hình k
ế
t c
ấ
u g
ồ
m có các nút và các
nhánh có hướng, ây là cách biể
u di
ễ
n cây
mã rút g
ọ
n. Hình 3.3 bi
ể
u di
ễ
n ví d
ụ
v
ề
ồ
hình k
ế
t c
ấ
u cho b
ộ
mã 00, 01, 100, 1010,

lOMoARcPSD|36067889
Hình 3.3: Ví dụ về ồ hình kết cấu
Một từ mã ược biểu diễn bởi một vòng kín xuất phát từ nút gốc theo các nhánh có
hướng qua các nút trung gian và trở về kết thúc tại nút gốc. Trị của các nhánh ược ghi ở
ầu xuất phát của nhánh và ở phía bên trái. Dấu V là dấu “hoặc” có nghĩa là một nhánh
có thể ại diện cho trị bên trái hoặc trị bên phải của dấu V; các nút ược ánh số theo thứ tự
xa dần nút gốc (số ghi trong vòng tròn của nút). Thứ tự trị các ký hiệu lấy theo thứ tự
các nhánh trên ường i.
Đồ hình kết cấu không chỉ ược dùng ể mô phỏng bản thân mã mà còn ược dùng ể
xét cách vận hành của thiết bị mã hoá và giải mã.
3.2.2.3. Hàm cấu trúc mã
Hàm cấu trúc mã thể hiện một ặc tính quan trọng của mã là sự phân bố các từ mã theo
ộ dài, ký hiệu bằng (
).
Ví dụ 3-4: Bộ mã 00, 01, 100, 1010, 1011 có hàm (
) dưới dạng sau:
(
) = 2, khi
= 2
1, khi
= 3
2, khi
= 4
Từ hàm cấu trúc có thể phân biệt ược mã ều hoặc không ều. Trường hợp hàm cấu
trúc bằng không với tất cả các từ mã trừ từ mã ban ầu, ây là loại mã ều. Nếu hàm cấu
trúc có hai hoặc nhiều giá trị khác không, ây là loại mã không ều. Cũng từ hàm cấu trúc
có thể xác minh mã thỏa mãn iều kiện phân tách ược hay không.
Kết luận:
Trên ây là những phương pháp biểu diễn mã có thể áp dụng cho bất cứ loại mã nào.
Tuy nhiên, vẫn có những phương pháp biểu diễn tổng quát khác có tính chất bao trùm
hơn mà có thể phân thành hai phương pháp chủ yếu sau: phương pháp biểu diễn hình
học và phương pháp biểu diễn ại số. Với phương pháp biểu diễn hình học, các từ mã có
ộ dài ược biểu diễn bằng một véctơ hay một iểm ( ầu mút vectơ) trong không gian
chiều. Bộ mã là một hệ iểm trong không gian ó. Với phương pháp biểu diễn ại số, bộ mã
ược xem như một cấu trúc ại số nhất ịnh. Các loại mã ược phân loại và nghiên cứu theo
các cấu trúc ại số sử dụng ể biểu diễn bộ mã.

lOMoARcPSD|36067889
3.2.3. Điều kiện phân tách của mã hiệu
3.2.3.1. Điều kiện ể mã phân tách ược
Các tin tức mã hoá khi truyền i ược trình bày dưới dạng một dãy ký hiệu liên tiếp
nhau. Muốn giải mã, hay muốn khôi phục các tin từ dãy ký hiệu mã nhận ược, iều kiện
trước tiên là trong dãy ký hiệu liên tiếp ó phải có quy luật ảm bảo sự phân tách một cách
duy nhất các từ mã. Nói một cách khác chúng phải có quy luật ể phân biệt ược các ký
hiệu ầu của mỗi từ mã. Nếu iều kiện này không ược thỏa mãn thì từ một chuỗi ký hiệu
mã nhận ược, có thể có nhiều cách ể tách nó ra thành các từ mã hoặc không thể tách nó
ược. Điều này làm cho bản tin nhận ược sau giải mã có thể không giống với bản tin ã
phát. Có thể tìm hiểu kỹ hơn qua các ví dụ sau ây:
Ví dụ 3-5: Xét bộ mã
1
= {0, 10, 11} mã hóa cho nguồn = {, , } theo quy luật:
; ; 11.
Giả sử phía phát gửi i bản tin = , lúc ó chuỗi từ mã tương ứng ược phát i
là = 0100011.
Vấn ề là phía thu sau khi nhận ược chuỗi từ mã làm sao có thể nhận biết ược bản
tin tương ứng mà bên phát ã phát i.
Cần chú ý là giữa từ mã và tin ược mã hóa có quan hệ một - một thì việc giải mã ở
phía thu sẽ bao gồm việc tách úng từ mã nhận ược (tách mã) và chuyển ngược từ mã
thành tin tương ứng. Việc chuyển từ mã thành tin sẽ ược thực hiện dễ dàng nhờ một sơ
ồ giải mã xác ịnh. Việc tách mã là một thuật toán kiểm tra tính úng ắn của một số tiêu
chuẩn ược gọi là iều kiện phân tách của mã hiệu. Việc kiểm tra này ược bắt ầu từ ký
hiệu mã ầu tiên của chuỗi cho ến khi có thể ngắt ược một từ mã thì nó sẽ ngắt từ mã và
lại coi ký hiệu tiếp theo là ký hiệu ầu tiên của chuỗi mới và kiểm tra tiếp.
Chẳng hạn, với chuỗi ký hiệu mã nhận ược như trên thì phía thu chỉ có một khả năng
ể tách mã hợp lý là: 0 | 10 | 0 | 0 | 11 và xác ịnh ược bản tin ã ược gửi i là
.
Ví dụ 3-6: Xét bộ mã
2
= {0, 10, 01} mã hóa cho nguồn = {, , } theo quy luật:
0; ; 01.
Giả sử phía thu nhận ược chuỗi ký hiệu = 01010 và thực hiện quá trình tách mã. Ở
ây, phía thu có thể thực hiện ược ba khả năng tách mã hợp lý sau:
0 | 10 | 10
01 | 0 | 10
01 | 01 | 0

lOMoARcPSD|36067889
Vì vậy phía thu sẽ không biết ược chính xác phía phát ã gửi i bản tin nào trong 3
bản tin sau: hay hay . Một bộ mã như vậy không phù hợp cho việc tách mã
và ược gọi là mã không thể giải mã duy nhất hay còn gọi là mã không phân tách ược.
Vì vậy iều kiện ể một bộ mã có thể giải mã duy nhất hay phân tách ược là bất kỳ
dãy các từ mã nào của bộ mã cũng không ược trùng với một dãy các từ mã khác của
cùng bộ mã.
Ví dụ 3-7: Xét bộ mã
3
= {010, 0101, 10100} mã hóa cho nguồn = {, , } theo quy
luật: ; ; 10100.
Giả sử phía thu nhận ược một chuỗi ký hiệu là 01010100101 và thực hiện quá trình
tách mã. Ở ây chỉ có một cách tách mã duy nhất là:
0101 | 010 | 0101.
nhưng việc tách mã trở nên khó khăn hơn so với bộ mã
1
|. Chẳng hạn, lúc gặp chuỗi
010 thì chưa chắc chắn ó là một từ mã vì có thể là phần ầu của từ mã 0101, iều này phụ
thuộc vào ký hiệu i ngay sau chuỗi 010. Nếu ký hiệu i ngay sau chuỗi này là 0 thì có thể
khẳng ịnh ược 010 là từ mã và 0 là phần ầu của một từ mã sau ó. Còn nếu ký hiệu ngay
sau là 1 thì không thể khẳng ịnh vì có hai khả năng: hoặc 010 là một từ mã và 1 là phần
ầu của từ mã khác hoặc 0101 là một từ mã.
Nguyên nhân của iều này là do trong bộ mã có một từ mã này là phần ầu (prefix)
của một từ mã khác (có thể hiểu Prefix là phần còn lại của từ mã sau khi bỏ i một số ký
hiệu cuối cùng, một từ mã thường ược ọc từ trái sang phải nên ký hiệu ầu tiên của từ mã
là ký hiệu bên trái nhất và ký hiệu cuối cùng là ký hiệu bên phải nhất). Và ó cũng chính
là nguyên nhân và bản chất của việc một dãy ký hiệu có thể tách thành hai dãy từ mã
khác nhau.
Mã có tính prefix là bộ mã không có bất kỳ từ mã nào là prefix của một từ mã khác
trong cùng bộ mã. Mã prefix chỉ có duy nhất một cách tách thành các từ mã thành phần
nên ây là bộ mã phân tách ược.
3.2.3.2. Bảng thử mã và ộ chậm giải mã
Dựa vào tính prefix trên, ể nhận biết một bộ mã (dĩ nhiên không phải mã prefix) có
phân tách ược hay không, người ta thường dùng một công cụ gọi là bảng thử mã. Bản
chất của bảng thử mã là phân tích những từ mã dài thành những từ mã ngắn dần.
Cách thực hiện bảng thử mã như sau:
- Đem các từ mã xếp thành một cột, theo thứ tự của từ mã từ nhỏ ến lớn, ánh dấu cột là
cột 1.

lOMoARcPSD| 36067889
- Trong cột này, ối chiếu các từ mã ngắn với từ mã dài hơn, nếu từ mã ngắn là prefix
của từ mã dài thì ghi tiếp phần còn lại vào cột tiếp theo và ánh dấu là cột 2.
- Tiếp tục ối chiếu các tổ hợp mã trong cột 1 và cột 2 với nhau, nếu chuỗi nào trong cột
này là prefix của chuỗi trong cột kia, phần còn lại sẽ ược ghi vào cột 3.
- Tiếp tục theo qui tắc này nếu ang xét ở cột thứ j thì ối chiếu các chuỗi trong cột này
với cột 1. Nếu có chuỗi nào trong cột này là prefix trong cột kia thì phần còn lại sẽ ược ghi
vào cột j +1. Thực hiện cho ến khi không thể iền thêm ược nữa hoặc cột mới thêm vào
trùng với một cột trước ó hoặc có một chuỗi trong cột mới trùng với một từ mã.
Ta có ịnh lý sau:
Định lý: Điều kiện cần và ủ ể mã có tính phân tách là không có một tổ hợp mã nào trong
các cột 2, trùng với một từ mã trong cột 1.
Thực vậy, vì từ cột 2 là những phần còn lại của từ mã dài (chuỗi cuối) mà prefix
của nó ã trùng với từ mã khác hoặc phần cuối của từ mã khác. Nếu một chuỗi cuối trùng
với một từ mã khác thì chắc chắn có lớn hơn một cách phân tách chuỗi mã nhận ược
thành các từ mã. Hay nói cách khác nếu ịnh lý trên không thoả mãn thì sẽ tồn tại một
cách ghép các từ mã thành chuỗi mã, mà trong nó tạo ra một oạn ký hiệu mã trùng với
một từ mã khác với các từ mã ược ghép thành chuỗi.
Độ chậm giải mã là số ký hiệu cần phải nhận ược ủ ể có thể phân tách (nhận dạng)
ược từ mã. Đối với mã có thể phân tách, ộ chậm giải mã thường là hữu hạn, nhưng cũng
có trường hợp ộ chậm giải mã là vô hạn.
Ví dụ 3-8: Bảng thử mã phân tách của bộ mã 00, 01, 100, 1010, 1011 ược cho như ở bảng
3.1.
Bảng 3.1: Bảng thử mã của bộ mã 00, 01, 100, 1010, 1011
Cột 1 Cột 2
00
01
100
1010
1011
Bảng thử 3.1 cho thấy cột 2 trống, nghĩa là bộ mã phân tách ược. Rõ ràng trong
trường hợp này không có từ mã nào trùng với phần ầu (prefix) của từ mã khác nên khi
nhận ủ số ký hiệu của một từ mã thì không có từ mã nào khác nhận các ký hiệu mã này

lOMoARcPSD|36067889
làm phần ầu nữa nên ây chính là thời iểm ngắt mã. Độ chậm giải mã của mã này bằng ộ
dài từ mã.
Ví dụ 3-9: Xét tính phân tách của bộ mã 10, 100, 01, 011.
Bảng thử mã phân tách của bộ mã 10, 100, 01, 011 ở bảng 3.2.
Trong các cột từ cột 2, 3,… của bảng thử này không có tổ hợp mã nào trùng với từ
mã trong cột 1, nhưng có thể iền các cột ến vô hạn mà không gặp cột trống. Như vậy ộ
chậm giải mã là vô hạn, tuy vậy mã vẫn có thể phân tách ược.
Bảng 3.2: Bảng thử mã của bộ mã 10, 100, 01, 011
Cột 1
Cột 2
Cột 3
Cột 4
Cột 5
.... *
10
0
1
0
1
100
1
11
00
11
01
0
1
0
011
00
11
00
Bảng thử mã phân tách cho phép ánh giá ộ chậm giải mã. Nếu là số hiệu cột rỗng,
thì ộ chậm giải mã
ược tính theo:
[
1
2 ]
2
]
(3.4)
trong ó:
và
là ộ dài từ mã ngắn nhất và dài nhất, [] là ký hiệu chỉ phần nguyên
của .
3.2.3.3. Bất ẳng thức Kraft
Điều kiện tồn tại một mã thỏa mãn tính prefìx ược xác ịnh bằng bất ẳng thức Kraft
như sau:
Bất ẳng thức Kraft: Nếu một dãy số nguyên
1
,
2
thoả mãn iều kiện:
=1
1 (3.5)
thì sẽ tồn tại một mã có tính prefix, cơ số và dãy số nguyên trên là các ộ dài của các
từ mã trong bộ mã.
Độ chậm giải mã của mã prefix bằng ộ dài của từ mã dài nhất.

lOMoARcPSD|36067889
3.2.4. Mã hệ thống
3.2.4.1. Mã hệ thống tổng quát
Mã hệ thống là một loại mã mà mỗi từ mã của nó ược xây dựng bằng cách liên kết
một số từ mã của một bộ mã gốc. Vì bộ mã gốc có tính phân tách nên bộ mã hệ thống
cùng có tính phân tách. Nếu bộ mã gốc có tính prefix thì bộ mã hệ thống cũng có tính
prefix. Hiện nay, thường sử dụng một số từ mã của bộ mã gốc làm các tổ hợp tạo thành
phần ầu của từ mã hệ thống và gọi nó là các tổ hợp ầu. Các tổ hợp còn lại của bộ mã gốc
ược sử dụng làm các tổ hợp kết thúc của từ mã hệ thống và gọi nó là các tổ hợp cuối. Từ
mã của mã hệ thống ược tạo ra bằng cách nối các tổ hợp ầu lại với nhau và nối thêm một
tổ hợp cuối.
Để biểu diễn mã hệ thống có thể dùng cách biểu diễn mã bất kỳ, ể thấy ó là mã hệ
thống thường biểu diễn các tổ hợp ầu và các tổ hợp cuối rồi biểu diễn sự liên kết các tổ hợp
này ể tạo thành từ mã. Cách biểu diễn thuận tiện ối với mã hệ thống là ồ hình kết cấu với
một chút thay ổi. Trong ồ hình kết cấu này, chỉ những tổ hợp ầu mới kết thúc ở nút gốc,
còn các tổ hợp cuối sẽ kết thúc ở một nút kết thúc riêng. Sự thay ổi này cho phép phân biệt
tổ hợp cuối và tổ hợp ầu, ồng thời cho phép xác ịnh một từ mã của mã hệ thống. Từ mã của
mã hệ thống sẽ là trình tự các trị ược biểu diễn bằng các nhánh i từ nút gốc, có thể vòng
qua nút gốc một số lần với các ường i khác nhau, rồi kết thúc ở một nút kết thúc.
Việc giải mã ối với mã hệ thống phải qua hai bước. Bước thứ nhất, tách chuỗi ký
hiệu mã nhận ược thành chuỗi các tổ hợp ầu và các tổ hợp cuối. Bước thứ hai, tìm các
tổ hợp cuối và xác ịnh iểm kết thúc từ mã tại ây.
Phương pháp giải mã hệ thống bằng ồ hình kết cấu thực hiện như sau: xuất phát từ
nút gốc theo ường mũi tên của các nhánh một cách tuần tự, mỗi khi quay về gốc là kết
thúc một tổ hợp ầu và khi vào ường cụt là kết thúc tổ hợp cuối cùng, ồng thời kết thúc
từ mã hệ thống.
3.2.4.2. Mã hệ thống có tính prefix
Mã hệ thống có tính prefix ược xây dựng từ một bộ mã gốc có tính prefix bằng
cách lấy một số từ mã của mã prefix gốc làm tổ hợp ầu và các từ mã còn lại làm tổ hợp
cuối. Ghép các tổ hợp ầu với nhau và nối một trong các tổ hợp cuối vào thành từ mã của
mã mới gọi là mã hệ thống có tính prefix.
Ví dụ 3-10: Lấy bộ mã prefix 1, 00, 010, 011 làm gốc, trong ó các tổ hợp 1, 00, 010 là
tổ hợp ầu, 011 làm tổ hợp cuối. Các tổ hợp ược hình thành như sau ều có thể là từ mã
của mã hệ thống:
1011, 11011, 00011, 100011, 010011, 11010011,...

lOMoARcPSD|36067889
Khi giải mã phải qua hai bước. Bước thứ nhất, từ dãy ký hiệu nhận ược phân tách
thành dãy các tổ hợp ầu và tổ hợp cuối. Bước thứ hai, phân tách thành dãy các tổ hợp
của mã hệ thống.
Với bộ mã trên, khi nhận ược tin dưới dạng dãy ký hiệu mã:
11011010011101100011010011 Bước
1: Tách thành dãy các tổ hợp ầu và tổ hợp cuối
1-1-011-010-1-011-00-011-010-011 Bước
2: Phân tách thành dãy các tổ hợp mã của hệ thống
11011-0101011-00011-010011
3.2.4.3. Mã có dấu phân tách
Các loại mã hệ thống có tính prefix ều có tính phân tách ược, nhưng các thiết bị
tách từ mã ối với các loại mã ó ều phức tạp. Để có thể sử dụng những thiết bị ơn giản
cho phân tách từ mã và cho phép phân tách mã trong iều kiện có nhiễu, cần phải xây
dựng những loại mã có dấu phân tách. Những lý luận về mã hệ thống giúp nhận thấy
rằng nếu mỗi từ mã có một tổ hợp cuối và tổ hợp cuối của mọi từ mã là giống nhau thì
mỗi khi tìm thấy tổ hợp cuối này sẽ tìm thấy iểm kết thúc của một từ mã. Như vậy, có
thể sử dụng tổ hợp cuối này ể phân tách mã và nó ược gọi là dấu phân tách. Mã dùng
dấu phân tách ể ngắt các từ mã ược gọi là mã có dấu phân tách.
Tóm lại, mã có dấu phân tách là một loại mã mà mỗi từ mã ược giới hạn bởi một
dấu hiệu ặc biệt gọi là dấu phân tách. Dấu phân tách là một dấu hiệu có thế là một tổ
hợp các ký hiệu mã mà cũng có thể không phải là ký hiệu mã. Ví dụ, một bài viết là một
cách mã hóa thông tin trao ổi giữa con người với nhau. Nếu coi bài viết này ược mã hóa
bởi các ký hiệu mã là bộ chữ cái thì dấu phân tách không phải là ký hiệu mã. Nhưng nếu
coi bài viết ược mã hóa bằng bộ chữ mở rộng (gồm cả dấu) thì dấu phân tách là một ký
hiệu mã. Thường trong mã hóa, dấu phân tách là một tổ hợp ặc biệt không có trong từ
mã hoặc trong chuỗi liên tục các từ mã. Một trường hợp thường gặp trong mã hóa, mã
có dấu phân tách là một trường hợp riêng của mã hệ thống có tính prefix.
Trường hợp mã có tính prefix khi phân tách một từ mã, cần phải biết ược ít nhất tất
cả các ký hiệu của từ mã cần phân tách. Việc phân tách một từ mã là việc nhận dạng dãy
ký hiệu của một từ mã cụ thể. Việc này phải ược thực hiện với mọi từ mã của bộ mã.
Trường hợp mã có dấu phân tách, ể tách một từ mã ã cho, chỉ cần nhận dạng dấu
phân tách. Nếu dấu phân tách là một dấu hiệu ặc biệt mà nhiễu trong ường truyền không
làm nó chuyển thành một ký hiệu mã thì mã này cho phép chống nhiễu. Nếu dấu phân
tách là tổ hợp ký hiệu mã của dấu phân tách thì việc nhận dạng này ược thực hiện bằng

lOMoARcPSD|36067889
cách làm trễ oạn mã dài bằng dấu phân tách nhờ một thanh ghi dịch và so sánh oạn mã
này với dấu phân tách. Nếu ầu ra của mạch so sánh cho biết sự giống nhau thì sẽ nhận
ược một dấu phân tách và ã kết thúc một từ mã. Cấu trúc phân tách từ mã nêu trên ược
gọi là bộ lọc tuyến tính iều chỉnh theo dấu phân tách.
Với mã có dấu phân tách là một trường hợp riêng của mã hệ thống, khi ó ược gọi
là mã hệ thống có dấu phân tách thì từ mã của nó gồm phần ầu (là các từ mã của bộ mã
gốc có tính prefix) và phần cuối (là một từ mã của bộ mã gốc) là dấu phân tách. Dấu
phân tách này sẽ không trùng với bất kỳ một oạn mã nào trong từ mã cũng như do xếp
các từ mã tạo thành.
Ví dụ 3-11: Mã hệ thống có dấu phân tách là bộ mã ược xây dựng từ bộ mã gốc 1, 01, 001
với tổ hợp cuối hay dấu phân tách là 001 và các tổ hợp ầu là 1, 01 sẽ có các từ mã:
01111001, 111101001, 010101001,...
Nếu nhận ược chuỗi ký hiệu mã:
0111100101010100111110100101111001
có thể dễ dàng tách ra ược các từ mã:
01111001-010101001-111101001-01111001
bằng bộ lọc tuyến tính iều chỉnh theo dấu phân tách 001, gồm thanh ghi dịch 3 bít mà
các ký hiệu mã của chuỗi mã nhận ược khi i qua nó. Đầu ra mỗi bít thanh ghi dịch ược
ưa ến ầu vào một mạch ồng dấu. Ba ầu vào còn lại của mỗi mạch sẽ theo thứ tự là 0, 0,
l. Đầu ra 3 mạch ồng dấu sẽ qua một mạch ngưỡng mà chỉ khi cả 3 ầu vào của mạch
ngưỡng là 1 thì ầu ra của nó mới bằng 1. Khi ầu ra của mạch ngưỡng là 1, sẽ có dấu
phân tách trên thanh ghi dịch hay nói cách khác ã xác ịnh ược iểm kết thúc của từ mã.
3.2.5. Phát hiện và sửa lỗi
Việc phát hiện lỗi và sửa lỗi phụ thuộc vào tính chất thống kê của kênh và nhiễu. Có
hai loại lỗi:
- Lỗi ộc lập thống kê: các lỗi xuất hiện riêng lẻ, không liên quan lẫn nhau.
- Lỗi cụm: lỗi liên quan chặt chẽ với nhau, thường xuất hiện cùng một lúc.
3.2.5.1. Nguyên tắc phát hiện lỗi của mã hiệu
Khả năng phát hiện lỗi của một mã hiệu dựa trên một ý tưởng rất ơn giản: nếu mã
hiệu là tập hợp những từ mã có ộ dài thì số các từ mã (tổ hợp mã mang tin) ược chọn
phải nhỏ hơn tổng số các tổ hợp ký hiệu mã. Số các tổ hợp không làm từ mã ược gọi
là tổ hợp cấm. Khi chịu tác ộng của nhiễu, một từ mã chuyển ổi sai thành một từ mã

lOMoARcPSD|36067889
khác thì không thể phát hiện ược lỗi sai, nếu chuyển ổi thành tổ hợp cấm thì sẽ phát hiện
ược ã thu sai, do vậy khả năng phát hiện lỗi ược tăng cường nếu số tổ hợp cấm tăng lên.
Một bộ mã cho phép phát hiện lỗi phải là bộ mã ược xây dựng sao cho mọi từ mã
bị lỗi trên ường truyền phải ược chuyển thành tổ hợp cấm.
3.2.5.2. Nguyên tắc sửa lỗi của mã hiệu
Cơ chế sửa lỗi của mã hiệu ồng thời cũng là nguyên lý giải mã phải dựa vào tính
thống kê của kênh ể ảm bảo lỗi tối thiểu. Nói một cách khác khi nhận ược một tổ hợp
cấm, thiết bị sửa lỗi có nhiệm vụ quy về từ mã phát i với xác suất lỗi tối thiểu.
Muốn vậy cần phải dựa vào tính chất nhiễu trong kênh ể phân nhóm các tổ hợp cấm,
mỗi nhóm tương ứng với một từ mã mà chúng có khả năng bị chuyển ổi sang nhiều nhất.
Một bộ mã cho phép sửa ược lỗi là một bộ mã ược xây dựng sao cho mỗi từ mã khi
bị lỗi sẽ chuyển thành những tổ hợp cấm và là những tổ hợp cấm của chỉ riêng nó.
Ví dụ 3-12: Mã hiệu gồm 4 từ mã 0001, 0101, 1000, 1100 khi bị sai cụm gồm 2 ký hiệu
kế cận (véc tơ sai 0011, 0110, 1100) sẽ chuyển thành 12 tổ hợp cấm theo cụm. Cơ chế
sửa sai dựa theo bảng giải mã 3.3.
Bảng 3.3: Bảng giải mã cho mã hiệu gồm 4 từ mã 0001, 0101, 1000, 1100
Từ mã 0001 0101 1000 1100
0010 0110 1011 1111
Tổ hợp cấm 0111 0011 1110 1010
1101 1001 0100 0000
Khi nhận ược các tổ hợp cấm 0010 và 1011, tương ứng sẽ giải mã về 0001 và 1000.
3.3. MÃ HÓA NGUỒN
3.3.1. Một số khái niệm chung
Mã hóa nguồn là phép biến ổi ầu tiên cho nguồn nguyên thủy, ầu vào của phép
biến ổi này có thể là nguồn tin rời rạc hoặc nguồn tin nguyên thủy. Trong cả hai trường
hợp mục ích chính của phép mã hóa nguồn là biểu diễn thông tin với tài nguyên tối thiểu.
Về bản chất, mã hóa nguồn là quá trình rút ngắn các bit tín hiệu dư thừa ể có thể sử
dụng tối a dung lượng của kênh truyền. Với nguồn thông tin ở ây có thể là dữ liệu thoại,
số liệu hay hình ảnh.
Tín hiệu ược mã hóa thành các bit thông tin theo những quy tắc khác nhau, ể nhằm
ạt ược tới giới hạn Entropi của nguồn (Entropi chỉ ra lượng thông tin có trong mỗi ký

lOMoARcPSD| 36067889
tự, vì tần xuất xuất hiện của mỗi ký tự là khác nhau, nên mỗi ký tự mang một lượng
thông tin khác nhau)
Các vấn ề cần nghiên cứu ối với mã hóa nguồn là: mã hóa nguồn liên tục, mã hóa
nguồn rời rạc và nén dữ liệu.
Đối với nguồn rời rạc do tạo ra các tin rời rạc thể hiện là chuỗi các ký hiệu ngẫu
nhiên. Do ó, khi mã hóa nguồn rời rạc, vấn ề cơ bản là thay ổi bảng chữ cái và phân bố
xác suất ể giảm bớt lượng ký hiệu cần dùng. Như vậy cần quan tâm: Entropi của nguồn
trước khi mã hóa; Entropi của nguồn sau khi mã hóa; Hiệu quả của phép mã hóa; Giới
hạn của phép mã hóa. Trường hợp mã hóa cho nguồn rời rạc không nhớ: sử dụng từ mã
có ộ dài cố ịnh hoặc từ mã có ộ dài thay ổi (phương pháp mã hoá nguồn nổi tiếng như:
Huffman, Shanon Fano). Với nguồn dừng rời rạc: thường sử dụng thuật toán mã hoá
nguồn Lempel-Ziv.
Đối với nguồn liên tục do tạo ra tín hiệu liên tục thể hiện một quá trình ngẫu nhiên
liên tục. Trong các hệ thống truyền thông, nguồn liên tục thường ược biến ổi thành nguồn
rời rạc, xử lý và truyền tới phía thu lại biến ổi thành nguồn liên tục.
Mô hình toán học của nguồn thông tin:
Các nguồn thông tin tạo ra các bản tin một cách ngẫu nhiên, nghĩa là ầu ra của
nguồn ược ặc trưng bởi các luật thống kê. Nguồn tin là một quá trình ngẫu nhiên. Ngược
lại, nếu biết chính xác ầu ra của nguồn thì việc nhận ược nó không còn ý nghĩa và sẽ
không cần phải truyền nó i nữa.
Dạng ơn giản nhất của nguồn rời rạc là nguồn tạo ra một chuỗi các ký hiệu từ một
bảng chữ cái hữu hạn. Ví dụ một nguồn nhị phân tạo ra một chuỗi các ký hiệu nhị phân
như 1001011101..., từ bảng chữ cái bao gồm hai ký hiệu là {0, 1}. Tổng quát, nguồn rời
rạc có thể tạo ra một chuỗi các ký hiệu trong ký hiệu của bảng chữ cái {
1
,
2
}.
Để xây dựng ược mô hình toán học cho một nguồn rời rạc, giả sử rằng mỗi chữ cái
trong bảng chữ cái {
1
,
2
} có xác suất xuất hiện là
. Với:
= ( =
và
1
= 1 (3.6)
Xét hai mô hình toán học của nguồn rời rạc. Mô hình thứ nhất, nguồn rời rạc không
nhớ (DMS) nếu ký hiệu xuất hiện một cách ộc lập với nhau. Mô hình thứ hai, nguồn
dừng rời rạc nếu các mối liên hệ thống kê giữa các thời iểm không phụ thuộc vào thời
gian (hay còn gọi nguồn rời rạc có nhớ). Với nguồn rời rạc, vấn ề cơ bản là thay ổi bảng
chữ cái và phân bố xác suất ể giảm bớt số lượng ký hiệu cần dùng.
Nguồn liên tục tạo ra một tín hiệu, một thể hiện của một quá trình ngẫu nhiên.
Nguồn liên tục có thể ược biến thành một chuỗi các biến ngẫu nhiên (liên tục) bằng phép

lOMoARcPSD|36067889
lấy mẫu. Lượng tử hóa cho phép biến ổi các biến ngẫu nhiên này thành các biến ngẫu
nhiên rời rạc, với sai số nhất ịnh.
3.3.2. Mã hóa cho các nguồn tin rời rạc
Trong chương II ã giới thiệu o ộ thông tin cho biến ngẫu nhiên rời rạc . Khi là
ầu ra của một nguồn rời rạc, Entropy () ặc trưng cho lượng tin trung bình phát ra bởi
nguồn. Trong phần này xem xét quá trình mã hóa ầu ra của một nguồn.
Giả sử nguồn rời rạc gồm ký hiệu {
1
,
2
}, với xác suất xuất hiện các ký
hiệu tương ứng là {
1
,
2
}. Mã hóa nguồn chính là quá trình biểu diễn các ký hiệu
của nguồn bởi các chuỗi
có chiều dài
(
= [
1
,
2
,
= 0/1).
Yêu cầu của bộ mã hóa nguồn:
- Các từ mã biểu diễn ở dạng nhị phân.
- Quá trình mã hóa sao cho việc giải mã là duy nhất.
- Để ánh giá hiệu quả của bộ mã hóa nguồn thường thông qua việc so sánh Entropy
H(X) với số lượng bit trung bình dùng ể biểu diễn từ mã (Hiệu suất mã hóa).
3.3.2.1 Mã hóa nguồn rời rạc không nhớ
Giả sử rằng DMS gồm L ký hiệu {
1
,
2
}, với xác suất xuất hiện các ký hiệu
tương ứng là {
1
,
2
}. Entropy của DMS là:
(
=1
(
)(
2
(3.7)
a) Mã hóa với từ mã có chiều dài bằng nhau:
Tất cả các ký hiệu của nguồn ược mã hóa bằng các từ mã có chiều dài bằng nhau
(từ mã bit). Đây là quá trình mã hóa không tổn thất, và việc giải mã là dễ dàng và duy
nhất. Ví dụ: mã ASCII, mã EBCDIC, mã Baudot…Giả sử nguồn gồm ký hiệu ồng xác
suất. Để mã hóa dùng từ mã bit thì có hai khả năng: =
2
khi là lũy thừa của 2
( = 2
). Và khi không phải là lũy thừa của 2, thì
2
+ 1.
Lúc ó, hiệu suất mã hóa của nguồn DMS:
()
2
= = (3.8)
Quan sát thấy rằng khi L là lũy thừa của 2 và các ký hiệu ồng xác suất, = (),
do ó ạt hiệu suất 100%. Tuy nhiên nếu L không phải là lũy thừa của 2 nhưng các ký hiệu
nguồn ồng xác suất. Hiệu suất mã:
=
()
=
2
(3.9)

lOMoARcPSD| 36067889
2+1
Khi lớn thì log
2
L lớn vì vậy hiệu suất mã hóa cao. Ngược lại, khi nhỏ, hiệu suất
sẽ rất thấp. Để thực hiện mã hóa mong muốn thì phải mã hóa từng khối ký hiệu một
lúc. Quá trình mã hóa ký hiệu cùng một lúc ược thực hiện như sau:
Số ký hiệu có thể có của nguồn là
. Chọn chiều dài từ mã mã hóa là , yêu cầu
giá trị của N phải thỏa mãn:
2
2
=
2
(3.10) Do
N phải là số nguyên, nên hiệu suất mã hóa:
() ()
2
= = = (3.11)
2+1
Vì vậy, chọn lớn thì hiệu suất sẽ cao (dù cho nhỏ).
b) Mã hóa với từ mã có chiều dài thay ổi:
Mã hoá nguồn sử dụng với từ mã có ộ dài thay ổi thường sử dụng phương pháp mã
hóa thống kê tối ưu. Mục tiêu của mã hoá thống kê tối ưu là mã hóa tin rời rạc với số
lượng các ký hiệu mã nhị phân tối thiểu. Do ó mã hóa thống kê tối ưu thuộc loại mã nén
dữ liệu.
Khi các ký tự của nguồn có xác suất xảy ra không giống nhau, một phương pháp
mã hóa hiệu quả hơn là sử dụng các từ mã có chiều dài thay ổi (VLC). Một ví dụ như
vậy về mã hóa là mã Morse. Trong VLC, các từ mã ngắn ược gán tương ứng các giá trị
xác suất cao và các từ mã dài ứng với các giá trị xác suất thấp. Tốc ộ bít cần ể mã hóa
các kí hiệu này là nghịch ảo của logarit của xác suất, tức là log
2
. Do ó, Entropy của các
kí hiệu là số bít trung bình tối thiểu cần ể biểu diễn các kí hiệu là:
(
=1
log
2
(3.12)
Mục tiêu cơ bản là xây dựng một phương pháp mã hóa có tính hệ thống ể tạo ra các
từ mã có ộ dài thay ổi, giải mã duy nhất và có hiệu quả theo nghĩa trung bình các ký hiệu
nhị phân ứng với một ký hiệu của nguồn ( ộ dài trung bình của từ mã), phải tối thiểu.
=
=1
(
) (3.13)
trong ó:
là ký hiệu thứ của nguồn và
là số ký hiệu nhị phân ứng với từ mã của
.
Điều kiện tồn tại một mã thỏa mã tính prefix (giải mã ược) ược xác ịnh bởi bất ẳng thức
Kraft.
Định lý về giới hạn trên và dưới của chiểu dài trung bình từ mã:
Định lý: Gọi là một nguồn rời rạc không nhớ với entrôpi hữu hạn () bít với các ký
hiệu
,1 i L, với các xác suất xuất hiện tương ứng
, 1 i L. Có thể xây dựng

lOMoARcPSD|36067889
một mã hiệu nhị phân có tính prefix và có ộ dài từ mã trung bình thỏa mãn bất ẳng
thức:
( < () + 1 (3.14)
Mã hóa thống kê tối ưu có ưu iểm là hệ số nén tương ối cao, phương pháp thực
hiện tương ối ơn giản, òi hỏi ít bộ nhớ. Nhược iểm của nó là phải chứa cả bảng mã vào
tệp tin nén thì phía nhận mới có thể giải mã ược, do ó hiệu suất nén chỉ cao khi thực hiện
các tệp tin lớn.
Tiếp theo sẽ xem xét quá trình mã hóa nguồn cho nguồn rời rạc không nhớ có xác
suất xuất hiện không giống nhau bằng các từ mã có ộ dài thay ổi.
b1) Mã thống kê tối ưu Shannon - Fano
Độc lập với nhau, nhưng Shannon và Fano ã xây dựng phương pháp lập mã thống
kê tối ưu trên cùng một cơ sở: ộ dài từ mã tỷ lệ nghịch với xác suất xuất hiện.
Các bước ể lập mã:
Bước 1: Sắp xếp các tin
của nguồn theo thứ tự xác suất giảm dần.
Bước 2: Chia thành hai nhóm tin sao cho tổng xác suất mỗi nhóm tương ồng nhau (bằng
nhau hoặc gần bằng nhau).
Bước 3: Mỗi nhóm gán cho một ký hiệu mã (0, 1).

lOMoARcPSD|36067889
= =
()
=1
Ví dụ 3-13: Cho nguồn tin X = {
}, i = 1. . .8, có các lớp tin và xác suất xuất hiện tương
ứng (
) = {0,25; 0,125; 0,0625; 0,0625; 0,25; 0,125; 0,0625; 0,0625}. Hãy lập mã
thống kê tối ưu Shannon - Fano cho nguồn tin trên và tính hiệu suất mã.
Quá trình mã hóa:
Đầu tiên, sắp xếp nguồn tin giảm dần theo xác suất xuất hiện, ghi vào bảng 3.4 theo
mẫu.
Các thông số tối ưu:
Bướ
c 4: L
ặ
p l
ại bướ
c 2 và 3 cho các nh
óm con cho ế
n khi không th
ể
ti
ế
p t
ục ượ
c n
ữ
a.
Bước 5: Đọ
c t
ừ
mã tương ứ
ng v
ớ
i m
ỗ
i tin là t
ổ
h
ợ
p t
ấ
t c
ả
các ký hi
ệ
u mã c
ủ
a các nhóm
mà l
ớp tin ó phụ
thu
ộ
c, l
ấ
y t
ừ
nhóm l
ớn ế
n nhóm nh
ỏ
(tính t
ừ
trái sang ph
ả
i).
Sơ ồ
gi
ả
i thu
ật ể
l
ậ
p mã Shannon- Fano:
N
hư minh họ
a trên hình 3.4.
Hình 3.4: Sơ ồ
gi
ả
i thu
ật ể
l
ậ
p mã Shannon- Fano
Các thông s
ố
t
ối ưu
:
-
Th
ử
b
ất ẳ
ng th
ứ
c Kraft (
2
=1
, d
1)
ấ
u b
ằng ượ
c x
ả
y ra.
Hi
-
ệ
u su
ấ
t mã:
()
(
)
2
(
)
=1
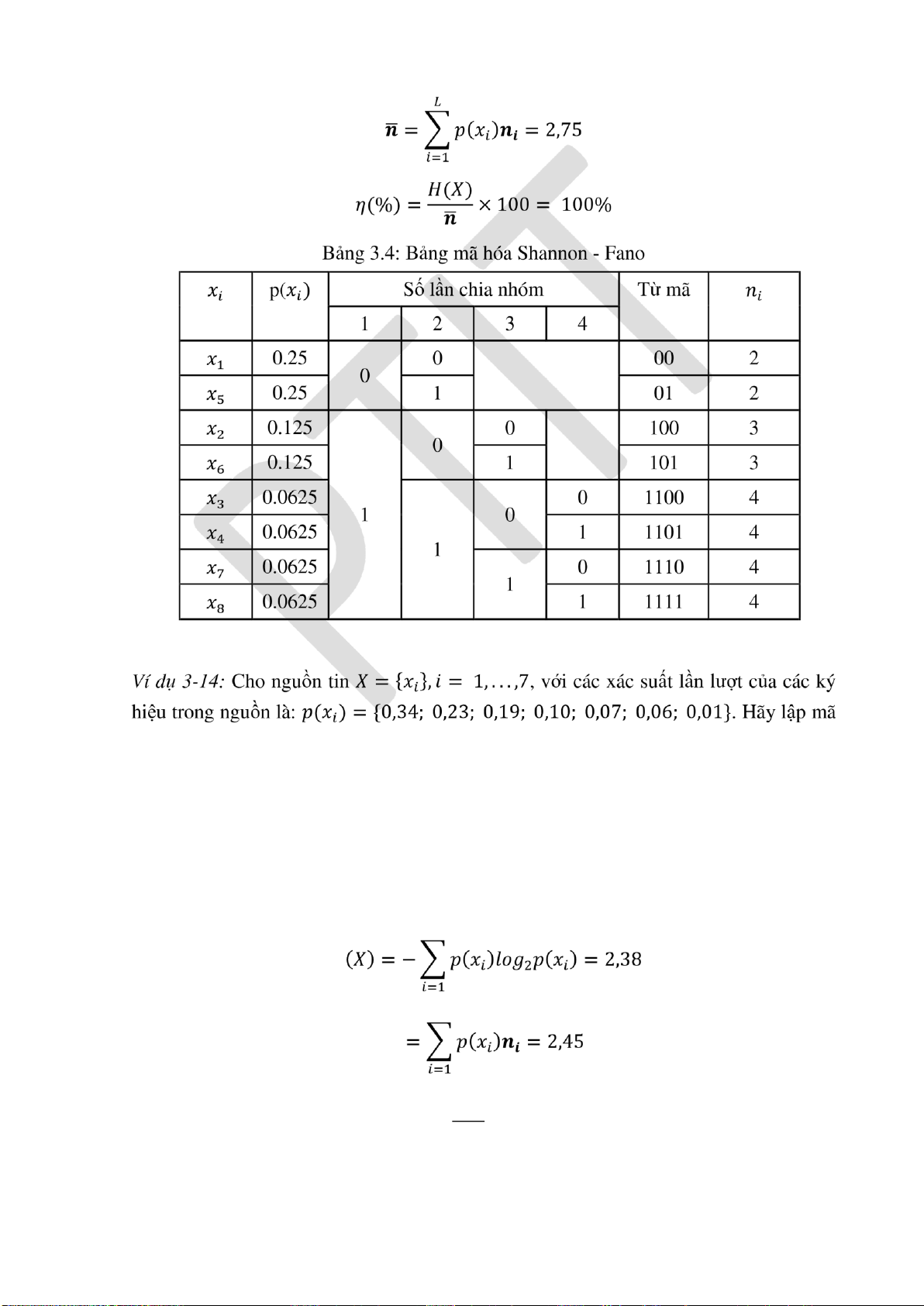
lOMoARcPSD|36067889
thống kê tối ưu Shannon - Fano cho nguồn tin trên và tính hiệu suất mã.
Quá trình mã hóa:
Sắp xếp nguồn tin với các ký hiệu giảm dần theo xác suất xuất hiện, ghi vào bảng mã
3.5.
Các thông số tối ưu:
()
(%) = × 100 = 97%

lOMoARcPSD|36067889
hóa cho một ký hiệu của nguồn là cực thiểu. Phương pháp mã hóa này cho một bộ mã có
tính prefix và tất nhiên quá trình giải mã là duy nhất.
Các bước lập mã:
Bước 1: Sắp xếp các tin
của nguồn theo thứ tự xác suất giảm dần.
Bước 2: Chọn hai lớp tin có xác suất nhỏ nhất gán cho mỗi lớp tin một ký hiệu mã (0,1).
Bước 3: Thay thế hai lớp tin nhỏ nhất này bằng một lớp tin mới có xác suất bằng tổng hai
xác suất.
Bước 4: Coi như có nguồn tin mới, quay lại làm từ bước 1 cho ến khi tổng hai xác suất
bằng 1 thì dừng lại.
Bước 5: Đọc từ mã tương ứng với mỗi lớp tin là tổ hợp các ký hiệu mã gán cho các nhóm
mà lớp tin ó phụ thuộc vào, lấy từ nút gốc ến nút lá (tính từ phải sang trái).
Sơ ồ giải thuật tạo mã: Như minh họa trên hình 3.5.
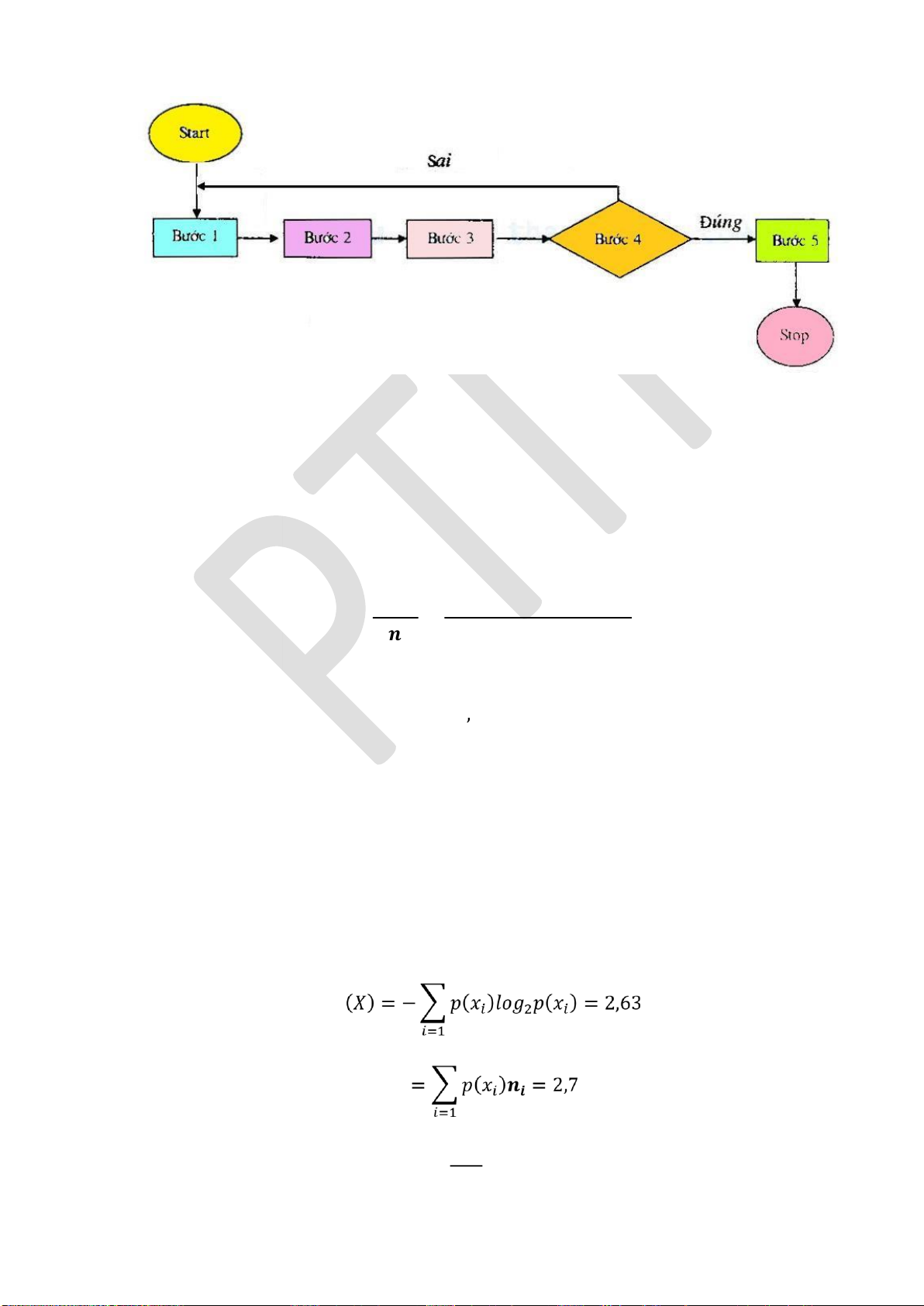
lOMoARcPSD|36067889
Quá trình mã hóa:
Đầu tiên sắp xếp nguồn tin giảm dần theo xác suất xuất hiện, ghi vào bảng 3.6 theo
mẫu.
Các thông số tối ưu:
()
(%) =
Hình 3.5
:
Sơ ồ
gi
ả
i thu
ật ể
l
ậ
p mã Huffman
Các thông s
ố
t
ối ưu
-
Th
ử
b
ất ẳ
ng th
ứ
c Kraft (
2
=1
1)
, d
ấ
u b
ằng ượ
c x
ả
y ra.
-
Hi
ệ
u su
ấ
t mã:
=
()
=
(
)
2
(
)
=1
(
)
=1
Xét ví d
ụ
c
ủa phương pháp này.
Ví d
ụ
3-15:
Cho ngu
ồ
n tin
=
{
}
,2,...,
=1
8
có các lớp tin và
xác su
ấ
t xu
ấ
t hi
ệ
n
tương ứ
ng
(
)={0,36
; 0,14; 0,13; 0,12; 0,1; 0,09,0,04;
0,02}
.
Hãy lập mã thống kê tối ưu Huffman cho nguồn tin trên và tính hiệu suất bộ mã
.
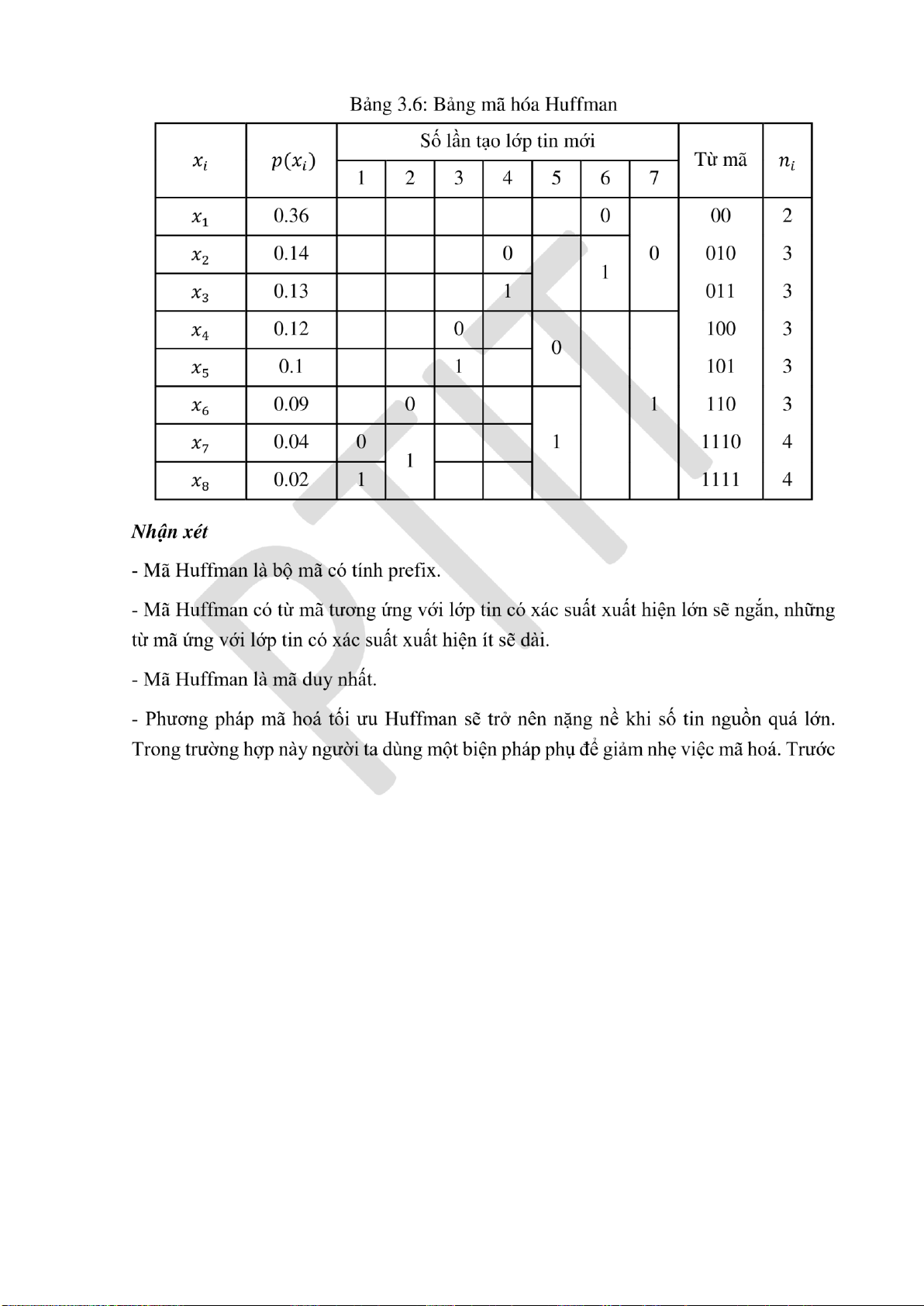
lOMoARcPSD|36067889
tiên liệt kê các tin nguồn theo thứ tự xác suất giảm dần, sau ó ghép thành từng nhóm
những tin có xác suất gần bằng nhau. Dùng mã ều ể mã hoá các tin trong cùng một
nhóm. Sau ó, xem các nhóm tin như một khối tin và dùng phương pháp mã hoá Huffman
ể mã hoá các khối tin. Từ mã cuối cùng tương ứng mỗi tin nguồn gồm 2 phần: mã
Huffman và mã ều. b3) Kết luận:
Mã hóa thống kê tối ưu có các ặc iểm:
- Mã thống kế tối ưu là mã có ộ dài từ mã của các lớp tin tỷ lệ nghịch với xác suất
xuất hiện của chúng.
- Đây là bộ mã của phép mã hóa tối ưu cho nguồn vì kết quả mã hoá là một bộ mã có
chiều dài trung bình là nhỏ nhất trong tất cả các phép mã hóa cho nguồn.
- Các ký hiệu khác nhau của bộ mã phải ồng xác suất, có như vậy lượng tin mỗi ký
hiệu mới ạt trị số cực ại.

lOMoARcPSD|36067889
- Xác suất xuất hiện ký hiệu trong từ mã không phụ thuộc vào sự có mặt của các ký
hiệu ra trước.
- Thử bất ẳng thức Kraft
=1
2
, dấu bằng ược xảy ra vì vậy ây là bộ mã
có tính prefix.
3.3.2.2. Mã hoá nguồn dừng rời rạc
Các thuật toán mã hóa thống kê tối ưu phải biết xác suất xuất hiện của tất cả các tin.
Tuy nhiên, trong thực tế, tính chất thống kê của nguồn thường không biết trước và mỗi
chúng ta thường ước lượng các giá trị xác suất của nguồn rời rạc bằng cách quan sát một
chuỗi dài các ký hiệu.
Ngược lại, thuật toán mã hóa nguồn Lampel-Ziv lại ộc lập với tính chất thống kê
của nguồn do ó rất thích hợp ể mã hóa nguồn dừng rời rạc. Thuật toán ược Jacob Braham
Ziv ưa ra lần ầu tiên năm 1977, sau ó phát triển thành một họ giải thuật nén từ iển là LZ.
Năm 1984, Terry Welch cải tiến giải thuật LZ thành một giải thuật tốt hơn LZW. Không
cần biết trước xác suất phân bố của các ký hiệu.Thuật toán ược thực hiện bằng cách xây
dựng các từ iển. Từ iển ược xây dựng ồng thời với quá trình ọc dữ liệu. Sự có mặt của
một chuỗi con trong từ iển khẳng ịnh rằng chuỗi ó ã từng xuất hiện trong phần dữ liệu ã
ọc. Thuật toán liên tục “tra cứu” và cập nhật từ iển sau mỗi lần ọc một ký tự ở dữ liệu
ầu vào. Do kích thước bộ nhớ không phải vô hạn và ể ảm bảo tốc ộ tìm kiếm, từ iển chỉ
giới hạn 4096 ở phần tử dùng ể lưu lớn nhất là 4096 giá trị của các từ mã. Như vậy ộ dài
lớn nhất của mã là 12 bít (4096 = 2
12
). Được ứng dụng rộng rãi trong nén số liệu các
file máy tính, các tiện ích nén/giãn trong UNIX. Thường ược dùng ể nén các loại văn
bản, ảnh en trắng, ảnh màu, ảnh a mức xám...
Và là chuẩn nén cho các dạng ảnh GIF và TIFF.
Ví dụ 3-16: Xét một chuỗi số nhị phân:
10101101001001110101000011001110101100011011
Hãy lập mã cho chuỗi trên sử dụng thuật toán Lempel – Ziv.
Quá trình mã hóa:
Bước 1: Chia chuỗi ký hiệu trên thành các chuỗi con (cụm):
1,0,10,11,01,00,100,111,010,1000,011,001,110,101,10001,1011. Rõ ràng là mỗi chuỗi
con trong chuỗi là ghép của chuỗi con cũ và một ký hiệu mới.
Bước 2: Lập bảng mã hóa (bảng từ iển)
Để mã hóa các chuỗi con, cần xây dựng một bảng từ iển như bảng 3.7. Do chuỗi
ký hiệu có 16 chuỗi con, cần dùng từ mã 4 bit ể biểu diễn vị trí trong từ iển.
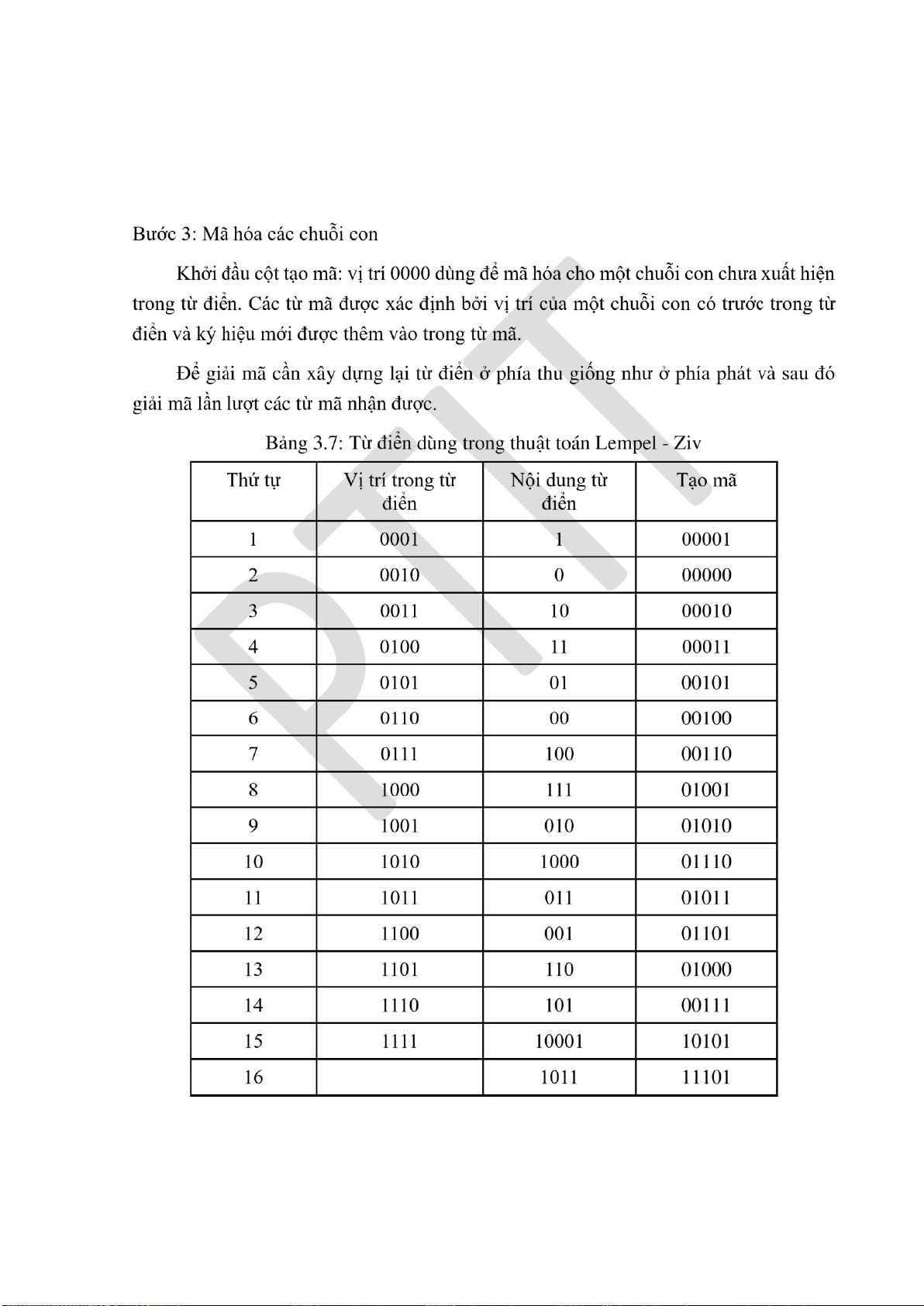
lOMoARcPSD|36067889
Các vị trí của từ iển liên tiếp nhau, bắt ầu bằng 1 và tăng dần (trong trường hợp
này là 16). Trong cột vị trí: iền giá trị nhị phân 4 bit tăng dần, loại trừ 0000.
Cột nội dung: iền vào giá trị các chuỗi con, mỗi chuỗi con trên một hàng theo thứ
tự tương ứng.
Ớ ví dụ trên, mã hóa 44 ký hiệu nhị phân của nguồn thành 16 từ mã, mỗi từ mã có
ộ dài 5 bit, như vậy là không thực hiện việc nén số liệu do chuỗi ký hiệu quá ngắn. Thuật
toán sẽ hiệu quả hơn khi chuỗi ký hiệu ủ dài và có nén số-liệu ở ầu ra của nguồn.
3.3.3. Mã hóa cho các nguồn tin liên tục

lOMoARcPSD|36067889
Nguồn tương tự sinh ra các bản tin () là một thể hiện cụ thể của quá trình ngẫu
nhiên (). Khi () là một quá trình ngẫu nhiên dừng, có trải phổ hữu hạn, có thể sử
dụng ịnh lý lấy mẫu ể biểu diễn () qua một chuỗi các mẫu lấy theo tốc ộ Nyquist.
Sử dụng ịnh lý lấy mẫu, tín hiệu ở ầu ra của một nguồn tương tự ược biểu diễn một
cách tương ương bằng một chuỗi các mẫu rời rạc theo thời gian. Sau ó các mẫu ược
lượng tử hóa theo biên ộ và ược mã hóa. Một dạng ơn giản của mã hóa là biểu diễn mỗi
mức biên ộ rời rạc bằng một dãy các ký hiệu nhị phân. Như vậy nếu biên ộ tín hiệu có
mức rời rạc, ta cần =
2
bit cho một mẫu trong trường hợp là lũy thừa của 2 và
2
+ 1 khi không phải là lũy thừa của 2. Mặt khác, nếu các mức không ồng
xác suất xuất hiện và biết xác suất của các mức tín hiệu ầu ra thì có thể sử dụng phương
pháp mã hóa Huffman (mã hóa theo Entrôpi) ể tăng hiệu quả mã hóa.
Lượng tử hóa biên ộ của một mẫu tín hiệu tạo nên hiệu quả trong việc nén số liệu
nhưng ồng thời cũng tạo nên một sự sai lệch nào ó của tín hiệu hay còn gọi là sự suy
giảm tính trung thực của tín hiệu. Trong phần này cũng sẽ xét việc tối thiểu hóa sai lệch.
3.3.3.1. Hàm tốc ộ - méo
Trong quá trình lượng tử hóa tín hiệu cần quan tâm trước tiên tới méo tín hiệu khi
các mẫu của nguồn ược lượng tử hóa thành một số hữu hạn các mức. Méo nghĩa là có một
sự sai khác giữa giá trị thực của các mẫu tín hiệu {
} với các giá trị lượng tử hóa tương
ứng
, ược ký hiệu là (
,
).
Hàm tốc ộ - méo (()): Biểu diễn tốc ộ lập tin lý thuyết nhỏ nhất ể có sai số nhỏ hơn
D, lượng tin tối thiếu ể biểu diễn nguồn với sai số D:
() = min (, ) (3.15)
(|):[(,
trong ó: (, ) là lượng tin tương hỗ trung bình giữa .
Như vậy:
- Rõ ràng () là tốc ộ bít nhỏ nhất ảm bảo một sai lệch xác ịnh.
- Cho một nguồn tin với phân bố xác suất nguồn cho trước, các mẫu tín hiệu ược lượng tử
hóa với sai số d x x( ,
~
) .
- Sai số nhỏ òi hỏi tốc ộ truyền tin lớn và ngược lại.
- Hàm tốc ộ tạo tin sai lệch biểu diễn liên hệ giữa sai số và tốc ộ truyền tin.
Xác ịnh sai số:
Nguồn sau khi lấy mẫu gồm nhiều mẫu. Với mỗi mẫu, ký hiệu sai lệch là (
,
).

lOMoARcPSD|36067889
=
1
(
)
)
2
]
=
1
[
(
)
)
(
]
2
0
Sai lệch có thể ược ịnh nghĩa theo nhiều cách: sai lệch bình phương
(
,
) = (
)
2
(3.16)
Sai số trên tập các biến ngẫu nhiên là kỳ vọng toán học của D:
= [(
,
)]
=1
[(
,
)] = [(, )] (3.17)
3.3.3.2. Kỹ thuật lượng tử hóa
Lượng tử hóa là phép diễn tả một dải liên tục các giá trị của biên ộ tín hiệu bằng
một tập hữu hạn các giá trị biên ộ rời rạc. Lượng tử hóa tín hiệu sẽ làm méo tín hiệu
trong phạm vi mà người thiết kế có thể ịnh trước. Bộ lượng tử bit có thể có = 2
mức biên ộ rời rạc.
a) Lượng tử tuyến tính
Trong lượng tử tuyến tính các giá trị lượng tử phân bố ều trong toàn bộ tín hiệu,
khoảng cách giữa hai giá trị gần nhau nhất ược gọi là bước lượng tử. Độ méo tín hiệu
lượng tử tỷ lệ với bình phương bước lượng tử, bước lượng tử tỷ lệ nghịch với số giá trị
rời rạc. Méo lượng tử hóa ược tính là lỗi bình phương trung bình như sau:
= [(
(3.18)
trong ó: () là biên ộ tín hiệu ược lấy mẫu tại thời iểm ,
() biểu diễn giá trị lượng
tử gần () nhất. Méo lượng tử và chất lượng của bộ lượng tử ược ánh giá qua tỷ số
công suất tín hiệu / nhiễu lượng tử (). Bộ iều chế xung mã (PCM) dùng phép lượng
tử 8 bit / mẫu trong iện thoại thương mại. Nếu phép lượng tử là tuyến tính sẽ có công
thức liên hệ như sau:
() = 6,02 + (3.19)
trong ó = 4,77 ối với giá trị ỉnh của SNR và = 0 ối với SNR trung bình. Từ phương
trình trên ta thấy là cứ thêm một bit lượng tử thì SNR ược tăng thêm 6 dB. b) Lượng tử
phi tuyến
Méo lượng tử có thể ược giảm thiểu nếu phân bố các giá trị lượng tử một cách thích
hợp (không phải cách ều như lượng tử tuyến tính). Phân bố này dựa trên hàm mật ộ xác
suất (PDF) như sau:
2 2
[(
()) ] =
()] () (3.20)
Từ phương trình trên ta thấy méo trung bình có thể ược giảm thiểu bằng cách giảm
giá trị (
())
2
tại những nơi có giá trị () lớn. Tức các giá trị lượng tử phải
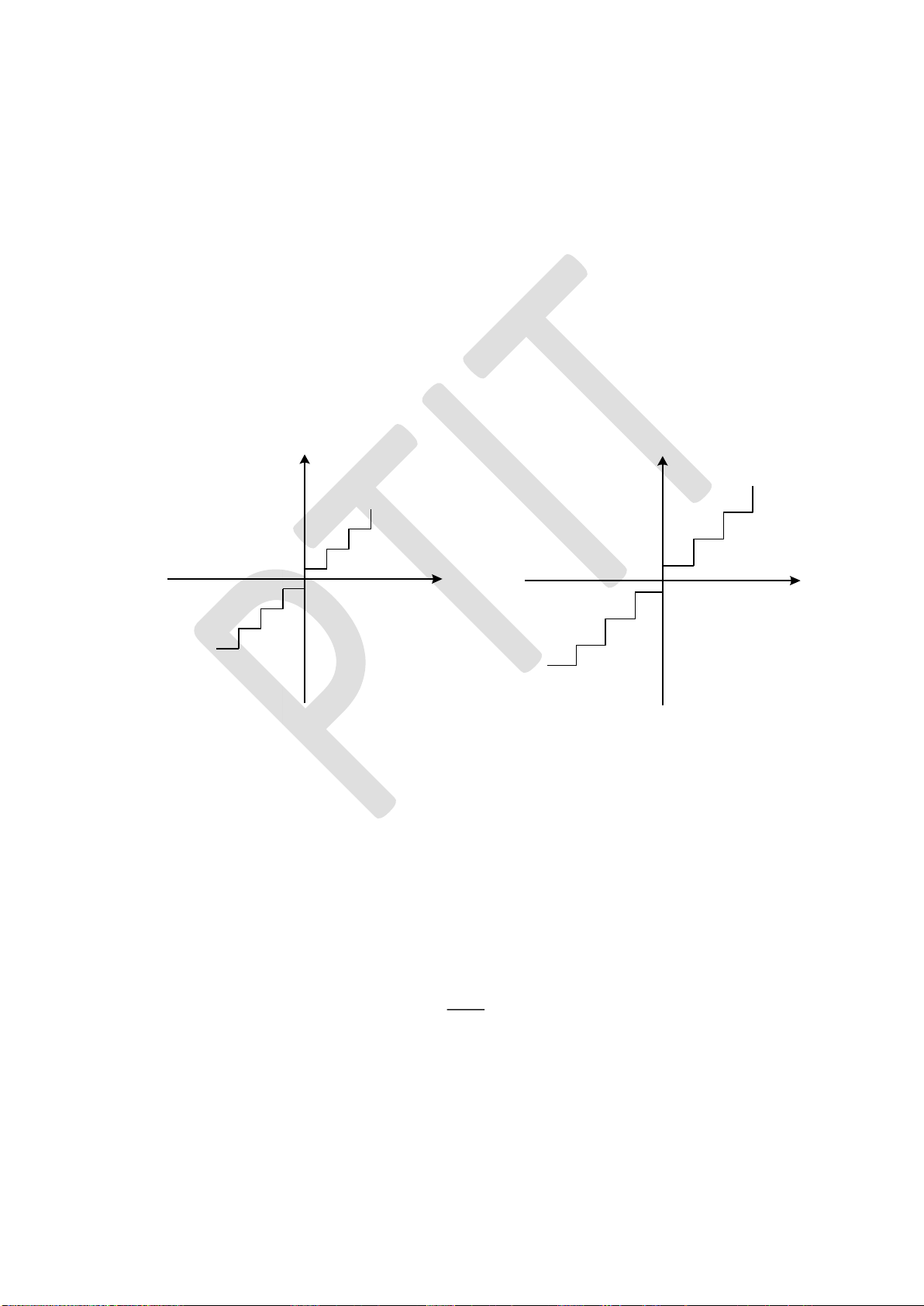
lOMoARcPSD|36067889
‘nhiều’ tại những vùng biên ộ có xác suất cao (tiếng nói nhỏ), còn ‘ít’ tại những vùng
biên ộ có xác suất thấp (tiếng nói lớn). Một phương pháp thường dùng trong iện thoại là
bộ lượng tử Loga với hai kỹ thuật là luật dùng ở Bắc Mỹ và luật dùng ở châu Âu.
Tín hiệu trước hết ược i qua bộ “nén” (dạng hàm Loga) và sau ó i vào bộ lượng tử tuyến
tính.
hay một tổ hợp bit ể biểu diễn. Ở phép lượng tử vectơ thì một nhóm mẫu biên ộ ứng với
một nhóm mẫu lượng tử sẽ tương ứng với một tổ hợp bit ược gọi là một vectơ lượng tử
trong không gian vectơ lượng tử (với lượng tử thường số mẫu bằng 1). Số mẫu trong
nhóm lượng tử gọi là một vectơ mẫu ược lượng tử. Do tính chất tương quan giữa các
mẫu trong tiếng nói mà phép lượng tử vectơ tạo nên mã có ộ nén cao với:
2
= (bit/mẫu) (3.21)
trong ó: là số chiều của vectơ không gian lượng tử; là mức lượng tử trong không
gian vectơ n chiều và là số bit mã hóa trên một mẫu.
Lỗi lượng tử vectơ ược coi là khoảng cách Euclit giữa vectơ lượng tử và vectơ ầu
vào. Được sử dụng cho bộ mã hóa nguồn âm có tốc ộ bit thấp.
c) Lượng tử thích nghi
Như ã nói ở trên là có sự khác nhau của
PDF
trong thời
gian dài và thời gian
ngắn ối với tiếng nói. Sự thay ổi theo thời gian của tiếng nói tạo nên một dải ộng lớn
cỡ 40 dB). Do vậy bộ lượng tử cần ược iều chỉnh thích hợp bằng cách tăng bước
(
lượng tử khi công suất tín hiệu lối vào tăng và giảm khi công suất tín hiệu lối vào giảm
khi ó số mức lượng tử không thay ổi) ta gọi ó là lượng tử thích nghi.
(
f
Q
x
)
(
f
Q
(
x
)
a.
b.
Hình 3.6
:
Lượng tử thích nghi
d)
Lượng tử vectơ
Trong phép lượng tử thông thường mỗi mẫu biên ộ ứng với một giá trị lượng tử
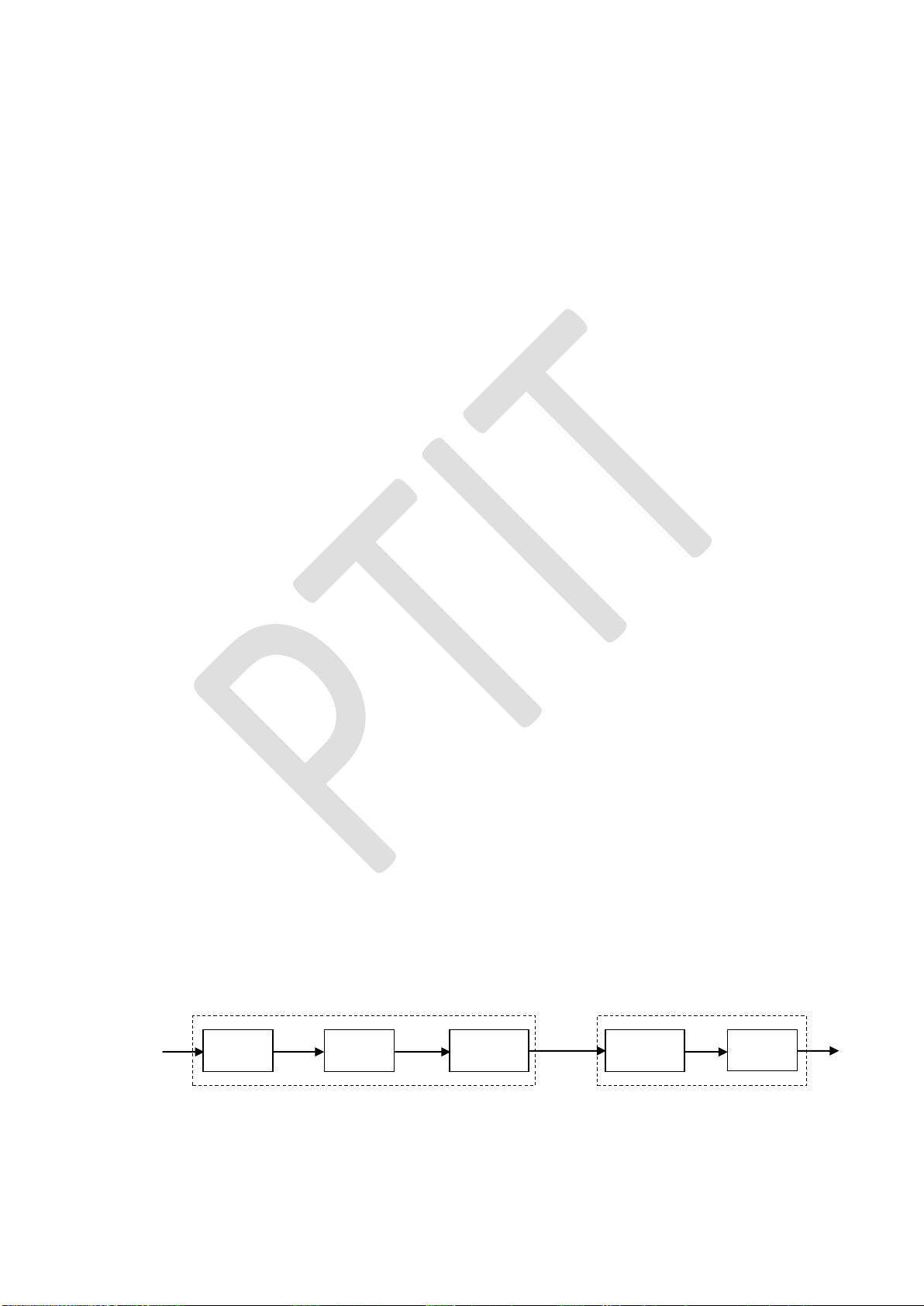
lOMoARcPSD|36067889
3.3.3.3. Kỹ thuật mã hóa nguồn tương tự
Thuật toán mã hoá nguồn tương tự có thể ược xem xét thông qua dạng tiêu biểu
của nó là mã hoá tín hiệu tiếng nói (biến ổi tín hiệu thoại tương tự thành tín hiệu số).
Các bộ mã hoá tiếng nói thường ược chia thành 3 loại chính là bộ mã hoá dạng sóng
miền thời gian, mã hóa dạng sóng miền tần số và mã hoá dựa trên mô hình. Nội dung
của phương pháp mã hoá dạng sóng thời gian là dạng sóng của tín hiệu tiếng nói liên tục
ược rời rạc hoá nhờ lấy mẫu và sau ó ược số hoá nhờ mã hoá nhị phân các giá trị ại diện
cho mức của các mẫu dạng sóng tiếng nói. Phương pháp mã hóa dạng sóng miền tần số
dạng sóng tín hiệu ược chia thành các dải con có tần số khác nhau, mã hóa ộc lập cho
các dải băng. Cơ sở của phương pháp mã hóa dựa trên mô hình nguồn phát âm là việc
phân tích cơ quan phát thanh của con người và quá trình tạo ra âm thanh tiếng nói. Hiển
nhiên, tiếng nói hoàn toàn ược xác ịnh bởi các thông số của mạch lọc và các thông số
kích thích. Mã hoá nguồn phát thanh là việc mã hoá các thông số kích thích và lọc của
mô hình tiếng nói nói trên thành các tín hiệu số. Thay vì truyền i các chuỗi bít mã các
giá trị mẫu dạng sóng tiếng nói như trong phương pháp mã hoá dạng sóng ã nêu trên,
các chuỗi bít mã các thông số của mô hình tạo tiếng nói ược truyền i trong phương pháp
mã hoá nguồn phát âm. Tiếng nói iện tử ược tái tạo lại ở phần thu nhờ các mạch iện tử
thực hiện tổng hợp tiếng nói dựa trên các thông số kích thích và lọc nhận ược. Một trong
các bộ mã hoá tiếng nói tiêu biểu cho phương pháp mã hoá nguồn phát âm là bộ mã hoá
dự oán tuyến tính (LPC), ầu tiên ược phát triển cho các ứng dụng quân sự. Tuy nhiên kỹ
thuật này khá phức tạp, có ộ trễ cao, giá thành ắt bù lại có tỷ lệ nén lớn và cho tốc ộ bit
mã hóa thấp.
a) Mã hóa dạng sóng thời gian a-1)
Phương pháp iều chế xung mã PCM
PCM ược ặc trưng bởi ba quá trình. Đó là lấy mẫu, lượng tử hoá và mã hoá. Ba
quá trình này gọi là chuyển ổi A/D. Muốn khôi phục lại tín hiệu analog từ tín hiệu số
phải trải qua hai quá trình: Giải mã – dãn số và lọc thông thấp. Hai quá trình này gọi là
chuyển ổi D/A.
Tín hiệu
analog
B
ộ
mã hoá-
nén s
ố
B
ộ
l
ấ
y
m
ẫ
u
B
ộ
lượ
ng
t
ử
hoá
B
ộ
gi
ả
i mã
-
dãn s
ố
B
ộ
l
ọ
c
th
ấ
p
Đườ
ng
truy
ề
n
V
PAM
Tín hi
ệ
u
analog
Chuy
ển đổ
i A/D
Chuy
ển đổ
i D/A
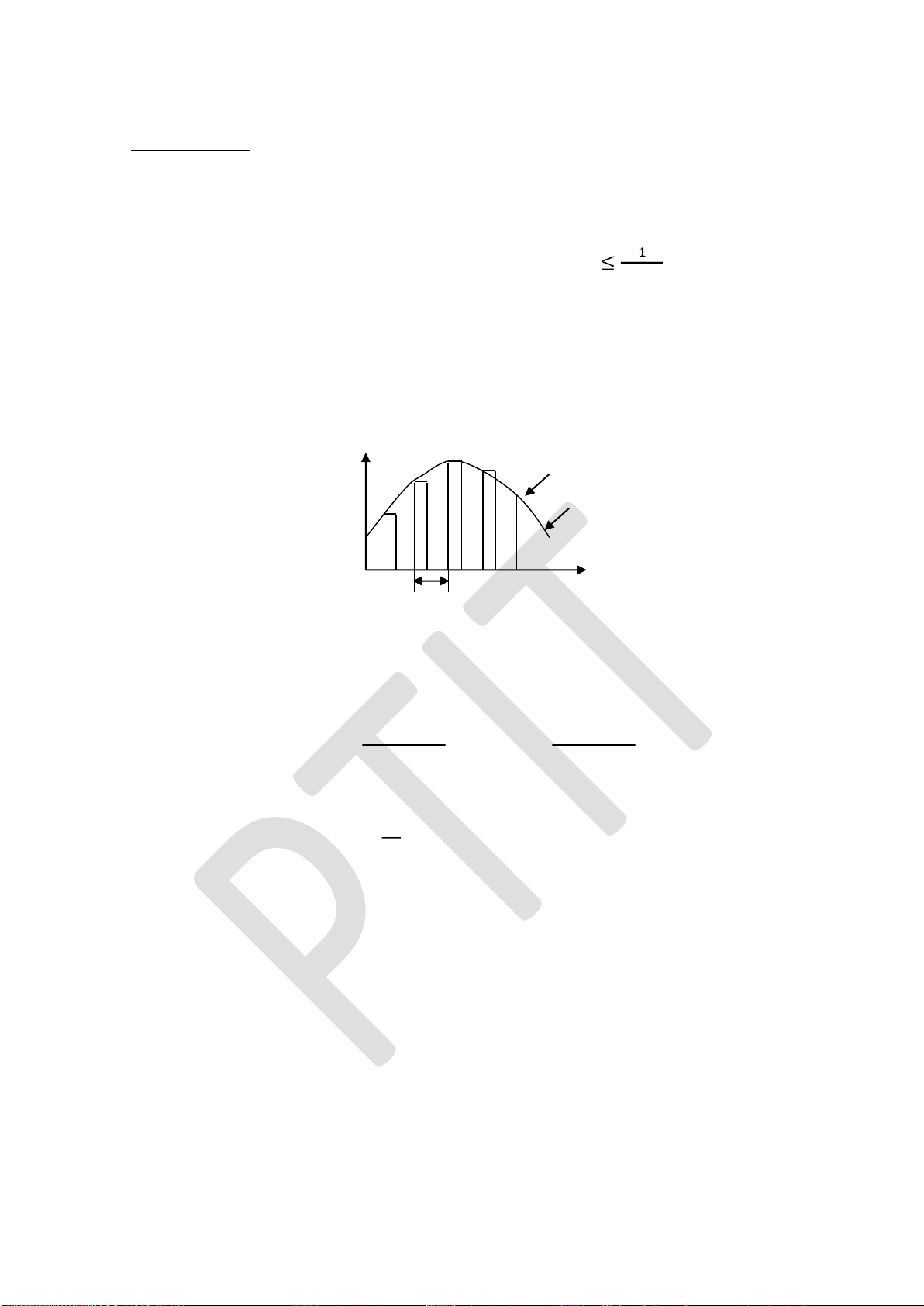
lOMoARcPSD|36067889
Hình 3.7: Sơ ồ khối quá trình chuyển ổi A/D và D/A trong hệ thống PCM
Chuyển ổi A/D:
- Lấy mẫu: Quá trình chuyển ổi tín hiệu tương tự thành dãy xung iều biên (V
PAM
). Chu
kỳ của dãy xung lấy mẫu (T
m
) ược xác ịnh theo ịnh lý lấy mẫu của Nyquist:
2
(3.22)
trong ó
là tần số lớn nhất trong băng phổ của tín hiệu tương tự.
S(t) Xung lấy mẫu
Tín hiệu analog
t
T
m
Hình 3.8: Lấy mẫu tín hiệu tương tự
Tín hiệu thoại có băng tần hữu hiệu từ 0,3 ến 3,4 KHz. Từ biểu thức (3.22), có thể lấy
chu kỳ lấy mẫu tín hiệu thoại là:
1 1
=
2×4000 ()
= 125 <
2×3400 ()
(3.23) Hoặc
tần số lấy mẫu tín hiệu thoại:
1
=
= 8000 () = 8 () (3.24)
- Lượng tử hóa: Lượng tử hóa nghĩa là chia biên ộ của tín hiệu thành các khoảng ều
hoặc không ều, mỗi khoảng là một bước lượng tử, biên ộ tín hiệu ứng với ầu hoặc cuối
của mỗi bước lượng tử gọi là một mức lượng tử. Sau khi có các mức lượng tử thì biên ộ
của các xung mẫu ược làm tròn ến mức gần nhất. Mục ích của lượng tử hoá ể khi thực
hiện mã hoá giá trị mỗi xung lấy mẫu thành một từ mã có số lượng bit ít nhất.
Quá trình lượng tử hoá có mô hình toán học như sau:
=
+
(3.25)
là giá trị
lượng tử của
và
là sai số lượng tử (thường coi ó là nhiễu cọng).
Có hai phương pháp lượng tử hoá: Đều và không ều.
Lượng tử hoá ều: chia biên ộ các xung lấy mẫu thành các khoảng ều nhau, mỗi khoảng
là một bước lượng tử ều, ký hiệu là . Các ường song song với trục thời gian là các mức

lOMoARcPSD| 36067889
lượng tử. Sau ó làm tròn biên ộ xung lấy mẫu tới mức lượng tử gần nhất sẽ nhận ược
xung lượng tử. Nếu biên ộ của tín hiệu analog biến thiên trong khoảng từ -a ến a thì số
lượng mức lượng tử và có mối quan hệ sau ây:
= 2/ (3.26)
Làm tròn biên ộ xung lấy mẫu gây ra méo lượng tử. Biên ộ xung méo lượng tử nằm
trong giới hạn từ - /2 ến + /2. Công suất méo lượng tử P
MLT
ược xác ịnh theo biểu thức
sau ây:
/2 2
() =
12
2
(3.27)
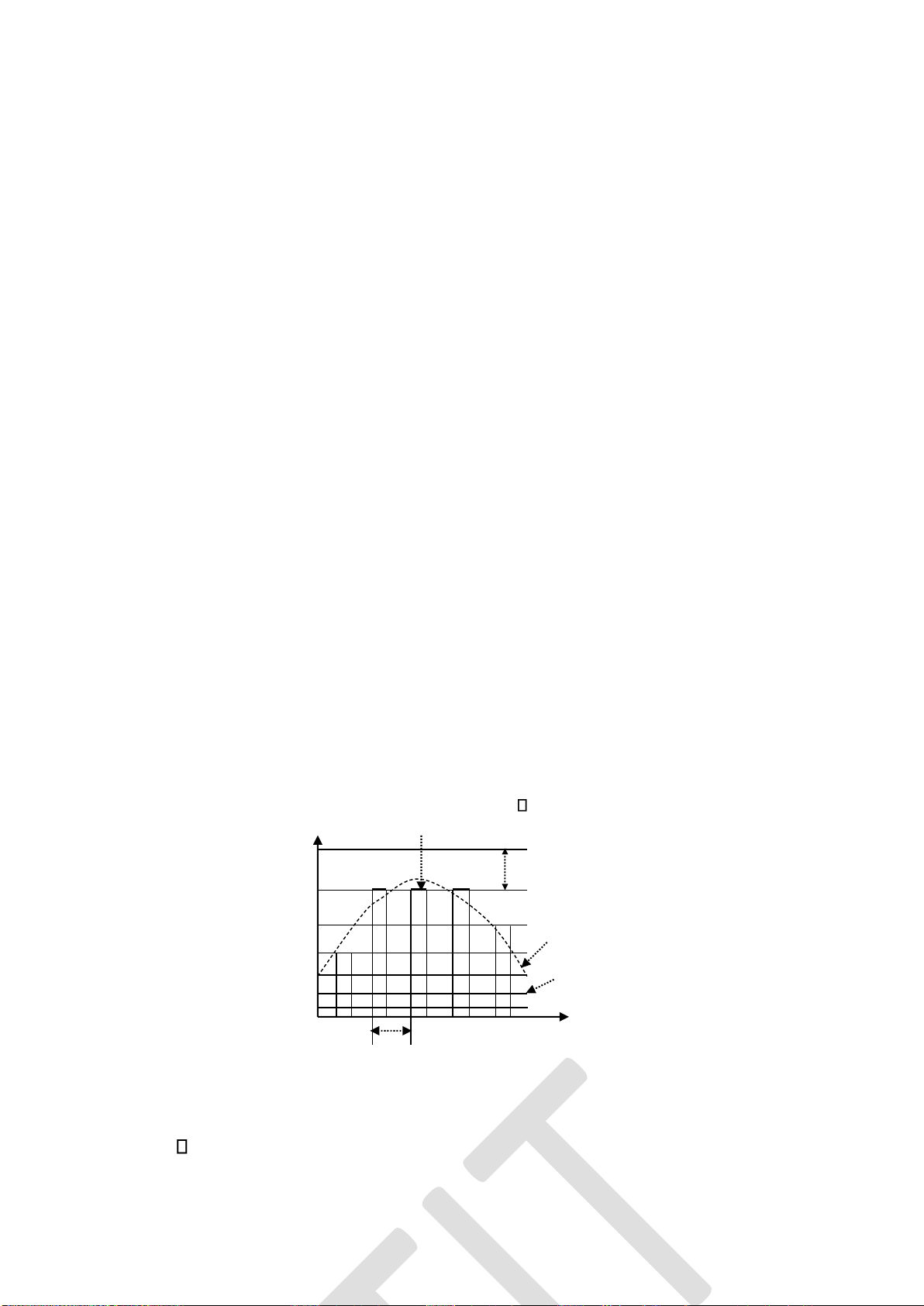
lOMoARcPSD| 36067889
có cường ộ yếu tạo thành. Vì thế nếu sử dụng lượng tử hoá ều sẽ làm giảm chất lượng
tín hiệu thoại tại ầu thu. Muốn khắc phục nhược iểm này, trong thiết bị ghép kênh PCM
chỉ sử dụng lượng tử hoá không ều.
Lượng tử hoá không ều: Trái với lượng tử hoá ều, lượng tử hoá không ều chia biên ộ
xung lấy mẫu thành các khoảng không ều theo nguyên tắc khi biên ộ xung lấy mẫu càng
lớn thì ộ dài bước lượng tử càng lớn, như trên hình 3.10. Lượng tử hoá không ều ược
thực hiện bằng cách sử dụng bộ nén.
S(t) Xung lượng tử
7
i
- Bước lượng tử không ều
6
5
Tín hiệu analog
4
3 Mức lượng tử
2
1
0 t
Tm
Hình 3.10: Lượng tử hoá không ều
- Mã hóa:
Đặc tính biên ộ bộ mã hoá - nén số
Chức năng của mã hoá là chuyển ổi biên ộ xung lượng tử thành một từ mã gồm
một số bit nhất ịnh. Theo kết quả nghiên cứu và tính toán của nhiều tác giả thì trong

lOMoARcPSD| 36067889
trường hợp lượng tử hoá ều, biên ộ cực ại của xung lấy mẫu tín hiệu thoại bằng 4096 .
Do ó mỗi từ mã phải chứa 12 bit, dẫn tới hậu quả là tốc ộ bit mỗi kênh thoại lớn gấp 1,5
lần tốc ộ bit tiêu chuẩn 64 Kbit/s. Muốn nhận ược tốc ộ bít tiêu chuẩn, thường sử dụng
bộ nén có ặc tính biên ộ dạng logarit, còn ược gọi là bộ nén analog. Biểu thức toán học
của bộ nén analog theo tiêu chuẩn Châu Âu có dạng:
y
111 Axlnlnln
AAx
A khi
khi
01A
xx
1
A
1
(3.28)
trong ó: A= 87,6 ặc trưng cho mức ộ nén, x = V
vào
/ V
vào max
; y = V
ra
/ V
ra max
.
Từ biểu thức (3.28) xây dựng ược ường cong thể hiện ặc tuyến bộ nén A. Đặc tuyến
bộ nén phải ối xứng với ặc tuyến bộ dãn ể không gây ra méo tín hiệu khi khôi phục tín
hiệu tại ầu thu. Dạng ường cong ặc tuyến của bộ nén và bộ dãn như hình 3.11.
Tuy nhiên, do bộ nén tương tự tại phía mã hoá và bộ dãn tương tự tại phía giải mã
chứa các diode bán dẫn nên gây ra méo phi tuyến. Trong PCM sử dụng bộ mã hoá - nén
số và bộ giải mã- dãn số ể loại trừ méo phi tuyến. Tóm lại, sử dụng mã hoá- nén số vừa
ạt ược mục tiêu lượng tử hoá không ều, vừa ạt ược mục tiêu mỗi từ mã chỉ có 8 bit.
Biên ộ ra Đặc tuyến nén
+
1
Đặc tuyến dãn
-1
Biên ộ vào
+
1
-1
Hình 3.11: Đặc tuyến bộ nén và bộ dãn analog
Chuyển ổi D/A:

lOMoARcPSD|36067889
Bộ giải mã - dãn số có chức năng chuyển ổi mỗi từ mã 8 bit thành một xung lượng
tử ã bị nén và sau ó dãn biên ộ xung tới giá trị như khi chưa bị nén. Dãy xung ầu ra bộ
giải mã - dãn số qua bộ lọc thông thấp có tần số cắt bằng 3,4 KHz ể khôi phục lại tín
hiệu thoại tương tự. a-2) Điều xung mã vi sai DPCM
Như ta ã biết, PCM ược thực hiện bằng cách mã hóa các giá trị mẫu ược lượng tử
hóa của tín hiệu liên tục lối vào. Số bit mã cần thiết, chẳng hạn cho tín hiệu iện thoại,
như phần trước ã trình bày, ã ược CCITT xác ịnh phải là 8 bít. Tốc ộ tín hiệu thoại PCM
như vậy là 64 Kbit/s, chiếm phổ tần khá lớn. Những rung ộng chuẩn chu kỳ của thanh
huyền và các chuyển ộng hạn chế của các bộ phận thuộc cơ quan phát âm như môi và
lưỡi thực tế tạo ra các mẫu âm thanh rất tương quan trong tín hiệu âm hữu thanh. Ngược
lại, các âm vô thanh thì có xu hướng không tương quan. Trong àm thoại, một người àm
thoại tiêu biểu thường nói trong 40% thời gian và ối với các giai oạn tiếng nói tích cực
(giai oạn có nói trong cuộc àm thoại) thì các âm hữu thanh xảy ra gấp 4 lần so với các
âm vô thanh. Sự trội hơn hẳn của các âm hữu thanh có nghĩa là tính tương quan trong
các tín hiệu âm thoại có thể khai thác ược một cách có hiệu quả. Do tính tương quan cao
của các mẫu tiếng nói, sai lệch giữa hai mẫu kế nhau thường khá nhỏ so với giá trị của
từng mẫu.Vì vậy, thay vì mã hóa các giá trị mẫu tiếng nói như với PCM, chỉ cần mã hóa
sai lệch giữa các mẫu tiếng nói liên tiếp. Do ó, chỉ cần một số bit ít hơn ể mã.
Mã hóa: Đây chính là nguyên tắc của iều chế xung vi sai DPCM. DPCM sử dụng
bộ lọc ể hạn chế dải tần tín hiệu thoại analog ến 3,4 KHz. Bộ lấy mẫu có tần số lấy mẫu
f
m
= 8 KHz. X
n
là giá trị biên ộ xung lấy mẫu hiện tại.
là giá trị biên ộ các xung lấy
mẫu trước ó.
là giá trị dự oán của biên ộ xung lấy mẫu tiếp theo:
X
ˆ
n
p
a X
i
~
n i
(3.29)
i 1
trong ó:
là hệ số dự oán, ược chọn ể tối thiểu hoá sai số giữa giá trị biên ộ xung lấy
mẫu hiện tại
và giá trị dự oán của biên ộ xung lấy mẫu tiếp theo.
là giá trị dự oán
biên ộ xung lấy mẫu tiếp theo, ược ngoại suy từ p giá trị xung lấy mẫu trước ó. e
n
là hiệu
số, hay còn gọi là vi sai giữa
và
. e
n
ược mã hoá thành 4 bit.
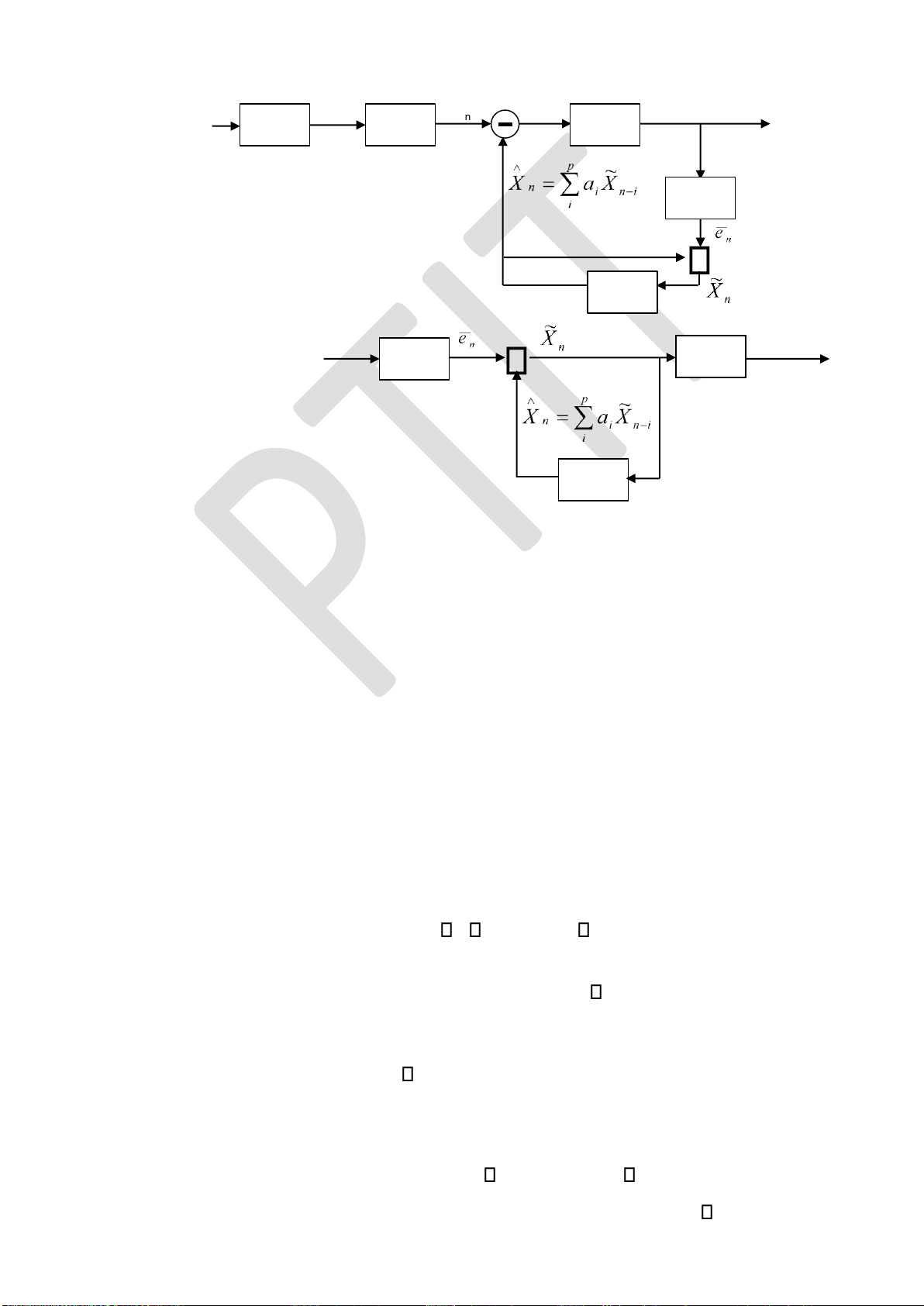
lOMoARcPSD|36067889
a-3) Điều chế Delta (DM)
Khác với PCM và DPCM, trong iều chế Delta mỗi từ mã chỉ có một bit (-1 hoặc
+1). Mặt khác ể tránh méo tín hiệu analog tại phía thu, tần số lấy mẫu tại phía phát lớn
hơn nhiều lần so với tần số lấy mẫu của PCM và DPCM (
= 8 ). Tần số lấy mẫu
của DM ược xác ịnh theo biểu thức sau ây:
()
2
()
/ (3.30)
trong ó:
()
(KHz) là tần số lấy mẫu của DM,
()
(KHz) là tần số cực ại của tín hiệu
tương tự,
(V) là biên ộ cực ại của tín hiệu tương tự, (V) là bước lượng tử ều.
Mã hóa: Tín hiệu tương tự ược lấy mẫu theo chu kỳ
()
(
()
= 1/
()
). Thiết
lập hàm bậc thang, mỗi bậc bằng theo nguyên tắc khi sườn tín hiệu tăng thì bậc thang
i lên, khi sườn tín hiệu nằm ngang thì bậc thang cũng nằm ngang, khi sườn tín hiệu giảm
thì bậc thang i xuống. Tại thời iểm lấy mẫu nếu giá trị tín hiệu () lớn hơn giá trị hàm
bậc thang trước ó một chu kỳ thì nhận ược > 0 và mã hoá thành +1. Ngược lại, tại
thời iểm lấy mẫu mà giá trị của () bé hơn giá trị hàm bậc thang thì < 0 và ược mã
Hình 3.12
:
Sơ ồ
kh
ố
i mã hóa và gi
ả
i mã DPCM
Gi
ả
i mã
:
Tín hi
ệ
u DPCM t
ại ầ
u vào là các t
ừ
mã 4 bit. Sau khi gi
ả
i mã, m
ỗ
i t
ừ
mã
ượ
c chuy
ể
n thành m
ột xung có biên ộ
b
ằ
ng
và ược ưa tớ
i b
ộ
c
ộ
ng. M
ột ầ
u vào
khác c
ủ
a b
ộ
c
ộng ượ
c n
ố
i t
ới ầ
u ra b
ộ
d
ự
oán. Đầ
u ra b
ộ
c
ộ
ng xu
ấ
t hi
ệ
n m
ộ
t xung
l
ấ
y m
ẫu có biên ộ
b
ằ
ng xung l
ấ
y m
ẫ
u phía phát. Dãy xung l
ấ
y m
ẫ
u qua b
ộ
l
ọc ể
khôi
ph
ụ
c l
ạ
i tín hi
ệu tương tự
.
B
ộ
gi
ả
i
mã
B
ộ
l
ọ
c
B
ộ
d
ự
oán
Tín hi
ệ
u
DPCM
Tín hi
ệ
u
tương tự
Máy thu
B
ộ
l
ọ
c
B
ộ
l
ấ
y
m
ẫ
u
B
ộ
mã
hoá
B
ộ
gi
ả
i
mã
B
ộ
d
ự
oán
Tín hi
ệ
u
tương
t
ự
Tín hi
ệ
u
DPCM
X
n
e
n
Máy phát
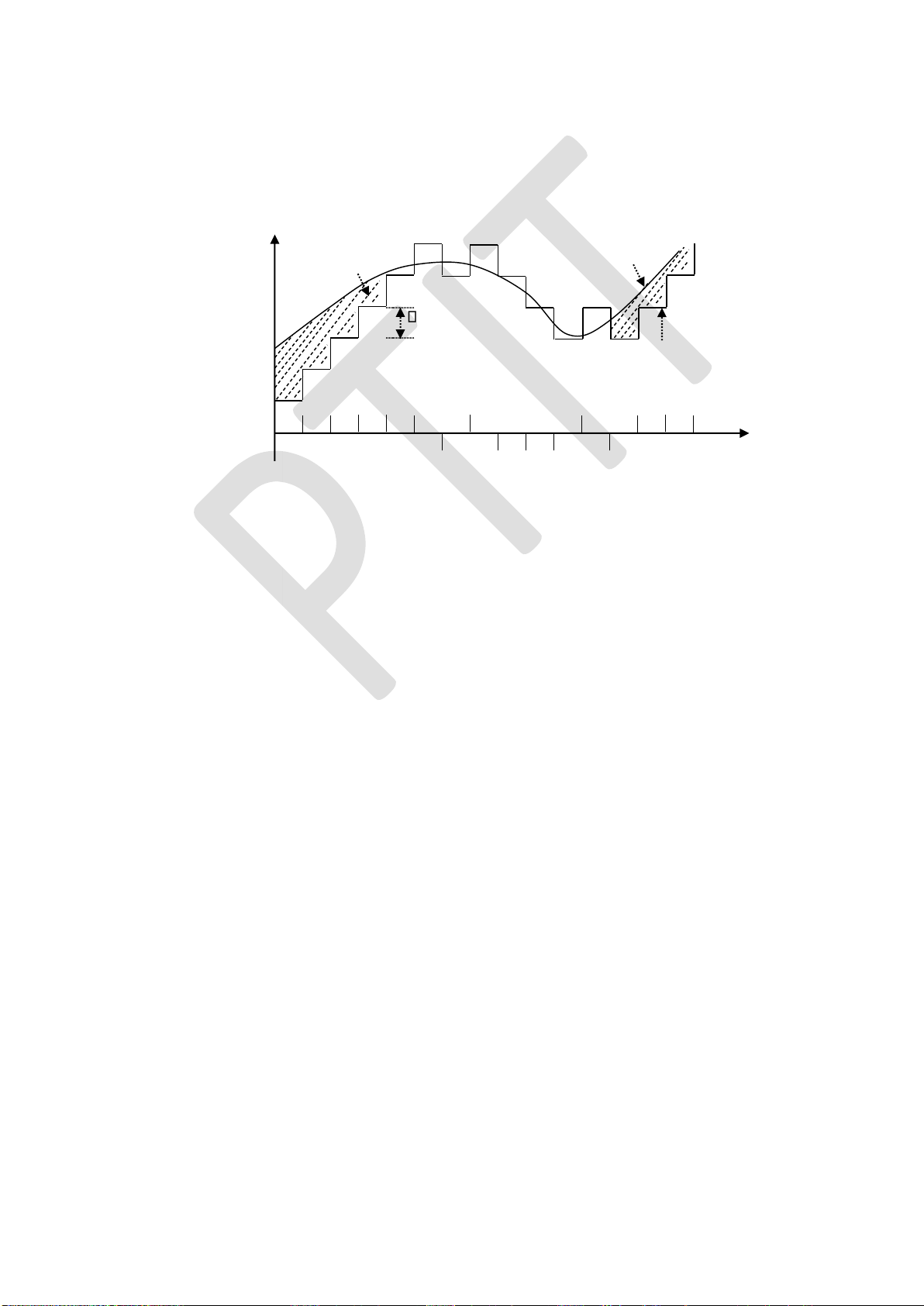
lOMoARcPSD| 36067889
hoá thành 0. Trong quãng thời gian sườn tín hiệu tăng hoặc giảm nhanh thì hàm bậc
thang tăng hoặc giảm không kịp và gây ra quá tải sườn.
Biên ộ
Quá tải sườn Tín hiệu analog
Hàm bậc thang
Tín hiệu DM
0
t
Hình 3.13: Chuyển ổi A/D trong DM
Giải mã: Tại phía thu tái lập lại hàm bậc thang dựa vào kết quả giải mã. Nhận ược một
dãy các bit 1, bộ tích phân tại máy thu tạo ra dãy bậc thang i lên, nhận ược dãy các bit 1
và 0 an xen nhau thì bộ tích phân tạo ra dãy bậc thanh nằm ngang và nhận ược dãy các
bit 0 thì bộ tích phân tạo lập dãy bậc thang i xuống. Tín hiệu dạng bậc thang qua bộ lọc
tách ra giá trị trung bình của hàm bậc thang và ó là ộng tác khôi phục lại tín hiệu tương
tự. Vì tín hiệu tương tự tại ầu ra bộ lọc là giá trị trung bình của hàm bậc thang nên trong
quãng thời gian quá tải sườn thì dạng sóng tín hiệu tương tự thu ược bị lệch so với dạng
sóng tương tự tại phía phát. Do ó quá tải sườn gây ra méo tín hiệu. Để khắc phục méo
tín hiệu do quá tải sườn cần sử dụng kỹ thuật iều chế Delta thích ứng (ADMo). a-4) Điều
chế xung mã vi sai thích ứng (ADPCM)
Như ta ã trình bày trong phần trên, tốc ộ bit của tín hiệu PCM gồm các từ mã 8 bit
và tín hiệu tiếng nói ược lấy mẫu với tần số 8 KHz bằng 64 Kbit/s. Nếu số lượng bit của
từ mã giảm còn 4 như trong iều chế mã xung vi sai (DPCM) thì tốc ộ bit giảm và chỉ
bằng 32 Kbit/s. Có xu hướng tiêu chuẩn hóa quốc tế tốc ộ 32 Kbit/s ối với tín hiệu mã
tiếng nói nhờ sử dụng ADPCM. Vấn ề này ược phản ánh trong khuyến nghị G.721 của
CCITT (nay ITU-T), có liên quan ến iều chế mã xung vi sai tự thích nghi 32 Kbit/s và
các tài liệu khác.
Bộ lượng tử hóa tự thích nghi thay ổi bước lượng tử của nó phù hợp với phương
sai của các xung lấy mẫu tín hiệu i qua. Các thuật toán ược phát triển cho iều chế mã
xung vi sai khi mã hóa tín hiệu tiếng nói bằng cách sử dụng bộ lượng tử hóa và bộ dự
oán tự thích nghi, trong ó các hệ số thay ổi có chu kỳ ể phản ánh thống kê của tín hiệu

lOMoARcPSD|36067889
vào. Hơn nữa truyền các hệ số dự oán ến máy thu, và như vậy làm tăng số bit truyền và
tốc ộ bit, bộ dự oán thu tính các hệ số riêng của nó.
b. Mã hóa dạng sóng trong miền tần số
Mã hóa ược tiến hành theo các vùng tần số. Phổ của tín hiệu tiếng nói ược chia
thành các dải hẹp hoặc biến ổi thành các tần số rời rạc và ược mã hóa ộc lập với nhau.
Tùy theo mức ộ quan trọng của các dải tần con hay tần số rời rạc mà số bit sử dụng mã
hóa nhiều hay ít.
b-1) Mã hóa theo băng con (SBC)
Phổ của tín hiệu ược chia thành 4 ến 8 dải con bằng các bộ lọc. Các băng con ược
di chuyển biên trái về 0 ể có thể dùng tốc ộ lấy mẫu Nyquist ở trong miền thời gian và
ược lấy mẫu với số bít khác nhau phụ thuộc biên ộ phổ và tiêu chuẩn thính giác của con
người.
b-2) Mã hóa biến ổi thích nghi
Mã hóa biến ổi thích nghi là kỹ thuật mã hóa trong miền tần số dùng phương pháp
chuyển ổi toán học. Có tốc ộ mã hóa trong khoảng 9,6 – 20 Kbit/s. Các mẫu tín hiệu
trong một cửa sổ ược biến ổi thành một tập các tần số rời rạc, biên ộ của các tần số này
ược lượng tử và mã hóa riêng biệt ể truyền i. Tại bộ thu các hệ số lượng tử ược biến ổi
ngược ể tạo lại tín hiệu ban ầu. Ví dụ như mã hóa biến ổi cosin rời rạc (DCT). Trên thực
tế DCT hay IDCT ược tính theo thuật toán nhanh ể áp ứng thời gian thực tế và việc thiết
kế bước lượng tử khác nhau ở các tần số khác nhau cũng ược thực hiện theo thời gian
ược truyền như thông tin tiêu ề (cỡ 2 Kbit/s) số bit lượng tử ở tần số rời rạc tỷ lệ với
năng lượng của nó. Ngoài ra còn có các phép chuyển ổi KLT, DFT...
c) Mã hóa nguồn dựa trên mô hình phát âm
Kỹ thuật này dùng ể tách các thông số của nguồn âm và mã hóa các thông số này
truyền ến nơi thu. Tại nơi thu các thông số này ược giải mã ể iều khiển một nguồn âm
tương tự như nơi phát ể tái tạo lại tín hiệu. Các bộ phát âm có tốc ộ bit rất thấp nhưng
phức tạp và phụ thuộc vào nguồn âm. Bộ mã hóa dựa trên mô hình làm việc rất tốt với
tốc ộ bit thấp từ 2 ến 5 Kbit/s và ví dụ iển hình của các bộ mã hóa tham số là bộ mã hóa
dự oán tuyến tính LPC và bộ mã hóa dự oán tuyến tính kích thích hỗn hợp MELP. c-1)
Mã hóa LPC
Mô hình này coi cơ quan phát âm như bộ lọc cực với hàm truyền ược mô tả:
H z( )
M
G
(3.31)
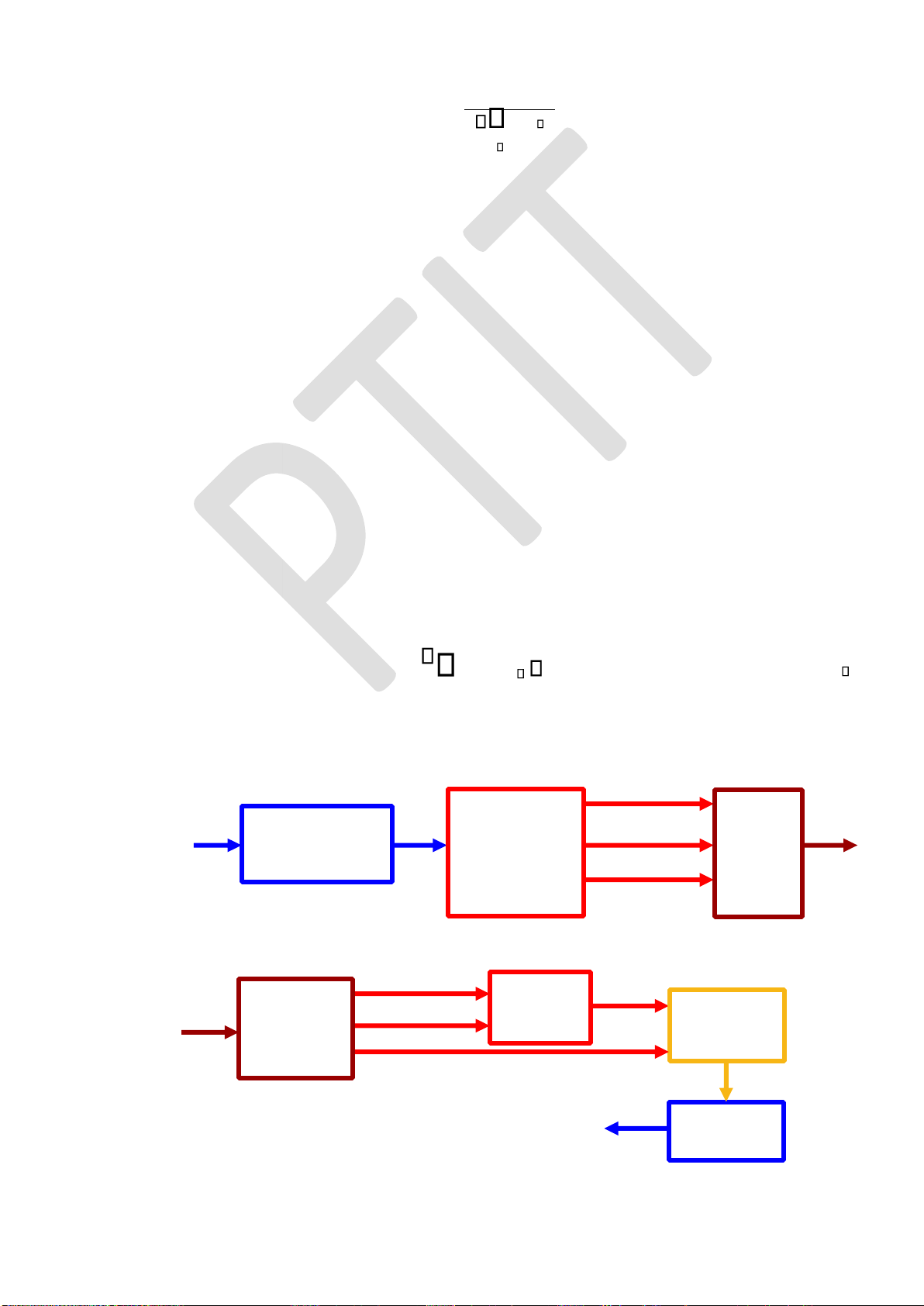
lOMoARcPSD|36067889
1 b zk k
k 1
trong ó: G là hệ số khuếch ại, z
-1
biểu diễn toán tử trễ ơn vị. Kích thích bộ lọc hoặc là
xung với tần số pitch hoặc nhiễu trắng ngẫu nhiên tùy thuộc oạn tiếng nói là hữu thanh
hay vô thanh.
Các hệ số của bộ lọc ược xác ịnh dùng kỹ thuật dự oán tuyến tính giống như trong bộ
ADPCM. Song thay cho việc truyền các giá trị lượng tử của tín hiệu lỗi giữa mẫu tiên
oán và mẫy thực (ADPCM), hệ thống LPC truyền chỉ những ặc tính chọn lọc của tín
hiệu lỗi ó là các thông số như: hệ số khuếch ại, tần số pitch, quyết ịnh hữu thanh hay vô
thanh, cho phép xấp xỉ tín hiệu lỗi chính xác. Tại bộ thu các thông tin trên ược dùng ể
tái tạo lại tín hiệu lỗi ể kích thích bộ lọc tổng hợp. Còn bộ lọc tổng hợp tại bộ thu ược
iều khiển bởi các hệ số ự oán nhận ược. Trên thực tế nhiều bộ LPC phát các hệ số bộ lọc
trong ó ã biểu diễn tín hiệu lỗi và có thể tổng hợp trực tiếp tại bộ thu.
Xác ịnh hệ số dự oán: tín hiệu dự oán là một tổng có trọng số của p mẫu trước ó (p dài
từ 10 – 15).
s
n
p
a s
k n k
e
n
(3.32) k 1
trong ó: e
n
là lỗi dự oán.
Hình 3.14: Sơ ồ bộ mã hóa LPC
Hình 3.15: Sơ ồ bộ giải mã LPC
Lấy mẫu
f
s
=8000 mẫu/s
a
{
p
)}
k
(
Xác ịnh âm
hữu thanh hay
vô thanh và
kích thích
Tín hiệu
thoại
Mã hóa
Pitch
Kích thích
Bộ lọc IIR
H(z)
Lọc thông
thấp
a
{
p
)}
k
(
Bộ tạo tín
hiệu
Tín hiệu
thoại
Giải mã
Pitch
Kích thích

lOMoARcPSD|36067889
Các hệ số dự oán ược xác ịnh qua việc làm tối thiểu năng lượng trung bình E của
tín hiệu lỗi:
N N
p
2
E e
n
2
a s
k n k
(3.33)
n 1
n
1 k 0
Với
0
. Thường lỗi ược tính trong cửa sổ 10ms tương ứng với N = 80. Cho
vi phân của E theo a
m
bằng 0 ta có:
E N p p N p
am n 12sn m k 0a sk n k k 0 1n sn m n k k s a k 0C amk k 0
(3.34)
Với C
m
là hệ số tương quan giữa các mẫu r, m. Sau khi xác ịnh C
m
giải phương
trình trên có thể xác ịnh ược các hệ số dự oán. Các hệ số dự oán thường không ược mã
hóa truyền i trực tiếp (vì cần ến 8 -10 bit/ hệ số) mà truyền các hệ số phản ánh (chúng
có dải ộng nhỏ hơn chỉ cần 6 bit/ hệ số). Như vậy một bộ dự oán bậc 10 tổng số bit dùng
cho các thông số mô hình trên 1 frame là 72 (bao gồm 5 cho khuếch ại và 6 cho chu kỳ
pitch). Nếu các thông số ược ước lượng lại cứ sau 15 – 30ms thì tốc ộ bit sẽ là 2400 –
4800 bit/s. Việc mã hóa các hệ số phản ánh có thể ược cải tiến khi dùng thêm các bộ
biến ổi phi tuyến ( ặt trước bộ mã hóa) sẽ làm giảm ộ nhạy của các hệ số phản ánh ối với
lỗi lượng tử. Chúng thường dùng là biến ổi tỷ số loga (LAR).
LAR k
n
( ) tanh (
1
R k
n
( ))log
10
1
1 R k
R k
n
n
( )
( )
(3.35)
Các LPC khác nhau trong cách tạo ra tín hiệu lỗi tại bộ thu. Có 3 cách cơ bản: cách
thứ nhất rất phổ biến dùng 2 nguồn kích thích tại bộ thu, một nguồn là nhiễu trắng và
nguồn kia là oạn xung có chu kỳ pitch, việc chọn nguồn này hay nguồn kia kích thích
phụ thuộc vào quyết ịnh voice/unvoice của bộ phát. Kỹ thuật này gặp khó khăn trong
việc tách thông tin về pitch ở bộ phát (ngoài ra sự ồng pha giữa các thành phần hài của
xung kích thích tạo nên tiếng ù trong tiếng nói tổng hợp).
c-2) LPC kích thích bằng a xung (MPE-LPC)

lOMoARcPSD| 36067889
Việc kích thích bằng xung ơn/ chu kỳ pitch luôn làm méo tín hiệu. Atal ã ề nghị
dùng nhiều xung (8 xung/chu kỳ) và iều chỉnh vị trí và biên ộ các xung này ể tối thiểu
lỗi trung bình bình phương có tính tới trọng số thụ cảm. Kỹ thuật này ược gọi là MPE-
LPC làm chất lượng tiếng nói tốt hơn không chỉ do lỗi dự oán ược xấp xỉ tốt hơn mà còn
do nó không òi hỏi tách pitch. Số xung có thể giảm với voive có pitch cao bằng cách kết
hợp một bộ lọc tuyến tính với vòng pitch trong bộ tổng hợp. c-3) LPC kích thích bằng
mã (CELP)
Ở phương pháp này bộ mã hóa và giải mã có chung một bảng mã tín hiệu kích
thích ngẫu nhiên (nhiễu trắng Gauss). Với mỗi tín hiệu tiếng nói bộ phát sẽ tìm trong
bảng mã tín hiệu kích thích lên bộ lọc LPC cho tín hiệu gần giống nhất, sau ó chỉ việc
truyền chỉ số của tín hiệu kích thích này ến bộ thu. Dựa vào chỉ số này bộ thu sẽ tìm ra
tín hiệu kích thích thích hợp. Bộ mã hóa theo kỹ thuật này òi hỏi hơn 500 triệu phép tính
nhân và cộng/ giây. Chúng có thể cho chất lượng tiếng nói cao với việc kích thích ược
mã hóa 0,25 bit/mẫu và có tốc ộ 4,8 Kbit/s.
3.4. MÃ HÓA KÊNH
Thông tin truyền qua kênh thường bị nhiễu phá hoại gây ra các lỗi nên cần phải có
các phương pháp mã hóa có khả năng phát hiện lỗi/ sửa lỗi.
Định lý Shannon mã hóa kênh có nhiễu ở chương II ã chỉ ra rằng: nếu thông lượng
kênh lớn hơn tốc ộ lập tin của nguồn thì có thể truyền tin với sai số nhỏ tuỳ ý. Định lý
này là cơ sở lý thuyết của các loại mã chống nhiễu.
Mã hóa kênh là biện pháp dùng các mã hiệu cho phép phát hiện lỗi hoặc có khả
năng tự sửa lỗi ể mã hóa tín hiệu truyền qua kênh. Mã hóa kênh nhằm cải tiến kỹ thuật
truyền tin cho phép tín hiệu phát i có khả năng chống lại ảnh hưởng của nhiễu. Mã hóa
kênh làm giảm lỗi bit hoặc giảm tỷ số năng lượng bít trên mật ộ nhiễu yêu cầu tại ầu thu.
Có hai hướng tiếp cận cơ bản ể sửa lỗi. Cách tiếp cận thứ nhất liên quan ến việc
phát hiện ra các lỗi và yêu cầu lặp lại tự ộng (ARQ) khi nhận thấy các lỗi này. Hướng
tiếp cận này ngầm ịnh rằng có sẵn một kênh phản hồi ngoài kênh truyền chính ể có thể
chuyển các thông báo yêu cầu truyền lại. Trên thực tế, do vậy, kỹ thuật ARQ này ược
sử dụng rộng rãi trong các hệ thống truyền thông máy tính thông qua các ường dây iện
thoại (vốn có sẵn kênh báo hiệu kèm theo). Cách tiếp cận thứ hai, ó là sửa lỗi trước
(FEC), liên quan ến việc phát hiện lỗi và cố gắng ể sửa lỗi ó. FEC là kỹ thuật ược sử
dụng ến khi mà một kênh phản hồi không tồn tại, do ó việc truyền các thông báo yêu
cầu truyền lại là không thể thực hiện dễ dàng, và kể cả khi có sẵn một kênh như vậy, thì
kỹ thuật này vẫn tối ưu hơn nhiều, vì nhiều khi chỉ vì sai một vài bit mà phải truyền lại
cả một lượng thông tin lớn, thì rất không hiệu quả. Một trường hợp sử dụng FEC là trong
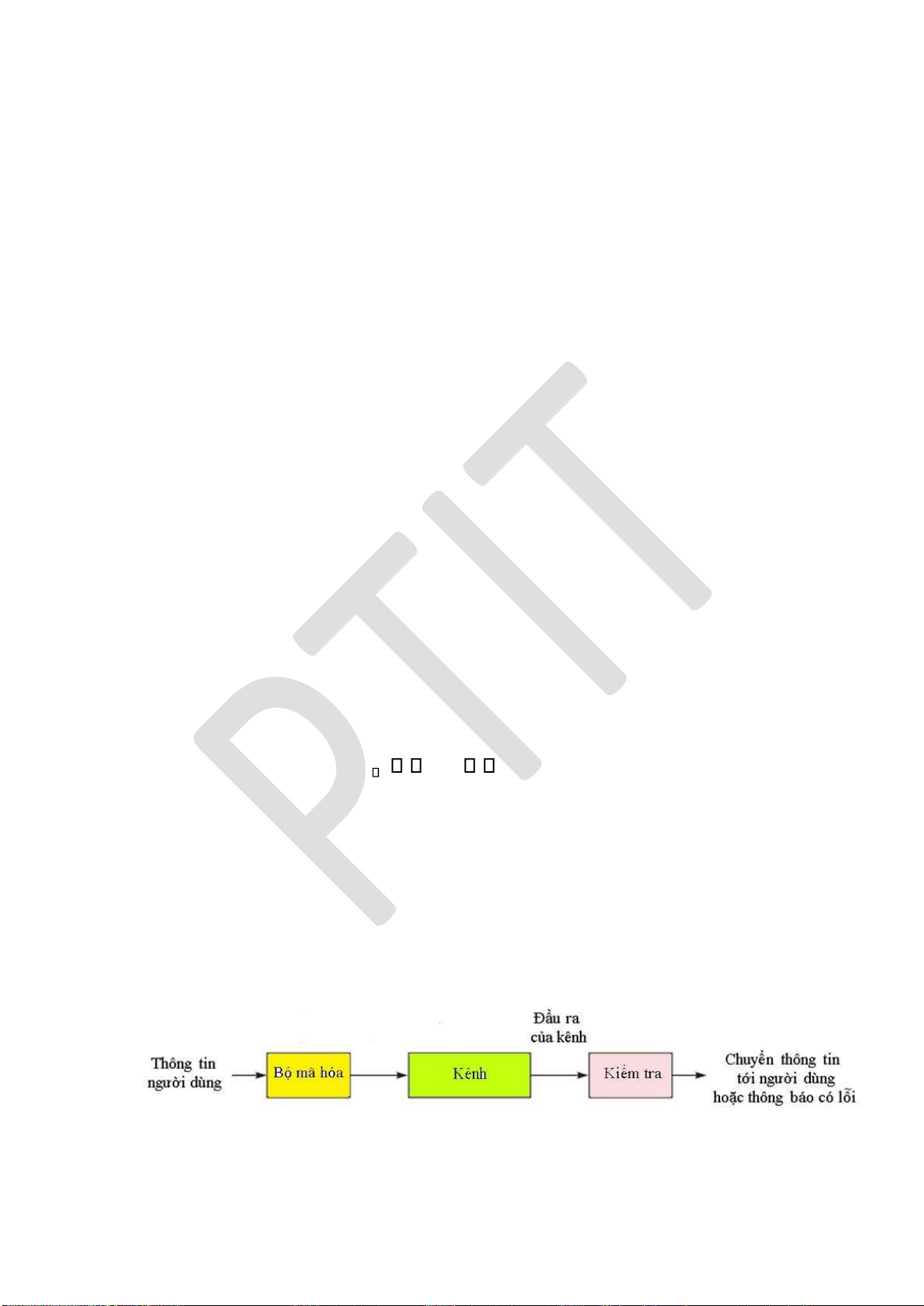
lOMoARcPSD|36067889
thông tin vệ tinh và thông tin vũ trụ. Một ứng dụng gần ây của FEC là trong các ĩa CD.
Nó ã cung cấp một khả năng áng kinh ngạc, ó là khả năng tái tạo lại âm thanh hoàn hảo,
kể cả khi mặt ĩa có bị xước hoặc dính bụi bẩn. Tuy nhiên, với cả hai hướng tiếp cận này,
chúng ta nhận thấy rằng ều cần bước ầu tiên: Phát hiện lỗi. Sự khác biệt giữa 2 hướng
tiếp cận này chỉ là ARQ “lãng phí” băng thông ể truyền lại, trong khi FEC thì yêu cầu
các bít dư thừa ược ưa vào thông tin truyền i thông qua các quá trình xử lý ể có thể sửa
ược lỗi ở phía thu.
Trong mục này sẽ khảo sát kỹ bốn loại mã chống nhiễu ược dùng rộng rãi nhất
trong truyền số liệu ó là: Mã kiểm tra chẵn lẻ (Parity), Mã a thức (Mã vòng kiểm tra
(CRC)), Mã khối tuyến tính (mã Hamming); Mã tích chập.
3.4.1. Mã kiểm tra chẵn lẻ
3.4.1.1. Mã kiểm tra chẵn lẻ ơn
Mã ơn giản nhất là mã kiểm tra chẵn lẻ ơn. Với một chuỗi k bit thông tin, nó sẽ
thêm vào 1 bit kiểm tra ể tạo nên một từ mã. Kiểm tra chẵn lẻ ảm bảo rằng tổng số bit 1
trong từ mã là chẵn. Bit kiểm tra trong trường hợp này gọi là bit chẵn lẻ. Mã phát hiện
lỗi này ược sử dụng trong bảng mã ASCII, với mỗi ký tự sẽ ược thể hiện bằng 7 bit, và
8 bit nếu tính cả 1 bit chẵn lẻ ược thêm vào. Mã này là một ví dụ về một mã tuyến tính
iển hình vì bit chẵn lẻ ược tính toán bằng việc cộng modulo 2 của toàn bộ các bit thông
tin.
b
k 1
b
1
b
2
... b
k
mod2
(3.36)
trong ó: b
1
, b
2
,…, b
k
là các bit thông tin.
Nhắc lại về phép cộng modulo 2: 0 + 0 = 0; 0 + 1 = 1, 1 + 0 = 1; 1 + 1 = 0. Do ó,
nếu như số bit mang thông tin có chẵn số 1 thì bit chẵn lẻ sẽ mang giá trị là 0, và ngược
lại. Kết quả là, dựa theo luật trên sẽ có với một dòng bit sử dụng mã chẵn lẻ ể kiểm tra,
thì số bit 1 (kể cả bit chẵn lẻ) thì luôn là số chẵn. Đây là ý tưởng về mã kiểm tra chẵn lẻ
ơn.
Hình 3.16: Hệ thống phát hiện lỗi thông thường
Nếu một từ mã bị 1 lỗi ơn trong quá trình truyền dẫn, thì phía thu sẽ nhận ược dòng
bit với số bit 1 là số lẻ, và lỗi ã ược phát hiện. Nói cách khác, tổng quát hơn, nếu như từ mã
có một số lẻ các lỗi thì chuỗi bit ầu ra sẽ có một số lẻ bit 1. Do ó, bit chẵn lẻ ơn có thể cho
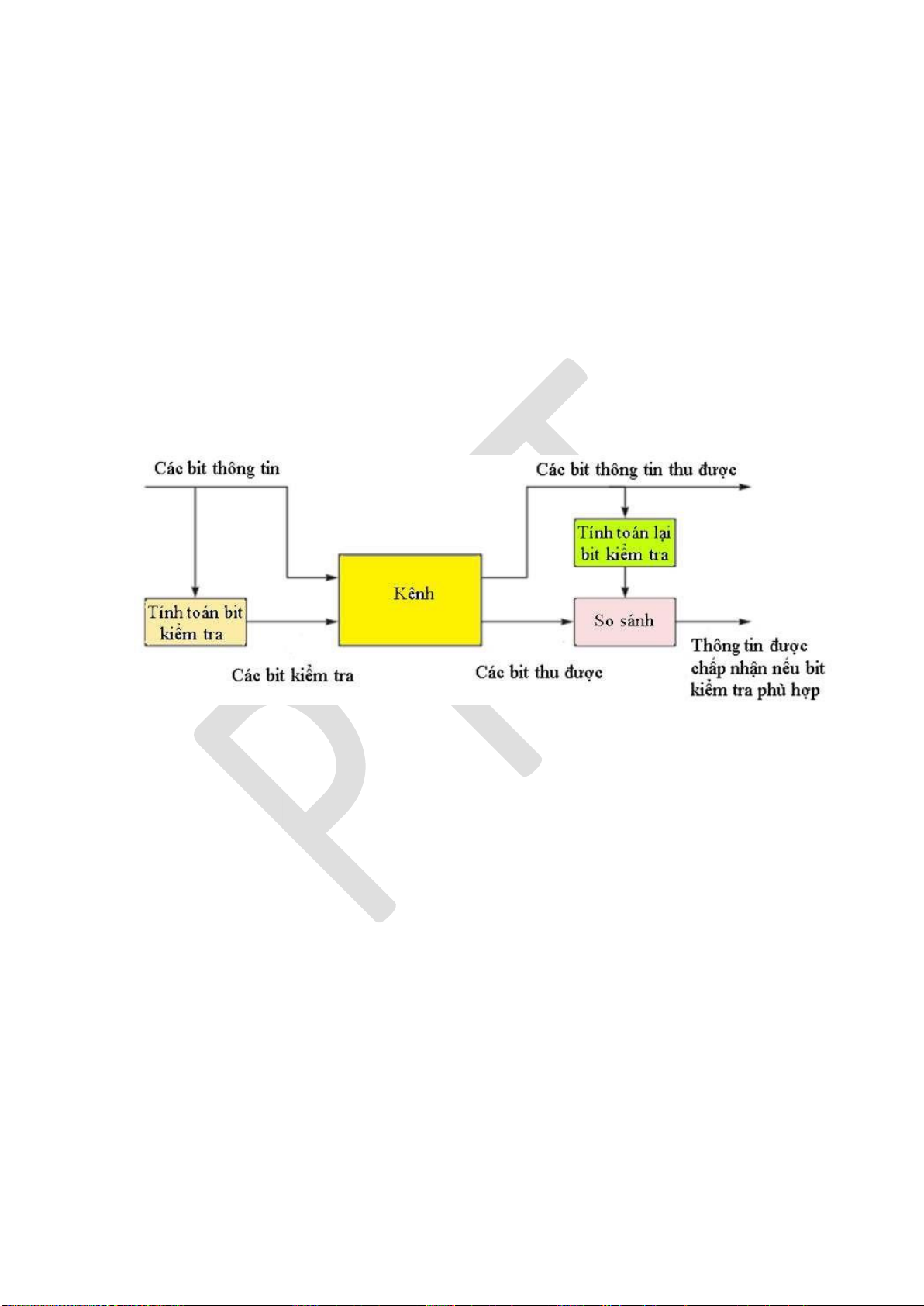
lOMoARcPSD| 36067889
phép chúng ta phát hiện ra tất cả các ký tự bị lỗi nếu như số lỗi là số lẻ. Tuy nhiên, nó sẽ
hoàn toàn không có tác dụng trong các trường hợp số lỗi xuất hiện là chẵn. Trong các trường
hợp ó, số bit 1 vẫn là chẵn, và mã này sẽ không thể phát hiện ược lỗi. Dù sao thì bit chẵn
lẻ ơn vẫn có thể cung cấp một khả năng phát hiện lỗi nào ó, cụ thể là một nửa số trường
hợp có thể xảy ra lỗi, và số lỗi có thể phát hiện phụ thuộc vào giá trị k của từng chuỗi mã
ược gắn bit kiểm tra.
Hình 3.17 chỉ ra cách thay thế ể xem xét ví dụ này. Ở ầu phát một tổng kiểm tra
ược tính toán từ các bit thông tin và ược truyền i cùng với các bit này. Ở phía thu, tổng
kiểm tra ược tính toán lại, dựa trên thông tin thu nhận ược. Tổng kiểm tra nhận ược và
tổng kiểm tra ược tính toán lại ược em ra so sánh, và sẽ có thông báo lỗi nếu chúng
không khớp với nhau.
Hình 3.17: Hệ thống phát hiện lỗi sử dụng các bit kiểm tra
Ví dụ ơn giản này có thể ược sử dụng ể trình bày về hai yếu tố cơ bản cần thiết
trong việc nhìn nhận việc phát hiện lỗi. Thứ nhất ó là việc phát hiện lỗi yêu cầu về sự
tồn tại của sự dư thừa, nghĩa là phải thêm vào các bit ể kiểm tra chứ không ơn thuần tận
dụng toàn bộ băng thông cho việc truyền các bit thông tin. Với một mã kiểm tra chẵn lẻ
ơn có ộ dài là k+1, k bit là các bit thông tin, còn 1 bit còn lại là bit chẵn lẻ. Do ó, 1/(k+1)
các bit phát bị thừa.
Yếu tố thứ 2 có thể nhận ra ó là tất cả các kỹ thuật phát hiện lỗi ều không thể phát
hiện ược một số lỗi. Thông thường, một kỹ thuật phát hiện lỗi sẽ luôn luôn thất bại trong
việc phát hiện các lỗi truyền dẫn làm biến ổi một từ mã thành một từ mã khác. Ví dụ với
mã kiểm tra chẵn lẻ ơn, nếu như số lỗi xuất hiện là chẵn thì từ mã sẽ bị biến ổi thành
một từ mã khác ược hiểu là úng, và mã sẽ không thể phát hiện ược lỗi.
Do ó, trong việc lựa chọn mã phát hiện lỗi, người ta luôn cố gắng lựa chọn các mã
ít có khả năng biến ổi các lỗi thành các từ mã hợp lệ, dựa trên các lỗi thường xảy ra trên
kênh truyền dẫn hiện có. Để minh họa cho việc này, chúng tôi giả sử miêu tả một tập
các khối bit nhị phân như trên hình 3.18, với các từ mã ược ký hiệu bởi x và các từ không
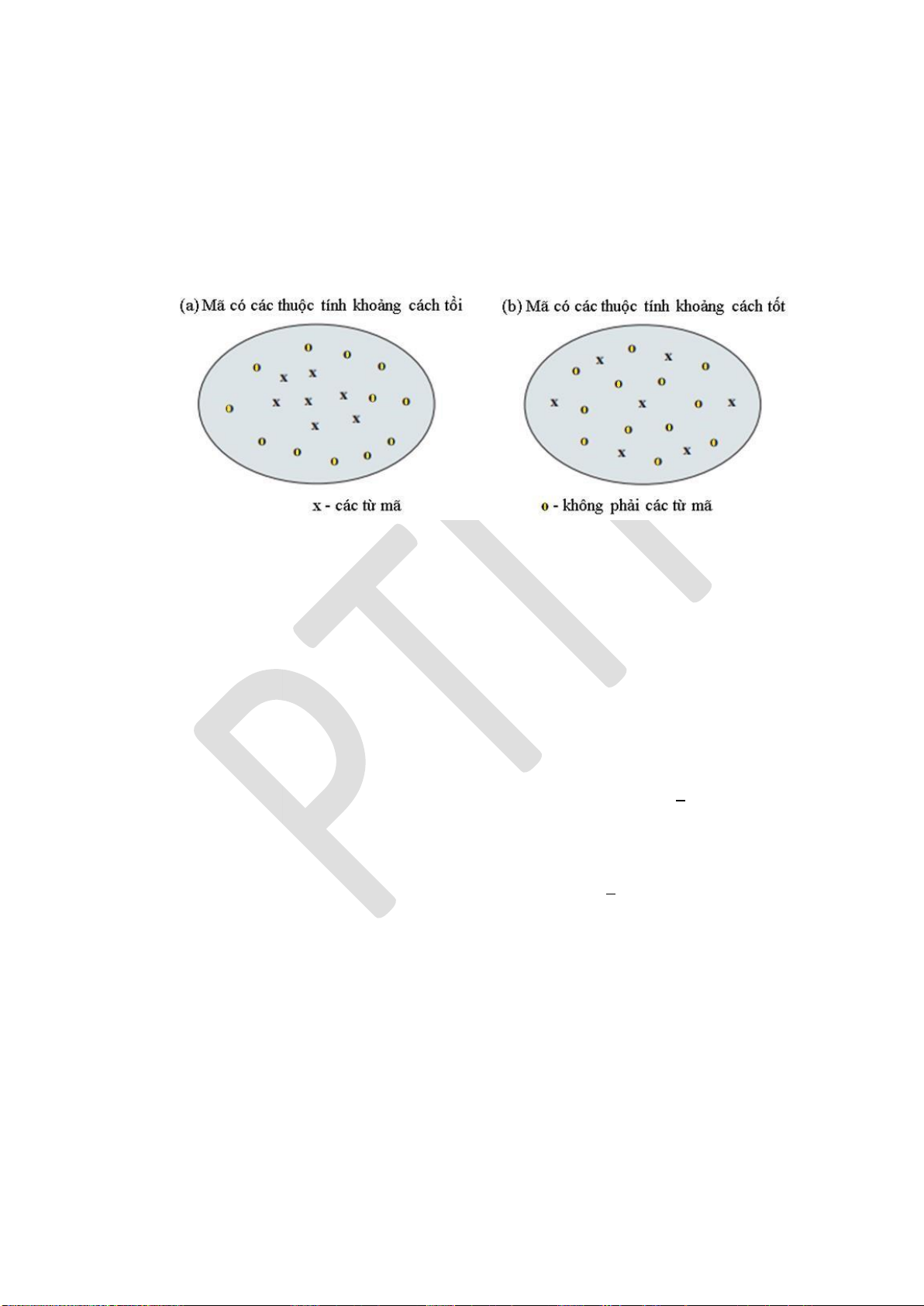
lOMoARcPSD|36067889
phải từ mã ký hiệu là o. Để giảm thiểu khả năng phát hiện sai lỗi, chúng tôi muốn rằng
các từ mã ược sinh luôn cách càng xa nhau càng tốt. Do ó trên hình 3.18a là một mã
không tốt, vì các từ mã ở quá gần nhau. Ở hình 3.18b thì khác, ây là một tập mã tốt vì
khoảng cách giữa các từ mã là tối a. Sự hiệu quả của một mã phụ thuộc hoàn toàn vào
loại lỗi mà nó sẽ gặp phải trên kênh truyền. Tiếp theo, chúng ta sẽ xem xét hiệu quả của
bộ mã kiểm tra chẵn lẻ ược em ra làm ví dụ như thế nào.
Hình 3.18: Các thuộc tính khoảng cách của các mã
Hiệu quả của các mã phát hiện lỗi
Hiệu quả của một mã phát hiện lỗi ược o bằng khả năng mà hệ thống thất bại trong
việc phát hiện lỗi từ kênh truyền sử dụng mã ó. Để tính toán xác suất này, chúng ta cần
biết về xác xuất xuất hiện của các loại lỗi. Những xác suất này dựa vào các tính chất ặc
trưng của kênh truyền. Chúng ta sẽ nhìn nhận ba dạng lỗi của kênh: lỗi vectơ ngẫu nhiên,
lỗi bit ngẫu nhiên và lỗi liên hoàn.
Giả sử chúng ta truyền một từ mã có n bit. Ta ịnh nghĩa vectơ e = (e
1,
e
2
,…,
e
n
) với
mỗi phần tử e
i
=1 là tương ương với một lỗi xuất hiện lại bit có vị trí i trong số các bit
truyền i và e
i
=0 nếu như ngược lại. Trong trường hợp tổng quát, ta có số vectơ lỗi có thể
xuất hiện là 2
n
. Trong mô hình kênh xác suất của vectơ lỗi e xuất hiện không phụ thuộc
vào số lỗi mà nó có. Do ó vectơ lỗi (1, 0, 0,…, 0) cũng có xác suất xảy ra giống như xác
suất của vectơ lỗi (1, 1, 1,…, 1). Mã kiểm tra chẵn lẻ ơn sẽ thất bại trong việc phát hiện
ra các vectơ lỗi với số số 1 là chẵn. Do ó, với mô hình kênh có vectơ lỗi ngẫu nhiên, xác
suất phát hiện lỗi sai là ½.
Bây giờ sẽ xem xét mô hình lỗi bit ngẫu nhiên, với các lỗi bít xuất hiện ộc lập với
các lỗi khác. Truyền thông vệ tinh cho ta một ví dụ của kênh loại này. Ta coi p là xác
suất xuất hiện một lỗi trong kênh truyền ơn bit. Lúc này xác suất của một vectơ lỗi với j
lỗi sẽ là p
j
(1 – p)
n-j
, vì với mỗi lỗi trong j lỗi xuất hiện sẽ có xác suất p và mỗi phép
truyền úng trong số n-j phép truyền úng sẽ có xác suất là 1 – p. Viết lại xác suất này ta
sẽ có:

lOMoARcPSD|36067889
p[ ]e (1 p)
n w( )e
p
w( )e
(1 p) (
n
p
)
w( )e
(3.37)
1 p
Ở ây, w(e) ược ịnh nghĩa là trọng số, hay số các số 1 có trong vectơ e. Với nhiều
kênh truyền thông ang ược sử dụng, xác suất của bit lỗi nhỏ hơn rất nhiều so với một,
do ó p<1/2 và p/(1-p)<1. Điều này ược ngầm hiểu rằng trong kênh lỗi bit ngẫu nhiên,
xác xuất của một vectơ e giảm khi số bit lỗi tăng (số 1 trong vectơ tăng). Điều ó có nghĩa
là, một lỗi xảy ra ở ít ký tự sẽ có khả năng cao hơn so với một lỗi xảy ra ở nhiều ký tự
cùng lúc. Do vậy, kênh này có mục ích ánh xạ một từ mã ược truyền vào trong một khối
bit nhị phân ược phân bố xung quanh từ mã.
Mã kiểm tra chẵn lẻ ơn sẽ thất bại nếu số lỗi là số chẵn. Do ó, trong mô hình bit lỗi
ngẫu nhiên, ta sẽ có công thức:
[á ] = [á ý ô á ]
= [á ý ó 1]
= 2
n
p
2
(1 p)
n 2
4
n
p
4
(1 p)
n 4
... (3.38)
Tổng này ược cộng tới khi n ạt ược số lỗi lớn nhất mà kênh có thể mắc phải cùng 1
lúc. Trong công thức trước chúng ta ã ề cập ến việc tính biểu thức:
n n! (3.39)
jj n
!
j !
Với là số bit 1 và là số bit 0 tồn tại trong vectơ lỗi. Trong bất kỳ một hệ
thống truyền dẫn nào ang ược sử dụng, xác suất của một bit lỗi () luôn luôn nhỏ hơn
rất nhiều so với 1. Vì vậy, có thể sử dụng một công thức tính gần úng:
p
i
(1 p)
j
p
i
(1 pj) p
i
(3.40)
Nếu như p = 10
-3
thì
p
2
(1 p)
n 2
10
-6
và
p
4
(1 p)
n 4
10
-12
. Do ó xác xuất của việc
phát hiện sai lỗi sẽ ược quyết ịnh hầu hết bởi hạng tử ầu tiên trong công thức trên. Ví
dụ, nếu có n=32 và p=10
-4
. Lúc này sẽ nhận ược xác xuất phát hiện sai lỗi chỉ là 5×10
-6
,
giảm i khoảng 2 bậc.
Có thể nhận thấy một khoảng cách lớn giữa hiệu năng ạt ược khi sử dụng 2 mô
hình kênh ã ược nêu ở trên. Nhiều kênh truyền thông tổng hợp các yếu tố của cả hai

lOMoARcPSD|36067889
dạng kênh này, và nó ược gọi là mô hình kênh kết hợp. Thời gian truyền với tỉ lệ lỗi thấp
an xen với thời gian có sự xuất hiện của nhiều cụm lỗi. Thời gian truyền dẫn với tỉ lệ lỗi
thấp tương tự như mô hình kênh lỗi bit ngẫu nhiên, và thời gian còn lại thì tương tự với
mô hình kênh vectơ lỗi ngẫu nhiên. Xác suất của việc phát hiện lỗi sai ối với mã chẵn lẻ
ơn sẽ nằm âu ó giữa xác suất của 2 mô hình kênh này. Nói chung, các phép o phải thống
kê ể có thể phân loại và sử dụng ược từng loại kênh riêng biệt.
3.4.1.2. Mã kiểm tra chẵn lẻ 2 chiều
Một phương pháp ơn giản ể nâng cao năng lực phát hiện lỗi của mã chẵn lẻ ơn ó
là sắp xếp các bit thông tin theo từng cột, mỗi cột có k bit, như ta thấy trên hình 3.19.
Bit cuối cùng ở mỗi cột là bit kiểm tra cho các bit thông tin nằm trong cột ó. Lưu ý rằng
cột cuối cùng là một “từ mã kiểm tra” cho m cột phía trước nó. Các bit ngoài cùng bên
phải của mỗi dòng là bit kiểm tra cho toàn bộ các bit trong dòng ó. Ma trận mã hóa cuối
cùng ảm bảo rằng mỗi hàng ều ược kiểm tra chẵn lẻ.
Nếu một, hai, hoặc 3 lỗi xuất hiện ở bất cứ âu trong ma trận bit trong quá trình ược
truyền i, nó sẽ khiến cho ít nhất một hàng có mã kiểm tra sai, như ta thấy trên hình 3.20.
Tuy nhiên, một vài trường hợp với 4 bit lỗi vẫn không thể ược phát hiện, cũng ược thể
hiện trên hình vẽ.
Hình 3.19: Mã kiểm tra chẵn lẻ hai chiều
Mã kiểm tra chẵn lẻ hai chiều là một ví dụ khác về mã tuyến tính. Nó có ưu iểm là
khả năng phát hiện lỗi có thể ược ịnh nghĩa một cách trực quan, tuy nhiên hiệu năng
không thực sự tốt. Những loại mã tốt hơn sẽ ược ề cập ến trong một phần khác, nói về
các mã tuyến tính.

lOMoARcPSD| 36067889
Quá trình mã hóa lấy () và tạo ra a thức từ mã () chứa các bít thông tin và các
bit bổ sung ể kiểm tra, và nó thỏa mãn một khuôn mẫu nào ó. Để phát hiện lỗi, phía thu
kiểm tra ể xem khuôn mẫu ó có ược áp ứng không. Trước khi giải thích cụ thể quá trình
này, cần xem lại về a thức số học.
Mã a thức sử dụng a thức số học ể tính toán từ mã tương ứng với a thức thông tin.
Hình 3.21 ưa ra ví dụ về a thức cộng, nhân và chia sử dụng các hệ số nhị phân.
Chú ý rằng với hệ nhị phân, ta có
+
= (1 + 1)
= 0. Cụ thể hơn, khi phép chia ược
hoàn thành, phần dư () sẽ có bậc nhỏ hơn bậc của a thức chia. Trong ví dụ này a thức
Hình 3.20: Các ký t
ự
l
ỗ
i có th
ể
và không th
ể
b
ị
phát hi
ệ
n c
ủ
a mã hai chi
ề
u
3.4.2
. Các mã a thứ
c
Bây gi
ờ
s
ẽ
xem xét h
ọ
các mã
a thứ
c
ượ
c s
ử
d
ụ
ng r
ộ
ng rãi trong phát hi
ệ
n l
ỗ
i
và s
ử
a l
ỗi. Các mã a thứ
c có th
ể
ượ
c th
ự
c hi
ệ
n d
ễ
dàng thông qua các m
ạ
ch thanh ghi
d
ị
ch vì th
ế
chúng là các mã iề
u khi
ể
n l
ỗi ượ
c s
ử
d
ụ
ng r
ộ
ng rãi nh
ất. Mã a thứ
c t
ạ
o
ra các bit ki
ể
m tra nh
ờ
vi
ệ
c ki
ể
m
tra các bit dư theo chu kỳ
(CRC). Vì v
ậ
y mã
a thứ
c
còn ượ
c bi
ết ến như là các mã CRC.
Trong mã a thứ
c, các ký hi
ệ
u thông tin, t
ừ
mã và
vectơ
l
ỗi ượ
c bi
ể
u di
ễ
n b
ằ
ng
các a thứ
c nh
ị
phân. Bit thông tin th
ứ
(
1
,
2
1
,
0
)
ượ
c s
ử
d
ụng ể
hình
thành nên a thứ
c thông tin c
ủ
a m
ứ
c
1
:
()=
1
1
+
2
2
+
+
1
+
0
(3.41)

lOMoARcPSD| 36067889
chia có bậc 3, vì vậy quá trình chia tiếp diễn cho ến khi phần dư có bậc nhỏ hơn hoặc bằng
2.

lOMoARcPSD| 36067889
Việc tính toán các bit kiểm tra ộ dư theo chu kỳ ược mô tả như sau:
Bước 1: Đầu tiên a thức thông tin ược nhân với
.
() = 11 + 22 1+1 + 0 (3.43)
Nếu hình dung rằng bit thông tin ang ở vị trí thấp hơn trong chuỗi ghi có ộ dài
, phép nhân ưa các bit thông tin tới vị trí cao nhất của , vì số hạng cao nhất của ()
có ể ạt ược là . Trường hợp này ược thể hiện trong hình 3.22. Đa thức thông tin là
() =
3
+
2
, do ó kết quả ầu tiên thu ược là
3
() =
6
+
5
. Sau 3 bước dịch sang
bên trái, thành phần của thanh ghi dịch là (1, 1, 0, 0, 0, 0, 0).
Bước 2: Bao gồm chia
() cho () ể xác ịnh phần dư (). Các số hạng bao gồm
trong phép chia ược ưa ra trong giải thích sau:
Hình 3.21: S
ố
h
ọc a thứ
c
M
ột a thức mã ược xác ị
nh
b
ằng a thứ
c sinh
()
c
ủ
a nó.
Ở
ây, giả
s
ử
r
ằ
ng
chúng ta a
ng làm vi
ệ
c v
ới mã trong ó có
bit t
ừ
mã, bao g
ồ
m
bit thông tin và
bit ki
ể
m tra. Chúng ta nh
ắ
c t
ớ
i lo
ạ
i mã
(
,
)
. Đa thứ
c sinh cho lo
ạ
i mã này có b
ậ
c
và có d
ạ
ng:
(
)
=
+
1
1
+
+
1
+1
(3.42)
t
rong ó:
1
,
2
là các s
ố
nh
ị
phân.
Trong ph
ầ
n ti
ế
p theo là ví d
ụ
bi
ể
u di
ễ
n cho mã
(7
,
4)
v
ới a thứ
c sinh:
(
)
=
3
+
+1
.

lOMoARcPSD| 36067889
() = (). () + () (3.44)
Đa thức dư () cung cấp các bit kiểm tra ộ dư theo chu kỳ (CRC). Trong ví dụ ưa ra
ở hình 3.22, chúng ta có
6
+
5
= (). (
3
+
2
+ ) + ; có nghĩa là () =
.
Vì a thức chia () có bậc nên phần dư () có thể có bậc cao nhất là .
Vì vậy () có nhiều nhất là số hạng. Nói về thanh ghi có chiều dài như ã ược
giới thiệu phía trên, () có thể có bậc thấp hơn . Nhắc lại rằng bậc cao hơn ã
ược chiếm bởi các bit thông tin. Do ó chúng ta thấy rằng quá trình mã hóa này giới thiệu
một a thức nhị phân trong ó số hạng có vị trí cao hơn là các bit thông tin và các số
hạng có vị trí thấp hơn là các bit kiểm tra dư thừa theo chu kỳ. Trong ví dụ ở hình
Hình 3.22: Ví d
ụ
v
ề
mã hóa CRC
Bướ
c 3
:
Thu ượ
c t
ừ
mã nh
ị
phân
()
b
ằ
ng cách c
ộ
ng thêm ph
ần dư
()
vào
(
)
.
(
)
=
(
)
+
(
)
(3.45)
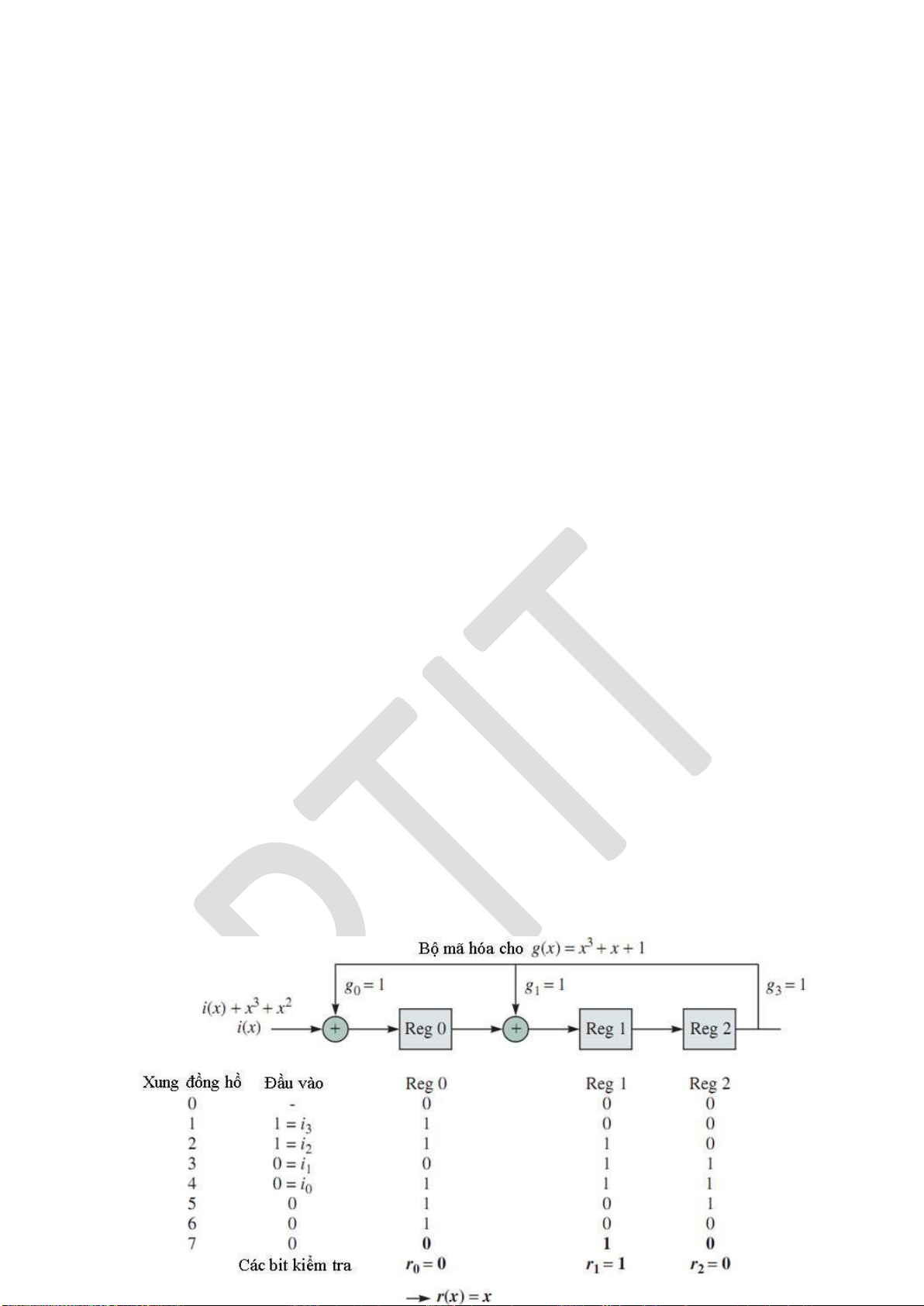
lOMoARcPSD| 36067889
3.22, phép chia
3
() cho () cho a thức dư () = . Đa thức từ mã sẽ là
6
+
5
+
, tương ứng với chuỗi từ mã nhị phân (1, 1, 0, 0, 0, 1, 0). Chú ý rằng 4 vị trí ầu tiên
chứa 4 bit thông tin còn 3 bit sau chứa các bit CRC.
Trong hình 3.21, cho thấy ở phép chia thông thường chia 122 cho 35 ược thương
số là 3 và dư 17 (122 = 3.35 +17). Chú ý rằng bằng cách trừ i phần dư 17 ở cả 2 bên, ta
có 122-17 = 3.35 do ó 122 – 17 chia hết cho 35. Tương tự, a thức từ mã () chia hết
cho () vì:
() =
() + () = (). () + () + () = (). () (3.46)
Trong ó ã sử dụng phép tính toán trong cơ số 2 là () + () = 0. Sự tương ương
này có nghĩa là tất cả từ mã ược nhân với a thức sinh (). Đó chính là mẫu sẽ ược kiểm
tra ở phía thu. Máy thu có thể kiểm tra ể xem mẫu này có ược thỏa mãn không bằng cách
chia a thức nhận ược cho (). Nếu phần dư khác 0 thì một lỗi ược phát hiện.
Một thuật toán quen thuộc hơn về việc mang các oạn chữ viết có thể ược sử dụng
ể tạo ra mạch các thanh ghi dịch hồi tiếp thực thi phép chia. Các tap hồi tiếp trong mạch
này ược xác ịnh bằng các hệ số của a thức sinh. Hình 3.23 là một mạch chia có a thức
sinh g(x) = x
3
+ x + 1. Hình vẽ cũng chỉ ra trạng thái của các thanh ghi bởi vì thuật toán
thực hiện phép chia tương tự như trong ví dụ mã hóa trước ó.
Một mạch chia tương tự như vậy dùng bộ mã hóa có thể ược sử dụng ở phía thu ể
làm rõ a thức nhận ược có khớp với a thức từ mã hay không.
Bảng 3.8 dưới ây giới thiệu các a thức sinh sau khi ã chuẩn hóa. Các a thức CRC-
12 và CRC-16 ược giới thiệu như một phần của giao thức ồng bộ bit IBM cho iều khiển
lỗi trong tuyến truyền thông. Đa thức CCITT-16 ược sử dụng trong chuẩn HDLC và
trong XMODEM. Đa thức CCITT-32 ược sử dụng trong chuẩn IEEE 802 LAN và trong
modem chuẩn CCITT V.42. Cuối cùng CRC-8 và CRC-10 gần ây ược sử dụng trong
các mạng ATM.

lOMoARcPSD|36067889
Hình 3.23: Mạch các thanh ghi dịch cho a thức sinh
Bảng 3.8: Các a thức sinh chuẩn
3.4.3. Mã khối tuyến tính
Trong lý thuyết mã hóa, mã khối là một tập hợp bao gồm nhiều mã sửa lỗi mã hóa
dữ liệu theo từng khối. Có rất nhiều loại mã khối khác nhau, ược sử dụng rộng rãi trong
nhiều ứng dụng thực tiễn. Một nguyên nhân khiến mã khối hữu ích như vậy là nó cho
phép sử dụng một cách thống nhất các phương pháp từ lý thuyết mã hóa, toán học, và
khoa học máy tính ể nghiên cứu về các giới hạn của mã khối. Các giới hạn ó thường ở
dạng bất ẳng thức liên hệ các tham số của mã, chẳng hạn như tỉ lệ và khả năng phát hiện
và sửa lỗi.
Mã sửa lỗi ược dùng ể truyền dữ liệu số một cách áng tin cậy trên một kênh liên
lạc có nhiễu. Khi cần truyền nhiều dữ liệu bằng mã khối, người gửi chia dữ liệu thành
nhiều phần nhỏ. Mỗi phần nhỏ ược gọi là một thông iệp và thuật toán mã hóa khối mã
hóa mỗi thông iệp thành một từ mã còn ược gọi là một khối trong mã hóa khối. Người
gửi gửi tất cả các khối cho người nhận, sau ó người nhận sử dụng thuật toán phục hồi lại
thông iệp ban ầu từ các khối có lỗi.
Mã khối ược gọi là tuyến tính nếu thỏa mãn sự kết hợp tuyến tính bất kỳ hai từ mã
nào ó cũng là một từ mã thuộc mã ó. Trong trường hợp nhị phân, tổng của 2 từ mã bất kỳ
cũng là một từ mã. Mã khối tuyến tính ược ặc trưng bởi các tham số dưới ây: Độ dài khối
bản tin ; Đô dài từ mã ; Khoảng cách Hamming cực tiểu d
m
; Tỉ lệ mã = /.
Sơ ồ khối tổng quát bộ mã khối tuyến tính (n, k) như ưa ra trên hình 3.24.

lOMoARcPSD|36067889
Hình 3.24: Sơ ồ khối tổng quát bộ mã khối tuyến tính (n, k)
Ở ây, các bản tin k bit hình thành nên 2
k
chuỗi các bản tin riêng biệt nhau hay còn
gọi là k-tuples. Các khối n bit cũng hình thành nên 2
n
các chuỗi bit riêng biệt hay còn
gọi là n-tuples. Quá trình mã hóa có nhiệm vụ gán mỗi một trong số 2
k
các bản tin -
ktuples vào một trong số 2
n
các chuỗi bit riêng biệt - n-tuples.
Ví dụ 3-17: Xem xét việc gán mã hóa sau ây cho mã khối tuyến tính (6, 3). Có 2
k
= 2
3
=
8 vectơ bản tin và do ó tương ứng với 8 từ mã. Có 2
n
= 2
6
= 64 (6- tuples trong không
gian vectơ V
6
).
Chúng ta có thể thấy rằng tám từ mã thể hiện trong Bảng 3.9 dưới ây hình thành
nên một không gian con của V
6
(vectơ có các thành phần toàn 0 và tổng của hai từ mã
bất kỳ tạo nên một từ mã thành phần khác trong không gian con). Do vậy, các từ mã này
ại diện cho một mã khối tuyến tính.
Do một tập hợp các từ mã tạo thành một mã khối tuyến tính là một không gian con
k chiều của không gian vectơ nhị phân n chiều (k <n). Chúng ta luôn có thể tìm thấy một
tập hợp các n-tuples, ít hơn 2
k
có thể tạo ra tất cả 2
k
từ mã của không gian con. Tập các
vectơ (từ mã) ược tạo ra ược xem như là sự mở rộng của các không gian con. Tập nhỏ
nhất của các từ mã ộc lập tuyến tính ược gọi là một cơ sở của không gian con, và số
lượng các vectơ trong tập cơ sở này là kích thước của không gian con. Bất kỳ tập cơ sở
nào của k ộc lập tuyến tính trong n-tuples: V
1
, V
2
…. V
k
có thể ược sử dụng ể tạo ra các
vectơ mã khối tuyến tính theo yêu cầu, vì mỗi vectơ mã là tổ hợp tuyến tính của V
1
, V
2
….
V
k
. Do vậy, mỗi một tập của 2
k
từ mã (U) có thể ược mô tả bởi:
U=m
1
V
1
+m
2
V
2
+…..+m
k
V
k
với m
i
= 0 hoặc 1 là các chữ số bản tin và i = 1, ..., k.
Bảng 3.9: Cấp phát các từ mã cho các bản tin
Vectơ bản tin Từ mã
000 000000
100 110100
010 011010
110 101110
001 101001
101 011101
011 110011
111 000111

lOMoARcPSD|36067889
Trên thực tế, hoạt ộng của bộ lập mã ược biểu diễn toán học ở dạng ma trận tạo
mã/ma trận sinh G hay a thức tạo mã g(x).Tổng quát, chúng ta có thể ịnh nghĩa một ma
trận sinh qua ma trận k n sau ây:
V1 v11 v12 v1n
V2 v21 v22 v2n (3.47) G
Vk vk1 vk2 vkn
Các vectơ mã, theo quy ước, thường ược xem như là các vectơ hàng. Như vậy, bản
tin m, một chuỗi k bit tin, ược hiển thị dưới ây như là một vectơ hàng (ma trận 1 k: ma
trận có một hàng và k cột):
m = m
1
, m
2
, …. , m
k
Việc tạo ra từ mã U ược viết bằng ký hiệu ma trận như là tích m và G:
U = mG (3.48)
Chặng hạn, chúng ta có thể có một ma trận sinh:
V
1
1 1 0 1 0 0
G V
2 0 1 1 0 1 0 (3.49)
V
3
1 0 1 0 0 1
Ở ây, V
1
, V
2
, V
3
là ba vectơ ộc lập tuyến tính (một tập hợp con của 8 vectơ mã) có thể
tạo ra tất cả các vectơ mã. Ví dụ, từ mã U
4
cho vectơ bản tin thứ tư 1 1 0 sử dụng ma
trận sinh của biểu thức (3.49):
V
1
U
4
1 10
V
2
1.V
1
1.V
2
0.V
3
V
3
110100 011010 000000
1101110

lOMoARcPSD|36067889
3.4.3.1. Các mã khối tuyến tính hệ thống
Mã khối tuyến tính hệ thống (n, k) là ánh xạ từ một vectơ bản tin k bit thành từ mã
n bit mà ở ó k bit của bản tin trùng với k bit của từ mã. Các số còn lại (n-k) giành cho
các bit kiểm tra chẵn lẻ. Một mã khối tuyến tính hệ thống sẽ có ma trận sinh ược biểu
diễn có dạng:
p11 p12 ... p1,(n k ) 1 0 ... 0
G P I
k
p
21
p
22
... p
2
,(n k
)
0 1 ...
0 (3.50)
pk1 pk2 ... pk n k,( ) 0 0 ... 1
trong ó: P là ma trận chẵn lẻ và là một phần của ma trận sinh; p
ij
= 0 hoặc 1, và ma trận
I
k
(có kích thước k×k) là ma trận ơn vị (những phần tử trên ường chéo chính có giá trị
bằng 1 còn các phần tử khác có giá trị lại bằng 0). Lưu ý rằng ma trận sinh dạng hệ thống
thì ộ phức tạp mã hóa giảm vì không cần thiết phải lưu trữ ma trận ơn vị trong ma trận
sinh. Bằng cách kết hợp các biểu thức (3.49) và (3.50) mỗi từ mã ược thể hiện như sau:

lOMoARcPSD| 36067889
u u1, p21 p22 ... p2,(n k ) 0 1 ... 0
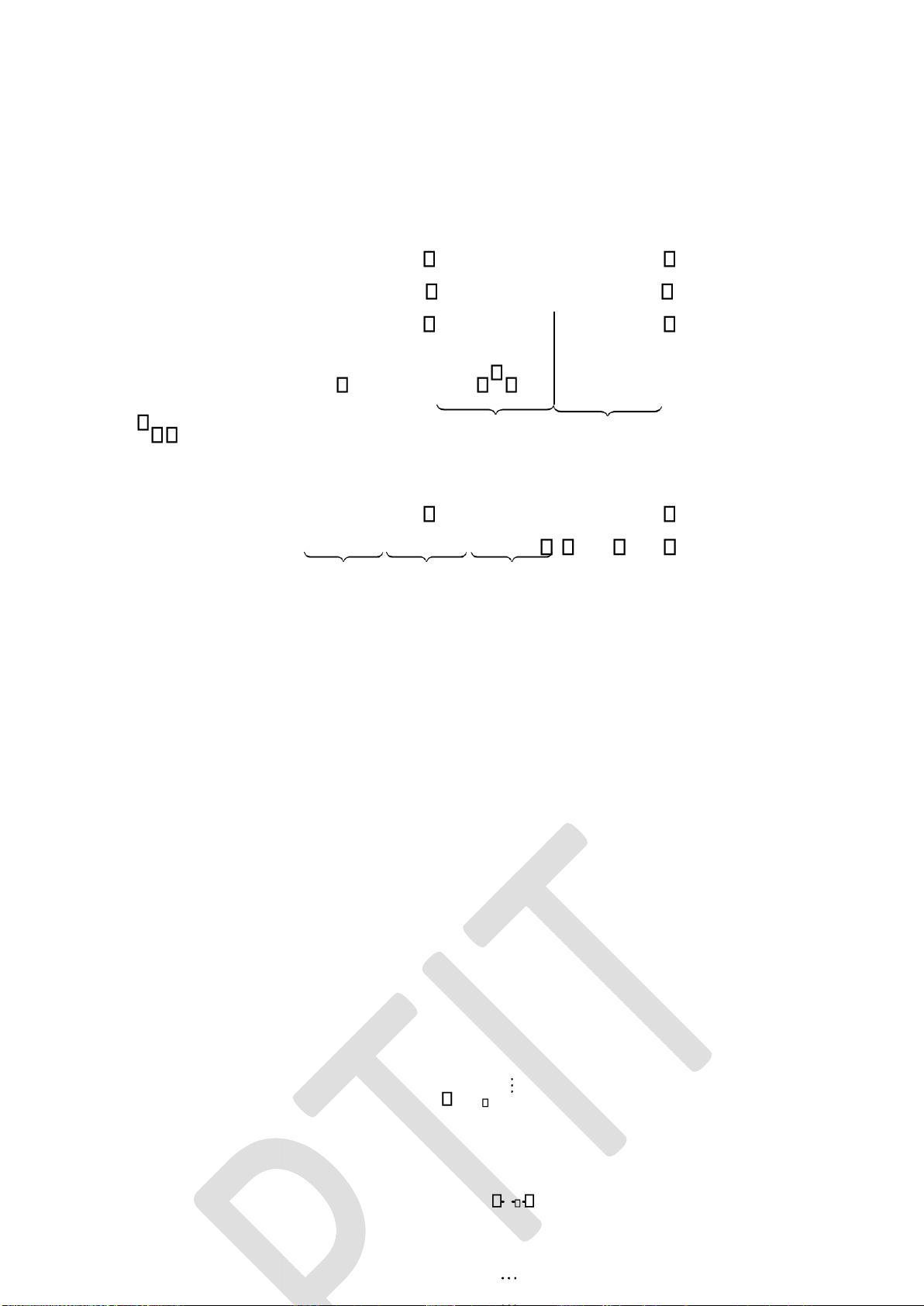
lOMoARcPSD|36067889
Các từ mã hệ thống ôi khi ược viết sao cho các bit tin ở phần bên trái của từ mã
phát hiện lỗi hoặc sửa lỗi của mã.
Đối với ví dụ 3.17 về mã (6, 3) ở trên, các từ mã ược mô tả như sau:
1 1 0 1 0 0
U m m m [ 1, 2, 3] 0 110 11 00 10
01 (3.53)
P I3
U m m m m m m m m m 13, 1 2, 2 3, 1, 2, 3
(3.54)
u
1
u
2
u
3
u4 u5 u6
Biểu thức (3.54) cho biết thông tin cụ thể về cấu trúc của mã khối tuyến tính. Có
thể thấy rằng các bit dự phòng ược tạo ra theo nhiều cách. Các bit chẵn lẻ ầu tiên là tổng
của các bit tin ầu tiên và thứ ba của bản tin, tương ứng, bit chẵn lẻ thứ hai là tổng của
các bit tin ầu tiên và thứ hai, và bit chẵn lẻ thứ ba là tổng của các bit tin thứ hai và thứ
ba. Cấu trúc như vậy cho biết rằng so sánh với kiểm tra tính chẵn lẻ ơn hoặc tái tạo các
chữ số lặp lại ơn giản, khả năng ể phát hiện và sửa lỗi của mã khối tuyến tính là lớn hơn.
3.4.3.2. Ma trận kiểm tra chẵn lẻ
Ma trận H, ược gọi là ma trận kiểm tra chẵn lẻ, cho phép giải mã các vectơ nhận
ược. Đối với mỗi ma trận sinh G (k×n), tồn tại một ma trận H (n-k)×n, sao cho các hàng
của G là trực giao với các hàng của H, nghĩa là G.H
T
= 0, với H
T
là ma trận chuyển vị
của H, và 0 là ma trận với k×(n-k) phần tử có giá trị 0. H
T
là ma trận n×(n-k) có các hàng
là các cột của H và có các cột là các hàng của H. Để thực hiện ầy ủ các yêu cầu trực giao
cho một từ mã hệ thống, các thành phần của ma trận H ược viết như sau:
H [I
n k
P
T
] (3.55) Do ó,
ma trận H
T
ược viết như sau:
I

lOMoARcPSD|36067889
HT n k (3.56a)
P
1 0 0
0 1 1
HT p011
p
012
p
1,(1n k ) (3.56b)
p21
p
22
p
2,(
n k
)
pk1 pk2 pk n k,( )
Điều ó chứng tỏ rằng UH
T
là kết quả của mỗi từ mã U ược tạo ra bởi G và ma trận
H
T
:
UHT p p p p1 1, 2 2,..., pn k pn k 0
Ở ây, các bit chẵn lẻ p
1
, p
2
, …, p
n-k
ược xác ịnh trong biểu thức (3.52). Do vậy, ma
trận kiểm tra chẵn lẻ H ược xây dựng ể áp ứng yêu cầu trực giao ã nói ở trên và chúng
ta có thể sử dụng nó ể kiểm tra xem một vectơ nhận ược có là một từ mã hợp lệ của tập
các từ mã chưa. U là một từ mã ược tạo ra bởi ma trận G nếu và chỉ nếu UH
T
= 0.
3.4.3.3. Kiểm tra Syndrome
Gọi r r r
1 2
, ,...,r
n
là một vectơ nhận ược (một trong số 2
n
bộ từ mã – n-tuples)
kết quả từ việc truyền tải của U u u
1
,
2
,...,u
n
(một trong số 2
k
bộ từ mã) Do ó, chúng ta
có thể biểu diễn r qua biểu thức dưới ây:
r U e
(3.57)
Ở ây, e e e
1
,
2
,...,e
n
là một vectơ lỗi hoặc mẫu lỗi gây ra bởi kênh truyền dẫn.
Có tổng cộng 2 1
n
khả năng các mẫu lỗi khác không trong không gian của 2
n
từ mã.
Syndrome của r ược ịnh nghĩa là:
S rH
T
(3.58)

lOMoARcPSD| 36067889
Syndrome là kết quả kiểm tra chẵn lẻ, thực hiện trên r ể xác ịnh xem liệu r có là
một từ mã hợp lệ của bộ từ mã. Nếu trên thực tế, r là một từ mã của bộ từ mã thì
Syndrome S có giá trị bằng 0. Nếu phát hiện r có bit lỗi thì Syndrome có giá trị khác 0.
Nếu r chứa các lỗi có thể sửa ược, Syndrome sẽ có một số giá trị khác không trong thành
phần dành cho các mẫu báo lỗi cụ thể. Bộ giải mã, tùy thuộc vào lỗi ó ể thực hiện FEC
hoặc ARQ, sau ó sẽ thực hiện các biện pháp ể xác ịnh vị trí các lỗi và sửa chữa chúng
(FEC), hoặc nếu không nó sẽ yêu cầu truyền lại (ARQ). Kết hợp các biểu thức (3.57) và
(3.58), Syndrome của r ược xác ịnh:
S (U e H)
T
UH
T
eH
T (3.59)
Tuy nhiên, UH
T
= 0 cho tất cả các từ mã của tập từ mã, do ó:
S eH
T
(3.60)
Từ các biến ổi trên, bắt ầu với biểu thức (3.57) và kết thúc với biểu thức (3.60) là
bằng chứng cho thấy rằng các kiểm tra Syndrome, cho dù thực hiện ở trên vectơ mã bị lỗi
hoặc trên các mẫu lỗi ều mang lại Syndrome tương tự nhau. Một tính chất quan trọng của
mã khối tuyến tính, nền tảng cho quá trình giải mã, là ánh xạ giữa các mẫu lỗi có thể sửa
ược và Syndrome là ánh xạ 1:1.
Dưới ây là 2 thuộc tính bắt buộc của ma trận kiểm tra chẵn lẻ:
(1) Không có cột nào của H chứa toàn các phần tử có giá trị 0, hoặc một lỗi ở vị trí từ mã
tương ứng khác sẽ không ảnh hưởng ến Syndrome và sẽ không phát hiện ược.
(2) Tất cả các cột của H phải là duy nhất. Nếu hai cột của H giống hệt nhau, các lỗi trong
hai vị trí từ mã tương ứng sẽ không thể phân biệt ược.
Ví dụ 3-18: Kiểm tra Syndrome
Giả sử từ mã U = 1 0 1 1 1 0 từ ví dụ nêu ở trên ược truyền và nhận ược vectơ r
= 0 0 1 1 10, các bit tận cùng bên trái nhận ược bị lỗi. Tìm giá trị vectơ Syndrome
lOMoARcPSD| 36067889
Một mã khối tuyến tính ược ặc trưng bởi hai số nguyên, n và k, và một ma trận
lập mã, còn số nguyên n là tổng số bit hay ký hiệu của từ mã ầu ra của bộ lập mã. R=k/n
ược gọi là tốc ộ mã, là số o ể ánh giá lượng dư ược bổ sung. Khác với mã khối tuyến
tính, mã chập ược ặc trưng bởi ba số nguyên: n, k và N, trong ó N ược gọi là ộ dài ràng
buộc (Contraint length); nó thể hiện số lần dịch cực ại của nhóm k bit bản tin mà sau ó
nhóm k bit này không còn gây ảnh hưởng ến ầu ra của bộ tạo mã. Một ặc tính quan trọng
của các mã chập khác biệt so với các mã khối là bộ tạo mã của chúng có bộ nhớ, nên
quá trình tạo ra n phần tử ở ầu ra của các bộ lập mã này không chỉ phụ thuộc vào k bit
ầu vào mà còn phụ thuộc vào (N-1) tập hợp k bit ầu vào trước ó.
T
SrH
và xác minh r
ằ
ng nó b
ằ
ng
T
eH
.
Ta có:
Syndrome c
(
ủ
a
vectơ
t
ừ
mã l
ỗ
i)
Ti
ế
p theo, xác minh Syndrome c
ủ
a
vectơ
t
ừ
mã l
ỗ
i có gi
ống như Syndrome củ
a
các m
ẫ
u l
ỗ
i gây ra l
ỗ
i:
100000
100
T
T
H
SeH
(Syndrome c
ủ
a mô hình l
ỗ
i)
3.4.4
. Các mã ch
ậ
p
hay a thứ
c t
ạ
o mã. S
ố
nguyên
k
là s
ố
bit hay ký hi
ệ
u c
ủ
a kh
ố
i b
ả
n tin
ở
ầ
u vào c
ủ
a b
ộ
1
0
0
1
0
0
0
1
0
001110
0
1
1
0
1
1
1
1
0
1
100
11
,
11
,
T
SrH

lOMoARcPSD|36067889
3.4.4.1. Tạo mã chập
Mã chập ược tạo ra bằng cách cho chuỗi thông tin truyền qua hệ thống các thanh
ghi dịch tuyến tính có số trạng thái hữu hạn. Cho số lượng thanh ghi là N, mỗi thanh ghi
dịch có k ô nhớ và ầu ra bộ mã chập có n hàm ại số tuyến tính. Số ô nhớ của bộ ghi dịch
là N×k.
Giả thiết, bộ mã chập làm việc với các chữ số nhị phân, thì tại mỗi lần dịch sẽ có k
bit thông tin ầu vào ược dịch vào thanh ghi thứ nhất và tương ứng có k bit thông tin
trong thanh ghi dịch cuối cùng ược ẩy ra ngoài mà không tham gia vào quá trình tạo
chuỗi bit ầu ra. Đầu ra nhận ược chuỗi n bit mã từ n bộ cộng module 2. Như vậy, giá trị
chuỗi kênh ầu ra không chỉ phục thuộc vào k bit thông tin ầu vào hiện tại mà còn phụ
thuộc vào (N-1)k bit trước ó, ược gọi là mã chập (n, k, L) với L=N-1.
Giả sử u là vectơ ầu vào, x là vectơ từ mã tương ứng ược mã hóa, bây giờ chúng ta
mô tả cách tạo ra x từ u. Để mô tả bộ mã hóa chúng ta phải biết sự kết nối giữa thanh ghi
ầu vào và ầu ra. Cách tiếp cận này có thể giúp chúng ta chỉ ra sự tương tự và khác nhau
với mã khối. Điều này có thể dẫn tới những ký hiệu phức tạp và nhằm nhấn mạnh tới cấu
trúc ại số của mã chập, nó sẽ làm giảm i tính quan tâm cho mục ích giải mã của chúng ta.
Do vậy, chúng ta chỉ phác họa tiếp cận này một cách sơ lược. Sau ó, mô tả mã hóa sẽ ược
ưa ra với những quan iểm khác.
Để mô tả bộ mã hóa như hình 3.25, chúng ta sử dụng N ma trận bổ sung
G G G
1
,
2
...,
N
bao gồm k hàng và n cột. Ma trận G
i
mô tả sự kết nối giữa oạn thứ i của k ô
nhớ trong thanh ghi lối vào với n ô của thanh ghi lối ra. Kết quả là “1” trong G
i
nghĩa là
có kết nối, là “0” nghĩa là không kết nối. Do ó chúng ta có thể ịnh nghĩa ma trận sinh
của mã chập như sau:
G
1
G
2
... G
N
G1 G2 ... GN
G G1 G2 ... GN (3.61)
Và tất cả các lối vào khác trong ma trận bằng 0. Do ó nếu lối vào là vectơ u, tương
ứng vectơ mã hóa là:
G
1
G2
...
...
...
G
N
...
...
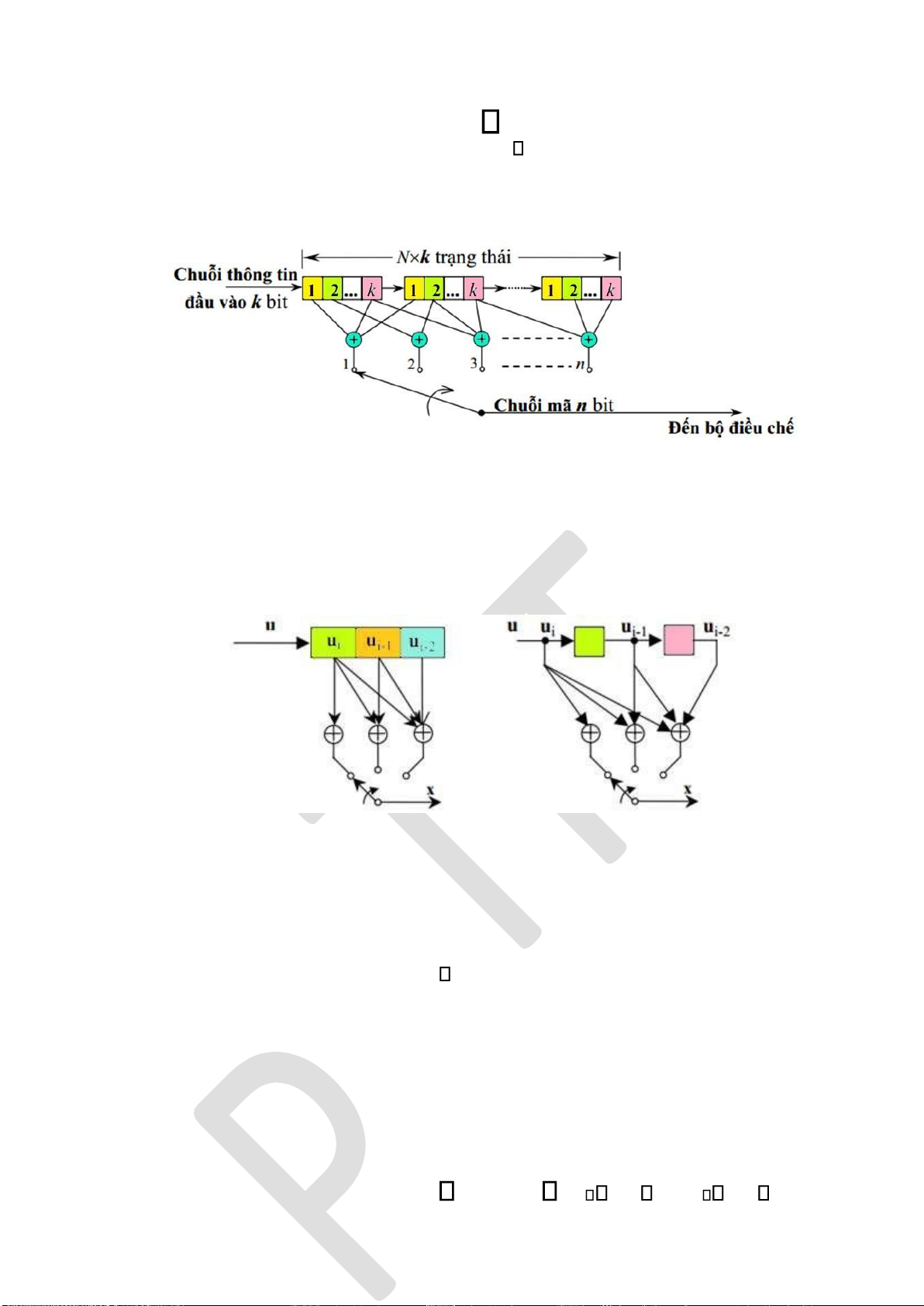
lOMoARcPSD|36067889
x uG
(3.62)
1
G
2
0 1 1 và G
3
0 0 1 .
Do ó ma trận sinh từ (3.47) là:
Hình 3.25
:
Sơ ồ
t
ổ
ng quan b
ộ
mã ch
ậ
p
Xem xét m
ộ
t s
ố
ví d
ụ
minh h
ọ
a:
Ví d
ụ
3-19
:
Xét mã ch
ậ
p (3, 1, 2). Hai gi
ản ồ
tương ương có bộ
mã hóa ượ
c minh
h
ọ
a
ở
hình 3.26.
Hình 3.26: Gi
ản ồ
tương ương cho bộ
mã ch
ậ
p (3, 1, 2)
B
ộ
th
ứ
nh
ấ
t s
ử
d
ụ
ng thanh ghi v
ớ
i 3 ô nh
ớ, ngượ
c l
ạ
i b
ộ
th
ứ
hai s
ử
d
ụ
ng 2 ô nh
ớ
,
m
ỗi ô coi như mộ
t b
ộ
tr
ễ
ơn vị
. L
ối ra thanh ghi ượ
c thay th
ế
b
ở
i b
ộ
tính toán ọ
c
ượ
c chu
ỗ
i ra c
ủ
a 3 b
ộ
c
ộ
ng. B
ộ
mã hóa ược quy ị
nh b
ở
i 3 ma tr
ậ
n b
ổ
sung (trong
th
ự
c t
ế
là 3
vectơ
hàng do
k
là:
=1)
111
G
;

lOMoARcPSD|36067889
111 011 001 000 ... ... ...
000 111 011
001 000 ...
...
Từ (3.62) có thể suy ra: Nếu chuỗi thông tin ầu vào là u = (11011 …) ược mã hóa
thành chuỗi x = (111100010110100…). Lưu ý rằng, chuỗi mã hóa có thể ược tạo bằng
tổng modul 2 các hàng của
G
tương ứng với “1” trong chuỗi thông tin.
Ví dụ 3-20: Xét mã (3, 2, 1). Bộ mã hóa ược minh họa ở hình 3.27. Bây giờ mã ược xác ịnh
thông qua 2 ma trận:
1 0 1
G1 0 1 0
0 0 1
G
000
...
000
...
111
...
011
...
001
...
000
...
...
...
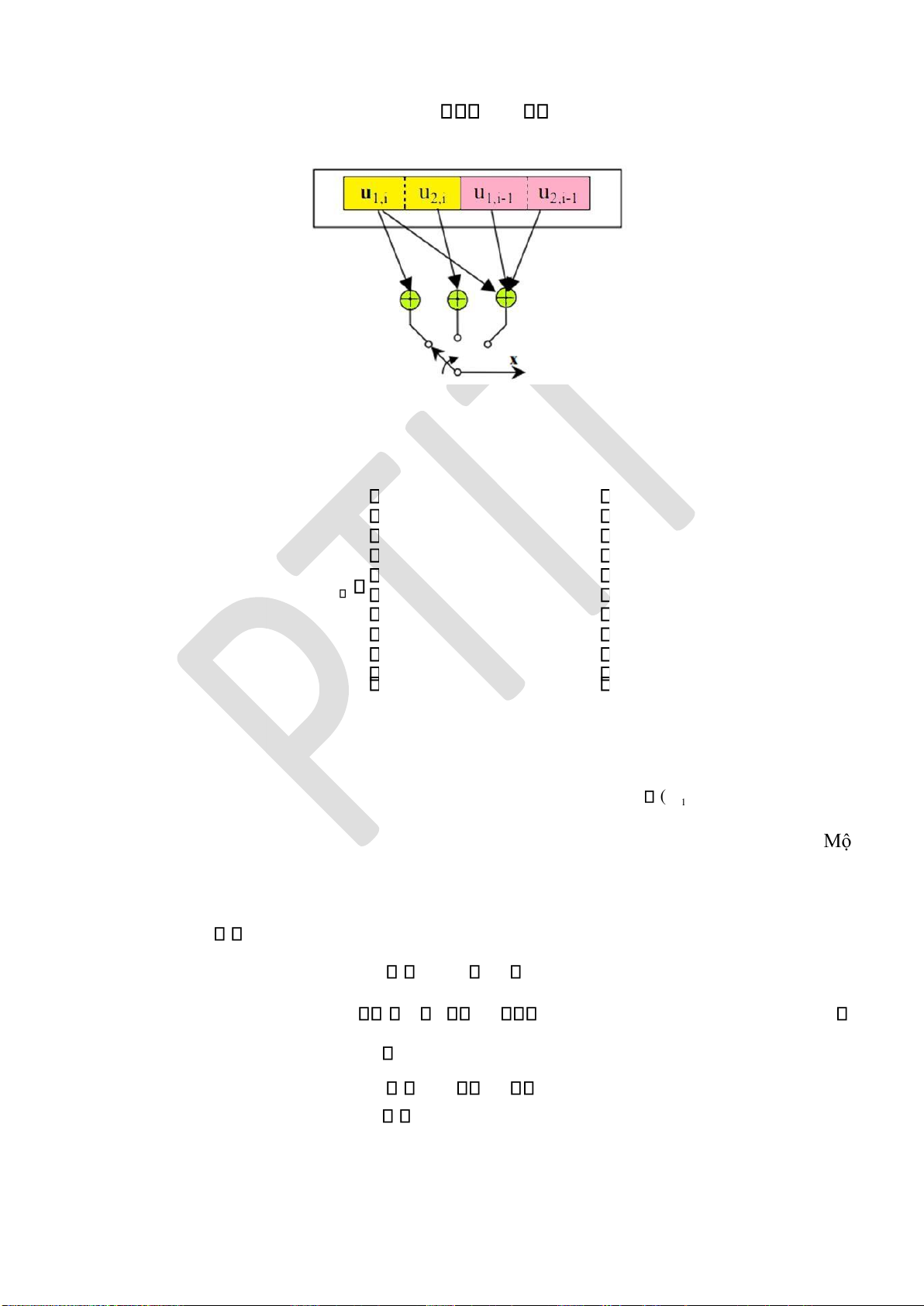
lOMoARcPSD|36067889
G2 0 0 1
Một
cách tương tự ta cũng có thể biểu diễn ma trận sinh: ,G ,...,G )
2N
.
dịch k=1, chiều dài chuỗi ầu ra n = 3 tức là mã (3, 1, 2) và ma trận sinh của mã chập có
dạng sau: g
1
100
G
g
2
G
101
G
(4,5,7) (3.63)
...
111
g
3
Sơ ồ mã chập ược biểu diễn như hình 3.28:
Hình 3.27: B
ộ
mã ch
ậ
p (3, 2, 1)
Ma tr
ận sinh ượ
c t
ạ
o ra:
000
101
...
...
001
...
001
...
000
010
101
000
001
...
000
010
...
000
001
000
101
000
000
001
000
000
010
001
000
000
...
...
...
...
...
G
Chu
ỗ
i thông tin
u
=
(11011011…)
ượ
c mã hóa thành chu
ỗ
i mã
x
=
(111010100110…)
.
1
(
GG
Ví d
ụ
3-21
:
Cho b
ộ
mã ch
ậ
p có chi
ề
u dài ràng bu
ộ
c
N
= 3, s
ố
ô nh
ớ
trong m
ỗ
i thanh ghi
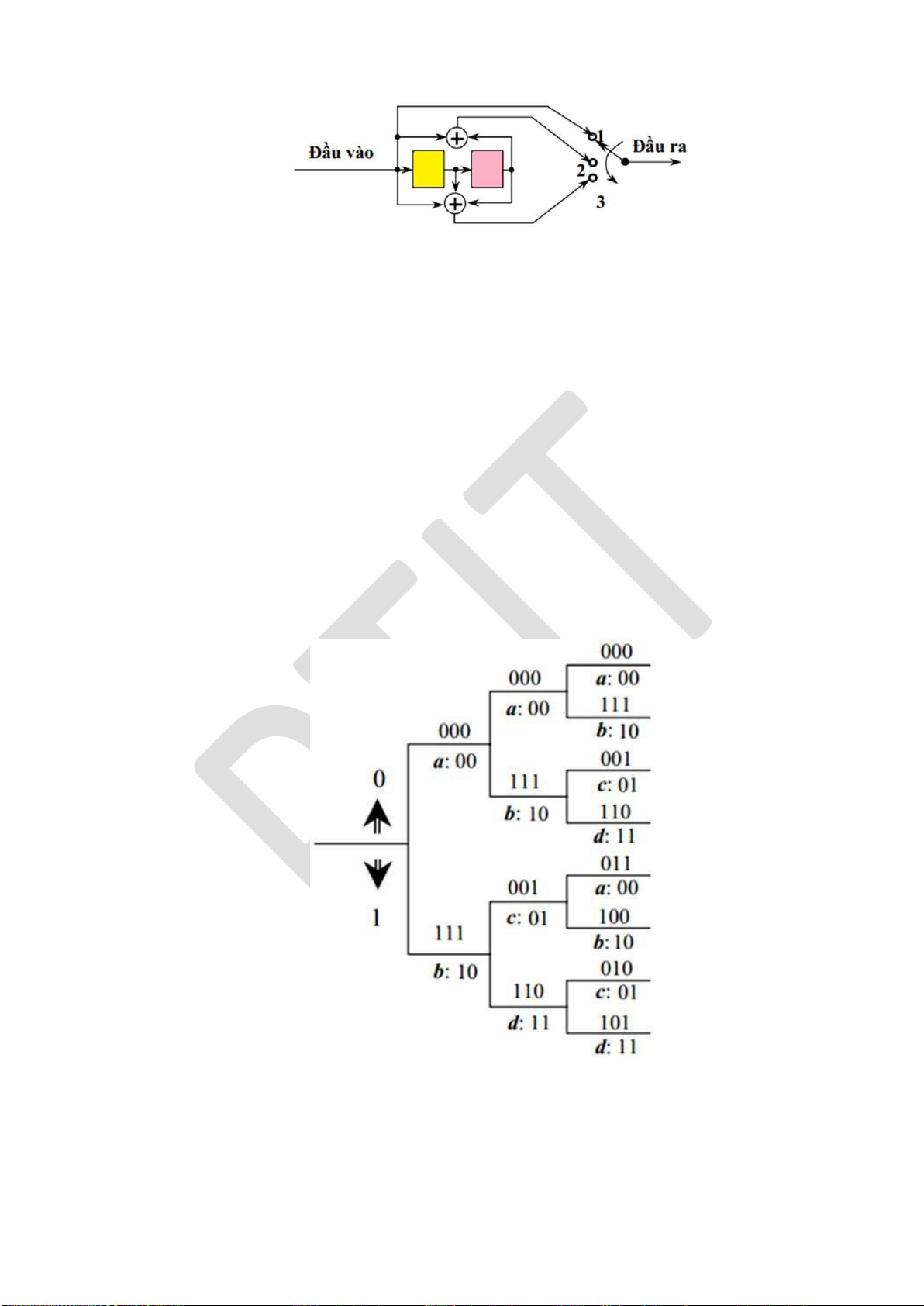
lOMoARcPSD|36067889
Hình 3.28: Sơ ồ bộ mã chập với n = 3, k = 1, N = 3
3.4.4.2. Biểu diễn mã chập
Có ba phương pháp ể biểu diễn mã chập ó là: sơ ồ trạng thái, sơ ồ hình cây, và sơ
ồ lưới. Để làm rõ các phương pháp này ta tập trung phân tích dựa trên ví dụ 3.6.
Hình 3.29: Sơ ồ hình cây của bộ mã chập với n = 3, k = 1, N = 3 (ví dụ 3.21)
Từ sơ ồ hình cây có thể thực hiện mã hóa bằng cách dựa vào các bit ầu vào và thực
hiện lần lượt theo các nhánh của cây, ta sẽ nhận ược tuyến mã, từ ó ta nhận ược dãy các
chuỗi ầu ra.
b) Sơ ồ trạng thái
a)
Sơ ồ
hình cây
T
ừ
ví d
ụ
3-21, gi
ả
thi
ế
t tr
ạng thái ban ầ
u c
ủ
a thanh ghi d
ị
ch trong b
ộ
mã ề
u là
tr
ạ
ng thái toàn 0. N
ếu bit vào ầ
u tiên là bit 0 (
k
=1)
thì ầ
u ra ta nh
ận ượ
c chu
ỗ
i 000
(
n
=3)
. Còn n
ếu bit ầ
u tiên vào b
ằng 1 thì ầ
u ra ta nh
ậ
n chu
ỗ
i bit 111. N
ếu bit vào ầ
u
tiên là bit “1” và bit vào tiếp theo là bit “0” thì chuỗ
i th
ứ
nh
ất là “111” và chuỗ
i th
ứ
hai
là chu
ỗi “001”. Với cách mã hóa như vậ
y, ta có th
ể
bi
ể
u di
ễ
n mã ch
ập theo sơ ồ
d
ạ
ng
hình cây
–
hình 3.29.

lOMoARcPSD| 36067889
Sơ ồ trạng thái ược thực hiện bằng cách ơn giản sơ ồ 4 trạng thái có thể có của bộ
mã (a, b, c và d tương ứng với các trạng thái 00, 10, 01, 11) và trạng thái chuyển tiếp có
thể ược tạo ra từ trạng thái này chuyển sang trạng thái khác, quá trình chuyển tiếp có thể
là:
0
,
1
,
0
,
1
,
0
,
1
,
0
,
1
(3.64)
Ký hiệu
1
là quá trình chuyển tiếp từ trạng thái sang trạng thái với bit
ầu vào là bit “1”.
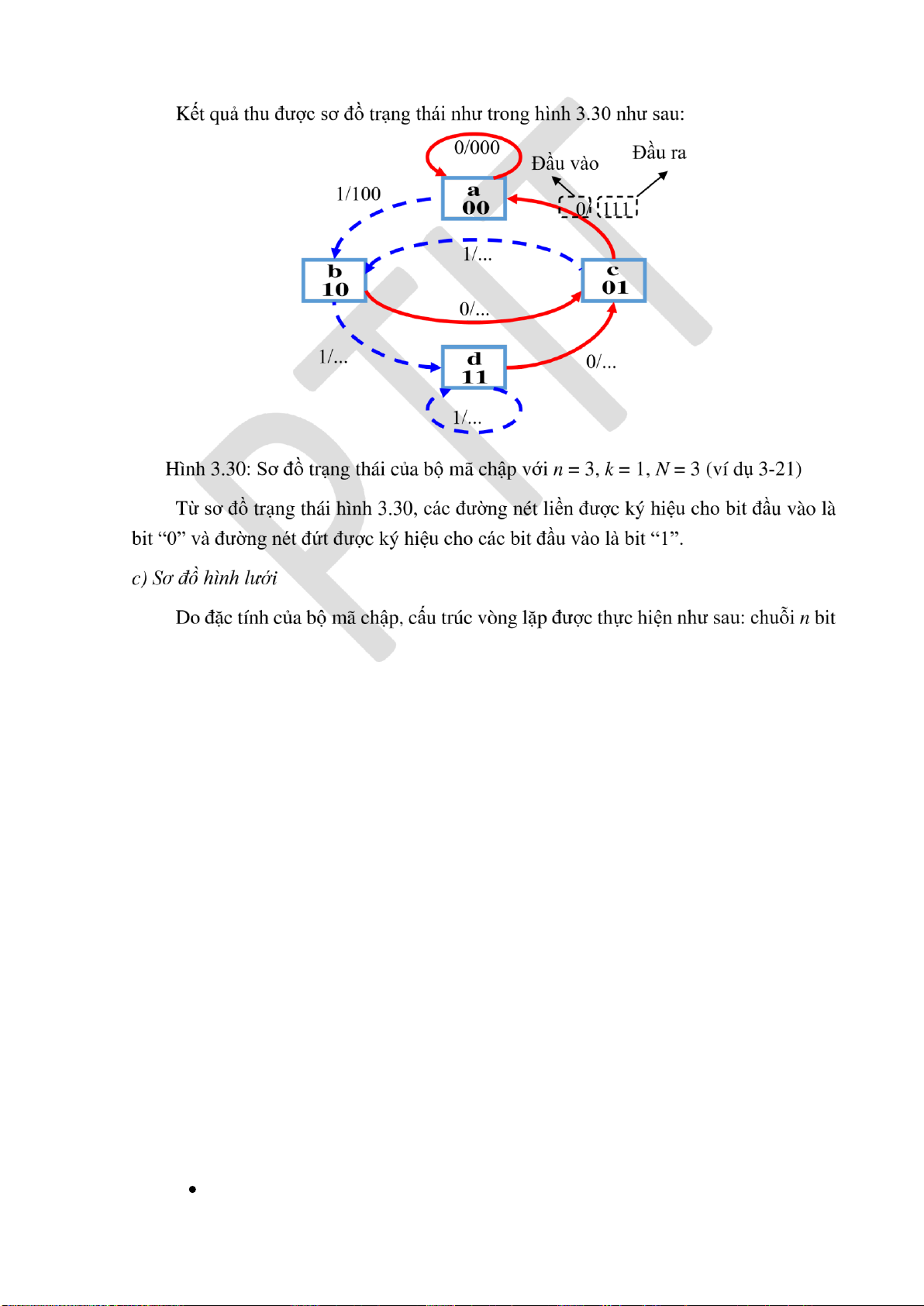
lOMoARcPSD|36067889
ầu ra phụ thuộc vào chuỗi k bit ầu vào hiện tại và (N-1) chuỗi ầu vào trước ó hay (N-
1)×k bit ầu vào trước ó. Từ ví dụ 3.6, có chuỗi 3 bit ầu ra phụ thuộc vào 1 bit ầu vào
hoặc là “1” hoặc là “0” và 4 trạng thái có thể có của hai thanh ghi dịch, ký hiệu là a =
“00”; b = “10”; c = “01”; d = “11”. Nếu ặt tên cho mỗi nút trong sơ ồ hình cây tương
ứng với 4 trạng thái của thanh ghi dịch, ta thấy rằng tại tầng thứ 3 có 2 nút mang nhãn a
và 2 nút mang nhãn b, 2 nút mang nhãn c và 2 nút mang nhãn d. Bây giờ ta quan sát tất
cả các nhánh bắt nguồn từ 2 nhánh có nhãn giống nhau (trạng thái giống nhau) thì tạo ra
chuỗi ầu ra giống nhau, nghĩa là hai nút có nhãn giống nhau thì có thể coi như nhau. Với
tính chất ó có thể biểu diễn mã chập bằng sơ ồ dạng hình lưới gọn hơn, trong ó các ường
nét liền ược ký hiệu cho bit ầu vào là bit “0” và ường nét ứt còn lại ứng với bit ầu vào
là bit “1”.
Chuỗi thu
a
000
111
b
001
c
110 010
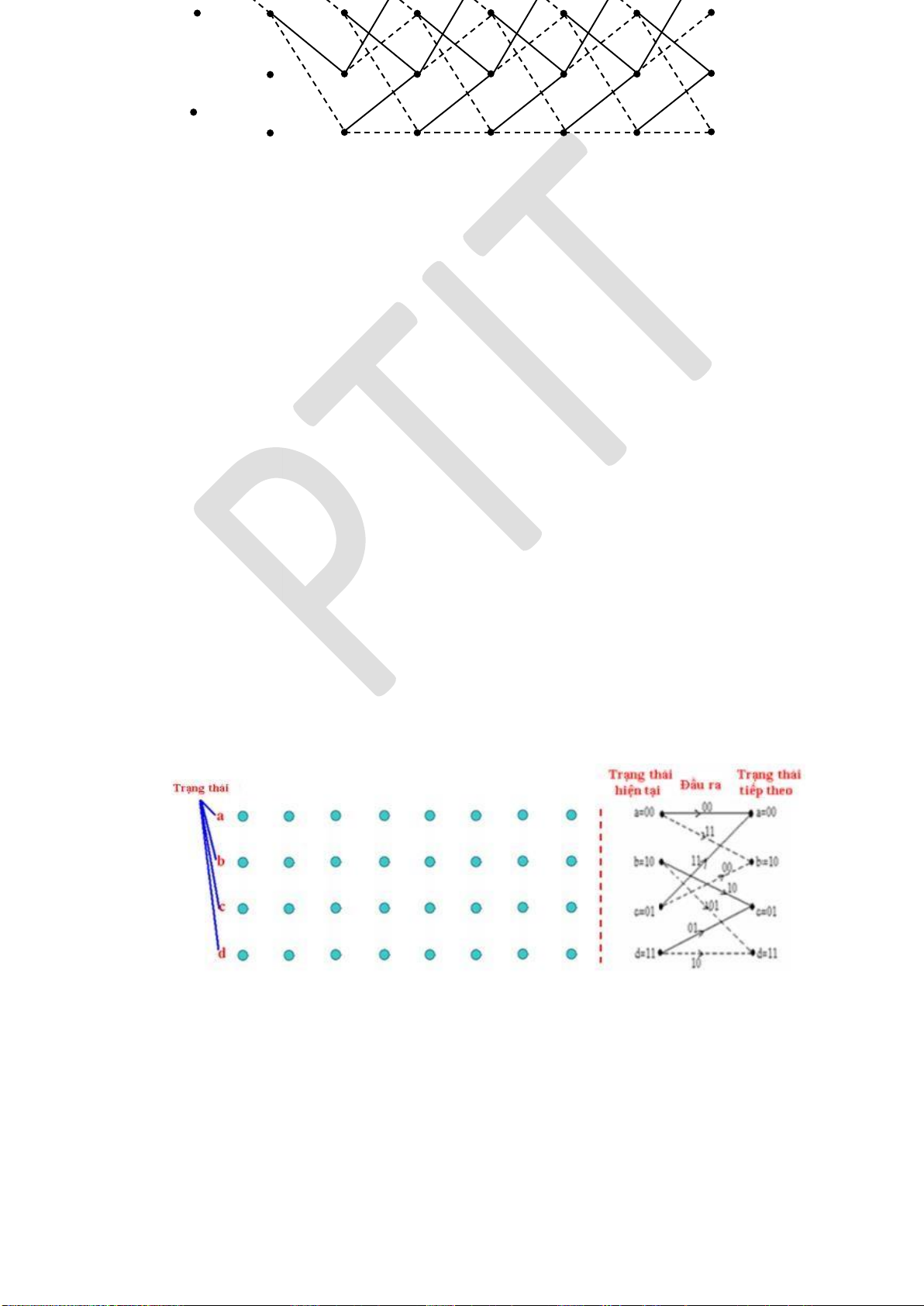
lOMoARcPSD|36067889
d
101
Hình 3.31: Sơ ồ hình lưới bộ mã chập với n = 3, k = 1, N = 3 (ví dụ 3-20)
(Trạng thái ban ầu toàn bằng “0”)
So với sơ ồ hình lưới và hình cây thì sơ ồ trạng thái là ơn giản nhất.
3.4.4.3. Giải mã mã chập bằng thuật toán Viterbi
Giải mã mã chập bằng thuật toán Viterbi là phương pháp giải mã phổ biến nhất
hiện nay. Ở ây, thuật toán Viterbi dựa trên cơ sở giải mã kế cận gần nhất. Thuật toán
tính khoảng cách Hamming (gọi là metric) giữa các tín hiệu thu ở thời iểm t
i
và tất cả
các ường trong lưới dẫn ến mỗi nút trạng thái ở cùng thời iểm t
i
. Khi hai ường cùng ến
một nút trạng thái, chọn ra ường có khoảng cách Hamming ngắn hơn, gọi là ường sống
sót. Việc chọn ường sống sót ược thực hiện cho tất cả các trạng thái ở tất cả các thời
iểm.
Ví dụ 3-22: Xét quá trình giải mã Viterbi cho mã tích chập (2, 1, 2); Phía phát cần truyền
bản tin gồm 12 bit; Chuỗi dữ liệu thu ược ở phía thu gồm 24 bit như sau:
Y = 110111000110001111101100 Quá
trình giải mã ược thực hiện như sau:
Bước 1: Xây dựng lưới mã theo thời gian như sau:
Bước 2: Tính chỉ số o của nhánh
Bắt ầu từ nút trạng thái a (có giá trị chạy bằng 0), lần lượt tính chỉ số o của các
nhánh có thể có dựa vào dữ liệu thu và sơ ồ lưới mã. Tính chỉ số o của từng nhánh dựa
vào khoảng cách Hamming.
Bước 3: Tính giá trị chạy tại mỗi nút
Cộng giá trị chạy của nút trước ó với chỉ số o của nhánh chuyển trạng trạng thái giữa
hai nút này.
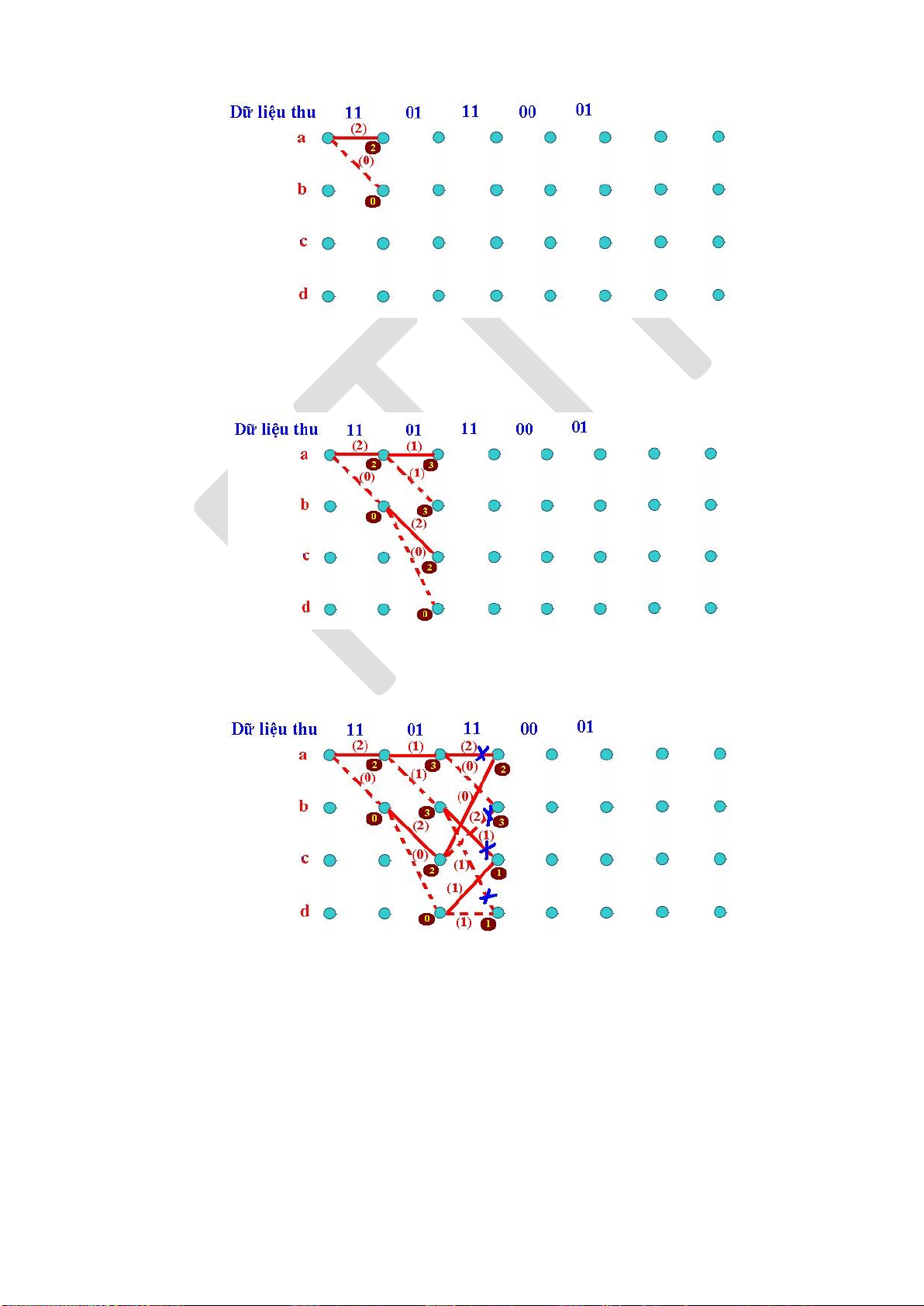
lOMoARcPSD|36067889
Quá trình ược lặp lại cho ến khi hết dữ liệu.
Bước 5: Xác ịnh ường mã tối ưu
Từ trạng thái cuối cùng (trạng thái a), i ngược lại (từ phải sang trái) ể xác ịnh ường
mã còn tồn tại ây là ường mã tối ưu.
Bước 6: Xác ịnh dữ liệu thu
Từ ường mã tối ưu, xác ịnh ược dữ liệu thu.
Ta thu ược sơ ồ ầy ủ như sau:
Bước 4: Bướ
c l
ặ
p
L
ặ
p l
ạ
i quá trình tính toán cho t
ấ
t c
ả
các chuy
ể
n tr
ạ
ng thái có th
ể
có t
ạ
i các nút.
Trong quá trình l
ặ
p n
ế
u có các
nhánh ế
n cùng m
ộ
t nút, nhánh nào t
ạ
o ra giá tr
ị
ch
ạ
y t
ạ
i nút
ó lớn hơn sẽ
b
ị
lo
ạ
i b
ỏ
.

lOMoARcPSD|36067889
1- Nêu ý nghĩa của mã hóa và iều kiện ể mã phân tách ược.
2- Trình bày khái niệm về mã có tính prefix, mã hệ thống, mã hệ thống có tính prefix
và mã có dấu phân tách.
3- Trình bày khái niệm mã hiệu và các thông số cơ bản của mã hiệu.
4- Vẽ sơ ồ khối và trình bày nguyên tắc mã hóa và giải mã của phương pháp iều xung
mã (PCM)?
5- Vẽ sơ ồ khối và trình bày nguyên tắc mã hóa và giải mã của phương pháp iều xung
mã vi sai (DPCM)?
6- Vẽ sơ ồ khối và trình bày nguyên tắc mã hóa và giải mã của phương pháp mã hóa dự
oán tuyến tính (LPC)?
7- Cho nguồn không nhớ 531; 0; 1; 3; 5} với xác suất tương ứng
{0,05; 0,1; 0,1; 0,15; 0,05; 0,25; 0,3}. a)
Tìm Entropy của nguồn?
b) Nếu nguồn ược mã hoá sang các bit nhị phân dùng phương pháp mã hoá Fano,
hãy thực hiện quá trình mã hoá ó và cho biết hiệu suất bộ mã?
c) Giả sử nguồn ược lượng tử theo nguyên tắc:
Q( 5) Q( 3)4
Chu
ỗ
i d
ữ
li
ệu thu ượ
c: 110111001000
3.5
.
TỔNG KẾT CHƯƠNG
Chương 3
ã cung cấp những
vấn ề cơ bản trong mã hóa như: khái niệm mã hóa,
mã hiệu, ưa ra các thông số cơ bản của mã hiệu
,
iều kiện thiết lập mã và các phương
pháp biểu diễn mã. Trên cơ sở ó ã nghiên cứu cụ thể các phương pháp mã hóa nguồn,
mã hóa kênh. Trong ó ã trình bày khái niệm mã hóa thống kê tối ưu
và mã hóa chống
nhiễu
,
các bước mã hóa/giải mã của
các phương pháp mã hóa thống kê
tối ưu
và các
phương pháp mã hóa chống nhiễu
.
Câu hỏi/bài tập chương 3
lOMoARcPSD|36067889
Q( 1) Q(0) Q(1) 0
Q Q(3) (5) 4
Tìm Entropy của nguồn lượng tử?
8- Cho chuỗi nhị phân sau:
00010010000001100001000000010000001010000100000011010000000110 Hãy
thực hiện mã hóa nguồn Lempel-Ziv?
9- Cho nguồn không nhớ 531; 0; 1; 3; 5} với xác suất tương ứng
{0,05; 0,1; 0,1; 0,15; 0,05; 0,25; 0,3}. a)
Tìm Entropy của nguồn?
b) Nếu nguồn ược mã hoá sang các bit nhị phân dùng phương pháp mã hoá Huffman,
hãy thực hiện quá trình mã hoá ó và cho biết hiệu suất bộ mã? 10- Nguồn DMS
có 7 ký hiệu với xác suất xuất hiện như sau:
u
i
u
1
u
2
u
3
u
4
u
5
u
6
u
7
p
i
0,34 0,23 0,19 0,1 0,07 0,06 0,01
a) Tìm Entropy của nguồn?
b) Nếu nguồn ược mã hoá sang các bit nhị phân dùng phương pháp mã hoá Huffman,
hãy thực hiện quá trình mã hoá ó và cho biết hiệu suất bộ mã?
11- Cho mã tích chập (2, 1, 2) với các a thức sinh: g
(1)
= (1, 1, 1); g
(2)
= (1, 0, 1)
a) Vẽ sơ ồ mã hóa?
b) Vẽ sơ ồ trạng thái và sơ ồ lưới mã?
c) Giả sử chuỗi dữ liệu vào 1010. Hãy xác ịnh dữ liệu mã hóa?
d) Giả sử dữ liệu thu ược là Y. Hãy thực hiện việc giải mã dùng giải thuật Viterbi
trong các trường hợp sau: Y = 1110001011; Y = 1110101011; Y = 1110111001?
12- Cho mã Hamming (7, 4) với: c m m
1
1 2
m
3
; c
2
m
2
m
3
m
4
; c m m
3
1 2
m
4
a) Vẽ sơ ồ khối bộ mã hóa và giải thích?
b) Tìm từ mã với chuỗi bit tin tức vào M = [0 1 1 1]?
c) Giả sử lỗi trên kênh truyền và máy thu ược từ mã Y = [0 1 1 1 0 1 0]. Xây dựng
sơ ồ khối giải mã Syndrome và giải thích. Chứng minh máy thu sửa ược lỗi ơn?
13- Cho mã tích chập (3, 1, 2) với các a thức sinh: g
(1)
= (1,1,1); g
(2)
= (1,0,1); g
(3)
=
(1,1,0)
a) Vẽ sơ ồ mã hóa?
b) Vẽ sơ ồ trạng thái và sơ ồ lưới mã?
c) Giả sử chuỗi dữ liệu vào 00110. Hãy xác ịnh dữ liệu mã hóa?

lOMoARcPSD|36067889
- CHƯƠNG 4 -
GHP KÊNH
Trong hệ thống truyền tin ể nâng cao hiệu suất sử dụng môi trường truyền dẫn cần
phải thực hiện chức năng ghép kênh. Trong chương này sẽ ề cập các nội dung liên quan
ến các kỹ thuật ghép kênh và ứng dụng ghép kênh trong hệ thống truyền thông số.
4.1. TỔNG QUAN VỀ KỸ THUẬT GHÉP KÊNH
Ghép kênh là kỹ thuật liên quan ến việc chia sẻ các tài nguyên của mạng qua một
số tuyến truyền dẫn thông tin. Tài nguyên mạng, vấn ề quan tâm ầu tiên ối với chúng ta
là băng thông, có ơn vị là Hz ối với các hệ thống truyền dẫn tương tự và là bit/s ối với
các hệ thống truyền dẫn số. Trong phần này chúng ta xem xét các kỹ thuật ghép kênh
ược sử dụng ể chia sẻ các tuyến truyền dẫn kết nối một nhóm người dùng. Những kỹ
thuật này cơ bản ược sử dụng trong các mạng iện thoại và trong các dịch vụ quảng bá.
Hình 4.1a chỉ ra ví dụ trong ó ba cặp người dùng trao ổi thông tin qua việc sử dụng
ba cặp ường dây. Việc bố trí này sẽ hoàn toàn dành riêng các tài nguyên mạng, ó là các
ường dây ối với mỗi cặp người dùng, là kiểu iển hình trong mạng thoại thời kỳ phát triển

lOMoARcPSD|36067889
ầu. Tuy nhiên, cách thức tiếp cận nhanh chóng trở thành không phổ biến và không hiệu
quả khi số người dùng tăng lên. Phương thức tiếp cận hiệu quả hơn là chia sẻ ộng các
tài nguyên này, ó là các tuyến truyền dẫn kết nối một nhóm người dùng.
Trong hình 4.1b cho thấy cách thức bộ ghép kênh cho phép chia sẻ tài nguyên này.
Khi một người dùng ở một ầu cuối này muốn trao ổi thông tin với một người dùng ở một
ầu cuối khác, bộ ghép kênh sẽ gán một tuyến truyền dẫn nào ó trong suốt khoảng thời
gian có cuộc gọi. Khi cuộc gọi hoàn thành, tuyến truyền dẫn này ược ưa trở về trạng thái
sẵn sàng ể phục vụ các yêu cầu tuyến truyền dẫn mới.
Lưu ý: hai bộ ghép kênh cần phải trao ổi thông tin với nhau ể thiết lập và giải phóng
tuyến truyền dẫn.
Tuyến truyền dẫn ấu nối hai bộ ghép kênh ược gọi là trung kế. Ban ầu, mỗi trung
kế chỉ có một tuyến truyền dẫn ơn, khi ó, tín hiệu báo hiệu cho một kết nối sẽ ược mang
trên tuyến truyền dẫn này. Tuy nhiên, những tiến bộ về công nghệ truyền dẫn ã làm cho
tuyến truyền dẫn ơn có băng thông lớn có thể truyền dẫn nhiều kết nối. Trên quan iểm
thiết lập kết nối, một tuyến như vậy ược xem là tương ương với một số trung kế. Bàn
luận về một số cách tiếp cận khác ể thông tin từ nhiều kết nối vào một tuyến truyền dẫn
ơn sẽ ề cập ến sau ây.

lOMoARcPSD|36067889
Hình 4.2: Ghép kênh phân chia theo tần số FDM
Khoảng những năm 1930 FDM ược ưa vào mạng iện thoại. Bộ ghép kênh tương
tự ã thực hiện ghép 12 kênh thoại vào một tuyến truyền dẫn. Mỗi tín hiệu thoại chiếm
một khoảng băng thông 4 KHz. Bộ ghép kênh này iều chế mỗi tín hiệu thoại sao cho
mỗi tín hiệu chiếm một khoảng băng thông 4 KHz trong dải từ 60 ến 108 KHz. Tín hiệu
Hình 4.1: Ghép kênh
4.2
. K
Ỹ
THU
Ậ
T GHÉP KÊNH
4.2.1
. K
ỹ
thu
ậ
t ghép kênh phân chia theo t
ầ
n s
ố
(FDM)
Giả sử tuyến truyền dẫn có băng thông (Hz) lớn hơn nhiều so với băng thông ược
yêu cầu bởi một kết nối ơn. Ví dụ, trong hình 4.2a, mỗi ngườ
i dùng
có tín hiệu với
băng thông
W
(Hz), và kênh có băng thông khả dụng lớn hơn
3
W
(Hz). Tr
ong ghép kênh
phân chia tần số (FDM), băng thông này ược chia thành một số băng tần nhỏ
hơn gọ
i
là các băng con
, m
ỗi băng con ượ
c
cấp cho tín hiệu của một kết nối riêng lẻ. Bộ ghép
kênh gán băng con ó cho mỗi kết nối và sử dụng iều chế ể ặt tín hiệu của kết nối
ó vào băng con thích hợp. Quá trình này ưa ến một tín hiệu kết hợp toàn phần mang
tất cả các kết nối như chỉ ra ở hình 4.2b. Tín hiệu ghép
k
ế
t
hợp ược truyền
i, và bộ
tách kênh khôi phục các tín hiệu tương ứng ối với mỗi kết nối. Việc giảm số lượng
tuyến truyền dẫn cần ược thực hiện ể giảm chi phí tổng của hệ thống ó.
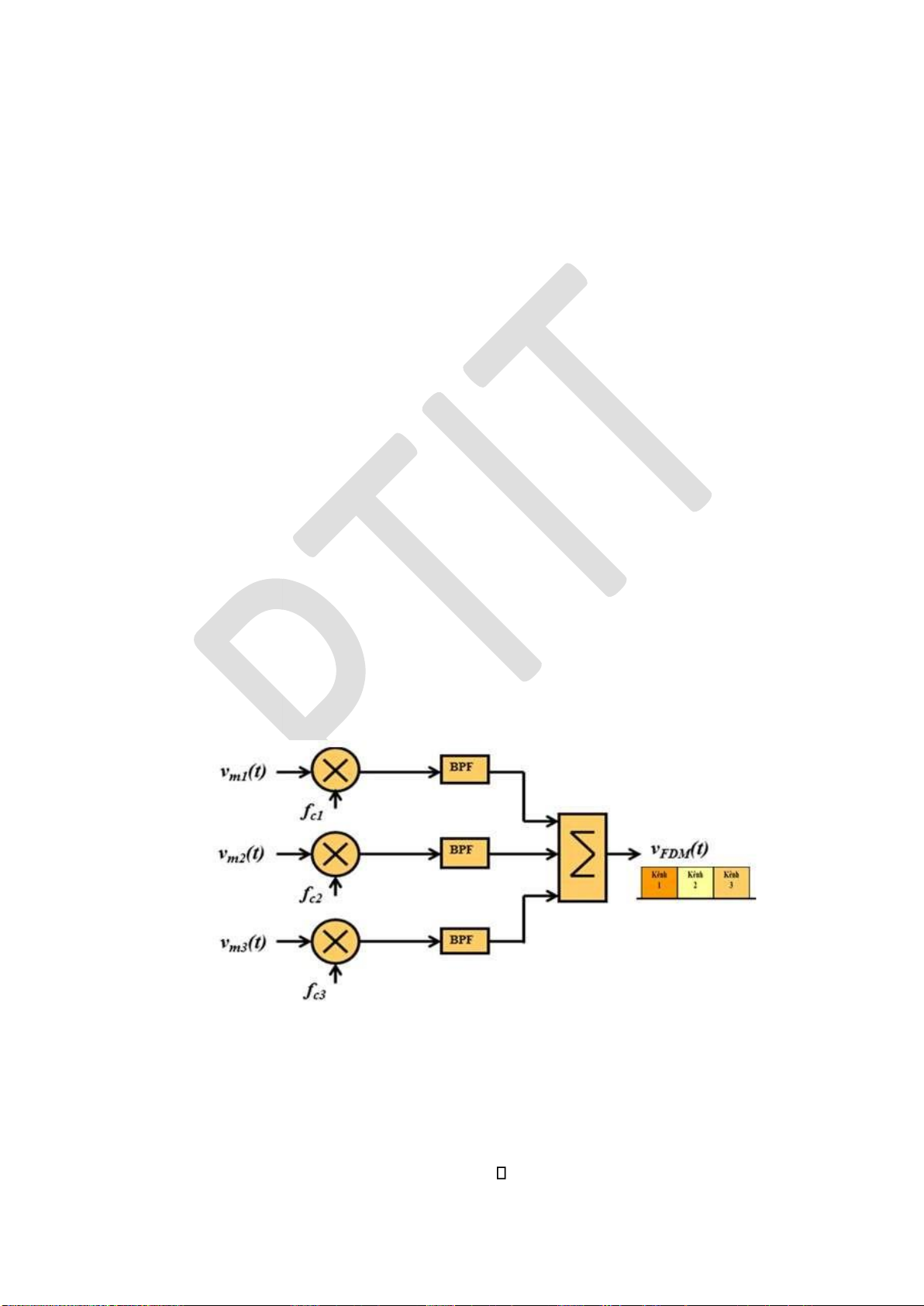
lOMoARcPSD| 36067889
ghép kết hợp này ược gọi là một nhóm. Phân cấp các bộ ghép kênh tương tự cũng ã ược
ịnh nghĩa. Ví dụ, siêu nhóm (mang 60 tín hiệu thoại) ược tạo ra qua việc ghép 5 nhóm,
mỗi nhóm có băng thông 48 KHz, vào dải tần số từ 312 ến 552 KHz. Lưu ý, với mục ích
ghép kênh, mỗi nhóm ược xử lý như tín hiệu riêng lẻ. Sau ó, 10 siêu nhóm có thể ược
ghép thành siêu siêu nhóm gồm có 600 tín hiệu thoại chiếm dải tần số từ 564 ến 3084
KHz.
Các ví dụ tương tự về FDM là phát thanh quảng bá, truyền hình quảng bá và truyền
hình cáp. Trong ó, mỗi trạm có dải tần số ã ược gán. Các trạm trong phát thanh AM, FM
và truyền hình ược gán tương ứng các dải tần số là 10 KHz, 200 KHz và 6 MHz. FDM
cũng ược sử dụng trong iện thoại di ộng gồm nhiều khoảng tần số, iển hình mỗi khoảng
là 25 ến 30 KHz, ược dùng chung bởi những người dùng trong cùng một vùng phủ. Mỗi
người dùng ược gán khoảng tần số cho mỗi hướng. Lưu ý: trong FDM thông tin của
người dùng có thể ở dạng tương tự hoặc dạng số.
Ví dụ về hệ thống FDM gồm 3 kênh ược mô tả ở hình 4.3.
Phía phát: Mỗi tín hiệu vào v
m
(t) (có băng thông f
m
) ược ưa vào các bộ nhân (bộ iều chế)
ể nhân với các tần số sóng mang khác nhau, chẳng hạn f
c1
ối với v
m1
(t), f
c2
ưới với v
m2
(t)
và f
c3
ối với v
m3
(t). Đầu ra của bộ nhân sẽ là tín hiệu DSBSC (Double SideBand
Suppressed Carrier). Sau ó ược chuyển qua bộ lọc BPF có băng thông f
c
+f
m
hoặc f
c
-f
m
.
Đầu ra của bộ lọc BPF sẽ là tín hiệu LSB (Lower SideBand- băng dưới) hoặc USB
(Upper SideBand- băng trên). Các tín hiệu này sẽ ược ghép kênh với nhau.
Hình 4.3: Hệ thống FDM ghép 3 kênh thông tin ầu vào
Băng thông của tín hiệu ghép kênh FDM phụ thuộc vào số lượng sóng mang sử
dụng, N và ược xác ịnh như sau:
BW
FDM
N f
.
m
(4.1)
lOMoARcPSD| 36067889
Phía thu: Các bộ lọc băng tại nhánh phát và nhánh thu của mỗi kênh có băng tần như
nhau. Đầu vào nhánh thu có 3 bộ lọc băng nối song song và óng vai trò tách kênh. Bộ
iều chế tại nhánh phát sử dụng sóng mang nào thì bộ giải iều chế của kênh ấy cũng sử
dụng sóng mang như vậy. Tín hiệu kênh ược giải iều chế với sóng mang và ầu ra bộ giải
iều chế ngoài băng âm tần còn có các thành phần tần số cao. Bộ lọc thấp loại bỏ các
thành phần tần số cao, chỉ giữ lại băng âm tần.
Đối với trường hợp các tín hiệu vào là tín hiệu tiếng nói, trước khi iều chế tín hiệu
tiếng nói phải qua bộ lọc thấp ể hạn chế băng tần từ 0,3 ến 3,4 kHz. Sau ó băng tần này
ược iều chế theo phương thức iều biên với sóng mang
ể ược hai băng bên. Dạng tín
hiệu iều biên ầu ra các bộ iều chế (bộ nhân) như hình 4.4.
Đặc tính suy hao - tần số của bộ lọc băng
Băng tần thoại Băng dướ
i Băng trên
f (kHz)
0,3 3,4
fc
Hình 4.4: Tín hiệu iều biên trong cấp iều chế kênh
4.2.2. Kỹ thuật ghép kênh phân chia theo thời gian (TDM)
Khi có nhiều tín hiệu có tần số hoặc băng tần như nhau cùng truyền tại một thời
iểm phải sử dụng ghép kênh theo thời gian. Có thể ghép kênh theo thời gian (TDM) các
tín hiệu tương tự hoặc các tín hiệu số. Tương ứng là TDM tín hiệu tương tự và TDM tín
hiệu số.
Trong ghép kênh phân chia theo thời gian, truyền dẫn giữa các bộ ghép kênh ược
cung cấp bởi tuyến truyền dẫn số tốc ộ cao. Mỗi một kết nối tạo ra luồng thông tin số
ược chèn vào tuyến tốc ộ cao. Ví dụ trong Hình 4.5a, mỗi kết nối tạo ra tín hiệu – một
ơn vị thông tin với chu kỳ 3T giây. Đơn vị thông tin này có thể là bit, byte hoặc khối bit
có kích thước cố ịnh. Điển hình, tuyến truyền dẫn ược tổ chức thành các khung, lần lượt
ược chia thành các khe có ộ dài thời gian như nhau. Ví dụ, trong Hình 4.5b, tuyến truyền
dẫn có thể gửi một ơn vị thông tin với chu kỳ T giây, và tín hiệu ghép hợp có cấu trúc
khung gồm 3 khe, mỗi khe cho một người dùng. Trong khoảng thời gian thiết lập kết
nối, mỗi kết nối ược gán một khe thích hợp với thông tin ược tạo ra bởi kết nối.
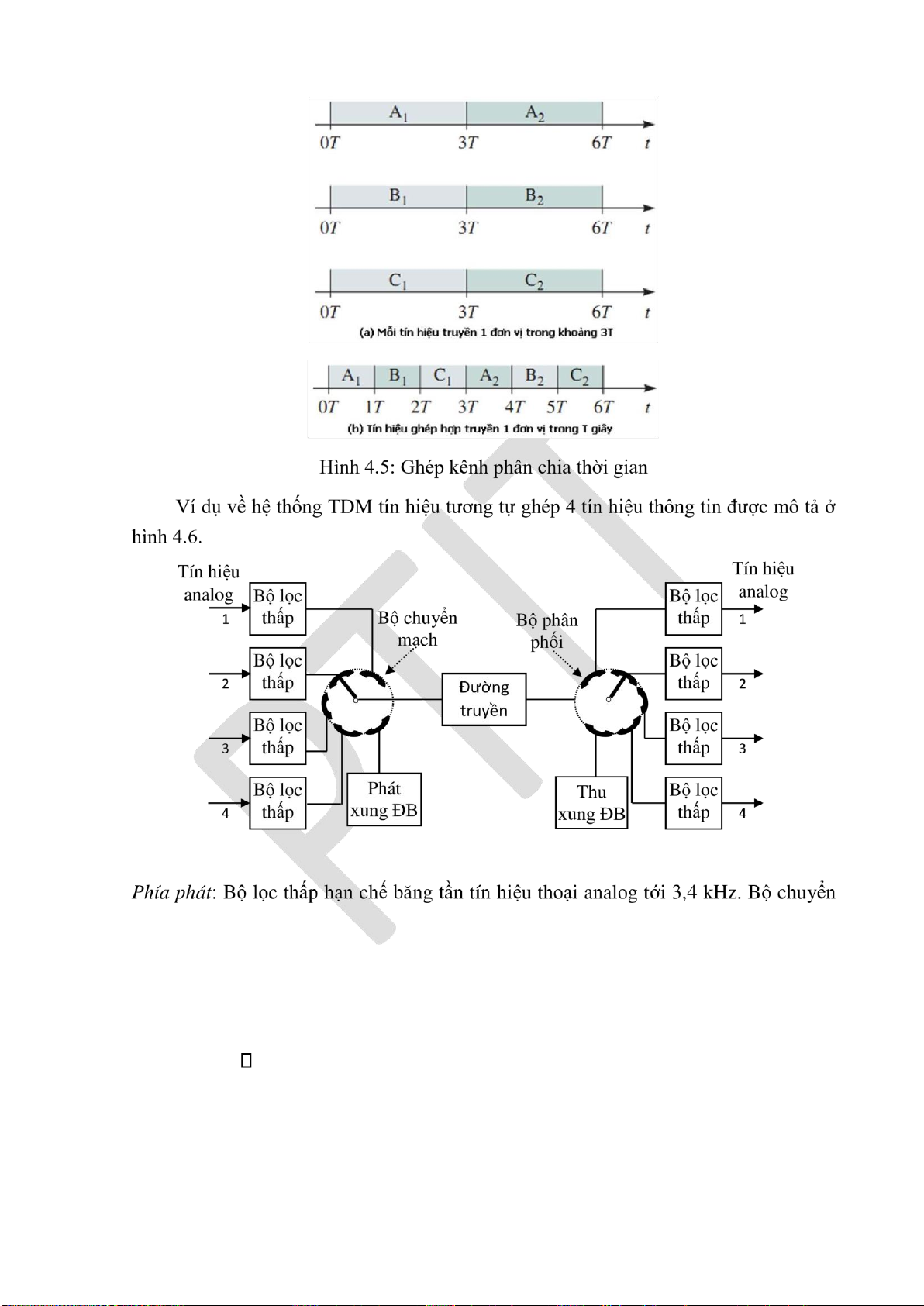
lOMoARcPSD| 36067889
Hình 4.6: Hệ thống TDM tín hiệu tương ghép 4 kênh thông tin
mạch óng vai trò lấy mẫu tín hiệu các kênh, vì vậy chổi của bộ chuyển mạch quay một
vòng hết 125 s, bằng một chu kỳ lấy mẫu. Chổi tiếp xúc với tiếp iểm tĩnh của kênh nào
thì một xung của kênh ấy ược truyền i. Trước hết một xung ồng bộ ược truyền i và tiếp
theo ó là xung của các kênh 1, 2, 3 và 4. Kết thúc một chu kỳ ghép lại có một xung ồng
bộ và ghép tiếp xung thứ hai của các kênh. Quá trình này cứ tiếp diễn liên tục theo thời
gian. Để phía thu hoạt ộng ồng bộ với phía phát, yêu cầu chổi của bộ phân phối quay
cùng tốc ộ và ồng pha với chổi của bộ chuyển mạch. Nghĩa là hai chổi phải tiếp xúc với
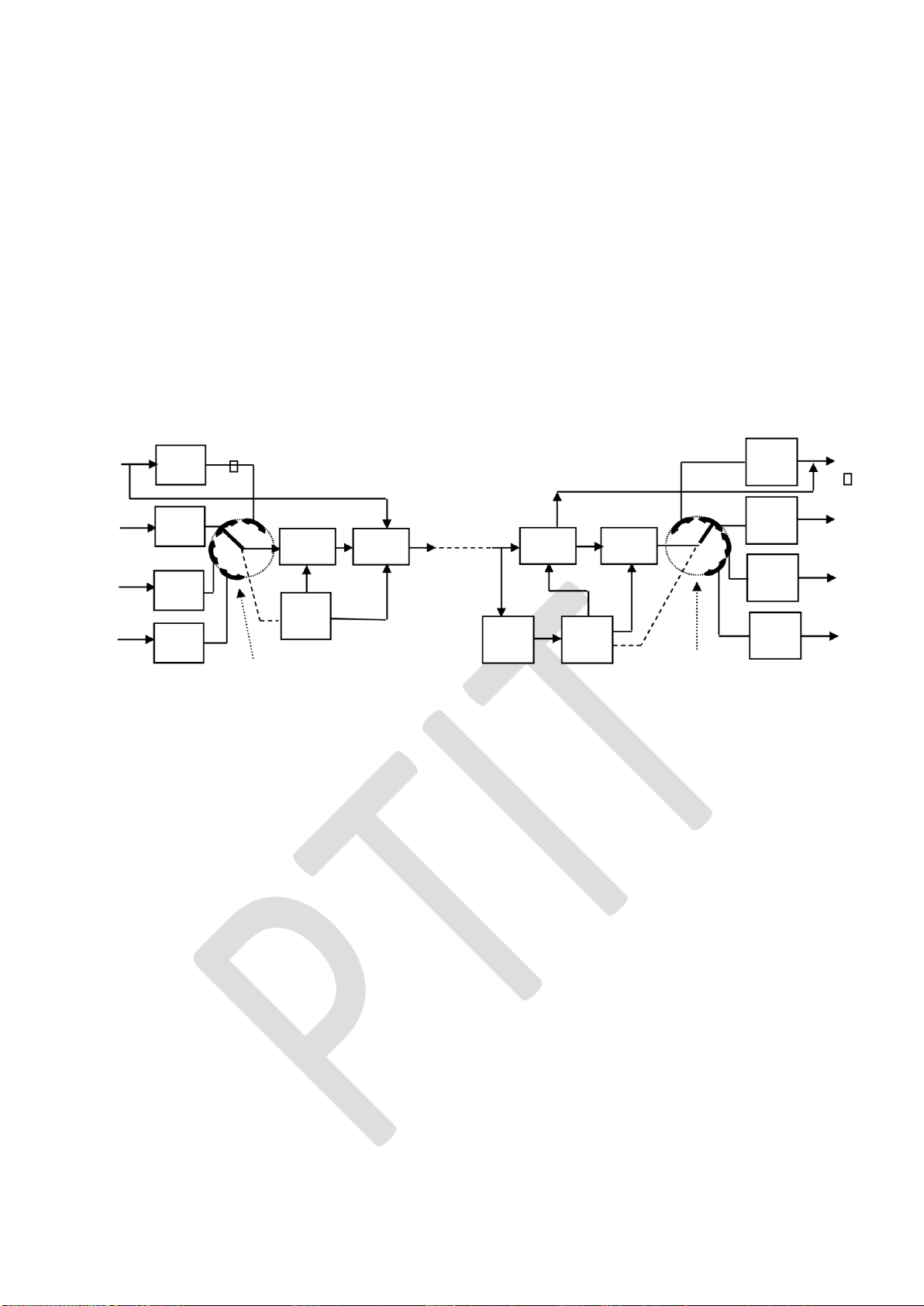
lOMoARcPSD| 36067889
tiếp iểm tĩnh tại vị trí tương ứng. Yêu cầu ồng bộ giữa máy phát và máy thu sẽ ược áp
ứng nhờ xung ồng bộ.
Phía thu: Sau khi tách dãy xung của các kênh cần khôi phục lại tín hiệu analog nhờ sử dụng
bộ lọc thấp giống như bộ lọc này tại phía phát.
Ví dụ về hệ thống TDM tín hiệu số ghép 3 tín hiệu thông tin ược mô tả ở hình
4.7.
Bộ lọc Bộ lọc
1 thấp Báo hiệu thấp 1
Các bit báo hiệu
Bộ lọc Bộ lọc
2 thấp
Bhoá ộ mã khung Tạo Đườ
ng truy
ền Tái tkhung ạo Bộ
mã
giả
i
B
thộ lấp ọc 2
Bộ lọc thấp
3
3
thấp Bộ tạo
4 Bthộ lấọp c xung Tbừộ mã ồ khung ng Đ. hồTách Bxung ộ tạ
o
Bộ phân
B
th
ộ l
ấ
ọ
p
c
4
Tín hiệu Bộ chuyển
phối Tín hianalog ệu analog mạch
Hình 4.7: Sơ ồ khối hệ thống TDM tín hiệu số
Quá trình hoạt ộng của bộ chuyển mạch và bộ phân phối ã ược trình bày trong phần
TDM tín hiệu tương tự. Sau ây trình bày hoạt ộng TDM tín hiệu số.
Phía phát: Sau khi lấy mẫu tín hiệu thoại analog của các kênh, xung lấy mẫu ược ưa vào
bộ mã hoá ể tiến hành lượng tử hoá và mã hoá mỗi xung thành một từ mã nhị phân gồm
8 bit. Các bit tin này ược ghép xen byte ể tạo thành một khung nhờ khối tạo khung.
Trong khung còn có từ mã ồng bộ khung ặt tại ầu khung và các bit báo hiệu ược ghép
vào vị trí ã quy ịnh trước. Bộ tạo xung ngoài chức năng tạo ra từ mã ồng bộ khung còn
có chức năng iều khiển các khối trong nhánh phát hoạt ộng.
Phía thu: Dãy tín hiệu số i vào máy thu. Dãy xung ồng hồ ược tách từ tín hiệu thu ể ồng
bộ bộ tạo xung thu. Bộ tạo xung phía phát và phía thu tuy ã thiết kế có tốc ộ bit như
nhau, nhưng do ặt xa nhau nên chịu sự tác ộng của thời tiết khác nhau, gây ra sai lệch
tốc ộ bit. Vì vậy dưới sự khống chế của dãy xung ồng hồ, bộ tạo xung thu hoạt ộng ổn
ịnh. Khối tái tạo khung tách từ mã ồng bộ khung ể làm gốc thời gian bắt ầu một khung,
tách các bit báo hiệu ể xử lý riêng, còn các byte tin ược ưa vào bộ giải mã ể chuyển mỗi
từ mã 8 bit thành một xung. Do bộ phân phối hoạt ộng ồng bộ với bộ chuyển mạch nên
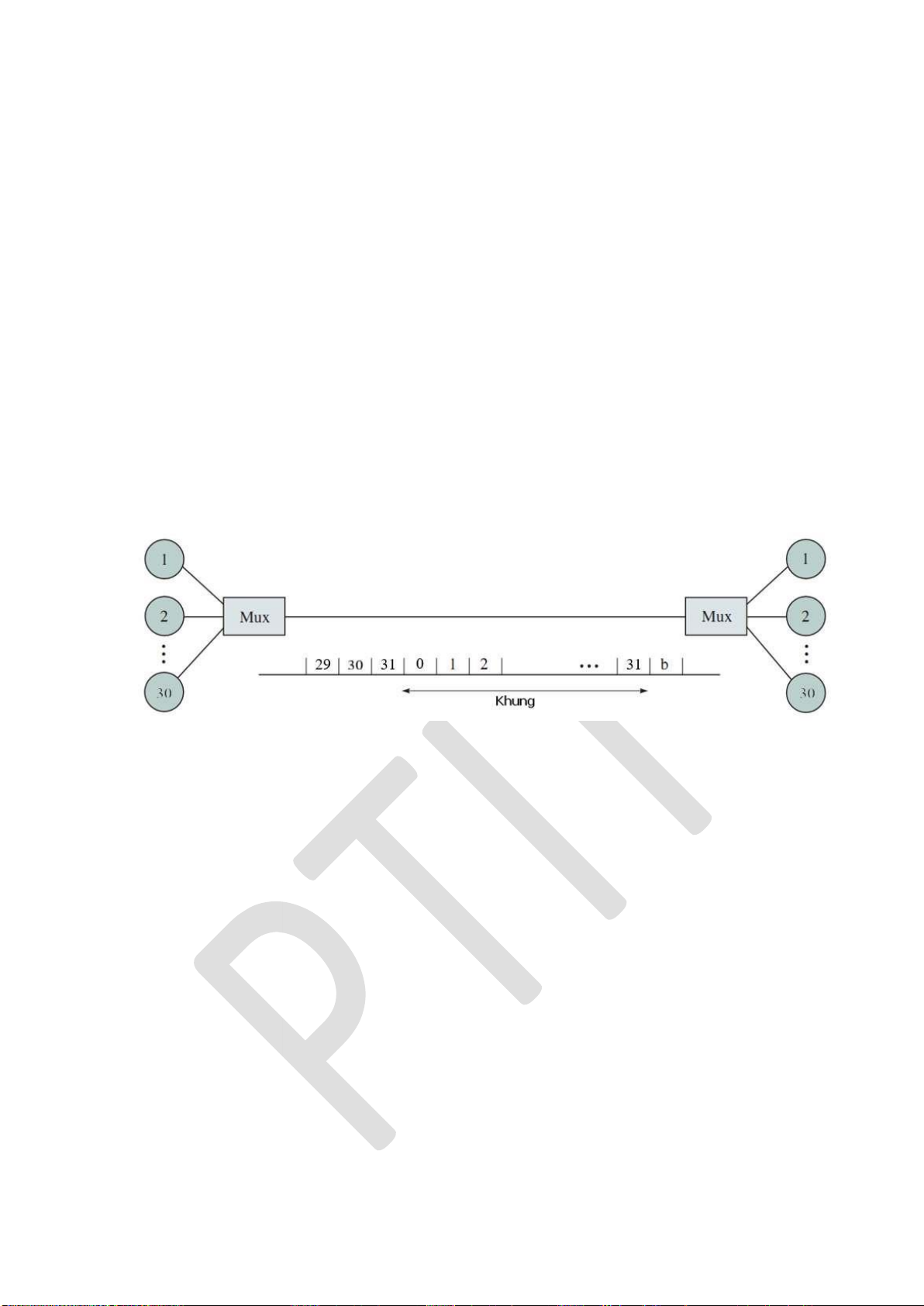
lOMoARcPSD| 36067889
xung của các kênh tại ầu ra bộ giải mã ược chuyển vào bộ lọc thấp của kênh tương ứng.
Đầu ra bộ lọc thấp là tín hiệu thoại analog. Bộ tạo xung phía thu iều khiển hoạt ộng của
các khối trong nhánh thu.
Giả sử tín hiệu thông tin ược lấy mẫu với tần số 8 KHz và ược mã hóa ở tốc ộ 8
Kbit/s. Chu kỳ của 1 khe thời gian: T
kênh
= T
lấy mẫu
= 1/8KHz = 125 μs. Chu kỳ của một
khung: T
khung
= số kênh × T
kênh
= 500 μs. Số bit trong mỗi kênh: 8 bit; Số bit trong mỗi
khung: 32 bit; Tốc ộ bit của mỗi kênh: f
b(kênh)
= f
b
= 8 Kbit/s; Tốc ộ bit của mỗi khung:
f
b(khung)
= số kênh × f
b
= 32 Kbit/s; Băng thông của hệ thống TDM: BW
TDM
= f
b(khung)
=
32 Kbit/s
TDM ược sử dụng trong mạng iện thoại vào những năm 1960. Hệ thống truyền dẫn
E1 truyền 30 kết nối iện thoại số như chỉ ra ở hình 4.8. Lưu ý, tín hiệu thoại số có ược
nhờ lấy mẫu tín hiệu thoại tương tự với tốc ộ 8000 lần/giây và mỗi mẫu ược bmã hóa là
8 bit.
Hình 4.8: Hệ thống truyền dẫn E1
Hệ thống E1 sử dụng khung truyền dẫn gồm 32 khe thời gian 8 bit. Mỗi khe mang
một mẫu PCM ối với một kết nối ơn. Khởi ầu mỗi khung ược chỉ ra bởi 1 từ mã ồng bộ
(khe ầu tiên khung). Tốc ộ của tuyến truyền dẫn:
(32×8) bit/khung × 8000 khung/giây = 2,048 Mbit/s
Hệ thống truyền dẫn E1 ược sử dụng ể truyền lưu lượng giữa các tổng ài iện thoại.
Sự gia tăng của lưu lượng mạng iện thoại và những tiến bộ về truyền dẫn số ã dẫn ến sự
phát triển của phân cấp ghép kênh số tiêu chuẩn. Những phân cấp truyền dẫn số này ịnh
nghĩa luồng ghép của lưu lượng iện thoại.
Hình 4.9 cho thấy các phân cấp truyền dẫn ã ược phát triển ở Bắc Mỹ, Nhật và
Châu Âu. Ở Bắc Mỹ và Nhật, luồng tín hiệu số 1 (DS1) tương ứng với ầu ra của bộ ghép
kênh T1, và là khối xây dựng cơ bản. Luồng tín hiệu DS2 có ược qua việc ghép 4 tín
hiệu DS1, và DS3 có tốc ộ 44,736 Mbps ược ghép từ 28 luồng tín hiệu DS1,... Ở Châu
Âu, CCITT ã phát triển một phân cấp số tương tự. Luồng tín hiệu E1 gồm 32 kênh tốc
ộ 64 Kbit/s tạo thành khối xây dựng cơ bản. Chỉ có 30 trong 32 kênh ược sử dụng làm
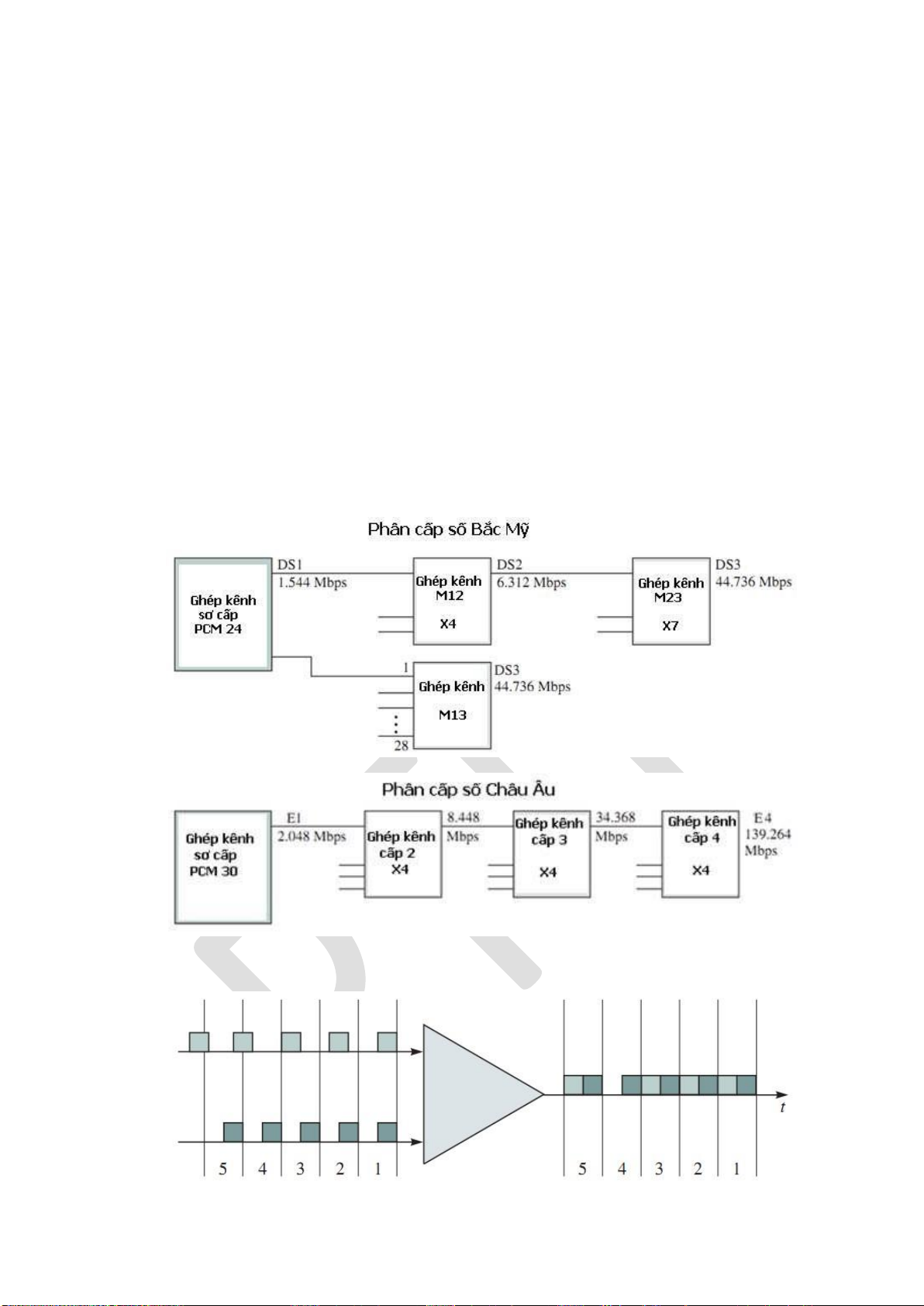
lOMoARcPSD|36067889
kênh thoại; một kênh khác dùng cho báo hiệu và một kênh còn lại ể ồng bộ khung và
bảo dưỡng tuyến truyền dẫn. Các mức cấp 2, 3, 4 của phân cấp có ược qua việc ghép 4
tín hiệu trong mức thấp hơn.
Hoạt ộng của bộ ghép kênh TDM liên quan chặt chẽ ến các vấn ề ồng bộ của luồng
ầu vào. Hình 4.10 chỉ ra 2 luồng số, mỗi luồng có tốc ộ danh ịnh là 1 bit/T giây, ược
ghép hợp thành một luồng tổng gửi i 2 bit/T giây. Điều gì sẽ xảy ra nếu một trong hai
luồng thành phần có tốc ộ chậm hơn 1/T bps? Mỗi T giây, bộ ghép kênh yêu cầu mỗi ầu
vào cung cấp 1 bit, tại một iểm nào ó ầu vào chậm không cung cấp ược bit ưa vào. Hiện
tượng này gọi là trượt bit. Lưu ý, bit ến muộn ược xem là bit ến sớm trong khoảng T
giây kế tiếp.
Ngược lại, nếu một trong hai luồng thành phần có tốc ộ nhanh hơn 1/T bps, tức là
các bit ến nhanh hơn việc chúng ược gửi i, các bit sẽ tích lũy tại bộ ghép kênh và thậm
chí bị mất.
Hình 4.10: Thời iểm tương ối của các luồng ầu vào và ầu ra trong bộ ghép kênh
Hình 4.9: Các phân cấp số cơ bản

lOMoARcPSD| 36067889
TDM
Để giải quyết các vấn ề về ồng bộ, thông thường các bộ ghép kênh TDM ã ược
thiết kế hoạt ộng ở tốc ộ cao hơn một chút tốc ộ ghép của các luồng ầu vào. Cấu trúc
khung của tín hiệu ầu ra bộ ghép kênh sẽ chứa các bit ược sử dụng ể chỉ thị ối với hiện
tượng trượt. Phương pháp này cho phép các luồng ược tách kênh úng.
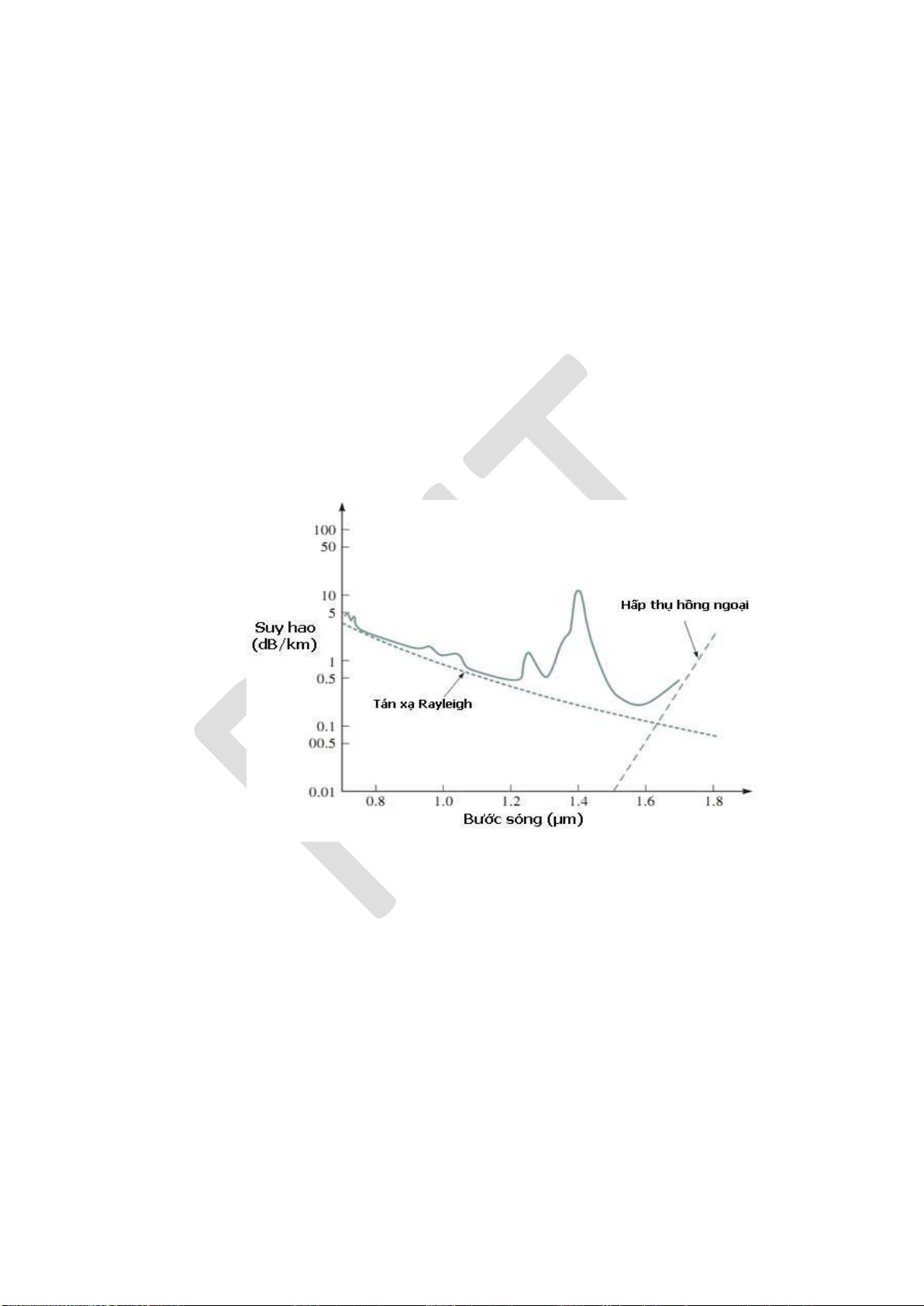
lOMoARcPSD|36067889
Lưu ý, việc ưa vào các bit phụ (bít chèn) ể giải quyết vấn ề trượt hàm ý rằng cấu trúc
khung của luồng ầu ra không ồng bộ hoàn toàn với cấu trúc khung của tất cả các luồng
vào. Để tách luồng ầu vào thành phần từ tín hiệu ã ghép, thì cần tách toàn bộ tín hiệu ã
ghép, tạo ra sự iều chỉnh ối với trượt, và sau ó lấy ra tín hiệu mong muốn. Kiểu bộ ghép
kênh này gọi là không ồng bộ bởi vì các khung ầu vào không ồng bộ với khung ầu ra.
4.2.3. Các kỹ thuật ghép kênh khác
4.2.3.1. Kỹ thuật ghép kênh phân chia theo bước sóng (WDM)
Hình 4.11: Mối quan hệ giữa suy hao và bước sóng sợi quang
dụng kỹ thuật ghép kênh phân chia bước sóng (WDM). WDM ược xem là phiên bản của
FDM ở miền quang, trong ó nhiều tín hiệu thông tin iều chế các tín hiệu quang tại các
bước sóng quang khác nhau (các màu). Tín hiệu nhận ược sau khi ghép sẽ ược truyền
ồng thời qua cùng một sợi quang như chỉ ra ở hình 4.12.
Các bộ ghép kênh quang (MUX) và tách kênh quang (DEMUX) có thể ược sử
dụng ể kết hợp và tách các tín hiệu quang (các bước sóng khác nhau). Ví dụ, các hệ
thống WDM sử dụng 16 bước sóng tại STM-16 ể cung cấp tốc ộ lên tới 16x2,5 Gbps =
40 Gbps. Hình 4.13 chỉ ra tín hiệu quang trong một hệ thống như vậy. Các hệ thống
Các hệ thống truyền dẫn sợi quang hiện nay có thể hoạt ộng ở tốc ộ từ hàng chục
Gb/s ến hàng nghìn Tb/s. Trong hình vẽ 4.11 cho thấy dải các bước sóng suy hao thấp
rộng khoảng 100 nm trong dải 1300 nm. Dải này tương ứng với băng thông 18 THz. Dải
khác khoảng 100 nm trong dải 1550 nm, cung cấp băng thông 19 THz. Rõ ràng công
nghệ ơn kênh hiện nay chưa khai thác triệt ể băng thông khả dụng này.
Thông tin ược mang bởi một sợi quang ơn có thể ược tăng
thông
qua việc sử
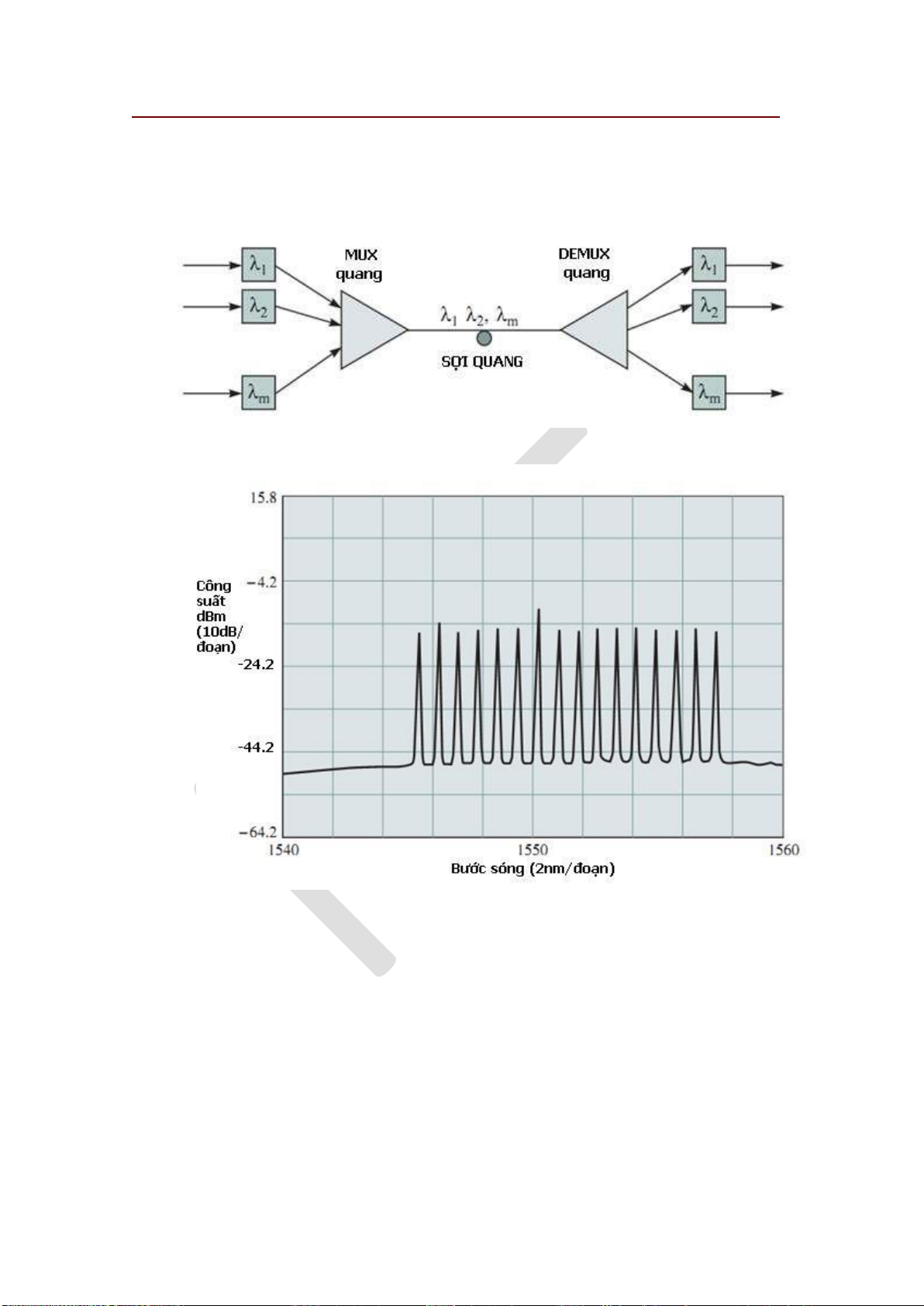
lOMoARcPSD|36067889
WDM có 32 bước sóng tại STM-64 có thể cho tốc ộ là 320 Gbps. Sự hấp dẫn của WDM
là sự tăng lên áng kể về băng thông khả dụng mà không phải ầu tư lớn cũng như triển
khai thêm sợi quang. Băng thông bổ sung có thể ược sử dụng ể truyền tải nhiều lưu
lượng.
Hình 4.13: Tín hiệu quang trong hệ thống WDM
có thể mang các luồng thông tin theo khuôn dạng SDH, trong khi các bước sóng khác
có thể mang thông tin khuôn dạng Gigabit Ethernet hoặc khuôn dạng truyền dẫn khác.
4.2.3.2. Kỹ thuật ghép kênh phân chia theo mã (CDM)
Ghép kênh phân chia theo mã chính là a truy nhập phân chia theo mã (CDMA).
Nguyên lý chung của CDMA ược thể hiện như hình 4.14.
Hình 4.12: Ghép kênh phân chia bước sóng WDM
Trong WDM, mỗi bước sóng ược iều chế riêng biệt, nên mỗi bước sóng không
cần mang thông tin theo khuôn dạng truyền dẫn giống nhau. Do vậy, một số bước sóng
lOMoARcPSD|36067889
Trong CDMA, nhiều người sử dụng có thể dùng chung tần số và trong cùng thời
gian. Để không gây nhiễu cho nhau, mỗi người sử dụng chỉ ược phép phát i một năng
lượng bit (
) nhất ịnh ể ảm bảo tỷ số
/
0
quy ịnh, trong ó
là năng lượng bit của
tín hiệu cần thu và
0
là mật ộ phổ tạp âm tương ương gây ra do các tín hiệu của người
sử dụng khác. Để giảm mật ộ phổ tạp âm cần phải trải phổ tín hiệu của người sử dụng
trước khi phát. Ngoài ra, ể máy thu có thể phân biệt ược tín hiệu cần thu với các tín hiệu
khác, mỗi tín hiệu phát i phải ược cài khẩu ngữ riêng theo một mã nhất ịnh. Có thể so
sánh CDMA như là nhiều người trong phòng nói chuyện với nhau từng ôi một theo các
ngôn ngữ khác nhau (các mã khác nhau). Nếu nói khẽ (
0
nhỏ) thì họ hoàn toàn không
gây nhiễu cho nhau. Hình 4.14 biểu thị N người sử dụng, mỗi người ược mã hoá bằng
một mã riêng, ược ký hiệu từ 1 ến N. Mỗi khối con ặc trưng cho sự chiếm tiềm năng vô
tuyến của người sử dụng: tần số, thời gian và
.
S: mã & E
b
f: tần số
1
N
Hình 4.14: Nguyên lý a truy nhập phân chia theo mã
Do ặc thù của di ộng nên khi một người sử dụng nào ó ến gần trạm gốc,
0
của
người ấy gây ra cho máy thu người khác sẽ lớn hơn (tiếng của người ấy nghe to hơn) và
gây nhiễu nhiều hơn cho máy thu người khác. Hiện tượng này ược gọi là hiện tượng gần
- xa. Để giảm ảnh hưởng của hiện tượng gần - xa, cần iều chỉnh công suất máy di ộng
thấp hơn khi nó tiến ến gần trạm gốc. Trong hệ thống CDMA, quá trình iều khiển công
suất ược tiến hành tự ộng. CDMA là phương thức a truy nhập có nhiều ưu iểm so với
các phương thức a truy nhập khác.
4.3. ỨNG DỤNG KỸ THUẬT GHÉP KÊNH TRONG HỆ THỐNG TRUYỀN
THÔNG SỐ
4.3.1. Kỹ thuật ghép kênh TDM-PCM
Kỹ thuật ghép kênh TDM-PCM tín hiệu thoại ược thể hiện ở sơ ồ hình 4.15. Kỹ
thuật này thực hiện ghép kênh TDM 30 kênh thoại, kênh ồng bộ và kênh báo hiệu thành
luồng số ầu ra có tốc ộ 2048 Kbit/s.

lOMoARcPSD| 36067889
Phía phát: Sử dụng bộ lọc thông thấp ể hạn chế băng tần tiếng nói từ 300 ến 3400 Hz,
tín hiệu ầu ra tại bộ lọc thông thấp ược chuyển ến bộ lấy mẫu. Bộ lấy mẫu óng vai trò là
một thiết bị chuyển mạch iện tử óng mở theo chu kỳ 125 s, tạo ra các xung mẫu có chu
kỳ 125 s. Bộ mã hoá biến ổi mỗi xung lấy mẫu thành các từ mã 8 bit và ưa ến khối ghép
kênh TDM tín hiệu thoại, tín hiệu ồng bộ và tín hiệu báo hiệu thành một
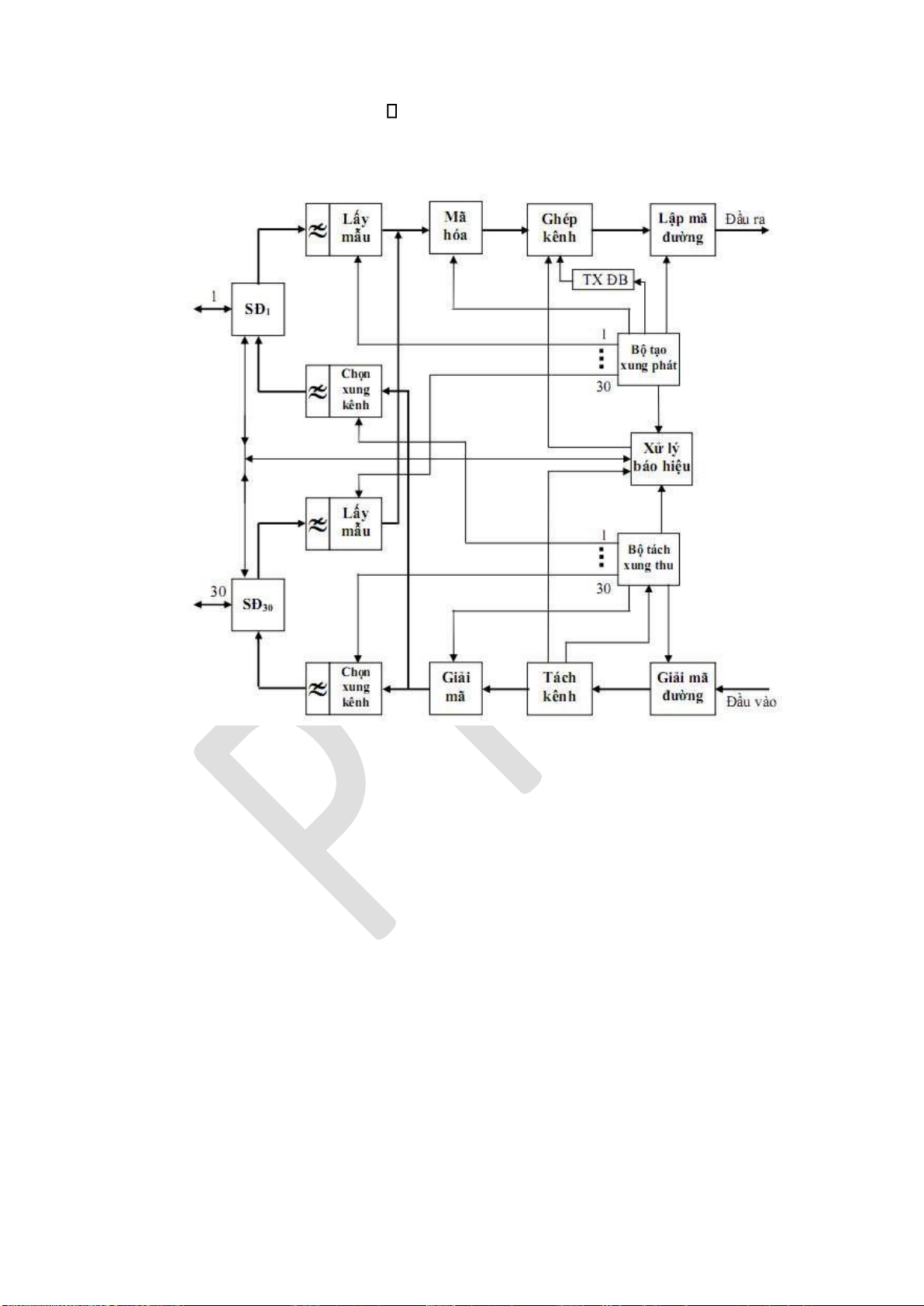
lOMoARcPSD|36067889
khung PCM-30 có thời hạn 125 s. Luồng bit nhị phân tại ầu ra bộ ghép kênh TDM ược
ưa qua Bộ mã hóa ường dây ể chuyển ổi khuôn dạng thích hợp với môi trường kênh
truyền.
các xung lượng tử, qua bộ chọn xung kênh và bộ lọc thông thấp tách ra tín hiệu thoại
analog của từng kênh. Bộ chọn xung kênh là một chuyển mạch iện tử óng mở theo tốc
ộ và pha của bộ lấy mẫu ở phía phát. Đầu vào bộ chọn xung kênh ấu song song với nhau
và mỗi bộ chỉ cho xung kênh mình i qua, tức là tách kênh theo thời gian ược thực hiện
tại ây.
Tín hiệu số ầu ra thiết bị PCM-30 ược sắp xếp thành khung và a khung trước khi
truyền.
Hình 4.15: B
ộ
ghép kênh TDM PCM-30
P
hía thu
:
L
uồng bit thu ược chuyển vào Bộ giải mã ường dây ể
chuy
ển thành các
luồng bit nhị phân. Mộ
t ph
ầ
n tín hi
ệ
u
ở
ầu ra bộ giải mã ường dây ược ưa vào khố
i
tách xung
ồ
ng b
ộ
ể
tách ra xung ồ
ng b
ộ
và ưa tớ
i kh
ố
i t
ạo xung thu ể
kích thích
b
ộ
chia xung và t
ạ
o ra các khe th
ời gian ồ
ng b
ộ
v
ớ
i phía phát. Ph
ầ
n tín hi
ệ
u còn l
ạ
i
ược ưa vào khối tách kênh TDM ể
tách lu
ồng bit ầ
u vào thành 30 kênh tho
ạ
i, kênh
báo hi
ệ
u. S
au ó các từ
mã 8 bit c
ủ
a 30 kênh tho
ại ưa tớ
i b
ộ
gi
ải mã ể
chuy
ể
n thành
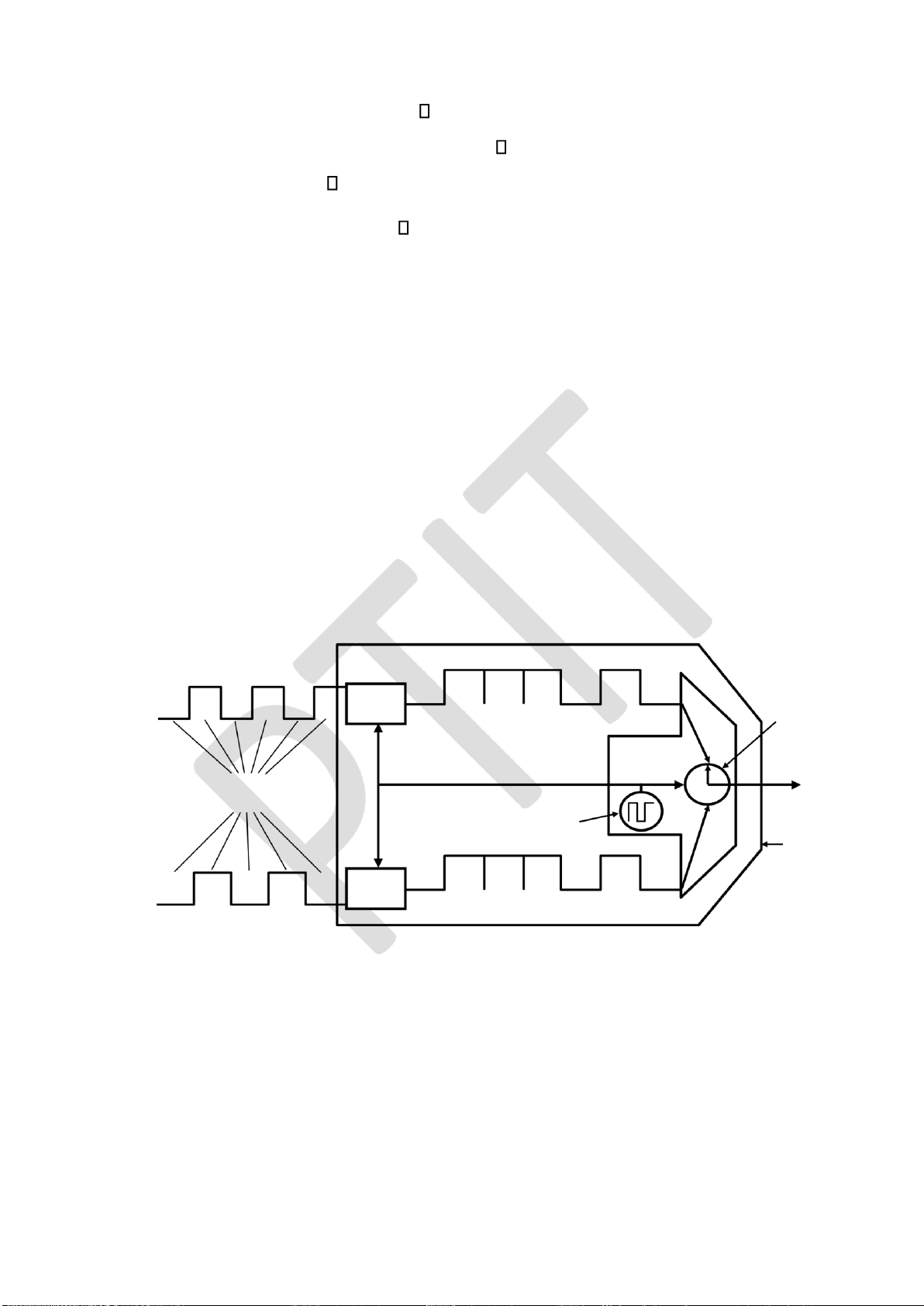
lOMoARcPSD| 36067889
Mỗi khung có thời hạn là 125 s, ược chia thành 32 khe thời gian và ánh số thứ tự
từ TS0 ến TS31. Mỗi TS có thời hạn là 3,9 s và ghép ược 8 bit dữ liệu. Tổng số bit
trong khung bằng: 8 bit 32 = 256 bit. Tốc ộ bit ầu ra PCM-30 ược tính như sau:
R
PCM-30
= 256 (bit/ khung) 8.10
3
(khung /s) = 2048 kbit/s
Đa khung của PCM-30 gồm 16 khung, ánh số thứ tự từ F0 ến F15.
Hiện nay ể ghép các luồng số tốc ộ thấp thành các luống số tốc ộ cao hơn có thể
sử dụng kỹ thuật ghép kênh cận ồng bộ PDH hoặc kỹ thuật ghép kênh ồng bộ SDH. Đối
với ghép kênh PDH là kỹ thuật ghép kênh không sử dụng ồng bộ tập trung, nghĩa là tất
cả các phần tử trong mạng không bị khống chế bởi một ồng hồ chủ. Mỗi thiết bị ghép
kênh trong mạng có một ồng hồ riêng. Chính vì vậy mà các luồng số tạo ra có sự chênh
lệch về tốc ộ bit, chẳng hạn như cho các tốc ộ bit 2048 Kbit/s ± 50ppm. Muốn ghép các
luồng số có tốc ộ bit khác nhau này thành một luồng số có tốc ộ cao hơn thì phải hiệu
chỉnh sao cho tốc ộ bit của chúng bằng tốc ộ bit của ồng hồ bộ ghép kênh nhờ chèn bit.
Sau khi chèn bit thì các luồng số ầu vào bộ ghép xem như ã ồng bộ về tốc ộ bit, nhưng
pha của chúng không ồng bộ với nhau. Kỹ thuật ghép kênh như vậy ược gọi là kỹ thuật
ghép kênh cận ồng bộ PDH (Hình 4.16).
Luồng số 2Mbit/s có
tốc độ bit định mức Chèn 6 5 4 3 2 1 6 5 4 3 2 1
Bit
chuyThiết bị ển mạch
J- Các bit chèn Tín hiệu ra
Các bit dữ
liệu đầu vào Bộ tạo xung đồng hồ
Bộ ghép kênh
5
4 3 2 1
Chèn
J 5 4 3 2 1
Luồng số 2Mbit/s có tốc Bit độ bit thấp hơn
định
Hình 4.16: Kỹ thuật ghép kênh cận ồng bộ PDH
Về tiêu chuẩn tốc ộ bit PDH, hiện nay trên thế giới có 3 tiêu chuẩn. Đó là tiêu
chuẩn Châu Âu, tiêu chuẩn Bắc Mỹ và tiêu chuẩn của Nhật Bản. ITU-T công nhận 4
mức ầu tiên theo tiêu chuẩn Châu Âu và 3 mức ầu tiên theo tiêu chuẩn Bắc Mỹ là các
mức truyền dẫn PDH quốc tế.
Sau ây sẽ trình bày cụ thể kỹ thuật ghép kênh ồng bộ SDH.
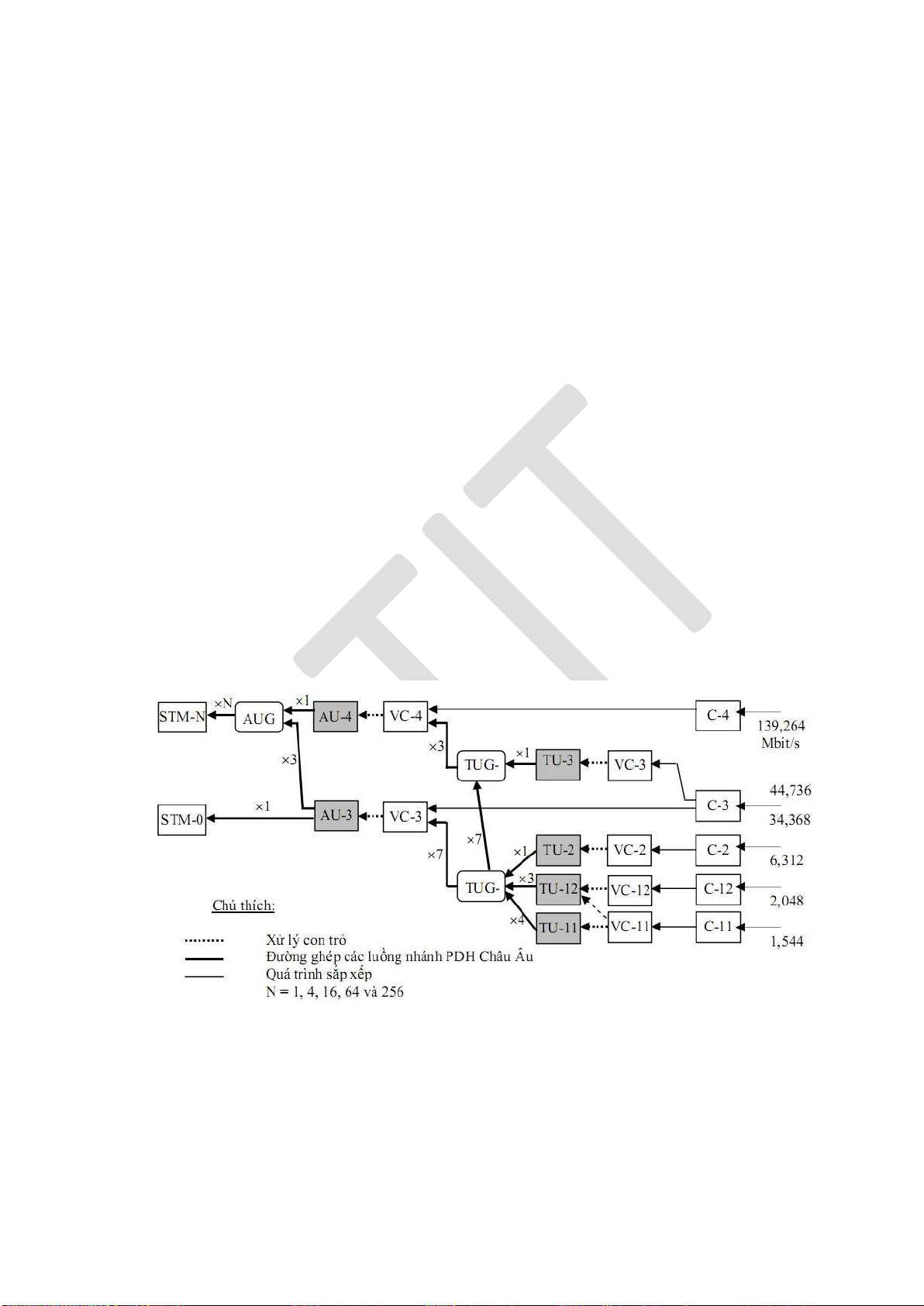
lOMoARcPSD|36067889
4.3.2. Kỹ thuật ghép kênh SDH
Ở kỹ thuật ghép kênh ồng bộ SDH, phía phát và phía thu ược duy trì ồng bộ liên
tục và tự ộng với các bộ phân phối của bộ ghép kênh và bộ phân kênh. Tốc ộ luồng bit
tổng ở ầu ra của bộ ghép kênh úng bằng N lần tốc ộ luồng bit của các luồng bit nhánh
cộng với tốc ộ của các thông tin phụ (ghép N luồng bit nhánh). Điều này có nghĩa là,
nếu không kể tới các thông tin phụ thì tần số nhịp của bộ ghép/tách kênh úng bằng N lần
tần số nhịp của các luồng nhánh ược ghép và quan hệ tốc ộ này phải ược duy trì một
cách liên tục và tự ộng trong suốt quá trình ghép/tách kênh.
Cụ thể, các bit hoặc các từ mã của các luồng nhánh ược sắp xếp liên tiếp tạo nên
Sơ ồ hình 4.17 thể hiện kỹ thuật ghép kênh ồng bộ SDH.
Hình 4.17: Kỹ thuật ghép kênh SDH (Khuyến nghị G.709 của ITU-T)
ITU-T ã qui ịnh sáu mức phương tiện truyền dẫn chung cho SDH là: các luồng ồng
bộ mức 0 (STM-0) có tốc ộ bit là 51,84 Mbit/s và các mức kế tiếp là mức 1 (STM1) có
tốc ộ bit là 155,52 Mbit/s, STM-4 có tốc ộ bit là 622,08 Mbit/s, STM-16 có tốc ộ bit là
luồng bit ghép (trừ các khe dành cho ồng bộ khung, thông tin báo hiệu và nghiệp vụ).
Hơn nữa, vị trí của các bit/từ mã của mỗi luồng nhánh chiếm một vị trí xác ịnh trong
luồng bit ghép, ược biết trước ở phía thu. Do ó, kỹ thuật ghép kênh ồng bộ SDH có
những ưu iểm nổi bật hơn so với kỹ thuật ghép kênh PDH là:
-
Hiệu quả sử dụng ường truyền cao;
-
Việc tách/ghép tại các trạm trung gian ược thực hiện một cách thuận tiện và linh hoạt.
-
Tốc ộ bit tiêu chuẩn cao, có khả năng truyền tải tín hiệu băng rộng.
-
Được tiêu chuẩn hoá quốc tế toàn cầu.
lOMoARcPSD| 36067889
2048,32 Mbit/s, STM-64 có tốc ộ bit là 9953,28 Mbit/s và STM-256 có tốc ộ bit là
39813,120 Mbit/s.
Mức STM-1 ược gọi là mức cơ bản trong SDH, cấu trúc khung STM-1 như trên
hình 4.18. Khung STM-1 có 9 hàng 270 cột. Độ dài khung bằng 125 s. Tổng số byte
trong khung STM-1 = 270 byte 9 = 2430 byte.
270 cột
9 cột 261 cột
Hàng 1
RSOH
AU-4 PTR Tải trọng 9 hàng
Hàng 4
MSOH
s
125
Hình 4.18: Cấu trúc khung STM-1
Trong SDH, VC-3 ược sử dụng ể truyền các luồng tốc ộ bit mức 3 (PDH) là 34368
Kbit/s; VC-4 ược sử dụng ể ghép 3 VC-3 hoặc 63 VC-12. VC-4 ược xác ịnh là lớp truyền
dẫn hỗ trợ cho các luồng ATM trong SONET và SDH. Ngoài ra, SDH hỗ trợ chuyển tải
VC-11 trên các kết nối lớp VC-12 bằng giải pháp tương thích ặc biệt.
Có hai phương pháp hình thành luồng tín hiệu STM-N. Phương pháp thứ nhất qua
AU-4 (Châu Âu) và phương pháp thứ hai qua AU-3 (Bắc Mỹ, Nhật Bản). Luồng tín hiệu
AU-4 ược hình thành từ một luồng nhánh 139264 Kbit/s, hoặc 3 luồng nhánh 34368
Kbit/s, hoặc 63 luồng 2048 Kbit/s thuộc phân cấp số PDH của Châu Âu. AU-3 ược hình
thành từ một luồng nhánh 44736 Kbit/s, hoặc 7 luồng nhánh 6312 Kbit/s, hoặc 28 luồng
1544 Kbit/s. Cũng có thể sử dụng 63 luồng 1544 Kbit/s thay thế cho 63 luồng 2048
Kbit/s ghép thành tín hiệu STM-1 qua TU-12,..., AU-4.
Như vậy, quá trình hình thành các luồng STM-N ược thực hiện qua hai bước ộc
lập. Bước thứ nhất hình thành luồng truyền dẫn ồng bộ mức 1 (STM-1) từ các luồng
nhánh PDH. Bước thứ hai hình thành các luồng truyền dẫn ồng bộ bậc cao mức N (STM-
N), thực hiện bằng cách ghép xen byte các luồng truyền dẫn ồng bộ mức 1 (STM-1)
hoặc các luồng truyền dẫn ồng bộ mức thấp hơn STM-M (M<N).
Ví dụ ghép 63 luồng VC-12 thành luồng STM-1 như sau (Hình 4.19):

lOMoARcPSD|36067889
Mỗi khung C-12 có 34 byte, tiếp nhận từ luồng số cận ồng bộ 2048 Kbit/s trong
125 s là 32 byte và ộn thêm 2 byte. Sau ó VC-12 bổ sung thêm một byte VC-4 POH ể
tạo thành khung VC-12 có 35 byte. Cứ 4 khung VC-12 tạo thành một a khung VC-
12.
TU-12 bổ sung thêm vào ầu khung VC-12 thứ nhất, thứ hai, thứ ba một byte con
trỏ TU-12 và byte dữ trữ vào ầu khung thứ tư ể tạo thành a khung TU-12. Như vậy mỗi
khung TU-12 có 4 cột 9 dòng (36 byte).
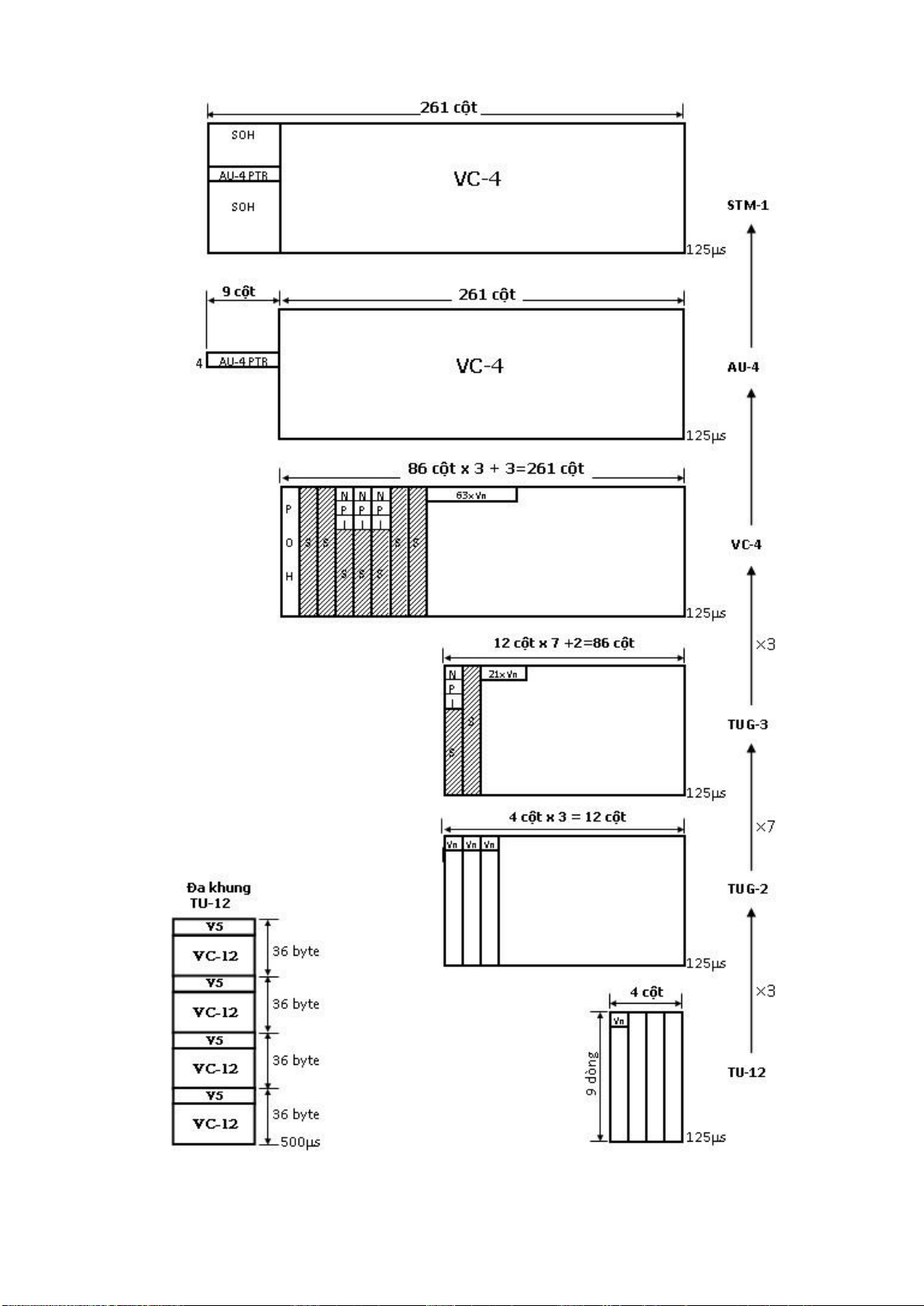
lOMoARcPSD|36067889
lOMoARcPSD|36067889
Hình 4.19: Quá trình ghép 63 luồng VC-12 thành luồng STM-1 Nguyên
tắc ghép xen byte N luồng tín hiệu STM-1 thành luồng tín hiệu STM-
N như sau: ầu tiên ghép byte thứ nhất của luồng tín hiệu STM-1 thứ
nhất, byte thứ nhất của STM-1 thứ hai, byte thứ nhất của STM-1 thứ
ba, byte thứ nhất của STM-1 thứ tư. Sau ó ghép byte thứ hai cũng theo
trình tự trên. Cứ ghép như vậy cho hết một chu trình 125 s. Quá trình
trên sẽ ược lặp lại trong mỗi chu trình. Như vậy, tốc ộ luồng tín hiệu
STM-N ầu ra lớn gấp N lần tốc ộ luồng tín hiệu STM-1 ầu vào.
Do ó, ể hình thành ược luồng tín hiệu STM-4 phải ghép xen byte 4 luồng tín hiệu
STM-1 như hình 4.20a. Luồng tín hiệu STM-16 ược hình thành bằng cách ghép xen byte
16 luồng tín hiệu STM-1 hoặc ghép xen nhóm 4 byte 4 luồng tín hiệu STM-4 như hình
4.20b. Luồng tín hiệu STM-64 thường hình thành từ 4 luồng tín hiệu STM-16. Tuy nhiên
cũng có thể sử dụng hỗn hợp nhiều loại luồng tín hiệu ồng bộ mức thấp ể tạo thành luồng
tín hiệu ồng bộ mức cao hơn.
STM-1#1 aaaa ... STM-4#1 aaaa ...
STM-1#2 bbbb ... dcbadcba ... STM-4#2 bbbb ... ddddccccbbbbaaaa ...
STM-1#3
cccc ... MUX STM- 4 STM-4#3 cccc ... MUX STM- 16
dddd ... dddd ...
STM-1#4 1/4 STM-4#4 4/16
(a) (b)
Hình 4.20: Kỹ thuật ghép các luồng tín hiệu STM-1 và STM-4 tương ứng thành các
luồng tín hiệu STM-4 và STM-16
4.4. TỔNG KẾT CHƯƠNG
Chương 4 ã ề cập những vấn ề cơ bản về ghép kênh: Giải thích các kỹ thuật ghép
kênh ược sử dụng ể chia sẻ các tài nguyên truyền dẫn, ặc biệt là ghép kênh phân chia
tần số (FDM) và ghép kênh phân chia thời gian (TDM). Đã trình bày cụ thể các kỹ thuật
ghép kênh TDM PCM, SDH: là các kỹ thuật minh họa cụ thể cho kỹ thuật ghép kênh
phân chia theo thời gian TDM.
Câu hỏi/bài tập chương 4
1- Vẽ và mô tả cấu trúc khung tín hiệu STM-1. Tính tốc ộ truyền tín hiệu của khung?
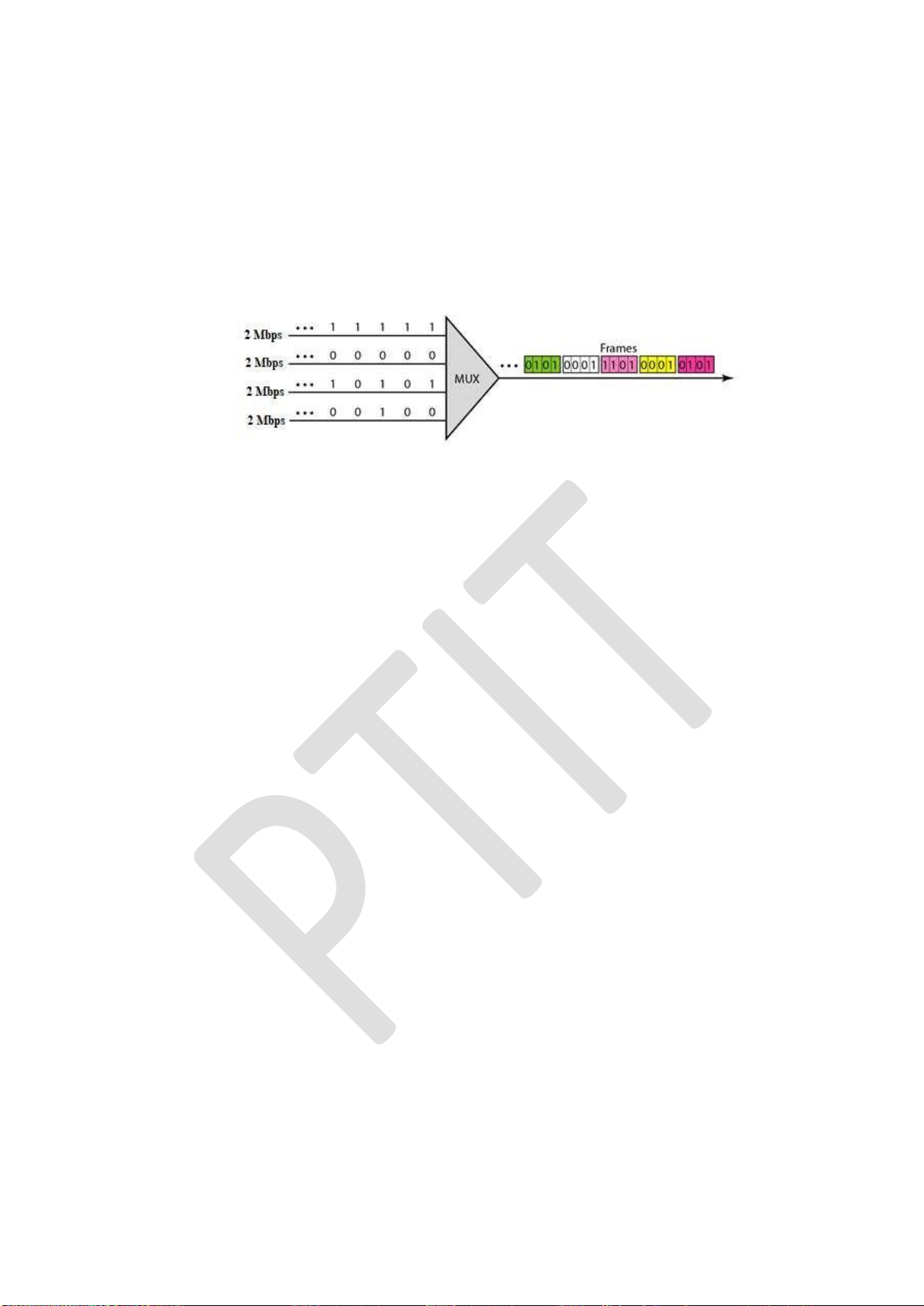
lOMoARcPSD|36067889
2- Vẽ sơ ồ khối và trình bày nguyên lý hoạt ộng của bộ ghép kênh TDM? Dùng TDM
ồng bộ ể ghép 4 kênh tín hiệu. Tốc ộ mỗi kênh 800 bps. Giả sử cấu trúc khung ghép
gồm 1 bit ồng bộ và 4 khe thời gian (mỗi khe chứa 1Byte). Hãy cho biết tốc ộ khung,
tốc ộ bit trên ường truyền?
3- Trình bày nguyên lý hoạt ộng của bộ ghép kênh TDM? So sánh giữa ghép kênh TDM
ồng bộ và TDM thống kê ? Cho bộ ghép kênh TDM như sau:
Hãy tính: khoảng thời gian của bit ầu vào, khoảng thời gian của bit ầu ra, tốc ộ bit
ầu ra, tốc ộ khung ầu ra. Biết rằng 1 bit ồng bộ ược thêm vào khung ghép ở ầu ra?
4- Trình bày nguyên lý hoạt ộng của bộ ghép kênh FDM? Hãy ưa ra cấu hình thiết kế
sử dụng FDM thích hợp cho trường hợp 4 kênh dữ liệu ầu vào bộ ghép, mỗi kênh có
tốc ộ 1 Mb/s, ược truyền qua kênh vệ tinh có băng thông 1 MHz.
5- Vẽ sơ ồ khối và mô tả nguyên tắc hoạt ộng của bộ ghép kênh PCM-30. Hãy xác ịnh
tốc ộ ầu ra của bộ ghép này.
6- Trình bày nguyên tắc hoạt ộng FDM? Giả sử rằng một kênh thoại chiếm một băng
thông 4 kHz. Sử dụng kỹ thuật FDM ghép ba kênh thoại vào một liên kết với băng
thông 12 kHz, từ băng tần 20-32 kHz. Vẽ cấu hình bộ MUX/DMUX của FDM. Giả
sử không có khoảng băng bảo vệ.
7- Vẽ sơ ồ khối, nêu chức năng các khối trong bộ ghép SDH tiêu chuẩn khi ghép các
luồng số PDH theo tiêu chuẩn Châu Âu. Dựa trên sơ ồ bộ ghép hãy tính tổng số luồng
E1, E3 và E4 khi ghép trong một luồng STM-4.
- CHƯƠNG 5 -
ĐIỀU CHẾ TÍN HIỆU
Trong các hệ thống truyền tin ể truyền tin tức i xa thì cần phải chuyển tin tức trong
một dạng năng lượng thích hợp với môi trường truyền lan. Dạng năng lượng ược dùng,
phải ít bị suy hao và bị biến dạng do tác ộng của nhiễu. Để thực hiện ược iều này cần
một phép biến ổi là iều chế. Chương này sẽ trình bày về iều chế tín hiệu.

lOMoARcPSD| 36067889
5.1. KHÁI NIỆM VỂ ĐIỀU CHẾ
Phần lớn các tín hiệu mang thông tin như hình ảnh, tiếng nói,... ều là các tín hiệu
tần số thấp và có phổ giới hạn từ f
m
ến f
M
với f
m
< f
M
. Chặng hạn như: tín hiệu tiếng nói
có phổ từ 300 Hz ến 3400 Hz và tín hiệu truyền hình có phổ từ 25 Hz ến 6,5 MHz.
Do ó không thể truyền trực tiếp các tín hiệu này i xa bằng sóng iện từ vì chúng
không thể bức xạ trực tiếp ược bằng Ăngten. Trong khi ó các tín hiệu radio tần số cao
lại có khả năng bức xạ tốt. Vì vậy cần phải dịch chuyển phổ của tín hiệu lên miền tần số
cao, quá trình này gọi là iều chế (Modulation).
Ngoài ra ể có thể tận dụng các ường truyền cáp kim loại (cáp xoắn ôi) cho việc
truyền số liệu giữa các máy tính ở những khoảng cách xa (ví dụ như liên lạc trong mạng
Internet) thì cần phải chuyển ổi các tín hiệu iện i ra từ các máy tính cho phù hợp với
ường truyền. Bởi vì ường truyền này ược thiết kế cho thông tin tiếng nói có băng thông
trong khoảng 300 - 3400Hz, nếu các tín hiệu dạng số tần số cao ược truyền trực tiếp trên
ường dây thoại thì chúng sẽ bị suy giảm và biến dạng, khi ến ầu thu sẽ không nhận ra
ược. Quá trình chuyển ổi này cũng ược gọi là iều chế,
Quá trình số hóa tín hiệu tương tự, quá trình chuyển từ tín hiệu iện sang tín hiệu
quang... ều là các quá trình iều chế, chúng có nhiệm vụ là chuyển tin tức trong một dạng
năng lượng thích hợp với môi trường truyền lan, trong ó dạng năng lượng ược dùng ít
bị tổn hao, biến dạng do tác ộng của nhiễu và có ộ phân biệt rõ ràng ể quá trình giải iều
chế có thể dễ dàng nhận dạng dù có bị nhiễu làm biến dạng phần nào.
Về mặt toán học ể mô tả quá trình iều chế, ta sử dụng hai hàm: Hàm tin () và
Hàm tải tin ().
Định nghĩa: Điều chế là quá trình cho hàm tin () tác ộng lên tải tin () sao cho nhận
ược một tín hiệu có phổ nằm ở miền tần số phù hợp với kênh truyền.
Sau iều chế sẽ nhận ược tín hiệu (), () ược gọi là tín hiệu iều chế, () ược gọi
là tín hiệu bị iều chế.
Dựa vào tính chất của tải tin và tín hiệu mang tin có thể phân làm các loại iều chế
cơ bản như sau:
- Điều chế các tín hiệu liên tục:
Tín hiệu mang tin () là tín hiệu tương tự, tần số thấp. Tải tin () là một tín hiệu
iều hòa tần số cao:

lOMoARcPSD| 36067889
() =
0
(
0
+
0
) =
0
(2
0
+
0
), với
0
ủ lớn (5.1) Có
thể chia iều chế các tín hiệu liên tục làm 3 loại chính:
a) Cho () tác ộng vào biên ộ của tải tin: iều biên (AM)
() =
0
. () (5.2)
b) Cho () tác ộng vào tần số của tải tin: iều tần (FM)
() =
0
. () (5.3)
c) Cho () tác ộng vào pha của tải tin: iều pha (PM)
() =
0
. () (5.4)
Điều tần và iều pha ược gọi là iều chế góc vì bản chất của chúng ều làm thay ổi góc
pha của tải tin.
- Điều chế xung:
Tín hiệu mang tin () là tín hiệu tương tự. Tải tin () là một dãy xung tuần hoàn:
() = (
0
) (5.5) Cho () tác
ộng vào các tham số của tải tin, ta có các loại iều chế xung sau:
a) Cho () tác ộng vào biên ộ của tải tin: iều biên xung (PAM)
b) Cho () tác ộng vào tần số của tải tin: iều tần xung (PFM)
c) Cho () tác ộng vào pha của tải tin: iều pha xung (PPM)
d) Cho () tác ộng vào ộ rộng của tải tin: iều rộng xung (PWM)
- Các phương pháp khoá dịch:
Tín hiệu mang tin () là dãy bít nhị phân, tải tin () là một dao ộng iều hoà:
() =
0
(
0
+
0
)
Cho () tác ộng vào các tham số biên ộ, tần số và pha của tải tin, ta có các phương
pháp iều chế khóa dịch sau:
a) Phương pháp iều chế khoá dịch biên ộ (ASK)
b) Phương pháp khóa dịch tần số (FSK)
c) Phương pháp khóa dịch pha (PSK)
d) Kết hợp giữa ASK và PSK ta có iều chế biên ộ cầu phương (QAM)
5.2. BIỂU DIỄN TÍN HIỆU

lOMoARcPSD|36067889
+
(
t
)
=
S
+
(
f
)
+
Nhiều tín hiệu mang thông tin ược truyền i dưới dạng iều chế. Kênh mà tín hiệu
iều chế truyền qua bị giới hạn trong dải thông ở miền tần số xung quanh tần số của sóng
mang như iều chế hai biên, lân cận tần số sóng mang như iều chế ơn biên. Tín hiệu và
kênh (hệ thống) thỏa mãn iều kiện dải thông nhỏ hơn nhiều so với tần số của sóng mang
gọi là tín hiệu và hệ thống băng hẹp. Việc iều chế ược thực hiện ở phía phát ể tạo ra tín
hiệu có dải tần hữu hạn và quá trình giải iều chế ược thực hiện ở phía thu ể khôi phục
lại thông tin. Không làm mất tính tổng quát cho việc biểu diễn toán học, ta có thể chuyển
các kênh và tín hiệu thông dải thành các kênh và tín hiệu tần số thấp một cách tương
ương. Thêm nữa, hiệu quả của các kỹ thuật iều chế và giải iều chế là ộc lập với tần số
của sóng mang và dải tần của kênh. Việc biểu diễn các tín hiệu có dải phổ hạn chế và
các hệ thống thông dải bằng các tín hiệu tần số thấp và các hệ thống thấp tương ương là
những vấn ề quan trọng cần xem xét.
5.2.1. Biểu diễn thông thấp tín hiệu và hệ thống truyền tin
5.2.1.1. Biểu diễn các tín hiệu có dải tần hữu hạn
Giả sử tín hiệu thực () có dải tần số nằm trong một dải tần hữu hạn lân cận tần
số
như trong hình 5.1. Đầu tiên ta xây dựng tín hiệu chỉ chứa các thành phần tần số
dương trong (). Tín hiệu như vậy có thể ược biểu diễn:
+
() = 2()() (5.6)
với () là biến ổi Fourier của () và () là biến ổi Fourier của hàm ơn vị.
Biểu diễn trong miền thời gian tín hiệu trong (5.6) là:
s e
df = F
1
1
[S(f)] (5.7)
Tín hiệu
+
() ược gọi là tín hiệu giải tích hay tín hiệu ường bao trước của ().
Chú ý rằng
1
[()] = () và:
1
[2()] = () +
(5.8)
Từ ó:
(5.9)

lOMoARcPSD|36067889
(
)
=
1
(
)
=
1
+
1
Hình 5.1: Phổ tín hiệu có dải tần hữu hạn
Ta ịnh nghĩa tín hiệu () là:
()
(5.10)
Tín hiệu () có thể xem như tín hiệu ra của bộ lọc với áp ứng xung:
() = , - (5.11)
Bộ lọc này ơn giản là bộ dịch pha 90
0
với tất cả tần số của tín hiệu vào.
Tín hiệu giải tích
+
() là tín hiệu có dải tần hữu hạn. Ta có thể nhận ược tín hiệu
tương ương tần số thấp bằng cách dịch chuyển tần số của
+
(). Ta ịnh nghĩa
() như
sau:
() =
+
( +
0
) (5.12) Biểu diễn
ở miền thời gian của tín hiệu này là:
() =
+
()
2
= [() + ()]
2
(5.13)
Hay một cách tương ương là:
() + () =
()
2
(5.14) Nói chung
tín hiệu
() là tín hiệu phức và có thể ược biểu diễn dưới dạng:
() = () + () (5.15)
Từ ó ta nhận ược:
() = ()2
()2
(5.16)
() = ()2
+ ()2
(5.17)
Biểu thức 5.16 là dạng biểu diễn mong muốn của của tín hiệu có dải tần hữu hạn.
Các thành phần tần số thấp x(t) và y(t) có thể xem như ược iều chế biên ộ với các tín

lOMoARcPSD|36067889
(
)
=
(
)
+
=
+
1
2
2
(
)
+
=
1
2
|
(
)
+
hiệu mang
c
t và
c
t tương ứng. Do các thành phần tín hiệu mang này ở dạng
pha vuông góc, x(t) và y(t) ược gọi là các thành phần vuông góc của tín hiệu thông giải
s(t).
Một cách biểu diễn khác của tín hiệu trong biểu thức 6.16 là:
() = {[() + ()]
2
} = {
()
2
} (5.18)
với: là ký hiệu phần thực của số phức. Tín hiệu tần số thấp
() thường ược gọi là
ường bao phức của tín hiệu thực () và là tín hiệu tần số thấp tương ương.
Cách biểu diễn thứ ba của tín hiệu có dải tần hữu hạn có ược bằng cách biểu diễn
() như sau:
() = ()
()
(5.19)
trong ó: a(t) =
2
() +
2
() và () =
()
()
Như vậy:
() = {
()
2
} = { ()
[2+()]
} = () [2
+ ()] (5.20)
Tín hiệu () ược gọi là ường bao của () và () là pha của (). Như vậy (5.16),
(5.18), (5.20) là các biểu diễn tương ương của tín hiệu có dải tần hữu hạn.
Biến ổi Fourier của ():
2
{[
()2
]}2
(5.11) Sử dụng ẳng thức:
Re() = ( +
) (5.22) Biểu
thức (5.21) trở thành:
() =
1
2 [
(
) +
)] (5.23)
ở ây
() là biến ổi Fourier của
(). Đây là mối liên hệ cơ bản giữa phổ của tín hiệu
thực có dải tần hữu hạn () và phổ của tín hiệu thông thấp tương ương
().
Năng lượng của tín hiệu () là:
= |
2
(5.24)

lOMoARcPSD|36067889
5.2.1.2. Biểu diễn hệ thống tuyến tính có dải tần hữu hạn
Hệ thống tuyến tính có thể ược biểu diễn hoặc qua áp ứng xung () hoặc qua áp
ứng tần số () là biến ổi Fourier của (). Do () là thực nên:
) = () (5.25)
Để chuyển hệ thống về hệ thống thông thấp tương ương, ta ịnh nghĩa
(
):
(), > 0
(
) = { 0, < 0 (5.26)
thì:
) = {0), , < 0> 0
(5.27)
Do (5.25) ta có:
() =
(
) +
)
(5.28) Biến ổi Fourier ngược của () cho ta áp ứng xung ():
(()2 ()2 = 2 ()2] (5.29)
với
() là biến ổi Fourier ngược của
(). Tổng quát áp ứng xung
() là áp ứng xung
của hệ thống thông thấp tương ương có giá trị phức.
5.2.2. Không gian tín hiệu
Do tín hiệu có các tính chất tương tự như các vectơ nên có thể sử dụng khái niệm
vectơ ể biểu diễn các tín hiệu.
5.2.2.1. Khái niệm không gian vectơ
Vectơ trong không gian chiều ược xác ịnh bởi thành phần [
1
,
2
, …,
]. Nó
cũng có thể ược biểu diễn là một tổ hợp tuyến tính của các vectơ ơn vị
, ,
nghĩa là:
=1
(5.30)
Theo ịnh nghĩa, vectơ ơn vị có ộ dài ơn vị và v
i
là ộ dài hình chiếu của vectơ trên
trục của vectơ ơn vị e
i
.

lOMoARcPSD|36067889
=
=
=
[
()
]
2
(
)
.
(
)
={
1
, =
0
,
Tích vô hướng của 2 vectơ n chiều
= [
11
12
…
1
] và
= [
21
22
…
2
] ược
ịnh nghĩa là:
.
=1
1
2
(5.31)
Hai vectơ
và
ược gọi là trực giao nếu
.
= 0. Tổng quát, tập hợp vectơ
, 1 là trực giao nếu:
= 0 (5.32) Với mọi 1
, và .
Chuẩn của vectơ , ký hiệu , ược ịnh nghĩa là:
=1
2
(5.33)
chính là ộ dài của vectơ v. Khi tập hợp vectơ ược gọi là trực chuẩn nếu chúng trực
giao và mỗi vectơ có chuẩn bằng ơn vị. Tập hợp vectơ ược gọi là ộc lập tuyến tính
nếu không một vectơ nào trong tập hợp ó là một tổ hợp tuyến tính của các vectơ còn lại.
5.2.2.2. Khái niệm về không gian tín hiệu
Cũng giống như trong không gian vectơ, ta có thể xây dựng các khái niệm tương
ứng cho tập hợp tín hiệu xác ịnh trong khoảng [a b] nào ó. Tích vô hướng của hai tín
hiệu phức
1
() và
2
(), ký hiệu là x
1
(t), x
2
(t), ược ịnh nghĩa là:
1
(),
2
(=
1
().
2
() (5.34)
Hai tín hiệu trực giao nếu tích vô hướng của chúng bằng 0. Chuẩn của một tín hiệu
ược ịnh nghĩa là:
(
|()|
2
(5.35)
Tập hợp tín hiệu ược gọi là trực chuẩn nếu chúng trực giao và chuẩn của chúng
bằng ợn vị. Tập m tín hiệu ược gọi là ộc lập tuyến tính nếu không có tín hiệu nào trong
số m tín hiệu ó biểu diễn ược bằng tổ hợp tuyến tính của các tín hiệu còn lại.
5.2.2.3. Khai triển trực giao tín hiệu
Giả sử s(t) là tín hiệu thực, xác ịnh và có năng lượng hữu hạn:
(5.36) Giả sử
tồn tại tập hợp các hàm {f
n
} là trực chuẩn theo nghĩa:

lOMoARcPSD|36067889
(5.37)
Ước lượng tín hiệu s(t) bằng một tổ hợp tuyến tính các hàm này, nghĩa là:
(
=1
() (5.38)
trong ó:
là các hệ số ước lượng s(t). Sai số phép ước lượng là:
() = (() (5.39)
Chọn các hệ số {
} ể cực tiểu hóa năng lượng của tín hiệu sai số. Khi ó s(t) ược
viết thành:
() =
=1
() (5.40)
Chúng ta hiểu rằng s(t) bằng khai triển chuỗi của nó theo ịnh nghĩa sai số có năng
lượng bằng 0. Khi mọi tín hiệu có năng lượng hữu hạn ều ược biểu diễn bằng khai triển
chuỗi theo dạng (5.40) thì tập hợp các hàm trực chuẩn {
()} ược gọi là hệ kín.
5.2.3. Biểu diễn các tín hiệu iều chế số
Khi truyền thông tin số qua kênh truyền, bộ iều chế là thiết bị biến ổi thông tin số
thành các tín hiệu tương tự phù hợp với các tính chất của kênh. Quá trình biến ổi gồm
chuyến dãy thông tin số {
} thành các khối =
2
các bit nhị phân và chọn một
trong = 2
tín hiệu xác ịnh có năng lượng hữu hạn {
(), m = 1, 2, . . . , M} ể truyền
mỗi khối qua kênh.
Khi việc biến ổi từ dãy số {
} thành tín hiệu phụ thuộc vào một hay nhiều tín hiệu
ã tạo ra trước ó thì bộ iều chế là có nhớ. Ngược lại, khi biến ổi dãy số {
} thành các tín
hiệu {
()}, không bị ràng buộc bởi các tín hiệu ã tạo ra trước ó thì bộ iều chế ược gọi
là không nhớ.
5.2.3.1. Các phương pháp iều chế không nhớ
Bộ iều chế trong một hệ thống truyền thông số biến ổi một dãy ký hiệu nhị phân
thành một tập các tín hiệu tương tự tương ứng. Các tín hiệu tương tự này có thể khác
nhau về biến ộ, pha hay tần số, hoặc ồng thời hại hay nhiều tham số của tín hiệu. Không
mất tính tổng quát, ta giả thiết tốc ộ số liệu ầu vào là bit/s trong mọi trường hợp.
a) Tín hiệu iều chế biên ộ xung (PAM)
Trong hệ thống PAM số, tín hiệu có thể biểu diễn theo dạng:
() = [
()
2
] =
() cos 2
(5.41)

lOMoARcPSD|36067889
(
)
=
(
)
2
=
1
2
trong ó:
{
} là ký hiệu giá trị biên ộ tương ứng với = 2
khối bít có thể
(hay là các ký hiệu). Các giá trị biên ộ tín hiệu,
lấy các giá trị (mức) rời rạc:
=
(2 ), = 1, 2, . . . , (d là ộ chênh lệch biên ộ giữa hai tín hiệu liên tiếp);
{( } là tín hiệu xung thực mà ộ rộng của nó sẽ ảnh hưởng tới phổ tín hiệu
truyền i. Tốc ộ ký hiệu trong hệ thống PAM là /, ó chính là tốc ộ thay ổi về biên ộ
của sóng mang thể hiện việc truyền thông tin mới. Khoảng thời gian
= 1/ gọi là
chu kỳ bit và khoảng thời gian = / =
, gọi là chu kỳ ký hiệu.
Các tín hiệu PAM mức có năng lượng:
(5.42)
trong ó:
là năng lượng của xung (). Rõ ràng các tín hiệu này là một chiều (N = 1) và
ược biểu diễn tổng quát như sau:
() =
() (5.43)
với: () cos 2
là ký hiệu một tín hiệu có năng lượng ơn vị và
, .
Sơ ồ không gian tín hiệu tương ứng với M = 2, M = 4 và M = 8 ược cho trên hình
5.2. Hệ thống PAM số còn ược gọi là iều chế khóa dịch biên ộ (ASK).
Quá trình biến ổi hay gán k bit thông tin thành M = 2
tín hiệu khác nhau về biên
ộ có thể thực hiện theo nhiều cách. Một cách ơn giản nhất là các tín hiệu kề nhau khác
nhau một ký hiệu nhị phân như trên hình 5.2. Loại biến ổi này gọi là mã hóa Gray. Loại
này hay ược sử dụng do phần lớn sai lỗi gây ra bởi nhiều sẽ biến một tín hiệu thành một
tín hiệu kề (hai tín hiệu có biên ộ liên tiếp nhau). Trong trường hợp như thế chỉ có 1 bit
bị sai lỗi trong dãy bit.
Khoảng cách Euclide giữa hai iểm tín hiệu là:
|
| =
| | (5.44)
Khoảng cách giữa hai iểm tín hiệu kề nhau có khoảng cách Euclide nhỏ nhất và
bằng:
()
= 2 (5.45)
=
1
2

lOMoARcPSD|36067889
Tín hiệu PAM trong công thức (5.38) là tín hiệu iều chế hai biên (DSB) và òi hỏi
ộ rộng dải thông của kênh bằng hai lần ộ rộng phổ của tín hiệu tần số thấp tương ương
ể truyền tải. Chúng ta có thể dùng tín hiệu PAM ơn biên (SSB) ược biểu diễn như sau:
= {
[() ± ()]
2
}, = 1,2, . . (5.46)
và () là biến ổi Hilbert của (). Như vậy dải phổ của tín hiệu SSB bằng nửa dải phổ
của tín hiệu DSB.
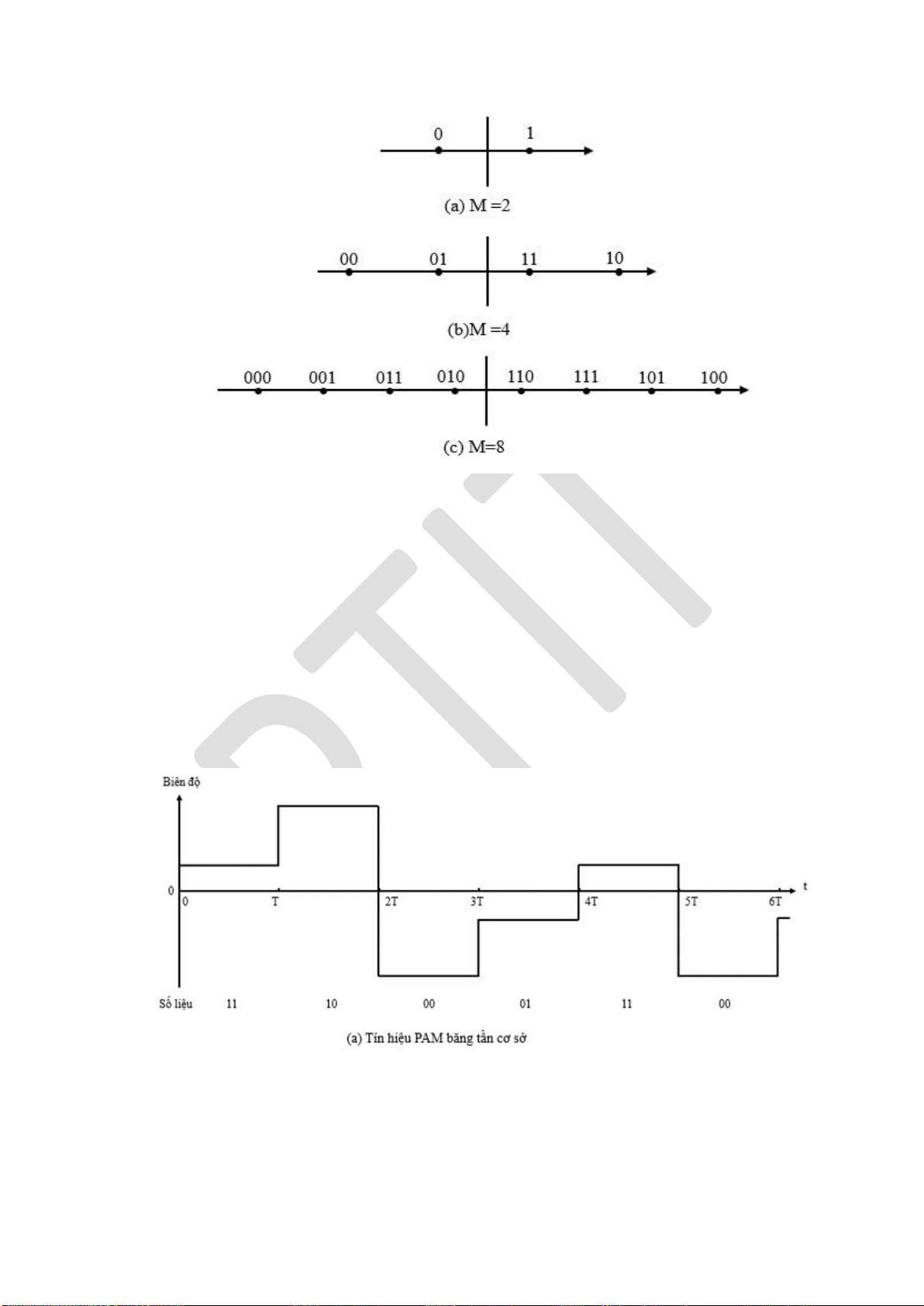
lOMoARcPSD|36067889
Hình 5.2
:
Sơ ồ không gian tín hiệu cho các tín hiệu PAM số
Tín hiệu PAM số có thể truyền trực tiếp qua kênh mà không cần
sóng mang. Trong
trường hợp này tín hiệu ược biểu
di
ễn như sau:
(
)
=
()
,
= 1,2...,
(5.47)
Tín hiệu này ược gọi là
tín hiệu băng tần cơ sở
. Ví dụ tín hiệu PAM băng tần cơ
sở bốn mức ược biểu diễn trên hình 5.3(a), còn trong trường hợp
có sóng mang là trên
hình 5.3
(
b).Trong trườ
ng h
ợ
p tín hi
ệ
u PAM nh
ị
phân (
=2
)
ta có
1
(
)
2
(
)
hai
tín hiệu có cùng năng lượng và hệ số tương quan chéo bằng
-1
.
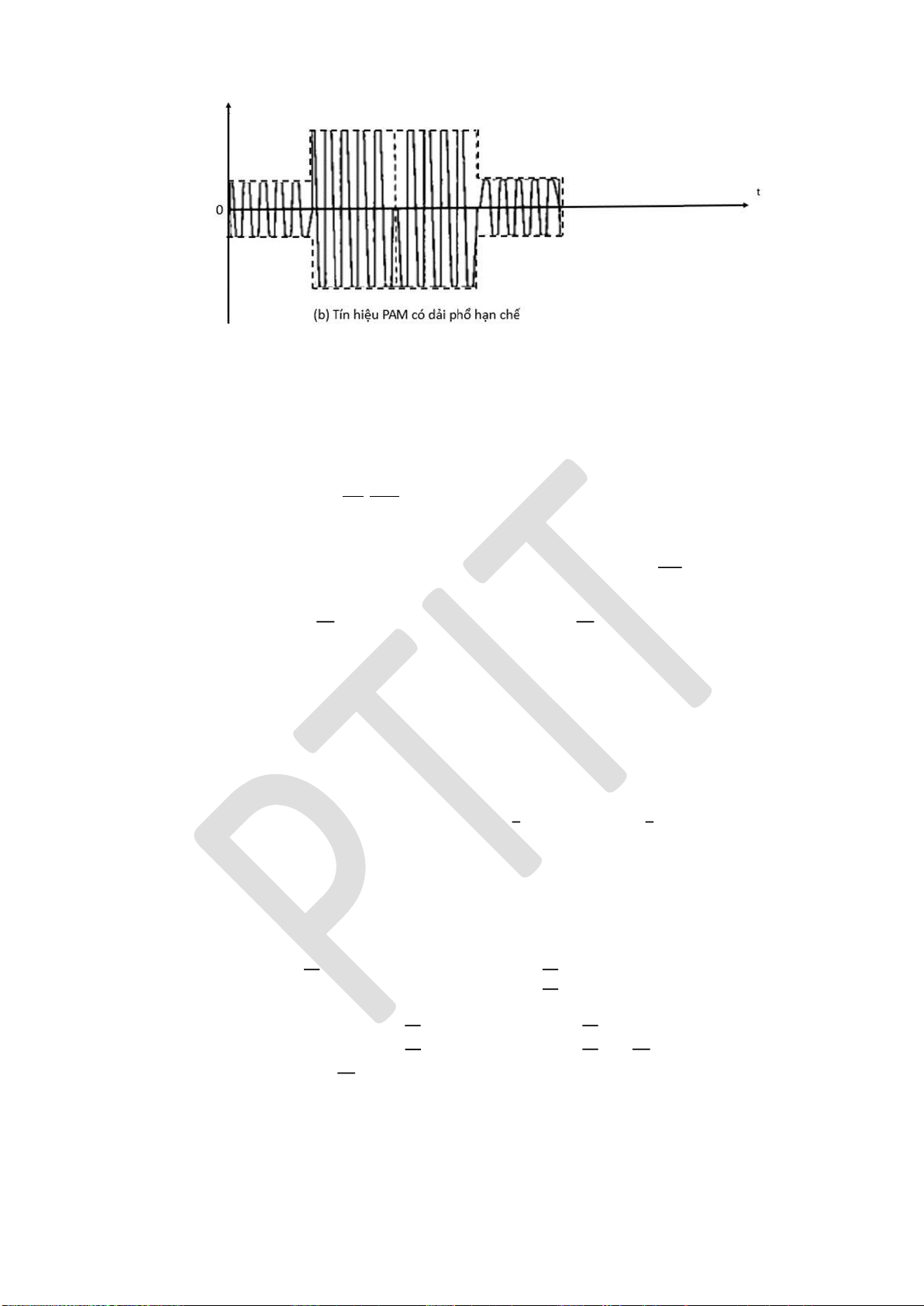
lOMoARcPSD|36067889
2
(
)
=
1
2
2
(
)
=
1
2
0
0
=
[
2
2
Hình 5.3: Tín hiệu PAM băng tần cơ sở và dải phổ hạn chế
b) Tín hiệu iều chế pha
Trong iều chế pha số, tín hiệu ược biểu diễn như sau:
2(1)
2
] = () cos [2
+ 2 ( 1)]
= [()
= ()
2
( 2
()
2
( 2
(5.48)
trong ó: = 1,2, . . , () là tín hiệu xung và
= 2( , = 1,
2, . . . , với là số lượng các giá trị pha của sóng mang.
Điều chế pha số ược gọi là iều chế khóa dịch pha (PSK).
Chú ý rằng các tín hiệu này có năng lượng bằng nhau, nghĩa là:
=
(5.40)
Hơn nữa, các tín hiệu ó có thể ược biểu diễn thành các tổ hợp tuyến tính của hai tín
hiệu trực giao
1
() và
2
() như sau:
s
m
(t) =
1
()
1
() +
2
()
2
() (5.50)
trong ó:
1
(
2
() cos 2
;
2
(
2
() sin 2
và các vectơ hai chiều
= [
1
2
] là:
2
(
2
( 1)].
Sơ ồ không gian tín hiệu với = 2, = 4 và = 8 ược cho trên hình 5.4.
Trường hợp = 2, ứng với các tín hiệu một chiều giống như tín hiệu PAM nhị phân.
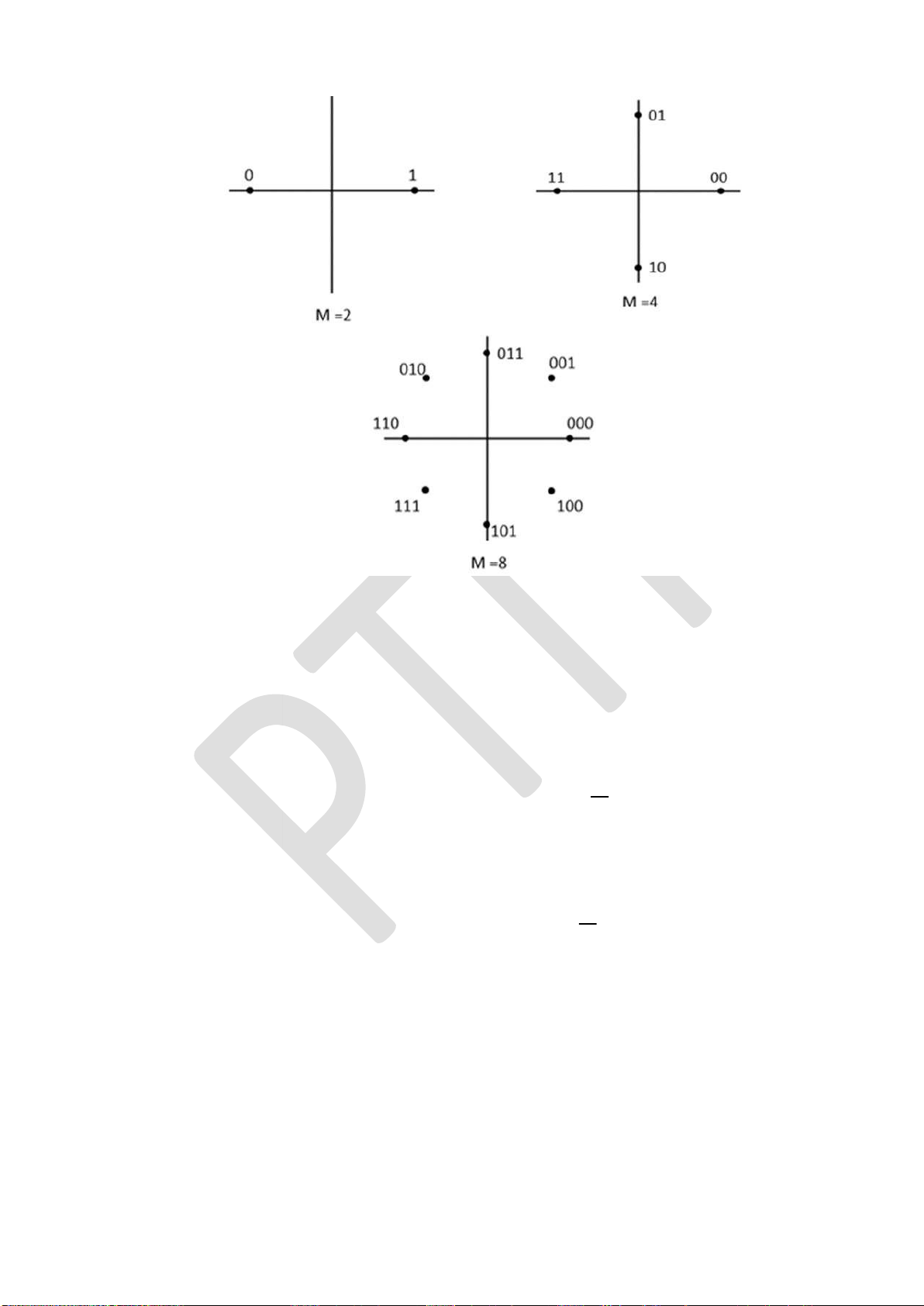
lOMoARcPSD|36067889
c) Điều chế biên ộ cầu phương (QAM)
Xét việc iều chế ồng thời hai ký hiệu bit bằng hai sóng mang vuông góc cos
2
và sin 2
. Phép iều chế này ược gọi là iều chế PAM vuông góc hay ều chế
biên ộ cầu phương (QAM) và tín hiệu iều chế là:
() = [(
+
)()
2
] =
() cos 2
cos 2
,
, (5.53)
Hình 5.4:
Sơ ồ
không gian tín hi
ệ
u c
ủ
a tín hi
ệ
u PSK
Quá trình bi
ến ổ
i hay gán
bit thông tin thành
=2
tín hi
ệ
u có pha khác nhau
có th
ể
th
ự
c hi
ệ
n theo nhi
ều cách. Mã Gray hay ượ
c s
ử
d
ụ
ng vì sai s
ố
do nhi
ễ
u t
ạ
o ra
nói chung ch
ỉ
làm sai m
ộ
t bit trong dãy
bit.
Kho
ả
ng cách Euclide gi
ữa hai iể
m tín hi
ệ
u là:
(
)
=
|
|
=
{
[
2
(
)
]}
1
/
2
(5.51)
Kho
ả
ng cách Euclide t
ố
i thi
ể
u
ứ
ng v
ới trườ
ng h
ợ
p |m-n|=1, t
ứ
c là hai tín hi
ệ
u có
pha k
ề
nhau là:
(
)
=
{
[
2
]}
2
/
1
(5.52)
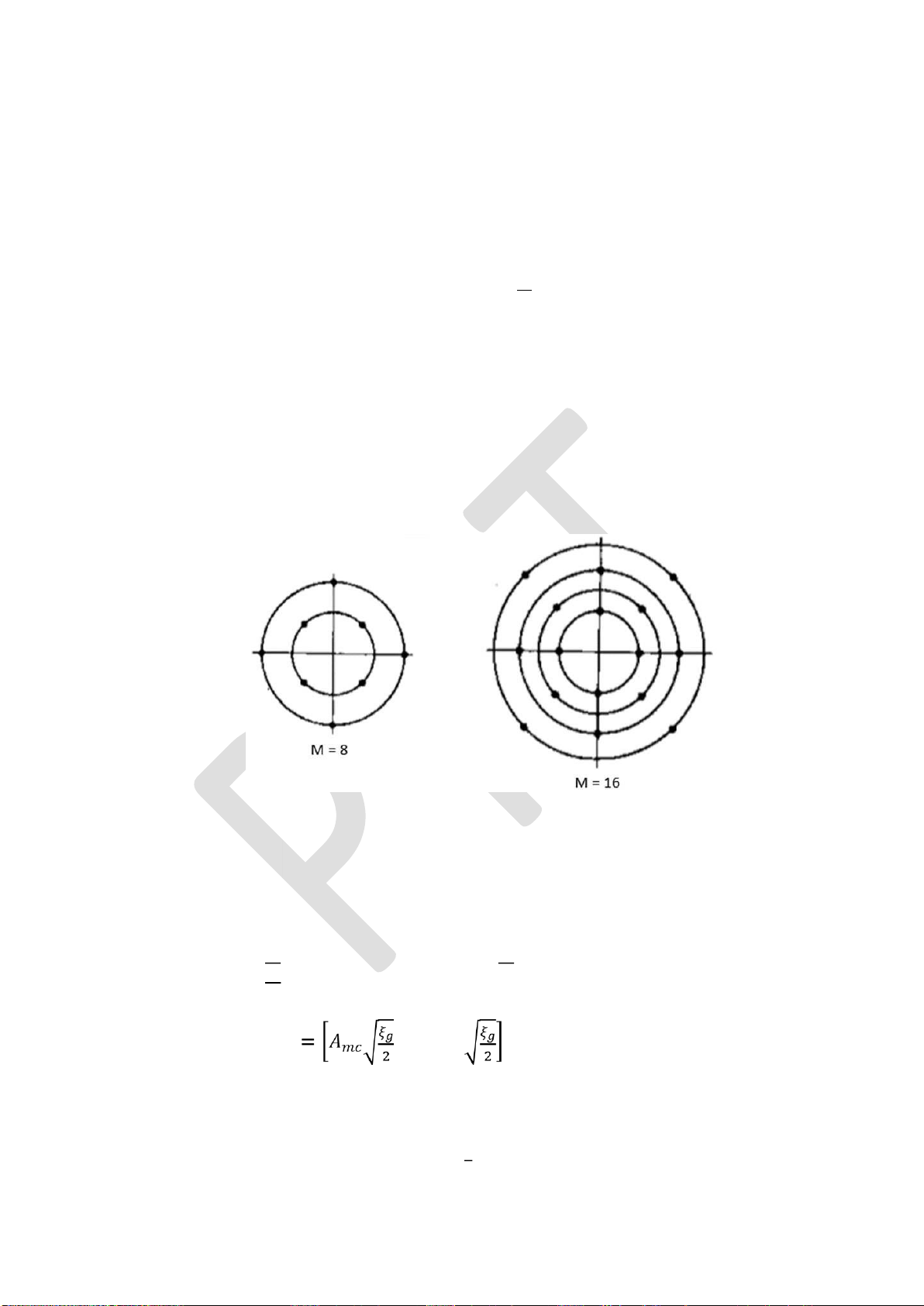
lOMoARcPSD|36067889
với:
và
là biên ộ sóng mang thông tin của hai thành phần vuông góc và () là
tín hiệu xung.
Tín hiệu QAM có thể ược biểu diễn theo cách khác:
() = [
()
2
] (5.54)
với: = ( 2 + 2)1/2và = .
Từ cách biểu diễn này ta thấy tín hiệu QAM là iều chế biên ộ và pha ồng thời.
Thực tế có thể kết hợp hệ thống PAM
1
mức biên ộ với hệ thống PSK
2
mức
= [
1
2
] là:
.
Khoảng cách Euclide giữa hai iểm tín hiệu là:
()
= |
| = {
1
2
[(
)
2
+ (
)
2
]} (5.56)
Trong trường hợp các giá trị biên ộ tín hiệu thuộc tập hợp các giá trị rời rạc
pha ể
t
ạ
o ra tín hi
ệ
u PAM-PSK v
ớ
i M =
1
2
tín hi
ệ
u khác nhau. N
ế
u
1
=
2
và
2
=
2
thì m
ộ
t tín hi
ệ
u PAM-PSK có th
ể
truy
ề
n t
ải ồ
ng th
ờ
i
+=
log
2
bi
t nhị
phân với tốc ộ ký
hi
ệ
u
/(+)
. Ví d
ụ
v
ề
sơ ồ
không gian tín hi
ệ
u PAM-PSK v
ớ
i
=8
và
=
16
trên hình 5.5.
Hình 5.5: Ví d
ụ
v
ề
sơ ồ
không gian tín hi
ệ
u PAM-PSK
Gi
ống như tín hiệ
u PSK, tín hi
ệ
u QAM có th
ể
bi
ể
u di
ễ
n b
ằ
ng t
ổ
h
ợ
p tuy
ế
n tính
c
ủ
a hai tín hi
ệ
u tr
ự
c giao
1
)
(
và
2
)
(
như sau:
(
)
=
1
(
)
1
)+
(
2
(
)
2
)
(
(5.55)
v
ớ
i :
1
(
)
=
2
g(t)cos2
;
2
(
)
=
2
g(t)sin2
và các vectơ hai chiề
u

lOMoARcPSD|36067889
{(2 }, = 1, 2, . . . , } sơ ồ không gian tín hiệu là hình chữ nhật như trên
hình 5.6. Khoảng cách Euclide giữa hai iểm kề là nhỏ nhất và bằng:
()
= 2
(5.57)
Hình 5.6: Sơ ồ không gian tín hiệu QAM chữ nhật
d) Tín hiệu nhiều chiều
Ta thấy rằng tín hiệu iều chế số cả về biên ộ và pha tương ứng với vectơ hay sơ ồ
không gian tín hiệu hai chiều. Nếu ta muốn xây dựng các tín hiệu tương ứng với các
vectơ trong không gian nhiều chiều hơn, có thể sử dụng hoặc miền thời gian hoặc miền
tần số, hoặc cả hai ể tăng số chiều của tín hiệu.
Giả sử ta có các vectơ tín hiệu N chiều, có thể chia khoảng thời gian
1
thành
khoảng thời gian nhỏ, mỗi khoảng thời gian nhỏ kéo dài trong T =
1
/. Trong mỗi
khoảng thời gian nhỏ có thể dùng tín hiệu PAM nhị phân (tín hiệu một chiều) ể truyền
một phần tử của vectơ tín hiệu chiều. Nếu chẵn, một khe thời gian có thể sử dụng
ể truyền ồng thời hai thành phần của vectơ chiều bằng cách iều chế biên ộ các sóng
mang vuông góc một cách ộc lập bởi các thành phần tương ứng. Như vậy vectơ tín hiệu
N chiều ược truyền trong ơn vị thời gian.
Cách khác, một dải tần số có ộ rộng ược chia thành khe tần số, mỗi khe
rộng , mỗi vectơ tín hiệu chiều ược truyền qua kênh bằng cách iều chế ồng thời
biên ộ của sóng mang trong khe tần số. Cần chú ý ộ phân tách tần số giữa các sóng
mang là ể không bị hiện tượng iều chế chéo giữa các tín hiệu trong sóng mang.
Nếu các sóng mang vuông góc ược sử dụng trong mỗi khe tần số, vectơ chiều (với
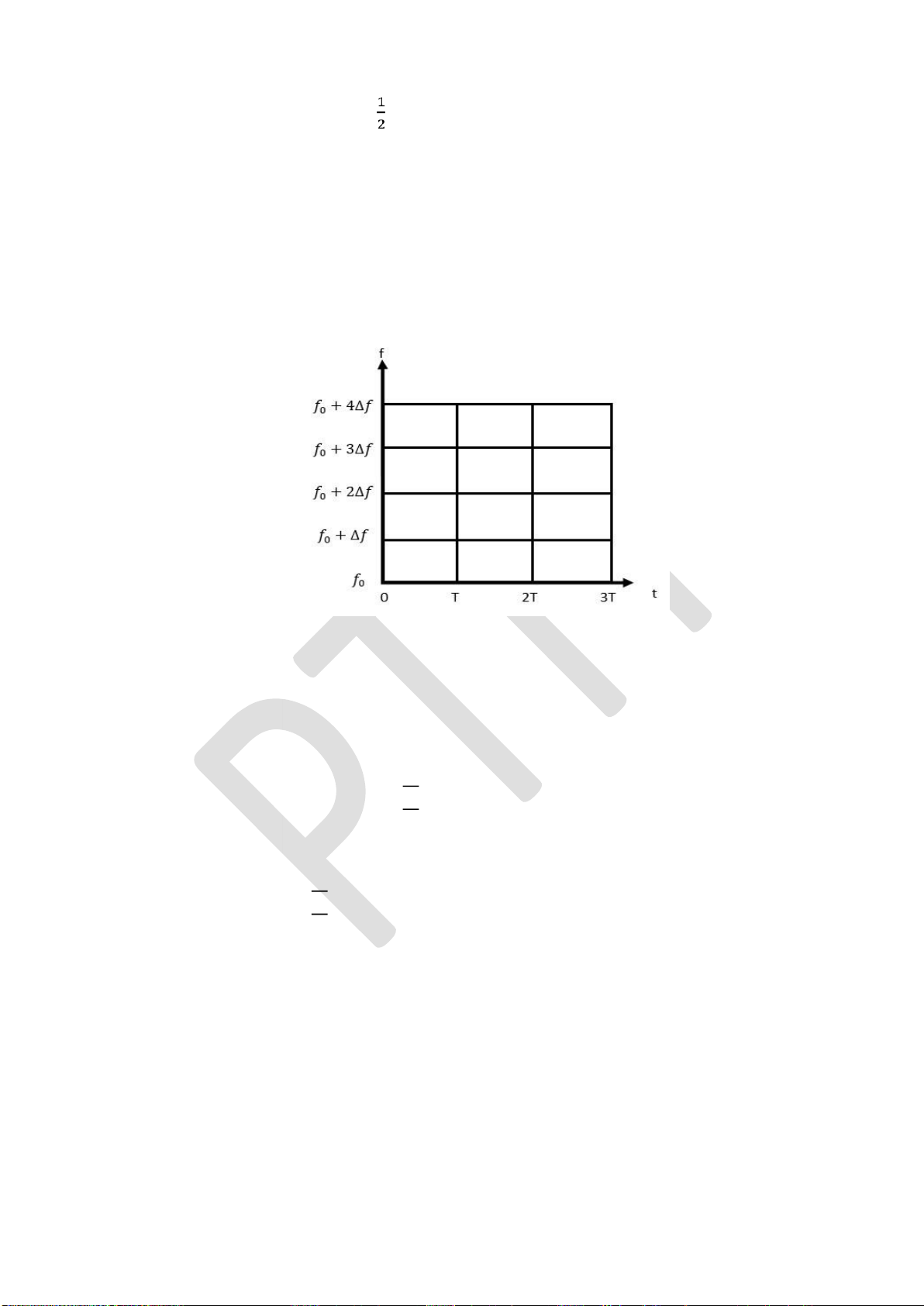
lOMoARcPSD|36067889
chẵn) có thể ược truyền trong khe tần số, làm giảm ộ rộng dải thông cần thiết i hai
lần.
Tổng quát hơn, có thể sử dụng ồng thời cả miền thời gian và miền tần số ể truyền
vectơ tín hiệu chiều. Ví dụ trên hình 5.7 trình bày việc chia trục thời gian và trục tần
số thành 12 khe. Với vectơ tín hiệu 12 chiều có thể truyền i bởi tín hiệu PAM hay vectơ
tín hiệu 24 chiều có thể truyền i bằng cách dùng hai sóng mang vuông góc (QAM) trong
mỗi khe.
(5.58)
Loại iều chế tần số này ược gọi là iều chế khóa dịch tần (FSK). Các tín hiệu này có
năng lượng bằng nhau và hệ số tượng quan chéo là:
Hình 5.7: Chia trục thời gian và trục tần số thành các khe
e)
Tín hiệu trực giao nhiều chiều
Ta xét việc
xây d
ự
ng
tín hi
ệ
u tr
ực giao có năng lượ
ng b
ằ
ng nhau
ở
các t
ầ
n s
ố
khác nhau
, ượ
c bi
ể
u di
ễ
n b
ở
i:
(
)
=
[
s
lm
(
t
)
e
c
t
]
=
2
[
2
+2
]
,
trong ó:
s
lm
(
t
)
=
2
e
j2
,=
là tín hi
ệ
u t
ầ
n s
ố
th
ấ
p
tương ương
.
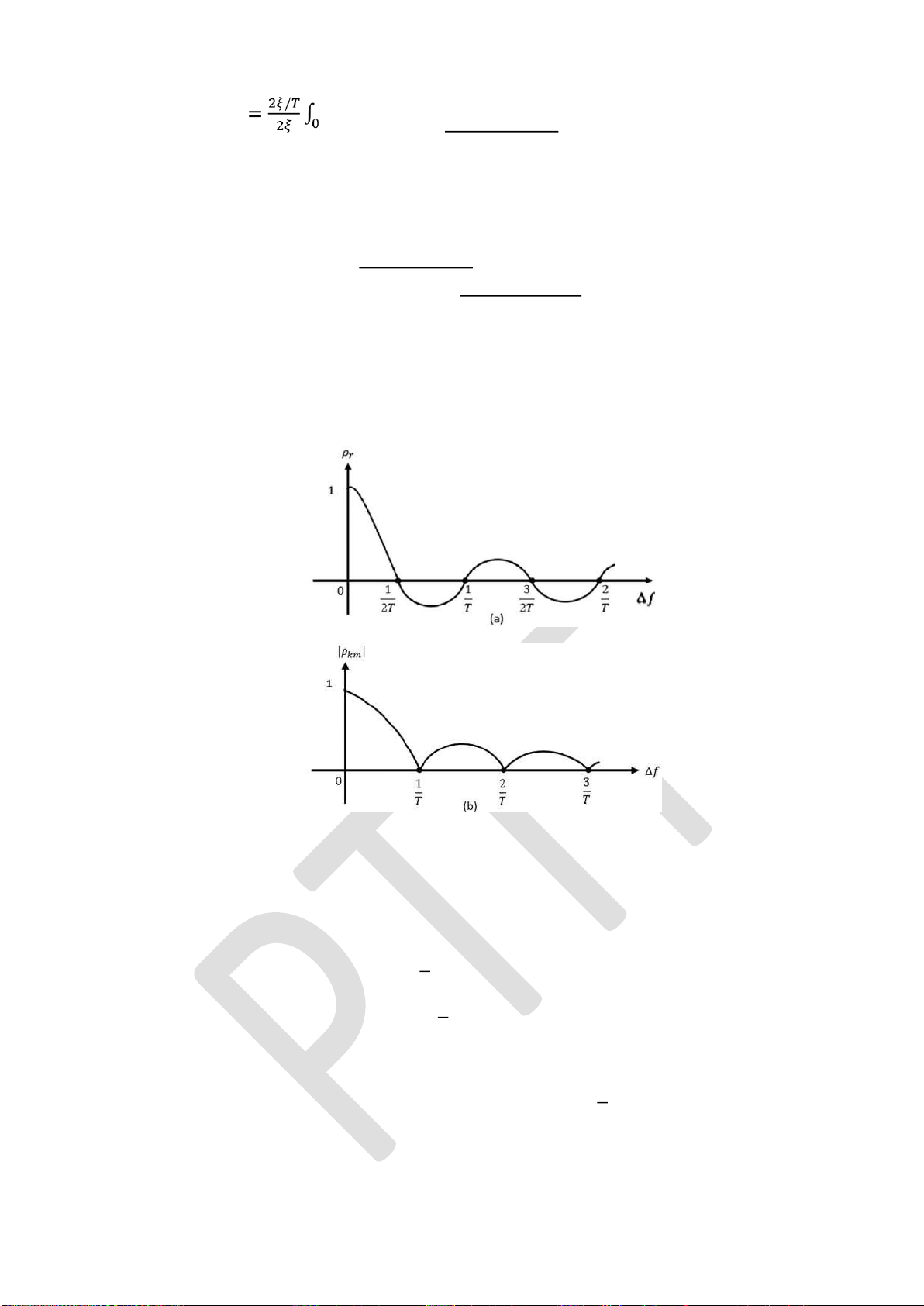
lOMoARcPSD|36067889
ej2() =
()
[
()
]
ej()
(5.59)
Phần thực của
là:
= (
) =
()
[()] cos[( )] =
2
[
()
2()] (5.60)
Ta thấy (
) = 0 khi = 1/2T và , Do |. | = 1 với hai khe tần
số kề nhau, = 1/2T biểu thị ộ phân tách tần số nhỏ nhất giữa các tín hiệu kề nhau ể
Hình 5.8: Bi
ể
u di
ễ
n h
ệ
s
ố
tương quan chéo theo ộ
phân tách t
ầ
n s
ố
ố
i v
ớ
i tín hi
ệ
u
FSK
Trong trườ
ng h
ợ
p
=1
/2T
, tín hi
ệ
u FSK
mức tương ương với các
vectơ
1
=
[
]
2
=
[
0
]
…………………………………
=
[
]
ở
ây
=
. Kho
ả
ng cách gi
ữ
a hai tín hi
ệ
u là:

lOMoARcPSD|36067889
thỏa mãn tính trực giao giữa tín hiệu. Đường biểu diễn (
) và |
| theo
trên hình 5.8. Chú ý là (
) = 0 tại các tần số là bội của 1/2. chiều:
(5.61)
()
với mọi m, k (5.62)
và ây cũng là khoảng cách nhỏ nhất giữa hai tín hiệu. Hình 5.9 biểu diễn sơ ồ không gian
tín hiệu với = = 2 và = = 3.
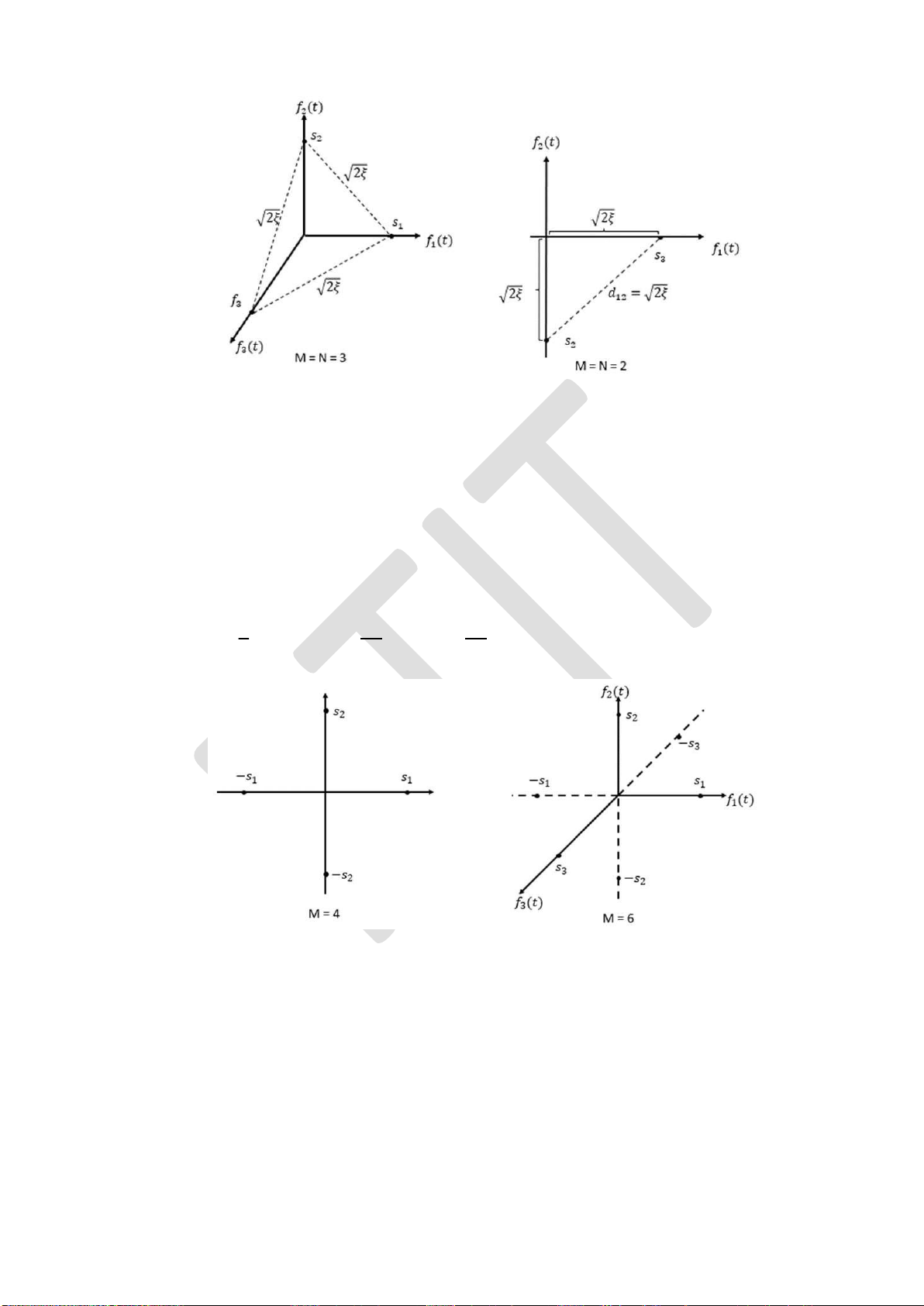
lOMoARcPSD| 36067889
= 0. Khoảng
Hình 5.9: Các tín hi
ệ
u tr
ự
c giao v
ớ
i
==2
và
==3
.
f) Tín hi
ệ
u tr
ự
c giao kép
T
ậ
p h
ợ
p
tín hiệu
tr
ự
c giao kép có th
ể
ượ
c xây d
ự
ng t
ừ
/2
các tín hi
ệ
u tr
ự
c
giao b
ằng cách ả
o d
ấ
u các tín hi
ệ
u tr
ự
c
giao. Như vậ
y ta c
ầ
n s
ố
chi
ề
u
=/2
cho
vi
ệ
c xây d
ự
ng t
ậ
p h
ợ
p
tín hi
ệ
u tr
ự
c giao kép. Hình 5.10 bi
ể
u di
ễ
n các tín hi
ệ
u tr
ự
c
giao kép v
ớ
i
=4
và
=6
.
Ta th
ấ
y r
ằ
ng s
ự
liên h
ệ
gi
ữ
a m
ộ
t c
ặ
p hai tín hi
ệ
u là
=1
ho
ặ
c
cách
=2
, ho
ặ
c
=
2
và
=
2
là khoảng cách nhỏ nhất giữa hai tín hiệu.

lOMoARcPSD|36067889
Hình 5.10: Sơ ồ không gian tín hiệu của tín hiệu trực giao kép với M = 4 và M = 6
5.2.3.2. Điều chế tuyến tính có nhớ
Các phương pháp iều chế tín hiệu xét ở phần 5.2.3.1 thuộc loại iều chế không nhớ
do không có sự liên hệ nào giữa tín hiệu ã truyền i với các tín hiệu tạo ra sau ó. Trong
phần này ta sẽ xét tới tín hiệu iều chế có sự phụ thuộc của tín hiệu ã truyền i với các tín
hiệu sẽ truyền sau ó. Sự phụ thuộc giữa các tín hiệu này thường có mục ích làm cho phổ
của tín hiệu truyền i thích hợp với các ặc iểm về tần số của kênh truyền.
Xét một số ví dụ về tín hiệu iều chế có nhớ và biểu diễn tính có nhớ bằng dãy
Markov. Giả thiết rằng các tín hiệu ở băng tần cơ sở. Đối với các tín hiệu có dải phổ hữu
hạn ược suy ra một cách tương tự.
Hình 5.11 biễu diễn ba tín hiệu băng tần cơ sở và dãy số liệu tương ứng. Tín hiệu
thứ nhất gọi là tín hiệu NRZ, nó là ơn giản nhất trong ba tín hiệu. Thông tin nhị phân 1
ược biểu diễn bởi một xung vuông biên ộ A và thông tin nhị phân 0 ược biểu diễn bởi
một xung vuông biên ộ -A. Như vậy phép iều chế tín hiệu NRZ là không nhớ và nó
tương ương với tín hiệu PAM nhị phân hay PSK nhị phân trong các hệ thống iều chế có
sử dụng tín hiệu sóng mang.
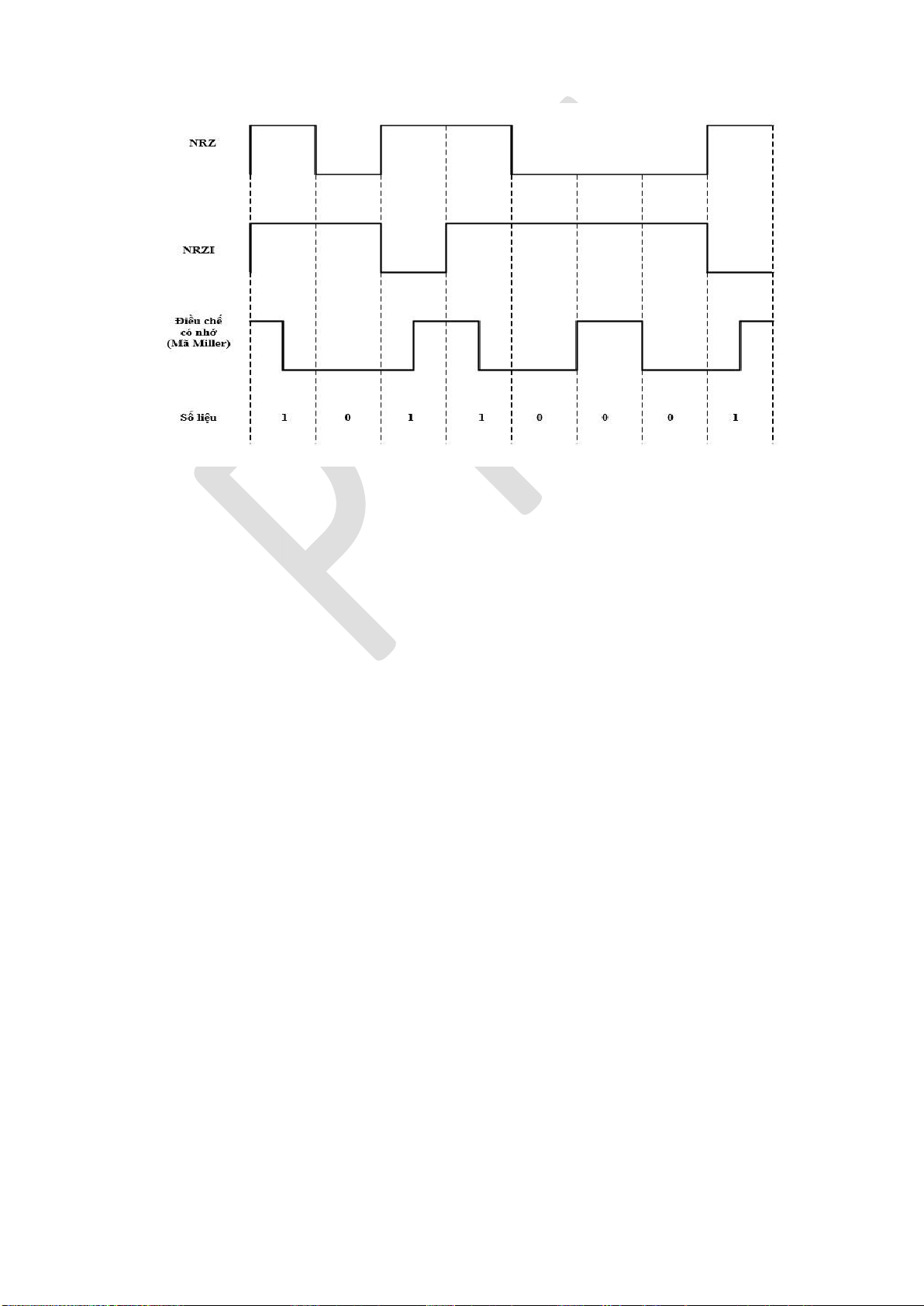
lOMoARcPSD|36067889
trong ó : {
} là dãy bit nhị phân ở ầu vào bộ mã hóa và {
} là dãy bit ra của bộ mã
hóa. Khi
= 1 thì tín hiệu truyền i là một xung vuông biên ộ , và khi
= 0 thì tín
hiệu truyền di là xung vuông biên ộ -A. Như vậy ầu ra của bộ mã hóa ược biến ổi thành
một trong hai loại tín hiệu giống hệt như mã NRZ,
Mã hóa vi sai là mã hóa có nhớ. Phối hợp sự hoạt ộng của bộ mã hóa và bộ iều chế
ược biểu diễn bởi sơ ồ trạng thái (dãy Markov) trên hình 5.12. Sơ ồ trạng thái có thể ược
mô tả bằng ma trận chuyển ổi tương ứng với hai khả năng có thể của ầu vào {0, 1}. Chú
ý rằng khi
= 0, bộ mã hóa giữ nguyên trạng thái. Ma trận chuyển ổi ứng với ầu vào
0 là:
1 0 (5.64)
1
= [ ]
0 1
= 1 nếu
làm bộ mã hóa chuyển từ trạng thái sang trạng thái . Tương tự ma trận
chuyển ổi trạng thái với
= 1 là:
0 1 (5.65)
Hình 5.11
:
Tín hiệu băng tần cơ sở
Tín hiệu NRZI khác với tín hiệu NRZ ở chỗ có sự chuyển ổi từ mức biên ộ này
sang mức biên ộ khác khi có
thông tin nh
ị
phân 1. Biên ộ
tín hi
ệu không thay ổ
i khi
truy
ề
n các bit 0. Ki
ể
u mã hóa tín hi
ệu như thế
ượ
c g
ọ
i là mã hóa vi sai. Thu
ậ
t toán mã
hóa ượ
c mô t
ả
toán h
ọc như sau:
=
1
(5.63)
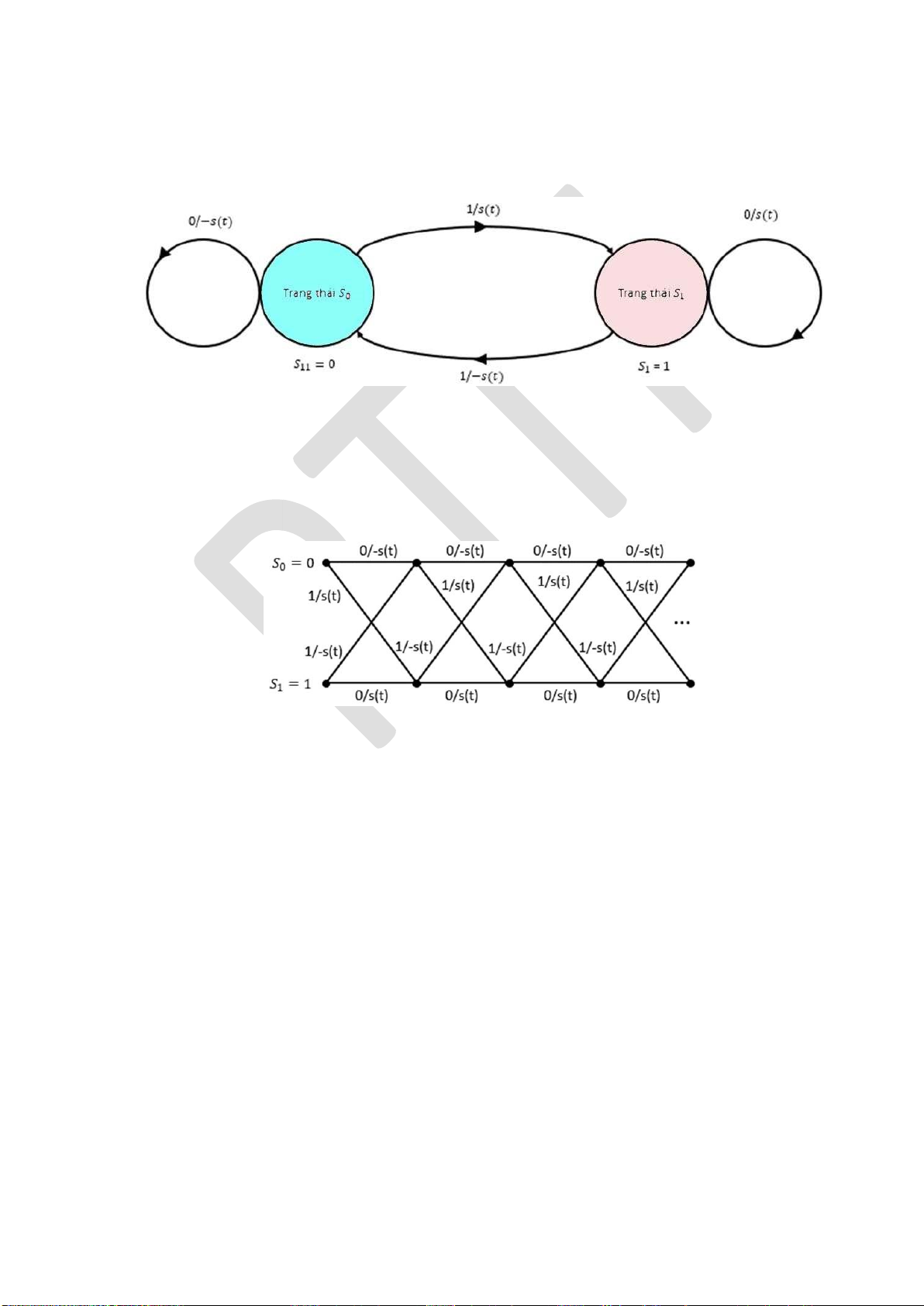
lOMoARcPSD| 36067889
2
= [ ]
1 0
Đó là hai ma trận chuyển ổi trạng thái ặc trưng cho tín hiệu NRZI.
Hình 5.13: Sơ ồ lưới ối với tín hiệu NRZI
Tín hiệu tạo ra bởi iều chế trễ cũng có nhớ. Xét phương pháp Miller và sử dụng
mã NRZI ể truyền số liệu ã ược mã vuông góc. Loại iều chế số này ược sử dụng nhiều
Hình 5.12
:
Lưu ồ trạng thái của tín hiệu NRZI
Một cách khác ể thể hiện quá trình nhớ là bằng sơ ồ lưới. Sơ ồ lưới ối với tín
hiệu NRZI trên hình 5.13. Sơ ồ này cho chúng ta các thông tin về sự phụ thuộc của các
tí
n hiệu giống như lưu ồ trạng thái.
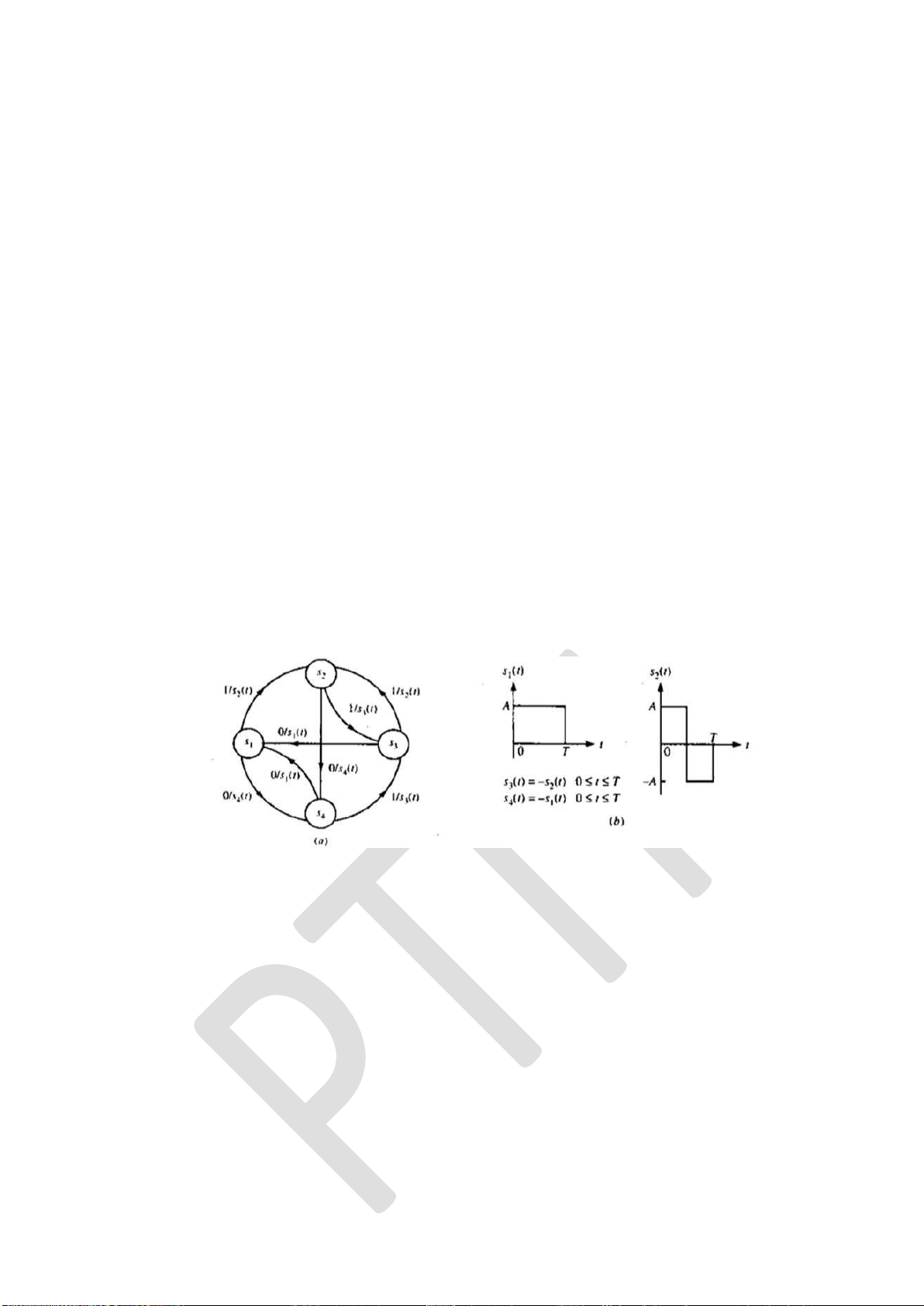
lOMoARcPSD| 36067889
trong việc ghi lên băng từ, ĩa từ số. Tín hiệu ược biểu diễn bởi sơ ồ trạng thái có 4 trạng
thái trên hình 5.14(a). Có hai tín hiệu cơ bản là
1
() và
2
()và hai tín hiệu ối
1
()
và
2
() ược sử dụng ể truyền thông tin nhị phân. Các tín hiệu này hình 5.14(b). Quá
trình biến ổi từ các bit thành các tín hiệu tương ứng ược cho trên lưu ồ trạng thái. Ma
trận chuyển ổi trạng thái ặc trưng cho quá trình mã hóa và iều chế dễ dàng nhận ược từ
lưu ồ trạng thái. Với
= 0, ta có:
0
1
= [
0
1
1
và khi
= 1 thì ma trận chuyển ổi là:
0
0
0
0
0
0
0
0
1
1
(5.66)
]
0
0
0
1
= [
0
0
0
1
0
1
0
0
1
0
1
0
0
(5.67)
]
0
0
Hai ma trận này ặc trưng cho phương pháp mã hóa Miller.
Hình 5.14: Lưu ồ trạng thái
(a) Các tín hiệu cơ bản; (b) Cho quá trình iều chế tín hiệu số có nhớ
Các kỹ thuật iều chế có nhớ như NRZI và mã hóa Miller ược tổng quát hóa bởi
dãy Markov trạng thái với các xác suất các trạng thái dùng {
, } và các
xác suất chuyển ổi {
, , = 1,2} Xác suất chuyến ổi
ký hiệu xác suất tín
hiệu
() ược truyền sau tín hiệu
() ở khoảng thời gian ngay trước ó. Các xác suất
chuyển ổi ược sắp xếp thành dạng ma trận như sau:
11 12 1
21 22 2
= [
] (5.68)

lOMoARcPSD|36067889
1 2
P ược gọi là ma trận xác suất chuyển ổi. Ma trận xác suất chuyển ổi có thể dễ dàng
nhận ược từ ma trận chuyển ổi {
} và các xác suất tương ứng của các ký hiệu vào (các
xác suất {
}. Mối liên hệ cơ bản ó là:
2
=1
(5.69)
trong ó:
1
= (
= 0) và
2
= (
= 1).
Với tín hiệu NRZI và xác suất
1
=
2
=1/ 2, ma trận xác suất chuyển ổi là:
1/2
= [
1/2
1/2
] (5.70)
1/2
Tương tự ma trận chuyển ổi cho mã Miller với xác suất xuất hiện các ký hiệu ầu vào
như nhau
1
=
2
=
1
2
hay
1
=
2
=
3
=
4
=
1
4
là:
0
0
= [
1/2
1/2
1/2
0
1/2
0
0
1/2
0
1/2
1/2
1/2
] (5.71)
0
0
Ma trận xác suất chuyển ổi ược sử dụng trong việc xác ịnh các tính chất về phổ của
các tín hiệu iều chế số có nhớ.

lOMoARcPSD|36067889
. () (5.72)
0
. () (5.74)
x
() =
0
[
0
. +
0
] (5.76)
x
() =
0
[
0
+
. +
0
] (5.77)
.
5.3
ĐIÊU CHẾ
TÍN HI
Ệ
U
TƯƠNG TỰ
5.3.1
. Điề
u ch
ế
tín hi
ệ
u liên t
ụ
c
5.3.1.1.
Điề
u ch
ế
góc
a) Tín hi
ệu iề
u ch
ế
góc
-
Xét tín hi
ệu iề
u pha:
Độ
l
ệ
ch pha t
ứ
c th
ờ
i t
ỷ
l
ệ
v
ớ
i
()
:
(
)
=
0
Bi
ể
u th
ứ
c c
ủ
a tín hi
ệu iề
u pha là:
x
(
)
=
0
(
)
=
0
[
0
.
(
)
+
]
(5.73)
Xét tín hi
-
ệu iề
u t
ầ
n:
T
ầ
n s
ố
t
ứ
c th
ờ
i c
ủ
a tín hi
ệ
u t
ỷ
l
ệ
v
ớ
i s(t):
(
)
=
0
Bi
ể
u th
ứ
c c
ủ
a tín hi
ệu iề
u t
ầ
n là:
x
(
)
=
0
(
)
=
0
[
()
]
=
0
[
0
()
]
(5.75)
-
Xét trườ
ng h
ợ
p riêng:
()=
, bi
ể
u th
ứ
c c
ủ
a tín hi
ệu iều pha, iề
u t
ầ
n tr
ở
thành:

lOMoARcPSD|36067889
Nếu ổi gốc thời gian thích hợp, ta có biểu thức chung của tín hiệu iều biên góc như
sau:
() =
0
(
0
+ . ) (5.78)
trong ó: là chỉ tiêu iều biên góc, chính là ộ lệch cực ại của pha so với giá trị trung bình.
Đối với tín hiệu iều pha, ta có:
(5.79)
Đối với tín hiệu iều tần, ta có:
= (5.80)
b) Thực hiện iều chế và giải iều chế góc
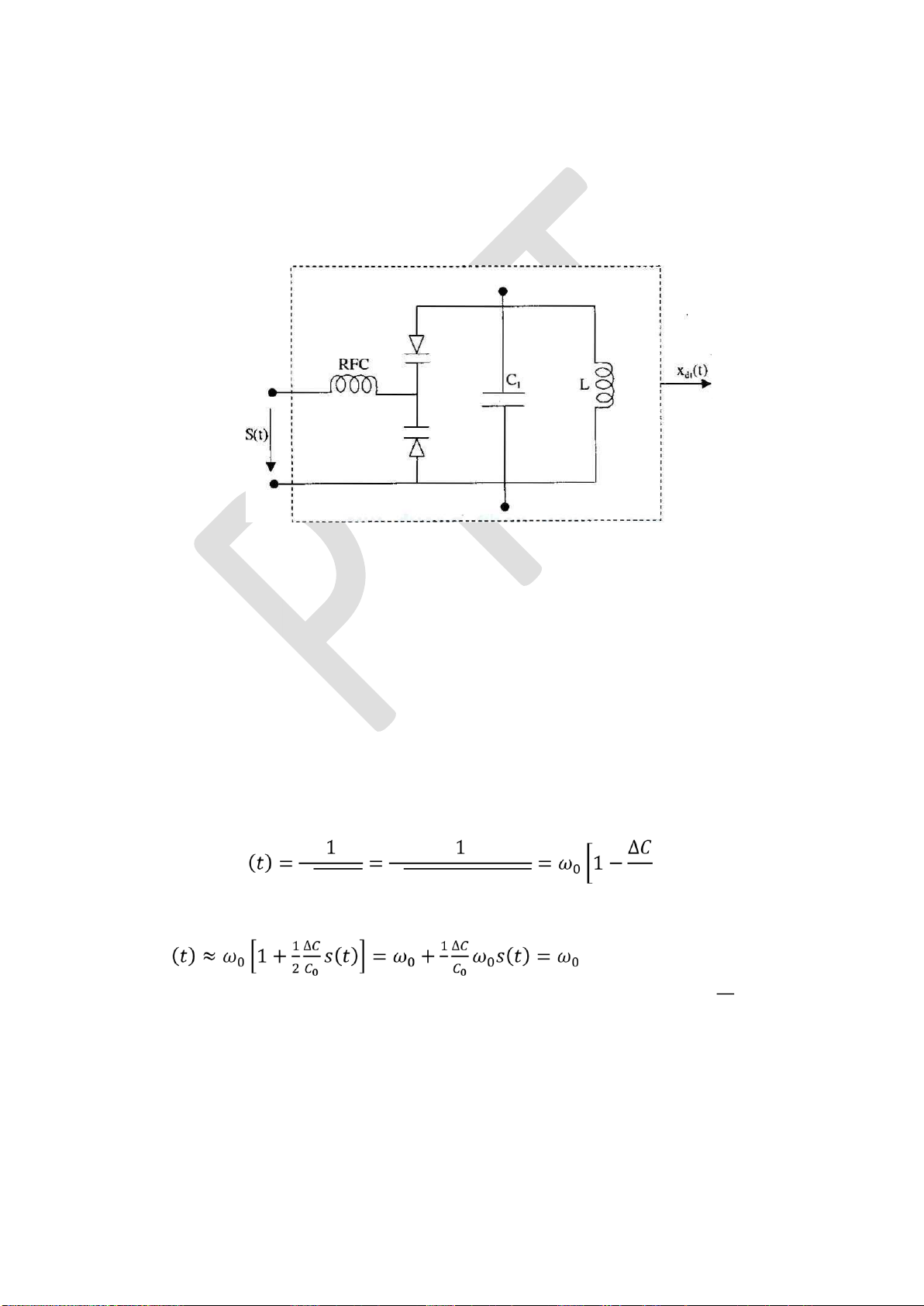
lOMoARcPSD|36067889
(5.81)
()]
() (
0
()) 0
. () (do
1) (5.82)
2 0
Vậy ta nhận ược một tín hiệu iều tần.
Giải iều chế: Có hai phương pháp giải iều tần ó là giải iều tần bằng mạch tách ường bao
và giải iều tần dùng vòng khoá pha.
Hình 5.16 là sơ ồ khối của bộ giải iều tần dùng vòng khóa pha (PLL). Đây là
b-1)
Đ
i
ề
u t
ầ
n:
Điề
u ch
ế
:
Ta c
ầ
n ph
ải làm thay ổ
i t
ầ
n s
ố
t
ứ
c th
ờ
i c
ủ
a m
ộ
t b
ộ
t
ạo dao ộ
ng hình sin
theo hàm tin
()
b
ằ
ng cách s
ử
d
ụ
ng m
ộ
t b
ộ
iề
u khi
ể
n b
ằng iệ
n áp (VCO):
Để
th
ự
c
hi
ệ
n b
ộ
t
ạo dao ộ
ng này, s
ử
d
ụ
ng b
ộ
t
ạo dao ộng LC dùng iố
t bi
ế
n dung. Ph
ầ
n th
ụ
ộ
ng c
ủ
a m
ạ
ch t
ạo dao ộ
n
g này ượ
c th
ể
hi
ệ
n trong hình 5-1.
Hình 5.15: Ph
ầ
n th
ụ
ộ
ng c
ủ
a m
ạ
ch t
ạo dao ộ
ng LC
Trong m
ạch iệ
n hình 5.15, ta có:
(
)
=
v
(
)+
1
=[
v0
(
)
]+
1
=
(
v0
+
1
)
(
)
=
0
(
)
T
ầ
n s
ố
dao
ộ
ng t
ứ
c th
ờ
i c
ủ
a m
ạ
ch t
ạo dao ộ
ng LC này là:
1
/
2
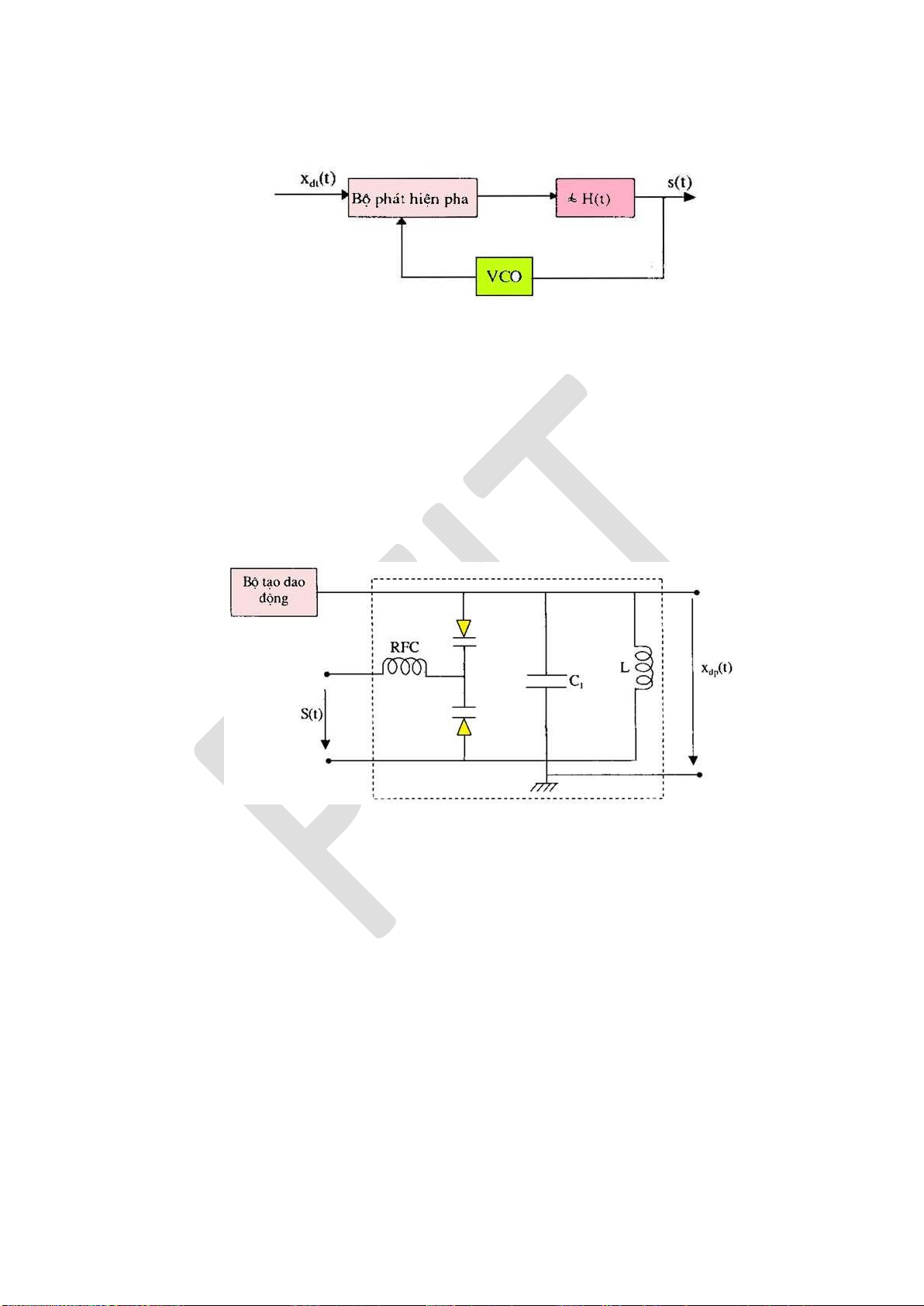
lOMoARcPSD|36067889
một hệ thống kín gồm 3 thành phần chính, bao gồm: một bộ phát hiện pha, một bộ lọc
thông thấp và một bộ tạo dao ộng iều khiển bằng iện áp (VCO).
Hình 5.16: Giải iều tần dùng vòng khóa dịch pha
Khi cho một tín hiệu iều tần qua một mạch vòng khoá pha, khi mạch khóa thì tín
b-2) Điều pha:
hi
ệ
u ra c
ủ
a b
ộ
l
ọ
c thông th
ấ
p t
ỷ
l
ệ
v
ớ
i tín hi
ệ
u mang tin
()
.
Điề
u ch
ế
Cho tín hi
:
ệu iề
u hòa t
ầ
n s
ố
0
qua m
ộ
t m
ạ
ch c
ộng hưở
ng có d
ị
ch pha thay
ổi ượ
c theo
()
như
hình 5.17, ta s
ẽ
nh
ận ượ
c tín hi
ệu iề
u pha c
ủ
a
()
. Các thông
s
ố
c
ủ
a m
ạ
ch t
ạo dao ộng ược xác ịnh tương tự
như
trong bi
ể
u th
ứ
c (5.81), (5.82).
Do ó pha của
i
ệ
n áp ra c
ủ
a m
ạ
ch c
ộng hưở
ng LC s
ẽ
thay ổ
i theo
()
do ặ
c
tuy
ế
n pha c
ủ
a m
ạ
ch c
ộng hưở
ng xung quanh
0
x
ấ
p x
ỉ
tuy
ế
n tính, vì l
ệ
ch c
ộng hưở
ng
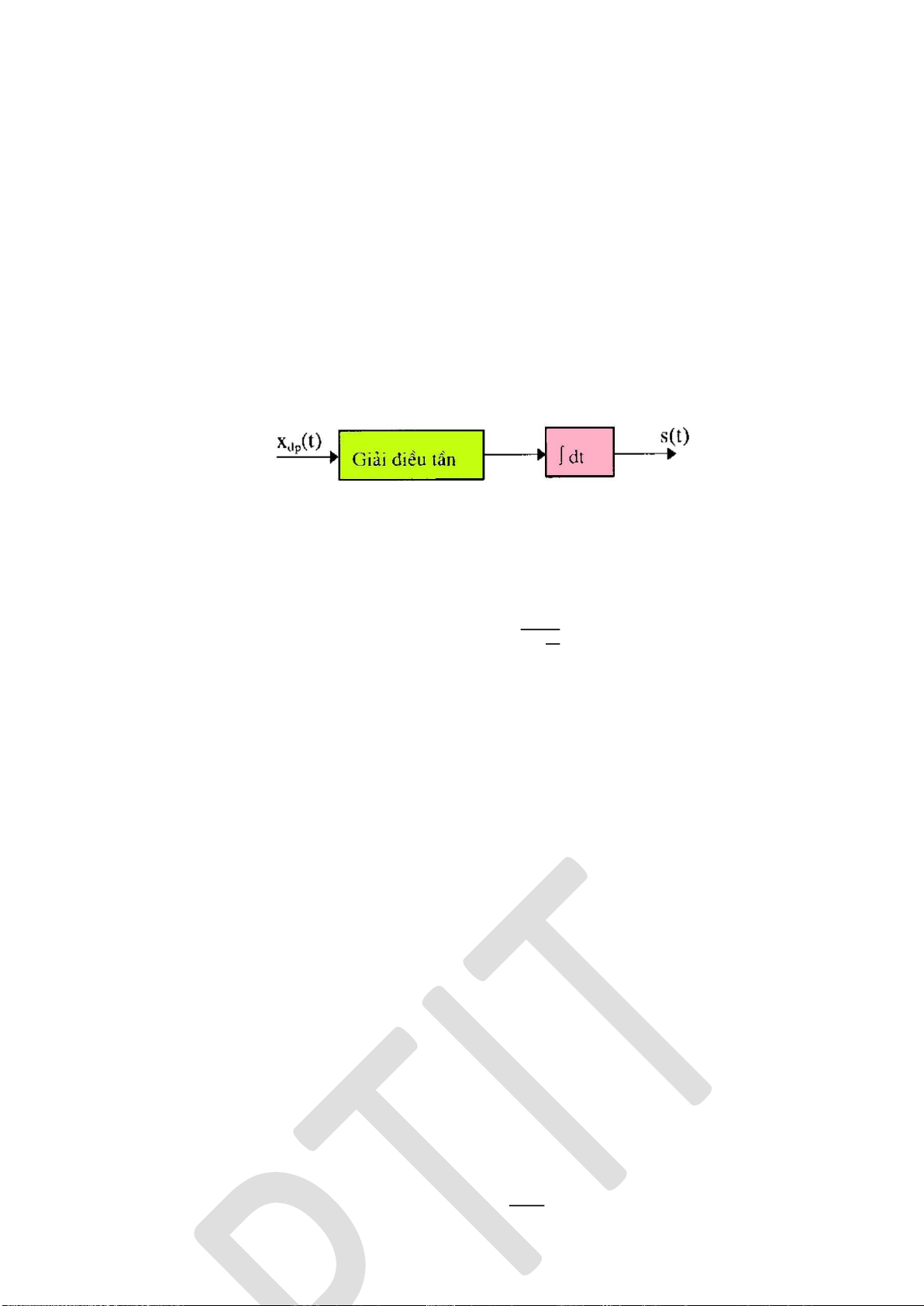
lOMoARcPSD|36067889
Hĩnh 5.17: Phần thụ ộng của mạch tạo dao ộng LC
Khi () thay ổĩ theo () thì tần số cộng hưởng của mạch cũng sẽ thay ổi
nhỏ nên nhận ược ở ầu ra của mạch tín hiệu iều pha theo ().
Giải iều chế: Ta có thể khôi phục lại ược () từ tín hiệu iều pha bằng cách ưa tín hiệu
iều pha qua một bộ giải iều tần rồi lấy tích phân tín hiệu nhận ược, như minh họa trên
hình 5.18.
Hình 5.18: Giải iều pha
Mạch tích phân thường ược thực hiện xấp xỉ bằng bộ lọc thông thấp tần số cắt
có
hàm truyền:
() =
1
(5.83)
1+
5.3.1.2. Điều biên
Tín hiệu mang tin () là thực, biên ộ ược chuẩn hóa sao cho |( và có phổ
hữu hạn trong khoảng 0 <
< || <
. Tín hiệu này có thể coi là tín hiệu dải hẹp có
bề rộng phổ:
=
(5.84)
0
là tần số của tải tin (hay sóng mang) (), giả thiết:
= 2
<<
0
= 2
0
(5.85) Tải
tin () là một tín hiệu iều hòa tần số
0
:
() =
0
(
0
+
0
) =
0
(2
0
+
0
) (5.86)
Nguyên lý của iều biên là biến ổi biên ộ không ổi
0
của tải tin thành biên ộ ()
phụ thuộc vào ().
Thực hiện iều biên: Ta sử dụng một bộ khuyếch ại iều khiển bằng iện áp G như trên
hình 5.19.

lOMoARcPSD|36067889
1
1
1
0
v()
= (5.87)
0
Khi ưa tải tin () = (
0
+
0
) vào ầu vào của bộ khuếch ại có iện áp iều
khiển là:
v() =
0
[1 + ()] (5.88)
thì sẽ nhận ược ở ầu ra của bộ khuếch ại:
() = () =
0
[1 + ()]cos(
0
+
0
)
=
0
[1 + ()]cos(
0
+
0
) = ()cos(
0
+
0
) (5.89) Tín
hiệu () ở ầu ra nhân ược chính là tín hiệu iều biên của ().
Hình 5.19: Thực hiện iều biên
Thực hiện giải iều biên: Có hai phương pháp thông dụng ể giải iều biên, ó là: tách ường
bao và giải iều biên ồng bộ.
Xét cụ thể phương pháp tách ường bao như sau: Một bộ tách hình bao lý tưởng là
một mạch iện sinh ra một tín hiệu ở ầu ra tỷ lệ thuận với ường bao thực của tín hiệu vào.
Tín hiệu vào là tín hiệu iều biên ():
() = ()(
0
+
0
) Tín
hiệu ra () của bộ tách ường bao lý tưởng là:
() = () (5.90)
Mạch tách ường bao (hình 5.20) là một iốt D (giả thiết là lý tưởng) nối với một iện
trở R và tụ iện C. Điốt D mở ối với phần dương của tín hiệu vào. Khi iện áp tăng, D mở
tụ C ược nạp tới giá trị ỉnh của (). Khi iện áp ầu vào giảm i, D khóa, tụ C phóng iện
qua R cho ến khi iện áp vào tăng tới giá trị làm cho D lại mở.
Hằng số phóng: = , khi chọn thích hợp: . Trong thực tế, ta
chọn: = thì tín hiệu ra () xấp xỉ là ường bao của tín hiệu vào () với ộ

lOMoARcPSD| 36067889
méo không áng kể. Trái lại, nếu chọn quá nhỏ hoặc quá lớn thì tín hiệu ra của mạch
tách ường bao sẽ bị méo lớn.
Hình 5.20: Mạch tách ường bao
5.3.2. Điều chế xung
Ban ầu, ể truyền tiếng nói trong các mạng viễn thông thường chỉ dựa trên kỹ thuật
truyền tương tự, nhưng ở những khoảng cách xa, ộ rõ của tiếng nói có thể kém i. Do bị
suy hao và bị nhiễu nên có thể sẽ khó nghe hoặc không nhận ra người nói ang nói gì. Do
vậy các tín hiệu tương tự ược khuếch ại ở những khoảng cách nhất ịnh, tuy nhiên nhiễu
cũng ược khuếch ại và mỗi tầng khuếch ại sau khi kết nối ều làm tích lũy nhiễu. Để cải
thiện chất lượng truyền dẫn cần phải sử dụng các phương pháp iều chế tín hiệu xung
(còn gọi là số hóa) ể chuyển ổi từ tín hiệu tiếng nói (liên tục) sang tín hiệu dạng số và ở
ầu nhận cần phải giải iều chế một lần nữa thành âm thanh.
Ở ây có sự khác nhau quan trọng giữa các ặc tính của hai phương pháp truyền dẫn này
là trong các hệ thống chuyển mạch số, thông tin ược tái tạo và ược phát i hoàn toàn
không bị nhiễu. Việc khảo sát các phương pháp iều chế ra tín hiệu số nhằm xác ịnh
phương pháp tốt nhất cho mọi loại môi trường truyền là iều hết sức quan trọng. Chúng
ta sẽ cụ thể hóa kỹ thuật số như sau:
Tải tin () là một dãy xung vuông tuần hoàn chu kỳ
cho ở công thức (5.5) như
trên Hình 5.21.
Hình 5.21: Tải tin của tín hiệu iều biên xung

lOMoARcPSD|36067889
Tải tin () có bốn tham số: Biên ộ ; Tần số
=
1
; Thời iểm xuất hiện của xung
thứ :
=
0
+
và Độ rộng xung: .
Cho hàm tin () tác ộng vào từng tham số trên, sẽ nhận ược bốn loại iều biên
xung tương ứng: iều biên xung (PAM), iều pha xung (PPM), iều tần xung (PFM), iều
rộng xung (PWM).
Tín hiệu iều biên xung sẽ có dạng tổng quát:
(
(
0
) (5.91)
Các tham số biên ộ
, ộ rộng
, chu kỳ
, thời iểm xuất hiện xung
0
phụ thuộc
vào , tương ứng với iều biên xung (PAM), iều rộng xung (PWM), iều tần xung (PFM),
iều pha xung (PPM).
5.3.2.1. Điều biên xung (PAM)
Tín hiệu iều biên xung là tín hiệu có biên ộ mang tin (hình 5.22) tuân theo quy luật
sau:
= (
) (5.92)
Thực hiện iều biên xung là lấy mẫu tín hiệu () dựa trên ịnh luật lấy mẫu của
Shannon, thay thế nó bằng một hàm rời rạc là những mẫu của hàm trên lấy tại những
thời iểm rời rạc.
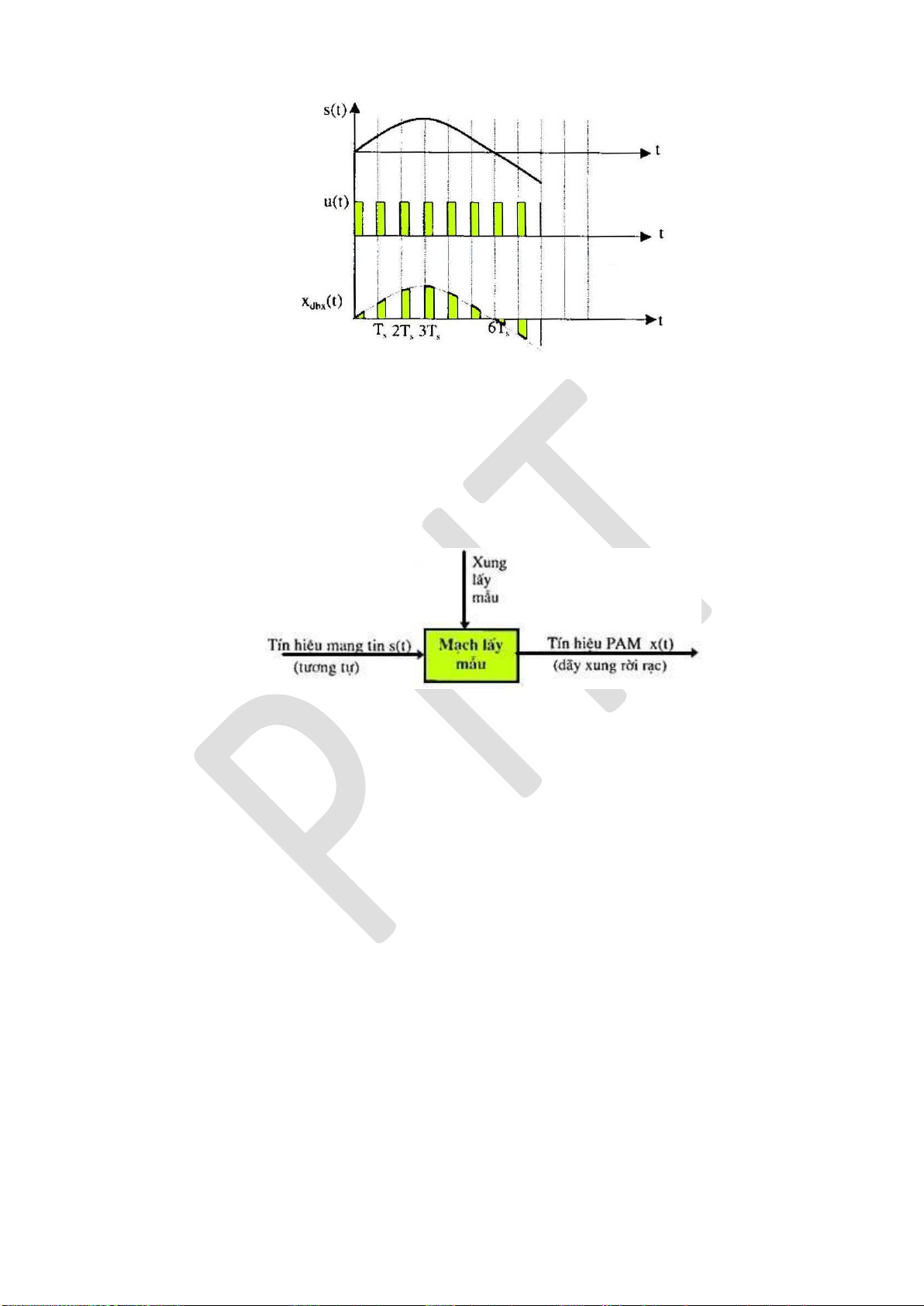
lOMoARcPSD|36067889
Điều biên xung (PAM) vẫn chưa phải là quá trình số hoá vì dạng iều chế này lấy
xung có bề rộng cố ịnh nhưng có chiều cao (biên ộ) thay ổi theo tín hiệu iều chế. Điều
chế biên ộ xung rất nhạy cảm với nhiễu nhiệt và nhiễu xuyên âm, nhiễu sẽ tác ộng lên
ỉnh xung và hình thành tạp âm trên kênh khi giải iều chế.
5.3.2.2. Điều pha xung (PPM)
Tín hiệu iều pha xung là tín hiệu có pha (hay thời iểm xuất hiện của xung) mang tin
luân theo quy luật sau:
Hình 5.22: Tín hiệu
iề
u biên xung
N
ế
u t
ầ
n s
ố
l
ấ
y m
ẫu ≥
2 l
ầ
n t
ầ
n s
ố
cao nh
ấ
t c
ủ
a tín hi
ệ
u
(
)
thì phép lấy mẫu bảo
toàn thông tin của tín hiệu. Ví dụ tiếng nói có tần số lớn nhất là 3400Hz thì cần lấy mẫu
với tần số
nhỏ nhất là
6800
Hz.
Hình 5.23
ưa ra
sơ
ồ tổng quát
c
ủ
a l
ấ
y m
ẫ
u.
Hình 5.23:
Điề
u biên xung
Tín hi
ệ
u mang tin
()
ược ưa ến ầ
u vào c
ủ
a m
ạ
ch l
ấ
y m
ẫ
u. Xung l
ấ
y m
ẫ
u
()
là m
ộ
t dãy xung vuông tu
ầ
n hoàn chu k
ỳ
. Đầ
u ra là tín hi
ệu iề
u biên xung
()
là một dãy xung mà biên ộ mỗi xung bằng
v
ới biên ộ
c
ủ
a tín hi
ệu tương tự
g
ố
c t
ạ
i
th
ời iể
m l
ấ
y m
ẫ
u. Các
xung này ượ
c t
ạ
o ra có t
ầ
n s
ố
ả
m b
ảo ị
nh lý l
ấ
y m
ẫ
u. Do
ó,
có th
ể
khôi ph
ụ
c (quá trình gi
ải iề
u biên) l
ạ
i chính xác tín hi
ệ
u
()
t
ừ
tín hi
ệu iề
u
biên xung n
ế
u tín hi
ệ
u
()
ượ
c l
ấ
y m
ẫ
u
ở
t
ầ
n s
ố
.
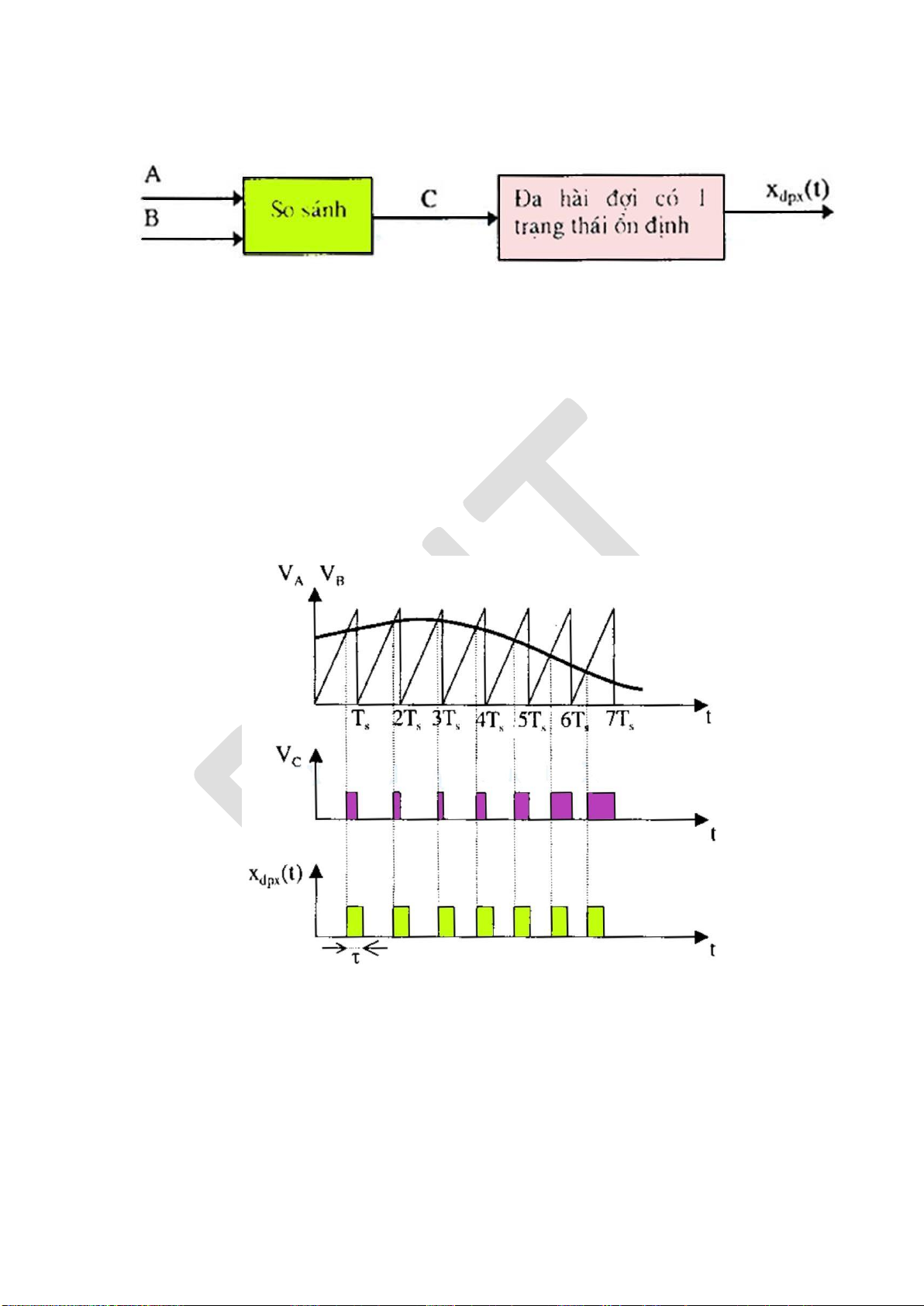
lOMoARcPSD|36067889
0
=
0
. (
) (5.93)
Có thể thực hiện iều pha xung bằng sơ ồ khối mạch như trên hình 5.24.
Hình 5.24: Mạch iều pha xung
Đầu vào A là tín hiệu
, ó là xung răng cưa tuần hoàn chu kỳ
.
Đầu vào B là tín hiệu:
= [1 + . ()] có dạng tín hiệu trong mạch như minh
h
ọ
a trên hình 5.25.
Tín hi
ệu ầ
u vào
ở
A ượ
c so sánh v
ớ
i tín hi
ệu ầ
u vào
ở
B, cho th
ấ
y m
ộ
t dãy
xung vuông có th
ời iể
m xu
ấ
t hi
ện xung mang tin nhưng có ộ
r
ộ
ng xung khác
. Nếu
ta cho tín hi
ệ
u
ở
C
i qua một a hài ợ
i có m
ộ
t tr
ạ
ng thái
ổn ịnh (ộ
r
ộ
ng xung
)
thì
s
ẽ
nh
ận ượ
c m
ộ
t tín hi
ệu iề
u pha xung.
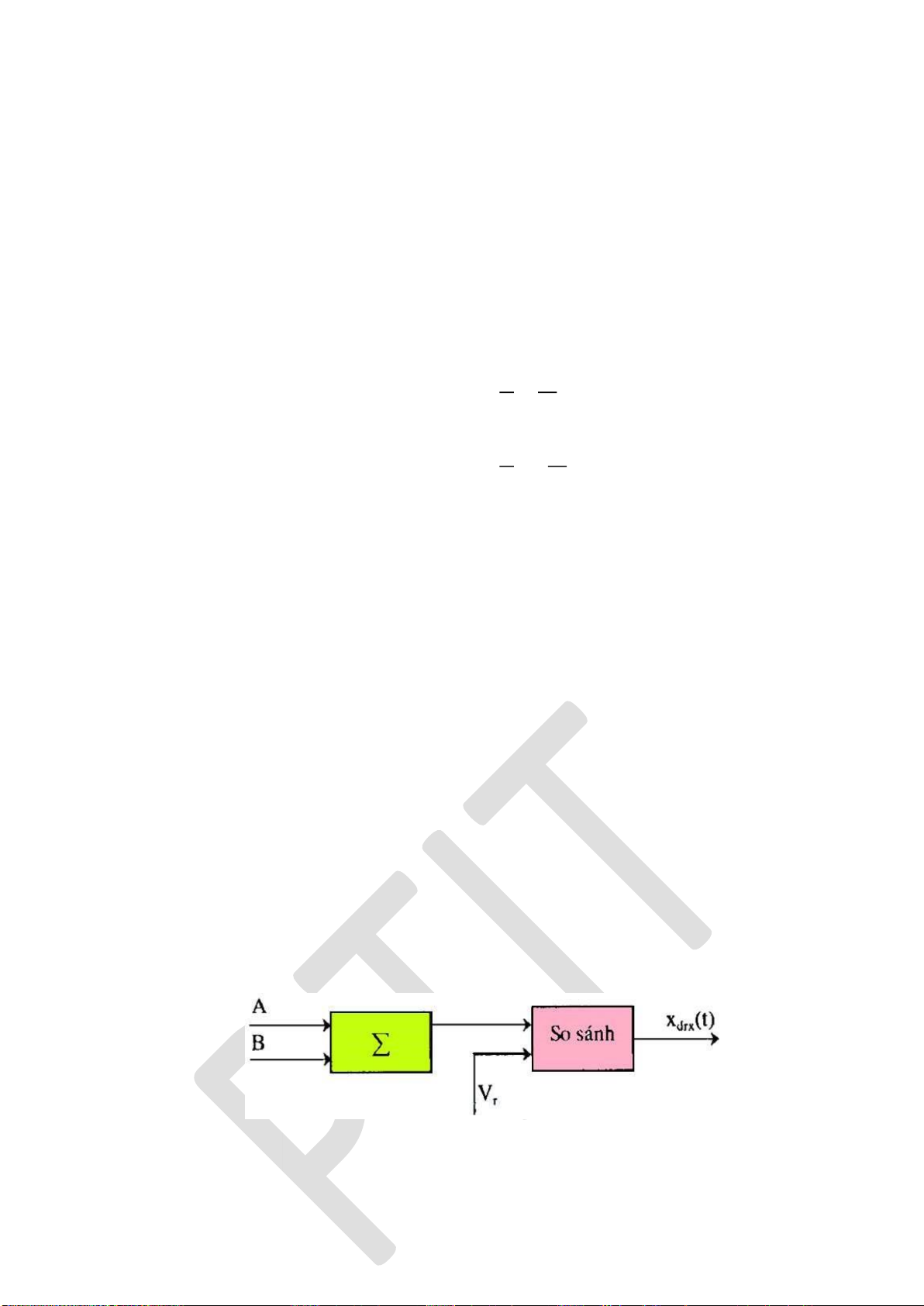
lOMoARcPSD|36067889
Hình 5.25: Tín hiệu iều pha xung Pha
của xung ược xác ịnh một cách rõ ràng như sau:
Xét trong một chu kỳ:
=
0
(5.94)
mà
=
tại thời iểm mạch so sánh chuyển trạng thái, do ó:
0
= [1 + . ()] (5.95)
0
=
0
+
0
(
) (5.96)
= ( + 0) + 0 () (5.97)
Đây là tín hiệu iều pha xung.
5.3.2.3. Điều rộng xung (PWM)
Tín hiệu iều rộng xung là tín hiệu có ộ rộng xung mang tin tuân theo quy luật:
= . (
) (5.98)
Trong dạng iều chế này, giữ biên ộ xung cố ịnh, nhưng bề rộng xung thay ổi. Cạnh
của xung dịch theo tín hiệu mang tin làm bề rộng xung thay ổi theo. Khi nhiễu làm thay
ổi biên ộ xung sẽ không ảnh hưởng ến tín hiệu gốc vì biên ộ xung không mang thông tin
nào. Tuy vậy, nhiễu cũng làm xáo trộn cạnh của xung bởi hiện tượng méo dạng khi
truyền.
Có 3 cách iều rộng xung: Giữ nguyên sườn trước, thay ổi sườn sau; Giữ nguyên
sườn sau, thay ổi sườn trước và Giữ nguyên iểm giữa, thay ổi ộ rộng.
Ta xét cách thứ nhất là giữ nguyên sườn trước, thay ổi sườn sau.
Mạch iện thực hiện iều rộng xung như hình 5.26.
Hình 5.26: Mạch iều rộng xung

lOMoARcPSD| 36067889
Đầu vào A là tín hiệu
= (); Đầu vào B (
) là tín hiệu răng cưa tuần hoàn chu
kỳ
;
là iện áp tham chiếu.
Dạng tín hiệu trong mạch iều rộng xung như hình 5.27.
Tín hiệu ở iểm C là tổng hai tín hiệu
,
, nó ược so sánh với tín hiệu
cho ở
ầu ra một dãy xung vuông có ộ rộng xung mang tin.
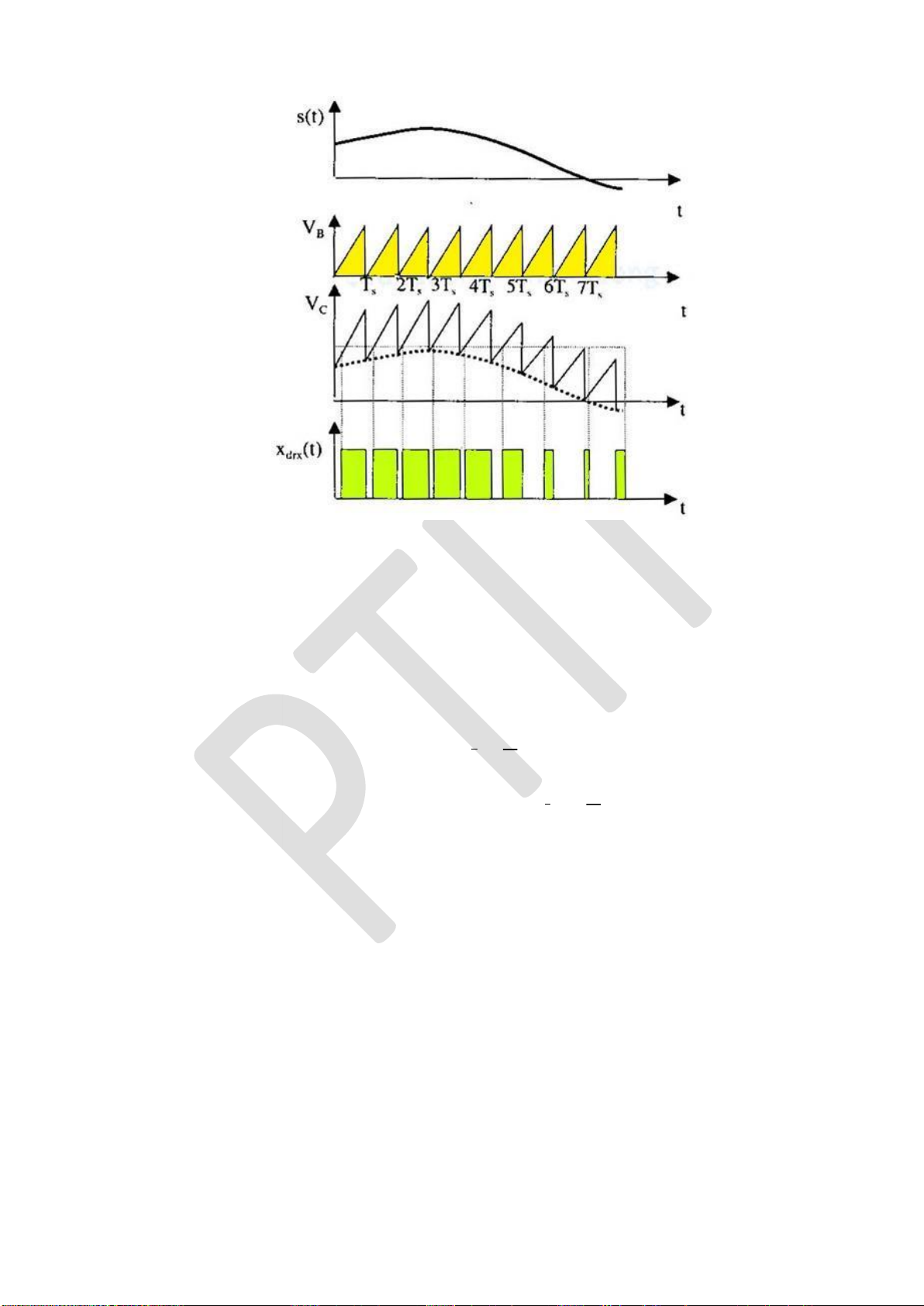
lOMoARcPSD| 36067889
() (5.101)
(5.102)
Hình 5.27: D
ạ
ng tín hi
ệ
u trong m
ạ
ch
iề
u r
ộ
ng xung
Độ
r
ộng xung ược xác ị
nh c
ụ
th
ể
như sau:
T
ạ
i th
ời iể
m m
ạ
ch so sánh chuy
ể
n tr
ạ
ng thái, ta có:
+
=
=
(5.99)
0
+
(
)
=
(5.100)
=
0
+
1
0
=
=
(
0
)
+
1
0
(
)
Đây là tín hiệu iề
u r
ộ
ng xung.
Đố
i v
ớ
i hai cách còn l
ạ
i, m
ạch iệ
n v
ẫn như
hình 5.26 tuy nhiên ch
ỉ
thay ổ
i tín
hi
ệ
u
là tín hiệu xung răng
cưa tuầ
n hoàn chu k
ỳ
d
ốc sườ
n sau ho
ặ
c d
ố
c c
ả
hai m
ộ
t
cách tương ứ
ng.
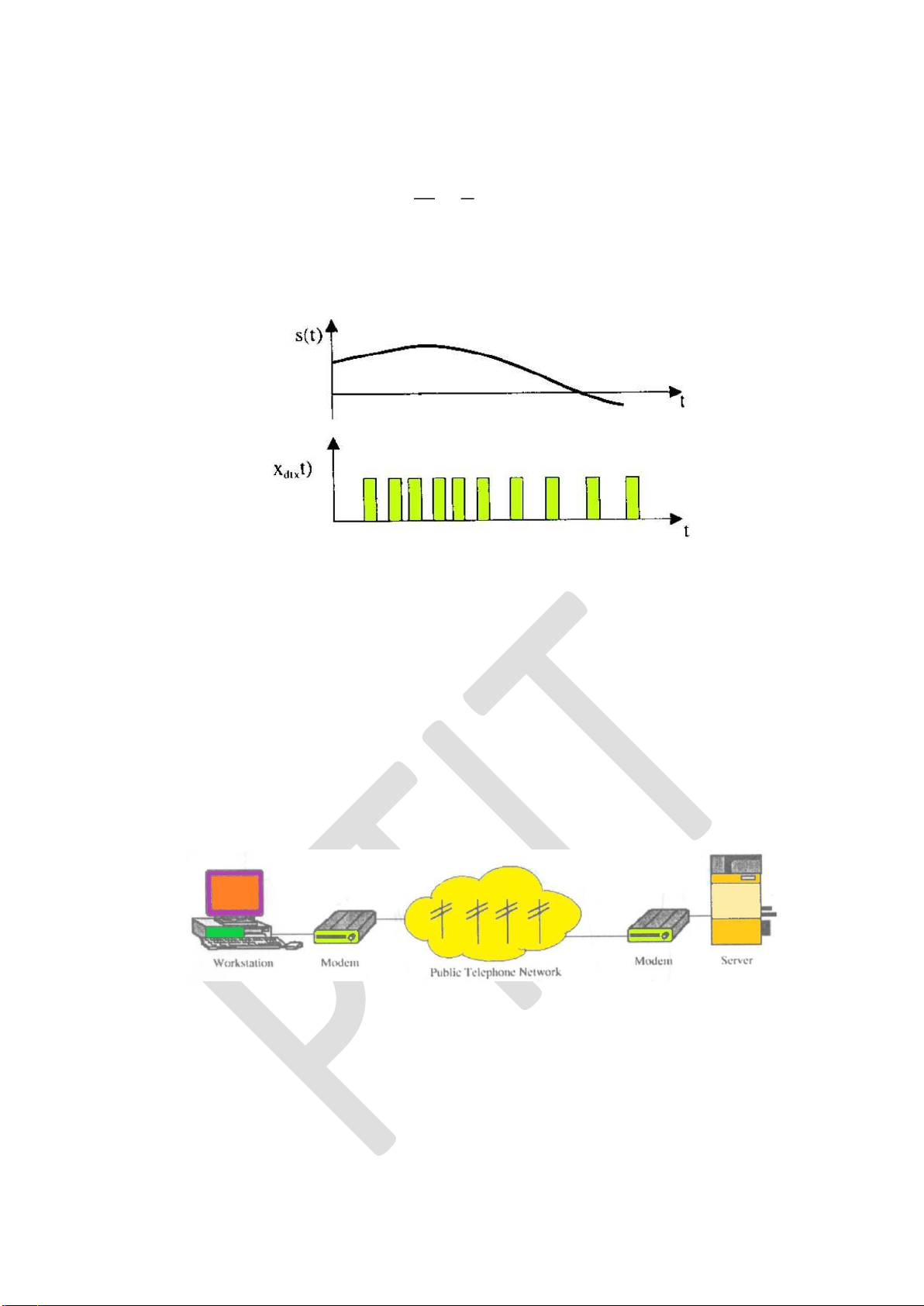
lOMoARcPSD|36067889
5.3.2.4. Điều tần xung (PFM)
Tín hiệu iều tần xung là tín hiệu có tần số mang tin.
1 1
= . (
) (5.103)
Phương pháp iều chế này ược xem như tương ương với iều rộng xung. Dạng
tín hiệu iều tần xung ược thể hiện trong hình 5.28.
Hình 5.28: Tín hiệu iều tần xung
5.4. ĐIỀU CHẾ TÍN HIỆU SỐ
Khi muốn truyền số liệu giữa các máy tính trên các ường truyền cáp kim loại (cáp
xoắn ôi) có sẵn như hình 5.29, cần chuyển ổi các tín hiệu i ra từ các máy tính sang dạng
phù hợp với ường truyền. Đường truyền này ược thiết kế cho thông tin tiếng nói có băng
thông trong khoảng 300-3400 Hz. Chính vì lý do này không thể ặt hai mức iện áp từ
DTE trực tiếp lên ường dây. Vì vậy, dữ liệu nhị phân cần ược chuyển ổi sang dạng tương
thích với tín hiệu iện thoại tại DTE phát và chuyển ổi ngược lại thành dạng nhị phân lại
ầu thu.
Hình 5.29: Đường truyền số liệu giữa các máy tính trên ường truyền cáp xoắn ôi
Đối với truyền hình cáp CATV cũng vậy, tín hiệu số từ các trung tâm truyền hình
cáp sẽ ược chuyển ổi thành tín hiệu tương tự tần số vô tuyến ể ghép kênh trên các cáp
ồng trục và ến máy thu hình của các thuê bao.
Mạch iện thực hiện hoạt ộng chuyển ổi từ tín hiệu băng gốc số sang tín hiệu liên
tục (hình sin) băng tần thích hợp gọi là bộ iều chế (Modulator), và mạch iện thực hiện
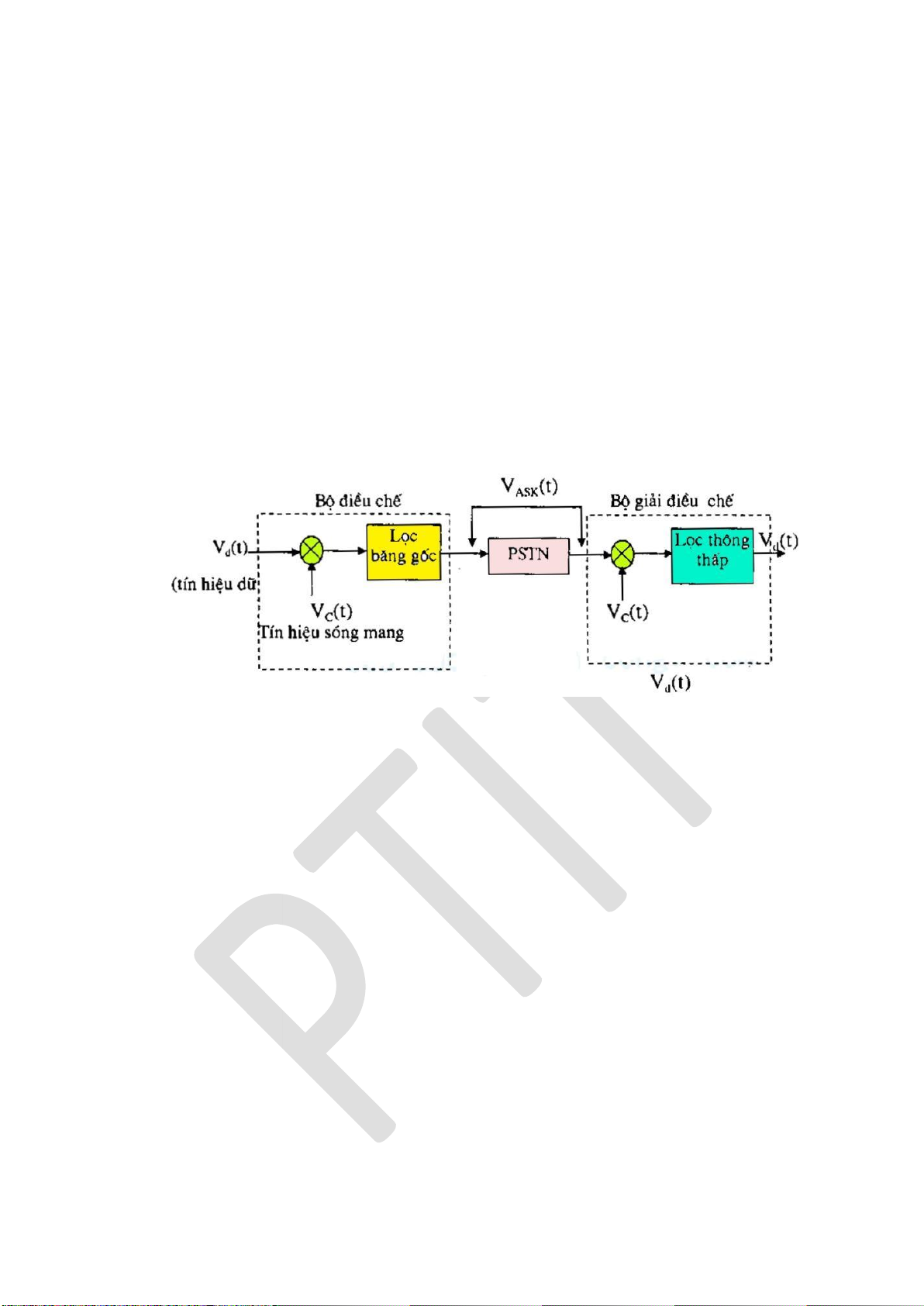
lOMoARcPSD| 36067889
hoạt ộng chuyển ổi ngược lại ược gọi là bộ giải iều chế (Demodulator). Vì mỗi liên kết
ều cần cả hai mạch, chúng kết hợp lại thành một thiết bị chung gọi là Modem.
Để thực hiện iều chế, phải thay ổi biên ộ, tần số và pha của tín hiệu sóng mang
hình sin theo sự biến ổi của dữ liệu nhị phân cần truyền. Dữ liệu nhị phân ược truyền
chỉ yêu cầu hai mức tín hiệu, sự chuyển mạch tín hiệu giữa hai mức mang ý nghĩa khóa
vì vậy ba loại iều chế trên ược gọi là iều chế khóa dịch biên ộ (ASK), khoá dịch tần số
(FSK) và khoá dịch pha (PSK). Ngoài ra hiện nay còn kết hợp ASK với PSK gọi là iều
chế QAM.
5.4.1. Điều chế khóa dịch biên ộ (ASK)
Nguyên lý hoạt ộng cơ bản của ASK ược minh hoạ trong hình 5.30 và dạng sóng ơn
giản ở hình 5.31.
Hình 5.30: Sơ ồ mạch
Nguyên lý của ASK là biên ộ của tín hiệu sóng mang ược chuyển ổi giữa hai mức
dữ liệu với tốc ộ ược xác ịnh bởi tốc ộ bít của tín hiệu nhị phân ược truyền. Sóng mang
có tần số thuộc băng thông ường truyền. Kích thước băng thông yêu cầu ược xác ịnh bởi
tốc ộ của tín hiệu, tốc ộ càng cao thì kích thước băng thông yêu cầu càng lớn. Trong
thực tế các phương pháp iều chế khác nhau òi hỏi ộ rộng băng thông khác nhau, nên
việc ánh giá mức băng thông yêu cầu ứng với mỗi phương pháp là rất cần thiết.
Về mặt toán học, hoạt ộng iều chế ASK, PSK, FSK tương ương với việc nhân tín
hiệu sóng mang với tín hiệu dữ liệu nhị phân. Sóng mang có tần số riêng
và biên ộ
không ổi biểu diễn dưới dạng biểu thức iện áp:
() = cos
; (
: /) (5.104)
Một tín hiệu số mang tin tuần hoàn ơn cực với biên ộ không ổi và tần số cơ bản
0
ược khai triển theo chuỗi fourier như sau:

lOMoARcPSD|36067889
() = 1/2 + 2/(
0
3
0
+ 1/5 5
0
(5.105)
Suy ra ASK có thể biểu diễn:
() =
() ×
() (5.106)
Do ó:
() = 1/2 cos
+ 2/(cos
.
0
cos
. 3
0
+. . . )
Suy ra:
= 1/2 cos
+ 1/[cos(
0
) + cos(
+
0
) cos(
3
0
)
cos(
+ 3
0
) +. . . ] (5.107)
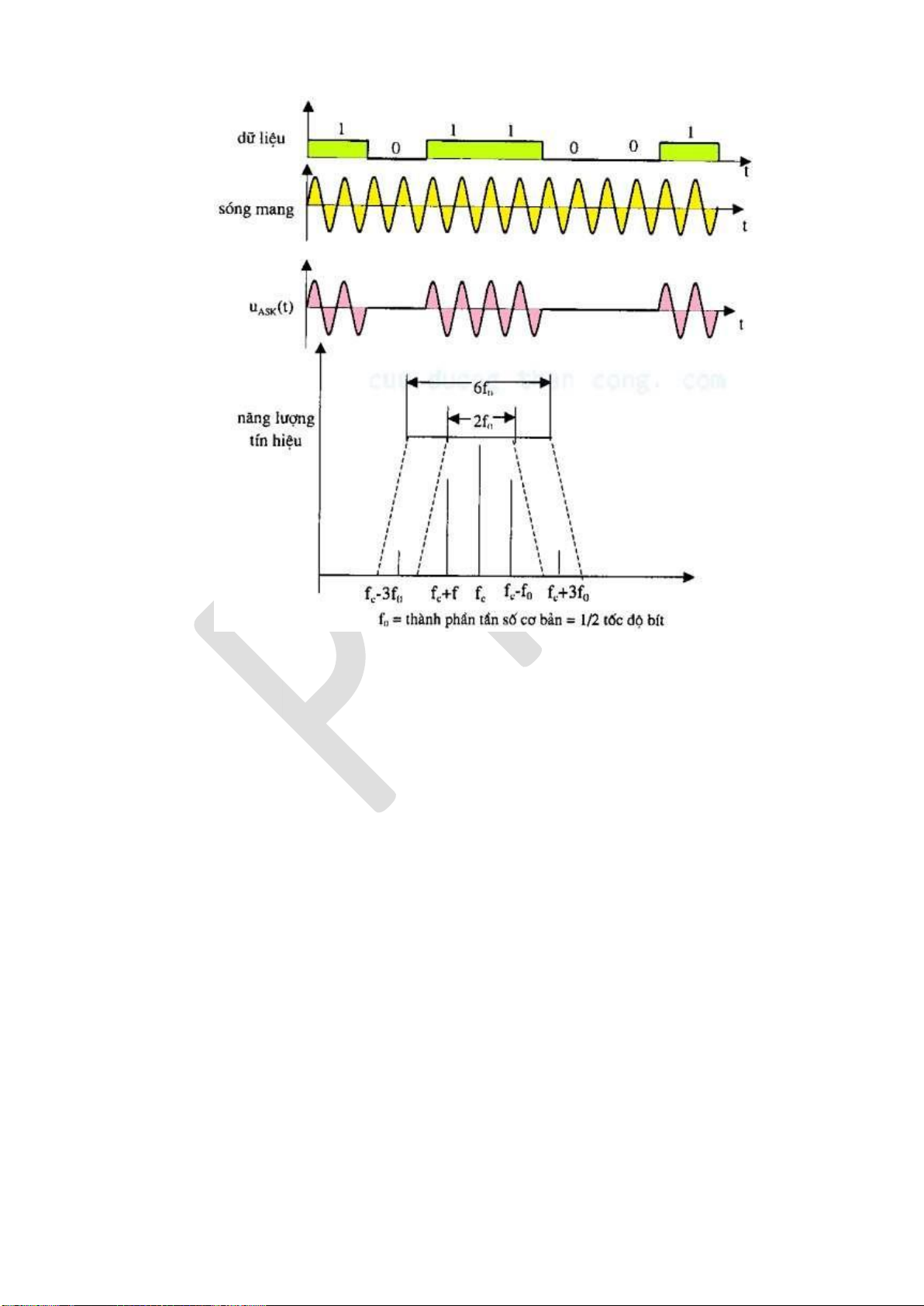
lOMoARcPSD| 36067889
0
hình 5.31.
Băng thông càng lớn thì tín hiệu thu càng trung thực. Tuy nhiên, hiệu quả hoạt ộng
có thể ạt ược nếu băng thông của kênh ủ chỗ ể cho thành phần tần số cơ bản của dòng
dữ liệu 101010... vì băng thông yêu cầu trong các dòng dữ liệu có thứ tự khác ều nhỏ
hơn. Gọi
0
là tần số cơ bản của tín hiệu dữ liệu theo tuần tự 101010...
0
bằng nửa tốc
ộ bit (bit/s), suy ra băng thông tối thiểu của ASK bằng với tốc ộ bit tính sang ơn vị Hz,
2
0
hoặc ể thu ược thành phần hài bậc 3 thì phảỉ gấp ba lần tốc ộ bit tính sang Hz, 6
0
.
Từ hình 5.31 có thể thấy rằng ối với ASK tín hiệu sóng mang hiện diện trong tín
hiệu thu ngay cả khi không có tín hiệu thồng tin
0
, 3
0
,... trong ó. Từ công thức Nyquist,
suy ra với tín hiệu nhị phân thì tốc ộ số liệu tối a ạt ược bằng hai lần băng thông. Vì thế,
Hình 5.31: D
ạng sóng và băng thông
Chúng ta th
ấ
y tín hi
ệ
u
ASK tương ương vớ
i tín hi
ệ
u s
ố
li
ệ
u ngu
ồ
n chuy
ể
n d
ị
ch
sang d
ạ
ng t
ầ
n s
ố
c
ủ
a sóng mang, bên c
ạ
nh
ó còn có hai thành phầ
n t
ầ
n s
ố
cơ bả
n
(
(
0
)
và
(
+
0
)
)
và hai thành ph
ầ
n hài b
ậ
c cao (
(
3
0
)
và
(
+3
)
)
.
Tất cả hình thành nên biên tần cơ bản, do ó bảng thông của ASK ược trình bày trên

lOMoARcPSD| 36067889
giả sử việc khôi phục lại tín hiệu số liệu ược thực hiện bởi mạch giải iều chế. Tại ây tín
hiệu thu lại ược nhân một lần nữa với sóng mang cùng dạng. Từ ó sinh ra hai phiên bản
của tín hiệu thu: thành phần bao quanh tần số 2
(
+
) và thành phần bao quanh tần
số bằng 0 (
-
). Cả hai phiên bản ều chứa thông tin trong hai biên tần, nhưng thành
phần sau cùng ược chọn bằng cách cho i qua bộ lọc thông thấp. Bộ lọc thông này ược
thiết kế ể chỉ cho các tần số từ 0 ến
0
hoặc nếu hài bậc 3 nhân ược thì từ 0 ến 3
0
. Do
vậy ở ầu ra của bộ lọc chính là phiên bản của tín hiệu dữ liệu truyền bị giới hạn băng
tần.
Mặc dù ASK là phương pháp thực hiện ơn giản, dễ bị ảnh hưởng bởi nhiễu, khó
ồng bộ và thường dùng trong cáp quang. Gần ây tất cả các hệ thống truyền dẫn ều ược
thực hiện bởi kỹ thuật số và ASK có cơ hội tham gia và thường ược dùng kết hợp với
PSK ể thiết kế các Modem tốc ộ cao.
5.4.2. Phương pháp iều chế khoá dịch tần số (FSK)
Nguyên lý hoạt ộng cơ bản ược minh họa trong hình 5.32.
Để tránh vấn ề thay ổi biên ộ, với FSK dùng hai tín hiệu sóng mang phân biệt tần
số nhưng có cùng biên ộ và cố inh, một cho bít nhị phân ‘0’, một cho bit nhị phân ‘1’.
Nguyên lý của FSK là hai giá trị nhị phân ược biểu diễn bởi hai tín hiệu tần số
khác nhau. Hoạt ộng iều chế tương ương với sự tổng hợp các ầu ra của hai bộ iều chế
ASK riêng biệt: một thực hiện trên sóng mang thứ nhất dùng phần gốc của tín hiệu dữ
liệu (mức cao) và một thực hiện sóng mang thứ hai dùng phẫn bù của tín hiệu dữ liệu
(mức 0).
Về mặt toán học, có thể biểu diễn tín hiệu FSK như sau:
Hai sóng mang có tần số riêng
1
và
2
, biên ộ không ổi biểu diễn dưới dạng biểu
thức iện áp.
1
() = cos
1
; (
1
: /)
2
() = cos
2
; (
2
: /)
Một tín hiệu số mang tin tuần hoàn ơn cực với biên ộ không ổi và tần số cơ bản
0
ược khai triển theo chuỗi fourier như sau:
() = 1/2 + 2/(
0
1/3 3
0
+ 1/5 5
0
() = cos
1
.
() + cos
1
.
() (5.108)
Trong ó
() là phần bù của tín hiệu dữ liệu gốc
().
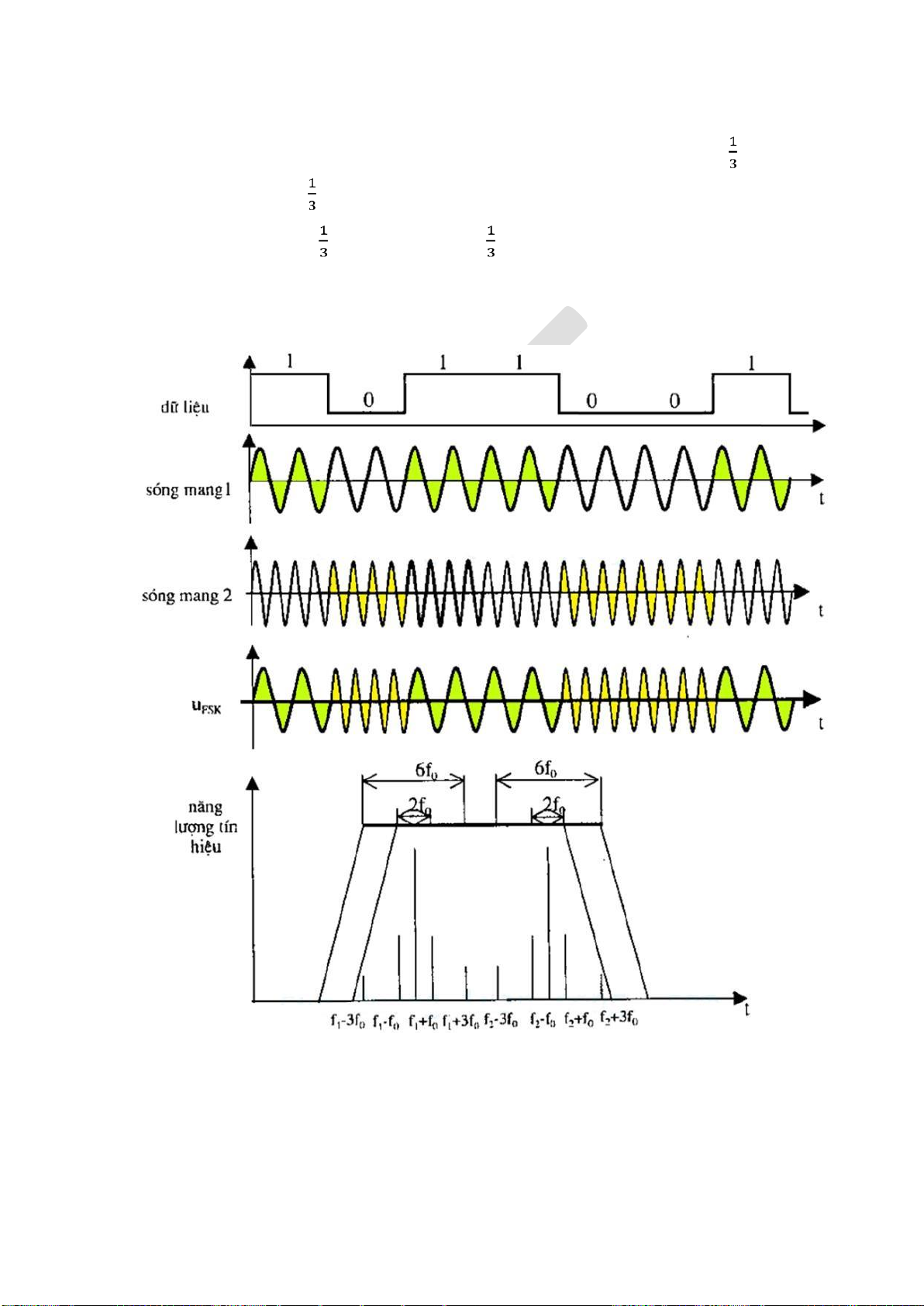
lOMoARcPSD|36067889
Do ó:
() = 1/2 cos
1
+ 1/[cos(
1
0
) + cos(
1
+
0
) cos(
1
3
0
) cos(
1
+ 3
0
) +. . . ] + 1/2 cos
2
+ 1/[cos(
2
0
) +
cos(
2
+
0
) cos(
2
3
0
) cos(
2
+ 3
0
) +. . . ] (5.109) Có thể suy
ra băng thông của FSK một cách ơn giản là tổng hợp hai sóng mang
Hình 5.32: Tín hiệu iều chế FSK và băng thông
Như ã ề cập ở phần trước, tín hiệu có tần số cao nhất ược tạo ra từ dãy bit 1011001...
với FSK vì tín hiệu nhị phân 0 và 1 iều chế lên các sóng mang riêng rẽ, nên băng thông
tối thiểu cho mỗi sóng mang bằng một nửa tốc ộ bít, nghĩa là thành phần tần số cơ bản
iề
u ch
ế
ASK riêng bi
ệ
t
ở
t
ầ
n s
ố
góc
1
và
2
.
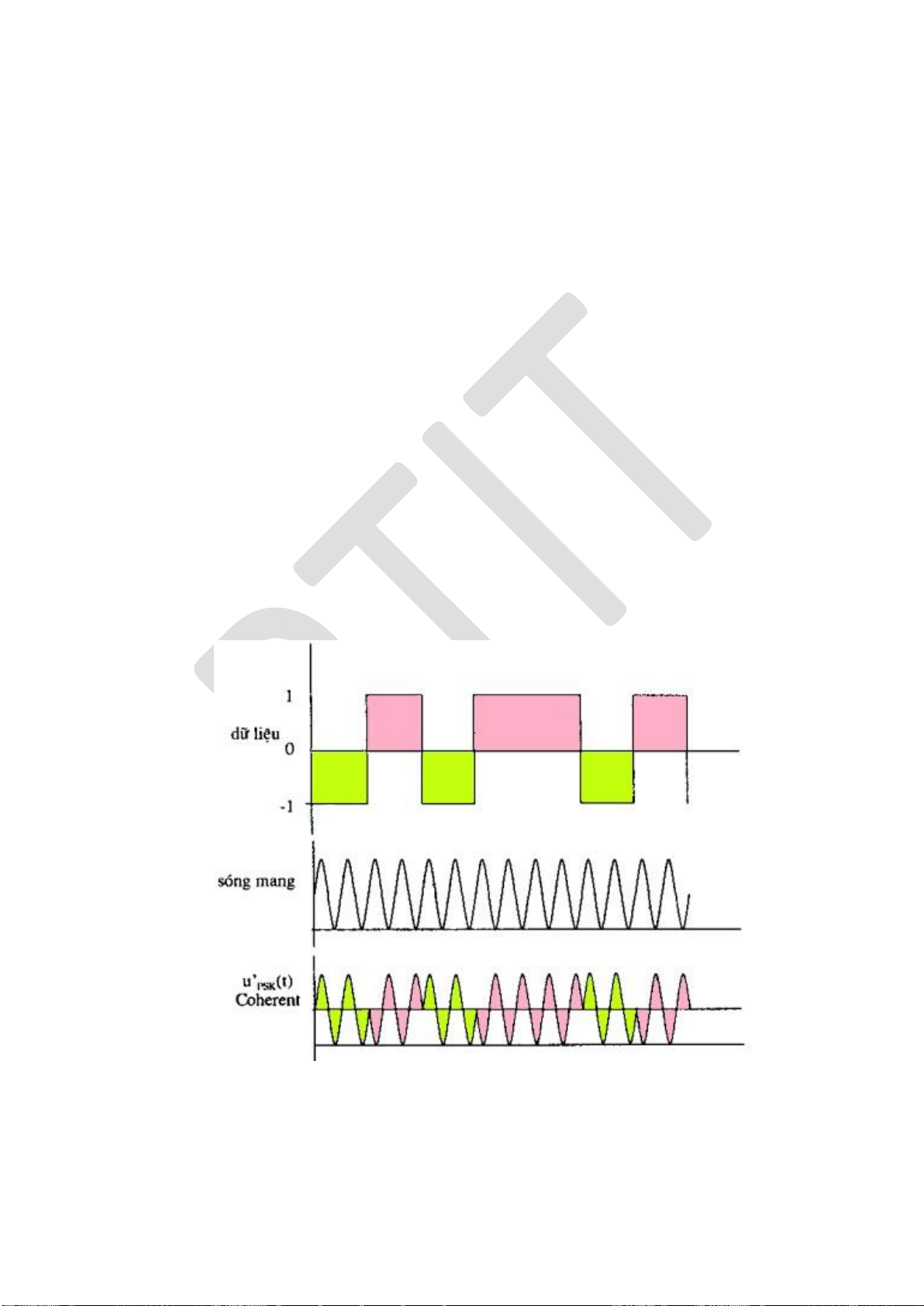
lOMoARcPSD|36067889
lớn nhất cho mỗi sóng mang
0
bằng một nửa so với ASK. Do ó nếu giả sử chỉ thư ược
thành phần tần số cơ bản thì băng thồng tổng cộng bằng 4
0
cộng với khoảng dịch tần
. Tuy nhiên vì
0
bằng một nửa so với ASK nôn băng thông tổng bằng với băng thông
tổng cho ASK cộng với khoảng dịch tần. Tương tự nếu cặp hài bậc 3 ược thu thì băng
thông bằng 6
0
cộng với khoảng dịch tần.
Hình 5.33: Tín hiệu 2-PSK
Kỹ thuật
FSK
có tỷ suất lỗi thấp hơn ASK, thường dùng trong truyền số liệu qua
ường iện thoại (tần số thấp), hoặc trong mạng
không dây (tần số
cao).
5.4.3.
Phương pháp iề
u ch
ế
khoá d
ị
ch pha (PSK)
Nguyê
n lý của PSK là tần số và biên ộ của sóng mang ược giữ không ổi trong
khi pha của nó ược dịch theo mỗi
bit
của dòng dữ liệu truyền.
Xét loại PSK thứ nhất dùng hai tín hiệu sóng mang cố ịnh ại diện cho
bit 0 và 1,
hai sóng mang khác pha nhau 180°. Vì tín hi
ệ
u này ch
ỉ
là ngh
ịch ả
o c
ủ
a tín hi
ệ
u kia
nên lo
ại này ượ
c g
ọ
i là k
ế
t h
ợ
p pha
PSK còn ượ
c g
ọ
i là 2-PSK.
Ở
ây, tín hiệ
u b
ả
ng g
ố
c
()
là xung NRZ
lưỡ
ng c
ự
c nh
ậ
n
=2
giá trị như ở
hình 5.33
, nên dạng sóng ã iều chế có dạng giống như ASK ảo pha, một
symbol
của
tín hiệu iều chế mang thông tin của 1
bit.
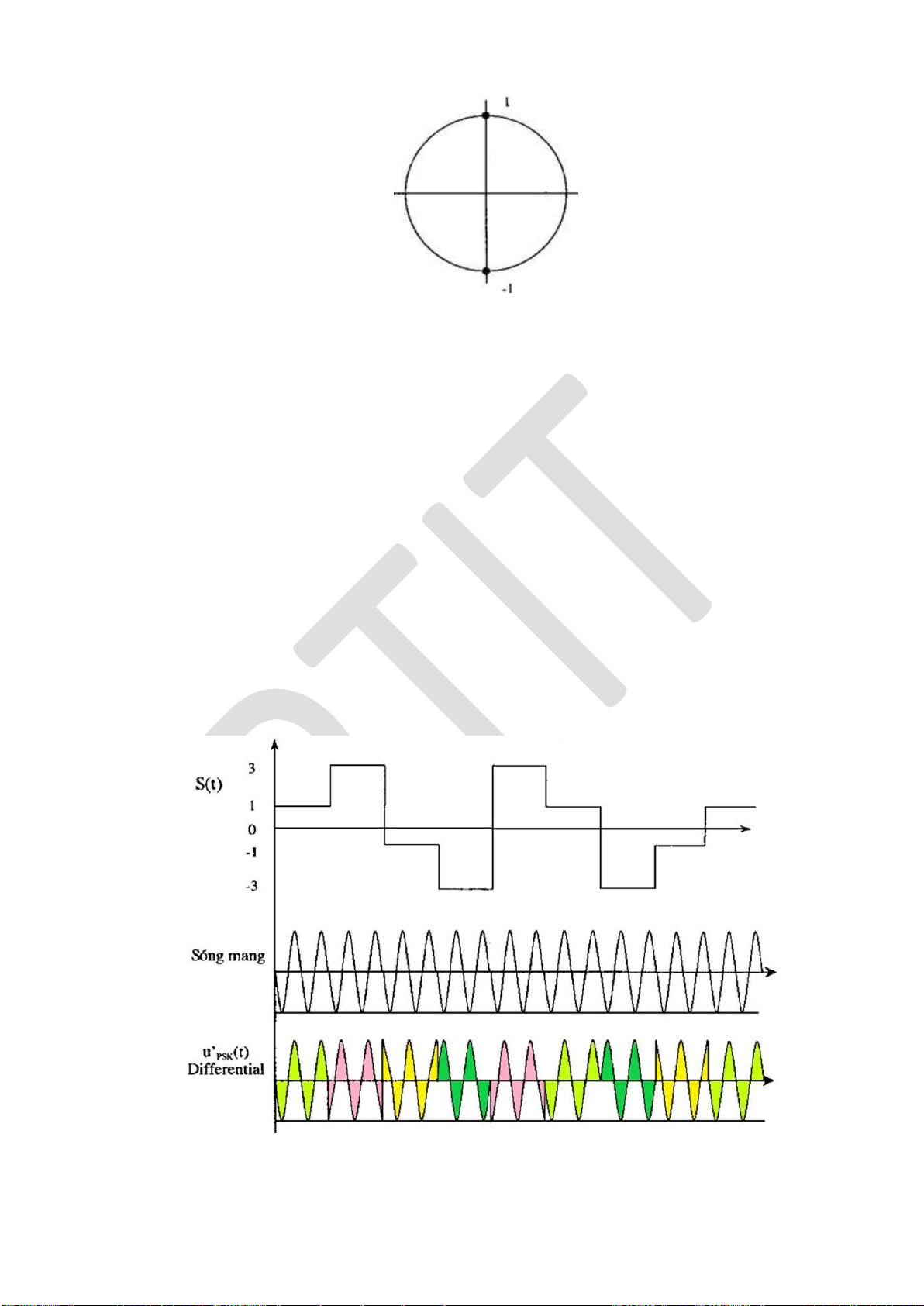
lOMoARcPSD|36067889
Hình 5.35: Tín hiệu 4-PSK
Hình 5.34: Sơ ồ pha 2
PSK
-
Điều bất tiện của loại này là tại máy thu òi hỏi phải có sóng mang tham chiếu ể
so pha với tín hiệu thu, do ó cần thực hiện ồng bộ pha
giữa máy thu và máy phát. Kết
quả là dẫn ến mạch giải iều chế phức tạp hơn.
Lo
ạ
i PSK th
ứ
hai ta xét t
ớ
i là PSK vi phâ
n còn ượ
c g
ọ
i là 4-PSK. Tín hi
ệu băng
g
ố
c là m
ộ
t xung NRZ
lưỡ
ng c
ự
c nh
ậ
n n = 4 giá tr
ị
, thì m
ộ
t d
ạng sóng ã iề
u ch
ế
như
hình 5.35.
V
ớ
i lo
ạ
i này s
ự
d
ị
ch pha x
ả
y ra t
ạ
i m
ỗ
i bit không c
ầ
n quan tâm t
ớ
i chu
ỗ
i bit 0
hay bit
1
đang đượ
c truy
ề
n. M
ộ
t s
ự
d
ịch pha 90° tương ứ
ng v
ớ
i tín hi
ệ
u hi
ệ
n hành
ch
ỉ
đị
nh 0 là bít k
ế
ti
ế
p trong khi s
ự
d
ị
ch pha 270° ch
ỉ
bit
1
. Như vậ
y m
ạ
ch gi
ải điề
u
ch
ế
ch
ỉ
c
ầ
n
xác định độ
l
ớ
n c
ủ
a s
ự
d
ị
ch pha thay vì ph
ải xác đị
nh giá tr
ị
tuy
ệt đố
i
c
ủ
a t
ừ
ng pha.
Ở
m
ạch điề
u ch
ế
ch
ỉ
khi nào thay đổ
i tr
ạ
ng thái c
ủ
a d
ữ
li
ệ
u m
ới đổ
i
pha c
ủ
a sóng mang.
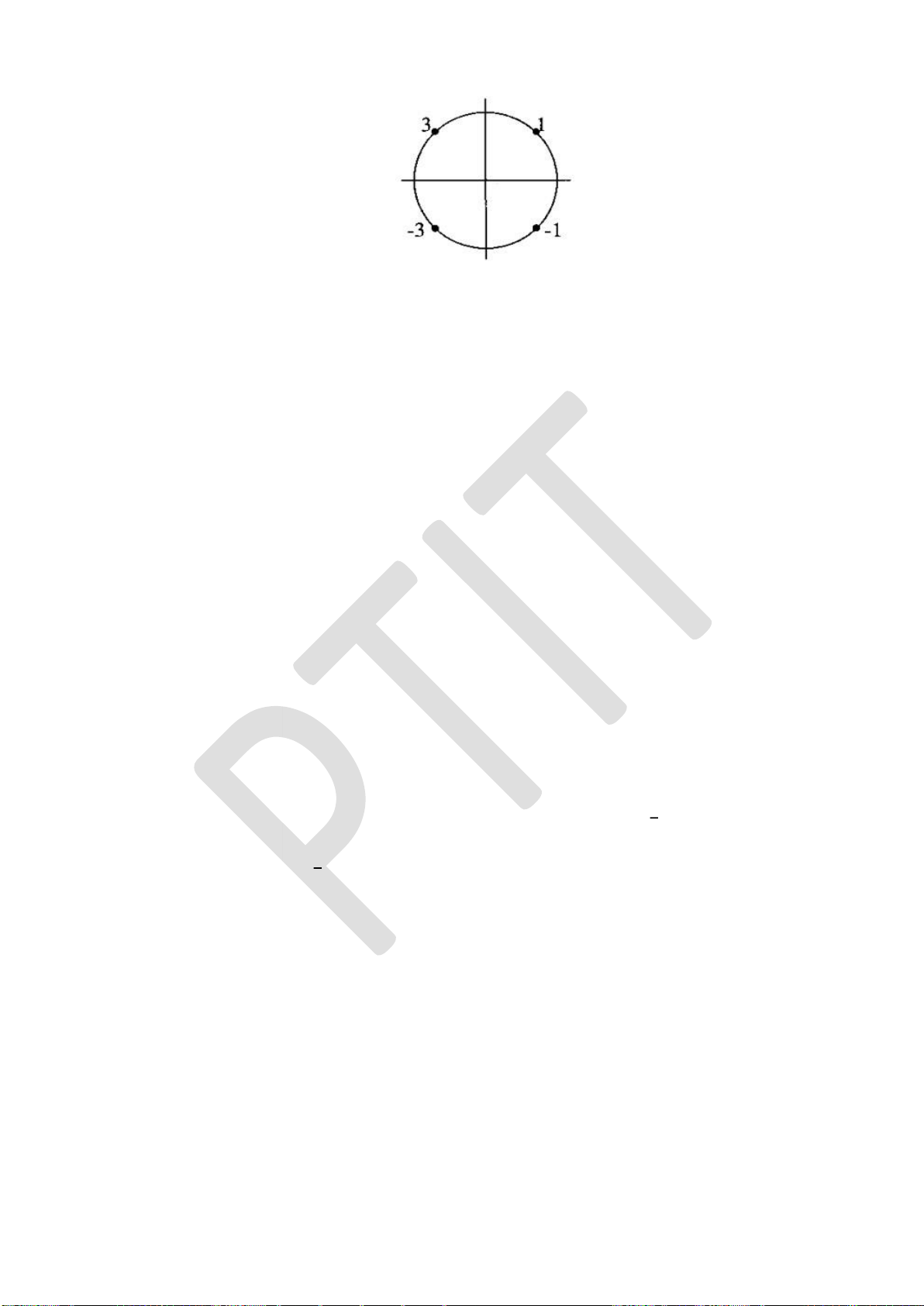
lOMoARcPSD|36067889
1
3
1
3
Hình 5.36: Sơ ồ pha 4-PSK
Hình 5.36 biểu diễn sơ ồ pha tín hiệu 4-PSK. Giống như 2-PSK, nếu tín hiệu băng
gốc không bị giới hạn băng thông, thì tín hiệu 4-PSK cũng dịch chuyển tức thời trên
vòng tròn ơn vị.
Về mặt toán học, có thể xác ịnh bãng thông PSK. Ở ây trình bày tín hiệu số nhị phân
dưới dạng lưỡng cực vì mức tín hiệu âm sẽ là kết quả ổi pha 180° của sóng mang.
Sóng mang có tần số riêng
và biên ộ không ổi biểu diền dưới dạng biểu thức iện
áp:
() = cos
; (
: /)
Một tín hiệu số mang tin tuần hoàn ơn cực với biên ộ tổng hợp và tần số cơ bản
0
ược khai triển toán học theo chuỗi fourier như sau:
() = 4/(
0
3
0
+ 1/5 5
0
(5.110)
Suy ra:
() = 4/(
.
0
. 3
0
= 2/[cos(
0
) + cos(
0
+
0
) cos(
3
0
)
cos(
+ 3
0
) +. . . ] (5.111)
Từ công thức trên ta thấy phổ tần số PSK giống như ASK chỉ khác là không có
thành phần sóng mang. Do ó, băng thông của tín hiệu PSK sẽ ược thể hiện như ở hình
5.37. Giả sử chỉ thành phần tần số cơ bản của dãy 101100... ược nhận thì băng thông tồi
thiểu bằng 2
0
, bằng giá trị tốc ộ bit. Tuy nhiên, do vắng mặt thành phần sóng mang
nên có nhiều năng lượng trong biên tần ơn (data), iều ó giúp PSK chống nhiễu tốt hơn
ASK hay FSK. Giới hạn băng của tín hiệu từ
ến
+
0
, có nghĩa là băng thông bằng
0
và ạt ược tốc ộ Nyquist. Hầu hết năng lượng nhận ược thuộc về tín hiệu mang thông
tin,
+
0
(do không có
).
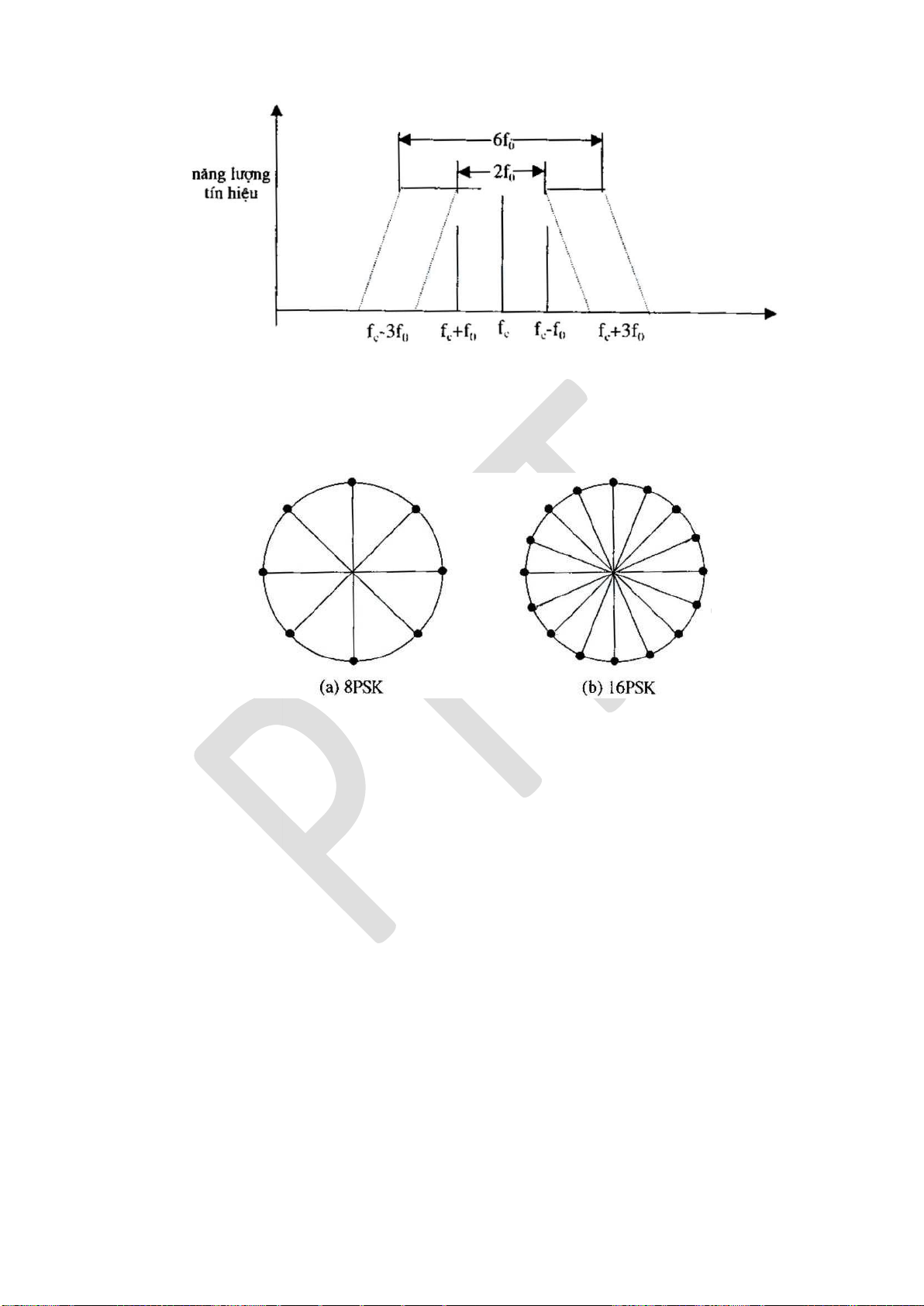
lOMoARcPSD| 36067889
Ngày nay các thiết bị truyền dẫn và chuyển mạch kỹ thuật số ã và ang ược dùng
Hình 5.37: Băng thông PSK
Bên cạch 2
-
PSK và 4-PSK,
còn có PSK nhiều pha. Hình 5.38 ưa ra các sơ ồ
pha
ối với 8
-
PSK và 16-PSK.
Hình 5.38
:
PSK nhiều pha
trong mạng truyền tin
hiện ại. Kết quả ứng dụng ó, tạo iều kiện ạt ược tốc ộ
bit
vượt xa tốc ộ có ược theo các phương pháp iều chế cơ bản kể trên nhờ sử dụng các
phương pháp iều chế phức tạp hơn. Trong các phương pháp nhằm gia tăng tốc ộ, tồn
tại hai khuynh hướng: hoặc nhiều mức tín hiệu hoặc kết hợp
các phương pháp iều chế
cơ bản, ặc biệt là ASK và PSK. Loại iều chế kết hợp giữa ASK và PSK gọi là biên ộ
cầu phương QAM.

lOMoARcPSD|36067889
5.4.4. Điều chế biên ộ cầu phương (QAM)
5.4.4.1. Biểu diễn tín hiệu cầu phương
Trước khi mô tả iều chế biên ộ cầu phương, hãy xét biểu diễn cầu phương của các
tín hiệu. Một tín hiệu hình sin: cos(
0
+ ) có pha xác ịnh ược trình bày bằng ịnh lý
cộng của hàm lượng giác như sau:
cos(
0
+ ) = cos . cos
0
sin . sin
0
Trong biểu thức này, cos
0
và sin
0
là các tín hiệu hàm sin có hiệu số pha là
90° và cắt nhau vuông góc trong biểu ồ pha. Cos và tương ứng sin là các hệ số của
chúng có thể biểu diễn tất cả các iểm tín hiệu của sóng iều chế nhiều mức bằng cách
chọn thích hợp các hệ số này.
5.4.4.2. Biểu diễn iều pha QAM
Xét biểu diễn cầu phương của 4-PSK. 4-PSK có thể ược coi là trường hợp riêng
của iều chế QAM trong ó sự thay ổi về biên ộ của sóng mang bằng 0. Sóng 4-PSK ()
có thể ược biểu diễn là tổng của hai tín hiệu hình sin vuông góc với nhau như sau:
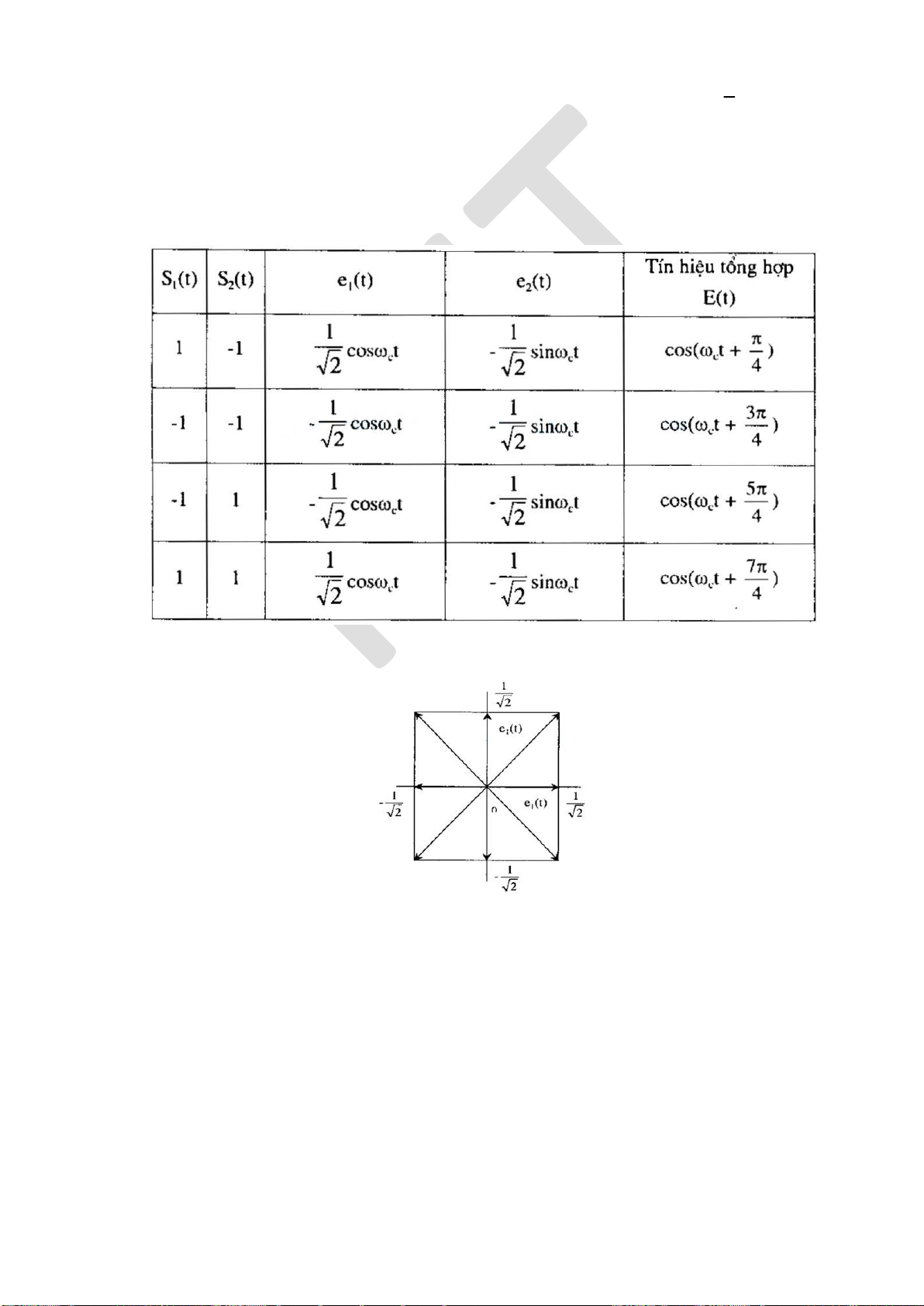
lOMoARcPSD|36067889
Hình 5.39: Sóng 4-PSK bao gồm các tín hiệu trực giao
Nếu
1
() và
2
() là các sóng iều biên có hai giá trị thì có thể kết hợp chúng ể tạo
thành các sóng iều chế có 4 iểm tín hiệu. Vì quỹ tích véctơ của các tín hiệu bị giới hạn
băng thông không dịch chuyển trên ường tròn ơn vị nên các sóng thu ược khác với tín
hiệu 4-PSK chuẩn, Tuy nhiên vì chúng có cùng một biên ộ cố ịnh tại thời iểm tách sóng
nên có thể coi chúng như là PSK.
Tín hiệu nhận ược bằng cách kết hợp hai sóng iều biên (AM) vuông góc với nhau
ược gọi là sóng iều chế biên ộ cẩu phương (QAM). Sóng QAM có hai ưu iểm là: nó có
(
)
=
1
(
)
+
2
(
)
={
1
(
)
.cos
0
+
2
(
)
.sin
0
}/
2
B
ả
ng 5.1 cho th
ấ
y hai tín hi
ệ
u
băng
g
ố
c
1
(
)
,
2
(
)
và các tín hiệu tổng tạo thành
từ chúng.
Bảng 5.1: Bảng biểu diễn trực giao 4
-
PSK
Những tín hiệu
này ược mồ tả t
rong hình 5.39.
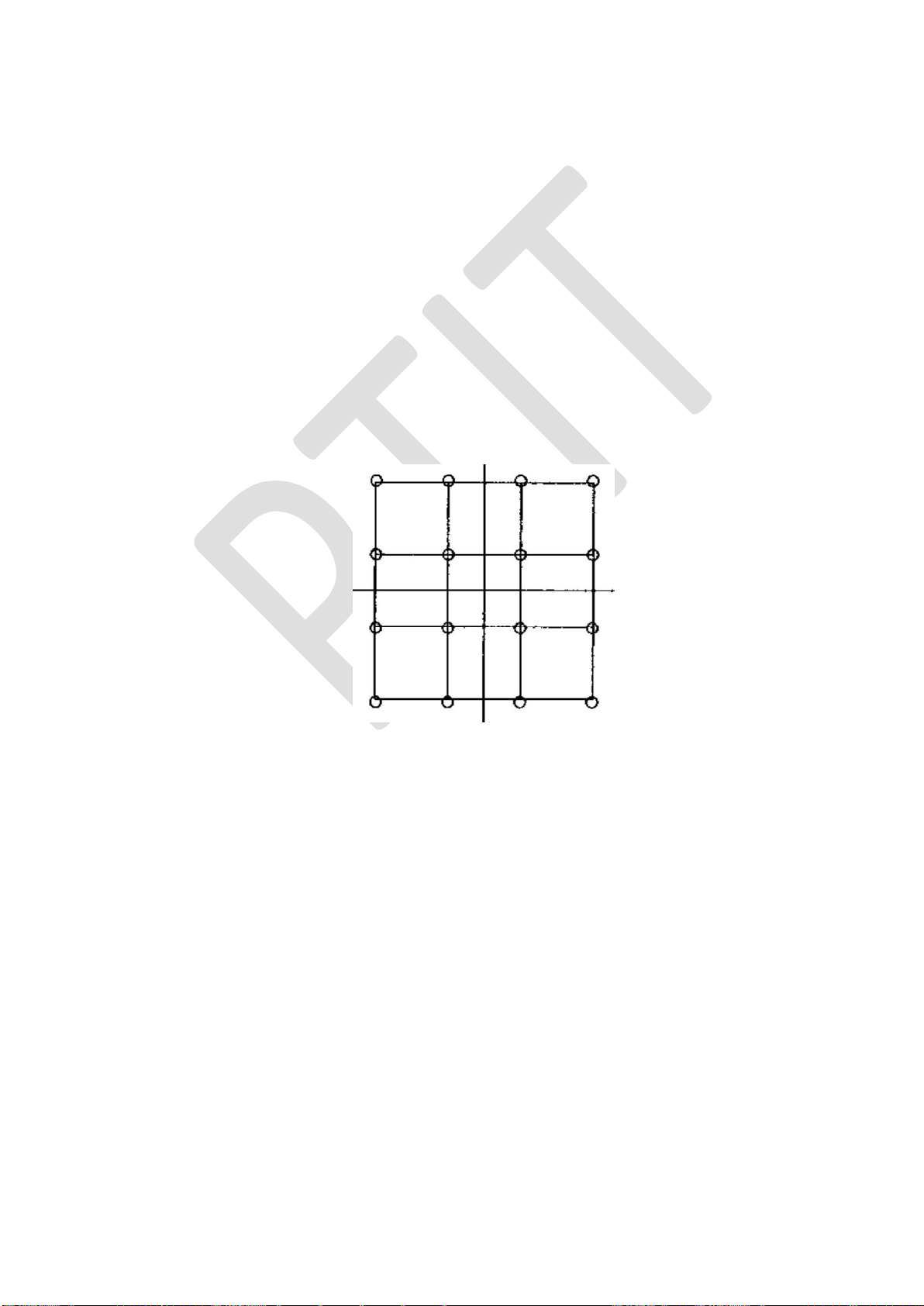
lOMoARcPSD|36067889
thể biển diễn ược từ hai tín hiệu iều chế biên ộ cơ sở và có thể chọn một iểm bất kỳ trên
biểu ổ không gian tín hiệu như là một iểm tín hiệu.
5.4.4.3. QAM nhiều trạng thái
QAM cho phép sắp xếp ngẫu nhiên các iểm tín hiệu cũng như dễ dàng thực hiện
iều chế và giải iều chế tín hiệu nhờ tính chất cầu phương của các tín hiệu. Ngoài ra, cách
sắp xếp hình chữ nhật thường ược sử dụng khi tham số C/N òi hỏi khá cao. Hình 5.40
cho thấy cách sắp xếp các iểm tín hiệu ối với iều chế biên ộ cầu phương 16 mức (16-
QAM). QAM nhiều trạng thái có thể ược tạo thành bởi hai tín hiệu iều chế biên ộ trực
giao có mức, vì vậy có 2
iểm tín hiệu. Khi = 2 thì QAM giống hệt cách sắp xếp tín
hiệu của 4-PSK. Khi = 4 thì iều chế là 16-QAM, khi = 8 hoặc 16 thì iều chế tương
ứng là 64-QAM hoặc 256-QAM.
Hình 5.40: Biểu ồ không gian tín hiệu 16-QAM
5.5. TỔNG KẾT CHƯƠNG
Chương 5 ã trình bày cụ thể về khái niệm iều chế, cách biểu diễn tín hiệu. Trên cơ
sở ó ã trình bày cụ thể về iều chế cho tín hiệu tương tự, bao gồm iều chế tín hiệu liên
tục và iều chế xung. Phần cuối của chương ã phân tích về iều chế tín hiệu số, bao gồm:
Điều chế khóa dịch biên ộ (ASK), Điều chế khóa dịch tần số (FSK), Điều chế khóa dịch
pha (PSK) và Điều chế biên ộ cầu phương (QAM).
Câu hỏi/bài tập chương 5
1- Nêu khái niệm và phân loại các phương pháp iều chế tín hiệu?
2- Trình bày tóm tắt các cách biểu diễn các tín hiệu có dải tần hữu hạn?
3- Trình bày phương thức iều chế và giải iều chế ASK?
4- Trình bày phương thức iều chế và giải iều chế FSK?
5- Trình bày phương thức iều chế và giải iều chế PSK?

lOMoARcPSD| 36067889
6- Trình bày phương thức iều chế và giải iều chế QAM?
7- Vẽ và giải thích sơ ồ iều chế và giải iều chế BPSK? Cho chuỗi tín hiệu số 01101…,
tốc ộ bit là 2 Mbps, ược iều chế bằng phương pháp BPSK. Biên ộ 5V.
Tần số sóng mang 8MHz. Pha ối với bit ‘1’ là 180
0
, pha ối với bit ‘0’ là 0
0
. a) Vẽ
tín hiệu BPSK?
b) Tính tốc ộ Baud?
c) Vẽ giản ồ trạng thái pha của tín hiệu BPSK?
8- Vẽ và giải thích sơ ồ iều chế và giải iều chế QPSK? Cho một chuỗi tín hiệu số
0110101100…, tốc ộ bit là 10 Gbps, ược iều chế bằng phương pháp 4-PSK (QPSK).
Biết sóng mang có biên ộ 5V, tần số 20 GHz và pha ược biểu diễn như sau: ‘00’ pha
0
0
; ‘01’ pha 90
0
; ‘10’ pha 180
0
; ‘11’ pha 270
0
. a) Vẽ tín hiệu QPSK.
b) Tính tốc ộ Baud.
c) Vẽ giản ồ trạng thái pha của tín hiệu QPSK.
9- Cho tín hiệu số 01010, tốc ộ bít là 5 bit/s, ược iều chế bằng phương pháp ASK.
Với tần số sóng mang là f
C
bằng 20Hz, biên ộ ối với bit “1” là 5V, biên ộ ối với bit
“0” là 2V và pha ban ầu của sóng mang là 180
0
.
a- Vẽ tín hiệu ASK b- Tín hiệu ASK có phải là tín hiệu iều hòa hay
không? Giải thích?
c- Tính tốc ộ baud.
10- Cho tín hiệu số 01101, tốc ộ bít là 5 bit/s, ược iều chế bằng phương pháp FSK.
Biên ộ sóng mang là 5V, tần số ối với bit “1” là 20 Hz, tần số ối với bit “0” là 10
kHz và pha ban ầu của sóng mang là 180
0
.
a- Vẽ tín hiệu FSK b- Tín hiệu FSK có phải là tín hiệu iều hòa hay
không?Giải thích. c- Tính tốc ộ baud.

lOMoARcPSD|36067889
- CHƯƠNG VI -
NHIỄU VÀ BỘ THU TỐI ƯU
Trong hệ thống truyền tin, chất lượng tin tức nhận ược phụ thuộc rất nhiều vào
chất lượng của kênh truyền tin và cấu trúc máy thu. Kênh truyền tin có thể hiểu là một
môi trường ể truyền lan tín hiệu mang tin ồng thời cũng chịu sự tác ộng của nhiễu. Nhiễu
là loại tín hiệu không mong muốn. Nó tác ộng vào tín hiệu mang tin trên kênh truyền
làm cho thông tin sai lệch và mất chính xác. Đối với các bộ thu việc chọn ược một cấu
trúc thu tối ưu là rất quan trọng. Do ó, nội dung của chương này sẽ ề cập ến một số vấn
ề cơ bản về nhiễu và bộ thu tối ưu.
6.1. NHIỄU
6.1.1. Định nghĩa và phân loại nhiễu
Định nghĩa: Nhiễu là các tín hiệu ngẫu nhiên hoặc xác ịnh bất kỳ không mong muốn,
gây nhiễu loạn ối với tín hiệu mong muốn cần ược khôi phục chính xác trong một hệ
thống. Nói cách khác, một tín hiệu bất kỳ gây nhiễu loạn thường là sự dao ộng ngẫu
nhiên của iện áp hoặc dòng iện có xu hướng che khuất các tín hiệu mong muốn ược gọi
là nhiễu.
Phân loại nhiễu: Nhiễu ược phát sinh từ nhiều nguồn khác nhau và có thể ược phân
loại thành 2 loại chính: Thứ nhất là do con người tạo ra và thứ hai là tự nhiên xảy ra.
Các loại nhiễu do con người tạo ra trên thực tế có thể phát sinh từ bất kỳ một
phần nào của thiết bị iện tử hoặc của thiết bị iện tử và bao gồm những vấn ề như thu
nhận iện từ của các tín hiệu bức xạ khác, bộ lọc cấp nguồn không phù hợp…. Các loại
nhiễu do con người tạo ra ều có một ặc tính chung là ảnh hưởng của chúng có thể ược
loại bỏ hoặc ược giảm thiểu ở mức tối thiểu nhờ thiết kế và thực thi kỹ thuật cẩn thận.
Nhiễu gây ra bởi nhiễu tự nhiên không thể kiểm soát ược một cách trực tiếp và các
ặc tính của chúng có thể ược mô tả tốt nhất bằng thống kê. Nhiễu tự nhiên ến từ chuyển
ộng nhiệt ngẫu nhiên của các iện tử, sự hấp thụ khí quyển và các nguồn vũ trụ.
6.1.2. Các tham số ặc trưng mô tả nhiễu
Vì nhiễu chủ yếu là ngẫu nhiên trong tự nhiên, ược mô tả tốt nhất thông qua các ặc
tính thống kê của nó. Trong phần này sẽ trình bày và phân tích về các tham số chính và
các quan hệ lẫn nhau ối với mô tả nhiễu. Mà không i sâu vào chi tiết của các biến ngẫu
nhiên và các quy trình ngẫu nhiên, các biểu thức ược ưa ra ể mô tả nhiễu thông qua mật
ộ phổ công suất (miền tần số) hoặc hàm tự tương quan (miền thời gian). Phần này ưa ra
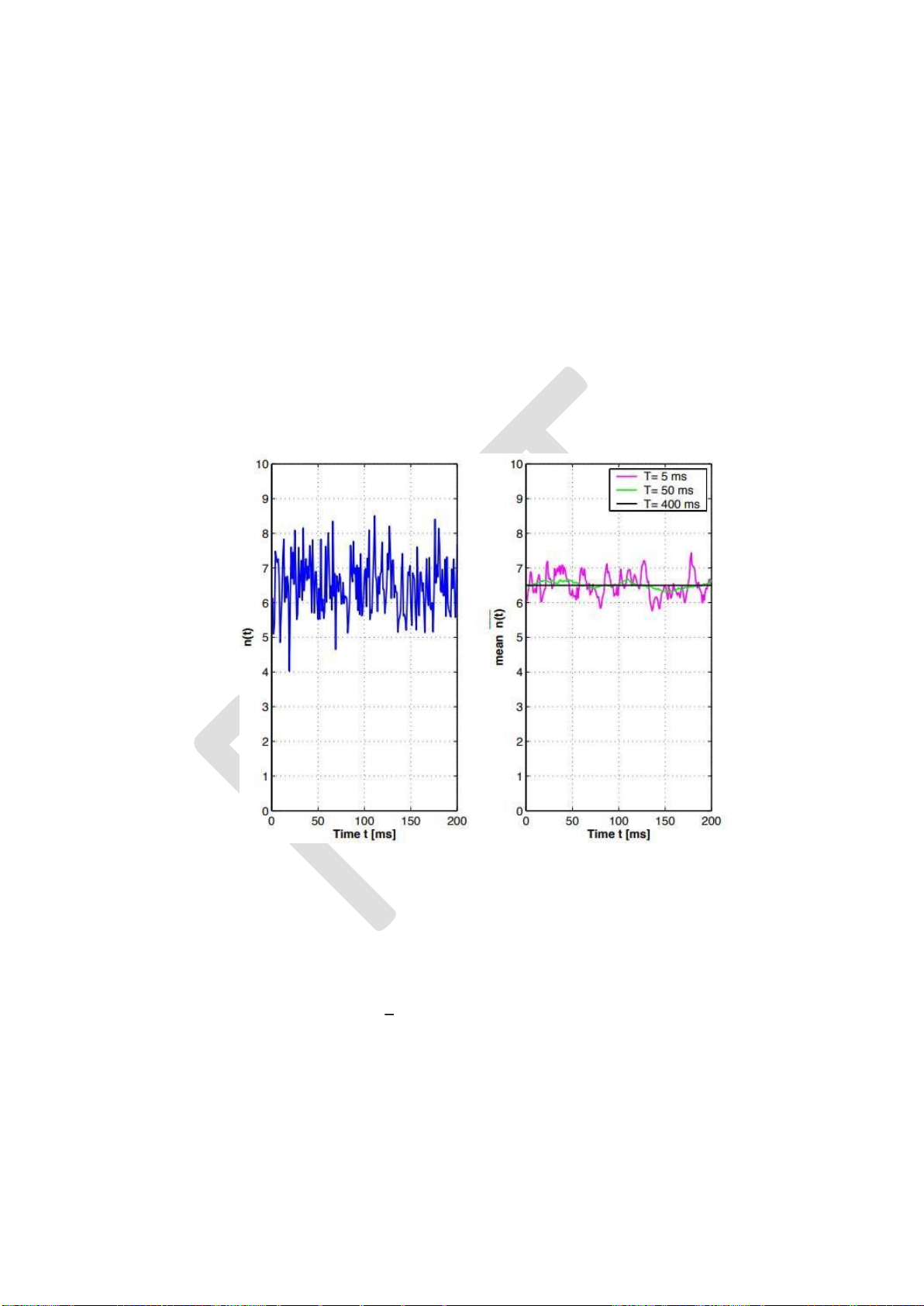
lOMoARcPSD|36067889
một ánh giá sơ lược về một số nguyên tắc cơ bản, có thể tìm thấy mô tả ầy ủ trong tài
liệu [Papoulis, 1984, Proakis, 1989]. Cần lưu ý rằng mô tả là hợp lệ cho cả tín hiệu ngẫu
nhiên và xác ịnh.
6.1.2.1. Biểu diễn nhiễu trung bình theo thời gian
Ở dạng trung bình của bất kỳ tín hiệu nào, dù là ngẫu nhiên hay xác ịnh, chúng ta tìm
thấy các tham số cho biết iều gì ó về tín hiệu. Nhưng nhiều thông tin chi tiết về tín hiệu
bị mất trong quá trình này. Tuy nhiên, trong trường hợp nhiễu ngẫu nhiên, ây là con số
hữu ích duy nhất.
Giá trị trung bình của () ược ký hiệu là ( hoặc {()} và bằng: ( = {()}
= lim
1
/2
/2
() (6.1)
trong ó: (
ược gọi là DC hoặc giá trị trung bình của (). Thực tế ể tính giá trị trung
bình, phải chọn thời gian trung bình ủ lớn ể làm bằng phẳng các biến ộng của ()
một cách thỏa áng. Hình 6.1 cho thấy giá trị trung bình ( ược tính bằng cách trượt
Gi
ả
s
ử
()
là iệ
n áp ho
ặc dòng iệ
n nhi
ễ
u ng
ẫ
u nhiên. D
ạng sóng iển hình ượ
c
minh h
ọ
a trong hình 6.1. Bây gi
ờ
chúng ta xác ịnh các ại lượ
ng th
ố
ng kê sau c
ủ
a
()
:
Hình 6.1: D
ạ
ng sóng nhi
ễ
u ng
ẫ
u nhiên và giá tr
ị
trung bình c
ủ
a nó
Giá tr
ị
trung bình

lOMoARcPSD|36067889
2
(
)
một cửa sổ trung tâm tại và kéo dài từ /2 ến + /2 trên (). Chúng ta thấy
rằng ối với thời gian trung bình bé = 5 vẫn có một lượng dao ộng áng kể trong khi
= 400 cửa sổ bao phủ toàn bộ thời gian tín hiệu kết quả là một giá trị trung bình
không ổi.
Giá trị bình phương- trung bình
() = { ()} = lim
/2
/2
|()|
2
(6.2)
Trị bình phương trung bình
) ược xác ịnh theo biểu thức (6.2) cho biết công
suất trung bình () theo thời gian của (). Căn bậc hai của
) ược gọi là giá trị căn
bậc hai bình phương trung bình (RMS) của (). Ưu iểm của ký hiệu RMS là các ơn vị
của giống với ().
6.1.2.2. Chuyển ổi Fourier
Định nghĩa của phép chuyển ổi Fourier [Stremler, 1982] ược ưa ra như sau:
(()} = ()
2
(6.3)
và chuyển ổi Fourier ngược:
(
1
{()} = ()
2
(6.4)
Nếu tín hiệu () là tín hiệu công suất, tức là tín hiệu có công suất hữu hạn nhưng
năng lượng vô hạn, tích phân trong (6.3) sẽ phân kỳ. Tuy nhiên, xét trong trường hợp
thực tế của một thời gian quan sát hữu hạn và giả sử rằng tín hiệu bằng 0 bên ngoài
khoảng thời gian này, là tương ương ể nhân tín hiệu với hàm cổng ơn vị (/).
Trong trường hợp này, chuyển ổi Fourier có thể ược viết là:
/2
2
(6.5)
() =
{()(/
/2
()
Lưu ý là phép nhân với hàm trong miền thời gian là tương ương với một tích chập
bởi một hàm trong miền tần số.
6.1.2.3. Các hàm tương quan
Sau ây, hai hàm thống kê ược giới thiệu ể sử dụng khảo sát sự giống nhau giữa các hàm
ngẫu nhiên.

lOMoARcPSD|36067889
Hàm tự tương quan
Hàm tự tương quan {
()( + )} =
() của tín hiệu () ược ịnh nghĩa là
[Stremler, 1982]:
{
()( + )} ( + ) (6.6)
trong ó:
() là liên hợp phức của (). Lưu ý rằng chỉ số phụ
ược thêm vào hàm tự
tương quan () ể biểu thị biến ngẫu nhiên hoặc hàm ược xem xét. Hàm tự tương quan
(6.6) thường ược sử dụng trong phân tích tín hiệu, nó ưa ra một phép o tương tự của tín
hiệu () với chính nó so với sự dịch chuyển thời gian tương ối bằng . Đối với các tín
hiệu thời gian thay ổi chậm, các giá trị tín hiệu không thay ổi nhanh chóng theo thời
gian sẽ dẫn ến một hàm tự tương quan phẳng
(). Mặt khác, các tín hiệu nhiễu có xu
hướng biến ộng nhanh làm phát sinh hàm tự tương quan với ỉnh nhọn tại = 0 (không
dịch chuyển thời gian) và nhanh chóng giảm xuống 0 khi tăng .
Như ví dụ ở hình 6.2 và 6.3 hiển thị các tín hiệu thời gian và các hàm tự tương
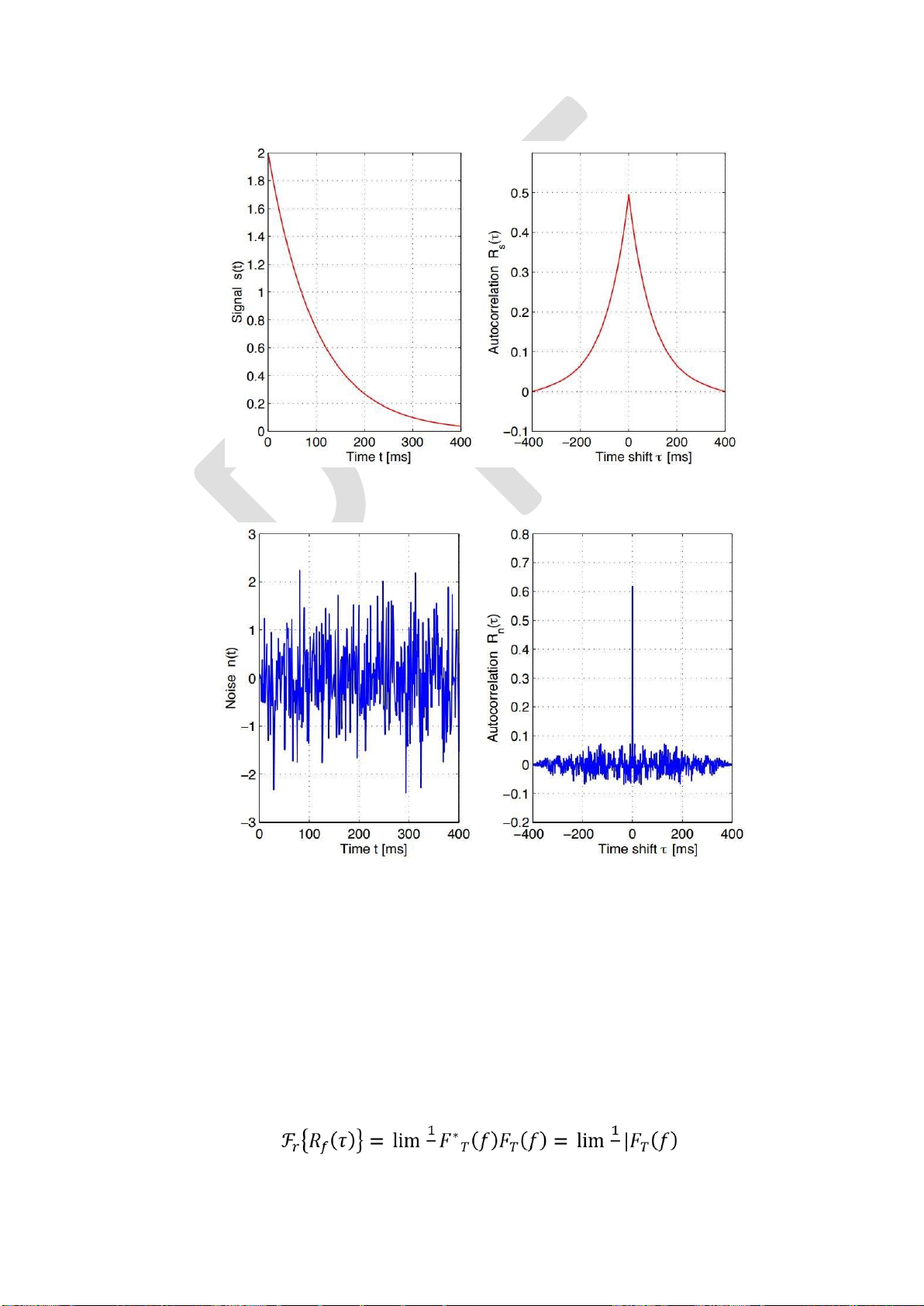
lOMoARcPSD|36067889
Hình 6.3: Tín hiệu thời gian và hàm tự tương quan của dạng sóng nhiễu ngẫu nhiên
Khi xử lý các biến ngẫu nhiên, hàm tự tương quan
() là một ại lượng thống kê mô
tả quá trình ngẫu nhiên. Lưu ý rằng khi ặt = 0 trong biểu thức (6.6) thu ược
(0) =
{
2
()} =
) là công suất trung bình của tín hiệu như ã thấy bằng cách so sánh với
biểu thức (6.2). Một lần nữa, lưu ý rằng ịnh nghĩa
() như ược cho bởi biểu thức (6.6)
là chỉ hợp lệ nếu quá trình ngẫu nhiên là cả dừng và ergodic.
Phép biến ổi Fourier ( ối với ) khi lấy cả hai vế của (6.6) [Proakis, 1989] sẽ bằng:
|
2
(6.7)
quan tương ứ
ng cho c
ả
tín hi
ệ
u nhi
ễ
u ng
ẫu nhiên và hàm mũ.
Hình 6.2: Tín hi
ệ
u th
ờ
i gian và hàm t
ự
tương quan củ
a d
ạ
ng sóng nhi
ễu hàm mũ

lOMoARcPSD|36067889
(
)
=
lim
1
(
)
/2
2
/
Do ó, chúng ta có kết luận quan trọng là tích phân tương quan dẫn ến
() tương ứng
với một phép nhân trong miền tần số. Hoặc nói cách khác là thay vì ánh giá tích phân
trong biểu thức (6.6), chúng ta có thể tính chuyển ổi Fourier của () theo biểu thức
(6.5), xác ịnh |
()|
2
và sử dụng phép biến ổi Fourier ngược ể lấy
(). Giới hạn
trong biểu thức (6.7) chủ yếu ề cập về thời gian quan sát hữu hạn, thực tế thì giới
hạn này có nghĩa là phải quan sát tín hiệu trong một khoảng thời gian hợp lý.
Hàm tương quan chéo
Một hàm liên quan chặt chẽ ến hàm tự tương quan, có thể ược sử dụng như một phép o
tương tự giữa hai tín hiệu khác nhau, ó là hàm tương quan chéo. Với hai dạng sóng ()
và (), hàm tương quan chéo {
()( + )} =
() ược ịnh nghĩa là:
{
()( + )} =
( + ) (6.8)
Tự tương quan ược coi là một trường hợp ặc biệt của tương quan chéo, vì có thể
thu ược bằng cách ặt () = () trong (6.8). Giải thích mối tương quan chéo giữa hai
tín hiệu là tương tự như tín hiệu tự tương quan, với ưu iểm là thông tin bổ sung chẳng
hạn như sự dịch chuyển thời gian giữa hai tín hiệu tương tự có thể ược giảm i.
Nói chung, khi các tín hiệu không tương quan ược thêm vào, công suất trung bình
của tổng bằng tổng các công suất trung bình của các tín hiệu.
Một ứng dụng hữu ích của các hàm tương quan là tách các tín hiệu bị che bởi nhiễu
cộng. Hình 6.4 cho thấy dạng sóng thời gian () cho kết quả khi nhiễu ngẫu nhiên ()
từ hình 6.3 ược thêm vào tín hiệu () của hình 6.2. Rõ ràng là dạng sóng tín hiệu bị
nằm trong một lượng nhiễu áng kể và sẽ rất khó ể tách () ra khỏi (). Tuy nhiên,
hàm tự tương quan
() có thể nhận ược từ quá trình tự tương quan của các tín hiệu
tổng
+
(). Việc tách các tín hiệu bị che bởi nhiễu cộng là một vấn ề chính khi xử lý
hệ thống truyền tin.
Hình 6.4: Tín hiệu thời gian và hàm tự tương quan của nhiễu cộng dạng sóng hàm mũ
6.1.2.4. Mật ộ phổ công suất
Xem xét việc xử lý các tín hiệu bị cắt ngắn, tức là các tín hiệu chỉ ược xét trong một
khoảng thời gian hữu hạn /2, /2]. Giả sử tín hiệu bằng 0 khi ở ngoài khoảng thời
gian này và việc biểu diễn toán học là không phức tạp như ối với các tín hiệu thời gian
vô hạn. Định lý Parseval cho các tín hiệu bị cắt ngắn là:
/2
/2
|()|
2
|
()|
2
(6.9)

lOMoARcPSD|36067889
1
|
(
)
|
2
/2
2
/
=
lim
1
2
=
lim
1
|
|
2
/2
2
/
=
Lưu ý có sự giống nhau giữa số hạng ầu tiên trong (6.9) và công suất trung bình ()
theo thời gian của một tín hiệu như ã cho trong (6.2), nên ta có:
= lim |
()|
2
(6.10)
Tích phân ầu tiên trong phương trình (6.10) cho thấy rằng ể nhận ược tổng công
suất của một tín hiệu, chúng ta phải cộng công suất thành phần của mỗi lần tăng khi thực
hiện tích phân theo thời gian . Việc ánh giá tích phân trong một khoảng thời gian hữu
hạn sẽ ưa ra ược công suất tín hiệu trong thời gian này. Vì vậy, tích phân ầu tiên cũng
có giá trị trong mỗi khoảng thời gian. Tuy nhiên, phương trình của Parseval ề xuất một
phương pháp thứ hai ể tính công suất tổng trong miền tần số. Số hạng cuối cùng trong
(6.10) cho thấy rằng tổng của |()|
2
trên tất cả các tần số cũng cho kết quả là công
suất tổng . Định nghĩa hàm mật ộ phổ công suất () có ơn vị W/Hz như là tích phân
của nó theo tần số là bằng công suất tổng:
() |
()|
2
(6.11)
Ngoài ra, cần lưu ý là () cũng cho công suất trên mỗi lần tăng tần số, có nghĩa là sự
tích hợp của hàm mật ộ công suất trên một dải tần số sẽ cho công suất tổng trong
khoảng tần số này. Trong iều kiện nhất ịnh (ược áp ứng cho hầu hết các tín hiệu quan
tâm thực tế) () liên quan ến |
()|
2
như sau:
|()|
2
() = lim (6.12)
Thông qua (6.7) mối quan hệ giữa mật ộ phổ công suất và dạng chuyển ổi Fourier
của hàm tự tương quan ược cho:
(
()} (6.13)
Khi ánh giá phân bố của công suất nhiễu theo tần số, mật ộ phổ công suất () phải là
hàm ể kiểm tra, chứ không phải là chuyển ổi Fourier. Đó là do chuyển ổi Fourier của
một ại lượng ngẫu nhiên cũng là một ại lượng ngẫu nhiên nên không mang lại bất kỳ
thông tin hữu ích nào. Như chúng ta ã biết, ối với các tín hiệu ngẫu nhiên cần phải khảo
sát các ặc tính thống kê. Do ó, trong trường hợp này cần quan tâm ến nội dung tần số
của nhiễu, chúng ta tính chuyển ổi Fourier của hàm tự tương quan như ã cho trong biểu
thức trên.
Từ các biểu thức (6.10), (6.11) và 6.6) ta có:

lOMoARcPSD|36067889
=
() ( ) () =
(0) (6.14)
Biểu thức (6.14) ược sử dụng ể tính công suất tổng bằng cách sử dụng tín hiệu miền
thời gian, hàm mật ộ phổ công suất hoặc hàm tự tương quan.
6.1.3. Một số loại nhiễu cơ bản
6.1.3.1. Nhiễu trong hệ thống tuyến tính
Khi thiết kế và mô tả các hệ thống truyền tin, nhiễu là một yếu tố quan trọng phải
ược tính ến. Nói chung, các nguồn nhiễu vật lý khác nhau ngoài các nguồn nhiễu do
con người tạo ra khác cũng góp phần vào nhiễu tổng trong hệ thống.Trong phần sau sẽ
khảo sát nhiễu trong hệ thống bất biến thời gian tuyến tính (LTI).
a) Nhiễu trắng giới hạn băng tần
Để mô tả nhiễu, sử dụng tham số mật ộ phổ công suất. Chúng ta biết nhiễu ngẫu
nhiên có xu hướng dao ộng nhanh, giả sử iện áp nhiễu () có hàm tự tương quan là:
() =
2
0
() (6.15)
trong ó: () là hàm xung. Do ó,
() = 0 với mọi , iều này cho thấy tín hiệu
nhiễu hoàn toàn không tương quan ngoại trừ tại dịch chuyển thời gian bằng không.
Chuyển ổi Fourier của mật ộ phổ công suất
() là:
(
()} =
2
0
[W/Hz] (6.16)
Mật ộ phổ công suất là không ổi ối với tất cả các tần số, do ó nó chứa tất cả các
thành phần tần số với trọng số công suất bằng nhau. Loại nhiễu này ược coi là nhiễu
trắng tương tự như ánh sáng trắng. Hệ số một phần hai trong (6.16) là cần thiết ể có mật
ộ phổ công suất hai phía.
Một vấn ề nẩy sinh khi tính toán công suất tổng của nhiễu trắng, vì:
(6.17)
iều này nghĩa là công suất là một ại lượng vô hạn và do ó không thể sử dụng ể mô tả bất
kỳ quá trình vật lý nào.
Tuy nhiên, ây lại là một mô hình tốt cho nhiều trường hợp trong ó có băng thông
hữu hạn qua hệ thống. Trong trường hợp này, mật ộ phổ công suất ược giả thiết là bằng
phẳng trong băng thông o hữu hạn, khi ó sẽ giới hạn công suất nhiễu tổng. Trong trường

lOMoARcPSD|36067889
hợp này nhiễu trắng giới hạn băng tần sẽ xuất hiện dưới dạng nhiễu trắng ối với hệ thống
o.
Công suất nhiễu trắng giới hạn băng tần là không phụ thuộc vào việc chọn tần số
hoạt ộng
0
. Do ó, nếu () là nhiễu trắng trung bình bằng 0 với mật ộ phổ công suất
bằng
0
/2 [W/Hz], thì với băng thông công suất nhiễu là:
2
0
2 2
=
0
[] (6.18)
b) Truyền nhiễu qua hệ thống LTI
Chuyển ổi tín hiệu vào () qua hệ thống bất biến thời gian tuyến tính (LTI) ược
mô tả trong miền thời gian thông qua tích chập:
() = ( ) (6.19)
trong ó: () là tín hiệu ầu ra và () là áp ứng xung của hệ thống LTI. Nếu tín hiệu ầu
vào là ngẫu nhiên, iều cần quan tâm là mật ộ phổ công suất
() của tín hiệu ầu ra.
Thay (6.19) vào (6.6) và thực hiện phép chuyển ổi các biến, sẽ thu ược hàm tự tương
quan của tín hiệu ầu ra [Proakis, 1989]:
( +
() (6.20)
từ ó thông qua (6.13) sẽ thu ược ():
(
()} =
()|()|
2
(6.21)
Do ó, chúng ta có kết quả quan trọng là phổ mật ộ công suất của tín hiệu ầu ra là
tích của phổ mật ộ công suất ầu vào nhân với bình phương ộ lớn của hàm truyền tần số.
Nếu muốn có hàm tự tương quan, thì dễ dàng tính ược phổ mật ộ công suất thông qua
(6.21) và sau ó thực hiện chuyển ổi ngược:
(
1
{
(
1
{
(|()|
2
} (6.22)
Nếu tín hiệu ầu vào ngẫu nhiên là nhiễu trắng
() với mật ộ phổ công suất
0
/2,
thì (6.21) trở thành:
() =
2
0
|()|
2
(6.23)
c) Băng tần nhiễu tương ương
Công suất nhiễu tổng ầu ra hệ thống với hàm truyền tần số ã biết |()| có thể ược
tính bằng cách sử dụng (6.21) và (6.14). Nếu nhiễu ầu vào là nhiễu trắng, ta có:
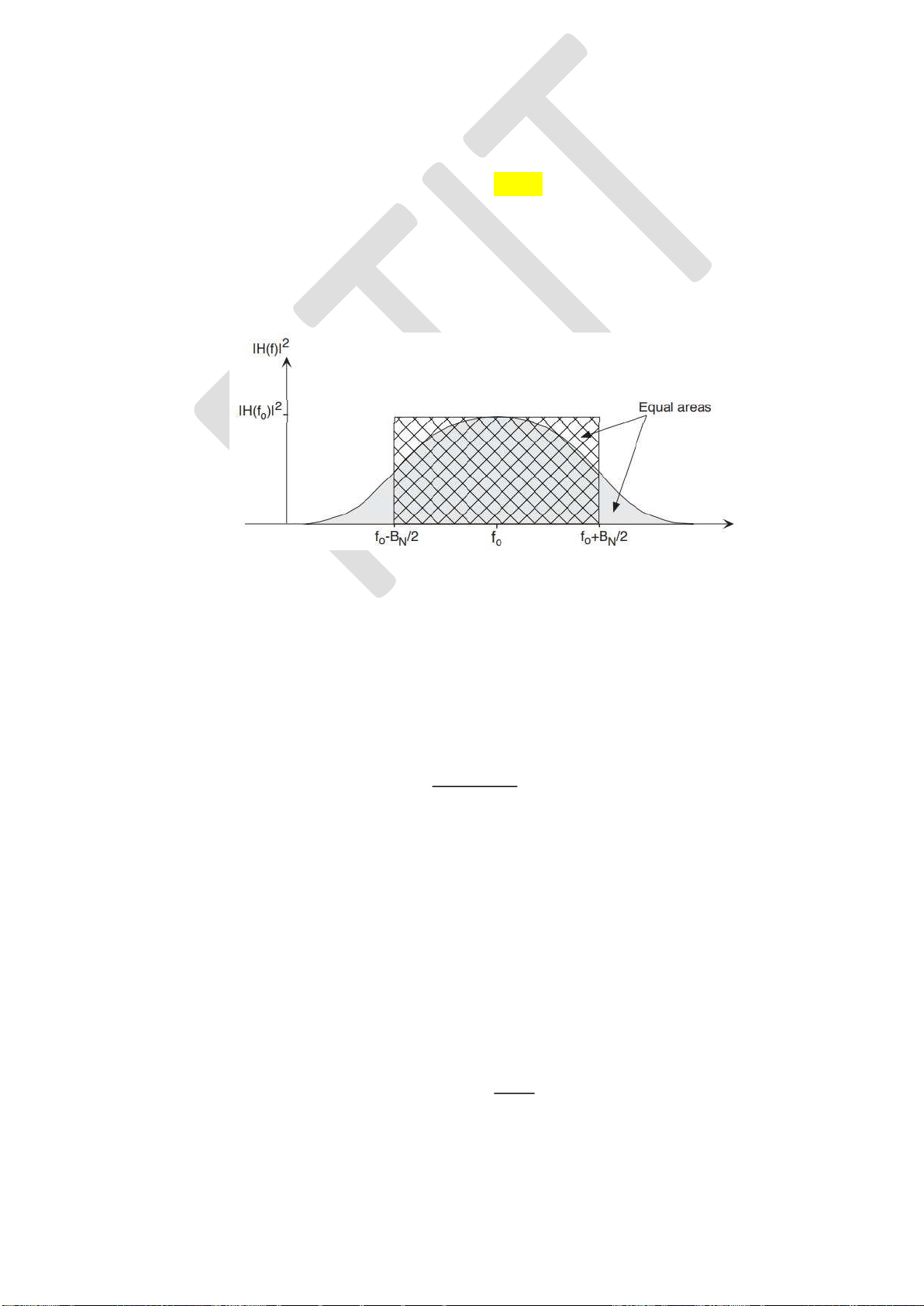
lOMoARcPSD|36067889
=
(
)
=
0
|
(
)
0
|
2
(6.24)
Tích phân là một hằng số ối với một hàm truyền tần số hệ thống ã cho. Chúng ta
muốn có một biểu thức ơn giản tương tự như (4.25) cho công suất nhiễu ầu ra. Cách tiếp
cận là xác ịnh băng thông nhiễu tương ương
của bộ lọc lý tưởng sao cho công suất
nhiễu ầu ra từ bộ lọc lý tưởng và hệ thống thực tế là bằng nhau. Như trong hình 6.5, giả
thiết rằng hàm truyền tần số của các bộ lọc lý tưởng là phẳng và bằng (
0
) trong băng
thông
quanh tần số trung tâm
0
và bằng không ở ngoài
.
Hình 6.5: Đồ thị của băng tần nhiễu tương ương Do
ó, công suất nhiễu ầu ra của bộ lọc lý tưởng là:
0
+
/2
2
=
0
|()|
2
(6.25)
=
0
0
/2
|()| Từ (6.24) và (6.25), ta có:
0
|()|
2
=
|()|
2 []
(6.26)
Định nghĩa về băng thông nhiễu tương ương,
cho phép thảo luận các hệ thống
tuyến tính thực tế bằng cách sử dụng các hệ thống tương ương lý tưởng của chúng.
d) Tỷ số tín hiệu trên nhiễu
Đặt công suất tín hiệu ầu vào thiết bị là
) và công suất nhiễu ầu vào của thiết
bị là
). Tỷ số tín hiệu trên nhiễu ầu vào
ược ịnh nghĩa là tỷ số của công suất
tín hiệu khả dụng tổng với công suất nhiễu khả dụng tổng tại ầu vào và cho bởi:
)
=
)
(6.27)

lOMoARcPSD|36067889
Do ó, SNR cho biết lượng công suất nhiễu so với công suất tín hiệu. Rõ ràng tỷ số
tín hiệu trên nhiễu ở ầu ra của thiết bị là tương tự như biểu thức trên. Ngoài ra, ịnh nghĩa
của SNR không phụ thuộc vào nguồn và loại nhiễu.
SNR là tỷ số công suất thường ược biểu thị bằng Decibel:
= 10
10
() (6.28)
Do ó, SNR= 13 dB nghĩa là công suất tín hiệu lớn hơn hai mươi lần so với công
suất nhiễu, trong khi SNR= 0 dB nghĩa là công suất tín hiệu bằng công suất nhiễu.
6.1.3.2. Nhiễu xẩy ra tự nhiên
Nhiễu vô tuyến tự nhiên trong các hệ thống viễn thông vừa ược thu bởi ăng ten
cũng như ược tạo ra trong chính hệ thống. Ảnh hưởng ầu tiên ược tính ến là sự óng góp
của nhiễu nhiệt ăng-ten. Suy hao do hơi nước và oxy, mây và lượng mưa kèm theo nhiễu
nhiệt, chớp và các khí quyển khác làm suy hao thêm SNR. Ngoài ra, ăng ten thu có thể
thu ược nhiễu ngoài trái ất có nguồn gốc nhiệt hoặc không nhiệt.
Phần này sẽ ưa ra một cái nhìn tổng quan về các loại nhiễu xuất hiện tự nhiên khác
nhau và xác ịnh các ại lượng thích hợp ể mô hình hóa ảnh hưởng của nhiễu này. Trước
hết, chúng ta xét ịnh luật bức xạ Planck, là cơ sở cho các loại nhiễu.
Luật Planck
Năm 1900, Max Planck tìm ra ịnh luật liên quan ến phát xạ iện từ từ vật en ở trạng
thái cân bằng nhiệt. Vật en ược ịnh nghĩa ơn giản là một vật lý tưởng, hoàn toàn không
trong suốt có thể hấp thụ tất cả các phát xạ tới ở mọi tần số, không phản xạ lại bất kỳ tần
số nào. Một vật ở trạng thái cân bằng nhiệt ộng phát ra môi trường một lượng năng lượng
bằng với lượng mà nó hấp thụ từ môi trường. Do ó, ngoài việc là một bộ hấp thụ hoàn
hảo, vật en còn là một bộ phát hoàn hảo. Điểm chính của nguồn gốc Planck là năng
lượng chỉ có thể ược trao ổi dưới dạng các phần rời rạc hoặc lượng tử bằng , trong ó
là hằng số Planck = 6,626 × 10
34
[] và là tần số tính bằng Hz.
Khi ó, năng lượng của mức (trạng thái) cơ bản bằng 0, của mức ầu tiên , của
mức thứ hai , v.v. Tổng quát:
= với = 0,1, 2 (6.29)
trong ó: là số mức (trạng thái). Với số lượng tử năng lượng
(còn gọi là các nguyên
tố năng lượng) ở mức sẽ cho năng lượng của mức ó là
. Năng lượng tổng thu
ược bằng cách cộng dồn trên tất cả các trạng thái, do ó:
=
0
. 0 +
1
+
2
+
3
(6.30)

lOMoARcPSD| 36067889
Theo cơ học lượng tử, xác suất chiếm một mức năng lượng i xuống với
/
trong ó: . Khi ó, số lượng tử năng lượng
1
ở mức ầu tiên ược cho bằng số ở trạng thái
cơ bản
0
nhân với xác suất
/
. Tương tự
2
=
1
/
=
0
/
, v.v. Số
lượng tử năng lượng tổng là:
= 0(1 + / + / + / (6.31)
Để xác ịnh năng lượng trung bình, chúng ta chia năng lượng tổng cho số lượng tử
năng lượng tổng và có thể ược ơn giản hóa bằng:
( =
/
(6.32)
Sử dụng mật ộ các mode, tìm ra ịnh luật Planck cho bức xạ vật en. Được biểu thị
bằng ộ sáng của năng lượng phát xạ từ vật en cho như sau:
3
1
() =
2
/
1
(6.33)
a) Phát xạ nhiệt
Trong hệ thống luôn tồn tại phát xạ nhiệt và ược tạo ra thông qua chuyển ộng nhiệt
ngẫu nhiên của các iện tử trong môi trường dẫn như iện trở. Đường i của mỗi iện tử là
ngẫu nhiên do tương tác với các iện tử khác. Hiệu ứng thuần của chuyển ộng iện tử là
một dòng iện ngẫu nhiên chạy trong môi trường dẫn với giá trị trung bình bằng không.
Mật ộ phổ công suất của nhiễu nhiệt ược ưa ra bởi luật phân bố Planck (6.32). Đối với
dải nhiệt ộ và tần số bình thường thấp hơn dải quang học, tham số / là rất nhỏ, do
ó
/
/ và (6.32) ược tính gần úng bằng:
() = (6.34)
Mật ộ phổ công suất theo (6.34) không phụ thuộc vào tần số và do ó ược gọi là phổ
nhiễu trắng. Trong băng thông , công suất nhiễu khả dụng khi ó là:
= (6.35)
Biểu thức trên cho thấy rằng nếu băng thông ược cố ịnh thì sẽ biết ược nhiệt ộ ể
tính công suất nhiễu. Đây là lý do, tại sao thường nói ến nhiệt ộ nhiễu khi ề cập ến công
suất nhiễu (ngay cả khi nguồn nhiễu không phải là nhiệt).
Với = 300 , tức là ở nhiệt ộ phòng, sẽ nhận ược công suất nhiễu là −114 dBm
trên băng thông 1 MHz. Cần nhớ giá trị này như một tham khảo và sử dụng ể tính công
suất nhiễu gần úng cho một băng thông nhất ịnh. Ví dụ, công suất nhiễu cho hệ thống
20 MHz sẽ là −101 dBm.

lOMoARcPSD| 36067889
b) Nhiễu ngoài trái ất
Không gian vũ trụ phần lớn là nguồn nhiễu băng thông rộng, có thể coi là sóng iện
từ phẳng. Phát xạ vũ trụ phải ược tính ến nếu búp sóng chính hoặc búp sóng phụ của ăng
ten thu hướng vào không gian vũ trụ. Các nguồn nhiễu là cả phát xạ nhiệt và không phát
nhiệt từ Mặt trời, Mặt trăng, Sao và các hành tinh và từ những nơi khác trong thiên hà
của chúng ta và các thiên hà khác.
Nếu sự phát xạ có nguồn gốc nhiệt thì sự óng góp của nó ối với công suất nhiễu
ược mô tả thông qua ộ sáng phổ như ược cho trong (4.40), là mật ộ công suất tính bằng
W trên một ơn vị góc khối trên một ơn vị diện tích trên Hz. Tại các tần số vô tuyến trong
ó , ộ sáng phổ
ược ưa ra bởi ịnh luật Rayleigh-Jeans:
2
=
2 [
2
..
] (6.36)
trong ó:
là nhiệt ộ sáng, λ là bước sóng và k là hằng số Boltzmann.
Công suất nhiễu thực tế nhận ược trong dải tần hẹp phụ thuộc vào hướng của búp
sóng chính và các búp sóng phụ của ăng ten thu và vùng hiệu dụng của ăng ten. Như
vậy, ộ sáng phổ của nguồn mở rộng là một hàm liên quan trực tiếp ến tọa ộ anten. Đối
với các nguồn rời rạc (chẳng hạn như Mặt trời), nằm trong búp sóng chính của ăng ten
và ối diện một góc khối
nhỏ hơn nhiều so với góc khối của chùm tia chính ăng ten,
thì mật ộ công suất phổ là:
2
2
2
. ] (6.37) =
[.
Trong trường hợp tổng quát,
thay ổi theo
trong ó ược gọi là chỉ số phổ. Đối
với sự phát xạ nhiệt của vật en . Đối với phát xạ không nhiệt (6.36) vẫn có thể
ược sử dụng nhưng nhiệt ộ sáng
không còn liên quan ến phát xạ nhiệt mà là nhiệt ộ
sáng ẳng trị, ngoài ra chỉ số phổ phải ược xác ịnh chính xác.
Bức xạ nền: Toàn bộ vũ trụ bị bão hòa với bức xạ nền vô tuyến, tàn tích của một vụ nổ
lớn. Sau vụ nổ lớn, sự hình thành của vật chất, không gian và thời gian hầu như không
còn gì, nhiệt ộ phổ biến lúc ầu rất cao. Tuy nhiên, khi vũ trụ mở rộng nhiệt ộ xuống
khoảng −270 ◦C, nhiệt ộ như ngày nay. Sự mở rộng không gian ã kéo dài bước sóng
phát xạ iện từ cho ến khi i vào phạm vi sóng vô tuyến. Ngày nay, phát xạ ược o một
cách ồng ều từ mọi hướng của không gian, do ó có thuật ngữ "bức xạ nền". Nó sẽ "làm
nóng" bất kỳ vật thể có nhiệt thấp ến nhiệt ộ không gian là 3 (lưu ý rằng ộ không tuyệt
ối Kelvin là 273
0
).
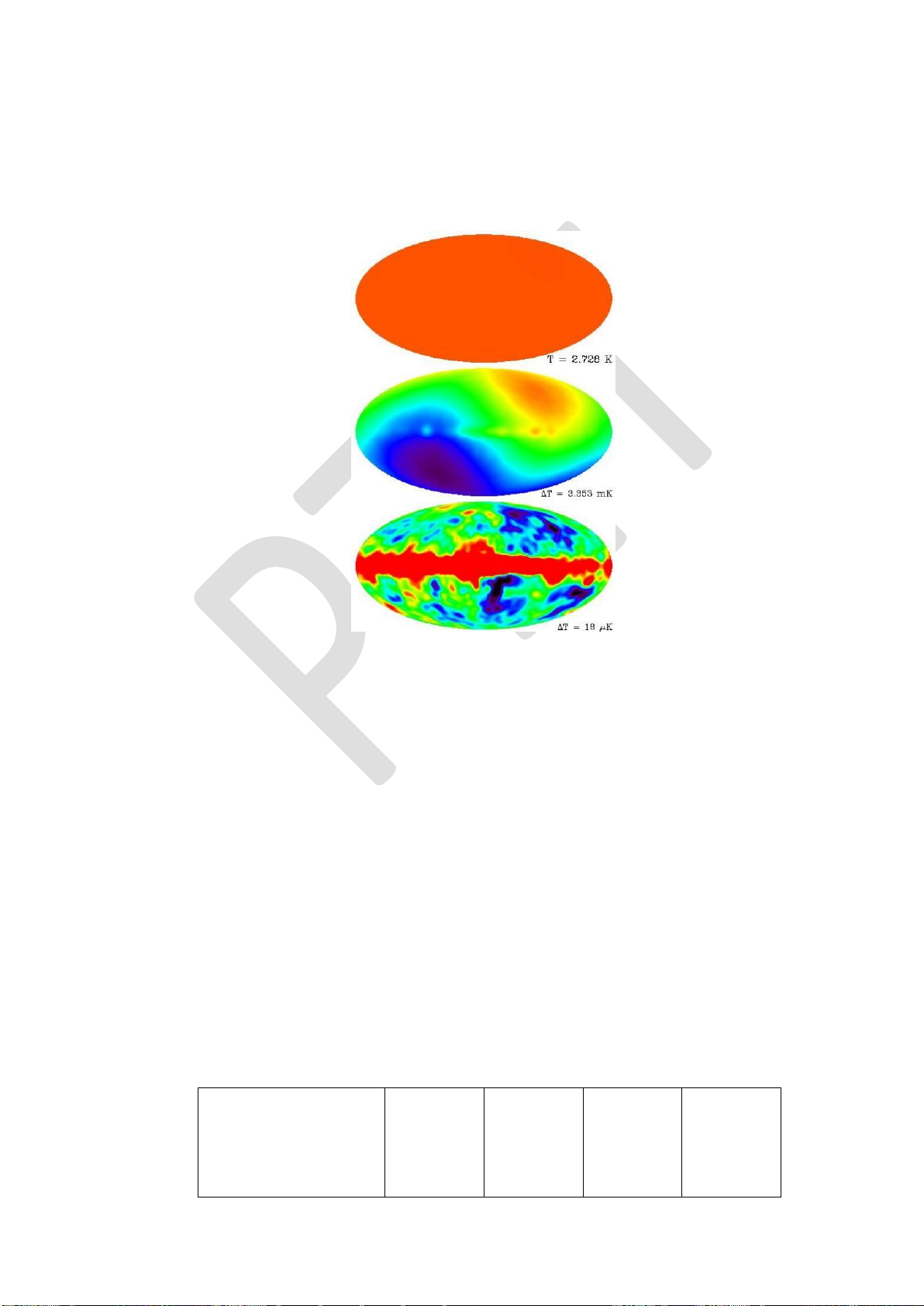
lOMoARcPSD|36067889
Nhiệt ộ của phát xạ nền vô tuyến vũ trụ ược xác ịnh với vệ tinh COBE trong hai
năm ầu quan sát ầu tiên như trên hình 6.6. Mặt phẳng của dải Ngân hà nằm ngang ở giữa
mỗi bức tranh. Dải nhiệt ộ là 0-4K cho ảnh trên cùng, 3,3mK cho ảnh giữa và 18µK cho
ảnh dưới cùng.
năng lượng bị hấp thụ một phần bởi khí quyển và ược phát xạ lại dưới dạng nhiễu. Nhiệt
ộ nhiễu hấp thụ hiệu dụng,
ược cho dưới dạng hàm của nhiệt ộ môi trường xung
quanh,
và suy hao,
là:
=
(
1) (6.38)
Lưu ý là
không giống với nhiệt ộ vật lý (môi trường xung quanh) của khí quyển
và tăng khi suy hao khí quyển ngày càng tăng. Bảng 6.1 cho thấy một số giá trị của
và
khi nhiệt ộ môi trường
là 300.
Bảng 6.1: Nhiệt ộ nhiễu hấp thụ cho các giá trị suy hao khác nhau khi
= 300
[]
0
1
3
10
[ ô ]
1
1,26
2
10
Hình 6.6: Nhi
ệt ộ
c
ủ
a phát x
ạ
n
ề
n vô tuy
ến vũ trụ
c) Nhi
ễ
u h
ấ
p th
ụ
Khi m
ộ
t v
ậ
t h
ấ
p th
ụ
năng lượng thì năng lượng tương tự
s
ẽ
ượ
c phát x
ạ
thành
nhi
ễ
u
như chỉ
ra trong lý thuy
ế
t phát x
ạ
v
ật en. Nế
u không, nhi
ệt ộ
c
ủ
a m
ộ
t v
ậ
t s
ẽ
tăng lên và nhiệt ộ
c
ủ
a nh
ữ
ng v
ậ
t khác gi
ả
m xu
ống. Trong trườ
ng h
ợp ăng
ten b
-
ứ
c x
ạ
,

lOMoARcPSD| 36067889
[]
0
78
300
2700
Suy hao của bầu khí quyển phụ thuộc nhiều vào tần số. Hơi nước và oxy gây ra
suy hao khí quyển lớn ở dải tần 20GHz và 60GHz. Dải tần dưới 10GHz thể hiện nhiệt ộ
nhiễu thấp nhất.
d) Các nguồn nhiễu tự nhiên khác
Nhiễu bắn: loại nhiễu này xảy ra khi việc ịnh lượng hạt tải iện tử trở nên rõ ràng. Nó
phát sinh trong các thiết bị vật lý khi một hạt tích iện di chuyển qua một gradient thế
năng mà không có va chạm và với thời gian bắt ầu ngẫu nhiên. Đây là trường hợp xảy
ra trong các ống chân không do sự phát xạ ngẫu nhiên của các iện tử từ catốt và trong
nhiều linh kiện bán dẫn do sự khuếch tán của các hạt tải thiểu số, tạo ra và tái tổ hợp
ngẫu nhiên của các cặp iện tử-lỗ trống. Đối với những trường hợp này, mật ộ phổ công
suất tương ối bằng phẳng với các tần số theo thứ tự 1/, trong ó là thời gian chuyển
tiếp hoặc thời gian sống của các hạt mang. Xét theo dòng trung bình, mật ộ phổ công
suất là:
= () + 2()
2
(6.39)
trong ó: q là iện tích iện tử = 1,6. 10
19
[]. Số hạng ầu tiên trong (6.39) tương ứng với
AC hoặc phần dao ộng của dòng nhiễu và số hạng thứ hai tương ứng với giá trị trung
bình khác không.
Nhiễu /: rất nhiều thành phần thể hiện nhiễu 1/ xuất hiện ở tần số thấp (tùy thuộc
vào quá trình dưới 1MHz, 10kHz hoặc 1kHz). Có một số giả thuyết về nguồn gốc của
nhiễu này và nó rất khó ể o do tần số thấp.
6.2. BỘ THU TỐI ƯU
6.2.1. Khái niệm về bộ thu tối ưu
Xét trường hợp ơn giản nhất khi dạng của tín hiệu trong kênh không bị méo và chỉ
bị nhiễu cộng. Khi ó ở ầu vào của máy thu sẽ có tổng của tín hiệu và nhiễu:
() =
( ) + () (6.40)
trong ó: là hệ số truyền của kênh (thông thường ), giả thiết = const,
là thời gian giữ chậm tín hiệu của kênh,
() là nhiễu cộng, là một hàm ngẫu nhiên,
Trường tin ầu vào {
} = , khi ó các
() là các tín hiệu phát
tương ứng với các tin
.

lOMoARcPSD|36067889
Do () là một quá trình ngẫu nhiên nên () cũng là một quá trình ngẫu nhiên.
Vậy khi nhận ược () ta có thể ề ra giả thiết sau:
1.
1
()(
1
) ã ược truyền i và trong quá trình truyền
1
() ược cộng thêm
một nhiễu: () = (
1
( )
2.
2
()(
2
) ã ược truyền i và trong quá trình truyền
2
() ược cộng thêm
một nhiễu: () = (
2
( )
………………..
M.
()(
) ã ược truyền i và trong quá trình truyền
() ược cộng thêm một
nhiễu: () = (
( )
Nhiệm vụ của bộ thu là phải chọn một trong giả thuyết này trong khi nó chỉ biết
một số tính chất của nguồn tín hiệu và dạng của tín hiệu nhận ược (). Rõ ràng là mỗi
một giả thuyết ều có một xác suất lỗi tương ứng vì () là một hàm ngẫu nhiên. Như
vậy máy thu phải chọn một lời giải nào ó trong iều kiện bất ịnh. Việc xét các quy luật
chọn lời giải trong iều kiện bất ịnh chính là nội dung của bài toán thống kê. Vì vậy thu
tín hiệu khi có nhiễu là một bài toán thống kê.
Nhiệm vụ của máy thu là phải chọn lời giải do ó máy thu còn ược gọi là sơ ồ giải.
Yêu cầu lớn nhất của sơ ồ giải là phải cho ra lời giải úng (phát
phải tìm ược
).
Trong thực tế có rất nhiều sơ ồ giải. Trong tất cả các sơ ồ giải có thể có thì tại một sơ ồ
bảo ảm xác suất thu lớn phải úng là lớn nhất (xác suất giải sai là bé nhất). Sơ ồ này ược
gọi là sơ ồ giải tối ưu. Máy thu xây dựng theo sơ ồ giải ó ược gọi là máy thu tối ưu (hay
máy thu lý tưởng).
6.2.2. Các vấn ề thu tối ưu
6.2.2.1. Thế chống nhiễu
Có thể dùng xác suất thu úng ể ánh giá ộ chính xác của một hệ thống truyền tin
một cách ịnh lượng. Để ánh giá ảnh hưởng của nhiễu lên ộ chính xác của việc thu, người
ta ưa ra khái niệm tính chống nhiễu của máy thu. Nếu cùng một mức nhiễu, máy thu nào
ó có xác suất thu úng là lớn hơn thì ược coi là có tính chống nhiễu lớn. Hiển nhiên rằng
tính chống nhiễu của máy thu tối ưu là lớn nhất và ược gọi là thế chống nhiễu.
6.2.2.2. Hai loại sai lỗi khi chọn giả thuyết
Sai lỗi loại 1: Gọi
1
là giả thuyết về tin
1
ã gửi i. Nội dung của sai lầm này là bác bỏ
1
mà thực tế là nó úng. Tức là quả thực
1
gửi i mà ta không gửi. Sai lầm 1 là bỏ sót
tin (hay mục tiêu).

lOMoARcPSD|36067889
Sai lỗi loại 2: Thừa nhận
1
trong khi thực tế nó sai. Tức là thực ra không có
1
mà ta
lại bảo là có. Sai lầm loại này gọi là nhầm tin hoặc báo ộng nhầm.
Bình thường, không có iều kiện gì ặc biệt, sự tồn tại của hai loại sai lỗi trên là
không “ngang quyền” (không gây tác hại như nhau).
6.2.2.3. Tiêu chuẩn Kachennhicov
Thông thường khái niệm tối ưu là phải hiểu theo một nghĩa nào ó, tức là tối ưu
theo một tiêu chuẩn nào ó. Thông thường trong thông tin "thu tối ưu" ược hiểu theo
nghĩa như sau (do Kachennhicov ề ra và gọi là tiêu chuẩn Kachennhicov).
Trong cùng một iều kiện ã cho trong số hai hay nhiều sơ ồ giải, sơ ồ nào ảm bảo
xác suất giải úng lớn nhất thì ược gọi là tối ưu.
Hạn chế: Không ề cập ến các loại sai lỗi, tức là coi chúng tồn tại "ngang quyền" nhau.
Ưu iểm: Đơn giản, dễ tính toán, dễ thực hiện.
Ngoài tiêu chuẩn Kachennhicov còn có một số những tiêu chuẩn khác như:
Neyman-Pearson, Bayes, Vald …. Những tiêu chuẩn này khắc phục ược nhược iểm trên
nhưng khá phức tạp nên không dùng trong thông tin.
6.2.2.4. Xử lý tối ưu các tín hiệu
Nhiệm vụ của máy thu là cho ta các lời giải
. Quá trình thực hiện nhiệm vụ này
ược gọi là quá trình xử lý tín hiệu. Trong quá trình xử lý tín hiệu thường phải thực hiện
các phép toán tuyến tính hoặc phi tuyến nhờ các mạch tuyến tính hoặc phi tuyến (ví dụ:
biến tần, tách sóng, lọc, hạn chế, nhân, chia, tích phân, bình phương, khuếch ại …). Quá
trình xử lý tín hiệu trong máy thu tối ưu ược gọi là xử lý tối ưu tín hiệu. Xử lý ể nhận
lời giải có xác suất lỗi bé nhất. Trước kia việc tổng hợp các máy thu (xây dựng sơ ồ giải)
chỉ căn cứ vào các tiêu chuẩn chất lượng mang tính chất chức năng mà không mang tính
chất thống kê. Ảnh hưởng của nhiễu lên chất lượng của máy thu chỉ ược tính theo tỷ số
tín hiệu /nhiễu. Tức là việc tổng hợp máy thu tối ưu trước ây chỉ chủ yếu dựa vào trực
giác, kinh nghiệm, thí nghiệm. Ngày nay lý thuyết truyền tin ã cho phép bằng toán học
tổng hợp ược máy thu tối ưu ("Tối ưu" lúc này mới mang tính chất ịnh lượng) tức là dựa
vào các tiêu chuẩn tối ưu bằng công cụ thống kê toán học người ta ã xác ịnh ược quy tắc
giải tối ưu.
6.2.2.5. Xác suất giải sai và quy tắc giải tối ưu
Cho
là tín hiệu ã gửi i, xác suất ể gửi tín hiệu này i là (
), (
) ược gọi là
xác suất tiên nghiệm
1
(
) = 1). Giả thiết là
() có thời hạn ,
() ược gọi

lOMoARcPSD| 36067889
là các tín hiệu nguyên tố ứng với các dấu mã. Ở máy thu nhận ược (). Từ () qua sơ
ồ giải sẽ có lời giải
nào ó. Nếu nhận ược
thì coi rằng
ã ược gửi i. Như vậy
ã
ược gửi i với một xác suất (
/) ược gọi là xác suất hậu nghiệm. Do ó, xác suất giải
sai sẽ là:
(/,
(
/) (6.41)
Từ (6.41) ta sẽ tìm ra quy tắc giải tối ưu (theo tiêu chuẩn Kachennhicov). Để tìm
ra quy tắc giải tối ưu xét hai sơ ồ giải sau:
Sơ ồ 1: Từ () cho ta
1
Sơ ồ 2: Từ () cho ta
2
Nếu (/,
1
) < (/,
2
) (6.42) thì ta sẽ coi sơ ồ thứ nhất tối ưu hơn sơ ồ
thứ hai.
Từ (6.41) và (6.42) (
1
/) > (
2
/) (6.43)
Tức là xác suất chọn lời giải sai (/,
) càng nhỏ nếu xác suất hậu nghiệm
tương ứng (
/) càng lớn.
Ta xét sơ ồ, khi ó ta có thể coi ( 1) hệ thức sau:
(
/) > (
/) với {
(6.44)
Nếu có ( hệ thức này thì ta coi sơ ồ giải chọn
sẽ là tối ưu (theo nghĩa
Kachennhicov) vì nó ảm bảo xác suất lỗi là bé nhất, biểu thức (6.44) chính là quy tắc
giải tối ưu. Sơ ồ giải thỏa mãn biểu thức (6.44) chính là sơ ồ giải tối ưu.
6.2.3. Bộ thu tối ưu cho kênh có nhiễu cọng Gaussian
Khái niệm về kênh gaussian ã ược trình bày trong mục 2.2.3.1. Trong phần này sẽ
i vào phân tích về bộ thu tối ưu cho kênh có nhiễu cọng Gaussian.
Đầu tiên xác ịnh mô hình toán học của tín hiệu ở ầu vào của bộ thu. Giả thiết rằng
thiết bị phát truyền thông tin số qua tín hiệu {
(), }, mỗi tín hiệu
ược truyền trong một khoảng thời gian và ta xét việc truyền thông tin trong khoảng 0
.
Tín hiệu khi truyền qua kênh bị ảnh hưởng của nhiễu cộng gaussian, tín hiệu nhận
ược trong khoảng thời gian là:
() =
() + (), (6.45)
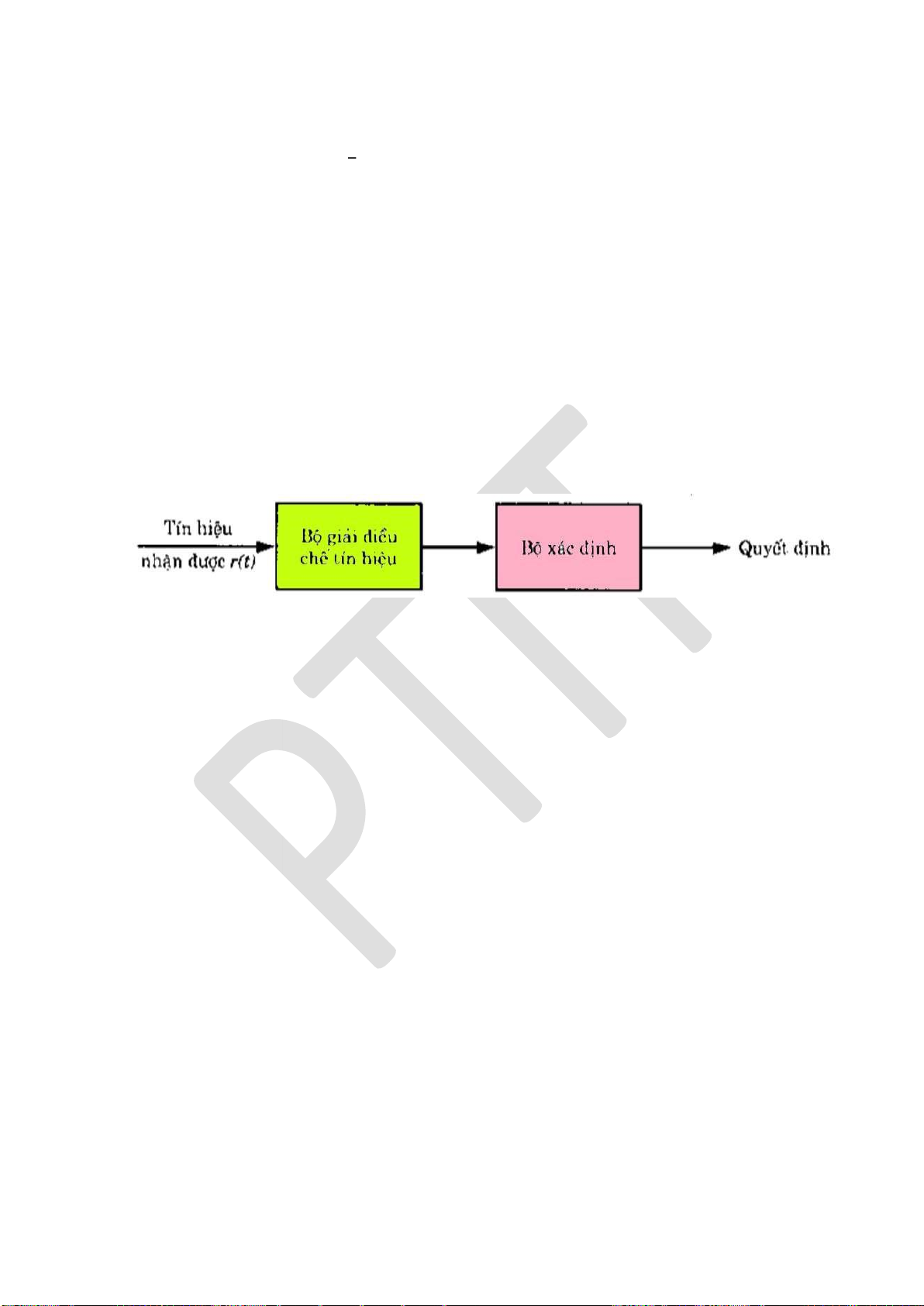
lOMoARcPSD|36067889
với () là một thể hiện của quá trình ngẫu nhiên nhiễu cộng gaussian (AWGN) với mật
ộ phổ công suất
() =
1
2
0
[/]. Dựa trên tín hiệu () thu ược, mong muốn
thiết kế một bộ thu tối ưu theo nghĩa nó cực tiểu hóa xác suất lỗi.
Cấu trúc cơ bản của bộ thu như trên hình 6.7, bao gồm 2 khối chức năng chính.
Khối thứ nhất là bộ giải iều chế tín hiệu và khối thứ hai là bộ xác ịnh tín hiệu. Chức
năng của bộ giải iều chế tín hiệu là chuyển tín hiệu thu ược () thành một vectơ chiều
= {
1
2
} với là số chiều của tín hiệu truyền i. Chức năng bộ xác ịnh tín hiệu
là xác ịnh tín hiệu nào trong tín hiệu ã ược truyền i dựa trên vectơ .
Có hai cách thực hiện giải iều chế tín hiệu ược xét dưới ây. Cách thứ nhất dựa
trên tính tương quan của tín hiệu và cách thứ hai dựa vào bộ lọc phối hợp. Bộ xác ịnh
tối ưu tiếp sau bộ giải iều chế tín hiệu ược thiết kết ể cực tiểu hóa xác suất lỗi.
Hình 6.7: Bộ thu tín hiệu
6.2.3.1. Bộ giải iều chế tương quan
Bộ giải iều chế tương quan phân giải tín hiệu nhận ược ở phía thu thành các vectơ
chiều. Nói cách khác, tín hiệu và nhiễu ược khai triển thành chuỗi tuyến tính của các
hàm trực giao cơ sở {
()}. Giả thiết hàm cơ sở {
()} tương ứng với các vectơ sinh
của không gian vectơ, như vậy mọi tín hiệu có thể phát i {
(), } ều có
thể biểu diễn thành một tổ hợp tuyến tính của {
()}. Trong trường hợp có nhiễu, các
hàm {
()} không tạo nên không gian nhiễu. Tuy nhiên, thành phần nhiễu nằm ngoài
không gian tín hiệu, không ảnh hưởng tới bộ xác ịnh tín hiệu.
Giả thiết tín hiệu thu, () ược cho qua một băng song song gồm bộ tương quan
chéo ể khai triển () theo hàm cơ sở {
()} như trên hình 6.8.
Ta có thể biểu diễn tín hiệu () trong khoảng thời gian 0 như sau:
(
=1
() + ) (6.46)
Thành phần ) ược ịnh nghĩa là:
() = (
=1
() (6.47)
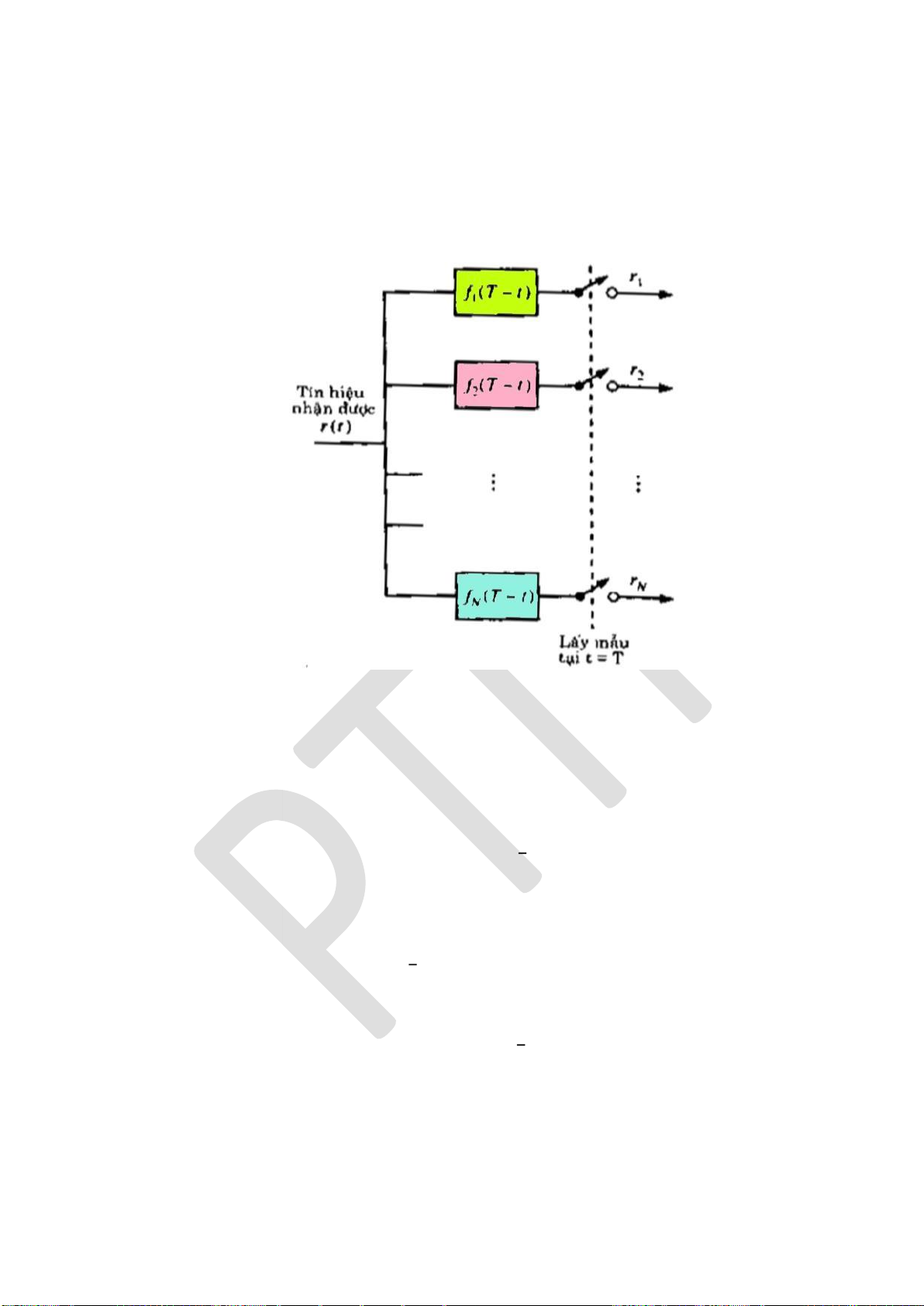
lOMoARcPSD| 36067889
là quá trình nhiễu gausian có giá trị trung bình bằng 0 biểu diễn sự khác nhau giữa nhiễu
nguyên thủy () với thành phần tương ứng với sự khai triển () theo các hàm cơ sở
{
()}. Chúng ta sẽ thấy dưới ây rằng
() không ảnh hưởng tới việc xác ịnh tín hiệu
nào ã truyền i. Do ó việc xác ịnh tín hiệu có thể dựa hoàn toàn trên tín hiệu ầu ra bộ
tương quan và các thành phần nhiễu
=
+
, .
với
Hình 6.8: B
ộ
gi
ải iề
u ch
ế
tương quan
Do các tín hi
ệ
u
{
(
)}
là xác ị
nh nên các thành ph
ầ
n tín hi
ệu cũng xác ị
nh. Các
thành ph
ầ
n nhi
ễ
u
{
}
có phân b
ố
gausian.
Phương sai củ
a các thành ph
ầ
n nhi
ễ
u là:
(
)
=
1
2
0
(6.48)
=1
khi
=
và b
ằng 0 trong các trườ
ng h
ợp khác. Như vậ
y
thành ph
ầ
n
c
ủ
a nhi
ễ
u
{
}
là các bi
ế
n ng
ẫu nhiên gausian không có tương qua
n, giá tr
ị
trung bình
b
ằ
ng 0 và
phương
sai chung
2
=
1
2
0
. Như vậ
y các tín hi
ệ
u ra c
ủ
a b
ộ
tương quan
{
}
là các bi
ế
n ng
ẫ
u nhiên gaussian v
ới phương sai là:
2
=
2
=
1
2
0
(6.49)

lOMoARcPSD|36067889
Do các thành phần của nhiễu {
} là các biến ngẫu nhiên gaussian không tương
quan nên chúng ộc lập thống kê. Từ ó các tín hiệu ầu ra của bộ tương quan {
} cũng là
các biến ngẫu nhiên gaussian ộc lập thống kê. Hàm mật ộ phân bố xác suất có iều kiện
của các biến ngẫu nhiên = {
1
2
} là:
, (6.50)
(0) 0
Cuối cùng ta muốn chứng tỏ rằng các tín hiệu ầu ra bộ tương quan (
1
2
) là
ủ ể xác ịnh tín hiệu nào ã truyền i từ phía phát, không cần thêm thông tin từ phần còn lại
của nhiễu
(). Thực vậy,
() không có liên hệ với tín hiệu {
}:
[
()
] = [
()]
+ [
()
] = [
()
]
= {[(
=1
()]
0
[()()]
()
=1
(
)
()
1 1
= 2
0
(
2
0
() = 0 (6.51)
Do
() và {
} là các biến ngẫu nhiên gaussian không tương quan nên chúng ộc
lập thống kê. Như vậy
() không chứa thông tin ảnh hưởng tới việc xác ịnh tín hiệu
nào ã ược truyền i mà tất cả thông tin ể xác ịnh ều ở các tín hiệu {
}. Như vậy
() có
thể bỏ qua.
6.2.3.2. Bộ giải iều chế dùng bộ lọc phối hợp
Để thay một băng bộ tương quan ể tạo ra các tín hiệu {
}, có thể sử dụng một
băng gồm bộ lọc tuyến tính. Giả sử áp ứng xung của bộ lọc là:
() =
( (6.52)
với {
()} là hàm cơ sở và
() = 0 với ngoài khoảng [0, ]. Đầu ra của các bộ
lọc này tương ứng khi ta lấy mẫu các tín hiệu ra tại thời iểm = là:
(
0
()
() =
, (6.53)
Như vậy, các mẫu ầu ra của bộ lọc tại thời iểm = chính là tập giá trị {
} nhận
ược từ bộ tương quan tuyến tính.
Một bộ lọc mà áp ứng xung () = ( ) với () xác ịnh trong khoảng 0
ược gọi là bộ lọc phối hợp với tín hiệu (). Ví dụ về tín hiệu và bộ lọc phối hợp
trên hình 6.9. Đáp ứng của tín hiệu () ở ầu ra bộ lọc là:
(
0
()( + ) (6.54)
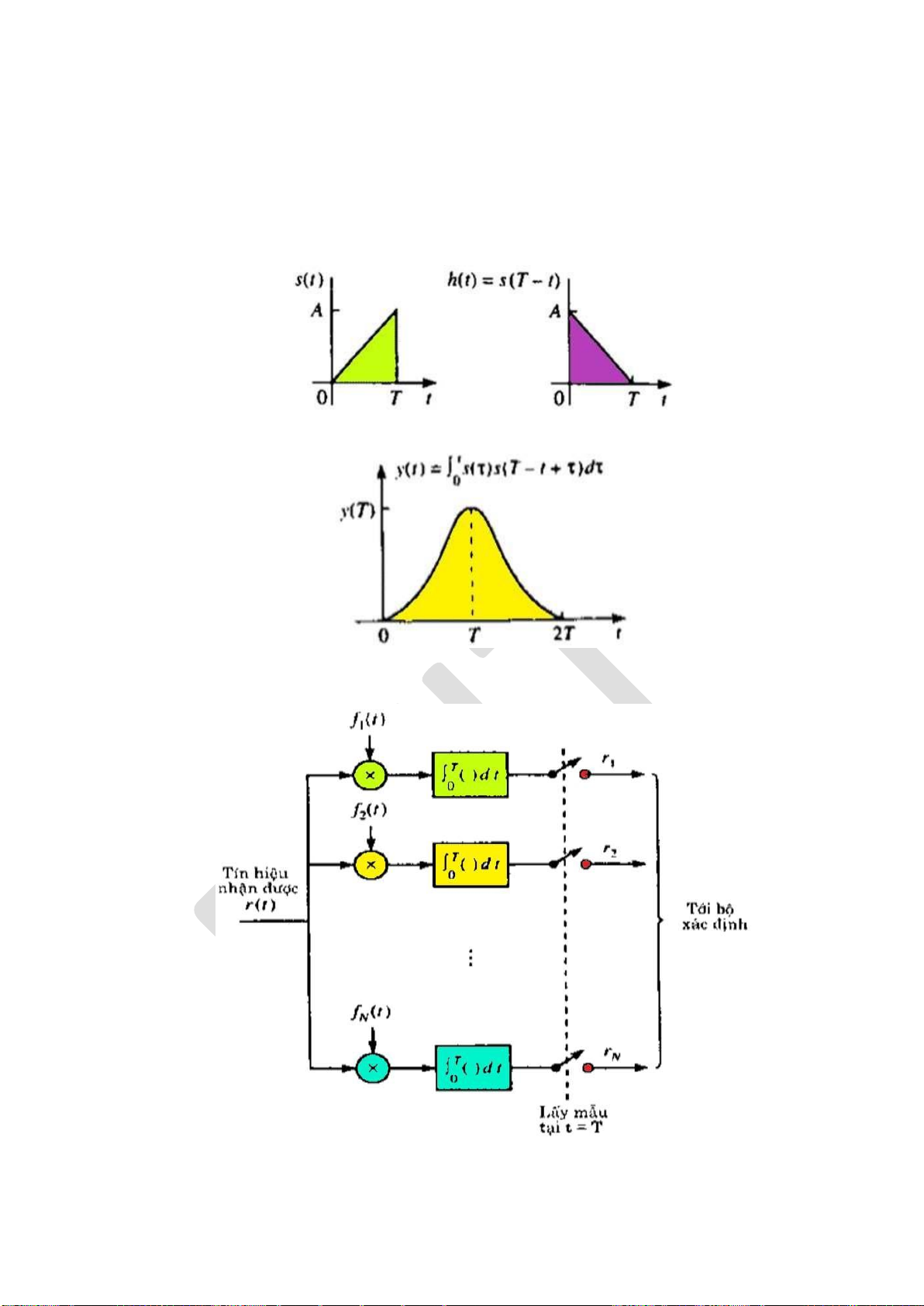
lOMoARcPSD|36067889
chính là hàm tự tương quan của tín hiệu (). Hình 6.10 biểu diễn () với tín hiệu ()
trên hình 6.9. Hàm tự tương quan () là hàm chẵn ối với và có một cực ại tại =
.
Với bộ giải iều chế ược mô tả ở trên, bộ lọc phối hợp là phối hợp với các hàm
cơ sở {
()}. Hình 6.11 mô tả bộ giải iều chế loại này.
Hình 6.9: tín hi
ệ
u s(t) và b
ộ
l
ọ
c ph
ố
i h
ợ
p
Hình 6.10
Đầ
:
u ra b
ộ
l
ọ
c ph
ố
i h
ợ
p là hàm t
ự
tưng quan củ
a s(t)
Hình 6.11: B
ộ
gi
ải iề
u ch
ế

lOMoARcPSD|36067889
(
)
=
|
(
)
|
2
=
2
(
)
0
=
1
2
Tính chất của bộ lọc phối hợp:
- Nếu tín hiệu () bị ảnh hưởng bởi nhiễu AWGN thì bộ lọc với áp ứng xung phối
hợp với () sẽ cực ại hóa tỷ số tín hiệu trên nhiễu (SNR). Giá trị SNR cực ại của bộ lọc
phối hợp là: 2
= (6.55)
0
- Tỷ số tín hiệu trên nhiễu cực ại SNR
0
của bộ lọc phối hợp phụ thuộc vào năng
lượng của tín hiệu () chứ không phụ thuộc vào tính chất của tín hiệu (). Đây là tính
chất quan trọng thứ hai của bộ lọc phối hợp.
Biểu diễn bộ lọc phối hợp trong miền tần số:
Do () = ( ) nên ta có:
() =
()
2
(6.56)
Ta thấy rằng áp ứng tần số của bộ lọc phối hợp là liên hợp phức của tín hiệu truyền
i nhân với
2
, biểu diễn trễ khoảng thời gian . Nói cách khác, |()| = |()|, áp
ứng biên ộ của bộ lọc phối hợp giống với phổ biên ộ của tín hiệu truyền i và pha của
() ngược với pha của ().
Tín hiệu () với phổ () ược i qua một bộ lọc phối hợp, tín hiệu ra của bộ lọc
có phổ () = |()|
2
2
, tương ứng với tín hiệu ra khi lấy mẫu tín hiệu ra tại thời
iểm = , là:
(6.57)
Nhiễu ở ầu ra của bộ lọc phối hợp có phổ mật ộ công suất:
0
() = |()|
2
0
(6.58) Như vậy, công suất nhiễu ở ầu ra của bộ lọc là:
1
= 2
0
(6.59) Tỷ số tín
hiệu trên nhiễu ược cho bởi:
2
2
0
=
=
1
2
0 =
0 (6.60)

lOMoARcPSD|36067889
6.2.3.3. Bộ xác ịnh tối ưu
Rõ ràng là với tín hiệu truyền qua kênh có nhiễu AWGN thì vectơ = [
1
2
]
ược ưa qua bộ giải iều chế chứa mọi thông tin cần thiết. Trong phần này sẽ trình bày
luật xác ịnh tối ưu dựa trên vectơ . Giả thiết tín hiệu truyền qua các kênh là không nhớ
trong các khoảng thời gian của một tín hiệu.
Ta muốn thiết kế một bộ xác ịnh tín hiệu có thể xác ịnh tín hiệu ã truyền i từ phía
phát dựa vào vectơ thu ược xác suất xác ịnh úng bằng cực ại. Xét luật xác ịnh dựa trên
xác suất hậu nghiệm là xác suất ã phát
khi ã thu ược vectơ , ược ịnh nghĩa như sau:
(í | ),
và ký hiệu gọn lại là (
| ). Tiêu chuẩn xác ịnh dựa trên sự lựa chọn tín hiệu tương
ứng với giá trị cực ại của tập hợp các xác suất hậu nghiệm là {(
| )}. Sau ó chứng
tỏ rằng tiêu chuẩn này sẽ cực ại hóa xác suất xác ịnh úng (có nghĩa là cực tiểu hóa xác
suất lỗi). Tiêu chuẩn này ược gọi là tiêu chuẩn cực ại hóa xác suất hậu nghiệm (MAP).
Theo luật Bayes, xác suất hậu nghiệm ược xác ịnh bởi:
(
|) =
(|
(
)
)
()
(6.61)
với (|
) là hàm mật ộ phân bố xác suất có iều kiện của vectơ nhận ược khi ã xác ịnh
ược truyền i và (
) là xác suất tiên nghiệm của tín hiệu thứ ược truyền i. Mẫu
số của (6.61) ược biểu diễn như sau:
(
=1
(|
)(
) (6.62)
Từ (6.61) và (6.62) thấy rằng ể xác ịnh ược xác suất hậu nghiệm (
|) cần phải
biết xác suất tiên nghiệm (
) và hàm mật ộ phân bố xác suất có iều kiện (|
) với
. Có thể thấy mẫu số của (6.61) ộc lập với tín hiệu truyền i và như vậy
luật xác ịnh dựa trên việc tìm tín hiệu làm cực ại (
|) tương ương với việc tìm tín
hiệu làm cực ại (|
).
Hàm mật ộ phân bố xác suất là (|
) thường ược gọi là hàm khả năng
(likelihood function). Tiêu chuẩn xác ịnh dựa trên việc cực ại hóa (|
) ối với tín
hiệu thường ược gọi là tiêu chuẩn cực ại khả năng (ML). Ta thấy rằng bộ xác ịnh dựa
trên tiêu chuẩn MAP và dựa trên tiêu chuẩn ML mang lại các kết quả giống nhau nếu
các xác suất tiên nghiệm (
) là bằng nhau, hay các tín hiệu {
} là ồng xác suất.

lOMoARcPSD|36067889
Đối với kênh có nhiễu AWGN, hàm có khả năng (|
) ược xác ịnh bởi (6.50).
Để ơn giản tính toán, ta làm việc với loga tự nhiên của (|
) là hàm ơn iệu.
ln (|
ln
2
(6.63)
Tìm cực ại của ln (|
) theo
tương ương với việc tìm tín hiệu
ể cực tiểu
hóa khoảng cách Euclide:
(,
=1
(
)
2
(6.64)
Với kênh có nhiễu AWGN, luật xác ịnh dựa trên tiêu chuẩn ML trở thành việc tìm
tín hiệu
có khoảng cách tới vectơ nhận ược nhỏ nhất. Ta gọi luật xác ịnh này là xác
ịnh khoảng cách cực tiểu.
Một cách diễn giải khác là luật xác ịnh tối ưu dựa trên tiêu chuẩn ML có thể nhận
ược bằng cách khai triển (6.64) thành:
(, =1 2 =1 =1 2
= ||
2
2
+ |
|
2
= 1,2 (6.65)
Do thành phần ||
2
là không ổi với mọi giá trị (,
), nên có
thể bỏ qua khi so sánh và sẽ có tập hợp khoảng cách khác:
,
+ |
|
2
(6.66)
Việc chọn tín hiệu
cực tiểu hóa ,
) tương ương với việc chọn tín hiệu
làm cực ại khoảng cách (,
,
), có nghĩa là:
(,
) = 2
|
|
2
(6.67)
Thành phần
biểu thị hình chiếu của vectơ nhận ược trên mỗi vectơ trong tập
vectơ ứng với tập tín hiệu phát i. Giá trị mỗi hình chiếu này là ộ o ộ liên quan giữa
các vectơ nhận ược tín hiệu thứ m. Do lý do này ta gọi (,
), m=1, 2, …, M là các ộ
tương quan cho việc xác ịnh tín hiệu nào ã truyền i. Thành phần |
|
2
=
, = 1,2, .
. , có thể bỏ qua nếu các tín hiệu có cùng năng lượng trong việc tính các ộ tương quan
(,
) hay các khoảng cách (,
) (,
).
Dễ thấy rằng các ộ tương quan có thể biểu diễn thành:
(,
0
()
()
, = 1,2, . . , (6.68)
Do ó các giá trị này có thể tạo ra bởi một bộ giải iều chế xác ịnh tương quan chéo
giữa tín hiệu nhận ược () với tín hiệu có thể truyền i ở phía phát và thêm vào ầu ra

lOMoARcPSD|36067889
của mỗi bộ tương quan năng lượng của tín hiệu tương ứng trong trường hợp các tín hiệu
năng lượng khác nhau. Một cách tương ương, tín hiệu thu ược có thể cho qua một băng
gồm bộ lọc phối hợp với các tín hiệu {
()} và lấy mẫu tại = . Như vậy bộ thu
tối ưu (giải iều chế và xác ịnh) có thể xây dựng như trên hình 6.12.
Ta thấy rằng bộ xác ịnh tối ưu ML tính toán tập hợp khoảng cách (,
) hay
,
) và chọn tín hiệu tương ứng với khoảng cách nhỏ nhất. Bộ xác ịnh tối ưu ML
có thể tính ộ tương quan (,
) và chọn tín hiệu có ộ tương quan với lớn nhất.
Những iều vừa xây dựng là xét trong trường hợp các tín hiệu là ồng xác suất. Tuy
nhiên, khi các tín hiệu là không ồng xác suất thì bộ xác ịnh tối ưu MAP sẽ dựa trên xác
suất (
|), hay các ộ o (,
) = (|
)(
).
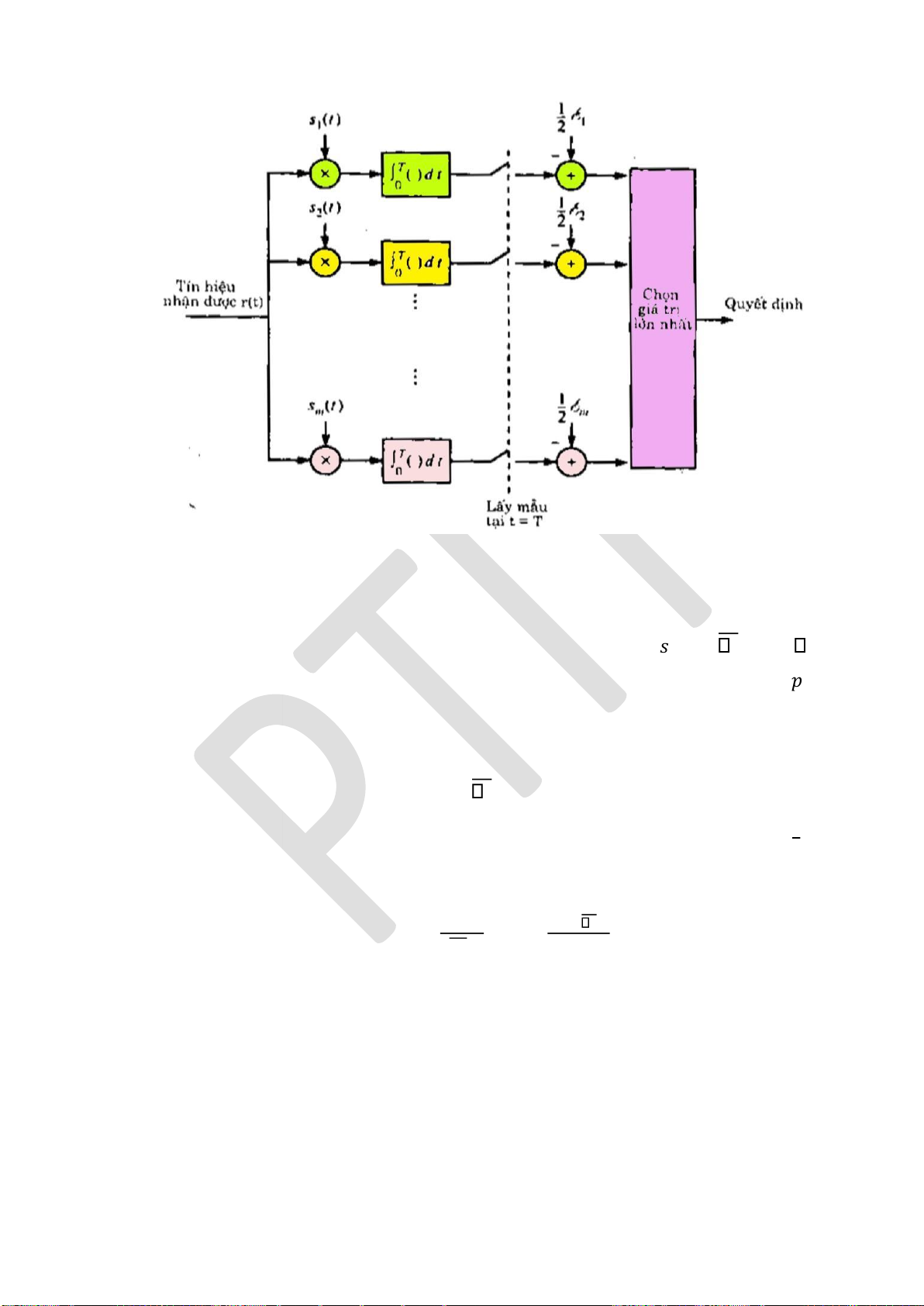
lOMoARcPSD|36067889
Hình 6.12: Th
ự
c hi
ệ
n b
ộ
thu t
ối ưu vớ
i kênh có nhi
ễ
u AWGN
Ví d
ụ
1.1.3:
Xét tính hi
ệ
u PAM nh
ị
phân v
ới hai iể
m tín hi
ệ
u
1
2
=
, v
ớ
i
là
năng lượ
ng
ứ
ng v
ớ
i m
ộ
t bit. Xác su
ấ
t tiên nghi
ệ
m là
(
)
=
và
(
)
. Ta
xác ịnh các ộ
o cho bộ
xác ị
nh t
ối ưu MAP khi tín hiệ
u b
ị
nhi
ễ
u AWGN.
Vectơ
tín hi
ệ
u nh
ận ược ố
i v
ớ
i tín hi
ệ
u PAM nh
ị
phân là:
=±
+
(
)
(6.69)
v
ớ
i
)
(
là bi
ế
n ng
ẫ
u nhiên gaussian có tr
ị
trung bình b
ằng 0 và phương
sai
2
=
1
2
0
.
Hàm m
ật ộ
phân b
ố
xác su
ất có iề
u ki
ệ
n
(
|
)
c
ủ
a hai tín hi
ệ
u là:
(
|
1
)
=
1
2
exp
[
(
)
2
2
2
]
(6.70)

lOMoARcPSD|36067889
(|
2
)
2
2
(6.71)
Các khoảng cách (,
) và (,
) là:
(,
1
)
2
2
(6.72)
( )
2
(,
2
)
2
2
(6.73)
Nếu (,
1
) > (,
2
) ta xác ịnh tín hiệu là
1
và ngược lại là tín hiệu
2
.
Luật xác ịnh có thể biểu diễn như sau:
(,1) >1
1
(,2) <
2
Nhưng:
(6.74)
(,1)
(6.75)
(,2) 2
nên (6.74) trở thành:
=
exp
[
(
+
)
2
(
)
2
2
]
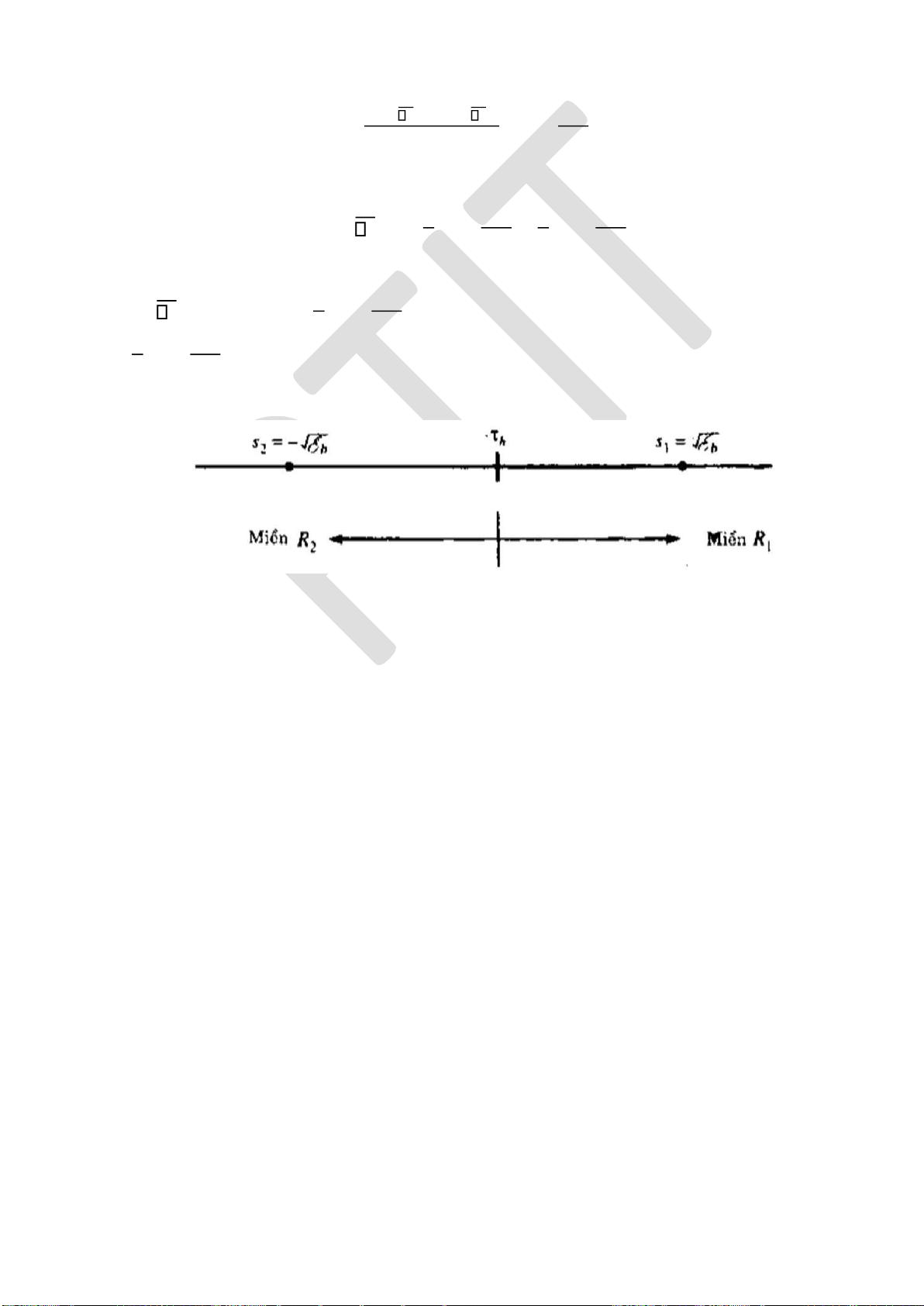
lOMoARcPSD| 36067889
(6.77)
1
4
0 = 0. Nếu
Trong trường hợp các xác suất tiên nghiệm không bằng nhau, cần phải biết các giá
trị này và giá trị
0
ể tính giới hạn
.
(
+
)
2
(
)
2
2
2
<
2
>
1
(6.76)
hay tương ương:
<
2
>
1
1
2
2
=
1
4
0
Đó là dạ
ng cu
ố
i c
ủ
a b
ộ
xác ị
nh t
ối ưu. Nó tính các bộ
tương quan
(
,
)
=
và so sánh v
ớ
i
1
4
0
. Hình 6.13 v
ẽ
hai iể
m tín hi
ệ
u
1
và
2
. Gi
ớ
i h
ạ
n
ký hi
ệ
u là
. Giá tr
ị
này ph
ụ
thu
ộ
c vào
0
và
. N
ế
u
=1/2
,
>1/2
, tín hi
ệ
u
1
có xác su
ấ
t l
ớn hơn và
<0
và mi
ề
n
1
l
ớn hơn miề
n
2
.
Hình 6.13: Bi
ể
u di
ễ
n không gian tín hi
ệ
u cho b
ộ
xác ị
nh t
ối ưu tín
hi
ệ
u PAM nh
ị
phân

lOMoARcPSD|36067889
=
±
Chúng ta kết thúc phần này với việc chứng minh rằng luật xác ịnh dựa trên tiêu
chuẩn cực ại khả năng tối thiểu hóa xác suất lỗi khi tín hiệu ồng xác suất tiên nghiệm.
Ký hiệu
là miền của không gian chiều mà trong ó ta xác ịnh tín hiệu
() ã ược truyền i khi nhận vectơ = [
1
2
]. Xác suất xác ịnh nhầm khi ó là:
(|
(|
) (6.78)
là miền bù của
. Xác suất lỗi trung bình là:
(=1 1 (|=1 1 (|)
=1
1
(|
)] (6.79)
() ược cực tiểu hóa bởi việc lựa chọn tín hiệu
nếu (|
) > (|
) với mọi
. Khi tín hiệu không ồng xác suất, ta có thể chứng minh một cách tổng quát là
tiêu chuẩn MAP làm cực tiểu hóa xác suất lỗi trung bình.
6.2.3.4. Bộ xác ịnh dãy cực ại khả năng
Khi tín hiệu không nhớ, bộ xác ịnh ký hiệu-ký hiệu mô tả ở trên là tối ưu theo nghĩa
nó cực tiểu hóa xác suất lỗi. Mặt khác, khi tín hiệu truyền i có nhớ, có nghĩa là các tín
hiệu trong các khoảng thời gian liên tiếp có ảnh hưởng lẫn nhau, thì bộ xác ịnh tối ưu là
bộ xác ịnh dựa trên dãy các ký hiệu nhận ược trong các khoảng thời gian liên tiếp. Dưới
ây sẽ xét hai kiểu xác ịnh khác nhau. Trong phần ầu sẽ xét thuật toán xác ịnh dãy khả
năng cực ại bằng cách tìm khoảng cách Euclide nhỏ nhất trong lưới ặc trưng cho tín hiệu
truyền i. Trong phần sau, sẽ xét thuật toán cực ại hóa xác suất hậu nghiệm, từ ó cho phép
xác ịnh trên cơ sở ký hiệu-ký hiệu và mỗi ký hiệu ược xác ịnh dựa trên dãy các vectơ tín
hiệu nhận ược.
Để xây dựng thuật toán xác ịnh dãy cực ại khả năng, xét tín hiệu NRZI mà quá
trình nhớ ược ặc trưng bởi lưới. Tín hiệu ược truyền là tín hiệu PAM nhị phân. Như vậy
có thể có hai tín hiệu ược truyền i tương ứng với hai iểm tín hiệu
1
2
= với
là năng lượng ứng với một bit. Đầu ra của bộ lọc phối hợp hay bộ giải iều chế tương
quan với tín hiệu PAM nhị phân ở khoảng thời gian tín hiệu thứ là:
+
(6.80)
với
là biến ngẫu nhiên gaussian có giá trị trung bình bằng 0 và phương sai
2
=
1
2
0
. Hàm mật ộ phân bố xác suất có iều kiện hai tín hiệu có thể truyền i là:

lOMoARcPSD|36067889
(
)
=
{
1
(
)
,
2
(
)
(
,
(
)
)
=
(
(
)
)
=1
(
|
1
) (6.81)
(
|
2
) (6.82)
Giả sử ta nhận ược một dãy các tín hiệu ở ầu ra của bộ lọc phối hợp
1
,
2
.
Do nhiễu trên kênh là nhiễu trắng có phân bố gaussian và ( ), ( ) với
là trực giao, dẫn tới (
) = 0 với . Như vậy dãy
1
,
2
cũng là nhiễu
trắng. Từ ó, với mỗi dãy tín hiệu truyền i
()
, hàm mật ộ phân bố xác suất ồng thời của
1
,
2
là tích của hàm mật ộ phân bố xác suất biên:
(12 |()=1 =1 1 (
)
(6.83)
ở ây
hoặc
. Như vậy với dãy
1
,
2
nhận ược, bộ xác ịnh sẽ
tìm dãy
()
} làm cực ại hàm mật ộ phân bố xác suất có iều kiện (
1
2
|
()
).
Bộ xác ịnh như thế ược gọi là bộ xác ịnh dãy cực ại hóa khả năng.
Lấy loga của (6.83) và bỏ qua các thành phần ộc lập với (
1
2
), ta tìm ược
một bộ xác ịnh dãy cực ại khả năng ể chọn dãy
()
ể làm cực tiểu khoảng cách Euclide:
2
(6.84)
Khi tìm trong lưới dãy làm cực tiểu ộ ài (,
()
), ta có thể phải tính ộ dài
(,
()
) cho mọi dãy có thể. Với tín hiệu NRZI chẳng hạn, khi iều chế nhị phân, số
lượng các dãy là 2
với là số tín hiệu ở ầu ra bộ giải iều chế, nhưng có thể giảm số
lượng dãy phải tìm trong lưới nhờ áp dụng thuật toán Viterbi. Thuật toán Viterbi là thuật
toán tìm trong lưới ể xác ịnh dãy ML. Chúng ta mô tả thuật toán này ối với tín hiệu
NRZI. Giả sử rằng quá trình tìm kiếm khởi ầu ở trạng thái
0
. Lưới tương ứng trên hình
6.14.

lOMoARcPSD|36067889
0
(
1
1
,
)
=
(
1
)
2
+
(
2
+
)
2
1
(
0
1
,
)
=
(
1
+
)
2
+
(
2
)
2
1
(
1
0
,
)
=
(
1
)
2
+
(
2
)
2
Hình 6.14: Lưới tương ứng với tín hiệu NRZI
Tại thời iểm = , nhận ược
1
=
1
()
+
1
, từ bộ iều chế và tại thời iểm
= 2 nhận ược
2
=
2
()
+
2
. Do tín hiệu có nhớ 1 bit, ta ký hiệu = 1, có thể thấy
lưới tiến tới trạng thái bình thường của nó sau hai chuyển ổi. Sau khi nhận ược
2
tại
thời iểm = 2, có hai ường tín hiệu i vào mỗi nút và hai ường tín hiệu i ra khỏi mỗi
nút. Hai ường vào nút
0
tại thời iểm = 2 tương ứng với các bit thông tin (0, 0) và
(1, 1) hay hai iểm tín hiệu . Hai ường vào nút
1
tại thời
iểm = 2 tương ứng với các bit thông tin (0, 1) và (1, 0) hay tại hai iểm tín hiệu
.
Với hai ường tín hiệu vào nút
0
ta tính hai khoảng cách Euclide:
(6.85)
(6.86)
Thuật toán Viterbi so sánh hai khoảng cách này và bỏ i khoàng cách lớn hơn.
Đường ứng với khoảng cách nhỏ hơn ược lưu trữ và gọi là ường sống sót tại thời iểm
= 2. Việc bỏ qua một trong hai ường không cần xét tới tính tối ưu của việc tìm kiếm
bởi vì mọi sự mở rộng ường với khoảng cách lớn sau thời iểm = 2 luôn có ộ o lớn
hơn so với ường còn lại ược mở rộng theo úng ường như thế sau thời iểm =
2.
Tương tự, hai ường vào nút
1
tại thời iểm = 2, ta tính hai khoảng cách Euclide:
(6.87)
(6.88)
So sánh hai ộ o này và ường tín hiệu ứng với ộ o lớn hơn bị bỏ qua. Như vậy, tại
thời iểm = 2, ta còn hai ường còn lại, một ường tại nút
0
và một ường tại nút
1
.
Đường tín hiệu tại các nút
0
và
1
sau ó ược mở rộng dọc theo hai ường còn lại.
Sau khi nhận ược
3
tại thời iểm = 3, ta tính hai ộ o của hai ường vào trạng thái
0
. Giả sử các ường còn lại tại thời iểm = 2 là (0,0) tại
0
và (0,1) tại
1
. Hai ộ o
cho hai ường vào
0
tại = 3 là:

lOMoARcPSD|36067889
(6.89)
(6.90)
So sánh hai ộ o này với nhau và ường với ộ o lớn hơn bị bỏ qua. Quá trình này cứ
tiếp tục mỗi khi nhận ược một tín hiệu mới từ bộ giải iều chế. Tương tự, hai ộ o của hai
ường vào trạng thái
1
tại thời iểm = 3 là:
(6.91)
(6.92)
Như vậy, thuật toán Viterbi tính toán hai ộ o của hai ường tín hiệu vào một nút tại
mỗi giai oạn của quá trình tìm kiếm và bỏ qua một ường tại mỗi nút. Hai ường còn lại
sau ó ược mở rộng tới trạng thái tiếp theo. Như vậy, số ường tìm kiếm trong cây giảm i
hai lần tại mỗi giai oạn.
Ta tạo ra ược một cách dễ dàng lưới tìm kiếm cho iều chế M mức theo thuật toán
Viterbi. Ví dụ iều chế có nhớ với = 4 ược ặc trưng bởi lưới 4 trạng thái trên
6.2.4. Hiệu năng của bộ thu tối ưu
hình 6.15. M
ỗ
i tr
ạng thái có hai ườ
ng tín hi
ệu vào và hai ườ
ng tín hi
ệ
u ra kh
ỏ
i nút.
Quá trình nh
ớ
c
ủ
a tín hi
ệ
u là
=1
. Thu
ật toán Viterbi cho 4 ườ
ng còn l
ạ
i t
ạ
i m
ỗ
i giai
oạn và các ộ
o tương ứng. Hai ộ
o tương ứ
ng v
ới hai ường vào và 1 ườ
ng b
ị
b
ỏ
qua t
ạ
i m
ỗi giai oạn. Như vậ
y thu
ậ
t toán Viberti c
ự
c ti
ể
u hóa s
ố
ườ
ng tìm ki
ế
m trên
lướ
i trong vi
ệc xác ị
nh dãy ML.
Hình 6.15: M
ột giai oạ
n c
ủa lướ
i
ứ
ng v
ới iề
u ch
ế
có nh
ớ
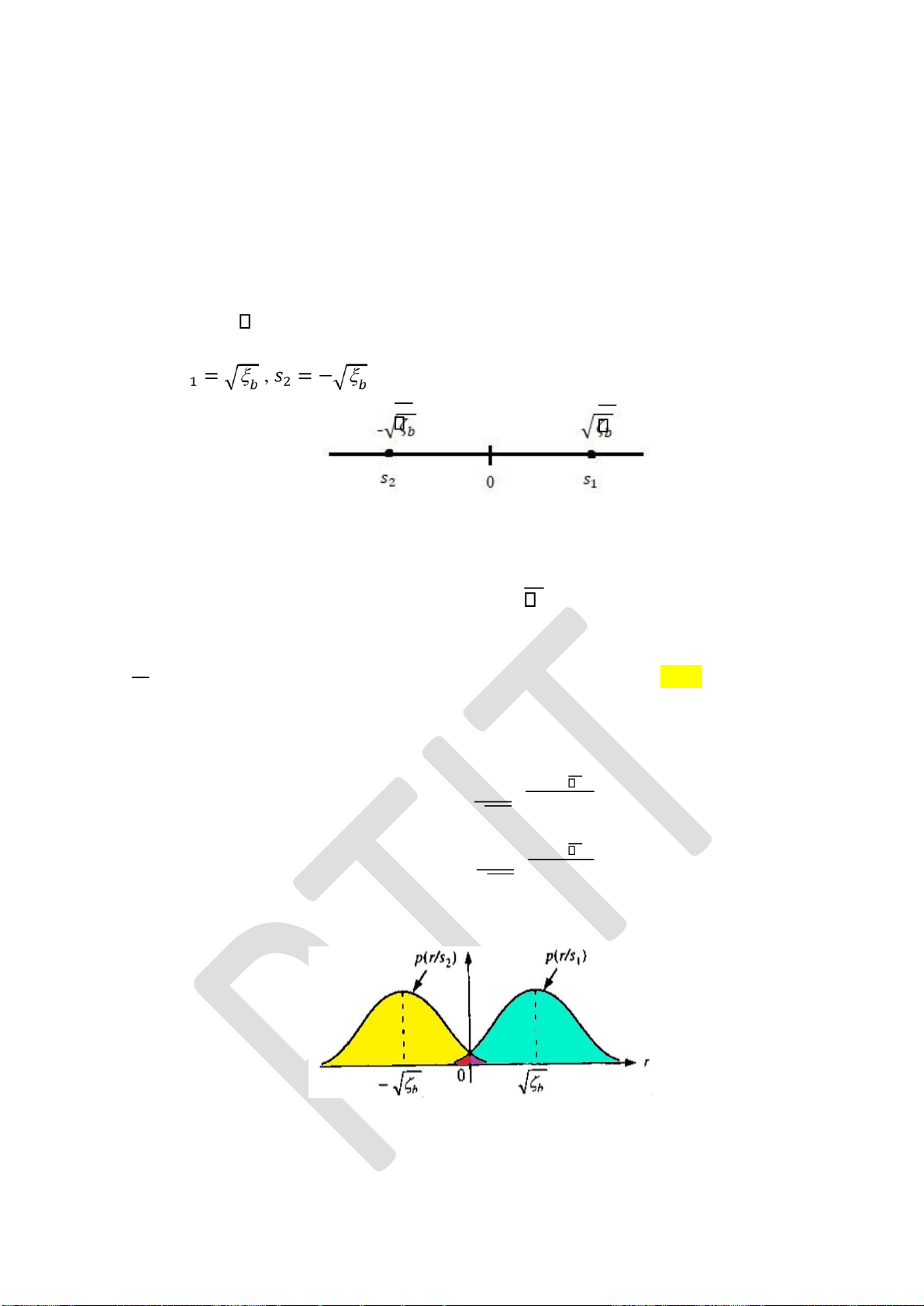
lOMoARcPSD|36067889
Trong phần này chỉ tập trung vào xem xét hiệu năng của bộ thu tối ưu ối với tín
hiệu không nhớ.
6.2.4.1. Xác suất lỗi với tín hiệu nhị phân
Ta xét tín hiệu PAM nhị phân với hai tín hiệu
1
() = () và
2
(() với
() là một xung bất kỳ khác 0 trong khoảng 0 và bằng 0 tại thời các thời iểm
thời gian khác. Do
1
(
2
() nên các tín hiệu này ngược pha với nhau. Năng lượng
xung () là
. Tín hiệu PAM là một chiều và biểu diễn hình học ơn giản là vectơ một
chiều . Hình 6.16 biểu diễn hai tín hiệu.
Hình 6.16: Hai tín hiệu của tín hiệu PAM nhị phân
Giả thiết tín hiệu
1
() ược truyền i và tín hiệu thu ược sau bộ giải iều chế là:
2 =
=
1
+
=
+
(6.93)
v
ớ
i n là thành ph
ầ
n nhi
ễ
u c
ộ
ng gaussian có giá tr
ị
trung bình b
ằng 0 và phương sai
0
2
. T
rong trườ
ng h
ợ
p này, lu
ật xác ị
nh d
ựa trên ộ
tương quan
(
6.67)
s
ẽ
so sánh
v
ớ
i
c
ậ
n 0. N
ế
u
>0
thì s
ẽ
quy
ết ị
nh tín hi
ệ
u truy
ền i là
1
(
)
và n
ế
u
<0
thì quy
ết ị
nh
tín hi
ệ
u truy
ền i là
2
(
)
, hai hàm xác su
ất có iề
u ki
ệ
n là:
(|
1
=
)
1
0
(
)
2
0
(6.94)
(|
2
=
)
1
0
+
(
)
2
0
Hai hàm m
ật ộ
xác su
ất này ượ
c bi
ể
u di
ễ
n trên hình 6.17.
Hình 6.17: Hai hàm m
ật ộ
phân b
ố
xác su
ấ
t c
ủ
a hai tín hi
ệ
u
Gi
ả
thi
ế
t
1
(
)
truy
ền i, xác xuấ
t l
ỗ
i là xác su
ất ể
<0
, nghĩa là:

lOMoARcPSD|36067889
(6.95)
(| dr
= = ( ) (6.96)
Với () ược ịnh nghĩa trong (2.35). Tương tự, nếu
2
() ược truyền i thì xác suất
ể > 0 à (| Nếu giả thiết
1
() và
2
() có xác suất truyền i như nhau
thì giá trị trung bình của xác suất lỗi là:
= [(|
1
) + (|
2
)]/2 = ( (6.97)
Ta có thể nhận thấy có hai tính chất quan trọng sau. Thứ nhất, xác suất lỗi chỉ phụ
2
thuộc vào tỷ số mà không phụ thuộc vào tính chất của tín hiệu
và nhiễu. Thứ hai,
2
0

lOMoARcPSD| 36067889
, ta có:
iểm tín hiệu.
1
2

lOMoARcPSD|36067889
.
Hình 6.18: Các iểm tín hiệu của tín hiệu nhị phân trực giao
Ta thay vào biểu thức ộ o tương quan trong (6.67) ể nhận ược (,
1
) và (,
2
). Xác suất lỗi là xác suất ể (,
2
) > (,
1
).
(|
1
) = [(,
2
) > (,
1
)] = [ (6.101)
Do
1
và
2
là các biến ngẫu nhiên gaussian ộc lập thống kê có giá trị trung bình
bằng 0 và phương sai
2
0
, biến ngẫu nhiên x =
2
-
1
cũng là biến ngẫu nhiên
gaussian có giá trị trung bình bằng 0 và phương sai
0
. Do ó:
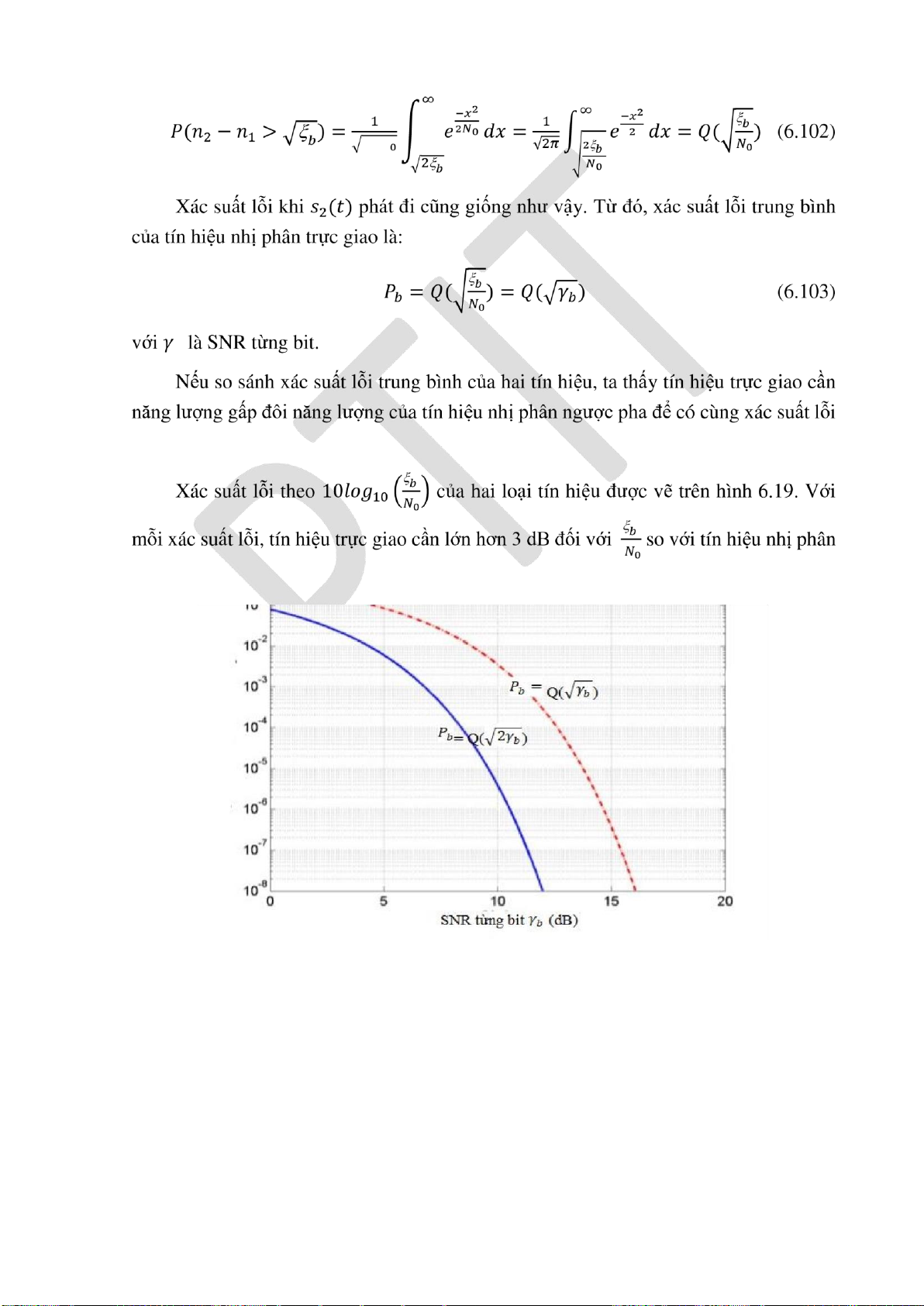
lOMoARcPSD| 36067889
2

lOMoARcPSD|36067889
trung bình.
ngược pha.
Hình 6.19: Xác suất lỗi cho các tín hiệu nhị phân
6.2.4.2. Xác suất lỗi tín hiệu trực giao M mức
Với các tín hiệu trực giao cùng năng lượng, bộ xác ịnh tối ưu sẽ chọn tín hiệu có ộ
o tương quan chéo lớn nhất với vectơ , nghĩa là:
(,
) = .
=1
, (6.104)
Để tính xác suất lỗi, ta giả sử tín hiệu
1
ược truyền i. Vectơ tín hiệu thu ược là:
= [
] (6.105)
với:
1
,
2
là các biến ngẫu nhiên gaussian ộc lập thống kê, có giá trị trung bình
bằng 0 và phương
2
=
0
. Đầu ra của dãy M bộ tương quan là:
(,
1
) = +
1
)
(,
2
) = (6.106)
………………………
(,
) =

lOMoARcPSD|36067889
1
=
+
1
1
(
1
)=
1
0
(
1
)
2
0
(
(
)
=
1
0
2
0
Khi chuẩn hóa bằng cách chia tất cả các biểu thức (6.106) cho , hàm mật ộ phân
bố xác suất của tín hiệu ở ầu ra bộ tự tương quan thứ nhất ( ) là:
(6.107)
và các hàm mật ộ phân bố xác suất của các tín hiệu ầu ra 1 bộ tương quan khác là:
, (6.108)
Xác suất xác ịnh úng là:
(
2
<
1
,
3
<
1
<
1
|
1
) (
1
)
1
(6.109)
với: P(
<
1
|
1
) là xác suất ồng thời ể tất cả
2
,
3
ều nhỏ
hơn
1
. Do {
} là ộc lập thống kê nên xác suất ồng thời là tích của 1 xác suất sau:
(
(
)
, = 2, . . , (6.110)
Các xác suất này là giống nhau với và xác suất ồng thời là lũy thừa
bậc 1 của một xác suất. Từ ó, xác suất xác ịnh úng là:
1
dx
) (
1
)
1
(6.111)
và xác suất lỗi ký hiệu là:
(6.112)
2
1 ( 1
dx ) ] 2 dy (6.113)
Xác suất lỗi khi 1 tín hiệu còn lại ược truyền i cũng úng như vậy. Do tín
hiệu là ồng khả năng khi truyền nên
là xác suất lỗi trung bình của một ký hiệu.
Khi so sánh hiệu quả các phương pháp iều chế số, ta muốn biểu diễn xác suất lỗi
theo tỷ số SNR từng bit là thay cho SNR từng ký hiệu . Với =
2
, mỗi ký hiệu
2
2
1
2
0

lOMoARcPSD|36067889
(
)
2
1
1
0 0
gồm bit thông tin và
=
và ta có thể thay vào (6.113).
Đôi khi ta cũng muốn chuyển xác suất lỗi ký hiệu thành dạng tương ương là xác
suất lỗi từng bit. Với các tín hiệu trực giao ồng xác suất, lỗi của các ký hiệu là ồng khả
năng và bằng:
=
(6.114)
1
Số lượng trung bình các bit bị lỗi trong ký hiệu có ộ dài là:
1
2
= 2
1
(6.115)
=1
và xác suất lỗi trung bình một bit là:
21
=
2
1
2
, 1 (6.116)
Đồ thị trên hình 6.20 biểu diễn xác suất lỗi bit theo SNR từng bit . Ta thấy rằng
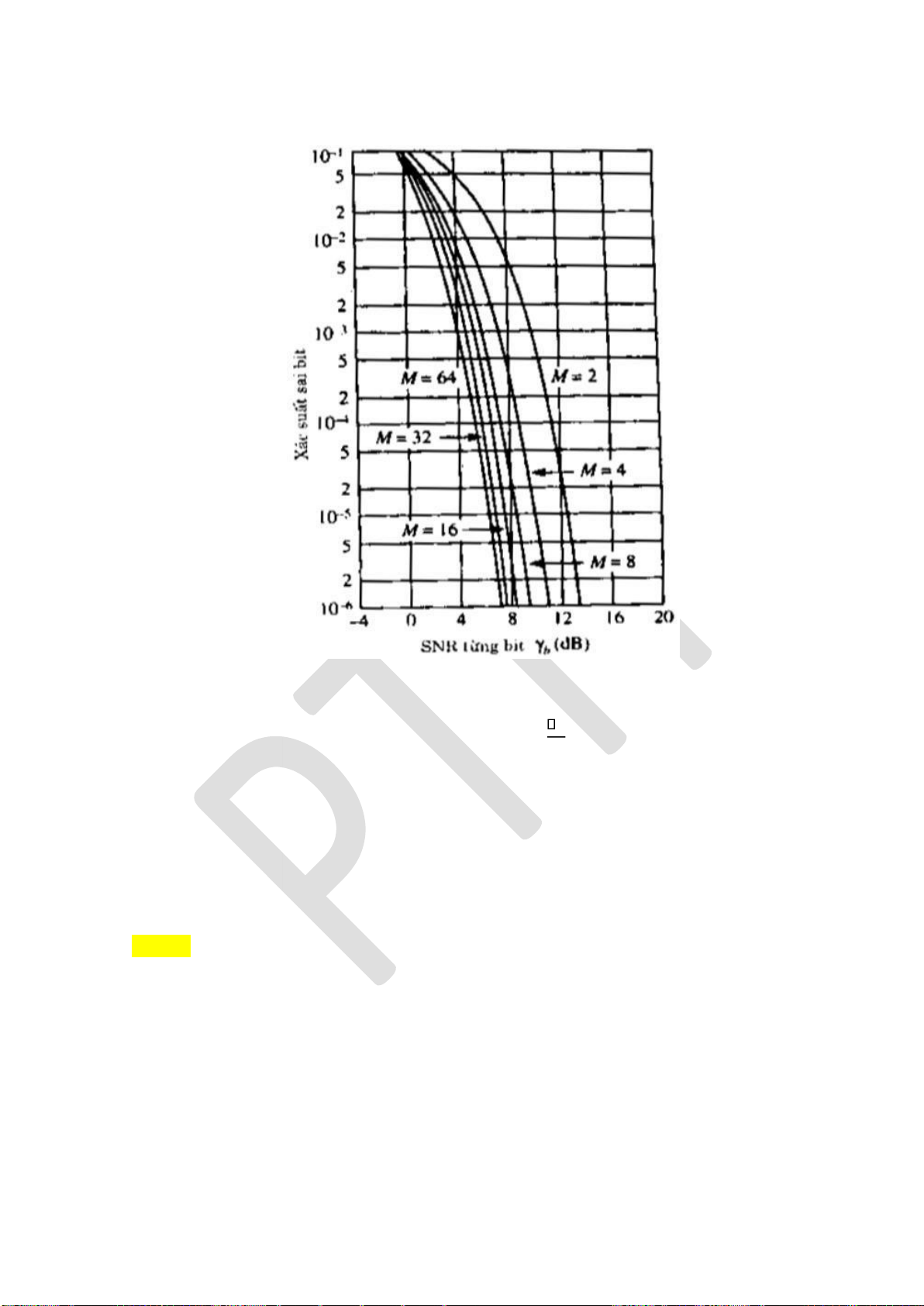
lOMoARcPSD| 36067889
0 khi tăng
số lượng tín hiệu M, có thể giảm SNR từng bit ể có cùng một xác suất lỗi. ể xác
suất lỗi bé tùy ý khi
hiệu.
Hình 6.20:
Xác suất lỗi
bit ối với thu liên kết tín hiệu trực giao
V
ấn ề
bây gi
ờ
là
xác ị
nh gi
ớ
i h
ạn dướ
i c
ủ
a
0
. Câu tr
ả
l
ời ược trình bày dưới ây.
Ta kh
ả
o sát
ảnh hưở
ng lên xác su
ấ
t l
ỗ
i
khi tăng
c
ủ
a các tín hi
ệ
u tr
ực giao. Để
ơn giả
n trong bi
ể
u di
ễ
n toán h
ọ
c
, trướ
c h
ết ta xác ị
nh gi
ớ
i h
ạ
n trên c
ủ
a xác su
ấ
t l
ỗ
i ký
(6.113)
. N
ế
u ta xét b
ộ
xác ị
nh tín hi
ệ
u tr
ự
c giao
m
ức như mộ
t b
ộ
ưa ra
1
quy
ế
t

lOMoARcPSD|36067889
Nhắc lại rằng xác suất lỗi của các ký hiệu trực giao nhị phân ược xác ịnh bởi
ịnh giữa ầu ra của bộ tương quan (,
) với ầu ra khác (,
),
thì xác suất lỗi bị chặn trên giới hạn hợp của sự kiện. Điều ó có nghĩa là nếu
biểu thị sự kiện (,
) > (,
) với thì ta có
=
=1
=1
(
)
và:
(M
2
= ( (6.117)
Giới hạn này có thể ơn giản hơn nữa nếu xét giới hạn trên của :
<
2
0
(6.118)
và
<
2
0 = 2
.
2
0 . Như vậy:
(
2 2)
0
< 2
2
(6.119)
lớn hơn 22 hay:
Khi (hay ), xác suất lỗi tiến t
ới 0, do ó
0
> 22 = 1,39 (1,42 ) (6.120)
0
Giới hạn trên của xác suất lỗi chỉ ra rằng nếu > 1,42 , ta có thể giảm tùy
ý
. Tuy nhiên giới hạn hợp không phải là giới hạn trên chặt do giới hạn trên của hàm
> 4ln2.
là không chặt. Về sau ta sẽ thấy giới hạn xét ở trên là tương ối chặt với
0
0
< 4ln2, giới hạn trên chặt hơn của
là:
Với
2

lOMoARcPSD|36067889
(
2
=
1
2
)
0
< 2 (6.121)
Khi thì
0, ta có:
> ln2 = 0,693 1,6 dB) (6.122)
0
Như vậy, 1,6 là giá trị cực tiểu của SNR từng bit ể có thể giảm xác suất lỗi
nhỏ tùy ý khi . Giới hạn này gọi là giới hạn Shannon cho kênh có nhiễu cộng
gaussian (AWGN).
6.2.4.3. Xác suất lỗi tín hiệu mã nhị phân M mức
Các tín hiệu mã nhị phân ược biểu diễn bởi các vectơ tín hiệu:
= [
1
2
], = 1, 2, . . . . , . (6.123)
Với
= ± / với mọi và , là ộ dài của từ mã và cũng là số chiều của các tín
hiệu.
Nếu
()
là khoảng cách Euclide nhỏ nhất giữa tín hiệu thì xác suất lỗi ký hiệu
có giới hạn trên là:
()
2
()
2
< (
= (
(
2
0
)
(
4
0
)
]
(6.124)
< 2
Khoảng cách Euclide nhỏ nhất phụ thuộc vào việc chọn từ mã, nghĩa là phụ thuộc
vào việc thiết kế mã.
6.2.4.4. Xác suất lỗi tín hiệu PAM M mức
Tín hiệu PAM M mức ược biểu diễn hình học bởi M iểm tín hiệu trong không gian
một chiều với giá trị:
, m= 1,2, .... , M (6.125)
với:
là năng lượng xung cơ bản () .Các giá trị biên ộ là:
lOMoARcPSD| 36067889
(6.126)
(6.127)
=
(
2
)
,
=1,2,....,
và kho
ả
ng cách Ecuclide gi
ữa hai iể
m tín hi
ệ
u k
ế
nhau là
2
:
=
1
=1
=
2
2
(
2
)
2
=1
=
2
2
[
1
3
(
2
1
)
]
=
1
6
(
2
1
)
2
M
ột cách tương ương, ta có thể
ặc trưng các tín hiệ
u này b
ở
i công su
ấ
t trung
bình:
=
=
1
6
(
2
1)
2
(6.128)
Xác su
ấ
t l
ỗ
i trung bình cho tín hi
ệ
u PAM M m
ứ
c có th
ể
xác ị
nh theo lu
ậ
t c
ực ạ
i
hóa ộ
o tương quan trong (
. B
6.67)
ộ
xác ị
nh so sánh tín hi
ệ
u
ở
ầ
u ra b
ộ
gi
ải iề
u
ch
ế
v
ớ
i
1
c
ậ
n t
ại iể
m gi
ữ
a các giá tr
ị
biên ộ
như trên hình 6.21
và quy
ết ị
nh
ch
ọ
n các giá tr
ị
biên ộ
sát
nh
ấ
t.
lOMoARcPSD|36067889
Hình 6.21: Các cận là iểm giữa các giá trị biên ộ liên tiếp
Việc ánh dấu các cận cho phép tính xác suất lỗi. Nếu giá trị biên ộ thứ ược truyền
i thì tín hiệu ầu ra bộ giải iều chế là:
=
+ (6.129)
với là biến ngẫu nhiên có giá trị trung bình bằng 0 và phương sai
1
2
0
. Nếu tất cả
các giá trị biên ộ là ồng xác suất tiên nghiệm thì xác suất xác ịnh ký hiệu sai trung bình
là xác suất ể giá trị biến ngẫu nhiên vượt qua một nửa hiệu giá trị biên ộ của hai mức
liên tiếp. Tuy nhiên khi một trong hai giá trị biên ộ ±( truyền i, sai số chỉ xảy ra
theo một chiều. Ta có:
= 12/0
(| | > 2
0
/2
/2
)
(6.130)
/0 0
Xác suất lỗi trong (6.130) có thể ược biểu diễn theo công suất trung bình truyền i.
Từ (6.128) và từ:
2
=
(
2
1
6
)
0
(6.131)
Thay
2
vào (6.130) ta nhận ược xác suất lỗi ký hiệu trung bình theo công suất
trung bình là:
(6.132)
=
1
2
2
1
)
=
1
2

lOMoARcPSD|36067889
=
2
(
1
)
(
6
(
2
1
)
0
)
=
2
(
1
)
(
6
(
2
1
)
0
)
=
2
(
1
)
(
(
6
2
)
(
2
1
)
0
)
trong ó:
=
là năng lượng trung bình.
Khi vẽ xác suất lỗi ký hiệu cho tín hiệu PAM mức, ta dùng SNR như tham số.
Do =
và =
2
, (6.132) có thể viết thành:
(6.133)
với:
=
là năng lượng trung bình ứng với một bit và
/
0
là SNR trung
bình ứng với một bit. Hình 6.22 vẽ xác suất lỗi ký hiệu theo 10
10
(
/
0
) với
là tham số. SNR theo bit tăng 4 dB khi tăng gấp ôi và giữ nguyên xác suất lỗi.
6.2.4.5. Xác suất lỗi tín hiệu PSK M mức
Tín hiệu iều chế pha số có thể biểu diễn như sau:
() = () cos [2
+
2
( , (6.134)
và biểu diễn vectơ tương ứng:
( ( 1) ] (6.135)
với:
=
1
2
là năng lượng mỗi tín hiệu và () là xung của tín hiệu truyền i. Do các
tín hiệu có cùng năng lượng, bộ xác ịnh tối ưu trong (6.67) tính các ộ o tương quan:
(,
) = .
, = 1, (6.136)
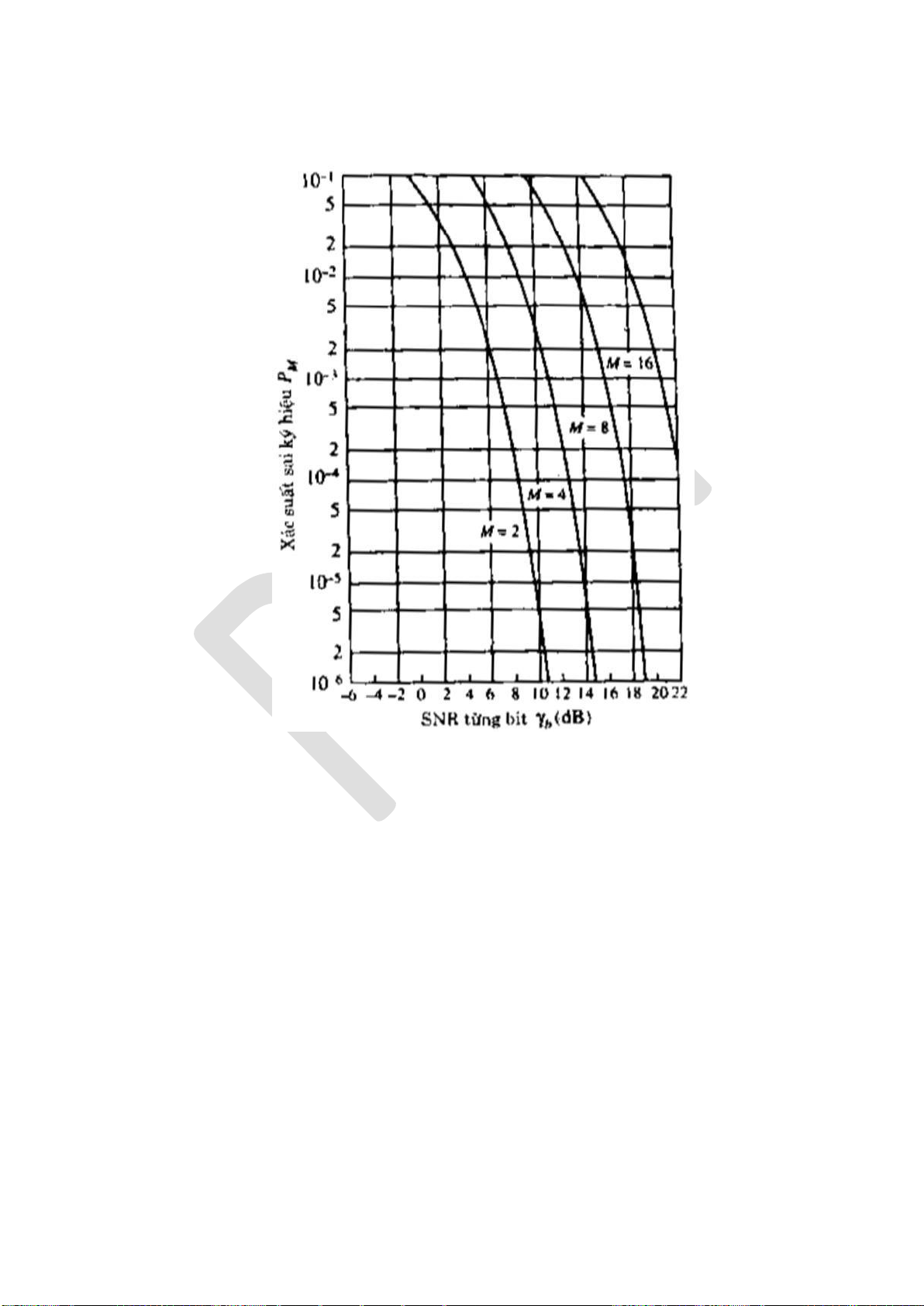
lOMoARcPSD| 36067889
Nói cách khác, vectơ tín hiệu thu ược = [
1
2
] ược chiếu trên vectơ tín hiệu
và
sẽ
chọn tín hiệu ứng với hình chiếu lớn nhất. xác ịnh pha này tính pha của tín hiệu ứng với
và chọn vectơ tín hiệu
có pha gần với nhất. Pha của là:
Hình 6.22:
Xác suất lỗi
tín hiệu PAM
B
ộ
xác ịnh tương quan mô tả
ở
trên là tương ương vớ
i b
ộ
xác ị
nh pha mà b
ộ

lOMoARcPSD|36067889
2
= arctag
1 (6.137)
Ta sẽ các ịnh hàm mật ộ phân bố xác suất của
, từ ó sẽ tính xác suất lỗi. Xét
trường hợp tín hiệu truyền i có pha
= 0, ứng với tín hiệu
1
().Vectơ tín hiệu truyền
i là :
(6.138)
và vectơ tín hiệu thu ược có các thành phần :
(6.139) Do
1
và
2
là hai biến ngẫu nhiên ồng thời nên và
21 = 22 = 20 = 2 .Ta có:
(
1
,
2
) =
(6.140) Hàm mật ộ phân bố xác suất của
, ược xác ịnh khi ổi biến từ (
1
,
2
)
thành:
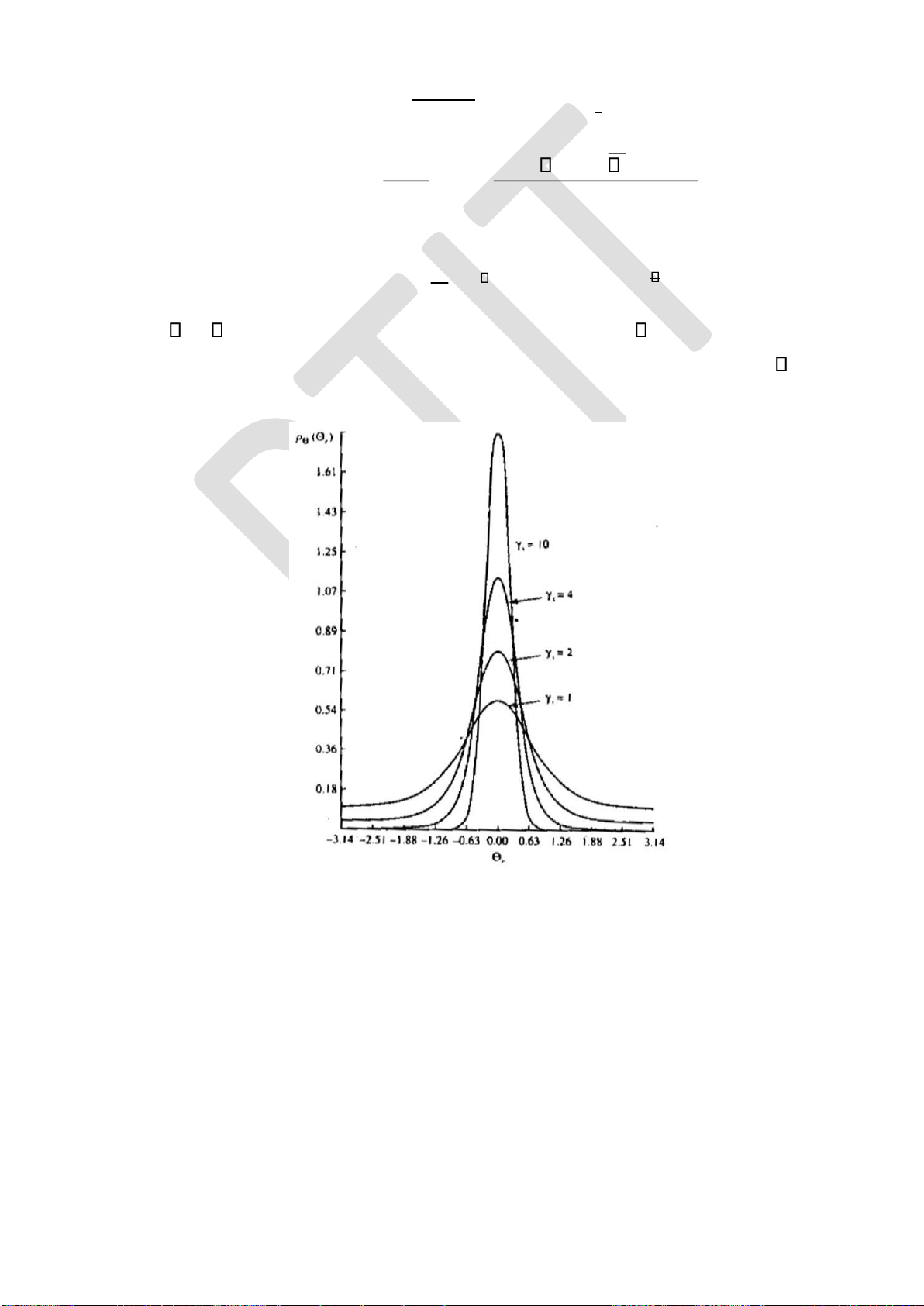
lOMoARcPSD| 36067889
2
=
1
2
+
2
2
,
=
arctag
1
2
(6.141)
,
(
,
)
=
2
2
[
2
+
2
cos
2
2
]
L
ấ
y tích phân c
ủ
a
,
(
,
)
theo V ta có
(
)
:
(
)
=
,
(
,
)
0
=
1
2
2
sin
2
(
4
cos
)
/2
0
(6.142)
v
ớ
i:
=
/
0
. Hình 6.23 v
ẽ
(
)
v
ớ
i m
ộ
t s
ố
giá tr
ị
c
ủ
a
, khi tín hi
ệ
u truy
ền i
có pha b
ằ
ng 0. Chú ý r
ằ
ng
(
)
càng h
ẹ
p và c
ực ạ
i t
ạ
i
=0
càng cao n
ế
u
càng
l
ớ
n.
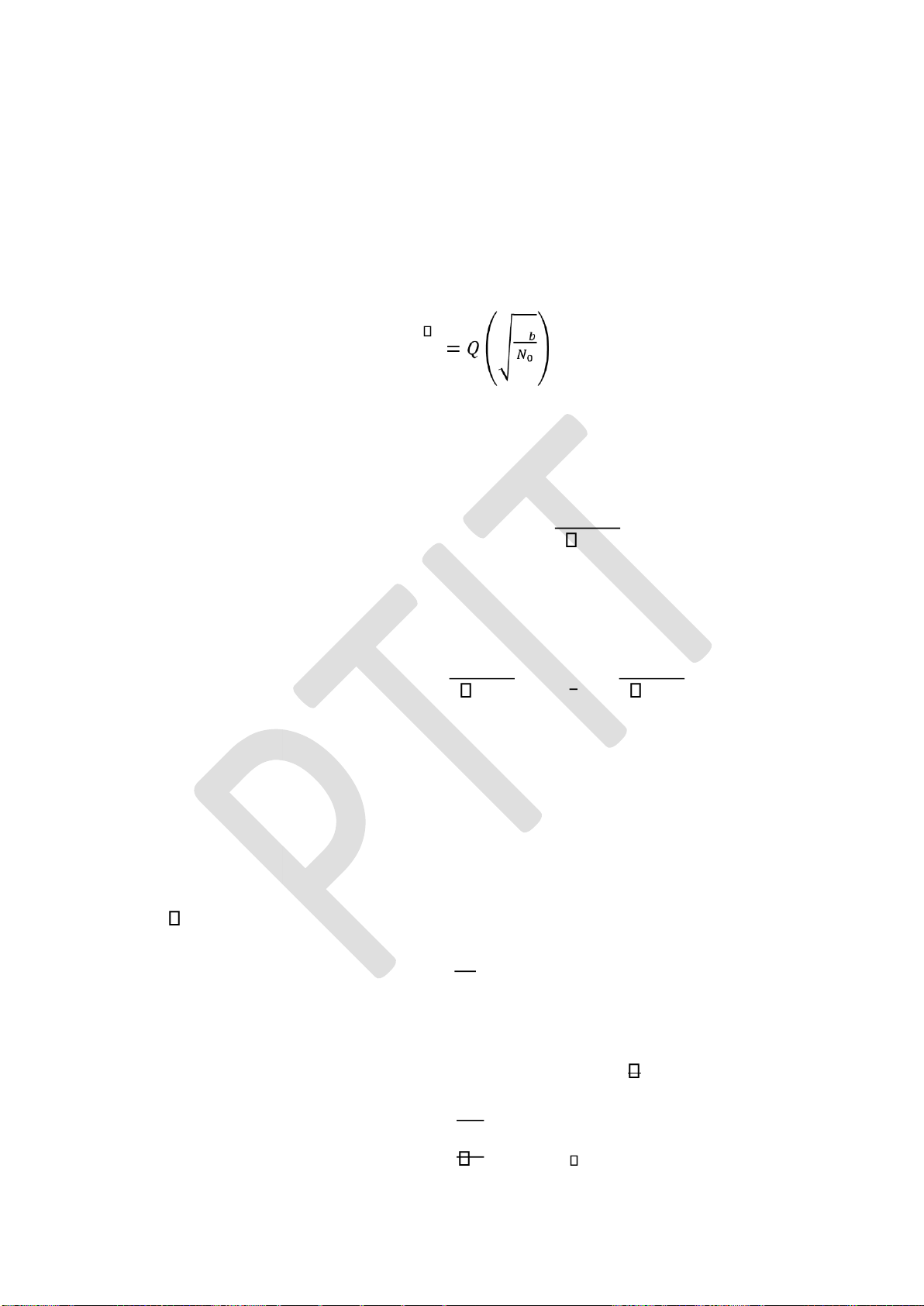
lOMoARcPSD|36067889
2
)
2
=
[
(
2
/
0
)]
2
4
=2
(
2
/
0
)[
1
2
(
2
/
0
)]
Hình 6.23: Hàm mật ộ phân bố xác suất
(
)
Khi
1
() ược truyền i, việc xác ịnh bị sai nếu nhiễu làm pha nằm ngoài khoảng
/
/. Như vậy, xác suất lỗi ký hiệu là:
/
/
(
)
(6.143)
Với iều chế pha nhị phân thì xác suất lỗi là:
2
2
(6.144)
Với = 4 ta có hai tín hiệu iều chế pha nhị phân và có pha vuông góc. Nếu không
có hiện tượng xuyên nhiễu giữa các tín hiệu trong hai sóng mang vuông góc thì xác suất
lỗi bit giống trong (6.144). Mặt khác, xác xuất lỗi ký hiệu với = 4 ược xác ịnh qua:
(6.145)
với:
là xác suất thu úng ký hiệu 2 bit. Chú ý rằng (6.145) rút ra từ tính ộc lập thống
kê của nhiễu cộng tác ộng lên hai thành phần vuông góc. Như vậy, xác suất lỗi ký hiệu
với = 4 là:
(6.146)
Với M > 4 thì xác suất lỗi ký hiệu
ược tính theo (6.142) bằng phương pháp số.
Hình 6.24 biểu diễn xác suất này theo SNR. Với
= 10
5
, sai khác giữa = 4 và
= 8 xấp xỉ 4dB và giữa = 8 và = 16 xấp xỉ 5dB. Với lớn, phải tăng gấp ôi số
pha tín hiệu cần tăng 6dB/bit ể có cùng một xác suất lỗi.
Để xấp xỉ xác suất lỗi ký hiệu khi lớn và SNR lớn, trước tiên ta xấp xỉ
(
).
Với
/
0
và |
/2 ta có:
(
2
cos
22
(6.147)
Thay (6.147) vào (6.143) và ổi biến từ
, thành
sin
, ta có:
/ sin2
cos

lOMoARcPSD|36067889
/
2
(6.148)
với =
2
và
=
.
2
sin
)
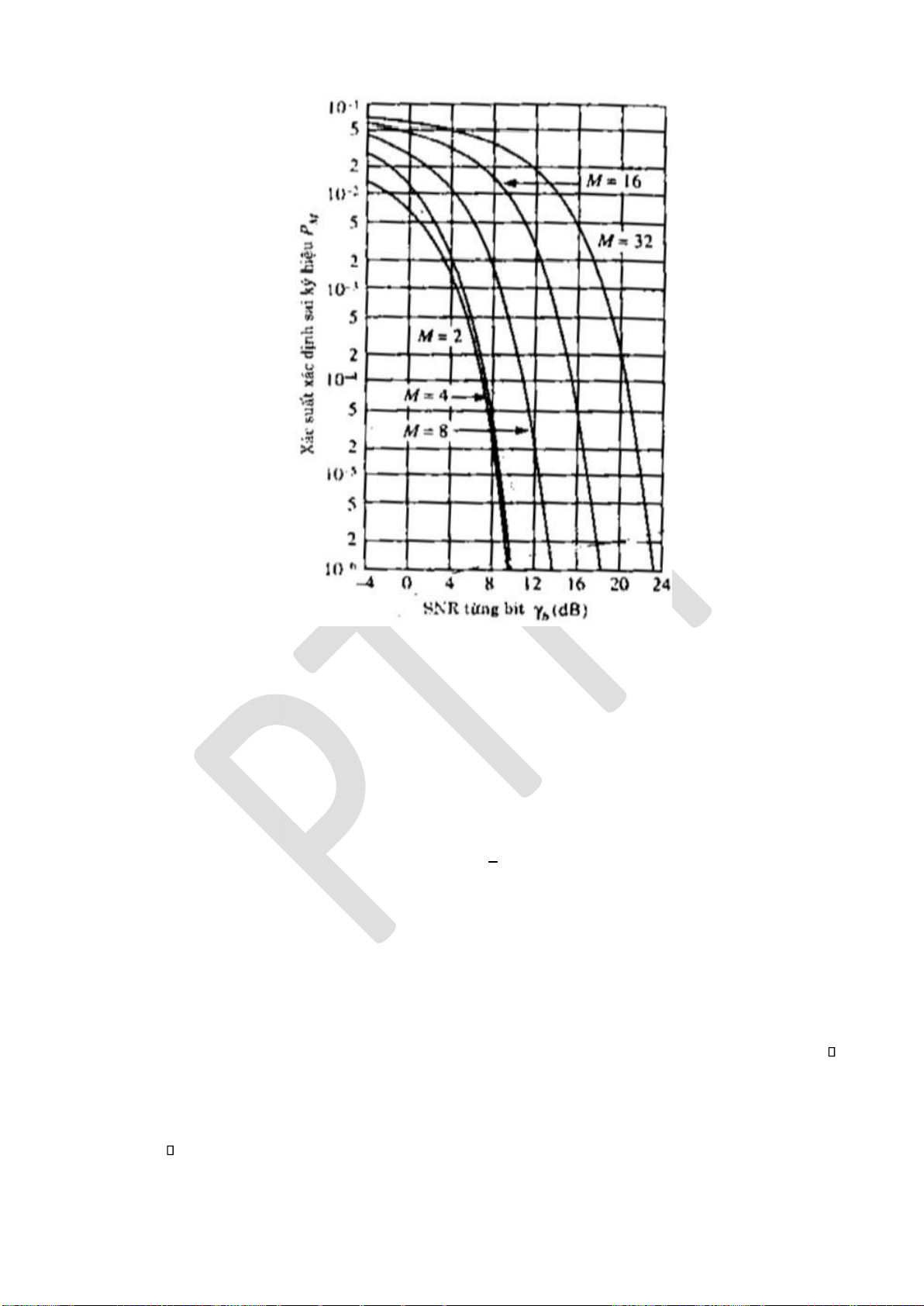
lOMoARcPSD|36067889
Trong việc giải iều chế tín hiệu PSK, ta giả thiết bộ giải iều chế xác ịnh chính
lý phi tuyến và tạo nên ộ dịch pha.Ví dụ với tín hiệu PSK nhị phân, tín hiệu thường ược
bình phương ể loại bỏ sự iều chế và thành phần tần số gấp ôi ược lọc và chia ôi tần số ể
xác ịnh tần số sóng mang và góc pha .Các phép biến ổi ó tạo nên sự dịch pha 180
trong pha sóng mang. Có thể loại bỏ dịch pha bằng cách mã hóa trong các pha khác nhau
giữa các tín hiệu liên tiếp. Với mã PSK nhị phân, bit thông tin 1 tạo dịch pha sóng mang
180 so với pha của tín hiệu trước ó và bit thông tin 0 không tạo dịch pha ối với tín hiệu
ã phát trước ó. Tín hiệu PSK ược xây dựng từ việc mã hóa như thế gọi là mã hóa vi sai.
Hình 6.24: Xác su
ấ
t l
ỗ
i ký hi
ệ
u v
ớ
i tín hi
ệ
u PSK
Xác su
ấ
t l
ỗ
i bit cho tín hi
ệ
u PSK
m
ứ
c có th
ể
rút ra t
ừ
vi
ệ
c bi
ến ổ
i ký hi
ệ
u
bit thành tín hi
ệu tương ứ
ng.
Khi mã Gray ượ
c s
ử
d
ụ
ng cho quá trình bi
ến ổ
i, hai ký
hi
ệ
u
bit ượ
c chuy
ể
n thành hai tín hi
ệ
u k
ề
nhau và sai khác v
ề
pha ch
ỉ
cho m
ộ
t bit.
V
ớ
i các l
ỗ
i
thông thườ
ng thì các ký hi
ệ
u
bit ch
ỉ
có 1 bit b
ị
l
ỗ
i. Xác su
ấ
t l
ỗ
i
bit ố
i v
ớ
i
tín hi
ệ
u PSK
m
ứ
c là:
1
(6.149)
xác pha sóng mang. Th
ự
c t
ế
, pha sóng mang
ượ
c tính t
ừ
tín hi
ệ
u thu qua vài phép x
ử
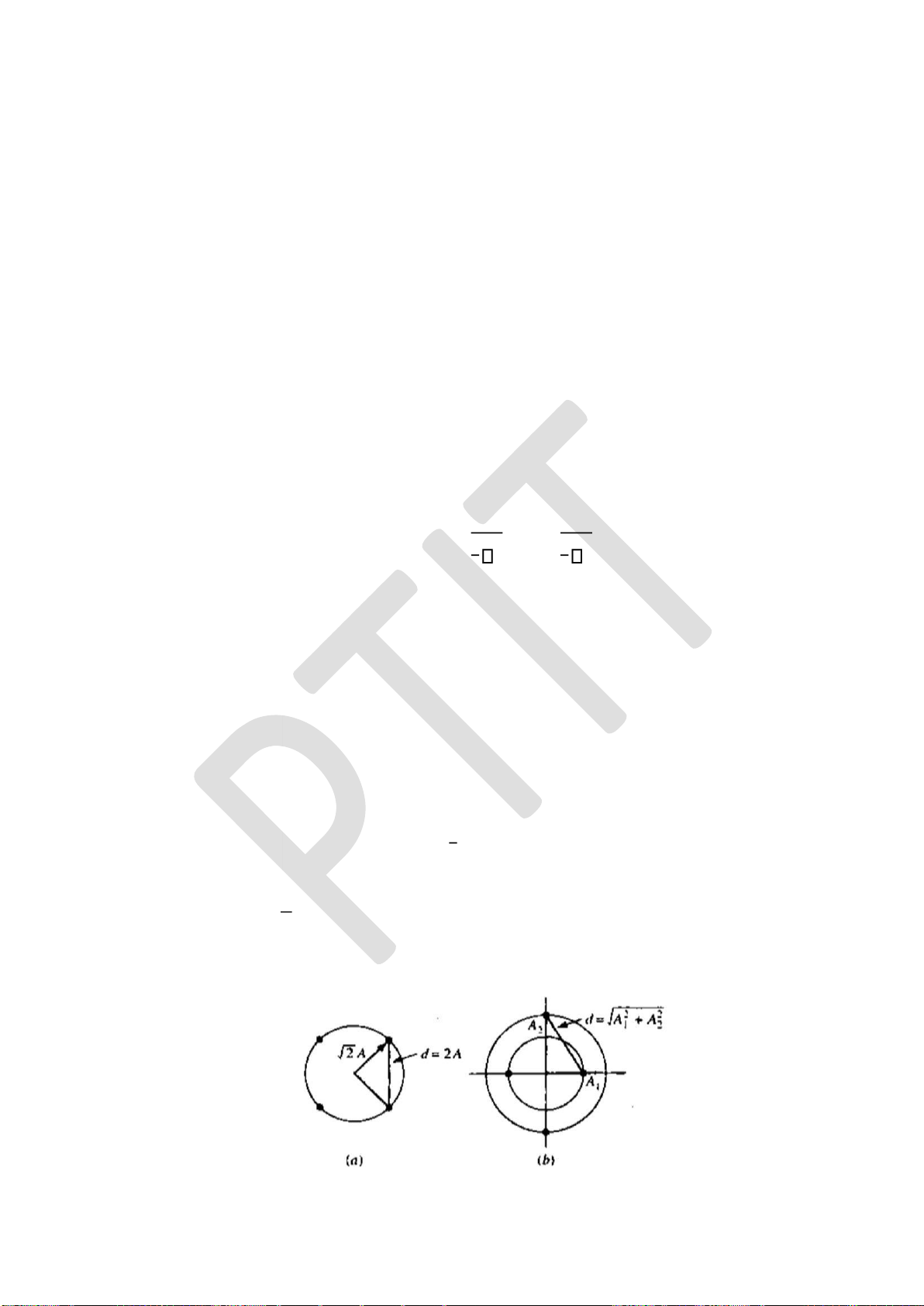
lOMoARcPSD|36067889
=
[
1
2
1
2
]
1
4
3
Bộ giải iều chế ứng với tín hiệu PSK mã hóa vi sai ược thực hiện như ã mô tả ở
trên và bỏ qua sự dịch pha.Tiếp theo bộ xác ịnh là bộ so sánh pha, nó so sánh pha của
tín hiệu thu qua hai khoảng thời gian tín hiệu liên tiếp ể xác ịnh thông tin. Bộ giải iều
chế liên kết tín hiệu PSK mã hóa vi sai tạo nên xác suất lỗi lớn hơn so với tín hiệu PSK
mã hóa pha tuyệt ối do việc giải iều chế pha sai dẫn tới việc giải mã sai trong hai khoảng
thời gian tín hiệu liên tiếp. Như vậy xác xuất lỗi trong trường hợp này gấp ôi xác xuất
lỗi ối với mã hóa pha tuyệt ối.
6.2.4.6. Xác suất lỗi tín hiệu QAM
Tín hiệu QAM có thể ược biểu diễn như sau:
() =
()2
()2
(6.150)
với:
và
là biên ộ của các thành phần vuông góc (chúng mang thông tin) và ()
là tín hiệu xung. Vectơ biểu diễn tín hiệu này là:
(6.151)
Để xác ịnh xác suất lỗi tín hiệu QAM, ta phải xác ịnh các iểm tín hiệu. Bắt ầu với
tín hiệu QAM với = 4 iểm. Hình 6.25 mô tả hai tập hợp bốn iểm tín hiệu. Tập hợp
thử nhất là tín hiệu iều chế pha bốn mức và tập hợp thứ hai là tín hiệu QAM hai mức
biến ộ, ký hiệu
1
và
2
với bốn giá trị pha. Do xác suất lỗi gắn với khoảng cách nhỏ
nhất giữa hai iểm tín hiệu và ta có
()
= 2 với cả hai loại tín hiệu. Công suất trung
bình của tín hiệu phát i (trên cơ sở tất cả các tín hiệu là ồng xác suất) với tín hiệu bốn
mức pha là:
= . 4.2
2
= 2
2
(6.152)
Với tín hiệu hai mức biên ộ, bốn mức pha, các iểm tín hiệu nằm trên hai ường tròn
bán kính , và
()
= 2, ta có:
= [2.3. ² + 2²] = 2² (6.153)
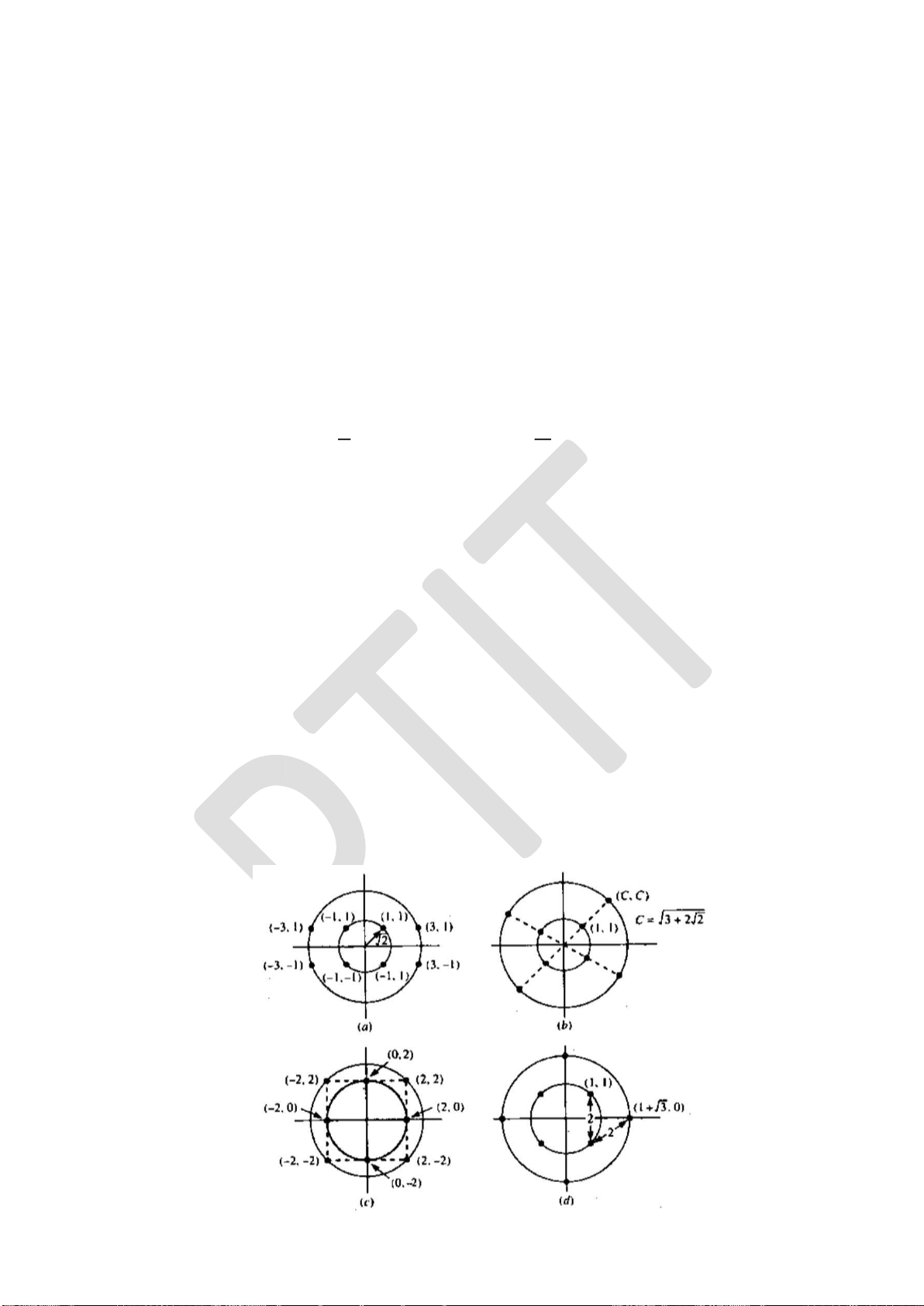
lOMoARcPSD| 36067889
=
1
(
2
+
2
)
=1
=
2
(
2
+
2
)
=1
Hình 6.25: Hai tập hợp 4 iểm tín hiệu
Như vậy với các ứng dụng trong thực tế, tỷ lệ sai số của hai tín hiệu này là như
nhau. Nói cách khác, không có sự khác biệt giữa hai loại tín hiệu này khi sử dụng trong
thực tế.
Xét trường hợp tín hiệu QAM với = 8. Có nhiều tập hợp các iểm tín hiệu, và ta
xét bốn tập hợp các iểm tín hiệu như trên hình 6.26, tất cả các loại tín hiệu ầu có hai mức
biên ộ và khoảng cách nhỏ nhất giữa hai iểm tín hiệu là 2. Các giá trị
(
,
) ược chuẩn hóa bởi . Giả sử các tín hiệu ống xác suất, công suất trung bình
của tín hiệu truyền i là:
(6.154)
với (
,
) là tọa ộ các iểm tín hiệu ã ược chuẩn hóa bởi A.
Hai tập hợp tín hiệu (a) và (c) có các iểm tín hiệu trong một hình chữ nhật và
= 6
2
. Tín hiệu trong hình (b) có công suất trung bình
= 6,83
2
và hình (d) là
= 4,73
2
. Như vậy tín hiệu (d) yêu cầu công suất thấp hơn 1 dB so với tín hiệu thứ
nhất và 1,6 dB so với tín hiệu thứ hai với cùng một xác suất lỗi. Loại tín hiệu này là loại
tín hiệu QAM với = 8 tốt nhất do yêu cầu về công suất nhỏ nhất với khoảng cách cực
tiểu giữa hai iểm tín hiệu ã cho.
Với , có nhiều khả năng lựa chọn tín hiệu QAM trong không gian hai chiều.
Ví dụ ta có thể chọn tín hiệu nhiều mức biên ộ như trên hình 5.5. Loại tín hiệu QAM
với = 16 này là mở rộng của tín hiệu QAM với = 8 tối ưu. Tuy nhiên loại tín hiệu
này không phải là tốt nhất trong kênh AWGN (loại tín hiệu QAM với = 16 trong
hình 5.5).

lOMoARcPSD|36067889
=
(
)
2
=2
(
1
)
(
3
1
0
)
[
(
3
(
1)
0
)]
2
(
3
(
1)
0
)
Hình 6.26: Bốn tập hợp iểm tín hiệu QAM tám iểm (M=8)
Tập hợp tín hiệu QAM chữ nhật có ưu iểm là dễ dàng tạo ra từ hai tín hiệu PAM
iều chế vào các tín hiệu pha vuông góc. Hơn nữa, chúng dễ dàng trong giải iều chế. Mặc
dù chúng không phải là tín hiệu QAM với tốt nhất, công suất trung bình yêu
cầu chỉ lớn hơn một chút so với tín hiệu tối ưu ể cho cùng một xác suất lỗi (với cùng
một khoảng cách cực tiểu). Vì những lý do ó, tín hiệu QAM mức hình chữ nhật thường
ược sử dụng trong thực tế.
Tín hiệu QAM chữ nhật với = 2
với chẵn tương ương với hai tín hiệu PAM
trong các tín hiệu mang vuông góc, mỗi tín hiệu có
/2
iểm tín hiệu. Do các tín
hiệu trong các thành phần pha vuông góc có thể phân tách một cách rõ ràng tại bộ giải
iều chế, xác suất lỗi của tín hiệu QAM có thể xác ịnh dễ dàng từ xác suất lỗi của tín hiệu
PAM. Xác suất xác ịnh úng của tín hiệu QAM mức là:
(6.155)
với: là xác suất lỗi của tín hiệu PAM mức với một nửa công suất trung bình trong
mỗi tín hiệu vuông góc của tín hiệu QAM tương ương. Sửa ổi xác suất lỗi của tín hiệu
PAM M mức, ta có:
(6.156)
với:
/
0
là SNR trung bình của mỗi ký hiệu. Xác suất lỗi ký hiệu tín hiệu QAM M
mức là:
)² (6.157)
Chú ý rằng kết quả này úng với k chẵn. Với k lẻ thì không có hệ thống PAM
mức tương ương. Tuy nhiên có thể dễ dàng xác ịnh tốc ộ xác ịnh sai cho tập hợp các iểm
tín hiệu hình chữ nhạt. Nếu sử dụng bộ xác ịnh tối ưu dựa trên ộ o khoảng cách thì xác
suất lỗi ký hiệu bị chặn trên bởi:
(6.158)

lOMoARcPSD|36067889
với và
/
0
là SNR trung bình từng ký bit. Xác suất lỗi ký hiệu ược vẽ trên
hình 6.27 theo SNR trung bình từng bit.
Với tín hiệu QAM không chữ nhật, ta có thể xác ịnh giới hạn trên của xác suất lỗi
bằng cách sử dụng giới hạn hợp:
< ( (6.159)
với:
()
là khoảng cách Euclide cực tiểu giữa hai iểm tín hiệu. Giới hạn này không
chặt khi lớn. Khi lớn, ta có thể xấp xỉ . bằng cách thay bằng M
n
, là số iểm
kề lớn nhất với khoảng cách
()
.
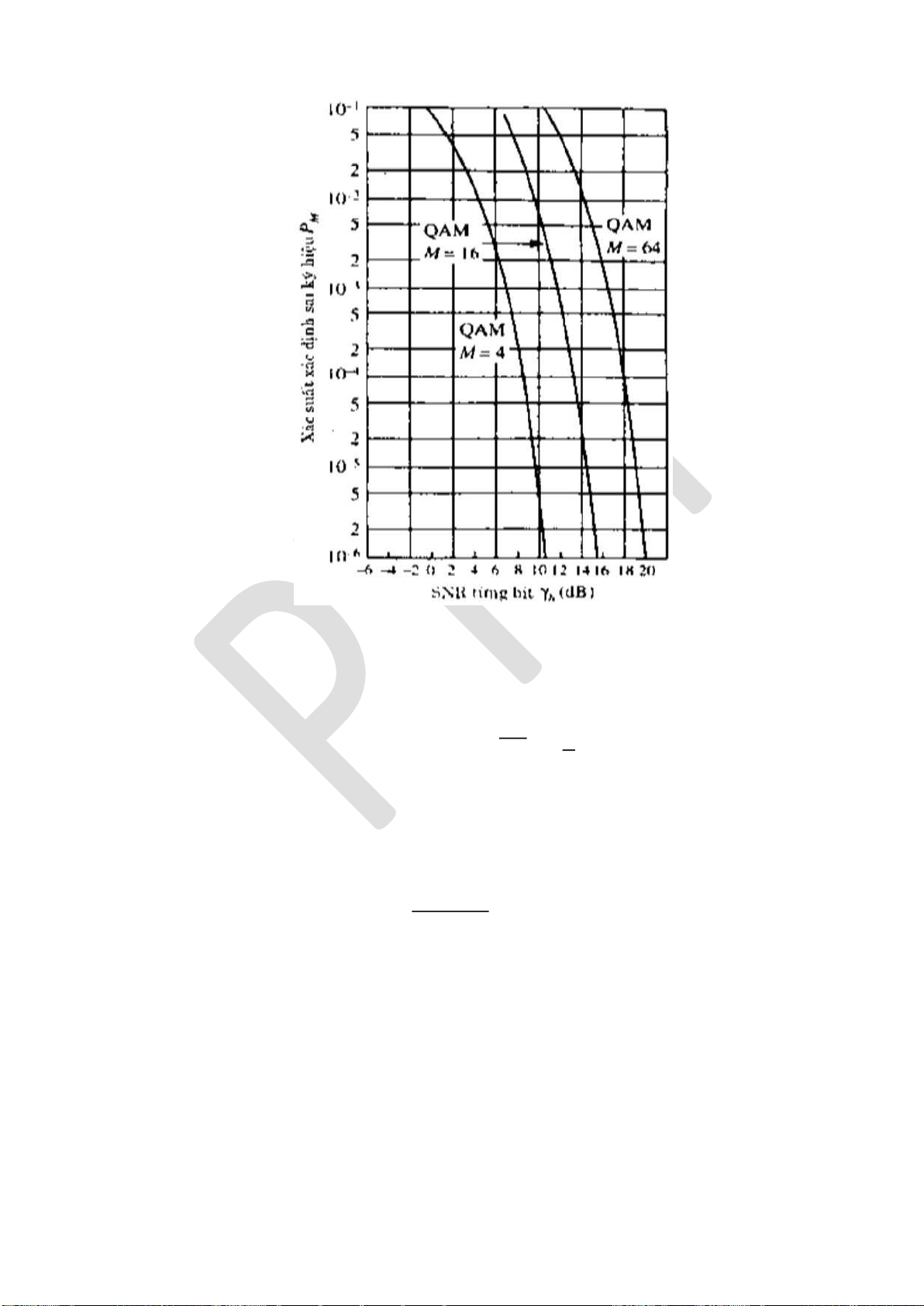
lOMoARcPSD|36067889
=
2
2
(/)
(6.161)
Với = 4 thì
= 1. Như vậy tín hiệu PSK và QAM bốn mức có hiệu quả tương
ương nhau với cùng SNR từng ký hiệu. Mặt khác, nếu > 4 thi
> 1 nên tín hiệu
QAM mức có ộ hiệu quả cao hơn so với tín hiệu PSK mức. Bảng 6.2 cho ta một
số liệu về tỷ số
Bảng 6.2: Lợi về SNR của tín hiệu QAM so với tín hiệu PSK
Hình 6.27:
Xác suất lỗi ký hiệu của
tín hiệu QAM
Ta có thể so sánh hiệu quả hai tín hiệu QAM và PSK với cùng một giá trị M và hai
tín
hiệu cùng có hai chiều. Xác s
u
ấ
t l
ỗ
i ký hi
ệ
u c
ủ
a tín hi
ệ
u PSK
M
m
ứ
c là:
(
2
)
(6.160)
v
ớ
i:
là SNR c
ủ
a t
ừ
ng ký hi
ệ
u. Do các xác su
ấ
t l
ỗ
i
ề
u ph
ụ
thu
ộc vào ố
i s
ố
c
ủ
a hàm
nên ta
có thể so sánh các ối số
này v
ớ
i nhau. T
ỷ
s
ố
hai ố
i s
ố
này là:
3
/
(1)

lOMoARcPSD|36067889
6.3. TỔNG KẾT CHƯƠNG
Chương 6 ã trình bày cụ thể về những vấn ề cơ bản của nhiễu như: ịnh nghĩa và
phân loại nhiễu, ưa ra các tham số ặc trưng mô tả nhiễu và giới thiệu một số loại nhiễu
cơ bản. Phần cuối của chương ã phân tích về bộ thu tối ưu, bao gồm: Khái niệm về bộ
thu tối ưu, Các vấn ề thu tối ưu và Bộ thu tối ưu cho kênh có nhiễu cọng Gaussian.
Câu hỏi/bài tập chương 6
1- Nêu ịnh nghĩa và phân loại nhiễu trong hệ thống truyền tin?
2- Trình bày về nhiễu trắng giới hạn băng tần?
3- Hãy trình bày các loại nhiễu xẩy ra trong tự nhiên?
4- Trình bày khái niệm về bộ thu tối ưu?
5- Vẽ sơ ồ cấu trúc của bộ thu cơ bản và cho biết các chức năng của các khối trong sơ
ồ?
6- Vẽ sơ ồ và nêu nguyên tắc hoạt ộng của bộ giải iều chế tương quan?
7- Vẽ sơ ồ và nêu nguyên tắc hoạt ộng của bộ giải iều chế dùng bộ lọc phối hợp?
8- Vẽ sơ ồ và nêu nguyên tắc hoạt ộng của bộ thu tối ưu với kênh có nhiễu AWGN
9- Cho hệ thống BPSK truyền qua kênh AWGN với mật ộ phổ công suất
0
=
2
10
10
[/],
=
2
/2, T là chu kỳ của bít và A là biên ộ tín hiệu. Xác ịnh giá
trị của A ể xác suất lỗi bít ạt ược 10
-6
, nếu tốc ộ dữ liệu là: a) 10Kb/s; b) 100Kb/s; c)
1Mb/s.
10- Một hệ thống truyền tin số QAM có tốc ộ 2400 symbol/s (baud). Nhiễu cộng ược giả
sử là nhiễu trắng và phân bố Gauss. Xác ịnh
/
0
ể ạt ược xác suất lỗi
10
5
với tốc ộ bit tương ứng là: a) 4800 bit/s; b) 9600 bit/s; c)19200 bit/s; d) Hãy
nhận xét dựa trên các kết quả nhận ược ở các câu trên.

lOMoARcPSD|36067889
Học viện Công nghệ Bưu chính Viễn thông
Downloaded by D?a (nyeonggot7@gmail.com)
- TÀI LIỆU THAM KHẢO-
[1] Bài giảng môn Truyền dẫn số, Học viện Công nghệ Bưu chính Viễn thông, 2014.
[2] Trần thị Ngân, Giáo trình“Cơ sở lý thuyết truyền tin”, Nhà xuất bản Hà Nội, 2007.
[3] PGS.TS. Nguyễn Bình, Bài giảng“Lý thuyết thông tin”, Học viện Công nghệ Bưu
chính Viễn thông, 2006.
[4] Đặng Văn Chuyết, Nguyễn Tuấn Anh, “Cơ sở lý thuyết truyền tin” tập 1. Nhà xuất
bản Giáo dục, 2003.
1995.
[5]
Stefan Host,
“Information and Communication Theory”
, IEEE Press, John Wiley &
Sons, 2019.
[6]
Wim C. van Etten,
“Introduction to Random Signals and Noise”
, John Wiley &
Sons, 2005.
[7]
John. G. Proaskis,
“Digital Communication”
, McGraw- Hill International Editions,

lOMoARcPSD| 36067889
Học viện Công nghệ Bưu chính Viễn thông
Downloaded by D?a (nyeonggot7@gmail.com)
221
Bấm Tải xuống để xem toàn bộ.




