


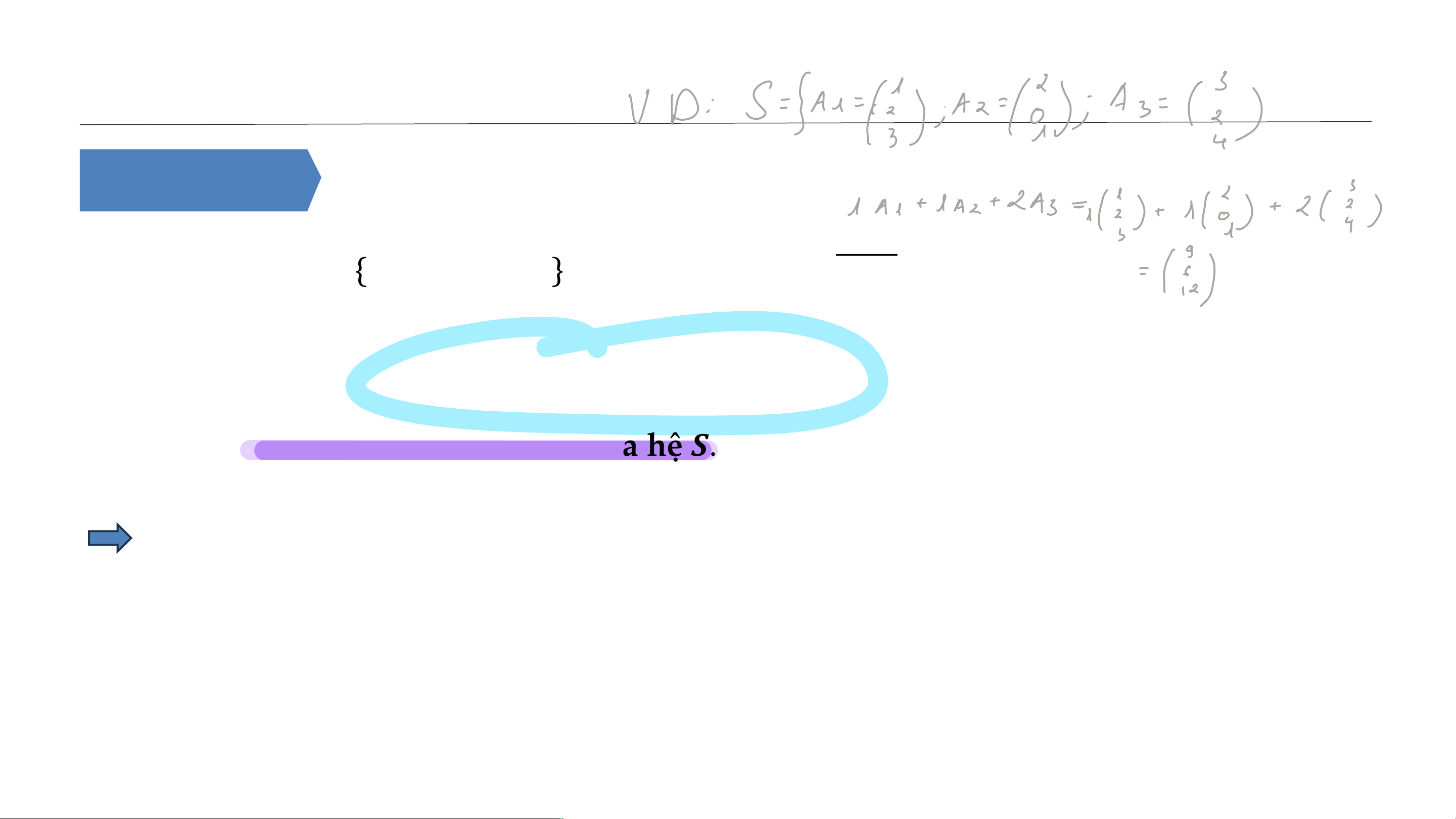




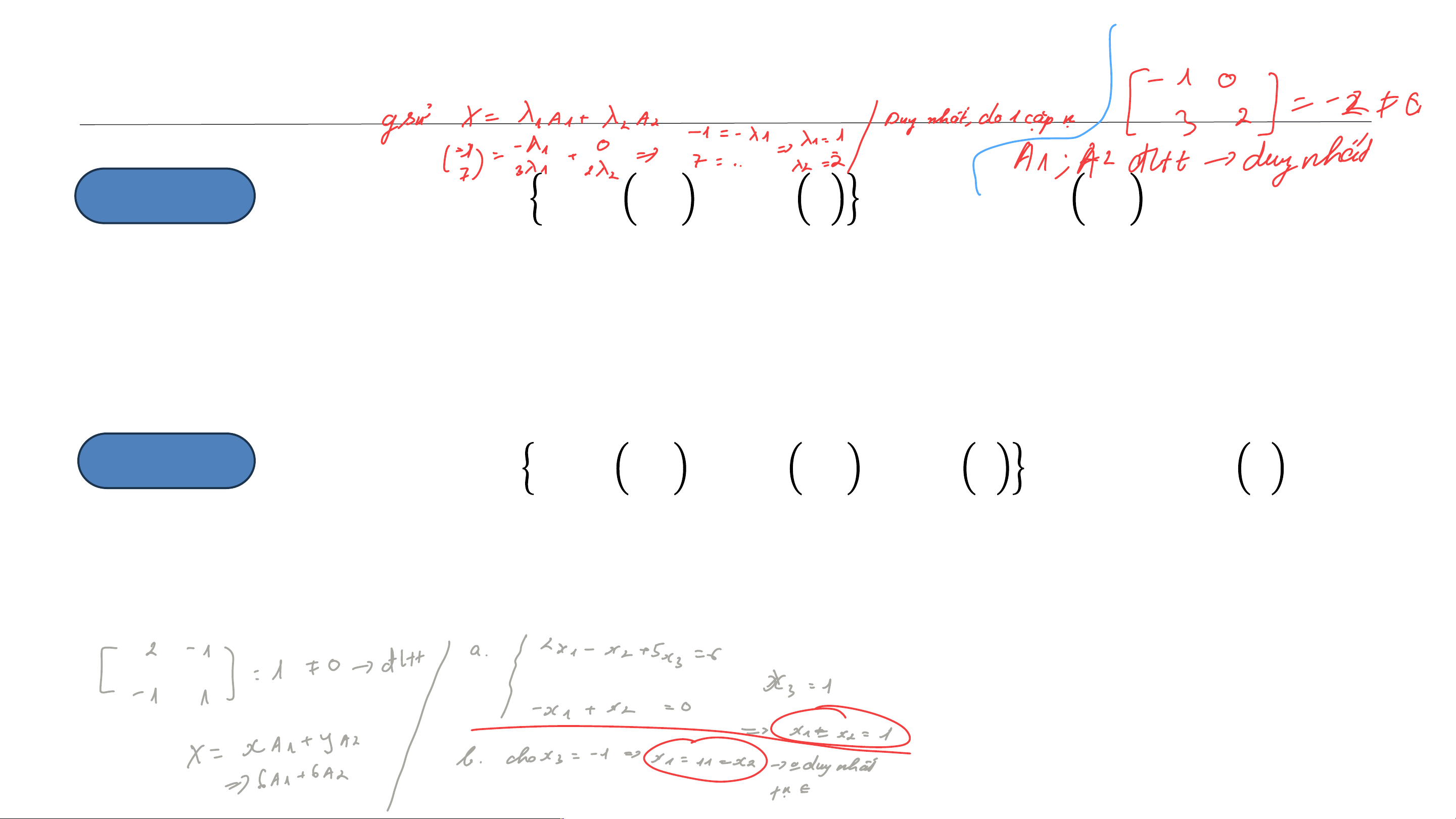


Preview text:
TOÁN CAO CẤP 1 TOÁN CAO CẤP 1 TỔNG QUAN MÔN HỌC
CHƯƠNG 1: KHÔNG GIAN VÉC TƠ ℝ𝑛
CHƯƠNG 2: MA TRẬN – ĐỊNH THỨC
CHƯƠNG 3: HỆ PHƯƠNG TRÌNH TUYẾN TÍNH
CHƯƠNG 4: HÀM SỐ MỘT BIẾN SỐ
CHƯƠNG 5: GIỚI HẠN VÀ SỰ LIÊN TỤC CỦA HÀM SỐ MỘT BIẾN SỐ
CHƯƠNG 6: ĐẠO HÀM VÀ VI PHÂN CỦA HÀM SỐ MỘT BIẾN SỐ CHƯƠNG 7: TÍCH PHÂN
CHƯƠNG 8: HÀM SỐ NHIỀU BIẾN SỐ BỘ MÔN TOÁN 2
CHƯƠNG 1: KHÔNG GIAN VÉC TƠ ℝ𝑛 1.1
Không gian véc tơ 𝒏 chiều ℝ𝒏 1.2
Các mối liên hệ tuyến tính trong ℝ𝒏 1.3
Cơ sở của không gian véc tơ ℝ𝒏 1.4
Cơ sở và hạng của hệ véc tơ 1.5 Bài tập BỘ MÔN TOÁN 3
1.1. KHÔNG GIAN VÉC TƠ 𝒏 CHIỀU ℝ𝒏 1.1.1. Các định nghĩa 1.1.2 Các phép toán 1.1.3
Không gian véc tơ n chiều ℝ𝒏 BỘ MÔN TOÁN 4
1.1.1. CÁC ĐỊNH NGHĨA Định nghĩa 1 𝒙𝟏 𝒙
Mỗi bộ gồm 𝒏 số thực 𝒙 𝟐
𝟏, 𝒙𝟐, … , 𝒙𝒏 được xếp có thứ tự dưới dạng cột …
hoặc dạng hàng 𝒙 𝒙
𝟏, 𝒙𝟐, … , 𝒙𝒏 gọi là một véc tơ 𝒏 chiều. 𝒏
Số thực 𝒙𝒊 được gọi là thành phần thứ 𝒊 của véc tơ đó, 𝒊 = 𝟏, 𝒏.
Các véc tơ thường kí hiệu bằng các chữ cái in hoa như 𝑿, 𝒀, 𝑨, 𝑩, … Định nghĩa 2
Véc tơ không 𝒏 chiều: 𝑶𝒏 = 𝟎, 𝟎, … , 𝟎 . Định nghĩa 3
Các véc tơ đơn vị 𝒏 chiều:
𝑬𝟏 = 𝟏, 𝟎, … , 𝟎 , 𝑬𝟐 = 𝟎, 𝟏, … , 𝟎 ,..., 𝑬𝒏 = 𝟎, … , 𝟎, 𝟏 . Định nghĩa 4
Hai véc tơ 𝒏 chiều bằng nhau
𝑿 = 𝒙𝟏, 𝒙𝟐, … , 𝒙𝒏 , 𝑿 = 𝒀 ⟺ 𝒙 𝒀 = 𝒚
𝒊 = 𝒚𝒊, ∀𝒊 = 𝟏, 𝒏. BỘ MÔN TOÁN 5
𝟏, 𝒚𝟐, … , 𝒚𝒏 . 1.1.2. CÁC PHÉP TOÁN
Cho hai véc tơ 𝒏 chiều 𝑿 = 𝒙𝟏, 𝒙𝟐, … , 𝒙𝒏 , 𝒀 = 𝒚𝟏, 𝒚𝟐, … , 𝒚𝒏 và 𝝀 ∈ ℝ.
Phép cộng hai véc tơ
𝑿 + 𝒀 = 𝒙𝟏 + 𝒚𝟏, 𝒙𝟐 + 𝒚𝟐, … , 𝒙𝒏 + 𝒚𝒏 .
Phép nhân một số thực với một véc tơ
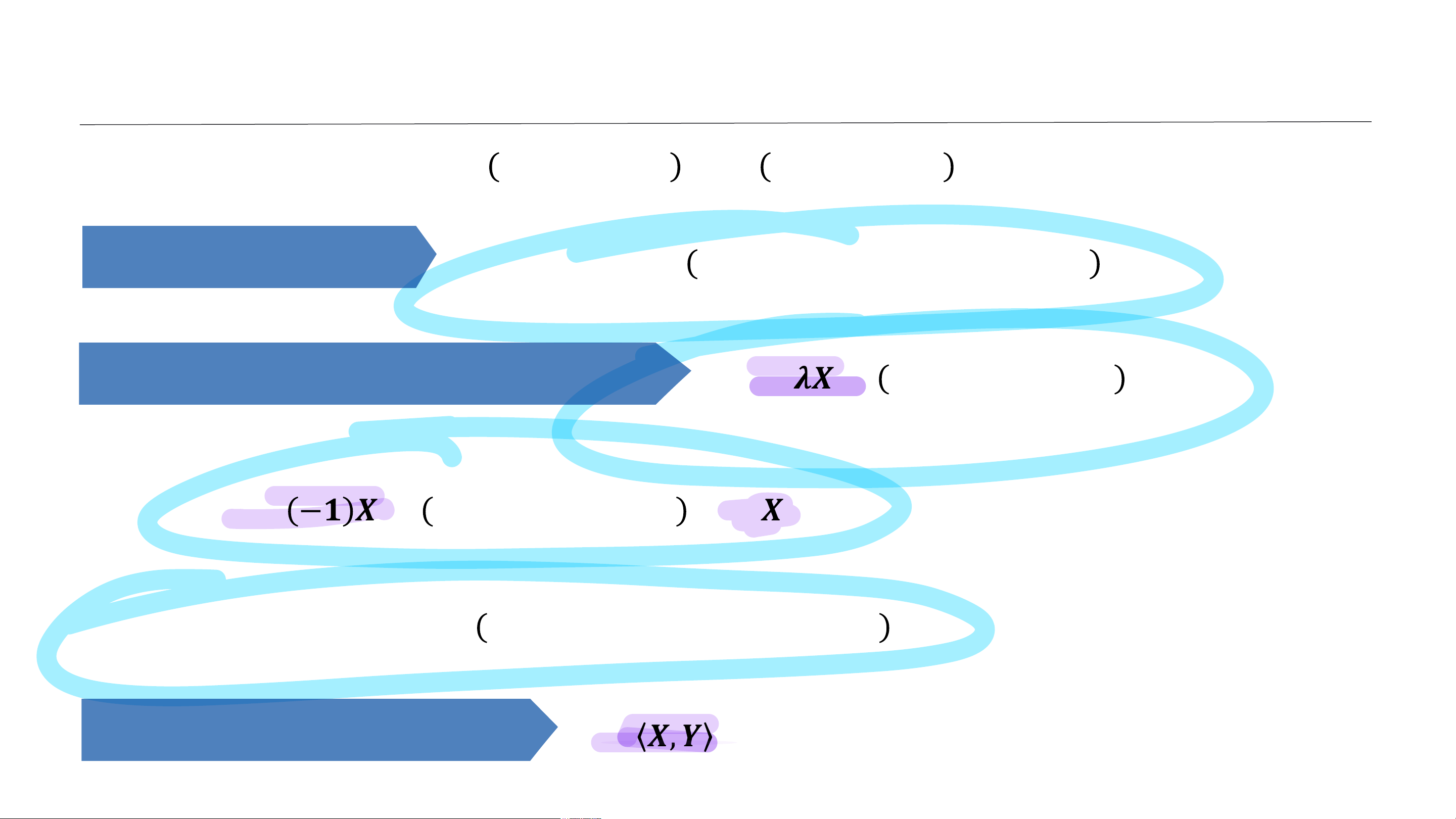
𝝀𝑿 = 𝝀𝒙𝟏, 𝝀𝒙𝟐, … , 𝝀𝒙𝒏 . Đặc biệt:
−𝟏 𝑿 = −𝒙𝟏, −𝒙𝟐, … , −𝒙𝒏 ≔ −𝑿 và
𝑿 − 𝒀 ≔ 𝑿 + (−𝒀) = 𝒙𝟏 − 𝒚𝟏, 𝒙𝟐 − 𝒚𝟐, … , 𝒙𝒏 − 𝒚𝒏 .
Tích vô hướng của hai véc tơ
𝑿, 𝒀 = 𝒙𝟏𝒚𝟏 + 𝒙𝟐𝒚𝟐 + ⋯ + 𝒙𝒏𝒚𝒏. BỘ MÔN TOÁN 6 1.1.2. CÁC PHÉP TOÁN Ví dụ 1.1:
Cho 𝑿 = 𝟐, 𝟏, 𝟑 ; 𝒀 = 𝟏, −𝟏, 𝟎 . Hãy tính:
a) 𝑿 + 𝒀
b) 𝑿 − 𝒀
c) 𝟐𝑿
d) 𝑿 + 𝟑𝒀
e) 𝟑𝑿 − 𝟐𝒀 f) 𝑿, 𝒀 BỘ MÔN TOÁN 7
1.1.3. KHÔNG GIAN VÉC TƠ n CHIỀU ℝ𝒏 Định nghĩa
Tập hợp tất cả các véc tơ n chiều cùng với hai phép toán: phép cộng hai véc tơ và phép
nhân một số thực với một véc tơ được gọi là không gian véc tơ n chiều. Kí hiệu: ℝ𝒏. BỘ MÔN TOÁN 8
1.2. CÁC MỐI LIÊN HỆ TUYẾN TÍNH TRONG ℝ𝒏 1.2.1.
Tổ hợp tuyến tính 1.2.2
Độc lập tuyến tính - phụ thuộc tuyến tính BỘ MÔN TOÁN 9
1.2.1. TỔ HỢP TUYẾN TÍNH Định nghĩa 1
Cho hệ véc tơ 𝑺 = 𝑨𝟏, 𝑨𝟐, … , 𝑨𝒎 ⊂ ℝ𝒏, 𝝀𝒊 ∈ ℝ, ∀𝒊 = 𝟏, 𝒎.
Biểu thức có dạng
𝝀𝟏𝑨𝟏 + 𝝀𝟐𝑨𝟐 + ⋯ + 𝝀𝒎𝑨𝒎
được gọi là một tổ hợp tuyến tính của hệ 𝑺. Nhận xét:
• Mỗi tổ hợp tuyến tính của hệ 𝑺 là một véc tơ 𝒏 chiều.
• Có vô số tổ hợp tuyến tính của hệ 𝑺 cho trước. BỘ MÔN TOÁN 10
1.2.1. TỔ HỢP TUYẾN TÍNH Định nghĩa 2
Ta nói véc tơ 𝒏 chiều 𝑿 được biểu diễn tuyến tính qua hệ 𝑺 (hay véc tơ 𝑿 là tổ hợp
tuyến tính của hệ 𝑺) nếu tồn tại các số thực 𝝀𝟏, 𝝀𝟐, … , 𝝀𝒎 sao cho:
𝑿 = 𝝀𝟏𝑨𝟏 + 𝝀𝟐𝑨𝟐 + ⋯ + 𝝀𝒎𝑨𝒎. Nhận xét:
• Véc tơ 𝑶𝒏 được biểu diễn tuyến tính qua mọi hệ véc tơ 𝒏 chiều.
• Mọi véc tơ 𝒏 chiều 𝑿 đều được biểu diễn tuyến tính qua hệ n véc tơ đơn vị 𝒏 chiều.
• Nếu véc tơ 𝒏 chiều 𝑿 được biểu diễn tuyến tính qua hệ 𝑺 thì véc tơ 𝑿 luôn được biểu
diễn tuyến tính qua mọi hệ véc tơ 𝒏 chiều chứa hệ 𝑺. BỘ MÔN TOÁN 11
1.2.1. TỔ HỢP TUYẾN TÍNH Ví dụ 1.2: BỘ MÔN TOÁN 12 AnTran
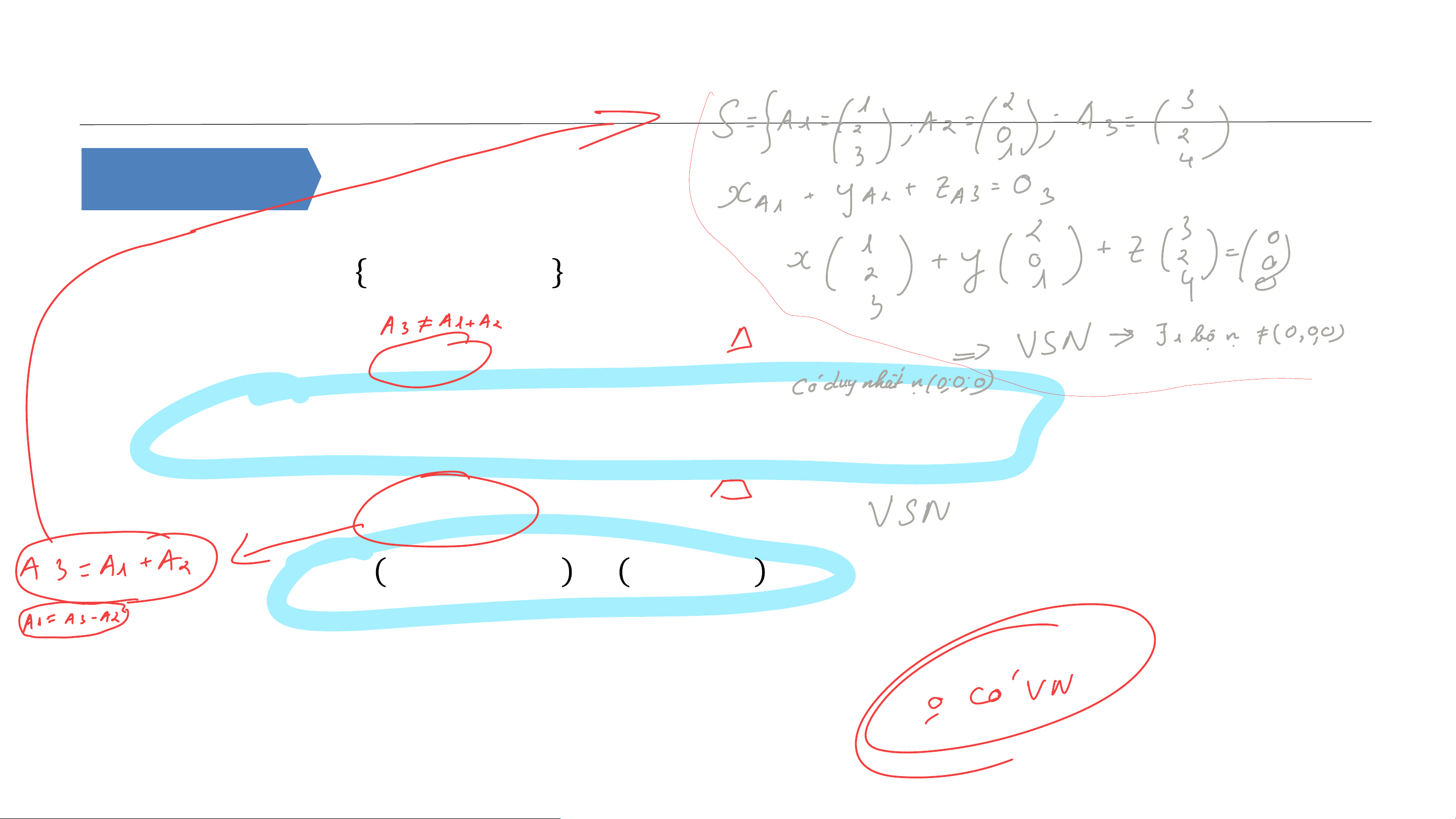
1.2.2. ĐỘC LẬP TUYẾN TÍNH - PHỤ THUỘC TUYẾN TÍNH Định nghĩa 3
Cho hệ véc tơ 𝑺 = 𝑨𝟏, 𝑨𝟐, … , 𝑨𝒎 ⊂ ℝ𝒏.
• Hệ 𝑺 được gọi là độc lập tuyến tính (ĐLTT) nếu
𝝀𝟏𝑨𝟏 + 𝝀𝟐𝑨𝟐 + ⋯ + 𝝀𝒎𝑨𝒎 = 𝑶𝒏 ⇔ 𝝀𝟏 = 𝝀𝟐 = ⋯ = 𝝀𝒎 = 𝟎.
• Hệ 𝑺 được gọi là phụ thuộc tuyến tính (PTTT) nếu
∃ 𝝀𝟏, 𝝀𝟐, … , 𝝀𝒎 ≠ 𝟎, 𝟎, … , 𝟎 sao cho
𝝀𝟏𝑨𝟏 + 𝝀𝟐𝑨𝟐 + ⋯ + 𝝀𝒎𝑨𝒎 = 𝑶𝒏. BỘ MÔN TOÁN 13
1.2.2. ĐỘC LẬP TUYẾN TÍNH - PHỤ THUỘC TUYẾN TÍNH Ví dụ 1.3: BỘ MÔN TOÁN 14
1.2.2. ĐỘC LẬP TUYẾN TÍNH - PHỤ THUỘC TUYẾN TÍNH Một số tính chất
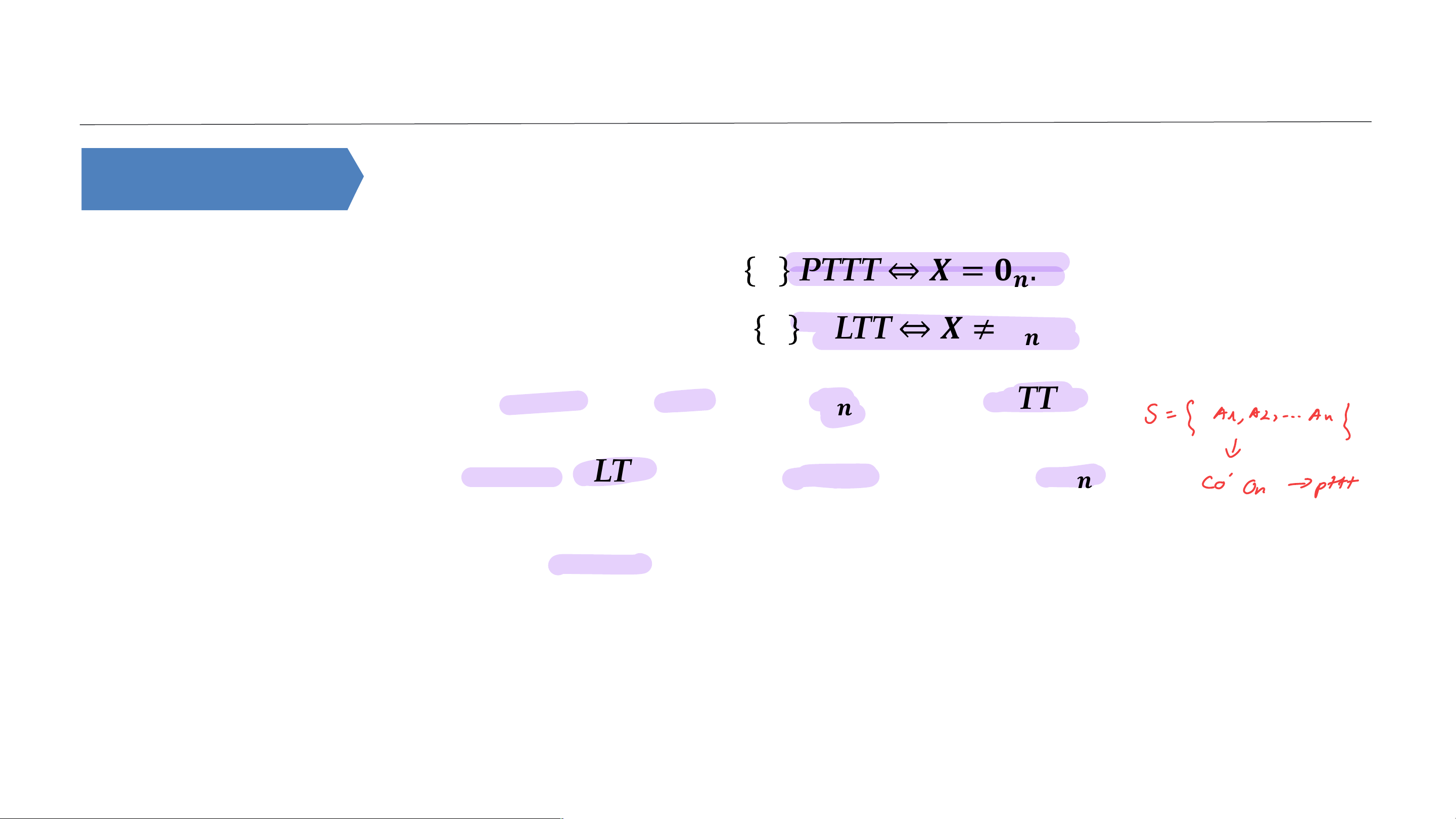
• Tính chất 1: Hệ chỉ gồm một véc tơ 𝒏 chiều 𝑿 PTTT ⇔ 𝑿 = 𝟎𝒏.
Hệ chỉ gồm một véc tơ 𝒏 chiều 𝑿 ĐLTT ⇔ 𝑿 ≠ 𝟎𝒏.
• Tính chất 2: Trong ℝ𝒏, nếu một hệ có chứa véc tơ 𝟎𝒏 thì hệ đó PTTT.
Hệ quả: Trong ℝ𝒏, nếu một hệ ĐLTT thì hệ đó không chứa véc tơ 𝟎𝒏.
• Tính chất 3: Nếu một hệ véc tơ PTTT thì mọi hệ chứa nó cũng PTTT.
Hệ quả: Nếu một hệ ĐLTT thì mọi hệ con khác rỗng của nó cũng ĐLTT. BỘ MÔN TOÁN 15
1.2.2. ĐỘC LẬP TUYẾN TÍNH - PHỤ THUỘC TUYẾN TÍNH Một số định lý
• Định lý 1. Hệ 𝑺 gồm m véc tơ (𝒎 ≥ 𝟐) PTTT khi và chỉ khi trong hệ tồn tại một véc
tơ được biểu diễn tuyến tính qua các véc tơ còn lại.
• Định lý 2. Nếu một véc tơ được biểu diễn tuyến tính qua một hệ ĐLTT thì sự biểu diễn
đó là duy nhất.
• Định lý 3. Trong không gian ℝ𝒏 cho hai hệ véc tơ:
Hệ (1): 𝑨𝟏, 𝑨𝟐, . . . , 𝑨𝒎 và hệ (2): 𝑩𝟏, 𝑩𝟐, . . . , 𝑩𝒌 .
Nếu mỗi véc tơ của hệ (1) đều được biểu diễn tuyến tính qua các véc tơ của hệ (2) và
𝒎 > 𝒌 thì hệ (1) PTTT. BỘ MÔN TOÁN 16
1.2.2. ĐỘC LẬP TUYẾN TÍNH - PHỤ THUỘC TUYẾN TÍNH −𝟏 𝟎 −𝟏 Ví
dụ 1.4 : Cho hệ véc tơ 𝑺 = 𝑨𝟏 = ; 𝑨
và véc tơ 𝑿 = . 𝟑 𝟐 = 𝟐 𝟕
a) Véc tơ 𝑿 có được biểu diễn tuyến tính qua hệ 𝑺 hay không?
b) Sự biểu diễn tuyến tính ở câu a) có duy nhất không? 𝟐 −𝟏 𝟓 𝟔 Ví
dụ 1.5: Cho hệ véc tơ 𝑺 = 𝑨𝟏 = ; 𝑨 ; 𝑨
và véc tơ 𝑿 = . −𝟏 𝟐 = 𝟏 𝟑 = 𝟎 𝟎
a) Véc tơ 𝑿 có được biểu diễn tuyến tính qua hệ 𝑺 hay không?
b) Sự biểu diễn tuyến tính ở câu a) có duy nhất không? BỘ MÔN TOÁN 17
1.3. CƠ SỞ CỦA KHÔNG GIAN VÉC TƠ ℝ𝒏 1.3.1.
Hệ véc tơ độc lập tuyến tính cực đại trong ℝ𝒏 1.3.2
Cơ sở của không gian véc tơ ℝ𝒏 BỘ MÔN TOÁN 18
1.3.1. HỆ VÉC TƠ ĐỘC LẬP TUYẾN TÍNH CỰC ĐẠI TRONG ℝ𝒏 Định nghĩa 1
Cho hệ 𝒎 véc tơ 𝒏 chiều 𝑨𝟏, 𝑨𝟐, . . . , 𝑨𝒎 𝟏 .
Hệ (1) được gọi là hệ véc tơ độc lập tuyến tính cực đại (ĐLTTCĐ) trong không gian ℝ𝒏
nếu hệ đó đồng thời thỏa mãn hai điều kiện: • Hệ (1) ĐLTT.
• Nếu thêm bất kỳ một véc tơ nào của không gian ℝ𝒏 vào hệ đã cho thì hệ mới PTTT. Chú ý:
Hai điều kiện trên tương đương với mọi véc tơ trong ℝ𝒏 đều được biểu diễn tuyến tính
duy nhất qua hệ véc tơ (1). BỘ MÔN TOÁN 19