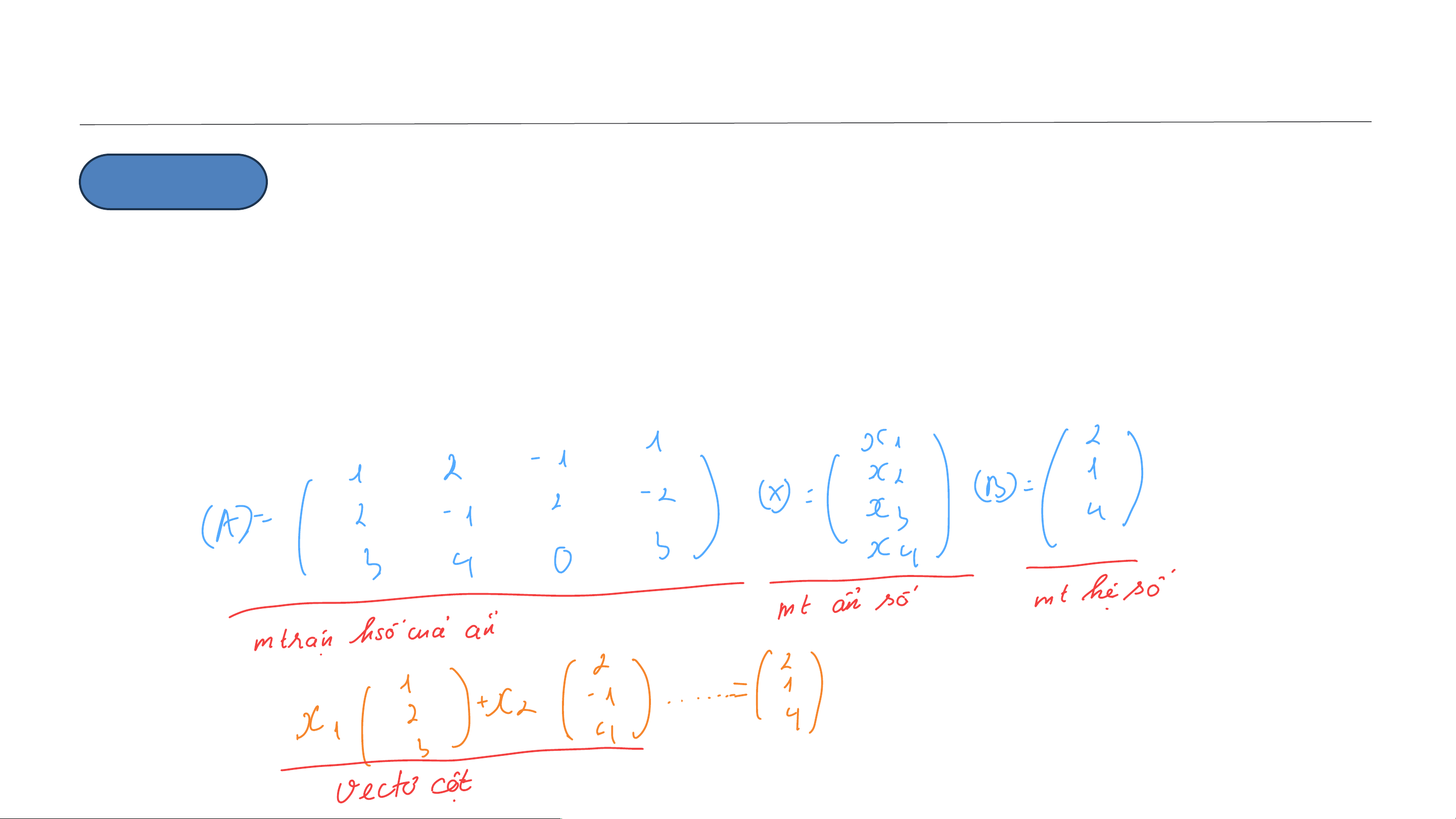








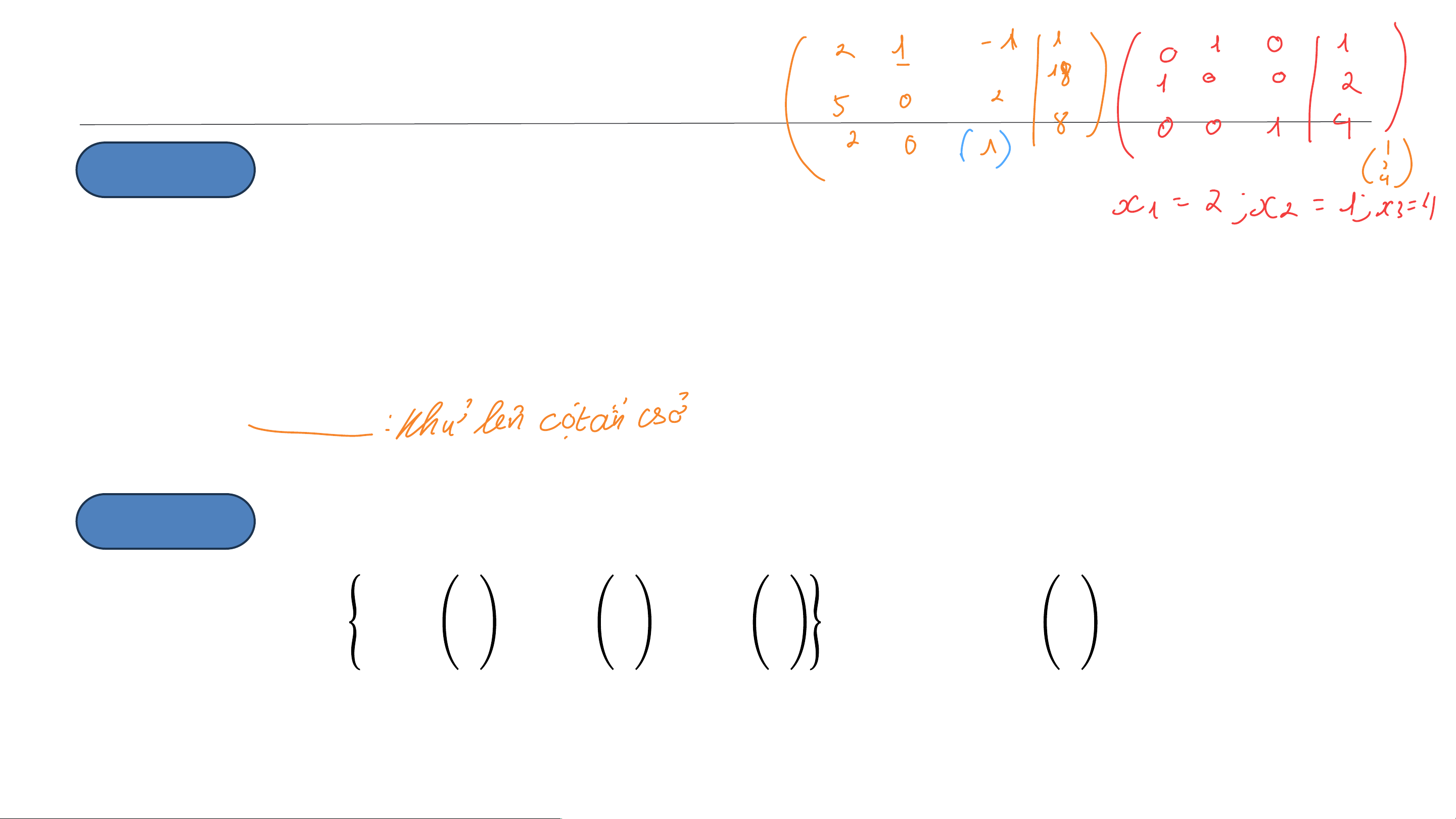




Preview text:
CHƯƠNG 3
HỆ PHƯƠNG TRÌNH TUYẾN TÍNH 1 BỘ MÔN TOÁN
CHƯƠNG 3: HỆ PHƯƠNG TRÌNH TUYẾN TÍNH 3.1
Mô tả hệ phương trình tuyến tính 3.2
Hệ phương trình tuyến tính tổng quát 3.3
Hệ ràng buộc tuyến tính 3.4 Bài tập 2 BỘ MÔN TOÁN
3.1. MÔ TẢ HỆ PHƯƠNG TRÌNH TUYẾN TÍNH 3.1.1.
Các dạng hệ phương trình tuyến tính tổng quát 3.1.2
Nghiệm của hệ phương trình tuyến tính 3.1.3
Các phép biến đổi sơ cấp lên hệ phương trình tuyến tính 3 BỘ MÔN TOÁN
3.1.1. CÁC DẠNG HỆ PHƯƠNG TRÌNH TUYẾN TÍNH TỔNG QUÁT Dạng tường minh
Hệ phương trình tuyến tính gồm 𝒎 phương trình, 𝒏 ẩn số có dạng tường minh là: 𝒂𝟏𝟏𝒙𝟏 + 𝒂𝟏𝟐𝒙𝟐 + . . . + 𝒂𝟏𝒏𝒙𝒏 = 𝒃𝟏 𝒂 ൞ 𝟐𝟏𝒙𝟏 + 𝒂𝟐𝟐𝒙𝟐 + . . . + 𝒂𝟐𝒏𝒙𝒏 = 𝒃𝟐 (𝟑. 𝟏) . . . . . . . . . . . . . . . . . . . . . . . . . . .
𝒂𝒎𝟏𝒙𝟏 + 𝒂𝒎𝟐𝒙𝟐 + . . . + 𝒂𝒎𝒏𝒙𝒏 = 𝒃𝒎
(trong đó: 𝒙𝒋 là các ẩn số; 𝒂𝒊𝒋, 𝒃𝒊 là các hệ số thực với 𝒊 = 𝟏, 𝒎, 𝒋 = 𝟏, 𝒏). Dạng ma trận 𝑨𝑿 = 𝑩, 𝒂𝟏𝟏 𝒂𝟏𝟐 . . . 𝒂𝟏𝒏 𝒙𝟏 𝒃𝟏 𝒂 𝒙 𝒃 trong đó: 𝑨 = 𝟐𝟏 𝒂𝟐𝟐 . . . 𝒂𝟐𝒏 ; 𝟐 𝟐 . . . . . . . . . . . . . 𝑿 = ⋮ , 𝑩 = ⋮
𝒂𝒎𝟏 𝒂𝒎𝟐 . . . 𝒂𝒎𝒏 𝒙𝒏 𝒃𝒎
𝑨: ma trận hệ số của ẩn; 𝑿: ma trận ẩn số; 𝑩: ma trận hệ số vế phải. 𝒙 Dạng véc tơ
𝟏𝑨𝟏 + 𝒙𝟐𝑨𝟐+. . . +𝒙𝒏𝑨𝒏 = 𝑩, (𝑨𝒋 là véc tơ cột thứ j của ma trận 𝑨). 4 BỘ MÔN TOÁN
3.1.1. CÁC DẠNG HỆ PHƯƠNG TRÌNH TUYẾN TÍNH TỔNG QUÁT Ví dụ 3.1:
Viết dạng ma trận, dạng véc tơ của hệ phương trình sau: 𝒙𝟏 + 𝟐𝒙𝟐 − 𝒙𝟑 + 𝒙𝟒 = 𝟐 ቐ𝟐𝒙𝟏 − 𝒙𝟐
+ 𝟐𝒙𝟑 − 𝟐𝒙𝟒 = 𝟏 . 𝟑𝒙𝟏 + 𝟒𝒙𝟐 + 𝟑𝒙𝟒 = 𝟒 5 BỘ MÔN TOÁN
3.1.2. NGHIỆM HỆ PHƯƠNG TRÌNH TUYẾN TÍNH Định nghĩa
Bộ 𝒏 số thực 𝒙𝟎 𝟎 𝟎
𝟏, 𝒙𝟐, … , 𝒙𝒏 được gọi là nghiệm của hệ phương trình tuyến tính (3.1) nếu khi thay 𝒙 𝟎
𝒋 = 𝒙𝒋 , ∀𝒋 = 𝟏, 𝒏 vào hệ thì ta được 𝒎 đồng nhất thức. Nhận xét
• Từ dạng véc tơ của hệ (3.1), nếu véc tơ 𝑿 𝟎 𝟎 𝟎
𝟎 = 𝒙𝟏, 𝒙𝟐, … , 𝒙𝒏 là nghiệm của hệ thì ta có đẳng thức: 𝒙𝟎 𝟎 𝟎
𝟏𝑨𝟏 + 𝒙𝟐𝑨𝟐+. . . +𝒙𝒏𝑨𝒏 = 𝑩.
Như vậy, đi tìm 𝑿𝟎 thực chất là đi tìm một biểu thị tuyến tính của véc tơ 𝑩 qua hệ
𝑨𝟏, 𝑨𝟐, . . . , 𝑨𝒏 .
• Từ dạng ma trận của hệ (3.1), để tìm nghiệm của hệ thì ta đi tìm một ma trận 𝑿 thoả
mãn phương trình: 𝑨𝑿 = 𝑩. 6 BỘ MÔN TOÁN
3.1.2. NGHIỆM HỆ PHƯƠNG TRÌNH TUYẾN TÍNH Ví
dụ 3.2 :
Cho hệ phương trình sau: −𝟐 𝟎 𝟒 𝟐 𝟑𝟔 𝒙𝟏 𝟑
+ 𝒙𝟐 𝟏 + 𝒙𝟑 −𝟏 + 𝒙𝟒 𝟑 = 𝟏𝟎 . 𝟎 𝟑 −𝟏 −𝟐 −𝟏𝟔
a) Viết dạng ma trận của hệ phương trình trên.
b) Thông qua dạng ma trận của hệ đã cho, chứng minh 𝑿𝟎 = −𝟒; 𝟏; 𝟑; 𝟖 là một nghiệm của hệ. 7 BỘ MÔN TOÁN
3.1.2. NGHIỆM HỆ PHƯƠNG TRÌNH TUYẾN TÍNH Ví dụ 3.3 :
(Tự đọc) Một hãng dự tính sẽ sản xuất 4 loại sản phẩm (SP) A, B, C, D từ 3
loại nguyên liệu (NL) I, II, III. Định mức về số đơn vị (đv) NL mỗi loại cần sử dụng để
sản xuất ra 1 đơn vị SP được cho ở bảng sau: SP A B C D NL I 3 2 4 3 II 2 1 3 1 III 4 2 2 1
a)Hãy lập hệ phương trình xác định phương án sản xuất của hãng biết hãng dùng hết 215
đv NL I, 100 đv NL II và 165 đv NL III.
b) Kiểm tra xem các véc tơ 𝑿𝟎 = 𝟐𝟎; 𝟐𝟓; 𝟎; 𝟑𝟓 và 𝑿𝟏 = 𝟏𝟓; 𝟐𝟎; 𝟒𝟎; 𝟎 có là phương án 8
sản xuất không? Vì sao? BỘ MÔN TOÁN
3.1.3. CÁC PHÉP BIẾN ĐỔI SƠ CẤP LÊN HỆ PHƯƠNG TRÌNH TUYẾN TÍNH Định nghĩa 1
Các phép biến đổi sơ cấp (BĐSC) lên hệ phương trình tuyến tính là:
• Đổi chỗ hai phương trình cho nhau.
• Nhân hai vế của một phương trình với một số khác 0.
• Nhân hai vế của một phương trình với một số rồi cộng vào một phương trình khác. Định lý
Các phép biến đổi sơ cấp không làm thay đổi tập nghiệm của hệ phương trình tuyến tính. 9 BỘ MÔN TOÁN
3.1.3. CÁC PHÉP BIẾN ĐỔI SƠ CẤP LÊN HỆ PHƯƠNG TRÌNH TUYẾN TÍNH Định nghĩa 2 • ෩
𝑨 = 𝑨 𝑩 : gọi là ma trận hệ số mở rộng.
• Mỗi hệ phương trình tuyến tính tương ứng với một ma trận ෩
𝑨 và ngược lại. Nhận xét
Thực hiện phép BĐSC lên hệ phương trình tuyến tính thực chất là BĐSC lên hệ véc tơ
dòng của ma trận ෩ 𝑨. 10 BỘ MÔN TOÁN
3.2. HỆ PHƯƠNG TRÌNH TUYẾN TÍNH TỔNG QUÁT 3.2.1.
Điều kiện tồn tại nghiệm 3.2.2 Phương pháp giải 11 BỘ MÔN TOÁN
3.2.1. ĐIỀU KIỆN TỒN TẠI NGHIỆM
Xét dạng véc tơ của hệ phương trình tuyến tính tổng quát:
𝒙𝟏𝑨𝟏 + 𝒙𝟐𝑨𝟐+. . . +𝒙𝒏𝑨𝒏 = 𝑩 (3.2). Định lý
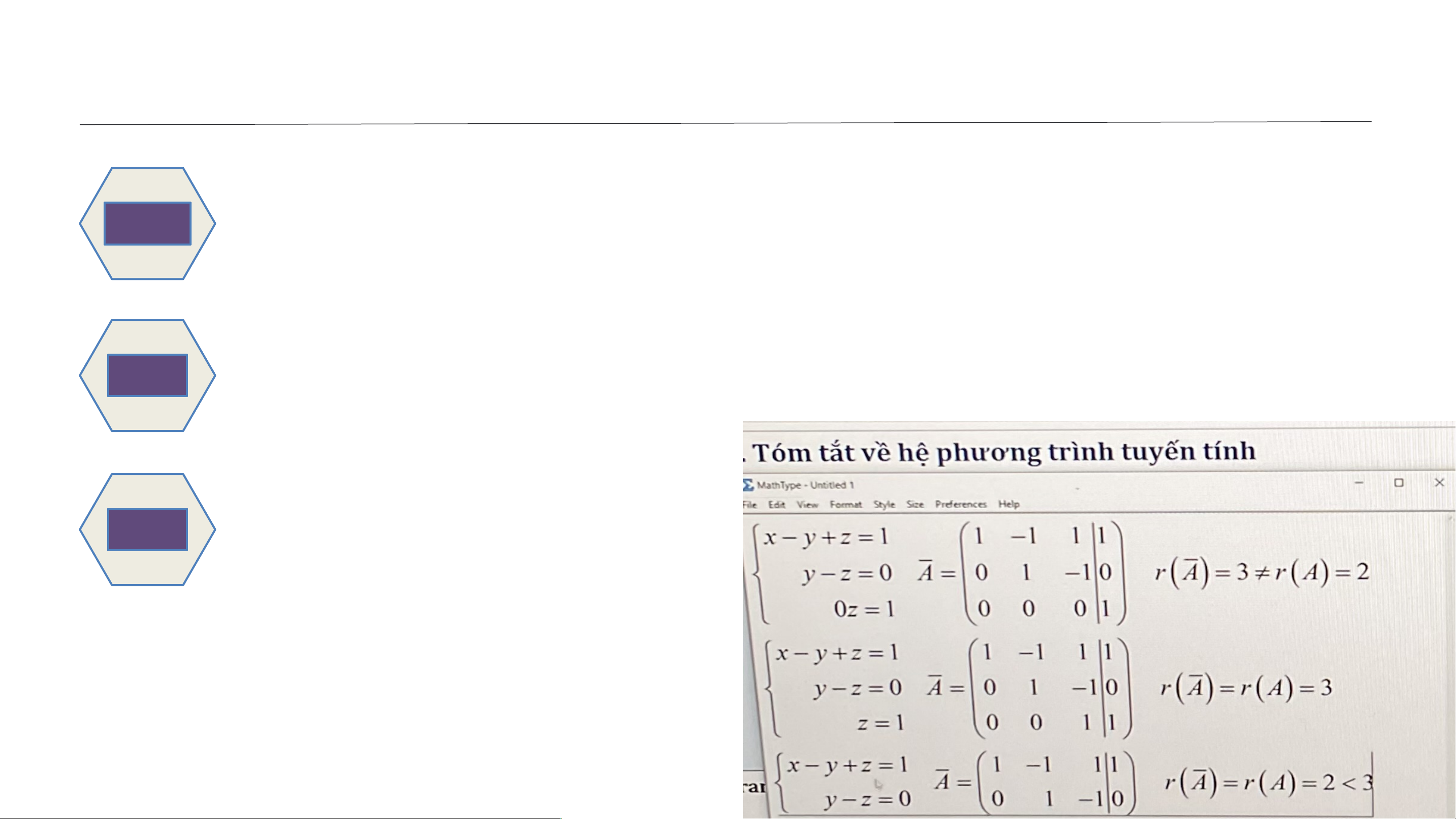
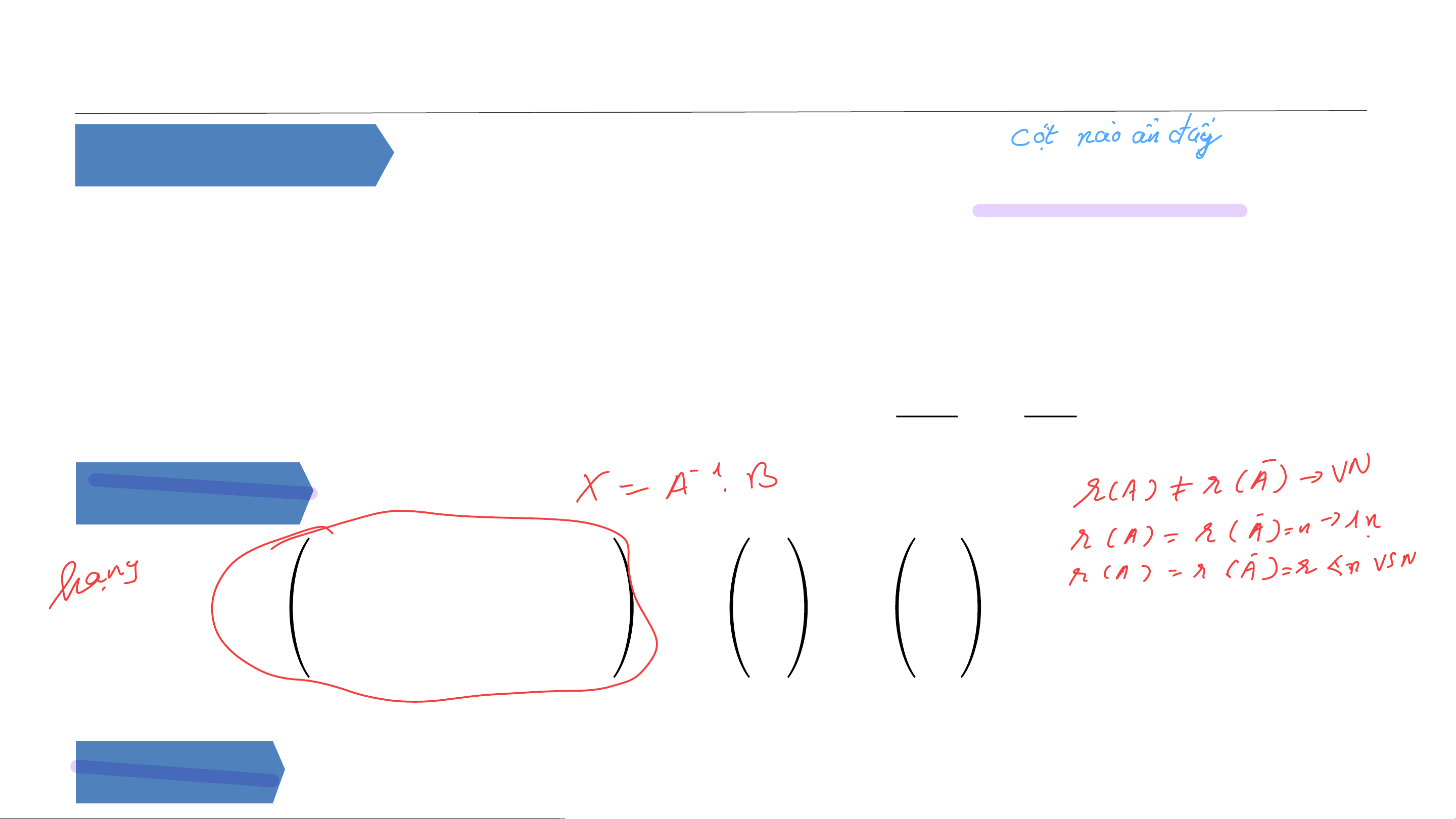
Hệ (3.2) có nghiệm khi và chỉ khi véc tơ 𝑩 biểu thị tuyến tính qua hệ 𝑨𝟏, 𝑨𝟐, . . . , 𝑨𝒏 , tức là: 𝒉 𝑨 = 𝒉 ෩ 𝑨 . Hệ quả
Đối với hệ phương trình tuyến tính gồm 𝒎 phương trình, 𝒏 ẩn số thì:
• Hệ vô nghiệm khi và chỉ khi 𝒉 𝑨 < 𝒉 ෩ 𝑨 .
• Hệ vô số nghiệm khi và chỉ khi 𝒉 𝑨 = 𝒉 ෩ 𝑨 = 𝒓 < 𝒏.
• Hệ có nghiệm duy nhất khi và chỉ khi 𝒉 𝑨 = 𝒉 ෩ 𝑨 = 𝒏. 12 BỘ MÔN TOÁN
3.2.2. PHƯƠNG PHÁP GIẢI Bước 1: Lập ma trận ෩
𝑨 = 𝑨 𝑩 . Khử toàn phần lên hàng của ෩
𝑨 , đưa ෩ 𝑨 thành ෩
𝒁 = 𝒁 𝑻 , với 𝒁 là
ma trận có tối đa các cột đơn vị khác nhau (hay số véc tơ đơn vị khác nhau bằng số dòng khác không). Bước 2:
Viết hệ phương trình ứng với ma trận ෩ 𝒁.
Các ẩn tương ứng với các cột đơn vị khác nhau gọi là các ẩn cơ sở.
Các ẩn còn lại gọi là ẩn tự do. Bước 3:
Đặt các ẩn tự do bằng các tham số khác nhau (𝜶, 𝜷, 𝜸, …), biểu diễn các ẩn cơ sở theo các
ẩn tự do, ta được nghiệm tổng quát.
Từ nghiệm tổng quát, cho ẩn tự do bằng giá trị cụ thể ta được nghiệm riêng. 13
Từ nghiệm tổng quát, cho tất cả các ẩn tự do bằng 0 ta được nghiệm cơ sở. BỘ MÔN TOÁN
3.2.2. PHƯƠNG PHÁP GIẢI
Chú ý: Trong quá trình khử toàn phần nếu xuất hiện dấu hiệu:
❑ Có 1 dòng mà tất cả các phần tử đều bằng 0 thì ta bỏ dòng đó đi và tiếp tục khử.
❑ Có 1 dòng mà các phần tử bên trái bằng 0 còn phần tử bên phải khác 0 thì hệ vô nghiệm. Ví dụ 3.4 : Giải các AnTran
hệ phương trình tuyến tính sau: 𝟐𝒙 𝟐𝒙 𝟏
+ 𝟑𝒙𝟐 − 𝟕𝒙𝟑 + 𝟓𝒙𝟒 = 𝟑 𝟏 + 𝒙𝟐 − 𝒙𝟑 = 𝟏 𝟑𝒙 a) ቐ𝟑𝒙 𝟏 + 𝟐𝒙𝟐 − 𝒙𝟑 + 𝟑𝒙𝟒 = 𝟕 𝟏 −
𝒙𝟐 + 𝟑𝒙𝟑 = 𝟏𝟕 . b) . 𝒙 𝟐𝒙 𝟏 − 𝟐𝒙𝟑 + 𝒙𝟒 = 𝟎 𝟏 + 𝒙𝟑 = 𝟖 𝒙𝟏 + 𝒙𝟐
− 𝟑𝒙𝟑 + 𝟐𝒙𝟒 = 𝟏 𝟐𝒙𝟏 + 𝒙𝟐 − 𝒙𝟑 + 𝒙𝟒 = 𝟒 𝟑𝒙 c) 𝟏 + 𝟐𝒙𝟐 + 𝒙𝟑 − 𝒙𝟒 = 𝟗 −𝒙 . 𝟏 + 𝟐𝒙𝟐 + 𝒙𝟑 + 𝟑𝒙𝟒 = 𝟏𝟑 𝒙𝟐 − 𝒙𝟑 + 𝟑𝒙𝟒 = 𝟕 14 BỘ MÔN TOÁN
3.2.2. PHƯƠNG PHÁP GIẢI
Ví dụ 3.5: Cho hệ phương trình tuyến tính sau: 𝒙𝟏 + 𝒙𝟐 + 𝒙𝟑 + 𝒙𝟒 = 𝟏𝟓 ቐ𝟐𝒙𝟏 + 𝒙𝟐
+ 𝟕𝒙𝟑 + 𝟑𝒙𝟒 = 𝟑𝟕 . 𝒙𝟏
+ 𝟐𝒙𝟐 − 𝟐𝒙𝟑 + 𝒙𝟒 = 𝟏𝟕
a) Bằng phương pháp khử toàn phần, tìm công thức nghiệm tổng quát của hệ trên với
𝒙𝟏, 𝒙𝟐, 𝒙𝟒 là ẩn cơ sở.
b) Chỉ ra một nghiệm riêng của hệ thoả mãn 𝟐𝒙𝟐 − 𝟒𝒙𝟑 − 𝒙𝟒 = 𝟐𝟕.
Ví dụ 3.6: Cho hệ véc tơ 𝟏 𝟐 𝟏 𝟑
𝑺 = 𝑨𝟏 = 𝟏 , 𝑨𝟐 = 𝟑 , 𝑨𝟑 = 𝟏 và véc tơ 𝑩 = 𝟓 . 𝟐 𝟏 𝟑 𝟕
a) CMR hệ 𝑺 là một cơ sở của không gian ℝ𝟑.
b) Tìm hệ số phân tích (hay toạ độ) của véc tơ 𝑩 qua cơ sở 𝑺 bằng phương pháp khử 15 BỘ MÔN TOÁN toàn phần.
3.3. HỆ RÀNG BUỘC TUYẾN TÍNH 3.3.1. Một số khái niệm
Phương pháp tìm một nghiệm không âm của hệ phương 3.3.2
trình tuyến tính tổng quát 3.3.3
Phương pháp tìm một nghiệm không âm của hệ hỗn hợp 3.3.4
Một số ví dụ minh hoạ kinh tế 16 BỘ MÔN TOÁN
3.3.1. MỘT SỐ KHÁI NIỆM Véc tơ không âm
𝑿 = 𝒙𝟏; 𝒙𝟐; . . . ; 𝒙𝒏 được gọi là véc tơ không âm nếu 𝒙𝒊 ≥ 𝟎,∀𝒊 = 𝟏, . . , 𝒏. Kí hiệu: 𝑿 ≥ 𝟎𝒏. Nghiệm không âm 𝑿 𝟎 𝟎 𝟎 𝑻
𝟎 = 𝒙𝟏; 𝒙𝟐; . . . ; 𝒙𝒏
được gọi là nghiệm không âm của hệ phương trình tuyến tính
𝑨𝑿 = 𝑩 nếu 𝑿𝟎 là nghiệm của hệ và 𝑿𝟎 ≥ 𝟎𝒏.
Hệ ràng buộc tuyến tính dạng chính tắc
Là hệ ràng buộc tuyến tính có dạng: 𝒂𝟏𝟏𝒙𝟏 + 𝒂𝟏𝟐𝒙𝟐 + … + 𝒂𝟏𝒏𝒙𝒏 = 𝒃𝟏 𝒂𝟐𝟏𝒙𝟏 + 𝒂𝟐𝟐𝒙𝟐 + … + 𝒂𝟐𝒏𝒙𝒏 = 𝒃𝟐 … 𝒂𝒎𝟏𝒙𝟏 + 𝒂𝒎𝟐𝒙𝟐 + … +
𝒂𝒎𝒏𝒙𝒏 = 𝒃𝒎
𝒙𝒋 ≥ 𝟎; ∀𝒋 = 𝟏, 𝟐, … , 𝒏. 17 BỘ MÔN TOÁN
3.3.1. MỘT SỐ KHÁI NIỆM
Hệ ràng buộc tuyến tính (Tự đọc)
• Hệ gồm các phương trình và bất phương trình tuyến tính gọi là hệ ràng buộc tuyến
tính (hay hệ hỗn hợp).
• Nhận xét: Mọi hệ hỗn hợp đều đưa được về hệ ràng buộc tuyến tính dạng chính tắc.
Chẳng hạn: Với mỗi 𝒊 = 𝟏, 𝟐, … , 𝒎,
❑ Nếu 𝒂𝒊𝟏𝒙𝟏 + 𝒂𝒊𝟐𝒙𝟐 + ⋯ + 𝒂𝒊𝒏𝒙𝒏 ≤ 𝒃𝒊 thì ta thêm ẩn bù 𝒙𝒑 ≥ 𝟎 và viết lại dưới dạng:
𝒂𝒊𝟏𝒙𝟏 + 𝒂𝒊𝟐𝒙𝟐 + ⋯ + 𝒂𝒊𝒏𝒙𝒏 + 𝒙𝒑 = 𝒃𝒊, ൝ 𝒙𝒑 ≥ 𝟎.
❑ Nếu 𝒂𝒊𝟏𝒙𝟏 + 𝒂𝒊𝟐𝒙𝟐 + ⋯ + 𝒂𝒊𝒏𝒙𝒏 ≥ 𝒃𝒊 thì ta thêm ẩn bù 𝒙𝒒 ≥ 𝟎 và viết lại dưới dạng:
𝒂𝒊𝟏𝒙𝟏 + 𝒂𝒊𝟐𝒙𝟐 + ⋯ + 𝒂𝒊𝒏𝒙𝒏 − 𝒙𝒒 = 𝒃𝒊, ൝ 𝒙 18 𝒒 ≥ 𝟎. BỘ MÔN TOÁN
3.3.2. PHƯƠNG PHÁP TÌM MỘT NGHIỆM KHÔNG ÂM CỦA
HỆ PHƯƠNG TRÌNH TUYẾN TÍNH TỔNG QUÁT Bước 1: Lập ma trận ෩
𝑨 = 𝑨 𝑩 . Nếu trong 𝑩 có thành phần âm thì nhân dòng tương ứng với −𝟏 . Bước 2:
Khử toàn phần lên hàng của ෩ 𝑨 , đưa ෩ 𝑨 về ෩
𝒁 = 𝒁 𝑻 sao cho 𝒁 có tối đa cột véc tơ đơn vị
khác nhau. Mỗi bước khử đảm bảo vế phải luôn không âm bằng cách:
❑ Chọn cột xoay 𝑨𝒋 là cột có ít nhất một thành phần dương. 𝟎
❑ Trên cột 𝑨𝒋 , chọn phần tử xoay như sau: 𝟎 𝒃 𝒃 𝐦𝐢𝐧 𝒊 ∶ 𝒂 > 𝟎 = 𝒊𝟎 ⟹ 𝒂 : là phần tử xoay. 𝒂 𝒊𝒋 𝒊 𝒊𝒋 𝟎 𝒂 𝟎𝒋𝟎 𝟎 𝒊𝟎𝒋𝟎 Bước 3: Từ ma trận ෩
𝒁 viết hệ phương trình tương ứng và tìm nghiệm cơ sở của nó.
Nghiệm cơ sở chính là nghiệm không âm cần tìm của hệ. 19 BỘ MÔN TOÁN
3.3.2. PHƯƠNG PHÁP TÌM MỘT NGHIỆM KHÔNG ÂM CỦA
HỆ PHƯƠNG TRÌNH TUYẾN TÍNH TỔNG QUÁT Chú ý:
Trong quá trình khử toàn phần, có thể xuất hiện một trong hai trường hợp sau:
• Có 1 dòng mà các phần tử bên trái 𝒂𝒊𝒋 ≤ 𝟎, ∀𝒋, còn phần tử bên phải 𝒃𝒊 > 𝟎 thì hệ
phương trình không có nghiệm không âm.
• Có hiện tượng xoay vòng: tại một bước khử nào đó, một cột véc tơ trong cơ sở (tức là,
cột véc tơ đơn vị) có thể bị loại ra khỏi cơ sở và thay bằng một cột véc tơ khác. AnTran 20 BỘ MÔN TOÁN