Bài giảng chương 2: Suy luận toán học môn Toán rời rạc | Đại học Kỹ thuật - Công nghệ Cần Thơ

TOÁN RỜI RẠC DISCRETE MATHEMATICS LÊ THỊ PHƯƠNG DUNG Thời gian thi cuối kỳ Tuần 16 của HK Nội dung 1. Mệnh đề và vị từ 2. Suy luận toán học 3. Phép đếm 4. Quan hệ 5. Đại số Bool
6. Lý thuyết chia và đồng dư Tài liệu tham khảo
 Kenneth Rosen, “Toán học rời rạc”, bản dịch của NXB KH&KT.
 Nguyễn Đức Nghĩa, Nguyễn Tô Thành, “Toán rời rạc”, NXB ĐHQG Hà Nội.
 Đỗ Đức Giáo, “Toán rời rạc”, NXB ĐHQG Hà Nội.
 Đỗ Đức Giáo, “Hướng dẫn giải bài tập Toán rời rạc”, NXB Giáo Dục.
 Nguyễn Tiến Quang, “Bài tập số học”, NXB Giáo Dục.  ……..
Chương 2: Suy luận toán học  Các quy tắc suy luận
 Các phương pháp chứng minh Các quy tắc suy luận  Xét mệnh đề
, trong đó là giả thiết là kết luận. Từ giả thiết
, chúng ta sử dụng các quy tắc suy luận/các phương pháp chứng minh để đưa ra kết luận  Ví dụ:
“Nếu hôm nay trời mưa thì cô ấy không đến. Nếu cô ấy không đến
thì ngày mai cô ấy đến. Vì vậy, nếu hôm nay trời mưa thì ngày mai
cô ấy đến.” Hai câu đầu tiên là giả thiết, câu cuối cùng là kết luận
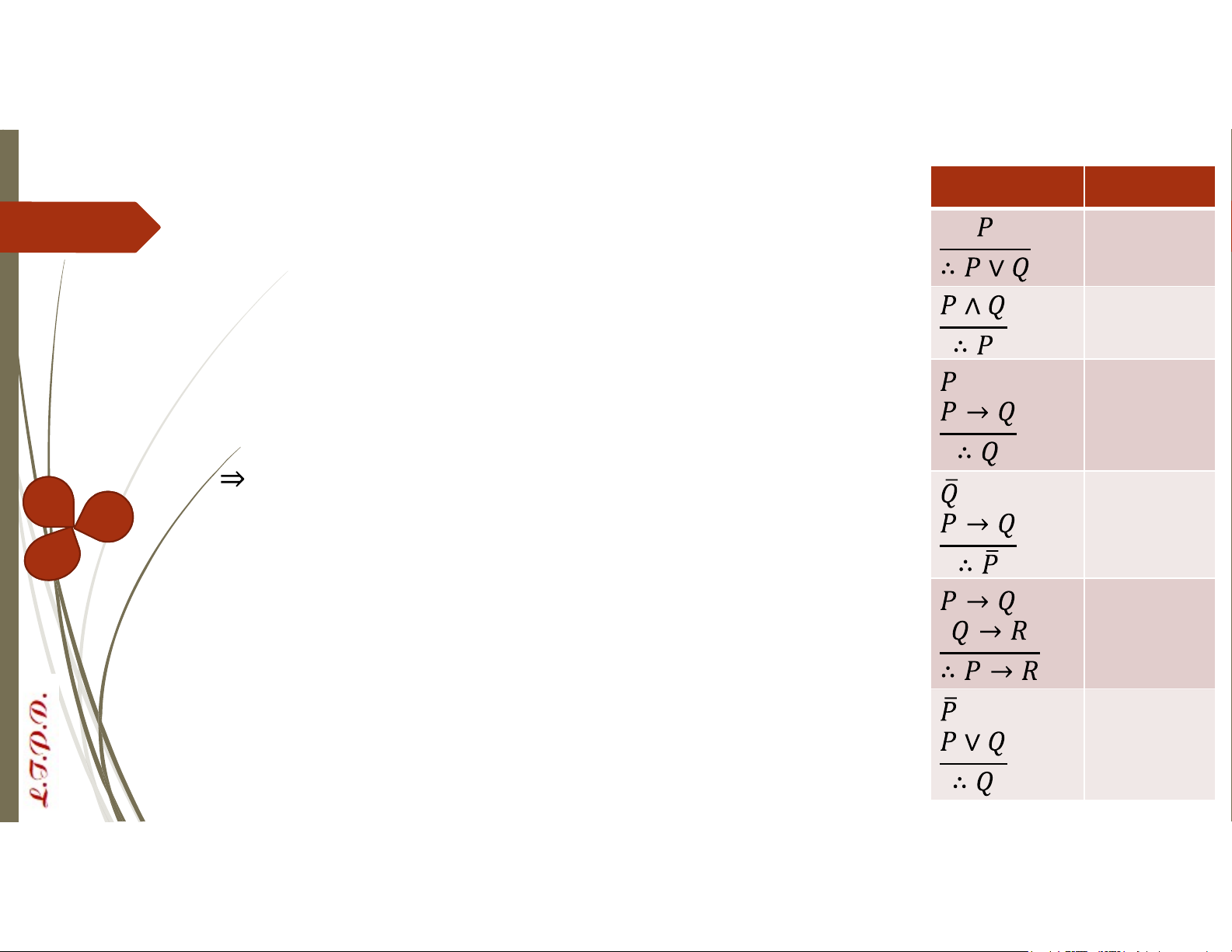
“An giỏi toán. Do đó, An giỏi toán hoặc tin” Câu đầu là giả thiết, câu cuối là kết luận Quy tắc CáHcằn q g đ uúny t g ắc suy luận Tên Cộng Rút gọn Khẳng định Phủ định
Tam đoạn luận giả định Tam đoạn luận tuyển Quy tắc Tên Các quy tắc suy luận Cộng  Ví dụ: Rút gọn
“Nếu hôm nay trời mưa thì cô ấy không đến. Nếu cô
ấy không đến thì ngày mai cô ấy đến. Vì vậy, nếu hôm Khẳng
nay trời mưa thì ngày mai cô ấy đến.” định Quy tắc … Phủ định
“An giỏi toán. Do đó, An giỏi toán hoặc tin” Quy tắc … Tam đoạn
“Nếu hôm nay tuyết rơi thì trường học đóng cửa. Hôm luận giả
nay trường học không đóng cửa. Do đó, hôm nay đã định không có tuyết rơi.” Tam đoạn Quy tắc … luận tuyển Quy tắc Tên Các quy tắc suy luận Cộng  Ví dụ: Rút gọn
“Nếu hôm nay trời mưa thì cô ấy không đến. Nếu cô
ấy không đến thì ngày mai cô ấy đến. Vì vậy, nếu hôm Khẳng
nay trời mưa thì ngày mai cô ấy đến.” định Đặt: Phủ định P = “Hôm nay trời mưa”
Q = “Cô ấy không đến” Tam đoạn
R = “Ngày mai cô ấy đến” luận giả định Biểu thức: Tam đoạn
Quy tắc Tam đoạn luận giả định luận tuyển Quy tắc Tên Các quy tắc suy luận Cộng  Ví dụ: Rút gọn
“An giỏi toán. Do đó, An giỏi toán hoặc tin” Khẳng định Đặt: P = “An giỏi toán” Phủ định Q = “An giỏi tin” Biểu thức: Tam đoạn Quy tắc Cộng luận giả định Tam đoạn luận tuyển Quy tắc Tên Các quy tắc suy luận Cộng  Ví dụ: Rút gọn
“Nếu hôm nay tuyết rơi thì trường học đóng cửa. Hôm
nay trường học không đóng cửa. Do đó, hôm nay đã Khẳng không có tuyết rơi.” định Phủ định Đặt:
P = “Hôm nay tuyết rơi”
Q = “Trường học đóng cửa” Tam đoạn luận giả Biểu diễn: định Quy tắc Phủ định Tam đoạn luận tuyển Quy tắc Tên Các quy tắc suy luận Cộng  Ví dụ: Rút gọn
“Hôm nay trời nóng trên 100 độ hoặc sự ô nhiễm là
nguy hại. Hôm nay nhiệt độ ngoài trời thấp hơn 100 Khẳng
độ. Do đó, sự ô nhiễm là nguy hại.” định
Quy tắc Tam đoạn luận tuyển Phủ định Tam đoạn luận giả định Tam đoạn luận tuyển Quy tắc Tên Các quy tắc suy luận Cộng  Ví dụ: Rút gọn
“Nếu tôi làm bài tập này cả đêm thì tôi có thể trả lời
được tất cả các bài tập. Nếu tôi trả lời được tất cả các Khẳng
bài tập thì tôi sẽ hiểu được tài liệu này. Do đó, nếu tôi định
làm được bài tập này cả đêm thì tôi sẽ hiểu được tài liệu này.” Phủ định
Quy tắc Tam đoạn luận giả định Tam đoạn luận giả định Tam đoạn luận tuyển Quy tắc Tên Các quy tắc suy luận Cộng
 VD: Dùng các quy tắc suy luận chứng minh rằng Rút gọn Khẳng định Phủ định
--------------------------------- Tam đoạn Khẳng định 1 và 3 luận giả
Tam đoạn luận tuyển 2 và 3 định Khẳng định 4 và 5 Tam đoạn luận tuyển Quy tắc Tên Các quy tắc suy luận Cộng
 VD: Dùng các quy tắc suy luận chứng minh rằng Rút gọn Khẳng định Phủ định Tam đoạn
--------------------------------- luận giả Từ 1 và 2 định Từ 4 và 5 Tam đoạn luận Từ 3 và 6 tuyển Các quy tắc suy luận
 VD: “Nếu bạn đã giải hết bài tập trong sách Toán rời rạc này thì bạn nắm
vững logic. Bạn nắm vững logic. Vậy, bạn đã giải hết bài tập trong sách Toán rời rạc này.” Quy tắc …
Đặt: P = “Bạn đã giải hết bài tập trong sách Toán rời rạc này”
Q = “Bạn nắm vững logic” Biểu diễn: Đây là một tiếp liên
Một suy diễn như trên được gọi là ngụy biện
 Ngụy biện hay ngộ nhận kết quả là phương pháp chứng minh sai, suy luận
không dựa vào hằng đúng mà chỉ dựa vào một tiếp liên Các quy tắc suy luận VD: Cho 2 giả thiết:
- Môn Logic là khó hoặc không có nhiều sinh viên thích môn Logic.
- Nếu môn Toán là dễ thì Logic là không khó.
Hãy xác định xem các khẳng định sau là có dựa trên cơ sở của các giả thiết đã cho hay không:
a/ Môn toán là không dễ nếu nhiều sinh viên thích môn logic.
b/ Không có nhiều sinh viên thích môn logic nếu môn toán là không dễ.
c/ Môn toán là dễ hoặc môn logic là khó.
d/ Môn logic là không khó hoặc môn toán là không dễ.
e/ Nếu không có nhiều sinh viên thích môn logic khi đó hoặc là môn toán
không dễ hoặc là logic không khó. Các quy tắc suy luận VD: Gợi ý cách làm bài:
1. Đặt các mệnh đề đơn
2. Biểu diễn hai giả thiết thành biểu thức
3. Biểu diễn kết luận thành biểu thức
4. Suy diễn từ giả thiết đến kết luận:
a. Cách 1: Dùng các quy tắc suy luận (vừa học)
b. Cách 2: Dùng quy tắc tương đương logic CM “giả thiết  kết luận = T” Các quy tắc suy luận VD: Cho 2 giả thiết:
- Môn logic là khó hoặc không có nhiều sinh viên thích môn logic.
- Nếu môn toán là dễ thì logic là không khó. Đặt:
 P = “Môn logic là khó”
 Q = “Nhiều sinh viên thích môn logic”
 R = “Môn Toán là dễ”
Hai giả thiết được biểu diễn:   hoặc Các quy tắc suy luận P = “Môn logic là khó”
Q = “Nhiều sinh viên thích môn logic” R = “Môn Toán là dễ” • 𝑃 ∨ 𝑄
• 𝑅 → 𝑃 hoặc 𝑅 ∨ 𝑃
a/ Môn toán là không dễ nếu nhiều sinh viên thích môn logic. Biểu thức kết luận:
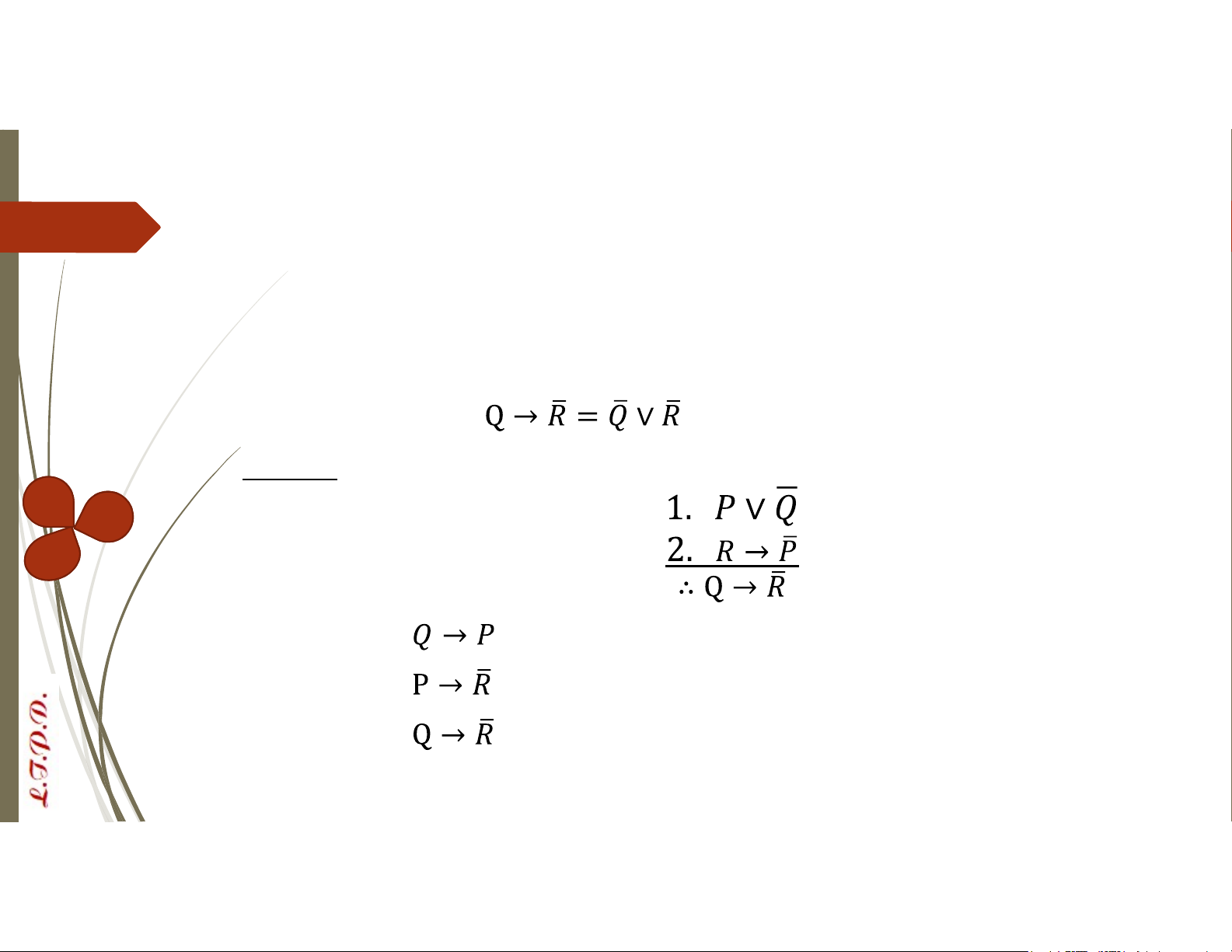
Cách 1: Dùng quy tắc suy luận 3. (từ 1) 4. (từ 2) 5. (từ 3 và 4)
Vậy kết luận trong phát biểu a/ là có cơ sở Các quy tắc suy luận P = “Môn logic là khó”
Q = “Nhiều sinh viên thích môn logic” R = “Môn Toán là dễ” • 𝑃 ∨ 𝑄
• 𝑅 → 𝑃 hoặc 𝑅 ∨ 𝑃
a/ Môn toán là không dễ nếu nhiều sinh viên thích môn logic. Biểu thức kết luận:
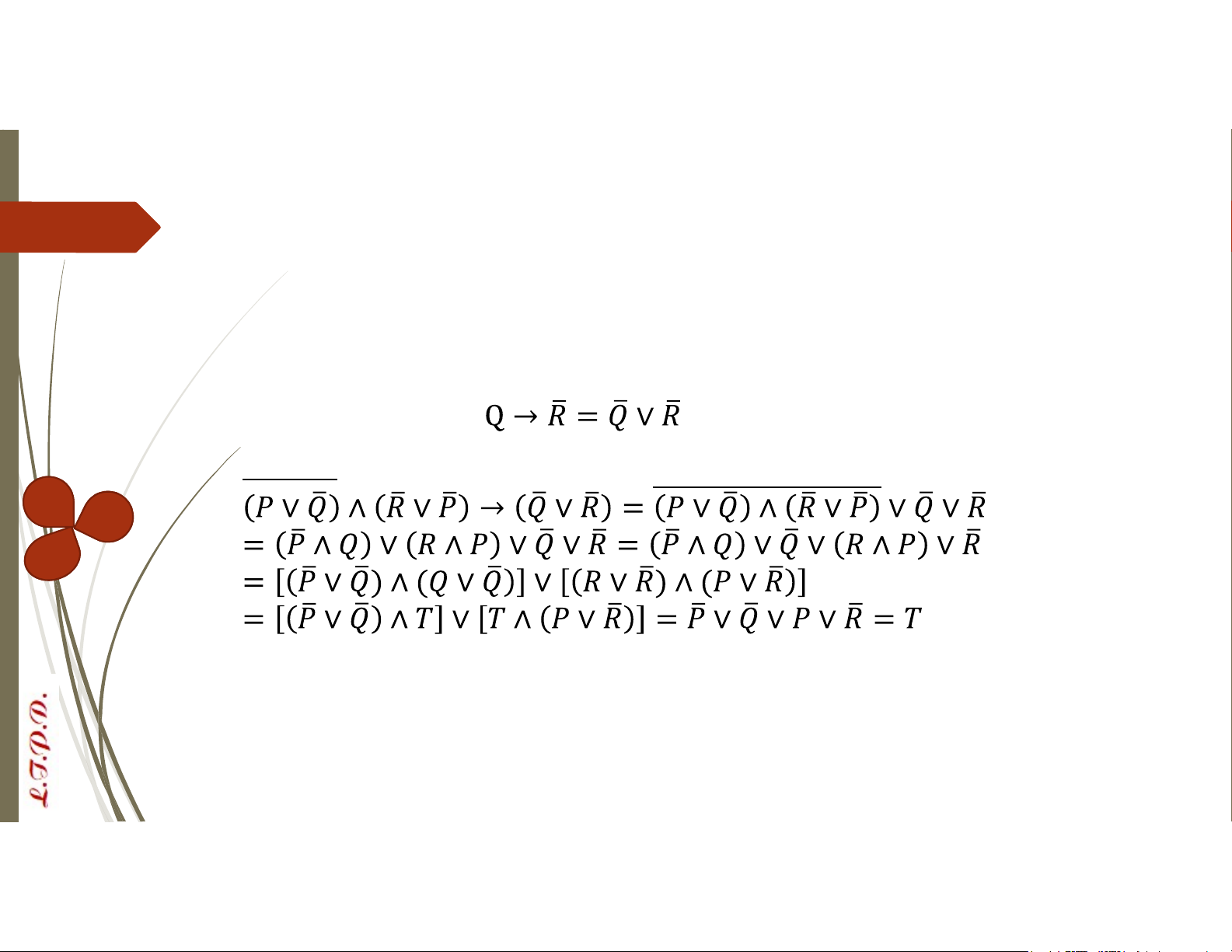
Cách 2: Dùng quy tắc tương đương logic
Vậy kết luận trong phát biểu a/ là có cơ sở
b/ Không có nhiều sinh viên thích môn logic nếu môn toán là không dễ. Các quy tắc suy luận P = “Môn logic là khó”
Q = “Nhiều sinh viên thích môn logic” R = “Môn Toán là dễ” • 𝑃 ∨ 𝑄
• 𝑅 → 𝑃 hoặc 𝑅 ∨ 𝑃
b/ Không có nhiều sinh viên thích môn logic nếu môn toán là không dễ. Biểu thức kết luận:
Nếu mệnh đề “giả thiết kết luận” = T thì phát biểu trong câu b/ là có cơ sở Ta xét:
Đây là một tiếp liên. Vậy kết luận trong phát biểu b/ là không có cơ sở
c/ Môn toán là dễ hoặc môn logic là khó. Các quy tắc suy luận P = “Môn logic là khó”
Q = “Nhiều sinh viên thích môn logic” R = “Môn Toán là dễ” • 𝑃 ∨ 𝑄
• 𝑅 → 𝑃 hoặc 𝑅 ∨ 𝑃
c/ Môn toán là dễ hoặc môn logic là khó. Biểu thức kết luận:
Nếu mệnh đề “giả thiết kết luận” = T thì phát biểu trong câu c/ là có cơ sở Ta xét:
Đây là một tiếp liên. Vậy kết luận trong phát biểu c/ là không có cơ sở
d/ Môn logic là không khó hoặc môn toán là không dễ. Các quy tắc suy luận P = “Môn logic là khó”
Q = “Nhiều sinh viên thích môn logic” R = “Môn Toán là dễ” • 𝑃 ∨ 𝑄
• 𝑅 → 𝑃 hoặc 𝑅 ∨ 𝑃
d/ Môn logic là không khó hoặc môn toán là không dễ. Biểu thức kết luận:
Nếu mệnh đề “giả thiết kết luận” = T thì phát biểu trong câu d/ là có cơ sở Ta xét:
Vậy kết luận trong phát biểu d/ là có cơ sở
e/ Nếu không có nhiều sinh viên thích môn logic khi đó hoặc là môn toán
không dễ hoặc là logic không khó. Các quy tắc suy luận P = “Môn logic là khó”
Q = “Nhiều sinh viên thích môn logic” R = “Môn Toán là dễ” • 𝑃 ∨ 𝑄
• 𝑅 → 𝑃 hoặc 𝑅 ∨ 𝑃
e/ Nếu không có nhiều sinh viên thích môn logic khi đó hoặc là môn toán
không dễ hoặc là logic không khó. Biểu thức kết luận:
Nếu mệnh đề “giả thiết kết luận” = T thì phát biểu trong câu e/ là có cơ sở Ta xét:
Vậy kết luận trong phát biểu e/ là có cơ sở
Các phương pháp chứng minh  Cho mệnh đề
, trong đó P là giả thiết và Q là kết luận của bài toán, việc
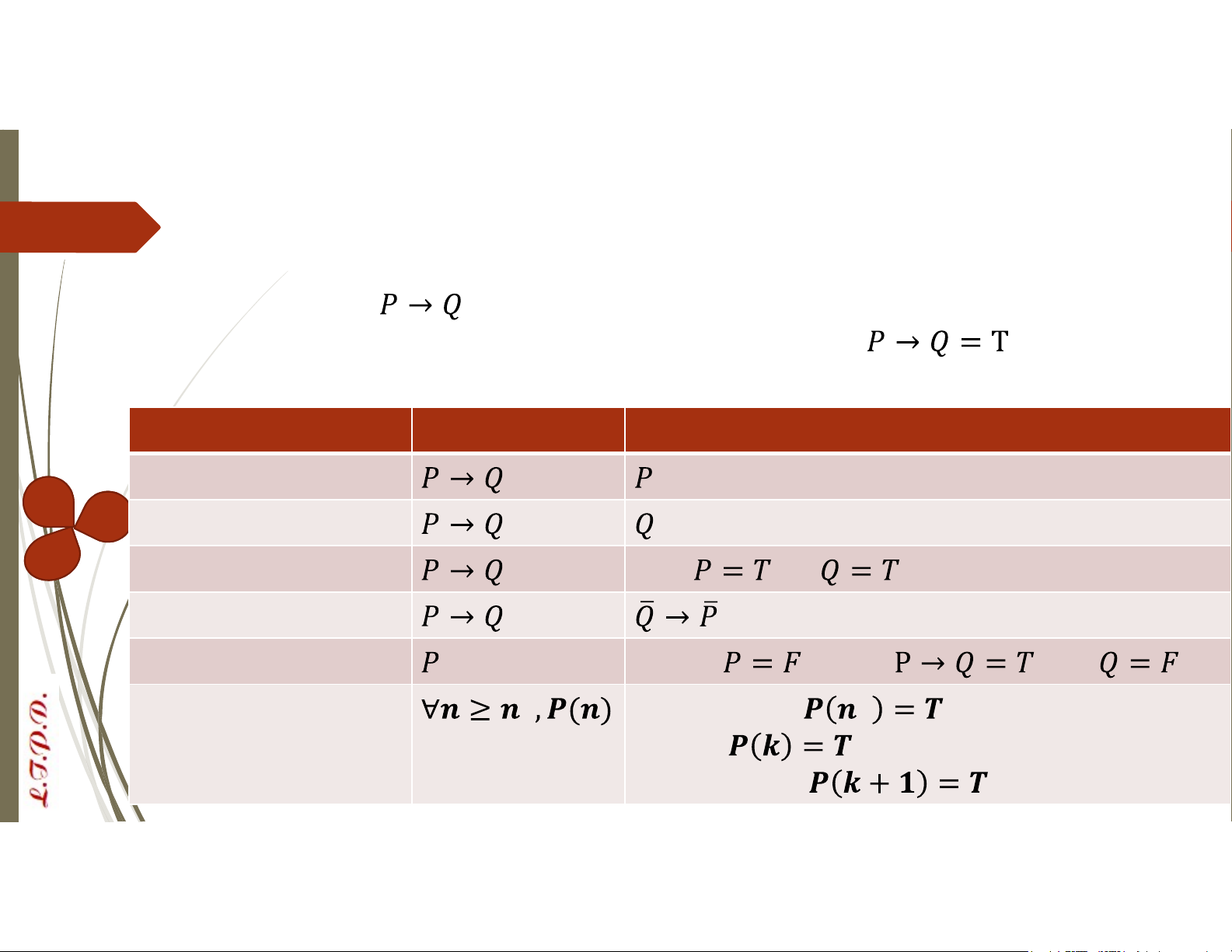
đi từ giả thiết đến kết luận là đi chứng minh mệnh đề Phương pháp Thực hiện Cách chứng minh Rỗng sai Tầm thường đúng Trực tiếp Nếu thì Gián tiếp Phản chứng Giả sử đi đến , với Quy nạp 𝟎 Kiểm chứng 𝟎 Giả sử Chứng minh
Các phương pháp chứng minh  VD: Cho “Nếu thì ”. Chứng minh rằng Ta có “Nếu thì ” Vì giả thiết “ ” nên
(Không cần xét đến kết luận “ ”)
Phương pháp chứng minh Rỗng  VD: Cho “Nếu và thì ”. Chứng minh Ta có Do đó “ ” Vậy
bất chấp giả thiết là đúng hay sai
Phương pháp chứng minh Tầm thường
Các phương pháp chứng minh
 VD: Chứng minh rằng nếu lẻ thì lẻ
Giả sử rằng giả thiết lẻ là đúng. Đặt , với , ta có là lẻ Vậy nếu lẻ thì lẻ
Phương pháp chứng minh Trực tiếp  VD: Cho “Nếu thì ”. Chứng minh rằng với mọi Giả sử , tức là: , với . Ta có: Vậy nếu thì
Phương pháp chứng minh Trực tiếp
Các phương pháp chứng minh
 VD: Chứng minh định lý “Nếu
là số lẻ thì là số lẻ” Giả sử chẵn, tức là , với , ta có là chẵn Vậy nếu
là số lẻ thì là số lẻ
Phương pháp chứng minh Gián tiếp
Các phương pháp chứng minh
 VD: Cho 7 đoạn thẳng có độ dài lớn hơn 10 và nhỏ hơn 100. Chứng minh rằng luôn
tìm được 3 đoạn để có thể ghép thành một tam giác.
Sử dụng phương pháp chứng minh Phản chứng Gọi
là độ dài các đoạn thẳng được sắp xếp theo thứ tự tăng dần ta có 10
100. Ta cần tìm được ba đoạn liên tiếp sao cho tổng độ
dài của hai đoạn đầu lớn hơn đoạn cuối
Giả sử không thể tìm được 3 đoạn để có thể ghép thành một tam giác, tức là ta có: Vì 𝑎 > 10 ∀𝑖 = 1,2, … , 7
Mâu thuẫn với giả thiết
Vậy luôn tồn tại được 3 đoạn để
tức là luôn tìm được 3
đoạn để có thể ghép thành một tam giác
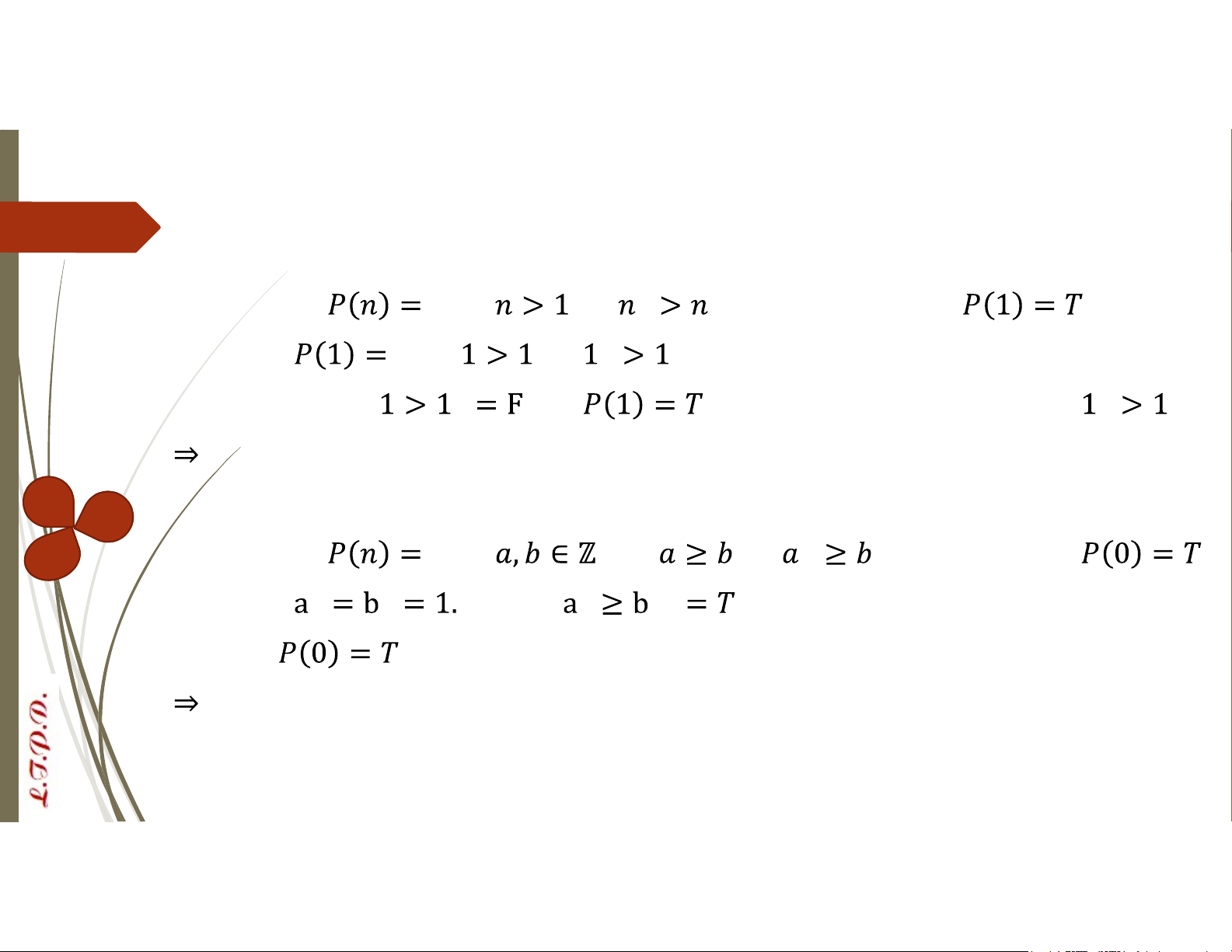
Các phương pháp chứng minh VD: Với
là số nguyên. Chứng minh mệnh đề , với
Sử dụng phương pháp chứng minh Quy nạp  Với : và . Ta được
 Giả sử điều cần chứng minh đúng với giá trị , tức là:
 Chứng minh điều này cũng đúng với giá trị Tức là: ( ) Ta có: ( )
 Vậy điều cần chứng minh đúng với mọi số nguyên
Các phương pháp chứng minh
VD: Sử dụng phương pháp quy nạp chứng minh các biểu thức sau: n n a n 2 n(n n 2 )( 1  ) i i n  ) 1 b) i.2  2  (n  1 ). 1 2 ) c  i(i !)(n )! 1 1  i1 i 1  i1 6
Cách giải: Ghi nhớ 3 bước trong chứng minh quy nạp Đặt - B1: Kiểm chứng Tức là thế
ở hai vế và chứng minh hai vế bằng nhau - B2: Giả sử Thế
ở cả hai vế và giả sử hai vế bằng nhau
- B3: Sử dụng giả thuyết quy nạp ở B2 là , chứng minh Tức là thế
ở cả hai vế và chứng minh hai vế bằng nhau
Các phương pháp chứng minh n 2 n(n  )( 1 2n  ) 1 VD a) Đặt i  với mọi số nguyên i1 6 - B1: Kiểm chứng Vế trái = Vế phải = ( )( . )
Vì vế trái=vế phải nên - B2: Giả sử tức là: ( )( ) - B3: Kiểm chứng tức là cần chứng minh: ( )( )( ) Vế trái= ( )( )
(do giả thuyết quy nạp B2) ( )( )( ) = vế phải Vậy với mọi số nguyên
Các phương pháp chứng minh
 Chứng minh từng trường hợp: Để chứng minh ta có
thể sử dụng tương đương logic
 VD: Chứng minh rằng “Nếu không chia hết cho 3 thì không chia hết cho 3” Đặt:
“ không chia hết cho 3” và Q “ không chia hết cho 3” “ chia cho 3 dư 1” và “ chia cho 3 dư 2” Để chứng minh , ta chứng minh
Các phương pháp chứng minh
 VD: Chứng minh rằng “Nếu không chia hết cho 3 thì không chia hết cho 3” Đặt:
“ không chia hết cho 3” và Q “ không chia hết cho 3” “ chia cho 3 dư 1” và “ chia cho 3 dư 2” Để chứng minh , ta chứng minh Giả sử đúng, tức là với Khi đó: chia cho 3 dư 1 Do đó, (1) Giả sử đúng, tức là với Khi đó: chia cho 3 dư 1 Do đó, (2)
Từ (1) và (2) suy ra nếu không chia hết cho 3 thì không chia hết cho 3
Các phương pháp chứng minh
VD: Một lớp học có 20 học sinh. Các học sinh tham gia vào 3 nhóm năng khiếu:
nhóm Toán có 17 em, nhóm Văn có 13 em và Anh văn có 11 em. Chứng minh rằng
trong lớp có em tham gia đồng thời cả 3 nhóm.
 Gọi là số nhóm mà học sinh tham gia, với . Khi đó:
 Giả sử không tồn tại một học sinh nào tham gia cả 3 nhóm. Tức là . Ta có:  Từ (1) và (2) suy ra 41 là một mâu thuẫn.
 Vậy trong lớp có em tham gia đồng thời cả 3 nhóm.
Các phương pháp chứng minh VD: Chứng minh rằng
luôn chia hết cho 3 với mọi  Đặt Xét hai trường hợp: Nếu thì Ngược lại, đặt . Khi đó: Do đó BÀI TẬP Chứng minh quy nạp: n n(n  n )( 1  n )( 2  i i(  i )( 1  ) 2  ) 3 n i1 4  i   1 1 i1 i (  )! 1 (n  )! 1 n 1 n(n   ) 3 n i1 i i (  i )( 1  ) 2 ( 4 n  n )( 1  ) 2  i1 3 . 2  n 3 1 i1 n n(n  n 2 )( 1  i i(  ) 2  ) 7 i1 6 BÀI TẬP
1. Xét xem G có là hệ quả của F không? F = (PQ)(QR) G = P (Q R)
2. Xét xem suy luận sau đây có hợp logic không?
Nếu Hân về nhà muộn thì mẹ Hân rất giận. Nếu Hùng thường vắng nhà thì mẹ Hùng
rất buồn. Nếu mẹ Hân giận hoặc mẹ Hùng buồn thì cô Hoa sẽ đến chia sẻ và an ủi. Mà
cô Hoa không đến chia sẻ và an ủi. Vậy Hân về nhà sớm và Hùng rất ít khi vắng nhà.
3. Cho vị từ P(x,y)=“x là ước của y”, không gian vị từ là tập Viết
biểu thức logic của các khẳng định sau đây, cho biết chân trị và giải thích lý do
a. Với mọi x, tồn tại y sao cho x là ước của y
b. Tồn tại y, sao cho với mọi x, x là ước của y 4. Chứng minh quy nạp: n i1 3 . 2  n 3 1 i1