Bài Tập Toán Rời Rạc | Đại học Kỹ thuật - Công nghệ Cần Thơ

BÀI TẬP TOÁN RỜI RẠC Chương 1 1. Cho mệnh đề
p: ” nhiệt độ dưới 0” q: ” tuyết rơi”
Sử dụng p, q và các liên từ logic để viết các mệnh đề sau:
a. Nhiệt độ dưới không và tuyết rơi
b. Nhiệt độ dưới không nhưng không có tuyết rơi
c. Nhiệt độ không dưới không và không có tuyết rơi
d. Có tuyết rơi hoặc nhiệt độ dưới không hoặc cả hai
e. Nếu nhiệt độ dưới không thì cũng có tuyết rơi
f. Nhiệt độ dưới không là điều kiện cần và đủ để có tuyết rơi
2. Diễn đạt mệnh đề logic thành các câu thông thường p: “bạn bị cúm”
q: “bạn thi trượt kỳ thi cuối khóa”
r: “bạn được lên lớp” a. p q b. q r c. q r d. p v q v r e. (p r ) v (q r )
3. Lập bảng giá trị chân lý cho các mệnh đề phức hợp sau: a. p  q b. p v p c. ( p v q ) q d.(p v q) (p  q) e. p  q f. p  q g. (p  q) v p  q h. p q k. (p q) v (p q) l. p q) v ( p q) m.(q v q) v r n. (p  q) v r o. (p v q)  r
4. Xác định giá trị của x mỗi khi gặp câu lệnh dưới đây trong một chương trình máy
tính nếu trước câu lệnh x=1; a. if 1+2 =3 then x:=x+1;
b. if (1+1=3) or (2+2=3) then x:=x+1;
c. if (1+1=2) xor (1+2=3) then x:=x+1;
d. if (2+3=5) and (3+4=7) then x:=x+1;
5. Tìm OR bit, AND bit, XOR bit của các cặp xâu nhị phân a. 1011110 ; 0100001 b. 11110000 ; 10101010
6. Xác định các biểu thức sau: a. 11000  (01011 v 11011) b. (01111  10101) v 01000
c. (01010  11011)  01000
d. (11011 v 01010)  (10001 v 11011)
7. Sử dụng bảng chân lý để chứng minh các luật
8. Chứng minh các mệnh đề kéo theo sau đây là hằng đúng ( bằng 2 cách) a. (p  q) p b. p (p v q) c. p (p q) d. (p  q) (p q) e. (p q) p f. ( p q) q
9. Chứng minh các tương đương sau: a. p q và (p  q) v ( p  q) b. p q và q p c. p q và p q d. (p  q) và p q e. ( p q) và p q
10. Cho Q(x) là câu “ x+1=x ”. Tìm chân lý  x Q(x) trong không gian thực
11. Cho câu Q(x,y): “x+y=0” Xác định chân lý của các lượng từ:  y  x Q(x,y),  x  y Q(x,y)
12. Cho P(x,y) là câu :” x đã học môn y” . Với không gian của x là tập hợp các sinh
viên trong lớp và không gian của y là tập hợp các môn tin học
Diễn đạt các biểu thức logic chứa lượng từ sau sang câu : a.  x  y P(x,y) b.  x  y P(x,y) c.  x  y P(x,y) d.  y  x P(x,y) e.  y  x P(x,y) f.  x  y P(x,y)
13. Cho P(x) là câu “ x nói được tiếng Nga”
Q(x) là câu:” x biết C++”
Cho không gian đối với các lượng từ là tập hợp tất cả các sinh viên ở trường.
Diễn đạt câu sau bằng cách dùng các lượng từ và liên từ logic
a. Có một sinh viên ở trường nói được tiếng Nga và biết C++
b. Có một sinh viên ở trường nói được tiếng Nga nhưng không biết C++
c. Mọi sinh viên ở trường đều nói được tiếng Nga hoặc biết C++
d. Không có sinh viên ở trường nói được tiếng Nga hoặc biết C++
14. Cho P(x) là câu:’ X học ở lớp hơn 5 h mỗi ngày trong tuần”
ở đây không gian là tập các sinh viên. Hãy diễn đạt các lượng từ sau thành câu: a.  x P(x) b.  x P(x) c.  x P(x) d.  x P(x)
15. Suy luận nào được sử dụng trong các lập luận cho dưới đây:
a. An học giỏi môn toán . Do đó An học giỏi môn toán hoặc lý
b. Bình học giỏi toán và tin. Do đó Bình học giỏi tin
c. Nếu trời mưa thì bể bơi sẽ đóng cửa. Trời mưa do đó bể bơi đóng cửa
d. Nếu hôm nay tuyết rơi thì trường đại học sẽ đóng cửa. Hôm nay trường đại học
không đóng cửa. Do vậy hôm nay đã không có tuyết rơi.
e. Nếu tôi đi bơi thì tôi sẽ phơi nắng được nhiều. Nếu tôi phơi nắng nhiều thì tôi sẽ rám
nắng. Do đó nếu tôi đi bơi thì tôi rám nắng
f. Tối nay tôi đi xem phim hoặc tôi ở nhà làm bài tập lớn. Tối nay tôi đã không đi xem
phim. Do vậy tôi đã làm bài tập lớn 1 1 1
16. Tìm công thức tính tổng + +...
bằng cách quan sát giá trị của biểu thức 2 4 n 2
này với giá trị nhỏ của n. Dùng phương pháp quy nạp toán học để chứng minh kết quả của bạn. 2 n(n  ) 1 
17. Chứng minh rằng 13 + 23 + ...+ n3=   với n nguyên dương  2  (n  )( 1 2n  )( 1 2n  ) 3
18. Chứng minh rằng 12 + 32 +... + (2n+1)2 = ( ) với n nguyên không 3 âm
19. Chứng minh rằng 1.1!+2.2!+... n.n!= (n+1)!-1 với n nguyên dương
20. Chứng minh rằng n5- n chia hết cho 5 với n nguyên không âm
21. Chứng minh rằng n3 - n chia hết cho 6 với n nguyên không âm
22. Chứng minh rằng n2- 1 chia hết cho 8 với n nguyên dương lẻ
23. Máy trả tiền ATM ở ngân hàng chỉ có hai loại tiền 20$ và 50$. Máy có thể trả các
khoản tiền là bao nhiêu nếu số tờ giấy bạc thuộc hai loại trên là không hạn chế.Hãy
chứng minh câu trả lời của bạn bằng quy nạp toán học Chương 2
1. Một tòa nhà có 27 tầng, mỗi tầng có 37 văn phòng. Hỏi có bao nhiêu văn phòng trong tòa nhà đó?
2. Một phiếu trắc nghiệm đa lựa chọn gồm 10 câu. Mỗi câu hỏi có 4 phương án trả lời :
a. Có bao nhiêu cách điền vào phiếu trắc nghiệm nếu mọi câu hỏi đều được trả lời?
b. Có bao nhiêu cách điền phiếu trắc nghiệm nếu có thể bỏ trống?
3. Có bao nhiêu người có họ tên viết tắt bằng 3 chữ cái ?
4. Có bao nhiêu người có họ tên viết tắt bằng 3 chữ cái trong đó không chữ cái nào được lặp lại?
5. Có bao nhiêu người có họ tên viết tắt bằng 3 chữ cái trong đó trong đó chữ cái đầu tiên là chữ A?
6. Có bao nhiêu xâu nhị phân độ dài bằng 8
7. Có bao nhiêu xâu nhị phân độ dài bằng 10 và có bít cuối và bit đầu là 1
8. Có bao nhiêu xâu nhị phân độ dài bằng 6 hoặc ít hơn?
9. Có bao nhiêu xâu gồm 3 chữ số thập phân :
a. Không chứa cùng một chữ số 3 lần
b. Bắt đầu bằng chữ số lẻ ? c. Có đúng 2 chữ số 4
10. Có bao nhiêu biển đăng ký xe nếu dùng 3 chữ số theo sau là 3 chữ cái hoặc 3 chữ
cái theo sau là 3 chữ số ?
11. Có bao nhiêu biển đăng ký xe nếu dùng 2 chữ số theo sau là 4chữ cái hoặc 2chữ cái theo sau là 4 chữ số ?
12. Có bao nhiêu xâu nhị phân có độ dài bằng 8 và có 2 bít đầu là 0
13. Mỗi sinh viên trong lớp hoặc giỏi toán rời rạc hoặc giỏi tin hoặc giỏi cả hai môn
này. Trong lớp có bao nhiêu sinh viên nếu 38 người giỏi tin (kể cả người giỏi cả 2 môn),
23 người giỏi toán ( kể cả giỏi cả hai môn) và 7 người giỏi cả hai môn?
14. Chứng tỏ rằng trong bất kỳ tập hợp gồm 6 lớp học nào cũng có ít nhất hai lớp gặp
nhau cùng 1 ngày, các lớp học nghỉ thứ 7
15. Trong một ngăn tủ có chứa một tá tất màu nâu, một tá tất màu đen. Một người lấy
các chiếc tất một cách ngẫu nhiên trong bóng tối. Anh ta cần phải lấy ra bao nhiêu chiếc
tất để chắc chắn rằng mình có ít nhất 2 chiếc tất cùng màu?
16. Mỗi sinh viên trong một trường đại học đều quê ở 1 trong 50 tỉnh. Cần tuyển bao
nhiêu sinh viên để đảm bảo có ít nhất 100 người cùng tỉnh?
17. Giả sử một tổ có 9 sinh viên
a. Chứng tỏ rằng trong tổ có ít nhất 5 sinh viên nam hoặc ít nhất có 5 sinh viên nữ.
b. Chứng tỏ rằng trong tổ có ít nhất 3 sinh viên nam hoặc ít nhất 7 sinh viên nữ
18. Một mạng máy tính gồm có 6 máy. Mỗi máy nối trực tiếp hoặc không nối với các
máy khác. Chỉ ra rằng có ít nhất 2 máy mà số các máy khác nối với chúng là bằng nhau
19. Một người bán hàng định đi bán tại 8 thành phố. Hành trình bắt đầu tại một thành
phố và đi đến 7 thành phố khác theo bất kỳ thứ tự nào. Hỏi có thể đi qua tất cả các thành
phố bằng bao nhiêu lộ trình khác nhau?
20. Có bao nhiêu thứ tự có thể xảy ra trong cuộc thi chạy giữa 5 vận động viên?
21. Bao nhiêu khả năng có thể xảy ra đối với các vị trí thứ nhất, thứ nhì, thứ ba trong
cuộc đua có 12 con ngựa, nếu mọi thứ tự tới đích đều có thể xảy ra?
22. Có 6 ứng cử viên chức thống đốc bang. Tính số cách in tên của các ứng cử viên trên phiếu bầu cử?
23. Có một nhóm sinh viên gồm n nam và n nữ. Có bao nhiêu cách xếp thành một hàng
sao cho nam nữ đứng xen nhau?
24. Có bao nhiêu cách chọn một tập hợp 2 số nguyên dương nhỏ hơn 100?
25. Có bao nhiêu cách chọn một tập hợp 5 chữ từ bảng chữ cái tiếng Anh?
26.Trong bảng chữ cái tiếng Anh có 21 phụ âm và 5 nguyên âm. Bao nhiêu xâu gồm 6 chữ thường gồm:
a. Đúng một nguyên âm. 6.5.21.21.21.21.21
b. Ít nhất một nguyên âm
c. Đúng hai nguyên âm c(6,2).5.5.21.21.21.21 d. Ít nhất 2 nguyên âm.
27. Giả sử một tổ bộ môn có 10 nam và 15 nữ. Có bao nhiêu cách chọn một hội đồng
gồm 6 ủy viên trong đó:
a. Số ủy viên nam bằng số ủy viên nữ
b. Số ủy viên nam ít hơn số ủy viên nữ
28. Có bao nhiêu xâu nhị phân chứa đúng 8 số 0 và 10 số 1 và ngay sau mỗi số 0 nhất thiết là một số 1?
29. Có bao nhiêu xâu nhị phân có độ dài 10 chứa ít nhất 3 số 0 và ít nhất 3 số 1?
30. Có bao nhiêu xâu chứa 3 chữ cái tiếp theo là 3 chữ số, nếu các chữ cái hoặc các chữ
số không xuất hiện quá 1 lần
31. Một câu lạc bộ có 25 thành viên
a. Có bao nhiêu cách chọn 4 thành viên vào ủy ban thường trực?
b. Có bao nhiêu cách chọn chủ tịch, phó chủ tịch, thư ký và thủ quỹ?
32. Tên file, tên thư mục trong môi trường DOS được quy định gồm 2 phần: phần tên
và phần mở rộng. Phần tên gồm tối đa 8 ký tự, phần mở rộng tối đa 3 ký tự và có thể có
hoặc không. Các ký tự trong tên file, tên thư mục chỉ gồm các chữ cái( không dấu,
không phân biệt chữ hoa, thường), chữ số hoặc dấu gạch chân. Có thể có bao nhiêu tên file, thư mục khác nhau?
33.Tìm hoán vị theo thứ tự từ điển đi liền sau hoán vị sau: a. 1432 b. 54123
34. Sử dụng thuật toán sinh hoán vị hãy tạo ra hoán vị của 4 số nguyên dương đầu tiên theo thứ tự từ điển
35. Sử dụng thuật toán sinh tổ hợp liệt kê tất cả các tổ hợp chập 3 của tập S = {1, 2, 3, 4, 5 } Chương 3
1.a.Liệt kê tất cả các cặp được sắp trong quan hệ R= {(a,b)| b chia hết cho a }trên tập {1,2,3,4,5,6}
b. Biểu diễn quan hệ trên bằng đồ thị
c. Biểu diễn quan hệ trên dạng ma trận
2. Đối với mỗi quan hệ cho dưới đây trên tập {1,2,3,4} hãy xác định xem nó có là phản
xạ, đối xứng hay bắc cầu không ?
a. {(2,2), (2,3), (2,4), (3,2), (3,3), (3,4)}
b. {(1,1), (1,2), (2,1), (2,2), (3,3), (4,4)} c. {(2,4), (4,2)} d. {(1,2),(2,3),(4,4)}
e. {(1,1), (2,2), (3,3),(4,4) }
f. {(1,3), (1,4), (2,3), (2,4), (3,1), (3,4)}
3. Cho một ví dụ về một quan hệ trên tập {1,2,3,4} có tính chất
a. Phản xạ,đối xứng, không bắc cầu
b. Không phản xạ, đối xứng, bắc cầu.
c. Phản xạ, đối xứng, bắc cầu.
4. Làm thế nào có thể xây dựng bao đóng phản xạ, bao đóng đối xứng của một quan
hệ?. Tìm bao đóng phản xạ, đối xứng của quan hệ
R={(1,2), (2,3), (2,4), (3,1)} trên A={ 1,2,3,4}
5. a.Một bao đóng bắc cầu có thể nhận được bằng cách gộp tất cả các cặp (a,c) sao cho
(a,b) và ( b,c) thuộc quan hệ đó không?
b. Mô tả hai thuật toán tìm bao đóng bắc cầu
c. Tìm bao đóng bắc cầu của quan hệ
R= {(1,1), (1,3), (2,1), (2,3), (2,4), (3,2), (3,4), (4,1)} trên A={ 1,2,3,4}
6. a.Chứng minh quan hệ đồng dư theo modul m là một quan hệ tương đương với mọi m nguyên dương lớn hơn 1
b. Chứng minh quan hệ {(a,b)|a   b (mod 7)} là một quan hệ tương đương trên tập số nguyên
7. Thế nào là các lớp tương đương của một quan hệ tương đương?
Xác định các lớp tương đương của quan hệ đồng dư theo modul 5
8. Cho S là tập tất cả các xâu chữ cái tiếng Anh. Hãy xác định xem các quan hệ cho
dưới đây có là phản xạ, đối xứng, bắc cầu hay không?
a. R = {(a,b)| a và b không có chữ cái nào chung} 1
b. R2 = {(a,b)| a và b có chiều dài khác nhau}
c. R3 = {(a,b)| a dài hơn b}
9. Trong số các quan hệ cho trên tập mọi người dưới đây, quan hệ nào là quan hệ tương đương?
a. {(x,y)| x và y sinh cùng ngày giờ}
b. {(x,y)| x và y sinh cùng năm}
c. {(x,y)| x và y ở cùng thành phố}
10. Cho R là quan hệ trên tập tất cả các cặp số nguyên dương được sắp sao cho
((a,b),(c,d))  R nếu và chỉ nếu ad=bc. Chứng minh rằng R là một quan hệ tương đương.
11. Tìm quan hệ tương đương nhỏ nhất trên tập {a,b,c,d,e}chứa quan hệ {(a,b), (d,c),(d,e)}. Chương 4
1. Có 4 đôi bóng thi đấu vòng tròn một lượt. Kết quả là đội 1 thắng cả 3 đội còn lại, đội
2 thắng đội 3 & 4, đội 4 thắng đội 3. Hãy dùng đồ thị để mô hình hoá kết quả các trận
đấu trên (đội i thắng đội j được biểu diễn bởi 1 cung (i,j) ).
2. Cho các đồ thị sau, hãy lập ma trận kề của chúng(ma trận zêrô-một). 1 3 4 4 3 1 5 5 2 4 2 3 1 2
3. Cho ma trận kề của đồ thị có hướng, hãy biểu diễn đồ thị đó. a. b.  1 0 0 0   1 1 0 0       1 0 0 1   1 1 0 0   1 0 0 1   1 1 1 0       1 0 1 1   1 1 1 0 
4. Cho đồ thị G =(X,U) như hình vẽ
a. Hãy tìm ma trận biểu diễn tương ứng với đồ thị G không trọng số
b. Tìm đường đi ngắn nhất từ đỉnh A đến các đỉnh khác. Độ dài của đường đi là bao nhiêu ? A 14 B 5 C 7 3 8 1 1 16 4 9 8 4 1 G 21 D F E 10 4 21
5. Đường đi ngắn nhất giữa hai đỉnh trong đồ thị có trọng số có là duy nhất không nếu
trong số của các cạnh phân biệt là khác nhau?
6. Giả sử rằng đơn đồ thị phẳng liên thông có 20 đỉnh, mỗi đỉnh đều có bậc bằng 3. Biểu
diễn phẳng của đồ thị này chia mặt phẳng thành bao nhiêu miền ?
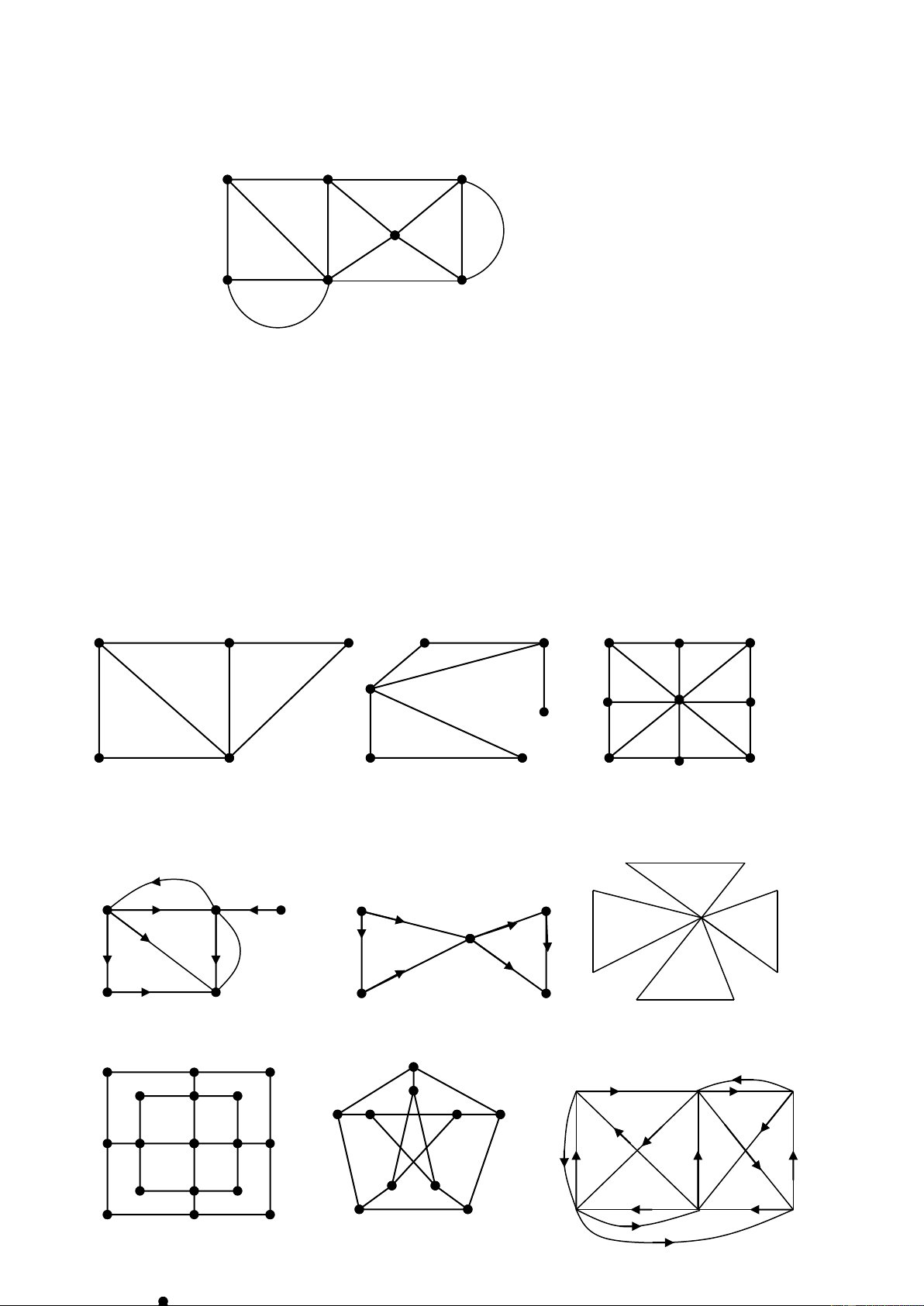
7. Trong các đồ thị sau, đồ thị nào là đồ thị Euler, nửa Euler, Hamilton, nửa Hamilton? Nêu rõ lý do. A B C D E F G H I
8. Tìm cây khung nhỏ nhất theo thuật toán Kruskal và Prim cho bởi đồ thị sau: A 18 B E 12 13 7 10 11 11 9 16 C D H 20 F
9. Tìm đường đi ngắn nhất từ đỉnh a đến đỉnh e trong các đồ thị có trọng số sau: b 5 c d 5 b d 5 4 2 2 4 4 a 2 1 4 2 e a 1 1 e 3 4 3 6 5 6 5 h g f c f
10. Tìm cây khung nhỏ nhất của các đồ thị trong câu 9 theo thuật toán Kruskal và thuật toán Prim.
11. Tìm cây khung lớn nhất của các đồ thị trong câu 9 theo thuật toán tựa Kruskal và thuật toán tựa Prim.
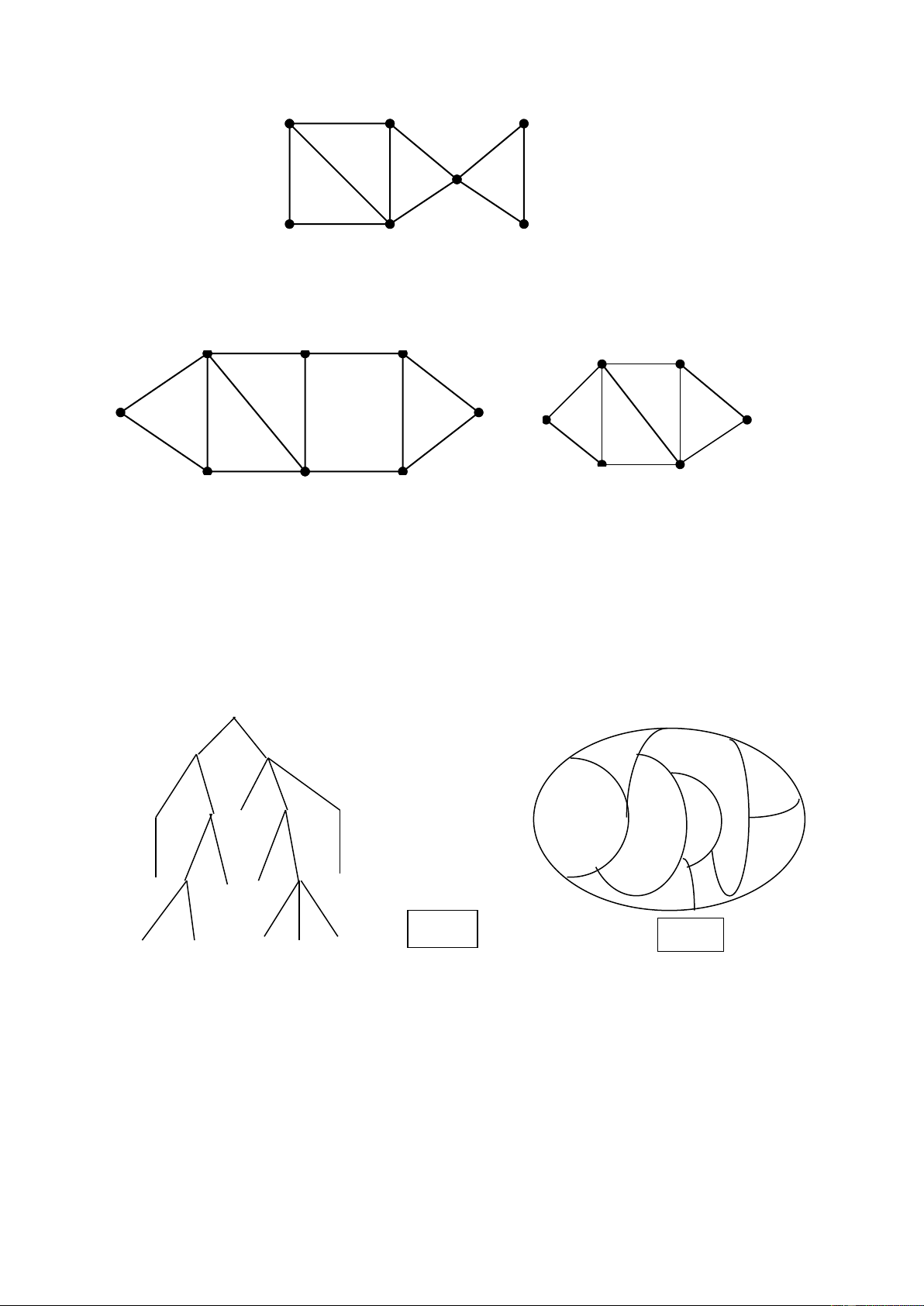
12. Xây dựng đồ thị đối ngẫu của bản đồ H1, sau đó tìm số màu cần tô bản đồ sao cho
không có hai miền kề nhau có cùng một số màu A B C D E F D E F X G A H C G H I J K L B M N O H2 Q H1
13.Duyệt cây H2 bằng các
P phương pháp tiền tự, trung tự, hậu tự
14.Cần bao nhiêu đợt thi để không có sinh viên nào phải thi 2 môn cùng một đợt thi,
biết rằng có 8 môn thi được đánh số từ 1 đến 8 và có các cặp môn thi có chung sinh viên
là: (1,2), (1,3), (1,4), (2,4), (2,5), (2,8), (3,45 ), (3,5), (3,7), (4,5), (5,7), (5,8), (6,7), (6,8)
Vẽ đồ thị mô tả bài toán, giải bài toán sử dụng thuật toán tô màu đồ thị.