Bài giảng Chương 4: Thống kê mô tả môn Xác suất thống kê | Đại học Duy Tân

❳⑩❈ ❙❯❻❚ ❚❍➮◆● ❑➊ ❚!♥ ❚❤➜% ❚&
✣➔ ◆➤♥❣✱ ✷✵✶✾ ❚!♥ ❚❤➜% ❚& ✶✴✷✻
❈❤"#♥❣ ✹✿ ❚❤)♥❣ ❦➯ ♠- .↔
✶✳ ❚-♥❣ .❤➸ ✈➔ ♠➝✉
❛✳ ❈→❝ ❦❤→✐ ♥✐➺♠✿
✲ ❚!♥❣ $❤➸ ✿ "➟♣ ❤&♣ "♦➔♥ ❜+ ❝→❝ ♣❤➛♥ "/ "❤0♥❣ ♥❤➜" "❤❡♦ ❞➜✉ ❤✐➺✉ ♥❣❤✐➯♥ ❝9✉✳ ❚<♥❣
"❤➸ ❝> "❤➸ ❤?✉ ❤↕♥ ❤♦➦❝ ✈C ❤↕♥✳
✲ ▼➝✉✿ ♠+" "➟♣ ❝♦♥ ❜➜" ❦➻ ❝G❛ "<♥❣ "❤➸✳ ❙0 ❧K&♥❣ ♣❤➛♥ "/ ❝G❛ ♥> ✤K&❝ ❣M✐ ❧➔ ❦➼❝❤
"❤KO❝ ❤❛② ❝Q ♠➝✉✳
✲ *❤➨♣ ❧➜② ♠➝✉✿ ✈✐➺❝ ❝❤M♥ ♠+" "➟♣ ❝♦♥ ❜➜" ❦➻ ❝G❛ "<♥❣ "❤➸✳
✲ ▼➝✉ ♥❣➝✉ ♥❤✐➯♥✿ ♠+" ♠➝✉ ❧➔ ♥❣➝✉ ♥❤✐➯♥ ♥➳✉ ✈✐➺❝ ❝❤M♥ ❝→❝ ❝→ "❤➸ ✤K&❝ "✐➳♥ ❤➔♥❤
✤+❝ ❧➟♣ ✈➔ ❝> ①→❝ U✉➜" ❝❤M♥ ♥❤K ♥❤❛✉✳
❱➲ ♠➦" "♦→♥ ❤M❝✱ ♠+" ♠➝✉ ♥❣➝✉ ♥❤✐➯♥ ❦➼❝❤ "❤KO❝ n "Y "<♥❣ "❤➸ ❝> ♣❤➙♥ ♣❤0✐ "❤❡♦ ❜✐➳♥
♥❣➝✉ ♥❤✐➯♥ X ❝> "❤➸ ①❡♠ ♥❤K ♠+" ❜+ n ❜✐➳♥ ♥❣➝✉ ♥❤✐➯♥ {X1, X2, ..., Xn} ✤+❝ ❧➟♣ ✈➔
❝> ❝[♥❣ ♣❤➙♥ ♣❤0✐ ✈O✐ X✳ ❚!♥ ❚❤➜% ❚& ✷✴✷✻
✲ ❈❤♦ ♠➝✉ ♥❣➝✉ ♥❤✐➯♥ {X1, X2, ..., Xn}✳ ❑❤✐ ✤>✿
✰ ❇+ n ❣✐→ "`a {x1, x2, ..., xn} ❝b "❤➸ c✉❛♥ "❤✉ ✤K&❝ ✤K&❝ ❣M✐ ❧➔ ♠➝✉ $❤3❝ ♥❣❤✐➺♠✳
✰ ▼+" ❤➔♠ ✭✤♦ ✤K&❝✮ T = T(X1, X2, ..., Xn) ✤K&❝ ❣M✐ ❧➔ ♠+" $❤6♥❣ ❦➯ "`➯♥ ♠➝✉
♥❣➝✉ ♥❤✐➯♥ {X1, X2, ..., Xn}✳
❜✳ >❤➨♣ ❧➜② ♠➝✉ ✤E♥ ❣✐↔♥✿
✲ ▲➜② ❝> ❤♦➔♥ ❧↕✐✿ ❈❤M♥ ♥❣➝✉ ♥❤✐➯♥ ♠+" ❝→ "❤➸ "Y "<♥❣ "❤➸✱ ❣❤✐ ❧↕✐ ❝→❝ ❞➜✉ ❤✐➺✉ ❝➛♥
c✉❛♥ "➙♠ ✈➔ ❤♦➔♥ "`↔ ❧↕✐ ✈➔♦ "<♥❣ "❤➸ "`KO❝ ❦❤✐ ❝❤M♥ "✐➳♣ ❧➛♥ U❛✉✳
✲ ▲➜② ❦❤C♥❣ ❤♦➔♥ ❧↕✐✿ "Ki♥❣ "j "`➯♥✱ ♥❤K♥❣ ♣❤➛♥ "/ ✤K&❝ ❧➜② `❛ ❦❤C♥❣ "`↔ ❧↕✐ ✈➔♦
"<♥❣ "❤➸ "`KO❝ ❦❤✐ ❝❤M♥ "✐➳♣✳ ❚!♥ ❚❤➜% ❚& ✸✴✷✻
✷✳ ❇↔♥❣ &➛♥ ()✱ &➛♥ (✉➜&
❛✳ ▼➝✉ ❦❤2♥❣ ❣❤➨♣ ❧6♣ ✲ ❇↔♥❣ %➛♥ '(✿
●✐→ %-. x1 x2 ✳✳✳ xm
❚➛♥ '( n1 n2 ✳✳✳ nm
%-♦♥❣ ✤3 x1, ..., xm ❧➔ ❝→❝ ❣✐→ %-. ❦❤→❝ ♥❤❛✉ ✈<✐ '( ❧➛♥ ①✉➜% ❤✐➺♥ ❧➔ n1, ..., nm✳
✲ ❇↔♥❣ %➛♥ '✉➜%✿ ●✐→ %-. x1 x2 ✳✳✳ xm
❚➛♥ '✉➜% f1 f2 ✳✳✳ fm m %-♦♥❣ ✤3 f P i = ni/n, n =
ni✳ ●✐→ %-. fi ✤@A❝ ❣B✐ ❧➔ ➛♥ #✉➜ ①✉➜% ❤✐➺♥ ❝C❛ xi %-♦♥❣ i=1 ♠➝✉✳ ❚!♥ ❚❤➜% ❚& ✹✴✷✻ ❱➼ ❞: ✶
❑❤↔♦ #→ ✉+✐ ❝.❛ ♠1 ♥❤2♠ ❤3❝ ✈✐➯♥ ❤3❝ ❛♥❤ ✈➠♥ ↕✐ ♠1 8✉♥❣ ➙♠ ♥❣♦↕✐ ♥❣;✱ ❛ ❤✉
✤>?❝ ❜↔♥❣ #A ❧✐➺✉ #❛✉✿ ❚✉+✐
✶✺ ✶✻ ✶✼ ✶✽ ✶✾ ❙A ❧>?♥❣ ✹ ✻ ✸ ✺ ✼ ❱➼ ❞: ✷
❑❤↔♦ #→ ♥❣➝✉ ♥❤✐➯♥ ♠1 ♥❤2♠ ♥❣>P✐ ✈➲ ✈✐➺❝ ❤3 #R ❞T♥❣ ♣❤>V♥❣ ✐➺♥ ❣➻ ❤>P♥❣ ①✉②➯♥
♥❤➜ ✤➸ ✤3❝ ❜→♦✿ ❜→♦ ❣✐➜②✱ ♠→② ➼♥❤✱ ✤✐➺♥ ❤♦↕✐ ❤❛② ♠→② ➼♥❤ ❜↔♥❣✳ ❑➳ ^✉↔ ✤>?❝ ❤➸
❤✐➺♥ ♥❤> #❛✉✿
_❤>V♥❣ ✐➺♥ ❇→♦ ❣✐➜② ▼→② ➼♥❤ ✣✐➺♥ ❤♦↕✐ ▼→② ➼♥❤ ❜↔♥❣ ❙A ❧>?♥❣ ✺ ✷✵ ✺✵ ✶✺ ❚!♥ ❚❤➜% ❚& ✺✴✷✻
❜✳ ▼➝✉ ❣❤➨♣ ❧6♣
❑❤✐ %❛ %❤✉ ✤@A❝ ♠➝✉ ❞H ❧✐➺✉ ✈<✐ ♥❤✐➲✉ ❣✐→ %-. ❦❤→❝ ♥❤❛✉ %❤➻ ♥❣@K✐ %❛ %✐➳♥ ❤➔♥❤ ❝❤✐❛
♠✐➲♥ ❣✐→ %-. %❤➔♥❤ ♥❤✐➲✉ ❦❤♦↔♥❣ [ai 1, ai) ❦❤M♥❣ ❣✐❛♦ ♥❤❛✉✳ − ✲ ❇↔♥❣ %➛♥ '(✿
❑❤♦↔♥❣ ❣✐→ %-. [a0, a1) [a1, a2) ✳✳✳ [am 1, am) − ❚➛♥ '( n1 n2 ✳✳✳ nm
✲ ❇↔♥❣ %➛♥ '✉➜%✿
❑❤♦↔♥❣ ❣✐→ %-. [a0, a1) [a1, a2) ✳✳✳ [am 1, am) − ❚➛♥ '✉➜% f1 f2 ✳✳✳ fm
◆❤➟♥ ①➨&✿ ❚❤M♥❣ %❤@K♥❣ ❝→❝ ❦❤♦↔♥❣ ❝❤✐❛ ❝3 ✤N ❞➔✐ ❜➡♥❣ ♥❤❛✉✳ ❚✉② ♥❤✐➯♥✱ %T② %❤✉N❝
✈➔♦ ♠U❝ ✤➼❝❤ ♥❣❤✐➯♥ ❝W✉ ♠➔ %❛ ❝3 %❤➸ ❝3 ♥❤H♥❣ ❝→❝❤ ❝❤✐❛ ❦❤♦↔♥❣ ❦❤→❝ ♥❤❛✉✳ ❚!♥ ❚❤➜% ❚& ✻✴✷✻ ❱➼ ❞# ✸
❈➙♥ #❤% ✶✵✵ #(→✐ #→♦ ✈-❛ #❤✉ ❤♦↕❝❤✱ #❛ ✤45❝ ❜↔♥❣ 9: ❧✐➺✉ 9❛✉✿
❑❤:✐ ❧45♥❣ ✭❣✮ ❬✶✵✵❀✶✷✵✮ ❬✶✷✵❀✶✹✵✮ ❬✶✹✵❀✶✻✵✮ ❬✶✻✵❀✶✽✵✮ ❬✶✽✵❀✷✵✵✮ ❙: #(→✐ ✶✷ ✶✾ ✸✶ ✷✸ ✶✺ ❱➼ ❞# ✹
❑❤↔♦ 9→# #❤K✐ ❣✐❛♥ #(✉♥❣ ❜➻♥❤ ✭#➼♥❤ ❜➡♥❣ ❣✐K✮ ♠➔ ♠Q# ♥❣4K✐ #- ✤Q #✉R✐ ✶✺ #(S ❧➯♥ ❞➔♥❤
✤➸ ✤W❝ #✐♥ #X❝ #❤K✐ 9Y ♦♥❧✐♥❡ #(♦♥❣ ♠Q# ♥❣➔② S ♠Q# #❤➔♥❤ ♣❤:✱ 9: ❧✐➺✉ ✤45❝ #❤➸ ❤✐➺♥ S ❜↔♥❣ 9❛✉✿ ✣Q #✉R✐
❬✶✺✱✷✵✮ ❬✷✵✱✸✵✮ ❬✸✵✱✹✵✮ ❬✹✵✱✺✵✮ ≥ 50
❚❤K✐ ❣✐❛♥ #(✉♥❣ ❜➻♥❤ ✶✱✶ ✷✱✷ ✷✱✼ ✶✱✾ ✵✱✼ ❚!♥ ❚❤➜% ❚& ✼✴✷✻
✸✳ ❈→❝ *+ ✤➦❝ ./0♥❣ ♠➝✉
❛✳ ❚/✉♥❣ ❜➻♥❤ ✈➔ ♣❤0>♥❣ *❛✐ ♠➝✉
❈❤♦ {x1, x2, ..., xn} ❧➔ ♠➝✉ () ❧✐➺✉ ❝-❛ ❜✐➳♥ ♥❣➝✉ ♥❤✐➯♥ X✳
✲ ❚7✉♥❣ ❜➻♥❤ ♠➝✉✱ ❦➼ ❤✐➺✉ ❧➔ x✱ ✤=>❝ ?➼♥❤ ?❤❡♦ ❝A♥❣ ?❤B❝✿ n x 1 X x = 1 + x2 + ... + xn = xi n n i=1
✲ D❤=E♥❣ (❛✐ ♠➝✉✱ ❦➼ ❤✐➺✉ ❧➔ s2✱ ✤=>❝ ?➼♥❤ ?❤❡♦ ❝A♥❣ ?❤B❝✿   n n 1 X 1 X s2 = (xi − x)2 = x2 n − 1 n − 1  i − n(x)2 i=1 i=1
✲ ✣G ❧➺❝❤ ❝❤✉➞♥ ♠➝✉✱ ❦➼ ❤✐➺✉ s✱ ✤=>❝ ?➼♥❤✿ √ s = s2 ❚!♥ ❚❤➜% ❚& ✽✴✷✻ ◆❤➟♥ ①➨.✿
✐✮ ❑❤✐ ♠➝✉ ✤=>❝ ❝❤♦ K ❞↕♥❣ ❜↔♥❣ ?➛♥ ()✿ X x1 x2 ✳✳✳ xm ni n1 n2 ✳✳✳ nm
✲ ❑➼❝❤ ?❤=P❝ ♠➝✉✿ n = n1 + n2 + ... + nm✳ m
✲ ❚7✉♥❣ ❜➻♥❤ ♠➝✉✿ 1 x = P nixi✳ n i=1 " # m
✲ D❤=E♥❣ (❛✐ ♠➝✉✿ 1 s2 = P nix2 . n − 1 i − nx2 i=1 ❚!♥ ❚❤➜% ❚& ✾✴✷✻
✐✐✮ ❑❤✐ ♠➝✉ ' ❞↕♥❣ ❜↔♥❣ ❣❤➨♣ ❧1♣✿ X a0 − a1 a1 − a2 ✳✳✳ am 1 − am − ni n1 n2 ✳✳✳ nm
45♦♥❣ ✤8 ak 1 − ak = [ak 1; ak)✳ − − ✣➦4 ak x 1 + ak − k =
4❛ ✤<=❝ ♠➝✉ ❞↕♥❣ 4❤✉ ❣?♥✿ 2 ❳ x1 x2 ✳✳✳ xm ni n1 n2 ✳✳✳ nm ❚!♥ ❚❤➜% ❚& ✶✵✴✷✻
✐✐✐✮ ❚➼♥❤ x ✈➔ s ❜➡♥❣ ♠→② 4➼♥❤ ❈❆❙■❖ ❋❳✺✼✵❱◆ S▲❯❙✳
✲ ▼♦❞❡ → ✸ → ✶
✲ ❇➟4✴4➢4 4➛♥ `a✿ ❙❤✐❢4 → ❙❊❚❯S → ❘❊S▲❆❨ ✭↓✮ → ✹✭❙4❛4✮
✲ ◆❤➟♣ `a ❧✐➺✉✱ ❦➳4 4❤l❝ ♥❤➟♣✿ ❜➜♠ ❆❈
✲ ▲➜② x✿ ❙❤✐❢4 → ✶ → ✹ → ✷ → ❂
✲ ▲➜② s✿ ❙❤✐❢4 → ✶ → ✹ → ✹ → ❂ ❱➼ ❞# ✺
❈❤✐➲✉ ❝❛♦ ✭♠➨+✮ ❝-❛ ✶✵ 0✐♥❤ ✈✐➯♥ ✤↕✐ ❤6❝✿
1.75, 1.69, 1.70, 1.82, 1.68, 1.72, 1.70, 1.67, 1.71, 1.68
❚➼♥❤ +:✉♥❣ ❜➻♥❤ ♠➝✉✱ ♣❤AB♥❣ 0❛✐ ♠➝✉ ✈➔ ✤D ❧➺❝❤ ❝❤✉➞♥ ♠➝✉✳ ✣→♣ ()✳ ¯ x = 1, 712; s2 = 0.00197; s = 0.0444 ❚!♥ ❚❤➜% ❚& ✶✶✴✷✻ ❱➼ ❞# ✻
❉♦❛♥❤ +❤✉ X ✭+:✐➺✉ ✤J♥❣✮ +:♦♥❣ ✶✵✵ ♥❣➔② ✤AL❝ ❝❤6♥ ♥❣➝✉ ♥❤✐➯♥ ❝-❛ ✶ ❝M❛ ❤➔♥❣✿ X
✶✾✱✵ ✲ ✶✾✱✹ ✶✾✱✹ ✲ ✶✾✱✽ ✶✾✱✽ ✲ ✷✵✱✷ ✷✵✱✷ ✲ ✷✵✱✻ ✷✵✱✻ ✲ ✷✶✱✵ ni 15 25 30 20 10
❚➻♠ +:✉♥❣ ❜➻♥❤ ♠➝✉ ✈➔ ✤D ❧➺❝❤ ❝❤✉➞♥ ♠➝✉✳
●✐↔✐✳ ❉↕♥❣ 4❤✉ ❣?♥✿ X
✶✾✱✷ ✶✾✱✻ ✷✵ ✷✵✱✹ ✷✵✱✽ ni 15 25 30 20 10
❈→❝ `a ✤➦❝ 45<♥❣ ♠➝✉✿ ¯ x = 19, 94; s = 0, 48 ❚!♥ ❚❤➜% ❚& ✶✷✴✷✻
❜✳ ❚#✉♥❣ ✈( ♠➝✉
❙➢♣ ①➳♣ ♠➝✉ () ❧✐➺✉ -❤❡♦ -❤1 -2 -➠♥❣ ❞➛♥✱ ❣✐↔ (: x1 ≤ x2 ≤ ... ≤ xn✳ !✉♥❣ ✈& ♠➝✉✱ ❦➼
❤✐➺✉ xmed✱ ①→❝ ✤A♥❤ ❜C✐✿  x , ♥➳✉ n ❧➫✱ n+1  x 2 med = x n + x n +1 2 2  ♥➳✉ n ❝❤➤♥✳  2
❝✳ ❍➺ ./ 012♥❣ 3✉❛♥ ♠➝✉
❈❤♦ {(x1, y1); (x2, y2); ...; (xn, yn)} ❧➔ ♠➝✉ ❤❛✐ ❝❤✐➲✉ ❝K❛ ✈❡❝-M ♥❣➝✉ ♥❤✐➯♥ (X, Y )✳ ❍➺
+, -.♥❣ /✉❛♥ ♠➝✉ ✤OP❝ ①→❝ ✤A♥❤ ❜C✐✿ Pn (xi − x)(yi − y) r = i=1 pPn (x (y i=1 i − x)2 Pn i=1 i − y)2 ❚!♥ ❚❤➜% ❚& ✶✸✴✷✻ ✸✳ ❇✐➸✉ ✤:
❛✳ ❇✐➸✉ ✤: ❝❤♦ ❞> ❧✐➺✉ #@✐ #↕❝✿
✲ ❇✐➸✉ ✤5 ❝7 ✿ ✤R -❤A ❣R♠ ❝→❝ ❝S- ❤➻♥❤ ❝❤U ♥❤➟- ❝W ❝❤✐➲✉ ❝❛♦ ❜➡♥❣ -➛♥ () ✭-➛♥ (✉➜-✮ -OM♥❣ 1♥❣✳
✲ ✣❛ ❣✐→❝ ➛♥ +, ✿ ✤O\♥❣ ❣➜♣ ❦❤]❝ ♥)✐ ❝→❝ ✤✐➸♠ (x1, n1), ..., (xk, nk) -_➯♥ ♠➦- ♣❤➥♥❣✳
✲ ✣❛ ❣✐→❝ ➛♥ +✉➜ ✿ ✤O\♥❣ ❣➜♣ ❦❤]❝ ♥)✐ ❝→❝ ✤✐➸♠ (x1, f1), ..., (xk, fk) -_➯♥ ♠➦- ♣❤➥♥❣✳
✲ ❇✐➸✉ ✤5 ❤➻♥❤ !>♥✿ ❤➻♥❤ -_b♥ ✤OP❝ ❝❤✐❛ _❛ ❝→❝ ♣❤➛♥ ❝W ❞✐➺♥ -➼❝❤ -➾ ❧➺ ✈d✐ -➛♥ (✉➜- ✭-➛♥ ()✮ -OM♥❣ 1♥❣✳ ❚!♥ ❚❤➜% ❚& ✶✹✴✷✻ ❱➼ ❞E ✼ ❈❤♦ ❞B ❧✐➺✉✿ X ✶ ✷ ✸ ✹ ✺ ❚➛♥ +, ✶✷ ✸✵ ✷✵ ✶✶ ✼
❚➛♥ +✉➜ ✵✳✶✺ ✵✳✹ ✵✳✸ ✵✳✶✹ ✵✳✶
❍➣② ✈➩ ❝→❝ ❜✐➸✉ ✤5✿
✲ ❜✐➸✉ ✤5 ❝7 ✭ ➛♥ +,✱ ➛♥ +✉➜ ✮
✲ ✤❛ ❣✐→❝ ➛♥ +,✱ ➛♥ +✉➜
✲ ❜✐➸✉ ✤5 ❤➻♥❤ !>♥ ❚!♥ ❚❤➜% ❚& ✶✺✴✷✻ ❚!♥ ❚❤➜% ❚& ✶✻✴✷✻ ❚!♥ ❚❤➜% ❚& ✶✼✴✷✻ ❚!♥ ❚❤➜% ❚& ✶✽✴✷✻
❜✳ ❇✐➸✉ ✤' ❝❤♦ ❞, ❧✐➺✉ ❧✐➯♥ 12❝✿
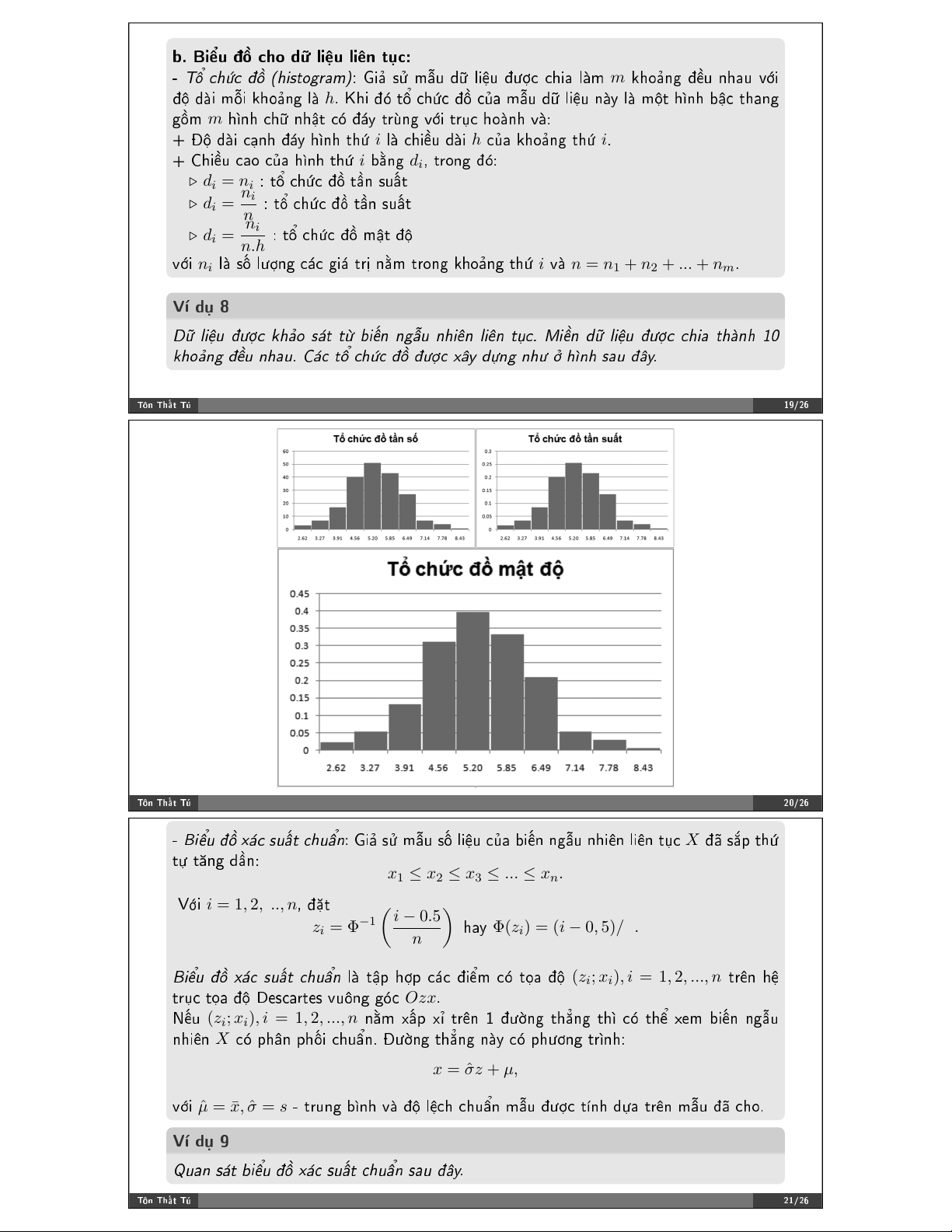
✲ ❚! ❝❤$❝ ✤& ✭❤✐)*♦❣-❛♠✮✿ ●✐↔ %& ♠➝✉ ❞+ ❧✐➺✉ ✤/0❝ ❝❤✐❛ ❧➔♠ m ❦❤♦↔♥❣ ✤➲✉ ♥❤❛✉ ✈;✐
✤< ❞➔✐ ♠=✐ ❦❤♦↔♥❣ ❧➔ h✳ ❑❤✐ ✤@ AB ❝❤C❝ ✤D ❝E❛ ♠➝✉ ❞+ ❧✐➺✉ ♥➔② ❧➔ ♠❣D♠ m ❤➻♥❤ ❝❤+ ♥❤➟A ❝@ ✤→② AKL♥❣ ✈;✐ AKM❝ ❤♦➔♥❤ ✈➔✿
✰ ✣< ❞➔✐ ❝↕♥❤ ✤→② ❤➻♥❤ A❤C i ❧➔ ❝❤✐➲✉ ❞➔✐ h ❝E❛ ❦❤♦↔♥❣ A❤C i✳
✰ ❈❤✐➲✉ ❝❛♦ ❝E❛ ❤➻♥❤ A❤C i ❜➡♥❣ di✱ AK♦♥❣ ✤@✿
⊲ di = ni ✿ AB ❝❤C❝ ✤D A➛♥ %✉➜A ni ⊲ di =
✿ AB ❝❤C❝ ✤D A➛♥ %✉➜A nni ⊲ di =
✿ AB ❝❤C❝ ✤D ♠➟A ✤< n.h
✈;✐ ni ❧➔ %V ❧/0♥❣ ❝→❝ ❣✐→ AKW ♥➡♠ AK♦♥❣ ❦❤♦↔♥❣ A❤C i ✈➔ n = n1 + n2 + ... + nm✳ ❱➼ ❞2 ✽
❉2 ❧✐➺✉ ✤67❝ ❦❤↔♦ )→* *; ❜✐➳♥ ♥❣➝✉ ♥❤✐➯♥ ❧✐➯♥ *A❝✳ ▼✐➲♥ ❞2 ❧✐➺✉ ✤67❝ ❝❤✐❛ *❤➔♥❤ ✶✵
❦❤♦↔♥❣ ✤➲✉ ♥❤❛✉✳ ❈→❝ *! ❝❤$❝ ✤& ✤67❝ ①➙② ❞M♥❣ ♥❤6 N ❤➻♥❤ )❛✉ ✤➙②✳ ❚!♥ ❚❤➜% ❚& ✶✾✴✷✻ ❚!♥ ❚❤➜% ❚& ✷✵✴✷✻
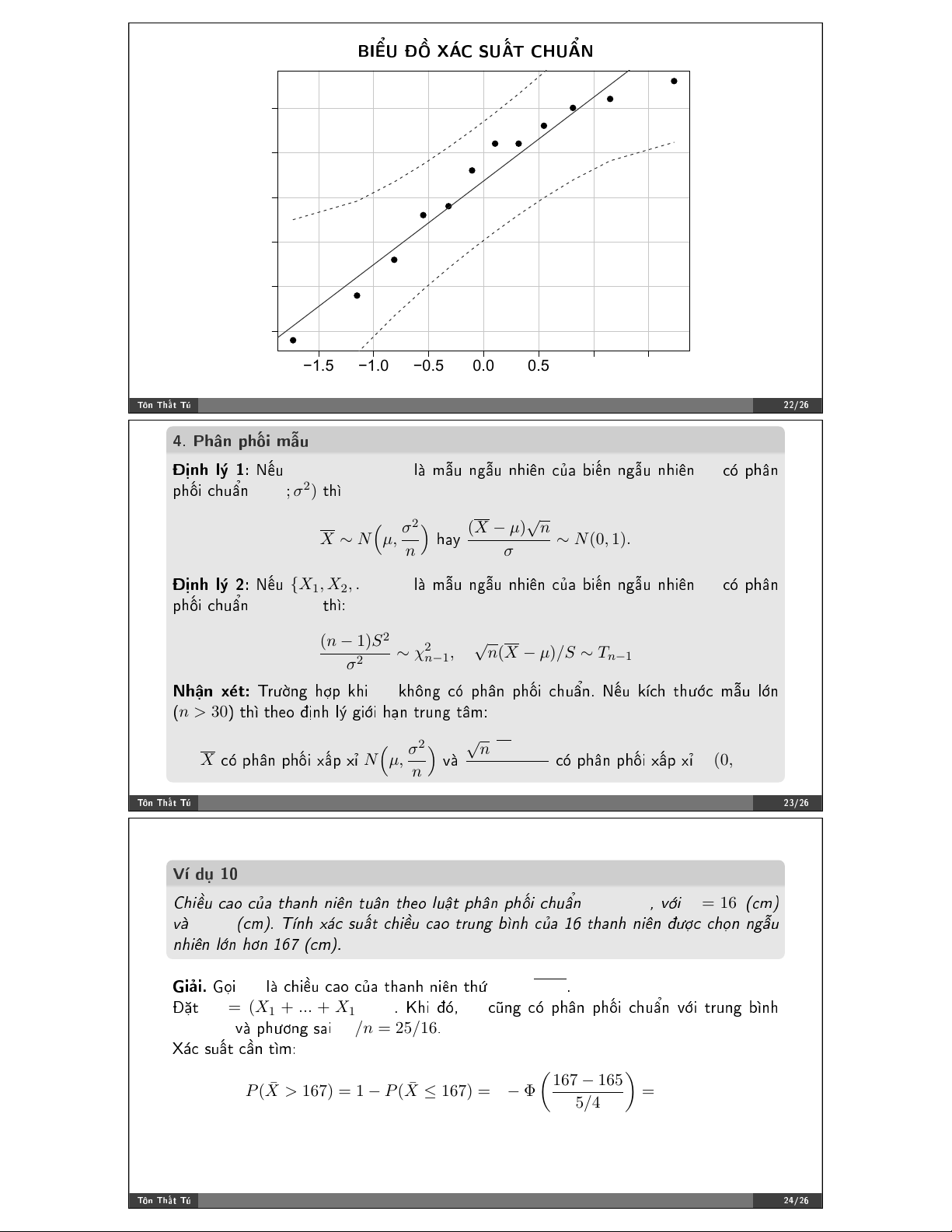
✲ ❇✐➸✉ ✤& ①→❝ )✉➜* ❝❤✉➞♥✿ ●✐↔ %& ♠➝✉ %V ❧✐➺✉ ❝E❛ ❜✐➳♥ ♥❣➝✉ ♥❤✐➯♥ ❧✐➯♥ AM❝ X ✤➣ %➢♣ A❤C A] A➠♥❣ ❞➛♥✿
x1 ≤ x2 ≤ x3 ≤ ... ≤ xn.
❱;✐ i = 1, 2, ..., n✱ ✤➦A i − 0.5 z 1 i = Φ−
❤❛② Φ(zi) = (i − 0, 5)/n. n
❇✐➸✉ ✤% ①→❝ )✉➜+ ❝❤✉➞♥ ❧➔ "➟♣ ❤&♣ ❝→❝ ✤✐➸♠ ❝- ".❛ ✤0 (zi; xi), i = 1, 2, ..., n "1➯♥ ❤➺
"15❝ ".❛ ✤0 ❉❡8❝❛1"❡8 ✈✉;♥❣ ❣-❝ Ozx✳
◆➳✉ (zi; xi), i = 1, 2, ..., n ♥➡♠ ①➜♣ ①➾ "1➯♥ ✶ ✤EF♥❣ "❤➥♥❣ "❤➻ ❝- "❤➸ ①❡♠ ❜✐➳♥ ♥❣➝✉
♥❤✐➯♥ X ❝- ♣❤➙♥ ♣❤L✐ ❝❤✉➞♥✳ ✣EF♥❣ "❤➥♥❣ ♥➔② ❝- ♣❤EP♥❣ "1➻♥❤✿ x = ˆ σz + ˆ µ,
✈R✐ ˆµ = ¯x, ˆσ = s ✲ "1✉♥❣ ❜➻♥❤ ✈➔ ✤0 ❧➺❝❤ ❝❤✉➞♥ ♠➝✉ ✤E&❝ "➼♥❤ ❞V❛ "1➯♥ ♠➝✉ ✤➣ ❝❤♦✳ ❱➼ ❞# ✾
◗✉❛♥ )→+ ❜✐➸✉ ✤% ①→❝ )✉➜+ ❝❤✉➞♥ )❛✉ ✤➙②✳ ❚!♥ ❚❤➜% ❚& ✷✶✴✷✻
❇■➎❯ ✣➬ ❳⑩❈ ❙❯❻❚ ❈❍❯❽◆ 6.5 6.0 5.5 5.0 4.5 4.0 •1.5 •1.0 •0.5 0.0 0.5 1.0 1.5 ❚!♥ ❚❤➜% ❚& ✷✷✴✷✻
✹✳ 1❤➙♥ ♣❤6✐ ♠➝✉
✣;♥❤ ❧= ✶✿ ◆➳✉ {X1, X2, ..., Xn} ❧➔ ♠➝✉ ♥❣➝✉ ♥❤✐➯♥ ❝-❛ ❜✐➳♥ ♥❣➝✉ ♥❤✐➯♥ X ❝0 ♣❤➙♥
♣❤3✐ ❝❤✉➞♥ N(µ; σ2) 5❤➻ √ σ2 n X ∼ N µ, ❤❛② (X − µ) ∼ N(0, 1). n σ
✣;♥❤ ❧= ✷✿ ◆➳✉ {X1, X2, ..., Xn} ❧➔ ♠➝✉ ♥❣➝✉ ♥❤✐➯♥ ❝-❛ ❜✐➳♥ ♥❣➝✉ ♥❤✐➯♥ X ❝0 ♣❤➙♥
♣❤3✐ ❝❤✉➞♥ N(µ; σ2) 5❤➻✿ (n − 1)S2 √ ∼ χ2 , n(X − µ)/S ∼ Tn σ2 n 1 1 − −
◆❤➟♥ ①➨D✿ ❚:;<♥❣ ❤=♣ ❦❤✐ X ❦❤?♥❣ ❝0 ♣❤➙♥ ♣❤3✐ ❝❤✉➞♥✳ ◆➳✉ ❦➼❝❤ 5❤;B❝ ♠➝✉ ❧B♥
✭n > 30✮ 5❤➻ 5❤❡♦ ✤H♥❤ ❧I ❣✐B✐ ❤↕♥ 5:✉♥❣ 5➙♠✿ √ σ2 n(X − µ)
X ❝0 ♣❤➙♥ ♣❤3✐ ①➜♣ ①➾ N µ, ✈➔
❝0 ♣❤➙♥ ♣❤3✐ ①➜♣ ①➾ N(0, 1) n S ❚!♥ ❚❤➜% ❚& ✷✸✴✷✻ ❱➼ ❞H ✶✵
❈❤✐➲✉ ❝❛♦ ❝(❛ )❤❛♥❤ ♥✐➯♥ )✉➙♥ )❤❡♦ ❧✉➟) ♣❤➙♥ ♣❤1✐ ❝❤✉➞♥ N(µ; σ2)✱ ✈5✐ µ = 165✭❝♠✮
✈➔ σ = 5✭❝♠✮✳ ❚➼♥❤ ①→❝ ?✉➜) ❝❤✐➲✉ ❝❛♦ )A✉♥❣ ❜➻♥❤ ❝(❛ ✶✻ )❤❛♥❤ ♥✐➯♥ ✤HI❝ ❝❤J♥ ♥❣➝✉
♥❤✐➯♥ ❧5♥ ❤L♥ ✶✻✼ ✭❝♠✮✳
●✐↔✐✳ ●P✐ Xi ❧➔ ❝❤✐➲✉ ❝❛♦ ❝-❛ 5❤❛♥❤ ♥✐➯♥ 5❤R i, i = 1, 16✳ ✣➦5 ¯
X = (X1 + ... + X16)/16✳ ❑❤✐ ✤0✱ ¯
X ❝W♥❣ ❝0 ♣❤➙♥ ♣❤3✐ ❝❤✉➞♥ ✈B✐ 5:✉♥❣ ❜➻♥❤
µ = 165 ✈➔ ♣❤;X♥❣ Y❛✐ σ2/n = 25/16✳
❳→❝ Y✉➜5 ❝➛♥ 5➻♠✿ 167 − 165 P ( ¯ X > 167) = 1 − P ( ¯ X ≤ 167) = 1 − Φ = 0.0548 5/4 ❚!♥ ❚❤➜% ❚& ✷✹✴✷✻ ❱➼ ❞# ✶✶
✣➸ ♥❣❤✐➯♥ ❝(✉ ✈➲ ,❤➙♠ ♥✐➯♥ ❝/♥❣ ,→❝ ✭,➼♥❤ ,34♥ ♥➠♠✮ ❝7❛ ♥❤➙♥ ✈✐➯♥ 9 ♠:, ❝/♥❣ ,② ❧=♥✱
♥❣?@✐ ,❛ ❦❤↔♦ D→, ,❤➙♠ ♥✐➯♥ ❝7❛ ✶✵✵ ♥❤➙♥ ✈✐➯♥ ✤?H❝ ❝❤I♥ ♥❣➝✉ ♥❤✐➯♥ ,3♦♥❣ ❝/♥❣ ,②✳
❑➳, N✉↔ ♥❤? D❛✉✿ ❚❤➙♠ ♥✐➯♥
✺✲✼ ✽✲✶✵ ✶✶✲✶✸ ✶✹✲✶✻ ✶✼✲✶✾ ❙Z ♥❤➙♥ ✈✐➯♥ ✽ ✷✶ ✸✻ ✷✺ ✶✵
❛✳ ❍➣② ,➼♥❤ ❣✐→ ,3^ ,3✉♥❣ ❜➻♥❤ ♠➝✉ ✈➔ ❣✐→ ,3^ ✤: ❧➺❝❤ ❝❤✉➞♥ ♠➝✉✳
❜✳ ●✐↔ De ,❤➙♠ ♥✐➯♥ ❝/♥❣ ,→❝ ❝7❛ ♥❤➙♥ ✈✐➯♥ 9 ❝/♥❣ ,② ,3➯♥ ❧➔ ❜✐➳♥ ♥❣➝✉ ♥❤✐➯♥ X ❝f ❦g
✈I♥❣ ❧➔ ✶✷ ♥➠♠ ✈➔ ✤: ❧➺❝❤ ❝❤✉➞♥ ❧➔ ✸ ♥➠♠✳ ❚➼♥❤ ①→❝ D✉➜, ✤➸ ,3✉♥❣ ❜➻♥❤ ♠➝✉ ♥❤➟♥ ❣✐→
,3^ ❧=♥ ❤k♥ ✶✷✱✺ ♥➠♠✳ ❚!♥ ❚❤➜% ❚& ✷✺✴✷✻
●✐↔✐✳ ❉↕♥❣ $❤✉ ❣'♥✿ ❚❤➙♠ ♥✐➯♥ ✻ ✾ ✶✷ ✶✺ ✶✽
❙5 ♥❤➙♥ ✈✐➯♥ ✽ ✷✶ ✸✻ ✷✺ ✶✵
❛✳ ❈→❝ >5 ✤➦❝ $AB♥❣ ♠➝✉✿ ¯x = 12, 24; s = 3, 27✳
❜✳ ❚❤❡♦ ✤G♥❤ ❧I ❣✐J✐ ❤↕♥ $A✉♥❣ $➙♠ ¯
X ❝K ♣❤➙♥ ♣❤5✐ ①➜♣ ①➾ ❝❤✉➞♥ N(12; 32/100) =
N (12; 0, 09)✳ ❉♦ ✤K✿ 12, 5 − 12 P ( ¯ X > 12, 5) = 1 − Φ √ = 0.0478 0, 09 ❚!♥ ❚❤➜% ❚& ✷✻✴✷✻