











Preview text:
❳⑩❈ ❙❯❻❚ ❚❍➮◆● ❑➊ ❚!♥ ❚❤➜% ❚&
✣➔ ◆➤♥❣✱ ✷✵✶✾ ❚!♥ ❚❤➜% ❚& ✶✴✹✵
❈❤"#♥❣ ✺✳ ()❝ ❧",♥❣ -❤❛♠ 01
✶✳ ,-❝ ❧01♥❣ ✤✐➸♠
✶✳✶ ✣6♥❤ ♥❣❤➽❛
✲ ❈❤♦ ♠➝✉ ♥❣➝✉ ♥❤✐➯♥ {X1, X2, ..., Xn} +, +-♥❣ +❤➸ ❝0 ♣❤➙♥ ♣❤3✐ ♣❤4 +❤✉5❝ ✈➔♦
+❤❛♠ 93 θ ❝❤:❛ ❜✐➳+✳ ❑❤✐ ✤0✱ ♠5+ ❤➔♠ ✭+❤3♥❣ ❦➯✮ ˆθ = ˆθ(X1, ..., Xn) ✤:D❝ ❣E✐ ❧➔ ♠5+
!❝ ❧ $♥❣ ❝G❛ +❤❛♠ 93 θ✳
✲ ❱I✐ ♠5+ ♠➝✉ ❣✐→ +KL ❝4 +❤➸ {x1, x2, ..., xn} +❛ +❤✉ ✤:D❝ ♠5+ ❣✐→ +KL ❝4 +❤➸ ❝G❛ ˆθ✳
❑❤✐ ✤0✱ ❣✐→ +KL ˆθ(x1, ..., xn) ✤:D❝ ❣E✐ ❧➔ !❝ ❧ $♥❣ ✤✐➸♠ ❝G❛ +❤❛♠ 93 θ ❞N❛ +K➯♥ ♠➝✉ ❣✐→ +KL {x1, x2, ..., xn}✳ ❚!♥ ❚❤➜% ❚& ✷✴✹✵
✶✳✷ :❤➙♥ ❧♦↕✐ 0-❝ ❧01♥❣
✲ OI❝ ❧:D♥❣ ˆθ = ˆθ(X1, ..., Xn) ✤:D❝ ❣E✐ ❧➔ !❝ ❧ $♥❣ ❦❤-♥❣ ❝❤➺❝❤ ❝G❛ +❤❛♠ 93 θ ♥➳✉ E(ˆ θ) = θ✳
❚K♦♥❣ +K:Q♥❣ ❤D♣ ♥❣:D❝ ❧↕✐ +❤➻ +❛ ❣E✐ ˆθ ✤:D❝ ❣E✐ ❧➔ !❝ ❧ $♥❣ ❝❤➺❝❤ ✈➔ ❣✐→ +KL b(θ) = E(ˆ
θ) − θ ✤:D❝ ❣E✐ ❧➔ ✤/ ❝❤➺❝❤ ❝0❛ !❝ ❧ $♥❣✳
✲ OI❝ ❧:D♥❣ ˆθ = ˆθ(X1, ..., Xn) ✤:D❝ ❣E✐ ❧➔ !❝ ❧ $♥❣ ❦❤-♥❣ ❝❤➺❝❤ 2✐➺♠ ❝➟♥ ❝G❛ +❤❛♠ 93 θ ♥➳✉ lim E(ˆ θ) = θ. n→+∞
✲ ❈❤♦ ˆθ1 ✈➔ ˆθ2 ❧➔ ❤❛✐ :I❝ ❧:D♥❣ ❦❤T♥❣ ❝❤➺❝❤ ❝G❛ +❤❛♠ 93 θ✳ ❚❛ ♥0✐ :I❝ ❧:D♥❣ ˆθ1 ❤✐➺✉
5✉↔ ❤7♥ :I❝ ❧:D♥❣ ˆθ2 ♥➳✉ D(ˆθ1) < D(ˆθ2)✳
✲ OI❝ ❧:D♥❣ ˆθ ❝G❛ θ ❧➔ :I❝ ❧:D♥❣ ❦❤T♥❣ ❝❤➺❝❤ ✈➔ ❝0 ♣❤:V♥❣ 9❛✐ D(ˆθ) ❜➨ ♥❤➜+ ✤:D❝
❣E✐ ❧➔ !❝ ❧ $♥❣ 282 ♥❤➜2✳ ❚!♥ ❚❤➜% ❚& ✸✴✹✵
!❝ ❧$%♥❣ ❦❤*♥❣ ❝❤➺❝❤ ❝,❛ ./✉♥❣ ❜➻♥❤ ✈➔ ♣❤$6♥❣ 7❛✐
✣:♥❤ ❧;✿ ❈❤♦ ❜✐➳♥ ♥❣➝✉ ♥❤✐➯♥ X ❝,❛ ♠/0 01♥❣ 0❤➸ ❝3 E(X) = µ, D(X) = σ2✳ ●✐↔ 78
{X1, X2, ..., Xn} ❧➔ ♠➝✉ ♥❣➝✉ ♥❤✐➯♥ ❝,❛ X✳ ❑❤✐ ✤3✿ n ✐✮ 1 X = P X n
i ❧➔ ?@❝ ❧?A♥❣ ❦❤C♥❣ ❝❤➺❝❤ ❝,❛ µ✳ i=1 n ✐✐✮ 1 S2 = P (X n − 1
i − X)2 ❧➔ ?@❝ ❧?A♥❣ ❦❤C♥❣ ❝❤➺❝❤ ❝,❛ σ2✳ i=1
◆❤➟♥ ①➨.✿ ❈3 0❤➸ ❝❤E♥❣ ♠✐♥❤ ✤?A❝ F➡♥❣✿ n n − 1 1 X E(S2) = σ2 ✈@✐ S2 = (X ∗ n ∗ n i − ¯ X)2 i=1
✣✐➲✉ ♥➔② ❝3 ♥❣❤➽❛ S2 ❧➔ ?@❝ ❧?A♥❣ ❝❤➺❝❤ ✭❦❤C♥❣ ❝❤➺❝❤ 0✐➺♠ ❝➟♥✮ ❝,❛ σ2✱ ❞♦ ✤3 ♥3 ∗
✓❦❤C♥❣ ✤?A❝ ❝❤R♥✔ ❧➔♠ ♣❤?U♥❣ 7❛✐ ♠➝✉✳ ❚!♥ ❚❤➜% ❚& ✹✴✹✵
!❝ ❧$%♥❣ ❦❤*♥❣ ❝❤➺❝❤ ❝,❛ .➾ ❧➺
✣:♥❤ ❧;✿ ❈❤♦ ❜✐➳♥ ♥❣➝✉ ♥❤✐➯♥ X ❝3 ♣❤➙♥ ♣❤W✐ ❇❡F♥♦✉❧❧✐ ✈@✐ 0❤❛♠ 7W p✳ ●R✐
(X1, X2, ..., Xn) ❧➔ ♠➝✉ ♥❣➝✉ ♥❤✐➯♥ ❝,❛ X✳ ❑❤✐ ✤3✿ ˆ X P = 1 + X2 + ... + Xn n
❧➔ ♠/0 ?@❝ ❧?A♥❣ ❦❤C♥❣ ❝❤➺❝❤ ❝,❛ 0❤❛♠ 7W p✳
B ♥❣❤➽❛✿ ◆➳✉ ❞➜✉ ❤✐➺✉ A ❝3 0➾ ❧➺ p ❝❤?❛ ❜✐➳0✱ ✈➔ 0F♦♥❣ ♠➝✉ ✤✐➲✉ 0F❛ ❦➼❝❤ 0❤?@❝ n ❝3 k
❝→ 0❤➸ ♠❛♥❣ ❞➜✉ ❤✐➺✉ A✱ 0❤➻ 0➛♥ 7✉➜0 fn = k/n ❧➔ ♠/0 ?@❝ ❧?A♥❣ ❦❤C♥❣ ❝❤➺❝❤ ❝,❛ p✳ ❚!♥ ❚❤➜% ❚& ✺✴✹✵ ❱➼ ❞G ✶
✲ ❈❤♦ ❜✐➳♥ ♥❣➝✉ ♥❤✐➯♥ X ❝- ❦/ ✈1♥❣ µ ✈➔ ♣❤45♥❣ 6❛✐ σ2 ❝❤4❛ ❜✐➳8✳ ✣➸ 4<❝ ❧4>♥❣
❝❤♦ µ ✈➔ σ2 ♥❣4?✐ 8❛ 8✐➳♥ ❤➔♥❤ ✤✐➲✉ 8B❛ ♠➝✉ ❦➼❝❤ 8❤4<❝ ✷✵✵ ✈➔ 8➼♥❤ ✤4>❝ 8B✉♥❣ ❜➻♥❤ ✈➔
♣❤45♥❣ 6❛✐ ❝❤✉➞♥ ♠➝✉✿ ¯ x = 125, 8; s2 = 2, 76
❑❤✐ ✤-✱ 8❛ ❝- 8❤➸ ①❡♠ µ ≈ 125, 8 ✈➔ σ2 ≈ 2, 76✳
✲ ✣➸ 4<❝ ❧4>♥❣ 8➾ ❧➺ p ❝P 8B✐ Q♥❣ ❤R ❝❤♦ S♥❣ ❝P ✈✐➯♥ ❆✱ ♥❣4?✐ 8❛ ❦❤↔♦ 6→8 ♥❣➝✉ ♥❤✐➯♥
4000 ♥❣4?✐ 8❤➻ ❝- ✷✻✹✵ ♥❣4?✐ Q♥❣ ❤R S♥❣ ❝P ✈✐➯♥ ♥➔②✳ ◆❤4 ✈➟②✱ 8❛ ❝- 8❤➸ ①❡♠ 8➾ ❧➺ Q♥❣
❤R S♥❣ ❝P ✈✐➯♥ ❆ ①➜♣ ①➾✿ p ≈ 2640/4000 = 0, 66 ❚!♥ ❚❤➜% ❚& ✻✴✹✵ X θ {X1, X2, ..., Xn} L = L(X1, ..., Xn) U = U (X1, ..., Xn) α ∈ (0, 1)
P (L < θ < U ) = 1 − α. (L, U ) θ 1 − α α U − L (L, U ) θ 1 − α 1 − α α1, α2 ∈ (0, 1) α1 + α2 = α Gn = Gn(X1, ..., Xn, θ) Gn Gn n → ∞ θ Gn θ a b P (Gn ≤ a) = α1 P (Gn < b) = 1 − α2
a < Gn(X1, ..., Xn, θ) < b θ L, U
P (L < θ < U ) ≥ 1 − α. α1 = 0 α2 = 0
✷✳✷ ❑❤♦↔♥❣ (✐♥ ❝➟② ❝❤♦ ❦➻ ✈0♥❣ ❦❤✐ ✤➣ ❜✐➳( ♣❤67♥❣ 8❛✐
❇➔✐ (♦→♥✳ ❈❤♦ ❜✐➳♥ ♥❣➝✉ ♥❤✐➯♥ X ❝-❛ ♠01 12♥❣ 1❤➸ ❝4 ♣❤➙♥ ♣❤7✐ ❝❤✉➞♥ N(µ; σ2) ✈:✐
µ ❝❤;❛ ❜✐➳1 ✈➔ σ2 ✤➣ ❜✐➳1✳ ❚➻♠ ❦❤♦↔♥❣ 1✐♥ ❝➟② ❝❤♦ µ ✈:✐ ♠E❝ F ♥❣❤➽❛ α✳
●>✐ ?✳ ◆➳✉ {X1, X2, ..., Xn} ❧➔ ♠➝✉ ♥❣➝✉ ♥❤✐➯♥ ❝-❛ X 1❤➻ X − µ Z = √ ∼ N(0; 1). σ/ n
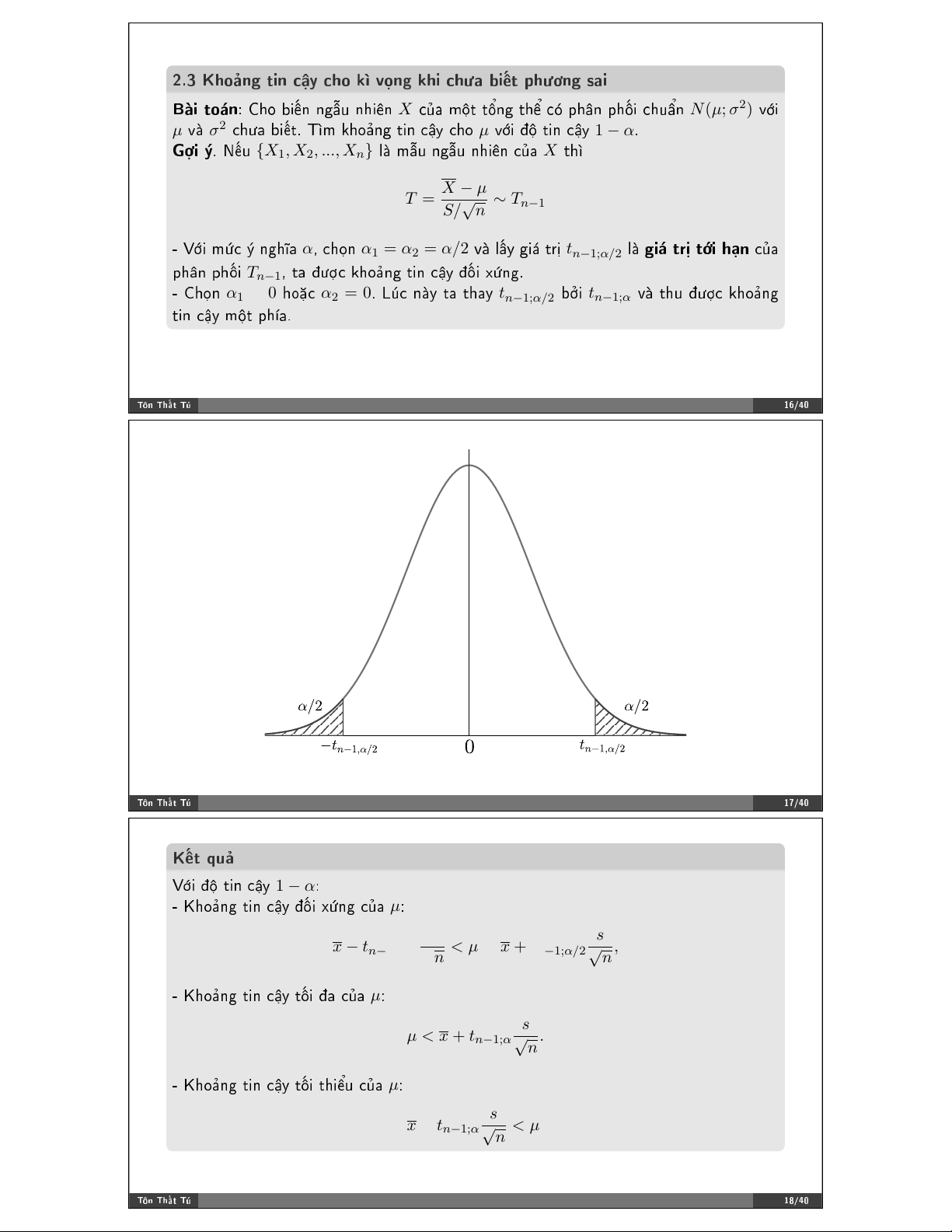
✲ ❱:✐ α ∈ (0; 1)✱ ❝❤M♥ α1 = α2 = α/2 ✈➔ zα/2 = Φ−1(1 − α) ❧➔ ❣✐→ (@A (B✐ ❤↕♥ ♠E❝ 2
α/2 ❝-❛ ♣❤➙♥ ♣❤7✐ ❝❤✉➞♥ 1➢❝✱ ❣✐↔✐ ❜➜1 ♣❤;P♥❣ 1Q➻♥❤✿ σ σ
−zα/2 < Z < zα/2 ⇔ X − zα/2 √ < µ < X + z √ n α/2 n
1❛ ✤;S❝ ❦❤♦↔♥❣ 1✐♥ ❝➟② ✤7✐ ①E♥❣✳
✲ ◆➳✉ ❝❤M♥ α1 = 0 ❤♦➦❝ α2 = 0✳ ▲W❝ ♥➔② 1❛ 1❤❛② zα/ ❜X✐ 2
zα ✈➔ 1❤✉ ✤;S❝ ❦❤♦↔♥❣ 1✐♥
❝➟② ♠01 ♣❤➼❛✳ ❚!♥ ❚❤➜% ❚& ✶✵✴✹✵ ❚!♥ ❚❤➜% ❚& ✶✶✴✹✵ ❛✳ ❑➳( D✉↔
❱:✐ ✤0 1✐♥ ❝➟② 1 − α✿
✲ ❑❤♦↔♥❣ 1✐♥ ❝➟② ✤7✐ ①E♥❣ ❝-❛ µ✿ σ σ
x − zα/2 √ < µ < x + z √ , n α/2 n
✲ ❑❤♦↔♥❣ 1✐♥ ❝➟② 17✐ ✤❛ ❝-❛ µ✿ σ µ < x + zα √ . n
✲ ❑❤♦↔♥❣ 1✐♥ ❝➟② 17✐ 1❤✐➸✉ ❝-❛ µ✿ σ µ > x − zα √ . n ❚!♥ ❚❤➜% ❚& ✶✷✴✹✵ ❱➼ ❞# ✷
❑❤"✐ ❧%&♥❣ ✭❦❣✮ ❝-❛ ♠01 1❤✐➳1 ❜4 ❝5 ♣❤➙♥ ♣❤"✐ ❝❤✉➞♥ N(µ; σ2) ✈;✐ σ = 0.2 ✭❦❣✮✳ ❈❤>♥
♥❣➝✉ ♥❤✐➯♥ ✷✺ 1❤✐➳1 ❜4 ♥❣%C✐ 1❛ 1➼♥❤ ✤%&❝ 1F✉♥❣ ❜➻♥❤ ♠➝✉ x = 65, 1 ✭❦❣✮✳ ❱;✐ ✤0 1✐♥ ❝➟②
✾✺✪ ❤➣② 1➻♠ ❦❤♦↔♥❣ 1✐♥ ❝➟② ✭✤"✐ ①Q♥❣✮ ❝❤♦ ❦❤"✐ ❧%&♥❣ 1F✉♥❣ ❜➻♥❤ ❝-❛ 1❤✐➳1 ❜4 ♥➔②✳ ❈❤♦ ❜✐➳1 z0,025 = 1, 96✳ ●✐↔✐✳
✲ ❈→❝ $% ✤➦❝ ()*♥❣ ♠➝✉✿ n = 25; ¯x = 65, 1✳
✲ ✣3 (✐♥ ❝➟②✿ 1 − α = 0, 95 ⇒ α = 0, 05; zα/2 = z0,025 = 1, 96✳
✲ ❙❛✐ $% *9❝ ❧*;♥❣✿ σ 0, 2 ε = zα/2 √ = 1, 96 ∗ √ = 0, 0784 n 25
✲ ❑❤♦↔♥❣ (✐♥ ❝➟② ❝❤♦ ❦❤%✐ ❧*;♥❣ ()✉♥❣ ❜➻♥❤ µ ❝C❛ (❤✐➳( ❜E ♥➔②✿ ¯
x − ε < µ < ¯x + ε ⇔ 65, 02 < µ < 65, 18 ❚!♥ ❚❤➜% ❚& ✶✸✴✹✵
❜✳ ❱➜♥ ✤➲ ❝/ ♠➝✉
❚H ❝I♥❣ (❤J❝ ❦❤♦↔♥❣ (✐♥ ❝➟② ❝❤♦ µ (❛ (❤➜② )➡♥❣ $❛✐ $% ❝C❛ *9❝ ❧*;♥❣ |x − µ| ❜➨ ❤N♥ ❤♦➦❝ ❜➡♥❣ σ zα/ ✳ 2 √n
✲ ❙❛✐ $% *9❝ ❧*;♥❣✿ σ ε = zα/2 √n
✲ ✣✐➲✉ ❦✐➺♥ ❤↕♥ ❝❤➳✿ ε < ∆ ✈9✐ ∆ > 0 ❝❤♦ ()*9❝✳ σ ε = zα/2 √ < ∆ n
✲ ●✐↔✐ ❜➜( ♣❤*N♥❣ ()➻♥❤ (❤❡♦ n✿ z 2 α/ n > 2σ . ∆ ❚!♥ ❚❤➜% ❚& ✶✹✴✹✵ ❱➼ ❞# ✸
❚FT ❧↕✐ ✈;✐ ❱➼ ❞W ✷ ♥➳✉ ②➯✉ ❝➛✉ Y❛✐ Y" %;❝ ❧%&♥❣ ❦❤Z♥❣ ✈%&1 [✉→ ✵✱✵✺ 1❤➻ ✈;✐ ✤0 1✐♥ ❝➟②
✾✽✪ 1❛ ❝➛♥ ❝❤>♥ 1"✐ 1❤✐➸✉ ❜❛♦ ♥❤✐➯✉ 1❤✐➳1 ❜4 ✤➸ ❦❤↔♦ Y→1❄ ❈❤♦ ❜✐➳1 z0,01 = 2, 326✳ ●✐↔✐✳
✲ ❙❛✐ $% *9❝ ❧*;♥❣✿ σ ε = zα/2 √n
✲ ✣✐➲✉ ❦✐➺♥ ❤↕♥ ❝❤➳✿ ε < ∆ = 0, 05✳ ✲ ❙✉② )❛✿ z 2 α/ n > 2σ . ∆
✲ ✣3 (✐♥ ❝➟②✿ 1 − α = 0, 98 ⇒ α = 0, 2; zα/2 = z0,01 = 2, 326✳ ❉♦ ✤W✿ 2, 326 ∗ 0, 22 n > = 86, 56 0, 05
❱➟②✱ ❦➼❝❤ (❤*9❝ ♠➝✉ (%✐ (❤✐➸✉ ❝➛♥ ❦❤↔♦ $→(✿ n = 87 ❚!♥ ❚❤➜% ❚& ✶✺✴✹✵
✷✳✸ ❑❤♦↔♥❣ )✐♥ ❝➟② ❝❤♦ ❦➻ ✈1♥❣ ❦❤✐ ❝❤2❛ ❜✐➳) ♣❤27♥❣ 8❛✐
❇➔✐ )♦→♥✿ ❈❤♦ ❜✐➳♥ ♥❣➝✉ ♥❤✐➯♥ X ❝-❛ ♠01 12♥❣ 1❤➸ ❝4 ♣❤➙♥ ♣❤7✐ ❝❤✉➞♥ N(µ; σ2) ✈:✐
µ ✈➔ σ2 ❝❤<❛ ❜✐➳1✳ ❚➻♠ ❦❤♦↔♥❣ 1✐♥ ❝➟② ❝❤♦ µ ✈:✐ ✤0 1✐♥ ❝➟② 1 − α✳
●=✐ >✳ ◆➳✉ {X1, X2, ..., Xn} ❧➔ ♠➝✉ ♥❣➝✉ ♥❤✐➯♥ ❝-❛ X 1❤➻ X − µ T = √ ∼ T S/ n n−1
✲ ❱:✐ ♠I❝ J ♥❣❤➽❛ α✱ ❝❤M♥ α1 = α2 = α/2 ✈➔ ❧➜② ❣✐→ 1PQ tn
❧➔ ❣✐→ )?@ )A✐ ❤↕♥ ❝-❛ −1;α/2
♣❤➙♥ ♣❤7✐ Tn−1✱ 1❛ ✤✲ ❈❤M♥ α1 = 0 ❤♦➦❝ α2 = 0✳ ▲V❝ ♥➔② 1❛ 1❤❛② tn ❜W✐ t −1;α/2
n−1;α ✈➔ 1❤✉ ✤1✐♥ ❝➟② ♠01 ♣❤➼❛✳ ❚!♥ ❚❤➜% ❚& ✶✻✴✹✵ ❚!♥ ❚❤➜% ❚& ✶✼✴✹✵ ❑➳) C✉↔
❱:✐ ✤0 1✐♥ ❝➟② 1 − α✿
✲ ❑❤♦↔♥❣ 1✐♥ ❝➟② ✤7✐ ①I♥❣ ❝-❛ µ✿ s s x − tn √ < µ < x + t √ , −1;α/2 n n−1;α/2 n
✲ ❑❤♦↔♥❣ 1✐♥ ❝➟② 17✐ ✤❛ ❝-❛ µ✿ s µ < x + tn . −1;α √n
✲ ❑❤♦↔♥❣ 1✐♥ ❝➟② 17✐ 1❤✐➸✉ ❝-❛ µ✿ s x − tn < µ. −1;α √n ❚!♥ ❚❤➜% ❚& ✶✽✴✹✵ ◆❤➟♥ ①➨&✿
✐✮ ❑❤✐ n > 30✿ tn ✳ −1;α/2 ≈ zα/2
✐✐✮ ❑❤✐ ❦➼❝❤ )❤*+❝ ♠➝✉ ❧+♥ ✭n > 30✮ )❤❡♦ ✤5♥❤ ❧6 ❣✐+✐ ❤↕♥ )9✉♥❣ )➙♠ ❦➳) <✉↔ )9➯♥ ✈➝♥
→♣ ❞C♥❣ ✤*D❝ ❞E )❤✐➳✉ ❣✐↔ )❤✐➳) ✈➲ ✤✐➲✉ ❦✐➺♥ ♣❤➙♥ ♣❤H✐ ❝❤✉➞♥ ❝J❛ ❜✐➳♥ ♥❣➝✉ ♥❤✐➯♥ X✳ ❱➼ ❞+ ✹
▼!" ♠➝✉ ✶✻ ♣✐♥ ❞,♥❣ ❝❤♦ 1♠❛3"♣❤♦♥❡ ✤67❝ ❝❤8♥ ♥❣➝✉ ♥❤✐➯♥ ❝:❛ ❝;♥❣ "② ❆ ❝> "✉?✐ "❤8
"3✉♥❣ ❜➻♥❤ "➼♥❤ "3➯♥ ♠➝✉ x = 24308 ✭❣✐D✮ ✈➔ ✤! ❧➺❝❤ ❝❤✉➞♥ ♠➝✉ s = 727 ✭❣✐D✮✳ ●✐↔ 1N
3➡♥❣ "✉?✐ "❤8 ♣✐♥ 1♠❛3"♣❤♦♥❡ ❝> ♣❤➙♥ ♣❤Q✐ ❝❤✉➞♥✳ ❱S✐ ✤! "✐♥ ❝➟② ✾✺✪✱ ❤➣② "➻♠ ❦❤♦↔♥❣
"✐♥ ❝➟② ❝❤♦ "✉?✐ "❤8 "3✉♥❣ ❜➻♥❤ ❝:❛ ♣✐♥ 1♠❛3"♣❤♦♥❡ ✤67❝ 1↔♥ ①✉➜" ❜]✐ ❝;♥❣ "② ❆✳ ❈❤♦
❜✐➳" t15;0,025 = 2, 1314✳ ❚!♥ ❚❤➜% ❚& ✶✾✴✹✵
●✐↔✐✳ ❚❤❡♦ ❣✐↔ )❤✐➳)✿ n = 16; ¯ x = 24308; s = 727
✣O )✐♥ ❝➟②✿ 1 − α = 0, 95 ⇒ α = 0, 05; tn−1;α/2 = t15;0,025 = 2, 1314 ❙❛✐ SH✿ s 727 ε = tn √ = 2, 1314 ∗ √ = 387, 382 −1;α/2 n 16
❑❤♦↔♥❣ )✐♥ ❝➟② ❝❤♦ )✉T✐ )❤U )9✉♥❣ ❜➻♥❤ ❝J❛ ♣✐♥ S♠❛9)♣❤♦♥❡✿ ¯
x − ε < µ < ¯x + ε ⇔ 23920.618 < µ < 24695.382 ❚!♥ ❚❤➜% ❚& ✷✵✴✹✵ ❱➼ ❞+ ✺
◆➠♥❣ 1✉➜" ✭"↕✴❤❛✮ ❝:❛ ♠!" ❧♦↕✐ ❝➙② "3d♥❣ "✉➙♥ "❤❡♦ ❧✉➟" ♣❤➙♥ ♣❤Q✐ ❝❤✉➞♥✳ ❍➣② "➻♠ 6S❝
❧67♥❣ ❦❤♦↔♥❣ ✤Q✐ ①f♥❣ ♥➠♥❣ 1✉➜" "3✉♥❣ ❜➻♥❤ ❝:❛ ♠!" ❧♦↕✐ ❝➙② "3d♥❣ ♥➔② ✈S✐ ✤! "✐♥ ❝➟②
✾✺✪ "3➯♥ ❝g 1] ❜↔♥❣ 1Q ❧✐➺✉ ✤✐➲✉ "3❛ 1❛✉ ✤➙②✿
◆➠♥❣ 1✉➜"✭"↕✴❤❛✮
✹✷✲✹✼ ✹✼✲✺✷ ✺✷✲✺✼ ✺✼✲✻✷ ✻✷✲✻✼
❙Q ✤✐➸♠ "❤✉ ❤♦↕❝❤ ✷ ✺ ✶✹ ✶✵ ✺
❈❤♦ ❜✐➳" z0,05 = 1, 645; z0,025 = 1, 96; z0,02 = 2, 054; z0,01 = 2, 326✳
●✐↔✐✳ ❉↕♥❣ )❤✉ ❣U♥✿
◆➠♥❣ S✉➜)✭)↕✴❤❛✮
✹✹✱✺ ✹✾✱✺ ✺✹✱✺ ✺✾✱✺ ✻✹✱✺
❙H ✤✐➸♠ )❤✉ ❤♦↕❝❤ ✷ ✺ ✶✹ ✶✵ ✺ ❚!♥ ❚❤➜% ❚& ✷✶✴✹✵
❈→❝ #$ ✤➦❝ '()♥❣ ♠➝✉✿ n = 36; ¯ x = 56, 028; s = 5, 321
✣1 '✐♥ ❝➟②✿ 1 − α = 0, 95 ⇒ α = 0, 05; tn−1;α/2 ≈ zα/2 = z0,025 = 1, 96 ❙❛✐ #$✿ s 5, 321 ε = tn √ = 1, 96 ∗ √ = 1, 738 −1;α/2 n 36
❑❤♦↔♥❣ '✐♥ ❝➟② ❝❤♦ ♥➠♥❣ #✉➜' '(✉♥❣ ❜➻♥❤✿ ¯
x − ε < µ < ¯x + ε ⇔ 54, 29 < µ < 57, 766 ❚!♥ ❚❤➜% ❚& ✷✷✴✹✵
✷✳✹ ❑❤♦↔♥❣ )✐♥ ❝➟② ❝❤♦ ♣❤/0♥❣ 1❛✐ ✭✤5❝ )❤➯♠✮
❇➔✐ )♦→♥✿ ❈❤♦ ❜✐➳♥ ♥❣➝✉ ♥❤✐➯♥ X ❝A❛ ♠1' 'B♥❣ '❤➸ ❝D ♣❤➙♥ ♣❤$✐ ❝❤✉➞♥ N(µ; σ2) ✈I✐
µ ✈➔ σ2 ❝❤)❛ ❜✐➳'✳ ❚➻♠ ❦❤♦↔♥❣ '✐♥ ❝➟② ❝❤♦ σ2 ✈I✐ ✤1 '✐♥ ❝➟② 1 − α✳
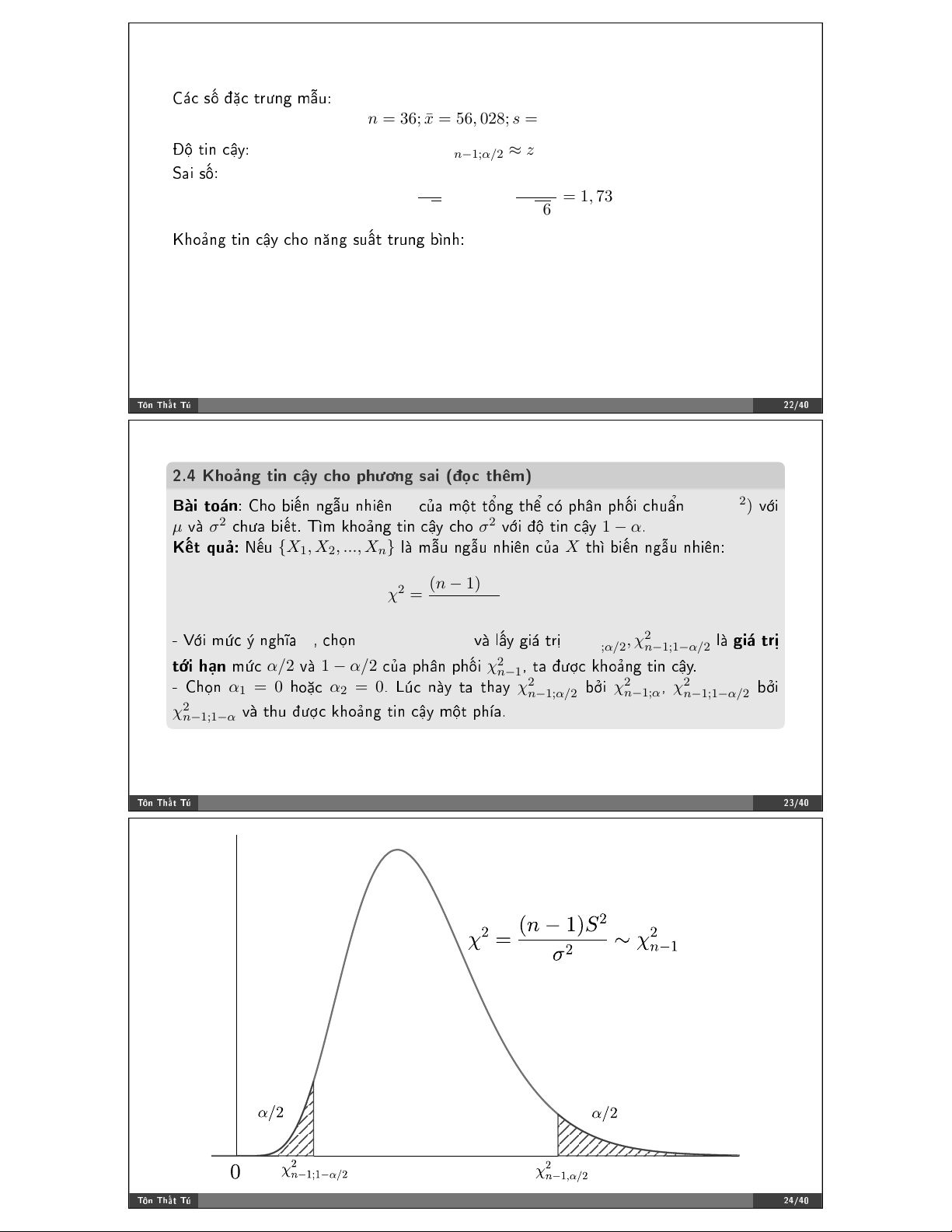
❑➳) =✉↔✿ ◆➳✉ {X1, X2, ..., Xn} ❧➔ ♠➝✉ ♥❣➝✉ ♥❤✐➯♥ ❝A❛ X '❤➻ ❜✐➳♥ ♥❣➝✉ ♥❤✐➯♥✿ (n − 1)S2 χ2 = ∼ χ2 . σ2 n−1
✲ ❱I✐ ♠R❝ S ♥❣❤➽❛ α✱ ❝❤V♥ α1 = α2 = α/2 ✈➔ ❧➜② ❣✐→ '(W χ2 , χ2 ❧➔ ❣✐→ )@A n−1;α/2 n−1;1−α/2
)B✐ ❤↕♥ ♠R❝ α/2 ✈➔ 1 − α/2 ❝A❛ ♣❤➙♥ ♣❤$✐ χ2 ✱ '❛ ✤)X❝ ❦❤♦↔♥❣ '✐♥ ❝➟②✳ n−1
✲ ❈❤V♥ α1 = 0 ❤♦➦❝ α2 = 0✳ ▲Z❝ ♥➔② '❛ '❤❛② χ2 ❜[✐ χ2 ✱ χ2 ❜[✐ n−1;α/2 n−1;α n−1;1−α/2 χ2
✈➔ '❤✉ ✤)X❝ ❦❤♦↔♥❣ '✐♥ ❝➟② ♠1' ♣❤➼❛✳ n−1;1−α ❚!♥ ❚❤➜% ❚& ✷✸✴✹✵ ❚!♥ ❚❤➜% ❚& ✷✹✴✹✵ ❑➳" #✉↔
❱!✐ ✤$ %✐♥ ❝➟② 1 − α✿
✲ ❑❤♦↔♥❣ %✐♥ ❝➟② ❤❛✐ ♣❤➼❛ ❝❤♦ σ2✿ (n − 1)s2 (n − 1)s2 < σ2 < , χ2 χ2 n−1;α/2 n−1;1−α/2
✲ ❑❤♦↔♥❣ %✐♥ ❝➟② %4✐ ✤❛ ❝❤♦ ♣❤56♥❣ 7❛✐ σ2✿ (n − 1)s2 0 < σ2 < . χ2n−1;1−α
✲ ❑❤♦↔♥❣ %✐♥ ❝➟② %4✐ %❤✐➸✉ ❝❤♦ ♣❤56♥❣ 7❛✐ σ2✿
(n − 1)s2 < σ2 < +∞. χ2n−1;α ❚!♥ ❚❤➜% ❚& ✷✺✴✹✵ ❱➼ ❞) ✻
▼!" ❞➙② ❝❤✉②➲♥ "+ ✤!♥❣ ✤.♥❣ ❣↕♦ ✈➔♦ ❜❛♦ ✤56❝ ❦✐➸♠ ";❛✳ ❈➙♥ "❤> ✷✺ ❜❛♦ ❣↕♦ ❞♦ ❞➙②
❝❤✉②➲♥ ♥➔② "❤+❝ ❤✐➺♥ "❤➻ "➼♥❤ ✤56❝ ✤! ❧➺❝❤ ❝❤✉➞♥ ❦❤F✐ ❧56♥❣ ❣↕♦ ♠G✐ ❜❛♦ s = 0, 15
✭❦❣✮✳ ❱K✐ ✤! "✐♥ ❝➟② ✾✺✪ "➻♠ ❦❤♦↔♥❣ "✐♥ ❝➟② ❝❤♦ ♣❤5Q♥❣ R❛✐ ❝S❛ ❦❤F✐ ❧56♥❣ ❣↕♦ ✤56❝
✤.♥❣ ❝❤♦ ♠G✐ ❜❛♦ ❜T✐ ❞➙② ❝❤✉②➲♥ ♥➔②✳ ●✐↔ "❤✐➳" ❦❤F✐ ❧56♥❣ ❣↕♦ ✤56❝ ✤.♥❣ ❝❤♦ ♠G✐ ❜❛♦
"✉➙♥ "❤❡♦ ❧✉➟" ♣❤➙♥ ♣❤F✐ ❝❤✉➞♥✳ ❈❤♦ ❜✐➳"✿ χ2 = 39, 364✱ χ2 = 12, 401. 24;0.025 24;0.975
✣→♣ ./✿ 0, 0137 < σ2 < 0, 0435✳ ❚!♥ ❚❤➜% ❚& ✷✻✴✹✵
✷✳✺ ❑❤♦↔♥❣ "✐♥ ❝➟② ❝❤♦ "✛ ❧➺
❇➔✐ "♦→♥✿ ❳➨% ❞➜✉ ❤✐➺✉ A %@♦♥❣ %A♥❣ %❤➸ ❝B %➾ ❧➺ ❧➔ p ✭❝❤5❛ ❜✐➳%✮✳ ✣➸ ❦❤↔♦ 7→% ❣✐→ %@M p
%❛ %✐➳♥ ❤➔♥❤ ✤✐➲✉ %@❛ ♠$% ♠➝✉ ❦➼❝❤ %❤5!❝ n✳ ●✐↔ 7R %@♦♥❣ ♠➝✉ ♥➔② ❝B k ♣❤➛♥ %R ♠❛♥❣
❞➜✉ ❤✐➺✉ A✳ ❍➣② %➻♠ ❦❤♦↔♥❣ %✐♥ ❝➟② ❝❤♦ p✳ ❑➳" #✉↔✿
✲ ●W✐ X ❧➔ 74 ♣❤➛♥ %R ♠❛♥❣ ❞➜✉ ❤✐➺✉ A %@♦♥❣ ♠➝✉ ❦➼❝❤ %❤5!❝ n✱ %❛ ❝B X ∼ B(n, p)✳
❚❤❡♦ ✤M♥❤ ❧[ ❣✐!✐ ❤↕♥ %➼❝❤ ♣❤➙♥ ▼♦✐✈@❡✲▲❛♣❧❛❝❡✱ ❜✐➳♥ ♥❣➝✉ ♥❤✐➯♥✿ X − np Z =
❝B ♣❤➙♥ ♣❤4✐ ①➜♣ ①➾ ❝❤✉➞♥ %➢❝ N(0, 1)✳ pnp(1 − p)
✲ ❱!✐ α ∈ (0; 1) ❝❤♦ %@5!❝✱ ❝❤W♥ α1 = α2 = α/2 %❛ ✤5e❝ ❦❤♦↔♥❣✿ r r p(1 − p) p(1 − p) ˆ p − zα/2 < p < ˆ p + z n α/2 n ✈!✐ ˆp = X/n = k/n✳ ❚!♥ ❚❤➜% ❚& ✷✼✴✹✵ ❚!♥ ❚❤➜% ❚& ✷✽✴✹✵
▼➦" ❦❤→❝✱ ❞♦ ˆp ❧➔ ♠-" ./❝ ❧.0♥❣ ❝3❛ p ♥➯♥ "❛ ❝6 "❤➸ ①❡♠ p ≈ ˆp ❦❤✐ n ❧/♥✳
✣✐➲✉ ❦✐➺♥✿ nˆp > 5 ✈➔ n(1 − ˆp) > 5✳ ❛✳ ❑➳, -✉↔
❱/✐ ✤- "✐♥ ❝➟② 1 − α✿
✲ ❑❤♦↔♥❣ "✐♥ ❝➟② ✤E✐ ①F♥❣ ❝❤♦ p✿ r r ˆ p(1 − ˆ p) ˆ p(1 − ˆ p) ˆ p − zα/2 < p < ˆ p + z . n α/2 n
✲ ❑❤♦↔♥❣ "✐♥ ❝➙② "E✐ ✤❛ ❝❤♦ p✿ r ˆp(1 − ˆp) p < ˆ p + zα . n
✲ ❑❤♦↔♥❣ (✐♥ ❝➟② (-✐ (❤✐➸✉ ❝❤♦ p✿ r ˆp(1 − ˆp) p > ˆ p − zα . n ❚!♥ ❚❤➜% ❚& ✷✾✴✹✵ ❱➼ ❞# ✼
●✐❡♦ ✹✵✵ ❤↕( ✤➟✉ ①❛♥❤ (❤➻ ❝1 ✺✵ ❤↕( ❦❤4♥❣ ♥↔② ♠➛♠✳ ❱<✐ ✤= (✐♥ ❝➟② ✾✽✪✱ ❤➣② (➻♠✿
❛✮ ❑❤♦↔♥❣ (✐♥ ❝➟② ✤F✐ ①G♥❣ ❝❤♦ (➾ ❧➺ ❤↕( ♥↔② ♠➛♠✳
❜✮ ❑❤♦↔♥❣ (✐♥ ❝➟② (F✐ (❤✐➸✉ ❝❤♦ (➾ ❧➺ ❤↕( ❦❤4♥❣ ♥↔② ♠➛♠✳
❈❤♦ ❜✐➳( z0,05 = 1, 645; z0,025 = 1, 96; z0,02 = 2, 054; z0,01 = 2, 326✳ ●✐↔✐✳
❛✳ ✲ ❚➾ ❧➺ ♠➝✉✿ k 400 − 50 ˆ p = = = 0, 875✳ n 400
✲ ✣9 (✐♥ ❝➟②✿ 1 − α = 0, 98 ⇒ α = 0, 02; zα/2 = z0,01 = 2, 326 r r ✲ ❙❛✐ ;-✿ ˆ p(1 − ˆ p) 0, 875 ∗ (1 − 0, 875) ε = zα/2 = 2, 326 ∗ = 0, 0385 n 400
✲ ❑❤♦↔♥❣ (✐♥ ❝➟② ❝❤♦ (➾ ❧➺ ❤↕( ♥↔② ♠➛♠ ♣✿ ˆ p − ε < p < ˆ
p + ε ⇔ 0, 8365 < p < 0, 9135 ❚!♥ ❚❤➜% ❚& ✸✵✴✹✵
❜✳ ✲ ❚➾ ❧➺ ♠➝✉✿ k 50 ˆ p = = = 0, 125 n 400
✲ ✣, -✐♥ ❝➟②✿ 1 − α = 0, 98 ⇒ α = 0, 02; zα = z0,02 = 2, 054 ✲ ❙❛✐ 56✿ r r ˆ p(1 − ˆ p) 0, 125 ∗ (1 − 0, 125) ε = zα = 2, 054 ∗ = 0, 034 n 400
✲ ❑❤♦↔♥❣ -✐♥ ❝➟② -6✐ -❤✐➸✉ ❝❤♦ -➾ ❧➺ ❤↕- ❦❤?♥❣ ♥↔② ♠➛♠ ♣✿ p > ˆ p − ε ⇔ p > 0, 091 ❚!♥ ❚❤➜% ❚& ✸✶✴✹✵ ❜✳ ◆❤➟♥ ①➨(
✐✮ ❑❤♦↔♥❣ (✐♥ ❝➟② ❝❤♦ 12 ❧45♥❣ ❝→ (❤➸
❚B ❦❤♦↔♥❣ -✐♥ ❝➟② ❝❤♦ -➾ ❧➺ -❛ ❝C -❤➸ 5✉② D❛ ❦❤♦↔♥❣ -✐♥ ❝➟② ❝❤♦ 56 ❧EF♥❣ ❝→ -❤➸ ♠❛♥❣
❞➜✉ ❤✐➺✉ ♥❣❤✐➯♥ ❝K✉ ❤♦➦❝ 56 ❧EF♥❣ ❝→ -❤➸ ❝M❛ -N♥❣ -❤➸✳ ❈P -❤➸✿
✲ ●R✐ ❑ ✈➔ ◆ ❧➛♥ ❧EF- ❧➔ 56 ❧EF♥❣ ❝→ -❤➸ ♠❛♥❣ ❞➜✉ ❤✐➺✉ ♥❣❤✐➯♥ ❝K✉ ✈➔ 56 ❧EF♥❣ ❝→ -❤➸
❝M❛ -N♥❣ -❤➸✳ ❑❤✐ ✤C✱ -➾ ❧➺ ❞➜✉ ❤✐➺✉ ♥❣❤✐➯♥ ❝K✉✿ K p = (1) N
✲ ❉Y❛ -D➯♥ ♠➝✉ ✤✐➲✉ -D❛✱ -❛ E[❝ ❧EF♥❣ ✤EF❝ ❦❤♦↔♥❣ -✐♥ ❝➟② ❝❤♦ -➾ ❧➺ ♣✿ p1 < p < p2 (2)
❚B ✭✶✮ ✈➔ ✭✷✮ 5✉② D❛ ❦❤♦↔♥❣ -✐♥ ❝➟② ❝❤♦ ❣✐→ -D` ❑ ❤♦➦❝ ◆✳ ❚!♥ ❚❤➜% ❚& ✸✷✴✹✵ ❱➼ ❞; ✽
❚!♦♥❣ ♠&' ❝✉&❝ ❜➛✉ ❝, - ♠&' ✤/❛ ♣❤34♥❣ ❝5 ✶✵✵✵✵ ❝, '!✐✳ ◆❣3;✐ '❛ ♣❤<♥❣ ✈➜♥ ♥❣➝✉
♥❤✐➯♥ ✸✵✵ ❝, '!✐ '❤➻ '❤➜② ❝5 ✶✺✻ ♥❣3;✐ F♥❣ ❤& ❝❤♦ G♥❣ ❝, ✈✐➯♥ ❆✳ ❱J✐ ✤& '✐♥ ❝➟② ✾✺✪
'➻♠ ❦❤♦↔♥❣ '✐♥ ❝➟② ✭✤Q✐ ①G♥❣✮ ❝❤♦ TQ ❧3V♥❣ ❝, '!✐ - ✤/❛ ♣❤34♥❣ ♥➔② F♥❣ ❤& ❝❤♦ G♥❣ ❝, ✈✐➯♥ ❆✳
●✐↔✐✳ ●R✐ ❑ ❧➔ 56 ❧EF♥❣ ❝a -D✐ b ✤`❛ ♣❤Ec♥❣ ♥➔② M♥❣ ❤, K♥❣ ❝a ✈✐➯♥ ❆✳ ❚❛ ❝C -➾ ❧➺ M♥❣
❤, K♥❣ ❝a ✈✐➯♥ ❆✿ p = K/10000✳
❚➾ ❧➺ ♠➝✉✿ ˆp = k/n = 156/300 = 0, 52
✣, -✐♥ ❝➟②✿ 1 − α = 0, 95 ⇒ α = 0, 05; zα/2 = z0,025 = 1, 96 ❙❛✐ 56✿ r ˆp(1 − ˆp) r 0, 52 ∗ 0, 48 ε = zα/2 = 1, 96 ∗ = 0, 0565 n 300
❑❤♦↔♥❣ -✐♥ ❝➟② ❝❤♦ -➾ ❧➺ M♥❣ ❤,✿ ˆ p − ε < p < ˆ
p + ε ⇔ 0, 4635 < p < 0, 5765 ❚B ✤C✱ 5✉② D❛✿
0, 4635 < K/10000 < 0, 5765 ⇔ 4635 < K < 5765 ❚!♥ ❚❤➜% ❚& ✸✸✴✹✵ ❱➼ ❞# ✾
✣➸ "#❝ ❧"&♥❣ )* ❧"&♥❣ ❝→ ❝, -.♦♥❣ ❤1✱ ♥❣"3✐ -❛ ❧➔♠ ♥❤" )❛✉✳ ❇➢- ♥❣➝✉ ♥❤✐➯♥ ✺✵✵ ❝♦♥
❝→✱ )❛✉ ✤, ✤→♥❤ ❞➜✉ ✈➔♦ ❝→❝ ❝♦♥ ❝→ ✤➣ ✤"&❝ ❜➢- ✈➔ -❤↔ ❝❤G♥❣ -❛ ①✉*♥❣ ❤1✳ ❙❛✉ ✤, ❜➢-
♥❣➝✉ ♥❤✐➯♥ ✷✵✵ ❝♦♥ ❝→ ✤➸ ❦✐➸♠ -.❛ -❤➻ -❤➜② ❝, ✸✵ ❝♦♥ ❝, ✤→♥❤ ❞➜✉✳ ❱#✐ ✤P -✐♥ ❝➟② ✾✵✪
-➻♠ ❦❤♦↔♥❣ -✐♥ ❝➟② ✤*✐ ①T♥❣ ❝❤♦ )* ❧"&♥❣ ❝→ ❝, -.♦♥❣ ❤1✳
●✐↔✐✳ ●!✐ ◆ ❧➔ &' ❧()♥❣ ❝→ ./♦♥❣ ❤2✳ ❚❛ ❝6 .➾ ❧➺ ❝→ ✤()❝ ✤→♥❤ ❞➜✉✿ p = 500/N✳
❚➾ ❧➺ ♠➝✉✿ ˆp = k/n = 30/200 = 0, 15
✣A .✐♥ ❝➟②✿ 1 − α = 0, 9 ⇒ α = 0, 1; zα/2 = z0,05 = 1, 645 ❙❛✐ &'✿ r ˆp(1 − ˆp) r 0, 15 ∗ 0, 85 ε = zα/2 = 1, 645 ∗ = 0, 0415 n 200
❑❤♦↔♥❣ .✐♥ ❝➟② ❝❤♦ .➾ ❧➺ ❝→ ✤()❝ ✤→♥❤ ❞➜✉✿ ˆ p − ε < p < ˆ
p + ε ⇔ 0, 1085 < p < 0, 1915
❚G ✤6✱ &✉② /❛✿
0, 1085 < 500/N < 0, 1915 ⇔ 2610, 9 < N < 4608, 3 ❚!♥ ❚❤➜% ❚& ✸✹✴✹✵
✐✐✮ ❱➜♥ ✤➲ ✈➲ ❝0 ♠➝✉
✲ ❙❛✐ &' (J❝ ❧()♥❣✿ r ˆp(1 − ˆp) ε = zα/2 n
✲ ✣✐➲✉ ❦✐➺♥ ❤↕♥ ❝❤➳✿ ε ≤ ∆✱ ∆ > 0 ❝❤♦ ./(J❝✳
✲ ●✐↔ &O ❣✐→ ./P ˆp ❦❤Q♥❣ ❜✐➳♥ ✤A♥❣ ❧J♥ ❦❤✐ .➼♥❤ .➼♥❤ ./➯♥ ❝→❝ ♠➝✉ ❦❤→❝ ♥❤❛✉✱ ❦❤✐ ✤6✿ z 2 α/ n ≥ 2 ˆ p(1 − ˆ p). ∆
✲ ❚/♦♥❣ ./(U♥❣ ❤)♣ ❦❤Q♥❣ ❝6 ❞W ❧✐➺✉ ✤➸ .➼♥❤ ❣✐→ ./P ˆp✱ &O ❞Y♥❣ ❜➜. ✤➥♥❣ .❤[❝ ˆp(1 − ˆp) ≤
1/4 .❛ .❤✉ ✤()❝ ❜➜. ✤➥♥❣ .❤[❝✿ 1 z 2 α/ n ≥ 2 . 4 ∆ ❚!♥ ❚❤➜% ❚& ✸✺✴✹✵ ❱➼ ❞# ✶✵
▼P- ❝✉P❝ ❦❤↔♦ )→- )T❝ ❦❤V❡ ❝P♥❣ ✤1♥❣ ✤❛♥❣ ✤"&❝ ❧➯♥ ❦➳ ❤♦↕❝❤ -.♦♥❣ ♠P- ❦❤✉ ✈Z❝ ✤[
-❤\ ❧#♥ ✈#✐ ♠]❝ ✤➼❝❤ "#❝ -➼♥❤ -✛ ❧➺ -.➫ ❡♠ -b ✵ ✤➳♥ ✶✹ -✉e✐ ❝❤"❛ ✤"&❝ -✐➯♠ ❝❤f♥❣ ❜↕✐
❧✐➺- ✤➛② ✤f✳ ❈→❝ ♥❤➔ -e ❝❤T❝ ❝f❛ ❞Z →♥ ♠✉*♥ -✛ ❧➺ ♠➝✉ ❝f❛ -.➫ ❦❤[♥❣ ✤"&❝ -✐➯♠ ❝❤f♥❣
✤➛② ✤f k/n ♣❤↔✐ ♥➡♠ -.♦♥❣ ❦❤♦↔♥❣ ❝f❛ -✛ ❧➺ -❤Z❝ p ✈#✐ )❛✐ )* ±0, 05 ✈#✐ ①→❝ )✉➜- -*✐
-❤✐➸✉ ✾✽✪✳ ❍V✐ ❦➼❝❤ -❤"#❝ ♠➝✉ ✤✐➲✉ -.❛ -*✐ -❤✐➸✉ ❧➔ ❜❛♦ ♥❤✐➯✉❄
❈❤♦ ❜✐➳- z0,05 = 1, 645; z0,025 = 1, 96; z0,02 = 2, 054; z0,01 = 2, 326✳
●✐↔✐✳ ❙❛✐ &' (J❝ ❧()♥❣✿ r ˆp(1 − ˆp) ε = zα/2 n
✣✐➲✉ ❦✐➺♥✿ ε ≤ ∆ = 0, 05✳ ❙✉② /❛✿ z 2 α/ n ≥ 2 ˆ p(1 − ˆ p). ∆ ❚!♥ ❚❤➜% ❚& ✸✻✴✹✵
❱➻ ˆp ❝❤$❛ ❜✐➳) ♥➯♥ →♣ ❞/♥❣ ❜➜) ✤➥♥❣ )❤4❝ ˆp(1 − ˆp) ≤ 1/4 )❛ )❤✉ ✤$6❝✿ 1 z 2 α/ n ≥ 2 . 4 ∆
✣9 )✐♥ ❝➟②✿ 1 − α = 0, 98 ⇒ α = 0, 02; zα/2 = z0,01 = 2, 326✳ ❉♦ ✤?✿ 1 2, 326 2 n ≥ = 541, 0276 4 0, 05 ❱➟②✱ n = 542✳ ❚!♥ ❚❤➜% ❚& ✸✼✴✹✵ ❱➼ ❞# ✶✶
❙↔♥ ❧$%♥❣ ❣↕♦ ❜→♥ +❛ -+♦♥❣ ✶ ♥❣➔② ❝2 ♣❤➙♥ ♣❤6✐ ❝❤✉➞♥✳ ✣✐➲✉ -+❛ =↔♥ ❧$%♥❣ ❜→♥ +❛ -+♦♥❣
✶✷✵ ♥❣➔②✱ -❛ ✤$%❝ ❜↔♥❣ =6 ❧✐➺✉ =❛✉✿
❙↔♥ ❧$%♥❣ ✭❦❣✮ ✹✵✵✲✹✹✵ ✹✹✵✲✹✽✵ ✹✽✵✲✺✷✵ ✺✷✵✲✺✻✵ ✺✻✵✲✻✵✵ ✻✵✵✲✻✹✵ ✻✹✵✲✻✽✵ ❙1 ♥❣➔② ✹ ✾ ✶✺ ✷✸ ✸✵ ✷✷ ✶✼
❛✮ ❱F✐ ✤G -✐♥ ❝➟② ✾✺✪ -➻♠ ❦❤♦↔♥❣ -✐♥ ❝➟② ✤6✐ ①P♥❣ ❝❤♦ =6 -✐➲♥ ❜→♥ +❛ -+✉♥❣ ❜➻♥❤ -+♦♥❣
♠G- ♥❣➔②✳ ❇✐➳- ❣✐→ ♠S✐ ❦❣ ❣↕♦ ❧➔ ✶✺✳✵✵✵ ✤T♥❣✳
❜✮ ◆❣➔② ❝2 =↔♥ ❧$%♥❣ ❣↕♦ ❜→♥ +❛ ❦❤V♥❣ ♥❤W ❤X♥ ✺✻✵ ❦❣ ✤$%❝ ❣Z✐ ❧➔ ♥❣➔② ❝❛♦ ✤✐➸♠✳ ❱F✐
✤G -✐♥ ❝➟② ✾✽✪✱ -➻♠ ❦❤♦↔♥❣ -✐♥ ❝➟② ✤6✐ ①P♥❣ ❝❤♦ =6 ♥❣➔② ❝❛♦ ✤✐➸♠ -+♦♥❣ ✶✵✵✵ ♥❣➔② ❜→♥✳
❈❤♦ ❜✐➳- z0,05 = 1, 645; z0,025 = 1, 96; z0,02 = 2, 054; z0,01 = 2, 326✳ ❚!♥ ❚❤➜% ❚& ✸✽✴✹✵ ●✐↔✐✳
❛✳ ❉↕♥❣ )❤✉ ❣B♥✿
❙↔♥ ❧$%♥❣ ✭❦❣✮ ✹✷✵ ✹✻✵ ✺✵✵ ✺✹✵ ✺✽✵ ✻✷✵ ✻✻✵ ❙0 ♥❣➔② ✹ ✾ ✶✺ ✷✸ ✸✵ ✷✷ ✶✼
❈→❝ DE ✤➦❝ )G$♥❣ ♠➝✉✿ n = 120; ¯x = 566, 67; s = 64
✣9 )✐♥ ❝➟②✿ 1 − α = 0, 95 ⇒ α = 0, 05; tn−1;α/2 = t119;0,025 ≈ z0,025 = 1, 96✳ ❙❛✐ DE✿ s 64 ε = tn √ = 1, 96 ∗ √ = 11, 45 −1;α/2 n 120
❑❤♦↔♥❣ )✐♥ ❝➟② ❝❤♦ ❦❤E✐ ❧$6♥❣ ❣↕♦ )G✉♥❣ ❜➻♥❤ ❜→♥ ✤$6❝ )G♦♥❣ ✶ ♥❣➔②✿ ¯
x − ε < µ < ¯x + ε ⇔ 555, 22 < µ < 578, 12
❑❤♦↔♥❣ )✐♥ ❝➟② ❝❤♦ DE )✐➲♥ ❚ ✭♥❣➔♥ ✤T♥❣✮ )G✉♥❣ ❜➻♥❤ ❜→♥ ✤$6❝ )G♦♥❣ ✶ ♥❣➔②✿
555, 22 ∗ 15 < T < 578, 12 ∗ 15 ⇔ 8328, 3 < T < 8671, 8 ❚!♥ ❚❤➜% ❚& ✸✾✴✹✵
❜✳ ●#✐ ❑ ❧➔ () ♥❣➔② ❝❛♦ ✤✐➸♠ 34♦♥❣ ✶✵✵✵ ♥❣➔②✳ ❚❛ ❝8 3➾ ❧➺ ♥❣➔② ❝❛♦ ✤✐➸♠✿ p = K/1000✳
❚➾ ❧➺ ♠➝✉ ♥❣➔② ❝❛♦ ✤✐➸♠✿ k 30 + 22 + 17 ˆ p = = = 0, 575 n 120
✣? 3✐♥ ❝➟②✿ 1 − α = 0, 98 ⇒ α = 0, 02; zα/2 = z0,01 = 2, 326✳ ❙❛✐ ()✿ r r ˆ p(1 − ˆ p) 0, 575 ∗ (1 − 0, 575) ε = zα/2 = 2, 326 ∗ = 0, 105 n 120
❑❤♦↔♥❣ 3✐♥ ❝➟② ❝❤♦ 3➾ ❧➺ ♥❣➔② ❝❛♦ ✤✐➸♠ ♣✿ ˆ p − ε < p < ˆ
p + ε ⇔ 0, 47 < p < 0, 68 ❙✉② 4❛✿
0, 47 < K/1000 < 0, 68 ⇔ 470 < K < 680 ❚!♥ ❚❤➜% ❚& ✹✵✴✹✵



