Bài giảng Chương 6: Kiểm định giả thuyết thống kê môn Xác suất thống kê | Đại học Duy Tân
Bài giảng Chương 6: Kiểm định giả thuyết thống kê môn Xác suất thống kê | Đại học Duy Tân. Tài liệu được sưu tầm giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời bạn đọc đón xem.
Môn: Xác xuất thống kê (STA 151) 144 tài liệu
Trường: Đại học Duy Tân 1.9 K tài liệu
Tác giả:
Preview text:
❳⑩❈ ❙❯❻❚ ❚❍➮◆● ❑➊ ❚!♥ ❚❤➜% ❚&
✣➔ ◆➤♥❣✱ ✷✵✶✾ ❚!♥ ❚❤➜% ❚& ✶✴✸✽
❈❤"#♥❣ ✻✿ ❑✐➸♠ ✤-♥❤ ❣✐↔ /❤✉②➳/ /❤3♥❣ ❦➯
✶✳ ❈→❝ ❦❤→✐ ♥✐➺♠
✶✳✶ ●✐↔ 6❤✉②➳6 6❤:♥❣ ❦➯
✲ ●✐↔ #❤✉②➳# #❤(♥❣ ❦➯ ❧➔ ❝→❝ ❦❤➥♥❣ ✤+♥❤ ✈➲ ♣❤➙♥ ♣❤0✐ ❝2❛ 45♥❣ 4❤➸ ♥❣❤✐➯♥ ❝8✉✳ ❈< 4❤➸✱
✤> ❧➔ ❝→❝ ❦❤➥♥❣ ✤+♥❤ ✈➲ ❣✐→ 4?+ ❝❤@❛ ❜✐➳4 ❝2❛ 4❤❛♠ D0 ✤0✐ ✈E✐ ♣❤➙♥ ♣❤0✐ ✤➣ ❜✐➳4✱ ❝→❝
❦❤➥♥❣ ✤+♥❤ ✈➲ ❞↕♥❣ ♣❤➙♥ ♣❤0✐ ❝❤@❛ ❜✐➳4 ❤❛② ✈➲ ♠0✐ J✉❛♥ ❤➺ ❣✐L❛ ❝→❝ ❜✐➳♥ ♥❣➝✉ ♥❤✐➯♥✳ ❱➼ ❞? ✶
✰ ●.✐ µ ❧➔ #✉1✐ #❤. #2✉♥❣ ❜➻♥❤ ❝6❛ ♥❣89✐ ❱✐➺# ◆❛♠✳ ●✐↔ #❤✉②➳# #❤(♥❣ ❦➯ ❝? #❤➸ ❧➔✿
µ = 60 ✭#✉1✐✮ ❤♦➦❝ µ > 60✱ ❤♦➦❝ µ 6= 60✱ ✳✳✳
✰ ●.✐ p ❧➔ #➾ ❧➺ ♣❤➳ ♣❤➞♠ ❝6❛ ♥❤➔ ♠→② ❆✳ ●✐↔ #❤✉②➳# #❤(♥❣ ❦➯ ❝? #❤➸ ❧➔✿ p < 0, 1
❤♦➦❝ p = 0, 1 ❤♦➦❝ p 6= 0, 1❀ ✳✳✳
❑❤✐ ♥❣❤✐➯♥ ❝8✉ 4❛ ❝> 4❤➸ ✤@❛ ?❛ ♥❤✐➲✉ ❣✐↔ 4❤✉②➳4 ❦❤→❝ ♥❤❛✉✳ ❚?♦♥❣ ❝❤@R♥❣ ♥➔②✱ ❝❤S♥❣
4❛ ❝❤➾ ❦❤↔♦ D→4 ❜➔✐ 4♦→♥ ❦✐➸♠ ✤+♥❤ ✈E✐ ❤❛✐ ❣✐↔ 6❤✉②➳6 ♠➔ 4❤U✐✳ ❚!♥ ❚❤➜% ❚& ✷✴✸✽
✲ ❇➔✐ #♦→♥ ❦✐➸♠ ✤O♥❤ ❣✐↔ #❤✉②➳# ❧➔ ❜➔✐ 4♦→♥ ❣V♠ ♠W4 ❝➦♣ ❣✐↔ 4❤✉②➳4 4❤0♥❣ ❦➯ ♠➙✉ 4❤✉➝♥
♥❤❛✉ ✤@Y❝ ✤@❛ ?❛ ①❡♠ ①➨4 ✤➸ ❝❤]♥ ♠W4 ❣✐↔ 4❤✉②➳4 ✤S♥❣✳ ▼W4 4?♦♥❣ ❤❛✐ ❣✐↔ 4❤✉②➳4 ✤>
✤@Y❝ ❣✐↔ ✤+♥❤ ❜❛♥ ✤➛✉ ❧➔ ❣✐↔ 4❤✉②➳4 ✤S♥❣✱ ❣]✐ ❧➔ ❣✐↔ #❤✉②➳# ❣(❝ ✈➔ ✤@Y❝ ❦➼ ❤✐➺✉ ❧➔ H0✳
●✐↔ 4❤✉②➳4 ❝b♥ ❧↕✐ ❣]✐ ❧➔ ✤(✐ #❤✉②➳#✱ ✤@Y❝ ❦➼ ❤✐➺✉ ❧➔ H1✳
(H0 : ❣✐↔ 4❤✉②➳4 ❣0❝ H1 : ✤0✐ 4❤✉②➳4
✲ ❑✐➸♠ ✤O♥❤ ❣✐↔ #❤✉②➳# ❧➔ ♣❤@R♥❣ ♣❤→♣ Dc ❞<♥❣ ♠➝✉ ❞L ❧✐➺✉ 4❤✉ ✤@Y❝ ✤➸ ✤@❛ ?❛ J✉②➳4
✤+♥❤ ❜→❝ ❜d H0 ❤❛② ❝❤➜♣ ♥❤➟♥ H0✳ ❚!♥ ❚❤➜% ❚& ✸✴✸✽
✶✳✷ ◆❣✉②➯♥ ❧* ①→❝ .✉➜0 ♥❤2 ✈➔ ①→❝ .✉➜0 ❧5♥
✲ ◆❣✉②➯♥ ❧➼ ①→❝ +✉➜- ♥❤/✿ ▼#$ ❜✐➳♥ ❝* ❝+ ①→❝ .✉➜$ 1➜$ ♥❤3 ❣➛♥ ❜➡♥❣ ✵ $❤➻ ❜✐➳♥ ❝* ✤+
❤➛✉ ♥❤: ❦❤<♥❣ ①↔② 1❛ ❦❤✐ $❤@❝ ❤✐➺♥ ♣❤➨♣ $❤D ♠#$ ❧➛♥✳
✲ ◆❣✉②➯♥ ❧➼ ①→❝ +✉➜- ❧0♥✿ ▼#$ ❜✐➳♥ ❝* ❝+ ①→❝ .✉➜$ ❣➛♥ ❜➡♥❣ ✶ $❤➻ ❜✐➳♥ ❝* ✤+ ❤➛✉ ♥❤: .➩
①↔② 1❛ ❦❤✐ $❤@❝ ❤✐➺♥ ♣❤➨♣ $❤D✳
✶✳✸ ❚❤8♥❣ ❦➯ ❦✐➸♠ ✤>♥❤
●K✐ {X1, X2, ..., Xn} ❧➔ ♠#$ ♠➝✉ ♥❣➝✉ ♥❤✐➯♥ $O② P✳ ❚❛ ①➙② ❞@♥❣ ♠#$ $❤*♥❣ ❦➯ T =
T (X1, X2, ..., Xn) ✈➔ .➩ .D ❞U♥❣ ♥+ ✤➸ ✤:❛ 1❛ W✉②➳$ ✤X♥❤ ❜→❝ ❜3 ❤❛② ❝❤➜♣ ♥❤➟♥ ❣✐↔
$❤✉②➳$ H0✳ ▲[❝ ♥➔②✱ T ✤:]❝ ❣K✐ ❧➔ -❤1♥❣ ❦➯ ❦✐➸♠ ✤7♥❤ ✭❤❛② -✐➯✉ ❝❤✉➞♥ ❦✐➸♠ ✤7♥❤✮✳
❱a✐ α ∈ (0, 1) ❝❤♦ $1:a❝✱ $❛ ❝+ $❤➸ ①➙② ❞@♥❣ ♠✐➲♥ Wα .❛♦ ❝❤♦✿
P (T ∈ Wα|H0 ✤[♥❣) = α
▲[❝ ✤+✱ ♠✐➲♥ Wα ✤:]❝ ❣K✐ ❧➔ ♠✐➲♥ ❜→❝ ❜/ ✈0✐ ♠<❝ = ♥❣❤➽❛ α✳ ❚!♥ ❚❤➜% ❚& ✹✴✸✽
✶✳✸ ❈→❝ ❜A5❝ 0✐➳♥ ❤➔♥❤
❑❤✐ ❝❤♦ $1:a❝ ♠e❝ P ♥❣❤➽❛ α $❛ ❝+ $❤➸ .D ❞U♥❣ ❝→❝ ❜:a❝ ❣]✐ P .❛✉ ✤➙② ✤➸ $✐➳♥ ❤➔♥❤
❣✐↔✐ ❜➔✐ $♦→♥ ❦✐➸♠ ✤X♥❤✿
✲ ❳→❝ ✤X♥❤ ❣✐↔ $❤✉②➳$ H0, H1 ✈➔ ♣❤→$ ❜✐➸✉ ❜➔✐ $♦→♥✳
✲ ❈❤K♥ $❤*♥❣ ❦➯ ❦✐➸♠ ✤X♥❤ T ✈➔ $➼♥❤ ❣✐→ $1X ❝j❛ ♥+ $1➯♥ ♠➝✉ ❞k ❧✐➺✉ $❤✉ ✤:]❝ ✭❦➼ ❤✐➺✉ ❧➔ Ts✮✳
✲ ❳→❝ ✤X♥❤ ♠✐➲♥ ❜→❝ ❜3 Wα ✈a✐ ♠e❝ P ♥❣❤➽❛ α ❝❤♦ $1:a❝✳
✲ ❑➳$ ❧✉➟♥✿ ◆➳✉ Ts ∈ Wα $❤➻ ❜→❝ ❜3 ❣✐↔ $❤✉②➳$ H0✳ ◆❣:]❝ ❧↕✐✱ $❛ ❝❤:❛ ❝+ ❝n .o ❜→❝
❜3 H0 ♥➯♥ $↕♠ $❤p✐ ❝❤➜♣ ♥❤➟♥ ❣✐↔ $❤✉②➳$ ♥➔②✳ ❚!♥ ❚❤➜% ❚& ✺✴✸✽
✶✳✹ ❙❛✐ ❧➛♠ ❦❤✐ ❦✐➸♠ ✤>♥❤
✲ ❙❛✐ ❧➛♠ ❧♦↕✐ ■✿ ❙❛✐ ❧➛♠ ♠➢❝ ♣❤↔✐ ❦❤✐ ❜→❝ ❜3 H0 ♥❤:♥❣ $1♦♥❣ ❦❤✐ $❤@❝ $➳ ❧➔ H0 ❧➔ ❣✐↔
$❤✉②➳$ ✤[♥❣✳ ❑➼ ❤✐➺✉✿ α✳
✲ ❙❛✐ ❧➛♠ ❧♦↕✐ ■■✿ ❙❛✐ ❧➛♠ ♠➢❝ ♣❤↔✐ ❦❤✐ ❝❤➜♣ ♥❤➟♥ H0 $1♦♥❣ ❦❤✐ $❤@❝ $➳ ❧➔ H0 ❧➔ ❣✐↔
$❤✉②➳$ .❛✐✳ ❑➼ ❤✐➺✉✿ β✳
❇↔♥❣ ❞:a✐ ✤➙② $u♥❣ ❤]♣ ❧↕✐ ❝→❝ $1:p♥❣ ❤]♣✿ ❚❤@❝ $➳ H ◗✉②➳$ ✤X♥❤ 0 ✤[♥❣ H0 .❛✐ ❇→❝ ❜3 H0
.❛✐ ❧➛♠ ❧♦↕✐ ■
W✉②➳$ ✤X♥❤ ✤[♥❣ ❈❤➜♣ ♥❤➟♥ H0
W✉②➳$ ✤X♥❤ ✤[♥❣
.❛✐ ❧➛♠ ❧♦↕✐ ■■ ◆❤: ✈➟②✱
α = P (❜→❝ ❜3 H0 ⑤ H0 ✤[♥❣),
β = P (❝❤➜♣ ♥❤➟♥ H0 ⑤ H0 .❛✐) ❚!♥ ❚❤➜% ❚& ✻✴✸✽
✷✳ ❑✐➸♠ ✤'♥❤ ❣✐↔ ,❤✉②➳, ✈➲ ❦➻ ✈4♥❣ ❝6❛ ♣❤➙♥ ♣❤:✐ ❝❤✉➞♥
✷✳✶ ❑❤✐ ♣❤=>♥❣ ?❛✐ ✤➣ ❜✐➳,
❈❤♦ ❜✐➳♥ ♥❣➝✉ ♥❤✐➯♥ X ❝,❛ ♠/0 01♥❣ 0❤➸ ❝3 ♣❤➙♥ ♣❤6✐ ❝❤✉➞♥ N(µ; σ2) ✈9✐ ❦➻ ✈<♥❣ µ
❝❤=❛ ❜✐➳0 ✈➔ ♣❤=?♥❣ @❛✐ σ2 ✤➣ ❜✐➳0✳
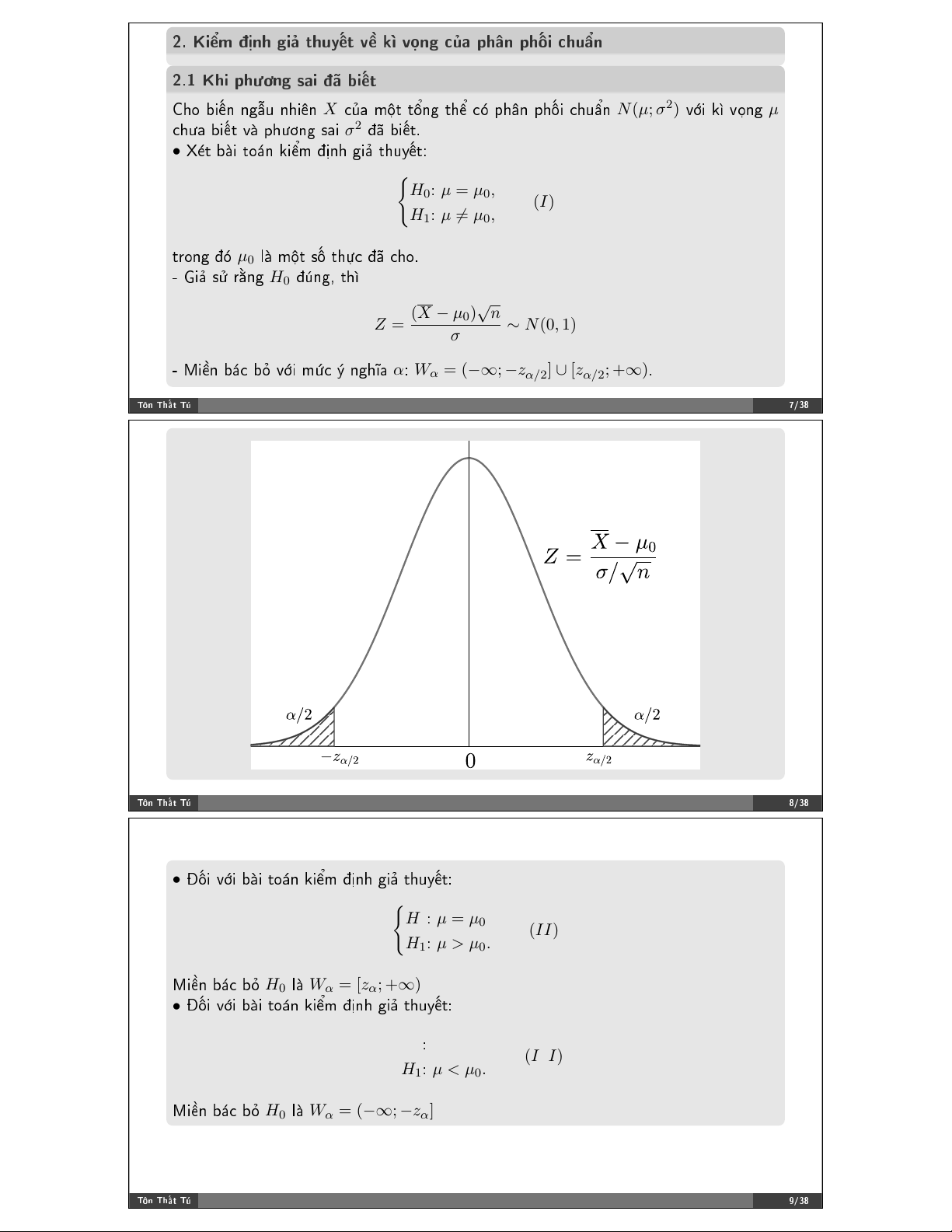
• ❳➨0 ❜➔✐ 0♦→♥ ❦✐➸♠ ✤G♥❤ ❣✐↔ 0❤✉②➳0✿ (H0✿ µ = µ0, (I) H1✿ µ 6= µ0,
0K♦♥❣ ✤3 µ0 ❧➔ ♠/0 @6 0❤M❝ ✤➣ ❝❤♦✳
✲ ●✐↔ @P K➡♥❣ H0 ✤R♥❣✱ 0❤➻ √ (X − µ n Z = 0) ∼ N(0, 1) σ
✲ ▼✐➲♥ ❜→❝ ❜V ✈9✐ ♠W❝ X ♥❣❤➽❛ α✿ Wα = (−∞; −zα/2] ∪ [zα/2; +∞)✳ ❚!♥ ❚❤➜% ❚& ✼✴✸✽ ❚!♥ ❚❤➜% ❚& ✽✴✸✽
• ✣6✐ ✈9✐ ❜➔✐ 0♦→♥ ❦✐➸♠ ✤G♥❤ ❣✐↔ 0❤✉②➳0✿ (H0✿ µ = µ0 (II) H1✿ µ > µ0.
▼✐➲♥ ❜→❝ ❜V H0 ❧➔ Wα = [zα; +∞)
• ✣6✐ ✈9✐ ❜➔✐ 0♦→♥ ❦✐➸♠ ✤G♥❤ ❣✐↔ 0❤✉②➳0✿ (H0✿ µ = µ0 (III) H1✿ µ < µ0.
▼✐➲♥ ❜→❝ ❜V H0 ❧➔ Wα = (−∞; −zα] ❚!♥ ❚❤➜% ❚& ✾✴✸✽ ❇➔✐ #♦→♥ ■■ ❇➔✐ #♦→♥ ■■■ ❚!♥ ❚❤➜% ❚& ✶✵✴✸✽ ❱➼ ❞# ✷
◆❣✉#♥ ❝➜♣ ✤✐➺♥ ❝❤♦ ♠→② 0➼♥❤ ✤↕0 0✐➯✉ ❝❤✉➞♥ ❧➔ ✶✾ ✈♦❧0✳ ✣♦ ♥❣✉#♥ ❝➜♣ ✤✐➺♥ ❝<❛ ♠>0 ♠➝✉
✷✺ B↕❝ ♣✐♥ ✤CD❝ ❝❤E♥ ♥❣➝✉ ♥❤✐➯♥ ❝<❛ ❤➣♥❣ B↔♥ ①✉➜0 ❆ ♥❣CJ✐ 0❛ 0➼♥❤ ✤CD❝ x = 19, 25
✈♦❧0✳ ●✐↔ BL ♥❣✉#♥ ❝➜♣ ✤✐➺♥ ♥➔② ❝M ♣❤➙♥ ♣❤O✐ ❝❤✉➞♥ ✈P✐ ✤> ❧➺❝❤ ❝❤✉➞♥ σ = 0, 5 ✈♦❧0✳ ❱P✐
♠R❝ S ♥❣❤➽❛ α = 0, 05 ❤➣② ❦✐➸♠ ✤W♥❤ ❣✐↔ 0❤✉②➳0 ❣O❝ H0✿ µ = 19 ✭✈♦❧0✮ ✈P✐ ✤O✐ 0❤✉②➳0
H1✿ µ > 19 ✭✈♦❧0✮✱ 0]♦♥❣ ✤M µ ❧➔ ♥❣✉#♥ ❝➜♣ ✤✐➺♥ 0]✉♥❣ ❜➻♥❤ ❝<❛ ❧♦↕✐ B↕❝ ♣✐♥ 0]➯♥✳
❈❤♦ ❜✐➳0 z0.1 = 1.282; z0.05 = 1.645; z0.025 = 1.96; z0.02 = 2.054, z0.01 = 2.326
●✐↔✐✳ ❇➔✐ #♦→♥ ❦✐➸♠ ✤,♥❤✿ (H0 : µ = 19 H1 : µ > 19
❈→❝ 12 ✤➦❝ #45♥❣ ♠➝✉✿ n = 25; ¯x = 19, 25✳ √ √
●✐→ #4, ❝;❛ #❤2♥❣ ❦➯ ❦✐➸♠ ✤,♥❤✿ (¯ x − µ n (19, 25 − 19) 25 z = 0) = = 2, 5✳ σ 0, 5
▼?❝ @ ♥❣❤➽❛✿ α = 0, 05 ⇒ zα = z0,05 = 1, 645✳
▼✐➲♥ ❜→❝ ❜D✿ Wα = [1, 645; +∞)✳
❱➻ z ∈ Wα ♥➯♥ #❛ ❜→❝ ❜D ❣✐↔ #❤✉②➳# H0 ✈➔ ❝❤➜♣ ♥❤➟♥ H1✳ ❚!♥ ❚❤➜% ❚& ✶✶✴✸✽ ❱➼ ❞# ✸
❚]♦♥❣ ♥➠♠ 0]CP❝ ❦❤O✐ ❧CD♥❣ 0]✉♥❣ ❜➻♥❤ ❝<❛ ❜c ①✉➜0 ❝❤✉#♥❣ d ♠>0 0]❛♥❣ 0]↕✐ ❧➔ ✸✽✵❦❣✳
◆➠♠ ♥❛② ♥❣CJ✐ 0❛ →♣ ❞i♥❣ 0❤L ♠>0 ❝❤➳ ✤> ➠♥ ♠P✐ ✈P✐ ❤② ✈E♥❣ ❧➔ ❜c B➩ 0➠♥❣ 0]E♥❣
♥❤❛♥❤ ❤k♥✳ ❙❛✉ 0❤J✐ ❣✐❛♥ →♣ ❞i♥❣ 0❤L✱ ♥❣CJ✐ 0❛ ❝❤E♥ ♥❣➝✉ ♥❤✐➯♥ ✺✵ ❝♦♥ ❜c ①✉➜0 ❝❤✉#♥❣
✤❡♠ ❝➙♥ ✈➔ 0➼♥❤ ✤CD❝ ❦❤O✐ ❧CD♥❣ 0]✉♥❣ ❜➻♥❤ ❝<❛ ❝❤n♥❣ ❧➔ x = 390❦❣✳ ❱P✐ ♠R❝ S ♥❣❤➽❛
α = 0, 02 ❝M 0❤➸ ❝❤♦ ]➡♥❣ ❦❤O✐ ❧CD♥❣ 0]✉♥❣ ❜➻♥❤ ❝<❛ ❜c ①✉➜0 ❝❤✉#♥❣ ✤➣ 0➠♥❣ ❧➯♥ ❦❤p♥❣❄
●✐↔ BL ]➡♥❣ ❦❤O✐ ❧CD♥❣ ❝<❛ ❜c ❝M ♣❤➙♥ ♣❤O✐ ❝❤✉➞♥ ✈P✐ ✤> ❧➺❝❤ ❝❤✉➞♥ σ = 25, 2❦❣✳
❈❤♦ ❜✐➳0 z0.1 = 1.282; z0.05 = 1.645; z0.025 = 1.96; z0.02 = 2.054, z0.01 = 2.326
●✐↔✐✳ ●N✐ µ✭❦❣✮ ❧➔ ❦❤2✐ ❧5R♥❣ #4✉♥❣ ❜➻♥❤ ❝;❛ ❜S ①✉➜# ❝❤✉U♥❣✳ ❚❤❡♦ ❣✐↔ #❤✐➳#✱ #❛ ❝Y ❜➔✐
#♦→♥ ❦✐➸♠ ✤,♥❤✿ (H0 : µ = 380 H1 : µ > 380 √ √
●✐→ #4, ❝;❛ #❤2♥❣ ❦➯ ❦✐➸♠ ✤,♥❤✿ (¯ x − µ n (390 − 380) 50 z = 0) = = 2, 806✳ σ 25, 2
▼?❝ @ ♥❣❤➽❛✿ α = 0, 02 ⇒ zα = z0,02 = 2, 054✳ ▼✐➲♥ ❜→❝ ❜D✿ Wα = [2, 054; +∞)✳
❱➻ z ∈ Wα ♥➯♥ #❛ ❜→❝ ❜D ❣✐↔ #❤✉②➳# H0✳ ❱➟②✱ ✈Z✐ ♠?❝ @ ♥❣❤➽❛ ✷✪ ❦❤2✐ ❧5R♥❣ #4✉♥❣ ❜➻♥❤
❜S ①✉➜# ❝❤✉U♥❣ ✤➣ #➠♥❣ ❧➯♥✳ ❚!♥ ❚❤➜% ❚& ✶✷✴✸✽
❑❤→✐ ♥✐➺♠ ♣✲❣✐→ *+,
✲❣✐→ %&' %()♥❣ +♥❣ ✈-✐ ♠/% %❤1♥❣ ❦➯ ❦✐➸♠ ✤'♥❤ ❧➔ ♠+❝ ①→❝ :✉➜% %❤➜♣ ♥❤➜% ✭✤(?❝ %➼♥❤
❞B❛ %&➯♥ ❣✐→ %&' %❤B❝ ♥❣❤✐➺♠ ❝E❛ %❤1♥❣ ❦➯ ♥➔②✮ ♠➔ %❛ ❝❤➜♣ ♥❤➟♥ ❣✐↔ %❤✉②➳% H0✳
◗✉② %➢❝ ❦✐➸♠ ✤'♥❤✿
✲ ◆➳✉ ♣✲❣✐→ %&' ≤ α %❤➻ ❜→❝ ❜R ❣✐↔ %❤✉②➳% H0✳
✲ ◆➳✉ ♣✲❣✐→ %&' > α %❤➻ ❝❤(❛ ❝S ❝) :T ❜→❝ ❜R ❣✐↔ %❤✉②➳% H0✳
❑❤✐ ♠+❝ V ♥❣❤➽❛ α ❦❤X♥❣ ✤(?❝ ❝❤➾ &❛ %❤➻ %❛ %❤(Z♥❣ :♦ :→♥❤ ♥S ✈-✐ ♠+❝ ✺✪✳
✣1✐ ✈-✐ ✸ ❜➔✐ %♦→♥ T %&➯♥✿ ❇➔✐ %♦→♥ ✭■✮ ✭■■✮ ✭■■■✮
♣✲❣✐→ %&' 2(1 − Φ(|z|)) 1 − Φ(z) Φ(z) ❚!♥ ❚❤➜% ❚& ✶✸✴✸✽
✷✳✷ ❑❤✐ ♣❤/0♥❣ 1❛✐ ❝❤/❛ ❜✐➳*
❈❤♦ ❜✐➳♥ ♥❣➝✉ ♥❤✐➯♥ X ❝E❛ ♠/% %d♥❣ %❤➸ ❝S ♣❤➙♥ ♣❤1✐ ❝❤✉➞♥ N(µ; σ2) ✈-✐ ❦➻ ✈g♥❣ µ
❝❤(❛ ❜✐➳% ✈➔ ♣❤()♥❣ :❛✐ σ2 ❝❤(❛ ❜✐➳%✳
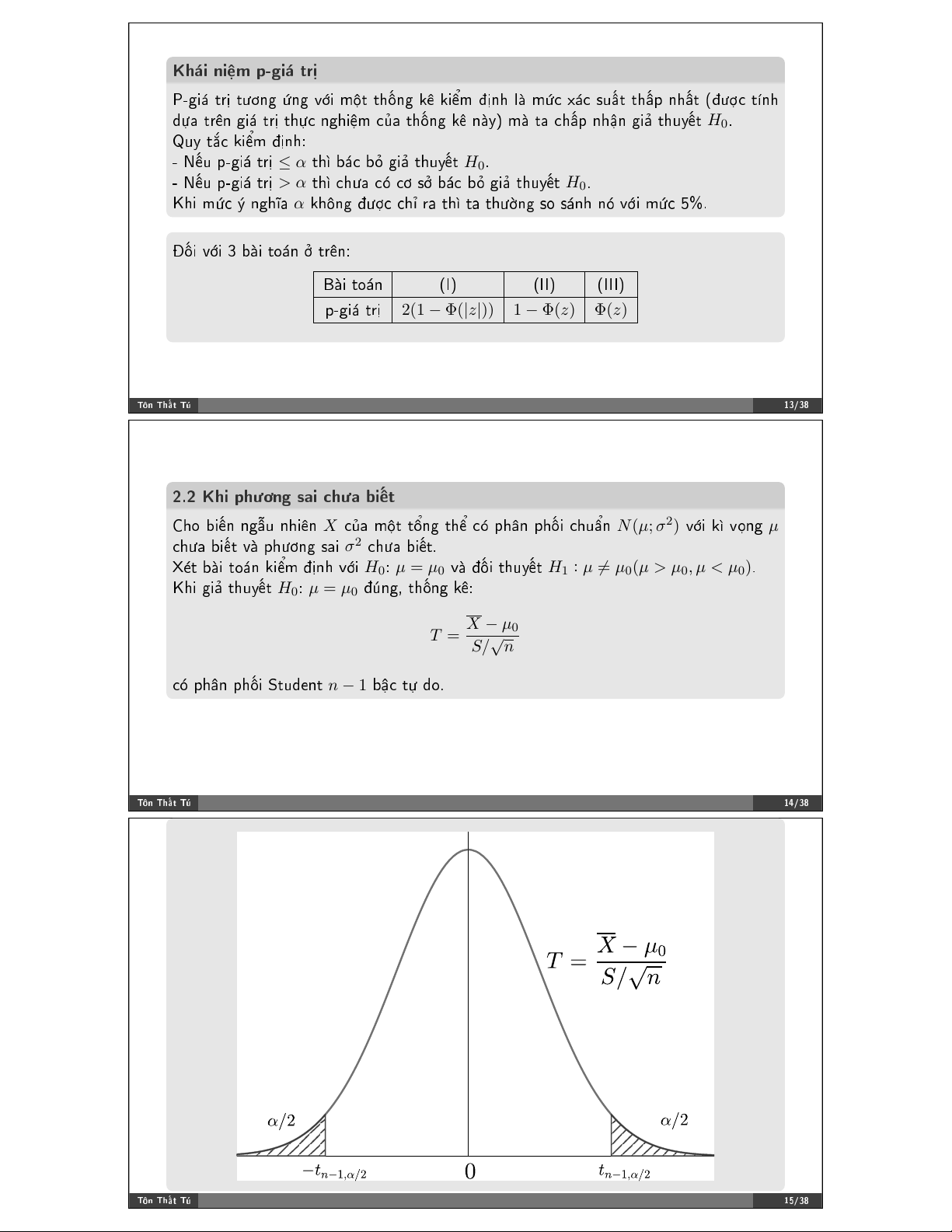
❳➨% ❜➔✐ %♦→♥ ❦✐➸♠ ✤'♥❤ ✈-✐ H0✿ µ = µ0 ✈➔ ✤1✐ %❤✉②➳% H1 : µ 6= µ0(µ > µ0, µ < µ0)✳
❑❤✐ ❣✐↔ %❤✉②➳% H0✿ µ = µ0 ✤j♥❣✱ %❤1♥❣ ❦➯✿ X − µ T = 0 √ S/ n
❝S ♣❤➙♥ ♣❤1✐ ❙%✉❞❡♥% n − 1 ❜➟❝ %B ❞♦✳ ❚!♥ ❚❤➜% ❚& ✶✹✴✸✽ ❚!♥ ❚❤➜% ❚& ✶✺✴✸✽
❈❤♦ ❜✐➳♥ ♥❣➝✉ ♥❤✐➯♥ X ∼ N(µ; σ2) ✈,✐ σ2 ❝❤.❛ ❜✐➳0✳
●✐↔ 0❤✉②➳0 ❣5❝ H0✿ µ = µ0
●✐→ 089 0❤5♥❣ ❦➯ ❦✐➸♠ ✤9♥❤✿ x − µ √ t = 0 n s ✣5✐ 0❤✉②➳0 ▼✐➲♥ ❜→❝ ❜A H0 ♣✲❣✐→ 089 H1✿ µ 6= µ0
(−∞; −tn−1;α/2] ∪ [tn−1;α/2; +∞) 2P (Tn−1 > |t|) H1✿ µ > µ0 [tn−1;α; +∞) P (Tn−1 > t) H1✿ µ < µ0 (−∞; −tn−1;α] P (Tn−1 < t)
❚8♦♥❣ 08.E♥❣ ❤F♣ n > 30✿ tn−1;α ≈ zα✳ ❚!♥ ❚❤➜% ❚& ✶✻✴✸✽ ❱➼ ❞# ✹
❚✉"✐ $❤& $'✉♥❣ ❜➻♥❤ ❝-❛ ♠0$ ❧♦↕✐ ❜4♥❣ ✤➧♥ ❞♦ ♥❤➔ ♠→② ❆ <↔♥ ①✉➜$ ❦❤✐ ❝❤A❛ ❝↔✐ $✐➳♥ ❦➽
$❤✉➟$ ❧➔ ✷✵✵✵ ❣✐G✳ ❙❛✉ $❤G✐ ❣✐❛♥ ❝↔✐ $✐➳♥ ❦➽ $❤✉➟$ ♥❣AG✐ $❛ ❝❤&♥ ♥❣➝✉ ♥❤✐➯♥ ✷✺ ❜4♥❣ ✤➧♥
❝❤♦ ❧➢♣ $❤O ♥❣❤✐➺♠✳ ❑➳$ R✉↔ $❤S❝ ♥❣❤✐➺♠ $❤✉ ✤AT❝ $✉"✐ $❤& $'✉♥❣ ❜➻♥❤ ♠➝✉ x = 2102
❣✐G ✈➔ ✤0 ❧➺❝❤ ❝❤✉➞♥ ♠➝✉ s = 15 ❣✐G✳ ❱X✐ ♠Y❝ Z ♥❣❤➽❛ 0, 025 ❝4 $❤➸ ❦➳$ ❧✉➟♥ ✏<❛✉ ❦❤✐
❝↔✐ $✐➳♥ ❦➽ $❤✉➟$✱ $✉"✐ $❤& ❜4♥❣ ✤➧♥ ❝4 $➠♥❣ ❧➯♥✑ ❦❤`♥❣❄ ❇✐➳$ $✉"✐ $❤& ❜4♥❣ ✤➧♥ ❝4 ♣❤➙♥
♣❤d✐ ❝❤✉➞♥✳ ❈❤♦ ❜✐➳$ t24;0,025 = 2, 063✳
●✐↔✐✳ ●G✐ µ✭❣✐E✮ ❧➔ 0✉L✐ 0❤G 08✉♥❣ ❜➻♥❤ ❝N❛ ❧♦↕✐ ❜P♥❣ ✤➧♥ R❛✉ ❝↔✐ 0✐➳♥✳ ❚❛ ❝P ❜➔✐ 0♦→♥ ❦✐➸♠ ✤9♥❤✿ (H0 : µ = 2000 H1 : µ > 2000
✲ ❈→❝ R5 ✤➦❝ 08.♥❣ ♠➝✉✿ n = 25; ¯x = 2102; s = 15 ❚!♥ ❚❤➜% ❚& ✶✼✴✸✽
✲ ❚❤5♥❣ ❦➯ ❦✐➸♠ ✤9♥❤✿ √ √ (¯ x − µ n (2102 − 2000) 25 t = 0) = = 34 s 15
✲ ▼T❝ U ♥❣❤➽❛✿ α = 0, 025; tn−1;α = t24;0,025 = 2, 063
✲ ▼✐➲♥ ❜→❝ ❜A✿ Wα = [2, 063; +∞)
❱➻ t ∈ Wα ♥➯♥ 0❛ ❜→❝ ❜A H0 ✈➔ ❝❤➜♣ ♥❤➟♥ H1✳ ❱➟②✱ R❛✉ ❝↔✐ 0✐➳♥ ❦[ 0❤✉➟0 0✉L✐ 0❤G ❜P♥❣
✤➧♥ ✤➣ 0➠♥❣ ❧➯♥✳ ❚!♥ ❚❤➜% ❚& ✶✽✴✸✽ ❱➼ ❞# ✺
▼!" ①➼ ♥❣❤✐➺♣ ❝, ✺✵✵✵ ❝/♥❣ ♥❤➙♥ ❝1♥❣ 2↔♥ ①✉➜" ♠!" ❧♦↕✐ 2↔♥ ♣❤➞♠✳ ❚❤❡♦ ❞?✐ "❤@✐ ❣✐❛♥
❤♦➔♥ "❤➔♥❤ 2↔♥ ♣❤➞♠ ❝C❛ ✶✵✵ ❝/♥❣ ♥❤➙♥✱ "❛ ✤GH❝ ❜↔♥❣ 2J ❧✐➺✉ 2❛✉✿
❚❤@✐ ❣✐❛♥ ✭♣❤✮ ✷✽✲✸✵ ✸✵✲✸✷ ✸✷✲✸✹ ✸✹✲✸✻ ✸✻✲✸✽ ✸✽✲✹✵ ❙J ❝/♥❣ ♥❤➙♥ ✺ ✶✺ ✷✺ ✸✵ ✷✵ ✺
❛✮ ❚➻♠ ❦❤♦↔♥❣ "✐♥ ❝➟② ✤J✐ ①Y♥❣ ❝❤♦ "❤@✐ ❣✐❛♥ ❤♦➔♥ "❤➔♥❤ "Z✉♥❣ ❜➻♥❤ ✈\✐ ✤! "✐♥ ❝➟② ✾✵✪✳
❜✮ ❈/♥❣ ♥❤➙♥ ❝, "❛② ♥❣❤➲ ❝❛♦ ♥➳✉ "❤@✐ ❣✐❛♥ ❤♦➔♥ "❤➔♥❤ ✶ 2↔♥ ♣❤➞♠ ❞G\✐ ✸✷♣❤✳ ❱\✐
✤! "✐♥ ❝➟② ✾✺✪✱ "➻♠ ❦❤♦↔♥❣ "✐♥ ❝➟② ✤J✐ ①Y♥❣ ❝❤♦ 2J ❝/♥❣ ♥❤➙♥ ❝, "❛② ♥❣❤➲ ❝❛♦ ❝C❛ ①➼ ♥❣❤✐➺♣✳
❝✮ ❳➼ ♥❣❤✐➺♣ d✉② ✤e♥❤ ✤e♥❤ ♠Y❝ ❤♦➔♥ "❤➔♥❤ "Z✉♥❣ ❜➻♥❤ ✶ 2↔♥ ♣❤➞♠ ❧➔ ✸✹ ♣❤f"✳ ❈, g
❦✐➳♥ ❝❤♦ Z➡♥❣ ✤e♥❤ ♠Y❝ ♥➔② ❝, ❤↕✐ ❝❤♦ ❝/♥❣ ♥❤➙♥✳ ❱\✐ ♠Y❝ g ♥❣❤➽❛ ✷✪ ❤➣② ♥❤➟♥ ①➨" ✈➲ g ❦✐➳♥ ✤,✳
❈❤♦ ❜✐➳" z0.1 = 1.282; z0.05 = 1.645; z0.025 = 1.96; z0.02 = 2.054, z0.01 = 2.326 ❚!♥ ❚❤➜% ❚& ✶✾✴✸✽
●✐↔✐✳ ❛✳ ❉↕♥❣ &❤✉ ❣)♥✿
❚❤,✐ ❣✐❛♥ ✭♣❤✮ ✷✾ ✸✶ ✸✸ ✸✺ ✸✼ ✸✾ ❙8 ❝:♥❣ ♥❤➙♥ ✺ ✶✺ ✷✺ ✸✵ ✷✵ ✺
❈→❝ ?8 ✤➦❝ &BC♥❣ ♠➝✉✿ n = 100; ¯x = 34, 2; s = 2, 494
✣G &✐♥ ❝➟②✿ 1 − α = 0, 9 ⇒ α = 0, 1; tn−1;α/2 = t99;0,05 ≈ z0,05 = 1, 645 ❙❛✐ ?8✿ s 2, 494 ε = tn √ = 1, 645 ∗ √ = 0, 41 −1;α/2 n 100
❑❤♦↔♥❣ &✐♥ ❝➟② ❝❤♦ &❤,✐ ❣✐❛♥ ❤♦➔♥ &❤➔♥❤ &B✉♥❣ ❜➻♥❤✿ ¯
x − ε < µ < ¯x + ε ⇔ 33, 79 < µ < 34, 61 ❚!♥ ❚❤➜% ❚& ✷✵✴✸✽
❜✳ ●)✐ ❑ ❧➔ ?8 ❝:♥❣ ♥❤➙♥ ❝R &❛② ♥❣❤➲ ❝❛♦✳ ❚➾ ❧➺ ❝:♥❣ ♥❤➙♥ ❝R &❛② ♥❣❤➲ ❝❛♦✿ p = K/5000✳
❚➾ ❧➺ ♠➝✉ ❝:♥❣ ♥❤➙♥ ❝R &❛② ♥❣❤➲ ❝❛♦✿ ˆ p = k/n = (5 + 15)/100 = 0, 2
✣G &✐♥ ❝➟②✿ 1 − α = 0, 95 ⇒ α = 0, 05; zα/2 = z0,025 = 1, 96 ❙❛✐ ?8✿ r ˆp(1 − ˆp) r 0, 2 ∗ 0, 8 ε = zα/2 = 1, 96 ∗ = 0, 0784 n 100
❑❤♦↔♥❣ &✐♥ ❝➟② ❝❤♦ &➾ ❧➺ ❝:♥❣ ♥❤➙♥ ❝R &❛② ♥❣❤➲ ❝❛♦✿ ˆ p − ε < p < ˆ
p + ε ⇔ 0, 1216 < p < 0, 2784
❙✉② B❛✿ 0, 1216 < K/5000 < 0, 2784 ⇔ 608 < K < 1392✳ ❚!♥ ❚❤➜% ❚& ✷✶✴✸✽
❝✳ ●#✐ µ ✭♣❤✮ ❧➔ +❤,✐ ❣✐❛♥ ❤♦➔♥ +❤➔♥❤ +1✉♥❣ ❜➻♥❤ ✶ 6↔♥ ♣❤➙♠ ❝:❛ ❝;♥❣ ♥❤➙♥✳ ❚❛ ❝= ❜➔✐
+♦→♥ ❦✐➸♠ ✤B♥❤✿ (H0 : µ = 34 H1 : µ > 34
✲ ❚❤E♥❣ ❦➯ ❦✐➸♠ ✤B♥❤✿ √ √ (¯ x − µ n (34, 2 − 34) 100 t = 0) = = 0, 802 s 2, 494
✲ ▼H❝ I ♥❣❤➽❛✿ α = 0, 02; tn−1;α = t99;0,02 ≈ z0,02 = 2, 054
✲ ▼✐➲♥ ❜→❝ ❜L✿ Wα = [2, 054; +∞)
❱➻ t /∈ Wα ♥➯♥ +❛ ❝❤N❛ ❝= ❝O 6P ❜→❝ ❜L H0✳ ❱➟②✱ ✤B♥❤ ♠H❝ T✉② ✤B♥❤ ❦❤;♥❣ ❣➙② ❤↕✐ ❝❤♦ ❝;♥❣ ♥❤➙♥✳ ❚!♥ ❚❤➜% ❚& ✷✷✴✸✽
✸✳ ❙♦ $→♥❤ ❤❛✐ ❦+ ✈-♥❣ ❝0❛ ❤❛✐ ♠➝✉ ✤5❝ ❧➟♣
❈❤♦ X ✈➔ Y ❜✐➳♥ 6E ♥❣➝✉ ♥❤✐➯♥ ❝:❛ ❤❛✐ +Z♥❣ +❤➸ ✤[❝ ❧➟♣ ♥❤❛✉ ✈➔ ❧➛♥ ❧N]+ ❝= ♣❤➙♥ ♣❤E✐
❝❤✉➞♥ N(µx; σ2x) ✈➔ N(µy; σ2y) ✈_✐ ♣❤NO♥❣ 6❛✐ σ2x, σ2y ❝❤N❛ ❜✐➳+✳
❳➨+ ❜➔✐ +♦→♥ ❦✐➸♠ ✤B♥❤ ✈_✐ H0 : µx − µy = ∆0
✈➔ ✤E✐ +❤✉②➳+ H1 : µx − µy 6= ∆0(µx − µy > ∆0, µx − µy < ∆0)✳
●✐↔ 6b (x1, ..., xm) ✈➔ (y1, ..., yn) ❧➔ ❝→❝ ♠➝✉ +❤✉ ✤N]❝ +c X ✈➔ Y +NO♥❣ H♥❣✳
❈❤➾ ①➨= =>?@♥❣ ❤A♣ ❦❤✐ ❝B ♠➝✉ ❧C♥ ✭♠✱♥❃✸✵✮✳
❑❤✐ ✤=✱ →♣ ❞f♥❣ ✣B♥❤ ❧➼ ❣✐_✐ ❤↕♥ +1✉♥❣ +➙♠ +❛ ❝=✿ (X − Y ) − (µ Z = x − µy) r S2 S2 x + y m n
❝= ♣❤➙♥ ♣❤E✐ ①➜♣ ①➾ ♣❤➙♥ ♣❤E✐ ❝❤✉➞♥ +➢❝ N(0; 1)✳ ❚!♥ ❚❤➜% ❚& ✷✸✴✸✽
X ∼ N(µx; σ2x) ✈➔ Y ∼ N(µy; σ2y) +1♦♥❣ ✤= σ2x ✈➔ σ2y ✤➲✉ ❝❤N❛ ❜✐➳+❀ m > 30 ✈➔ n > 30✳
●✐↔ +❤✉②➳+ +❤E♥❣ ❦➯ H0✿ µx − µy = ∆0
●✐→ +1B +❤E♥❣ ❦➯ ❦✐➸♠ ✤B♥❤✿ x − y − ∆ z = 0 r s2 s2 x + y m n ✣E✐ +❤✉②➳+ ▼✐➲♥ ❜→❝ ❜L H0 ♣✲❣✐→ +1B H1✿ µx − µy 6= ∆0
(−∞; −zα/2] ∪ [zα/2; +∞) 2(1 − Φ(|z|)) H1✿ µx − µy > ∆0 [zα; +∞) 1 − Φ(z) H1✿ µx − µy < ∆0 (−∞; −zα] Φ(z) ❚!♥ ❚❤➜% ❚& ✷✹✴✸✽
◆❤➟♥ ①➨&✿ ❑❤✐ ∆0 = 0✱ ❝→❝ ❜➔✐ (♦→♥ ❦✐➸♠ ✤/♥❤ (0➯♥ (❤23♥❣ ✤25❝ ✈✐➳( ❧↕✐ ❞2;✐ ❞↕♥❣✿ (H (I) 0 : µx = µy H1 : µx 6= µy (H (II) 0 : µx = µy H1 : µx < µy (H (III) 0 : µx = µy H1 : µx > µy
❚❤>♥❣ ❦➯ ❦✐➸♠ ✤/♥❤ (0? (❤➔♥❤✿ x − y z = rs2 s2 x + y m n ❚!♥ ❚❤➜% ❚& ✷✺✴✸✽ ❱➼ ❞+ ✻
◆❣"#✐ %❛ ❝➙♥ %*➫ ,- ,✐♥❤ / ❤❛✐ ❦❤✉ ✈3❝ %❤➔♥❤ %❤5 ✈➔ ♥6♥❣ %❤6♥✱ ❦➳% 9✉↔ %❤✉ ✤"<❝✿ ❑❤✉ ✈3❝ ❙@ %*➫
❚*✉♥❣ ❜➻♥❤ ♠➝✉ F❤"-♥❣ ,❛✐ ♠➝✉ ◆6♥❣ %❤6♥ m = 60 x = 3, 0 ❦❣ s2x = 0, 4 ❦❣2 ❚❤➔♥❤ %❤5 n = 50 y = 3, 1 ❦❣ s2y = 0, 5 ❦❣2
❱H✐ ♠I❝ J ♥❣❤➽❛ 0, 05 ❝L %❤➸ ❝♦✐ ❦❤@✐ ❧"<♥❣ %*✉♥❣ ❜➻♥❤ ❝P❛ %*➫ ,- ,✐♥❤ / ❤❛✐ ❦❤✉ ✈3❝
❦❤→❝ ♥❤❛✉ ❦❤6♥❣❄ ❇✐➳% ❦❤@✐ ❧"<♥❣ %*➫ ,- ,✐♥❤ / ❤❛✐ ❦❤✉ ✈3❝ ❝L ♣❤➙♥ ♣❤@✐ ❝❤✉➞♥✳ ❈❤♦ ❜✐➳% z0.025 = 1.96
●✐↔✐✳ ●A✐ µx, µy ✭❦❣✮ ❧➔ ❦❤>✐ ❧25♥❣ (0✉♥❣ ❜➻♥❤ ❝F❛ (0➫ IJ I✐♥❤ ? ♥K♥❣ (❤K♥ ✈➔ (❤➔♥❤ (❤/✳
❚❛ ❝M ❜➔✐ (♦→♥ ❦✐➸♠ ✤/♥❤✿ (H0 : µx = µy H1 : µx 6= µy
❚❤>♥❣ ❦➯ ❦✐➸♠ ✤/♥❤✿ ¯ x − ¯y 3, 0 − 3, 1 z = = = −0, 774 q p s2 0, 4/60 + 0, 5/50 x/m + s2 y/n ❚!♥ ❚❤➜% ❚& ✷✻✴✸✽
▼O❝ P ♥❣❤➽❛✿ α = 0, 05; zα/2 = z0,025 = 1, 96✳
▼✐➲♥ ❜→❝ ❜S✿ Wα = (−∞; −1, 96] ∪ [1, 96; +∞)
❱➻ z /∈ Wα ♥➯♥ (❛ ❝❤2❛ ❝M ❝J I? ❜→❝ ❜S ❣✐↔ (❤✉②➳( H0✳ ❱➟②✱ ❦❤K♥❣ ❝M IX ❦❤→❝ ❜✐➺( ✈➲
❦❤>✐ ❧25♥❣ (0✉♥❣ ❜➻♥❤ ❝F❛ (0➫ IJ I✐♥❤ ? ❤❛✐ ✈Z♥❣ (0➯♥✳ ❱➼ ❞+ ✼
◆❣"#✐ %❛ %✐➳♥ ❤➔♥❤ ♠X% ❝✉X❝ ♥❣❤✐➯♥ ❝I✉ ✤➸ ,♦ ,→♥❤ ♠I❝ ❧"-♥❣ %*✉♥❣ ❜➻♥❤ ❝P❛ ♣❤Z ♥[
,♦ ✈H✐ ♠I❝ ❧"<♥❣ %*✉♥❣ ❜➻♥❤ ❝P❛ ♥❛♠ ❣✐H✐ %*♦♥❣ ♠X% ❝6♥❣ %② ❧H♥✳ ▼X% ♠➝✉ ❣^♠ ✶✵✵ ♣❤Z
♥[ ❝L ♠I❝ ❧"-♥❣ %*✉♥❣ ❜➻♥❤ ✼✱✷✸ ✤6❧❛✴❣✐# ✈H✐ ✤X ❧➺❝❤ ❝❤✉➞♥ ✶✱✻✹ ✤6❧❛✴❣✐#✳ ▼X% ♠➝✉
❣^♠ ✼✺ ♥❛♠ ❣✐H✐ ❝L ♠I❝ ❧"<♥❣ %*✉♥❣ ❜➻♥❤ ❧➔ ✽✱✵✻ ✤6❧❛✴❣✐# ✈H✐ ✤X ❧➺❝❤ ❝❤✉➞♥ ❧➔ ✶✱✽✺
✤6❧❛✴❣✐#✳ ❱H✐ ♠I❝ J ♥❣❤➽❛ ✶✪ ,@ ❧✐➺✉ ♥➔② ❝L ❝❤I♥❣ ♠✐♥❤ ✤"<❝ ♠I❝ ❧"-♥❣ %*✉♥❣ ❜➻♥❤
❝P❛ ♣❤Z ♥[ %*♦♥❣ ❝6♥❣ %② ❧➔ %❤➜♣ ❤-♥ ♥❛♠ ❣✐H✐ ❤❛② ❦❤6♥❣ ❄ ❈❤♦ ❜✐➳% z0,01 = 2, 326✳ ❚!♥ ❚❤➜% ❚& ✷✼✴✸✽
●✐↔✐✳ ●!✐ µx, µy ✭✤%❧❛✴❣✐*✮ ❧➔ ♠.❝ ❧01♥❣ 34✉♥❣ ❜➻♥❤ ❝9❛ ♥: ✈➔ ♥❛♠ ❣✐<✐✳ ❚❛ ❝? ❜➔✐ 3♦→♥ ❦✐➸♠ ✤D♥❤✿ (H0 : µx = µy H1 : µx < µy
❚❤F♥❣ ❦➯ ❦✐➸♠ ✤D♥❤✿ ¯ x − ¯y 7, 23 − 8, 06 z = = = −3, 08 q p s2 1, 642/100 + 1, 852/75 x/m + s2 y/n
▼.❝ I ♥❣❤➽❛✿ α = 0, 01; zα = z0,01 = 2, 326✳
▼✐➲♥ ❜→❝ ❜L✿ Wα = (−∞; −2, 326]
❱➻ z ∈ Wα ♥➯♥ 3❛ ❜→❝ ❜L ❣✐↔ 3❤✉②➳3 H0✳ ❱➟②✱ ❧01♥❣ 34✉♥❣ ❜➻♥❤ ❝9❛ ♥: ❣✐<✐ 3❤➜♣ ❤1♥ U♦
✈<✐ ♥❛♠ ❣✐<✐ 34♦♥❣ ❝%♥❣ 3②✳ ❚!♥ ❚❤➜% ❚& ✷✽✴✸✽
✹✳ ❑✐➸♠ ✤)♥❤ ❣✐↔ -❤✉②➳- ✈➲ -➾ ❧➺
❈❤♦ 3➼♥❤ ❝❤➜3 A ❝? 3➾ ❧➺ ❧➔ p ✭❝❤0❛ ❜✐➳3✮ 34♦♥❣ 3Z♥❣ 3❤➸✳ ❳➨3 ❜➔✐ 3♦→♥ ❦✐➸♠ ✤D♥❤ ❣✐↔ 3❤✉②➳3✿ H0 : p = p0
✈➔ ✤F✐ 3❤✉②➳3 H1 : p 6= p0(p > p0, p < p0)✳
❈❤!♥ ♠]3 ♠➝✉ ♥❣➝✉ ♥❤✐➯♥ ❦➼❝❤ 3❤0<❝ n✱ ✤➦3 (1,
♣❤➛♥ 3a i ❝? 3➼♥❤ ❝❤➜3 ❆ Xi = 0,
♣❤➛♥ 3a i ❦❤%♥❣ ❝? 3➼♥❤ ❝❤➜3 ❆ ✈➔ ˆ X P =
1 + X2 + ... + Xn ✲ 3➾ ❧➺ ♣❤➛♥ 3a ❝? 3➼♥❤ ❝❤➜3 A✳ n
❑❤✐ H0 ✤%♥❣✱ ✈*✐ n ✤+ ❧*♥✱ -❤❡♦ ✣1♥❤ ❧➼ ❣✐*✐ ❤↕♥ -4✉♥❣ -➙♠✿ ˆ P − p Z = 0 pp0(1 − p0)/n
❝: ♣❤➙♥ ♣❤<✐ ①➜♣ ①➾ ♣❤➙♥ ♣❤<✐ ❝❤✉➞♥ -➢❝ N(0; 1)✳ ❚!♥ ❚❤➜% ❚& ✷✾✴✸✽
❈❤♦ ˆp = k/n ❧➔ ♠D- E*❝ ❧EF♥❣ ❝+❛ -✛ ❧➺ p -J ♠D- ♠➝✉ ❦➼❝❤ -❤E*❝ n✳
●✐↔ -❤✉②➳- ❣<❝ H0✿ p = p0 √
●✐→ -41 -❤<♥❣ ❦➯ ❦✐➸♠ ✤1♥❤✿ (ˆ p − p n z = 0) pp0(1 − p0) ✣<✐ -❤✉②➳- ▼✐➲♥ ❜→❝ ❜W H0 ♣✲❣✐→ -41 H1 : p 6= p0
(−∞; −zα/2] ∪ [zα/2; +∞) 2(1 − Φ(|z|)) H1✿ p > p0 [zα; +∞) 1 − Φ(z) H1✿ p < p0 (−∞; −zα] Φ(z) ❚!♥ ❚❤➜% ❚& ✸✵✴✸✽ ❱➼ ❞# ✽
●✐→♠ ✤%❝ ♠'( ❝)♥❣ (② (✉②➯♥ ❜% ✾✵✪ 3↔♥ ♣❤➞♠ ❝8❛ ❝)♥❣ (② ✤↕( (✐➯✉ ❝❤✉➞♥ ;✉%❝ ❣✐❛✳
▼'( ❝)♥❣ (② ❦✐➸♠ ✤@♥❤ ✤'❝ ❧➟♣ ✤➣ (✐➳♥ ❤➔♥❤ ❦✐➸♠ (F❛ ✷✵✵ 3↔♥ ♣❤➞♠ ❝8❛ ❝)♥❣ (② ✤H (❤➻
(❤➜② ❝H ✶✻✽ 3↔♥ ♣❤➞♠ ✤↕( ②➯✉ ❝➛✉✳ ❱P✐ ♠Q❝ R ♥❣❤➽❛ α = 0, 1 ❝H (❤➸ ❝❤♦ F➡♥❣ (✛ ❧➺ 3↔♥
♣❤➞♠ ✤↕( (✐➯✉ ❝❤✉➞♥ ;✉%❝ ❣✐❛ (❤➜♣ ❤X♥ ✾✵✪ ❦❤)♥❣❄ ❈❤♦ ❜✐➳( z0,1 = 1, 282✳
●✐↔✐✳ ●!✐ p ❧➔ %➾ ❧➺ (↔♥ ♣❤➞♠ ✤↕% %✐➯✉ ❝❤✉➞♥ 4✉5❝ ❣✐❛ ❝8❛ ❝9♥❣ %②✳ ❇➔✐ %♦→♥ ❦✐➸♠ ✤A♥❤✿ (H0 : p = 0, 9 H1 : p < 0, 9
❚➾ ❧➺ ♠➝✉✿ ˆp = k/n = 168/200 = 0, 84
❚❤5♥❣ ❦➯ ❦✐➸♠ ✤A♥❤✿ √ √ (ˆ p − p n (0, 84 − 0, 9) 200 z = 0) = √ = −2, 83 pp 0, 9 0(1 − p0) ∗ 0, 1
▼F❝ G ♥❣❤➽❛✿ α = 0, 1 ⇒ zα = z0.1 = 1.282✳
▼✐➲♥ ❜→❝ ❜K✿ Wα = (−∞; −1, 282]✳
❱➻ z ∈ Wα ♥➯♥ ❜→❝ ❜K H0✳ ❱➟②✱ %✛ ❧➺ (↔♥ ♣❤➞♠ ✤↕% %✐➯✉ ❝❤✉➞♥ 4✉5❝ ❣✐❛ %❤➜♣ ❤R♥ ✾✵✪✳ ❚!♥ ❚❤➜% ❚& ✸✶✴✸✽ ❱➼ ❞# ✾
▼'( ❦❤✉ ✈\❝ ❝H ✶✵✵✵✵ ❤' ❣✐❛ ✤➻♥❤ 3✐♥❤ 3%♥❣ ✈➔ ❝→❝ ❤' ] ✤➙② ❝❤➾ 3` ❞b♥❣ ❣❛ ❝8❛ ✷ ❝)♥❣
(② ❆ ✈➔ ❇✳ ✣✐➲✉ (F❛ ✽✵✵ ❤' (❤➻ ❝H ✻✵✵ ❤' ❞g♥❣ ❣❛✱ (F♦♥❣ ✤H ✸✻✵ ❤' ❞g♥❣ ❣❛ ❝8❛ ❝)♥❣ (② ❆✳
❛✮ ❱P✐ ✤' (✐♥ ❝➟② ✾✺✪✱ (➻♠ ❦❤♦↔♥❣ (✐♥ ❝➟② ✤%✐ ①Q♥❣ ❝❤♦ 3% ❧mn♥❣ ❤' ❞g♥❣ ❣❛ ] ❦❤✉ ✈\❝ ♥➔②✳
❜✮ ❈H R ❦✐➳♥ ❝❤♦ F➡♥❣ ❣❛ ❝8❛ ❝)♥❣ (② ❆ ✤mn❝ ❝→❝ ❤' (❤➼❝❤ ❞g♥❣ ❤X♥✳ ❱P✐ ♠Q❝ R ♥❣❤➽❛
✷✪ ❤➣② ♥❤➟♥ ①➨( ✈➲ R ❦✐➳♥ ➜②✳
●✐↔✐✳ ❛✳ ●!✐ ❑ ❧➔ (5 ❧WX♥❣ ❤Y ❞[♥❣ ❣❛ \ ❦❤✉ ✈^❝ ♥➔②✳ ❚❛ ❝_ %➾ ❧➺ ❤Y ❞[♥❣ ❣❛✿ p = K/10000✳
❚➾ ❧➺ ♠➝✉✿ ˆp = k/n = 600/800 = 0, 75✳
✣Y %✐♥ ❝➟②✿ 1 − α = 0, 95 ⇒ α = 0, 05; zα/2 = z0,025 = 1, 96✳ ❙❛✐ (5✿ r ˆp(1 − ˆp) r 0, 75 ∗ 0, 25 ε = zα/2 = 1, 96 ∗ = 0, 03 n 800
❑❤♦↔♥❣ %✐♥ ❝➟② ❝❤♦ %➾ ❧➺ ❤Y ❞[♥❣ ❣❛✿ ˆp − ε < p < ˆp + ε ⇔ 0, 72 < p < 0, 78
❙✉② b❛✿ 0, 72 < K/10000 < 0, 78 ⇔ 7200 < K < 7500✳ ❚!♥ ❚❤➜% ❚& ✸✷✴✸✽
❜✳ ●!✐ p ❧➔ %➾ ❧➺ ❤Y ❞[♥❣ ❣❛ ❝8❛ ❝9♥❣ %② ❆✳ ❇➔✐ %♦→♥ ❦✐➸♠ ✤A♥❤✿ (H0 : p = 0, 5 H1 : p > 0, 5
❚➾ ❧➺ ♠➝✉✿ ˆp = k/n = 360/600 = 0, 6
●✐→ %bA ❝8❛ %❤5♥❣ ❦➯ ❦✐➸♠ ✤A♥❤✿ √ √ (ˆ p − p n (0, 6 − 0, 5) 600 z = 0) = √ = 4, 9 pp 0, 5 0(1 − p0) ∗ 0, 5
▼F❝ G ♥❣❤➽❛✿ α = 0, 02 ⇒ zα = z0.02 = 2, 054✳
▼✐➲♥ ❜→❝ ❜K✿ Wα = [2, 054; +∞)✳
❱➻ z ∈ Wα ♥➯♥ ❜→❝ ❜K H0✳ ❱➟②✱ (↔♥ ♣❤➞♠ ❣❛ ❝8❛ ❝9♥❣ %② ❆ ✤WX❝ W❛ %❤➼❝❤ ❤R♥✳ ❚!♥ ❚❤➜% ❚& ✸✸✴✸✽
✺✳ ❙♦ $→♥❤ ❤❛✐ *➾ ❧➺
❳➨" "➼♥❤ ❝❤➜" A ❝( "➾ ❧➺ ❧➔ p1 ✈➔ p2 ❝❤.❛ ❜✐➳" "3♦♥❣ ❤❛✐ "6♥❣ "❤➸ ✤9❝ ❧➟♣ ♥❤❛✉✳ ❳➨" ❜➔✐
"♦→♥ ❦✐➸♠ ✤A♥❤ ✈B✐ ❣✐↔ "❤✉②➳" ❣E❝✿ H0 : p1 = p2
✈➔ ✤E✐ "❤✉②➳" H1 : p1 6= p2(p1 > p2, p1 < p2)✳
●✐↔ HI ˆp1 = k1/n1 ✈➔ ˆp2 = k2/n2 ❧➛♥ ❧.K" ❧➔ .B❝ ❧.K♥❣ ❝L❛ p1 ✈➔ p2 "M ❤❛✐ ♠➝✉ ♥❣➝✉
♥❤✐➯♥ ✤9❝ ❧➟♣ ❦➼❝❤ "❤.B❝ n1 ✈➔ n2 ".P♥❣ Q♥❣✳
❑❤✐ ❣✐↔ "❤✉②➳" H0 ✤S♥❣✱ "❤E♥❣ ❦➯ ˆ p k Z = 1 − ˆ p2 ✈B✐ ˆp = 1 + k2 s 1 1 n1 + n2 ˆ p(1 − ˆ p) + n1 n2
❝( ♣❤➙♥ ♣❤E✐ ①➜♣ ①➾ ♣❤➙♥ ♣❤E✐ ❝❤✉➞♥ "➢❝ N(0, 1)✳ ❚!♥ ❚❤➜% ❚& ✸✹✴✸✽
●✐↔ HI ˆp1 = k1/n1 ✈➔ ˆp2 = k2/n2 ❧➛♥ ❧.K" ❧➔ .B❝ ❧.K♥❣ ❝L❛ p1 ✈➔ p2 "M ❤❛✐ ♠➝✉
♥❣➝✉ ♥❤✐➯♥ ✤9❝ ❧➟♣✳
✲ ●✐↔ "❤✉②➳" ❣E❝ H0✿ p1 = p2
✲ ●✐→ "3A "❤E♥❣ ❦➯ ❦✐➸♠ ✤A♥❤✿ ˆ p k z = 1 − ˆ p2 ✈B✐ ˆp = 1 + k2 s 1 1 n1 + n2 ˆ p(1 − ˆ p) + n1 n2 ✣E✐ "❤✉②➳" ▼✐➲♥ ❜→❝ ❜] H0 ♣✲❣✐→ "3A H1 : p1 6= p2
(−∞; −zα/2] ∪ [zα/2; +∞) 2(1 − Φ(|z|)) H1 : p1 > p2 [zα; +∞) 1 − Φ(z) H1 : p1 < p2 (−∞; −zα] Φ(z) ❚!♥ ❚❤➜% ❚& ✸✺✴✸✽ ❱➼ ❞1 ✶✵
❑✐➸♠ $%❛ ♥❣➝✉ ♥❤✐➯♥ ❝→❝ /↔♥ ♣❤➞♠ ❝3♥❣ ❧♦↕✐ ❞♦ ❤❛✐ ♥❤➔ ♠→② /↔♥ ①✉➜$ $❤✉ ✤=>❝ ❞? ❧✐➺✉✿
◆❤➔ ♠→② ❙D /↔♥ ♣❤➞♠ ✤=>❝ ❦✐➸♠ $%❛ ❙D ♣❤➳ ♣❤➞♠ ❆ ✶✵✵✵ ✷✺ ❇ ✾✻✵ ✸✵
❱Q✐ ♠R❝ S ♥❣❤➽❛ α = 0, 05 ❝U $❤➸ ❝♦✐ $✛ ❧➺ ♣❤➳ ♣❤➞♠ ❝W❛ ❤❛✐ ♥❤➔ ♠→② $%➯♥ ❜➡♥❣ ♥❤❛✉
❦❤Z♥❣❄ ❈❤♦ ❜✐➳$ z0.025 = 1.96
●✐↔✐✳ ●^✐ p1, p2 ❧➔ "➾ ❧➺ ♣❤➳ ♣❤➞♠ ❝L❛ ♥❤➔ ♠→② ❆✱ ❇ ".P♥❣ Q♥❣✳ ❚❛ ❝( ❜➔✐ "♦→♥ ❦✐➸♠ ✤A♥❤✿ (H0 : p1 = p2 H1 : p1 6= p2 ❚!♥ ❚❤➜% ❚& ✸✻✴✸✽
❈→❝ #➾ ❧➺ ♠➝✉✿ ˆ
p1 = k1/n1 = 25/1000 = 0, 025; ˆ p2 = k2/n2 = 30/960 = 0, 03125 ˆ
p = (k1 + k2)/(n1 + n2) = (25 + 30)/(1000 + 960) = 0, 028
●✐→ #-. ❝/❛ #❤2♥❣ ❦➯ ❦✐➸♠ ✤.♥❤✿ ˆ p 0, 025 − 0, 03125 z = 1 − ˆ p2 = = −0, 838 s p 1 1
0, 028 ∗ (1 − 0, 028)(1/1000 + 1/960) ˆ p(1 − ˆ p) + n1 n2
▼:❝ ; ♥❣❤➽❛✿ α = 0, 05 ⇒ zα/2 = z0.025 = 1, 96✳
▼✐➲♥ ❜→❝ ❜@✿ Wα = (−∞; 1, 96] ∪ [1, 96; +∞)✳
❱➻ z /∈ Wα ♥➯♥ ❝❤C❛ ❝D ❝E FG ❜→❝ ❜@ H0✳ ❱➟②✱ #➾ ❧➺ ♣❤➳ ♣❤➞♠ ❝/❛ ❤❛✐ ♥❤➔ ♠→② ❦❤O♥❣
❝D FP ❦❤→❝ ❜✐➺#✳ ❚!♥ ❚❤➜% ❚& ✸✼✴✸✽ ❱➼ ❞# ✶✶
❈!♥❣ $② ♥&'❝ ❣✐↔✐ ❦❤→$ ✤❛♥❣ ♥❣❤✐➯♥ ❝1✉ ✈✐➺❝ ✤&❛ ✈➔♦ ♠8$ ❝!♥❣ $❤1❝ ♠'✐ ✤➸ ❝↔✐ $✐➳♥ ;↔♥
♣❤➞♠ ❝>❛ ♠➻♥❤✳ ❱'✐ ❝!♥❣ $❤1❝ ❝B ❦❤✐ ❝❤♦ ✺✵✵ ♥❣&E✐ ❞G♥❣ $❤H $❤➻ ❝I ✶✷✵ ♥❣&E✐ &❛ $❤➼❝❤
♥I✳ ❱'✐ ❝!♥❣ $❤1❝ ♠'✐ ❦❤✐ ❝❤♦ ✶✵✵✵ ♥❣&E✐ ❦❤→❝ ❞G♥❣ $❤➻ ❝I ✸✵✵ ♥❣&E✐ ❜↔♦ &❛ $❤➼❝❤
❤&O♥❣ ✈P ♥➔②✳ ❱'✐ ♠1❝ Q ♥❣❤➽❛ ✷✪ ❤➣② ❦✐➸♠ ✤P♥❤ ①❡♠ ❝!♥❣ $❤1❝ ♠'✐ ✤&❛ ✈➔♦ ❝I ❧➔♠
$➠♥❣ $➾ ❧➺ ♥❣&E✐ &❛ $❤➼❝❤ $❤1❝ ✉Z♥❣ ❝>❛ ❝!♥❣ $② ❤❛② ❦❤!♥❣ ❄ ❈❤♦ ❜✐➳$ z0,02 = 2, 054✳
●✐↔✐✳ ●Q✐ p1, p2 ❧➔ #➾ ❧➺ ♥❣CR✐ C❛ #❤➼❝❤ ♥CT❝ ✉2♥❣ ✈T✐ ❝O♥❣ #❤:❝ ❝V ✈➔ ♠T✐✳ ❚❛ ❝D ❜➔✐
#♦→♥ ❦✐➸♠ ✤.♥❤✿ (H0 : p1 = p2 H1 : p1 < p2
❈→❝ #➾ ❧➺ ♠➝✉✿ ˆp1 = 0, 24; ˆp2 = 0, 3; ˆp = 0, 28✳
●✐→ #-. #❤2♥❣ ❦➯ ❦✐➸♠ ✤.♥❤✿ z = −2, 39
▼✐➲♥ ❜→❝ ❜@✿ Wα = (−∞; −2, 054]✳
❱➻ z ∈ Wα ♥➯♥ ❜→❝ ❜@ ❣✐↔ #❤✉②➳# H0✳
❱➟②✱ ❝O♥❣ #❤:❝ ♠T✐ ✤C❛ ✈➔♦ ✤➣ ❧➔♠ #➠♥❣ #➾ ❧➺ ♥❣CR✐ C❛ #❤➼❝❤ #❤:❝ ✉2♥❣ ❝/❛ ❝O♥❣ #②✳ ❚!♥ ❚❤➜% ❚& ✸✽✴✸✽
Tài liệu liên quan:
-
Bài giảng Chương 5. Ước lượng tham số môn Xác suất thống kê | Đại học Duy Tân
3 2 -
Bài giảng Chương 4: Thống kê mô tả môn Xác suất thống kê | Đại học Duy Tân
3 2 -
Bài giảng Chương 3. Vectơ ngẫu nhiên môn Xác suất thống kê | Đại học Duy Tân
3 2 -
Bài giảng Chương 1: Xác suất môn Xác suất thống kê | Đại học Duy Tân
3 2