

































Preview text:
lOMoARcPSD|36149638 VẬT
LÝ ĐẠI CƯƠNG 1
CHƯƠNG I: ĐỘNG HỌC CHẤT ĐIỂM Bài 1.1) MỞ ĐẦU I.
Chuyển động và hệ quy chiếu
- Chuyển động là sự thay đổi vị trí trong không gian theo thời gian của vật thể này so với vật thể khác.
- Khi chúng ta nói một chiếc máy bay đang bay trên bầu trời thì có nghĩa là chúng ta đã tạm quy
ước bầu trời đứng yên và chiếc máy bay đang chuyển động đối với bầu trời. Như vậy khái niệm
chuyển động là một khái niệm có tính tương đối, điều đó thể hiện ở chỗ: Một vật chuyển động là
phải chuyển động so với vật nào, chứ không có khái niệm chuyển động chung chung.
- Vật này được quy ước là đứng yên thì vật kia chuyển động và ngược lại.
- Khi chúng ta nói: một chiếc xe đang chuyển động trên đường thì thực tế chúng ta đã ngầm quy
ước với nhau rằng chiếc xe đó chuyển động so với đường hay cây cối, nhà cửa ở bên đường. Nên
nói đầy đủ hơn phải là: chiếc xe đang chuyển động so với con đường. Như vậy không thể nói một
chuyển động mà không chỉ ra được một vật mà đối với nó thì vật này chuyển động.
- Vật được coi là đứng yên để xét chuyển động của vật khác được gọi là vật làm “mốc” hay “hệ quy chiếu”.
- Để thuận lợi cho việc nghiên cứu chuyển động người ta gắn vào hệ quy chiếu một hệ toạ độ,
chẳng hạn hệ toạ độ Descartes Oxyz (Renè Descartes1596 - 1650 người Pháp) II.
Chất điểm và hệ chất điểm
- Chất điểm: Chất điểm là vật mà kích thước của nó nhỏ hơn nhiều so với quãng đường mà nó đi
được (nhỏ hơn từ vài trăm đến vài ngàn lần). Một vật có thể được xem là chất điểm hoặc không
phải là chất điểm, điều này phụ thuộc vào độ dài quãng đường chuyển động của vật đó chứ không
phụ thuộc vào kích thước của nó.
- Ví dụ: Chiếc xe tải trong quãng đường chuyển động từ Bắc vào Nam có thể coi là chất điểm.
- Hệ chất điểm: Là tập hợp hai hay nhiều chất điểm mà khoảng cách giữa các chất điểm là không
đổi hoặc chuyển động của chất điểm này phụ thuộc các chất điểm khác. III.
Phương trình chuyển động của chất điểm
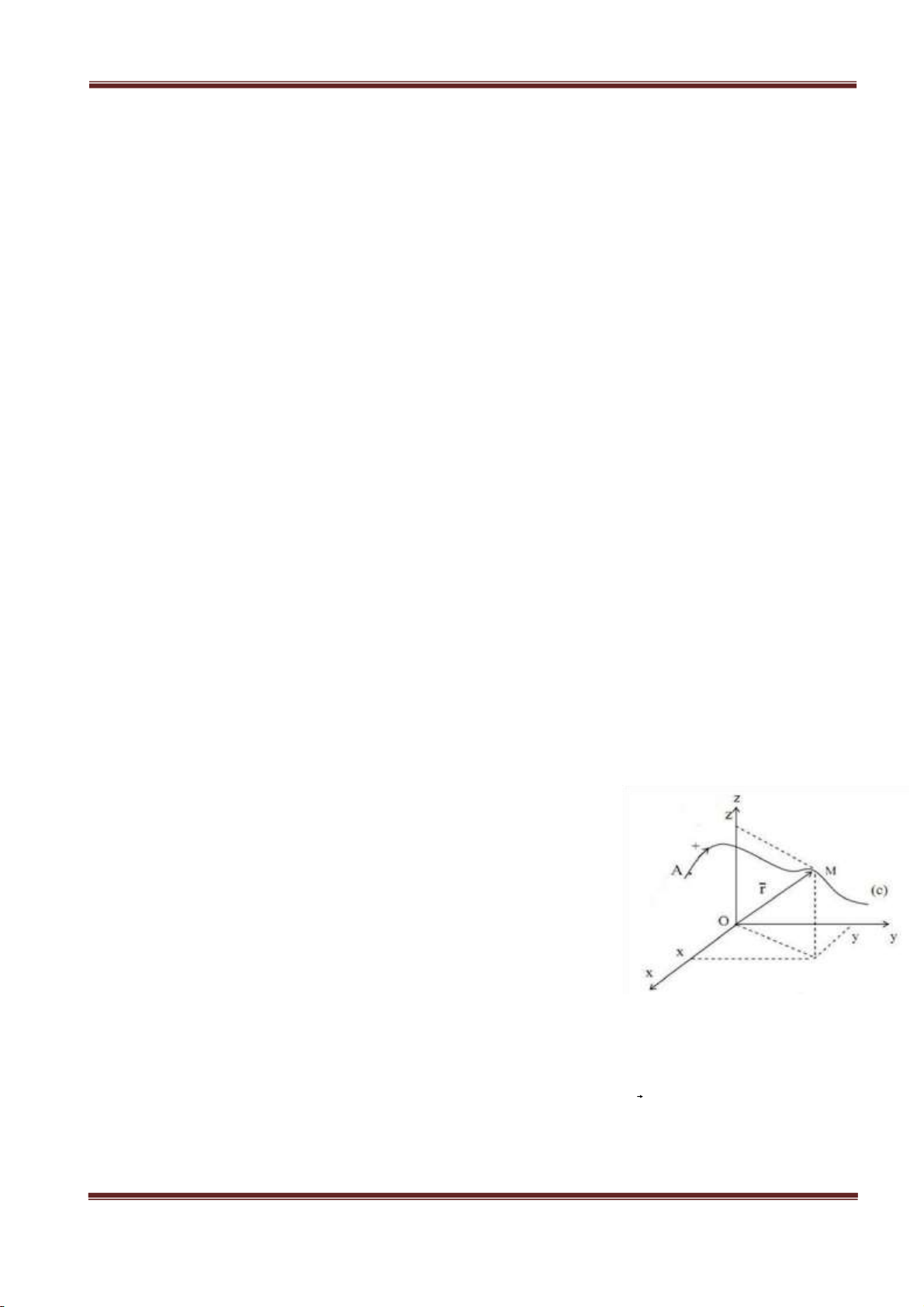
- Xét một chất điểm chuyển động theo đường cong bất kỳ AB
trong hệ quychiếu O,x,y,z (Hình 1.1).
- Giả sử rằng tại thời điểm t vị trí của chất điểm là M trên đường
cong AB, M là một điểm nên hoàn toàn được xác định bởi ba
toạ độ x, y và z (ta hay nói là ba toạ độ của điểm M). Nhưng vì
chất điểm chuyển động nên x,y,z thay đổi theo thời gian. Nghĩa
là ba toạ độ là hàm của thời gian: x = x(t) y = y(t) (1.1). z = z(t)
Hình 1.1: Tọa độ của chất điểm
- (Trong trường hợp chuyển động thẳng nếu ta chọn hệ tọa độ sao cho chuyển động dọc theo trục
Ox thì: x = x(t); y = 0; z = 0). Việc xác định chuyển động của chất điểm bằng hệ phương trình
(1.1) gọi là phương pháp tọa độ và phương trình đó gọi là phương trình chuyển động dạng tọa độ Descartes.
- Điểm M cũng hoàn toàn được xác định nếu biết vector r⃗ và các cosin chỉ phương của nó, vì r⃗=x
i⃗+ y ⃗j+z ⃗k . (1.2) Nhưng do M chuyển động nên r⃗ thay đổi cả phương, chiều và độ lớn theo
thời gian: r⃗ ¿r⃗ (t) . (1.3) Đây là phương trình chuyển động dạng vector trong đó r⃗ được gọi là
Bộ môn Vật Lý 1 lOMoARcPSD| 36149638 VẬT
LÝ ĐẠI CƯƠNG 1
bán kính vector hay vector định vị. Chúng ta cũng không quên rằng để xác định vector này còn
cần ba cosin chỉ phương nữa.
- Ta cũng có thể biểu diễn chuyển động bằng một cách khác là: chọn trên quỹ đạo một gốc tọa độ,
chẳng hạn A và như vậy đoạn đường mà chất điểm đi được, được xác định so với A bằng cung s,
và cũng như trên s là một hàm của thời gian: s=s(t).(1.4). Phương trình này là phương trình chuyển
động dạng quỹ đạo. Phương pháp này gặp khó khăn ở chỗ là phải biết trước dạng quỹ đạo của
chuyển động. s được gọi là hoành độ cong. IV. Quỹ đạo 1) Quỹ đạo
- Quỹ đạo của một chất điểm là quỹ tích của tất cả những điểm trong không gian mà chất điểm đã
đi qua trong suốt quá trình chuyển động của nó.
- Như vậy quỹ đạo của một chất điểm thực tế chính là đường đi của nó trong không gian.
2) Phương trình quỹ đạo
- Phương trình quỹ đạo của một chất là phương trình biểu diễn mối liên hệ giữa các toạ độ chuyển
động của chất điểm trong không gian.
- Nghĩa là phương trình quỹ đạo có dạng: F(x,y,z)=0 (1.5)
- Và nếu biết phương trình quỹ đạo thì biết được dạng quỹ đạo của chất điểm đó.
Ví dụ 1: Một chất điểm chuyển động theo phương trình: x = 2 cos t ω;y = 4 sin t ω . a.
Đây là phương trình quỹ đạo hay phương trình chuyển động của chất điểm?
b. Tìm dạng quĩ đạo của chất điểm V. Hoành độ cong
- Giả sử quỹ đạo của chất điểm là một đường cong (C) ( hình 1.1). Trên đường cong (C) ta chọn
một điểm A nào đó là gốc và một chiều dương theo chiều chuyển động của chất điểm. Khi đó tại
mỗi thời điểm t, vị trí M của chất điểm trên đường cong (C) được xác định bởi trị đại số của cung , kí hiệu là: AM s (1.6)
- Người ta gọi s là hoành độ cong của chất điểm chuyển động. Khi chất điểm chuyển động, s là
hàm của thời gian t, tức là: s s t( ) (1.7)
- Véc tơ vi phân hoành độ cong d s⃗
Phương trùng với tiếp tuyến của quỹ đạo tại điểm đang xét.
Hướng theo chiều chuyển động.
Độ lớn bằng vi phân hoành độ cong ds. Bài 1.2)
VECTƠ VẬN TỐC CỦA CHẤT ĐIỂM I. Định nghĩa
- Để chứng tỏ sự cần thiết của việc đưa ra khái niệm vận tốc ta lấy ví dụ sau đây: hai xe cùng xuất
phát từ một nơi, cùng một lúc và cùng đến đích vào một thời điểm. Nhưng chúng ta không thể
nói được xe nào đã chuyển động nhanh hay chậm hơn xe nào nếu không biết được xe nào đã tiêu
tốn ít hay nhiều thời gian hơn cho chuyển động (vì có thể quãng đường đi của hai xe là như nhau
hoặc khác nhau). Như vậy để so sánh các chuyển động với nhau thì phải so sánh quãng đường
mà chúng đi được trong cùng một thời gian, hay tốt nhất là cùng một đơn vị thời gian, quãng
Bộ môn Vật Lý 2 lOMoARcPSD|36149638 VẬT
LÝ ĐẠI CƯƠNG 1
đường đi trong một đơn vị thời gian đó được gọi là vận tốc. Như vậy có thể định nghĩa vận tốc như sau:
“Vận tốc của một chuyển động là đại lượng đặc trưng cho sự nhanh hay chậm của một
chuyển động, có trị số bằng quãng đường mà chất điểm đi được trong một đơn vị thời gian”.
- Để đặc trưng cho cả phương, chiều của chuyển động, điểm đặt của vận tốc, thì vận tốc là một đại lượng vector. II. Vectơ vận tốc
Vận tốc trung bình của một chuyển động trên một đoạn đường nào đó nói chung khác với vận
tốc tại một thời điểm bất kỳ trên quỹ đạo. Bởi vậy ta thường gặp hai loại vận tốc.
1) Vận tốc trung bình
- Vận tốc trung bình của một chuyển động là quãng
đường trung bình mà chuyển động đi được trong một đơn vị thời gian.
- Trong hệ đơn vị SI đơn vị thời gian là một giây
ngoài ra nếu không sử dụng hệ đơn vị SI thì ta có
thể lấy các đơn vị khác như:
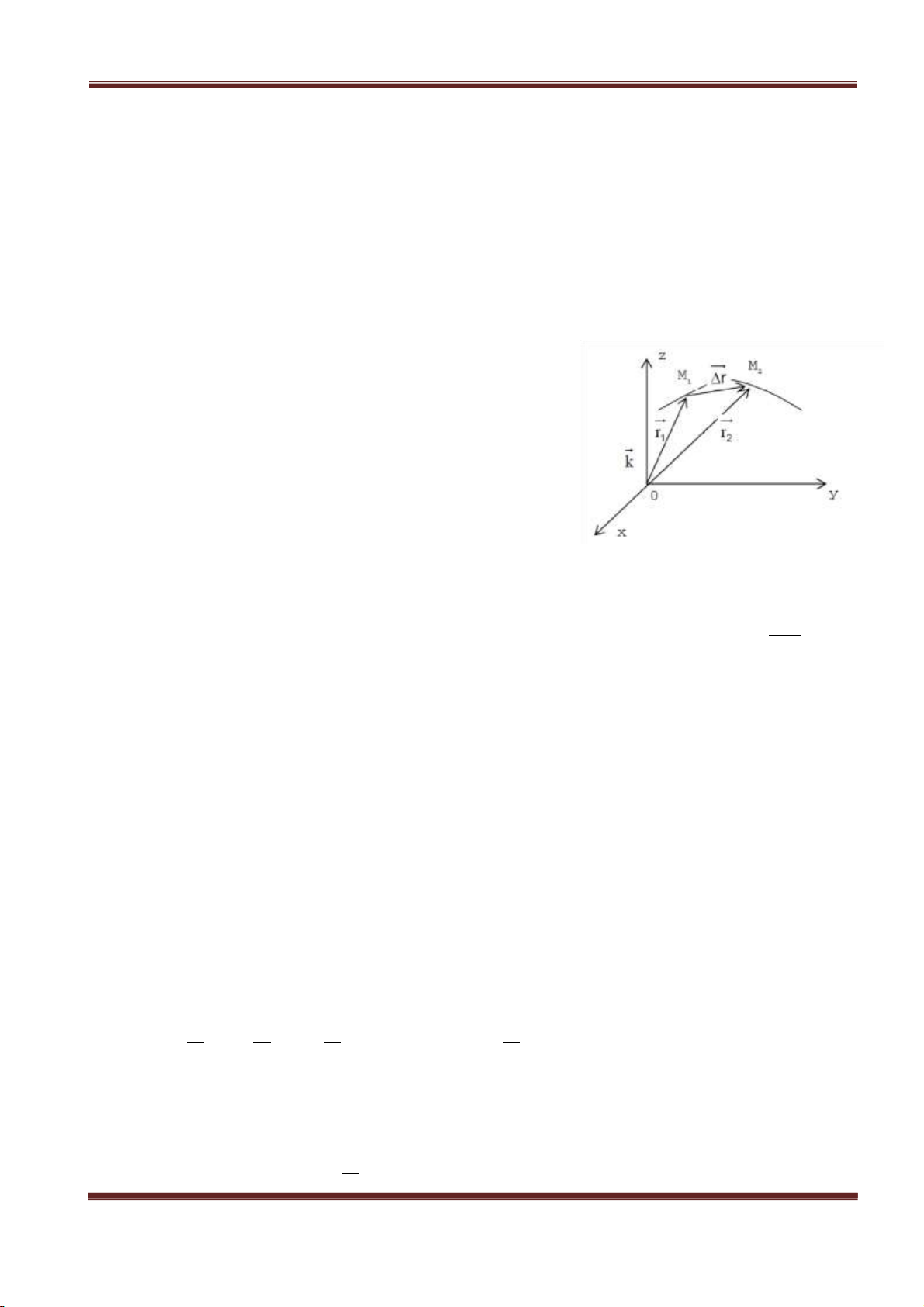
Hình 1.2: vec tơ vận tốc của chất điểm
giờ, phút, ngày, tuần .v..v..
- Giả sử tại thời điểm t chất điểm ở vị trí M được 1
xác định bởi bán kính vector r⃗=r⃗1 .
- Đến thời điểm t + Δt vị trí của chất điểm là M2: r⃗2=r⃗+∆r⃗
- Như vậy trong thời gian Δt chất điểm đi được một đoạn ∆ S đường
ΔS , nên theo định nghĩa của chúng ta thì vận tốc trung bình chính là: vtb= ∆t (1.8)
2) Vận tốc tức thời
- Vận tốc tức thời của một chuyển động là vận tốc của nó tại một thời điểm nào đó trên quỹ đạo
của chuyển động của nó.
- Việc xác định vận tốc của chất điểm tại một thời điểm bất kỳ trên quỹ đạo lại có ý nghĩa hơn vận
tốc trung bình, vì đó mới là vận tốc thực của chuyển động.
- Để có biểu thức tính vận tốc tức thời ta có nhận xét như sau: nếu Δt → 0thì M → M và do đó 2 1 vtb
→vt . Nghĩa là vận tốc trung bình trên đoạn đường ngắn M
được xem là vận tốc tại 1M2 điểm M
. Nói như vậy có nghĩa là: Vận tốc tức thời của một chất điểm tại một thời điểm 1 hay vt
nào đó trên quỹ đạo bằng đạo hàm bậc nhất của bán kính vector theo thời gian tại điểm đó.
- Vector vận tốc có độ lớn bằng độ lớn của vận tốc, có phương là phương của tiếp tuyến tại điểm
đang xét, có chiều là chiều của chuyển động. III.
Vectơ vận tốc trong hệ tọa độ Đê - các
Do trong hệ tọa độ Đêcác thì r⃗=x i⃗+ y ⃗j+z ⃗k
dxdt ⃗+ dydt ⃗j+ dzdt k⃗=vx ⃗i+v y ⃗j+v z dzdt k⃗ (1.9) v⃗= i dx
Bộ môn Vật Lý 3 lOMoARcPSD| 36149638 VẬT
LÝ ĐẠI CƯƠNG 1 v x= dt v v iớv y= dy (1.11) dt
{ dz v z= dt Bài 1.3)
VECTƠ GIA TỐC CỦA CHẤT ĐIỂM I.
Định nghĩa và biểu thức vectơ gia tốc
1) Khái niệm và định nghĩa -
Đối với những chuyển động không đều thì vận
tốc liên tục thay đổi, để đặc trưng cho sự thay đổi
nhanh hay chậm của vận tốc người ta đưa ra khái niệm
Hình 1.3: vec tơ gia tốc của chất
gia tốc với ý nghĩa tương tự như vận tốc. điểm
“Gia tốc của một chuyển động là đại lượng đặc trưng cho sự thay đổi nhanh hay chậm
của vận tốc, có trị số bằng lượng vận tốc thay đổi trong một đơn vị thời gian”.
2) Gia tốc trung bình -
Tương tự như vận tốc ta cũng xét hai thời điểm trên quỹ đạo: -
Tại thời điểm t (M ) vị trí và vận tốc của chất điểm được xác định bằng 1 r⃗ và v⃗ . -
Đến thời điểm t + Δt (M ) vị trí và vận tốc của chất điểm được xác 2
định bằng: r⃗+∆r⃗ và v⃗+∆v⃗ . ∆ v -
Vậy độ tăng trung bình của vận tốc trong một đơn vị thời gian là: atb= ∆t (1.12)
(a là gia tốc trung bình của chuyển động của chất điểm đang xét ở trên đoạn đường M tb 1M2)
3) Gia tốc tức thời -
Hoàn toàn lập luận tương tự như đối với vận tốc, gia tốc tức thời của
mộtchất điểm tại một thời điểm nào đó chính là kết quả của giới hạn sau đây:
a⃗= lim ∆∆t⃗v = ddtv⃗ = ddt2r⃗2 (1.13) ∆t→ 0 -
Dạng thành phần của a⃗ là:
⃗+a y ⃗j+az dzdt k⃗ (1.14) a⃗=ax i
Bộ môn Vật Lý 4 lOMoARcPSD|36149638 VẬT
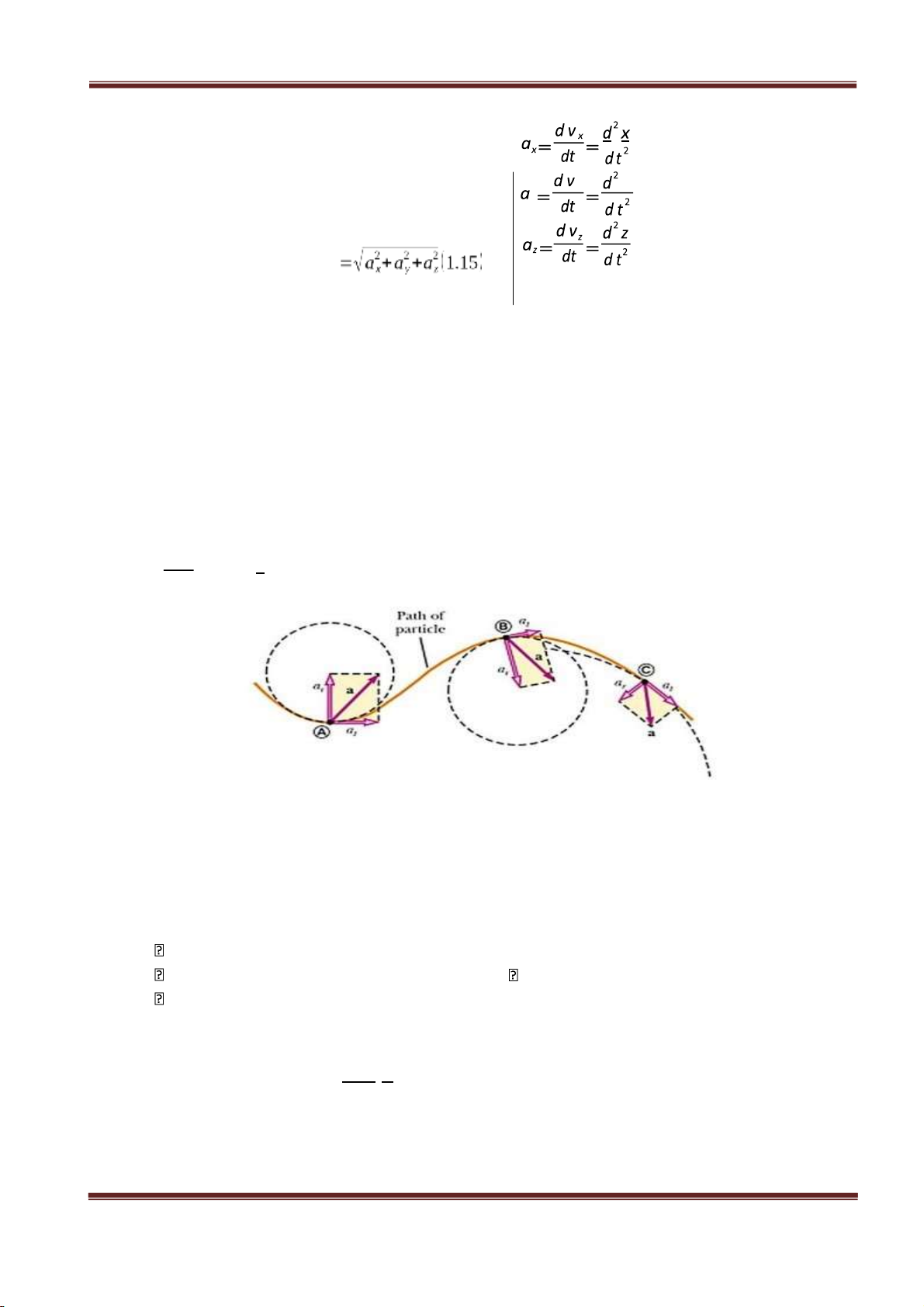
LÝ ĐẠI CƯƠNG 1 y y y a v iớ (1.16) II.
Gia tốc tiếp tuyến và gia tốc pháp tuyến 1) Khái niệm -
Nguyên nhân của chuyển động cong về một phía nào đó của chất điểm
là do trên đoạn đường đó vector gia tốc lệch về phía đó của quỹ đạo. -
Vector gia tốc cũng như mọi vector khác đều có thể phân tích trên hai
hay ba phương bất kỳ tuy nhiên để thuận lợi cho việc tính toán người
ta phân tích nó lên hai phương đặc biệt là pháp tuyến và tiếp tuyến với quỹ đạo
a⃗ =a⃗n+a⃗t (1.17)
2) Dạng vector của gia tốc pháp tuyến: a⃗n=
ddt⃗vn= vR2 n⃗ (1.18)
Hình 1.4: Gia tốc tiếp tuyến và gia tốc pháp tuyến a a → → - Vậy: n
đặc trưng cho sự biến thiên về phương của vectơ vận tốc, n có:
Phương trùng với pháp tuyến của quỹ đạo tại M
Có chiều hướng về tâm của quỹ đạo v2 an
Có độ lớn r (1.19)
( n⃗ là vector đơn vị có phương pháp tuyến với quỹ đạo, có chiều ngược với vector bán kính tại đó).
3) Dạng vector của gia tốc tiếp tuyến: dv d2s Giat
cố ti pế tuy nế at= = - dt dt2 (1.20)
Bộ môn Vật Lý 5 lOMoARcPSD| 36149638 VẬT
LÝ ĐẠI CƯƠNG 1
Kết luận: aτ đặc trưng cho sự biến thiên của vectơ vận tốc về độ lớn
Có phương trùng với tiếp tuyến của quỹ đạo tại M.
Có chiều là chiều chuyển động khi v tăng và chiều ngược lại khi v giảm.
Có độ lớn bằng đạo hàm độ lớn vận tốc theo thời gian. → → → =a +a a -
Gia tốc toàn phần: t n (1.21) → v
an=0 : không thay đổi phương: chuyển động thẳng v
aτ =0 : → không thay đổi chiều và giá trị: chuyển động cong đều. → v
a= 0 : không thay đổi phương chiều và giá trị: chuyển động thẳng đều.
(Trong đó R là bán kính chính khúc của đường tròn mật tiếp tại điểm đang xét (đã được minh hoạ trên hình 1.4))
Ví dụ 2: Một hòn đá được thả rơi theo phương thẳng đứng với phương trình: {x=3t +2} y=t
a) Xác định dạng quỹ đạo chuyển động của hòn đá.
b) Viết phương trình vận tốc và xác định độ lớn của vận tốc hòn đá tại thời điểm sau khi hòn đá được thả rơi 3s
c) Viết phương trình gia tốc và xác định độ lớn của gia tốc hòn đá tại thời điểm sau khi hòn đá được thả rơi 5s
Ví dụ 3: Một quả cầu chuyển động với phương trình vận tốc như sau: v⃗ =4t3i⃗+2t2⃗j+(3t+1)⃗k a)
Tính độ lớn vận tốc của quả cầu tại thời điểm t=5s.
b) Viết phương trình gia tốc và xác định độ lớn của gia tốc vật tại thời điểm sau khi vật được thả rơi 5s.
Ví dụ 4: Một chiếc xe chuyển động trên một quỹ đạo tròn, bán kính bằng 50m.Quãng đường được đi
trên quỹ đạo được xác định bởi công thức: s = - 0,5t2+ 10t + 10 .Tìm vận tốc, gia tốc tiếp tuyến và gia
tốc pháp tuyến, gia tốc toàn phần của ôtô lúc t = 5 giây. Bài 1.4)
MỘT SỐ DẠNG CHUYỂN ĐỘNG CƠ THƯỜNG GẶP I.
Chuyển động thẳng biến đổi đều → =0 -
Là chuyển động có quỹ đạo thẳng và gia tốc a không đổi: an , Do đó: dv
a=aτ= dt =const⇒dv=adt v t
Bộ môn Vật Lý 6 lOMoARcPSD|36149638 VẬT
LÝ ĐẠI CƯƠNG 1
v 0 dv 0 a dt. ⇒v=v0+at (1.22)
Chuyển động chậm dần đều: a.v<0 (1.23)
Chuyển động nhanh dần đều: a.v>0 (1.24) ds
v=dt ⇒ds=vdt=(v0+at)dt -
Phương trình quãng đường: at2 s= 2 +vot (1.25)
- Lấy tích phân hai vế ta có: 2 2 =2as
- Khử thời gian t trong (1.22) ta được: v −v0 (1.26)
Ví dụ 5: Một ô tô bắt đầu rời bến, sau 20s đạt vận tốc 36km/h. Chiều dương là chiều chuyển động. Tính: a) Gia tốc của ô tô
b) Quãng đường ô tô đi trong 20s đó.
c) Nếu tiếp tục tăng tốc như vậy thì sau bao lâu nữa ô tô đạt vận tốc 54km/h. II.
Chuyển động tròn biến đổi đều
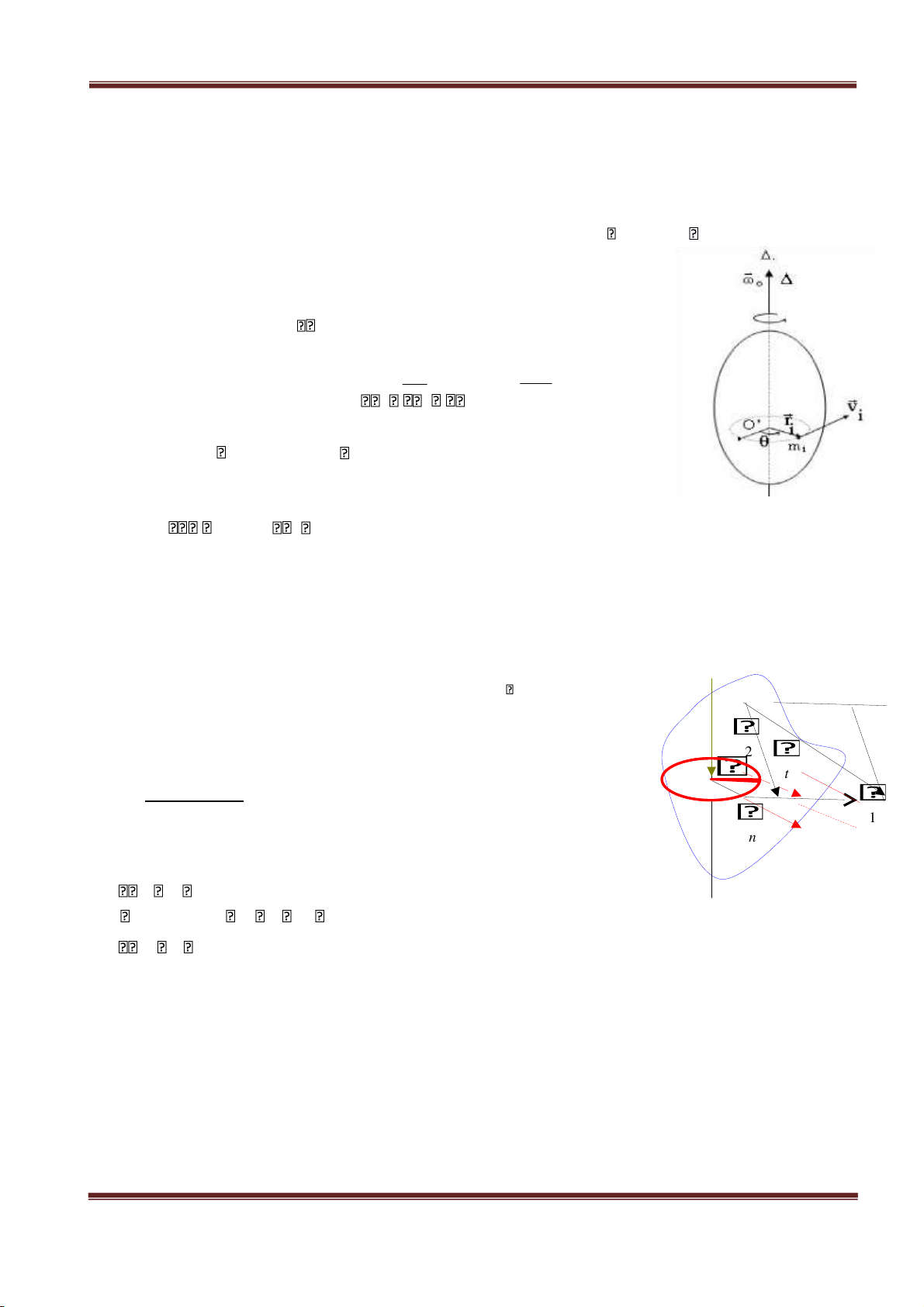
Trong chuyển động, nếu bán kính cong của quỹ đạo không thay đổi, chuyển động đó gọi là chuyển
động tròn. Trong chuyển động tròn, do có sự thay đổi của bán kính véc tơ r⃗=OM⃗ , ngoài các đại lượng
v, a, at , an người ta còn đưa ra các đại lượng vận tốc góc và gia tốc góc. 1) Vận tốc góc.
Giả sử chất điểm M chuyển động trên quỹ đạo tròn tâm O, bán kính R. Trong khoảng thời gian '
t t ' t chất điểm đi được quãng đường s bằng cung MM’ ứng với góc quay MOM của bán kính R = OM ( hình vẽ ).
Vận tốc góc trung bình. tb t (1.34)
Vận tốc góc tức thời. lim d dt t 0 t (1.35)
Vậy: Vận tốc góc bằng đạo hàm góc quay theo thời gian.
Hình 1.6: Chuyển động tròn
Đơn vị của vận tốc góc là rad/s
Trong chuyển động tròn đều thì const , người ta đưa ra khái nệm chu kì và tần số. 2 T
Chu kì T: Chu kì là thời gian cần thiết để chất điểm đi được một vòng. (1.36)
Bộ môn Vật Lý 7 lOMoARcPSD| 36149638 VẬT
LÝ ĐẠI CƯƠNG 1 f 1
Tần số f: Tần số là số vòng quay của chất điểm trong một đơn vị thời gian: 2 T (1.37)
Đơn vị của chu kì và tần số là giây (s) và héc (Hz).
Véc tơ vận tốc góc.
Véc tơ vận tốc góc ω⃗ là véc tơ có độ
lớn được định nghĩa ở (1.35), nằm trên trục
của vòng tròn quỹ đạo, chiều tuân theo quy tắc
vặn nút chai: Nếu quay cái vặn nút chai theo .
chiều chuyển động của chất điểm thì chiều tiến
của cái vặn nút chai chỉ chiều của véc tơ ⃗
*Liên hệ giữa v và ω⃗ : v R
Hình 1.7: quy tắc vặn nút chai (1.38) vận tốc góc -Dạng véc tơ: v R (1.39)
*Liên hệ giữa an và : an 2 .R (1.40) 2) Gia tốc góc.
Giả sử trong khoảng thời gian t t ' t
của chất điểm chuyển động tròn biến thiên một 2 d d lượng 2 dt dt ' . tb Gia tốc góc trung bình : t (1.41) lim
Gia tốc góc tức thời t 0 t (1.42)
Vậy: Gia tốc góc bằng đạo hàm vận tốc góc theo thời gian và bằng đoạ hàm bậc hai của góc quay
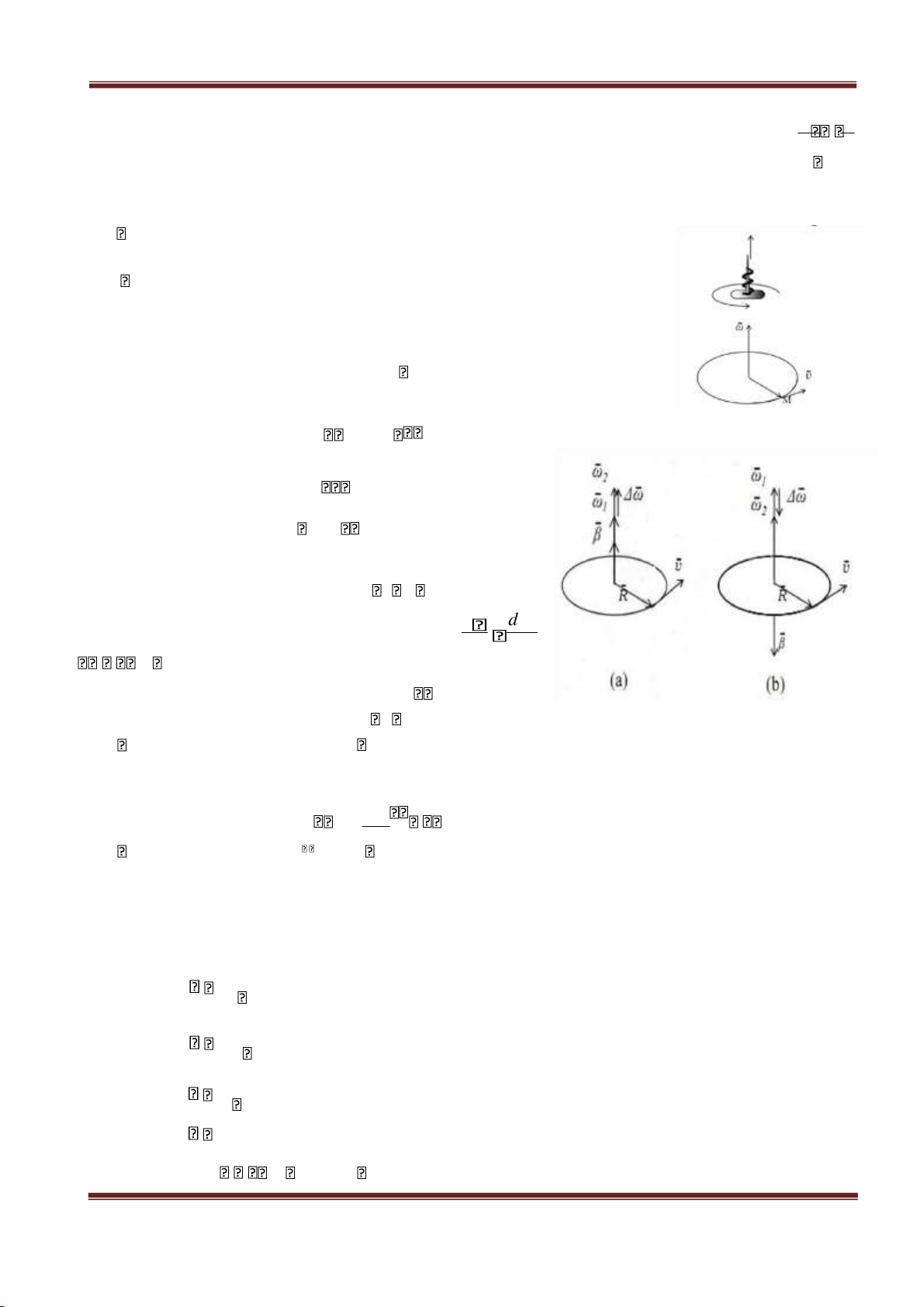
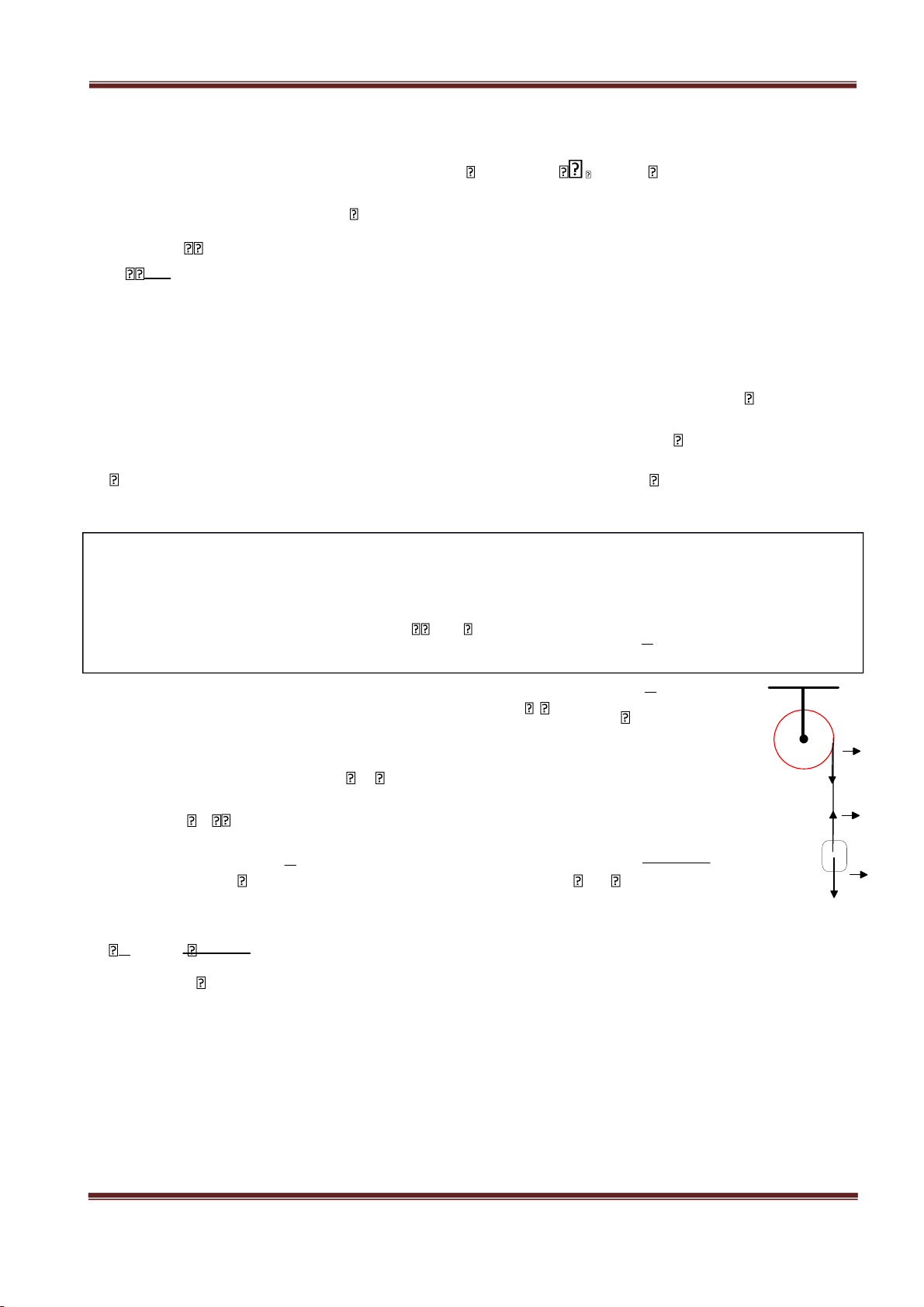
Hình 1.8: liên hệ giữa các vec tơ ⃗R,ω,⃗ v ,⃗ ⃗β theo thời gian.
Đơn vị của gia tốc góc là rad/s2.
a. chuyển động nhanh dần; b. chuyển động 0 +Khi
, tăng, chuyển động tròn nhanh chậm dần dần. 0 +Khi
, giảm, chuyển động tròn chậm dần. 0 +Khi
, không đổi, chuyển động tròn đều. const +Khi
, chuyển động tròn thay đổi đều, ta có: 0 t
Bộ môn Vật Lý 8 lOMoARcPSD|36149638 VẬT
LÝ ĐẠI CƯƠNG 1 t 2 0t 2 2 02 2
(1.43) Véc tơ gia tốc góc.
- Véc tơ gia tốc góc là véc tơ có trị số xác định theo (1.41), nằm trên trục của vòng⃗ tròn
quỹ đạo, cùng chiều với nếu tăng và ngược chiều với nếu giảm ( hình 1.8 ). ⃗ d
- Theo định nghĩa này ta có thể viết: dt (1.44) *Liên hệ giữa a a R t và : t Dạng véc tơ: at R
Ví dụ 6: Một đĩa đồng chất có dạng hình tròn có R = 30cm đang quay tròn đều quanh trục của nó. Biết
thời gian quay hết 1 vòng là 2s. Tính tốc độ dài, tốc độ góc của 2 điểm A, B nằm trên cùng 1 đường
kính của đĩa. Biết điểm A nằm trên vành đĩa, điểm B nằm trên trung điểm giữa tâm O của vòng tròn và vành đĩa. III.
Chuyển động với gia tốc không đổi
Nhiều khi ta phải xét chuyển động của một vật trong trường lực. Chẳng hạn một electron bay vào
trong một điện trường hoặc từ trường với vận tốc ban đầu v . Sau đây ta xét chuyển động của vật trong 0 trọng trường.
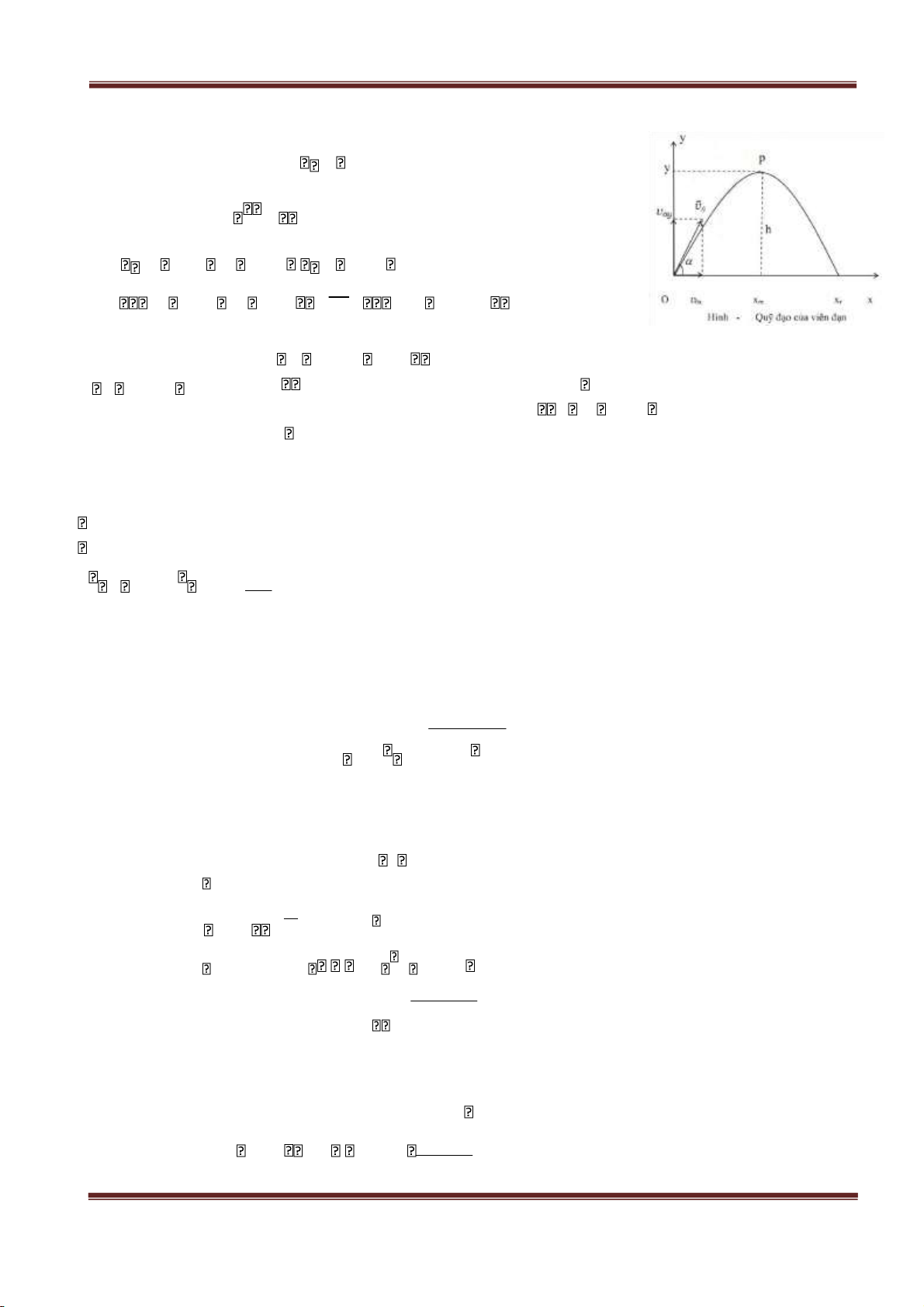
Bài toán: Một viên đạn được bắn lên từ mặt đất với vận tốc v0 hợp với phương nằm ngang một góc ,
bỏ qua sức cản của không khí.
a.Viết phương trình chuyển động của vật.
b.Tìm dạng quỹ đạo của vật.
c.Tìm thời gian kể từ lúc bắn đến lúc vật chạm đất.
d.Xác định tầm bay xa của vật.
e.Tìm độ cao lớn nhất mà viên đạn đạt tới.
f.Xác định bán kính cong của quỹ đạo của vật tại điểm cao nhất
Bài giải
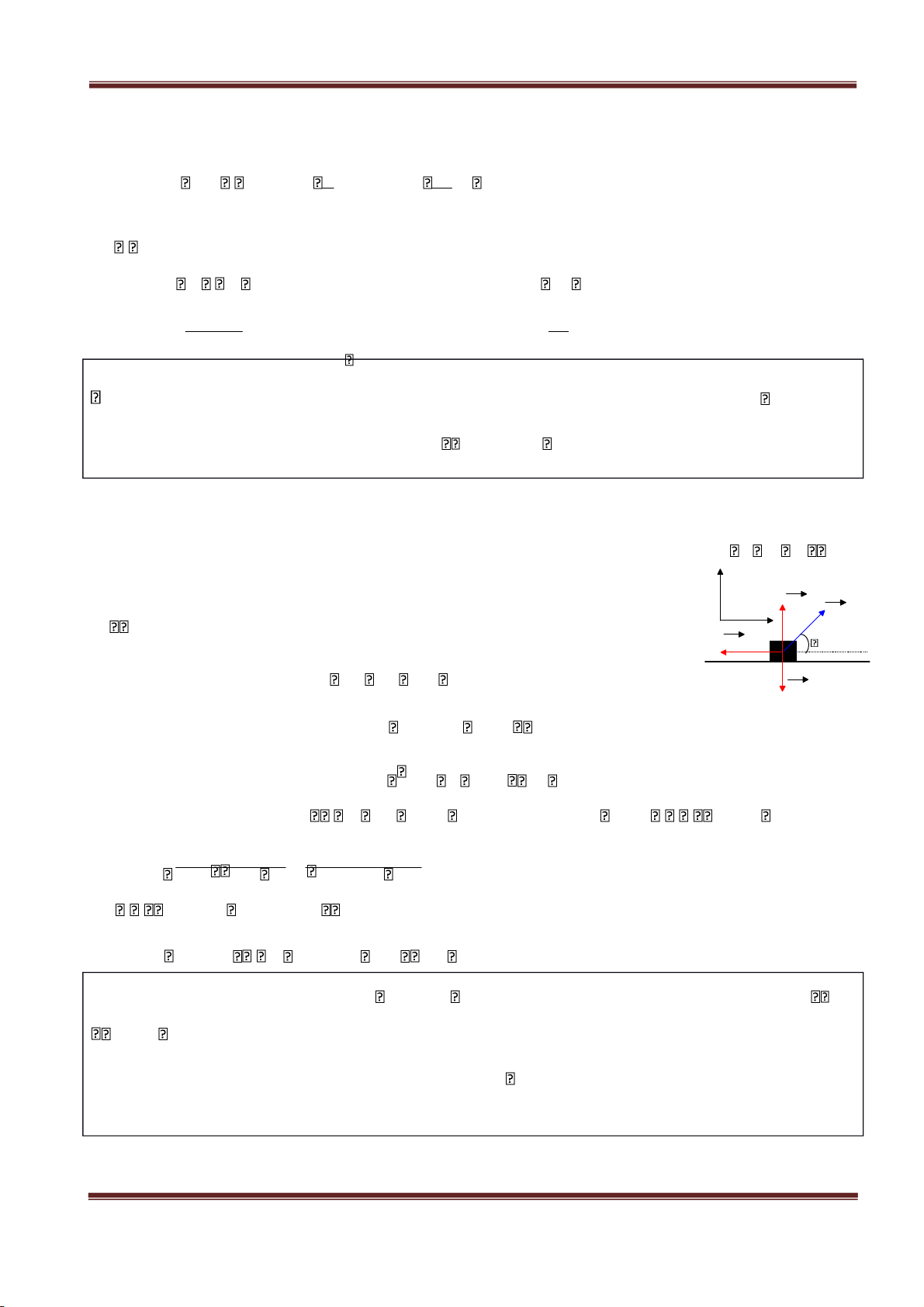
Ngay sau khi bắn lực tác dụng vào vật là trọng lực luôn thẳng đứng hướng xuống, nên gia tốc⃗
của vật trong suốt quá trình chuyển động là a g luôn thẳng đứng hướng xuống. Chọn trục toạ độ Oxy,
gốc O tại vị trí bắn, Ox nằm ngang, Oy thẳng hướng lên ( hình vẽ ).
Bộ môn Vật Lý 9 lOMoARcPSD| 36149638 VẬT
LÝ ĐẠI CƯƠNG 1
Ta phân tích chuyển động của vật thành hai thành phần trên trục ⃗ ax 0 Ox và Oy. Ta có: a ay g
C1 v tx ( 0) v0 cos vx v0 cos Với
C2 v ty ( 0) v0 sin vy v0 sin
gt Hình 1.5: Chuyển động ném xiên dy (1.27) Lại có: vy v0 sin gt Vậy dt dx x v t0 cos x dt v0 cos v 2 gt y v t0 sin 2 (1.28)
Phương trình quỹ đạo. g 2 2v cos
- Từ (1.28) khử t ta được: y xtan 2 2 0 x (1.29)
- Vậy quỹ đạo của vật là một parabol, có bề lõm quay xuống (nhánh phải của hình 1.5 ).
Thời gian chuyển động.
Khi chạm đất thì y = 0, từ (1.28) ta có: t 0(loai) g v0 sin t t 2 0 t 2v0 sin g (1.30)
Độ cao cực đại.
Khi đạt tới điểm cao nhất P, vận tốc của viên đạn theo phương Oy bằng không. Từ (1.27) ta được: v0 sin vy v0 sin gtP 0 tP g
Bộ môn Vật Lý 10 lOMoARcPSD|36149638 VẬT
LÝ ĐẠI CƯƠNG 1 2g y 2 2 Max v0 sin v0 sing g v. 0 2sing2 yMax v 2 2 0 sin (1.31) Tầm bay xa.
Khi chạm đất viên đạn cách gốc O một đoạn L = xmax , khi đó y = 0. L x 2 Max v0 sin2
Từ (1.28) và (1.29) ta được: g (1.32) Bán kính
cong của quỹ đạo tại điểm cao nhất.
a an g v; y 0;v vx an g vx2 Ở điểm cao nhất thì R R v02 cos2 g Từ đó suy ra: (1.33)
Bài toán ném ngang chính là bài toán ném xiên với góc ném 00
Bài toán rơi tự do: chuyển động thẳng nhanh dần đều với gia tốc rơi là gia tốc trọng trường và vận tốc đầu bằng 0
Ví dụ 7: Một quả cầu được ném theo phương ngang từ độ cao 80m. sau khi ném được 3s vận tốc của
quả cầu hợp với phương ngang một góc 450 . a) Tính vận tốc ban đầu của quả cầu.
b) Quả cầu chạm đất lúc nào, ở đâu, với vận tốc bao nhiêu.
Ví dụ 8: Từ độ cao 120m người ta thả một vật thẳng đứng xuống với v = 10m/s, g = 10m/s2. a)
Sau bao lâu vật chạm đất.
b) Tính vận tốc của vật lúc vừa chạm đất.
CHƯƠNG 2: ĐỘNG LỰC HỌC CHẤT ĐIỂM
Động lực học là phần cơ học nghiên cứu mối quan hệ giữa sự biến đối chuyển động (trạng thái)
của vật với sự tương tác giữa vật với các vật khác quanh nó. Bài 2.1)
CÁC ĐỊNH LUẬT NEWTON I.
Định luật 1 Newton
Phát biểu: “Khi một chất điểm cô lập (không chịu một tác động nào từ bên ngoài) nếu đang đứng yên,
nó sẽ tiếp tục đứng yên, nếu đang chuyển động thì chuyển động của nó là thẳng đều.” Biểu thức:
Chất điểm đứng yên: v=0
Chất điểm chuyển động thẳng đều: v=const
Ý nghĩa: Một chất điểm cô lập bảo toàn trạng thái chuyển động của nó. Tính chất bảo toàn trạng thái
chuyển động gọi là quán tính, vì vậy định luật 1 Newton còn gọi là định luật quán tính. II.
Định luật 2 Newton Phát biểu:
• Chuyển động của một chất điểm chịu tác dụng của các lực có tổng hợp lực ⃗F≠0 là một chuyển động có gia tốc.
Bộ môn Vật Lý 11 lOMoARcPSD| 36149638 VẬT
LÝ ĐẠI CƯƠNG 1
• Gia tốc chuyển động của chất điểm tỉ lệ với tổng hợp lực tác dụng ⃗F và tỉ lệ nghịch với khối lượng
của chất điểm đó. Biểu thức: F⃗ a⃗= m
Điều kiện áp dụng của định luật II: trong hệ qui chiếu quán tính và trong cơ học cổ điển khi khối lượng coi là bất biến.
III. Định luật 3 Newton
Phát biểu: Nếu vật A tác dụng vào vật B một lực ⃗F AB thì vật B sẽ tác dụng vào vật A một lực ⃗FBA .
Hai lực này tồn tại đồng thời, cùng đường tác dụng, ngược chiều và bằng nhau về độ lớn. Biểu thức:
⃗F AB=−⃗FBA A B F F BA AB Bài 2.2)
CÁC LOẠI LỰC CƠ HỌC
Trong phạm vi cơ học cổ điển, xét về bản chất có ba loại lực cơ học: lực hấp dẫn, lực đàn hồi và lực ma sát.
Theo định luật II Newton, mặc dầu một lực bất kì được đo bằng tích số khối lượng và gia tốc
mà lực truyền cho vật, nhưng trong tự nhiên không có lực nào phụ thuộc vào gia tốc của vật. Lực trong
tự nhiên chỉ phụ thuộc vào vị trí và vận tốc của vật. I.
Lực hấp dẫn – Trọng lực
Mọi vật trong tự nhiên đều hút lẫn nhau bởi các lực có cùng bản chất gọi là lực hấp dẫn. Lực hấp dẫn
giữa các vật, đóng vai trò cực kì quan trọng trong tự nhiên. Nó chi phối mọi chuyển động của các vật thể
trong tự nhiên: từ chuyển động của các hành tinh quanh Mặt Trời, chuyển động của Mặt Trăng quanh
Trái Đất, sự rơi của mọi vật về bề mặt Trái Đất, sự tồn tại lớp khí quyển quanh Trái Đất, hiện tượng thủy triều… Lực hấp dẫn
Qui luật về tương tác hấp dẫn giữa hai chất điểm được Newton tìm ra và phát biểu dưới dạng định luật vạn vật hấp dẫn
Nội dung: “Hai chất điểm bất kì luôn hút nhau bởi một lực gọi là lực hấp dẫn. Lực này có độ lớn tỷ lệ
với tích khối lượng của hai chất điểm và tỷ lệ nghịch với bình phương khoảng cách giữa chúng.” Biểu thức. m m1 2 F G r 2 . Độ lớn: ⃗ m m12 r⃗ F G r3 . Dạng vector:
G 6,67.10 11 Nm2 / kg 2 là hằng số hấp dẫn vũ trụ. Trọng lực
Bộ môn Vật Lý 12 lOMoARcPSD|36149638 VẬT
LÝ ĐẠI CƯƠNG 1
Khái niệm trọng lực được xây dựng từ lực hấp dẫn và lực quán tính li tâm do Trái Đất không đứng yên
mà chuyển động tự quay quanh mình nó. Các giá trị tính toán cho thấy, lực li tâm có giá trị nhỏ hơn rất
nhiều giá trị của lực hấp dẫn, vì vậy ⃗ ⃗
trong thực tế thường bỏ qua lực li tâm, khi đó P Fhd . Do vậy, khái niệm trọng lực, một cách gần đúng
được vận dung như sau. Khái niệm: Theo nghĩa gần đúng trọng lực là lực hấp dẫn do Trái đất hút vật và định bởi: ⃗ ⃗ ⃗ P Fhd mg . Đặc điểm:
- Phương của trọng lực là phương thẳng đứng, chiều hướng về tâm Trái đất
- Độ lớn trọng lực P mg
- Điểm đặt: đặt vào vật khảo sát.
Trọng lượng và trọng lực.
Trọng lượng: của một vật thường được xem lực hấp dẫn tác động lên vật thể đó.
Trọng lực: Lực trái đất tác động trên một vật để hút vật về hướng Trái đất.
Trọng lượng của một vật là độ lớn của trọng lực tác dụng lên vật ấy. II. Lực đàn hồi
Trong khuôn khổ chương 2 ta chỉ xét một số lực mang tính chất là lực đàn hồi Phản lực
Khi một vật chuyển động trên một mặt phẳng thì vật này tác dụng lên mặt đó một lực nén. Theo định
luật 3 Newton, mặt phẳng cũng sẽ tác dụng ngược lại vật một lực ⃗N gọi là phản lực. Lực căng dây
Giả sử có một vật bị buộc vào một sợi dây, giả thiết rằng khi đó dây bị căng. Tại những điểm trên dây
sẽ xuất hiện những lực gọi là lực căng.
Trong các bài toán thông thường, lực căng có cường độ không đổi dọc theo một sợi dây.
Bộ môn Vật Lý 13 lOMoARcPSD| 36149638 VẬT
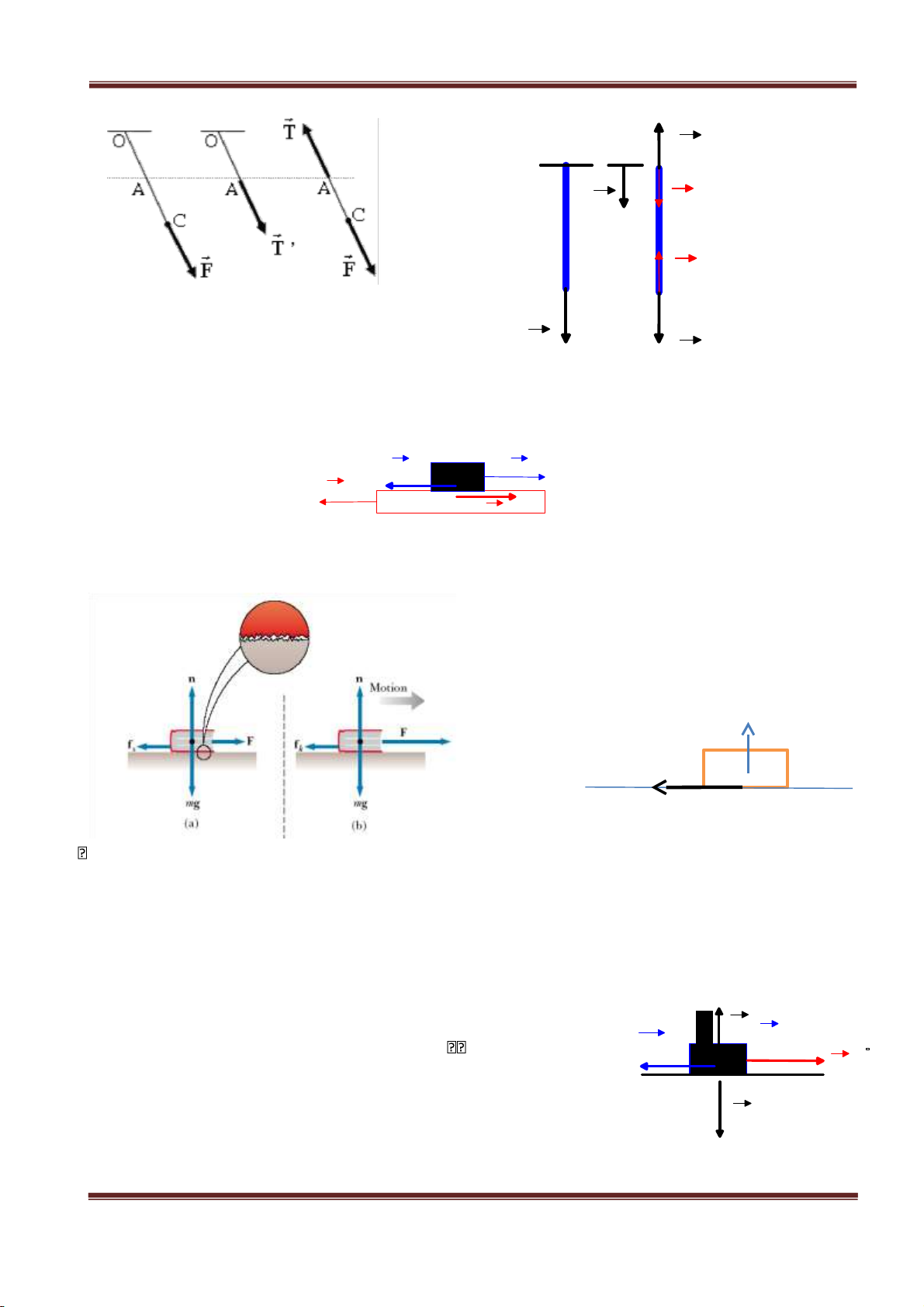
LÝ ĐẠI CƯƠNG 1 A F' A F" T' T B B F F III. Lực ma sát
Khi vật A tiếp xúc vật B mà giữa chúng có chuyển động tương đối với nhau thì ở mặt tiếp xúc xuất hiện
các lực luôn hướng ngược chiều chuyển động tương đối giữa các vật. Các lực đó gọi là lực ma sát. v f AB BA A
Khi hai vật rắn tiếp xúc v BA
nhau,thì lực ma sát gọi là ma sát khô
(bao gồm ma sát trượt, ma B f
sát nghỉ và ma sát lăn). Khi vật rắn AB
chuyển trong môi trường lỏng và khí, lực ma sát gọi là ma sát nhớt.
Nguyên nhân chủ yếu sinh ra hiện tượng ma sát là do sự gồ ghề, mấp mô của mặt tiếp xúc và do sự tương
tác giữa các nguyên tử, phân tử ở những vùng tiếp xúc thực sự giữa các vật. Lực ma sát nghỉ. ⃗ ⃗
Xét vật A và B tiếp xúc với nhau và B cố định. Tác dụng lực F lên vật A, phương F luôn tiếp tuyến ⃗
mặt tiếp xúc, độ lớn của F thay đổi được. Thực nghiệm cho thấy: ⃗
- Khi độ lớn của F nhỏ, vật A vẫn đứng yên. Điều đó chứng tỏ mặt ⃗ ⃗ m' N v AB = 0
tiếp xúc tác dụng lên A một lực tiếp tuyến f f msn
F . Lực tiếp tuyến msn A F ⃗
fmsn do mặt tiếp xúc tác dụng lên A lúc này gọi là lực ma sát nghĩ. Q ⃗
- Khi tăng dần độ lớn của F , A vẫn đứng yên điều đó chứng tỏ lực
Bộ môn Vật Lý 14 lOMoARcPSD|36149638 VẬT
LÝ ĐẠI CƯƠNG 1
⃗ ma sát nghĩ có độ lớn tăng dần
và luôn bằng độ lớn của ngoại lực F F F . ⃗
M thì A bắt đầu trượt trên mặt tiếp xúc. FM là
- Khi độ lớn của F đạt đến giá trị nhất định giá trị lớn nhất của lực ma sát nghỉ. ⃗
- Khi tăng áp lực vuông góc Q, (chẳng hạn bỏ thêm gia trọng m’ lên vật A), độ lớn cực đại của ma sát nghĩ F N
M tăng. Nhiều kết quả thí nghiệm cho thấy FM n
, trong đó n là hệ số ma sát nghĩ phụ
thuộc và bản chất của bề mặt tiếp xúc.
Vậy, lực ma sát nghỉ có đặc điểm:
Xuất hiện khi vật này có xu hướng trượt (nhưng chưa trượt) trên mặt tiếp xúc của vật khác.
Phương tiếp tuyến với mặt tiếp xúc, chiều ngược chiều xu hướng trượt của vật trên mặt tiếp xúc.
Độ lớn fmsn thay đổi, 0 fmsn n N
Lực ma sát trượt. ⃗
Khi vật A đã trượt trên mặt tiếp xúc. Nếu ngừng tác dụng của ngoại lực F vật sẽ chuyển động chậm
dần và dừng lại. Điều đó chứng tỏ, khi vật A trượt trên mặt tiếp xúc, mặt tiếp tác dụng lên nó một lực,
cản trở chuyển động tương đối của nó so mặt sàn. Lực này có phương tiếp tuyến mặt tiếp xúc và ngược
hướng với hướng trượt tương đối của vật so mặt tiếp xúc. Nhiều thí nghiệm khác đã cho thấy lực ma
sát trượt có đặc điểm:
Xuất hiện ở mặt tiếp xúc khi vật này trượt tương đối so vật kia.
Phương tiếp tuyến với mặt tiếp xúc, chiều ngược chiều trượt của vật khảo sát
Độ lớn tỷ lệ với áp lực vuông góc với mặt tiếp xúc fmst
tQ t N (2.11) Chú ý: -
t là hệ số ma sát trượt hầu như không phụ thuộc diện tích mặt tiếp xúc mà phụ thuộc tính chất của mặt tiếp xúc. -
Hệ số ma sát trượt thường nhỏ hơn hệ số ma sát nghĩ, nhưng trong một số trường hợp chúngxấp xĩ
bằng nhau t n Lực ma sát lăn.
Lực ma sát lăn có các đặc điểm sau: •
Xuất hiện khi vật này lăn trên vật kia. •
Phương tiếp tuyến mặt tiếp xúc, chiều cản trở chuyển động của vật khảo sát • N
Độ lớn tỷ lệ với phản lực vuông góc fmsl l (2.12) •
Hệ số ma sát lăn nhỏ hơn nhiều hệ số ma sát trượt Bài 2.3)
PHƯƠNG TRÌNH CƠ BẢN ĐỘNG LỰC HỌC
Phương pháp động lực học là phương pháp vận dụng các định luật Newton giải bài toán cơ
bản của động lực học.
Hai bài toán cơ bản của cơ học gồm:
Bộ môn Vật Lý 15 lOMoARcPSD| 36149638 VẬT
LÝ ĐẠI CƯƠNG 1
Bài toán thuận. Biết các lực tác dụng lên vật, cần xác định tính chất chuyển động của vật. Các bước tiến
hành để giải bài toán này như sau: - Chọn hệ qui chiếu.
- Chỉ ra các lực tác dụng lên vật và biểu diễn chúng.
- Viết phương trình cơ bản của động lực học
Σ⃗Fx=ma⃗x
Σ⃗F y=ma⃗y
- Chiếu xuống các trục tọa độ cần thiết Ox Oy Oz, , ax,ay ,az . Từ đó suy ra phương trình chuyển động.
Bài toán ngược. Biết tính chất chuyển động của vật, xác định các lực tác dụng lên vật.
- Từ tính chất chuyển động, vận dụng công thức động học suy ra gia tốc của vật.
Chỉ ra các lực tác dụng lên vật và biểu diễn chúng.Viết phương trình cơ bản của động lực học
Σ⃗Fx=ma⃗x
Σ⃗F y=ma⃗y
- Chiếu xuống các trục tọa độ cần thiết Ox Oy Oz, ,
. Từ đó suy ra các lực tác dụng cần tìm.
Các ví dụ minh họa ⃗
Ví dụ 1: Một người kéo khúc gỗ có dạng hình hộp trượt trên mặt phẳng ngang với lực kéo F lập với
phương ngang góc 300. Độ lớn của F 100N , khối lượng khúc gỗ m 50kg , hệ số ma sát giữa vật và mặt phẳng ngang là 0,1.
a) Sau thời gian bao lâu vật trượt được quãng đường 48m.
b) Nếu 0 , thì thời gian trên là bao nhiêu.
Xét hệ qui chiếu Oxy gắn mặt đất , trục Ox trùng hướng chuyển động. y a) 300. N
Các lực tác dụng lên vật như hình vẽ. x F O ma F ⃗
⃗ P⃗ N⃗ f⃗ms (1) fms
Phương trình động lực học:
Chiếu (1) xuống hai trục Ox và Oy,( ay 0 do vật chỉ trượt theo phương ngang): P max F cos fms (1) may 0 F sin N P(2) .
Từ (2): fms N (P F sin ). Thế vào (1) : ax F cos mP F sin 0,8m s/ 2 (3) 1 2 s v t0 at
Bộ môn Vật Lý 16 lOMoARcPSD|36149638 VẬT
LÝ ĐẠI CƯƠNG 1
Vật chuyển động biến đổi đều theo chiều dương ta chọn nên quãng đường đi định bởi: 2 . 2s t 0,v0 0 s 1 at 2 t 60s
Từ điều kiện ban đầu: 2
. Vậy thời gian cần tìm là: a 0 b) .
ax F P 1,9m s/ 2 t 2s 25s Từ (3) m
. Nên thời gian cần tìm là a ⃗
Ví dụ 2: Một vật có khối lượng m 1kg dưới tác dụng của lực F có hướng lập với phương ngang góc
thì bắt đầu chuyển động nhanh dần đều trên mặt phẳng nằm ngang với độ lớn gia tốc a 0,2m s/ 2
. Hệ số ma sát trượt giữa vật và mặt ngang là 0,1. Lấy g 10/ s2 . Xác định độ lớn của F⃗ nếu: a)
α=300 , b) α=00 Giải.
Xét hệ qui chiếu Oxy gắn mặt đất , trục Ox trùng hướng chuyển động. Theo đề bài ay 0 a ax 0,2m s/ 2 . y N x F a) 300 O
Các ngoại lực tác dụng lên vật như hình vẽ. f ms
Phương trình chuyển động ma F ⃗
⃗ P⃗ N⃗ f⃗ms P max F cos fms (1)
Chiếu (1) xuống hai trục Ox và Oy có: may 0 F sin N P(2) .
Từ (2) biểu thức lực ma sát fms
N (P F sin ). Thế vào (1): max F cos P F sin . F max
mg 1.0,2 0,1.1.10 1,3N Do đó cos sin 0,86 0,1.0,5 . b) 00.
Khi đó N P và fms N P nên F max mg 1,2N . Ví dụ 3 2kg m 2kg 0,1
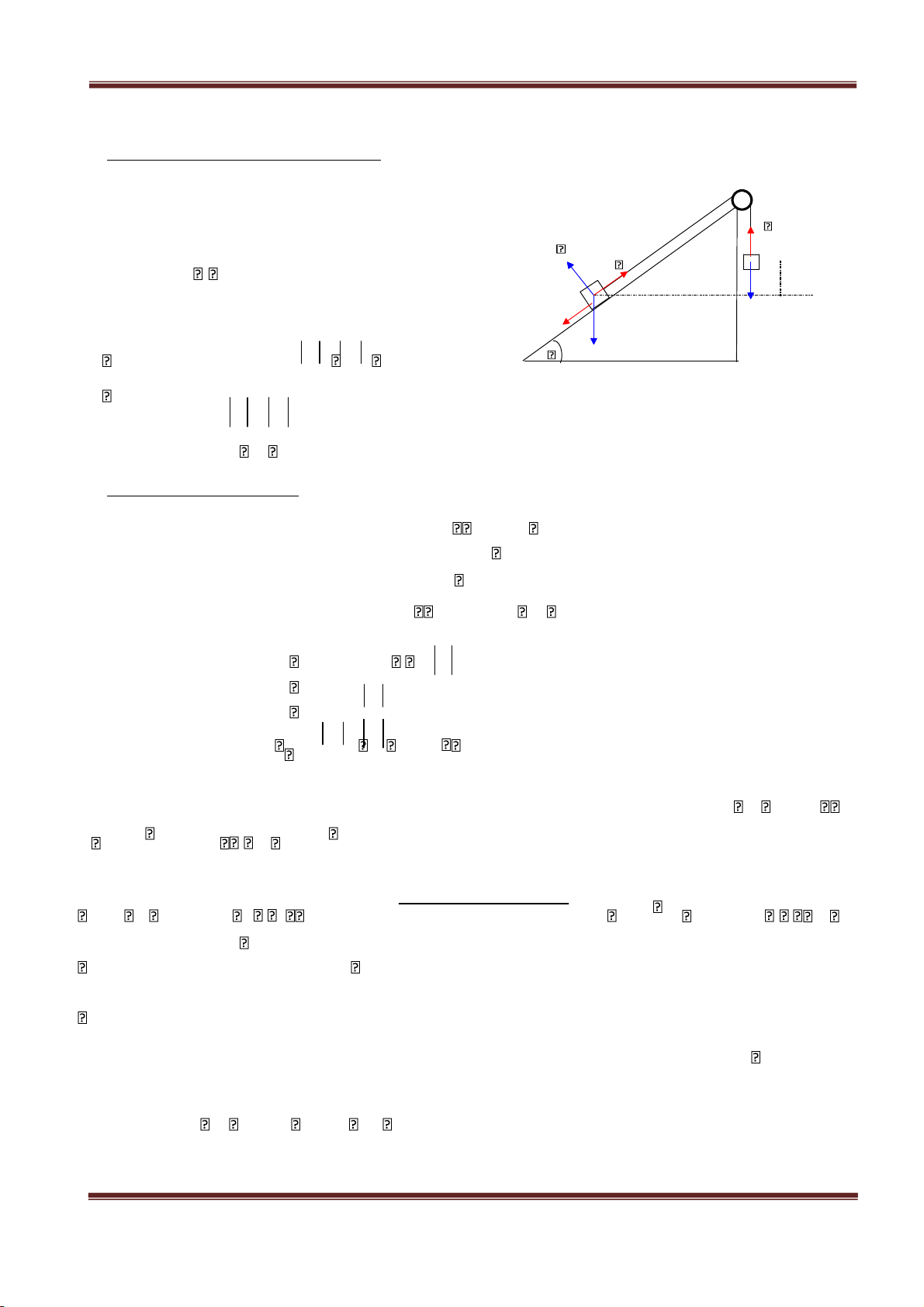
: Cho cơ hệ như hình vẽ . m1 , 2
. Hệ số ma sát giữa m2 và sàn nghiêng là , 30 ;g 10m s/ 0
2 . Bỏ qua khối lượng ròng rọc, dây không dãn, khối lượng không đáng kể. Tại thời
điểm ban đầu vật m1 ở vị trí cao hơn vật m2 một đoạn h 1m ..
1. Chỉ ra các lực tác dụng lên các vật. Hệ vật chuyển động theo chiều nào? Tại sao?
2. Tìm gia tốc của các vật và sức căng dây, áp lực lên trục của ròng rọc.
3. Sau bao lâu hai vật có độ cao ngang nhau? Khi đó vận tốc mỗi vật là bao nhiêu?
Bộ môn Vật Lý 17 lOMoARcPSD| 36149638 VẬT
LÝ ĐẠI CƯƠNG 1 Giải.
1. Các lực tác dụng lên vật như hình vẽ.
Coi hai vật là một hệ thì các ngoại lực tác dụng lên hệ là C ⃗ ⃗ ⃗ ⃗ N P P, , 1
1 2 và lực ma sát. N không gây ra chuyển độngcho m 1 2
vật. Do P sin P 2
1 vì vậy m1 đi xuống, m2 đi lên Theo h m 2 đề: P P 1 2
dây không dãn nên a⃗
1 a⃗2 a .
khối lượng dây không đáng kể, và do bỏ quakhối ⃗ ⃗
lượng ròng ròng T T T1 2 .
2. Tìm gia tốc, sức căng dây.
m a1 ⃗1 P⃗1 T⃗1 ⃗ ⃗ ⃗
Viết phương trình chuyển động cho mỗi vật: m a P T 2 2 2
2 . Chiếu xuống chiều dương là chiều
m a1 ⃗1 P1T⃗1 ⃗ ⃗
chuyển động của mỗi vật: m a2 2 T2 P2 sin fms (a).
Lại chiếu phương trình chuyển động củam2 theo phương vuông góc chuyển động; 0 N P2 cos N
P2 cos . Nên fms
N P2 cos . Thế vào hệ (a). (1)
m a2 T m aP12 sin P 1 T P2
cos (2)a P1 P2 (sinm1 m 2 cos ) 2 1,818m s/ .
a⃗1 hướng thẳng đứng xuống và a⃗2 hướng lên dọc mặt nghiêng và cùng có độ lớn 1,818m s/ 2 Vậy
Từ (1) suy ra: T P m a
m g ( a) 16,364N 1 1 1
. Hướng các sức căng dây như hình vẽ. ⃗ ⃗
Bộ môn Vật Lý 18 lOMoARcPSD|36149638 VẬT
LÝ ĐẠI CƯƠNG 1
Tìm áp lực Q lên trục ròng rọc. Do tác dụng của các sức căng dây T ở hai bên ròng rọc, trục ròng ⃗
rọc bị nén. Từ hình vẽ, tứ giác CC C C Q 12
3 là hình thoi với góc C
, nên có phương là phân giác Q 2T cos 30,24N
của góc C và có độ lớn:C 2 T' T' C2T' Q T' C 4 C3
3. Sau bao lâu hai vật ở ngang nhau hai vật ở ngang nhau.
Khi hai vật ở ngang nhau, vật m1 đi được đoạn đường s1 , vật m2 đi được đoạn đường s2 . Ta có: s s sin h 2 1
, do hai vật đều chuyển động theo chiều dương với vận tốc đầu bằng không nên at 2 at 2 2h 2 s1 s2 ; (1 sin ) h t 0,8( )s 2 2 a(1 sin ) 3,104 .
Bộ môn Vật Lý 19 lOMoARcPSD| 36149638 VẬT
LÝ ĐẠI CƯƠNG 1
CHƯƠNG 3: ĐỘNG LỰC HỌC HỆ CHẤT ĐIỂM – ĐỘNG
LỰC HỌC VẬT RẮN. Bài 3.1)
KHỐI TÂM – ĐỊNH LUẬT BẢO TOÀN ĐỘNG LƯỢNG I. Khối tâm
1) Khái niệm khối tâm và ý nghĩa vật lý.
Khối tâm G của hệ là một trong các yếu tố đặc trưng cho sự phân bố khối lượng của vật .
Chuyển động của vật rắn, đặc biệt là chuyển động quay, sự phân bố khối lượng của vật ảnh hưởng khá
lớn chuyển động của vật. (quạt trần khi quay bị đảo, đó là do trục quay không đi qua khối tâm; bánh xe
đạp khi một số nan hoa (căm) gãy bị đảo cũng do nguyên nhân tương tự…)
Trong kĩ thuật việc xác định đúng vị trí khối tâm là đặc biệt quan trọng. Thực nghiệm cho thấy, nếu hệ
có một tâm hay một đường hay một mặt đối xứng thì khối tâm nằm trên tâm, đường hay mặt đó. Trong
trọng trường đều và vì hệ khảo sát chiếm miền không gian không lớn nên vị trí khối tâm trùng với vị
trí trọng tâm (điểm đặt của trọng lực). Tuy nhiên, khái niệm khối tâm luôn tồn tại, còn trọng tâm chỉ
tồn tại trong trường trọng lực. 2) Định nghĩa khối tâm
Khối tâm G được định nghĩa xuất phát từ bài toán tìm điểm đặt (trọng tâm) của hệ hai chất điểm.
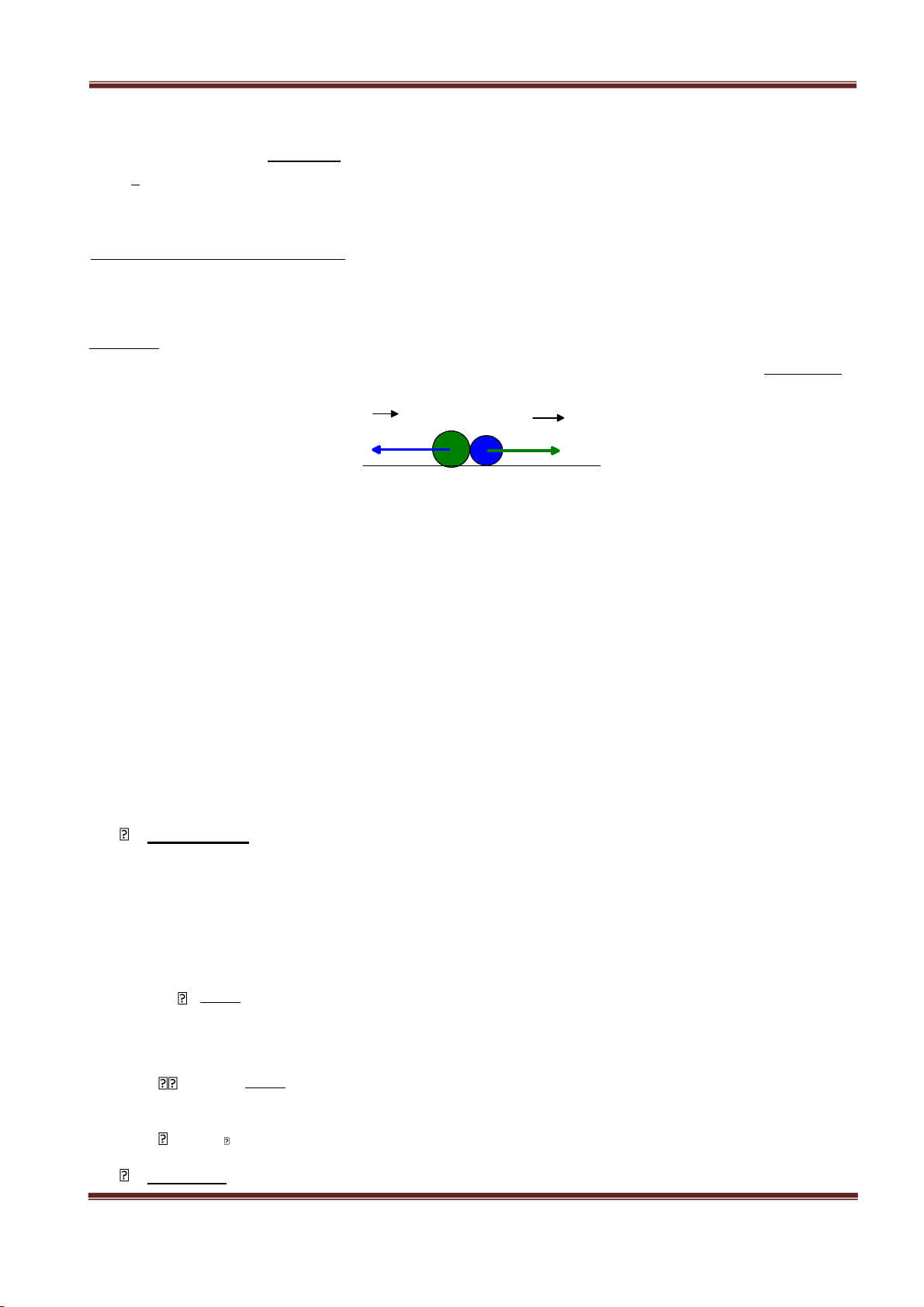
Xét hai chất điểm M1, M 2 có khối lượng tương ứng m1, m2 . Gọi ⃗p1 , ⃗p2 là trọng lực tác dụng lên
mỗi chất điểm. Giả sử trọng trường là đều thì ⃗p1 // ⃗p2 . Gọi G là điểm đặt của tổng hai
M G1 p2 m2 M1 G M2 M G p m 2 1
1 . Do hai vector ⃗M1G↑↓⃗M2G2 lực đó thì
⃗M1G −m1 P
nên ta có: ⃗M2G= m2 1 P2
Điểm G thỏa mãn hệ thức m1⃗M1G+m2⃗M2G=0 là khối tâm của hệ hai chất điểm. Suy
rộng cho hệ gồm n chất điểm, khối tâm G của hệ là điểm thỏa mãn:
m1⃗M1G+m2⃗M2G+m3⃗M3G+mi⃗M i G…+mn⃗M nG=0 (3.1)
Vậy: khối tâm G của hệ n chất điểm là một điểm thỏa : n ∑mi⃗Mi G=0 (3.2) i=1
3) Công thức xác định vị trí khối tâm đối với một điểm gốc O.
Hệ chất điểm khối lượng phân bố rời rạc.
Xét chất điểm thứ i của hệ, từ hình vẽ ta có OG⃗=⃗OM i+⃗Mi G M2 G
Nên miOG⃗=mi⃗OM i+mi⃗M iG (a).
Lấy tổng (a) với n chất điểm n
⃗OG=∑n mi⃗OMi+∑n mi⃗Mi G Mi
Bộ môn Vật Lý 20 lOMoARcPSD|36149638 VẬT
LÝ ĐẠI CƯƠNG 1 ∑mi R . i=1 r O i=1 i=1 i
Để ý (3.2) ta có công thức xác định vị trí khối tâm G đối với gốc tọa độ O nào đó là: n n ∑m ∑ i⃗OM i mi r⃗i OG⃗= i 1 1 = n hay ⃗R= i= n ∑ m ∑ i mi i=1 i=1
Vậy, vị trí khối tâm G của hệ đối với gốc O xác định bởi vector ⃗R=OG⃗ thỏa mãn công thức: n ∑mi r⃗i ⃗R= i=1n (3.3) ∑ mi i=1 x m xi i G M y m yi i G M zG m zi i
Trong hệ trục tọa độ Descartes, các thành phần của tọa độ khối tâm là: M (3.4)
Vật rắn khối lượng phân bố liên tục.
Gọi dm là khối lượng chứa trong nguyên tố thể tích dV, khi đó vị trí khối tâm vật rắn định bởi: 1 xG M vat xdm 1
Bộ môn Vật Lý 21 lOMoARcPSD| 36149638 VẬT
LÝ ĐẠI CƯƠNG 1 yG M vat ydm ⃗ R ⃗ V dmrM (3.5) hay zG M1 vat zdm dm M
Khi khối lượng phân bố đều dm dV M; V dV V ta có công thức: 1 xG V V xdV 1
xG m1.0 29m am11 3m a1 95 a 50cm
yG m1.0 2m1.0 3m a1 1 a 30cm Vậy 9m1 3
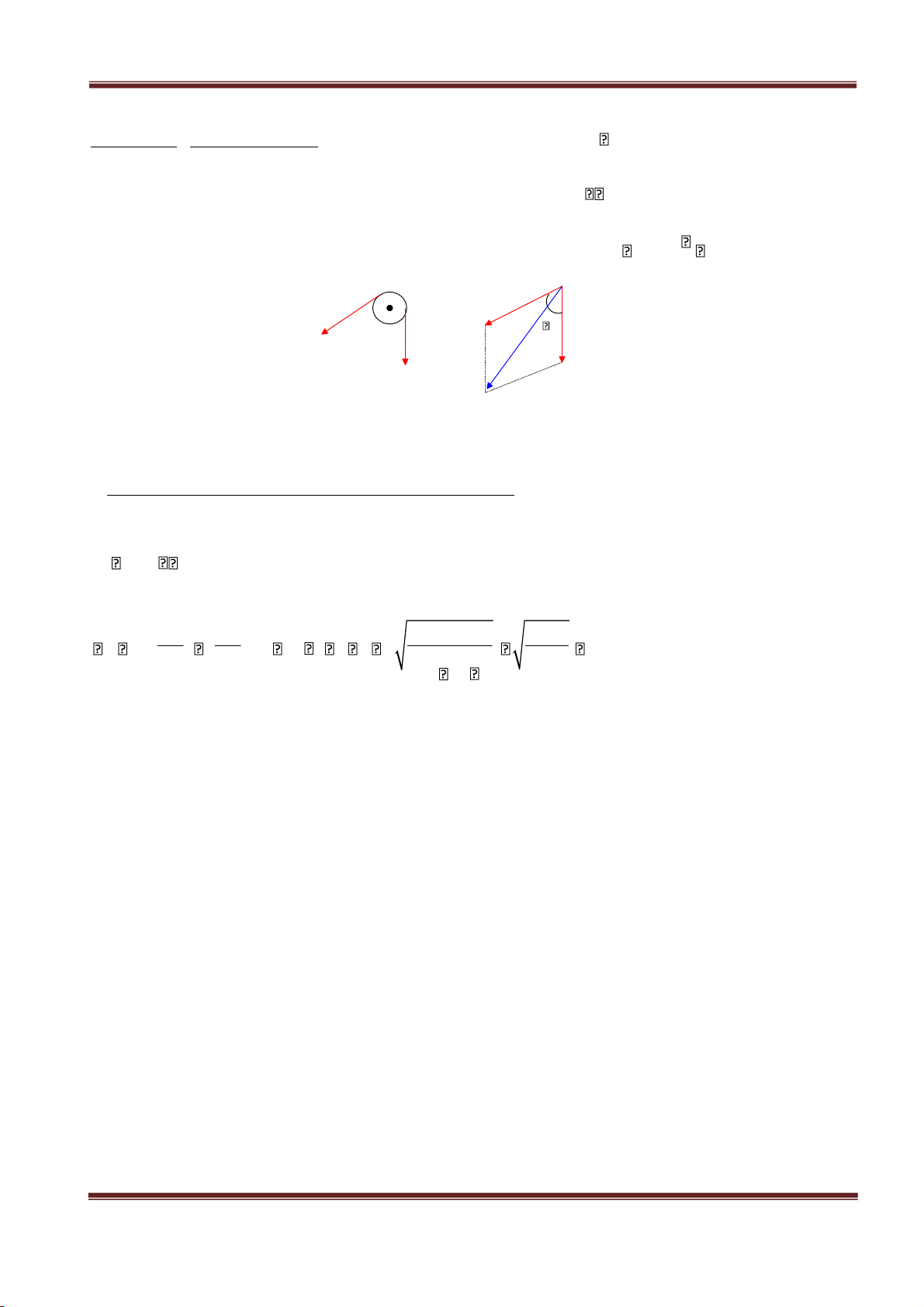
Ví dụ 2: Xác định khối tâm của một dây loại đồng nhất khối lượng m được uốn thành một cung tròn
bán kính R và góc ở tâm là 2 . Giải
Bộ môn Vật Lý 22 lOMoARcPSD|36149638 VẬT
LÝ ĐẠI CƯƠNG 1
Chọn trục tọa độ Ox trùng phân giác của góc ở tâm 2 . dl
Vì khối lượng phân bố đều nên Ox cũng là trục đối xứng của vật. Như vậy
khối tâm của vật nằm trên trục Ox (hình vẽ). Do đó vị trí khối tâm của d R 1 x m L xdm x z G G 0 1 xG xdm yG 0 m cung tròn là . Cần tìm L ?
Xét nguyên tố độ dài dl dl dl Rd dm Rd
có khối lượng dm , do nên
. Tọa độ của yếu tố x 1
1 2 cos . d 1 R2 sin
này là x Rcos . Vậy G L xdm m m
m . Do đó Rcos . Rd R 2R2 sin Rsin xG
xG m2 R m .
4) Vận tốc khối tâm G. Tọa độ khối tâm n ⃗R
M i=1 mi r⃗i (3.7)
Lấy đạo hàm theo thời gian (3.7) ta có công thức xác định vận tốc khối tâm: m
d(¿dt¿ir⃗i)= M1 ∑=n mi
ddt(r⃗i)= M1 ∑i=n1 mi ⃗vi i 1 ⃗ 1 n v⃗¿ dt M i=1 . n
Do ⃗p=∑ mi v⃗i
là tổng động lượng của hệ, nên vận tốc khối tâm định bởi:
i=1 v⃗= ⃗p (3.8) M
Vận tốc chuyển động của khối tâm bằng tỷ số động lượng của cả hệ chia cho khối lượng của hệ.
Từ (3.8), suy ra cách xác định động lượng của hệ: mi n ∑¿⃗vG (3.9) i=1
Bộ môn Vật Lý 23 lOMoARcPSD| 36149638 VẬT
LÝ ĐẠI CƯƠNG 1 ⃗p=¿
Động lượng của hệ được xác định bằng cách nhân khối lượng của hệ với vận tốc của khối tâm. 5)
Phương trình chuyển động của khối tâm G. Gia
tốc chuyển động của khối tâm của hệ định bởi: a⃗=
ddt⃗vG hay a⃗ = M1 ∑=n mi dt = M ∑i=n1 mi a⃗i i 1
Trong đó mia⃗i=⃗Fi là ngoại lực tác dụng lên chất điểm thứ i của hệ.
Nên ∑mi a⃗i=∑ F⃗i=F⃗ là tổng các ngoại lực tác dụng lên hệ. Như vậy
phương trình chuyển động của khối tâm G là:
mi a⃗G F⃗i Ma⃗G F⃗ (3.10)
Khối tâm của hệ chuyển động như một chất điểm có khối lượng bằng tổng khối lượng của hệ và chịu
tác dụng của một lực bằng tổng các ngoại lực tác dụng lên hệ.
Công thức (3.10) cho ta rút ra một kết luận lý thú là: khi ném một cái thước, mặc dù quĩ đạo của các
phần tử thuộc cái thước rất phức tạp (vừa bay vừa xoay) nhưng ta thấy toàn thể cái thước vẫn vạch nên
một đường cong Parabol tựa như chuyển động của một chất điểm chuyển động dưới tác dụng của trọng lực. II.
Định luật bảo toàn động lượng trong hệ cô lập.
Nội dung định luật: Khi các chất điểm trong hệ chỉ tương tác với nhau (hệ cô lập), tổng động lượng
của hệ trước và sau tương tác không thay đổi. …
Hay ⃗phệ=∑ ⃗pi=⃗const ⃗ ⃗ ⃗ ⃗
Trong đó p p ... p ... 1 2
là tổng động lượng các chất điểm trước tương tác, p1 2 là tổng động lượng
các chất điểm sau tương tác.
Trong thực tế không có hệ cô lập, nhưng có thể áp dụng định luật cho các trường hợp sau:
- Nếu theo phươngOx , hệ không chịu tác dụng của ngoại lực thì theo phương đó bảo toàn. - Hệ có
nội lực lớn hơn rất nhiều ngoại lực (bài toán va chạm, nổ do thời gian tương tác rất ngắn nên ngoại
lực nhỏ hơn nhiều nội lực).
Ví dụ 3: Một toa xe goòng chở đầy cát khối lượng 800kg đang chuyển động với tốc độ 5m s/ trên đường
ray thẳng thì một hòn đá khối lượng 8kg bay với tốc độ 20m s/ đến cắm vào toa xe cát theo hướng lập
với hướng chuyển động góc 300. Xác định vận tốc của toa xe ngay sau đó. Giải.
Hệ tương tác là toa xe cát và hòn đá. Xét hệ qui chiếu Oxy (hướng x
Ox, trùng hướng chuyển động của xe). v2
Bộ môn Vật Lý 24 lOMoARcPSD|36149638 VẬT
LÝ ĐẠI CƯƠNG 1 , ,
Kí hiệu v v⃗ ⃗1 1 là vận tốc của toa xe trước và sau tương tác; v v⃗2 ⃗2 là v1
vận tốc của đá trước và sau tương tác
Theo hướng Ox hệ kín nên động lượng của hệ theo hướng này bảo toàn. Ta có:
m v1 1x m v22x m v1 1 x m v2 2 x
v1 x v2 x vx vx
m v1 1x m v2 2x m v1 1 m v2 2 cos 5,12m s/ m1 m2 vx
v1x v1 5m s v/ ; 2 x v2 cos m1 m2 .
Bộ môn Vật Lý 25 lOMoARcPSD|36149638
VẬT LÝ ĐẠI CƯƠNG 1
Bài 3.2) PHƯƠNG TRÌNH CƠ BẢN CỦA CHUYỂN ĐỘNG VẬT RẮN QUAY
QUANH MỘT TRỤC CỐ ĐỊNH
I. Đặc điểm của chuyển động quay của vật rắn quanh một trục cố định. Mọi điểm
trên vật chuyển động vạch nên các đường tròn có tâm trên trục quay,
mặt phẳng đường tròn vuông góc trục quay.
• Trong cùng một khoảng thời gian mọi điểm trên vật đều quay được cùng một góc quay .
• Tại một thời điểm mọi điểm trên vật đều có cùng giá trị đại số của ⃗ d d d 2 ⃗ dt
vận tốc góc và gia tốc góc : dt ; dt .
• Vận tốc dài và gia tốc tiếp tuyến của điểm cách trục quay r định bởi: v⃗
r⃗ ; a⃗t ⃗ r⃗ ⃗
II. Mô men của lực F đối với trục
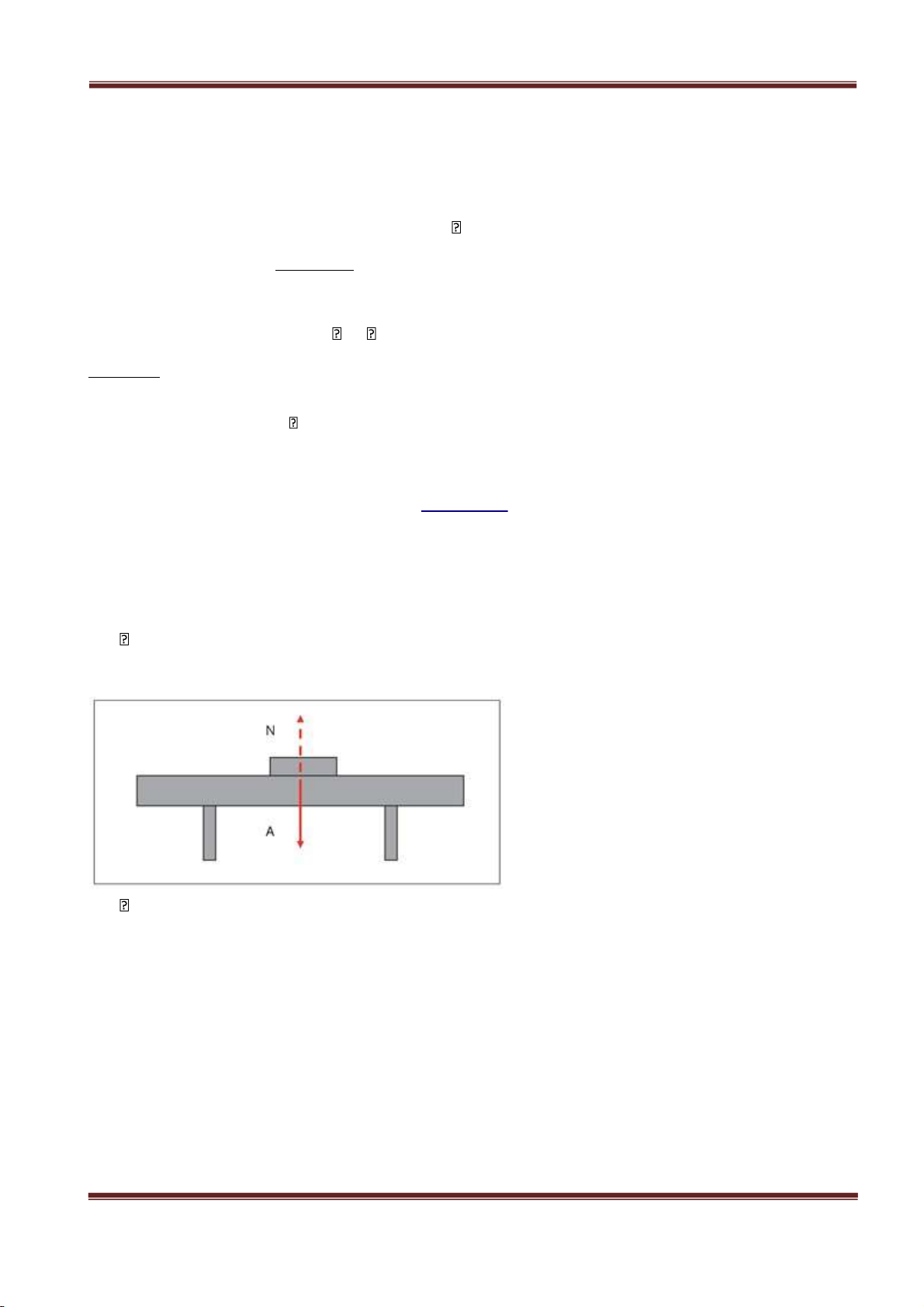
1) Tác dụng của lực trong chuyển động quay quanh một trục.
• Khi vật rắn chuyển động quay quanh một trục, chỉ có các thành ⃗ ⃗ phần lực tiếp tuyến với
quĩ đạo của điểm đặt mới gây ra tác dụng M F ( ) quay cho vật.⃗ ⃗ F 2 F t r •
Chứng minh : Xét lực F có phương bất kì tác dụng lên điểm M F F ⃗ 1 F
thuộc vật rắn. Phân tích F thành các thành phần n ⃗ ⃗ ⃗ F F1 F2 ⃗ ⃗ ⃗ ⃗ ⃗ ⃗
⃗ F Ft Fn F2 F F F 1 t n . Từ hình vẽ ta có: ⃗ F -
2 : song song trục quay không gây ra tác dụng quay mà chỉ có tác dụng làm vật trượt dọc theo trục. ⃗ F -
n vuông góc trục quay, không gây ra tác dụng quay chỉ có thể làm vật
Bộ môn Vật Lý 1 lOMoARcPSD| 36149638
VẬT LÝ ĐẠI CƯƠNG 1
rắn ép vào trục quay (vật rắn có xu hướng dời theo phương vuông góc trục) ⃗
Như vậy tác dụng quay của lực F có được là do tác dụng của thành phần lực tiếp tuyến của nó.
2) Mô men của lực đối với trục quay ⃗
Mô men của lực Ft đối với trục quay là đại lượng đặc trưng cho tác dụng quay của vật quanh trục đó và định bởi: M⃗ F⃗ t
r⃗ F⃗t (3.12) ⃗ ⃗ M F Như vậy, t có: • ,
phương vuông góc mặt phẳng (r F⃗ ⃗t ) nên trùng trục quay. • chiều: nắm tay phải ⃗ ⃗ M F • độ lớn: t
r F. t sin90 r F. t . Chú ý: ⃗ ⃗
• Trong chuyển động quay, mô men của lực F cũng chính bằng mô men của lực Ft . ⃗
• Giá của lực F đi qua trục quay không gây ra mô men quay. III.Phương trình cơ bản của
chuyển động quay của vật rắn. ⃗ ⃗
Phương trình: dạng vector: M I hoặc dạng đại số: M I (3.11) Trong đó: ⃗ -
M là tổng mô men của các ngoại lực tác dụng lên vật rắn đối với trục . n
Bộ môn Vật Lý 2 lOMoARcPSD|36149638
VẬT LÝ ĐẠI CƯƠNG 1 -
I là mô men quán tính của vật rắn đối trục định bởi I
i 1 Ii và Ii m ri i2 là mô men quán tính
của chất điểm i đối với trục ⃗ d -
dt là gia tốc góc của vật rắn.
Mô men quán tính: Đại lượng Ii đo bằng tích số khối lượng và bình phương khoảng cách từ chất điểm
đến trục quay gọi là mô men quán tính của chất điểm thứ i đối với trục quay. Tức là Ii m ri i2
Ví dụ 4: Cho cơ hệ như hình vẽ. A là một đĩa tròn đồng chất có khối lượng m 2,5kg 1 và có bán kính
R 20cm có thể quay quanh trục nằm ngang. Vật nặng B có khối lượng m2 1,2kg treo vào đầu một sợi
dây. Bỏ qua khối lượng của dây, dây không trượt trên đĩa và bỏ qua ma sát giữa đĩa và trục. Tìm 1 2
mR gia tốc của vật A ,B và sức căng dây. Mô men quán tính của đĩa định bởi: 2 Giải. ⃗
Các lực tác dụng lên các vật như hình vẽ. T T . T gây ra mô men quay cho đĩa A 1 2 A T R. I
.(1) với I 2 m R1 . T'
Vật A chuyển động quay quanh trục cố định nên có:
Vật B chuyển động tịnh tiến: m g2 T m a2 (2) R Mặt khác a at (3). T
Từ (1) và (3): T 12 m a1
thế vào (2) ta tìm được a m12 m g12m2 và B P1 T 1 m a1 m g12 2 m1 2m2 . Bài 3.3) MÔMEN QUÁN TÍNH I. Định nghĩa.
Bộ môn Vật Lý 3 lOMoARcPSD| 36149638
VẬT LÝ ĐẠI CƯƠNG 1
Cùng với khối tâm G, mô men quán tính là một trong những đại lượng đặc trưng cho sự phân bố khối
lượng của vật rắn đối với một trục Công thức: •
Nếu vât rắn gồm các chất điểm phân bố rời rạc mô men quán tính của vật đối với trục quay n I m ri i2 định bởi: i 1 . I r dm2 •
Nếu vật rắn có khối lượng phân bố liên tục, thay tổng bằng tích phân: VR II. Mô men quán
tính đối với trục quay đi qua khối tâm:
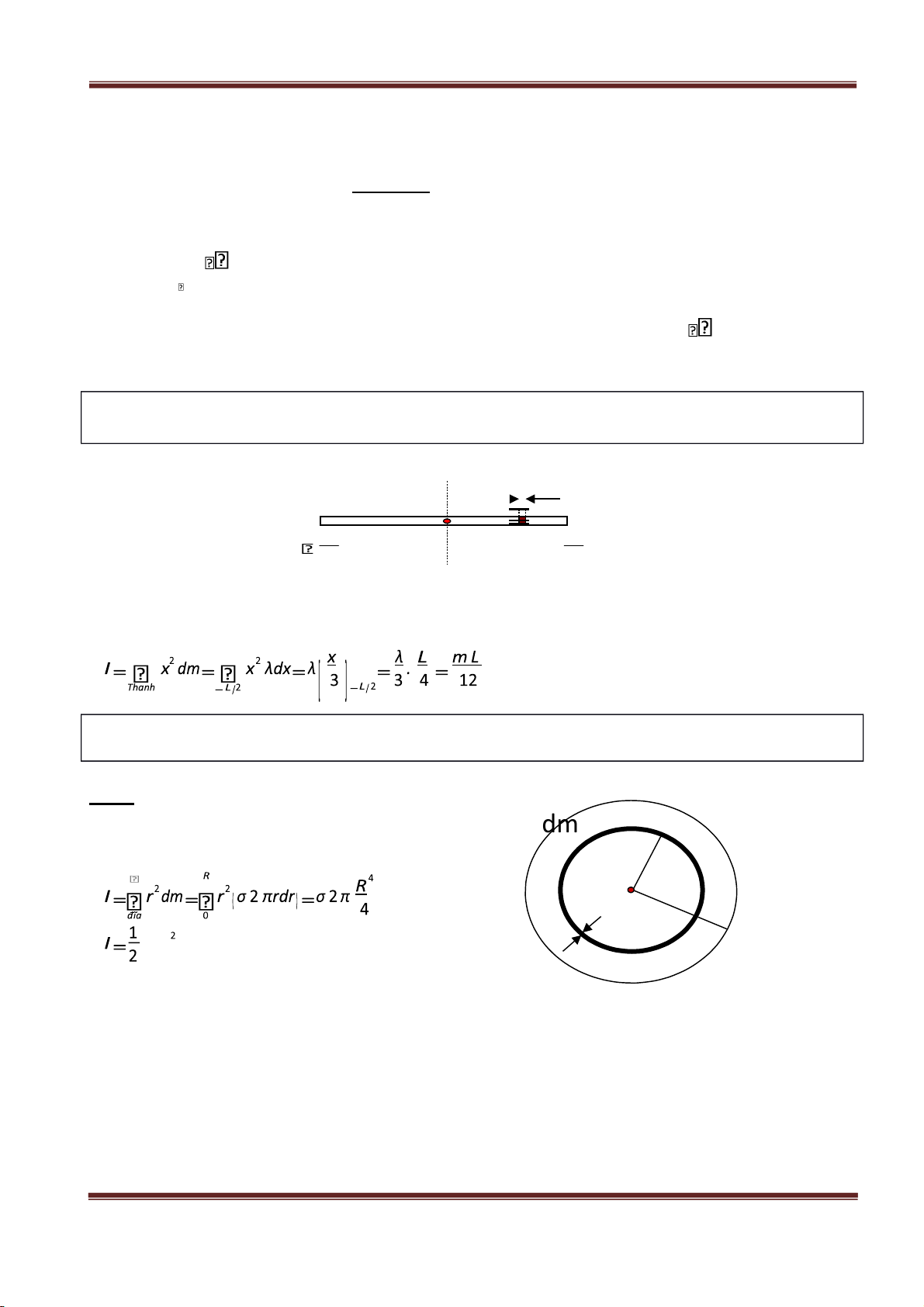
Ví dụ 5 : Tìm công thức xác định mô men quan tính của một thanh dài l , khối lượng m, mật độ dài λ
đối với trục đi qua khối tâm của thanh và vuông góc thanh. Giải: d L 2 x L x 2
Chia thanh thành những đoạn nhỏ dx, dx cách khối tâm một khoảng x, đoạn dx có khối lượng dm=λdx.
Mô men quán tính của thanh đối với trục quay qua khối tâm : ❑
Ví dụ 6 : Tìm công thức xác định mô men quan tính của một đĩa đặc đồng chất, khối lượng m,bán kính
R, mật độ mặt σ đối với trục đi qua khối tâm của đĩa và vuông góc mặt phẳng đĩa. Giải :
Chia đĩa tròn thành những vành tròn bán kính r dày dr. dm
Vành tròn có khối lượng dm = σ2πrdr. r
Mô men quán tính của đĩa : O dr R
m R trong đó m = σπR 2 L/2 L/2 3 3 2
Bộ môn Vật Lý 4 lOMoARcPSD|36149638
VẬT LÝ ĐẠI CƯƠNG 1
Mô men quán tính của một số vật có hình dạng đặc biệt đối với trục đi qua khối tâm : • MR
Vành tròn hoặc trụ rỗng: IG 2 ; 1 2 IG MR •
Hình trụ đặc hoặc đĩa đặc: 2 . 1 2
l khối lượng m: IG 12 Ml . • Thanh đồng chất dài 2 2 IG MR • Khối cầu đặc: 5 . 2 2 •
Khối cầu rỗng : IG= 3 M R a2+b2 •
Hình chữ nhật có các cạnh a và b: 1 ) IG= 12 M ¿ 1 2 • Hình Vuông cạnh a : IG= 6 M a III.
Mômen quán tính đối với trục quay không đi qua khối tâm
Định lí Huygen – Steiner: Để tính mô men quán tính của vật đối trục bất kì song song trục đi qua khối
tâm và cách trục này đoạn d, ta dùng công thức:
I IG md 2 (3.12)
Công thức là nội dung của định lí Huygen – Steiner.
Ví dụ 7: Tìm công thức xác định mô men quan tính của một thanh dài l , khối lượng m đối với trục đi
qua một đầu thanh và vuông góc thanh. IG ml2
Giải. Mô men quán tính đối với qua khối tâm (G ở chính giữa thanh): . Do đó mô men 1 G m l 2 1 2 ml 2 2 3
quán tính đối trục đi qua một đầu thanh là: I I md 12 ml 2
Bộ môn Vật Lý 5 lOMoARcPSD| 36149638
VẬT LÝ ĐẠI CƯƠNG 1 Ví dụ 8 kg m/ m
: Một đĩa bằng đồng có khối lượng riêng 8,9.103
3 có bề dày b 4.10 2 . Đĩa bị khoét
thủng một lỗ tròn bán kính R / 2 như hình vẽ. Tìm mô men quán tính của đĩa đã bị khoét đối với trục đi
qua tâm đĩa và vuông góc đĩa. Giải.
Để giải quyết bài toán ta tiến hành như sau:
- Xác định khối tâm của các vật đồng chất. Khối tâm của đĩa chưa bị khoét là O, củađĩa tròn bán O kính r R / 2 là 1
- Tính mô men quán tính của đĩa chưa bị khoét đối với trục đi ta tâm G là I0 R R
Tính mô men quán tính của đĩa tròn bên trái có bán kính r R / 2 , đối với trục qua O1 O
0 1 song song trục qua G, dùng công thức Huyghen suy ra mô men quán tính của nó đối
với trục qua G là I01 .
Mô men quán tính của đĩa bị khoét đối I
với trục qua G cần tìm đinh bởi: I IO 01 . Ta có: 1 2 I0 mR
Mô men quán tính của đĩa chưa bị khoét lỗ đối với trục qua G định bởi: 2 . Với m V S b. b R2 . m R1
Mô men quán tính của lỗ tròn bên trái đối với trục qua O1 là IO1 1 m1 R2 2 18 2 với 2 2 2 4 m1 S b1 b R 1
b R2 . Nên mô men quan tính của đĩa bên trái đối với trục qua G theo 1 R 2 1
Huyghen – Steiner: I1G I 1 2 m 2 8 m R1 2 14 m R1 2 83m R1 2 O 1
Vậy mô men quán tính của đĩa bị khoét đối với trục qua G vuông góc đĩa là :
Bộ môn Vật Lý 6 lOMoARcPSD|36149638
VẬT LÝ ĐẠI CƯƠNG 1 1 2 3m R 2 1 1 R2 m m 1
I I0 I01 mR 2 8 8 . 1 2 I 5 bR4 m b R 2 và vào m1 4
b R suy ra kết quả. 32 Thay
CHƯƠNG 6: NGUYÊN LÝ I NHIỆT ĐỘNG HỌC Bài 6.1)
MỘT SỐ KHÁI NIỆM I.
Thông số trạng thái – Phương trình trạng thái:
Thông số trạng thái : Khi nghiên cứu một vật nếu thấy tính chất của nó thay đổi ta nói
rằng trạng thái của vật đã thay đổi. Như vậy các tính chất của vật biểu hiện trạng thái của
vật, mỗi tính chất thường được đặc trưng bởi một đại lượng vật lí và như vậy trạng thái
của một vật được xác định bởi một tập hợp xác định các đại lượng vật lí. Các đại lượng
vật lý này gọi là các thông số trạng thái.
Để biểu diễn trạng thái của một khối khí nhất định, người ta thường dùng ba thông số trạng
thái: thể tích V; áp suất p và nhiệt độ T của khối khí.
Phương trình trạng thái là phương trình thể hiện sự phụ thuộc của các thông số trạng thái với nhau.
Phương trình tổng quát: f p V T, , 0 II.
Áp suất – Nhiệt độ:
Áp suất: là đại lượng vật lý bằng lực nén vuông góc lên một đơn vị diện tích. Nếu kí
hiệu Fn là lực nén vuông góc lên ΔS thì áp suất p được xác định: S p F n Đơn vị :
N2 Pa(pascal) at
9,81.104Pa5Pa 736 760mmHgmmHg m atm 1,013.10
Nhiệt độ: là đại lượng vật lí đặc trưng cho mức độ chuyển động hỗn loạn của các phân tử cấu tạo nên vật.
Trong hệ SI đơn vị của nhiệt độ là Kelvin (thang nhiệt độ tuyệt đối), kí hiệu là K. Ngoài ra, để
o đo nhiệt độ, người ta thường dùng đơn vị C (thang nhiệt độ bách phân).
Mối liên hệ giữa các đơn vị nhiệt độ: T = t + 273,16
Bộ môn Vật Lý 7 lOMoARcPSD| 36149638
VẬT LÝ ĐẠI CƯƠNG 1
Trong tính toán người ta thường lấy: T = t + 273
T: là nhiệt độ trong thang tuyệt đối, t là nhiệt độ trong thang bách phân. III.
Phương trình trạng thái khí lý tưởng 1) Các định luật thực nghiệm về chất khí:
Định luật Boyle - Mariotte: “Trong quá trình đẳng nhiệt của một khối khí nhất định,
áp suất tỉ lệ nghịch với thể tích”.
Hay: “Trong quá trình đẳng nhiệt, thể tích của khối khí nhân với áp suất của lượng khí đó là
một đại lượng không đổi”. pV. const -
Biểu thức: p↝ 1 hay V
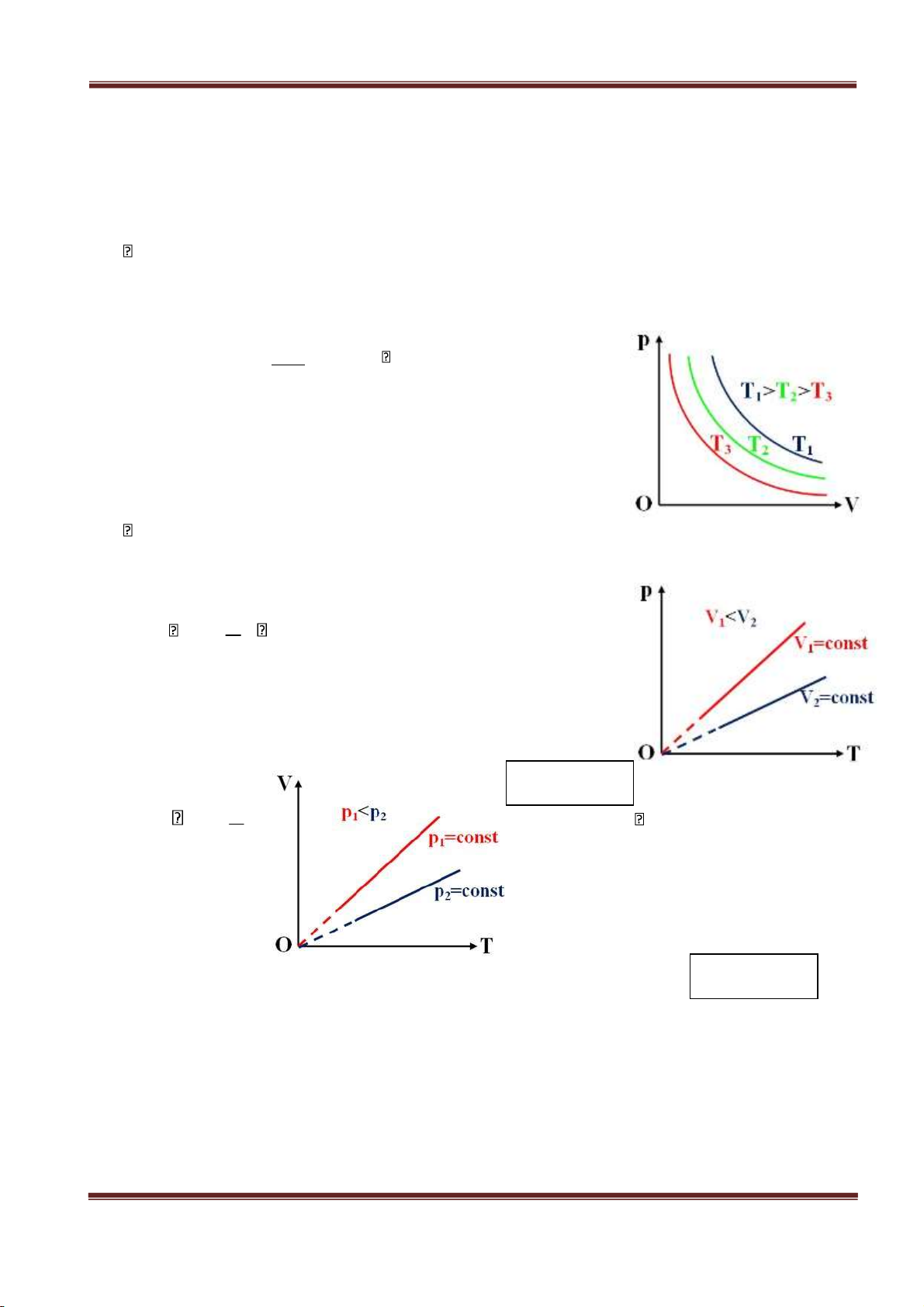
Đường đẳng nhiệt: Trong hệ tọa độ (p,V), đường đẳng nhiệt là đường
hypebol. Ứng với nhiệt độ khác nhau ta có các đường đẳng nhiệt khác
nhau (hình 6-1). Nhiệt độ càng cao, đường đẳng nhiệt càng xa gốc tọa
độ. Tập hợp các đường đẳng nhiệt gọi là họ đường đẳng nhiệt.
Các định luật Gay - Luytsac:
a. “Trong quá trình đẳng tích của một khối khí, áp suất tỉ lệ với nhiệt độ tuyệt đối”.Hình 6-1 p -
p T hay T const
Đường đẳng tích: Trong hệ tọa độ (p,T), đường đẳng tích là đường thẳng
có phương đi qua gốc tọa độ O (hình 6-2a)
b. “ Trong quá trình đẳng áp của một khối khí, thể tích tỉ lvới nhiệt độ tuyệt đối”. V Hình 6-2a - V T hay T const
Đường đẳng áp: Trong
hệ tọa độ (V,T), đường đẳng áp là đường thẳng có phương đi
qua gốc tọa độ O (Hình 6-2b). 2) Phương trình
trạng thái khí lý tưởng: • Khí lý
tưởng là khối khí tuân theo hai định luật Boyle – Hình 6-2b
Mariotte và Gay – Luytsac.
Ở điều kiện tiêu chuẩn, một khối khí lý tưởng có: T0=273,16K;
p0=1atm=1,033at=1,013.105Pa; V0=22,41m3
• Phương trình trạng thái khí lý tưởng: Thể hiện mối liên hệ giữa 3 thông số trạng thái: p, V, T.
Bộ môn Vật Lý 8 lOMoARcPSD|36149638
VẬT LÝ ĐẠI CƯƠNG 1
Đối với 1 kilomol khí Clapayron và Mendeleev đã tìm ra phương trình sau: pV RT.
Đối với một khối khí có khối lượng m, pt Clapayron pV
- Mendeleev được viết: m pV. RT =const pV. nRT hay T
3) Giá trị của hằng số khí lý tưởng:
Theo định luật Avogadro, ở nhiệt độ T và áp suất p giống nhau, 1kmol chất khí bất kỳ đều chiếm cùng
một thể tích. Ở đktc, 1kmol KLT có: T0=273,16K; p0=1atm=1,033at=1,013.105Pa; V0=22,41m3 p V.
1,013.105 N .22,41m3 R 0 0 m2 8,31.103 J nT. 0 1kmol.273,16K kmol K.
Nếu m[kg,g]; n[kmol,mol]; p[Pa, N/m2]; V[m3] thì: 3 J 8,31 J R 8,31.10 kmol K. mol K.
Nếu m[kg,g]; n[kmol,mol]; p[at]; V[m3,lit] thì: m .3 at lit.at
R 0,0848 0,0848 kmol K. mol K.
Ví dụ 1: Một bình kín chứa 14g N2 ở áp suất 1at và nhiệt độ 270C. Sau khi hơ nóng, áp suất trong
bình tăng lên đến 5at. Tính:
a) Nhiệt độ của khối khí sau khi hơ nóng. b) Thể tích của bình. Giải:
a) Vì bình kín và coi sự giãn nở của bình là không đáng kể nên quá trình hơ nóng khối khí trong bình
là quá trình đẳng tích.
p1 p2 T2 p T2. 1 5 300 1500K T1 T2 p1 1 b) Thể tích của bình:
Từ phương trình trạng thái của khí lí tưởng : m m RT1
14.8,31.300 12,72.10 ( 3 m3) pV. RT V p1 28.9,81.104
Bộ môn Vật Lý 9 lOMoARcPSD| 36149638
VẬT LÝ ĐẠI CƯƠNG 1 (hayV 12.72(lit))
Bài 6.2) NỘI NĂNG CỦA HỆ NHIỆT ĐỘNG - CÔNG VÀ NHIỆT I.
Hệ nhiệt động - Trạng thái cân bằng và quá trình cân bằng.
Hệ nhiệt động : Một tập hợp các vật được xác định hoàn toàn bởi các thông số vĩ mô, độc lập
với nhau, được gọi là hệ vĩ mô hay hệ nhiệt động (gọi tắt là hệ).
Các vật ngoài hệ là ngoại vật đối với hệ hay môi trường xung quanh của hệ.
Nếu hệ và môi trường không trao đổi nhiệt thì hệ cô lập đối với ngoại vật về phương diện nhiệt:
ta nói rằng giữa hệ và ngoại vật có một vỏ cách nhiệt. Nếu hệ và ngoại vật trao đổi nhiệt nhưng không
sinh ra công do sự nén hoặc dãn nở thì hệ cô lập đối với ngoại vật về phương diện cơ học.
Hệ gọi là cô lập nếu nó hoàn toàn không tương tác và trao đổi năng lượng với môi trường ngoài.
Định nghĩa trạng thái cân bằng và quá trình cân bằng:
Trạng thái cân bằng của hệ là trạng thái không biến đổi theo thời gian và tính bất biến đó không
phụ thuộc vào các quá trình của ngoại vật.
Quá trình cân bằng là một quá trình biến đổi gồm một chuỗi liên tiếp các trạng thái cân bằng.
Quá trình cân bằng theo định nghĩa trên chỉ là một quá trình lí tưởng, không có trong thực tế.
Tuy nhiên nếu quá trình thực hiện rất chậm để có đủ thời gian thiết lập lại sự cân bằng mới thì quá
trình đó được coi là quá trình cân bằng. Ví dụ: Nén khối khí trong xi – lanh bằng pit – tông một cách vô cùng chậm chạp. II. Nội năng.
- Năng lượng của hệ nhiệt động (W) là đại lượng đặc trưng cho mức độ vận động của hệ.
- Mỗi trạng thái vận động ứng với 1 năng lượng xác định, khi trạng thái của hệ thay đổi thì năng
lượng của hệ cũng thay đổi theo.
- Năng lượng của hệ nhiệt động là 1 hàm trạng thái. (Nghĩa là: độ biến thiên năng lượng của hệ
trong 1 quá trình biến đổi chỉ phụ thuộc vào trạng thái đầu và trạng thái cuối).
- Năng lượng hệ = Động năng do chuyển động cơ + Thế năng do tương tác với môi trường ngoài
+ Nội năng do vận động bên trong hệ.
- Nội năng (U): là phần năng lượng tương ứng với những chuyển động hỗn loạn bên trong của các
phân tử, nguyên tử.. bao gồm động năng của các phân tử vi mô, thế năng tương tác giữa các phân tử đó.
- Đối với hệ nhiệt động: W≈U
- Khi khảo sát sự biến đổi của hệ nhiệt động, người ta quan tâm đến độ biến thiên nội năng ∆U
nên việc chọn gốc nội năng không quan trọng (thường chọn U =0 ở T 0 0=0K). III.
Công và nhiệt của hệ nhiệt động
Công là dạng truyền năng lượng do lực làm hệ dịch chuyển hay thay đổi thể tích của hệ.
Quy ước: A>0 nếu hệ nhận công từ môi
trường A<0 nếu bản thân hệ sinh
công. Đơn vị của công: Jun [J].
Bộ môn Vật Lý 10 lOMoARcPSD|36149638
VẬT LÝ ĐẠI CƯƠNG 1
Nhiệt là đại lượng đặc trưng cho mức độ trao đổi năng lượng thông qua chuyển động
hỗn loạn của các phân tử trong hệ.
Quy ước: Q>0 nếu hệ nhận nhiệt từ môi trường ngoài.
Q<0 nếu bản thân hệ tỏa nhiệt ra môi trường ngoài.
Đơn vị của nhiệt: Jun [J] hoặc Calo [Cal] (Với 1Cal=4,18J) Lưu ý:
- Công và nhiệt chỉ xuất hiện trong quá trình biến đổi trạng thái của hệ, không phải là đại lượng
đặc trưng cho mỗi trạng thái xác định như năng lượng => Công và nhiệt không phải là năng
lượng. Công và nhiệt không phải là những hàm trạng thái mà là những hàm quá trình.
- Công và nhiệt có mối liên hệ chặt chẽ với nhau: A Q.
Thí dụ: + Cọ xát hệ => Thực hiện công, đồng thời sinh nhiệt (hệ nóng lên).
+ Nung nóng hệ => Truyền nhiệt cho hệ, đồng thời thể tích giãn nở chứng tỏ cũng thực hiện công. Bài 6.3)
NGUYÊN LÝ I NHIỆT ĐỘNG HỌC I.
Các cách phát biểu nguyên lý I nhiệt động học:
Phát biểu 1: “Trong một quá trình biến đổi, độ biến thiên nội năng của hệ bằng tổng công và
nhiệt mà hệ nhận được trong quá trình biến đổi đó”.
U A Q hay dU A Q
Quy ước: A và Q là công và nhiệt mà hệ nhận được từ môi trường thì:
A’=-A và Q’=-Q là công sinh ra và nhiệt tỏa ra môi trường.
Từ biểu thức nguyên lý I, suy ra: Q U A A U Q ' hay '
Phát biểu 2: “Trong một quá trình biến đổi, nhiệt truyền cho hệ bằng tổng độ biết thiên nội năng
của hệ và công do hệ sinh ra trong quá trình biến đổi đó”. Hay: “Trong một quá trình biến đổi,
công mà hệ nhận được bằng tổng độ biết thiên nội năng của hệ và nhiệt do hệ tỏa ra trong quá trình biến đổi đó”.
Các đại lượng U , A và Q có thể dương hoặc âm:
A>0 và Q>0 ⇒ U >0 : nội năng của hệ tăng.
A<0 và Q<0 ⇒ U <0 : nội năng của hệ giảm. II.
Hệ quả của nguyên lý I nhiệt động học:
Nếu hệ nhận công, nhận nhiệt: A>0 và Q>0 thì nội năng của hệ tăng: ∆U>0 hay U2>U1.
Nếu hệ sinh công, tỏa nhiệt: A<0 và Q<0 thì nội năng của hệ giảm:
∆U<0 hay U2 Nếu hệ cô lập không trao đổi công và nhiệt với môi trường ngoài: A=0 và Q=0 thì nội năng của
hệ được bảo toàn: ∆U=0 hay U2=U1=const
Định luật bảo toàn và chuyển hóa năng lượng: Năng lượng không tự sinh ra và cũng không tự
mất đi, nó chỉ chuyển hóa từ dạng này sang dạng khác, truyền từ hệ này sang hệ khác.
Bộ môn Vật Lý 11 lOMoARcPSD| 36149638
VẬT LÝ ĐẠI CƯƠNG 1
Nếu hệ cô lập gồm 2 vật chỉ trao đổi nhiệt với nhau: Q=Q ’ giả sử vật 1+Q2=0 hay Q1=-Q2=Q2
1 thu nhiệt thì vật 2 tỏa nhiệt và ngược lại.
Nếu hệ biến đổi theo 1 chu trình kín: Sau một dãy các biến đổi hệ trở về trạng thái ban đầu
U2=U1. Phương trình trạng thái khí lý tưởng: ∆U=U2-U1=A+Q=0 Suy ra: A Q Q' hay Q A A'
Vậy: Nếu hệ nhận công thì sẽ tỏa nhiệt; ngược lại, nếu hệ nhận nhiệt thì sẽ sinh công. III.
Ý nghĩa vật lý của nguyên lý I nhiệt động học:
Nguyên lý I nhiệt động học đóng vai trò rất quan trọng trong việc nhận thức tự nhiên cũng như
trong khoa học, kỹ thuật. “Nguyên lý I là một quy luật tuyệt đối của thiên nhiên (Ăngghen)”.
Từ hệ quả của nguyên lý ta thấy rằng không thể có một máy nào làm việc tuần hoàn sinh công
mà lại không nhận thêm năng lượng từ bên ngoài hoặc sinh công lớn hơn năng lượng truyền cho
nó. Những máy này được gọi là động cơ vĩnh cửu loại 1.
Như vậy nguyên lý thứ nhất của nhiệt động học khẳng định rằng “Không thể chế tạo động cơ vĩnh cửu loại I”. Bài 6.4)
ỨNG DỤNG NGUYÊN LÝ I ĐỂ KHẢO SÁT CÁC QUÁ TRÌNH CÂN
BẰNG CỦA KHÍ LÝ TƯỞNG I.
Biểu thức công, nhiệt và độ biến thiên nội năng trong quá trình cân
bằng Biểu thức công mà hệ nhận được trong quá trình cân bằng:
- Công mà khối khí nhận được khi pit – tông dịch chuyển một đoạn dl x2 x1 0 ⃗ ⃗ A F dl. F dl. p S dl. . p dV.
- Công mà hệ nhận được trong quá trình nén cân bằng từ V1 V2: 2 V 2 A A pdV. 1 V 1
Biểu thức nhiệt mà hệ nhận được trong quá trình cân bằng:
- Nhiệt dung riêng (c) của một chất là đại lượng vật lý có giá trị bằng nhiệt lượng cần thiết truyền
cho 1 đơn vị khối lượng để nhiệt độ của nó tăng thêm 1 độ. c 1 . Q m dT
- Nhiệt dung phân tử (nhiệt dung mol C): C
.c là khối lượng của 1mol chất đó. m Q CdT
Bộ môn Vật Lý 12 lOMoARcPSD|36149638
VẬT LÝ ĐẠI CƯƠNG 1
Trong hệ đơn vị SI đơn vị của c là J/kg.độ(K), đơn vị của C là J/mol.K
Biểu thức nội năng của khí lý tưởng trong quá trình cân bằng:
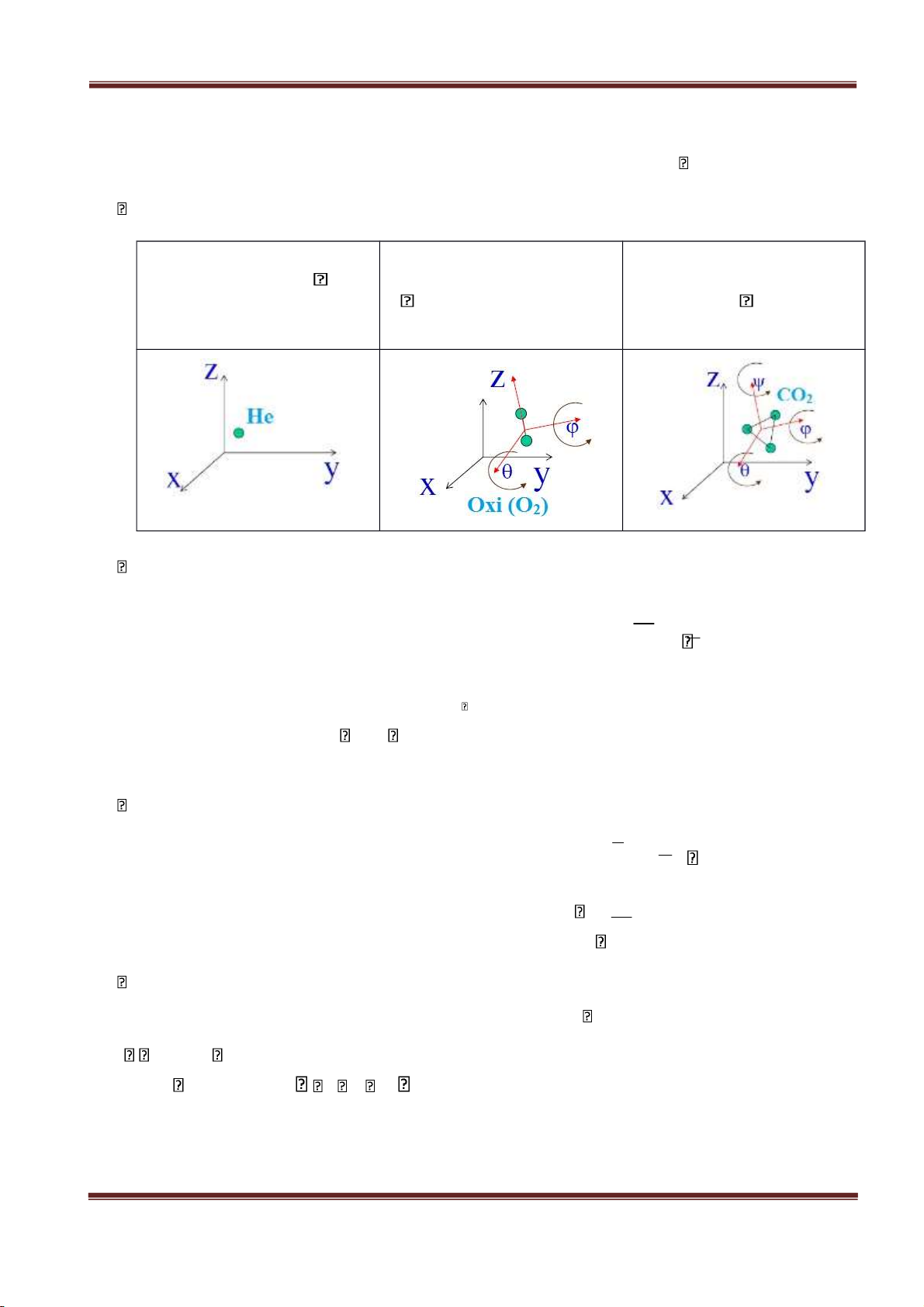
Khái niệm về bậc tự do (i): bậc tự do i là số tọa độ độc lập cần thiết để mô tả chuyển động của một phân tử khí.
TH1 : Phân tử khí đơn nguyên TH2 : Phân tử khí lưỡng
TH3 : Phân tử khí có từ 3
tử (He, Ne, Ar,.) thì: i 3 nguyên tử (H nguyên tử trở lên (O 2 , O 2 , CO,…) thì 3 , CH 4 , i 5 NO i 2 ,…) thì: 6
Định luật phân bố đều năng lượng theo bậc tự do: “Động năng trung bình của phân tử khí được
phân bố đều cho các bậc tự do của phân tử; ứng với mỗi bậc tự do, động năng bằng 1/2.k .T” B i Wđ k TB
Tổng quát: Động năng trung bình của phân tử khí có i bậc tự do: 2 R 23 J K/ kB 1,38.10 N A (hằng số Boltzmann)
Biểu thức nội năng của khí lý tưởng: i U = N .W0 A đ RT
Nội năng của 1kmol khí lý tưởng có NA phân tử: 2 m iR U= n.U0 T 2
Nội năng của n(kmol) hay m(kg) khí lý tưởng:
Nhận xét: Nội năng (U) của một khối khí chỉ phụ thuộc vào nhiệt độ (T).
Trong một quá trình biến đổi bất kỳ mà nhiệt độ thay đổi từ T1 T2 thì độ biến thiên nội năng: m iR U T 2 T T2 T1
Ví dụ 2: Sau khi nhận được nhiệt lượng Q = 150 cal, nhiệt độ của m = 40,3 g khí ôxi tăng từ t1 =
Bộ môn Vật Lý 13 lOMoARcPSD| 36149638
VẬT LÝ ĐẠI CƯƠNG 1 o
16 C tới t2 = 40oC. Hỏi quá trình hơ nóng đó được tiến hành trong điều kiện nào?
Giải : Quá trình hơ nóng thì không thể đẳng nhiệt hay đoạn nhiệt được chỉ có thể là đẳng tích và
đẳng áp. Ta tính nhiệt dung mol sau đó so sánh với nhiệt dung mol đẳng áp và nhiệt dung mol đẳng tích.
Dùng công thức tính nhiệt lượng:
Q mC T C Q 32.150.4,18 20,7 J m T 40,3.24 mol K.
Tính thử nhiệt dung mol đẳng tích rồi so sánh i 5 J
CV R .8,31 20,7 2 2 mol K.
Vậy quá trình hơ nóng đó được tiến hành trong điều kiện đẳng tích II.
Ứng dụng: quá trình đẳng tích, đẳng áp, đẳng nhiệt và đoạn nhiệt
Quá trình đẳng tích: V1 V2 =cons ,t dV 0
P =const hay P1 P2
Theo ĐL Gay-Luytsac, liên hệ p – T: T T1
T2 Công mà khối khí nhận vào: V 2 A12 p dV. 0 V1 m iR U12 . (T2 T1) 2
Độ biến thiên nội năng:
Q12 m.C (V T2 T1) CV iR
Nhiệt mà khối khí nhận vào: 2
Ví dụ 3: Một bình kín giãn nở kém thể tích 2l, đựng 12g khí nitơ ở nhiệt độ 10oC. Sau khi hơ nóng,
áp suất trung bình lên tới 104 mmHg. Tìm nhiệt lượng mà khối khí đã nhận được Giải:
Bình kín, giãn nở kém tức là quá trình đẳng tích A=0 U A Q Theo nguyên lý I:
Bộ môn Vật Lý 14 lOMoARcPSD|36149638
VẬT LÝ ĐẠI CƯƠNG 1 m m iR i m m i m Q U CV T (T2 T1) (
RT2 RT1) (p V2 2 RT1) 2 2 2
Thay số vào với i=5 (khí lưỡng nguyên tử), đổi áp suất từ đơn vị mmHg sang N/m2
V2 V1 V 2.10 3 m3 (Pa), 5 4 3 12 .8,31.(10 273)) U .(10 .133,3.2.10 2 28 U 4,1KJ P =const
Quá trình đẳng áp: P1 2 V V1 V2 =const hay
Theo ĐL Gay-Luytsac, liên hệ V – T: T T1 T2 V 2 A12
p dV. p V( 2 V1) 0
Công mà khối khí nhận vào: V1 m iR U12 . (T2 T1) 2
Độ biến thiên nội năng: m
Q12 .C (P T2 T1)
Nhiệt mà khối khí nhận vào:
Mặt khác, theo ng/lý I, ta có: m iR m m iR Q12 U12 A12 . (T2 T1) .R(T2 T1) ( R)(T2 T1) 2 2 m iR Q12 U12 A12 . (T2 T1) 0 2 CP iR R (i 2)R CV R
Bộ môn Vật Lý 15 lOMoARcPSD| 36149638
VẬT LÝ ĐẠI CƯƠNG 1
Suy ra: Nhiệt dung mol đẳng áp: 2 2 R Hệ thức Maye: C CP V
Ví dụ 4: Hơ nóng đẳng áp 2 kmol khí cácbonic cho đến khi nhiệt độ tăng thêm 50oC. Tìm:
a. Độ biến thiên nội năng của khối khí
b. Công do khí giãn nở sinh ra
c. Nhiệt lượng truyền cho khí Giải:
Khí CO2 là khí ba nguyên tử nên bậc tự do i = 6 m iR 6 6 J U12 .
(T2 T1) .2000.8,31.50 2,5.10 2 2 KJ A12 p V( 2 V1) nR(T2 T1) nR T 2000.8,31.50 831 ( .pV nRT) Q
U A' 3331J
Quá trình đẳng nhiệt T1 T2 = cons ,t T0
Theo ĐL Boyle-Mariotte, liên hệ p – V:
pV. = const hay p V1. 1 p V2. 2
Công mà khối khí nhận vào: V2 V 2 dV V2
A12 V 1p dV. V 1 p .V .11 V p1 1V .ln V1 m V2 m
RT1,2.ln p2 A12 RT1,2.ln V1 p1
Độ biến thiên nội năng: m iR U12 . (T2 T1) 0 2
Nhiệt mà khối khí nhận vào:
Bộ môn Vật Lý 16 lOMoARcPSD|36149638
VẬT LÝ ĐẠI CƯƠNG 1 Q12
U12 A12 0 A12 m V2 m RT1,2.ln p2 Q12 A12 RT1,2.ln V1 p1
Ví dụ 5: Nén đẳng nhiệt 3l không khí ở áp suất 1at. Tìm nhiệt tỏa ra biết rằng thể tích cuối cùng
bằng 1/10 thể tích ban đầu. Giải U12 0
Quá trình là nén đẳng nhiệt nên: m V2 p1 V .ln1 V2 Q12 A12 RT.ln V1 V1
Chú ý đổi hết đơn vị về SI: P(Pa), V(m3) 3 V2 1.9,81.10 .3.104 .ln 1 678J Q12 p1 V .ln1 V1 10
Quá trình đoạn nhiệt
Quá trình đoạn nhiệt: là quá trình biến đổi trạng thái mà trong đó hệ không trao đổi nhiệt với môi
trường ngoài: Q 0 hay Q 0
Ví dụ: Quá trình nén hoặc làm giãn nở khối khí trong 1 bình có vỏ cách nhiệt lý tưởng
Theo ng/lý I NĐH, ta có: dU
A Q A 0 m iR m U .
T dU .C dTV 2 m dV dA p dV. .RT V m m dV dT R dV C dTV
RT 0 Suy ra: V T CV V R R d(lnT)
d(lnV) 0 d(lnT lnV) 0(*) CV CV Cp i 2
Bộ môn Vật Lý 17 lOMoARcPSD| 36149638
VẬT LÝ ĐẠI CƯƠNG 1 C i Đặt: V
là chỉ số đoạn nhiệt ( hệ số Poisson) R Cp CV 1 CV CV (*) d(lnT (
1)lnV 0 d(lnT lnV 1 ) 0 d(ln .T V 1 ) 0 ln .T V 1 = const T V. 1 = const hay TV1 1. 1 = T .2 2V 1 m pV RT Từ pt trạng thái: p.V = const Pt
liên hệ p – V trong quá trình đoạn nhiệt: hay p V. = p .V 1 1 2 2
T .p1 = const
Pt liên hệ p – T trong quá trình đoạn nhiệt: hay
T p1 . 11 = T p2 . 21 0
Nhiệt mà khối khí nhận vào: Q12 m iR U12 . (T2 T1) 2
Độ biến thiên nội năng: U Q U
Theo ng/lý I NĐH, công mà khối khí nhận vào: A12 12 12 12 pV m RT i 2 i 1 Từ pt trạng thái: và i 2 1 A12
U12 i (p V2 2 pV1 1) (p V2 2 pV1 1)
Bộ môn Vật Lý 18 lOMoARcPSD|36149638
VẬT LÝ ĐẠI CƯƠNG 1 Ta viết lại: 2 1
Ví dụ 6: 1kg không khí ở nhiệt độ 30oC và áp suất 1,5at được giãn đoạn nhiệt đến áp suất 1at. Hỏi:
a. Thể tích không khí tăng lên bao nhiêu lần?
b. Nhiệt độ không khí sau khi giãn?
c. Công do không khí sinh ra khi giãn nở? Giải 1 1 1 ,4
a. p V1. 1 = p .2 V2 VV2 pp1 VV2 pp1 11,5 1,34 1 2 1 2 1 1.4 1 b. TV1. 1 1 = T .2 V2 1 T2 T1. VV12 1 ,134 270K
c. Không khí bao gồm 80% N2 và 20% O2 (các khí khác chiếm lượng ko đáng kể) -> khối lượng mol
tính trung bình ra xấp xỉ 29g m iR 1000 5 4J A12 U12 Q12 U12 . (T2 T1) . .8,31. 270 303 2,4.10 2 29 2
Bộ môn Vật Lý 19 lOMoARcPSD| 36149638
VẬT LÝ ĐẠI CƯƠNG 1 CHƯƠNG VII:
NGUYÊN LÝ II NHIỆT ĐỘNG HỌC Bài 7.1)
QUÁ TRÌNH THUẬN NGHỊCH VÀ KHÔNG THUẬN NGHỊCH I.
Những hạn chế của nguyên lý I nhiệt động học:
Theo nguyên lý I nhiệt động học, công và nhiệt hoàn toàn tương đương nhau, công có
thể chuyển hóa hoàn toàn thành nhiệt và nhiệt cũng có thể chuyển hóa hoàn toàn thành công.
Nhưng thực nghiệm chứng tỏ rằng, nhiệt không thể chuyển hóa hoàn toàn thành công.
Nguyên lý I nhiệt động học không cho biết chiều diễn biến của quá trình truyền nhiệt
trong hệ nhiệt động. Thực tế chứng minh rằng, nhiệt truyền từ hệ có nhiệt độ cao hơn sang
hệ có nhiệt độ thấp hơn.
Mặt khác, nguyên lý I nhiệt động học cũng không đề cập đến chất lượng nhiệt như thế
nào. Thực nghiệm chứng tỏ rằng, hệ nhiệt động thu nhiệt từ nguồn có nhiệt độ cao hơn sẽ
sinh công nhiều hơn so với trường hợp thu nhiệt từ nguồn có nhiệt độ thấp hơn. Nguyên lý
II sẽ khắc phục các hạn chế trên. II.
Quá trình thuận nghịch và không thuận nghịch:
1) Quá trình thuận nghịch:
Một quá trình biến đổi từ trạng thái (1) sang trạng thái (2) được gọi là thuận
nghịch khi có thể tiến hành biến đổi theo chiều ngược lại từ (2) về (1) qua tất cả các trạng
thái trung gian như chiều thuận, nhưng không làm biến đổi hệ cũng như môi trường xung quanh.
Với khái niệm như trên, quá trình thuận nghịch phải là quá trình cân bằng, điều
này chỉ xảy ra đối với các hệ nhiệt động lý tưởng.
2) Quá trình không thuận nghịch:
Quá trình không thuận nghịch là quá trình khi tiến hành theo chiều ngược, hệ
không đi qua đầy đủ các trạng thái trung gian như chiều thuận, sau khi đưa hệ về trạng
thái ban đầu thì môi trường xung quanh hệ sẽ bị biến đổi.
Quá trình không thuận nghịch là quá trình thường xảy ra với các hệ nhiệt động trong thực tế. III. Ý nghĩa:
Trên nguyên tắc, muốn thực hiện một quá trình biến đổi thuận nghịch phải tránh mọi mất
mát nhiệt do ma sát và phải đảm bảo mọi trạng thái trung gian là trạng thái cân bằng. Vì vạy,
quá trình thuận nghịch là quá trình lý tưởng, thực tế chỉ tồn tại quá trình không thuận nghịch.
Tuy nhiên, việc nghiên cứu các quá trình này đóng vai trò quan trọng trong công trình nghiên
cứu nguyên lý II nhiệt động học.
Bộ môn Vật Lý 20 lOMoARcPSD|36149638
VẬT LÝ ĐẠI CƯƠNG 1 Bài 7.2)
NGUYÊN LÝ II NHIỆT ĐỘNG HỌC
Nguyên lý II nhiệt động học ra đời nhằm nghiên cứu, phân tích hoạt động của các
máy nhiệt. Để phát biểu nguyên lý II, trước hết ta hãy xem xét đến các máy nhiệt. I. Máy nhiệt:
Máy nhiệt là một hệ hoạt động tuần hoàn biến đổi công thành nhiệt và biến đổi nhiệt
thành công thông qua các quá trình biến đổi trạng thái.
Hai bộ phận quan trọng của máy nhiệt là tác nhân và các nguồn nhiệt. Tác nhân là các
chất vận chuyển trong máy nhiệt làm nhiệm vụ biến nhiệt thành công và ngược lại. Khi máy
hoạt động, tác nhân trao đổi nhiệt với các nguồn nhiệt có nhiệt độ không đổi, sự trao đổi
nhiệt với tác nhân không làm ảnh hưởng đến nhiệt độ của nó. Thông thường, có 2 nguồn
nhiệt, nguồn có nhiệt độ cao gọi là nguồn nóng (T ), nguồn có nhiệt độ thấp gọi là nguồn h lạnh (Tc).
Tất cả các máy nhiệt đều hoạt động tuần hoàn và tác nhân trong máy biến đổi theo chu
trình. Có hai loại máy nhiệt là động cơ nhiệt và máy làm lạnh.
1) Động cơ nhiệt:
Động cơ nhiệt là máy có nhiệm vụ biến nhiệt thành công. Ví dụ: động cơ hơi nước, động
cơ đốt trong, động cơ phản lực,…
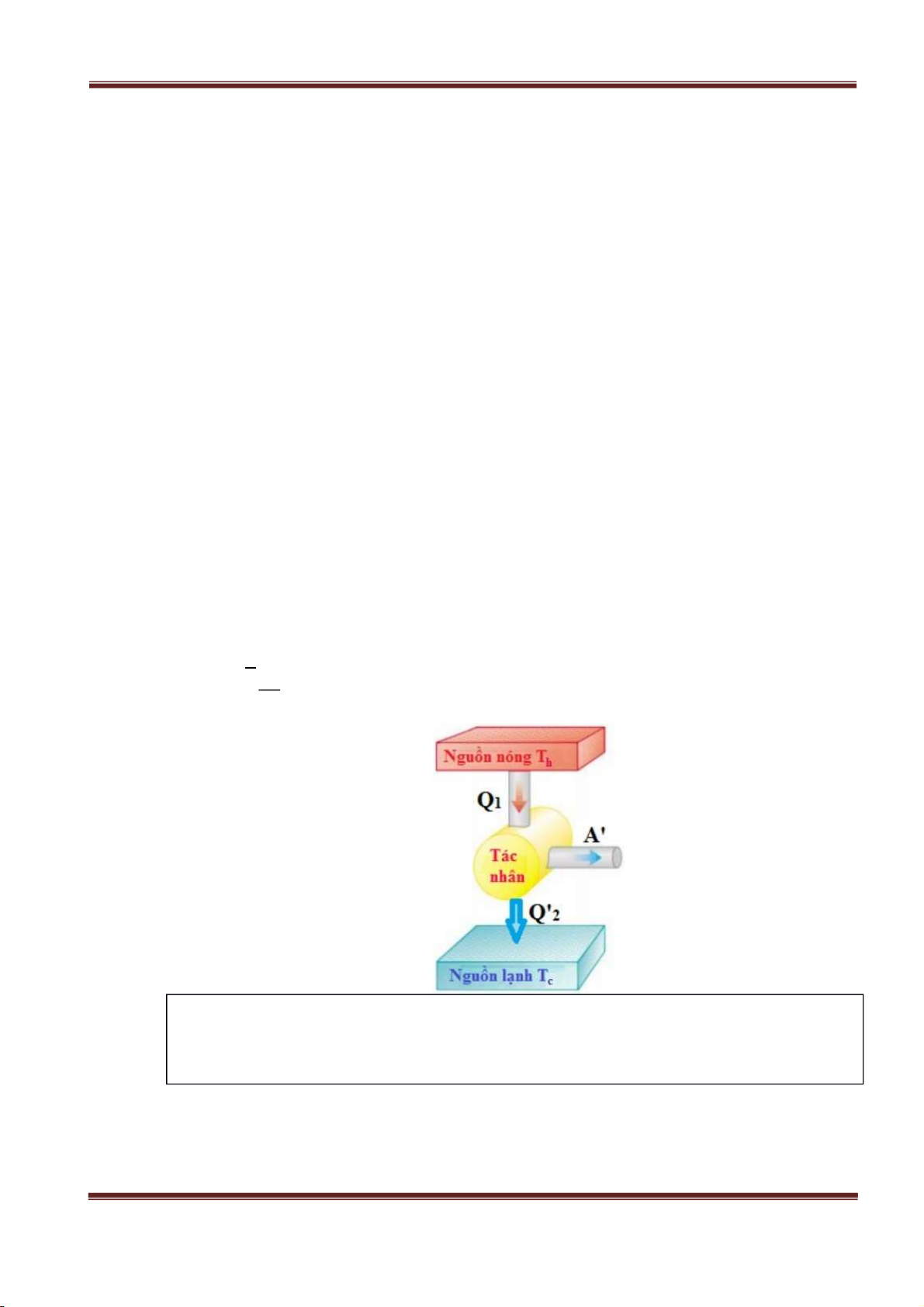
Khi động cơ nhiệt hoạt động, trong một chu trình tác nhân nhận từ nguồn nóng một nhiệt
lượng Q1 và nhả ra cho nguồn lạnh một nhiệt lượng Q'2 đồng thời sinh công A'=Q1−Q'2 thì hiệu
suất được tính như sau: A' Q'2 η= =1− Q1 Q1
Ví dụ 1 : Một động cơ nhiệt nhận từ nguồn nóng 52kcal và trả cho nguồn lạnh 12kcal nhiệt
lượng trong mỗi chu trình. Tính hiệu suất của động cơ.
Ví dụ 2 : Một động cơ nhiệt có hiệu suất 30% nhận từ nguồn nóng 50kcal nhiệt lượng
trong mỗi chu trình. Tính công do động cơ sinh ra trong mỗi chu trình.
2) Máy làm lạnh: (SV tham khảo)
Bộ môn Vật Lý 21 lOMoARcPSD| 36149638
VẬT LÝ ĐẠI CƯƠNG 1
Máy làm lạnh là máy có nhiệm vụ biến công thành nhiệt. Ví dụ: tủ lạnh, máy điều hòa, máy làm đá,…
Trong một chu trình, tác nhân tiêu thụ một công A và lấy một nhiệt lượng Q2 từ nguồn
lạnh thì hệ số làm lạnh được tính như sau: Q2 ε= A II.
Phát biểu nguyên lý II nhiệt động học:
Nguyên lý II được rút ra từ thực nghiệm. Có nhiều cách phát biểu nguyên lý II.
1) Phát biểu của Clausius: “Nhiệt không thể tự truyền từ vật lạnh hơn sang vật nóng hơn”.
2) Phát biểu của Thompson: “Không thể chế tạo được một máy hoạt động tuần hoàn biến đổi
liên tục nhiệt thành công nhờ làm lạnh một vật mà môi trường xung quanh không chịu một
sự thay đổi đồng thời nào”. Bài 7.3)
CHU TRÌNH CARNOT – ĐỊNH LÝ CARNOT I. Chu trình Carnot:
Các máy nhiệt đều hoạt động theo các chu trình, trong đó máy nhiệt đạt hiệu suất cao
nhất là khi hoạt động theo chu trình Carnot thuận nghịch do nhà bác học người Pháp Sadi
Carnot (1793 – 1832) phát minh vào năm 1824.
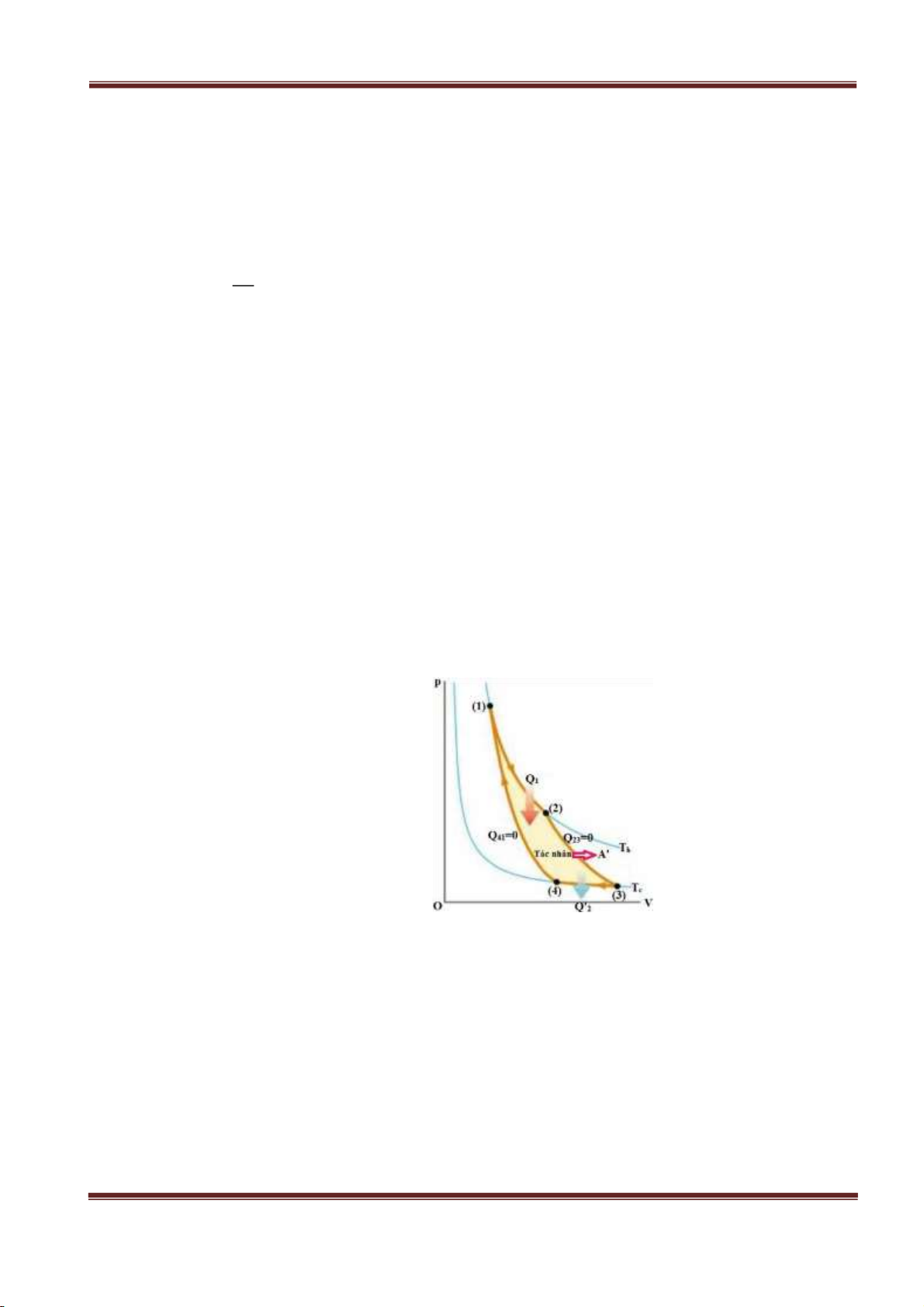
Một chu trình Carnot thuận nghịch gồm: 2 quá trình đẳng nhiệt và 2 quá trình đoạn
nhiệt thuận nghịch xen kẽ nhau có đồ thị trong hệ tọa độ (p, V) như hình vẽ.
• Quá trình dãn đẳng nhiệt (1) → (2): hệ nhận từ nguồn nóng T h nhiệt lượng
Q1=Q12 nên giãn nở từ thể tích V1→V2 nên tác nhân sinh công A'12 cho môi trường ngoài.
• Quá trình dãn đoạn nhiệt (2) → (3): hệ cô lập không trao đổi nhiệt với môi trường ngoài
Q23=0 , tiếp tục sinh công A'23 nên nhiệt độ giảm từ T h→Tc .
• Quá trình nén đẳng nhiệt (3) → (4): hệ nhận công A34 và nhả cho nguồn lạnh T c nhiệt
lượng Q'2=−Q34 .
• Quá trình nén đoạn nhiệt (4) → (1): hệ cô lập không trao đổi nhiệt với môi trường ngoài
Q41=0 , tiếp tục nhận công A41 nên nhiệt độ tăng từ T c →T h và kết thúc một chu trình.
Bộ môn Vật Lý 22 lOMoARcPSD|36149638
VẬT LÝ ĐẠI CƯƠNG 1 II.
Hiệu suất động cơ Carnot – Định lý Carnot:
Hiệu suất động cơ Carnot:
Với 2 quá trình đẳng nhiệt, nhiệt nhận từ nguồn nóng và nhả cho nguồn lạnh là: m V2 ' −m V4 m V3
Q1=Q12= μ RT h .ln
V1 và Q2=−Q34= μ RT c .ln V3= μ RTc .ln V4
Với 2 quá trình đoạn nhiệt, ta có:
T hV γ2−1=T c V3γ−1 và T hV γ1−1=T c V γ4−1 T c
Suy ra, hiệu suất của động cơ Carnot: ηc=1− T h
Vậy: hiệu suất của chu trình Carnot thuận nghịch chỉ phụ thuộc vào nhiệt độ của nguồn nóng và nguồn lạnh.
Ví dụ 3: Nhiệt độ của nguồn nóng và nguồn lạnh của một động cơ nhiệt làm việc theo chu
trình Carnot lần lượt là 2270C và 270C. Khi tốn một nhiệt lượng 4,18kJ thì có thể sinh công tối đa bằng bao nhiêu?
Ví dụ 4: Khi hoạt động theo chu trình Carnot, động cơ nhận được năng lượng 10kcal từ
nguồn nóng và thực hiện một công 12kJ. Biết nhiệt độ của nguồn nóng là 1270C, tính nhiệt
lượng động cơ nhả ra cho nguồn lạnh và nhiệt độ của nguồn lạnh.
Ví dụ 5: Một động cơ nhiệt hoạt động theo chu trình Carnot thuận nghịch. Biết công mà động
cơ sinh ra sau mỗi chu trình là 7350J, nhiệt độ nguồn nóng là 1000C, nhiệt độ nguồn lạnh là 00C. Tính:
a) Hiệu suất của động cơ.
b) Nhiệt lượng động cơ nhận được từ nguồn nóng trong một chu trình.
c) Nhiệt lượng động cơ nhả ra cho nguồn lạnh trong một chu trình.
Ví dụ 6: Một động cơ nhiệt làm việc theo chu trình carnot, có công suất P=500W. Nhiệt
độ của nguồn nóng là 2270C, nhiệt độ của nguồn lạnh là 270C. Tính: a) Nhiệt lượng mà tác
nhân nhận được từ nguồn nóng trong 1s.
b) Nhiệt lượng mà tác nhân nhả ra cho nguồn lạnh trong 1s. Định lý Carnot:
- Hiệu suất của tất cả các động cơ thuận nghịch chạy theo chu trình Carnot với cùng nguồn
nóng và nguồn lạnh đều bằng nhau và không phụ thuộc vào tác nhân cũng như cách chế tạo máy. Tc
ηc1=ηc2=1−T h
- Hiệu suất của động cơ không thuận nghịch luôn nhỏ hơn hiệu suất của động cơ thuận nghịch. ηktn <ηtn Hệ quả:
Từ định lý Carnot, ta rút ra được các kết luận sau:
- Hiệu suất cực đại là hiệu suất của động cơ hoạt động theo chu trình Carnot thuận nghịch.
Bộ môn Vật Lý 23 lOMoARcPSD| 36149638
VẬT LÝ ĐẠI CƯƠNG 1 ηmax=ηCtn
Giải thích hạn chế thứ nhất của nguyên lý I nhiệt động học: Trong thực tế, không thể tăng
nhiệt độ nguồn nóng T h→∞ và hạ nhiệt độ nguồn lạnh T c →0(K ) nên ηmax<1 . Vì vậy, không
thể biến hoàn toàn nhiệt thành công.
Giải thích hạn chế thứ hai của nguyên lý I nhiệt động học: Hai động cơ nhiệt hoạt động với
nhiệt độ nguồn lạnh bằng nhau, động cơ nào có nhiệt độ nguồn nóng cao hơn sẽ có hiệu suất
lớn hơn, từ đó sinh công nhiều hơn. Vì vậy, ta nói nhiệt lượng lấy từ nguồn có nhiệt độ cao
hơn sẽ có chất lượng cao hơn nhiệt lượng lấy từ nguồn có nhiệt độ thấp hơn.
- Muốn tăng hiệu suất của động cơ nhiệt, ta phải nâng cao nhiệt độ T h của nguồn nóng hoặc
hạ thấp nhiệt độ T c của nguồn lạnh. Ngoài ra, ta có thể chế tạo động cơ càng gần động cơ
Carnot thuận nghịch càng tốt. III. Biểu thức định lượng nguyên lý II nhiệt động học: ' ' Q T Q T Q Q -
Từ định lý Carnot và hệ quả, ta có: η≤ηC ↔ Q1 T h Q1 Th T h T c -
Trong trường hợp tổng quát, nếu tác nhân trao đổi nhiệt với n
nguồn nhiệt có nhiệt độ
T1,T2,…,Tn và nhận được nhiệt lượng tương ứng Q1,Q2,…,Qn thì biểu thức định lượng nguyên
lý II được viết dưới dạng: Q Q Q n Q T1 T2 Tn hay∑i=1 Ti
Trong đó: Dấu “=” ứng với chu trình thuận nghịch; Dấu
“<” ứng với chu trình không thuận nghịch.
- Nếu trong một chu trình, hệ lần lượt tiếp xúc với vô số nguồn nhiệt có nhiệt độ T biến thiên
liên tục, mỗi quá trình tiếp xúc là một quá trình vi phân, hệ nhận nhiệt δQ . Khi đó, biểu thức
trên được viết dưới dạng vi phân gọi là bất đẳng thức Clausius: T
Bài 7.4) HÀM ENTROPI – NGUYÊN LÝ TĂNG ENTROPI I. Hàm Entropi:
Bộ môn Vật Lý 24 lOMoARcPSD|36149638
VẬT LÝ ĐẠI CƯƠNG 1
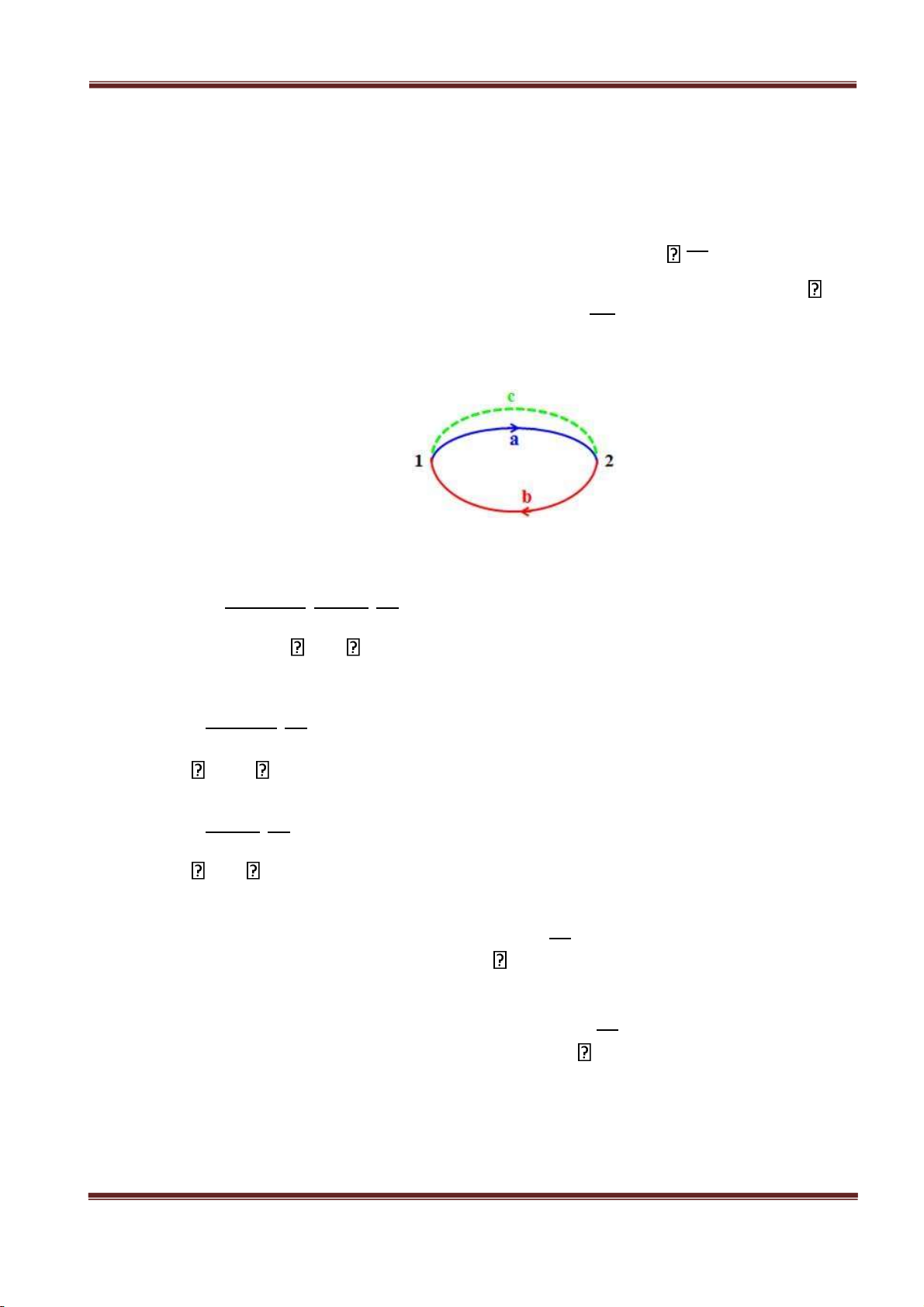
- Xét hệ biến đổi theo một chu trình gồm hai quá trình thuận nghịch 1a2 và 2b1, suy ra chu
trình 1a2b1 là thuận nghịch. Theo bất đẳng thức Clausius, ta có: ❑ δQ ❑ δQ ❑ δQ ∮ 1a
2b1 T =0↔1 a2 T +2 b1 T =0
- Vì quá trình biến đổi 2b1 là thuận nghịch nên ta có thể viết: ❑ δQ ❑ δQ 2 b1 T =−1 b2 T Suy ra: ❑ δQ ❑ δQ 2 δQ 1 a2 T =1 b2 T = 1 T δQ
- Vậy: đối với quá trình thuận nghịch,
T không phụ thuộc vào quá trình biến đổi hệ từ trạng
thái (1) sang trạng thái (2) mà chỉ phụ thuộc vào hai trạng thái ấy. Nghĩa là, nó phụ δQ
thuộc vào tính chất nội tại của hệ nhiệt động. Do đó, T phải đại diện cho một độ biến
thiên vi phân của một biến số trạng thái nào đó của hệ, người ta gọi biến số này là Entropi S của hệ.
- Vì Entropi là hàm trạng thái nên độ biến thiên Entropi phải như nhau với mọi quá trình biến
đổi giữa hai trạng thái, với quá trình thuận nghịch ta có thể viết hệ thức sau: 2 δQ
ΔS12=S2−S1= T 1 - Tính chất:
• S là hàm trạng thái, không phụ thuộc vào quá trình biến đổi của hệ từ trạng thái này sang trạng thái khác.
Bộ môn Vật Lý 25 lOMoARcPSD| 36149638
VẬT LÝ ĐẠI CƯƠNG 1
• S có tính cộng được. Nghĩa là, Entropi của toàn hệ bằng tổng Entropi từng phần của hệ.
• Entropi được xác định sai khác một hằng số cộng So : S=So+ δQT với So là Entropi ở
trạng thái gốc. Nếu quy ước So=0 tại T =0(K ) thì δQ Entropi được định bởi: S= T • Đơn vị Entropi: [J/K] II.
Nguyên lý tăng Entropi:
- Xét hệ biến đổi theo một chu trình gồm hai quá trình 1a2 là thuận nghịch và 2b1 là không
thuận nghịch, suy ra chu trình 1a2b1 là không thuận nghịch. Theo bất đẳng thức Clausius, ta có: ❑ δQ ❑ δQ ❑ δQ ∮ 1a
2b1 T <0↔1 a2 T +2 b1 T <0
- Vì quá trình biến đổi 2b1 là thuận nghịch nên ta có thể viết: ❑ δQ ❑ δQ 2 b1 T =−1 b2 T Suy ra: ❑ δQ ❑ δQ 1 a2 T <1
b2 T =ΔS12 2 δQ
Vậy: Với quá trình thuận nghịch: ΔS12= 1 T 2 δQ
Với quá trình không thuận nghịch: ΔS12> 1 T 2
Bộ môn Vật Lý 26 lOMoARcPSD|36149638
VẬT LÝ ĐẠI CƯƠNG 1 δQ
- Từ các kết quả trên, nguyên lý II có thể được viết dưới dạng: ΔS12≥ T 1
δQ Phương trình vi phân: dS≥ T
- Trong trường hợp hệ cô lập không trao đổi nhiệt với môi trường ngoài, ta có:
δQ=0→ ΔS≥0
• Dấu “=” ứng với quá trình thuận nghịch:
ΔS12=S2−S1=0→S2=S1=const :
Entropi của hệ không đổi.
• Dấu “>” ứng với quá trình không thuận nghịch:
ΔS12=S2−S1>0→S2>S1 :
Entropi của hệ luôn tăng.
Trong thực tế, các quá trình nhiệt động đều là không thuận nghịch nên ta có nguyên lý tăng
Entropi như sau: “Mọi quá trình nhiệt động xảy ra trên thực tế trong một hệ cô lập, Entropi
của hệ luôn luôn tăng”. Hệ quả:
o Một hệ cô lập không thể hai lần đi qua cùng một trạng thái. (Vì nếu vậy, S sẽ trở lại giá trị ban đầu).
o Một hệ cô lập ở trạng thái cân bằng khi Entropi của nó cực đại. (Vì khi hệ đã ở trạng thái
cân bằng thì quá trình không thuận nghịch cũng kết thúc, S không tăng).
o Entropi của hệ cũng là hàm trạng thái như năng lượng, nhưng không bảo toàn như năng
lượng. (Vì S luôn tăng). III.
Ý nghĩa thống kê của Entropi:
Nguyên lý II cho thấy nhiệt không thể tự truyền tự vật lạnh sang vật nóng và Entropi
của hệ cô lập không thể giảm. Nói cách khác, hệ luôn có xu hướng biến đổi từ trạng thái
không cân bằng về trạng thái cân bằng. Một khi về trạng thái cân bằng rồi, hệ không thể tự
động trở lại trạng thái không cân bằng nữa.
Entropi là thước đo mức độ hỗn loạn của các phân tử trong hệ. Khi Entropi tăng (ví
dụ hệ được làm nóng) thì tính hỗn loạn của các phân tử cũng tăng, tính trật tự cũng giảm và
ngược lại. Nguyên lý II chỉ áp dụng cho hệ vĩ mô gồm rất nhiều phân tử, khi đó có thể bỏ
qua ảnh hưởng của những thăng giáng. IV.
Độ biến thiên Entropi của khí lý tưởng:
Xét khối khí lý tưởng có quá trình biến đổi cân bằng từ trạng thái 1 ( p1,V1,T1 ) sang trạng thái 2 (
p2,V2,T2 ); 1.
Quá trình đoạn nhiệt: 2 δQ
δQ=0 nên ΔS12= T =0 1
Nhận xét: Quá trình đoạn nhiệt là quá trình đẳng Entropi.
Bộ môn Vật Lý 27 lOMoARcPSD| 36149638
VẬT LÝ ĐẠI CƯƠNG 1
2. Quá trình thuận nghịch bất kỳ:
- Theo nguyên lý I, ta có: dU=δQ+δA→δQ=dU−δA
Với: U= mμ CV T →dU= mμ CV dT
và δA=−p.dV =−μm RT dVV δQ m dT m dV 2 δQ T2 m dT V 2 m dV Suy ra:
= μ CV T + μ R V → ΔS12= T = T1 μ CV T + V 1 μ R V T 1 Vậy:
ΔS12=mμ CV .ln T
T12+ mμ R.ln VV 12
- Nếu thay hệ thức Mayer: Cp−CV =R và phương trình trạng thái: p1V1 p2V2 T2 p2V 2 = → = T1 T2 T1 p1V 1
thì độ biến thiên Entropi còn được tính theo biểu thức sau:
ΔS12= mμ CV .ln
pp21 + mμ Cp .ln VV12
Xét quá trình đẳng tích: V 2=m
1=V2→ΔS12=mμ CV .ln TT1 μ CV .ln pp21
Nhận xét: Quá trình làm nóng đẳng tích diễn ra theo chiều tăng Entropi. m V 2 m T2 • =
Xét quá trình đẳng áp:
p1= p2→ ΔS12= μ Cp .ln V 1 μ C p.ln T1
Nhận xét: Quá trình làm nóng hay giãn nở đẳng áp diễn ra theo chiều tăng Entropi. • m
Xét quá trình đẳng nhiệt: T1=T2→ ΔS12=mμ R.ln
VV21=−μ R.ln pp21 Nhận xét:
Quá trình làm giãn nở đẳng nhiệt diễn ra theo chiều tăng Entropi.
Bộ môn Vật Lý 28



