Bài giảng Cơ Nhiệt Môn Vật lý đại cương | Đại học Tài nguyên và Môi trường Hà Nội

CHƯƠNG I: ĐỘNG HỌC CHẤT ĐIỂM Bài 1.1) MỞ ĐẦU I.
Chuyển động và hệ quy chiếu
- Chuyển động là sự thay đổi vị trí trong không gian theo thời gian của vật thể này so với vật thể khác.
- Khi chúng ta nói một chiếc máy bay đang bay trên bầu trời thì có nghĩa là chúng ta đã tạm quy
ước bầu trời đứng yên và chiếc máy bay đang chuyển động đối với bầu trời. Như vậy khái niệm
chuyển động là một khái niệm có tính tương đối, điều đó thể hiện ở chỗ: Một vật chuyển động
là phải chuyển động so với vật nào, chứ không có khái niệm chuyển động chung chung.
- Vật này được quy ước là đứng yên thì vật kia chuyển động và ngược lại.
- Khi chúng ta nói: một chiếc xe đang chuyển động trên đường thì thực tế chúng ta đã ngầm quy
ước với nhau rằng chiếc xe đó chuyển động so với đường hay cây cối, nhà cửa ở bên đường.
Nên nói đầy đủ hơn phải là: chiếc xe đang chuyển động so với con đường. Như vậy không thể
nói một chuyển động mà không chỉ ra được một vật mà đối với nó thì vật này chuyển động.
- Vật được coi là đứng yên để xét chuyển động của vật khác được gọi là vật làm “mốc” hay “hệ quy chiếu”.
- Để thuận lợi cho việc nghiên cứu chuyển động người ta gắn vào hệ quy chiếu một hệ toạ độ,
chẳng hạn hệ toạ độ Descartes Oxyz (Renè Descartes1596 - 1650 người Pháp) II.
Chất điểm và hệ chất điểm
- Chất điểm: Chất điểm là vật mà kích thước của nó nhỏ hơn nhiều so với quãng đường mà nó đi
được (nhỏ hơn từ vài trăm đến vài ngàn lần). Một vật có thể được xem là chất điểm hoặc không
phải là chất điểm, điều này phụ thuộc vào độ dài quãng đường chuyển động của vật đó chứ
không phụ thuộc vào kích thước của nó.
- Ví dụ: Chiếc xe tải trong quãng đường chuyển động từ Bắc vào Nam có thể coi là chất điểm.
- Hệ chất điểm: Là tập hợp hai hay nhiều chất điểm mà khoảng cách giữa các chất điểm là không
đổi hoặc chuyển động của chất điểm này phụ thuộc các chất điểm khác. III.
Phương trình chuyển động của chất điểm
- Xét một chất điểm chuyển động theo đường cong bất kỳ AB
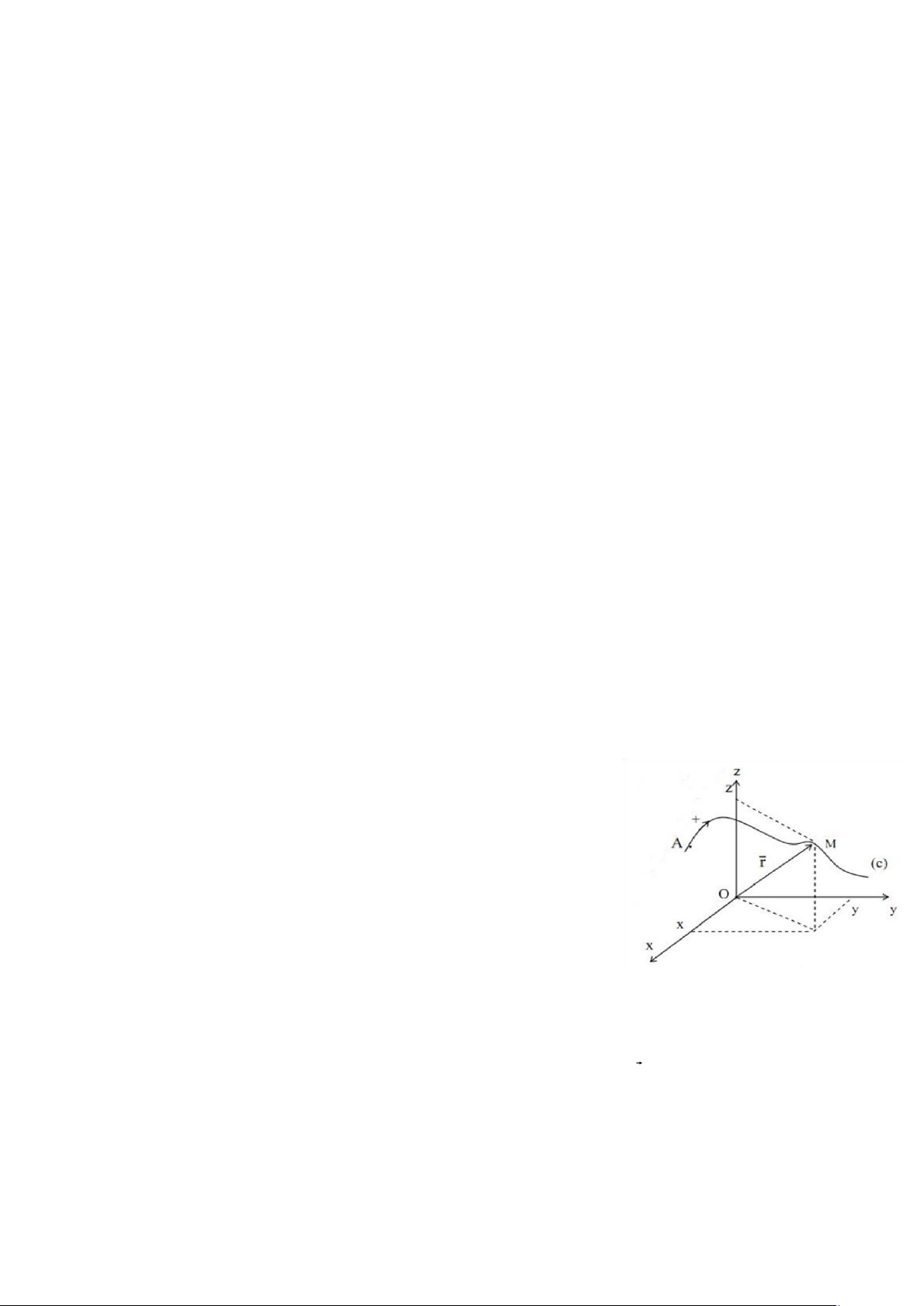
trong hệ quychiếu O,x,y,z (Hình 1.1).
- Giả sử rằng tại thời điểm t vị trí của chất điểm là M trên đường
cong AB, M là một điểm nên hoàn toàn được xác định bởi ba
toạ độ x, y và z (ta hay nói là ba toạ độ của điểm M). Nhưng vì
chất điểm chuyển động nên x,y,z thay đổi theo thời gian. Nghĩa
là ba toạ độ là hàm của thời gian: x = x(t) y = y(t) (1.1). z = z(t)
Hình 1.1: Tọa độ của chất điểm
- (Trong trường hợp chuyển động thẳng nếu ta chọn hệ tọa độ sao cho chuyển động dọc theo trục
Ox thì: x = x(t); y = 0; z = 0). Việc xác định chuyển động của chất điểm bằng hệ phương trình
(1.1) gọi là phương pháp tọa độ và phương trình đó gọi là phương trình chuyển động dạng tọa độ Descartes.
- Điểm M cũng hoàn toàn được xác định nếu biết vector r⃗ và các cosin chỉ phương của nó, vì
r⃗=xi⃗+ y ⃗j+zk⃗. (1.2) Nhưng do M chuyển động nên r⃗ thay đổi cả phương, chiều và độ lớn theo
thời gian:r⃗¿r⃗ (t ). (1.3) Đây là phương trình chuyển động dạng vector trong đór⃗ được gọi là
bán kính vector hay vector định vị. Chúng ta cũng không quên rằng để xác định vector này còn
cần ba cosin chỉ phương nữa.
- Ta cũng có thể biểu diễn chuyển động bằng một cách khác là: chọn trên quỹ đạo một gốc tọa độ,
chẳng hạn A và như vậy đoạn đường mà chất điểm đi được, được xác định so với A bằng cung
s, và cũng như trên s là một hàm của thời gian: s=s(t).(1.4). Phương trình này là phương trình
chuyển động dạng quỹ đạo. Phương pháp này gặp khó khăn ở chỗ là phải biết trước dạng quỹ
đạo của chuyển động. s được gọi là hoành độ cong. IV. Quỹ đạo 1) Quỹ đạo
- Quỹ đạo của một chất điểm là quỹ tích của tất cả những điểm trong không gian mà chất điểm đã
đi qua trong suốt quá trình chuyển động của nó.
- Như vậy quỹ đạo của một chất điểm thực tế chính là đường đi của nó trong không gian.
2) Phương trình quỹ đạo
- Phương trình quỹ đạo của một chất là phương trình biểu diễn mối liên hệ giữa các toạ độ chuyển
động của chất điểm trong không gian.
- Nghĩa là phương trình quỹ đạo có dạng: F(x,y,z)=0 (1.5)
- Và nếu biết phương trình quỹ đạo thì biết được dạng quỹ đạo của chất điểm đó.
Ví dụ 1: Một chất điểm chuyển động theo phương trình: x = 2 cos t ω;y = 4 sin t ω . a. Đây
là phương trình quỹ đạo hay phương trình chuyển động của chất điểm?
b. Tìm dạng quĩ đạo của chất điểm V. Hoành độ cong
- Giả sử quỹ đạo của chất điểm là một đường cong (C) ( hình 1.1). Trên đường cong (C) ta chọn
một điểm A nào đó là gốc và một chiều dương theo chiều chuyển động của chất điểm. Khi đó tại
mỗi thời điểm t, vị trí M của chất điểm trên đường cong (C) được xác định bởi trị đại số của cung , kí hiệu là: (1.6)
- Người ta gọi s là hoành độ cong của chất điểm chuyển động. Khi chất điểm chuyển động, s là
hàm của thời gian t, tức là: (1.7)
- Véc tơ vi phân hoành độ congd s⃗
 Phương trùng với tiếp tuyến của quỹ đạo tại điểm đang xét.
 Hướng theo chiều chuyển động.
 Độ lớn bằng vi phân hoành độ cong ds. Bài 1.2)
VECTƠ VẬN TỐC CỦA CHẤT ĐIỂM I. Định nghĩa
- Để chứng tỏ sự cần thiết của việc đưa ra khái niệm vận tốc ta lấy ví dụ sau đây: hai xe cùng xuất
phát từ một nơi, cùng một lúc và cùng đến đích vào một thời điểm. Nhưng chúng ta không thể
nói được xe nào đã chuyển động nhanh hay chậm hơn xe nào nếu không biết được xe nào đã tiêu
tốn ít hay nhiều thời gian hơn cho chuyển động (vì có thể quãng đường đi của hai xe là như nhau
hoặc khác nhau). Như vậy để so sánh các chuyển động với nhau thì phải so sánh quãng đường
mà chúng đi được trong cùng một thời gian, hay tốt nhất là cùng một đơn vị thời gian, quãng
đường đi trong một đơn vị thời gian đó được gọi là vận tốc. Như vậy có thể định nghĩa vận tốc như sau:
“Vận tốc của một chuyển động là đại lượng đặc trưng cho sự nhanh hay chậm của một
chuyển động, có trị số bằng quãng đường mà chất điểm đi được trong một đơn vị thời gian”.
- Để đặc trưng cho cả phương, chiều của chuyển động, điểm đặt của vận tốc, thì vận tốc là một đại lượng vector. II. Vectơ vận tốc
Vận tốc trung bình của một chuyển động trên một đoạn đường nào đó nói chung khác với
vận tốc tại một thời điểm bất kỳ trên quỹ đạo. Bởi vậy ta thường gặp hai loại vận tốc.
1) Vận tốc trung bình
- Vận tốc trung bình của một chuyển động là quãng
đường trung bình mà chuyển động đi được trong một đơn vị thời gian.
- Trong hệ đơn vị SI đơn vị thời gian là một giây
ngoài ra nếu không sử dụng hệ đơn vị SI thì ta có
thể lấy các đơn vị khác như:
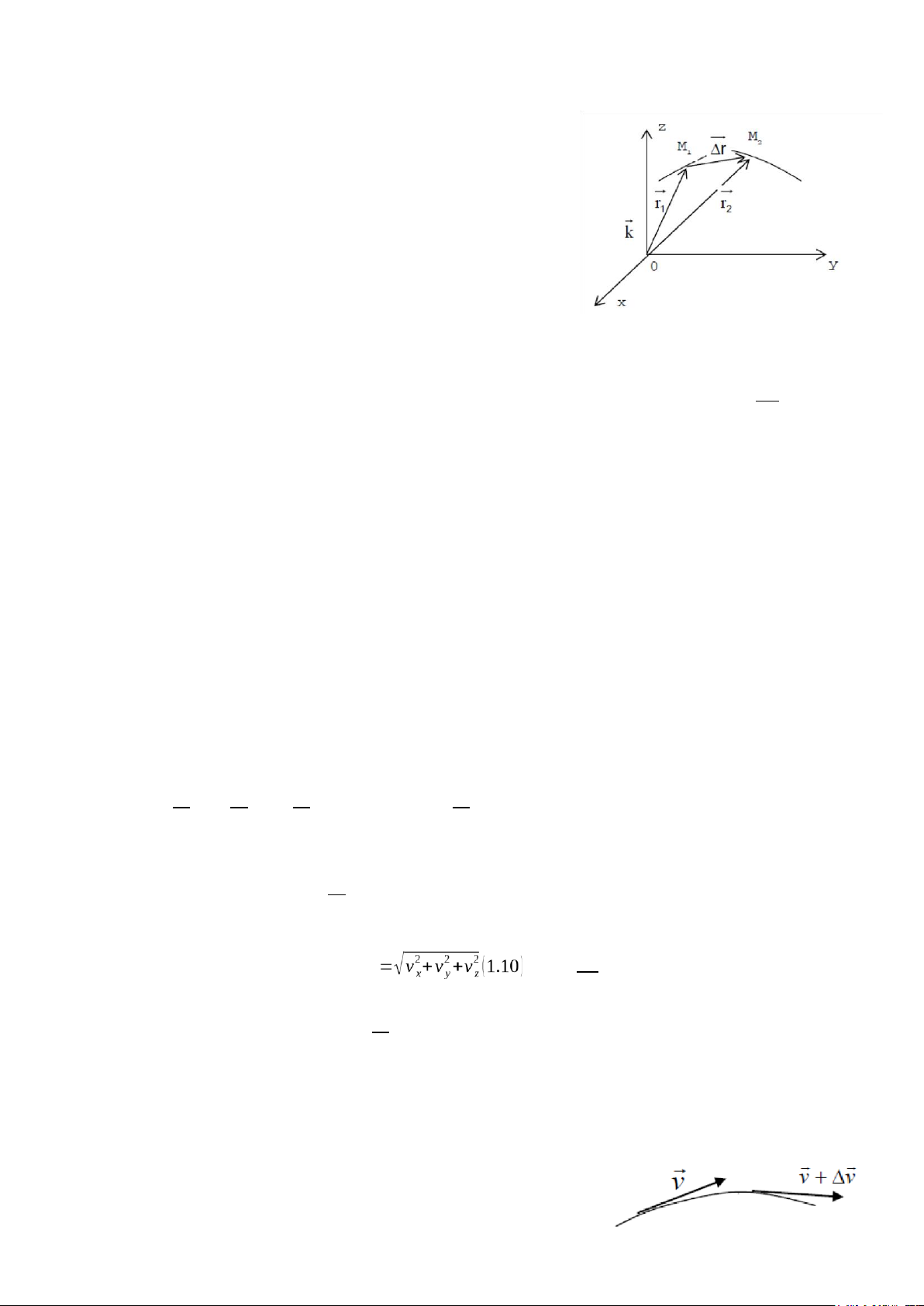
Hình 1.2: vec tơ vận tốc của chất điểm
giờ, phút, ngày, tuần .v..v..
- Giả sử tại thời điểm t chất điểm ở vị trí M1 được
xác định bởi bán kính vector r⃗=r⃗1.
- Đến thời điểm t + Δt vị trí của chất điểm là M2: r⃗2=r⃗+∆r⃗
- Như vậy trong thời gian Δt chất điểm đi được một đoạn ∆S đường
ΔS , nên theo định nghĩa của chúng ta thì vận tốc trung bình chính là: vtb= ∆t (1.8)
2) Vận tốc tức thời
- Vận tốc tức thời của một chuyển động là vận tốc của nó tại một thời điểm nào đó trên quỹ đạo
của chuyển động của nó.
- Việc xác định vận tốc của chất điểm tại một thời điểm bất kỳ trên quỹ đạo lại có ý nghĩa hơn vận
tốc trung bình, vì đó mới là vận tốc thực của chuyển động.
- Để có biểu thức tính vận tốc tức thời ta có nhận xét như sau: nếu Δt → 0thì M2→ M1và do đó vtb
→vt. Nghĩa là vận tốc trung bình trên đoạn đường ngắn M1M2 được xem là vận tốc tại điểm M1
hay vt. Nói như vậy có nghĩa là: Vận tốc tức thời của một chất điểm tại một thời điểm nào đó
trên quỹ đạo bằng đạo hàm bậc nhất của bán kính vector theo thời gian tại điểm đó.
- Vector vận tốc có độ lớn bằng độ lớn của vận tốc, có phương là phương của tiếp tuyến tại điểm
đang xét, có chiều là chiều của chuyển động. III.
Vectơ vận tốc trong hệ tọa độ Đê - các
Do trong hệ tọa độ Đêcác thì r⃗=xi⃗+ y ⃗j+zk⃗
dxdt ⃗+ dydt ⃗j+ dzdt k⃗=vx ⃗i+v y ⃗j+v z dzdt k⃗ (1.9) v⃗= i dx vx= dt v
vớiv y= dy (1.11) dt
{ dz v z= dt Bài 1.3)
VECTƠ GIA TỐC CỦA CHẤT ĐIỂM I.
Định nghĩa và biểu thức vectơ gia tốc
1) Khái niệm và định nghĩa -
Đối với những chuyển động không đều thì vận
tốc liên tục thay đổi, để đặc trưng cho sự thay đổi nhanh
hay chậm của vận tốc người ta đưa ra khái niệm gia tốc
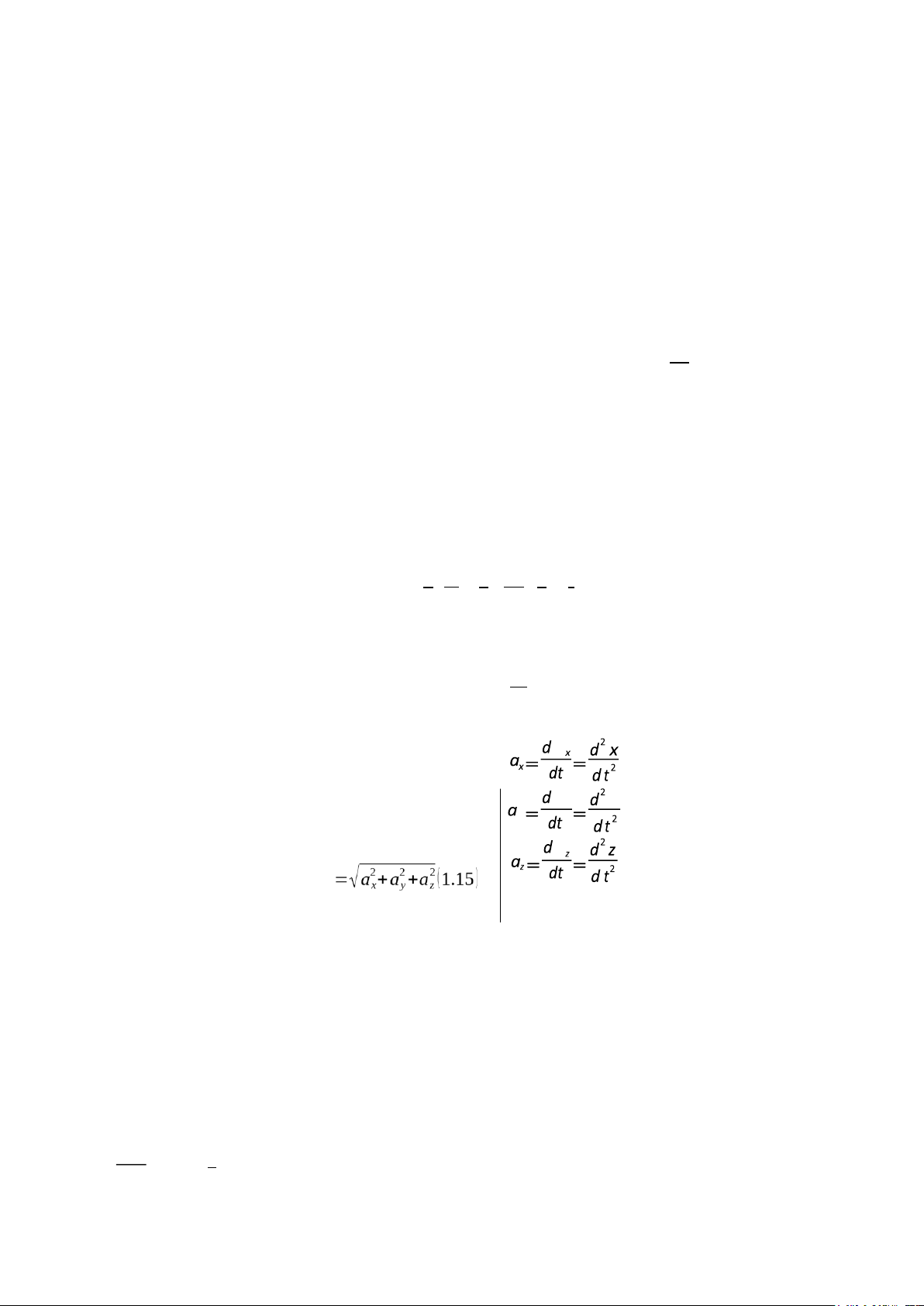
Hình 1.3: vec tơ gia tốc của chất
với ý nghĩa tương tự như vận tốc. điểm
“Gia tốc của một chuyển động là đại lượng đặc trưng cho sự thay đổi nhanh hay chậm
của vận tốc, có trị số bằng lượng vận tốc thay đổi trong một đơn vị thời gian”.
2) Gia tốc trung bình -
Tương tự như vận tốc ta cũng xét hai thời điểm trên quỹ đạo: -
Tại thời điểm t (M1) vị trí và vận tốc của chất điểm được xác định bằng r⃗ và v⃗. -
Đến thời điểm t + Δt (M2) vị trí và vận tốc của chất điểm được xác định
bằng:r⃗+∆r⃗ vàv⃗+∆v⃗. ∆v -
Vậy độ tăng trung bình của vận tốc trong một đơn vị thời gian là:atb= ∆t (1.12)
(atb là gia tốc trung bình của chuyển động của chất điểm đang xét ở trên đoạn đường M1M2)
3) Gia tốc tức thời -
Hoàn toàn lập luận tương tự như đối với vận tốc, gia tốc tức thời của
mộtchất điểm tại một thời điểm nào đó chính là kết quả của giới hạn sau đây:
a⃗= lim ∆∆⃗vt =ddtv⃗ = dd2tr⃗2 (1.13) ∆t →0
- Dạng thành phần củaa⃗là:
⃗+a y ⃗j+az dzdt k⃗ (1.14) a⃗=ax i v v y y (1.16) y v a với II.
Gia tốc tiếp tuyến và gia tốc pháp tuyến 1) Khái niệm -
Nguyên nhân của chuyển động cong về một phía nào đó của chất điểm là
do trên đoạn đường đó vector gia tốc lệch về phía đó của quỹ đạo. -
Vector gia tốc cũng như mọi vector khác đều có thể phân tích trên hai hay
ba phương bất kỳ tuy nhiên để thuận lợi cho việc tính toán người ta phân
tích nó lên hai phương đặc biệt là pháp tuyến và tiếp tuyến với quỹ đạo
a⃗=a⃗n+a⃗t
(1.17) 2) Dạng vector của gia tốc pháp tuyến: a⃗n=
ddt⃗vn = vR2 n⃗ (1.18)
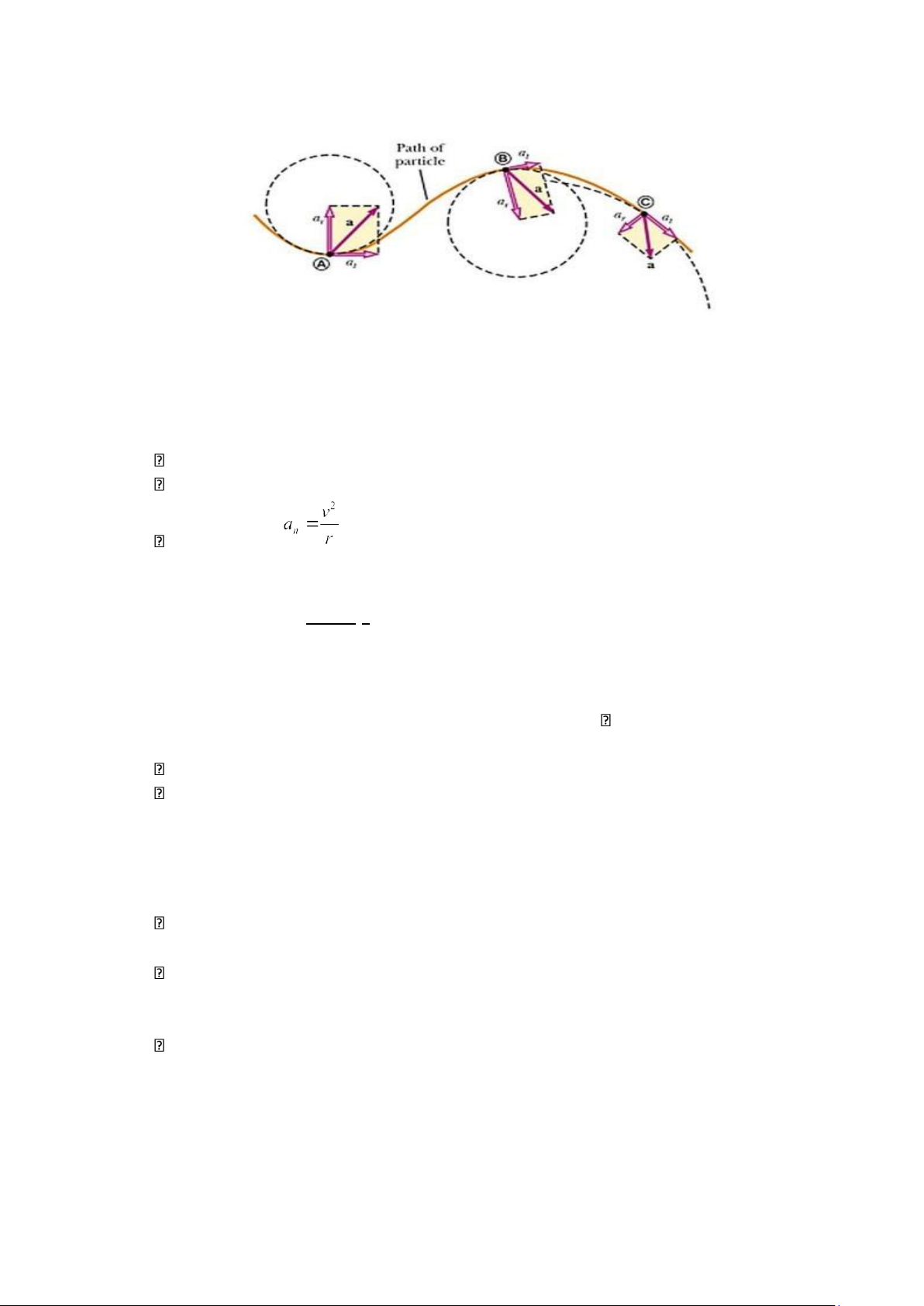
Hình 1.4: Gia tốc tiếp tuyến và gia tốc pháp tuyến a a → → -
Vậy: n đặc trưng cho sự biến thiên về phương của vectơ vận tốc, n có: 
Phương trùng với pháp tuyến của quỹ đạo tại M 
Có chiều hướng về tâm của quỹ đạo  Có độ lớn (1.19)
(n⃗là vector đơn vị có phương pháp tuyến với quỹ đạo, có chiều ngược với vector bán kính tại đó).
3) Dạng vector của gia tốc tiếp tuyến: dv d2s
Giatốctiếptuyến at= = - dt dt2 (1.20)
Kết luận: aτ đặc trưng cho sự biến thiên của vectơ vận tốc về độ lớn 
Có phương trùng với tiếp tuyến của quỹ đạo tại M. 
Có chiều là chiều chuyển động khi v tăng và chiều ngược lại khi v giảm. 
Có độ lớn bằng đạo hàm độ lớn vận tốc theo thời gian. → → → -
Gia tốc toàn phần: =a +a t n (1.21) a → 
an=0 : v không thay đổi phương: chuyển động thẳng v 
aτ =0 : → không thay đổi chiều và giá trị: chuyển động cong đều. → 
a= 0 : v không thay đổi phương chiều và giá trị: chuyển động thẳng đều.
(Trong đó R là bán kính chính khúc của đường tròn mật tiếp tại điểm đang xét (đã được minh hoạ trên hình 1.4)) x y=t
Ví dụ 2: Một hòn đá được thả rơi theo phương thẳng đứng với phương trình: { =3t+2} a)
Xác định dạng quỹ đạo chuyển động của hòn đá. b)
Viết phương trình vận tốc và xác định độ lớn của vận tốc hòn đá tại thời điểm sau khi
hòn đá được thả rơi 3s c)
Viết phương trình gia tốc và xác định độ lớn của gia tốc hòn đá tại thời điểm sau khi hòn đá được thả rơi 5s
Ví dụ 3: Một quả cầu chuyển động với phương trình vận tốc như sau: v⃗=4 t3i⃗+2t2
⃗j+(3t+1)⃗k a) Tính độ lớn vận tốc của quả cầu tại thời điểm t=5s.
b) Viết phương trình gia tốc và xác định độ lớn của gia tốc vật tại thời điểm sau khi vật được thả rơi 5s.
Ví dụ 4: Một chiếc xe chuyển động trên một quỹ đạo tròn, bán kính bằng 50m.Quãng đường được
đi trên quỹ đạo được xác định bởi công thức: s = - 0,5t2+ 10t + 10 .Tìm vận tốc, gia tốc tiếp tuyến
và gia tốc pháp tuyến, gia tốc toàn phần của ôtô lúc t = 5 giây. Bài 1.4)
MỘT SỐ DẠNG CHUYỂN ĐỘNG CƠ THƯỜNG GẶP I.
Chuyển động thẳng biến đổi đều → -
Là chuyển động có quỹ đạo thẳng và gia tốc a không đổi: a =0 n , Do đó: dv
a=aτ= dt =const⇒dv=adt
⇒v=v +at 0 (1.22) 
Chuyển động chậm dần đều: a.v<0 (1.23) 
Chuyển động nhanh dần đều: a.v>0 (1.24) ds
v=dt ⇒ds=vdt=(v0+at)dt -
Phương trình quãng đường: at2 s= 2 +vot (1.25)
- Lấy tích phân hai vế ta có: 2 2
- Khử thời gian t trong (1.22) ta được: v −v =2as 0 (1.26)
Ví dụ 5: Một ô tô bắt đầu rời bến, sau 20s đạt vận tốc 36km/h. Chiều dương là chiều chuyển động. Tính: a) Gia tốc của ô tô
b) Quãng đường ô tô đi trong 20s đó.
c) Nếu tiếp tục tăng tốc như vậy thì sau bao lâu nữa ô tô đạt vận tốc 54km/h. II.
Chuyển động tròn biến đổi đều
Trong chuyển động, nếu bán kính cong của quỹ đạo không thay đổi, chuyển động đó gọi là chuyển
động tròn. Trong chuyển động tròn, do có sự thay đổi của bán kính véc tơ r⃗=⃗OM, ngoài các đại lượng
v, a, at , an người ta còn đưa ra các đại lượng vận tốc góc và gia tốc góc. 1) Vận tốc góc.
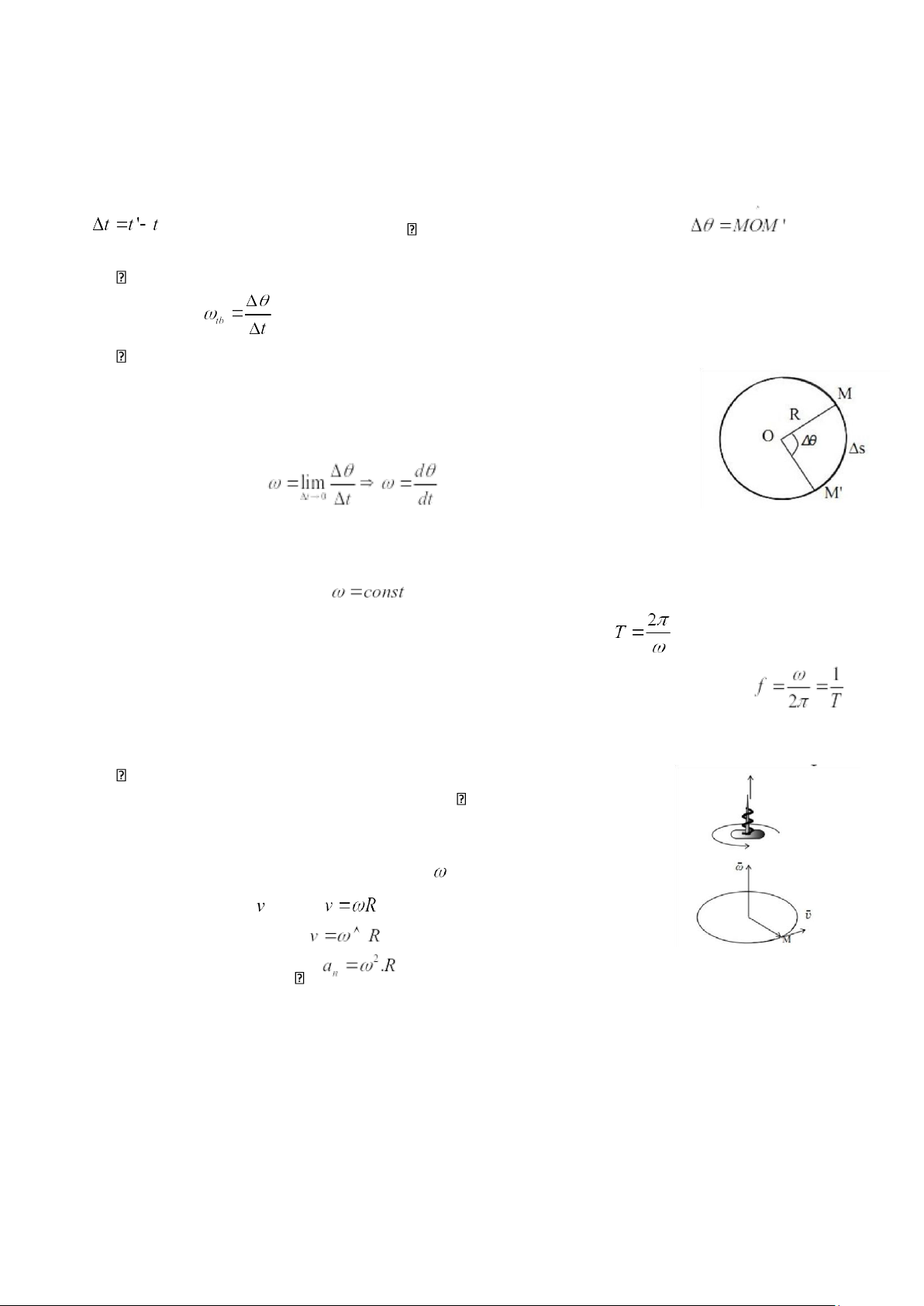
Giả sử chất điểm M chuyển động trên quỹ đạo tròn tâm O, bán kính R. Trong khoảng thời gian
chất điểm đi được quãng đường s bằng cung MM’ ứng với góc quay của bán kính R = OM ( hình vẽ ).
 Vận tốc góc trung bình. (1.34)
 Vận tốc góc tức thời. (1.35)
Hình 1.6: Chuyển động tròn
Vậy: Vận tốc góc bằng đạo hàm góc quay theo thời gian. Đơn
vị của vận tốc góc là rad/s
Trong chuyển động tròn đều thì
, người ta đưa ra khái nệm chu kì và tần số.
Chu kì T: Chu kì là thời gian cần thiết để chất điểm đi được một vòng. (1.36)
Tần số f: Tần số là số vòng quay của chất điểm trong một đơn vị thời gian: (1.37)
Đơn vị của chu kì và tần số là giây (s) và héc (Hz).
 Véc tơ vận tốc góc.
Véc tơ vận tốc góc ω⃗ là véc tơ có độ lớn  được định nghĩa ở (1.35),
nằm trên trục của vòng tròn quỹ đạo, chiều tuân theo quy tắc vặn nút chai:
Nếu quay cái vặn nút chai theo chiều chuyển động của chất điểm thì chiều
tiến của cái vặn nút chai chỉ chiều của véc tơ .
*Liên hệ giữa vàω⃗: (1.38) -Dạng véc tơ: (1.39)
*Liên hệ giữa an và : (1.40) 2) Gia tốc góc.
Hình 1.7: quy tắc vặn nút chai
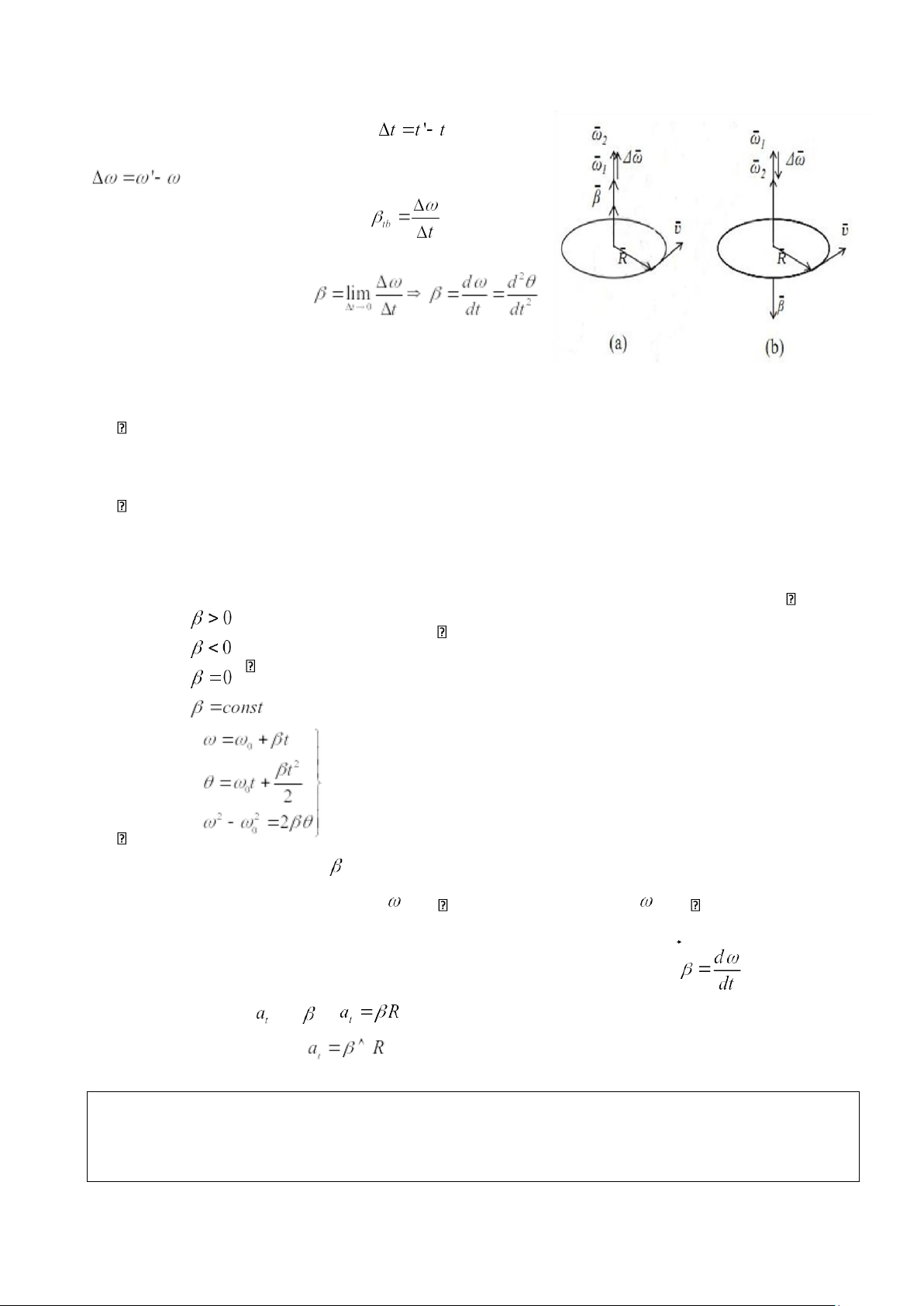
Giả sử trong khoảng thời gian vận tốc góc
của chất điểm chuyển động tròn biến thiên một lượng .
 Gia tốc góc trung bình : (1.41)
 Gia tốc góc tức thời (1.42)
Vậy: Gia tốc góc bằng đạo hàm vận tốc góc theo thời gian và bằng đoạ hàm bậc hai của góc
quay theo Hình 1.8: liên hệ giữa các vec tơ ⃗R,ω⃗,v⃗ ,⃗β thời gian.
Đơn vị của gia tốc góc là rad/s2. a. chuyển động nhanh dần; b. chuyển động +Khi ,  tăng, chuyển
động tròn nhanh dần. chậm dần +Khi ,  giảm, chuyển động tròn chậm dần. +Khi
,  không đổi, chuyển động tròn đều. +Khi
, chuyển động tròn thay đổi đều, ta có: (1.43)  Véc tơ gia tốc góc.
- Véc tơ gia tốc góc là véc tơ có trị số xác định theo (1.41), nằm trên trục của vòng tròn
quỹ đạo, cùng chiều với nếu  tăng và ngược chiều với nếu  giảm ( hình 1.8 ). - Theo
định nghĩa này ta có thể viết: (1.44) *Liên hệ và : giữa Dạng véc tơ:
Ví dụ 6: Một đĩa đồng chất có dạng hình tròn có R = 30cm đang quay tròn đều quanh trục của nó. Biết
thời gian quay hết 1 vòng là 2s. Tính tốc độ dài, tốc độ góc của 2 điểm A, B nằm trên cùng 1 đường
kính của đĩa. Biết điểm A nằm trên vành đĩa, điểm B nằm trên trung điểm giữa tâm O của vòng tròn và vành đĩa. III.
Chuyển động với gia tốc không đổi
Nhiều khi ta phải xét chuyển động của một vật trong trường lực. Chẳng hạn một electron bay vào
trong một điện trường hoặc từ trường với vận tốc ban đầu v0. Sau đây ta xét chuyển động của vật trong trọng trường.
Bài toán: Một viên đạn được bắn lên từ mặt đất với vận tốc v0 hợp với phương nằm ngang một góc ,
bỏ qua sức cản của không khí.
a.Viết phương trình chuyển động của vật.
b.Tìm dạng quỹ đạo của vật.
c.Tìm thời gian kể từ lúc bắn đến lúc vật chạm đất.
d.Xác định tầm bay xa của vật.
e.Tìm độ cao lớn nhất mà viên đạn đạt tới.
f.Xác định bán kính cong của quỹ đạo của vật tại điểm cao nhất Bài giải
Ngay sau khi bắn lực tác dụng vào vật là trọng lực luôn thẳng đứng hướng xuống, nên gia tốc
của vật trong suốt quá trình chuyển động là
luôn thẳng đứng hướng xuống. Chọn trục toạ độ Oxy,
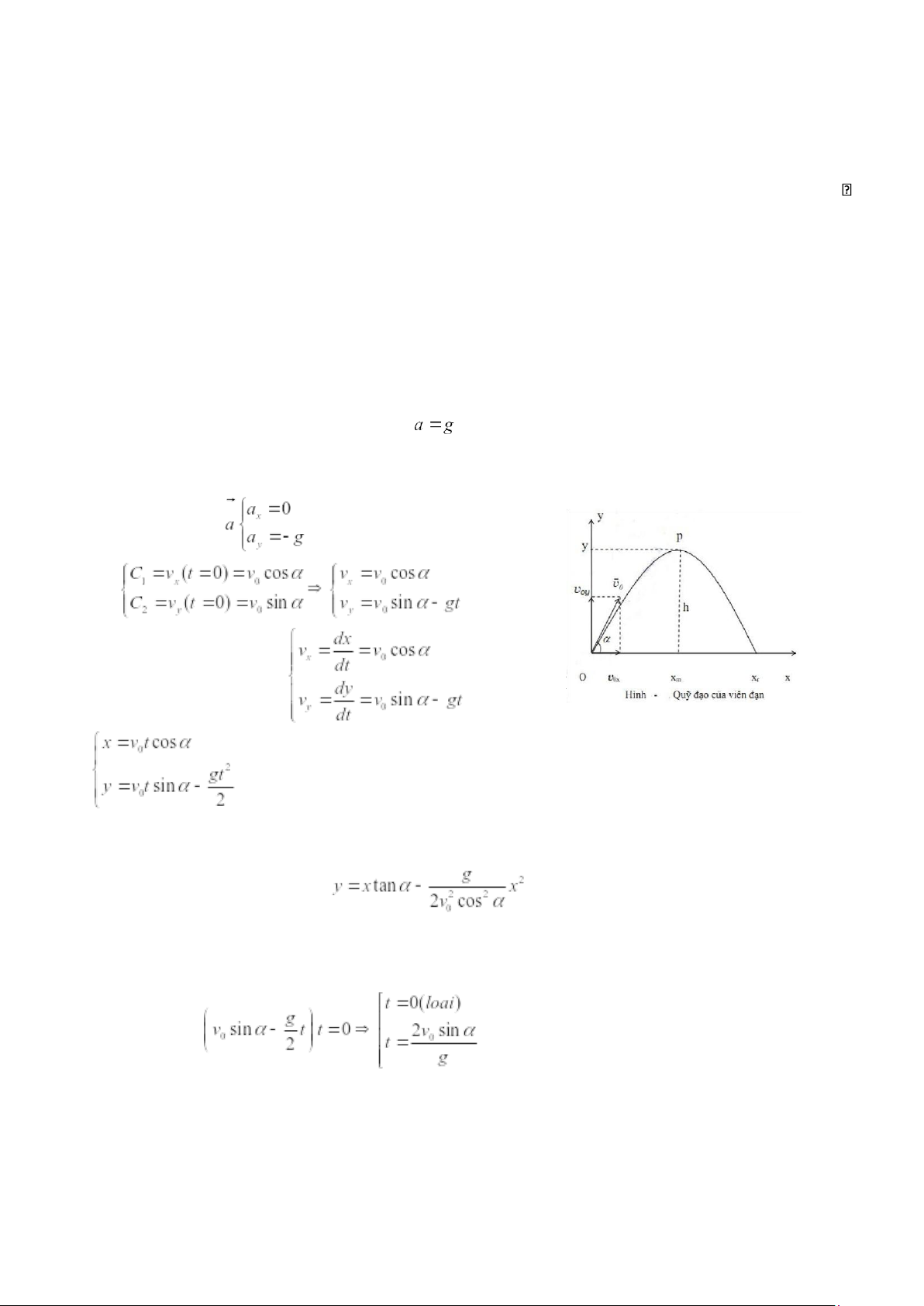
gốc O tại vị trí bắn, Ox nằm ngang, Oy thẳng hướng lên ( hình vẽ ). Ta phân tích chuyển động của vật
thành hai thành phần trên trục Với (1.27) Ox và Oy. Ta có:
Hình 1.5: Chuyển động ném xiên Lại có: Vậy (1.28)
Phương trình quỹ đạo.
- Từ (1.28) khử t ta được: (1.29)
- Vậy quỹ đạo của vật là một parabol, có bề lõm quay xuống (nhánh phải của hình 1.5 ).
Thời gian chuyển động.
Khi chạm đất thì y = 0, từ (1.28) ta có: (1.30) Độ cao cực đại.
Khi đạt tới điểm cao nhất P, vận tốc của viên đạn theo phương Oy bằng không. Từ (1.27) ta được: (1.31) Tầm bay xa.
Khi chạm đất viên đạn cách gốc O một đoạn L = xmax , khi đó y = 0.
Từ (1.28) và (1.29) ta được: (1.32) Bán kính cong của quỹ đạo tại điểm cao (1.33)
nhất. Ở điểm cao nhất thì Từ đó suy ra:
Bài toán ném ngang chính là bài toán ném xiên với góc ném 00
Bài toán rơi tự do: chuyển động thẳng nhanh dần đều với gia tốc rơi là gia tốc trọng trường và vận tốc đầu bằng 0
Ví dụ 7: Một quả cầu được ném theo phương ngang từ độ cao 80m. sau khi ném được 3s vận tốc
của quả cầu hợp với phương ngang một góc 450 . a) Tính vận tốc ban đầu của quả cầu.
b) Quả cầu chạm đất lúc nào, ở đâu, với vận tốc bao nhiêu.
Ví dụ 8: Từ độ cao 120m người ta thả một vật thẳng đứng xuống với v = 10m/s, g = 10m/s2.
a) Sau bao lâu vật chạm đất.
b) Tính vận tốc của vật lúc vừa chạm đất.
CHƯƠNG 2: ĐỘNG LỰC HỌC CHẤT ĐIỂM
Động lực học là phần cơ học nghiên cứu mối quan hệ giữa sự biến đối chuyển động (trạng thái)
của vật với sự tương tác giữa vật với các vật khác quanh nó. Bài 2.1)
CÁC ĐỊNH LUẬT NEWTON I.
Định luật 1 Newton
Phát biểu: “Khi một chất điểm cô lập (không chịu một tác động nào từ bên ngoài) nếu đang đứng yên,
nó sẽ tiếp tục đứng yên, nếu đang chuyển động thì chuyển động của nó là thẳng đều.” Biểu thức:
Chất điểm đứng yên: v=0
Chất điểm chuyển động thẳng đều: v=const
Ý nghĩa: Một chất điểm cô lập bảo toàn trạng thái chuyển động của nó. Tính chất bảo toàn trạng thái
chuyển động gọi là quán tính, vì vậy định luật 1 Newton còn gọi là định luật quán tính.
II. Định luật 2 Newton Phát biểu:
• Chuyển động của một chất điểm chịu tác dụng của các lực có tổng hợp lực ⃗F≠0 là một chuyển động có gia tốc.
• Gia tốc chuyển động của chất điểm tỉ lệ với tổng hợp lực tác dụng ⃗F và tỉ lệ nghịch với khối lượng
của chất điểm đó. Biểu thức: ⃗F a⃗= m
Điều kiện áp dụng của định luật II: trong hệ qui chiếu quán tính và trong cơ học cổ điển khi khối lượng coi là bất biến.
III. Định luật 3 Newton
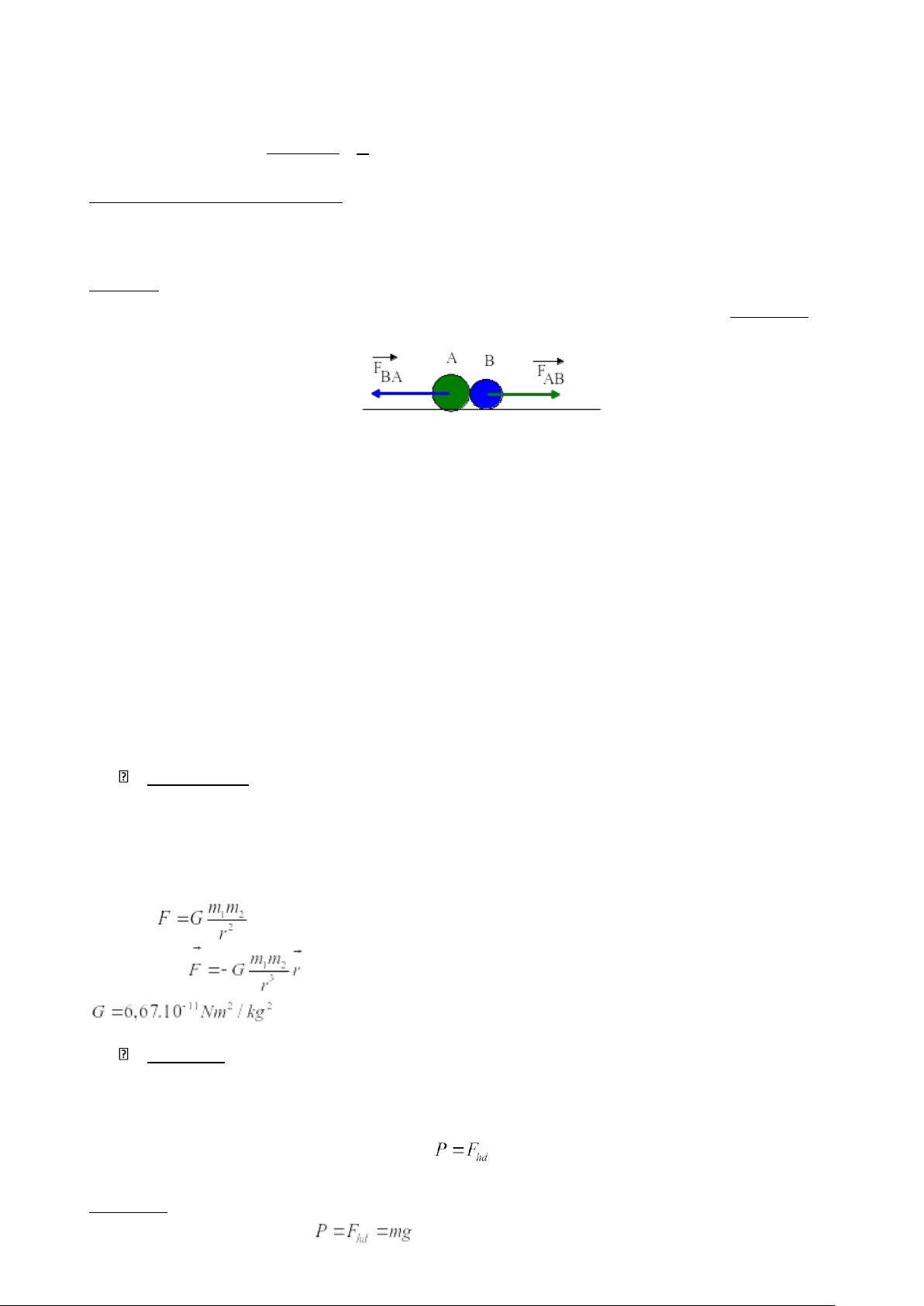
Phát biểu: Nếu vật A tác dụng vào vật B một lực ⃗FAB thì vật B sẽ tác dụng vào vật A một lực⃗FBA. Hai
lực này tồn tại đồng thời, cùng đường tác dụng, ngược chiều và bằng nhau về độ lớn. Biểu thức:
⃗FAB=−⃗FBA Bài 2.2)
CÁC LOẠI LỰC CƠ HỌC
Trong phạm vi cơ học cổ điển, xét về bản chất có ba loại lực cơ học: lực hấp dẫn, lực đàn hồi và lực ma sát.
Theo định luật II Newton, mặc dầu một lực bất kì được đo bằng tích số khối lượng và gia tốc mà
lực truyền cho vật, nhưng trong tự nhiên không có lực nào phụ thuộc vào gia tốc của vật. Lực trong tự
nhiên chỉ phụ thuộc vào vị trí và vận tốc của vật. I.
Lực hấp dẫn – Trọng lực
Mọi vật trong tự nhiên đều hút lẫn nhau bởi các lực có cùng bản chất gọi là lực hấp dẫn. Lực hấp dẫn
giữa các vật, đóng vai trò cực kì quan trọng trong tự nhiên. Nó chi phối mọi chuyển động của các vật
thể trong tự nhiên: từ chuyển động của các hành tinh quanh Mặt Trời, chuyển động của Mặt Trăng quanh
Trái Đất, sự rơi của mọi vật về bề mặt Trái Đất, sự tồn tại lớp khí quyển quanh Trái Đất, hiện tượng thủy triều…  Lực hấp dẫn
Qui luật về tương tác hấp dẫn giữa hai chất điểm được Newton tìm ra và phát biểu dưới dạng định luật vạn vật hấp dẫn
Nội dung: “Hai chất điểm bất kì luôn hút nhau bởi một lực gọi là lực hấp dẫn. Lực này có độ lớn tỷ lệ
với tích khối lượng của hai chất điểm và tỷ lệ nghịch với bình phương khoảng cách giữa chúng.” Biểu thức. Độ lớn: . Dạng vector: . là hằng số hấp dẫn vũ trụ.  Trọng lực
Khái niệm trọng lực được xây dựng từ lực hấp dẫn và lực quán tính li tâm do Trái Đất không đứng yên
mà chuyển động tự quay quanh mình nó.
Các giá trị tính toán cho thấy, lực li tâm có giá trị nhỏ hơn rất nhiều giá trị của lực hấp dẫn, vì vậy
trong thực tế thường bỏ qua lực li tâm, khi đó
. Do vậy, khái niệm trọng lực, một cách gần đúng được vận dung như sau.
Khái niệm: Theo nghĩa gần đúng trọng lực là lực hấp dẫn do Trái đất hút vật và định bởi: . Đặc điểm:
- Phương của trọng lực là phương thẳng đứng, chiều hướng về tâm Trái đất - Độ lớn trọng lực
- Điểm đặt: đặt vào vật khảo sát.
Trọng lượng và trọng lực.
Trọng lượng: của một vật thường được xem lực hấp dẫn tác động lên vật thể đó.
Trọng lực: Lực trái đất tác động trên một vật để hút vật về hướng Trái đất.
Trọng lượng của một vật là độ lớn của trọng lực tác dụng lên vật ấy. II. Lực đàn hồi
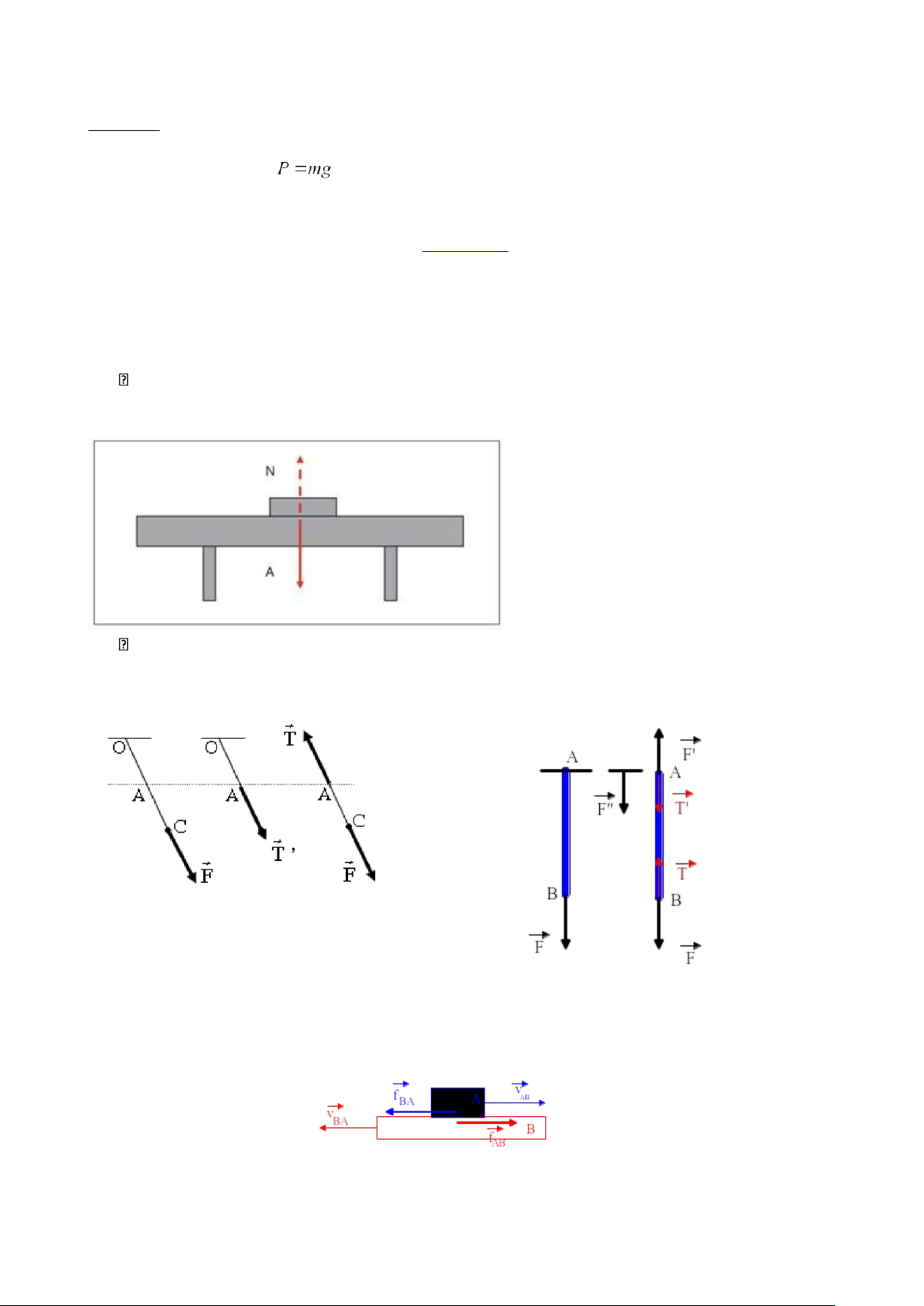
Trong khuôn khổ chương 2 ta chỉ xét một số lực mang tính chất là lực đàn hồi  Phản lực
Khi một vật chuyển động trên một mặt phẳng thì vật này tác dụng lên mặt đó một lực nén. Theo định
luật 3 Newton, mặt phẳng cũng sẽ tác dụng ngược lại vật một lực ⃗N gọi là phản lực.  Lực căng dây
Giả sử có một vật bị buộc vào một sợi dây, giả thiết rằng khi đó dây bị căng. Tại những điểm trên dây
sẽ xuất hiện những lực gọi là lực căng.
Trong các bài toán thông thường, lực căng có cường độ không đổi dọc theo một sợi dây. III. Lực ma sát
Khi vật A tiếp xúc vật B mà giữa chúng có chuyển động tương đối với nhau thì ở mặt tiếp xúc xuất
hiện các lực luôn hướng ngược chiều chuyển động tương đối giữa các vật. Các lực đó gọi là lực ma sát.
Khi hai vật rắn tiếp xúc
nhau,thì lực ma sát gọi là ma sát khô
(bao gồm ma sát trượt, ma
sát nghỉvà ma sát lăn). Khi vật rắn chuyển trong môi trường
lỏng và khí, lựcma sát gọi là ma sát nhớt.
Nguyên nhân chủ yếu sinh ra hiện tượng ma sát là do sự gồ ghề, mấp mô của mặt tiếp xúc và do sự
tương tác giữa các nguyên tử, phân tử ở những vùng tiếp xúc thực sự giữa các vật.  Lực ma sát nghỉ.
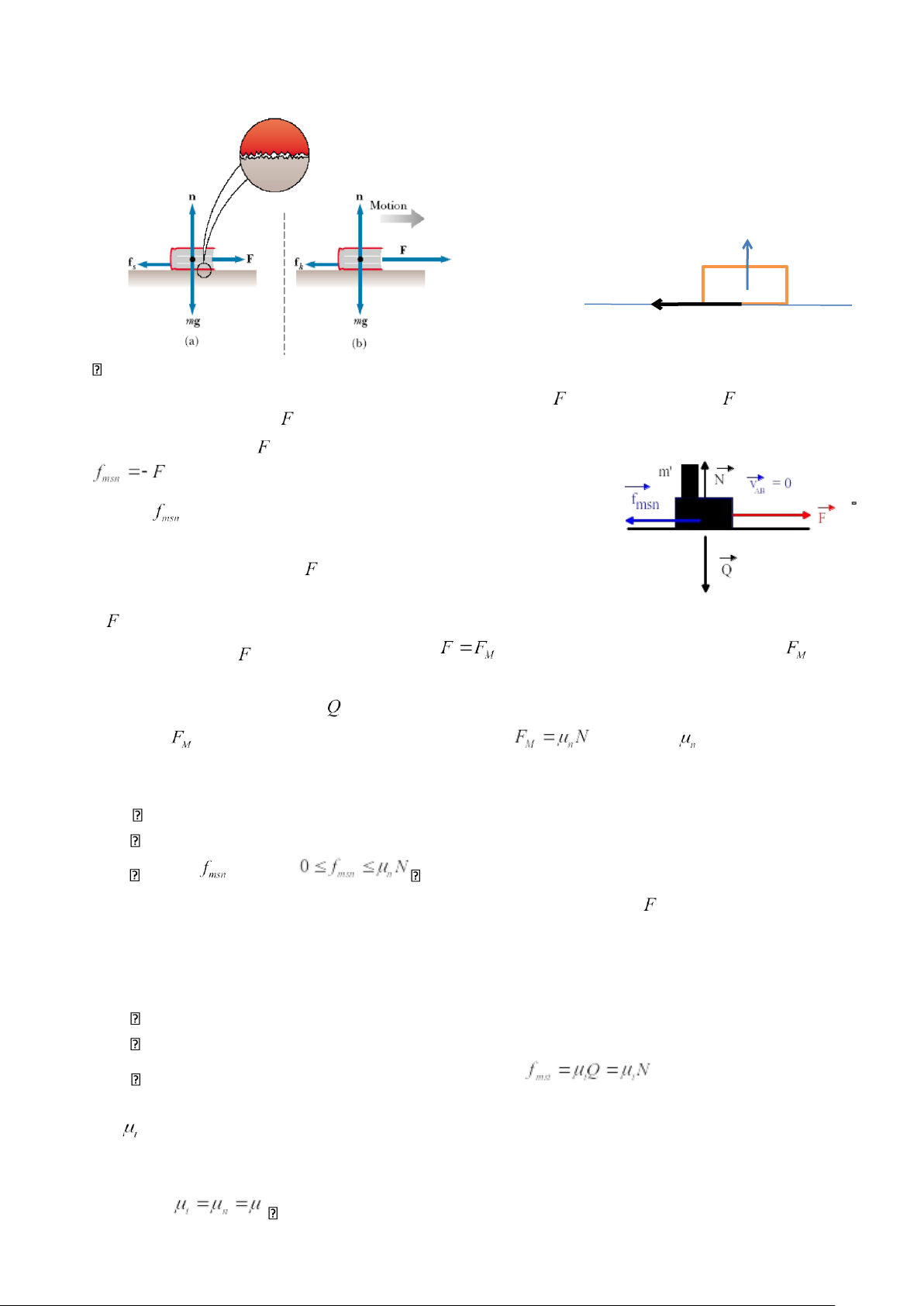
Xét vật A và B tiếp xúc với nhau và B cố định. Tác dụng lực lên vật A, phương luôn tiếp tuyến
mặt tiếp xúc, độ lớn của thay đổi được. Thực nghiệm cho thấy: - Khi độ lớn của nhỏ, vật A vẫn đứng
yên. Điều đó chứng tỏ mặt tiếp xúc tác dụng lên A một lực tiếp tuyến . Lực tiếp tuyến
do mặt tiếp xúc tác dụng lên A lúc này gọi là lực ma sát nghĩ.
- Khi tăng dần độ lớn của , A vẫn đứng yên điều đó chứng tỏ lực
ma sát nghĩ có độ lớn tăng dần và luôn bằng độ lớn của ngoại lực .
- Khi độ lớn của đạt đến giá trị nhất định
thì A bắt đầu trượt trên mặt tiếp xúc. là giá
trị lớn nhất của lực ma sát nghỉ.
- Khi tăng áp lực vuông góc , (chẳng hạn bỏ thêm gia trọng m’ lên vật A), độ lớn cực đại của ma sát nghĩ
tăng. Nhiều kết quả thí nghiệm cho thấy , trong đó là hệ số ma sát nghĩ
phụ thuộc và bản chất của bề mặt tiếp xúc.
Vậy, lực ma sát nghỉ có đặc điểm:
Xuất hiện khi vật này có xu hướng trượt (nhưng chưa trượt) trên mặt tiếp xúc của vật khác.
Phương tiếp tuyến với mặt tiếp xúc, chiều ngược chiều xu hướng trượt của vật trên mặt tiếp xúc. Độ lớn thay đổi, 
Lực ma sát trượt.
Khi vật A đã trượt trên mặt tiếp xúc. Nếu ngừng tác dụng của ngoại lực vật sẽ chuyển động chậm
dần và dừng lại. Điều đó chứng tỏ, khi vật A trượt trên mặt tiếp xúc, mặt tiếp tác dụng lên nó một lực,
cản trở chuyển động tương đối của nó so mặt sàn. Lực này có phương tiếp tuyến mặt tiếp xúc và ngược
hướng với hướng trượt tương đối của vật so mặt tiếp xúc. Nhiều thí nghiệm khác đã cho thấy lực ma
sát trượt có đặc điểm:
Xuất hiện ở mặt tiếp xúc khi vật này trượt tương đối so vật kia.
Phương tiếp tuyến với mặt tiếp xúc, chiều ngược chiều trượt của vật khảo sát
 Độ lớn tỷ lệ với áp lực vuông góc với mặt tiếp xúc (2.11) Chú ý: -
là hệ số ma sát trượt hầu như không phụ thuộc diện tích mặt tiếp xúc mà phụ thuộc tính chất của mặt tiếp xúc.
- Hệ số ma sát trượt thường nhỏ hơn hệ số ma sát nghĩ, nhưng trong một số trường hợp chúngxấp xĩ bằng nhau
 Lực ma sát lăn.
Lực ma sát lăn có các đặc điểm sau: •
Xuất hiện khi vật này lăn trên vật kia. •
Phương tiếp tuyến mặt tiếp xúc, chiều cản trở chuyển động của vật khảo sát •
Độ lớn tỷ lệ với phản lực vuông góc (2.12) •
Hệ số ma sát lăn nhỏ hơn nhiều hệ số ma sát trượt Bài 2.3)
PHƯƠNG TRÌNH CƠ BẢN ĐỘNG LỰC HỌC
 Phương pháp động lực học là phương pháp vận dụng các định luật Newton giải bài toán cơ bản
của động lực học.
Hai bài toán cơ bản của cơ học gồm:
Bài toán thuận. Biết các lực tác dụng lên vật, cần xác định tính chất chuyển động của vật. Các bước tiến
hành để giải bài toán này như sau: - Chọn hệ qui chiếu. -
Chỉ ra các lực tác dụng lên vật và biểu diễn chúng. -
Viết phương trình cơ bản của động lực học
Σ⃗F x=m⃗ax
Σ⃗F y=ma⃗y -
Chiếu xuống các trục tọa độ cần thiết
. Từ đó suy ra phương trình chuyển động.
Bài toán ngược. Biết tính chất chuyển động của vật, xác định các lực tác dụng lên vật. -
Từ tính chất chuyển động, vận dụng công thức động học suy ra gia tốc của vật.
Chỉ ra các lực tác dụng lên vật và biểu diễn chúng.Viết phương trình cơ bản của động lực học
Σ⃗F x=m⃗ax
Σ⃗F y=ma⃗y -
Chiếu xuống các trục tọa độ cần thiết
. Từ đó suy ra các lực tác dụng cần tìm. 
Các ví dụ minh họa
Ví dụ 1: Một người kéo khúc gỗ có dạng hình hộp trượt trên mặt phẳng ngang với lực kéo lập với phương ngang góc . Độ lớn của , khối lượng khúc gỗ , hệ số ma sát giữa vật và mặt phẳng ngang là . a) Sau
thời gian bao lâu vật trượt được quãng đường 48m. b)
Nếu , thì thời gian trên là bao nhiêu.
Các lực tác dụng lên vật như hình vẽ.
Phương trình động lực học: (1)
Chiếu (1) xuống hai trục Ox và Oy,(
do vật chỉ trượt theo phương ngang): . . Thế vào (1) : (3)
Vật chuyển động biến đổi đều theo chiều dương ta chọn nên quãng đường đi định bởi:
Từ điều kiện ban đầu:
. Vậy thời gian cần tìm là: .
Xét hệ qui chiếu Oxy gắn mặt đất , trục Ox trùng hướng chuyển động. a) . Từ (2): . b) Từ (3)
. Nên thời gian cần tìm là
Ví dụ 2: Một vật có khối lượng
dưới tác dụng của lực có hướng lập với phương
ngang góc thì bắt đầu chuyển động nhanh dần đều trên mặt phẳng nằm ngang với độ lớn gia tốc . Lấy
. Hệ số ma sát trượt giữa vật và mặt ngang là
. Xác định độ lớn của nếu: a) α=300, b)α=00 Giải.
Xét hệ qui chiếu Oxy gắn mặt đất , trục Ox trùng hướng chuyển động. Theo đề bài a) .
Các ngoại lực tác dụng lên vật như hình vẽ. . b) Khi đó
Phương trình chuyển động
Chiếu (1) xuống hai trục Ox và Oy có: .
Từ (2) biểu thức lực ma sát . Thế vào (1): Do đó . . và nên .
Ví dụ 3: Cho cơ hệ như hình vẽ . , . Hệ số ma sát giữa và sàn nghiêng là ,
. Bỏ qua khối lượng ròng rọc, dây không dãn, khối lượng không đáng
kể. Tại thời điểm ban đầu vật ở vị trí cao hơn vật một đoạn ..
1. Chỉ ra các lực tác dụng lên các vật. Hệ vật chuyển động theo chiều nào? Tại sao?
2. Tìm gia tốc của các vật và sức căng dây, áp lực lên trục của ròng rọc.
3. Sau bao lâu hai vật có độ cao ngang nhau? Khi đó vận tốc mỗi vật là bao nhiêu? Giải.
1. Các lực tác dụng lên vật như hình vẽ.
Coi hai vật là một hệ thì các ngoại lực tác dụng lên hệ là
và lực ma sát. không gây ra chuyển độngcho vật. Do
vì vậy đi xuống, đi lên Theo đề: 
dây không dãn nên . 
khối lượng dây không đáng kể, và do bỏ quakhối
lượng ròng ròng .
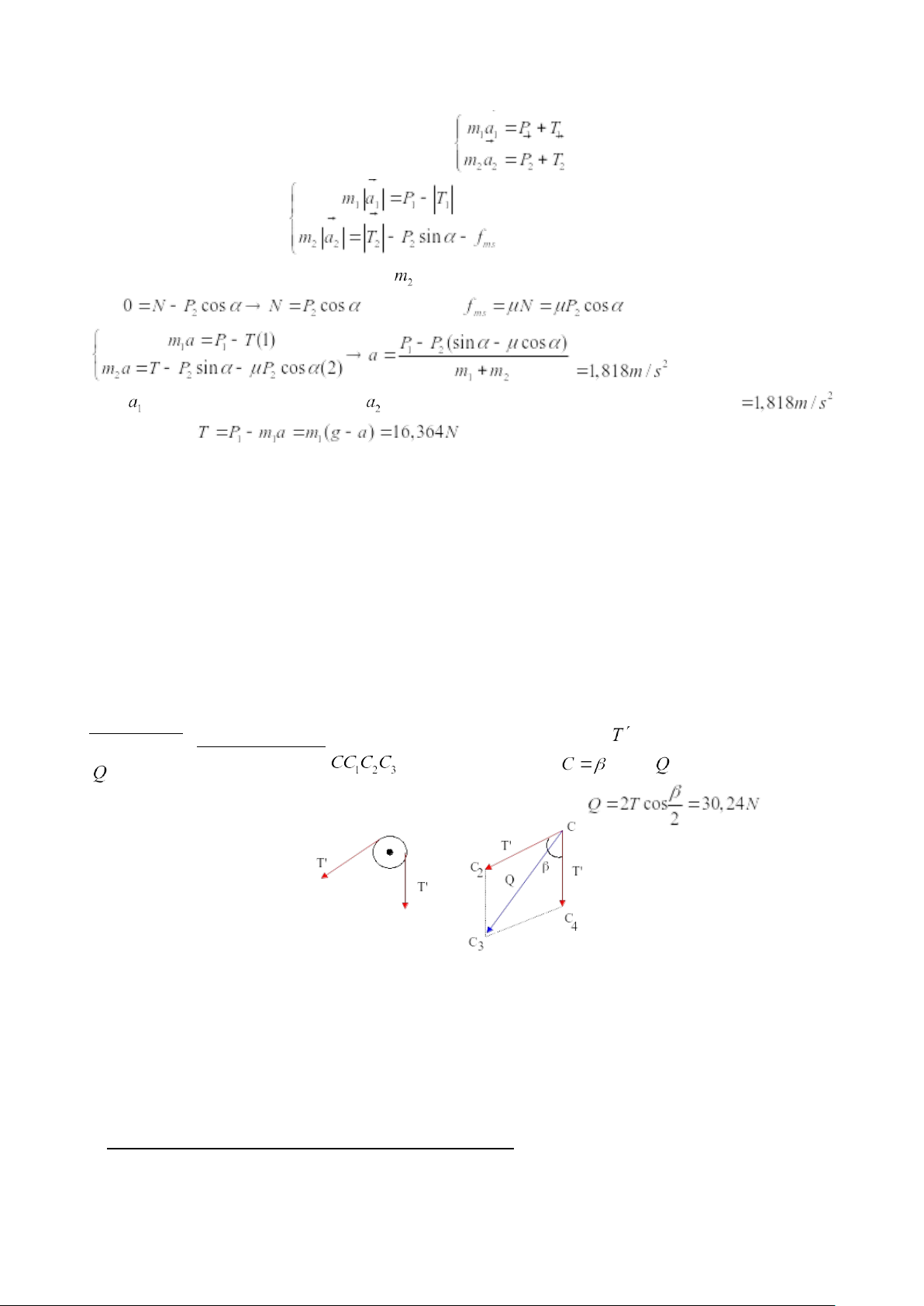
2. Tìm gia tốc, sức căng dây. .
Viết phương trình chuyển động cho mỗi vật:
chuyển động của mỗi vật: ( a).
Lại chiếu phương trình chuyển động của theo phương vuông góc chuyển động; . Nên
Vậy hướng thẳng đứng xuống và hướng lên dọc mặt nghiêng và cùng có độ lớn Từ (1) suy ra:
. Hướng các sức căng dây như hình vẽ.
Chiếu xuống chiều dương là chiều . Thế vào hệ (a). .
Tìm áp lực lên trục ròng rọc . Do tác dụng của các sức căng dây ở hai bên ròng rọc, trục ròng rọc bị là hình thoi với góc
, nên có phương là phân giác nén. Từ hình vẽ, tứ giác của góc C và có độ lớn:
3. Sau bao lâu hai vật ở ngang nhau hai vật ở ngang nhau.
đi được đoạn đường , vật
, do hai vật đều chuyển động theo chiều dương với vận tốc đầu bằng không nên
Khi hai vật ở ngang nhau, vật
đi được đoạn đường . Ta có: .
CHƯƠNG 3: ĐỘNG LỰC HỌC HỆ CHẤT ĐIỂM – ĐỘNG
LỰC HỌC VẬT RẮN. Bài 3.1)
KHỐI TÂM – ĐỊNH LUẬT BẢO TOÀN ĐỘNG LƯỢNG I. Khối tâm
1) Khái niệm khối tâm và ý nghĩa vật lý.
Khối tâm G của hệ là một trong các yếu tố đặc trưng cho sự phân bố khối lượng của vật .
Chuyển động của vật rắn, đặc biệt là chuyển động quay, sự phân bố khối lượng của vật ảnh hưởng khá
lớn chuyển động của vật. (quạt trần khi quay bị đảo, đó là do trục quay không đi qua khối tâm; bánh xe
đạp khi một số nan hoa (căm) gãy bị đảo cũng do nguyên nhân tương tự…)
Trong kĩ thuật việc xác định đúng vị trí khối tâm là đặc biệt quan trọng. Thực nghiệm cho thấy, nếu hệ
có một tâm hay một đường hay một mặt đối xứng thì khối tâm nằm trên tâm, đường hay mặt đó. Trong
trọng trường đều và vì hệ khảo sát chiếm miền không gian không lớn nên vị trí khối tâm trùng với vị
trí trọng tâm (điểm đặt của trọng lực). Tuy nhiên, khái niệm khối tâm luôn tồn tại, còn trọng tâm chỉ
tồn tại trong trường trọng lực. 2) Định nghĩa khối tâm
Khối tâm G được định nghĩa xuất phát từ bài toán tìm điểm đặt (trọng tâm) của hệ hai chất điểm. Xét hai chất điểm
có khối lượng tương ứng
. Gọi ⃗p1, ⃗p2 là trọng lực tác dụng
lên mỗi chất điểm. Giả sử trọng trường là đều thì ⃗p1 // ⃗p2. Gọi G là điểm đặt của tổng hai lực đó thì 2 M1 G M
⃗M1G↑↓⃗M2G . Do hai vector 2 ⃗M P 1G −m1
nên ta có: ⃗M2G = m2 1 P2
Điểm G thỏa mãn hệ thức m1⃗M1G+m2⃗M2G=0 là khối tâm của hệ hai chất điểm. Suy
rộng cho hệ gồm n chất điểm, khối tâm G của hệ là điểm thỏa mãn:
m1⃗M1G+m2⃗M2G+m3⃗M3G+mi⃗M iG…+mn⃗M nG=0 (3.1)
Vậy: khối tâm G của hệ n chất điểm là một điểm thỏa : n
∑ mi⃗M iG=0 (3.2) i=1
3) Công thức xác định vị trí khối tâm đối với một điểm gốc O. 
Hệ chất điểm khối lượng phân bố rời rạc. Xét chất điểm thứ i của hệ, từ hình vẽ ta có
⃗OG=⃗OMi+⃗MiG
Nên miOG⃗=mi⃗OMi+mi⃗M iG (a).
Lấy tổng (a) với n chất điểm n n n
∑ mi⃗OG=∑ mi⃗OM i+∑ mi⃗M iG i=1 i=1 i=1 . n ∑mi⃗OMi
Để ý (3.2) ta có công thức xác định vị trí khối tâm G đối với gốc tọa độ O nào đó là: ⃗OG= i=1 n ∑ mi i=1 n ∑ mi r⃗i hay ⃗R= i=1n ∑mi i=1
Vậy, vị trí khối tâm G của hệ đối với gốc O xác định bởi vector ⃗R=⃗OG thỏa mãn công thức: n ∑ mi r⃗i ⃗R= i=1n (3.3) ∑mi i=1
Trong hệ trục tọa độ Descartes, các thành phần của tọa độ khối tâm là: (3.4) 
Vật rắn khối lượng phân bố liên tục.
Gọi dm là khối lượng chứa trong nguyên tố thể tích dV, khi đó vị trí khối tâm vật rắn định bởi:  1 xG  M vatxdm  1 yG  M vatydm   1
 zG M vatzdm (3.5) hay
Khi khối lượng phân bố đều ta có công thức: