Bài giảng: Đạo hàm và vi phân | Giải tích 1 | Đại học Bách Khoa Hà Nội

PGS. TS. Nguyễn Xuân Thảo thao.nguyenxuan@hust.edu.vn GIẢI TÍCH I BÀI 3
§1.9. ĐẠO HÀM VÀ VI PHÂN  Đặt vấn đề
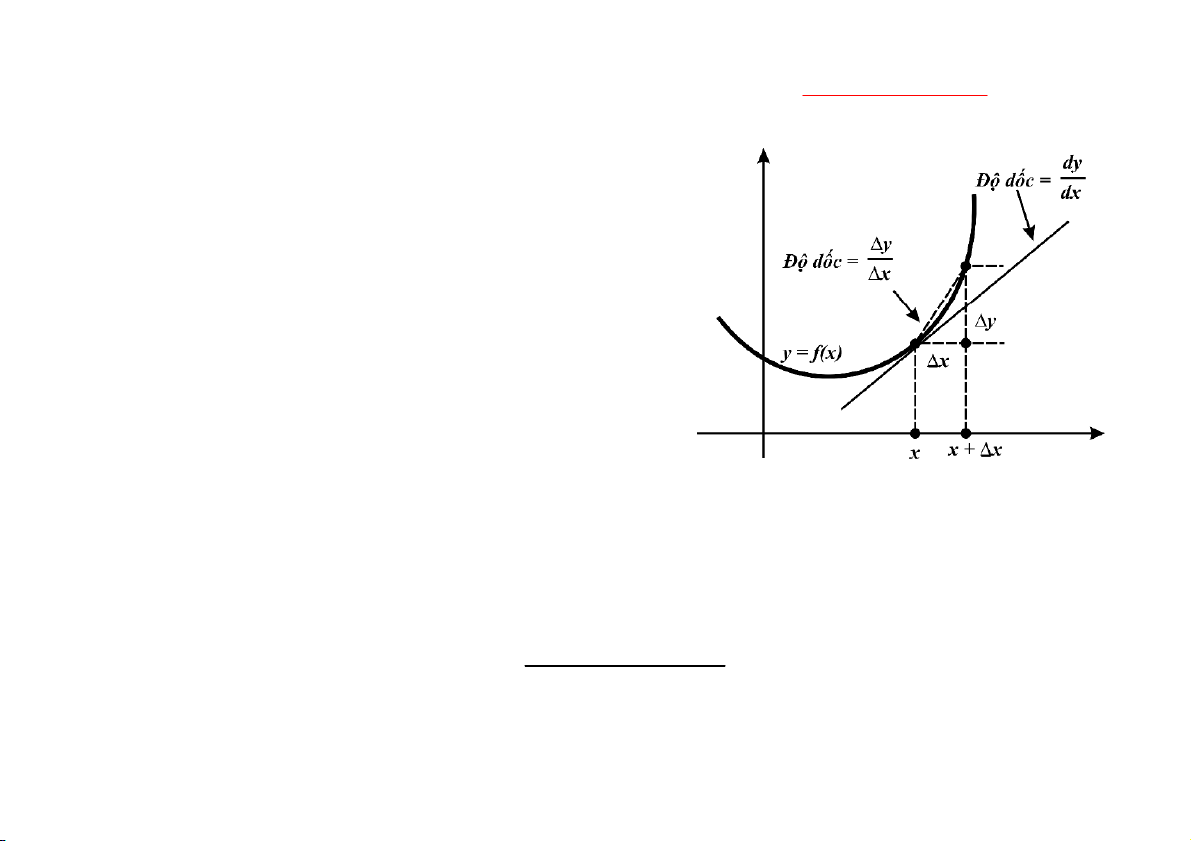
 Bài toán cơ bản của phép tính vi phân là: tính độ dốc của tiếp tuyến
I. Định nghĩa. f(x) xác định trong , f'(x0) = a  U x  0 0 f (x  x)  f (x )   0 0 lim  a x0 x 1
PGS. TS. Nguyễn Xuân Thảo thao.nguyenxuan@hust.edu.vn
Ví dụ 1. y = 2010, tính y' Ví dụ 2. y = x3, tính y' GIẢI 2
PGS. TS. Nguyễn Xuân Thảo thao.nguyenxuan@hust.edu.vn (x  3 x)  3 (x ) +)  y (x )  0 0 lim  0 x 0 x 2 2 3 2 3x x  3x x  x 3x x +)  0 0 lim  0 lim  2 3x0. x 0 x x0 x
Ví dụ 3. y = ax, 0 < a  1, tính y'
Ví dụ 4. y = |x|, xét y'(0), y'(-1) GIẢI 3
PGS. TS. Nguyễn Xuân Thảo thao.nguyenxuan@hust.edu.vn  , x x  0 +) y (x )    y  ( 1)  1.  , x x  0 0  x  0 x +) y (0)  lim  lim x 0 x x0 x  1, x  0    1, x  0
Hàm số không có đạo hàm tại x=0. 4
PGS. TS. Nguyễn Xuân Thảo thao.nguyenxuan@hust.edu.vn a) Ý nghĩa hình học
f'(x0) là hệ số góc của tiếp
tuyến với đồ thị hàm số y = f(x) tại x = x0.
b) Ý nghĩa cơ học. Xét chất điểm M chuyển động
thẳng, không đều với quãng đường là S(t) tính từ
điểm O nào đó. Khi đó vận tốc tức thời tại t0 là S(t )  S(t ) v(t )  0 lim  S 0 (t0) t t0 t  t0 5
PGS. TS. Nguyễn Xuân Thảo thao.nguyenxuan@hust.edu.vn
Ví dụ 5. Một người đi xe máy với vận tốc 30km/h
trong nửa đầu tiên của đoạn đường và 20km/h trong
nửa thứ hai. Hỏi vận tốc trung bình là bao nhiêu?
(26 km/h, 25 km/h; 24 km/h, 23 km/h)
Ví dụ 6. Một tên lửa bắn thẳng lên từ mặt đất với vận
tốc ban đầu v0 m/s và đạt độ cao trong t giây là S = tv0  16t2
a) Tìm vận tốc ở thời điểm t
b) Mất bao lâu để tên lửa đạt tới độ cao tối đa?
c) Tính vận tốc tên lửa khi chạm đất
d) Vận tốc ban đầu là bao nhiêu để tên lửa chạm đất sau khi bắn 15 giây. 6
PGS. TS. Nguyễn Xuân Thảo thao.nguyenxuan@hust.edu.vn
c) Ý nghĩa thực tế. dy là tốc độ biến đổi của y theo dx x.
Ví dụ 7. Cho hình tròn bán kính r, ta có S = r2, ta có
S' = 2r. Như vậy tốc độ biến đổi diện tích của một
hình tròn theo bán kính chính bằng chu vi của nó.
Ví dụ 8. Một cái thang dài 13ft đứng dựa vào bức
tường thì chân thang bị trượt ra xa bức tường với tốc
độ không đổi 6ft/s. Đầu trên của chiếc thang chuyển
động xuống dưới nhanh như thế nào khi chân thang cách tường 5ft ? 7
PGS. TS. Nguyễn Xuân Thảo thao.nguyenxuan@hust.edu.vn
Ví dụ 9. Người ta hút dầu ra khỏi thùng để làm sạch
nó. Biết sau khi hút t phút lượng dầu còn lại trong
thùng là V = 40(50  t)2 lít.
a) Tìm lượng dầu hút trung bình trong 20 phút đầu tiên. 2  2 40.50 40.30 (v   3200 (l/p)) tb 20
b) Tìm tốc độ dầu được hút ra khỏi thùng tại thời điểm t = 20 phút. (v 20  2 (40.50  v )  20 2400 (l/p)) t 8
PGS. TS. Nguyễn Xuân Thảo thao.nguyenxuan@hust.edu.vn
Ví dụ 10. Một cái thùng hình nón với đỉnh ở phía dưới
có chiều cao 12 ft và đường kính đáy là 12ft được
bơm đầy nước với tốc độ không đổi là 4ft3/phút. Hãy
tính tốc độ biến đổi chiều cao cột nước khi 1
a) nước sâu 2ft (y 2  )  1
b) nước sâu 8ft. (y8  ) 1  6 Ví dụ 11 a)(K57). Chứng minh rằng: 2 1) 2arctan  arcsin x x  ,  x  1 1 2 x 9
PGS. TS. Nguyễn Xuân Thảo thao.nguyenxuan@hust.edu.vn 2x 5 2)  2arccot x  arccos  ,  x  1 1 2 x 2  1 xar cot x  0
b)(K58)Tính f (x), biết : f (x)   2 x  0 x  0  2 1 2 ar cot  x x  0 (f (x)   2 x 1 4 x )   0 x  0 10
PGS. TS. Nguyễn Xuân Thảo thao.nguyenxuan@hust.edu.vn
c)(K59) 1) CMR : Phương trình 5 x  sinx  2x  2 có duy nhất nghiệm thực.  2   2)Tính x
f (0), biết f (x)  3x  e x  0 , (3)  0 x  0 GIẢI 11
PGS. TS. Nguyễn Xuân Thảo thao.nguyenxuan@hust.edu.vn 2    x   3x  e  0 1 +) (0)  lim  lim x f  3    3 x x  0 x   x e 2 0 0 1      +) f (0)  3.
d)(K64) 1) Không khí được bơm vào một quả bóng
bay hình cầu với tốc độ 3 100cm / . s Tính tốc độ tăng
lên của bán kính quả bóng, khi bán kính quả bóng 1 bằng 50 cm. ( m / s ) 10  0 GIẢI 12
PGS. TS. Nguyễn Xuân Thảo thao.nguyenxuan@hust.edu.vn 4 +)  dV dR V  3 R    2 4 R 3 dt dt dR 1 dV 1 1 +)   100  m / . s 2 2 dt  4 R dt  4 (50) 10  0 2
2) Tính đạo hàm của  arctan x y ,x  1. 1 2 x 2 ( ) 1 2 x
2. Đạo hàm một phía, mối liên hệ với liên tục, đạo hàm của hàm ngược. a) Đạo hàm một phía. Định nghĩa. 13
PGS. TS. Nguyễn Xuân Thảo thao.nguyenxuan@hust.edu.vn f x x f x f x  0         0 0 0 lim ; x 0 x  f x x f x f x  0         0 0 0 lim x0 x
Nhận xét.  f'(x0)  f'(x0 + 0) = f'(x0  0)
Ví dụ 1. a) y  1 x , xét y'(1 0) b(K60) y   2
1 x , tính các đạo hàm phải, trái tại điểm 1 (2; -2; 2; -2)  1  
c(K61) Tính f (0), biết f (x)  x e x   0. (0)  0 x   0 14
PGS. TS. Nguyễn Xuân Thảo thao.nguyenxuan@hust.edu.vn  x arctan 3x x  0
d(K64) Cho hàm số f (x)   .  x ae  bsin x x   3 0
Tìm a, b để f (x) khả vi tại x=0. (a  0;b  3 ) GIẢI 15
PGS. TS. Nguyễn Xuân Thảo thao.nguyenxuan@hust.edu.vn
+) f (x) khả vi tại x=0, nên f(x) liên tục tại x=0, do đó  
f (0 )  f (0 )  f (0)  lim ( x arctan 3x )  3 lim ( x ae  b sin x)  0   x 0 x0  0  . a
+) f (x) khả vi tại x=0  f(0)  f (0) x arctan 3x  0 b sin x  0  lim  lim   x 0 x  0 x 0 x  0  3  . b
Do đó f(x) khả vi x=0 khi a  0;b  3. 16
PGS. TS. Nguyễn Xuân Thảo thao.nguyenxuan@hust.edu.vn
b) Liên hệ đạo hàm và liên tục.
 f'(x0)  f(x) liên tục tại x0.
Ngược lại không đúng, ví dụ  3 y x liên tục tại x0 = 0 nhưng  f'(0).
c) Đạo hàm của hàm số ngược
+) Hàm số x = (y) có hàm ngược y = f(x)
+) y = f(x) liên tục tại x0 = (y0) +) '(y0)  0 1
Khi đó ta có f x0  . y0 
Ví dụ 2. y = arccot x, tính y'. 17
PGS. TS. Nguyễn Xuân Thảo thao.nguyenxuan@hust.edu.vn GIẢI 1
+) y = arccot x liên tục và x=coty có x    0 2 sin y 1 1 1 +) y(x)    2 sin y     . x(y ) 1 2 cot y 1 2 x
Ví dụ 3. a) y = arcsin x, tính y'.
b) (K58) 1. Cho các hàm f, g khả vi ; g là hàm ngược 1 của f. Đặt G(x) 
. Tính G(2) , biết f(3)=2, g  x  1 f (3)  1 ( ) 9 18
PGS. TS. Nguyễn Xuân Thảo thao.nguyenxuan@hust.edu.vn
2. Cho các hàm f, g khả vi ; g là hàm ngược của f. Đặt  ( ) ( ) g x G x e
. Tính G(2), biết f(3)=2, f (3)  1 ( 3 e )
3. Cho các hàm f, g khả vi ; biết f (g(x))  x, f  x   2 ( ) 1 (f (x )) . Tính ( g x) (arctanx+C) GIẢI 2) 19
PGS. TS. Nguyễn Xuân Thảo thao.nguyenxuan@hust.edu.vn +)  G  g g(2) e  g 3 (2) (2) (2)e 1 +) g(2)   1 G(2)  3 e . f (3)
c(K59) Chứng minh rằng hàm số f x  x   2 ( ) 2
2 ln(x  1) có hàm số ngược  1 g x  1
( ) f (x ). Tính g(2). ( ) 2 20
PGS. TS. Nguyễn Xuân Thảo thao.nguyenxuan@hust.edu.vn d(K64) Hàm số f x  3
( ) x  x có hàm số ngược 1
y  g(x). Tính g(2). ( ) 4 GIẢI 21
PGS. TS. Nguyễn Xuân Thảo thao.nguyenxuan@hust.edu.vn +) f (1)  2; f (1)  4  0. 1 1 +)  g(2)   . f (1) 4
3. Phép toán và công thức.
a) Phép toán. Các hàm f, g khả vi tại x0 
 (f  g)'(x0) = f'(x0)  g'(x0)
 (f.g)'(x0) = f'(x0)g(x0) + f(x0)g'(x0)   f  f  x g x  g x f x  x0  0  0  0  0    , g(x0)  0.  g  2 g  x0  22
PGS. TS. Nguyễn Xuân Thảo thao.nguyenxuan@hust.edu.vn
b) Đạo hàm các hàm sơ cấp cơ bản.
Ta dẫn ra công thức của một vài hàm
 c' = 0  (x)' = x  1 1
 (ax)’ = ax lna  log a x   x lna 1 1  tan x    arccos x   2 cos x 1 2 x 1  arccot x    1 2 x 23
PGS. TS. Nguyễn Xuân Thảo thao.nguyenxuan@hust.edu.vn
Ví dụ 1 (K52). Tìm k để hàm số f x  liên tục tại x = 0   arcsinxk 1  cos , x  0 a) f x    x (k > 2) 0, x  0   k 1  arctan x  sin , x  0 b) f x    x (k > 2) 0, x   0 GIẢI a) 24
PGS. TS. Nguyễn Xuân Thảo thao.nguyenxuan@hust.edu.vn +) x  0  k 1 f   x  (arcsin x) 1 1 1  k cos  (arcsinx )k  ( )  ( sin ) 1 2 2 x x x x k 1 (arcsin x) 1 1 1  k cos  (arcsin x)k sin 1 2 2 x x x x 2 1 k x 1 1  (arcsin x) [k cos  sin ] 2 x 1 2 x arcsin x x x 25
PGS. TS. Nguyễn Xuân Thảo thao.nguyenxuan@hust.edu.vn +) f (x )  f (0) arcsink x 1 f (0)  lim  lim cos  0  k  1. x0 x  0 x0 x x 1
+) lim f( x)  f(0)  lim
(arcsin x)k  0  k  2. x  x  2 0 0 x
Ví dụ 2 (K57). Tính f (0), ở đó 1 1 4 2  x cos x , x 0 f (x) 4 (0) x ln 2 1 2x       0, x  0 26
PGS. TS. Nguyễn Xuân Thảo thao.nguyenxuan@hust.edu.vn
c) Đạo hàm của hàm hợp. dy(u) du(x)  (u ), (x )  0 0
y = y(u(x)) có đạo hàm tại du dx x0 và có dy(u(x)) dy (u) du(x) (x )  (u )  0 0 ( 0 x ). dx du dx
Ví dụ 1. y = (x  1)(x  2) ... (x  2009), tính y'(1). (2008!) 2  x, x  2  Ví dụ 2. y  
 2  x  x  3, 2  x  3, tính y'. x  3, x   3 27
PGS. TS. Nguyễn Xuân Thảo thao.nguyenxuan@hust.edu.vn 1, x  2 
( 2x  1,  2  x  3)  1, x  3
Ví dụ 3. y = xx, x>0, tính y'. GIẢI 28
PGS. TS. Nguyễn Xuân Thảo thao.nguyenxuan@hust.edu.vn +)  xln ( ) x  ( )  u f x e f x e ,u  x ln . x df (x) df (u) du(x) +)    u e (1 ln x) dx du dx  x lnx (1 ln )  x e x x (1 ln x).
Ví dụ 4. Chứng minh rằng:
- Đạo hàm của hàm chẵn là hàm lẻ (K58) GIẢI 29
PGS. TS. Nguyễn Xuân Thảo thao.nguyenxuan@hust.edu.vn +) Do f chẵn, nên có
( )  ( ),  d ( )  d f x f x x f x f (x) dx dx d d df (x) +) f (x ) (x) 
 f (x )  f (x ) d(x) dx dx  f (x) là hàm lẻ.
- Đạo hàm của hàm lẻ là hàm chẵn (K58)
- Đạo hàm của hàm tuần hoàn là hàm tuần hoàn có cùng chu kì x Ví dụ 5. y = x x , tính y’. 30
PGS. TS. Nguyễn Xuân Thảo thao.nguyenxuan@hust.edu.vn
Ví dụ 6 (K53). Chứng minh rằng
a) 3arctan x  arctan( x  2)  4arctan( x 1), x  0
b) 2arccot x  arccot(x  2)  3arccot(x  1), x  0 GIẢI a) 31
PGS. TS. Nguyễn Xuân Thảo thao.nguyenxuan@hust.edu.vn
+) arctan(x  2)  3arctan( x 1)  arctan(x 1) 3arctan x (1)
+) f(t)  arctan(t 1)  3arctan ,t t [ ; x x  1], x  0  1 3  1 1  f  2 (t )        1 (t  2 1) 1 2 t  1 (t  2 1) 1 2 t  1 2 t
 0,t  0  f (t) nghịch biến trên [x;x+1], do đó
f (x  1)  f ( x)  (1). Ví dụ 7 (K50). 2
a) CMR arctanx4  arctany4  ln x ,  x, y: x  y > 0. 2 y 32
PGS. TS. Nguyễn Xuân Thảo thao.nguyenxuan@hust.edu.vn 2
b) CMR arccotx4  arccoty4  ln y ,  x, y: x  y > 0. 2 x
Ví dụ 8 (K56). CMR f(x) liên tục với mọi x.   2 1 x arccot , x  0 a)f (x)   x 0, x  0   2 1 x arctan , x  0 b)f (x)   x 0, x  0 33
PGS. TS. Nguyễn Xuân Thảo thao.nguyenxuan@hust.edu.vn    3 1 x sin , x  0  3 1 x cos , x  0 c)f (x)   x d)f (x)   x 0, x  0 0, x  0 4. Vi phân
a) Định nghĩa. f(x) xác định trong U , nếu có  x  0 0
f (x )  Ax  ( 0
x ), ở đó A chỉ phụ thuộc vào x0
chứ không phụ thuộc vào x, (x) là VCB cấp cao
hơn so với x thì ta nói f(x) khả vi tại x0 và có df (x )   0 A . x
Ví dụ 1. y = 2x + 3, tính dy. GIẢI 34
PGS. TS. Nguyễn Xuân Thảo thao.nguyenxuan@hust.edu.vn
+) y(x)  y(x  x)  y(x)  [2(x  x)  3]  [2x  3]
+)  2x  0  x  A  2 
, (x )  0  x  dy   2 x.
b) Ý nghĩa hình học. Nếu A  0 thì f (x )  df (x ).
Nhận xét Ax là tuyến tính đối với x nên nó đơn giản hơn f nhiều.
c) Ứng dụng tính gần đúng.
f(x0 + x)  f(x0) + df(x0).
Ví dụ 2. 1) Tính gần đúng 4,01. 35
PGS. TS. Nguyễn Xuân Thảo thao.nguyenxuan@hust.edu.vn 2  0,06 2)(K59) Tính gần đúng 3 . (1,02) 2  0,06
3)(K64) Tính gần đúng 3 7,988. (1,999) GIẢI 36
PGS. TS. Nguyễn Xuân Thảo thao.nguyenxuan@hust.edu.vn
+) f( x)  3 x, x  8, x  0,012  0
3 7,988  f (x  x)  f (x )  f (x  0 0 0 ) . x 1 1 1
+) f( x )  3 8  2,f (x )    0 0 2 3 3 x 8 12 x 3 1 7,988  2   (0,012)  1,999. 12 37
PGS. TS. Nguyễn Xuân Thảo thao.nguyenxuan@hust.edu.vn
Ví dụ 3. Một mảnh kim loại hình vuông, mỗi cạnh
20cm, khi nung nóng mỗi cạnh dãn ra 0,1cm. Tính
gần đúng phần diện tích mảnh kim loại dãn ra.
d) Liên hệ giữa đạo hàm và khả vi
f'(x0) = A  df(x0) = Ax. Ví dụ 4. d  6 x  4 3x   d  1 2 x   x d e  Ví dụ 5. d  3 x     x  GIẢI 38
PGS. TS. Nguyễn Xuân Thảo thao.nguyenxuan@hust.edu.vn  x   x  1  x d e d e d e  +) d  3 x           x  2 3x dx  x  2 3x dx  x  1 x  x x e x e e (x  1) +)   ,x  0. 2 2 4 3x x 3x
e) Tính bất biến của vi phân cấp 1
y = f(x) khả vi, x = (t) khả vi  dy = f'(x)dx.
5. Đạo hàm và vi phân cấp cao a) Đạo hàm cấp cao.
Định nghĩa. f(n)(x) = (f(n  1)(x))' , n  2. Ví dụ 1. 39
PGS. TS. Nguyễn Xuân Thảo thao.nguyenxuan@hust.edu.vn  y = x, (n)    ( 1)...     (  1) n y n x ,  .  n       y = sinx, y  sin  x  n   2  n       y = cosx, y  o c s  x  n   2 
Quy tắc.  f(n)(x), g(n)(x) thì có
1) (f(x)  g(x))(n) = f(n)(x)  g(n)(x) n
2) f  x.g  xn k k   C f x  nk g  x  n k0 (Quy tắc Leibnitz). 40
PGS. TS. Nguyễn Xuân Thảo thao.nguyenxuan@hust.edu.vn
Ví dụ 2. y = x lnx, tính y(5)
Ví dụ 3. y = sinax cosbx, tính y(20)
Ví dụ 4. y = x2 cosx, tính y(30) 1 Ví dụ 5. y  , tính y(n) 2 x  1
Ví dụ 6 a)(K50). Tính y(n),   n 1 2 1)  x n  y (  2 2 x e n 1 2x) 2 x e n  n  1 2 !3 2) y  x ln(1 3x) ( 3x  n) 1 3xn GIẢI 1) 41
PGS. TS. Nguyễn Xuân Thảo thao.nguyenxuan@hust.edu.vn +) 2x (k ) k        2 ( ) 1 2 , ( ) ( ) ( 2) x f x x g x e g x e , 1 2x, k  0 (k)  f (x)   2, k  1   0, k   2 n (n) k (k ) (n  f (x)   k ) C f (x)g (x) n k 0 1 k (k ) (n   k ) C f (x)g (x) n k 0 +) 0 n 2x 1 n1   C  x  e  C   2 (1 2 )( 2) ( 2)( 2) x n n e 42
PGS. TS. Nguyễn Xuân Thảo thao.nguyenxuan@hust.edu.vn n 2x n 2x n         2 (1 2 )( 2) ( 2) ( 2) x x e n e e (n 1  2x). 1 (50) b (K63) Cho f ( x)  . 2 Tính y (x). x  2x  1 51! ( ,x  1) (x  52 1) GIẢI 43
PGS. TS. Nguyễn Xuân Thảo thao.nguyenxuan@hust.edu.vn 1 +)f (x)  , (x  2 1) ( 50 (50) 1)  51! 51! +)f (x)   , x  1. (x  52 1) (x  52 1) HAVE A GOOD UNDERSTANDING! 44