





Preview text:
CHÀO MỪNG CÁC EM
ĐẾN VỚI BÀI HỌC HÔM NAY! KHỞI ĐỘNG
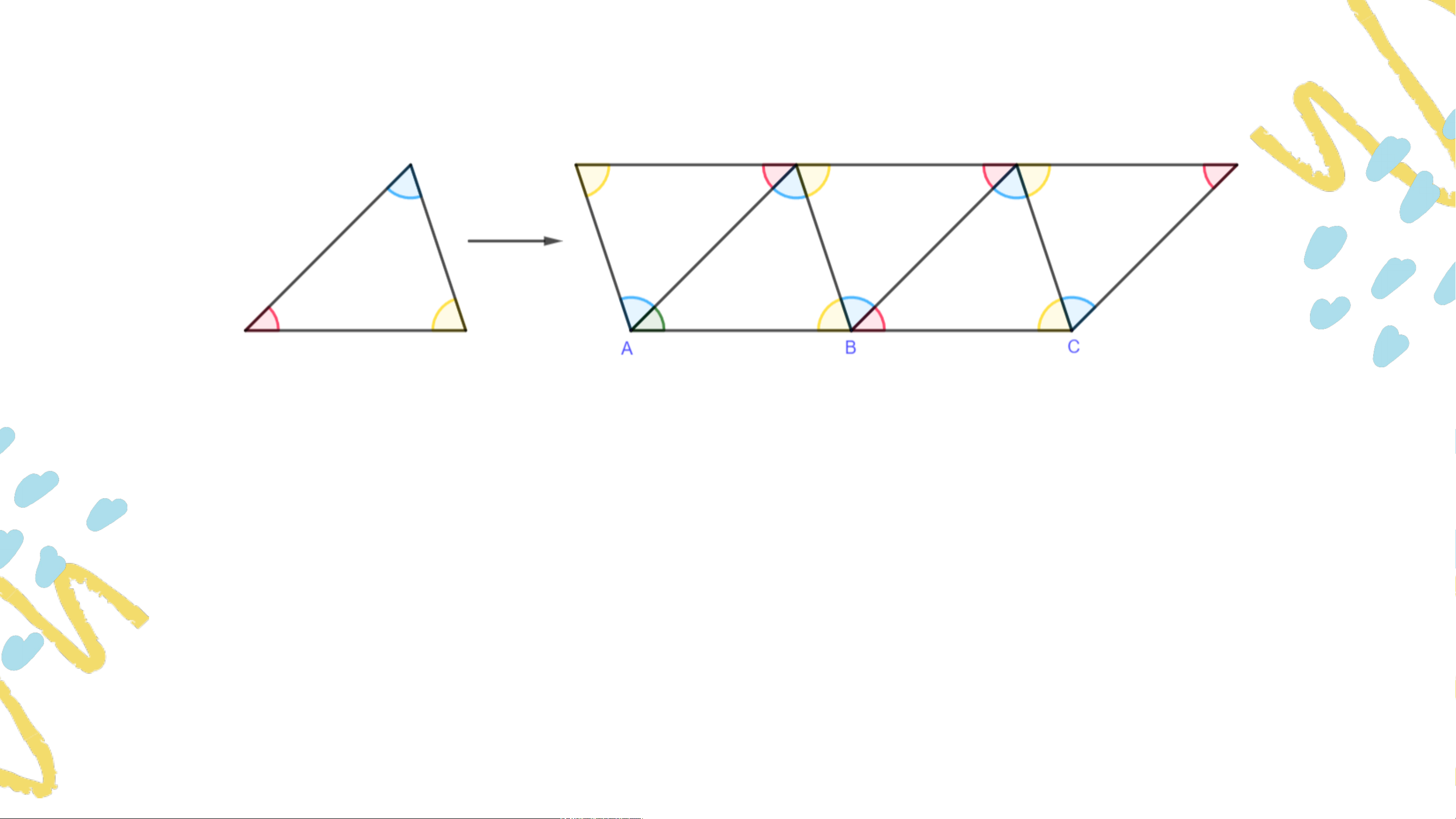
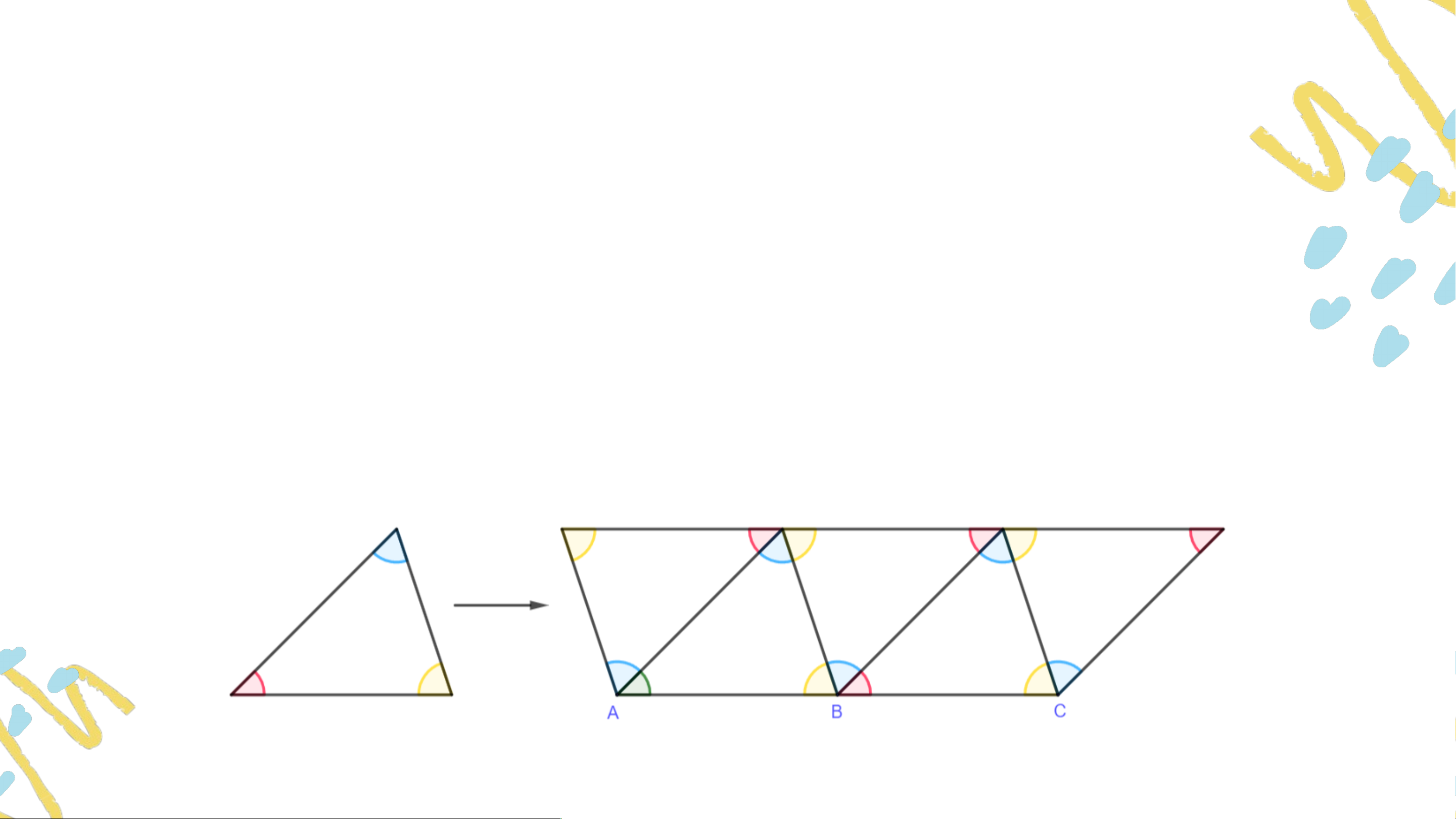
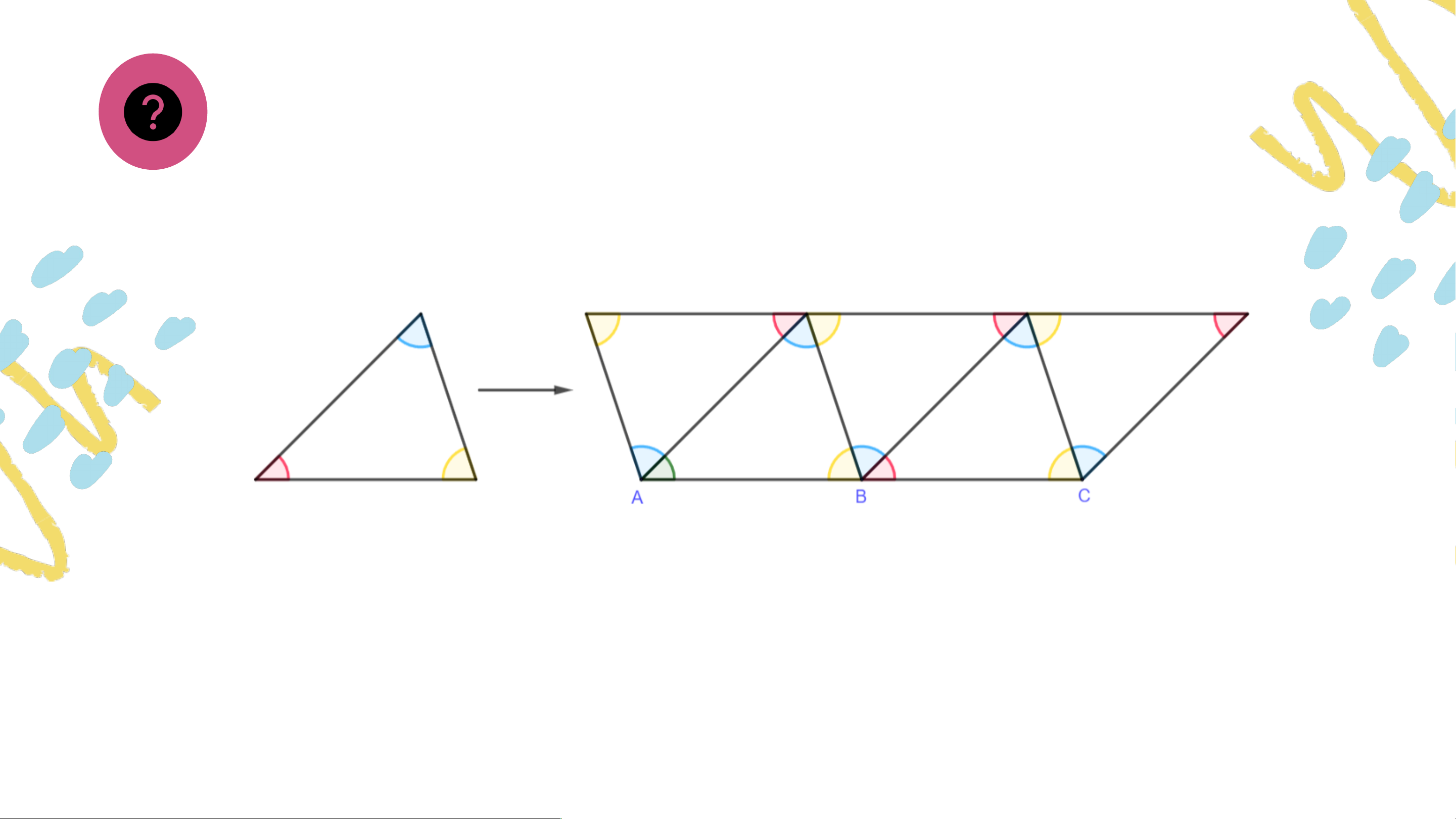
• Người ta có thể xếp các viên gạch hình tam giác giống hệt nhau để trang trí.
• Em có nhận xét gì về ba góc tại mỗi đỉnh chung của ba tam giác?
• Từ đó em rút ra kết luận gì về vị trí của ba điểm ? Trả lời:
- Tổng ba góc tại mỗi đỉnh chung của ba tam giác bằng 180 độ. - Ba điểm thẳng hàng. CHƯƠNG IV. TAM GIÁC BẰNG NHAU
BÀI 12: TỔNG CÁC GÓC TRONG MỘT TAM GIÁC NỘI DUNG BÀI HỌC
01 Tổng các góc trong một tam giác.
02 Góc ngoài của tam giác.
1. Tổng các góc trong một tam giác
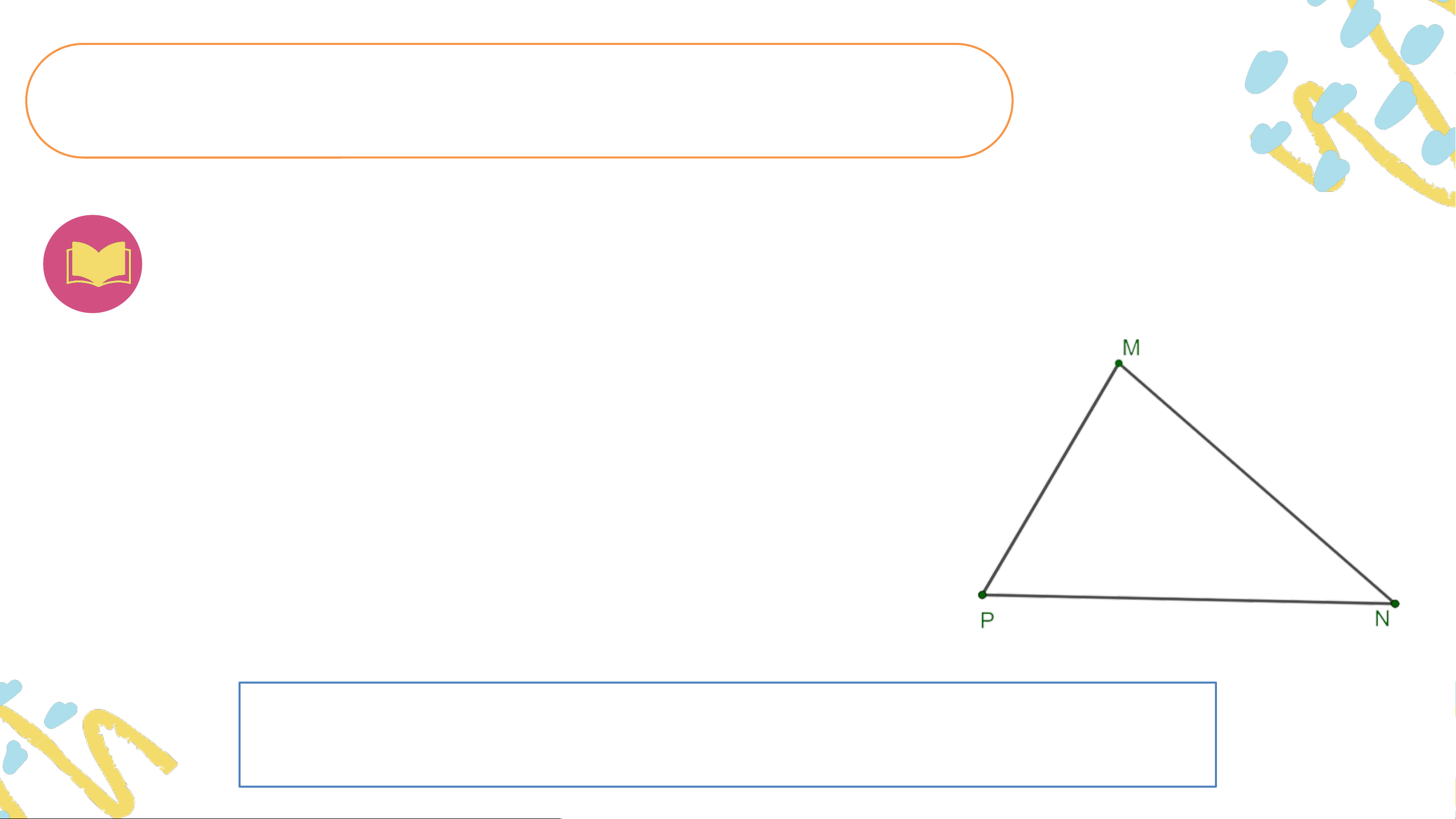
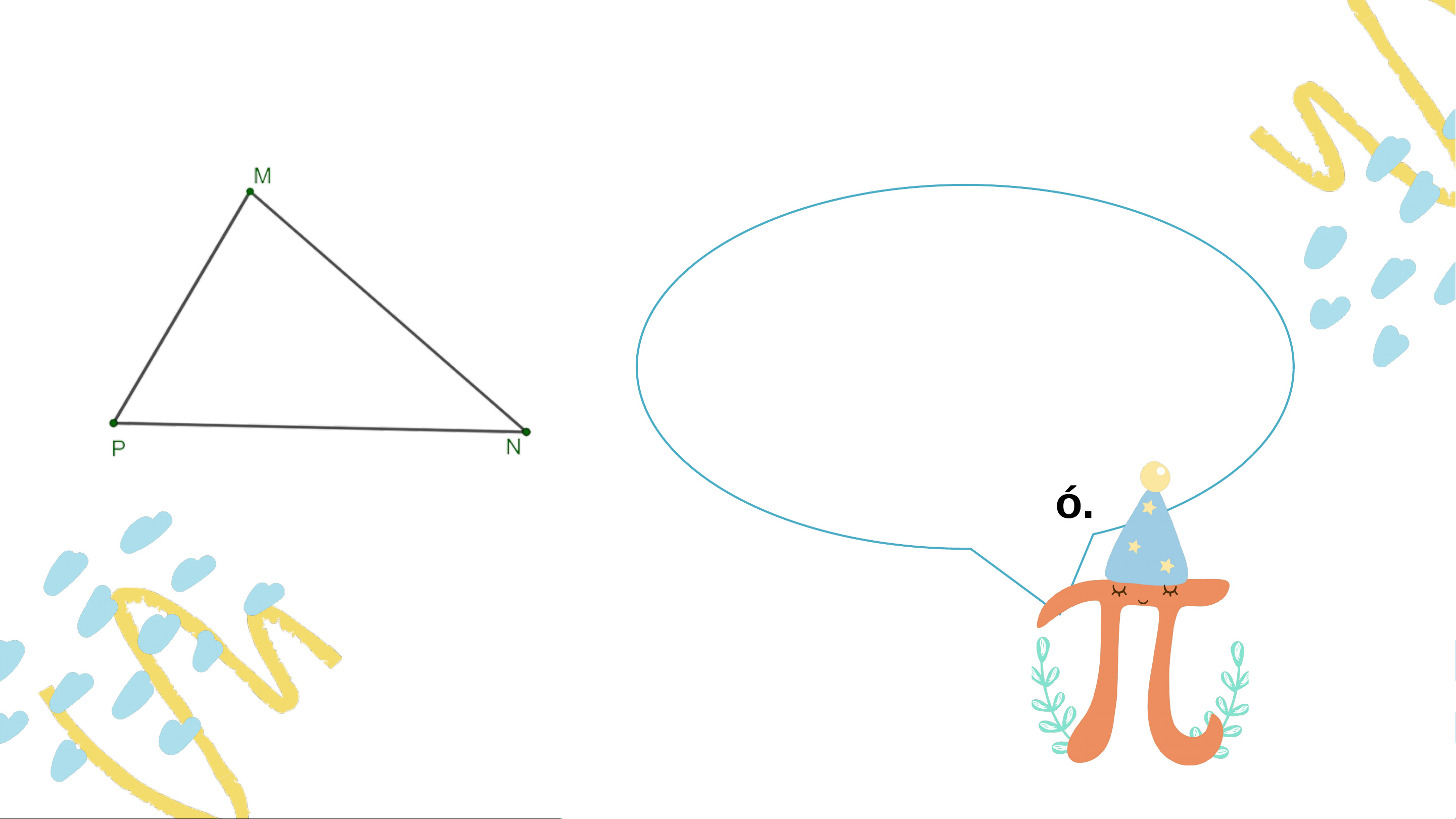
HĐ1. Vẽ tam giác bất kì, đo ba góc của tam giác đó.
- Tổng số đo 3 góc của tam giác bằng bao nhiêu?
- So sánh kết quả của em với các bạn và rút ra nhận xét.
Tổng số đo 3 góc của tam giác bằng HĐ2.
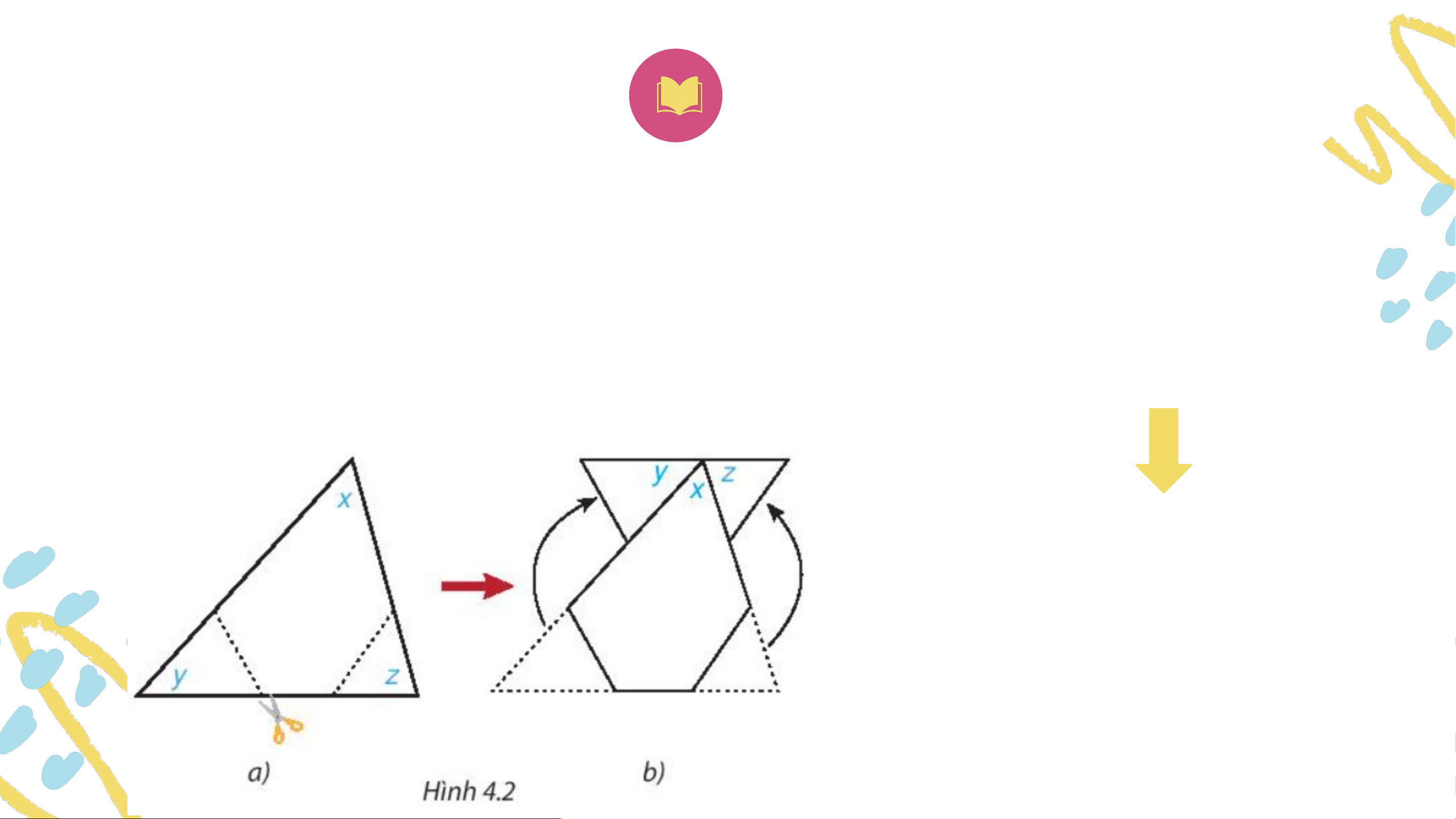
- Cắt một hình tam giác bằng giấy bất kì. Đánh dấu 3 góc là .
- Cắt hai góc và ghép lên góc như hình vẽ. Từ đó, em hãy dự
đoạn tổng số đo các góc của tam giác ban đầu. Tổng số đo các góc của tam giác ban đầu là . Đị Đ nh l n í: í: Tổng 3 Tổ ng 3 góc tro g ng một ta óc tro m ng một ta gi g ác á bằng c bằng . GT KL
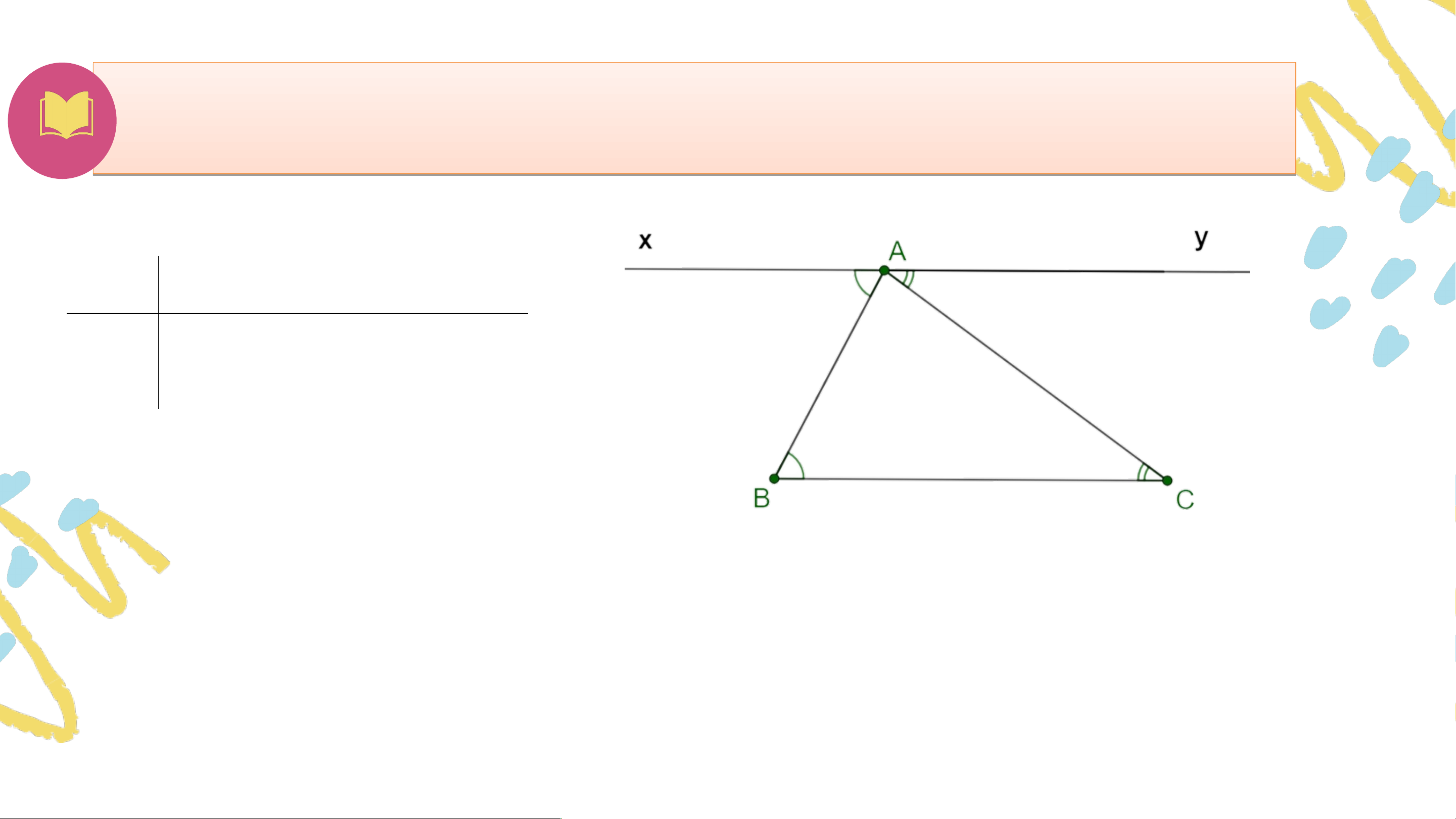
Qua kẻ đường thẳng song song với . (các cặp góc so le trong) Do đó . Tổng 3 góc trong
một tam giác là tổng số đo 3 góc trong tam giác đó.
Tổng 3 góc tại mỗi đỉnh chung của 3 tam giác
(chẳng hạn tại ) bằng bao nhiêu độ? Ba điểm có thẳng hàng không? Trả lời:
Tổng 3 góc tại mỗi đỉnh chung của 3 tam giác bằng . Ba điểm thẳng hàng. Ví dụ
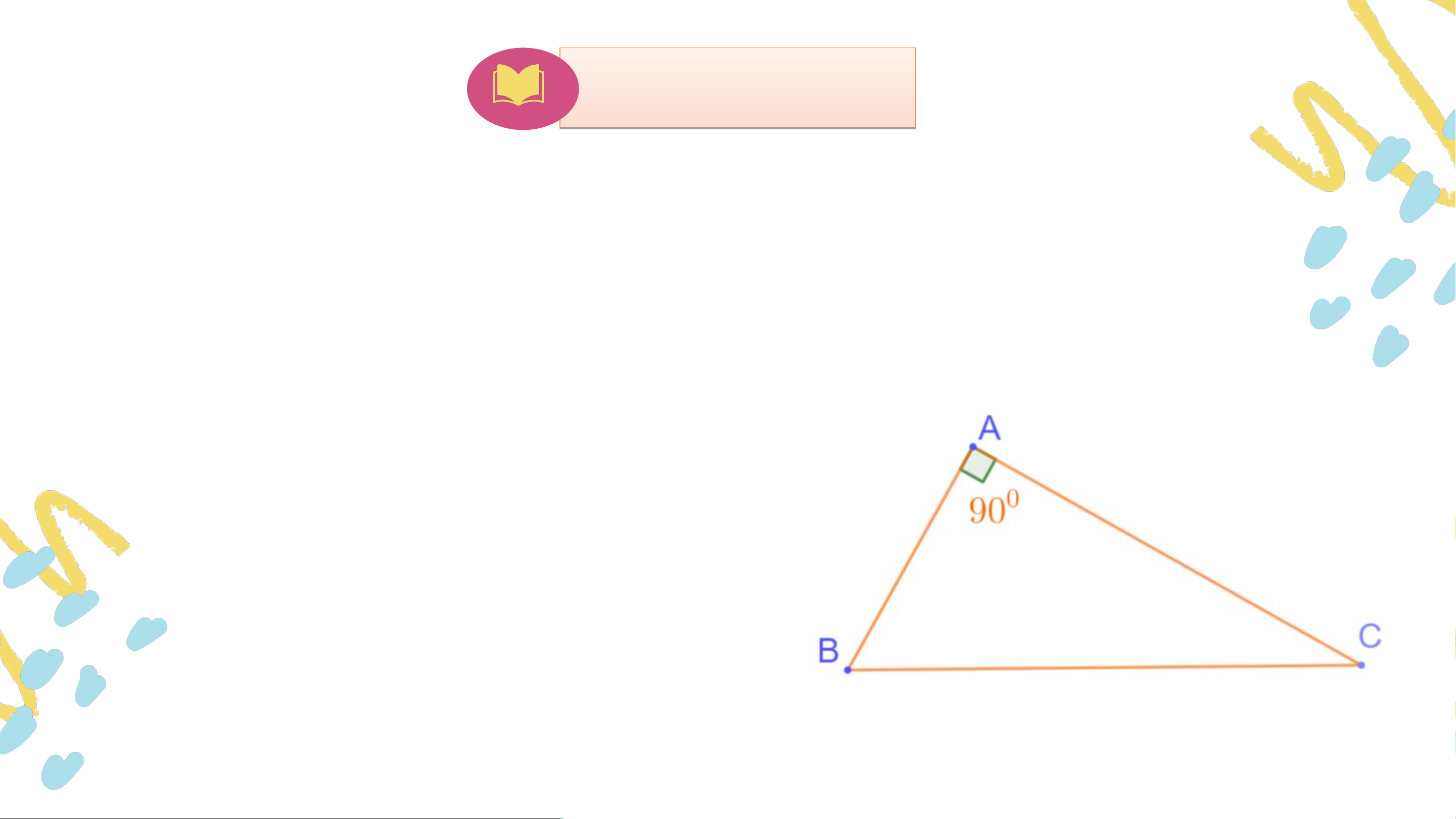
Tính số đo các góc trong hình sau. Giải Trong tam giác ta có: Do đó: . Trong tam giác ta có: Do đó, . Trong tam giác ta có: Do đó, . Chú ý:
Tam giác có 3 góc đều nhọn là tam giác nhọn.
Tam giác có 1 góc tù là tam giác tù.
Tam giác có 1 góc vuông là tam giác vuông. LUY L ỆN TẬP.
Cho tam giác vuông tại . Tính tổng hai góc và . Giải Xét tam giác ta có: Nhận xét Hai Ha góc gó có tổng tổn g bằ b ng ằ ng gọ g i ọ là hai h gó g c ó phụ p nh hụ au nh . au Vậy tron tro g n tam ta giác g iác vuô u ng ô , ng hai ha góc gó nhọ n n họ n phụ p nh hụ au nh . au
2. Góc ngoài của một tam giác VẬN DỤNG ẬN .
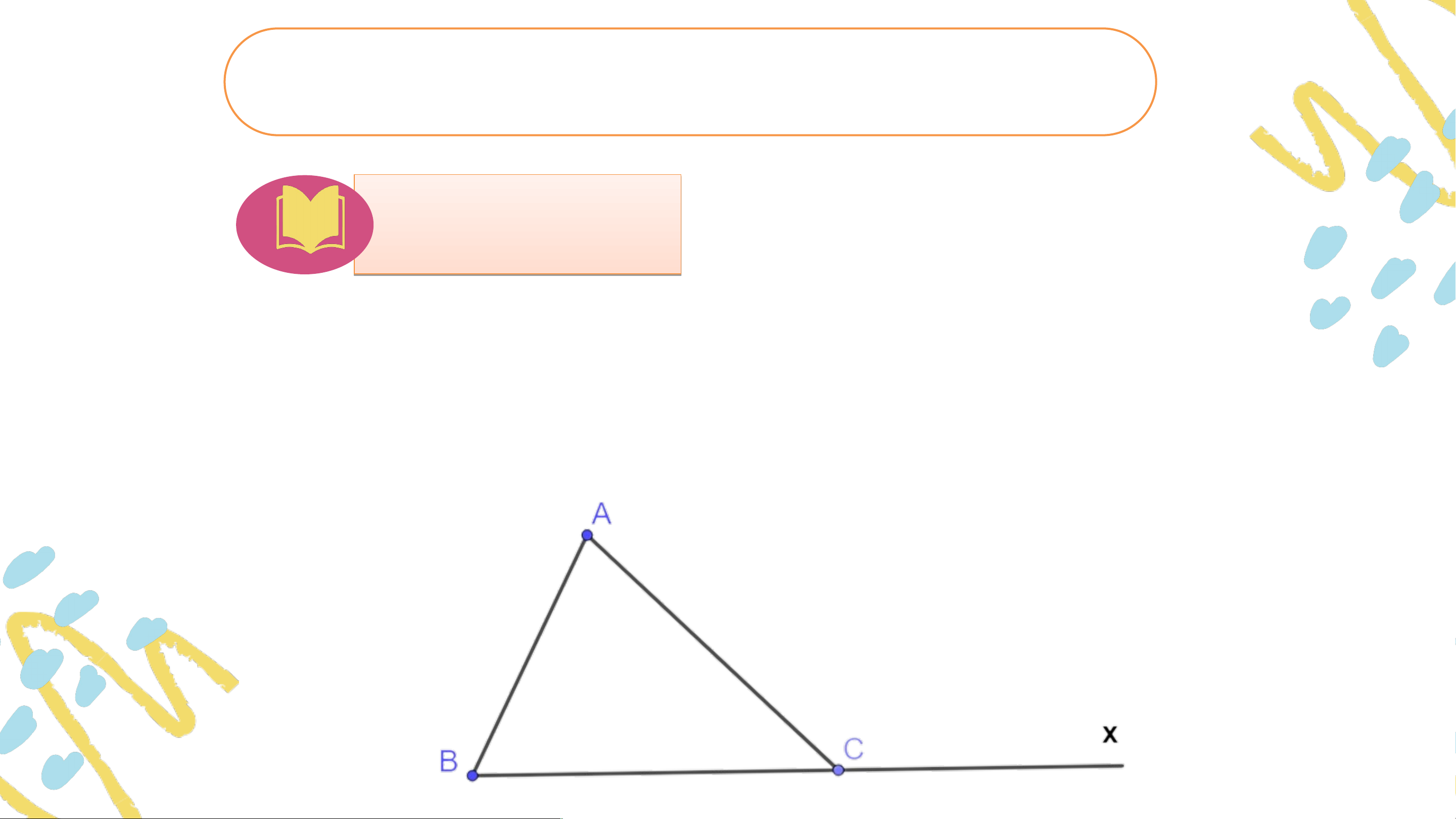
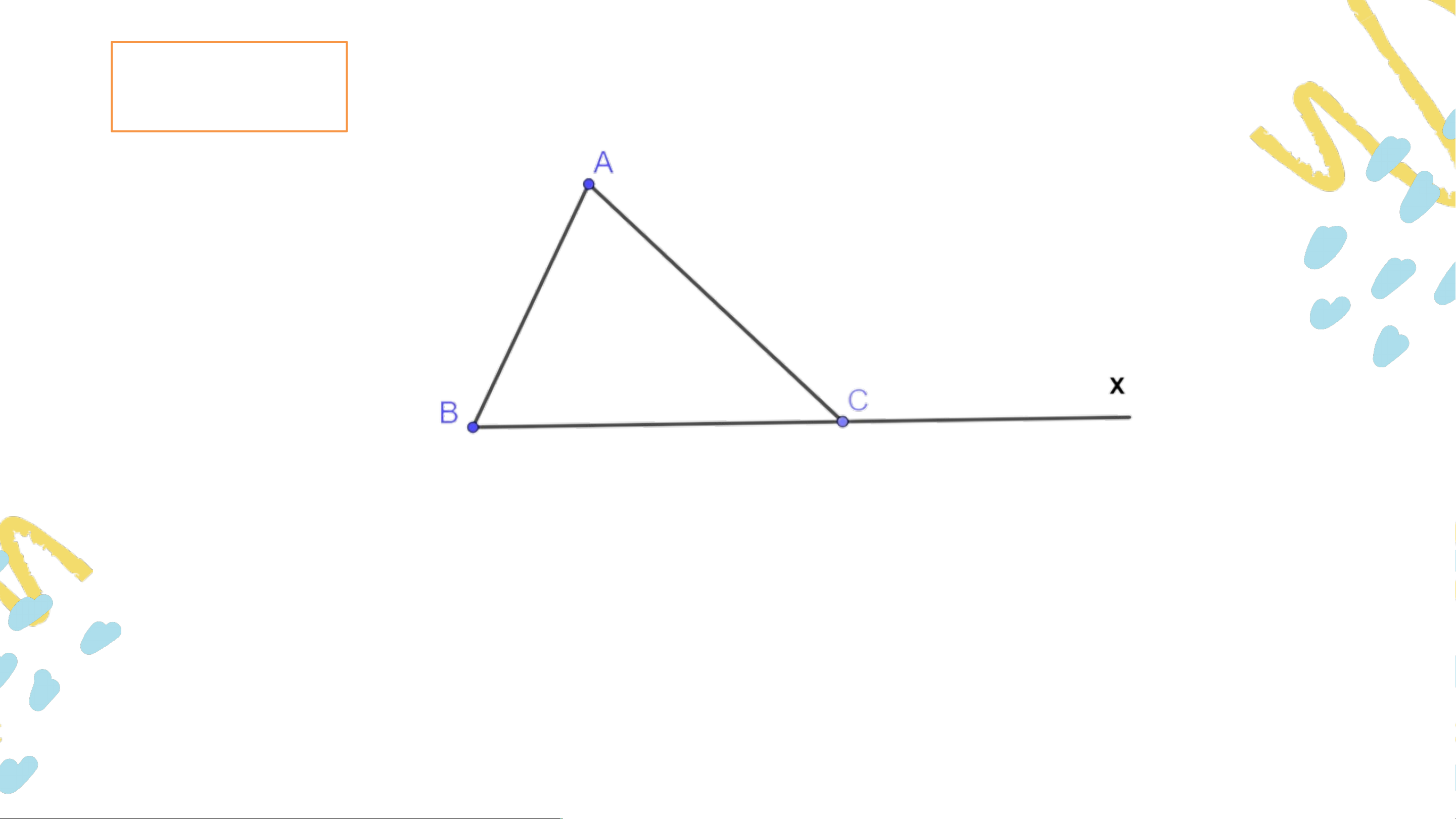
Cho tam giác và là tia đối của tia . Chứng mình rằng: . Trả lời:
+ Vì là tia đối của tia nên và là hai góc kề bù. (1) + Xét tam giác ABC có: (2) Từ (1) và (2) suy ra: . Nhận xét:
Góc gọi là góc ngoài tại của tam giác .
Góc không kề với hai góc và của tam giác .
Mỗi góc ngoài của một tam giác có số đo bằng
tổng số đo hai góc trong không kề với nó. LUYỆN TẬP
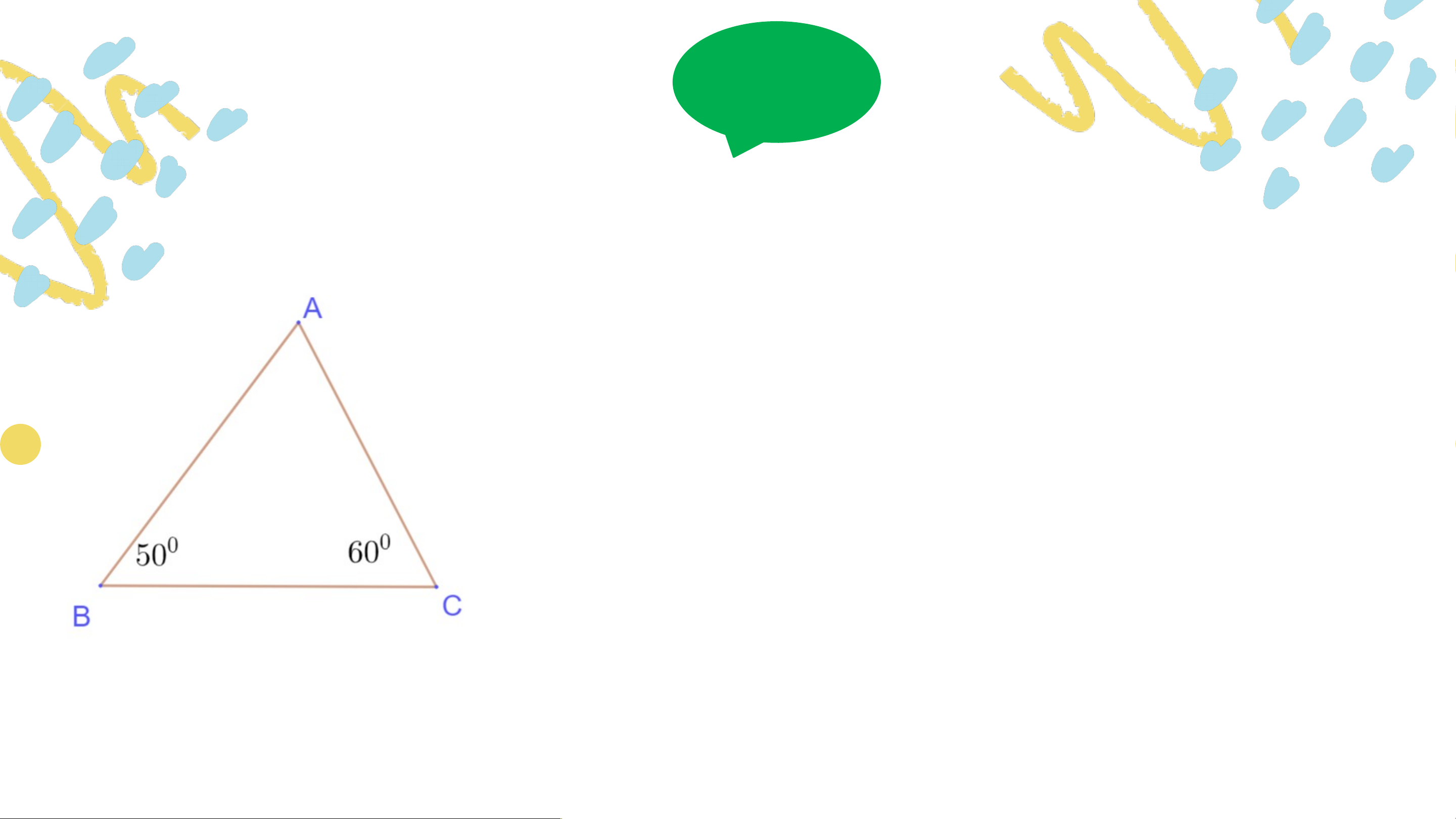
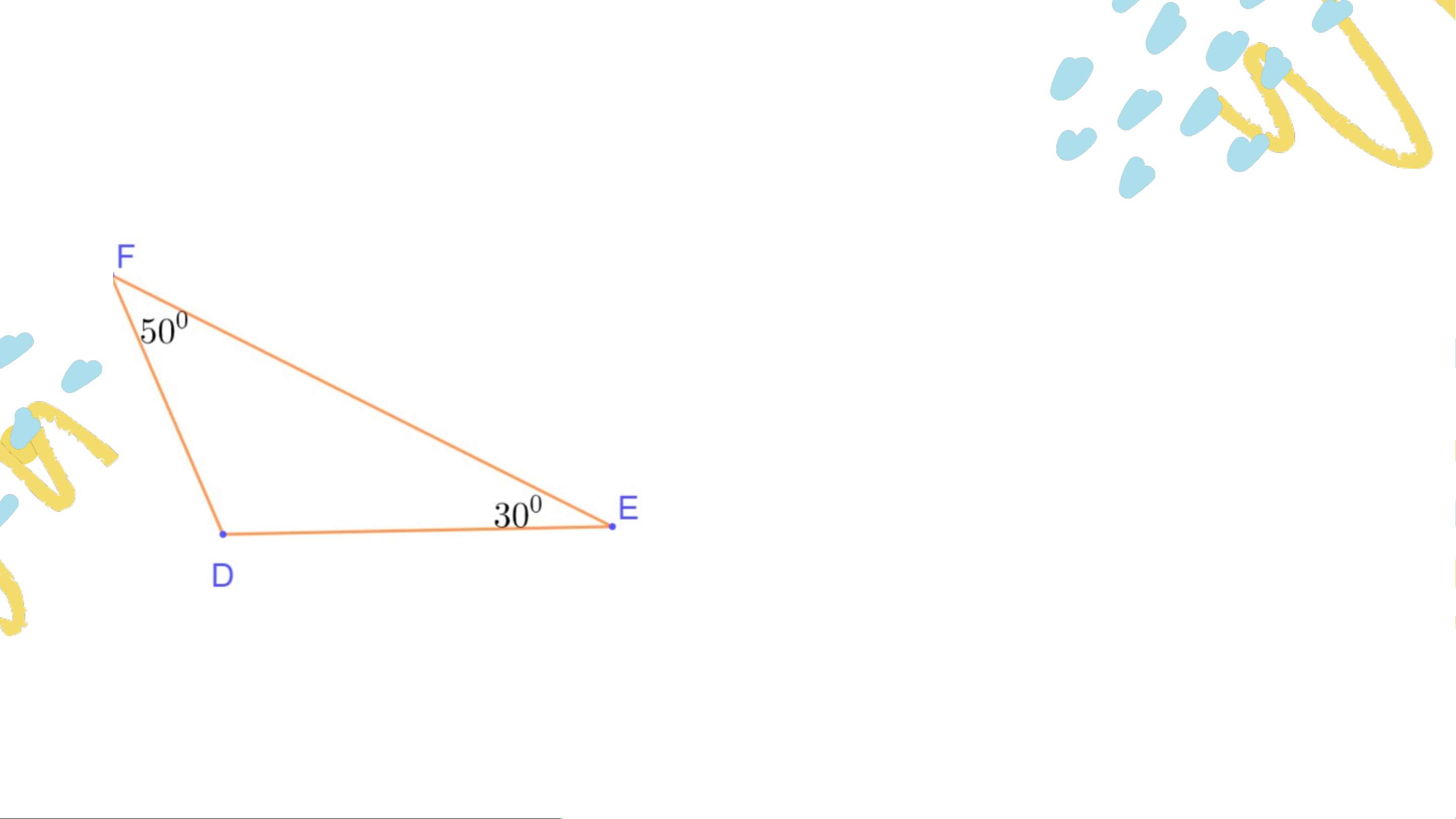
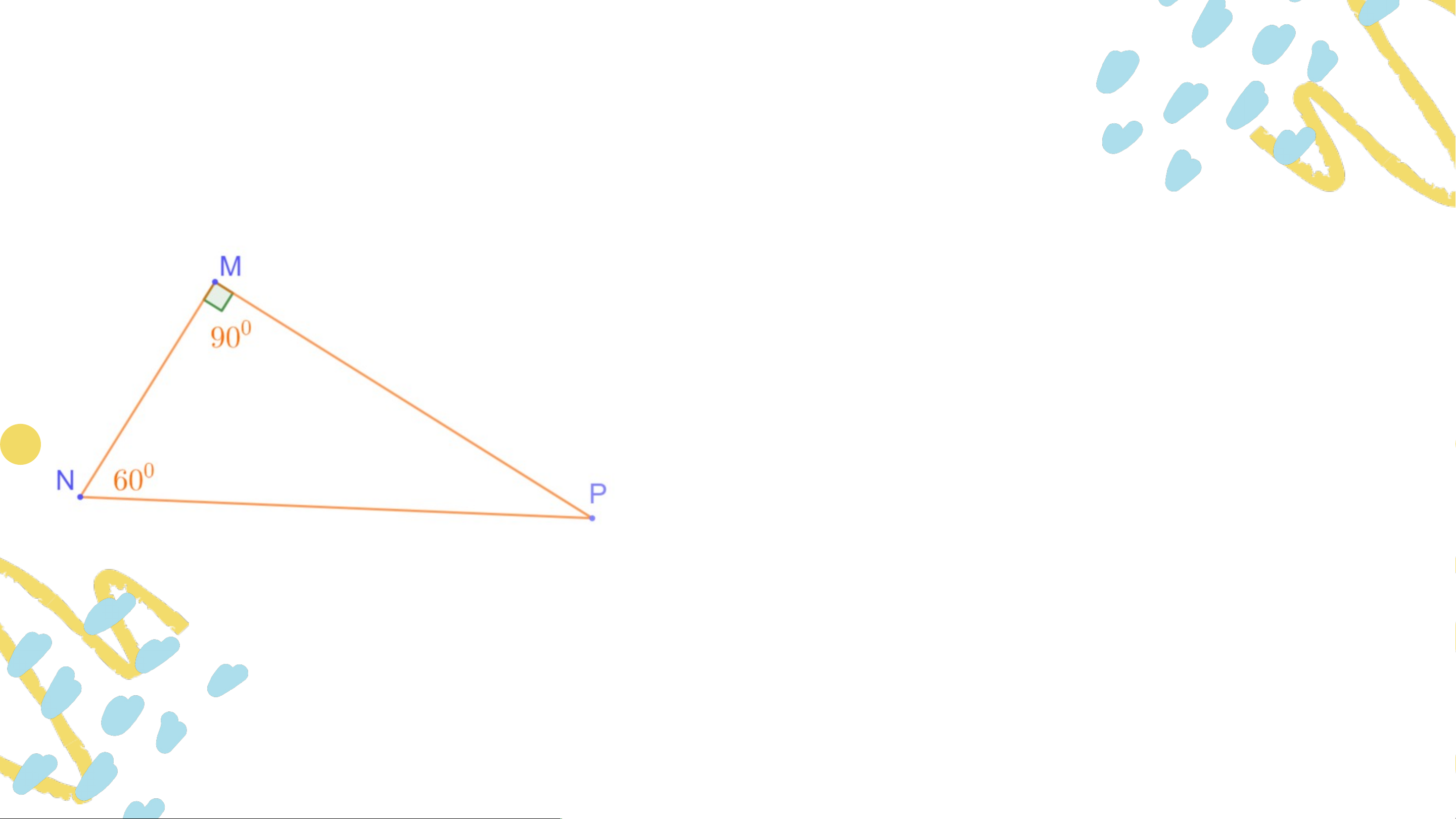
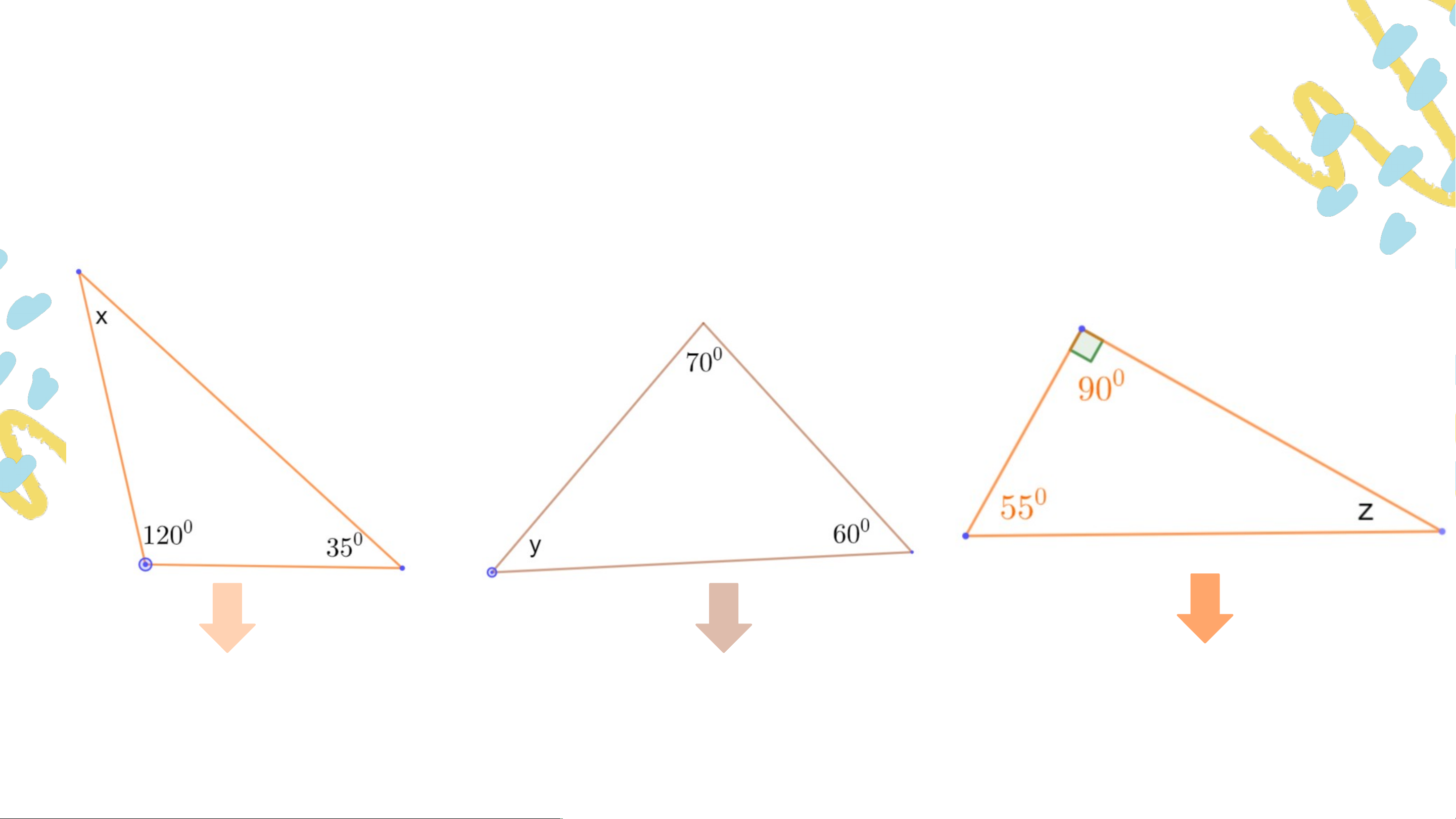
Bài 4.1 (SGK – tr.62) Tính các số đo trong các hình sau . .
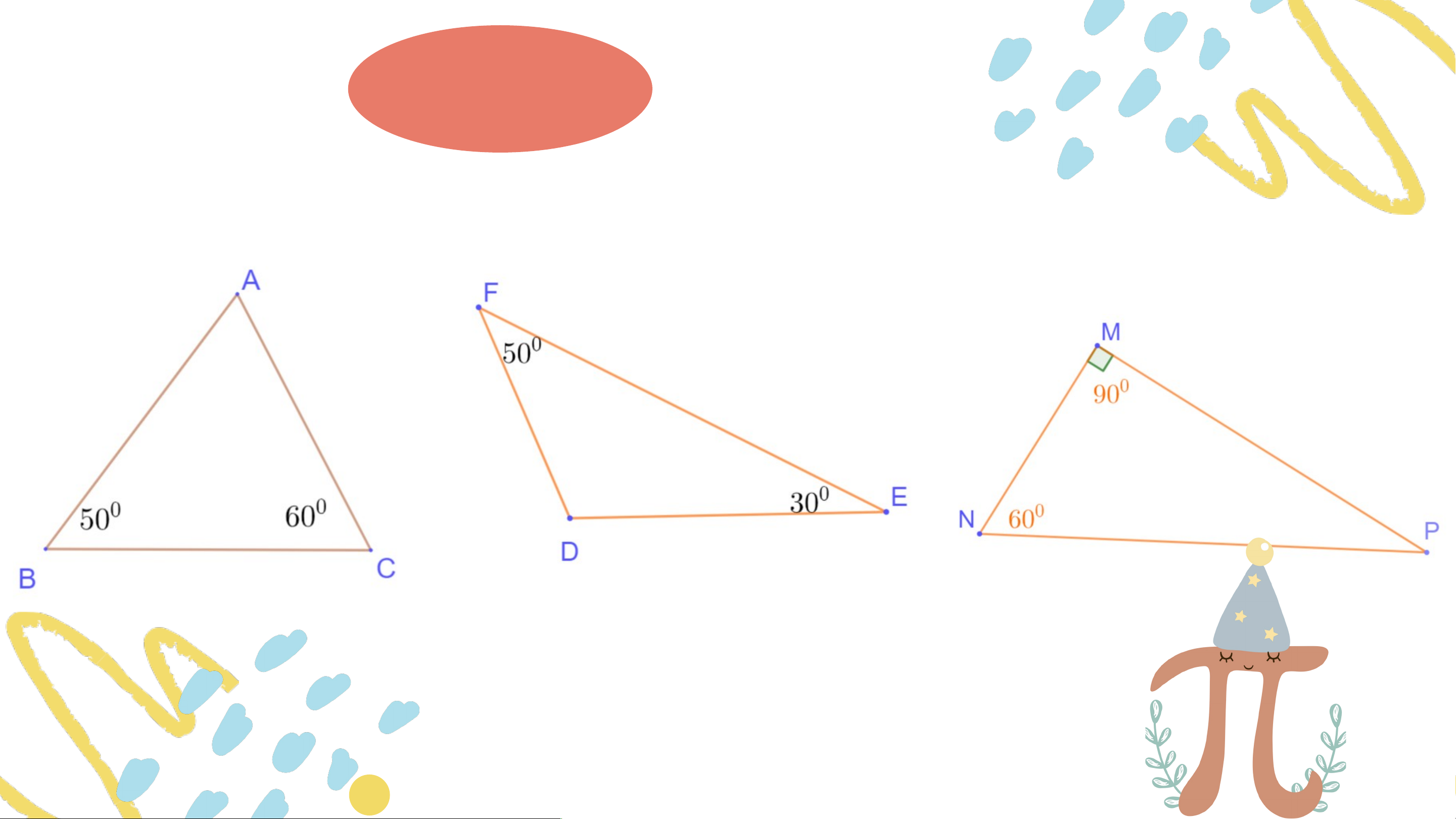
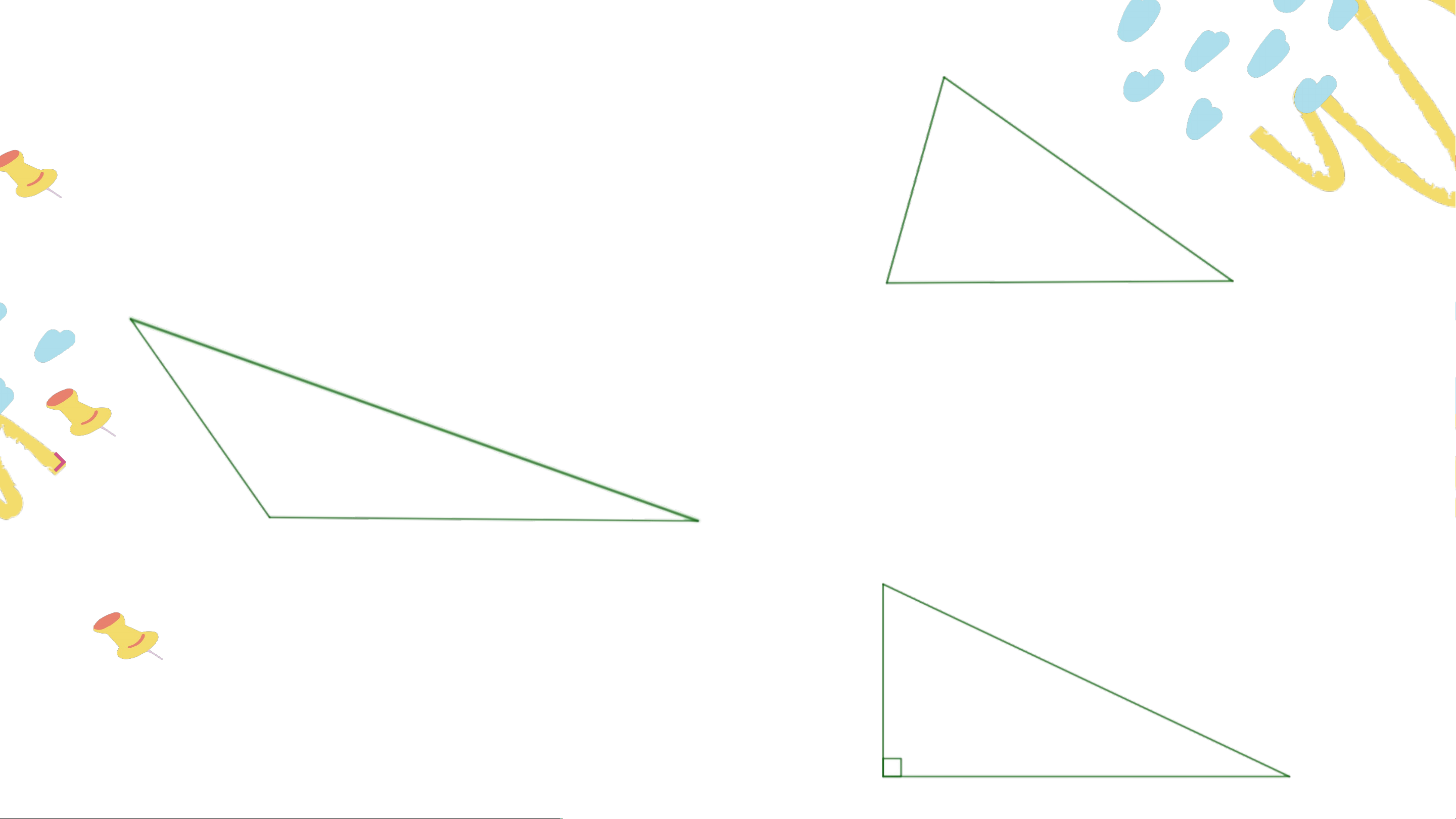
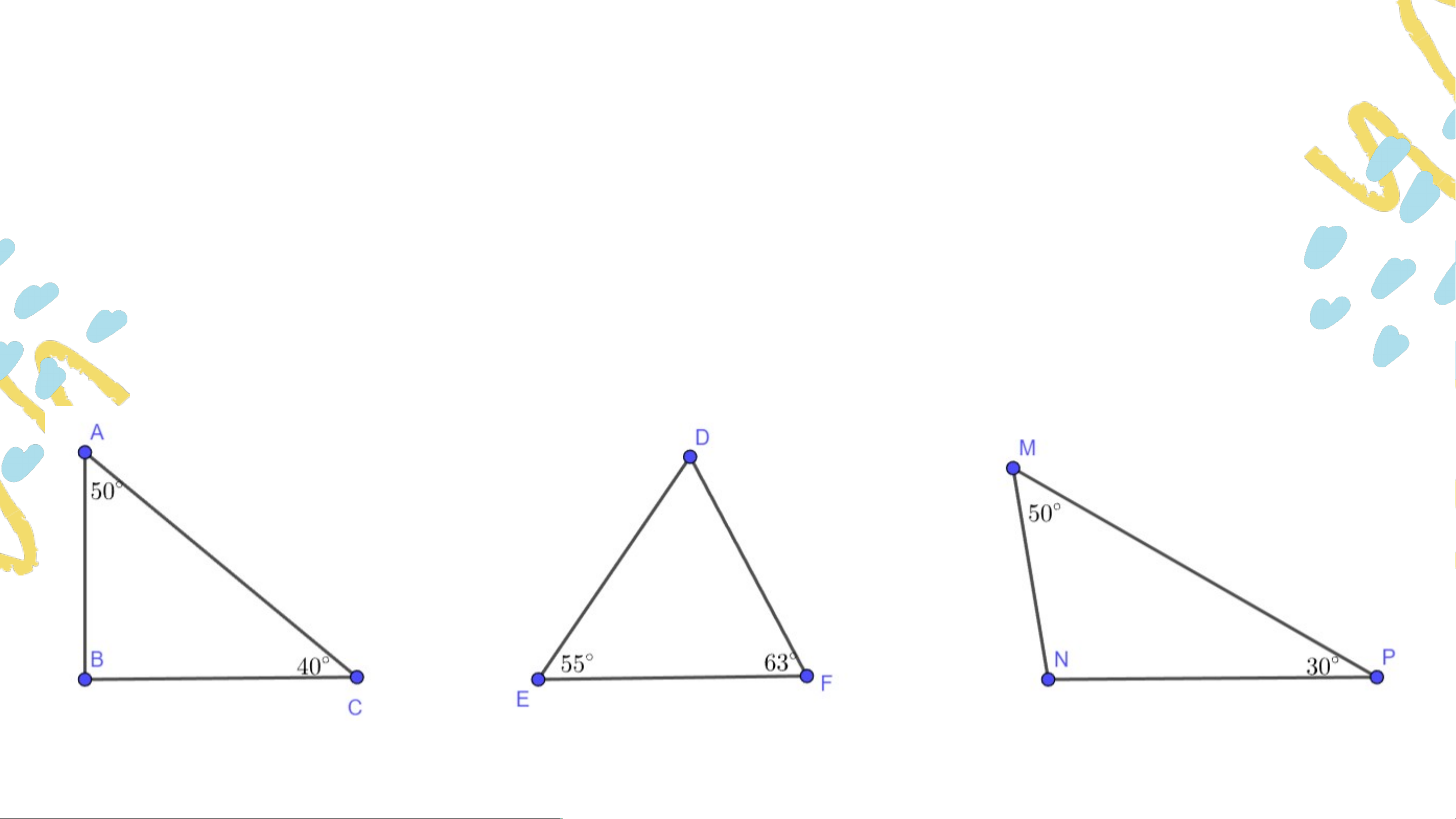
Bài 4.2 (SGK – tr.62) Trong các tam giác dưới đây,
tam giác nào là tam giác nhọn? Tam giác vuông? Tam giác tù? Trả lời:
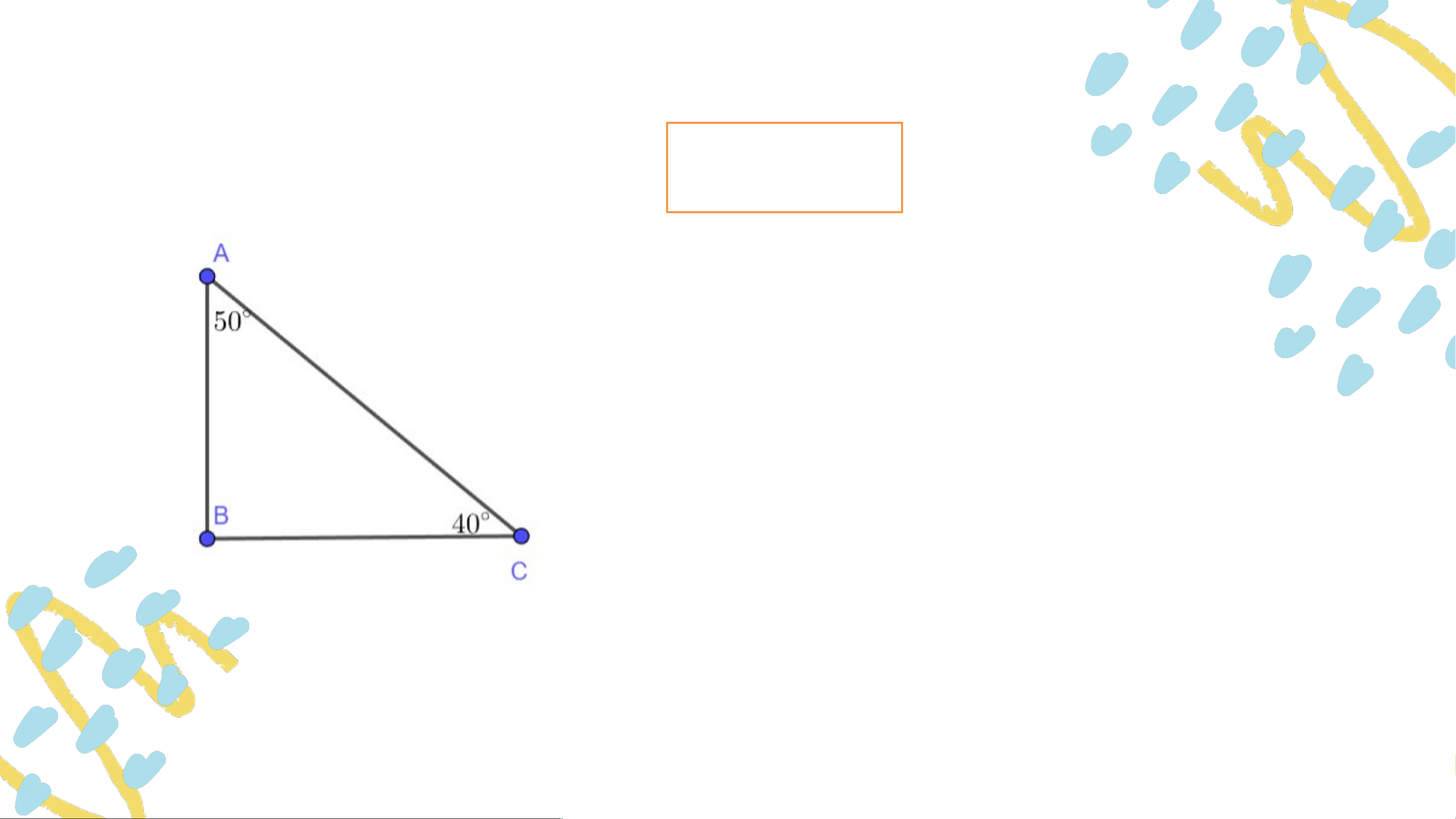
Tam giác là tam giác vuông.
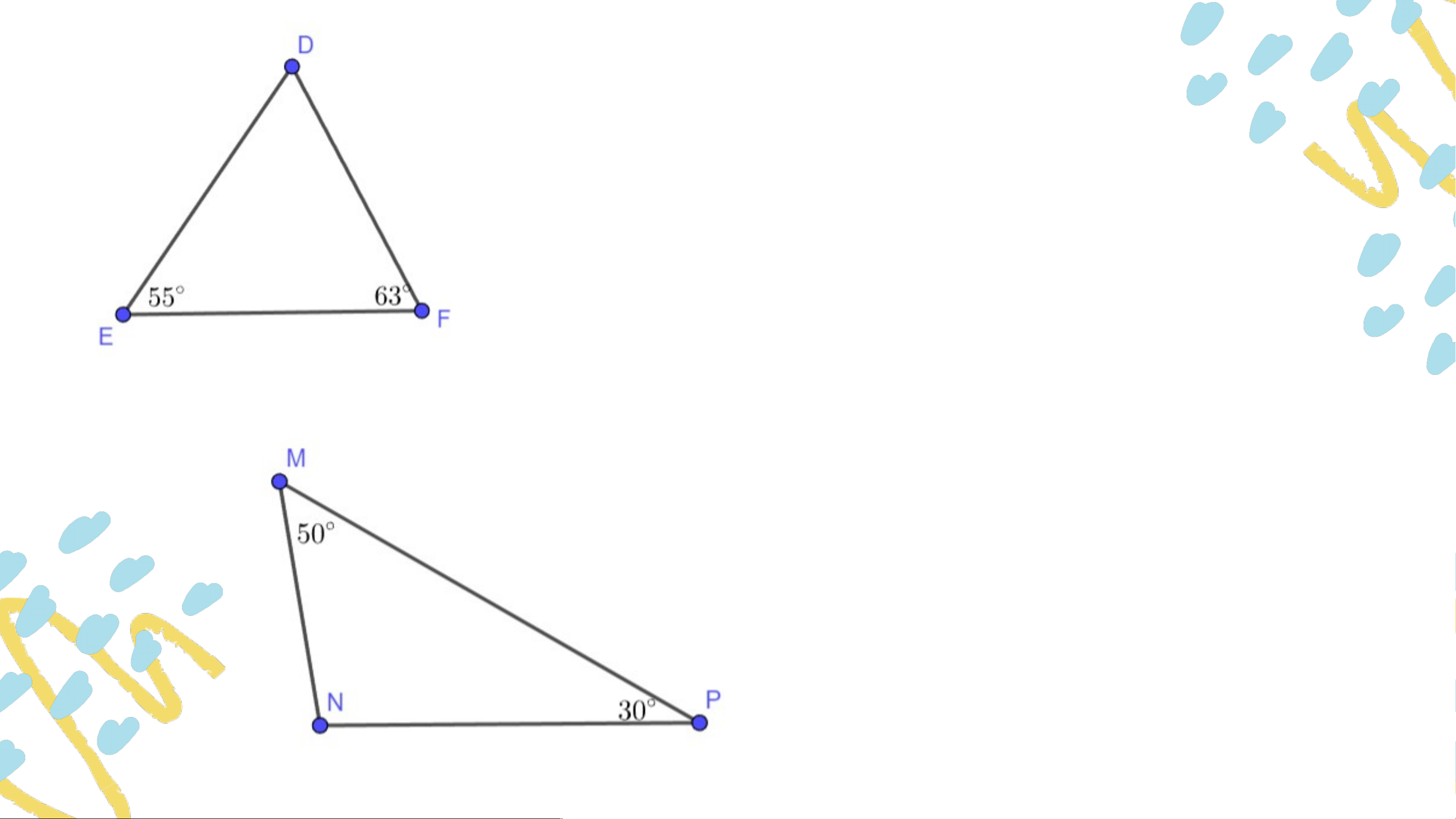
Tam giác là tam giác nhọn. Tam giác là tam giác tù. VẬN DỤNG
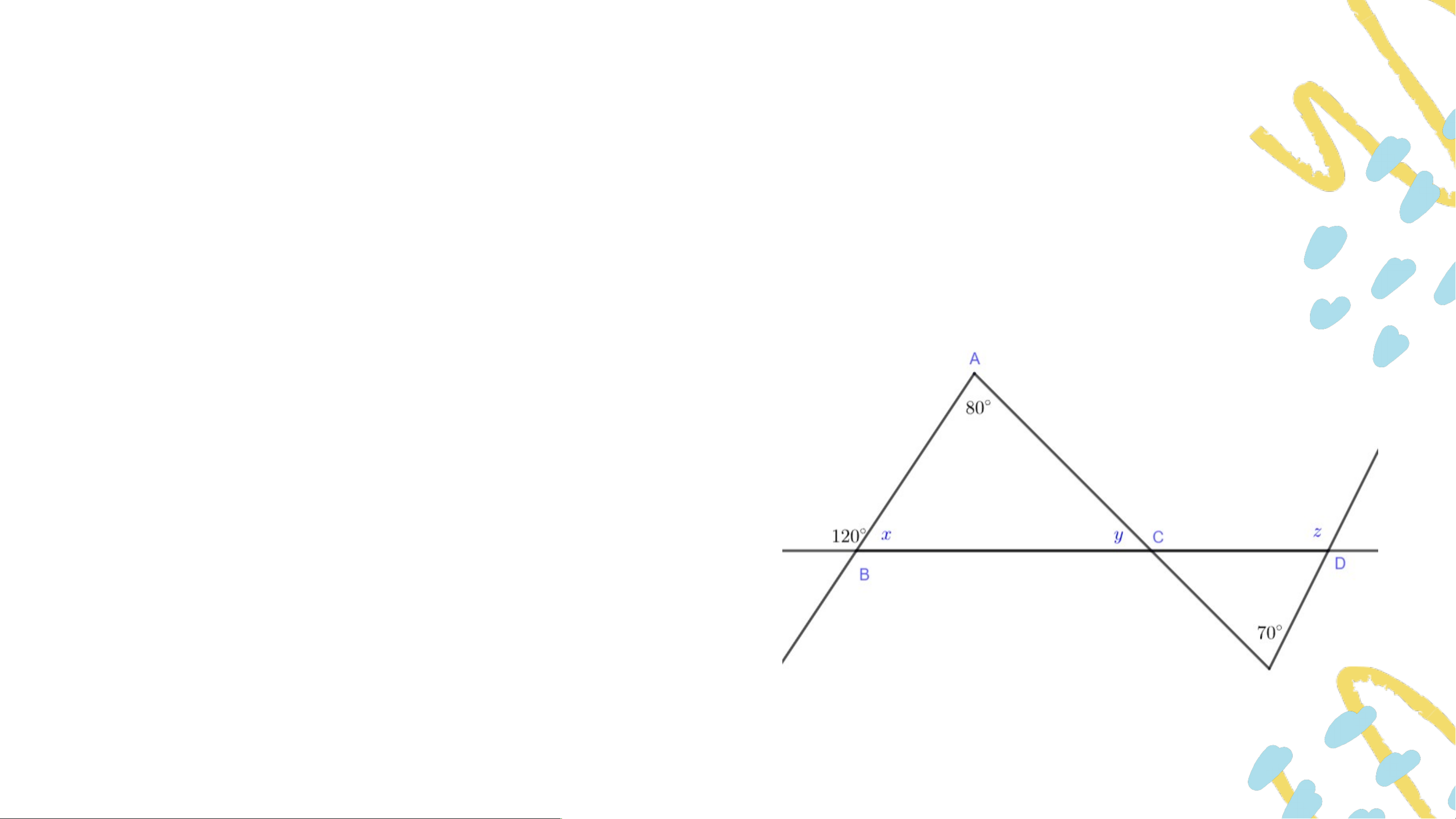
Bài 4.3 (SGK – tr.62) Tính các số đo trong Hình 4.8. Giải • (góc ngoài của tam giác)
HƯỚNG DẪN VỀ NHÀ 01 02 03 Ôn lại kiến Hoàn thành bài tập Chuẩn bị thức đã học. trong SBT. bài mới. CẢM ƠN CÁC EM
ĐÃ LẮNG NGHE BÀI GIẢNG! Join Now
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27




