CHÀO MỪNG CÁC EM
ĐẾN VỚI TIẾT HỌC
Khối lượng Trái Đất khoảng 5,9724. 1024 kg.
Khối lượng Sao Hỏa khoảng 6,417. 1023kg. Khối lượng Sao Hỏa bằng khoảng bao nhiêu
lần khối lượng Trái Đất? 6,417. 1023 5,9724. 1024
BÀI 3: PHÉP TÍNH LUỸ
THỪA VỚI SỐ MŨ TỰ NHIÊN
CỦA MỘT SỐ HỮU TỈ (4 tiết) NỘI DUNG BÀI HỌC Tích và thương của Phép tính luỹ thừa với hai luỹ thừa cùng cơ số mũ tự nhiên số
Luỹ thừa của một luỹ Luyện tập thừa
I. PHÉP LUỸ THỪA VỚI SỐ MŨ TỰ NHIÊN
HĐ1 Viết các tích sau dưới dạng luỹ thừa a) 7.7.7.7.7 = 75 b) 12.12. … .12 = 12𝑛 𝑛 thừa số 12
Với 𝑛 là một số tự nhiên lớn hơn 1, lũy thừa bậc 𝑛 của
một số hữu tỉ 𝑥, kí hiệu 𝑥𝑛, là tích của 𝑛 thừa số 𝑥:
𝑥𝑛 = 𝑥. 𝑥. … . 𝑥 (𝑥 ∈ ℚ, 𝑛 ∈ ℕ, 𝑛 > 1) 𝑛 thừa số 𝑥
Số 𝑥 được gọi là cơ số, 𝑛 được gọi là số mũ.
Quy ước: 𝑥1 = 𝑥𝑥0 = 1(𝑥 ≠ 0) Chú ý:
❑ 𝑥𝑛 đọc là "𝑥 mũ 𝑛" hoặc "𝑥 lũy thừa 𝑛" hoặc "lũy thừa bậc 𝑛 của 𝑥𝑛"
❑ 𝑥2 còn được gọi là "𝑥 bình phương" hay "bình phương của 𝑥"
❑ 𝑥3 còn được đọc là "𝑥 lập phương" hay "lập phương của 𝑥" Ví dụ 1
Viết mỗi tích sau dưới dạng một luỹ thừa −5 −5 −5 −5 −5 4 a) 7 . 7 . 7 . 7 = 7
b) −0,4 . −0,4 . −0,4 . −0,4 . −0,4 = −0,4 5 * Lưu ý:
Để viết lũy thừa bậc 𝑛 của phân số 𝑎 , ta phải viết 𝑎 𝑏 𝑏 𝑎 𝑛
trong dấu ngoặc ( ), tức là . 𝑏
𝑎 𝑛 = 𝑎𝑛 𝑏 𝑏𝑛
(𝑎, 𝑏 ∈ ℤ, 𝑏 ≠ 0) Ví dụ 2 So sánh −3 2 −3 2 a) 5 và 52 2 −3 2 −3 −3 −3 . −3 −3 2 −3 −3 2 = 5 = 5 . 5 = 5.5 = 52 . Vậy 5 52 2 3 23 b) 3 và 33 2 3 2 2 2 2.2.2 23 2 3 23
3 = 3 . 3 . 3 = 3.3.3 = 33 . Vậy 3 = 33 Luyện tập 1
Tính thể tích một bể nước dạng hình lập phương có độ dài cạnh là 1,8 m. Giải 𝑉 = 1,8 3 = 5,832 (𝑚3) Luyện tập 2 Tính −3 3 −3 −3 −3 −3 . −3 . −3 −27 a) = = 4 = 4 . 4 . 4 4.4.4 64 . 1 5 1 1 1 1 1 1.1.1.1.1 1 b) = = 2
2 . 2 . 2 . 2 . 2 = 2.2.2.2.2 32 . IV. LUYỆN TẬP
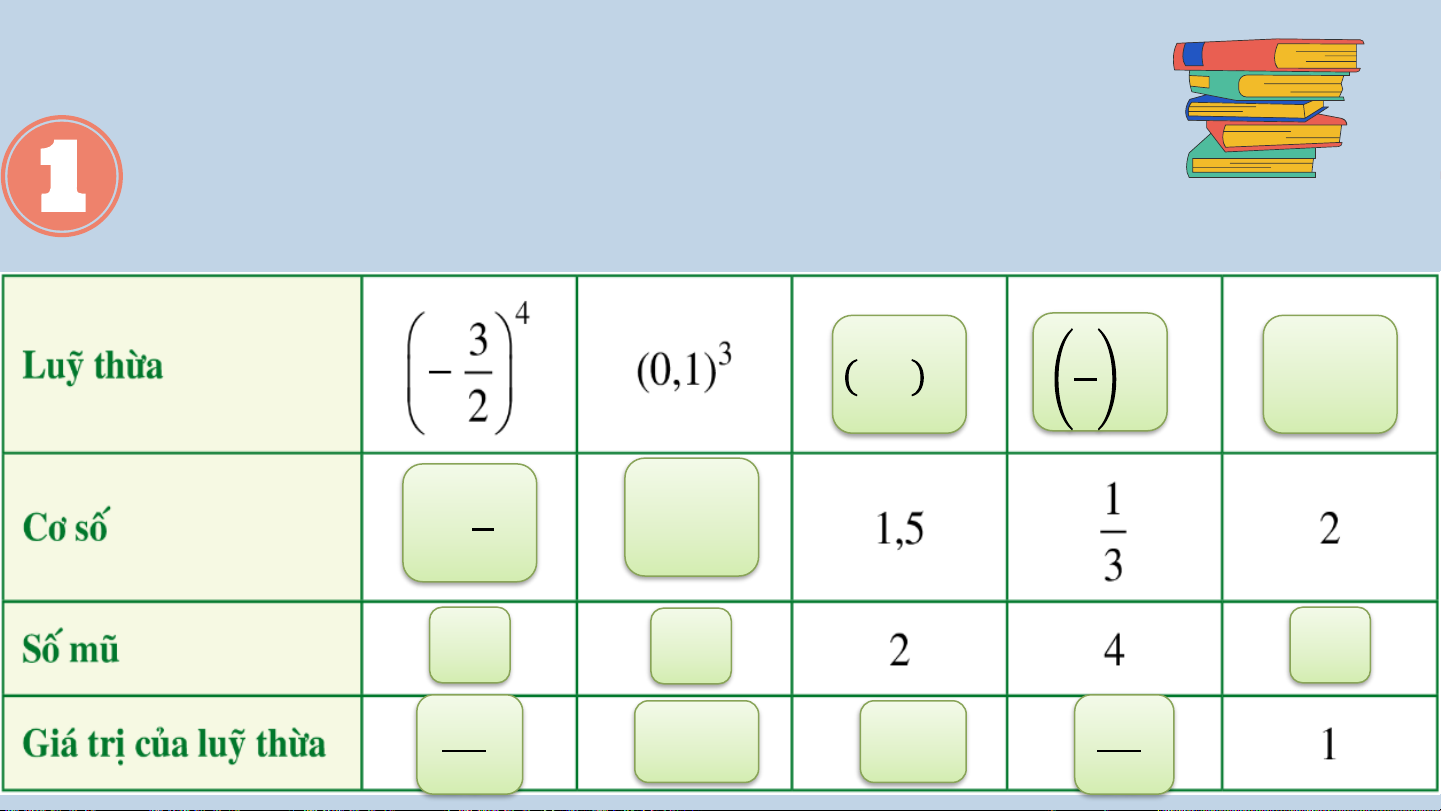
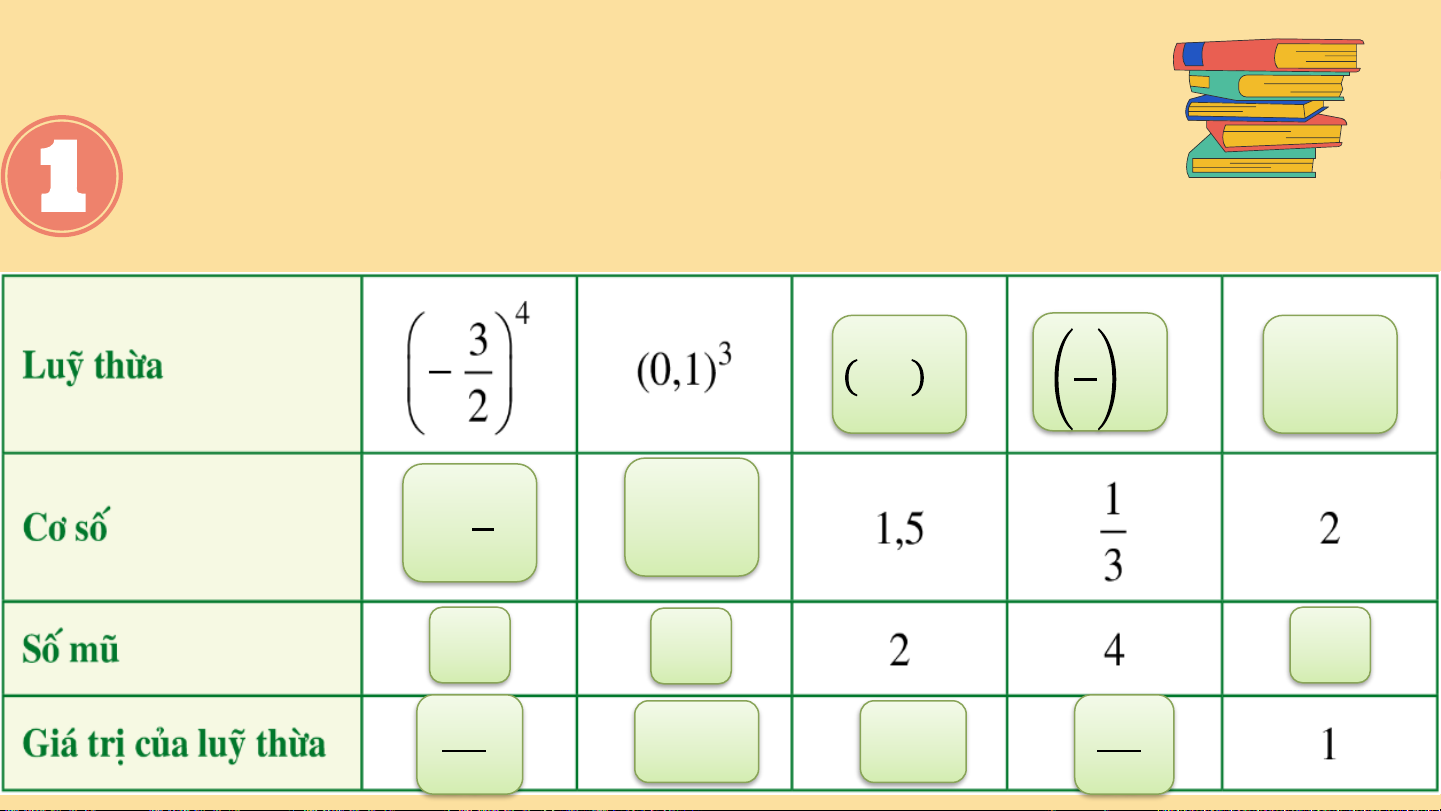
Tìm số thích hợp cho ? trong bảng 4 1,5 2 1 20 3 3 − 0,1 2 4 3 0 81 0,001 2,25 1 16 81
II. TÍCH VÀ THƯƠNG CỦA HAI LUỸ THỪA CÙNG CƠ SỐ
HĐ2 Viết kết quả của các phép tính sau dưới dạng luỹ thừa
a) 2𝑚. 2𝑛 = 2𝑚+𝑛 𝑚, 𝑛 ∈ ℕ
b) 3𝑚∶ 3 𝑛= 3𝑚−𝑛 (𝑚 ≥ 𝑛) Quy tắc:
Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên
cơ số và cộng các số mũ.
𝑥𝑚. 𝑥𝑛 = 𝑥𝑚+𝑛
Khi chia hai lũy thừa cùng cơ số (khác 0), ta
giữ nguyên cơ số và lấy số mũ của lũy thừa bị
chia trừ đi số mũ của lũy thừa chia.
𝑥𝑚: 𝑥𝑛 = 𝑥𝑚−𝑛 𝑥 ≠ 0, 𝑚 ≥ 𝑛 Ví dụ 3
Viết kết quả của mỗi phép tính sau dưới dạng một luỹ thừa −5 4 −5 3 −5 4+3 −5 7 a) 9 . 9 = 9 = 9 b)
−0,8 5: −0,8 2 = −0,8 5−2 = −0,8 3 Luyện tập 3
Viết kết quả của mỗi phép tính sau dưới dạng một luỹ thừa 6
a) 5. 1,2 8 = 1,2. 1,2 8 = 1,2 1+8 = 1,2 9 −4 7 16 −4 7 −4 2 −4 7−2 −4 5 b) 9 : 81 = = = 9 : 9 9 9 So sánh 1 2 1 6 1 4 2
a) −2 4. −2 5 và −2 12 ∶ −2 3 b) 2 . 2 và 2
−2 4. −2 5 = −2 4+5 = −2 9 1 2 1 6 1 2+6 1 8 2 . 2 = 2 = 2
−2 12: −2 3 = −2 12−3 = −2 9 1 4 2 1 4.2 1 8 = =
⇒ −2 4. −2 5 = −2 12∶ −2 3 2 2 2 1 2 1 6 1 4 2 ⇒ 2 . 2 = 2 c) 0,3 8: 0,3 2 và 0,3 2 3
0,3 8: 0,3 2 = 0,3 8−2 = 0,3 6 ; 0,3 2 3 = 0,3 2.3 = 0,3 6 ⇒ 0,3 8: 0,3 2 = 0,3 2 3 3 5 3 3 3 2 d) − 2 : −2 và 2 3 5 3 3 3 5−3 3 2 3 2 − 2 : −2 = −2 = − 2 = 2 3 5 3 3 3 2 ⇒ − 2 : −2 = 2
III. LUỸ THỪA CỦA LUỸ THỪA
HĐ3 So sánh 153 2 và 153.2 Ta có
153 2 = 153. 153 = 153+3 = 156 153.2 = 156 Vậy 153 2 = 153.2
Khi tính lũy thừa của một lũy thừa, ta
giữ nguyên cơ số và nhân hai số mũ: 𝑥𝑚 𝑛 = 𝑥𝑚.𝑛
Viết kết quả của mỗi phép tính sau dưới dạng luỹ Ví dụ 4 thừa của a. −2 3 5 −2 3.5 −2 15 7 = 7 = 7 = 𝑎15 a) b)
0,1 2 4 = 0,1 2.4 = 0,1 8 = 𝑎8 Ví dụ 5 Viết 218 dưới dạng: a) Luỹ thừa của 22 218 = 22.9 = 22 9 b) Luỹ thừa của 8 218 = 23.6 = 23 6 = 86 Viết Luyện
kết quả của mỗi phép tính sau dưới tập 4
dạng luỹ thừa của a. −1 3 4 a) ta có: 6 = 𝑎 3.4 = 𝑎12 = 𝑎3 4 Với 𝑎 = −16 b) Với 𝑎 = −0,2 ta có: −0,2 4 5 = 𝑎 4.5 = 𝑎20 = 𝑎4 5 IV. LUYỆN TẬP
Tìm số thích hợp cho ? trong bảng 4 1,5 2 1 20 3 3 − 0,1 2 4 3 0 81 0,001 2,25 1 16 81 So sánh 1 2 1 6 1 4 2
a) −2 4. −2 5 và −2 12 ∶ −2 3 b) 2 . 2 và 2
−2 4. −2 5 = −2 4+5 = −2 9 1 2 1 6 1 2+6 1 8 2 . 2 = 2 = 2
−2 12: −2 3 = −2 12−3 = −2 9 1 4 2 1 4.2 1 8 = =
⇒ −2 4. −2 5 = −2 12∶ −2 3 2 2 2 1 2 1 6 1 4 2 ⇒ 2 . 2 = 2 c) 0,3 8: 0,3 2 và 0,3 2 3
0,3 8: 0,3 2 = 0,3 8−2 = 0,3 6 ; 0,3 2 3 = 0,3 2.3 = 0,3 6 ⇒ 0,3 8: 0,3 2 = 0,3 2 3 3 5 3 3 3 2 d) − 2 : −2 và 2 3 5 3 3 3 5−3 3 2 3 2 − 2 : −2 = −2 = − 2 = 2 3 5 3 3 3 2 ⇒ − 2 : −2 = 2
Tìm 𝒙, biết 2 7 2 6 a) 1,2 3. 𝑥 = 1,2 5 b) 3 : 𝑥 = 3 7 6 𝑥 = 1,2 5: 1,2 3 2 2 𝑥 = 3 : 3 𝑥 = 1,2 2 2 𝑥 = 3 𝑥 = 1,44
Viết kết quả của mỗi phép tính sau dưới dạng luỹ thừa của a. 8 3 4 2 8 3 8 8 4 8 a) . = 𝑎4 , với 𝑎 = 9 . 3 . 3 = 9 9 = 9 9 1 7
b) 4 .0,25 = 0,25 7.0,25 = 0,258 = 𝑎8 ,với 𝑎 = 0,25 −1 −1 6 −1 −1 5 c)
−0,125 6: 8 = 8 : 8 = 8 = 𝑎5, 1 với 𝑎 = − 8 −3 3 2 −3 3.2 −3 6 −3 d) 2 = 2 = 2 = 𝑎6 ,với 𝑎 = 2 Vận dụng
Biết vận tốc ánh sáng xấp xỉ bằng 299 792 458 𝑚/𝑠 và ánh sáng
Mặt Trời cần khoảng 8 phút 19 giây mới đến được Trái Đất.
Khoảng cách giữa Mặt Trời và Trái Đất xấp xỉ bằng bao nhiêu ki-lô-mét? Giải
Ta có: 299792458 ≈ 300000000 = 3.108 (m/s)
Đổi 8 phút 19 giây = 499 giây ≈ 500 giây
Khoảng cách giữa Mặt Trời và Trái Đất là:
3.108. 500 = 3.108. 5.102 = 15.108(𝑘𝑚) 33
Hai mảnh vườn có dạng hình
vuông. Mảnh vườn thứ nhất có độ
dài cạnh là 19,5 m. Mảnh vườn
thứ hai có độ dài cạnh là 6,5
m. Diện tích mảnh vườn thứ nhất
gấp bao nhiêu lần diện tích mảnh vườn thứ hai? Giải
Diện tích hình vuông thứ nhất là: (19,5)2 = 380,25 (m2)
Diện tích hình vuông thứ hai là: (6,5)2 = 42,25 (m2)
Ta có: 380,25 ∶ 42,25 = 9380,25 ∶ 42,5 = 9
⇒ Diện tích mảnh vườn thứ nhất gấp 9 lần diện
tích mảnh vườn thứ hai. a) (3,147)3 ≈ 31,167
b) (−23,457)5 ≈ −7101700,278 4 4 c) = 256 −5 625 5 d) (0,12)2. −13 ≈ −3,107.10−4 28 TRÒ CHƠI HÁI CAM 5 Câu hỏi 1 −1 : Tính: =? 2 1 −1 A. C. 32 32 1 −1 B. D. 10 10
Câu hỏi 2: Lũy thừa với số mũ lẻ của một số hữu tỉ âm mang dấu: A. Dương C. Âm khi số mũ âm B. Âm D. Không xác định Câu hỏi 3: Tính nhanh 𝑀
= (100 − 1). (100 − 22). (100 − 32) … (100 − 502) A. 0 C. Không xác định B. 100 D. Đáp án khác 2 Câu hỏi 2
4: Kết quả của phép tính + 1 là: 5 2 9 41 A. C. 10 100 81 B. D. Kết quả khác 100 15 Câu hỏi 3
5: Kết quả của phép tính . 0,36 5là: 5 125 3125 A. C. 27 243 25 243 B. D. 127 3125
HƯỚNG DẪN VỀ NHÀ Ôn lại kiến thức Hoàn thành các bài
Chuẩn bị bài mới “Thứ tự đã học trong bài tập còn lại trong
thực hiện các phép tính. SGK và SBT
Quy tắc dấu ngoặc”. CẢM ƠN CÁC EM ĐÃ
LẮNG NGHE BÀI GIẢNG!
Document Outline

• Slide 1
• Slide 2
• Slide 3
• Slide 4
• Slide 5
• Slide 6
• Slide 7
• Slide 8
• Slide 9
• Slide 10
• Slide 11
• Slide 12
• Slide 13
• Slide 14
• Slide 15
• Slide 16
• Slide 17
• Slide 18
• Slide 19
• Slide 20
• Slide 21
• Slide 22
• Slide 23
• Slide 24
• Slide 25
• Slide 26
• Slide 27
• Slide 28
• Slide 29
• Slide 30
• Slide 31
• Slide 32
• Slide 33
• Slide 34
• Slide 35
• Slide 36
• Slide 37
• Slide 38
• Slide 39
• Slide 40
• Slide 41
• Slide 42
• Slide 43
• Slide 44
• Slide 45