CHÀO MỪNG CÁC EM
ĐẾN VỚI BUỔI HỌC NGÀY HÔM NAY! KHỞI ĐỘNG
Ta cần thực hiện phép chia sau: x3 + 1 : x2 − x + 1 .
Làm thế nào để thực hiện được phép chia một đa thức cho một đa thức khác?
CHƯƠNG VI: BIỂU THỨC ĐẠI SỐ
BÀI 5: PHÉP CHIA ĐA THỨC MỘT BIẾN NỘI DUNG BÀI HỌC 1
Chia đơn thức cho đơn thức 2
Chia đa thức cho đơn thức 3
Chia đa thức một biến đã sắp xếp
Chia đơn thức cho đơn thức
Thảo luận nhóm hoàn thành HĐ1 HĐ 1: Giải Thực hiện phép tính:
a) 𝑥5: 𝑥3 = 𝑥5 − 3 = 𝑥2. a) 𝑥5: 𝑥3
b) 4𝑥3 : 𝑥2 = 4 . 𝑥3: 𝑥2 b) 4𝑥3 : 𝑥2 = 4 . 𝑥3 − 2 = 4𝑥. 𝑎𝑥𝑚 𝑎 𝑥𝑚
c) 𝑎𝑥𝑚 : 𝑏𝑥𝑛 (𝑎 ≠ 0; 𝑏 ≠ 0;
c) 𝑎𝑥𝑚 : 𝑏𝑥𝑛 = 𝑏𝑥𝑛 = 𝑏 . 𝑥𝑛
𝑚, 𝑛 ∈ ℕ, 𝑚 ≥ 𝑛).
= 𝑎 ∶ 𝑏 . 𝑥𝑚−𝑛
(𝑎 ≠ 0; 𝑏 ≠ 0; 𝑚, 𝑛 ∈ ℕ; 𝑚 ≥ 𝑛). KẾT LUẬN
Muốn chia đơn thức 𝐴 cho đơn thức 𝐵(𝐵 ≠ 0) khi số mũ của biến trong 𝐴
lớn hơn hoặc băng số mū của biến đó trong 𝐵, ta làm như sau:
- Chia hệ số của đơn thức 𝐴 cho hệ số của đơn thức B;
- Chia luỹ thừa của biến trong 𝐴 cho luỹ thừa của biến đó trong B;
- Nhân các kết quả vừa tìm được với nhau. • Chú ý: 𝑎 𝑎
𝑎𝑥𝑚 : 𝑏𝑥𝑛 = 𝑏 ⋅ 𝑥𝑚:𝑥𝑛 = 𝑏 ⋅ 𝑥𝑚−𝑛
(𝑎 ≠ 0; 𝑏 ≠ 0; 𝑚, 𝑛 ∈ ℕ; 𝑚 ≥ 𝑛).
Ví dụ 1 (SGK – tr64) Tính: a) 12𝑥4 : 6𝑥2 ;
b) −24𝑥𝑚 : 6𝑥𝑛 (𝑚, 𝑛 ∈ ℕ, 𝑚 ≥ 𝑛). Giải
a) 12𝑥4 : 6𝑥2 = 12: 6 . 𝑥4: 𝑥2 = 2𝑥4−2 = 2𝑥2.
b) −24𝑥𝑚 ∶ 6𝑥𝑛 = [(−24): 6] ⋅ 𝑥𝑚: 𝑥𝑛 = −4𝑥𝑚−𝑛. LUYỆN TẬP 1 Tính: a) 3𝑥6 : 0,5𝑥4 ;
b) −12𝑥𝑚+2 : 4𝑥𝑛+2 (𝑚, 𝑛 ∈ ℕ; 𝑚 ≥ 𝑛). Giải
𝑎) (3𝑥6): (0,5𝑥4) = 3: 0,5 . (𝑥6: 𝑥4) = 6𝑥2.
𝑏) −12𝑥𝑚 + 2 : 4𝑥𝑛 + 2 = −12: 4 . 𝑥𝑚 + 2: 𝑥𝑛 + 2
= −3 . 𝑥𝑚+2−𝑛−2 = −3𝑥𝑚−𝑛.
Chia đa thức cho đơn thức
Thảo luận nhóm hoàn thành HĐ2 HĐ 2:
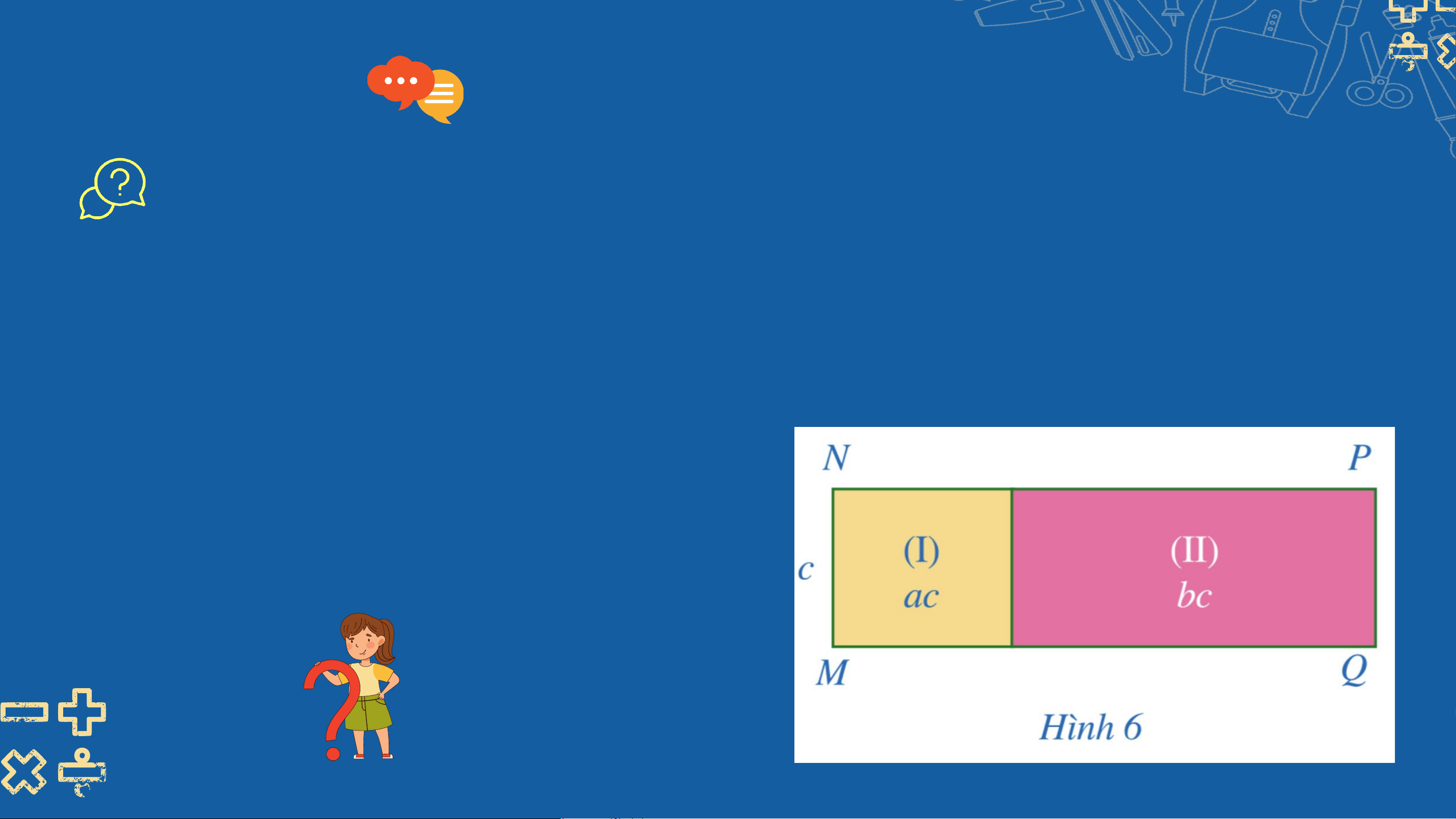
Ở Hình 6, diện tích các hình chữ nhật (I), (II) lần lượt là 𝐴 = 𝑎𝑐, 𝐵 = 𝑏𝑐. Biết 𝑀𝑁 = 𝑐. a) Tính 𝑁𝑃.
b) So sánh: (𝐴 + 𝐵): 𝑐 và 𝐴: 𝑐 + 𝐵: 𝑐. Giải
a) Độ dài cạnh kề với MN của hình chữ nhật
(I) là A: 𝑐 = 𝑎𝑐 ∶ 𝑐 = 𝑎.
Độ dài cạnh kề với PQ của hình chữ nhật
(II) là B: 𝑐 = 𝑏𝑐 ∶ 𝑐 = 𝑏. Khi đó NP = 𝑎 + 𝑏. Giải
b) Diện tích MNPQ bằng tổng diện tích hai hình chữ nhật (I) và (II) bằng ac + bc.
Khi đó độ dài NP là thương trong phép chia diện tích hình chữ nhật MNPQ cho MN.
Hay NP = (ac + bc) : c = (A + B) : c. * Chú ý:
Mà NP = a + b = A : c + B : c. (A + B) : C = A : C = B : C
Do đó (A + B): c = A : c + B : c.
(A – B) : C = A : C – B : C
HĐ 3: Cho đa thức 𝑃(𝑥) = 4𝑥2 + 3𝑥 và đơn thức 𝑄(𝑥) = 2𝑥.
(𝐴 − 𝐵): 𝐶 = 𝐴: 𝐶
a) Hãy chia từng đơn thức (của biến 𝑥 ) có trong đa thức
𝑃(𝑥) cho đơn thức 𝑄(𝑥).
b) Hãy cộng các thương vừa tìm được. Giải
a) 4𝑥2 ∶ 2𝑥 = 4 ∶ 2 . (𝑥2 ∶ 𝑥) = 2𝑥. 3
3𝑥 ∶ 2𝑥 = 3 ∶ 2 . 𝑥 ∶ 𝑥 = 2
b) 4𝑥2 ∶ 2𝑥 + 3𝑥 ∶ 2𝑥 = 2𝑥 + 32 KẾT LUẬN
Muốn chia đa thức 𝑃 cho đơn thức 𝑄(𝑄 ≠ 0) khi số mũ
của biến ở mỗi đơn thức của P lớn hơn hoặc bằng số
mũ của biến đó trong 𝑄, ta chia mỗi đơn thức của đa
thức 𝑃 cho đơn thức 𝑄 rồi cộng các thương với nhau.
Ví dụ 2 (SGK – tr65)
Tính: 9𝑥6 + 6𝑥4 − 𝑥2 : 3𝑥2 . Giải
9𝑥6 + 6𝑥4 − 𝑥2 : 3𝑥2
= 9𝑥6 : 3𝑥2 + 6𝑥4 : 3𝑥2 − 𝑥2 : 3𝑥2 1
= 9: 3 ⋅ 𝑥6: 𝑥2 + 6: 3 . 𝑥4: 𝑥2 − 3 . 𝑥2:𝑥2 1 = 3𝑥4 + 2𝑥2 − 3 LUYỆN TẬP 2 Tính: 1 1 1
2 𝑥4 − 4 𝑥3 + 𝑥 : − 8 𝑥 Giải 1 1 −1 1 −1 1 −1 −1
2 𝑥4 − 4 𝑥3 + 𝑥 : 8 𝑥 = (2 𝑥4: 8 𝑥) − 4 𝑥3: ( 8 𝑥) + (𝑥: 8 𝑥) = −4𝑥3 + 2𝑥2 − 8 3
Chia đa thức một biến đã sắp xếp
Thảo luận nhóm hoàn thành HĐ4
HĐ 4: Thực hiện phép chia: a) 2𝑥2 + 5𝑥 + 2 : (2𝑥 + 1)
* Để thực hiện phép chia ta làm như sau: 2𝑥2 + 5𝑥 + 2 2𝑥 + 1 _
• Lấy 2x2 chia cho 2x được x, viết x. 2𝑥2 + 𝑥 𝑥 + 2
- Lấy x nhân với 2x + 1 được 2x2 + x, viết 2x2 + x. 4𝑥 + 2 _
- Lấy 2x2 + 5x + 2 trừ đi 2x2 + x được 4x + 2, viết 4𝑥 + 2 4x + 2. • Lấy 0
4x chia cho 2x được 2, viết 2.
- Lấy 2 nhân với 2x + 1 được 4x + 2, viết 4x + 2. Vậy:
- Lấy 4x + 2 trừ 4x + 2 được 0, viết 0.
(2x2 + 5x + 2):(2x + 1) = x + 2
b) 3𝑥3 − 5𝑥2 + 2 : 𝑥2 + 1 .
• Lấy 3x3 chia cho x2 được 3x, viết 3x. _ 3𝑥3 − 5𝑥2 + 2 𝑥2 + 1 -
Lấy 3x nhân với x2 + 1 được 3x3 + 3x, viết 3x3 + 3x. -
Lấy 3x3 - 5x2 + 2 trừ đi 3x3 + 3x được -5x2 - 3x + 2, 3𝑥3 + 3𝑥 3𝑥 − 5 viết -5x2 - 3x + 2. • Lấy −5𝑥2 − 3𝑥 + 2
-5x2 chia cho x2 được -5, viết -5. _ -
Lấy -5 nhân với x2 + 1 được -5x2 - 5, viết -5x2 - 5. −5𝑥2 − 5 -
Lấy -5x2 - 3x + 2 trừ đi -5x2 - 5 được -3x + 7, viết −3𝑥 + 7 -3x + 7.
• Bậc của đa thức -3x + 7 bằng 1, nhỏ hơn bậc của Vậy: (3x3 - 5x2 + 2)
đa thức x2 + 1 bằng 2 nên phép chia kết thúc. = (3x-5).(x2 +1)+(-3x+7) KẾT LUẬN
Để chia một đa thức cho một đa thức khác đa thức không (cả hai đa thức đều
đã thu gọn và sắp xếp các đơn thức theo số mũ giảm dần của biến) khi bậc
của đa thức bị chia lớn hơn hoặc bằng bậc của đa thức chia, ta làm như sau: Bước 1:
• Chia đơn thức bậc cao nhất của đa thừc bị chia cho đơn thức bậc cao nhất của đa thức chia
• Nhân kết quả trên với đa thức chia và đặt tích dưới đa thức bị chia sao cho
hai đơn thức có cùng số mũ của biến ở cùng cột
• Lấy đa thức bị chia trừ đi tích đặt dưới để được đa thức mới. KẾT LUẬN Bước 2:
Tiếp tục quá trình trên cho đến khi nhận được đa thức không hoặc đa thức
có bậc nhỏ hơn bậc của đa thức chia.
Tính: a) 6𝑥2 − 13𝑥 + 6 : (−3𝑥 + 2);
Ví dụ 3 (SGK – tr66)
b) 8𝑥2 − 10𝑥 + 5 : (−2𝑥 + 1). Giải Vậy:
6𝑥2 − 13𝑥 + 6 ∶ −3𝑥 + 2 = −2x + 3 Ta còn viết:
6𝑥2 − 13𝑥 + 6 = (−3𝑥 + 2)(−2x + 3) Giải
Vậy: 8𝑥2 − 10𝑥 + 5 : −2𝑥 + 1 = −4𝑥 + 3 dư 2
Ta còn viết: 8𝑥2 − 10𝑥 + 5 = −2𝑥 + 1 −4x + 3 + 2 LUYỆN TẬP 3
Tính: a) 𝑥3 + 1 : 𝑥2 − 𝑥 + 1
b) (8𝑥3 − 6𝑥2 + 5): 𝑥2 + 𝑥 + 1 Giải a) _ 𝑥3 + 1 𝑥2 − 𝑥 + 1 𝑥3 − 𝑥2 + 𝑥 𝑥 + 1 𝑥2 − 𝑥 + 1
Vậy 𝑥3 + 1 : 𝑥2 − 𝑥 + 1 𝑥2 − 𝑥 + 1 = 𝑥 + 1.4 0 Giải b) 8𝑥3 − 6𝑥2 + 5 𝑥2 + 𝑥 + 1 _ 8𝑥3 + 8𝑥2 + 8𝑥 8𝑥 − 14 _ −14𝑥2 − 8𝑥 + 5 −14𝑥2 − 14𝑥 − 14 6𝑥 + 19
Vậy: 8𝑥3 − 6𝑥2 + 5 = 8𝑥 − 14 . 𝑥2 + 𝑥 + 1 + 22𝑥 + 19 . NHẬN XÉT
- Khi chia đa thức 𝐴 cho đa thức 𝐵 của cùng một biến (𝐵 ≠ 0), có hai khả năng xảy ra:
• Phép chia có dư bằng 0 . Trong trường hợp này ta nói đa thức 𝐴 chia hết cho đa thức 𝐵.
• Phép chia có dư là đa thức 𝑅(𝑅 ≠ 0) với bậc của 𝑅 nhỏ hơn bậc của 𝐵.
Phép chia trong trường hợp này được gọi là phép chia có dư.
- Người ta chứng minh được rằng đối với hai đa thức tùy ý 𝐴 và 𝐵 của cùng
một biến (𝐵 ≠ 0), tồn tại duy nhất một cặp đa thức 𝑄 và 𝑅 sao cho 𝐴 =
𝐵. 𝑄 + 𝑅, trong đó 𝑅 bằng 0 hoặc bậc của 𝑅 nhỏ hơn bậc của 𝐵. Như vậy,
đa thức 𝐴 chia hết cho đa thức 𝐵 khi và chi khi 𝑅 = 0. LUYỆN TẬP Bài 1 Tính Giải a) 4𝑥3 ∶ −2𝑥2 ;
𝑎) (4𝑥3): (−2𝑥2) = 4: −2 . (𝑥3: 𝑥2) = −2𝑥. b) −7𝑥2 ∶ (6𝑥); −7
𝑏)(−7𝑥2) ∶ 6𝑥 = −7 ∶ 6 . (𝑥2 ∶ 𝑥) = 6 c) −14𝑥4 ∶ −8𝑥3 . 𝑐) −14𝑥4 : −8𝑥3 7
= −14 ∶ −8 . (𝑥4 ∶ 𝑥3) = 4𝑥 Bài 2 Giải Tính
𝑎) 8𝑥3 + 2𝑥2 − 6𝑥 ∶ 4𝑥
= 8𝑥3 ∶ 4𝑥 + 2𝑥2 ∶ 4𝑥 − 6𝑥 ∶ 4𝑥
a) 8𝑥3 + 2𝑥2 − 6𝑥 : ( 4𝑥); 1 3 = 2𝑥2 +
b) 5𝑥3 − 4𝑥 : (−2𝑥); 2 𝑥 − 2
𝑏) 5𝑥3 − 4𝑥 ∶ −2𝑥
c) −15𝑥6 − 24𝑥3 : −3𝑥2 .
= 5𝑥3 ∶ −2𝑥 − 4𝑥 ∶ −2𝑥 −5 −5
= 2 𝑥2 − (−2) = 2 𝑥2 + 2 Bài 2 Giải Tính
𝑐) −15𝑥6 − 24𝑥3 ∶ −3𝑥2
a) 8𝑥3 + 2𝑥2 − 6𝑥 : ( 4𝑥);
= −15𝑥6 ∶ −3𝑥2 − 24𝑥3 ∶ −3𝑥2
b) 5𝑥3 − 4𝑥 : (−2𝑥); = 5𝑥4 − −8𝑥
c) −15𝑥6 − 24𝑥3 : −3𝑥2 . = 5𝑥4 + 8𝑥. Bài 3 Tính Giải
a) 𝑥2 − 2𝑥 + 1 : (𝑥 − 1); a)
b) 𝑥3 + 2𝑥2 + 𝑥 : 𝑥2 + 𝑥 ; 𝑥2 − 2𝑥 + 1 𝑥 − 1 _ 𝑥2 − 𝑥 𝑥 − 1
c) −16𝑥4 + 1 : −4𝑥2 + 1 − 𝑥 + 1 _
d) −32𝑥5 + 1 : (−2𝑥 + 1). − 𝑥 + 1 0 Giải b) c) 𝑥3 + 2𝑥2 + 𝑥 𝑥2 + 𝑥 + 1 −16𝑥4 + 1 _ −4𝑥2 + 1 _ 𝑥3 + 𝑥2 −16𝑥4 + 4𝑥2 𝑥 + 1 4𝑥2 + 1 𝑥2 + 𝑥 −4𝑥2 + 1 𝑥2 + 𝑥 −4𝑥2 + 1 0 0 d) −32𝑥5 + 1 _ −2𝑥 + 1 −32𝑥5 + 16𝑥4
16𝑥4 + 8𝑥3 + 4𝑥2 + 2𝑥 + 1 −16𝑥4 + 1 _ −16𝑥4 + 8𝑥3 _ −8𝑥3 + 1 −8𝑥3 + 4𝑥2 _ −4𝑥2 + 1 −4𝑥2 + 2𝑥 −2𝑥 + 1 −2𝑥 + 1 0 Bài 4 Tính
a) 6𝑥2 − 2𝑥 + 1 : (3𝑥 − 1);
b) 27𝑥3 + 𝑥2 − 𝑥 + 1 : (−2𝑥 + 1);
c) 8𝑥3 + 2𝑥2 + 𝑥 : 2𝑥3 + 𝑥 + 1 ;
d) 3𝑥4 + 8𝑥3 − 2𝑥2 + 𝑥 + 1 : (3𝑥 + 1). Giải a) c) _ 6𝑥2 − 2𝑥 + 1 3𝑥 − 1 2𝑥3 + 𝑥 + 1 _ 8𝑥3 + 2𝑥2 + 𝑥 6𝑥2 − 2𝑥 2𝑥 8𝑥3 + 4𝑥 + 4 4 1 −3𝑥 − 4 Giải −2𝑥 + 1 27𝑥3 + 𝑥2 − 𝑥 + 1 b) _ 27 27𝑥3 − −27 29 25 2 𝑥2 2 𝑥2 − 4 𝑥 − 8 29 _ 2 𝑥2 − 𝑥 + 1 29 29 2 𝑥2 − 4 𝑥 25 _ 4 𝑥 + 1 29 25 4 𝑥 − 8 33 8 d)
3𝑥4 − 8𝑥3 − 2𝑥2 + 𝑥 + 1 3𝑥 + 1 _ 3𝑥4 + 𝑥3 7 13 22 𝑥3 − 7𝑥3 − 2𝑥2 + 𝑥 + 1 3 𝑥2 − 9 𝑥 + 27 _ 7 7𝑥3 + 3𝑥2 −13 _ 3 𝑥2 + 𝑥 + 1 −13 13 3 𝑥2 − 9 𝑥 22 _ 9 𝑥 + 1 22 22 9 𝑥 + 27 5 27
BÀI TẬP TRẮC NGHIỆM 3 −1 Câu 1. Tính 4 𝑥3 : 2 𝑥2 −3 3 A. 𝑥 B. 𝑥 2 2 3 −3 C. 𝑥 D. 𝑥 4 4
BÀI TẬP TRẮC NGHIỆM −1
Câu 2. Tính (𝑥3 − 3𝑥2 + 6𝑥): 3 𝑥 A. 3𝑥2 + 9𝑥 – 18 B. – 3𝑥2 + 9𝑥 – 18 −1 −1 C. 𝑥2 + 9𝑥 – 18 D. 𝑥2 − 9𝑥 – 18 3 3
BÀI TẬP TRẮC NGHIỆM
Câu 3. Rút gọn đa thức 2𝑥
𝑄(𝑥) = 3 3 − 1 + 15𝑥2 − 10𝑥 :(−5𝑥) − (3𝑥 − 1) A. 4x B. 4x -4 C. -4x – 4 D. -4x
BÀI TẬP TRẮC NGHIỆM
Câu 4. Tính (3𝑥3 – 7𝑥2 + 4𝑥 – 4) ∶ 𝑥 – 2 A. 3𝑥2 − 𝑥 – 18 B. 3𝑥2 − 𝑥 + 18 C. −3𝑥2 − 𝑥 – 2 D. 3𝑥2 − 𝑥 + 2
BÀI TẬP TRẮC NGHIỆM
Câu 5. Số dư của phép chia đa thức 4𝑥4 – 2𝑥2 + 7 cho 𝑥 + 3 A. 313 B. 3x C. 21x D. 21 BÀI TẬP THÊM Giải Câu 1. Tính: a) 75𝑥5 : 3𝑥3
a) 75𝑥5 : 3𝑥3 = 75: 3 ⋅ 𝑥5: 𝑥3 = 25, 𝑥5−3 = 25𝑥2 b) − 5 𝑥4 : 1 𝑥 2 2 b) 5 1 5 1 c) −9𝑥3 : − 2 𝑥2 − 5
2 𝑥4 : 2 𝑥 = − 2 : 2 ⋅ 𝑥4: 𝑥
d) 8𝑥𝑛+2 : 3𝑥4 (𝑛 ∈ ℕ, 𝑛 ≥ 2). = −5𝑥4−1 = −5𝑥3 BÀI TẬP THÊM Giải Câu 1. Tính: 2 2 a) 75𝑥5 : 3𝑥3
c) −9𝑥3 : − 5𝑥2 = (−9): −5 ⋅ 𝑥3:𝑥2 b) − 5 𝑥4 : 1 𝑥 2 2 45 = 2 𝑥 c) −9𝑥3 : − 2 𝑥2 8 5 d)
8𝑥𝑛+2 : 3𝑥4 = 3 ⋅ 𝑥𝑛+2:𝑥4
d) 8𝑥𝑛+2 : 3𝑥4 (𝑛 ∈ ℕ, 𝑛 ≥ 2). 8 8
= 3𝑥𝑛+2−4 = 3𝑥𝑛−2 BÀI TẬP THÊM
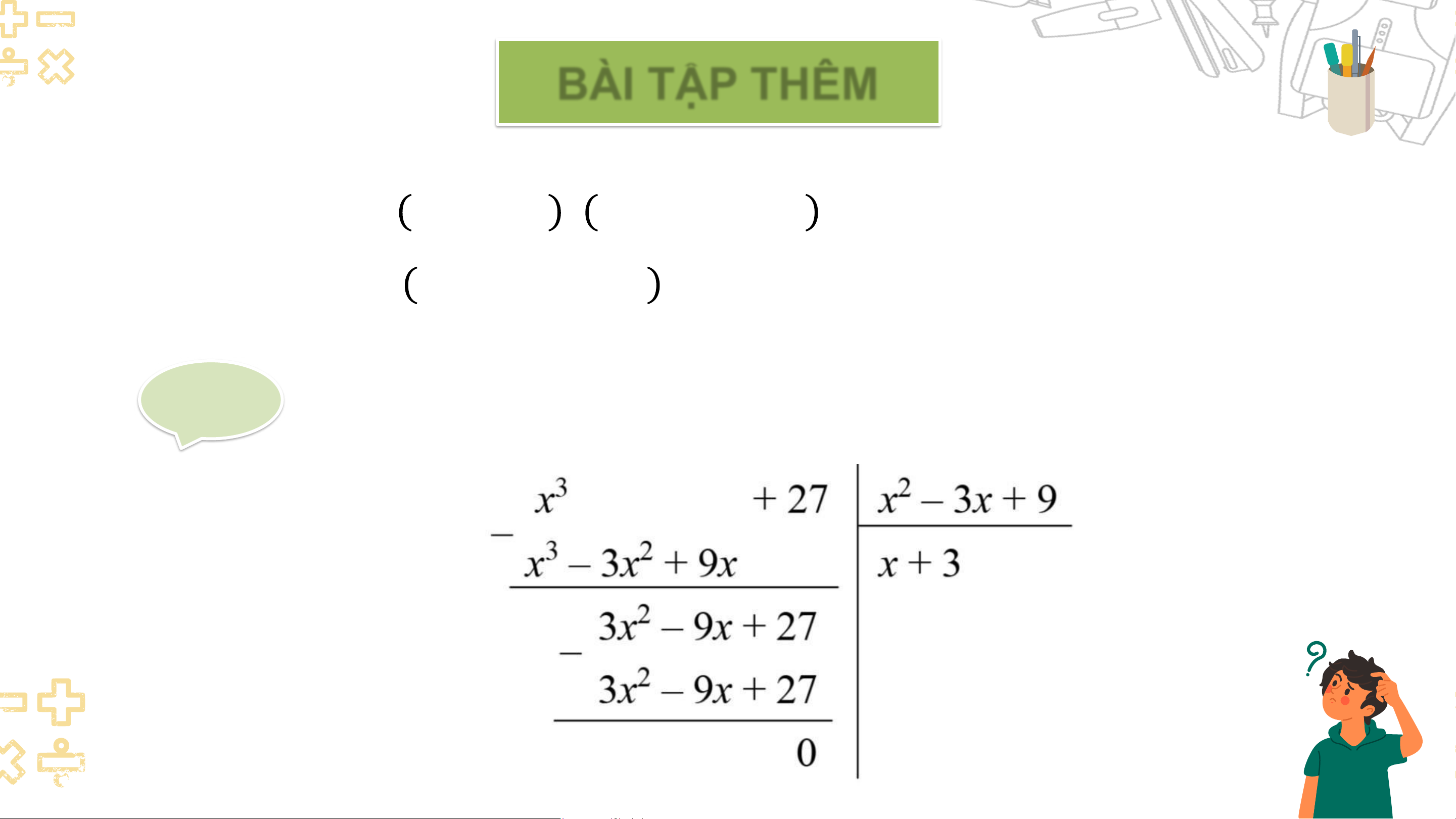
Câu 2. Tính: a) 𝑥3 + 27 : 𝑥2 − 3𝑥 + 9
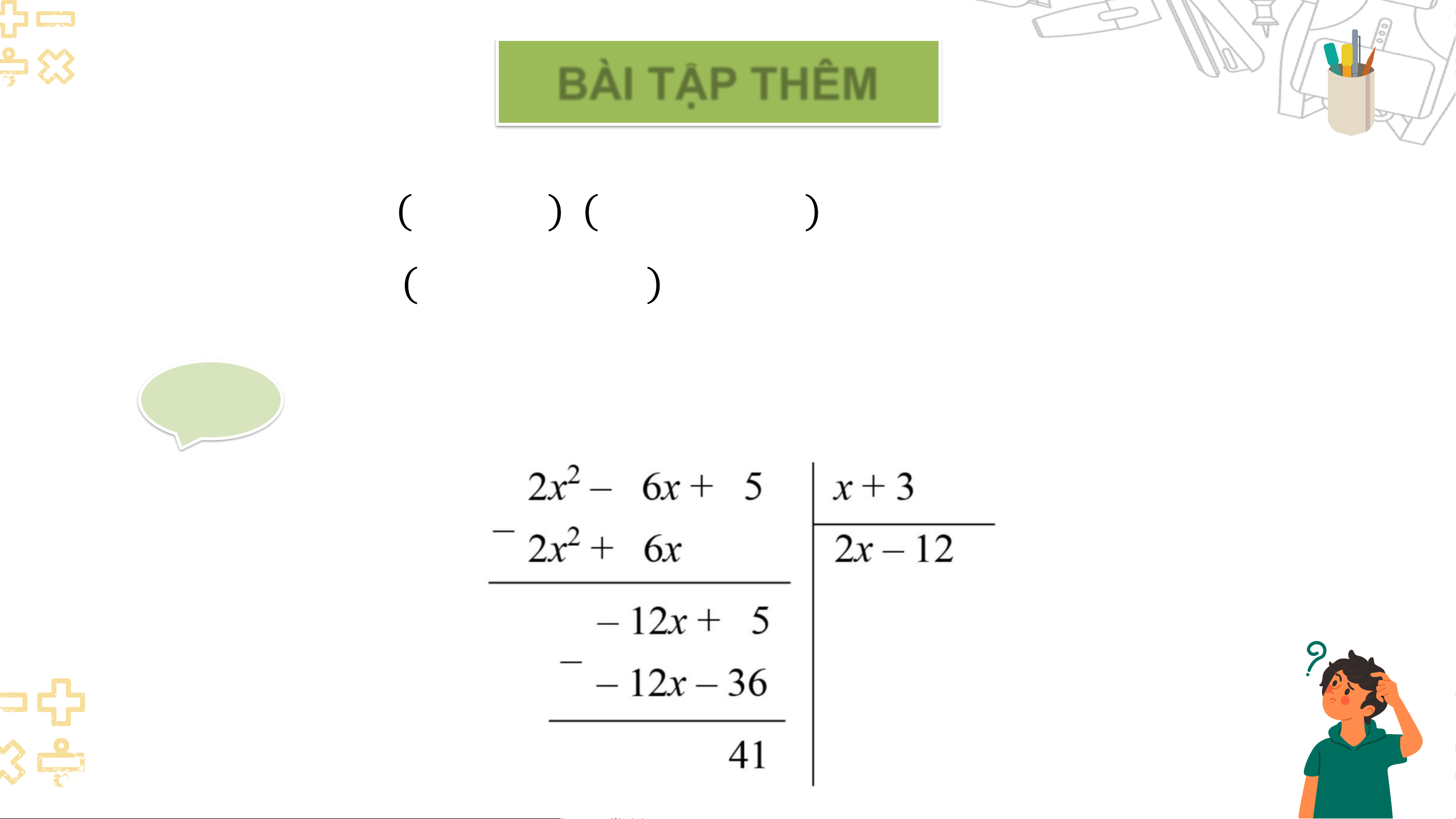
b) 2𝑥2 − 6𝑥 + 5 : (𝑥 + 3). Giải a) BÀI TẬP THÊM
Câu 2. Tính: a) 𝑥3 + 27 : 𝑥2 − 3𝑥 + 9
b) 2𝑥2 − 6𝑥 + 5 : (𝑥 + 3). Giải b) VẬN DỤNG Bài 5
Một công ty sau khi tăng giá 30 nghìn đồng mỗi sản phẩm so với
giá ban đầu là 2𝑥 (nghìn đồng) thì có doanh thu là 6𝑥2 + 170𝑥 + 1200
(nghìn đồng). Tính số sản phẩm mà công ty đó đã bán được theo 𝑥. Giải
Giá sản phẩm sau khi đã tăng giá là 2𝑥 + 30 (nghìn đồng).
Khi đó số sản phẩm mà công ty bán được là thương trong phép chia
6𝑥2 + 170𝑥 + 1200 cho 2𝑥 + 30.
Thực hiện phép tính ta được:
(6𝑥2 + 170𝑥 + 1200): 2x + 30 = 3x + 40
Vậy số sản phẩm mà công ty đó đã bán được là 3𝑥 + 40 sản phẩm. Bài 6
Một hình hộp chữ nhật có thể tích là 𝑥3 + 6𝑥2 + 11𝑥 + 6 cm3 . Biết
đáy là hình chữ nhật có các kích thước là 𝑥 + 1 (cm) và 𝑥 + 2 (cm).
Tính chiều cao của hình hôp chữ nhật đó theo 𝑥. Giải
Diện tích đáy của hình hộp chữ nhật là:
𝑥 + 1 𝑥 + 2 = 𝑥 . 𝑥 + 𝑥 . 2 + 1 . 𝑥 + 1 . 2 = 𝑥2 + 2𝑥 + 𝑥 + 2
= 𝑥2 + 3𝑥 + 2 (𝑐𝑚2). Giải
Chiều cao của hình hộp chữ nhật là thương trong phép chia thể tích
hình hộp chữ nhật cho diện tích đáy của hình hộp chữ nhật đó.
Thực hiện phép tính ta được:
𝑥3 + 6𝑥2 + 11𝑥 + 6 : 𝑥2 + 3𝑥 + 2 = 𝑥 + 3
Vậy chiều cao của hình hộp chữ nhật đó là 𝑥 + 3 cm.
HƯỚNG DẪN VỀ NHÀ • Chuẩn bị bài mới * Ghi nhớ * Hoàn thành các “Bài tập kiến thức trong bài. bài tập trong SBT.
cuối chương VI” CẢM ƠN CÁC EM
ĐÃ CHÚ Ý LẮNG NGHE!
Document Outline

• Slide 1
• Slide 2
• Slide 3
• Slide 4
• Slide 5
• Slide 6
• Slide 7
• Slide 8
• Slide 9
• Slide 10
• Slide 11
• Slide 12
• Slide 13
• Slide 14
• Slide 15
• Slide 16
• Slide 17
• Slide 18
• Slide 19
• Slide 20
• Slide 21
• Slide 22
• Slide 23
• Slide 24
• Slide 25
• Slide 26
• Slide 27
• Slide 28
• Slide 29
• Slide 30
• Slide 31
• Slide 32
• Slide 33
• Slide 34
• Slide 35
• Slide 36
• Slide 37
• Slide 38
• Slide 39
• Slide 40
• Slide 41
• Slide 42
• Slide 43
• Slide 44
• Slide 45
• Slide 46
• Slide 47
• Slide 48
• Slide 49
• Slide 50
• Slide 51
• Slide 52