Bài giảng điện tử môn Toán 7 Chương 2 Bài 1: Số vô tỉ. Căn bậc hai số học (Tiết 16) | Chân trời sáng tạo

Bài giảng điện tử môn Toán 7 Chương 2 Bài 1: Số vô tỉ. Căn bậc hai số học (Tiết 16) | Chân trời sáng tạo được VietJack sưu tầm và soạn thảo để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

26 13 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Giáo án Toán 7

Môn: Toán 7

Sách: Chân trời sáng tạo

Thông tin:

28 trang 6 tháng trước

Tác giả:

Profile Mai Nguyệt
C
H
À
O
M
Ừ
N
G
C
Á
C
E
M
Đ
Ế
N
V
Ớ
I
T
I
Ế
T
H
Ọ
C
!

 !"#$%&'()*
+),$-.!/'0
1+1*2 1345
)6(7%"815
90:%;<=0(>%3
?% 13 :!9<42(6!*@)A:
$#!+%89BC! >9%86
% D! DE%')FG8!B%H
;<)(#$9,I
Bài học hôm nay sẽ trả lời cho chúng ta
câu hỏi trên
;<)(#$9,I
@JH?KLMN-OG@P-QRS
?KQT-E0JUF
RQVWAXGYZQ[SAXGY
-;#$ 
C!; D\!9,I
Z,có số hữu tỉ nào
mà bình phương lên
bằng 2.
J @S]^_S`GQPaaQbG-cR?KQd^N
@QVWAXGYQeGQQfGQZSgGQh-H
a)Hãy thực hiện các phép chia sau đây rồi làm tiếp câu b:
3:2=?; 37:25=?; 5:3=?; 1:9=?.
b)Dùng kết quả trên để viết các số sau đây dưới dạng số thập phân:
; ; ;
3
2
=…
37
25
=…
5
3
=…
1
9
=…
ZJiEj9!klF
J @S]^_S`GQPaaQbG-cR?KQd^N
@QVWAXGYQeGQQfGQZSgGQh-H
a)Kết quả các phép chia là:
3:2= ; 37:25= ; 5:3=; 1:9=
b)Dùng kết quả trên để viết các số sau đây dưới dạng số thập phân:
3
2
=𝟏 , 𝟓 ;
37
25
=𝟏 , 𝟒 𝟖 ;
5
3
=𝟏 , 𝟔𝟔𝟔…;
1
9
=𝟎 , 𝟏𝟏𝟏….
8
Với một số hữu tỉ ta chỉ có hai trường hợp sau:
bằng một phân số thập phân thì kết quả của phép chia
là số thập phân bằng với phân số thập phân đó.
J @S]^_S`GQPaaQbG-cR?KQd^N
Trường hợp 1: (xem SGK/tr30)
3
2
=
15
10
=𝟏 , 𝟓 ;
37
25
=
148
100
=𝟏 ,𝟒𝟖;
9
Với một số hữu tỉ ta chỉ có hai trường hợp sau:
không bằng bất cứ phân số thập phân nào thì kết quả của phép
chia không bao giờ dừng và có chữ số hoặc cụm chữ số sau
dấu phẩy lặp đi lặp lại.
Trường hợp 2: (xem SGK/tr30)
3
2
=
15
10
=𝟏 , 𝟓 ;
37
25
=
148
100
=𝟏 ,𝟒𝟖 ;
(xem SGK/tr30)
10
Chú ý(xem SGK/tr30)
J @S]^_S`GQPaaQbG-cR?KQd^N
Số 0,8(3) đọc là 0,8 chu kì 3;
số 2,6(12) đọc là 2,6 chu kì 12
.
Chú ý:
11
J @S]^_S`GQPaaQbG-cR?KQd^N
Số 0,8(3) đọc là 0,8 chu kì 3;
số 2,6(12) đọc là 2,6 chu kì 12
.
Chú ý:
Người ta chứng minh được rằng:
Mỗi số hữu tỉ được biểu diễn bởi một số thập
phân hữu hạn hoặc vô hạn tuần hoàn.
KTTT:
12
J @S]^_S`GQPaaQbG-cR?KQd^N
Ví dụ 1: (xem SGK/tr31)
5
4
=𝟏 ,𝟐𝟓 ;
171
500
=𝟎 , 𝟑𝟒𝟐;
431
165
=𝟐 , 𝟔(𝟏𝟐);
=
\?KLMN
@QVWAXGYQeGQQfGQZSgGQh-H
Z\iEj9!kJF
M
N
D
C
A
B
Cho 2 hình vuông ABCD và AMBN như hình bên
Cho biết cạnh AM = 1dm.
Em hãy cho biết diện tích hình vuông ABCD gấp
mấy lần diện tích hình vuông AMBN .
Tính diện tích hình vuông ABCD.
Hãy biểu diễn diện tích hình vuông ABCD theo độ dài đoạn AB.
\?KLMN
Z\iEj9!kJF
M
N
D
C
A
B
Giải:
Ta thấy diện tích hình vuông AMBN bằng 2 lần diện tích
tam giác ANB và diện tích hình vuông ABCD bằng 4
lần diện tích tam giác ANB. Do đó, diện tích hình vuông
ABCD gấp 2 lần diện tích hình vuông AMBN .
Diện tích hình vuông AMBN là: 1.1 = 1
Do diện tích hình vuông ABCD gấp 2 lần diện tích hình
vuông AMBN nên diện tích hình vuông ABCD là 2
Diện tích hình vuông ABCD là:
(đơn vị diện tích).
15
Z\i: (xem SGK/tr31)
16
\?KLMN
Mỗi số thập phân vô hạn
không tuần hoàn là biểu diễn thập
phân của một số, số đó gọi là số vô tỉ.
KTTT:
Tập hợp số vô tỉ được kí hiệu là: I
Chú ý:
17
LB15\: (xem SGK/tr31)
12
25
=𝟎 , 𝟒 𝟖 ;
Y<H
27
2
=𝟏𝟑, 𝟓 ;
\HEj?YZ!k\F
Hoàn thành các phát biểu sau:
a)Số a = 5,123 là một số thập phân hữu hạn nên a là số I
b)Số b = 6,15555…=6,1(5) là một số thập phân vô hạn tuần
hoàn nên b là số ..?...
c)G8!:%)(
2,*9,mL)I
d)Cho biết số c = 2,23606… là một số thập phân vô hạn không
tuần hoàn. Vậy c là số ..?....
\HEj?YZ!k\F
Hoàn thành các phát biểu sau:
a)Số a = 5,123 là một số thập phân hữu hạn nên a là số ..?.
b)Số b = 6,15555…=6,1(5) là một số thập phân vô hạn
tuần hoàn nên b là số ..?...
c)G8!:%)(
2,*9,mL)I
d)Cho biết số c = 2,23606… là một số thập phân
vô hạn không tuần hoàn. Vậy c là số ..?....
Y<H
,$
,$
#$
#$
Vận
dụng
Vận
dụng
0
2
.
_QVWAXGYLPG_nGY.
Hãy so sánh hai số hữu tỉ: 0,834 và .
HOẠT ĐỘNG CẶP ĐÔI
op4mHSuy nghĩ, thảo luận thực hiện yêu cầu của
Vận Dụng 1trang 31 SGK.
- Thời gian: 2 phút
Vận
dụng
Vận
dụng
0
2
.
Hãy so sánh hai số hữu tỉ: 0,834 và .
Y<H
Mẫu chung của 500 và 6
là 1500
Vì 1251>1250 nên
Vậy lqkr >
Hết
giờ
000
1
0
2
0
3
0
4
0
5
0
6
0
7
0
8
0
9
1
0
BT TRẮC NGHIỆM CỦNG CỐ:
-2JHPhân số nào dưới đây viết được dưới dạng
số thập phân vô hạn tuần hoàn?
A.
3
8
2
5
B.
54
165
C.
D.
2291
100
Hết
giờ
000
1
0
2
0
3
0
4
0
5
0
6
0
7
0
8
0
9
1
0
BT TRẮC NGHIỆM CỦNG CỐ:
Câu 2: a21+%20%1+1*
2#*I
A.
7
6
52
165
B.
17
160
C.
D.
5
18
BÀI TẬP TRẮC NGHIỆM CỦNG CỐ
Câu 3. Viết số dưới dạng số thập phân là:
A.0,25. B. 0,2(5). C.0,(25). D.0,(025).
Câu 4. Viết số thập phân 0,52 dưới dạng phân số tối giản là:
25
99
Hết
giờ
000
1
0
2
0
3
0
4
0
5
0
6
0
7
0
8
0
9
1
0
-2sPhát biểu nào dưới đây !?
RSố vô tỉ là số viết được dưới dạng số thập phân vô
hạn không tuần hoàn
@Số vô tỉ là số viết được dưới dạng số thập phân vô
hạn tuần hoàn
-Số 0 không phải số hữu tỉ dương và cũng không là
số hữu tỉ âm.
_ Mỗi số thâp phân hữu hạn hoặc vô hạn tuần hoàn
biểu diễn một số hữu tỉ.
BT TRẮC NGHIỆM CỦNG CỐ:
HƯỚNG DẪN VỀ NHÀ
1. - Học bài và xem lại tất cả các bài tập đã giải
2. Hoàn thành bài tập 1 trang 33SGK
3. Đọc và nghiên cứu trước nội dung 3,4 của bài để tiết
sau học
CẢM ƠN CÁC EM ĐÃ
CHÚ Ý LẮNG NGHE
| 1/28
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

CHÀO MỪNG CÁC EM
ĐẾN VỚI TIẾT HỌC!
Trong chương này, các em sẽ tìm hiểu về số thực. Tập
hợp số thực bao gồm các số hữu tỉ đã học và một loại số
mới là số vô tỉ. Chúng ta cũng sẽ học cách viết số thực
dưới dạng thập phân, cách biểu diễn số thực trên trục số
và cách làm tròn một số thực; đồng thời vận dụng các
kiến thức đó vào giải quyết một số vấn đề thực tiễn. Số
được biểu diễn trong bức tranh khảm trên sân một tòa nhà tại Berlin, Đức.
Tỉ số giữa chu vi với đường kính của bất kì đường tròn nào
đều bằng nhau và bằng  
(đọc là pi). Người ta tính được:
có phải là một số hữu tỉ không?
có phải là một số hữu tỉ không?
Bài học hôm nay sẽ trả lời cho chúng ta câu hỏi trên
Bài 1: SỐ VÔ TỈ. CĂN BẬC HAI SỐ HỌC (Tiết 16 )
A.HOẠT ĐỘNG KHỞI ĐỘNG
Có số hữu tỉ nào mà bình phương
của nó bằng 2 hay không?
Không có số hữu tỉ nào
mà bình phương lên bằng 2.
B. HOẠT ĐỘNG HÌNH THÀNH KIẾN THỨC:
1. BIỂU DIỄN THẬP PHÂN CỦA SỐ HỮU TỈ
Khám phá 1 (xem sgk trang 30)
a)Hãy thực hiện các phép chia sau đây rồi làm tiếp câu b: 3:2=?; 37:25=?; 5:3=?; 1:9=?.
b)Dùng kết quả trên để viết các số sau đây dưới dạng số thập phân: 3 1 ; ; ; 2 =… 37 25 =… 5 3 =… 9 =…
B. HOẠT ĐỘNG HÌNH THÀNH KIẾN THỨC:
1. BIỂU DIỄN THẬP PHÂN CỦA SỐ HỮU TỈ
a)Kết quả các phép chia là:
3:2= ; 37:25= ; 5:3=; 1:9=
b)Dùng kết quả trên để viết các số sau đây dưới dạng số thập phân: 3 37
2 =𝟏 , 𝟓 ;
25 =𝟏, 𝟒𝟖; 5 1
3 =𝟏 , 𝟔𝟔𝟔 … ;
9 =𝟎 , 𝟏𝟏𝟏 … . 1. B
IỂU DIỄN THẬP PHÂN CỦA SỐ HỮU TỈ
Với một số hữu tỉ ta chỉ có hai trường hợp sau:
Trường hợp 1: (xem SGK/tr30)
bằng một phân số thập phân thì kết quả của phép chia
là số thập phân bằng với phân số thập phân đó. 3 15 37 148
2 = 10 =𝟏 , 𝟓 ; 25 = 10 0 =𝟏 ,𝟒𝟖 ; 8
Với một số hữu tỉ ta chỉ có hai trường hợp sau:
Trường hợp 2: (xem SGK/tr30)
không bằng bất cứ phân số thập phân nào thì kết quả của phép chi
a không bao giờ dừng và có chữ số hoặc cụm chữ số sau
dấu phẩy lặp đi lặp lại. (xem SGK/tr30) 3 15 148
2 = 10 =𝟏 , 𝟓 ; 37
25 = 10 0 =𝟏 ,𝟒𝟖 ; 9
1. BIỂU DIỄN THẬP PHÂN CỦA SỐ HỮU TỈ
Chú ý(xem SGK/tr30)
Chú ý: Số 0,8(3) đọc là 0,8 chu kì 3;
số 2,6(12) đọc là 2,6 chu kì 12 . 10
1. BIỂU DIỄN THẬP PHÂN CỦA SỐ HỮU TỈ
Chú ý: Số 0,8(3) đọc là 0,8 chu kì 3;
số 2,6(12) đọc là 2,6 chu kì 12 . K T T
T: Người ta chứng minh được rằng:
Mỗi số hữu tỉ được biểu diễn bởi một số thập
phân hữu hạn hoặc vô hạn tuần hoàn. 11
1. BIỂU DIỄN THẬP PHÂN CỦA SỐ HỮU TỈ
Ví dụ 1: (xem SGK/tr31) 5 171
4 =𝟏 ,𝟐𝟓 ;
500 =𝟎 , 𝟑𝟒𝟐 ; 431
165 =𝟐 , 𝟔(𝟏𝟐); = 12
B. HOẠT ĐỘNG HÌNH THÀNH KIẾN THỨC: 2. SỐ VÔ TỈ
Khám phá 2 (xem sgk trang 31) M
Cho 2 hình vuông ABCD và AMBN như hình bên
Cho biết cạnh AM = 1dm. A B
Em hãy cho biết diện tích hình vuông ABCD gấp N
mấy lần diện tích hình vuông AMBN . D C
Tính diện tích hình vuông ABCD.
Hãy biểu diễn diện tích hình vuông ABCD theo độ dài đoạn AB. 2. SỐ VÔ TỈ
Khám phá 2 (xem sgk trang 31) M Giải: A B
Ta thấy diện tích hình vuông AMBN bằng 2 lần diện tích
tam giác ANB và diện tích hình vuông ABCD bằng 4 N
lần diện tích tam giác ANB. Do đó, diện tích hình vuông D C
ABCD gấp 2 lần diện tích hình vuông AMBN .
Diện tích hình vuông AMBN là: 1.1 = 1
Do diện tích hình vuông ABCD gấp 2 lần diện tích hình
vuông AMBN nên diện tích hình vuông ABCD là 2
Diện tích hình vuông ABCD là: (đơn vị diện tích).
Khám phá 2 : (xem SGK/tr31) 15 2. SỐ VÔ TỈ K
TT T : Mỗi số thập phân vô hạn
không tuần hoàn là biểu diễn thập
phân của một số, số đó gọi là số vô tỉ.
Chú ý: Tập hợp số vô tỉ được kí hiệu là: I 16
Ví dụ 2: (xem SGK/tr31) 17 Giải: 12 27
25 =𝟎 , 𝟒𝟖;
2 =𝟏𝟑, 𝟓 ;
Thực hành 2: ( xem SGK trang 32)
Hoàn thành các phát biểu sau:
a)Số a = 5,123 là một số thập phân hữu hạn nên a là số ..?.
b)Số b = 6,15555…=6,1(5) là một số thập phân vô hạn tuần hoàn nên b là số ..?...
c)Người ta chứng minh được là một số
thập phân vô hạn không tuần toàn. Vậy là số ..?....
d)Cho biết số c = 2,23606… là một số thập phân vô hạn không
tuần hoàn. Vậy c là số ..?....
Thực hành 2: ( xem SGK trang 32) Giải:
Hoàn thành các phát biểu sau:
a) Số a = 5,123 là một số thập phân hữu hạn nên a là số ..? h.ữu tỉ
b)Số b = 6,15555…=6,1(5) là một số thập phân vô hạn
tuần hoàn nên b là số ..? h ... ữu tỉ
c) Người ta chứng minh được là một số
thập phân vô hạn không tuần toàn. Vậy là số ..?.... vô tỉ
d)Cho biết số c = 2,23606… là một số thập phân
vô hạn không tuần hoàn. Vậy c là số ..?.... vô tỉ
D. HOẠT ĐỘNG VẬN DỤNG. Vận ận dụng
Hãy so sánh hai số hữu tỉ: 0,834 và . 02.
HOẠT ĐỘNG CẶP ĐÔI
- Yêu cầu: Suy nghĩ, thảo luận thực hiện yêu cầu của Vận Dụng 1trang 31 SGK. - Thời gian: 2 phút Vận dụng
Hãy so sánh hai số hữu tỉ: 0,834 và . Giải: Mẫu chung của 500 và 6 là 1500 02. Vì 1251>1250 nên Vậy 0,834 >
BT TRẮC NGHIỆM CỦNG CỐ:
Câu 1: Phân số nào dưới đây viết được dưới dạng
số thập phân vô hạn tuần hoàn? A 3 54 2291 2 . B. 8 C. D. 5 16 5 1 00 Hết 0 10 0giờ 0 1 2 3 4 5 6 7 8 9 0
BT TRẮC NGHIỆM CỦNG CỐ:
Câu 2: Phân số nào dưới đây viết được dưới dạng
số thập phân hữu hạn? A 7 17 5 52 . B. 6 160 C. D. 16 5 18 Hết 0 10 0giờ 0 1 2 3 4 5 6 7 8 9 0
BÀI TẬP TRẮC NGHIỆM CỦNG CỐ 25
Câu 3. Viết số dưới dạng số thập phân là: 99 A.0,25. B. 0,2(5). C.0,(25). D.0,(025).
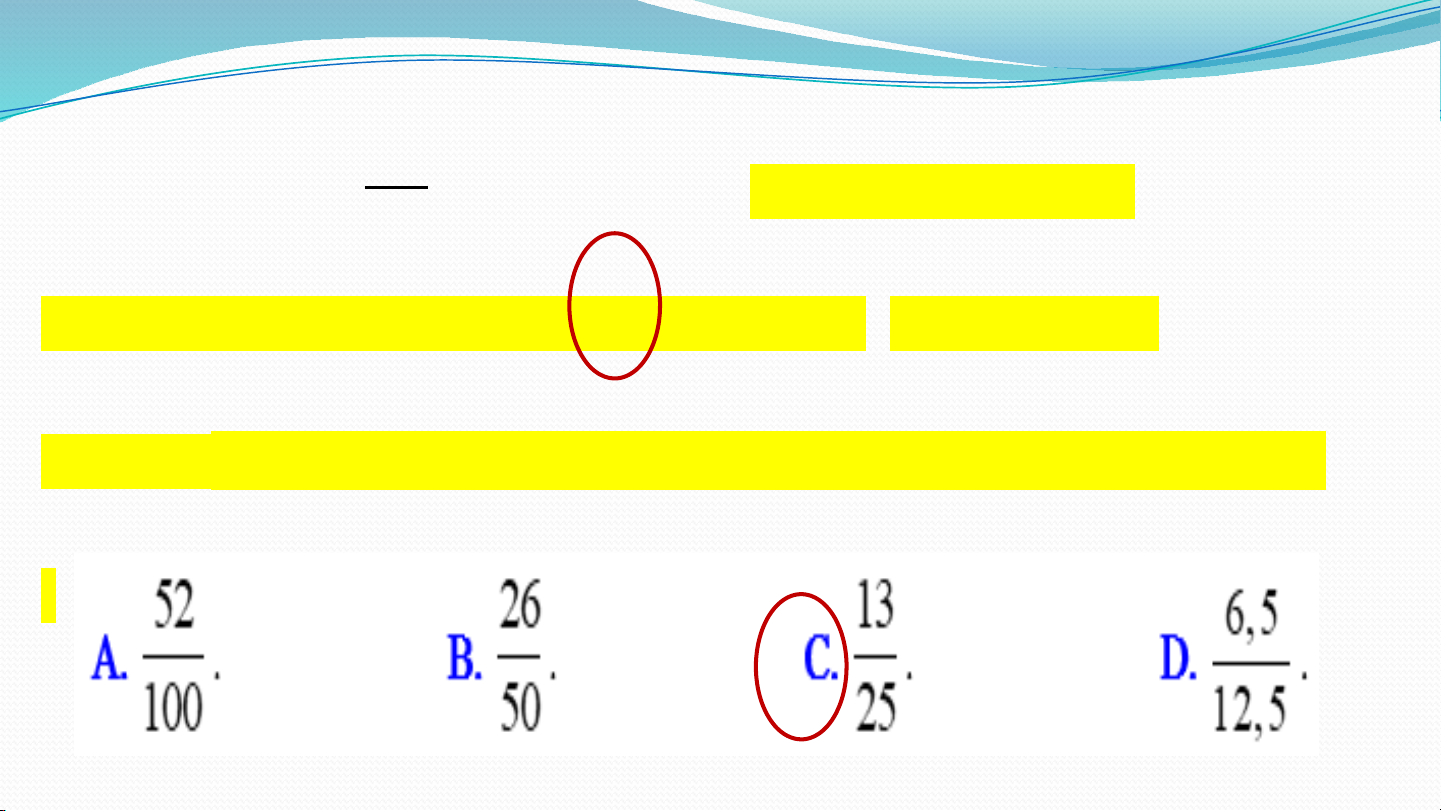
Câu 4. Viết số thập phân 0,52 dưới dạng phân số tối giản là:
BT TRẮC NGHIỆM CỦNG CỐ:
Câu 5. Phát biểu nào dưới đây sai?
A. Số vô tỉ là số viết được dưới dạng số thập phân vô hạn không tuần hoàn
B. Số vô tỉ là số viết được dưới dạng số thập phân vô hạn tuần hoàn
C. Số 0 không phải số hữu tỉ dương và cũng không là số hữu tỉ âm.
D. Mỗi số thâp phân hữu hạn hoặc vô hạn tuần hoàn Hết
biểu diễn một số hữu tỉ. 0 10 0giờ 0 1 2 3 4 5 6 7 8 9 0 HƯỚNG DẪN VỀ NHÀ
1. - Học bài và xem lại tất cả các bài tập đã giải
2. Hoàn thành bài tập 1 trang 33SGK
3. Đọc và nghiên cứu trước nội dung 3,4 của bài để tiết sau học CẢM ƠN CÁC EM ĐÃ CHÚ Ý LẮNG NGHE
Document Outline

  • Slide 1
  • Slide 2
  • Slide 3
  • Slide 4
  • A.HOẠT ĐỘNG KHỞI ĐỘNG
  • Slide 6
  • Slide 7
  • Slide 8
  • Slide 9
  • Slide 10
  • Slide 11
  • Slide 12
  • Slide 13
  • Slide 14
  • Slide 15
  • Slide 16
  • Slide 17
  • Slide 18
  • Slide 19
  • Slide 20
  • Slide 21
  • Slide 22
  • Slide 23
  • Slide 24
  • BÀI TẬP TRẮC NGHIỆM CỦNG CỐ
  • Slide 26
  • HƯỚNG DẪN VỀ NHÀ
  • Slide 28