Bài giảng điện tử môn Toán 7 Chương 8 Bài 11: Bài tập cuối chương 8 | Chân trời sáng tạo

Bài giảng điện tử môn Toán 7 Chương 8 Bài 11: Bài tập cuối chương 8 | Chân trời sáng tạo được VietJack sưu tầm và soạn thảo để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

24 12 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Giáo án Toán 7

Môn: Toán 7

Sách: Chân trời sáng tạo

Thông tin:

19 trang 6 tháng trước

Tác giả:

Profile Mai Nguyệt
TIẾT 1
1
2
3
4
5
1
2
3
4
5
CHÚC MỪNG ĐỘI BẠN THỎ
CONGRATULATIONS RABBIT TEAM
CHÚC MỪNG ĐỘI BẠN CỌP
CONGRATULATIONS TIGER TEAM
AI LÊN CAO HƠN
Tiết Bài ÔN TẬP CHƯƠNG 8
Tiết Bài ÔN TẬP CHƯƠNG 8
Tổng số đo ba góc của một tam giác bằng 180
0
Trong một tam giác, tổng độ dài hai cạnh bất kì bao giờ cũng
lớn hơn độ dài cạnh còn lại.
Các trường hợp bằng nhau của hai tam giác
Các trường hợp bằng nhau của hai tam giác vuông.
Tam giác cân và tính chất của tam giác cân.
Tiết Bài ÔN TẬP CHƯƠNG 8
Tiết Bài ÔN TẬP CHƯƠNG 8
Bài 1: Tìm số đo x ở các hình vẽ sau
x
50
°
65
°
A
B
C
x
°
H
G
I
x
51
°
K
E
D
F
Hình 1
Hình 2
Hình 3
Tiết Bài ÔN TẬP CHƯƠNG 8
Tiết Bài ÔN TẬP CHƯƠNG 8
Bài 1: Tìm số đo x ở các hình vẽ sau
x
50
°
65
°
A
B
C
Hình 1
Giải
µ
µ µ
0
0 0 0
0 0 0
0 0 0
0
ABC,
A B C 180
50 180
65 50
115 65
x + 65
x = 180 -
x = 180
x = 65
Xeùt coù:
(toång ba goùc trong tam giaùc)
Vaäy
Tiết Bài ÔN TẬP CHƯƠNG 8
Tiết Bài ÔN TẬP CHƯƠNG 8
Bài 1: Tìm số đo x ở các hình vẽ sau
x
°
H
G
I
Hình 2
Giải
µ µ
µ
µ
0
0
0
IHG, IH IG
IHG
H G
H 69
G 69
I
x = 69
Xeùt coù:
caân taïi
Do ñoù
Maø
Neân
Vaäy
Tiết Bài ÔN TẬP CHƯƠNG 8
Tiết Bài ÔN TẬP CHƯƠNG 8
Bài 1: Tìm số đo x ở các hình vẽ sau
x
51
°
K
E
D
F
Hình 3
Giải
· ·
·
·
·
·
·
·
0
0
0
0
0
DEK ,
DEK EDK 90
KDF EDK 90 2
DEK KDF
DEK 51
KDF 51
K
(1)
x = 51
Xeùt vuoâng taïi coù:
Maët khaùc ta coù
Töø (1) vaø 2 suy ra
Maø
Neân
Vaäy
Tiết Bài ÔN TẬP CHƯƠNG 8
Tiết Bài ÔN TẬP CHƯƠNG 8
Bài 2: Hãy chỉ ra các cặp tam giác bằng nhau trong hình sau và cho biết chúng bằng
nhau theo trường hợp nào?
Hình 1
A
B
D
C
I
E
H
G
F
Hình 2
Tiết Bài ÔN TẬP CHƯƠNG 8
Tiết Bài ÔN TẬP CHƯƠNG 8
Bài 2: Hãy chỉ ra các cặp tam giác bằng nhau trong hình sau và cho biết chúng bằng
nhau theo trường hợp nào?
Hình 1
A
B
D
C
Giải
AC
ABC CDA
AB = CD
BC = AD
= (c.c.c)
Xeùt ABC vaø CDA, coù:
laø caïnh chung
Do ño ù
Tiết Bài ÔN TẬP CHƯƠNG 8
Tiết Bài ÔN TẬP CHƯƠNG 8
Bài 2: Hãy chỉ ra các cặp tam giác bằng nhau trong hình sau và cho biết chúng bằng
nhau theo trường hợp nào?
I
E
H
G
F
Hình 2
Giải
·
·
EFI HGI,
EIF HIG
EFI HGI
IF = IG
IE = IH
ù = (c.g.c)
Xeùt vaø coù:
(hai goùc ñoái ñænh)
Do ño
Tiết Bài ÔN TẬP CHƯƠNG 8
Tiết Bài ÔN TẬP CHƯƠNG 8
K
N
M
B
C
A
GT
KL
AM BC
b)
Baøi 3:
MK A
Cho tam giaùc ABC caân taïi A, tia phaân giaùc cuûa goùc A caét BC taïi M.
a) Chöùng minh:
Ve õMN vuoâng goùc AB taïi N, laáy ñieåm K treân caïnh AC sao cho AN = AK.
Chöùng minh C
· ·
·
1
ABC BAM CAM BAC
2
MN AB
A,
N, AN = AK
caân taïi
taïi
a) AM BC
b) MK AC
Tiết Bài ÔN TẬP CHƯƠNG 8
Tiết Bài ÔN TẬP CHƯƠNG 8
K
N
M
B
C
A
GT
KL
Giải
Baøi 3:
· ·
·
1
ABC BAM CAM BAC
2
MN AB
A,
N, AN = AK, K AC
caân taïi
taïi
a) AM BC
b) MK AC
· ·
ABM ACM,
BAM CAM
ABM ACM
coù:
AB = AC (gt)
(gt)
AM
=
a
(c.g.
)
c)
Xeùt vaø
laø caïnh chung
Do ñoù
·
·
·
·
·
·
0
0
AMB AMC
AMB AMC 180
AMB AMC 90
ø
AM BC
(hai goùc töông öùng)
Ma (hai goùc ke àbuø)
Neân
Vaäy
Tiết Bài ÔN TẬP CHƯƠNG 8
Tiết Bài ÔN TẬP CHƯƠNG 8
K
N
M
B
C
A
GT
KL
Giải
Baøi 3:
· ·
·
1
ABC BAM CAM BAC
2
MN AB
A,
N, AN = AK, K AC
caân taïi
taïi
a) AM BC
b) MK AC
·
·
· ·
ANM AKM,
NAM KAM BAM CAM
ANM AKM
coù:
AN = AK (gt)
( = )
AM
ù = (c.g.
)
c)
b
Xeùt vaø
do
laø caïnh chung
Do ño
· ·
·
·
0
0
ANM AKM
ANM 90
AKM 90
A
ø (gt)
MK C
(hai goùc töông öùng)
Ma
Neân
Vaäy
Bài 4: Một khung treo quần áo hình tam
giác có thiết kế như hình 1, các thiết kế
mặt bên trái của khung được vẽ lại như
hình 2. Biết góc HIG bằng 16 độ
a) Tính số đo góc IMN.
b) Chứng minh: MN song song AB.
B
N
G
H
I
M
A
Hình 1
Hình 2
Bài 4:
B
N
G
H
I
M
A
Hình 1
Hình 2
a) Tính số đo góc IMN.
Giải
· ·
· ·
·
· ·
·
· ·
·
0
0
0 0
0
0
IMN
IMN INM
IMN INM 180 HIG
180 HIG
IMN INM
2
180 16
IMN INM 82
2
IMN 82
ù IM = IN (gt)
ù I
(1)
Ta co
Do ño caân taïi
Maø
Vaäy
Bài 4:
B
N
G
H
I
M
A
Hình 1
Hình 2
b) Chứng minh: MN song song AB.
Giải
·
·
·
·
·
·
·
0
Vì
IAB
IAB IBA
180 HIG
IAB IBA
2
IMN IAB
IA = IM + MA
IB = IN + NB
IM = IN, MA = NB (gt)
IA = IB
ù I
(2)
(1) (2)
MN // AB
Maø
Neân
Do ño caân taïi
Maø
Töø vaø suy ra ôû vò trí ñoàng vò
Neân
HƯỚNG DẪN HỌC SINH TỰ HỌC
HƯỚNG DẪN HỌC SINH TỰ HỌC
-
Xem lại các kiến thức và các dạng bài tập của
chương 8.
-
Hệ thống kiến thức chương 8 bằng sơ đồ tư duy.
-
Làm các bài tập còn lại trong sách bài tập.
HƯỚNG DẪN HỌC SINH TỰ HỌC
HƯỚNG DẪN HỌC SINH TỰ HỌC
-
Xem lại các kiến thức và các dạng bài tập của
chương 8.
-
Hệ thống kiến thức chương 8 bằng sơ đồ tư duy.
-
Làm các bài tập còn lại trong sách bài tập.
| 1/19
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

TIẾT 1
CHÚC MỪNG ĐỘI BẠN THỎ
CHÚC MỪNG ĐỘI BẠN CỌP 5
CONGRATULATIONS RABBIT TEAM
CONGRATULATIONS TIGER TEAM 5 4 4 3 3 2 2 AI LÊN CAO HƠN 1 1 Tiết iế B ài ÔN T ài ẬP C ÔN T H ẬP C ƯƠ Ư NG 8 G
Tổng số đo ba góc của một tam giác bằng 1800
Trong một tam giác, tổng độ dài hai cạnh bất kì bao giờ cũng
lớn hơn độ dài cạnh còn lại.
Các trường hợp bằng nhau của hai tam giác
Các trường hợp bằng nhau của hai tam giác vuông.
Tam giác cân và tính chất của tam giác cân. Tiết iế B ài ÔN T ài Ô ẬP C N T H ẬP C ƯƠ Ư NG 8 G
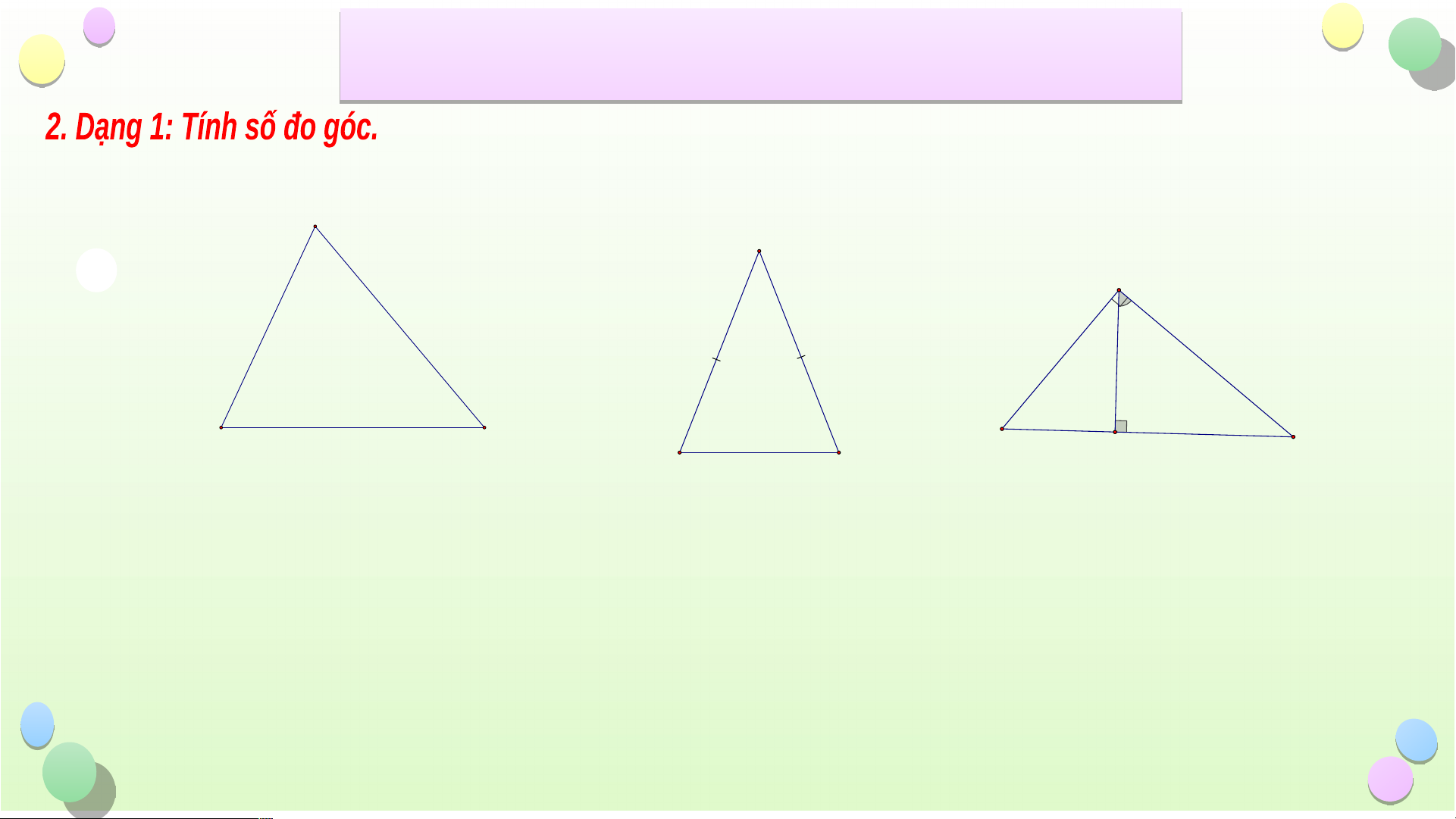
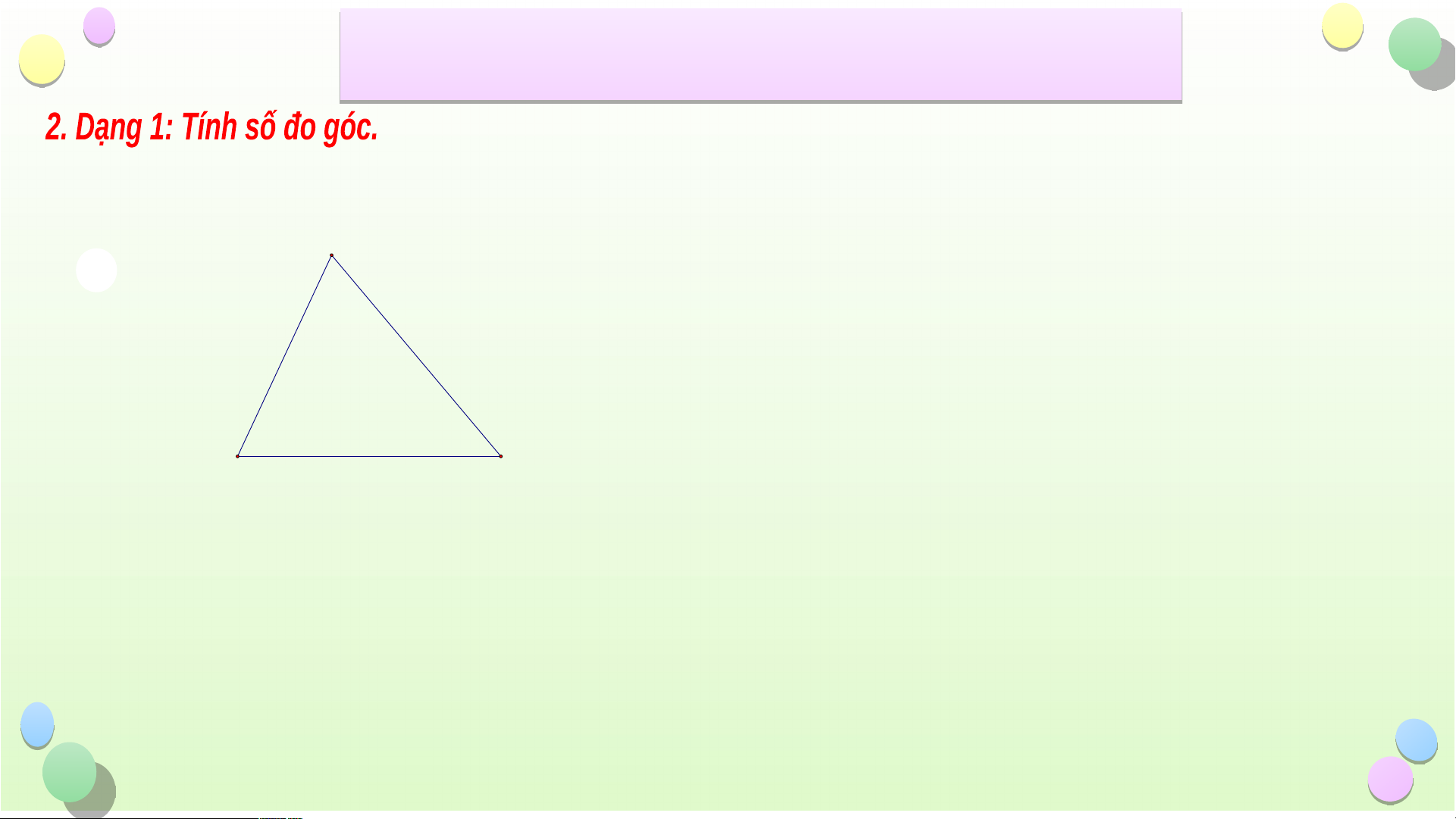
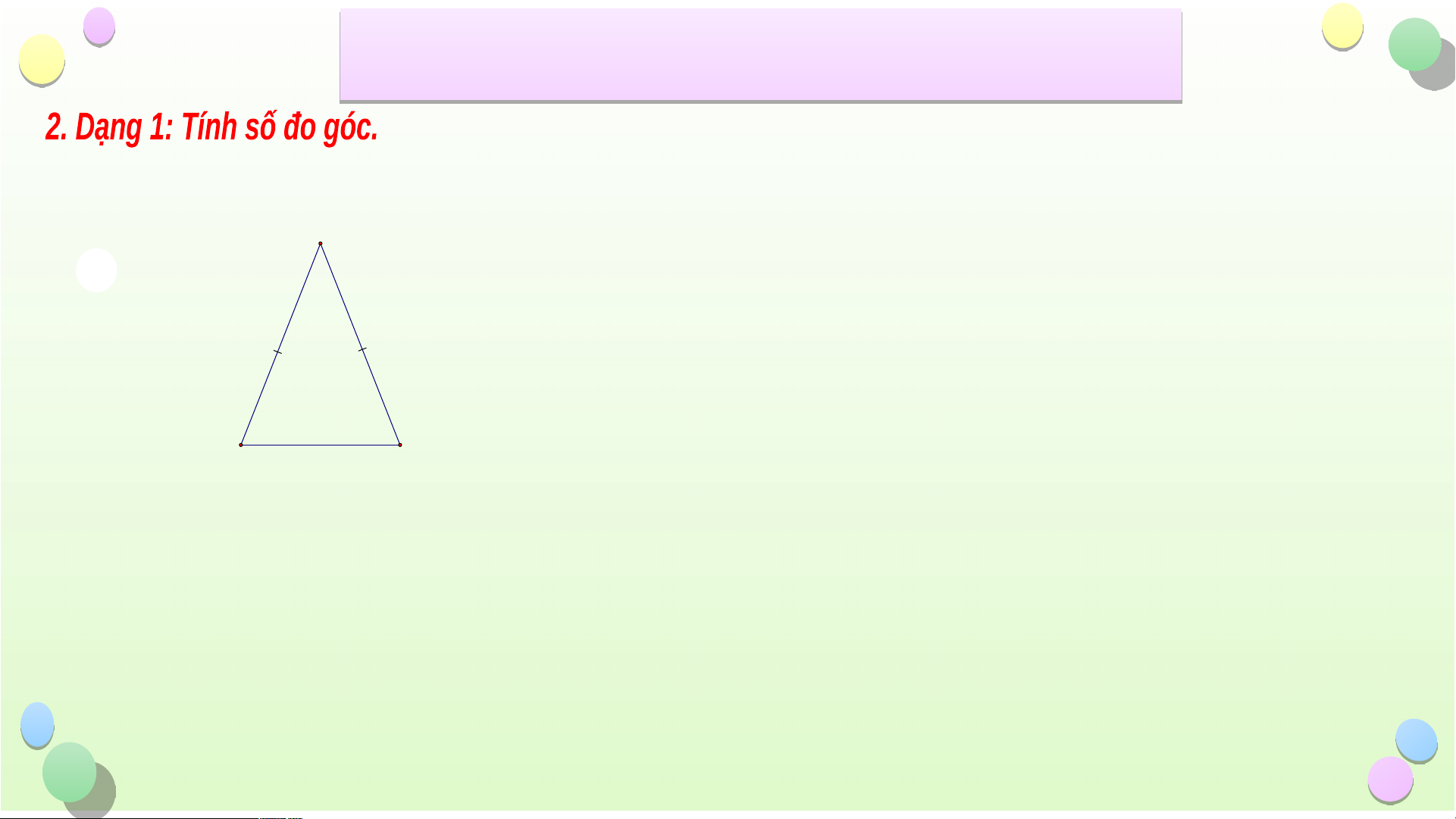
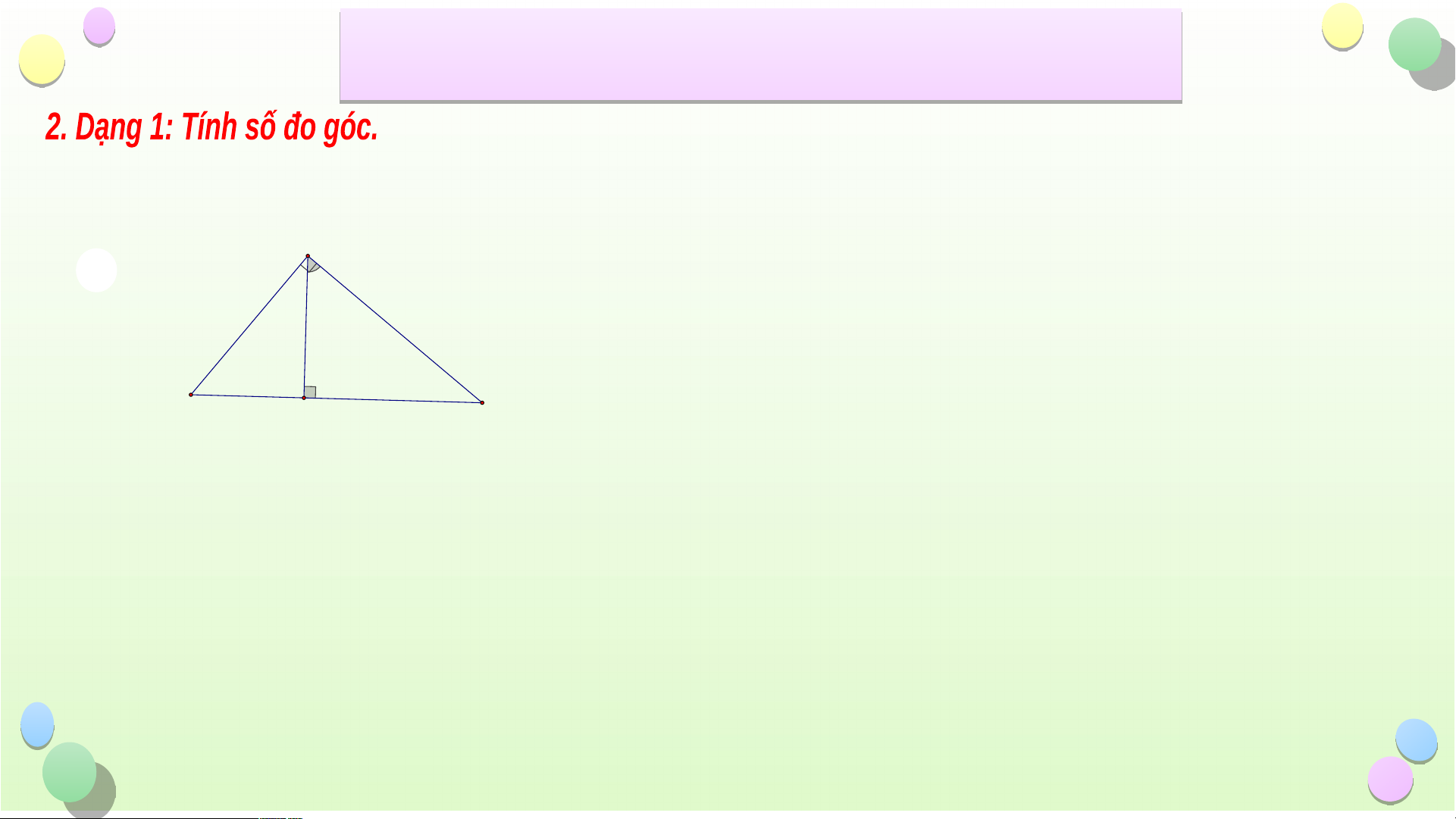
Bài 1: Tìm số đo x ở các hình vẽ sau A x I D x 65° 50° 51° B C 69° x E K F Hình 1 H G Hình 2 Hình 3 Tiết iế B ài ÔN T ài Ô ẬP C N T H ẬP C ƯƠ Ư NG 8 G
Bài 1: Tìm số đo x ở các hình vẽ sau A Giải x Xe  ù t ABC, coù: µ µ µ 0 A  B  C 180  (toång ba goù c trong tam giaù c) 0 0 0  x + 65  50 180  65° 50° B C 0 x = 180 -  0 0 65  50  Hình 1 0 0 0 x = 180  115 65  0 Va äy x = 65 Tiết iế B ài ÔN T ài Ô ẬP C N T H ẬP C ƯƠ Ư NG 8 G
Bài 1: Tìm số đo x ở các hình vẽ sau Giải I Xeù t I  HG, coù : I H I  G  I  HG caâ n taïi I µ µ Do ño H ù G  69° x µ 0 H G Ma H ø 6  9 Hình 2 µ 0 Neân G 6  9 0 Va äy x = 69 Tiết iế B ài ÔN T ài Ô ẬP C N T H ẬP C ƯƠ Ư NG 8 G
Bài 1: Tìm số đo x ở các hình vẽ sau Giải D x Xeù t D  EK vuoâ ng taïi K, coù: · · 0 DEK  EDK 90  (1) 51° · · 0 E Maët khaù c ta co K ù DF  EDK 90   2 K F Hình 3 Töø (1) vaø  · · 2 suy ra D EK K  DF · 0 Ma D ø EK 5  1 · 0 Neân K DF 51  0 Va äy x = 51 Tiết iế B ài ÔN T ài Ô ẬP C N T H ẬP C ƯƠ Ư NG 8 G
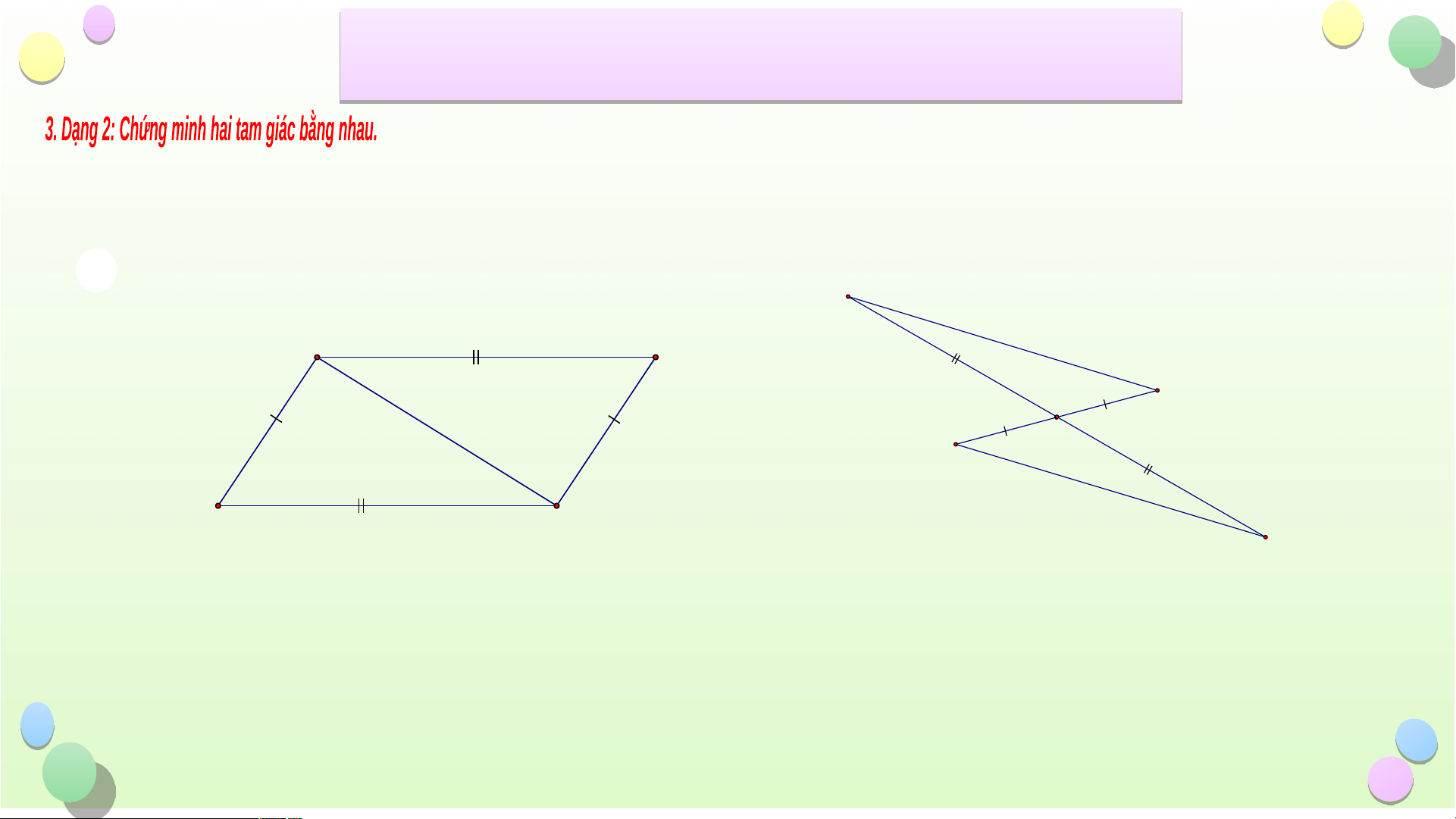
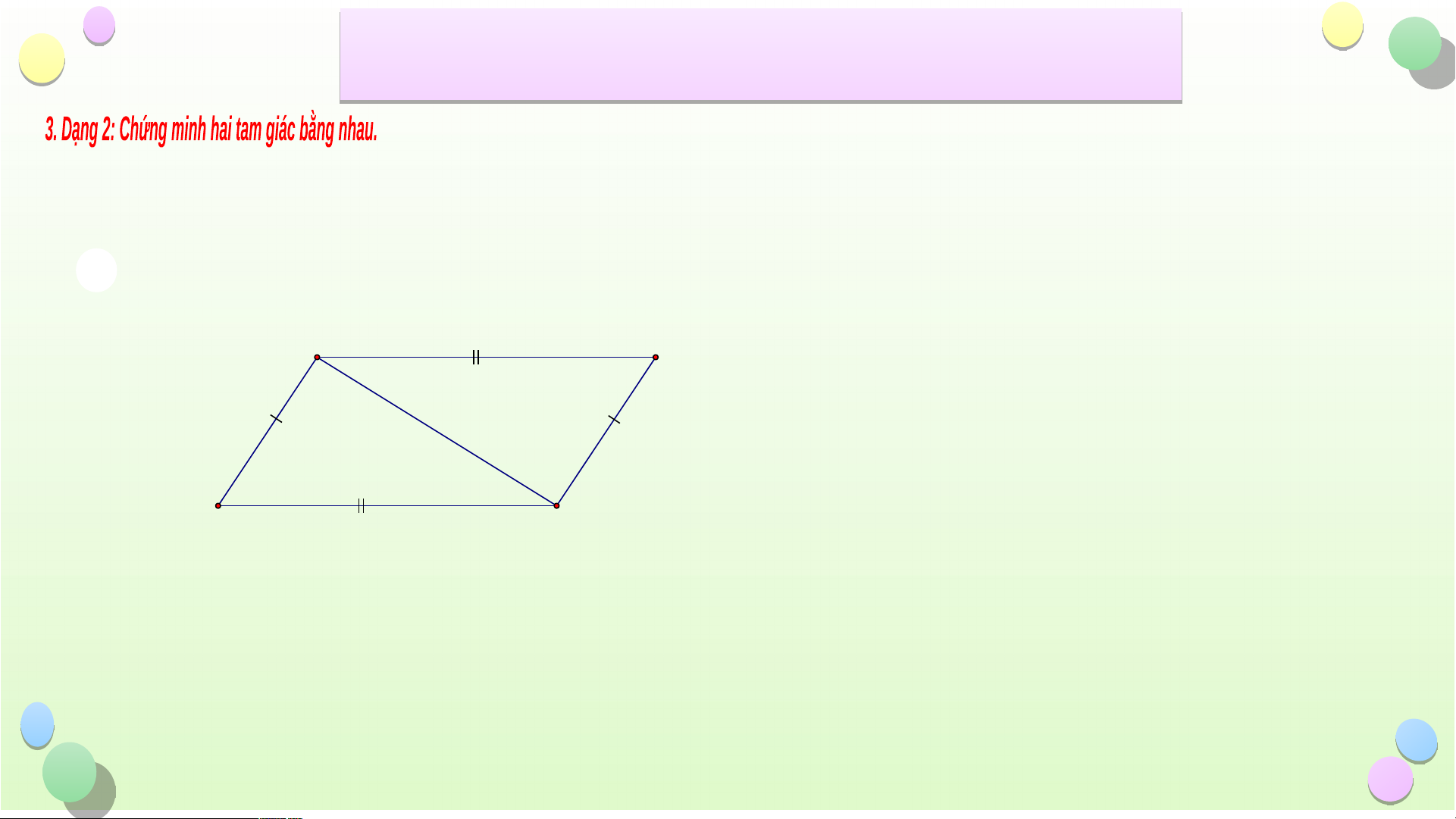
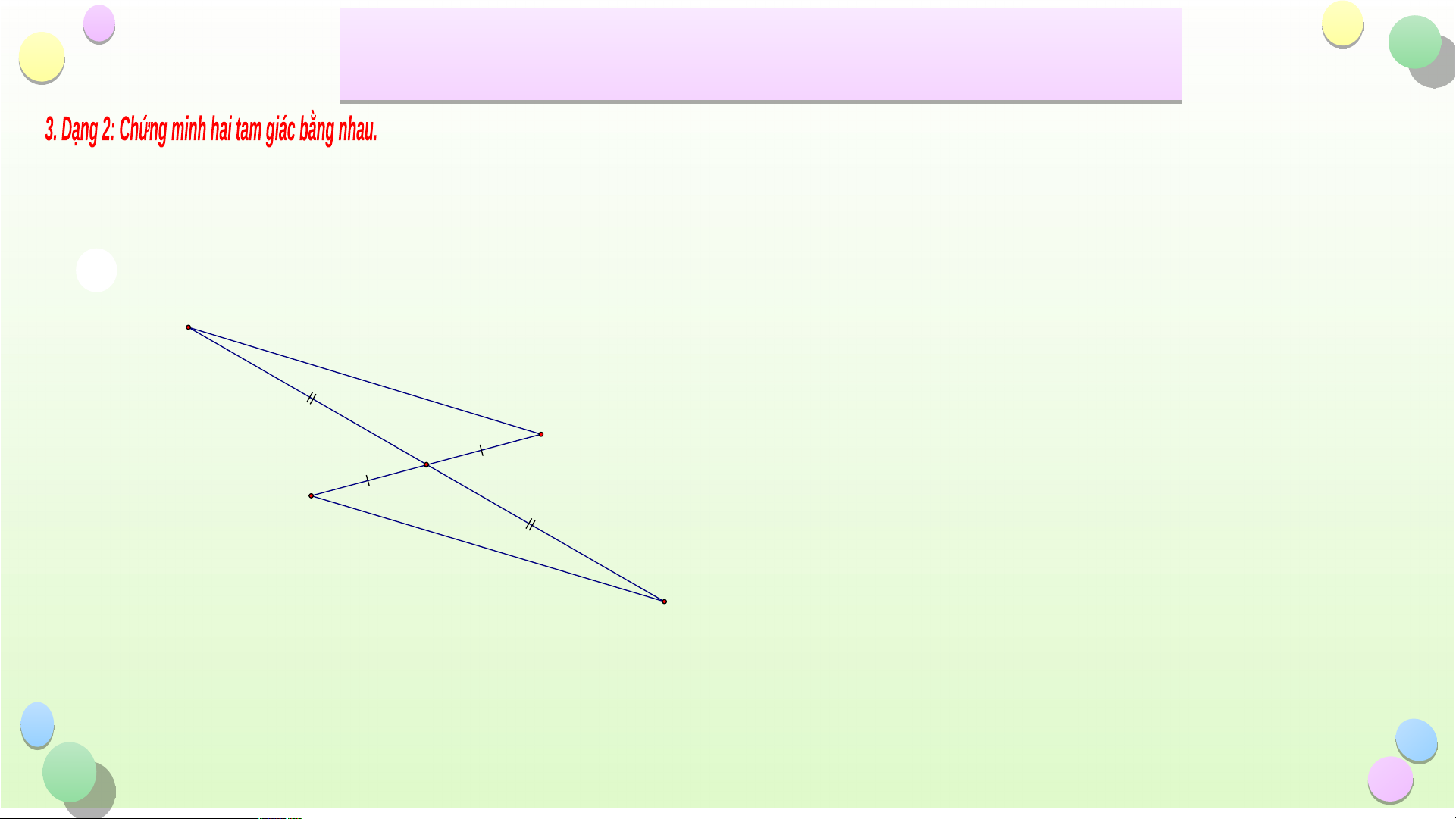
Bài 2: Hãy chỉ ra các cặp tam giác bằng nhau trong hình sau và cho biết chúng bằng
nhau theo trường hợp nào? E A B F I G D C H Hình 2 Hình 1 Tiết iế B ài ÔN T ài Ô ẬP C N T H ẬP C ƯƠ Ư NG 8 G
Bài 2: Hãy chỉ ra các cặp tam giác bằng nhau trong hình sau và cho biết chúng bằng
nhau theo trường hợp nào? Giải A B Xe  ù t ABC va  ø CDA, coù: AB = CD A C laø caïnh chung BC = AD D C Do ño ùA  BC = C  DA (c.c.c) Hình 1 Tiết iế B ài ÔN T ài Ô ẬP C N T H ẬP C ƯƠ Ư NG 8 G
Bài 2: Hãy chỉ ra các cặp tam giác bằng nhau trong hình sau và cho biết chúng bằng
nhau theo trường hợp nào? Giải E Xeù t E  FI v a  ø HGI, coù: IF = IG F · · E IF H  IG (hai goù c ñoái ñæ nh) I G IE = IH Do ñ ù o EFI = HG  I (c.g.c) H Hình 2 Tiết iế B ài ÔN T ài Ô ẬP C N T H ẬP C ƯƠ Ư NG 8 G Baøi 3: Cho tam giaù
c ABC caân taïi A, tia phaân giaù c cuû a goù c A caét BC taïi M. a) Chöù ng minh: A M BC b) Ve õMN vuoâng goù
c AB taïi N, laáy ñieåm K treân caïnh AC sao cho AN = AK. Chöù ng min h MK AC A · · 1 · A  BC caâ n taïi A, B AM C  AM  BAC GT 2
MN  AB taïi N, AN = AK KL a) AM BC N K b) MK AC B M C Tiết iế B ài ÔN T ài Ô ẬP C N T H ẬP C ƯƠ Ư NG 8 G Baøi 3: A · · 1 · A  BC caâ n taïi A, B AM C  AM  BAC GT 2
MN  AB taïi N, AN = AK, K AC KL a) AM BC N K b) MK AC B M C Giải a ) Xe ù t A  BM vaø A  CM, coù : · ·  AMB A  MC (hai goù c töông öù ng) AB = AC (gt) · · 0 Ma A ø MB  AMC 180  (hai goù c ke àbuø) · · B AM CA  M (gt) · · 0 Neân A MB A  MC 90  AM laø caïnh chung Va äy AM BC Do ñ où A
 BM = ACM (c.g.c) Tiết iế B ài ÔN T ài Ô ẬP C N T H ẬP C ƯƠ Ư NG 8 G Baøi 3: A · · 1 · A  BC caâ n taïi A , B AM C  AM  BAC GT 2
MN  AB taïi N, AN = AK, K AC KL a) AM BC N K b) MK AC B M C Giải ) b Xe ù t A  NM v aø A  KM, coù : · ·  ANM A  KM (hai goù c töông öù ng) AN = AK (gt) · 0 Ma A ø NM 90  (gt) · · · · NAM K  AM (do B AM C = AM) · 0 Neân A KM 90  AM laø caïnh chung Va äy MK  AC Do ñ ù o A  NM = A  KM (c.g.c) I
Bài 4: Một khung treo quần áo hình tam
giác có thiết kế như hình 1, các thiết kế
mặt bên trái của khung được vẽ lại như M N
hình 2. Biết góc HIG bằng 16 độ a) Tính số đo góc IMN. A B
b) Chứng minh: MN song song AB. H G Hình 1 Hình 2 Giải Bài 4: a) Tính số đo góc IMN. I Ta c ù o IM = IN (gt) Do ñ ù
o IMN caân taïi I · · M N  IMN I  NM · · 0 · Ma I øMN  INM 1  80  HIG A B 0 · · · 180  HIG  IMN I  NM  (1) H G 2 0 0 · · 180  16 0 Hình 1 Hình 2  IMN I  NM  8  2 2 · 0 Vaäy I MN 8  2 Giải Bài 4:
b) Chứng minh: MN song song AB. I Vì IA = IM + MA IB = IN + NB M a I øM = IN, MA = NB (gt) M N Neâ n IA = IB Do ñ ù o I  AB caâ n taïi I A B · ·  IAB I  BA H G 0 · · · 180  HIG Ma I øAB  IBA  (2) 2 Hình 1 Hình 2 · · T ö ( ø1) v a ( ø2) suy ra I MN I  AB ôû vò trí ñoàng vò Neâ n MN // AB HƯỚNG Ư DẪ D N HỌC SIN ỌC H TỰ H TỰ ỌC Ọ
- Xem lại các kiến thức và các dạng bài tập của chương 8.
- Hệ thống kiến thức chương 8 bằng sơ đồ tư duy.
- Làm các bài tập còn lại trong sách bài tập. HƯỚNG Ư DẪ D N HỌC SIN ỌC H TỰ H TỰ ỌC Ọ
- Xem lại các kiến thức và các dạng bài tập của chương 8.
- Hệ thống kiến thức chương 8 bằng sơ đồ tư duy.
- Làm các bài tập còn lại trong sách bài tập.
Document Outline

  • Slide 1
  • Slide 2
  • Slide 13
  • Slide 14
  • Slide 15
  • Slide 16
  • Slide 17
  • Slide 18
  • Slide 19
  • Slide 20
  • Slide 21
  • Slide 22
  • Slide 23
  • Slide 24
  • Slide 25
  • Slide 26
  • Slide 27
  • Slide 28
  • Slide 29