Bài giảng điện tử môn Toán 7 Chương 8 Bài 11: Bài tập cuối chương 8 (Tiết 2) | Chân trời sáng tạo
Bài giảng điện tử môn Toán 7 Chương 8 Bài 11: Bài tập cuối chương 8 (Tiết 2) | Chân trời sáng tạo được VietJack sưu tầm và soạn thảo để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!
Chủ đề: Giáo án Toán 7
Môn: Toán 7
Sách: Chân trời sáng tạo
Thông tin:
Tác giả:
Preview text:
TIẾT 2 non Ong học việc
Caâu 1 :So saùnh caùc goùc cuûa tam giaùc ABC, bieát AB = 3cm, AC = 5cm, BC = 4cm. µ µ µ A. A B C µ µ µ B. C B A µ µ µ C. B C A
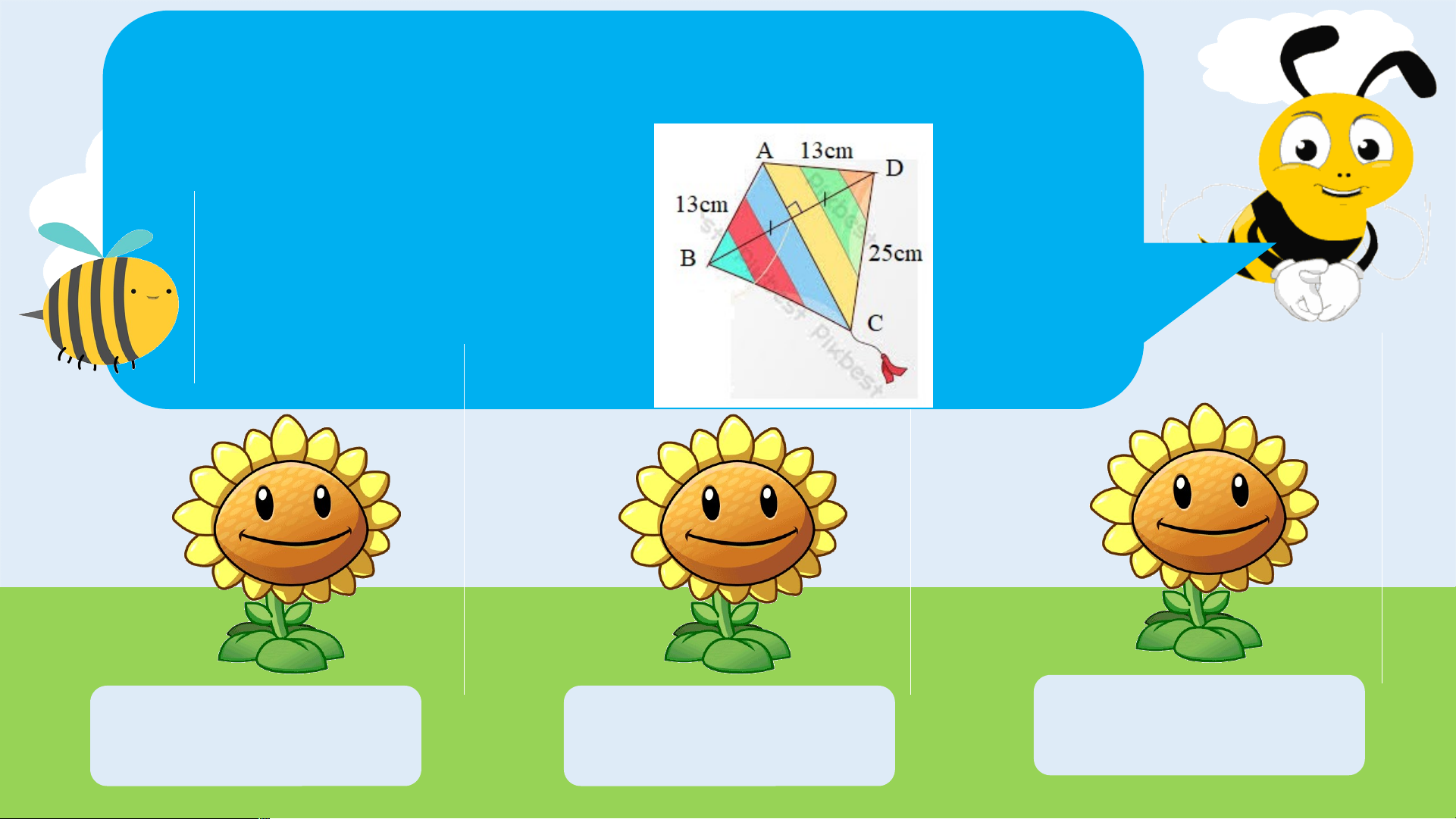
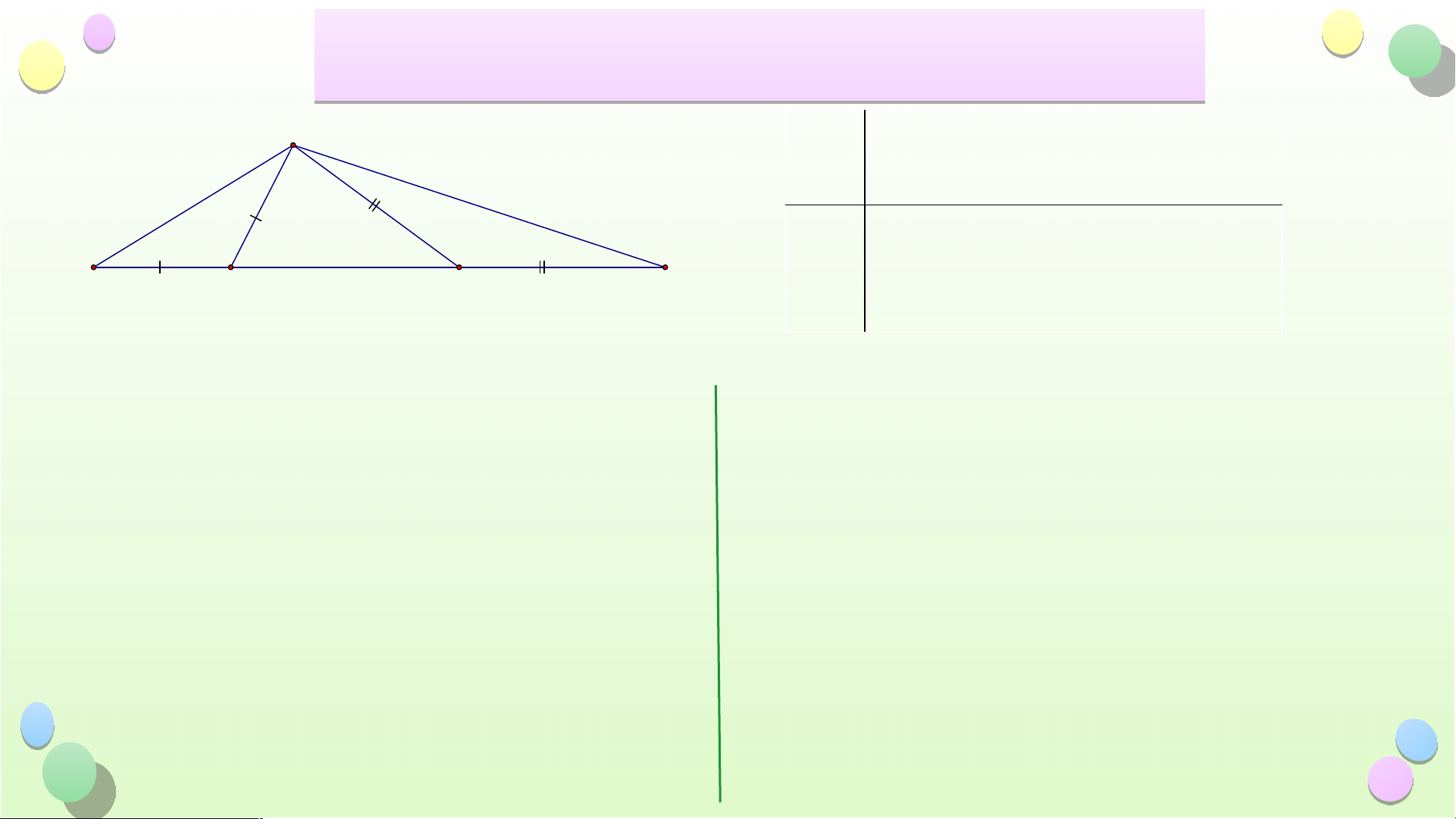
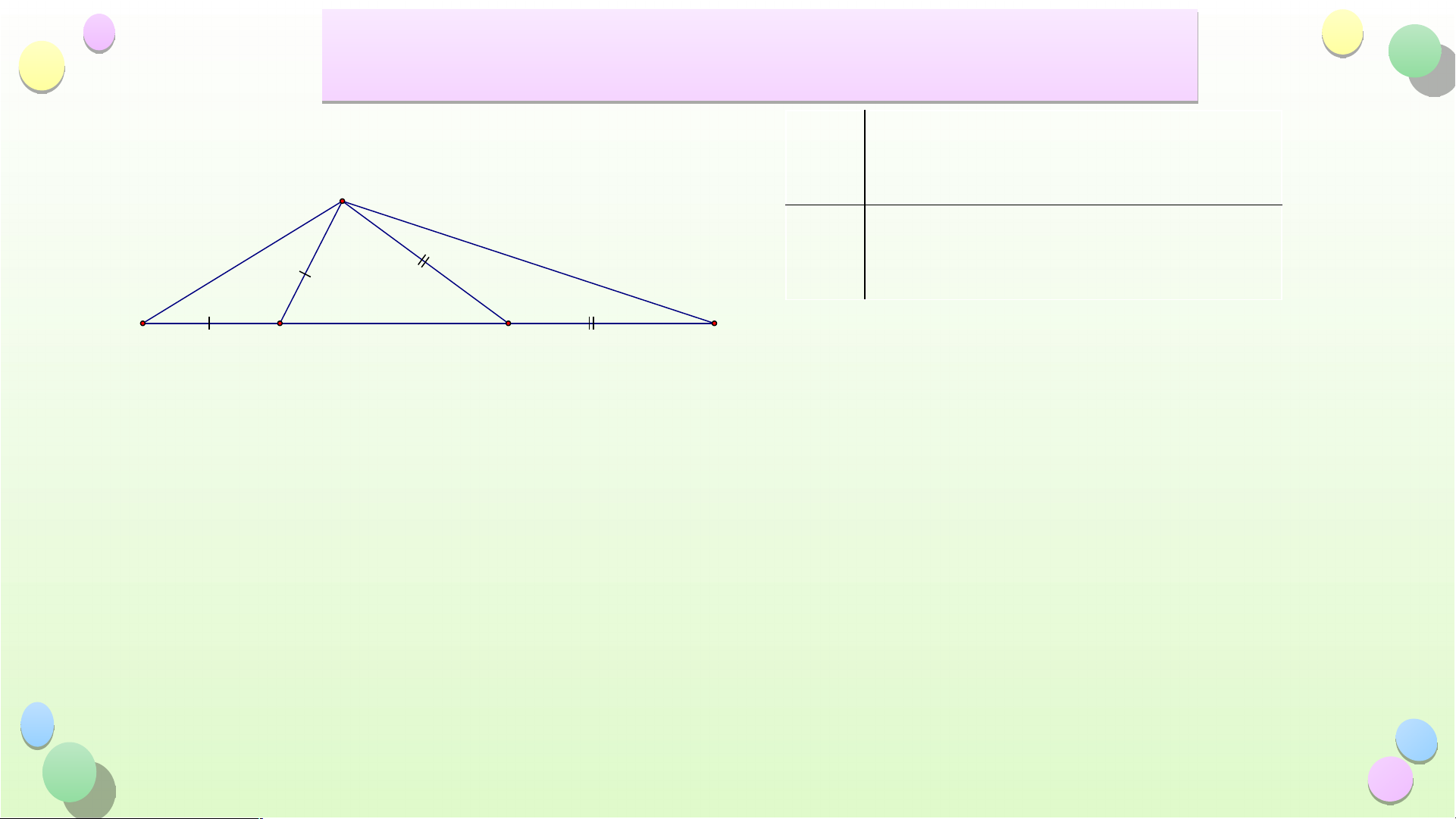
Câu 2: Để thiết kế một con diều người ta làm các thanh
AB, AD, CB, CD (hình sau). Biết CD = 25cm. Hỏi BC dài bao nhiêu? A. BC = 25 cm B. BC = 13 cm C. BC = 48 cm
Câu 3: Trọng tâm của tam giác là
A. Giao điểm ba đường cao của tam giác
B. Giao điểm ba đường trung trực của tam giác
C. Giao điểm ba đường trung tuyến của tam giác A. Giao điểm ba đường B. Giao điểm ba đường C. Giao điểm ba đường cao của tam giác trung trực của tam giác trung tuyến của tam giác Caâu 4 :Cho tam giaù c ABC vôù i G laø troïng taâm cuû a tam giaù c, A GM AM laø
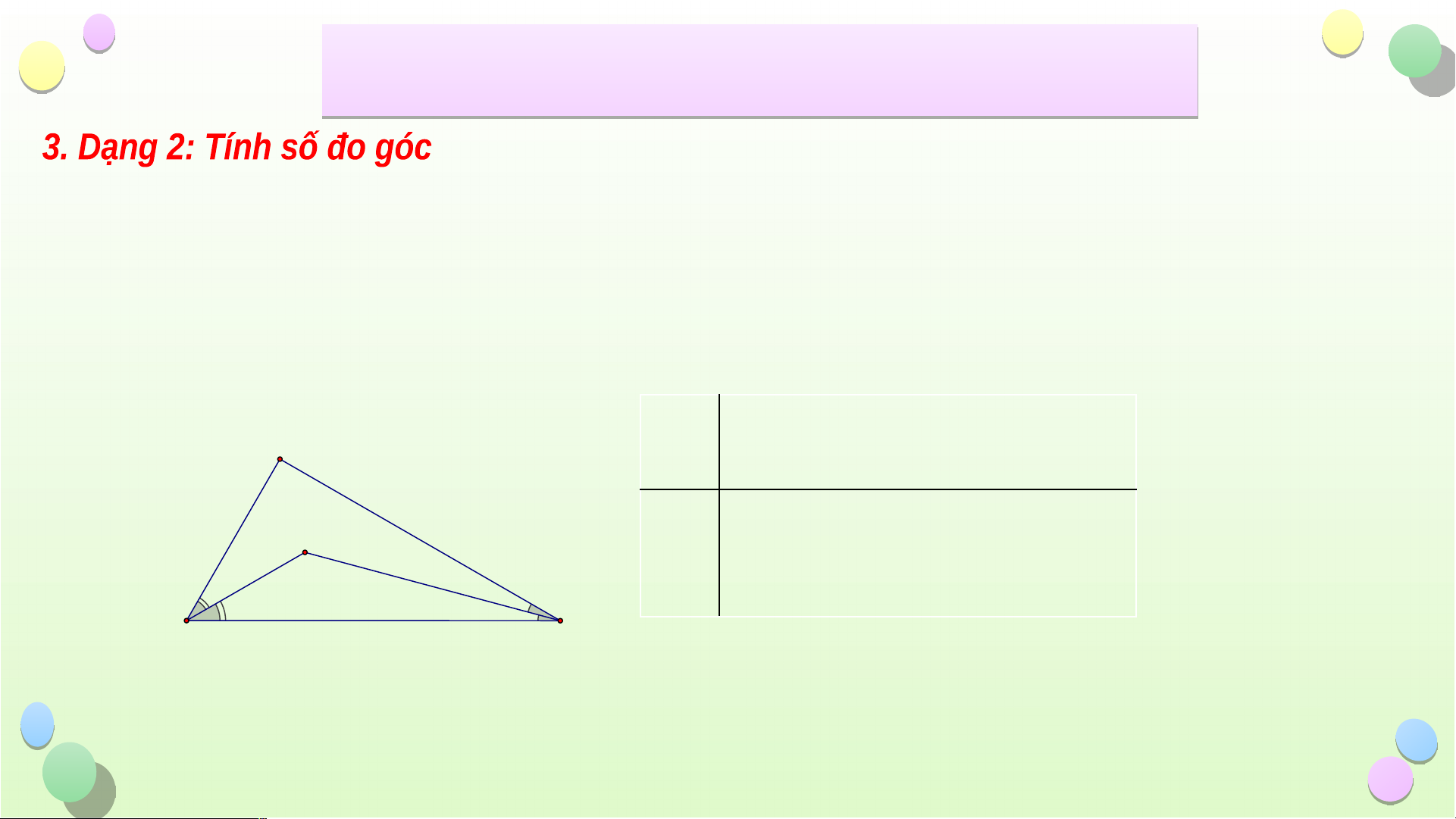
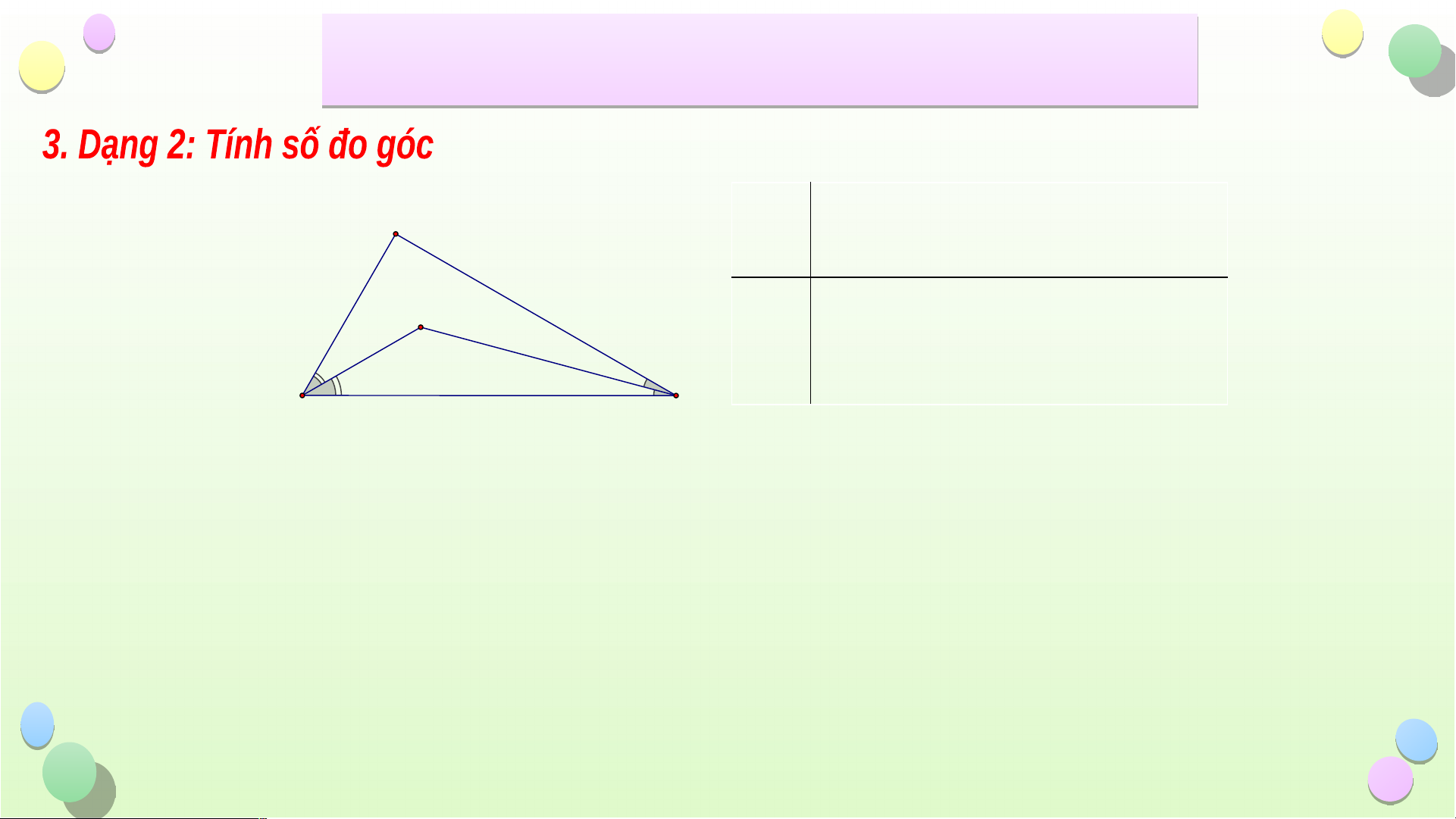
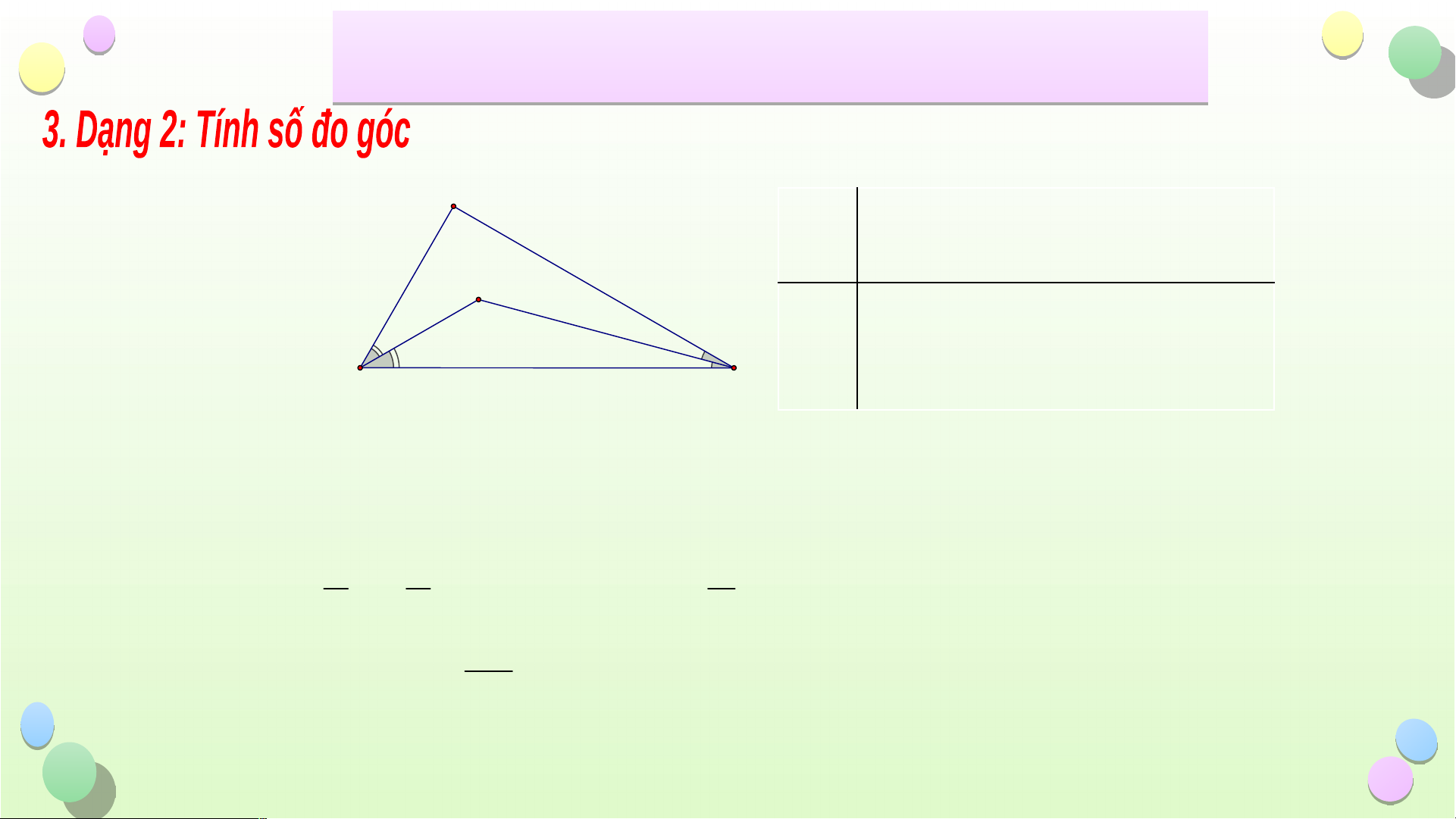
ñöôøng trung tuyeán (hình sau). Tæ soá baèng AG G GM GM 1 GM 1 A. 2 B. C. B AG AG 3 AG 2 M C GM 1 GM A. 2 GM 1 B. C. AG AG 3 AG 2 µ 0 Caâu 5: C ho tam giaù c ABC bieát B 7 0 , A µ 0 C 60 . Tia phaâ n giaù c cuûa goù c B vaø goù
c C caét nhau taïi M (hình beân). M Tính soá ño goù c MAB B C B. 500 A. 250 C. 600 Tiết iế B ài ÔN T ài ẬP C ÔN T H ẬP C ƯƠ Ư NG 8 G
Quan hệ giữa cạnh và góc trong một tam giác
Quan hệ giữa đường vuông góc và đường xiên
Tính chất của đường trung trực
Tính chất ba đường trung trực của tam giác
Đường trung tuyến và tính chất ba đường trung tuyến của tam giác
Đường cao và tính chất ba đường cao của tam giác
Tính chất ba đường phân giác của tam giác của tam giác Tiết iế 2 B 2 ài ÔN T ài ẬP ÔN T CH ẬP ƯƠ Ư NG 8
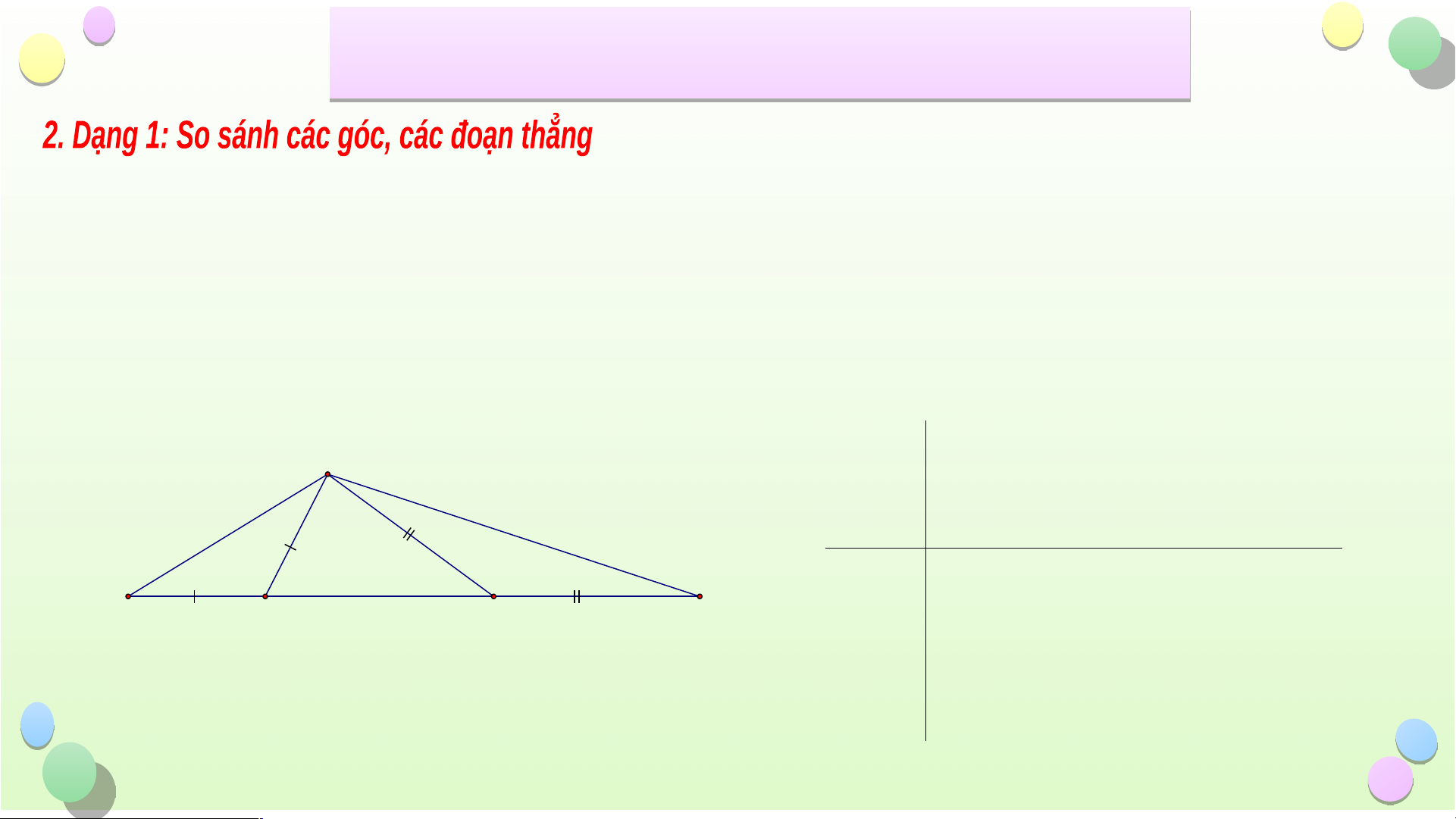
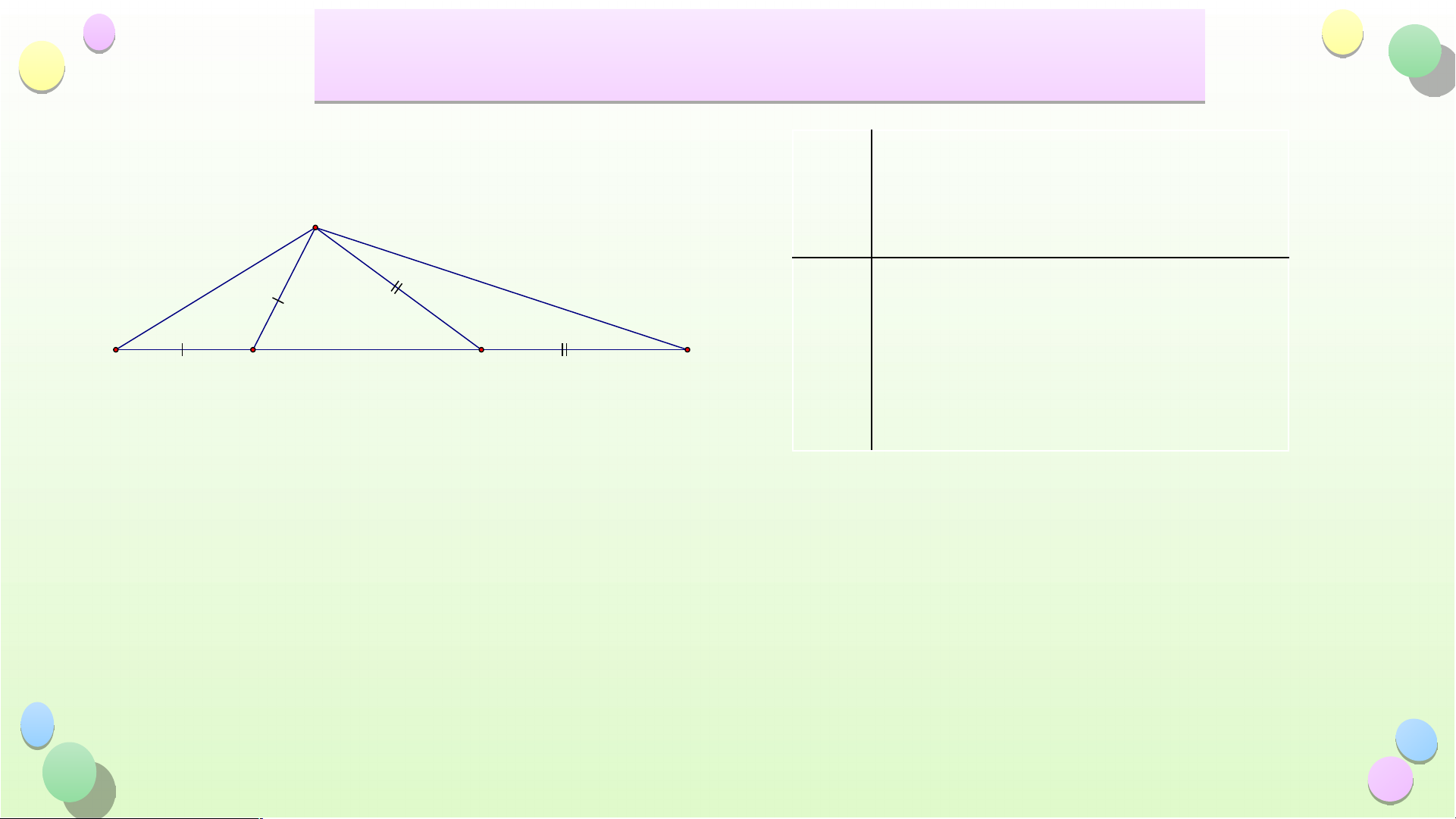
Bài 1: Cho tam giác ABC có AB > AC. Trên tia đối của tia BC lấy điểm M sao
cho BM = BA. Trên tia đối của tia CB lấy điểm N sao cho CN = CA
a) Hãy so sánh các góc ACB và ABC
b) Hãy so sánh các góc ANB và AMC
c) Hãy so sánh các đoạn thẳng AM và AN Giải A GT A BC, AB AC, AB B M, AC C N · · a) So saù nh A CB va A ø BC N M C B KL · · b) So saù nh A NB va A ø MC c) So saù n h AM v ø a AN Tiết Tiế 2 Bài Ô 2 N Bài Ô T ẬP CH T ƯƠ Ư NG 8 Bài 1: ABC, AB AC, Giải A GT AB B M, AC C N · · KL a) So saùnh A CB va A ø BC N M · · C B b) So saù nh A NB va A ø MC c) So saù n h AM v a A ø N a) Xeù t A BC, coù : AB > AC · · ACB > ABC (goù c ñoái dieän vôù i caïnh lôù n hôn) · · Vaäy ACB >ABC Tiết Tiế 2 Bài Ô 2 N Bài Ô T ẬP CH T ƯƠ Ư NG 8 Bài 1: A A BC, AB AC, GT Giải AB B M, AC C N · · b) So saù nh A NB va A ø MC N M KL C B c) So saù n h AM v ø a AN b) Ta coù: · · · · · 0 0 Do A
NB NAC ACN 1 80 A CB + A CN 180 (hai goù c ke àbuø) · · 0 · · Ne ân A 2 NB A CN 1 80 (2) 0 A BC A BM 180 (hai goù c ke àbuø) Chöù
ng minh töông töï, ta coù: · · Ma A ø CB A BC (chöù ng minh treân) · · 0 A 2 MC A BM 1 80 (3) · · Neân A CN A BM (1) · · Tö (1 ø
), (2), (3) suy r a A NB AMC Vì A CN caâ n taïi C (d o AC = CN) · · Vaäy A NB AMC · · ANB NAC Tiết Tiế 2 Bài Ô 2 N Bài Ô TẬ T P CH P ƯƠ Ư NG 8 Bài 1: A BC, AB AC, A GT Giải AB B M, AC C N KL c) So saùn h AM v ø a AN N M C B c) Xeù t A MN, c ù o: · · A NB > A MC (chöù ng minh treân) · · Hay A NM AMN
AM AN (caïnh ñoá i dieän vôù i goù c lôù n hôn) Va äy AM > AN Tiết Tiế 2 Bài Ô 2 N Bài Ô TẬ T P CH P ƯƠ Ư NG 8 µ µ µ Baø i 2:C ho tam giaù c ABC co A ù B C. Hai ñöôø ng phaân giaù c cuû a goù c B vaø goù c C caét nhau taïi O. a) Tính soá ño goù c A. b) Tính soá ño goù c BOC. µ µ µ A BC, A B C A Giải GT µ µ BO, C O laø tia phaân giaù c cuû aB , C O µ KL a) A ? · b) B OC ? B C Tiết Tiế 2 Bài Ô 2 N Bài Ô TẬ T P CH P ƯƠ Ư NG 8 Baø i 2 : µ µ µ ABC, A B C A GT µ µ Giải BO, C O laø tia phaân giaù c cuû aB , C O µ a) A ? KL · b) B OC ? B C a) Xe ù t ABC, c ù : o µ µ µ 0 A B C 18 0 (toå ng ba goù c cuû a tam giaù c) µ µ µ Ma A ø B C (gt) µ 0 Neân A 2 180 µ 0 A 90 µ 0 Vaäy A 9 0 Tiết Tiế t 2 Bài ÔN T 2 Ậ Bài ÔN T P CH P ƯƠ Ư NG 8 A Baø i 2 : µ µ µ A BC, A B C Giải GT µ µ BO, C O laø tia phaân giaù c cuû aB , C O µ a) A ? KL · B C b) B OC ? b) Xe ù t B OC, c ù : o · · · 0 BOC OBC OCB 1 80 (toå ng ba goù c cuû a tam giaù c) µ µ µ · B C A 0 · 0 µ µ µ B
OC = 180 ha y B OC = 180 (do A B C) 2 2 2 0 · 90 0 0 B OC = 180 1 35 2 · 0 Vaäy B OC 1 35 Tiết iế 2 Bài Ô 2 N Bài Ô T ẬP CH T ƯƠ Ư NG 8
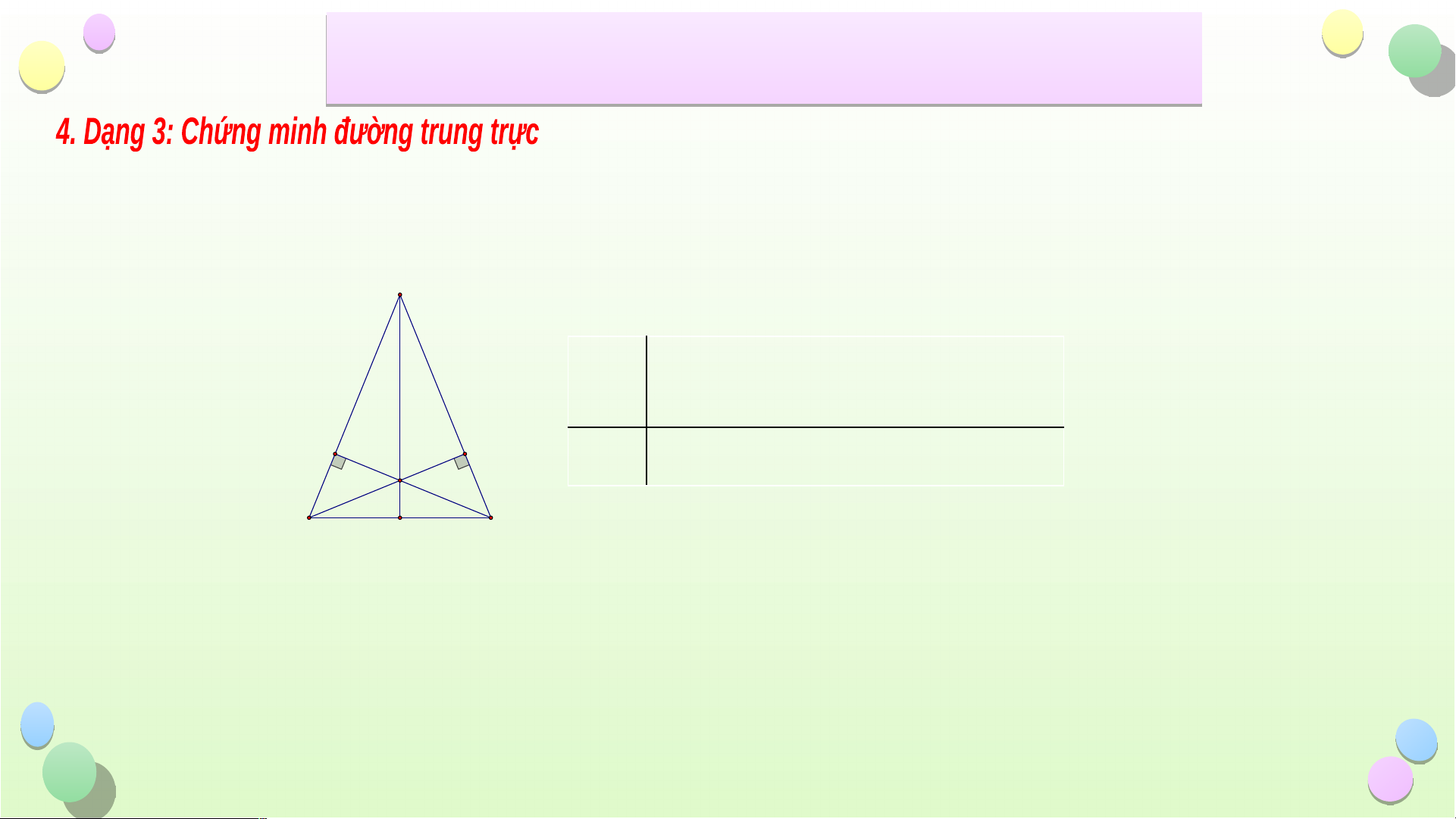
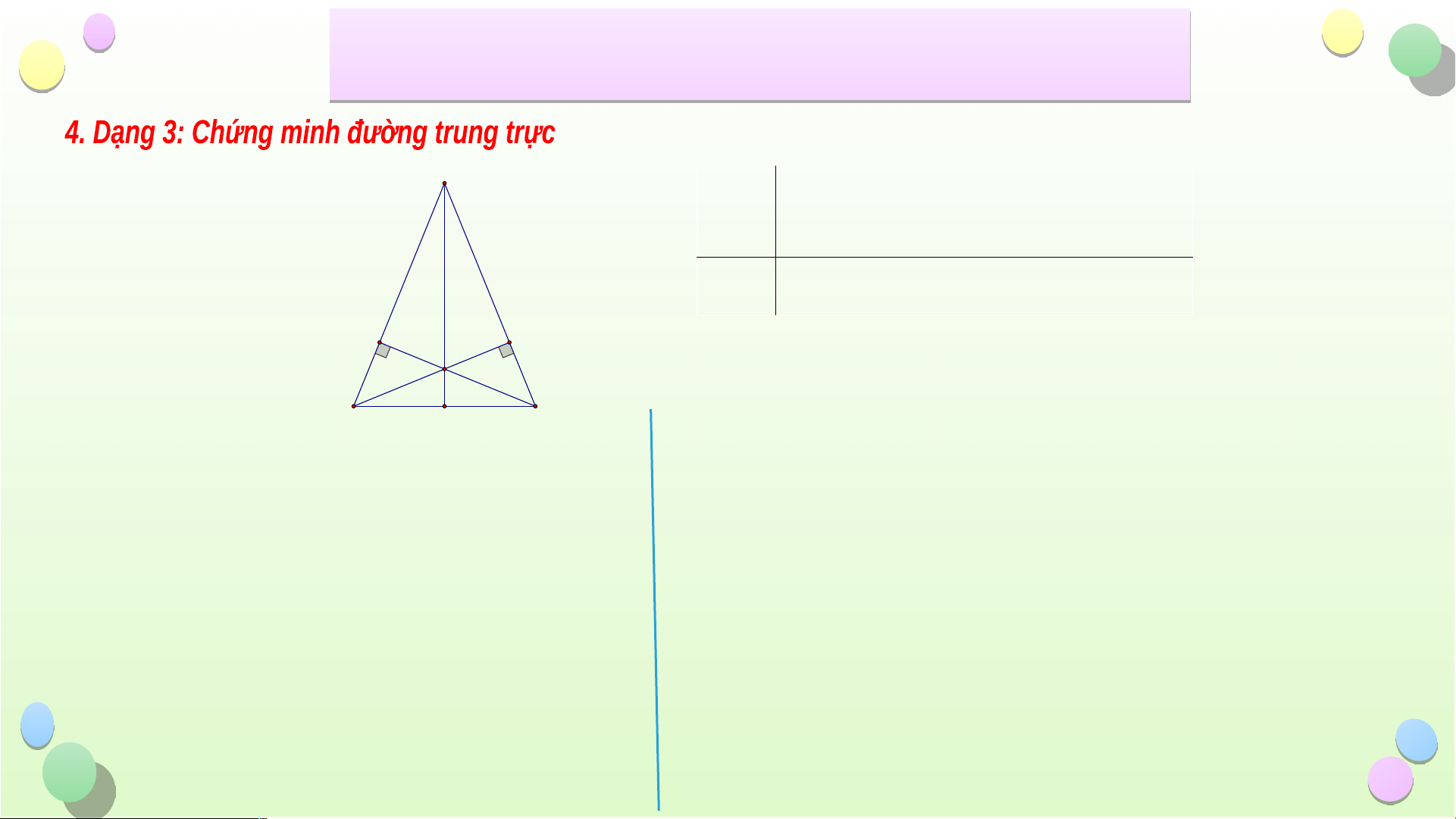
Bài 3: Cho tam giác ABC cân tại A, hai đường cao BE và CF cắt nhau tại H.
Chứng minh AH là đường trung trực của BC A Giải A BC caâ
n taïi A, BE AC taïi E,
GT CF AB taïi F, BE CF = {H} F E H
KL AH laø ñöôøng trung tröïc cu û a BC B N C Tiết iế 2 B 2 ài ÔN T ài ẬP ÔN T CH ẬP ƯƠ Ư NG 8 Bài 3: A A BC caâ
n taïi A, BE AC taïi E, GT Giải
CF AB taïi F, BE CF = {H}
KL AH laø ñöôøng trung tröïc cu û a BC F E H B N C Xe ù t A BN vuoâ ng taïi N v aø A CN vuoâ ng taïi N, coù: Goïi N laø giao ñieåm cuû a A H v ø a BC) AN laø caïnh chung Xe ù t A BC, coù : AB=AC (d o A BC caâ n taïi A)
BE AC taïi E
, CF AB taïi F A
BN ACN (caïnh huyeà n-goù c nhoïn) Ma B ø E CF = {H}
BN = CN (hai caïnh töông öù ng) Neân H laø tröïc taâm cuû a tam gia ù c ABC M a A ø B = AC (gt)
AH BC taïi N Vaäy AH laø
ñöôøng trung tröïc cu û a BC.
Bài 4: Trên bản đồ quy hoạch một khu dân cư có ba điểm dân cư A, B, C, tìm địa
điểm M để xây dựng một trường học sao cho trường học này cách đều ba điểm dân cư đó. Giải
Vì điểm M để xây dựng một trường học cách đều ba điểm dân cư
Nên điểm M cần tìm là giao điểm của hai đường trung trực của hai đoạn AB và AC. HƯỚNG Ư DẪ D N HỌC SIN ỌC H TỰ H TỰ ỌC Ọ
- Xem lại các kiến thức và các dạng bài tập của chương 8.
- Hệ thống kiến thức chương 8 bằng sơ đồ tư duy.
- Làm các bài tập còn lại trong sách bài tập.
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20