Bài giảng điện tử môn Toán 7 Chương 8 Bài 2: Tam giác bằng nhau C - G - C (Tiết 53) | Chân trời sáng tạo

Bài giảng điện tử môn Toán 7 Chương 8 Bài 2: Tam giác bằng nhau C - G - C (Tiết 53) | Chân trời sáng tạo được VietJack sưu tầm và soạn thảo để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem! 

19 10 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Giáo án Toán 7

Môn: Toán 7

Sách: Chân trời sáng tạo

Thông tin:

14 trang 6 tháng trước

Tác giả:

Profile Mai Nguyệt

KIỂM TRA BÀI CŨ:

A B C
ABC
!
!"
#
$ $"
#"
Trả lời:
Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia
thì hai tam giác đó bằng nhau.
!
!"
#
$ $"
#"
%&'()
ABC
CBA
!#!"#"
!$!"$"
#$#"$"
*+
CBA
ABC
KIỂM TRA BÀI CŨ:
!
!"
#
$ $"
#"
KHỞI ĐỘNG
Như vậy, ở trường hợp thứ nhất ta chỉ cần xét 3
cạnh là có thể biết hai tam giác bằng nhau.
Tương tự, trong trường hợp nếu ta chỉ xét hai
cạnh và góc xen giữa thì có nhận biết được hai tam
giác bằng nhau hay không?
AB = A’B’
thì hai tam giác ABC và A’B’C’ bằng nhau???
Nếu
, ,
B B
BC = B’C’
Bài HAI TAM GIÁC BẰNG NHAU
*--.(/0
A
B
C
1(!2-
34

1(!2-
34

1(!2-
34
!#'!$
1(!2-
34
!#'!$
1(2-
34
!$'#$
1(2-
34
!$'#$
5-3
4!$'
#$6($
5-3
4!$'
#$6($
Nếu hai cạnh và góc xen giữa của tam giác này bằng hai
cạnh và góc xen giữa của tam giác kia thì hai tam giác đó
bằng nhau
%&'()
ABC
A B C
AB = A’B’
ABC
A B C
*+
Ta thừa nhận tính chất cơ bản sau:
!
#
$
!"
$"
#"
, ,
B B
BC = B’C’
!
#
7
$
Chứng minh hai tam giác trong hình vẽ đã cho bằng nhau .
BC = DC
AC cạnh chung
BCA = DCA
ABC ADC c g c
Vì:
$89$+':;<=2>6
?@
D
C
B
A
A ABC ACD
B ABC ADC
C BAC ACD
B CAB ACD
Câu 2
$!#$(!#!$*.
4!#'!$6/?7<A;
!7!A1BC6?#A'
$7$B8sai
D
!#A$7##CC$

$#7$A77CC$
ABC
DEF
EF G HF G IFA E F
G < AB DE AC DF
A ABC DFE
B ABC EDF
D ABC DEF 
Câu 3 $
CJ?K;?8/6?@.
.
C ABC DEF
' (
Cho 2 tam giác như hình vẽ có:
!
#
$
!" #"
$"
Chú ý: Với trường hợp bằng nhau thứ hai, góc bằng nhau
phải là góc xen giữa.
Góc A’ có phải là góc
xen giữa hai cạnh
A’C’ và B’C’ không?
Bài tập 1:
Hai tam giác đó có bằng nhau không?
< <
<
< <
BC B C
B B
AC A C
Trên mỗi hình H1, H2, H3 có các tam giác nào
bằng nhau? Vì sao?
L
(H2)
1
C
M
Bài tập:
(H1)
!
#
$7
A
9
N
(H3)
O
%
P
9
N
ABD AED c g c
Q+)!#!A
!
9
!
N
!74
GHK KIG c g c
Q+)1LCM
L1C
1CM
1C4
MNP
MQP
'
C0(
(2-3

Q+)
0
R
%S
R
$TK(4(

DẶN DÒ
| 1/14
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

KIỂM TRA BÀI CŨ:
Phát biểu trường hợp bằng nhau thứ nhất của tam giác ?  A BC = (c A
 ' B 'C ' . c. c) khi nào? A A’ B C C’ B’ KIỂM TRA BÀI CŨ: Trả lời: A A’ B C C’ B’
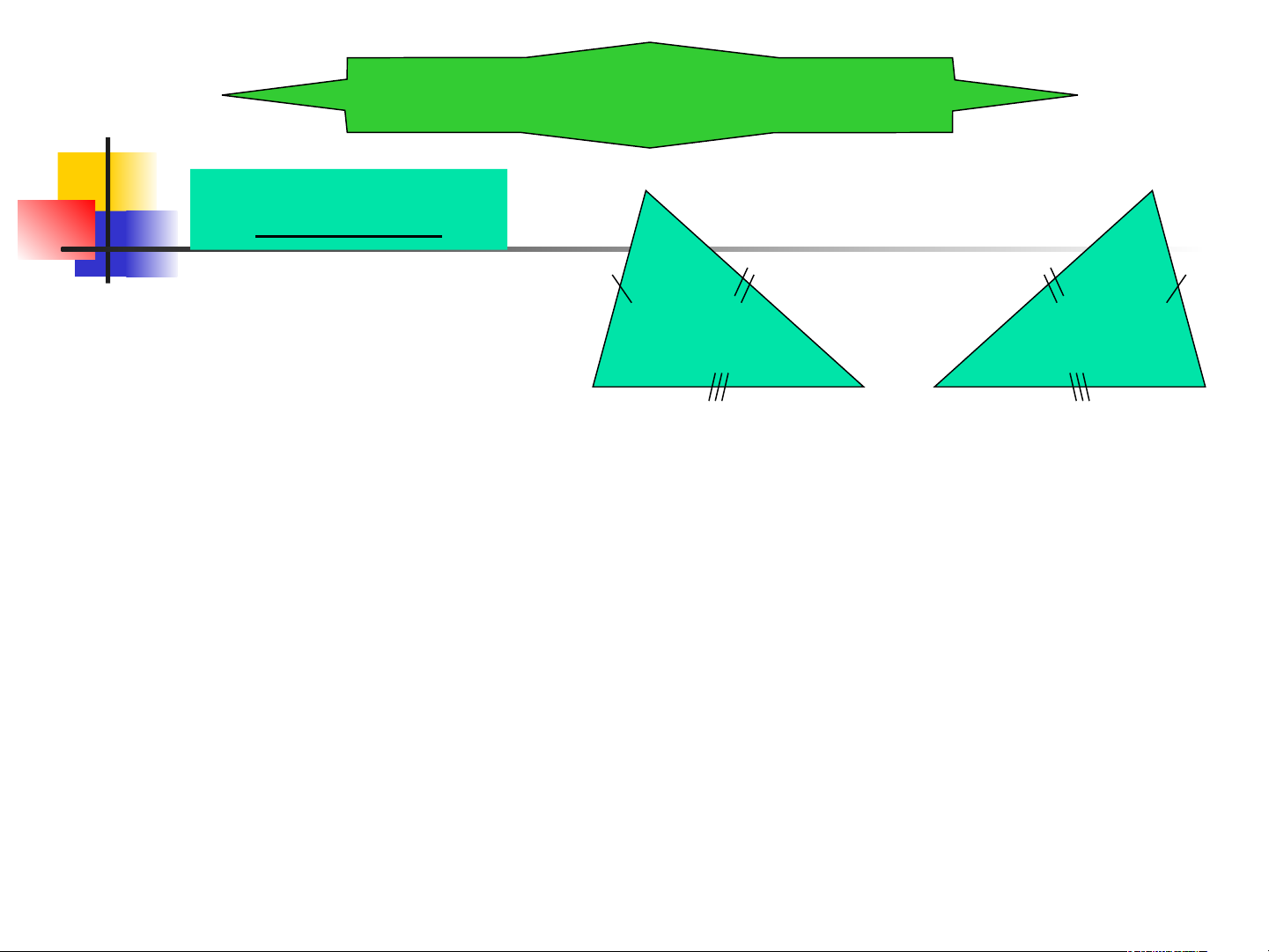
Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia
thì hai tam giác đó bằng nhau. Nếu  A và BC ' AB ' c C'ó: AB = A’B’ AC = A’C’ BC = B’C’ Thì = ABC  (c ' AB'C' . c. c) KHỞI ĐỘNG
Như vậy, ở trường hợp thứ nhất ta chỉ cần xét 3
cạnh là có thể biết hai tam giác bằng nhau.
Tương tự, trong trường hợp nếu ta chỉ xét hai
cạnh và góc xen giữa thì có nhận biết được hai tam
giác bằng nhau hay không? A A’ Nếu AB = A’B’ ˆ ˆ B B ' B C C’ B’ BC = B’C’
thì hai tam giác ABC và A’B’C’ bằng nhau???
Bài HAI TAM GIÁC BẰNG NHAU
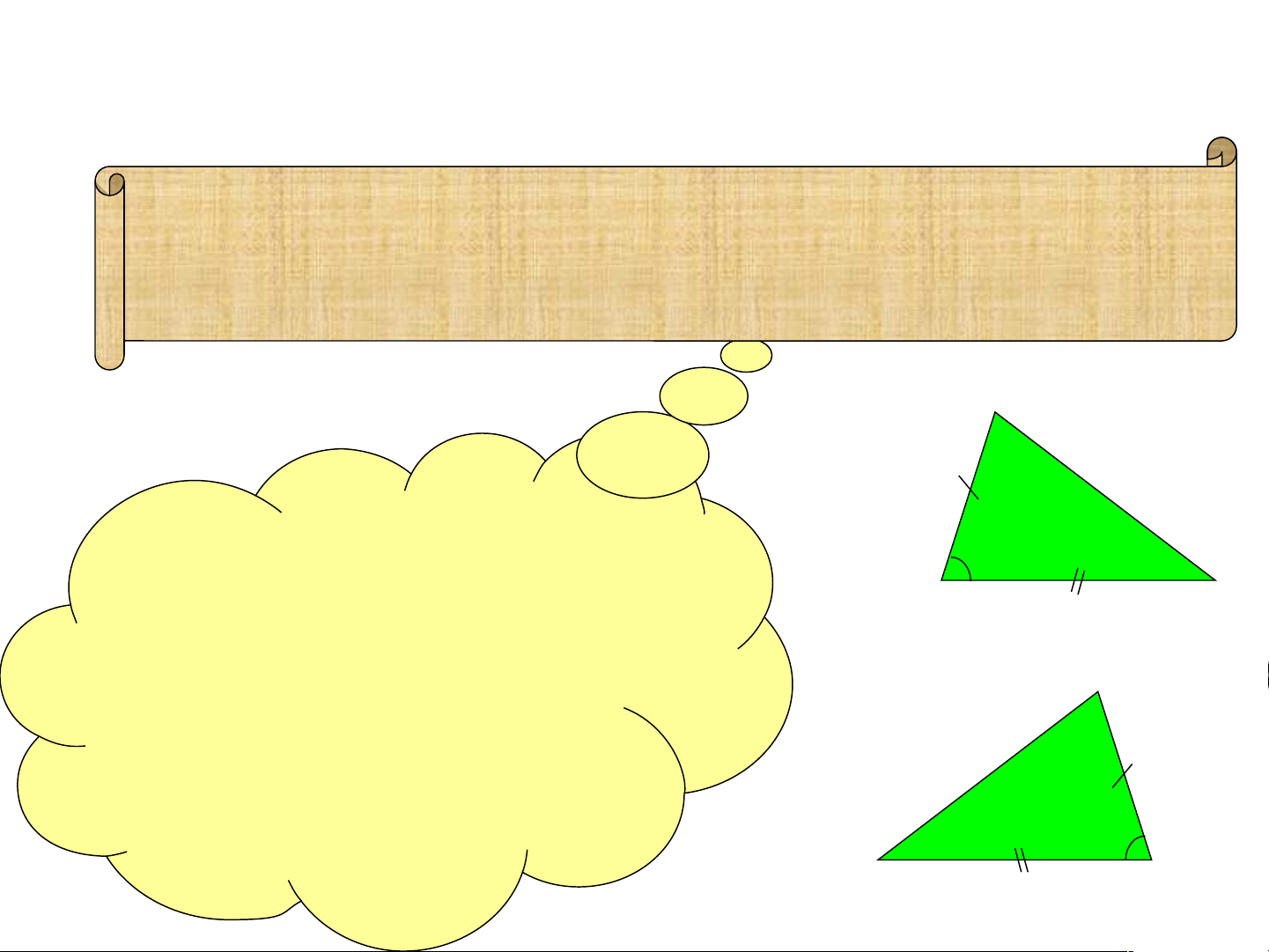
Theo em hai tam giác trên có bằng nhau hay không ? G X ó Genc A cgi xen Aữa ữ hai a cạnh A C A C v à à A giữa ữ h a ai cạ ai n cạ h A B B AC và B là A và gócC A C G G óc Gó A óc c xe A nào n xex nen e giữ gi gi a ữữ ha aa h a i ha c ai ạ c nh ạ cạn cạ nhh A nà C o nà ? o và B và C B B C
Ta thừa nhận tính chất cơ bản sau:
Nếu hai cạnh và góc xen giữa của tam giác này bằng hai
cạnh và góc xen giữa củ
a tam giác kia thì hai tam giác đó bằng nhau A Nếu  A B và C A ' B ' Cc'ó: AB = A’B’ B C ˆ ˆ B B ' A’ BC = B’C’ Thì ABC = A  ' B 'C ' C’ B’
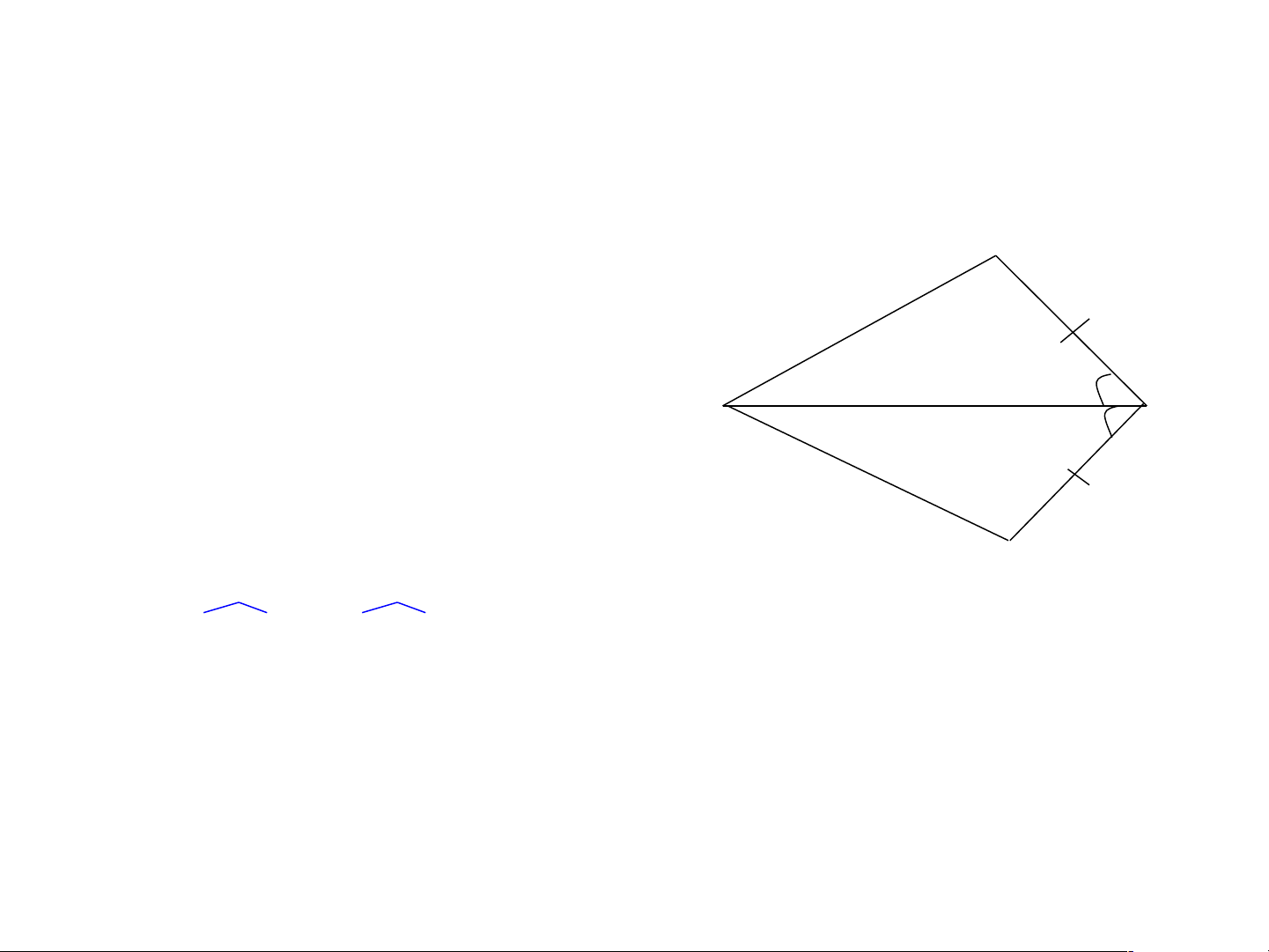
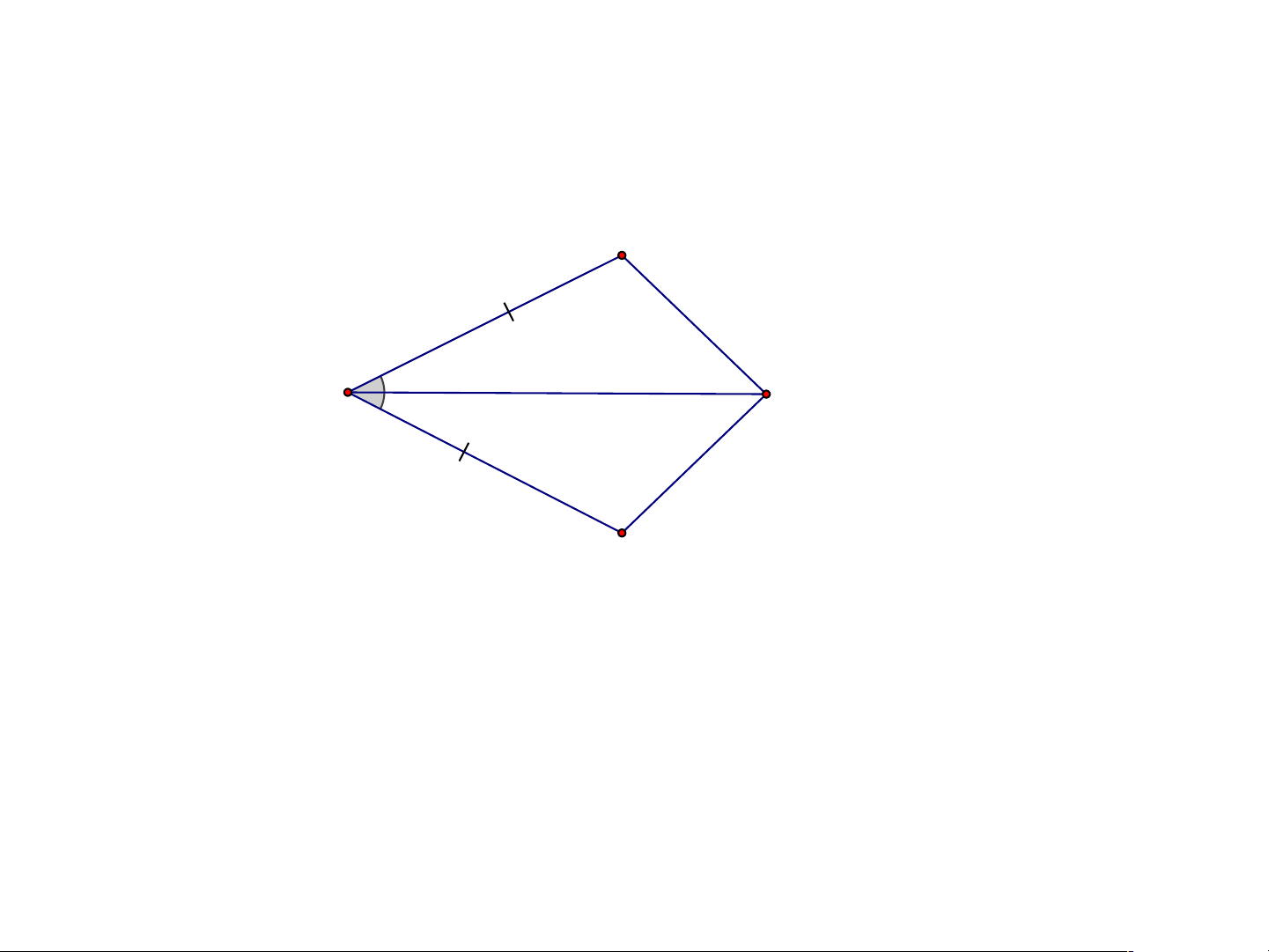
Chứng minh hai tam giác trong hình vẽ đã cho bằng nhau . B A C ABC ADC( . c g.c) Vì: BC = DC D BCA = DCA AC cạnh chung
Câu 1 Cho hình vẽ sa. u, nhận xét nào là đúng? B C A D . A ABC ACD . B ABC ADC C. BAC ACD . B CAB ACD Câu 2
Cho tam giác ABC có AB=AC. Trên các
cạnh AB và AC lấy các điểm D,E sao cho
AD=AE. Gọi K là giao điểm của BE và CD. Chọn câu sai. A.BE=CD B. BK= KC C. BD= CE D .DK =KC ABC và DEF
Câu 3 Cho hai tam giác có  o  o  o A 50  ; E 70  ; F 6
 0 ; ABDE, AC DF
. Khẳng định nào sau đây là đúng?. . . A ABC DFE .
B ABC EDF .
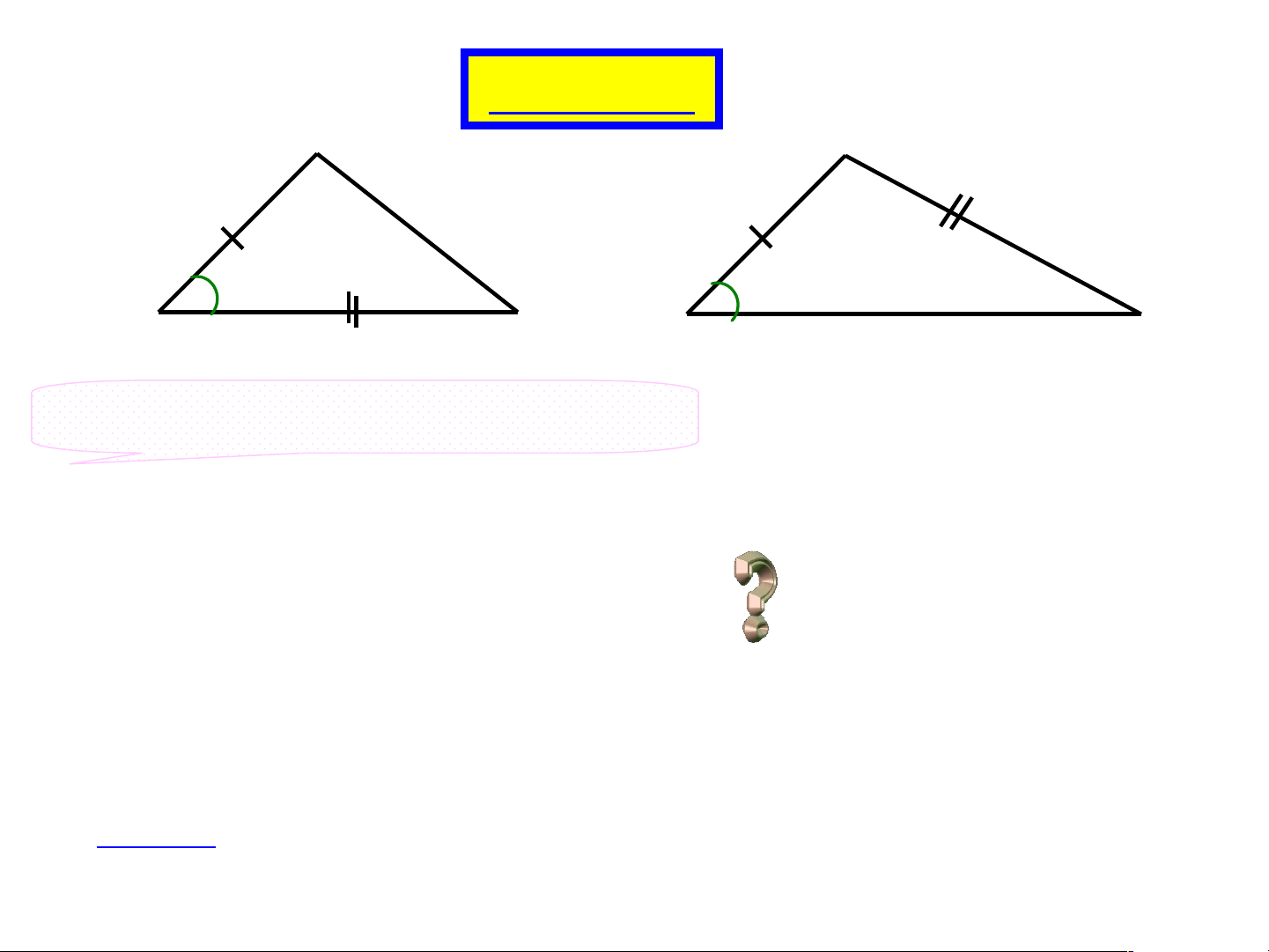
D ABC DEF C. ABC   DEF Bài tập 1: C C’ A B A’ B’
Cho 2 tam giác như hình vẽ có: , , BC B C ,
Góc A’ có phải là góc   B B xen giữa hai cạnh , ,
A’C’ và B’C’ không? AC A C
Hai tam giác đó có bằng nhau không?
Chú ý: Với trường hợp bằng nhau thứ hai, góc bằng nhau
phải là góc xen giữa. Bài tập:
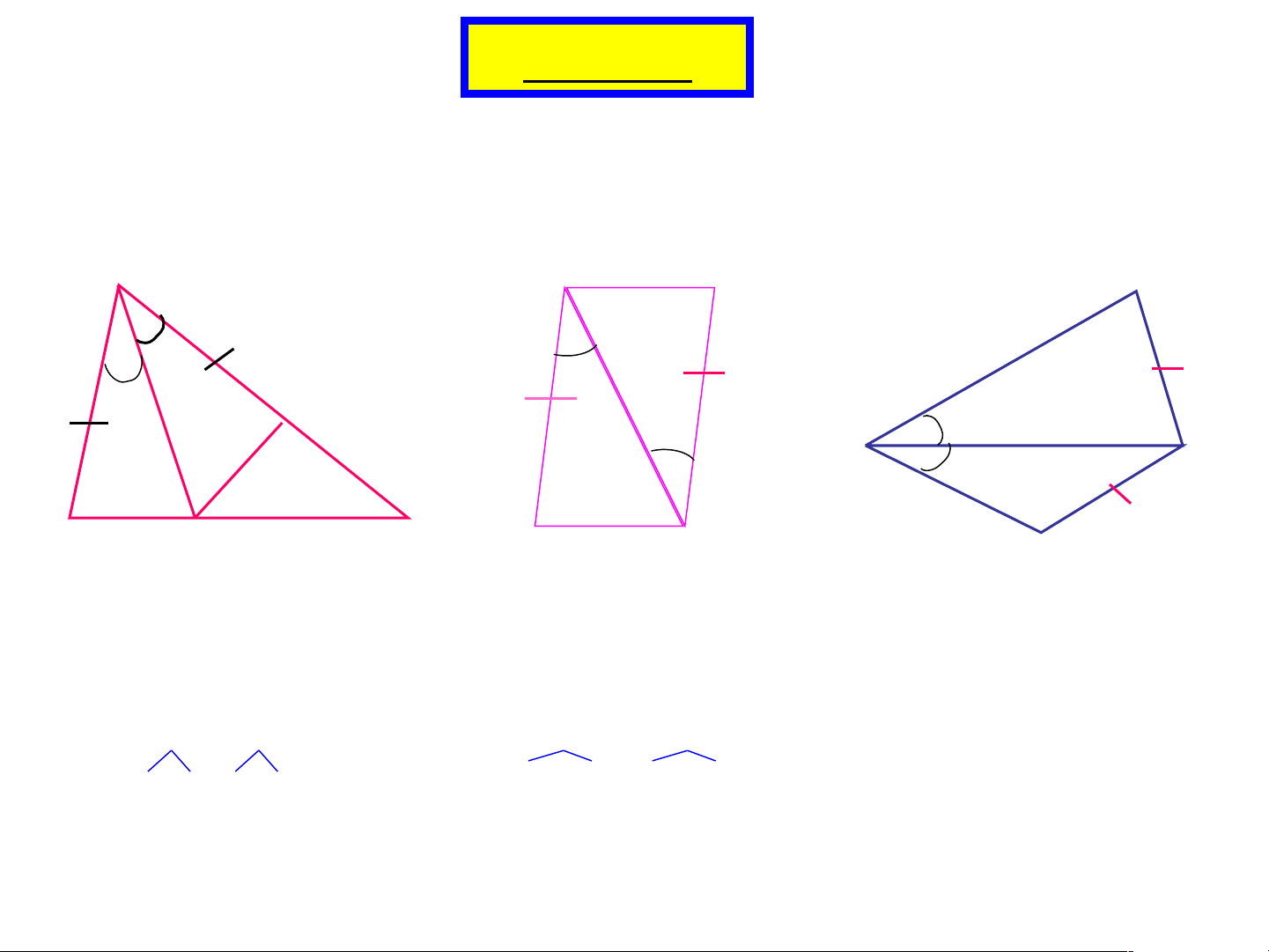
Trên mỗi hình H1, H2, H3 có các tam giác nào bằng nhau? Vì sao? A G I N 2 E 1 1 M P 2 B D C H K Q (H1) (H2) (H3) ABD AED( . c g.c) GHK KIG( . c g.c)
MNP và MQP Vì: AB = AE Vì: GH = KI không bằng nhau A = A Vì: Không có 1 2 HGK = GKI góc xen giữa AD cạnh chung GK cạnh chung bằng nhau DẶN DÒ
- Nắm trường hợp bằng nhau thứ hai của tam giác
-Chuẩn bị thường hợp bằng nhau góc cạnh góc của hai tam giác .
Document Outline

  • PowerPoint Presentation
  • Slide 2
  • Slide 3
  • Slide 4
  • Slide 5
  • Slide 6
  • Slide 7
  • Slide 8
  • Slide 9
  • Slide 10
  • Slide 11
  • Slide 12
  • Slide 13
  • Slide 14