Bài giảng tuần 2.
1. Định luật Gauss (Ostradskyi-Gauss, Định luật O-G, sách của Lương Duyên Bình...)
Câu đố: Vậy Radio là do ai phát minh ra? Telefon?
Trả lời: Radio là do ông Radio-novic, Telefon-ovic!
1.1 - Đo độ lớn của điện tích thế nào?
- Thế thì "đo" là gì?
- "Đo" có nghĩa là lấy đơn vị của một cái khác để xác định độ lớn của một cái chưa biết, ví dụ khi may
quần áo thì người ta ướm cái thước vào cánh tay để xem cánh tay dài bao nhiêu "thước"
Một ví dụ nữa, các bạn đo cân nặng bằng cách nào? Chúng ta đứng lên bàn cân và nhìn kim chỉ số cân,
vậy thì độ lệch của kim, hay chính là độ xoắn của lò xò bên dưới chính là thước đo cân nặng
Thực tế thì ngày nay hầu hết các đại lượng cần đo như khối lượng, nhiệt độ, áp suất, độ dài, độ sáng, độ
rọi, cường độ dòng, hiệu điện thế, tốc độ, gia tốc,... lương, chuyển khoản,...tất cả đều đo so sánh bằng một đại
lượng duy nhất là ???? điện thế, cái hiện thị lên màn hình smartphone.
Muốn đo điện tích thì chúng ta phải dùng thứ chúng ta đã biết, ví dụ tiếng kêu của cái máy cảm biến điện
thế, đưa cái máy lại gần Q thì điện áp tăng lên, nếu vượt ngưỡng 3V thì kêu tách một cái. Và chúng ta đưa cái
máy đi vòng quanh Q (cả 3-chiều xyz) và đếm số tiếng kêu.
Định nghĩa 1: Độ lớn điện tích là số đường sức trên một đơn vị diện tích bên ngoài Q.
Đ/N này của Faraday, ông đo lực tác dụng mà Q tác dụng lên điện tích q0
(điện tích tiêu chuẩn). Lực = 1C
tác dụng cộng được nên có nhiều đường sức trên một đơn vị diện tích thì F lớn. N
- Mật độ đường sức:   F
(số đường sức đếm được trên mặt cầu bao quanh Q chia cho diện tích mặt S
cầu) (mặt bất kỳ cũng được, nhưng đơn giản nhất hãy chọn mặt cầu) N
Suy ra ngay từ hình học:   F
, còn thì không phụ thuộc N
r vì số lượng tia đường sức mà Q phát ra 4 r  là không đổi.
Hệ quả: là Mật độ đường sức giảm theo r . Dễ hiểu thôi, vì định luật Coulomb đã nói là l 2 ực F mà Q t/d giảm theo r2.
Đường sức của điện trường: Đường sức là tia tưởng tượng là dọc theo nó có lực (bằng 1 đơn vị) t/d lên điện tích q0 . Vậy Q c = 1C
àng lớn thì số đg sức / 1 đv S càng lớn, vì F có tính cộng được. 1 Qq
Định luật Coulomb: 0 F  2 4 r 0
Nếu quy định q0 là điện tích tiêu chuẩn (để nhiều người đo khác nhau có thể đồng nhất số liệu) = 1C thì
chúng ta có thể viết lại định luật Coulomb như sau: F 1 Q  2 q 4 r 0 0
Như thế này thì lực đo được sẽ đồng nhất với mọi người đo, vì nó không phụ thuộc q nữa, có thể là bao 0
nhiêu cũng được, miễn là nó không thay đổi khi đo. F  1 Q 
Cường độ điện trường: E    2  q 4 r 0  0 
Như vậy đối với mỗi điện tích Q thì có một cường độ điện trường xác định. Đây là véc tơ như F, là hàm của biến r E  1 Q r  2 40 r
Hướng của E không phụ thuộc tích Qq0 mà chỉ phụ thuộc dấu của Q, nếu Q dương thì đường sức đi từ tâm
mặt cầu ra ngoài, và ngược lại nếu Q âm thì đường sức đi từ ngoài vào tâm mặt cầu.
E phụ thuộc vào r nhưng cũng phụ thuộc vào 0 E
(độ thẩm của chân không). Hơn nữa nếu chúng ta đo
trong môi trường thì giá trị của E (dĩ nhiên là cả F) sẽ còn phụ thuộc độ thẩm của môi trường.
Độ thẩm điện của môi trường: Thực nghiệm chỉ ra, độ thẩm của môi trường  là một con số (không đơn
vị) chỉ bội số của 0  N Ví dụ, không khí  , 1  ...    Dầu 2  . Gốm
10000 . Gốm trọng tụ khổng lồ thường làm bằng vật liệu perovskite ABO (A= Ca, B=T  10000 3 i: CaTiO3, ... BaTiO , CaMnO 3 ...): 3 .
Môi trường cách điện cần có  lớn, cho nên tại sao vỏ bu-gi được bọc sứ (Al2O dạng men lỏng) 3
Như vậy độ thẩm tổng thể là  0. Vậy định luật Coulomb phải được viết lại thành: 1 Qq0 F  2
, suy ra cường độ điện trường: 4 r 0 E Q , r    1 ,  0 2 4 r 0
Cảm ứng điện: Cường độ điện trường vẫn phụ thuộc r và 0 !
Liệu có đại lượng nào chỉ phụ thuộc r mà không phụ thuộc vào  0 ?
Rất đơn giản chúng ta có thể tạo ra đại lượng đó bằng cách chia E cho 0 :   
D r E r , ,  1 Q Q 0    2 2  4 r 4r 0 Viết gọn lại thành:  D  Q r  Q DS Sr  
Phát biểu: Đại lượng D được gọi là
Cẩm ứng điện của môi trường, là đại lượng véc tơ như E.
Hãy thể hiện véc tơ D:  Q
D   ... nhưng giải tích véc tơ không có phép chia véc tơ !!! S
Cho nên chỉ còn 1 cách viết :
Q D  S
Câu hỏi: phép nhân véc tơ nào cho kết quả là đại lượng vô hướng (Q là vô hướng)?
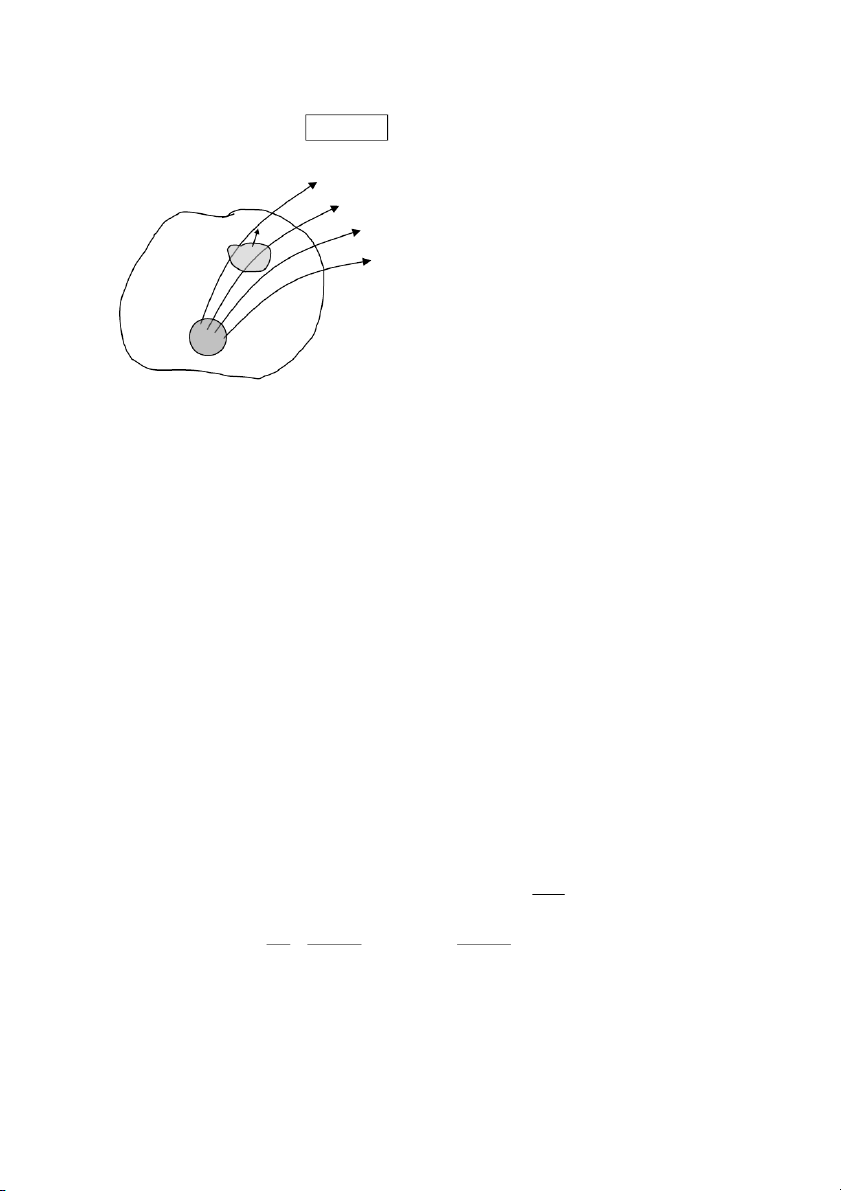
Trả lời: Là phép nhân vô hướng (.), suy ra, cách thể hiện cuối cùng của cảm ứng điện là: Q D S  Xem hình bên dưới. S dS Véc tơ pháp tuyến 
n xyz được định nghĩa là véc tơ có độ dài = 1 và vuông góc với mặt tại vị trí xyz. Định luật Gauss
Muốn tìm điện tích Q thì chúng ta phải cầm máy đo chạy vòng quanh mặt , hoặc thể hiện bằng toán học S
là lấy tích phân của cảm ứng điện theo dS trên toàn mặt S:
Q D  S
d , thường được viết như sau Q D  S
d (dạng tích phân của định luật S Gauss) Q   D n Còn S d n  dS : dS S
Ví dụ, nếu là mặt cầu thì S
D// n tại mọi vị trí trên mặt cầu, nên:
D n Dncos0 Dn  Q   DdS S
Dạng vi phân của Q D S  là dQ D  d
 S của định luật Gauss dS dS S Q
Định luật Gauss là bài toán về tích phân mặt của tích vô hướng hai véc tơ thay đổi liên tục tên mặt đó.
Định luật này về toán học là cho phép hạ bậc của tích phân từ bậc 2 xuống bậc 1. Tai sao? Q 
 DdS --- viết như thế này là bậc 1 vì chỉ có 1 biến là , nhưng có thể viết tích dS S
phân này như sau, do dS i(diện tích) = dxdy:   Q  Ddxdy  
D xydy dx    S x  y 
Lấy tích phân nhiều lớp rất phức tạp, và thông qua phép tính véc tơ Gauss hạ bậc tích phân này xuống bậc
1. Còn 1 định lí nữa gọi là định lí Stokes cho phép hạ bậc tích phân từ bậc 3 xuống bậc 2.
Muốn áp dụng định luật Gauss thì mấy kỹ thuật sau:
1. Cần lưu í, nếu mặt S không chứa điện tích, thì có bao nhiêu đường sức đi vào S sẽ có bấy nhiêu đi ra
nên kết quả tích phân phải bằng 0: DdS  , 0 vì 0   Q S
2. Nên chọn mặt có tính chất sao cho D không đổi, hoặc = 0, thì lúc đó có thể bỏ D ra ngoài dấu tích phân,
và bài toán còn lại là tính diện tích của mặt S. Ví dụ, mặt cầu, hình lập phương, hình trụ...
Bài tập ứng dụng về mặt cầu:
Tìm D trên mặt cầu bán kính r bao quanh điện tích Q.
Giải: Áp dụng công thức Q 
 DdS . Thấy rằng nếu r không đổi thì D cũng không đổi, nên trên bề mặt S
mặt cầu bán kính r bao quanh Q thì độ lớn của D là không đổi, vậy bỏ D ra ngoài dấu tích phân.   2 Q
Q  DdS D dS  DS D4 r  D    2   4r S  S  D Q Qq0 E    F Eq  2 0 2 
... đây chính là định luật Coulomb! 4 r 4 r 0 0 0 Bài về tụ điện:
Chúng ta biết là tụ điện gồm hai bản tụ tích điện trái dấu Q+, Q-, điện trường E bên trong bản tụ là không
đổi. Vậy, có mấy lưu í sau:
1. Tổng điện tích Q+ + Q- = 0, do |Q+| = |Q-| nên nếu chúng ta chọn mặt S bao quanh cả hai bản tụ thì kết
quả tích phân Gauss phải bằng 0, còn nếu S bao quanh 1 bản tụ thì tích phân sẽ là +Q hay -Q tùy trường hợp.
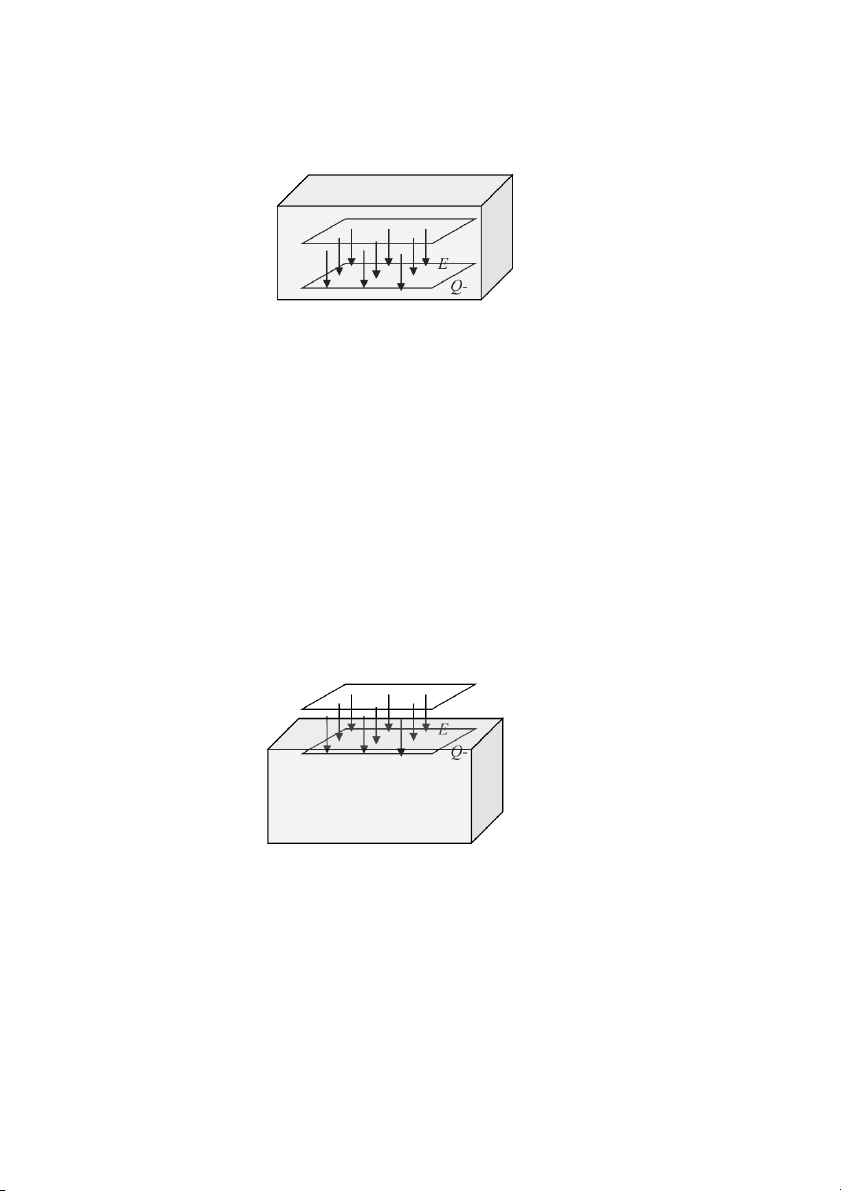
2. Chọn mặt S bao quanh như thế nào cho đơn giản nhất? Q+
Nếu chọn mặt S như hình vẽ:
- bên trong tụ thì E = const và // với pháp tuyến của mặt, cùng chiều với pháp tuyến mặt Q+ và ngược
chiều pháp tuyến mặt Q-, như vậy khi nhân D n D(Q )
 và  D(Q ) .
- ở bốn mặt bao quanh thì E=0, cho nên D n 0 
- vậy nếu lấy tích phân Gauss trên mặt S ta có:
Q D ndS  D ndS  D ndS S hai mat đáy 4 mat xung quanh Q  DndS 
0  DndS hai mat đáy 4mat xung quanh hai mat đáy Q 
D ndS D  0   D hai mat đáy
- như vậy, kết quả đúng, mặt S bao quanh cả hai bản tụ nên lượng điện tích chứa trong mặt S phải là 0. Bài về về nhà:
Xác định lượng điện tích chứa trong mặt S như hình sau (chỉ bao quanh bản tụ âm). Định luật Gauss nói
rằng lượng điện tích trong mặt này phải là -Q. Bạn tính tích phân Gauss! Q+ S Bài giảng tuần 3
2. Điện thế (dịch từ tiếng Trung, thế năng - potential của điện trường - electric field)
- Câu hỏi: Vậy công A mà
điện trường thực hiện là bao nhiêu?
Tức là công A làm q chuyển F=kQq/r2
động từ r đến vô cùng = ? Q+ q+ - Trả lời:
Hệ quả của lực F:
(1) điện tích q sẽ chuyển động, gia tốc a= F/m thế nhưng lực này giảm q
dần theo r nên gia tốc cũng giảm theo r
(2) tuy vậy, q sẽ chuyển động từ vị trí r cho đến vô vùng Kết luận:
(1) nếu 2 điện tích cùng dấu để gần nhau thì khoảng cách của chúng
tăng lên từ r đến vô vùng
(2) ngược lại, nếu 2 điện tích trái dấu thì chúng sẽ hút nhau sao cho
khoảng cách giảm liên tục từ vô cùng đến 0 r2   A  F  r d  r r  1  2 1 r   
Ar    Fdr (vì F //r )   r
- Kết luận: công điện trường thực hiện là một số dương = kQq/r; A càng lớn nếu   dr  1  A  r kQq    kQq     2r r  r  r  1 1  kQq A kQq r        0   r  r
r càng nhỏ, A = vô cùng nếu r = 0; A = 0 nếu r = vô cùng (nhớ A là công mang q từ một điểm r đến vô cùng) kQ - Nếu chọn là 1C thì q A 
: Công mà điện trường của Q thực hiện lên điện tích cùng dấu có giá trị q = 1C tỉ r r lệ nghịch với r.
- Định nghĩa điện thế U: + Điện thế U là để mang điện tích
công mà chúng ta phải thực hiện
= 1C từ vô cùng đến vị trí q r, vậy U r  kQ   A   r
Vậy điện thế là khả năng sinh công của điện trường, phụ thuộc r r
+ Thông thường các bạn có thể nhớ nhanh: Điện thế (Thế năng) là công âm !
+ Điện thế = thế năng của điện trường (do Q gây ra) Mọi loại Thế năng (hấp dẫn, điện...) = công âm
Trong thực tế ứng dụng thì chúng ta không thể mang đến vô vùng được, nên người ta xác định hiệu hai thế năng q
U(r1)-U(r2) = hiệu điện thế:
U r   U r  kQ  kQ   1 1   r  r      kQ   1 2 kQ 1 2       r r r r rr 1  2   2 1   1 2  r 
Đối với điện tích điểm hiệu điện thế giữa hai điểm r   1
 r2 = r là: U kQ 2r Qq F kQ
Nhắc lại: Định luật Coulomb F k   E   (E làcuong đo) 2 2
suy ra U E r  r q r
Chính là công thức tụ điện: Hiệu điện thế giữa hai bản tụ = cường độ điện trường  khoảng cách hai bản tụ!
Thế năng, điện thế, hiệu điện thế là các đại lượng vô hướng, chỉ phụ thuộc độ lớn của r, không phụ thuộc phương!
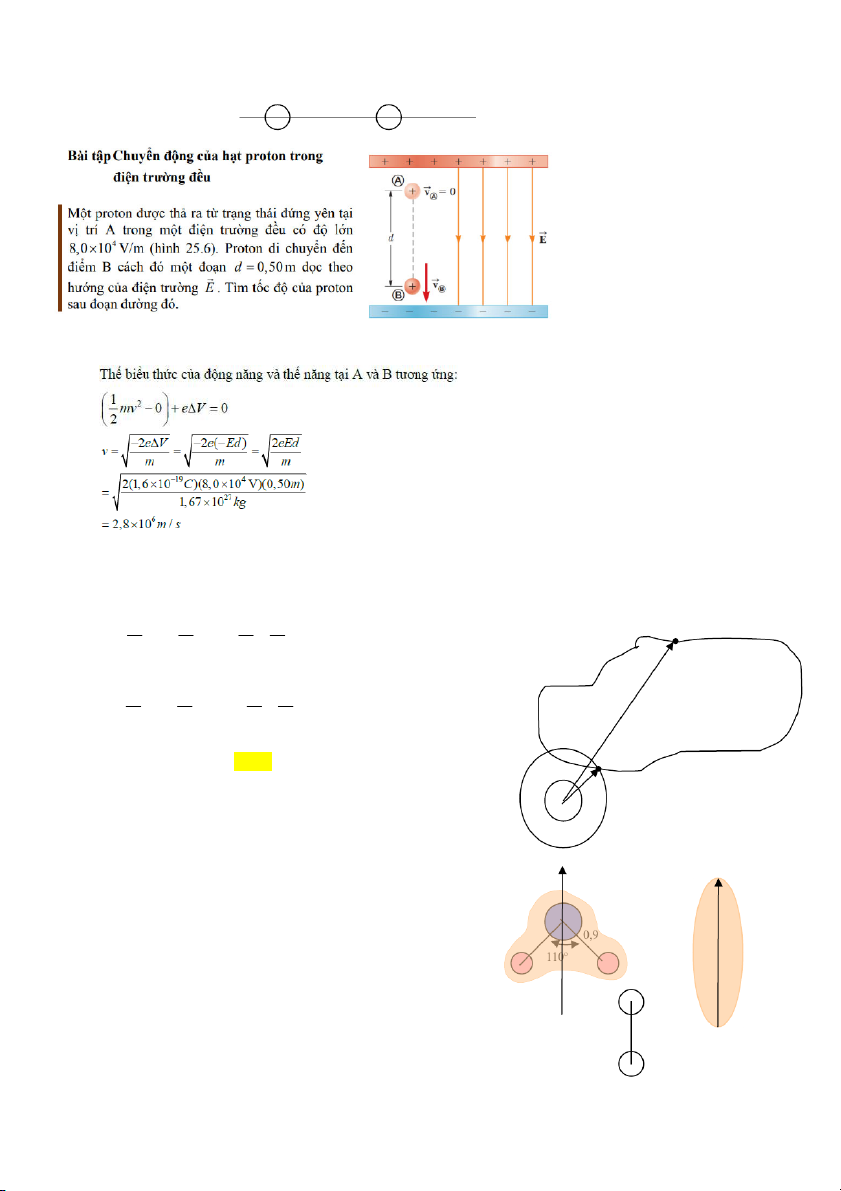
Bài tập 1: Bài tập về tụ điện. Theo định nghĩa, tụ điện phẳng gồm hai bản tụ rộng hơn nhiều so với khoảng cách
hai bản đó, nên điện trường giữa hai bản tụ. Cho E = const ,
d = 1mm E = 12V/m, tính U. r  d
  U Ed
Nhớ đổi đơn vị ra m (d) E=const d
U = 12(V/m).0,001(m)=0,012V S
Bài tập 2: Cho 1 ắc quy ô tô có hiệu điện thế giữa hai cực là 12 V. Ắc quy gồm 6 ắc quy nhỏ ghép song song, mỗi
ăc quy nhỏ lại gồm 12 ắc quy con ghép nối tiếp. Khoảng cách giữa hai điện cực Chì của ắc quy con là 5mm. Hỏi
điện trường E giữa hai bản tụ của ắc quy con là bao nhiêu?
- Cũng ứng dụng công thức r d   U
 Ed . Giải đúng thì U = 1V, E = 1V / 0,005 m = 200 V/m.
- Hệ quả quan trọng đối với điện thế U
(1) Điện thế là đại lượng vô hướng (cũng như công A, U luôn vô hướng, U cũng luôn vô hướng): suy
ra là điện thế U trên một mặt cầu bao quanh điện tích Q là như nhau, cho nên người ta gọi mặt cầu bán kính r là
mặt đẳng thế ("đẳng" = "bằng")
- Câu hỏi 1: cho mặt cầu bán kính r bao quanh điện tích Q, hỏi hiệu điện thế U giữa hai điểm bất kỳ trên
mặt đó là bao nhiêu? Trả lời: bằng 0
- Câu hỏi 2: cho 2 mặt cầu bán kính R > r bao quanh điện tích Q, hỏi hiệu điện thế giữa hai điểm bất kỳ  r  R 
trên hai mặt cầu là bao nhiêu? Trả lời: U
 Er , chính xác là U kQ  !  rR 
(2) Chính vì nó là vô hướng nên Điện thế có tính cộng được: điện thế do hai điện tích khác nhau gây ra
tại một điểm có thể cộng lại thành 1 giá trị chung.
Bài tập: cho Q = 1C, Q 1 = 2
2C, đặt cách nhau 1m, tìm các điểm nằm trên đường thẳng nối Q Q 1 sao cho 2 U = 0.
Khối lượng proton: 1,672×10−27 kg
Điện tích proton: 1,602 × 10−19 C
Những bài tập này có trong TLTK đã đưa lên WSMH, tuần 3, "Điện thế"
- Định lí về trường lực có thế năng "Công trên đường bất kỳ khép kín luôn bằng 0"
+ Công dịch chuyển q = 1C từ A đến B: Q Q  1 1  U   k   k kQ B AB    r r r r A B  B A 
+ Vậy công dịch chuyển từ B đến A là: Q Q  1 1  U k r BA    k   kQ   r r r r B B A  B A 
Suy ra, công chuyển dịch điện tích từ A đến B xong lại về A,
tức theo đường khép kín :
 A = 0, đây chính là lí do vì sao mà
điện tích như electron có thể chuyển động quanh hạt nhân trên  A
các đường khép kín mà không tốn công, vây nó không bao giờ Q+ r
rơi vào hạt nhân được. Electron chuyển động trên các mặt đẳng A thế!
- Một trường lực bất kỳ, ví dụ từ trường, lực hấp dẫn, lực Q- 
ma sát, lực lò xo, nếu có thế năng thì công trên đường khép Q-=0,2e
kín luôn = 0, và ngược lại, chỉ khi nào công trên đường
khép kín =0 thì trường lực đó mới gọi là trường lực THẾ nm (có thế năng). d=0,5nm Q+ Q- d Q+=0,2e Q+
- Lưỡng cực điện:
+ Định nghĩa: là hệ hai điện tích bằng nhau trái dấu cách một khoảng r thường nhỏ, ví dụ quan trọng nhất là phân tử nước H O 2
+ Lưỡng cực:vì nó có hai cực cùng độ lớn điện tích nhưng ngược dấu.
+ Môment lưỡng cực : được hiểu là p p=Qd
Khi đặt lưỡng cực trong điện trường xoay chiều (lò vi sóng đổi chiều sóng giữa hai thành lò khoảng 10 lần / 1 9
giây, tức là f=1 GHz) thì lưỡng cực này nó lúc lắc vì có xu hướng định hướng theo điện trường, vậy phân tử nước
dao động, thì sinh nhiệt, nên nước nóng lên.
Đây cũng chính là lí do vì sao áp đt di động vào tay thấy nóng, không phải vì pin mà vì sóng di động (2,4 GHz nó
làm nóng H O trong da !) --- tại sao nhiều người vẫn tin rằng sóng di động làm hại sức khỏe, người phản đối t 2 hì
nói sóng đt quá yếu, người ủng hộ chỉ ra có phụ cấp độc hại cho cán
bộ làm việc trong môi trường sóng vi ba (GHz). Cứ làm việc gần đài
phát thanh, trạm thu phát di động, radar là có phụ cấp, ví dụ bộ đội
thông tin có phụ cấp độc hại. 2   d r
Bài tập. Cho lực F  a m m
của một trường lực hướng tâm bất 2 dt 2 r  
kỳ (lò xo, hấp dẫn, tĩnh điện), hãy tìm A  F  r d r r ?   dọc theo 1 2 1 r
một đường  bất kỳ như hình vẽ.
Đây là bài tập về giải tích véc tơ. x
Nếu bằng giải tích véc tơ r    2 2 r 2 r2   d r  d  r d  r2 2 r 1 r d   m   1 v F  r d m   r d m   m  v d v   d v v   2  mv T  T      2    2 r 1 dt dt dt 2 2 r r r r r r 1 v 1 1 1 1 1 2 v
Định lí công - động năng: Công thực hiện trong trường lực thế = hiệu hai động năng Điện dung 1. Tụ điện
- Hệ có hai bản cực có khả năng tích điện: có những trường hợp biên, ví dụ, điện dung của một điện tích Q hình cầu bán kính R? - Những hệ chính:  S + Tụ phẳng: C 0  (S = diện tích bản Q+ d Q+
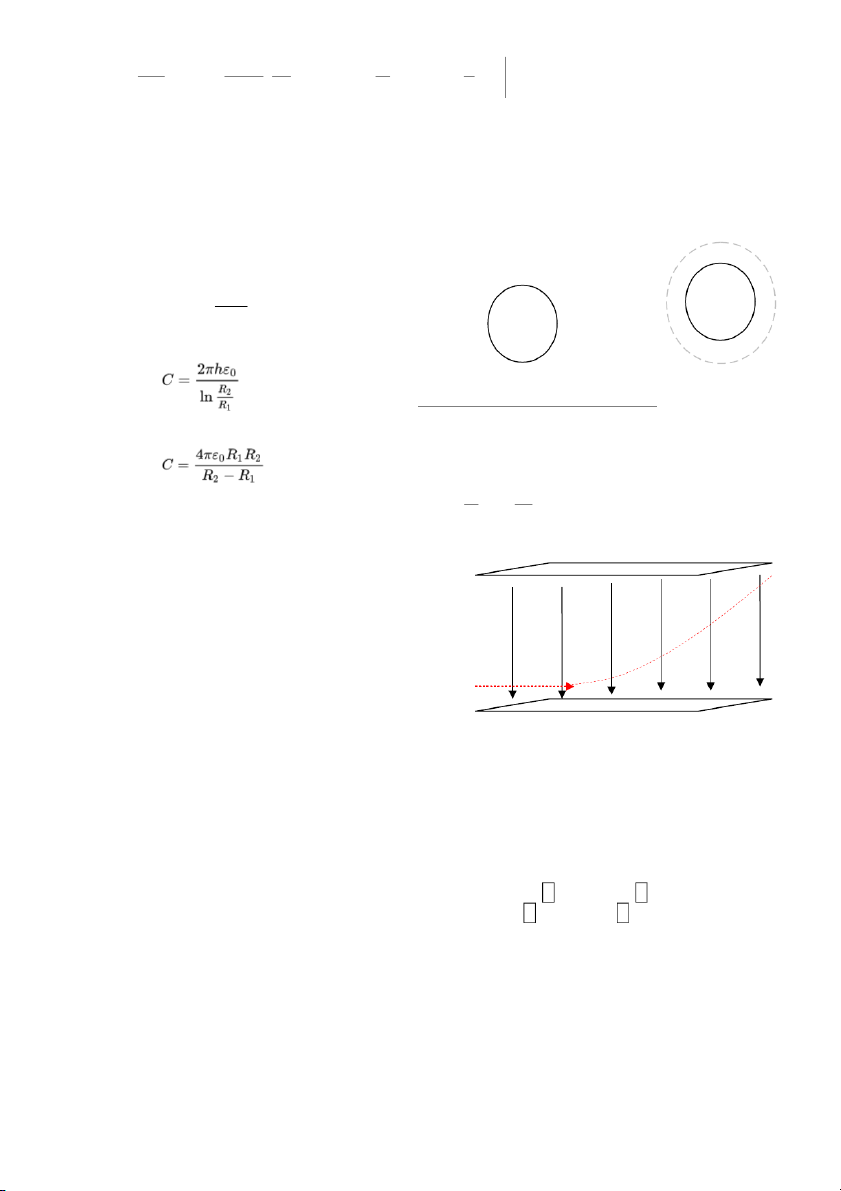
tụ, khoảng cách 2 bản tụ) d + Tụ trụ:
, h = chiều dài tụ, Đây là tụ điện Q-
R1 và R2 là bán kính của hai mặt trụ Q- + Tụ cầu 1 1
- Tụ mắc // cộng dồn, tụ mắc nối tiếp thì cộng dồn nghịch đảo   C i Ci
Câu 17: Một electron bay vào khoảng
giữa 2 bản của một tụ điện phẳng có các
bản nằm ngang, hướng bay song song với các bản, vận tốc bay v 6 o = 10 (m/s). Chiều
dài của tụ điện là L = 5 cm, cường độ điện
trường giữa hai bản của tụ điện là E = 100
(V/m). Tính độ lệch quỹ đạo sau khi ra khỏi tụ.
Từ trường (tuần 5)
- Khái niệm: lực hút phát sinh từ kim loại sắt Fe và oxit sắt (đá nam châm) Fe3O4.
- Sắt Fe: kim loại có tính chất từ hóa được, cấu trúc điện tử thì Fe có 1 điện tử tự do trên lớp 3d (Fe là kim loại
3d), trong bảng tuần hoàn Fe vị trí 26, nó có 26 proton và 26 electron (điện tử)
- 26 điện tử phân bố trên các quỹ đạo khác nhau, lần lượt là:
+ lớp đầu tiên: 1s (quỹ đạo tròn, mặt cầu R ~ 10-11 m): có 2 điện tử  quay thuận  quay ngược
+ lớp thứ 2: 2s (quỹ đạo tròn, mặt cầu R ~ 10-11 m): có 2 điện tử  quay thuận  quay ngược
+ lớp thứ 2: 2p (đã bị định hướng x,y,z nên ta có 3 quỹ đạo p là p (2 e), p x (2 e), p y z (2 e)
+ lớp thứ 3: 3s (2e), 3p(2e+2e+2e), 3d (d , d x
y,dz, dxy, dx2-y2): tất cả chứa được 10e, nhưng Fe chỉ có 8e trên
quỹ đạo 3d: dx (), dy (), dz (), dxy (), dx2-y2()
+ 2e trên 3dxy (), dx2-y2() tạo ra tính sắt từ: bị định hướng song song trong từ trường ngoài
+ trong Fe3O thì tính sắt từ duy trì ngay cả khi không có từ trường ngoài : đây là cục nam châm 4
- Bản chất từ trường là gì: là tác dụng lực giữa hai đối tượng có tính sắt từ (ferroelectric) do điên tử quay quanh
trục (như trái đất quay quanh trục), lõi trái đất là sắt nên trái đất có từ tính yếu - Về thuật ngữ:
+ từ trường (tiếng Trung): magnetic field (tiếng Latin)
+ nam-châm (tiếng Trung phiên âm từ
): từ tính (magnetic, magnetism) magnet
- Từ trường được biết đến từ khi nào: la-bàn (tiếng Trung phiên âm từ ) compas
- Elon Musk: tweet thách đấu (đánh nhau) với Putin ai thua thì mất Ucraina, trong câu tweet, ông ta viết tên của
Ucraina là " Україна " -- thể hiện rất rõ quan điểm trung thực của văn hóa phương tây, người ta ưu tiên viết tên trong văn bản gốc.
Mô tả từ trường như thế nào?
- Vì nó thể hiện tác dụng lực -- rất tự nhiên nếu chúng ta mô tả từ trường bằng các mũi tên:
Quy ước về lực từ đi ra từ cực Bắc đi vào cực Nam
- Cực Bắc: (B) tiếng Việt, trong tiếng Anh (trên mạng) : kí hiệu là N (North)
- Cực Nam: (N) tiếng Việt, trong tiếng Anh: S (South) S N B N B N Đúng Sai Đúng
- Thể hiện từ trường qua đường sức: Faraday, từ cái thể hiện này lộ ra một khái niệm mới là từ trường về cơ bản
là một trường lực tương tự điện trường và trường hấp dẫn.
- Nhắc lại: hai cực cùng dấu đẩy nhau, trái dấu hút nhau, tương tự điện trường
- Tuy nhiên đặc tính tác dụng lực của từ trường khác với của điện trường:
 đường sức điện trường là các đường thẳng, còn của từ trường là các đường cong
 điện trường: các đường thẳng đi đến vô cùng, không quay lại, còn từ trường thì các đường sức là các
đường khép kín : là các vòng khép kín
 điện trường: lực bị phân tán, trường lực phân tán: công A thực hiện trên
đường khép kín bao quanh điện tích = 0, đường đẳng thế luôn vuông
góc với đường sức điện trường
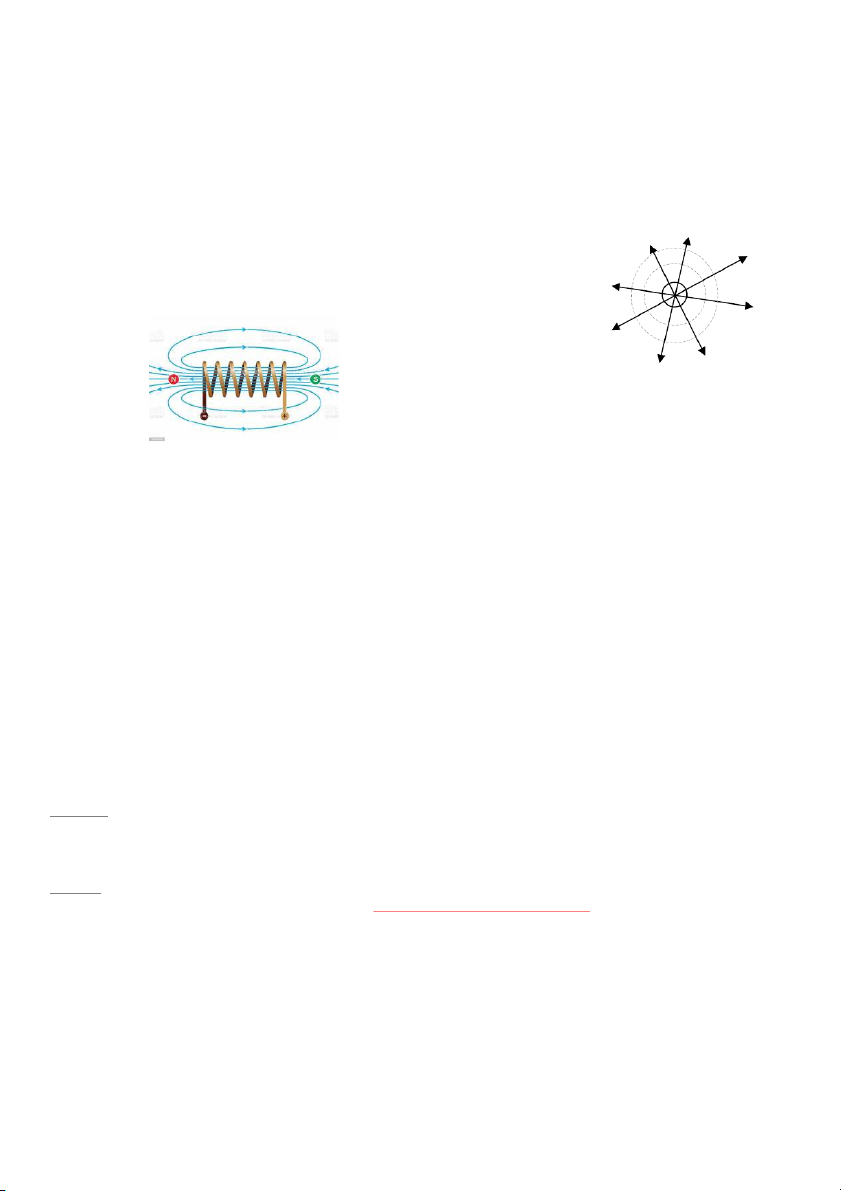
 từ trường: lực quay vòng, trường lực xoáy: thử vẽ một từ trường
Các đường sức đi xuyên qua lòng ống thành các đường khép kín: nếu có 1 nam châm nhỏ chạy
vòng quanh các đường sức khép kín này thì nó không mất công nào - suy ra 0   A
- Đơn vị của cường độ điện trường: Véc tơ cường độ điện trường là H, H - Henry
- Độ thẩm từ (Magnetic permeability): B    H  0
, trong đó 0 độ từ thẩm chân không,  độ từ thẩm môi trường
(là một con số không đơn vị). Đơn vị của B: là Tesla (đo từ trường lớn), Gauss (đo từ trường nhỏ) 1T = 10000 G
 từ trường trái đất: ~1G = 10-4 T
 nam châm điện (10k vòng): 300 -500 G, có thể tạo được nam châm điện từ 1T đến 20T
 từ trường của máy cộng hưởng từ hạt nhân: 1T
 từ trường của sao nơ tron: 10 T 8
 không gian vũ trụ: 10-10 T, vào cỡ 1 G 
 từ trường thấp nhất trong PTN mà con người tạo được: 10-14 T, 0.1 nG (tạo được bằng cách nào?
màn chắn từ là màn chắn sóng điện từ)
- Từ trường và điện trường là hai khái niệm tương đối, từ trường là do điện trường chuyển động gây ra, từ trường
là hệ quả (theo thuyết) tương đối của điện trường chuyển động với vận tốc ánh sáng (lí do trực quan là ánh sáng
chỉ tác dụng lên mắt người, vật chất, thông qua thành phần điện - tại sao chúng ta nhìn rõ hơn thông qua kính lọc
polaroid, vì nó loại thành phần gây nhiễu là từ trường)
Câu hỏi:Chất lượng ảnh (image) được đo bằng đơn vị nào?
chúng ta vẫn dùng thuật toán tăng chất lượng ảnh, vấn đề là chất lượng định nghĩa thế nào? tại sao đt
smartphone thế hệ mới lại có nhiều camera hơn là 1?
Trả lời: thuật toán không thể làm thay đổi được số photon bắt trên thấu kính máy ảnh và ghi nhớ trong bộ nhớ
máy ảnh - chất lượng ảnh về vật lí được đo bằng số photon mà thấu kính bắt được.
- muốn tăng chất lượng ảnh: một là tăng số thấu kính, tăng kích thước ống kính; hai là dùng bộ lọc, lọc bớt
phần từ, dùng phần mềm, chỉnh thời gian phơi sáng lâu hơn - liên quan đến chống rung máy ảnh khi phơi sáng
lâu, vì sao iPhone chụp tốt, còn thuật toán thì dùng bộ lọc, lấy ảnh chỉ do 1 loại bước sóng gây ra, ví dụ chỉ lấy
phần ảnh cho sóng hồng ngoại ghi trên bộ nhớ ...
- Liên hệ giữa B (độ thẩm từ) và H (cường độ từ trường): B    H 0
- Nhắc lại công thức liên hệ độ thẩm điện và cường độ điện trường: D    E 0
- Từ trường tạo ra từ rất nhiều cách khác nhau: cuộn dây có dòng điện chạy qua, một sợi dây có dòng chạy qua cũng gây ra từ trường
 cuộn dây có nhiều cấu hình: cuộn trụ thẳng, cuộn xoắn vòng tròng, dây thẳng, dây tròn ,...
 Bài tập: Google đọc thêm về từ trường trái đất
Định luật Gauss cho từ trường
- với điện trường thì do các đường sức là đường mở nên D d  S Q  
nếu S bao quanh điện tích S
- với từ trường do các đường sức là đóng nên B d 0   S
: có bao nhiêu đường sức đi ra thì có bấy nhiêu đi vào, S
bất kể mặt S là mặt nào, có bao quanh nam châm hay không cũng không quan trọng
- Kết luận: Không có từ tích riêng biệt, không thể tách cực bắc và cực nam của một nam châm, một điện tích quay
quanh trục riêng chỉ có 2 cách duy nhất, tạo ra 2 nam châm ngược cực