Bài giảng Giải tích 2 | Trường Đại học Kỹ thuật - Công nghệ Cần Thơ
Bài giảng Giải tích 2 | Trường Đại học Kỹ thuật - Công nghệ Cần Thơ. Tài liệu được sưu tầm giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời bạn đọc đón xem.
Môn: Giải tích 2 (CT) 3 tài liệu
Trường: Trường Đại học Kỹ thuật - Công nghệ Cần Thơ 150 tài liệu
Tác giả:
Preview text:
PGS.TS. Phạm Ngọc Anh BÀI GIẢNG GIẢI TÍCH 2
NHÀ XUẤT BẢN THÔNG TIN VÀ TRUYỀN THÔNG-2015 51 89/176-05 Mã số: 8I092M5 TT-05 Lời nói đầu
Trong hoạt động khoa học và kỹ thuật thường gặp nhiều vấn đề có liên quan
đến hàm nhiều biến số và các ứng dụng của chúng. Do vậy, giải tích hàm nhiều biến
số là một môn học đang giữ một vị trí quan trọng trong các lĩnh vực ứng dụng và
trong hệ thống các môn học của Học viện Công nghệ Bưu chính Viễn thông. Các
kiến thức và phương pháp tiếp cận của giải tích hàm nhiều biến số đã hỗ trợ hiệu
quả các kiến thức nền tảng cho các môn học như vật lý, xác suất thống kê, toán kỹ
thuật, toán rời rạc và các môn chuyên ngành khác.
Bài giảng "Giải tích hàm nhiều biến số" được biên soạn lại theo chương trình
qui định của Học viện cho hệ đại học chuyên ngành Điện tử-Viễn thông-Công nghệ
thông tin với hình thức đào tạo theo tín chỉ. Do đối tượng sinh viên rất đa dạng với
trình độ cơ bản khác nhau, chúng tôi đã cố gắng tìm cách tiếp cận đơn giản và hợp
lý để trình bày nội dung theo phương pháp dễ hiểu hơn, nhằm giúp cho sinh viên
nắm được các kiến thức cơ bản nhất.
Để vừa ôn tập, vừa tự kiểm tra kiến thức và để hình dung được mức độ của một
đề thi hết môn, sau mỗi phần lý thuyết quan trọng chúng tôi thường đưa ra các ví
dụ minh họa chi tiết. Nội dung được chia thành 4 chương. Chương 1 dành cho phép
tính vi phân của hàm nhiều biến số. Chương 2 và 3 trình bày chi tiết về tích phân
đường và tích phân mặt. Phương trình vi phân và các phương pháp giải được đưa
ra trong chương 4. Các khái niệm và công thức được trình bày tương đối đơn giản
và được minh họa bằng nhiều ví dụ với các hình vẽ sinh động. Các chứng minh khó
được lược bớt có chọn lọc để giúp cho giáo trình không quá cồng kềnh nhưng vẫn
đảm bảo được, để tiện cho sinh viên học tập chuyên sâu và tra cứu phục vụ quá
trình học tập các môn học khác. Cuối mỗi chương học đều có các bài tập để sinh
viên tự giải nhằm giúp các em hiểu sâu sắc hơn về lý thuyết và rèn luyện kỹ năng thực hành.
Tác giả hy vọng rằng giáo trình này có ích cho các em sinh viên và các bạn đồng
nghiệp trong quá trình học tập và giảng dạy về môn học giải tích hàm nhiều biến
số. Tác giả cũng cám ơn mọi ý kiến góp ý để giáo trình bài giảng này được hoàn
thiện hơn nhằm nâng cao chất lượng dạy và học môn học này. Tác giả Mục lục
Lời nói đầu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . iii
Mục lục . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . iv
1 Phép tính vi phân hàm nhiều biến 2
1.1 Không gian Rn . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
1.1.1 Các phép toán . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
1.1.2 Chuẩn và hàm khoảng cách. . . . . . . . . . . . . . . . . . . . 2 1.1.3
Tôpô. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
1.2 Hàm số nhiều biến . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3 1.2.1
Mặt cầu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
1.2.2 Mặt Elipxoit . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
1.2.3 Mặt hypeboloit 1 tầng . . . . . . . . . . . . . . . . . . . . . . 5
1.2.4 Mặt hypeboloit 2 tầng . . . . . . . . . . . . . . . . . . . . . . 6
1.2.5 Mặt paraboloit-eliptic . . . . . . . . . . . . . . . . . . . . . . 6
1.2.6 Mặt trụ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
1.2.7 Mặt nón bậc hai . . . . . . . . . . . . . . . . . . . . . . . . . 8
1.3 Giới hạn hàm nhiều biến số . . . . . . . . . . . . . . . . . . . . . . . 9
1.4 Hàm số liên tục . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
1.5 Đạo hàm riêng và vi phân toàn phần của hàm nhiều biến số . . . . . 11 1.5.1
Đạo hàm riêng . . . . . . . . . . . . . . . . . . . . . . . . . . 11
1.5.2 Hàm khả vi . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
1.6 Đạo hàm theo phương và hướng . . . . . . . . . . . . . . . . . . . . . 14
1.7 Quan hệ giữa đạo hàm theo phương và đạo hàm riêng . . . . . . . . . 15
1.8 Đạo hàm riêng của hàm hợp . . . . . . . . . . . . . . . . . . . . . . . 16
1.9 Đạo hàm riêng và vi phân cấp cao . . . . . . . . . . . . . . . . . . . . 17
1.10 Công thức Taylor của hàm 2 biến số . . . . . . . . . . . . . . . . . . 19
1.11 Hàm ẩn . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21
1.12 Cực trị của hàm nhiều biến . . . . . . . . . . . . . . . . . . . . . . . 23
1.12.1 Định nghĩa . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23 MỤC LỤC v
1.12.2 Cực trị không điều kiện . . . . . . . . . . . . . . . . . . . . . 23
1.12.3 Cực trị có điều kiện . . . . . . . . . . . . . . . . . . . . . . . . 27
1.13 Giá trị lớn nhất và nhỏ nhất . . . . . . . . . . . . . . . . . . . . . . . 29
1.13.1 Định nghĩa . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
1.13.2 Phương pháp tìm . . . . . . . . . . . . . . . . . . . . . . . . . 29
1.14 Bài tập Chương 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31 2 TÍCH PHÂN BỘI 36
2.1 Tích phân phụ thuộc tham số . . . . . . . . . . . . . . . . . . . . . . 36
2.1.1 Tích phân xác định . . . . . . . . . . . . . . . . . . . . . . . . 36
2.2 Tích phân kép . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46
2.2.1 Định nghĩa . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46
2.2.2 Điều kiện khả tích . . . . . . . . . . . . . . . . . . . . . . . . 46 2.2.3 Các tính chất.
. . . . . . . . . . . . . . . . . . . . . . . . . . 48
2.2.4 Định lý Fubini. . . . . . . . . . . . . . . . . . . . . . . . . . . 48
2.2.5 Công thức đổi biến. . . . . . . . . . . . . . . . . . . . . . . . 52
2.2.6 Ứng dụng của tích phân kép. . . . . . . . . . . . . . . . . . . 55
2.3 Tích phân bội. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 60
2.3.1 Định nghĩa. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 60
2.3.2 Công thức tính . . . . . . . . . . . . . . . . . . . . . . . . . . 61
2.4 Bài tập Chương 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 65
3 TÍCH PHÂN ĐƯỜNG VÀ MẶT 69
3.1 Tích phân đường loại 1 . . . . . . . . . . . . . . . . . . . . . . . . . . 69
3.1.1 Định nghĩa . . . . . . . . . . . . . . . . . . . . . . . . . . . . 69
3.1.2 Tính chất . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 69
3.1.3 Công thức tính . . . . . . . . . . . . . . . . . . . . . . . . . . 70
3.2 Tích phân đường loại 2 . . . . . . . . . . . . . . . . . . . . . . . . . . 74 3.2.1
Định nghĩa . . . . . . . . . . . . . . . . . . . . . . . . . . . . 74
3.2.2 Nhận xét . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 75
3.2.3 Tích chất và ý nghĩa cơ học của tích phân đường loại 2 . . . . 75
3.2.4 Cách tính tích phân đường loại 2 . . . . . . . . . . . . . . . . 76
3.2.5 Chú ý . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 77
3.2.6 Công thức Green . . . . . . . . . . . . . . . . . . . . . . . . . 79
3.2.7 Định lý 4 mệnh đề tương đương . . . . . . . . . . . . . . . . . 82
3.3 Tích phân mặt loại 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . 87 MỤC LỤC 1
3.3.1 Các khái niệm về mặt . . . . . . . . . . . . . . . . . . . . . . 87
3.3.2 Định nghĩa . . . . . . . . . . . . . . . . . . . . . . . . . . . . 89
3.3.3 Cách tính . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 89
3.3.4 Tính chất cơ học của tích phân mặt loại 1 . . . . . . . . . . . 91
3.3.5 Tích phân mặt loại 2 . . . . . . . . . . . . . . . . . . . . . . . 92
3.3.6 Định nghĩa . . . . . . . . . . . . . . . . . . . . . . . . . . . . 92
3.3.7 Cách tính . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 92
3.4 Quan hệ giữa các tích phân . . . . . . . . . . . . . . . . . . . . . . . 95 3.4.1
Công thức Stokes . . . . . . . . . . . . . . . . . . . . . . . . 95
3.4.2 Công thức Ostrogradski . . . . . . . . . . . . . . . . . . . . . 97
3.5 Véc tơ rôta và trường thế . . . . . . . . . . . . . . . . . . . . . . . . . 98
3.6 Bài tập Chương 3 . . . . . . . . . . . . . . . . . . . . . . . . . . . 100
4 PHƯƠNG TRÌNH VÀ HỆ PHƯƠNG TRÌNH VI PHÂN 104
4.1 Khái niệm chung về phương trình vi phân . . . . . . . . . . . . . . . 104
4.1.1 Các bài toán . . . . . . . . . . . . . . . . . . . . . . . . . . . . 104
4.1.2 Định nghĩa . . . . . . . . . . . . . . . . . . . . . . . . . . . . 105
4.2 Phương trình vi phân cấp một . . . . . . . . . . . . . . . . . . . . . . 105
4.2.1 Định nghĩa và sự tồn tại nghiệm . . . . . . . . . . . . . . . . . 105
4.3 Phương trình tách biến . . . . . . . . . . . . . . . . . . . . . . . . . . 106
4.3.1 Phương trình tuyến tính . . . . . . . . . . . . . . . . . . . . . 109
4.3.2 Phương trình Bernoulli . . . . . . . . . . . . . . . . . . . . . . 110
4.3.3 Phương trình vi phân toàn phần . . . . . . . . . . . . . . . . . 112
4.4 Phương trình vi phân cấp hai . . . . . . . . . . . . . . . . . . . . . . 113
4.4.1 Định nghĩa và sự tồn tại nghiệm . . . . . . . . . . . . . . . . . 113
4.4.2 Phương trình khuyết . . . . . . . . . . . . . . . . . . . . . . . 114
4.4.3 Phương trình vi phân tuyến tính cấp 2 . . . . . . . . . . . . . 116
4.4.4 Cấu trúc nghiệm . . . . . . . . . . . . . . . . . . . . . . . . . 116
4.4.5 Phương trình vi phân tuyến tính cấp 2 với hệ số hằng số . . . 119
4.5 Hệ phương trình vi phân . . . . . . . . . . . . . . . . . . . . . . . . . 126
4.5.1 Hệ phương trình vi phân cấp 1 . . . . . . . . . . . . . . . . . 126
4.5.2 Phương pháp giải hệ phương trình vi phân cấp 1 . . . . . . . 126
4.5.3 Phương pháp giải hệ phương trình vi phân cấp 1 với hệ số
hằng số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 127
4.6 Bài tập Chương 4 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 129
Tài liệu tham khảo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 134 Chương 1
Phép tính vi phân hàm nhiều biến 1.1 Không gian Rn 1.1.1 Các phép toán Cho hai véc tơ
x = (x1, x2, ..., xn) ∈ Rn, y = (y1, y2, ..., yn) ∈ Rn.
Khi đó, ta nhắc lại các phép toán quen thuộc trong không gian n chiều Rn: + Phép cộng và trừ:
x ± y = (x1 ± y1, x2 ± y2, ..., xn ± yn).
+ Phép nhân véc tơ với một số thực:
λx = (λx1, λx2, ..., λxn), ∀λ ∈ R.
+ Phép nhân vô hướng hai véc tơ:
hx, yi = x1y1 + x2y2 + ... + xnyn.
Khi đó, ta có véc tơ x vuông góc với y khi và chỉ khi x1y1 + x2y2 + ... + xnyn = 0.
+ Góc giữa 2 véc tơ x 6= 0 và y 6= 0 xác định bởi công thức: x cos(x, y) = 1y1 + x2y2 + ... + xnyn p p . x2 + x2 + ... + x2 y2 + y2 + ... + y2 1 2 n 1 2 n
1.1.2 Chuẩn và hàm khoảng cách.
Cho véc tơ x = (x1, x2, ..., xn) ∈ Rn. Khi đó, chuẩn của véc tơ x là một số thực
được ký hiệu bởi kxk và được xác định bởi q kxk = x2 + x2 + ... + x2 . 1 2 n 1.2 Hàm số nhiều biến 3
Chuẩn có các tính chất cơ bản sau:
+ kxk ≥ 0 ∀x ∈ Rn và kxk = 0 khi và chỉ khi x = 0.
+ kλxk = |λ|kxk ∀x ∈ Rn, λ ∈ R.
+ kx + yk ≤ kxk + kyk ∀x, y ∈ Rn.
Khi đó, khoảng cách giữa x ∈ Rn và y ∈ Rn được xác định bởi công thức d(x, y) = kx − yk. 1.1.3 Tôpô.
Cho x ∈ Rn, ǫ > 0. Khi đó
+ B(x, ǫ) = {y ∈ Rn : ky − xk < ǫ} gọi là hình cầu mở có tâm tại điểm x và bán kính là ǫ. + ¯
B(x, ǫ) = {y ∈ Rn : ky − xk ≤ ǫ} gọi là hình cầu đóng có tâm tại điểm x và bán kính là ǫ.
+ Điểm x ∈ M ⊆ Rn gọi là điểm trong, nếu tồn tại một hình cầu mở B(x, ǫ) sao
cho B(x, ǫ) ⊆ M. Tập hợp các điểm trong của M được gọi là phần trong của M và ký hiệu bởi intM.
+ Tập M ⊆ Rn gọi là tập mở, nếu intM = M.
+ Cho M ⊆ Rn. Điểm x được gọi là điểm biên của M, nếu với mọi ǫ > 0 thì B(x, ǫ)
chứa những điểm thuộc M và những điểm không thuộc M. Tập hợp các điểm biên
của M được ký hiệu là ∂M.
+ Tập M ⊆ Rn gọi là một tập đóng, nếu ∂M ⊆ M.
+ Tập M ⊆ Rn gọi là bị chặn bởi α > 0, nếu kxk ≤ α ∀x ∈ M.
+ Tập M ⊆ Rn gọi là tập compact, nếu M là tập đóng và bị chặn. 1.2 Hàm số nhiều biến
Cho ∅ 6= D ⊆ Rn. Khi đó, ánh xạ f : D → R xác định bởi
x = (x1, x2, ..., xn) ∈ D 7−→ y = f(x1, x2, ..., xn) ∈ R
được gọi là một hàm số nhiều biến, Tập D được gọi là miền xác định của hàm số f.
Các số x1, x2, ..., xn được gọi là các biến số của hàm số f.
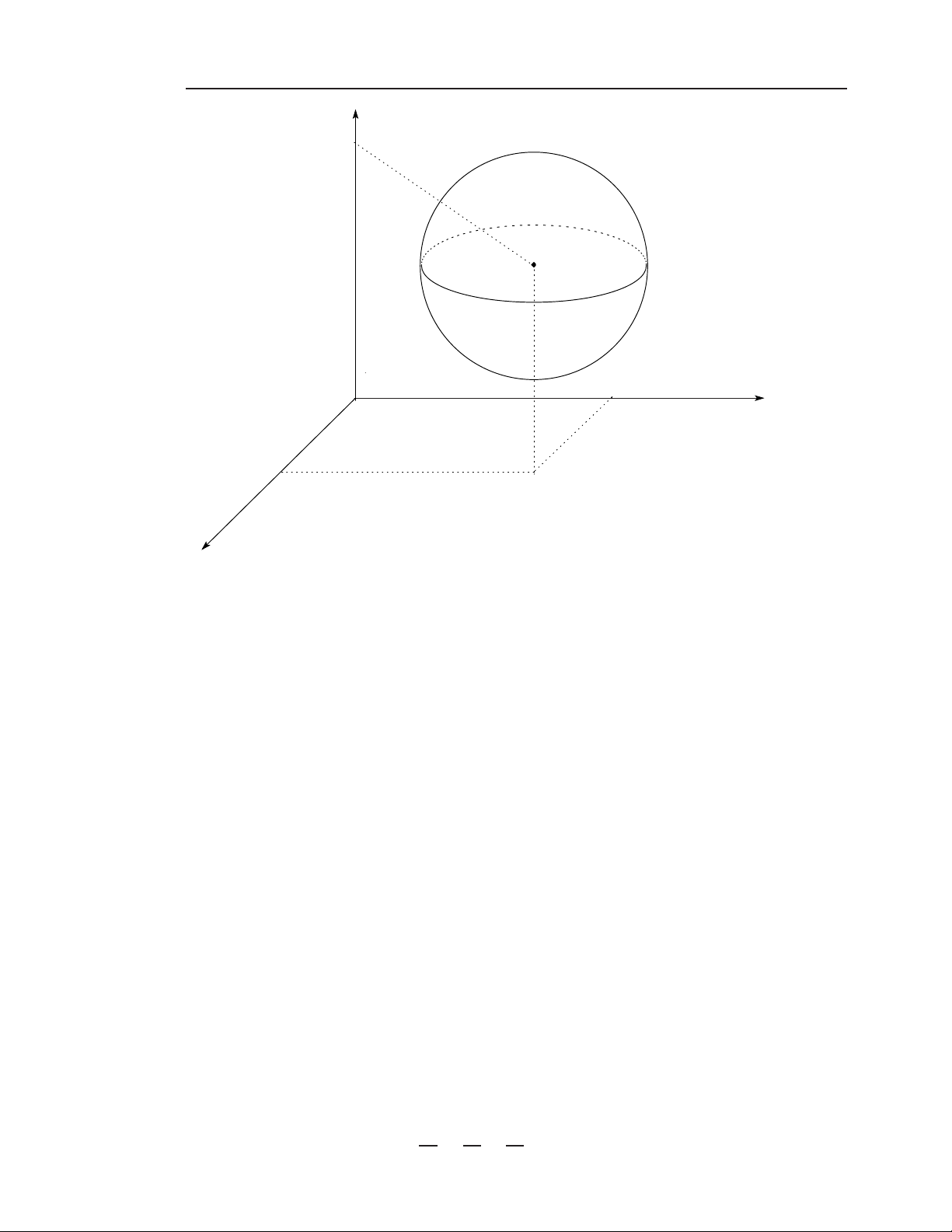
Ví dụ 1.1. Cho R > 0. Tìm miền xác định của hàm số q f (x) = R2 − x2 . 1 − x2 2 − ... − x2 n 4
Phép tính vi phân hàm nhiều biến z c I b y O a x Hình 1.1: Mặt cầu. Giải.
Theo định nghĩa, miền xác định D được xác định bởi
D ={x ∈ Rn : R2 − x21 − x22 − ... − x2n ≥ 0}
={x ∈ Rn : kx − 0k2 ≤ R2} = ¯ B(0, R).
Dưới đây là một số mặt bậc 2 thường gặp trong không gian R3. 1.2.1 Mặt cầu Phương trình:
(S) = {(x, y, z) ∈ R3 : (x − a)2 + (y − b)2 + (z − c)2 = R2}.
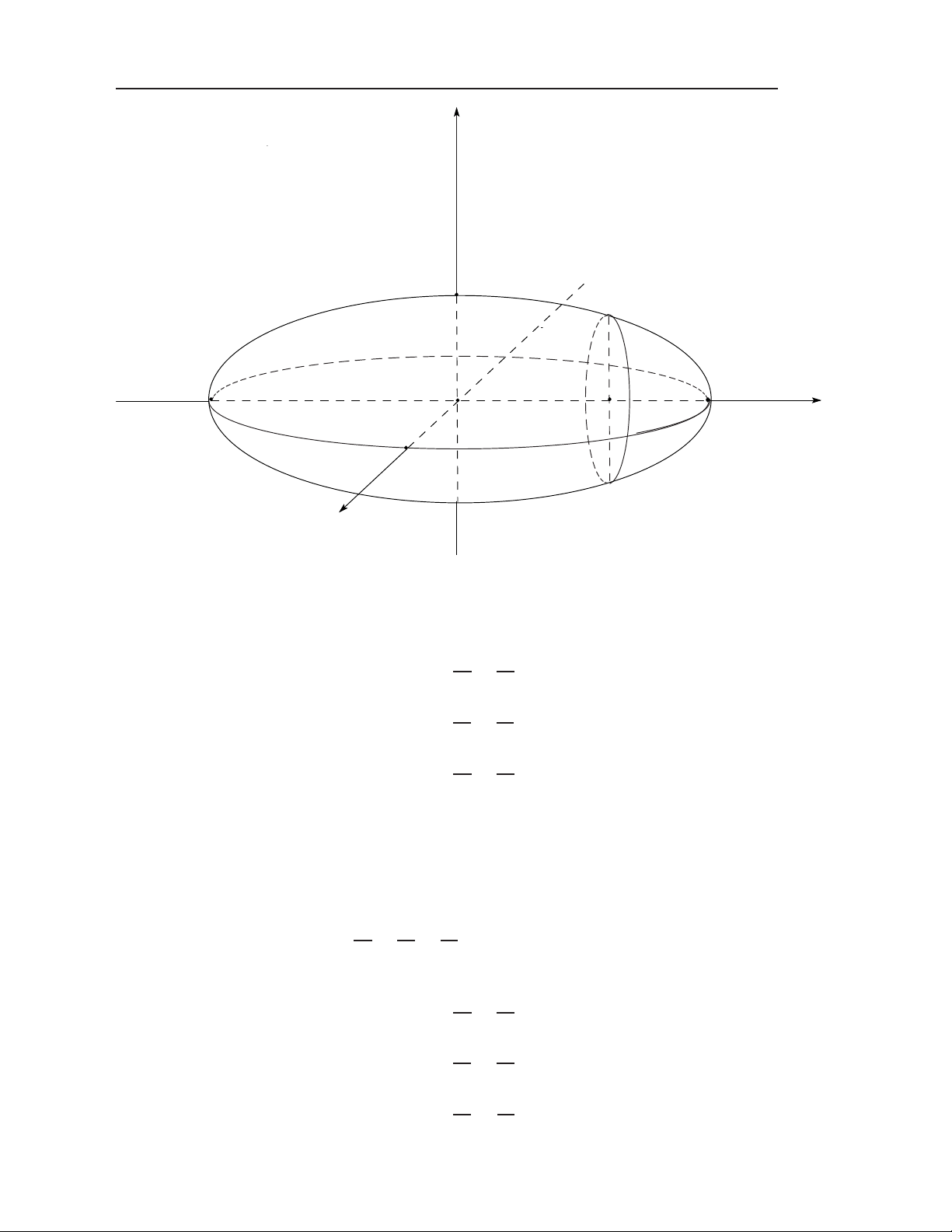
Khi đó, điểm I(a, b, c) gọi là tâm và R gọi là bán kính của mặt cầu (S). 1.2.2 Mặt Elipxoit Phương trình: x2 y2 z2 (E) : + + = 1 (a, b, c > 0). a2 b2 c2 1.2 Hàm số nhiều biến 5 z c b y O a x Hình 1.2: Mặt elipxoit. Các mặt cắt x2 y2 (Oxy) z = 0 : + = 1. a2 b2 y2 z2 (Oyz) x = 0 : + = 1. b2 c2 x2 z2 (Oxz) y = 0 : + = 1. a2 c2
1.2.3 Mặt hypeboloit 1 tầng Phương trình: x2 y2 z2 (H1) : + − = 1 (a, b, c > 0). a2 b2 c2 Các mặt cắt x2 y2 (Oxy) z = 0 : + = 1. a2 b2 y2 z2 (Oyz) x = 0 : − = 1. b2 c2 x2 z2 (Oxz) y = 0 : − = 1. a2 c2 6
Phép tính vi phân hàm nhiều biến z b y O a x
Hình 1.3: Mặt hypeboloit 1 tầng.
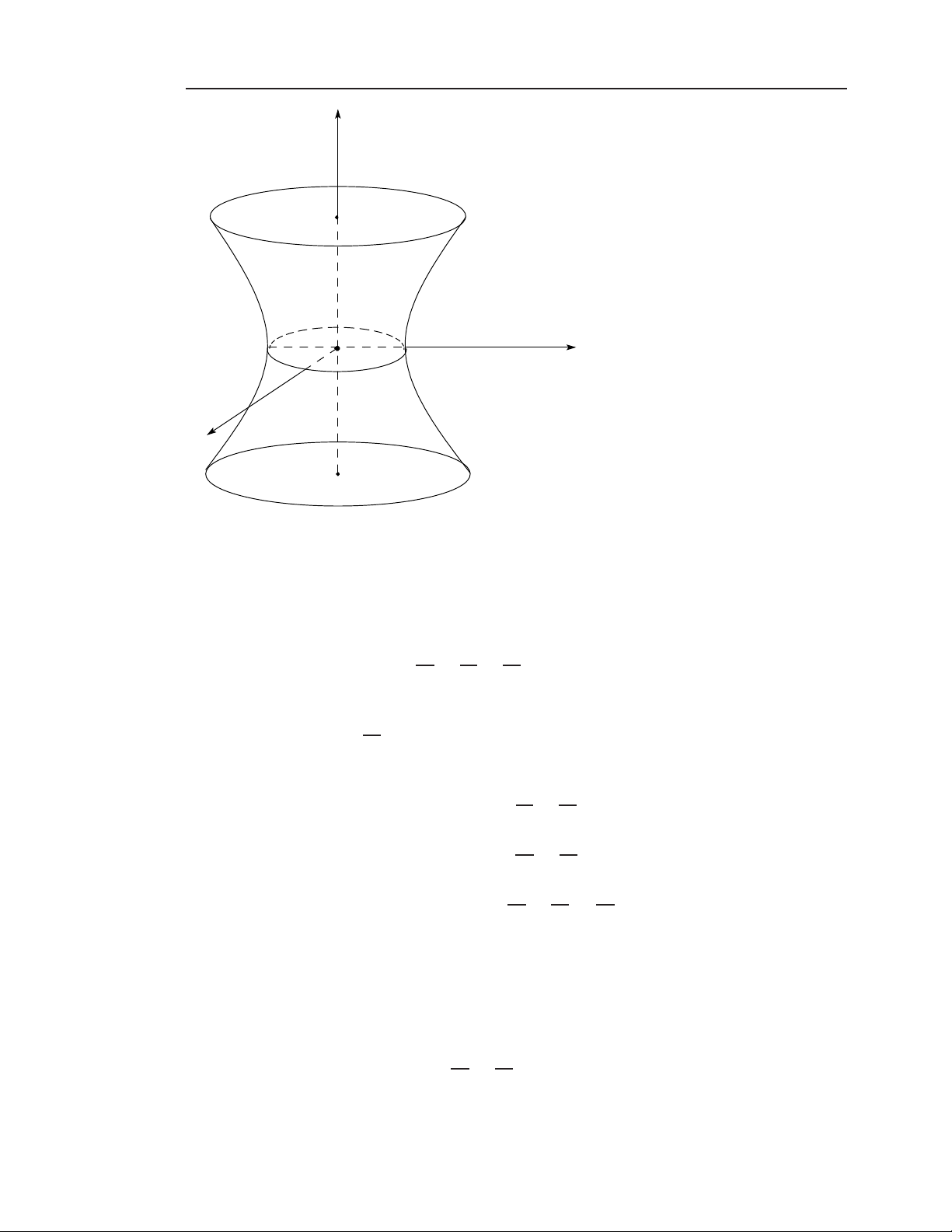
1.2.4 Mặt hypeboloit 2 tầng Phương trình: x2 y2 z2 (H2) : + − = −1 (a, b, c > 0). a2 b2 c2 Điều kiện
z2 − 1 ≥ 0 ⇔ z ∈ (−∞,−c] ∪ [c,+∞). c2 Các mặt cắt y2 z2 (Oyz) x = 0 : − = −1. b2 c2 x2 z2 (Oxz) y = 0 : − = −1. a2 c2 x2 y2 h2 (P ) z = h > c : + = − 1. a2 b2 c2 1.2.5 Mặt paraboloit-eliptic Phương trình: x2 y2 (P E) : + = 2z (p, q > 0), p q
với điều kiện z ≥ 0. Các mặt cắt (Oyz) x = 0 : y2 = 2qz. 1.2 Hàm số nhiều biến 7 z c y O −c x
Hình 1.4: Mặt hypeboloit 2 tầng. (Oxz) y = 0 : x2 = 2pz. x2 y2 (P ) z = h > 0 : + = 2h. p q z y O x
Hình 1.5: Mặt paraboloit-eliptic. 8
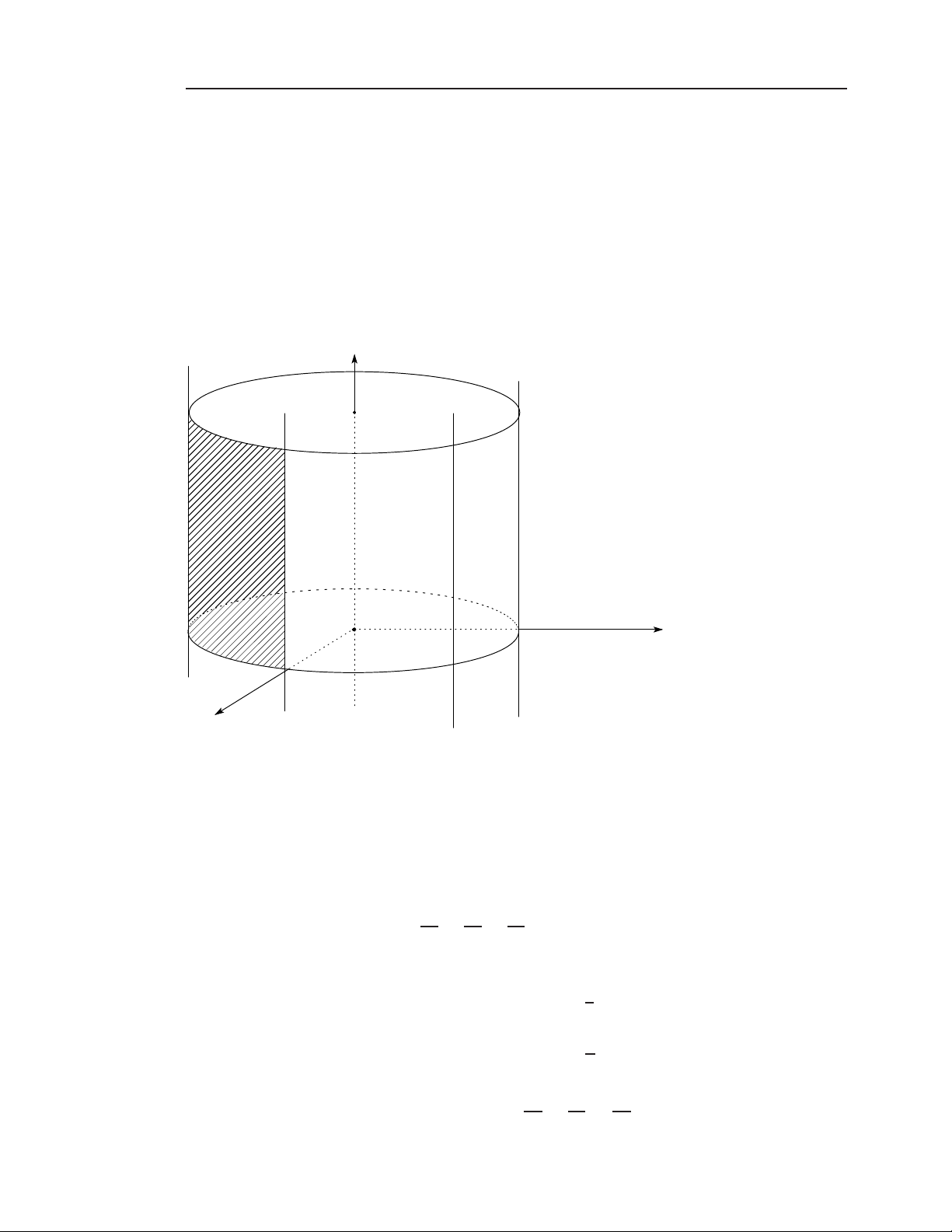
Phép tính vi phân hàm nhiều biến 1.2.6 Mặt trụ Phương trình:
(Tz) : f (x, y) = 0 song song với trục Oz,
(Ty) : g(x, z) = 0 song song với trục Oy,
(Tx) : f (y, z) = 0 song song với trục Ox,
trong đó f, g, h : D ⊆ R2 → R. z y O x
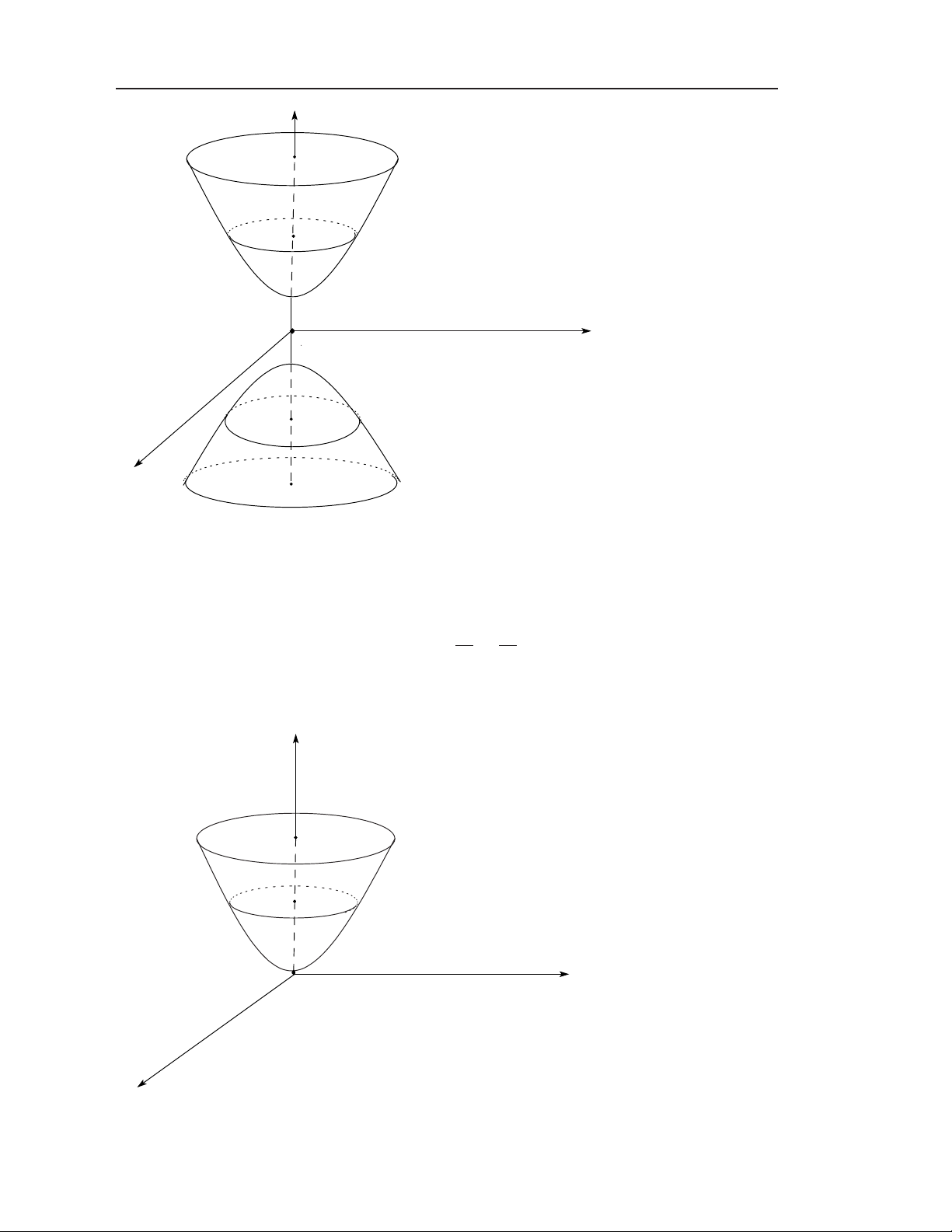
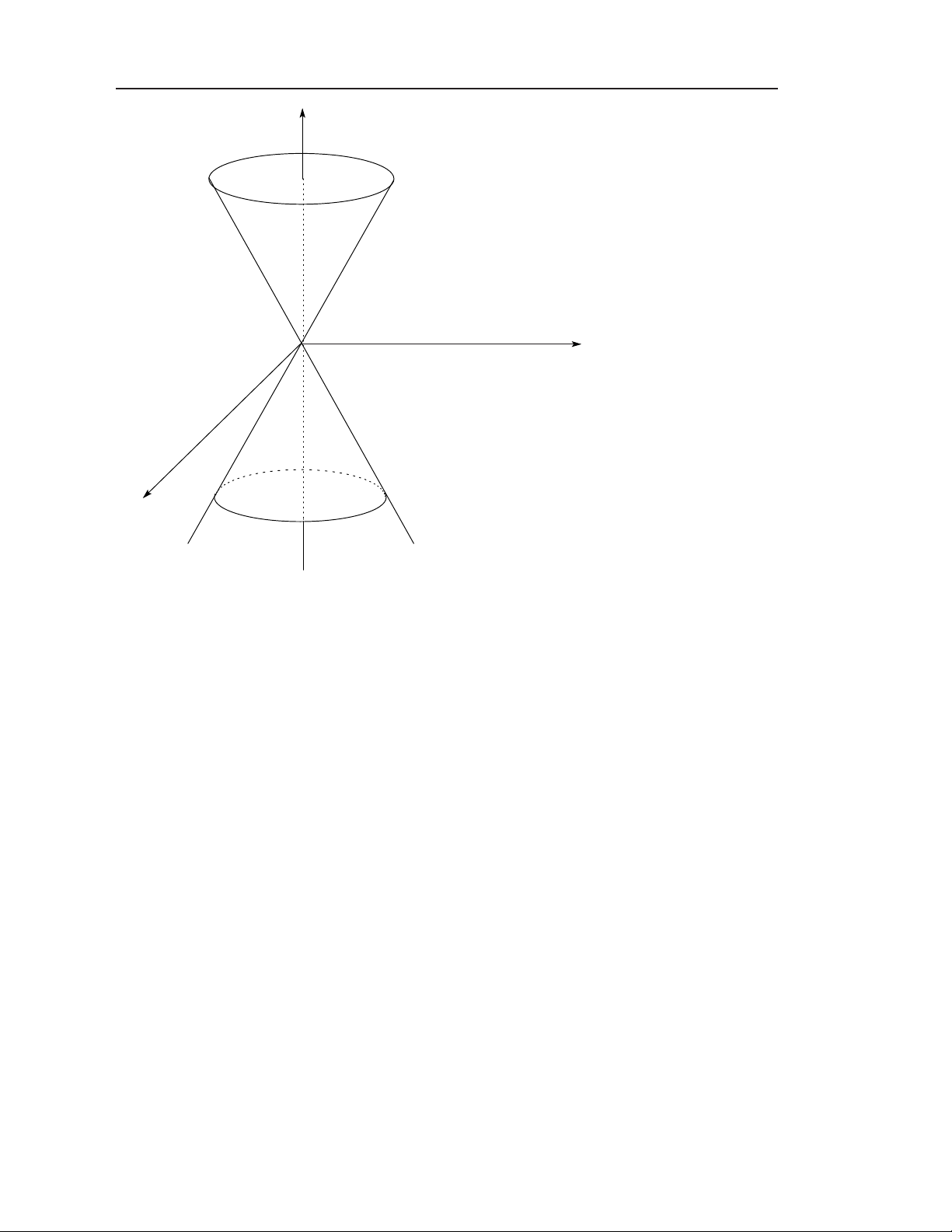
Hình 1.6: Mặt trụ song song Oz. 1.2.7 Mặt nón bậc hai Phương trình: x2 y2 z2 (N) : + − = 0 (a, b, c > 0). a2 b2 c2 Các mặt cắt b (Oyz) x = 0 : y = ± z. c a (Oxz) y = 0 : x = ± z. c x2 y2 h2 (P ) z = h > 0 : + = . a2 b2 c2
1.3 Giới hạn hàm nhiều biến số 9 z y O x
Hình 1.7: Mặt nón bậc hai.
1.3 Giới hạn hàm nhiều biến số
Để hiểu về giới hạn hàm nhiều biến số trong không gian Rn, ta có thể nghiên
cứu thông qua giới hạn của hàm hai biến số. Một dãy điểm {Mn} ⊂ R2 được gọi là
dần tới điểm M0 ∈ R2, viết tắt là Mn → M0 khi n → ∞ hay lim Mn = M0, nếu n→∞
với mọi ǫ > 0 tồn tại số tự nhiên n(ǫ) sao cho
Mn ∈ B(M0, ǫ) ∀n ≥ n(ǫ).
Trong trường hợp đặc biệt: Nếu lim xn = x0 và lim yn = y0 thì điểm Mn(xn, yn) → n→∞ n→∞ M0(x0, y0) khi n → ∞.
Cho một hàm 2 biến số z = f(x, y), xác định trong hình cầu có tâm tại điểm
M0 ∈ R2 và bán kính ǫ > 0, có thể trừ điểm M0. Khi đó, số m được gọi là giới hạn
của hàm f(x, y) khi (x, y) dần tới M0(x0, y0), ký hiệu lim f(M) = m, nếu với mọi M →M0
dãy điểm bất kỳ {Mn} ⊂ R2 sao cho lim Mn = M0 thì n→∞ lim f (Mn) = m. n→∞
Ta có thể chứng minh được rằng: lim f(M) = m khi và chỉ khi M →M0
∀ǫ > 0, ∃δ > 0, ∀M ∈ B(M0, δ) ⇒ |f(M) − m| < ǫ. 10
Phép tính vi phân hàm nhiều biến
Ví dụ 1.2. Tìm giới hạn x2y I1 = lim . (x,y)→(0,0) 2x2 + y2 Giải.
Hàm số f(x, y) = x2y xác định trên D = R2\{(0, 0)}. Từ bất đẳng thức 2x2+y2 x2 x2 1 ≤ = ∀(x, y) ∈ D, 2x2 + y2 2x2 2
ta có |f(x, y)| ≤ 1|y| với mọi (x, y) ∈ D. Do đó 2 x2y 1 0 ≤ lim |y| = 0. (x,y)→(0,0) 2x2 + y2 ≤ lim (x,y)→(0,0) 2 Vậy I1 = 0.
Ví dụ 1.3. Tìm giới hạn xy I2 = lim . (x,y)→(0,0) 2x2 + y2 Giải. Hàm số f(x, y) = xy
xác định trên D = R2\{(0, 0)}. Ta xét 2 trường hợp đặc 2x2+y2 biệt sau:
+ Điểm (x, y) ∈ (d1) : y = x. Khi đó (x, y) → (0, 0) khi và chỉ khi x → 0. Khi đó, ta có xy x2 1 I2 = lim = lim = . (x,y)→(0,0) 2x2 + y2 x→0 2x2 + x2 3
+ Điểm (x, y) ∈ (d2) : y = 3x. Khi đó (x, y) → (0, 0) khi và chỉ khi x → 0. Khi đó, ta có xy 3x2 3 I2 = lim = lim = . (x,y)→(0,0) 2x2 + y2 x→0 2x2 + 9x2 11
Do vậy I2 không tồn tại. 1.4 Hàm số liên tục
Cho hàm số z = f(x, y) xác định trên miền D và điểm M0 ∈ D. Khi đó,
+ Hàm số f liên tục tại điểm M0 nếu tồn tại giới hạn lim f (M) = f (M0). M →M0
+ Hàm số f liên tục trên miền D nếu f liên tục tại mọi điểm M ∈ D.
+ Hàm số f liên tục đều trên miền D nếu với mọi ǫ > 0, tồn tại δ > 0 sao cho
∀(x, y), (x′, y′) ∈ D : k(x, y) − (x′, y′)k < δ ⇒ |f(x, y) − f(x′, y′)| < ǫ.
Bằng cách dùng định nghĩa, ta có chú ý sau.
1.5 Đạo hàm riêng và vi phân toàn phần của hàm nhiều biến số 11
Chú ý 1.1. + Nếu hàm f : D ⊆ R2 → R liên tục đều trên miền D, thì f liên tục
trên miền D. Điều ngược lại không đúng.
+ Nếu f liên tục trên miền D và D là tập compact, thì f liên tục đều trên miền D.
+ Nếu f liên tục trên miền compact D, thì f đạt giá trị lớn nhất và nhỏ nhất trên miền D.
1.5 Đạo hàm riêng và vi phân toàn phần của hàm nhiều biến số
Cho hàm số z = f(x) với x = (x1, ..., xn) xác định trên miền D ⊆ Rn và điểm ¯ x = (¯ x1, ¯ x2, ..., ¯ xn) ∈ D. 1.5.1 Đạo hàm riêng
Nếu hàm một biến số x1 7−→ f(x1, ¯x2, ..., ¯xn) có đạo hàm tại x1, thì đạo hàm đó
được gọi là đạo hàm riêng của f theo ẩn x1 tại điểm ¯x và được ký hiệu ∂f f ′x (¯x) hay (¯ x). 1 ∂x1
Bằng cách hiểu tương tự, ta cũng có các đạo hàm riêng của f theo ẩn xi (i = 1, 2, ..., n) tại điểm ¯ x và được ký hiệu ∂f f ′ (¯ x) hay (¯ x). xi ∂xi
Ví dụ 1.4. Tìm các đạo hàm riêng của hàm số sau: f (x, y) = x2 tan(x3 + 2y). Giải. ∂f 1 3x4 = 2x tan(x3 + 2y) + x2. .3x2 = 2x tan(x3 + 2y) + . ∂x cos2(x3 + 2y) cos2(x3 + 2y) ∂f 1 2x2 = x2. .2 = . ∂y cos2(x3 + 2y) cos2(x3 + 2y) 1.5.2 Hàm khả vi
Cho hàm nhiều biến f : D ⊆ Rn → R và điểm ¯x = (¯x1, ¯x2, ..., ¯xn) ∈ D.
+ Với mỗi x = (x1, x2, ..., xn) ∈ D, đặt ∆x = x i i − ¯ xi ∀i = 1, 2, ..., n, 12
Phép tính vi phân hàm nhiều biến
và ∆x = (∆x , ∆ , ..., ∆ ) được gọi là số gia của đối số. Khi đó 1 x2 xn ∆f =f (x) − f(¯x) =f (¯ x + ∆x) − f(¯x) =f (¯ x1 + ∆x , ¯ x , ..., ¯ x ) − f(¯x 1 2 + ∆x2 n + ∆xn 1, ¯ x2, ..., ¯ xn)
được gọi là số gia của hàm số tại điểm ¯x.
+ Nếu số gia của hàm số có dạng ∆f = A1∆x + A + ... + A + α + α + ... + α , 1 2∆x2 n∆xn 1∆x1 2∆x2 n∆xn
trong đó Ai(i = 1, 2, ..., n) chỉ phụ thuộc vào ¯x, không phụ thuộc vào ∆x = (∆x , ∆ , ..., ∆ ) và 1 x2 xn
lim αk = 0 ∀k = 1, 2, ..., n, ∆x→0
thì hàm số f được gọi là khả vi tại điểm ¯x. Khi đó df = A1∆x + A + ... + A 1 2∆x2 n∆xn
được gọi là vi phân toàn phần của f tại điểm ¯x.
+ Hàm số f được gọi là khả vi trên miền D, nếu f khả vi tại mọi điểm ¯x ∈ D.
Định lý 1.1. Nếu hàm f : D ⊆ Rn → R có các đạo hàm riêng liên tục trong một
lân cận của điểm ¯x ∈ D, thì f sẽ khả vi tại điểm ¯x và ∂f ∂f ∂f df = (¯ x)∆ + (¯ x)∆ + ... + (¯ x)∆ . ∂x x1 x2 xn 1 ∂x2 ∂xn
Chứng minh: Theo định nghĩa, ta có ∆f =f (¯ x1 + ∆x , ¯ x , ..., ¯ x ) − f(¯x 1 2 + ∆x2 n + ∆xn 1, ¯ x2, ..., ¯ xn) =f (¯ x1 + ∆x , ¯ x , ..., ¯ x ) − f(¯x , ..., ¯ x ) 1 2 + ∆x2 n + ∆xn 1, ¯ x2 + ∆x2 n + ∆xn + · · · + f (¯ x1, ¯ x2, ...¯
xn−1, ¯xn + ∆x ) − f(¯x n 1, ¯ x2, ..., ¯ xn).
Theo công thức số gia giới nội, tồn tại các số θ1, θ2, ..., θn ∈ (0, 1) sao cho f (¯ x1, ..., ¯ xi−1, ¯xi + ∆x , ..., ¯x ) − f(¯x , ..., ¯ x ) i n + ∆xn 1, ..., ¯ xi, ¯ xi+1 + ∆xi+1 n + ∆xn ∂f = (¯ x , ..., ¯ x )∆ . ∂x 1, ..., ¯ xi−1, ¯xi + θi∆xi n + ∆xn xi i
Do các đạo hàm riêng liên tục trong lân cận của điểm ¯x nên ∂f ∂f (¯ x , ..., ¯ x ) = (¯ x) + α ∂x 1, ..., ¯ xi−1, ¯xi + θi∆xi n + ∆xn i(∆x), i ∂xi
trong đó lim αi(∆x) = 0 ∀i = 1, 2, ..., n. Do vậy, định lý được chứng minh. ∆x→0
1.5 Đạo hàm riêng và vi phân toàn phần của hàm nhiều biến số 13
Chú ý 1.2. Trong trường hợp hàm 3 biến số f(x, y, z) có các đạo hàm riêng liên
tục trong lân cận của điểm (x0, y0, z0), theo định lý trên, ta có ∂f ∂f ∂f ∆f = (x (x (x ∂x
0, y0, z0)∆x + ∂y 0, y0, z0)∆y + ∂z 0, y0, z0)∆z + α∆x + β∆y + γ∆z. p Đặt ρ = ∆2 và x + ∆2 y + ∆2 z ǫ = 1(α∆ ρ
x + β∆y + γ∆z ). Khi đó, theo bất đẳng thức Bunhiacôpski, ta có q 1
(α2 + β2 + γ2)(∆2x + ∆2y + ∆2z) p |ǫ| = |α∆ p = α2 + β2 + γ2. ρ x + β∆y + γ∆z | ≤ ∆2 + ∆2 + ∆2 x y z Do đó lim ǫ = 0 (∆x,∆y,∆z)→0 và
α∆x + β∆y + γ∆z = o(ρ). Như vậy ∂f ∂f ∂f ∆f = (x (x (x ∂x
0, y0, z0)∆x + ∂y 0, y0, z0)∆y + ∂z 0, y0, z0)∆z + o(ρ).
Khi các số ∆x, ∆y, ∆z khá nhỏ, ta có ∂f ∂f ∂f ∆f ≈ (x (x (x ∂x
0, y0, z0)∆x + ∂y 0, y0, z0)∆y + ∂z 0, y0, z0)∆z. hay ∂f ∂f
f (x0 + ∆x, y0 + ∆y, z0 + ∆z) ≈f(x0, y0, z0) + (x (x ∂x
0, y0, z0)∆x + ∂y 0, y0, z0)∆y ∂f + (x ∂z 0, y0, z0)∆z . (1.1)
Ví dụ 1.5. Dùng vi phân, tính xấp xỉ giá trị biểu thức sau: 1, 02 S = arctan . 0, 95 Giải: Từ 1 + 0, 02 S = arctan , 1 − 0, 05
ta đặt x0 = 1, y0 = 1, ∆x = 0, 02, ∆y = −0, 05 và f(x, y) = arctan x. Khi đó y ∂f −y ∂f x = , = . ∂x x2 + y2 ∂y x2 + y2 14
Phép tính vi phân hàm nhiều biến
Theo công thức (1.1) cho hàm số có 2 biến, ta có
∆f = f (x0 + ∆x, y0 + ∆y) − f(x0, y0) ∂f ∂f ≈ (x (x ∂x 0, y0)∆x + ∂y 0, y0)∆y. Do đó S = f (x0 + ∆x, y0 + ∆y) = ∆f + f (x0, y0) ∂f ∂f ≈ (x (x ∂x
0, y0)∆x + ∂y 0, y0)∆y + f(x0, y0) 1 × 0, 02 + 1 × 0, 05 = f (1, 1) + 2 π = + 0, 035 4 ≈ 0, 82 (rad).
1.6 Đạo hàm theo phương và hướng
Cho véc tơ d ∈ D ⊆ Rn, f : D → R và ¯x ∈ D và λ > 0 sao cho ¯x + λd ∈ D. Nếu
tồn tại giới hạn (hữu hạn) f (¯ x + λd) − f(¯x) lim , λ→0+ λ
thì giới hạn này được gọi là đạo hàm theo phương d của hàm f tại điểm ¯x và được
ký hiệu bởi Ddf(¯x). Véc tơ d0 := 1 d là véc tơ đơn vị và thường gọi là hướng của kdk
của véc tơ d. Khi đó, Dd f(¯x) được gọi là đạo hàm theo hướng d của hàm f tại điểm 0 ¯ x.
Ví dụ 1.6. Tìm đạo hàm theo phương Ddf(¯x) của hàm số f(x, y, z) = 2x+3y +z2,
trong đó d = (1, 2, 0), ¯x = (3, −1, 1). Giải:
Theo định nghĩa, đạo hàm Ddf(¯x) được xác định bởi công thức f (¯ x + λd) − f(¯x) Ddf (¯ x) = lim λ→0+ λ
f (3 + λ, −1 + 2λ, 1) − f(3, −1, 1) = lim λ→0+ λ
2(3 + λ) + 3(−1 + 2λ) + 12 − (2.3 + 3.(−1) + 12) = lim λ→0+ λ = 8.
Dựa vào định nghĩa, ta có nhận xét sau:
1.7 Quan hệ giữa đạo hàm theo phương và đạo hàm riêng 15
Chú ý 1.3. Giả sử {e1, e2, ..., en} là một hệ cơ sở trực chuẩn trong Rn, hay
ei = (0, 0, · · · , 0, 1, 0, · · · , 0) (1 ở vị trí thứ i), và hàm số f(x) tồn tại các đạo hàm
riêng trên D và ¯x ∈ D. Khi đó ∂f De f (¯ x) = (¯ x) ∀i = 1, 2, ..., n. i ∂xi
1.7 Quan hệ giữa đạo hàm theo phương và đạo hàm riêng
Cho hàm f : D ⊆ Rn → R khả vi tại điểm ¯x ∈ D. Khi đó, đạo hàm theo phương
d = (d1, d2, ..., dn) được xác định bởi công thức: ∂f ∂f ∂f Ddf (¯ x) = (¯ x)d (¯ x)d (¯ x)d ∂x 1 + 2 + ... + n. (1.2) 1 ∂x2 ∂xn
Chứng minh: Theo định nghĩa, hàm số f khả vi tại điểm ¯x hay ∆f = A1∆x + A + ... + A + α + α + ... + α , 1 2∆x2 n∆xn 1∆x1 2∆x2 n∆xn
trong đó ¯x + ∆x ∈ D, ∆f = f(¯x + ∆x) − f(¯x), Ai = ∂f (¯x), lim α ∂x i = 0 với mọi i ∆x→0
i = 1, 2, ..., n. Dùng công thức trên với ∆x = λd i i, ta có f (¯ x + λd) − f(¯x) Ddf (¯ x) = lim ∆x→0 λ
= lim (A1d1 + ... + Andn + α1d1 + ... + αndn) ∆x→0 ∂f ∂f ∂f = (¯ x)d (¯ x)d (¯ x)d ∂x 1 + 2 + ... + n. 1 ∂x2 ∂xn
Ví dụ 1.7. Tìm đạo hàm theo phương d = (−1, 3) tại điểm ¯x = (e, e2) của hàm số f (x, y) = ln(x2 + y). Giải.
Tính các đạo hàm theo phương ∂f 2x = , ∂x x2 + y ∂f 1 = . ∂y x2 + y Khi đó ∂f 2x 1 (¯ x) = (¯ x) = , ∂x x2 + y e ∂f 1 1 (¯ x) = (¯ x) = . ∂y x2 + y 2e2
