





















































































































Preview text:
lOMoAR cPSD| 35883770
BỘ GIÁO DỤC VÀ ĐÀO TẠO
TRƯỜNG ĐẠI HỌC CẦN THƠ ---0O0---
BÀI GIẢNG MÔN HỌC
XÁC SUẤT THỐNG KÊ
Biên soạn: TS. TRẦN VĂN LÝ LƯU HÀNH NỘI BỘ lOMoAR cPSD| 35883770 MỤC LỤC
Chƣơng I: KHÁI NIỆM XÁC SUẤT
VÀ CÁC CÔNG THỨC TÍNH XÁC SUẤT CƠ BẢN ................ 1
§ 1. GIẢI TÍCH TỔ HỢP ...................................................................................... 1
1.1. Quy tắc nhân ............................................................................................ 1
1.2. Chỉnh hợp ................................................................................................. 2
1.3. Hoán vị ..................................................................................................... 3
1.4. Chỉnh hợp lặp ........................................................................................... 3
1.5. Tổ hợp ...................................................................................................... 3
§ 2. PHÉP THỬ VÀ BIẾN CỐ ............................................................................. 7
2.1. Khái niệm phép thử và biến cố ................................................................ 7
2.2. Các loại biến cố ........................................................................................ 7
2.3. Các dạng quan hệ giữa các biến cố .......................................................... 9
§ 3. ĐỊNH NGHĨA XÁC SUẤT ......................................................................... 12
3.1. Định nghĩa xác suất theo lối cổ điển ...................................................... 12
3.2. Định nghĩa xác suất theo tần suất .......................................................... 13
3.3. Định nghĩa xác suất theo quan điểm hình học ....................................... 14
3.4. Các tính chất cơ bản của xác suất .......................................................... 16
§ 4. CÔNG THỨC CỘNG VÀ CÔNG THỨC NHÂN XÁC SUẤT ................. 20
4.1. Công thức cộng ...................................................................................... 20
4.2. Công thức nhân xác suất ........................................................................ 22
§ 5. CÔNG THỨC XÁC SUẤT ĐẦY ĐỦ − CÔNG THỨC BAYES
VÀ CÔNG THỨC BERNOULLI ............................................................... 29
5.1. Công thức xác suất đầy đủ và công thức Bayes ..................................... 29
5.2. Công thức Bernoulli ............................................................................... 31
Chƣơng II: ĐẠI LƢỢNG NGẪU NHIÊN
VÀ MỘT SỐ PHÂN PHỐI THÔNG DỤNG ............................. 36
§ 1. KHÁI NIỆM ĐẠI LƢỢNG NGẪU NHIÊN
VÀ LUẬT PHÂN PHỐI XÁC SUẤT ......................................................... 36
1.1. Khái niệm đại lƣợng ngẫu nhiên ........................................................... 36
1.2. Các loại đại lƣợng ngẫu nhiên ............................................................... 37
1.3. Luật phân phối xác suất của đại lƣợng ngẫu nhiên ............................... 37
§ 2. CÁC THAM SỐ CỦA ĐẠI LƢỢNG NGẪU NHIÊN ............................... 43
2.1. Kỳ vọng .................................................................................................. 43
2.2. Phƣơng sai ............................................................................................. 46
2.3. Độ lệch tiêu chuẩn.................................................................................. 47
2.4. Mode ...................................................................................................... 48
§ 3. CÁC PHÂN PHỐI RỜI RẠC THÔNG DỤNG ........................................... 50 i
3.1. Phân phối nhị thức ................................................................................. 50 lOMoAR cPSD| 35883770
3.2. Phân phối Poisson .................................................................................. 52
3.3. Phân phối siêu bội .................................................................................. 57
§ 4. CÁC PHÂN PHỐI LIÊN TỤC THÔNG DỤNG ........................................ 57
4.1. Phân phối chuẩn ..................................................................................... 57
4.2. Phân phối 2 (khi − bình phƣơng) ....................................................... 59
4.3. Phân phối student ................................................................................... 60
4.4. Phân phối mũ ......................................................................................... 61
4.5. Phân phối đều ........................................................................................ 62
§ 5. ĐẠI LƢỢNG NGẪU NHIÊN HAI CHIỀU ............................................... 65
5.1. Hàm phân phối xác suất ......................................................................... 65
5.2. Bảng phân phối xác suất của đại lƣợng ngẫu nhiên hai chiều rời rạc ... 66
5.3. Hàm mật độ của đại lƣợng ngẫu nhiên hai chiều liên tục ..................... 67
5.4. Các tham số đặc trƣng của đại lƣợng ngẫu nhiên hai chiều .................. 69
§ 6. HÀM CỦA CÁC ĐẠI LƢỢNG NGẪU NHIÊN ....................................... 75
6.1. Hàm của một đại lƣợng ngẫu nhiên ...................................................... 75
6.2. Hàm của hai đại lƣợng ngẫu nhiên ........................................................ 76
Chƣơng III: TỔNG THỂ VÀ MẪU ................................................................. 80
§ 1. ĐẠI LƢỢNG NGẪU NHIÊN GỐC VÀ MẪU NGẪU NHIÊN ................ 80
1.1. Khái niệm tổng thể và mẫu .................................................................... 80
1.2. Đại lƣợng ngẫu nhiên gốc và mẫu ngẫu nhiên ...................................... 80
1.3. Các thống kê (đặc trƣng) của mẫu ngẫu nhiên ...................................... 82
§ 2. CÁC PHƢƠNG PHÁP TÍNH THAM SỐ MẪU CỤ THỂ ........................ 85
2.1. Các tham số mẫu cụ thể ......................................................................... 85
2.2. Sắp xếp số liệu ....................................................................................... 85
2.3. Các phƣơng pháp tính ........................................................................... 86
Chƣơng IV: ƢỚC LƢỢNG CÁC THAM SỐ
CỦA ĐẠI LƢỢNG NGẪU NHIÊN ........................................... 91
§ 1. ƢỚC LƢỢNG ĐIỂM ................................................................................. 91
1.1. Đặt vấn đề .............................................................................................. 91
1.2. Các phƣơng pháp ƣớc lƣợng ................................................................ 91
§ 2. PHƢƠNG PHÁP KHOẢNG TIN CẬY ..................................................... 96
2.1. Đặt vấn đề .............................................................................................. 96
2.2. Phƣơng pháp ......................................................................................... 96
2.3. Ƣớc lƣợng trung bình ........................................................................... 97
2.4. Ƣớc lƣợng tỷ lệ ................................................................................... 101
2.5. Ƣớc lƣợng phƣơng sai........................................................................ 103
Chƣơng V: KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ ................................ 109
§ 1. CÁC ĐỊNH NGHĨA VÀ PHƢƠNG PHÁP KIỂM ĐỊNH ........................ 109
1.1. Các khái niệm và định nghĩa ............................................................... 109
1.2. Kiểm định giả thuyết thống kê lOMoAR cPSD| 35883770
về các tham số của đại lƣợng ngẫu nhiên ............................................ 110
1.3. Nguyên tắc kiểm định .......................................................................... 111
§ 2. MỘT SỐ BÀI TOÁN KIỂM ĐỊNH .......................................................... 112
2.1. Kiểm định giả thuyết về trung bình ..................................................... 112
2.2. Kiểm định giả thuyết về tỷ lệ ............................................................... 114
2.3. Kiểm định giả thuyết về phƣơng sai .................................................... 115
2.4. Kiểm định giả thuyết về sự so sánh của hai trung bình ....................... 116
2.5 Kiểm định giả thuyết về sự so sánh của hai tỷ lệ ................................. 117
2.6 Kiểm định sự độc lập ........................................................................... 118
Chƣơng VI: TƢƠNG QUAN VÀ HỒI QUY ................................................ 125
§ 1. HỆ SỐ TƢƠNG QUAN THỰC NGHIỆM ............................................... 125
1.1. Hệ số tƣơng quan lý thuyết.................................................................. 125
1.2. Ƣớc lƣợng hệ số tƣơng quan thực nghiệm ......................................... 126
§ 2. HỒI QUY TUYẾN TÍNH .......................................................................... 128
2.1. Kỳ vọng có điều kiện ........................................................................... 128
2.2. Hàm hồi quy ......................................................................................... 128
2.3. Ƣớc lƣợng hàm hồi quy tuyến tính ..................................................... 128
2.4. Mối liên hệ giữa tƣơng quan và hồi quy.............................................. 131
§ 3. TƢƠNG QUAN BẢNG ............................................................................ 132
CÁC BẢNG SỐ ................................................................................................. 138
TÀI LIỆU THAM KHẢO ................................................................................ 144 iii lOMoAR cPSD| 35883770 lOMoAR cPSD| 35883770 CHƯƠNG I
KHÁI NIỆM XÁC SUẤT
VÀ CÁC CÔNG THỨC TÍNH XÁC SUẤT CƠ BẢN
§ 1. GIẢI TÍCH TỔ HỢP 1.1. Quy tắc nhân
Giả sử một công việc có thể chia làm k giai đoạn:
− Giai đoạn 1 có n1 cách thực hiện.
− Giai đoạn 2 có n2 cách thực hiện. …
− Giai đoạn k có nk cách thực hiện.
Khi đó, số cách thực hiện công việc là n = n1n2…nk (1.1)
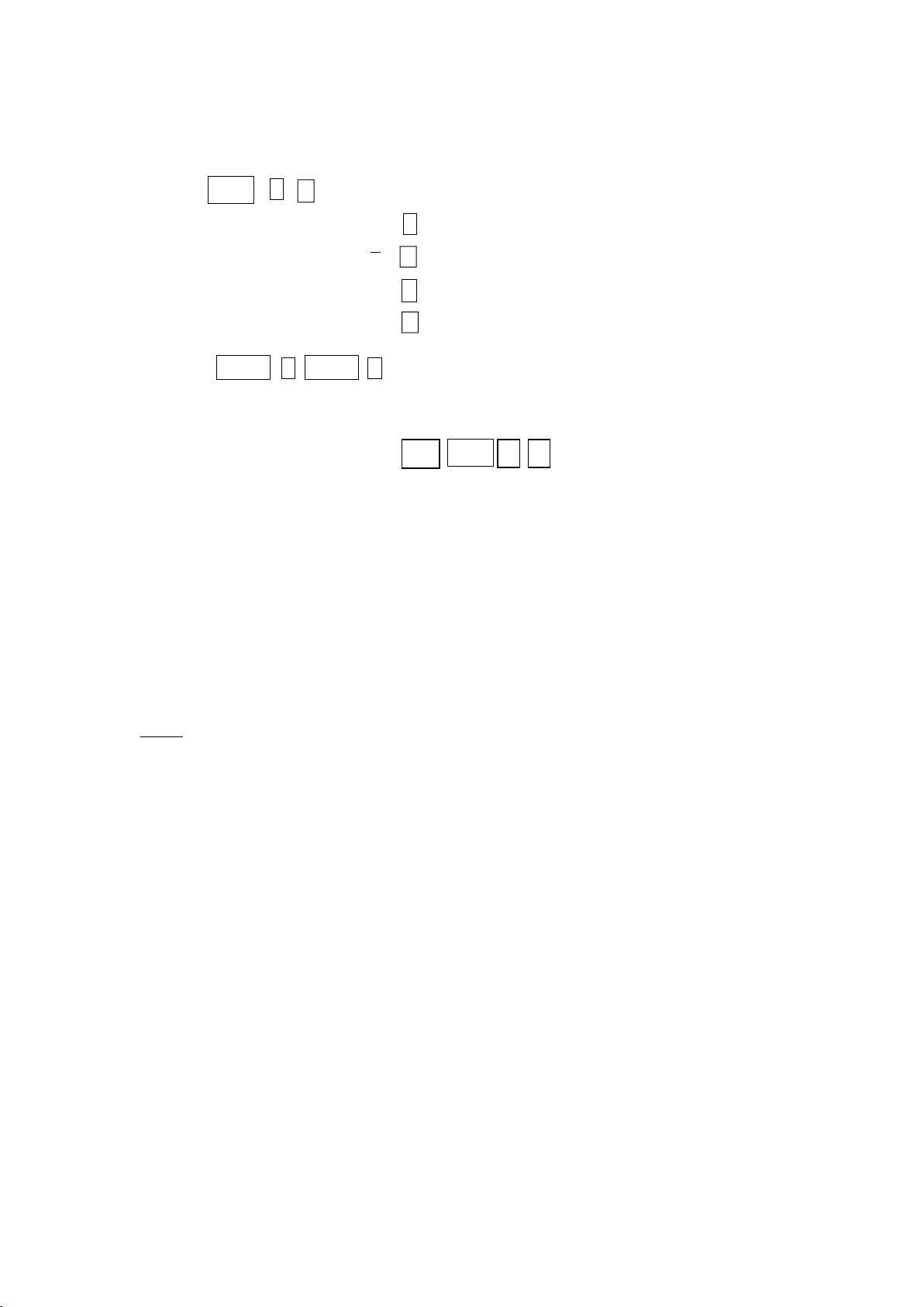
Ví dụ 1: Với 2 bi đen và 3 bi trắng, muốn chọn ra một cặp bi 1 đen và 1
trắng, hỏi có bao nhiêu cách chọn? 4 1 5 2 6 3 Hình 1.1 Giải
Việc chọn ra một cặp bi đen−trắng có thể tiến hành qua hai giai đoạn:
− Chọn 1 bi đen: có n1 = 2 cách.
− Chọn 1 bi trắng: có n2 = 3 cách.
Vậy có tất cả n = n1n2 = 2.3 = 6 cách khác nhau để thực hiện công việc.
Ví dụ 2: Một đề thi trắc nghiệm ngoại ngữ gồm có ba phần. Phần thứ nhất
có 5 câu hỏi, mỗi câu có cho sẵn 4 phương án trả lời. Phần thứ hai có 10 câu
hỏi, mỗi câu có 2 cách trả lời đúng hoặc sai. Phần thứ ba là một đoạn văn bản
có 4 ô trống ứng với 4 từ khác nhau cho trước. Hỏi khi thí sinh làm bài một cách
ngẫu nhiên thì có tất cả bao nhiêu cách giải khác nhau? 1 lOMoAR cPSD| 35883770 GIẢI TÍCH TỔ HỢP Giải
Để xác định tổng số cách làm bài ngẫu nhiên của thí sinh, ta sẽ tìm riêng số
cách làm ở từng phần rồi nhân số cách làm của ba phần với nhau:
− Trong phần thứ nhất, vì mỗi câu hỏi có 4 cách chọn phƣơng án khác
nhau nên phần này (5 câu) có số cách làm là n1 = 4.4.4.4.4 = 1024
− Với 10 câu trong phần thứ hai, do mỗi câu có 2 cách chọn đúng hoặc sai
nên số cách khác nhau để làm cho phần này là n2 = 210 = 1024
− Ở phần ba, để chọn từ điền vào ô trống thứ nhất có 4 cách và chọn từ
cho các ô thứ hai, thứ ba, thứ tƣ có số cách chọn lần lƣợt là 3, 2,1. Do đó, số cách làm cho phần này là n3 = 4.3.2.1 = 24
Tóm lại, đề thi trắc nghiệm trên có số cách làm ngẫu nhiên là n = n1.n2.n3 = 25165824 1.2. Chỉnh hợp a) Định nghĩa
Một chỉnh hợp chập k của n phần tử (k n) là một nhóm gồm k phần tử
khác nhau, có phân biệt thứ tự, chọn từ tập hợp n phần tử cho trƣớc. b) Công thức tính
Số chỉnh hợp chập k của n phần tử đƣợc kí hiệu là k A n và đƣợc tính bởi k n! A = = n(n − 1)…(n − k + 1) (1.2) n (n − k)! CHÚ Ý 1 i) n! = 1.2…n ii) 0! = 1
Ví dụ 3: Từ một lớp học có 50 sinh viên chọn ngẫu nhiên ra một nhóm 3
sinh viên để lập ban cán sự lớp gồm lớp trưởng, lớp phó học tập và lớp phó văn
thể. Hỏi có bao nhiêu cách chọn tất cả? Giải
Mỗi cách chọn ra một nhóm 3 sinh viên để lập một ban cán sự lớp là một
chỉnh hợp chập 3 của 50 phần tử (vì các sinh viên trong nhóm có hai đặc điểm là
khác nhau và có quy định thứ tự lớp trƣởng, lớp phó học tập, lớp phó văn thể).
Do đó, tổng số cách chọn ban cán sự cho lớp là 3 A = 50.49.48 = 117600 50 2
CHƢƠNG I: KHÁI NIỆM XÁC SUẤT VÀ NHỮNG CÔNG THỨC TÍNH XÁC SUẤT CƠ BẢN lOMoAR cPSD| 35883770 GIẢI TÍCH TỔ HỢP 1.3. Hoán vị a) Định nghĩa
Một hoán vị của n phần tử là một cách sắp xếp thứ tự của n phần tử đó. b) Công thức tính
Số hoán vị của n phần tử đƣợc kí hiệu Pn và đƣợc xác định nhƣ sau Pn = n! (1.3)
Ví dụ 4: Hỏi khi xếp 4 quyển giáo trình khác nhau lên một kệ sách thì có
bao nhiêu cách xếp? Giải
Vì mỗi cách xếp các quyển giáo trình lên kệ sách là một hoán vị của 4 phần
tử nên số cách sắp xếp tất cả là P4 = 1.2.3.4 = 24 1.4. Chỉnh hợp lặp a) Định nghĩa
Một chỉnh hợp lặp chập k của n phần tử (k có thể lớn hơn n) là một nhóm
gồm k phần tử có phân biệt thứ tự, trong đó có thể có những phần tử giống nhau
chọn từ tập hợp n phần tử cho trƣớc. b) Công thức tính
Số chỉnh hợp lặp chập k của n phần tử đƣợc kí hiệu là k Bn và đƣợc tính bởi k Bn = nk (1.4)
Ví dụ 5: Có bao nhiêu cách lập nên một số tự nhiên gồm 3 chữ số chọn từ 2 chữ số 1 và 5? Giải
Mỗi cách lập nên một số tự nhiên gồm 3 chữ số chọn từ 2 chữ số đã cho là
một chỉnh hợp lặp chập 3 của 2 phần tử. Số cách lập là 3 B = 23 = 8 2
Các số đó gồm 111, 115, 151, 511, 155, 515, 551 và 555. 1.5. Tổ hợp a) Định nghĩa
Một tổ hợp chập k của n phần tử (k n) là một nhóm gồm k phần tử khác
nhau, không phân biệt thứ tự, chọn từ tập hợp n phần tử cho trƣớc. b) Công thức tính
Số tổ hợp chập k của n phần tử đƣợc kí hiệu là k C n và đƣợc tính bởi k C = n! = n(n − 1)...( n − k + 1) (1.5) n k!(n − k)! k!
CHƢƠNG I: KHÁI NIỆM XÁC SUẤT VÀ NHỮNG CÔNG THỨC TÍNH XÁC SUẤT CƠ BẢN 3 lOMoAR cPSD| 35883770 GIẢI TÍCH TỔ HỢP CHÚ Ý 2 i) C k
n = Cn − k n ii) 0 n 1 n − 1 C
= C = 1, C = C = n n n n n k = k iii) C C + n Ck − 1 n − 1 n − 1
Ví dụ 6: Từ một lô hàng có 20 sản phẩm chọn kiểm tra ngẫu nhiên 15 sản
phẩm. Hỏi có bao nhiêu cách chọn? Giải
Do mỗi cách chọn ra một mẫu kiểm tra là một tổ hợp chập 15 của 20 phần
tử nên tổng số cách chọn khác nhau là 15 20.19.18.17.16 C = 5 = C 19.3.17.6 = 5814 = 20 20 5!
Ví dụ 7: Một trường đại học cử 8 sinh viên xuất sắc đi du học ở các nước
A, B, C và D qua 3 đợt. Đợt một chọn ngẫu nhiên 3 sinh viên cử đi học ở nước A.
Đợt hai, từ 5 sinh viên còn lại chọn ra ngẫu nhiên 3 sinh viên cử đi học ở 3 nước
B, C và D, mỗi sinh viên một nước. Đợt ba, chọn từ 4 nước A, B, C, D ra 2 nơi
(có thể giống nhau) để cử 2 sinh viên còn lại đi du học. Hỏi nhà trường có thể
thực hiện công việc trên với bao nhiêu cách khác nhau? Giải
Việc đếm số cách khác nhau để nhà trƣờng cử 8 sinh viên xuất sắc đi du
học có thể chia làm 3 giai đoạn:
− Chọn 3 sinh viên cử đi học đợt một: vì mỗi cách chọn ra một nhóm 3
sinh viên để cử đi học ở nƣớc A là một tổ hợp chập 3 của 8 phần tử nên số cách chọn là 8.7.6 = 56 C3 = 8 3!
− Chọn 3 sinh viên cử đi học đợt hai: việc chọn ra 3 sinh viên khác nhau
từ 5 sinh viên còn lại để cử đi học ở các nƣớc B, C, D (mỗi sinh viên một nƣớc)
là một việc chọn lựa có tính thứ tự nên mỗi cách chọn là một chỉnh hợp chập 3
của 5 phần tử. Do đó có số cách chọn là 3 A = 5.4.3 = 60 5
− Cử 2 sinh viên còn lại đi học đợt ba: mỗi cách chọn ra 2 nƣớc (có thể
trùng giống nhau) từ 4 nƣớc A, B, C, D cho 2 sinh viên còn lại đi học là một
chỉnh hợp lặp chập 2 của 4 phần tử. Do đó, số cách khác nhau để thực hiện đợt này là 2 B = 42 = 16 4
Theo quy tắc nhân, số cách khác nhau để nhà trƣờng cử 8 sinh viên đi du học là 56.60.16 = 53760 4
CHƢƠNG I: KHÁI NIỆM XÁC SUẤT VÀ NHỮNG CÔNG THỨC TÍNH XÁC SUẤT CƠ BẢN lOMoAR cPSD| 35883770 GIẢI TÍCH TỔ HỢP CHÚ Ý 3
Trong lý thuyết xác suất ta rất hay phải tìm số cách làm khác nhau khi lấy
ngẫu nhiên k phần tử từ n phần tử trong một đám đông. Tùy thuộc vào tính chất
của nhóm k phần tử lấy ra mà số cách đƣợc xác định dựa vào các khái niệm và
công thức tính trong giải tích tổ hợp.
− Nếu k phần tử lấy ra khác nhau từng đôi và không kể tính thứ tự thì mỗi
cách lấy k phần tử nhƣ vậy tƣơng ứng với một tổ hợp chập k của n phần tử.
− Nếu k phần tử lấy ra khác nhau từng đôi và có tính thứ tự thì mỗi cách
lấy khi đó tƣơng ứng với một chỉnh hợp chập k của n phần tử. Đặc biệt, khi k = n
thì mỗi cách thực hiện công việc ứng với một hoán vị của n phần tử.
− Nếu trong k phần tử lấy ra có tính thứ tự và có những phần tử trùng lặp
lại thì mỗi cách lấy ứng với một chỉnh hợp lặp chập k của n phần tử.
Cụ thể hơn, khi lấy ra k phần tử (từ n phần tử cho trƣớc) theo phƣơng thức
lấy một lƣợt thì số cách lấy đƣợc xác định theo nghĩa tổ hợp. Trong trƣờng hợp k
phần tử lấy ra đƣợc thực hiện theo phƣơng thức lấy lần lƣợt, nếu lấy không hoàn
lại thì xác định theo nghĩa chỉnh hợp, còn nếu lấy có hoàn lại thì số cách lấy đƣợc
xác định theo nghĩa chỉnh hợp lặp. CHÚ Ý 4
Trong Excel, các công thức tính của giải tích tổ đƣợc xác định bởi các hàm sau • n! = FACT(n) (1.6) k • C n = COMBIN(n,k) (1.7) k • B n = POWER(k,n) (1.8) k • A n = FACT(n)/FACT(n − k) (1.9) BÀI TẬP 1 .
i/ Xếp ngẫu nhiên 5 hành khách lên đoàn tàu có 5 toa sao cho mỗi ngƣời lên
một toa, hỏi có bao nhiêu cách xếp?
ii/ Số cách xếp tùy ý 3 hành khách lên đoàn tàu có 5 toa là (a) 15 (b) A 3 3 (c) B (d) C3 5 5 5 2 .
Có bao nhiêu cách xếp thẳng hàng 6 sinh viên sao cho hai sinh viên định
trƣớc luôn đƣợc xếp cạnh nhau? (a) 5! (b) 6! (c) 5!.2 (d) 6!.2 3 .
Một giải bóng đá gồm 14 đội đá vòng tròn hai lƣợt đi và về, hỏi phải tổ
chức tất cả bao nhiêu trận đấu? (a) A 2 2 (d) 28 (b) B2 (c) C 14 1 4 1 4 4 .
Một lô hàng có 10 sản phẩm trong đó có 4 phế phẩm. Có bao nhiêu cách lấy
ra 3 sản phẩm sao cho trong đó có đúng một phế phẩm? (a) C3 .4 (c) 4. B2 10 6 (b) 4. A 2 (d) 4. C 26
CHƢƠNG I: KHÁI NIỆM XÁC SUẤT VÀ NHỮNG CÔNG THỨC TÍNH XÁC SUẤT CƠ BẢN 5 lOMoAR cPSD| 35883770 GIẢI TÍCH TỔ HỢP 5 .
Tung đồng thời 3 con xúc xắc khác nhau, xét số chấm xuất hiện ở mặt trên
các con xúc xắc, hỏi có bao nhiêu trƣờng hợp khác nhau có thể xảy ra? (a) 18 (c) 216 (b) 36 (d) một số khác 6 .
Lớp có 50 sinh viên trong đó có A và B. Có bao nhiêu cách cử 4 sinh viên
đi du học sao cho 4 sinh viên đó
a/ Cùng học ở một nƣớc?
b/ Học ở 4 nƣớc khác nhau?
c/ Học ở 4 nƣớc khác nhau trong đó có A và B?
d/ Cùng học ở một nƣớc trong đó có A và B? 7 .
Có bao nhiêu số điện thoại gồm 6 chữ số trong đó có đúng một cặp số trùng
(và không có hơn 2 chữ số trùng)? 8 .
Trong một cuộc họp tất cả mọi ngƣời đều bắt tay nhau và ngƣời ta đếm
đƣợc tất cả có 1225 cái bắt tay. Hỏi cuộc họp đó có bao nhiêu ngƣời? 9 .
Có mấy cách xếp r quả cầu khác nhau vào n hộp lớn?
10 . Có năm lá phiếu có ghi số từ 1 đến 5. Xếp ngẫu nhiên 5 phiếu cạnh nhau.
a/ Có bao nhiêu cách xếp khác nhau tất cả?
b/ Có bao nhiêu cách xếp để số chẵn luôn cạnh nhau?
c/ Có bao nhiêu cách xếp để số chẵn, lẻ xen kẽ nhau? 6
CHƢƠNG I: KHÁI NIỆM XÁC SUẤT VÀ NHỮNG CÔNG THỨC TÍNH XÁC SUẤT CƠ BẢN lOMoAR cPSD| 35883770 PHÉP THỬ VÀ BIẾN CỐ
§ 2. PHÉP THỬ VÀ BIẾN CỐ
2.1. Khái niệm phép thử và biến cố a) Phép thử
Trong thực tế ta rất thƣờng phải quan sát một sự việc hay một nhóm sự việc
nào đó mà kết quả của nó không thể dự báo trƣớc đƣợc. Khi đó, ta nói rằng ta xét
một phép thử ngẫu nhiên.
Phép thử ngẫu nhiên có thể chỉ là một thao tác đơn giản nào đó. Chẳng hạn
tung đồng xu lên để quan sát xem nó lật mặt nào, hay kiểm tra thử một sản phẩm
xem chất lƣợng có tốt không … Phép thử cũng có thể là cả một quá trình phức
tạp bao gồm nhiều giai đoạn, phải quan sát phân tích trong một thời gian dài nhƣ
nghiên cứu về một giống cây trồng, về một quy trình sản xuất mới ... b) Biến cố
Biến cố hay còn gọi là sự kiện đƣợc hiểu là một kết quả nào đó có liên quan
trong phép thử (kể cả những dạng kết quả không bao giờ xảy ra).
Ví dụ 1: Xét phép thử tung một con xúc xắc cân đối đồng chất và quan sát
số chấm xuất hiện ở mặt trên của nó. Trong phép thử này có một số dạng biến cố
thường được xét đến như sau:
− Xúc xắc xuất hiện mặt 1 chấm, 2 chấm, …, 6 chấm.
− Xúc xắc xuất hiện mặt có số chấm chẵn, lẻ.
− Xúc xắc xuất hiện mặt có số chấm nhỏ hơn 3, nhỏ hơn 5, …
2.2. Các loại biến cố
a) Biến cố chắc chắn
Biến cố chắc chắn là biến cố nhất định xảy ra khi thực hiện phép thử. Thí
dụ, trong phép thử tung xúc xắc cân đối đồng chất, biến cố xúc xắc xuất hiện
mặt có số chấm nhỏ hơn 7 là biến cố chắc chắn.
Biến cố chắc chắn đƣợc kí hiệu là .
b) Biến cố không thể
Biến cố không thể là biến cố nhất định không xảy ra khi thực hiện phép thử.
Khi tung một xúc xắc, biến cố xúc xắc xuất hiện mặt nhỏ hơn 1 là biến cố không thể.
Biến cố không thể đƣợc kí hiệu là Ø.
c) Biến cố ngẫu nhiên
Biến cố ngẫu nhiên là biến cố có thể xảy ra và cũng có thể không xảy ra khi
thực hiện phép thử. Các biến cố nhƣ xúc xắc xuất hiện mặt có số chấm chẵn, mặt
có số chấm nhỏ hơn 3 hay mặt 1 chấm, 2 chấm, … là những biến cố ngẫu nhiên.
Các biến cố ngẫu nhiên đƣợc kí hiệu A, B, C, …, A1, A2, …
d) Biến cố thuận lợi
Biến cố A đƣợc gọi là biến cố thuận cho biến cố B nếu khi A xảy ra thì sẽ kéo theo B xảy ra.
CHƢƠNG I: KHÁI NIỆM XÁC SUẤT VÀ NHỮNG CÔNG THỨC TÍNH XÁC SUẤT CƠ BẢN 7 lOMoAR cPSD| 35883770 PHÉP THỬ VÀ BIẾN CỐ
Kí hiệu : A B (hay A B).
Ví dụ 2: Gọi Ai là biến cố xúc xắc xuất hiện mặt i chấm (i = 1, 2, …, 6 ) và
A là biến cố xúc xắc xuất hiện mặt lẻ. Ta có A1, A3 và A5 là các biến cố thuận lợi cho biến cố A.
e) Biến cố tương đương
Biến cố A đƣợc gọi là tƣơng đƣơng biến cố B khi và chỉ khi nếu biến cố A
xảy ra thì sẽ kéo theo biến cố B xảy ra và ngƣợc lại. Kí hiệu : A = B.
Ví dụ 3: Xét phép thử tung đồng thời 2 xúc xắc. Gọi A là biến cố được
tổng số chấm là 12 và B là biến cố cả 2 xúc xắc đều xuất hiện mặt 6, ta có A = B;
Biến cố tổng số chấm bằng 8 và biến cố cả 2 xúc xắc đều xuất hiện mặt 4 chấm
là hai biến cố không tương đương nhau. f) Biến cố tổng
Biến cố C đƣợc gọi là tổng của hai biến cố A và B khi và chỉ khi nếu C xảy
ra thì có ít nhất một trong hai biến cố A hoặc B xảy ra và ngƣợc lại.
Kí hiệu : C = A + B (hay C = A B).
Ví dụ 4: Hai xạ thủ bắn mỗi người một viên đạn vào cùng một bia. Gọi A
là biến cố người thứ nhất bắn trúng, B là biến cố người thứ hai bắn trúng và C là
biến cố bia bị trúng đạn. Khi đó ta có C = A+B. g) Biến cố tích
Biến cố C đƣợc gọi là tích của hai biến cố A và B khi và chỉ khi nếu C xảy
ra thì đồng thời cả hai biến cố A và B đều xảy ra và ngƣợc lại.
Kí hiệu : C = A.B (hay C = A B).
Ví dụ 5: Một đường dây điện có 2 nhánh được mắc song song. Gọi A và B
lần lượt là biến cố dòng điện ở nhánh thứ nhất và thứ hai bị khóa; C là biến cố
đường dây điện không hoạt động. Ta có C = AB. CHÚ Ý 1
Các định nghĩa về biến cố tổng và tích có thể mở rộng ra cho tổng và tích
của nhóm nhiều hơn hai biến cố.
Ví dụ 6: Từ 4 lô sản phẩm lấy ra ngẫu nhiên mỗi lô 1 sản phẩm. Gọi Ai là
biến cố sản phẩm lấy ra từ lô i là phế phẩm (i = 1, 2, 3, 4); A là biến cố trong 3
sản phẩm lấy ra có ít nhất một phế phẩm; B là biến cố cả 3 sản phẩm lấy ra đều là phế phẩm. Ta có A = A1 + A2 + A3 + A4 B = A1A2A3A4
h) Biến cố sơ cấp
Biến cố sơ cấp là biến cố không thể phân tích thành những biến cố nhỏ hơn
đƣợc nữa. Biến cố không phải là biến cố sơ cấp đƣợc gọi là biến cố phức hợp. 8
CHƢƠNG I: KHÁI NIỆM XÁC SUẤT VÀ NHỮNG CÔNG THỨC TÍNH XÁC SUẤT CƠ BẢN lOMoAR cPSD| 35883770 PHÉP THỬ VÀ BIẾN CỐ CHÚ Ý 2
Mọi biến cố phức hợp đều có thể phân tích thành tổng của các biến cố sơ
cấp. Đặc biệt, biến cố chắc chắn là tổng của tất cả các biến cố sơ cấp và đƣợc gọi
là không gian các biến cố sơ cấp.
Trong ví dụ 2, các biến cố A1, A3, A5 là những biến cố sơ cấp; còn biến cố
A (xúc xắc xuất hiện mặt lẻ) là biến cố phức hợp và ta có A = A1 + A3 + A5.
i) Biến cố đối lập
Biến cố “không xảy ra biến cố A” đƣợc gọi là biến cố đối lập của biến cố A. Kí hiệu A .
Thí dụ, với A là biến cố xúc xắc xuất hiện mặt lẻ thì A là biến cố xúc xắc
xuất hiện mặt chẵn. Với các biến cố trong ví dụ 6, ta có A = A 1 A 2 A 3 A 4
B = A 1 + A 2 + A 3 + A 4 CHÚ Ý 3 i) A = A ii)
A + A = ; A A = Ø
iii) A. = A; A.Ø = Ø iv)
A + B = A.B ; AB = A + B v)
Nếu A B thì A.B = A
vi) A(BC) = (AB)C; A(B + C) = AB + AC
2.3. Các dạng quan hệ giữa các biến cố
a) Quan hệ xung khắc
Hai biến cố A và B đƣợc gọi là xung khắc nhau nếu chúng không thể đồng
thời xảy ra trong một phép thử. Khi đó, A.B = Ø.
Nhóm biến cố mà hai biến cố tùy ý đều xung khắc nhau đƣợc gọi là nhóm
biến cố xung khắc từng đôi.
b) Quan hệ độc lập
Hai biến cố đƣợc gọi là độc lập nhau nếu việc xảy ra hay không xảy ra của
biến cố này không phụ thuộc vào việc xảy ra hay không xảy ra của biến cố kia và ngƣợc lại.
Nhóm biến cố mà mỗi biến cố đều độc lập với biến cố tích của tổ hợp tùy ý
lấy từ những biến cố còn lại đƣợc gọi là nhóm biến cố độc lập toàn phần.
CHƢƠNG I: KHÁI NIỆM XÁC SUẤT VÀ NHỮNG CÔNG THỨC TÍNH XÁC SUẤT CƠ BẢN 9 lOMoAR cPSD| 35883770 PHÉP THỬ VÀ BIẾN CỐ BÀI TẬP
1 . Ba ngƣời mỗi ngƣời bắn một viên đạn vào cùng một bia, gọi Ai là biến cố
ngƣời thứ i bắn trúng (i = 1, 2, 3). Hãy xét những biểu diễn đƣa ra sau đây
cho những biến cố phức hợp qua các biến cố sơ cấp A1, A2 và A3 là đúng hay sai.
BIẾN CỐ PHỨC HỢP VÀ BIỂU DIỄN ĐỀ NGHỊ ĐÚNG SAI a/
A : {chỉ có ngƣời thứ nhất bắn trúng} → A = A1 b/
B : {cả 3 ngƣời đều bắn trúng} → B = A1A2A3 c/
C : {ngƣời đầu bắn trúng ngƣời thứ ba bắn trƣợt} → C = A1 A 3 d/
D : {có đúng một ngƣời bắn trúng} → D = A1+A2+A3 e/
E : {có đúng hai ngƣời bắn trúng} → E = A1A2 + A1A3 + A2A3 f/
F : {có ít nhất hai ngƣời bắn trúng}
→ F = A1A2 A 3 + A1 A 2A3 + A 1A2A3 + A1A2A3 g/
G : {có không quá hai ngƣời bắn trúng} → G = F h/
H : {không có ai bắn trúng} → H = B
2 . Kiểm tra ngẫu nhiên mỗi lô một sản phẩm với năm lô sản phẩm khác nhau.
Mỗi sản phẩm hoặc là chính phẩm hoặc là phế phẩm. Gọi Ai là biến cố sản
phẩm kiểm tra của lô thứ i là chính phẩm (i = 1, 2, 3, 4, 5). Hãy biểu diễn
qua những biến cố Ai các biến cố sau
a/ Cả 5 sản phẩm đều là phế phẩm.
b/ Có ít nhất một chính phẩm.
c/ Có không quá một chính phẩm.
d/ Với biến cố có 2 phế phẩm và 3 chính phẩm thì có bao nhiêu trƣờng
hợp khác nhau tất cả? Hãy chỉ ra một trƣờng hợp đại diện. 3 .
Có 2 hộp chứa các viên bi. Mỗi hộp chứa n bi, trong đó có k bi đỏ (2Chọn từ mỗi hộp ngẫu nhiên 2 bi. Gọi:
Ai là biến cố chọn đƣợc i bi đỏ từ hộp thứ I (i =0,1,2).
Bi là biến cố chọn đƣợc i bi đỏ từ hộp thứ II (i =0,1,2).
Chọn một câu sai trong các câu sau:
(a) Biến cố chọn đƣợc 0 bi đỏ trong 4 bi lấy ra là A0B0.
(b) Biến cố chọn đƣợc 3 bi đỏ trong 4 bi lấy ra là A1B2.
(c) Biến cố chọn đƣợc 4 bi đỏ trong 4 bi lấy ra là A2B2.
(d) Biến cố chọn đƣợc 0 bi đỏ hoặc 4 bi đỏ trong 4 bi lấy ra là A0B0 + A2B2. 4 .
Khi thực hiện một phép thử, có một trong ba biến cố xảy ra là A1, A2 và A3.
Khi đó, trong các khẳng định sau khẳng định nào là sai:
(a) A1, A2 là hai biến cố đối lập.
(b) A1, A2 là hai biến cố xung khắc.
(c) A1 + A2 + A3 là một biến cố chắc chắn.
(d) A3 là biến cố thuận lợi cho biến cố chắc chắn. 10
CHƢƠNG I: KHÁI NIỆM XÁC SUẤT VÀ NHỮNG CÔNG THỨC TÍNH XÁC SUẤT CƠ BẢN lOMoAR cPSD| 35883770 PHÉP THỬ VÀ BIẾN CỐ
5 . Ba ngƣời cùng bắn vào một mục tiêu. Gọi Ak là biến cố ngƣời thứ k bắn
trúng mục tiêu (k = 1, 2, 3). Biến cố A1 + A2 + A3 chỉ cho trƣờng hợp nào sau đây?
(a) Chỉ có ngƣời thứ nhất bắn trúng mục tiêu.
(b) Chỉ có một ngƣời bắn trúng mục tiêu.
(c) Chỉ có hai ngƣời bắn trúng mục tiêu.
(d) Có ngƣời bắn trúng mục tiêu.
6 . Một chi tiết đƣợc lấy ngẫu nhiên có thể là chi tiết loại 1 (biến cố A) hoặc
chi tiết loại 2 (biến cố B) hoặc chi tiết loại 3 (biến cố C). Biến cố nào sau
đây là biến cố không thể? (a) A+B (b) AB + C (c) AC (d) A + B 7 .
Gọi A là biến cố sinh con trai, B là biến cố sinh con có trọng lƣợng hơn
3kg. Câu nào sau đây đúng?
(a) A và B là 2 biến cố xung khắc.
(b) A và B là 2 biến cố đối lập.
(c) A và B là 2 biến cố độc lập.
(d) AB là biến cố chắc chắn. 8 .
Chọn câu đúng trong các câu sau:
(a) Hai biến cố xung khắc thì đối lập.
(b) Hai biến cố độc lập khi và chỉ khi chúng không đồng thời xảy ra trong một phép thử.
(c) Hai biến cố xung khắc khi và chỉ khi chúng không đồng thời xảy ra trong một phép thử.
(d) Hai biến cố đối lập khi và chỉ khi chúng không đồng thời xảy ra trong một phép thử.
CHƢƠNG I: KHÁI NIỆM XÁC SUẤT VÀ NHỮNG CÔNG THỨC TÍNH XÁC SUẤT CƠ BẢN 11 lOMoAR cPSD| 35883770 ĐỊNH NGHĨA XÁC SUẤT
§ 3. ĐỊNH NGHĨA XÁC SUẤT
3.1. Định nghĩa xác suất theo lối cổ điển
Giả sử một phép thử có n biến cố sơ cấp đồng khả năng có thể xảy ra, trong
đó có m biến cố thuận lợi cho biến cố A. Khi đó, xác suất xảy ra biến cố A đƣợc
kí hiệu là P(A) và đƣợc định nghĩa m P(A) = (1.10) n
Ví dụ 1: Xét phép thử tung một con xúc xắc cân đối đồng chất và quan sát
số chấm xuất hiện ở mặt trên của nó. Phép thử có n = 6 biến cố sơ cấp đồng khả
năng: xúc xắc xuất hiện mặt 1 chấm, 2 chấm, …, 6 chấm. Gọi A là biến cố xúc
xắc xuất hiện mặt lẻ, A có m = 3 biến cố sơ cấp thuận lợi gồm các mặt 1 chấm, 3
chấm và 5 chấm. Do đó biến cố A có xác suất m 3 P(A) = = = 0,5 n 6 CHÚ Ý 1
Các biến cố sơ cấp đồng khả năng của phép thử thƣờng đƣợc nói gọn là các
trƣờng hợp đồng khả năng và các biến cố sơ cấp thuận lợi cho biến cố A đƣợc
gọi là các trƣờng hợp thuận lợi cho A. m
Soá tröôøng hôïp thuaän lôïi cho A P(A) = = n
Soá tröôøng hôïp ñoàng khaû naêng
Ví dụ 2: Tung đồng thời 2 con xúc xắc cân đối đồng chất khác nhau, gọi A
là biến cố tổng số chấm xuất hiện mặt trên các xúc xắc bằng 8. Tính P(A). Giải
Số trƣờng hợp đồng khả năng : n = 6.6 = 36
Số trƣờng hợp thuận lợi cho A : m = 5 m 5 Do đó P(A) = = = 0,138889. n 36
Ví dụ 3: Lấy ngẫu nhiên ra 3 lá bài từ một cỗ bài tây 52 lá, tính xác suất
sao cho 3 lá bài lấy ra: a) đều là lá hình,
b) có 1 lá đỏ và 2 lá đen. Giải
Số trƣờng hợp đồng khả năng khi lấy ngẫu nhiên 3 lá bài từ 52 lá bài là n = C3 = 22100 52
a) Gọi A là biến cố 3 lá bài lấy ra đều là lá hình.
Biến cố A có số trƣờng hợp thuận lợi 12
CHƢƠNG I: KHÁI NIỆM XÁC SUẤT VÀ NHỮNG CÔNG THỨC TÍNH XÁC SUẤT CƠ BẢN lOMoAR cPSD| 35883770 ĐỊNH NGHĨA XÁC SUẤT mA = C3 = 220 1 2 m 220 Do đó P(A) = A = = 0,009955 n 22100
b) Gọi B là biến cố trong 3 lá bài lấy ra có 1 lá đỏ và 2 lá đen.
Việc xác định số trƣờng hợp thuận lợi cho B có thể chia làm hai bƣớc
− Chọn 1 lá đỏ: có n1 = 26 cách
− Chọn 2 lá đen: có n2 = C2 = 325 26
Vậy, theo qui tắc nhân, số trƣờng hợp thuận lợi cho biến cố B là mB = n1n2 = 8450
Suy ra P(B) = mB = 8450 = 0,382353 n 22100
3.2. Định nghĩa xác suất theo tần suất a) Tần suất
Giả sử thực hiện n lần một phép thử giống nhau, trong đó biến cố A xảy ra
m lần (m đƣợc gọi là tần số của biến cố A). Tần suất của biến cố A đƣợc kí hiệu
là fn(A) và đƣợc xác định m f (1.11) n(A) = n b) Xác suất
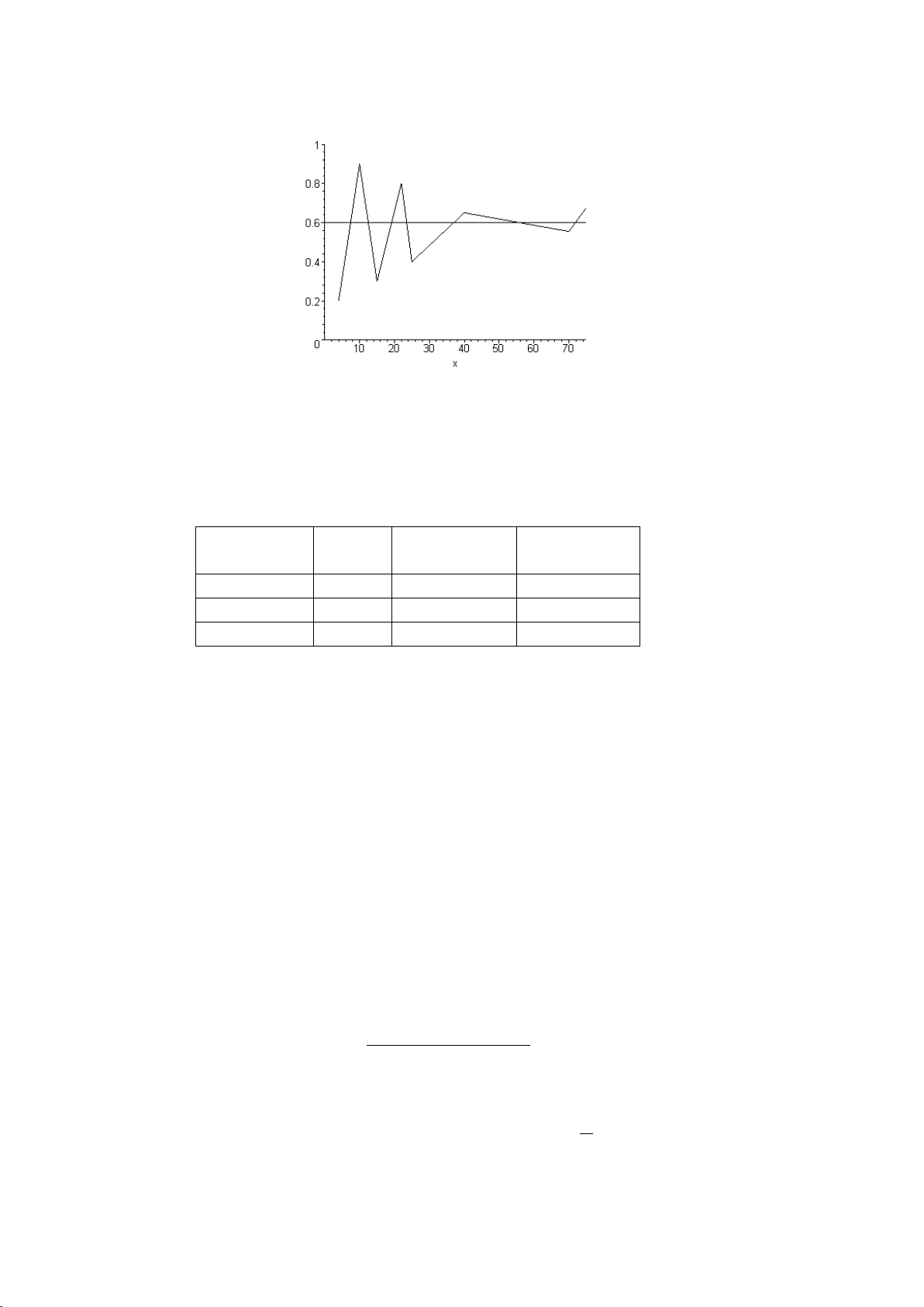
Cho số lần thực hiện phép thử n tăng lên vô hạn lần, nếu tần suất fn(A) của
biến cố A dần về một giá trị hữu hạn thì giá trị đó đƣợc định nghĩa là xác suất xảy ra biến cố A. m P(A) = lim fn(A) = lim (1.12) n→ n→ n CHÚ Ý 2
Ở cách định nghĩa trên, việc cho số lần thực hiện phép thử tăng lên vô hạn
lần là một cách nói mang tính chất lý thuyết. Trong thực tế, chỉ cần với số lần
thực hiện phép thử đủ lớn thì có thể lấy giá trị tần suất khi đó xấp xỉ cho giá trị xác suất.
CHƢƠNG I: KHÁI NIỆM XÁC SUẤT VÀ NHỮNG CÔNG THỨC TÍNH XÁC SUẤT CƠ BẢN 13 lOMoAR cPSD| 35883770 ĐỊNH NGHĨA XÁC SUẤT fn(A) n Hình 1.2
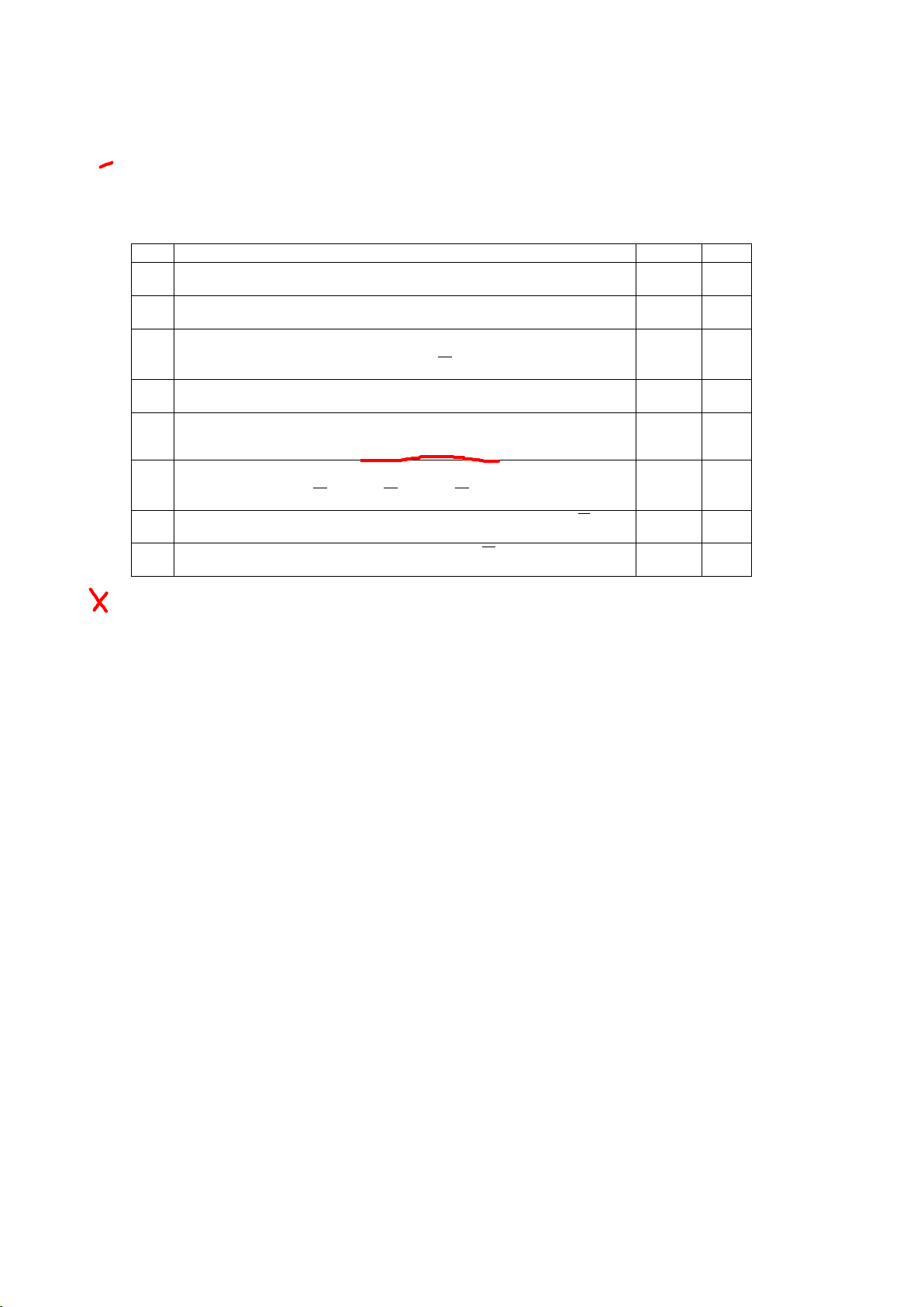
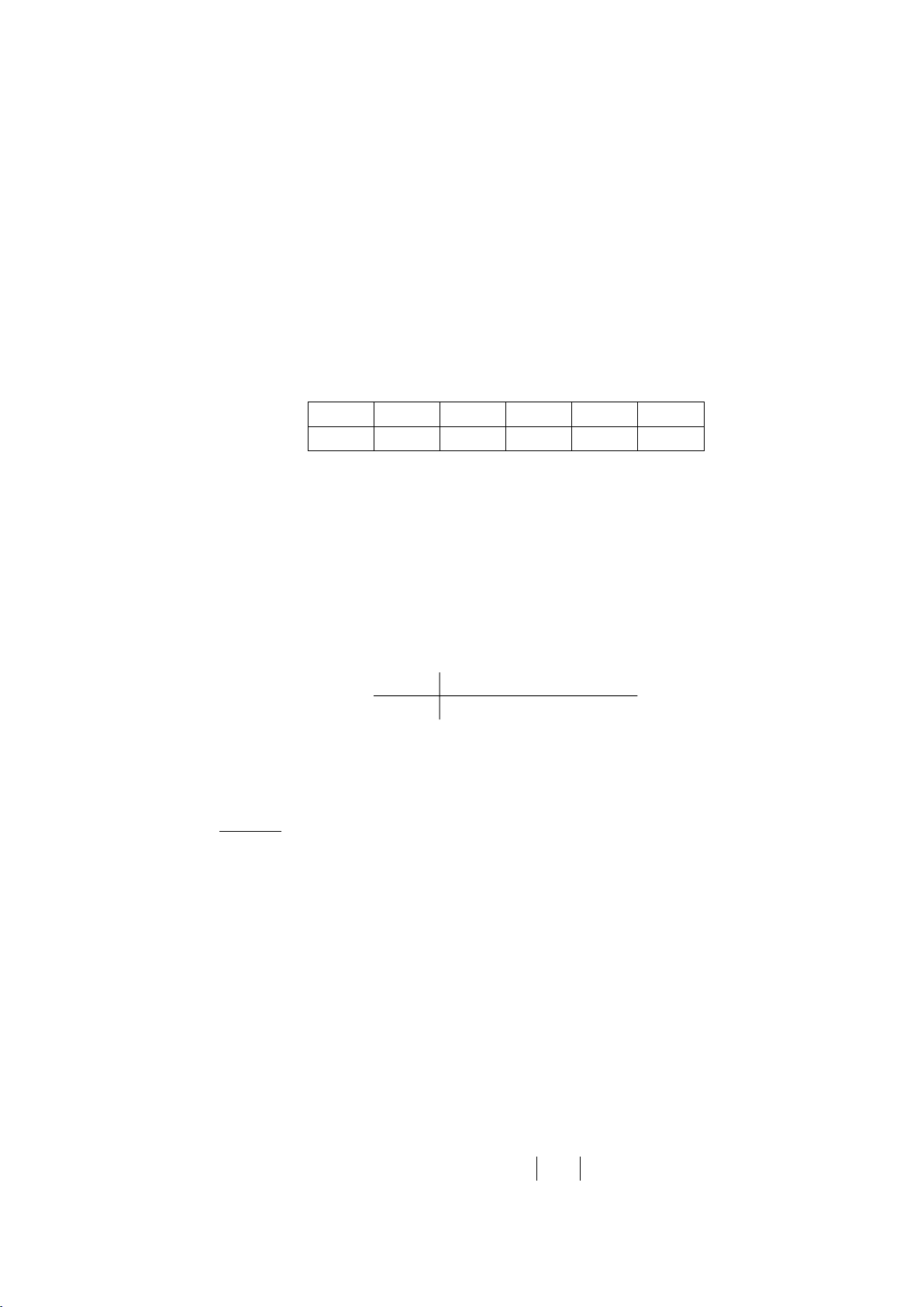
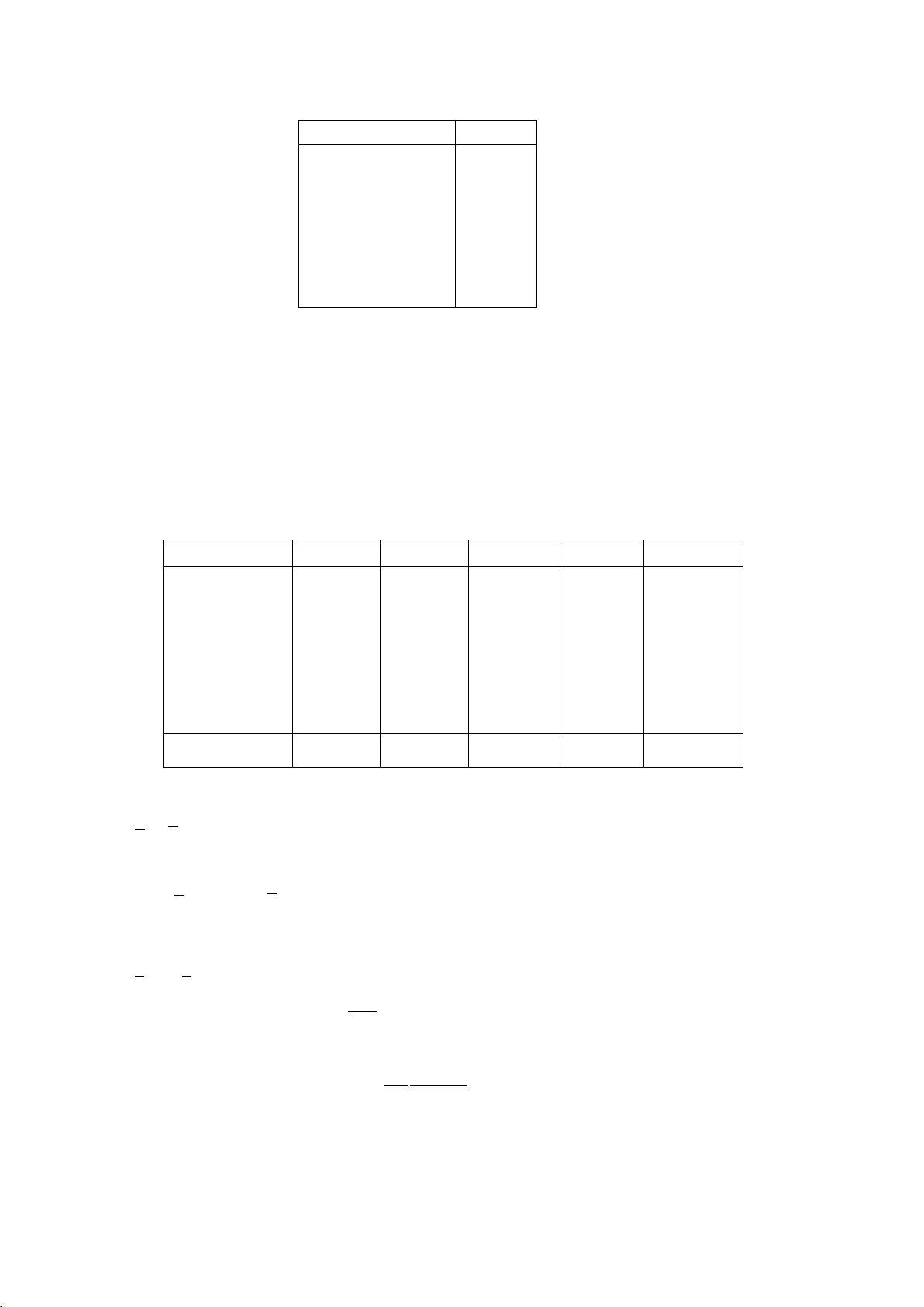
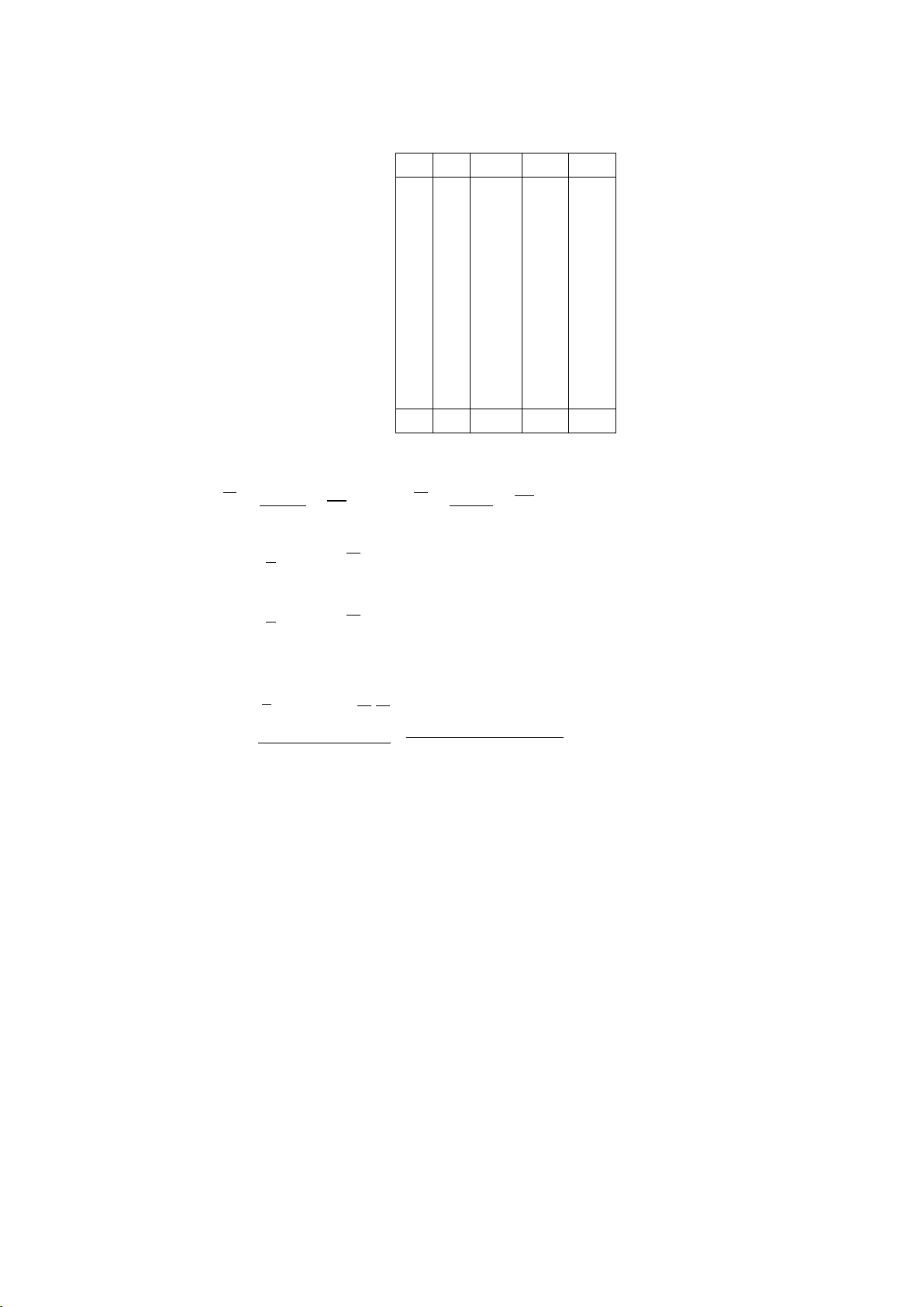
Ví dụ 4: Theo lối cổ điển, dễ xác định được xác suất đồng xu lật mặt sấp
khi tung là 0,5. Một số nhà khoa học đã kiểm tra về giá trị xác suất này theo khái niệm tần suất: Người làm Số lần Số lần được Tần suất lật Thí nghiệm tung mặt sấp mặt sấp Buyffon 4040 2048 0,5069 Pearson 12000 6019 0,5016 Pearson 24000 12012 0,5005
Cách định nghĩa xác suất theo tần suất còn đƣợc gọi là định nghĩa theo quan
điểm thống kê. Trong thực tế, có không ít biến cố khó có thể xác định xác suất
xảy ra theo lối cổ điển. Nghĩa là không thể nào xác định đƣợc số trƣờng hợp
đồng khả năng của phép thử cũng nhƣ số trƣờng hợp thuận lợi cho biến cố. Khi
đó ngƣời ta thống kê một mẫu quan sát và dùng giá trị tần suất để ƣớc lƣợng cho
giá trị xác suất. Phƣơng pháp này đƣợc áp dụng có hiệu quả trong việc tìm ra qui
luật diễn biến phức tạp về thời tiết, tỷ lệ phế phẩm, lập kích thƣớc quần áo may
sẵn, trong nhân chủng học, trong xã hội học, … Chẳng hạn, nhờ thống kê ngƣời
ta xấp xỉ xác suất sinh con trai là 0,518.
3.3. Định nghĩa xác suất theo quan điểm hình học
Xét một phép thử có tập hợp các trƣờng hợp đồng khả năng đƣợc biểu diễn
bởi miền hình học với độ đo (độ dài, diện tích, thể tích) hữu hạn khác 0, biến
cố A đƣợc biểu diễn bởi miền con DA. Khi đó, xác suất xảy ra biến cố A đƣợc xác định Ñoä ño cuûa mieàn D P(A) = A (1.13) Ñoä ño cuûa mieàn
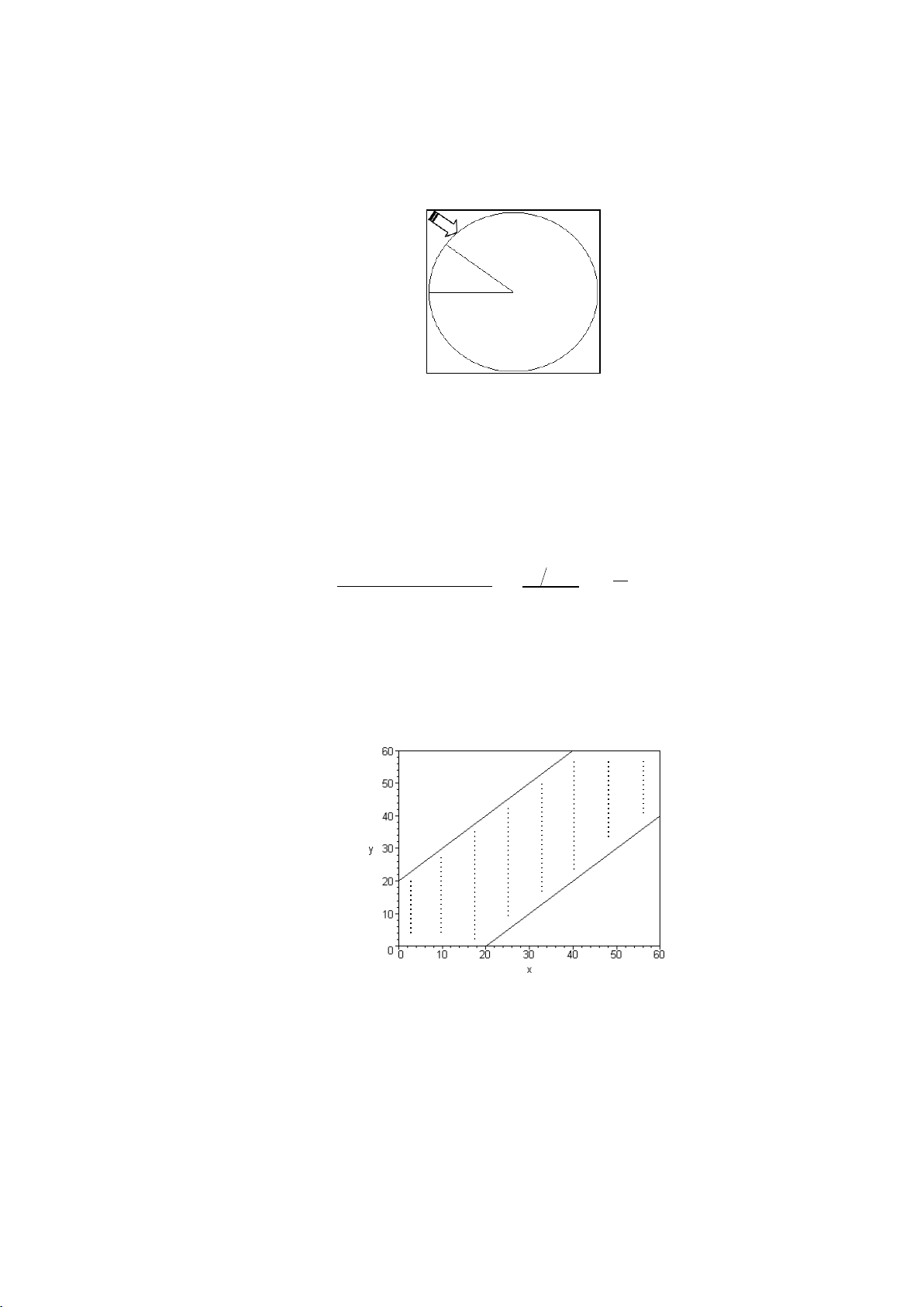
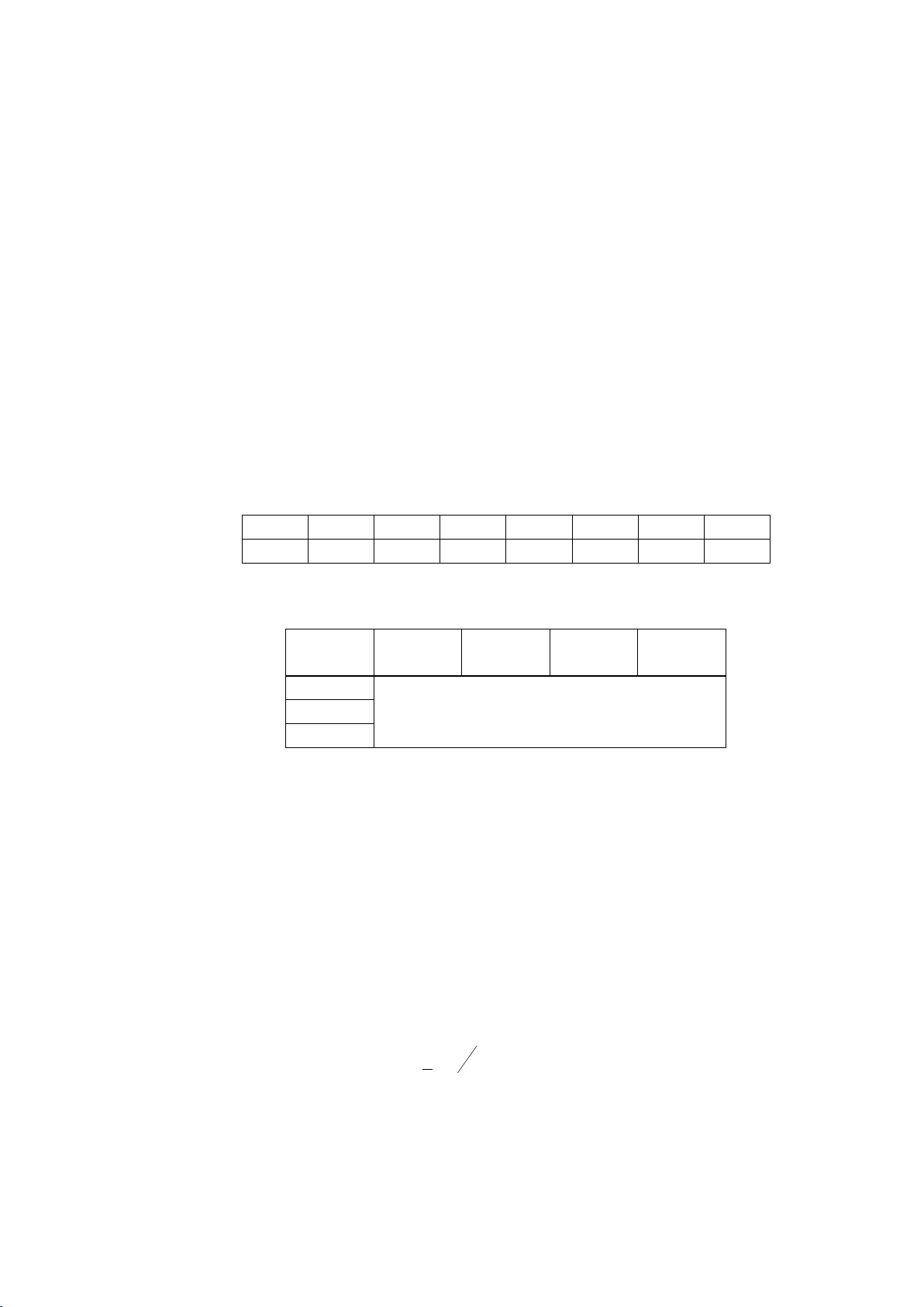
Ví dụ 5: Quay một đĩa tròn có bán kính R quanh 1 trục ở tâm. Trên biên π
của đĩa tròn có 1 cung a là cung được thưởng với số đo là
. Khi đĩa dừng lại, 6 14
CHƢƠNG I: KHÁI NIỆM XÁC SUẤT VÀ NHỮNG CÔNG THỨC TÍNH XÁC SUẤT CƠ BẢN lOMoAR cPSD| 35883770 ĐỊNH NGHĨA XÁC SUẤT
nếu mũi tên chỉ ở cung a thì người chơi được thưởng. Hãy xác định xác suất
được thưởng trong trò chơi này. Giải a Hình 1.3
Mỗi trƣờng hợp đồng khả năng có thể tƣơng ứng với 1 điểm trên biên của
đĩa tròn. Gọi A là biến cố ngƣời chơi đƣợc thƣởng. Mỗi trƣờng hợp thuận lợi cho
A tƣơng ứng với 1 điểm của cung a.
Xác suất đƣợc thƣởng đƣợc tính bởi Ñoä daøi cuûa cung a ( 6)R 1 P(A) = = = = 0,083333 Chu vi cuûa ñóa troøn 2R 12
Ví dụ 6: Hai người hẹn gặp nhau tại một địa điểm vào khoảng từ 13 giờ
đến 14 giờ. Họ quy ước rằng người đến trước sẽ chỉ đợi 20 phút, nếu không gặp
sẽ ra về. Giả sử việc đến điểm hẹn của mỗi người là ngẫu nhiên. Hãy xác định
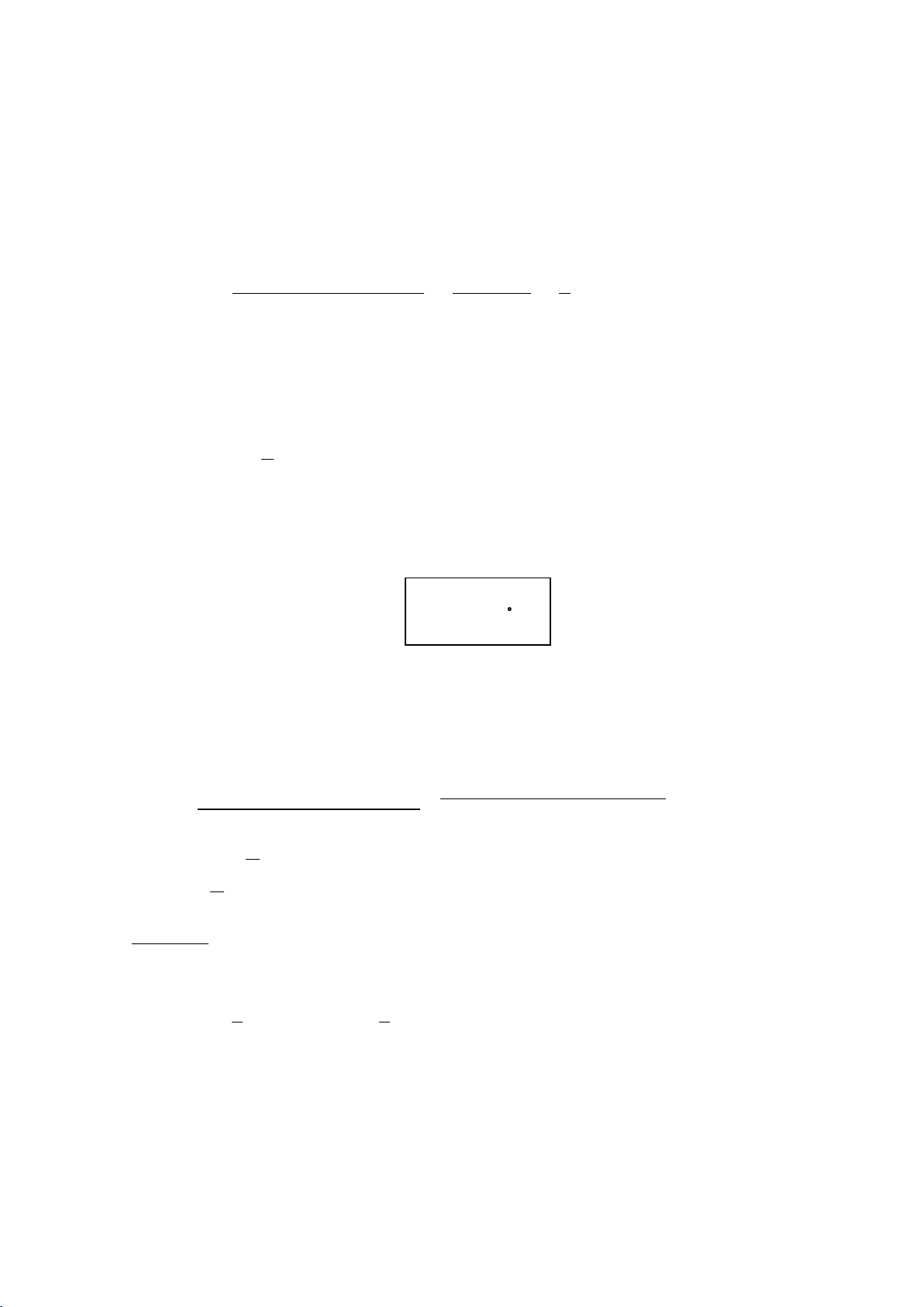
xác suất để hai người gặp nhau. y = x + 20 DA y = x − 20 Hình 1.4 Giải
Lấy gốc thời gian là 13 giờ, gọi x là thời điểm đến của ngƣời thứ nhất, y là
thời điểm đến của ngƣời thứ hai và đơn vị tính là phút.
Tập hợp các trƣờng hợp đồng khả năng có thể xảy ra là tập hợp các điểm (x;y) thuộc miền
= {(x;y) : 0 x 60, 0 y 60}
CHƢƠNG I: KHÁI NIỆM XÁC SUẤT VÀ NHỮNG CÔNG THỨC TÍNH XÁC SUẤT CƠ BẢN 15 lOMoAR cPSD| 35883770 ĐỊNH NGHĨA XÁC SUẤT
Gọi A là biến cố hai ngƣời gặp nhau. Khi đó tập các trƣờng hợp thuận lợi
cho A là tập các điểm (x;y) thuộc miền
DA = {(x;y) : |y − x| 20}
= {(x;y) : x − 20 y x + 20}
Xác suất hai ngƣời gặp nhau Dieän tích cuûa mieàn DA 60 2 − 40 2 5 P(A) = = = 0,555556 = 60 2 9 Dieän tích cuûa mieàn
3.4. Các tính chất cơ bản của xác suất i)
0 P(A) 1 với mọi biến cố A ii)
P( ) = 1, P(Ø) = 0
iii) Nếu A B thì P(A) P(B) iv) P(A) + P( A ) = 1
Ví dụ 7: Trong hình chữ nhật xác định một điểm A. Ném ngẫu nhiên
một chất điểm vào hình chữ nhật, tính xác suất sao cho chất điểm không trúng vào điểm A. A Hình 1.5 Giải
Gọi A là biến cố chất điểm trúng vào điểm A. Với cách định nghĩa xác suất
theo quan điểm hình học, ta có 0
P(A) = Dieän tích cuûa ñieåm A = = 0
Dieän tích hình chöõ nhaät Ω
Dieän tích hình chöõ nhaät Ω Mà P(A) + P( A ) = 1
Suy ra P( A ) = 1 − P(A) = 1 CHÚ Ý 3
Trong ví dụ trên, mặc dù P(A) = 0 nhƣng khi ném chất điểm vẫn có thể trúng điểm A, tức là biến
cố A vẫn có thể xảy ra. Nghĩa là biến cố có xác suất 0 vẫn có thể xảy ra. Biến cố nhƣ vậy đƣợc gọi là biến
cố “hầu không thể”.
Tƣơng tự dù P( A ) = 1 nhƣng biến cố A cũng có thể không xảy ra khi chất điểm trúng vào điểm
A. Các biến cố có xác suất bằng 1 nhƣng có thể không xảy ra nhƣ vậy đƣợc gọi là biến cố “hầu chắc chắn”. 16
CHƢƠNG I: KHÁI NIỆM XÁC SUẤT VÀ NHỮNG CÔNG THỨC TÍNH XÁC SUẤT CƠ BẢN lOMoAR cPSD| 35883770 ĐỊNH NGHĨA XÁC SUẤT
Ví dụ 8: Từ một lô có 20 sản phẩm, trong đó có 6 phế phẩm, lấy ngẫu
nhiên ra 5 sản phẩm. Tính xác suất sao cho trong các sản phẩm lấy ra có:
a) Đúng 2 phế phẩm.
b) Ít nhất 1 phế phẩm. Giải
a) Gọi A là biến cố có đúng 2 phế phẩm trong 5 sản phẩm lấy ra. Theo
định nghĩa xác suất cổ điển ta có C C 2 3 P(A) = 6 14 = 0,352167 5 C 20
b) Gọi B là biến cố trong 5 sản phẩm lấy ra có ít nhất 1 phế phẩm. Xác suất
xảy ra biến cố A đƣợc tính theo xác suất của biến cố đối lập nhƣ sau C5
P(B) = 1 − P( B ) = 1 − 14 = 1 − 0,129128 = 0,870872. 5 C 20 CHÚ Ý 4 x n−x C C
Khi tính xác suất theo định nghĩa cổ điển rất hay tính theo theo dạng giá trị M N−M , trong n C N
Excel giá trị này đƣợc tính theo hàm x n−x C C
M N−M = HYPGEOMDIST(x,n,M,N). (1.14) n C N BÀI TẬP
1 . Chọn ngẫu nhiên một tờ vé số có 5 chữ số. Tính xác suất chọn đƣợc vé có
các chữ số đôi một khác nhau trong đó có số 1 và số 5.
2 . Khi gọi điện thoại một khách hàng quên mất 3 chữ số cuối đành chọn ngẫu
nhiên 3 số. Tính xác suất ngƣời đó thực hiện đƣợc cuộc liên lạc khi chỉ nhớ
là 3 chữ số đó khác nhau và số cuối là số chẵn. 1 1 a) b) 5.9.8 103 1 1 c) d) 3 C 10.9.8 1 0
3 . Có 6 quyển sách khác nhau gồm 1 quyển tiếng Nhật, 2 quyển tiếng Nga và
3 quyển tiếng Pháp. Xếp ngẫu nhiên các quyển sách đó lên một cái kệ, tính
xác suất sao cho quyển tiếng Nhật đƣợc xếp giữa hai quyển tiếng Nga. 2!3!3! 3!3! a) b) 6! 6! 2!3! 2!4! c) d) 6! 6!
CHƢƠNG I: KHÁI NIỆM XÁC SUẤT VÀ NHỮNG CÔNG THỨC TÍNH XÁC SUẤT CƠ BẢN 17 lOMoAR cPSD| 35883770 ĐỊNH NGHĨA XÁC SUẤT
4 . Có 5 hành khách bƣớc ngẫu nhiên lên một đoàn tàu có 10 toa. Tính xác suất
sao cho có 2 hành khách lên cùng một toa, ba hành khách còn lại lên ba toa khác. 1 A 5 a) b) 10 104 105 3 2 4 C C A c) 50 .10.9.8 5 d) 5 10 5 10 10 5 .
Từ 8 đôi giày cùng số nhƣng khác màu nhau, lấy ngẫu nhiên một lƣợt ra 6
chiếc. Tính xác suất các chiếc giày lấy ra không tạo nên đôi nào. 16.14.12.10.8.6 C 6 .26 8 a) b) 6 C 16 C 6 16 C6 .26 8.C4 .24 8 7 c) d) A 6 C 6 16 16 6 .
Gieo đồng thời 3 con xúc xắc cân đối, đồng chất. Tìm xác suất sao cho tổng
số chấm ở mặt trên các con xúc xắc bằng 8. a) 12 b) 18 63 63 c) 21 d) 36 63 63
7 . Một đề thi trắc nghiệm gồm 10 câu hỏi, ở mỗi câu hỏi có cho sẵn 5 phƣơng
án trả lời, trong đó chỉ có 1 phƣơng án đúng. Thí sinh làm bài bằng cách: ở
mỗi câu hỏi chọn 1 trong 5 phƣơng án trả lời đã cho và sẽ đƣợc 1 điểm nếu
chọn đƣợc câu trả lời đúng, còn nếu chọn sai sẽ không có điểm ở câu đó.
Tìm xác suất để đƣợc 5 điểm khi làm bài một cách ngẫu nhiên. C 5 .4 5 C 5 .4 5 a) 10 b) 10 510 105 C 5 C 5 c) 10 d) 10 510 105 8
. Bỏ ngẫu nhiên 3 lá thƣ vào 3 phong bì đã viết sẵn tên của 3 ngƣời nhận.
Tính xác suất sao cho không thƣ nào đến đúng địa chỉ của ngƣời nhận. 1 2 a) b) 3! 3! c) 3 d) 4 3! 3! 9 .
Một hộp có 3 bi đỏ, 2 bi trắng và 1 bi xanh. Lấy ngẫu nhiên từ hộp ra 2 bi. Tính
xác suất sao cho 2 bi lấy ra cùng màu. 1 3 (a) (c) 2 C 2 C 6 6 2 4 (b) (d) C 2 6 C 2 6 18
CHƢƠNG I: KHÁI NIỆM XÁC SUẤT VÀ NHỮNG CÔNG THỨC TÍNH XÁC SUẤT CƠ BẢN lOMoAR cPSD| 35883770 ĐỊNH NGHĨA XÁC SUẤT
10 . Khi gọi điện thoại một khách hàng quên mất 3 chữ số cuối đành chọn ngẫu
nhiên 3 số. Tính xác suất ngƣời đó thực hiện đƣợc cuộc liên lạc trong các trƣờng hợp sau:
a/ Khách hàng đó không nhớ đƣợc thông tin nào khác.
b/ Khách hàng đó chỉ nhớ là 3 chữ số đó khác nhau.
c/ Khách hàng đó nhớ là 3 chữ số đó khác nhau và số cuối là số chẵn.
11 . Có 10 quyển sách khác nhau gồm 1 quyển tiếng Nhật, 2 quyển tiếng Nga, 3
quyển tiếng Pháp và 4 quyển tiếng Anh. Xếp ngẫu nhiên các quyển sách đó
lên một cái kệ, tính xác suất sao cho:
a/ Những quyển sách cùng một ngôn ngữ đƣợc xếp cạnh nhau.
b/ Ba quyển bằng tiếng Pháp đƣợc xếp cạnh nhau.
c/ Hai quyển tiếng Nga không đƣợc xếp cạnh nhau.
d/ Quyển tiếng Nhật đƣợc xếp giữa hai quyển tiếng Nga.
12 . Gieo đồng thời 2 con xúc xắc cân đối, đồng chất. Tìm xác suất sao cho:
a/ tổng số chấm ở mặt trên con xúc xắc bằng 9;
b/ số chấm ở mặt trên 2 con xúc xắc bằng nhau.
13 . Một chiếc hộp đựng 6 quả cầu trắng, 4 quả cầu đỏ và 2 quả cầu đen. Chọn
ngẫu nhiên 6 quả cầu. Tìm xác suất để chọn đƣợc 3 quả trắng, 2 quả đỏ và 1 quả đen.
14 . Giả sử có 10 khách hàng vào 1 gian hội chợ có 3 quầy, mỗi ngƣời chỉ tới 1
quầy. Tìm các xác suất:
a/ Có 4 ngƣời đến quầy số 1.
b/ Có 4 ngƣời đến 1 quầy nào đó.
c/ Có 4 ngƣời đến quầy 1 và 3 ngƣời đến quầy 2.
15 . Bỏ ngẫu nhiên 6 lá thƣ vào 6 phong bì đã viết sẵn tên của 6 ngƣời nhận. Tính xác suất:
a/ Cả 6 thƣ đều đến đúng địa chỉ.
b/ Lá thƣ thứ nhất đến đúng địa chỉ.
c/ Chỉ có 1 lá thƣ đến đúng địa chỉ.
d/ Chỉ lá thƣ thứ nhất đến đúng địa chỉ.
16 . Trong 1 tuần lễ có 7 tai nạn giao thông. Tính xác suất để mỗi ngày có đúng một tai nạn.
17 . Đƣờng dây cáp ngầm nối một tổng đài với một trạm dài 1km. Tính xác suất
của sự kiện dây cáp bị đứt nơi cách tổng đài không dƣới 800m.
18 . Kẽ trên mặt phẳng các đƣờng thẳng song song cách đều nhau một khoảng
6cm. Gieo ngẫu nhiên lên mặt phẳng một đồng xu có bán kính 1cm. Tìm
xác suất sao cho đồng xu không cắt đƣờng thẳng nào cả.
19 . Một đoạn thẳng có độ dài a đƣợc bẻ làm ba đoạn. Tính xác suất để ba đoạn
đó tạo thành một tam giác.
CHƢƠNG I: KHÁI NIỆM XÁC SUẤT VÀ NHỮNG CÔNG THỨC TÍNH XÁC SUẤT CƠ BẢN 19 lOMoAR cPSD| 35883770
CÔNG THỨC CỘNG VÀ CÔNG THỨC NHÂN XÁC SUẤT
§ 4. CÔNG THỨC CỘNG VÀ CÔNG THỨC NHÂN XÁC SUẤT
4.1. Công thức cộng
a) Công thức cộng với tổng hai biến cố
Với A và B là hai biến cố tùy ý, ta có
P(A + B) = P(A) + P(B) − P(AB) (1.15)
Đặc biệt, khi A và B xung khắc nhau thì P(A + B) = P(A) + P(B) (1.16) Chứng minh
Giả sử phép thử có số trƣờng hợp đồng khả năng là n. Các biến cố A, B lần lƣợt có số trƣờng hợp thuận lợi là mA, mB.
• Nếu A và B là hai biến cố xung khắc nhau thì trƣờng hợp nào đã thuận lợi cho A sẽ không thuận
lợi cho B và ngƣợc lại. Do vậy, số trƣờng hợp thuận lợi cho A + B khi này là mA + B = mA + mB. Do đó m m + m m m A B A + B P(A + B) = A+B = = n n n n P(A + B) = P(A) + P(B)
• Nếu A và B là hai biến cố không xung khắc nhau thì trong các trƣờng hợp có thể xảy ra có những
trƣờng hợp vừa thuận lợi cho A vừa thuận lợi cho B (giả sử có mAB trƣờng hợp dạng này). Đó là những
trƣờng hợp thuận lợi cho biến cố tích AB.
Khi đó, A + B có số trƣờng hợp thuận lợi là mA+B = mA + mB − mAB. Ta có m m + m − m m m m P(A + B) = A+B A AB AB A = = + B − AB n n n n n
P(A + B) = P(A) + P(B) − P(AB)
Ví dụ 1: Một cơ quan có tất cả 100 nhân viên, trong đó có 40 nữ. Trong
50 nhân viên có nhà ở gần cơ quan có 15 nữ. Chọn ngẫu nhiên một nhân viên,
tính xác suất sao cho chọn được người thuộc diện phải trực cơ quan vào ban
đêm. Biết rằng theo quy định của cơ quan, nhân viên nào hoặc là nam hoặc có
nhà gần cơ quan thì thuộc diện phải trực đêm. Giải
Gọi A là biến cố nhân viên đƣợc chọn là nam, B là biến cố nhân viên đƣợc
chọn có nhà gần cơ quan và C là biến cố ngƣời đƣợc chọn thuộc diện phải trực đêm.
Theo quy định của cơ quan, ta có C = A + B Do đó P(C) = P(A + B) Và theo công thức cộng 20
CHƢƠNG I: KHÁI NIỆM XÁC SUẤT VÀ NHỮNG CÔNG THỨC TÍNH XÁC SUẤT CƠ BẢN lOMoAR cPSD| 35883770
CÔNG THỨC CỘNG VÀ CÔNG THỨC NHÂN XÁC SUẤT
P(A + B) = P(A) + P(B) − P(AB) 60 = + 50 − 35 = 0,75 100 100 100
Vậy xác suất cần tìm là P(C) = 0,75.
Ví dụ 2: Chọn ngẫu nhiên một số điện thoại có 6 chữ số, tính xác suất sao
cho số được chọn: a) có chữ số 1,
b) có chữ số 1 và chữ số 2. Giải
a) Gọi A là biến cố chọn đƣợc số điện thoại có chữ số 1. Xác suất xảy ra
biến cố A đƣợc tính theo biến cố đối lập 96 P(A) = 1 − P( A ) = 1 − = 1 − 0,531441 = 0,468559 10 6
b) Gọi B là biến cố chọn đƣợc số điện thoại có chữ số 2. Với C là biến cố
chọn đƣợc số vừa có chữ số 1 và chữ số 2, ta có C = A.B
Suy ra C có biến cố đối lập C = A + B
Theo công thức cộng ta có
P( C ) = P( A + B ) = P( A ) + P( B ) − P( A B ) Trong đó 96 86 P( A ) = P( B ) = , P( A B ) = 10 6 10 6 Suy ra 96 86 P( C ) = 2. − 10 6 10 6
Do đó, xác suất chọn đƣợc số điện thoại có chữ số 1 và chữ số 2 là 96 86
P(C) = 1 − P( C ) = 1 − 2. + = 0,199262 10 6 10 6
b) Công thức cộng tổng quát
Với các biến cố tùy ý A1, A2, …, An ta có n
P(A1 + A2 + ... + An ) = P(A ) − A ) i P(Ai j i =1 i j + P(A A A ) − i j k
... + (−1)n −1P(A1A2...An ) (1.17) i jk
Nếu các biến cố A1, A2, …, An tạo nên nhóm biến cố xung khắc từng đôi thì
P(A1 + A2 + ...+ An ) = P(A1) + P(A2) + … + P(An) (1.18)
CHƢƠNG I: KHÁI NIỆM XÁC SUẤT VÀ NHỮNG CÔNG THỨC TÍNH XÁC SUẤT CƠ BẢN 21 lOMoAR cPSD| 35883770
CÔNG THỨC CỘNG VÀ CÔNG THỨC NHÂN XÁC SUẤT
Ví dụ 3: Một hộp chứa các viên bi với kích cỡ giống nhau trong đó có 5 bi
đỏ, 4 bi xanh, 3 bi vàng và 2 bi trắng. Từ hộp lấy ngẫu nhiên 3 bi, tính xác suất
lấy được 3 bi cùng màu. Giải
Gọi A là biến cố lấy đƣợc 3 bi cùng màu; A1, A2, A3 lần lƣợt là biến cố 3 bi
lấy ra có cùng màu đỏ, cùng màu xanh và cùng màu vàng. Ta có A = A1 + A2 + A3
Do đó P(A) = P(A1 + A2 + A3)
Vì các biến cố A1, A2, A3 đôi một xung khắc nhau nên C3 + C3 1 P(A +
1 + A2 + A3) = P(A1) + P(A2) + P(A3) = 5 4 = 0,041209 3 C C 3 C 3 14 14 14 Vậy P(A) = 0,041209.
Ví dụ 4: Bỏ ngẫu nhiên 4 lá thư vào 4 phong bì tương ứng đã ghi sẵn địa
chỉ. Tính xác suất sao cho có ít nhất một lá thư được bỏ đúng phong bì của nó. Giải
Gọi Ai là biến cố thƣ thứ i (i = 1,2,3,4) đƣợc bỏ đúng phong bì và A là biến cố cần tính xác suất. Ta có A = A1 + A2 + A3 + A4
Theo công thức cộng với các biến cố tùy ý, ta có P(A) = P(A1 + A2 + A3 + A4)
= [P(A1) + P(A2) + P(A3) + P(A4)] − [P(A1A2) + P(A1A3) + P(A1A4)
+ P(A2A3) + P(A2A4) + P(A3A4)] + [P(A1A2A3) + P(A1A2A4)
+ P(A1A3A4) + P(A2A3A4)] − P(A1A2A3A4) 3! 2! 1 = 4. − 6. + 4 − 1 1 1 = − 1 + − 1 = 0,625. 4! 4! 4! 4! 1! 2! 3! 4! 4.2.
Công thức nhân xác suất
a) Xác suất có điều kiện
Xác suất của biến cố A đƣợc xác định khi biến cố B đã xảy ra đƣợc gọi là
xác suất có điều kiện của biến cố A (với điều kiện B). Kí hiệu : P(A/B).
Ví dụ 5: Từ một hộp có 5 sản phẩm với 2 phế phẩm, lấy lần lượt không
hoàn lại ra 2 sản phẩm. Gọi A, B lần lượt là biến cố sản phẩm lấy lần thứ nhất,
thứ hai là phế phẩm. Tính các xác suất P(B/A) và P(B/ A ). Giải
Nếu biến cố A xảy ra thì trong hộp chỉ còn 4 sản phẩm với 1 phế phẩm. Do đó 22
CHƢƠNG I: KHÁI NIỆM XÁC SUẤT VÀ NHỮNG CÔNG THỨC TÍNH XÁC SUẤT CƠ BẢN lOMoAR cPSD| 35883770
CÔNG THỨC CỘNG VÀ CÔNG THỨC NHÂN XÁC SUẤT 1 P(B/A) = = 0,25 4
Khi biến cố A xảy ra thì trong 4 sản phẩm còn lại vẫn còn đủ 2 phế phẩm. Suy ra 2 = 0,5 P(B/ A ) = 4 CHÚ Ý 1
Nếu A và B là hai biến cố độc lập nhau thì
P(A/B) = P(A) và P(B/A) = P(B) CHÚ Ý 2
Gọi n là số trƣờng hợp đồng khả năng của phép thử, mB là số trƣờng hợp thuận lợi cho biến cố B,
mAB số trƣờng hợp thuận lợi cho cả 2 biến cố A và B.
Xét trong trường hợp biến cố B đã xảy ra, số trƣờng hợp đồng khả năng khi đó là mB và số
trƣờng hợp thuận lợi cho biến cố A là mAB. Do đó m P(A/B) = AB m B m AB n P(AB) Suy ra P(A/B) = = m B P(B) n
Rút ra công thức tính xác suất có điều kiện P(AB) P(A/B) = (1.19) P(B)
Ví dụ 6: Có 20 tấm thẻ được ghi số từ 1 đến 20. Chọn ngẫu nhiên một thẻ.
Tính xác suất sao cho thẻ chọn ra ghi số chia hết cho 3 khi biết số đó chia hết cho 2. Giải
Gọi A và B lần lƣợt là biến cố số trên thẻ lấy ra chia hết cho 2 và 3, cần tính P(A/B) .
Vì biến cố A có 10 trƣờng hợp thuận lợi (với các thẻ có số chẵn) nên 10 P(A) = = 0,5 20
Mặt khác, do AB là biến cố thẻ chọn ra có số chia hết cho 6 nên có 3 trƣờng
hợp thuận lợi (gồm các số 6, 12, 18). Suy ra 3 P(AB) = = 0,15 20
Theo công thức xác suất có điều kiện ta có
CHƢƠNG I: KHÁI NIỆM XÁC SUẤT VÀ NHỮNG CÔNG THỨC TÍNH XÁC SUẤT CƠ BẢN 23 lOMoAR cPSD| 35883770
CÔNG THỨC CỘNG VÀ CÔNG THỨC NHÂN XÁC SUẤT P(AB) 0,15 P(B/A) = = = 0,3. P(A) 0,5
b) Công thức nhân với tích của hai biến cố
Từ công thức xác suất có điều kiện ta có P(AB) = P(A).P(B/A) (1.20) Hay P(AB) = P(B).P(A/B) (1.21)
Nếu A và B là hai biến cố độc lập nhau thì P(AB) = P(A).P(B) (1.22)
Ví dụ 7: Một chùm có 5 chìa khóa, trong đó có 2 chìa mở được cửa. Thử
lần lượt từng chìa cho đến khi nào mở được cửa thì dừng. Tính xác suất để việc
thử dừng lại ở lần thử thứ hai. Giải
Gọi Ai là biến cố lần thử thứ i mở đƣợc cửa, A là biến cố việc thử dừng ở
lần thử thứ hai. Ta phải có A = A 1A2 Suy ra P(A) = P( A 1A2)
Áp dụng công thức nhân với hai biến cố tùy ý P( A 3 2 1A2) = P( A 1).P(A2/ A 1) = . = 0,3. 5 4
Vậy xác suất cần tìm là P(A) = 0,3.
Ví dụ 8: Có hai hộp chứa các viên bi, mỗi hộp chứa 5 bi với số bi đỏ lần
lượt là 1 và 3. Từ mỗi hộp lấy ngẫu nhiên ra một bi.
a) Tính xác suất sao cho hai bi lấy ra đều là bi đỏ.
b) Biết hai bi lấy ra có đúng một bi đỏ, tính xác suất bi đỏ đó là bi của hộp thứ nhất. Giải
Gọi Ai là biến cố bi lấy từ hộp thứ i là bi đỏ (i = 1,2).
a) Gọi A là biến cố lấy đƣợc hai bi đỏ. Ta có A = A1A2 P(A) = P(A1A2)
Vì A1 và A2 là hai biến cố độc lập nên P(A 3 1A2) = P(A1).P(A2) = 1 . = 0, 12. 5 5
b) Gọi B là biến cố trong hai bi lấy ra có đúng 1bi đỏ. Cần tính P(A1/B) = ?
Theo công thức xác suất có điều kiện ta có 24
CHƢƠNG I: KHÁI NIỆM XÁC SUẤT VÀ NHỮNG CÔNG THỨC TÍNH XÁC SUẤT CƠ BẢN lOMoAR cPSD| 35883770
CÔNG THỨC CỘNG VÀ CÔNG THỨC NHÂN XÁC SUẤT P(A B) 1 P(A1/B) = P(B) Trong đó B = A 1 A 2 + A 1A2 A1B = A1 A 2 Do đó
P(B) = P(A1 A 2 + A 1A2) = P(A1 A 2) + P( A 1A2) 2 4 3
= P(A1).P( A 2) + P( A 1)P(A2) = 1 . + . = 0,56 5 5 5 5 1 2 P(A1B) = P(A1 A 2) = . = 0,08 5 5 0,08 1 Suy ra P(A = 1/B) = = 0,142857. 0,56 7
c) Công thức nhân tổng quát
Với A1, A2, …, An là các biến cố tùy ý ta có
P(A1A2…An) = P(A1)P(A2/A1)P(A3/A1A2)…P(An/A1…An − 1) (1.23)
Nếu các biến cố A1, A2, …, An tạo nên nhóm độc lập toàn phần thì
P(A1A2…An) = P(A1)P(A2)…P(An) (1.24)
Ví dụ 9: Chia 9 hộp sữa (có 3 hộp kém phẩm chất) ra làm ba phần bằng
nhau. Tính xác suất sao cho mỗi phần đều có một hộp kém phẩm chất. Giải
Gọi Ai là biến cố phần thứ i (i = 1,2,3) có hộp kém phẩm chất và A là biến
cố cần tính xác suất. Ta có A = A 1A2A3 Do đó P(A) = P(A 1A2A3) Theo công thức nhân C1 C2 C1 C2
P(A1A2) = P(A1).P(A2/A1)P(A3/A1A2) = 3 6 . 2 4 .1 = 0,321429 3 C C 3 9 6
CHƢƠNG I: KHÁI NIỆM XÁC SUẤT VÀ NHỮNG CÔNG THỨC TÍNH XÁC SUẤT CƠ BẢN 25 lOMoAR cPSD| 35883770
CÔNG THỨC CỘNG VÀ CÔNG THỨC NHÂN XÁC SUẤT BÀI TẬP
1 . Một số điện thoại có sáu chữ số. Ngƣời gọi quên chữ số cuối cùng, ngƣời
đó quay một cách ngẫu nhiên. Tìm xác suất để ngƣời đó thực hiện đƣợc
cuộc liên lạc mà không phải quay quá ba lần. a) 0,1 b) 0,2 c) 0,3 d) 0,4
2 . Có bốn linh kiện trong một mạch điện chúng có thể bị hỏng một cách độc
lập trong khoảng thời gian T với xác suất tƣơng ứng 0,1; 0,3; 0,2; 0,3. Tìm
xác suất để mạch bị hỏng trong thời gian T nếu mạch mắc nối tiếp. a) 0,0018 b) 0,0082 c) 0,6472 d) 0,3528
3 . Một xạ thủ bắn vào bia cho đến khi trúng thì dừng. Tìm xác suất để xạ thủ
đó dừng bắn ở lần thứ ba, biết rằng xác suất bắn trúng ở mỗi lần bắn là 0,7. a) 0,063 b) 0,027 c) 0,343 d) 0,147
4 . Một bình có 8 bi trắng, 6 bi vàng, 5 bi đỏ và 1 bi xanh. Chọn ngẫu nhiên 3
bi từ bình. Tìm xác suất để 3 bi đƣợc chọn có 3 màu khác nhau. C3 + C3 + C3 8 6 5 a) b) 8.6.5 + 8.6 + 8.5 + 6.5 3 C C 3 20 20 − C 3 C3 C3 c) 5 d) 20 5 3 3 C C 20 20
5 . Một lô hàng có 10 chính phẩm và 5 phế phẩm. Lần thứ nhất chọn ngẫu
nhiên không hoàn lại 5 sản phẩm và lần thứ 2 cũng chọn không hoàn lại
thêm 5 sản phẩm nữa. Tính xác suất đê lần thứ nhất đƣợc 5 chính phẩm, lần
thứ 2 đƣợc 2 chính phẩm và 3 phế phẩm. C C 2 3 (C 2 )2 5 2 2 C C C a) 5 5 5 b) d) 5 C 5 c) 10 5 5 5 5 10 C C C 15 15 15
6 . Cho biết một vận động viên bắn súng có xác suất bắn trúng bia ở mỗi viên
là 0,9. Tính xác suất có ít nhất 1 viên đạn trúng bia khi vận động viên đó bắn 2 viên. (a) 0,81 (c) 0,198 (b) 0,01 (d) 0,99 7 .
Xét quan hệ giữa xác suất của các biến cố Al, A2 và A1 + A2. Trong các kết
quả sau kết quả nào là đúng:
(a) P(A1 + A2) = 0,6; P(A1) = 0,7; P(A2) = 0,2; P(A1A2) = 0
(b) P(A1 + A2) = 0,6; P(A1) = 0,7; P(A2) = 0,2; P(A1A2) = 0,1
(c) P(A1 + A2) = 0,6; P(A1) = 0,7; P(A2) = 0,2; P(A1A2) = 0,2
(d) P(A1 + A2) = 0,6; P(A1) = 0,7; P(A2) = 0,2; P(A1A2) = 0,3 26
CHƢƠNG I: KHÁI NIỆM XÁC SUẤT VÀ NHỮNG CÔNG THỨC TÍNH XÁC SUẤT CƠ BẢN lOMoAR cPSD| 35883770
CÔNG THỨC CỘNG VÀ CÔNG THỨC NHÂN XÁC SUẤT 8 .
Một hộp có 3 bi đỏ, 2 bi trắng và 1 bi xanh. Lấy ngẫu nhiên từ hộp ra 2 bi.
Tính xác suất sao cho 2 bi lấy ra cùng màu. 1 3 (a) (c) C 2 6 C 2 6 2 4 (b) (d) C 2 C 2 6 6
9 . Hai xạ thủ bắn mỗi ngƣời 1 viên đạn vào cùng một mục tiêu với xác suất
trúng lần lƣợt là 0,7 và 0,9. Tính xác suất mục tiêu bị trúng đúng 1 viên đạn. (a) 0,03 (c) 0,63 (b) 0,34 (d) 0,97
10 . Cho biết P(A) = 0,2; P(B) = 0,4; B(A/B) = 0,1. Khi đó, P(B/A) có giá trị là: (a) 0,1 (c) 0,3 (b) 0,2 (d) 0,4
11 . Nếu P(A+B+C) = 0,3; P(A) = P(B) = P(C) = 0,2; P(AB) = P(AC) = P(BC)
= 0,1 thì P(ABC) có giá trị là: (a) 0 (c) 0,2 (b) 0,1 (d) 1
12 . Sinh viên đƣợc cộng điểm thƣởng nếu có đƣợc ít nhất 1 trong 2 loại chứng
chỉ quốc gia về ngoại ngữ hay tin học. Lớp với 100 sinh viên có 60 sinh
viên có chứng chỉ ngoại ngữ, 40 sinh viên có chứng chỉ tin học, 30 sinh
viên vừa có chứng chỉ ngoại ngữ vừa có chứng chỉ tin học. Chọn ngẫu
nhiên một sinh viên trong lớp, xác suất chọn đƣợc sinh viên đƣợc cộng điểm thƣởng là: (a) 0,3 (c) 0,6 (b) 0,4 (d) 0,7
13 . Hai khách hàng chọn mua ngẫu nhiên mỗi ngƣời một con gà tại một quầy
có 10 con gà (với 3 gà bệnh). Xác suất để cả 2 khách hàng đều mua phải gà bệnh là: (a) 6/90 (c) 6/100 (b) 9/100 (d) 9/90
14 . Một hộp có năm tấm phiếu trong đó có một phiếu trúng thƣởng. Năm ngƣời
lần lƣợt mỗi ngƣời rút ngẫu nhiên một phiếu.
a/ Hỏi rút trƣớc hay rút sau có lợi?
b/ Câu trả lời có khác không nếu trong năm phiếu có hai phiếu thƣởng?
c/ Xét khi trong năm phiếu có hai phiếu thƣởng, nếu có hai ngƣời nào đó
rút đƣợc phiếu thƣởng thì dừng lại. Tính xác suất sao cho khi đến ngƣời
thứ ba rút xong thì dừng lại.
CHƢƠNG I: KHÁI NIỆM XÁC SUẤT VÀ NHỮNG CÔNG THỨC TÍNH XÁC SUẤT CƠ BẢN 27 lOMoAR cPSD| 35883770
CÔNG THỨC CỘNG VÀ CÔNG THỨC NHÂN XÁC SUẤT
15 . Chọn ngẫu nhiên một tờ vé số có sáu chữ số, tính xác suất sao cho chọn đƣợc vé:
a/ Có các chữ số 1, 2, 3.
b/ Có số 1 và có số chẵn.
c/ Có số 1 và là số chẵn.
16 . Một hộp có chín viên bi giống nhau trên đó lần lƣợt ghi các số tự nhiên từ 1
đến 9. Từ hộp lấy ngẫu nhiên ra ba bi.
a/ Tính xác suất sao cho ba bi lấy ra đều là bi có số chẵn.
b/ Tính xác suất sao cho ba bi lấy ra đều là bi có số chẵn nếu biết rằng
trong các bi lấy ra có ít nhất một bi có số chẵn.
c/ Tính xác suất trong 3 bi lấy ra có bi mang số 8.
d/ Tính xác suất trong 3 bi lấy ra có bi mang số 8 nếu biết rằng trong các bi
lấy ra có ít nhất một bi có số chẵn.
17 . Có bốn linh kiện trong một mạch điện chúng có thể bị hỏng một cách độc
lập trong khoảng thời gian T với xác suất tƣơng ứng 0,1; 0,3; 0,2; 0,3. Tìm
xác suất để mạch bị hỏng trong thời gian T nếu mạch mắc song song.
18 . Một xạ thủ bắn vào bia cho đến khi trúng thì dừng. Tìm xác suất để xạ thủ
đó dừng bắn ở lần thứ tƣ, biết rằng xác suất bắn trúng ở mỗi lần bắn là 0,7.
19 . Một bình có 8 bi trắng, 6 bi vàng, 5 bi đỏ và 1 bi xanh. Chọn ngẫu nhiên 3
bi từ bình. Tìm xác suất để:
a/ 3 bi đƣợc chọn có màu khác nhau;
b/ 3 bi đƣợc chọn cùng màu;
c/ trong 3 bi đƣợc chọn phải có ít nhất 1 bi đỏ.
20 . Một công ty cần tuyển 2 nhân viên. Có 6 ngƣời nộp đơn trong đó có 4 nữ và
2 nam. Khả năng đƣợc tuyển của mỗi ngƣời là nhƣ nhau.
a/ Tính xác suất để 2 nữ đƣợc chọn nếu biết rằng ít nhất 1 nữ đƣợc chọn.
b/ Giả sử Hoa là một trong 4 nữ. Tính xác suất để Hoa đƣợc chọn. Tính
xác suất để Hoa đƣợc chọn nếu biết rằng ít nhất 1 nữ đã đƣợc chọn.
21 . Hộp thứ nhất có 5 bi đỏ và 3 bi trắng. Hộp thứ 2 có 8 bi đỏ và 2 bi trắng.
Lấy ngẫu nhiên mỗi hộp ra 2 bi.
a/ Tìm xác suất để lấy đƣợc 3 bi đỏ.
b/ Nếu lấy đƣợc 3 đỏ và 1 bi trắng, tìm xác suất để bi trắng là của hộp thứ nhất.
22 . Một đoàn tàu gồm 3 toa đỗ ở sân ga. Có 5 hành khách bƣớc lên tàu. Mỗi
hành khách độc lập với nhau chọn ngẫu nhiên 1 toa. Tính xác suất để mỗi
toa đều có ít nhất 1 hành khách mới bƣớc lên. 28
CHƢƠNG I: KHÁI NIỆM XÁC SUẤT VÀ NHỮNG CÔNG THỨC TÍNH XÁC SUẤT CƠ BẢN lOMoAR cPSD| 35883770
CÔNG THỨC XÁC SUẤT ĐẦY ĐỦ, CÔNG THỨC BAYES VÀ CÔNG THỨC BERNOULLI
§ 5. CÔNG THỨC XÁC SUẤT ĐẦY ĐỦ − CÔNG THỨC BAYES
VÀ CÔNG THỨC BERNOULLI
5.1. Công thức xác suất đầy đủ và công thức Bayes
a) Nhóm biến cố đầy đủ và xung khắc từng đôi
Nhóm biến cố A1, A2, …, An đƣợc gọi là nhóm đầy đủ và xung khắc từng
đôi nếu hai biến cố tùy ý trong nhóm đều xung khắc nhau và có thêm tính chất A1 + A2 + ... + An = CHÚ Ý 1
Nếu A1, A2, …, An là là nhóm đầy đủ và xung khắc từng đôi thì
P(A1) + P(A2) + … + P(An) = 1
b) Công thức xác suất đầy đủ
Giả sử các biến cố A1, A2, …, An lập nên nhóm đầy đủ và xung khắc từng
đôi. Với B là biến cố tùy ý, ta có n P(B) = P(A )P(B/ A ) (1.25) i i i=1
= P(A1)P(B/A1) + P(A2)P(B/A2) + … + P(An)P(B/An) Chứng minh
Vì A1, A2, …, An là nhóm là nhóm đầy đủ và xung khắc từng đôi nên A1 + A2 + ...+ An = Suy ra B = B = (A
1 + A2 + ...+ An)B = A1B + A2 B+ ...+ AnB Do đó
P(B) = P(A1B + A2 B + ...+ AnB)
Mặt khác, vì A1 + A2 + ...+ An là nhóm xung khắc từng đôi nên A1B, A2 B, ..., AnB cũng là nhóm
xung khắc từng đôi. Do vậy
P(A1B + A2 B + ...+ AnB) = P(A1B) + P(A2 B) + … + P(AnB)
= P(A1)P(B/A1) + P(A2)P( B/A2) + … + P(An)P(B/An) Tóm lại
P(B) = P(A1)P(B/A1) + P(A2)P( B/A2) + … + P(An)P(B/An)
Ví dụ 1: Có ba lô sản phẩm, mỗi lô có 10 sản phẩm với số phế phẩm lần
lượt là 1, 2, 3. Từ mỗi lô lấy ngẫu nhiên một sản phẩm. Sau đó, từ ba sản phẩm
bên ngoài chọn ra một sản phẩm. Tính xác suất sao cho sản phẩm chọn ra lần sau là phế phẩm. Giải
Gọi B là biến cố sản phẩm chọn ra lần sau là phế phẩm, Ai là biến cố sản
phẩm chọn ra lần sau là sản phẩm của lô thứ i (i = 1,2,3).Khi đó, các biến cố A1,
A2 và A3 tạo nên nhóm đầy đủ và xung khắc từng đôi.
CHƢƠNG I: KHÁI NIỆM XÁC SUẤT VÀ NHỮNG CÔNG THỨC TÍNH XÁC SUẤT CƠ BẢN 29 lOMoAR cPSD| 35883770
CÔNG THỨC XÁC SUẤT ĐẦY ĐỦ, CÔNG THỨC BAYES VÀ CÔNG THỨC BERNOULLI
Theo công thức xác suất đầy đủ ta có
P(B) = P(A1)P(B/A1) + P(A2)P(B/A2) + P(A3)P(B/A3) 1 1 1 2 1 3 = . + . + . = 0,2 3 10 3 10 3 10
Vậy xác suất cần tìm là P(B) = 0,2. c) Công thức Bayes
Giả sử B là một biến cố đã xảy ra và {A1, A2, …, An } là nhóm đầy đủ và
xung khắc từng đôi, ta có P(A )P(B/ A ) i i P(A , (i = 1,2, …, n) (1.26) i/B) = P(B) P(A )P(B/ A ) Hay P(A i i i/B) = , (i = 1,2, …, n) (1.27) n P(A )P(B/ A ) i i i=1 Chứng minh
Theo công thức nhân, với mọi i = 1, 2, …, n ta có
P(AiB) = P(Ai)P(B/Ai) = P(B)P(Ai/B) Suy ra P(A )P(B / A ) i i P(Ai/B) = P(B) n
Hơn nữa, theo công thức xác suất đầy đủ thì P(B) = P(A )P(B / A ) nên có thể viết i i i=1 P(A )P(B / A ) i i P(A i/B) = n P(A )P(B / A ) i i i=1
Ví dụ 2: Một nhà máy có ba phân xưởng I, II và III cùng sản xuất một loại
sản phẩm. Các phân xưởng có tỷ lệ đóng góp trên tổng sản phẩm của nhà máy
lần lượt là 30%, 50% và 20%. Tỷ lệ phế phẩm của phân xưởng I là 3%, của phân
xưởng II là 2% và của phân xưởng III là 4%. Chọn ngẫu nhiên một sản phẩm
của nhà máy để kiểm tra.
a) Tính xác suất sao cho sản phẩm kiểm tra là phế phẩm.
b) Giả sử sản phẩm kiểm tra là phế phẩm, tìm xác suất sao cho sản phẩm
đó là do phân xưởng I sản xuất. Giải
Gọi Ai là biến cố sản phẩm kiểm ta là sản phẩm của phân xƣởng thứ i (i =1,
2, 3). Các biến cố A1, A2, A3 tạo nên nhóm đầy đủ và xung khắc từng đôi.
a) B là biến cố sản phẩm kiểm tra là phế phẩm. Theo công thức xác suất đầy đủ ta có
P(B) = P(A1)P(B/A1) + P(A2)P(B/A2) + P(A3)P(B/A3)
= 0,3.0,03 + 0,5.0,02 + 0,2.0,04 = 0,027 30
CHƢƠNG I: KHÁI NIỆM XÁC SUẤT VÀ NHỮNG CÔNG THỨC TÍNH XÁC SUẤT CƠ BẢN lOMoAR cPSD| 35883770
CÔNG THỨC XÁC SUẤT ĐẦY ĐỦ, CÔNG THỨC BAYES VÀ CÔNG THỨC BERNOULLI b) Tính P(A1/B). P(A )P(B/ A ) Áp dụng công thức Bayes P(A i i i/B) = P(B) 0,3.0,03 Suy ra P(Ai/B) = = 0,3333. 0,027
Ví dụ 3: Một mạch điện gồm hai bộ phận độc lập được mắc nối tiếp, với
xác suất bị hỏng trong thời gian nào đó của mỗi bộ phận lần lượt là 0,01 và
0,015. Ở một thời điểm trong khoảng thời gian trên người ta thấy mạch điện
ngừng làm việc (do bộ phận nào đó hỏng), tìm xác suất để chỉ bộ phận thứ nhất hỏng. Giải
Gọi Ai là biến cố bộ phận thứ i bị hỏng (i = 1, 2) và B là biến cố mạch điện không làm việc.
Đặt B0 = A 1 A 2, B1 = A1 A 2, B2 = A 1A2, B3 = A1A2. Cần tính P(B1/B) = ?
Vì {B0, B1, B2, B3} là nhóm đầy đủ và xung khắc từng đôi nên theo công thức Bayes, ta có P(B )P(B/ B ) P(B 1 1 1/B) = 3 P(B )P(B/ B ) i i i=0 Trong đó
P(B0) = P( A 1 A 2) = P( A 1)P( A 2) = 0,99.0,985 = 0,97515
Tƣơng tự P(B1) = 0,00985; P(B2) = 0,01485; P(B3) = 0,00015
Mặt khác P(B/B0) = 0; P(B/B1) = 1; P(B/B2) = 1; P(B/B3) = 1 0,00985 Suy ra P(B1/B) = = 0,396378. 0,00985 + 01485 + 0,00015 CHÚ Ý 2
Trong công thức xác suất đầy đủ và công thức Bayes, điều kiện
A1 + A2 + ... + An = có thể thay bởi B A1 + A2 + ... + An .
5.2. Công thức Bernoulli
a) Dãy phép thử Bernoulli
Một dãy n phép thử giống nhau đƣợc gọi là dãy Bernoulli nếu thỏa đồng thời ba điều kiện sau i)
Các phép thử độc lập nhau. ii)
Ở mỗi phép thử chỉ có hai dạng kết quả: hoặc xảy ra biến cố A hoặc xảy ra biến cố A .
iii) P(A) = p không đổi đối với mọi phép thử.
Việc kiểm tra một dãy phép thử qua bộ ba điều kiện trên đƣợc gọi là kiểm
tra theo lƣợc đồ Bernoulli. Xác suất p xảy ra biến cố A gọi là xác suất thành
công. Các thí nghiệm giống nhau đƣợc xem là tạo nên dãy Bernoulli nếu chúng
CHƢƠNG I: KHÁI NIỆM XÁC SUẤT VÀ NHỮNG CÔNG THỨC TÍNH XÁC SUẤT CƠ BẢN 31 lOMoAR cPSD| 35883770
CÔNG THỨC XÁC SUẤT ĐẦY ĐỦ, CÔNG THỨC BAYES VÀ CÔNG THỨC BERNOULLI
đƣợc thực hiện độc lập nhau; đồng thời ở mỗi thí nghiệm chỉ quan tâm hai dạng
kết quả là thành công hoặc thất bại (không xét dạng kết quả chỉ thành công một
phần) với xác suất thành công nhƣ nhau.
Thí dụ, một xạ thủ bắn các phát súng có xác suất trúng bia đều nhƣ nhau
với sự kiện mong muốn là đạn trúng bia, hay việc ta tung một con xúc xắc và
quan tâm xem xúc xắc có lật mặt chẵn hay không, … tạo nên các dãy phép thử Bernoulli.
b) Công thức Bernoulli
Xác suất sao cho trong n phép thử Bernoulli biến cố A xảy ra đúng k lần
đƣợc tính bởi công thức Bernoulli nhƣ sau
Pn(k) = Ck .pk .q n−k , k = 0, 1, …, n (1.28) n
Trong đó p = P(A) và q = 1 − p.
Ví dụ 4: Tung một con xúc xắc cân đối đồng chất năm lần liên tiếp, tính
xác suất sao cho có đúng hai lần xúc xắc xuất hiện mặt có số chấm nhỏ hơn 3. Giải
Gọi A là biến cố xúc xắc xuất hiện mặt có số chấm nhỏ hơn 3. Ta có 2 1 p = P(A) = = 6 3
Năm lần tung xúc xắc với sự kiện A quan tâm nhƣ trên thỏa các điều kiện
của lƣợc đồ Bernoulli nên có thể tƣơng ứng với dãy n = 5 phép thử Bernoulli.
Theo công thức Bernoulli thì xác suất cần tìm đƣợc tính nhƣ sau 1 2 2 3
P5(2) = C2 . . = 0,329218 5 3 3
Ví dụ 5: Một đề thi trắc nghiệm có 100 câu hỏi, mỗi câu hỏi có cho sẵn 4
phương án trả lời, trong đó chỉ có 1 phương án đúng nhất. Tính xác suất sao cho
khi thí sinh làm bài một cách ngẫu nhiên thì chọn được đúng 50 câu đúng. Giải
Xem việc chọn phƣơng án trả lời cho mỗi câu hỏi nhƣ một phép thử, ta có
100 phép thử độc lập nhau.
Gọi A là biến cố chọn đƣợc phƣơng án đúng. Ở mỗi phép thử ta đều có
p = P(A) = 0,25 : không đổi
Vậy biến cố A và dãy phép thử hiểu nhƣ trên tạo nên dãy phép thử Bernoulli.
Áp dụng công thức tính xác suất Bernoulli ta có:
P100(50) = C50 .(0,25)50.(0,75)50 = 4,50731E-08 100 32
CHƢƠNG I: KHÁI NIỆM XÁC SUẤT VÀ NHỮNG CÔNG THỨC TÍNH XÁC SUẤT CƠ BẢN lOMoAR cPSD| 35883770
CÔNG THỨC XÁC SUẤT ĐẦY ĐỦ, CÔNG THỨC BAYES VÀ CÔNG THỨC BERNOULLI CHÚ Ý 3
Để tính các giá trị xác suất theo công thức Bernoulli, Excel sử dụng các hàm sau n−k • k k n−k k k = BINOMDIST(k,n,p,FALSE) (1.29) = Cn .p .q Cn .p .(1 - p) k • i i n−i Cn .p .(1-p) = BINOMDIST(k,n,p,TRUE) (1.30) i=0 BÀI TẬP
1 . Trong một lớp học, tỉ lệ sinh viên tham dự đầy đủ một môn học là 60%,
trong số đó xác suất để một sinh viên thi đạt môn học đó là 85%. Chọn
ngẫu nhiên một sinh viên của lớp. Khả năng để sinh viên này đến lớp đầy
đủ và không thi đạt môn này là: (a) 0,75 (b) 0,09 (c) 0,51 (d) 0,15
2 . Có hai lô sản phẩm: lô I có 5 sản phẩm với 2 phế phẩm, lô II với 4 sản
phẩm đều là chính phẩm. Lấy 1 sản phẩm từ lô I bỏ sang lô II, sau đó từ lô
II lấy ngẫu nhiên 1 sản phẩm. Tính xác suất sản phẩm lấy từ lô II là phế phẩm? (a) 1/20 (b) 1/25 (c) 1/10 (d) 2/25
3 . Một kiện hàng gồm 100 sản phẩm, trong đó có 10 phế phẩm. Chọn ngẫu
nhiên lần lƣợt có hoàn lại 5 sản phẩm để kiểm tra. Xác suất để trong 5 sản
phẩm lấy ra có 2 phế phẩm đƣợc tính bởi cách nào sao đây? (a) C 2 (0,1)2 (0,9)3 5 (b) 2 C (0,6)2 (0,4)4 100 C 2 C 4 (c) 10 90 6 C 100 C 2 (d) 10 6 C 100
4 . Tung đồng xu 3 lần, xác suất có đúng 2 lần đồng xu lật mặt sấp là: (a) 1/8 (b) 2/3 (c) 3/8 (d) 1/2
5 . Một nhà máy có hai phân xƣởng với tỷ lệ phế phẩm lần lƣợt là 4%, 8%. Số
sản phẩm do phân xƣởng thứ nhất sản xuất ra gấp ba lần số sản phẩm của
phân xƣởng thứ hai. Chọn kiểm tra ngẫu nhiên 1 sản phẩm của nhà máy.
Tính xác suất sao cho sản phẩm kiểm tra là phế phẩm? (a) 0,02 (b) 0,05 (c) 0,12 (d) 0,2
6 . Một hộp có 12 cây viết với 8 cây còn mới và 4 cây đã có sử dụng rồi. Lần
thứ nhất từ hộp lấy 1 cây viết để dùng, sau đó trả trở lại hộp. Lần thứ hai
cũng từ hộp đó lấy ngẫu nhiên một cây viết để sử dụng thì thấy đó là cây
viết còn mới. Tính xác suất cây viết lấy lần thứ nhất cũng là cây viết mới. 7 2 (a) (c) 11 3 4 7 (b) (d) 11 18
CHƢƠNG I: KHÁI NIỆM XÁC SUẤT VÀ NHỮNG CÔNG THỨC TÍNH XÁC SUẤT CƠ BẢN 33 lOMoAR cPSD| 35883770
CÔNG THỨC XÁC SUẤT ĐẦY ĐỦ, CÔNG THỨC BAYES VÀ CÔNG THỨC BERNOULLI 7 .
Tung đồng xu 5 lần, tính xác suất sao cho có đúng 2 lần đồng xu lật mặt sấp. 2 1 2 1 3 1 5 (d) (a) 5 (b) C2 (c) C3 C3 5 2 5 2 5 2
8 . Một nhà máy sản xuất ra một loại sản phẩm đƣợc gia công qua ba công
đoạn độc lập nhau. Xác suất bị khuyết tật ở các công đoạn lần lƣợt là 2%,
3% và 5%. Nếu sản phẩm bị khuyết tật cả ba công đoạn thì chắc chắn trở
thành phế phẩm; bị khuyết tật ở hai công đoạn thì khả năng trở thành phế
phẩm là 60%; còn nếu bị khuyết tật ở một công đoạn thì khả năng trở thành
phế phẩm là 30%. Chọn ngẫu nhiên một sản phẩm của nhà máy, tính xác
suất sản phẩm đó là phế phẩm.
9 . Một lô sản phẩm gồm ba loại do ba phân xƣởng khác nhau sản xuất. Trong
đó số sản phẩm do các phân xƣởng II và III đều gấp đôi số sản phẩm do
phân xƣởng I sản xuất. Tỷ lệ phế phẩm của các phân xƣởng lần lƣợt là 3%,
5%, 4%. Chọn ngẫu nhiên một sản phẩm trong lô.
a/ Tính xác suất để sản phẩm chọn ra là phế phẩm.
b/ Nếu sản phẩm lấy ra là phế phẩm thì khả năng sản phẩm đó do phân
xƣởng nào sản xuất ra cao hơn?
10 . Một lô hàng có sáu sản phẩm không rõ chất lƣợng cụ thể (mọi giả thiết về
số sản phẩm tốt có trong lô hàng lúc đầu đều đồng khả năng). Từ lô hàng
chọn ngẫu nhiên ra hai sản phẩm.
a/ Tính xác suất để hai sản phẩm chọn ra đều là sản phẩm tốt.
b/ Tính xác suất sao cho các sản phẩm còn lại trong hộp chỉ còn một sản
phẩm tốt biết hai sản phẩm lấy ra đều tốt.
11 . Hộp thứ nhất có sáu bi, trong đó có hai bi đỏ. Hộp thứ hai có năm bi, trong
đó có ba bi đỏ. Lần thứ nhất lấy 3 bi ở hộp thứ nhất bỏ sang hộp thứ hai.
Sau đó, lần thứ hai, từ hộp thứ hai lấy ra ngoài 2 bi.
a/ Tính xác suất sao cho các bi lấy lần thứ hai đều đỏ.
b/ Giả sử lần thứ hai lấy đƣợc 2 bi đỏ, tính xác suất để trong 3 bi lấy lần thứ nhất có 1 bi đỏ.
12 . Một hộp có sáu quả bóng bàn, trong đó có bốn quả còn mới. Lần đầu lấy ra
hai quả để thi đấu, sau đó trả trở lại hộp. Sau đó lần thứ hai lại lấy tiếp ra
hai quả nữa. Giả sử hai quả bóng lấy lần sau đều mới, tính xác suất để các
quả lấy lần đầu cũng đều là những quả bóng mới.
13 . Một lô hàng có 30 sản phẩm (trong đó có 12 sản phẩm loại A) đƣợc đóng
gói để gửi cho khách hàng. Nơi nhận kiểm tra thì thấy thất lạc một sản
phẩm. Với những sản phẩm còn lại, chọn ngẫu nhiên một sản phẩm thì thấy
đó là sản phẩm loại A. Tính xác suất để sản phẩm phất lạc cũng là sản phẩm loại A.
14 . Một công ty lớn A hợp đồng sản suất bo mạch 40% đối với công ty B và
60% đối với công ty C. Công ty B lại hợp đồng 70% bo mạch nó nhận đƣợc
từ công ty A với công ty D và 30 % với công ty E. Khi các bo mạch đƣợc
hoàn thành từ các công ty C, D, E chúng đƣợc đƣa đến công ty A để gắn
vào các model khác nhau của máy tính. Biết rằng các công ty C, D và E lần 34
CHƢƠNG I: KHÁI NIỆM XÁC SUẤT VÀ NHỮNG CÔNG THỨC TÍNH XÁC SUẤT CƠ BẢN lOMoAR cPSD| 35883770
CÔNG THỨC XÁC SUẤT ĐẦY ĐỦ, CÔNG THỨC BAYES VÀ CÔNG THỨC BERNOULLI
lƣợt có tỷ lệ bo mạch bị hƣ trong thời gian bảo hành sau khi bán lần lƣợt là
1%, 2% và 3%. Tính xác suất sao cho một bo mạch chọn ngẫu nhiên của
công ty A bị hƣ trong thời gian bảo hành.
15 . Biết một ngƣời có nhóm máu AB có thể nhận của bất kỳ nhóm máu nào.
Nếu ngƣời đó có nhóm máu thuộc vào các nhóm còn lại (A, B hoặc O) thì
chỉ có thể nhận của ngƣời cùng nhóm máu hoặc nhóm máu O. Cho biết tỷ
lệ ngƣời có nhóm máu O, A, B và AB trong một vùng lần lƣợt là 10%,
20%, 30% và 40%. Chọn ngẫu nhiên một ngƣời cần tiếp máu và một ngƣời
cho máu của vùng đó. Tính xác suất sao cho sự truyền máu đƣợc thực hiện.
16 . Tính xác suất sao cho trong năm lần tung xúc xắc cân đối đồng chất có:
a/ Đúng hai lần xúc xắc xuất hiện mặt có số chấm nhỏ hơn 3.
b/ Có ít nhất một lần xúc xắc xuất hiện mặt có số chấm nhỏ hơn 3.
Để xác suất sao cho có ít nhất một lần xúc xắc xuất hiện mặt có số chấm nhỏ
hơn 3 không bé hơn 0,9 thì phải tung xúc xắc ít nhất bao nhiêu lần?
17 . Có hai kiện hàng chứa rất nhiều sản phẩm với tỷ lệ phế phẩm lần lƣợt là
10%, 20%. Từ mỗi kiện lấy ngẫu nhiên 2 sản phẩm, tính xác suất sao cho
trong 4 sản phẩm lấy ra có đúng 3 phế phẩm.
18 . Một công nhân đi làm ở thành phố khi trở về nhà có hai cách: hoặc đi theo
đƣờng ngầm hoặc đi theo lối cầu. Biết rằng nếu đi theo lối đƣờng ngầm thì
có khả năng 75% trƣờng hợp ông ta về đến nhà trƣớc 6 giờ; còn nếu đi theo
lối cầu thì khả năng này chỉ có 40%. Tuy nhiên ông ta thích đi theo lối cầu
hơn, có đến 2/3 trƣờng hợp ông ấy về nhà theo lối cầu. Tìm xác suất để
công nhân đó về theo lối cầu biết rằng ông ta về đến nhà sau 6 giờ.
19 . Có 3 hộp, mỗi hộp 10 viên bi và số bi trắng ở mỗi hộp lần lƣợt là 3, 5, 7.
a/ Chọn ngẫu nhiên mỗi hộp 1 bi. Tính xác suất để đƣợc 3 bi trắng.
b/ Chọn ngẫu nhiên 1 hộp rồi từ hộp đó chọn ra 3 bi. Tính xác suất để đƣợc 3 bi trắng.
c/ Lấy ngẫu nhiên từ mỗi hộp ra 1 bi rồi từ 3 bi lấy ra 1 bi. Tính xác suất
để viên bi lấy ra sau là bi trắng.
d/ Lấy ngẫu nhiên 1 hộp rồi từ hộp đó lấy ra 1 bi. Tính xác suất để đƣợc bi trắng.
20 . Ba khẩu súng bắn vào mục tiêu, có 2 viên đạn bắn trúng. Tìm xác suất để
viên thứ nhất bắn trúng nếu xác suất bắn trúng của viên thứ nhất, thứ 2, thứ
3 tƣơng ứng bằng 0,3; 0,4; 0,5.
CHƢƠNG I: KHÁI NIỆM XÁC SUẤT VÀ NHỮNG CÔNG THỨC TÍNH XÁC SUẤT CƠ BẢN 35 lOMoAR cPSD| 35883770 CHƯƠNG II
ĐẠI LƯỢNG NGẪU NHIÊN
VÀ MỘT SỐ PHÂN PHỐI THÔNG DỤNG
§ 1. KHÁI NIỆM ĐẠI LƯỢNG NGẪU NHIÊN
VÀ LUẬT PHÂN PHỐI XÁC SUẤT
1.1. Khái niệm đại lượng ngẫu nhiên
Nội dung đƣợc xét ở chƣơng thứ nhất chủ yếu là các vấn đề xoay quanh
khái niệm xác suất của một biến cố nào đó trong phép thử ngẫu nhiên. Qua đó,
giới thiệu một số cách khác nhau định nghĩa cho khái niệm xác suất, các tính chất
cơ bản của xác suất, các công thức tính xác suất, … Trong chƣơng thứ hai này
phép thử ngẫu nhiên đƣợc nghiên cứu ở mức độ khái quát hơn. Ở đây phép thử,
hiện tƣợng ngẫu nhiên đƣợc xét nhờ vào một dạng đại lƣợng số nhận các giá trị
biến thiên theo kết quả của phép thử ngẫu nhiên. Trong lý thuyết xác suất dạng
đại lƣợng nhƣ vậy gọi là đại lƣợng ngẫu nhiên hay biến ngẫu nhiên.
Đại lƣợng ngẫu nhiên đƣợc hiểu là đại lƣợng nhận các giá trị (hay khoảng
giá trị) có thể của nó với một xác suất nhất định phụ thuộc vào kết quả của phép
thử ngẫu nhiên. Các đại lƣợng ngẫu nhiên thƣờng đƣợc kí hiệu là X, Y, Z, X1, X2, …
Ví dụ 1: Gọi X là số lần đồng xu lật mặt sấp khi tung đồng xu 5 lần liên
tiếp. Khi đó, X là một đại lượng ngẫu nhiên với các giá trị có thể gồm 0, 1, 2, 3, 4 và 5.
Đại lượng ngẫu nhiên X nhận một trong các giá trị có thể của nó với một
xác suất nhất định phụ thuộc vào kết quả của quá trình phép thử. Chẳng hạn, nếu
trong 5 lần tung có đúng 2 lần đồng xu lật mặt sấp thì X khi đó nhận giá trị bằng
2; xác suất để nó nhận giá trị này được viết là P(X = 2) và được tính bởi công thức Bernoulli như sau
P(X = 2) = P (2) = C 2 .(0,5)2 .(0,5)3 = 0,3125 5 5
(do 5 lần tung đồng xu tạo nên dãy Bernoulli với xác suất lật mặt sấp p = 0,5)
Với mỗi phép thử ngẫu nhiên đều có thể xây dựng một đại lƣợng ngẫu
nhiên tƣơng ứng để khảo sát. Thí dụ, với phép thử tung xúc xắc có thể xét trên
đại lƣợng ngẫu nhiên chỉ cho số chấm xuất hiện ở mặt trên của nó, kiểm tra chất
lƣợng của một mẫu các sản phẩm có thể xét qua đại lƣợng ngẫu nhiên chỉ cho số
phế phẩm trong mẫu, … Những phép thử nhƣ vậy gọi là phép thử có tính định
lƣợng (các kết quả có dạng là những giá trị số).
Với những phép thử có tính chất định tính (phép thử quan tâm đến tính
chất), để xây dựng đại lƣợng ngẫu nhiên tƣơng ứng ta gắn mỗi một trạng thái kết
quả với một giá trị số. Chẳng hạn, xét với phép thử lấy ngẫu nhiên một viên bi
xem có phải là bi đỏ hay không, nếu là bi đỏ thì ta gắn với giá trị 1, còn nếu 36
CHƢƠNG II: ĐẠI LƢỢNG NGẪU NHIÊN VÀ MỘT SỐ PHÂN PHỐI THÔNG DỤNG lOMoAR cPSD| 35883770
ĐẠI LƢỢNG NGẪU NHIÊN VÀ LUẬT PHÂN PHỐI XÁC XUẤT
không phải là bi đỏ thì sẽ gắn với giá trị 0. Khi đó ta có đại lƣợng ngẫu nhiên với
hai giá trị có thể là 0 và 1.
1.2. Các loại đại lượng ngẫu nhiên
Dựa trên đặc điểm của tập hợp những giá trị có thể nhận, các đại lƣợng
ngẫu nhiên đƣợc xét với hai dạng cơ bản là đại lƣợng ngẫu nhiên rời rạc và đại
lƣợng ngẫu nhiên liên tục.
a) Đại lượng ngẫu nhiên rời rạc
Đại lƣợng ngẫu nhiên rời rạc là đại lƣợng mà các giá trị có thể của nó tạo
nên một tập hợp hữu hạn hay vô hạn đếm đƣợc các giá trị rời rạc, cách quãng nhau.
Số chấm xuất hiện ở mặt trên xúc xắc, số cuộc gọi điện thoại đến một trung
tâm bƣu điện trong một thời gian nào đó, … là những đại lƣợng ngẫu nhiên rời rạc.
b) Đại lượng ngẫu nhiên liên tục
Đại lƣợng ngẫu nhiên liên tục là đại lƣợng mà các giá trị có thể của nó lấp
kín liên tục một khoảng nào đó trên trục số.
Thí dụ, chiều cao của các sinh viên, nhiệt độ không khí tại thành phố Cần
thơ ở một thời điểm nào đó trong ngày, … là những đại lƣợng ngẫu nhiên liên tục.
1.3. Luật phân phối xác suất của đại lượng ngẫu nhiên
Luật phân phối xác suất là quy luật thể hiện mối quan hệ giữa tập hợp, các
khoảng giá trị có thể nhận đƣợc và những xác suất tƣơng ứng để đại lƣợng ngẫu
nhiên nhận các giá trị, khoảng giá trị đó. Ba hình thức thƣờng đƣợc dùng để phản
ánh cho luật phân phối xác suất của đại lƣợng ngẫu nhiên gồm: bảng phân phối
xác suất, hàm mật độ xác suất và hàm phân phối xác suất.
a) Bảng phân phối xác suất
Bảng phân phối xác suất phản ánh luật phân phối xác suất của đại lƣợng
ngẫu nhiên rời rạc. Trong đó ghi rõ các giá trị có thể có và những xác suất tƣơng
ứng của đại lƣợng ngẫu nhiên.
Giả sử đại lƣợng ngẫu nhiên rời rạc X có n giá trị có thể x1, x2, …, xn và các
xác suất tƣơng ứng p1, p2, …, pn. Khi đó, bảng phân phối xác suất của X đƣợc lập dƣới dạng X x1 x2 … xn P p1 p2 … pn CHÚ Ý 1
Trong bảng phân phối xác suất nhƣ trên, ta có: i)
pi = P(X = xi) với i = 1, 2, …, n ii) pi 0 với mọi i n iii) pi = 1 (2.1) i=1
CHƢƠNG II: ĐẠI LƢỢNG NGẪU NHIÊN VÀ MỘT SỐ PHÂN PHỐI THÔNG DỤNG 37 lOMoAR cPSD| 35883770
ĐẠI LƢỢNG NGẪU NHIÊN VÀ LUẬT PHÂN PHỐI XÁC SUẤT
Ví dụ 2: Một lô có 5 ống nghiệm, trong đó có 2 ống kém phẩm chất. Lấy
ngẫu nhiên từ lô ra 3 ống nghiệm để sử dụng. Gọi X là số ống nghiệm kém phẩm
chất trong 3 ống nghiệm lấy ra. Hãy lập bảng phân phối xác suất của X. Giải
Đại lƣợng ngẫu nhiên X có 3 giá trị có thể gồm 0, 1 và 2 với các xác suất tƣơng ứng C 3 P(X = 0) = 3 = 0,1 C 3 5 C 1C 2 P(X = 1) = 2 3 = 0,6 3 C 5 C 2C 1 P(X = 2) = 2 3 = 0,3 3 C 5
Vậy X có bảng phân phối xác suất X 0 1 2 P 0,1 0,6 0,3
b) Hàm mật độ xác suất
Hàm mật độ f(x) của đại lƣợng ngẫu nhiên liên tục X là một hàm không âm
xác định trên toàn trục số sao cho b
P(a X b) = f (x)dx với mọi a, b (2.2) a CHÚ Ý 2
Hàm mật độ f(x) có các tính chất sau i) f(x) 0 với mọi x + ii) f(x)dx = 1 (2.3) −
Ví dụ 3: Cho biết tuổi thọ của một dụng cụ điện là một đại lượng ngẫu
nhiên liên tục X (tính theo đơn vị năm) có hàm mật độ xác suất
0 neáu x [0;3] f(x) =
kx(3 - x) neáu x [0;3] a) Tìm hằng số k.
b) Biết loại dụng cụ trên được bảo hành với thời gian là 1 năm. Tính xác
suất sao cho một dụng cụ chọn ngẫu nhiên bị hỏng trong thời gian bảo hành. Giải
a) Vì f(x) là hàm mật độ xác suất nên + 3 2
f (x)dx= 1 kx(3 − x)dx = 1 k = 9 − 0 38
CHƢƠNG II: ĐẠI LƢỢNG NGẪU NHIÊN VÀ MỘT SỐ PHÂN PHỐI THÔNG DỤNG lOMoAR cPSD| 35883770
ĐẠI LƢỢNG NGẪU NHIÊN VÀ LUẬT PHÂN PHỐI XÁC XUẤT
b) Xác suất cần tìm đƣợc tính bởi 1 1 2 7
P(0 X 1) = f (x)dx = x(3 − x)dx = 9 27 0 0 CHÚ Ý 3
Xác suất đại lƣợng ngẫu nhiên liên tục nhận giá trị cụ thể tại một điểm luôn triệt tiêu bằng 0.
Thật vậy, nếu X là đại lƣợng ngẫu nhiên liên tục có hàm mật độ f(x) và x0 là một giá trị tùy ý, ta có x0 P(X = x f (x)dx = 0 0) = P(x X x ) = 0 0 x0
c) Hàm phân phối xác suất
Hàm phân phối xác suất của đại lƣợng ngẫu nhiên X đƣợc kí hiệu là F(x)
và đƣợc xác định trên toàn trục số bởi công thức F(x) = P(X < x) (2.4) CHÚ Ý 4
Nếu X là đại lƣợng ngẫu nhiên rời rạc có các giá trị có thể x1, x2, …, xn với
các xác suất tƣơng ứng p1, p2, …, pn thì X có hàm phân phối xác định bởi F(x) = p (2.5) i x i x
Nếu X là đại lƣợng ngẫu nhiên liên tục có hàm mật độ f(x) thì x F(x) = f(t)dt (2.6) −
Ví dụ 4: Hãy xác định hàm phân phối xác suất của đại lượng ngẫu nhiên
rời rạc X có bảng phân phối xác suất sau đây X −1 2 5 P 0,5 0,3 0,2 Giải Nếu x −1
thì F(x) = pi = 0 (vì không có giá trị xi nào thỏa xi < 1). x i x
Nếu −1< x 2 thì F(x) = pi = 0,5 (có xi = −1 < x) x i x
Nếu 2 < x 5 thì F(x) = pi = 0,5 + 0, 3 = 0,8 (có −1 và 2 nhỏ hơn x) x i x
Nếu x > 5 thì F(x) = pi = 0,5 + 0, 3 + 0,2 = 1 (vì mọi xi đều nhỏ hơn x) x i x
CHƢƠNG II: ĐẠI LƢỢNG NGẪU NHIÊN VÀ MỘT SỐ PHÂN PHỐI THÔNG DỤNG 39 lOMoAR cPSD| 35883770
ĐẠI LƢỢNG NGẪU NHIÊN VÀ LUẬT PHÂN PHỐI XÁC SUẤT
Tóm lại, X có hàm phân phối xác suất 0 neáu x - 1
F(x) = 0,5 neáu -1 x 2
0,8 neáu 2 x 5 1 neáu x 5
Đồ thị của hàm phân phối xác suất F(x) của đại lƣợng rời rạc X nhƣ trên có dạng hàm bậc thang Hình 2.1
Ví dụ 5: Cho đại lượng ngẫu nhiên liên tục X có hàm mật độ xác suất 0 f(x) =
neáu x 0;
sinx neáu x0; 2
Hãy xác định hàm phân phối xác suất của X. Giải x
Nếu x < 0 thì F(x) = f (t)dt = 0 − x x sin t 1− cosx
Nếu x [0; ] thì F(x) = f (t)dt = dt = 2 2 − 0 x sin t
Nếu x > thì F(x) = f (t)dt = dt = 1 2 − 0
Vậy X có hàm phân phối xác suất 0 neáu x 0
1- cosx neáu F(x) = x 0; 2 1 neáu x 40
CHƢƠNG II: ĐẠI LƢỢNG NGẪU NHIÊN VÀ MỘT SỐ PHÂN PHỐI THÔNG DỤNG lOMoAR cPSD| 35883770
ĐẠI LƢỢNG NGẪU NHIÊN VÀ LUẬT PHÂN PHỐI XÁC XUẤT CHÚ Ý 5
Hàm phân phối xác suất F(x) có các tính chất sau i)
0 F(x) 1 với mọi x ii)
F(− ) = 0, F(+ ) = 1
iii) F(x) là hàm không giảm
iv) Nếu X là đại lƣợng ngẫu nhiên rời rạc thì P(a X < b) = F(b) − F(a) v)
Nếu X là đại lƣợng ngẫu nhiên liên tục có hàm mật độ xác suất f(x) và
hàm phân phối xác suất F(x) thì F’(x) = f(x) Và P(a X BÀI TẬP
1 . Có hai lô sản phẩm, mỗi lô có sáu sản phẩm với số phế phẩm lần lƣợt là hai
và ba. Lấy một sản phẩm từ lô thứ nhất bỏ sang lô thứ hai, sau đó từ lô thứ
hai lấy ngẫu nhiên ra hai sản phẩm. Gọi X là số phế phẩm trong hai sản phẩm lấy ra lần sau.
a/ Hãy lập bảng phân phối xác suất của X.
b/ Tìm hàm phân phối xác suất của X. c/ Tính P(0 < X < 4). 2 .
Cho đại lƣợng liên tục X có hàm mật độ xác suất ax 2 (1 − x), x [0;1] f (x) = 0, x [0;1] a/ Tìm hằng số a.
b/ Tìm hàm phân phối xác suất của X.
c/ Tính P(0,5 < X < 2). 3 .
Cho đại lƣợng ngẫu nhiên liên tục X có hàm phân phối xác suất 0, neâùu x 0 1 2 F(x) =
x (9 − 2x), neâùu 0 x 3 27 1, neâùu x 3 a/ Tính P(2 < X < 5). b/
Tìm hàm mật độ xác suất của X. 4 .
Cho đại lƣợng ngẫu nhiên liên tục X có hàm mật độ xác suất ax 2 (6 − x), x [0;6] f (x) = 0, x [0;6] a/ Tìm hằng số a. b/Tính P(X > 2).
c/ Tìm k để P(X < k) = 1/9.
CHƢƠNG II: ĐẠI LƢỢNG NGẪU NHIÊN VÀ MỘT SỐ PHÂN PHỐI THÔNG DỤNG 41 lOMoAR cPSD| 35883770
ĐẠI LƢỢNG NGẪU NHIÊN VÀ LUẬT PHÂN PHỐI XÁC SUẤT 5 .
Cho đại lƣợng ngẫu nhiên liên tục X có hàm mật độ xác suất 2 0, neâùu x [0; ] 3 f(x) = 2
a(2x − 3x2 ), neâùu x [0; ] 3 a/ Tìm hằng số a.
b/Tính xác suất sao cho trong năm lần quan sát độc lập về X có đúng hai lần 1
X nhận giá trị trong khoảng ( ;1). 3 6 .
Tìm hằng số a chƣa biết trong hàm mật độ xác suất của đại lƣợng liên tục X sau đây: 0, f (x) = x [0;1] ax(1 − x), x [0;1] (a) a = 2 (b) a = 4 (c) a = 6 (d) a = 8 7 .
Tính P(−5 < X < 2) với đại lƣợng ngẫu nhiên liên tục X có hàm phân phối xác suất 0, neâùu x 0 1 F(x) =
x2 (9 − 2x), neâùu 0 x 3 27 1, neâùu x 3 7 20 17 10 (a) (b) (c) (d) 27 27 27 27 8 .
Cho đại lƣợng ngẫu nhiên liên tục X có hàm mật độ phân phối xác suất: 0 neáu x 0
F(x) = k(1 − cos x ) neuá x 0; . 1 neáu x
Hằng số k có giá trị là: (a) 0,5 (b) 1,5 (c) 2 (d) 2,5 9 .
Cho đại lƣợng ngẫu nhiên liên tục có hàm mật độ xác suất 0 x 0;1 f(x) = neáu 1 neáu x 0;1 1
Xác suất P(−1 < X < ) có giá trị là: 3 (a) 0 (b) 1/3 (c) 2/3 (d) 1 42
CHƢƠNG II: ĐẠI LƢỢNG NGẪU NHIÊN VÀ MỘT SỐ PHÂN PHỐI THÔNG DỤNG lOMoAR cPSD| 35883770
CÁC THAM SỐ CỦA ĐẠI LƢỢNG NGẪU NHIÊN § 2.
CÁC THAM SỐ CỦA ĐẠI LƯỢNG NGẪU NHIÊN 2.1. Kỳ vọng a) Định nghĩa
Kỳ vọng của đại lƣợng ngẫu nhiên X đƣợc kí hiệu là E(X) (hay M(X)) và
đƣợc xác định là tổng (tích phân) của các tích giữa các giá trị có thể có của X với
các xác suất (giá trị hàm mật độ) tƣơng ứng.
Nếu X là đại lƣợng ngẫu nhiên rời rạc có các giá trị có thể x1, x2, …, xn với
các xác suất tƣơng ứng p1, p2, …, pn thì X có kỳ vọng n E(X) = x (2.7) i pi i=1
Nếu X là đại lƣợng ngẫu nhiên liên tục có hàm mật độ f(x) thì + E(X) = xf(x)dx (2.8) −
Ví dụ 1: Giả sử điểm thi môn xác suất − thống kê của lớp gồm 100 sinh
viên có 10 sinh viên được điểm 10, 30 sinh viên được điểm 8, 40 sinh viên điểm 6
và 20 sinh viên điểm 4. Chọn ngẫu nhiên một sinh viên của lớp. Gọi X là điểm thi
của sinh viên đó. Hãy tính kỳ vọng E(X) của X. Giải
Đại lƣợng ngẫu nhiên X có bảng phân phối xác suất X 4 6 8 10 P 0,2 0,4 0,3 0,1 Do đó X có kỳ vọng
E(X) = 4.0,2 + 6.0,4 + 8.0,3 + 10.0,1 = 6,6
Ví dụ 2: Cho đại lượng ngẫu nhiên liên tục X có hàm mật độ xác suất 0 f(x) =
neáu x a;b 1
neáu x a;b b − a
Tính kỳ vọng E(X) của X. Giải Ta có + b x a + b E(X) = xf(x)dx = dx = b − a 2 − a
CHƢƠNG II: ĐẠI LƢỢNG NGẪU NHIÊN VÀ MỘT SỐ PHÂN PHỐI THÔNG DỤNG 43 lOMoAR cPSD| 35883770
CÁC THAM SỐ CỦA ĐẠI LƢỢNG NGẪU NHIÊN b) Tính chất i)
Với C là một hằng số và X là đại lƣợng ngẫu nhiên tùy ý ta có E(C) = C E(CX) = CE(X) ii)
Với X và Y là hai đại lƣợng ngẫu nhiên tùy ý ta có E(X Y) = E(X) E(Y)
iii) Nếu X và Y là hai đại lƣợng ngẫu nhiên phân phối độc lập nhau thì E(XY) = E(X)E(Y)
Ví dụ 3: Có ba lô sản phẩm, mỗi lô 10 sản phẩm với số phế phẩm lần lượt
là 1, 2 và 3. Tung một khối tứ diện đều (trong đó có 1 mặt một chấm, 1 mặt hai
chấm và 2 mặt ba chấm ) cho khối tứ diện rơi xuống mặt bàn. Nếu mặt i chấm
của tứ diện chạm bàn thì từ lô thứ i lấy ra 1 sản phẩm (i = 1, 2, 3). Gọi X là số
chấm của mặt tứ diện chạm bàn, Y là số phế phẩm lấy ra và đặt Z = XY. Tính E(X), E(Y) và E(Z). Giải Tính E(X)
Đại lƣợng ngẫu nhiên X có bảng phân phối xác suất X 1 2 3 P 0,25 0,25 0,5
Suy ra E(X) = 1.0,25 + 2.0,25 + 3.0,5 = 2,25. Tính E(Y)
Đại lƣợng ngẫu nhiên Y có hai giá trị có thể là 0 và 1.
Các xác suất tƣơng ứng
P(Y=0) = P(X=1)P(Y=0/x=1) + P(X=2)P(Y=0/X=2) + P(X=3)P(Y=0/X=3)
= 0,25.0,9 + 0,25.0,8 + 0,5.0,7 = 0,775 P(Y=1) = 1 − P(Y=0) = 0,225
Suy ra Y có bảng phân phối xác suất Y 0 1 P 0,775 0,225 Do đó E(Y) = 0,225. Tính E(Z)
Đại lƣợng ngẫu nhiên Z = XY có các giá trị có thể 0, 1, 2, 3 X Z 1 2 3 0 0 0 0 Y 1 2 3 1 44
CHƢƠNG II: ĐẠI LƢỢNG NGẪU NHIÊN VÀ MỘT SỐ PHÂN PHỐI THÔNG DỤNG lOMoAR cPSD| 35883770
CÁC THAM SỐ CỦA ĐẠI LƢỢNG NGẪU NHIÊN Xác suất tƣơng ứng
P(Z = 1) = P([X=1].[Y=1]) = P(X=1).P(Y=1/X=1) = 0,25.0,1 = 0,025
P(Z = 2) = P([X=2].[Y=1]) = P(X=2).P(Y=1/X=2) = 0,25.0,2 = 0,05
P(Z = 3) = P([X=3].[Y=1]) = P(X=3)P(Y=1/X=3) = 0,5.0,3 = 0,15
P(Z = 0) = 1 − P(Z = 1) − P(Z = 2) − P(Z = 3) = 0,775
Vậy Z có bảng phân phối xác suất Z 0 1 2 3 P 0,775 0,025 0,05 0,15
Suy ra Z có kỳ vọng E(Z) = 1.0,025 + 2.0,05 + 3.0,15 = 0,565 Nhận xét
Do hai đại lƣợng X và Y trong ví dụ trên không độc lập nhau nên
E(Z) = E(XY) = 0,565 0.50625 = E(X)E(Y) c) Ý nghĩa
Trong ví dụ 1 ta thấy kỳ vọng của đại lƣợng ngẫu nhiên X (chỉ điểm thi của
sinh viên) chính là trung bình các giá trị có thể của X (điểm trung bình của lớp) 10.10 + 8.30 + 6.40 + 4.20 E(X) = = 6,6 100
Tuy nhiên điều này không đúng trong mọi trƣờng hợp. Chẳng hạn xét đại
lƣợng ngẫu nhiên rời rạc Y có bảng phân phối xác suất nhƣ sau Y −4 4 P 0,25 0,75 Ta có E(Y) = 2 nhƣng Y có
trung bình hai giá trị có thể của nó là
0. Ở đây do giá trị 4 có xác suất
tƣơng ứng lớn hơn nên kỳ vọng Trung bình E(X)
nghiêng về giá trị này hơn. Giống 0
nhƣ phải chọn lựa một điểm tựa giữa
giá trị kỳ vọng là 2 và giá trị trung
bình là 0 để cân bằng hai giá trị có
thể −4 và 4 thì ta sẽ chọn ở giá trị kỳ Trọng tâm
vọng. Qua đó ta thấy kỳ vọng còn
phản ánh trọng tâm phân phối xác Hìmh 2.2
suất của đại lƣợng ngẫu nhiên.
Nhìn chung thì kỳ vọng của đại lƣợng ngẫu nhiên thƣờng gần với giá trị
trung bình. Do đó ngƣời ta hay dùng giá trị kỳ vọng để xấp xỉ giá trị trung bình
(hay ngƣợc lại) và một số trƣờng hợp không có sự phân biệt giữa hai loại giá trị
này. Đồng thời giá trị kỳ vọng cũng thể hiện cho biết trọng tâm phân phối xác
suất của đại lƣợng ngẫu nhiên.
Tóm lại kỳ vọng của đại lƣợng ngẫu nhiên xấp xỉ giá trị trung bình và phản
ánh trọng tâm xác suất của đại lƣợng ngẫu nhiên.
CHƢƠNG II: ĐẠI LƢỢNG NGẪU NHIÊN VÀ MỘT SỐ PHÂN PHỐI THÔNG DỤNG 45 lOMoAR cPSD| 35883770
CÁC THAM SỐ CỦA ĐẠI LƢỢNG NGẪU NHIÊN 2.2. Phương sai a) Định nghĩa
Phƣơng sai của đại lƣợng ngẫu nhiên X đƣợc kí hiệu là Var(X) (hay V(X)
hoặc D(X)) và đƣợc định nghĩa bởi công thức Var(X) = E{[X − E(X)]2} (2.9)
Ví dụ 4: Cho đại lượng ngẫu nhiên rời rạc X có bảng phân phối xác suất X 0 1 2 3 P 0,1 0,2 0,3 0,4 Tính a) E(X) b) E(Y) với Y = X2
c) E(Z) với Z = [X − E(X)]2 d) Var(X) Giải a) E(X) = 2
b) Đại lƣợng Y = X2 có bảng phân phối xác suất Y 0 1 4 9 P 0,1 0,2 0,3 0,4
Suy ra E(Y) = 0.0,1 + 1.0,2 + 4.0,3 + 9.0,4 = 5
c) Ta có Z = [X − E(X)]2 = (X − 2)2. Do đó Z có bảng phân phối xác suất Z 0 1 4 P 0,3 0,6 0,1
Suy ra E(Z) = 0.0,3 + 1.0,6 + 4.0,1 = 1
d) Var(X) = E{[X − E(X)]2} = E(Z) = 1 CHÚ Ý 1
Từ công thức định nghĩa phƣơng sai, ta rút ra công thức tính tƣơng đƣơng khác Var(X) = E(X2) − [E(X)]2 (2.10) Trong đó
− Nếu X là đại lƣợng ngẫu nhiên rời rạc có các giá trị có thể x1, x2, …, xn
với các xác suất tƣơng ứng p1, p2, …, pn thì n E(X2) = xi 2 pi (2.11) i=1
− Nếu X là đại lƣợng ngẫu nhiên liên tục có hàm mật độ f(x) thì 46
CHƢƠNG II: ĐẠI LƢỢNG NGẪU NHIÊN VÀ MỘT SỐ PHÂN PHỐI THÔNG DỤNG lOMoAR cPSD| 35883770
CÁC THAM SỐ CỦA ĐẠI LƢỢNG NGẪU NHIÊN + E(X2) = x 2f(x)dx (2.12) −
Ví dụ 5: Tính phương sai của đại lượng ngẫu nhiên liên tục X có hàm mật độ xác suất 0 f(x) =
neáu x a;b 1
neáu x a;b b − a Giải
Ta có Var(X) = E(X2) − [E(X)]2 a + b
Trong ví dụ 2 ta đã tính đƣợc E(X) = 2 + b x 2
Mặt khác E(X2) = x 2f(x)dx = dx = a 2 + ab + b2 b − a 3 − a a 2 + ab + b2 a + b 2 ( a − b)2 Suy ra Var(X) = − = 3 2 6 b) Tính chất i)
Với C là một hằng số và X là đại lƣợng ngẫu nhiên tùy ý ta có Var(C) = 0 Var(CX) = C2.Var(X) ii)
Nếu X và Y là hai đại lƣợng ngẫu nhiên phân phối độc lập nhau thì Var(X Y) = Var(X) +Var(Y) c) Ý nghĩa
Theo trên ta biết giá trị kỳ vọng phản trọng tâm phân phối xác suất của đại
lƣợng ngẫu nhiên . Do đó |X − E(X)| xác định cho các khoảng cách từ các giá trị
có thể có đến trọng tâm phân phối xác suất. Suy ra [X − E(X)]2 xác định cho bình
phƣơng các khoảng cách từ các giá trị có thể có đến trọng tâm phân phối xác
suất. Do vậy, giá trị phƣơng sai Var(X) = E{[X − E(X)]2} chính là giá trị trung
bình của các bình phƣơng các khoảng cách từ các giá trị có thể có đến trọng tâm
phân phối xác suất. Nghĩa là đại lƣợng ngẫu nhiên có phƣơng sai lớn thì các
khoảng cách từ các giá trị có thể có đến trọng tâm phân phối xác suất lớn (tức là
có độ phân tán lớn) và ngƣợc lại. Như vậy tham số phương sai phản ánh độ phân
tán của đại lượng ngẫu nhiên.
2.3. Độ lệch tiêu chuẩn
Độ lệch tiêu chuẩn của đại lƣợng ngẫu nhiên X đƣợc kí hiệu là (X) hay
X và đƣợc xác định bởi (X) = Var (X) (2.13)
CHƢƠNG II: ĐẠI LƢỢNG NGẪU NHIÊN VÀ MỘT SỐ PHÂN PHỐI THÔNG DỤNG 47 lOMoAR cPSD| 35883770
CÁC THAM SỐ CỦA ĐẠI LƢỢNG NGẪU NHIÊN 2.4. Mode
Tham số Mode của đại lƣợng ngẫu nhiên X đƣợc viết là Mod(X) và đƣợc
hiểu là một giá trị của X có khả năng xảy ra cao nhất, còn đƣợc gọi là giá trị tin chắc nhất.
Nếu X là đại lƣợng ngẫu nhiên rời rạc có các giá trị có thể x1, x2, …, xn với
các xác suất tƣơng ứng p1, p2, …, pn thì
Mod(X) = xi có xác suất pi lớn nhất (2.14)
Nếu X là đại lƣợng ngẫu nhiên liên tục có hàm mật độ f(x) thì
Mod(X) = x0 sao cho f(x) đạt giá trị lớn nhất tại x = x0 (2.15)
Ví dụ 6: Tìm tham số Mode của đại lượng ngẫu nhiên X có hàm mật độ 0 f(x) =
neáu x [0;3]
2 x(3 - x) neáu x [0;3] 9 Giải
Ta chỉ cần xét trên đoạn [0;3]. 2 Ta có f’(x) = (3 − 2x) 9 3 Do đó f’(x) = 0 x = 2 Mặt 3
khác f(0) = f(3) = 0, f( ) = 0,5 2 3
Suy ra f(x) đạt giá trị lớn nhất bằng 0,5 tại x = 2 3 Do đó Mod(X) = 2 BÀI TẬP 1 .
Chọn một câu đúng trong các câu sau về phƣơng sai Var(X) và kỳ vọng
E(X) của đại lƣợng ngẫu nhiên X:
(a) Var(X) = 10, E(X2) = 18, E(X) = 3.
(b) Var(X) = 10, E(X2) = 19, E(X) = 3.
(c) Var(X) = 10, E(X2) = 19, E(X) = 2.
(d) Var(X) = 10, E(X2) = 18, E(X) = 2. 2 .
Cho đại lƣợng ngẫu nhiên rời rạc X có: X 0 1 2 3 P 0,1 0,2 0,4 0,3 Xét 2 kết luận: l) E(X) = l,9 2) Var(X) = D(X) = 0,89. 48
CHƢƠNG II: ĐẠI LƢỢNG NGẪU NHIÊN VÀ MỘT SỐ PHÂN PHỐI THÔNG DỤNG lOMoAR cPSD| 35883770
CÁC THAM SỐ CỦA ĐẠI LƢỢNG NGẪU NHIÊN
(a) Chỉ có kết luận l) đúng.
(b) Chỉ có kết luận 2) đúng.
(c) Cả hai kết luận 1) và 2) đều đúng.
(d) Cả hai kết luận l), 2) đều sai. 3 .
Tính E(X) cuûa ñaïi löôïng lieân tuïc X coù haøm maät ñoä xaùc suaát ax 2 (1 − x), x [0;1] f (x) = 0, x [0;1] (a) − 0.6 (b) 0.6 (c) 0 (d) 1 4 .
Cho X và Y là hai đại lƣợng ngẫu nhiên có E(X) = 2 và E(Y) = 3. Xét hai kết luận: l) E(XY) = 6. 2) E(X+Y) = 5.
Chọn một câu trả lời đúng trong các câu sau:
(a) Chỉ có kết luận 1) đúng.
(b) Chỉ có kết luận 2) đúng.
(c) Cả hai kết luận l) và 2) đều đúng.
(d) Cả hai kết luận l) và 2) đều sai. 5 .
Cho đại lƣợng ngẫu nhiên rời rạc X có bảng phân phối xác suất X −1 1 2 P 0,25 0,25 0,5
Đại lƣợng Y = 2X − 1 có kỳ vọng E(Y) bằng: (a) 0 (b) 1 (c) 2 (d) 3 6 .
Cho đại lƣợng X có E(X) = 1,6 và có bảng phân phối xác suất X −2 0 2 4 P p 0,1 p’ 0,5
Trƣờng hợp nào sau đây đúng? (a) p = p’ = 0,1 (c) p = 0,1; p’ = 0,3 (b) p = 0,3; p’ = 0,1 (d) p = p’ = 0,3 7 .
Cho đại lƣợng ngẫu nhiên rời rạc X có hai giá trị 1 và 2 với các xác suất
P(X=1) = 0,6; P(X=2) = 0,4. Câu nào sau đây đúng? (a) Mod(X) = 0,6 (b) E(X) = 1,2 (c) Var(X) = 0,24 0 neáu x 1
(d) X có hàm phân phối xác suất F(x) = 0,6 neuá 1 x 2 0,4 neuá x 2 8 .
Cho X là đại lƣợng ngẫu nhiên liên tục có hàm phân phối xác suất F(x). Với
a < b, câu nào sau đây sai? (a) P(X = 0) = 0. b (d) E(X) = xF (x)dx (b) F(a) F(b). a (c) P(a < X
CHƢƠNG II: ĐẠI LƢỢNG NGẪU NHIÊN VÀ MỘT SỐ PHÂN PHỐI THÔNG DỤNG 49 lOMoAR cPSD| 35883770
CÁC PHÂN PHỐI RỜI RẠC THÔNG DỤNG
§ 3. CÁC PHÂN PHỐI RỜI RẠC THÔNG DỤNG
3.1. Phân phối nhị thức a) Định nghĩa
Đại lƣợng ngẫu nhiên rời rạc X đƣợc gọi là phân phối xác suất theo quy luật
nhị thức với các giá trị đặc trƣng là n và p nếu X có các giá trị có thể gồm 0, 1, 2,
…, n và các xác suất tƣơng ứng đƣợc tính nhƣ sau P(X = x) = Cx .px .qn−x ; x = 0, 1, …, n (2.16) n
Kí hiệu : XB(n;p) hay X~B(n;p).
b) Các tham số đặc trưng Nếu XB(n;p) thì i) E(X) = np ii)
Var(X) = npq với q = 1 − q
iii) np − q Mod(X) np + p
Ví dụ 1: Xác suất thành công của một thí nghiệm sinh hóa là 90%. Một
nhóm gồm 25 sinh viên tiến hành cùng thí nghiệm trên độc lập với nhau.
a) Tính xác suất sao cho có ít nhất 23 thí nghiệm thành công.
b) Tìm độ lệch tiêu chuẩn của số thí nghiệm thành công.
c) Xác định số thí nghiệm thành công tin chắc nhất. Giải
Gọi X là số thí nghiệm thành công trong các thí nghiệm của nhóm sinh viên. Ta có: XB(25;0,9). a) Xác suất cần tìm
P(X 23) = P(X = 23) + P(X = 24) +P(X = 25) Do XB(25;0,9) nên P(X = 23) = C23 25 .(0,9) 23.(0,1) 2
P(X = 24) = C24.(0,9) 24.(0,1) 1 25 P(X = 25) = C25 25 .(0,9) 25.(0,1) 0 Suy ra
P(X 23) = C9 .(0,9) 9.0,1 + C9 .(0,9) 9.0,1 +C25.(0,9) 25.(0,1) 0 = 0,537094 10 10 25 b) Ta có (X) = Var (X) .
Mặt khác do XB(25;0,9) nên Var(X) = npq = 25.0,9.0,1 Suy ra (X) = 1,5.
c) Số thí nghiệm thành công tin chắc nhất chính là tham số Mode của X.
Do X có phân phối nhị thức nên 50
CHƢƠNG II: ĐẠI LƢỢNG NGẪU NHIÊN VÀ MỘT SỐ PHÂN PHỐI THÔNG DỤNG lOMoAR cPSD| 35883770
CÁC PHÂN PHỐI RỜI RẠC THÔNG DỤNG
np − q Mod(X) np + p
22,5 − 0,1 Mod(X) 22,5 + 0,9 Mod(X) = 23
c) Các công thức tính gần đúng
Nếu XB(n;p) và n khá lớn, p không quá gần 0 và 1thì i) P(X = x0) 1 f (u ) (2.17) 0 npq ii)
P(x1 X x2) (u2) − (u1) (2.18) Trong đó u − np q = 1 − p, u i i = (i = 0, 1, 2) npq 1 −u2 f(u) = e
2 (hàm Gauss, là hàm chẵn) 2 1 u −t2
(u) = e 2 dt (hàm Laplace, là hàm lẻ) 2 0
Ví dụ 2: Xác suất để một chiếc đinh ốc đạt loạt A trong quá trình sản xuất
hàng loạt là 0,8. Tính xác suất sao cho trong 900 đinh ốc được sản xuất ra có
a) Đúng 714 đinh ốc loại A.
b) Từ 708 đến 744 đinh ốc loại A. Giải
Gọi X là số đinh ốc đạt loại A trong 900 đinh ốc sản xuất ra. Ta có XB(900;0,8).
Do n = 900 khá lớn và p = 0,8 không quá gần 0 và 1 nên có thể vận dụng
các công thức tính gần đúng.
a) Xác suất sao cho trong các đinh ốc sản xuất ra có đúng 714 đạt loại A có
thể đƣợc xấp xỉ theo hàm Gauss
714 − 900.0,8 f (−0,5) f (0,5) 1 P(X = 714) f = =
900.0,8.0,2 900.0,8.0,2 12 12 Mà f(0,5) = 0,3521 0,3521 Suy ra P(X = 714) = 0,029342. 12
b) Với hàm Laplace, xác suất trong 900 đinh ốc sản xuất ra có từ 708 đến
744 đinh ốc loại A đƣợc tính gần đúng nhƣ sau
744 − 900.0,8 708 − 900.0,8
P(708 X 732) − 900.0,8.0,2 900.0,8.0,2
CHƢƠNG II: ĐẠI LƢỢNG NGẪU NHIÊN VÀ MỘT SỐ PHÂN PHỐI THÔNG DỤNG 51 lOMoAR cPSD| 35883770
CÁC PHÂN PHỐI RỜI RẠC THÔNG DỤNG
P(708 X 732) (2)− (−1) = (2)+ (1)
P(708 X 732) 0,47725 + 0,34134 = 0,81859
3.2. Phân phối Poisson a) Định nghĩa
Đại lƣợng ngẫu nhiên rời rạc X đƣợc gọi là phân phối xác suất theo luật
Poisson với giá trị đặc trƣng a nếu X có các giá trị có thể gồm 0, 1, 2, … và các
xác suất tƣơng ứng đƣợc tính bởi công thức x a − P(X = x) = e a , x = 0, 1, 2, … (2.19) x!
Kí hiệu: X P(a) hay X ~ P(a). CHÚ Ý 1
Nếu XB(n;p) và n khá lớn, p khá gần 0 thì đại lƣợng X có thể xấp xỉ nhƣ
phân phối Poisson với giá trị đặc trƣng a = np. Khi đó
P(X = x) = Cx .p x .q n−x a x − e a , x = 0, 1, 2, … n x!
b) Các tham số đặc trưng Nếu X P(a) thì i) E(X) = Var(X) = a ii) a − 1 Mod(X) a
Ví dụ 3: Xác suất một người bị phản ứng khi tiêm huyết thanh là 0,002.
a) Tính xác suất sao cho trong 2000 người tiêm huyết thanh có đúng 2
người bị phản ứng.
b) Tìm số người bị phản ứng tin chắc nhất trong 2000 người tiêm. Giải
Gọi X là số ngƣời bị phản ứng trong 2000 ngƣời tiêm huyết thanh. Ta có XB(2000;0,002).
Ta thấy n = 2000 khá lớn và p = 0,002 khá bé nên có thể xấp xỉ
X P(a) với a = np = 2000.0,002 = 4 Do đó 2 4 − a) P(X = 2) = e 4 = 0,146525. 2!
b) Số ngƣời bị phản ứng tin chắc nhất Mod(X) đƣợc xác định bởi a − 1 Mod(X) a 3 Mod(X) 4
Suy ra Mod(X) = 3 hoặc Mod(X) = 4. CHÚ Ý 2 52
CHƢƠNG II: ĐẠI LƢỢNG NGẪU NHIÊN VÀ MỘT SỐ PHÂN PHỐI THÔNG DỤNG lOMoAR cPSD| 35883770
CÁC PHÂN PHỐI RỜI RẠC THÔNG DỤNG
Ngƣời đầu tiên mô tả phân phối Poisson là Simeon Denis Poisson vào năm
1837. Trong thực tế ứng dụng, có nhiều đại lƣợng tuân theo luật Poisson. Thí dụ
nhƣ các đại lƣợng chỉ số cuộc điện thoại nhận đƣợc ở một trạm điện thoại trong
một phút, số khách hàng đến ngân hàng đối với mỗi chu kỳ một giờ đồng hồ, số
máy bị hỏng trong một ngày, … là những dạng đại lƣợng phân phối xác suất theo
quy luật Poisson. Nhìn chung, các đại lƣợng có dạng chỉ cho số lƣợng dòng vào
của một hệ phục vụ (quán bia, hiệu cắt tóc, hiệu sửa xe, trạm điện thoại hay một
cửa hàng nào đó, …) là các đại lƣợng ngẫu nhiên tuân theo luật Poisson.
Ví dụ 4: Số khách hàng vào một cửa hàng bách hóa trong một giờ là đại
lượng ngẫu nhiên tuân theo quy luật Poisson với mật độ trung bình là 8 khách hàng trong một giờ.
a) Tìm xác suất để trong một giờ có 4 khách hàng.
b) Tìm xác suất để trong một giờ có không quá 4 khách hàng. Giải
Gọi X là số khách hàng vào cửa hàng trong một giờ. Ta có X P(8).
a) Xác suất để trong một giờ có 4 khách hàng đến cửa hàng 4 8 − P(X = 4) = e 8 = 0,057252 4!
b) Xác suất để trong một giờ có 4 khách hàng đến cửa hàng 4 8k −8 P(X 4) = = 0,099632 k! e k=0
c) Số khách hàng tin chắc nhất là tham số Mod(X) do đó a − 1 Mod(X) a 7 Mod(X) 8
Do đó Mod(X) = 7 hoặc Mod(X) = 8.
3.3. Phân phối siêu bội a) Định nghĩa
Đại lƣợng ngẫu nhiên X đƣợc gọi là phân phối xác suất theo luật siêu bội
với các giá trị đặc trƣng N, M và n nếu X có các giá trị có thể gồm 0, 1, 2, …, n
và các xác suất tƣơng ứng đƣợc tính bởi Cx Cn−x
P(X = x) = M N−M , x = 0, 1, 2, …, n (2.20) C n N
Kí hiệu XH(N;M;n) hay X~H(N;M;n).
b) Các tham số đặc trưng Nếu X H(N;M;n) thì M i) E(X) = np với p = N
CHƢƠNG II: ĐẠI LƢỢNG NGẪU NHIÊN VÀ MỘT SỐ PHÂN PHỐI THÔNG DỤNG 53 lOMoAR cPSD| 35883770
CÁC PHÂN PHỐI RỜI RẠC THÔNG DỤNG N − n ii) Var(X) = npq với q = 1 − p N −1
Ví dụ 5: Trong một hộp đèn 15 bóng có 5 bóng kém chất lượng. Chọn
ngẫu nhiên không hoàn lại 10 bóng. Tìm phương sai của số bóng kém chất lượng trong mẫu chọn ra. Giải
Gọi X là số bóng kém chất lƣợng trong 10 bóng chọn ra.
Ta có X H(15;5;10). Do đó N − n Var(X) = npq 5 10 5 = 10 = 0,793651 N −1 15 15 14 CHÚ Ý 3
Nếu X H(N;M;n) và N khá lớn so với n thì đại lƣợng X có thể xấp xỉ nhƣ M
phân phối nhị thức XB(n;p) với hai giá trị đặc trƣng n và p = . Khi đó N x n−x C C P(X = x) = M N−M Cx x n−x n .p .q
, q = 1 − p; x = 0, 1, 2, …, n n C M
Ví dụ 6: Từ một lô hàng có 10000 sản phẩm với 8000 sản phẩm loại I, lấy
ngẫu nhiên ra 100 sản phẩm. Tính xác suất sao cho có ít nhất 72 sản phẩm loại I
trong các sản phẩm lấy ra. Giải
Gọi X là số sản phẩm loại I trong 100 sản phẩm lấy ra.
Ta có X H(10000;8000;10).
Do N = 10000 lớn hơn khá nhiều so với n = 100 nên M XB(100;0,8) với p = = 8000 = 0,8 N 10000
Xét trong phân phối nhị thức XB(100;0,8), vì n = 100 khá lớn, p = 0,8
không quá gần 0 và 1 nên xác suất cần tìm đƣợc xấp xỉ bằng hàm Laplace 100 −100.0,8 72 −100.0,8
P(72 X 100) − 100.0,8.0,2 100.0,8.0,2
= (5) − (−2) = (5) + (2) = 0,5 + 0,4772 = 0,9772 CHÚ Ý 4
Khi vận dụng các hàm Excel, tính cho các xác suất tƣơng ứng trong phân phối nhị thức và phân
phối siêu bội đƣợc giới thiệu ở các phần trƣớc. Đối với phân phối Poisson XP(a), xác suất đƣợc tính nhƣ sau x a • −a P(X = x) = e
= POISSON(x,a,FALSE), x = 0, 1, 2, … x! 54
CHƢƠNG II: ĐẠI LƢỢNG NGẪU NHIÊN VÀ MỘT SỐ PHÂN PHỐI THÔNG DỤNG lOMoAR cPSD| 35883770
CÁC PHÂN PHỐI RỜI RẠC THÔNG DỤNG x x a • − a P(X x) = e
= POISSON(x,a,TRUE), x = 0, 1, 2, … k=0 k! BÀI TẬP
1 . Trong 1 ca làm việc một máy tự động sản xuất đƣợc 100 sản phẩm. Xác
suất để 1 sản phẩm đƣợc sản xuất ra bị hƣ là 0,1. Giả thiết rằng quá trình
máy sản xuất ra các sản phẩm là độc lập với nhau.
a/ Tìm quy luật phân phối xác suất của số phế phẩm trong ca.
b/ Tìm số phế phẩm trung bình, số phế phẩm tin chắc nhất và độ lệch
chuẩn của số phế phẩm trong ca.
2 . Một xạ thủ bắn vào bia với xác suất trúng là 0,6. Tìm xác suất sao cho trong 100 phát bắn vào bia có: a/ 50 phát trúng bia.
b/ Không quả 50 phát trúng bia.
3 . Xác suất sinh con trai ở 1 nhà hộ sinh là 0,51. Tìm xác suất sao cho trong
1000 ca đến sinh số bé trai bé hơn số bé gái.
4 . Trong một kho chứa bóng đèn tỷ lệ bóng hoỏng là 50/00 . Xếp các bóng đèn thành từng lô 1000 bóng.
a/ Tính xác suất sao cho trong mỗi lô có không quá 1 bóng đèn bị hỏng.
b/ Tìm số bóng hỏng tin chắc nhất trong lô.
5 . Từ 1 lô hàng gồm 400 sản phẩm, trong đó có 100 sản phẩm loại A, lấy ngẫu
nhiên 80 sản phẩm. Tính số sản phẩm loại A trung bình và độ lệch chuẩn
của số sản phẩm loại A có trong 80 sản phẩm lấy ra.
6 . Trong 1 lô hàng gồm 10000 sản phẩm (trong đó có 4000 sản phẩm loại 1).
Lấy ngẫu nhiên không hoàn lại từ lô ra 10 sản phẩm. Tìm các xác suất sau đây:
a/ Có 3 sản phẩm loại 1 trong 10 sản phẩm lấy ra.
b/ Có ít nhất 1 sản phẩm loại 1 trong 10 sản phẩm lấy ra. 7 .
Cho đại lƣợng ngẫu nhiên X có phân phối siêu bội H(1000;100;10). Xét hai kết luận: 1) E(X) = 1. 2) (X) = 3 .
Chọn một câu đúng trong các câu sau:
(a) Chỉ có kết luận 1) đúng.
(b) Chỉ có kết luận 2) đúng.
(c) Cả hai kết luận 1) và 2) đều sai.
(d) Cả hai kết luận l) và 2) đều đúng. 8 .
Cho đại lƣợng ngẫu nhiên X có phân phối nhị thức B(100;0,1). Đại lƣợng
Y = 10X + 99 có phƣơng sai Var(Y) bằng: (a) 9 (b) 90 (c) 900 (d) 999 9 .
Cho đại lƣợng ngẫu nhiên X có phân phối Poisson P(3). X có giá trị tin chắc nhất (Mod(X)) là
CHƢƠNG II: ĐẠI LƢỢNG NGẪU NHIÊN VÀ MỘT SỐ PHÂN PHỐI THÔNG DỤNG 55 lOMoAR cPSD| 35883770
CÁC PHÂN PHỐI RỜI RẠC THÔNG DỤNG (a) 0 hoặc 1. (c) 2 hoặc 3. (b) 1 hoặc 2. (d) 3 hoặc 4.
10 . Cho đại lƣợng ngẫu nhiên X có phân phối nhị thức B(3;0,5). Xác suất P(X = 1) có giá trị là (a) 0,15 (b) 0,225 (c) 0,375 (d) 0,5
11 . Cho đại lƣợng ngẫu nhiên X có phân phối siêu bội H(100;50;10).
Đại lƣợng Y = 2X2 có kỳ vọng E(Y) là (a) 59,5 (b) 59 (c) 59,05 (d) 59,09
12 . Cho đại lƣợng ngẫu nhiên X có phân phối siêu bội H(6;4;2).
Khi đó xác suất P(X = 0) có giá trị là 1 C 2 (a) 2 (c) 4 C 4 C 2 6 1 (b) 2 (d) C 2 6 C 2 6
13 . Cho hai đại lƣợng ngẫu nhiên X và Y độc lập nhau, với X có phân phối
Poisson P(2), Y có phân phối nhị thức B(25; 0,8). Var( X − Y) có giá trị là: (a) 6 (b) 2 (c) 2,8 (d) 1,2
14 . Cho đại lƣợng ngẫu nhiên liên tục X có phân phối Poisson P(4). Khi đó, E(2X) có giá trị là: (a) 2 (b) 4 (c) 6 (d) 8
15 . Có hai lô sản phẩm: lô I có 5 sản phẩm với 2 phế phẩm, lô II với 4 sản
phẩm đều là chính phẩm. Lấy 1 sản phẩm từ lô I bỏ sang lô II, sau đó từ lô
II lấy ngẫu nhiên 1 sản phẩm. Tính xác suất sản phẩm lấy từ lô II là phế phẩm? (a) 1/20 (b) 1/25 (c) 1/10 (d) 2/25
16 . Nếu đại lƣợng ngẫu nhiên liên tục X phân phối Poisson P(5) thì xác suất
P(X = 2) đƣợc tính bởi: 52 25 e −5 (a) (c) 2!e −5 5! 52 e −5 25 (b) (d) 2! 5!e −5 56
CHƢƠNG II: ĐẠI LƢỢNG NGẪU NHIÊN VÀ MỘT SỐ PHÂN PHỐI THÔNG DỤNG lOMoAR cPSD| 35883770
CÁC PHÂN PHỐI LIÊN TỤC THÔNG DỤNG
§ 4. CÁC PHÂN PHỐI LIÊN TỤC THÔNG DỤNG
4.1. Phân phối chuẩn a) Định nghĩa
Đại lƣợng ngẫu nhiên liên tục X đƣợc gọi là phân phối xác suất theo quy
luật chuẩn với các giá trị đặc trƣng là và 2 nếu X có hàm mật độ xác suất nhƣ sau (x−)2 1 − f(x) = e 22 (2.21) 2
Kí hiệu : XN( ; 2) hay X~N( ; 2).
b) Các tham số đặc trưng
Nếu XN( ; 2) thì i) E(X) = Mod(X) = ii) Var(X) = 2
Các kết quả trên có thể nhận thấy một cách trực quan nhờ vào dạng đồ thị
của hàm phân phối chuẩn 3 2 1 Hình 2.3 Qua đồ thị ta thấy
• Phân phối chuẩn XN( ; 2) đối xứng qua trục đi qua điểm .
• là điểm mà hàm mật độ của phân phối chuẩn đạt cực đại.
• càng lớn thì phân phối chuẩn càng phân tán ( 1 > 2 > 3).
c) Phân phối chuẩn hóa
Đại lƣợng ngẫu nhiên X phân phối xác suất theo luật chuẩn nếu có trung
bình = 0 và phƣơng sai 2 = 1 đƣợc gọi là phân phối xác suất theo luật chuẩn hóa.
Kí hiệu: X N(0;1) hay X~N(0;1).
CHƢƠNG II: ĐẠI LƢỢNG NGẪU NHIÊN VÀ MỘT SỐ PHÂN PHỐI THÔNG DỤNG 57 lOMoAR cPSD| 35883770
CÁC PHÂN PHỐI LIÊN TỤC THÔNG DỤNG CHÚ Ý 1 • X −
Nếu X có phân phối chuẩn N( ; 2) thì U = có phân phối chuẩn hóa N(0;1).
• Phân phối chuẩn hóa có hàm mật độ là hàm Gauss 1 −u2 f(u) = e 2 (2.24) 2
Đồ thị của hàm mật độ phân phối chuẩn hóa có dạng hình chuông nhận trục
tung làm trục đối xứng và tạo với trục hoành một miền phẳng có giá trị diện tích bằng 1. Hình 2.4
• Phân phối chuẩn hóa có hàm phân phối xác suất 1 u −t2
(u) = e 2 dt (với (−u) = 1 − (u)) (2.23) 2 −
Các giá trị thƣờng dùng của hàm phân phối (u) đƣợc tính sẵn lập thành
một bảng số với lƣu ý (−u) = 1 − (u). d) Phân vị chuẩn
Phân vị chuẩn mức xác suất đƣợc kí hiệu là z và đƣợc định nghĩa là một
giá trị của đại lƣợng ZN(0;1) sao cho P(Z < z ) = .
Các giá trị thƣờng dùng của phân vị chuẩn đƣợc tính sẵn lập thành một bảng số.
CHÚ Ý 2 z = −z . 1−
e) Các công thức tính xác suất
Nếu XN( ; 2) thì x − i)
P(X < x) = x − = 0,5 + . (2.24) 58
CHƢƠNG II: ĐẠI LƢỢNG NGẪU NHIÊN VÀ MỘT SỐ PHÂN PHỐI THÔNG DỤNG lOMoAR cPSD| 35883770
CÁC PHÂN PHỐI LIÊN TỤC THÔNG DỤNG − − x − x − ii)
P(x < X < x ) = x 2 − x1 = 2 − 1 (2.25) 1 2
iii) P(|X − | < ) = 2 − 1 = 2 . (2.26) 1 u −t2 1 u −t2 Trong đó (u) =
e 2 dt , (u) = e 2 dt (Lƣu ý: 2 − 2 0 (u) = (u) + 0,5).
Ví dụ 1: Trong hệ thống tỷ giá hối đoái thả nổi, sự biến động của tỷ giá
hối đoái chịu sự tác động của rất nhiều nhân tố và có thể xem như biến ngẫu
nhiên phân phối chuẩn. Giả sử ở một giai đoạn nào đó tỷ giá của USD với VND
có trung bình là 15500 đồng và độ lệch tiêu chuẩn là 500 đồng. Tìm xác suất để
trong một ngày nào đó
a) Tỷ giá sẽ thấp hơn 14500 đồng.
b) Tỷ giá sẽ cao hơn 16000 đồng.
c) Tỷ giá sẽ nằm trong khoảng từ 14500 đồng đến 16500 đồng. Giải
Gọi X là đại lƣợng chỉ cho tỷ giá hối đoái của USD với VND. Ta có XN(15500;5002).
a) Ta có P(X < 14500) = 14500 −15500 = (2) = 0,9772 500 b) Xác suất cần tìm
P(X > 16000) = 1 − P(X < 16000) = 1 − 16000 −15500 500
= 1 − (1) = 1 − 0,8413 = 0,1587. c) Ta có
P(14500 < X < 16500) = 16500 −15500 − 14500 −15500 500 500
= (2)− (−2) =2 (2)−1 = 2.0,9772−1 = 0,9544
4.2. Phân phối 2 (khi − bình phương) a) Định nghĩa
Đại lƣợng ngẫu nhiên V đƣợc gọi là phân phối xác suất theo luật 2 với n
bậc tự do, kí hiệu V 2 (n) hay V ~ 2 (n) , nếu V đƣợc xác định bởi V = X2 + X2 + ... + X2 (2.27) 1 2 n Trong đó • X i
N(0;1) với mọi i = 1, 2, …, n.
CHƢƠNG II: ĐẠI LƢỢNG NGẪU NHIÊN VÀ MỘT SỐ PHÂN PHỐI THÔNG DỤNG 59 lOMoAR cPSD| 35883770
CÁC PHÂN PHỐI LIÊN TỤC THÔNG DỤNG
• Các đại lƣợng X1, X2, …, Xn có phân phối độc lập nhau. CHÚ Ý 3
Phân phối 2 với n bậc tự do có hàm mật độ 0, neáu x 0 −x n −1 fn(x) = e 2 x 2 neáu x 0 (2.28) n 2 2 (n ) 2 + Trong đó (x) = t x−1e−tdt (Hàm Gamma) 0 b) Các tham số
Nếu V 2 (n) thì E(V) = n và Var(V) = 2n. c) Phân vị 2
Phân vị 2 mức xác suất và n bậc tự do đƣợc kí hiệu là 2 (n) và đƣợc
định nghĩa là một giá trị của đại lƣợng V 2 (n) sao cho P(V > 2 (n) ) = .
Các giá trị thƣờng dùng của phân vị 2 đƣợc tính sẵn lập thành một bảng số.
4.3. Phân phối student a) Định nghĩa
Đại lƣợng ngẫu nhiên T đƣợc gọi là phân phối xác suất theo quy luật
student với n bậc tự do, kí hiệu TT(n) hay T ~T(n) , nếu X đƣợc xác định bởi U n T = (2.29) V Trong đó
• UN(0;1), V 2 (n).
• Các đại lƣợng U và V có phân phối độc lập nhau. CHÚ Ý 4
Hàm mật độ của đại lƣợng ngẫu nhiên có phân phối student với n bậc tự do có dạng x 2 −n+1 2 n +1 1 + n 2 fn(x) = n (2.30) n 2 60
CHƢƠNG II: ĐẠI LƢỢNG NGẪU NHIÊN VÀ MỘT SỐ PHÂN PHỐI THÔNG DỤNG lOMoAR cPSD| 35883770
CÁC PHÂN PHỐI LIÊN TỤC THÔNG DỤNG + Trong đó (x) = t x−1e−tdt (Hàm Gamma) 0 b) Các tham số Nếu n
TT(n) thì E(T) = 0 và Var(T) = . n − 2 c) Phân vị student
Phân vị student mức xác suất và n bậc tự do đƣợc kí hiệu là t (n) và
đƣợc định nghĩa là một giá trị của đại lƣợng TT(n) sao cho P(T > t (n) ) = .
Các giá trị thƣờng dùng của phân vị student đƣợc tính sẵn lập thành một bảng số. 4.4. Phân phối mũ a) Định nghĩa
Đại lƣợng ngẫu nhiên X đƣợc gọi là có phân phối mũ với tham số 0
nếu nó có hàm mật độ xác suất. e−x nếu f (x) = x 0 (2.31) 0 nếu x 0 CHÚ Ý 5
Nếu X có phân phối mũ với tham số thì hàm phân phối xác suất của X là x
F(x) = e−xdt = 1− e−x với x>0 0 và F(x) = 0 với x 0
b) Các tham số đặc trưng
Nếu X là đại lƣợng ngẫu nhiên có phân phối mũ với tham số thì + + + 1 • Kỳ vọng của X là −x −x −x dx =
E(X) = xe dx = − xe + e 0 0 0 + 1
• Phƣơng sai của X là Var (X) = x 2 e−x dx − 2 0
Tích phân từng phần ta đƣợc + + − −
x 2 e x dx − 1 = − x 2 e −x + + x dx = 2 0 2 xe 0 2 0 2 Do đó Var (X) = 1 2
Ví dụ 2: Giả sử tuổi thọ (tính bằng năm) của một mạch điện tử trong máy
tính là một đại lượng ngẫu nhiên có phân phối mũ với kỳ vọng là 6,25. Thời gian
CHƢƠNG II: ĐẠI LƢỢNG NGẪU NHIÊN VÀ MỘT SỐ PHÂN PHỐI THÔNG DỤNG 61 lOMoAR cPSD| 35883770
CÁC PHÂN PHỐI LIÊN TỤC THÔNG DỤNG
bảo hành của mạch điện tử này là 5 năm. Hỏi có bao nhiêu phần trăm mạch điện
tử bán ra phải thay thế trong thời gian bảo hành? Giải
Gọi X là tuổi thọ của mạch . Thì X có phân phối mũ Ta có 1 = = 1 E(X) 6,25 − 5
P(X 5) = F(5) = 1− e−5 = 1− e 6,25 = 1− e−0,8 = 1− 0,449 = 0,5506
Vậy có khoảng 55% số mạch điện tử bán ra phải thay thế trong thời gian bảo hành .
c) Ứng dụng thực tế
Khoảng thời gian giữa hai lần xuất hiện của một biến có phân phối mũ.
Chẳng hạn khoảng thời gian giữa hai ca cấp cứu ở một bệnh viện, giữa hai lần
hỏng hóc của một cái máy, giữa hai trận lụt hay động đất là những đại lƣợng
ngẫu nhiên có phân phối mũ .
4.5. Phân phối đều a) Định nghĩa
Đại lƣợng ngẫu nhiên liên tục X đƣợc gọi là phân phối đều trên đoạn [a,b]
nếu là hàm mật độ xác suất có dạng 1
nếu x a,b f (x) = b − a (2.32) nếu 0
x a,b NHẬN XÉT
Nếu X có phân phối đều trên a, b thì hàm phân phối của X cho bởi F(x) = 0 nếu x a x x d(x) x − a F(x) = f (x)dx = =
nếu a x b − b - a b − a a F(x) = 1 nếu x b CHÚ Ý 6
Giả sử (,) a, b. Xác suất để X rơi vào (,) là −
P( X ) = f (x)dx = b − a
b) Các tham số đặc trưng b xdx 1 b2 − a 2 a + b E(X) = = = b − a b − a 2 2 a
(kỳ vọng là điểm trung bình điểm của[a,b]. 62
CHƢƠNG II: ĐẠI LƢỢNG NGẪU NHIÊN VÀ MỘT SỐ PHÂN PHỐI THÔNG DỤNG lOMoAR cPSD| 35883770
CÁC PHÂN PHỐI LIÊN TỤC THÔNG DỤNG b x 2 dx 2 1 x 3 b = − a + b Var (X) = − E(X) b − a 3 2 a b − a a ( ( = b2 + ab + a 2 a + b)2 b − a)2 − = 3 4 12
Mod(X) là bất cứ điểm nào trên [a,b].
Ví dụ 3: Lịch chạy của xe buýt tại 1 trạm xe buýt như sau: chiếc xe buýt
đầu tiên trong ngày sẽ khởi hành từ tra45mna2y lúc 7 giờ, cứ sau mỗi 15 phút sẽ
có 1 xe khác đến trạm. Giả sử một hành khách đến trạm trong khoảng thời gian 7
giờ đến 7g30. Tìm xác suất để hành khách này chờ. a) Ít hơn 5 phút b) Ít nhất 12 phút Giải
Gọi X là số phút sau 7 giờ mà hành khách đến trạm X là đại lƣợng ngẫu
nhiên có phân phối đều trong khoảng (0,30)
a) Hành khách sẽ chờ ít hơn 5 phút nếu đến trạm giữa 7g10 và 7g15 hoặc
giữa 7g25 và 7g30. Do đó xác suất cần tìm là 1
P(10 X 15) + P(25 X 30) = 5 + 5 = 30 30 3
b) Hành khách sẽ chờ ít nhất 12 phút nếu đến trạm giữa 7giờ và 7giờ 3
phút hoặc giữa 7u15 và 7g18 phút. Xác suất cần tìm là 1
P(0 X 3) + P(15 X 18) = 3 + 3 = 30 30 5 CHÚ Ý 5
Có thể dùng các hàm Excel để tính các giá trị của hàm mật độ, hàm phân phối trong phân phối
chuẩn, phân phối chuẩn hóa cũng nhƣ tra tìm các giá trị phân vị: ( )2 x− 1 − • f(x) = e 22
= NORMDIST(x, , ,FALSE) (2.33) 2 ( t − )2 x − • 1 F(x) = e 2
dt = NORMDIST(x, , ,TRUE) (2.34) 2 0 1 u • (u) = −t 2 e 2 dt = NORMSDIST(x) (2.35) 2 −
• Cho V 2 (n), ta có
− Xác suất P(V > x) = CHIDIST(x,n) (2.36) − 2
Phân vị ;n = CHIINV(1− ,n) (2.37) • Cho TT(n), ta có
− Xác suất P(T > x) = TDIST(x,n,1) và P(|T| > x) = TDIST(x,n,2) (2.38)
− Phân vị t ;n = TINV((1− )*2,n) (2.39)
CHƢƠNG II: ĐẠI LƢỢNG NGẪU NHIÊN VÀ MỘT SỐ PHÂN PHỐI THÔNG DỤNG 63 lOMoAR cPSD| 35883770
CÁC PHÂN PHỐI LIÊN TỤC THÔNG DỤNG BÀI TẬP
1 . Trọng lƣợng của 1 loại trái cây là đại lƣợng ngẫu nhiên phân phối theo quy
luật chuẩn với trung bình là 250g và phƣơng sai là 25. Quả đƣợc gọi là loại
1 nếu có trọng lƣợng từ 255g trở lên. Tìm tỷ lệ quả loại 1 của loại trái cây đó.
2 . Chiều cao nam giới đã trƣởng thành là một đại lƣợng ngẫu nhiên phân phối
theo quy luật chuẩn N(160;36). Tìm xác suất để khi chọn ngẫu nhiên 4 nam
thì có ít nhất 1 ngƣời có chiều cao nằm trong khoảng (158;162).
3 . Một chi tiết máy đƣợc gọi là đạt tiêu chuẩn kỹ thuật nếu nhƣ đƣờng kính
của nó sai lệch so với đƣờng kính thiết kế (đƣờng kính trung bình) không
quá 0,33 cm về giá trị tuyệt đối. Cho biết đƣờng kính của loại chi tiết máy
đó là đại lƣợng ngẫu nhiên phân phối xác suất theo quy luật chuẩn với độ lệch tiêu chuẩn là 0,3.
Tìm số chi tiết máy đạt tiêu chuẩn trung bình khi sản xuất 100 chi tiết máy.
4 . Cho XN(10;4) , tính các xác suất sau a/ P(− 5 < X < 12,13) c/ P(X < 0,21) b/ P(|X − 10| < 1,64) d/ P(X > 13,25) 5 .
Tra bảng phân vị student và phân vị 2 tìm các giá trị phân vị sau a/ t0,9;15 e/ 2 0,99;24 b/ t0,975;27 f/ 2 0,95;20 c/ t0,995;30 d/ 2 0,05;12 6 .
Cho đại lƣợng X phân phối theo quy luật chuẩn với hàm mật độ f(x) = x 2 +1 1 x− e 2
. Trƣờng hợp nào dƣới đây cho kỳ vọng và phƣơng sai của X là 2 đúng? (a) E(X) = Var(X) = 0 (c) E(X) = 1, Var(X) = 0 (b) E(X) = 0, Var(X) = 1 (d) E(X) = Var(X) = 1 7 .
Cho X là đại lƣợng ngẫu nhiên liên tục có phân phối chuẩn N(10; 100). Kết quả nào sau đây là sai:
(a) P(0 < X < ) = 0,5
(c) P(10 < X < 16) = 0,2257 (b) P(X > 14) = 0,3446 (d) P(X < 8) = 0,4207 64
CHƢƠNG II: ĐẠI LƢỢNG NGẪU NHIÊN VÀ MỘT SỐ PHÂN PHỐI THÔNG DỤNG lOMoAR cPSD| 35883770
ĐẠI LƢỢNG NGẪU NHIÊN HAI CHIỀU § 5.
ĐẠI LƯỢNG NGẪU NHIÊN HAI CHIỀU
Trong thực tế nhiều khi phải xét đồng thời nhiều đại lƣợng khác nhau có
quan hệ tƣơng hỗ và dẫn tới khái niệm đại lƣợng ngẫu nhiên nhiều chiều. Chẳng
hạn khi nghiên cứu một chi tiết máy, ta quan tâm đồng thời đến nhiều khía cạnh
khác nhau nhƣ trọng lƣợng, kích thƣớc (riêng nó đã là nhiều chiều), chất lƣợng,
chất liệu... Việc nghiên cứu riêng rẽ từng khía cạnh có thể cho ta các thông tin không đầy đủ.
Để cho đơn giản, ta nghiên cứu đại lƣợng ngẫu nhiên 2 chiều (X,Y), trong
đó X và Y là các đại lƣợng một chiều. Hầu hết các kết quả có thể mở rộng khá dễ
dàng cho đại lƣợng n chiều. Nếu X và Y là rời rạc, ta có đại lƣợng ngẫu nhiên hai
chiều rời rạc; nếu chúng liên tục, ta có đại lƣợng hai chiều liên tục. Sẽ phức tạp
hơn với trƣờng hợp một đại lƣợng là rời rạc và một đại lƣợng là liên tục mà ta không xét ở đây.
5.1. Hàm phân phối xác suất a) Định nghĩa
Hàm phân phối xác suất của đại lƣợng hai chiều ( X; Y) đƣợc xác định nhƣ sau F (x, y) = P (X(2.40) b) Tính chất
Tƣơng tự nhƣ trƣờng hợp một chiều, ta có thể dẫn ra một số tính chất của
hàm phân phối hai chiều. (i ) 1 F (x,y) 0.
(ii ) F(x,y) không giảm theo từng đối số.
(iii ) F(−,y) = F(x,−) = 0, F( +,+ ) = 1.
(giá trị hiểu theo nghĩa lấy giới hạn) (iv ) P(x 1 X CHÚ Ý 1
F (x, +) = P (XF (+ ; y) = P (X <+ ; YCác hàm F1(x), F2(y) là các phân phối của riêng từng thành phần X và Y
tƣơng ứng; chúng đƣợc gọi là các phân phối biên của đại lƣợng hai chiều (X, Y).
Đó cũng chính là các phân phối (một chiều) thông thƣờng của X và Y. CHÚ Ý 2
Hai đại lƣợng ngẫu nhiên X và Y đƣợc gọi là độc lập nếu F(x.y) = F1(x) F2(y) (2.41)
Tất nhiên nếu X và Y độc lập, ta có thể nghiên cứu riêng rẽ từng đại lƣợng
theo các phƣơng pháp đã có và từ các phân phối biên của X và Y có thể xác định
đƣợc phân phối của (X,Y) theo (2.41). Tuy nhiên chúng không đủ để xác định
phân phối đồng thời nếu X và Y không độc lập.
CHƢƠNG II: ĐẠI LƢỢNG NGẪU NHIÊN VÀ MỘT SỐ PHÂN PHỐI THÔNG DỤNG 65 lOMoAR cPSD| 35883770
ĐẠI LƢỢNG NGẪU NHIÊN HAI CHIỀU
5.2. Bảng phân phối xác suất của đại lượng ngẫu nhiên hai chiều rời rạc
Bảng phân phối xác suất của đại lƣợng (X,Y) rời rạc có dạng Y y1 y2 ... yj ... ym X j x1 P11 P12 ... P1j ... P1m p1(x1) x P P ... P ... P . 2 . 21 . 22 . . 2j . . 2m p1( x . 2) . . . .. . .. . . x P P P P . i . i 1 p x . i 2 ... . i j ... . i m 1(. i) . . . . . . xn Pn 1 Pn 2 ... Pn j ... Pn m p1(xn) P2(y1) P2(y2) ... P2(yj) ... P2(ym) 1 i
Trong đó pij = P(X=xi,Y=yj) là xác suất đồng thời để X lấy giá trị
xi, i = 1, n và Y lấy giá trị yj, j=1, m . Bảng này có thể trở thành vô hạn khi n,m nhận giá trị . CHÚ Ý 3
Ta có thể tìm đƣợc hàm phân phối xác suất từ bảng phân phối xác suất F(x,y) = p (2.42) ij x i x yiy
Các phân phối biên của đại lƣợng hai chiều có thể đƣợc xác định
P(X= xi) = p1(xi) = p , i = 1, n (2.43) ij j
P(Y= yi) = p2(yi) = p , i = 1, m (2.44) ij j
Ví dụ 1: Cho bảng phân phối đồng thời của X và Y Y 1 2 3 X 1 0,1 0,25 0,1 2 0,15 0,05 0,35
Tìm luật phân phối xác suất của các đại lượng X và Y, sau đó tính F (2,3). Giải
Lấy tổng hàng và tổng cột tƣơng ứng của bảng số, ta có các phân phối biên cần tìm X 1 2 Y 1 2 3 P 0,45 0,55 P 0,25 0,3 0,45 Việc
tính F(2,3) dựa vào (2.42):
F(2,3) = p = p + p = 0,35 ij 11 12 xi 2 y j 3 66
CHƢƠNG II: ĐẠI LƢỢNG NGẪU NHIÊN VÀ MỘT SỐ PHÂN PHỐI THÔNG DỤNG lOMoAR cPSD| 35883770
ĐẠI LƢỢNG NGẪU NHIÊN HAI CHIỀU
Từ CHÚ Ý 2, hai đại lƣợng rời rạc X, Y đƣợc gọi là độc lập nếu với mọi
cặp giá trị xi, yj ta luôn có Pij = p1 (xi) p2 ( yj);
i = 1, n ; j = 1, m (2.45)
Rõ ràng trong thí dụ 1 ta thấy p11 = 0,1 p1(1).p2(1) = 0,1125. Vậy hai đại
lƣợng X và Y ở đây không độc lập.
Bây giờ giả sử Y lấy một giá trị cố định nào đó và ta muốn quan tâm đến
luật phân phối xác suất của X có bị ảnh hƣởng không. Theo công thức xác suất
có điều kiện ở chƣơng I P(X = x ; Y = y ) P( X = x i k i /Y = yk) = , i = 1, n (2.46) P(Y = y ) k
Vậy ta có thể định nghĩa luật phân phối có điều kiện của X biết Y nhận giá
trị yk cụ thể. Tƣơng tự có thể xác luật phân phối có điều kiện của Y biết X nhận
một giá trị cụ thể nào đó.
Ví dụ 2: Tìm phân phối có điều kiện của X biết rằng Y = 1 trong bài toán ở thí dụ 1. Giải Ta có P(X = 1, Y = 1) P(X = 1/ Y = 1) = = p 0,10 11 = = 0,4 P(Y = 1) p (1) 0,25 2 0,15 P(X = 2 / Y = 1) = P21 = = 0,6 P (1) 0,25 2
Bảng phân phối xác suất có điều kiện của X biết Y = 1 là X 1 2 P(x/Y=1) 0,4 0,6
5.3. Hàm mật độ của đại lượng ngẫu nhiên hai chiều liên tục
Khái niệm hàm phân phối xác suất của đại lƣợng hai chiều (X,Y) liên tục đã
đƣợc xét ở định nghĩa 5.1 . Ta sẽ đƣa ra khái niệm hàm mật độ của (X,Y) nhƣ sau: a) Định nghĩa
Nếu hàm phân phối F(x,y) của đại lượng hai chiều (X,Y) có dạng x y
F(x, y) = f (u, v)dudv (2.47) −−
trong đó f(x,y)>0, thì hàm f(x,y) được gọi là hàm mật độ của đại lượng
(X,Y), hay hàm mật độ đồng thời của X và Y.
Về mặt hình học, hàm F(x,y) có thể xem nhƣ là một mặt cong trong R3 và
đƣợc gọi là mặt phân phối xác suất. Nếu F(x,y) liên tục theo cả hai đại lƣợng thì
CHƢƠNG II: ĐẠI LƢỢNG NGẪU NHIÊN VÀ MỘT SỐ PHÂN PHỐI THÔNG DỤNG 67 lOMoAR cPSD| 35883770
ĐẠI LƢỢNG NGẪU NHIÊN HAI CHIỀU F(x, y) f (x, y) = (2.48) xy
Dạng hàm phân phối thƣờng khá phức tạp, nên ngƣời ta hay dùng hàm mật độ. b) Tính chất
Hàm mật độ đại lƣợng hai chiều(X,Y) có các tính chất quan trọng sau: (i ) f(x,y) 0 ++
(ii ) f (x, y)dxdy = 1 −−
(iii ) P[(X,Y) D] = f (x, y)dxdy D CHÚ Ý 4
Các hàm mật độ biên của đại lƣợng (X;Y) đƣợc xác định bởi: + f (x) = 1
f (x, y)dy − + f ( y) = 2
f (x, y)dx − F Để 1 ý f
và là mật độ của đại lƣợng thành phần X,
1 (x) cũng chính bằng x
tƣơng tự đối với f ( y) . 2
Ví dụ 3: Tìm các hàm mật độ biên của đại lượng (X,Y) có hàm mật độ hai chiều
f (x, y) = 1
, x, y R
2 (1 + x2 )(1 + y 2 ) Giải Dễ thấy 1 + 1 1 f (x) = dy = 1 2 − (1+ x 2 )(1+ y2 ) (1+ x 2 )
Do x và y đối xứng nhau nên ta cũng đƣợc kết quả tƣơng tự với f2(x).
c) Hàm mật độ có điều kiện
Hai đại lƣợng ngẫu đƣợc gọi là độc lập, nếu f (x, y) = f (x)f (y) 1 2
Nếu mật độ đồng thời của X và Y không bằng tích các mật độ biên f và f 1 2
ta nói X và Y không độc lập. Trong trƣờng hợp đó có thể đƣa vào khái niệm hàm
mật độ có điều kiện của thành phần X biết Y = y đƣợc xác định là f (x, y) (x y) = = f (x, y) (2.49) + f (y) 2 f (x, y)dx − 68
CHƢƠNG II: ĐẠI LƢỢNG NGẪU NHIÊN VÀ MỘT SỐ PHÂN PHỐI THÔNG DỤNG lOMoAR cPSD| 35883770
ĐẠI LƢỢNG NGẪU NHIÊN HAI CHIỀU
Tƣơng tự (x y) là hàm mật độ có điều kiện của Y biết X = x cụ thể nào
đó, nó sẽ bằng f(x,y)/f1(x). Chú ý rằng các mật độ có điều kiện cũng thoả mãn
các tính chất của hàm mật độ bình thƣờng.
Ví dụ 4: Cho hàm mật độ đồng thời f (x) = x + y,0 x, y 1. Xác định các
hàm mật độ có điều kiện. Giải
Trƣớc hết ta phải tính các f (x) và f (y) là các mật độ biên 1 2 1 1 f (x) = 1
(x + y)dy = x + ,0 x 1; 2 0 1
Tƣơng tự f (y) = y + ,0 y 1; 2 2
Từ đó, với 0 y 1, ta có x + y 0 x 1 , (x y) = y + 0,5 0, x [0,1]
Và với 0 x 1 x + y , 0 y 1 (y x) = x + 0,5 0, y [0,1]
Để ý là hàm mật độ có điều kiện (x y) là hàm của x, đồng thời nếu coi y
là tham số thì nó cũng là hàm của y. Ta có f (x, y) = f (y)(x y) = f (x)(y x) và 2 1
rõ ràng nếu (x y) = f (x) (hoặc (y x) = f (y)) thì X và Y độc lập. 1 2
5.4. Các tham số đặc trưng của đại lượng ngẫu nhiên hai chiều
a) Các tham số đặc trưng của đại lượng thành phần
Các đại lƣợng X và Y đã có các số đặc trƣng quan trọng là kỳ vọng và
phƣơng sai. Ở đây ta nhắc lại kết quả đã biết có để ý đến các khái niệm mới ở
chƣơng này, các công thức chỉ viết cho đại lƣợng X, đối với Y hoàn toàn tƣơng
tự . − Nếu X là đại lƣợng rời rạc
E(X) = x p (x ) = x p(x , x ); i 1 i i i j i i j
Var (X) = (x − EX)2 p (x ) = x 2 p(x , x ) − (E(X))2 . i 1 i i i j i i j
− Nếu X là đại lƣợng liên tục + ++ E(X) = xf (x)dx = (x, y)dxdy; 1 xf − −− + ++
Var (X) = (x − EX)2 f (x)dx = 1
x 2 f (x, y)dxdy − (E(X)) 2 . − −−
CHƢƠNG II: ĐẠI LƢỢNG NGẪU NHIÊN VÀ MỘT SỐ PHÂN PHỐI THÔNG DỤNG 69 lOMoAR cPSD| 35883770
ĐẠI LƢỢNG NGẪU NHIÊN HAI CHIỀU
b) Hiệp phương sai và hệ số tương quan
Hiệp phƣơng sai của hai đại lƣợng X và Y đƣợc ký hiệu là và đƣợc XY định nghĩa
= E[(X − EX)(Y − EY)] = E(XY) − E(X)E(Y) XY
Chú ý là phép toán lấy E ở bên ngoài dấu ngoặc móc không giống trƣờng
hợp đại lƣợng một chiều. Phụ thuộc vào (X;Y) là rời rạc hay liên tục, ta có
= x x p(x , x ) − E(X)E(Y) (2.50) XY i j i j i j = (2.51) XY
xyf (x, y)dxdy − E(X)E(Y) −−
Dễ thấy phƣơng sai là trƣờng hợp riêng của hiệp phƣơng sai khi X = Y và Var (X) =
. Hiệp phƣơng sai đƣợc dùng làm độ đo quan hệ giữa hai đại lƣợng XX
X và Y; nếu chúng đồng đại lƣợng cùng nhau thì hiệp phƣơng sai dƣơng, nếu
chúng nghịch đại lƣợng ta có hiệp phƣơng sai âm.
Ta biết nếu X và Y độc lập thì E(XY) = E(X)E(Y), điều đó kéo theo hiệp
phƣơng sai của hai đại lƣợng độc lập bằng 0. Nhƣng điều ngƣợc lại không chắc
đúng. Vì vậy ta đƣa vào khái niệm mới: nếu
= 0 , ta nói rằng X và Y không XY tƣơng quan.
Rõ ràng khái niệm độc lập là mạnh hơn không tƣơng quan. Nhiều khi để
đơn giản ký hiệu, ngƣời ta tập hợp các hiệp phƣơng sai của một vectơ ngẫu
nhiên vào một ma trận gọi là ma trận hiệp phƣơng sai; trong trƣờng hợp đại
lƣợng hai chiều (X,Y) đó là Var (X) XY = Var (Y) YX
Trên đƣờng chéo chính là các phƣơng sai, và do = XY YX nên ma trận này đối xứng .
Hiệp phƣơng sai có hạn chế cơ bản là khó xác định đƣợc miền biến thiên,
nó thay đổi từ cặp biến này sang cặp biến khác. Chƣa kể về mặt vật lý nó có đơn
vị đo bằng bình phƣơng đơn vị đo của X và Y ( nếu chúng cùng đơn vị đo). Vì
thế ngƣời ta đƣa ra một số đặc trƣng khác gọi là hệ số tƣơng quan, ký hiệu là rXY,
đƣợc xác định nhƣ sau: r = XY (2.52) XY X Y
Có thể chứng minh rằng r
1.Nếu r = 1, ta có hai đại lƣợng X và Y XY XY
tƣơng quan dạng tuyến tính (tức là tồn tại a và b sao cho Y=aX + b); còn nếu r
= 0 thì X và Y không tƣơng quan. Nói chung 0 r 1, trong trƣờng hợp XY XY
này ta nói rằng hai đại lƣợng X và Y tƣơng quan với nhau. Hai đại lƣợng tƣơng
quan thì phụ thuộc (không độc lập), nhƣng ngƣợc lại chƣa chắc đúng. 70
CHƢƠNG II: ĐẠI LƢỢNG NGẪU NHIÊN VÀ MỘT SỐ PHÂN PHỐI THÔNG DỤNG lOMoAR cPSD| 35883770
ĐẠI LƢỢNG NGẪU NHIÊN HAI CHIỀU
Ví dụ 5: Tính hiệp phương sai và hệ số tương quan của X và Y trong thí dụ 1. Giải
Ta phải tính Var(X), Var(Y) và E(XY) − E(X)E(Y). Hai bảng phân phối
biên đã tìm đƣợc trong thí dụ 1: X 1 2 Y 1 2 3 P 0,45 0,55 P 0,25 0,3 0,45
Ta có ngay E(X) = 1,55 ; E(Y) = 2,20; Var(X) = 0,2475; Var(Y) = 0,66. Tính
E(XY) = x x p(x , y ) = i j i j i j
= 1.1.0,10 +1.2.0,25 +1.3.0,10 + 2.1.0,15 + 2.2.0,05 + 2.3.0,35 = 3.50. Từ đó hiệp phƣơng sai
= E(XY) − E(X)E(Y) = 3,50 −1,55.2,20 = 0,09 . XY
Hệ số tƣơng quan đƣợc tính = XY = 0,09 0,22 XY Var (X).Var (Y) 0,2475 .0,66
Ví dụ 6: Đại lượng ngẫu nhiên hai chiều (X,Y) có hàm mật độ 1 ,
4x 2 + y 2 4
f (x, y) = 2
0, 4x 2 + y 2 4
Chứng tỏ X và Y phụ thuộc và tính hiệp phương sai . XY Giải
Các hàm mật độ biên đƣợc tính + 2 1 − x 2 , x 1 f (x) = f (x, y)dy = 1 − 0, x 1 + 1 4 − y2 , y 2 f (y) = f (x, y)dy = 2 2 − 0, y 2
Do f (x, y) f (x)f (y) nên X và Y phụ thuộc. 1 2
Vì f (x) và f (y) là các hàm chẵn nên đồ thị đối xứng qua các trục tƣơng 1 2
ứng và E(X) = E(Y) = 0, từ đó = XY xyf (x; y)dxdy −−
CHƢƠNG II: ĐẠI LƢỢNG NGẪU NHIÊN VÀ MỘT SỐ PHÂN PHỐI THÔNG DỤNG 71 lOMoAR cPSD| 35883770
ĐẠI LƢỢNG NGẪU NHIÊN HAI CHIỀU 1 1 2 1−x 2 = 2 xdx
ydy = 0 (Tích phân trong lấy theo hàm lẻ có cận đối xứng). −1 −2 1−x 2
Rõ ràng X và Y không tƣơng quan, nhƣng vẫn phụ thuộc nhau.
c) Các số đặc trưng có điều kiện
Dùng các khái niệm xác suất có điều kiện và hàm mật độ có điều kiện ta có
thể định nghĩa kỳ vọng có điều kiện của đại lƣợng ngẫu nhiên X với Y = y là một
giá trị xác định nhƣ sau:
E(X y) = x P(X = x Y = y) (X rời rạc), (2.53) i i i
E(X y) = x(x y)dx (X liên tục) (2.54) −
Tƣơng tự, ta định nghĩa cho kỳ vọng có điều kiện E(Y x) là một hàm phụ
thuộc x, và trong thống kê ngƣời ta gọi là hàm hồi quy của Y đối với X. Đồ thị
của hàm đó trên mặt phẳng tọa độ Đề-Các có tên gọi là đƣờng hồi quy. Sau này
ta sẽ dùng hồi quy để biểu diễn sự phụ thuộc tƣơng quan giữa các đại lƣợng ngẫu nhiên (xem chƣơng VI).
Để ý là các kỳ vọng có điều kiện E(X Y) , E(Y X) ( cũng nhƣ các số đặc
trƣng có điều kiện khác) là các đại lƣợng ngẫu nhiên nên đến lƣợt mình nó lại có
thể có những đặc số tƣơng ứng.
Ví dụ 7: Cho bảng phân phối của đại lượng (X,Y) Y 1 2 3 X 2 0,15 0,08 0,27 4 0,10 0,20 0,20
Tính các kỳ vọng có điều kiện E( X y1); E(Y x2 ) Giải Ta có p 0,15 P(X=2 Y = 1) = 11 = = 0,6; p (1) 0,25 2 p 0,10 P(X=4 Y = 1) = 21 = = 0,4 p (1) 0,25 2
Từ đó E(X = 4 Y = 1) = 2.06 + 4.0,4 = 2,8 Tƣơng tự p 0,10 P(X=1 X = 4) = 21 = = 0,2; p (4) 0,50 2 p 0,20 P(Y=2 X = 4) = 22 = = 0,4; p (4) 0,50 2 72
CHƢƠNG II: ĐẠI LƢỢNG NGẪU NHIÊN VÀ MỘT SỐ PHÂN PHỐI THÔNG DỤNG lOMoAR cPSD| 35883770
ĐẠI LƢỢNG NGẪU NHIÊN HAI CHIỀU p 0,20 P(Y=3 X = 4) = 23 = = 0,4 p (4) 0,50 2
Và từ đó suy ra E (Y X = 4) = 1.0,2 + 2.0,4 + 3.0,4 = 2,2
Cuối cùng, lƣu ý đến một số tính chất của kỳ vọng có điều kiện E (Y X )
(i) với mọi g liên tục E[g (X)Y X ] = g(X)E(Y X ) ;
(ii) E ( X1 + X2 X ) = E (X1 X ) + E(X2 X );
(iii) Nếu X, Y độc lập E (Y X ) = E (Y) ;
(iv) E [E(Y X ) ] = E(Y) BÀI TẬP
1 . Một túi chứa 10 thẻ đổ và 6 thẻ xanh. Chọn ngẫu nhiên ra 3 tấm thẻ (không hoàn lại).
a/ Gọi X là số thẻ đỏ. Tìm phân bố xác xuất của X, E(X) và Var(X).
b/ Giả sử rút mỗi thẻ đỏ đƣợc 5 điểm và rút mỗi thẻ xanh đƣợc 8 điểm. Gọi
X là số điểm tổng cộng trên 3 thẻ rút ra. Tìm phân bố xác xuất của Y. Tìm EY, DY. 2 .
Các ĐLNN X và Y có bảng phân bố xác xuất đồng thời nhƣ sau : Y 1 2 3 X 1 0,12 0,15 0,03 2 0,28 0,35 0,07
a/ Chứng minh rằng X và Y độc lập.
b/ Tìm quy luật phân bố của Z = XY. Từ đó tính E(Z) và kiểm tra rằng E(Z) = E(X) + E(Y).
3 . Số trẻ em sinh ra trong một tuần của làng A nào đó là một ĐLNN X có phân phối xác xuất là X 0 1 2 3 P 0,4 0,3 0,2 0,1
Số ngƣời chết trong 1 tuần ở làng A đó là một ĐLNN Y có phân bố xác xuất là Y X 0 1 2 3 4 P 0,1 0,3 0,4 0,15 0,05
Giả sử rằng X và Y độc lập
a/ Tìm phân bố xác xuất đồng thời của X và Y, b/ Tính P X Y.
CHƢƠNG II: ĐẠI LƢỢNG NGẪU NHIÊN VÀ MỘT SỐ PHÂN PHỐI THÔNG DỤNG 73 lOMoAR cPSD| 35883770
ĐẠI LƢỢNG NGẪU NHIÊN HAI CHIỀU 4 .
Cho X, Y là hai ĐLNN có phân bố xác suất đồng thời nhƣ sau : Y −1 1 X −1 1/6 1/4 0 1/6 1/8 1 1/6 1/8 Hãy tính E(X), E(Y), và r XY XY. 5 .
Cho X, Y là hai ĐLNN có phân bố xác suất đồng thời nhƣ sau : Y − 1 0 1 X −1 4/15 1/15 4/15 0 1/15 2/15 1/15 1 0 2/15 0
a/ Tính E(X), E(Y), XY và rXY.
b/ X và Y có độc lập hay không? 6 .
Cho X, Y có hàm mật độ đồng thời là
cx neáu 0 y x 1 f (x , y) = 0 neáu traùi laïi a/ Tìm c.
b/ Tìm các hàm mật độ của X và Y.
c/ X và Y có độc lập hay không ? 7 .
Cặp (X, Y) có hàm mật độ là 1 x 2 y 2 neáu + 1 f (x , y) = 6 9 4 0 neáu traùi laïi
Tìm hàm mật độ của X và Y. 8 .
Cho ĐLNN hai chiều (X, Y) có hàm mật độ f (x , y) = ( )
1 + x 2 )(1 + y 2 a/ Tìm hằng số c.
b/ Tìm hàm phân bố của (X, Y).
c/ X và Y có độc lập không ?
d/ Tìm xác suất để điểm (X, Y) rơi vào hình chử nhật với các đỉnh là
A(1,1), B( 3,1), C(1,0) và D( 3,1). 9 .
Giả sử X và Y là hai ĐLNN độc lập có phân phối đều trên 0,2.
Tính P XY 1, Y 2X, X 2Y.
10 . Hai ngƣòi bạn hẹn gặp nhau tại một vƣờn hoa trong khoảng từ năm đến 6
giờ để cùng đi thăm thầy giáo cũ. Họ quy ƣớc rằng sẽ đợi nhau không quá 5
phút. Tính xác suất để họ cùng đi đến nhà thầy giáo. 74
CHƢƠNG II: ĐẠI LƢỢNG NGẪU NHIÊN VÀ MỘT SỐ PHÂN PHỐI THÔNG DỤNG lOMoAR cPSD| 35883770
HÀM CỦA CÁC ĐẠI LƢỢNG NGẪU NHIÊN § 6.
HÀM CỦA CÁC ĐẠI LƯỢNG NGẪU NHIÊN
6.1. Hàm của một đại lượng ngẫu nhiên
Nếu ta xác định Z = g(X) là một hàm của đại lƣợng ngẫu nhiên X thì Z trở
thành một đại lƣợng ngẫu nhiên mới. Nếu X rời rạc thì Z là đại lƣợng rời rạc, còn
nếu X liên tục thì Z cũng liên tục. Vấn đề đặt ra là tìm cách xác định luật phân
phối của Z qua luật phân phối đã biết của X. Ở đây ta chỉ xét các trƣờng hợp đơn
giản khi hàm g không quá phức tạp.
a) Trường hợp X rời rạc
Ví dụ 1: Cho đại lượng ngẫu nhiên X có luật phân phối X −2 −1 0 1 2 P 0,1 0,2 0,3 0,2 0,2
Xác định luật phân phối của Z = X2 và tìm kỳ vọng của Z. Giải
Dễ thấy P(Z = 0) = P(X = 0) = 0,3.
Z = 1 X = −1 hoặc X = 1, suy ra P (Z = 1) = 0,2 + 0,2 = 0,4.
Z = 4 X = −2 hoặc X = 2, suy ra P ( Z = 4) = 0,1 + 0,2 = 0,3.
Từ đó bảng phân phối của Z = X2 là Z 0 1 4 P 0,3 0,4 0,3
Xuất phát từ luật phân phối trên, ta có
E(Z) = z P(Z = z ) = 0.0,3 +1.0,4 + 4.0,3 = 1,6 i i i CHÚ Ý
Trong trƣờng hợp Z = g(X) tổng quát, ta có thể tính trực tiếp kỳ vọng của Z
không cần qua luật phân phối của nó
E(Z) = g(x )P(X = x ) = g(x )p i i i i (2.55) i i
Trong ví dụ trên, dễ thấy
E(Z) = (−2)2.0,1 + (−1)2.0,2 + 02.0,3 +11.0,2 + 22.0,2 = 1,6. (2.56)
b) Trường hợp X liên tục
Khi X là đại lƣợng ngẫu nhiên liên tục, vấn đề sẽ phức tạp hơn. Giả sử X có
hàm mật độ f(x) đã biết và Z = g(X), trong đó g là hàm đơn điệu sao cho tồn tại
hàm ngƣợc X = (Z) = g−1(Z).
Khi đó hàm mật độ của (z) của đại lƣợng Z = g(X) sẽ là
(z) = f ψ(z) ψ' (z) .
CHƢƠNG II: ĐẠI LƢỢNG NGẪU NHIÊN VÀ MỘT SỐ PHÂN PHỐI THÔNG DỤNG 75 lOMoAR cPSD| 35883770
HÀM CỦA CÁC ĐẠI LƢỢNG NGẪU NHIÊN
Ví dụ 2: Đại lượng ngẫu nhiên X tuân theo luật phân phối mũ với tham số 1
= . Tìm luật phân phối xác suất của đại lượng Z = X3. 2 Giải
Vì hàm y = x3 là đơn điệu tăng và khả vi, do đó có thể áp dụng công thức
(z) = f ψ(z) ψ' (z) . 1
Dễ thấy (y) = y 3 = x,
Mặt khác do hàm mật độ của X có dạng f(x) = e-x , x > 0
nên nếu đặt (z) là hàm mật độ của Z = X3, ta có 1 −2 λ 3 = = − 3 = z (z) f ψ(z) ψ' (z) λe λ . z z , z 0 3 3 33 z2 e−λ
6.2. Hàm của hai đại lượng ngẫu nhiên
Xét đại lƣợng ngẫu nhiên Z = g(X,Y), trong đó (X;Y) là đại lƣợng ngẫu
nhiên 2 chiều đã biết luật phân phối xác suất. Nếu g là một hàm tùy ý thì bài toán
xác định luật phân phối của Z qua luật phân phối của (X;Y) sẽ rất phức tạp. Ta sẽ
xét một trƣờng hợp đơn giản g(X,Y) = X + Y.
a) Trường hợp các đại lượng X, Y rời rạc
Theo công thức xác suất đầy đủ (tổng lấy theo i sao cho xi + yi = zk):
P(Z = zk) = P(X = x ; Y = z − x ) (hoặc =
− y ;Y = y )) i k i
P( X = zk j j i i
= P(X = x )P(Y = z − x X = x ) i k i i i Nếu X và Y độc lập
P(Z = zk) = P(X = x )P(Y = z − x ) i k i i
Ví dụ 3: Cho luật phân phối của (X, Y) có dạng Y 2 3 4 X 1 0 0,15 0,05 2 0,20 0,10 0 3 0,25 0,05 0,20
Xác định luật phân phối xác suất của Z = X + Y. Giải
Tập giá trị của Z = X + Y là { 3,,4,5,6,7}, từ đó
P(Z = 3) = P( X= 1, Y = 2) = 0
P(Z = 4) = P(X=1,Y=3) +P(X=2, Y= 2) = 0,15 + 0,20 = 0,35 76
CHƢƠNG II: ĐẠI LƢỢNG NGẪU NHIÊN VÀ MỘT SỐ PHÂN PHỐI THÔNG DỤNG lOMoAR cPSD| 35883770
HÀM CỦA CÁC ĐẠI LƢỢNG NGẪU NHIÊN
P(Z = 5) = P(X=1,Y=4)+P(X=2,Y=3)+P(X=3,Y=2) = 0,05 +0,10 +0,25 = 0,40;
P(Z=6) = P(X=2,Y=4)+P(X=3,Y=3) = 0 + 0,05 = 0,05;
P(Z=7) = P(X=3, Y = 4) = 0,20.
Từ đó bảng phân phối xác suất của Z là Z 4 5 6 7 P 0,35 0,4 0,05 0,2
Ví dụ 4: Cho X và Y là đại lượng ngẫu nhiên độc lập tuân theo luật
Poisson với các tham số tương ứng và . Tìm luật phân phối của Z = X+Y Giải Theo công thức P(Z = z − k) = P(X = x )P(Y = z x ) ta có i k i i z − λx μz−x P(Z = z) = e λ e−μ ; x, y,z N x=0 x! (z − x)!
Nhân và chia vế phải với z! (λ + μ) e−(λ+μ) z −(λ+μ) x x z−x P(Z = z) = z! C λ μ = e z z! x=0
Hệ thức cuối cho thấy Z = X + Y cũng tuân theo luật Poisson với tham số + .
b) Trường hợp các đại lượng X,Y liên tục
Gọi (z) là hàm phân phối của đại lƣợng Z = X+Y, ta có
(z) = P (Z< z) = P (X + Y < z)
Biểu diễn tập giá trị của ( X, Y) sao cho X + Y < z là miền D nên theo tính
chất (iii) của hàm mật độ 2 chiều +z−x
(z) = P(( X ,Y) D) = f (x, y)dxdy = f(x, y)dydx D −−
Lấy đạo hàm hai vế theo z và gọi (z) = '(z) là mật độ của Z + (z) = f(x, z − x)dx −
Tƣơng tự nếu ta thay đổi trình tự lấy tích phân + (z) = f(z − y,y)dy −
Trong trƣờng hợp riêng, khi X và Y độc lập, ta có + +
(z) = f (x)f (z − x)dx = (z − y)f (y)dy 1 2 f1 2 − −
CHƢƠNG II: ĐẠI LƢỢNG NGẪU NHIÊN VÀ MỘT SỐ PHÂN PHỐI THÔNG DỤNG 77 lOMoAR cPSD| 35883770
HÀM CỦA CÁC ĐẠI LƢỢNG NGẪU NHIÊN
Ví dụ 5: Cho hai đại lượng X, Y độc lập cùng với phân phối đều trên đoạn
[ 0,1] ( tức hàm mật độ f1 (x) = f2(x) =1 khi x [ 0,1]). Tìm hàm mật độ và hàm
phân phối của Z = X + Y. Giải
Để ý rằng cả hai hàm mật độ của X và Y đều bằng 0 khi đối số nằm ngoài
[ 0,1]. Gọi (z) là hàm mật độ của Z = X + Y, ta có 1
(z) = f (x)f (z − x)dx 1 2 0
Do f1(x) và f2(x) có giá trị khác không trên [0,1], nên (z) chỉ có thể có giá
trị khác không trên [0,2]. Ta tính lần lƣợt: Nếu z 0, (z) = 0; Nếu 0 < z 1, ta có z 1
(z) = f (x)f (z − x)dx + (x)f (z − x)dx; 1 2 f1 2 0 z z
Do tích phân thứ hai bằng 0 bởi f2 = 0 suy ra (z) = dx = z; 0
Nếu 1 < z 2 hay 0 z-1 1
(z) = f (x)f (z − x)dx + f (x)f (z − x)dx; 1 2 1 2 0 z-1 1
Do tích phân thứ hai bằng 0 bởi f2 0, suy ra (z) = dx = 2 − z; z −1 Nếu z >2 , (z) = 0
Từ đó mật độ của Z = X +Y sẽ là 0, z 0, z, 0 z 1, (z) = 2 − z, 1 z 2, 0, z 2
Đại lƣợng ngẫu nhiên Z có hàm mật độ nhƣ trên đƣợc gọi là tuân theo luật
phân phối tam giác, hay phân phối Xim-xơn. Việc tìm hàm phân phối của Z không có gì phức tạp: 0 z 0, z2 0 z 1, (z) = 2 1− (2 − z)2 1 z 2, 2 1, z 2, 78
CHƢƠNG II: ĐẠI LƢỢNG NGẪU NHIÊN VÀ MỘT SỐ PHÂN PHỐI THÔNG DỤNG lOMoAR cPSD| 35883770
HÀM CỦA CÁC ĐẠI LƢỢNG NGẪU NHIÊN
c) Các số đặc trưng của hàm các đại lượng ngẫu nhiên
Khi muốn tính các số đặc trƣng (kỳ vọng, phƣơng sai,...) của đại lƣợng
ngẫu nhiên Z = g( X,Y), đã biết luật phân phối xác suất của Z, ta không gặp trở
ngại gì lớn. Tuy nhiên việc xác định luật phân phối của Z khá phức tạp. Trong
thực tế nhiều khi ta chỉ cần quan tâm đến các số đặc trƣng của Z là đủ.
Chẳng hạn trong trƣờng hợp khi X và Y là các đại lƣợng rời rạc và đã biết
phân phối đồng thời p(xi ; yj ).
E(Z) = E[g(X, Y)] = g(x y )p(x ; y ). i j i j i j
Nếu (X,Y) liên tục có hàm mật độ f(x,y) thì
E(Z) = g(x, y)f(x, y)dxdy. R 2 BÀI TẬP 1.
Cho X và Y là hai đại lƣợng độc lập có phân phối nhƣ sau: X 12 20 30 Y 2 3 P 0,2 0,3 0,5 P 0,4 0,6
Đặt Z1 = X + Y, Z2 = XY. Tìm bảng phân phối xác suất của Z1 và Z2. 2.
Cho đại lƣợng ngẫu nhiên hai chiều (X, ) có bảng phân phối xác suất Y 10 11 12 13 X 1 0,01 0,10 0,20 0,08 2 0,06 0,12 0,21 0,02 3 0,02 0,09 0,05 0,04
Tìm phân phối xác suất của Z = X + Y. 3.
Cho X, Y là các đại lƣợng ngẫu nhiên độc lập XP(3), YP(5). Đặt Z = X + Y.
a) Hãy tìm phân phối của Z. b) Hãy tính P(X=3/Z=4). 4.
Giả sử X và Y là các đại lƣợng ngẫu nhiên độc lập với XB(4;0,5),
YB(10;0,4). Tìm phân phối xác suất của Z = X + Y. 5.
Cho X, Y là các đại lƣợng ngẫu nhiên độc lập.
X có hàm mật độ xác suất: f(x) = e− x nếu x > 0 ( = 0 nếu x 0). 1 − y Y có hàm mật độ g(y) = e
2 nếu y > 0 ( = 0 nếu x 0). 2
Tìm hàm mật độ Z = X + Y.
CHƢƠNG II: ĐẠI LƢỢNG NGẪU NHIÊN VÀ MỘT SỐ PHÂN PHỐI THÔNG DỤNG 79 lOMoAR cPSD| 35883770 CHƢƠNG III TỔNG THỂ VÀ MẪU
§ 1. ĐẠI LƢỢNG NGẪU NHIÊN GỐC VÀ MẪU NGẪU NHIÊN
1.1. Khái niệm tổng thể và mẫu a) Tổng thể
Đối tƣợng nghiên cứu của xác suất thống kê là các đại lƣợng biến thiên.
Chúng có thể biểu thị về số lƣợng, chất lƣợng, đặc tính của các vấn đề kinh tế, xã
hội, kỹ thuật đƣợc quan tâm. Tổng thể nghiên cứu trong thống kê đƣợc hiểu là
tập hợp tất cả các phần tử mang những thông tin liên quan đến một vấn đề cần
khảo sát nào đó. Kí hiệu số phần tử của tổng thể là N.
Khi khảo sát về chiều cao trung bình của các sinh viên của một trƣờng đại
học thì tổng thể nghiên cứu là tập hợp tất cả các sinh viên đang theo học ở trƣờng
đó. Muốn tính thu nhập trung bình của một hộ gia đình ở thành phố Cần thơ thì
tổng thể sẽ là tất cả các hộ của thành phố.
Kỳ vọng của đại lƣợng ngẫu nhiên gốc E(X) = m đƣợc gọi là trung bình của
tổng thể và phƣơng sai Var(X) = 2 cũng đƣợc gọi là phƣơng sai của tổng thể.
Giả sử tổng thể có N phần tử với đại lƣợng ngẫu nhiên gốc X. Giá trị của X
trên phần tử thứ i là Xi (i = 1, 2, …, N), tức N trị số của X là X1, X2, …, XN. Khi
đó X có bảng phân phối xác suất X X1 X2 … XN P 1 1 … 1 N N N Tổng 1 N
thể có kỳ vọng m = E(X) = X (3.1) N i i=1 Phƣơng 2 = 1 N sai tổng thể Var (X) = 1 N (X − m)2 X2 − m2 (3.2) i = i N i=1 N i=1
Ví dụ 1: Một công ty có N = 25 nhân viên. Lương tháng X (đơn vị triệu
đồng) của các nhân viên như sau
3,0 3,5 3,8 4,4 4,5 3,2 3,8 4,0 4,0 5,0 4,4 5,0 4,5
5,0 4,5 3,8 3,5 3,2 4,0 4,4 4,5 3,5 3,5 4,0 4,4
Tính trung bình và phương sai của trị số lương tháng các nhân viên của công ty. Giải 80
CHƢƠNG III: TỔNG THỂ VÀ MẪU lOMoAR cPSD| 35883770
ĐẠI LƢỢNG NGẪU NHIÊN GỐC VÀ MẪU NGẪU NHIÊN
Tổng thể các nhân viên trong công ty có trung bình trị số lƣơng 3,0 + 3,5 + ... + 4,4 m = = 4,056 25 ( Phƣơng sai 3,0)2 + (3,5)2 + ... + (4,4)2 2 =
− (4,056 )2 = 0,318464 25 CHÚ Ý
Nếu đại lƣợng gốc X có trị số Xi lập lại Ni lần. Khi đó các trị số có thể sắp
xếp lại theo mức giá trị Xi tăng dần Xi X1 X2 … Xk Ni N1 N2 … Nk k
Với Ni là tần số xuất hiện của giá trị Xi; N = N . i i=1
Khi đó, trung bình tổng thể 1 N m = E(X) = N X (3.3) i i N i=1 Phƣơng sai tổng thể 1 2 = Var (X) = N 1 N (X − m)2 = i i N N X2 − m2 (3.4) N i i i=1 N i=1
Chẳng hạn trong Ví dụ 1, các trị số của tổng thể X có thể ghi lại dƣới dạng bảng nhƣ sau Xi 3,0 3,2 3,5 3,8 4,0 4,4 4,5 5,0 Ni 1 2 4 3 4 4 4 3 Tính toán khi này:
(3,0).1+ (3,2).2 + ... + (5,0).3 m = = 4,056 25 (
3,0)2 .1+ (3,2)2 .2 + ... + (5,0)2 .3 2 = − (4,056 )2 = 0,318464 25 b) Phƣơng pháp mẫu
Trong thực tế, khó có thể (và thƣờng là không thể) khảo sát tất cả các phần
tử của tổng thể. Từ tổng thể ngƣời ta kiểm tra, quan sát trên một nhóm phần tử
đại diện gọi là mẫu. Số phần tử nằm trong mẫu gọi là kích thƣớc mẫu hay cỡ
mẫu, kí hiệu n. Với các thông tin thu đƣợc từ mẫu, bằng các phƣơng pháp khoa
học ngƣời ta rút ra kết luận chung cho cả tổng thể. Phƣơng pháp làm việc nhƣ
vậy đƣợc gọi là phƣơng pháp mẫu.
Có hai phƣơng thức cơ bản thƣờng đƣợc dùng để lấy một mẫu đại diện từ tổng thể:
− Lấy mẫu có hoàn lại: chọn ngẫu nhiên từ tổng thể ra một phần tử để
kiểm tra, ghi lại các số đặc trƣng cần thiết từ phần tử đó, sau đó trả nó trở lại tổng
thể trƣớc khi chọn tiếp ngẫu nhiên lần sau. Kết quả ở từng lần chọn độc lập với nhau.
CHƢƠNG III: TỔNG THỂ VÀ MẪU 81 lOMoAR cPSD| 35883770
ĐẠI LƢỢNG NGẪU NHIÊN GỐC VÀ MẪU NGẪU NHIÊN
− Lấy mẫu ngẫu nhiên không hoàn lại: tƣơng tự nhƣ trên, chỉ khác ở chỗ
là các phần tử đƣợc chọn ra sẽ không đƣợc trả lại tập ban đầu. Khi đó các kết quả
ở các lần chọn phụ thuộc nhau.
Quay giải nhất của xổ số gồm năm chữ số bằng cách dùng một bộ số, một
bàn quay và quay 5 lần, đó là lấy mẫu có hoàn lại năm lần. Kiểm tra một số hộp
sữa để đánh giá chất lƣợng của lô sữa, những hộp sữa đƣợc lấy ngẫu nhiên ra
chính là lấy mẫu không hoàn lại.
1.2. Đại lƣợng ngẫu nhiên gốc và mẫu ngẫu nhiên
Trong phân tích thống kê ngƣời ta chấp nhận giả thiết rằng các phần tử của
một tổng thể nào đó đều đƣợc cảm sinh bởi một đại lƣợng ngẫu nhiên gốc. Trong
thực hành đại lƣợng ngẫu nhiên gốc thƣờng tuân theo luật phân phối chuẩn, hoặc
chƣa biết rõ dạng, hoặc chƣa biết tham số. Việc phân tích lý thuyết để xác định
xác định thông phân phối của đại lƣợng gốc sẽ dựa trên các nghiên cứu mẫu ngẫu nhiên.
Tiến hành n quan sát độc lập về đại lƣợng ngẫu nhiên gốc X (xác định cho
dấu hiệu nào đó trên các phần tử của tổng thể). Ta gọi Xi là đại lƣợng ngẫu nhiên
chỉ kết quả quan sát lần thứ i về đại lƣợng ngẫu nhiên X. Khi đó tập hợp n đại
lƣợng ngẫu nhiên WX = (X1, X2,…. Xn) đƣợc gọi là mẫu ngẫu nhiên có kích thƣớc n.
Nhƣ vậy mẫu ngẫu nhiên cỡ n thực chất là n đại lƣợng ngẫu nhiên độc lập,
cùng phân phối nhƣ đại lƣợng ngẫu nhiên gố X của tổng thể nghiên cứu.
Ta gọi xi là giá trị thu đƣợc trong lần quan sát thứ i. Khi đó
wx = (x1, x2,... , xn) là n giá trị cụ thể ta quan sát đựợc. Đó là một giá trị cụ thể mà
ngẫu nhiên WX = (X1, X2,…., Xn) nhận đƣợc.
Từ nay về sau khi nói rằng ta có một mẫu ngẫu nhiên cỡ n rút ra từ đại
lƣợng ngẫu nhiên X (theo phƣơng thức lấy mẫu có hoàn lại), ta sẽ hiểu đó là n
đại lƣợng ngẫu nhiên độc lập, cùng phân phối nếu ta không quan tâm đến kết quả
cụ thể đã quan sát đƣợc mà ta muốn nghiên cứu tính chất chung của mẫu, của các
đặc trƣng mẫu; còn ta sẽ hiểu đó là n giá trị cụ thể quan sát đựợc, nếu ta quan tâm
đến kết quả cụ thể và cần những tính toán cụ thể.
1.3. Các thống kê (đặc trƣng) của mẫu ngẫu nhiên
Xét WX = (X1, X2,…. Xn) là mẫu ngẫu nhiên rút ra từ đại lƣợng ngẫu nhiên
gốc X có E(X) = m và Var(X) = 2. a) Trung bình mẫu 1 n X = X (3.5) n i i=1
Do X1, X2,…. Xn là các đại lƣợng ngẫu nhiên độc lập, cùng phân phối nhƣ
X nên X là một đại lƣợng ngẫu nhiên. NHẬN XÉT
Theo tính chất của kỳ vọng và phƣơng sai ta có: 1 n n.E(X) E( X ) = E(X ) = = m i n n i=1 82
CHƢƠNG III: TỔNG THỂ VÀ MẪU lOMoAR cPSD| 35883770
ĐẠI LƢỢNG NGẪU NHIÊN GỐC VÀ MẪU NGẪU NHIÊN 1 n n.Var (X) 2 Var( X ) = Var (X ) = = 2 i n i=1 n 2 n
Nhƣ vậy trung bình mẫu ngẫu nhiên có kỳ vọng bằng trung bình tổng thể và
phƣơng sai bằng 1/n lần phƣơng sai tổng thể.
b) Phƣơng sai mẫu ngẫu nhiên 1 1 1 1 S2 = (X − 2 X )2 = i X2 − i X (3.6) n i−1 n i−1 Ta có )2 2 1 n ( − )− ( − E(S ) = E X m X m i n i−1 1 = E(X − m)2 − E (X − m)2 n i i=1 1 2 n −1 =
nVar(X) − Var (X) = 2 − = .2 n n n
Nghĩa là kỳ vọng của phƣơng sai mẫu ngẫu nhiên khác với phƣơng sai tổng thể n −1 E(S2) = 2 . n
c) Phƣơng sai mẫu điều chỉnh 1 n n S’2 = (X − X)2 = S2 (3.7) n −1 i i=1 n −1 Khi đó n n −1 E (S’2) = E(S2 ) = n . .2 = 2 n −1 n −1 n
Nhƣ vậy về mặt kỳ vọng thì X và S’2 đúng bằng trung bình và phƣơng sai của tổng thể.
d) Độ lệch tiêu chuẩn của mẫu ngẫu nhiên S = S2 (3.8)
e) Độ lệch tiêu chuẩn điều chỉnh S'= S'2 (3.9)
f) Phân bố xác suất của trung bình và phƣơng sai mẫu
Theo [6], nếu (X1, X2,…. Xn) là mẫu ngẩu nhiên đƣợc rút ra từ đại lƣợng
ngẫu nhiên ngẫu nhiên X có phân phối chuẩn N (;2 ) thì:
• n X có phân phối chuẩn N(n , n 2 ). 2
• X có phân phối chuẩn N ( ; ). n
CHƢƠNG III: TỔNG THỂ VÀ MẪU 83 lOMoAR cPSD| 35883770
ĐẠI LƢỢNG NGẪU NHIÊN GỐC VÀ MẪU NGẪU NHIÊN ( • nS2 n −1)S'2 có phân phối 2 n−1 . 2 = 2
• X và S2 độc lập với nhau. X − X − • T = n −1 hoặc T =
có phân phối Student với n −1 bậc n S S2 tự do.
Nếu (X1, X2,…. Xn) là mẫu từ đại lƣợng ngẫu nhiên ngẫu nhiên chuẩn
N ( ; 2 ) , còn (Y1,Y2,.. ,Ym) là mẫu từ đại lƣợng ngẫu nhiên ngẫu nhiên chuẩn 1 1
N ( ; 2 ) độc lập với mẫu trên. Khi đó: 1 1 • 2 2 1 + X Y N ( 2 1 ; ). 2 m n (
X − Y)− ( − ) (n + m − 2).n.m 1 2 • T = (
có phân phối Student với n + m). ( n.S 2 + m.S 2) x y
n + m – 2 bbậc tự do, trong đó S2 , S2 là hai phƣơng sai mẫu tƣơng ứng với mẫu x y X và mẫu Y. 84
CHƢƠNG III: TỔNG THỂ VÀ MẪU lOMoAR cPSD| 35883770
CÁC PHƢƠNG PHÁP TÍNH THAM SỐ MẪU
§ 2. CÁC PHƢƠNG PHÁP TÍNH THAM SỐ MẪU CỤ THỂ
2.1. Các tham số mẫu cụ thể
Xét mẫu cụ thể wx = (x1 , x2 , ..., xn) là một giá trị của mẫu ngẫu nhiên
WX = (X1 , X2 , ..., Xn). Ta có • 1 n
Trung bình mẫu cụ thể: x = x n i (3.10) i =1 1 1
• Phƣơng sai mẫu cụ thể: s2 = n (x x2 − n i − (x)2 (3.11) x)2 = n n i i =1 i =1 • n
Phƣơng sai điều chỉnh của mẫu cụ thể: s'2 = s2 (3.12) n −1
• Độ lệch tiêu chuẩn: s = s2 (3.13)
• Độ lệch tiêu chuẩn điều chỉnh: s' = s'2 (3.14)
Ví dụ 2: Từ tổng thể các trị số lương ở Ví dụ 1, ta lấy mẫu n = 5 giá trị ở
các vị trí 1, 5, 10, 15, 20, 25 được mẫu cụ thể wx = (3,0; 4,5; 5,0; 4,5; 4,4). Mẫu 3,0 + 4,5 + 5,0 + 4,5 + 4,4
wx có trung bình x = = 4,28. 5 Phương sai mẫu
(3,0)2 + (4,5)2 + (5,0)2 + (4,5)2 + (4,4)2 s2 = − (4,28)2 = 0,4535. 5 5
Phương sai điều chỉnh s'2 = .0,4536 = 0,567. 4
Độ lệch tiêu chuẩn s = 0,4536 = 0, 6735.
Độ lệch tiêu chuẩn điều chỉnh s’ = 0,567 = 0, 753.
2.2. Sắp xếp số liệu
Trƣờng hợp mẫu wx = (x1 , x2 , ..., xn) có kích thƣớc n tƣơng đối lớn thì việc
xác định các tham số x , s2, s'2 theo các công thức trên sẽ mất nhiều công sức.
Khi đó, nếu không cần độ chính xác cao, ta thƣờng sắp xếp các số liệu ban đầu
của mẫu lại, lập nên một mẫu các điểm đại diện, rồi xác định các tham số mẫu
dựa vào mẫu các điểm đại diện đó:
− Chia các giá trị trong wx ra thành các khoảng giá trị x'i _ x"i (thƣờng
chia thành các khoảng có độ dài nhƣ nhau) và xác định tần số ni tƣơng ứng ở mỗi
khoảng (số giá trị trong wx nằm trong khoảng x'i _ x"i). Khi đó, ta đƣợc một mẫu
dƣới dạng các khoảng giá trị: x'i _ x"i ni x'1 _ x"1 n1 x'2 _ x"2 n2 ⁝ ⁝ x'k _ x"k nk
CHƢƠNG III: TỔNG THỂ VÀ MẪU 85 lOMoAR cPSD| 35883770
CÁC PHƢƠNG PHÁP TÍNH THAM SỐ MẪU k Trong đó ni = n i =1
− Từ mẫu các khoảng giá trị, lập mẫu các điểm đại diện: xi ni x1 n1 x2 n2 ⁝ ⁝ xk nk
Với xi là một giá trị đƣợc chọn bất kỳ trong khoảng x'i _ x"i x ' + " (thƣờng x ta lấy x i i
i là điểm giữa của x'i _ x"i , tức xi = ) 2
Ví dụ 3: Đo ngẫu nhiên chiều cao của 40 thanh niên ta được các số liệu
xếp theo thứ tự tăng dần (tính theo đơn vị cm):
152 154 155 156 157 157 157 158 158 159
159 160 160 161 161 161 161 162 162 162
163 163 164 164 164 164 165 165 166 167
167 167 168 168 169 169 170 171 172 172
Có thể chia các số liệu thu được làm 4 khoảng: khoảng [152;157) có 4 giá
trị, khoảng [157;162) có 13 giá trị, khoảng [162;167) có 12 giá trị, khoảng [167;172] 11 giá trị.
Khi tính các đặc trưng mẫu số liệu đã cho một cách tương đối có thể tính
theo các giá trị trung tâm của các lớp khoảng được chia ra như trên.
Các khoảng xi’ − xi’’ Giá trị trung tâm xi Tần số ni [152;157) 154,5 4 [157;162) 159,5 13 [162;167) 164,5 12 [167;172] 172,5 11
2.3. Các phƣơng pháp tính
Cho mẫu cụ thể dƣới dạng xi ni x1 n1 x2 n2 ⁝ ⁝ xk nk
Khi đó có thể xác định các tham số mẫu bởi 1 trong 2 phƣơng pháp sau a) Tính trực tiếp Dùng các công thức 1 k x = n x i i (3.15) n i =1 86
CHƢƠNG III: TỔNG THỂ VÀ MẪU lOMoAR cPSD| 35883770
CÁC PHƢƠNG PHÁP TÍNH THAM SỐ MẪU 1 k s2 = n n x2 − i i (x)2 (3.16) i =1 n s'2 = s2 (3.17) n −1
Ví dụ 4: Tính trung bình, phương sai, phương sai điều chỉnh, độ lệch tiêu
chuẩn và độ lệch tiêu chuẩn điều chỉnh của mẫu số liệu sau xi 5 10 15 20 25 ni 15 25 30 20 10 Giải Ta có bảng tính x 2 i ni xini xi ni 5 15 75 375 10 25 250 2500 15 30 450 6750 20 20 400 8000 25 10 250 6250 n = 100 1425 23875 Suy ra 1425 − 1 Trung bình mẫu x = k nx = = 14,25. i i n i =1 100 1 k − 23875 Phƣơng sai mẫu s2 = − n n x2 − (14,25)2 i i (x)2 = 100 = 238,75. i =1 n 100
− Phƣơng sai điều chỉnh s'2 = s2 = 238,75 = 241,1616. n − 1 99
− Độ lệch tiêu chuẩn s = s2 = 15,45154.
− Độ lệch tiêu chuẩn s = s2 = 15,52938.
b) Phƣơng pháp đổi biến (thay đổi gốc tính và đơn vị tính)
Khi các giá trị xi quá lớn hoặc là các giá trị số có nhiều chữ số lẻ thì ta có
thể xác định các tham số mẫu một cách gián tiếp thông qua các giá trị (biến) mới
ui dễ tính toán hơn ( ui là những số nguyên gần 0). • x − x Công thức đổi biến u i 0 i = (3.18) h
• Các bƣớc thực hiện
− Chọn x0 : là giá trị xi ứng với ni lớn nhất (hoặc là giá trị ở khoảng giữa). − Chọn h :
+ Nếu các giá trị xi cách đều nhau một khoảng là h0 thì chọn h = h0.
CHƢƠNG III: TỔNG THỂ VÀ MẪU 87 lOMoAR cPSD| 35883770
CÁC PHƢƠNG PHÁP TÍNH THAM SỐ MẪU
+ Nếu các giá trị xi không cách đều nhau ta chọn h là ƣớc số chung lớn
nhất của các khoảng cách x − i x0 (i=1,2,...,k).
− Xác định các giá trị ui theo công thức (3.17), lập bảng tính để xác định
trung bình và phƣơng sai theo các giá trị ui ( u và s 2u ): x 2 i ni ui niui niui 1 1 u = k u n ; s2 = k u 2 n − u 2 n i i u i i i=1 n i=1
− Xác định x và s2 ( trung bình và phƣơng sai theo các giá trị ban đầu xi) từ u và u s 2 bởi các công thức x = h u + x0 (3.19) s2 = h2 u .s 2 (3.20)
Ví dụ 5: Kiểm tra trọng lượng của một số sản phẩm người ta thu được các số liệu sau
Trọng lượng xi (g) 70,75 75,75 80,75 85,75 90,75 Số sản phẩm ni 12 20 40 20 8
Tính trung bình và phương sai của mẫu số liệu trên. Giải − Chọn x 80,75 x i
0 = 80,75; h = 5 với công thức đổi biến ui = . 5 Ta lập bảng tính x 2 i ni ui niui niui 70,75 12 −2 −24 48 75,75 20 −1 −20 20 80,75 40 0 0 0 85,75 20 1 20 20 90,75 8 2 16 32 n = 100 −8 120 Ta có 1 k u = u n = − 0,08 n i i i=1 1 s2 = k
u 2 n − u 2 = 1,2 − (−0,08)2 = 1,1936 u n i i i=1 Suy ra
x = h u + x0 = 5(−0,08) + 80,75 = 80,35 s2 = h2 u .s 2 = 25.1,1936 = 29,84 88
CHƢƠNG III: TỔNG THỂ VÀ MẪU lOMoAR cPSD| 35883770
CÁC PHƢƠNG PHÁP TÍNH THAM SỐ MẪU BÀI TẬP 1.
Cho 8 kết quả đo đạc về đại lƣợng X bởi cùng một máy không có sai số hệ thống
369 378 315 420 385 401 372 383 Tính x,s2 ,s'2 ,s,s'. 2.
Số liệu đo điện trở của 20 tụ điện nhƣ sau
4,45 4,45 4,40 4,42 4,45 4,38 4,42 4,36 4,35 4,40
4,42 4,44 4,36 4,32 4,44 4,38 4,39 4,40 4,42 4,45
Xác định trung bình mẫu và phƣơng sai mẫu của số liệu đo điện trở. 3.
Chiều cao (cm) của 100 sinh viên nam ở một trƣờng đại học cho bởi
bảng dƣói đây. Hãy sắp xếp các số liệu trên thành bảng bằng cách
chia số liệu thành các khoảng thích hợp.
152 168 160 148 155 145 159 161 145
157 164 154 155 149 158 160 166 158
170 148 152 173 167 151 162 169 151
156 173 153 157 151 161 154 159 161
166 157 149 164 160 170 173 67 170
152 168 160 148 155 145 159 161 145
157 164 154 155 149 158 160 166 158
170 148 152 173 167 151 162 169 151
156 173 153 157 151 161 154 159 161
166 157 149 164 160 170 173 67 170 4.
Theo dõi năng suất của 11 hécta lúa ở một vùng, ngƣời ta thu đƣợc kết quả cho ở bảng sau: Năng suất (tạ/ha) Diện tích (ha) 30 – 35 7 35 – 40 12 40 – 45 18 45 – 50 27 50 – 55 20 55 – 60 8 60 – 65 5 65 − 70 3
Tính giá trị trung bình, phƣơng sai và phƣơng sai điều chỉnh của mấu cụ thể này.
CHƢƠNG III: TỔNG THỂ VÀ MẪU 89 lOMoAR cPSD| 35883770
CÁC PHƢƠNG PHÁP TÍNH THAM SỐ MẪU 5.
Quan sát về thời gian cần thiết để sản suất một chi tiết máy ta thu
đƣợc các số liệu cho ở bảng sau: Khoảng thời gian (phút) Số quan sát 20 – 25 2 25 – 30 14 30 – 35 26 35 – 40 32 40 – 45 14 45 – 50 8 50 – 55 4
Tính giá trị trung bình, phƣơng sai và phƣơng sai điều chỉnh của mẫu. 6.
Thống kê số hàng bán đƣợc trong một ngày bán đƣợc số lƣợng hàng
tƣơng ứng, ta có bảng số liệu sau:
Lƣợng hàng bán trong ngày (kg) Số ngày (ni) 100 – 200 5 200 – 250 12 250 – 300 56 300 – 350 107 350 – 400 75 400 – 450 70 450 – 500 35 500 – 550 30 550 – 700 10
Tính giá trị trung bình mẫu và nêu ý nghĩa của nó. 7.
Các kết quả về việc đo độ bền các sợi chỉ ta thu đƣợc bảng số liệu (đơn vị gam) Độ bền
120- 140- 160- 180- 200- 220- 240- 260- của sợi 140 160 180 200 220 240 260 280 Số các sợi 1 4 10 14 12 6 2 1
Hãy xác định độ bền trung bình, phƣơng sai và độ lệch chuẩn điều chỉnh của mẫu trên. 8.
Điều tra doanh số hàng tháng (đơn vị triệu đồng) của 100 hộ kinh
doanh một ngành hàng, ta thu đƣợc các số liệu sau:
Doanh số xi 10,1 10,2 10,4 10,5 10,7 10,8 10,9 11 11,3 11,4 Số hộ ni 2 3 8 13 25 20 12 10 6 1
Tìm doanh số trung bình và độ phân tán của các doanh số so với
doanh số trung bình của các hộ nói trên. 90
CHƢƠNG III: TỔNG THỂ VÀ MẪU lOMoAR cPSD| 35883770 CHƢƠNG IV
ƢỚC LƢỢNG CÁC THAM SỐ
CỦA ĐẠI LƢỢNG NGẪU NHIÊN
§ 1. ƢỚC LƢỢNG ĐIỂM
1.1. Đặt vấn đề
Giả sử tổng thể ứng với đại lƣợng ngẫu nhiên X có tham số (trung bình,
tỷ lệ, phƣơng sai) chƣa biết. Ta cần xác định xem nhận giá trị nào hay nói cách
khác là ta cần ƣớc lƣợng tham số . Dựa vào mẫu ngẫu nhiên
WX = (X1, X2, ..., Xn) ta sẽ xây dựng một hàm ˆ (X1, X2, ..., Xn) để khi mẫu nhận
một giá trị cụ thể (x1, x2, …,xn) thì xác định đƣợc một giá trị
0 = ˆ (x1, x2, …,xn) ƣớc lƣợng cho . Cách ƣớc lƣợng tham số nhƣ vậy gọi là ƣớc lƣợng điểm.
1.2. Các phƣơng pháp ƣớc lƣợng điểm
Từ mẫu ngẫu nhiên WX = (X1, X2, ..., Xn), ta xây dựng thống kê
= (X1, X2, ..., Xn) để ƣớc lƣợng cho . Tùy thuộc vào những tiêu chuẩn khác
nhau, ta có các dạng ƣớc lƣợng khác nhau cho tham số .
a) Ƣớc lƣợng không chệch
Thống kê = (X1, X2, ..., Xn) được gọi là ước lượng không chệch của
tham số nếu E( ˆ) = . NHẬN XÉT
Giả sử là ƣớc lƣợng không chệch của tham số θ . Ta có
E(− θ) = E() − E(θ) = θ − θ = 0
Vậy ƣớc lƣợng không chệch là ƣớc lƣợng có sai số trung bình bằng 0.
CHÚ Ý Nhƣ đã nêu ở chƣơng III, ta có
− Trung bình của ngẫu nhiên X là ƣớc lƣợng không chệch của trung bình
của tổng thể m vì E(X) = m.
− Phƣơng sai điều chỉnh của mẫu ngẫu nhiên là ƣớc lƣợng không chệch
của phƣơng sai của tổng thể σ 2 vì E(S 2 ) = 2 .
CHƢƠNG IV: ƢỚC LƢỢNG CÁC THAM SỐ CỦA ĐẠI LƢỢNG NGẪU NHIÊN 91 lOMoAR cPSD| 35883770 ƢỚC LƢỢNG ĐIỂM
Ví dụ 1: Cân thử 100 trái cây của nông trường ta có kết quả như sau
Trọng lượng (g) Số trái 35 - 55 3 55 - 75 10 75 - 95 25 95 - 115 35 115 - 135 20 135 - 155 6 155 - 175 1
a/ Tìm ước lượng không chệch cho trọng lượng trung bình của một trái
cây trong nông trường.
b/ Tìm ước lượng không chệch cho đại lượng biểu thị độ đồng đều của các
trái cây trong nông trường.
c/ Nếu xem các trái có trọng lượng không quá 95 g là trái loại II. Tìm ước
lượng không chệch của trái loại II trong nông trường. Giải
Ta xác định các tham số mẫu dùng để ƣớc lƣợng. Trọng lƣợng x 2 i ni ui niui niui 35 - 55 45 3 −3 −9 27 55 - 75 65 10 −2 −20 40 75 - 95 85 25 −1 25 25 95 - 115 105 35 0 0 0 115 - 135 125 20 1 20 20 135 - 155 145 6 2 12 24 155 - 175 165 1 3 3 8 n = 100 −19 145 Ta có 1 k u = u n = − 0,19 n i i i=1 1 k 2 s =
u 2 n − u 2 = 1,2 − (−0,08)2 = 1,414. u i i n i=1 Suy ra x = h u + x0 = 101,2. 100
sˆ 2 = h2.s 2 = 566 s2 = .566 = 571,7 s = 23,9 u 99 Tỷ 3 + 10 + 25
lệ trái loại II trong mẫu f = = 0,38. 100 92
CHƢƠNG IV: ƢỚC LƢỢNG CÁC THAM SỐ CỦA ĐẠI LƢỢNG NGẪU NHIÊN lOMoAR cPSD| 35883770 ƢỚC LƢỢNG ĐIỂM Từ đó ta suy ra
a/ Ƣớc lƣợng không chệch của trọng lƣợng trung bình của các trái cây trong nông trƣờng là x = 101,2g
b/ Ƣớc lƣợng không chệch của đại lƣợng biểu thị độ phân tán của trọng lƣợng các trái cây là: s = 23,9g
c/ Ƣớc lƣợng không chệch của tỷ lệ trái loại II của nông trƣờng là: f = 0,38 = 38%
b) Ƣớc lƣợng hiệu quả
Giả sử là ƣớc lƣợng không chệch của tham số θ . Theo bất đẳng thức Tchebychev ta có ( ) Var( )
P − E() ε 1− ε2 ( ) Var( ) Vì
E() = θ nên P − θ ε 1− ε2 (
Ta thấy Var( ) càng nhỏ thì P − E() ε) càng gần 1. Do đó ta sẽ chọn
với Var( ) nhỏ nhất .
Ước lượng không chệch được gọi là ước lượng có hiệu quả của tham số
θ nếu Var( ) nhỏ nhất trong các ước lượng của θ . CHÚ Ý
Ngƣời ta chứng minh đƣợc rằng nếu là ƣớc lƣợng hiệu quả của θ thì phƣơng sai của nó là 1 Var (ˆ) = (4.1) ln f (x, ) n.E( ) 2
Trong đó f (x,) là hàm mật độ xác suất của đại lƣợng ngẫu nhiên gốc.
Mọi ƣớc lƣợng không chệch cho θ luôn có phƣơng sai lớn hơn Var (ˆ) trong
(4.1) là giới hạn Crame - Rao. NHẬN XÉT σ2
Nếu đại lượng ngẫu nhiên gốc X Nμ;
thì trung bình mẫu X là ước n
lượng hiệu quả của kỳ vọng E(X) = . 1 n σ2 Thật vậy, ta biết X = X N(μ( ) n i i=1 n
Mặt khác, do X có phân phối chuẩn nên nếu f(x, μ) là hàm mật độ của Xi thì
CHƢƠNG IV: ƢỚC LƢỢNG CÁC THAM SỐ CỦA ĐẠI LƢỢNG NGẪU NHIÊN 93 lOMoAR cPSD| 35883770 ƢỚC LƢỢNG ĐIỂM
f(x, μ) = 1 e−(x −μ)2 /2σ2 σ 2π x − μ Ta có lnf(x, μ) = μ σ2 2 lnf(x, μ) x − μ 2 n Suy ra nE = nE = . μ σ2 σ2
Do đó Var( X) chính bằng nghịch đảo 2 / n .
Vậy X là ƣớc lƣợng hiệu quả của .
c) Ƣớc lƣợng vững
Thống kê = (X1, X2, ..., Xn) được gọi là ước lượng vững của tham số
nếu 0 ta có lim P( ˆ −θ ε) =1 n→
Nếu là ƣớc lƣợng không chệch của và lim Var () = 0 thì ˆ là ƣớc n→ lƣợng vững của .
d) Phƣơng pháp ƣớc lƣợng hợp lý tối đa
Giả sử W = (X , X ,..., X ) là mẫu ngẫu nhiên đƣợc tạo nên từ đại lƣợng X 1 2 n
ngẫu nhiên gốc X có mẫu cụ thể w = (x , x
) và thống kê = (X1, X2, x 1 2 ,..., xn ..., Xn)
Xét hàm hợp lý L(x , x ,..., x , θ)của đối số θ xác định nhƣ sau: 1 2 n − Nếu X rời rạc :
L(x , x ,..., x ,) = P(X = x / ,..., X = x / ) 1 2 n 1 1 n n (4.2) n = P(X = x / ) (4.3) i i i=1 L(x =
1, x2 ,..., x ,θ) là xác suất để nhận đƣợc mẫu cụ thể w (x , x ,..., x ) . n x 1 2 n
− Nếu X liên tục có hàm mật độ xác suất f (x, )
L(x , x ,..., x ,) = f (x ,)f (x ,)...f (x ,) 1 2 n 1 2 n
L(x , x ,..., x , θ) là mật độ xác suất tại điểm w = (x , x ,..., x ) 1 2 n x 1 2 n
Giá trị o = (x , x ,..., x 1 2
n ) được gọi là ước lượng hợp lý tối đa nếu ứng với
giá trị này của hàm hợp lý đạt cực đại. CHÚ Ý
Vì hàm L và lnL đạt cực đại tại cùng một giá trị nên khi tìm ƣớc lƣợng
hợp lý tối đa ta xét lnL thay vì xét L. Ta thực hiện qua các bƣớc sau 94
CHƢƠNG IV: ƢỚC LƢỢNG CÁC THAM SỐ CỦA ĐẠI LƢỢNG NGẪU NHIÊN lOMoAR cPSD| 35883770 ƢỚC LƢỢNG ĐIỂM − lnL Tìm . θ − lnL Giải phƣơng trình ( Phƣơng trình hợp lý). θ
Giả sử phƣơng trình có nghiệm là = (x , x ,..., x ) o 1 2 n − 2lnL Tìm đạo hàm cấp hai θ 2 lnL = Nếu tại 0 mà (x , x ,..., x ) là o 1 2 n
<0 thì lnL đạt cực đại. Khi đó θ
ƣớc lƣợng điểm hợp lý tối đa của .
CHƢƠNG IV: ƢỚC LƢỢNG CÁC THAM SỐ CỦA ĐẠI LƢỢNG NGẪU NHIÊN 95 lOMoAR cPSD| 35883770
PHƢƠNG PHÁP KHOẢNG TIN CẬY
§ 2. PHƢƠNG PHÁP KHOẢNG TIN CẬY
2.1. Đặt vấn đề
Ƣớc lƣợng điểm có một nhƣợc điểm cơ bản là không thể biết đƣợc độ chính
xác cũng nhƣ xác suất để ƣớc lƣợng đó chính xác. Đặc biệt là khi kích thƣớc mẫu
nhỏ sự sai lệch của ƣớc lƣợng so với giá trị thật khá lớn và chỉ với một số khó
đánh giá đƣợc khả năng mắc sai lầm khi ƣớc lƣợng là bao nhiêu. Để khắc phục
những hạn chế đó, ngƣời ta thực hiện ƣớc lƣợng bằng một khoảng giá trị. Rõ
ràng ƣớc lƣợng khoảng có độ tin cậy cao hơn nhiều và cho phép xác định khách
quan sai số ƣớc lƣợng. Tất nhiên một khoảng ƣớc lƣợng vẫn có thể sai giống nhƣ
mọi ƣớc lƣợng khác, nhƣng so với ƣớc lƣợng điểm, xác suất sai lầm có thể biết
và trong chừng mực nào đấy có thể hy vọng kiểm soát đƣợc. Nói nhƣ vậy không
có nghĩa là không nên dùng ƣớc lƣợng điểm nữa. Nó vẫn cho ta một thông tin
quan trọng và ƣớc lƣợng khoảng sẽ đƣợc xây dựng xung quang ƣớc lƣợng điểm.
Từ đó, để ƣớc lƣợng một tham số , phƣơng pháp khoảng tin cậy xây dựng
một thống kê nào đó có luật phân phối xác định không phụ thuộc vào (nhƣng
thống kê lại phụ thuộc). Dựa vào thống kê đó, ta tìm đƣợc khoảng giá trị ( 1; 2)
để ƣớc lƣợng cho tham số . Khoảng ƣớc lƣợng ( 1; 2) còn đƣợc gọi là khoảng
tin cậy của ƣớc lƣợng. Điều kiện đặt ra đối với khoảng tin cậy ( 1; 2) là phải
chứa đƣợc tham số với một xác suất khá cao. Trong phƣơng pháp này, ngƣời
ta ấn định một số xác suất khá bé và buộc xác suất để tham số rơi vào
khoảng tin cậy ( 1; 2) phải đạt bằng 1 − :
P( 1 < < 2) = 1 − (4.4)
Giá trị xác suất cho trƣớc đƣợc gọi là mức ý nghĩa của ƣớc lƣợng và
1 − đƣợc gọi là độ tin cậy của ƣớc lƣợng.
Các giá trị 1và 2 tạo nên khoảng tin cậy đƣợc xác định bằng phƣơng pháp
mẫu. Từ tổng thể lập mẫu ngẫu nhiên WX = (X1, X2, ..., Xn). Dùng mẫu ngẫu nhiên WX lập các hàm
1(X1, X2, ..., Xn) và 1(X1, X2, ..., Xn) (4.5)
Với một mẫu giá trị cụ thể wx = (x1, x2, ..., xn) của WX, thay vào các hàm
(4.5) tính các giá trị 1và 2 giới hạn nên khoảng tin cậy:
1 = 1(x1, x2, ..., xn) và 2 = 2(x1, x2, ..., xn)
Bằng phƣơng pháp thiết lập các hàm 1(X1, X2, ..., Xn) và 2(X1, X2, ...,
Xn) thích hợp thì các giá trị 1, 2 tính đƣợc từ mẫu cụ thể wx sẽ thỏa điều kiện
đặt ra là P( 1 < < 2) = 1 − . 96
CHƢƠNG IV: ƢỚC LƢỢNG CÁC THAM SỐ CỦA ĐẠI LƢỢNG NGẪU NHIÊN lOMoAR cPSD| 35883770
PHƢƠNG PHÁP KHOẢNG TIN CẬY 2.2. Phƣơng pháp
− Từ tổng thể lập mẫu nhiên WX = (X1, X2, ..., Xn).
− Với mẫu ngẫu nhiên WX xây dựng một thống kê có chứa tham số cần ƣợc lƣợng : U = f(X1, X2, ..., Xn, )
Ngoài điều kiện phải chứa tham số , yêu cầu quan trọng đặt ra với thống
kê U là có thể xấp xỉ về một trong những dạng phân phối thông dụng nhƣ phân
phối chuẩn hóa, phân phối student hay phân phối khi_bình phƣơng,…
− Khi biết đƣợc dạng phân phối của U, với mức ý nghĩa cho trƣớc có
thể tìm đƣợc các giá trị u1 và u2 sao cho
P(u1 < U < u2) = 1 − (4.6)
− Biến đổi (4.3) đƣa về dạng P( 1 < < 2) = 1 − .
Khi đó ( 1; 2) là khoảng tin cậy cần tìm.
2.3. Ƣớc lƣợng trung bình
Giả sử đại lƣợng ngẫu nhiên X (xác định cho một chỉ tiêu nào đó trên các
phần tử của tổng thể) có phân phối theo luật chuẩn N(m; 2) với trung bình m =
E(X) chƣa biết. Với mức ý nghĩa cho trƣớc ta xây dựng khoảng tin cậy
(m1;m2) để ƣớc lƣợng cho trung bình m sao cho P(m1 < m < m2) = 1 − .
Từ tổng thể với đại lƣợng ngẫu nhiên gốc X, lập mẫu ngẫu nhiên WX = (X1,
X2, ..., Xn) có kích thƣớc n. Tùy thuộc vào đặc điểm đại lƣợng ngẫu nhiên X biết
phƣơng sai hay chƣa và kích thƣớc mẫu n có lớn hay không, việc lập nên khoảng
tin cậy (m1;m2) đƣợc xác định trong các trƣờng hợp khác nhau.
a) Trƣờng hợp 1: Biết phƣơng sai Var(X) = σ 2 .
Từ mẫu ngẫu nhiên WX = (X1, X2, ..., Xn), lập thống kê X − m U =
n ( X là trung bình mẫu ngẫu nhiên)
Theo phân bố xác suất của trung bình mẫu đã xét ở chƣơng III, ta có UN(0;1).
Chọn cặp giá trị 1 và 2 sao cho 1 + 2 = , tìm các phân vị chuẩn u 1 và u 1 − 2 P(U < u ) = 1 (4.7) 1 P(U < u ) = 1 − 1 − 2 (4.8) 2
Vì phân vị chuẩn có tính chất u u = − nên từ (4.7) ta có 1 − 1 1 P(U < − u ) = 1 − 1 (4.9) 1
Lấy (4.8) trừ (4.9) vế theo vế ta đƣợc P(U < u ) − P(U < − u ) = 1 − 1 − 1 − 2 − 1 2 1
CHƢƠNG IV: ƢỚC LƢỢNG CÁC THAM SỐ CỦA ĐẠI LƢỢNG NGẪU NHIÊN 97 lOMoAR cPSD| 35883770
PHƢƠNG PHÁP KHOẢNG TIN CẬY P(− u < U < u ) = 1 − 1 − 1 − 1 2 X − m P(− u < < u n ) = 1 − 1 − 1 − 1 2 P( X − u < m < X + u ) = 1 − 1 − − 2 n 1 1 n Đặt m u 1 = X − u và m 1 − 2 = X + − 2 n 1 1 n
Khi đó, khoảng giá trị (m1;m2) sẽ thỏa điều kiện đặt ra cho khoảng tin cậy là
P(m1 < m < m2) = 1 − CHÚ Ý 1 Nếu ta chọn
thì khoảng tin cậy lúc đó có dạng đối xứng với 1 = 2 = 2
trung tâm là trung bình mẫu X .
Khi đó, nếu đặt = 1 − thì 2 u = u = u 1− 2 1− 1 Và nếu đặt = u thì n
m1 = X − và m2 = X −
Giá trị đƣợc gọi là độ chính xác của ƣớc lƣợng. CHÚ Ý 2
Trong thực hành, khi có mẫu cụ thể wx = (x1, x2, ..., xn) và mức ý nghĩa
đƣợc ấn định trƣớc thì khoảng tin cậy (m1;m2) cho tham số trung bình m đƣợc
tìm tuần tự qua các bƣớc sau:
− Với mẫu cụ thể wx, tính trung bình mẫu x .
− Với mức ý nghĩa , tính = 1 −
, rồi tra tìm phân vị chuẩn u . 2 −
Tính độ chính xác = u . (4.10) n
− Xác định khoảng tin cậy (m1;m2) = ( x − ; x + ). (4.11)
Ví dụ 2: Biết trọng lượng của một loại sản phẩm là đại lượng ngẫu nhiên
X (kg) phân phối theo luật chuẩn có phương sai Var(X) = 2 = 0,01kg. Để ước
lượng trọng lượng trung bình m = E(X) của các sản phẩm, người ta kiểm tra một
mẫu gồm 25 sản phẩm và tính được trọng lượng trung bình trong mẫu này là
5,2kg. Hãy tìm khoảng tin cậy 99% của trọng lượng trung bình m. 98
CHƢƠNG IV: ƢỚC LƢỢNG CÁC THAM SỐ CỦA ĐẠI LƢỢNG NGẪU NHIÊN lOMoAR cPSD| 35883770
PHƢƠNG PHÁP KHOẢNG TIN CẬY Giải
Kích thƣớc của mẫu đã cho là n = 25 và trung bình mẫu là x = 5,2; Đại
lƣợng X có độ lệch tiêu chuẩn = 0,1.
Độ tin cậy của ƣợc lƣợng là 1 − = 0,99. Do đó = 1 − = 0,995. 2
Tra phân vị chuẩn ta đƣợc u = u 0,995 = 2,5758. 0,1 Độ chính xác = u = 2,5758. = 0,051516. n 5 Suy ra
m1 = x − = 5,2 − 0,051516 = 5,148484
m2 = x + = 5,2 + 0,051516 = 5,251516
Vậy khoảng tin cậy 99% của m là (m1;m2) = (5,148484;5,251516). Tức là
với độ tin cậy và thông tin mẫu đã cho thì trọng lƣợng trung bình của các sản
phẩm đƣợc ƣớc lƣợng từ 5,148484 kg đến 5,251516 kg.
b) Trƣờng hợp 2: Chƣa biết phƣơng sai Var(X), n 30.
Về phƣơng pháp cũng tƣơng tự trƣờng hợp 1, chỉ khác là trong trƣờng hợp
này trƣớc hết phải ƣớc lƣợng 2 bằng phƣơng sai mẫu điều chỉnh S’2 (đƣợc xác
định từ mẫu ngẫu nhiên WX) và ƣớc lƣợng đƣợc dựa vào thống kê: X − m U = n S
Trong thực hành, khoảng tin cậy cũng đƣợc lập dƣới dạng
(m1;m2) = ( x − ; x + ) Với độ chính xác s = u (4.12) n
(s là độ lệch tiêu chuẩn điều chỉnh của mẫu cụ thể)
Ví dụ 3: Cân thử trọng lượng của một số gói mì ăn liền thì thu được các số liệu sau
Khoảng trọng lượng (g) [70;75) [75;80) [80;85) [85;90) Số gói mì 11 32 44 13
Với mức ý nghĩa 2%, hãy dùng mẫu số liệu trên để ước lượng trọng
lượng trung bình các gói mì. Giải
Gọi X là trọng lƣợng của các gói mì, cần ƣớc lƣợng cho trung bình
m = E(X) trong trƣờng hợp chƣa biết Var(X), kích thƣớc mẫu n = 100 > 30.
CHƢƠNG IV: ƢỚC LƢỢNG CÁC THAM SỐ CỦA ĐẠI LƢỢNG NGẪU NHIÊN 99 lOMoAR cPSD| 35883770
PHƢƠNG PHÁP KHOẢNG TIN CẬY
Mẫu số liệu đƣợc cho dƣới dạng khoảng, mỗi khoảng lấy giá trị đại diện
xi là giá trị ở giữa khoảng xi 72,5 77,5 82,5 87,5 ni 11 32 44 13
Với mẫu của các giá trị đại diện, ta có x = 80,45; s 4,27.
Mức ý nghĩa = 0,02 = 1 − = 0,99 u = u 0,99 = 2,3263. 2 s 4,27 Độ chính xác = = 2,3263. u = 0,99333. n 10 Suy ra
m1 = x − = 80,45 − 0,99333 = 79,45667
m2 = x + = 80,45 + 0,99333 = 81,44333
Vậy với mức ý nghĩa 2% trọng lƣợng trung bình m của các gói mì đƣợc
ƣớc lƣợng trong khoảng (m1;m2) = (79,45667g;81,44333g).
c) Trƣờng hợp 3: Chƣa biết phƣơng sai Var(X), n < 30
và X có phân phối chuẩn. Chọn X − m thống kê U = n . S'
Mặc dù dựa trên thống kê U cũng giống nhƣ trong trƣờng hợp 2 nhƣng
khi chƣa biết Var(X), n < 30 và X có phân phối chuẩn thì thống kê U khi này
sẽ đƣợc xấp xỉ về phân phối student với n − 1 bậc tự do T(n−1).
Do đó, khi tính độ chính xác, giá trị phân vị chuẩn sẽ đƣợc thay bằng
phân vị student t (n −1) với mức xác suất = và n − 1 bậc tự do: /2 2 s
= t (n −1) . (4.13) /2 n
Ví dụ 4: Để ước lượng đường kính trung bình của các viên bi sắt,
người ta kiểm tra trên một số bi:
Đường kính ni (mm) 6,5 7,0 7,5 8,0 8,5 Số bi ni 1 7 12 3 2
Cho biết đường kính của các viên bi là đại lượng phân phối theo luật
chuẩn. Hãy ước lượng đường kính trung bình của các viên bi với độ tin cậy 95%. 100
CHƢƠNG IV: ƢỚC LƢỢNG CÁC THAM SỐ CỦA ĐẠI LƢỢNG NGẪU NHIÊN lOMoAR cPSD| 35883770
PHƢƠNG PHÁP KHOẢNG TIN CẬY Giải
Gọi X là đại lƣợng chỉ đƣờng kính của các viên bi, cần ƣớc lƣợng cho
trung bình m = E(X) trong trƣờng hợp X có phân phối chuẩn, chƣa biết
Var(X) và kích thƣớc mẫu n = 25 < 30.
Với mẫu đã cho ta có x = 7,46; s = 0,48.
Độ tin cậy 1 − = 0,95 = = 0,025. 2
Tra phân vị student với n − 1 = 24 bậc tự do, ta đƣợc t0,025(24) = 2,0639 s 0,48 Độ chính xác = t = 2,0639. = 0,198134. ;n−1 n 5 Suy ra
m1 = x − = 7,46 − 0,198134 = 79,45667
m2 = x + = 7,46 + 0,198134 = 81,44333
Vậy với mức ý nghĩa 2% trọng lƣợng trung bình m của các gói mì đƣợc
ƣớc lƣợng trong khoảng (m1;m2) = (79,45667g;81,44333g).
2.4. Ƣớc lƣợng tỷ lệ a) Đặt vấn đề
Tổng thể chia làm hai loại phần tử, những phần tử có tính chất A và
không có tính chất A. Giả sử tỷ lệ p các phần tử có tính chất A chƣa biết. Với
mức ý nghĩa cho trƣớc và một mẫu gồm n quan sát độc lập (X1,X2, ... Xn)
ta xây dựng khoảng tin cậy (p1;p2) để ƣớc lƣợng cho p sao cho
P(p1 < p < p2) = 1 − CHÚ Ý 3
Các đại lƣợng Xi trong mẫu quan sát đƣợc xác định bởi
0 neáu phaàn töû trong laàn quan saùt thöù i khoângcoù tính chaát A X = i 1
neáu phaàn töû trong laàn quan saùt thöù i coù tính chaát A b) Phƣơng pháp
Giả sử trong mẫu n phần tử quan sát có m phần tử mang tính chất A.
Khi đó, tỷ lệ phần tử có tính chất A trong mẫu là F = m . n n Với p(1− p)
n đủ lớn, ta có Fn N(p; ), q = 1 − p. n − Chọn (F p) n thống kê U = n . Ta có UN(0;1). p(1− p)
CHƢƠNG IV: ƢỚC LƢỢNG CÁC THAM SỐ CỦA ĐẠI LƢỢNG NGẪU NHIÊN 101 lOMoAR cPSD| 35883770
PHƢƠNG PHÁP KHOẢNG TIN CẬY Ta có 1 − = 1 − − 2 2
= P(U < u ) − P(U < u ) = P(U < u ) − P(U < − u ) 1− 1− 1− 2 2 2 2 (F − p) n = P(− u < n
< U < u ) = P(− u < u ) 1− 1− 1− 1− p(1− p) 2 2 2 2 p(1− p) p(1− p) = P(F − − n u < p < Fn u ), = 1 − n n 2 p(1− p)
Do đó, nếu đặt = u
, p1 = Fn − , p2 = Fn + thì n
P(p1 < p < p2) = 1 − p(1− p) F (1− F ) n n
Khi n đủ lớn có thể xấp xỉ n n
Khi đó, khoảng tin cậy của tỷ lệ p đƣợc lập dƣới dạng
(p1;p2) = (Fn − ;Fn + )
Trong đó, độ chính xác đƣợc tính bởi F (1− F ) n n = u với = 1 − n 2 CHU Ý 4
Khi thực hành tính toán, với mẫu quan sát cỡ n, xác định tần số m của
các phần tử có tính chất quan tâm xuất hiện trong mẫu và tính tỷ lệ mẫu m f = . n
Tìm phân vị chuẩn u = u , tính độ chính xác 1− 2 f (1− f ) = u (4.14) n
Lập khoảng tin cậy: (p1;p2) = (f − ;f + ). (4.15)
Ví dụ 5: Mở thử 200 hộp của một kho đồ hộp, người ta thấy có 8 sản
phẩm bị biến chất. Với độ tin cậy 95%, hãy ước lượng tỷ lệ đồ hộp bị biến chất ở kho đó. Giải
Gọi p là tỷ lệ đồ hộp bị biến chất trong kho. Ta cần tìm khoảng tin cậy 95% cho p.
Tỷ lệ đồ hộp bị biến chất trong mẫu n = 200 quan sát f = 0,04. 102
CHƢƠNG IV: ƢỚC LƢỢNG CÁC THAM SỐ CỦA ĐẠI LƢỢNG NGẪU NHIÊN lOMoAR cPSD| 35883770
PHƢƠNG PHÁP KHOẢNG TIN CẬY
Độ tin cậy 1 − = 0,95 = 1 − = 0,975 u = u 0,975 = 1,96. 2 Độ 0,04.0,96 chính xác = 1,96 = 0,027159. 200 Khoảng tin cậy
(p1;p2) = (0,04 − 0,027159;0,04 + 0,027159) = (0,012841;0,067159).
2.5. Ƣớc lƣợng phƣơng sai
Giả sử đại lƣợng ngẫu nhiên X phân phối theo quy luật chuẩn có
phƣơng sai Var(X) = 2 chƣa biết. Cho trƣớc mức ý nghĩa và một mẫu cụ thể wx có kích thƣớc n x … i x1 x2 xk n … i n1 n2 nk k
(ni là tần số của giá trị xi, n = n ) i 1
Ta lập khoảng tin cậy ( 2 1, 2 2) để ƣớclƣợng cho 2 thoả điều kiện
P( 2 1< 2 < 2 2) = 1 −
Theo lý thuyết mẫu, nếu biết E(X) = thì thống kê ( 2 = n x − i )2 i có phân phối 2
với n bậc tự do; còn khi E(X) chƣa biết 2 (n −1)S'2 thì thống kê 2 =
có phân phối 2 với n − 1 bậc tự do (Với S'2 là 2
phƣơng sai điều chỉnh của mẫu).
Từ đó, tùy theo trung bình của X đã biết hay chƣa mà các giá trị 2 1 và 2 đƣợc 2
xác định khác nhau trong hai trƣờng hợp sau đây.
a) Biết E(X) = . Ta có k −
n (x ) 2 i i 2 = i=1 1 2 2 (4.16) k − n (x )2 i i 2 = i=1 2 2 1− 2 (n 2
i là tần số ứng với giá trị xi;
, 2 là các phân vị khi bình phƣơng n 1− 2 2 bậc
tự do với mức xác suất lần lƣợt là 1− , ) 2 2
CHƢƠNG IV: ƢỚC LƢỢNG CÁC THAM SỐ CỦA ĐẠI LƢỢNG NGẪU NHIÊN 103 lOMoAR cPSD| 35883770
PHƢƠNG PHÁP KHOẢNG TIN CẬY
b) Chƣa biết E(X). Khi đó
2 = (n −1)s '2 1 2 2 (4.17)
2 = (n −1)s '2 2 2 1− 2
(s'2 là phƣơng sai điều chỉnh của mẫu cụ thể; 2 , 2 là các phân vị khi 1− 2 2
bình phƣơng n − 1 bậc tự do với mức xác suất lần lƣợt là 1− , ) 2 2
Ví dụ 6: Cho biết khối lượng của một loại sản phẩm là đại lượng X
phân phối theo luật chuẩn với kỳ vọng E(X) = 30. Cân thử từng sản phẩm của
một mẫu ngẫu nhiên gồm 25 đơn vị sản phẩm, ta có kết quả Khối lượng xi (g) 29,3 29,7 30 30,5 30,7 Số sản phẩm ni 4 5 8 5 3
Với độ tin cậy 95% hãy tìm khoảng tin cậy cho phương sai Var(X) = 2 Giải 5
Với mẫu số liệu đã cho ta có n (x − 30 i )2 = 5,13. i i=1
Ta dùng (4.16) đƣợc khoảng tin cậy cần tìm là 5,13 5,13 5,13 5,13 ; = ; = (0,1262;0,391). 2 2 40,65 13,12 0,025;25 0,975;25
Ví dụ 7: Để tham khảo độ chính xác của một dụng cụ đo chiều dài
người ta đo trên cùng một mục tiêu 30 lần bằng dụng cụ ấy. Kết quả nhận
được s2 = 0,05. Hãy tìm ước lượng cho độ phân tán sai số X của dụng cụ đó.
Cho biết đại lượng đo cho sai số ngẫu nhiên có dạng phân phối chuẩn. Giải
Do E(X) chƣa biết nên khoảng tin cậy đƣợc tìm theo (4.17). Ta có 2 2 = 45,7 ; = 16 . 0,975;29 0,025;29
Với s’2 = 0,05 khoảng tin cậy (4.17) tìm đƣợc là (0,032; 0,09) CHÚ Ý 5
Khi xác định một số ƣớc lƣợng cũng nhƣ tính các tham số hay dùng trong ƣớc lƣợng nhƣ s’ và
s’2 có thể dùng các bảng tính trong Excel.
Thí dụ, đo sức bền chịu lực của một loại ống công nghiệp ngƣời ta thu đƣợc bộ số liệu sau
4500 6500 5000 5200 4800 4900 5125 6200 5375 (9 ống) 104
CHƢƠNG IV: ƢỚC LƢỢNG CÁC THAM SỐ CỦA ĐẠI LƢỢNG NGẪU NHIÊN lOMoAR cPSD| 35883770
PHƢƠNG PHÁP KHOẢNG TIN CẬY
Hãy xây dựng khoảng tin cậy 95% cho sức bền trung bình của loại ống trên.
Khi dùng bảng tính Excel ta thực hiện qua các bƣớc sau Nhập số liệu A B C D E F G H K 1
4500 6500 5000 5200 4800 4900 5125 6200 5375
Chọn lần lƣợt đơn lệnh Tools và lệnh Data Analysis.
Chọn chƣơng trình Descriptive Statistics trong hộp thoại Data Analysis rồi nhấp OK.
Trong hộp thoại , ấn định lần lƣợt các chi tiết: ▪
Input Range (phạm vi đầu vào) : $A$1:$K$1 ▪
Group By (cách sắp xếp theo hàng hay cột) : Rows ▪
Labels in Fisrt Row/Column (nhãn dữ liệu) ▪
Confidence Level (mức tin cậy) ▪
Output Range (phạm vi đầu ra) ▪
Summary Statistics (kết quả tóm tắt) A B 1 Mean
5288.889 Trung bình mẫu x 2 Standard Error
218.4268 Sai số chuẩn s' n 3 Median 5125 Trung vị 4 Mode #N/A Giá trị mode 5 Standard Deviation
655.2804 Độ lệch tiêu chuẩn điều chỉnh s’ 6 Sample Variance
429392.4 Phương sai điều chỉnh s’2 7 Kurtosis
0.245489 Diễn tả đặc điểm thuộc về đỉnh của dạng phân phối dữ liệu 8 Skewness
1.049589 Phản ánh mức độ bất đối xứng của dạng phân phối dữ liệu 9 Range
2000 Khoảng quan sát 10 Minimum
4500 Giá trị quan sát nhỏ nhất 11 Maximum
6500 Giá trị quan sát lớn nhất 12 Sum
47600 Tổng các giá trị quan sát 13 Count
9 Kích thước mẫu n 14 Phân vị Student t 2.306006 15 Độ chính xác 503.6934
Do ƣớc lƣợng có độ tin cậy 1 − = 0.95 = 1−
= 0.975, chọn ô B14 nhập biểu 2
thức = TINV((1− )*2,n −1) = TINV((1−0.975)*2,8) đƣợc giá trị phân vị student với
mức xác suất 0.975 và 8 bậc tự do là 2.306006. Chọn ô s'
B15 nhập biểu thức = B2*B14 để tính độ chính xác = t . = 503.6934 n
Kết quả: Khoảng tin cậy 95% ( x ) = (5288.889 503.6934).
CHƢƠNG IV: ƢỚC LƢỢNG CÁC THAM SỐ CỦA ĐẠI LƢỢNG NGẪU NHIÊN 105 lOMoAR cPSD| 35883770
PHƢƠNG PHÁP KHOẢNG TIN CẬY BÀI TẬP
1 . Khi kiểm tra 400 sản phẩm của nhà máy thì thấy có 80 sản phẩm loại 2.
Hãy dùng mẫu kiểm tra này để ƣớc lƣợng tỷ lệ sản phẩm loại 2 của nhà
máy với độ tin cậy 96%? a/ (0.166052;0.233948) c/ (0,1068;0,6308) b/ (0,1608;0,3608) d/ (0.159712;0.240288)
2 . Cho biết trọng lƣợng của các gói mì ăn liền có độ lệch tiêu chuẩn là =
2,5g. Khi muốn dùng mẫu thống kê có kích thƣớc n = 100 để ƣớc lƣợng
trọng lƣợng trung bình của các gói mì với độ chính xác = 0,49g thì độ tin
cậy tƣơng ứng của ƣớc lƣợng là bao nhiêu? a/ 95% b/ 96% c/ 98% d/ 99%
3 . Tiến hành quan sát về số lít xăng bán đƣợc trong một số ngày ở một trạm
xăng ngƣời ta thu đƣợc kết quả sau: xi (lít) 200 220 240 260 280 300 320 ni (số ngày) 5 8 12 25 30 16 4 3.1 /
Ƣớc lƣợng số lít xăng bán đƣợc trung bình trong ngày với độ tin cậy 99%? a/ (257,7;273,7) c/ (259,4;269,4) b/ (260,5;280,5) d/ (260,2;280,2) 3.2 /
Xem những ngày bán không đến 250 lít xăng là những ngày "ế
hàng". Ƣớc lƣợng tỷ lệ những ngày "ế hàng" với độ tin cậy 95%. a/ (0.161059;0.338941) c/ (0.149281;0.350719) b/ (0.138456;0.361544) d/ (0.16513;0.33487)
3.3 / Với thông tin mẫu có đƣợc, hỏi muốn ƣớc lƣợng tỷ lệ những ngày "ế
hàng" với độ tin cậy là 99% và độ chính xác tối đa là 0,05 thì phải lấy mẫu
thống kê với kích thƣớc tối thiểu là bao nhiêu ngày? a/ 497 b/ 498 c/ 499 d/ 500
4 . Do mắc phải 1 số sai sót khi lắp ráp, một dây chuyền đóng gói 1 loại sản
phẩm cho ra những sản phẩm có trọng lƣợng không nhƣ nhau. Qua tính
toán độ sai lệch ở từng khâu, ngƣời ta xác định đƣợc độ lệch tiêu chuẩn của
trọng lƣơng các sản phẩm đó là 0,8. Kiểm tra một số sản phẩm thì thu đƣợc các số liệu sau
Khoảng trọng lƣợng(g) Số sản phẩm [6,25;7,25) 18 [7,25;8,25) 32 [8,25;9,25) 44 [9,25;10,25) 6
4.1 / Hãy chỉ ra khoảng tin cậy của trọng lƣợng trung bình các sản phẩm với độ tin cậy 95%. a/ (7,94392;8.31608) c/ (7,96568;8,29432) b/ (7,92392;8.33608) d/ (7,9732;7,9732) 106
CHƢƠNG IV: ƢỚC LƢỢNG CÁC THAM SỐ CỦA ĐẠI LƢỢNG NGẪU NHIÊN lOMoAR cPSD| 35883770
PHƢƠNG PHÁP KHOẢNG TIN CẬY 4.2 /
Nếu muốn ƣớc lƣợng với độ dài khoảng tin cậy là 0,1728 thì độ tin
cậy của ƣớc lƣợng là bao nhiêu? a/ 72% b/ 82% c/ 92% d/ 95% 5 .
Cân thử 100 quả của 1 loại trái cây, ngƣời ta thu kết quả nhƣ sau: Trọng lƣợng (g) 95 − 100 100 − 105 105 − 110 110 − 115 115 − 120 120 − 125 125 − 130 Số quả 5 12 18 20 23 15 7
a/ Ƣớc lƣợng trọng lƣợng trung bình của loại trái cây trên với độ tin cậy 95%.
b/ Với mẫu đã cho, nếu cho rằng trung bình của loại trái cây này trong
khỏang (111,8433;114,8567) thì độ tin cậy của ƣớc lƣợng này là bao nhiêu?
c/ Những quả có trọng lƣợng từ 120g trở lên gọi là loại 1. Hãy ƣớc lƣợng
trung bình và tỷ lệ quả loại 1 với độ tin cậy 99%. Cho biết trọng lƣợng
các trái cây có phân phối chuẩn.
6 . Tiến hành quan sát về số lít xăng bán đƣợc trong một số ngày ở một trạm
xăng ngƣời ta thu đƣợc kết quả sau: xi (lít) 200 220 240 260 280 300 320 ni (số ngày) 5 8 12 25 30 16 4
a/ Ƣớc lƣợng số lít xăng bán đƣợc trung bình trong ngày với độ tin cậy 99%.
b/ Xem những ngày bán không đến 250 lít xăng là những ngày "ế hàng".
Ƣớc lƣợng tỷ lệ những ngày "ế hàng" với độ tin cậy 95%.
c/ Với thông tin mẫu có đƣợc, hỏi muốn ƣớc lƣợng tỷ lệ những ngày "ế
hàng" với độ tin cậy là 99% và độ chính xác tối đa là 0,05 thì phải lấy
mẫu thống kê với kích thƣớc tối thiểu là bao nhiêu ngày?
7 . Hàm lƣợng dầu trung bình trong một loại trái cây lúc đầu là 10%. Ngƣời ta
chăm bón bằng một loại phân N và sau một thời gian kiểm tra một số trái
thì thu đƣợc kết quả sau: Hàm lƣợng xi (%) 2 4 6 8 10 12 14 Số trái ni 76 90 80 70 84 115 110
a/ Một báo cáo cho rằng sau khi dùng loại phân N hàm lƣợng dầu trung
bình trong loại trái cây trên có thay đổi. Với mức ý nghĩa 1%, hãy cho
kết luận về báo cáo đó.
b/ Tìm khoảng ƣớc lƣợng cho hàm lƣợng dầu trung bình của loại trái cây
trên sau chăm bón với độ tin cậy 95%.
c/ Những trái có hàm lƣợng dầu từ 11% trở lên đƣợc gọi là loại A. Hãy ƣớc
lƣợng tỷ lệ trái loại A với độ tin cậy 99%.
d/ Ƣớc lƣợng hàm lƣợng dầu trung bình của các trái loại A với độ tin cậy 99%
8 . Kiểm tra ngẫu nhiên 16 lô thuốc mới nhập về tìm đƣợc độ phân tán của
thành phần chính trong mỗi viên thuốc là s’2 = 0,775 gr2. Với độ tin cậy
95% hãy ƣớc lƣợng độ phân tán của thành phần chính trong mỗi viên thuốc
CHƢƠNG IV: ƢỚC LƢỢNG CÁC THAM SỐ CỦA ĐẠI LƢỢNG NGẪU NHIÊN 107 lOMoAR cPSD| 35883770
PHƢƠNG PHÁP KHOẢNG TIN CẬY
của cả lô thuốc đó. Biết trọng lƣợng thành phần chính trong mỗi viên thuốc phân phối chuẩn.
9 . Lãi suất cổ phiếu của một công ty trong vòng 5 năm qua là 15%, 10%, 20%,
7%, 14%. Với độ tin cậy 90% hãy ƣớc lƣợng độ phân tán của lãi suất cổ
phiếu của công ty đó. Biết lãi suất cổ phiếu là biến ngẫu nhiên phân phối chuẩn.
10 . Để nghiên cứu độ ổn định của một máy gia công, ngƣời ta lấy ngẫu nhiên
25 chi tiết do máy đó gia công, đem đo và thu đƣợc các kích thƣớc sau:
24,1 27,2 26,7 23,6 26,4 25,8 27,3 23,2 26,9 27,1 22,7 26,9 24,8
24,0 23,4 24,5 26,1 25,9 25,4 22,9 26,4 25,4 23,3 23,0 24,3.
Với độ tin cậy 95% hãy ƣớc lƣợng độ phân tán của kích thƣớc các chi tiết
do máy đó gia công. Biết kích thƣớc chi tiết đƣợc gia công là đại lƣợng ngẫu nhiên phân phối chuẩn. 108
CHƢƠNG IV: ƢỚC LƢỢNG CÁC THAM SỐ CỦA ĐẠI LƢỢNG NGẪU NHIÊN lOMoAR cPSD| 35883770 CHƢƠNG V
KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ § 1.
CÁC ĐỊNH NGHĨA VÀ PHƢƠNG PHÁP KIỂM ĐỊNH
1.1. Các khái niệm và định nghĩa
Kiểm định giả thuyết thống kê là một vấn đề quan trọng của Thống kê. Nội
dung công việc ở đây là căn cứ các số liệu thu đƣợc để đƣa ra một kết luận về
một giả thuyết thống kê nào đó mà ta quan tâm.
a) Giả thuyết thống kê
Trong các bài toán nghiên cứu thống kê có khi ta cần đánh giá những giả
định về giá trị trung bình của một đại lƣợng nào đó, hoặc một tỷ lệ nào đó, hoặc
ta cần so sánh hai dụng cụ cân đo, hai phƣơng pháp làm thí nghiệm … xem có
hiệu quả chất lƣợng nhƣ nhau không. Nói chung là phải xem xét những giả định
về các vấn đề thống kê. Chúng ta phải đƣa ra nhận định về tính thừa nhận đƣợc
hay không thừa nhận đƣợc của các giả định về các vấn đề thống kê. Các giả định
về các vấn đề thống kê đƣợc gọi là các giả thuyết thống kê. Các giả thuyết thống
kê thƣờng gặp là các giả thiết nói về các tham số, các dạng quy luật phân phối, về
tính độc lập của đại lƣợng ngẫu nhiên. Chẳng hạn nhƣ giả thuyết cho rằng đại
lƣợng ngẫu nhiên nào đó có phân phối theo luật chuẩn, giả thuyết cho rằng trọng
lƣợng trung bình của một loại sản phẩm nào đó có xu hƣớng giảm sút, giả thuyết
cho rằng tuổi thọ trung bình của hai loại bóng đèn A và B là nhƣ nhau, …. Trong
phạm vi của giáo trình này ta chỉ xét những giả thuyết thống kê nói về các tham
số của đại lƣợng ngẫu nhiên. Các giả thuyết thống kê đƣợc kí hiệu là H0. b) Giả thuyết đối
Giả thuyết đƣa ra kiểm định H0 đƣợc gọi là giả thuyết gốc. Giả thuyết trái
ngƣợc với giả thuyết gốc đƣợc gọi là giả thuyết đối hay đối thuyết, kí hiệu H1.Ta
thừa nhận khi đã chọn cặp giả thuyết H0 và H1 thì việc chấp nhận H0 sẽ chính là
bác bỏ H1 và ngƣợc lại.
c) Kiểm định giả thuyết thống kê
Khi có hai giả thuyết H0 và H1 thì kiểm định giả thuyết là đƣa ra một quy
tắc, dựa vào đó để lựa chọn H0 hay H1. Trong lý thuyết thống kê, xuất phát từ
một mẫu ngẫu nhiên X1, X2, …, Xn (chọn từ một đại lƣợng X chƣa biết phân phối
hoặc có phân phối F(X, ) nhƣng chƣa biết ) ta chia tập hợp giá trị có thể của
mẫu ngẫu nhiên (còn gọi là không gian mẫu) thành hai miền loại trừ nhau W và
W . Giả thiết H0 đƣợc chấp nhận khi mẫu nằm trong vùng W , còn bị bác bỏ khi
nằm trong vùng W. Đây chính là quy tắc kiểm định giả thuyết thống kê.
CHƢƠNG V: KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 109 lOMoAR cPSD| 35883770
KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ
d) Sai lầm loại 1 & sai lầm loại 2
Khi kiểm định một giả thuyết thống kê có thể mắc một trong hai dạng sai lầm sau
− Sai lầm loại 1: Bác bỏ một giả thuyết đúng.
− Sai lầm loại 2: Chấp nhận một giả thuyết sai.
Nếu muốn làm giảm xác suất mắc sai lầm loại 1 thì sẽ làm tăng xác suất
mắc sai lầm loại 2 (và ngƣợc lại) khi kiểm định. e) Mức ý nghĩa α
Là xác suất mắc phải sai lầm loại 1. Khi kiểm định giả thuyết thống kê,
ngƣời ta thƣờng ấn định trƣớc mức ý nghĩa (là một xác suất khá nhỏ, chẳng
hạn 1%, 5%, …) rồi tìm cách hạn chế xác suất mắc sai lầm loại 2. f) Giá trị quan sát
Tùy theo nội dung kiểm định, với mẫu các số liệu x1, x2, …, xn lấy từ tổng
thể, bằng phƣơng pháp khoa học phù hợp, phƣơng pháp kiểm định thống kê xác
định một giá trị cụ thể dùng để quan sát đƣa ra kết luận kiểm định. Giá trị đó
đƣợc gọi là giá trị quan sát hay là giá trị kiểm định. Kí hiệu u0. g) Miền bác bỏ
Là một miền giá trị W đƣợc
xác định từ mức ý nghĩa sao cho nếu giá
trị quan sát u0 thuộc trong đó thì sẽ bác bỏ giả thuyết H0.
1.2. Kiểm định giả thuyết thống kê về các tham số của đại lƣợng ngẫu nhiên a) Bài toán
Giả sử tổng thể nghiên cứu (tƣơng ứng với đại lƣợng ngẫu nhiên gốc X) có
tham số (trung bình, tỷ lệ hoặc phƣơng sai) chƣa biết. Dựa vào một cơ sở nào
đó ngƣời ta đƣa ra một mức giá trị giả thuyết cho . Cho trƣớc mức ý nghĩa 0
và một mẫu số liệu có kích thƣớc n, xét các dạng kiểm định:
(1) Kiểm định hai phía H : = 0 0 . H : θ θ 1 0
(2) Kiểm định phía phải H : 0 0 .
H : θ θ 1 0
(3) Kiểm định phía trái H : 0 0 H : θ θ 1 0 110
CHƢƠNG V: KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ lOMoAR cPSD| 35883770
KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ
1.3. Nguyên tắc kiểm định
Từ mẫu ngẫu nhiên WX = (X1, X2, …, Xn) chọn thống kê ˆ (X1, X2, …, Xn)
sao cho nếu H0 đúng thì P( ˆ W ) = .
• Lấy mẫu quan sát cụ thể wx = (x1, x2, …, xn) của mẫu ngẫu nhiên
WX = (X1, X2, …, Xn) , xác định giá trị quan sát u0 = ˆ (x1, x2, …, xn).
• Từ mức ý nghĩa , xác định miền bác bỏ W . • Kết luận
− Nếu u0 W thì bác bỏ giả thuyết H0 , thừa nhận đối thuyết H1.
− Nếu u0 W thì thừa nhận H0, bác bỏ H1.
CHƢƠNG V: KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 111 lOMoAR cPSD| 35883770
KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ § 2.
MỘT SỐ BÀI TOÁN KIỂM ĐỊNH
2.4. Kiểm định giả thuyết về trung bình
Giả sử đại lƣợng ngẫu nhiên X có trung bình E(X) = m chƣa biết. Cho trƣớc
mức ý nghĩa và mẫu số quan sát có kích thƣớc n. Có ba dạng kiểm định về giá
trị giả thuyết m0 đối với trung bình m : (1) H : m = m : m m : m m 0 0 H và (3) H , (2) 0 0 0 0 H : m m 0 H : m m 0 H : m m 1 1 1 0
Theo nguyên tắc kiểm định chung nêu ở mục 1.3, tùy theo đại lƣợng X biết
phƣơng sai hay chƣa và mẫu có kích thƣớc nhỏ hay lớn mà giá trị quan sát và
miền bác bỏ đƣợc xác định khác nhau trong ba trƣờng hợp sau đây.
a) Biết Var(X) = 2 , n 30 (hoặc n < 30, X có phân phối chuẩn)
• Từ mức ý nghĩa xác định miền bác bỏ W :
− Nếu kiểm định ở dạng (1) thì W = (− ; − u ) ( u ;+ ). 1− 1− 2 2
− Nếu kiểm định ở dạng (2) thì W = ( u ; + ). 1−
− Nếu kiểm định ở dạng (3) thì W = (− ; − u ). 1− Trong đó u và u 1−
1− là các giá trị phân vị chuẩn. 2
• Từ các số liệu của mẫu cụ thể tính x , từ đó tính giá trị quan sát: (x − m ) n 0 u0 = (5.1)
• Quan sát giá trị u0 và miền giá trị W , dựa trên nguyên tắc chung kết luận.
Ví dụ 1: Kiểm tra độ dài X của 16 chi tiết cùng loại thu được trung bình
mẫu của các độ dài đó x = 10,1. Cho biết X N(m;1), với mức ý nghĩa = 0,05
hãy kiểm định giả thuyết H0 cho rằng E(X) = m = 10,5. Giải
Do không nhắc tới đối thuyết trong yêu cầu, nên ta chọn H1: E(X) 10,5. Ở đây = 1 nên ta có 10,1−1,5 u = 16 = −1,6. 0 1
Mức ý nghĩa = 0,05 u = u = u 0,975 = 1,96. 1− 2
Miền bác bỏ W = (− ;−1,96) (1,96;+ ). Ta có u 0 W Giả thuyết H 0 chấp nhận đƣợc. 112
CHƢƠNG V: KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ lOMoAR cPSD| 35883770
KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ
b) Chƣa biết Var(X), n 30
Quy tắc kiểm định tiến hành nhƣ trƣờng hợp a), chỉ khác là trong công thức
xác định giá trị quan sát u0 , giá trị đƣợc thay bởi độ lệch tiêu chuẩn điều chỉnh s'.
Ví dụ 2: Độ bền của một loại dây thép sản xuất theo công nghệ cũ là 150.
Sau khi cải tiến kỹ thuật người ta lấy mẫu gồm 100 sợi dây thép để thử độ bền thì
thấy độ bền trung bình là 155 và s’ = 25. Với = 0,05 hỏi công nghệ mới có tốt
hơn công nghệ cũ hay không? Giải
Ở đây n = 100 khá lớn nên không cần giả thuyết chuẩn đối với độ bền của
loại dây thép. Rõ ràng để so sánh hai công nghệ sản xuất trên ta chỉ có thể so
sánh độ bền trung bình m của phƣơng pháp sau với 150 là trung bình của độ bền
theo phƣơng pháp cũ. Nếu m > 150 thì coi nhƣ phƣơng pháp sau tốt hơn phƣơng
pháp cũ, còn nếu m 150 thì ta nói ngƣợc lại. Do đó, ta chọn dạng kiểm định H : m m = 150 (2): 0 0 H : m m 1 0
Mẫu quan sát có x = 155, s = 25, n = 100. X − m 155 −150 Tính u = 0 n = 100 = 2 . 0 s' 25
Mức ý nghĩa = 0,05 u = u = 1,645. 1− 0,95
Miền bác bỏ W = ( u 1− ; + ) = (1,645;+ ).
Ta có u0 W . Do đó ta bác bỏ giả thuyết H
0, chấp nhận đối thuyết H1.
Nghĩa là ta có thể cho rằng việc cải tiến kỹ thuật là có hiệu quả.
c) Chƣa biết Var(X), n < 30, X có phân phối chuẩn • Miền bác bỏ W
− Nếu kiểm định ở dạng (1) thì W =(− ; − t ) ( t ;+ ), /2 /2
− Nếu kiểm định ở dạng (2) thì W = ( t ; + ),
− Nếu kiểm định ở dạng (3) thì W = (− ; − t ).
Trong đó t và t t
là các phân vị student với bậc tự do k = n − 1. /2 1− •
(x − m ) n Giá trị quan sát u 0 0 = (5.2) s
Trong đó x là trung bình, s là độ lệch tiêu chuẩn và n là kích thƣớc của mẫu quan sát.
CHƢƠNG V: KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 113 lOMoAR cPSD| 35883770
KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ
Ví dụ 3: Kết quả đo chiều cao (cm) của 24 trẻ em 2 tuổi cho bởi bảng số liệu sau 84,4 89,9
89,0 81,9 87,0 78,5 84,1 86,3 81,3 86,8
83,4 89,8 85,4 80,6 85,0 82,5 85,4 85,0
85,5 81,6 80,6 80,0 80,784,3
Chiều cao chuẩn của trẻ em 2 tuổi ở vùng đó là 86,5cm. Hỏi với = 0,01
có sự khác biệt đáng kể của chiều cao nhóm trẻ so với chuẩn hay không? Giải
Chú ý là ta có thể coi kết quả đo nhƣ là mẫu chọn từ tập nền có phân phối
chuẩn (đó cũng là ý nghĩa ứng dụng của phân phối chuẩn rất hay gặp trong thực
tế). Ở đây ta xét giả thuyết H0 : m = m0 = 86,5 với đối thuyết H1 : m 86, (m là
chiều cao trung bình của nhóm trẻ đang khảo sát) và = 0,01.
Trƣớc hết từ mẫu số liệu với n = 24 ta tính đƣợc x = 84,1; s = 3,11. X − m 84,1 − 86,5 Giá trị quan sát u = 0 n = 24 −3,81 . 0 s' 3,11
Mức ý nghĩa = 0,01 t (23) = 2,807. 0,005
Miền bác bỏ W = (− ;−2,807)) (2,807;+ ) u0 W . Do đó ta
không có cơ sở chấp nhận giả thuyết H0 và nhóm trẻ trên có chiều cao lệch đáng kể so với chuẩn.
2.5. Kiểm định giả thuyết về tỷ lệ
Giả sử tỷ lệ các phần tử có tính chất A trong tổng thể là giá trị p chƣa biết. Xét các kiểm định: (1) H : m = m : m m : m m 0 0 H và (3) H , (2) 0 0 0 0 H : m m 0 H : m m 0 H : m m 1 1 1 0
• Miền bác bỏ đƣợc xác định tƣơng tự nhƣ trong kiểm định trung bình:
− Nếu kiểm định ở dạng (1) thì W = (− ; − u ) ( u ;+ ). 1− 1− 2 2
− Nếu kiểm định ở dạng (2) thì W = ( u ; + ). 1−
− Nếu kiểm định ở dạng (3) thì W = (− ; − u ). 1−
• Với mẫu quan sát kích thƣớc n, xác định tỷ lệ f các phần tử có tính chất
A trong mẫu (tỷ lệ mẫu), tính giá trị quan sát: (f − p0 ) n u0 = (5.3) p (1− ) 0 p0 114
CHƢƠNG V: KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ lOMoAR cPSD| 35883770
KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ
Ví dụ 4: Giám đốc một công ty tuyên bố 90% động cơ của công ty đạt
chuẩn quốc gia. Một hãng độc lập kiểm tra 200 động cơ của công ty thì thấy có
168 đạt yêu cầu. Với mức = 0,05 ta có thể cho rằng tuyên bố trên là vượt quá thực tế hay không? Giải
Tỷ lệ mẫu của số động cơ đạt yêu cầu là f = 168/200 = 0,84 hơi thấp làm
chúng ta nghi ngờ. Gọi p là xác suất gặp một động cơ đạt tiêu chuẩn quốc gia của
công ty nọ. Nếu p < 0,9 thì nghĩa là tuyên bố của vị giám đốc cao hơn thực tế,
còn p 0,9 thì ngƣợc lại. Ta sẽ kiểm định giả thuyết H0 : p 0,9 với đối thuyết
H1 : p < 0,9 ( = 0,05). 0,84 − 0,9 Tính u = 200 −2,83. 0 0,9.0,1
Mức ý nghĩa = 0,05 u = u 1− 0,955 = 1,645.
Miền bác bỏ W = (− ;−1,645). Ta có u 0 W Giả thuyết H
0 không thể chấp nhận đƣợc, ta chấp nhận
đối thuyết cho rằng tuyên bố của công ty nọ là vƣợt quá thực tế.
2.6. Kiểm định giả thuyết về phƣơng sai
Xét đại lƣợng ngẫu nhiên X có phân phối chuẩn với phƣơng sai Var(X) = 2
chƣa biết. Kiểm định mức giá trị giả thuyết 2 cho 2 với các dạng: 0 H : 2 = 2 H H 0 0 0 : 2 2 : 2 2 0 0 0 (1) , (2) và (3) H : 2 2 H : 2 2 H : 2 2 1 0 1 0 1 0 • Miền bác bỏ W :
− Nếu kiểm định ở dạng (1) thì W =(− ; 2 (n −1) ) ( 2 (n −1) ;+ ), 1− 2 2
− Nếu kiểm định ở dạng (2) thì W = ( 2 (n −1) ; + ),
− Nếu kiểm định ở dạng (3) thì W 2 = (− ; 1− (n −1) ). • Giá trị quan sát: (n −1)s2 u0 = (5.4) 2 0
Trong đó s’2 là phƣơng sai điều chỉnh và n là kích thƣớc của mẫu quan sát.
CHƢƠNG V: KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 115 lOMoAR cPSD| 35883770
KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ
Ví dụ 5: Chủ hảng sản xuất cho biết độ lệch chuẩn của sai số đo ( dung
sai) của thuyết bị cao nhất là 5 đơn vị. Người ta kiểm tra 19 thuyết bị đo thì thấy
s’2 = 33. Với = 0,05 có kết luận gì về ý kiến của chủ hãng trên ? Giải
Giả thuyết gốc là H0 : 2 σ 2 = 25; ta chọn đối thuyết là H 0 1 : 2 > 25 18.33 Tính u 0 = 23,76 . 25
Tra phân vị khi _bình phƣơng 20,05(18) = 28,9 .
Miền bác bỏ W = (28,9 ;+ ). Ta có u 0 W Giả thuyết H 0 chấp nhận đƣợc.
2.7. Kiểm định giả thuyết về sự so sánh của hai trung bình
Giả sử hai đại lƣợng ngẫu nhiên X,Y độc lập, cùng phân phối theo quy luật
chuẩn với E(X), E(Y) chƣa biết. Cần kiểm định các dạng: (1) H : E(X) = E(Y) H : E(X) E(Y) : E(X) E(Y) 0 và (3) H , (2) 0 0 H : E(X) E(Y) H : E(X) E(Y) H : E(X) E(Y) 1 1 1
Để kiểm định các dạng trên, miền bác bỏ đƣợc xác định theo các giá trị
phân vị chuẩn tƣơng tự trƣờng hợp a) trong kiểm định trung bình. Giá trị quan sát
đƣợc tính giống nhau với cả ba dạng theo công thức x − y u0 = (5.5) var(X ) + var(Y ) m n
Trong đó x là trung bình, m là kích thƣớc mẫu quan sát lấy từ tổng thể
tƣơng ứng với đại lƣợng X; còn y là trung bình, m là kích thƣớc mẫu quan sát
lấy từ tổng thể tƣơng ứng với đại lƣợng Y. CHÚ Ý
Trƣờng hợp Var(X), Var(Y) chƣa biết và m, n khá lớn thì giá trị Var(X)
đƣợc thay bằng phƣơng sai điều chỉnh của mẫu tƣơng ứng đại lƣợng X (ký hiệu
sx’2) và Var(Y) đƣợc thay bằng sy’2 tƣơng ứng.
Ví dụ 6: Hai máy tự động dùng để cắt thanh kim loại do cùng một kỹ thuật
viên phụ trách và cân chỉnh. Người ta chọn ngẫu nhiên 36 thanh kim loại do mỗi
máy cắt ra thì thấy độ dài trung bình mẫu và độ lệch điều chỉnh tương ứng
x = 12,5cm; sx = 1,2cm và y = 12,2cm; sy = 1,4cm. Với mức ý nghĩa 1%, nếu
nói rằng chiều dài các thanh kim loại do máy 1 cắt nói chung lớn hơn chiều dài
của các thanh kim loại của máy 2 cắt hay không? Biết chiều dài thanh kim loại
do các máy đó cắt ra có phân phối chuẩn. 116
CHƢƠNG V: KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ lOMoAR cPSD| 35883770
KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ Giải
Gọi X, Y lần lƣợt là chiều dài của các thanh kim loại do hai máy cắt ra. Cần
kiểm định giả thuyết H0: E(X) E(Y) với đối thuyết H1: E(X) > E(Y). 12,5 −12,2 Giá trị quan sát u0 = = 0,976. (1,2)2 + (1,4)2 36 36
Miền bác bỏ W = ( u ;+ ) = (2,326 ;+ ). 1− Ta có u 0 W
Chấp nhận giả thuyết H
0, bác bỏ đối thuyết H1.
2.8. Kiểm định giả thuyết về sự so sánh của hai tỷ lệ
Xét p1 và p2 lần lƣợt là tỷ lệ các phần tử có tính chất A tƣơng ứng trong 2
tổng thể khác nhau. Khi xét những giả định so sánh về hai tỷ lệ này ta có có dạng kiểm định sau: (1) H : p = p H : p p : p p 0 1 2 và (3) H , (2) 0 1 2 0 1 2 H : p p p p 2 H : p 2 H : p 1 1 1 1 1 1 2
• Miền bác bỏ: xác định tƣơng tự nhƣ trong kiểm định tỷ lệ. • Giá trị quan sát: f − f u 1 2 0 = (5.6) 1 p (1− 1 p ) + * * m n Trong đó
− f1 là tỷ lệ phần tử có tính chất A, m là kích thƣớc mẫu quan sát lấy từ
tổng thể ứng với tỷ lệ p1.
− f2 là tỷ lệ phần tử có tính chất A, m là kích thƣớc mẫu quan sát lấy từ
tổng thể ứng với tỷ lệ p2. + − mf nf p 1 2 * = . m + n
Ví dụ 7: Theo dõi số tai nạn lao động của hai phân xưởng trong sáu
tháng, ta có số liệu sau: phân xưởng I: 2/200 công nhân; phân xưởng II 12/800
công nhân. Với mức = 0,05 hỏi có sự khác nhau đáng kể về chất lượng công
tác bảo hộ lao động hay không ở hai phân xưởng trên? Giải
Ta phải kiểm định giả thuyết về sự bằng nhau của hai tỷ lệ tai nạn lao động:
H0 : p1 = p2 với H1 : p1 p2.
Với p1, p2 lần lƣợt là tỷ lệ bị tai nạn lao động ở hai phân xƣởng. Trƣớc tiên dễ thấy
f = 2 = 0,01; n = 200; f = 12 = 0,015; n = 800; p = 140 = 0,14. 1 200 1 2 800 2 * 1000
CHƢƠNG V: KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 117 lOMoAR cPSD| 35883770
KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ Từ đó: 0,01 − 0,015 u 160 0 = −0,182 0,14.0,86
Tra phân vị chuẩn u = u = u 0,975 = 1,96. 1− 2
Miền bác bỏ W = (− ;−1,96) (1,96;+ ). Ta có u 0 W Giả thuyết H
0 chấp nhận đƣợc. Điều đó có nghĩa là
không có cơ sở cho rằng có sự khác biệt đáng kể về chất lƣợng công tác bảo hộ
lao động ở hai phân xƣởng.
2.9. Kiểm định sự độc lập a) Bài toán
Giả sử ta cần nghiên cứu đồng thời hai dấu hiệu X và Y, với X có h dấu hiệu
thành phần {x ,x ,..., x }; Y có c dấu hiệu thành phần {y , y ,..., y }. Chọn một 1 2 h 1 2 c
mẫu gồm n phần tử, quan sát đồng thời hai dấu hiệu X và Y ta có bảng số liệu sau: Y y ….. y 1 y2 c X x n n 1 n11 12 1c x n ….. n 2 n21 22 2c ⁝ ⁝ ⁝ ⁝ ⁝ x n ….. n h nh1 h 2 hc
Với một mức ý nghĩa cho trƣớc, ta cần kiểm tra X và Y có độc lập nhau không?
b) Các bƣớc thực hiện
Ta có thể thực hành theo các bƣớc sau:
• Bước 1: Chọn giả thiết H và đối thiết H :
H: X và Y độc lập,
H : X và Y phụ thuộc.
• Bước 2: Tìm miền bác bỏ: W =
( 2 ((h −1)(c −1)), + )
Trong đó 2 ((h −1)(c −1)) là phân vị khi bình phƣơng bậc tự do (h −1)(c −1) , mức xác suất .
• Bước 3: Tính giá trị quan sát: ( n − n ) 2 2 = h c ij ij (4.12) qs i=1 j=1 nij Trong đó 118
CHƢƠNG V: KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ lOMoAR cPSD| 35883770
KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ
n : Tần số thực tế ứng với các phần tử đồng thời mang dấu hiệu ij
(x , y ) đƣợc xác định từ mẫu chọn ra, i j
n : Tần số lý thuyết ứng với các phần tử đồng thời mang dấu hiệu ij
(x , y ) . Tần số lý thuyết đƣợc xác định bởi i j n = h c i j ij . n Với
hi: Tổng số liệu của hàng thứ i,
cj: Tổng số liệu của cột j.
• Bước 4: Trả lời.
Ví dụ 8: Nghiên cứu 200 cặp vợ chồng có thời gian kết hôn trên 5 năm để
tìm hiểu có mối quan hệ giữa thời gian tìm hiểu trước hôn nhân và tình trạng
hiện tại của cuộc hôn nhân hay không. Có 3 mức độ thời gian tìm hiểu trước hôn
nhân là ngắn, trung bình và dài. Cũng có 3 mức độ tình trạng hôn nhân hiện tại
là hạnh phúc, không hạnh phúc và ly dị. Phỏng vấn 200 người ta có số liệu sau: Ngắn Trung bình Dài Hạnh phúc 38 58 54 Không hạnh phúc 12 14 4 Ly dị 10 8 2
Với độ tin cậy 95%, đánh giá xem có mối quan hệ giữa thời gian tìm hiểu
trước hôn nhân và tình trạng hiện tại của cuộc hôn nhân hay không? Giải
* Chọn H: Không có mối quan hệ giữa thời gian tìm hiểu trƣớc hôn nhân
và tình trạng hiện tại của cuộc hôn nhân,
H : Có mối quan hệ giữa thời gian tìm hiểu trƣớc hôn nhân và tình trạng
hiện tại của cuộc hôn nhân. * Miền bác bỏ W =
( 2 ((h −1)(c −1)), + ) = ( 2 (4), + ) = (9.488; + ). 0.05
* Ta tính đƣợc các tần số lý thuyết bởi bảng sau: Ngắn Trung bình Dài Hạnh phúc 45 60 45 Không hạnh phúc 9 12 9 Ly dị 6 8 6
Do đó giá trị quan sát đƣợc xác định cụ thể nhƣ sau: (38 − 45)2 (58 − 60)2 (2 − 6)2 2 = + + + = 12.4. qs ... 45 60 2
CHƢƠNG V: KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 119 lOMoAR cPSD| 35883770
KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ Ta có 2 W qs
nên ta bác bỏ giả thiết, chấp nhận đối thiết. Vậy có đủ
bằng chứng thống kê kết luận có mối quan hệ giữa thời gian tìm hiểu
trƣớc hôn nhân và tình trạng hiện tại của cuộc hôn nhân. CHÚ Ý
Các trƣờng hợp kiểm định so sánh hai trung bình trong Excel đƣợc thực hiện bởi đơn lệnh: Tools,
Data Analysis, z-Test: Two Sample for Means (hay z-Test: Paired Two Sample for Means hay z-Test:
Paired Two Sample Assuming Equal Variances hay z-Test: Paired Two Sample Assuming Unequal Variances ) BÀI TẬP
1 . Chọn khẳng định đúng/sai trong các trƣờng hợp sau Đúng Sai a/
Kiểm tra ngẫu nhiên 81 sản phẩm thấy khối lƣợng trung
bình là 210g với độ lệch tiêu chuẩn điều chỉnh là 36g. Với
mức ý nghĩa 1% nếu nói rằng trọng lƣợng thực sự của các
sản phẩm là thấp hơn mức ghi ngoài bao bì là 225g thì đúng hay sai? b/
Một dây chuyền sản xuất tự động lúc đầu tỷ lệ sản phẩm
loại I là 85%. Sau một thời gian sản xuất ngƣời ta nghi
ngờ tỷ lệ sản phẩm loại I không còn nhƣ trƣớc nữa. Để
kiểm tra về điều này, ngƣời ta tiến hành kiểm tra 640 sản
phẩm thì thấy có 512 sản phẩm loại I. Với độ tin cậy 99%
hãy cho biết điều nghi ngờ trên đúng hay sai? c/
Trọng lƣợng của 1 loại sản phẩm do 1 nhà máy sản xuất
là đại lƣợng ngẫu nhiên phân phối theo quy luật chuẩn với
trọng lƣợng trung bình là 500 g. Nghi ngờ trọng lƣợng
của loại sản phẩm này có xu hƣớng giảm sút, ngƣời ta cân
thử 25 sản phẩm và tính đƣợc trung bình x = 495 và độ
lệch tiêu chuẩn điều chỉnh s’ = 10. Với mức ý nghĩa 5%,
có thể kết luận nghi ngờ trên là đúng hay sai? d/
Sau khi áp dụng một biện pháp cải tiến mới, nhà máy báo
cáo rằng tỷ lệ phế phẩm đã giảm xuống chỉ còn 2%. Tuy
nhiên, có ý kiến cho rằng tỷ lệ phế phẩm của nhà máy sau
cải tiến vẫn còn cao hơn mức báo cáo. Ngƣời ta kiểm tra
thử 800 sản phẩm thì thấy có 24 phế phẩm. Với mức ý
nghĩa 0,05 hãy cho biết ý kiến trên là đúng hay sai? e/
Hai máy cắt dây thép có độ lệch chuẩn tƣơng ứng 1=
0,26 cm và 2= 0,31 cm. Ngƣời ta chọn ngẫu nhiên 50
dây thép do mỗi máy cắt ra thì thấy độ dài trung bình mẫu
tƣơng ứng x 1= 142,6 cm và x 2 = 142,3 cm. Với mức ý
nghĩa 1%, nếu nói rằng hai máy cắt dây cùng độ dài thì đúng hai sai? 120
CHƢƠNG V: KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ lOMoAR cPSD| 35883770
KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ f/
Theo phƣơng pháp thứ nhất thì khi thực hiện 200 thí
nghiệm thì có 12 thí nghiệm thất bại. Với phƣơng pháp
thứ hai thì có 5 thí nghiệm thất bại khi thực hiện 100 thí
nghiệm. Khi đƣa ra kết luận với mức ý nghĩa 0,05 cho
rằng phƣơng pháp thứ hai tốt hơn phƣơng pháp thứ nhất thì đúng hay sai? g/
Tỷ lệ mắc bệnh sốt rét ở một huyện miền núi là 7%.
Trong lần kiểm tra sức khoẻ ngẫu nhiên 350 ngƣời thấy
có 30 ngƣời mang vi trùng sốt rét. Với độ tin cậy 95%,
nếu khẳng định tỷ lệ mắc bệnh sốt rét của vùng đã tăng lên thì đúng hay sai? h/
Chiều cao trung bình của 100 nam sinh lớp 12 ở một
trƣờng trung học nội thành là 1,68m với độ lệch tiêu
chuẩn điều chỉnh mẫu là 6cm. Trong khi kiểm tra 120 em
ở lớp 12 của một huyện ngoại thành thì có chiều cao trung
bình là 1,64m với độ lệch chuẩn điều chỉnh mẫu là 5cm.
Với mức ý nghĩa 1% nếu kết luận rằng học sinh nội thành
phát triển thể lực tốt hơn học sinh ngoại thành thì đúng hay sai? i/
Giám đốc một công ty tuyên bố 90% động cơ của công ty
đạt chuẩn quốc gia. Một hãng độc lập kiểm tra 200 động
cơ của công ty thì thấy có 168 đạt yêu cầu. Với mức ý
nghĩa 5% nếu xem tuyên bố trên là vƣợt quá thực tế thì đúng hay sai? j/
Theo dõi số tai nạn lao động ở hai xí nghiệp trong thành
phố ta thấy: Ở xí nghiệp I có 500 công nhân với 28 ngƣời
bị tai nạn trong sáu tháng đầu năm. Cũng 6 tháng đó xí
nghiệp II có 20 ngƣời bị tai nạn trong số 400 công nhân.
Với độ tin cậy 99% nếu xem chất lƣợng công tác phòng
hộ lao động ở xí nghiệp I kém hơn xí nghiệp thì đúng hay sai?
2 . Một cuộc nghiên cứu cho thấy một ngƣời Mỹ trƣởng thành sau 1 năm đọc
trung bình 10 cuốn sách. Một mẫu ngẫu nhiên gồm 136 ngƣời đƣợc phỏng
vấn cho thấy trung bình họ đọc 12 cuốn sách trong 1 năm với độ lệch tiêu
chuẩn điều chỉnh là 9 cuốn. Nhận định xem có phải thực ra một ngƣời Mỹ
trung bình đọc nhiều hơn 10 cuốn sách trong một năm hay không. Mức ý nghĩa = 5%.
3 . Một nhà sản xuất bánh ngọt tuyên bố rằng mỗi chiếc bánh của họ trung bình
có 88 calo. Một mẫu ngẫu nhiên với 36 chiếc bánh đƣợc kiểm tra cho thấy
lƣợng calo trung bình trong mỗi chiếc bánh là 90 calo với độ lệch tiêu chuẩn
điều chỉnh là 4 calo. Với mức ý nghĩa 5%, kiểm tra xem có phải trên thực tế
mỗi chiếc bánh về trung bình chứa nhiều hơn 88 calo hay không.
4 . Một cuộc nghiên cứu giả thuyết rằng điểm trung bình trong kỳ thi tốt nghiệp
vừa qua là 9 ( thang điểm 20). Chọn ngẫu nhiên 400 thí sinh để kiểm tra ta
tính đƣợc trung bình mẫu là 9,2 với độ lệch tiêu chuẩn điều chỉnh là 2,4. Với
mức ý nghĩa 5% giả thuyết đã nêu có đúng không?
CHƢƠNG V: KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 121 lOMoAR cPSD| 35883770
KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ
5 . Năng suất lúa trung bình của giống lúa A đƣợc công bố là 43 tạ/ha. Một
nhóm gồm 60 thửa ruộng thí nghiệm đƣợc kiểm tra cho thấy năng suất trung
bình của nhóm là 46,2 tạ/ha với độ lệch tiêu chuẩn điều chỉnh là 12tạ/ha . Với
mức ý nghĩa = 5%, nhận định xem có phải là công bố là thấp hơn với sự thật hay không?
6 . Trong một cửa hàng lớn có rất nhiều quầy hàng, mỗi nhân viên bán hàng
trung bình một ngày bán đƣợc 780 ngàn đồng. Trong một ngày khuyến mại
80 nhân viên bán hàng mỗi ngƣời trung bình bán đƣợc 920 ngàn với độ lệch
tiêu chuẩn điều chỉnh là 620 ngàn. Với mức ý nghĩa = 0,1 kiểm định xem
trong ngày khuyến mại lƣợng hàng trung bình mỗi nhân viên bán đƣợc có
nhiều hơn ngày thƣờng hay không?
7 . Một loại dây cáp đƣợc dánh giá là có thể treo đƣợc vật nặng trung bình là
1800kg không đứt. Ngƣời ta đem thử một mẫu gồm 16 dây cáp trên và kết
quả cho thấy vật nặng trung bình dây cáp treo đƣợc là 1740kg với độ lệch
tiêu chuẩn điều chỉnh là 60kg. Với mức ý nghĩa = 0,05 nhận định xem sự
đáng gía có phải là quá cao không?
8 . Một công ty lớn nói rằng lƣơng trung bình mỗi kỹ sƣ của họ là
48.000USD/năm. Một thanh niên có ý định xin vào công ty thăm dò 12 kỹ sƣ
của công ty thì thấy rằng lƣơng trung bình của họ là 45,850USD với độ lệch
tiêu chuẩn điều chỉnh là 6 300 USD. Với mức ý nghĩa = 5% kiểm tra xem
có phải thông báo của công ty là quá sự thật hay không?
9 . Một vận động viên nói rằng trung bình một lần đẩy tạ anh ta đẩy đƣợc 43
mét. Huấn luyện viên kiểm tra anh ta đẩy tạ 10 lần thì thấy rằng khoảng cách
anh ta đẩy đƣợc trung bình là 40,6 mét với độ lệch tiêu chuẩn điều chỉnh là
3,8m. Dựa trên kết quả này ở mức 5% có thể coi rằng anh ta nói cƣờng điệu
khả năng của mình không?
10 .Một quán ăn nói với nhân viên thu thuế rằng trung bình một ngày họ có 32
khách. Kiểm tra ngẩu nhiên 2 ngày cho thấy số khách trung bình một ngày là
37,2 và độ lệch tiêu chuẩn điều chỉnh là 7,4. Với mức ý nghĩa 2% kiểm định
xem chủ quán nói có đúng hay không?
11 .Một tay đua xe đạp nói rằng mỗi ngày trung bình anh ta đạp xe ít nhất là 5
dặm (trong rất nhiều năm). Chọn ngẫu nhiên 8 ngày trong sổ tay anh ta thì
thấy các số liệu ghi quảng đƣờng anh ta đi nhƣ sau:
5,3 4,5 4,8 5,1 4,3 4,8 4,9 4,7.
Với mức = 5% có thể cho rằng anh ta nói có đúng hay không?
12 .Một tỉnh báo cáo rằng tỉ lệ học sinh đỗ tốt nghiệp của họ là 88%. Một mẫu
ngẫu nhiên gồm 100 em đƣợc chọn cho thấy trong đó chỉ có 82 em đỗ. Với
mức ý nghĩa = 5%, kiểm tra xem phải chăng báo cáo của tỉnh về tỷ lệ đỗ 88% là cao hơn sự thật.
13 .Một công ty tuyên bố rằng 40% dân chúng ƣa thích sản phẩm của công ty.
Một cuộc điều tra 400 ngƣời tiêu dùng cho thấy 125 ngƣời thích mua sản
phẩm của công ty. Với mức ý nghĩa 5% kiểm định xem có phải công ty nói quá sự thật hay không?
14 .Một cuộc nghiên cứu của Bộ Y tế cho rằng 12 % dân cƣ trong tỉnh A mắc
bệnh đau mắt hột. Chọn ngẫu nhiên 200 ngƣời để khám mắt, đã phát hiện 21
ngƣời bị đau mắt hột. Kiểm định xem tỷ lệ 12% đã nêu có đúng không với mức ý nghĩa = 0,01. 122
CHƢƠNG V: KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ lOMoAR cPSD| 35883770
KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ
15 .Một phƣơng pháp điều trị bệnh đƣợc quảng cáo rằng sẽ chữa khỏi cho 75%
bệnh nhân mắc bệnh A. Trong một nhóm 120 ngƣời sử dụng phƣơng pháp
điều trị này có 82 ngƣời khỏi. Với mức ý nghĩa = 0,05 nhận định xem lời
quảng cáo đó có phải là cao hơn thực tế hay không.
16 .Một trung tâm cai nghiện ma túy công bố rằng nhiều nhất là 22% số bệnh
nhân của họ mắc nghiện trở lại trong vòng 2 năm.Một cuộc nghiên cứu theo
dõi 35 bệnh nhân từ trung tâm này trở về cho thấy có 10 ngƣời mắc nghiện
trở lại. Với mức ý nghĩa 1% nhận định xem công bố của trung tâm có cao
hơn so với thực tế không.
17 .Trọng lƣợng sản phẩm X do nhà máy sản xuất ra là đại lƣợng ngẫu nhiên
phân phối chuẩn với độ lệch tiêu chuẩn là = 2kg và trọng lƣợng trung bình
là 20kg. Nghi ngờ máy hoạt động không bình thƣờng làm thay đổi trọng
lƣợng trung bình các sản phẩm ngƣời ta cân thử 100 sản phẩm và thu đƣợc kết quả sau:
Trọng lƣợng sản phẩm (kg) 19 20 21 22 23
Số sản phẩm tƣơng ứng 10 60 20 5 5
Với mức ý nghĩa 5% hãy kết luận về điều nghi ngờ nói trên.
18 .Một nhà máy sản suất bóng đèn cho rằng chất lƣợng bóng đèn sẽ đƣợc coi là
đồng đều nếu tuổi thọ của các bóng đèn có độ lệch chuẩn bằng 1000 giờ hoặc
ít hơn. Lấy ngẫu nhiên 10 bóng để kiểm tra thì tìm đƣợc độ lệch tiêu chuẩn
điều chỉnh là 1150. Vậy với mức ý nghĩa 5% có thể coi chất lƣợng bóng đèn
do công ty đó sản xuất là đồng đều hay không? Biết tuổi thọ bóng đèn phân phối theo luật chuẩn.
19 .Ngƣời ta thử độ chịu lực của 35 chốt khoá thì thấy rằng độ lệch chuẩn điều
chỉnh là 3,5pao (1 pao khoảng 450gam). Có thể cho rằng đảm bảo của ngƣời
sản xuất: độ lệch chuẩn thật bằng 3pao, là đúng không? Kiểm định với mức ý nghĩa 5%.
20 .Chọn ngẫu nhiên 47 vòng bi cùng loại thì thấy độ lệch tiêu chuẩn điều chỉnh
là là 0,003. Theo quảng cáo thì độ lệch chuẩn thực không vƣợt quá 0,0025.
Vậy ta có thể kết luận gì với độ tin cậy 95%?
21 .Kết quả thi môn học chung của sinh viên 3 khoa trong một trƣờng đại học
đƣợc thể hiện qua mẫu dƣới đây: Kết quả Giỏi Khá Trung bình Kém Khoa A 15 18 20 3 B 6 12 25 7 C 8 15 22 5
Với mức ý nghĩa 5% hãy kiểm tra xem kết quả thi môn học chung có phụ thuộc vào khoa hay không?
22 .Một cuộc thăm dò đƣợc tiến hành ở Mỹ bởi Viện nghiên cứu xã hội học nổi
tiếng Gallup để nghiên cứu mối quan hệ giữa nghề nghiệp của một ngƣời với
CHƢƠNG V: KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 123 lOMoAR cPSD| 35883770
KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ
quan niệm của ngƣời đó về tiêu chuẩn đạo đức và tính trung thực. Kết quả
khảo sát một mẫu ngẫu nhiên gồm 380 ngƣời cho ta số liệu sau đây: Nghề Quan niệm nghiệp Cao Trung bình Thấp Bác sĩ 53 35 10 Luật sƣ 24 43 27 Nhà kinh doanh 18 55 20 Nhà chính trị 14 43 38
Với mức ý nghĩa 5%, hãy xác định xem có mối quan hệ giữa nghề nghiệp với
quan niệm về tiêu chuẩn đạo đức và tính trung thực hay không?
23 .Khi kiểm tra một số sản phẩm do hai phân xƣởng của một nhà máy sản xuất,
ngƣời ta thu đƣợc các số liệu sau:
Số sản phẩm đƣợc kiểm tra Số phế phẩm Phân xƣởng I 100 5 Phân xƣởng II 200 12
Có ý kiến cho rằng quy trình sản xuất của phân xƣởng I tốt hơn ở phân
xƣởng II. Xét kiểm định về ý kiến này với mức ý nghĩa 1%:
a/ Chọn giả thuyết và đối thuyết?
b/ Tìm miền bác bỏ W của kiểm định ?
c/ Tính giá trị quan sát u0 ?
d/ Trả lời: ý kiến trên đó có chấp nhận đƣợc không ?
24 .Quan sát lƣợng bán ra của một mặt hàng ở một cửa hàng trong một số ngày,
ngƣời ta thu đƣợc các kết quả sau:
Lƣợng bán ra (kg/ngày) Số ngày 0 6 1 15 2 30 3 35 4 10 5 4
Xét kiểm định với độ tin cậy 99% về một báo cáo cho rằng trung bình mỗi
ngày cửa hàng bán đƣợc 3 kg về mặt hàng này:
a/ Chọn giả thuyết và đối thuyết?
b/ Tìm miền bác bỏ W của kiểm định?
c/ Tính các giá trị của thống kê mẫu x , S và S ' ?
d/ Tính giá trị quan sát u0 từ số liệu mẫu?
e/ Trả lời: báo cáo đúng hay sai? 124
CHƢƠNG V: KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ lOMoAR cPSD| 35883770 CHƢƠNG VI
TƢƠNG QUAN VÀ HỒI QUY § 1.
HỆ SỐ TƢƠNG QUAN THỰC NGHIỆM
Trong chƣơng II, khi xét về đại lƣợng ngẫu nhiên hai chiều (X,Y) ta đã giới
thiệu các đặc trƣng số đồng thời của hai đại lƣợng X, Y nhƣ hiệp phƣơng sai, hệ
số tƣơng quan, … Hệ số tƣơng quan rXY phản ánh mức độ phụ thuộc tuyến tính
giữa hai đại lƣợng ngẫu nhiên X và Y. Nhƣng khi chƣa biết phân phối của (X,Y)
thì hệ số tƣơng quan lý thuyết rXY cũng chƣa tìm đƣợc. Do đó ta tìm cách ƣớc
lƣợng rXY theo mẫu quan sát đƣợc.
Trƣớc hết ta nhắc lại định nghĩa về hệ số tƣơng quan lý thuyết, ý nghĩa và
các tính chất. Sau đó ta sẽ xét phƣơng pháp ƣớc lƣợng hệ số tƣơng quan thực nghiệm.
1.1. Hệ số tƣơng quan lý thuyết a) Hiệp phƣơng sai
Hiệp phƣơng sai XY của hai đại lƣợng X và Y đƣợc xác định
= E[(X − EX)(Y − EY)] = E(XY) − E(X)E(Y) XY Trong đó
− Nếu (X,Y) rời rạc thì
= x x p(x , x ) − E(X)E(Y), XY i j i j i j
− Nếu (X,Y) liên tục thì = XY
xyf (x, y)dxdy − E(X)E(Y) . −−
b) Hệ số tƣơng quan
Hai đại lƣợng X, Y có hệ số tƣơng quan đƣợc tính bởi r = XY XY X Y
Hệ số tƣơng quan đo mức độ phụ thuộc tuyến tính giữa X và Y, có các tính chất sau (i) |rXY| 1.
(ii) |rXY| = 1 thì X và Y có quan hệ phụ thuộc tuyến tính.
(iii) Nếu |rXY| càng gần 1 thì mối quan hệ tuyến tính giữa X và Y càng chặt chẽ.
(iv) |rXY| = 0 thì giữa X và Y không có phụ thuộc tuyến tính tƣơng quan.
CHƢƠNG VI: TƢƠNG QUAN VÀ HỒI QUY 125 lOMoAR cPSD| 35883770 TƢƠNG QUAN VÀ HỒI QUY
(v) Nếu rXY > 0 thì X và Y có tƣơng quan thuận (X tăng thì Y tăng). Nếu
rXY < 0 thì X và Y có tƣơng quan nghịch.
1.2. Ƣớc lƣợng hệ số tƣơng quan thực nghiệm
Giả sử hai đại lƣợng X, Y có hệ số tƣơng quan rXY chƣa biết, dựa trên một
mẫu quan sát thực nghiệm ta tính giá trị R để ƣớc lƣợng cho rXY. Giá trị R đƣợc
tính từ mẫu thực nghiệm đƣợc gọi là hệ số tƣơng quan thực nghiệm.
Quan sát (X,Y) n lần, ta đƣợc: X X1 X2 X3 ……. Xn Y Y1 Y2 Y3 ……. Yn
Hệ số tƣơng quan thực nghiệm của (X,Y) đƣợc xác định bởi 1 (X − X i )(Y − Y i ) n R = (6.1) S S X Y Trong đó X Yi X = i , Y = n n 1 2 1 2
S2 = X2 − X , S2 = Y2 − Y X n i Y n i
Công thức (6.1) không đƣợc dùng để tính toán vì X , Y thƣờng là các số lẻ,
do đó X − X , Y − Y cũng lẻ, tính toán thực hành mất nhiều công sức. Ta khai i i
triển và rút gọn tử số lại để dể dàng ứng dụng hơn. Ta có: 1 1 X Y − X − 1 X Y + X.Y Y i i n i i n n R = S S X Y 1 X Y − XY − XY + X.Y i n i = (n −1)S' S' X Y 1 X Y − X.Y i i R = n (6.2) S S X Y
Ví dụ 1: Gọi X là điểm Toán và Y là điểm Lý của một số thí sinh trong một
kỳ thi ghi nhận được như sau: X 4 5 2 6 9 8 5 7 3 8 Y 6 5 3 4 9 9 7 6 5 4
Hãy tính hệ số tương quan thực nghiệm R(X,Y) 126
CHƢƠNG VI: TƢƠNG QUAN VÀ HỒI QUY lOMoAR cPSD| 35883770 TƢƠNG QUAN VÀ HỒI QUY Giải Ta có bảng tính: X Y X2 XY Y2 4 6 16 24 36 5 5 25 25 25 2 3 4 6 9 6 4 36 24 16 9 9 81 81 81 8 9 64 72 81 5 7 25 35 49 7 6 49 42 36 3 5 9 15 25 8 4 64 32 16 57 58 373 366 374 Suy ra Y X 57 i = 58 = X = i = = 5,7 ; Y = 5,8 n 10 n 10 2 S = 1 2 = 2,193171 X X2 − X i
= 37,3 − (5,7)2 = 4,81 SX n 1 2 S = 2 Y Y2 − Y i
= 37,4 − (5,8)2 = 3,76 SY = 1,939072 n
Hệ số tƣơng quan thực nghiệm là: 1 X Y − X.Y i i R = 36,6 − 5,7.5,8 n = = 0,834761 S S X Y 2,193171 .1,939072
CHƢƠNG VI: TƢƠNG QUAN VÀ HỒI QUY 127 lOMoAR cPSD| 35883770 TƢƠNG QUAN VÀ HỒI QUY § 2.
HỒI QUY TUYẾN TÍNH
2.1. Kỳ vọng có điều kiện
Kỳ vọng có điều kiện của đại lƣợng ngẫu nhiên Y với X = x (x là một giá trị
không đổi) đƣợc xác định nhƣ sau:
E(Y x) = y P(Y = y X = x) (Y rời rạc), (6.3) i i i
E(Y x) = y(y x)dx (X liên tục). (6.4) − 2.2. Hàm hồi quy
Hàm hồi quy của Y đối với X đƣợc định nghĩa Y = f(X) = E(Y|x) (6.5) X
Nếu đồ thị của hàm hồi quy có dạng đƣờng thẳng thì hàm hồi quy có dạng
phƣơng trình Y = AX + B, gọi là hàm hồi quy tuyến tính. X
Nếu đồ thị của hàm hồi quy có dạng đƣờng cong thì hàm hồi quy có dạng
phƣơng trình Y = AX2 + BX + C, Y = AX3 + BX2 + CX + D, … X X
Ở đây ta chỉ xét dạng hàm hồi quy tuyến tính.
2.3. Ƣớc lƣợng hàm hồi quy tuyến tính
Xét hai đại lƣợng X và Y với hàm hồi qui của đại lƣợng Y đối với đại
lƣợng X có dạng tuyến tính Y = AX + B chƣa xác định đƣợc. X
Giả sử hai đại lƣợng X, Y có hệ số tƣơng quan rXY chƣa biết, dựa trên một
mẫu quan sát thực nghiệm ta tính giá trị R để ƣớc lƣợng cho rXY. Giá trị R đƣợc
tính từ mẫu thực nghiệm đƣợc gọi là hệ số tƣơng quan thực nghiệm.
Dựa vào mẫu quan sát thực nghiệm để tìm hàm hồi quy tuyến tính mẫu
Y = aX + b để ƣớc lƣợng cho Y = AX + B X X
Quan sát (X,Y) nhiều lần ta đƣợc X X1 X2 X3 ……. Xn Y Y1 Y2 Y3 ……. Yn
Sai số tại Xi khi chọn phƣơng trình hồi quy Y = aX + b là: X
Yi – (aXi +b) = Yi − aXi − b
Tổng bình phƣơng sai số là: S = (Y − aX − b) i i 2
Ta chọn (a, b) sao cho tổng bình phƣơng sai số S bé nhất. Muốn vậy thì: S = S 0 ; = 0 ; a b 128
CHƢƠNG VI: TƢƠNG QUAN VÀ HỒI QUY lOMoAR cPSD| 35883770 TƢƠNG QUAN VÀ HỒI QUY Ta có:
S = 2(Y − aX − b)(−1) b i i S
= 2(− Y + a(X )+ nb) = 0 a (X )+ nb = Y b i i i i
S = 2(Y − aX − b)(− X ) a i i i S
= 2(− X Y + a( X 2 )+ b( X ))= 0 a ( X 2 )+ b( X )= X Y a i i i i i i i i
Ta có hệ phƣơng trình xác định (a,b): a (X)+ nb = Y (6.6) ( X2 )+ b( X) = XY a
Giải hệ phƣơng trình này ta tính đƣợc (a,b): XY − X.Y a = , b = Y − a X (6.7) S 2 X Trong đó X Y 1 2 1 X = i , Y =
i , S2 = X2 − X , XY = X Y n X n n i n i i
Ví dụ 2: Thống kê ghi lại số thí sinh dự thi Đại học mỗi năm như sau: Năm
1991 1992 1993 1994 1995 1996 1997 1998 Số thí sinh (ngàn) 140 145 144 146 146 148 149 150
Hãy dự báo số thí sinh sẽ dự thi đại học năm 1999, 2000? Giải
Đặt: X = năm – 1991, Y = Số thí sinh – 140 (ngàn).
Để hình dung đƣợc phần nào sự thay đổi của Y theo X ta đặt các điểm quan sát lên đồ thị.
Ta thấy các điểm trên đồ thị phân bố gần nhƣ một đƣờng thẳng, ta tìm
phƣơng trình hồi quy có dạng Y = aX + b. X
CHƢƠNG VI: TƢƠNG QUAN VÀ HỒI QUY 129 lOMoAR cPSD| 35883770 TƢƠNG QUAN VÀ HỒI QUY Ta có bảng tính X Y X2 XY 0 0 0 0 1 5 1 5 2 4 4 8 3 6 9 18 4 6 16 24 5 8 25 40 6 9 36 54 7 10 49 70 28 48 140 219
Ta có hệ phƣơng trình xác định (a,b): a (X)+ nb = Y ( X2 )+ b( X) = XY a 28.a + 8.b = 48 140.a + 28.b = 219 196.a + 56.b = 336 280.a + 56.b = 438 102 84.a = 102 a = = 1,21 84 48 − 28.a b = = 1,75 8
Do đó phƣơng trình hồi quy là: Y = (1,21)X +1,75 X Dự báo: Năm 1999 (X = 8): Y= (1.21)(8)+ 1.75 = 11.43
Số thí sinh = 140 +0 11.43=151,43 ngàn. Năm 2000 (X = 9): Y = (1.21)(9) + 1.75 = 12.64
Số thí sinh = 140 +12.64 = 152,64 ngàn. CHÚ Ý
Hồi quy tuyến tính thƣờng đƣợc sử dụng để dự báo dân số, dự báo kinh tế,
dự báo giáo dục v.v… Giá trị dự báo chỉ có giá trị cho một tƣơng lai gần, nếu dự
báo xa quá thì sai số sẽ lớn. Để giảm thiểu sai số thì ta nên cập nhập lại phƣơng
trình hồi quy mỗi khi có thêm số liệu để những lần dự báo tiếp theo đƣợc chính xác hơn. 130
CHƢƠNG VI: TƢƠNG QUAN VÀ HỒI QUY lOMoAR cPSD| 35883770 TƢƠNG QUAN VÀ HỒI QUY
2.4. Mối liên hệ giữa tƣơng quan và hồi quy
Khi đã tính đƣợc hệ số tƣơng quan thực nghiệm, ta có thể dùng hệ số tƣơng
quan thực nghiệm để tìm phƣơng trình hồi quy mà không cần dùng đến dữ liệu quan sát. SY a = R S (6.8) X b = Y − a.X Thật vậy,
Hệ phƣơng trình hồi quy là: a (X)+ nb = Y ( X2 )+ b( X) = XY a
Chia phƣơng trình trên cho n, ta có: X Y a + b =
aX + b = Y b = Y − a.X n n Ta có: 1 2 2
S2 = X2 − X X2 = nS2 + nX X n X X X = X = n.X n 1 XY − XY R = n XY = nRS S + n.XY X Y S S X Y
Thay các tổng số này vào phƣơng trình sau, ta có: ( 2 )
a nS2 + nX + (Y − a.X)(nX)= nRS S Y + X X nXY 2 2
anS2 + n.a.X + n.XY − naX = nRS S Y + X X n.XY S a = R Y SX CHÚ Ý
(i ) Từ kết quả trên ta cũng rút ra đƣợc phƣơng trình hồi qui tuyến tính
thực nghiệm của Y đối với X cũng có thể tìm đƣợc qua công thức sau Y − Y X − X X = R (6.9) S S Y X
(ii ) Các hệ số c và d trong phƣơng trình hàm hồi qui tuyến tính X
= cY + d của X đối với Y đƣợc tìm tƣơng tự nhƣ với a và b chỉ khác là vai Y
trò của X và Y đƣợc thay đổi cho nhau.
CHƢƠNG VI: TƢƠNG QUAN VÀ HỒI QUY 131 lOMoAR cPSD| 35883770 TƢƠNG QUAN VÀ HỒI QUY § 3. TƢƠNG QUAN BẢNG
3.1. Trƣờng hợp nhiều số liệu (tƣơng quan bảng)
Trong trƣờng hợp có nhiều số liệu, thƣờng một giá trị của X ứng với nhiều
giá trị của Y và ngƣợc lại một giá trị của Y ứng với nhiều giá trị của X, và số liệu
thƣờng đƣợc dẫn về bảng tƣơng quan với dạng nhƣ sau: Y Y1 Y2 ... Yj ... Ym X j X1 n11 n12 ... n1j ... n1m n(X1) X n n ... n ... n n(X . 2 . 21 . 22 . .2j . . 2m . 2) . . . .. . .. . . X n n n n n(X . i . i 1 . i 2 ... . i j ... . i m . i) . . . . . . Xk nn 1 nn 2 ... nn j ... nn m n(Xn) n(Y1) n(Y2) ... n(Yj) ... n(Ym) n i
Tiến hành n quan sát về (X,Y), X nhận k giá trị x1, x2, …, xk; Y nhận m giá
trị y1, y2, …, ym. Dòng n(xi) ghi số lần X nhận giá trị xi; cột n(yj) ghi số lần Y
nhận giá trị yj; nij là số lần (X,Y) nhận cặp giá trị (xi,yj).
Các hệ số a, b của hàm hồi qui tuyến tính thực nghiệm Y = aX + b đƣợc X tìm bởi XY − X.Y a = , b = Y − a X S 2 X Trong đó X n(X ) Y n(Y ) X = i i , Y = j j , n n 1 2 S2 = X2n(X ) − X , X Y n XY = i i ij X n i i n
3.2. Tính toán trên mẫu số liệu cụ thể
Khi giải bài toán về tƣơng quan, ta phải đi tính các đặc trƣng mẫu XY , X ,
Y , sau đó tính các phƣơng sai thực nghiệm S2 , S 2 rồi đến R và phƣơng trình x y
hồi qui tuyến tính mẫu.
Thực chất là tính toán các đặc trƣng mẫu. Vì vậy ta có thể áp dụng các thủ
thuật tính toán nhƣ đổi biến, hỗ trợ máy tính, … Trƣờng hợp không quá nhiều số
liệu tính toán ta có thể tính trực tiếp trên bảng tính. 132
CHƢƠNG VI: TƢƠNG QUAN VÀ HỒI QUY lOMoAR cPSD| 35883770 TƢƠNG QUAN VÀ HỒI QUY
Ví dụ 3: Bảng sau đây cho ta quan sát thu nhập của 100 nhân viên ở một
cơ quan trong một tháng (tính theo đơn vị nghìn đồng): Nhóm Thu nhập Y
tuổi X 0 − 1 1 − 2 2 − 3 >3 20 − 30 10 10 30 − 40 16 15 10 40 − 50 10 10 10 50 − 60 4 5
Hãy tìm các hàm hồi qui tuyến tính thực nghiệm Y = aX + b, X = cY + d. X Y Giải
Lấy các giá trị đại diện cho các khoảng của X là 25; 35; 45; 55; và các giá
trị đại diện cho các khoảng của Y là 0,5; 1,5; 2,5; 3,5. Ta có bảng tính trực tiếp: Y 0,5 1,5 2,5 3,5 n(X 2 i) Xi n(Xi) Xi n(Xi) X 25 10 10 20 500 12500 625 875 35 16 15 10 41 1435 50225 840 1312,5 1225 45 10 10 10 30 1350 60750 675 1125 1575 55 4 5 9 495 27225 110 412,5 n(Yj) 4 31 35 30 n = 100 T1=3780 T2=150700 Yj n(Yj) 2 46,5 87,5 105 T3= 241 Y 2 j n(Yj) 1 69,75 218,75 367,5 T4= 657 T = 8775 Các đặc trƣng mẫu T T X = 1 = 37,8 ; 2 = 2 − (X)2 = 78,16 ; S X n n T T T
Y = 3 = 2,41; S2 = 4 − (Y)2 = 0,7619 ; XY = = 87,75 . n Y n n
Các hệ số của các hàm tƣơng quan tuyến tính: XY − X.Y a =
= −0,043; b = Y − a X = 4,04 S 2 X XY − X.Y c =
= −4,39; d = X − c Y = 48,38 S 2 Y
Ta đƣợc các hàm hồi qui tuyến tính Y = −0,043X + 4,04; X X Y = −4,39Y + 48,38
CHƢƠNG VI: TƢƠNG QUAN VÀ HỒI QUY 133 lOMoAR cPSD| 35883770 TƢƠNG QUAN VÀ HỒI QUY CHÚ Ý
Khi xây dựng các hàm hồi qui tuyến tính có thể sử dụng công thức (6.9) kết
hợp với phƣơng pháp đổi biến số tính các đặc trƣng mẫu X − X X'= 0 , X = h. X' + X0 h Y − Y Y'= 0 , Y = k.Y' + Y k 0 2 S = h 2 .S2 = , S2 k 2 .S2 X X' Y Y' Đặc biệt R = R’.
Lƣu ý là công thức tính XY qua X'Y' khá phức tạp, nhƣng ta không cần
tính XY khi sử dụng công thức (6.9).
Với ví dụ 3, lấy X0 = 35; h = 10; Y0 = 2,5; k = 1 ta có bảng tính sau Y 0,5 1,5 2,5 3,5 n(Xi) Xi n(Xi) X 2 n(Xi) i X X’ | Y’ −2 −1 0 1 25 −1 10 10 20 −20 20 0 −10 35 0 16 15 10 41 0 0 0 0 0 45 1 10 10 10 30 30 30 −10 0 10 55 2 4 5 9 18 36 −16 −10 n(Yj) 4 31 35 30 n = 100 T’1 = 28 T’2 = 86 Y’j n(Yj) −8 −31 0 30 T’3= −9 Y’ 2 n(Yj) j 16 31 0 30 T’4= 77 T’ = −36 Ta có T' X'= 1 = 0,28 X = 37,8 n T' 2 = 2 − (X')2 = 0,7816 S = 8,84 X' SX’ = 0,884 SX n T' Y'= 3 = −0,09 Y = 2,41 n T' 2 = 4 − S (Y')2 = 0,7619 = 0,873 Y' SY’ = 0,873 SY n T' X'Y' =
= −0,36 ; R = R’ = X'Y' − X' Y' = −0,434 n S S X' Y'
Hàm hồi qui tuyến tính của Y đối với X tìm bởi Y − Y X − X X = R S S Y X 134
CHƢƠNG VI: TƢƠNG QUAN VÀ HỒI QUY lOMoAR cPSD| 35883770 TƢƠNG QUAN VÀ HỒI QUY − Y 2,41 X − 37,8 Y = −0,043X + 4,03 X = (−0,434) 0,873 8,84 X
Hàm hồi qui tuyến tính của X đối với Y tìm bởi X − X Y − Y Y = R S S X Y − X 37,8 Y − 2,41 X = −4,39Y + 48,39 Y = (−0,434) 8,84 0,873 Y BÀI TẬP 1.
Cho các giá trị quan sát của hai đại lƣợng ngẫu nhiên X và Y ở bảng sau: X 5 10 10 10 15 15 15 20 20 20 Y 20 20 30 30 30 40 50 50 60 60
Giả sử X và Y có sự phụ thuộc tƣơpng quan tuyến tính. Tìm hàm hồi quy tuyến tính mẫu: Y = aX + b. X 2.
Ngƣời ta đo chiều dài vật đúc và khuôn thì thấy chúng lệch khỏi qui định nhƣ sau: X 0.90 1,22 1,32 0,77 1,30 1,20 1,32 0,95 0,45 1,30 1,20
Y -0,30 0,10 0,70 -0,28 0,25 0,02 0,37 -0,70 0,55 0,35 0,32
Trong đó X, Y là các độ lệch.
Xác định hệ số tƣơng quan. 3.
Số liệu thống kê nhằm nghiên cứu quan hệ giữa tổng sản phẩm nông
nghiệp Y với tổng giá trị tài sản cố định X của 10 nông trại (tính trên 100 ha) nhƣ sau :
X 11,3 12,9 13,6 16,8 18,8 20,0 22,2 23,7 26,6 27,5
Y 13,2 15,6 17,2 18,8 20,2 23,9 22,4 23,0 24,4 24,6
Xác định đƣờng hồi qui tuyến tính mẫu YX = aX + b. Sau đó tìm phƣơng
sai số thực nghiệm và khoảng tin cậy 95% cho hệ số góc của đƣờng hồi quy trên. 4.
Đo chiều cao X (cm) và trọng lƣợng Y (kg) của 100 học sinh, ta đƣợc kết quả sau :
X 145 - 150 150 - 155 155 - 160 160 - 165 165 - 170 Y 35 – 40 3 40 – 45 5 10 45 – 50 14 20 6 50 – 55 15 12 5 55 – 60 6 4
Giả thuyết X và Y có mối phụ thuộc tƣơng quan tuyến tính. Tính các
CHƢƠNG VI: TƢƠNG QUAN VÀ HỒI QUY 135 lOMoAR cPSD| 35883770 TƢƠNG QUAN VÀ HỒI QUY hàm hồ qui a) Y = aX + b. X b) X = cY + d. Y 5.
Theo dõi lƣợng phân bón và năng xuất lúa của 100 hecta kúa ở một
vùng, ta thu đƣợc bảng số liệu sau: X 120 140 160 180 200 Y 2,2 2 2,6 5 3 3,0 11 8 4 3,4 15 17 3,8 10 6 7 4,2 12
Trong đó X là phân bón (kg/ha) và Y là năng suất lúa (tấn/ha).
a) Hãy ƣớc lƣợng hệ số tƣơng quan tuyến tính r.
b) Tìm phƣơng trình tƣơng quan tuyến tính: Y = aX + b X 6.
Đo chiều cao và đƣơnf kính của một loại cây, ta đƣợc kết quả cho bởi bảng sau: X 6 8 10 12 14 Y 30 2 17 9 3 35 10 17 9 40 3 24 16 13 45 6 24 12 50 2 11 22
Trong đó X là đƣờng kính (cm)và Y là chiều cao(m)
a) Xác định hệ số tƣơng quan tuyến tính mấu r.
b) Tìm phƣơng trình hồi qui tuyến tính mẫu.
c) Các phƣơng trình trên sẽ thay đổi nhƣ thế nào nếu X đƣợc tính theo đơn vị là mét (m) ? 7.
Một công ty nhỏ quan tâm tới việc phân tích hiệu quả của việc quảng
cáo. Trong thời gian 5 tháng công ty thu đƣợc kết quả sau X 5 8 10 15 22 Y 6 15 20 30 39
Trong đó X là số tiền chi cho quảng cáo (đơn vị là trăm USD) còn Y là
tổng doanh thu (đơn vị là nghìn USD). Hãy xác định hệ số tƣơng quan. 8.
Một trƣờng đại học thu thập các số liệu về số chứng chỉ mà một sinh
viên theo học và số giờ học ở nhà của anh ta trong một tuần. X 20 25 30 50 20 23 Y 12 13 12 15 16 16
Ở đó X là số giờ học, Y là số chứng chỉ. Tìm hệ số tƣơng quan giữa X và
Y. Ở mức ý nghĩa = 5%, có sự tƣơng quan tuyến tính giữa hai biến nói ở trên không? 136
CHƢƠNG VI: TƢƠNG QUAN VÀ HỒI QUY lOMoAR cPSD| 35883770 TƢƠNG QUAN VÀ HỒI QUY 9.
Một nghiên cứu đƣợc tiến hành ở Mỹ để xác định mối quan hệ giữa
chiều cao của một ngƣời cỡ giày của họ.
Nhà nghiên cứu đã thu đƣợc số liệu sau X 66 63 67 71 62 Y 1 9 7 8 10 6 2 X 65 72 68 60 66 Y 1 1 1 8 12 10 5 8 2 2 2
Trong đó X là chiều cao (đơn vị là inches) còn Y là cở giày.
Hãy tính hệ số tƣơng quan giữa X và Y.
10. Tuổi và huyết áp của 10 bệnh nhân trẻ em (dƣới 14 tuổi) chọn ngẫu
nhiên đƣợc cho trong bảng sau đây: X 14 1 9 7 9 12 1 3 9 1 Y 100 83 112 152 104 90 92 85 120 130
Trong đó X là tuổi còn Y là huyết áp.
Tìm đƣờng hồi quy mẫu của Y đối với X.
Tính sai số tiêu chuẩn của đƣờng hồi quy.
CHƢƠNG VI: TƢƠNG QUAN VÀ HỒI QUY 137 lOMoAR cPSD| 35883770 CÁC BẢNG SỐ 1 −u2
Các giá trị hàm Gauss f(u) = e 2 2 f(u) y (u = x+y) 0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0
0.3989 0.3989 0.3989 0.3988 0.3986 0.3984 0.3982 0.3980 0.3977 0.3973
0.1 0.3970 0.3965 0.3961 0.3956 0.3951 0.3945 0.3939 0.3932 0.3925 0.3918
0.2 0.3910 0.3902 0.3894 0.3885 0.3876 0.3867 0.3857 0.3847 0.3836 0.3825
0.3 0.3814 0.3802 0.3790 0.3778 0.3765 0.3752 0.3739 0.3725 0.3712 0.3697
0.4 0.3683 0.3668 0.3653 0.3637 0.3621 0.3605 0.3589 0.3572 0.3555 0.3538
0.5 0.3521 0.3503 0.3485 0.3467 0.3448 0.3429 0.3410 0.3391 0.3372 0.3352
0.6 0.3332 0.3312 0.3292 0.3271 0.3251 0.3230 0.3209 0.3187 0.3166 0.3144
0.7 0.3123 0.3101 0.3079 0.3056 0.3034 0.3011 0.2989 0.2966 0.2943 0.2920
0.8 0.2897 0.2874 0.2850 0.2827 0.2803 0.2780 0.2756 0.2732 0.2709 0.2685
0.9 0.2661 0.2637 0.2613 0.2589 0.2565 0.2541 0.2516 0.2492 0.2468 0.2444 1
0.2420 0.2396 0.2371 0.2347 0.2323 0.2299 0.2275 0.2251 0.2227 0.2203
1.1 0.2179 0.2155 0.2131 0.2107 0.2083 0.2059 0.2036 0.2012 0.1989 0.1965
1.2 0.1942 0.1919 0.1895 0.1872 0.1849 0.1826 0.1804 0.1781 0.1758 0.1736
1.3 0.1714 0.1691 0.1669 0.1647 0.1626 0.1604 0.1582 0.1561 0.1539 0.1518
1.4 0.1497 0.1476 0.1456 0.1435 0.1415 0.1394 0.1374 0.1354 0.1334 0.1315
1.5 0.1295 0.1276 0.1257 0.1238 0.1219 0.1200 0.1182 0.1163 0.1145 0.1127
1.6 0.1109 0.1092 0.1074 0.1057 0.1040 0.1023 0.1006 0.0989 0.0973 0.0957
1.7 0.0940 0.0925 0.0909 0.0893 0.0878 0.0863 0.0848 0.0833 0.0818 0.0804 x
1.8 0.0790 0.0775 0.0761 0.0748 0.0734 0.0721 0.0707 0.0694 0.0681 0.0669
1.9 0.0656 0.0644 0.0632 0.0620 0.0608 0.0596 0.0584 0.0573 0.0562 0.0551 2
0.0540 0.0529 0.0519 0.0508 0.0498 0.0488 0.0478 0.0468 0.0459 0.0449
2.1 0.0440 0.0431 0.0422 0.0413 0.0404 0.0396 0.0387 0.0379 0.0371 0.0363
2.2 0.0355 0.0347 0.0339 0.0332 0.0325 0.0317 0.0310 0.0303 0.0297 0.0290
2.3 0.0283 0.0277 0.0270 0.0264 0.0258 0.0252 0.0246 0.0241 0.0235 0.0229
2.4 0.0224 0.0219 0.0213 0.0208 0.0203 0.0198 0.0194 0.0189 0.0184 0.0180
2.5 0.0175 0.0171 0.0167 0.0163 0.0158 0.0154 0.0151 0.0147 0.0143 0.0139
2.6 0.0136 0.0132 0.0129 0.0126 0.0122 0.0119 0.0116 0.0113 0.0110 0.0107
2.7 0.0104 0.0101 0.0099 0.0096 0.0093 0.0091 0.0088 0.0086 0.0084 0.0081
2.8 0.0079 0.0077 0.0075 0.0073 0.0071 0.0069 0.0067 0.0065 0.0063 0.0061
2.9 0.0060 0.0058 0.0056 0.0055 0.0053 0.0051 0.0050 0.0048 0.0047 0.0046 3
0.0044 0.0043 0.0042 0.0040 0.0039 0.0038 0.0037 0.0036 0.0035 0.0034
3.1 0.0033 0.0032 0.0031 0.0030 0.0029 0.0028 0.0027 0.0026 0.0025 0.0025
3.2 0.0024 0.0023 0.0022 0.0022 0.0021 0.0020 0.0020 0.0019 0.0018 0.0018
3.3 0.0017 0.0017 0.0016 0.0016 0.0015 0.0015 0.0014 0.0014 0.0013 0.0013
3.4 0.0012 0.0012 0.0012 0.0011 0.0011 0.0010 0.0010 0.0010 0.0009 0.0009
3.5 0.0009 0.0008 0.0008 0.0008 0.0008 0.0007 0.0007 0.0007 0.0007 0.0006
3.6 0.0006 0.0006 0.0006 0.0005 0.0005 0.0005 0.0005 0.0005 0.0005 0.0004
3.7 0.0004 0.0004 0.0004 0.0004 0.0004 0.0004 0.0003 0.0003 0.0003 0.0003
3.8 0.0003 0.0003 0.0003 0.0003 0.0003 0.0002 0.0002 0.0002 0.0002 0.0002
3.9 0.0002 0.0002 0.0002 0.0002 0.0002 0.0002 0.0002 0.0002 0.0001 0.0001 138 CÁC BẢNG SỐ lOMoAR cPSD| 35883770 CÁC BẢNG SỐ 1 u −t2
Các giá trị hàm Laplace (u) = e 2 dt 2 0 (u) y (u=x+y) 0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09
0.0 0.0000 0.0040 0.0080 0.0120 0.0160 0.0199 0.0239 0.0279 0.0319 0.0359
0.1 0.0398 0.0438 0.0478 0.0517 0.0557 0.0596 0.0636 0.0675 0.0714 0.0753
0.2 0.0793 0.0832 0.0871 0.0910 0.0948 0.0987 0.1026 0.1064 0.1103 0.1141
0.3 0.1179 0.1217 0.1255 0.1293 0.1331 0.1368 0.1406 0.1443 0.1480 0.1517
0.4 0.1554 0.1591 0.1628 0.1664 0.1700 0.1736 0.1772 0.1808 0.1844 0.1879
0.5 0.1915 0.1950 0.1985 0.2019 0.2054 0.2088 0.2123 0.2157 0.2190 0.2224
0.6 0.2257 0.2291 0.2324 0.2357 0.2389 0.2422 0.2454 0.2486 0.2517 0.2549
0.7 0.2580 0.2611 0.2642 0.2673 0.2704 0.2734 0.2764 0.2794 0.2823 0.2852
0.8 0.2881 0.2910 0.2939 0.2967 0.2995 0.3023 0.3051 0.3078 0.3106 0.3133
0.9 0.3159 0.3186 0.3212 0.3238 0.3264 0.3289 0.3315 0.3340 0.3365 0.3389
1.0 0.3413 0.3438 0.3461 0.3485 0.3508 0.3531 0.3554 0.3577 0.3599 0.3621
1.1 0.3643 0.3665 0.3686 0.3708 0.3729 0.3749 0.3770 0.3790 0.3810 0.3830
1.2 0.3849 0.3869 0.3888 0.3907 0.3925 0.3944 0.3962 0.3980 0.3997 0.4015
1.3 0.4032 0.4049 0.4066 0.4082 0.4099 0.4115 0.4131 0.4147 0.4162 0.4177
x 1.4 0.4192 0.4207 0.4222 0.4236 0.4251 0.4265 0.4279 0.4292 0.4306 0.4319
1.5 0.4332 0.4345 0.4357 0.4370 0.4382 0.4394 0.4406 0.4418 0.4429 0.4441
1.6 0.4452 0.4463 0.4474 0.4484 0.4495 0.4505 0.4515 0.4525 0.4535 0.4545
1.7 0.4554 0.4564 0.4573 0.4582 0.4591 0.4599 0.4608 0.4616 0.4625 0.4633
1.8 0.4641 0.4649 0.4656 0.4664 0.4671 0.4678 0.4686 0.4693 0.4699 0.4706
1.9 0.4713 0.4719 0.4726 0.4732 0.4738 0.4744 0.4750 0.4756 0.4761 0.4767
2.0 0.4772 0.4778 0.4783 0.4788 0.4793 0.4798 0.4803 0.4808 0.4812 0.4817
2.1 0.4821 0.4826 0.4830 0.4834 0.4838 0.4842 0.4846 0.4850 0.4854 0.4857
2.2 0.4861 0.4864 0.4868 0.4871 0.4875 0.4878 0.4881 0.4884 0.4887 0.4890
2.3 0.4893 0.4896 0.4898 0.4901 0.4904 0.4906 0.4909 0.4911 0.4913 0.4916
2.4 0.4918 0.4920 0.4922 0.4925 0.4927 0.4929 0.4931 0.4932 0.4934 0.4936
2.5 0.4938 0.4940 0.4941 0.4943 0.4945 0.4946 0.4948 0.4949 0.4951 0.4952
2.6 0.4953 0.4955 0.4956 0.4957 0.4959 0.4960 0.4961 0.4962 0.4963 0.4964
2.7 0.4965 0.4966 0.4967 0.4968 0.4969 0.4970 0.4971 0.4972 0.4973 0.4974
2.8 0.4974 0.4975 0.4976 0.4977 0.4977 0.4978 0.4979 0.4979 0.4980 0.4981
2.9 0.4981 0.4982 0.4982 0.4983 0.4984 0.4984 0.4985 0.4985 0.4986 0.4986 u (u) u (u) u (u) u (u) 3
0.4986500 3.5 0.4997673 4
0.4999683 4.5 0.4999966
3.1 0.4990323 3.6 0.4998409 4.1 0.4999793 4.6 0.4999979 (u) 0.5
3.2 0.4993128 3.7 0.4998922 4.2 0.4999866 4.7 0.4999987 với u 5
3.3 0.4995165 3.8 0.4999276 4.3 0.4999915 4.8 0.4999992
3.4 0.4996630 3.9 0.4999519 4.4 0.4999946 4.9 0.4999995 CÁC BẢNG SỐ 139 lOMoAR cPSD| 35883770 CÁC BẢNG SỐ 1 u t 2 −
Các giá trị hàm (u) = e 2 dt 2 − (u) y (u=x+y) 0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0
0.5000 0.5040 0.5080 0.5120 0.5160 0.5199 0.5239 0.5279 0.5319 0.5359
0.1 0.5398 0.5438 0.5478 0.5517 0.5557 0.5596 0.5636 0.5675 0.5714 0.5753
0.2 0.5793 0.5832 0.5871 0.5910 0.5948 0.5987 0.6026 0.6064 0.6103 0.6141
0.3 0.6179 0.6217 0.6255 0.6293 0.6331 0.6368 0.6406 0.6443 0.6480 0.6517
0.4 0.6554 0.6591 0.6628 0.6664 0.6700 0.6736 0.6772 0.6808 0.6844 0.6879
0.5 0.6915 0.6950 0.6985 0.7019 0.7054 0.7088 0.7123 0.7157 0.7190 0.7224
0.6 0.7257 0.7291 0.7324 0.7357 0.7389 0.7422 0.7454 0.7486 0.7517 0.7549
0.7 0.7580 0.7611 0.7642 0.7673 0.7704 0.7734 0.7764 0.7794 0.7823 0.7852
0.8 0.7881 0.7910 0.7939 0.7967 0.7995 0.8023 0.8051 0.8078 0.8106 0.8133
0.9 0.8159 0.8186 0.8212 0.8238 0.8264 0.8289 0.8315 0.8340 0.8365 0.8389 1
0.8413 0.8438 0.8461 0.8485 0.8508 0.8531 0.8554 0.8577 0.8599 0.8621
1.1 0.8643 0.8665 0.8686 0.8708 0.8729 0.8749 0.8770 0.8790 0.8810 0.8830
1.2 0.8849 0.8869 0.8888 0.8907 0.8925 0.8944 0.8962 0.8980 0.8997 0.9015
1.3 0.9032 0.9049 0.9066 0.9082 0.9099 0.9115 0.9131 0.9147 0.9162 0.9177
x 1.4 0.9192 0.9207 0.9222 0.9236 0.9251 0.9265 0.9279 0.9292 0.9306 0.9319
1.5 0.9332 0.9345 0.9357 0.9370 0.9382 0.9394 0.9406 0.9418 0.9429 0.9441
1.6 0.9452 0.9463 0.9474 0.9484 0.9495 0.9505 0.9515 0.9525 0.9535 0.9545
1.7 0.9554 0.9564 0.9573 0.9582 0.9591 0.9599 0.9608 0.9616 0.9625 0.9633
1.8 0.9641 0.9649 0.9656 0.9664 0.9671 0.9678 0.9686 0.9693 0.9699 0.9706
1.9 0.9713 0.9719 0.9726 0.9732 0.9738 0.9744 0.9750 0.9756 0.9761 0.9767 2
0.9772 0.9778 0.9783 0.9788 0.9793 0.9798 0.9803 0.9808 0.9812 0.9817
2.1 0.9821 0.9826 0.9830 0.9834 0.9838 0.9842 0.9846 0.9850 0.9854 0.9857
2.2 0.9861 0.9864 0.9868 0.9871 0.9875 0.9878 0.9881 0.9884 0.9887 0.9890
2.3 0.9893 0.9896 0.9898 0.9901 0.9904 0.9906 0.9909 0.9911 0.9913 0.9916
2.4 0.9918 0.9920 0.9922 0.9925 0.9927 0.9929 0.9931 0.9932 0.9934 0.9936
2.5 0.9938 0.9940 0.9941 0.9943 0.9945 0.9946 0.9948 0.9949 0.9951 0.9952
2.6 0.9953 0.9955 0.9956 0.9957 0.9959 0.9960 0.9961 0.9962 0.9963 0.9964
2.7 0.9965 0.9966 0.9967 0.9968 0.9969 0.9970 0.9971 0.9972 0.9973 0.9974
2.8 0.9974 0.9975 0.9976 0.9977 0.9977 0.9978 0.9979 0.9979 0.9980 0.9981
2.9 0.9981 0.9982 0.9982 0.9983 0.9984 0.9984 0.9985 0.9985 0.9986 0.9986 3
0.9987 0.9987 0.9987 0.9988 0.9988 0.9989 0.9989 0.9989 0.9990 0.9990 140 CÁC BẢNG SỐ lOMoAR cPSD| 35883770 CÁC BẢNG SỐ
Các giá trị phân vị chuẩn z ( =x+y) y 0.5
0.0000 0.0025 0.0050 0.0075 0.0100 0.0125 0.0150 0.0175 0.0201 0.0226
0.51 0.0251 0.0276 0.0301 0.0326 0.0351 0.0376 0.0401 0.0426 0.0451 0.0476
0.52 0.0502 0.0527 0.0552 0.0577 0.0602 0.0627 0.0652 0.0677 0.0702 0.0728
0.53 0.0753 0.0778 0.0803 0.0828 0.0853 0.0878 0.0904 0.0929 0.0954 0.0979
0.54 0.1004 0.1030 0.1055 0.1080 0.1105 0.1130 0.1156 0.1181 0.1206 0.1231
0.55 0.1257 0.1282 0.1307 0.1332 0.1358 0.1383 0.1408 0.1434 0.1459 0.1484
0.56 0.1510 0.1535 0.1560 0.1586 0.1611 0.1637 0.1662 0.1687 0.1713 0.1738
0.57 0.1764 0.1789 0.1815 0.1840 0.1866 0.1891 0.1917 0.1942 0.1968 0.1993
0.58 0.2019 0.2045 0.2070 0.2096 0.2121 0.2147 0.2173 0.2198 0.2224 0.2250
0.59 0.2275 0.2301 0.2327 0.2353 0.2378 0.2404 0.2430 0.2456 0.2482 0.2508 0.6
0.2533 0.2559 0.2585 0.2611 0.2637 0.2663 0.2689 0.2715 0.2741 0.2767
0.61 0.2793 0.2819 0.2845 0.2871 0.2898 0.2924 0.2950 0.2976 0.3002 0.3029
0.62 0.3055 0.3081 0.3107 0.3134 0.3160 0.3186 0.3213 0.3239 0.3266 0.3292
0.63 0.3319 0.3345 0.3372 0.3398 0.3425 0.3451 0.3478 0.3505 0.3531 0.3558
0.64 0.3585 0.3611 0.3638 0.3665 0.3692 0.3719 0.3745 0.3772 0.3799 0.3826
0.65 0.3853 0.3880 0.3907 0.3934 0.3961 0.3989 0.4016 0.4043 0.4070 0.4097
0.66 0.4125 0.4152 0.4179 0.4207 0.4234 0.4261 0.4289 0.4316 0.4344 0.4372
0.67 0.4399 0.4427 0.4454 0.4482 0.4510 0.4538 0.4565 0.4593 0.4621 0.4649
0.68 0.4677 0.4705 0.4733 0.4761 0.4789 0.4817 0.4845 0.4874 0.4902 0.4930
0.69 0.4958 0.4987 0.5015 0.5044 0.5072 0.5101 0.5129 0.5158 0.5187 0.5215 0.7
0.5244 0.5273 0.5302 0.5330 0.5359 0.5388 0.5417 0.5446 0.5476 0.5505
0.71 0.5534 0.5563 0.5592 0.5622 0.5651 0.5681 0.5710 0.5740 0.5769 0.5799
0.72 0.5828 0.5858 0.5888 0.5918 0.5948 0.5978 0.6008 0.6038 0.6068 0.6098
0.73 0.6128 0.6158 0.6189 0.6219 0.6250 0.6280 0.6311 0.6341 0.6372 0.6403 x
0.74 0.6433 0.6464 0.6495 0.6526 0.6557 0.6588 0.6620 0.6651 0.6682 0.6713
0.75 0.6745 0.6776 0.6808 0.6840 0.6871 0.6903 0.6935 0.6967 0.6999 0.7031
0.76 0.7063 0.7095 0.7128 0.7160 0.7192 0.7225 0.7257 0.7290 0.7323 0.7356
0.77 0.7388 0.7421 0.7454 0.7488 0.7521 0.7554 0.7588 0.7621 0.7655 0.7688
0.78 0.7722 0.7756 0.7790 0.7824 0.7858 0.7892 0.7926 0.7961 0.7995 0.8030
0.79 0.8064 0.8099 0.8134 0.8169 0.8204 0.8239 0.8274 0.8310 0.8345 0.8381 0.8
0.8416 0.8452 0.8488 0.8524 0.8560 0.8596 0.8632 0.8669 0.8706 0.8742
0.81 0.8779 0.8816 0.8853 0.8890 0.8927 0.8965 0.9002 0.9040 0.9078 0.9116
0.82 0.9154 0.9192 0.9230 0.9269 0.9307 0.9346 0.9385 0.9424 0.9463 0.9502
0.83 0.9542 0.9581 0.9621 0.9661 0.9701 0.9741 0.9782 0.9822 0.9863 0.9904
0.84 0.9945 0.9986 1.0027 1.0069 1.0110 1.0152 1.0194 1.0237 1.0279 1.0322
0.85 1.0364 1.0407 1.0451 1.0494 1.0537 1.0581 1.0625 1.0669 1.0714 1.0758
0.86 1.0803 1.0848 1.0893 1.0939 1.0985 1.1031 1.1077 1.1123 1.1170 1.1217
0.87 1.1264 1.1311 1.1359 1.1407 1.1455 1.1503 1.1552 1.1601 1.1650 1.1700
0.88 1.1750 1.1800 1.1850 1.1901 1.1952 1.2004 1.2055 1.2107 1.2160 1.2212
0.89 1.2265 1.2319 1.2372 1.2426 1.2481 1.2536 1.2591 1.2646 1.2702 1.2759 0.9
1.2816 1.2873 1.2930 1.2988 1.3047 1.3106 1.3165 1.3225 1.3285 1.3346
0.91 1.3408 1.3469 1.3532 1.3595 1.3658 1.3722 1.3787 1.3852 1.3917 1.3984
0.92 1.4051 1.4118 1.4187 1.4255 1.4325 1.4395 1.4466 1.4538 1.4611 1.4684
0.93 1.4758 1.4833 1.4909 1.4985 1.5063 1.5141 1.5220 1.5301 1.5382 1.5464
0.94 1.5548 1.5632 1.5718 1.5805 1.5893 1.5982 1.6072 1.6164 1.6258 1.6352
0.95 1.6449 1.6546 1.6646 1.6747 1.6849 1.6954 1.7060 1.7169 1.7279 1.7392
0.96 1.7507 1.7624 1.7744 1.7866 1.7991 1.8119 1.8250 1.8384 1.8522 1.8663
0.97 1.8808 1.8957 1.9110 1.9268 1.9431 1.9600 1.9774 1.9954 2.0141 2.0335
0.98 2.0537 2.0748 2.0969 2.1201 2.1444 2.1701 2.1973 2.2262 2.2571 2.2904
0.99 2.3263 2.3656 2.4089 2.4573 2.5121 2.5758 2.6521 2.7478 2.8782 3.0902 CÁC BẢNG SỐ 141 lOMoAR cPSD| 35883770 CÁC BẢNG SỐ
Các giá trị phân vị 2 (n) 2 (n) Mức xác suất 0.995 0.99 0.975 0.95 0.9 0.1 0.05 0.025 0.01 0.005 1
0.0000 0.0002 0.0010 0.0039 0.0158 2.7055 3.8415 5.0239 6.6349 7.8794 2
0.0100 0.0201 0.0506 0.1026 0.2107 4.6052 5.9915 7.3778 9.2104 10.5965 3
0.0717 0.1148 0.2158 0.3518 0.5844 6.2514 7.8147 9.3484 11.3449 12.8381 4
0.2070 0.2971 0.4844 0.7107 1.0636 7.7794 9.4877 11.1433 13.2767 14.8602 5
0.4118 0.5543 0.8312 1.1455 1.6103 9.2363 11.0705 12.8325 15.0863 16.7496 6
0.6757 0.8721 1.2373 1.6354 2.2041 10.6446 12.5916 14.4494 16.8119 18.5475 7
0.9893 1.2390 1.6899 2.1673 2.8331 12.0170 14.0671 16.0128 18.4753 20.2777 8
1.3444 1.6465 2.1797 2.7326 3.4895 13.3616 15.5073 17.5345 20.0902 21.9549 9
1.7349 2.0879 2.7004 3.3251 4.1682 14.6837 16.9190 19.0228 21.6660 23.5893 10
2.1558 2.5582 3.2470 3.9403 4.8652 15.9872 18.3070 20.4832 23.2093 25.1881 11
2.6032 3.0535 3.8157 4.5748 5.5778 17.2750 19.6752 21.9200 24.7250 26.7569 12
3.0738 3.5706 4.4038 5.2260 6.3038 18.5493 21.0261 23.3367 26.2170 28.2997 13
3.5650 4.1069 5.0087 5.8919 7.0415 19.8119 22.3620 24.7356 27.6882 29.8193 14
4.0747 4.6604 5.6287 6.5706 7.7895 21.0641 23.6848 26.1189 29.1412 31.3194 15
4.6009 5.2294 6.2621 7.2609 8.5468 22.3071 24.9958 27.4884 30.5780 32.8015 16
5.1422 5.8122 6.9077 7.9616 9.3122 23.5418 26.2962 28.8453 31.9999 34.2671 17
5.6973 6.4077 7.5642 8.6718 10.0852 24.7690 27.5871 30.1910 33.4087 35.7184 18
6.2648 7.0149 8.2307 9.3904 10.8649 25.9894 28.8693 31.5264 34.8052 37.1564 19
6.8439 7.6327 8.9065 10.1170 11.6509 27.2036 30.1435 32.8523 36.1908 38.5821 20
7.4338 8.2604 9.5908 10.8508 12.4426 28.4120 31.4104 34.1696 37.5663 39.9969
n 21 8.0336 8.8972 10.2829 11.5913 13.2396 29.6151 32.6706 35.4789 38.9322 41.4009 22
8.6427 9.5425 10.9823 12.3380 14.0415 30.8133 33.9245 36.7807 40.2894 42.7957 23
9.2604 10.1957 11.6885 13.0905 14.8480 32.0069 35.1725 38.0756 41.6383 44.1814 24
9.8862 10.8563 12.4011 13.8484 15.6587 33.1962 36.4150 39.3641 42.9798 45.5584
25 10.5196 11.5240 13.1197 14.6114 16.4734 34.3816 37.6525 40.6465 44.3140 46.9280
26 11.1602 12.1982 13.8439 15.3792 17.2919 35.5632 38.8851 41.9231 45.6416 48.2898
27 11.8077 12.8785 14.5734 16.1514 18.1139 36.7412 40.1133 43.1945 46.9628 49.6450
28 12.4613 13.5647 15.3079 16.9279 18.9392 37.9159 41.3372 44.4608 48.2782 50.9936
29 13.1211 14.2564 16.0471 17.7084 19.7677 39.0875 42.5569 45.7223 49.5878 52.3355
30 13.7867 14.9535 16.7908 18.4927 20.5992 40.2560 43.7730 46.9792 50.8922 53.6719
31 14.4577 15.6555 17.5387 19.2806 21.4336 41.4217 44.9853 48.2319 52.1914 55.0025
32 15.1340 16.3622 18.2908 20.0719 22.2706 42.5847 46.1942 49.4804 53.4857 56.3280
33 15.8152 17.0735 19.0467 20.8665 23.1102 43.7452 47.3999 50.7251 54.7754 57.6483
34 16.5013 17.7891 19.8062 21.6643 23.9522 44.9032 48.6024 51.9660 56.0609 58.9637
35 17.1917 18.5089 20.5694 22.4650 24.7966 46.0588 49.8018 53.2033 57.3420 60.2746
36 17.8868 19.2326 21.3359 23.2686 25.6433 47.2122 50.9985 54.4373 58.6192 61.5811
37 18.5859 19.9603 22.1056 24.0749 26.4921 48.3634 52.1923 55.6680 59.8926 62.8832
38 19.2888 20.6914 22.8785 24.8839 27.3430 49.5126 53.3835 56.8955 61.1620 64.1812
39 19.9958 21.4261 23.6543 25.6954 28.1958 50.6598 54.5722 58.1201 62.4281 65.4753
40 20.7066 22.1642 24.4331 26.5093 29.0505 51.8050 55.7585 59.3417 63.6908 66.7660
41 21.4208 22.9056 25.2145 27.3256 29.9071 52.9485 56.9424 60.5606 64.9500 68.0526
42 22.1384 23.6501 25.9987 28.1440 30.7654 54.0902 58.1240 61.7767 66.2063 69.3360
43 22.8596 24.3976 26.7854 28.9647 31.6255 55.2302 59.3035 62.9903 67.4593 70.6157
44 23.5836 25.1480 27.5745 29.7875 32.4871 56.3685 60.4809 64.2014 68.7096 71.8923
45 24.3110 25.9012 28.3662 30.6123 33.3504 57.5053 61.6562 65.4101 69.9569 73.1660 142 CÁC BẢNG SỐ lOMoAR cPSD| 35883770 CÁC BẢNG SỐ
Các giá trị phân vị Student t (n) t (n) Mức xác suất 0.1 0.05 0.025 0.01 0.005 0.0005 1
3.0777 6.3137 12.7062 31.8210 63.6559 636.5776 2 1.8856 2.9200 4.3027 6.9645 9.9250 31.5998 3 1.6377 2.3534 3.1824 4.5407 5.8408 12.9244 4 1.5332 2.1318 2.7765 3.7469 4.6041 8.6101 5 1.4759 2.0150 2.5706 3.3649 4.0321 6.8685 6 1.4398 1.9432 2.4469 3.1427 3.7074 5.9587 7 1.4149 1.8946 2.3646 2.9979 3.4995 5.4081 8 1.3968 1.8595 2.3060 2.8965 3.3554 5.0414 9 1.3830 1.8331 2.2622 2.8214 3.2498 4.7809 10 1.3722 1.8125 2.2281 2.7638 3.1693 4.5868 11 1.3634 1.7959 2.2010 2.7181 3.1058 4.4369 12 1.3562 1.7823 2.1788 2.6810 3.0545 4.3178 13 1.3502 1.7709 2.1604 2.6503 3.0123 4.2209 14 1.3450 1.7613 2.1448 2.6245 2.9768 4.1403 15 1.3406 1.7531 2.1315 2.6025 2.9467 4.0728 16 1.3368 1.7459 2.1199 2.5835 2.9208 4.0149 17 1.3334 1.7396 2.1098 2.5669 2.8982 3.9651 18 1.3304 1.7341 2.1009 2.5524 2.8784 3.9217 19 1.3277 1.7291 2.0930 2.5395 2.8609 3.8833 20 1.3253 1.7247 2.0860 2.5280 2.8453 3.8496 n 21 1.3232 1.7207 2.0796 2.5176 2.8314 3.8193 22 1.3212 1.7171 2.0739 2.5083 2.8188 3.7922 23 1.3195 1.7139 2.0687 2.4999 2.8073 3.7676 24 1.3178 1.7109 2.0639 2.4922 2.7970 3.7454 25 1.3163 1.7081 2.0595 2.4851 2.7874 3.7251 26 1.3150 1.7056 2.0555 2.4786 2.7787 3.7067 27 1.3137 1.7033 2.0518 2.4727 2.7707 3.6895 28 1.3125 1.7011 2.0484 2.4671 2.7633 3.6739 29 1.3114 1.6991 2.0452 2.4620 2.7564 3.6595 30 1.3104 1.6973 2.0423 2.4573 2.7500 3.6460 31 1.3095 1.6955 2.0395 2.4528 2.7440 3.6335 32 1.3086 1.6939 2.0369 2.4487 2.7385 3.6218 33 1.3077 1.6924 2.0345 2.4448 2.7333 3.6109 34 1.3070 1.6909 2.0322 2.4411 2.7284 3.6007 35 1.3062 1.6896 2.0301 2.4377 2.7238 3.5911 36 1.3055 1.6883 2.0281 2.4345 2.7195 3.5821 37 1.3049 1.6871 2.0262 2.4314 2.7154 3.5737 38 1.3042 1.6860 2.0244 2.4286 2.7116 3.5657 39 1.3036 1.6849 2.0227 2.4258 2.7079 3.5581 40 1.3031 1.6839 2.0211 2.4233 2.7045 3.5510 41 1.3025 1.6829 2.0195 2.4208 2.7012 3.5443 42 1.3020 1.6820 2.0181 2.4185 2.6981 3.5377 43 1.3016 1.6811 2.0167 2.4163 2.6951 3.5316 44 1.3011 1.6802 2.0154 2.4141 2.6923 3.5258 45 1.3007 1.6794 2.0141 2.4121 2.6896 3.5203 CÁC BẢNG SỐ 143 lOMoAR cPSD| 35883770
TÀI LIỆU THAM KHẢO
[1] Đặng Hấn. 1996. Xác Suất Thống Kê. NXB Thống Kê.
[2] Hoàng Ngọc Nhậm. 1995. Xác Suất Và Thống Kê Toán. Đại Học Kinh Tế TP HCM.
[3] Nguyễn Hữu Khánh. Xác Suất Thống Kê A. 2000. Đại Học Cần Thơ.
[4] Trần Văn Minh (chủ biên). Xác Suất Thống Kê Và Các Tính Toán
Trên Excel. 2001. NXB Giao Thông Vận Tải.
[5] Tống Đình Quỳ. 1999. Giáo Trình Xác Suất Thống Kê. NXB Giáo Dục.
[6] Đinh Văn Gắng. 2000. Lý Thuyết Xác Suất Và Thống Kê. NXB Giáo Dục.
[7] Nguyễn Bác Văn. 1996. Xác Suất Và Xử Lí Số Liệu Thống Kê. NXB Giáo Dục.
[8] Đào Hữu Hồ. 1996. Xác Suất Thống Kê. NXB ĐH QG HN.
[9] J.S Milton & Jesse C.Arnold.1998. Introduction To Probability And Statistics. Mcgraw-Hill, Inc.
[10] John J.Kinney.1997. Probability. John Willy & Sons, Inc.
[11] R. J. Barlow. 1989. Statistics. John Willy & Sons, Inc.
[12] Prem S.Mann. Statistics For Business And Economics. John Willy & Sons, Inc. 144 lOMoAR cPSD| 35883770
HƯỚNG DẪN SỬ DỤNG MÁY TÍNH BỎ TÚI 1) Máy tính fx500A 2) Máy tính fx500MS
• Mở thống kê: Mode • • Mở thống kê: Mode 2 • Nhập dữ liệu: • Nhập dữ liệu: x x n M x Shift n M 1 1 1 1 ⁝ ⁝ ⁝ ⁝ ⁝ ⁝ ⁝ ⁝ ⁝ x x n M x Shift n M k k k k • Tính: • Tính: n : Shift 6 n : Shift 1 3 x : Shift 7 x : Shift 2 1 sˆ : Shift 8 sˆ : Shift 2 2 s : Shift 9 s : Shift 2 3 • Thoát: Mode 0 • Thoát: Mode 1 3) Máy tính fx570MS
• Mở thống kê: Mode Mode 1
• Các bước tiếp theo tương tự máy tính fx500MS. 4) Máy tính fx570ES
• Mở thống kê: Shift Mode ▼ 4 1
• Nhập dữ liệu: Mode 3 1 X FREQ x n 1 1 ⁝ ⁝ AC x n k k 145 lOMoAR cPSD| 35883770 • Tính: Shift 1 5 n : 1 x : 2 3 sˆ : s : 4 • Thoát: Mode 1 Mode 1
5) Máy tính fx500ES, fx570ES-PLUS, fx570VN-PLUS: tương tự máy tính
fx570ES nhưng bước tính thì sử dụng: AC Shift 1 4
ĐỀ KIỂM TRA THAM KHẢO I.
1. Một chi tiết được lấy ngẫu nhiên có thể là chi tiết loại 1 (biến cố A) hoặc chi
tiết loại 2 (biến cố B) hoặc chi tiết loại 3 (biến cố C). Biến cố nào sau đây là biến cố không thể? (a) A+B (b) AB + C (c) AC (d) A + B
2. Cho đại lượng ngẫu nhiên liên tục X có phân phối nhị thức B(100; 0,2). Khi
đó, Var(2X + 5) có giá trị là: (a) 20 (b) 16 (c) 32 (d) 64
3. Ba người cùng bắn vào một mục tiêu. Gọi Ak là biến cố người thứ k bắn trúng
mục tiêu (k = 1, 2, 3). Biến cố A1 + A2 + A3 chỉ cho trường hợp nào sau đây?
(a) Chỉ có người thứ nhất bắn trúng mục tiêu.
(b) Chỉ có một người bắn trúng mục tiêu.
(c) Chỉ có hai người bắn trúng mục tiêu.
(d) Có người bắn trúng mục tiêu.
4. Gọi A là biến cố sinh con trai, B là biến cố sinh con có trọng lượng hơn 3kg. Câu nào sau đây đúng?
(a) A và B là 2 biến cố xung khắc.
(b) A và B là 2 biến cố đối lập.
(c) A và B là 2 biến cố độc lập.
(d) AB là biến cố chắc chắn.
5. Cho biết P(A) = 0,2; P(B) = 0,4; B(A/B) = 0,1. Khi đó, P(B/A) có giá trị là: 146 lOMoAR cPSD| 35883770 (a) 0,1 (b) 0,2 (c) 0,3 (d) 0,4
6. Nếu P(A+B+C) = 0,3; P(A) = P(B) = P(C) = 0,2; P(AB) = P(AC) = P(BC) =
0,1 thì P(ABC) có giá trị là: (a) 0 (b) 0,1 (c) 0,2 (d) 1
7. Cho đại lượng X phân phối theo quy luật chuẩn với hàm mật độ x 2 +1 1 x− f(x) = e 2
. Trường hợp nào dưới đây cho kỳ vọng và phương sai của 2 X là đúng? (a) E(X) = Var(X) = 0 (c) E(X) = 1, Var(X) = 0 (b) E(X) = 0, Var(X) = 1 (d) E(X) = Var(X) = 1
8. Cho đại lượng X có E(X) = 1,6 và có bảng phân phối xác suất X −2 0 2 4 P p 0,1 p’ 0,5
Trường hợp nào sau đây đúng? (a) p = p’ = 0,1 (c) p = 0,1; p’ = 0,3 (b) p = 0,3; p’ = 0,1 (d) p = p’ = 0,3
9. Cho đại lượng ngẫu nhiên liên tục X có hàm mật độ phân phối xác suất: 0 neáu x 0
F(x) = k(1 − cos x ) neuá x 0; . 1 neáu x
Hằng số k có giá trị là: (a) 0,5 (b) 1,5 (c) 2 (d)2,5 10. Cho đại lượng ngẫu nhiên liên tục X 0 x 0;1
có hàm mật độ xác suất f(x) = neáu . 1 neáu x 0;1
Xác suất P(0,6 < X < 1,2) có giá trị là: (a) 0,1 (b) 0,2 (c) 0,3 (d) 0,4
11. Cho đại lượng ngẫu nhiên rời rạc X có hai giá trị 1 và 2 với các xác suất
P(X=1) = 0,6; P(X=2) = 0,4. Câu nào sau đây đúng? (a) Mod(X) = 0,6 (b) E(X) = 1,2 (c) Var(X) = 0,24 0 neáu x 1
(d) X có hàm phân phối xác suất F(x) = 0,6 neuá 1 x 2 0,4 neuá x 2 147 lOMoAR cPSD| 35883770
12. Cho đại lượng ngẫu nhiên liên tục X có phân phối chuẩn N(5; 0,04). Khi đó,
E(X) và Var(X) có giá trị là: (a) E(X) = 5 ; Var(X) = 0,2 (c) E(X) = 5 ; Var(X) = 0,04 (b) E(X) = 25 ; Var(X) = 0,04 (d) E(X) = 25 ; Var(X) = 0,2
13. Cho X là đại lượng ngẫu nhiên liên tục có hàm phân phối xác suất F(x). Với
a < b, câu nào sau đây sai? (a) P(X = 0) = 0. (b) F(a) F(b). (c) P(a < X b (d) E(X) = xF(x)dx a
14. Một kiện hàng gồm 100 sản phẩm, trong đó có 10 phế phẩm. Chọn ngẫu
nhiên lần lượt có hoàn lại 5 sản phẩm để kiểm tra. Xác suất để trong 5 sản
phẩm lấy ra có 2 phế phẩm được tính bởi cách nào sao đây? (a) C 2 (0,1)2 (0,9)3 5 (b) 2 C (0,6)2 (0,4)4 100 C 2 C 4 (c) 10 90 6 C 100 C 2 (d) 10 6 C 100
15. Tung đồng xu 3 lần, xác suất có đúng 2 lần đồng xu lật mặt sấp là: (a) 1/8 (b) 2/3 (c) 3/8 (d) 1/2
16. Một kiện hàng có 15 sản phẩm, trong đó có 10 sản phẩm loại A. Kiểm tra lần
lượt không hoàn lại 2 sản phẩm của kiện hàng. Xác suất để 2 sản phẩm kiểm
tra có không quá 1 sản phẩm loại A là: (a) 2/21 (b) 3/7 (c) 4/7 (d) 10/21
17. Tín hiệu thông tin được phát 3 lần độc lập với xác suất thu được mỗi lần là
0,6. Số lần nguồn thu nhận được thông tin tin chắc nhất là: (a) 0 (b) 1 (c) 2 (d) 3
18. Bỏ ngẫu nhiên 4 lá thư vào 4 phong bì đã ghi sẵn địa chỉ tương ứng. Xác suất
sao cho ít nhất 2 thư bỏ đúng địa chỉ người nhận là: (a) 3/4 (b) 2/4 (c) 10/24 (d) 7/24
19. Trong một lớp học, tỉ lệ sinh viên tham dự đầy đủ một môn học là 60%,
trong số đó xác suất để một sinh viên thi đạt môn học đó là 85%. Chọn ngâu
xnhiên một sinh viên của lớp. Khả năng để sinh viên này đến lớp đầy đủ và
không thi đạt môn này là: (a) 0,75 (b) 0,09 (c) 0,51 (d) 0,15
20. Có hai lô sản phẩm: lô I có 5 sản phẩm với 2 phế phẩm, lô II với 4 sản phẩm
đều là chính phẩm. Lấy 1 sản phẩm từ lô I bỏ sang lô II, sau đó từ lô II lấy
ngẫu nhiên 1 sản phẩm. Tính xác suất sản phẩm lấy từ lô II là phế phẩm? (a) 1/20 (b) 1/25 (c) 1/10 (d) 2/25 148 lOMoAR cPSD| 35883770
21. Sinh viên được cộng điểm thưởng nếu có được ít nhất 1 trong 2 loại chứng
chỉ quốc gia về ngoại ngữ hay tin học. Lớp với 100 sinh viên có 60 sinh viên
có chứng chỉ ngoại ngữ, 40 sinh viên có chứng chỉ tin học, 30 sinh viên vừa có
chứng chỉ ngoại ngữ vừa có chứng chỉ tin học. Chọn ngẫu nhiên một sinh viên
trong lớp, xác suất chọn được sinh viên được cộng điểm thưởng là: (a) 0,3 (b) 0,4 (c) 0,6 (d) 0,7
22. Hai khách hàng chọn mua ngẫu nhiên mỗi người một con gà tại một quầy có
10 con gà (với 3 gà bệnh). Xác suất để cả 2 khách hàng đều mua phải gà bệnh là: (a) 6/90 (b) 9/100 (c) 6/100 (d) 9/90
2 3. Cho đại lượng ngẫu nhiên liên tục X có phân phối Poisson P(4). Khi đó, E(2X) có giá trị là: (a) 2 (b) 4 (c) 6 (d) 8
24. Cho hai đại lượng ngẫu nhiên X và Y độc lập nhau, với X có phân phối
Poisson P(2), Y có phân phối nhị thức B(25; 0,8). Var( X − Y) có giá trị là: (a) 6 (b) 2 (c) 2,8 (d) 1,2
25. Nếu đại lượng ngẫu nhiên liên tục X phân phối Poisson P(5) thì xác suất
P(X = 2) được tính bởi: 52 25 e −5 (a) (c) 2!e −5 5! 52 e −5 25 (b) (d) 2! 5!e −5
26. Cho X là đại lượng ngẫu nhiên liên tục có phân phối chuẩn N(10; 100). Kết quả nào sau đây là sai:
(a) P(0 < X < ) = 0,5 (b) P(X > 14) = 0,3446
(c) P(10 < X < 16) = 0,2257 (d) P(X < 8) = 0,4207
II. Một máy đóng gói được coi là đạt yêu cầu nếu có hơn 75% sản phẩm đạt
trọng lượng quy định nào đó. Chọn ngẫu nhiên 400 sản phẩm của một
máy thì thấy có 320 đạt trọng lượng quy định.
27. Khi ước lượng tỷ lệ p sản phẩm đạt yêu cầu của máy đang khảo sát, muốn đạt
được độ chính xác = 0,0392 thì độ tin cậy của ước lượng là bao nhiêu?
Với mức ý nghĩa 1%, kiểm định xem máy đang khảo sát hoạt động có đạt yêu cầu không?
28. Chọn giả thiết và đối thiết?
29. Tìm miền bác bỏ W của kiểm định ?
30. Tính giá trị quan sát u0 ?
31. Trả lời: máy có đạt yêu cầu hay không? III.
Mở thử 200 hộp của một kho đồ hộp, người ta thấy có 8 sản phẩm bị
biến chất. Với độ tin cậy 95%, hãy ước lượng tỷ lệ p đồ hộp bị biến chất ở kho đó. 149 lOMoAR cPSD| 35883770
32. Tính độ chính xác của ước lượng?
33. Tìm khoảng ước lượng?
IV. Trong một cửa hàng lớn có rất có rất nhiều quầy hàng, mỗi nhân viên
bán hàng trung bình một ngày bán được 780 nghìn đồng. Trong một
ngày khuyến mãi, lấy số liệu trên một số nhân viên thì thu được kết quả sau:
Số tiền bán hàng thu được (nghìn đồng) 700 750 800 850 Số nhân viên 30 35 20 10
Với mức ý nghĩa 5%, xét ý kiến cho rằng trong ngày khuyến mãi số tiền
trung bình m mỗi nhân viên bán hàng thu được có nhiều hơn ngày thường:
34. Chọn giả thiết và đối thiết?
35. Tìm miền bác bỏ W của kiểm định?
36. Tính giá trị quan sát u0 ?
37. Trả lời: ý kiến trên có chấp nhận được không?
Ước lượng số tiền bán hàng thu được trung bình m trên mỗi nhân viên trong
ngày khuyến mãi với độ tin cậy 95%:
38. Tính độ chính xác của ước lượng?
39. Tìm khoảng ước lượng?
40. Trong ước lượng trung bình trên, nếu độ chính xác của ước lượng = 1 thì
phải lấy số liệu mẫu tương ứng trên bao nhiêu nhân viên? 150




