Bài giảng môn Lý thuyết truyền tin | Học viện Công Nghệ Bưu Chính Viễn Thông

lOMoAR cPSD| 58736390
HỌC VIỆN CÔNG NGHỆ BƯU CHÍNH VIỄN THÔNG BÀI GIẢNG MÔN
LÝ THUYẾT TRUYỀN TIN Bộ môn :
Tín hiệu & Hệ thống - Khoa VT1
Học kỳ / Năm biên soạn : II/2022 BÀI GIẢNG MÔN LÝ THUYẾT TRUYỀN TIN lOMoAR cPSD| 58736390 Nội dung
▪ Chương 1 : Giới thiệu về lý thuyết truyền tin
▪ Chương 2 : Cơ sở lý thuyết truyền tin
▪ Chương 3 : Mã hóa
▪ Chương 4 : Ghép kênh
▪ Chương 5 : Điều chế tín hiệu
▪ Chương 6 : Nhiễu và bộ thu tối ưu www.ptit.edu.vn
BỘ MÔN: TH & HT - KHOA VT1 Trang 2 BÀI GIẢNG MÔN LÝ THUYẾT TRUYỀN TIN
Ch ương 6 - Nhiễu và bộ thu tối ưu . ▪ Nhiễu
. Định nghĩa và phân loại nhiễu
. Các tham số đặc trưng mô tả nhiễu
. Một số loại nhiễu cơ bản ▪ Bộ thu tối ưu
. Khái niệm về bộ thu tối ưu
. Các vấn đề thu tối ưu
. Bộ thu tối ưu cho kênh có nhiễu cọng Gaussian lOMoAR cPSD| 58736390 www.ptit.edu.vn
BỘ MÔN: TH & HT - KHOA VT1 Trang 3
6.1.1. Định nghĩa và phân loại nhiễu – Định nghĩa:
. Nhiễu là các tín hiệu ngẫu nhiên hoặc xác định bất kỳ không mong
muốn, gây nhiễu loạn đối với tín hiệu thông tin cần được khôi phục
chính xác trong một hệ thống.
. Nói cách khác, nhiễu là một tín hiệu bất kỳ gây nhiễu loạn thường
là sự dao động ngẫu nhiên của điện áp hoặc dòng điện có xu
hướng che khuất các tín hiệu thông tin.
– Phân loại nhiễu: Gồm 2 loại cơ bản
. Nhiễu do con người tạo ra: phát sinh từ bất kỳ phần nào của thiết
bị điện tử hoặc của thiết bị điện tử. Nhiễu này có thể được loại bỏ
hoặc giảm ở mức tối thiểu nhờ thiết kế và chế tạo cẩn thận.
. Nhiễu tự nhiên: không kiểm soát được trực tiếp và thường được
mô tả bằng thống kê. Nhiễu này là do chuyển động nhiệt ngẫu
11/05/2022 nhiên của các điện tử, sự hấp thụ khí quyển và các nguồn vũ trụ.5 lOMoAR cPSD| 58736390
6.1.2 . Các tham số đặc trưng mô tả nhiễu
– Vì nhiễu chủ yếu là ngẫu nhiên trong tự nhiên, được mô tả tốt nhất
thông qua các đặc tính thống kê của nó .
– Trong phần này sẽ trình bày và phân tích về các tham số chính và
các quan hệ lẫn nhau đối với mô tả nhiễu .
– C ác biểu thức được đưa ra để mô tả nhiễu thông qua mật độ phổ
công suất ( miền tần số) hoặc hàm tự tương quan mi ( ền thời gian ) . 6 lOMoAR cPSD| 58736390 lOMoAR cPSD| 58736390
6.1.2. Các tham số đặc trưng mô tả nhiễu
6.1.2.2 Chuyển đổi Fourier
– Định nghĩa của phép chuyển đổi Fourier [Stremler, 1982]: () = ℱ{()} = ∫ () (6.3)
– Chuyển đổi Fourier ngược: () = ℱ {()} = ∫ () (6.4)
. Nếu tín hiệu ()là tín hiệu công suất: tức là t/h có công suất hữu
hạn nhưng năng lượng vô hạn, tích phân trong (6.3) sẽ phân kỳ.
. Xét trường hợp thực tế: thời gian quan sát hữu hạn và giả sử tín
hiệu bằng 0 ở ngoài . Khi đó, chuyển đổi Fourier: (6.5) (/)- hàm cổng đơn vị.
Lưu ý: phép nhân với hàm trong miền thời gian là tương đương với
một tích chập bởi một hàm trong miền tần số. 10 lOMoAR cPSD| 58736390
6.1.2. Các tham số đặc trưng mô tả nhiễu
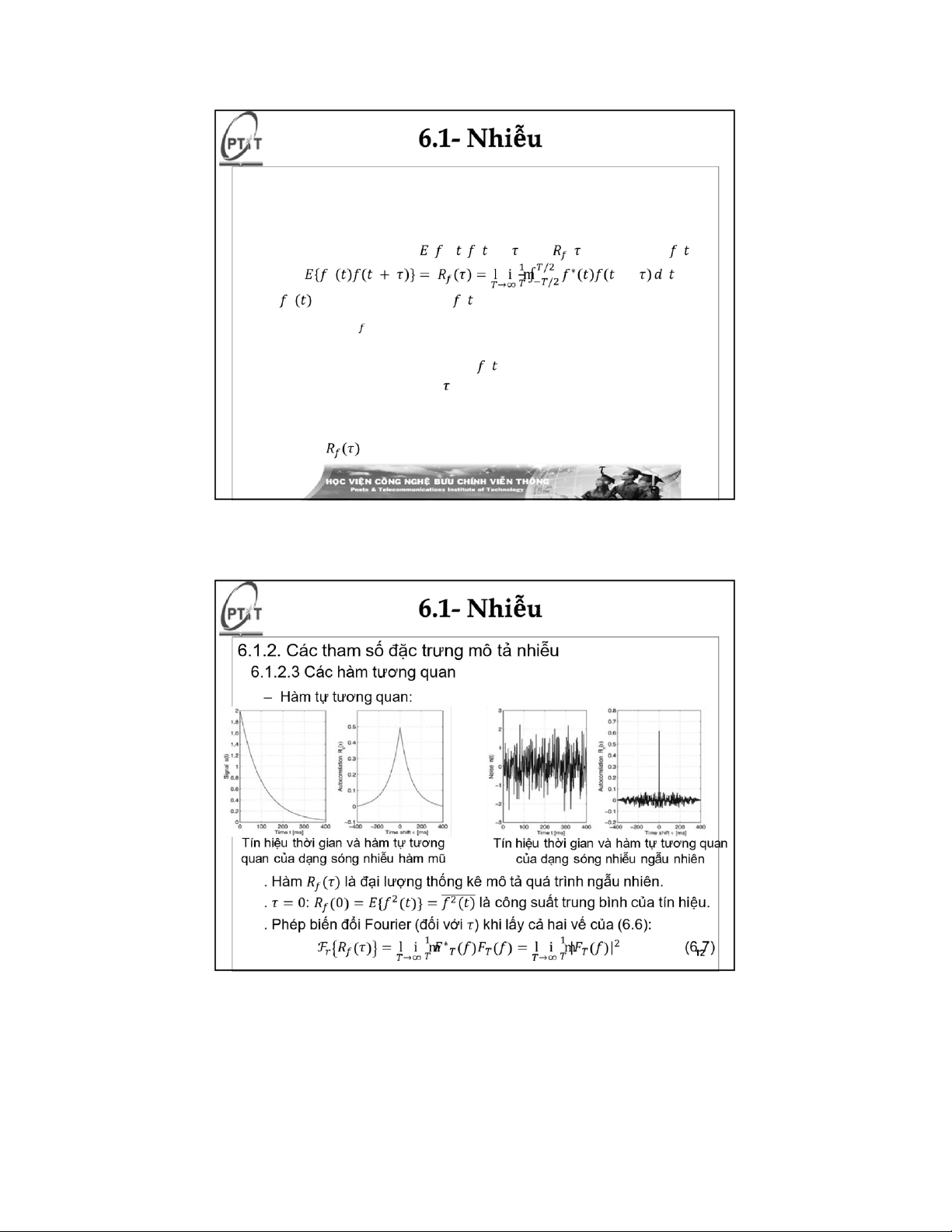
6.1.2.3 Các hàm tương quan – Hàm tự tương quan:
. Hàm tự tương quan {∗()( + )}= ()của tín hiệu (): ∗ + (6.6)
∗ là liên hợp phức của () chỉ số phụ : biểu thị biến ngẫu nhiên hoặc
hàm được xét . Hàm tự tương quan: sử dụng trong phân tích tín
hiệu, đưa ra một phép đo tương tự của tín hiệu ()với chính nó với
sự dịch chuyển thời gian tương đối bằng .
. Với các tín hiệu thời gian thay đổi chậm: các giá trị tín hiệu không
thay đổi nhanh theo thời gian sẽ dẫn đến một hàm tự tương quan
phẳng . Mặt khác, nhiễu có xu hướng biến động nhanh làm phát
sinh hàm tự tương quan với đỉnh nhọn tại =0(không dịch
11/05/2022 chuyển thời gian) và nhanh chóng giảm xuống 0 khi tăng . 11 lOMoAR cPSD| 58736390 lOMoAR cPSD| 58736390 lOMoAR cPSD| 58736390 lOMoAR cPSD| 58736390
6.1.3. Một số loại nhiễu cơ bản
6.1.3.1 Nhiễu trong hệ thống tuyến tính
– Băng tần nhiễu tương đương:
. Nếu nhiễu đầu vào là nhiễu trắng, công suất nhiễu tổng đầu ra hệ
thống với hàm truyền tần số đã biết là: =∫ = ∫ (6.24)
→ với một hàm truyền đã cho: tích phân là một hằng số.
. Để đơn giản khi tính : cách tiếp cận là xác định băng thông nhiễu
tương đương của bộ lọc lý tưởng sao cho công suất nhiễu đầu ra
từ bộ lọc lý tưởng và hệ thống thực tế là bằng nhau. . Do đó,
đầu ra của bộ lọc lý tưởng là: / = ∫ / = (6.25) . Từ (6.24), (6.25): =∫ (6.26)
cho phép thảo luận các hệ thống tuyến tính thực tế bằng cách
sử dụng các hệ thống lý tưởng tương đương. 18 lOMoAR cPSD| 58736390
6.1.3. Một số loại nhiễu cơ bản
6.1.3.2 Nhiễu xẩy ra tự nhiên
– Cơ sở cho các loại nhiễu này định luật bức xạ Planck: . Luật Planck:
➢ Năm 1900, Max Planck tìm ra định luật liên quan đến phát xạ
điện từ từ vật đen ở trạng thái cân bằng nhiệt.
➢ Vật đen được định nghĩa là một vật lý tưởng, hoàn toàn không
trong suốt có thể hấp thụ tất cả các phát xạ tới ở mọi tần số và
không phản xạ lại bất kỳ tần số nào.
➢ Một vật ở trạng thái cân bằng nhiệt động: lượng năng lượng
phát ra bằng với lượng mà nó hấp thụ từ môi trường.
➢ Do đó, vật đen là một bộ hấp thụ hoàn hảo thì nó còn là một bộ phát xạ hoàn hảo.
➢ Điểm chính của nguồn gốc Planck là năng lượng chỉ được trao
đổi dưới dạng các phần rời rạc hoặc lượng tử bằng ℎ, trong đó
ℎlà hằng số Planck ℎ=6,626×10 []và là tần số tính bằng Hz. 20 lOMoAR cPSD| 58736390
6.1.3. Một số loại nhiễu cơ bản
6.1.3.2 Nhiễu xẩy ra tự nhiên
– Cơ sở cho các loại nhiễu này định luật bức xạ Planck: . Luật Planck:
➢ Đặt là số mức (trạng thái), =0,1,2,…. và là số lượng tử năng
lượng ở mức . Năng lượng của mức là: ℎ.
➢ Theo cơ học lượng tử, xác suất chiếm một mức năng lượng đi
xuống là ∆/ . Khi đó, sẽ là: = /
với: =1,38×10 [ ]là hằng số Boltzmann, là nhiệt độ tuyệt đối
Kelvin, và ∆=ℎ là độ lệch năng lượng.
➢ Năng lượng trung bình là tỉ số giữa năng lượng tổng và số lượng
tử năng lượng tổng: (6.32)
➢ Sử dụng mật độ các mode, tìm ra định luật Planck cho bức xạ
vật đen. Được biểu thị bằng độ sáng của năng lượng phát xạ: ()= / (6.33) 11/05/2022 21
6.1.3. Một số loại nhiễu cơ bản
6.1.3.2 Nhiễu xẩy ra tự nhiên – Phát xạ nhiệt:
. Trong hệ thống luôn tồn tại phát xạ nhiệt thông qua chuyển động
nhiệt ngẫu nhiên của các điện tử trong môi trường dẫn.
. Hiệu ứng của chuyển động điện tử là một dòng điện ngẫu nhiên
chạy trong môi trường dẫn với giá trị trung bình bằng không.
. Mật độ phổ công suất của nhiễu nhiệt tuân theo luật phân bố Planck: =()
. Với dải nhiệt độ và tần số bình thường thấp hơn dải quang học,
tham số ℎ/ là rất nhỏ, do đó / ≈1+ℎ/ nên: = (6.34)
→ không phụ thuộc vào tần số nên gọi là phổ nhiễu trắng. . Trong băng thông
, công suất nhiễu khả dụng là: = (6.35)22 lOMoAR cPSD| 58736390
6.1.3. Một số loại nhiễu cơ bản
6.1.3.2 Nhiễu xẩy ra tự nhiên
– Nhiễu ngoài trái đất:
. Không gian vũ trụ phần lớn là nguồn nhiễu băng thông rộng, có thể
coi là sóng điện từ phẳng.
. Các nguồn nhiễu: phát xạ nhiệt và không phát xạ nhiệt từ Mặt trời,
Mặt trăng, Sao, các hành tinh và nơi khác trong các thiên hà. . Với
phát xạ nhiệt thì công suất nhiễu được mô tả qua độ sáng phổ, .
Theo định luật Rayleigh-Jeans, ở tần số vô tuyến ℎ≪ : = (6.36) ..
là nhiệt độ sáng, λ là bước sóng và k là hằng số Boltzmann. .
Tổng quát: thay đổi theo trong đó được gọi là chỉ số phổ. Đối với
sự phát xạ nhiệt của vật đen =−2.
. Với không phát xạ nhiệt:
không liên quan đến phát xạ nhiệt mà
11/05/2022 là nhiệt độ sáng đẳng trị và n phải được xác định chính xác. 23
6.1.3. Một số loại nhiễu cơ bản
6.1.3.2 Nhiễu xẩy ra tự nhiên – Bức xạ nền:
. Toàn bộ vũ trụ bị bão hòa với bức xạ nền vô tuyến, tàn tích của một vụ nổ lớn.
. Ngày nay, phát xạ được đo một cách đồng đều từ mọi hướng của
không gian, do đó có thuật ngữ "bức xạ nền".
. Bức xạ nền sẽ "làm nóng" bất kỳ vật thể có nhiệt thấp đến nhiệt độ
không gian là 3 (độ không tuyệt đối Kelvin là −273 )..
. Nhiệt độ của phát xạ nền vô tuyến vũ trụ
được xác định với vệ tinh COBE trong hai
năm đầu quan sát đầu tiên như hình vẽ. Mặt
phẳng của dải Ngân hà nằm ngang ở giữa mỗi
bức tranh. Dải nhiệt độ là 0-4K cho ảnh trên
cùng, 3,3mK cho ảnh giữa và 18µK cho ảnh dưới cùng. 24
6.1.3. Một số loại nhiễu cơ bản
6.1.3.2 Nhiễu xẩy ra tự nhiên lOMoAR cPSD| 58736390 – Nhiễu hấp thụ:
. Khi một vật hấp thụ năng lượng thì năng lượng tương tự sẽ được
phát xạ thành nhiễu như chỉ ra trong lý thuyết phát xạ vật đen. Nếu
không, nhiệt độ của một vật sẽ tăng lên và nhiệt độ của những vật khác giảm xuống.
. Trong trường hợp ăng-ten bức xạ, năng lượng bị hấp thụ một phần
bởi khí quyển và được phát xạ lại dưới dạng nhiễu.
. Nhiệt độ nhiễu hấp thụ hiệu dụng, được cho dưới dạng hàm của
nhiệt độ môi trường xung quanh, và suy hao, là: = (−1) (6.38)
Lưu ý: không giống với nhiệt độ vật lý (môi trường xung quanh) của
khí quyển và tăng khi suy hao khí quyển ngày càng tăng. Suy
hao của bầu khí quyển phụ thuộc nhiều vào tần số. 11/05/2022 25 lOMoAR cPSD| 58736390 lOMoAR cPSD| 58736390
6.2.1. Khái niệm về bộ thu tối ưu
– Nhiệm vụ của bộ thu: chọn một trong giả thuyết trong khi chỉ biết
một số tính chất của nguồn và dạng của tín hiệu nhận được .
– Mỗi một giả thuyết đều có một xác suất sai tương ứng vì ()là một hàm ngẫu nhiên.
– Do đó, máy thu phải chọn một lời giải nào đó trong điều kiện bất
định. Vì vậy thu tín hiệu khi có nhiễu là một bài toán thống kê.
– Việc máy thu chọn lời giải còn được gọi là sơ đồ giải.
– Yêu cầu của sơ đồ giải: phải cho ra lời giải đúng (phát phải tìm ).
– Thực tế có rất nhiều sơ đồ giải: tại một sơ đồ bảo đảm xác suất thu
lớn phải đúng là lớn nhất (xác suất giải sai là bé nhất). Sơ đồ này
được gọi là sơ đồ giải tối ưu.
– Máy thu xây dựng theo sơ đồ giải tối ưu được gọi là máy thu tối ưu
11/05/2022 (hay máy thu lý tưởng). 29 lOMoAR cPSD| 58736390 6.2. .
2 Các vấn đề thu tối ưu
6 . 2 . 2 . 1 Thế chống nhiễu
– Có thể dùng xác suất thu đúng để đánh giá độ chính xác của một
hệ thống truyền tin một cách định lượng .
– Để đánh giá ảnh hưởng của nhiễu lên độ chính xác của việc thu,
người ta đưa ra khái niệm tính chống nhiễu của máy thu .
– Nếu cùng một mức nhiễu, máy thu nào đó có xác suất thu đúng là
lớn hơn thì được coi là có tính chống nhiễu lớn .
– Hiển nhiên tính chống nhiễu của máy thu tối ưu là lớn nhất và
được gọi là thế chống nhiễu . 30 lOMoAR cPSD| 58736390
6.2.2. Các vấn đề thu tối ưu
6.2.2.3 Tiêu chuẩn Kachennhicov
– Thông thường khái niệm tối ưu là phải hiểu tối ưu theo một tiêu
chuẩn nào đó. Trong thông tin "thu tối ưu" được hiểu theo nghĩa như
sau (tiêu chuẩn Kachennhicov):
Trong cùng một điều kiện đã cho trong số hai hay nhiều sơ đồ giải,
sơ đồ nào đảm bảo xác suất giải đúng lớn nhất thì được gọi là tối ưu.
– Hạn chế: Không đề cập đến các loại sai lỗi, tức là coi chúng tồn tại "ngang quyền" nhau.
– Ưu điểm: Đơn giản, dễ tính toán, dễ thực hiện.
– Ngoài tiêu chuẩn Kachennhicov còn có một số những tiêu chuẩn
khác như: Neyman-Pearson, Bayes, Vald …. Những tiêu chuẩn này
khắc phục được nhược điểm trên nhưng khá phức tạp nên
không dùng trong thông tin. 32 lOMoAR cPSD| 58736390
6.2.2. Các vấn đề thu tối ưu
6.2.2.4 Xử lý tối ưu các tín hiệu
– Nhiệm vụ máy thu: cho các lời giải
nhờ quá trình xử lý tín hiệu.
– Trong quá trình xử lý tín hiệu: phải thực hiện các phép toán tuyến
tính hoặc phi tuyến nhờ các mạch tuyến tính hoặc phi tuyến.
– Quá trình xử lý tín hiệu trong máy thu tối ưu được gọi là xử lý tối ưu
tín hiệu. Xử lý để nhận lời giải có xác suất lỗi bé nhất.
– Trước kia việc xây dựng sơ đồ giải chỉ căn cứ các tiêu chuẩn chất
lượng mang tính chức năng mà không mang tính thống kê.
– Ảnh hưởng của nhiễu lên chất lượng của máy thu chỉ được tính
theo tỷ số tín hiệu /nhiễu. Tức là việc xây dựng sơ đồ giải tối ưu
trước đây chỉ dựa vào trực giác, kinh nghiệm, thí nghiệm.
– Ngày nay lý thuyết truyền tin cho phép bằng toán học xây dựng sơ
đồ giải tối ưu (tính định lượng), tức là dựa vào các tiêu chuẩn tối
ưu bằng thống kê toán học đã xác định được quy tắc giải tối ưu. 11/05/2022 33
6.2.2. Các vấn đề thu tối ưu
6.2.2.5 Xác suất giải sai và quy tắc giải tối ưu
– Cho là tín hiệu đã gửi đi với xác suất tiên nghiệm là ( ) ∑ =1. Giả thiết là có thời hạn .
– Ở máy thu nhận được (), qua sơ đồ giải sẽ có lời giải nào đó.
– Nếu nhận được thì coi
đã được gửi đi với một xác suất hậu nghiệm
(/). Xác suất giải sai sẽ là: /, =1−(/) (6.41)
– Từ (6.41) sẽ tìm ra quy tắc giải tối ưu (t/c Kachennhicov). Xét 2 sơ đồ giải:
Sơ đồ 1: Từ ()cho
và Sơ đồ 2: Từ ()cho .
– Nếu /, < /, (6.42): sơ đồ 1 tối ưu hơn sơ đồ 2.
– Từ (6.41) và (6.42) ⇒ (/)>(/) (6.43) – Xét
sơ đồ có: / > / với , (6.44)
– Nếu có (−1)hệ thức như (6.44) thì ta coi sơ đồ giải chọn sẽ là tối ưu vì đảm
bảo xác suất lỗi là bé nhất, đây chính là quy tắc giải tối ưu. Sơ đồ giải thỏa 11/05/2022
mãn biểu thức (6.44) chính là sơ đồ giải tối ưu. 34 20
Downloaded by To Nu (tonuwxa@gmail.com)