
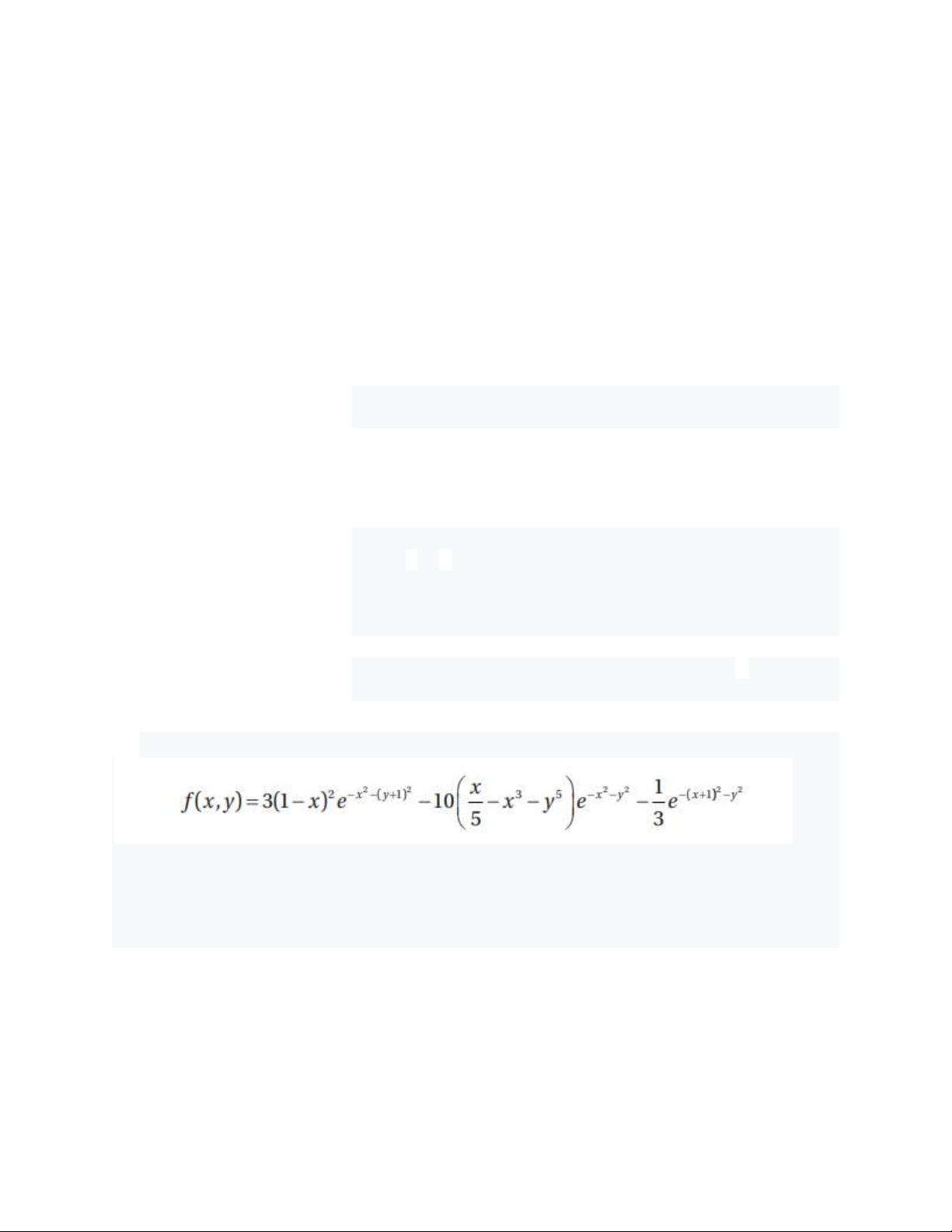


Preview text:
lOMoARcPSD|36442750
Chương 5: Các lệnh đồ họa đặc biệt
5.1 Đồ họa 2 chiều: FPLOT và EZPLOT
- Các lệnh vẽ đồ thị đường cong fplot và ezplot được thiết kế cho nhiều trường hợp
khác nhau mà không cần phải chỉ ra các chi tiết được tích hợp sẵn trong mỗi lần. Cú pháp của chúng như sau: fplot(‘f’, [xmin, xmax])
Vẽ đồ thị hàm giữa các giới hạn trong từng
trường hợp được cho trong bảng
fplot(‘f’,[xmin, xmax, ymin, ymax], S) Vẽ đồ thị hàm tại các khoảng biến thiên của x và
y, với các tùy chọn về màu sắc và ký tự được
cho bởi S. ymin và ymax kiểm soát các giá trị của trục tung
fplot(‘[f1,f2,...,fn]’,[xmin, xmax, ymin, Vẽ đồ thị các hàm f1, f2,..., fn trên cùng các trục ymax], S,t,n)
trong khoảng biến thiên của x và được chỉ định
với các tùy chọn về màu sắc và ký tự được xác định trong S
fplot(‘f’,[xmin, xmax],...,t)
Vẽ đồ thị của f sử dụng dung sai t
fplot(‘f’,[xmin, xmax],...,n)
Vẽ đồ thị của f với n>=1 ezplot(‘f’, [xmin, xmax]) Tương tự như fplot
ezplot(‘f’, [xmin, xmax, ymin, ymax])
Vẽ đồ thị hàm f(x,y) tại các khoảng biến thiên cho
trước của x và y . Không giống fplot, ezplot có thể là f(x,y) ezplot(x, y)
Vẽ đồ thị đường cong tham số x = x(t) và y = y(t) trên miền 0 < t < 2π ezplot(‘f’, [xmin, xmax])
Vẽ đồ thị đường cong tham số x = x(t) và y = y(t).
Đây là một biến thể có hai tham số chức năng
của ezplot(x,y); sự khác biệt duy nhất là tmin và
tmax được sử dụng thay vì từ 0 đến 2π. Vì vậy,
cú pháp là ezplot(fx,fy,[tmin tmax]) ezplot(‘f’)
Vẽ đồ thị đường cong f nằm trong [-2π, 2π] Ví dụ: -
Ví dụ đầu tiên, biểu diễn đồ thị của hàm f(x) = Sin(x)e-0,4x trên khoảng [0,10]. Hình
5-1 trình bày kết quả của cú pháp sau: >> x = 0:0.05:10;
>> y = sin(x) .* exp(-0.4*x); >> plot(x,y)
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 -
Biểu diễn của đường cong trước đó (Hình 5-2) cũng có thể được thực hiện bằng cú pháp sau:
>> ezplot('sin(x) * exp(-0.4*x)', [0,10]) -
Lưu ý rằng ezplot tự động đặt tiêu đề. Bạn cũng có thể có được biểu diễn đồ họa
tương tự bằng cách sử dụng lệnh sau:
>> fplot('sin(x) * exp(-0.4*x)', [0,10]) -
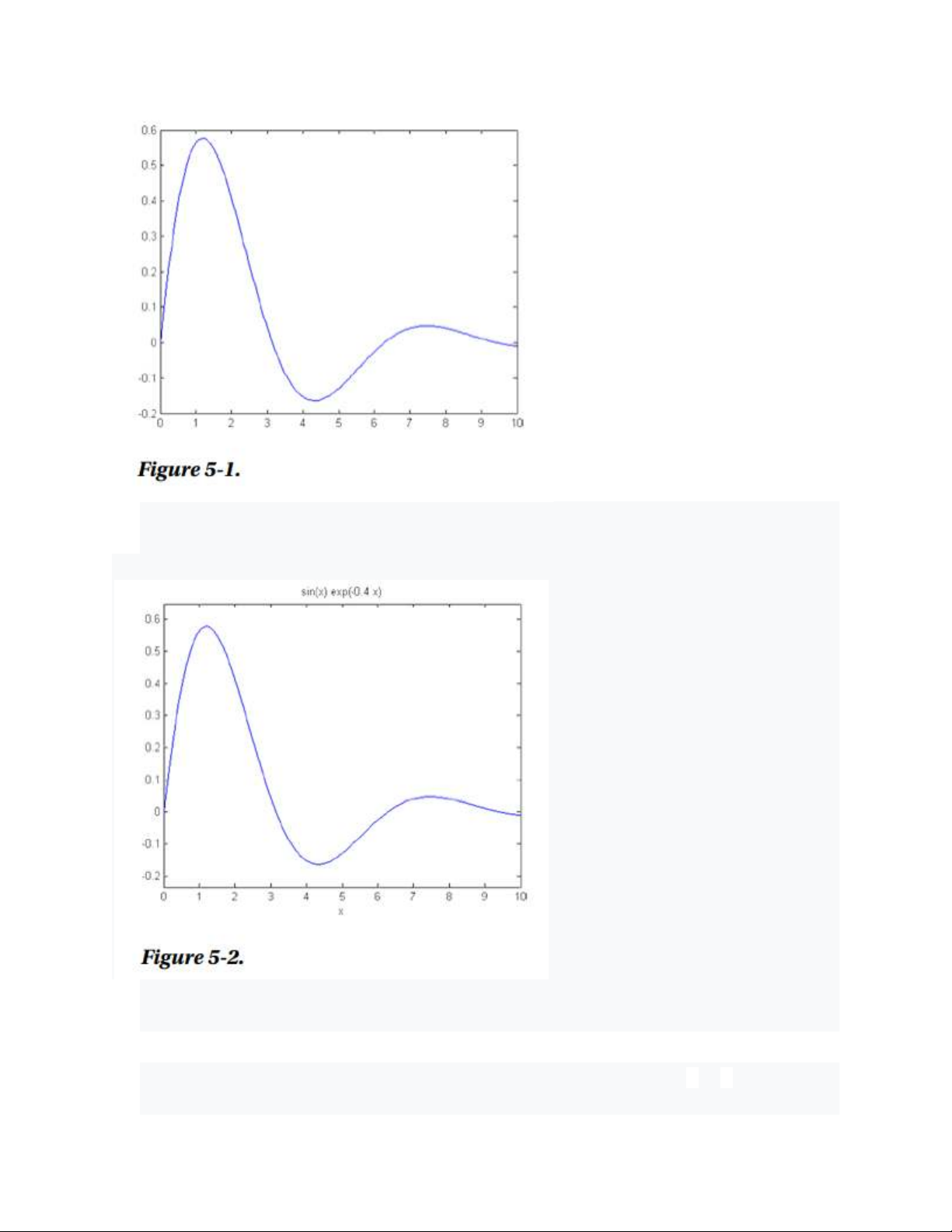
Hình 5-3 hiển thị đường cong cho x2 – y4 = 0 trong khoảng [-2π, 2π] sử dụng cú pháp sau:
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 >> ezplot('x^2-y^4') -
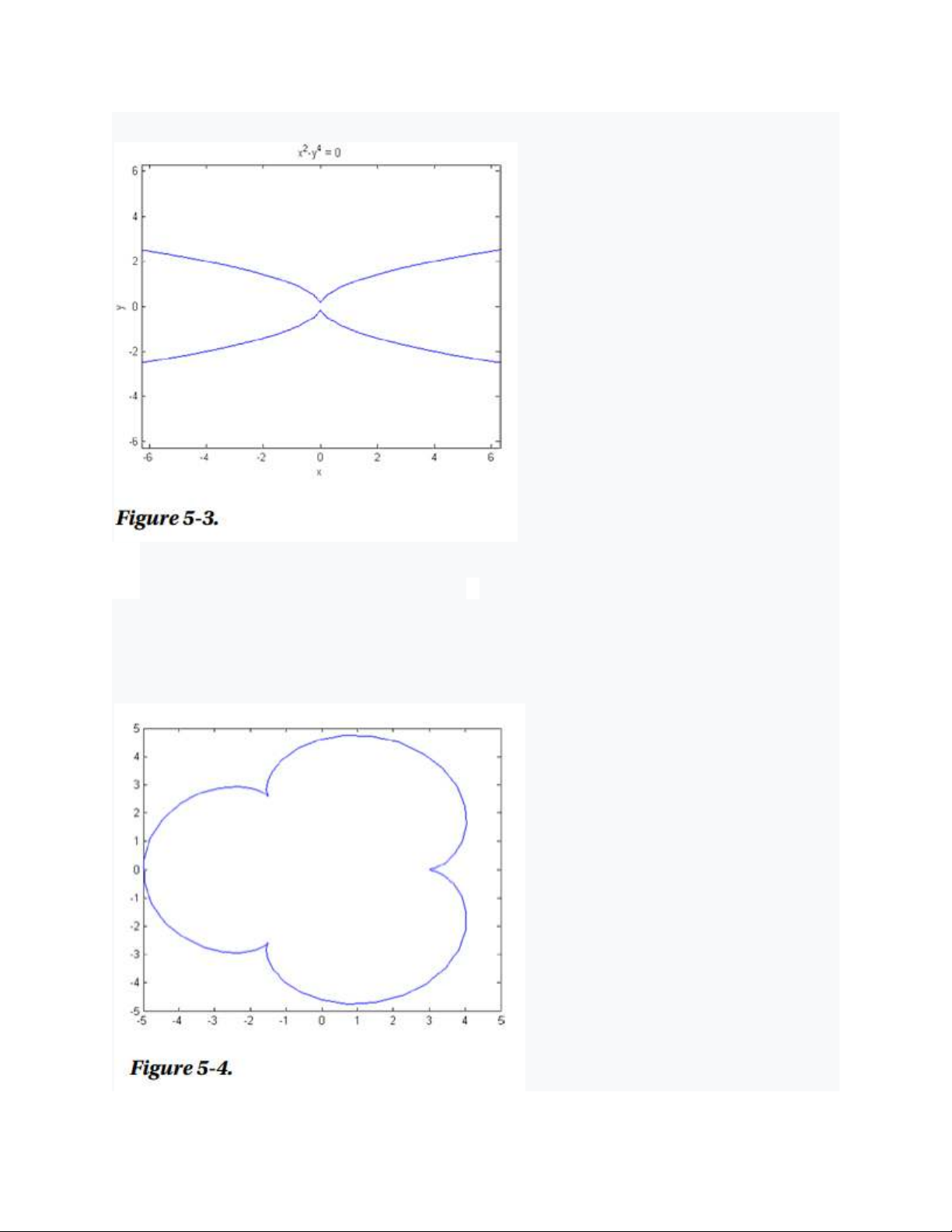
Sau đó, chúng ta vẽ đồ thị đường cong tham số – x(t) = 4cos(t) –cos(4t), y(t) =
4sin(t) –sin(4t) thay đổi t giữa 0 và 2π (Hình 5-4). Cú pháp như sau: >> t = 0:0.1:2*pi;
>> x = 4 * cos(t) - cos(4*t);
>> y = 4 * sin(t) - sin(4*t); >> plot(x,y)
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 -
Biểu đồ tương tự (Hình 5-5) có thể thu được bằng cách sử dụng cú pháp sau:
>> ezplot('4*cos(t) - cos(4*t)', '4*sin(t) - sin(4*t)', [0, 2*pi]) -
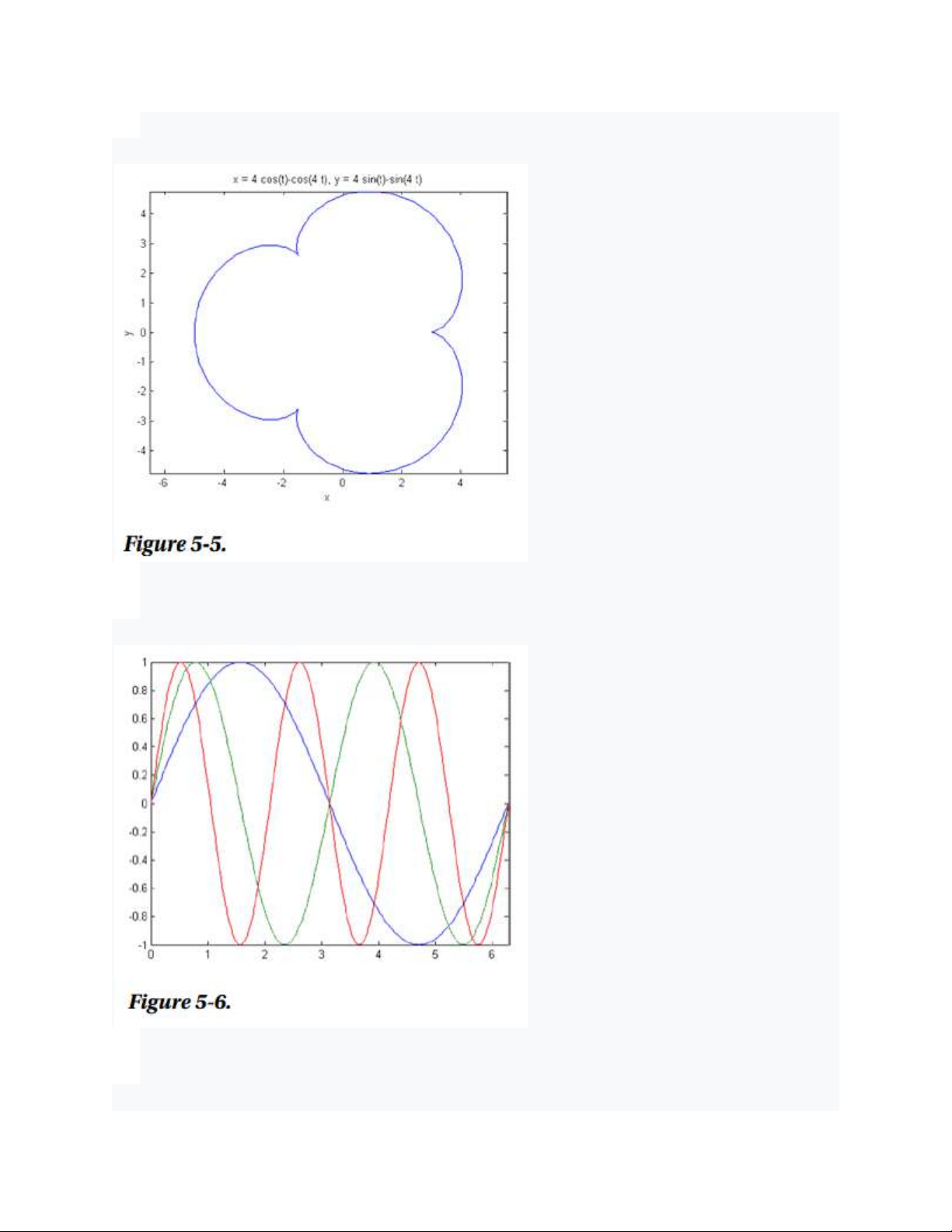
Tiếp theo, các đường cong Sine(x), Sine(2x) và Sine(3x) quanh các trục giống
nhau như trong Hình 5-6. Cú pháp như sau:
>> fplot('[sin(x), sin(2*x), sin(3*x)]', [0, 2*pi]) -
Chúng ta có thể thử biểu diễn mọi đường cong trước đó bằng các nét vẽ khác
nhau (Hình 5-7) bằng cách sử dụng cú pháp sau:
>> fplot('[sin(x), sin(2*x), sin(3*x)]', [0, 2*pi],'*')
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 -
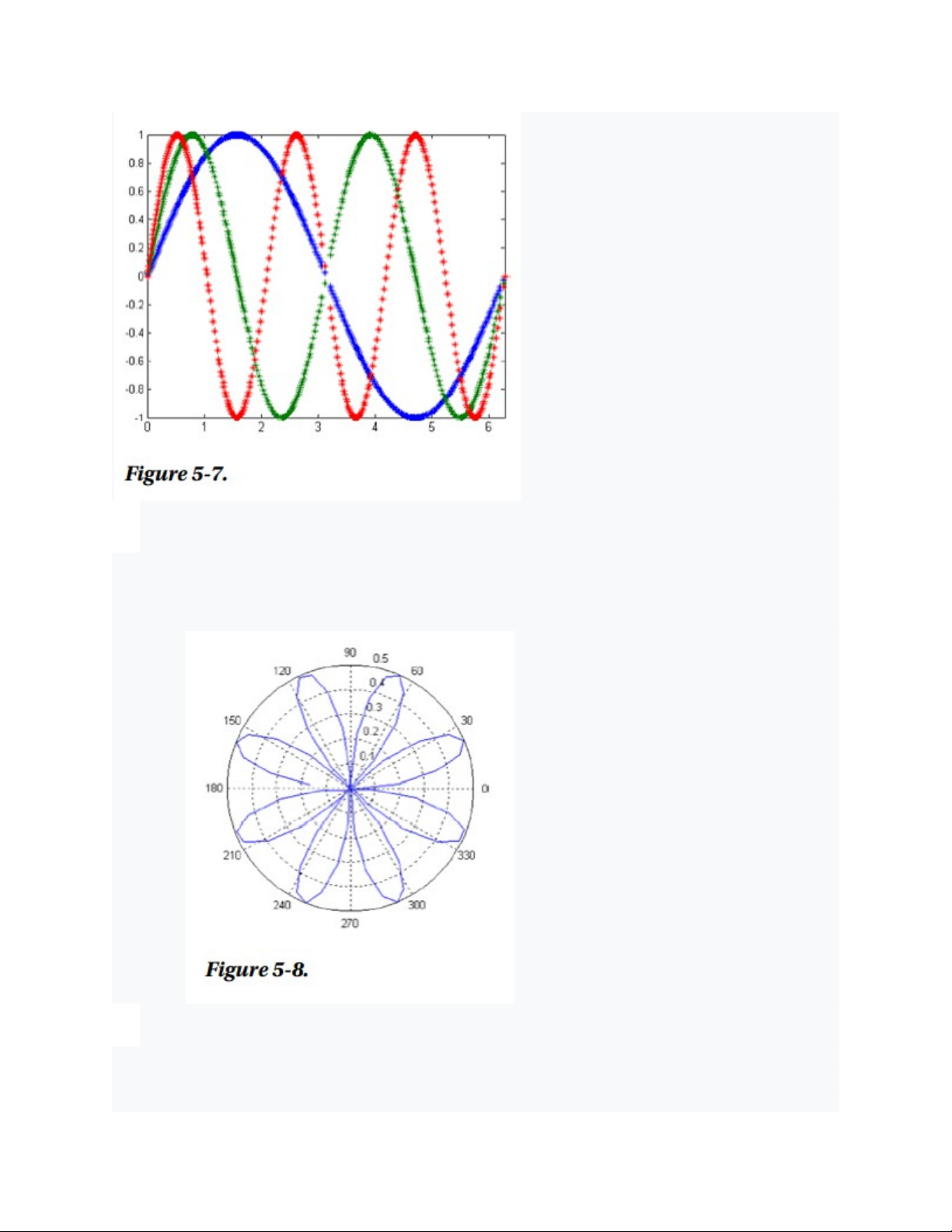
Dưới đây bạn sẽ tìm thấy cú pháp được sử dụng để biểu diễn đường cong cực r =
Sin(2a) Cos(2a) cho t giữa 0 và 2p (Hình 5-8). >> t = 0:0.1:2*pi;
>> r = sin(2*t).* cos(2*t); >> polar(t,r) -
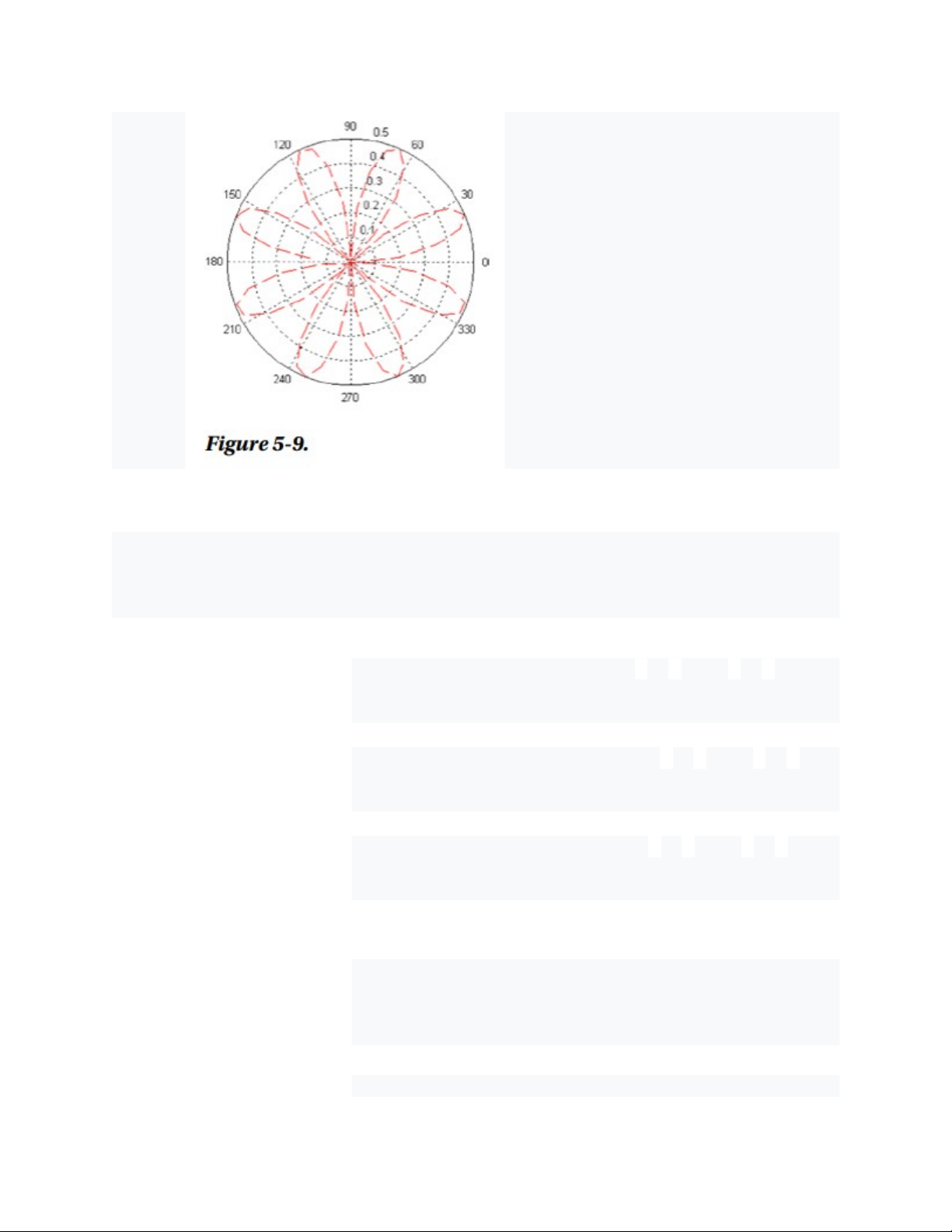
Ví dụ này cũng có thể biểu diễn đường cong cực bằng một đường nét đứt màu
đỏ (Hình 5-9) bằng cách sử dụng cú pháp sau >> t = 0:0.1:2*pi;
>> r = sin(2*t).*cos(2*t); >> polar(t,r,'--r')
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
5.2 Đồ họa 3 chiều với lệnh EZ
- Theo cách tương tự, các hàm ez được sử dụng để biểu diễn đồ họa hai chiều mà
không cần chỉ ra sự tồn tại của hình dạng mảng, đồ họa ba chiều của các đường cong,
bề mặt, đường viền, viền và các dạng khác của đồ họa cũng có thể được sử dụng, các lệnh sử dụng như sau: ezcontour(f)
Đồ thị hình bao của f(x,y) trong [-2π, 2π] x [-2π, 2π] ezcontour(f, domain)
Đồ thị hình bao của f(x,y) trong miền xác định ezcontour(...,n)
Đồ thị hình bao của f(x,y) trong lưới kích thước n x n ezcontourf(f)
Vẽ đồ thị hình bao của f(x,y) trong [-2π, 2π] x [-2π, 2π] ezcontourf(f, domain)
Vẽ đồ thị hình bao của f(x, y) trong miền đã cho ezcontourf(...,n)
Đồ thị hình bao của f(x, y) vẽ vào lưới n x n ezmesh(f)
Vẽ vào biểu đồ lưới của f(x,y) tại [-2π, 2π] x [-2π, 2π] ezmesh(f,domain)
Vẽ vào biểu đồ lưới của f(x,y) trong miền đã cho ezmesh(...,n)
Vẽ biểu đồ lưới của f(x,y) trong lưới nxn ezmesh(x, y, z)
Biểu đồ lưới cho x = x(t,u), y = y(t,u), z = z(t,u) trong đó t,u ∈ [-2π, 2π] ezmesh(x, y, z, domain)
Đồ thị lưới cho x = x(t,u), y = y(t,u), z = z(t,u) trong đó t,u ∈ miền ezmesh(..., ‘circ’)
Biểu đồ lưới của một hình tròn, không phải hình vuông
mặc định, nằm giữa trong miền ezmeshc(f)
Thực hiện kết hợp các biểu đồ dạng lưới và đường viền ezmeshc(f, domain)
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 ezmeshc(...,n) ezmeshc(x, y, z) ezmeshc(x, and z, domain) ezmeshc(..., ‘circ’) ezsurf(f)
Những lệnh này tạo màu cho bề mặt biểu đồ ezsurf(f, domain) ezsurf(...,n) ezsurf(x, y, z) ezsurf (x, y, z, domain) ezsurf(..., ‘circ’) ezsurfc(f)
Những lệnh này tạo ra các sơ đồ là sự kết hợp của đồ thị ezsurfc(f, domain)
bề mặt và đường viền ezsurfc(...,n) ezsurfc(x, y, z) ezsurfc(x, y, z, domain) ezsurfc(..., ‘circ’) ezplot3(x, y, z)
Đường cong tham số dạng 3D cho x = x(t), y = y(t), z = z(t) t ∈ [-2π, 2π] ezplot3(x, y, z, domain)
Đường cong tham số dạng 3D cho x = x(t), y = y(t), z = z(t) t ∈ miền ezplot3(..., ‘animate’)
Đường cong tham số sử dụng hoạt ảnh 3D ezpolar(f)
Vẽ đồ thị đường cong cực r = f(c) với c ∈ [0, 2π] ezpolar(f, [a, b])
Vẽ đồ thị đường cong cực r = f(c) với c ∈ [a, b] -
Dưới đây là đồ thị hình bao (Hình 5-10) của hàm số:
>> f = ['3 *(1-x)^2*exp(-(x^2)-(y + 1)^2)',...
'-10*(x/5-x^3-y^5)*exp(-x^2-y^2)','-1/3*exp(-(x + 1)^2 - y^2)'];
>> ezcontour(f,[-3,3],49) colormap summer
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 -
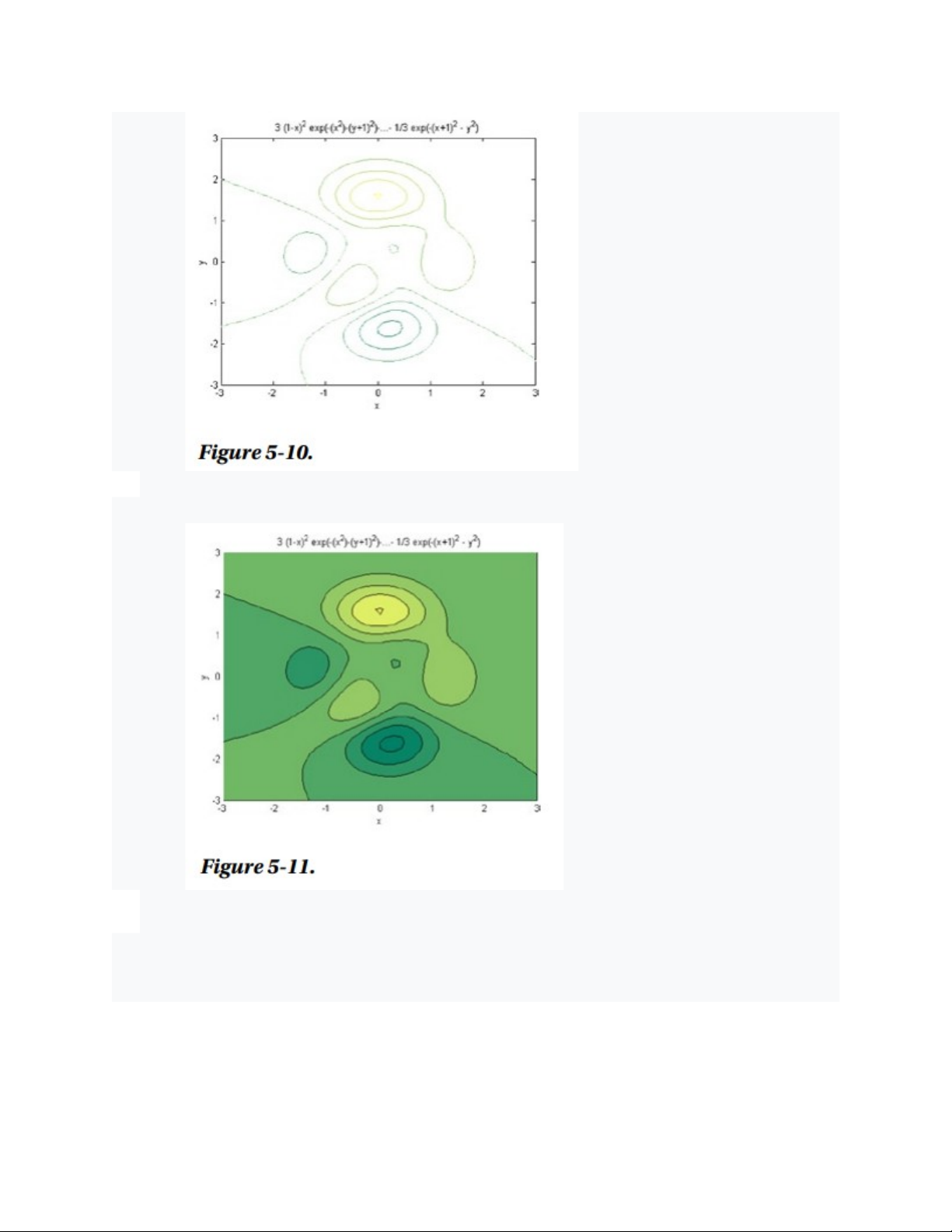
Sau đó tô màu vào đường viền trước đó (Hình 5-11).
>> ezcontourf(f,[-3,3],49) -
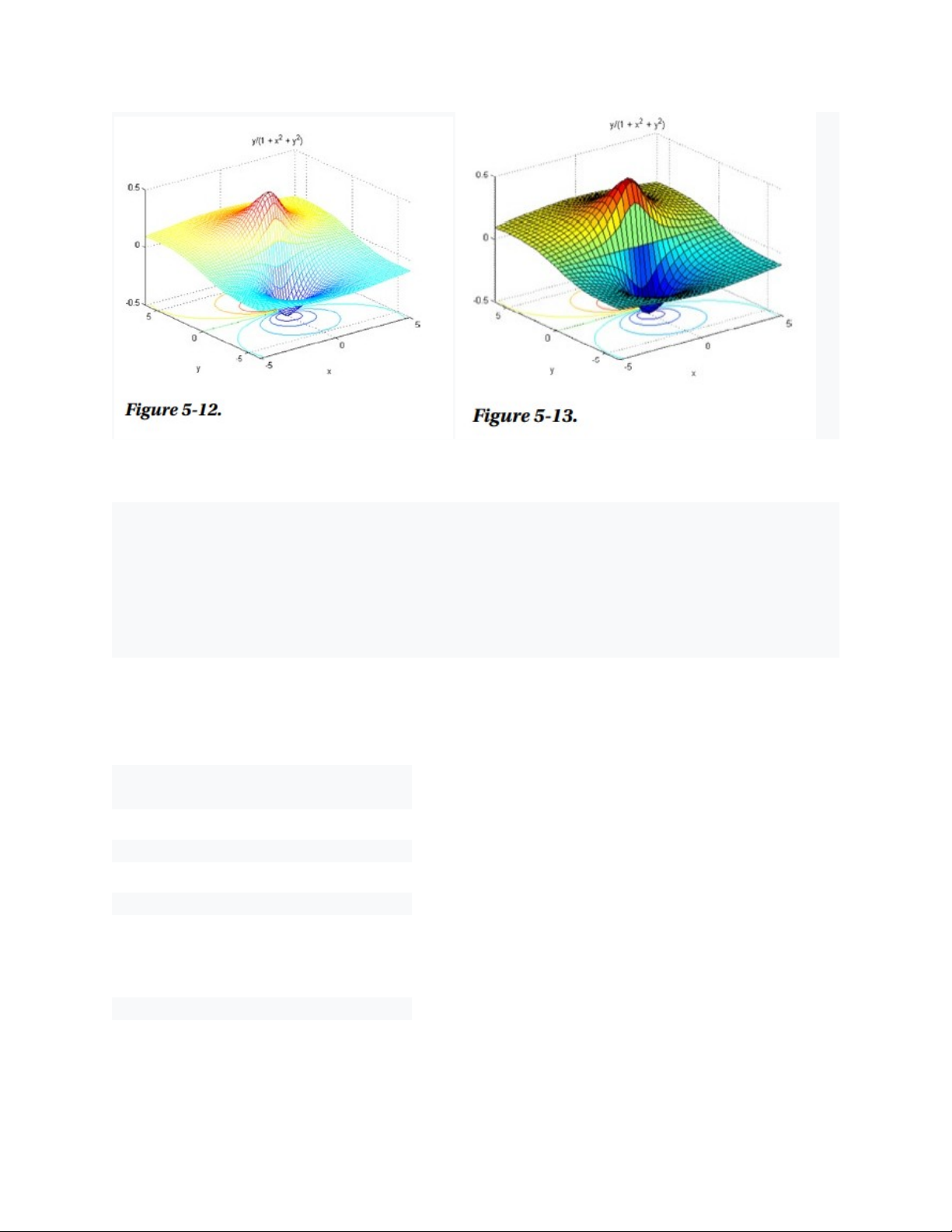
Trong ví dụ sau, chúng ta thực hiện đường viền lưới hỗn hợp (Hình 5-12) cho
chức năng biểu đồ, sau đó là bề mặt đồ họa và đường viền (Hình 5-13): f(x,y) =
>> ezmeshc('y /(1 + x^2 + y^2)', [- 5, 5, - 2*pi, 2*pi])
>> ezsurfc('y/(1 + x^2 + y^2)', [- 5, 5, - 2*pi, 2*pi], 35)
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
5.3 Các bước để đồ thị hóa dữ liệu
- Như chúng ta đã thấy, mô-đun cơ bản của MATLAB cung cấp nhiều tùy chọn khi nói
đến đại diện cho đồ họa. Nó cho phép vẽ đồ thị của các đường cong và bề mặt phẳng,
cho phép nhóm và chồng lên nhau. Nó cũng có thể để đưa màu sắc, lưới, khung, v.v.
vào đồ họa. Biểu diễn hàm ở dạng ẩn, rõ ràng và tọa độ tham số. Do đó, MATLAB là
phần mềm toán học với hiệu suất đồ họa cao, khác biệt so với nhiều công cụ tính toán
khác. MATLAB cũng cho phép đồ họa khung, đường, sao, biểu đồ, khối đa diện, bản đồ
địa lý và hình ảnh động. Việc tạo biểu đồ thường được thực hiện theo các bước sau: Các bước Ví dụ Chuẩn bị dữ liệu
x = 0:0.2:12; Y1 = besselj(1,x); Y2 = besselj(2,x); Y3 = besselj(3,x);
Chọn cửa sổ và xác định vị trí figure(1); subplot(2,2,1)
Sử dụng chức năng đồ họa h = plot(x,Y1,x,Y2,x,Y3);
Chọn các dòng và đặc điểm đánh
set(h,'LineWidth',2,{'LineStyle'}); set(h,{'Color'},
dấu (chiều rộng, màu sắc, ...) {'r';'g';'b'})
Giới hạn vị trí của trục, dấu và lưới axis([0,12,-0.5,1]) grid on
Đặt chú thích, nhãn và ghi chú
xlabel('Time'); ylabel('Amplitude')
legend(h,'First','Second','Third') title('Bessel Functions') [y,ix] = min(Y1); Xuất biểu đồ
print -depsc -tiff -r200 graphname
5.4 Các bước trình chiếu đồ họa 3D
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
- Mô-đun cơ bản của MATLAB cho phép đồ họa ba chiều cả đường, lưới và bề mặt.
Bạn có thể sử dụng tọa độ rõ ràng hoặc tham số. Các bước chung để thực hiện một đồ
thị ba chiều được trình bày trong bảng sau: Các bước Ví dụ 1. Chuẩn bị dữ liệu Z = peaks(20);
2. Lựa chọn cửa sổ và vị trí figure(1) subplot(2,1,2)
3. Sử dụng chức năng đồ họa 3D h = surf(Z); 4. Đặt màu và đổ bóng colormap hot shading interp set(h,'EdgeColor','k') 5. Thêm ánh sáng light('Position',[-2,2,20]) lighting phong material([0.4,0.6,0.5,30])
set(h,'FaceColor',[0.7 0.7 0],... 'BackFaceLighting','lit') 6. Đặt điểm nhìn view([30,25])
set(gca,'CameraViewAngleMode','Manual')
7. Giới hạn vị trí và đánh dấu trên trục axis([5 15 5 15 -8 8])
set(gca,'ZTickLabel','Negative||Positive')
8. Đặt tỷ lệ khung hình
set(gca, 'PlotBoxAspectRatio', [2.5 2.5 1])
9. Đặt chú thích biểu đồ và trục xlabel('X Axis') ylabel('Y Axis') zlabel('Function Value') title('Peaks') 10.In biểu đồ
set(gcf,'PaperPositionMode','auto') print -dps2 Ví dụ:
Xét bề mặt z = x2 - y2 trong [-2,2]x[-2,2]: thể hiện nó bằng ánh sáng mạnh và tô
màu xám đậm (Hình 5-25). Sau đó, biểu diễn trên cùng một trục, đường cong tập trung
từ bốn điểm nhìn khác nhau và được tô bóng bởi mặc định (Hình 5-26).
>> [X, and] = meshgrid(-2:0.05:2); Z = X .^ 2 – Y .^ 2;
surf(X,Y,Z),shading interp,brighten(0.75),colormap(gray(5))
>> [X, Y] = meshgrid(-2:0.05:2); Z = X .^ 2 – Y .^ 2; subplot(2,2,1)
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 surf(X,Y,Z) subplot(2,2,2) surf(X,Y,Z),view(-90,0) subplot(2,2,3) surf(X,Y,Z),view(60,30) subplot(2,2,4) surf(X,Y,Z),view(-10,30) -
Sau đó, MATLAB đọc một tệp và các thuộc tính thích hợp được sử dụng để tạo
biểu đồ đầy màu sắc trong Hình 5-27. >> load clown surface(peaks,flipud(X),... 'FaceColor','texturemap',... 'EdgeColor','none',... 'CDataMapping','direct') colormap(map) view(-35, 45) -
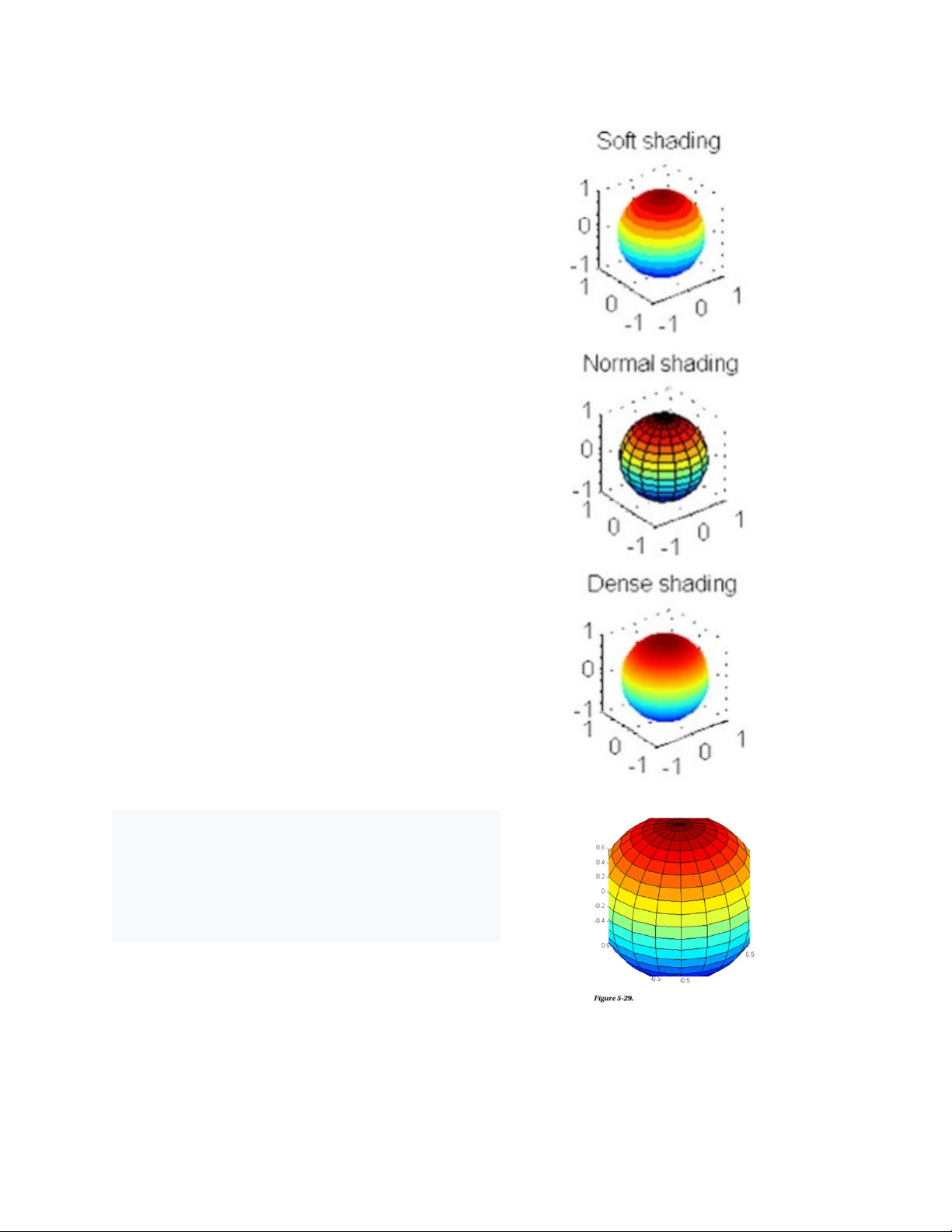
Chú hề của chúng ta có thể sử dụng một quả bóng, vì vậy hãy tạo một quả bóng
cho anh ấy. Các shader khác nhau được sử dụng cho hình cầu.
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 >> subplot(3,1,1) sphere(16) axis square shading flat title('Soft shading') subplot(3,1,2) sphere(16) axis square shading faceted title(' Normal shading') subplot(3,1,3) sphere(16) axis square shading interp title('Dense shading')
Ví dụ sau thay đổi tỷ lệ xuất hiện cho hình cầu: >> sphere
set(gca,'DataAspectRatio',[1 1 1],...
'PlotBoxAspectRatio',[1 1 1],'ZLim',[-0.6 0.6])
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Bây giờ đặt màu nền của hình hiện tại là màu trắng:
>> set(gcf, 'Color', 'w') -
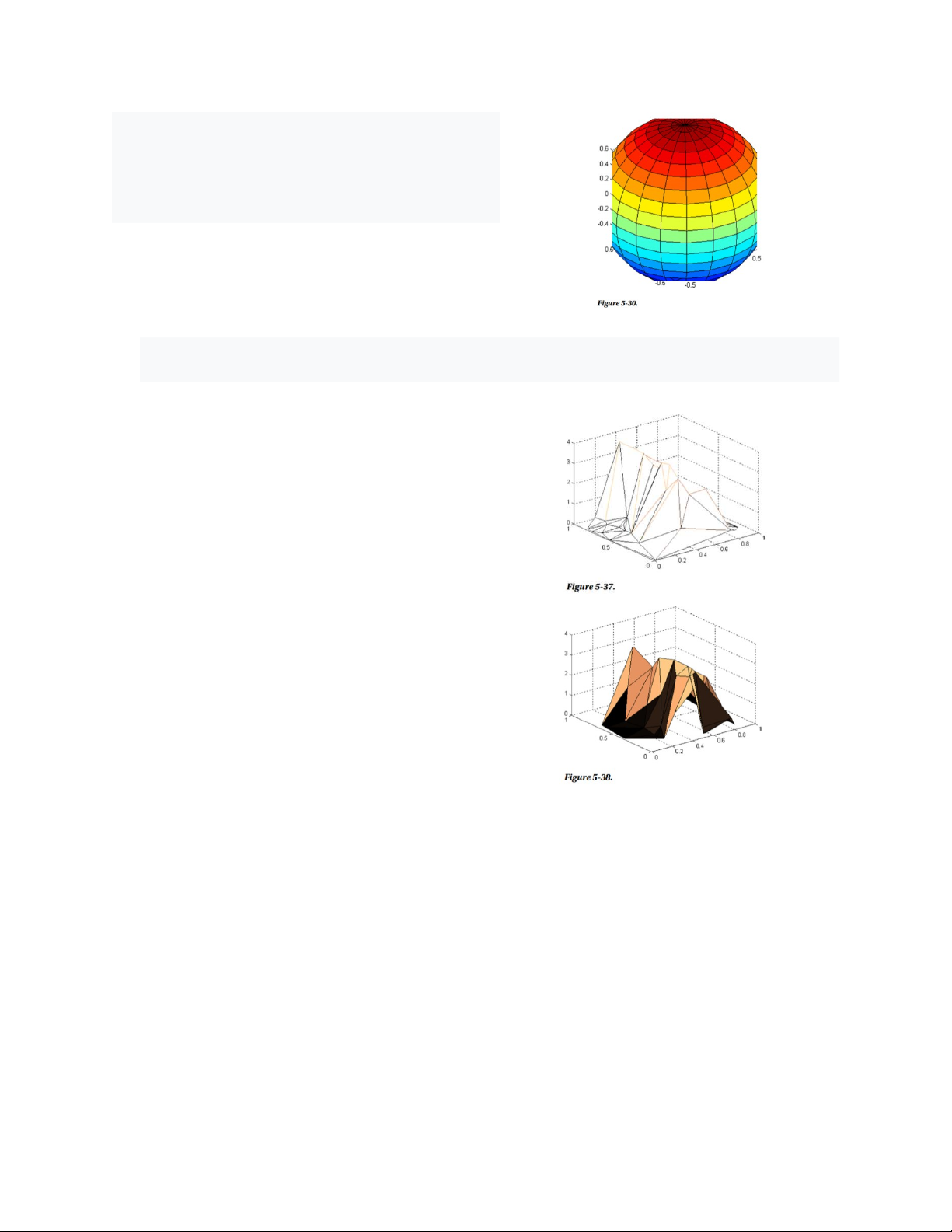
Dưới đây là hai ví dụ về đồ họa tam giác. Lưu ý rằng vì hàm rand là hàm được
sử dụng, kết quả của bạn sẽ không giống như những kết quả này. >> x = rand(1,50); y = rand(1,50); z = peaks(6*x-3,6*x-3); tri = delaunay(x,y); trimesh(tri,x,y,z) >> x = rand(1,50); y = rand(1,50); z = peaks(6*x-3,6*x-3); tri = delaunay(x,y); trisurf(tri,x,y,z); colormap copper
Downloaded by v?n ti?n Lê (vantienle525@gmail.com)


