TR
NG Đ I H C CÔNG NGH SÀI GÒN BAN KHOA H C C B N B MÔN TOÁN BÀI GI NG TOÁN CAO C P C1 (H Đ I H C)
Biên so n: TS TR N NG C H I
TP H CHÍ MINH − 2009 L U HÀNH N I B 1 Lời nói đ u _____________________
p bài gi ng Toán cao c p C1 (H đ i h c) đ c biên so n trên c sở đ c ng T
môn h c c a Tr ờng Đ i h c Công Ngh Sài Gòn; nhằm đáp ng yêu c u nâng cao ch t l
ng gi ng d y trong giai đo n nhà tr ờng th c hi n đào t o theo h c ch tín ch .
T p bài gi ng này ch a đ ng n i dung mà tác gi đã gi ng d y ở Tr ờng Đ i h c
Công Ngh Sài Gòn và các tr ờng đ i h c khác. Tác gi bày t lòng c m n đ i v i các
đồng nghi p ở Ban Khoa h c C b n - Tr ờng Đ i h c Công Ngh Sài Gòn đã đ ng
viên, đóng góp nhi u ý ki n quý báu cho vi c biên so n.
Tuy v y, thi u sót vẫn không th tránh kh i. Tác gi r t mong nh n đ c nh ng nh n
xét góp ý c a quý đồng nghi p cho t p bài gi ng này và xin chân thành cám n.
Tp. Hồ Chí Minh, tháng 09 năm 2009 Tác gi 2 M C L C CH
NG 1. PHÉP TÍNH VI PHÂN HÀM M T BI N A. HÀM S
1. HÀM S S C P C B N ........................................................................................... 5
2. HÀM S S C P .......................................................................................................... 9 B. GI I H N
1. Đ NH NGHƾA VÀ TÍNH CH T ................................................................................. 10 2. HÀM T NG Đ
NG ............................................................................................... 12
3. VÔ CÙNG BÉ (VCB) - VÔ CÙNG L N .................................................................... 16
4. D NG VÔ Đ NH 1∞ .................................................................................................... 22 C. LIÊN T C
1. Đ NH NGHƾA VÀ TÍNH CH T .................................................................................. 23
2. HÀM S LIÊN T C TRÊN M T ĐO N ................................................................... 25 D - Đ O HÀM VÀ VI PHÂN
1. KHÁI NI M Đ O HÀM ............................................................................................. 27 2. PH
NG PHÁP TÍNH Đ O HÀM ........................................................................... 30
3. VI PHÂN ....................................................................................................................... 34
4. Đ O HÀM VÀ VI PHÂN C P CAO .......................................................................... 36
5. QUI T C L’HOSPITAL ............................................................................................... 38
6. KHAI TRI N TAYLOR ............................................................................................... 43
7. NG D NG .................................................................................................................. 47
BÀI T P ........................................................................................................................... 53 CH
NG 2. PHÉP TÍNH TÍCH PHÂN HÀM M T BI N
A - TÍCH PHÂN B T Đ NH
1. KHÁI NI M V TÍCH PHÂN B T Đ NH ................................................................ 59 3 2. CÁC PH
NG PHÁP TÍNH TÍCH PHÂN ................................................................. 61
3. TÍCH PHÂN HÀM H U T ......................................................................................... 67 4. TÍCH PHÂN HÀM L
NG GIÁC ............................................................................. 71
5. TÍCH PHÂN HÀM VÔ T ............................................................................................ 73
B -TÍCH PHÂN XÁC Đ NH - TÍCH PHÂN SUY R NG
1. TÍCH PHÂN XÁC Đ NH ............................................................................................ 78
2. TÍCH PHÂN SUY R NG ............................................................................................ 84
3. NG D NG C A TÍCH PHÂN .................................................................................. 88 4. KHÁI NI M V PH
NG TRÌNH VI PHÂN ........................................................... 90
BÀI T P ........................................................................................................................... 95 CH
NG 3. PHÉP TÍNH VI PHÂN HÀM NHI U BI N
1. KHÁI NI M V HÀM NHI U BI N ........................................................................ 99
2. Đ O HÀM RIÊNG ..................................................................................................... 102
3. Đ O HÀM RIÊNG C A HÀM H P ........................................................................ 104
4. Đ O HÀM RIÊNG C A HÀM N .......................................................................... 105
5. VI PHÂN ..................................................................................................................... 107
6. C C TR .................................................................................................................... 109
7. C C TR CÓ ĐI U KI N ......................................................................................... 110
8. GIÁ TR L N NH T- GIÁ TR NH NH T .......................................................... 113
9. M T S BÀI TOÁN KINH T ................................................................................. 115
BÀI T P ......................................................................................................................... 118 4 CH NG 1
PHÉP TÍNH VI PHÂN HÀM M T BI N A. HÀM S 1. HÀM S S C P C B N
1.1. Hàm lũy thừa y = xα (α : Const)
Mi n xác đ nh D c a hàm s y = xα ph thu c vào α. Tr ờng h p α là s vô t , ta có
D = [0; +∞) n u α > 0; D = (0; +∞) n u α < 0.
1.2. Hàm s mũ: y = ax (0 < a ≠ 1 : Const)
Hàm s y = ax có mi n xác đ nh D = R, mi n giá tr là (0; +∞).
1.3. Hàm s logarit: y = logax (0 < a ≠ 1 : Const)
Hàm s y = logax có mi n xác đ nh D = (0; +∞), mi n giá tr là R. Nh c l i m t s công th c:
V i 0 < a, b ≠ 1; x, x1, x2 > 0 và y, α∈R, ta có: ⎧y = log x a y 1) ⎨
⇔ x = a . Ñaëc bieät, log 1 = 0; log a = 1. a a x ⎩ > 0 loga x 2) a = x.
3) log (x x ) = log (x ) + log (x ). a 1 2 a 1 a 2 x1 4) log ( ) = log (x ) - log (x ). a a 1 a 2 x2 1
Ñaëc bieät, log ( ) = - log (x). a a x 5) log (xα ) =α log (x). a a 1 6) log α ≠ α (x) = log (x) ( 0). a a α 7) log x = log b.log x; a a b log x a log x = . b log b a
8) lnx = log x : Logarit Neâpe cuûa x. e
lgx = log x : Logarit thaäp phaân cuûa x. 10
Ví d : Tính A = log1325. ln 25 Gi i: A = log 25 = ≈ 1,254947126 13 . ln13 5 1.4. Hàm s l ng giác và hàm ng c
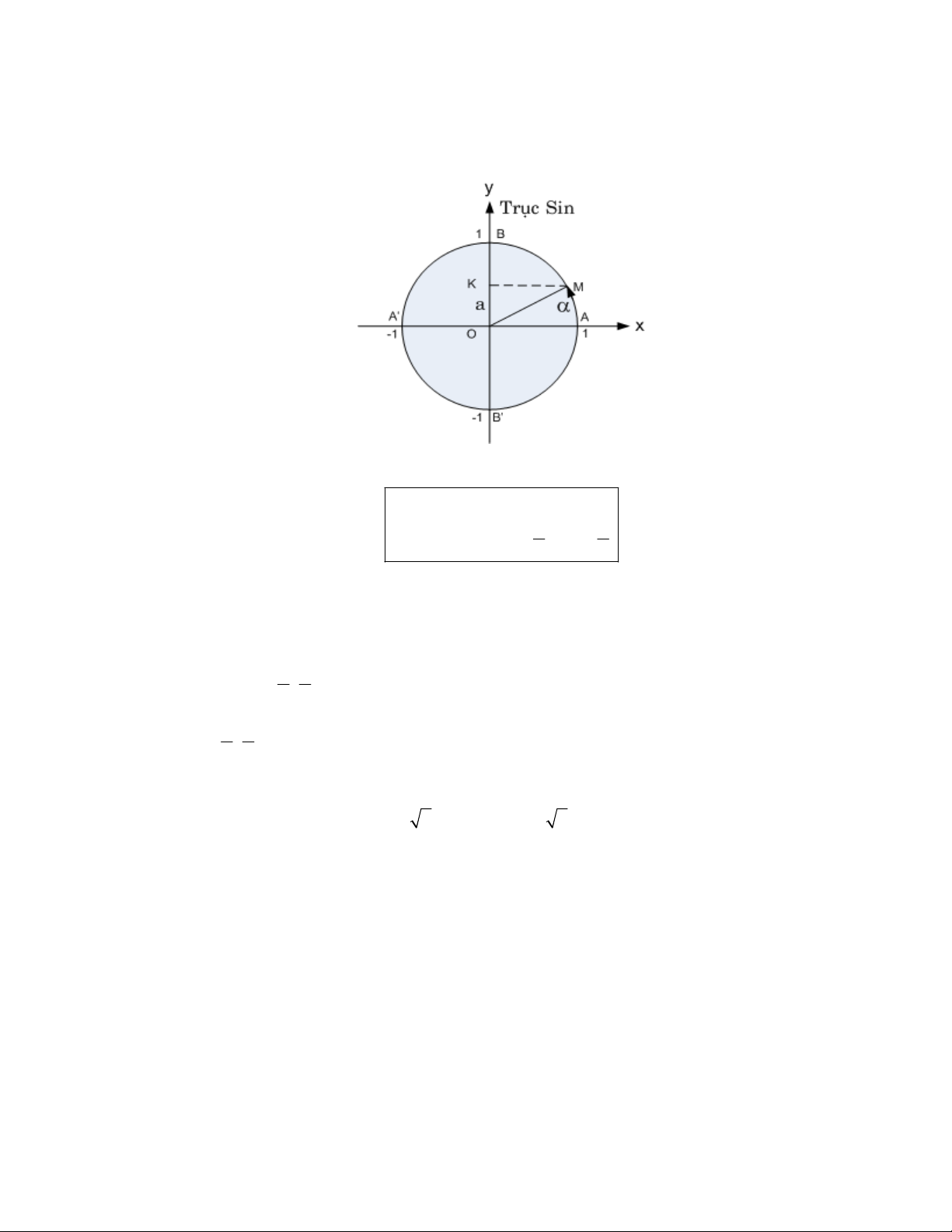
1.4.1. Hàm y = sinx và y =arcsinx:
V i −1 ≤ a ≤ 1, ta đ nh nghƿa: si ⎧ n α = a; ⎪ arcsin a = α ⇔ ⎨ π π − ≤ α ≤ . ⎪⎩ 2 2
Khi đó arcsina (−1 ≤ a ≤ 1) đ c xác đ nh duy nh t. Nh v y, y= arcsinx là hàm s có tính ch t sau: •
Mi n xác đ nh: D = [−1;1]. • π π Mi n giá tr : [− ; ]. 2 2 • π π ∀α ∈ [− ; ], a ∀ ∈ [ 1
− ;1];sinα = a ⇔ arcsin a = α. 2 2 •
y = arcsinx là hàm s lẻ, nghƿa là arcsin(−x) = − arcsinx.
Ví d : arcsin(1/2) = π/6; arcsin(− 3 /2) = − arcsin( 3 /2) = −π/3; arcsin(−1/2) = π/6;
arcsin(−3/4) = − arcsin(3/4) ≈ − 0,848062079; arcsin(−4) không tồn t i.
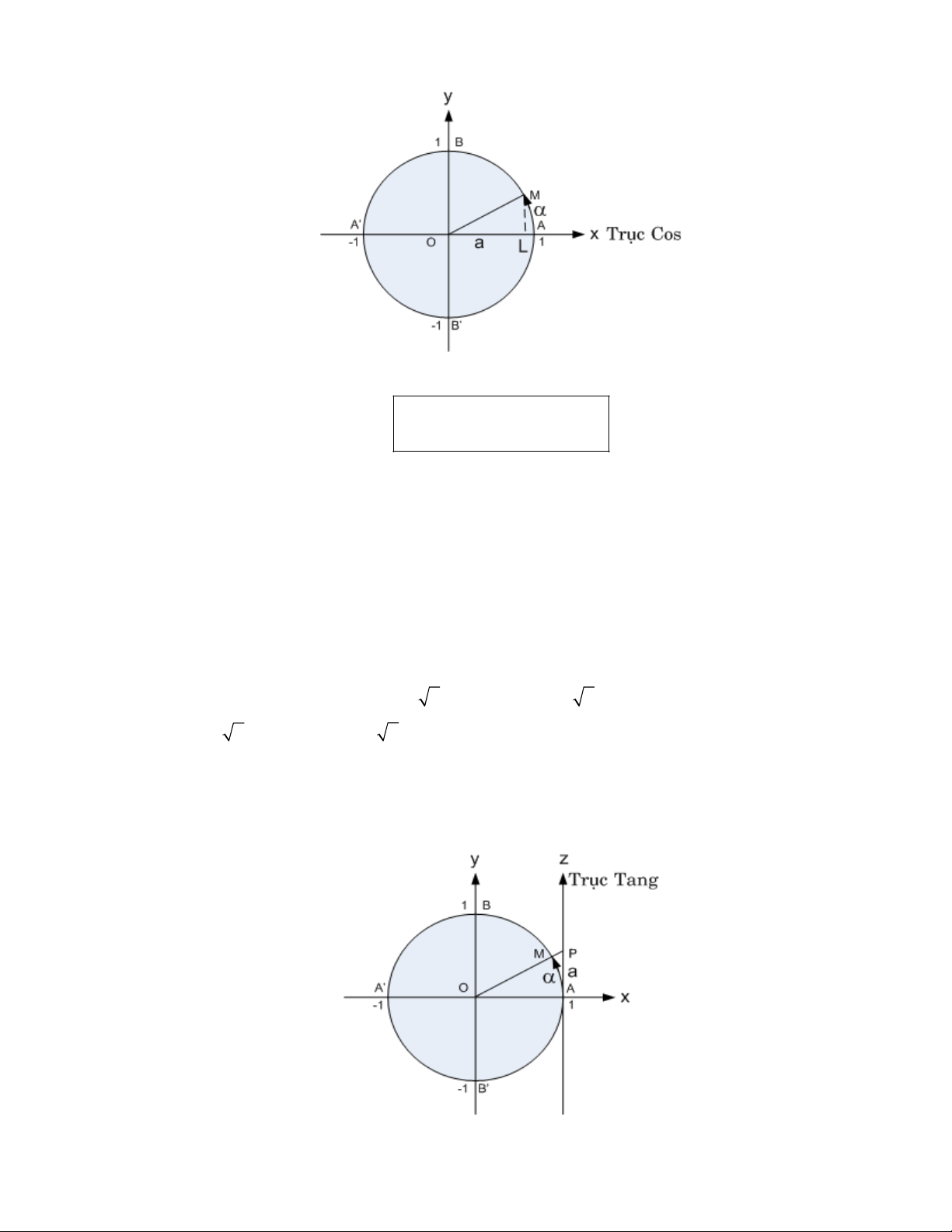
1.4.2. Hàm y = cosx và y =arccosx: 6
V i −1 ≤ a ≤ 1, ta đ nh nghƿa: ⎧cosα = a; arccos a = α ⇔ ⎨ 0 ⎩ ≤ α ≤ . π
Khi đó arccosa (−1 ≤ a ≤ 1) đ c xác đ nh duy nh t. Nh v y, y= arccosx là hàm s có tính ch t sau: •
Mi n xác đ nh: D = [−1;1]. • Mi n giá tr : [0; ] π . • ∀α ∈ [0; ] π , a ∀ ∈ [ 1
− ;1];cosα = a ⇔ arccosa = . α •
arccos(− x) = π − arccosx.
Ví d : arccos(1/2) = π/3; arccos(− 3 /2) = π − arccos( 3 /2) = π − π/6 = 5π/6;
arccos(− 2 /2) = π − arccos( 2 /2)= 3π/4; arccos(−3/4) = π - arccos(3/4)≈ 2,418858406;
arccos(− 4) không tồn t i.
1.4.3. Hàm y = tgx và y =arctgx: 7
V i a ∈ R, ta đ nh nghƿa: ⎧tgα = a; ⎪ arc tga = α ⇔ ⎨ π π − < α < . ⎪⎩ 2 2 Khi đó arctga đ
c xác đ nh duy nh t. Nh v y, y= arctgx là hàm s có tính ch t sau: •
Mi n xác đ nh: D = R. • π π Mi n giá tr : (− ; ). 2 2 • π π ∀α ∈ (− ; ), a
∀ ∈ ,tgα = a ⇔ arctga = . α 2 2 •
y = arctgx là hàm s lẻ, nghƿa là arctg(−x) = − arctgx.
Ví d : arctg1 = π/4; arctg(− 3 /3) = − arctg( 3 /3) = − π/6; arctg(−1)= −π/4;
arctg(3/4) ≈ 0,643501108; arctg(− 4) ≈ −1,3258.
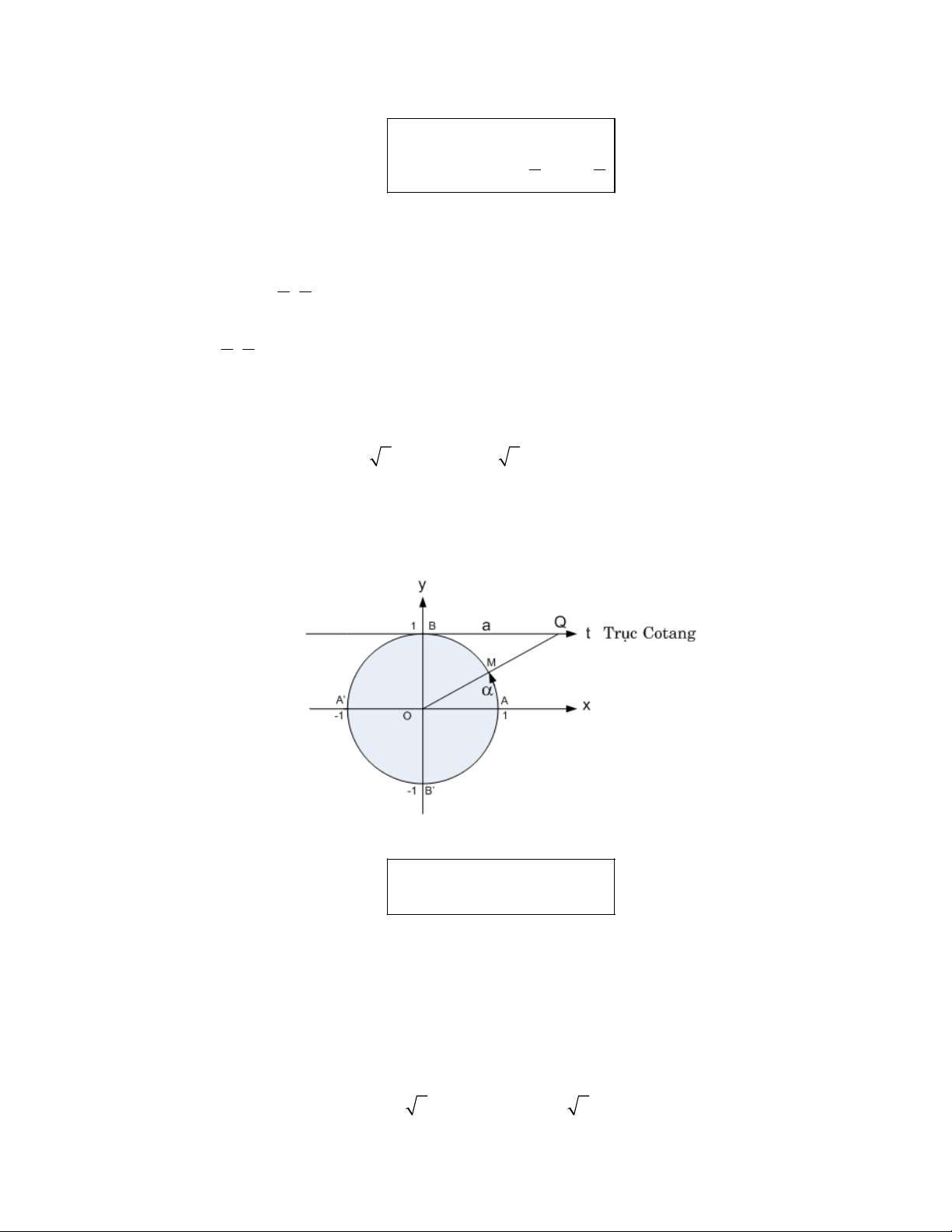
1.4.4. Hàm y = cotgx và y =arccotgx:
V i a ∈ R, ta đ nh nghƿa: co ⎧ tgα = a; arc cotga = α ⇔ ⎨ 0 ⎩ < α < . π Khi đó arccotga đ
c xác đ nh duy nh t. Nh v y, y= arccotgx là hàm s có tính ch t sau: •
Mi n xác đ nh: D = R. • Mi n giá tr : (0; ) π . • ∀α ∈ (0; ) π , a
∀ ∈ ,cot gα = a ⇔ arccot ga = . α •
arccotg(−x) = π − arccotgx.
Ví d : arccotg1 = π/4; arccotg(− 3 /3) = π − arccotg( 3 /3) = π − π/3 = 2π/3; 8
arccotg(− 3 ) = π − arccotg( 3 ) = π − π/6 = 5π/6;
arccotg(3/4) = π/2 − arctg(3/4) ≈ 0,927295218
arccotg(−4) = π/2 − arctg(−4) ≈ π/2 + arctg4 ≈ 2,89661399.
trong đó ta đã s d ng tính ch t sau: 1.4.5. Tính ch t:
1) V i m i −1 ≤ x ≤ 1, arcsinx + arccosx = π/2.
2) V i m i x, arctgx + arccotgx = π/2. 2. HÀM S S C P Hàm s s c p là hàm s đ
c xây d ng từ các hàm hằng và các hàm s s c p c b n qua
các phép toán đ i s : c ng, trừ, nhân, chia và phép h p n i ánh x .
Ví d : y = ln(1 + 2x) là m t hàm s s c p. ⎧sin 6x neáu x < 0; ⎪ y = x ⎨ không là hàm s s c p. ⎪cos3x neáu x ⎩ ≥ 0. 9 B. GI I H N
1. Đ NH NGHƾA VÀ TÍNH CH T
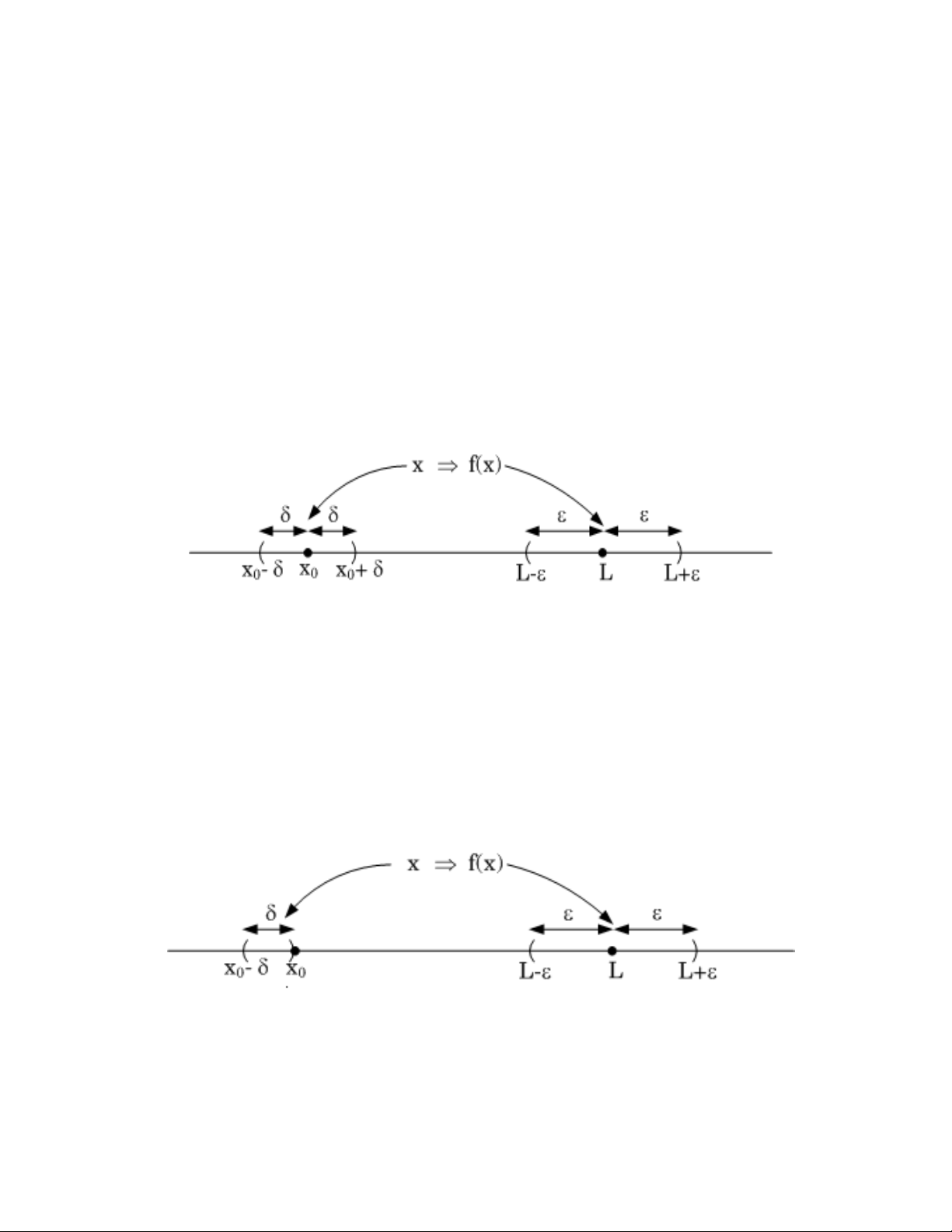
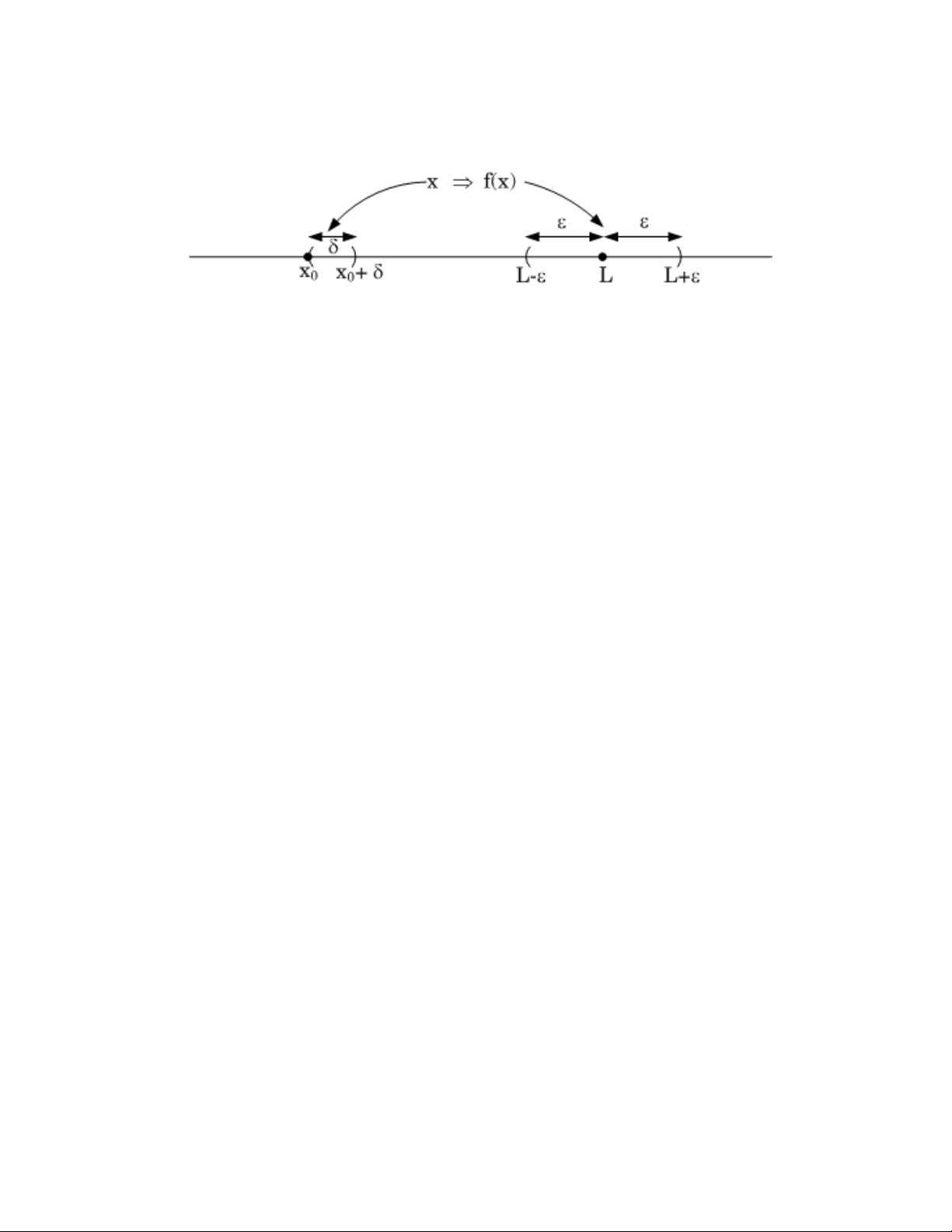
1.1. Đ nh nghƿa. 1) Cho hàm s f(x) xác đ nh trên m t kho ng ch a x0 (có th lo i trừ x0).
Ta nói f(x) có gi i h n là L∈ R khi x ti n v x0, n u f(x) có th g n L tùy ý khi x ti n sát đ n x0.
Ký hi u: lim f (x) = L hay f(x) → L khi x → x . 0 x→x0
Chính xác h n, theo ngôn ng toán h c, ta có:
lim f (x) = L ⇔ ∀ε > 0, ∃δ > 0,∀x ∈ , 0 |
< x − x |< δ ⇒|f (x) − L|< ε 0 x→x0
⇔ ∀ε > 0, ∃δ > 0,∀x ∈ , x − δ < x ≠ x < x + δ ⇒ | f (x) − L|< ε 0 0 0 Minh h a:
2) Cho hàm s f(x) xác đ nh trên m t kho ng có d ng (a;x0). Ta nói f(x) có gi i h n là L∈
R khi x ti n v x0 bên trái, n u f(x) có th g n L tùy ý khi x ti n sát đ n x0 v phía bên trái.
Ký hi u: lim f (x) = L hay f(x) → L khi x → x− . 0 x→x−0
Chính xác h n, theo ngôn ng toán h c, ta có:
lim f (x) = L ⇔ ∀ε > 0,∃δ > 0, x
∀ ∈ ,0 < x − x< δ ⇒|f(x) − L|< ε 0 x x− → 0 Minh h a:
3) Cho hàm s f(x) xác đ nh trên m t kho ng có d ng (x0;b). Ta nói f(x) có gi i h n là L∈
R khi x ti n v x0 bên ph i, n u f(x) có th g n L tùy ý khi x ti n sát đ n x0 v phía bên ph i.
Ký hi u: lim f (x) = L hay f(x) → L khi x → x+ . 0 x→x+0
Chính xác h n, theo ngôn ng toán h c, ta có: 10
lim f (x) = L ⇔ ∀ε > 0,∃δ > 0, x
∀ ∈ ,0 < x − x < δ ⇒|f(x) − L|< ε 0 x x+ → 0 Minh h a:
Nh v y, từ các đ nh nghƿa trên ta suy ra; ⎧lim f(x) = L; x→x+ ⎪ 0 lim f (x) = L ⇔ ⎨ x→x lim f (x) = L. 0 ⎪x→x−0 ⎩ 4) T ng t , ta đ nh nghƿa đ c các gi i h n: lim f (x) = + ; ∞ lim f (x) = − ; ∞ lim f (x) = ; ∞ ... . x→x x→x x→x 0 0 0
1.2. Đ nh lý. Cho các hàm s f(x), g(x) khi x→ x0. Khi đó, v i a, b ∈R, ta có:
1) N u f(x) →a, g(x) →b thì : f(x) + g(x) → a + b; f(x) – g(x) → a – b; f(x)g(x) → ab;
f(x)/g(x) → a/b (n u b ≠ 0).
2) N u f(x) →a, g(x) →∞ thì f(x) + g(x) → ∞.
3) N u f(x) →+∞, g(x) →+∞ thì f(x) + g(x) → +∞.
4) N u f(x) →a ≠ 0, g(x) →∞ thì f(x)g(x) → ∞.
5) N u f(x) →∞, g(x) →∞ thì f(x)g(x) →∞.
6) N u f(x) →a ≠ 0, g(x) →0 thì f(x)/g(x) → ∞.
7) N u f(x) →a, g(x) →+∞ thì f(x)/g(x) → 0.
8) N u f(x) →∞, g(x) →b thì f(x)/g(x) → ∞.
9) N u f(x) →a > 1, g(x) →+∞ thì f(x)g(x) → +∞.
N u f(x) →a v i 0 < a < 1, g(x) →+∞ thì f(x)g(x) → 0.
10) N u f(x) →a thì |f(x)| → |a|.
11) f(x) →0 ⇔ |f(x)| → 0.
12) (Gi i h n kẹp) Gi s f(x) ≤ h(x) ≤ g(x), ∀x khá g n x0 và f(x) → a; g(x) → a. Khi đó h(x) →a. 11
1.3. Đ nh lý. Cho f(x) là m t hàm s s c p xác đ nh t i x0. Khi đó lim f (x) = f (x ). 0 x→x0 1 − cos 2x 1 − cos π Ví d : 1) lim = = 2. π π x→ sin x 2 sin 2 1 + cos2x 2) lim
= ∞ (vì lim(1 + cos2x) = 1 + cos0 = 2 vaø limsin x = sin0 = 0) x 0 → sin x x→0 x→0
1.4. Các d ng vô đ nh trong gi i h n:
Có t t c 7 d ng vô đ nh trong gi i h n, đó là: 0 ∞ ∞ 0 0 ∞ − ; ∞ 0 ; ∞ ; ; 1 ; 0 ; ∞ . 0 ∞
1) D ng ∞ − ∞ : Khi f(x) → +∞ (− ∞) và g(x) → +∞ (− ∞) thì ta nói lim (f(x) – g(x)) có d ng vô đ nh ∞ − ∞ .
2) D ng 0∞ : Khi f(x) → 0 và g(x)→∞ thì ta nói lim f(x)g(x) có d ng vô đ nh 0∞ (L u
ý : f(x) → 0 không có nghƿa là f(x) ≡ 0). 3) T ng t cho 5 d ng còn l i.
Ta nói các d ng trên là các d ng vô d nh vì không có qui t c chung đ xác đ nh giá tr c a
gi i h n n u ch d a vào các gi i h n thành ph n.
Đ tính các gi i h n có d ng vô đ nh, ta c n bi n đổi đ làm m t đi d ng vô đ nh, g i là kh d ng vô đ nh. 2. HÀM T NG Đ NG
2.1. Đ nh nghƿa. Cho các hàm s f(x), g(x) xác đ nh và không tri t tiêu trên m t kho ng
ch a x0 (có th lo i trừ x0). Ta nói f(x) t ng đ
ng v i g(x) khi x →x0, ký hi u f(x)∼ g(x) khi f (x) x →x = 0, n u lim 1. x→x0 g(x) Nh v y, f (x) f (x) ∼ g(x) ⇔ lim = 1 x→x0 g(x) (f (x), g(x) ≠ 0) Các tính ch t sau đ c th a: 1) f(x) ∼ f(x).
2) f(x) ∼ g(x) ⇒ g(x) ∼ f(x). 12
3) f(x) ∼ g(x) và g(x) ∼ h(x) ⇒ f(x) ∼ h(x).
2.2. Đ nh lý. 1) N u f(x) → L ∈ R, L ≠ 0, thì f(x) ∼ L.
2) N u f(x) ∼ g(x) và g(x) → A thì f(x) → A. ⎧f (x)f (x) ∼ g (x)g (x); ⎧f (x) ∼ g (x); 1 2 1 2 ⎪ 3) N u 1 1 ⎨ thì f (x) g (x) ⎨ f (x) ∼ g (x). ⎩ 1 1 ∼ . 2 2 ⎪f (x) g (x) ⎩ 2 2 4) N u f(x) ∼ g(x) thì n n
f (x) ∼ g(x) (gi s các căn có nghƿa). Chú ý:
• Ta không th vi t f(x) ∼ 0 hay f(x) ∼ ∞ (ngay c khi f(x) →0 hay f(x) →∞) vì đi u này vô nghƿa! • ⎧f (x) ∼ g (x);
⎡f (x) + f (x) ∼ g (x) + g (x); 1 1 ⎨ ⇒ 1 2 1 2 f (x) ∼ g (x). ⎢ ⎩ f (x) ⎣ − f (x) ∼ g (x) − g (x). 2 2 1 2 1 2 f (x)
Ch ng minh: 1) N u f(x) → L∈ R, L≠ 0, thì lim
= 1 nên f(x) ∼ L (ở đây L đ c xem L nh hàm hằng). f (x)
2) N u f(x) ∼ g(x) và g(x) → A thì f (x) = g(x) → 1.A = A . g(x) ⎧f (x) ∼ g (x); 3) Gi s 1 1 ⎨ Khi đó f (x) ∼ g (x). ⎩ 2 2 f (x) f (x) 1 2 lim = lim = 1. g (x) g (x) 1 2 từ đó f (x)f (x) f (x) f (x) 1 2 1 2 lim = lim . lim = 1.1 = 1; g (x)g (x) g (x) g (x) 1 2 1 2 f (x) / f (x) f (x) f (x) 1 2 1 2 lim = lim / lim = 1 / 1 = 1. g (x) / g (x) g (x) g (x) 1 2 1 2 ⎧f (x)f (x) ∼ g (x)g (x); 1 2 1 2 ⎪ Suy ra f (x) g (x) ⎨ 1 1 ∼ . ⎪f (x) g (x) ⎩ 2 2
4) Gi s f(x) ∼ g(x). Khi đó n f (x) f (x) n lim = lim n = 1 = 1. n g(x) g(x) Suy ra n n f (x) ∼ g(x) . 13
2.3.M t s gi i h n và t ng đ ng c b n: GI I H N T NG Đ NG sin x lim = 1 sinx ∼ x khi x→0 (x: rad) (x: rad) x→0 x 1 − cos x 1 lim = (x: rad)
1 – cosx∼ 1 x2 khi x→0 (x: rad) 2 x 0 → x 2 2 tgx lim = 1 tgx ∼ x khi x→0 (x: rad) (x: rad) x 0 → x arc sin x lim = 1 arcsinx ∼ x khi x→0 x 0 → x arctgx lim = 1 arctgx ∼ x khi x→0 x 0 → x x e − 1 ex − 1∼ x khi x→0 lim = 1 x→0 x ln(1 + x) lim = 1 ln(1+ x) ∼ x khi x→0 x 0 → x (1 + x)α − 1
(1+x)α −1 ∼ αx khi x→0 (α ≠ 0) lim = α x→0 x • x x lim e = + ; ∞ lim e = 0. • Khi x→∞: x→+∞ x→−∞ • a lim ln x = + ; ∞ lim ln x = − . ∞
nxn + an−1xn−1+...+amxm ∼ amxm x x 0+ →+∞ → • Khi x→ 0: • lim tgx = + ; ∞ lim tgx = − . ∞ − + π π a x→ x→
nxn + an−1xn−1+...+amxm ∼ amxm 2 2
(m < n; an ≠ 0; am ≠ 0) • π π lim arctgx = ; lim arctgx = − . x→+∞ x 2 →−∞ 2 x 1 • ⎛ 1 ⎞ lim 1
⎜ + ⎟ = e; lim(1 + x)x = e. x→∞ x→0 x ⎝ ⎠
Ví d . Tính các gi i h n sau: 2 2 ln cos 2x (x − 5x + 4) arcsin(x − x) a) L = lim ; b) L = lim ; 1 2 2 x→0 x 1 → x (x + 3x) sin x (e − e)(1 − 4x − 3) 8 6 3x − 5x + 4x + 2 c) L = lim . 3 8 7 4 x→∞ x − 5x + 14x + 1 ln cos 2x Gi i. a) L = lim 1 2 x→0 (x + . Khi x→0 ta có 3x) sin x
lncos2x = ln[1 + (cos2x −1)] ∼ cos2x −1 ∼ − (1/2)(2x)2 = −2x2 (1) 14 x2 + 3x ∼ 3x (2) sinx ∼ x (3)
Từ (2) và (3) ta suy ra: (x2 + 3x)sinx ∼ 3x.x = 3x2 (4) Từ (1) và (4) ta suy ra: 2 ln cos 2x 2 − x 2 ∼ = − . 2 2 (x + 3x) sin x 3x 3 2 Do đó L = − . 1 3 2 2 (x − 5x + 4) arcsin(x − x) b) L = lim
. Đặt t = x − 1 ⇔ x = t+1 . Khi x→1 ta có t →0. Do đó 2 x x 1 → (e − e)(1 − 4x − 3) 2 2 2 2 (x − 5x + 4)arcsin(x − x) (t − 3t)arcsin(t + t) L = lim = lim . 2 x 1 → x t 0 → t (e − e)(1 − 4x − 3) e(e − 1)(1 − 1 + 4t) Khi t→0 ta có: t2 – 3t ∼ –3t, (1)
arcsin(t2 + t) ∼ t2 + t ∼ t. (2) Từ (1) và (2) ta có:
(t2 – 3t) arcsin(t2 + t) ∼ –3t.t ∼ –3t2. (3) Mặt khác, et – 1 ∼ t (4) 1 1 2
1 − 1 + 4t = 1 − (1 + 4t) ∼ − (4t) = −2t (5) 2 Từ (4) và (5) ta có: t 2
e(e − 1)(1 − 1 + 4t) ∼ et( 2 − t) = 2 − et (6) Từ (3) và (6) ta suy ra: 2 2 2 (t − 3t) arcsin(t + t) 3 − t 3 ∼ → . 2 t e(e − 1)(1 − 1 + 4t) 2e − t 2e 3 Do đó L = 2 . 2e 8 6 3x − 5x + 4x + 2 c) L = lim . 3 8 7 4 x→∞ x − 5x + 14x + Khi x→∞ ta có 1 3x8 – 5x6 + 4x + 2 ∼ 3x8 x8 – 5x7 + 14x4 + 1 ∼ x8 8 6 8 3x − 5x + 4x + 2 3x Suy ra ∼ → 3. Do đó L = 3. 8 7 4 8 x − 5x + 14x + 1 x 3 15
3. VÔ CÙNG BÉ (VCB)-VÔ CÙNG L N
3.1. VÔ CÙNG BÉ (VCB)
1) Đ nh nghƿa. Ta nói f(x) là m t VCB khi x→x = 0 n u lim f (x) 0. x→x0 f (x)
2) So sánh hai VCB: Cho f(x) và g(x) là VCB khi x → x = 0. Gi s lim . L x→ 0 x g(x)
a) N u L = 0 thì ta nói VCB f(x) có c p cao h n VCB g(x).
b) N u L =∞ thì ta nói VCB f(x) có c p th p h n VCB g(x).
c) N u 0 < L < + ∞ thì ta nói hai VCB f(x) và g(x) có cùng c p.
3) B c c a VCB khi x → 0: Cho f(x) là m t VCB khi x→0. Ta nói VCB f(x) có c p α khi ch n x làm VCB chính n u: f(x) ∼ axα khi x→0
trong đó a ≠ 0 và α > 0.
Nh n xét: Các đ nh nghƿa trong 2) và 3) t
ng thích nhau khi ta so sánh hai VCB khi x → 0.
Ví d : Khi x→0, 1 – cos4x là m t VCB c p 2 vì 1 2 2
1 − cos 4x ∼ (4x) = 8x . vaø coù cuøng caáp thaáp cao hôn 2
4) T ng (hi u) hai VCB: Cho f(x), g(x) là hai VCB khi x→ x0.
a) N u f(x) và g(x) không có cùng c p thì
⎧f(x) neáu f(x) coù caáp thaáp hôn g(x); f(x) + g(x) ∼ ⎨
g(x) neáu f(x) coù caáp cao hôn g(x). ⎩
b) N u f(x) và g(x) có cùng c p nh ng không t ng đ
ng thì f(x) − g(x) là VCB có cùng c p v i VCB f(x), h n n a ⎧f (x) ⎪ ∼ f (x) 1 ⎨
⇒ f(x) − g(x) ∼ f (x) − g (x). (*) 1 1 g(x) ⎪ ∼ g (x) ⎩ 1
Đặc bi t, cho f(x), g(x) là hai VCB khi x→0 có c p l n l t là α, β: f(x) ∼ axα (a ≠ 0); g(x) ∼ bxβ (b ≠ 0). Khi đó 16 ⎧axα neáu α < ; β ⎪
f (x) − g(x) ∼ ⎨−bxβ neáu α > ; β
⎪(a − b)xα neáu α = ;β a − b ≠ 0. ⎩
Chú ý: Tr ờng h p hai VCB f(x) và g(x) t ng đ
ng và f(x) ∼ f1(x), g(x) ∼ g1(x) thì f(x)
− g(x) là VCB có c p l n h n VCB f(x) nh ng (*) không còn đúng.
5) Qui t c gi l i VCB c p bé nh t (Qui t c ng t b VCB c p cao): Gi s khi x→x0, VCB f(x) đ
c phân tích thành tổng c a nhi u VCB, trong đó ch có m t VCB c p th p nh t là f0(x). Khi đó: f(x) ∼ f0(x) khi x→0.
Chú ý: Tr ờng h p có nhi u VCB c p bé nh t trong phân tích c a f(x) thì ta g p các VCB
đó l i, xem nh là m t VCB và dùng tính ch t 4b) ở trên đ kh o sát c p c a VCB đó, sau đó
m i có th áp d ng qui t c trên.
3.2. VÔ CÙNG L N (VCL)
1) Đ nh nghƿa: Ta nói f(x) là m t VCL khi x→x lim f (x) = ∞ 0 n u . x x → 0 f (x)
2) So sánh hai VCL: Cho f(x) và g(x) là VCL khi x → x = 0. Gi s lim . L
x→x0 g(x)
a) N u L = 0 thì ta nói VCL f(x) có c p th p h n VCL g(x).
b) N u L =∞ thì ta nói VCL f(x) có c p cao h n VCL g(x).
c) N u 0 < L < + ∞ thì ta nói hai VCL f(x) và g(x) có cùng c p.
3) B c c a VCL khi x → ∞: Cho f(x) là m t VCL khi x → ∞. Ta nói VCL f(x) có c p α
khi ch n x làm VCL chính n u: f(x) ∼ axα khi x → ∞
trong đó a ≠ 0 và α > 0.
Nh n xét: Các đ nh nghƿa trong 2) và 3) t
ng thích nhau khi ta so sánh hai VCL khi x → ∞.
Ví d : Khi x → ∞, 2x3 – 9x2 + 5x + 19 VCL c p 3 vì 3 2 3 2x – 9x + 5x + 19 ∼ 2x .
4) T ng (hi u) hai VCL: Cho f(x), g(x) là hai VCL khi x→ x0.
a) N u f(x) và g(x) không có cùng c p thì
⎧f(x) neáu f(x) coù caáp cao hôn g(x); f(x) + g(x) ∼ ⎨
g(x) neáu f(x) coù caáp thaáp hôn g(x). ⎩ 17
b) N u f(x) và g(x) có cùng c p nh ng không t ng đ
ng thì f(x) − g(x) là VCL có cùng c p v i VCL f(x), h n n a ⎧f (x) ⎪ ∼ f (x) 1 ⎨
⇒ f(x) − g(x) ∼ f (x) − g (x). (*) 1 1 g(x) ⎪ ∼ g (x) ⎩ 1
Đặc bi t, cho f(x), g(x) là hai VCL khi x → ∞ có c p l n l t là α, β: f(x) ∼ axα (a ≠ 0); g(x) ∼ bxβ (b ≠ 0). Khi đó ⎧axα neáu α > ; β ⎪
f (x) − g(x) ∼ ⎨−bxβ neáu α < ; β
⎪(a − b)xα neáu α = ;β a − b ≠ 0. ⎩
Chú ý: Tr ờng h p hai VCL f(x) và g(x) t ng đ
ng và f(x) ∼ f1(x), g(x) ∼ g1(x) thì f(x)
− g(x) có th không là VCL hoặc là VCL có c p nh h n VCL f(x) nh ng (*) không còn đúng.
5) Qui t c gi l i VCL c p cao nh t (Qui t c ng t b VCL c p th p): Gi s khi x→x0, VCL f(x) đ
c phân tích thành tổng c a nhi u VCL, trong đó ch có m t VCL c p cao nh t là fn(x). Khi đó f(x) ∼ fn(x) khi x→ x0.
Chú ý: Tr ờng h p có nhi u VCL c p cao nh t trong phân tích c a f(x) thì ta g p các
VCL đó l i, xem nh là m t đ i l
ng (có th là VCL nh ng cũng có th không), và dùng tính
ch t 4b) ở trên đ kh o sát đ i l
ng này, sau đó m i có th áp d ng qui t c trên.
Ví d : Tính các gi i h n sau: 2 2
L = lim( 3x − 4x + 2 − 3x + 4x − 1) 1 x→+∞ 2 2
L = lim( 3x − 4x + 2 − 3x + 4x − 1) 2 x→−∞ 2 2
L = lim( 3x − 4x + 2 − 2x + 4x − 1) 3 x→∞ 3 3 2 3 3
L = lim( 2x + 2x − 3x + 1 − 2x + 3x + 2) 4 x→∞ 3 3 2 3 2 3
L = lim( 2x + 9x + 1 + 10 + 3x − 2x ) 5 x→∞ 3 3 2 3 3
L = lim( 2x + 2x − 3x + 1 − x + 3x + 2) 6 x→∞ arc tg 2 2 (x + 4x) + ln(1 + 3tgx) − x L = lim 7 x→0 x arctg(4x) + cos 2x − e 2 3 2 3
(x − 6x + 8) arc tg(x − 8) + 2 ln(x − 4x + 5) + (x − 2) L = lim 8 4 x→2 x 2 2 (x 2)
(e − e )(2 − x + 2) + 2x − 8x + 9 − e − 18 Gi i. • 2 2
L = lim( 3x − 4x + 2 − 3x + 4x − 1) 1 x→+∞ Khi x→ +∞ ta có: 2 2
A := 3x − 4x + 2 ∼ 3x = |x| 3 = x 3. (1) 2 2
B := 3x + 4x − 1 ∼ 3x ∼ |x| 3 = x 3 (2)
(Nh v y, theo trên ta có A − B không là VCL hoặc là VCL c p nh h n 1, nh ng ch a xác
đ nh đ c c p chính xác là bao nhiêu). 2 2 A − B
Ta bi n đổi: A − B = A + . Khi x→ +∞ ta có B
A3 – B3 = (3x2 – 4x + 2) – (3x2 + 4x – 1) = – 8x + 3 ∼ – 8x (3) A + B = 2x 3 (do (1) và (2)) (4) Từ (3) và (4) ta suy ra: 8x 4 3 A – B = − → − khi x→ +∞ 2x 3 3 4 3 V y L − 1 = . 3 • 2 2
L = lim( 3x − 4x + 2 − 3x + 4x − 1) 2 x→−∞ Lý lu n t
ng t khi tính L1 và chú ý rằng khi x→ – ∞ ta có 2 2
3x − 4x + 2 ∼ 3x = |x| 3 = −x 3. 2 2
3x + 4x − 1 ∼ 3x ∼ |x| 3 = −x 3 4 3 Từ đó, ta tính đ c L = . 2 3 • 2 2
L = lim( 3x − 4x + 2 − 2x + 4x − 1) 3 x→∞ Khi x→ ∞ ta có 2 2
A := 3x − 4x + 2 ∼ 3x = |x| 3. 2 2
B := 2x + 4x − 1 ∼ 2x ∼ |x| 2.
Suy ra A − B ∼ |x|( 3 − 2) → +∞ khi x → ∞ . V y L3 = +∞. • 3 3 2 3 3
L = lim( 2x + 2x − 3x + 1 − 2x + 3x + 2) 4 x→∞ Khi x→ ∞ ta có 3 3 2 3 3 3
A := 2x + 2x − 3x + 1 ∼ 2x = x 2. (1) 3 3 3 3 3
B := 2x + 3x + 2 ∼ 2x = x 2. (2) 19
(Nh v y, theo trên ta có A − B không là VCL hoặc là VCL c p nh h n 1, nh ng ch a xác
đ nh đ c c p chính xác là bao nhiêu). 3 3 A − B Ta bi n đổi: A − B = 2 2 A + AB + . Khi x→ ∞ ta có B
A3 – B3 = (2x3 + 2x2 – 3x+1) – (2x3 + 3x + 2) = 2x2 – 6x – 1 ∼ 2x2 (3) A2 ∼ 2 3 x 4 ; AB ∼ 2 3 x 4 ; B2 ∼ 2 3 x
4 . Suy ra A2 + AB + B2∼ 3 2 3 x 4 (4) Từ (3) và (4) ta suy ra: 2 3 2x 2 2 A – B ∼ → = khi x→ ∞. 2 3 3 3x 4 3 4 3 3 2 V y L4 = . 3 • 3 3 2 3 2 3
L = lim( 2x + 9x + 1 + 10 + 3x − 2x ) 5 x→∞ Lý lu n t
ng t khi tính L4 và s d ng công th c: 3 3 A + B A + B = 2 2 A − AB + , B từ đó ta tính đ c L5 = 3 2 2 . • 3 3 2 3 3
L = lim( 2x + 2x − 3x + 1 − x + 3x + 2) 6 x→∞ Khi x→ ∞ ta có: 3 3 2 3 3 3
A := 2x + 2x − 3x + 1 ∼ 2x = x 2. 3 3 3 3 B := x + 3x + 2 ∼ x = x. Suy ra 3
A − B ∼ x( 2 − 1) → ∞ khi x → ∞ . V y L6 = ∞. 2 2 •
arc tg(x + 4x) + ln(1 + 3tgx) − x L = lim 7 x x 0 → arctg(4x) + cos2x − e Khi x→0 ta có:
* arctg(x2 + 4x)∼ x2 + 4x ∼ 4x, ln(1+ 3tgx) ∼ 3tgx ∼ 3x.
Suy ra arctg(x2 + 4x) + ln(1+ 3tgx)∼ 7x
Từ đó arctg(x2 + 4x) + ln(1+ 3tgx) – x2∼ 7x (1)
* arctg(4x) + cos2x – ex = arctg(4x) + (cos2x – 1) – (ex – 1) 20