Bài giảng về Ứng dụng hình học của Tích phân xác định | Đại học Bách khoa Hà Nội
Bài giảng về Ứng dụng hình học của Tích phân xác định của Đại học Bách Khoa Hà Nội với những kiến thức và thông tin bổ ích giúp sinh viên tham khảo, ôn luyện và phục vụ nhu cầu học tập của mình cụ thể là có định hướng ôn tập, nắm vững kiến thức môn học và làm bài tốt trong những bài kiểm tra, bài tiểu luận, bài tập kết thúc học phần, từ đó học tập tốt và có kết quả cao cũng như có thể vận dụng tốt những kiến thức mình đã học vào thực tiễn cuộc sống. Mời bạn đọc đón xem!
Preview text:
lOMoARcPSD|36442750
Ứng dụng tích phân xác định
I. Tính diện tích hình phẳng
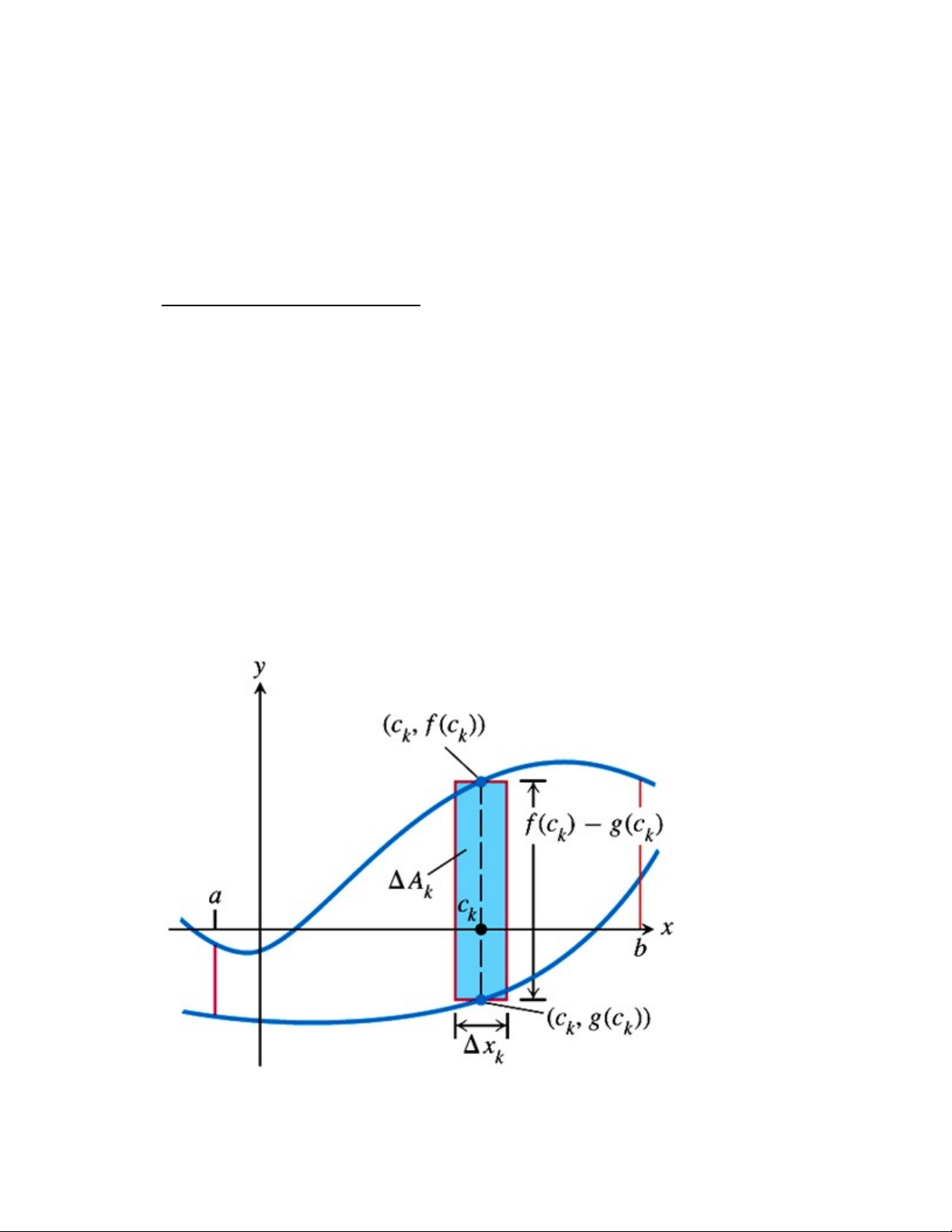
1. Đường cong cho trong hệ tọa độ Descarter Sơ đồ Tổng Tích phân:
i. Chia [a; b] thành n phần a ≡ x0 < x1 < ⋯ < xn ≡ b
ii. Khi đó diện tích S bằng tổng n hình thang cong Si
iii. Lấy xấp xỉ Sk ≈ Shình chữ nhật = dài ∗ rộng = |f(ck) − g(ck)|. ∆x 끫뢞
iv. 끫뢌 = ∫ |끫뢦(끫룊) − 끫뢨(끫룊)|끫뢢끫룊 끫뢜
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
• 끫료 = 끫뢦(끫룊), 끫료 = 끫뢨(끫룊), 끫뢜 ≤ 끫룊 ≤ b: 끫뢞
� |끫뢦(끫룊) − 끫뢨(끫룊)| 끫뢢끫룊 끫뢜
• 끫룊 = 끫뢦(끫료), 끫룊 = 끫뢨(끫료), 끫뢠 ≤ 끫료 ≤ 끫뢢: 끫뢢
� |끫뢦(끫료) − 끫뢨(끫료)| 끫뢢끫료 끫뢠 2. Đường cong tham số �끫룊 = 끫룊(끫룂) 끫료
, 끫뢜 ≤ 끫룂 ≤ 끫뢞: = 끫료(끫룂)끫뢞 끫뢞
� |끫료(끫룂)끫룊′(끫룂)| 끫뢢끫룂 = � |끫룊(끫룂)끫료′(끫룂)| 끫뢢끫룂 끫뢜 끫뢜
Trường hợp đường cong kín, không có khoảng chặn t,
ta tìm t=a, t=b sao cho (x(a),y(a))=(x(b),y(b))
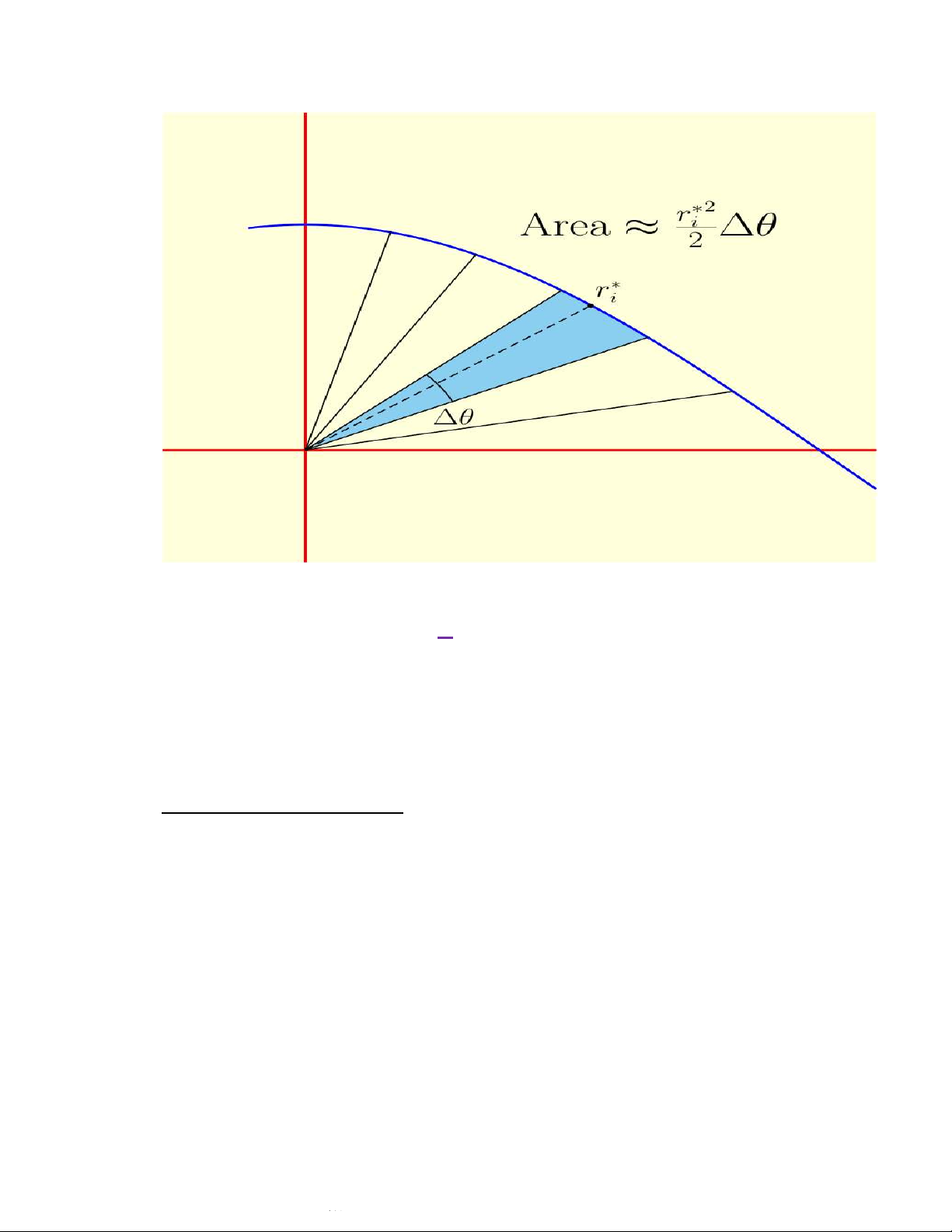
3. Đường cong trong hệ tọa độ cực Sơ đồ Tổng Tích phân:
i. Chia [α; β] thành n phần α ≡ φ ≡
0 < φ1< φ2<…< φn β
ii. Khi đó S bằng diện tích của n hình quạt gần tròn Si 1
iii. Lấy xấp xỉ Sk ≈ Squạt tròn = r2(φ 2 k)∆φ 1 끫뷺
iv. 끫뢌 = ∫ 끫뢾2(φ)dφ 2 끫뷸
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 r=r(φ), α ≤ φ ≤ β 1 끫뷸
� 끫뢾2(끫븢)끫뢢끫븢 2 끫뷺 II. Tính thể tích
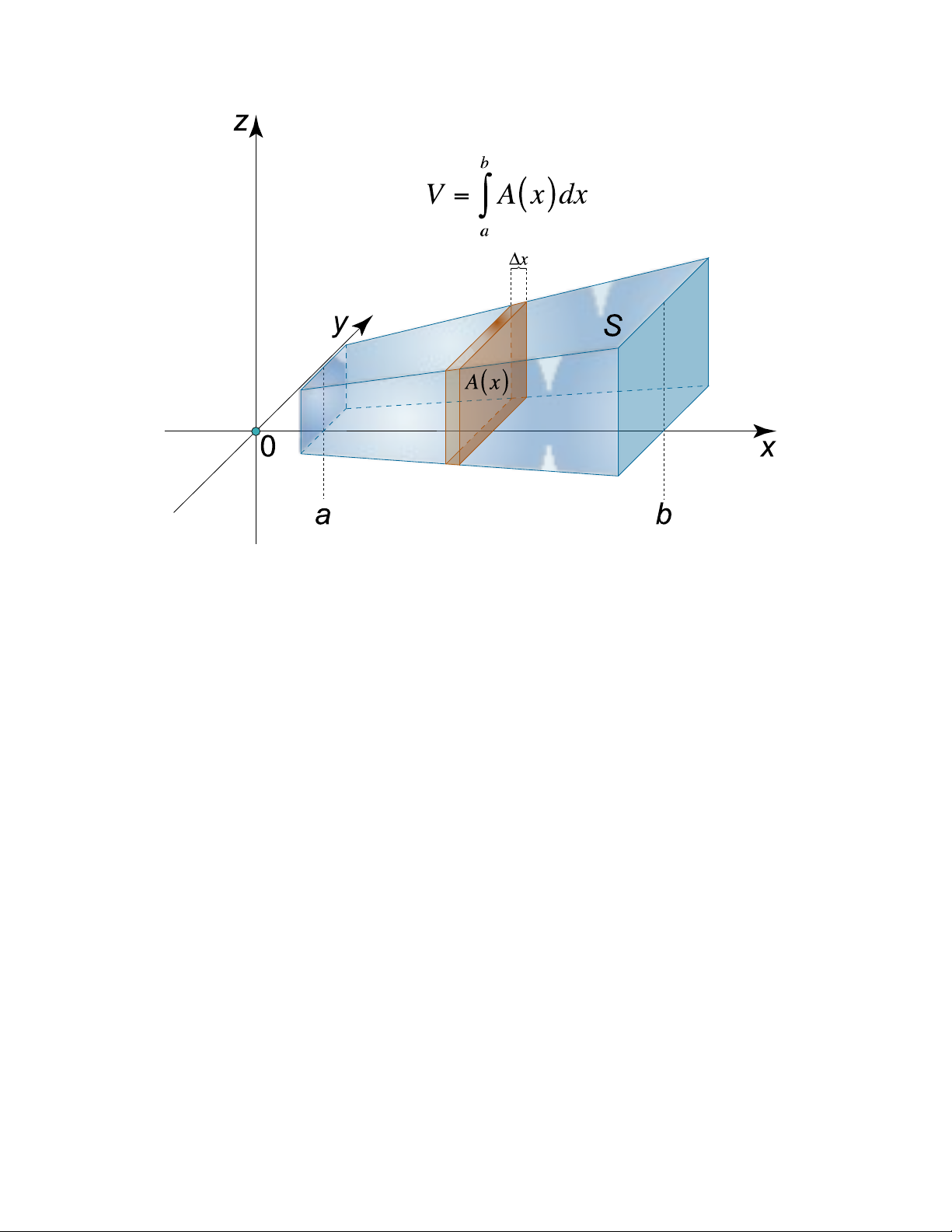
1. Thể tích vật thể với mặt cắt ngang đã biết Sơ đồ Tổng tích phân
i. Chia [a;b] thành n phần x ≡ ≡
0 aii. Khi đó A bằng tổng thể tích của n lát cắt Ai iii. Lấy xấp xỉ A ≈V ).∆x k
trụ=Diện tích đáy.Chiều cao= A(xk k 끫뢞
iv. A=∫ 끫롨(끫룊)끫뢢끫룊 끫뢜
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 b � A(x)dx a
trong đó hàm liên tục A(x) là diện tích của thiết diện thẳng
góc với trục Ox của vật thể
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
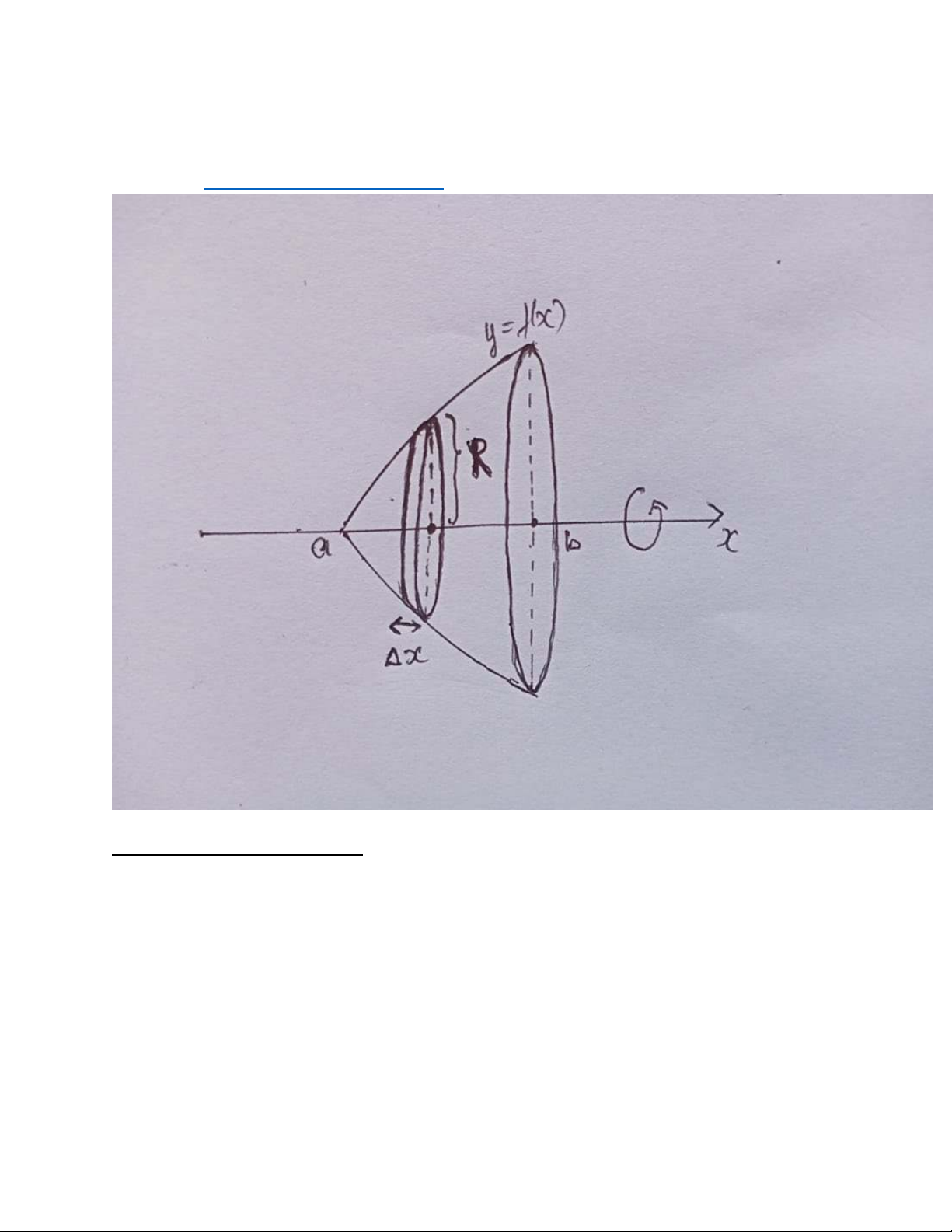
2. Thể tích vật thể tròn xoay a) Disk/Washer Method Sơ đồ Tổng Tích phân
i. Chia [a;b] thành n phần x ≡ ≡
0 aii. V bằng tổng thể tích của n lát cắt Vi iii. Lấy xấp xỉ V ≈V )∆x k trụ=πr2h=πr2(ck k 끫뢞
iv. V=끫븖 ∫ 끫뢊2(끫룊)끫뢢끫룊 끫뢜
, R(x) là khoảng cách từ vỏ hình trụ đến trục quay
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
• 끫료 = 끫뢦(끫룊), 끫료 = 0 , 끫뢜 ≤ 끫룊 ≤ 끫뢞, 끫뢼끫뢼끫뢜끫료 끫뢼끫뢼끫뢜끫뢼ℎ 끫뢄끫룊 끫뢞
끫븖 � 끫뢦2(끫룊)끫뢢끫룊 끫뢜
• 끫룊 = 끫뢨(끫료), 끫룊 = 0, 끫뢠 ≤ 끫료 ≤ 끫뢢, 끫뢼끫뢼끫뢜끫료 끫뢼끫뢼끫뢜끫뢼ℎ 끫뢄끫료 끫뢢
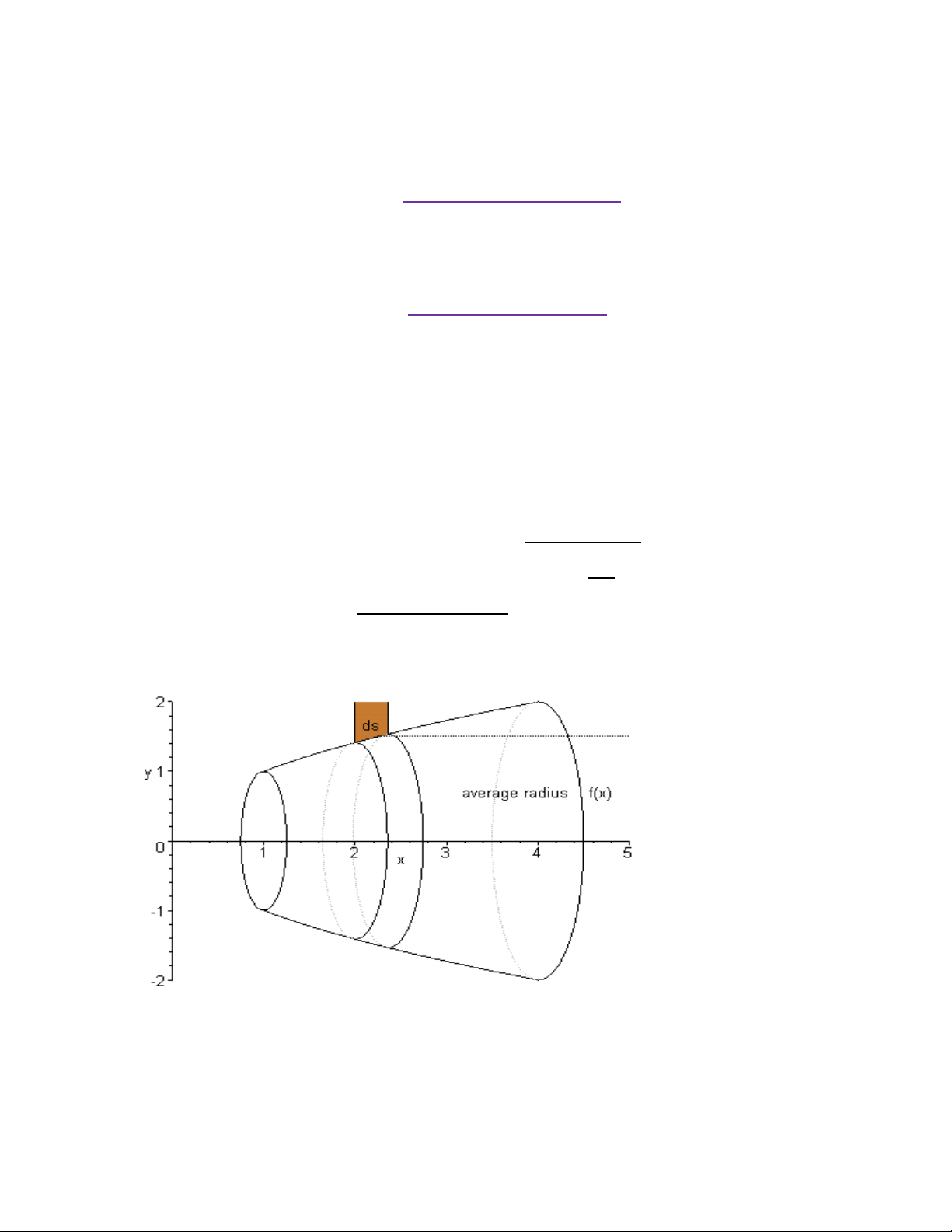
끫븖 � 끫뢨2(끫료)끫뢢끫료 끫뢠 b) Shell Method
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 Sơ đồ Tổng Tích phân:
i. Chia [a;b] thành n phần x ≡ ≡ 0 a
ii. Khi đó V bằng tổng thể tích n lớp vỏ hình trụ
iii. Thể tích của vỏ hình trụ gấp 2πrh lần độ dày nên
끫롨끫뢰 ≈ 2끫븖끫뢊(끫뢠끫뢰)ℎ(끫뢠끫뢰)∆끫룊끫뢰 끫뢞
iv. 끫롨 = 2끫븖 ∫ 끫뢊(끫룊)ℎ(끫룊)끫뢢끫룊 끫뢜
trong đó: R(x) là khoảng cách từ trục quay đến vỏ hình trụ
h(x) là chiều cao của hình trụ
• 끫료 = 끫뢦(끫룊), 끫료 = 0, 끫뢜 ≤ 끫룊 ≤ 끫뢞, 끫뢼끫뢼끫뢜끫료 끫뢼끫뢼끫뢜끫뢼ℎ 끫뢄끫료 끫뢞
2끫븖 � 끫룊끫뢦(끫룊)끫뢢끫룊 끫뢜
• 끫룊 = 끫뢨(끫료), 끫룊 = 0, 끫뢠 ≤ 끫료 ≤ 끫뢢, 끫뢼끫뢼끫뢜끫료 끫뢼끫뢼끫뢜끫뢼ℎ 끫뢄끫룊 끫뢢
2끫븖 � 끫료끫뢨(끫료)끫뢢끫료 끫뢠
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 c) Đường cong tham số • �끫룊 = 끫룊(끫룂) 끫료
, 끫뢜 ≤ 끫룂 ≤ 끫뢞 끫뢼끫뢼끫뢜끫료 끫뢼끫뢼끫뢜끫뢼ℎ 끫뢄끫룊 = 끫료(끫룂) 끫뢞
� |끫료2(끫룂)끫룊′(끫룂)| 끫뢢끫룂 끫뢜 • �끫룊 = 끫룊(끫룂) 끫료
, 끫뢜 ≤ 끫룂 ≤ 끫뢞 끫뢼끫뢼끫뢜끫료 끫뢼끫뢼끫뢜끫뢼ℎ 끫뢄끫료 = 끫료(끫룂) 끫뢞
� |끫룊2(끫룂)끫료′(끫룂)| 끫뢢끫룂 끫뢜
d) Đường cong trong hệ tọa độ cực Sơ đồ Tổng Tích phân:
xét cố định trên ∆φk sử dụng Shell Mothod ta có ∆끫뢒 2
끫뢰 = 2끫븖끫뢾2 sin(끫븢끫뢰) ∆끫뢾∆끫븢 => 끫뢒끫뢰 = 끫븖끫뢾3sin (끫븢 3 끫뢰)∆끫븢 끫뢞
=> 끫뢒 = ∫ 2 끫븖끫뢾3 sin(끫븢) 끫뢢끫븢 끫뢜 3
• 끫뢾 = 끫뢾(끫븢), 끫뷸 ≤ 끫븢 ≤ 끫뷺 끫뢼끫뢼끫뢜끫료 끫뢼끫뢼끫뢜끫뢼ℎ 끫룂끫뢾ụ끫뢠 끫뢠ự끫뢠 2끫븖 끫뷺
� 끫뢾3(끫븢)끫룀끫룀끫뢼끫븢끫뢢끫븢 3 끫뷸 • 끫뢾 끫븖
= 끫뢾(끫븢), 끫뷸 ≤ 끫븢 ≤ 끫뷺 끫뢼끫뢼끫뢜끫료 끫뢼끫뢼끫뢜끫뢼ℎ 끫븢 = 2 2끫븖 끫뷺
� 끫뢾3(끫븢)끫뢠끫뢠끫룀끫븢끫뢢끫븢 3 끫뷸
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
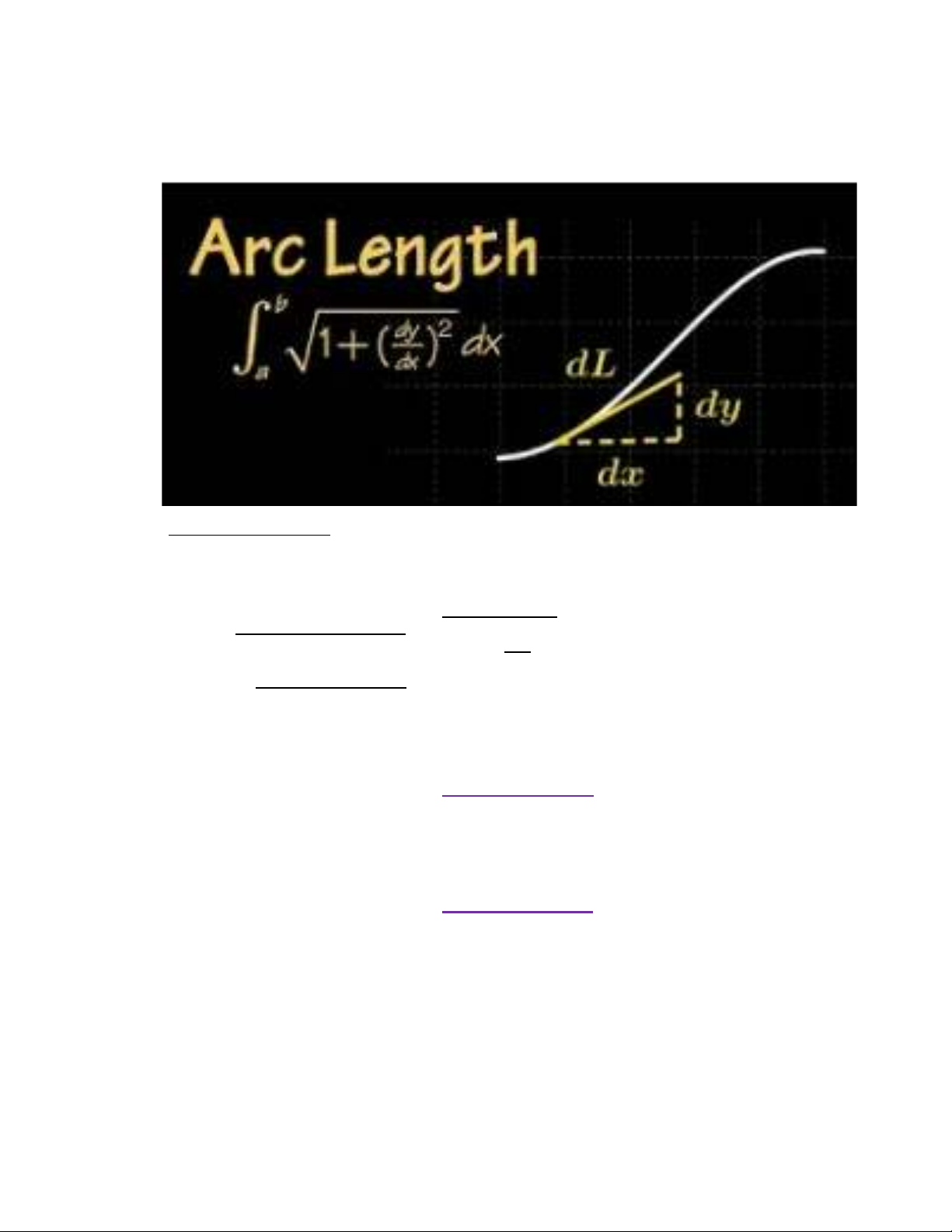
III. Tính độ dài cung phẳng
1. Đường cong trong hệ tọa độ Descartes Sơ đồ Vi phân i. Lấy x∈[a;b] lấy x+dx ii. dy=y(x+dx)-y(x) 2
iii. dL=�(끫뢢끫룊)2 + (끫뢢끫료)2=�1 + �끫뢢끫뢢� 끫뢢끫룊 끫뢢끫뢢 끫뢞
iv. L=∫ �1 + �끫료′(끫룊)�2끫뢢끫룊 끫뢜
• 끫료 = 끫료(끫룊), 끫뢜 ≤ 끫룊 ≤ 끫뢞, 끫료′(끫룊) 끫뢲끫룀ê끫뢼 끫룂ụ끫뢠 끫뢞
� �1 + �끫료′(끫룊)�2끫뢢끫룊 끫뢜
• 끫룊 = 끫뢨(끫료), 끫뢠 ≤ 끫료 ≤ 끫뢢, 끫룊′(끫료) 끫뢲끫룀ê끫뢼 끫룂ụ끫뢠 끫뢞
� �1 + �끫룊′(끫료)�2끫뢢끫료 끫뢜
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 2. �끫룊 = 끫룊(끫룂) 끫료 , a ≤ t ≤ b = 끫료(끫룂) 끫뢞
� �[끫룊′(끫룂)]2 + [끫료′(끫룂)]2 끫뢢끫룂 끫뢜
3. r=r(φ), a ≤ φ ≤ b 끫뢞
� �r2(φ) + [r′(φ)]2 끫뢢φ 끫뢜
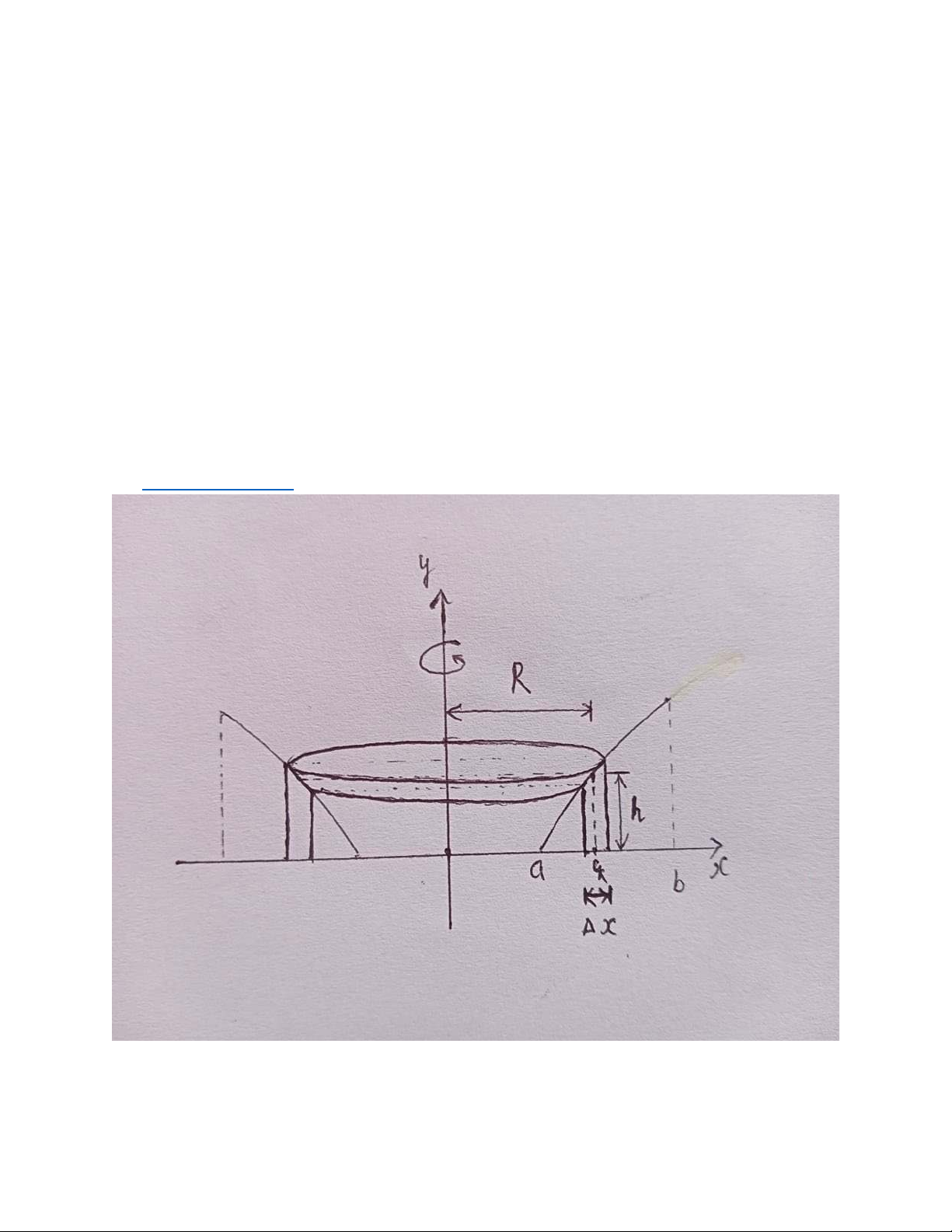
IV. Tính diện tích mặt tròn xoay
1. Đường cong trong hệ tọa độ Descartes Sơ đồ Vi phân i. Lấy x∈[a;b] lấy x+dx 2
ii. ds = 2π. r(ck). dL = 2πr(ck)�1 + �끫뢢끫뢢� 끫뢢끫룊 끫뢢끫뢢 끫뢞
iii. 끫룀 = ∫ 2끫븖끫뢾(끫룊)�1 + �끫료′(끫룊)�2끫뢢끫룊 끫뢜
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
• y=y(x), a ≤ x ≤ b, y’(x) liên tục, quay quanh Ox 끫뢞
2끫븖 � 끫료(끫룊)�1 + [끫료′(끫룊)]2 끫뢢끫룊 끫뢜
• y=y(x), a ≤ x ≤ b, y’(x) liên tục, quay quanh Oy 끫뢞
2끫븖 � 끫룊�1 + [끫료′(끫룊)]2 끫뢢끫룊 끫뢜
• x=x(y), c ≤ y ≤ d, x’(y) liên tục, quay quanh Oy 끫뢞
2끫븖 � 끫룊(끫료)�1 + [끫룊′(끫료)]2 끫뢢끫료 끫뢜
• x=x(y), c ≤ y ≤ d, x’(y) liên tục, quay quanh Ox 끫뢞
2끫븖 � 끫료�1 + [끫룊′(끫료)]2 끫뢢끫료 끫뢜 2. �끫룊 = 끫룊(끫룂) 끫료 , a ≤ t ≤ b = 끫료(끫룂) • Quay quanh Ox 끫뢞
2끫븖 � 끫료(끫룂)�[끫룊′(끫룂)]2 + [끫료′(끫룂)]2 끫뢢끫룂 끫뢜 • Quay quanh Oy 끫뢞
2끫븖 � 끫룊(끫룂)�[끫룊′(끫룂)]2 + [끫료′(끫룂)]2 끫뢢끫룂 끫뢜
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
3. Đường cong trong hệ tọa độ cực
• r=r(φ)≥0, sinφ≥0, a≤φ≤b, quay quanh trục cực 끫뢞
2끫븖 � 끫뢾(끫븢)끫룀끫룀끫뢼끫븢�r2(φ) + [r′(φ)]2 끫뢢φ 끫뢜
• r=r(φ)≥0, sinφ≥0, a≤φ≤b, quay quanh 끫븢 끫븖 = 2 끫뢞
2끫븖 � 끫뢾(끫븢)끫뢠끫뢠끫룀끫븢�r2(φ) + [r′(φ)]2 끫뢢φ 끫뢜
Downloaded by v?n ti?n Lê (vantienle525@gmail.com)