Bài tập buổi 5 - Giải thuật Prim và Kruskal môn Toán rời rạc | Học viện Công Nghệ Bưu Chính Viễn Thông

lOMoAR cPSD| 59031616 BÀI TẬP BUỔI 5
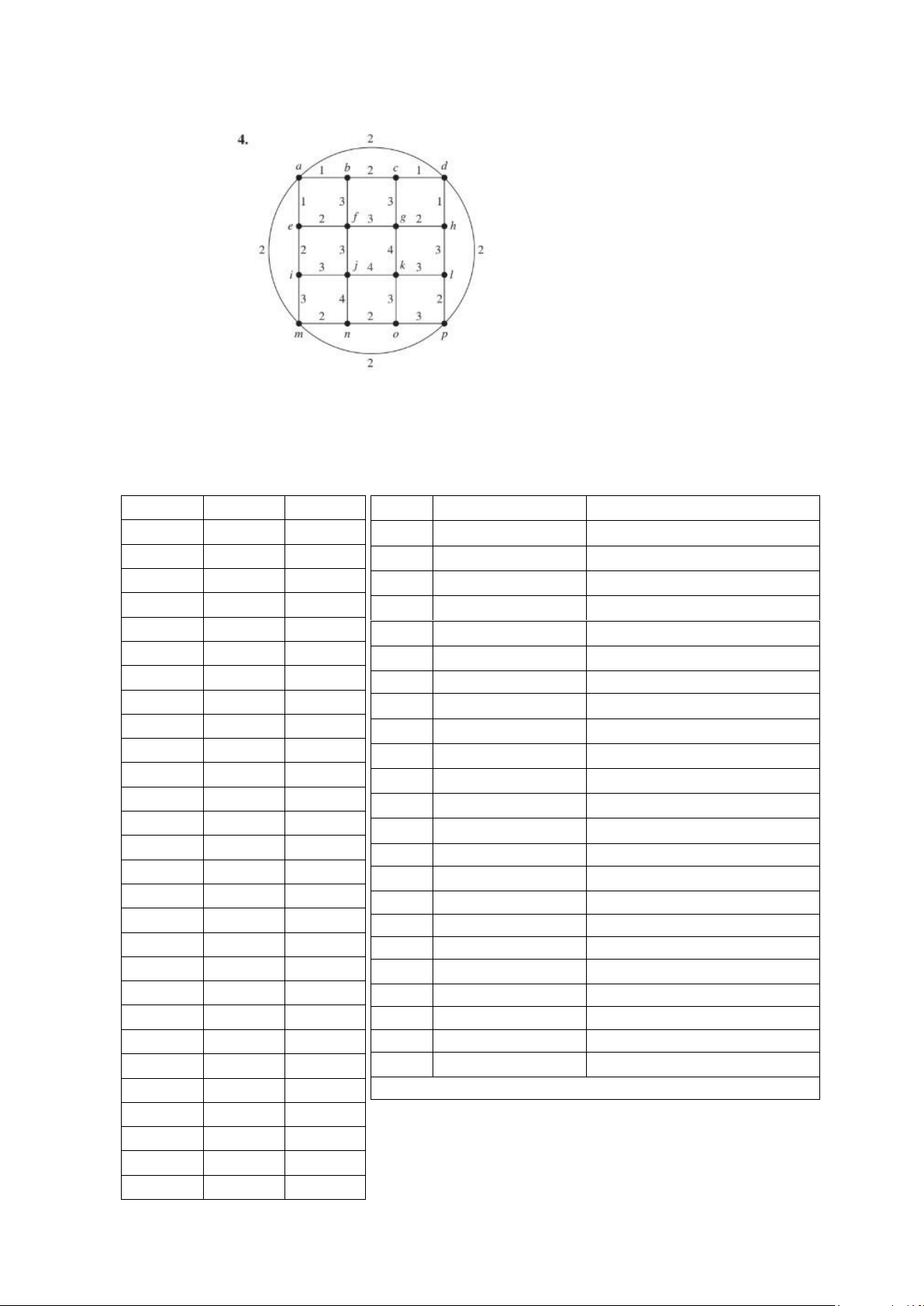
Bài tập 8 – 15 trang 840 và bài 19 trang 842 Bài 8: Bước 1: T = ∅; D(T) = 0;
Bước 2: Sắp xếp các cạnh theo
Bước 3: Lặp thứ tự tăng dần của trọng số. đầu cuối trọng số STT Cạnh được xét T ∪ e a b 1 1 E \ (a, b) T = T ∪ (a, b); D(T) = 1 a e 1 2 E = E \ (a, e) T = T ∪ (a, e); D(T) = 2 c d 1 3 E = E \ (c, d) T = T ∪ (c, d); D(T) = 3 d h 1 4 E = E \ (d, h) T = T ∪ (d, h); D(T) = 4 a d 2 5 E = E \ (a, d) T = T ∪ (a, d); D(T) = 6 a m 2 6 E = E \ (a, m) T = T ∪ (a, m); D(T) = 8 b c 2 7 E = E \ (b, c) Tạo nên chu trình d p 2 8 E = E \ (d, p) T = T ∪ (d, p); D(T) = 10 e f 2 9 E = E \ (e, f) T = T ∪ (e, f); D(T) = 12 e i 2 10 E = E \ (e, i) T = T ∪ (e, i); D(T) = 14 g h 2 11 E = E \ (g, h) T = T ∪ (g, h); D(T) = 16 l p 2 12 E = E \ (l, p) T = T ∪ (l, p); D(T) = 18 m n 2 13 E = E \ (m, n) T = T ∪ (m, n); D(T) = 20 m p 2 14 E = E \ (m, p) Tạo nên chu trình n o 2 15 E = E \ (n, o) T = T ∪ (n, o); D(T) = 22 b f 3 16 E = E \ (b, f) Tạo nên chu trình c g 3 17 E = E \ (c, g) Tạo nên chu trình f g 3 18 E = E \ (f, g) Tạo nên chu trình f j 3 19 E = E \ (f, j) T = T ∪ (f, j); D(T) = 25 h l 3 20 E = E \ (h, l) Tạo nên chu trình i j 3 21 E = E \ (i, j) Tạo nên chu trình i m 3 22 E = E \ (i, m) Tạo nên chu trình k l 3 23 E = E \ (k, l) T = T ∪ (k, l); D(T) = 28 k o 3
Bước lặp kết thúc vì |T| > N – 1 = 15 o p 3 g k 4 j k 4 j n 4 lOMoAR cPSD| 59031616
Bước 4: Trả lại kết quả:
T = {(a, b), (a, e), (c, d), (d, h), (a, d), (a, m), (d, p), (e, f), (e, i), (g, h), (l, p), (m, n), (n, o), (f, j), (k,
l)} D(T) = 1 + 1 + 1 + 1 + 1 + 1 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 3 + 3 = 28 Bài 9: a c 1 b
Bài 10: Giải thích cách hoạt động của thuật toán Prim và thuật toán Kruskal trong xây dựng rừng khung nhỏ nhất.
- Đối với thuật toán Kruskal:
+ Bước đầu tiên khởi tạo rừng khung T = ∅ và độ dài rừng khung là D(T) = 0.
+ Bước thứ hai là sắp xếp tập E cạnh rừng khung theo trọng số từ nhỏ đến lớn.
+ Bước thứ ba là lặp đến khi số cạnh trong rừng khung |T| > N – 1 hoặc tập cạnh rỗng. Khi đó mỗi
vòng lặp ta loại bỏ cạnh nhỏ nhất theo thứ tự ra khỏi tập cạnh E và kiểm tra xem khi cho cạnh đó
(e) vào tập cạnh T thì có tạo nên chu trình hay không nếu không thì thêm vào tập cạnh T và tăng
độ dài rừng khung là D(T) = D(T) + d(e).
+ Bước cuối cùng là trả về kết quả tập T và độ dài rừng khung D.
- Đối với thuật toán Prim:
+ Bước đầu tiên khởi tạo hai tập VH = {đỉnh bất kì} là tập các đỉnh đã xét và V = {các đỉnh còn lại
của G} là tập các đỉnh chưa xét. Tập cạnh rừng khung T = ∅và độ dài rừng khung D(T) = 0.
+ Bước thứ hai lặp đến khi V = ∅. Ta xét lần lượt từng đỉnh kề với đỉnh có trong tập VH với điều
kiện là có trọng số nhỏ nhất và chưa có trong tập VH. Khi đó T = T ∪ (u, v) và D(T) = D(T) + d(u,
v) với u ∈ VH và v ∈ V.
+ Bước ba là trả lại tập khung T và D(T).
Câu 11: Thay vì chọn những cạnh có trọng số nhỏ nhất, chỉ cần chọn những cạnh có trọng số lớn nhất ở bước 2.
Câu 12: Đối với thuật toán kruskal thì chỉ cần sắp xếp tập cạnh cây khung từ cao đến thấp là được.
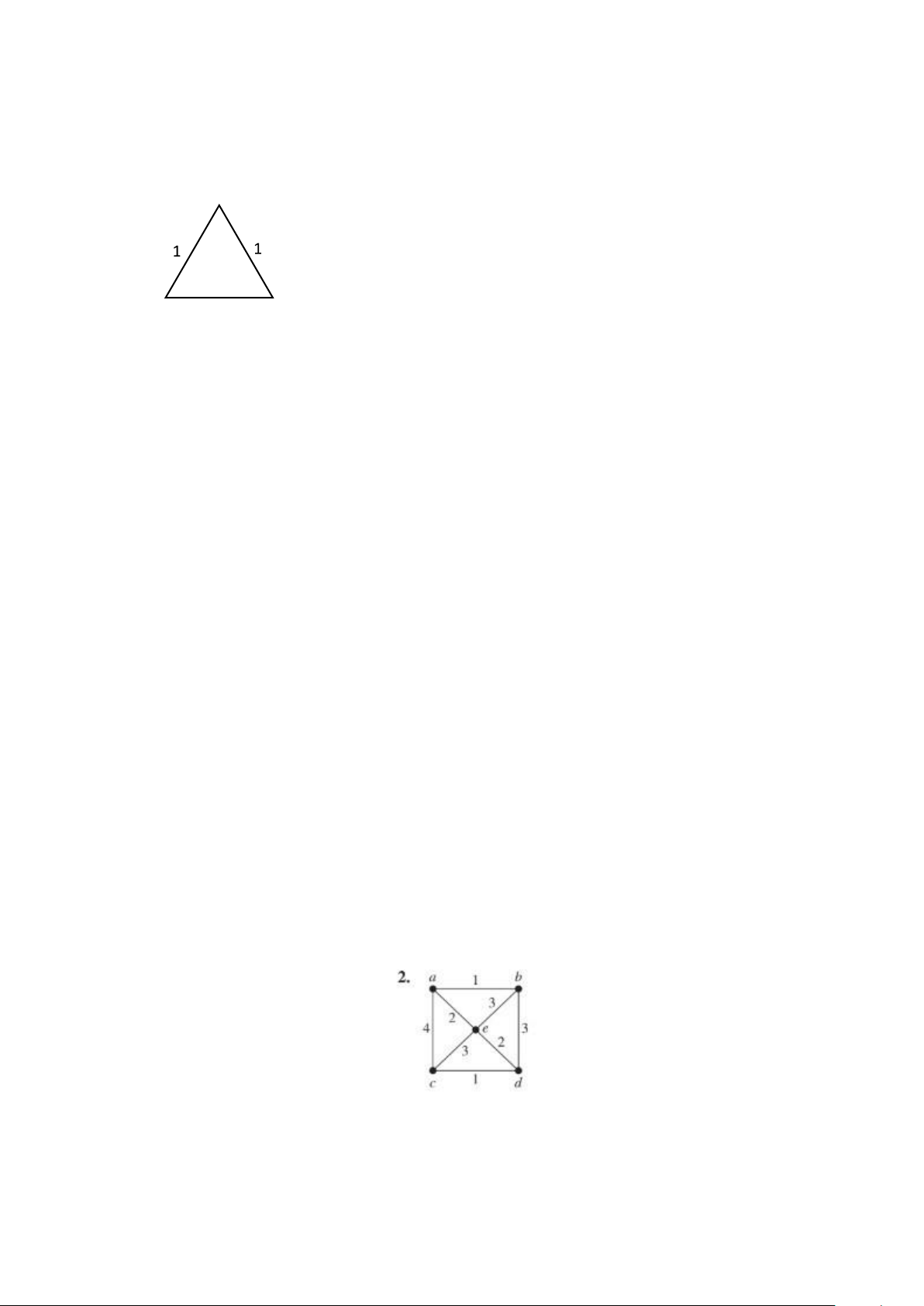
Câu 13: Cây khung lớn nhất của bài
T = {(a, c), (c, e), (e, b), (b, d)} ; D(T) = 4 + 3 + 3 + 3 = 13 lOMoAR cPSD| 59031616
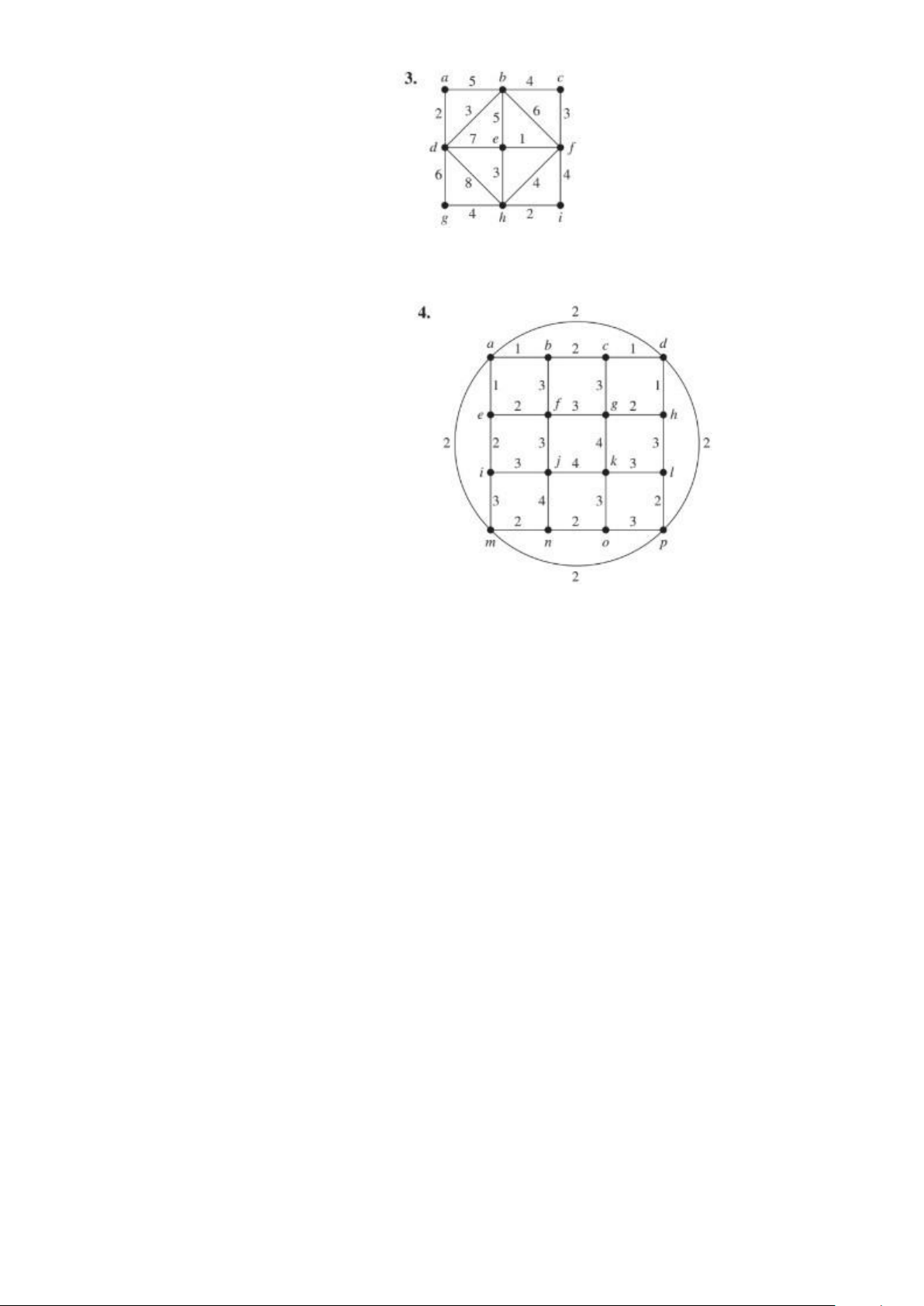
Câu 14: Cây khung lớn nhất của bài
T = {(d, h), (d, e), (d, g), (b, f), (a, b), (b, e), (b, c), (f, i)};
D(T) = 8 + 7 + 6 + 6 + 5 + 5 + 4 + 4 = 45
Câu 15: Cây khung lớn nhất của bài
T = {(g, k), (j, k), (j, n), (b, f), (c, g), (f, g), (h, l), (i,
j), (i, m), (k, l), (k, o), (o, p), (a, d), (a, m), (e, f)}
D(T) = 4 + 4 + 4 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 2 + 2 + 2 = 45 Bài 19 trang 842
- Đối với thuật toán Kruskal:
+ Bước đầu tiên khởi tạo rừng khung T = ∅ và độ dài rừng khung là D(T) = 0.
+ Bước thứ hai là sắp xếp tập E cạnh rừng khung theo trọng số từ nhỏ đến lớn.
+ Bước thứ ba là lặp đến khi số cạnh trong rừng khung |T| > N – 1 hoặc tập cạnh rỗng. Khi đó mỗi
vòng lặp ta loại bỏ cạnh nhỏ nhất theo thứ tự ra khỏi tập cạnh E và kiểm tra xem khi cho cạnh đó
(e) vào tập cạnh T thì có tạo nên chu trình hay không nếu không thì thêm vào tập cạnh T và tăng
độ dài rừng khung là D(T) = D(T) + d(e).
+ Bước cuối cùng là trả về kết quả tập T và độ dài rừng khung D.
- Đối với thuật toán Prim:
+ Bước đầu tiên khởi tạo hai tập VH = {đỉnh bất kì} là tập các đỉnh đã xét và V = {các đỉnh còn lại
của G} là tập các đỉnh chưa xét. Tập cạnh rừng khung T = ∅và độ dài rừng khung D(T) = 0.
+ Bước thứ hai lặp đến khi V = ∅. Ta xét lần lượt từng đỉnh kề với đỉnh có trong tập VH với điều
kiện là có trọng số nhỏ nhất và chưa có trong tập VH. Khi đó T = T ∪ (u, v) và D(T) = D(T) + d(u,
v) với u ∈ VH và v ∈ V.
+ Bước ba là trả lại tập khung T và D(T). lOMoAR cPSD| 59031616 Thuật toán Kruskal:
- Khởi tạo T = ∅ và D(T) = 0;
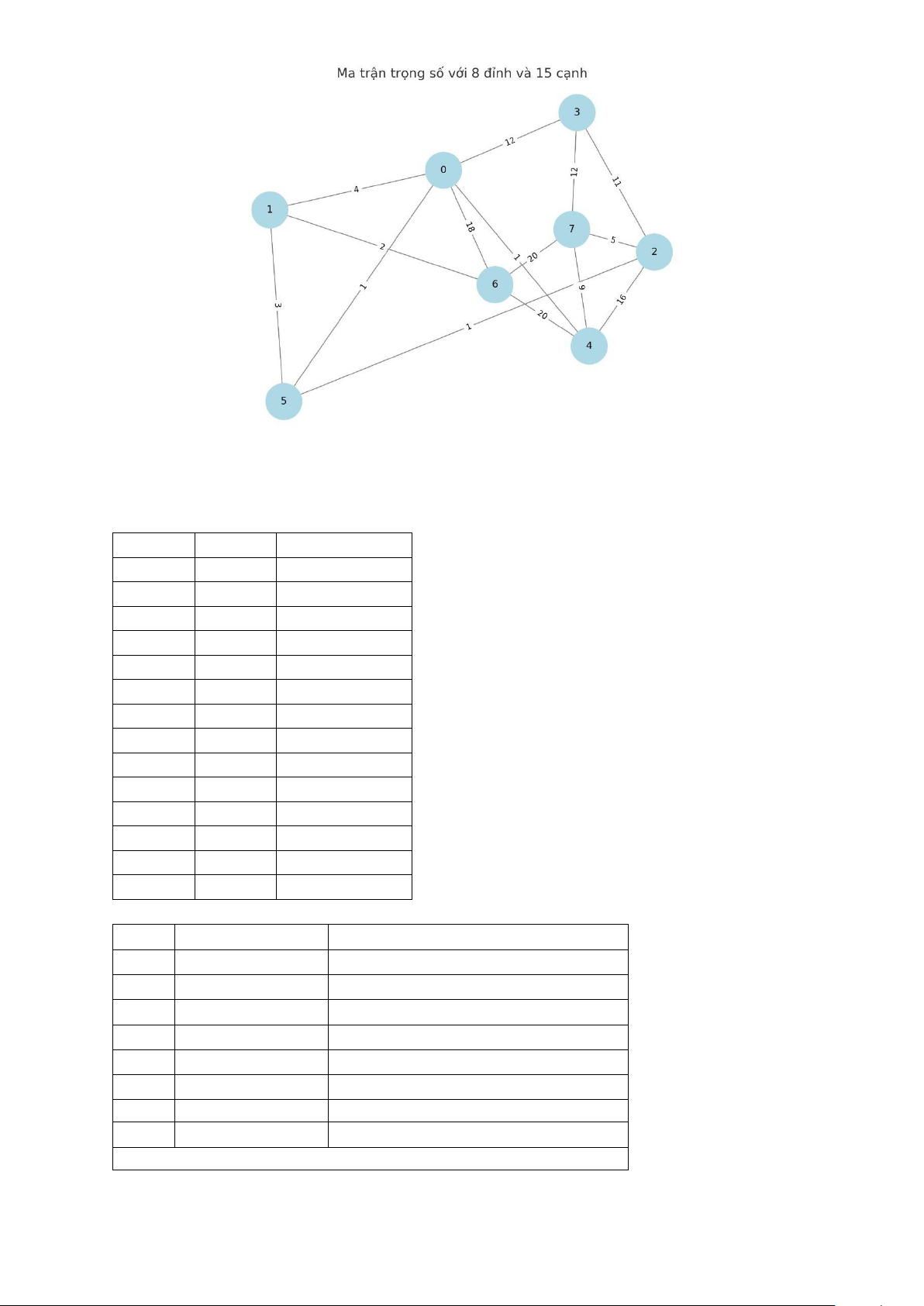
- Tạo tập E đỉnh đầu và cuối có trọng số giảm dần: Đầu Cuối Trọng số 1 5 1 1 6 1 3 6 1 2 7 2 2 6 3 3 8 5 5 8 9 3 4 11 1 4 12 4 8 12 3 5 16 1 7 18 5 7 20 7 8 20
- Lặp cho đến khi |T| > N – 1 và E ≠∅ STT Cạnh được xét T ∪ e 1 E \ (1, 5) T = T ∪ (1, 5); D(T) = 1 2 E = E \ (1, 6) T = T ∪ (1, 6); D(T) = 2 3 E = E \ (3, 6) T = T ∪ (3, 6); D(T) = 3 4 E = E \ (2, 7) T = T ∪ (2, 7); D(T) = 5 5 E = E \ (2, 6) T = T ∪ (2, 6); D(T) = 8 6 E = E \ (3, 8) T = T ∪ (3, 8); D(T) = 13 7 E = E \ (5, 8) Tạo nên chu trình 8 E = E \ (3, 4) T = T ∪ (3, 4); D(T) = 24
Bước lặp kết thúc vì |T| > N – 1 = 7 - Trả lại kết quả: lOMoAR cPSD| 59031616
+ T = {(1, 5), (1, 6), (3, 6), (2, 7), (2, 6), (3, 8)} + D(T) = 24 Thuật toán Prim:
T = ∅; D(T) = 0; V = {2, 3, 4, 5, 6, 7, 8}; VH = {1} e = (v,t) v V\v = ? VH∪ v = ? T, D(T) ∈V, t ∈ VH Có độ dài nhỏ nhất (1, 5) 2, 3, 4, 6, 7, 8 1, 5 T = T∪(1,5) D(T) = 0 + 1 (1, 6) 2, 3, 4, 7, 8 1, 5, 6 T = T∪(1, 6) D(T) = 1 + 1 (6, 3) 2, 4, 7, 8 1, 3, 5, 6 T = T∪(6, 3) D(T) = 2 + 1 (6, 2) 4, 7, 8 1, 2, 3, 5, 6 T = T∪(6, 2) D(T) = 3 + 3 (2, 7) 4, 8 1, 2, 3, 5, 6, 7 T = T∪(2, 7) D(T) = 6 + 2 (3, 8) 4 1, 2, 3, 5, 6, 7, 8 T = T∪(3, 8) D(T) = 8 + 5 (3, 4) ∅ 1, 2, 3, 4, 5, 6, 7, 8 T = T∪(3, 4) D(T) = 13 + 11
V = ∅: Kết thúc vòng lập
Kết quả T = {(1,5), (1, 6), (6, 3), (6, 2), (2, 7), (3, 8), (3, 4)}
D(T) = 1 + 1 + 1 + 3 + 2 + 5 + 11 = 24