Báo cáo bài tập lớn môn Toán rời rạc | Học viện Công Nghệ Bưu Chính Viễn Thông

lOMoAR cPSD| 59031616
HỌC VIỆN CÔNG NGHỆ BƯU CHÍNH VIỄN THÔNG
BÁO CÁO BÀI TẬP LỚN MÔN: TOÁN RỜI RẠC 1 Giảng viên
: Nguyễn Thị Mai Trang
Nhóm học phần : Nhóm 8
Nhóm bài tập lớn : Nhóm 6
Sinh viên thực hiện :
Nguyễn Trường Giang B23DCCN258
Ngô Hồng Phúc B23DCCN655 Lê Huy Hải B23DCCN272
Trần Văn Trung Hiếu B23DCCN314
Nguyễn Xuân Quang B23DCCN692 lOMoAR cPSD| 59031616 Họ và Tên 1.Lê Huy Hải 2.Nguyễn Trường Giang 3.Nguyễn Xuân Quang 4.Trần Văn Trung Hiếu 5.Ngô Hồng Phúc Nhóm học phần – Nhóm Nhóm 06 bài tập lớn hieutranvantrung4@gmail.com Bài lập trình Số 1 Môn Toán Rời Rạc 1 Giảng Viên Nguyễn Thị Mai Trang Ngày 15/11/2024
Bài 1: Một dãy số tự nhiên bất kì An = {a1, a2, ..., an} ược gọi là một
ường nguyên tố bậc k nếu tổng k phần tử liên tiếp bất kì của dãy số An là
một số nguyên tố (k ≤ n). Ví dụ dãy số A = {3, 27, 7, 9, 15} là một ường
nguyên tố bậc 3. Cho dãy số An. Hãy liệt kê tất cả các ường nguyên tố
bậc k có thể có ược tạo ra bằng cách tráo ổi các phần tử khác nhau của dãy số An. 1.1-Sơ ồ khối 1.Input:
• Cho 1 số nguyên n là số lưởng phần tử của dãy A.
• Cho dãy số A= (a1,a2,…,an) là các phần tử của dãy. • Cho 1 số tự nhiên k 2.Thứ tự nhập:
• Dòng 1: n (số lượng phần tử của dãy) lOMoAR cPSD| 59031616
• Dòng 2: Các phần tử của dãy A, cách nhau bằng dấu cách
• Dòng 3: Số tự nhiên k 3.Output
• In ra tổng số lượng dãy con thỏa mãn iều kiện.
• Liệt kê tất cả hoán vị của dãy A thoả mãn tạo thành 1
ường nguyên tố bậc k.
• In thời gian thực hiện ể tìm ra dãy thỏa mãn iều kiện.
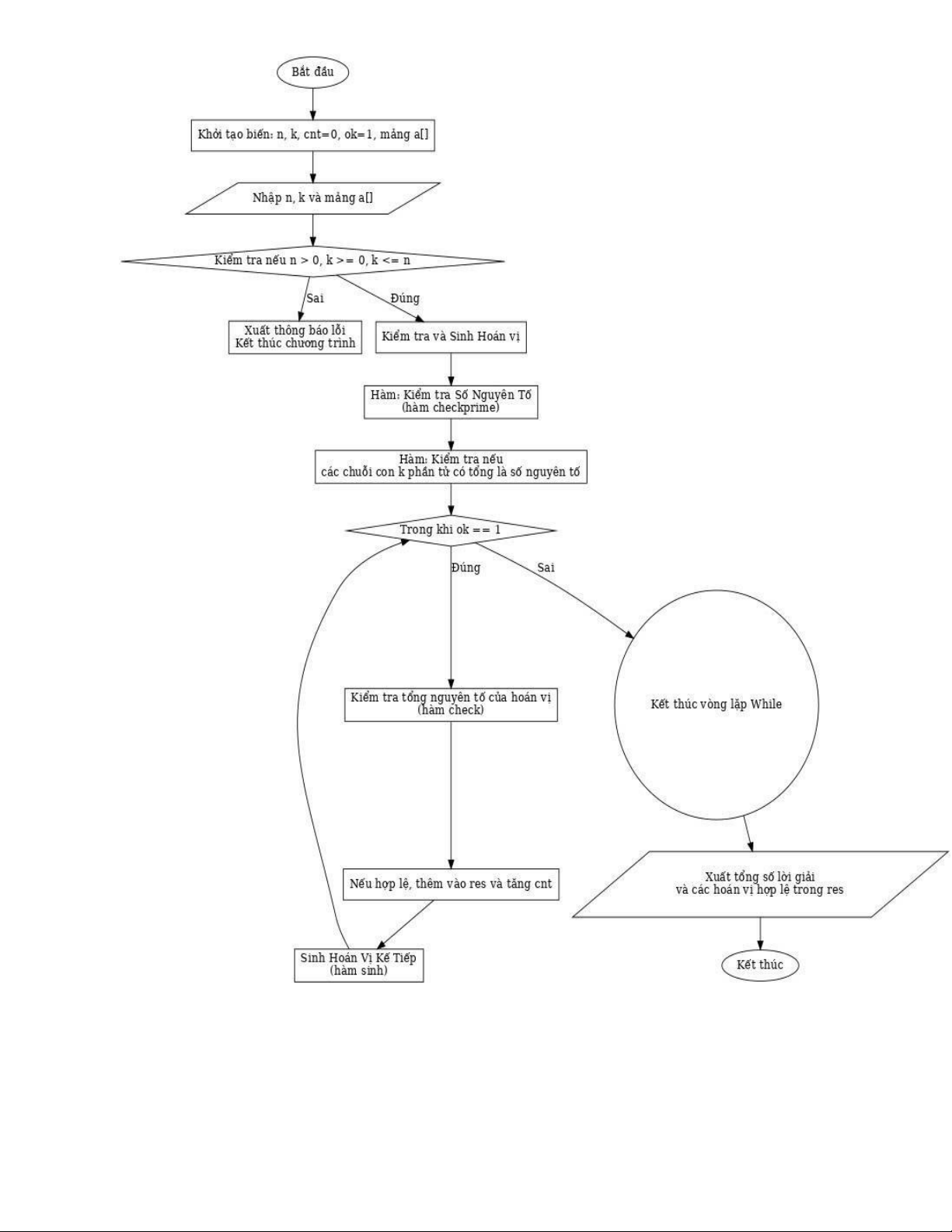
4. Sơ ồ khối thuật toán chính của bài: lOMoAR cPSD| 59031616
1.2 Chương trình trên ngôn ngữ C++ lOMoAR cPSD| 59031616 #include #define ll long long using namespace std;
ll n, a[100], ok, k, cnt = 0; vector> res;
// Hàm kiểm tra số nguyên tố int
checkprime(ll n) { if (n < 2)
return 0; if (n == 2) return 1;
for (ll i = 2; i <= sqrt(n); i++) { if (n % i == 0) return 0; } return 1; }
// Hàm kiểm tra nếu tổng của mọi chuỗi con k phần tử là số nguyên tố int check(ll a[], ll k) { ll sum = 0; for (ll i = 0; i < k; i++) { sum += a[i]; }
if (!checkprime(sum)) return 0; lOMoAR cPSD| 59031616
for (ll i = k; i < n; i++) {
sum = sum + a[i] - a[i - k]; if (!checkprime(sum)) return 0; } return 1; }
// Sinh hoán vị kế tiếp void sinh() {
ll i = n - 2; while (i >= 0 && a[i]
> a[i + 1]) { i--; } if (i == - 1) { ok = 0; } else { ll j = n - 1; while (a[i] > a[j]) j--; swap(a[i], a[j]); reverse(a + i + 1, a + n); } } int main() { cin >> n; lOMoAR cPSD| 59031616
for (ll i = 0; i < n; i++) cin >> a[i]; cin >> k;
if (n <= 0 || k <= 0 || k > n) {
cout << "Input error! Ensure N > 0, K > 0, and K <= N." << endl; return 0; }
auto start = chrono::high_resolution_clock::now();
ok = 1; while (ok) { if (check(a, k)) {
res.push_back(vector(a, a + n)); // Thêm hoán vị vào danh sách kết quả cnt++; } sinh(); } // In kết quả
cout << "The total number of solutions is " << cnt << endl;
for (const auto &tmp : res) { for (ll x : tmp) { cout << x << ' '; } cout << endl; } lOMoAR cPSD| 59031616
// Đo thời gian thực thi
auto end = chrono::high_resolution_clock::now();
chrono::duration elapsed = end - start;
cout << "Time to find the solution is " << elapsed.count() << " seconds" << endl; return 0; } 1.3 Kết quả lOMoAR cPSD| 59031616 lOMoAR cPSD| 59031616 lOMoAR cPSD| 59031616
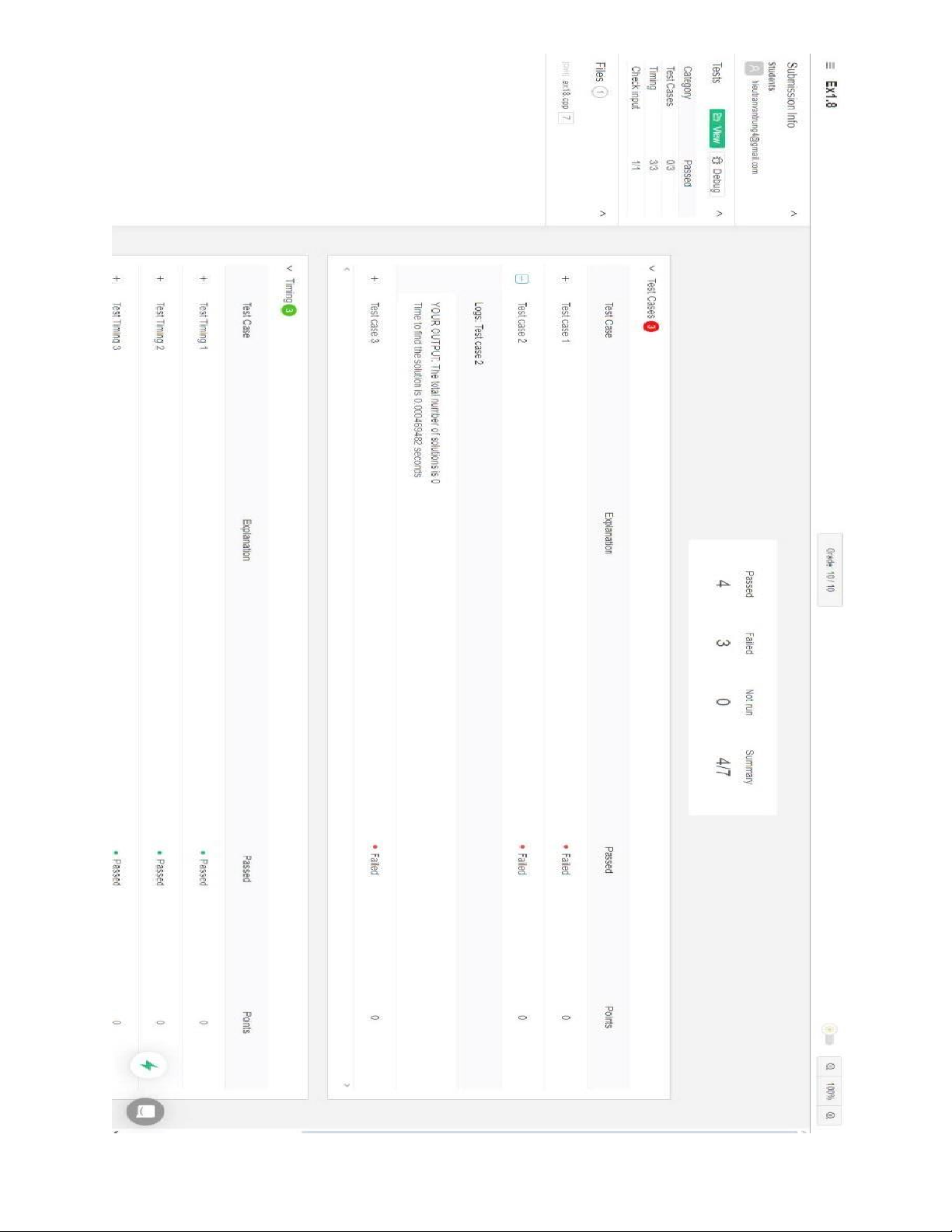
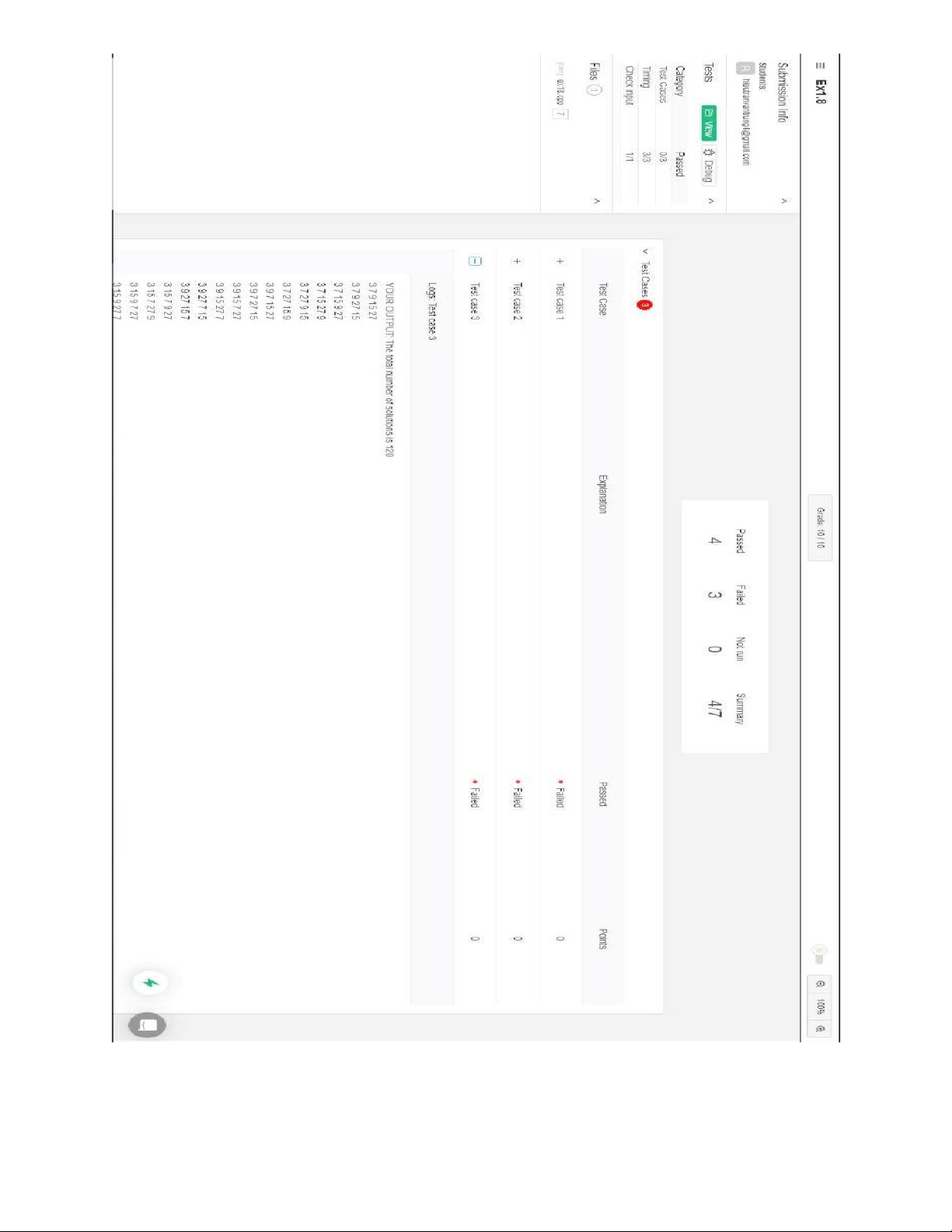
1.4 Kết quả chụp màn hình ã pass ví dụ : lOMoAR cPSD| 59031616