
Preview text:
lOMoAR cPSD| 59031616 BÀI TẬP BUỔI 9
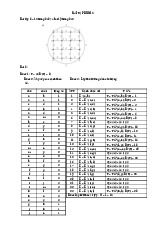
Minh họa thuật toán Dijkstra, Bellman-Ford và Floyd. Dijkstra:
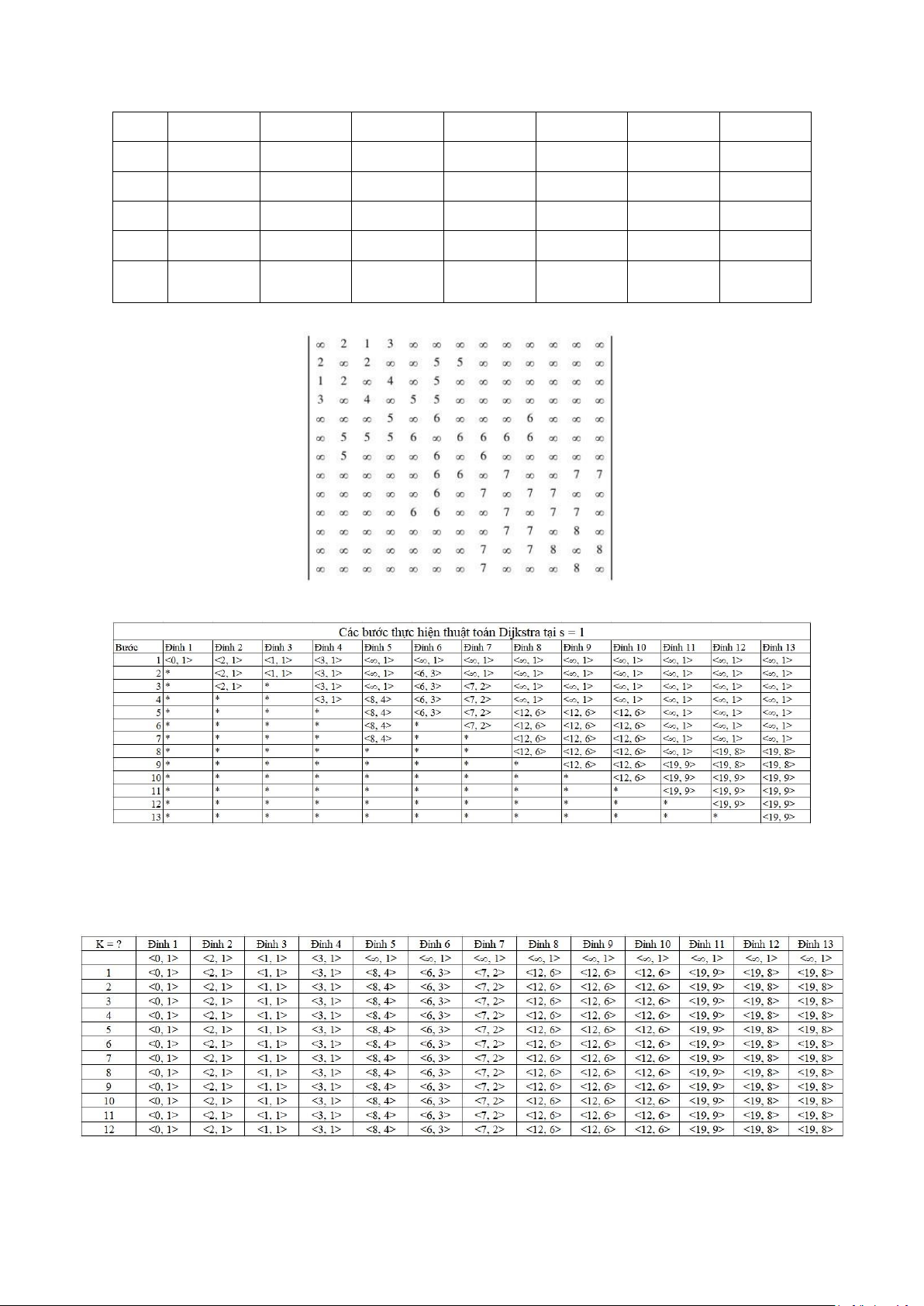
Các bước thực hiện thuật toán Dijkstra tại s = 1 Bướ Đỉnh 1 Đỉnh 2 Đỉnh 3 Đỉnh 4 Đỉnh 5 Đỉnh 6 Đỉnh 7 c 1 <0, 1> <11, 1> <65, 1> <17, 1> <65, 1> <65, 1> <65, 1> 2 * <11, 1> <23, 2> <17, 1> <65, 1> <21, 2> <27, 2> 3 * * <23, 2> <17, 1> <65, 1> <21, 2> <27, 2> 4 * * <23, 2> * <65, 1> <21, 2> <27, 2> 5 * * <23, 2> * <37, 3> * <27, 2> 6 * * * * <37, 3> * <27, 2> 7 * * * * <37, 3> * * Bellman-Ford: K Đỉnh 1 Đỉnh 2 Đỉnh 3 Đỉnh 4 Đỉnh 5 Đỉnh 6 Đỉnh 7 = ? <0, 1> <11, 1> <65, 1> <17, 1> <65, 1> <65, 1> <65, 1> 0 11 23 17 37 21 27 65 65 65 65 65 65 0 65 0 12 25 26 10 16 1 2 2 4 2 2 2 65 65 0 13 14 65 19 1 2 3 3 3 6 7 65 65 65 0 65 65 18 1 2 3 4 5 6 7 65 65 65 65 0 65 15 1 2 3 4 5 6 7 65 13 18 31 32 0 10 1 2 3 4 5 6 7 1 2 3 3 3 6 7 1 2 3 4 5 6 7 lOMoAR cPSD| 59031616 1 <0, 1> <11, 1> <23, 2> <17, 1> <37, 3> <21, 2> <27, 2> 2 <0, 1> <11, 1> <23, 2> <17, 1> <37, 3> <21, 2> <27, 2> 3 <0, 1> <11, 1> <23, 2> <17, 1> <37, 3> <21, 2> <27, 2> 4 <0, 1> <11, 1> <23, 2> <17, 1> <37, 3> <21, 2> <27, 2> 5 <0, 1> <11, 1> <23, 2> <17, 1> <37, 3> <21, 2> <27, 2> Floyd: Dijkstra: Bellman-Ford: Floyd: lOMoAR cPSD| 59031616 Mô tả thuật toán:
Thuật toán Dijkstra dùng để tìm đường đi ngắn nhất từ một điểm xuất
phát đến các điểm còn lại trong đồ thị có trọng số không âm. Nó hoạt động
bằng cách liên tục chọn đỉnh gần nhất chưa được xét, sau đó cập nhật khoảng
cách ngắn nhất đến các đỉnh kề nếu tìm được đường đi tốt hơn. Quá trình lặp
lại cho đến khi không còn đỉnh nào cần xét.
Thuật toán Bellman-Ford cũng dùng để tìm đường đi ngắn nhất từ một
đỉnh đến các đỉnh khác, nhưng cho phép trọng số âm. Nó lặp lại việc cập nhật
khoảng cách giữa các đỉnh qua các cạnh tối đa V-1 lần (với V là số đỉnh). Nếu
sau V-1 lần vẫn còn cập nhật được, chứng tỏ có chu trình âm.
Thuật toán Floyd-Warshall dùng để tìm đường đi ngắn nhất giữa mọi cặp
đỉnh trong đồ thị. Nó xét từng đỉnh làm điểm trung gian và cập nhật khoảng
cách giữa mọi cặp đỉnh nếu đi qua điểm trung gian đó giúp rút ngắn đường đi.