Bài Tập Chương 1 Môn Xác suất thống kê | Trường Đại học Kinh tế, Đại học Huế

lOMoAR cPSD| 58794847
Chương I. BIẾN CỐ NGẪU NHIÊN VÀ XÁC SUẤT
BT1. Một lô hàng gồm 100 sản phẩm, trong ó có 10 phế phẩm. Lấy ngẫu nhiên ra 20 sản
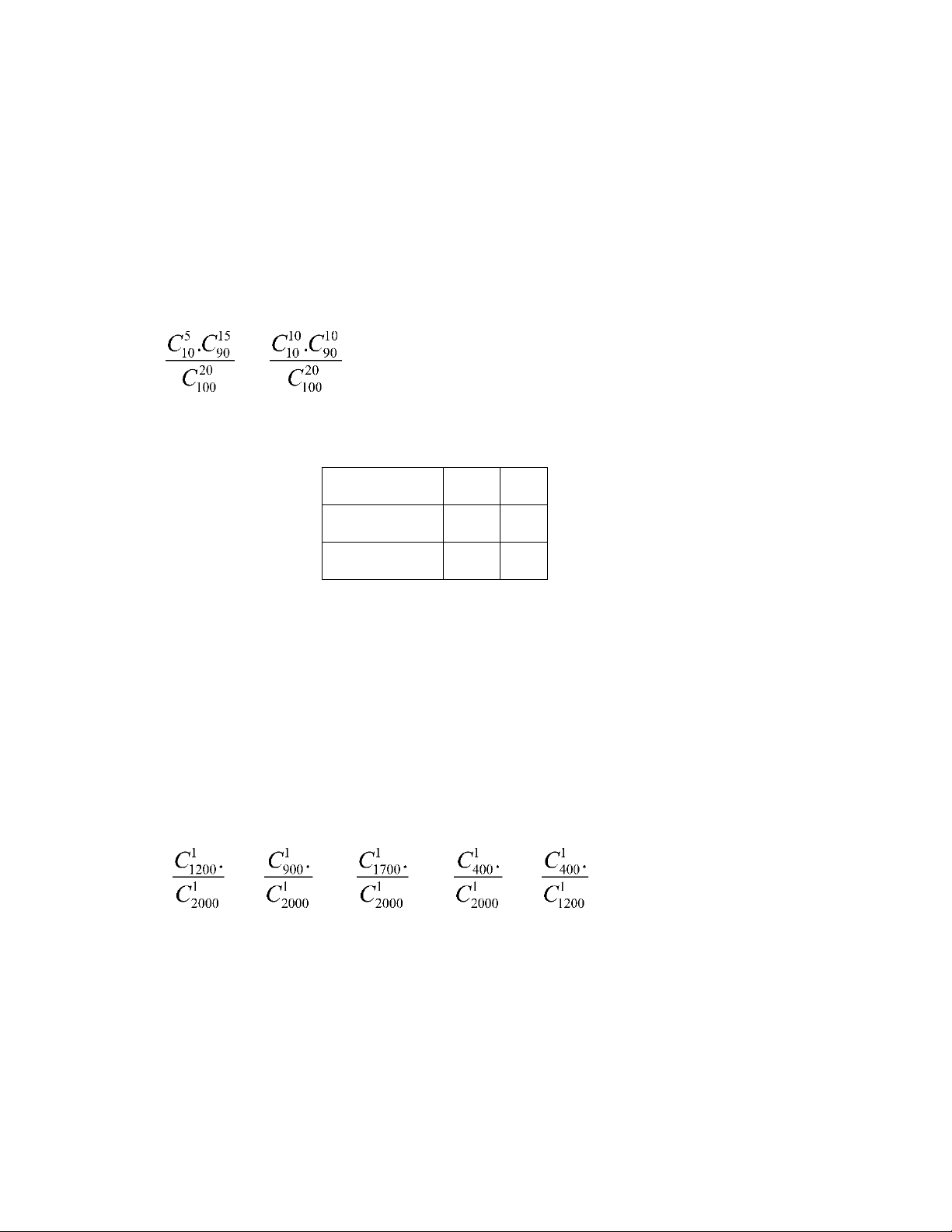
phẩm. Tính xác suất ể trong 20 sản phẩm lấy ra a. Có 5 phế phẩm. b. Bị cả 10 phế phẩm. c. Có úng 5 chính phẩm. ĐS a) b) c)0
BT2: Thống kê 2000 sinh viên một khoá của trường kinh tế theo giới tính và ngành học
thu ược các số liệu sau:
Ngành học Nam Nữ Học Kinh tế 400 500 Học QTKD 800 300
Lấy ngẫu nhiên một sinh viên khoá ó. Tìm xác suất ể ược a. Nam sinh viên
b. Sinh viên học kinh tế.
c. Hoặc nam sinh viên, hoặc học kinh tế.
d. Nam sinh viên và học kinh tế.
e. Nếu ã chọn ược một nam sinh viên thì xác suất ể người ó học kinh tế bằng bao nhiêu?. ĐS: a) b) c) d) e)
BT3. Xác suất ể mỗi doanh nghiệp sản xuất có mua bảo hiểm cháy nổ là 0,7. Kiểm tra ngẫu
nhiên 12 doanh nghiệp, tính xác suất ể:
a. Có úng 9 doanh nghiệp có mua bảo hiểm cháy nổ.
b. có ít nhất 10 doanh nghiệp mua bảo hiểm cháy nổ. lOMoAR cPSD| 58794847 ĐS:a)0,2397 ; b) 0,2528;
BT4: Ba sinh viên cùng làm bài thi , Xác suất làm ược bài của SV thứ nhất, thứ hai, thứ ba
lần lượt là 0,8; 0,7 và 0,6. Tính xác suất a. Cả 3 SV làm ược bài b. Có 2 SV làm ược bài
c. Có ít nhất một sinh viên không làm ược bài
d. Nếu hai SV làm ược bài, tính xác suất SV thứ nhất không làm ược bài
ĐS: a) 0,336; b)0,452; c)0,664; d)0,1858
BT5. Thống kê cho biết xác suất ể xạ thủ bắn trúng mục tiêu là 0,4.
a. Tính xác suất ể xạ thủ ó bắn 5 viên thì có 3 viên bắn trúng mục tiêu
b. Với xác suất không nhỏ hơn 0,9 xạ thủ ó cần bắn ít nhất bao nhiêu lần ể có ít nhất
một lần trúng mục tiêu.
ĐS: Xạ thủ ó bắn ít nhất 5 lần.
BT6. Tại một cửa hàng, xác suất ể khách hàng mua thiết bị iện tử là 0,4; xác suất khách
hàng cài ặt phần mềm là 0,3; nhưng với khách ã mua thiết bị thì xác suất ể sau ó cài ặt phần
mềm là 0,6. Hãy tính xác suất một khách hàng:
a. Mua thiết bị iện tử và cài ặt phần mềm.
b. Có thực hiện ít nhất một giao dịch.
c. Không thực hiện giao dịch nào.
d. Chỉ thực hiện úng một giao dịch.
e.Không cài ặt phần mềm biết người ó mua thiết bị iện tử
ĐS: a)0,24;b)0,46;c)0,54;d)0,22
BT7. Theo thống kê của trường Đại học A, tỷ lệ sinh viên trượt môn XSTK là 40%, trượt
môn Triết là 30%. Trong số sinh viên trượt môn XSTK có 50% sinh viên trượt môn Triết.
Gặp ngẫu nhiên 1 sinh viên. Tính xác suất
a. Sinh viên ó trượt cả 2 môn lOMoAR cPSD| 58794847
b. Sinh viên ó ậu cả 2 môn
c. Sinh viên ậu môn XSTK biết sinh viên ó trượt môn Triết.
d. Sinh viên ó ậu môn XSTK biết sinh viên ó ậu môn Triết
ĐS: a)0,2;b)0,5;c) 0,333;d) 0,714
BT8.Trên một bảng quảng cáo người ta mắc 2 hệ thống bóng èn. Hệ thống I gồm 2 bóng
mắc nối tiếp. hệ thống II gồm 2 bóng mắc song song . Khả năng bị hỏng của mỗi bóng èn
sau 6 giờ thắp sáng liên tục là 15% và việc hỏng các bóng coi như ộc lập. tính xác suất a. Hệ thống I bị hỏng
b. Hệ thống II không bị hỏng
c. Cả hai hệ thống bị hỏng
d. Chỉ có hệ thống I bị hỏng
ĐS:a)0,2775;b)0,9775;c)0,00624;c)0,2712
BT9. Có 3 cầu thủ chơi bóng rỗ. Khả năng ném trúng rỗ của các cầu thủ tương ứng là
0,7;0,8 và 0,85 .Tính xác suất ể
a. cả 3 cầu thủ ều ném trúng rỗ
b. có một càu thủ ném trúng rỗ.
c. chỉ có cầu thủ 1 ném trúng rỗ
d. có không quá 1 cầu thủ ném trúng rỗ
e. e.Có ít nhất 1 cầu thủ ném trúng rỗ
f. Nếu có một cầu thủ ném trúng rỗ. Tính xác suất ể cầu thủ thứ 2 ném trúng.
ĐS: a)0,476;b)0,108;c)0,119;d)0,117;e)0,991;f)0,333
BT10. Một người bắn bia với xác suất trúng là 0,7
a. Bắn liên tiếp 3 viên, tính xác suất ể có ít nhất một lần trúng bia
b. Hỏi phải bắn ít nhất mấy lần ể có xác suất ít nhất 1 lần bắn trúng bia ≥0,97. ĐS: a)0,973;b)3 lOMoAR cPSD| 58794847
BT11. Một người có nguyện vọng thi vào hai trường ại học. Đợt một thi vào trường A, khả
năng ỗ là 90%. Nếu ợt một người ó thi ỗ thì khả năng thi ỗ ợt hai vào trường B là 99%.
Ngược lại nếu lần thứ nhất thi trượt thì khả năng thi ỗ lần hai chỉ còn 50%. Tính xác suất ể
a. Người ó ỗ cả hai trường
b. Người ó chỉ ỗ một trường
c. Người ó chỉ ỗ trường B
d. Người ó không ỗ trường nào cả.
ĐS: a)0,891; b)0,059; c)0,05; d)0,05
BT12. Khả năng rủi ro khi ầu tư vào các dự án I ,II tương ứng là 8% và 6%, gặp rủi ro ồng
thời khi ầu tư cả 2 dự án là 4%.
a. Nếu dự án 1 gặp rủi ro, Tính xác suất ể dự án 2 gặp rủi ro
b. Tính xác suất Chỉ dự án I gặp rủi ro
c. Tính xác suất Chỉ 1 dự án gặp rủi ro
d. Tính xác suất Gặp rủi ro
e. Tính xác suất Không gặp rủi ro
ĐS:a) 0,5; b)0,04; c)0,06; d)0,1; e)0,9
BT13. Điều tra về việc tiêu thụ sản phẩm của công ty A cho thấy 30% các bà vợ thường
xem chương trình thể thao, 50% các ông chồng thường xem chương trình thể thao, song
nếu thấy vợ xem thì tỷ lệ chồng cùng xem là 60%. Lấy ngẫu nhiên một cặp vợ chồng. Tìm xác suất ể
a. Cả hai cùng thường xem chương trình thể thao
b. Có ít nhất một người thường xem
c. Không có ai thường xem
d. Nếu chồng xem thì vợ cùng xem
e. Nếu chồng không xem thì vợ vẫn xem
ĐS: a)0,18;b)0,62;c)0,38;d)0,36; e)0,24 lOMoAR cPSD| 58794847
BT14. Nhân viên tiếp thị i tiếp xúc với các khách hàng tiềm năng của công ty và khả năng
một khách hàng tiềm năng sau khi tiếp xúc với nhân viên tiếp thị sẽ mua hàng của công ty
là 75%. Hãy tính xác suất ể nhân viên tiếp thị i tiếp xúc với 6 khách hàng tiềm năng sẽ:
a. Bán ược hàng cho 4 người b.
Bán ược hàng cho ít nhất 1 người ĐS: a)0,2966;b)0,9996
BT15. Một sinh viên phải thi 3 môn một cách ộc lập với nhau, xác suất nhận ược cùng một
iểm số nào ó ở cả ba môn ều như nhau. Xác suất ể thi một môn ược iểm tám là 0,18; ược
iểm dưới tám là 0,65. Xác suất ể cả ba môn ều ược iểm mười là 0,000343. Tính xác suất ể
sinh viên thi ba môn ược ít nhất 28 iểm. Biết rằng iểm thi ược cho theo thang iểm mười, không có iểm lẻ. ĐS:0,00656
BT16.Một phân xưởng có 60 công nhân, trong ó có 40 nữ và 20 nam. Tỷ lệ công nhân nữ
tốt nghiệp phổ thông trung học là 15%, còn tỷ lệ này ối với nam là 20%.
a. Gặp ngẫu nhiên một công nhân của phân xưởng. Tìm xác suất ể người công nhân
tốt nghiệp phổ thông trung học là nữ.
b. Gặp ngẫu nhiên hai công nhân của phân xưởng. Tìm xác suất ể có ít nhất một người
tốt nghiệp phổ thông trung học trong số hai người gặp. ĐS: a)0,6; b)0,3056
BT17. Một cửa hàng bán một loại sản phẩm do hai công ty A và B cung cấp với tỷ lệ sản
phẩm của công ty A và B có trong cửa hàng tương ứng là 55% và 45%. Theo thống kê tỷ
lệ phế phẩm của công ty A và B tương ứng là 2% và 3%. Một khách hàng ến mua ngẫu
nhiên 1 sản phẩm của cửa hàng.
a. Tính xác suất ể khách hàng mua ược chính phẩm
b. Giả sử sản phẩm khách hàng mua là phế phẩm. Khi ó khả năng phế phẩm này do
công ty nào cung cấp là cao hơn.
ĐS:a)0,9755; b)Phế phẩm khách mua do công ty B cung cấp là cao hơn lOMoAR cPSD| 58794847
BT18.Có 2 xạ thủ loại 1 và 8 xạ thủ loại 2, xác suất bắn trúng ích của các xạ thủ theo thứ tự là 0,9 và 0,8
a. Lấy ngẫu nhiên một xạ thủ và cho xạ thủ ó bắn một viên ạn. Tính xác suất bắn trúng ích
b. Lấy ngẫu nhiên hai xạ thủ và mỗi người bắn một viên ạn thì khả năng hai viên ạn
cùng trúng ích là bao nhiêu?. ĐS:a)0,82; b)0,672
BT19. Có ba hộp ựng sản phẩm
Hộp I: có 15 sản phẩm tốt và 5 sản phẩm xấu
Hộp II: có 10 sản phẩm tốt và 5 sản phẩm xấu
Hộp III có 20 sản phẩm tốt và 10 sản phẩm xấu
Ta gieo một con xúc xắc cân ối và ồng chất, nếu xuất hiện mặt một chấm thì chọn hộp I,
nếu xuất hiện mặt 2 hoặc 3 chấm thì chọn hộp II, nếu xuất hiện một trong các mặt còn lại
thì chọn hộp III. Từ hộp ược chọn ó lấy ngẫu nhiên ra một sản phẩm.
a. Tính xác suất ể lấy ược sản phẩm tốt.
b. Giả sử lấy ược một sản phẩm xấu. Tính xác suất ể sản phẩm xấu thuộc hộp II. ĐS:a)0,6806; b)0,3479
BT20. Có hai hộp ựng sản phẩm, hộp thứ nhất có 12 sản phẩm tốt và 3 sản phẩm xấu, hộp
thứ hai có 10 sản phẩm tốt và 4 sản phẩm xấu.
a. Từ mỗi hộp lấy ra một sản phẩm. Tính xác suất ể lấy ược hai sản phẩm cùng loại.
b. Từ mỗi hộp lấy ra một sản phẩm. Tính xác suất ể lấy ược 1 sản tốt.
c. Từ mỗi hộp lấy ra 2 sản phẩm. Tính xác suất ể lấy ược 3 sản tốt và 1 sản phẩm xấu.
Nếu lấy ược 3 sản phẩm tốt và 1 sản phẩm xấu. Tính xác suất ể sản phẩm xấu thuộc hộp 2.
d. Từ hộp 1 lấy ra 3 sản phẩm và từ hộp 2 lấy ra 2 sản phẩm. tính xác suất ể số sản
phẩm tốt trong hai hộp bằng nhau.
e. Chọn ngẫu nhiên một hộp và từ ó lấy ra 2 sản phẩm. Tính xác suất ể lấy ược 2 sản
phẩm tốt. Biết xác suất lựa chọn các hộp lần lượt là 0,4 và 0,6. lOMoAR cPSD| 58794847
f. Từ hộp thứ nhất bỏ sang hộp thứ hai 1 sản phẩm, sau ó từ hộp thứ hai lấy ra một sản
phẩm. Tính xác suất ể lấy ược sản phẩm tốt.
g. Từ hộp thứ nhất bỏ sang hộp thứ hai 2 sản phẩm, sau ó từ hộp thứ hai lấy ra hai sản
phẩm. Tính xác suất ể lấy ược ít nhất một sản phẩm tốt.
h. Từ hộp 1 lấy ra 3 sản phẩm, từ hộp 2 lấy ra 2 sản phẩm. sau ó trong 5 sản phẩm ã
chọn lấy ra 2 sản phẩm. Tính xác suất ể lấy ược ít nhất một sản phẩm tốt.
ĐS:a)0,6286;b)0,3714;c)0,4458;0,6198;d)0,2412;
e)0,5481;f)0,72;g)0,9364; h)0,9505
BT 21. Một doanh nghiệp có 3 ịa iểm ưa thích như nhau ể ký gửi hàng bán. Xác suất bán
ược lô hàng ở ịa iểm thứ nhất, thứ hai, thứ ba tương ứng là: 0,6; 0,7; 0,8. Biết rằng ở mỗi
ịa iểm người ó ó ký gửi 3 lô hàng và có một ịa iểm bán ược một lô. Tìm xác suất ể ó là ịa iểm thứ nhất. ĐS:0,5026
BT22. Tỷ lệ người dân nghiện rượu ở một vùng là 10%. Biết tỷ lệ người bị viêm gan trong
số người nghiện rượu là 60%, tỷ lệ người bị viêm gan trong số người không nghiện rượu
là 40%.Lấy ngẫu nhiên 1 người,
a. Biết rằng người ó bị viêm gan, tính xác suất người ó nghiện rượu.
b.Nếu người ó không bị viêm gan, tính xác suất ể người ó nghiện rượu ĐS:a)0,1429 b)0,069
BT23. Trong một bệnh viện tỷ lệ bệnh nhân các tỉnh như sau: tỉnh A: 25%, tỉnh B :35%,
tỉnh C: 40%. Biết rằng tỷ lệ bệnh nhân là giáo viên của các tỉnh là: tỉnh A: 2% tỉnh B: 3%,
tỉnh C: 3,5%. Chọn ngẫu nhiên một bệnh nhân
a. Tính xác suất ể bệnh nhân ó là giáo viên.
b. Biết bệnh nhân ó là giáo viên. Tính xác suất ể ó là bệnh nhân của tỉnh C ĐS:a)0,0295 b)0,4746
BT24.Có hai hộp ựng mẫu hàng xuất khẩu. Hộp thứ nhất ựng 10 mẫu trong ó có 6 mẫu
loại A và 4 mẫu loại B. Hộp thứ hai ựng 10 mẫu trong ó có 3 mẫu loại A và 7 mẫu loại B lOMoAR cPSD| 58794847
a. Từ mỗi hộp lấy ngẫu nhiên ra một mẫu hàng. Tính xác suất ể hai mẫu hàng lấy ra cùng loại
b. Giả sử xác suất lựa chọn các hộp là 0,45 và 0,55
c. Chọn ngẫu nhiên một hộp và từ ó lấy ra một mẫu. tính xác suất ể mẫu lấy ra là loại B
d. Chọn ngẫu nhiên một hộp và từ ó lấy ngẫu nhiên ra một mẫu thì ược mẫu loại B.
Hỏi mẫu ó có khả năng thuộc hộp nào nhiều hơn.
e. d.lấy 2 mẫu từ hộp I bỏ sang hộp II, sau ó từ hộp II lấy ra một mẫu. Tính xác suất ể lấy ược mẫu loại B.
ĐS:a)0,46;b)0,565.c.hộp thuộc mẫu 2 nhiều hơn.d)0,673
BT25. Một dây chuyền láp ráp nhận các chi tiết từ hai nhà máy khác nhau. Tỷ lệ chi tiết do
nhà máy thứ nhất cung cấp là 60%, của nhà máy thứ hai là 40%. Tỷ lệ chính phẩm của nhà
máy thứ nhất là 90%, của nhà máy thứ hai là 85%. Lấy ngẫu nhiên một chi tiết trên dây
chuyền và thấy rằng nó tốt. Tìm xác suất ể chi tiết ó do nhà máy thứ nhất sản xuât. ĐS: 0,6136
BT26. Trong những hộ vay tiền của ngân hàng ể nuôi tôm, tỉ lệ hộ làm ăn không có lãi là
5%. Trong các hộ vay tiền ngân hàng ể nuôi tôm mà làm ăn không có lãi, tỉ lệ trả nợ ngân
hàng không úng hạn là 88%. Trong các hộ vay tiền ngân hàng ể nuôi tôm mà làm ăn có lãi,
tỉ lệ trả nợ ngân hàng không úng hạn là 2%.
a. Một hộ ã vay tiền của ngân hàng ể nuôi tôm, thì xác suất hộ ó không trả nợ ngân
hàng úng hạn là bao nhiêu?.
b. Một hộ nuôi tôm ã không trả nợ ngân hàng úng hạn, thì xác suất hộ ó làm ăn không có lãi là bao nhiêu.? ĐS:a)0,063;b)0,6984
BT27. Một công nhân i làm ở thành phố khi trở về nhà có hai ường, anh ta i theo ường thứ
nhất hoặc ường thứ hai. Biết rằng anh ta i ường thứ nhất trong 1/3 trường hợp; còn lại i
theo ường thứ 2. Nếu i lối ường thứ nhất 80% trường hợp anh ta về nhà trước 6 giờ, còn i
theo ường thứ hai chỉ 70% trường hợp. Tìm xác suất ể lOMoAR cPSD| 58794847
a. Anh ta về nhà sau 6 giờ.
b. Nếu anh ta về trước 6 giờ, tính xác suất ể anh ta i theo ường thứ 2. ĐS :a)0,2667 b)0,6364
BT28.Tỷ lệ phế phẩm của sản phẩm X là 20%, chính phẩm là 80%. Để ảm bảo chất lượng,
người ta cho kiểm tra các sản phẩm X trước khi ưa ra thị trường. Thiết bị kiểm tra tự ộng
có ộ chính xác 90% ối với chính phẩm, 95% ối với phế phẩm. Sản phẩm X ược ưa ra thị
trường nếu thiết bị kiểm tra tự ộng coi là chính phẩm.
a. Tính xác suất ể sản phẩm X ược ưa ra thị trường
b. Với các sản phẩm ược ưa ra thị trường thì khả năng sản phẩm là phế phẩm bằng bao nhiêu?
c. Tính xác suất ể thiết bị kiểm tra úng. ĐS:a)0,73 b)0,0137 c)0,91
BT29.Hội ồng quản trị doanh nghiệp gồm 7 thành viên và mọi vấn ề ược quyết ịnh theo a
số. Ông chủ tịch muốn thông qua một ề án kinh doanh do ông soạn thảo. Giả sử khả năng
ủng hộ hay phản ối của mỗi thành viên trong hội ồng là như nhau.
a. Tính xác suất ể ề án ược thông qua.
b. Giả sử hội ồng quản trị ngoài ông chủ tịch ra còn có hai thành viên khác là ảng viên
lập thành một chi bộ và chi bộ họp trù bị ể thông qua ề án cũng theo nguyên tắc a
số.Sau ó ra cuộc họp chung thì ảng viên phải tuân theo nghị quyết của chi bộ. Tính
xác suất ể ề án ược thông qua. ĐS:a)0,65625 b)0,71875
BT30. Trong một kho rượu, số lượng chai rượu loại A và loại B là như nhau. Người ta lấy
ngẫu nhiên ra một chai rượu trong kho và ưa cho 4 người sành rượu nếm thử ể xem ây là
loại rượu nào. Giả sử mỗi người có khả năng oán úng là 80%. Có 3 người kết luận chai
rượu loại A và một người kết luận chai rượu loại B. Vậy chai rượu ó thuộc loại A với xác suất là bao nhiêu? ĐS:0,941 lOMoAR cPSD| 58794847
BT31.Hai nhà máy cùng sản xuất một loại sản phẩm. Nhà máy I sản xuất gấp 3 lần nhà
máy số II. Tỷ lệ phế phẩm của nhà máy I và máy II tương ứng là 10% và 20%. Lấy ngẫu
nhiên một sản phẩm trong kho chung của hai nhà máy ể kiểm tra thì gặp phải phế phẩm.
Tính xác suất ể phế phẩm ó do máy thứ hai sản xuất ĐS:0,4
BT32. Bắn 3 phát vào một máy bay với xác suất trúng tương ứng là 0,4;0,5 và 0,7. Nếu
trúng một phát thì xác suất rơi máy bay là 0,2, nếu trúng hai phát thì xác suất rơi là 0,6, còn
nếu trúng cả 3 phát thì chắc chắn máy bay rơi. Tìm xác suất ể máy bay bị rơi. ĐS:0,458
BT33.Một công ty chế biến thủy sản có 3 xí nghiệp A,B,C cùng sản xuất một loại sản phẩm
với sản lượng tương ứng theo tỷ lệ 3:3:4. Tỷ lệ sản phẩm ạt tiêu chuẩn xuất khẩu trong xí
nghiệp A là 70%, trong xí nghiệp B là 65%, trong xí nghiệp C là 60%.
a. Tính tỷ lệ sản phẩm ạt tiêu chuẩn xuất khẩu nói chung của cả ba xí nghiệp
b. Chọn ngẫu nhiên 5 sản phẩm của công ty (loại sản phẩm do 3 xí nghiệp này sản
xuất), kiểm tra thì thấy tất cả ều ạt tiêu chuẩn xuất khẩu. Tính xác suất ể 5 sản phẩm ó là của xí nghiệp C. ĐS:a)0,645 b)0,007
BT34 Chủ cửa hàng nhập về một loại nước hoa. Ông ta biết trong số ó có hàng chính hãng và
hàng "nhái" và kinh nghiệm cho biết tỷ lệ hàng "nhái" là 30%. Ông ta lấy ngẫu nhiên một hộp
nước hoa rồi ưa cho 4 người thử ể xác ịnh xem ây là hàng loại nào. Giả sử xác suất oán úng
của mỗi người là 70%. Có 3 người kết luận hộp nước hoa ó là chính hãng và 1 người kết luận
hộp nước hoa là hàng "nhái". Vậy khi ó xác suất chọn ược hộp hàng "nhái" là bao nhiêu? ĐS: 0,073
BT35. Một lớp có số học sinh nam bằng 3 lần số học sinh nữ. Tỷ lệ học sinh nữ giỏi Toán là
30% và tỷ lệ học sinh nam giỏi toán là 40%. Chọn ngẫu nhiên một học sinh trong lớp này. Tính xác suất ể:
a. Học sinh này giỏi Toán
b. Học sinh này là nam biết rằng học sinh này giỏi Toán. lOMoAR cPSD| 58794847 ĐS:a) 0,375;b)0,8
BT36. Một nhà máy có ba phân xưởng I, II,III cùng sản xuất ra một loại sản phẩm. Phân xưởng
I, II,III sản xuất tương ứng 35%, 40%,25% sản lượng của nhà máy, với tỷ lệ phế phẩm tương
ứng của các phân xưởng lần lượt là 0,12;0,1;0,05. Lấy ngẫu nhiên một sản phẩm kiểm tra
a. Tính xác suất ể lấy ược phế phẩm.
b. Nếu lấy ược phế phẩm. Tính xác suất ể phế phẩm ó do phân xưởng III sản xuất. ĐS:a)0,0945;b)0,1323
BT37. Một nhà máy sản xuất với tỷ lệ phế phẩm là 12%.
a.Lấy ngẫu nhiên lần lượt 20 sản phẩm theo phương thức có hoàn lại. Tính xác suất ể
i. Có úng một phế phẩm
ii. Có ít nhất một phế phẩm
iii. Có nhiều nhất một phế phẩm
b.Phải quan sát ít nhất bao nhiêu sản phẩm ể xác suất nhận ược ít nhất một phế phẩm ≥0,95
ĐS.a)i.0,2115;ii.0,922;iii.0,2891;b)24
BT38.Một nhà máy sản xuất bóng èn, máy A sản xuất 25%, máy B 35%, máy C 40% số
bóng èn. Tỉ lệ sản phẩm hỏng của mỗi máy trên số sản phẩm do máy ó sản xuất lần lượt là
3%;2% và 1%. Một người mua một bóng èn do nhà máy ó sản xuất.
a. Tính xác suất ể sản phẩm này do nhà máy A sản xuất.
b. Tính xác suất ể sản phẩm này tốt .
c. Biết rằng sản phẩm này xấu, tính xác suất ể sản phẩm này do nhà máy C sản xuất.
ĐS; a)0,25;b)0,9815; c)0,2162
BT39. Một bộ ề thi có 20 câu hỏi. Sinh viên giỏi sẽ trả lời úng hết cả 20 câu. Sinh viên khá trả
lời úng 15 câu.Sinh viên trung bình trả lời úng 10 câu. Sinh viên kém trả lời úng 5 câu. Tỷ lệ
sinh viên giỏi, khá , trung bình và kém lần lượt là 10%,20%;30% và 40%. Một sinh viên lên
bắt thăm 3 câu từ 20 câu trên. Giám khảo thấy anh ta trả lời úng cả 3 câu. Tính xác suất anh ta là sinh viên khá lOMoAR cPSD| 58794847 ĐS:0,3713
BT40.Hai người cùng dự thi vào một trường ại học. Xác suất ể người thứ nhất thi ỗ là 0,8,
người thứ hai thi ỗ là 0,9. Xác suất có ít nhất một người thi ỗ là 0,99. Tính xác suất các biến cố sau ây
a. Cả hai người cùng thi ỗ
b. Chỉ có một người thi ỗ c. Cả hai ều trượt.
d. Nếu người thứ nhất thi ỗ. Tính xác suất ể người thứ hai thi trượt
ĐS: a)0,71;b)0,28; c)0,01;d)0,1125
BT41. Một nhà máy sản xuất ô tô gồm 4 phân xưởng A,B,C và D. Biết rằng mỗi phân xưởng
tham gia vào quá trình sản xuất lần lượt là 20%,10%;40% và 30%. Khả năng làm hỏng sản
phẩm của mỗi phân xưởng là 5%;2%;8% và 6%. Sau khi ô tô xuất xưởng, chọn ngẫu nhiên
một chiếc ô tô ể kiểm tra.
a. Tính xác suất ể chiếc ô tô kiểm tra bị hỏng
b. Giả sử chiếc ô tô kiểm tra bị hỏng. tính xác suất ể lỗi này do phân xưởng C gây ra. ĐS: a)0,062;b)0,516
BT42. Một nhà máy có 3 phân xưởng. Phân xưởng I ,II và III có tỷ lệ phế phẩm là 1%;5% và
8%. Biết rằng tỷ lệ tham gia chế tạo sản phẩm của 3 phân xưởng là 2:3:5. Từ kho của nhà máy
lấy ra ngẫu nhiên một sản phẩm ể kiểm tra
a.Tính xác suất ể lấy ược phế phẩm.
b.Giả sử lấy ược phế phẩm. Tính xác suất ể sản phẩm ó do phân xưởng II sản xuất. ĐS: a)0,057;b)0,263
BT43. Có 3 hộp ĩa mềm, mỗi hộp có 10 ĩa. Trong ó hộp I có 2 ĩa hư, hộp II có 3 ĩa hư và hộp III có 4 ĩa hư.
a. Chọn ngẫu nhiên một hộp và lấy ra một ĩa thì ược ĩa tốt. Tính xác suất ể ĩa này ược lấy ra từ hộp I
b. Lấy từ hộp I ra một ĩa, từ hộp II ra một ĩa. Từ hai ĩa ã chọn này lấy ra một ĩa.
Tính xác suất chọn ược ĩa tốt. lOMoAR cPSD| 58794847 ĐS:a) 0,381;b)0,75
BT44. Một nhà máy sản xuất bóng èn có hai phân xưởng I và II. Biết rằng phân
xưởng II sản xuất gấp 4 lần phân xưởng I, tỷ lệ bóng hỏng của phân xưởng I là 5%,
phân xưởng II là 8%. Một người mua 1 bóng èn do nhà máy sản xuất.
a. Xác suất ể người ó mua ược bóng không hỏng.
b. Biết người ó mua phải bóng không hỏng, tính xác suất ể bóng ó do phân xưởng II sản xuất.