Bài tập chương 1 Xác suất thống kê | Trường Đại học Công nghệ, Đại học Quốc gia Hà Nội
Bài tập chương 1 Xác suất thống kê | Trường Đại học Công nghệ, Đại học Quốc gia Hà Nội được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn sinh viên cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!
Môn: Xác suất thống kê (MAT1011)
Trường: Trường Đại học Công nghệ, Đại học Quốc gia Hà Nội
Thông tin:
Tác giả:
Thông tin :
Môn:
Trường:
Trường Đại học Công nghệ, Đại học Quốc gia Hà Nội
Tác giả:
Tài liệu liên quan:
Preview text:
\Bài tập chương 1: Biến cố và xác suất của biến cố
Bài 1. (Sách Walpole 2.26) Một nghiên cứu đã kết luận rằng 7 nguyên tắc sống khỏe sau đây có thể
nâng cao tuổi thọ trung bình 11 năm cho nam giới và 7 năm cho nữ giới. Đó là: 1) không hút thuốc
5) duy trì cân nặng hợp lý
2) thể dục thường xuyên 6) ăn sáng
3) hạn chế đồ uống có cồn 7) không ăn vặt 4) ngủ 7-8 tiếng/ngày
Hỏi có bao nhiêu cách một người có thể chọn 5 trong 7 nguyên tắc kể trên
a. nếu người đó đang vi phạm cả 7 nguyên tắc 7C5
b. nếu người đó không bao giờ dùng đồ uống có cồn và luôn ăn sang
Bài 2. (Sách Walpole 2.31) Nhân chứng của 1 vụ tai nạn ô tô mô tả cho cảnh sát rằng: Biển số xe gây
tai nạn có các chữ cái RLH cố định rồi đến 3 chữ số, trong đó chữ số đầu tiên là 5. Nhân chứng này
không nhớ được 2 chữ số cuối nhưng chắc chắn 3 chữ số khác nhau. Hãy cho biết số biển số đăng ký tối
đa mà cảnh sát sẽ phải kiểm tra.
Bài 3. (Sách Walpole 2.33) Một bài kiểm tra trắc nghiệm có 5 câu hỏi, mỗi câu có 4 phương án trả lời
với duy nhất 1 phương án đúng.
a. Có bao nhiêu cách khác nhau một sinh viên có thể làm bài kiểm tra này biết rằng sinh viên chỉ
được chọn 1 trả lời cho mỗi câu hỏi?
b. Có bao nhiêu cách khác nhau một sinh viên có thể làm bài kiểm tra này biết rằng sinh viên chỉ
được chọn 1 trả lời cho mỗi câu hỏi và tất cả đều sai?
Bài 4. (Sách Walpole 2.80) Xác suất 1 xe máy đi đổ xăng cần được thay dầu là 0.25; xác suất nó cần
thay lọc dầu mới là 0.40; và xác suất vừa cần thay dầu vừa cần thay lọc dầu mới là 0.14.
a. Nếu xe phải thay dầu, xác suất cần thay lọc dầu mới là bao nhiêu?
b. Nếu xe phải thay lọc dầu mới, xác suất cần thay dầu là bao nhiêu?
Bài 5. (Sách Walpole 2.87) Một nhân viên tư vấn bất động sản có 8 chìa khóa để mở một số căn nhà
mới. Chỉ 1 chìa có thể mở được mọi nhà, 7 chìa kia không mở được nhà nào trong các nhà đang xét.
Biết 40% trong số các nhà này luôn không khóa, các nhà còn lại luôn khóa. Hãy tính xác suất để nhân
viên này có thể mở một căn nhà nhất định nếu anh ta chọn ngẫu nhiên 3 trong 8 chìa trước khi rời văn phòng.
Bài 6. (Sách Walpole 2.89) Một phường có 2 xe cứu hỏa hoạt động độc lập. Xác suất để một xe có mặt khi cần là 0.96.
a. Tính xác suất không xe nào có mặt khi cần.
b. Tính xác suất duy nhất 1 xe có mặt khi cần.
Bài 7. (Sách Đ.H.T I.8) Ở một nước có 50 tỉnh, mỗi tỉnh có 2 đại biểu quốc hội. Người ta chọn ngẫu
nhiên 50 đại biểu trong số 100 đại biểu để thành lập 1 ủy ban. Tính xác suất để
a. Trong ủy ban có ít nhất 1 đại biểu của thủ đô.
b. Mỗi tỉnh đều có đúng 1 đại biểu trong ủy ban.
Bài 8. (Sách Đ.H.T I.16) Một đoàn tàu gồm 3 toa đỗ ở sân ga. Có 5 hành khách bước lên tàu. Mỗi hành
khách độc lập với nhau chọn ngẫu nhiên 1 toa. Tính xác suất để mỗi toa đều có ít nhất 1 hành khách mới bước lên.
Bài 9. (Sách Walpole 2.90) Trong 1 nghiên cứu về các dòng sông ô nhiễm, ta định nghĩa các biến cố A: dòng sông bị ô nhiễm
B: mẫu nước kiểm tra bị phát hiện ô nhiễm C: được phép câu cá Giả sử và . a. Tính P(ABC) b. Tính c. Tính P(C)
d. Tính xác suất dòng sông bị ô nhiễm nếu biết được phép câu cá và mẫu nước kiểm tra không bị phát hiện ô nhiễm.
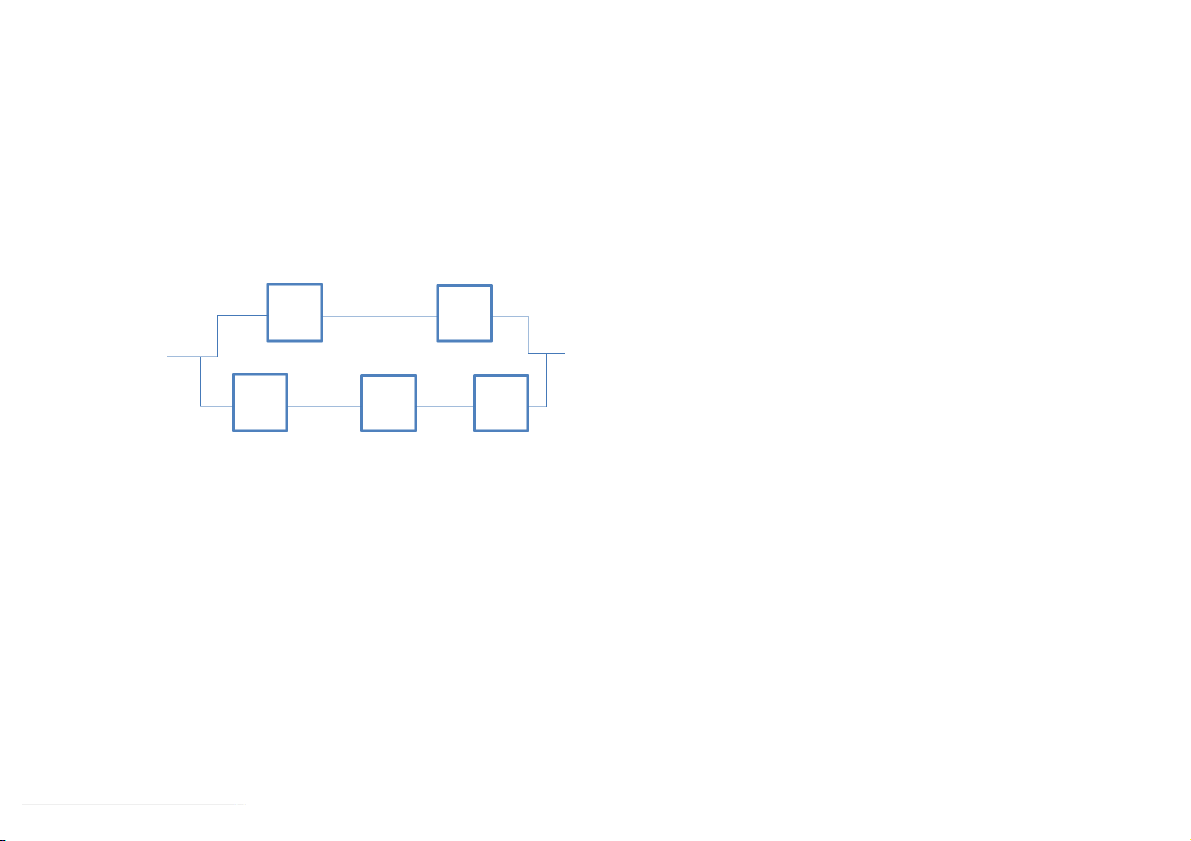
Bài 10. (Sách Walpole 2.93, 2.94) Xét mạch điện cho trong hình vẽ. Giả sử việc hỏng hóc của các thiết
bị thành phần diễn ra độc lập với nhau.
a. Tính xác suất để cả hệ thống hoạt động.
b. Biết hệ thống hoạt động, tính xác suất để A hỏng.
c. Biết hệ thống không hoạt động, tính xác suất để A hỏng. A B 0.7 0.7 C D E 0.8 0.8 0.7
Bài 11. (Sách Walpole 2.127) Việc nữ hoàng có mang gene dễ xuất huyết (hemophilia) hay không được
chuẩn đoán là 50-50. Nếu nữ hoàng mang gene này thì mỗi hoàng tử có 50% nguy cơ mang bệnh dễ
xuất huyết. Việc mang bệnh của các hoàng tử là độc lập với nhau. Nếu nữ hoàng không mang gene này
thì hoàng tử không bị bệnh dễ xuất huyết.
a. Biết rằng nữ hoàng có 3 hoàng tử không bị bệnh, tính xác suất nữ hoàng mang gene hemophilia. 1/9
b. Nếu có hoàng tử thứ tư, xác suất hoàng tử này bị bệnh dễ xuất huyết là bao nhiêu?
Bài 12. (Sách Đ.H.T 1.32) Một cặp trẻ sinh đôi có thể do cùng một trứng (sinh đôi thật), hay do hai
trứng khác nhau sinh ra (sinh đôi giả). Các cặp sinh đôi thật luôn có cùng giới tính. Đối với cặp sinh đôi
giả thì giới tính của mỗi đứa độc lập với nhau và có xác suất 0.5 là con trai. Thống kê cho thấy 34% cặp
sinh đôi đều là trai, 30% cặp sinh đôi đều là gái, và 36% cặp sinh đôi có giới tính khác nhau.
a. Tìm tỉ lệ cặp sinh đôi thật.
b. Chọn ngẫu nhiên một cặp sinh đôi thì được một cặp có cùng giới tính. Tính xác suất để đó là cặp sinh đôi thật.
Bài 13. (Monty Hall, xem slides) Có 3 cánh cửa. Đằng sau một cánh cửa là ô tô, hai cánh còn lại là hai
con dê. Nếu bạn chọn cửa 1, Monty Hall sẽ mở một trong hai cánh cửa còn lại thỏa mãn điều kiện đằng
sau cánh cửa đó là 1 con dê. Bạn có cơ hội chọn lại. Liệu chọn lại có giúp bạn có cơ hội rinh quà cao hơn không?