Bài tập Chương 2: Động lực học chất điểm môn Vật lý đại cương 2 | Đại học Bách Khoa Hà Nội

Chương 2
ĐỘNG LỰC HỌC CHẤT ĐIỂM
TÓM TẮT LÝ THUYẾT
1. Định luật II Newton hay F  m m
với F là tổng hợp lực tác dụng lên chất điểm; m khối lượng của
chất điểm; véc tơ gia tốc của chất điểm.
2. Trọng lực tác dụng lên vật có khối lượng m P  mg
3. Lực hướng tâm 2 v F  m (R )
là bán kính cong của quỹ đạo n R
4. Định lí về động lượng d - Định lí 1:  F ; (
là véc tơ động lượng của chất điểm) dt - Định lí 2:  2 1  t2
5. Biểu thức lực ma sát trượt (khô)
F  kN ; (k là hệ số ma sát, N )
là phản lực pháp tuyến ms
6. Định lí về mô men động lượng dL  M dt - Trong đó L 
là mô men động lượng của chất điểm. M 
là mô men của lực tác dụng lên chất điểm đối với gốc O.
- Trường hợp chất điểm chuyển động tròn, định lý có dạng d I dt - Với 2
I  mr là mô menquán tính của chất điểm đối với gốc O
7. Định luật Newton áp dụng cho chất điểm trong hệ qui chiếu phi quán tính
- Trong hệ quy chiếu O' chuyển động tịnh tiến so với hệ qui chiếu
quán tính O với gia tốc A m qt Với
là gia tốc chất điểm trong hệ O’; F ngoại lực tác dụng lên
chất điểm; F  mA là lực quán tính đặt lên chất điểm. qt BÀI TẬP VÍ DỤ
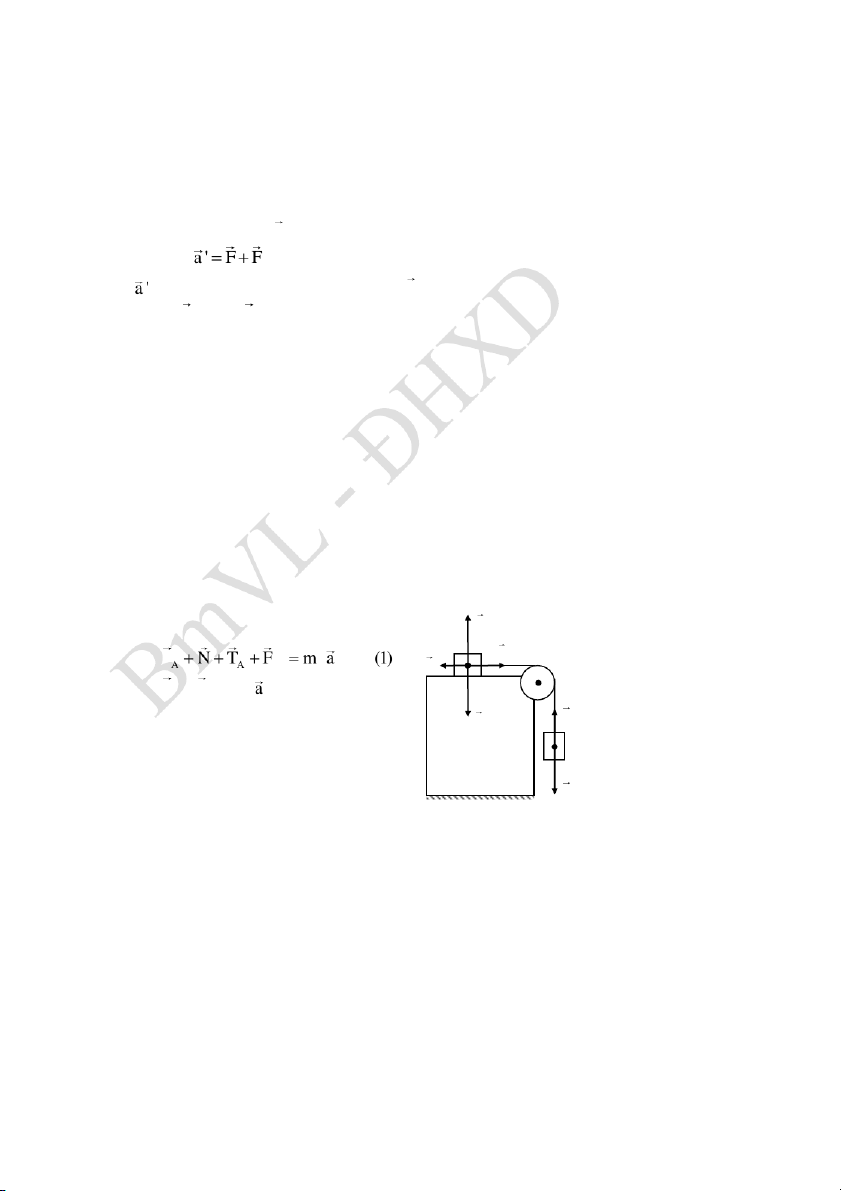
Ví dụ 1. Người ta gắn vào mép bàn một ròng rọc có khối lượng
không đáng kể. Hai vật A và B có khối lượng lần lượt m  200 g A
và m  300 g được nối với nhau bằng một sợi dây vắt qua ròng B
rọc. Ma sát giữa vật A và mặt bàn có k  0, 25 . Lấy 2 g  10m / s .
a. Xác định gia tốc chuyển động của hệ vật.
b. Tính lực căng của dây và lực nén lên trục của ròng rọc. Bỏ qua
khối lượng dây và ma sát ở ròng rọc.
c. Nếu thay đổi vị trí vật A và B cho nhau thì lực căng của dây sẽ
bằng bao nhiêu. Xem hệ số ma sát giữa vật và bàn vẫn như cũ. Lời giải
a. Xác định gia tốc của hệ
- Theo định luật II Newton ta có: N  A P TA ms A A  Fms P  T  m (2) B B B B
- Chiếu (1) và (2) tương ứng lên phương T P B
chuyển động của A và B, chọn chiều A
dương là chiều chuyển động, ta được: B T  F  m a (3) A ms A A  P P  T  m a (4) B B B B B 
- Ở đây ta chú ý, vì dây không giãn nên a  a  a , ròng rọc A B
không khối lượng nên T  T  T . A B
- Mặt khác F  kN  kP (do P  N ). Kết hợp với (3) và (4) ta ms A A có gia tốc của hệ: P  Fms P kP m km B B A B A a    g m  m m m m m A B A B A B 10 0,3 0,25.0,2   5  2 m/s  0,2 0,3
b. Tính lực căng của dây, lực nén lên trục ròng rọc
- Để xác định lực căng T, thay a vào (4) ta có:
T  T  P  m a  m (g  a)  0,3(10  5) 1,5 N B B B B  
- Ròng rọc chịu hai lực căng T và phản lực của trục ròng rọc, như
vậy ta thấy lực nén lên trục ròng rọc chính là hợp lực của hai lực
căng T, do đó ta có lực nén lên trục ròng rọc: Q  2T 1,5 2 N
c. Thay đổi vị trí vật A và B, ta cũng tính tương tự như trên và sẽ
tìm được những biểu thức về gia tốc của hệ và lực căng T của
dây tương tự như phần trên, chỉ khác là thay mA bằng mB và
thay mB bằng mA, dễ dàng thấy rằng lực căng T của dây vẫn không thay đổi.
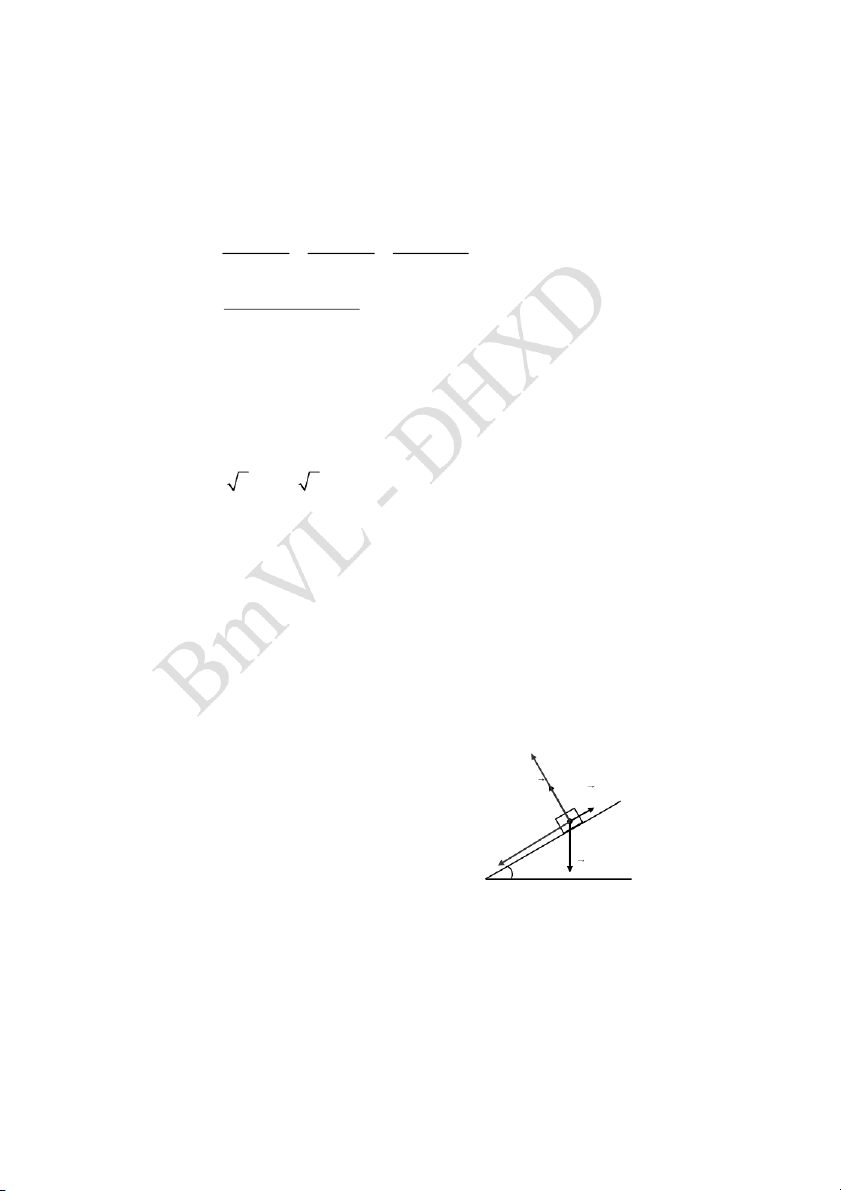
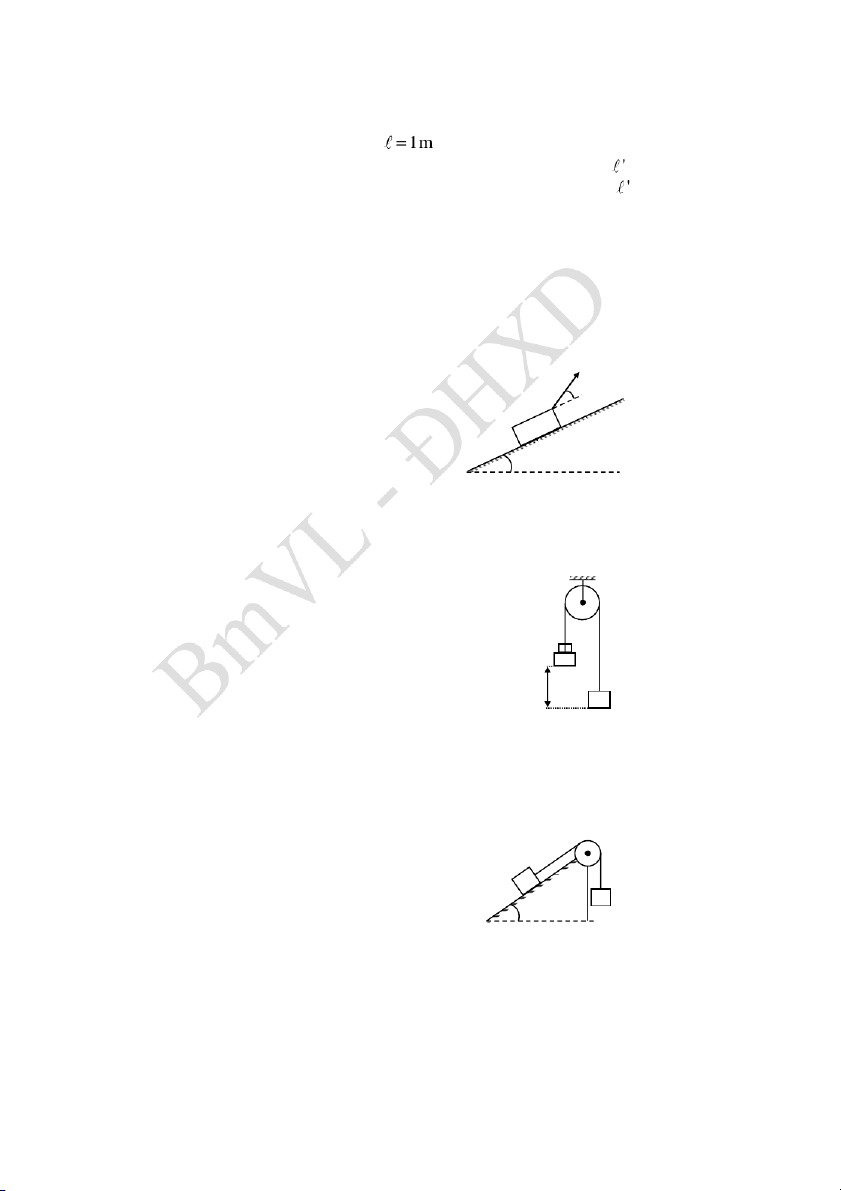
Ví dụ 2. Một vật đặt trên đỉnh dốc dài 165m, góc nghiêng của dốc
là  , hệ số ma sát giữa vật và mặt dốc k  0, 2 . Lấy 2 g  9,8m / s .
a. Với giá trị nào của  vật sẽ nằm yên mà không trượt. b. Cho 0
  30 . Hãy tìm thời gian vật trượt xuống hết đoạn dốc và
vận tốc của vật ở chân dốc. Lời giải y
a. Xác định giá trị của  để vật nằm cân bằng N Fmsn
- Chọn hệ trục xOy như hình vẽ. Khi vật nằm cân bằng ta có: O x  P P  N  F  0 (1) msn
- Chiếu (1) lên các trục Ox, Oy: Psin   F  0 (2) msn   N P cos  0 (3) - Từ (2) ta có F
 Psin  . Để vật nằm yên không bị trượt trên msn
dốc thì lực ma sát nghỉ  lực ma sát trượt, nên: F  kN  kPcos  msn 0
 Psin   kPcos   tg  k  0, 2    11
- Vậy để vật nằm yên trên mặt dốc thì 0  11 .
b. Tính thời gian trượt và vận tốc ở chân dốc khi 0   30 - Với 0
  30 , vật sẽ trượt trên mặt dốc, ta có: P  N  F  m (4) ms - Chiếu (4) lên Ox, Oy Psin   F  ma (5) ms   N P cos  0 (6)
- Từ (5) và (6) ta tìm được: a  g(sin   k cos )   9,8 0 0
sin 30 0, 2.cos30  3,2  2 m / s 
- Thời gian để vật trượt hết đoạn dốc s 165m (chú ý rằng vận tốc ban đầu bằng 0): 1 2s 2 s  at  t  10,16 s 2 a
- Vận tốc của vật ở chân dốc:
v  at  3, 2.10,16  32,5 m /s 
Ví dụ 3. Một chất điểm có khối lượng m được ném lên từ một điểm
O trên mặt đất, với vận tốc ban đầu v0 theo hướng nghiêng một góc
 với mặt phẳng ngang. Xác định mô men động lượng của chất
điểm đối với điểm O, tại thời điểm chất điểm đạt độ cao cực đại. (Áp dụng với: 0
m 100g;   30 ; v  25m / s ). 0 Lời giải
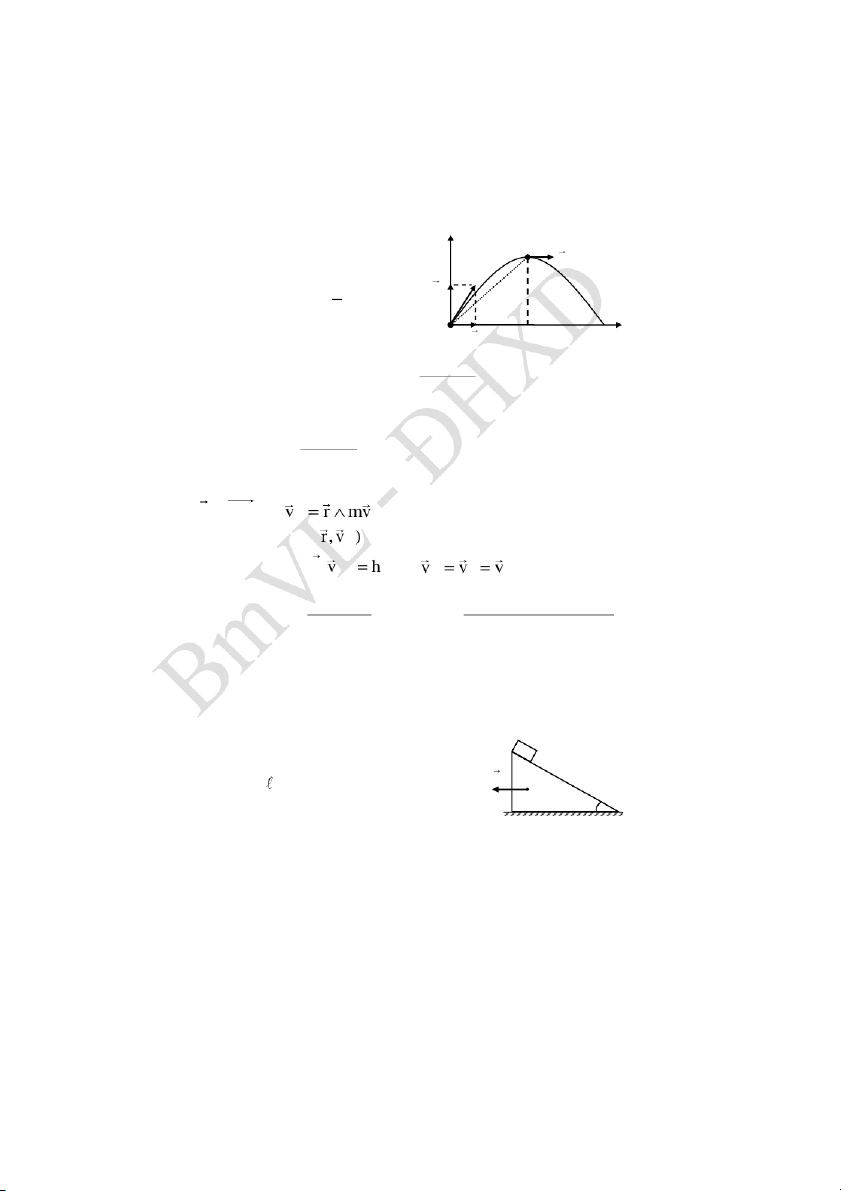
- Chọn hệ trục toạ độ xOy như hình vẽ, gốc thời gian là lúc ném.
- Phương trình chuyển động: y  A x  v cos  .t v o   A  voy r  y  v sin 1 2 .t gt h 0  2 max O
- Tại độ cao cực đại A ta có v  0 v x x y ox v sin  0
 v  v sin   gt  0  t   t y 0 1 g
- Thay vào phương trình chuyển động ta được: 2 v sin  0 h  y(t )  max 1 2g
- Mômen động lượng của chất điểm tại A đối với O: L  OA  m A A  L  mv r.sin( A A
- Mặt khác ta có: r.sin r, ; nên: A  max A x ox 2 2 3 2 v sin  mv sin  .cos  0 0     L  h mv  mv cos   max x 0 2g 2g - Thay số ta được:   2 L 28,18 kgm / s .
Ví dụ 4. Một vật khối lượng m đứng yên ở đỉnh một cái nêm nhờ
ma sát. Tìm thời gian vật trượt hết nêm khi cho nêm chuyển động
nhanh dần đều sang trái với gia tốc là a0 . Hệ m
số ma sát giữa mặt nêm và vật m là k, chiều
dài mặt nêm là , góc nghiêng là  và gia a0 tốc a  g.cot g   0   . Lời giải
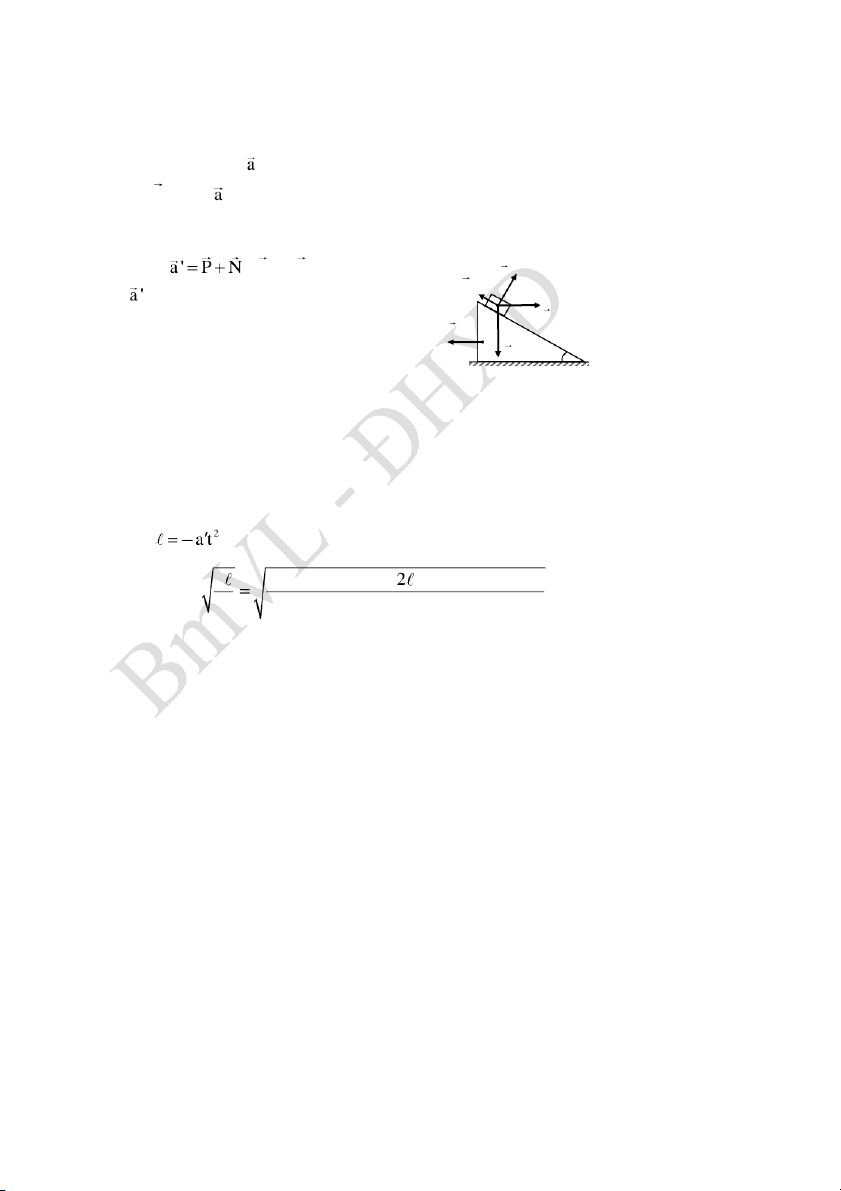
- Xét trong hệ quy chiếu gắn với nêm là hệ quy chiếu chuyển động tịnh tiến với gia tốc
, vật m sẽ chịu thêm lực quán tính: 0 F  m qt 0
- Áp dụng định luật Newton cho vật m trong hệ quy chiếu chuyển
động có gia tốc gắn với nêm, ta có phương trình chuyển động: m  F  F (1) ms qt N
với là gia tốc của vật m trong hệ quy chiếu Fms gắn với nêm. Fqt
- Chiếu (1) lên hướng chuyển động của vật: a0
ma '  Psin   F  F cos (2) P  ms qt
- Chiếu (1) lên hướng vuông góc với hướng chuyển động của vật
và chọn chiều dương hướng lên: 0  P
 cos  N  F sin  (3) qt
- Từ (2) và (3) suy ra gia tốc:
a  g sin  k cos   a cos  k sin  0  
- Để tìm thời gian vật trượt hết nêm, áp dụng phương trình: 1 2 2  t  a
g sin  k cos a cos  k sin  0  
- Chú ý: với a  g.cot g  để phản lực pháp tuyến 0   N  0 . BÀI TẬP ÁP DỤNG
2.1 Một người di chuyển một chiếc xe với vận tốc không đổi.
Lúc đầu người ấy kéo xe về phía trước, sau đó người ấy đẩy xe về
phía sau. Trong cả hai trường hợp, càng xe hợp với mặt phẳng ngang một góc .
 Hỏi trong trường hợp nào, người đó phải đặt lên
xe một lực lớn hơn. Biết trọng lượng của xe là P, hệ số ma sát giữa
bánh xe và mặt đường là k.
2.2 Một dây xích có chiều dài
được đặt trên mặt bàn sao
cho một phần của nó buông thõng xuống đất có chiều dài là .
Cho biết hệ số ma sát giữa xích và bàn là k 1/ 3. Tìm chiều dài
để dây xích bắt đầu trượt trên mặt bàn.
2.3 Một xe vận tải chạy trên đường nằm ngang với vận tốc không
đổi. Sau đó xe lên dốc, nghiêng với mặt nằm ngang một góc 0
 15 . Muốn xe vẫn chuyển động đều với vận tốc như cũ thì lực
kéo của động cơ phải lớn gấp bao nhiêu lần so với khi chạy trên
đường nằm ngang. Ma sát trong hai trường hợp đều có k  0,05.
2.4 Một vật khối lượng m được kéo đi với vận tốc không đổi bởi
một sợi dây trên một mặt phẳng nghiêng
có góc nghiêng  với mặt phẳng ngang. 
Hệ số ma sát giữa vật và mặt phẳng m
nghiêng bằng k. Xác định góc  giữa sợi
dây và mặt phẳng nghiêng để cho sức 
căng nhỏ nhất. Tính giá trị sức căng đó.
2.5 Hai vật có khối lượng m  300 g ; m  480 g được buộc 1 2
vào hai đầu một sợi dây vắt qua một ròng rọc có khối lượng không
đáng kể. Lúc đầu, giữ vật m1 ở dưới vật m2 một khoảng h  2m và
trên vật m2 có đặt vật m  200 g , sau thả cho hệ 3
vật chuyển động. Xác định:
a. Gia tốc của các vật và sức căng của dây.
b. Sau bao lâu vật m1 và m2 ở độ cao như nhau. m3
c. Lực tác dụng của vật m m2 3 lên vật m2 khi hệ
chuyển động. Bỏ qua khối lượng dây và ma sát ở h ròng rọc. m1
2.6 Có hai vật khối lượng m1, m2 liên kết với nhau bằng một sợi
dây vắt qua ròng rọc ở đỉnh của mặt phẳn nghiêng hợp với mặt ngang một góc .
 Vật m1 nằm trên phẳng nghiêng. Hệ số ma sát
giữa m1 và mặt nghiêng là k. Giả thiết lúc đầ u hai vật đứng yên.
a. Với điều kiện nào của tỉ số các khối lượng ( m / m ) để cho vật 2 1
m2: đi xuống; đi lên; đứng yên. m1 m2 
b. Xác định gia tốc của hệ vật trong hai trường hợp đầu. Bỏ qua
khối lượng ròng rọc và dây, ma sát ở ròng rọc không có.
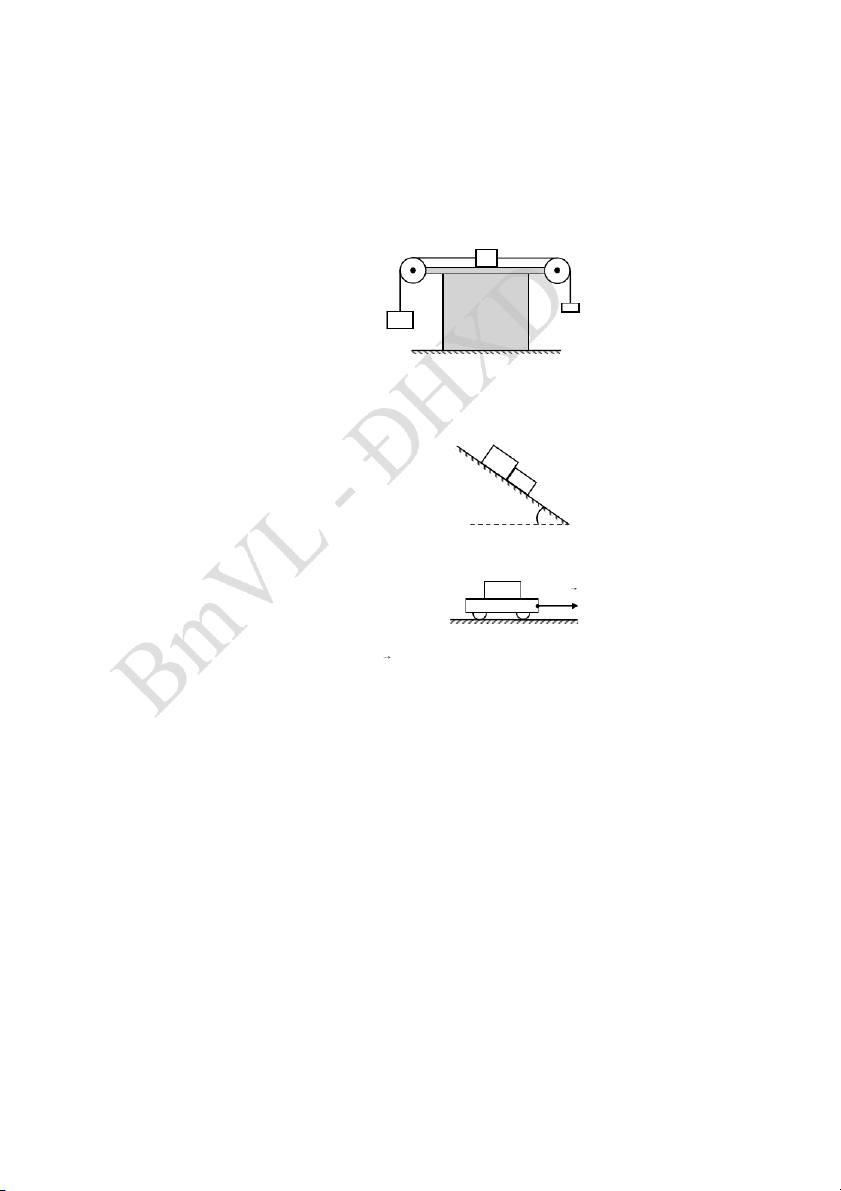
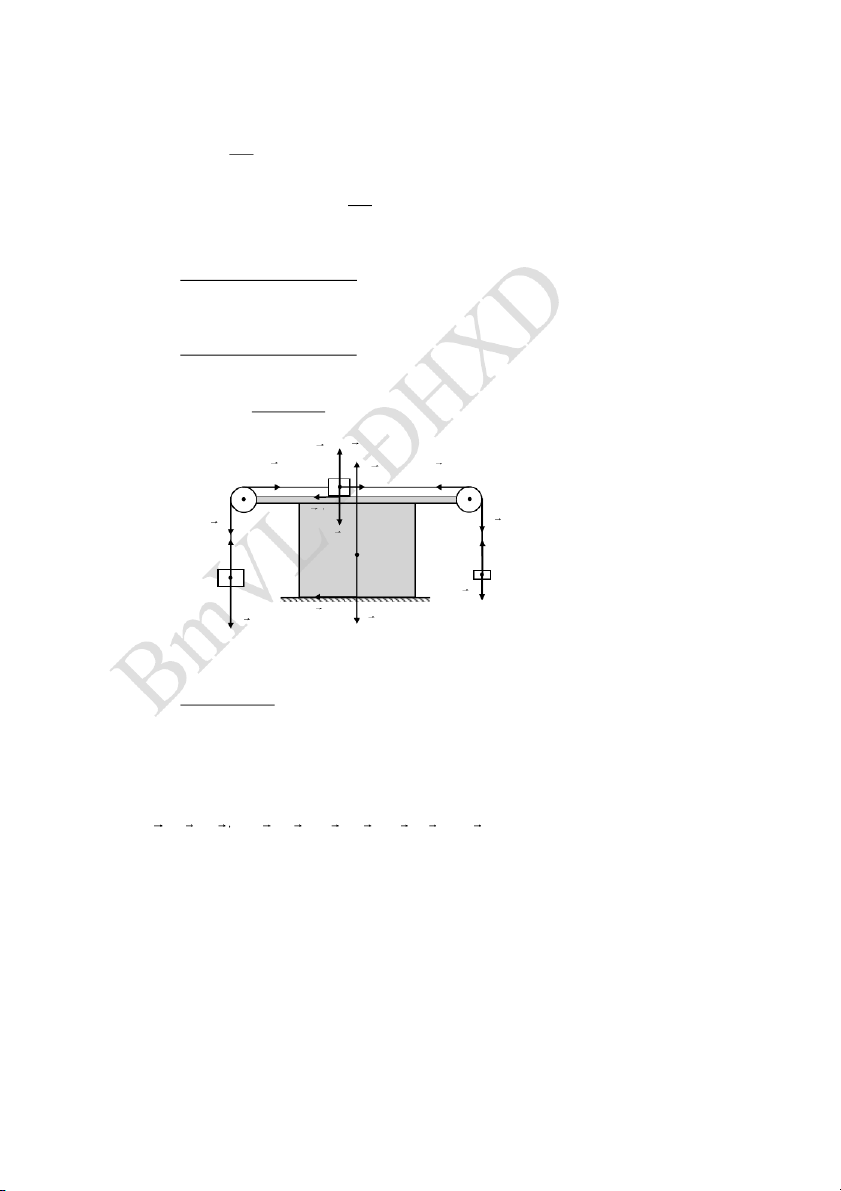
2.7 Trên một cái bàn có khối lượng M, đặt một hệ gồm ba vật có
khối lượng: m, 2m, 3m được liên kết với nhau bằng các sợi dây. Hệ
số ma sát giữa vật 2m và bàn là 2m
k  0,1. Hỏi hệ số ma sát giữa bàn
và mặt sàn phải có giá trị nhỏ nhất
bằng bao nhiêu để bàn đứng yên khi
hệ vật chuyển động. Bỏ qua khối M m
lượng dây và ròng rọc, ma sát ở các 3m
ròng rọc là không đáng kể.
2.8 Trên mặt nghiêng hợp với mặt ngang một góc 0   30 có đặt
hai vật tiếp giáp nhau khối lượng lần lượt là m  1kg , m  2 kg . 1 2
Hệ số ma sát giữa các vật và mặt nghiêng lần m2
lượt là k  0, 25 và k  0,1. 1 2 m1
a. Xác định lực tương tác giữa hai vật khi chuyển động. 
b. Góc nghiêng  phải có giá trị nhỏ nhất
bằng bao nhiêu để cho các vật có thể trượt xuống.
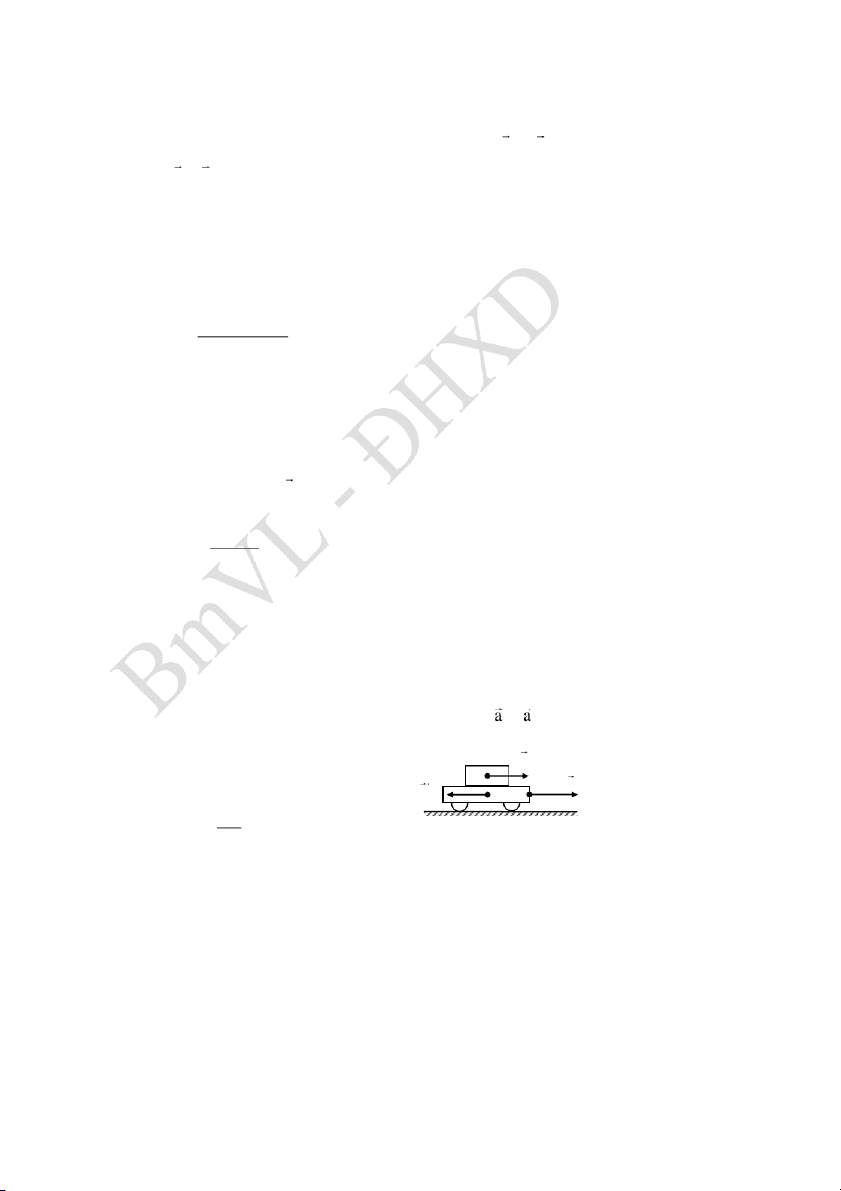
2.9 Một chiếc xe có khối lượng M  20kg
có thể chuyển động không ma sát trên mặt m F M
phẳng ngang. Trên xe đặt một hòn đá khối
lượng m  5kg . Hệ số ma sát giữa đá và xe là
k  0, 2. Người ta đặt lên xe một lực F có phương nằm ngang và
hướng dọc theo xe. Hỏi:
a. Muốn hòn đá không trượt trên xe khi xe chuyển động thì lực F
chỉ có thể có giá trị lớn nhất bằng bao nhiêu?
b. Nếu lực F  60 N hòn đá và xe sẽ chuyển động thế nào? Xác
định gia tốc của hòn đá và xe đối với mặt đất.
2.10 Một viên đạn khối lượng 10g chuyển động với vận tốc
v  200m / s xuyên thẳng vào một tấm gỗ và chui sâu vào một 0
đoạn . Biết thời gian chuyển động của đạn trong tấm gỗ là  4
t  4.10 s. Xác định lực cản trung bình của gỗ và độ xuyên của viên đạn. 
2.11 Một phân tử khí có khối lượng 23 m  4,65.10 g chuyển
động với vận tốc v 160 m / s tới va chạm đàn hồi vào thành bình với góc nghiêng 0
  60 so với pháp tuyến của thành bình. Tính
xung lượng của lực va chạm của phân tử khí lên thành bình.
2.12 Một vật có khối lượng m  1kg chuyển động thẳng trên mặt
sàn ngang theo phương x, với vận tốc ban đầu v 10m / s và chịu 0
lực cản F  rv , với r  1kg / s là hệ số cản và v là vận tốc chuyển c động của vật.
a. Chứng minh rằng vận tốc của vật giảm dần theo hàm số bậc
nhất của quãng đường đi.
b. Tính quãng đường đi được tới lúc dừng.
2.13 Một viên đạn có khối lượng m  10g bay theo phương ngang
trong không khí với vận tốc ban đầu v  500m / s . Cho biết lực 0
cản của không khí tỉ lệ và ngược chiều với vận tốc của viên đạn: F  rv với 3 
là hệ số cản của không khí. Bỏ qua c r 3,5.10 kg / s
ảnh hưởng của trọng lực. Hãy xác định:
a. Khoảng thời gian  để vận tốc viên đạn bằng một nửa vận tốc ban đầu v0.
b. Quãng đường viên đạn bay được theo phương ngang trong
khoảng thời gian  trên.
2.14 Một vật khối lượng m chuyển động từ dưới lên theo phương
thẳng đứng Ox với vận tốc ban đầu v0. Biết lực cản của không khí
tỉ lệ với bình phương vận tốc: 2
F  rv (r là hệ số tỉ lệ). Tính độ
cao cực đại vật lên được và thời gian vật lên đến độ cao cực đại.
2.15 Một chất điểm khối lượng m được ném lên từ một điểm O
trên mặt đất với vận tốc ban đầu v0 theo hướng nghiêng một góc 
với mặt phẳng ngang. Bỏ qua sức cản không khí. Hãy xác định tại
một thời điểm t và đối với điểm O.
a. Mô men ngoại lực tác dụng lên chất điểm.
b. Mô men động lượng của chất điểm.
2.16 Trên trần một thang máy đang đi lên với gia tốc 2
a 1,2 m/ s có gắn một lực kế. Đầu dưới lực kế có treo một ròng 0
rọc, người ta vắt qua ròng rọc một sợi dây và hai đầu dây treo hai
vật khối lượng lần lượt là m  200g , m  300 g . B ỏ qua khối 1 2
lượng và ma sát ở ròng rọc, dây không giã n và có khối lượng không á
đ ng kể đáng kể. Xác định:
a. Gia tốc của vật m1 so với đất và với thang máy.
b. Số chỉ trên lực kế.
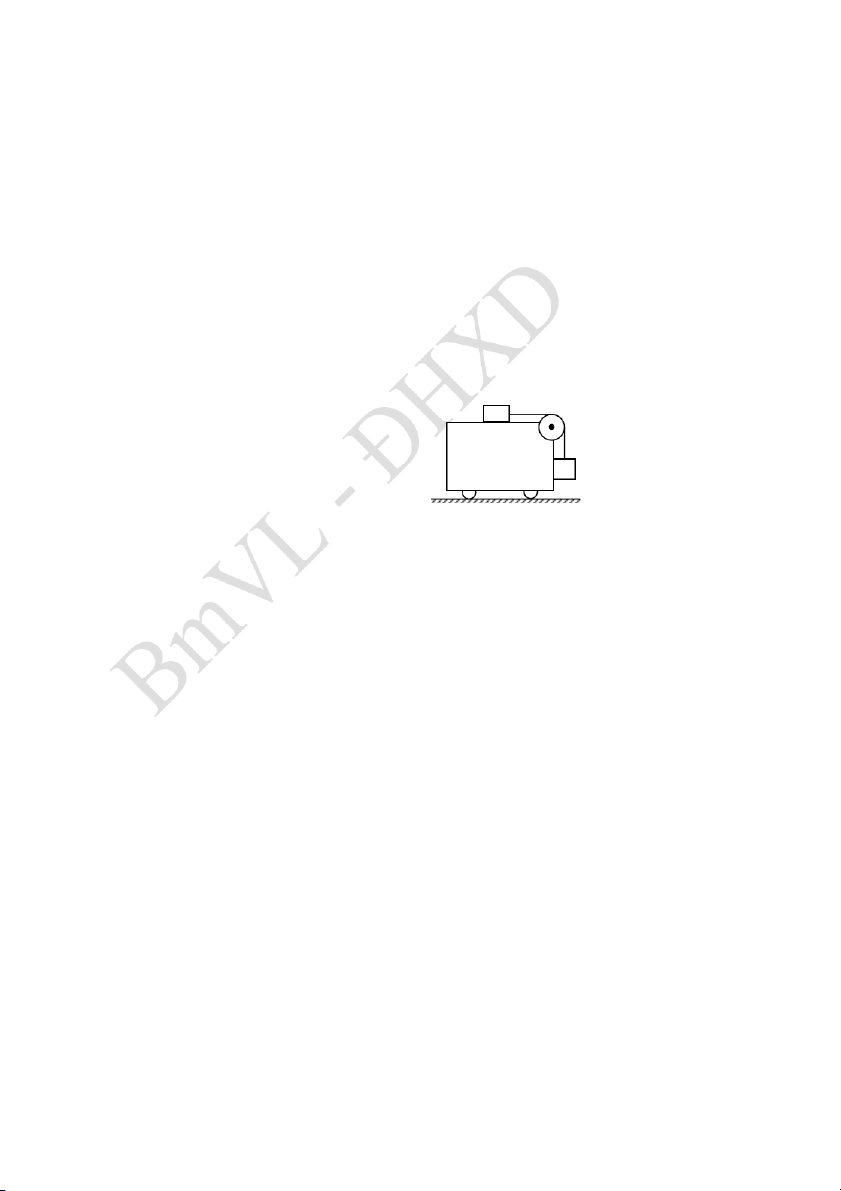
2.17 Cho hệ vật như hình vẽ bê . n Cần phải m1
dịch chuyển một chiếc xe theo phương
ngang với gia tốc nhỏ nhất bằng bao nhiêu
để cho các vật m1 và m2 không chu ển y m
động đối với xe. Cho khối lượng các vật 2
m  300 g , m  500 g ; hệ số ma sát giữa vật m 1 2 1, m2 và xe là
k  0, 2. Bỏ qua khối lượng ròng rọc và dây nối, ma sát ở ròng rọc không đáng kể.
2.18 Hỏi tàu hoả phải có vận tốc bằng bao nhiêu khi chạy qua một
đoạn đường vòng có bán kính R  98m để sợi dây treo quả cầu
buộc vào trần toa tàu lệch so với phương thẳng đứng một góc 0
  45 . Xác định sức căng của dây, biết khối lượng quả cầu là m  500g . Lấy 2 g  9,8m / s .
2.19 Một vật nhỏ khối lượng m  1kg được đặt trên một đĩa
phẳng ngang và cách trục quay của đĩa một khoảng r  0,5m . Hệ
số ma sát giữa vật và đĩa bằng k  0,25. Hỏi:
a. Lực ma sát phải có độ lớn bằng bao nhiêu để vật giữ trên đĩa,
nếu đĩa quay với vận tốc n 12 vòng/phút.
b. Với vận tốc góc nào của đĩa thì vật bắt đầu trượt khỏi đĩa.
2.20 Một máy bay thực hiện một vòng nhào lộn có bán kính 400m
trong mặt phẳng thẳng đứng với vận tốc 540km/h.
a. Xác định lực nén của phi công lên ghế máy bay ở điểm cao nhất
và thấp nhất của vòng nhào lộn, nếu khối lượngcủa phi công bằng 60kg.
b. Muốn cho người lái ở trạng thái không trọng lượng tại điểm cao
nhất của vòng nhào lộn thì vận tốc của máy bay phải bằng bao nhiêu ?
2.21 Một quả cầu khối lượng m  500g được treo vào đầu một sợi dây dài
. Quả cầu quay trong mặt phẳng nằm ngang
với vận tốc không đổi sao cho sợi dây vạch một mặt nón. Cho biết
góc tạo bởi sợi dây và phương thẳng đứng là 0
  30 . Xác định lực
căng dây, vận tốc dài và vận tốc góc của quả cầu.
HƯỚNG DẪN - LỜI GIẢI - ĐÁP SỐ
2.1 Trường hợp đẩy xe về phía sau F
phải dùng lực lớn hơn. F N 2
- Trường hợp kéo xe về phía trước, muốn
xe chuyển động đều phải có: F  F ,  1 F 1 ms
F  kN và N  P  F  P  Fsin  . ms 2 Fms P
- Hay: Fcos   k P  Fsin  N kP 1 F  F  cos  k sin F 
- Trường hợp đẩy xe về phía sau, xe chịu F2
trọng lực P , lực đẩy F , phản lực pháp P m F s
tuyến N ' và lực ma sát F
bằng cách phân tích tính tương tự: ms kP F  cos  ksin
- So sánh F và F' thấy F'  F , suy ra trường hợp đẩy xe về phía sau
phải dùng lực lớn hơn. 2.2   m
- Gọi P1 là trọng lượng của phần buông thõng; P2 là trọng lượng
của phần dây xích nằm trên mặt bàn. Muốn dây bắt đầu trượt phải
có P  F ; trong đó F  kP (chú ý: trọng lượng của các phần 1 ms ms 2
dây xích tỉ lệ với chiều dài), từ đó suy ra: k   m 1 k F
2.3 Đáp số 2  6,1 lần. F1
- Gọi F1, F2 là lực kéo của động cơ trên đường ngang và đường
dốc, muốn xe chuyển động đều thì tổng hợp lực tác dụng lên ôtô
gồm: lực kéo của động cơ, trọng lực P , phản lực pháp tuyến N của
mặt đường và lực ma sát của mặt đường F phải bằng không. ms F  P  N  F  0 ms
- Chiếu phương trình lên hướng chuyển động được biểu thức: F1, F2 và suy ra tỉ số F / F 2 1 mg sin  k cos 
2.4 Đáp số: tg  k; T  min 2 1  k -
Lực tổng hợp tác dụng lên vật:
F  T  P  N  F  0 (1) ms
- Chiếu (1) lên hướng chuyển động và lên phương vuông góc với
hướng chuyển động, ta có: T
 cos  P sin  F  0 (2) ms  T
 sin  N Pcos  0 (3)
 N  Pcos   Tsin
 F  kN  k P cos  Tsin ms   mg sin   k cos  - Thay vào (2) rút ra: T  cos  k sin
- Theo bất đẳng thức Bunhiacốpxki - Côsi:   2   2   2 2 cos k sin 1 k
cos   sin   const 1 cos - Vậy:    2 cos k sin lớn nhất khi:   tg  k k sin - Và cos ksin 2  1 k suy ra: max mgsin  k cos T  min 2 1 k 2.5 Đáp số: a.   2
a 3,8 m / s ; T  4, 08 N b. t  0,73 s c. F  1, 2 N 32   Hướng dẫn:
a. Viết phương trình của đinh luật II Niutơn cho từng vật: P  T  m 1 1 1 m  m T ' 2 3  2 23
- Chiếu lên phương trình chuyển động của hệ: m a  P  T (1) 1 1
m  m a  P  P  T (2) 2 3  2 3
- Chú ý: T  T và a là gia tốc của hệ. Từ (1) và (2) giải ra: a và T. h 1 h 2 b. Ta có: 2 s   at  t    0, 73 s 2 2 a 3,8
c. Tính F23. Xét riêng vật m3, ta có phương trình: m
F ; (F là lực do m2 tác dụng lên m3) hay: 3 2 3 23 23
m a  P  F  F  m g  a và F  F 3 3 23 23 3   32 23 2.6 Đáp số: m a. m 2 2 đi xuống:  sin  kcos m1 m m 2 2 đi lên:  sin  k cos m1 m m 2
2 đứng yên: sin   k cos    sin   k cos  m1 b. Trường hợp 1 m  m sin  k cos 2 1   a   g m  m 1 2 - Trường hợp 2 m sin   k cos  m 1   2 a   g m  m 1 2 0,6m 2.7 Đáp số: k  min M  5, 4m N N 2 T1 2m F T ms2 2 F T ' ms2 T ' 1 P 2 3 m 3m M P1 F P msn PM 3
- Khi bàn đứng yên, hệ vật chuyển động, ta tìm được gia tốc
chuyển động của hệ 3 vật: P  kP  P 3 2 1 a 
 0,3g (với g là gia tốc trọng trường) m  2m 3m
- Lực căng dây nối giữa vật 3m và 2m là: T  2,1mg ; giữa vật 2m 1 và m là: T  1,3mg . 2 -
Xét riêng bàn, để bàn đứng yên thì: T  T ' F
 P  P  T  T ' N  F  0 (1) 1 1 ms2 2 M 2 2 msn - Trong ó:
đ F là lực ma sát do vật 2m tác dụng lên bàn khi nó ms2
trượt trên mặt bàn, có: ' F
 2kmg  0,2mg. N là phản lực của ms2
mặt sàn tác dụng lên bàn; F
là tổng các lực ma sát nghỉ tác dụng msn lên các chân bàn.
- Chiếu (1) lên phương thẳng đứng, chọn chiều dương hướng lên
trên; và chiếu (1) lên phương ngang với chiều dương hướng sang phải, ta được:
T ' T ' P  P  N  0 (2) (với T '  T ; T '  T ) 1 2 2 M 1 1 2 2 ' T  F  T  F  0 (3) 1 ms2 2 msn
- Từ (2) ta có: N  T  T  P  P  M  5, 4m g 1 2 2 M   - Từ (3) ta có: ' F  T  F T  0,6mg msn 1 ms2 2 -
Để bàn đứng yên ta phải có điều kiện: F  F  k .N msn msM  b 0,6m
 0,6mg  k M  5, 4m g  k  b   b M  5, 4m 0,6m
- Vậy hệ số ma sát cực tiểu là: k  min M  5, 4m
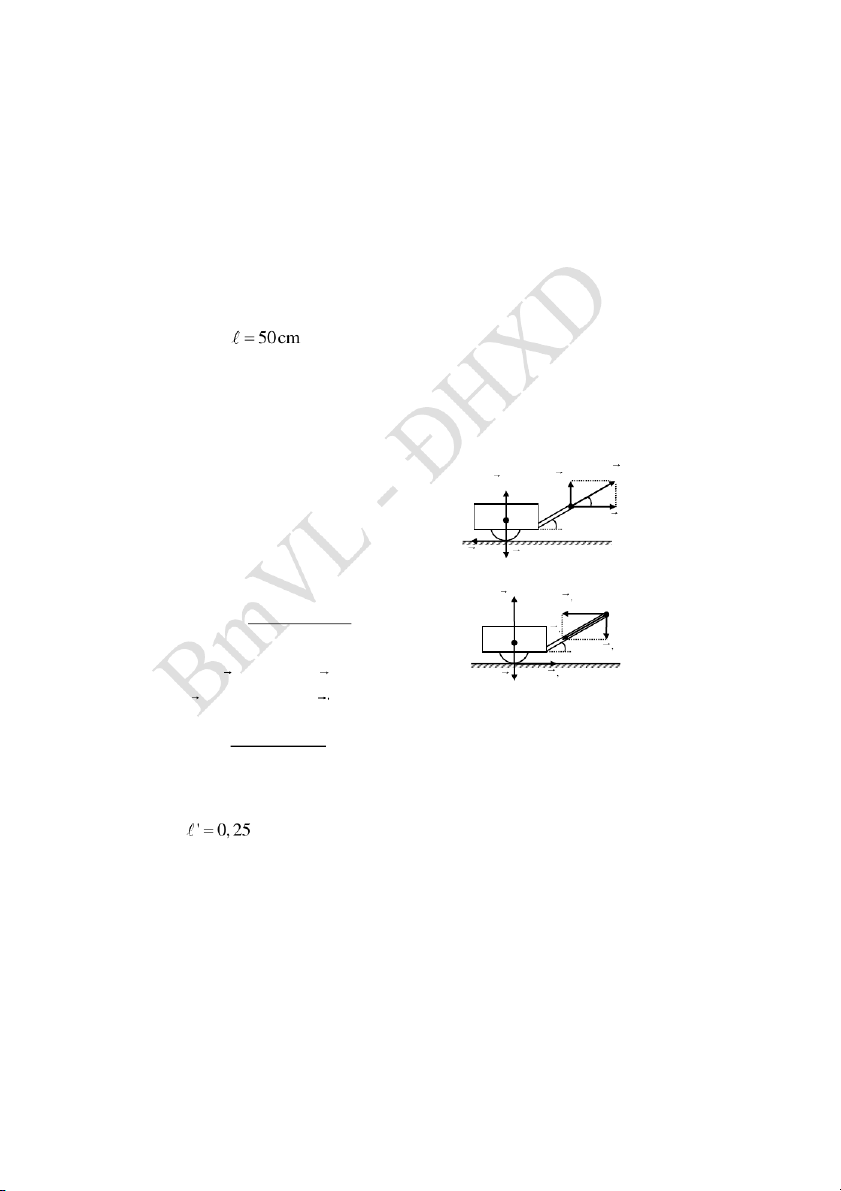
2.8 Đáp số: k k m m cos 1 2  a. 1 2 F  F   0,9 N 12 21   m  m 1 2 k m  k m b. 1 1 2 2 tg  hay 0 '   8 30 min m  m min 1 2 Hướng dẫn:
a. Xác định lực tương tác giữa hai vật
- Vì hệ số ma sát k  k , nên hai vật sẽ cùng trượt xuống trên mặt 1 2
nghiêng; áp dụng định luật II Newton cho hệ 2 vật tìm được gia tốc
a của hệ. Sau xét riêng từng vật m1 (hoặc m2), sẽ tính được lực tương tác F21(hoặc F12). b. Xác định góc  min
- Muốn hệ hai vật trượt xuống, các thành phần lực P , P của t1 t 2
trọng lực P , P theo hướng song song mặt nghiêng thoả mãn điều 1 2 kiện: P  P  F  F (1). F , F
là lực ma sát tác dụng lên t1 t 2 ms1 ms2 ms1 ms2
m1, m2 của mặt phẳng nghiêng.
P  m gsin; P  m g sin t1 1 t 2 2 F  k m g cos ;  F  k m g cos ms1 1 1 ms2 2 2 - Thay vào (1): k m  k m 1 1 2 2 tg  suy ra tg và  m  m min min 1 2 2.9 Đáp số: a. F  49 N max   b. a  1,96  2 m / s ; a  2,51  2 m / s 1 da 2 xe      Hướng dẫn:
a. Xác định lực cực đại F max
- Vì hòn đá không trượt trên xe, nên hệ (đá + xe) cùng chuyển động F với gia tốc a 
(1). Và lực do xe tác dụng lên đá khi chuyển m  M
đông (xét riêng hòn đá): F  ma (2) chính là lực ma sát nghỉ, da
muốn đá không trượt trên xe: ma  F (lực ma sát trượt). ms
F  kmg (là lực ma sát nghỉ cực đại). ms
- Từ (1) và (2): F  kg m  M thay số: F  49 N  F  49 N . max
b. Xác định gia tốc của hòn đá
- Với F  60 N  49 N hòn đá sẽ trượt trên xe. Gọi , là gia 1 2 tốc của hòn đá và xe.
- Với hòn đá: m a  F (1) F 1 1 ms ms m - : Với xe Ma  F  F (2) F 2 ms Fms M F - Từ (1) ms a   kg 1,96 m / s 1  2  m F F - Từ (2) ms  a   2,51 m / s 2  2  M
2.10 Đáp số: F  5  00 N ,  . tb   Hướng dẫn:
- Áp dụng định lý động lượng: mv  F .t suy ra: tb mv F  
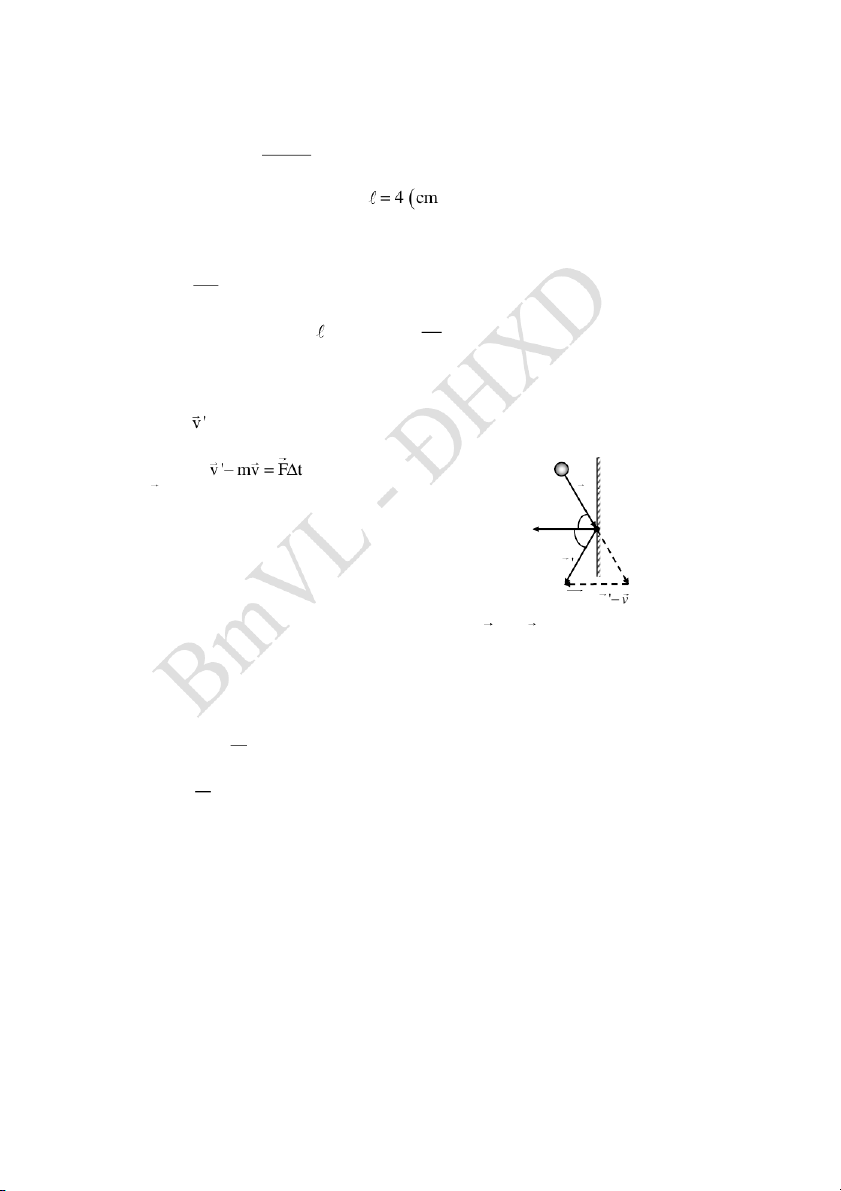
 500 N ; xem chuyển động của đạn trong gỗ là tb   t F chậm dần đều: 2 v  2a (gia tốc tb a   0). m  2.11 Đáp số: 24 F . t   7,44.10 Ns Hướng dẫn: - Gọi
là vận tốc của phân tử khí bật ra sau khi va chạm vào
thành bình; va chạm là đàn hồi v  v , áp dụng định lí động lượng: m (1) m
(F là lực so thành bình tác dụng lên phân tử khí v trong thời gian va chạm t  ). 
- Chiếu phương trình (1) lên phương pháp tuyến O
của thành bình, chiều (+) hướng ra, ta được: v
mv cos  mvcos  F.t    2mv cos   F. t  v v
- Lực do phân tử khí tác dụng lên thành bình F'  F  suy ra xung
lượng của lực do phân tử khí va chạm lên thành bình: 2  4 F t   2mvcos   7,44.10  N  s 2.12 Đáp số: r a. v  v  x 0 m m b. s  v 10 m 0   r Hướng dẫn:
a. Theo định luật II Newton dv ma  F  m  rv c dt mdv  r
 vdt; dx  vdt (phương trình chuyển động của vật là phương x) r mdv  rdx  dv   dx (1) m
- Lấy tích phân 2 vế của (1): v x r r dv   dx  v  v  x   (2) 0 m m v0 0
b. Cho v  0 suy ra quãng đường đi đến lúc dừng, từ (2) có: r 0  v  x 0 m m s  x  v  10 m 0   r 2.13 Đáp số: m a.   ln 2  1,98   s r r   t mv  b. 0 m x  1 e   714 m r   Hướng dẫn:
a. Theo định luật II Newton ta có: dv dv r m  rv    dt (1) dt v m
- Tích phân hai vế phương trình (1) ta được: v t r  t dv r v r m   dt  ln   t  v  v e   (2) 0 v m v m v 0 0 0 v m - Thay 0 v 
vào (2) tìm được   ln 2  1,98   s 2 r
b. Gọi x là quãng đường đi được theo phương ngang r r  t  t dx - Từ (2) ta có: m m v   v e  dx  v e dt (3) 0 0 dt
- Tích phân hai vế phương trình (3) ta được: x t r r  t mv   t  m 0 m dx  v e dt  x  1    e (4) 0  r 0 0  
- Thay t  1,98  s vào (4) ta được x  714 m m  r  2 m  rv 
2.14 Đáp số:   arctg v ; 0 h  ln1 0  rg  mg     2r  mg  Hướng dẫn:
- Theo định luật II Niutơn: dv dv r 2 m  mg  rv    dt dt mg 2 m v r mg dv r - Đặt   ta có   dt (1) r 2   v m
- Lấy tích phân từ v0 đến v ứng với thời gian từ t  0 đến t được:  v r  0 v    tg arctg   t   (2) m    
- Khi vật lên tới độ cao cực đại vận tốc v  0 . v r m v 0 0 arctg   t  0   arctg  m r   mg - Thay  
ta được thời gian chuyển động của vật: r m  r    arctg v 0  rg  mg    - Độ cao cực đại: t 2 m   v  m  rv  0 0 h  vdt   ln cosarctg   ln  1  r     2r mg 0      2.15 Đáp số: a. M  mg v cos t 0  1 b. L  mg v cos  2 t 0 2 Hướng dẫn:
- Xem bài mẫu (Ví dụ 2); chọn hệ toạ độ xOy; điểm O là gốc; trục
Ox nằm ngang, Oy thẳng đứng; gốc thời gian là lúc bắt đầu ném.
Ta có phương trình chuyển động: x   v cos t (1) 0    y  v sin  1 2  t   gt (2) 0  2 - Ngoài ra ta có: v  v cos (3) x 0  v  v sin  gt (4) y 0 
a. Mô men của trọng lực P  mg đối với điểm gốc O: M 
( là bán kính véc tơ xác định vị trí chất điểm
đối với điểm gốc O).
- Từ đó suy ra: M  Px  mg v cos t 0 
b. Mô men động lượng của chất điểm m với điểm gốc O: L  r  mv
- Từ đó suy ra độ lớn của mômen động lượng: F L  mxv  yv 0 a y x 
- Thay (1), (2), (3), (4) vào ta tính được: 1 T ' T ' L  mg v cos  2 t 0 2 T T 2 a 1 a F F qt1 qt 2 1 P 2 P