
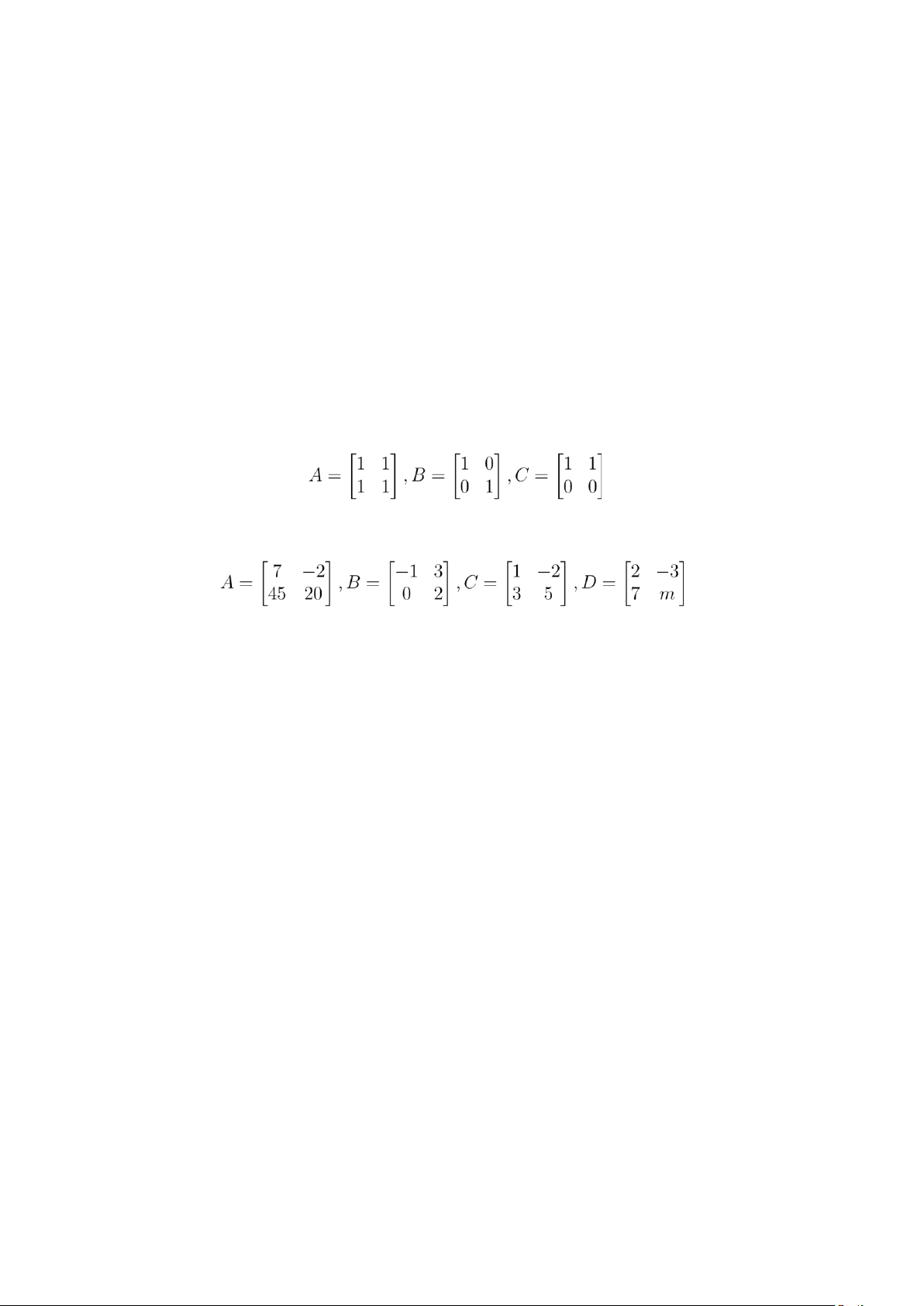


Preview text:
lOMoAR cPSD| 58800262 BÀI TẬP CHƯƠNG 3 Bài 1.
Tập hợp nào dưới đây là không gian véc tơ con của R4?
a) A = {(x,y,z,t) ∈ R4 | x2 + y2 + z2 + t2 = 0}.
b) B = {(x,y,z,t) ∈ R4 | x − 2y + 3z = 0}.
c) C = {(x,y,z,t) ∈ R4 | 2x − y + 3z = 0;z ≤ 0}.
d) D = {(x,y,z,t) ∈ R4 | xy − zt = 0}. Bài 2.
Tập hợp nào dưới đây là không gian véc tơ con của Rn?
a) W1 = {u = (x1,x2,...,xn) ∈ Rn | x1 = x2 = ... = xn}.
b) W2 = {u = (x1,x2,...,xn) ∈ Rn | x1 + x2 + ... + xn = 0}.
c) W3 = {u = (x1,x2,...,xn) ∈ Rn | x1 = x2 = ... = xn = 1}.
d) W4 = {u = (x1,x2,...,xn) ∈ Rn | x1 > 0}.
e) W5 = {u = (x1,x2,...,xn) ∈ Rn | x1 + xn = 1}.
Bài 3. Trong mỗi trường hợp dưới đây, hãy biểu diễn véc tơ v thành tổ hợp tuyến tính của v1,v2,v3.
a) v = (6,9,14);v1 = (1,1,2),v2 = (1,2,3),v3 = (1,1,1).
b) v = (−4,−4,3);v1 = (1,−13,8),v2 = (1,3,−2),v3 = (2,−2,1).
Bài 4. Tìm tất cả các giá trị của m sao cho u biểu diễn được thành tổ hợp tuyến tính của các véc tơ
u1,u2,u3.
a) u = (7,−2,m);u1 = (2,3,5),u2 = (3,7,8),u3 = (1,−6,1).
b) u = (1,3,5);u1 = (3,2,5),u2 = (2,4,7),u3 = (5,6,m).
Bài 5. Tìm điều kiện đối với a,b,c để véc tơ u = (a,b,c) ∈ R3 thuộc vào không gian véc tơ con sinh bởi các véc tơ dưới đây.
a) u1 = (2,3,−1),u2 = (1,4,7),u3 = (3,4,−3).
b) v1 = (2,−3,1),v2 = (1,−1,2),v3 = (5,−8,1). Bài 6.
Hệ véc tơ nào dưới đây là một hệ sinh của R3?
a) {u = (1,1,1),v = (2,2,0),w = (3,0,0)}. lOMoAR cPSD| 58800262
b) {u = (2,−1,3),v = (4,1,2),w = (8,−1,8)}.
c) {u = (3,1,4),v = (2,−3,5),w = (5,−2,9),s = (1,4,−1)}. Bài 7.
Hệ véc tơ nào dưới đây độc lập tuyến tính?
a) u = (4,−2,6),v = (6,−3,9) trong R3.
b) u = (2,−3,1),v = (3,−1,5),w = (1,−4,3) trong R3.
c) u = (5,4,3),v = (3,3,2),w = (8,1,3) trong R3.
d) u = (4,−5,2,6),v = (2,−2,1,3),w = (6,−3,3,9),s = (4,−1,5,6) trong R4.
Bài 8. Ba ma trận dưới đây có độc lập tuyến tính trong không gian véc tơ M2 các ma trận vuông cấp hai không? . Bài 9. Cho các ma trận .
Tìm m để A viết được thành một tổ hợp tuyến tính của các ma trận B,C,D. Biểu diễn A thành một tổ
hợp tuyến tính của các ma trận B,C,D với giá trị m vừa tìm được. Bài 10.
Hệ véc tơ nào dưới đây là cơ sở của không gian véc tơ R3?
a) (A) = {s1 = (1,3,−2),s2 = (4,−6,5)};
b) (B) = {u1 = (1,2,2),u2 = (3,6,5),u3 = (1,2,1)};
c) (C) = {v1 = (7,2,−6),v2 = (−3,−1,3),v3 = (2,1,−2)};
d) (D) = {w1 = (−3,2,1),w2 = (−1,5,2),w3 = (4,7,−1),w4 = (−5,2,4)}. Bài 11.
Hệ véc tơ nào dưới đây là cơ sở của không gian véc tơ R4?
a) S1 = {u1 = (1,0,−2,1),u2 = (2,1,−1,0),u3 = (1,1,−1,−2)};
b) S2 = {v1 = (1,3,2,−1),v2 = (−2,−5,−5,4),v3 = (−1,−2,−2,4),v4 = (−2,−3,−5,11)};
c) S3 = {w1 = (1,1,0,1),w2 = (2,1,3,1),w3 = (1,1,0,0),w4 = (3,2,3,1)}
Bài 12. Tìm một cơ sở và tính số chiều của các không gian con của R4 được xác định như sau.
a) Các véc tơ có dạng (a,b,c,0).
b) Các véc tơ có dạng (a,b,c,d) với c = a + b,d = a − b . lOMoAR cPSD| 58800262
c) Các véc tơ có dạng (a,b,c,d) với a = b = c = d. Bài 13.
Trong không gian véc tơ R3, cho các véc tơ
u = (1,−2,5);v1 = (1,1,1);v2 = (1,2,3);v3 = (2,−1,1).
a) Chứng minh rằng {v1,v2,v3} là một cơ sở của R3.
b) Tìm tọa độ của u trong cơ sở {v1,v2,v3}. Bài 14.
Trong không gian véc tơ M2 các ma trận vuông cấp hai, tìm tọa độ của ma trận trong cơ sở . Bài 15.
Tìm một hệ nghiệm cơ bản của hệ phương trình thuần nhất
Bài 16. Tìm một cơ sở và tính số chiều của không gian nghiệm của hệ phương trình 4x1 −
3x2 + x3 + x4 = 0
3x1 − x2 + 2x3 − 2x4 = 0
2x1 + x2 + x3 + 3x4 = 0 Bài 17.
Chứng minh rằng các tập con sau là các không gian con của R3.
V = {(x,y,z) ∈ R3 | x + 2y − z = 0},W = {(x,y,z) ∈ R3 | 3x − y + z = 0}.
a) Tìm một cơ sở của V,W,V ∩ W.
b) Tìm số chiều của các không gian V,W,V ∩ W. Bài 18.
Trong không gian vectơ R3, cho hệ vectơ
B = {(1,k,−1),(2,3,−1),(0,2k,1)}.
a) Tìm k để B là một cơ sở của R3.
b) Khi k = 1, B có phải là một cơ sở của R3 không? Nếu có, tìm ma trận chuyển từ cơ sở
B′ = {u1 = (0,0,1),u2 = (0,1,1),u3 = (1,0,1)} lOMoAR cPSD| 58800262 sang cơ sở B.
Bài 19. Tìm một cơ sở và tính số chiều của không gian véc tơ con của R4 sinh bởi hệ véc tơ sau.
a) S1 = {(−2,0,3,1);(1,2,−1,0);(−2,8,5,3);(−1,2,2,1)}.
b) S2 = {(1,0,0,−1);(2,1,1,0);(1,1,1,1);(1,2,3,4);(0,1,2,3)}.




