Bài tập Tập hợp và phương trình môn Toán cao cấp 2 | Học viện Công Nghệ Bưu Chính Viễn Thông

lOMoAR cPSD| 58800262
Toán cao cấp II – Chương 1
Bài tập 1: Hãy viết các tập hợp sau bằng cách liệt kê.
A là tập các số tự nhiên có hai chữ số và số hàng chục là 5.
B là tập các số tự nhiên là ước của 30.
C là tập các nghiệm thực của phương trình *Giải
Tập A: Các số tự nhiên có hai chữ số và chữ số hàng chục là 5 Các só đó
là:50, 51, 52, 53, 54, 55, 56, 57, 58, 59 Vậy:
A={50,51,52,53,54,55,56,57,58,59}
Tập B: Các số tự nhiên là ước của 30 Các uớc của 30 là: 1, 2, 3, 5, 6, 10, 15, 30 Vậy: B={1,2,3,5,6,10,15,30}
Tập C: Các nghiệm thựccủa phương trình x³-2x =0 Giải phương trình: x³-2x=0→x(x²-2)=0→x=0,x Vậy:
Bài tập 2: Hãy viết các tập hợp sau bằng cách chỉ ra thuộc tính đặc trưng. A = {3, 6, 9, 12, 15} B = {1, 4, 9} C = {−2, −1, 0, 1, 2} lOMoAR cPSD| 58800262 *Giải
A={3,6,9,12,15}→A={x∈N|x≤15,x chia hết cho 3}
B={1,4, 9} →B ={ x€N|x= k², k€N, x<10}
C={-2, -1, 0,1,2}→C={x€Z| -2≤ x ≤ 2 }
Bài tập 3: Cho A = {1, 2, 3} và B = {2, 3, 4}. Hãy viết ra các phần tử của A × B và
biểu diễn chúng trên mặt phẳng tọa độ. *Giải Cho: • A= {1, 2,3} • B ={2, 3,4} Tích Descartes:
A×B={ (a,b) | a ∈ A, b ∈ Bb} Liệt kê: A×B={(1,2),(1,3),(1,4), (2,2), (2,3), (2,4), (3,2), (3,3), (3,4)}
Tập này có thể biểu diễn là 9 điểm trên mặt phắng tọa độ .
Bài tập 4: Tìm các tập nghiệm của phương trình và bất phương trình sau, biểu diễn chúng trên trục số: a. x² - 4x + 3 = 0 b. x² - 4x + 3 > 3
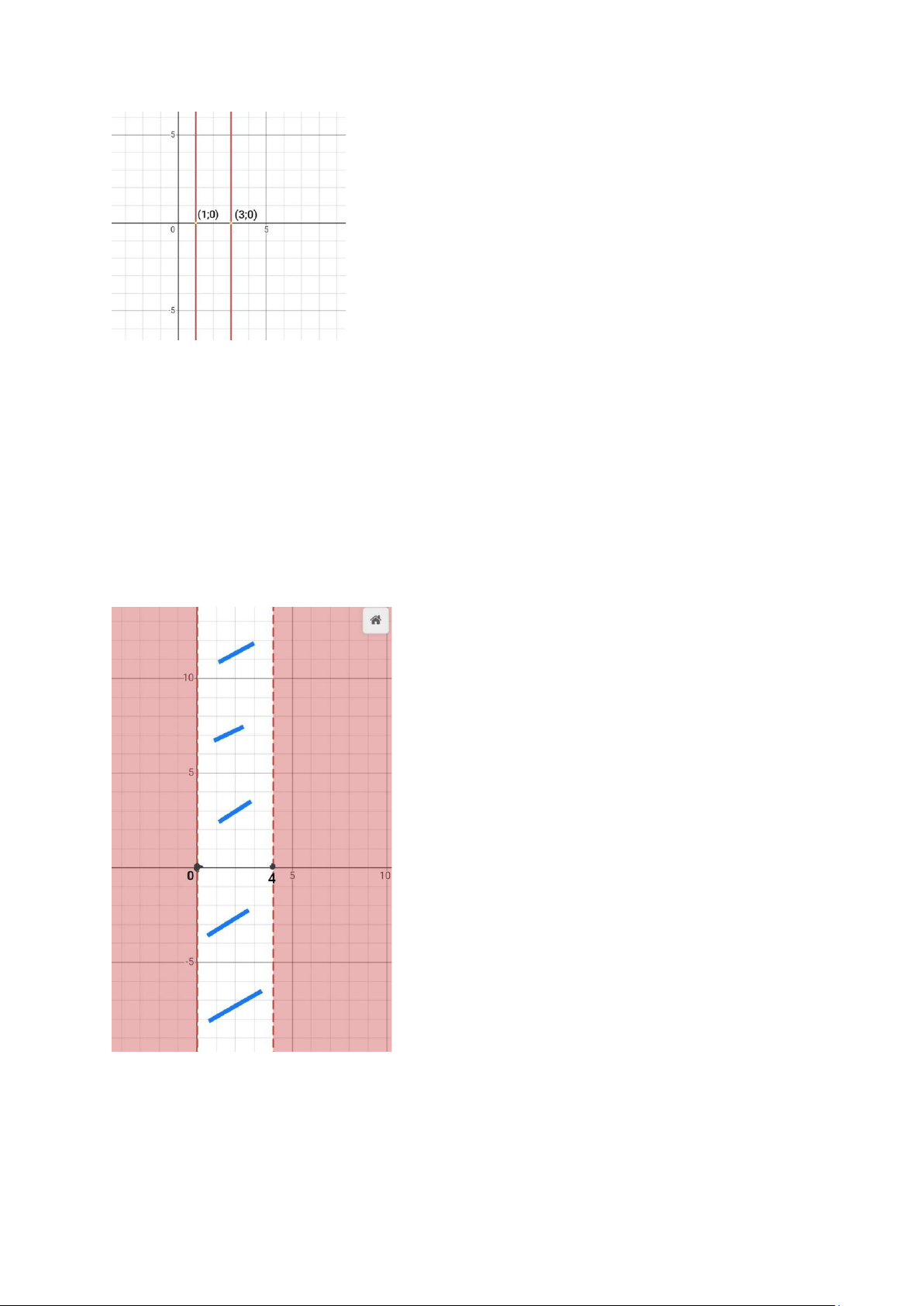
c. x² - 4x + 3 = 0*Giải a. x² − 4x + 3 = 0 ⇒ (x−1)(x−3) = 0 ⇒ x = 1 hoặc x = 3 Tập nghiệm: {1, 3} lOMoAR cPSD| 58800262 b. x² − 4x + 3 > 3 ⇒ x² − 4x > 0 ⇒ x(x − 4) > 0 ⇒ x < 0 hoặc x > 4
Tập nghiệm: (−∞, 0) ∪ (4, +∞)( biểu diễn là phần màu đỏ) Bài tập 5
Vớia<b∈ R,đặt [ a,b]={x ∈R∣a≤ x≤b}.Cho A=[1,2]vàB=[2,3] Hãy biểu diễn hình học tập hợp
A×B trên mặt phẳng toạ độ. lOMoAR cPSD| 58800262 Lời giải:
Tập A×B là tích Đề-các của hai đoạn:
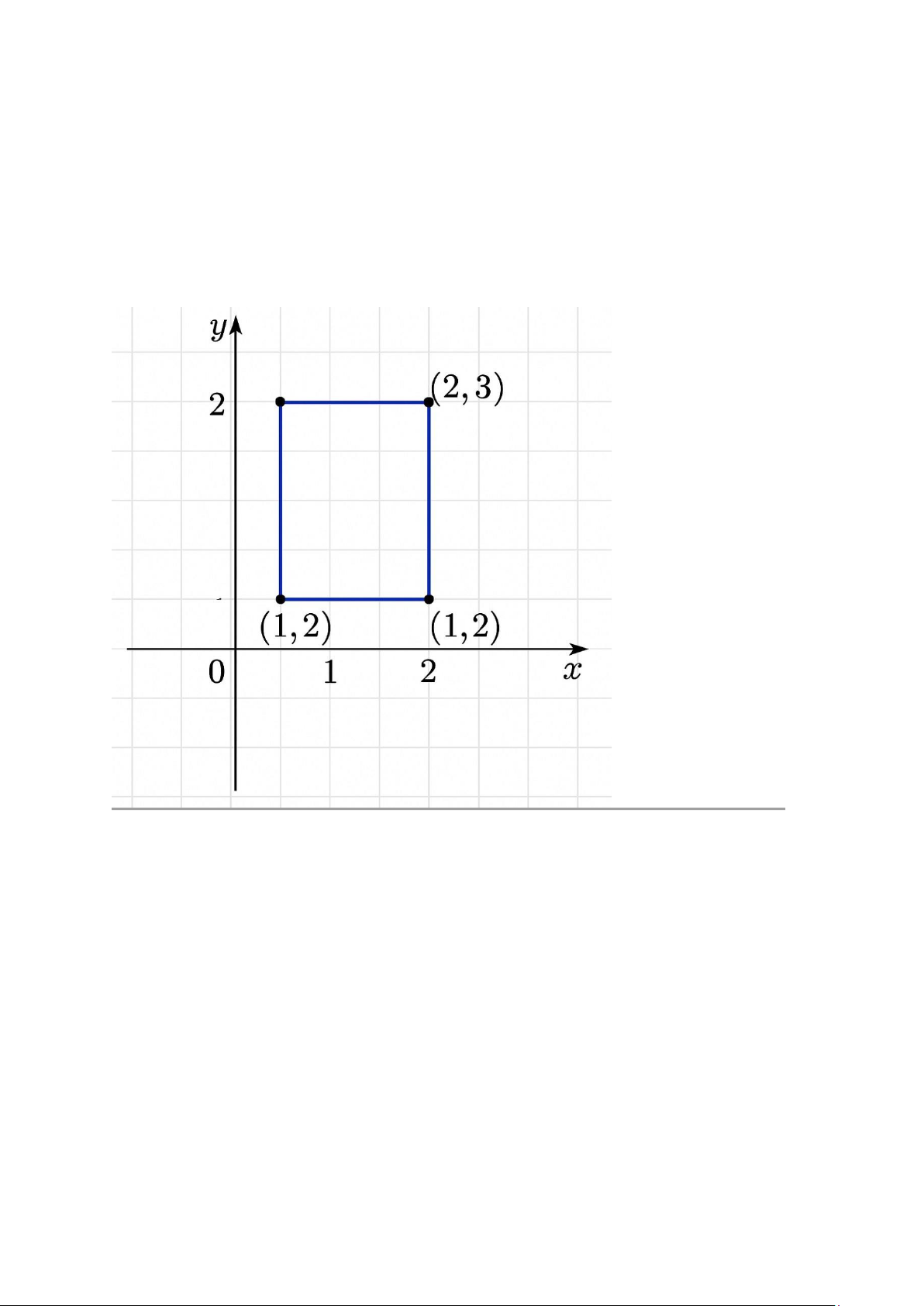
A×B={(x , y)∈R2∣1≤ x≤2,2≤ y≤3}
Đây là hình chữ nhật trên mặt phẳng tọa độ, có cạnh nằm song song với các trục: o
Trục hoành (x) chạy từ 1 đến 2.
o Trục tung (y) chạy từ 2 đến 3. Bài tập 6
Tìm tập các nghiệm của phương trình, bất phương trình và hệ phương trình sau, biểu
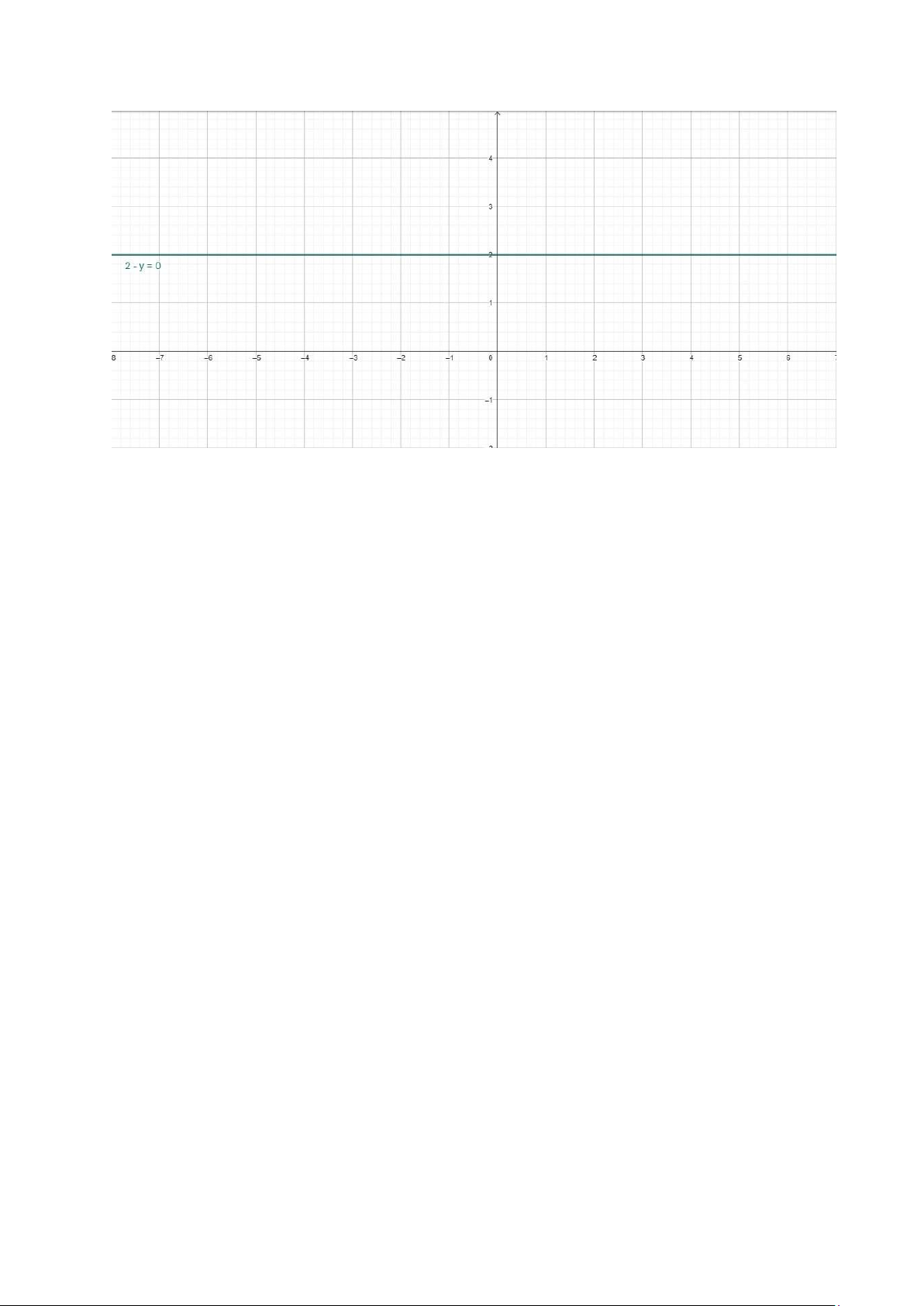
diễn trên mặt phẳng tọa độ: a. 2− y=0
⇒ y=2 ⇒ đường thẳng song song trục hoành, cắt trục tung tại y=2 lOMoAR cPSD| 58800262
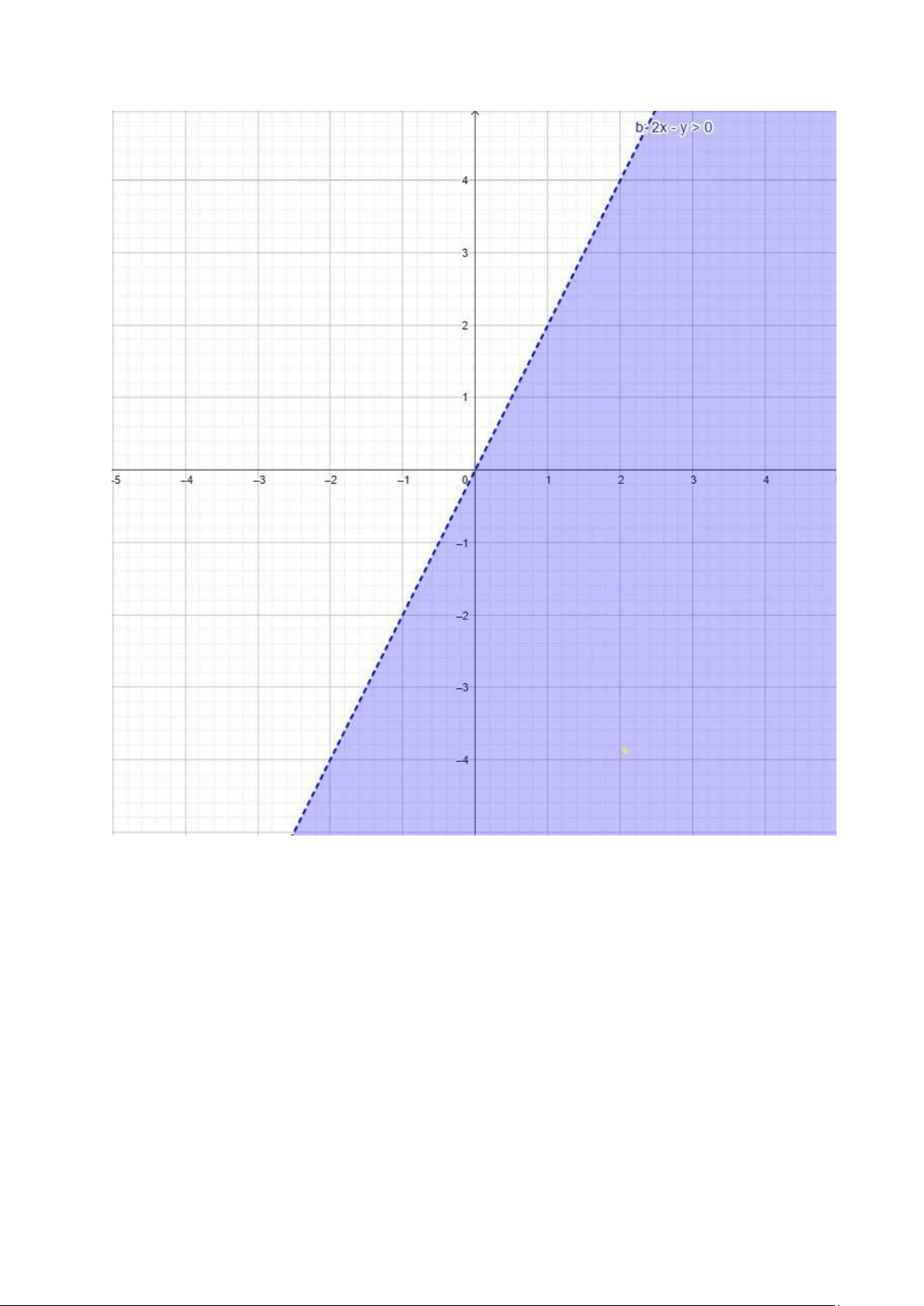
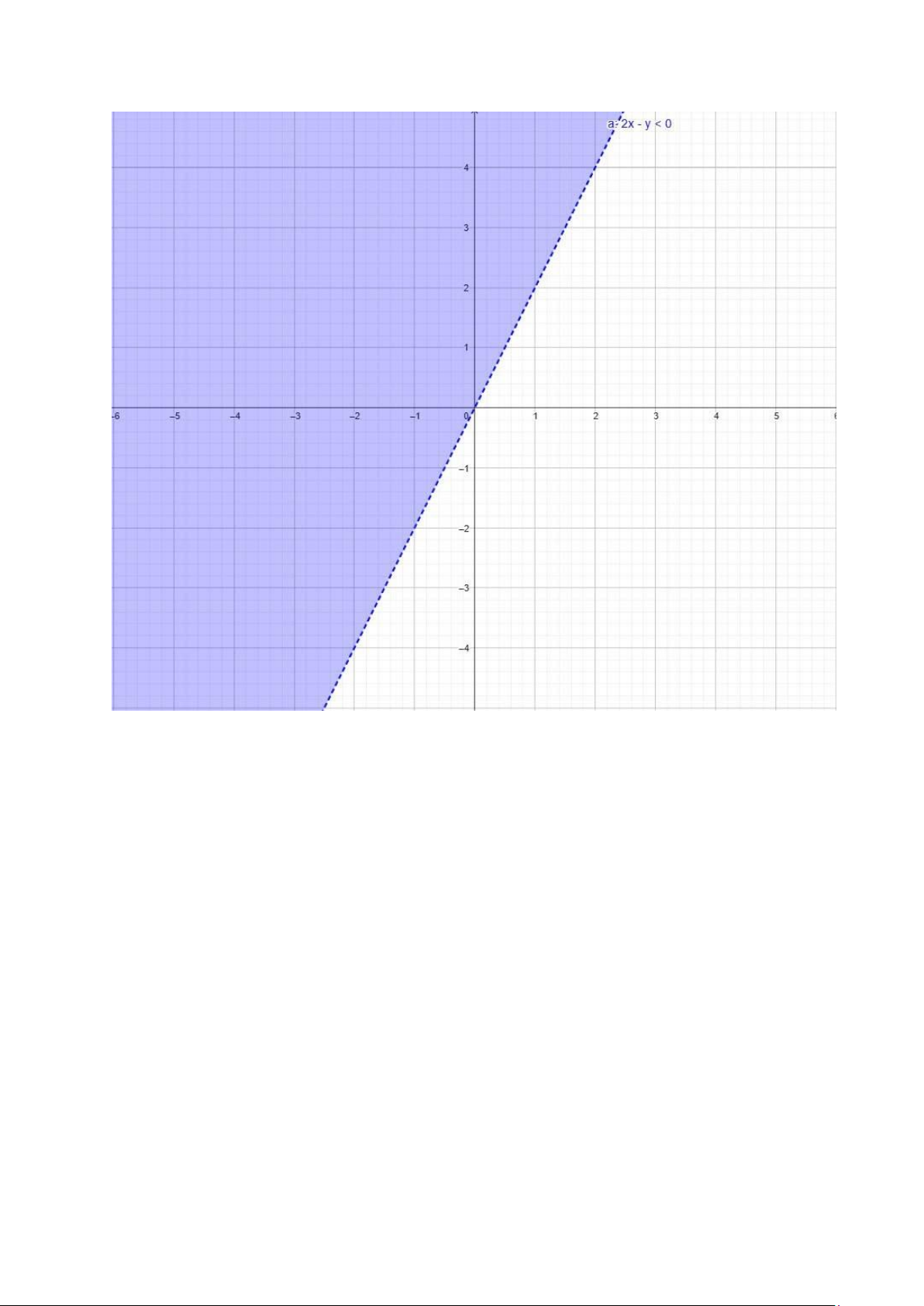
b. 2 x−y>0
⇔ y<2x ⇒ miền nằm dưới đường thẳng y=2x lOMoAR cPSD| 58800262
c.2x− y<0
⇔ y>2x ⇒ miền nằm trên đường y=2x lOMoAR cPSD| 58800262
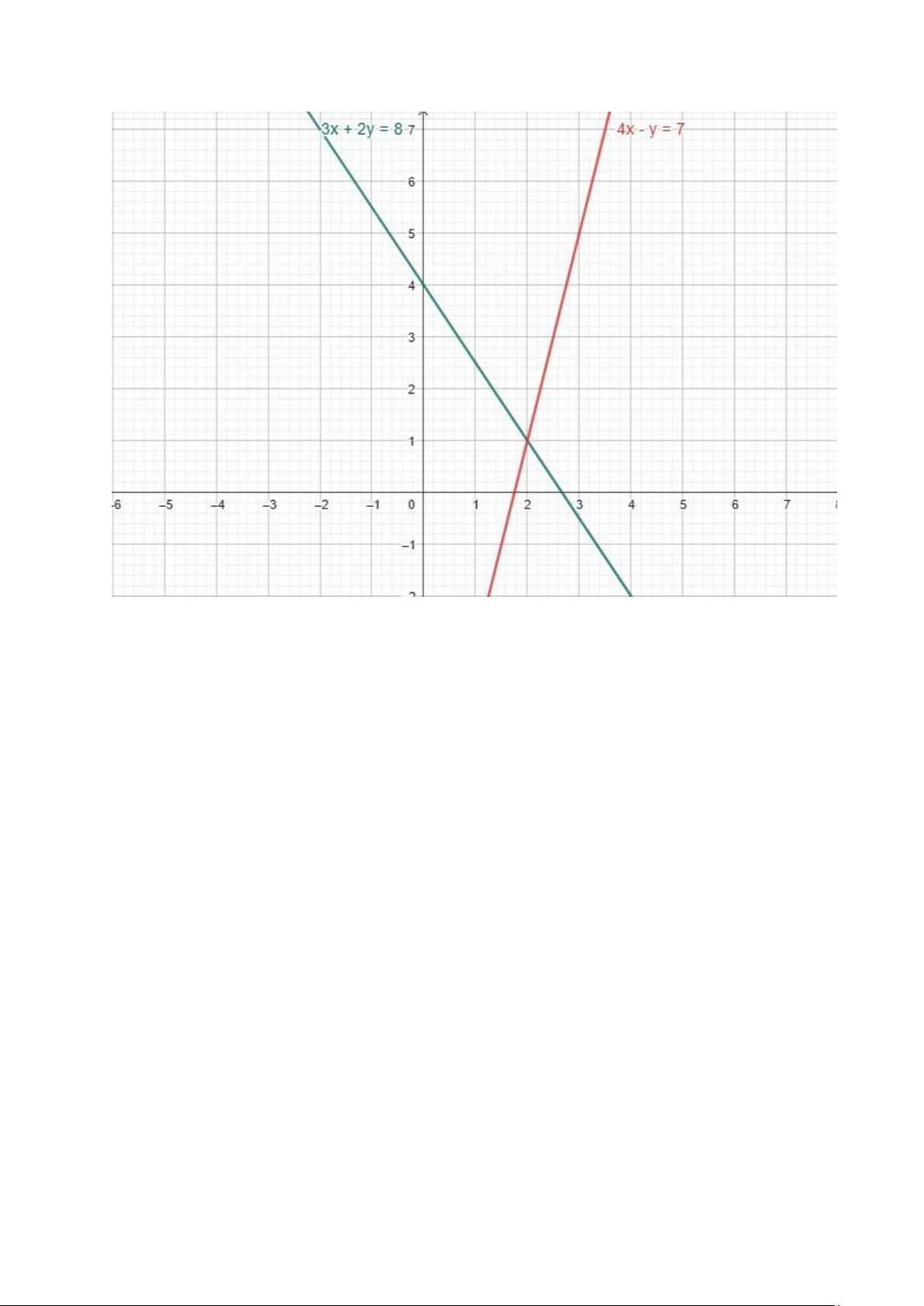
d. Hệ phương trình: 3x+2 y=8 { 4 x−y=7 Giải hệ:
1. Từ (2): y=4 x−7 2. Thay vào (1):
3 x+2(4 x−7)=8⇒3 x+8 x−14=8⇒11x=22⇒x=2⇒ y=4(2)−7=1 Nghiệm: (2,1) lOMoAR cPSD| 58800262
e. Hệ phương trình:
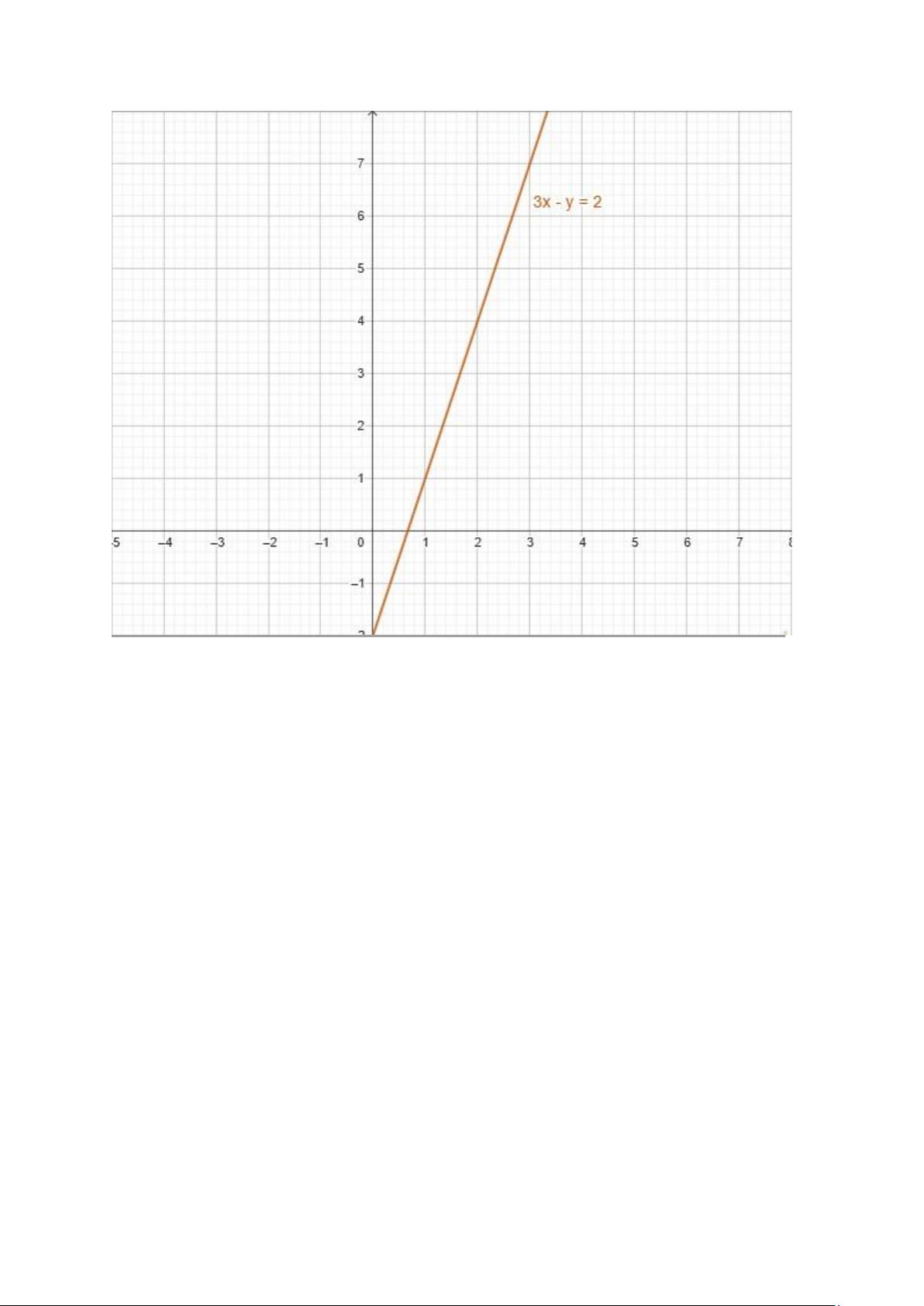
3 x−y=2 {−6 x+2 y=−4 Nhận thấy: •
Nhân phương trình (1) với 2: 6 x−2 y=4 •
Cộng với (2): (6 x−2 y)+(−6 x+2 y)=4−4=0→ Hệ có vô số nghiệm (hai phương trình tương đương).
→ Đây là một đường thẳng duy nhất:
3 x−y=2⇒ y=3x−2 lOMoAR cPSD| 58800262 Bài tập 7
Một hội nghị có 1000 người tham dự, trong đó số người không biết cả tiếng Anh và
tiếng Pháp là 20%. Số người còn lại có 50% biết nói tiếng Anh, và 40% biết nói tiếng
Pháp. Hỏi có bao nhiêu người biết nói cả hai thứ tiếng Anh và Pháp? Lời giải: Gọi: •
AA là tập hợp những người biết tiếng Anh. •
BB là tập hợp những người biết tiếng Pháp.
Tổng số người tham dự là: 1000
Số người không biết cả tiếng Anh và tiếng Pháp là 20%:1000×20%=200người
Vậy số người biết ít nhất một trong hai ngôn ngữ là:
1000−200=800người Giả sử trong 800 người này: lOMoAR cPSD| 58800262 •
50% biết tiếng Anh → ∣ A∣=800×50%=400 •
40% biết tiếng Pháp → ∣B∣=800×40%=320 •
Ta cần tìm số người biết cả hai thứ tiếng, tức là:
∣ A∩B∣=∣ A∣+∣B∣−∣ A∪B∣
Ở đây, ∣ A∪B∣=800vì 800 người là số người biết ít nhất một trong hai ngôn ngữ. Vậy:
∣ A∩B∣=400+320−800=−80
Kết quả này âm, điều đó cho thấy giả thiết ban đầu là sai: không thể có 50% biết
tiếng Anh và 40% biết tiếng Pháp trong số 800 người được, vì tổng của hai tỉ lệ này là
90%, nhỏ hơn 100%, tức là sẽ không đủ để có phần giao dương.
→ Do đó, 50% và 40% là tính trên toàn bộ 1000 người, chứ không phải chỉ 800
người biết ít nhất một ngôn ngữ. Ta sửa lại: •
Số người biết tiếng Anh: 1000×50%=500 •
Số người biết tiếng Pháp: 1000×40%=400 •
Số người biết ít nhất một ngôn ngữ: 1000−200=800 Vẫn dùng công thức giao của hai tập:
∣ A∩B∣=∣ A∣+∣B∣−∣ A∪B∣=500+400−800=100
Đáp số: 100 người biết cả hai thứ tiếng Anh và Pháp Bài tập 9
Biết rằng các số hữu tỉ a/b,c/d∈Q là bằng nhau nếu ad=cb
a. Quy tắc f :Q→Q cho ứng với a/bsố ab có là ánh xạ không?
Giả sử = (bằng nhau trong Q) • ab=1×2=2 • ab=2×4=8
→ Hai phân số bằng nhau nhưng ánh xạ lại khác nhau.
Không phải ánh xạ vì không xác định đơn trị trên Q (một phần tử ánh xạ ra nhiều giá trị). lOMoAR cPSD| 58800262 a 5 a
b. Quy tắc f: Q→Q, b → 3b Xét: =
f (1/2)= , f ( )= =
→ Kết quả giống nhau cho hai phân số bằng nhau.
Là ánh xạ vì xác định một giá trị duy nhất trên Q Bài tập 10
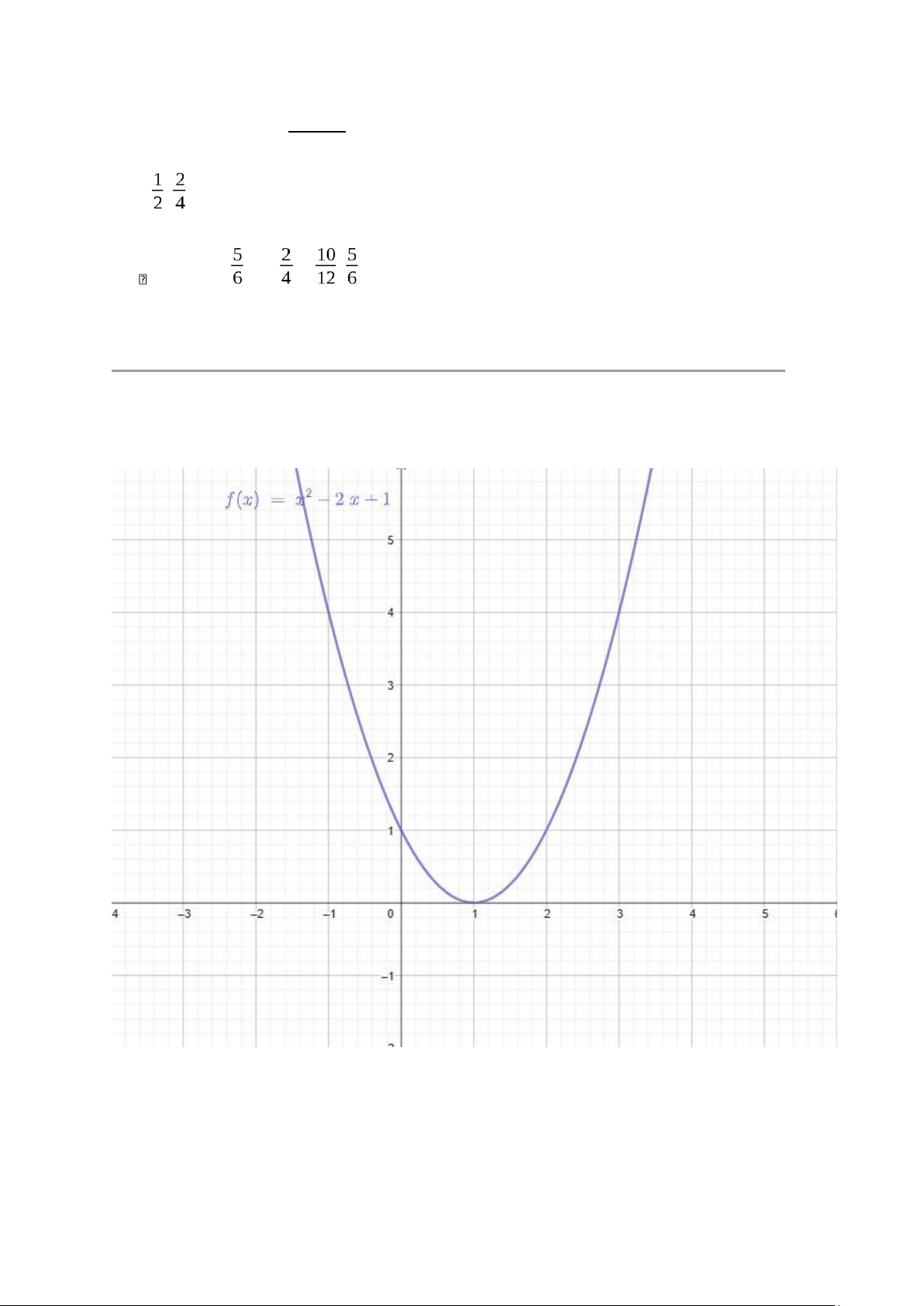
Chof :R→R, xácđịnhbởif (x)=x2−2 x+1=(x−1)2 Tính các giá trị sau và vẽ đồ thị của f.
1. f (0)=(0−1)2=1
2. f (1)=(1−1)2=0
3. f (−1)=(−1−1)2=4 4. f ([0,1]) lOMoAR cPSD| 58800262
f ( x )=(x−1)2đạt mintạix=1:f (1)=0
maxtại x=0:f (0)=1 →f ([0,1])=[0,1] 5. f−1(1)
(x−1)2=1⇒x−1=±1⇒ x=0hoặc2 →f −1(1)={0,2} 6.f−1(4)
Giải (x−1)2=4 ⇒x=−1hoặc3 →f −1(4)={−1,3} 7. f−1([1,4])
Tức là tìm tập x∈ Rsao cho(x−1)2∈[1,4]
→ 1≤(x−1)2≤4
→1≤∣x−1∣≤2 →
x−1∈[−2,−1]∪[1,2]
→x∈[−1,0]∪[2,3]
Bài tập 11: Tìm các ánh xạ gf và fg
Cho X = {1, 2, 3}, các ánh xạ f và g được định nghĩa bởi:
- f(1) = 1, f(2) = 3, f(3) = 2
- g(1) = 2, g(2) = 1, g(3) = 3
Ta cần tính hai ánh xạ hợp thành gf và fg:
1. Tính gf(x) = g(f(x)): - gf(1) = g(f(1)) = g(1) = 2 - gf(2) = g(f(2)) = g(3) = 3
- gf(3) = g(f(3)) = g(2) = 1 => gf = {1 → 2, 2 → 3, 3 → 1}
2. Tính fg(x) = f(g(x)): - fg(1) = f(g(1)) = f(2) = 3 - fg(2) = f(g(2)) = f(1) = 1 - fg(3) = f(g(3)) = f(3) = 2
=> fg = {1 → 3, 2 → 1, 3 → 2}
Bài tập 12: Chứng minh tính chất ánh xạ
Giả sử có các ánh xạ: f: X → Y, g: Y → Z và φ = g∘f: X → Z. Cần
chứng minh các mệnh đề sau: lOMoAR cPSD| 58800262
a. Nếu φ là đơn ánh thì f cũng là đơn ánh.Chứng
minh: Giả sử φ là đơn ánh, tức là: φ(x ) = φ(x ) ₁
₂ ⇒ x = x với mọi x , x ₁ ₂ ₁ ₂ ∈ X
⇒ g(f(x )) = g(f(x )) ₁₂ ⇒ x = x₁ ₂
⇒ f(x ) = f(x ) vì nếu không thì g sẽ đồng nhất 2 giá trị khác nhau, mâu thuẫn g₁ ₂
∘f đơn ánh → f đơn ánh.
b. Nếu φ là toàn ánh thì g cũng là toàn ánh.Chứng
minh: Giả sử φ là toàn ánh, tức là: ∀z ∈ Z, ∃x ∈
X sao cho φ(x) = z ⇔ g(f(x)) = z ⇒ ∀z ∈ Z, ∃y =
f(x) ∈ Y sao cho g(y) = z ⇒ g là toàn ánh.
c. Nếu φ là song ánh và f là toàn ánh thì g là song ánh. Chứng minh: -
Vì φ là đơn ánh ⇒ g∘f đơn ánh ⇒ f đơn ánh (từ (a)) ⇒ f là
song ánh (vì đã toàn ánh). -
Vì φ là toàn ánh ⇒ g toàn ánh (từ (b)) - Ta cần chứng minh g cũng đơn ánh:
Giả sử g(y ) = g(y ), ta cần chứng minh y = y .₁ ₂ ₁ ₂
Vì f là song ánh ⇒ ∃x , x ₁₂ ∈ X sao cho f(x ) = y , f(x ) = y₁ ₁ ₂ ₂
⇒ g(f(x )) = g(f(x )) ₁ ₂ ⇒ φ(x ) = ₁ φ(x₂)
⇒ x = x ₁ ₂ ⇒ y = y₁ ₂ ⇒ g đơn ánh ⇒ g song ánh.
Bài tập 13: Xét tính chất và tính nghịch đảo của ánh xạ Cho
ánh xạ f: ℂ → ℝ xác định bởi f(x) = x10+ 1. Xét các tính chất: 1. Đơn ánh:
Giả sử f(x ) = f(x ), tức là ₁ ₂
x101 + 1 = x102 + 1 ⇒ x101 = x102 .
Tuy nhiên, phương trình này có thể có nhiều nghiệm khác nhau (ví dụ x = 1, x ₁ ₂ = e2π i ) 10 ⇒ f không đơn ánh. 2. Toàn ánh:
f(x) = x10 + 1 với x 1
∈ ℂ thì giá trị f(x) thuộc ℂ, nhưng đề bài cho f: ℂ → ℝ nên ta xét f(x) ∈ ℝ. lOMoAR cPSD| 58800262
Tuy nhiên, với nhiều giá trị x phức thì x10 không phải là số thực 1 ⇒ f(x) không luôn
thuộc ℝ ⇒ không toàn ánh.
Vì vậy f không là ánh xạ từ ℂ → ℝ trừ khi giả sử x ∈ ℝ.
3. Nếu giả sử f: ℝ → ℝ thì x thì f(x) luôn > 1.
⇒ Không toàn ánh vì không đạt tới mọi giá trị thực. 4. f ¹(0): giải ⁻ x10 i
1 + 1 = 0 ⇒ x101 = -1 ⇒ x = e(2k+1)π , k = 0..9 10 ⇒ 10 nghiệm phức
⇒ f ¹(0) = {⁻ e(2k+1)π i }, k = 0..9} 10 5. f ¹(1): ⁻
x101 + 1 = 1 ⇒ x101 = 0 ⇒ x = 0 ⇒ f ¹(1) = {0}⁻
Bài tập 14: Chứng minh đẳng thức tập hợp
Cho A, B, C là các tập hợp tùy ý. Cần chứng minh các đẳng thức sau:
1. A \ (B ∩ C) = (A \ B) ∪ (A \ C)
- x ∈ A \ (B ∩ C) ⇔ x ∈ A và x ∉ (B ∩ C) ⇔ x ∈ A và (x ∉ B hoặc x ∉ C)
- ⇔ (x ∈ A và x ∉ B) hoặc (x ∈ A và x ∉ C) ⇔ x ∈ (A \ B) ∪ (A \ C)
2. A \ (B ∪ C) = (A \ B) ∩ (A \ C)
- x ∈ A \ (B ∪ C) ⇔ x ∈ A và x ∉ (B ∪ C) ⇔ x ∈ A và x ∉ B và x ∉ C
- ⇔ x ∈ (A \ B) và x ∈ (A \ C) ⇒ x ∈ (A \ B) ∩ (A \ C)
3. A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
- x ∈ A ∩ (B ∪ C) ⇔ x ∈ A và (x ∈ B hoặc x ∈ C)
- ⇔ (x ∈ A và x ∈ B) hoặc (x ∈ A và x ∈ C)
- ⇔ x ∈ (A ∩ B) ∪ (A ∩ C)
4. A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
- x ∈ A ∪ (B ∩ C) ⇔ x ∈ A hoặc (x ∈ B và x ∈ C)
- ⇔ (x ∈ A hoặc x ∈ B) và (x ∈ A hoặc x ∈ C)
- ⇔ x ∈ (A ∪ B) ∩ (A ∪ C)
Bài tập 15. Cho ánh xạ f : X→ X xác định sau đây. Hãy kiểm tra tính đơn ánh, toàn
ánh và song ánh của f. Tìm ánh xạ ngược của f nếu f là song ánh. lOMoAR cPSD| 58800262
1. X=R,Y =R và f (x)=x+7
2. X=R,Y =R và f (x)=x2+2 x−3. Tim f−1([−1,1])
3. X=[4,9],Y =[21,96] và f (x)=x2+2 x−3
4. X=R,Y =(0,+∞) và f (x)=ex+1
5. X=N ,Y =N và f (x)=x2+x
6. X=R,Y −R và f 2
x +1 x −x 7.
X=R,Y =R và f e −e x −x 8.
X=(0,+∞),Y=¿ và f e +e x
9. X=R,Y =(−1,1) và f (x)= ¿ x∨+1
10. X=R,Y =R+¿¿và f (x)=5x
11. X=¿,Y=¿ và f (x)=x2+5 Giải:
15.1. f(x) = x + 7, X = R, Y = R
Hàm số đơn ánh: vì x ≠ x ₁₂ ⇒ f(x ) ≠ f(x ).₁ ₂
Toàn ánh: với mọi y ∈ R, tồn tại x = y − 7 ∈ R sao cho f(x) = y. ⇒ f là song ánh.
Ánh xạ ngược: f ¹(y) = y − 7⁻
15.2. f(x) = x² + 2x − 3, X = R, Y = R
Không đơn ánh: vì parabol không đơn điệu. lOMoAR cPSD| 58800262
Không toàn ánh: f(x) ≥ −4, nên không đạt các giá trị nhỏ hơn −4.
⇒ Không song ánh, không có ánh xạ ngược. Tìm f ¹([−1, 1]) = {x ⁻
∈ R | −1 ≤ x² + 2x − 3 ≤ 1}
Giải bất phương trình kép:
15.3. f(x) = x² + 2x − 3, X = [4, 9], Y = [21, 96]
Trên đoạn [4, 9], f đồng biến, nên đơn ánh. f([4,
9]) = [21, 96] ⇒ toàn ánh. ⇒ f song ánh
Ánh xạ ngược: f ¹(y) = −1 − ⁻
(vì chọn nghiệm nằm trong miền xác định)
15.4. f(x) = ex+1, X = R, Y = (0,+∞)
f là hàm mũ, đồng biến trên R ⇒ đơn ánh
Với mọi y > 0, tồn tại x = ln(y) – 1S ⇒ toàn ánh ⇒ f song ánh
Ánh xạ ngược: f ¹(y) = ln(y) − 1⁻
15.5. f(x) = x(x+1), X = N, Y = N f là đơn ánh trên N
Không phải số tự nhiên nào cũng có dạng x(x+1) ⇒ không toàn ánh
⇒ Không song ánh, không có ánh xạ ngược
15.6. f(x) = 5x / (1 + x²), X = R, Y = R lOMoAR cPSD| 58800262
f không đơn ánh: vì f(x) = f(−x) f(x) ∈
(−1, 1) ⇒ không toàn ánh
⇒ f không song ánh, không có ánh xạ ngược
15.7. f(x) = (ex+1 − e−x) / 2, X = R, Y = R
Đây là hàm sinh hyperbol: f(x) = sinh(x)
Hàm đồng biến trên R, liên tục, và lim x→±∞ sinh(x) = ±∞ ⇒ Đơn ánh và toàn ánh ⇒ f là song ánh
Ánh xạ ngược: f ¹(y) = sinh ¹(y) = ln(y + ⁻ ⁻
15.8. f(x) = (ex+ e−x) / 2, X = (0, +∞), Y = [1, +∞)
Đây là hàm cosh(x) trên miền dương
cosh(x) ≥ 1 và đồng biến trên (0, ∞) ⇒ Đơn ánh và toàn ánh ⇒ f là song ánh
Ánh xạ ngược: f ¹(y) = ln(y + ⁻
15.9. f(x) = x / (|x| + 1), X = R, Y = (−1, 1)
Hàm lẻ, liên tục, đơn ánh trên từng nửa miền, nhưng không toàn ánh vì không đạt −1 và 1
Không có nghiệm tại x = 0 cho y = ±1
⇒ Không toàn ánh, nên không song ánh lOMoAR cPSD| 58800262 Không có ánh xạ ngược
15.10. f(x) =5x, X = R, Y = R⁺
Hàm mũ đồng biến, giá trị > 0 ⇒ Đơn ánh và toàn ánh ⇒ f là song ánh
Ánh xạ ngược: f ¹(y) = log (y)⁻ ₅
15.11. f(x) = x² + 5, X = (−∞, 0], Y = [5, +∞)
Trên miền (−∞, 0], f nghịch biến, liên tục ⇒ Đơn ánh và toàn ánh ⇒ f là song ánh Giải y = x² + 5 ⇒ x =
⇒ Ánh xạ ngược: f ¹(y) = −⁻
Bài tập 16: Tính các biểu thức phức Tính các biểu thức sau: 1. (1+i)6
2. (2+i)7 + (2−i)7 3. (1+2i)5 - (1−2i)5 Giải: 1. (1+i)6 = -8i
2. (2+i)7 + (2−i)7= -556 3. (1+2i)5 - (1−2i)5 = -76i Bài tập 17:
Biểu diễn cos(5x) và sin(5x) qua cos(x) và sin(x) Dựa theo công thức De Moivre:
(cos x+isinx)n= cos(nx) + i sin(nx) Với n = 5, ta có: lOMoAR cPSD| 58800262
(cos x+isinx)5 = cos(5x) + i sin(5x) Khai triển nhị thức Newton:
* cos5−k(x)* (isinx)k Phần thực (cos 5x):
cos(5x) = cos5(x) - 10cos3(x)* sin2x + 5 cosxsin4x
Thay sin2(x) = 1 - cos2(x), sin4(x) = (1 - cos2(x)¿2
cos(5x) = 16 cos5(x) - 20 cos3(x) + 5 cos(x) Phần ảo (sin 5x):
sin(5x) = 5 cos4(x) sin(x) - 10 cos2(x) sin3(x) + sin3x)
Thay cos2(x) = 1 - sin2(x), cos4(x) = (1 - sin2(x)¿2 sin(5x)
= 5 sin(x) - 20 sin3(x) + 16 sin5(x) Kết luận:
cos(5x) = 16 cos5 (x) - 20 cos3(x) + 5 cos(x)
sin(5x) = 5 sin(x) - 20 sin3(x) + 16 sin5(x) Bài tập
18 - Giải các phương trình sau:
a. Giải phương trình: x² + 3x + 12 = 0 Δ = b² -
4ac = 3² - 4×1×12 = 9 - 48 = -39 < 0 Phương trình có nghiệm phức: x =
b. Giải phương trình: x - 7x³ - 8 = 0⁶
Đặt y = x³, ta có phương trình: y² - 7y - 8 = 0 ⇒ y = ⇒ y = 8 hoặc y = -1 ⇒ x³ = 8 ⇒ x = 2 ⇒ x³ = -1 ⇒ x = -1
Các nghiệm thực: x = 2, x = -1
c. Giải phương trình: (x+i)15 + (x−i)15= 0
Đặt A = (x+i)15 + (x−i)15
Vì hai số là liên hợp bậc lẻ nên tổng của chúng là số thực gấp đôi phần thực.
Tổng bằng 0 khi phần thực = 0 ⇒ x = 0
Nghiệm: x = 0 Bài tập 19:
1. (1 + i)z + 3i·z= 2 + i lOMoAR cPSD| 58800262
Giả sử z = x + iy ⇒ z= x – iy Thay vào:
(1 + i)(x + iy) + 3i(x - iy) = 2 + i
→ (x + iy + ix - y) + 3i(x - iy) = 2 + i → (x
- y + i(x + y)) + 3i(x - iy) = 2 + i Tính tiếp: Thực: x - y Ảo: (x + y) + 3(x - iy)
→ (x - y) + i(x + y + 3x + 3y) = 2 + i
→ (x - y) + i(4x + 4y) = 2 + i → Hệ: x - y = 2 4x + 4y = 1 → x + y = 0.25
Giải hệ: x - y = 2 x + y = 0.25 → x = 1.125, y = -0.875
→ z = 1.125 - 0.875i 2.
z·z+ 3(z − z) = 4 − 3i
z·z= ¿z∨¿2¿= x2+ y2, z − z= 2iy → x2
+ y2+ 6iy = 4 − 3i Tách phần thực và ảo: x2+ y2= 4 6y = −3 ⇒ y = −0.5
→ x2= 4 − 0.25 = 3.75 ⇒ x = ± → z = ± − 0.5i
3. z+ 3(z +z)= 3i
Gọi z = x + iy → z= x - iy
→ x - iy + 3((x + iy) + (x - iy)) = 3i
= x - iy + 3(2x) = 3i → x - iy + 6x = 3i
→ 7x - iy = 3i → 7x = 0 và -iy = 3i → x = 0, y = -3
→ z = -3i 4. z·z+
3·z= −i
z = x + iy → z= x - iy, z·z= x² + y² →
x² + y² + 3(x - iy) = -i → (x² + y² + 3x) + (-3iy) = -i → Hệ: x² + y² + 3x = 0