






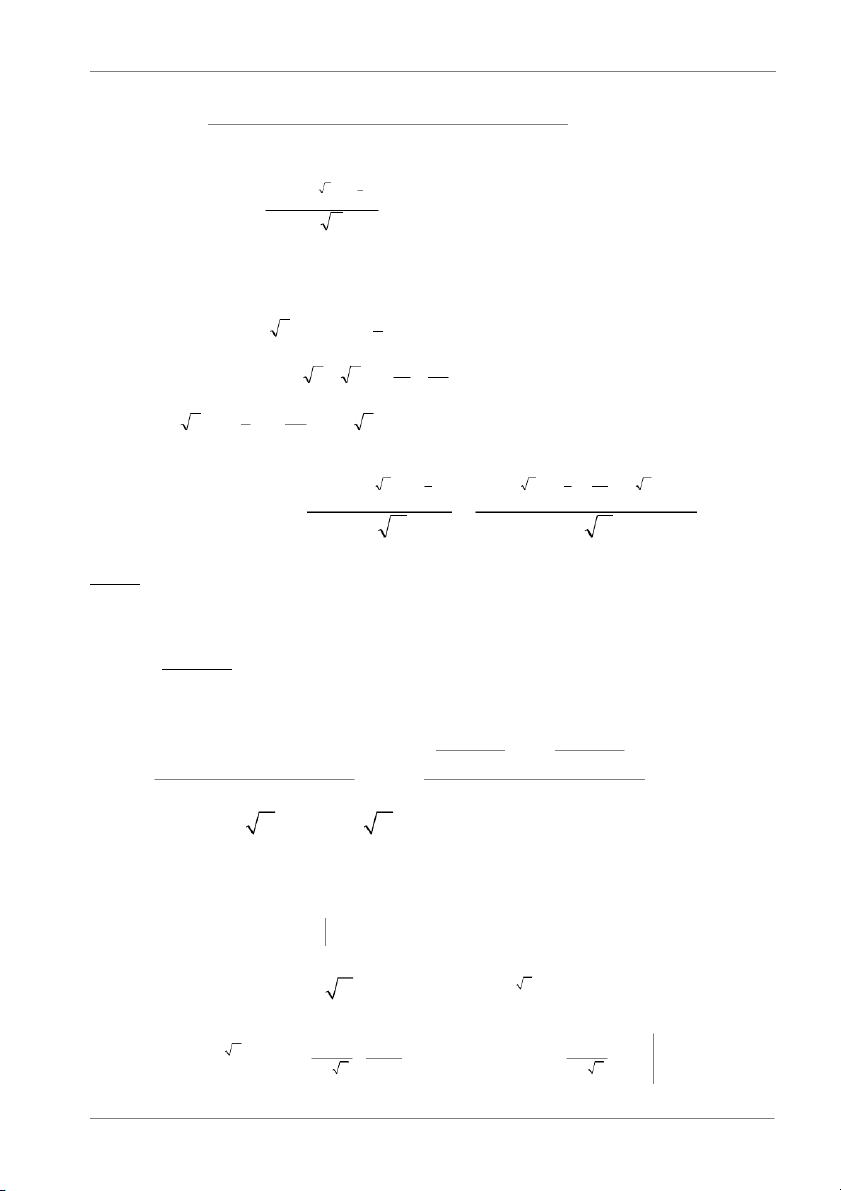
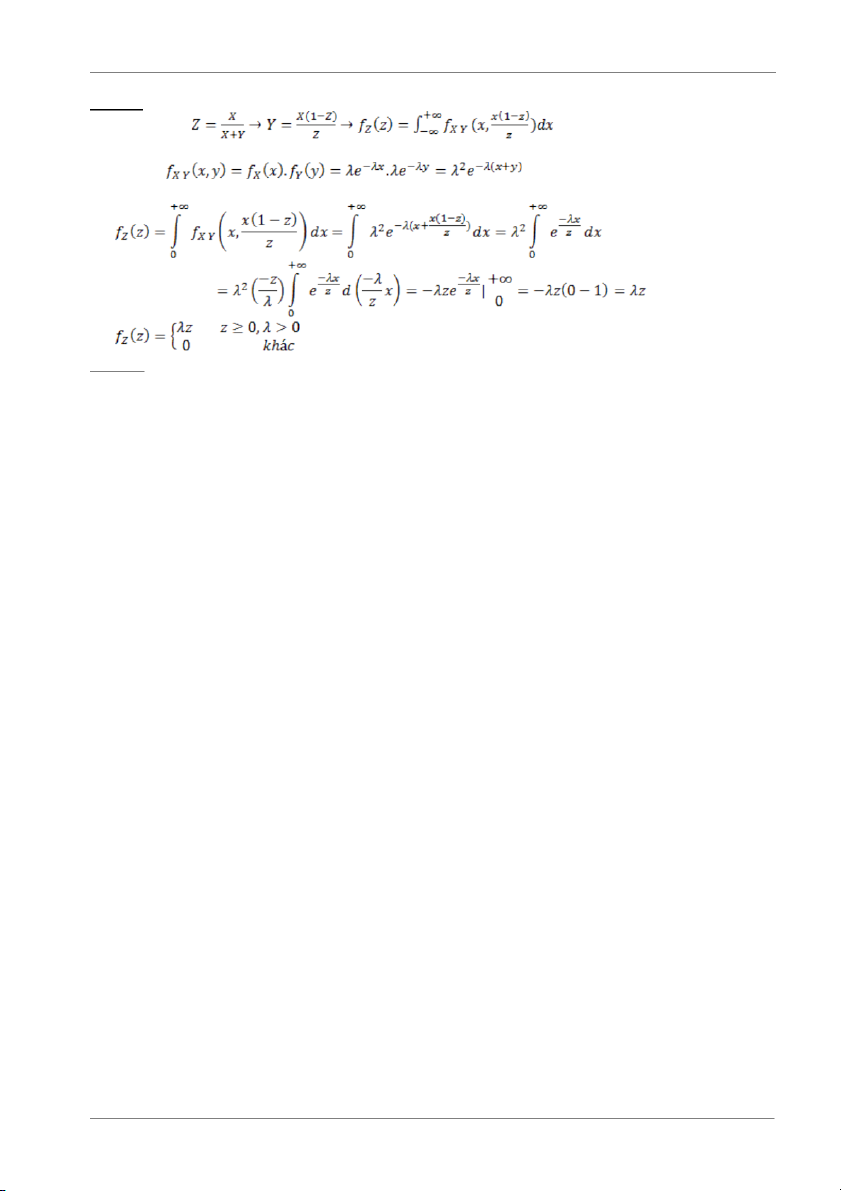



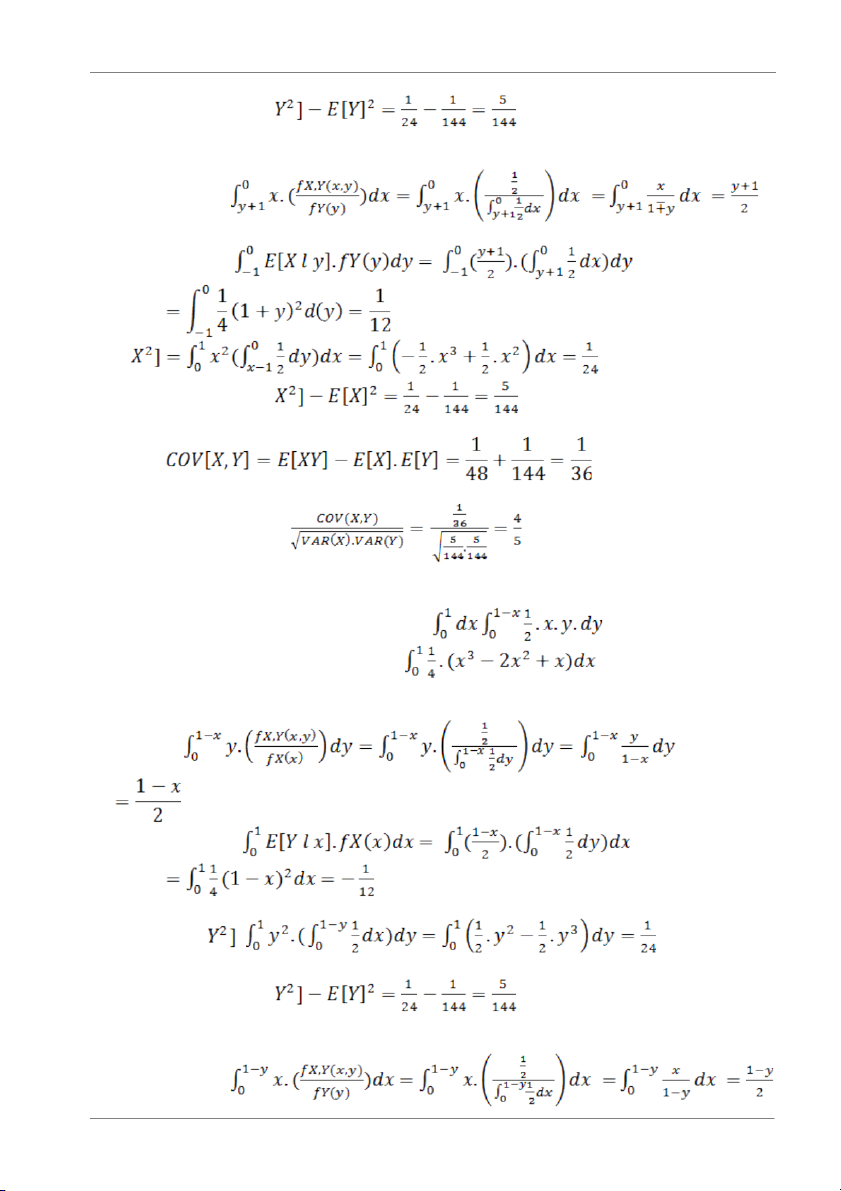
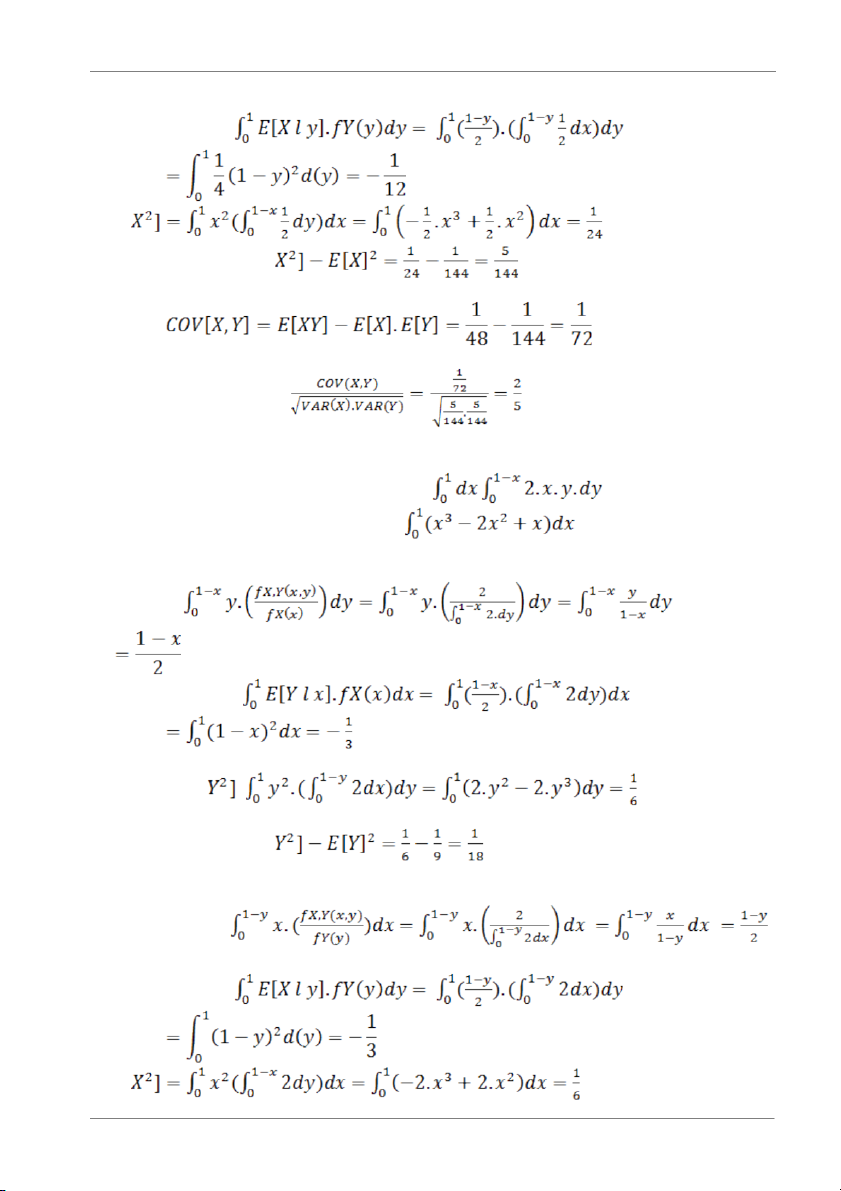

Preview text:
Xác suất thống kê –Chương 4
Cao Thành Lực - MAT1101 3 - 09020324 Chương 4:
BIẾN NGẪU NHIÊN NHIỀU CHIỀU Bài 2. X = I1 + I + 2 I3 + I4 Y = min(I , 1 I 2 , I3 , I4)
Z = max(I , I , I , 1 2 3 I 4 )
Ta có giá trị của x nhận các giá trị X = {0 , 1, 2 , 3, 4} , Y = {0 , 1} , Z = {0 , 1} 1
Mặt khác ta có X : β (4, ) 4 0 4 P[ X = ] 0 1 3 0 = C = 0.316 4 4 4 1 3 1 1 3 [X=1] =C P = 0.421 4 4 4 2 2 1 3 Vậy ta có 2 [X=2] =C P = 0.21 4 4 4 3 1 3 1 3 [X=3] =C P = 0.046 4 4 4 4 0 4 1 3 [X=4] =C P = 0.0039 4 4 4
Vậy ta có P[X = 0 , Y = 0 , Z = 0 ] = P[X = 0]P[Y=0/X=0] P[Z = 0/X=0 , Y = 0] = P[X=0] = 0.316
P[X=0 , Y = 1 , Z = 0] = P[X = 0 , Z = 1 , Y = 0] = P[X = 0, Y = 1 , Z = 1] = 0
Tương tự ta cũng có các giá trị
P [X = 1 , Y = 0 , Z = 1] = P[X = 1] = 0.421 Các trường hợp khác = 0 X = 2
P[X =2 , Y = 0 , Z = 1] = P[X = 2] = 0.21 X = 3
P[X = 3, Y = 0 , Z = 1] = P[X = 3] = 0.046 X = 4
P[X = 4 , Y = 0 , Z = 1] = P[X = 4] = 0.0039
Câu b , khi rút các quả bóng ra nhưng không trả lại vào hộp ta có
Các giá trị của X = {0 ,1 , 2, 3, 4} , Y = {0 , 1} , Z = {0 , 1} Bài 3
a, P[|X|< 5, Y<2, Z2 ≥ 2] = A
Do X, Y , Z là biến ngẫu nhiên độc lập
A = P[|X|< 5]. P[Y.2].P[Z 2≥ 2] = [F - x (5-) – F ( x -5)] .[Fy(2 )].P([- ∞ ,- 2 ] ∪ [ 2 ,+ ∞ ) = [Fx(5) - Fx(-5)].[F (2 y )].[Fz( 2 ) + (1-Fz( 2 )] b, Tương tự ta có
P[X<5, Y<0, Z=1] = P[X<5].P[Y<0].P[Z=1] = F - x(5-). Fy(0-).[Fz(1 )- Fz(1)]
C,P[min(X,Y,Z)>2] = P[X<2, Y>2, Z>2] = [1-F + x(2+)].[1-Fy(2+)].[1-Fz(2 )] Trang 1
Xác suất thống kê –Chương 4
Cao Thành Lực - MAT1101 3 - 09020324
d, P[Max(X, Y, Z)<6]=P[X<6, Y<6, Z<6] =F - x(6-). Fy(6-). Fz(6 ) Bài 4:
a. hàm xác suất đồng thời cho (X1,X2)
Vì các lần tung là độc lập và các kết cục của mỗi lần tung là đồng khả năng, ta có X1 1 2 3 4 5 6 X2 1 a a a a a a 2 a a a a a a 3 a a a a a a 4 a a a a a a 5 a a a a a a 6 a a a a a a Ta có: 36a = 1 1 ⇒ a = 36 Vậy ta có: X1 1 2 3 4 5 6 X2 1 1 1 1 1 1 1 36 36 36 36 36 36 1 1 1 1 1 1 2 36 36 36 36 36 36 1 1 1 1 1 1 3 36 36 36 36 36 36 1 1 1 1 1 1 4 36 36 36 36 36 36 1 1 1 1 1 1 5 36 36 36 36 36 36 1 1 1 1 1 1 6 36 36 36 36 36 36
X = min (X ,1 X 2 )
b. với Y = max(X1, X2 ) Bài 9: 2 2 − −by ax 2 2
f (x , y ) = axe bye
x > 0, y > 0, a > 0, b > 0 Trang 2
Xác suất thống kê –Chương 4
Cao Thành Lực - MAT1101 3 - 09020324 x 2 x 2 2 2 x 2 −ax −ax −ax −ax ax a) 2 2 2 2
F (x) = axe dx = −e d (− )= −e = 1− e X ∫ ∫ 2 0 0 0 y 2 2 −by −by Tương tự: 2 2
F (y ) = bye dy =1−e X ∫0 2 2 − ax b − y 2 2 1 − e 1 − e x > 0, y > 0
Suy ra F (x, y) = X 0 n u e ≠ b) Tìm P[X > Y] +∞ 2 − ax 2 P(X ) = axe dx = 1 ∫0 2 2 +∞ +∞ 2 b − y b − y b − x 2 2 2 P(Y ) = bye dy = −e = −e ∫x x 2 −bx 2
⇒ P(X > Y ) = −e
c) Tìm các hàm mật độ biên +∞ 2 +∞ 2 2 2 − −by − −by ax ax 2 2 2 2 f ( x) = axe bye dy = abxe ye dy X ∫ ∫ 0 0 +∞ 2 2 +∞ 2 − ax −by 2 2 1 − ax 1 −by 2 2 by 2 2 = abxe − e d (− ) ∫ 2 = abxe − e b b 0 0 2 2 a − x a − x 2 2 = axe (1− 0) = axe +∞ 2 2 2 b − − y −by ax 2 2 2 f ( y) = axe bye dx = bye X ∫ 0 Bài 10. a. b. Nếu hoặc thì hàm mật độ Nếu Nếu Trang 3
Xác suất thống kê –Chương 4
Cao Thành Lực - MAT1101 3 - 09020324 Nếu Nếu
c. Hàm mật độ biên của X Hàm mật độ biên của Y Bài 11. Miền giới hạn bởi : 2 2 x + y ≤ 1
Đặt x = r cos ϕ y = r sinϕ Định thức Jacobi dx dx ϕ cosϕ − r dr d sinϕ J = = = r dy dy sinϕ r cosϕ dr dϕ π 2 1 ⇒ ∫ ϕ
d ∫k.r.dr = 1 0 o 2 π ⇔ k ϕ d = 1 ⇔ π 1 k = 1 ⇔ = ∫ k 2 0 π Hàm mật độ biên : 1 1 1 f (x) X = = ∫ dy 0 π π 1 1 1 f ( ) y Y = = ∫ dx π π 0 Miền giới hạn bởi : (1) y = x +1 (2) y = -x + 1 (3) y = x – 1 (4) y = -x - 1 Trang 4
Xác suất thống kê –Chương 4
Cao Thành Lực - MAT1101 3 - 09020324 0 + x 1 1 0 1 1 − +x 0 0 dx kdy + dx kdy + dx kdy + dx kdy = 1 ∫ ∫ ∫ ∫ ∫ ∫ ∫ ∫ −1 0 0 − + x 1 0 0 1 − 1 − − x 0 1 1 0 1 ⇔ 1
( + x)dx + (x − ) 1 dx + (x − ) 1 dx + 1 ( + x)dx = ∫ ∫ ∫ ∫ k 1 − 0 0 − 1 1 1 ⇔ 2 = ⇔ k = k 2
Miền giới hạn bởi : y = -x + 1 1 1−x dx kdy = 1 ∫ ∫ 0 0 1 1 1 1 ⇔ 1 ( − x)dx = ⇔ = ⇔ = 2 ∫ k k 2 k 0 Bài 12:
Vecto ngẫu nhiên (X,Y) có hàm mật độ xác suất đồng thời − 2 − f ( , x y) = 2 x
y x > 0, y > 0 , e e X Y
Hãy tìm xác suất của các sự kiện sau: a.{X + Y ≤ 8} Ta có : 8 8− x 8 8− x
P[{X + Y ≤ 8}] = − x − 2 y − x − 2 2e dx e dy = e ( y dx −e ) ∫ ∫ ∫ 0 0 0 0 8 8 8 8 8 − x 2( x−8) − x 2 x−16 = 2 (− + 1) = − 2 . + 2 − x e e dx e e dx e dx ∫ ∫ ∫ x 16 = −2 − +2 − x e dx e dx ∫ ∫ 0 0 0 0 0 8 8 x −16 −x −8 −16 −8 −16 −8 = −2e − 2e
= −2e + 2e − 2e + 2= 2(e − 2e + 1) 0 0 .{ b X < Y} ∞ y ∞ y ∞
Ta có: P[{X < Y} ] −2 y − x 2 − y − x −2 = 2e dy e dx = 2e dy ( e − ) = 2 y e ( − y e − +1)dy ∫ ∫ ∫ 0 ∫ 0 0 0 0 ∞ ∞ ∞ ∞ 3 − y 2 2 − y 3 − y 2 = −2 + 2 = ( ) − ( − y e dy e dy e e ) ∫ ∫ 2 1 = (0 −1) − (0 −1) = 3 0 0 3 3 0 0 .{
c X − Y ≤ 10} ∞ 10+ y ∞ 10 + y ∞
P[{X −Y ≤10} ] −2 y − x −2 y − x −2 y −10 = 2e dy e dx = 2e dy(e ) = 2e ( − y −e +1)dy ∫ ∫ ∫ 0 ∫ 0 0 0 0 ∞ ∞ ∞ ∞ 3 − y 10 − 2 2 − y 3 − y 10 − 2 = −2 + 2 = ( ) − ( − y e dy e dy e e ) ∫ ∫ 3 0 0 0 0 2 2 10 − 10 (0 e ) (0 1) e − = − − − = − +1 3 3 Bài 13:
Cho X, Y có hàm mật độ xác suất đồng thời:
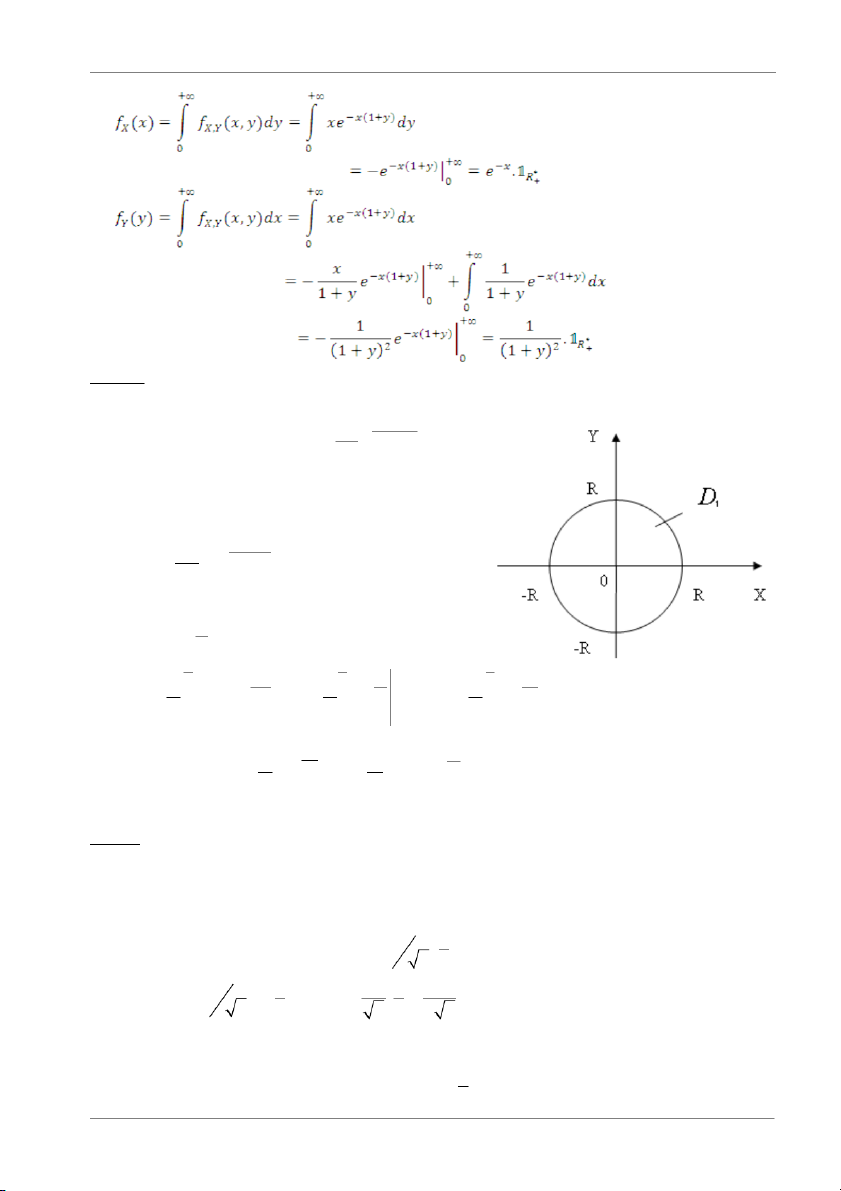
fX,Y(x,y) = xe-x(1+y) x > 0, y > 0
Hàm mật độ biên của X và củaY: Trang 5
Xác suất thống kê –Chương 4
Cao Thành Lực - MAT1101 3 - 09020324 Bài 14 : Lúc ρ = 0 ta có : −( 2 2 x +y ) f x y = e X Y ( , ) 1 2 , . 2π Lúc này 2 2 2
p X + Y < R
bằng 4 lần tích phân của hàm f x y Trên miền X Y , , ( ) 1 D 2 2 − x + y 4 2 P = e dxdy 2π ∫ 1 D
Chuyển sang tạo độ cực ta được. π 0≤ ϕ ≤ , 0≤ r ≤ R 2 π π R π 2 2 2 2 R − r 2 r 2 2 2 − 2 R ⇒ − 2 2 2 P = dϕ r .e dr = − e dϕ = − e −1 d ϕ π ∫ ∫ π ∫ π ∫ 0 0 0 0 0 2 2 2 R R − π − 2 2 = − e 1 − . =1 π − 2 e Bài 24:
X và Y là các biến ngẫu nhiên độc lập có phân phối đều trong đoạn [0,1] 2
a.Tính P[X < 1/2, |Y - 1| < 1/2] 1 2 1
P[X < 1/ 2,| Y −1|< 1/ 2] = P[0 < X < , < Y < 1] 2 2 1 1 1 1 1 = P[0 < X <
].P[ <Y < 1] = . = 2 2 2 2 2 2
b. Tính P[X/2 < 1, Y > 0] 1
P[X / 2 < 1,Y > 0] = P[0 < X < 1 / 2].P[Y > 0] = 2 Trang 6
Xác suất thống kê –Chương 4
Cao Thành Lực - MAT1101 3 - 09020324 c. Tính P[XY < 1/2] d. Tính P[min(X,Y) > 1/3] 2 2 4 [
P min(X ,Y ) > 1 / 3] = [
P X > 1 / 3].P[Y > 1 / 3] = . = 3 3 9 Bài 25. a. , ta có: Mặt khác: Suy ra:
Vậy X và Y là độc lập (đpcm) b. Ta có: Trong đó: Bài 40.
Một điểm X, Y, Z được chọn ngẫu nhiên trong hình cầu đơn vị
a. Tìm hàm mật độ đồng thời biên của X vàY: Trang 7
Xác suất thống kê –Chương 4
Cao Thành Lực - MAT1101 3 - 09020324 Nếu : Nếu khác:
b. Tìm hàm mật độ biên của X: Nếu : Nếu khác:
c. Cho trước Z, tìm hàm mật độ đồng thời có điều kiện của X và Y: Nếu : Nếu khác: không xác định
d. X, Y, Z có độc lập hay không:
Suy ra X, Y, Z không độc lập Bài 53
a,Tìm hàm mật độ xác suất đồng thời của các hàm sau : U = 1 X V = X + 1 X2
W = X + X + X 1 2 3 Ta có ma trận
U 1 0 0 X 1 V = 1 1 0 . X 2
W 1 1 1 X 3 X1 = U
⇒ X 2 = V −U X 3 =W V −
Ma trận Jacibian của phép biến đổi ngược là : 1 0 0 | ℑ|= −1 1 0 = 1 0 −1 1
Ta có hàm mật độ xác suất đồng thời được xác định theo công thức sau f ( 1 h ( , u , v ); w 2 h ( , u , v ); w 3 h ( , u , v )) w ( , u , v ) X ,Y , w f Z = U ,V ,W
|ℑ (x ,y ,z ) | Trang 8
Xác suất thống kê –Chương 4
Cao Thành Lực - MAT1101 3 - 09020324 f (h ( , u , v ); w h ( , u , v ); w h ( , u , v )). w | )( ℑ , u , v ) w | = 1 2 3 X , Y, Z
Ta có với X , X , 1
2 X 3 là các biến ngẫu nhiên có hàm phân phối đồng thời Gauss 1 ( 2 2 − x x + − 2x . 2 x + x ) 1 2 1 2 2 3
(x , x , x ) e f = (*) 1 2 3 X ,X , 1 2 X 3 π 2 π
Do đó hàm mật độ xác suất của U,V,W là f
( x , x , x ) = f ( , u v − , u w − ) 1 2 3 v 1
X , X2 ,X3 1
X , X2 , X3
Bằng việc thay thế x,y,z bởi u,v,w trong biến lũy thừa đi đến 2 2 1 − [(u) + ( u − + v) − 2 .( u u
− + v) + (−v + w)2 ] 2 2 2 = [ 2 2 2
− u + u + v − 2uv − uv 2 + 2 2 v w u + + − ] vw 2 2 2 3 2 = [( − 2 + 2) 2 w u + v + −(2 + 2)uv − ] vw 2 2 Thay vào ( * ) ta được 2 2 1 2 2 3 2 w −(x 1 x + 2 − 2 1 x .x2 + 3 x ) [ −(2 + 2 ) 2 u + v + (
− 2+ 2 )uv−vw] 2 2 2 f
( x , x , x ) e e = = 1 2 3 1
X , X2, X3 π 2 π π 2 π Bài 54:
Hàm mật độ xác suất đồng thời của X1 và X2 là: 2 ( 1 2 ) f (x , x )
f (x ). f (x ) x x e λ λ − + = = với x1,x2 ≥ 0 1 X ,X2 1 2 X1 1 X 2 2 X + X 1 2 M =
⇒ X + X = 2M ⇔ X = 2 − 1 2 1 M X 2 2 Thay vào V ta có: 2 2 X − − 1 X 2 X 2 X 1 ( + X M ) 2 ( X M ) 2 − + − 1 2 2 2 V = ⇔V = 2 2
⇔ X − X = 2 V ⇔ X = 2 V + X 1 2 1 2 ∞ ∞ 2 − λ( + 2 − ) 1 1 f (M ) = f
(x , 2M − x ) x M x dx = λ e dx M X ∫ ∫ 1, X 2 1 1 1 1 −∞ −∞ ∞ 2 2 ∞ − M λ 2 − 2 M = λ e λ = λ 1 dx e 1 x ∫ −∞ −∞ ∞ ∞ 2 −λ (x1 x + 1−2 V ) f (V ) = f
(x , x − 2 V )dx = λ e dx V ∫ ∫ 1 X , X 2 1 1 1 1 −∞ −∞ ∞ ∞ 2 ∞ 2 −2λ( − λ − λ x V 1 1 ) 2 x λ 1 −2 x λ 1 = λ e dx = e d ( ∫ ∫ −2λx ) = − e 1 1 − −∞ −∞ 2 V e 2λ 4 V e −∞ Trang 9
Xác suất thống kê –Chương 4
Cao Thành Lực - MAT1101 3 - 09020324 Bài 55. a.
b. Vì X và Y là những biến ngẫu nhiên mũ độc lập nên: Bài 59 : a. tìm E ( + )2 X Y E ( X + Y ) 2 2 2
= E X + 2X .Y +Y = +∞ +∞ +∞ +∞ +∞ +∞ ' = x f x y dy dx + x y f x y dy dx + y f x y dy dx X Y ∫ ∫ ( ' ',) ' ' ' ' 2 . X Y ∫ ∫ ( ' ',) ' ' ' X Y ∫ ∫ ( ' ', ) ' ' , , , −∞ −∞ −∞ −∞ −∞ −∞ +∞ +∞ +∞ +∞ ' = x f x dx + x y f x y dy dx + y f y dy ∫ X ( ') ' ' ' 2 . X Y ∫ ∫ ( ' ' , ) ' ' ' ∫ Y ( ' ) ' , −∞ −∞ −∞ −∞
= E X + 2E X .Y + E Y b. phương sai của (X+Y). V X +Y = E
( X +Y ) 2 − E + ( X Y ) 2
= E( X + 2X .Y +Y ) − E ( X ) + E (Y ) 2 2 2 2 2 = E( 2
X ) + 2E ( X .Y ) + E ( 2
Y ) − E ( X ) + 2E ( X ) .E( Y ) +E ( Y ) = E − + − + −
( X ) E ( X ) 2
2E ( X .Y ) 2E ( X ).E (Y ) E (Y ) E (Y ) 2 2 2
=V X + 2E ( X .Y ) −2 E( X) .E( Y) V + Y
c. phương sai của tổng bằng tổng các phương sai riêng biệt
trong trường hợp X,Y là các biến ngẫu nhiên độc lập. Trang 10
Xác suất thống kê –Chương 4
Cao Thành Lực - MAT1101 3 - 09020324
V [ X Y ] E ( X Y )2 + = + − E (X +Y ) 2
= E ( X +2 X.Y +Y ) − E( X ) + E( Y ) 2 2 2
E ( X ) 2E( X.Y ) E ( Y ) E( X) 2
2 E( X) .E( Y) E( Y) 2 2 2 = + + − + + E
( X ) E( X ) 2
2E ( X .Y ) 2E ( X ).E (Y ) E (Y ) E (Y ) 2 2 2 = − + − + −
=V [ X ] + 2E ( X .Y ) − 2E ( X ) .E (Y ) V + [Y ]
=V [ X ] + 2E ( X ) .E (Y ) −2E( X) .E( Y) V + [Y ]
= V [ X ] +V [Y ] Bài 61: Do X,Y là độc lập 2 x − => 2 e 1 f
(x, y) = f (x). f (y) = . X, Y X Y 2π 4 Vậy 2 x ∞ 3 − E[ 2 Y X ]= e 2 2 1 .y. . dxdy ∫ ∫ x π −∞ 1 2 4 − 2 x 2 ∞ 2 − ∞ 2 = 1 x .e 2 y 1 x 2 3 − . | dx 1 = 2 . dx ∫ − ∫ x e 4 2π 2 π −∞ 64 2 −∞ 2 x Đặt I= 2 2 . − dx ∫ x e do là hàm chẵn nên 2 ∞ −x π I = 2 . 2 2 dx = 2 = 2π 2 ∫x e 1 3 0 4. 2 1 => [ 2 E Y] = . 2π 2 X 64 2π Bài 66:
Hệ số tương quan và hiệp phương sai của hai biến ngẫu nhiên X,Y trong bài 11: f(x,y)=k a. Trường hợp 1 k=1/π Giả sử
là biến ngẫu nhiên có phân phối đều trên (0,2π).Giả sử X=cos ,Y=sin .Từ
ví dụ 4.42,ta có X,Y là 2 biến ngẫu nhiên phụ thuộc và không tương quan,E[X]=E[Y]=0
E[XY]=0 COV(X,Y)=E[XY]-E[Y].E[X]=0 b.Trường hợp 2:
+Với -1≤x≤0 và 0≤y≤1,khi đó k= ½
Tương quan của X và Y là: E[XY]= =
=0- ¼ .(1/4-2/3+1/2)= ¼ (3/4-2/3)=-1/48 Có: Trang 11
Xác suất thống kê –Chương 4
Cao Thành Lực - MAT1101 3 - 09020324 E[Y l x]= E[Y] = E[ = VAR[Y]=E[ Có: E[X l y]= E[X]= E[ VAR[X]=E[ Hiệp phương sai:
Hệ số tương quan được cho bởi: pX,Y= + Với -1
, -1≤y≤0 ,khi đó k= ½ :
Tương quan của X và Y là: E[XY]= =
=0- ¼ .(1/4-2/3+1/2)= ¼ (3/4-2/3)=-1/48 Có: E[Y l x]= E[Y] = Trang 12
Xác suất thống kê –Chương 4
Cao Thành Lực - MAT1101 3 - 09020324 E[ = VAR[Y]=E[ Có: E[X l y]= E[X]= E[ VAR[X]=E[ Hiệp phương sai:
Hệ số tương quan được cho bởi: pX,Y= + Với 0
Tương quan của X và Y là: E[XY]= = =1/48 Có: E[Y l x]= E[Y] = E[ = Trang 13
Xác suất thống kê –Chương 4
Cao Thành Lực - MAT1101 3 - 09020324 VAR[Y]=E[ Có: E[X l y]= E[X]= E[ VAR[X]=E[ Hiệp phương sai:
Hệ số tương quan được cho bởi: pX,Y=
+ Với 0≤x≤1 , 0≤y≤1 , k=1/2 :
Tương quan của X và Y là: E[XY]= = =1/48 Có: E[Y l x]= E[Y] = E[ = VAR[Y]=E[ Có: E[X l y]= Trang 14
Xác suất thống kê –Chương 4
Cao Thành Lực - MAT1101 3 - 09020324 E[X]= E[ VAR[X]=E[ Hiệp phương sai:
Hệ số tương quan được cho bởi: pX,Y= c.Trường hợp 3 :
+ Với 0≤x≤1 , 0≤y≤1 , k=2 :
Tương quan của X và Y là: E[XY]= = =1/12 Có: E[Y l x]= E[Y] = E[ = VAR[Y]=E[ Có: E[X l y]= E[X]= E[ Trang 15
Xác suất thống kê –Chương 4
Cao Thành Lực - MAT1101 3 - 09020324 VAR[X]=E[ Hiệp phương sai:
Hệ số tương quan được cho bởi: pX,Y= Bµi 68:
Hoµn thµnh nèt c¸c tÝnh to¸n ë vÝ dô 4.43 Ta có và Bài 69:
X là đầu vào của một kênh thông tin. X nhận giá trị ±1 với các khả năng như nhau. Giả sử đầu ra
của kênh là Y = X + N, với N là biến ngẫu nhiên Laplace với hàm mật độ: 1 α| | f (z ) z e α − =
− ∞ < z < +∞ N 2
Tìm hệ số tương quan giữa X và Y. E[X] = 0 VAR[X] = E[X2] = 1
Y = X + N → E[Y] = E[X + N] = E[X] + E[N] = 0 (do N là BNN Laplace) VAR[ ] Y = E Y + E [ ]2 Y = E Y = E ( X + N)2 2 2 2 = + [ ] 2 + = + [ ] 2 E X 2E XN E N 1 2E XN + 2 α
Hệ số tương quan giữa X và Y 2
E[XY ] − E[X ]E[Y ]
E[X ] + E[XN ] 1+ E[XN ] ρ= = = ( VAR X )VA ( R Y) + [ ] 2 2 1 2E XN + 1+ 2E XN + 2 [ ] 2 α α Trang 16




