







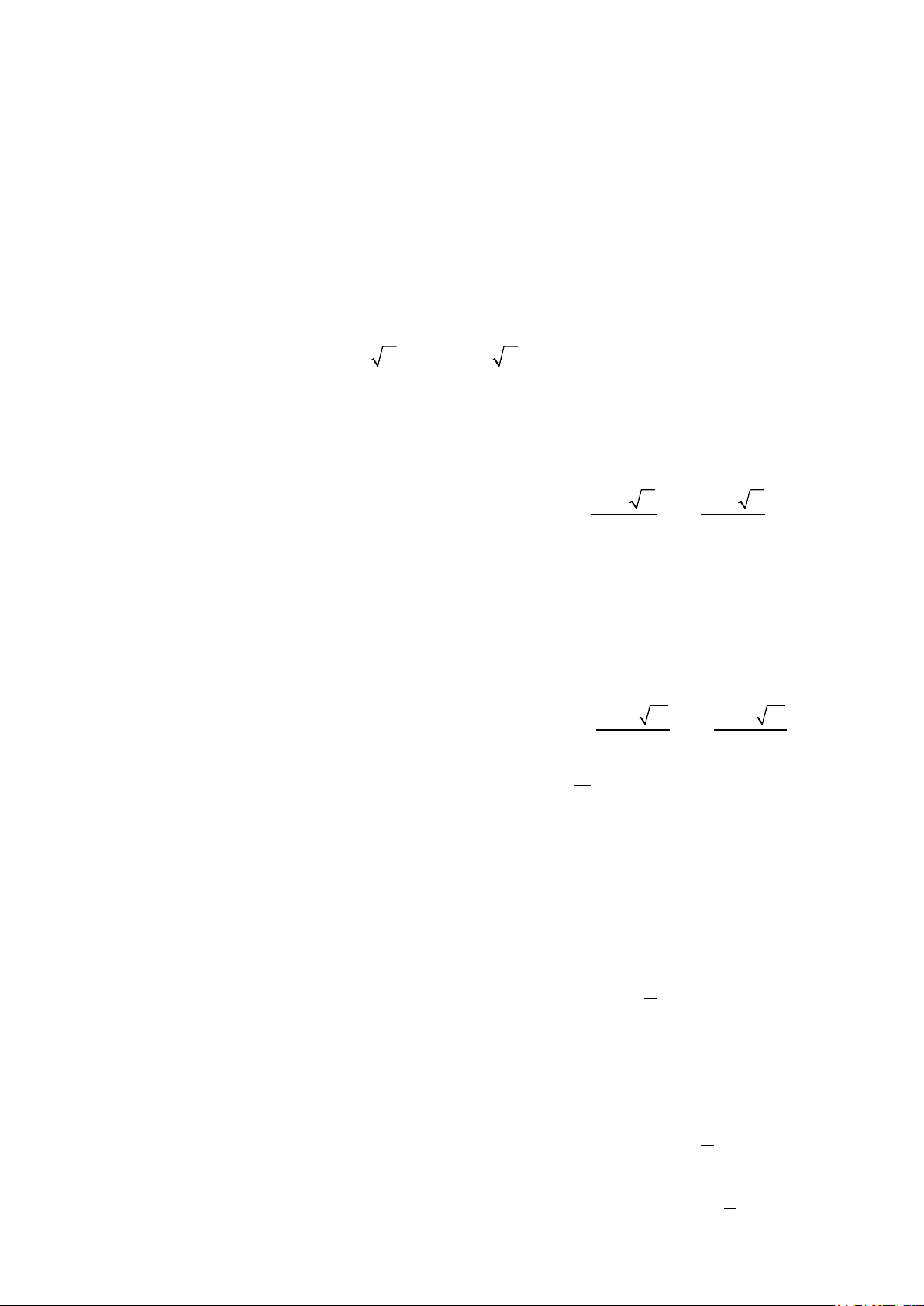

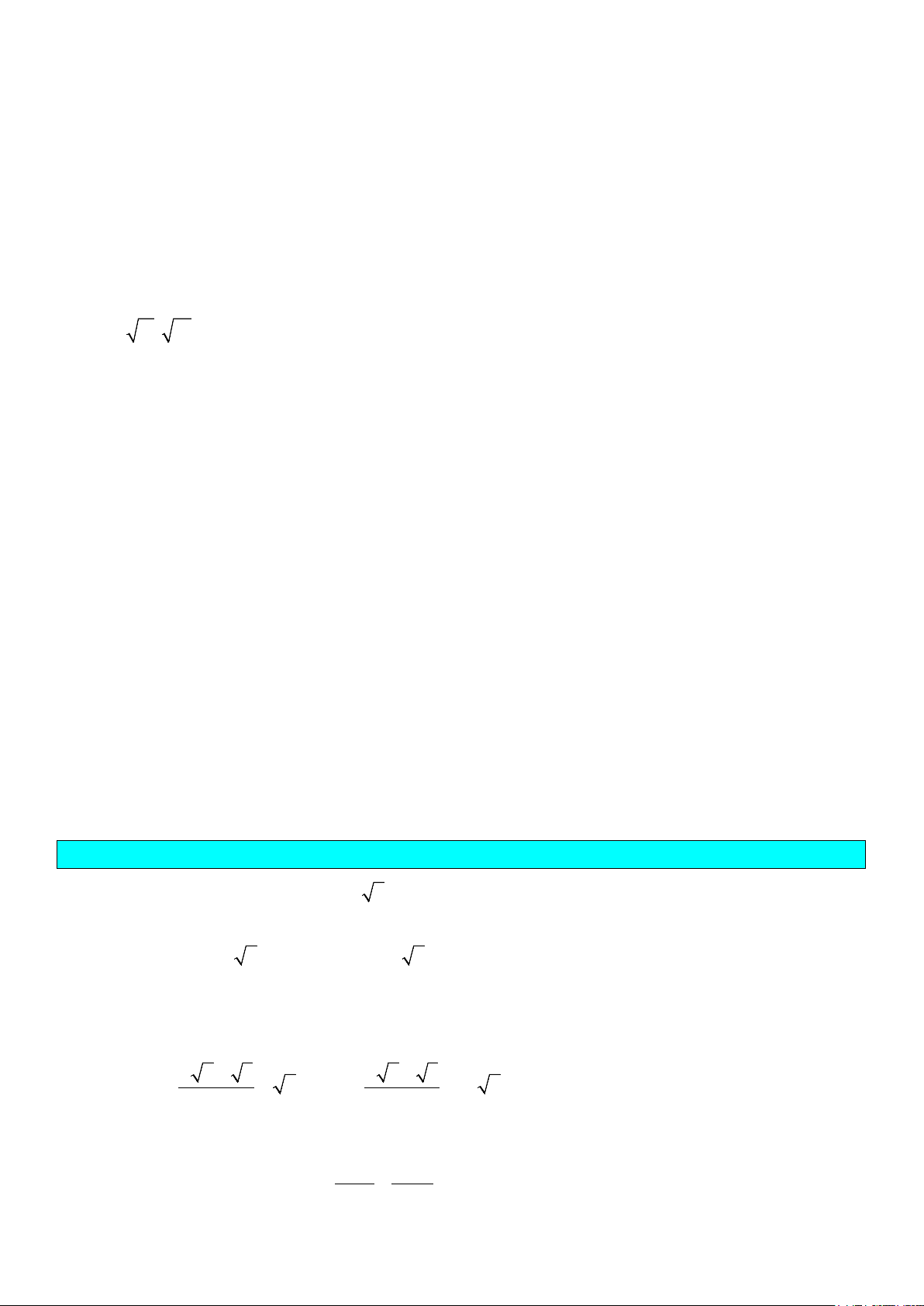








Preview text:
CHUYÊN ĐỀ 2_PHƯƠNG TRÌNH BẬC HAI VÀ HỆ THỨC VIÉT
A. KIẾN THỨC CƠ BẢN CẦN NẮM
1. Định nghĩa phương trình bậc hai một ẩn.
Phương trình bậc hai một ẩn (nói gọn là phương trình bậc hai) là phương trình có dạng 2
ax + bx + c = 0
trong đó x là ẩn; a,b,c là những số cho trước gọi là hệ số và a ≠ 0 .
2. Cách giải phương trình bậc hai một ẩn có dạng đặc biệt ( 2 2
ax + bx = 0;ax + c = 0. )
Dùng phương pháp đặt nhân tử chung hoặc dùng hằng đẳng thức để đưa vế trái về một bình phương.
Lưu ý: • Nếu A⋅ B = 0 thì A = 0 hoặc B = 0 . • Nếu 2
A = B(B ≥ 0) thì A = B hoặc A = − B .
3. Công thức nghiệm của phương trình bậc hai
Xét phương trình bậc hai một ẩn 2
ax + bx + c = 0(a ≠ 0). Tính biệt thức 2
∆ = b − 4ac . − + ∆ − − ∆
• Nếu Δ > 0 thì phương trình có hai nghiệm phân biệt: b = , b x x = . 1 2 2a 2a
• Nếu Δ = 0 thì phương trình có nghiệm kép: b x = x = − . 1 2 2a
• Nếu Δ < 0 thì phương trình vô nghiệm. Chú ý:
Xét phương trình bậc hai 2
ax + bx + c = 0(a ≠ 0), với b = 2b′ và 2
Δ′ = b′ − ac . − ′ + ′ − ′ − ′
• Nếu Δ′ > 0 thì phương trình có hai nghiệm phân biệt: b Δ b Δ x = , x = . 1 2 a a ′
• Nếu Δ′ = 0 thì phương trình có nghiệm kép: b x = x = − . 1 2 a
• Nếu Δ′ < 0 thì phương trình vô nghiệm. 4. Định lí Vi-et
Ta có định lí Viète như sau: b x + x = − 1 2
Nếu x , x là hai nghiệm của phương trình 2
ax + bx + c = 0(a ≠ 0) thì a 1 2 c x x = 1 2 a
5. Áp dụng định lí Vi-et để tính nhẩm nghiệm Xét phương trình 2
ax + bx + c = 0(a ≠ 0) .
- Nếu a + b + c = 0 thì phương trình có một nghiệm là x =1, còn nghiệm kia là c x = . 1 2 a
- Nếu a − b + c = 0 thì phương trình có một nghiệm là x = 1 − , còn nghiệm kia là c x = − 1 2 a
6. Tìm hai số khi biết tổng và tích của chúng
Nếu hai số có tổng bằng S và tích bằng P thì hai số đó là hai nghiệm của phương trình bậc hai: 2
x − Sx + P = 0
Điều kiện để có hai số đó là 2
S − 4P ≥ 0 .
MỘT SỐ LƯU Ý VÀ CÁC KẾT QUẢ CẦN NẮM KHI GIẢI CÁC BÀI TOÁN LIÊN QUAN ĐẾN ĐỊNH LÝ VI-ET
Bài toán thường gặp : Tìm m để phương trình 2
ax + bx + c = 0 (a ≠ 0) có hai nghiệm (phân biệt)
x , x thỏa mãn một biểu thức đối xứng đối với x , x 1 2 1 2 Quy trình
Bước 1. Tìm điều kiện để phương trình có hai nghiệm (phân biệt) x , x 1 2 • 2
ax + bx + c = 0 (a ≠ 0) có hai nghiệm x , x ⇔ ∆ ≥ 0 ( ' ∆ ≥ 0 1 2 ) • 2
ax + bx + c = 0 (a ≠ 0) có hai nghiệm phân biệt x , x ⇔ ∆ > 0 ( ' ∆ > 0 1 2 )
Bước 2. Biến đổi biểu thức đối xứng đối với x , x về tổng x + x và tích x .x 1 2 1 2 1 2
Bước 3. Sử dụng định lý Viet, ta có b x + x = − , c
x x = và thay vào biểu thức chứa tổng x + x và 1 2 a 1 2 a 1 2
tích x x ở trên. Giải ra m , đối chiếu điều kiện ở bước 1. 1 2
Một số phép biến đổi thường gặp 2 2 2 2
• x + x = x + x + 2x x – 2x x = x + x – 2x x 1 2 1 2 1 2 1 2 ( 1 2 )2 1 2 3 3 • x + x = (x + x )( 2 2
x + x – x x = x + x x + x – 3x x 1 2 1 2 1 2 1 2 ) ( 1 2 ) ( 1 2 )2 1 2 Hoặc 3 3 x + x = x + x – 3x x x + x . 1 2 ( 1 2 )2 1 2 ( 1 2 )
• x + x = (x )2 + (x )2 + 2x x – 2x x = (x + x )2 4 4 2 2 2 2 2 2 2 2 2 2 – 2x x . 1 2 1 2 1 2 1 2 1 2 1 2 • x – x thì xét 2 x – x = x – x = x + x – 4x x . 1 2 ( 1 2 )2 ( 1 2 )2 1 2 1 2
• x + x thì xét ( x + | x | = x + x + 2 x . x 1 2 )2 2 2 1 2 1 2 1 2 2 2 = x + x + 2 x x = x + x – 2x x + 2 x x . 1 1 1 2 ( 1 2 )2 1 2 1 2 Chú ý : 2 2 2
A = A , A ± B = (A ± B)2 , A . B = A.B .
IHỆ QUẢ CỦA ĐỊNH LÝ VIÉT Cho phương trình 2
ax + bx + c = 0 (a ≠ 0) có hai nghiệm x , x 1 2 . Định lý Viet: a + = − , . c x x x x = . 1 2 1 2 b a
Hệ quả 1. Nếu x =1 là nghiệm của phương trình thì 2 .1 a + .1
b + c = 0 hay a + b + c = 0 .
Ngược lại, nếu a + b + c = 0 thì x =1 là một nghiệm, nghiệm còn lại là c x = a
Hệ quả 2. Nếu x = 1
− là một nghiệm của phương trình thì 2 . a ( 1) − + . b ( 1)
− + c = 0 hay a − b + c = 0 .
Ngược lại, nếu a − b + c = 0 thì x = 1
− là một nghiệm,nghiệm còn lại là c x = − . a
Hệ quả 3. Nếu a và c trái dấu thì phương trình luôn có hai nghiệm phân biệt, đồng thời hai nghiệm luôn trái dấu nhau.
Hệ quả 4. Điều kiện để x > 0, x > 0 (cả hai nghiệm đều dương) là 1 2 x + x > 0 1 2 x x > 0 1 2
Hệ quả 5. Điều kiện để x < 0, x < 0 (cả hainghiệm đều âm) là 1 2 x + x < 0 1 2 x x > 0 1 2
Hệ quả 6. Điều kiện để x < 0 < x (cả hai nghiệm trái dấu ) là x .x < 0 hay a và c trái dấu. 1 2 1 2
DẠNG TOÁN CÓ THÊM ĐIỀU KIỆN PHỤ
Nếu bình phương hai vế ta cần thêm điều kiện phụ là hai vế lớn hơn hoặc bằng 0 . x + x ≥ 0
Nếu có x , x ta cần thêm diều kiện phụ là 1 2
x ≥ 0; x ≥ 0 ⇔ 1 2 1 2 x x ≥ 0 1 2 x + x > 0
Nếu x , x là độ dài hai cạnh đa giác ta cần thêm diều kiện phụ là: 1 2
x > 0, x > 0 ⇔ 1 2 1 2 x x > 0 1 2
DẠNG TOÁN SO SÁNH NGHIỆM VỚI SỐ 0 VÀ SỐ 𝜶𝜶 Cho phương trình 2
ax + bx + c = 0(a ≠ 0) có hai nghiệm x , x . 1 2 x + x > 0 1 2
x > 0, x > 0 ⇔ 1 2 x x > 0 1 2 x + x < 0 1 2
x < 0, x < 0 ⇔ 1 2 x x > 0 1 2
x < 0 < x ⇔ x x < 0 1 2 1 2 (
x −α + x −α > 0 1 ) ( 2 )
x > α, x > α ⇔ x −α > 0, x −α > 0 ⇔ 1 2 1 2 (
x −α x −α > 0 1 )( 2 ) (
x −α + x −α < 0 1 ) ( 2 )
x < α, x < α ⇔ x −α < 0, x −α < 0 ⇔ 1 2 1 2 (
x −α x −α > 0 1 )( 2 )
x < α < x ⇔ x −α < 0, x −α > 0 ⇔ x −α x −α < 0 1 2 1 2 ( 1 )( 2 )
B. BÀI TẬP VẬN DỤNG
Bài toán 1: phương trình bậc hai và ứng dụng vi-ét ( không chứa tham số )
Câu 1: Giải phương trình sau: 2
x + 2 2x = 6
Câu 2: Gọi x , x là các nghiệm của phương trình 2
x − 3x −10 = 0 . Không giải phương trình, hãy tính 1 2
giá trị của biểu thức: x +1 x +1 1 2 A = + x x 2 1
Câu 3: Cho phương trình 2
3x − 2x − 4 = 0 (1). Biết phương trình có hai nghiệm phân biệt x ; x . Tính 1 2 giá trị biểu thức: 1 1 A = + 2 2 x x 1 2
Câu 4: Cho phương trình 2
3x −11x −15 = 0 có 2 nghiệm là x , x Không giải phương trình, hãy tính giá 1 2
trị của biểu thức 3x 3x 1 2 A = + x x 2 1
Câu 5: Gọi x , x là hai nghiệm của phương trình 2
2x − 3x − 4 = 0 . Không giải phương trình, hãy tính 1 2
giá trị của biểu thức 2
A = (x + x ) + x x . 1 2 1 2
Câu 6: Cho phương trình: 2
2x − 4x − 3 = 0 có hai nghiệm là x ; x . Không giải phương trình, hãy tính 1 2
giá trị của biểu thức: A = (x − x )2 . 1 2
Câu 7: Cho phương trình 2
x − 4 3x + 8 = 0 có 2 nghiệm x ; x , không giải phương trình hãy tính giá trị 1 2 biểu thức: 3 3
Q = x + x 1 2
Câu 8: Cho phương trình: 2
4x − 5x − 3 = 0 có hai nghiệm là x , x . Không giải phương trình, hãy tính 1 2
giá trị của biểu thức S = x + x ; P = x x ; F = (x +1 x +1 − x − x . 1 )( 2 ) ( 1 2)2 1 2 1 2
Câu 9: Cho phương trình 2
3x + 5x − 6 = 0 có hai nghiệm x ,x . 1
2 Không giải phương trình, tính: 2 2x2 P = + 2x 1 x + x 1 2
Câu 10: a). Hãy tìm một phương trình bậc hai 2
ax + bx + c = 0 với các hệ số a,b,c là số nguyên nhận 5 2 x − = làm nghiệm. 3
b). Tính tổng lập phương hai nghiệm của phương trình vừa tìm được ở câu a)
Câu 11: Cho phương trình 2
x − 5x + a = 0 . Biết phương trình có một nghiệm là x = 6 − 2 5 . Tính giá trị của biểu thức 3 3
A = x − x + x − x − 285 1 1 2 2
Câu 12: Gọi x , x là hai nghiệm của phương trình: 2
3x + 5x − 6 = 0 . Không giải phương trình, tính các 1 2
giá trị của các biểu thức x x 1 2 D = + . x + 2 x + 2 2 1
Câu 13: Cho phương trình 2
x + 5x − 7 = 0 có hai nghiệm là x ; x . Không giải phương trình, hãy tính giá 1 2 trị của biểu thức 2 2
A = x + x − 2x x . 1 2 1 2
Câu 14: Cho phương trình 2
3x −12x − 5 = 0 có hai nghiệm là x , x . Không giải phương trình, hãy tính 1 2 2
giá trị của biểu thức:
x + 4x − x x 1 2 1 2 T = 2
4x + x + x x 1 2 1 2
Câu 15: Cho phương trình 2
x −12x + 4 = 0 có hai nghiệm dương phân biệt x , x . Không giải phương 1 2 2 2 +
trình, hãy tính giá trị của biểu thức x x 1 2 T = . x + x 1 2
Câu 16: Cho phương trình 2
x − x − 3 = 0 có hai nghiệm x , x . Không giải phương trình, hãy tính giá trị 1 2 của biểu thức A = 2 2
3x x + x + x (3x +1) 1 2 1 2 1
Câu 17: Cho phương trình 2
− 2x + 2x + 3 = 0 có 2 nghiệm phân biệt là x , x . Không giải phương trình, 1 2
hãy tính giá trị của biểu thức x +1 x +1 2 1 A = + 1− x 1− x 1 2
Câu 18: Cho phương trình 2
x − 4x + 3 = 0 có 2 nghiệm là x , x . Không giải phương trình, hãy tính giá 1 2 trị của biểu thức 5x − x x − 5x 1 2 1 2 A = − . x x 1 2
Câu 19: Cho phương trình 2
x −12x + 4 = 0 có hai nghiệm phân biệt x , x . Không giải phương trình hãy 1 2 x + x
tính giá trị của biểu thức 1 2 T = 2 2x + 24x − 4 1 2
Câu 20: Gọi x , x −
− = . Không giải phương trình, hãy tính giá 1
2 là hai nghiệm của phương trình: 2 x 4x 7 0 trị của biểu thức x x 1 2 T = + − 2. x x 2 2
Câu 21: Cho phương trình 2
2x − 3x −1 = 0 có hai nghiệm là x x , không giải phương trình hãy tính giá 1 2 trị của biểu thức x −1 x −1 1 2 A = + x +1 x +1 2 1
Câu 22: Cho phương trình: 2
x − 5x − 6 = 0 có hai nghiệm x , x . Hãy tính giá trị của biểu thức sau: A = 1 2 x x 1 2 + x −1 x −1 2 1
Câu 23: Cho phương trình: 2
x + 3x −10 = 0 có 2 nghiệm x , x . Tính giá trị biểu thức x + 2 x + 2 1 2 = + 1 2 A x x 2 1
Câu 24: Gọi x , x là hai nghiệm của phương trình: 2
x − x −1 = 0. Lập phương trình bậc hai có hai 1 2
nghiệm là x +1 x +1 2 1 ; x x 1 2
Câu 25: Cho phương trình 2
3x − 6x + 2 = 0 có hai nghiệm là x , x . Không giải phương trình, hãy tính 1 2
giá trị của biểu thức 2 2
A = x + x − x x . 1 2 1 2
Bài toán 2: các bài toán có liên qua đến tham số
Câu 1: Cho phương trình bậc hai 2
x − 6x + c = 0 có hai nghiệm phân biệt là x = 2x . Tính giá trị biểu 1 2 thức 3 3
S = x + x + 3x x x + x . 1 2 1 2 ( 1 2 )
Câu 2: Cho phương trình: 2
x + 5x + m = 0 (*) có một nghiệm là − 13 − 5 . Tìm tổng bình phương hai 2
nghiệm của phương trình trên.
Câu 3: Cho phương trình 2
mx + 2(m – 2) x + m – 3 = 0 (m là tham số). Khi phương trình có nghiệm, tìm
một hệ thức liên hệ giữa hai nghiệm của phương trình đã cho không phụ thuộc vào m .
Câu 4: Biết phương trình 2
2x + 4x + m = 0 ( m là tham số) có 1 nghiệm bằng 1.Tính tổng bình phương
hai nghiệm của phương trình.
Câu 5: Cho phương trình 2
x − (m +1)x −1 = 0 có nghiệm x =1− 2 . Tính bình phương của hiệu hai
nghiệm trong phương trình trên.
Câu 6: Biết rằng phương trình 2
x − 5x + a = 0 có hai nghiệm x , x , biết 5 13 1 2 x − =
. Tính giá trị của 1 2 biểu thức 2 2
x + x − 2x x . 1 2 1 2
Câu 7: Cho phương trình 2
x − 6x − 2m + 3 = 0. Tìm m để phương trình có hai nghiệm x , x thỏa mãn 1 2 2 2
x + x = 20. 1 2
Câu 8: Tìm tất cả các giá trị của tham số m để phương trình 2
x − 2mx + 4m − 4 = 0 có hai nghiệm x , x 1 2 thỏa mãn 2 2
x + x −8 = 0 . 1 2
Câu 9: Biết rằng phương trình bậc hai 2
x − 2x + m = 0 có một nghiệm là 2 x = . Tính tổng nghịch 3 −1
đảo bình phương hai nghiệm của phương trình trên.
Câu 10: Biết rằng phương trình bậc hai 2
x + 6x + a = 0 có một nghiệm là x = 3 − + 14 . Tìm tổng bình
phương hai nghiệm của phương trình trên.
Câu 11: Biết rằng phương trình bậc hai 2
x − 5x + m = 0 (m là tham số). Tìm m để phương trình có hai
nghiệm phân biệt sao cho tổng các bình phương của hai nghiệm bằng 13.
Câu 12: Phương trình 2
x − 2x − m +1 = 0 ( m là tham số) có một nghiệm là x =1+ 7 . Tính giá trị của biểu thức 2 2
A = x x + x x . 1 2 2 1
Câu 13: Phương trình 2
x + mx + 2m − 4 = 0 có x , x hai nghiệm và x = 1
− , tính giá trị của biểu thức 1 2 1 1 1 N = + x + 3 x + 3 1 2
Câu 14: Biết rằng phương trình bậc hai 2
x + 4x + m = 0 có một nghiệm là x = − 3 . Tìm tổng các nghịch
đảo hai nghiệm của phương trình trên.
Câu 15: Cho phương trình: 2
x − 2x + m −1 = 0 (1) với m là tham số. Tìm tất cả các giá trị của m để
phương trình có hai nghiệm phân biệt thỏa mãn: 1 1 x x −1 = + 1 2 x x 1 2
Câu 16: Cho phương trình: 2 x − 2(m − )
1 x − m − 3 = 0 . Tìm m để biểu thức 2 2
A = x + x đạt giá trị nhỏ 1 2 nhất.
Câu 17: Biết rằng phương trình bậc hai 2
2x − 4x + m = 0 có một nghiệm 2 10 x + = . Tính tổng nghịch 2
đảo hai nghiệm của phương trình trên.
Câu 18: Cho phương trình 2 x − (m + ) 2 2
3 x + m + 3 = 0 . Tìm m để phương trình có hai nghiệm phân biệt
x , x thỏa mãn (2x −1 2x −1 = 9 . 1 )( 2 ) 1 2
Câu 19: Cho phương trình 2 x − (m + ) 2 2
1 x + 4m − m = 0 . Tìm m để phương trình có hai nghiệm phân
biệt x , x sao cho biểu thức = −
đạt giá trị nhỏ nhất. 1 2 A x x 1 2
Câu 20: Cho phương trình 2
x + mx − 3 = 0 . Tìm m để phương trình có hai nghiệm phân biệt x , x thỏa 1 2
mãn x + x = 4 . 1 2
Câu 21: Cho phương trình 2
x + mx + 2m − 4 = 0 . Tìm m để phương trình có hai nghiệm phân biệt x , x 1 2
thỏa mãn x + x = 3. 1 2
Câu 22: Cho phương trình 2 2
x − 4x − m −1 = 0. Tìm m để phương trình có hai nghiệm phân biệt x , x 1 2
phân biệt thỏa mãn x = 5 − x . 2 1
Câu 23: Cho phương trình 2 x − 2(k − )
1 x − 4k = 0. Tìm k để phương trình có hai nghiệm phân biệt x , x 1 2
phân biệt thỏa mãn3x − x = 2 . 1 2
Câu 24: Cho phương trình 2
x − 6x + m + 3 = 0 . Tìm m để phương trình có hai nghiệm phân biệt x , x 1 2 phân biệt thỏa mãn 2 x = x . 2 1
Câu 25: Cho phương trình 2
x − (m − 3) x − 5 = 0 . Tìm m để phương trình có hai nghiệm x , x là các số 1 2 nguyên.
Câu 26: Cho phương trình 2
x − 20x + m + 5 = 0. Tìm m để phương trình có hai nghiệm x , x là các số 1 2 nguyên tố.
Câu 27: Cho phương trình 2
x − 2mx + m −1 = 0 . Tìm m đề phương trình có hai nghiệm phân biệt x , x 1 2
thỏa mãn x + x = 2. 1 2
Câu 28: Cho phương trình 2
x − (2m + 5) x + 2m +1 = 0. Tìm m để phương trình có hai nghiệm phân biệt
x , x mà biểu thức = −
đạt giá trị nhỏ nhất. 1 2 M x x 1 2
Câu 29: Cho phương trình 2
x − 5x + m −1 = 0 . Tìm m để phương trình có hai nghiệm phân biệt x , x sao 1 2 cho 2x = x . 1 2
Câu 30: Cho phương trình 2
x − (m + 5) x + 3m + 6 = 0 . Tìm m để phương trình có hai nghiệm phân biệt
x , x là độ dài của hai cạnh góc vuông của một tam giác vuông có độ dài cạnh huyền bằng 1 2 5.
Câu 31: Cho phương trình 2
x − (m − 2) x + m − 3 = 0 . Tìm m để phương trình có hai nghiệm phân biệt
x , x là độ dài hai cạnh của một tam giác vuông cân. 1 2
Câu 32: Cho phương trình 2
x + (m + 2) x − m − 4 = 0 . Tìm m để phương trình có hai nghiệm phân biệt
x , x thỏa mãn x < 0 ≤ x . 1 2 1 2 Vậy m > 4
− là giá trị cần tìm.
Câu 33: Cho phương trình 2
x + (m − 2) x + m − 5 = 0 . Tìm m để phương trình có hai nghiệm phân biệt
x , x thỏa mãn x ≤ 0 < x . 1 2 1 2
Câu 34: Cho phương trình 2
x + 2mx + 4m − 4 = 0 . Tìm m để phương trình có hai nghiệm phân biệt x , x 1 2
thoả mãn x < 2, x < 2 1 2
Câu 35: Cho phương trình 2
x − (m + 3)x + m −1 = 0 Tìm m để phương trình có hai nghiệm phân biệt thoả mãn 3
x < − < x . 1 2 2
CHUYÊN ĐỀ 2_PHƯƠNG TRÌNH BẬC HAI VÀ HỆ THỨC VIÉT
A. KIẾN THỨC CƠ BẢN CẦN NẮM
1. Định nghĩa phương trình bậc hai một ẩn.
Phương trình bậc hai một ẩn (nói gọn là phương trình bậc hai) là phương trình có dạng 2
ax + bx + c = 0
trong đó x là ẩn; a,b,c là những số cho trước gọi là hệ số và a ≠ 0 .
2. Cách giải phương trình bậc hai một ẩn có dạng đặc biệt ( 2 2
ax + bx = 0;ax + c = 0. )
Dùng phương pháp đặt nhân tử chung hoặc dùng hằng đẳng thức để đưa vế trái về một bình phương.
Lưu ý: • Nếu A⋅ B = 0 thì A = 0 hoặc B = 0 . • Nếu 2
A = B(B ≥ 0) thì A = B hoặc A = − B .
3. Công thức nghiệm của phương trình bậc hai
Xét phương trình bậc hai một ẩn 2
ax + bx + c = 0(a ≠ 0). Tính biệt thức 2
∆ = b − 4ac .
• Nếu Δ > 0 thì phương trình có hai nghiệm phân biệt: b − + ∆ , b x x − − ∆ = = . 1 2 2a 2a
• Nếu Δ = 0 thì phương trình có nghiệm kép: b x = x = − . 1 2 2a
• Nếu Δ < 0 thì phương trình vô nghiệm. Chú ý:
Xét phương trình bậc hai 2
ax + bx + c = 0(a ≠ 0), với b = 2b′ và 2
Δ′ = b′ − ac . − ′ + ′ − ′ ′
• Nếu Δ′ > 0 thì phương trình có hai nghiệm phân biệt: b Δ b − Δ x = , x = . 1 2 a a ′
• Nếu Δ′ = 0 thì phương trình có nghiệm kép: b x = x = − . 1 2 a
• Nếu Δ′ < 0 thì phương trình vô nghiệm. 4. Định lí Vi-et
Ta có định lí Viète như sau: b x + x = − 1 2
Nếu x , x là hai nghiệm của phương trình 2
ax + bx + c = 0(a ≠ 0) thì a 1 2 c x x = 1 2 a
5. Áp dụng định lí Vi-et để tính nhẩm nghiệm Xét phương trình 2
ax + bx + c = 0(a ≠ 0) .
- Nếu a + b + c = 0 thì phương trình có một nghiệm là x =1, còn nghiệm kia là c = . 1 x2 a
- Nếu a − b + c = 0 thì phương trình có một nghiệm là x = 1 − , còn nghiệm kia là c = − 1 x2 a
6. Tìm hai số khi biết tổng và tích của chúng
Nếu hai số có tổng bằng S và tích bằng P thì hai số đó là hai nghiệm của phương trình bậc hai: 2
x − Sx + P = 0
Điều kiện để có hai số đó là 2
S − 4P ≥ 0 .
MỘT SỐ LƯU Ý VÀ CÁC KẾT QUẢ CẦN NẮM KHI GIẢI CÁC BÀI TOÁN LIÊN QUAN ĐẾN ĐỊNH LÝ VI-ET
Bài toán thường gặp : Tìm m để phương trình 2
ax + bx + c = 0 (a ≠ 0) có hai nghiệm (phân biệt)
x , x thỏa mãn một biểu thức đối xứng đối với x , x 1 2 1 2 Quy trình
Bước 1. Tìm điều kiện để phương trình có hai nghiệm (phân biệt) x , x 1 2 • 2
ax + bx + c = 0 (a ≠ 0) có hai nghiệm x , x ⇔ ∆ ≥ 0 ( ' ∆ ≥ 0 1 2 ) • 2
ax + bx + c = 0 (a ≠ 0) có hai nghiệm phân biệt x , x ⇔ ∆ > 0 ( ' ∆ > 0 1 2 )
Bước 2. Biến đổi biểu thức đối xứng đối với x , x về tổng x + x và tích x .x 1 2 1 2 1 2
Bước 3. Sử dụng định lý Viet, ta có b x + x = − , c
x x = và thay vào biểu thức chứa tổng x + x và 1 2 a 1 2 a 1 2
tích x x ở trên. Giải ra m , đối chiếu điều kiện ở bước 1. 1 2
Một số phép biến đổi thường gặp 2 2 2 2
• x + x = x + x + 2x x – 2x x = x + x – 2x x 1 2 1 2 1 2 1 2 ( 1 2 )2 1 2 3 3 • x + x = (x + x )( 2 2
x + x – x x = x + x x + x – 3x x 1 2 1 2 1 2 1 2 ) ( 1 2 ) ( 1 2 )2 1 2 Hoặc 3 3 x + x = x + x – 3x x x + x . 1 2 ( 1 2 )2 1 2 ( 1 2 )
• x + x = (x )2 + (x )2 + 2x x – 2x x = (x + x )2 4 4 2 2 2 2 2 2 2 2 2 2 – 2x x . 1 2 1 2 1 2 1 2 1 2 1 2 • x – x thì xét 2 x – x = x – x = x + x – 4x x . 1 2 ( 1 2 )2 ( 1 2 )2 1 2 1 2
• x + x thì xét ( x + | x | = x + x + 2 x . x 1 2 )2 2 2 1 2 1 2 1 2 2 2 = x + x + 2 x x = x + x – 2x x + 2 x x . 1 1 1 2 ( 1 2 )2 1 2 1 2 Chú ý : 2 2 2
A = A , A ± B = (A ± B)2 , A . B = A.B .
IHỆ QUẢ CỦA ĐỊNH LÝ VIÉT Cho phương trình 2
ax + bx + c = 0 (a ≠ 0) có hai nghiệm x , x . 1 2 Định lý Viet: a + = − , . c x x x x = . 1 2 1 2 b a
Hệ quả 1. Nếu x =1 là nghiệm của phương trình thì 2 .1 a + .1
b + c = 0 hay a + b + c = 0 .
Ngược lại, nếu a + b + c = 0 thì x =1 là một nghiệm, nghiệm còn lại là c x = a
Hệ quả 2. Nếu x = 1
− là một nghiệm của phương trình thì 2 . a ( 1) − + . b ( 1)
− + c = 0 hay a − b + c = 0 .
Ngược lại, nếu a − b + c = 0 thì x = 1
− là một nghiệm,nghiệm còn lại là c x = − . a
Hệ quả 3. Nếu a và c trái dấu thì phương trình luôn có hai nghiệm phân biệt, đồng thời hai nghiệm luôn trái dấu nhau.
Hệ quả 4. Điều kiện để x > 0, x > 0 (cả hai nghiệm đều dương) là 1 2 x + x > 0 1 2 x x > 0 1 2
Hệ quả 5. Điều kiện để x < 0, x < 0 (cả hainghiệm đều âm) là 1 2 x + x < 0 1 2 x x > 0 1 2
Hệ quả 6. Điều kiện để x < 0 < x (cả hai nghiệm trái dấu ) là x .x < 0 hay a và c trái dấu. 1 2 1 2
DẠNG TOÁN CÓ THÊM ĐIỀU KIỆN PHỤ
Nếu bình phương hai vế ta cần thêm điều kiện phụ là hai vế lớn hơn hoặc bằng 0 . x + x ≥ 0
Nếu có x , x ta cần thêm diều kiện phụ là 1 2
x ≥ 0; x ≥ 0 ⇔ 1 2 1 2 x x ≥ 0 1 2 x + x > 0
Nếu x , x là độ dài hai cạnh đa giác ta cần thêm diều kiện phụ là: 1 2
x > 0, x > 0 ⇔ 1 2 1 2 x x > 0 1 2
DẠNG TOÁN SO SÁNH NGHIỆM VỚI SỐ 0 VÀ SỐ 𝜶𝜶 Cho phương trình 2
ax + bx + c = 0(a ≠ 0) có hai nghiệm x , x . 1 2 x + x > 0 1 2
x > 0, x > 0 ⇔ 1 2 x x > 0 1 2 x + x < 0 1 2
x < 0, x < 0 ⇔ 1 2 x x > 0 1 2
x < 0 < x ⇔ x x < 0 1 2 1 2 (
x −α + x −α > 0 1 ) ( 2 )
x > α, x > α ⇔ x −α > 0, x −α > 0 ⇔ 1 2 1 2 (
x −α x −α > 0 1 )( 2 ) (
x −α + x −α < 0 1 ) ( 2 )
x < α, x < α ⇔ x −α < 0, x −α < 0 ⇔ 1 2 1 2 (
x −α x −α > 0 1 )( 2 )
x < α < x ⇔ x −α < 0, x −α > 0 ⇔ x −α x −α < 0 1 2 1 2 ( 1 )( 2 )
B. BÀI TẬP VẬN DỤNG
Bài toán 1: phương trình bậc hai và ứng dụng vi-ét ( không chứa tham số )
Câu 1: Giải phương trình sau: 2
x + 2 2x = 6 Lời giải Ta có 2
x + 2 2x = 6 đưa về 2
x + 2 2x − 6 = 0
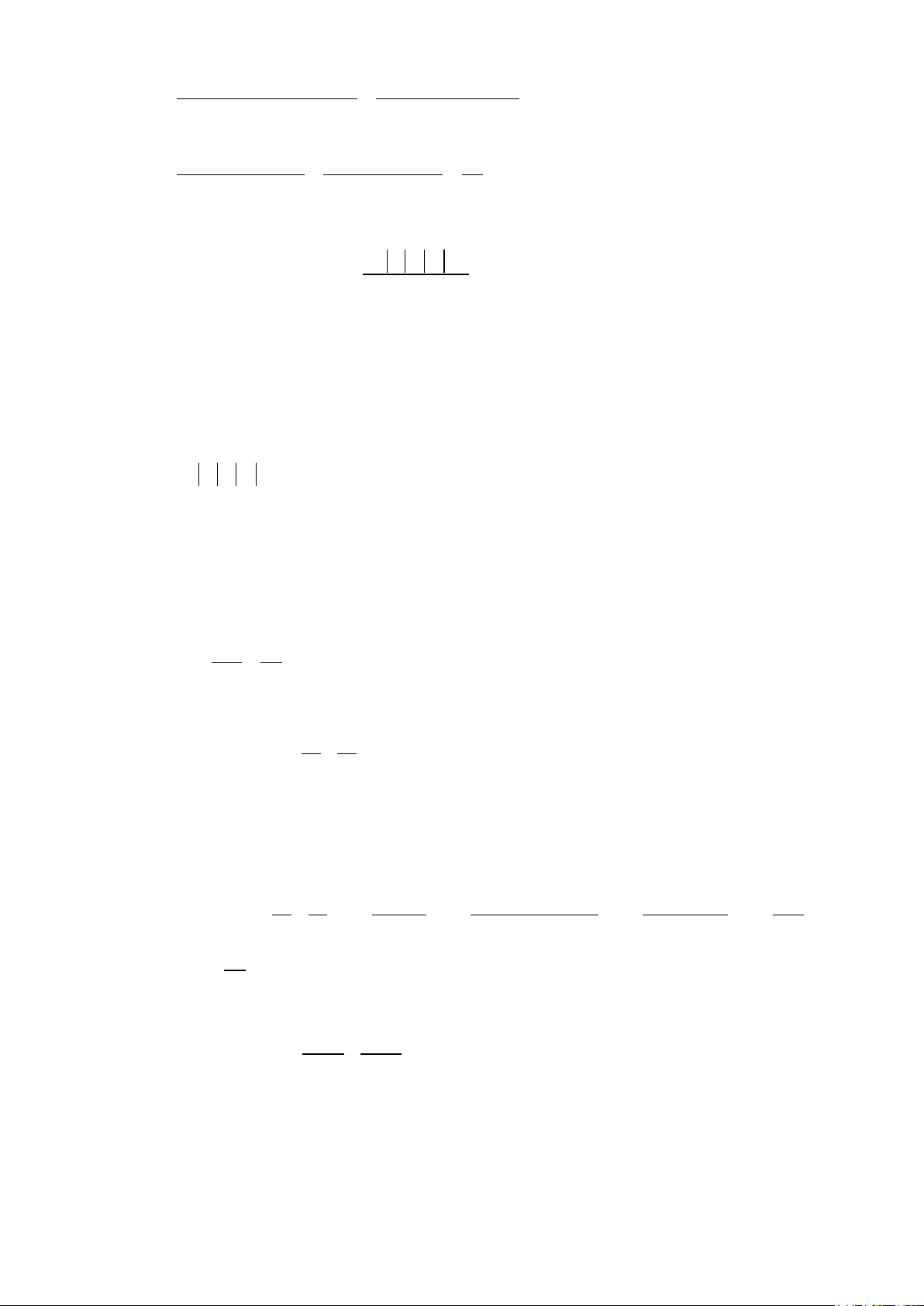
Tính được ∆ ' = 2 + 6 = 8 > 0 .
Khi đó, phương trình có 2 nghiệm phân biệt là: 2 8 x − + = = 2 và 2 8 x − − = = 3 − 2 1 1 2 1
Câu 2: Gọi x , x là các nghiệm của phương trình 2
x − 3x −10 = 0 . Không giải phương trình, hãy tính 1 2
giá trị của biểu thức: x +1 x +1 1 2 A = + x x 2 1 Lời giải Xét phương trình 2
x − 3x −10 = 0 . Ta có: 2 ∆ = ( 3 − ) − 4.( 10) −
= 49 > 0 . Suy ra phương trình có hai nghiệm phân biệt x , x . 1 2 x + x = 3 Theo hệ thức Viète: 1 2 . x .x = 10 − 1 2 Ta có x +1 x +1 1 2 A = + x x 2 1 2 2
x + x + x + x 1 1 2 2 = x .x 1 2
(x + x )2 − 2x .x + x + x 1 2 1 2 1 2 = x .x 1 2 2 3 − 2.( 10) − + 3 16 = = − 10 − 5 Vậy 16 A = − . 5
Câu 3: Cho phương trình 2
3x − 2x − 4 = 0 (1). Biết phương trình có hai nghiệm phân biệt x ; x . Tính 1 2 giá trị biểu thức: 1 1 A = + 2 2 x x 1 2 Lời giải Phương trình 2
3x − 2x − 4 = 0 (1) Ta có: . a c = 3.( 4 − ) = 12 − < 0
Suy ra phương trình (1) có 2 nghiệm phân biệt x ; x trái dấu 1 2
Áp dụng hệ thức Ta-lét ta có: −( 2 − ) 2 x + x = = 1 2 3 3 4 x x − = 1 2 3 Ta có: 1 1 A = + 2 2 x x 1 2 2 2 x + x 1 2 A = 2 2 x .x 1 2 2 2
x + x + 2x .x − 2x .x 1 2 1 2 1 2 A = 2 2 x .x 1 2
(x + x )2 − 2x .x 1 2 1 2 A = 2 2 x .x 1 2 2 2 4 2. − − 3 3 7 A = = 2 4 − 4 3 Vậy 7 A = 4
Câu 4: Cho phương trình 2
3x −11x −15 = 0 có 2 nghiệm là x , x Không giải phương trình, hãy tính giá 1 2
trị của biểu thức 3x 3x 1 2 A = + x x 2 1 Lời giải Ta có 3x + 4x = 3 1 2
⇔ (x + x ) + x = 6 1 2 2 ⇒ x = 9 − 2 Vì x = 9
− là nghiệm của phương trình nên ta có (− )2 9 − 5.( 9 − ) + m + 4 = 0. Tìm được m = 3 − ± 13
Câu 5: Gọi x , x là hai nghiệm của phương trình 2
2x − 3x − 4 = 0 . Không giải phương trình, hãy tính 1 2
giá trị của biểu thức 2
A = (x + x ) + x x . 1 2 1 2 Lời giải
Áp dụng định lí Vi-ét cho phương trình 2
2x − 3x − 4 = 0 , ta có : 3
x + x = , x x = 2 − . 1 2 1 2 2 2 Suy ra : 3 1 A = + ( 2) − = . 2 4
Câu 6: Cho phương trình: 2
2x − 4x − 3 = 0 có hai nghiệm là x ; x . Không giải phương trình, hãy tính 1 2
giá trị của biểu thức: A = (x − x )2 . 1 2 Lời giải
Phương trình có ac = 6
− < 0 nên luôn có 2 nghiệm phân biệt x , x 1 2
Theo hệ thức Viète, ta có: 3
x + x = 2; x x = − 1 2 1 2 2 Ta có:
A = (x − x )2 1 2
A = (x + x )2 − 4x x 1 2 1 2 2 3 A 2 4. − = − 2 A =10 Vậy A =10.
Câu 7: Cho phương trình 2
x − 4 3x + 8 = 0 có 2 nghiệm x ; x , không giải phương trình hãy tính giá trị 1 2 biểu thức: 3 3
Q = x + x 1 2 Lời giải Phương trình 2
x − 4 3x + 8 = 0 2
∆ ' = (2 3) −8 = 4 > 0 nên phương trình có hai nghiệm x1; x2
Áp dụng hệ thức Vi-ét ta có: x + x = 4 3 và x x = 8 1 2 1 2 Ta có: 3 3 Q = x + x 1 2 Q = (x + x )( 2 2
x − x x + x 1 2 1 1 2 2 ) Q = (x + x )( 2 2
x + 2x x + x − 3x x 1 2 1 1 2 2 1 2 )
Q = (x + x ) (x + x )2 −3x x 1 2 1 2 1 2
Q = (x + x )3 −3x x x + x 1 2 1 2 ( 1 2 )
Thay x + x = 4 3 và x x = 8 vào Q ta được: 1 2 1 2 = ( )3 Q 4 3 − 3.8.4 3 = 96 3
Câu 8: Cho phương trình: 2
4x − 5x − 3 = 0 có hai nghiệm là x , x . Không giải phương trình, hãy tính 1 2
giá trị của biểu thức S = x + x ; P = x x ; F = (x +1 x +1 − x − x . 1 )( 2 ) ( 1 2)2 1 2 1 2 Lời giải
Theo định lí Viète, ta có: b 5 S −
= x + x = − = ; c 3
P = x ⋅ x = = . 1 2 a 4 1 2 a 4
Ta có: F = (x + ) 1 (x + )
1 − (x − x )2 1 2 1 2 2 2
F = x x + x + x +1− x + 2x x − x 1 2 1 2 1 1 2 2 2 2
F = x x + x + x +1− x − 2x x − x + 4x x 1 2 1 2 1 1 2 2 1 2
F = 5x x + x + x +1− (x + x )2 1 2 1 2 1 2 2 3 − 5 5 49 F = 5. + +1 − − = . 4 4 4 16
Câu 9: Cho phương trình 2
3x + 5x − 6 = 0 có hai nghiệm x ,x . Không giải phương trình, tính: 1 2 2 2x2 P = + 2x 1 x + x 1 2 Lời giải
Chứng minh PT có 2 nghiệm phân biệt x , x 1 2 5 x + x − =
Theo định lý Viet ta có: 1 2 3 x x = 2 − 1 2 Theo đề Câu ta có : 2 + + (x + x )2 2 2 2 − 2x x + 2 2 2 2 2 x x x x x x x 1 2 1 2 1 2 86 − 2 2 1 1 2 2x + = = = 1 x + x x + x x + x 15 1 2 1 2 1 2
Câu 10: a). Hãy tìm một phương trình bậc hai 2
ax + bx + c = 0 với các hệ số a,b,c là số nguyên nhận 5 2 x − = làm nghiệm. 3
b). Tính tổng lập phương hai nghiệm của phương trình vừa tìm được ở câu a) Lời giải a). Ta có 5 2 x − = 3 3x = 5 − 2 3x + 2 = 5 ( x + )2 3 2 = 5 2 9x +12x + 4 = 5 2
9x +12x −1 = 0
Vậy phương trình bậc hai cần tìm là: 2
9x +12x −1 = 0 4 x + x − = 1 2
b). Theo hệ thức Vi-ét, ta có: 3 1 x .x − = 1 2 9 3 Ta có 3 3 4 1 − 4 − 76
x + x = x + x − 3x .x x + x − = − 3 − = 1 2 ( 1 2)3 1 2 ( 1 2 ) 3 9 3 27
Câu 11: Cho phương trình 2
x − 5x + a = 0 . Biết phương trình có một nghiệm là x = 6 − 2 5 . Tính giá trị của biểu thức 3 3
A = x − x + x − x − 285 1 1 2 2 Lời giải
Ta có x = 6 − 2 5 = 5 −1
Vì phương trình có một nghiệm là x = 6 − 2 5 nên thay x = 6 − 2 5 vào phương trình ta có a = 11 − + 7 5 x + x = 5
Áp dụng hệ thíc Viets ta có: 1 2 x .x = a 1 2 Ta có 3 3
A = x − x + x − x − 285 1 1 2 2 3 3
= x + x − (x + x ) −185 1 2 1 2 2 2
= (x + x )(x − x .x + x ) − 5 − 285 1 2 1 1 2 2 2
= (x + x ) (x + x ) − 3x .x − 290 1 2 1 2 1 2 2 = 5.5 − 3.( 11 − + 7 5) = 105 − 5
Vậy giá trị của biểu thức A là 105 − 5
Câu 12: Gọi x , x là hai nghiệm của phương trình: 2
3x + 5x − 6 = 0 . Không giải phương trình, tính các 1 2
giá trị của các biểu thức x x 1 2 D = + . x + 2 x + 2 2 1 Lời giải
Phương trình có tích ac = 3 . ( 6 − ) = 18
− < 0 nên có nghiệm phân biệt x , x . Theo định lý Viète, 1 2 ta có 5 x x − + = và x x = 2 − . 1 2 3 1 2 x , x ≠ 2 − 1 2 x x
x x + 2 + x x + 2 1 2 1 ( 1 ) 2 ( 2 ) D = + = x + 2 x + 2 x + 2 x + 2 2 1 ( 1 )( 2 ) ( 2 2
x + x + 2 x + x 1 2 ) ( 1 2) D =
x x + 2 x + x + 4 1 2 ( 1 2)
(x + x )2 − 2x x + 2 x + x 1 2 1 2 ( 1 2) D =
x x + 2 x + x + 4 1 2 ( 1 2) 2 5 − ( ) 5 2 . 2 2 − − − + ⋅ 3 3 31 D − = = (− ) 5 − 12 2 + 2 ⋅ + 4 3
Câu 13: Cho phương trình 2
x + 5x − 7 = 0 có hai nghiệm là x ; x . Không giải phương trình, hãy tính giá 1 2 trị của biểu thức 2 2
A = x + x − 2x x . 1 2 1 2 Lời giải
∆ = 25 + 28 = 53 > 0 nên pt có 2 nghiệm x2; x2. Theo Vi-et ta có x .x = 7; − x + x = 5 − 1 2 1 2 2 2
A = x + x – 2x x = (x + x – 4x x = (− )2 5 – 4.( 7 − ) = 53 1 2 )2 1 2 1 2 1 2 Vậy A = 53
Câu 14: Cho phương trình 2
3x −12x − 5 = 0 có hai nghiệm là x , x . Không giải phương trình, hãy tính 1 2 2
giá trị của biểu thức:
x + 4x − x x 1 2 1 2 T = 2
4x + x + x x 1 2 1 2 Lời giải
Phương trình đã cho là phương trình bậc hai của x có: ac = 3.( 5 − ) < 0
Nên phương trình đã cho có hai nghiệm phân biệt x ; x 1 2 b − 12 x + x = = = 4 1 2
- Theo định lý Vi-et, ta có: a 3 c 5 x x − = = 1 2 a 3 2 2
x + 4x − x x
x + x x + 4x − 2x x
x x + x + 4x − 2x x 1 2 1 2 1 1 2 2 1 2 1 ( 1 2 ) Do đó: 2 1 2 T = = = 2 2
4x + x + x x
4x + x + x x
4x + x x + x 1 2 1 2 1 2 1 2 1 2 ( 1 2 ) 5 4.4 2. − −
4x 4x 2x x 4(x x ) 2x x 3 + − + − 29 1 2 1 2 1 2 1 2 = = = = 4x + 4x 4(x + x ) 4.4 24 1 2 1 2
Vậy giá trị của biểu thức 29 T = 24
Câu 15: Cho phương trình 2
x −12x + 4 = 0 có hai nghiệm dương phân biệt x , x . Không giải phương 1 2 2 2 +
trình, hãy tính giá trị của biểu thức x x 1 2 T = . x + x 1 2 Lời giải 2
x −12x + 4 = 0 Xét ′ ′2 2
∆ = b − ac = ( 6) −
−1.4 = 32 > 0 nên phương trình có hai nghiệm phân biệt x , x 1 2
Áp dụng hệ thức Viète ta có: x + x =12; x x = 4 ⇒ x > 0, x > 0 1 2 1 2 1 2 Ta có: 2 x + x x + x
x + x − 2x x 12 − 2.4 2 ( 2 2 1 2 )2 ( ) 2 2 ( 2 2 2 1 2 1 2 )2 1 2 T = = = = = x x + ( x x ) 1156 2
x + x + 2 x x 12 + + 2 4 1 2 1 2 1 2 1 2 Nhận xét 2 2
x + x > 0 và x + x > 0 với mọi x , x > 0 suy ra T > 0 1 2 1 2 1 2 2
⇒ T = T = 1156 = 34 Vây T = 34 .
Câu 16: Cho phương trình 2
x − x − 3 = 0 có hai nghiệm x , x . Không giải phương trình, hãy tính giá trị 1 2 của biểu thức A = 2 2
3x x + x + x (3x +1) 1 2 1 2 1 Lời giải Xét phương trình 2
x − x − 3 = 0 có hai nghiệm x , x 1 2
Theo định lí Vi-et ta có: x + x =1; x x = 3 − 1 2 1 2 Khi đó A = 2 2
3x x + x + x (3x +1) 1 2 1 2 1
= 3x x (x + x ) + (x + x ) 1 2 1 2 1 2
= (3x x +1)(x + x ) 1 2 1 2 = [3.(-3)+1].1 = -8
Câu 17: Cho phương trình 2
− 2x + 2x + 3 = 0 có 2 nghiệm phân biệt là x , x . Không giải phương trình, 1 2
hãy tính giá trị của biểu thức x +1 x +1 2 1 A = + 1− x 1− x 1 2 Lời giải Vì 2 2
∆ = b − 4ac = 2 − 4.(− 2).3 = 4 +12 2 > 0
Nên phương trình có hai nghiệm phân biệt x , x . 1 2
Theo định lí Viète, ta có: b − 2 − 1 c 3 3
S = x + x = = =
; P = x .x = = = − 1 2 1 2 a − 2 2 a − 2 2 (x +1 1− x x +1 1− x 2 )( 2 ) ( 1 )( 1 ) 2 2 Do đó x +1 x +1
x − x +1− x + x − x +1− x 2 1 A = + 2 2 2 1 1 1 = + = 1− x 1− x (1− x 1− x 1− x 1− x
1− x − x + x x 1 ) ( 2 ) ( 2 ) ( 1 ) 1 2 2 1 1 2 2 1 3 2 2. − − − 2 − (x + x 2 − x + x − 2x x 2 − ( 2 S − 2P) 2 2 1 2 ) ( )2 2 2 1 2 1 2 3 = = = = =
1− (x + x + x x
1− x + x + x x 1− S + P 1 3 2 1 2 ) 1 2 ( 1 2) 1 2 1− + − 2 2
Câu 18: Cho phương trình 2
x − 4x + 3 = 0 có 2 nghiệm là x , x . Không giải phương trình, hãy tính giá 1 2 trị của biểu thức 5x − x x − 5x 1 2 1 2 A = − . x x 1 2 Lời giải Ta có: 2
x − 4x + 3 = 0 . Vì 2 2
∆ = b − 4ac = ( 4) − − 4.1.3 = 4 > 0.
Nên phương trình có hai nghiệm phân biệt x , x . 1 2 b S = x + x − = = 4 1 2
Theo định lí Vi-et, ta có: a . = . c P x x = = 3 1 2 a 5x − x x − 5x
(5x − x .x − x −5x .x 1 2 1 2 1 2 ) 2 ( 1 2 ) 1 A = − = x x x .x 1 2 1 2
5x .x − x − x + 5x .x 10x .x − ( 2 2 2 2 x + x 1 2 1 2 ) 1 2 2 1 1 2 A = = x .x x .x 1 2 1 2 P − ( 2 S − P) − ( 2 10. 2. 10.3 4 − 2.3) 20 A = = = P 3 3
Câu 19: Cho phương trình 2
x −12x + 4 = 0 có hai nghiệm phân biệt x , x . Không giải phương trình hãy 1 2 x + x
tính giá trị của biểu thức 1 2 T = 2 2x + 24x − 4 1 2 Lời giải x + x =12 Theo hệ thức Viet có: 1 2 x .x = 4 1 2
Nên x > 0, x > 0 1 2
Suy ra x + x = x + x =12 1 2 1 2
x là nghiệm của PT đã cho nên 2
x −12x + 4 = 0 hay 2
x =12x − 4 hay 2 2x = 24x −8 1 1 1 1 1 1 1 Suy ra 2
2x + 24x − 4 = 24x −8 + 24x − 4 1 2 1 2
= 24(x + x −12 = 24.12 −12 = 276 1 2 ) Vậy 12 1 T = = 276 24
Câu 20: Gọi x , x −
− = . Không giải phương trình, hãy tính giá 1
2 là hai nghiệm của phương trình: 2 x 4x 7 0 trị của biểu thức x x 1 2 T = + − 2. x x 2 2 Lời giải
Phương trình có ac = 7
− < 0 nên luôn có 2 nghiệm phân biệt x , x 1 2
Áp dụng hệ thức Viète ta có: x + x = 4; x x = 7 − . 1 2 1 2 2 2 x x x + x
(x + x − 2x x 4 − 2. 7 − 44 − 1 2 1 2 1 2 )2 2 1 2 ( ) Khi đó ta có:T = + − 2 = − 2 = − 2 = − 2 = x x x x x x 7 − 7 2 1 1 2 1 2 Vậy 44 T = − 7
Câu 21: Cho phương trình 2
2x − 3x −1 = 0 có hai nghiệm là x x , không giải phương trình hãy tính giá 1 2 trị của biểu thức x −1 x −1 1 2 A = + x +1 x +1 2 1 Lời giải Xét phương trình 2
2x − 3x −1 = 0 (1) có a = 2,b = 3, − c = 1 − Do . a c = 2
− < 0 nên pt(1) có hai nghiệm phân biệt x x 1 2 b − 3 x + x = = 1 2
Áp dụng hệ thức viete có a 2 c 1 x .x − = = 1 2 a 2 2 2 Do đó x −1 x −1 x + x − 2 1 2 1 2 A = + =
x +1 x +1 x .x + x + x +1 2 1 1 2 ( 1 2) 2 3 − 1 9 ( − − −
x + x )2 − 2x x − 2 2. 2 +1− 2 1 2 1 2 4 5 1 5 = 2 2 = = = . =
x x + x + x +1 1 − 3 1+1 4 2 8 1 2 ( 1 2) + +1 2 2
Câu 22: Cho phương trình: 2
x − 5x − 6 = 0 có hai nghiệm x , x . Hãy tính giá trị của biểu thức sau: A = 1 2 x x 1 2 + x −1 x −1 2 1 Lời giải PT: 2
x − 5x − 6 = 0 có hai nghiệm x ; x 1 2 x + x = 5
Áp dụng hệ thức Vi-et ta có: 1 2 x .x = 6 − 1 2
x x −1 + x x −1 1 ( 1 ) 2 ( 2 ) Khi đó: A = x x 1 2 + = x −1 x −1 (x −1 x −1 1 )( 2 ) 2 1 2 2 + − + (x + x )2 − − + 1 2
2 1x 2x ( 1x 2x ) 1 x 2 x ( 1x 2x) A = = − + + − + + 1 x 2 x ( 1x 2 x ) 1 x 2 x ( 1x 2 x ) 1 1 2 Vậy: A = 5 − 2.( 6) − − 5 16 − = 6 − − 5 +1 5
Câu 23: Cho phương trình: 2
x + 3x −10 = 0 có 2 nghiệm x , x . Tính giá trị biểu thức x + 2 x + 2 1 2 = + 1 2 A x x 2 1 Lời giải Phương trình 2
x + 3x −10 = 0 có hai nghiệm x và x . Theo định lý Viete, ta có 1 2 x + x = 3 − ; x .x = 10 − 1 2 1 2 x + 2 x + 2
x x + 2 + x . x + 2 1 ( 1 ) 2 ( 2 ) 1 2 A = + = x x x .x 2 1 1 2 2 2
x + 2x + x + 2x ( 2 2
x + x + 2x + 2x 1 2 ) ( 1 2 ) 1 1 2 2 A = = x .x x .x 1 2 1 2
(x + x )2 − 2x .x + 2 x + x 1 2 1 2 ( 1 2) A = x .x 1 2



