





















Preview text:
lOMoARcPSD|36442750
ĐẠI HỌC QUỐC GIA TP. HỒ CHÍ MINH
TRƯỜNG ĐẠI HỌC BÁCH KHOA
KHOA KHOA HỌC ỨNG DỤNG
BÁO CÁO BÀI TẬP LỚN
ĐẠI SỐ TUYẾN TÍNH TÊN ĐỀ TÀI
ỨNG DỤNG MÔ HÌNH MARKOV
TRONG THUẬT TOÁN GOOGLE PAGERANK LỚP L16, NHÓM 09 GVHD : ĐẶNG VĂN VINH Tp. HCM, 12/2021
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
ĐẠI HỌC QUỐC GIA TP. HỒ CHÍ MINH
TRƯỜNG ĐẠI HỌC BÁCH KHOA
KHOA KHOA HỌC ỨNG DỤNG
BÁO CÁO BÀI TẬP LỚN
ĐẠI SỐ TUYẾN TÍNH TÊN ĐỀ TÀI
ỨNG DỤNG MÔ HÌNH MARKOV
TRONG THUẬT TOÁN GOOGLE PAGERANK
DANH SÁCH THÀNH VIÊN NHÓM STT Họ và tên MSSV Nguyễn Đặng Cao Bằng 1 2110047 (Nhóm trưởng) 2 Nguyễn Quốc Đạt 2113142 3 Trần Thị Hải Dương 2110105
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 4 Trần Quốc Huy 2111363 5 Cao Anh Minh 2111728 6 Phạm Hồng Ngọc 2111861 7 Đặng Thị Như Quỳnh 2110426
TÓM TẮT BÀI BÁO CÁO
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 LỜI CẢM ƠN
Trong suốt quá trình thực hiện đề tài, nhóm chúng tôi đã nhận được nhiều
sự quan tâm, hướng dẫn và sự giúp đỡ của các thầy cô, anh chị và bè bạn.
Ngoài ra, nhóm cũng xin gửi lời cảm ơn chân thành đến thầy Đặng Văn
Vinh - giảng viên bộ môn “Đại số tuyến tính”. Nhờ sự hướng dẫn của thầy,
nhóm đã hoàn thành đề tài đúng tiến độ và giải quyết được những khó khăn
trong quá trình thực hiện. Sự hướng dẫn của thầy đã là kim chỉ nam cho mọi
hành động của nhóm và phát huy tối đa được mối quan hệ hỗ trợ giữa thầy và
trò trong môi trường giáo dục.
Lời cuối, xin gửi lời cảm ơn sâu sắc đến các cá nhân, các thầy cô đã dành
thời gian chỉ dẫn cho nhóm. Đây chính là niềm tin, nguồn động lực to lớn để
nhóm có thể hoàn thành tốt đề tài này.
Nhóm thực hiện 1
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 MỤC LỤC
DANH MỤC CÁC HÌNH ẢNH...............................................................................................3
DANH MỤC BẢNG BIỂU.......................................................................................................4
DANH MỤC CÁC TỪ VIẾT TẮT..........................................................................................5 CHƯƠNG 1.
MỞ ĐẦU.........................................................................................................1 CHƯƠNG 2.
CƠ SỞ LÝ THUYẾT.....................................................................................2 1. Markov: 2
1.1 Mô hình Markov:............................................................................................................2
1.2 Các loại xích Markov:....................................................................................................2
2. Google PageRank:.................................................................................................................3
2.3 Google Pagerank là gì?...................................................................................................3
2.4 Thuật toán của Google PageRank:.............................................................................4
2.5 Yếu tố hệ số đường dẫn trong công thức tính PageRank............................................5 CHƯƠNG 3.
MATLAB........................................................................................................7
1.Tổng quan về Matlab.............................................................................................................7
2. Các lệnh Matlab cơ bản được sử dụng trong bài toán......................................................7
2.1. LỆNH TITLE.................................................................................................................7
2.2 LỆNH FIND:...................................................................................................................7
2.3 LỆNH WHILE:...............................................................................................................8
2.4 LỆNH SUM:....................................................................................................................8
2.5 LỆNH BAR:....................................................................................................................9
2.6 LỆNH ZEROS:...............................................................................................................9
3. Biểu diễn thuật toán bằng ngôn ngữ Matlab:.................................................................10
3.1 Đoạn code hoàn chỉnh..................................................................................................10
3.2 Hình ảnh kết quả:.........................................................................................................11 2
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
CHƯƠNG 4. KẾT LUẬN...................................................................................................13
DANH MỤC TÀI LIỆU THAM KHẢO...............................................................................14 3
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
DANH MỤC CÁC HÌNH ẢNH
Hình ..........................................................................................................................
Hình .......................................................................................................................... 4
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
DANH MỤC BẢNG BIỂU
Bảng ................................................................................................................................
Bảng ................................................................................................................................ 5
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
DANH MỤC CÁC TỪ VIẾT TẮT 6
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 CHƯƠNG 0: ĐỀ BÀI Đề tài 15
1. Ứng dụng mô hình Markov trong thuật toán Google Pagerank.
2. Viết chương trình dùng thuật toán trên 7
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 CHƯƠNG 1. MỞ ĐẦU
Ngày nay khoa học ngày càng phát triển, với đà phát triển này việc ứng dụng
khoa học và sáng chế khoa học ở trường học là rất thiết thực và quan trọng.
Chính vì vậy, ngay từ năm đầu các giảng viên Trường ĐH Bách Khoa Tp.HCM
đã giúp cho các sinh viên ngành kỹ thuật làm quen với các ứng dụng lập trình ví
dụ như Chương trình Matlab.
Matlab là một môi trường tính toán số và lập trình cho phép tính toán số với
ma trận, vẽ đồ thị hàm số hay biểu đồ thông tin, thực hiện thuật toán, tạo các
giao diện người dùng và liên kết với những chương trình máy tính viết trên
nhiều ngôn ngữ lập trình khác. Với thư viện Toolbox, Matlab cho phép mô
phỏng tính toán, thực nghiệm nhiều mô hình trong thực tế và kỹ thuật. Với hơn
40 năm hình thành và phát triển, ngày nay với thiết kế sư dụng tương đối đơn
giản và phô thông, Matlab là công cụ tính toán hữu hiệu để giải quyết các bài toán kỹ thuật.
Vì vậy, đối với những bài toán trong Đại số tuyến tính, đặc biệt là các bài
toán ứng dụng các mô hình, ta có thể sử dụng các ứng dụng tính toán của Matlab
để giải quyết theo cách đơn giản, dễ hiểu và trực quan nhất, giúp chúng ta làm
quen và bổ sung thêm kỹ năng sử dụng các chương trình, ứng dụng cho sinh viên. 1
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 CHƯƠNG 2. CƠ SỞ LÝ THUYẾT 1. Markov: 1.1 Mô hình Markov:
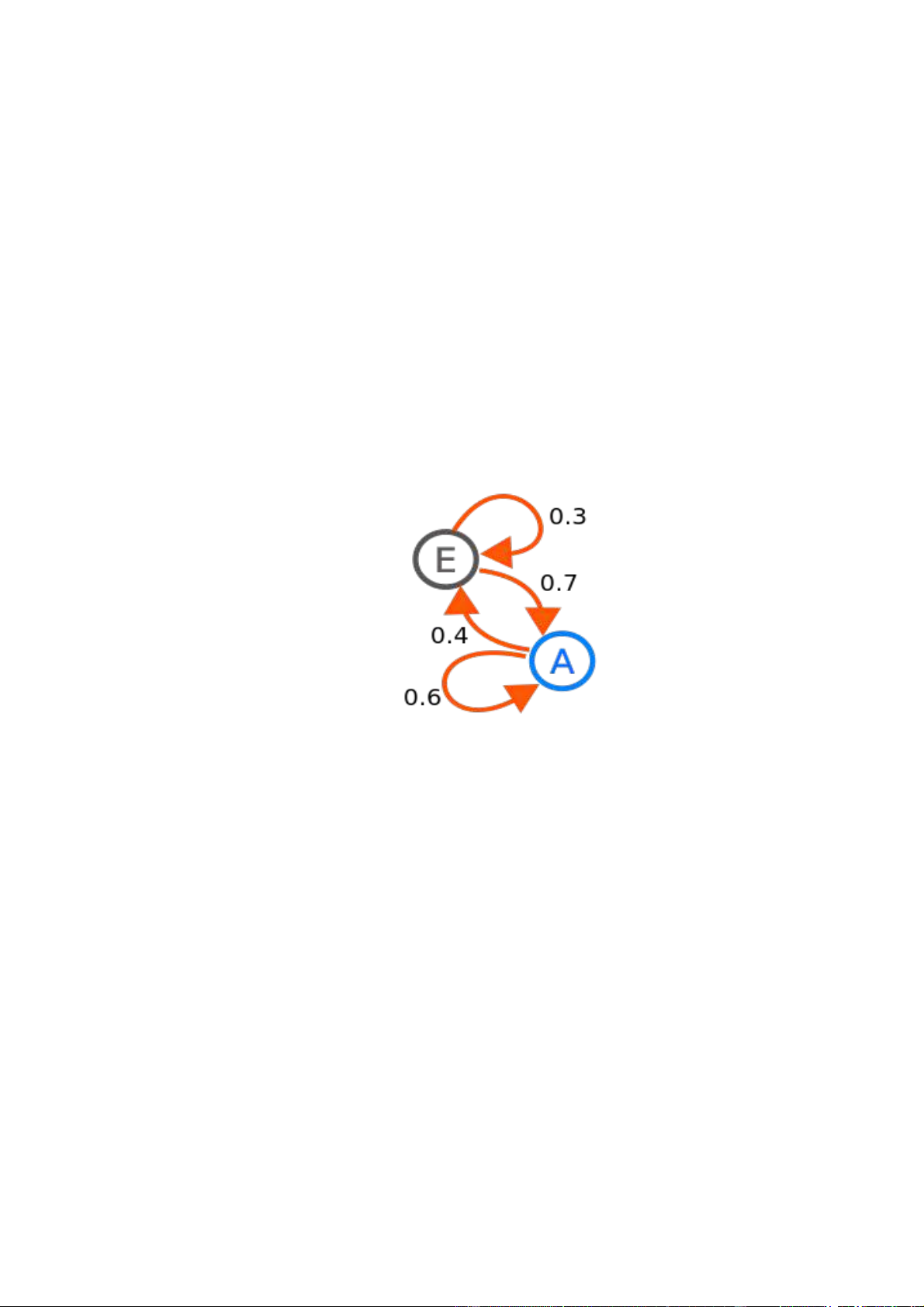
Mô hình Markov ( hay xích Markov ) là một quá trình ngẫu nhiên thỏa
mãn tính chất Markov (đôi khi được gọi là "tính không ghi nhớ"). Nói đơn giản,
nó là một quá trình mà các kết quả ở tương lai có thể được dự đoán chỉ dựa trên
trạng thái hiện tại và—quan trọng hơn—dự đoán ấy tốt bằng dự đoán dựa trên
toàn bộ lịch sử của quá trình đó. Nói cách khác, dựa trên trạng thái hiện tại của
hệ thống, những trạng thái quá khứ và tương lai là độc lập.
Sơ đồ biểu diễn một quá trình Markov với hai trạng thái E và A
Một xích Markov là một loại quá trình Markov có không gian trạng
thái rời rạc hoặc tập chỉ số rời rạc (thường biểu diễn thời gian), tuy nhiên không
có định nghĩa chính xác thống nhất. Thông thường, một xích Markov còn được
định nghĩa là một quá trình Markov trong thời gian liên tục hoặc rời rạc với
không gian trạng thái đếm được (tức thời gian bất kỳ), nhưng cũng có định
nghĩa khác coi xích Markov có thời gian rời rạc trong không gian trạng thái đếm
được hoặc liên tục (tức không gian trạng thái bất kỳ). 2
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 2. Google PageRank:
2.3 Google Pagerank là gì?
PageRank là một thuật toán của Google để đánh giá sự uy tín của trang
Web thông qua việt xem xét số lượng, chất lượng của các trang liên kết đến nó.
Mục đích của PageRank là đánh giá tầm quan trọng tương đối của website trong
toàn bộ hệ thống World Wide Web.
Nhà đồng sáng lập Google, Serge Brin và Larry Page đã phát minh ra
PageRank vào năm 1997 và sử dụng để xếp hạng trang web. Tên PageRank của
thuật toán được đặt theo tên của Larry Page.
Vì một số lý do, thanh công cụ PageRank đã bị Google gỡ bỏ vào năm
2016. Mặc dù thanh công cụ PageRank không còn, thuật toán PageRank vẫn còn
quan trọng trong việc đánh giá các web của Google.
Trong ví dụ trên, ta có 11 trang
web. Trang web B có nhiều trang web
liên kết với nó nhất, do đó rank của
trang web B đương nhiên là sẽ cao
nhất. Trang web C mặc dù số trang
web liên kết với nó ít hơn trang E
nhưng mà nó được trang B liên kết tới,
do đó nó sẽ có rank cao hơn trang E.
Như vậy kết quả rank cuối cùng của
một trang web dựa trên cáu trúc liên
kết của toàn bộ các trang web. Cách
tiếp cận này nghe mặc dù rất rộng và phức tạp, nhưng Page và Brin đã có thể đưa
nó vào thực tế bằng một thuật toán tương đối tầm thường.
2.4 Thuật toán của Google PageRank:
Thuật toán PageRank là một thuật toán học xếp hạng dựa trên phân tích đồ
thị liên kết giữa các trang web, mỗi trang web sẽ được xem như một đỉnh, mỗi
liên kết sẽ được xem như một cạnh của đồ thị.
Giả sử trang web A được các trang T1… Tn trỏ đến. Ta có công thức tính chỉ
số PageRank của trang A như sau: Thuật toán của Pagerank 3
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 Trong đó:
T: Số lượng và chất lượng Internal Links trên các trang
C; Số lượng Outlink trên mỗi trang
PR: Chỉ số PageRank trên từng trang
Tham số d (d: damping factor): Hệ số điều chỉnh (*) có thể được đặt trong
khoảng từ 0 đến 1. Đa phần thường lấy d là 0,85.
Tôi sẽ giải thích chi tiết hơn về tham số d trong phần kế tiếp.
Lưu ý: PageRank tạo một tỉ lệ % phân bố điểm số trên các trang Web, do đó
PageRank của tổng tất cả các trang Web sẽ là một.
Google định nghĩa 3 yếu tố trong khi phân tích đường dẫn của trang Web, đó là:
Số lượng và chất lượng của các Internal Link trỏ đến trang;
Số lượng Outlink trên mỗi trang;
Chỉ số PageRank của mỗi trang liên kết. .
Cách hoạt động của Google Pagerank 4
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
2.5 Yếu tố hệ số đường dẫn trong công thức tính PageRank
Bạn có thể tưởng tượng một xích Markov hữu hạn đồng nhất thời
gian như một cửa sổ Google vậy, hãy tưởng tượng về một hệ động lực ngẫu
nhiên… Mỗi lần click sẽ thay đổi trạng thái trong hệ thông qua những web ngẫu
nhiên… Tại mỗi thời điểm t sang t+1 web thứ i sẽ hiện lên các web thứ j theo
những đường link với xác suất nhất định.
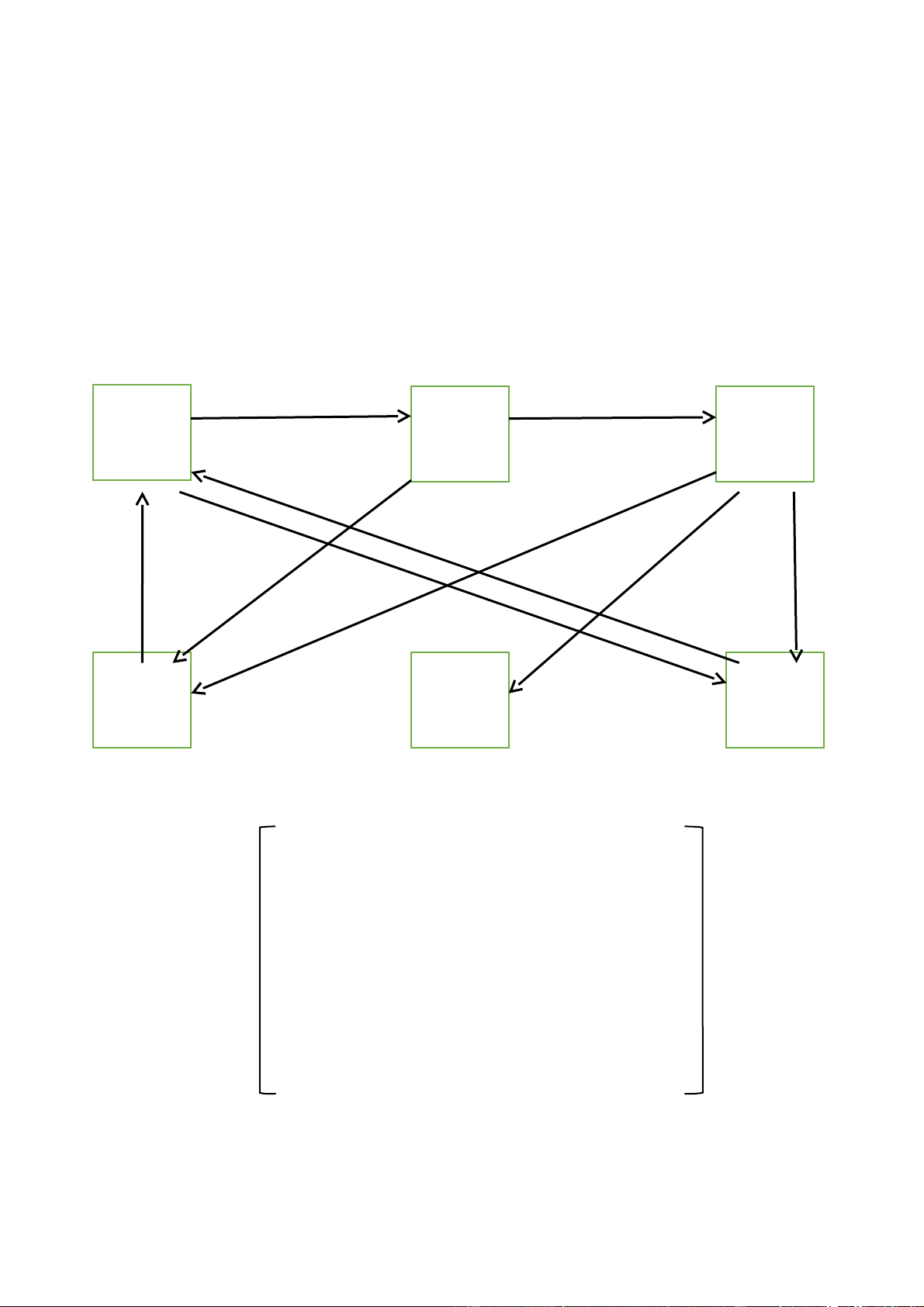
Đây là ví dụ cụ thể của nhóm đưa ra: 1 3 2 4 5 6
Dựa vào mô hình trên ta có ma trận A: 0.0 1.0 0.0 0.0 0.0 0.5 0.0 0.0 1.0 0.5 0.0 0.0 0.0 0.0 0.0 0,5 1.0 0.5 0.5 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.5 0.0 0.0 0.0 0.0 0.0 5
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Xác suất chuyển dịch trạng thái: Pr(=j|=i)= nếu có liên kết từ i sang j, ngược lại Pr(j|i).
Với là tổng số liên kết hướng từ i ra.
2.6 Phân bố dừng của xích Markov hữu hạn về thời gian:
Nếu như ma trận ngẫu nhiên cột (tổng thành phần từng cột bằng 1) mà ta
đang xét A là ma trận dương có từng thành phần >0 thì ma trận A chỉ có duy
nhất một phân bố dừng (duy nhất một vector riêng tương ứng trị riêng 1). Tất cả
trị riêng còn lại nhỏ hơn 1. 6
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 CHƯƠNG 3. MATLAB
1.Tổng quan về Matlab
-Matlab (viết tắt của Matrix Laborary) là một ngôn ngữ lập trình bậc cao bốn
thế hệ, môi trường để tính toán số học, trực quan và lập trình. Được phát triển bởi MathWorks.
-Nó cho phép thao tác với ma trận, vẽ biểu đồ với hàm và số liệu, hiện thực
thuật toán, tạo ra giao diện người dùng, bao gồm C,C++, Java và Fortran ; phân
tích dữ liệu, phát triển thuật toán, tạo các kiểu mẫu và ứng dụng.
Nó có rất nhiều lệnh và hàm toán học nhằm hỗ trợ đắc lực cho bạn trong việc
tính toán, vẽ các hình vẽ, biểu đồ thông dụng và thực thi các phương pháp tính toán.
2. Các lệnh Matlab cơ bản được sử dụng trong bài toán 2.1. LỆNH TITLE Công dụng:
Đặt tiêu đề cho đồ thị. Cú pháp:
Title(‘text 1’,’text 2’,...). Giải thích: text 1, text 2 chính là tiêu đề 2.2 LỆNH FIND: a) Công dụng:
Tìm phần tử trong vector hay ma trận theo yêu cầu. b) Cú pháp: k = find(x) [i,j] = find(x) 7
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 [i,j,s] = find(x) c) Giải thích:
k: chỉ vị trí của phần tử cần tìm trong vector.
i,j: chỉ số hàng và số cột tương ứng của phần tử cần tìm.
s: chứa giá trị của phần tử cần tìm.
x: tên vector, ma trận hay là yêu cầu đề ra. Nếu không
nêu ra yêu cầu thì mặc nhiên là tìm các phần tử khác 0. 2.3 LỆNH WHILE: a) Công dụng:
Dùng để thực hiện 1 công việc cần lặp đi lặp lại theo một quy luật, với số
bước lặp không xác định, phụ thuộc vào biểu thức luận lý. b) Cú pháp: while biểu thức luận lý thực hiện công việc; end c) Giải thích:
Biểu thức luận lý là các phép so sánh = =, <, >, <=, >=
Công việc chính là các lệnh cần thi hành, có thể có nhiều lệnh, kết thúc lệnh phải có dấu ;
Khi thực hiện xong công việc thì quay lên kiểm tra lại biểu thức luận lý,
nếu vẫn còn đúng thì tiếp tục thực hiện, nếu sai thì kết thúc. 2.4 LỆNH SUM: a) Công dụng:
Tính tổng của các phần tử. b) Cú pháp: s = sum(x) c) Giải thích:
s: là biến chứa kết quả. x: là tên ma trận.
Nếu x là ma trận thì s là tổng của các cột. 8
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 2.5 LỆNH BAR: a) Công dụng: Vẽ đồ thị dạng cột. b) Cú pháp: bar(x,y) c) Giải thích:
Vẽ giá trị x theo giá trị y. 2.6 LỆNH ZEROS: a) Công dụng:
Tạo ma trận mà giá trị của các phần tử b) Cú pháp: y = zeros(n) y = zeros(m,n) c) Giải thích: y: tên ma trận.
n: tạo ma trận có n hàng và n cột.
m, n: tạo ma trận có m hàng, n cột. 9
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
3. Biểu diễn thuật toán bằng ngôn ngữ Matlab:
3.1 Đoạn code hoàn chỉnh %% Class L16, Group 09 %% Teacher: Dang Van Vinh
%% Project: Google PageRank Algorithm %% Sparse matrices n = 6 i = [2 6 3 4 4 5 6 1 1] j = [1 1 2 2 3 3 3 4 6] G = sparse(i,j,1,n,n) spy(G) %% PageRank p = 0.85; delta = (1-p)/n; c = sum(G,1); k = find(c~=0); D = sparse(k,k,1./c(k),n,n); e = ones(n,1);j I = speye(n,n); x = (I - p*G*D)\e; x = x/sum(x) %% Conventional power method z = ((1-p)*(c~=0) + (c==0))/n; A = p*G*D + e*z; x = e/n; oldx = zeros(n,1); while norm(x - oldx) > .01 oldx = x; x = A*x; end 10
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 x = x/sum(x) %% Sparse power method G = p*G*D; x = e/n; oldx = zeros(n,1); while norm(x - oldx) > .01 oldx = x; x = G*x + e*(z*x); end x = x/sum(x) %% Inverse iteration x = (I - A)\e; x = x/sum(x) %% Bar graph bar(x) title('Page Rank') 11
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
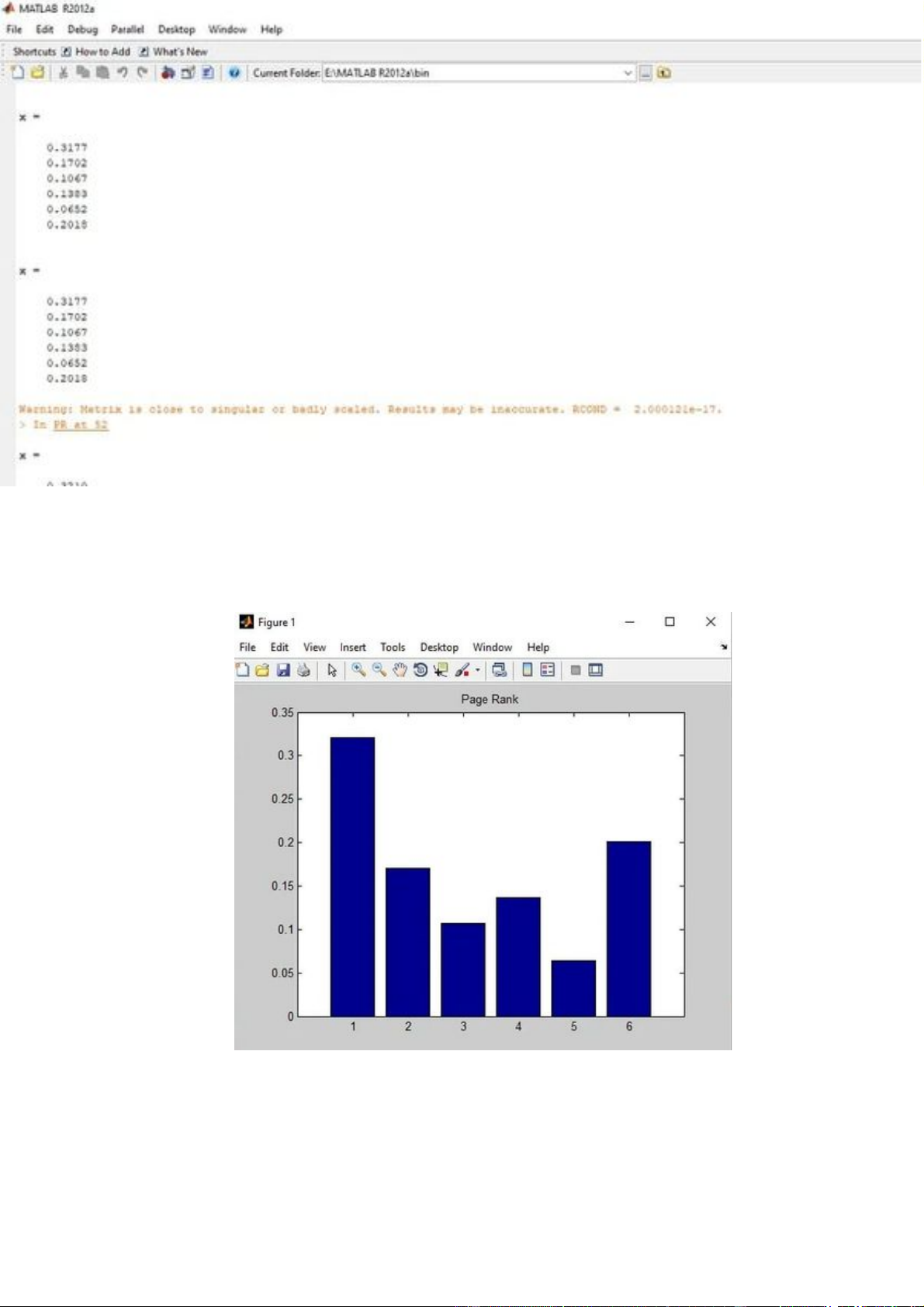
3.2 Hình ảnh kết quả: 12
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 13
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 CHƯƠNG 4. KẾT LUẬN
Như vậy, ta đã đi từ những vấn đề chung đến bài toán riêng khá phức tạp
đòi hỏi nhiều công việc tính toán với người giải quyết bài toán. Tuy nhiên, với
sự hỗ trợ của công cụ Matlab, việc giải quyết, khảo sát bài toán trở nên dễ dàng,
sinh động và trực quan hơn. * Ư u điểm
-Nhờ vào Matlap giúp việc tính toán dễ dàng, tiện lợi, cho kết quả chính xác như cách tính phổ thông.
-Giúp hiểu thêm về ứng dụng Matlab trong các bài toán kỹ thuật.
-Tiết kiệm thao tác và thời gian tính toán so với các cách tính phổ thông.
-Sử dụng các lệnh thông báo nội dung khiến cấu trúc sử dụng trở nên tương đối
đơn giản, dễ hiểu, dễ sử dụng và phù hợp với tất cả mọi người.
*Khuyết điểm
-Thiết kế đoạn code mất nhiều thời gian, công sức. -Đoạn code rườm rà.
-Còn mô phỏng trong phạm vi chủ đề được chỉ định, chưa sáng tạo sang các chủ
đề tính toán kĩ thuật khác. 14
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
DANH MỤC TÀI LIỆU THAM KHẢO
1. Xích Markov – Wikipedia tiếng Việt (https://vi.wikipedia.org/wiki/X %C3%ADch_Markov)
2. Giáo trình đại số tuyến tính – Đặng Văn Vinh– NXB. ĐHQG TP. Hồ Chí Minh
3. PageRank là gì? Cách tối ưu & Check Page Rank Website
(https://gtvseo.com/pagerank-la-gi/)
4. Các lệnh trong Matlab – Thủ thuật máy tính
(https://thuthuat.taimienphi.vn/cac-lenh-trong-matlab-32844n.aspx)
5. MatWorks – Makers of Matlab and Simulink
(https://www.mathworks.com/) 15
Downloaded by v?n ti?n Lê (vantienle525@gmail.com)




