
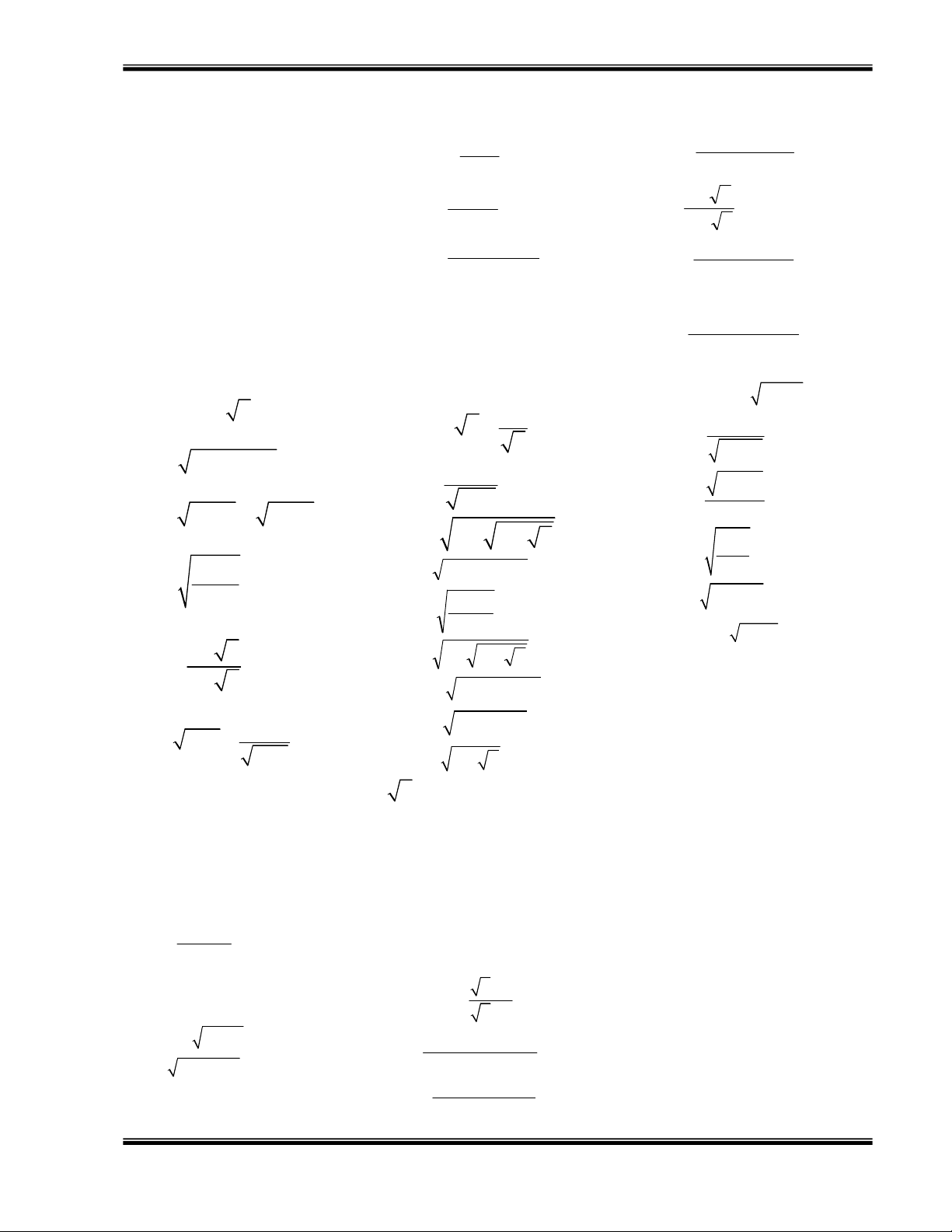
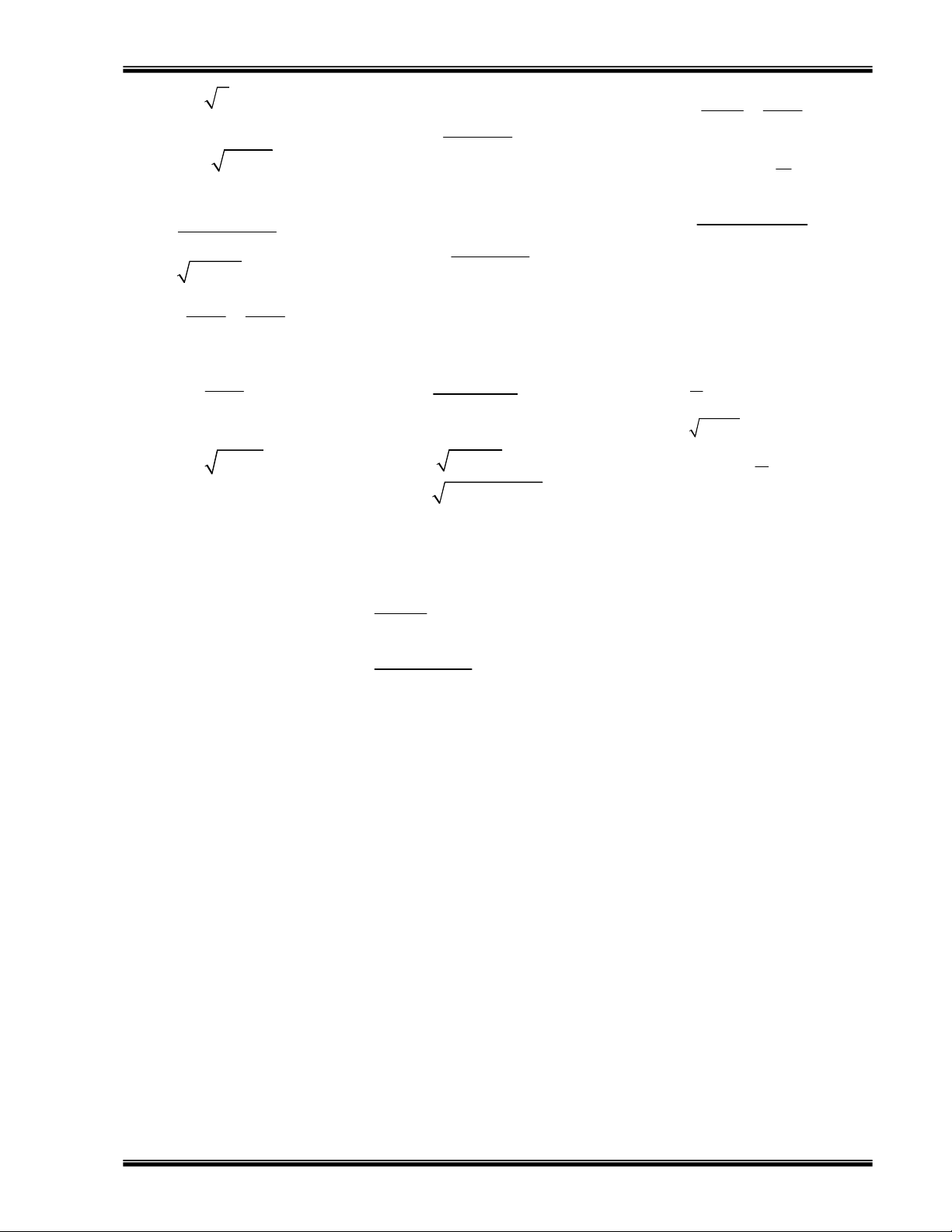

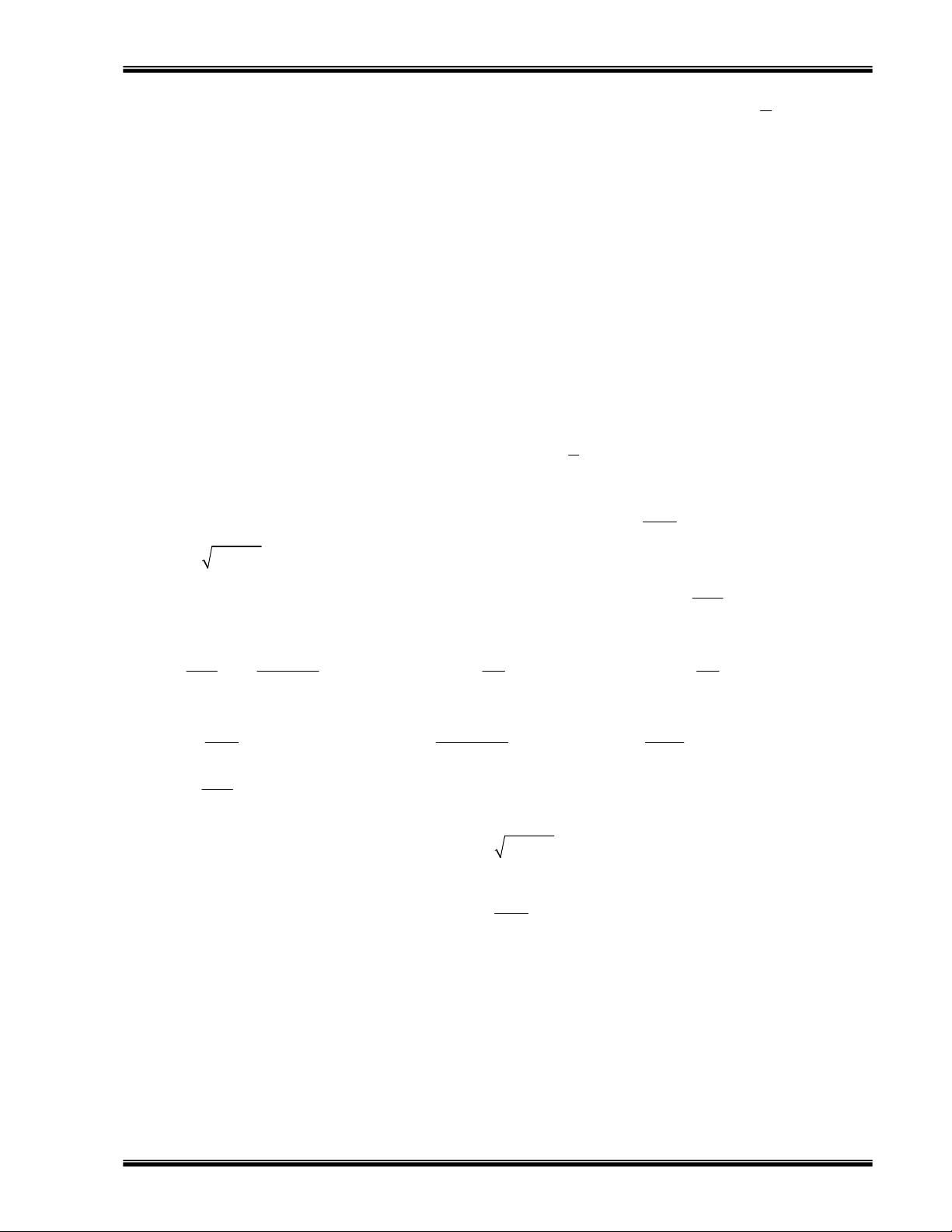


Preview text:
ĐẠI HỌC SƯ PHẠM HÀ NỘI ÑA Ñ ÏO ÏO HAØM A VAØ ÖÙN Ö G DU D ÏN U G CUÛA ÛA ÑA Ñ ÏO A HAØM A
VẤN ĐỀ 1: Tính đạo hàm bằng định nghĩa
Bài 1: Dùng định nghĩa tính đạo hàm của các hàm số sau tại điểm được chỉ ra: a) 2
y = f(x) = 2x − x + 2 tại x0 =1
b) y = f(x) = 3 − 2x tại x0 = –3 2x +1 π c) y = f(x) = tại x = = tại x x 0 = 2 d) y f(x) sin x 0 = −1 6 2 x + x +1 e) 3 y =f(x) = x tại x y =f(x) 0 = 1 f) = tại x x 0 = 0 − 1
Bài 2: Dùng định nghĩa tính đạo hàm của các hàm số sau tại điểm được chỉ ra:
a) y = x2 + 3x − x tại x =4 b) y =
x + 3 − x tại x =1. c) y =
x − x tại x =2. 0 0 0 π π
d) y = sin x + cos x tại x =0. e) y sin 2 = 2x tại x =
f) y = tan x +1 tại x = . 0 0 2 0 4
Bài 3: Dùng định nghĩa tính đạo hàm của các hàm số sau: a) 2 f(x) = x − 3x +1 b) 3
f(x) =x − 2x c) f(x) = x +1, (x > −1) 1 1 d) f(x) = e) f(x) = sin x f) f(x) = 2x − 3 cosx
VẤN ĐỀ 2: Tính đạo hàm bằng công thức
Bài 1: Tính đạo hàm của các hàm số 1 2 3 3 2 a) 5 4 3 2 y = x + x − x − x + 4x − 5 e) y = − x + x x. 2 3 2 2 x 3 1 1 1 b) 2 4 y = −
x + x − 0,5x f) 4 3 y =2x − x + 2 x − 5 3 4 3 = − + − 4 1 3 g) 5 3 y x 4x 2x 3 x c) y =2x − x + 2 x − 5 3 4 3 2 x x x d) 3 y = − +
− x + a (a là hằng số) 4 3 2
Bài 2: Tính đạo hàm của các hàm số sau: a) 2 y = (x + 3x)(2 − x) 3 2x k) y = 2x r) y = + 1 b) 2 y = (2x − ) 3 ( 5 x − 2x) x −1 2x +1 c) 2 2
y = (x + 1)(5 − 3x ) l) y = 5x − 3 1− 3x s) y = 2
d) y = x(2x −1)(3x + 2) 2 1 x + x + 1 + x − x m) y = 2 e) 2 2
y = (x − 2x + 3).(2x + 3) 2 1 x + x −1 − x + x t) y = f) 2 y = x x 2 x − 3x + 3 x −1 n) y = 2x −1 x −1 2 g) y = u) y = x + 1 − 4x − 3 2 2x − 4x +1 x −1 o) y = 2x + 10 x − 3 h) y = 4x − 3 2 2x 2 y x + 2x + 2 2 p) = − = x + 5x − 4 2 v) y i) y = x − 2x − 3 x + 1 3x − 6 2x −1 2 2x − 4x + 5 q) y = w) y = j) = ( + ) 1 y x 1 −1 x −1 x + x 2 1 1
Đại số và giải tích 11 Đạo hàm
ĐẠI HỌC SƯ PHẠM HÀ NỘI
Bài 3: Tính đạo hàm của các hàm số sau: a) 7 2
y = (x + x) 3 2x +1 1 h) y = k) y = 2 5 b) 3 2 2
y = (2x − 3x − 6x + 1) x −1 (x − x + 1) 2 c) 2 3 y = (1 − 2x ) (x +1) 1 − x i) y = l) y = 3 (x −1) 2 + x d) 2 32
y = (x − x ) 1 2 y 5x − 4x − 9 e) 2 3 2 2
y = (x − x + 1) (x + x + 1) j) = 2 2 m) y = (x − 2x + 5) − 2 2 x + 3x − 8 f) 2 4 y = (x + x +1) n) y = 1 ( + 2x)(2 + 3 2 x ) 3 ( − 4 3 x ) k) = ( − )4 2 y 3 2x g) 2 5 y 2 3 = (1 − 2x ) (2 − x ) 3 ( − x ) o) y = 2 1 − x + x
Bài 4: Tính đạo hàm của các hàm số sau: p) 2 y = (x − 2) x + 3 2 a) 2
y = x + x x + 1 1 g) y = x − 4x +1 y = x q) 2 x + 2 b) 2
y = 1 + 2x − x 1 + x h) y = 2 4 + x 1 − x r) y = c) 2 2 y =
x + 1 − 1 − x x i) y = x + x + x 3 x s) y = 2 x + 1 j) y = 2 2 x − 5x + 1 x −1 d) y = x 1 − x t) 3 y = (x − 2) k) y = 3 + 2x 2 u) = ( + − )3 y 1 1 2x 1 x − e) y =
l) y = 1 + x + x 1 + x m) 2 y = 2x − 5x + 2 3 3 1 n) y = x − x + 2 f) y = x −1 + x −1 o) y = x + x
Bài 5: Cho hàm số f (x) = 3x − 2 x . Tính f '(4); 2
f '(a ) trong đó a là hằng số khác 0
Bài 6: Cho n là số nguyên dương. Chứng minh rằng: n n 1 a) n n 1 (sin x.cosnx)' nsin − =
x.cos(n +1)x b) (sin x.sinnx)' n.sin − = x.sin(n +1)x c) n n 1 (cos x.sinnx)' n.cos − = x.cos(n +1)x d) n n 1 (cos x.cosnx)' n.cos − = − x.sin(n +1)x
Bài 7: Tính đạo hàm của các hàm số sau: 2 sin x i) 2 3 y = (2 + sin 2x) n) y=sinxcos2x a) y = 4 1 cos x + j)
o) y = (cos x − sin x)5 4 = ( 2 2 y sin cos x tan x) b) y = x.cosx p) 2 4
y = sin (cos(tan 3x))) + k) 2 x 1 y = cos 3 3 c) 3 y = sin (2x +1)
q) y = sin 2x cos 2x x 1 − r) 3
y = (sin x + cos x) ; e) 2 y = sin 2 + x sin 2x + cos 2x l) y =
s) y = 5sin x − 3cos x f) y = sin x + 2x
2 sin 2x − cos 2x 1 t) 2
y = sin(x − 3x + 2) h) 2 3 y = 2sin 4x − 3cos 5x m) y = 2 cos x 2 − sin x
Gv: Trần Quang Thuận Tel: 0912.676.613 – 091.5657.952
ĐẠI HỌC SƯ PHẠM HÀ NỘI u) y = sin x
b1) y = sin(cos x) + cos(sin x) 1 1 h1) y = − + v) 2 y = cos x x sin x cos x sin x c1) y = x − sin x 2 π
w) y = cos 2x + 1
i1) y = cos 2x − d1) 2
y = (sin x + cos x)
x) y = 2sin 3x cos5x 4 = − sin y x x x + cos x e1) 2 2 3cos 2 2cos 3
sin x − x cos x = y) y = j1) y 2 sin x − cos x 1+ cos 2x
cos x − x sin x f1) y = z) y = cos 2x 1− cos 2x sin x x g1) 4 4
y = cos x + sin x a1) y = + x sin x
Bài 8: Tính đạo hàm của các hàm số sau: x + 1 2 1 + tan 3x 1 a) y = tan f) y = j) 2 y = (1 + tan x) 2 2 1 − tan 3x 2 b) 3
y = tan x + cot 2x
g) y = tan(sin x) k) y = cot 2x π c) 2 y = cot x + 1 h) y = x tan x l) 3 y = cot (2x + ) ; 4
d) y = tan 3x − cot 3x i) y = tan x + cot x m) 2 3
y = tan (sin(cos 2x))
e) y = x cot x
Bài 9: Tính đạo hàm của hàm số đa thức 3 2
y = f (x) = ax + bx + cx + d + Bài 10: ax b
Cho hàm số y = f (x) =
(a, b, c, d là hằng số). Tính f '(x) cx + d 2 + + Bài 11: ax bx c
Cho hàm số y = f (x) =
(a, b, c, m, n là hằng số). Tính f '(x) mx + n
VẤN ĐỀ 3: Phương trình tiếp tuyến của đồ thị hàm số y = f(x)
Dạng 3.1 Viết phương trình tiếp tuyến của đồ thị hàm số y = f (x) tại điểm M (x ; f (x )) 0 0
Phương pháp: phương trình tiếp tuyến của đồ thị hàm số y = f (x) tại điểm M (x ; f (x )) là 0 0
y = f '(x )(x − x ) + f (x ) 0 0 0
Chú ý: +) Nếu bài toán yêu cầu viết phương trình tiếp tuyến tại điểm có hoành độ tiếp điểm x thì 0 vẫn là dạng toán này.
+) Nếu bài toán yêu cầu viết phương trình tiếp tuyến tại điểm có tung độ tiếp điểm y , ta 0
giải phương trình f (x) = y để tìm hoành độ tiếp điểm 0
Dạng 3.2: Viết phương trình tiếp tuyến của đồ thị hàm số y = f (x) , biết rằng tiếp tuyến đó có hệ số góc là k Phương pháp:
B1: Tính đạo hàm của hàm số y = f (x)
B2: Gọi M (x ; f (x )) là hoành độ tiếp điểm. Giải phương trình f (x ) = k để tìm hoành 0 0 0
độ tiếp điểm x 0
B3: Viết phương trình tiếp tuyến (dạng 3.1) 3
Đại số và giải tích 11 Đạo hàm
ĐẠI HỌC SƯ PHẠM HÀ NỘI
Dạng 3.3: Viết phương trình tiếp tuyến của đồ thị hàm số y = f (x) biết rằng tiếp tuyến đó đi qua điểm M(a;b). Phương pháp:
B1: Tính f '(x)
B2: Gọi M (x ; f (x )) là tiếp điểm. Khi đó phương trình tiếp tuyến tại tiếp điểm này là 0 0 0
y = f '(x )(x − x ) + f (x ) 0 0 0
Theo bài ra tiếp tuyến này đi qua điểm M nên ta có b = f '(x )(a − x ) + f (x ) (1) 0 0 0
B3: Giải phương trình (1) tìm hoành độ tiếp điểm và viết phương trình tiếp tuyến (dạng 1) Bài tập
Bài 1: Cho hàm số (C): 2
y = f(x) =x − 2x + 3. Viết phương trình tiếp với (C):
a) Tại điểm có hoành độ x0 = 1.
b) Song song với đường thẳng 4x – 2y + 5 = 0.
c) Vuông góc với đường thẳng x + 4y = 0.
d) Vuông góc với đường phân giác thứ nhất của góc hợp bởi các trục tọa độ. 2 2 − x + x
Bài 2: Cho hàm số y = f(x) = (C). x −1
a) Viết phương trình tiếp tuyến của (C) tại điểm M(2; 4).
b) Viết phương trình tiếp tuyến của (C) biết tiếp tuyến có hệ số góc k = 1. 3x +1
Bài 3: Cho hàm số y = f(x) = (C). 1− x
a) Viết phương trình tiếp tuyến của (C) tại điểm A(2; –7).
b) Viết phương trình tiếp tuyến của (C) tại giao điểm của (C) với trục hoành.
c) Viết phương trình tiếp tuyến của (C) tại giao điểm của (C) với trục tung. 1
d) Viết phương trình tiếp tuyến của (C) biết tiếp tuyến song song với d: y = x +100 . 2
e) Viết phương trình tiếp tuyến của (C) biết tiếp tuyến vuông góc với ∆: 2x + 2y – 5 = 0. Bài 4: 3 2
Cho hàm số (C): y = x − 3x .
a) Viết phương trình tiếp tuyến của đồ thị (C) tại điểm I(1, –2).
b) Chứng minh rằng các tiếp tuyến khác của đồ thị (C) không đi qua I. Bài 5: 2 Cho hàm số (C): y =
1− x − x . Tìm phương trình tiếp tuyến với (C): 1
a) Tại điểm có hoành độ x . 0 = 2
b) Song song với đường thẳng x + 2y = 0.
Bài 6: Gọi (C) là đồ thị của hàm số 3 2
y = x − 5x + 2
Viết phương trình tiếp tuyến của (C) sao cho tiếp tuyến đó
a) song song với đường thẳng y = −3x + 1 1
b) vuông góc với đường thẳng y = x − 4 7 c) đi qua điểm A(0;2) x + Bài 7 2
. Cho đường cong (C): y = x − 2
Viết phương trình tiếp tuyến của đồ thị (C) 4
Đại số và giải tích 11 Đạo hàm
ĐẠI HỌC SƯ PHẠM HÀ NỘI 1
a) tại điểm có hoành độ bằng 1
b) tại điểm có tung độ bằng 3
c) biết tiếp tuyến đó có hệ số góc là −4
Bài 8: Gọi (C) là đồ thị của hàm số 3
y = x − 3x + 2
Viết phương trình tiếp tuyến của (C) sao cho tiếp tuyến đó a) nhận điểm (
A 2;4) làm tiếp điểm
b) song song với đường thẳng y = 9x + 2 c) đi qua điểm B(0;2)
VẤN ĐỀ 4: Tính đạo hàm cấp cao
1. Để tính đạo hàm cấp 2, 3, 4, ... ta dùng công thức: (n) n 1 − / y = (y ) .
2. Để tính đạo hàm cấp n:
• Tính đạo hàm cấp 1, 2, 3, ... từ đó dự đoán công thức đạo hàm cấp n.
• Dùng phương pháp quy nạp toán học để chứng minh công thức đúng.
Bài 1: Cho hàm số f(x) = 3(x +1)cosx . π a) Tính f '(x),f ' (x) b) Tính f ' ( ) π , f ' ,f ' (1) 2
Bài 2: Tính đạo hàm của các hàm số đến cấp được chỉ ra: x − 3 a) y = cosx, y' ' b) 4 3 2
y = 5x − 2x + 5x − 4x + 7, y' c) y = , y' x + 4 d) 2 y = 2x − x , y' e) y = xsin x, y' f) y = x tan x, y' 1 g) 2 3 y = (x +1) ,y' h) 6 3 (4) y = x − 4x + 4, y i) (5) y = , y 1− x
Bài 3: Cho n là số nguyên dương. Chứng minh rằng: (n) n 1 ( 1 − ) n! π π a) = b) (n) n. (sinx) = sin x + c) (n) n. (cosx) = cos x + n 1 1+ x (1+ x) + 2 2
Bài 4: Tính đạo hàm cấp n của các hàm số sau: 1 1 x a) y = y = y = x b) c) + 2 2 x 2 − 3x + 2 x −1 1− x d) y = = = + 1 e) 2 y sin x f) 4 4 y sin x cos x + x
Bài 5: Chứng minh các hệ thức sau với các hàm số được chỉ ra: y = xsin x 2 y = 2x − x a) b)
xy' − 2(y'− sin x) + xy = 0 3 y y' +1 = 0 x − 3 y = x tan x y = c) 2 2 2 d) x + 4
x y' − 2(x + y )(1+ y) = 0 2 2y′ = (y − 1)y ' 5
Đại số và giải tích 11 Đạo hàm
ĐẠI HỌC SƯ PHẠM HÀ NỘI
VẤN ĐỀ 5: Các dạng toán khác
Bài 1: Giải phương trình f '(x) = 0 với:
a) f(x) = 3cosx − 4sin x + 5x
b) f(x) = cosx + 3 s ón + 2x −1 cos4x cos6x c) 2 f(x) = sin x + 2cosx d) f(x) = sin x − − 4 6 3π + x
e) f(x) = 1− sin(π + x) + 2 cos
f) f(x) = sin3x − 3 cos3x + 3(cosx − 3 sin x) 2
Bài 2: Giải phương trình f '(x) = g(x) với: 4 3 a) f(x) = sin 3x f(x) = sin 2x b) g(x) = sin 6x g(x) = 4 cos2x − 5sin 4x 2 x 2 2 x f(x) f(x) = 4x cos = 2x cos c) 2 d) 2 2 x g(x) = x − x sin x
g(x) = 8cos − 3 − 2xsinx 2
Bài 3: Giải bất phương trình f '(x) > g'(x) với: a) 3 2
f(x) = x + x − 2, g(x) = 3x + x + 2 2 b) 3 2 3 x
f(x) = 2x − x + 3, g(x) = x + − 3 2 2 c) 3 f(x) = , g(x) = x − x x
Bài 4: Chứng minh hàn số 6 6 2 2
y = sin x + cos x + 3sin x cos x có đạo hàm bằng 0 Bài 5: Chứng minh
a) y = tan x thỏa mãn hệ thức 2
y '− y −1 = 0
b) y = cot 2x thỏa mãn hệ thức 2
y '+ 2 y + 2 = 0
Bài 6: Giải phương trình y ' = 0 trong các trường hợp sau:
a) y = sin 2x − 2cos x b) 2
y = cos x + sin x c) y = 3sin 2x + 4cos 2x + 10x
d) y = tan x + cot x π Bài 7: cos x Tính f '
biết f (x) = 6 cos 2x
Bài 8: Xác định m để các bất phương trình sau nghiệm đúng với mọi x ∈ R: 3 mx 2 a) f '(x) > 0 vôùi f(x) = − 3x + mx − 5 3 3 2 mx mx b) f '(x) < 0 vôùi f(x) = − + (m + 1)x − 15 3 2
VẤN ĐỀ 6*: Tính tổng nhờ đạo hàm và tính giới hạn nhờ đạo hàm
Bài 1: Tính tổng sau: a) 2 1 ( ) 1 2 3 ... n P x x x nx − = + + + + b) 2 2 2 2 2 1 ( ) 1 2 3 ... n Q x x x n x − = + + + + 6
Đại số và giải tích 11 Đạo hàm
ĐẠI HỌC SƯ PHẠM HÀ NỘI
Bài 2: Tìm giới hạn sau: x + 8 − 3 3 x − 3x − 2 a) lim b) lim 2 x 1 → x + 2x − 3 x 1 → x −1 2 3
x + x + x + ... n + x − n c) lim x 1 → x −1
Bài 3: Chứng minh rằng a) 1 2 n 1 − n n 1 C 2C ... (n 1)C nC n2 − + + + − + = n n n n b) 0 1 2 n 1 − n n n 1 C 2C 3C ... nC (n 1)C 2 n2 − + + + + + + = + n n n n n
Bài 4: Tính các tổng sau: a) 1 2 3 19
S = C − 2C + 3C − ... + 19C − 20 20 20 20 20 b) 1 2 3 29
S = C − 2C + 3C − ... + 29C − 30 . 30 30 30 30
=================================== 7
Đại số và giải tích 11 Đạo hàm



