124 trang 4 lượt tải

bài tập -Đề thi TCC các năm

7

đề toán cao cấp

Tác giả:

Profile

Thu Hà Trương

1 giờ trước
Tải xuống
Báo cáo
Danh sách Quiz
Tải xuống
/124
HP: TOÁN CAO CẤP - BÀI TẬP THAM KHẢO
BỘ MÔN TOÁN - KHOA CNTT - HỌC VIỆN NÔNG NGHIỆP VIỆT NAM 1
Chương 1: Ma trận - Định thức - Hệ phương trình tuyến tính
Bài 1. Tìm các số
,,m n k
biết :
1)
x 3 x4 2 x
.
m n k
A B C
2)
2 x x 5
.
m n k
A B C
ĐS: 1)
2, 3, 4m n k
2)
2, 5, 2m n k
Bài 2. Cho các ma trận:
1 4 3
2 5 0
A



,
11
23
46
B





,
27
31
C



.
Tính
AB
,
BA
,
ABC
,
CB
.
ĐS:
4 10 15
3
1 14 18
t
AB




,
21 29
12 13
AB



,
1 1 3
8 23 6
16 46 12
BA






,
129 118
63 71
ABC



,
CB
Bài 3. Cho
3 3 3
0 1 1
658
A







,
1 2 2
3 2 1
0 1 1
B






và
I
là ma trận đơn vị cấp 3.
1) Tìm ma trận
X
sao cho
2 3 5A X I
.
2) Tính
2
AB
và
.
t
BA
. Từ đó hãy cho biết ma trận
B
có khả nghịch không ? nếu có, hãy suy
ra ma trận nghịch đảo của ma trận
B
.
3) Tìm
x
sao cho
det( ) 0B xI
. Tìm ma trận
Y
thỏa mãn:
( 3 ) 0B I Y
.
ĐS: 1)
11/ 3 2 2
0 1 2/ 3
4 10 / 3 7
X






; 2)
2
4 3 9
3 12 4
9 4 6
AB





;
.3
t
B A I
.
3)
3 13
3
2
xx

;
3 2 ,
t
Y z z z z
.
Bài 4. Cho hai ma trận
,AB
vuông cấp 3 có:
det(2 ) 4,A 
3
det( ) 8B
,
5
det( ) .
2
AB
Tính
det A
,
det B
,
det( )
tt
AB
,
41
det(5 )AB
,
2
det( )AB B
.
ĐS:
det 1/ 2;A 
det 2;B
det( ) 1;
tt
AB 
41
det(5 ) 125/ 32AB
;
2
det( ) 5AB B
.
Bài 5. Tìm hạng của các ma trận sau :
1 3 4 2
2 1 1 4
1 2 1 2
A





;
1 0 2
4 1 5
1 3 7
5 0 11
B







;
3 21 0 9 0
0 7 1 2 1
0 0 0 6 0
0 0 0 0 0
C






.
ĐS:
( ) 2; ( ) 3; ( ) 3r A r B r C
.
Bài 6. Cho ma trận:
0 1 2 3
1 2 3 0
2 0 1
3 0 1 2
A
m






.
1) Tính định thức của ma trận
A
theo
m
.
HP: TOÁN CAO CẤP - BÀI TẬP THAM KHẢO
BỘ MÔN TOÁN - KHOA CNTT - HỌC VIỆN NÔNG NGHIỆP VIỆT NAM 2
2) Sử dụng kết quả tính ở câu 1, hãy biện luận theo
m
hạng của ma trận
A
.
3) Khi
4m
hãy chứng tỏ rằng ma trận
A
khả nghịch.
Khi đó, hãy tính phần tử ở vị trí hàng 2 cột 3 của ma trận
1
A
.
ĐS: 1)
det 20( 3)Am
.
2) khi
3, ( ) 4m r A
; khi
3, ( ) 3m r A
.
3) Khi
4m
,
det 20 0A 
, chứng tỏ ma trận
A
khả nghịch.
Phần tử ở vị trí hàng 2 cột 3 của ma trận
1
A
là
32
32
0 2 3
11
( 1) . 1 3 0 ...
det 20
3 1 2
A
A
Bài 7. Cho ma trận
2 1 1
4 3 0 .
11
A
x





1) Tìm
x
để ma trận
A
khả nghịch và thỏa mãn
1
det 2A
.
2) Tìm ma trận nghịch đảo của
A
khi
2x
.
ĐS: 1)
3
4
x
; 2)
1
211
8/3 5/ 3 4/ 3
1/ 3 1/ 3 2 / 3
A





.
Bài 8. Cho hai ma trận:
23
11
A



và
1 1 2
2 2 3
B



.
1) Tìm ma trận nghịch đảo của
A
.
2) Tìm ma trận
X
sao cho
t
XA B
.
3) Tìm ma trận
Y
sao cho
AYA B
.
ĐS:
1)
1
1/ 5 3/ 5
1/ 5 2/ 5
A



; 2)
3/5 1/ 5
1/ 5 7 / 5
10
X






; 3) Không tồn tại ma trận
Y
.
Bài 9. Cho
1 2 3 4
0 1 2 1
0 0 3 2
A






và
5
7
6
B





. Tìm các ma trận
X
sao cho
AX B
.
ĐS:
21
0.5 4
,
3 1.5
z
z
Xz
z
z







.
Bài 10. Giải các hệ phương trình tuyến tính sau :
1)
2 4 0
3 2 8 0
4 7 0
x y z t
x y z t
x y z t
; 2)
3 2 3 4 1
2
6 5 6 4 5
7 5 7 8 0
x y z t
x y z
x y z t
x y z t
; 3)
4 3 1
5 5 2
7 2 3 10
2 3 5
x y z
x y z
x y z
x y z
.
ĐS: 1)
3 ; ; 0;x t y t z t
2)
4 5; 4 7; ,x t z y t z t
3) VN.
HP: TOÁN CAO CẤP - BÀI TẬP THAM KHẢO
BỘ MÔN TOÁN - KHOA CNTT - HỌC VIỆN NÔNG NGHIỆP VIỆT NAM 3
Bài 11. Cho hệ phương trình tuyến tính
1 2 3
1 2 3
2
1 2 3
2 3 4
3 5 11 17
4 10 ( 9) 5
x x x
x x x
x x m x m
. Tìm
m
để hệ này :
1) là hệ Cramer ; 2) có vô số nghiệm ; 3) vô nghiệm.
Khi hệ đã cho là hệ Cramer, hãy tính
2
x
theo
m
.
ĐS: 1)
1m 
;
2
2
2
5 2 7
1
mm
x
m

; 2)
1m 
3)
1m
Bài 12. Cho hai ma trận
1 0 0 2
1 2 2 2
1 3 3 1
3 0 1 2
A






và
1 0 0 2
1 1 2 2
1 1 1 1
3 1 1 1
B







.
1) Tìm phần tử nằm ở vị trí hàng 3, cột 2 của ma trận
2
A
.
2) Tính
AB
.
3) Chứng minh
A
khả nghịch. Tìm phần tử nằm ở vị trí hàng 1, cột 3 của ma trận
1
A
.
4) Tính
det( )AB
và
2
det( )A BA
.
ĐS: 1) Phần tử cần tìm là tích của “hàng 3 ma trận
A
” với “cột 2 ma trận
A
”;
2)
2 0 0 0
2 1 0 0
2 4 4 0
6 1 2 3
AB







; 4)
det( ) 24AB
;
2
det( ) 1008A BA
.
Bài 13. Có ba phụ huynh A, B, C dự định mua bốn món đồ: bút bi, bút chì, vở và hộp bút để trao phần
thưởng cuối năm. Số lượng muốn mua được cho trong bảng sau:
Đồ dùng
Phụ huynh
Bút bi
Bút chì
Vở
Hộp
bút
A
400
40
200
20
B
350
50
250
30
C
150
35
150
15
Ba người này có thể mua bốn món đồ ở hai cửa hàng CH1 và CH2 với giá bán mỗi loại ở từng cửa
hàng cho trong bảng sau:
Cửa hàng
Món đồ
CH 1
CH 2
Bút bi
3000 đ
3500đ
Bút chì
7000 đ
6500đ
Vở
5000đ
4800đ
Hộp bút
20000đ
17000đ
Hỏi mỗi phụ huynh A, B, C nên mua ở cửa hàng nào thì được rẻ hơn?
ĐS: A, B nên mua ở cửa hàng 1, C nên mua ở cửa hàng 2.
HP: TOÁN CAO CẤP - BÀI TẬP THAM KHẢO
BỘ MÔN TOÁN - KHOA CNTT - HỌC VIỆN NÔNG NGHIỆP VIỆT NAM 4
Bài 14. Một nhà máy sản xuất 3 loại sản phẩm A, B và C. Mỗi sản phẩm phải qua 3 công đoạn cắt, lắp
ráp và đóng gói với thời gian yêu cầu cho mỗi công đoạn được liệt kê ở bảng sau đây:
Sản phẩm A
Sản phẩm B
Sản phẩm C
Cắt
0.6 giờ
1 giờ
1.5 giờ
Lắp ráp
0.6 giờ
0.9 giờ
1.2 giờ
Đóng gói
0.2 giờ
0.3 giờ
0.5 giờ
Các bộ phận cắt, lắp ráp và đóng gói có số giờ công nhiều nhất trong mỗi tuần lần lượt là 380, 330 và
120 giờ công. Hỏi nhà máy phải sản xuất với số lượng mỗi loại là bao nhiêu theo mỗi tuần để nhà máy
hoạt động hết năng lực.
ĐS: Số lượng sản phẩm A, B, C lần lượt là 50, 200,100.
HP: TOÁN CAO CẤP - BÀI TẬP THAM KHẢO
BỘ MÔN TOÁN - KHOA CNTT - HỌC VIỆN NÔNG NGHIỆP VIỆT NAM 5
Chương 2: Phép tính vi phân hàm một biến
Bài 1. Hãy áp dụng định nghĩa để tính đạo hàm của các hàm số sau:
1)
11
23
f x x
2)
f x mx b
3)
2
59f t t t
4)
2
1.5 3.7f x x x
Bài 2. Cho hàm số
3
f x x
1) Nếu
0a
hãy dùng công thức hàm lũy thừa tính
'fa
2) Chứng minh rằng
'0f
không tồn tại.
Bài 3. Tính đạo hàm của các hàm số sau:
1)
1y x x
; 2)
2
43xx
y
x

; 3)
2
2xx
y
x
; 4)
2
3
1
vx
x




.
ĐS: 1)
31
'
2
2
yx
x

; 2)
3
3 2 3 1
'
22
yx
x
x
;
3)
3
1
'1y
x

; 4)
63
55
1 2 1
'1
3
3
v
xx
.
Bài 4. Viết phương trình đường tiếp tuyến với đường cong
4
yx
tại điểm
1;1
.Vẽ hình minh họa
kết quả.
ĐS:
13
44
yx
.
Bài 5. Giả sử rằng
2 3, 2 4, ' 2 2, ' 2 7f g f g
. Hãy tìm
'2h
khi:
1)
54h x f x g x
; 2)
h x f x g x
;
3)
fx
hx
gx
; 4)
1
gx
hx
fx
.
ĐS: 1)
43
; 2)
29
; 3)
13
16
; 4)
1.5
.
Bài 6. Tính đạo hàm của các hàm số sau:
1)
100
2
4F x x x
; 2)
3
4
1
1
gt
t
;
3)
ln(2 1)x
y
x
tại
1x
; 4)
2
2xx
ye
tại
0x
.
ĐS: 1)
99
2
' 100 4 2 4F x x x x
; 2)
3
4
4
12
'
1
t
gt
t

;
3)
2
'(1) ln3
3
y 
; 4)
'2y 
.
Bài 7. Tính
8
y
với:
1)
2
1
x
y
x
; 2)
2
1
43
y
xx

; 3)
3
1
x
y
x
.
HP: TOÁN CAO CẤP - BÀI TẬP THAM KHẢO
BỘ MÔN TOÁN - KHOA CNTT - HỌC VIỆN NÔNG NGHIỆP VIỆT NAM 6
ĐS: 1)
8
9
8!
1
y
x

; 2 )
11
1
11
!
2
31
n
n
nn
yn
xx







;
3)
21
11
33
21
1 1 4 ... 3 5 1 1 1 4 ... 3 2 1
33
n n n n
n
nn
y n x n x
Bài 8. Tính vi phân của các hàm số sau:
1)
2
sin2y x x
; 2)
2
ln 1yt
; 3)
1
1
u
y
u
; 4)
2
3
1yr

;
5)
2
1 .arccosy x x
tại
3
2
x
; 6)
3
1 tanf t t
tại
0t
.
ĐS: 1)
2
2 sin2 2 cos2dy x x x x dx
; 2)
2
2
1
t
dy dt
t
; 3)
2
2
1
dy du
u
;
4)
2
3
3
6
1
r
dy dr
r

; 5)
2
.arccos
'1
1
xx
y
x

33
1
26
dy dx
;
6)
2
2
3
1 1 1
'
3 cos
1 tan
ft
t
t
1
0
3
df dt
.
Bài 9. Tính
y
và
dy
tại giá trị đã cho của
x
và
dx x
:
1)
2
2 , 2, 0.4y x x x x
2)
; 4; 1y x x x
3)
5
, 8, 1y x x
x
4)
, 0, 0.5
x
y e x x
ĐS: 1)
0.8; 0.64dy y
2)
0.250; 0.236dy y
3)
0.078; 0.069dy y
4)
0.50; 0.65dy y
Bài 10. Hãy sử dụng xấp xỉ tuyến tính (vi phân) để tính gần đúng các giá trị sau:
1)
5
2.001
2)
0.015
e
3)
1
1002
4)
tan44
ĐS: 1)
32.08
2)
0.985
3)
0.998
4)
0.965
Bài 11. Một người nông dân muốn rào một khu đất rộng 1.5 triệu m
2
thành khu vườn hình chữ
nhật, sau đó chia khu vườn đất ra thành 2 phần diện tích bằng nhau bằng một hàng rào nằm song
song với mốt trong các cạnh của hình chữ nhật. Người nông dân phải làm thế nào để giảm tối đa
giá thành của hàng rào.
ĐS: Khu đất được chia thành 2 mảnh kích thước 1000m x 750m (cạnh chung dài 1000m)
HP: TOÁN CAO CẤP - BÀI TẬP THAM KHẢO - HỌC KÌ I NĂM HỌC 2017- 2018
BỘ MÔN TOÁN - KHOA CNTT - HỌC VIỆN NÔNG NGHIỆP VIỆT NAM 7
Bài 12. Một cái cốc uống nước hình nón được làm từ một
miếng bìa hình tròn bán kính R bằng cách cắt bỏ đi một
miếng hình quạt rồi dán các cạnh CA và CB lại với nhau
(xem hình vẽ bên). Hãy tìm dung tích lớn nhất của chiếc
cốc.
ĐS:
3
max
2
93
R
V
.
Bài 13. Một người phụ nữ đứng ở điểm A trên bờ của một
cái hồ nước hình tròn bán kính 2km. Người phụ nữ muốn
tới điểm C nằm đối diện phía bên kia hồ trong thời gian
ngắn nhất có thể. Cô ta có thể đi bộ với vận tốc 4km/h và
chèo thuyền với vận tốc 2km/h. Hỏi cô ta phải chọn hành
trình như thế nào?
ĐS: Thời gian đi
2cosy


;
0
2

.
Nhìn đồ thị hàm số ta thấy y nhỏ nhất khi
2
(
lớn nhất). Vậy cô ta không chèo thuyền mà đi bộ
nửa vòng hồ từ A đến C.
Bài 14. Hai cái cột thẳng đứng được gia cố bằng một dây
thừng PRS nối từ đỉnh của cột thứ nhất xuống một điểm R
trên mặt đất rồi nối tới đỉnh của cột thứ hai. Hãy chứng tỏ
rằng dây thừng sẽ có độ dài ngắn nhất khi
12

HP: TOÁN CAO CẤP - BÀI TẬP THAM KHẢO - HỌC KÌ I NĂM HỌC 2017- 2018
BỘ MÔN TOÁN - KHOA CNTT - HỌC VIỆN NÔNG NGHIỆP VIỆT NAM 8
Chương 3: Nguyên hàm – Tích phân
Bài 1. Tìm họ các nguyên hàm của các hàm số sau:
1)
2
2
( ) 1
3
x
fx
x
;
2)
1
()
12
gx
x
;
3)
4
( ) 3
x
h x e x
;
4)
( ) 3cos
3
l x x



;
5)
2
1
()
14
kx
x
;
6)
2
2
11
()
9
91
mx
x
x

.
ĐS: với
C
là hằng số tùy ý,
1)
2
2
()
6
x
F x x C
x
; 2)
1
( ) ln(1 2 )
2
G x x C
;
3)
4 3/2
32
()
43
x
H x e x C
; 4)
9
( ) sin
3
L x x C




;
5)
1
( ) arcsin(2 )
2
K x x C
; 6)
2
1 1 3
( ) ln 3 9 1 ln
3 6 3
x
M x x x C
x
.
Bài 2. Ký hiệu kích thước của một quần thể tại thời điểm
t
(đơn vị: năm) là
()Nt
. Khi đó, tốc độ
tăng trưởng của quần thể tại thời điểm
t
là
'( )
dN
Nt
dt
. Cho biết tốc độ tăng trưởng của quần thể
tại thời điểm
t
là
3sin(2 )
dN
t
dt
và biết
(0) 10 000N
, hãy tìm công thức biểu diễn
()Nt
.
ĐS:
3
( ) 1 cos(2 t)
2
Nt

.
Bài 3. Tìm nguyên hàm
F
của hàm số
f
biết
2
2
( ) 3
1
ft
t

và thỏa mãn
(1) 0F
.
ĐS:
( ) 2arctan 3( 1)
2
F t t t
Bài 4. Tính tích phân xác định của hàm số
f
trên đoạn
[0;2]
biết đồ thị hàm số
f
được cho như
hình vẽ sau:
1)
2)
3)
ĐS: 1)
5
6
; 2)
5
2
; 3)
4
3
.
Bài 5. 1) Cho biết
'( ) 12
x
f x x e

, hãy tính
(3) (0)ff
.
2) Cho biết
3
2
( ) 4f x dx
và
3
2
3 ( ) 2 ( ) 2f x g x dx

, hãy tìm
3
2
()g x dx
.
ĐS: 1)
3
3
0
(3) (0) '( ) .. 53f f f x dx e
; 2)
3
2
( ) 5g x dx

.
Bài 6. Tính diện tích hình phẳng giới hạn bởi các đường cong sau (yêu cầu vẽ hình minh họa và
đánh dấu phần hình giới hạn):
HP: TOÁN CAO CẤP - BÀI TẬP THAM KHẢO - HỌC KÌ I NĂM HỌC 2017- 2018
BỘ MÔN TOÁN - KHOA CNTT - HỌC VIỆN NÔNG NGHIỆP VIỆT NAM 9
1) các đường cong
2
2yx
,
3
3y x x
.
2) các đường cong
2
2y x x
,
x
ye
, đường thẳng
1, 2xx
.
3) các đường
sinyx
,
cos2yx
và
0,
2
xx

.
4) các đường
3
yx
và
1
y
x
và
1, 8xx
.
5) tam giác có ba đỉnh:
(0;0), (1;2), (4;1)A B C
.
6) các đường
3
x
y
,
2
x
y
và
1, 1xx
.
ĐS: 1)
5
11
6
; 2)
2
1
2e
e

; 3) 1;
4)
1
11 ln8
4
; 5)
7
11
2
; 6)
41
3ln3 2ln 2
.
Bài 7. Tính độ dài phần đường cong thuộc đồ thị hàm số:
1)
23
yx
từ điểm
(1;1)
đến điểm
(4;8)
;
2)
2
ln(1 )yx
với
1
0
2
x
;
3)
2
arcsin 1y x x
từ điểm
0x
đến
1
2
x
;
4)
1
.( 3)
3
y x x
với
19x
.
ĐS: 1)
125 13 13
27
; 2)
1
ln3
2
; 3)
2 3 2
; 4)
2
10
3
.
Bài 8. Tính các tích phân sau:
1)
2
ln
e
e
x dx
;
2)
1
3
2
0
4
x
dx
x
;
3)
/2
/4
1
tan
dx
x
;
4)
1
0
x
e dx
;
5)
2
1
x
xe dx

;
6)
0
1
34
dx
x

;
7)
2
1
4 4 5
dx
xx



;
8)
2
0
ln
1
x
dx
x

(HD:
1
u
x
)
ĐS: 1)
2
e
; 2)
16 7 5
3
; 3)
ln 2
; 4) 2
5)
2
1
4e
; 6)

; 7)
4
; 8) 0.
HP: TOÁN CAO CẤP - BÀI TẬP THAM KHẢO - HỌC KÌ I NĂM HỌC 2017- 2018
BỘ MÔN TOÁN - KHOA CNTT - HỌC VIỆN NÔNG NGHIỆP VIỆT NAM 10
Chương 4: Phép tính vi phân hàm nhiều biến
Bài 1. Tính vi phân toàn phần của các hàm 2 biến sau:
1)
2
2
( , ) 2 3 4
x
f x y x y x
y
; 2)
22
( , ) ln( 2 )f x y x y
tại điểm
(1;2)
;
3)
( , )
xy
f x y xe
; 4)
( ; ) arcsin( 2 )f x y x y
tại điểm
(0;0)
;
5)
( ; ) arctan
y
f x y
x
tại điểm
(1;1)
với
0,01x
và
0,02y
.
ĐS: 1)
2
3
2
12
( , ) (4 3) (2 )
2
x
df x y xy dx x dy
y
yx
; 2)
28
(1,2)
99
df dx dy
;
3)
2
( , ) (1 )
xy xy
df x y e xy dx x e dy
; 4)
(0,0) 2df dx dy
; 5)
0,015
.
Bài 2. Cho hàm số
22
( , ) .f x y x y
1) Hãy tính
(3,04;3,98).f
2) Hãy tính vi phân toàn phần của hàm số
f
tại điểm
(3;4).
3) hãy tính gần đúng
(3,04;3,98)f
bằng cách áp dụng công thức tính xấp xỉ:
''
0 0 0 0 0 0 0 0
( ; ) ( ; ) ( ; ) ( ; )
xy
f x x y y f x y f x y x f x y y
và đánh giá sai số.
ĐS: 1) 5,008193287 ; 2)
34
(3;4)
55
df dx dy
; 3) 5,008 và sai số là 2/10000
Bài 3. Tính
22
22
ff
A
xy



với:
1)
22
( , )f x y x y
; 2)
32
( , ) 3f x y x xy
;
3)
22
( , ) lnf x y x y
; 4)
( , ) cos cos
xy
f x y e y e x


.
ĐS: 1)
0A
; 2)
12Ax
; 3)
0A
; 4)
0A
.
Bài 4. Chứng tỏ rằng hàm số
.P bL K

(với
,,b

là các hằng số) (hàm sản xuất Cobb-
Douglas) thỏa mãn phương trình sau:
PP
L K P
LK



.
Bài 5. Tìm các điểm cực trị và giá trị cực trị (nếu có) của các hàm số sau:
1)
3 2 2 2
( , ) 8 12 24 6 1f x y x x y x y
2)
22
( , ) ( )
xy
f x y x y e

3)
( , ) (1 )f x y xy x y
4)
2
( , ) 3 2 2 3
y
f x y x e y
ĐS:
1) Hàm số đạt cực đại tại
(0,0)
, giá trị cực đại tại điểm đó là
(0,0) 1f
.
2) Hàm số đạt cực tiểu tại
( 2; 1)
và
( 2; 1) 1
CT
ff
.
3) Hàm số đạt cực đại tại
11
( ; )
33
và
1
27
CD
f
.
4) Hàm số đạt cực tiểu tại
0;0
và
0;0 5
CT
ff
.
HP: TOÁN CAO CẤP - BÀI TẬP THAM KHẢO - HỌC KÌ I NĂM HỌC 2017- 2018
BỘ MÔN TOÁN - KHOA CNTT - HỌC VIỆN NÔNG NGHIỆP VIỆT NAM 11
Bài 6. Một công ty sản suất hai loại mặt hàng với sản lượng sản phẩm lần lượt là
1
q
và
2
.q
Đơn
giá mỗi sản phẩm của hai mặt hàng tương ứng là
1
p
và
2
.p
Hàm tổng chi phí là
22
1 2 1 2 1 2
2 2 4 300.C q q q q q q
1) Lập hàm lợi nhuận của công ty.
2) Khi đơn giá của hai loại mặt hàng là
1
324p
và
2
524p
hãy xác định sản lượng tương
ứng của hai loại mặt hàng để lợi nhuận của công ty là lớn nhất.
ĐS:
22
1 1 2 2 1 2 1 2 1 2
1) 2 2 4 300p q p q q q q q q q
2)
1
120q
và
2
100q
HP: TOÁN CAO CẤP - BÀI TẬP THAM KHẢO - HỌC KÌ I NĂM HỌC 2017- 2018
BỘ MÔN TOÁN - KHOA CNTT - HỌC VIỆN NÔNG NGHIỆP VIỆT NAM 12
Chương 5: Phương trình vi phân
Bài 1. Giải các phương trình vi phân sau
1)
2
10x dy xydx
; 2)
1'
xx
e yy e
với điều kiện ban đầu
(0) 1y
;
3)
'
y
x
y
ye
x

; 4)
2
2
'
2
xy y
y
x xy
;
5)
2
2 ln
x
y xy e x

; 6)
2
11
cos
yy
x x x

;
7)
3
y xy xy
; 8)
2
ln
y
y y x
x

ĐS: 1)
2
1, 0, 1y C x y x
; 2)
2
2
1
2
y
x
e
ee
;
3)
ln ln | | ( 0)
c
y x c
x



; 4)
2
ln
Cx
yx
y
;
5)
2
( ln )
x
y e x x x C
; 6)
1
tany x C
x

;
7)
2
2
11
x
y Ce

; 8)
2
1
ln
2
y
x
Cx



.
Bài 2. (Mô hình tăng trưởng quần thể) Gọi số lượng cá thể của một quần thể tại thời điểm
t
là
( ).Pt
Tốc độ tăng trưởng của quần thể tại thời điểm
t
là đạo hàm
/.dP dt
Nhà sinh vật học, toán
học người Hà Lan Pierre – Francois Verhulst đưa ra mô hình cho sự phát triển của quần thể như
sau:
()
( ) 1 (1)
dP P t
kP t
dt M




trong đó
k
là hằng số tỷ lệ,
M
là hằng số cân bằng quần thể.
1) Hãy giải phương trình vi phân
(1).
2) Biết rằng
2; 2000000kM
và số lượng cá thể tại thời điểm ban đầu là
(0) 1000,P
hãy xác định công thức tính
()Pt
mô tả số lượng cá thể tại thời điểm
.t
ĐS: 1)
( ) , 0
1
kt
M
P t C
Ce

2)
2
2000000
()
1 1999
t
Pt
e
.
----------------------------- HẾT -----------------------------
................................... HẾT ...................................
Ghi chú: + Cán bộ coi thi không phải giải thích gì thêm
+ Sinh viên không được sử dụng tài liệu
Cán bộ ra đề Duyệt đề
Vũ Thị Thu Giang Vũ Thị Thu Giang
KHOA CÔNG NGHỆ THÔNG TIN
BỘ MÔN TOÁN
Đề số: 04
Ngày thi: 03/09/2020
ĐỀ THI KẾT THÚC HỌC PHẦN
Tên Học phần: Toán cao cấp
Thời gian làm bài: 75 phút
Loại đề thi: Tự luận
Câu I (2,0 điểm) Cho ma trận
1 1 2 1
2 0 1 , 2
1 2 1
AB
m

.
1. (1,0đ) Tính
2
t
AB
.
2. (1,0đ) Tìm điều kiện của tham số
m
để ma trận
A
khả nghịch. Khi đó, không tìm ma
trận nghịch đảo, hãy tính
1
det A
.
Câu II (1,5 điểm) Giải hệ phương trình tuyến tính
31
2 3 3 3
4 2 3 4.
x y z t
x y z t
x y z t
Câu III (1,5 điểm) Tính tích phân suy rộng
2
4
6
dx
xx


.
Câu IV (3,0 điểm)
1. (2,0đ) Tìm các điểm cực trị của hàm số
34
( ; ) 12 4 2020f x y x x y y
.
2. (1,0đ) Cho hàm số
2
( ; ) ln
x
g x y x
y




. Tìm vi phân toàn phần của hàm số
;g x y
tại
điểm
1;1
.
Câu V (2,0 điểm) Giải phương trình vi phân tuyến tính
32
3
'.
x
y
y x x e
x
................................... HẾT ...................................
Ghi chú: + Cán bộ coi thi không phải giải thích gì thêm
+ Sinh viên không được sử dụng tài liệu
Cán bộ ra đề Duyệt đề
Vũ Thị Thu Giang Vũ Thị Thu Giang
KHOA CÔNG NGHỆ THÔNG TIN
BỘ MÔN TOÁN
Đề số: 05
Ngày thi: 03/09/2020
ĐỀ THI KẾT THÚC HỌC PHẦN
Tên Học phần: Toán cao cấp
Thời gian làm bài: 75 phút
Loại đề thi: Tự luận
Câu I (2,0 điểm) Cho ma trận
1 1 2 1
2 0 1 , 2
1 2 1
AB
m

.
1. (1,0đ) Tính
2
t
BA
.
2. (1,0đ) Tìm điều kiện của tham số
m
để ma trận
A
khả nghịch. Khi đó, không tìm ma
trận nghịch đảo, hãy tính
1
det A
.
Câu II (1,5 điểm) Giải hệ phương trình tuyến tính
31
2 3 3 3
2 4 3 4
x y z t
x y z t
x y z t
.
Câu III (1,5 điểm) Tính tích phân suy rộng
2
4
6
dx
xx


.
Câu IV (3,0 điểm)
1. (2,0đ) Tìm các điểm cực trị của hàm số
34
( ; ) 12 4 2020f x y y y x x
.
2. (1,0đ) Cho hàm số
3
( ; ) ln
x
g x y x
y




. Tìm vi phân toàn phần của hàm số
;g x y
tại
điểm
1;1
.
Câu V (2,0 điểm) Giải phương trình vi phân tuyến tính
2
53
31
'.
x
ye
y
x x x
................................... HẾT ...................................
Ghi chú: + Cán bộ coi thi không phải giải thích gì thêm
+ Sinh viên không được sử dụng tài liệu
Cán bộ ra đề Duyệt đề
Lê Thị Diệu Thùy Vũ Thị Thu Giang
KHOA CÔNG NGHỆ THÔNG TIN
BỘ MÔN TOÁN
Đề số: 04
Ngày thi: 14/07/2020
ĐỀ THI KẾT THÚC HỌC PHẦN
Tên Học phần: Toán cao cấp
Thời gian làm bài: 75 phút
Loại đề thi: Tự luận
Câu I (2,0 điểm) Cho các ma trận
,,A B C
với
12
34
A



.
a) (0,5đ) Tính
t
AA
.
b) (1,0đ) Tìm ma trận
X
sao cho
2X A I
với
I
là ma trận đơn vị cấp 2. Ma trận
X
có
khả nghịch không?
c) (0,5đ) Biết rằng
3
,
m n k
BC

là các ma trận sao cho
AB C
. Tìm
, , .m n k
Câu II (1,5 điểm) Giải hệ phương trình tuyến tính
30
2 2 1
3 2 1.
x y z t
x y z t
x z t
Câu III (1,5 điểm) Tính tích phân suy rộng
0
2
( 3) .
x
x e dx

Câu IV (3,0 điểm)
a) (2,0đ) Tìm các điểm cực trị của hàm số
23
( ; ) 2 2020f x y x xy y y
.
b) (1,0đ) Cho hàm số
( ; ) ln
x
g x y x
y
. Tính
(1;1)
g
x
.
Câu V (2,0 điểm) Giải phương trình vi phân tuyến tính
2
2
' (3 sin 2 ) .
y
y x x
x
................................... HẾT ...................................
Ghi chú: + Cán bộ coi thi không phải giải thích gì thêm
+ Sinh viên không được sử dụng tài liệu
Cán bộ ra đề Duyệt đề
Lê Thị Diệu Thùy Vũ Thị Thu Giang
KHOA CÔNG NGHỆ THÔNG TIN
BỘ MÔN TOÁN
Đề số: 05
Ngày thi: 14/07/2020
ĐỀ THI KẾT THÚC HỌC PHẦN
Tên Học phần: Toán cao cấp
Thời gian làm bài: 75 phút
Loại đề thi: Tự luận
Câu I (2,0 điểm) Cho các ma trận
,,A B C
với
12
34
A



a) (0,5đ) Tính
t
AA
.
b) (1,0đ) Tìm ma trận
X
sao cho
3X I A
với
I
là ma trận đơn vị cấp 2. Ma trận
X
có
khả nghịch không?
c) (0,5đ) Biết rằng
4
,
m n k
BC

là các ma trận sao cho
AB C
. Tìm
, , .m n k
Câu II (1,5 điểm) Giải hệ phương trình tuyến tính
30
2 2 1
3 2 1.
x y z t
x y z t
x y t
Câu III (1,5 điểm) Tính tích phân suy rộng:
0
3
( 2) .
x
x e dx

Câu IV (3,0 điểm)
a) (2,0đ) Tìm các điểm cực trị của hàm số
32
( ; ) 2 2020f x y x x xy y
.
b) (1,0đ) Cho hàm số
( ; ) ln
y
g x y x
x
. Tính
(1;1)
g
x
.
Câu V (2,0 điểm) Giải phương trình vi phân tuyến tính
3
3
' (4 cos2 ) .
y
y x x
x
KHOA CÔNG NGHỆ THÔNG TIN
BỘ MÔN TOÁN
Đề số: 06
Ngày thi: 18/12/2019
ĐỀ THI KẾT THÚC HỌC PHẦN
Tên học phần: Toán cao cấp
Thời gian làm bài: 75 phút
Loại đề thi: Tự luận
Câu I (2.0 điểm) Cho ma trận
2 4 1 0
1 2 1 ; 2 1 .
2 0 1 1 3
x
AB
1) (0.5 điểm) Tìm phần tử thuộc hàng 1 cột 2 của ma trận
AB
và cho biết cấp của ma trận
.AB
2) (1.5 điểm) Với
1x
tìm ma trận nghịch đảo của ma trận
A
(nếu có).
Câu II (1.5 điểm) Giải hệ phương trình sau:
2 4 3
2 4 3
4 4 4 4
x y z t
x y z t .
x y z t
Câu III (2.5 điểm)
1) (1.0 điểm) Tìm đạo hàm và nguyên hàm của hàm số:
2
1
4
fx
x
.
2) (1.5 điểm) Tính độ dài đường cong
2
16yx
trên đoạn
0;2 2 .


Câu IV (2.0 điểm) Tìm các điểm cực trị (nếu có) của hàm số:
3 2 2
( , ) 3 6 6 8.f x y x y x xy
Câu V (2.0 điểm) Giải phương trình vi phân tuyến tính:
22
2
1.
x
y y x e
x
................................... HẾT ...................................
Ghi chú: + Sinh viên không được sử dụng tài liệu
+ Cán bộ coi thi không phải giải thích gì thêm
Cán bộ ra đề Duyệt đề
Lê Thị Diệu Thùy Phan Quang Sáng
KHOA CÔNG NGHỆ THÔNG TIN
BỘ MÔN TOÁN
Đề số: 07
Ngày thi: 18/12/2019
ĐỀ THI KẾT THÚC HỌC PHẦN
Tên học phần: Toán cao cấp
Thời gian làm bài: 75 phút
Loại đề thi: Tự luận
Câu I (2.0 điểm) Cho ma trận
2 4 2 1 0
1 2 ; 2 1 .
2 0 1 1 3
A x B
1) (0.5 điểm) Tìm phần tử thuộc hàng 2 cột 1 của ma trận
AB
và cho biết cấp của ma trận
.AB
2) (1.5 điểm) Với
1x
tìm ma trận nghịch đảo của ma trận
A
(nếu có).
Câu II (1.5 điểm) Giải hệ phương trình sau:
2 4 3
2 4 3
4 4 4 4
x y z t
x y z t .
x y z t
Câu III (2.5 điểm)
1) (1.0 điểm) Tìm đạo hàm và nguyên hàm của hàm số:
2
1
9
fx
x
.
2) (1.5 điểm) Tính độ dài đường cong
2
4yx
trên đoạn
[0;1].
Câu IV (2.0 điểm) Tìm các điểm cực trị (nếu có) của hàm số:
2 3 2
( , ) 3 6 6 9.f x y x xy y y
Câu V (2.0 điểm) Giải phương trình vi phân tuyến tính:
2
2
sin(2 ) .y y x x x
x
................................... HẾT ...................................
Ghi chú: + Sinh viên không được sử dụng tài liệu
+ Cán bộ coi thi không phải giải thích gì thêm
Cán bộ ra đề Duyệt đề
Lê Thị Diệu Thùy Phan Quang Sáng
KHOA CÔNG NGHỆ THÔNG TIN
BỘ MÔN TOÁN
Đề số: 08
Ngày thi: 20/12/2019
ĐỀ THI KẾT THÚC HỌC PHẦN
Tên Học phần: Toán cao cấp
Thời gian làm bài: 75 phút
Loại đề thi: Tự luận
Câu I (2.0 điểm) Cho ma trận
1 2 3
0 5 1
12
A
m





.
1. (0.75đ) Tìm phần tử nằm ở vị trí hàng 1 và cột 3 của ma trận
.
t
AA
theo
.m
2. (1.25đ) Tìm
m
để A khả nghịch. Khi đó không tìm ma trận
1
A
, hãy tính
1
det( )A
theo
.m
Câu II (1.5 điểm) Giải hệ phương trình
4 4 2 17
2 5 4 2 13.
3 8 3 25
x y z t
x y z t
x y z t
Câu III (1.5 điểm) Tính tích phân suy rộng
2
2
36
dx
x

.
Câu IV (3.0 điểm)
1. (1.0đ) Tìm vi phân toàn phần của
2
( , ) 3f x y x y y
tại điểm (2,1).
2. (2.0đ) Tìm các điểm cực trị (nếu có) của hàm số
( , ) 3ln 3ln 2 2f x y x y xy x y
(
,0xy
).
Câu V (2.0 điểm) Giải phương trình vi phân tuyến tính
3
3
' 2 1y y x
x
.
.................................. HẾT ...................................
Ghi chú: + Cán bộ coi thi không phải giải thích gì thêm
+ Sinh viên không được sử dụng tài liệu
Cán bộ ra đề Duyệt đề
Lê Thị Hạnh Phan Quang Sáng
KHOA CÔNG NGHỆ THÔNG TIN
BỘ MÔN TOÁN
Đề số: 09
Ngày thi: 20/12/2019
ĐỀ THI KẾT THÚC HỌC PHẦN
Tên Học phần: Toán cao cấp
Thời gian làm bài: 75 phút
Loại đề thi: Tự luận
Câu I (2.0 điểm) Cho ma trận
2 1 0
5 1 2
13
A
m





.
1. (0.75đ) Tìm phần tử nằm ở vị trí hàng 2 và cột 3 của ma trận
.
t
AA
theo
.m
2. (1.25đ) Tìm
m
để A khả nghịch. Khi đó không tìm ma trận
1
A
, hãy tính
1
det( )A
theo
.m
Câu II (1.5 điểm) Giải hệ phương trình
2 3 5
2 5 3 15 .
3 8 27 2 16
x y z t
x y z t
x y z t
Câu III (1.5 điểm) Tính tích phân suy rộng
2
1
26
dx
x

.
Câu IV (3.0 điểm)
1. (1.0đ) Tìm vi phân toàn phần của
2
( , ) 4 2f x y y x x
tại điểm (2,0).
2. (2.0đ) Tìm các điểm cực trị (nếu có) của hàm số
( , ) 8ln 8ln 2 2f x y x y xy x y
(
,0xy
).
Câu V (2.0 điểm) Giải phương trình vi phân tuyến tính
4
2 3 2
'
x
yy
xx

.
.................................. HẾT ...................................
Ghi chú: + Cán bộ coi thi không phải giải thích gì thêm
+ Sinh viên không được sử dụng tài liệu
Cán bộ ra đề Duyệt đề
Lê Thị Hạnh Phan Quang Sáng

Preview text:


HP: TOÁN CAO CẤP - BÀI TẬP THAM KHẢO
Chương 1: Ma trận - Định thức - Hệ phương trình tuyến tính
Bài 1. Tìm các số , m , n k biết : 1) A .BC 2) A .BC m x 3 n x 4 2 x k 2 m x n k x 5
ĐS: 1) m  2,n  3,k  4 2) m  2,n  5,k  2 1 1   1 4 3   2 7
Bài 2. Cho các ma trận: A    , B  2 3 , C    . 2 5 0      3 1 4 6   Tính  3 t A
B , AB , BA , ABC , CB .  1  1  3  4 10 15 21 29 1  29 118 ĐS:    3 t A B    , AB    , BA  8 23 6 , ABC    , CB  1  14 18 1  2 13     63 71 16 46 12    3  3  3 1 2 2    
Bài 3. Cho A  0 1 1    , B  3 2  1 
 và I là ma trận đơn vị cấp 3.  6 5 8     0 1 1  
1) Tìm ma trận X sao cho 2A  3X  5I . 2) Tính 2
A B và . t
B A . Từ đó hãy cho biết ma trận B có khả nghịch không ? nếu có, hãy suy
ra ma trận nghịch đảo của ma trận B . 3) Tìm x
sao cho det(B xI )  0 . Tìm ma trận Y thỏa mãn: (B  3I )Y  0 .  1  1/ 3 2  2  4 3  9 ĐS:     1) X  0 1  2  / 3 t   ; 2) 2 A B  3  12 4   ; . B A  3  I .  4 10 / 3 7      9 4 6     3   13 t
3) x  3  x
; Y  3z 2z z , z  . 2 5
Bài 4. Cho hai ma trận ,
A B vuông cấp 3 có: det(2 ) A  4  , 3
det(B )  8 , det( A B)  . 2
Tính det A, det B , det( t t A B ) , 4 1 det(5A B ) , 2
det(AB B ) . ĐS: det A  1
 / 2; det B  2; det( t t A B )  1  ; 4 1
det(5A B )  125 / 32 ; 2
det(AB B )  5 .
Bài 5. Tìm hạng của các ma trận sau :  1 0 2   3 21 0 9 0  1 3  4 2       4  1  5 0 7 1  2  1  A  2 1 1 4         ; B   ; C   .  1 3 7 0 0 0 6 0 1  2  1 2          5 0 11   0 0 0 0 0  ĐS: r( )
A  2; r(B)  3; r(C)  3 .  0 1  2 3   1  2 3 0
Bài 6. Cho ma trận: A     . 2 m 0 1      3 0 1  2
1) Tính định thức của ma trận A theo m .
BỘ MÔN TOÁN - KHOA CNTT - HỌC VIỆN NÔNG NGHIỆP VIỆT NAM 1
HP: TOÁN CAO CẤP - BÀI TẬP THAM KHẢO
2) Sử dụng kết quả tính ở câu 1, hãy biện luận theo m hạng của ma trận A .
3) Khi m  4 hãy chứng tỏ rằng ma trận A khả nghịch.
Khi đó, hãy tính phần tử ở vị trí hàng 2 cột 3 của ma trận 1 A .
ĐS: 1) det A  20(m 3) .
2) khi m  3, r( )
A  4 ; khi m  3, r( ) A  3 .
3) Khi m  4 , det A  20  0 , chứng tỏ ma trận A khả nghịch. 0 2 3 1 1
Phần tử ở vị trí hàng 2 cột 3 của ma trận 1  A là 3 2 A  ( 1  ) . 1  3 0  ... 32 det A 20 3 1  2 2 1 1    
Bài 7. Cho ma trận A  4 3 0 .   1 1 x   1) Tìm x 1
để ma trận A khả nghịch và thỏa mãn det  A   2 .
2) Tìm ma trận nghịch đảo của A khi x  2 .  2 1  1 ĐS: 3   1) x  ; 2) 1 A  8  / 3 5 / 3 4  / 3   . 4  1/ 3 1  / 3 2 / 3   2 3 1 1  2
Bài 8. Cho hai ma trận: A    và B    . 1 1   2 2 3
1) Tìm ma trận nghịch đảo của A .
2) Tìm ma trận X sao cho t XA B .
3) Tìm ma trận Y sao cho AYA B . 3 / 5 1  / 5 1  / 5 3 / 5 ĐS:   1) 1 A    ; 2) X  1/ 5 7
 / 5 ; 3) Không tồn tại ma trận Y . 1  / 5 2  / 5    1 0   1 2 3 4 5    
Bài 9. Cho A  0 1  2 1   và B  7
  . Tìm các ma trận X sao cho AX B. 0 0 3 2   6    2z 1   0.5z  4 ĐS: X    , z   . z    3 1.5z
Bài 10. Giải các hệ phương trình tuyến tính sau : 3
x  2y  3z  4t 1
x  4y  3z  1
x y  2z  4t  0   
x y z  2 
 5x  5y z  2 1) 3
x y  2z  8t  0; 2)  ; 3)  . 
6x  5y  6z  4t  5  
7x  2 y  3z  10 
x  4 y z  7t  0 
7x 5y  7z 8t  0  2
x  3y z  5
ĐS: 1) x  3t; y t; z  0; t  2) x  4
t z  5; y  4t  7; z,t  3) VN.
BỘ MÔN TOÁN - KHOA CNTT - HỌC VIỆN NÔNG NGHIỆP VIỆT NAM 2
HP: TOÁN CAO CẤP - BÀI TẬP THAM KHẢO x  2x  3x  4 1 2 3 
Bài 11. Cho hệ phương trình tuyến tính  3x  5x  11x  17
. Tìm m để hệ này : 1 2 3  2 4
x 10x  (m  9)x m  5  1 2 3
1) là hệ Cramer ; 2) có vô số nghiệm ; 3) vô nghiệm.
Khi hệ đã cho là hệ Cramer, hãy tính x theo m . 2 2   ĐS: 5m 2m 7 1) m  1  ; x  ; 2) m  1  3) m 1 2 2 1 m 1 0 0 2 1 0 0 2       1 2  2 2 1 1 2  2 
Bài 12. Cho hai ma trận A        và B . 1 3 3 1   1 1 1 1     3 0 1 2 3 1 1 1
1) Tìm phần tử nằm ở vị trí hàng 3, cột 2 của ma trận 2 A .
2) Tính A B .
3) Chứng minh A khả nghịch. Tìm phần tử nằm ở vị trí hàng 1, cột 3 của ma trận 1 A .
4) Tính det(A B) và 2 det(A B ) A .
ĐS: 1) Phần tử cần tìm là tích của “hàng 3 ma trận A ” với “cột 2 ma trận A ”; 2 0 0 0   2 1  0 0
2) A B           ; 4) det(A ) B 24 ; 2 det(A B ) A 1008 . 2 4 4 0   6 1 2 3
Bài 13. Có ba phụ huynh A, B, C dự định mua bốn món đồ: bút bi, bút chì, vở và hộp bút để trao phần
thưởng cuối năm. Số lượng muốn mua được cho trong bảng sau: Đồ dùng Bút bi Bút chì Vở Hộp bút Phụ huynh A 400 40 200 20 B 350 50 250 30 C 150 35 150 15
Ba người này có thể mua bốn món đồ ở hai cửa hàng CH1 và CH2 với giá bán mỗi loại ở từng cửa hàng cho trong bảng sau: Cửa hàng CH 1 CH 2 Món đồ Bút bi 3000 đ 3500đ Bút chì 7000 đ 6500đ Vở 5000đ 4800đ Hộp bút 20000đ 17000đ
Hỏi mỗi phụ huynh A, B, C nên mua ở cửa hàng nào thì được rẻ hơn?
ĐS: A, B nên mua ở cửa hàng 1, C nên mua ở cửa hàng 2.
BỘ MÔN TOÁN - KHOA CNTT - HỌC VIỆN NÔNG NGHIỆP VIỆT NAM 3
HP: TOÁN CAO CẤP - BÀI TẬP THAM KHẢO
Bài 14. Một nhà máy sản xuất 3 loại sản phẩm A, B và C. Mỗi sản phẩm phải qua 3 công đoạn cắt, lắp
ráp và đóng gói với thời gian yêu cầu cho mỗi công đoạn được liệt kê ở bảng sau đây: Sản phẩm A Sản phẩm B Sản phẩm C Cắt 0.6 giờ 1 giờ 1.5 giờ Lắp ráp 0.6 giờ 0.9 giờ 1.2 giờ Đóng gói 0.2 giờ 0.3 giờ 0.5 giờ
Các bộ phận cắt, lắp ráp và đóng gói có số giờ công nhiều nhất trong mỗi tuần lần lượt là 380, 330 và
120 giờ công. Hỏi nhà máy phải sản xuất với số lượng mỗi loại là bao nhiêu theo mỗi tuần để nhà máy
hoạt động hết năng lực.
ĐS: Số lượng sản phẩm A, B, C lần lượt là 50, 200,100.
BỘ MÔN TOÁN - KHOA CNTT - HỌC VIỆN NÔNG NGHIỆP VIỆT NAM 4
HP: TOÁN CAO CẤP - BÀI TẬP THAM KHẢO
Chương 2: Phép tính vi phân hàm một biến
Bài 1. Hãy áp dụng định nghĩa để tính đạo hàm của các hàm số sau: 1) f x 1 1  x
2) f x  mx b 2 3 3) f t  2  5t 9t 4) f x 2
1.5x x  3.7 Bài 2. Cho hàm số   3 f x x
1) Nếu a  0 hãy dùng công thức hàm lũy thừa tính f 'a
2) Chứng minh rằng f '0 không tồn tại.
Bài 3. Tính đạo hàm của các hàm số sau: 2 2 x  4x  3 2 x  2 x  1  1) y x x   1 ; 2) y  ; 3) y  ; 4) v x    . x x 3  x ĐS: 3 1 3 2 3 1 1) y '  x
; 2) y '  x   ; 2 3 2 x 2 2 x x 1 1 2 1 3) y '  1
; 4) v '  1  . 3 x 6 5 3 5 3 3 x x
Bài 4. Viết phương trình đường tiếp tuyến với đường cong 4 y
x tại điểm 1  ;1 .Vẽ hình minh họa kết quả. ĐS: 1 3 y x  . 4 4
Bài 5. Giả sử rằng f 2  3
 , g 2  4, f '2  2
 , g '2  7 . Hãy tìm h'2 khi:
1) hx  5 f x  4g x ;
2) hx  f xg x ; f x g x 3) h x    ; 4) h x    g x 1 . f xĐS: 13 1) 43  ; 2) 29  ; 3) ; 4) 1  .5. 16
Bài 6. Tính đạo hàm của các hàm số sau: 1
1) F x   x x 100 2 4
; 2) g t    ; t  3 4 1 ln(2x 1) 2 3) y
tại x  1 ; 4) x 2 x y e  
tại x  0 . x 3 ĐS: 12t
1) F x 
  x xx 99 2 ' 100 4 2 4
; 2) g 't     ; t  4 4 1 2 3) y '(1)   ln 3 ; 4) y '  2  . 3 8 Bài 7. Tính y với: 2 x 1 x 1) y y  ; 3) y  . 1 ; 2) x 2 x  4x  3 3 1 x
BỘ MÔN TOÁN - KHOA CNTT - HỌC VIỆN NÔNG NGHIỆP VIỆT NAM 5
HP: TOÁN CAO CẤP - BÀI TẬP THAM KHẢO n 1    ĐS: 8 8! n   1 1 1) y   y  n     ; 2 ) ! ; n 1  n 1  x  9 1 2  x 3 x  1      n 2 1 n 1  2 n n 1  1  n 3) y    1 n x    n x n   1 4...3 5 3 1   1 n   1 4...3 2  3 1 3 3
Bài 8. Tính vi phân của các hàm số sau: u 1  1) 2
y x sin 2x ; 2) 2
y  ln 1 t ; 3) y
; 4) y    r  2 3 1 ; u 1 3 5) 2
y  1 x .arccos x tại x  ; 6) f t  3
 1 tant tại t  0. 2 Đ 2t 2
S: 1) dy   2
2x sin 2x  2x cos 2xdx ; 2) dy
dt ; 3) dy du ; 2 1 tu  2 1 2 6r  . x arccos x  3    3 
4) dy   
dr ; 5) y '  1  dy      1dx     ; 1 r 3 3 2 1 x 2 6     1 1 1
6) f 't    df   1 0  dt . 3    2 2 3 cos 1 tan t t 3 Bài 9. Tính y
 và dy tại giá trị đã cho của x và dx x: 1) 2
y  2x x , x  2, x   0  .4 2) y x; x  4; x  1 5 3) y  , x  8, x  1 4) x
y e , x  0, x   0.5 x
ĐS: 1) dy  0.8; y   0.64    2) dy 0.250; y 0.236 3) dy  0  .078; y   0
 .069 4) dy  0.50; y   0.65
Bài 10. Hãy sử dụng xấp xỉ tuyến tính (vi phân) để tính gần đúng các giá trị sau: 1 1)  5 2.001 2) 0.015 e 3)
4) tan 44 1002
ĐS: 1) 32.08 2) 0.985
3) 0.998 4) 0.965
Bài 11. Một người nông dân muốn rào một khu đất rộng 1.5 triệu m2 thành khu vườn hình chữ
nhật, sau đó chia khu vườn đất ra thành 2 phần diện tích bằng nhau bằng một hàng rào nằm song
song với mốt trong các cạnh của hình chữ nhật. Người nông dân phải làm thế nào để giảm tối đa giá thành của hàng rào.
ĐS: Khu đất được chia thành 2 mảnh kích thước 1000m x 750m (cạnh chung dài 1000m)
BỘ MÔN TOÁN - KHOA CNTT - HỌC VIỆN NÔNG NGHIỆP VIỆT NAM 6
HP: TOÁN CAO CẤP - BÀI TẬP THAM KHẢO - HỌC KÌ I NĂM HỌC 2017- 2018
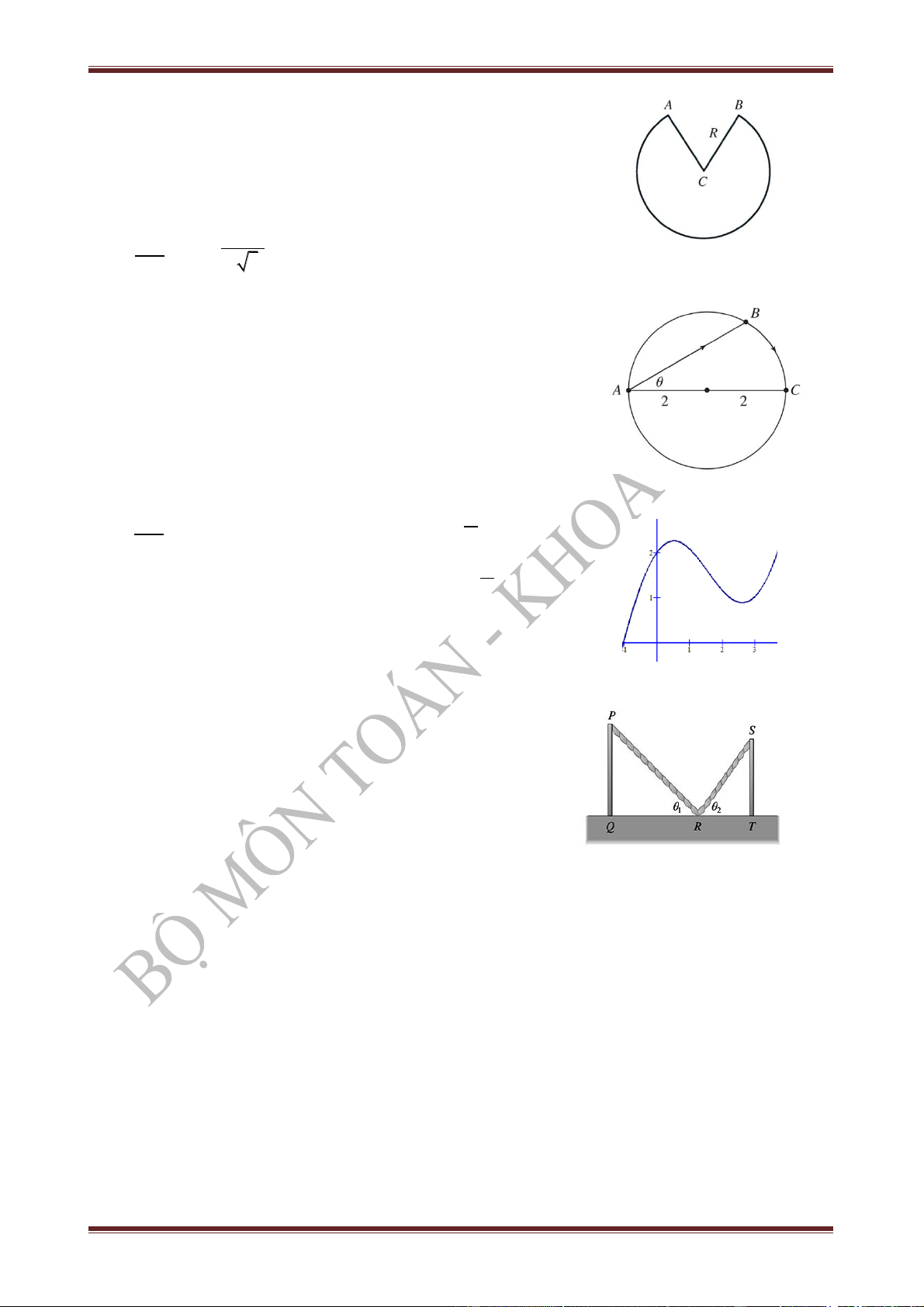
Bài 12. Một cái cốc uống nước hình nón được làm từ một
miếng bìa hình tròn bán kính R bằng cách cắt bỏ đi một
miếng hình quạt rồi dán các cạnh CA và CB lại với nhau
(xem hình vẽ bên). Hãy tìm dung tích lớn nhất của chiếc cốc. 3  ĐS: 2 R V  . max 9 3
Bài 13. Một người phụ nữ đứng ở điểm A trên bờ của một
cái hồ nước hình tròn bán kính 2km. Người phụ nữ muốn
tới điểm C nằm đối diện phía bên kia hồ trong thời gian
ngắn nhất có thể. Cô ta có thể đi bộ với vận tốc 4km/h và
chèo thuyền với vận tốc 2km/h. Hỏi cô ta phải chọn hành trình như thế nào?
ĐS: Thời gian đi y  2cos   ; 0    . 2 
Nhìn đồ thị hàm số ta thấy y nhỏ nhất khi   2
( lớn nhất). Vậy cô ta không chèo thuyền mà đi bộ
nửa vòng hồ từ A đến C.
Bài 14. Hai cái cột thẳng đứng được gia cố bằng một dây
thừng PRS nối từ đỉnh của cột thứ nhất xuống một điểm R
trên mặt đất rồi nối tới đỉnh của cột thứ hai. Hãy chứng tỏ
rằng dây thừng sẽ có độ dài ngắn nhất khi    1 2
BỘ MÔN TOÁN - KHOA CNTT - HỌC VIỆN NÔNG NGHIỆP VIỆT NAM 7
HP: TOÁN CAO CẤP - BÀI TẬP THAM KHẢO - HỌC KÌ I NĂM HỌC 2017- 2018
Chương 3: Nguyên hàm – Tích phân
Bài 1. Tìm họ các nguyên hàm của các hàm số sau: x 2 1    
1) f (x)  1  ; 2) g(x)  ; 3) 4 ( ) 3 x h x e x ; 2 3 x 1 2x    1 1 1 4) l(x)  3cos x   ; 5) k(x)  ; 6) ( m x)   .  3  2 2 1 4x 2  x  9 9x 1
ĐS: với C là hằng số tùy ý, 2 x 2 1
1) F (x)  x
  C ; 2) G(x)  ln(1 2x)  C ; 6 x 2 3    9  x 2 3) 4 3/ 2 H (x)  e
x C ; 4) L(x)  sin x C   ; 4 3   3  1 1 1 x  3 5) K (x) 
arcsin(2x)  C ; 6) 2 M (x) 
ln 3x  9x 1  ln  C . 2 3 6 x  3
Bài 2. Ký hiệu kích thước của một quần thể tại thời điểm t (đơn vị: năm) là N (t) . Khi đó, tốc độ tăng trưở dN
ng của quần thể tại thời điểm t là N '(t) 
. Cho biết tốc độ tăng trưởng của quần thể dt dN
tại thời điểm t là
 3sin(2t) và biết N(0) 10 000, hãy tìm công thức biểu diễn N(t) . dt ĐS: 3 N (t)  1cos(2 t) . 2 2
Bài 3. Tìm nguyên hàm F của hàm số f biết f (t)  3 
và thỏa mãn F(1)  0 . 2 1 t
ĐS: F(t) 
 2arctan t  3(t 1) 2
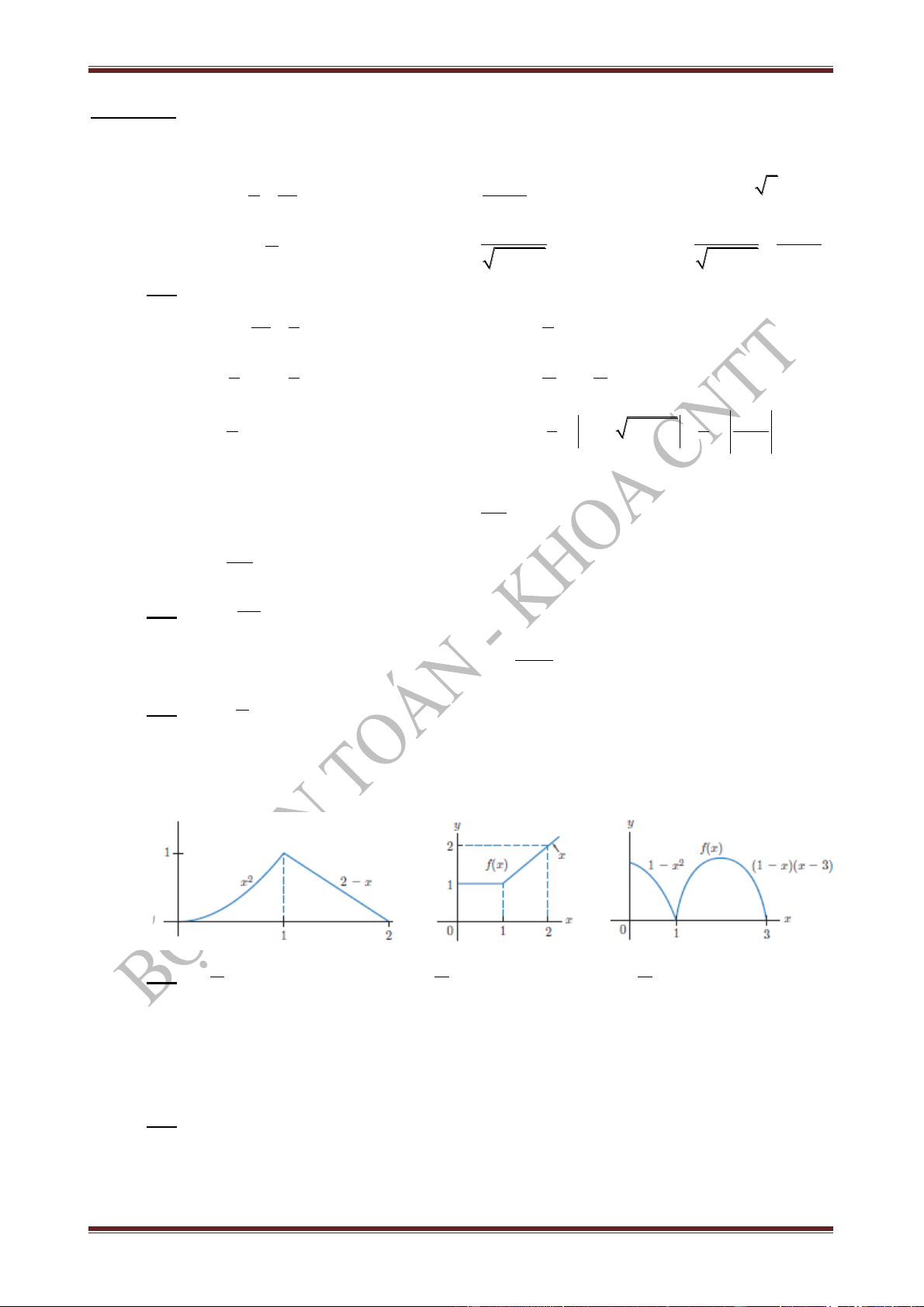
Bài 4. Tính tích phân xác định của hàm số f trên đoạn [0; 2] biết đồ thị hàm số f được cho như hình vẽ sau: 1) 2) 3) ĐS: 5 5 4 1) ; 2) ; 3) . 6 2 3 Bài 5. 1) Cho biết '( ) 12 x f x x e  
, hãy tính f (3)  f (0) . 3 3 3 2) Cho biết
f (x)dx  4 
và  3 f (x)  2g(x)dx  2 , hãy tìm g(x)dx  . 2  2  2  3 3 ĐS: 1) 3 f (3) f (0) f '(x)dx .. 53 e       ; 2)
g(x)dx  5   . 0 2 
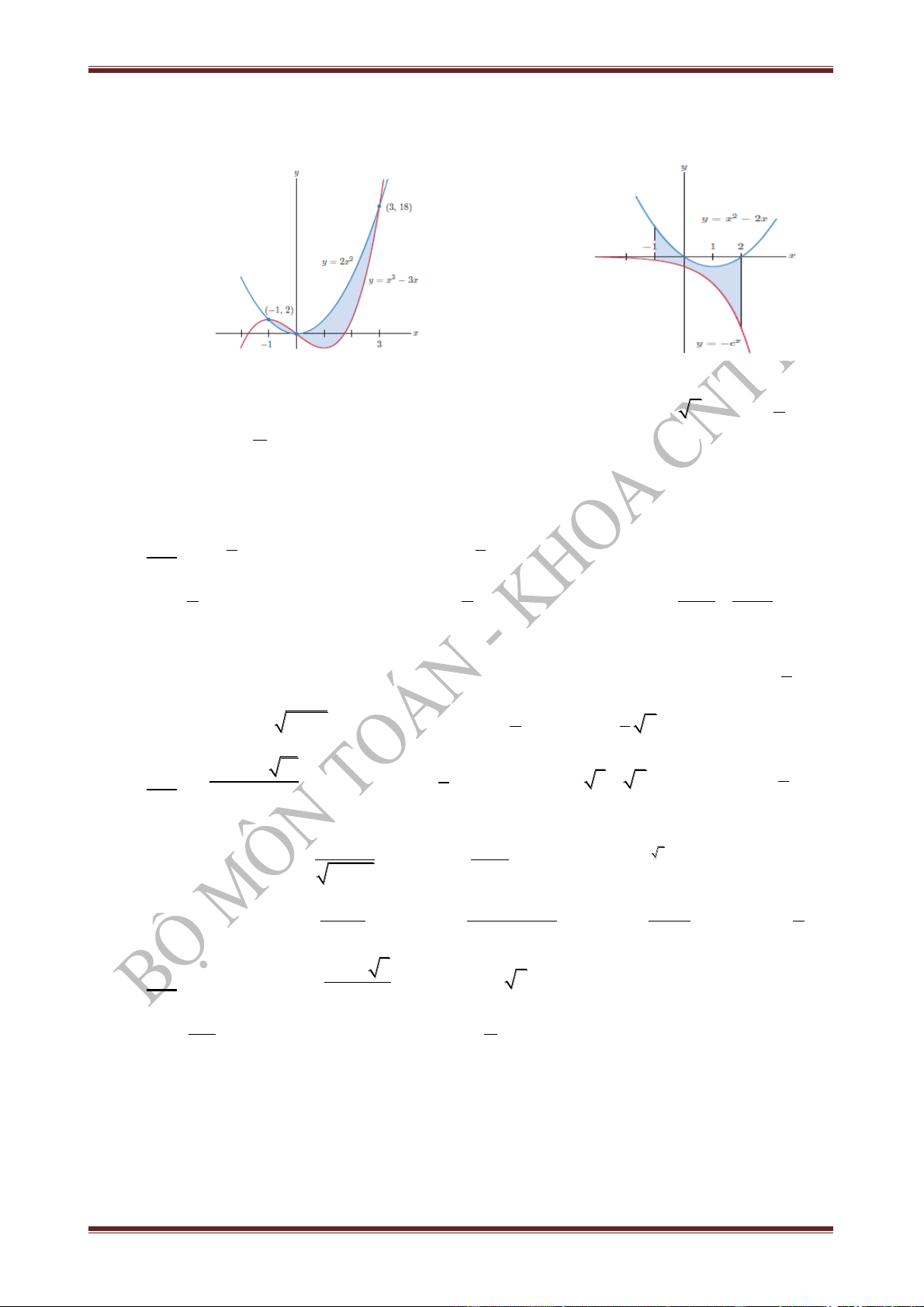
Bài 6. Tính diện tích hình phẳng giới hạn bởi các đường cong sau (yêu cầu vẽ hình minh họa và
đánh dấu phần hình giới hạn):
BỘ MÔN TOÁN - KHOA CNTT - HỌC VIỆN NÔNG NGHIỆP VIỆT NAM 8
HP: TOÁN CAO CẤP - BÀI TẬP THAM KHẢO - HỌC KÌ I NĂM HỌC 2017- 2018 1) các đường cong 2 y  2x , 2) các đường cong 2
y x  2x , 3
y x  3x . x y e
 , đường thẳng x  1  , x  2 .
3) các đường y  sin x , y  cos 2x 4) các đườ 1 ng 3 y x và y  và  x
và x  0, x  . 2
x  1, x  8 . 5) tam giác có ba đỉnh: 6) các đường 3x y  , 2x y  và ( A 0;0), (
B 1; 2), C(4;1) . x  1  , x 1. ĐS: 5 1 1) 11 ; 2) 2 e   2; 3) 1; 6 e 1 7 4 1 4) 11  ln 8 ; 5) 11 ; 6)  . 4 2 3ln 3 2 ln 2
Bài 7. Tính độ dài phần đường cong thuộc đồ thị hàm số: 1) 2 3
y x từ điểm (1;1) đến điểm (4;8) ; 1 2) 2
y  ln(1 x ) với 0  x  ; 2 1 1 3) 2
y  arcsin x  1 x từ điểm x  0 đến x  ; 4) y
x.(x  3) với 1  x  9 . 2 3  ĐS: 125 13 13 1 2 1) ; 2) ln 3 
; 3) 2 3  2 ; 4) 10 . 27 2 3
Bài 8. Tính các tích phân sau: 2  e 1 3 x / 2 1 1 1) x ln x dx  ; 2) dx  ; 3) dx  ; 4) e dx  ; 2  x tan x e 0 4  /4 0  0   1 1 ln x 1 5) 2  x xe dx  ; 6) dx  ; 7) dx  ; 8) dx  (HD: u  ) 3  4x 2 4x  4x  5 2 x 1 x 1   0  ĐS: 16 7 5 1) 2 e ; 2) ; 3) ln 2 ; 4) 2 3 1  5) ; 6)  ; 7) ; 8) 0. 2 4e 4
BỘ MÔN TOÁN - KHOA CNTT - HỌC VIỆN NÔNG NGHIỆP VIỆT NAM 9
HP: TOÁN CAO CẤP - BÀI TẬP THAM KHẢO - HỌC KÌ I NĂM HỌC 2017- 2018
Chương 4: Phép tính vi phân hàm nhiều biến
Bài 1. Tính vi phân toàn phần của các hàm 2 biến sau: x 1) 2 f ( ,
x y)  2x y  3x  4 ; 2) 2 2 f ( ,
x y)  ln(x  2y ) tại điểm (1; 2) ; 2 y 3) ( , ) xy
f x y xe ; 4) f ( ;
x y)  arcsin(x  2y) tại điểm (0;0) ; y 5) f ( ; x y)  arctan
tại điểm (1;1) với x   0,01 và y   0  ,02 . x Đ 1 2 x 2 8 S: 1) 2 df ( ,
x y)  (4xy
 3)dx  (2x
)dy ; 2) df (1, 2)  dx dy ; 2 3 2 y x y 9 9 3) xy 2 ( , )  (1 ) xy df x y e
xy dx x e dy ; 4) df (0, 0)  dx  2dy ; 5) 0  ,015. Bài 2. Cho hàm số 2 2 f ( , x y)  x y .
1) Hãy tính f (3, 04;3,98).
2) Hãy tính vi phân toàn phần của hàm số f tại điểm (3; 4).
3) hãy tính gần đúng f (3, 04;3,98) bằng cách áp dụng công thức tính xấp xỉ: ' ' f (x   ; x y y
 )  f (x ; y )  f (x ; y ) x
  f (x ; y ) y  và đánh giá sai số. 0 0 0 0 x 0 0 y 0 0 Đ 3 4 S: 1) 5,008193287 ; 2) df (3; 4)  dx
dy ; 3) 5,008 và sai số là 2/10000 5 5 2 2  ff
Bài 3. Tính A   với: 2 2 xy  1) 2 2 f ( ,
x y)  x y ; 2) 3 2 f ( ,
x y)  x  3xy ; 3) 2 2 f ( ,
x y)  ln x y ; 4) ( , ) x  cos  y f x y e y e cos x .
ĐS: 1) A  0 ; 2) A 12x ; 3) A  0 ; 4) A  0 .  
Bài 4. Chứng tỏ rằng hàm số P bL .K (với ,
b ,  là các hằng số) (hàm sản xuất Cobb- PP
Douglas) thỏa mãn phương trình sau: LK
     P. LK
Bài 5. Tìm các điểm cực trị và giá trị cực trị (nếu có) của các hàm số sau: 1) 3 2 2 2 f ( , x y)  8
x 12x y  24x  6y 1 2) 2 2 ( , ) ( ) x y f x y x y e    3) f ( ,
x y)  xy(1 x y) 4) 2 ( , )  3  2 y f x y x e  2y  3 ĐS:
1) Hàm số đạt cực đại tại (0, 0) , giá trị cực đại tại điểm đó là f (0, 0)  1.
2) Hàm số đạt cực tiểu tại ( 2  ; 1
 ) và f f ( 2  ; 1  )  1  . CT 1 1 1
3) Hàm số đạt cực đại tại ( ; ) và f  . 3 3 CD 27
4) Hàm số đạt cực tiểu tại 0;0 và ff 0;0  5. CT
BỘ MÔN TOÁN - KHOA CNTT - HỌC VIỆN NÔNG NGHIỆP VIỆT NAM 10
HP: TOÁN CAO CẤP - BÀI TẬP THAM KHẢO - HỌC KÌ I NĂM HỌC 2017- 2018
Bài 6. Một công ty sản suất hai loại mặt hàng với sản lượng sản phẩm lần lượt là q và q . Đơn 1 2
giá mỗi sản phẩm của hai mặt hàng tương ứng là p và p . Hàm tổng chi phí là 1 2 2 2
C q  2q q q  2q  4q  300. 1 2 1 2 1 2
1) Lập hàm lợi nhuận của công ty.
2) Khi đơn giá của hai loại mặt hàng là p  324 và p  524 hãy xác định sản lượng tương 1 2
ứng của hai loại mặt hàng để lợi nhuận của công ty là lớn nhất. ĐS: 2 2
1) p q p q q  2q q q  2q  4q  300 2) q  120 và q  100 1 1 2 2 1 2 1 2 1 2 1 2
BỘ MÔN TOÁN - KHOA CNTT - HỌC VIỆN NÔNG NGHIỆP VIỆT NAM 11
HP: TOÁN CAO CẤP - BÀI TẬP THAM KHẢO - HỌC KÌ I NĂM HỌC 2017- 2018
Chương 5: Phương trình vi phân
Bài 1. Giải các phương trình vi phân sau 1)  2 x  
1 dy xydx  0 ; 2) 1 x   ' x e
yy e với điều kiện ban đầu y(0)  1 ; y y 2 xy y 3) y ' xe  ; 4) y '  ; x 2 2x xy 2 1 1 5)   2 x y
xy e ln x ; 6) y  y  ; 2 x x cos x y 7) 3
y  xy  xy ; 8) 2 y 
y ln x x 2 y e ĐS: 1) 2 y C
x 1 , y  0, x  1; 2) 2 e  1 xe  ; 2  c Cx
3) y  x ln ln | | (c  0)   ; 4) y x ln ;  x  2 y 2 1 5) x
y e (x ln x x C) ; 6) y
tan x C ; x 2 1 7) 2 1 x y Ce  1; 8) y  . 2  ln x C x   2  
Bài 2. (Mô hình tăng trưởng quần thể) Gọi số lượng cá thể của một quần thể tại thời điểm t là
P(t). Tốc độ tăng trưởng của quần thể tại thời điểm t là đạo hàm dP / dt. Nhà sinh vật học, toán
học người Hà Lan Pierre – Francois Verhulst đưa ra mô hình cho sự phát triển của quần thể như sau: dPP(t)   kP(t) 1 (1)   dtM
trong đó k là hằng số tỷ lệ, M là hằng số cân bằng quần thể.
1) Hãy giải phương trình vi phân (1).
2) Biết rằng k  2; M  2000000 và số lượng cá thể tại thời điểm ban đầu là P(0)  1000,
hãy xác định công thức tính P(t) mô tả số lượng cá thể tại thời điểm t. Đ M 2000000
S: 1) P(t)  ,C  0 2) P(t)  . 1 ktCe 2 11999 t e
----------------------------- HẾT -----------------------------
BỘ MÔN TOÁN - KHOA CNTT - HỌC VIỆN NÔNG NGHIỆP VIỆT NAM 12 KHOA CÔNG NGHỆ THÔNG TIN
ĐỀ THI KẾT THÚC HỌC PHẦN BỘ MÔN TOÁN
Tên Học phần: Toán cao cấp Đề số: 04
Thời gian làm bài: 75 phút Ngày thi: 03/09/2020
Loại đề thi: Tự luận  1 1 2    1    
Câu I (2,0 điểm) Cho ma trận A  2 0 1 , B  2      .  1  2 m  1       1. (1,0đ) Tính 2 t A B .
2. (1,0đ) Tìm điều kiện của tham số m để ma trận A khả nghịch. Khi đó, không tìm ma
trận nghịch đảo, hãy tính  1 det A  .
Câu II (1,5 điểm) Giải hệ phương trình tuyến tính
x y z  3t 1 
 2x  3y  3z t  3
x  4y  2z 3t  4  . 
Câu III (1,5 điểm) Tính tích phân suy rộng  dx  . 2 6  x x 4 Câu IV (3,0 điểm)
1. (2,0đ) Tìm các điểm cực trị của hàm số 3 4 f ( ;
x y)  x 12x y  4 y  2020 .  x  2. (1,0đ) Cho hàm số 2 g( ; x y)  ln  x
 . Tìm vi phân toàn phần của hàm số g  ; x y tại  y  điểm 1;  1 .
Câu V (2,0 điểm) Giải phương trình vi phân tuyến tính 3y 3 2 y ' x   x x e . x
................................... HẾT ...................................
Ghi chú: + Cán bộ coi thi không phải giải thích gì thêm
+ Sinh viên không được sử dụng tài liệu Cán bộ ra đề Duyệt đề Vũ Thị Thu Giang Vũ Thị Thu Giang KHOA CÔNG NGHỆ THÔNG TIN
ĐỀ THI KẾT THÚC HỌC PHẦN BỘ MÔN TOÁN
Tên Học phần: Toán cao cấp Đề số: 05
Thời gian làm bài: 75 phút Ngày thi: 03/09/2020
Loại đề thi: Tự luận  1 1 2    1    
Câu I (2,0 điểm) Cho ma trận A  2 0 1 , B  2      .  1  2 m  1       1. (1,0đ) Tính 2 t B A .
2. (1,0đ) Tìm điều kiện của tham số m để ma trận A khả nghịch. Khi đó, không tìm ma
trận nghịch đảo, hãy tính  1 det A  .
Câu II (1,5 điểm) Giải hệ phương trình tuyến tính
x y z  3t 1 
 2x  3y  3z t  3 .
x  2y  4z 3t  4  
Câu III (1,5 điểm) Tính tích phân suy rộng  dx  . 2 6  x x 4 Câu IV (3,0 điểm)
1. (2,0đ) Tìm các điểm cực trị của hàm số 3 4 f ( ;
x y)  y 12 y x  4x  2020 .  x  2. (1,0đ) Cho hàm số 3 g( ; x y)  ln  x
. Tìm vi phân toàn phần của hàm số g  ; x y tại  y  điểm 1;  1 .
Câu V (2,0 điểm) Giải phương trình vi phân tuyến tính 2 3 1 x y e y '   . 5 3 x x x
................................... HẾT ...................................
Ghi chú: + Cán bộ coi thi không phải giải thích gì thêm
+ Sinh viên không được sử dụng tài liệu Cán bộ ra đề Duyệt đề Vũ Thị Thu Giang Vũ Thị Thu Giang KHOA CÔNG NGHỆ THÔNG TIN
ĐỀ THI KẾT THÚC HỌC PHẦN BỘ MÔN TOÁN
Tên Học phần: Toán cao cấp Đề số: 04
Thời gian làm bài: 75 phút Ngày thi: 14/07/2020
Loại đề thi: Tự luận 1  2
Câu I (2,0 điểm) Cho các ma trận , A ,
B C với A    . 3 4 a) (0,5đ) Tính t AA .
b) (1,0đ) Tìm ma trận X sao cho X  2A I với I là ma trận đơn vị cấp 2. Ma trận X có khả nghịch không?
c) (0,5đ) Biết rằng B , C  . Tìm , m , n k. m 3  n
là các ma trận sao cho AB C k
Câu II (1,5 điểm) Giải hệ phương trình tuyến tính
x y z  3t  0 
 2x y  2z t  1  3  x
z  2t  1  . 
Câu III (1,5 điểm) Tính tích phân suy rộng 0 2 (  3) x x e . dx  Câu IV (3,0 điểm)
a) (2,0đ) Tìm các điểm cực trị của hàm số 2 3 f ( ;
x y)  x  2xy y y  2020 . xg
b) (1,0đ) Cho hàm số g( ; x y)  ln x . Tính (1;1) y x  .
Câu V (2,0 điểm) Giải phương trình vi phân tuyến tính 2 y 2 y '
x (3  sin 2x) . x
................................... HẾT ...................................
Ghi chú: + Cán bộ coi thi không phải giải thích gì thêm
+ Sinh viên không được sử dụng tài liệu Cán bộ ra đề Duyệt đề Lê Thị Diệu Thùy Vũ Thị Thu Giang KHOA CÔNG NGHỆ THÔNG TIN
ĐỀ THI KẾT THÚC HỌC PHẦN BỘ MÔN TOÁN
Tên Học phần: Toán cao cấp Đề số: 05
Thời gian làm bài: 75 phút Ngày thi: 14/07/2020
Loại đề thi: Tự luận 1  2
Câu I (2,0 điểm) Cho các ma trận , A ,
B C với A    3 4
a) (0,5đ) Tính t A A .
b) (1,0đ) Tìm ma trận X sao cho X I  3A với I là ma trận đơn vị cấp 2. Ma trận X có khả nghịch không?
c) (0,5đ) Biết rằng B , C  . Tìm , m , n k. mn
k là các ma trận sao cho AB C 4
Câu II (1,5 điểm) Giải hệ phương trình tuyến tính
x y z  3t  0 
2x  2y z t 1 x3y  2t 1. 
Câu III (1,5 điểm) Tính tích phân suy rộng: 0 3 (  2) x x e . dx  Câu IV (3,0 điểm)
a) (2,0đ) Tìm các điểm cực trị của hàm số 3 2 f ( ;
x y)  x x  2xy y  2020 . yg
b) (1,0đ) Cho hàm số g( ; x y)  ln x . Tính (1;1) x x  .
Câu V (2,0 điểm) Giải phương trình vi phân tuyến tính 3y 3 y '
x (4  cos 2x) . x
................................... HẾT ...................................
Ghi chú: + Cán bộ coi thi không phải giải thích gì thêm
+ Sinh viên không được sử dụng tài liệu Cán bộ ra đề Duyệt đề Lê Thị Diệu Thùy Vũ Thị Thu Giang KHOA CÔNG NGHỆ THÔNG TIN
ĐỀ THI KẾT THÚC HỌC PHẦN BỘ MÔN TOÁN
Tên học phần: Toán cao cấp Đề số: 06
Thời gian làm bài: 75 phút Ngày thi: 18/12/2019
Loại đề thi: Tự luận 2 4 x  1 0    
Câu I (2.0 điểm) Cho ma trận A  1 2  1 ; B  2 1 .     2 0 1  1  3    
1) (0.5 điểm) Tìm phần tử thuộc hàng 1 cột 2 của ma trận AB và cho biết cấp của ma trận . AB
2) (1.5 điểm) Với x  1 tìm ma trận nghịch đảo của ma trận A (nếu có).
Câu II (1.5 điểm) Giải hệ phương trình sau:
x  2y  4z t  3 
2x y  4z t  3 .
x  4y  4z  4t  4   Câu III (2.5 điểm) 1
1) (1.0 điểm) Tìm đạo hàm và nguyên hàm của hàm số: f x  . 2 x  4
2) (1.5 điểm) Tính độ dài đường cong 2 y  16  x trên đoạ   n 0;2 2 .  
Câu IV (2.0 điểm) Tìm các điểm cực trị (nếu có) của hàm số: 3 2 2 f ( ,
x y)  x  3y  6x  6xy  8.
Câu V (2.0 điểm) Giải phương trình vi phân tuyến tính: 2 2 2 x y  y x e 1. x
................................... HẾT ...................................
Ghi chú: + Sinh viên không được sử dụng tài liệu
+ Cán bộ coi thi không phải giải thích gì thêm Cán bộ ra đề Duyệt đề Lê Thị Diệu Thùy Phan Quang Sáng KHOA CÔNG NGHỆ THÔNG TIN
ĐỀ THI KẾT THÚC HỌC PHẦN BỘ MÔN TOÁN
Tên học phần: Toán cao cấp Đề số: 07
Thời gian làm bài: 75 phút Ngày thi: 18/12/2019
Loại đề thi: Tự luận 2 4 2  1 0    
Câu I (2.0 điểm) Cho ma trận A  1 2  x ; B  2 1 .     2 0 1  1  3    
1) (0.5 điểm) Tìm phần tử thuộc hàng 2 cột 1 của ma trận AB và cho biết cấp của ma trận . AB
2) (1.5 điểm) Với x  1 tìm ma trận nghịch đảo của ma trận A (nếu có).
Câu II (1.5 điểm) Giải hệ phương trình sau:
x  2y  4z t  3 
2x y  4z t  3 .  4
x y  4z  4t  4   Câu III (2.5 điểm) 1
1) (1.0 điểm) Tìm đạo hàm và nguyên hàm của hàm số: f x  . 2 9  x
2) (1.5 điểm) Tính độ dài đường cong 2 y
4  x trên đoạn [0;1].
Câu IV (2.0 điểm) Tìm các điểm cực trị (nếu có) của hàm số: 2 3 2 f ( ,
x y)  3x  6xy y  6y  9.
Câu V (2.0 điểm) Giải phương trình vi phân tuyến tính: 2 2 y 
y x sin(2x)  . x x
................................... HẾT ...................................
Ghi chú: + Sinh viên không được sử dụng tài liệu
+ Cán bộ coi thi không phải giải thích gì thêm Cán bộ ra đề Duyệt đề Lê Thị Diệu Thùy Phan Quang Sáng KHOA CÔNG NGHỆ THÔNG TIN
ĐỀ THI KẾT THÚC HỌC PHẦN BỘ MÔN TOÁN
Tên Học phần: Toán cao cấp Đề số: 08
Thời gian làm bài: 75 phút Ngày thi: 20/12/2019
Loại đề thi: Tự luận  1 2 3   
Câu I (2.0 điểm) Cho ma trận A  0 5 1   .  1  2 m  
1. (0.75đ) Tìm phần tử nằm ở vị trí hàng 1 và cột 3 của ma trận . t A A theo . m
2. (1.25đ) Tìm m để A khả nghịch. Khi đó không tìm ma trận 1
A, hãy tính 1 det( A ) theo . m
Câu II (1.5 điểm) Giải hệ phương trình
x  4y  4z  2t 17 
2x  5y  4z  2t  13.
3x 8y 3z t  25   dx
Câu III (1.5 điểm) Tính tích phân suy rộng  . 2 3x  6 2 Câu IV (3.0 điểm)
1. (1.0đ) Tìm vi phân toàn phần của 2 f ( ,
x y)  x y  3  y tại điểm (2,1).
2. (2.0đ) Tìm các điểm cực trị (nếu có) của hàm số f ( ,
x y)  3ln x  3ln y xy  2x  2y ( , x y  0 ).
Câu V (2.0 điểm) Giải phương trình vi phân tuyến tính 3 3 y ' y  2x 1 . x
.................................. HẾT ...................................
Ghi chú: + Cán bộ coi thi không phải giải thích gì thêm
+ Sinh viên không được sử dụng tài liệu Cán bộ ra đề Duyệt đề
Lê Thị Hạnh Phan Quang Sáng KHOA CÔNG NGHỆ THÔNG TIN
ĐỀ THI KẾT THÚC HỌC PHẦN BỘ MÔN TOÁN
Tên Học phần: Toán cao cấp Đề số: 09
Thời gian làm bài: 75 phút Ngày thi: 20/12/2019
Loại đề thi: Tự luận  2 1 0  Câu I (2.0 điể  
m) Cho ma trận A  5 1 2   .  1  3 m  
1. (0.75đ) Tìm phần tử nằm ở vị trí hàng 2 và cột 3 của ma trận . t A A theo . m
2. (1.25đ) Tìm m để A khả nghịch. Khi đó không tìm ma trận 1
A, hãy tính 1 det( A ) theo . m
Câu II (1.5 điểm) Giải hệ phương trình
x  2y  3z t  5 
2x  5y  3z t  15 .
3x 8y  27z  2t 16   dx
Câu III (1.5 điểm) Tính tích phân suy rộng  . 2 2x  6 1 Câu IV (3.0 điểm)
1. (1.0đ) Tìm vi phân toàn phần của 2 f ( ,
x y)  y x  4  2x tại điểm (2,0).
2. (2.0đ) Tìm các điểm cực trị (nếu có) của hàm số f ( , x y)  8
 ln x 8ln y xy  2x  2y ( , x y  0 ).
Câu V (2.0 điểm) Giải phương trình vi phân tuyến tính 4 2 3x  2 y ' y  . x x
.................................. HẾT ...................................
Ghi chú: + Cán bộ coi thi không phải giải thích gì thêm
+ Sinh viên không được sử dụng tài liệu Cán bộ ra đề Duyệt đề
Lê Thị Hạnh Phan Quang Sáng

Tài liệu liên quan: