



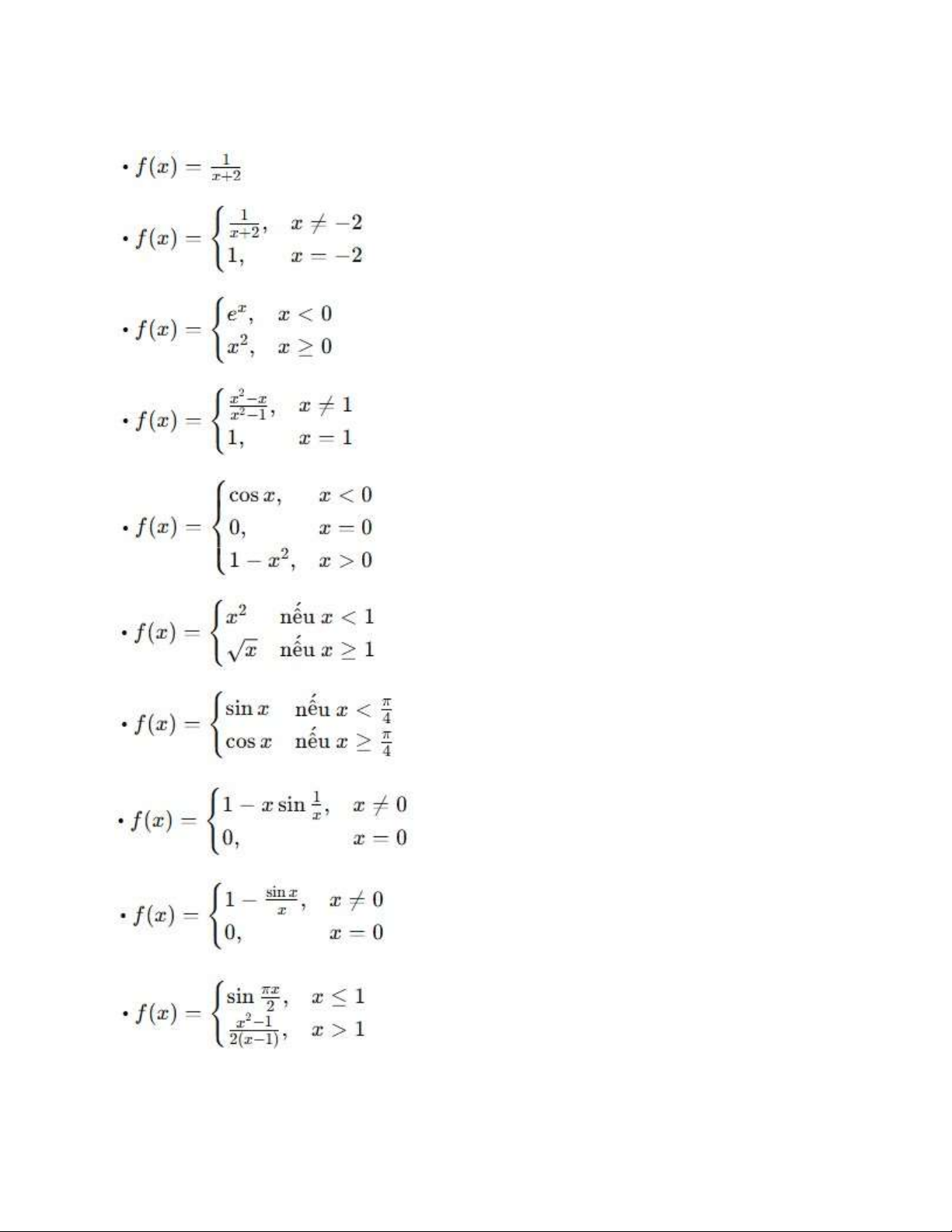










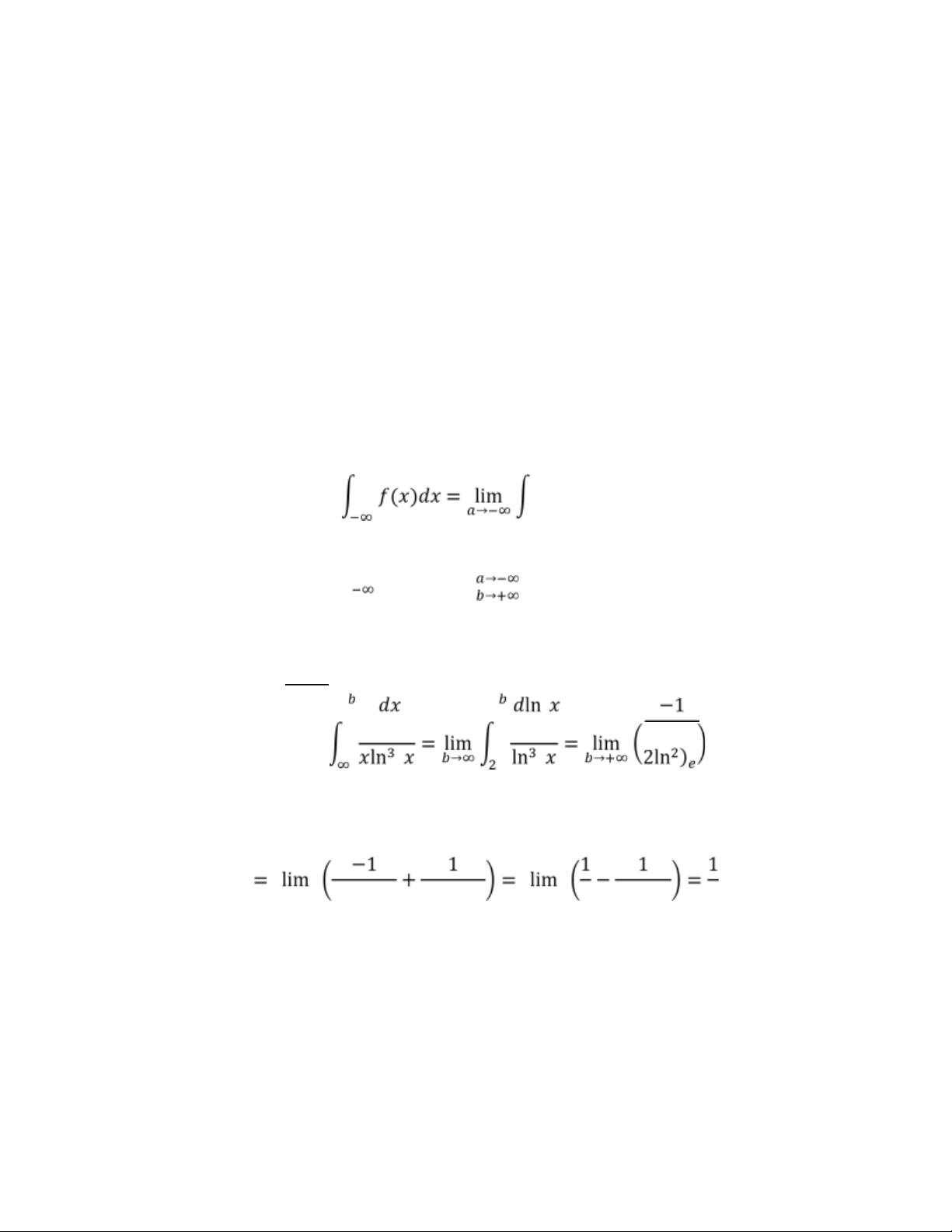



Preview text:
lOMoAR cPSD| 59735516 Chương 1
Bài 1: Tìm tập xác định của các hàm số sau
Bài 2: Tìm các hàm số f(x) và g(x) thỏa mãn F = f o g
Bài 3: Tìm hàm số chưa biết thỏa mãn f o g = h lOMoAR cPSD| 59735516
Bài 4: Tìm hàm nghịch của các hàm số sau lOMoAR cPSD| 59735516 Chương 2
Bài 1: Tính các giới hạn sau lOMoAR cPSD| 59735516 lOMoAR cPSD| 59735516
Bài 2: Xét tính liên tục của các hàm số sau trên R
Bài 3: Tìm a và b sao cho f(x) liên tục trên R lOMoAR cPSD| 59735516 lOMoAR cPSD| 59735516 TÍCH PHÂN I.
Tích phân không xác định – nguyên hàm a. Lý thuyết
• f x dx( ) = F x( )+C (với F’(x)=f(x))
• Bảng tích phân cơ bản 1. ∫ xn dx = x n+1 + C(n + 1) n+1 dx 2. ∫ = ln |x| + C x 3. ∫ ax dx = 1 ax + c lna 4. ∫ ex = ex + C. 5) ∫ cos xdx = cos x + C; ∫ sin xdx = cos x + C 6) ∫ chx = shx + C; ∫ shx = dx + C. dx dx 7. ∫ cos 2x = tan x + C; ∫ sin 2 x = −cot x + C x 8. x +a a a a arclot a + c1 lOMoAR cPSD| 59735516 9. C c| x −a 2a x+a ( x /a)
• Các phương pháp tính tích phân không xác định
1. Phương pháp đổi biến VD1: . Đặt
𝑡 ta có 𝑥 = 𝑡 2 + 5
⇒ 𝑑𝑥 = 2𝑡𝑑𝑡 vậy 𝐼 = ∫ (𝑡 2 + 5) ⋅ 𝑡 ⋅ 2𝑡𝑑𝑡 = 2∫ (𝑡 4 + 5𝑡 2 )𝑑𝑡 𝐶 . VD2:
Đặt 𝑡 = 1 − 𝑥 2 ta có: 𝐼 . VD3: I 1+𝑒𝑥.
Đặt 𝑡 = 1 + 𝑒 𝑥, khi đó 𝑒 𝑥 = 𝑡 − 1
⇒𝑒 𝑥 𝑑𝑥 = 𝑑𝑡 ⇒ (𝑡 − 1)𝑑𝑥 = 𝑑𝑡 𝑑𝑡 lOMoAR cPSD| 59735516 ⇒ 𝐼𝑑𝑥 ⇒ 𝐼𝑑𝑡 𝑡(𝑡 − 1) 𝑡 𝑡 − 1 𝑑𝑡 𝑑𝑡 𝐶 𝑡 − 1 𝑒 𝑥 𝑐
2. Phương pháp tích phân từng phần
Giả sử 𝑢 = 𝑢(𝑥) và v = v(x) là 2 hàm số có đạo hàm liên tục.
Ta có: (uv)’=uv’+uv’ Nên: d uv udv vdu( )= +
udv vdu d uv= − ( )
udv uv vdu= −
VD1: Tính 𝐼 = ∫ln 𝑥𝑑𝑥 Đặt 𝑢 = ln𝑥}
⇒ {𝑑𝑢 = 𝑥 1 𝑑𝑥 ⇒𝐼 = ∫ln 𝑥𝑑𝑥=𝑥ln𝑥 − ∫𝑥 𝑑𝑥 𝑑𝑣 = 𝑑𝑥 𝑣 = 𝑥 𝑥
VD2: Tính 𝐼 = ∫arctan𝑥𝑑𝑥. u = arctan 𝑥 Đặt 𝑑𝑣 = 𝑑𝑥 lOMoAR cPSD| 59735516 ⇒{𝑣𝑑𝑥==𝑥 𝑑𝑥 1
+1 𝑥 𝛼 => 𝐼 =𝑥arctan𝑥 − ∫ 1 +𝑥 𝑥 𝛼 𝑑𝑥= 𝑥arctan 𝑥 −21 ln(1 +𝑥 2 )+ 𝑐
Tổng quát: Thường sử dụng với các hàm
𝑓(𝑥) ⋅sin𝑥( Vs 𝑓(𝑥) là hàm đa thức ) 𝑓(𝑥) ⋅cos𝑥 𝐹 (𝑥) = {
𝑓(𝑥) ⋅ln𝑥 ⋅( trong TH nay đặt ln𝑥 = 4) 𝑓(𝑥)𝑒 𝑥
3. Tích phân trên các phân thức hữu tỉ 𝑃(𝑥) 𝑓(𝑥) = 𝑄(𝑥)
• Nếu bậc 𝑷(𝒙) lớn hơnQ(x): 𝑃(𝑥) 𝑅(𝑥) 𝑓(𝑥) = = ℎ(𝑥) + 𝑄(𝑥) 𝑄(𝑥) 𝑅(𝑥) Đưa về phân số tối giản 𝑄(𝑥) Lưu ý 𝐴 ∫
𝑑𝑥 = 𝐴 ⋅ln|𝑥 − 𝑎| + 𝐶 𝑥 − 𝑎 𝐴 1 1 ∫ ( 𝑥 − 𝑎)𝑘 𝑑𝑥 𝐶 lOMoAR cPSD| 59735516 𝑑𝑥
VD1: Tính 𝐼 =∫ 𝑥 2+6𝑥+25 𝑑𝑥𝑑(𝑥 + 3) 1 𝑥 + 3 𝐼 anctan + 𝑐 4 3 −1 VD2: Tính 𝐼. 3 = + 8 3 ( 𝑥 − 𝑑𝑥2)2 + 4 3 𝑥 − 2 𝑐 VD3: Tính 𝐼 = 1 𝑑𝑥 1 1 𝑑𝑥 1 1 𝑥 + 1/2 . lOMoAR cPSD| 59735516
• Tách thành phân thức đơn giản 2 VD1: Tính 𝐼 . 𝑥 2 + 2𝑥 + 6 𝑥 2 + 2𝑥 + 6 Ta có : 𝐴 = 𝑥 3 − 3𝑥 2 + 14𝑥 − 8
= (𝑥 −1)(𝑥 − 2)(𝑥 − 4) 𝐴 𝐵 𝐶 = + +
𝑥 − 1 𝑥 − 2 𝑥 − 4. Khử mẫu ta có.
𝑥 2 + 2𝑥 + 6 = 𝐴(𝑥 − 2)(𝑥 − 4) + 𝐵(𝑥 − 1)(𝑥 − 4) + (𝑥 − 1)(𝑥 − 2)
2 + 2𝑥 + 6 = (𝐴 + 𝐵 + 𝐶 )𝑥 2 + (−6𝐴 − 5𝐵 − 3𝐶 )𝑥 + (8𝐴 + 4𝐵 + 2𝐶 ) ⇔ 𝑥 𝐴 + 𝐵 + 𝐶 = 1 𝐴 = 3
{−6𝐴 − 5𝐵 − 3𝐶 = 2 ⇔ {𝐵 = −7 ⇒ 𝐼 = 3 ln |𝑥 − 1| − 7 ln |𝑥 − 2| + 5 ln |𝑥 − 4| + 8𝐴 + 4𝐵 + 2𝐶 = 6 𝐶 = 5 𝐶 2+1 VD2: 𝑑𝑥 Ta có: 𝑥
= 𝐴(𝑥 + 3) + 𝐵(𝑥 − 1)(𝑥 + 3) + 𝐶 (𝑥 − 1)2 (𝑥 + 3) + 𝐷(𝑥 − 1)3 𝐶 + 𝐷 = 0 𝐵 + 𝐶 − 3𝐷 = 1 lOMoAR cPSD| 59735516 ⇔ {
𝐴 + 2𝐵 − 5𝐶 + 3𝐷 = 0
3𝐴 − 3𝐵 + 3𝐶 − 𝐷 = 1
⇔𝐴= 112; 𝐵 = −5/32; 𝐶 = 5/32; 𝐵 = 3/8. 1 𝑑𝑥 3 𝑑𝑥 5 𝑑𝑥 5 𝑑𝑥 ⇒ 𝐼 𝑥 + 3 −1 3 5 𝑥 − 1 𝑐 b. Bài tập
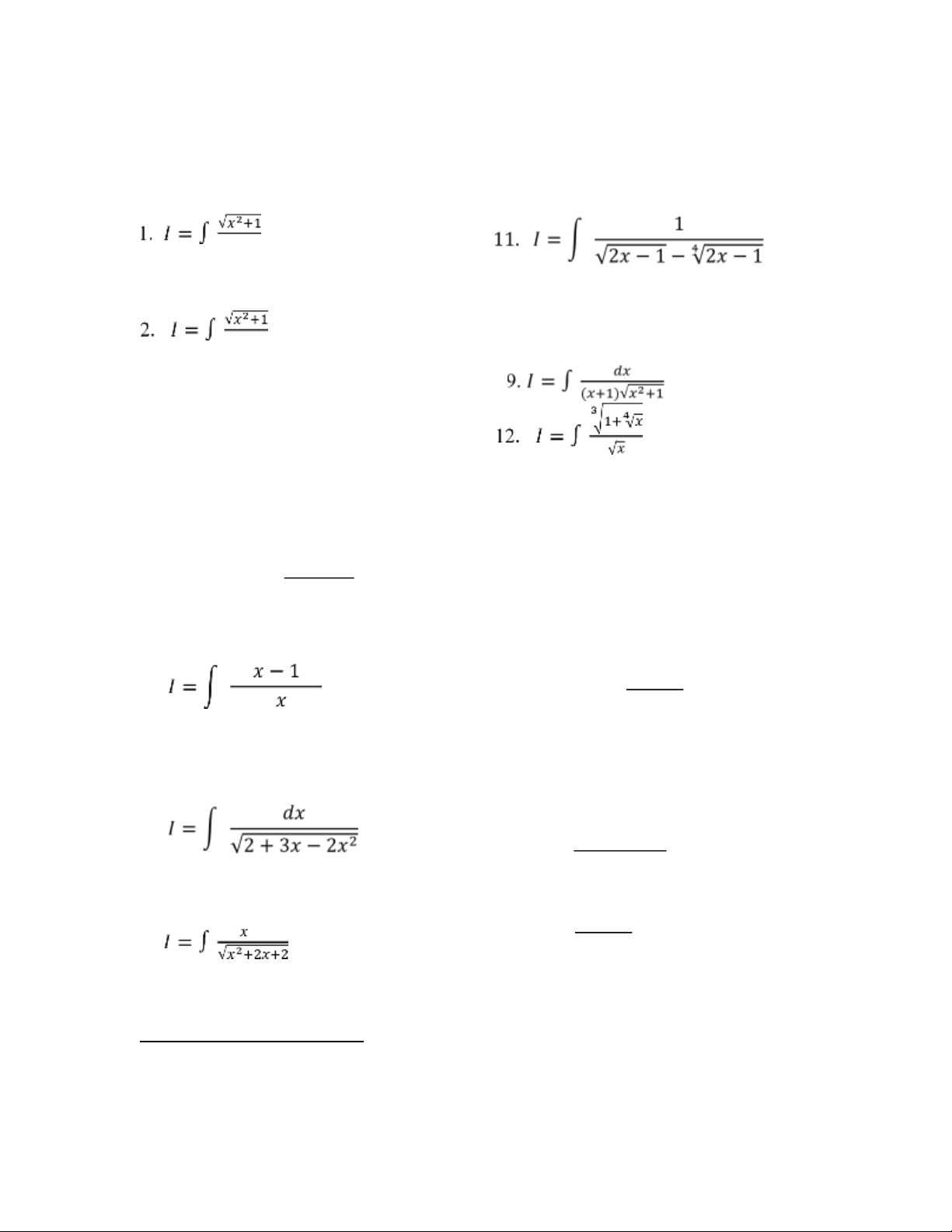
Bài 1. Tính các tích phân không xác định sau: x x−b2)2 a b 1. . 2. I = ∫ (x2 + 5)3 dx dx 7. I = ∫ dx 2 3. 2−3x I = ∫ 2 2 dx 6. I = ∫ ( a x x dx. x sin xcos x 8. I = ∫ 2x+1−5x−1 4.dx dx 9. I = ∫ cos 2x 5. I = ∫ dx. cosx−sin x
10. I = ∫(sin5x−sin 5x)dx. lOMoAR cPSD| 59735516
Bài 2. Tính các tích phân không xác định sau (BTVN): 2 𝑑𝑥 𝑑𝑥 𝑥 2 𝑑𝑥 𝑥
3 ⋅ 𝐼 = ∫ 𝑥ln𝑥𝑑𝑥. 4. 𝐼 = ∫ 𝑒 𝑥 cos 𝑥𝑑𝑥.
13. 𝐼 = ∫ sin1 𝑥cos3 𝑥𝑑𝑥 𝑑𝑥 5. 𝐼 = ∫ 2 14.𝐼 = ∫ cos2 𝑥2−5𝑥+7.
3𝑥sin+ 3𝑥𝑑𝑥. 𝑑𝑥 15.𝐼 =cos 2 𝑥 6. 𝑥 2 − − 1 𝑑𝑥 16. I = ∫ tan4 𝑥𝑑𝑥 7. 𝑑𝑥
17 . I = ∫ 1 + sin 𝑥 + cos 𝑥 𝑑𝑥 18. 𝐼 =∫ 1 +sin2 𝑥 . +3 8.𝑑𝑥 𝑥 + 3 lOMoAR cPSD| 59735516 19.I = ∫
20. 𝐼 = ∫𝑒 𝑥 sin2𝑥𝑑𝑥 𝑑𝑥 𝑥 4 √2𝑥 + 3 𝑑𝑥
21 . 𝐼 = ∫ 𝑥 + √ 1 + 𝑥 𝑥 II.
Tích phân xác định a. Lý thuyết
Cho hàm số f liên tục trên K và a, b là hai số bất kì thuộc K. Nếu F là một nguyên
hàm của f trên K thì hiệu số: F(b) - F(a) được gọi là tích phân của f từ a đến b.
Như vậy để tính được tích phân của các hàm cơ bản, ta làm như sau:
Bước 1. Tìm nguyên hàm của hàm số - gọi là F(x).
Bước 2. Tính F(b) - F(a) với a và b là hai cận tích phân. b. Bài tập
Bài 1. Tính các tích phân sau: 3
a) I = 1 (ex +4)dx
d) I = 2 9(sin2x+cos2 )x dx 0 lOMoAR cPSD| 59735516 e lnx x
b) I = 0 ex +2dx e) I =− 11( (xx++2)410)dx 4
c) I = 2sin .cosx xdx 0
III. Ứng dụng tích phân xác định Bài 1. Tính diện tích hình
phẳng giới hạn bởi a) Đường cong 𝑦 =
ln 𝑥, truc 𝑥 và đường thẳng 𝑥 = 𝑒 b) Đường con 𝑦 = 𝑥(𝑥 − 1)(𝑥 − 2) và trục x
Bài 2. Tính diện tích hình phẳng giới hạn bởi a) Đường cong 𝑦 =
ln(𝑥), trục 𝑥 và 𝑥 = 𝑒 b) 𝑦 = 𝑥(𝑥 − 1)(𝑥 −
2) và trục 𝑥 Bài
3. Tính độ dài cung: 𝐿
a. Trong đó: 𝐴(𝑎, 𝑓(𝑎); 𝐵(𝑏, 𝑓(𝑏)) IV.
Tích phân suy rộng a. Lý thuyết
1. Tích phân suy rộng loại 1. lOMoAR cPSD| 59735516
Tích phân suy rộng loại 1 của hàm số 𝑓(𝑥) trong [𝑎, +∞) được xác định bởi: +∞ 𝑏 ∫
𝑓(𝑥)𝑑𝑥 = lim ∫ 𝑓(𝑥)𝑑𝑥 𝑎 𝑏→+∞ 𝑎
Nếu ∃ giới hạn đó thì tích phân suy rộng trên được gọi là hội tụ, ngược lại nếu giới
hạn trên ∄ hoặc bằng ∞ thì tích phân trên gọi là phân kì Tương tự 𝑏 𝑏 𝑓(𝑥)𝑑𝑥 𝑎 +∞ 𝑏
∫ 𝑓(𝑥)𝑑𝑥= lim ∫ 𝑓(𝑥)𝑑𝑥 𝑎 ∞ 𝑑𝑥
VD1: I =∫𝑒𝑥 𝑥 ln3 𝑥 𝑝 𝐼 = lim 𝑏→+∞ 𝑒
𝑏→+∞ 2ln2 𝑏2 2ln2 𝑒 2 𝑏→+∞ 8 2ln2 𝑏 8 ⇒ Tích phân hội tụ
2. Tích phân suy rộng loại 2.
• Giả sử 𝑓(𝑥) liên tục [𝑎, 𝑏) và gián đoạn vô cực tại 𝑥 = 𝑏 lOMoAR cPSD| 59735516 lim 𝑓(𝑥) = ∞ 𝑥→𝑏− 𝑐
Nếu lim𝑐→𝑏− ∫𝑎 𝑓(𝑥)𝑑𝑥 Tồn tại (hữu hạn) thì GH đó gọi là tích phân suy rộng loại 2 𝑏
𝑐 của hàm 𝑓(𝑥) trên [𝑎, 𝑏) và
∫𝑎 𝑓(𝑥)𝑑𝑥 =
lim𝑐→𝑏−0 ∫𝑎 𝑓(𝑥)𝑑𝑥
• Giả sử 𝑓(𝑥) liên tục trong (𝑎, 𝑏] và gián đoạn vô cực tại 𝑥 = 𝑎 trong đó lim𝑓(𝑥)
= ∞ với 𝑥 → 𝑎 + 0(𝑎+ ) 𝑏
Nếu lim𝑐→𝑎+0 ∫0 𝑓(𝑥)𝑑𝑥∃ (hữu hạn) thì GH cũng gọi là Tích phân suy rộng của 𝑏
𝑓(𝑥) trên [𝑎, 𝑏) và kí hiệu là ∫𝑎 𝑓(𝑥)𝑑𝑥 𝑏 𝑏
Vậy ∫𝑎 𝑓(𝑥)𝑑𝑥 = lim𝑐→a+ ∫𝑐 𝑓(𝑥)𝑑𝑥
Giả sử 𝑓(𝑥) liên tục trên [𝑎, 𝑏], trừ điểm 𝑥 = 𝑥0 (𝑎 < 𝜔0 < 𝑏) mà tại đó 𝑓(𝑥) giá đoạn vô hạn lim 𝑓(𝑥) = ∞ 𝑥→𝑥0 𝑏 𝑏 𝑏
∫ 𝑓(𝑥)𝑑𝑥 = ∫ 𝑓(𝑥)𝑑𝑥 + ∫ 𝑓(𝑥)𝑑𝑥 𝑎 𝑎 𝑤
Theo định nghĩa trên ta có 𝑏 𝑐 𝑏 𝑓(𝑥)𝑑𝑥 lOMoAR cPSD| 59735516
Giống như tích phân suy rộng loại 1, tích phân suy rộng loại 2 cũng hội tụ nếu tích
phân tồn tại và phân kỳ nếu tích phân không tồn tại hoặc là giới hạn ∞. 1 𝑑𝑥 VD1: 𝐼 =∫0 √ 1−𝑥 𝑓 có 1
điểm gián đoạn vô cực tại 𝑥 = 1 ( 𝑥 ) = √ 1 − 𝑥 1 𝑑𝑥 𝑐 𝑑𝑥 Vậy ∫ = lim ∫ 𝑐 → 1 − 0 0 √ 1 − 𝑥 0 √ 1 − 𝑥 𝑐 = lim (−2√√1 − 𝑐 ] = 2 𝑐→1− 0 𝑐→ 𝑑𝑥 VD (1−𝑥)𝑚 𝑓
là gián đoạn vô cực tại 𝑥 = 1. 1 1 𝑑𝑥 𝑐 𝑑𝑥 (1− 𝑥)𝑚 (1 − 𝑥)−𝑚+1 𝑐 1 (1 − 𝑐 )−𝑚+1 = lim [− ⋅| ] = lim [ − ] 𝑐→1− −𝑚 + 1 𝑐→1− −𝑚 + 1 −𝑚 + 1.0 0 = lim {
1 [1 − (1 − 𝑐)1−𝑚 ]} 𝑐→1− 1 − 𝑚 1
𝑛ế𝑢𝑚 <
1𝐻ộ𝑖𝑡ụ Nếu { 1−𝑚 lOMoAR cPSD| 59735516
+∞𝑛ế𝑢𝑚>1𝑃ℎâ𝑛𝑘ỳ 𝜋/2 𝑑𝑥 VD3: 𝐼 = ∫0 cos 𝑥 1 𝑛 𝑓 gián đoạn tại 𝑥 𝜋/2 𝑑𝑥 𝑐 𝑑𝑥 ⇒ cos 𝑥 sin = 𝑥lim→/− 02 𝑥 𝑥→𝜋/2− 0 1 − sin2 . cos 1
= 𝑥lim→𝑛2− ∫0 (1 − sin𝑥)(1 + sin 𝑥) 𝑑sin 𝑥 𝑥 𝑥→ 1 + sin 𝑥 𝑐 1 + sin 𝑐 = lim | | = lim ln | | 𝜋 − ln 1 − − sin 𝑥 𝑥 → 𝜋 1 − sin 𝑥→2 0 2 𝑥 =+∞⇒ Phân kỳ VD 𝑥𝑑𝑥 𝑓(𝑥) =
𝑥ln2 𝑥 gián đoạn vô cực tại 𝑥 = 0 ⇒ 𝑥𝑑𝑥 𝑥𝑑𝑥 0+ 𝐶




