Bài tập Giải tích hàm nhiều biến | Toán Cao Cấp | Trường Đại học Thủy Lợi

Bài tập Giải tích hàm nhiều biến của Trường Đại học Thủy Lợi. Hi vọng tài liệu này sẽ giúp các bạn học tốt, ôn tập hiệu quả, đạt kết quả cao trong các bài thi, bài kiểm tra sắp tới. Mời các bạn cùng tham khảo chi tiết bài viết dưới đây nhé.

Môn:

Toán Cao Cấp (BLLLO2001) 14 tài liệu

Trường:

Đại học Thủy Lợi 221 tài liệu

Thông tin:
32 trang 4 tháng trước
Tác giả:
L
Lê Phương
docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Bài tập Giải tích hàm nhiều biến | Toán Cao Cấp | Trường Đại học Thủy Lợi

Bài tập Giải tích hàm nhiều biến của Trường Đại học Thủy Lợi. Hi vọng tài liệu này sẽ giúp các bạn học tốt, ôn tập hiệu quả, đạt kết quả cao trong các bài thi, bài kiểm tra sắp tới. Mời các bạn cùng tham khảo chi tiết bài viết dưới đây nhé.

108 54 lượt tải Tải xuống

Môn: Toán Cao Cấp (BLLLO2001) 14 tài liệu

Trường: Đại học Thủy Lợi 221 tài liệu

Thông tin:

32 trang 4 tháng trước

Tác giả:

Profile Lê Phương
lOMoARcPSD|40651217
OMoARcPSD|40651217
lOMoARcPSD|40651217
2022-2023
BÀI TẬP MÔN
GIẢI TÍCH HÀM NHIỀU BIẾN
TS. Nguyễn Hữu Thọ
Bài tập Giải tích hàm nhiều biến TS. Nguyễn Hữu Thọ
2022-2023
lOMoARcPSD|40651217
Bài tập buổi 1
HỆ TỌA ĐỘ TRONG ℝ
3
. CÁC MẶT CƠ BẢN. TỌA ĐỘ TRỤ, CẦU HÀM NHIỀU
BIẾN.MẶT PHẲNG TIẾP XÚC
18.4 ĐƯỜNG THẲNG VÀ MẶT PHẲNG
5. Viết phương trình tham số cho đường thẳng đi qua (2, 1,− −3) và song song với
(a) Véc tơ i + 4j−2k
x y + 7 z − 3
(b) Đường thẳng = =
3 −1 6
(c) Đường thẳng x = 2t −3, y = 3−2t z, = 5t −4 .
10. Tìm khoảng cách giữa các đường thẳng
x −2 y − 3 z x +1 y −2 z +1
(a) = = và = =
−1 4 2 1 0 2
(b) x = 2t −4, y = 4 −t z, = − 2t −1 và x = 4t −5, y = − 3t + 5, z = − 5t + 5
11. Tìm khoảng cách từ gốc toạ độ tới đường thẳng
x − 4 y −2 4 −z
= = .
3 4 5
17. Tìm khoảng cách giữa các mặt phẳng x −2y + 4z = 1 và 2x − 4y + 8z =−14.
18. Tìm phương trình của mặt phẳng sao cho song song với mặt phẳng 2x −5y + 3z = 7 và đi qua điểm (5,2,3 .)
18.5. MẶT TRỤ VÀ MẶT TRÒN XOAY (Tr. 45)
Vẽ mặt trụ của các p/trình trong các bài tập từ 1 dến 8. Gọi tên chúng nếu đã có tên từ trước.
1. y =x
2
2. y
2
+ =4z
2
16
3. x = siny 5. x + =3z 6
6. x
2
+ =z
2
9 7. y =e
x
8. Các đường sinh của mặt trụ song song với trục y . Giao của chúng với mặt phẳng xz là đường tròn với tâm
(0,0,a) và bán kính a . Vẽ mặt trụ và tìm phương trình của nó.
11. Tìm phương trình của mặt tròn xoay tạo ra khi quay đường tròn (y −b)
2
+ z
2
= a
2
(a < b) quanh:
(a) trục z (b) trục y .
Vẽ cả hai trường hợp.
B Ộ M Ô N T O Á N H Ọ C – T R Ư Ờ N G Đ Ạ I H Ọ C T H Ủ Y L Ợ I
Bài tập Giải tích hàm nhiều biến TS. Nguyễn Hữu Thọ
2022-2023
lOMoARcPSD|40651217
12. Trong mỗi trường hợp sau, viết phương trình của mặt tròn xoay tạo ra khi quay đường cong cho trước
quanh trục xác định, và vẽ các mặt cong:
(a) y = z
2
, trục y . (b) 9x
2
+ 4y
2
= 36, trục y .
1 |
(c) z = 4 − x
2
, trục z . (d) x = y
2
, trục x .
18.6. MẶT BẬC HAI (Tr. 50)
Vẽ và xác định các mặt cong trong các bài tập từ 114
1. 2x
2
+y
2
+ 4z
2
= 16 2. z
2
= 4(x
2
+y
2
)
3. z = 4(x
2
+ y
2
) 6. z = 4 − 2x
2
− 3y
2
11. 36x
2
+ 4y
2
+9z
2
= 36
19. Chỉ ra rằng hình chiếu trên mặt phẳng xy của giao tuyến hai mặt cong z = 1− x
2
và z = x
2
+ y
2
là 1 elip. (Gợi
ý: Tính z từ các phương trình trên).
20. Chỉ ra rằng hình chiếu trên mặt phẳng yz của giao tuyến của mặt phẳng x = 2y và paraboloid x = y
2
+z
2
là
một đường tròn.
21. Chỉ ra rằng hình chiếu trên mặt phẳng xy của giao tuyến của các paraboloid z = 3x
2
+ 5y
2
và z = −8 5x
2
−3y
2
là một đường tròn.
GỢI Ý
Dạng 1. Vẽ các mặt cong
+ Trước hết đưa về dạng phương trình chính tắc đã biết (xem các ví dụ tương ứng)
+ Sau đó thực hiện các bước tương tự
Trường hợp tổng quát
VD: Xét ( ):S z = + +m ax
2
by
2
+ Trước hết viết PT dưới dạng: z − = +m ax
2
by
2
+ Đổi hệ tọa độ:


Y
Z
X
= −
=
=
z
y
x
m
, thực tế phép biến đổi này đã dịch chuyển mặt phẳng tọa độ
xOy theo trục
Oz lêm trên |m | nếu m > 0 và xuống dưới |m | nếu m < 0 .
+ Trong hệ tọa độ mới OXYZ thì PT của ( ):S Z = +aX
2
bY
2
, đây là dạng chính tắc và ta đã có thể xác định
được mặt cong ( ).S
Bài tập Giải tích hàm nhiều biến TS. Nguyễn Hữu Thọ
2022-2023
lOMoARcPSD|40651217
Dạng 2. Giao tuyến giữa 2 mặt cong và tìm phương trình hình chiếu của giao tuyến đó lên một mặt
phẳng tọa độ.
Xét bài toán: Tìm giao tuyến của hai mặt cong (S
1
): F x y z( , , )=a và (S
2
):G x y z( , , ) =b ; sau đó tìm hình
chiếu của giao tuyến đó lên mặt phẳng tọa độ Oxy . Giải:
+ Gọi ( )C là giao tuyến của ( )S
1
và (S
2
), khi đó phương trình của ( )C là: G x y zF x y z(( , ,, , ))
==ba (1)
+ Gọi ( )C
*
là hình chiếu của ( )C lên mặt phẳng Oxy , phương trình mặt phẳng Oxy là z =0.
2 |
+ Từ hệ (1) ta khử biến z và nhận được phương trình: H x y( , ) = 0 : đây chính là phương trình hình chiếu
( )C
*
của ( )C lên mặt phẳng Oxy .
Chú ý: Nếu ta xét hình chiếu của ( )C lên mặt Oxz (có phương trình y =0) hoặc lên mặt Oyz (có phương
trình x =0 ), thì từ (1) ta sẽ khử biến y (tương ứng biến x ) ta sẽ nhận được phương trình của hình chiếu
tương ứng.
Bài tập Giải tích hàm nhiều biến TS. Nguyễn Hữu Thọ
2022-2023
lOMoARcPSD|40651217
3 |
Bài tập Giải tích hàm nhiều biến TS. Nguyễn Hữu Thọ
2022-2023
lOMoARcPSD|40651217
Bài tập buổi 2
HÀM NHIỀU BIẾN. ĐẠO HÀM RIÊNG. MẶT PHẲNG TIẾP XÚC
19.1. HÀM SỐ NHIỀU BIẾN (Tr. 61)
Tìm miền xác định của các hàm số được cho từ bài tập 1 đến 12:
xy 1 1
1. f x y( , ) = 2. f x y( , ) = +
x y
3. f x y( , ) = xy 5. f x y( , ) = ln(y − 3 )x
7. f x y z( , , ) = 9. f x y z( , , ) = − − −16 x
2
y
2
z
2
11. f x y z( , , ) xy lnz 3tan z 12. f x y z( , , )= ln(x
2
+y
2
+z
2
−1)
19.2. ĐẠO HÀM RIÊNG (Tr. 68)
∂ z ∂ z
Trong các bài tập từ 1 đến 14, tìm và .
∂ x ∂ y
2y
2
3. z = 7. z = x tan2y +y tan3x
3x +1
10. z = xye
xy
12. z = tan
−1
x
13. z =e
y
lnx
2
y
Trong các bài tập từ 15 đến 18, tìm các đạo hàm riêng đối với x y z, , .
16. w = sin
−1
z
, xy
y
17. w = x ln ,
z
∂ z ∂ z
21. Chỉ ra rằng tất cả các hàm số z = f x y( , ) sau đây thoả mãn phương trình x +y = 0:
∂ x ∂ y
x x
2y x
−
2 2 2
1
x y z
+ +
Bài tập Giải tích hàm nhiều biến TS. Nguyễn Hữu Thọ
2022-2023
lOMoARcPSD|40651217
(a) z = ; (b) z = ; y
x +y
2y
2
xy
2
(c) z =
ln
x
2
; (d) z
=
x
3
+y
3 .
5
2x y
4
5x y
2 3
, chỉ ra rằng x ∂ z +y ∂ z = 5z :
23. Nếu z = − +x
∂ x ∂ y
∂
2
z ∂
2
z
Trong các bài tập từ 24 tới 28, kiểm tra lại =
∂ ∂y x ∂ ∂x y
24. z = tan
−1
x
y
∂
2
f ∂
2
f
29. Chỉ ra rằng mỗi hàm số trong các hàm số sau đây thoả mãn phương trình Laplace: + = 0
∂x
2
∂y
2
(a) f x y( , ) = ln(x
2
+y
2
) (b) f x y( , ) =e
x
siny .
(c) f x y( , ) =e
−3x
cos3y (d) f x y( , ) = tan
−1
y
x
∂2f ∂2f
30. Chỉ ra rằng mỗi hàm số trong các hàm số sau đây thoả mãn phương trình truyền sóng:
a
2 ∂x
2
=
∂t
2
(a) f x t( , ) = (x +at)
3
(b) f x t( , ) = (x −at)
5
.
(c) f x t( , ) = sin(x +at) (d) f x t( , ) =e
x at−
19.3 MẶT PHẲNG TIẾP XÚC ĐỐI VỚI MẶT CONG (Tr.74)
Trong các bài tập 1 đến 10, tìm mặt phẳng tiếp xúc với các mặt cong cho trước tại các điểm tương ứng.
1. z = (x
2
+y
2 2
) , (1;2;25) 4. z = x
2
+xy +y
2
−10y + 5, (3;2;4)
5. z = x
2
−2y
2
, (3; 2;1)
7. z =e
y
cos ,x (0;0;1)
8. z = tan
−1
x
, y
4; 4;
π.

4
Bài tập Giải tích hàm nhiều biến TS. Nguyễn Hữu Thọ
2022-2023
lOMoARcPSD|40651217
GỢI Ý
1. Các bài toán tính đạo hàm riêng
+ Trước hết cần thuộc các công thức tính đạo hàm của hàm một biến số
+ Khi tính đạo hàm riêng đối với hàm số nhiều biến cần lưu ý: Khi tính đạo hàm riêng theo biến nào thì ta sẽ
thức hiện các quy tắc tính đạo hàm theo biến đó như việc tính đối với hàm một biến (đối với biến mà ta
đang quan tâm) còn các biến còn lại ta coi như là hằng số đối với biến mà ta đang thực hiện lấy đạo hàm.
5 |
2. Dạng bài toán: Viết phương trình tiếp diện đối với mặt cong ( ):Sz = f x y( ; ) tại điểm P x y z(
0
;
0
;
0
).
Giải:
(Chú ý, đây là bài toán viết phương trình tiếp diện đối với mặt cong, mặt cong này là đồ thị của một hàm số 2
biến số ; ta cần phân biệt rõ vì sắp tới chúng ta sẽ có dạng bài tập: Viết phương trình mặt phẳng tiếp diện đối
với một mặt cong, mặt cong này là đồ thị của một phương trình 3 biến F x y z( ; ; ) =c (với c là hằng số))
+ Trước hết: Kiểm tra điểm P x y z
(
0
;
0
;
0
) có thuộc mặt cong ( )S hay không (thông qua việc kiểm chứng đẳng
thức z
0
= f x y(
0
;
0
).
∂f ∂f ∂f ∂f
+ Tính các ĐHR: ∂x và ∂y và tính các giá trị các ĐHR đó tại (
x y
0
;
0
), tức là
∂x
(x y
0
;
0
)và
∂y
(x y
0
;
0
)
+ Phương trình tiếp diện cần
tìm:
Bài tập Giải tích hàm nhiều biến TS. Nguyễn Hữu Thọ
2022-2023
z −z
0
= f x y
x
(
0
,
0
)(x −x
0
)+ f x y
y
(
0
,
0
)(y −y
0
)
lOMoARcPSD|40651217
Bài tập buổi 3
ĐẠO HÀM THEO HƯỚNG. GRADIENT
19.5 ĐẠO HÀM THEO HƯỚNG VÀ GRADIENT(Tr.82)
1. Tìm gradient của f tại P nếu
(a) f x y z( , , )= xy +xz +yz , P = −( 1;3;5) (b) f x y z( , , )=e
xy
cosz , P =(0;2;0)
(c) f x y z(
, ,
)= ln(x
2
+y
2
+z
2
), P =(1;2;−2) (d)
f x y z
(
, ,
) =
xy
, P =(2;−1;5) z
2. Tìm đạo hàm theo hướng của f tại P theo hướng véc tơ đưa ra:
(a) f x y z( , , )= xy
2
+x z
2
+yz , P =(1;1;2), i + 2j− k ;
(b) f x y z( , , )= ln(x
2
+y
2
+z
2
), P
=
(0;0;1), véc tơ từ P đến Q(2;2;0);
(c) f x y z( , , )= x siny +y sinz +z sinx , P =(1;0;0), 2 3i +2j;
(d) f x y z( , , )= xye
z
+yze
x
, P =(1,0,0), véc tơ từ P đến Q(2;2;1).
Bài tập Giải tích hàm nhiều biến TS. Nguyễn Hữu Thọ
2022-2023
lOMoARcPSD|40651217
3. Tìm giá trị lớn nhất của đạo hàm theo hướng của f tại P và hướng mà đạo hàm hàm theo hướng đạt giá trị
lớn nhất:
(a) f x y z( , , )= sinxy + cosyz , P = −( 3;0;7);
(b) f x y z( , , )=e
x
cosy +e
y
cosz +e
z
cosx , P =(0;0;0);
(c) f x y z( , , )= 2xyz +y
2
+z
2
, P =(2;1;1); (d) f x y z( , , )=e
xyz
, P =(2;1;1).
4. Nên di chuyển theo hướng nào, bắt đầu từ gốc toạ độ, để nhận được tốc độ giảm nhanh nhất của hàm số
f x y z(
, ,
)=(2− −x y)
3
+(3x +2y − +z 1)
2
?
5. Tìm véc tơ đơn vị pháp tuyến của mặt xyz = 4 tại điểm (2;− −2; 1).
2 2
df (4;1;0):
6. Nếu f x y z( , , ) = x + 4y − 8z , tìm tại ds
x −4 y −1 z
(a) Dọc theo đường = = theo hướng giảm của x ;
2 1 −2
(b) Dọc theo pháp tuyến của m/phẳng 3(x − 4)−(y − +1) 2z = 0 theo hướng tăng của x ; (c) Theo
hướng mà hàm f tăng nhanh nhất.
7. Giả sử rằng nhiệt độ T tại điểm P = (x y z, , ) được xác định bởi T = 2x
2
−y
2
+ 4z
2
. Tìm tốc độ biến thiên của T
tại điểm (1;−2;1) theo hướng của véc tơ 4i − +j 2k. Theo hướng nào T tăng nhanh nhất tại điểm này?
Tốc độ tăng lớn nhất đó là bao nhiêu?
8. Tìm tiếp diện và pháp tuyến của hyperboloid x
2
+y
2
−z
2
= 5 tại điểm (4;5;6).
19.3. MẶT PHẲNG TIẾP XÚC (Tr. 74)
Tìm mặt phẳng tiếp xúc với các mặt cong cho trước tại các điểm tương ứng
9. xy
2
+yz
2
+zx
2
= 25, (1;2;3) 10. z
3
+xyz = 33, (1;2;3).
7 |
GỢI Ý
1. Để tính đạo hàm theo hướng của hàm f x y z( , , ) ta cần biết 3 yếu tố : Công thức hàm số, điểm cần tính
đạo hàm và hướng mà ta quan tâm.
+ Khi biết đủ 3 yếu tố đó thì chúng ta có thể tính được đạo hàm mong muốn. Các bước tính đạo
hàm theo hướng của hàm số w = f x y z( , , ) tại điểm P x y z
0
(
0
,
0
,
0
) theo hướng v = (a b c; ; ) ≠ 0 như sau :
Bước 1 : Tính grad f sau đó tính giá trị gradient của hàm số w = f x y z( , , ) tại điểm P x y z
0
(
0
,
0
,
0
) :
Bài tập Giải tích hàm nhiều biến TS. Nguyễn Hữu Thọ
2022-2023
lOMoARcPSD|40651217
grad f .
P x y z
0 0 0 0
(
, )
Bước 2 : Tính độ dài véc tơ v = (a b c; ; ) : v = a
2
+b
2
+c
2
sau đó xét : u = v
v
=


a
v v v
;
b
;
c


, đây chính là véc tơ đơn vị theo hướng của
véc tơ v.
Bước 3 : Khi đó, đạo hàm của hàm số w = f x y z( , , ) tại điểm P x y z
0
(
0
,
0
,
0
) theo hướng v = (a
b c; ; ) ≠ 0 được xác định bởi : =(grad f 0 ).u
df
ds
P
2. Bài toán: Viết phương trình tiếp diện và pháp tuyến của mặt cong ( )S có phương trình F x y z( , , ) = c
0
tại điểm
P x y z
0
(
0
,
0
,
0
), (ở đây
c
0
là hằng số đối với cá biến x y z, , ).
(Chú ý: Cách gải này áp dụng đối với trường hợp mặt cong ( )S được xác định bởi một phương trình 3
biến x y z, , .)
Cách giải: + Do
P x y z
0
(
0
,
0
,
0
) ( )∈ S nên F x y z
(
0
,
0
,
0
) =
c
0
, nên ( )S chính là một mặt mức của hàm số w = F x
y z( , , ) tại điểm
P x y z
0
(
0
,
0
,
0
).
+ Tính grad f , khi đó
N = gradf0 = ∂ ∂xf P0 i + ∂ ∂yf P0 j+ ∂ ∂zf P0 k= ∂ ∂xf  P0 ; ∂ ∂yf 
 P0 ; ∂ ∂zf P0
P 
chính là véc tơ pháp tuyến của mặt phẳng tiếp xúc (tiếp diện) với mặt cong( )S tại điểm P x y z
0
(
0
,
0
,
0
), từ
đó phương trình tiếp diện cần tìm xác định bởi:
Bài tập Giải tích hàm nhiều biến TS. Nguyễn Hữu Thọ
2022-2023
lOMoARcPSD|40651217

∂ ∂xf
 0 (x −x0)+ ∂ ∂yf P0 (y
−y0)+ ∂ ∂zf P0 (z −z0)= 0; P
Bài tập Giải tích hàm nhiều biến TS. Nguyễn Hữu Thọ
2022-2023
lOMoARcPSD|40651217
+ Pháp tuyển của mặt cong( )S tại điểm
P x y z
0
(
0
,
0 0
, ) chính là đường thẳng vuông góc với mặt cong( )S tại
điểm
P x y z
0
(
0
,
0 0
, ) và cũng chính là đường thẳng vuông góc với tiếp diện của mặt cong( )S tại điểm
P x y z
0
(
0
,
0 0
, ), do đó pháp tuyến này nhận véc tơ pháp tuyến của tiếp diện như là một véc tơ chỉ phương, nên
phương trình pháp tuyến xác định bởi:
(x −x
0
) ( y −y
0
) ( z −z
0
)
= =
∂ ∂xf P0 ∂ ∂yf  P0 ∂ ∂zf P
0
(hoặc ta có thể viết dưới dạng phương trình tham số sau:
yx ==yx00 ++f P  P tyx( ) .( )00
z = z0 + f P tz( )0
3. Hướng tăng của x (hoặc hướng tăng theo x ) chính là hướng theo véc tơ đơn vị i trên trục Ox , hướng giảm
của x (hoặc hướng giảm theo x ) chính là hướng theo véc tơ đối của véc tơ đơn vị i trên trục Ox , cũng
tương tự đối với các biến còn lại.
4. Cách xác định véc tơ theo hướng tăng của x dọc theo đường thẳng ( )d cho trước: có 2 cách
Cách 1: Trên đường thẳng ( )d lấy hai điểm
M x y z
1 1 1 1
( ; ; ) và
M x y z
2
(
2
;
2 2
; ). Giả sử
x
1
<
x
2
, khi đó véc tơ v =
M M
1 2
chính là véc tơ dọc theo nó sẽ theo hướng tăng của x dọc theo đường thẳng ( )d .
Cách 2: + Xác định véc tơ chỉ phương của đường thẳng ( )d : u
d
= (a b c; ; ).
+ Tính tích vô hướng:
u
d
=⋅ i m (vì xét hướng tăng hay giảm của x nên ta xét tích vô hướng của
VTCP với véc tơ đơn vị i trên trục Ox , còn nếu muốn xét hướng tăng hay giảm đối với các biến khác thì ta
xét tích vô hướng giữa VTCP cuat đường thẳng với các véc tơ đơn vị của trục tọa độ tương ứng).
+ Khi đó: Nếu
u
d
=⋅ i m > 0 thì góc giữa véc tơ
u
d
và véc tơ đơn vị i là góc nhọn và véc tơ
u
d
chính là véc
tơ xác định hướng dọc theo đường thẳng ( )d theo hướng tăng của x , còn lúc này véc tơ đối của véc tơ u
d
chính là véc tơ xác định hướng dọc theo đường thẳng ( )d theo hướng giảm của x .
Bài tập Giải tích hàm nhiều biến TS. Nguyễn Hữu Thọ
2022-2023
lOMoARcPSD|40651217
Nếu
u
d
=⋅ i m < 0 thì góc giữa véc tơ
u
d
và véc tơ đơn vị i là góc tù và véc tơ
u
d
chính là véc
tơ xác định hướng dọc theo đường thẳng ( )d theo hướng giảm của x , còn lúc này véc tơ đối của véc tơ u
d
chính là véc tơ xác định hướng dọc theo đường thẳng ( )d theo hướng tăng của x .
Bài tập buổi 4
ĐẠO HÀM HÀM HỢP, HÀM ẨN.
19.6 QUY TẮC DÂY CHUYỀN ĐỐI VỚI ĐẠO HÀM RIÊNG (Tr. 88)
dw
Trong các bài tập 1 đến 4, hãy tìm theo hai cách, dt
(a) Bằng cách sử dụng quy tắc dây chuyền và biểu diễn tất cả các số hạng theo t .
(b) Đổi biến trước khi lấy đạo hàm.
1. w =e
x y
2
+
2
, x = cost , y = sint .
2. w = xy +yz +zx , x = 3t
2
, y =e
t
, z =e
−t
.
4. w = ln(x
4
+2x y
2
+3y
2
), x = t , y = 2t
2
.
∂w w
Trong các bài tập 5 và 6, hãy tìm và bởi quy tắc dây chuyền và kiểm tra kết quả tìm được bằng cách sử
∂t u
dụng phương pháp khác.
x
6. w
=
2 2
, x tcosu , y tsinu x +y
7. Nếu f là một hàm nào đó (có đạo hàm liên tục) chứng minh rằng w = f x(
2
−y
2
) là một nghiệm của phương
∂w ∂w
trình đạo hàm riêng: y +x = 0.
∂x ∂y
Bài tập Giải tích hàm nhiều biến TS. Nguyễn Hữu Thọ
2022-2023
lOMoARcPSD|40651217
(Gợi ý: Đặt u = x
2
−y
2
⇒w = f u( ) và áp dụng quy tắc dây chuyền với trường hợp chỉ có một biến trung gian u
)
2 2 2 2
∂w ∂w
9. Nếu w = f x(−y y, −x ), chứng minh rằng: y +x = 0.
∂x ∂y
(Gợi ý:

u
v = −
= −
y
x
2
2
x
y
2
2
=⇒ w
f u v( ; ) và áp dụng quy tắc dây chuyền với trường hợp có hai biến trung gian u

và v ).
10. Nếu w = f y −x z, −y, chứng minh rằng: x2 ∂∂wx +y2 ∂∂wy +z2 ∂∂wz = 0.
 xy yz
14. Nếu w =
f x y
(
,
) ở đó x = r cosθ và y = r sinθ , chứng minh rằng:
∂w 2 + ∂∂wy 2 = ∂∂wr 2 + r 12
∂∂wθ  2.
∂ x
15. Nếu là hằng số và w = f x y( , ) ở đó x = u cosα−v sinα và y = u sinα + v cosα, chứng minh rằng
∂w2 +∂∂wy 2 = ∂∂wu 2 +∂∂wv 2 .
∂ x
16. Nếu w = f x y( , ) ở đó x = e
u
cosv và y = e
u
sinv , chứng minh rằng
∂∂ wx 2 + ∂∂ wy 2 = e−2u ∂∂ wu 2
+ ∂∂ wv 2  .
19.10 HÀM ẨN (Tr. 115)
dy
Trong bài tập 1 đến 6, sử dụng công thức (11) để tính
. dx
Bài tập Giải tích hàm nhiều biến TS. Nguyễn Hữu Thọ
2022-2023
lOMoARcPSD|40651217
1. y
2
−3x
2
− =1 0.
2. x
6
+2y
4
= 1.
3. x siny = x + y .
6. e
x
siny = e
y
cosx .
Trong bài tập 7 đến 10, sử dụng công thức (15) và (16) để tính ∂z / ∂x và ∂z / ∂y .
8. tan
−1
x + tan
−1
y + tan
−1
z = 9 .
9. z = xy sinxz .
GỢI Ý
1. Khi sử dụng quy tắc dây chuyền cần chú ý khi lấy đạo hàm theo biến ta đang quan tâm mà hàm số
đó là hàm một biến đối với biến đó thì ta sử dụng ký hiệu “d thẳng” theo kiểu đạo hàm thường (đạo hàm
của hàm một biến); còn khi hàm số đó là hàm nhiều hơn một biến đối với những biến ta cần lấy đạo hàm
thì ta phải sử dụng ký hiệu của đạo hàm riêng của hàm số đáng xét theo biến lấy đạo hàm.
2. Có những trường hợp chúng ta cần tạo ra một hoặc nhiều biến trung gian sau đó mới sử dụng công
thức đạo hàm hàm hợp tương ứng.
3. Khi sử dụng công thức đạo hàm của hàm ẩn, trước hết ta cần chuyển phương trình xác định hàm
ẩn về dạng: F x y( ; ) = c hoặc F x y z( ; ; ) = c (trong đó c là hằng số đối với cá biến).
Bài tập buổi 5
CỰC TRỊ TỰ DO
19.7 CỰC TRỊ TỰ DO (tr.94)
Trong các bài tập từ 1 đến 8, tìm điểm tới hạn và phân loại chúng bởi việc kiểm tra đạo hàm cấp 2.
Bài tập Giải tích hàm nhiều biến TS. Nguyễn Hữu Thọ
2022-2023
lOMoARcPSD|40651217
1. z = 5x
2
− 3xy + y
2
− 15x − y + 2.
2. z = 2x
2
+ xy + 3y
2
+ 10x − 9y + 11.
3. z = x
5
+y
4
−5x −32y −3 .
4. z = x
2
+y
3
−6xy .
5. z = x y
2
+ 3xy − 3x
2
− 4x + 2y .
6. z = 3xy
2
+ y
2
− 3x − 6x + 7 .
7. z = x
3
+ y
3
+ 3xy + 5 .
8. z = xy(2x + 4y + 1).
9. Đối với mỗi hàm số z = f x y( , ) dưới đây, chứng minh rằng f f
x
,
y
và D đều bằng 0 tại gốc và hãy chứng tỏ
rằng tại điểm gốc: (a) đạt giá trị cực tiểu, (b) đạt giá trị cực đại, (c) là điểm yên ngựa
(a) f x y(
,
) = x
4
+ y
4
. (b) f x y(
,
) = −x
4
− y
4
. (c) f x y(
,
) = x y
33
.
14. Hàm số z = (y − x
2
)(y − 2x
2
) có điểm yên ngựa tại (0;0).
(a) Kiểm tra (0;0)là điểm tới hạn.
(b) Chứng tỏ rằng kiểm tra đạo hàm cấp hai triệt tiêu để khẳng định điểm tới hạn là một điểm yên
ngựa là sai.
(c) Chứng tỏ rằng điểm tới hạn này là điểm yên ngựa bằng việc kiểm tra trực tiếp dấu của hàm số tại
lân cận điểm (0;0)
19. Tìm khoảng cách từ gốc toạ độ đến mặt phẳng x + 2y + 3z = 14.
(Gợi ý: Đánh giá nhỏ nhất w = x
2
+y
2
+z
2
khi coi y và z như các biến độc lập).
Bài tập buổi 6
CỰC TRỊ CÓ ĐIỀU KIỆN
Bài tập Giải tích hàm nhiều biến TS. Nguyễn Hữu Thọ
2022-2023
lOMoARcPSD|40651217
19.8 CỰC TRỊ CÓ ĐIỀU KIỆN (tr.103)
Giải các bài dưới đây bằng phương pháp nhân tử Lagrange.
1. Một hình chữ nhật với các cạnh song song với các trục toạ độ nội tiếp trong một miền bị chặn bởi các trục
toạ độ và đường thẳng x + 2y = 2. Tìm diện tích lớn nhất của hình chữ nhật này.
2. Tìm hình chữ nhật có chu vi lớn nhất (với các cạnh song song với các trục toạ độ), nội tiếp trong ellipse x
2
+
4y
2
= 4 .
3. Tìm hình chữ nhật có diện tích lớn nhất (với các cạnh song song với các trục toạ độ), nội tiếp trong ellipse x
2
+ 4y
2
= 4 .
6. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số f x y( , ) = 2x
2
+ +y y
2
trên đường tròn x
2
+y
2
= 1.
7. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số f x y( , ) = x
2
−xy +y
2
trên đường tròn x
2
+y
2
= 1.
Bài tập bổ xung :
1. Tìm cực trị có điều kiện của hàm số f x y( , ) = −x
2
+ xy − y
2
với điều kiện x
2
+ y
2
= 1.
2. Tìm cực trị có điều kiện của hàm số f x y( , ) = x
2
+ +x 2y
2
với điều kiện x
2
+y
2
= 1.
Bài tập Giải tích hàm nhiều biến TS. Nguyễn Hữu Thọ
2022-2023
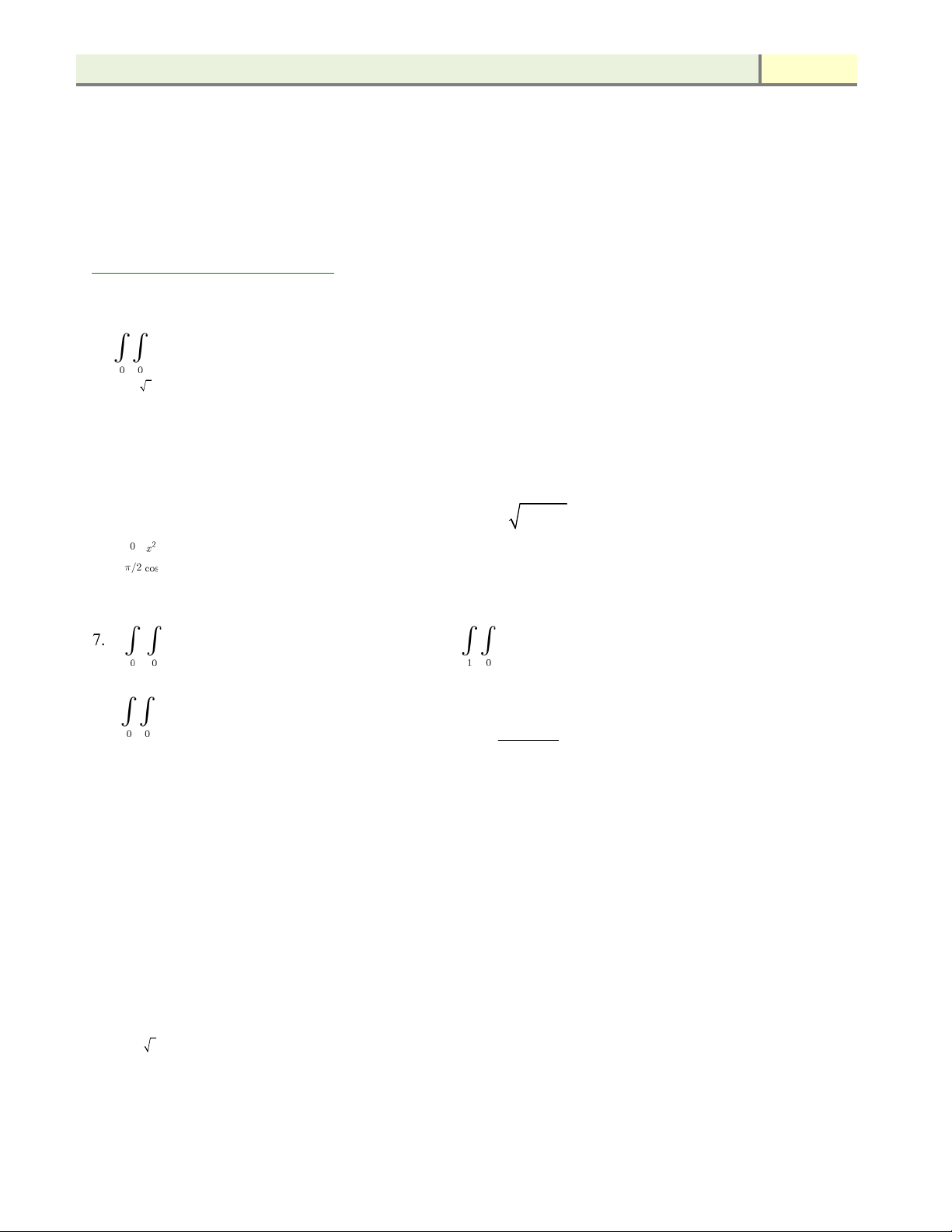
2.
0 0
∫∫
lOMoARcPSD|40651217
Bài tập buổi 7
TÍCH PHÂN BỘI HAI
20.1. TÍCH PHÂN LẶP (Tr. 119)
Xác định miền lấy tích phân của các tích phân lặp trong bài tập 1 và 2.
1 y
1. f x y dxdy( , )
4 x
f x y dydx( , )
Tính mỗi một tích phân lặp trong bài tập từ 3 đến 14. Cũng như vẽ miền lấy tích phân R.
1 x 4 y
3. ∫∫ (2x + 2
y dydx
) 5. ∫∫ 3 y
2
+ 9dxdy
0 0 x
3 lny
ydydx 9. ye dxdy
x
π x 2 2x
dydx
11. x cosydydx 13. ∫∫ .
1
x
(x + y)2
Trong các bài tập từ 15 đến 18, với việc đổi thứ tự lấy tích phân viết một tích phân lặp tương đương
2 e
2
17. ∫∫ f x y dxdy( , )
1 ey
Trong các bài tập từ 19 đến 24, với việc đổi thứ tự lấy tích phân viết một tích phân lặp tương đương và
tính cả hai tích phân đó.
1 1
19. ∫∫ 2x dxdy
3
0y 2 1
21. ∫∫ (5 − 2x −
y dydx
)
0 0
Bài tập Giải tích hàm nhiều biến TS. Nguyễn Hữu Thọ
2022-2023
| 1/32

Tài liệu khác của Đại học Thủy Lợi