









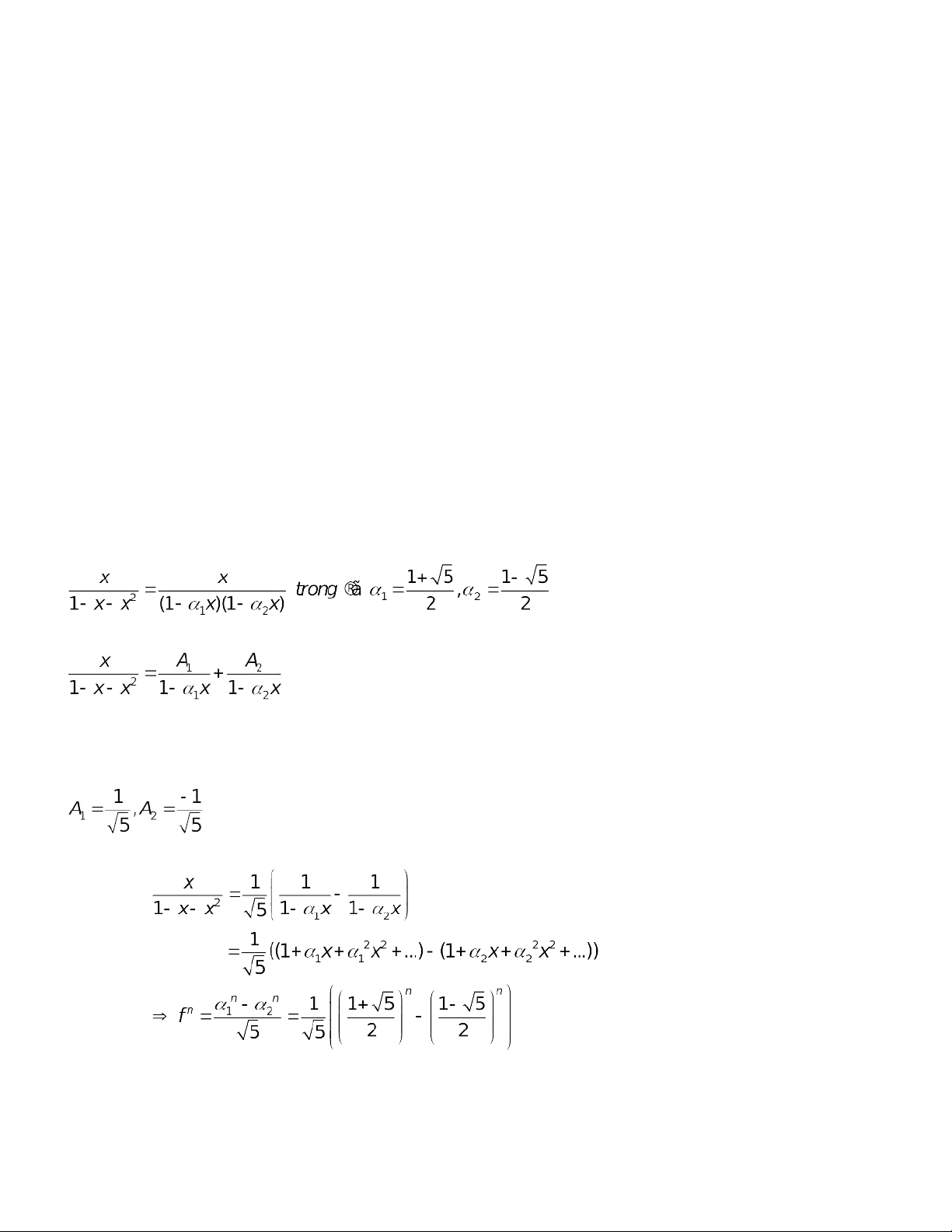








Preview text:
PHẦN MỞ ĐẦU ***
I.Lý do chọn đề tài
Dãy số và toán rời rạc là những dạng toán rất hay gặp trong các kì thi chọn học sinh giỏi như
kì thi chọn học sinh giỏi toán quốc gia, quốc tế. Trong cấu trúc đề thi toán quốc gia năm 2008-
2009, 2009-2010 thì cả 2 dạng toán trên đều có với tổng số điểm của 2 bài là 8/20.
Sách về dãy số và toán rời rạc về trên thị trường hiện nay khá nhiều và khá đầy đủ nhưng
học sinh vẫn thường lúng túng khi gặp các bài về 2 dạng toán này.
Hàm sinh là một trong những sáng tạo thần tình, bất ngờ, nhiều ứng dụng của toán rời
rạc. Hàm sinh chuyển những bài toán về dãy số thành những bài toán về hàm số. Điều này rất
tuyệt vời vì chúng ta đã có trong tay cả một cỗ máy lớn để làm việc với các hàm số. Nhờ vào
hàm sinh, chúng ta có thể áp dụng cỗ máy này vào các bài toán dãy số. Chúng ta có thể sử dụng
hàm sinh trong việc giải các dạng toán về phép đếm, ứng dụng trong toán rời rạc
Vì thế tôi xin được trao đổi với quí đồng nghiệp một số vấn đề về hàm sinh và ứng dụng
của hàm sinh trong một số bài toán dãy số và toán rời rạc
II. Mục đích của đề tài
Tôi chọn đề tài về “hàm sinh và một số ứng dụng” nhằm cung cấp một kiến thức mà theo
tôi còn khá mới trong chương trình toán phổ thông. Tuy nhiên ứng dụng của hàm sinh trong
học chuyên thì rất lớn. Các chuyên đề bồi dưỡng học sinh giỏi luôn là những lĩnh vực khó khăn,
nhất là chuyên đề toán rời rạc. Học sinh thường có tâm lí sợ, bỏ qua dạng toán này. Hàm sinh
sẽ cung cấp cho học sinh một cách nhìn mới về dãy số,về toán rời rạc, đặc biệt là bài toán đếm .
Với kiến thức về hàm sinh, tôi tin học sinh sẽ thấy hứng thú, tự tin hơn đối với các bài
toán về dãy số và toán rời rạc, hứng thú hơn với viêc học chuyên, khơi dậy lòng say mê tìm
tòi những cái mới ở các em.
III. Nhiệm vụ của đề tài
Đề tài “Hàm sinh và một số ứng dụng” có nhiệm vụ cung cấp những kiến thức cơ bản
nhất về hàm sinh và một số ứng dụng của hàm sinh trong các bài toán dãy số, toán tổ hợp. Qua
đó người đọc có thể hiểu được phần nào các khái niệm, các tính chất và các ứng dụng của hàm
sinh trong việc giải một số dạng toán.
Đề tài này đặc biệt hữu ích cho những người dạy và học chuyên, phần nào giúp cho học
sinh tiếp cận với 1 kiến thức còn khá mới trong chương trình toán phổ thông.
IV. Đối tượng nghiên cứu
Đối tượng nghiên cứu của đề tài “Hàm sinh và một số ứng dụng” chủ yếu là về hàm
sinh, các bài toán về dãy số, các bài toán về toán rời rạc đặc biệt là bài toán đếm.
V.Phương pháp nghiên cứu
Phương pháp nghiên cứu của đề tài chủ yếu là phương pháp phân tích, tổng hợp.
tương tự hoá, tổng quát hoá. PHẦN NỘI DUNG ***
CHƯƠNG I: NHỮNG CƠ SỞ KHOA HỌC I. Cơ sở lý luận
Các bài toán về dãy số, các bài toán đếm, một bộ phận khá lớn của toán rời rạc, từ trước
đến nay vẫn luôn là trở ngại khá lớn cho bất kì học sinh phổ thông nào. Bài toán về dãy số, bài
toán đếm có muôn màu muôn vẻ, biến ảo khôn lường, do vậy nếu ai đó thấy mình đã thành
thạo trong nhiều bài toán đó, ấy là đã có tư duy đủ tốt để sẵn sàng đón nhận các thử thách từ
nhiều lĩnh vực khoa học khác nhau cũng như từ thực tế cuộc sống. Việc trình bày một bài toán
đếm hay một bài về dãy số cũng không hề dễ dàng và càng cần có một tư duy thông suốt mạch
lạc. Vì vậy để rèn luyện tư duy, đặc biệt là đối với học sinh giỏi thi quốc gia thì không thể quên
bài toán rời rạc mà một phần của nó là bài toán đếm cũng như các bài toán về dãy số.
Hàm sinh là một phương pháp hữu dụng để giải các bài toán đếm và các bài toán về dãy
số. Khái niệm hàm sinh đơn giản nhưng ứng dụng thì rất tuyệt vời. II. Cơ sở pháp lí
Dãy số và toán rời rạc là những chuyên đề khó, nhưng nếu học sinh học chuyên toán thi
đây là 2 chuyên đề bắt buộc mà học sinh phải làm quen và nghiên cứu. Học tốt 2 chuyên đề này
học sinh có thể làm được đến 40% bài thi chọn đội tuyển học sinh thi quốc gia.
Hàm sinh là một khái niệm tương đối mới đối với toán phổ thông nhưng cũng được nhiều
người nghiên cứu và phát triển.
III. Cơ sở thực tiễn
Dãy số và toán rời rạc là những dạng toán rất hay gặp trong các kì thi chọn học sinh giỏi
như kì thi chọn học sinh giỏi toán quốc gia, quốc tế. Trong cấu trúc đề thi toán quốc gia năm
2008-2009, 2009-2010 thì cả 2 dạng toán trên đều có với tổng số điểm của 2 bài là 8/20.
Sách về dãy số và toán rời rạc về trên thị trường hiện nay khá nhiều và khá đầy đủ nhưng
học sinh vẫn thường lúng túng khi gặp các bài về 2 dạng toán này.
Khái niệm, công thức về hàm sinh tuy đơn giản nhưng ứng dụng thì rất lớn. Làm quen với
hàm sinh, học sinh có thể nhìn các bài toán khó của dãy số và bài toán đếm dưới một góc nhìn
khác dễ hiểu hơn, đa dạng hơn, linh hoạt hơn. Nắm chắc khái niệm và ứng dụng của hàm sinh
, học sinh sẽ tự tin và hứng thú hơn đối với việc học chuyên, tự tin hơn khi gặp những bài toán khó.
Ch¬ng II: Nh÷ng néi dung s¸ng kiÕn cô thÓ ¸p dông trong qu¸ tr×nh c«ng t¸c vµ gi¶ng d¹y
I. Những kiến thức cơ bản về hàm sinh
Trong bài viết này, các dãy số sẽ được để trong ngoặc < > để phân biệt với các đối tượng toán học khác. 1. Hàm sinh
Hàm sinh thường của dãy số vô hạng là chuỗi luỹ thừa hình thức
G(x) = g0 + g1x + g2x2 + g3x3 …
Ta gọi làm sinh là chuỗi hình thức bởi vì thông thường ta sẽ chỉ coi x là một ký hiệu thay
thế một số. Chỉ trong một vài trường hợp ta sẽ cho x nhận các giá trị thực, vì thế ta gần như
cũng không để ý đến sự hội tụ của các chuỗi. Có một số loại hàm sinh khác nhưng trong bài
này, ta sẽ chỉ xét đến hàm sinh thường.
Trong bài này, ta sẽ ký hiệu sự tương ứng giữa một dãy số và hàm sinh bằng dấu mũi tên hai chiều như sau g0 + g1x + g2x2 + g3x3 +…
Ví dụ, dưới đây là một số dãy số và hàm sinh của chúng
<0, 0, 0, 0, …> 0 + 0.x + 0.x2 + 0.x3 + … = 0
<1, 0, 0, 0, …> 1 + 0.x + 0.x2 + 0.x3 + … = 1
<3, 2, 1, 0, …> 3 + 2x + x2 + 0.x3 + … = x2 + 2x + 3
Quy tắc ở đây rất đơn giản: Số hạng thứ i của dãy số (đánh số từ 0) là hệ số của xi trong hàm sinh.
Nhắc lại công thức tính tổng của các số nhân lùi vô hạn
Đẳng thức này không đúng với |z| 1, nhưng một lần nữa ta không quan tâm đến vấn đề
hội tụ. Công thức này cho chúng ta công thức tường minh cho hàm sinh của hàng loạt các dãy số
<1, 1, 1, 1, …> 1 + x + x2 + x3 + … = 1/(1-x)
<1, -1, 1, -1, …> 1 - x + x2 - x3 + … = 1/(1+x)
<1, a, a2, a3, …> 1 + ax + a2x2 + a3x3 + … = 1/(1-ax)
<1, 0, 1, 0, 1, 0, ...> 1 + x2 + x4 + … = 1/(1-x2)
2.Các phép toán trên hàm sinh
Phép màu của hàm sinh nằm ở chỗ ta có thể chuyển các phép toán thực hiện trên dãy số
thành các phép toán thực hiện trên các hàm sinh tương ứng của chúng. Chúng ta cùng xem
xét các phép toán và các tác động của chúng trong thuật ngữ dãy số.
2.1. Nhân với hằng số
Khi nhân hàm sinh với một hằng số thì trong dãy số tương ứng, các số hạng sẽ được nhân
với hằng số đó. Ví dụ
<1, 0, 1, 0, 1, 0, ...> 1 + x2 + x4 + … = 1/(1-x2) Nhân hàm sinh với 2, ta được
2/(1-x2) = 2 + 2x2 + 2x4 + … là hàm sinh của dãy số <2, 0, 2, 0, 2, 0, …>
Quy tắc 1. (Quy tắc nhân với hằng số) Nếu F(x) thì cF(x) Ch ứ n g m i nh .
= c(f cf00 ++ f (cf1x+f1)x + (cf2x2 +2 f)3xx23 ++ (cf …3))x3 + … = cF(x). 2.2. Cộng
Cộng hai hàm sinh tương ứng với việc cộng các số hạng của dãy số theo đúng chỉ số. Ví
dụ, ta cộng hai dãy số trước đó
<1, 1, 1, 1, …> 1/(1-x)
+ <1, -1, 1, -1, …> 1/(1+x)
<2, 0, 2, 0, …> 1/(1-x) + 1/(1+x)
Bây giờ ta thu được hai biểu thức khác nhau cùng sinh ra dãy (2, 0, 2, 0, …).
Nhưng điều này không có gì ngạc nhiên vì thực ra chúng bằng nhau:
1/(1-x) + 1/(1+x) = [(1+x) + (1-x)]/(1-x)(1+x) = 2/(1-x2)
Quy tắc 2. (Quy tắc cộng) Nếu F(x), G(x) thì F(x) + G(x) Ch ứ n g m i nh .
f0+g0+ (f12+ +g …) + (g1)x + (f20+ g+2 g)x12x + g + …2x2 + …) = (f0 + f1x + f2x = F(x) + G(x)
2.3. Dịch chuyển sang phải
Ta bắt đầu từ một dãy số đơn giản và hàm sinh của nó
<1, 1, 1, 1, …> 1/(1-x)
Bây giờ ta dịch chuyển dãy số sang phải bằng cách thêm k số 0 vào đầu
<0, 0, …, 0, 1, 1, 1, …> xk + xk+1 + xk+2 + … = xk(1+x+x2 + …) = xk/(1-x)
Như vậy, thêm k số 0 vào đầu dãy số tương ứng với việc nhân hàm sinh với xk.
Điều này cũng đúng trong trường hợp tổng quát. Quy tắc 3.
(Quy tắc dịch chuyển phải) Nếu , f1, f 2, …> F(x)
xk.F(x) (có k số 0) Ch ứ n g mi nh.
<0, …, 0, f0, f1, f2, …> = x k(f f00 x+k f1+x + f f1xk+1 2x2 ++ f …)2xk+2 + … = xkF(x) 2.4. Đạo hàm
Điều gì sẽ xảy ra nếu ta lấy đạo hàm của hàm sinh? Chúng ta hãy bắt đầu từ việc lấy đạo hàm
của một hàm sinh đã trở nên quen thuộc của dãy số toàn 1:
Ta tìm được hàm sinh cho dãy số <1,2,3,4..>!
Tổng quát, việc lấy đạo hàm của hàm sinh có hai tác động lên dãy số tương ứng: các số
hạng được nhân với chỉ số và toàn bộ dãy số được dịch chuyển trái sang 1 vị trí.
Quy tắc 4. (Quy tắc đạo hàm) Nếu f1, f2, …> F(x) thì dF(x)/dx Ch ứ n g mi nh.
= (d/dx)(f f1 + 2f02 x + 3f+ f1x + f3x22 x+2 … + f3x3 + …) = dF(x)/dx
Quy tắc đạo hàm là một quy tắc rất hữu hiệu. Trong thực tế, ta thường xuyên cần đến một
trong hai tác động của phép đạo hàm, nhân số hạng với chỉ số và dịch chuyển sang trái. Một
cách điển hình, ta chỉ muốn có một tác động và tìm cách “vô hiệu hoá” tác động còn lại. Ví dụ,
ta thử tìm hàm sinh cho dãy số <0, 1, 4, 9,16, …>. Nếu ta có thể bắt đầu từ dãy <1, 1, 1, 1, …>
thì bằng cách nhân với chỉ số 2 lần, ta sẽ được kết quả mong muốn
<0.0, 1.1, 2.2, 3.3, …> = <0, 1, 4, 9, …>
Vấn đề là ở chỗ phép đạo hàm không chỉ nhân số hạng dãy số với chỉ số mà còn dịch
chuyển sang trái 1 vị trí. Thế nhưng, quy tắc 3 dịch chuyển phải cho chúng ta cách để vô hiệu
hoá tác động này: nhân hàm sinh thu được cho x.
Như vậy cách làm của chúng ta là bắt đầu từ dãy số <1, 1, 1, 1, …>, lấy đạo hàm, nhân
với x, lấy đạo hàm rồi lại nhân với x.
<1, 1, 1, 1, …> 1/(1-x)
<1, 2, 3, 4, …> (d/dx)(1/(1-x)) = 1/(1-x)2
<0, 1, 2, 3, 4, …> x/(1-x)2
<1, 4, 9, 16, …> (d/dx)( x/(1-x)2) = (1+x)/(1-x)3
<0, 1, 4, 9, 16, …> x(1+x)/(1-x)3
Như vậy hàm sinh cho dãy các bình phương là x(1+x)/(1-x)3.
3. Các hàm sinh thường gặp 3.1.Định lí nhị thức mở rộng
Với u là một số thực và k là số nguyên không âm. Lúc đó hệ số nhị thức mở rộng
được định nghĩa như sau Định lí 2
Định lý này có thể được chứng minh khá dễ dàng bằng cách sử dụng định lý Taylor
Ví dụ. Tìm khai triển luỹ thừa của các hàm sinh (1+x)-n, (1-x)-n
Giải: Theo dịnh lý nhị thức mở rộng, có thể suy ra Hàm số Khai triển luỹ thừa ak 1 (-1)k ak (1+x)n k+1 (k+1)ak 1 nếu và 0 trong TH ngược lại (-1)s nếu k=s.r và 0 trong TH ngược lại Ln(1+x) 0 khi k=0 và Ln(1-x) 0 khi k=0 và arctgx 0 vpí k chẵn và 1/k với k lẻ
II. Ứng dụng của hàm sinh trong dãy số Dạng 1:
Tìm số hạng tổng quát của dãy số * Phương pháp là - Để tìm dãy số
Ta xét hàm sinh sinh bởi dãy
- Dựa vào đặc điểm của dãy ta tìm được F(x)
- Đồng nhất thức sẽ thu được dãy
Bài 1.Tìm số hạng tổng quát của dãy số
Chẳng hạn dưới đây là hàm sinh cho dãy số Fibonacci:
<0, 1, 1, 2, 3, 5, 8, 13, …> x/(1-x-x2)
Chúng ta thấy dãy số Fibonacci biến đổi khá khó chịu, nhưng hàm sinh của nó thì rất đơn giản.
Chúng ta sẽ thiết lập công thức tính hàm sinh này và qua đó, tìm được công
thức tường minh tính các số hạng tổng quát của dãy số Fibonacci. Dĩ nhiên, chúng ta đã biết
công thức tính số hạng tổng quát của dãy Fibonacci trong phần phương pháp giải các phương
trình sai phân tuyến tính hệ số hằng. Nhưng điều này không ngăn cản chúng ta một lần nữa
tìm cách giải thích sự xuất hiện của phương trình đặc trưng, cách xử lý trường hợp nghiệm
kép thông qua công cụ hàm sinh. Hơn nữa, phương pháp hàm sinh còn giúp chúng ta giải
quyết hàng loạt các bài toán về dãy số đệ quy khác nữa, trong đó có những phương trình mà
chúng ta hoàn toàn bó tay với các phương pháp khác. * Tìm hàm sinh
Ta bắt đầu bằng cách nhắc lại định nghĩa của dãy Fibonacci: f0 = 0 f1 = 1 fn = fn-1 + fn-2 với n 2
Ta có thể khai triển đẳng thức cuối cùng thành dãy vô hạn các đẳng thức. Như thế
dãy số Fibonacci xác định bởi f0 = 0 f1 =1 f2 = f1 + f0 f3 = f2 + f1 f4 = f3 + f2 …
Bây giờ, cách làm tổng quát của chúng ta là: định nghĩa F(x) là hàm sinh của dãy số ở
bên trái của các đẳng thức, chính là các số Fibonacci. Sau đó chúng ta tìm được hàm sinh cho
dãy số ở vế phải. Cho hai vế bằng nhau và ta giải ra được hàm sinh F(x). Ta hãy cùng làm
điều này. Đầu tiên ta định nghĩa
F(x) = f0 + f1x + f2x2 + f3x3 + f4x4 + … Bây giờ, ta cần tìm hàm sinh cho dãy số
<0, 1, f1+f0, f2+f1, f3+f2, …>
Một trong những cách tiếp cận là tách các dãy số của chúng ta thành cách dãy mà chúng
ta đã biết hàm sinh, sau đó áp dụng Quy tắc cộng <0, 1, 0, 0, 0, …> x
+<0<0<0, 1+f, f, 0, f0, f001, f, f, f112, f+, ff203, ...> , f, …> 2+f 1 , f x3 xF(x)2+F(x)f2, …> x + xF(x) + x2F(x)
Dãy số này gần như là dãy số nằm ở vế phải của dãy Fibonacci, chỉ có 1 khác biệt
duy nhất là 1+f0 ở vị trí thứ hai. Nhưng do f0 = 0 nên điều này không có ý nghĩa gì.
Như vậy, ta có F(x) = x + xF(x) + x2F(x) và từ đó F(x) = x/(1-x-x2), đó chính là công
thức mà chúng ta đã nói đến ở phần đầu.
* Tìm công thức tường minh
Tại sao chúng ta lại phải tìm hàm sinh của một dãy số? Có một vài câu trả lời cho câu
hỏi này, nhưng dưới đây là một trong những câu trả lời đó: nếu ta tìm được hàm sinh cho một
dãy số, trong nhiều trường hợp, ta có thể tìm được công thức tường minh cho các số hạng của
dãy số đó, và đây là điều rất cần thiết. Ví dụ công thức tường minh cho hệ số của xn trong
khai triển của x/(1-x-x2) chính là công thức tường minh cho số hạng thứ n của dãy số Fibonacci.
Như vậy công việc tiếp theo của chúng ta là tìm các hệ số từ hàm sinh. Có một vài cách
tiếp cận cho bài toán này. Đối với các hàm phân thức, là tỷ số của các đa thức, chúng ta có thể
sử dụng phương pháp phân tích thành các phân thức sơ cấp mà chúng ta đã biết ở phần tích
phân các hàm hữu tỷ. Ta có thể tìm được dễ dàng các hệ số cho các phân thức sơ cấp, từ đó
tìm được các hệ số cần tìm.
Ta sẽ thử làm cho hàm sinh của dãy số Fibonacci. Đầu tiên, ta phân tích mẫu số ra thừa số
Tiếp theo ta sẽ tìm các hằng số A1,A2 sao cho
Ta có thể làm điều này bằng phương pháp hệ số bất định hoặc thay x các giá trị khác
nhau để thu được các phương trình tuyến tính đối với A1, A2. Ta có thể tìm được A1, A2 từ
các phương trình này. Thực hiện điều này, ta được
Thay vào đẳng thức nói trên ta được
Đây chính là công thức mà ta cũng đã tìm được trong phần giải các phương trình sai phân
tuyến tính hệ số hằng. Cách tiếp cận mới này làm sáng tỏ thêm một số vấn của phương pháp
đã đề cập tới. Nói riêng, quy tắc tìm nghiệm của phương trình sai phân trong trường hợp
phương trình đặc trưng có nghiệm kép là hệ quả của quy tắc tìm khai triển phân thức sơ cấp! , thoả mãn: Bài 2. Tìm dãy Lời giải: sinh bởi dãy
, tương tự như bài tập 1 ta có phương trình: ( Mẫu thức có ) =
. Đồng nhất thức ta được:
Bài 3. Tìm số hạng tổng quát cúa dãy thoả mãn éét hàm sinh Lời giải: Đặt ta có phương trình: Viết f(x) dưới dạng
Quy đồng mẫu số rồi đồng nhất hệ số ta thu được: Vậy: Ta có :
Bài 4. Tìm công thức tính số hạng tổng quát cho cấp số nhân cộng, tức là dãy số xác định bởi
a0 = a, an = axn-1 + d với mọi n = 1, 2, 3, …
Đặt F(x) = a0 + a1x + a2x2 + a3x3 + …
Ta có F(x) = a0 + a1x + a2x2 + a3x3 + …
= a0 + (qa0 + d)x + (qa1+d)x2 + (qa2+d)x3 + …
= a0 + qx(a0+a1x+a2x2+…) + dx(1+x+x2+…) = a + qxF(x) + dx/(1-x)
Cuối cùng, áp dụng các công thức khai triển quen thuộc, ta được
Bài 5.Tìm công thức tổng quát của dãy số cho bởi a0 = 1, an = 2an-1 + 3n với n = 1, 2, 3, .. LG:
Theo đúng sơ đồ trên, ta xét F(x) = a0 + a1x + a2x2 + a3x3 + … Và thực hiện việc khai triển vế phải:
F(x) = a0 + a1x + a2x2 + a3x3 + …
= a0 + (2a0+3)x + (2a1+32)x2 + (2a2+33)x3 + …
= (1 + 3x + (3x)2 + (3x)3 + …) + 2x(a0+a1x+a2x2+…)
= 1/(1-3x) + 2xF(x) Từ đó suy ra
Áp dụng công thức khai triển luỹ thừa cho các hàm số thường gặp, ta tìm được an = 3n+1 – 2n+1.
Bài 6.Tìm công thức tổng quát của dãy số cho bởi a0 = 1, an= 2an-1 + n.3n.
LG: Đặt F(x) = a0 + a1x + a2x2 + a3x3 + … éét
F(x) = a0 + a1x + a2x2 + a3x3 + …
= a0 + (2a0+1.3)x + (2a1+2.32)x2 + (2a2+3.33)x3 + …
= 1 + 3x(1 + 2.(3x) + 3(3x)2 + …) + 2x(a0+a1x+a2x2+…) = 1 + 3x/(1-3x)2 + 2xF(x) Từ đó suy ra Suy ra an = 3(n+1)3n – 9.3n + 7.2n = (n-2)3n+1 + 7.2n.
Bài 7.Tìm công thức tổng quát của dãy số xác định bởi a0 = 1, a1 = 4,
an = 4(an-1-an-2) với mọi n = 2, 3, 4, … LG:
Theo sơ đồ chung, ta xét F(x) = a0 + a1x + a2x2 + a3x3 + a4x4 + …
Bỏ qua hai số hạng đầu, các số hạng từ a2 trở đi được tính theo các số hạng trước đó Từ đó
F(x) = a0 + a1x + (4a1-4a0)x2 + (4a2-4a1)x3 + (4a3-4a2)x4 + …
= 1 + 4x + 4x(a1x+a2x2+a3x3+…) – 4x2(a0+a1x+a2x2+…)
= 1 + 4x + 4x(F(x)-1) – 4x2F(x)
F(x) = 1/(1-2x)2 = 1 + 2.2x + 3.22x2 + … Suy ra an = (n+1)2n. Dạng 2:Tính tổng 1. Phương pháp Để tính tổng ta xét hàm sinh: (*)
Sau đó sử dụng phương pháp đổi tổng để tính về phải của (*) rồi đồng nhất thức 2 vế ta được
f(n). 2. Bài tập áp dụng
Bài 1. Tính tổng sau: xét hàm sinh: Lời giải: Đặt biến đổi F(x) ta có:
Vậy F(x) chính là hàm sinh của dãy Fibonacci, do đó:
Bài 2.Tính tổng sau: Lời giải: Đặt xét hàm sinh: Đồng nhất thức ta có:
Bài 3. Tính tổng sau: Lời giải: Đặt xét hàm sinh:
Mặt khác theo công thức triển khai Newton ta có: đồng nhất thức ta có Bài 4. a) Tính tổng sau: b) Tính tổng sau: Lời giải: a) Ta có: b) Đặt xét hàm sinh: Áp dụng câu a ta có Khi x = 2 ta có
do đó đồng nhất các hệ số ta có:
Đồng nhất thức ta được
Bài 5. Tính tổng sau: Lời giải: éét hàm sinh của dãy ta có :



